Prerpints.org logo
Preprint
Article

Regional Gravity Field Modeling Using Band-Limited SRBFs: A Case Study in Colorado

Altmetrics

Downloads

107

Views

21

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

30 August 2023

Posted:

31 August 2023

You are already at the latest version

Alerts
Abstract
The use of spherical radial basis functions (SRBFs) in regional gravity field modeling has become popular in recent years. However, to our knowledge, their potential for combining gravity data from multiple sources, particularly data with different spectrum information in the frequency domain, has not been extensively explored. Therefore, band-limited SRBFs, which have good lo-calization characteristics in the frequency domain, are the main tool in this study. We propose a residual and a-prior accuracy comparative analysis method to determine the optimal degree of expansion of SRBFs for gravity data. Using this methodology, we constructed a high-resolution geoid model called ColSRBF2023 in Colorado. The degrees of expansion for terrestrial and airborne data were set to 5200 and 1840, respectively. Results indicate that ColSRBF2023 has a standard deviation (STD) value of 2.3 cm compared to the GSVS17 validate data. This value is 2-6 mm lower than models obtained using different degrees of expansion for gravity data and models from other institutions considered in this study. Additionally, at the 1'×1' grid in the entire target area, ColSRBF2023 has an STD value of 2.4 cm when compared to the validation model. This value is also the best among the options examined in this study. These findings highlight the importance of determining the optimal expansion degree of gravity data, particularly when constructing high-resolution gravity field models in rugged mountainous regions.
Keywords: 
Subject: Environmental and Earth Sciences  -   Remote Sensing

1. Introduction

Gravity data is crucial for studying the Earth's gravity field and for establishing the International Height Reference System (IHRS). To evaluate the repeatability of gravity potential values and compare different gravimetric geoid models, the Joint Working Group (JWG) 2.2.2 of the International Association of Geodesy (IAG) initiated the Colorado geoid experiment in 2017.The experiment involved the use of various modeling methods and the comparison of corresponding geoid models. In this context, the National Geodetic Survey (NGS) provided terrestrial gravity data , airborne gravity data, GPS/leveling data, and a digital elevation model (DEM) for a mountainous region in Colorado, which allowed the comparison of different methods for geoid computation using the same input dataset. Currently, global gravity field models (GGMs) are routinely used to provide long wavelength information of gravity fields, while other data types provide medium and short wavelengths. In addition to GGMs, terrestrial gravity data are the most widely used data type in gravity field modeling. However, in areas that are challenging to access (e.g., polar regions, mountains, forests, coastal areas, oceans) or in very large areas exceeding 10,000 km2, airborne gravity almost becomes the only viable option [1].
When using airborne gravimetry for the local geoid improvement, there are two main challenges that need to be addressed. Firstly, airborne gravity observations are taken at scattered points along flight trajectories, and a downward continuation technique must be employed [2-4]. However, the downward continuation process is an unstable procedure that amplifies high-frequency noise, leading to a reduction in the quality of airborne data. Secondly, the spectral range of airborne gravity data is uncertain. The flight altitude determines the resolution of the data, but the topographic heights beneath the flight lines often vary significantly. For example, in the mentioned study, the flight lines ranged from 5200 m to 7200 m above the ellipsoid, while the corresponding topographic heights varied from 932 m to 4376 m. This variation makes it challenging to obtain a reasonable resolution from the airborne gravity data. Secondly, airborne gravity data containing high-frequency noise and a series of filtering and estimation techniques are usually needed, which further exacerbate the uncertainty in the spectral information of airborne gravity data. To date, it is widely believed that the spectral range of airborne gravity data is approximately 2-3000, more detailed investigation is still necessary. It has been observed that using airborne gravity signals beyond their corresponding spherical harmonic (SH) degree can introduce modeling errors [5]. Therefore, finding and modeling this useful information provided by airborne gravimetry has become a critical issue in local geoid enhancement.
Several methods can be employed to model airborne gravity data for local geoid refinement, including the well-known least square collocation (LSC) method [6], least squares spectral combination method [7,8], and Slepian functions [9]. In this study, we have chosen to use band-limited spherical radial basis functions (SRBFs) for local geoid refinement. The justifications for this choice are as follows. First, the SRBF expression includes a continuation factor, allowing the establishment of observation equations directly at scattered points of observation without the need for gridding or downward continuation. This feature enables the assignment of observation errors to specific observables in space. Li utilized a set of band-limited SRBFs to model airborne gravity data and demonstrated that the SRBF method could effectively recover the gravity field while exhibiting filtering properties due to its design in the frequency domain [10]. Second, the band-limited SRBFs can be adjusted flexibly based on the spectrum information of the gravity data, which justifies their use in this study. This flexibility allows for better adaptation to the specific characteristics of the data. Third, SRBFs can express almost all types of gravity data, which form the basis for combining multisource gravity data to build a high-resolution regional gravity field. Additionally, experiments have shown that SRBFs are computationally efficient and do not require a covariance model like the LSC method, which is sometimes time-consuming[11]. Other examples and explanations of SRBFs can also be found in [12-21] and references therein.
In this study, our main focus is on refining the regional gravity field model in Colorado using band-limited SRBFs. To determine the optimal spectral information of the gravity data, we propose a residual and a-prior accuracy comparative analysis method. The organization of this work is as follows: This work is organized as follows: In Section 2, we introduce the study area in Colorado and describe the available data. We also outline the procedure for data preprocessing. In Section 3, we present the fundamental concepts of SRBFs and the parameter estimation procedure. This includes the formulation of observation equations, estimation of unknown coefficients, and calculation of gravitational functionals. In Section 4, we explain the computation procedure, which involves the RCR procedure, the residual and a-prior accuracy comparative analysis method, and how we combine different datasets. Section 5 presents our models as well as the validation of the results. Finally, Section 6 provides the conclusions and present potential future research directions.

2. Theory and Methods

A residual harmonic function T r e s x outside a sphere of radius R can be written as a finite sum of SRBFs:
T r e s x = ∑ i = n N α i Ψ i x , x i
where x = r ∙ r = r c o s φ c o s λ , c o s φ s i n λ , s i n φ T is the position vector of the observation point P, λ is the spherical longitude, φ is the spherical latitude, and r = R + h , with h being the spherical height of P above sphere Ω R with radius R. x i = R ∙ r i are the position vectors of the SRBFs. N is the number of SRBFs, T r e s x is the residual disturbing potential, and α i is the unknown coefficient. Ψ x , x i is an SRBF, the specific expression for which is [22,23]
Ψ x , x i = ∑ n m i n n m a x k n 2 n + 1 4 π R r n + 1 P n r T r i
where k n is the kernel function that defines the spectral properties of the SRBFs, R is the mean radius of Earth, P n is the Legendre polynomial of degree n , and r T r i is the spherical distance between x and x i . n m i n and n m a x are the minimum and maximum degrees of expansion, respectively. The SRBF in Eq. (2) is band-limited since the kernel functions are zero for each degree beyond n m a x or below n m i n .
This general expression (Eq. (2)) needs to be adapted for describing different gravitational functionals. We use observations that are given in terms of gravity disturbances δ g , which can be expressed as the gradient of the disturbing potential T . In spherical approximation, the magnitude of the gravity disturbance can be written as [24]
δ g = − ∂ T ∂ r
From the SRBF expression for the disturbing potential (Eq. (1)), the residual terrestrial gravity disturbances at the Earth’s surface and the residual airborne gravity disturbances at flight altitude can be written as
δ g r e s t e r x t e r = ∑ i = 1 N α i ∑ n m i n n t e r k n n + 1 r t e r 2 n + 1 4 π R r t e r n + 1 P n r t e r T r i = ∑ i = 1 N α i Ψ δ g x t e r , x i δ g r e s a i r x a i r = ∑ i = 1 N α i ∑ n m i n n a i r k n n + 1 r a i r 2 n + 1 4 π R r a i r n + 1 P n r a i r T r i = ∑ i = 1 N α i Ψ δ g x a i r , x i .
where x t e r and x a i r represent the position vectors of terrestrial gravity disturbances and airborne gravity disturbances, respectively. n t e r and n a i r are the maximum degrees of expansion of the terrestrial gravity disturbances and airborne gravity disturbances, respectively. Ψ δ g x , x i is the adapted SRBF of δ g ( x ) .
For terrestrial gravity observations, it is difficult to obtain a more appropriate expansion degree due to their uneven distribution. For airborne gravity data, however, due to their high altitudes and the low-pass filtering process, it is also not a simple task to determine optimal spectral information either. In this study, we provide a way to determine the optimal degree of series expansion for gravity data ( n t e r and n a i r ), which will be introduced in Section 3.1.
In Eq. (4), terrestrial gravity disturbances and airborne gravity disturbances have the same SRBF coefficients α i ( i = 1 , … , N ) , and we can thus combine these expressions to form our observation equations (Gauss–Markov model)
y 1 y 2 = A 1 A 2 α + e 1 e 2
where y 1 and y 2 are the vectors of the terrestrial gravity disturbances and airborne gravity disturbances, and A 1 and A 2 are the design matrices. α are the unknown SRBF coefficients, and e 1 and e 2 are the vectors of stochastic observation errors with expectation E e = 0 and dispersion D { e } = C . C = d i a g ( C 1 , C 2 ) is the variance‒covariance matrix of the observed error and meets C l = σ l 2 P l − 1 ( l = 1,2 ) , P 1 and P 2 is the observation weight matrix for group l ( l = 1,2 ) .
Usually, the normal equation matrix of Eq. (5) is ill conditioned and a stabilization is needed to make the computation of a solution possible. Moreover, since the true accuracy of the two datasets is not exactly known, it is especially necessary to determine reasonable weights when building the gravity field model by combining terrestrial and airborne gravity data. All of these requirements can be met using the variance component estimation method (VCE) [25]
1 σ 1 2 A 1 T P 1 A 1 + 1 σ 2 2 A 2 T P 2 A 2 + 1 σ μ 2 I α = 1 σ 1 2 A 1 T P 1 y 1 + 1 σ 2 2 A 2 T P 2 y 2
where σ 1 2 and σ 2 2 are the variance factors of terrestrial gravity disturbances and airborne gravity disturbances, respectively. σ μ 2 is the unknown prior variance factor, which is also a regularization parameter, and I is the unit matrix. The variance factor σ l 2 is usually determined based on an iterative method. That is, the initial variance factors σ l , 0 2 and σ μ , 0 2 are first given, and then the initial SRBF coefficients are estimated with the least squares estimation method. Then, the residuals of the least square values of the observation groups are further obtained, and the new variance factor can be calculated by
σ l , i 2 = e ^ l , i T P l e ^ l , i r l , i
σ ^ μ , i 2 = e ^ μ , i T P μ e ^ μ , i r μ , i
where e ^ l , i T and e ^ μ , i are the residuals of the observation groups after the i th iteration, and r l , i and r μ , i are redundant numbers, which can be expressed as
r l , i = n l − 1 σ l , i 2 t r A l , i T P l A l , i N i − 1 = n l − 1 σ l , i 2 t r N l , i N i − 1
r μ , i = u − 1 σ μ 2 t r P μ N i − 1
where n l represents the number of gravity observations in group l , u is the number of coefficients of SRBFs, A l , i is the design matrix at the i th iteration of the observations in group l , N l , i is the matrix of the normal equation at the i th iteration of the observations in group l , and N i is the total normal equation matrix of all observations at the i th iteration. t r stands for trace operation.
After the new variance factor is calculated, the next loop is entered until the convergence condition of the following equation is satisfied
m a x | σ ^ l , i 2 − σ ^ l , i − 1 2 | σ ^ l , i 2 ≤ τ l = 1,2
where τ is the convergence threshold, and we set τ = 0.01 . σ ^ l , i 2 is the variance factor of the l th group of observations after i th iteration.
Applying the least-squares method to Eq. (6), the unknown coefficients are estimated as
α ^ = 1 σ 1 2 A 1 T P 1 A 1 + 1 σ 2 2 A 2 T P 2 A 2 + 1 σ μ 2 I − 1 1 σ 1 2 A 1 T P 1 y 1 + 1 σ 2 2 A 2 T P 2 y 2
Inserting the coefficients of Eq. (12) back into Eq. (1), we can obtain the residual disturbing potential T r e s ( x ) .
Residual height anomaly is related to the residual disturbing potential T r e s ( x ) by
ζ r e s ( x ) = T r e s ( x ) γ
where γ is the normal gravity and ζ r e s ( x ) is the residual height anomaly.
Then, during the recovery procedure, we add back the height anomaly component of the GGM and the topographic effects, and a full-wavelength height anomaly ζ x can be obtained.
Finally, the geoid undulation can be obtained by the following conversion:
N x = ζ x + Δ g B x γ H ,
where H is the orthometric height, N x is the geoid undulation, and Δ g B is the simple Bouguer anomaly. Higher-order terms of the separation term [26] are not considered here to be consistent previously published procedures.

3. Gravity Data Processing and Analysis

3.1. Area of Interest

The Colorado geoid computation experiment is a collaborative effort involving the international geodetic community [27]. The study region is located between -110° and -102° longitude and between 35° and 40° latitude, primarily within the state of Colorado, USA. The area is characterized by rugged terrain in most of its part, which is evident in the topographic map displayed in Figure 1(a). The average elevation in this region is approximately 2,017 m. The highest peak reaches an elevation of 4,376 m, while the lowest point is at 932 m above sea level. In the central part of the study area lies the St. Louis Valley, which is an extensive depositional basin situated at high altitude. It covers an approximate area of 21,000 km2. To the west of the St. Louis Valley are the San Juan Mountains, which is a rugged mountain range in the Rocky Mountains. The eastern part of the study area consists of a plateau where the terrain is relatively flatter compared to other regions. This geographical information is important in understanding the characteristics and challenges of the study area for refining the regional gravity field model in Colorado.

3.2. Datasets Used for Modeling

The available data for the Colorado geoid computation experiment include terrestrial and airborne gravity data, GSVS17 GPS/leveling data, and Global Geopotential Models (GGMs). The terrestrial gravity data were provided by the National Geodetic Survey (NGS) and consist of 59,303 values obtained from over 137 survey campaigns, covering the entire area of the Colorado geoid project (see Figure 1 (b)). Grigoriadis et al. studied the spatial density of the point values for the area, and the results found that only 21.25% of the total cells of the 1 ' grid contain at least 1 point value, and approximately 50% of the cells of the 2 ' grid contain at least one value [28]. Therefore, it is more reasonable to build a geoid model with a resolution of less than 2 ' × 2 ' .
The raw airborne data use the Gravity for the Redefinition of the American Vertical Datum (GRAV-D) Block MS05. The north-south track spacing is 10 km, while the east-west cross track spacing is 80 km. The mean flight altitude is approximately 6,200 m. Figure 1 (b) illustrates the distribution of the survey lines in the area. As shown in Figure 1 (b), the lines are relatively evenly distributed and cover most of the study area. However, the coverage of airborne and terrestrial gravity data does not overlap completely. The airborne gravity data cover the latitudes between 35 ° ≤ φ ≤ 38.3 and longitudes between − 109 ° ≤ λ ≤ − 102 ° , There are no airborne data available for latitudes between 38.3 ° < φ ≤ 40 ° and longitudes between − 110 ° ≤ λ < − 109 ° (Figure 1 (b)). Moreover, the raw gravity data from MS05 are subject to biases between different tracks. Therefore, data from MS05 were debiased using the maximum median technique [29] and then resampled to 1 Hz. Finally, a dataset consisting of 283,716 data points was obtained. In addition, Childers et al. define the Fourier wavelength of the smallest recoverable feature as [30]
λ f = 1.54 × Z c
where Z c is the height of the measurement point above the center of the spherical body that causes the anomaly. In this study, the average altitude of the aircraft is 6.2 km, and the average topographic height is approximately 2 km; then, the distance of Z c is approximately 4.2 km. By substituting Z c = 4.2 into Equation (15), the minimum resolvable wavelength is calculated to be 6468 m, corresponding to a spherical harmonic degree of approximately 3000. However, this is just a rough estimate of the resolution since the study area is mountainous, and the topographic heights vary significantly.
Additionally, a total of 222 benchmarks of GSVS17 (Geoid Slope Validation Survey 2017) profile data [31] were provided by the NGS. These benchmarks are spaced approximately 1.6 km along Highway US 160 from Durango to Walsenburg. The accuracy of the geoid undulations inferred from the GPS-based ellipsoidal heights and the leveling-based orthometric heights is estimated to be approximately 1.5 cm. In addition to the comparisons made for the GSVS17 locations, entire geoid grids (at a 1 ' resolution) were compared based on the mean of all submitted models to assess the model’s performance over the entire area. Furthermore, the reference frame used for 3-D positioning of all three types of data (terrestrial gravity, airborne gravity, and GSVS17) is the IGS Reference Frame 2008 (IGS08) [32] on the Geodetic Reference System 1980 (GRS80) ellipsoid [33].

3.3. Data Preprocessing

In the original terrestrial data, there are cases in which several gravity observations are located at the same position, for which we only use the first of these observations (1090 points deleted). However, if the points sharing the same location but had a height difference of more than 3 m or a gravity difference of 2 mGal, then these points were both removed. Hence, 1215 points in total were excluded from the dataset (see Figure 1 (b)). Finally, a total of 58088 terrestrial gravity observations in the modeling area were obtained. Moreover, since the measurements are provided in orthometric heights H, we transform them to ellipsoidal heights using the geoid model 'GEOID 18B' provided by the National Geodesy Survey.
The airborne data had a dense distribution, resulting in a large design matrix. To simplify the computations, the sampling interval was reduced from 1 Hz to 1/8 Hz, and an average spatial interval of approximately 1 km along-track was obtained. This resulted in a total of 31,527 airborne gravity observations in the modeling area.
Then, for both types of observations, the following data preprocessing steps are performed:
① The observations were converted from absolute gravity g to gravity disturbance δ g by subtracting the normal gravity γ at the ellipsoidal height h of the observations
δ g = g − γ
② The atmospheric correction for the gravity disturbance δ g A T M was calculated using the method proposed by Torge [34]
δ g A T M = 0.874 − 9.9 × 10 − 5 H × 3.56 × 10 − 9 H 2
③ The atmospheric correction was added to the observations.
δ g = δ g 0 + δ g A T M

3.4. Remove Procedure

Gravity data obtained in a limited area cannot resolve long wavelengths in the gravity field. Therefore, the remove–compute–restore (RCR) procedure is usually utilized to remove the low-frequency and high-frequency signals of gravity data before modeling. However, when applying the RCR procedure, it is important to assess the performance of the Global Gravity Models (GGMs) used, as the error of the GGMs accumulates as expansion degrees increase. In this study, five combined GGMs are investigated: EGM2008 [35], XGM2019e_2159 [36], SGG-UGM-2 [37], XGM2016 [38], and GECO [39]. These models were chosen because they have relatively high accuracies and better spatial resolutions compared to other GGMs. The error degree variance offers insight into the error of a GGM, and it supplies a rudimentary quality assessment [40]. Figure 2 shows the degree-wise accumulated geoid errors of the five GGMs. EGM2008 exhibits a relatively large error, which rapidly increases from degrees 30-220, reaching approximately 7.3 cm at degree 220, and then slowly increases to 8.2 cm at the highest degree. On the other hand, models like XGM2019e_2159, SGG-UGM-2, and GECO, which have similar expansion degrees, show reduced errors of approximately 3.1 cm, 1.9 cm, and 4.3 cm, respectively. The significant error in EGM2008 in the frequency bands between degrees 30-220 is mainly due to the lack of data from the Gravity field and steady-state Ocean Circulation Explorer (GOCE) satellite. In contrast, the other three models are developed using GOCE data, resulting in better qualities in these frequency bands. Among the investigated models, XGM2016 exhibits the minimum cumulative geoid height error. Up to degree 719, the cumulative geoid height error of XGM2016 is approximately 1.1 cm, which is significantly lower than the corresponding values of the other four GGMs. Therefore, the XGM2016 model up to degree 719 is chosen for the RCR procedure. It is important to note that the error degree variances only provide a global mean of the internal error and cannot be considered as a realistic error estimate [41].
Another important factor that influences the performance of geoid modeling is topographic effects, which play a key role, especially in mountainous areas, since they can smooth the input observations and are of utmost importance for obtaining a good least-square fit. The topographic model dV_ELL_Earth2014 [42] from degree 720 to degree 2159 and a residual terrain model ERTM2160 [43] from degree 2160 to degree ~80,000 are removed from the terrestrial data. Similarly, for the airborne data, the effect of dV_ELL_Earth2104 from degree 720 to degree n a i r is removed. It is worth noting that using different topographic models above degree 2160 for the terrestrial and airborne data is reasonable because both the dV_ELL_Earth2014 and ERTM2160 models are derived from the same original data and contain the same signal [44]. This approach ensures consistency and avoids introducing additional errors due to the use of different models. Notably, for airborne data, the effect of dV_ELL_Earth2104 from degree 720 to degree n a i r is removed. In contrast, previous studies have utilized different degrees for removing topographic contributions in airborne data. However, we propose that removing topographic effects with degrees exceeding the optimal expansion degree of the gravity data may introduce modeling errors. Therefore, in this study, we remove the topographic contributions up to the expansion degree of the airborne data.
Figure 3 illustrates the distributions of the terrestrial and airborne gravity disturbances before and after the removal of the GGM and topographic effects. Figure 3(c) and 3(d) clearly show that the gravity disturbances become significantly smoother in the middle part of the study area after subtracting the contributions of the GGM and topographic effects.
Table 1 presents the statistical results of the gravity observations. The standard deviations of the terrestrial and airborne gravity disturbances are reduced from 38.72 to 6.90 mGal and from 29.56 to 3.35 mGal, respectively, after removing the contributions of the GGM and topographic effects. The standard deviation of the terrestrial data is reduced by 42.15% after subtracting the GGM and further reduced by 82.18% after including the topographic effects. Similarly, the airborne observations are reduced by 72.40% after subtracting the GGM and further reduced by 88.67% after including the topographic effects. The significant reduction in standard deviation indicates that the removal of the GGM and topographic effects leads to a smoother gravity field, enabling a better least-square fit in the gravity field modeling using SRBFs. It is worth noting that the smoothing effects are more pronounced in the terrestrial observations compared to the airborne observations after including the topographic model (Table 1). This is due to the fact that the short wavelength signal of the gravity field decreases with height, and the airborne gravity data are less sensitive to the short wavelength part compared to the terrestrial gravity data. Consequently, subtracting the topographic effects has a greater influence on the terrestrial gravity data compared to the airborne gravity data. Illustrating the smoothing effects and quantifying the reduction in standard deviation demonstrates the importance of removing the GGM and topographic contributions in order to improve the quality and accuracy of gravity field modeling.

4. Gravity Field Modeling

In the gravity field modeling based on band-limited SRBFs, several parameters and procedures were considered. The following configurations were used:
① Geocentric gravitational constant ( G M ): 3.986 004 415× 10 14 m 3 / s 2 .
② Average density of topographic masses ( ρ 0 ): 2670 k g / m 3 .
③ Geoid computations were performed in the tidefree system. GRS80 was used as the reference ellipsoid, and the conventional constants are referred to Moritz (2000).
Apart from these fundamental parameters, four important factors that influence the performance of SRBFs were also taken into account, namely, (1) the type of the SRBFs, (2) the location of the SRBFs, (3) the extensions of the data area and (4) the bandwidth parameters. Considering these parameters and procedures helps to ensure an effective and accurate gravity field modeling process based on band-limited SRBFs. Next, we introduce the model configuration for gravity field modeling based on band-limited SRBFs.
4.1.1. The Type of The SRBFs
There are many types of SRBFs that can be used for gravity field modeling, such as the Shannon functions, the Blackman functions, the Poisson functions, and the cubic polynomial functions. The Shannon function is a reproducing kernel of the space spanned by all solid spherical harmonics of degrees n = n m i n ⋯ n m a x [45]. As a result, it does not smooth the gravity signal in this spectral band. However, other types of SRBFs (e.g., Blackman functions, Poisson functions and cubic polynomial functions), with nonconstant kernel functions might smooth some gravity field harmonics. Though some harmonic properties are still remaining in the recovered signal, they might be significantly suppressed. Therefore, one has to be careful when interpreting results based on the SRBFs with smoothing kernel functions. Moreover, Bentel et al. studied the performance of different types of SRBFs, and the results show that the Shannon SRBFs lead to the same results as with spherical harmonics both in theory and in practice. Therefore, in this study, the Shannon kernel functions are used, the specific form of which is
k n = 1 n ϵ [ n m i n , n m a x ] 0 e l s e
4.1.2. Type of Grids
The location of the SRBFs depends on the type and number of grid points. There are many types of grids that can be used for regional gravity field modeling, such as the Driscoll-Healy grid, the triangle vertex grid and the Fibonacci grid. Eicker analyzed the advantages and disadvantages of different types of grids, and the results show that both the Reuter grids [46] and the triangle vertex grids are suitable for gravity field modeling with SRBFs. Bentel et al. noted that different types of grids do not differ significantly, especially compared to the other three factors that influence the modeling results. In addition, the control parameter β of the Reuter grid is related to the maximum expansion degree of SRBFs, which also facilitates gravity field modeling. We set β = n m a x , where n m a x is the maximum degree of the series expansion of SRBFs.
4.1.3. The Extensions of the Target, Observation, and Computation Area
In regional gravity modeling, the extension of the target area ∂ Ω T , the observation area ∂ Ω O , and the computation area ∂ Ω C needs to be defined carefully. At the edge of the observation area ∂ Ω O , the unknown coefficients cannot be appropriately estimated, which provokes edge effects. In general, the target area ∂ Ω T should be smaller than the observation area ∂ Ω O because the modeling accuracy gradually increases as the target area decreases. However, this operation reduces the target area, which sometimes resulting in a significant waste of gravity data. Moreover, the computation area ∂ Ω C should be larger than the observation area ∂ Ω O [47]. Otherwise, related computations may fail in gravity field modeling. Therefore, to minimize the edge effects in the computation, ∂ Ω T ⊂ ∂ Ω O ⊂ ∂ Ω C should be satisfied. In addition, the margins η need to be defined between the three areas. In our case, the target area ∂ Ω T is given to be between −109 ° and −103 ° and 36 ° and 39 ° . Therefore, the margin size η T , O between ∂ Ω T and ∂ Ω O is fixed to 1 °
The determination of the margin size η C , O between ∂ Ω C and ∂ Ω O follows the empirical formula described by Liu et al. [20]
η C , O ≈ 360 n m a x c o s ( φ m a x )
where φ m a x is the maximum latitude value of the target area. In this study, the value η C , O ≈ 0.1 ° follows, and the reason will be explained in section 4.1.4. Figure 4 visualizes the target area, the observation area, the computation area, and the margins.
4.1.4. Maximum and Minimum Degree of Expansion
The maximum degree of expansion of SRBFs is usually determined by high-resolution gravity data, which can be determined by empirical rules [48]
n m a x ≤ π R R e s o l
where Resol represents the resolution of the gravity data. In this study, the spatial resolution of terrestrial data is higher than that of airborne data. Therefore, the maximum expansion degree of SRBFs is mainly decided by the terrestrial data. Moreover, Liu et al. claimed that the average spatial interval of terrestrial gravity data is approximately 3.5 km, so they expanded the SRBFs to degree 5600, and signal frequencies higher than the maximum degree were not modeled. However, the maximum expansion degree determined by Liu et al. may be problematic, since Grigoriadis et al. stated that only about 50% of the cells in the 2 ' × 2 ' grid contained at least one value, which suggests that the data distribution may not be suitable to support such a high maximum degree of expansion. Therefore, this current study suggests that better results may be achieved by expanding the terrestrial gravity data to degrees less than 5400. However, determining the optimal spectral range for both terrestrial and airborne gravity data is difficult due to factors such as high altitude and uneven distribution of observations. To address this issue, we propose the residual and a-priori accuracy comparative analysis method, which will be discussed in detail in section 4.2.
For the minimum degree of expansion, Bucha et al. noted that there is still useful gravity information below the cutoff degree of the Global Geopotential Model (GGM). They concluded that starting the series expansion of SRBFs at a lower degree, such as 0, can help capture this useful part of the signal. This method has been commonly used in local gravity field modeling. However, the current study notes that this method is not always effective. In this study, since the contributions of XGM2016 up to degree 719 has been subtracted from the original signals, we set n m i n = 720 . By using this minimum degree starting from 720 instead of 0, we obtained better results, at least in the Colorado region of this study.

4.2. Residual and A-prior Accuracy Comparative Analysis Method

To efficiently use the gravity data for gravity field modeling, the residual and a-prior accuracy comparative analysis method is proposed to determine the optimal expansion degree of the gravity data. The procedure is as follows.
Step 1: In a large search interval, certain degrees with a large step size are selected as the maximum degree of expansion for the data. Using the gravity data available, the terrestrial-only and airborne-only SRBF models are built and the coefficients of SRBFs are estimated using the Variance Component Estimation (VCE) method. The modeling residuals of the gravity data are then statistically analyzed. The degree that yields the minimum root mean square (RMS) values of the residual with respect to the a-priori accuracy is identified as the initial degree.
Step 2: A smaller range around the initial degree is defined with a smaller degree step size. New SRBF models are built within this range. The differences between these models and GSVS17 data are calculated to obtain the STD value for each model. Finally, the model that has the smallest STD value is determined, and the corresponding expansion degree is considered as the optimal expansion degree of the gravity data.
It is important to note that Step 1 helps save calculation time and improve efficiency. Due to the large amount of gravity data, calculating the STD value for the geoid height difference for each model would require significant computational time. By initially selecting a larger degree range, the computational effort is reduced. In Step 2, external data (GSVS17) is used to assess the quality of the SRBF model within a smaller range. This is because there is some uncertainty in both the a-priori accuracy of terrestrial and airborne data. By incorporating external data within a smaller degree range, the computational effort is further reduced.

4.3. Gravity Field Modeling with SRBFs

We combine the terrestrial data and the airborne data using the Gauss–Markov model (Eq. (5)). Saleh et al. studied the qualities of the terrestrial gravity database of NGS, and the results show that the accuracy of terrestrial data is approximately 2.2 mGal [49]. Moreover, Varga et al. estimated the accuracy of terrestrial gravity data assuming that the errors are uncorrelated and obtained an accuracy of 2.6 mGal [50]. In addition, other scholars have estimated terrestrial gravity data at 1 mGal [51] or 3 mGal [52,53]. However, it seems that the accuracy of 1 mGal may be overstated, while the accuracy of 3 mGal may be understated. Therefore, we set the a-prior accuracy of the terrestrial gravity data to 2.2 mGal, which is essentially consistent with the results of Saleh et al. Moreover, the a-priori accuracy of the airborne gravity data is approximately 1.6-2 mGal [53], and we take the median value of 1.8 mGal as its a-priori accuracy.
The determination of the optimal expansion degree of terrestrial and airborne gravity data is conducted using the residual and a prior accuracy comparative analysis method. Figure 5 illustrates the procedure for finding the optimal degree of expansion. To fully demonstrate the difference caused by the degree of expansion of SRBFs, the STD of the differences between the geoid heights of the SRBF model and the GSVS17-derived geoid heights were also calculated. Figure 5a (Step 1) shows that a search range of 3600 to 5400, with a step size of 300, is selected for the terrestrial gravity data. For the airborne gravity data, a search range of 1600 to 3000, with a step size of 100, is chosen. It is observed that when the expanding degrees of the terrestrial and airborne data are 5100 and 1800, respectively, the RMS values of the residuals closely match their a-priori accuracy. Hence, these degrees are set as the initial values of expansion for the terrestrial and airborne gravity data (depicted by the black line in Figure 5a and b).Then, in Step 2, a smaller search interval of 4800 to 5400, with a step size of 100, is selected for the terrestrial data. For the airborne data, a search interval of 1800 to 1850, with a step size of 10, is chosen. It is observed that when the expanding degrees of the terrestrial and airborne data are 5200 and 1840, respectively, the geoid height differences reach their minimum value (depicted by the red line in Figure 5a and b).
In addition, as shown in Figure 5, although the residuals of the gravity disturbances decrease with an increase in the degree of expansion, the corresponding geoid accuracy does not exhibit the same trend. In fact, the increase of the expansion degree only improves the agreement between the recovered signal and the original signal, but it can also lead to overfitting of the observed values when the degree exceeds the optimal expansion degree of the SRBFs. Thus, the quality of the geoid does not always improve with increasing expansion degree. Additionally, the modeling error of airborne gravity data rapidly increases after the expansion degree surpasses 2200, whereas the corresponding change in terrestrial gravity data is not as significant. This indicates that the expansion degree of airborne gravity data may be more sensitive than that of terrestrial gravity data. In addition, according to the estimated resolution formula given by Eq. (15), the spherical harmonic degree of airborne gravity data is approximately 3000, whereas the optimal degree detected in our study is 1840. The STD values of geoid height differences calculated using these two degrees are approximately 0.158 m and 0.030 m, respectively (Figure 5 (b)), resulting in a difference of approximately 0.13 m. This highlights the influence of the expansion degree of the airborne gravity data on the modeling results. Moreover, the resolution of the airborne data explored in this study is approximately 10.6 km, which is larger than that of the NGS at 6.5 km. However, in terms of external accuracy, the resolution determined for the airborne data in this study seems to be more reliable than the aforementioned approach.

5. Evaluation of the Combined Solution

In this section, we compute two sets of output gravity functionals. The first is the geoid heights at the GSVS17 benchmarks, at which fourteen groups have provided geoid height results. The second is a grid model from 36 ° to 39 ° and −109 ° to −103 ° with a resolution of 1 ' × 1 ' . Fourteen groups have provided the geoid height grid model, and the comparison between our models and the mean of all the models are given.

5.1. Comparing to Models with Different Expanding Degrees of SRBFs

According to Eq. (6), there are two variables that need to be determined: the relative weight ω between the two types of observations and the regularization parameter λ . Both of these variables are determined through the VCE method, which is an iterative process to estimate the variance factors of different observation types and the prior information. Figure 6 illustrates how the variance factors of the gravity data change during the iteration process.
As seen from Figure 6, the iteration starts with the initial values of σ 1 2 = 6.25 m G a l 2 , σ 2 2 = 3.24 m G a l 2 and σ μ 2 = 1 × 10 − 13 , and after approximately 4 iterations, the variance factors tend to stabilize, and convergence is reached. The result of the finally obtained variance factors is σ 1 2 = 5.56 m G a l 2 , σ 2 2 = 4.15 m G a l 2 , and σ μ 2 = 1.17 × 10 − 13 , respectively. The relative weight ω between the airborne data and the terrestrial data is approximately 1.34:1, and the regularization parameter λ is approximately 4752 upon converting mGal to m / s 2 ( 1 m G a l = 1 × 10 − 5 m / s 2 ). It is worth noting that this result differs from that of Liu et al., who obtained variance factors of σ 1 2 = 6.13 m G a l 2 , σ 2 2 = 1.61 m G a l 2 , and σ μ 2 = 8.17 × 10 − 14 . Such a result is possible if both the terrestrial gravity data and the airborne gravity data are expanded to the same higher degree of 5600 [20]. Since the standard deviation of the residual airborne gravity data is small, the fitting effect is definitely better than that of terrestrial gravity data. However, it should be noted that the estimated variance factors actually represent the quality of the least-squares fit rather than the accuracy of the data itself.
To assess how our geoid model benefits from the residual and a prior accuracy comparative analysis method, our optimal computed model is compared to the model obtained with different maximum and minimum degrees of expansion of gravity data. Each model was then compared to the GSVS17 validation data, and the differences between the geoid height results and the validation data were recorded in Table 2.
The results of the investigation revealed that the geoid models obtained by setting the expansion degrees to 5600 (Model I) or 5200 (Model III) for both terrestrial and airborne gravity data, with a minimum expansion degree of 0, performed the worst with a standard error (STD) of 3.1 cm. However, when the minimum degree of expansion was changed to 720 (Models II and IV), the STD reduced to 2.6 cm. This suggests that the accuracy of the XGM2016 model up to degree 719 is higher than the residual components of the gravity data. Consequently, including the residual signals from degrees 0 to 719 does not contribute to improving the accuracy of the geoid model. This finding highlights the importance of considering the minimum expanding degree in regional gravity field modeling based on SRBFs. We note that this factor is often overlooked in previous studies. The quality of the XGM2016 model and its contribution to the overall accuracy of the geoid model should be taken into account when determining the appropriate expanding degrees for gravity data.
The optimal solution for our geoid model is Model VI, which is obtained by setting the expansion degrees to n t e r = 5200 , n a i r = 1840 and n m i n = 720 . When compared to the GSVS17 validation data, the geoid height differences have a STD value of approximately 2.3 cm, which is the smallest among all six selected models (Table 2). The improved performance of Model VI can be attributed to the introduction of a residual and a-priori accuracy comparative analysis method, as well as the special treatment of the minimum expansion degree of the SRBFs. Comparing Model VI to Model II and Model V, which have the same expansion degree of terrestrial data but different expansion degrees of airborne data, we find that Model II has an STD of 2.6 cm, while Model V has an STD of 2.5 cm, which are increased by 3 mm and 2 mm, respectively, compared to the STD value of Model VI. Therefore, when aiming to construct a geoid model with an accuracy of 1 cm, it is necessary to consider the potential impact of different expansion degrees of the gravity data.

5.2. GSVS17 Comparisons

To further evaluate the quality of the optimal geoid model (hereinafter referred to as ColSRBF2023), five geoid models are downloaded from the International Service for the Geoid (ISG) for accuracy comparison. The five models are ColFFTW2020 from Aristotle University of Thessaloniki (AUTh), ColSRBF2019 from the Deutsches Geodätisches Forschungsinstitut (DGFI), ColUNBSH2019 from the Geospatial Information Authority of Japan (GSI), ColRLSC2019 from the Institute for Astronomical and Physical Geodesy (IAPG) and ColWLSC2020 from the Politecnico di Milano (Polimi). The reason for choosing the five models is that all five models use the same RCR procedure. For example, they all use the same reference gravity field model (XGM2016 up to degree 719) and the same methods for removing the topographic effects [53]. Therefore, compared with the above models, they can better reflect the differences caused by different modeling methods. It is important to note that there is a bias of approximately 87 cm between the geopotential value of the reference level used in our experiment and that defined by the NAVD88 datum, which is tied to the tide gauge at Rimouski [54]. This bias has been subtracted in the comparison. Figure 7 shows the differences between the geoid heights obtained by different models and GSVS17-derived geoid heights, and Table 3 lists the geoid height differences of each model along the GSVS17 profile.
Figure 7 shows that the differences between each model and GSVS17 generally follow a similar trend. The STD values of the geoid height differences range from 2.3 cm to 3.9 cm, as listed in Table 3. The model with the smallest STD value is ColSRBF2023, which has a difference of approximately 2.3 cm. Table 3 also provides the range of differences for each model relative to GSVS17. The differences range from 11.3 cm for the ColSRBF2023 model to 22.8 cm for ColWLSC2020, with an average value of 15.7 cm. These values are quite significant considering the target accuracy of 1 cm for geoid modeling. However, considering the uneven distribution of observations, the result is still quite satisfactory.
In addition, as shown in Figure 7, the differences are clear around the point numbers (Nos.) of 100 and 200, with maximum and minimum deviations of 7.9 cm and -14.9 cm, respectively. This may be attributed to the scarcity of terrestrial gravity data in this section (see Figure 1). Notably, around Nos. 100 and 200, the terrain changes are more significant, and the ColSRBF2023 model is significantly improved compared with the other five models, which indicates the effectiveness of the residual and a-prior accuracy comparative analysis method proposed in this study. These values are quite significant considering the target accuracy of 1 cm for geoid modeling.

5.3. Area Comparison of Geoid Grids

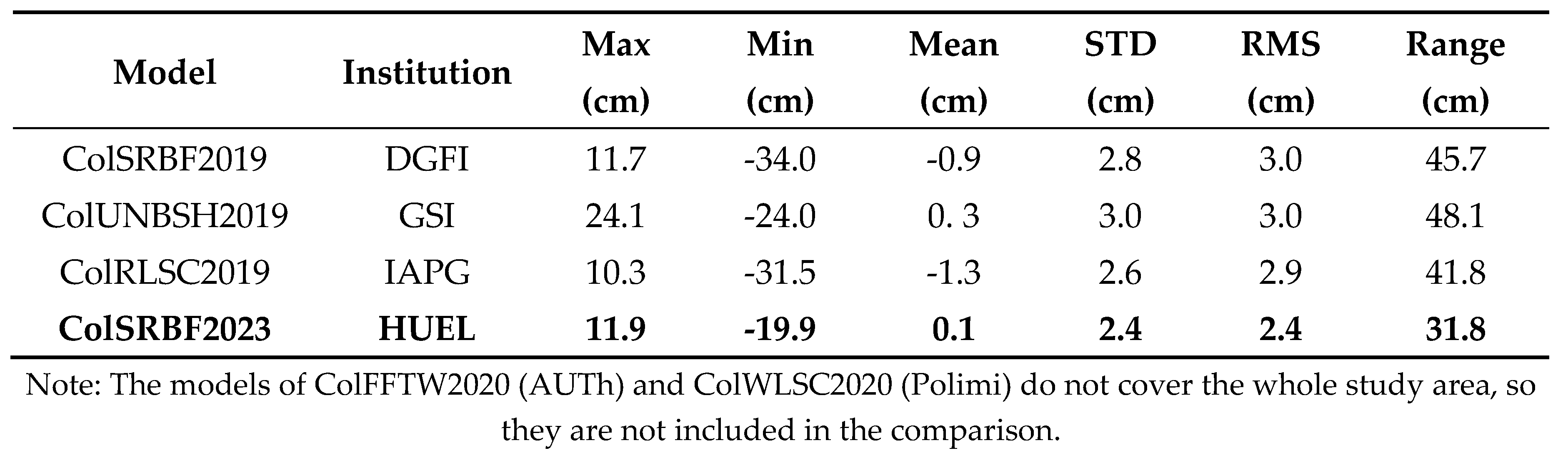
Since GSVS17 is located in a relatively flat area, comparison with GSVS17 may misrepresent the error of the entire study area. Therefore, we employ the average value of the geoid models submitted to ISG as a calibration model to further evaluate the accuracy of ColSRBF2023. Specifically, the geoid heights of the target area (36 ° N-39 ° N, 109 ° W-103 ° W) with a resolution of 1 ' × 1 ' are first calculated by ColSRBF2023, and then the geoid heights are compared with the calibration model. Figure 8a visualizes the geoid model for the whole target area ∂ Ω T , with a grid resolution of 1 ' × 1 ' , and Figure 8b shows the geoid height differences w.r.t. the calibration geoid model. Table 4 provides the statistics of these differences.
From Figure 8b, we can see that large differences are mainly concentrated on the east and west sides of the target area (dark blue and dark red blocks in Figure 8b). These areas are characterized by drastic elevation variations and sparse distribution of gravity data, highlighting the importance of gravity data density and quality. In other areas (yellow and light blue regions in Figure 8b), the differences are relatively small, generally not exceeding ±5 cm. Furthermore, in terms of RMS of the differences, ColSRBF2023 has a value of 2.4cm, while the other three models are 3.0cm, 3.0 cm and 2.9 cm, respectively. ColSRBF2023 has the smallest RMS value among all the models compared, and the accuracy improved by 5-6 mm. Additionally, the model with the largest range of differences is ColUNBSH2019 (GSI), reaching 48.1 cm. ColSRBF2023 performs slightly better, with an average range of 31.8 cm (Table 4). The overall average range of differences for all models is 41.8 cm, which reflects the significant challenge of achieving 1 cm accuracy in geoid modeling in mountainous areas.
In general, the optimal model in this study is the combined geoid model ColSRBF2023 obtained by setting the expansion degree of terrestrial and airborne gravity data n t e r = 5200 , n a i r = 1840 and n m i n = 720 , respectively (Table 2), the STD and RMS errors of which are 2.4 cm and 2.4 cm, respectively. The distribution of the difference is relatively uniform, which indicates the effectiveness of the residual and a-prior accuracy comparative analysis method and the treatment of the minimum degree of expansion of SRBFs.

6. Summary and Outlook

After the earlier work undertaken by Schmidt et al., Eicker, and Klees et al., SRBFs have been widely used for regional gravity field modeling in the last two decades. In this study, we combine terrestrial gravity data, airborne gravity data, GGMs and topographic models to calculate a high-resolution geoid model in Colorado based on band-limited SRBFs. Detailed explanations are given regarding the determination of the optimal expansion degree of gravity data: the optimal maximum expansion degree of terrestrial and airborne gravity data and the minimum expansion degree of gravity data. The main conclusions are as follows.
(1) The residual and a-priori accuracy comparative analysis method has proven to be effective in determining the expansion degree of gravity data. Using this method, we were able to determine the optimal expansion degree of terrestrial and airborne data to be 5200 and 1840, respectively. Additionally, the accuracy of our optimal geoid model, ColSRBF2023, was found to be 2.3 cm, which is the smallest compared to the other geoid models in this study. This implies that the expansion degrees of gravity data have influence on the modeling results, and cannot be overlooked when aiming for geoid modeling at the centimeter-level accuracy. Furthermore, the residual and a-priori accuracy comparative analysis method can also be utilized to detect the spectral information of gravity signals. This means that the method can provides valuable insights into the nature and characteristics of the gravity signals, enhancing our understanding of the geoid modeling process.
(2) The minimum degree of expansion of the gravity data also plays a role in the modeling result. If the expansion degree is not properly determined, it can lead to a geoid height error of ~5 mm. This highlights the importance of accurately determining the minimum expansion degree to achieve the desired level of accuracy in geoid modeling.
(3) By combining gravity data with different spectra using band-limited SRBFs, favorable modeling results can be achieved. Compared with ColSRBF2019, ColUNBSH2019, ColRLSC2019 and ColWLSC2020 submitted to ISG by different institutions, the ColSRBF2023 model showed a reduction in STD value of approximately 0.2-1.6 cm.
(4) Comparisons are also made with the mean results of all the contributions. Our geoid grid model for the whole study area delivers an STD value of 2.4 cm, which is also a small value for all participants. Moreover, there is favorable agreement between the STD error with regards to the area mean solutions and the STD error w.r.t. the GSVS17 GPS/leveling data, which shows the reliability of our geoid model ColSRBF2023.
All in all, in this study, we aimed to enhance the accuracy of the geoid model in Colorado using band-limited SRBFs. To achieve this, an investigation and determined the optimal expansion degrees for both terrestrial and airborne gravity data were conducted. The highest accuracy geoid model was obtained when the maximum expansion degrees for terrestrial and airborne gravity data were set to 5600 and 1840, respectively, while the minimum expansion degrees for both data types were set to 720.The study demonstrated the significance of accurately determining the spectral information of gravity data, particularly in regions with high topography, to improve the accuracy of geoid models. In future studies, we plan to perform further analyses of the remaining error sources in the determination of geoid models based on band-limited SRBFs, including the effect of the cutoff degree of the GGM, topographic reductions, and different approaches for handling airborne data, thereby furthering our contribution to the 1-cm geoid experiment of Colorado.

Author Contributions

Conceptualization, Z.M.; methodology Z.M.; funding acquisition and project administration, Z.M. and J.L; software, Z.M.; supervision and validation, M.Y.; writing—original draft, Z.M.; writing—review and editing, J.L. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the National Natural Science Foundation of China, grant

Data Availability Statement

The terrestrial gravity data, the airborne gravity data, and the point file of the GSVS17 GPS/leveling data used in this study were provided by the National Geodetic Survey, for the ’1 cm Geoid Experiment.’ The airborne gravity data are freely available on https://www.ngs.noaa.gov/GRAV-D/data_products.shtml. All data for this paper are properly cited and referred to in the reference list.

Acknowledgments

The authors are very grateful to the NGS, the ISG and the ICGEM for providing gravity, GPS/leveling, geoid and GGM data.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Varga, M.; Pitoňák, M.; Novák, P.; Bašić, T. Contribution of GRAV-D airborne gravity to improvement of regional gravimetric geoid modelling in Colorado, USA. J. Geod. 2021, 95, 1–23. [Google Scholar] [CrossRef]
  2. Forsberg, R.; Tscherning, C.C. The use of height data in gravity field approximation by collocation. J. Geophys. Res. 1981, 86, 7843–7854. [Google Scholar] [CrossRef]
  3. Novák, P.; Heck, B. Downward continuation and geoid determination based on band-limited airborne gravity data. J. Geod. 2002, 76, 269–278. [Google Scholar] [CrossRef]
  4. Hwang, C.; Hsiao, Y.S.; Shih, H.C.; Yang, M.; Chen, K.H.; Forsberg, R.; Olesen, A.V. Geodetic and geophysical results from a Taiwan airborne gravity survey: data reduction and accuracy assessment. J. Geophys. Res 2007, 112, B04407. [Google Scholar] [CrossRef]
  5. Willberg, M.; Zingerle, P.; Pail,R. Integration of airborne gravimetry data filtering into residual least-squares collocation: example from the 1 cm geoid experiment. J. Geod. 2020, 94, 1–17. [Google Scholar] [CrossRef]
  6. Tscherning, C.C. Geoid determination by 3D least-squares collocation; Sanso F, lecture notes in earth system sciences 110. Springer, Berlin, 2013, 311–336. [CrossRef]
  7. Kern, M.; Schwarz, K.K.P.P.; Sneeuw, N. A study on the combination of satellite, airborne, and terrestrial gravity data. J. Geod. 2003, 77, 217–225. [Google Scholar] [CrossRef]
  8. Shih, H.C.; Hwang, C.; Barriot, J.P.; Mouyen, M.; Corréia, P; Lequeux, D. ; Sichoix, L. High-resolution gravity and geoid models in Tahiti obtained from new airborne and land gravity observations: data fusion by spectral combination. Earth Planets & Space. 2015, 67, 124. [Google Scholar] [CrossRef]
  9. Simons, F.J.; Dahlen, F.A. Spherical Slepian functions and the polar gap in geodesy. Geophys. J. Int. 2006, 166, 1039–1061. [Google Scholar] [CrossRef]
  10. Li, X. Using radial basis functions in airborne gravimetry for local geoid improvement. J. Geod. 2017, 92, 471–485. [Google Scholar] [CrossRef]
  11. Wittwer, T. Regional gravity field modelling with radial basis functions; Delft University of Technology: Delft, The Netherlands, 2009. [Google Scholar]
  12. Schmidt, M.; Fengler; M. ; Mayer-Guerr, T.; Eicker, A.; Kusche, J.; Sanchez, L.; Han, S.C. Regional gravity field modeling in terms of spherical base functions. J Geod. 2007, 81, 17–38. [Google Scholar] [CrossRef]
  13. Klees, R.; Tenzer, R.; Prutkin, I.; Wittwer, T. A data-driven approach to local gravity field modelling using spherical radial basis functions. J. Geod. 2008, 82, 457–471. [Google Scholar] [CrossRef]
  14. Eicker, A. Gravity field refinement by radial basis functions from in-situ satellite data; Universität Bonn, Bonn, Germany, 2008.
  15. Bentel, K.; Schmidt, M.; Denby, C.R. Artifacts in regional gravity representations with spherical radial basis functions. J. Geod. Sci. 2013, 3, 173–187. [Google Scholar] [CrossRef]
  16. Lieb, V.; Schmidt, M.; Dettmering, D.; Börger, K. Combination of various observation techniques for regional modeling of the gravity field. J. Geophys. Res. Solid. Earth. 2016, 121, 3825–3845. [Google Scholar] [CrossRef]
  17. Bucha, B.; Janák, J.; Papčo, J.; Bezděk, A. High-resolution regional gravity field modelling in a mountainous area from terrestrial gravity data. Geophys. J. Int. 2016, 207, 949–966. [Google Scholar] [CrossRef]
  18. Klees, R.; Slobbe, D.; Farahani, H. A methodology for least-squares local quasi-geoid modelling using a noisy satellite-only gravity field model. J. Geod. 2018, 92, 431–442. [Google Scholar] [CrossRef]
  19. Slobbe, C.; Klees, R.; Farahani, HH.; Huisman, L.; Alberts,B. ; Voet, P.; Doncker, F.D. The Impact of Noise in a GRACE/GOCE Global Gravity Model on a Local Quasi-Geoid. J. Geophys. Res. Solid. Earth. 2019, 124, 3219–3237. [Google Scholar] [CrossRef]
  20. Liu, Q.; Schmidt, M.; Sánchez, L. Willberg, M. Regional gravity field refinement for (quasi-) geoid determination based on spherical radial basis functions in Colorado. J. Geod. 2020, 94, 99. [Google Scholar] [CrossRef]
  21. Liu, Y.S.; Lou, L.Z. Unified land–lcean quasi-geoid computation from heterogeneous data sets based on radial basis functions. Remote Sens. 2022, 14, 3015. [Google Scholar] [CrossRef]
  22. Freeden, W.; Gervens, T.; Schreiner, M. Constructive approximation on the sphere with applications to geomathematics; Oxford University Press on Demand, New York, USA, 1998.
  23. Schmidt, M.; Fengler, M.; Mayer-Guerr, T.; Eicker, A.; Kusche, J.; Sanchez, L.; Han, SC. Regional gravity field modeling in terms of spherical base functions. J. Geod. 2007, 81, 17–38. [Google Scholar] [CrossRef]
  24. Heiskanen, W.A.; Moritz, H. Physical geodesy. W.H. Freeman and Company, San Francisco, 1967.
  25. Koch, K.R. , Kusche, J. Regularization of geopotential determination from satellite data by variance components. J Geod. 2002, 76, 259–268. [Google Scholar] [CrossRef]
  26. Flury, J.; Rummel, R. On the geoid–quasigeoid separation in mountain areas. J. Geod. 2009, 83, 829–847. [Google Scholar] [CrossRef]
  27. Wang, Y.M. , Li, X., Ahlgren, K., Krcmaric, J. Colorado geoid modeling at the US National Geodetic Survey. J Geod. 2020, 94, 106. [Google Scholar] [CrossRef]
  28. Grigoriadis, V.N.; Vergos, G.S.; Barzaghi, R; Carrion, D. ; Koç, Ö. Collocation and FFT-based geoid estimation within the Colorado 1 cm geoid experiment. J. Geod. 2021, 95, 52. [Google Scholar] [CrossRef]
  29. Wang, Y.M.; Holmes, S., Li,X., and Ahlgren,K. NGS Annual Experimental Geoid Models – xGEOID17: What is new and the results; IAG-IASPEI, Kobe, Japan, 2017.
  30. Childers, V.A.; Bell, R.E.; Brozena, J.M. Airborne gravimetry: an investigation of filtering. Geophysics. 1999, 64, 61–69. [Google Scholar] [CrossRef]
  31. van Westrum, D.; Ahlgren, K.; Hirt, C.; Guillaume, S. A. Geoid Slope Validation Survey (2017) in the rugged terrain of Colorado, USA. J. Geod. 2021, 95, 9. [Google Scholar] [CrossRef]
  32. Rebischung, P.; Griffiths, J.; Ray, J.; Schmid, R.; Collilieux, X.; Garayt, B. IGS08: the IGS realization of ITRF2008. GPS. Solut. 2012, 16, 483–494. [Google Scholar] [CrossRef]
  33. Moritz, H. Geodetic Reference System 1980. J. Geod. 2000, 74, 128–133. [Google Scholar] [CrossRef]
  34. Torge, W. Gravimetry. Walter de Gruyter, Berlin, 1989.
  35. Pavlis, N.K.; Holmes, S.A.; Kenyon, S.C.; and Factor, J.K. The Development and Evaluation of the Earth Gravitational Model 2008 (EGM2008). J. Geophys. Res. 2012, 117, B04406. [Google Scholar] [CrossRef]
  36. Zingerle, P. , Pail, R., Gruber, T., Oikonomidou, X. The Experimental Gravity Field Model XGM2019e. Potsdam, Germany, 2019, Germany. [Google Scholar]
  37. Liang W.; Li J.; Xu, X; Zhang, S.; Zhao, Y. A High-Resolution Earth’s Gravity Field Model SGG-UGM-2 from GOCE, GRACE, Satellite Altimetry, and EGM2008. Engineering, 2020, 860-878. [CrossRef]
  38. Pail, R. , Fecher, T., Barnes, D., Factor, J. F., Holmes, S. A., Gruber, T., et al.. Short Note: the Experimental Geopotential Model XGM2016. J. Geod. 2018, 92, 443–451. [Google Scholar] [CrossRef]
  39. Gilardoni, M. , Reguzzoni, M., and Sampietro, D. GECO: a Global Gravity Model by Locally Combining GOCE Data and EGM2008. Stud. Geophys. Geod. 2015, 60, 228–247. [Google Scholar] [CrossRef]
  40. Pail, R. , Bruinsma, S., Migliaccio, F., Förste, C., Goiginger, H., Schuh,W.-D., et al. First GOCE Gravity Field Models Derived by Three Different Approaches. J. Geod. 2011, 85, 819–843. [Google Scholar] [CrossRef]
  41. Wu, Y.; He, X.; Luo, Z.; Shi, H. An Assessment of Recently Released High-Degree Global Geopotential Models Based on Heterogeneous Geodetic and Ocean Data. Front. Earth Sci. 2021, 9, 749611. [Google Scholar] [CrossRef]
  42. Rexer, M. , Hirt, C. , Claessens, S., Tenzer, R. Layer-based modelling of the Earth’s gravitational potential up to 10-km scale in spherical harmonics in spherical and ellipsoidal approximation. Surv. Geophys. 2016, 37, 1035–1074. [Google Scholar] [CrossRef]
  43. Hirt, C.; Kuhn, M.; Claessens, S.; Pail, R.; Seitz, K.; Gruber, T. Study of the Earth’s short-scale gravity field using the ERTM2160 gravity model. Comput. Geosci. 2014, 73, 71–80. [Google Scholar] [CrossRef]
  44. Rexer, M.; Hirt, C.; Claessens, S.; Tenzer, R. Layer-based modelling of the Earth’s gravitational potential up to 10-km scale in spherical harmonics in spherical and ellipsoidal approximation. Surv Geophys. 2016, 37, 1035–1074. [Google Scholar] [CrossRef]
  45. Freeden,W. ; Schneider, F. An integrated wavelet concept of physical geodesy. J. Geod. 1998, 72, 259–281.
  46. Reuter,R. Über Integralformeln der Einheitssphäre und harmonische Splinefunktionen. RWTH Aachen University, Aachen, Germany,1982.
  47. Naeimi, M.; Flury, J.; Brieden, P. On the regularization of regional gravity field solutions in spherical radial base functions. Geophys. J. Int. 2015, 202, 1041–1053. [Google Scholar] [CrossRef]
  48. Naeimi,M. Inversion of satellite gravity data using spherical radial base functions. Leibniz Universität Hannover, Hannover, Germany, 2013.
  49. Saleh, J. , Li, X.,Wang, Y., Roman, D., Smith, D. Error analysis of the NGS’ surface gravity database. J. Geod. 2013, 87, 203–221. [Google Scholar] [CrossRef]
  50. Varga, M.; Pitoňák, M.; Novák, P.; Bašić, T. Contribution of GRAVD airborne gravity to improvement of regional gravimetric geoid modelling in Colorado, USA. J. Geod. 2021, 95, 53. [Google Scholar] [CrossRef]
  51. Işık, M.S.; Erol, B.; Erol, S.; Sakil, F.F. High-resolution geoid modeling using least squares modification of stokes and hotine formulas in Colorado. J. Geod. 2021, 95, 49. [Google Scholar] [CrossRef]
  52. Jiang, T. , Dang, Y.M., Zhang, C.Y. Gravimetric geoid modeling from the combination of satellite gravity model, terrestrial and airborne gravity data: a case study in the mountainous area, Colorado. Earth, Planets and Space. 2020, 72, 189. [Google Scholar] [CrossRef]
  53. Wang, Y.M.; Sánchez, L.; Ågren, J. Colorado geoid computation experiment: overview and summary. J. Geod. 2021, 95, 127. [Google Scholar] [CrossRef]
  54. Zilkoski, D.B.; Richards, J.H.; Young, G.M. Results of the general adjustment of the North American Vertical Datum of 1988. Surv. Land. Inf. Syst. 1992, 52, 133–149. [Google Scholar]
  55. Bai, H.; Ming, Z.; Zhong, Y. Evaluation of evapotranspiration for exorheic basins in China using an improved estimate of terrestrial water storage change. Journal of Hydrology. 2022, 610, 127885. [Google Scholar] [CrossRef]
Preprints 83671 g001
Figure 1. a Topographic heights in the Colorado area; b Datasets: Terrestrial gravity data (blue), duplicated points (purple) and airborne gravity observations (orange), GSVS17 benchmarks (red) and the target area (black rectangle).
Figure 1. a Topographic heights in the Colorado area; b Datasets: Terrestrial gravity data (blue), duplicated points (purple) and airborne gravity observations (orange), GSVS17 benchmarks (red) and the target area (black rectangle).
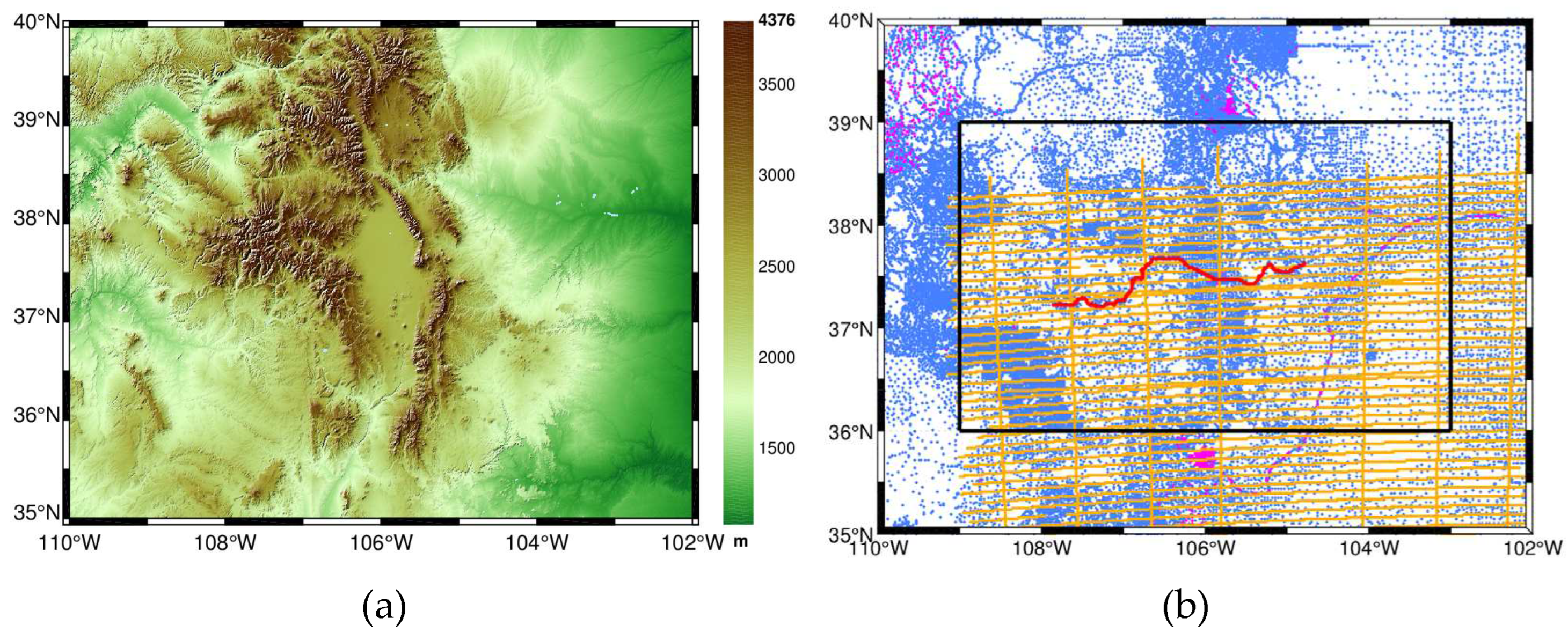
Preprints 83671 g001
Preprints 83671 g002
Figure 2. Cumulative geoid errors of different GGMs.
Figure 2. Cumulative geoid errors of different GGMs.
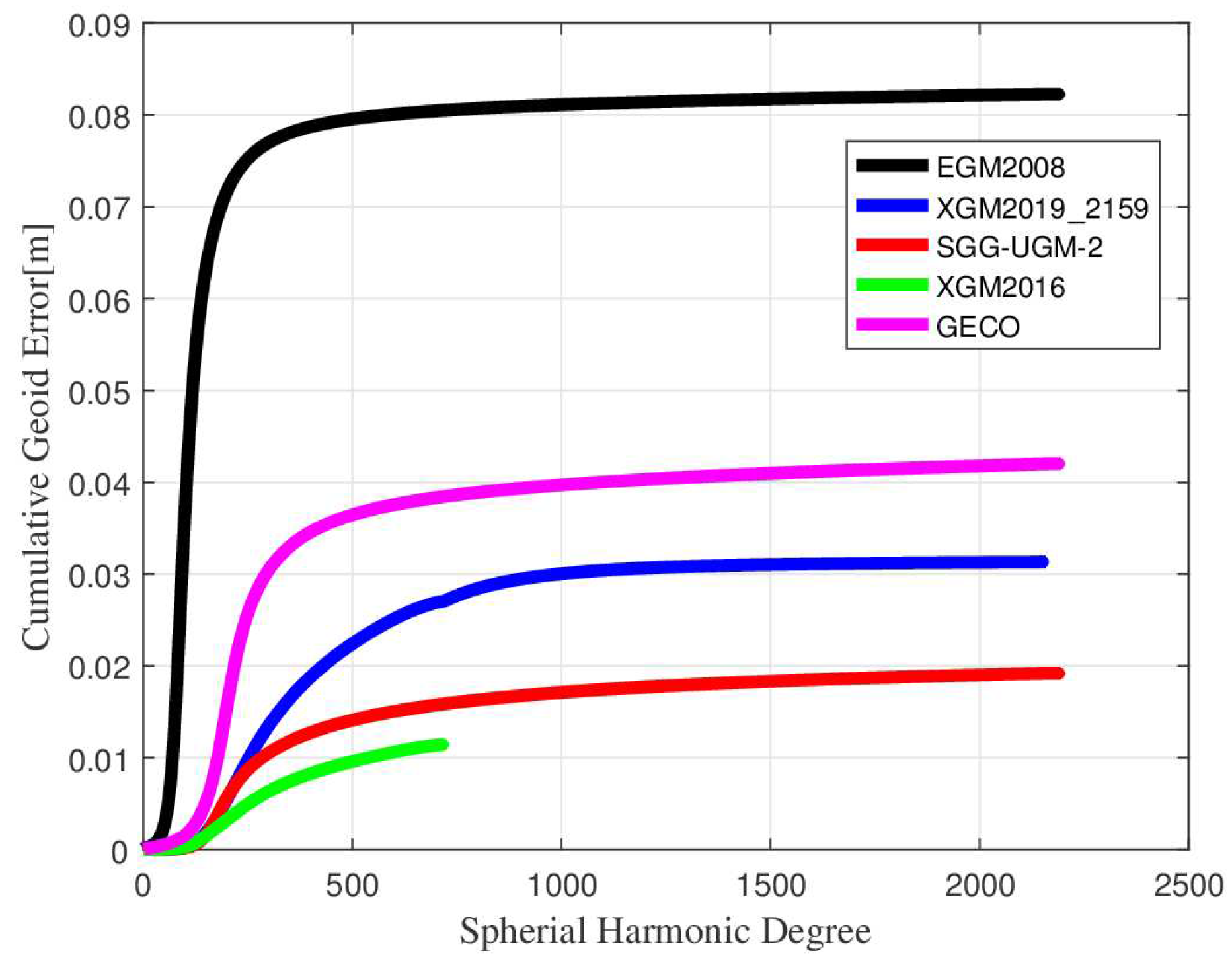
Preprints 83671 g002
Preprints 83671 g003
Figure 3. a, b Gravity observations ( δ g ); c, d remaining parts after both the GGM and topographic reduction ( δ g − δ g G G M − δ g R T M ) for the terrestrial data (left column) and airborne data (right column).
Figure 3. a, b Gravity observations ( δ g ); c, d remaining parts after both the GGM and topographic reduction ( δ g − δ g G G M − δ g R T M ) for the terrestrial data (left column) and airborne data (right column).
Preprints 83671 g003
Preprints 83671 g004
Figure 4. The extensions of the computation areas 𝜕𝛺C, observation area 𝜕𝛺O and target area𝜕𝛺T.
Figure 4. The extensions of the computation areas 𝜕𝛺C, observation area 𝜕𝛺O and target area𝜕𝛺T.
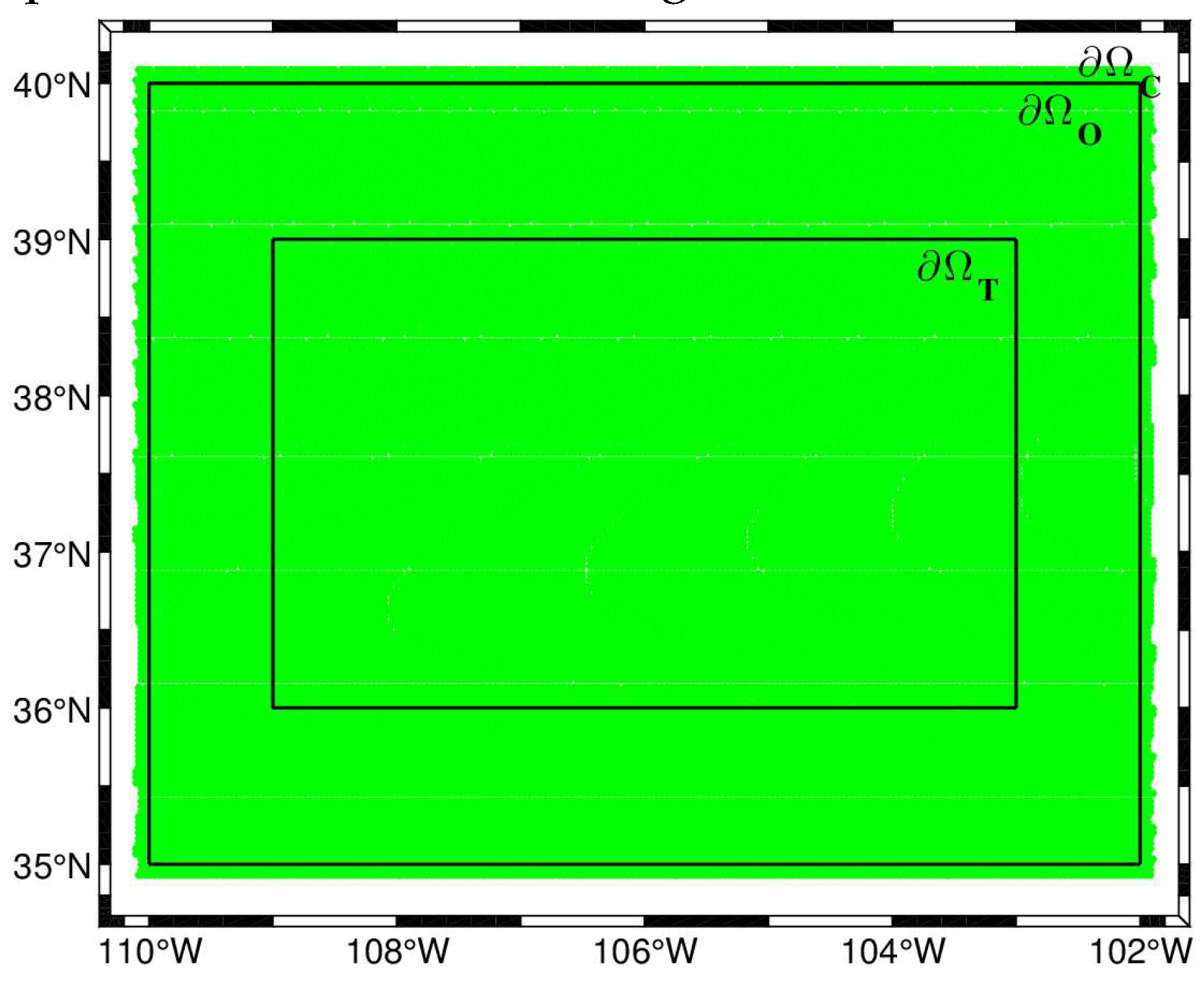
Preprints 83671 g004
Preprints 83671 g005
Figure 5. Residual and a-prior accuracy comparative analysis method used to find the optimal expansion degree of the terrestrial gravity data (a) and airborne gravity data (b). Blue: RMS value of the modeling residuals (mGal). Purple: Geoid accuracy of the terrestrial-only and airborne-only models (m).
Figure 5. Residual and a-prior accuracy comparative analysis method used to find the optimal expansion degree of the terrestrial gravity data (a) and airborne gravity data (b). Blue: RMS value of the modeling residuals (mGal). Purple: Geoid accuracy of the terrestrial-only and airborne-only models (m).
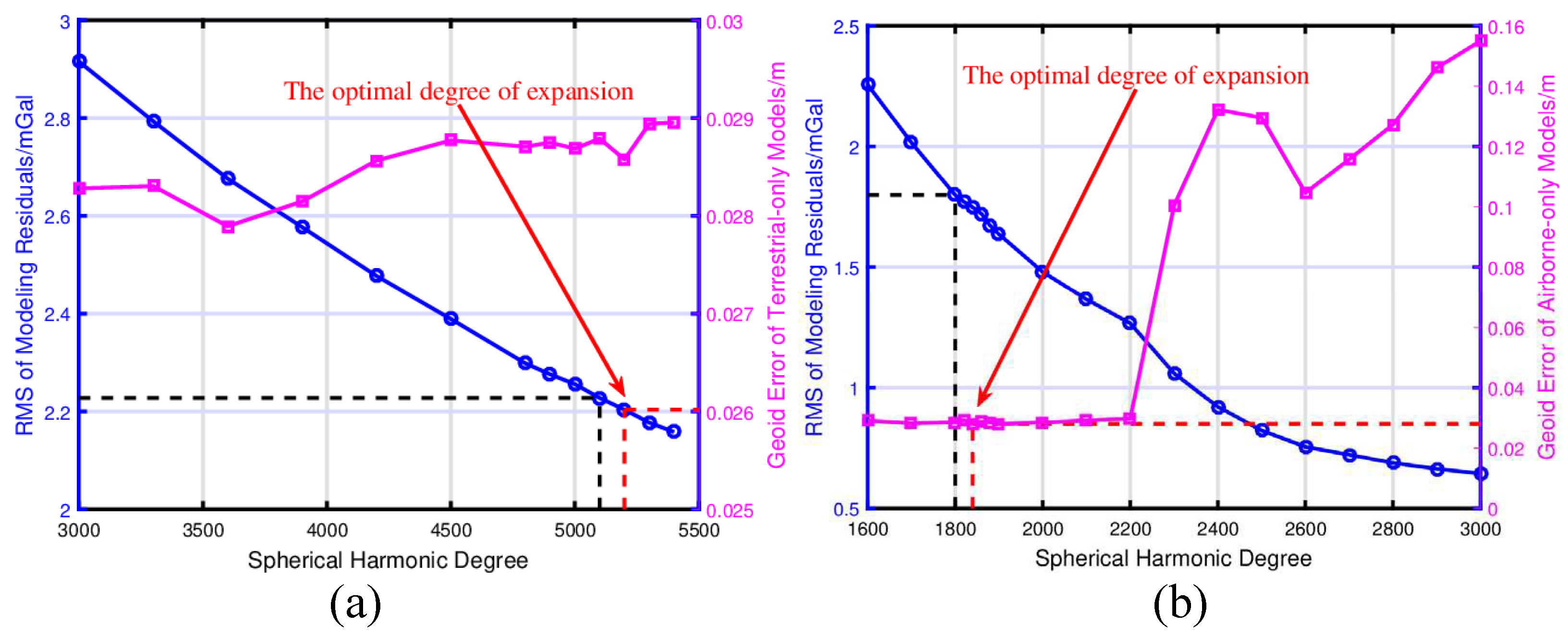
Preprints 83671 g005
Preprints 83671 g006
Figure 6. Changes in variance factors of gravity data with the number of iterations.
Figure 6. Changes in variance factors of gravity data with the number of iterations.
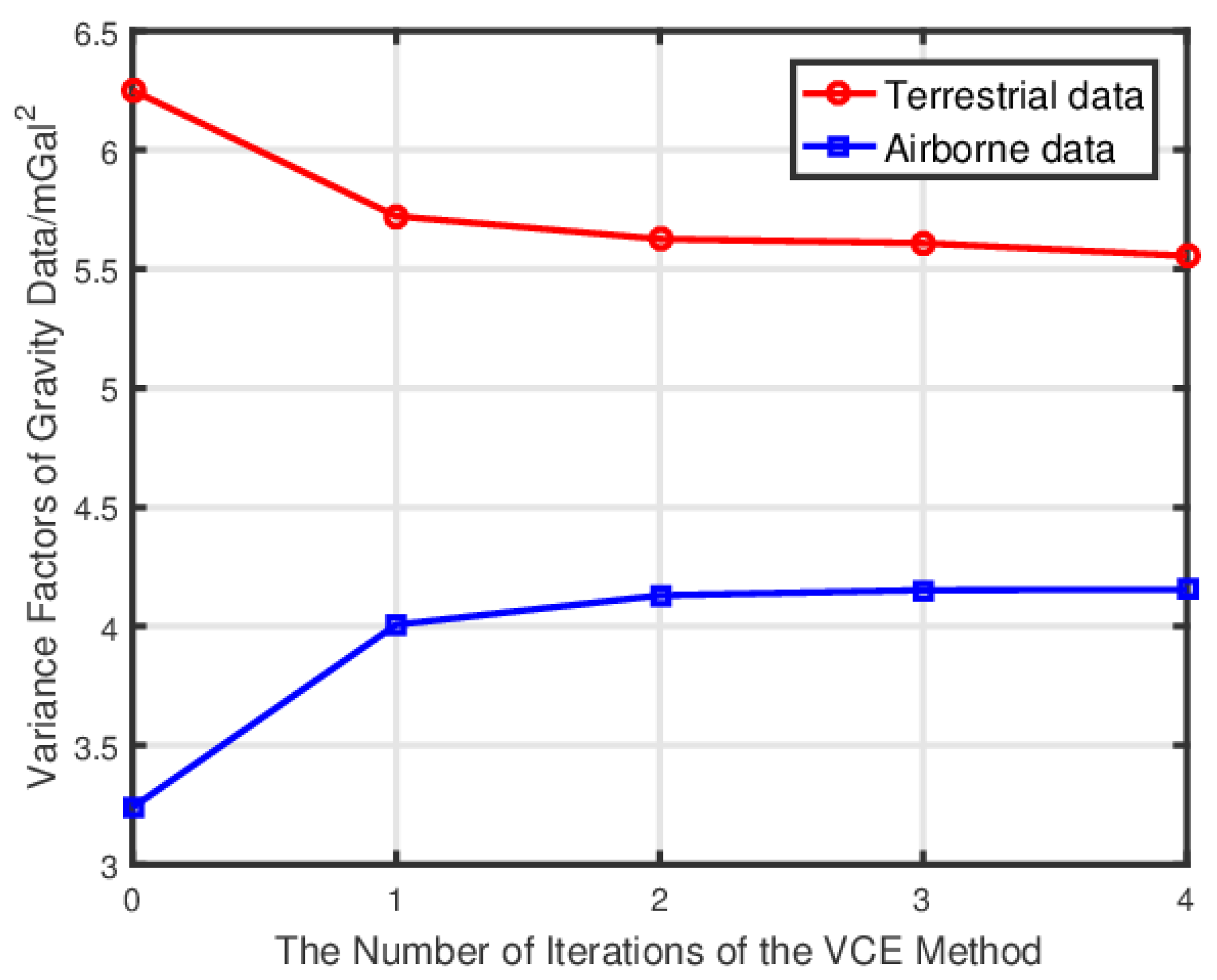
Preprints 83671 g006
Preprints 83671 g007
Figure 7. Geoid height differences on the GSVS17 benchmarks ( N M o d e l − N G S V S 17 ). 87 cm is subtracted from the models
Figure 7. Geoid height differences on the GSVS17 benchmarks ( N M o d e l − N G S V S 17 ). 87 cm is subtracted from the models
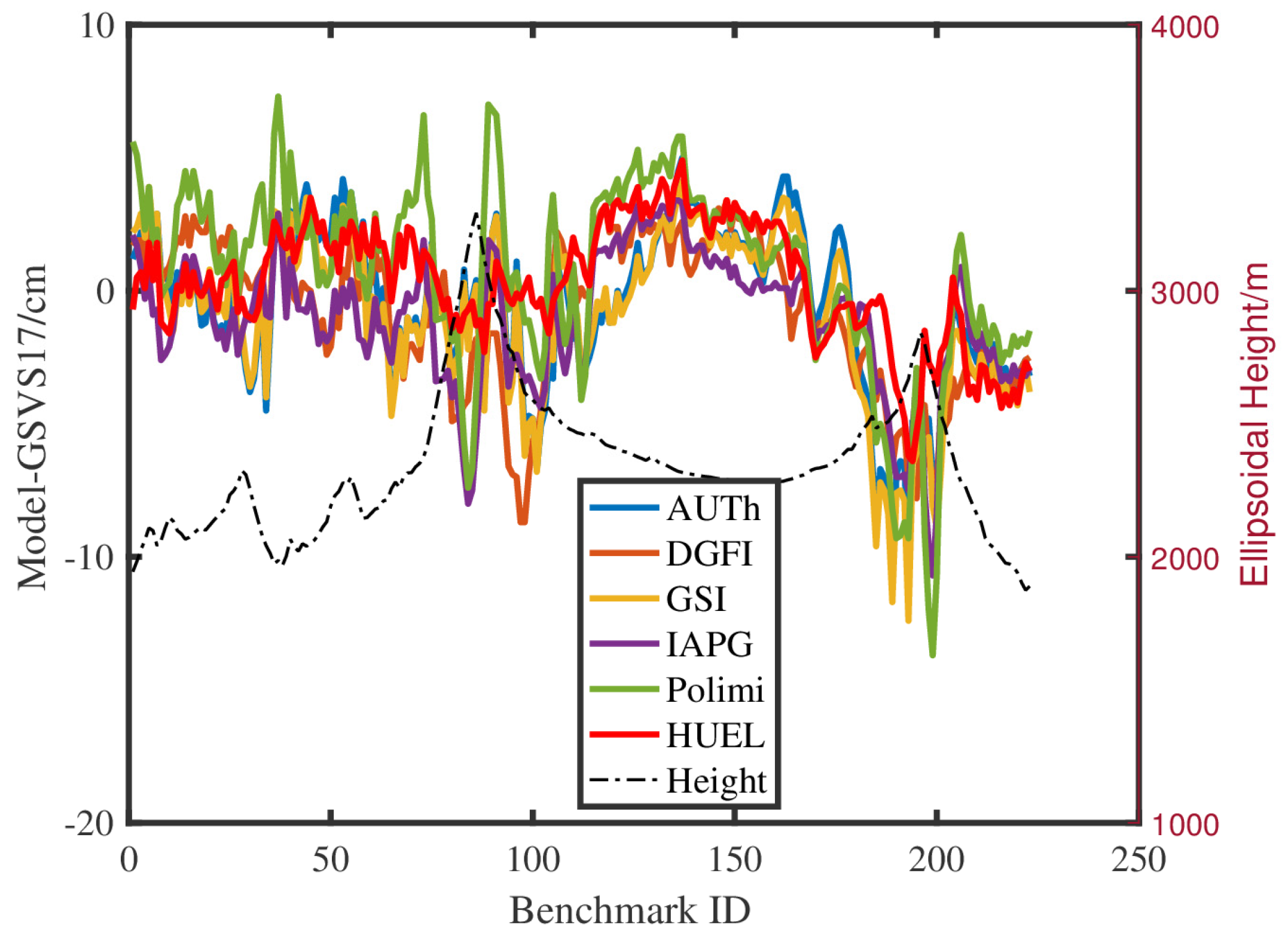
Preprints 83671 g007
Preprints 83671 g008
Figure 8. a The distributions of geoid heights of ColSRBF2023 at the 1 ' × 1 ' grid. b The distributions of differences between ColSRBF2023 and the mean geoid model at the 1 ' × 1 ' grid.
Figure 8. a The distributions of geoid heights of ColSRBF2023 at the 1 ' × 1 ' grid. b The distributions of differences between ColSRBF2023 and the mean geoid model at the 1 ' × 1 ' grid.
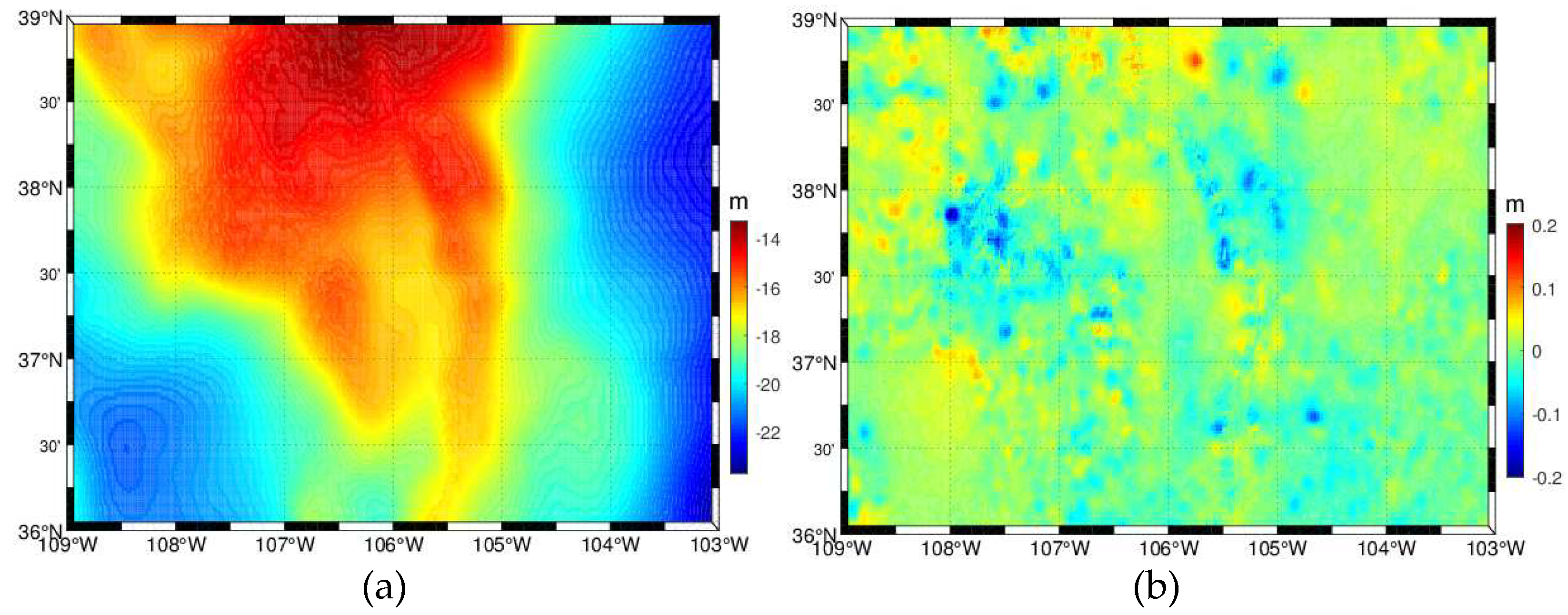
Preprints 83671 g008
Table 1. Statistics of the gravity observations.
Table 1. Statistics of the gravity observations.
Data Max (mGal) Min (mGal) Mean (mGal) STD (mGal)
Terrestrial   δ g 207.88 -146.36 0.35 38.72
Terrestrial   δ g − δ g G G M 137.40 -151.34 -5.64 22.40
Terrestrial   δ g − δ g G G M − δ g R T M 75.328 -135.86 0.76 6.90
Airborne   δ g 123.24 -43.88 7.33 29.56
Airborne   δ g − δ g G G M 68.25 -43.06 0.06 8.16
Airborne   δ g − δ g G G M − δ g R T M 19.01 -18.97 0.10 3.35
Table 2. Comparison of the combined models based on different expansion degrees of SRBFs.
Table 2. Comparison of the combined models based on different expansion degrees of SRBFs.
Model n t e r n a i r n m i n Max (cm) Min (cm) Mean (cm) STD (cm)
Model I 5600 5600 0 93.6 79.6 88.6 3.1
Model II 5600 5600 720 92.0 80.8 87.1 2.6
Model III 5200 5200 0 94.0 80.5 89.1 3.1
Model IV 5200 5200 720 91.8 81.1 87.0 2.6
Model V 5200 3000 720 91.9 80.1 87.0 2.5
Model VI 5200 1840 720 91.9 80.0 87.3 2.3
Table 3. Statistics of geoid height differences on the GSVS17 benchmarks ( N M o d e l − N G S V S 17 ). 87 cm is subtracted from the models
Table 3. Statistics of geoid height differences on the GSVS17 benchmarks ( N M o d e l − N G S V S 17 ). 87 cm is subtracted from the models
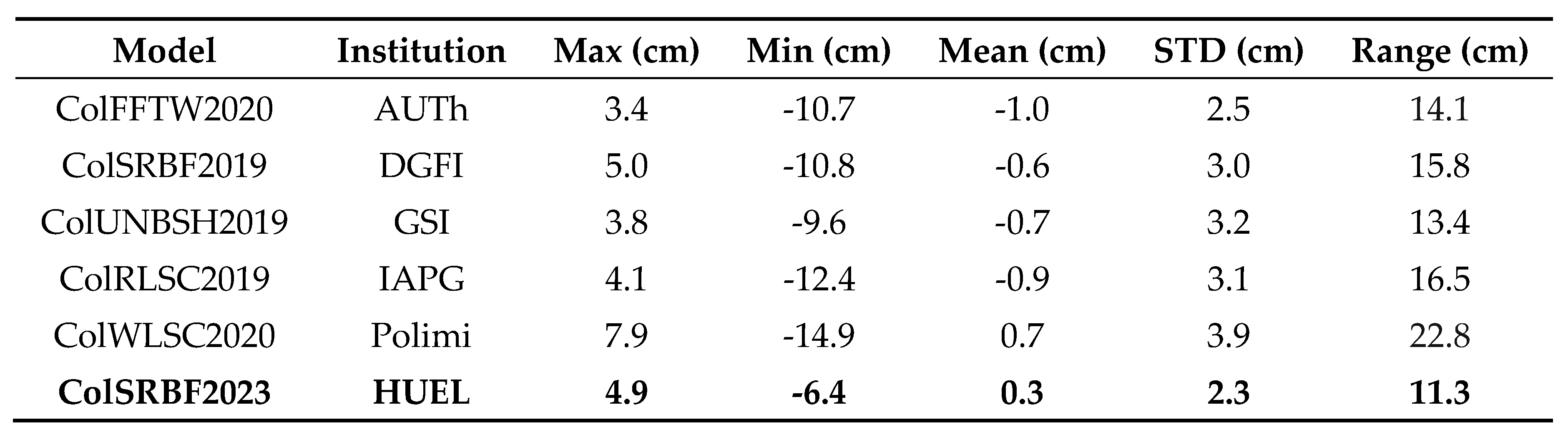
Preprints 83671 g010
Table 4. Statistics of the differences among the individual geoid models and the mean geoid models at the 1 ' × 1 ' grid.
Table 4. Statistics of the differences among the individual geoid models and the mean geoid models at the 1 ' × 1 ' grid.
Preprints 83671 g009
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated