Target Localization and Grasping of NAO robot Based on YOLOv8 network and Monocular Ranging

As a typical visual positioning system, monocular ranging is widely used in various fields. However, when the distance increases, there is a greater error. YOLOv8 network has the advantages of fast recognition speed and high accuracy. This paper proposes a method by combining YOLOv8 network recognition with a monocular ranging method to achieve target localization and grasping for the NAO robots. By establishing a visual distance error compensation model and applying it to correct the estimation results of the monocular distance measurement model, the accuracy of the NAO robot's long-distance monocular visual positioning is improved. Additionally, a grasping control strategy based on pose interpolation is proposed. Throughout, the proposed method's advantage in measurement accuracy was confirmed via experiments, and the grasping strategy has been implemented to accurately grasp the target object.

Keywords:

Subject: Computer Science and Mathematics - Robotics

1. Introduction

With the rapid development of robotics technology, robots have been widely used in various fields such as transportation, welding, and assembly [1]. However, the precise positioning and grasping of robots are key technologies and prerequisites for them to carry out a variety of tasks. Zhang L. et al. proposed a robotic grasping method that uses the deep learning method YOLOv3 and the auxiliary signs to obtain the target location [2]. Huang M. et al. proposed a multi-category SAR image object detection model based on YOLOv5s, to address the issues caused by complex scenes [3]. Tan L.et al. adopted the hollow convolution to resample the feature image to improve the feature extraction and target detection performance [4]. The improved YOLOv4 algorithm has been adopted by numerous studies to facilitate target detection in robotic vision, aiming to enhance detection accuracy [5,6]. Sun Y.et al. constructed the error compensation model based on Gaussian process regression (GPR), effectively improved the accuracy of positioning and grasping for large-sized objects [7]. This study focuses on the target localization and grasping of the NAO robot [8], and the target object is recognized through YOLOv8 network training [9].

The main contributions include: 1) A monocular ranging model is established for the NAO robot to achieve initial location of the target; 2) We propose a visual distance error compensation model to improve the NAO robot's distance ranging error within 2cm; 3) The multi-point measurement compensation technology is proposed to estimate the target’s position and pose, and ultimately achieve grasping the target.

This paper is organized as follows: In Section 2, relevant target recognition and Localization technology is reviewed. In Section 3, the visual distance error compensation model is established to improve the long-distance monocular visual positioning accuracy of the Nao robot. In Section 4, a grasp control strategy based on pose interpolation is proposed to realize the pose estimation and smooth grasping. The experiment and results analysis are given in Section 5. Finally, the conclusions are drawn in Section 6.

2. Target Recognition and Localization Technology

Target recognition based on traditional color segmentation has high requirements for the environment in which the target object is situated. The YOLOv8 network, through training, can extract feature points from target to achieve target recognition [11]. The Nao robot operate using a single camera. Hence this study employs the monocular vision localization techniques [12,13,14]. First, the position coordinates of the target center under the image coordinate system are obtained through target detection using the YOLOv8 network. Then the relationship between the location coordinates and image coordinates was determined using the monocular vision positioning model; Finally, obtain the location coordinates of the target under the NAO robot coordinate system, and acquire the pose of the target object by measuring the endpoint and the center point of the target object, thereby ensuring that the NAO robot can accurately grasp the object.

The principle of monocular ranging based on the YOLOv8 algorithm is shown in Figure 1. The system mainly consists of three components: target detection, internal and external parameter acquisition, and monocular ranging.

2.1. Target recognition based on YOLOv8 network

YOLOv8 is a deep neural network architecture used for target detection tasks, as shown in Figure 2, the network consists of four main components.

At the input end, the Mosaic data enhancement is used. The backbone network adopts the Context modules (C2f) based on ELAN structure, and the Neck module adopts the Path Aggregation Network (PAN) structure [15]. The output end uses the Task Aligned Assignor (TAA), the Distribution Focal Loss (DFL) and the Complete Intersection Over Union (CIOU) loss function [16,17] to achieve accurate and efficient target detection.

2.2. Modeling of monocular ranging

Based on the NAO robot, a monocular ranging model is employed, utilizing the pinhole perspective principle as depicted in Figure 3. The relationship between the camera coordinate system

X c - Y c - Z c

and the image coordinate system

X - Y

in the camera imaging model is represented. The point

M

, possesses coordinates

(X c, Y c, Z c)

, corresponds to the point

m

in the

(X, Y)

coordinate system, with coordinates

(X, Y)

. The relationship between image coordinates and actual spatial coordinates is depicted by Equation (1).

[\begin{matrix} X \\ Y \\ 1 \end{matrix}] = \frac{1}{Z_{c}} [\begin{matrix} f & 0 & 0 & 0 \\ 0 & f & 0 & 0 \\ 0 & 0 & 1 & 0 \end{matrix}] [\begin{matrix} X_{c} \\ Y_{c} \\ Z_{c} \\ 1 \end{matrix}]

(1)

The center point

(u_{0}, v_{0})

of the image pixel is taken as the origin of the image coordinate system. The transformation relationship is depicted in Equation (2), where

d x

and

d y

represent the size of each pixel, and

u

and

v

correspond to the pixel coordinates of the target point.

\{\begin{matrix} x = (u - u_{0}) d_{x} \\ y = (v - v_{0}) d_{y} \end{matrix}

(2)

Figure 4 shows the monocular ranging model established for the NAO robot. The robot is positioned at the origin

O_{W}

within the coordinate system

O_{W} X_{W} Y_{W} Z_{W}

. Point

O

serves as the camera position, and

O_{1} x y

represents the image coordinate system. The endpoints

Q_{1} 、 Q_{2}

of the target rod correspond to

q_{1} 、 q_{2}

in the image coordinate system, respectively. Taking point

Q_{1}

as an example, based on the principles of triangle similarity, the corresponding relationships of various angles can be obtained. So then, the X-coordinate

P_{X 1}

of point

Q_{1}

can be derived, as depicted in Equation (3).

P_{X 1} = \frac{H}{t a n (α + a r c t a n (\frac{v - v_{0}}{f_{y}}))}

(3)

The monocular ranging model for the NAO robot can be simplified into a perspective view, as shown in Figure 5. There,

θ_{1}

represents the angle between point

Q_{1}

and the principal optical axis in the horizontal direction. As a result, the distance between the target point and the robot in the Y-axis direction can be obtained. This is formulated in Equations (4), where

φ

denotes the angle of the NAO robot's head in the horizontal direction.

{P_{Y 1} = Y}_{1} = P_{X 1} \times \tan (θ_{1} + φ)

(4)

Similarly, one can derive the coordinates the position coordinates

{(X}_{W 2}, Y_{W 2})

of point

Q_{2}

under the robot's coordinate system can be obtained.

By using the monocular ranging model established in Figure 4, range measurements are performed on the two end points of the target bar, thereby obtaining the coordinate values of

Q_{1}

and

Q_{2}

, which are

{(P}_{X 1}, P_{Y 1})

and

{(P}_{X 2}, P_{Y 2})

, respectively. Consequently, the deflection angle of the target rod on the

O w X w Y w

plane

ϵ

can be obtained, as demonstrated in Equation (5).

ϵ = a r c t a n (\frac{P_{X 1} - P_{X 2}}{|P_{Y 1}| + |P_{Y 2}|})

(5)

3. Modeling Visual Distance Error Compensation

Based on the established monocular ranging model of the NAO robot, the distance in the X-axis direction of the robot's coordinate system is related to the

γ

angle in a tangent function relationship, as shown in Figure 6(a). The further away, the smaller the

γ

angle. This results in larger measurement errors for distances that are further away.

Therefore, an error compensation model is established to reduce the measurement errors when the target object is at a distance. The error term

k

, as denoted in Equation (6), has a relationship with the measured distance

d_{m}

of the target rod. The relationship is depicted in Figure 6(b).

k = d_{r} / d_{m}

(6)

A function between the actual measurement distance and the error coefficient is established as shown in Equation (7). The values of

a_{1}

a_{2}

a_{3}

a_{4}

, and

a_{5}

are respectively set to -0.6654、2.686、-3.612、1.636、0.7746.

k = a_{1} x^{4} + a_{2} x^{3} + a_{3} x^{2} + a_{4} x + a_{5}

(7)

The target coordinates after compensation are given by Equation (8).

\{\begin{matrix} X_{1} = P_{X 1} \times k \\ Y_{1} = P_{Y 1} \end{matrix}

(8)

4. Pose-Interpolated Grasping Control Strategy

4.1. Linear Path Interpolation

The path of the NAO robotic arm end effector from the start point to the end point follows a linear trajectory. Therefore, interpolation is applied to the straight path between the start and end points. Let the positional coordinates of workspace start and end points be denoted as

A = (x_{a}, y_{a}, z_{a})

and

B = (x_{b}, y_{b}, z_{b})

, respectively. The distance between the start and end points is

L = \sqrt{{(x_{b} - x_{a})}^{2} + {(y_{b} - y_{a})}^{2} + {(z_{b} - z_{a})}^{2}}

, A point

P_{i}

on the line segment

A B

can be represented as

P_{i} = P_{a} + (P_{b} - P_{a}) S (t) / L ， t \in [0, T]

, and its coordinates are denoted as Equation (9):

\{\begin{matrix} x_{i} = x_{a} + \frac{S (t) (x_{b} - x_{a})}{L} \\ y_{i} = y_{a} + \frac{S (t) (y_{b} - y_{a})}{L} \\ z_{i} = z_{a} + \frac{S (t) (z_{b} - z_{a})}{L} \end{matrix}

(9)

The interpolation curves of displacement, velocity, and acceleration are depicted in Figure 7. The arm velocity and acceleration both become zero at the start and end of the movement, ensuring the stability of the robot arm throughout its motion.

Substituting the

S (t)

from the acceleration-uniform-deceleration trajectory into the

x_{i}

, results in the arm's linear motion trajectory in space, as shown in Figure 8. It is evident that the points are densely packed at the ends of the straight line, while the middle portion is evenly distributed. This arrangement achieves the effect of acceleration-uniform-deceleration.

4.2. Position Interpolation

By employing the fourth-order polynomial interpolation method for trajectory planning, the robotic arm's motion can smoothly connect to the constant velocity trajectory from the beginning and end points.

The arm end displacement, velocity, and acceleration functions are expressed as

S (t)

V (t)

, and

A (t)

. The distance between the start and end points is denoted as

L

, and the velocity constant is represented as

V_{m}

, the time intervals for the three phases are represented as

t \in [0, T / 4, 3 T / 4, T]

S (t)

V (t)

, and

A (t)

of these three phases can be represented by the Equation (10-12) respectively. The acceleration phase

t \in [0, T / 4]

S_{1} (t)

V_{1} (t)

, and

A_{1} (t)

are:

\{\begin{matrix} S_{1} (t) = - \frac{V_{m}}{2 t_{1}^{3}} t^{4} + \frac{V_{m}}{t_{1}^{2}} t^{3} \\ V_{1} (t) = - \frac{{2 V}_{m}}{t_{1}^{3}} t^{3} + \frac{{3 V}_{m}}{t_{1}^{2}} t^{2} \\ A_{1} (t) = - \frac{{6 V}_{m}}{t_{1}^{3}} t^{2} + \frac{{6 V}_{m}}{t_{1}^{2}} t \end{matrix}

(10)

The constant velocity phase

t \in [T / 4,3 T / 4]

S_{2} (t)

V_{2} (t)

, and

A_{2} (t)

are:

\{\begin{matrix} S_{2} (t) = V_{m} t - V_{m} t_{1} / 2 \\ V_{2} (t) = V_{m} \\ A_{2} (t) = 0 \end{matrix}

(11)

The deceleration phase

t \in [3 T / 4, T]

S_{3} (t)

V_{3} (t)

, and

A_{3} (t)

are:

\{\begin{matrix} S_{3} (t) = b_{4} t^{4} + b_{3} t^{3} + b_{2} t^{2} + b_{1} t^{1} + b_{0} \\ V_{3} (t) = 4 b_{4} t^{3} + {3 b}_{3} t^{2} + 2 b_{2} t + b_{1} \\ A_{3} (t) = 12 b_{4} t^{2} + {6 b}_{3} t + 2 b_{2} \end{matrix}

(12)

4.3. Pose Interpolation

There are two methods for solving the pose of the robotic arm: the Euler method and the quaternion method. However, the Euler method struggles with issues such as singularities and coupling of angular velocities. Therefore, the quaternion method is chosen to interpolate the arm posture of the NAO robot.

The relationship between the quaternion

q_{t}

and arm end pose matrix

R

is as shown in the Equation (13-17), where

I

is the identity matrix and

ω

is the anti-symmetric matrix.

{\begin{cases} q_{t} = [q_{0}, q_{1}, q_{2}, q_{3}] = [q_{0}, q_{x}] \\ R = I + 2 q_{0} ω + 2 ω^{2} \end{cases}

(13)

Convert the initial rotation matrix

R_{b}

and the final rotation matrix

R_{f}

into quaternions. And then attitude angle

θ

is obtained.

\{\begin{matrix} q_{b} = [b_{0}, b_{1}, b_{2}, b_{3}] \\ q_{f} = [f_{0}, f_{1}, f_{2}, f_{3}] \\ θ = \cos^{- 1} (q_{b} ∙ q_{f}) \end{matrix}

(14)

At a certain moment

t

within this period

T

, the rotation matrix is represented by the quaternion

q_{t}

as follows:

q_{t} = x q_{b} + y q_{f}

(15)

where

x

y

are real numbers, and the attitude angle

\frac{t}{T} θ

between the initial quaternion

q_{b}

and the quaternion

q_{t}

at time

t

is defined. The attitude angle

(1 - \frac{t}{T}) θ

between the quaternion

q_{t}

at time t and the final quaternion

q_{f}

is defined. Therefore, the quaternion pose interpolation matrix is:

q_{t} = \frac{q_{b} \sin ((1 - \frac{t}{T}) θ)}{\sin θ} + \frac{q_{f} \sin (\frac{t}{T} θ)}{\sin θ}

(16)

By performing position interpolation, the displacement matrix

P

can be obtained. Similarly, through pose interpolation, the rotation matrix

R

can be derived. By combining the displacement matrix

P

and the rotation matrix

R

, the pose interpolation matrix is obtained. Subsequently, by solving the inverse kinematics of the pose interpolation matrix, the angle values of various joints during the NAO robot arm's motion process can be determined.

Conduct simulation experiments for arm trajectory planning by using MATLAB, take two points coordinates as the starting and ending points of the arm movement, as illustrated in Equation (17).

{\begin{cases} x y z_begin = [0.1817, - 0.1362, 0.0633] \\ x y z_fin = [0.12, - 0.01, 0.03] \end{cases}

(17)

Using these two points as the starting point and end point for trajectory planning, the corresponding pose interpolation matrix is substituted into the inverse kinematics equation, and arm motion simulation is performed using MATLAB to obtain the variation curve of the 5 joints in the NAO robotic arm.

The variation curves of the 5 joints’ angles of the arm from the start point to the end point are depicted in Figure 9. From the joint variation curves in the graph, it's evident that the NAO robotic arm can move smoothly from the start point to the end point.

5. Experiments and Results Analysis

5.1. Object Detection Experiment

In this experiment, the NAO robot's bottom camera collected 100 images of the target rod at different angles, which were then processed through rotation and mirroring. Subsequently, the yolov8 network was trained for 800 rounds, with approximately 300 images per round. The original image captured by the NAO robot's camera is depicted in Figure 10(a). The target bar is identified using the Yolov8 network, resulting in a binary image of the target object as shown in Figure 10(b).

After obtaining the edge point information of the target object, as shown in Figure 11a,b, data processing is employed to extract the pixel coordinates of the object's center point and endpoints, and then the target is localized.

The rod is positioned in front of the NAO robot at distances ranging from 0.25m to 1.30m, with intervals of 0.05m. Multiple experiments are conducted at each position to calculate an average value. From Table 1, it can be observed that the farther the target is from the robot, the larger the error becomes. Beyond 60cm, the distance error exceeds the requirements for the task.

To address the issue of significant measurement error when the target's position exceeds 60cm, experiments were conducted using the improved monocular distance model with error compensation.

The target was placed in front of the NAO robot at distances ranging from 0.25m to 1.30m. From Table 2, it can be observed that the minimum error between the actual and measured positions is 0.13cm, and the maximum error is 1.93cm. Whether the target's position is before or after 0.6m, the error does not exceed 0.02m.

As shown in Figure 12, the monocular distance measurement with the integrated error compensation model effectively reduces the distance error for positions that are farther away in the X-axis direction of the robot's coordinate system.

The rod was placed at 90cm in the robot's X-direction, with distances of 0cm, 20cm, and 40cm in the Y-direction. Each position underwent 10 tests, as shown in Table 3. The RMSEs of the three points are 0.644cm, 0.574cm and 1.077cm, respectively. It is evident that the NAO robot can accurately measure distances in the Y-axis direction, meeting the subsequent precision requirements.

After obtaining the position of the target rod, using the pixel coordinates of the two end points of the rod, the end point positions are calculated to determine the deviation angle of the rod. At a position of 60cm in the robot's X-axis direction, measurements were taken for deviation angles α of 30°, 45°, and 60°. As shown in Table 4, the RMSEs are 0.820°, 0.904° and 0.901° respectively, so the NAO robot can effectively measure the deviation angle of the rod, providing a foundation for accurate grasping.

5.2. Object Grasping Experiment

Due to the low friction between the ground and the feet of the NAO robot, it can experience slipping during walking, especially over longer distances. To mitigate this issue, a method involving measuring, short-distance walking, adjustment, and then measuring again. This approach ensures that the NAO robot can walk to the vicinity of the target rod with the correct orientation. Subsequently, adjust its crouching posture using the choreograph software. This ensures that the target rod is within the NAO robot's workspace. The internal API can obtain the position of its end effector. By combining this information with the known coordinates of the target's center point, the robot can accurately grasp the target at its center position. This process is illustrated in Figure 13.

6. Conclusions

This paper combines YOLOv8 network recognition with monocular ranging methods to recognize and locate the target object. NAO robot acquires the pose information of the target object through its own monocular vision sensor, builds a visual distance error compensation model based on monocular ranging to compensate for distance errors, then moves near the target, and grasps the target object by adjusting its attitude.

In the experiments, it is observed that the visual distance error compensation to the monocular ranging model effectively can improve the accuracy of the NAO robot’s distance measurement. The error between actual position and measurement position is controlled within 2cm. Furthermore, by utilizing pose interpolation techniques, the pose of the finger is adjusted to align with the target at a constant level. The experimental results show that the rotation angle error is controlled within 2°. These results indicate that the NAO robot can precisely estimate the target distance and pose, then facilitate precise walking and posture adjustments to ensure accurate object grasping.

Author Contributions

Conceptualization, Y.J. and S.W.; methodology, S.W.; software, Z.S.; validation, X.X. and G.W.; investigation, Y.J.; writing—original draft preparation, Z.S.; writing—review and editing, Y.J. and S.W.; project administration, H.L. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the National Natural Science Foundation of China (Grant No. 62073297), and the Natural Science Foundation of Henan Province (Grant No. 222300420595), and Henan Science and Technology research project (Grant No. 222102520024, No. 222102210019, No. 232102221035).

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

Liu, H.; Wu, B.; Li, J. The development process and social significance of humanoid robot. Public Communication of Science & Technology 2020,12(22),109-111. [CrossRef]
Zhang, L.; Zhang, H.; Yang, H.; Bian, G. B.; Wu, W. Multi-target detection and grasping control for humanoid robot NAO. International Journal of Adaptive Control and Signal Processing 2019, 33.7, 1225–1237. [Google Scholar] [CrossRef]
Huang, M.; Liu, Z.; Liu, T.; Wang, J. CCDS-YOLO: Multi-Category Synthetic Aperture Radar Image Object Detection Model Based on YOLOv5s. Electronics 2023, 12, 3497. [Google Scholar] [CrossRef]
Tan, L.; Lv, X.; Lian, X.; Wang, G. YOLOv4_Drone: UAV image target detection based on an improved YOLOv4 algorithm. Computers & Electrical Engineering 2021, Volume 93, 107261. [CrossRef]
Tian, M.; Li, X.; Kong, S.; Wu, L.; Yu, J. A modified YOLOv4 detection method for a vision-based underwater garbage cleaning robot. Frontiers of Information Technology & Electronics Engineering 2022, 23(8),1217-1228. [CrossRef]
Fu, H.; Song, G.; Wang, Y. Improved YOLOv4 marine target detection combined with CBAM. Symmetry 2021, 13(4), 623. [Google Scholar] [CrossRef]
Sun, Y.; Wang, X.; Lin, Q.; Shan, J.; Jia, S.; Ye, W. A high-accuracy positioning method for mobile robotic grasping with monocular vision and long-distance deviation. Measurement 2023, Volume 215, 112829. [Google Scholar] [CrossRef]
Liang, Z. Research on Target Grabbing Technology Based on NAO Robot. Doctoral ChangChun University of Technology, ChangChun, 2021.
Terven, J.; Cordova-Esparza, D. A comprehensive review of YOLO: From YOLOv1 to YOLOv8 and beyond. arXiv 2023, preprint arXiv, 2304.00501. [CrossRef]
Jin, Y.; Wen, S.; Shi, Z.; Li, H. Target Recognition and Navigation Path Optimization Based on NAO Robot. Appl. Sci. 2022, 12, 8466. [Google Scholar] [CrossRef]
Li, Y.; Fan, Q.; Huang, H.; Han, Z.; Gu, Q. A Modified YOLOv8 Detection Network for UAV Aerial Image Recognition. Drones 2023, 7, 304. [Google Scholar] [CrossRef]
He, M.; Zhu, C.; Huang, Q.; Ren, B.; Liu, J. A review of monocular visual odometry. The Visual Computer 2020, 36(5), 1053–1065. [Google Scholar] [CrossRef]
Kim, M.; Kim, J.; Jung, M.; Oh, H. Towards monocular vision-based autonomous flight through deep reinforcement learning. Expert Systems with Applications 2022, 198, 116742. [Google Scholar] [CrossRef]
Yang, M.; Wang, Y.; Liu, Z.; Zuo, S.; Cai, C.; Yang, J.; Yang, J. A monocular vision-based decoupling measurement method for plane motion orbits. Measurement 2022, 187, 110312. [Google Scholar] [CrossRef]
Yu, H.; Li, X.; Feng, Y.; Han, S. Multiple attentional path aggregation network for marine object detection. Applied Intelligence 2023, 53(2), 2434–2451. [Google Scholar] [CrossRef]
Feng, C.; Zhong, Y.; Gao, Y.; Scott, M. R.; Huang, W. Tood: Task-aligned one-stage object detection. In 2021 IEEE/CVF International Conference on Computer Vision (ICCV) (pp. 3490-3499), Montreal, QC, Canada, October 2021. 20 October.
Li, X.; Wang, W.; Wu, L.; Chen, S.; Hu, X.; Li, J. . Yang, J. Generalized focal loss: Learning qualified and distributed bounding boxes for dense object detection. Advances in Neural Information Processing Systems 2020, 33, 21002–21012. [Google Scholar]

Figure 1. Schematic diagram of monocular ranging based on YOLOv8.

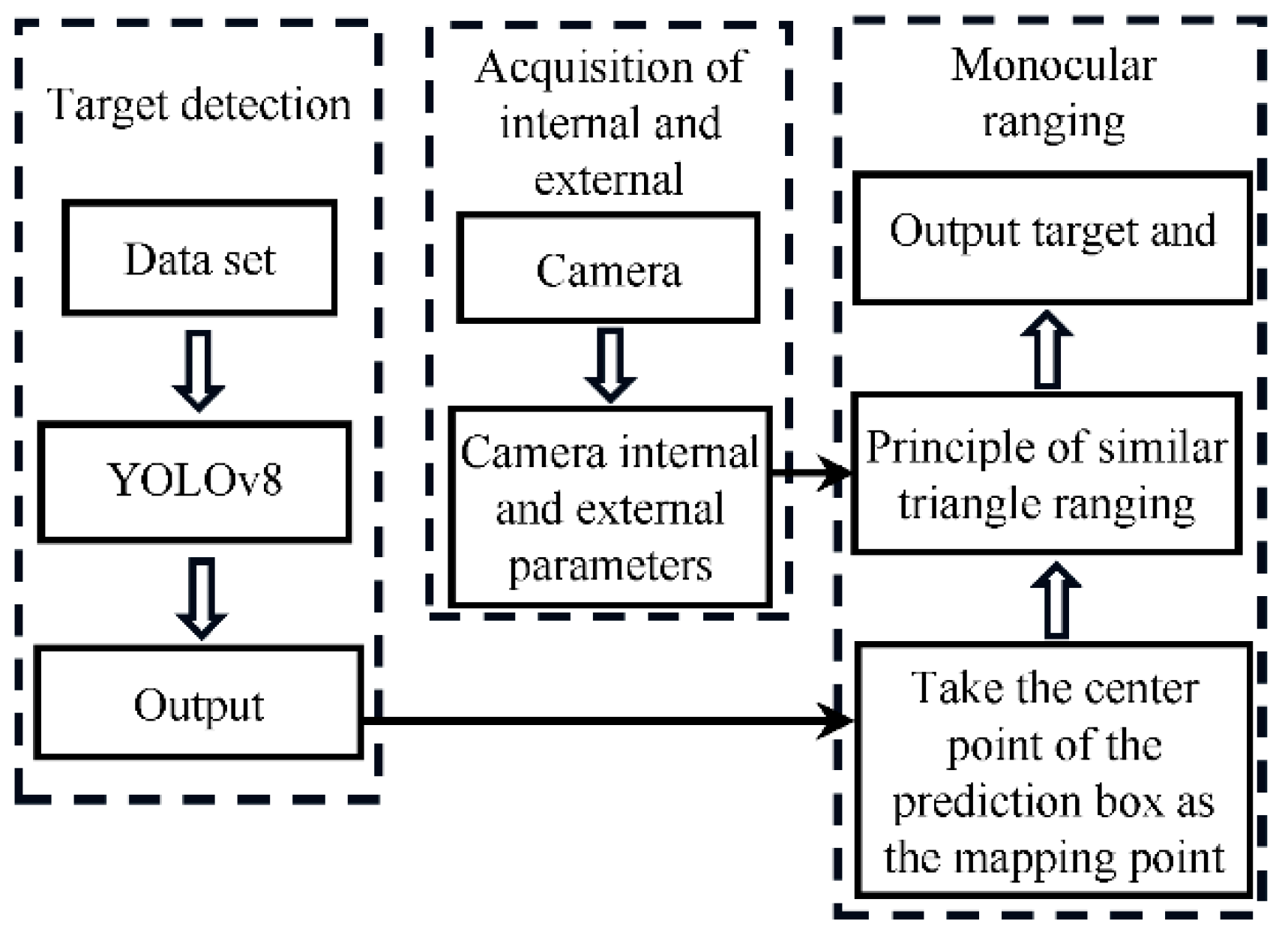
Figure 2. The network model of YOLOv8.

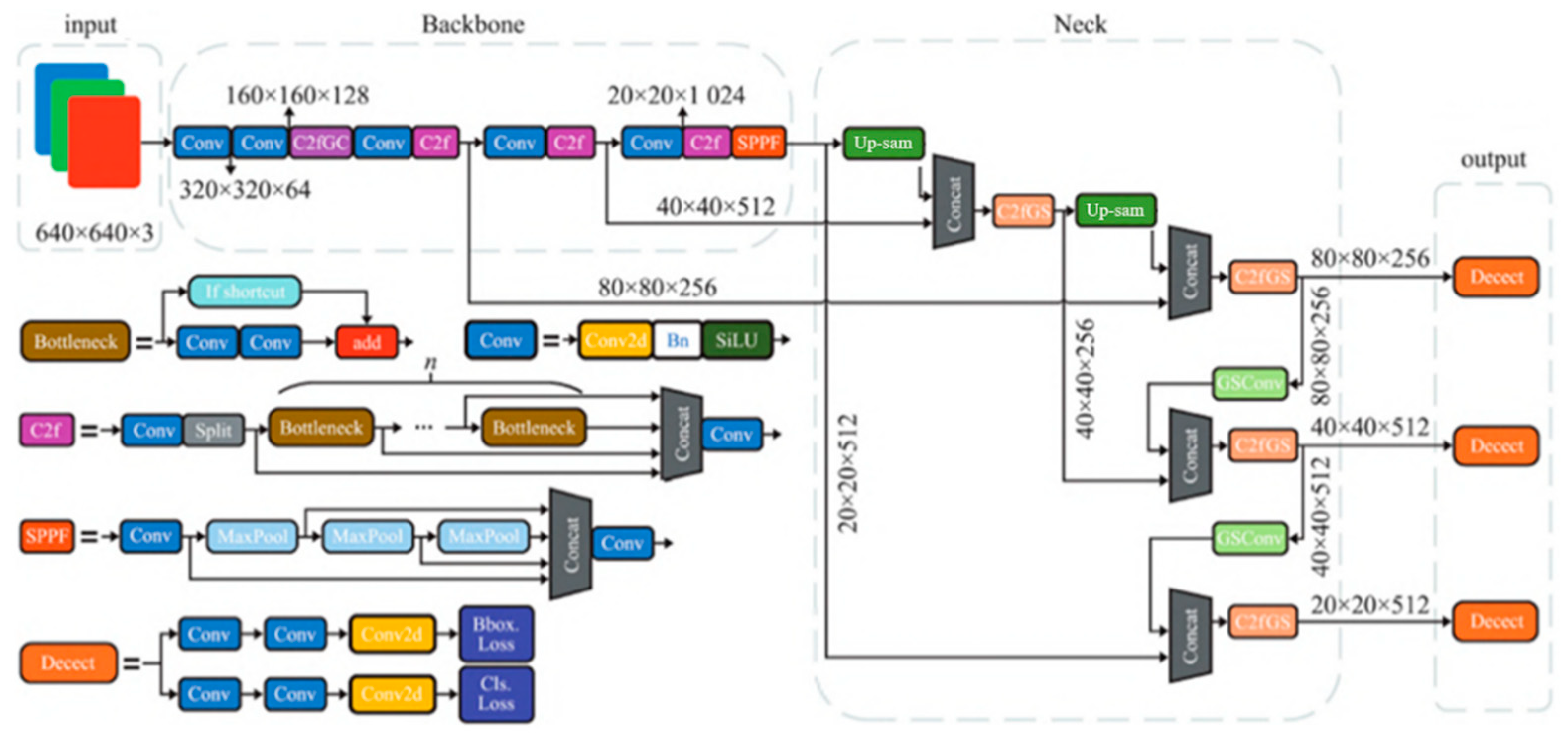
Figure 3. The pinhole imaging model.

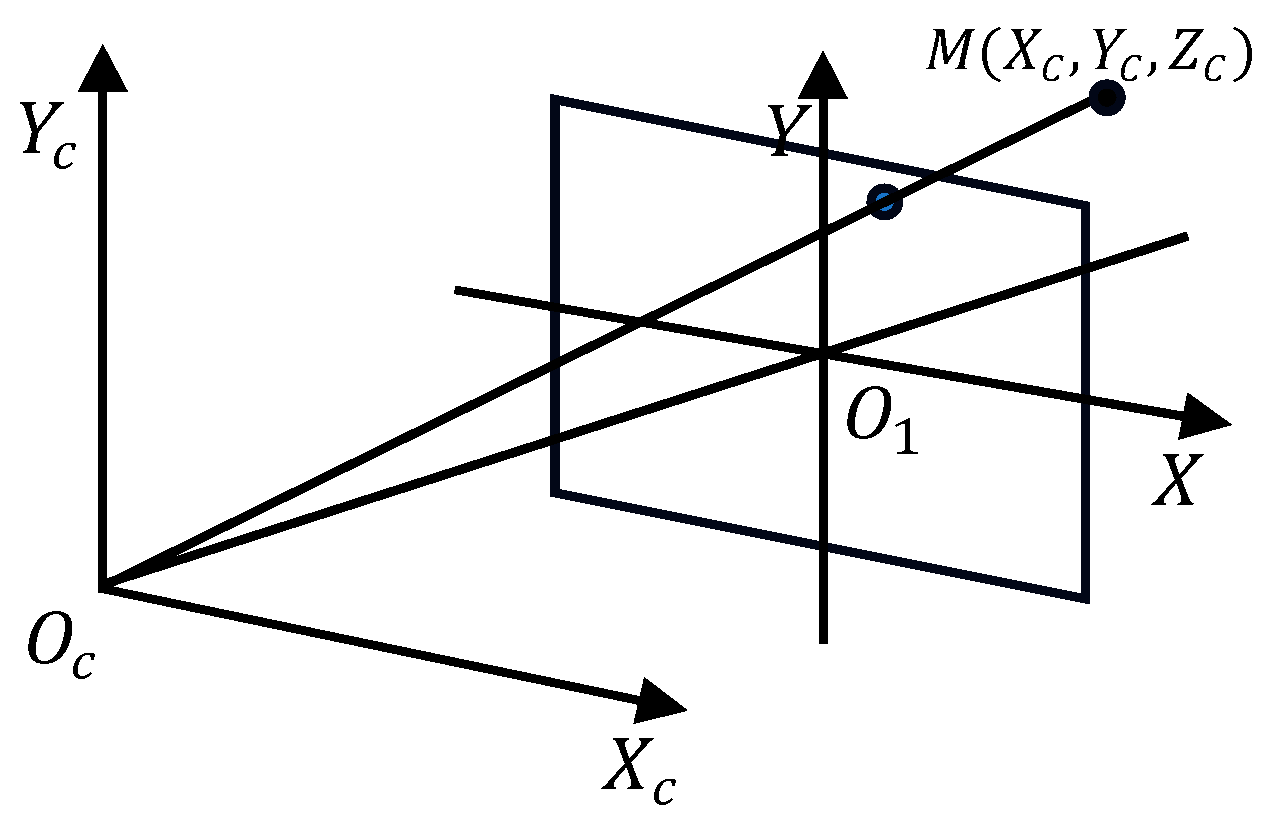
Figure 4. The monocular ranging model for the NAO robot.

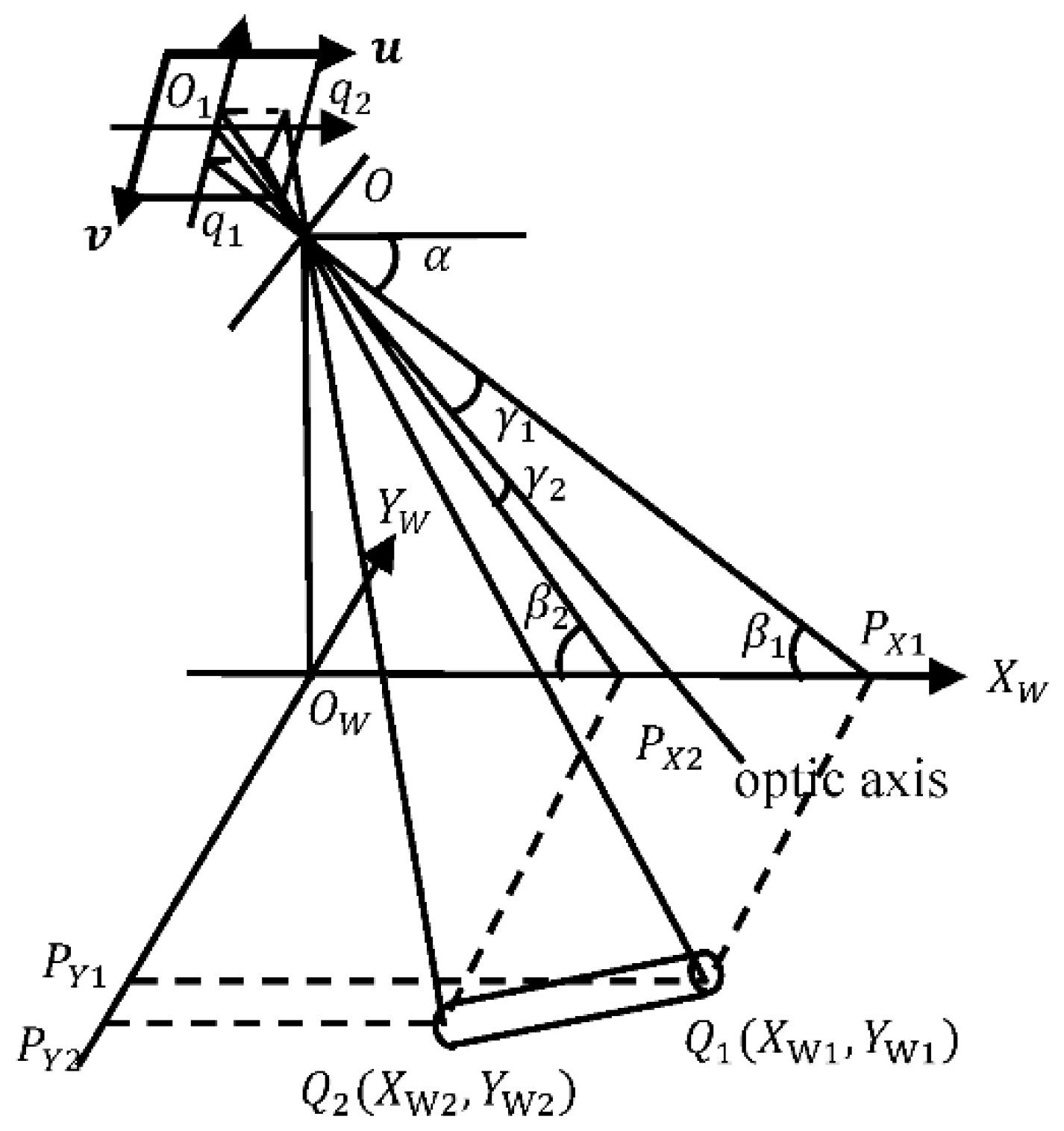
Figure 5. Vertical view of the monocular ranging model.

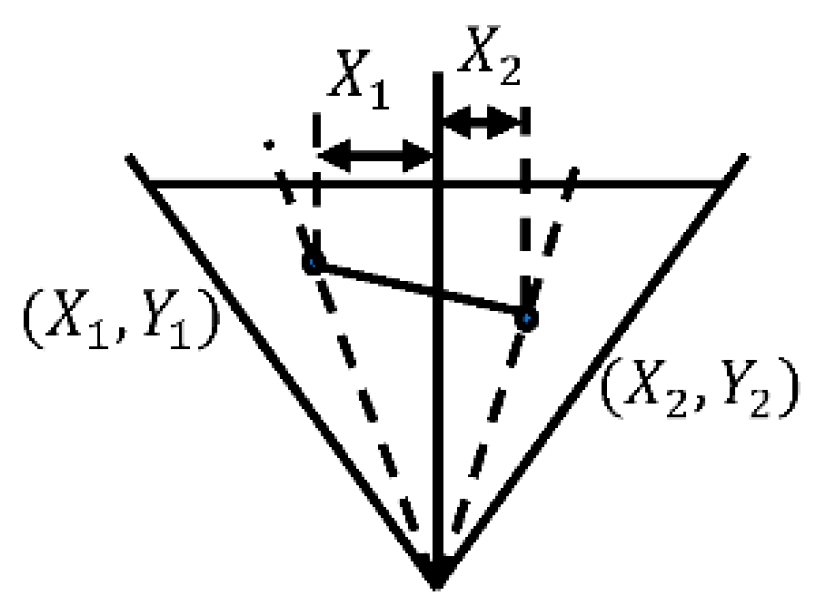
Figure 6. (a) Relationship between the γ angle and the measured distance; (b) Relationship between the measured distance and error coefficient

k

Figure 6. (a) Relationship between the γ angle and the measured distance; (b) Relationship between the measured distance and error coefficient

k

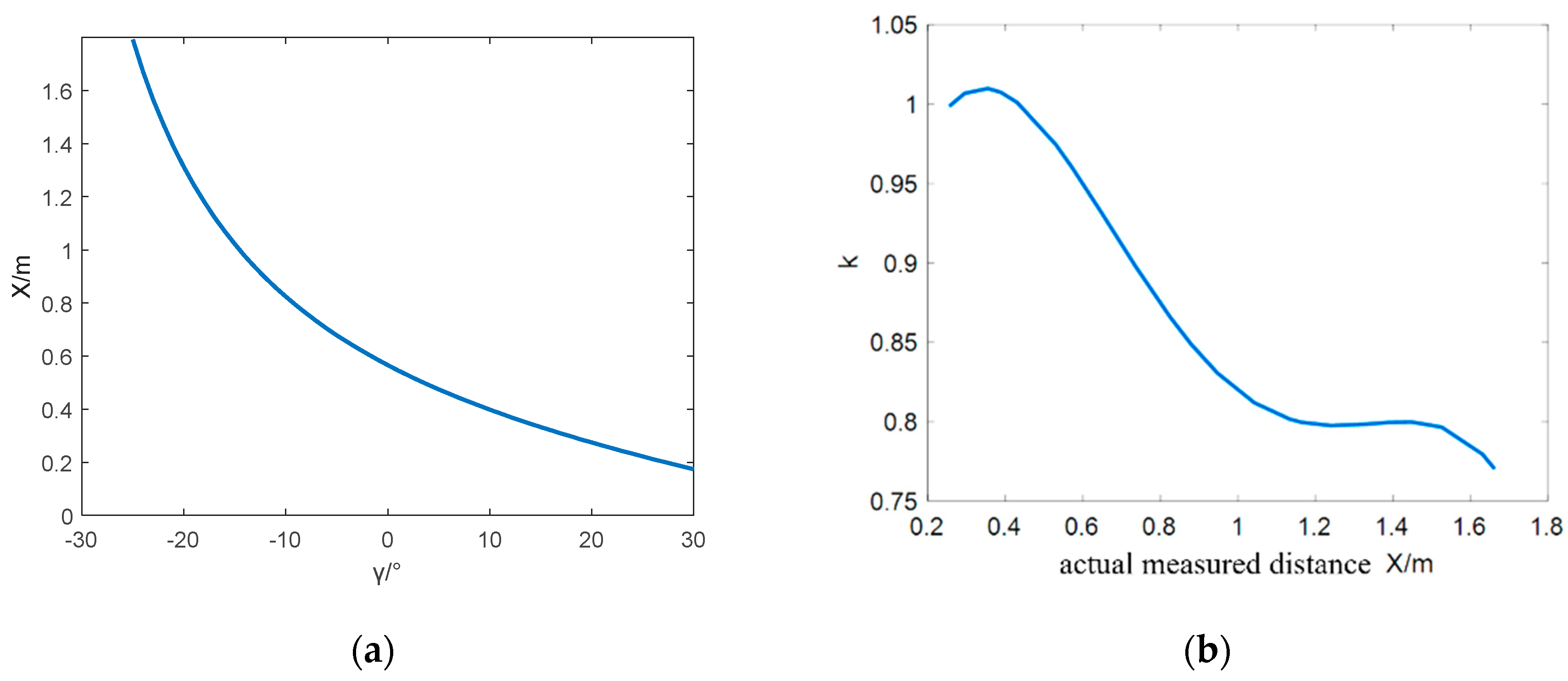
Figure 7. Interpolation curves for displacement, velocity, and acceleration.

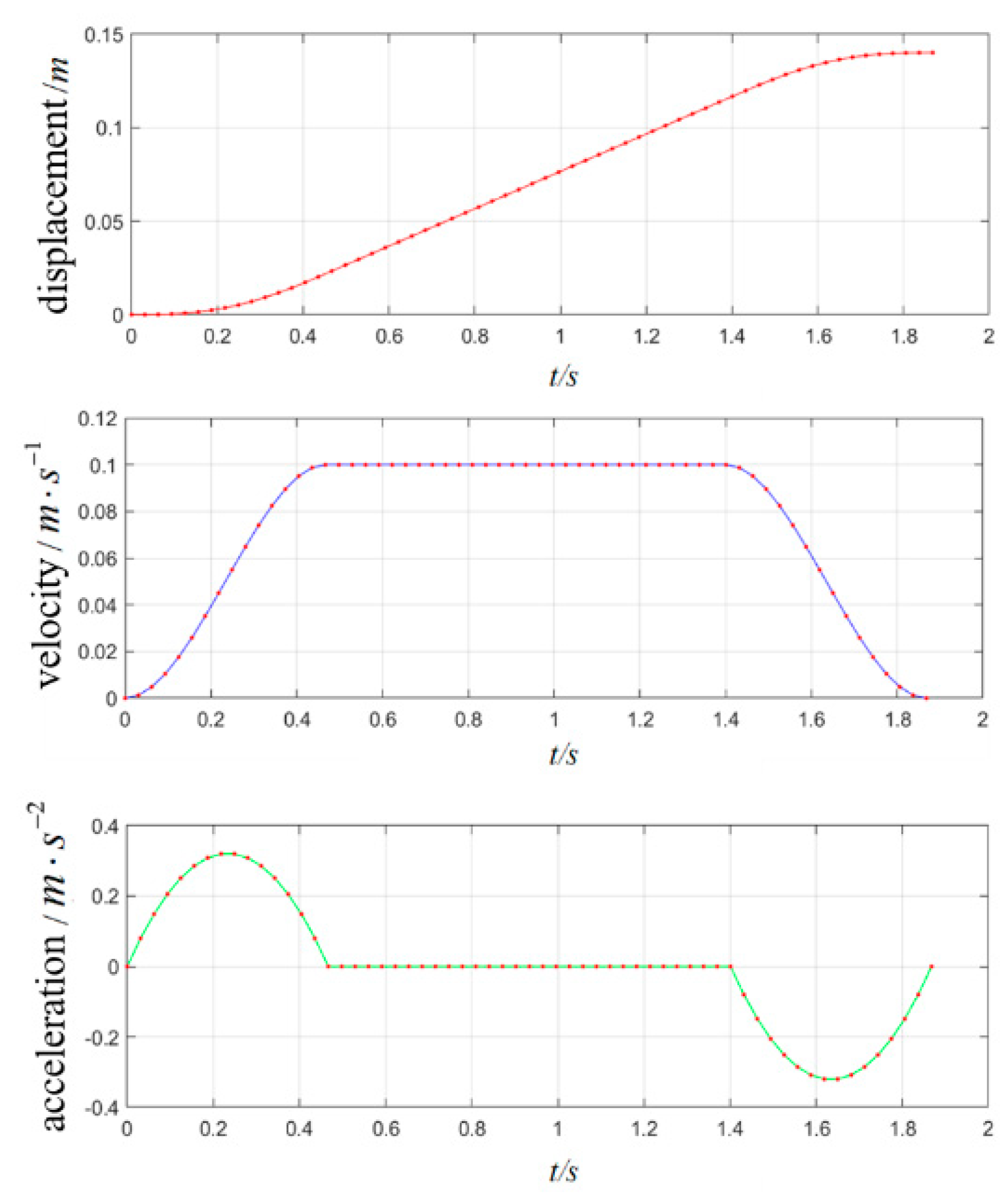
Figure 8. Linear motion interpolation diagram.

Figure 9. Joint angle motion curves.

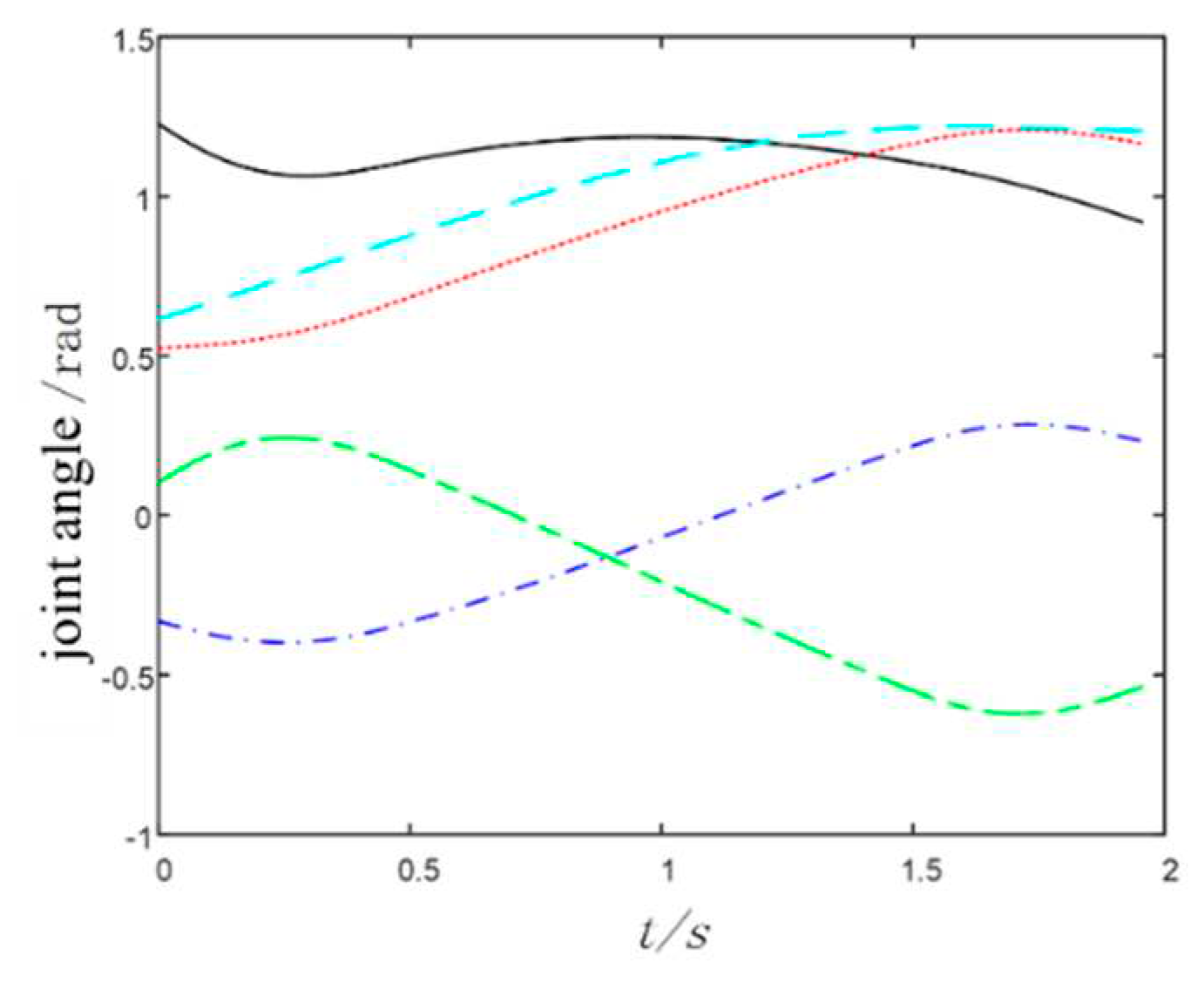
Figure 10. (a) Original image captured by NAO robot; (b) Original image captured by NAO robot.

Figure 11. (a) Endpoints of the Target Object; (b) Edge of the Target Object.

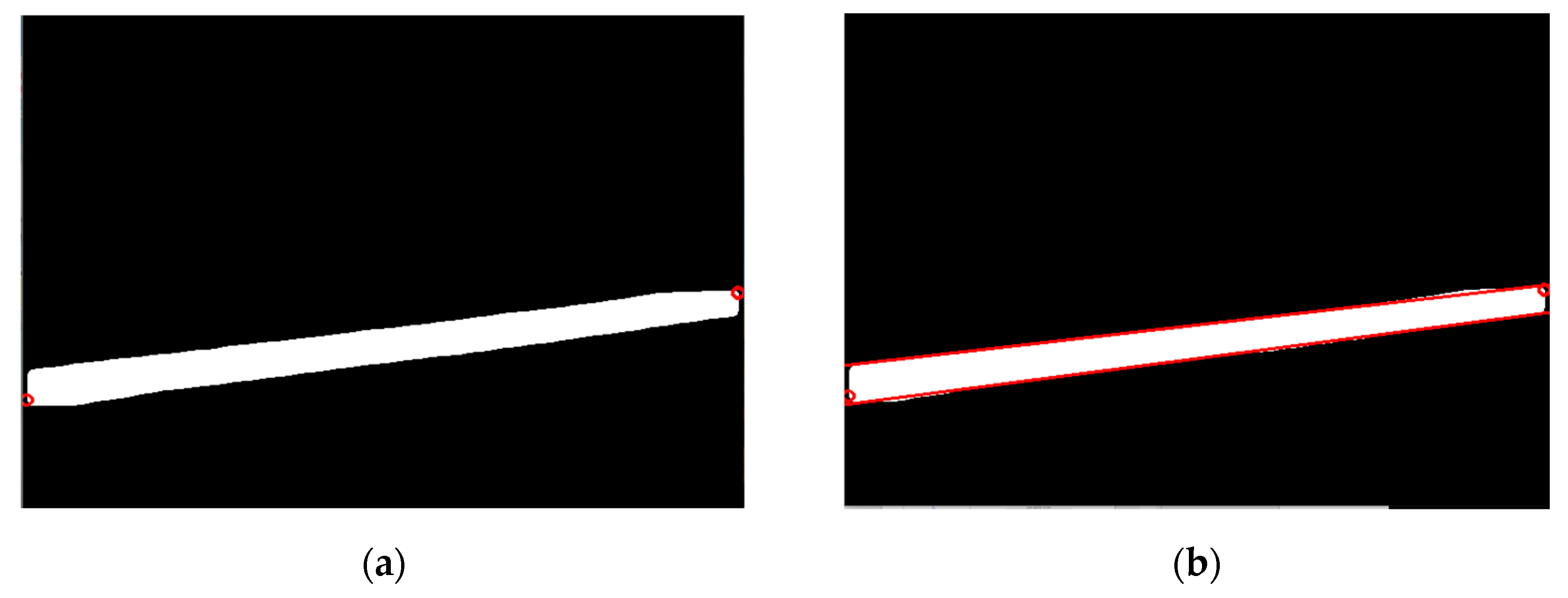
Figure 12. Comparison of measured distances before and after error compensation.

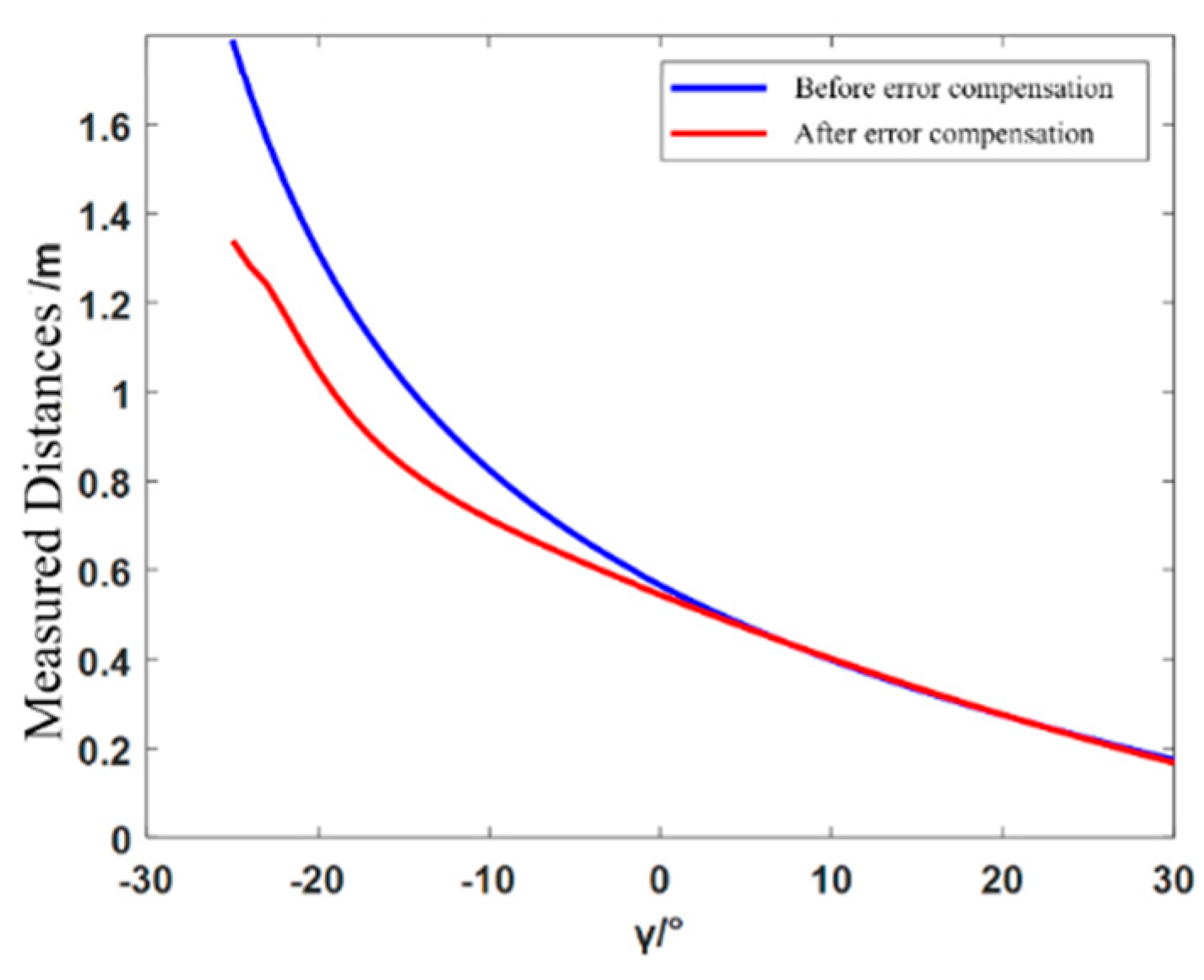
Figure 13. NAO robot grasping process.

Table 1. Actual and measured positions of the target before improvement.

Actual Position (cm)	Measured Position (cm)	Actual Position (cm)	Measured Position (cm)
25	25.50	80	94.71
30	29.49	85	104.26
35	35.45	90	113.50
40	38.83	95	116.43
45	43.84	100	123.99
50	52.94	105	133.08
55	57.17	110	139.06
60	64.80	115	144.73
65	73.69	120	152.62
70	82.55	125	163.13
75	87.94	130	166.29

Table 2. Actual and measured positions of the target after error compensation.

Actual Position (cm)	Measured Position (cm)	Actual Position (cm)	Measured Position (cm)
25	25.47	80	78.67
30	29.69	85	84.64
35	35.80	90	90.96
40	39.12	95	93.10
45	43.08	100	98.80
50	51.60	105	106.25
55	54.89	110	111.18
60	60.37	115	115.75
65	66.13	120	121.56
70	71.46	125	127.16
75	74.64	130	128.07

Table 3. Actual and measured distances in the Y-axis direction after error compensation.

Actual Distance (cm)	0	20	40
Index
1	0.8	20.4	41.2
2	0.7	20.9	40.4
3	0.8	19.5	40.4
4	0.6	20.4	41.5
5	0.8	20.3	40.4
6	0.6	19.7	41.7
7	0.4	20.2	41.4
8	0.5	20.9	41.5
9	0.6	20.8	39.6
10	0.5	20.5	40.4

Table 4. Actual deviation angle vs. measured deviation angle.

$α / °$	30	45	60
Index
1	30.48	45.66	60.85
2	30.76	45.69	59.36
3	30.53	45.93	58.82
4	31.22	45.87	59.56
5	29.87	46.05	60.59
6	30.82	45.92	60.89
7	30.63	46.15	61.35
8	29.08	45.56	61.09
9	29.35	44.58	60.53
10	31.34	46.37	59.02

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Target Localization and Grasping of NAO robot Based on YOLOv8 network and Monocular Ranging

Abstract

1. Introduction

2. Target Recognition and Localization Technology

2.1. Target recognition based on YOLOv8 network

2.2. Modeling of monocular ranging

3. Modeling Visual Distance Error Compensation

4. Pose-Interpolated Grasping Control Strategy

4.1. Linear Path Interpolation

4.2. Position Interpolation

4.3. Pose Interpolation

5. Experiments and Results Analysis

5.1. Object Detection Experiment

5.2. Object Grasping Experiment

6. Conclusions

Author Contributions

Funding

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe