Prerpints.org logo
Preprint
Article

Parametric Optimisation of Hypersonic Re-entry Capsules with Air-Duct Systems

This version is not peer-reviewed.

Submitted:

31 August 2023

Posted:

05 September 2023

You are already at the latest version

Abstract
This study focuses on the aerodynamic optimization of the re-entry capsule (REC) Orion Crew Exploration Vehicle (CEV) module, evaluating its performance using computational fluid dynamics (CFD). Three different models, namely Baseline, 2-Duct, and 4-Duct, are investigated under a wide range of flow speeds, from supersonic (Ma=1.6) to hypersonic (Ma=6) regimes. Thermofluids aspects, drag coefficient, surface heat flux, and the effectiveness of the modified geometry are assessed using aerodynamic and temperature-based models. The results show that the introduction of ducts in the 2-Duct and 4-Duct models leads to an average decrease in the drag coefficient of approximately 2.1% and 2.9%, respectively, compared to the baseline model, across all Mach numbers. The maximum reduction in drag coefficient is 3.55%, observed at Ma=1.4 using the 4-Duct capsule. However, it is found that the addition of extra ducts to the model increases the maximum heat transfer rate. Specifically, the heat flux is increased by up to 69% for the 4-Duct model at Ma=6, compared to the baseline model. On average, the heat flux is increased by approximately 28.6% for all conditions. The findings indicate that the introduction of ducts in the REC model improves its aerothermodynamic performance by reducing drag but also increases the heat transfer rate on the surface.
Keywords: 
Subject: 
Engineering  -   Aerospace Engineering

1. Introduction

The exploration of space and missions to other celestial bodies, particularly Mars, has brought attention to the significance of safe and dependable space travel. Re-Entry Capsules (REC) have been instrumental in the history of human spaceflight, ensuring the safe return of astronauts, scientific experiments and samples from space and delivering payloads to Earth. REC pass through hypersonic flow during their return journey, characterized by speeds exceeding five times the speed of sound (Mach > 5), which pose unique challenges in both experimental and modelling studies due to its high temperatures, velocities, and exceptional conditions [1]. Understanding hypersonic flow involves grasping physical flow phenomena, such as shock waves, flow separation, and boundary layer transition [2].
Recent studies have focused on the use of CFD simulations to optimize the aerodynamic performance of REC [3,4]. Simulations have been used to investigate the effects of capsule geometry, such as the shape of the nose and the position of the heat shield, on the aerodynamic performance of the capsule. Aerodynamic optimization of REC, such as space shuttles and REC, is crucial for ensuring safe and efficient re-entry into the Earth's atmosphere. The objective of this research is to aerodynamically optimise a REC – Orion CEV – in order to reduce drag and the heat flux generation on the capsule’s surface. The final goal is to design a safe, more efficient, and reliable REC that can withstand the extreme conditions of hypersonic flight.
Shifting the focus towards the aerothermal effects on a capsule’s surface, the Two-Temperature (TT) model can accurately predict the heat flux peaks [5]. In [5,6], the TT model has shown good prediction of heat flux distributions on REC. The simulation results of the TT model correlated well with experimental data. The latter study found that the relative error of heat flux at stagnation point is 1.54%, far less than 27.1% of the One-Temperature (OT) model and the relative error of heat flux at shoulder is 1.33%, 13.3% less than that of the OT model. Several studies have validated the S S T /   k − ω turbulence model alongside the Two-Temperature to predict heat flux. Both the turbulence model and TT model are available in the ANSYS FLUENT package [7].
In [8], researchers attempted to overcome the aerodynamic optimisation problem through introducing a front facing cavity that induces an opposing jet effect on the front of the blunt body, which helped reducing the peak heat flux on a blunt body by upwards of 33% compared to an unmodified blunt body. The latter finding has been inferred in [9], which has led to a net decrease in heat flux values, thereby improving heat transfer characteristics of the vehicle. The reduction in heat fluxes was found to be upwards of 36% and 21% for Mach speeds of 7 and 3 respectively. The undulation did not seem to affect aerodynamic characteristics of lift-drag even with altering the angle of attack. However, the optimized model in terms of both aerodynamic and aerothermodynamics characteristics and its underlying flow physics is yet to be studied. However, we aim in this study to explore the effects of re-introducing air through ducts to recreate this effect by affecting the separation point.
According to [10], the addition of a duct on around the capsule geometry can help with aerodynamic performance. The research concluded that the addition of a circumventing duct reduced the ballistic coefficient significantly and led to an increase in drag due to the modified flow around and through the constant duct surrounding the baseline model. It was concluded that the pressure drag of the ducted capsule was due to two components: the pressure difference across the capsule that produces an axial force on the vehicle, and the pressure difference across the duct that produces a normal force on the duct. Having a duct around the vehicle showed positive effects, thus this research aims to explore the effects of ducts.
Although there have been many studies on the aerothermodynamics of REC like shapes, little has been made to cover the full aspects associated with air-ducts systems and underlying physics. In contrast to previous studies, we have accounted for the effects of air ducts on a modified Orion CEV capsule and underlying physics in a rarefied hypersonic flow regime. The benchmark model is inspired by [11], but using CFD modelling in our study instead of the Direct Simulation Monte Carlo method. The key underlying physics include shockwaves, heat flux generation, surface temperatures, drag, and the flow pattern of the hypersonic flow. Section 2 demonstrates the relevant computational aerothermodynamic equations used in this study, Section 3 of the research defines the system design and parameters, Section 4 presents the results, and Section 5 summarizes the findings. The research aims to contribute to a better understanding of the underlying physics and aerodynamics associated with air-duct systems for REC.

2. Aerothermodynamic models

In supersonic flights ( Ma > 1 ), shockwaves begin to form around the body of the object, one of which a bow shock is curved and detached from the body to form at the upfront. This is commonly observed when the fluid experiences a sharp increase in pressure and temperature and a decrease in density. The conical shape of REC is designed to induce a bow shock, significantly increasing drag on the aircraft, and decelerating the REC velocity from 17500 mph to a safe parachute deployment speed range (100 – 160 mph [12]). Understanding the characteristics of bow shocks provides valuable insights into the aerodynamic forces acting on the capsule during re-entry. Bow shocks result in isentropic compression and rapid deceleration of the medium, leading to high temperatures, sometimes reaching up to 12200 K.
Another significant source of heating during re-entry is the viscous interaction between the free-stream air and the body surface of the re-entry vehicle. As high-velocity fluid is slowed down by viscous effects in the boundary layer, a large amount of kinetic energy is converted into heating through viscous dissipation [2,13]. This process is observed in a flat plate hypersonically amplified boundary layer. The thick boundary layer can interact with the inviscid flow, inducing viscous interactions that can have important effects on the surface-pressure distribution, lift, drag, and stability of hypersonic vehicles. Viscous interaction also leads to increased skin friction and heat transfer, making it essential to accurately model the boundary layer and viscous effects for a hypersonic simulation.

2.1. One-temperature model

The computational fluid dynamic (CFD) method is used to solve the 3D Reynolds-average Navier–Stokes (RANS) equations in transient-state in a coupled, implicit, second-order upwind solver. The κ - ω SST turbulence model is implemented. The transport equations for κ − ω can be described as:
𝜕 𝜕 t ρ κ + ∇ · ρ υ ⃑ κ = ∇ · Γ κ ∇ κ + G κ − Υ κ ,
𝜕 𝜕 t ρ ω + ∇ · ρ υ ⃑ ω = ∇ · Γ ω ∇ κ + G ω − Υ ω + D ω ,
where ρ is density of fluid, κ is turbulence kinetic energy,   ω is turbulence dissipation, υ ⃑ is three-dimensional flow velocity vector, Γ κ and Γ ω are the kinetic and dissipation diffusion rates, respectfully, G κ and G ω are the kinetic and dissipation energy generation rates, respectfully, Υ κ and Υ ω are kinetic and dissipation energy rates, respectfully, generated due to turbulence, and D ω is the orthogonal divergence term due to dissipation. The traditional solution to the energy equation in RANS equations assumes that the number of molecular collisions is sufficient for the flow to reach the local thermodynamic equilibrium state. This is called the One-Temperature (OT) model and is shown in the following form:
𝜕 𝜕 t ρ E + ∇ · υ ⃑ ρ E + p = ∇ · q − ∑ j ∇ · h j   J ⃑ j + S v + S h ,
where E = h − p ρ + v 2 2 is total fluid energy, h is fluid enthalpy, q = k · ∇ T is heat conduction, k is fluid thermal conductivity, ∑ j ∇ · h j   J ⃑ j is energy transfer due to component diffusion, S v is energy change due to viscous dissipation, and S h is energy source term.

2.2. Two-Temperature model

In hypersonic flows, the high velocities and short residence times of fluid elements prevent them from reaching local thermodynamic equilibrium. This means that the various components of the fluid (e.g., electrons, ions, and neutrals) can have significantly different temperatures. This departure from thermal equilibrium is referred to as thermal non-equilibrium. To accurately model the energy relaxation process and account for the non-equilibrium effects, the Two-Temperature (TT) model is employed. In contrast to the OT model, where a single temperature is assumed for the entire gas, the TT model considers the separate temperatures for electrons and heavy particles (atoms and molecules) within the gas.
The TT model is particularly suitable for simulating hypersonic flows because it better captures the energy exchange and relaxation phenomena between different species in the gas. It provides a more accurate representation of the flow field and can yield improved predictions compared to the OT model. To account for the thermal non-equilibrium in hypersonic flows, we have adopted the TT model in our aerothermodynamic simulation to better predict the energy relaxation process in hypersonic flight. Both, the translational rotational and electron vibration temperatures, T t r and T v e , respectively, are accounted for in the heat flux as:
q = k t r ∇ T t r + k v e ∇ T v e .

2.3. Electronic vibration

In the TT model, the translational and rotational energy modes of the components are assumed to be in equilibrium at one temperature. The vibrational and electron energy patterns of the components are assumed to be in equilibrium at another temperature. A system of conservation equations is solved, which includes the Navier–Stokes equations and one additional transport equation that models the conservation of vibrational-electronic energy [14]:
𝜕 𝜕 t ρ e v e + ∇ · ρ e v e V = − ∇ · q v e − ∑ j ∇ · e v e , i J ⃑ j + S v e + S c v ,
where, e v e is the electron vibration energy, q v e is the heat conduction due to electron vibration, ∇ e v e , i J i is the change in electron vibration energy due to component diffusion, S v e is the relaxation value between vibration and translational modes, and S c v is the energy cause by change in electron vibration energy due to chemical reaction.

3. Parametric design

The 3D, steady-state, double-precision, implicit density-based solver of flux type AUSM is used for all the computational simulations. Reynolds Averaged Navier Stokes (RANS) equations are solved to get the smooth variation of the averaged velocity and the pressure fields in a turbulent flow. The S S T / k – ω has been used to close the RANS equations as has a high accuracy for flows with adverse pressure gradients, separation, and reattachment better than other models [15]. Viscous heating, compressibility effects and production limiter were toggled to capture the heat flux generated due to viscous effects.

4.1. Parameters

To properly initialise the inlets and outlets of the model, a global operating condition of 0   P a was set, as to normal practice in hypersonic flow modelling. The inlet was set as a pressure far-field, as shown in Table 1.
In Table 1, four data points were utilised to study the effects on the unmodified and modified capsule through both a supersonic and hypersonic flow regime. The air properties play an important role in modelling the flow around the capsule. In compressible flow and boundary layer settings, air loses the properties of an ideal gas. Chemical reactions of dissociation, recombination and ionization begin to play an essential part in the heat flux generation and transfer near the stagnation point [16]. However, as mentioned before, chemical kinetics are beyond the scope of the research. Thus, an ideal gas condition was assumed for the air, to closely model compressibility effects, while saving on the computational power that chemically reacting flow requires. Moreover, a pressure far-field boundary condition can only be used with ideal gas law in Fluent. On the other hand, due to the changing physical properties of air with temperature, the Boltzmann-kinetic theory [17], Eucken-relation [18], and Blottner curve fit [19], were used to obtain the thermodynamics and transport properties. For instance, density is calculated using the ideal gas, specific heat capacity is determined using Boltzmann-kinetic theory, thermal conductivity is based on Eucken-relation, and viscosity is approximated using Blottner curve fit.

4.2. Geometry and design conditions

The baseline model/geometry of this research focuses on NASA’s latest Orion CEV module. The geometry dimensions are adopted from [10]. A summary of the free stream boundary conditions is shown in Table 2.
SolidWorks 2019 was used to model the Orion CEV geometry adopted from the research done by mentioned in the literature review. The reference geometry can be seen in Figure 1, and the newly created geometry (in millimetres) can be seen below.
Multiple models were created to aid in the CFD processes. A 3D representation of the capsule was recreated to aid as the baseline of the study, a 2D cross-section surface of the ducted 3D geometry can be seen in Figure 2.
The ducts were positioned in a crown pattern with a radius half of the ablative heat shield region. The ducts themselves had an arbitrary diameter of 250   m m . The IGS CAD of the geometry is imported into ANSYS Design Modeller for the CFD set-up and modelling. A Far-field computational domain is modelled using ANSYS Design Modeller around the capsule’s geometry following the importation process. The domain is a capped 50   m cylinder from one side, with a hemisphere radius of 50   m . A symmetry line through the XY plane is made split the domain and reduce the number of elements for computational efficiency. This is done with the assumption that the flow is symmetric along the XY plane. The computational domain can be seen in Figure 3.

4.3. Meshing

The domain was meshed using ANSYS-Fluent [7], to utilise its capability of producing polyhedral mesh elements. Polyhedral elements are known for their ability to handle stretched cells and to predict recirculating flows accurately, which is useful in the case of hypersonic flow. Moreover, polyhedral mesh automatically creates prismatic elements at the boundary and walls thereby overcoming the inability of tetrahedral mesh to resolve boundary layers. Furthermore, each polyhedral element is equivalent to 4 tetra-elements, hence, helps save on computation time and lowers the overall number of elements. To better capture the near wall effects such the boundary layer, separation points, and viscous heating, inflation layers were added to better enhance the accuracy of the model. The meshed domain is illustrated in Figure 4.
As for any project involving computational modelling and simulation with a discretised domain, a mesh independence study is essential in validating the numerical solution obtained from the simulation is both accurate and reliable. The mesh independence study was conducted on the capsule at a speed of Mach 6 and a pressure of 1064, as shown in Figure 5.
As can be seen in the figure above, the drag coefficient decreases with the increase in number of elements. Towards the end of the plot no significant change can be seen between the points, indicating a successful mesh convergence. The quick convergence is a result of Full-Multi Grid Initialisation, a unique function within Ansys which allows the user to achieve convergence with a coarse mesh, such as this case (Ansys Fluent Academic is limited to 512,000 elements). Therefore, a mesh size of 506425 was chosen, as the model converged. All subsequent simulations will be conducted with those number of elements.

4.4. Full-Multi Grid Initialisation

Full-Multi Grid (FMG) Initialisation is a method available in ANSYS Fluent. It is used to obtain better initial approximate solutions to complex flow problems such as hypersonic flow, rotating spiral flows in ducts, or expanding flow in ducts. These initial solutions help accelerate the flow convergence at a minimum cost to the overall computational expense. During FMG initialization, the inviscid Euler Equations are solved using first order discretization to obtain an approximate solution. FMG Initialization is useful for complex flow problems involving large pressure and velocity gradients on large meshes. It can be used with both pressure and density-based solvers, but only in steady mode [7]. FMG had a major role in accelerating the convergence. Given the 512k cell limit in Ansys, for the most part, the obtainable mesh can be treated as a coarse mesh relative to other hypersonic flow models which utilise millions of cells to achieve numerical convergence without FMG.

4. Results

Mach speeds, drag coefficient, surface heat flux, static pressure, and static temperature wese investigated for 4 different models, the baseline capsule to serve as a reference, a 2-duct capsule, and a 4-duct capsule to capture the effects of adding ducts into the capsule’s geometry has on the aerodynamic forces and heat reduction capabilities. The boundary conditions, air properties, and inlet/outlet properties were kept standard across all four simulations to allow for a valid comparison. Additionally, all the simulations were conducted with a zero angle of attack to the flow. Mach, pressure, and temperature contours are utilised as a visual aid and a comparison tool. In addition to that, surface heat flux reports and drag coefficient monitors are also being used to quantify the effects of altering the geometry. All the simulations were run until the residual values reached the convergence criterion of 10 e − 5 .

3.1. Baseline Capsule

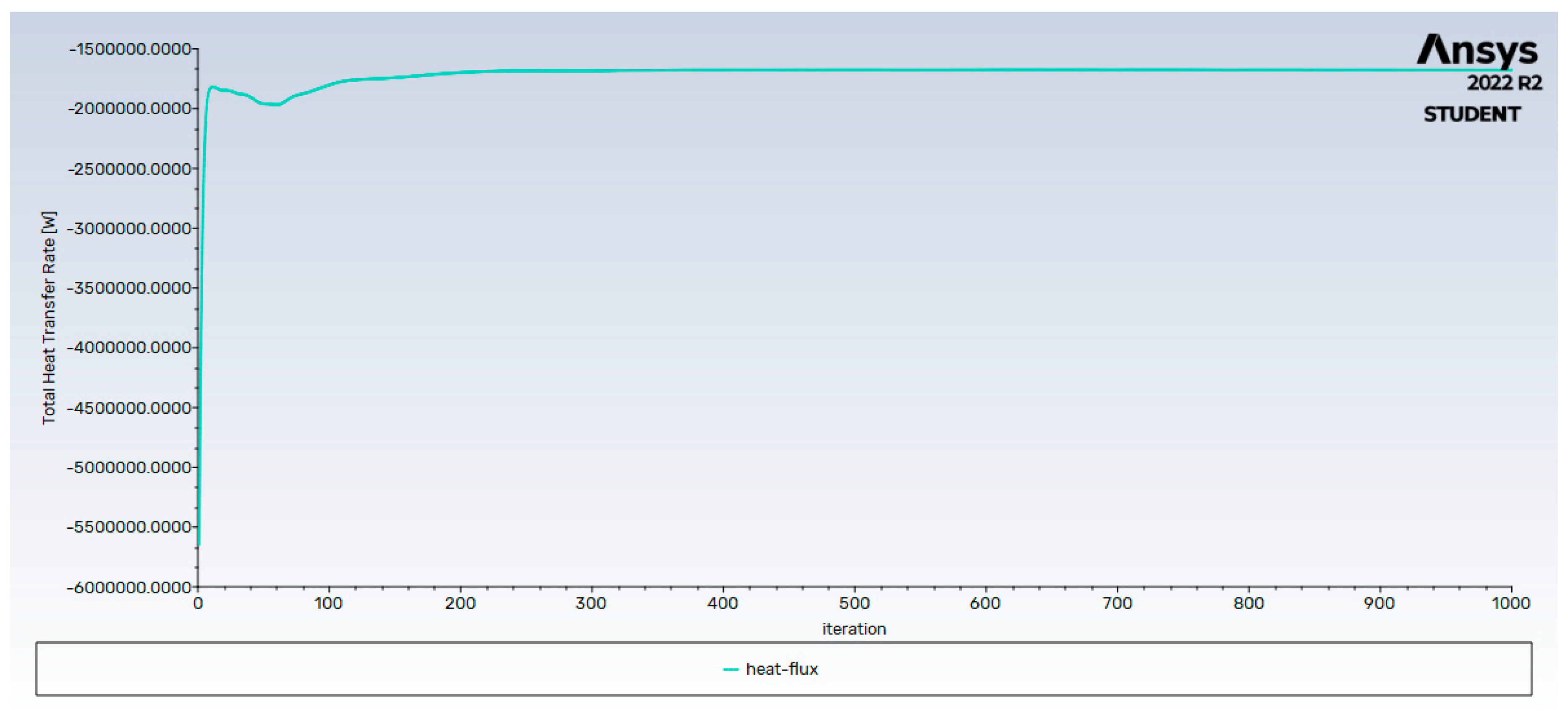
Simulating the baseline capsule at with no alterations at Mach 5 conditions, shows the reference pressure, temperature, heat flux, and Mach contours. The baseline capsule at Mach 5 converged to a drag coefficient of 1.125 and a total surface heat flux value of − 1677208.10   W / m 2 , as can be seen in both Figure 7 and Figure 8.
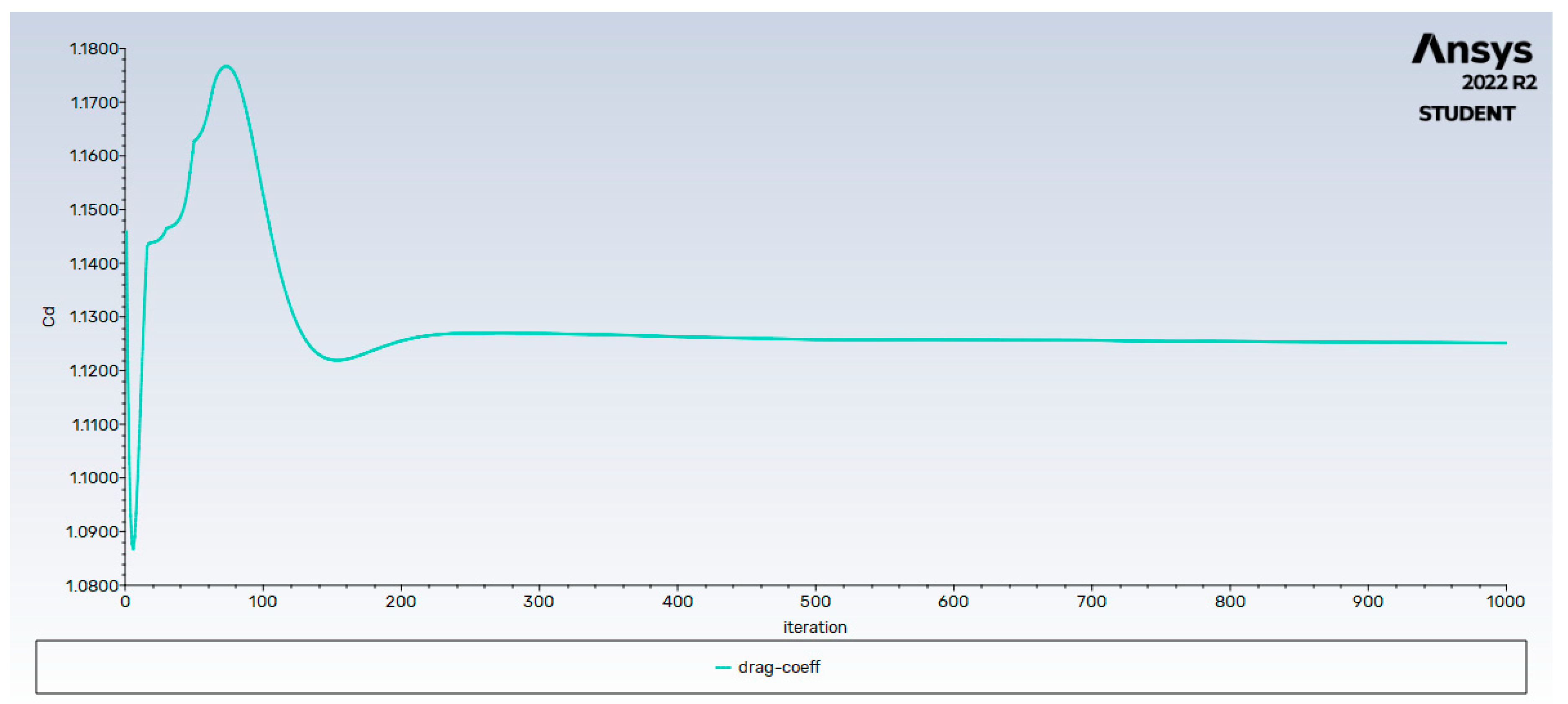
Preprints 83876 g006
Figure 6. Drag coefficient monitor plot of the unmodified capsule at Ma = 5
Figure 6. Drag coefficient monitor plot of the unmodified capsule at Ma = 5
Preprints 83876 g006
Preprints 83876 g007
Figure 7. Total heat flux monitor plot of the unmodified capsule at Ma = 5
Figure 7. Total heat flux monitor plot of the unmodified capsule at Ma = 5
Preprints 83876 g007
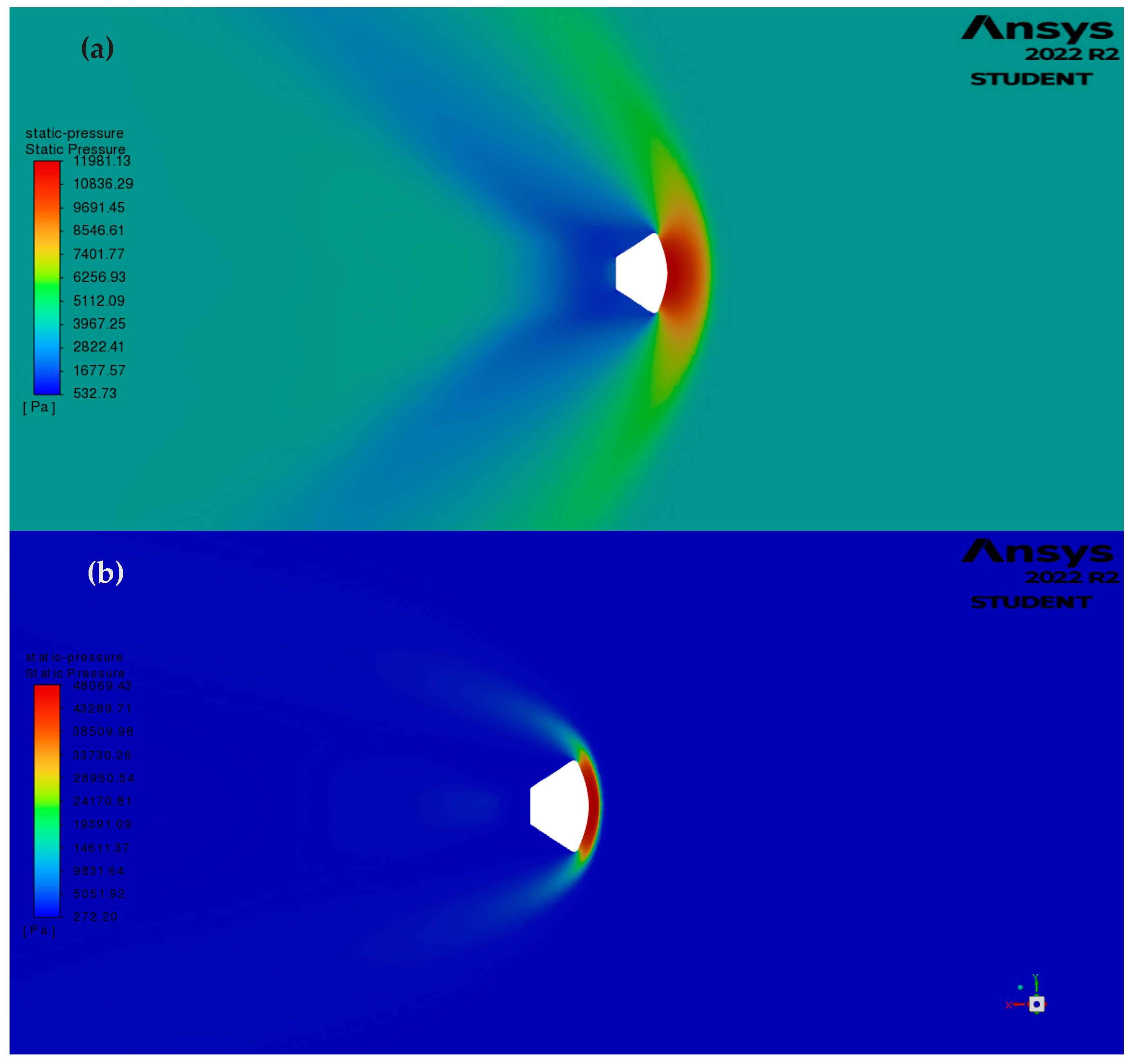
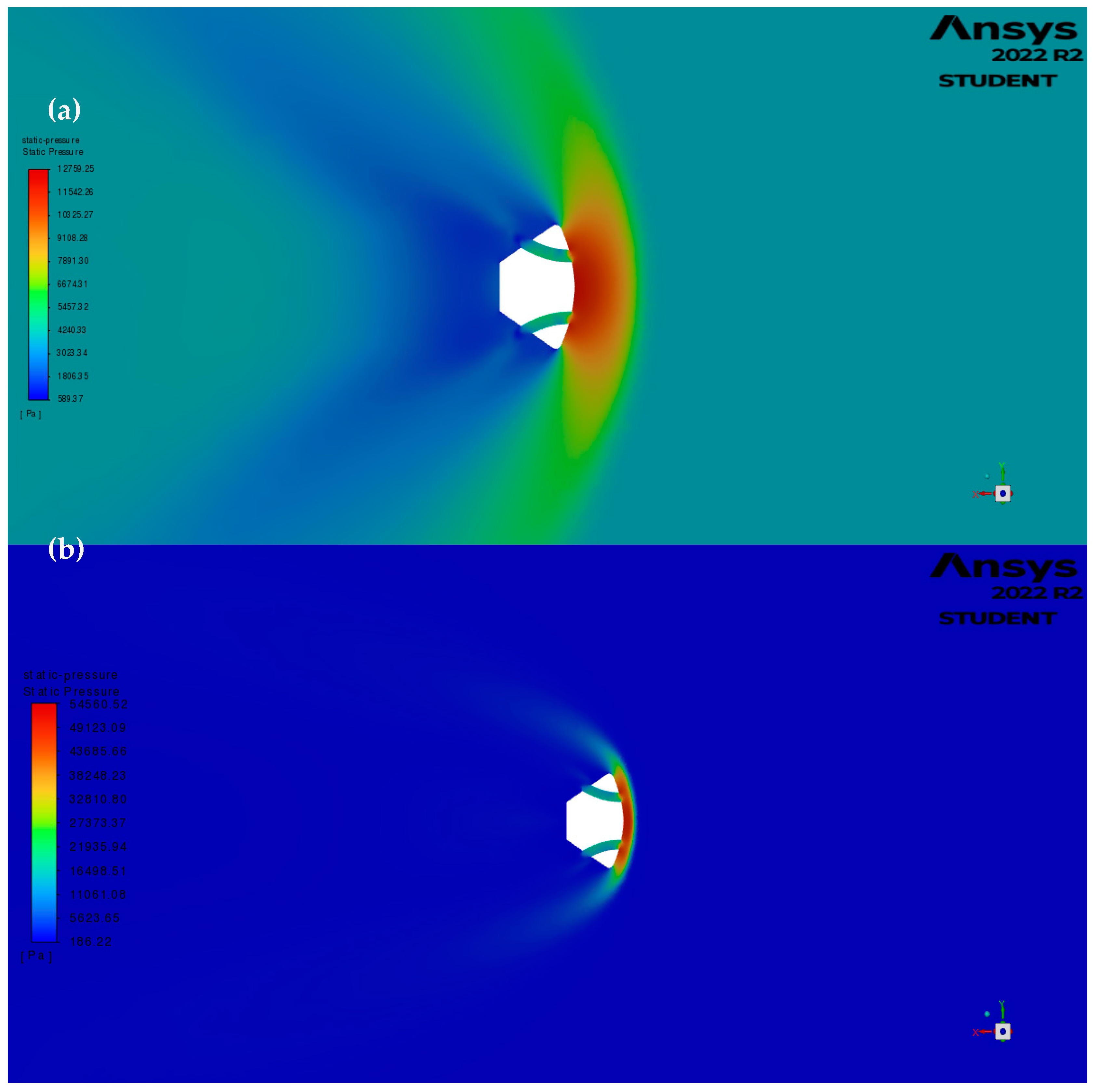
It has been observed that the all the Mach, Temperature, and Pressure contours change with the increase in Mach number. Initially, at relatively low Mach number ( 1.4 ≤ Ma ≤ 3 ), the pressure contour can be seen showing a weak Bow shock distribution around the capsule ablative heat shield. When transitioning to hypersonic flow speeds ( Ma = 6 ), the distributions transition to that of a strong Bow Shock distribution, where the pressure increase is concentrated close to the ablative shield rather than at a larger angle to the capsule at lower speeds. Furthermore, the Bow Shock to surface distance is observed to decrease with higher Mach numbers. At Ma = 1.4 near the shoulder of the capsule, the Prandtl-Meyer expansion fan can be observed. The pressure around the point can be seen ranging from a high-pressure value to a low-pressure value. The same effect cannot be observed at Ma = 6 , as the Prandtl-Meyer affect is limited to sonic and supersonic flows [20]. The static pressure contour comparison can be seen in Figure 9.
Preprints 83876 g008
Figure 8. Static pressure contours of baseline model (a) Ma = 1.4 , (b) Ma = 6 .
Figure 8. Static pressure contours of baseline model (a) Ma = 1.4 , (b) Ma = 6 .
Preprints 83876 g008
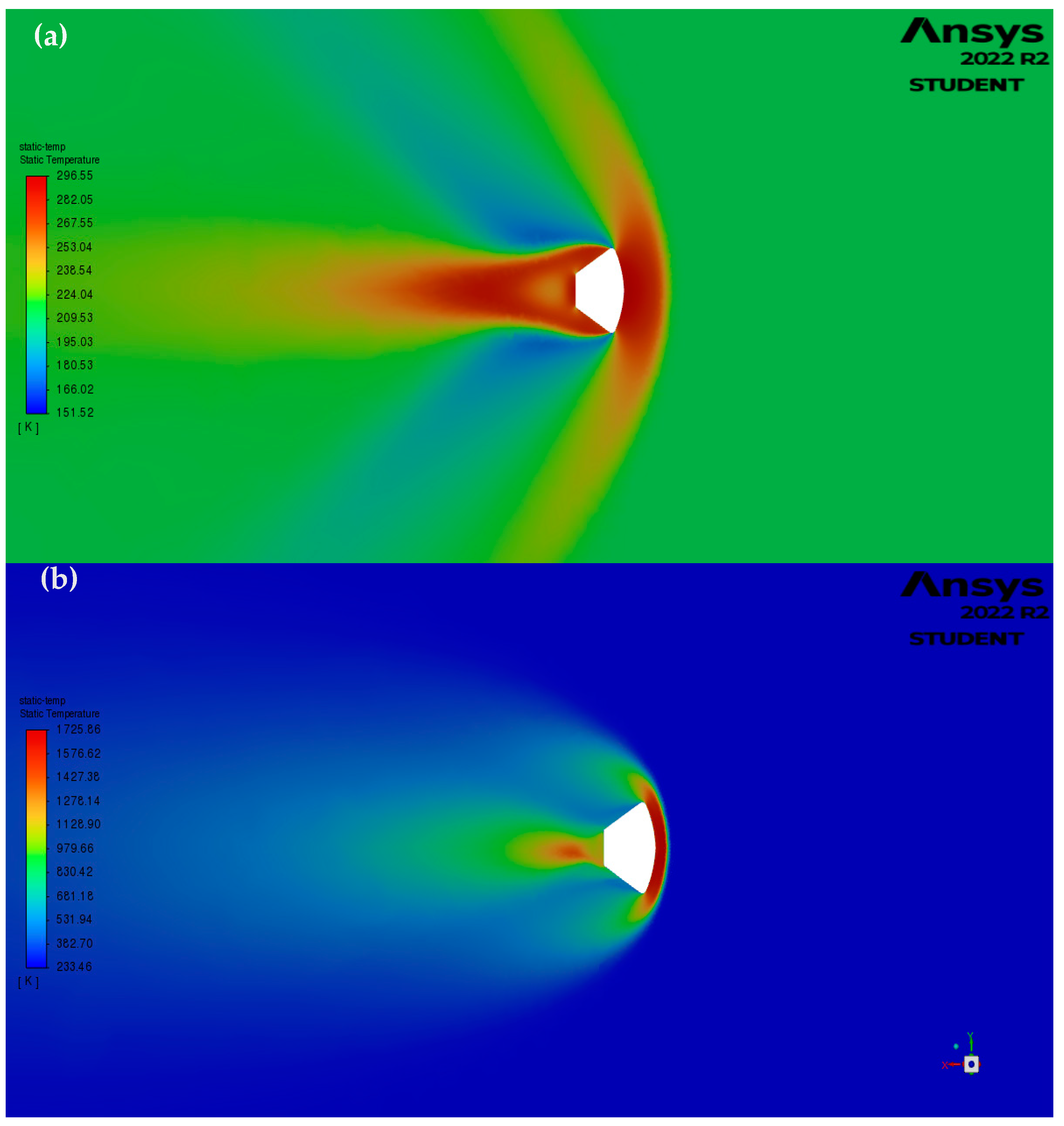
The same transition of the Bow Shock formation and angle can be seen with the static temperature distribution. More importantly, at Ma = 1.4 the high temperature regions are located towards the front of the capsule at the stagnation point and behind the capsule at the recirculating and viscous flow regions. At Ma = 6 , the relatively high temperature regions are mainly observed in front of the capsule. Although the recirculating region has a higher absolute temperature compared to the Ma = 1.4 contour, relatively the high temperature is restricted to the ablative heat shield at the bow shock region. This could be an affect attributed to the more compressed Bow Shock and the separation point, located further towards the apex of the capsule in higher flow regimes, effectively reducing the vorticity region and the distance for the recompression shock to form. The static temperature contours are illustrated in Figure 10.
Preprints 83876 g009
Figure 9. Static Temperature Contours of Baseline Model (a) Ma = 1.4 , (b) Ma = 6 .
Figure 9. Static Temperature Contours of Baseline Model (a) Ma = 1.4 , (b) Ma = 6 .
Preprints 83876 g009
The Mach speed contours provide more insight on the effects of hypersonic flows. Regions of acceleration and deceleration can help locate the vorticity regions and recompression region around the baseline capsule. Regions of stagnations and separation (where vorticity begins to happen) are easily identifiable as the low Mach blue regions, where the stagnation and vorticity occurs. The same Prandtl-Meyers effects can be observed in the 1.4 Mach contours as well. The Mach contours are further illustrated in Figure 11.
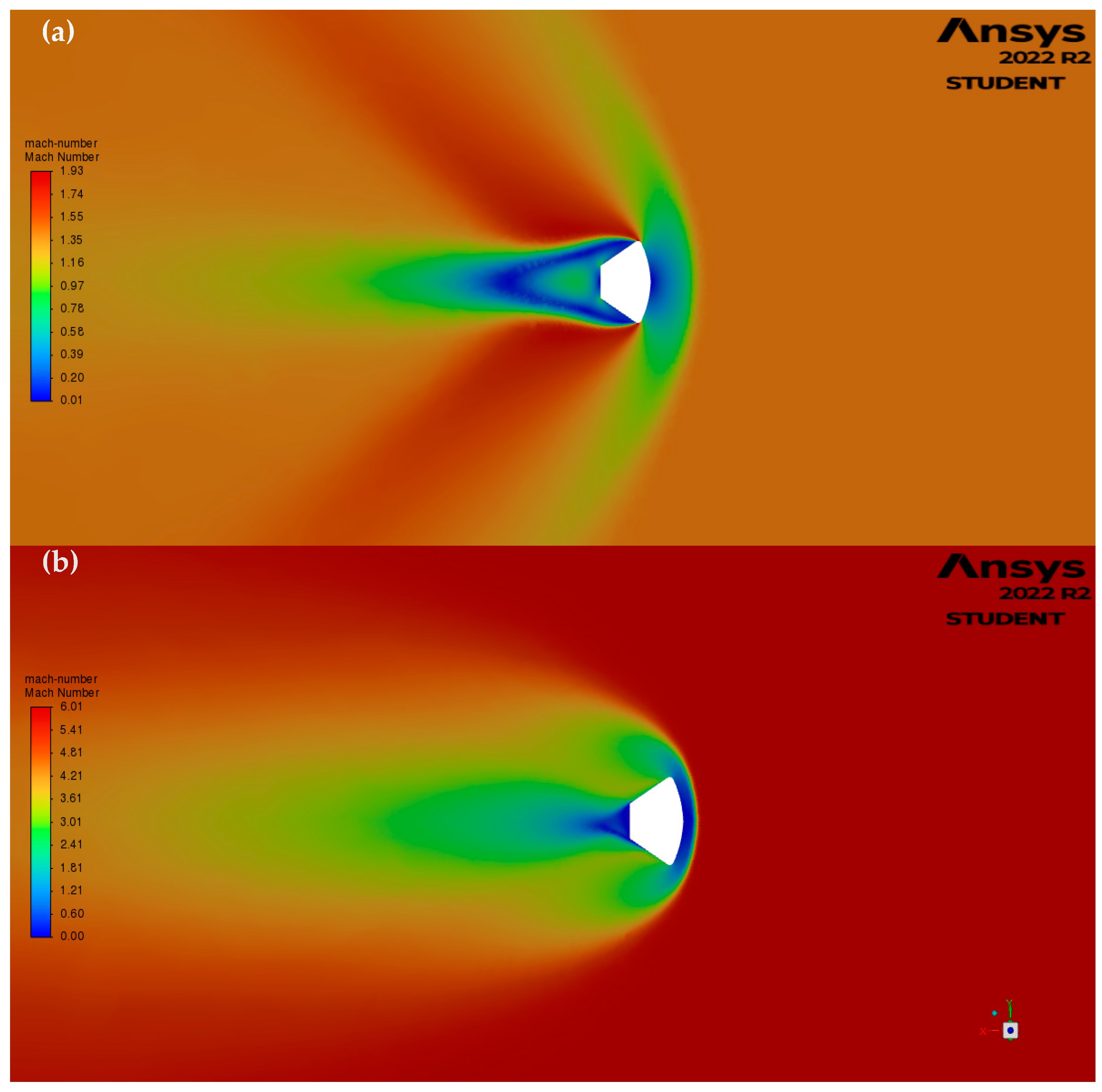
Preprints 83876 g010
Figure 10. Mach Contours of Baseline Model (a) Ma = 1.4 , (b) Ma = 6 .
Figure 10. Mach Contours of Baseline Model (a) Ma = 1.4 , (b) Ma = 6 .
Preprints 83876 g010
Regarding the total heat transfer on the capsule’s surface. The flux probe tool was used to extract the total heat flux generated on the surface of the capsule. The drag coefficient was also extracted for each Mach speed, as can be seen in Table 3.

3.2. Modified Capsule

Many of observable phenomena seen on the baseline capsule can be observed in both the 2-Duct and 4-Duct models. The main differences are observed within the maximum static pressure and temperature values. It is evident from the geometry alone that the introduction of duct into the capsule would firstly, create a path for the flow at the bow shock to flow. Secondly, the duct diameter is small compared to the capsule diameter, therefore compression of the air that goes through the duct is imminent. This compression leads to an increase of pressure and temperature. Visually, the 2-Duct and 4-Duct contour are similar and thus, only the 2-Duct will be used. In terms of the static pressure contour, visually the 1.4 Mach contour has a similar distribution to the baseline model. The significant difference can be seen towards the apex where an additional wave can be seen exiting the ducts. A 6.50% increase in the peak static pressure can be observed between the baseline and 2-Duct model at Mach 1.6 and a 13.5% increase at Mach 6. The static pressure distribution is further illustrated in Figure 12.
Preprints 83876 g011
Figure 11. Static Pressure Contours of 2-Duct Model (a) Ma=1.4, (b) Ma=6.
Figure 11. Static Pressure Contours of 2-Duct Model (a) Ma=1.4, (b) Ma=6.
Preprints 83876 g011
On the other hand, the static temperature contour showed a noticeable change in temperature distribution. Intuitively, the maximum temperature increased due to the added compression which occurs in the ducts. However, a negligible increase was observed in the Mach 1.4 case and a -0.62% decrease in the maximum static temperature at Mach 6. At a speed of Mach 1.4, the size of the wake region is significantly larger than that seen in Figure 13 and Figure 14. The increase in size can be seen to be a result of the addition of the 2 air ducts on the capsule. The compressed air can be observed to expand as it exits the duct creating a cold spot in the distribution. As for the Mach 6 case, the size wake region increases significantly. High temperatures can be observed in the recirculation and separation region.
Preprints 83876 g012
Figure 12. Static temperature contours of 2-duct model (a) M a = 1.4 , (b) M a = 6 .
Figure 12. Static temperature contours of 2-duct model (a) M a = 1.4 , (b) M a = 6 .
Preprints 83876 g012
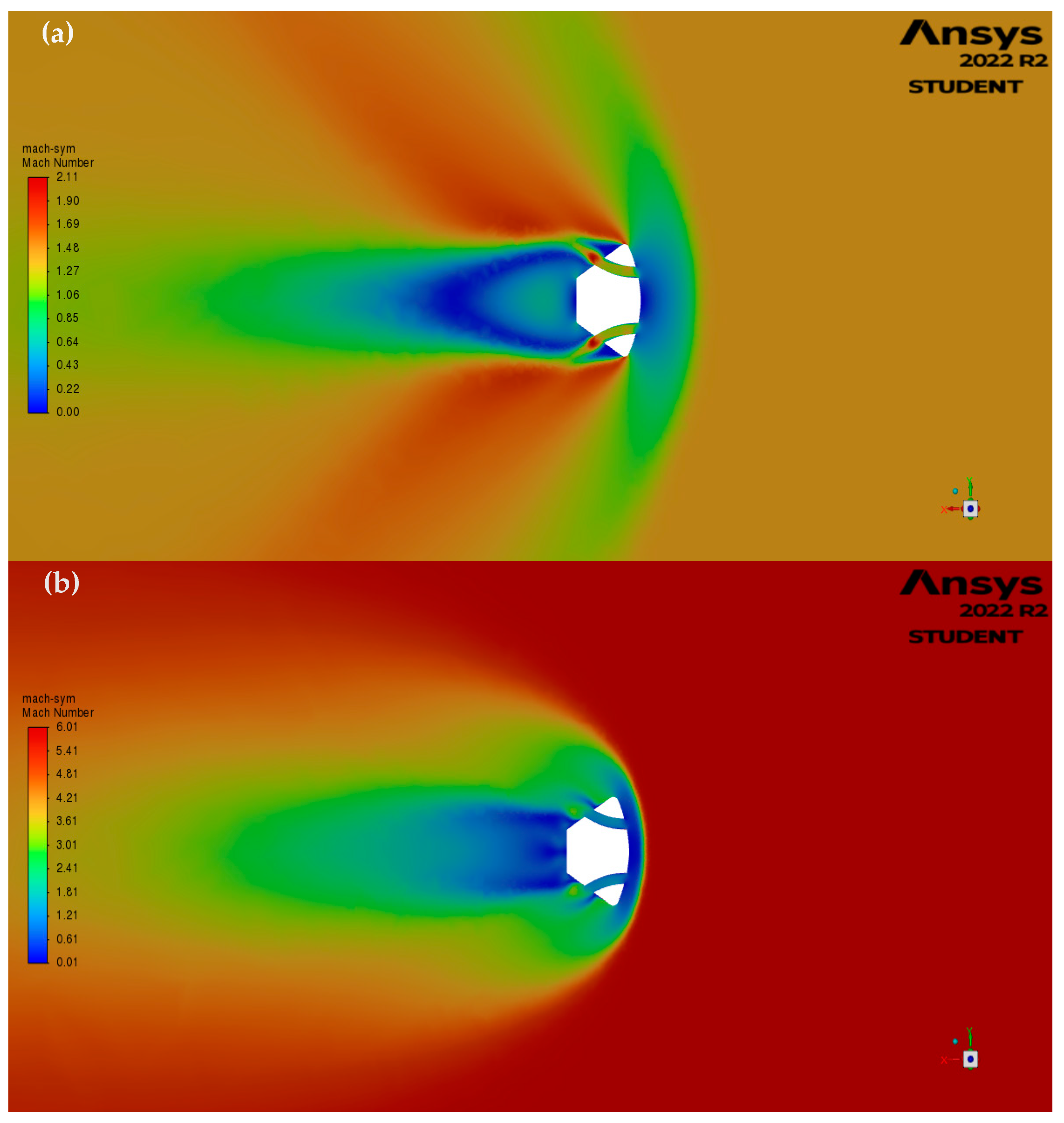
Similarly, the Mach contour shows an expanded wake with pushed back recompression shock zone. At Ma = 1.4 , the air passing through duct from the shock region can be seen accelerating as it leaves and reattaching within the outer inviscid flow. The same cannot be said at M a = 6 , but more deceleration can be detected near the apex point of the capsule.
Preprints 83876 g013
Figure 13. Mach contours of 2-duct model (a) M a = 1.4 , (b) M a = 6 .
Figure 13. Mach contours of 2-duct model (a) M a = 1.4 , (b) M a = 6 .
Preprints 83876 g013
A similar summary of both the 2-Duct and 4-Duct model can be seen in Table 4. From data in Table 2, Table 3 and Table 4 one can see that all 3 models have a similar trend in the drag coefficient.
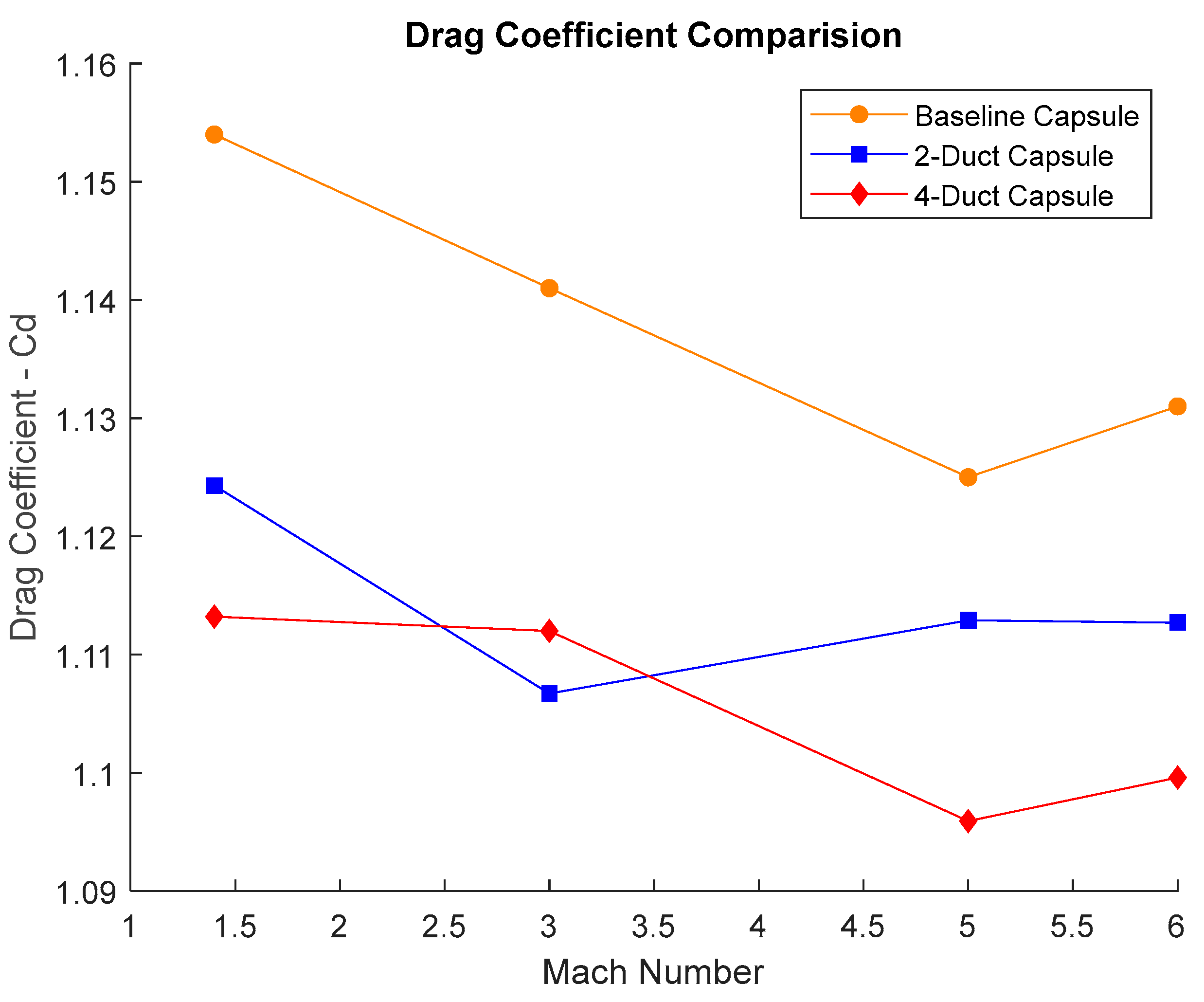
Preprints 83876 g014
Figure 14. Drag coefficient result comparison.
Figure 14. Drag coefficient result comparison.
Preprints 83876 g014
With the increase in Mach number the drag coefficient of the capsule can be seen to decrease. A similar trend was observed in [10]. Moreover, the addition of the ducts to the capsule result in an overall decrease in the drag coefficient across all Mach numbers. The maximum decrease is between the 4-Duct capsule and the Baseline, which showed a decrease of 3.55% at Ma=1.4. The average decrease across all Ma is 2.07% and 2.86% for the 2-Duct and 4-Duct Models respectively.
The heat flux on the other hand, initially showed a decrease in heat flux at Ma = 1.4 , but later displayed an increase in total surface heat flux around the capsule with the increase in Mach numbers. The increase is attributed to the number of ducts and subsequently the increased surface area and contact between the capsule and the air.
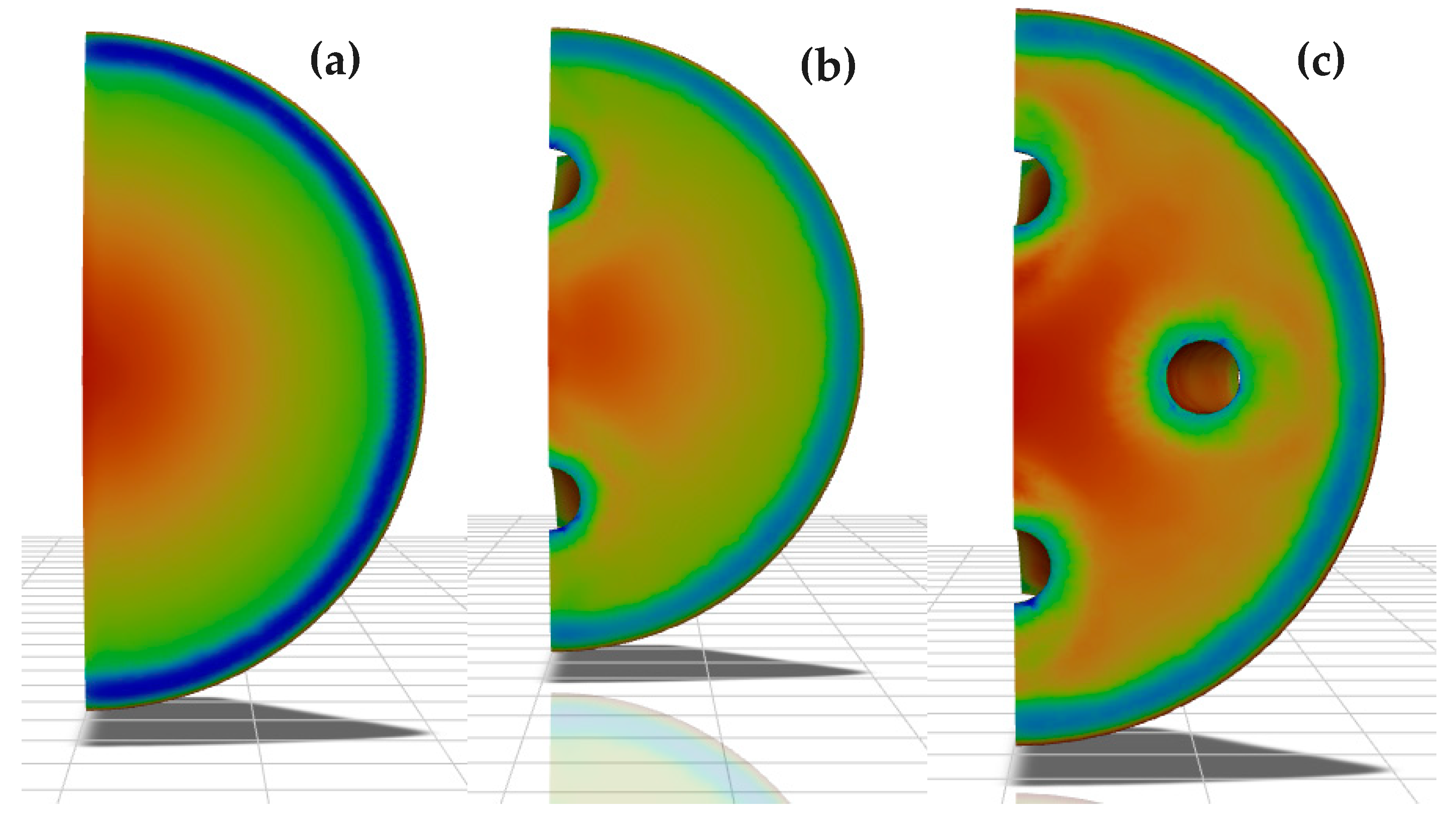
Preprints 83876 g015
Figure 15. Surface heat flux distribution at Ma = 6 for (a) baseline model, (b) 2-duct model, and (c) 4-duct model.
Figure 15. Surface heat flux distribution at Ma = 6 for (a) baseline model, (b) 2-duct model, and (c) 4-duct model.
Preprints 83876 g015
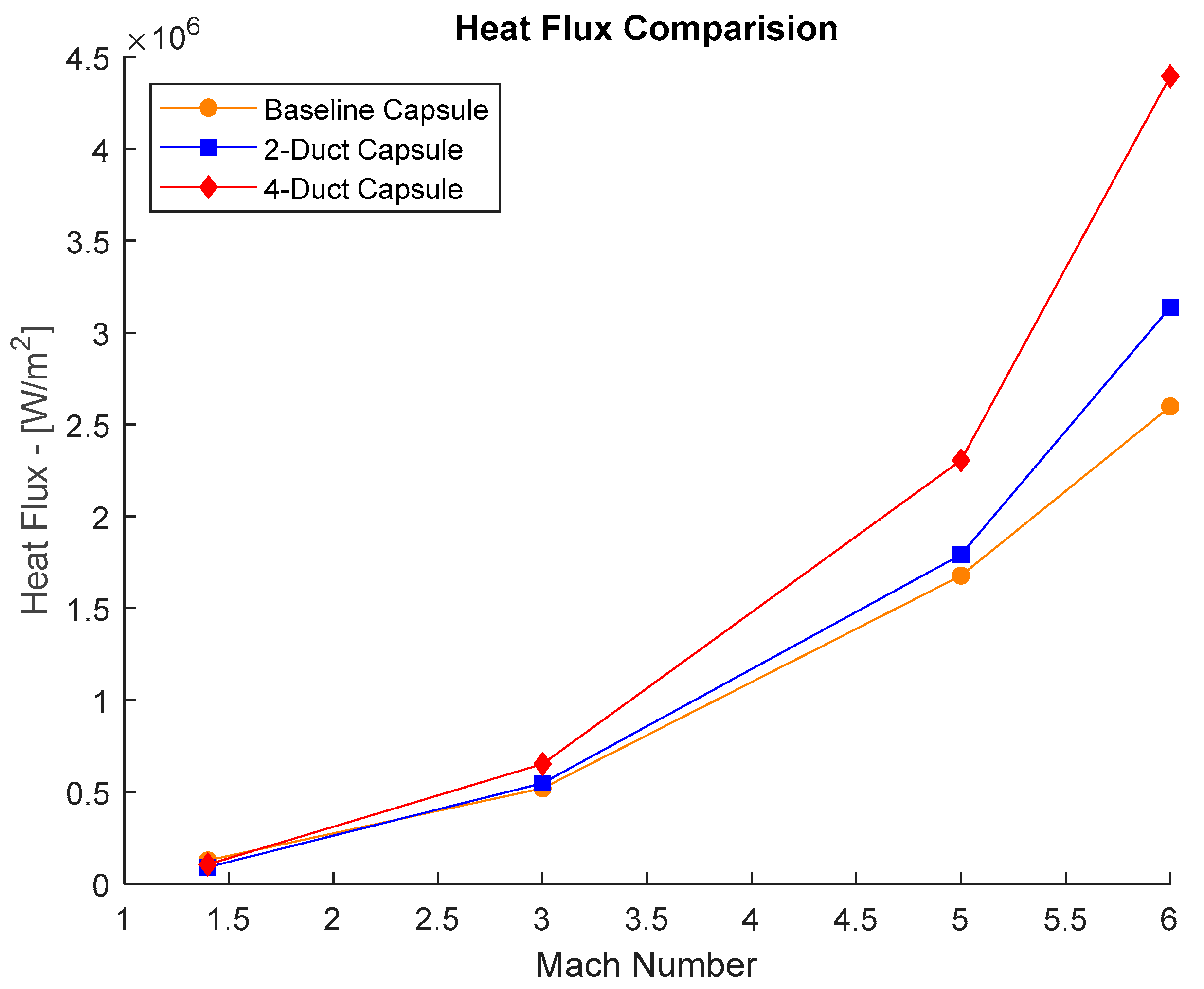
Preprints 83876 g016
Figure 16. Heat flux versus Ma various set-ups.
Figure 16. Heat flux versus Ma various set-ups.
Preprints 83876 g016
The plot shows the effects and trend of increasing the number of ducts on the heat flux on the capsules surface.

5. Conclusion

This study aimed to optimise a re-entry aircraft’s geometry to enhance its aerodynamic performance and reduce heat generation. A CFD simulation was carried out using ANSYS Fluent on a baseline Orion CEV module and modified Orion capsules created on SolidWorks. The geometry was created with stability in mind, thus even number of ducts in a crown pattern were added. The baseline module was created and tested, along with the two modified models to validate the efficacy of the aerodynamic optimisation choice. All three models were investigated under various flow conditions ranging from supersonic speeds of Mach 1.4 to Hypersonic Speeds of Mach 6. The use of ducts in the 2-Duct and 4-Duct Models was found to reduce the drag coefficient by an average of 2.07% and 2.86%, respectively, across all Mach numbers when compared to the unmodified model. The maximum decrease was observed in the 4-Duct model, which showed a decrease of 3.55% at Mach 1.4. However, the addition of extra ducts resulted in an increase in the maximum heat transfer rate. The heat flux increased by up to 69% between the 4-Duct model and the baseline model, with an average increase of around 28.6%. It should be noted that at Mach 1.4 both the 2-Duct and 4-Duct models had a heat flux reduction of 29.4% and 17.7% respectively.
All in all, the aerodynamic optimisation showed satisfying results in terms of drag reduction, however at the cost of increased heat flux in the ducts and more turbulent wakes at the end of the capsule with the increase in Mach number and the number of ducts. The research touched on the challenges of modelling hypersonic flows effectively. Hypersonic flow always involves sacrificing accuracy in one or more areas of the simulation. In this case the heat generation accuracy was sacrificed by assuming ideal non-reactive gas. Nonetheless, the results are a fair estimation of the trend that might arise with the addition of the optimisation geometry. As technology continues to advance, the optimization process will likely become more efficient and effective, aiming for safer and more REC vehicles in the future.

References

  1. Lin, P.; Liu, X.; Xiong, N.; Wang, X.; Shang, M.; Liu, G.; Tao, Y. Numerical Study on the Influence of Wall Temperature Gradient on Aerodynamic Characteristics of Low Aspect Ratio Flying Wing Configuration. Sci Rep 2021, 11, 16295. [Google Scholar] [CrossRef] [PubMed]
  2. Anderson, J.D. Hypersonic and High-Temperature Gas Dynamics; AIAA education series; Third edition.; American Institute of Aeronautics and Astronautics; American Institute of Aeronautics and Astronautics, Inc: Reston, Virginia, 2019; ISBN 978-1-62410-514-2. [Google Scholar]
  3. Carandente, V.; Zuppardi, G.; Savino, R. Aerothermodynamic and Stability Analyses of a Deployable Re-Entry Capsule. Acta Astronautica 2014, 93, 291–303. [Google Scholar] [CrossRef]
  4. Mungiguerra, S.; Zuppardi, G.; Savino, R. Rarefied Aerodynamics of a Deployable Re-Entry Capsule. Aerospace Science and Technology 2017, 69, 395–403. [Google Scholar] [CrossRef]
  5. Singh, N.; Schwartzentruber, T.E. Aerothermodynamic Correlations for High-Speed Flow. J. Fluid Mech. 2017, 821, 421–439. [Google Scholar] [CrossRef]
  6. Sun, J.; Zhu, H.; Xu, D.; Cai, G. Aerodynamic Thermal Simulation and Heat Flux Distribution Study of Mechanical Expansion Reentry Vehicle. Aerospace 2023, 10, 310. [Google Scholar] [CrossRef]
  7. ANSYS, Inc. Ansys® 2022.
  8. Visakh, P.; Akhil, J.; Nagaraja, S.R. Effect of Counter Flowing Jet on Heat Transfer and Drag in Hypersonic Re-Entry Vehicle. IOP Conf. Ser.: Mater. Sci. Eng. 2018, 377, 012163. [Google Scholar] [CrossRef]
  9. Kaushikh, K.; Arunvinthan, S.; Pillai, S.N. Aerodynamics and Aerothermodynamics of Undulated Re-Entry Vehicles. Acta Astronautica 2018, 142, 95–102. [Google Scholar] [CrossRef]
  10. Anbu Serene Raj, C.; Narasimhavaradhan, M.; Vaishnavi, N.; Arunvinthan, S.; Al Arjani, A.; Nadaraja Pillai, S. Aerodynamics of Ducted Re-Entry Vehicles. Chinese Journal of Aeronautics 2020, 33, 1837–1849. [Google Scholar] [CrossRef]
  11. Palharini, R.C.; Santos, W.F.N. The Impact of the Length-to-Depth Ratio on Aerodynamic Surface Quantities of a Rarefied Hypersonic Cavity Flow. Aerospace Science and Technology 2019, 88, 110–125. [Google Scholar] [CrossRef]
  12. Potvin, J.; Montanez, R.; Peek, G.; Potvin, J.; Montanez, R.; Peek, G. The Parks College Ram-Air Parachute Deployment Study - A Status Report. In Proceedings of the 14th Aerodynamic Decelerator Systems Technology Conference; American Institute of Aeronautics and Astronautics: San Francisco,CA,U.S.A., June 3 1997.
  13. Sazhin, S.S.; Al Qubeissi, M.; Xie, J.-F. Two Approaches to Modelling the Heating of Evaporating Droplets. International Communications in Heat and Mass Transfer 2014, 57, 353–356. [Google Scholar] [CrossRef]
  14. Fossati, M.; Mogavero, A.; Herrera-Montojo, J.; Scoggins, J.B.; Magin, T. A Kinetic BGK Edge-Based Scheme Including Vibrational and Electronic Energy Modes for High-Mach Flows. Computers & Fluids 2019, 185, 1–12. [Google Scholar] [CrossRef]
  15. Menter, F.R.; Lechner, R.; Matyushenko, A. Best Practice: RANS Turbulence Modeling in Ansys CFD; RANS Turbulence Modeling in Ansys CFD; Ansys Germany GmbH: Ansys Germany GmbH, 2023; p. 95.
  16. Dobrov, Y.; Gimadiev, V.; Karpenko, A.; Volkov, K. Numerical Simulation of Hypersonic Flow with Non-Equilibrium Chemical Reactions around Sphere. Acta Astronautica 2022, 194, 468–479. [Google Scholar] [CrossRef]
  17. Bais, S. The Equations: Icons of Knowledge; 1st ed.; Amsterdam University Press, 2005; ISBN 978-90-485-0539-5.
  18. Istomin, V.A.; Kustova, E.V.; Mekhonoshina, M.A. Validity of Eucken Formula and Stokes’ Viscosity Relation in High-Temperature Electronically Excited Gases.; Xi’an, China, 2014; pp. 1229–1236.
  19. Alkandry, H.; Boyd, I.; Martin, A. Comparison of Models for Mixture Transport Properties for Numerical Simulations of Ablative Heat-Shields. In Proceedings of the 51st AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition; American Institute of Aeronautics and Astronautics: Grapevine (Dallas/Ft. Worth Region), Texas, January 7 2013.
  20. Emanuel, G. Shock Waves in Gases. In Handbook of Shock Waves; Elsevier, 2001; pp. 185–262 ISBN 978-0-12-086430-0.
Preprints 83876 g001
Figure 1. Geometry drawing schematics in millimetres.
Figure 1. Geometry drawing schematics in millimetres.
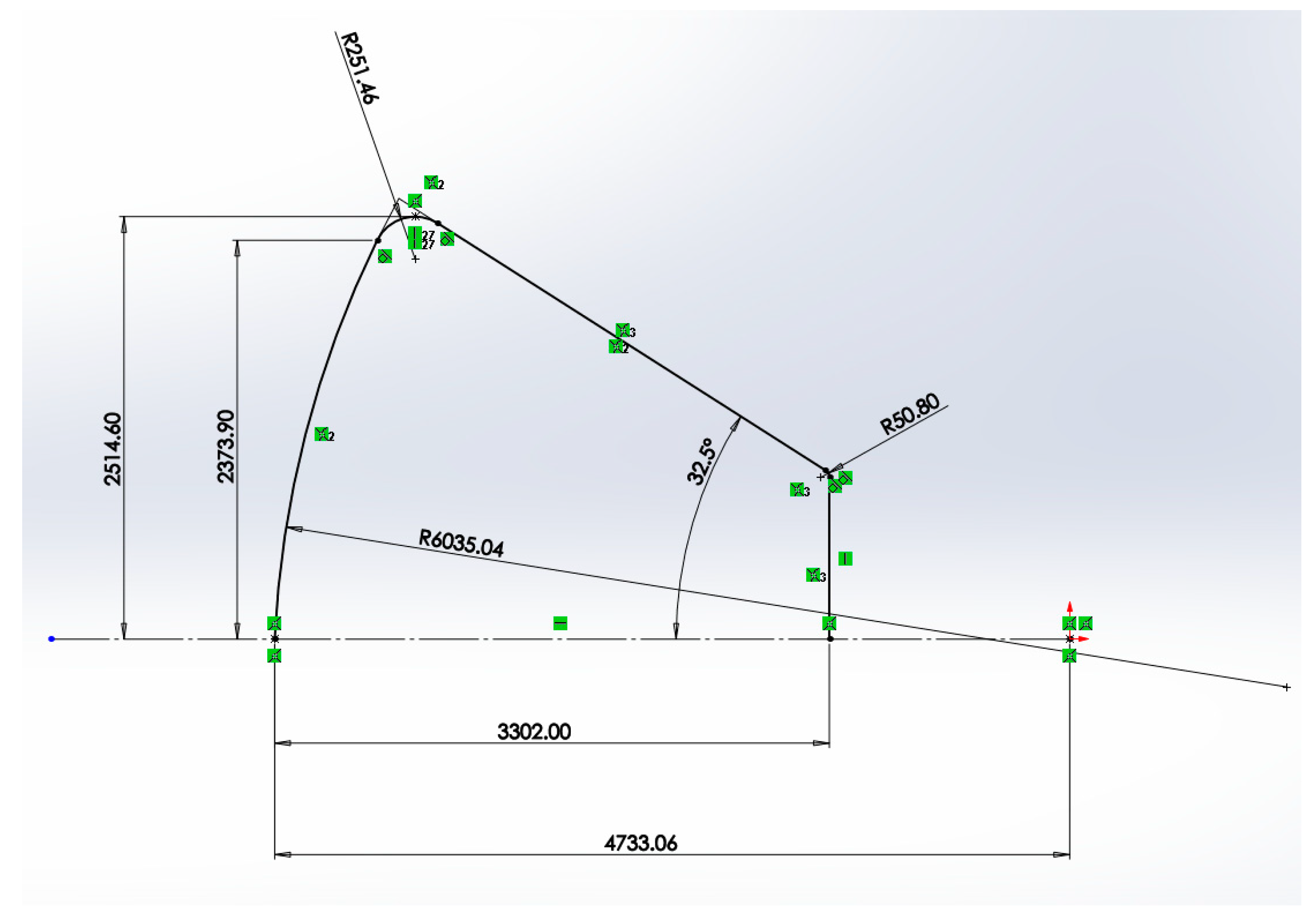
Preprints 83876 g001
Preprints 83876 g002
Figure 2. 3D baseline model (left) and cross-sectional view of the ducted model (right).
Figure 2. 3D baseline model (left) and cross-sectional view of the ducted model (right).
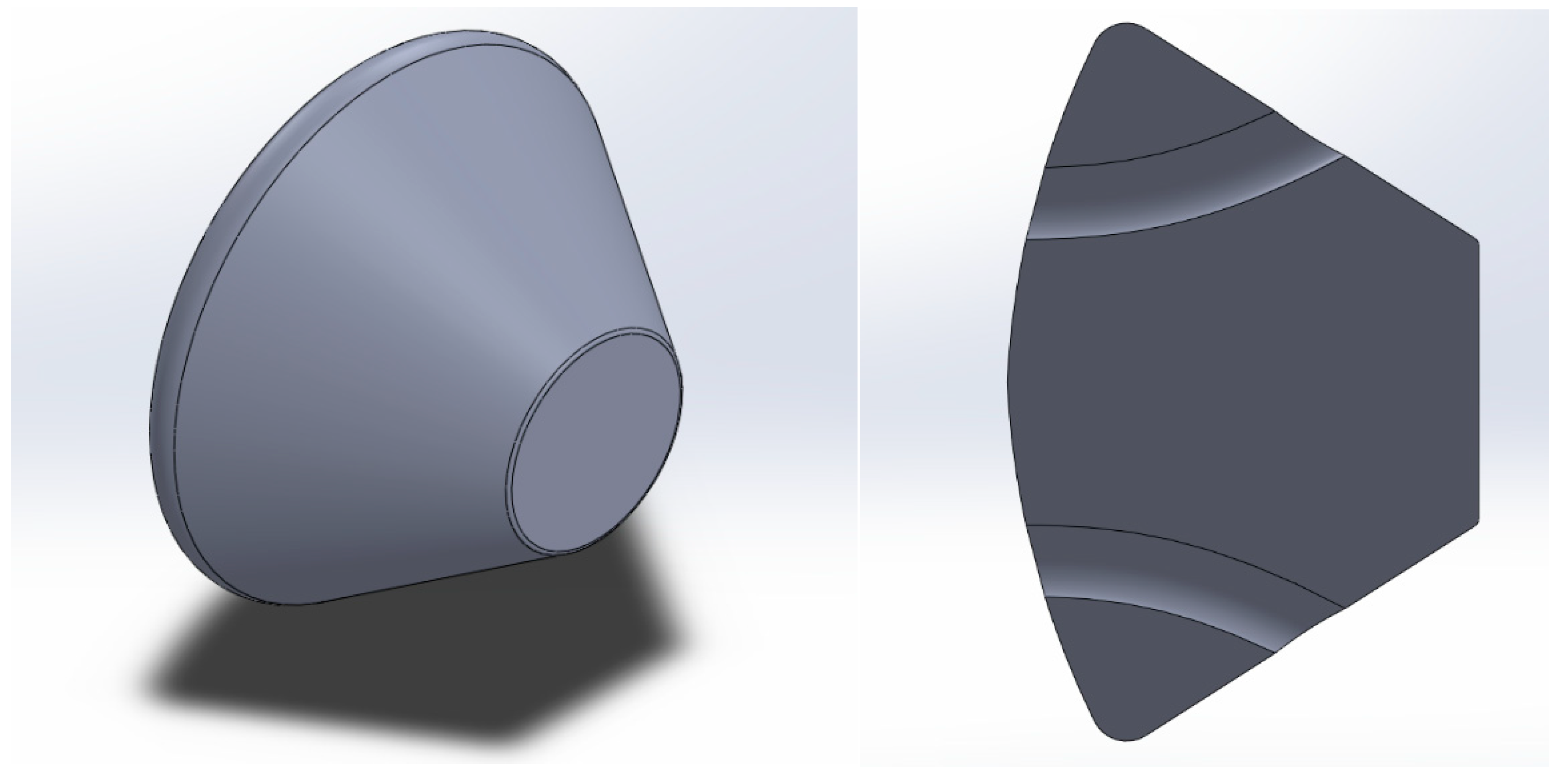
Preprints 83876 g002
Preprints 83876 g003
Figure 3. Computational domain geometry.
Figure 3. Computational domain geometry.
Preprints 83876 g003
Preprints 83876 g004
Figure 4. Meshed computational domain of the benchmark (unmodified) capsule, showing (a) Cross section of far-field region and (b) side view of capsule body.
Figure 4. Meshed computational domain of the benchmark (unmodified) capsule, showing (a) Cross section of far-field region and (b) side view of capsule body.
Preprints 83876 g004
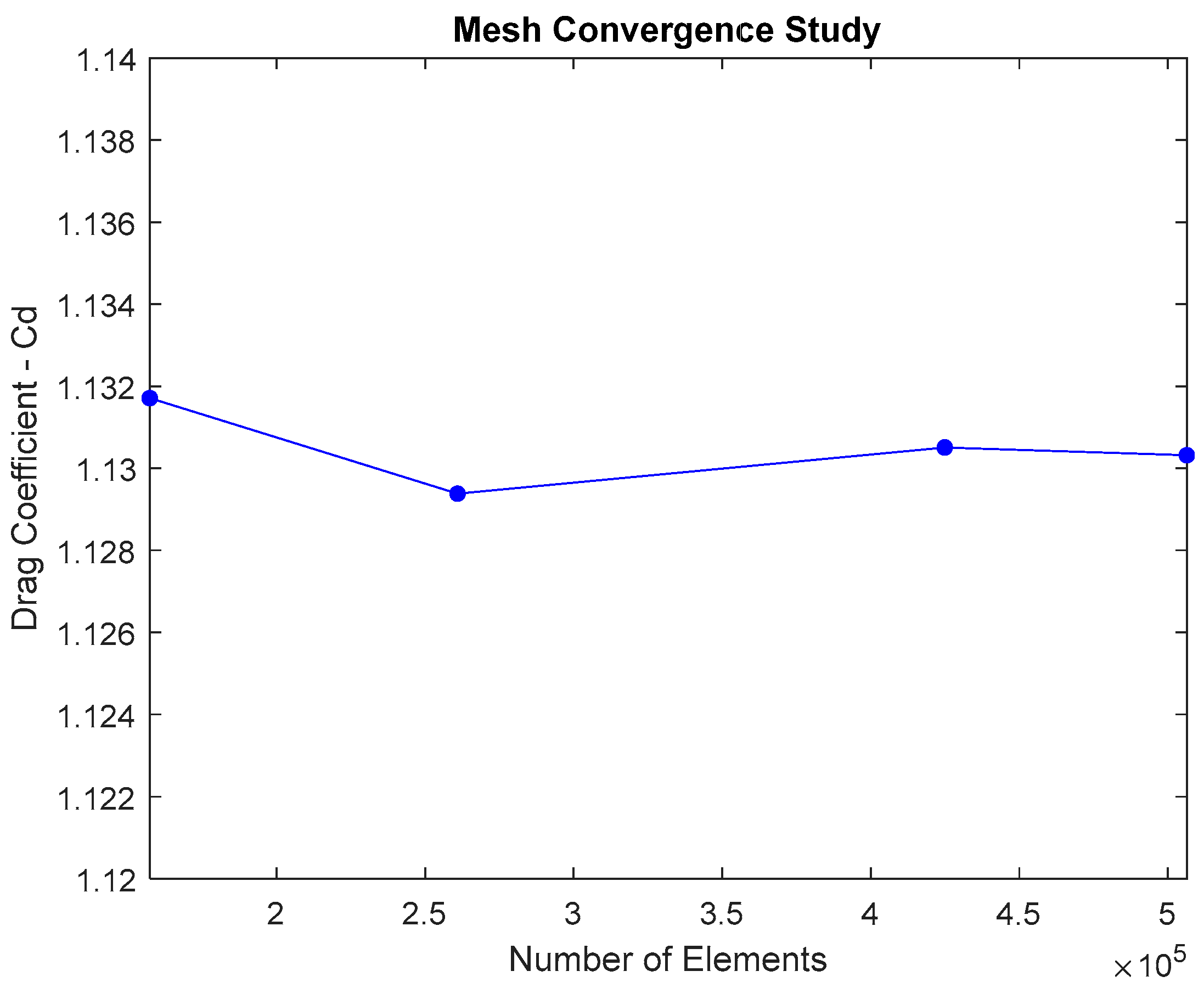
Preprints 83876 g005
Figure 5. Drag coefficient versus number of elements, revealing the mesh convergence attempt.
Figure 5. Drag coefficient versus number of elements, revealing the mesh convergence attempt.
Preprints 83876 g005
Table 1. Input parameters.
Table 1. Input parameters.
Ma Pressure (Pa) Temperature (K)
1.4 3952 213
3 2073 224
5 1238 232
6 1064 234
Table 2. Free stream boundary conditions.
Table 2. Free stream boundary conditions.
Ma Pressure   ( P a ) Temperature   ( K )
0.5 7550 110
0.7 7000 165
1.2 4519 210
1.4 3952 213
2 2891 219
3 2073 224
5 1238 232
6 1064 234
Table 3. Drag coefficient and heat flux summary of baseline capsule.
Table 3. Drag coefficient and heat flux summary of baseline capsule.
Ma Drag coefficient (CD) Heat   flux   ( W / m 2 )
1.4 1.1542 -127375.04
3 1.1411 -519027.80
5 1.1251 -1677208.10
6 1.1305 -2598212.20
Table 4. 2-duct and 4-duct model summary.
Table 4. 2-duct and 4-duct model summary.
2-Duct Model 4-Duct Model
Ma Drag Coefficient (CD) Heat   Flux   ( W / m 2 ) Drag Coefficient (CD) Heat   Flux   ( W / m 2 )
1.4 1.1243 -89887.47 1.1132 -104853.12
3 1.1067 -546800.49 1.1120 -651584.71
5 1.1129 -1791674.70 1.0959 -2304337.20
6 1.1127 -3136208.00 1.0996 -4394655.00
Table 5. Drag coefficient increase compared to baseline data.
Table 5. Drag coefficient increase compared to baseline data.
2-Duct Model 4-Duct Model
Ma % Decrease to Baseline % Decrease to Baseline
1.4 -2.594 -3.552
3 -3.020 -2.557
5 -1.086 -2.599
6 -1.575 -2.731
Average -2.069 -2.860
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated