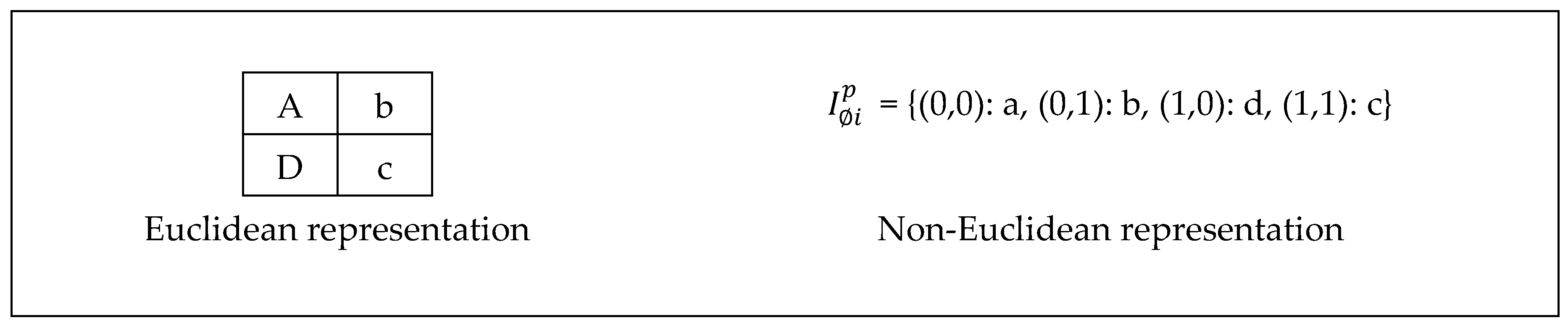Deep Learning in Medical Image Registration: Introduction and Survey

Preprint

Review

Deep Learning in Medical Image Registration: Introduction and Survey

Altmetrics

Downloads

167

Views

Comments

Ahmad Hammoudeh^*,Stéphane Dupont

This version is not peer-reviewed

This preprints belongs to the Topic

Artificial Intelligence in Medical Imaging and Image Processing

Submitted:

01 September 2023

Posted:

05 September 2023

You are already at the latest version

Alerts

Abstract

Image registration (IR) is a process that deforms images to align them with respect to a reference space, making it easier for medical practitioners to examine various medical images in a standardized reference frame, such as having the same rotation and scale. This document introduces image registration using a simple numeric example. It provides a definition of image registration along with a space-oriented symbolic representation. This review covers various aspects of image transformations, including affine, deformable, invertible, and bidirectional transformations, as well as medical image registration algorithms such as Voxelmorph, Demons, SyN, Iterative Closest Point, and SynthMorph. It also explores atlas-based registration and multistage image registration techniques, including coarse-fine and pyramid approaches. Furthermore, this survey paper discusses medical image registration taxonomies, datasets, evaluation measures, such as correlation-based metrics, segmentation-based metrics, processing time, and model size. It also explores applications in image-guided surgery, motion tracking, and tumor diagnosis. Finally, the document addresses future research directions, including the further development of transformers.

Keywords:

Subject: Computer Science and Mathematics - Computer Vision and Graphics

1.0. Image registration etymology

1.1. Registration in Dictionaries

When a novice human reads or hears the concept of “image registration” for the first time, the word “registration” may not provide a clue about what image registration engineers do. A curious non-native English speaker may look for a hint in a dictionary such as Oxford or Cambridge, but no related senses (Table 2). In the dictionary, the word “registration” is mainly associated with an entry in an official record or list, such as the addition of a new citizen to a national register or the enrollment of a student in a course (an entry in the record of enrolled students). Similarly, the license plate on a car is called a registration number in British English (an entry in the record of licensed cars). A related sense is found in Merriam-Webster's dictionary under the word “register,” but not under the word “registration,” which defines “register” (noun) as a correct alignment.

1.2. Registration in the printing industry

In the printing industry, registration is the process of getting an image printed at the same location on the paper each time. It also means the perfect alignment of printing components (e.g., dots, lines, colors) with respect to each other. Figure 1 shows an example of printing misalignments. The misalignment in early printing machines depended on the initial settings in addition to the movement of a paper while it runs through the printing machine. Hence, marks like crosshairs were used to be printed on paper boundaries to check a popper alignment/registration (Stallings, 2010). You may have seen a crosshair like the one shown on the right of Figure 1 in some old documents. In addition to ink printing on papers, registration covered other kinds of printing such as embossing and metallic foiling.

In color printing, basic colors were printed one color after another. For example, the basic colors of the CMYK color model are cyan, magenta, yellow, and key/black, which form the acronym of CMYK. A misalignment between colors may result in overlapping replicas (Wikipedia 2023).

In summary, the concept of image registration in computer vision seems to have been influenced by the printing industry. In computer vision, it is common to call a computer image that will be aligned a “moving image” and the reference image a “fixed image”. The naming of a “moving” and a “fixed” image suit the movement of a paper in a printing process, however, it is still very common to read “moving image” and “fixed image” in computer image registration papers, despite the lack of a moving part as IR is done digitally by computer algorithms only. The sense of registration in the printing industry can be seen as a narrow case of an expanding IR arena. IR includes aligning identical images, aligning images of non-rigid objects, and aligning images of different objects and/or different dimensions (like aligning a 2D X-ray image with a 3D MRI image).

In the previous paragraphs, a connection was drawn between the concept of IR and the registration printing industry. A potential, but less obvious, connection is between IR and registration in the music industry. Registration is known to organists (musicians who play organ) as the selection of organ stops. An organ stop is a part of an organ that controls the flow of the air to certain pipes, hence basically a musician combines stops to generate sounds. What is common between organ registration and IR is that both are processes of finding a configuration for an intended outcome. That outcome is a melody in the case of organ registration and an aligned image in the case of IR. Can organ registration be considered a type of IR? Answering such questions entails a full technical definition of image registration.

2.0. Image registration definition

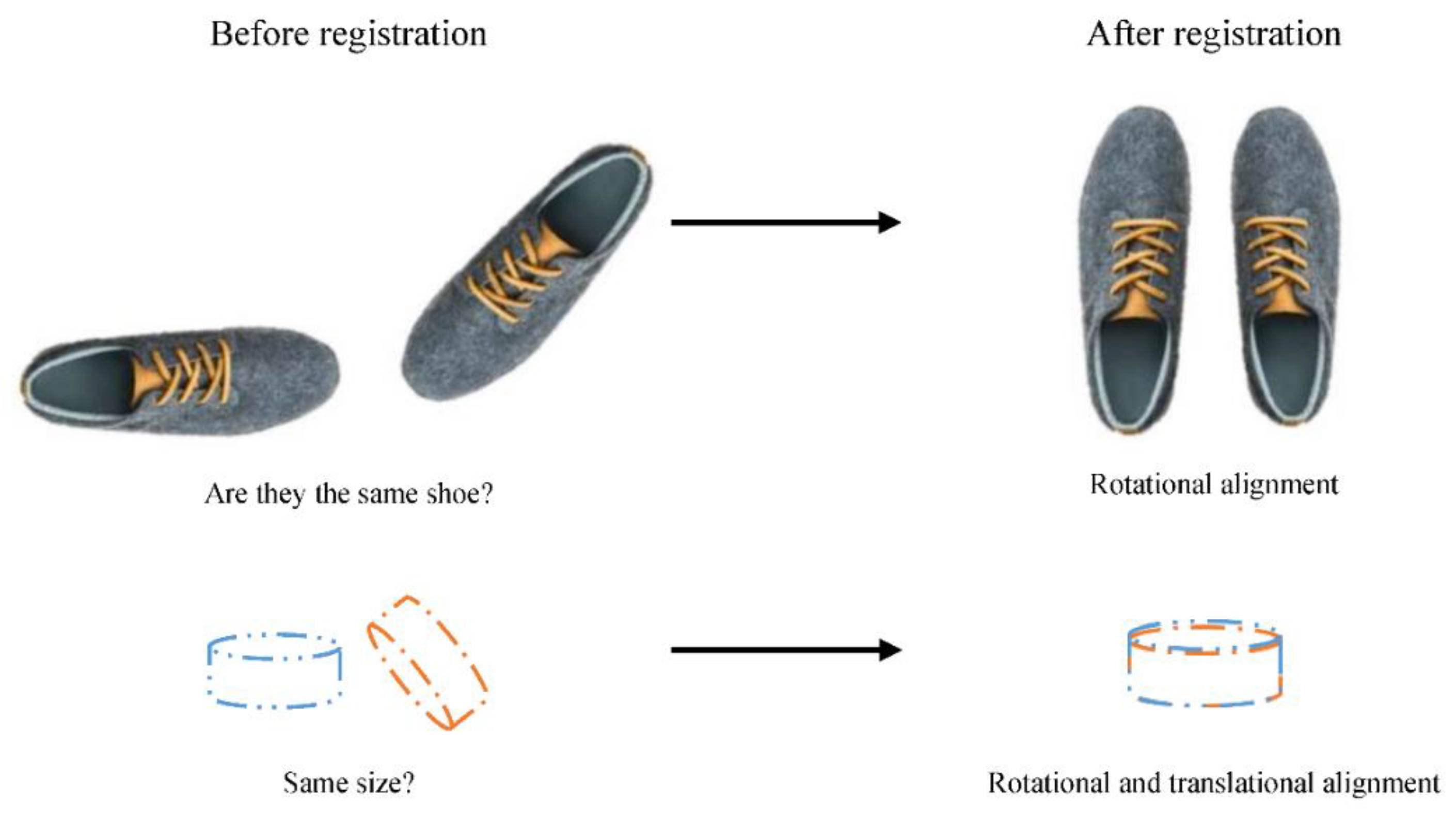
Humans align objects mentally before deciding whether two rotated objects are similar or not according to cognitive psychology (Cooper, 1975). Likewise, it is easier for medical practitioners to compare aligned medical images. To demonstrate this, a reader can compare the left side and the right side of Figure 2.

2.1. IR definitions in the literature

Image registration definitions in the literature of medical image registration can be categorized into three main definitions:

Definition 1.

Finding a transformation between two images that are related to each other such that the images are of the same object or similar objects, the same region, or similar regions (Stewart et al., 2004).

Definition 2.

The process of overlaying two or more images of the same scene taken at different times, from different viewpoints, and/or by different sensors (Zitova et al., 2003).

Definition 3.

The process of transforming different images into one coordinate system with matched content (Chen, X., Wang, et al, 2022).

Each definition imposed a constraint. The first definition limited registration to two images like the definitions in (Decuyper et al., 2021; Talwar et al., 2021; Fitzpatrick et al., 2000). The second definition limited registration to images of the “same scene” like the definition in (Abbasi et al., 2022). The third definition entailed a “coordinate system” like the definitions in (Haskins et al., 2020; Chen, X. et al 2021).

2.2. IR definition

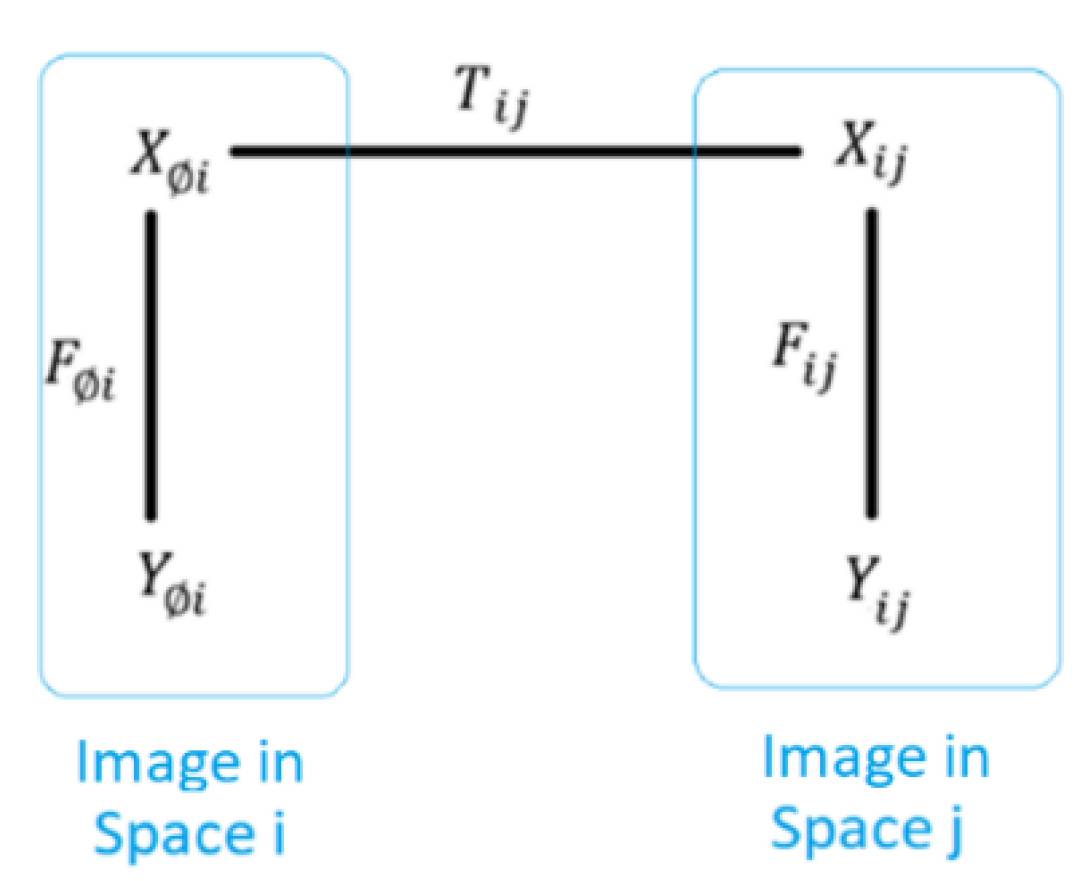
Briefly, Image registration is an alignment of images. The alignment is finding a space k (not necessarily a coordinate system) in which a correspondence relation is satisfied such that correspondent elements are in proximity. For instance, given an image

I_{\emptyset i}^{p}

= <

X_{\emptyset i}^{p}

Y_{\emptyset i}^{p}

>, and

I_{\emptyset j}^{q}

= <

X_{\emptyset j}^{q}

Y_{\emptyset j}^{q}

> with a correspondence set between them

C_{i j}^{p q}

= {(

{x e}_{\emptyset i}^{p}

{y e}_{\emptyset i}^{p}

)↔(

{x e}_{\emptyset j}^{q}

{y e}_{\emptyset j}^{q}

)}, the images p and q can be registered if there is a space k in which the correspondent points are positioned at the same location or nearby locations. That can be expressed as in Equation 1.

T i k ({x e}_{\emptyset i}^{p}, {y e}_{\emptyset i}^{p}) \approx T j k ({x e}_{\emptyset j}^{q}, {y e}_{\emptyset j}^{q}) f o r \forall c o r r e s p o n d e n c e p o i n t s \in C_{i j}^{p q}

(1)

where - (

{x e}_{\emptyset i}^{p}

{y e}_{\emptyset i}^{p}

)↔(

{x e}_{\emptyset j}^{q}

{y e}_{\emptyset j}^{q}

) are correspondent points between image p in space i, and image q in space j,

T_{i k}, T_{j k}

transformations map spaces i, and j (respectively) to space k.

An image is a representation of a function that maps a space/set X called domain to a space/set Y called co-domain. This definition may seem a generic definition that goes beyond digital graphics in the sense that a mathematical function y=x² can be considered an image under this definition, which is true. The discussion of what is an image and what is not is beyond the scope of this document. However, interested readers are referred to (Mitchel, 1984) who provided an interesting discussion based on Wittgenstein’s philosophy, in which Mitchell thinks of a family of images that includes graphical, optical, mental, and verbal images. This definition aligns with the classical concept of a digital image. A digital graphical image, which is a discrete function, can be thought of as a set of samples (e.g., recorded by a sensor) from a continuous function. That continuous function is a scene/object/manifold in the world. However, a sensor is no longer essential to acquire a digital graphical image since digital graphical images can be created virtually, using graphics tools or deep learning (GANs for example).

3.0. Introductory example

Readers who have some knowledge of image processing or modern algebra are advised to skip this section which targets novice readers. This section demonstrates an image transformation pipeline using a simple example (see Figure 3).

3.1. Image representations

Let P be a 2D digital image of 2x2 pixels in a Euclidean space as shown in Figure 4. The domain values

X_{\emptyset i}^{p}

can be represented in a set of tuples {(m, n)} where m, n are integers,

0 \leq m < 2, 0 \leq n < 2

. Explicitly

X_{\emptyset i}^{p}

= {(0,0), (0,1), (1,0), (1,1)}, where the first number in the tuple is the row and the second is the column in which a pixel is located such that counting starts from the top left corner of the image. The codomain values

Y_{\emptyset i}^{p}

is a set of 2x2 = 4 items, each item represents a color.

Y_{\emptyset i}^{p}

= {(a), (b), (c), (d)}. Colors in this example were represented as symbols for simplicity. There are multiple other ways to represent the domain/codomain values. For example, the codomain values of an RGB image consist of 3 numbers that represent the intensities of the basic colors (red, green, blue), which if mixed yield the color of the pixel.

F_{\emptyset i}^{p}

is a mapping between

X_{\emptyset i}^{p} & Y_{\emptyset i}^{p}

like how the blue lines in Figure 5 connect elements in the left rectangle (domain values) to elements in the right rectangle (co-domain values).

F_{\emptyset i}^{p}

can be represented, in some other cases, by an algebraic expression between X and Y.

3.2. Image transformation

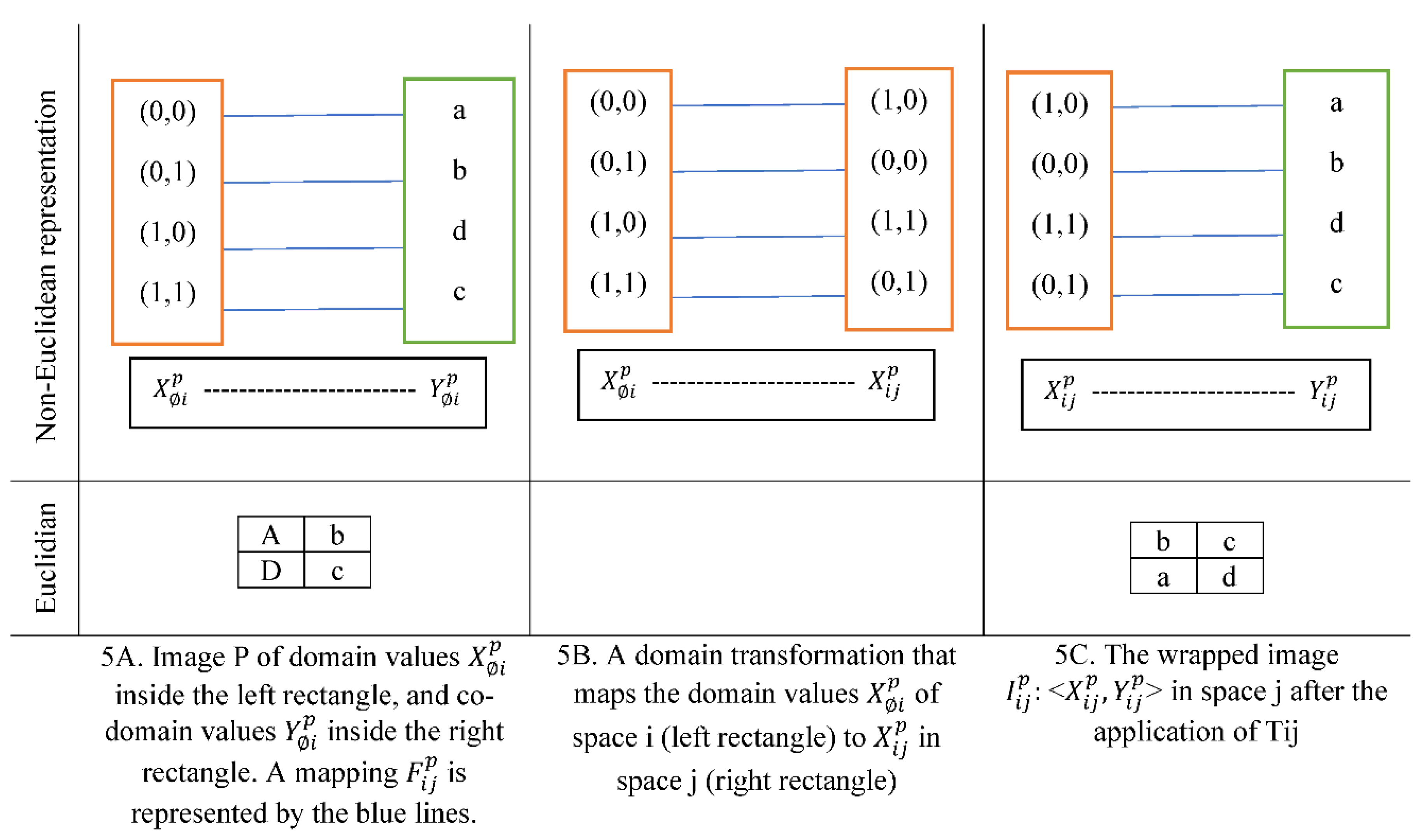
A toy example of image transformation is represented in Figure 5. T_ij is a domain transformation that relocates pixels 1 unit in a counterclockwise rotation. T_ij shown in Figure 5B replaced the domain values with new ones. For example, the domain value (0,0) in Figure 5A became (1,1) in Figure 5C.

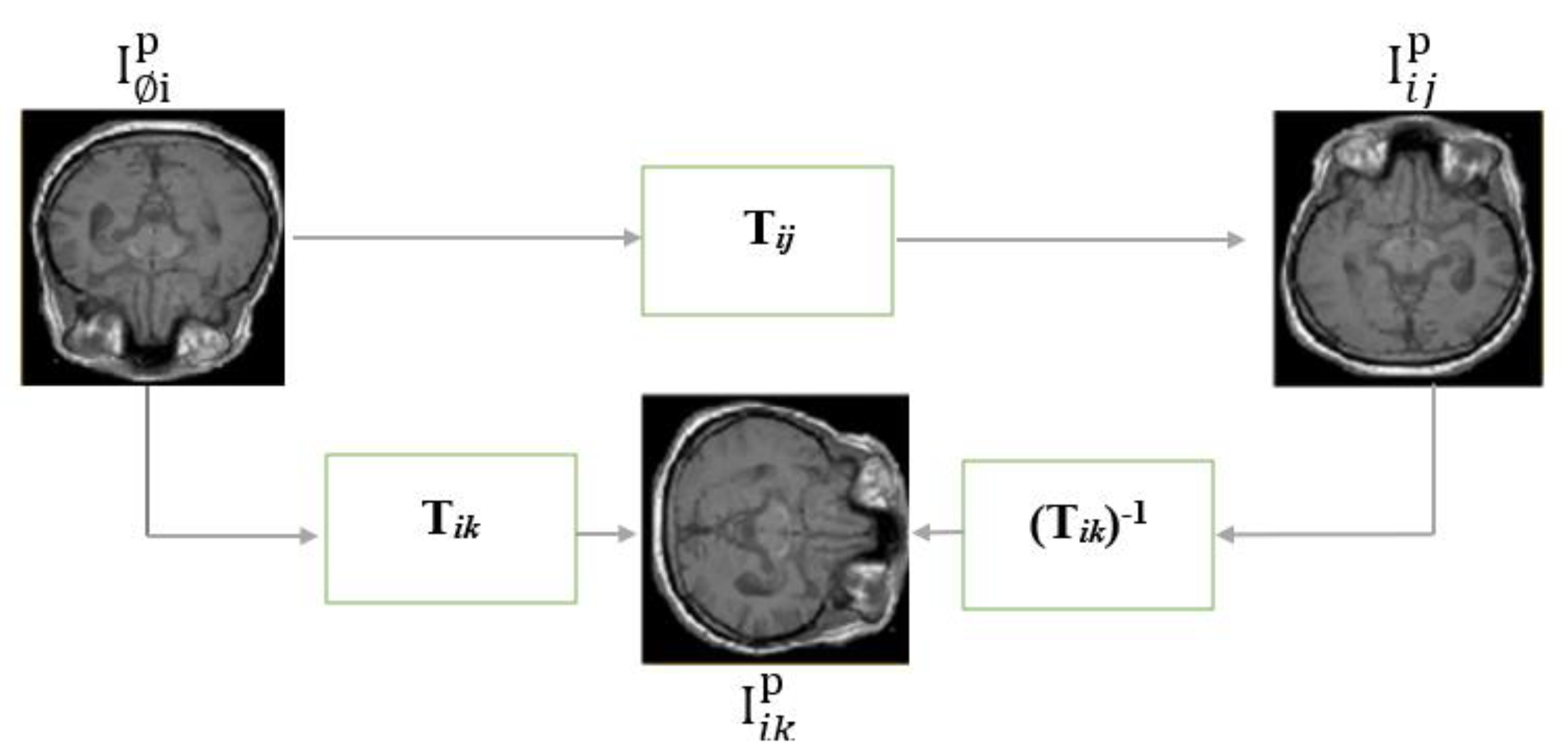
3.3.1. Image deformation using a displacement field

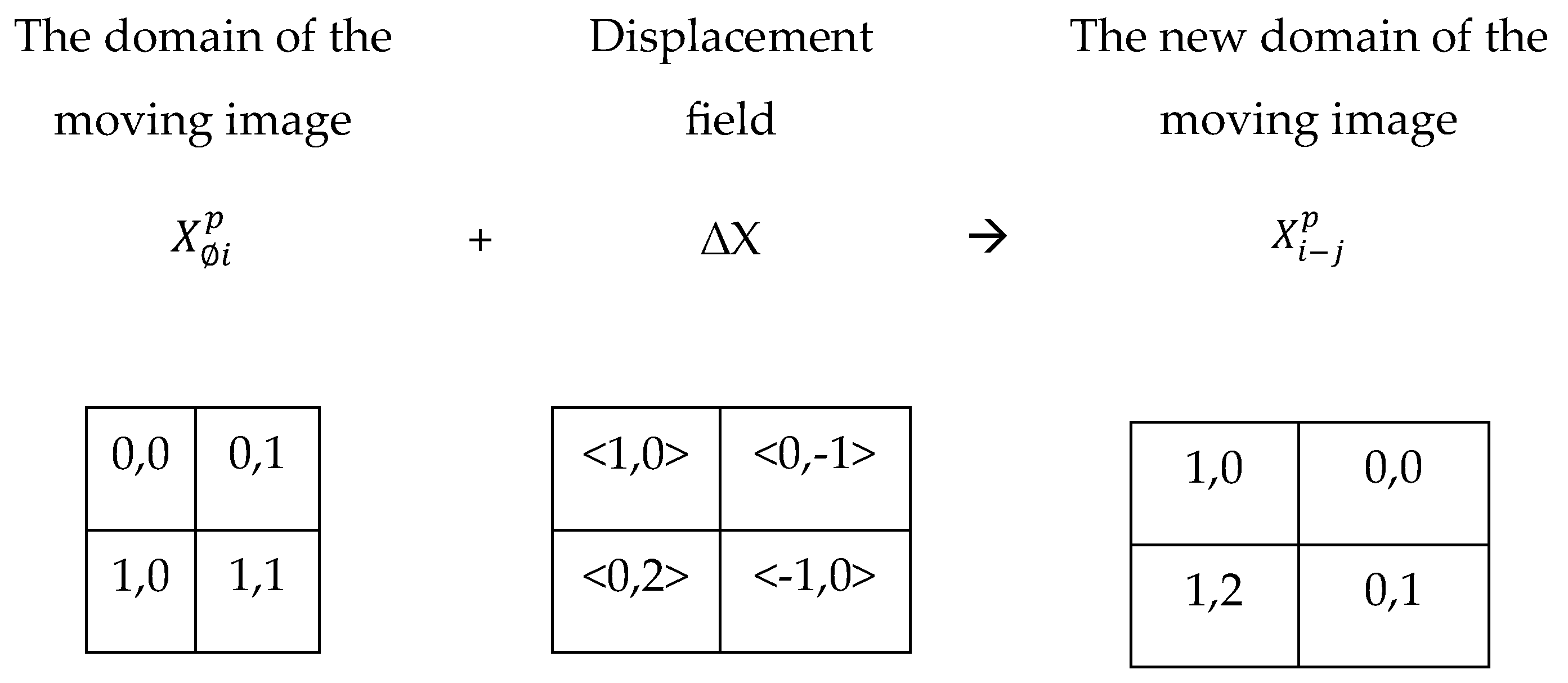
A displacement field

∆ X

represents domain relocation distances (see Equation 2), such that a 2D displacement value of <1,-1> moves a pixel 1 unit on the horizontal axis and -1 unit on the vertical axis.

X_{i - j}^{p} = T_{i - j} (X_{\emptyset i}^{p}) = X_{\emptyset i}^{p} + ∆ X

(2)

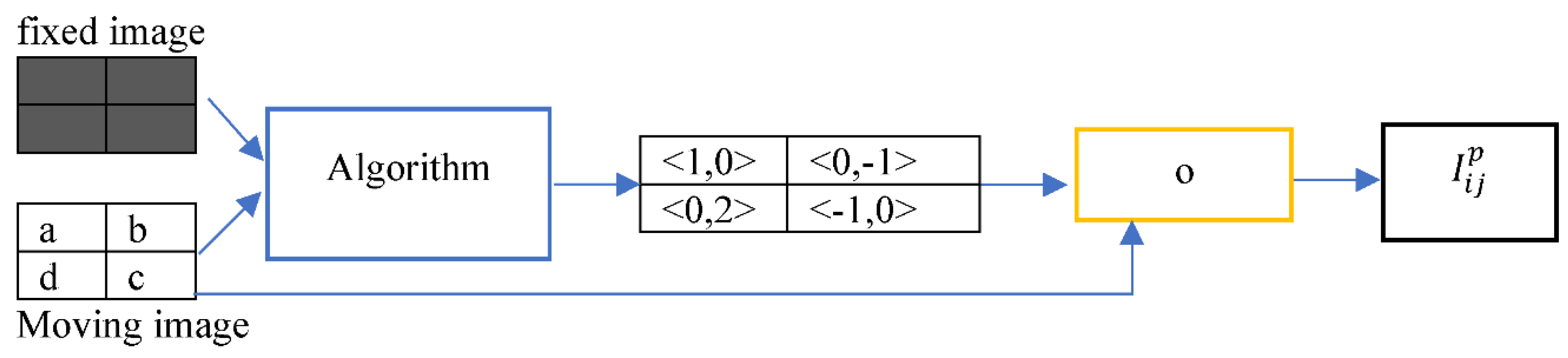
Figure 6 shows a displacement field ∆X estimated by an algorithm given a pair of fixed and moving images. The moving image

I_{\emptyset i}^{p}

= {‘0,0’: a, ‘0,1’: b, ‘1,0’: d, ‘1,1’: c}.The displacement field estimated by a registration algorithm is ∆X = {‘0,0’: <1,0>, ‘0,1’: <0,-1>, ‘1,0’: <0,2>, ‘1,1’: <-1,0>}. The goal is to obtain a transformed image

I_{i j}^{p}

by deforming the moving image

I_{\emptyset i}^{p}

The wrapping operation ‘o’ shown in Figure 6 consists of a domain deformation of a moving image followed by resampling. The replacement of the domain of the moving image

X_{\emptyset i}^{p}

by the domain of the wrapped image before any post-processing

X_{i - j}^{p}

yields a wrapped image

I_{i - j}^{p}

shown below. Figure 7 demonstrates how

X_{i - j}^{p}

was obtained by the addition of ∆X to

X_{\emptyset i}^{p}

I_{\emptyset i}^{p}

= {‘0,0’: a, ‘0,1’: b, ‘1,0’: d, ‘1,1’: c}

I_{i - j}^{p}

= {‘1,0’: a, ‘0,0’: b, ‘1,2’: d, ‘0,1’: c}

3.3. post-processing

A domain transformation may relocate pixels to locations that violate space constraints. A constraint that is commonly violated after a domain transformation of a digital graphical image is that domain values should be uniformly distributed integers. For example, a domain value of (0.3, 0.17) violates the mentioned constraint since 0.3 and 0.17 are not integers. Such violations can be fixed in a post-processing step called ‘resampling’. Resampling estimates codomain values

Y_{i j}^{p}

for post-processed domain values

X_{i j}^{p}

that don’t violate the space constraints. The selection of

X_{i j}^{p}

is known in the literature as ‘grid generation’. Resampling is done under the assumption that the post-processed image <

X_{i j}^{p}, Y_{i j}^{p}

> and the preprocessed image <

X_{i - j}^{p}, Y_{i - j}^{p}

> are discrete samples from the same function/manifold. Hence

Y_{i j}^{p}

can be interpolated based on

Y_{i - j}^{p}

. The Interpolations list includes but is not limited to linear, bilinear, and spline interpolations.

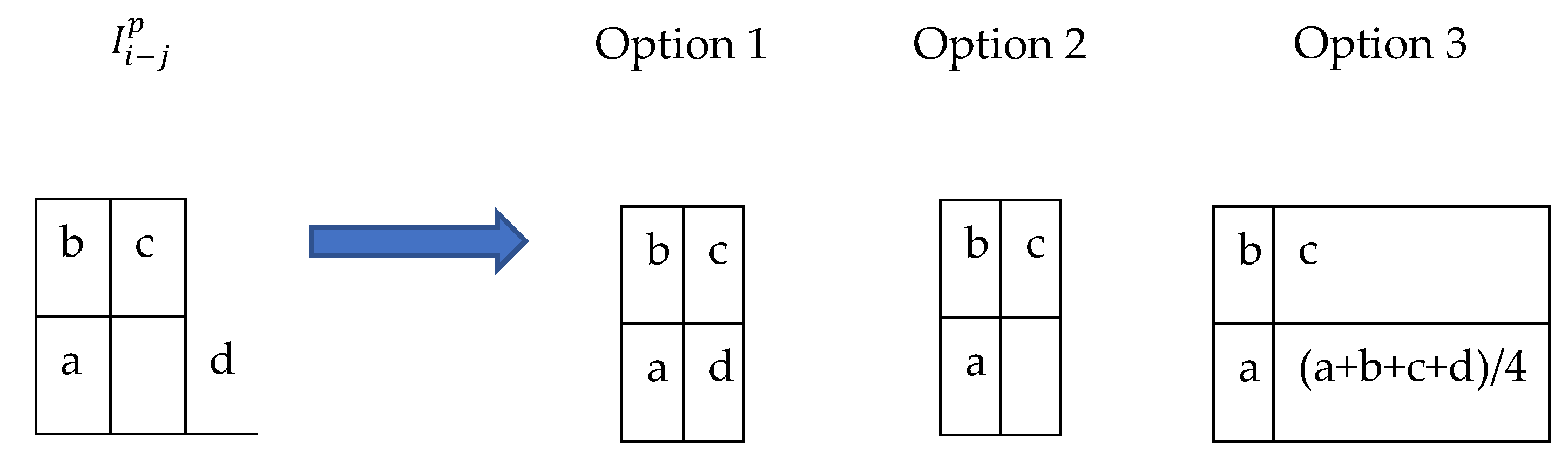
An example of post-processing is shown in Figure 8. Pixel d is out of the image boundaries. A potential fix is just to move the pixel d one step to the left to be in the empty cell at <1,1>. Another option is just to delete pixel d without filling the empty cell, another option is to fill the empty cell with the average of its surrounding pixels.

4.0. Review criterion

This work reviewed medical image registration (MIR). The list of surveyed work was collected by searching using the keywords medical image registration in the Scopus database. The search query was limited to open-access MIR papers written in English and published between 2021 and 2022. The number of retrieved records was 270, out of which 38 papers were excluded based on the abstract for their irrelevance (e.g., they are about medical images but not MIR). Other 41 papers were excluded as the authors could not find open-access versions of those papers as of December 2022. Out of 191 papers, 96 have been reviewed at the time of writing this draft in addition to 10 papers published before 2021. The research questions and sub-questions of this work are shown in Table 3. Preprints 84038 i002

Table 3. The questions of interest in this survey.

Research question	Sub-questions
What was the research pipeline of MIR in 2021 and 2022?	What were the proposed approaches of MIR?
	What were the evaluation criteria?
	What MIR datasets were used
	What were the applications/use cases of MIR?

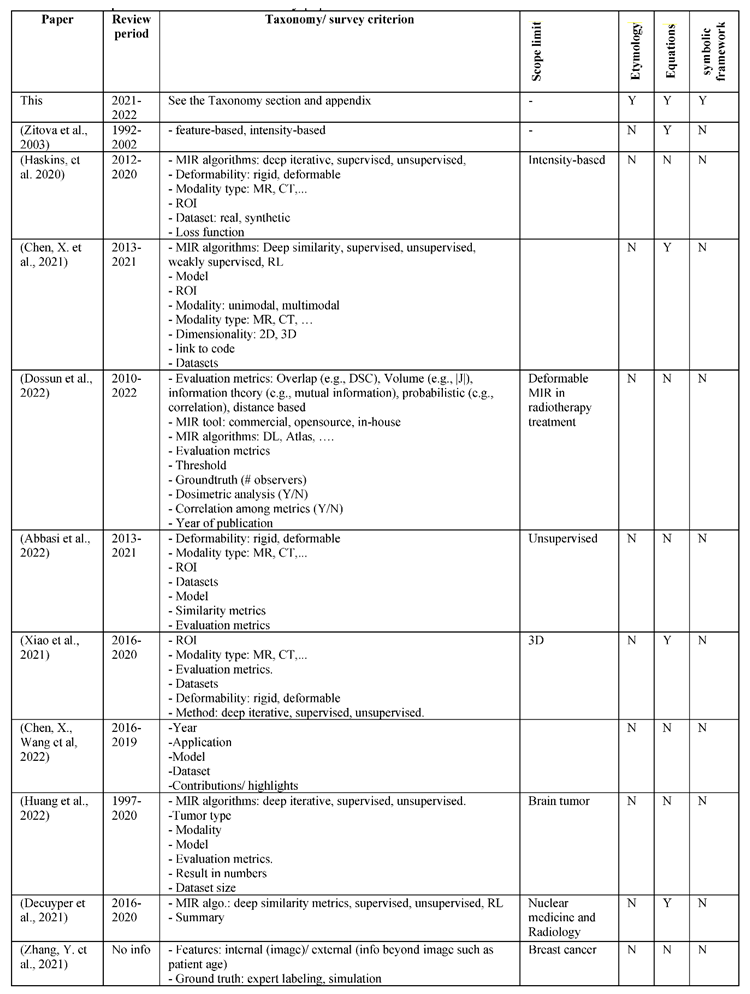
5.0. Related survey papers

Table 4 compares this work to related survey papers that appeared in the search query in section 6. Two highly cited review papers (Zitova et al., 2003; Haskins et al., 2020) were added to the table although they were published before 2021.

It could be in the interest of novice readers to read about the evolvement of IR concept and its etymology (see section 1) in addition to a simple numeric example that demonstrates the basics of IR (see section 3) since no review paper was found that addresses these parts to the best of the authors’ knowledge. Advanced users could be interested in the novel constraint-based analyses of IR introduced in the previous sections. Different from other survey papers shown in Table 4 which were mainly descriptive with no or just a few equations, this survey introduced a symbolic framework of the IR components (see the nomenclature) that has been used to express tens of equations.

Zitova et al. (2003) structured their paper based on the classical IR pipeline starting with feature detection, followed by feature matching, mapping function, image transformation, and resampling.

Haskins, et al. (2020) tracked the development of MIR algorithms covering 1) deep iterative methods that are based on similarity estimation, 2) supervised transformation estimation which entails ground truth labels that are not easily affordable, and 3) unsupervised transformation estimation methods which overcome the challenge of ground truth labels. Finally, 4) weakly supervised approaches were discussed.

Chen, X. et al. (2021) first provided a framework for image registration. Then explained the basic units of DL and reviewed DL methods such as deep similarity, supervised, unsupervised, weakly supervised, and RL. The authors discussed the challenges of MIR: 1) different preprocessing steps lead to different results, 2) a few studies quantify the uncertainty of predicted registration, and 3) limited data (small scale). Finally, possible research directions were highlighted: 1) hybrid models (classical methods and deep learning), and 2) Boosting MIR performance with priors.

Table 4. Comparison of related MIR survey papers.

Dossun et al. (2022) reviewed the performance of deformable IR in radiotherapy treatments in real patients. First, the scope of the paper and the paper selection process were explained. Then a taxonomy of MIR evaluation metrics was mentioned but no explanation or formula was provided. A table of 7 pages compared the surveyed papers. Then, statistics and figures summarized the results showing, for example, that the distribution of the ROIs was 36% for the prostate, 33% for the head and neck, and 26% for the thorax. Another figure showed the most frequent evaluation metrics ordered as the following: DSC > HD > TRE.

Abbasi et al. (2022) reviewed the evaluation metrics of unsupervised MIR in a sample of 55 papers. The statistics showed that: 1) the majority of papers were handling unimodal registration (82%), 2) a private dataset was more likely to be used than a publicly available dataset, 3) most papers worked with MR images (61%), and 4) the most researched ROI was the brain at 44%, then the heart at 15%.

Xiao et al. (2021) started with a brief introduction to deep learning, then provided a statistical analysis of a selected sample of 3D MIR papers that covered the distribution of ROI (Brain 40%, lung: 24%), modality (MR-MR: 46%, CT-CT: 24%), MIR methods: (unsupervised: 43%, supervised: 40%, deep iterative: 19%), and evaluation metrics (74% label based, 18% deformation based, 12% image-based). The MIR methods were reviewed based on the taxonomy (deep iterative methods, supervised, and unsupervised).

Chen, X., Wang, et al. (2022) reviewed medical image analysis covering four areas: image classification, detection, segmentation, and registration. First, the paper gave an overview of deep learning and its methods: supervised, unsupervised, and semi-supervised. Then it addressed ideas of DL that were shown to improve the outcomes: attention, involvement of domain knowledge, and uncertainty estimation. Then the paper briefly reviewed classification, detection, segmentation, and registration. Finally, the paper highlighted ideas for future improvement that included the idea of a fully end-to-end deep learning model for MIR. In addition to the incorporation of domain knowledge. They also highlighted important points for large-scale applications of deep learning in clinical settings such as having large datasets publicly available as well as producible codes. They also highlighted the need for more clinical-based evaluation and the involvement of domain experts from the medical field in the evaluation rather than limiting the evaluation to theoretical evaluation metrics.

Huang et al. (2022) reviewed AI applications in brain tumor imaging from a medical practitioner’s perspective. They pointed out the lack and the need for studies about the use of AI tools in routine clinical practice to characterize the validity and utility of the developed AI tools.

Zhang, Y. et al. (2021) elaborated on AI registration success, and highlighted challenges 1) the lack of large databases with precise annotation, 2) the need for guidance from medical experts in some cases, 3) having different opinions of experts in the case of some ambiguous images. 4) excluding non-imaging data of the patient, like age, and medical history, and 5) the interpretability of AI models.

Decuyper et al. (2021) started with an explanation of DL components covering neural network layers (CNNs, activations, normalization, pooling, and dropout), and DL architecture (e.g., Resnet, GANs, U-Net). Then the paper explained medical image acquisition and reconstruction. After a brief elaboration on IR categories, the paper elaborated on their challenges: 1) traditional iterative methods work well with unimodal images but poorly with multimodal images, or in the presence of noise, 2) deep iterative methods imply non-convex optimization that is difficult to converge, 3) In RL, deformable transformation results in a high dimensional space of possible actions, which makes it computationally difficult to train RL agents. Most previous works dealt with rigid transformation (low dimensional search space), 4) supervised learning approaches need ground-truth labels, and 5) unsupervised approaches face difficulty in back-propagating the gradients due to the multiple different steps. Finally, specific application areas were reviewed: chest pathology, breast cancer, cardiovascular diseases, abdominal diseases, neurological diseases, and whole-body imaging.

6.0. Taxonomies

A registration algorithm consists of a set of assumptions (prior knowledge), and a margin of uncertainty (the unknown part), which is expressed using variables (e.g., model parameters). For example, if a programmer knows exactly how to register any images in a similar way to having a formula that finds the roots of any quadratic equation, then s/he will just embed that prior knowledge (the formulae) in the code. However, there is no such a generic formula yet for most IR cases. Accordingly, variables are made and adjusted using an optimization method.

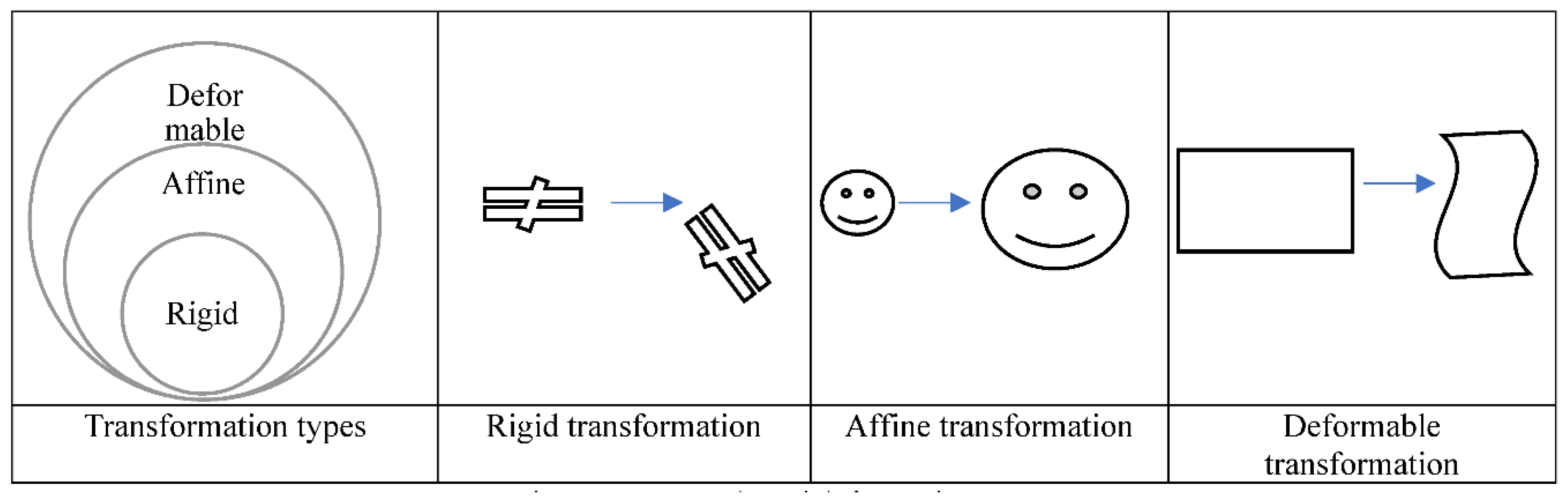
6.1. Deformation types

Transformation functions in MIR can be categorized based on their deformability into rigid, affine, and deformable transformations as shown in Figure 9.

In physics, the shape and size of a rigid body do not change under force. When you push a small solid steel bar, the location and/or the orientation of the bar may change, but the bar itself remains the same (e.g., the same mass, shape, and size). Likewise, a rigid transformation preserves the distances between every pair of points. Accordingly, rotations and translations are rigid transformations or proper rigid transformations in the distinction of reflections which are called improper rigid transformations as they do not preserve the handedness.

A rigid transformation T_ij preserves the distances between any two points on the object of interest, such that the constraint

||{x k}_{\emptyset i}^{p} - {x l}_{\emptyset i}^{p}|| = ||{x k}_{i j}^{p} - {x l}_{i j}^{p}||

holds for every pair of points k, l ∈ the set Mp. A rigid transformation can be expressed as in Equation 6.

v^{~} = T_{i j} (v) = A v + b

(6)

where v^~ is a newly transformed vector after the application of a rigid transformation to a vector v, which could be a position of a point in Euclidian space. b is a translation vector, and A is an orthogonal transformation (see the appendix for definition) such as orientation.

A rigid transformation is a subcategory of a bigger group of transformations called Affine transformations. Affine transformations preserve parallelism and lines, but no constraints on the preservation of distances. Thus, it can be expressed as in Equation 6 above used earlier for rigid transformation except that A is a linear transformation/matrix with no orthogonality constraint. In an affine registration, the transformation T_ij imposes the constraint

T_{i j} ({x k}_{\emptyset i}^{p} - {x l}_{\emptyset i}^{p}) = T_{i j} ({x k}_{\emptyset i}^{p}) - T_{i j} ({x l}_{\emptyset i}^{p}) = {x k}_{i j}^{p} - {x l}_{i j}^{p}

for every point k, l ∈ the set M_p. Scaling and shear mapping are examples of an affine, but not rigid, transformation.

The formula of a 2D proper rigid transformation (rotation and translation) is shown in Equation 7. The variables are the rotation angle θ, the translation on the x-axis

b x

, and the translation on the y-axis

b y

v^{~} = [\begin{matrix} c o s (θ) & - s i n (θ) \\ s i n (θ) & c o s (θ) \end{matrix}] v + [\begin{matrix} b x \\ b y \end{matrix}]

(7)

The formula of a proper rigid transformation in a 3D space consists of 6 unknown variables: 3 rotation angles (

θ x, θ y, θ z

), and 3 translations (bx, by, bz) as shown in Equation 8, where the subscriptions x, y, z are 3 perpendicular coordinates.

v^{~} = [\begin{matrix} 1 & 0 & 0 \\ 0 & c o s (θ x) & - s i n (θ x) \\ 0 & s i n (θ x) & c o s (θ x) \end{matrix}] [\begin{matrix} c o s (θ y) & 0 & s i n (θ y) \\ 0 & 1 & 0 \\ - s i n (θ y) & 0 & c o s (θ y) \end{matrix}] [\begin{matrix} c o s (θ z) & - s i n (θ z) & 0 \\ s i n (θ z) & c o s (θ z) & 0 \\ 0 & 0 & 1 \end{matrix}] v + [\begin{matrix} \begin{matrix} b x \\ b y \end{matrix} \\ b z \end{matrix}]

(8)

Transformations that do not preserve the rigidity or affinity constraints are called deformable transformations.

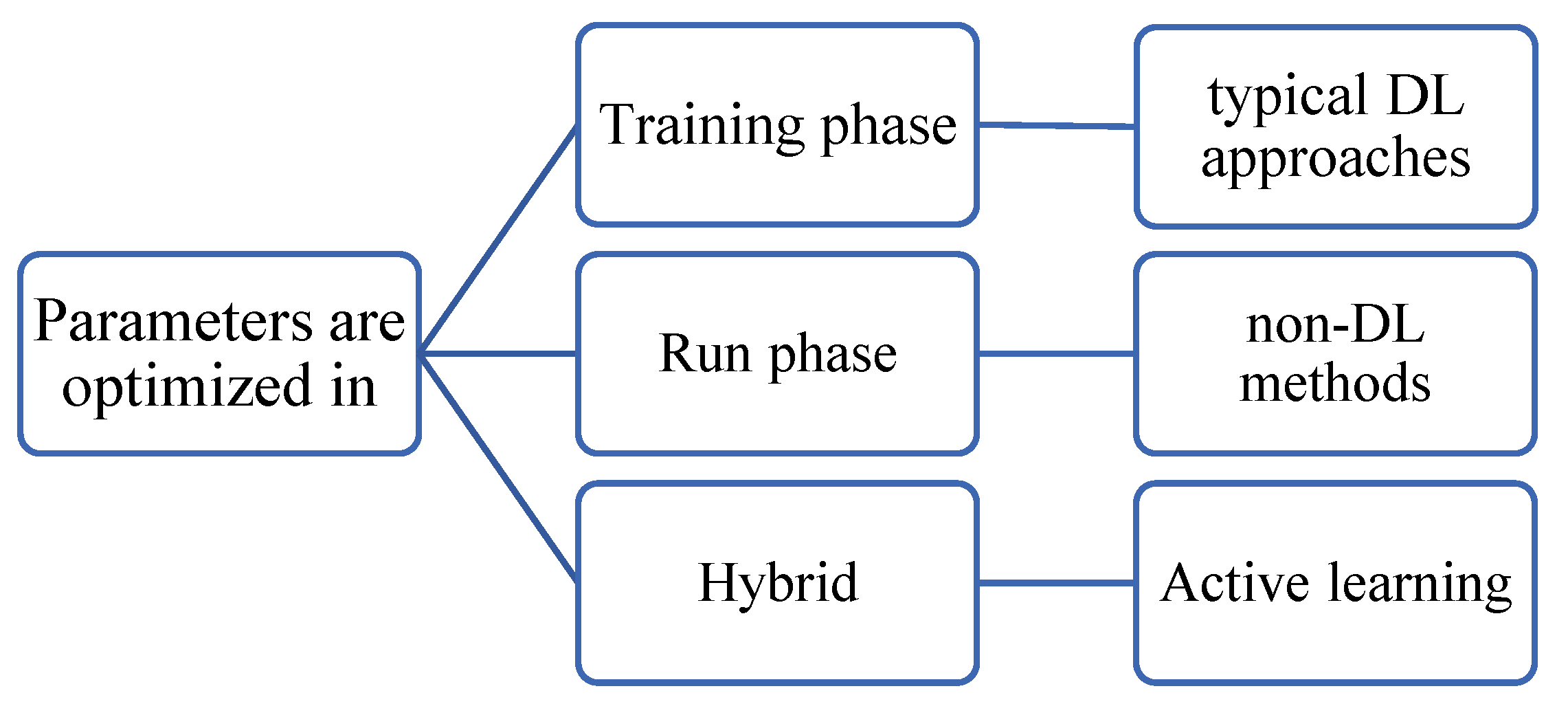
6.2. Optimization phase

Image registration entails an optimization step in which a model’s parameters are adjusted to minimize/maximize an objective function. Optimization can occur, as shown in Figure 10, 1) during the development phase as in DL approaches, or 2) during the running phase such as in iterative methods, or 3) in both e.g., active learning approaches, or a test-time training as called in (Zhu et al., 2021). The objective function of MIR is expressed in Equation 9 as a weighted sum of two components: the first quantifies the registration error that represents the proximity between the predicted registration and the correct one, and the second is a regularization component.

Loss = registration_error + regularization

(9)

The optimization methods such as gradient descent, evolutionary algorithms, and search are iterative. Hence the optimization step adds a time overhead to the phase in which it takes place. Thus, DL approaches take a long training time, but shorter registration time.

Approaches that run optimization in both phases aim at further improving the registration despite a slight increase in the computation time. To reduce the run-time overhead, the bulk optimization of the model parameters occurs in the training phase while just slight finetuning occurs during the run phase to customize the results (Zhu et al., 2021).

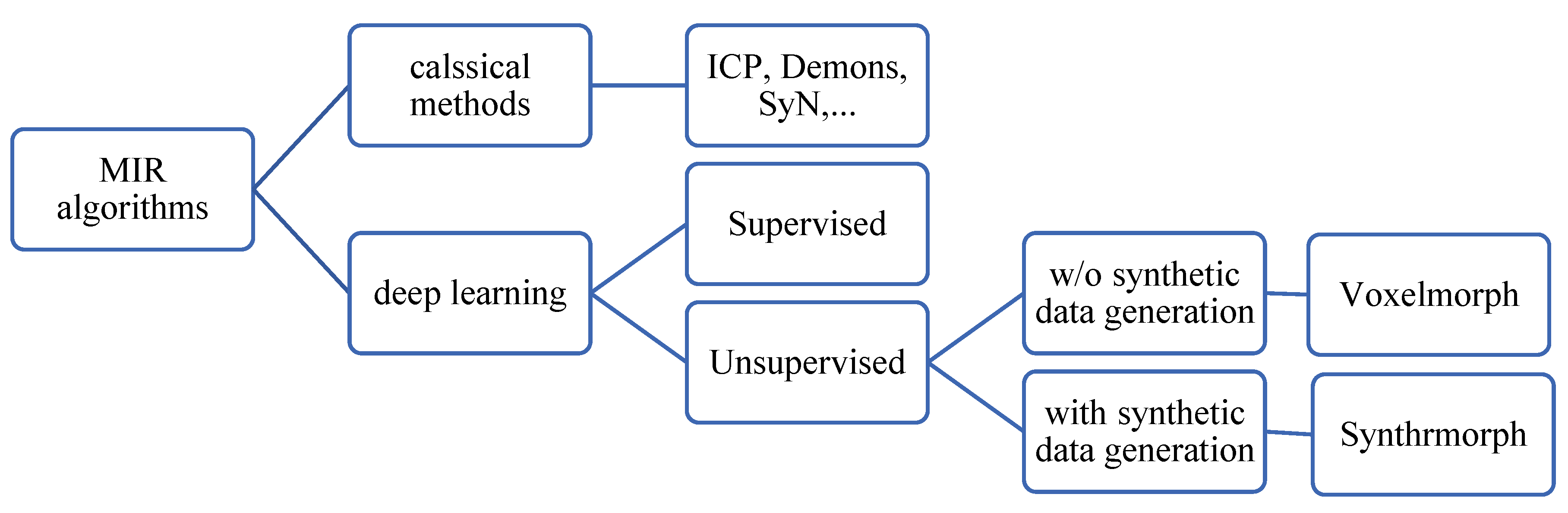
6.3. MIR algorithms

This section discusses selected registration algorithms. Mainly the algorithms that were used as baselines against which the performance of a new algorithm is compared. A taxonomy of MIR algorithms is shown in Figure 11.

6.3.1. Deep learning approaches

Deep learning approaches use multiple layers of neural networks. Neural networks can estimate the transformation function in the registration problem entirely using unknown variables (called neurons). Hence, the transformation function in this case is considered an implicit function in distinction with explicit transformation functions which assumes a tractable formula of the transformation functions such as rigid transformations shown in Equations 6-8. DL approaches were also called earlier “non-parametric methods”.

directly supervised deep learning approaches.

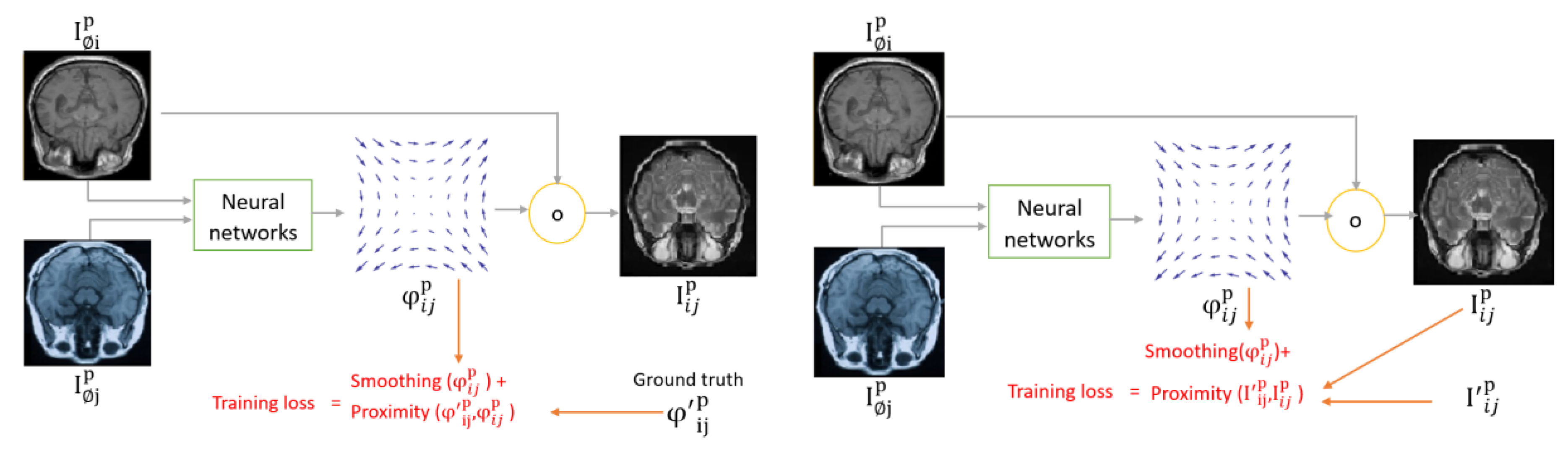
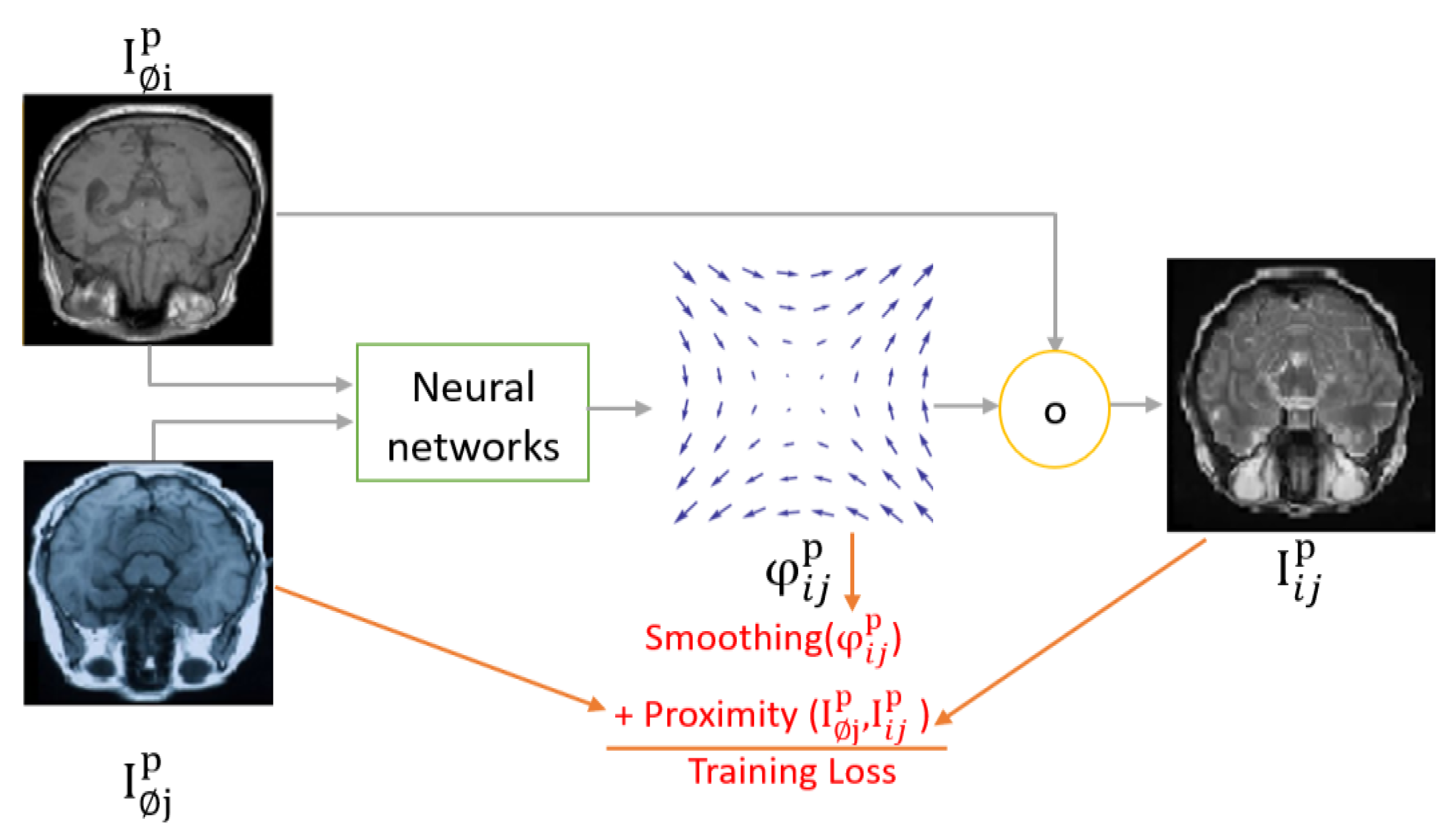
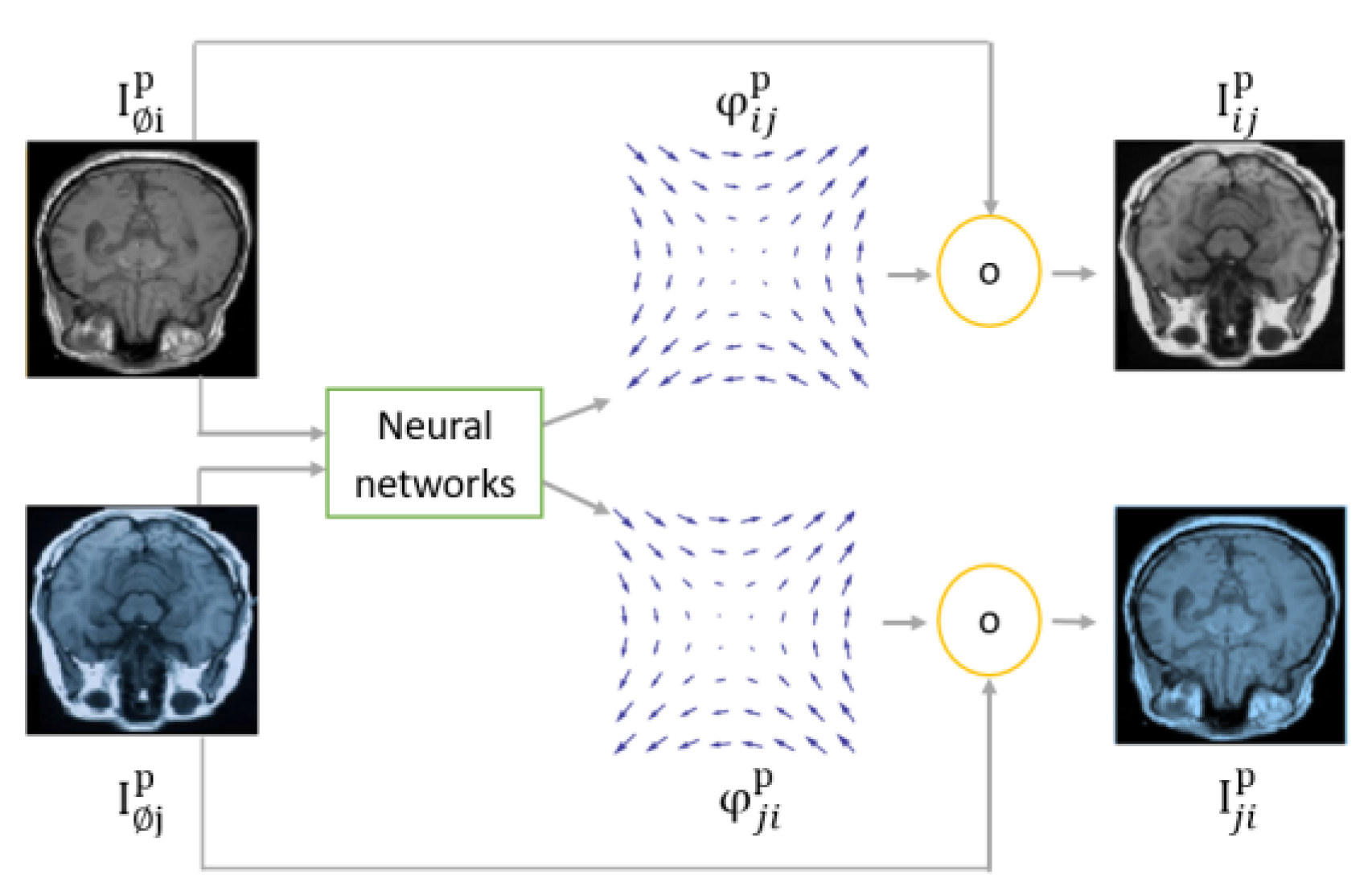
The diagram of directly supervised image registration approaches is shown in Figure 12. Initially, input images are fed to neural networks which produce a registration field. The registration field is applied to the fixed image to relocate its pixels in a process called spatial transformation represented as a yellow circle in the figures below.

The main question is how neural networks learn to estimate the registration field. In the directly supervised approach, A ground truth label is provided during the training phase. The ground truth label could be the registration field as shown in Figure 12 (left), or the wrapped image as shown in Figure 12 (right). A challenge of directly supervised MIR approaches is their need for ground truth labels, which entails medical experts annotating a large number of images. To overcome ground truth labels, unsupervised MIR has been proposed.

b. Unsupervised deep learning approach: Voxelmorph

Unsupervised MIR approaches do not entail an external supervision signal. Instead, the fixed image (input) was assumed to replace the ground truth label of the registered image

< {X_{i j}^{p}}^{'}, {Y_{i j}^{p}}^{'} > \approx < X_{\emptyset j}^{p}, Y_{\emptyset j}^{p} >

as in Voxelmorph (Balakrishnan et el., 2019). This assumption is useful when the fixed image and the moving image have similar modalities/co-domains. However, the assumption may not work well if the fixed image and the registered image are of different modalities (e.g., one is 3D MRI, and the other is 2D X-ray) unless a way is developed to bridge the gap between the two modalities. This has been reported by the results shown in Synthmorph (Hoffmann et al., 2021). Even for images of the same modality, co-domain dissimilarities can be a problem with this approach. For example, if the contrast of the fixed image is different than that of the moving image, then the mean square error MSE(

Y_{\emptyset j}^{p}

Y_{i j}^{p}

) may not represent the error adequately. However, another loss function like cross-correlation “CC” is more resilient against the contrast problem than MSE due to its scale invariance property. CC (Y1, Y2) = CC (Y1, α

\times

Y2) where α is a scale number.

MIR using Voxelmorph yielded results much faster than non-deep learning MIR methods without degradation of the registration quality. Voxelmorph cut the registration runtime to minutes/seconds compared to hours needed by non-deep learning methods used before Voxelmorph. Voxelmorph superseded non-deep learning methods when segmentation labels were added to the registration.

c. Unsupervised approach with synthetic data: Synthrmorph

If it is difficult to get ground-truth labels, why not generate them? Synthmorph (Hoffmann et al., 2021) proposed training Voxelmorph on synthetic data (randomly generated fixed and moving images). Synthmorph generated images in two steps, first segmentation labels were generated randomly, then fixed, and moving images were generated given the segmentation label. The results yielded by Synthrmorph were superior to classical methods even when the images were of different modalities.

6.3.2. non-deep learning methods:

MIR methods that do not involve deep neural networks are called ‘non-deep learning methods’, ‘classical methods’, or ‘iterative methods.’

Iterative Closest Point (ICP)

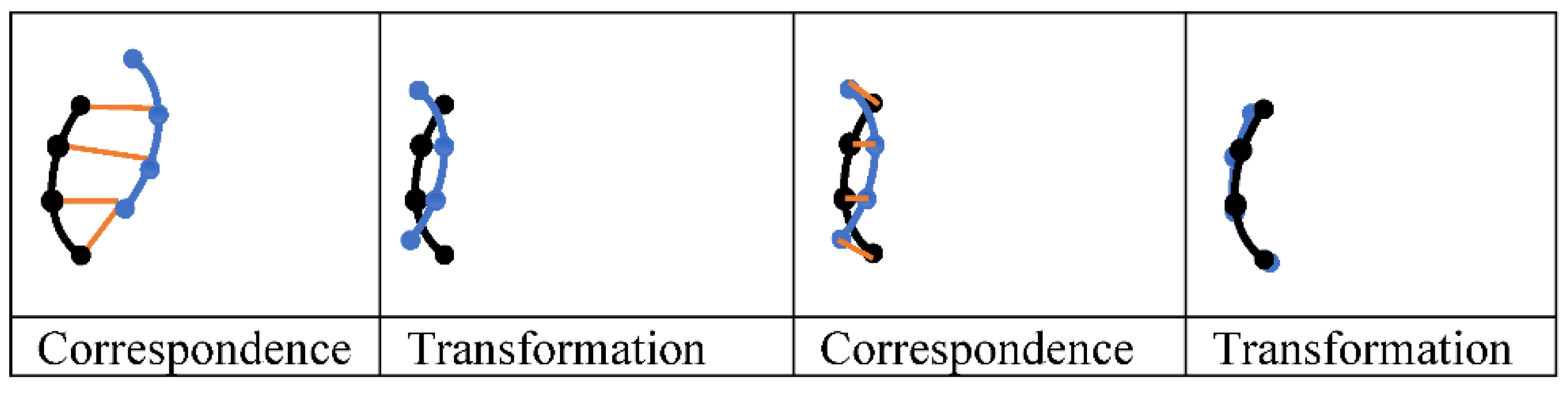
ICP (Arun, 1987; Estépar, 2004; Bouaziz, 2013) alternates between two goals: the establishment of a correspondence

C_{i j}^{p q}

, and finding a transformation

T_{i j}

that optimizes a loss function. A loss function quantifies the quality of a registration (see section 7). A demonstration of the ICP process is shown in Figure 13. Let the moving image be a blue line of 4 marked points, and the fixed image a similar black line. The loss function can be a point-wise Euclidean distance. First, 1) a correspondence is established between the points on each line such that each point is matched with its closest neighboring point. Notice that the correspondence is not 1-to-1 as the two bottom black points are matched with the same point, and the top blue point is not matched, 2) the blue line was translated to minimize the distance between the two lines, 3) another correspondence was found (1-to-1 correspondence this time), and 4) the black line was transformed (rotation and translation) based on the new correspondence.

ICP, like other iterative approaches, takes longer registration time than DL approaches. The establishment of a correspondence between nearest neighbors is straightforward but not always optimal and it sticks in local optima.

b. Demons

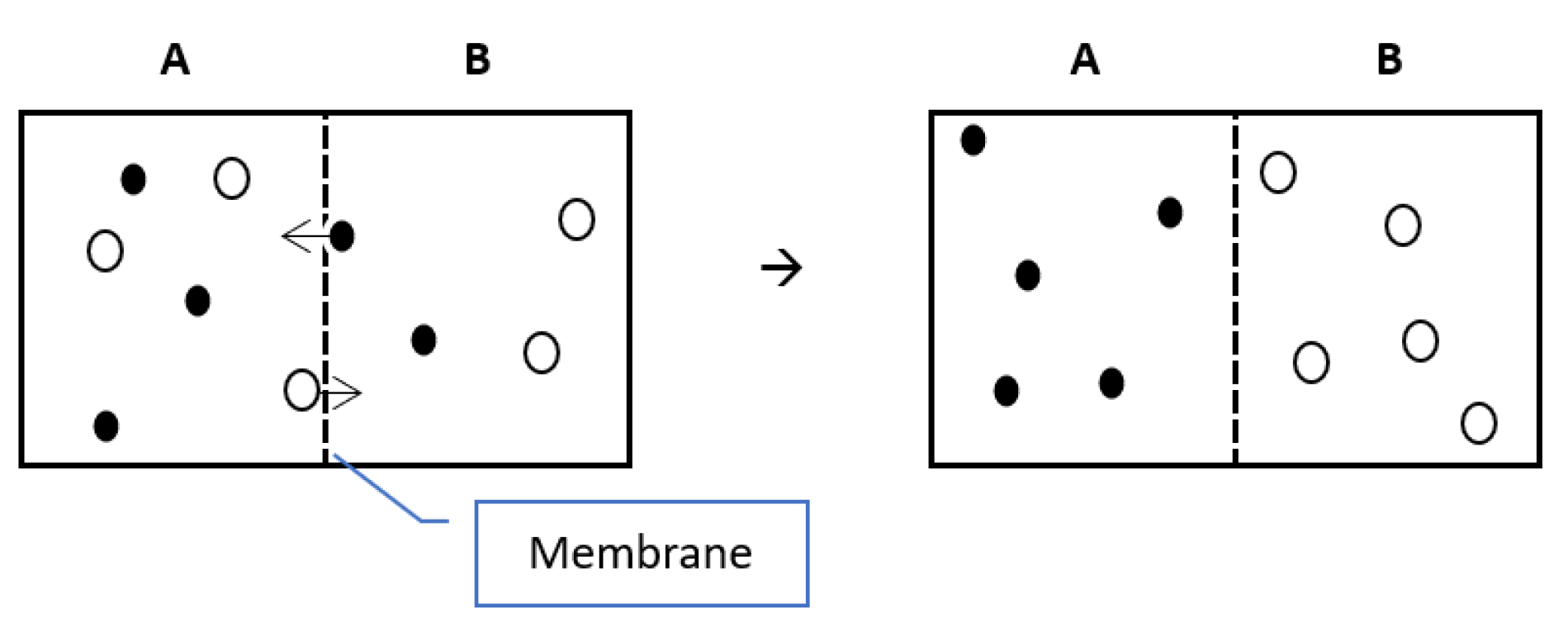
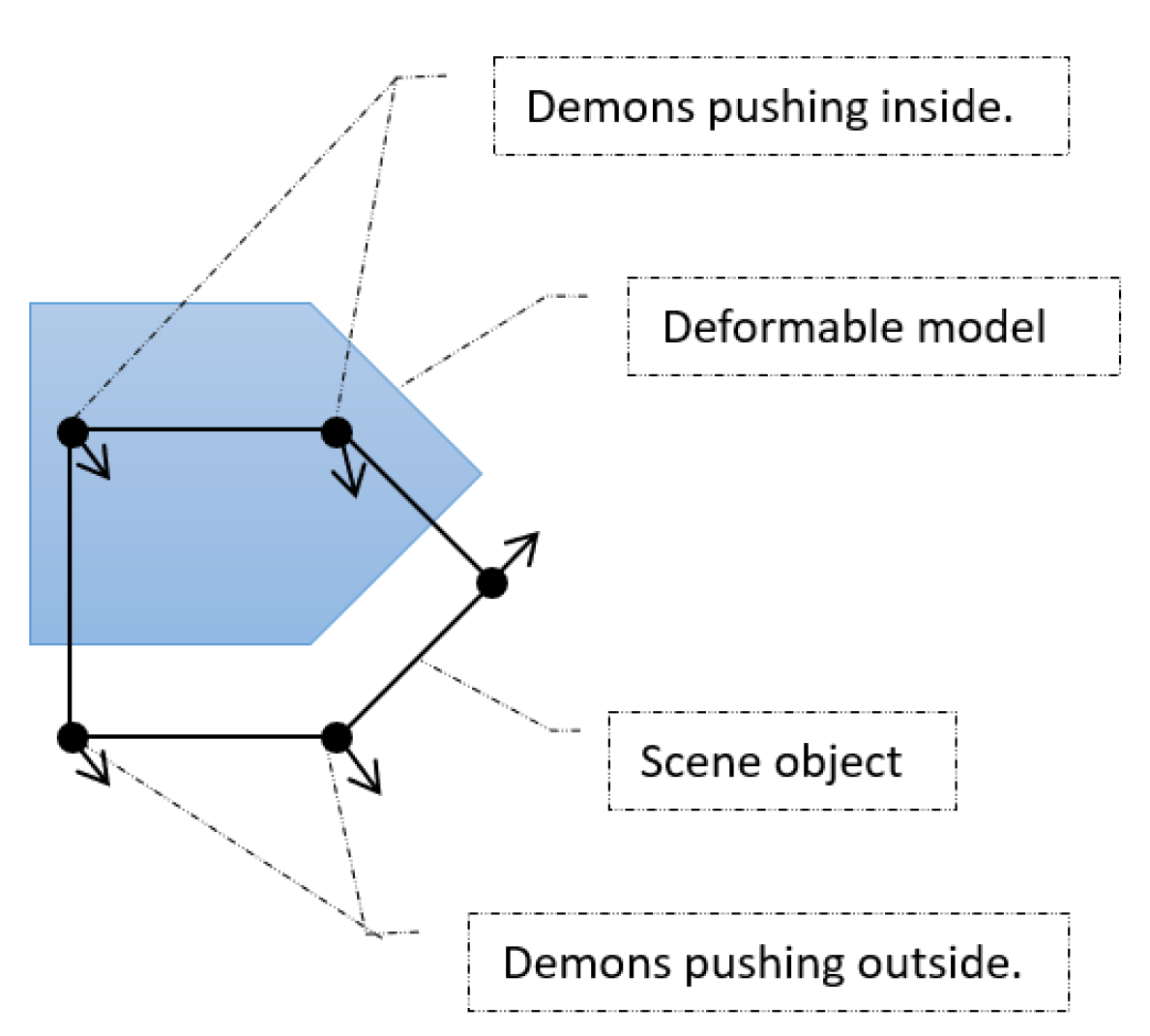
A deformable IR approach was proposed by Thirion (1996). The name of the Demons approach was influenced by Maxwell’s Demons paradox in Thermodynamics. Maxwell assumed a membrane that allows particles of type A to pass in one direction, while particles of type B can pass in the opposite direction, which will end up having all particles of type A on one side of the membrane and particles of type B on the other side as shown in Figure 15. That state of organized particles corresponds to a decrease in entropy, which contradicts the second law of thermodynamics. The solution to that paradox was that the demons generate entropy to organize the particles resulting in a greater total entropy than that was before the separation of the particles.

Influenced by Maxwell’s demons, Thirion suggested distributing particles (demons) on the boundaries of an object (see Figure 16) such that a demon will push locally either inside or outside the object based on a prediction of a binary classifier. It has been shown that what Thirion’s demons do is object matching using optical flow.

c. Symmetric Image normalization (SyN)

The main idea of SyN is to assume a symmetric and invertible transformation. Instead of transforming space i to j, SyN symmetrically transforms both space i & space j to an intermediate space such that

T_{j k} = T_{i k}^{- 1}

. In this case

T_{i k}

can be seen as half a step forward towards space j, and

T_{j k}

is half a step backward towards i (see Figure 17). The symmetric invertibility constraint of SyN can be expressed as in Equation 10

\exists k \in s p a c e : T_{i j} (I_{i}) = T_{k j} ((T_{i k} (I_{i})), w h e r e T_{k j} = T_{i k}^{- 1}

(10)

SyN was shown to supersede Demons in providing correlated results with human experts (Avants et al., 2008).

d. Registration software tools.

NiftyReg is a publicly available software for image registration. The software was developed initially by University College London and then King’s College London. The software uses two methods: 1) Reg Aladin, which is a block matching algorithm for global registration based on Ourselin et. al. (2001). 2) RegF3D (fast free form deformation) based on Modat et al (2010).

Advance Normalization Tools (ANT) is another stable software for MIR and statistical analysis. ANT yields stable results such that the registration does not change every time the software is run (Avants et al., 2014). A Python version of NiftyReg and ANTs was wrapped in a package called Nipype (Neuroimaging in Python pipelines & interfaces).

ANTs on Github: https://github.com/ANTsX/ANTs

Chen, T. et al., (2002) compared three registration tools: SPM12, FSL, and AFNI. SPM12 was recommended for novice users in the area of medical image analysis. It provided stable outcome images of “maximum contrast information” needed for tumor diagnosis. AFNI was recommended for advanced users and researchers due to the advanced capabilities needed for tasks such as volume estimation. FSL was considered for mid-level users.

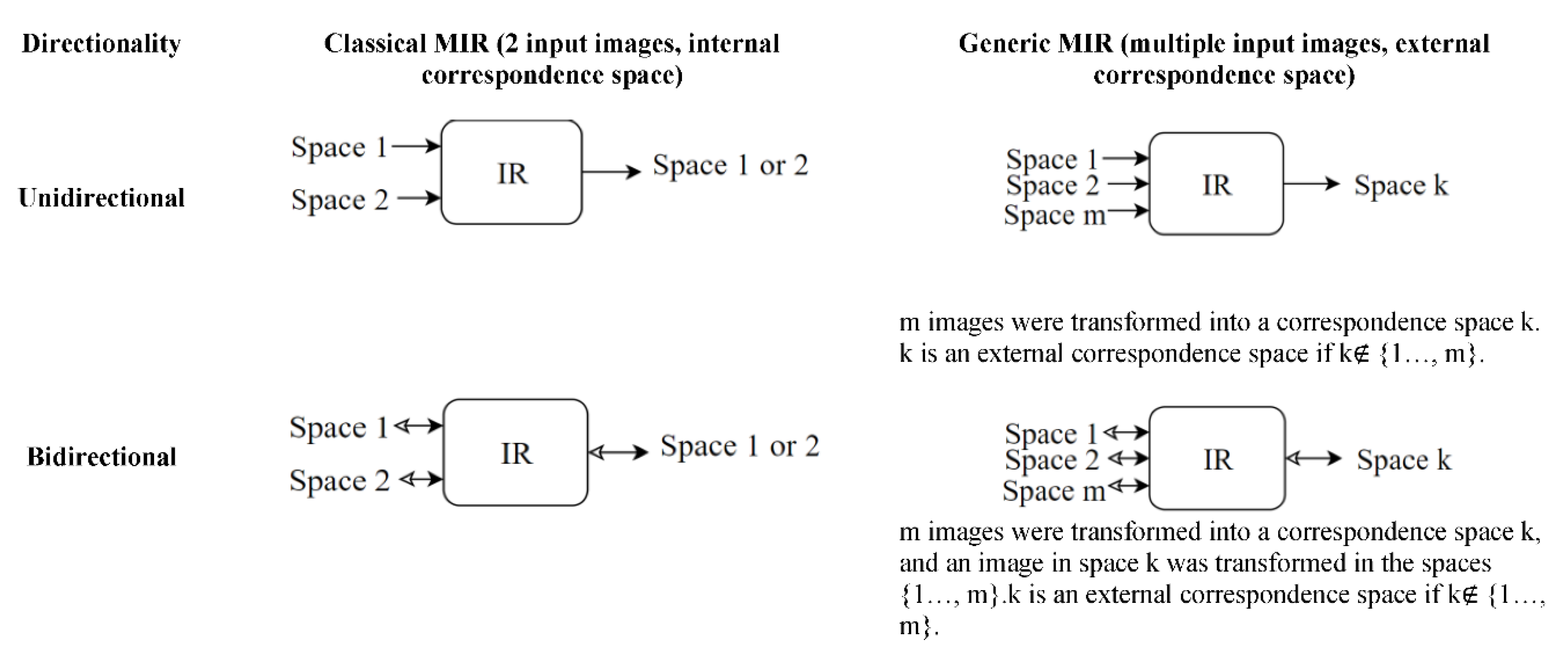
6.4. Correspondence space

MIR alignment occurs in a correspondence space k. The correspondence space can be the space in which an input image is located (internal), or it can be a new space (external). MIR in an internal correspondence space has been the most common among MIR methods. Examples of MIR in an internal space can be seen in the methods mentioned earlier, which included a transformation from the space of a moving image (i) to the space of the fixed image (j). An example of MIR in external space is Atlas-based registration.

Atlas-based registration

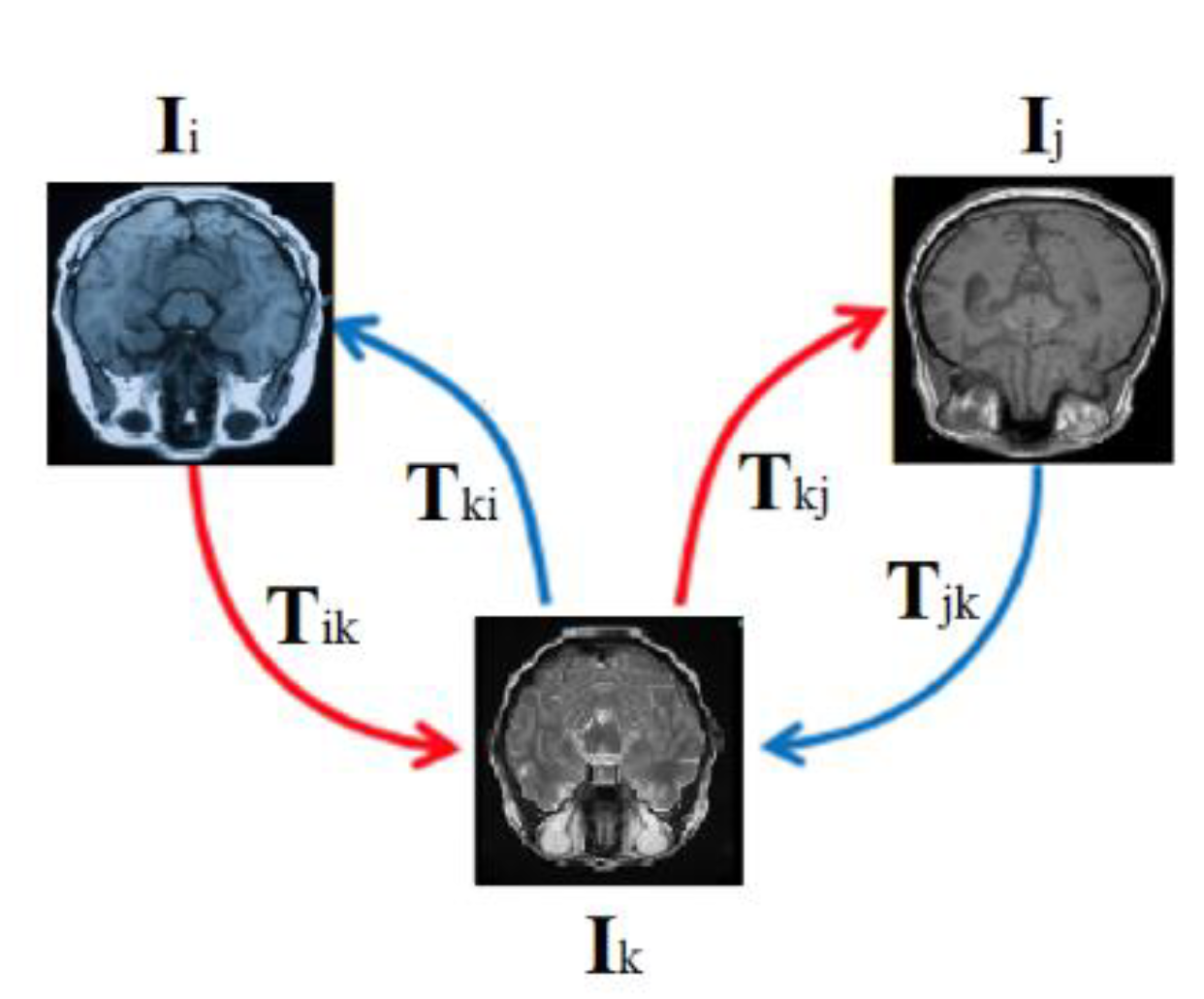
An Atlas is a standard or a reference image that represents a population of images. One way to form an Atlas of a brain is by finding the average image of a population of brain images, which is expected to be smooth and symmetrical. However, that is not the only way. (Dey et al., 2021) suggested an atlas generated by GANS. Another way to form an atlas is by IR in an external correspondence space. An example of atlas-based registration is the Aladdin framework (Ding, Z. et al., 2022) shown in Figure 18. Aladdin transformations are bidirectional and invertible.

Invertibility: for a transformation $T_{i j}$ , there is an inverse transformation $T_{i j}^{- 1}$
Bidirectionality: A bidirectional registration maps spaces in both directions from i to k and vice versa ( $T_{i \leftrightarrow k} : T_{i k}$ , and $T_{k i}$ ). Accordingly, a bidirectional IR model (Ding, W. et al.,2022; Ye et al.,2021) can yield two wrapped images $I_{i j}, I_{j i}$ . On the other side, a unidirectional registration maps a single space i into another j but not vice versa. An example of an invertible bidirectional MIR model in an internal correspondence space, namely Inversenet (Nazib et al., 2022), is shown in Figure 19.

The bidirectionality in an external correspondence space enables more transformation paths between spaces given three anchors as shown in Figure 18: fixed image I_i, moving image I_j, and an external correspondence space/Atlas I_k. Potential transformation paths were expressed in Equations 11-17 below. The dissimilarities between the left and right sides of the equations below were used as losses of an MIR model (Ding, Z. et al. 2022).

T_{k i} (T_{i k} (I_{\emptyset i})) = I_{\emptyset i}

(11)

T_{k i} (T_{j k} (I_{\emptyset j})) \approx I_{\emptyset i}

(12)

T_{k i} (I_{\emptyset j}) = I_{k i} \approx I_{\emptyset i}

(13)

T_{k j} (T_{j k} (I_{\emptyset j})) = I_{\emptyset j}

(14)

T_{k j} (T_{i k} (I_{\emptyset i})) \approx I_{\emptyset j}

(15)

T_{k j} (I_{\emptyset k}) = I_{k j} \approx I_{\emptyset j}

(16)

T_{k i} (I_{\emptyset i}) = T_{j k} (I_{\emptyset j})

(17)

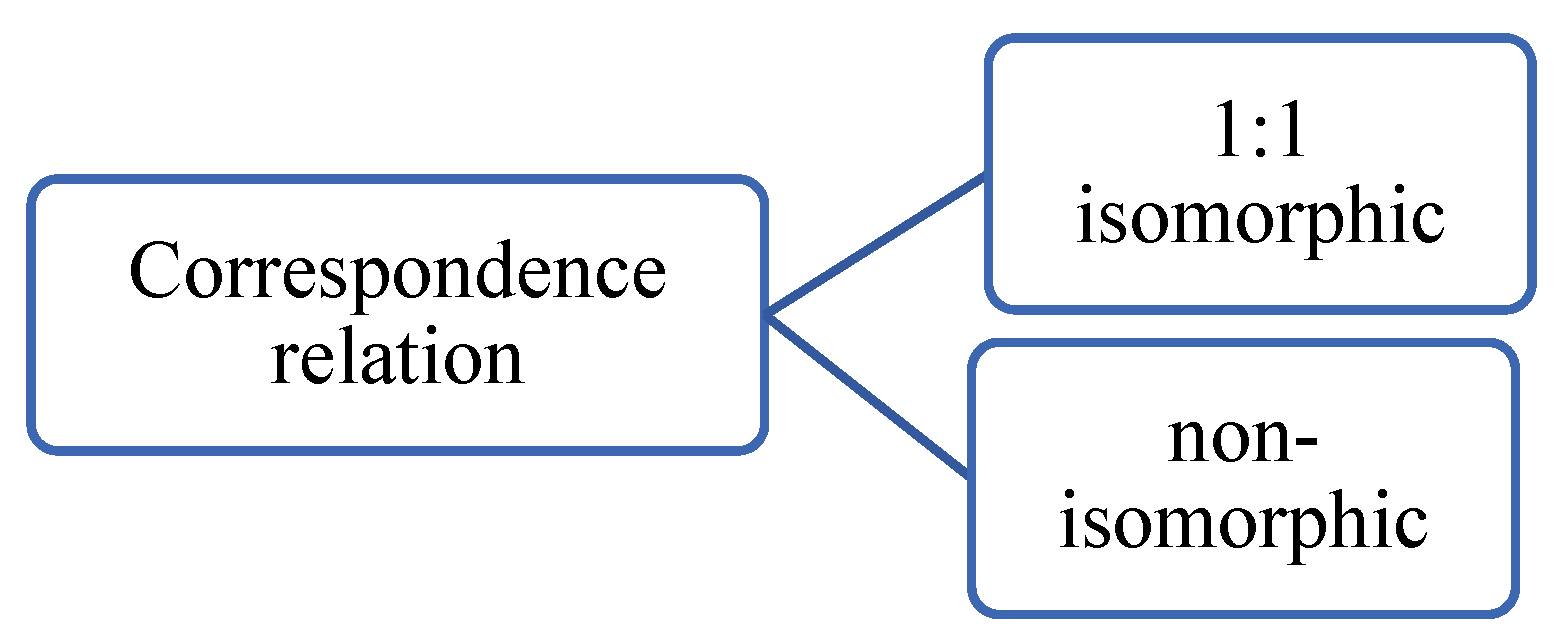
6.5. Correspondence relation

Correspondence relations can be categorized into isomorphic and non-isomorphic. Isomorphism entails a one-to-one correspondence relation between images. A special case of isomorphism is diffeomorphism which entails invertible and differentiable transformation. An example of non-isomorphism is a change of the topology such as that shown in Figure 22. A special case of non-isomorphism is a many-to-many correspondence as in metamorphism.

Figure 21. Correspondence relation taxonomy.

Figure 22. An example of metamorphism.

The spatial transformation unit imposes isomorphism, since the registration field just maps a single pixel from one location to another single point only, which is a 1:1 correspondence. However, the resampling step can affect the 1:1 correspondence relation, for example, if two nearby points are merged in the target image, which makes metamorphism possible but no guarantees. Diffeomorphism can be achieved by an integral

\int

before a spatial transformation.

Metamorphosis (Maillard et al., 2022) is a deep learning model that addresses metamorphic registration. Metamorphosis estimated the wrapped image without an explicit spatial transformation unit. However, alternative constraints were added as 2 equations embedded in the network as layers. However, no information if a spatial transformation holds implicitly. Metamorphosis superseded diffeomorphic registration methods especially when the ground truth correspondence was metamorphic. However, its runtime was 10-20 times that of Voxelmorph. The runtime is defined in section 7 (evaluation measures).

6.6. Multistage image registration

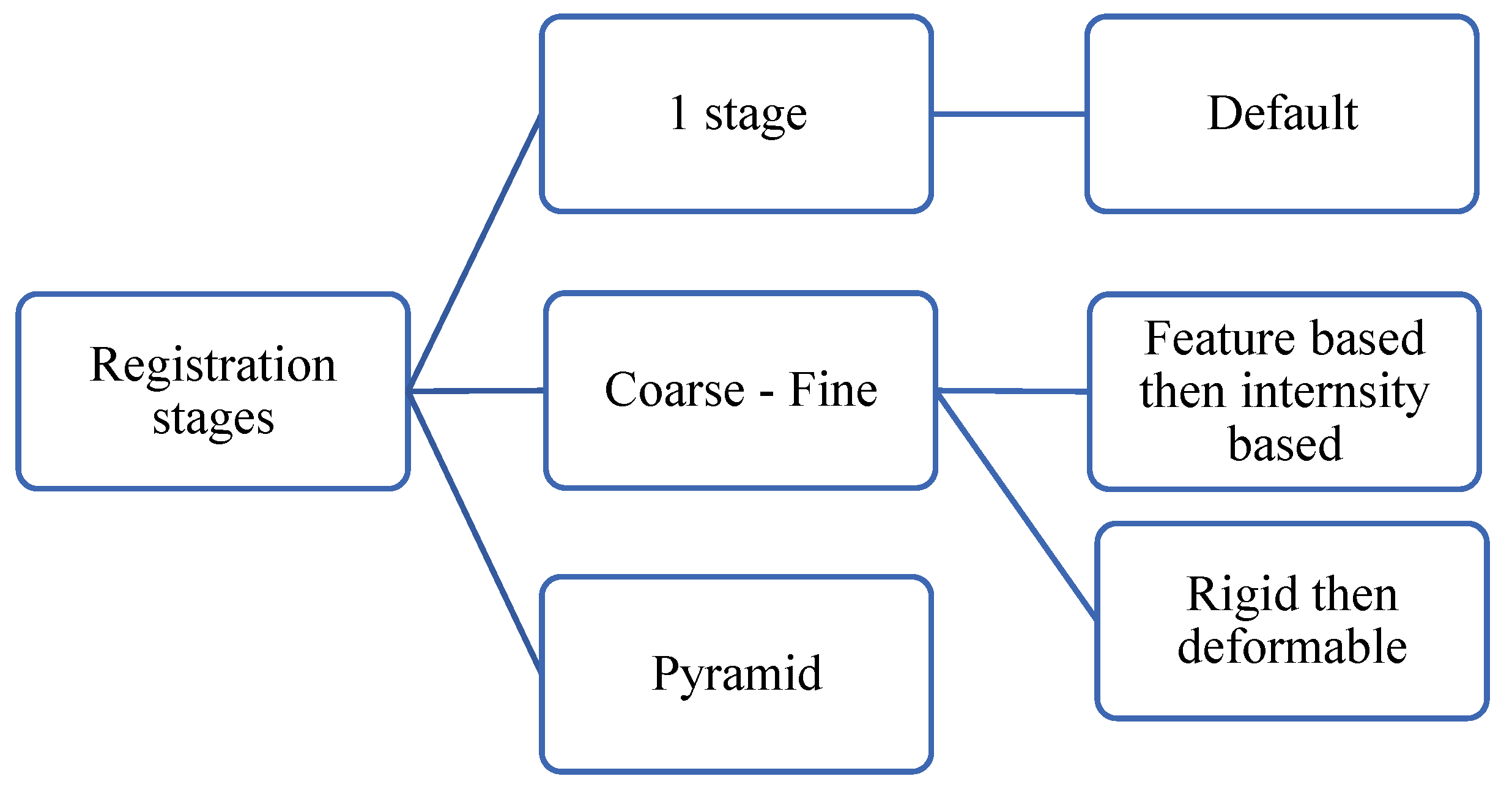
Instead of solving the registration problem for high-resolution images entirely in a big dimensional space, the registration problem can be conquered into multiple registration problems of various scales. Figure 23 shows a taxonomy of multistage image registration. Multistage MIR approaches save computational resources and time in addition to the enhancement of registration results.

6.6.1. Coarse-fine registration:

A coarse-fine registration (Himthani et al., 2022; Naik et al., 2022; Saadat et al., 2022; Van Houtte et al.,2022) consists of two stages: The first stage is called coarse registration, which aims at finding a fast registration solution but not optimal. That solution is fine-tuned later in the second stage. For example, the coarse registration could be an affine registration that aligns the position and orientation while the fine-tuned registration could be a deformable registration method that aligns deformed parts.

The parameters of a rigid transformation of a high-resolution image can be found using a downscaled version of the image, which would save computation time and energy. The parameters of a rigid transformation are either independent of the scale (e.g., rotation) or linearly dependent (translations). Assume an image of 1000x1000 pixels and its lower resolution version of 100x100 (downscaling by 10). Scaling does not affect angles, hence if an object is rotated by 30 degrees in the downscaled image, it will be also rotated by the same angle in the high-resolution image. However, distances between objects do change according to a fixed scale. If the distance between 2 objects in the low-resolution image is 25 units, then the equivalent distance in the high-resolution image will be 10×25 = 250, where 10 is the scaling ratio between the two images. Hence a solution for a rigid registration problem can be solved in a downscaled version of the images and then transferred to the higher resolution image.

6.6.2. Pyramid image registration.

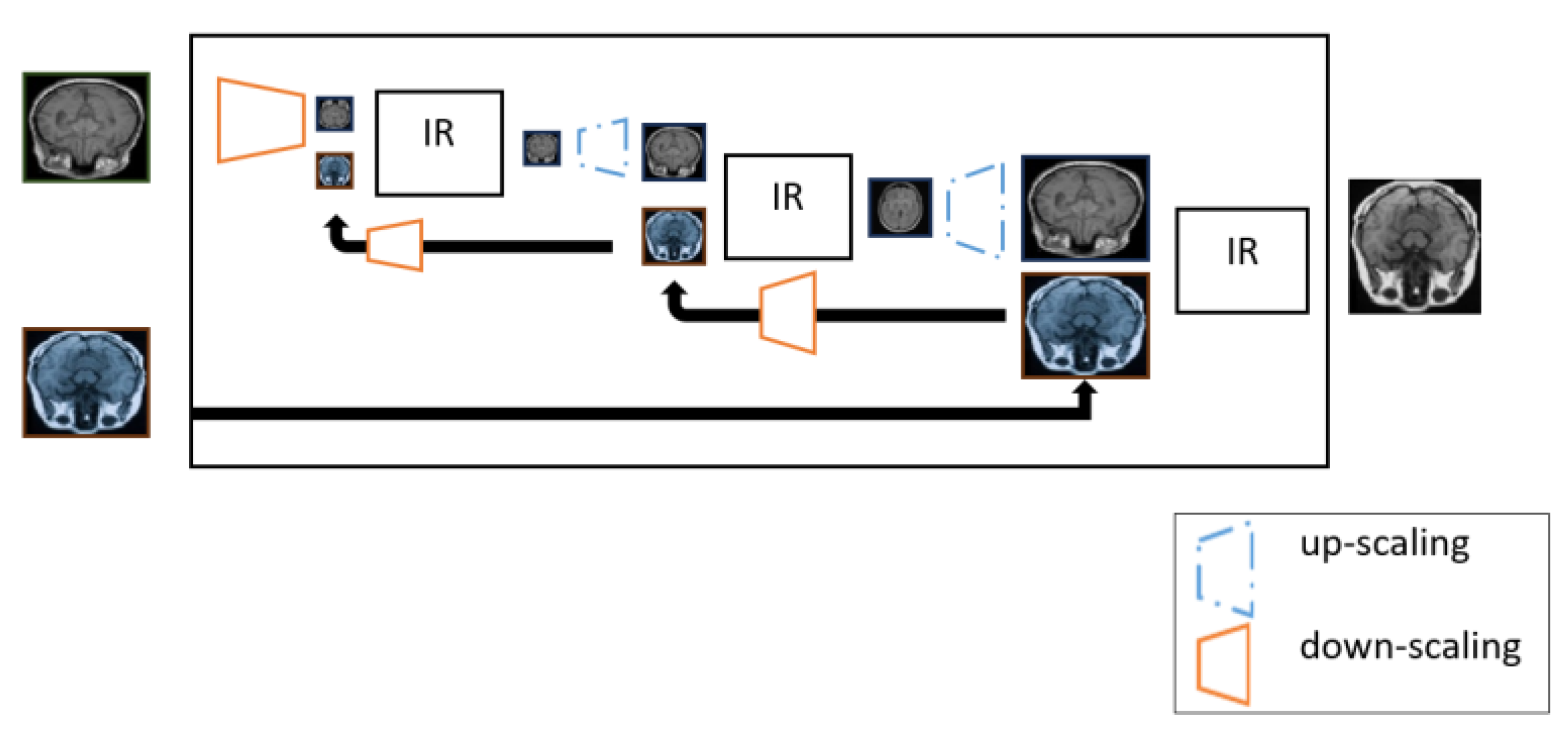
A pyramid consists of multi-scale images, where registration occurs at multiple stages. The idea of a pyramid representation has been well-studied in classical computer vision (Adelson et al., 1984) and utilized later in deep learning architectures such as Pyramid GANs (Denton et al., 2015; Lai et al., 2017). A pyramid registration (Wang et al., 2022; Chen, J. et al. 2022, Zhang, L. et al., 2021) starts with a downscaled version of the moving image followed by several operations of registration and upscaling as shown in Figure 24. After every registration step, the proximity between the wrapped image and the downscaled fixed image improves. Multi-stage registration can be seen as a sort of curriculum learning (Bengio et al., 2009) such that the first stages learn to solve easier problems and later stages learn the more difficult tasks.

6.7. Space Geometry

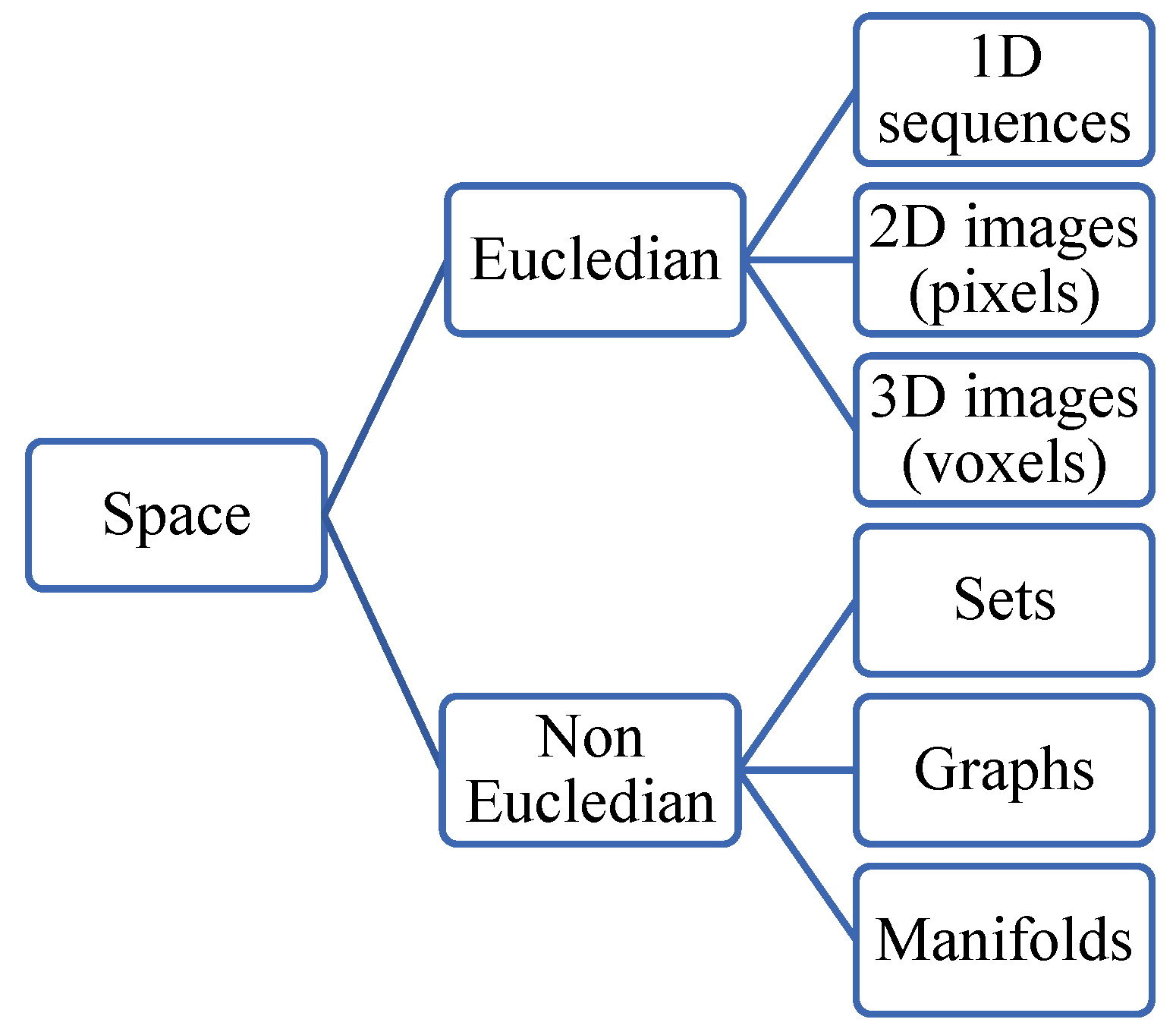
A taxonomy of spaces has been proposed GDL is shown in Figure 25. A space can be Euclidean-like RGB images (pixels distributed regularly in a rectangle). Non-Euclidean spaces are represented in sets, graphs, meshes, or manifolds. Examples of MIR for non-Euclidean data, specifically 3D point clouds, have been presented in (Terpstra et al., 2022; Su et al., 2021).

6.8. Other taxonomies

6.8.1. Feature-based and pixel-based

Feature-based and pixel-based taxonomy depends on the type of inputs to the registration algorithm. A feature-based registration involves an explicit feature extraction or selection, thus the input to the registration algorithm is not the image itself but representative features of that image such as its histogram (Ban et al., 2022). In pixel-based approaches, images are fed directly to the model without feature extraction. In general, DL registration approaches are pixel-based as neural networks can extract features implicitly.

6.8.2. Medical imaging modalities

Medical imaging modalities are imaging techniques (Kasban et al., 2015) used to visualize the body and its components. The main medical imaging modalities in MIR are:

X-ray

X-ray uses ionizing radiation (X-rays) to produce two-dimensional images of bones and dense tissues. X-rays are absorbed differently by different tissues, allowing visualization of structures like bones, lungs, and some organs. X-rays are quick and relatively inexpensive, thus suitable for some diagnostic purposes, such as detecting fractures, lung infections, and dental issues. However, they provide limited details about soft tissues.

b. Computed Tomography (CT) scan

CT scan, also known as CAT (Computerized Axial Tomography), is a non-invasive imaging technique that uses X-rays to create detailed cross-sectional images of the body. A CT scan provides a more detailed view of bones, blood vessels, and solid organs compared to traditional X-rays. It is especially useful for imaging areas like the brain, chest, abdomen, and pelvis. However, they involve exposure to ionizing radiation, and repeated scans should be minimized to reduce radiation exposure. During a CT scan, the X-ray source rotates around the patient, and multiple X-ray images are captured from different angles. These images are then processed by a computer to create cross-sectional slices, allowing doctors to visualize the body in detail. CT scans are commonly used in emergencies, trauma cases, and cancer staging, among other applications.

c. Magnetic Resonance Imaging (MR)

MRI uses strong magnetic fields and radio waves to create detailed images of tissues, organs, and the central nervous system. It provides high-resolution, multi-planar images, making it ideal for diagnosing conditions in the brain, spinal cord, muscles, and joints. MRI does not use ionizing radiation, which makes it safer, but it can be more time-consuming and expensive compared to X-rays and CT scans.

d. Ultrasound (US)

Ultrasound, also known as sonography, uses high-frequency sound waves to create real-time images of internal organs and structures. It is commonly used for imaging the abdomen, pelvis, heart, and developing fetus during pregnancy. Ultrasound is non-invasive and does not involve ionizing radiation. It provides real-time imaging and is excellent for assessing blood flow and certain soft tissue abnormalities. However, it may not provide as detailed images as MRI and CT.

e. Positron Emission Tomography (PET)

PET is a functional imaging technique that provides information about metabolic activity and cellular function. It involves the injection of a radioactive tracer that emits positrons. The interaction between the tracer and tissues produces gamma rays, which are detected by the PET scanner. PET is valuable in oncology (cancer imaging) and neurology (e.g., detecting Alzheimer's disease). PET can be combined with CT imaging to provide both functional and anatomical information in a single scan.

MIR is considered “unimodal” when there are no modality differences between the images involved in the registration process, otherwise, the registration is considered “multimodal”. See Figure 26. An example of a unimodal registration is when both moving and fixed images are X-rays. An example of multimodal registration is when a fixed image is of the T1-weighted MRI modality and the moving image of the T2-weighted MRI. T2-weighted MRI enhances the signal of the water and suppresses the signal of the fatty tissue while MRI/T1 does the opposite.

7.0. Evaluation measures

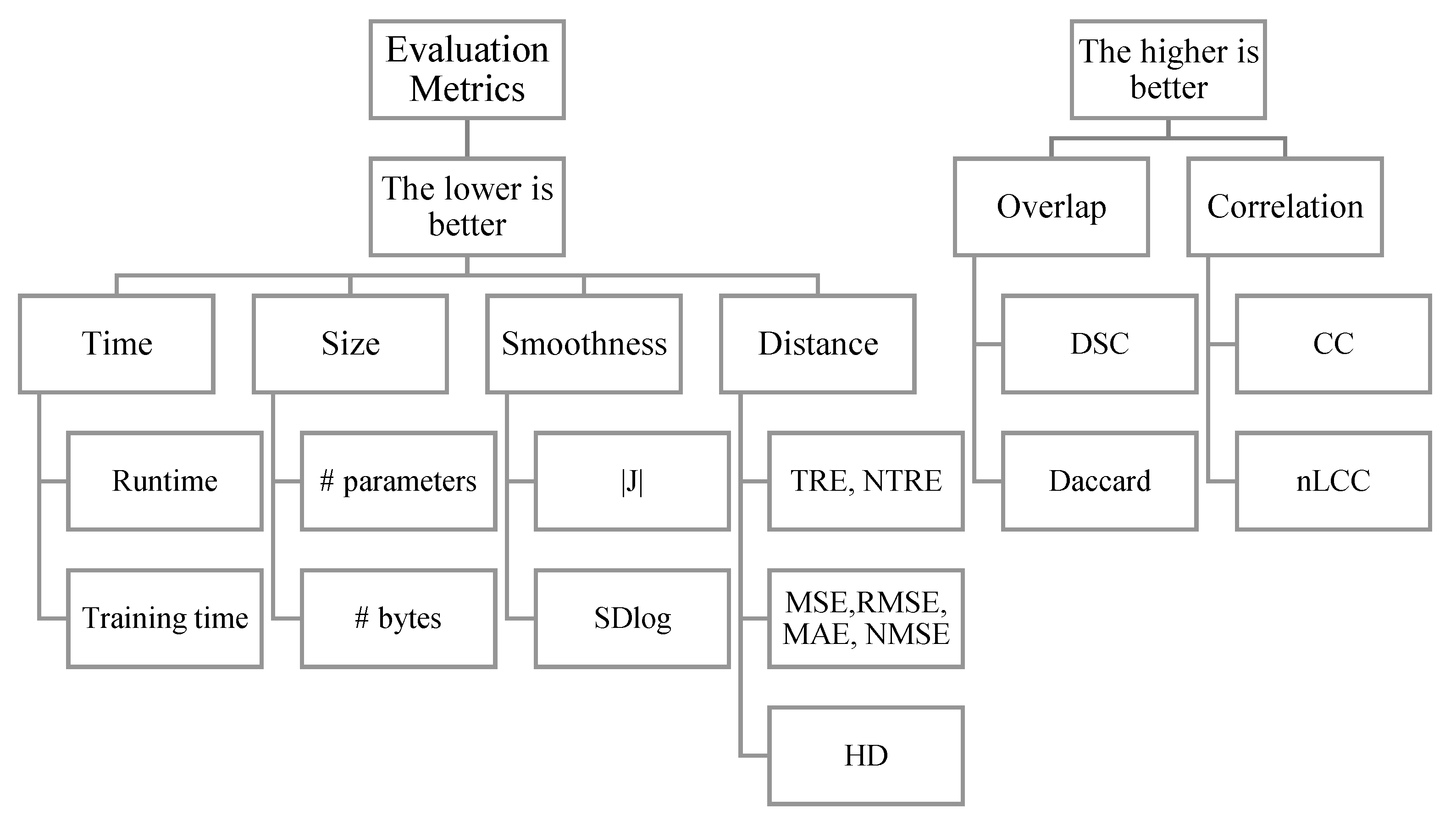
IR evaluation measures can be categorized as shown in Figure 27 into 1) time-based measures that focus on the time needed to finish a task, 2) size-based measures that focus on the memory resources that an MIR algorithm occupies, 3) smoothness measures that focus on the smoothness of the registration field (expressed by Jacobian), and 4) proximity-based measures that find the deviation of a registration outcome from the ground-truth. proximity can be expressed using distances between objects in a space, overlap between sets, or correlations between variables.

7.1. Time

a): Average registration runtime RT:

The runtime (RT) is the average registration time per image. The registration time is measured from the moment

t_{r, s t a r t}^{p}

at which an image p is loaded until obtaining the registered image at time

t_{r, e n d}^{p}

including the post-processing time. See Equation 18. Where N is the number of examples in a dataset.

R T = \frac{\sum_{p = 1}^{N} (t_{r, e n d}^{p} - t_{r, s t a r t}^{p})}{N}

(18)

In practice, getting the registration outcome in a short time is a desired property. The Voxelmorph algorithm, which uses deep learning for medical image registration, has shown an RT reduction from hours to seconds while keeping almost the same performance. The computation time of a registration process depends on the software as well as the hardware (Alcaín et al., 2021). Thus, a fair comparison of registration algorithms entails testing the computation time on the same hardware. The shorter RT of Voxelmorph compared to iterative approaches can be attributed partially to the hardware, where matrix multiplication processes used in DL are faster when run with a GPU. However, even on CPUs, Voxelmorph remains faster than iterative methods on a scale of minutes for voxelmorph to hours for iterative methods. The main reason for the longer RT in iterative approaches is the optimization done during the runtime, however, Voxelmorph-like approaches do not optimize the variables during the run phase, instead, all the variables are optimized in the training phase before the run time.

b) Average training time DT is the training time divided by the number of examples in the training dataset.

7.2. Distance-based measures

The distance can be chosen to be between co-domain values or domain values. The distance can be measured between selected points (landmarks) or all points.

a): Codomain distance: MSE, RMSE

The Euclidean point-wise distance between codomain values can be calculated using the mean square error (MSE), and root mean square error (RMSE) measure as in Equations 19, and 20 respectively.

M S E = \frac{1}{N} \sum_{p = 1}^{N} \frac{1}{L p} \sum_{e = 1}^{L p} {{D i s t (y e'}_{i j}^{p}, {y e}_{i j}^{p})}^{2}

(19)

R M S E = \sqrt{M S E}

(20)

b) Domain distance: TRE

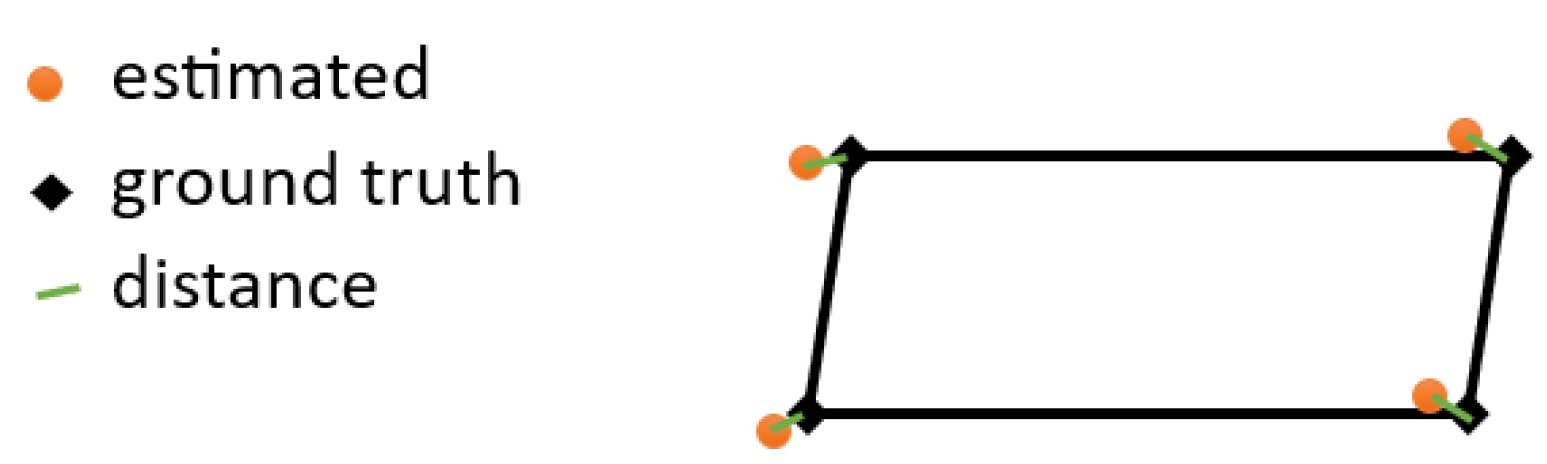
TRE (target registration error) is a distance-based metric that measures the deviation between points of two domains. See the deviation between estimated and ground truth points in Figure 28. The distance is used to represent the registration error since a perfect registration would locate correspondent points ideally at the same position. In the case of ground truth labels

X_{i j}^{'}

and predictions

X_{i j}

, TRE is shown in Equation 21.

T R E = R M S E (X_{i j}^{'}, X_{i j}) = \sqrt{\frac{1}{N} \sum_{p = 1}^{N} {e r r o r ({M'}_{i j}^{p}, M_{i j}^{p})}^{2}} = \sqrt{\frac{1}{N} \sum_{p = 1}^{N} \sum_{e = 1}^{M p} {{D i s t (x e'}_{i j}^{p}, {x e}_{i j}^{p})}^{2}}

(21)

where

{x e}_{i j}^{p} \in M_{i j}^{p}, {x e'}_{i j}^{p} \in {M'}_{i j}^{p}, {w i t h a c o r r o s o n d e n c e (x e'}_{i j}^{p} \leftrightarrow {x e}_{\emptyset j}^{p})

c) Domain distance: NTRE

TRE is affected by the scale of an image as well as the number of landmarks, the more landmarks in an image the higher the accumulative error could be. The normalized target to registration error (NTRE) is scale independent as shown in Equation 22.

N T R E = \sqrt{\frac{1}{N} \sum_{p = 1}^{N} \frac{\sum_{e = 1}^{M p} {{D i s t (x e'}_{i j}^{p}, {x e}_{i j}^{p})}^{2}}{\sum_{e = 1}^{M p} {{(x e'}_{i j}^{p})}^{2}}}

(22)

d) Domain distance: Hausdorff distance HD

HD measures how far two sets are from each other as in Equations 23 and 24 below.

H D (A, B) = m a x {\underset{a \in A}{\sup (} \inf_{b \in B} (D i s t (a, b))), \underset{b \in B}{\sup (} \inf_{a \in A} (D i s t (a, b))}

(23)

H D ({M'}_{i j}^{p}, M_{i j}^{p}) = \frac{1}{N} \sum_{p = 1}^{N} m a x {\underset{{m'}_{ij}^{p} \in {M'}_{ij}^{p}}{\sup (} \inf_{m_{ij}^{p} \in M_{ij}^{p}} (D i s t ({m'}_{i j}^{p}, m_{i j}^{p}))), \underset{m_{ij}^{p} \in M_{ij}^{p}}{\sup (} \inf_{{m'}_{ij}^{p} \in {M'}_{ij}^{p}} (D i s t ({m'}_{i j}^{p}, m_{i j}^{p}))

(24)

where

-: sup() is the supremum
-: inf() is the infimum
-: Dist (a,b) is the distance between point a in the first set and point b in the second set.

\inf_{b \in B} (d (a, b))

is the infimum distance between point a and all the points in set B

H D 95

metric replaces the supremum in the equation by the 95 percentile, which results in less sensitivity to outliers.

e) Domain distance: Center of mass COM measures the displacement between two the center of two sets A, B as shown in Equations 25 and 26

COM(A, B) = dist( Center(A), Center(B) )

(25)

C e n t e r (A) = m e a n (x), \forall x \in A

(26)

7.3. Segmentation measures

The dice similarity coefficient (DSC) measures the overlap between two segmentation sets

L_{\emptyset j}^{p}

L_{i j}^{p}

as in Equation 27 below.

D S C (L_{\emptyset j}^{p}, L_{i j}^{p}) = \frac{{2 | L}_{\emptyset j}^{p} \cap L_{i j}^{p} |}{| L_{\emptyset j}^{p} | + | L_{i j}^{p} |}

(27)

DSC is equivalent to the F1 score used in classification problems, where the segmentation problem is a classification problem on the pixel level, in which a pixel/point is assigned to a segmentation label that could be true or false. F1 = 2TP/(FP+FN +2TP).

The daccard coefficient is similar to DSC with a slight modification shown in Equation 28.

D a c c a r d (L_{\emptyset j}^{p}, L_{i j}^{p}) = \frac{{| L}_{\emptyset j}^{p} \cap L_{i j}^{p} |}{| L_{\emptyset j}^{p} \cup L_{i j}^{p} |}

(28)

7.4. Correlation measures

It has been reported that cross-correlation is a better objective function than MSE, and RMSE for image registration (Zitova et al., 2003; Haskins et al., 2020). cross-correlation “CC” is more resilient against the contrast problem than MSE due to its scale invariance property. CC (Y1, Y2) = CC (Y1, α

\times

Y2) where α is a scale number.

7.5. The smoothness of the registration field

A non-smooth registration field can relocate a pixel far away from all its adjacent pixels after registration, however, a smooth registration field is more likely to keep nearby pixels relatively close to each other after relocation. The smoothness can be expressed using the determinant of the Jacobian

|J (φ)|

7.6. Model size

A model size can be expressed by the number of bytes that a model occupies in a storage device or the total number of its parameters.

7.7. Clinical-based evaluation

Virtual evaluation using computer-based metrics (above) may not always align perfectly with the practical evaluation by medical experts. Thus, clinical-based evaluation and involvement of domain experts from the medical field have been recommended by Chen, X., Wang et al. (2022) to characterize the reliability of MIR tools (Huang et al., 2022).

The challenges of MIR assessment included 1) the lack of ground truth labels in practical scenarios makes it difficult to evaluate an MIR outcome convincingly. 2) Medical experts’ assessment could be subjective and may vary among experts. 3) Instable outcomes of some MIR algorithms, which yield different outcomes of different registration qualities for the same input image. 4) the quality of data can have a substantial impact on registration results, making it challenging to compare algorithms across datasets with varying quality (Chen, T. et al.,2022).

8.0. Medical imaging datasets

A list of public datasets used in the literature was summarized in Table 5. The datasets were categorized based on the region of interest (ROI) such as brain, chest, …etc., and the medical imaging type.

9.0. Medical applications

Changing the frame of reference might mislead humans (like the phenomenon of not recognizing an object if it has been flipped (e.g., old/young lady face in Figure 2). Hence, it is easier for medical practitioners to evaluate a medical image in a standard reference frame (e.g., orientation, scale). Thus, registration is an essential part of medical diagnoses that depend on imaging technologies. IR was applied in retina imaging (Ho et al., 2021), breast imaging (Ringel et al., 2022; Ying et al., 2022), HIFU treatment of heart arrhythmias (Dahman et al., 2022), and cross-staining alignment (Wang et al., 2022). Selected applications of MIR are discussed below.

9.1. Image-guided surgery

Image-guided surgery (IGS) incorporates imaging modalities such as CT, and US to assist surgeons during surgical procedures. For example, surgeons can visualize internal anatomy, pinpoint the location of tumors or lesions, and determine optimal incision points. Image-guided surgery enables surgeons to precisely target specific areas, and avoid critical structures during a procedure.

Before an IGS, a patient's preoperative images are loaded into a software or surgical navigation system. The collected images are then aligned with images taken during the surgery (inter-operative) using registration algorithms. Having images with key points/landmarks improves the registration process in terms of speed and precision. The landmarks can be selected manually by medical experts on computer software (Schmidt et al., 2022; Wang, Y. et al., 2022), or they could be fiducial markers, which are small devices placed in a patient’s body such as the injection of gold seeds to mark a tumor before radiation therapy. The number of landmarks needed for a precise registration can be reduced by the integration of semantic segmentation in addition to the use of a standard template (atlas) instead of preoperative images as shown by (Su et al., 2021). An alignment with no landmarks was tested by (Robertson et al., 2022) for catheter placement in non-immobilized patients.

To mention some examples of the use of MIR for IGS, 2D inter-operative and 3D preoperative images were aligned in real-time surgical navigation systems (Ashfaq et al., 2022). A similar alignment of 2D-3D was needed for the deep brain stimulation procedure which involves the placement of neuro-electrodes into the brain to treat movement disorders such as Parkinson, and Dystonia (Uneri et al., 2021). A real-time biopsy navigation system was developed by (Dupuy et al., 2021) to align 2D US inter-operative images with 3D TRUS preoperative images and to estimate in real-time the biopsy target of a prostate based on its previous trajectory.

9.2. Tumor diagnosis and therapy

A tumor is an abnormal mass or growth of cells in the body. Tumors can develop in various tissues or organs and can be either benign or malignant. Benign tumors are non-cancerous and typically do not invade nearby tissues or spread to other parts of the body. Benign tumors are generally not life-threatening, but medical attention and/or treatment are still required. Malignant tumors, on the other side, are cancerous. They have the potential to invade surrounding tissues and can spread to other parts of the body through the bloodstream or lymphatic system. Malignant tumors grow rapidly and can be life-threatening. Medical experts often diagnose a tumor and plan therapy depending on the tumor’s growth over time as recorded in aligned medical images. Accordingly, MIR has been used for radiotherapy (Fu et al., 2022; Vargas-Bedoya et al., 2022) and proton therapy (Hirotaki et al., 2022).

9.3. Motion processing

The human body experience normal deformation over time, some deformations occur at a slower pace such as the growth of bones over a lifetime (e.g., a human height grows from afew feet in newborns to several feet in adults) while some deformations occur at a faster pace such as heartbeats. The heart experiences alternating contractions and relaxations while pumping blood at a frequency of 1-3 beats per second. MIR helps to analyze such temporospatial deformations and resulting movements.

The cardiac motion was tracked by (Ye et al., 2021) using tagging magnetic resonance imaging (t-MRI), where an unsupervised bidirectional MIR model estimated the motion field between consecutive frames. (Upendra et al., 2021) focused on motion extraction from 4D cardiac CMRI (Cine Magnetic Resonance Imaging), mainly the development of patient-specific right ventricle (RV) models based on kinematic analysis. A DL deformable MIR was used to estimate the motion of the RV and generate isosurface meshes of cardiac geometry.

Respiratory movement can affect the quality of medical imaging by causing motion blur. To overcome this (Hou et al., 2022) proposed an unsupervised MIR framework for respiratory motion correction in PET (Positron Emission Tomography) images. (Chaudhary et al., 2022) focused on lung tissue expansion which is typically estimated by registering multiple scans. To reduce the number of needed scans, Chaudhary et al., (2022) proposed the use of generative adversarial learning to estimate local tissue expansion of lungs from a single CT scan.

2D-3D motion registration of bones was addressed in (Djurabekova et al., 2022) by manipulating segmented bones from static scans and matching digitally reconstructed radiographs to X-ray projections. The bones were, particularly foot and ankle structure.

10.0. Other research directions

10.1. Transformers

Transformers are a DL architecture that uses the attention mechanism solely dispensing with conventional and recurrent units (Vaswani et al., 2017). Transformers have contributed to noticeable improvements in computer vision, audio processing, and language processing tasks (Lin et al, 2022). The improvement can be seen in products like GPT-2, and ChatGPT which are examples of Generative Pre-trained Transformers (GPT). Transformers can be decomposed into basic/abstract mathematical components that distinguished them from recurrent and convolutional networks: 1) the position encoding, which explicitly feeds the position of a token as an input, 2) the product operation between features which is manifested explicitly in the product between the key and the query of the attention mechanism, and implicitly within the exponential function of the SoftMax (

e^{a + b} = e^{a} \times e^{b}

). 3) the exponential function which represents a transformation into another space.

In MIR, (Mok et al., 2022) proposed the use of the attention mechanism for affine MIR such that multi-head attention was used in the encoder, and convolutional units in the decoder. Transformers were embedded partially for deformable MIR in Transmorph (Chen, J. et al., 2022). Transmorph is a coarse-fine IR such that affine alignment is conducted in the first stage followed by deformable alignment in the second stage. The latter stage is a Voxelmorph-like registration with U-Net architecture except that the encoder part consists of transformers instead of ConvNets. Transmorph introduced transformers (self-attention blocks) as a part of the encoder only but not the decoder. Ma et al. (2022) attributed the difficulty of developing transformers for MIR to the large number of trainable parameters of a transformer unit compared to convolutional units. To reduce the number of parameters, the authors proposed the use of both convolution units and transformer units in an MIR model - SymTrans (Ma et al., 2022). SymTrans embedded transformers in both the encoder and the decoder (2 blocks in the encoder and 2 in the decoder).

The utilization of transformers in MIR was not as fast and revolutionary as it was in other domains. That could be attributed to the relatively small number of images in MIR datasets compared to other tasks. For example, millions of images were used for the ViLT model (Kim et al., 2021), and up to 0.8 billion images for the GiT model (Wang, J. et al., 2022).

10.2. No Registration

Another potential research direction is the elimination of the image registration step from the medical image analysis pipeline. In theory, an end-to-end deep learning model learns an automatic medical image analysis task (e.g., disease detection) without an explicit registration step. In (Chen, X., Zhang, et al, 2022), the authors proposed the elimination of the registration step entirely by the development of a breast cancer prediction model using vision transformers and multi-view images.

11.3 Other research directions explored before include Fourier transform-based IR (Zitova et al., 2003), Reinforcement learning based IR (Chen, X. et al., 2021; George et al., 2021; Sutton et al., 1994), and GANs-based MIR (Xiao et al., 2021; Chaudhary et al., 2022; Dey et al., 2021; Goodfellow et al., 2020). There could be further research interest in the mentioned MIR research directions in the future.

Acknowledgments

This work was funded partially by Service Public de Wallonie Recherche under grant n°2010235 ARIAC by digitalwallonia4.ai.

Nomenclature & Abbreviations

Table 1.A. Nomenclature.

b_x	translation on the X-axis
b_y	translation on the Y-axis
b_z	translation on the Z-axis
$C_{i j}^{p q}$	correspondence of image p in space i and image q in space j
DT	average training time
E	the total number of elements in a set
e (as in xe)	stands for the order of an element in a set $X_{\emptyset i}^{p} = {{x 1}_{\emptyset i}^{p}, {x 2}_{\emptyset i}^{p}, {x 3}_{\emptyset i}^{p}, \dots \dots {x E}_{\emptyset i}^{p}}$ , $Y_{\emptyset i}^{p} = {{y 1}_{\emptyset i}^{p}, {y 2}_{\emptyset i}^{p}, {y 3}_{\emptyset i}^{p}, \dots \dots {y E}_{\emptyset i}^{p}}$
$F_{i j}^{p}$	a mapping between $X_{i j}^{p} & Y_{i j}^{p}$ such that $Y_{i j}^{p} = F_{i j}^{p} (X_{i j}^{p})$
$I_{\emptyset i}^{p} (o r I_{i}^{p})$	< $X_{\emptyset i}^{p}, Y_{\emptyset i}^{p}$ > an image P that connects $X_{\emptyset i}^{p}$ and $Y_{\emptyset i}^{p}$
$L_{\emptyset i}^{p}$	$l a b e l s a s s o c i a t e d w i t h I_{\emptyset i}^{p} t h a t d e s c r i b e p r o p e r t i e s o f e l e m e n t s i n I_{\emptyset i}^{p}$ such as a segmentation category
Lp	the number of points in image P
$M_{\emptyset i}^{p}$	$a s e t o f m a r k s t h a t i n c l u d e s s e l e c t e d e l e m e n t s o r p o i n t s o f i m a g e P s u c h t h a t M_{\emptyset i}^{p} \in I_{\emptyset i}^{p}$
Mp	the number of landmarks in image P
N	the number of examples/samples in a dataset
O	an objective function that yields a smaller value when the registration is closer to the desired. For example, O = $\sum_{p = 1}^{N} {(Y_{\emptyset j}^{p} - Y_{i j}^{p})}^{2}$ which measures the square difference between a registered codomain $Y_{i j}^{p}$ and a ground truth $Y_{\emptyset j}^{p}$
RT	average registration runtime
$T_{i j}$	a domain mapping between $X_{\emptyset i} & X_{\emptyset j}$
$t_{r, s t a r t}^{p}$	the time at which image p is loaded to an IR model
$t_{r, e n d}^{p}$	the time at which image p is registered
\|\| v \|\|	length of vector v
$X_{\emptyset i}^{p} (o r X_{i}^{p})$	domain values of an image p in space i, where ∅ is a reference unknown codomain (used with raw data). p is an index of a registration example in a dataset.
$X_{i j}$	the transformed domain after applying $T_{i j} t o X_{\emptyset i}$ such that $X_{i j} = T_{i j} (X_{\emptyset i})$
$X_{i - j}$	$t h e o u t c o m e o f a p p l y i n g T_{i - j} t o X_{\emptyset i} s u c h t h a t X_{i - j} = T_{i - j} (X_{\emptyset i})$ but before any postprocessing like resampling
xe	element number e in a set X, $X_{\emptyset i}^{p} = {{x 1}_{\emptyset i}^{p}, {x 2}_{\emptyset i}^{p}, {x 3}_{\emptyset i}^{p}, \dots \dots {x E}_{\emptyset i}^{p}}$ ,
$Y_{\emptyset i}^{p} (o r Y_{i}^{p})$	codomain values of an image p in space i, where ∅ is a reference unknown codomain (used with raw data). p is an index of a registration example in a dataset.
$Y_{i - j}$	$c o d o m a i n v a l u e s a f t e r a t r a n s f o r m a t i o n T_{i - j}$ but before any post-processing (e.g., interpolation)
ye	element number e in a set Y, $Y_{\emptyset i}^{p} = {{y 1}_{\emptyset i}^{p}, {y 2}_{\emptyset i}^{p}, {y 3}_{\emptyset i}^{p}, \dots \dots {y E}_{\emptyset i}^{p}}$
$∆_{i j}^{p}$	a displacement field that transforms image p from space i to j.
$φ_{i j}^{p}$	a registration field that transforms image p from space i to j.
θ	rotation angle
$^{'}$	the apostrophe indicates ground truth, for example, < ${X'}_{i j}^{p}$ , ${Y'}_{i j}^{p}$ > is the ground truth outcome <domain and codomain> of image p after IR to space j.
$^{~}$	the ~ sign indicates a post-transformation outcome.
#	number of
Σ	standard deviation
∩	Intersection
∪	Union

Table 1.B. Abbreviations.

2D	two dimensional
3D	three dimensional
AI	artificial intelligence
CC	cross-correlation
COM	center of mass
CMYK	a color system in which cyan, magenta, yellow, and black are the basic colors
CT	computerized tomography
CNNs	convolutional neural networks
Dist	distance measure
DL	deep learning
DSC	dice score
e.g.	for example
F1	F score
FN	false negative
FP	false positive
GANs	generative adversarial networks
HD	Hough distance
IR	image registration
Inf	Infimum
i.e.	that is
J	Jacobian
JOCA	the determinant of Jacobian
MIR	medical image registration
ML	machine learning
MR	magnetic resonance imaging
MSE	mean square error
N	No
nCC	normalized cross-correlation
nLCC	normalized local cross-correlation
NN	neural networks
PET	positron emission tomography
Prox	a proximity measure
RGB	a color system in which red, green, and blue are the basic colors
RL	reinforcement learning
RMSE	root mean square error
ROI	region of interest
SDlogJ	standard deviation of log Jacobian
Sup	Supremum
TRE	target registration error
TN	true negative
TP	true positive
w/o	Without
US	ultra-sound
Y	Yes

Appendix A.

Table A1. Comparison table of surveyed papers

Paper	Modality	Modals	Directionality	Correspondence	Stages	Approach	ROI
(Andreadis et al., 2022)	Unimodal		Uni	1-to-1	1	Classical	Bladder
(Ashfaq et al., 2022)	Multimodal	MR	Uni	1-to-1	1	Classical	Brain
(Ban et al., 2022)	Multimodal	CT-Xray	Uni	1-to-1	1	Classical	Head
(Bashkanov et al., 2021)	Multimodal	MR - TRUS	Uni	1-to-1	Coarse-f.	Supervised	Prostate
(Begum et al., 2022)	Multimodal	CT - MR	Uni			Classical	Brain & Abdomen
(Burduja et al., 2021)	Unimodal	CT	Uni	1-to-1	1	Unsupervised	Liver
(Chaudhary et al., 2022)	Unimodal	CT	Uni	1-to-1	1	Unsupervised	Lung
(Chen, J. et al., 2022)			Uni	1-to-1	Pyramid	Unsupervised	Brain
(Dahman et al., 2022)	Multimodal	US - CT	Uni	1-to-1	1	Supervised	Heart
(Dey et al., 2021)	Unimodal	MR	Uni	1-to-1		Unsupervised	Brain
(Dida et al., 2022)	Unimodal	CT	Uni	1-to-1	1	Classical	Lung
(Ding, W. et al., 2022)	Multimodal	CT - MR	Bi	1-to-1	1	Unsupervised
(Ding, Z. et al., 2022)	Unimodal	MR	Bi	1-to-1	1	Unsupervised	Knee
(Djurabekova et al., 2022)	Multimodal	2D - 3D	Uni	1-to-1	1	Classical	Bones
(Dupuy et al., 2021)	Multimodal	US - TRUS	Uni	1-to-1	1	Supervised	Prostate
(Fu et al., 2022)	Unimodal	CT	Uni			Software	Liver
(Gao et al., 2022)	Unimodal	CT	Uni	1-to-1	Coarse-f.	Unsupervised	Spine
(George et al., 2021)	Unimodal		Uni	1-to-1	1	RL	Eye
(Himthani et al., 2022)	Unimodal	MR	Uni	1-to-1	Coarse-f.	Classical	Brain
(Hirotaki et al., 2022)	Multimodal	CT-Xray	Uni	1-to-1	1	Software	Lung, head, neck
(Ho et al., 2021)	Unimodal		Uni	1-to-1	Coarse-f.	Unsupervised	Eye
(Hou et al., 2022)	Unimodal	PET	Uni	1-to-1	1	Unsupervised	Heart
(Kujur et al., 2022)	Multimodal	MR	Uni	1-to-1	1	Classical	Brain
(Lee et al., 2022)	Unimodal	CT	Uni	1-to-1	1	Supervised	Kidney
(Li et al., 2022)	Unimodal	MR	Uni	1-to-1	1	Unsupervised	Brain
(Liu et al., 2021)	Unimodal		Uni	1-to-1	1	Classical	Tissues
(Ma et al., 2022)	Unimodal	MR	Uni	1-to-1	1	Unsupervised	Brain
(Maillard et al., 2022)	Unimodal	MR	Uni	Metamorphic m:n	1	Neuro-symbolic	Brain
(Meng et al., 2022)	Unimodal	MR	Uni	1-to-1	1	Unsupervised	Brain
(Mok et al., 2022)	Unimodal	MR	Uni	1-to-1	Coarse-f.	Unsupervised	Brain
(Naik et al., 2022)	Multimodal	CT-Xray	Uni	1-to-1	Coarse-f.	Classical	Spine
(Nazib et al., 2021)	Unimodal	MR	Bi	1-to-1	1	Unsupervised	Brain
(Park et al., 2022)	Unimodal	CT/MR	Uni	1-to-1	1	Unsupervised
(Ringel et al., 2022)	Unimodal	MR	Uni	1-to-1	1	Classical	Breast
(Robertson et al., 2022)	Multimodal	CT/MR - video		1-to-1	Coarse-f.	Software	Head
(Saadat et al., 2022)	Multimodal	CT-Fluoroscopy	Uni	1-to-1	Coarse-f.	Classical	Bones
(Saiti et al., 2022)	Multimodal	CT	Uni	1-to-1	1	Supervised
(Santarossa et al., 2022)	Multimodal	IR-FAF/OCT	Uni	1-to-1	1	Classical	Eye
(Schmidt et al., 2022)			Uni	1-to-1	Coarse-f.	Unsupervised	Veins
(Su et al., 2021)	Unimodal	CT/MR	Uni	1-to-1		Classical
(Terpstra et al., 2022)		MR	Uni	1-to-1	1	Supervised	Abdomen
(Uneri et al., 2021)	Unimodal		Uni	1-to-1		Classical	Brain
(Upendra, & Hasan et al., 2021)		MR	Uni	1-to-1	1	Unsupervised	Heart
(Upendra, & Hasan et al., 2021)	Unimodal	MR	Uni	1-to-1	1	Supervised	Blood
(Van et al., 2022)	Multimodal	CT-Xray	Uni	1-to-1	Coarse-f.	Unsupervised	Bones
(Vargas-Bedoya et al., 2022)	Unimodal	CT	Uni	1-to-1	1	Classical	Brain & Abdomen
(Vijayan et al., 2021)	Multimodal	CT	Uni	1-to-1	1		Bones
(Wang, C. et al., 2022)	Unimodal		Uni	1-to-1	Coarse-f.+ pyramid	Classical	Breast & prostate
(Wang, H. et al., 2022)	Unimodal	IR	Uni	1-to-1	1	Classical	Breast
(Wang, D. et al., 2022)	Unimodal	CT	Uni	1-to-1	Coarse-f.	Classical	Bones
(Wang, Z. et al., 2022)	Unimodal	MR					Brain
(Wu et al., 2022)	Unimodal	MR	Uni	1-to-1	1	Classical	Brain
(Xu et al., 2021)	Multimodal	CT - MR	Uni	1-to-1	Coarse-f.	Unsupervised	Abdomen
(Yang, Q. et al., 2021)	Unimodal	MR	Uni	1-to-1	1	Unsupervised	Prostate
(Yang, Y. et al., 2021)	Unimodal	greyscale	Uni	1-to-1	Coarse-f.	Classical	Brain
(Yang et al., 2022)	Multimodal	MR	Uni	1-to-1	1	Unsupervised	Prostate
(Ye et al., 2021)	Unimodal	MR	Bi	1-to-1	1	Unsupervised	Heart
(Ying et al., 2022)	Unimodal	MR	Uni	1-to-1	1	Classical	Breast
(Zhang, G. et al., 2021)	Unimodal		Uni	1-to-1	Pyramid	Unsupervised	Brain
(Zhang, L. et al., 2021)	Unimodal	MR	Uni	1-to-1	Pyramid	Unsupervised	Brain
(Zhu et al., 2021)	Unimodal	MR	Uni	1-to-1	Pyramid	Unsupervised	Head

References

Abbasi, S., Tavakoli, M., Boveiri, H. R., Shirazi, M. A. M., Khayami, R., Khorasani, H., ... & Mehdizadeh, A. (2022). Medical image registration using unsupervised deep neural network: A scoping literature review. Biomedical Signal Processing and Control, 73, 103444. [CrossRef]
Adelson, E. H., Anderson, C. H., Bergen, J. R., Burt, P. J., & Ogden, J. M. (1984). Pyramid methods in image processing. RCA engineer, 29(6), 33-41. 6).
Alcaín, E., Fernández, P. R., Nieto, R., Montemayor, A. S., Vilas, J., Galiana-Bordera, A., ... & Torrado-Carvajal, A. (2021). Hardware architectures for real-time medical imaging. Electronics, 10(24), 3118. [CrossRef]
Andreadis, G., Bosman, P. A., & Alderliesten, T. (2022, April). Multi-objective dual simplex-mesh based deformable image registration for 3D medical images-proof of concept. In Medical Imaging 2022: Image Processing (Vol. 12032, pp. 744-750). SPIE. [CrossRef]
Arun, K. S., Huang, T. S., & Blostein, S. D. (1987). Least-squares fitting of two 3-D point sets. IEEE Transactions on pattern analysis and machine intelligence, (5), 698-700.
Ashfaq, M., Minallah, N., Frnda, J., & Behan, L. (2022). Multi-Modal Rigid Image Registration and Segmentation Using Multi-Stage Forward Path Regenerative Genetic Algorithm. Symmetry, 14(8), 1506. [CrossRef]
Avants, B. B., Epstein, C. L., Grossman, M., & Gee, J. C. (2008). Symmetric diffeomorphic image registration with cross-correlation: evaluating automated labeling of elderly and neurodegenerative brain. Medical image analysis, 12(1), 26-41. [CrossRef]
Avants, B. B., Tustison, N. J., Stauffer, M., Song, G., Wu, B., & Gee, J. C. (2014). The Insight ToolKit image registration framework. Frontiers in neuroinformatics, 8, 44. [CrossRef]
Balakrishnan, G., Zhao, A., Sabuncu, M. R., Guttag, J., & Dalca, A. V. (2019). VoxelMorph: a learning framework for deformable medical image registration. IEEE transactions on medical imaging, 38(8), 1788-1800. [CrossRef]
Ban, Y., Wang, Y., Liu, S., Yang, B., Liu, M., Yin, L., & Zheng, W. (2022). 2D/3D multimode medical image alignment based on spatial histograms. Applied Sciences, 12(16), 8261. [CrossRef]
Bashkanov, O., Meyer, A., Schindele, D., Schostak, M., Tönnies, K. D., Hansen, C., & Rak, M. (2021, April). Learning Multi-Modal Volumetric Prostate Registration With Weak Inter-Subject Spatial Correspondence. In 2021 IEEE 18th International Symposium on Biomedical Imaging (ISBI) (pp. 1817-1821). IEEE. [CrossRef]
Begum, N., Badshah, N., Rada, L., Ademaj, A., Ashfaq, M., & Atta, H. (2022). An improved multi-modal joint segmentation and registration model based on Bhattacharyya distance measure. Alexandria Engineering Journal, 61(12), 12353-12365. [CrossRef]
Bengio, Y., Louradour, J., Collobert, R., & Weston, J. (2009, June). Curriculum learning. In Proceedings of the 26th annual international conference on machine learning (pp. 41-48).
Bouaziz, S., Tagliasacchi, A., & Pauly, M. (2013, August). Sparse iterative closest point. In Computer graphics forum (Vol. 32, No. 5, pp. 113-123). Oxford, UK: Blackwell Publishing Ltd.
Bronstein, M. M., Bruna, J., Cohen, T., & Veličković, P. (2021). Geometric deep learning: Grids, groups, graphs, geodesics, and gauges. arXiv preprint arXiv:2104.13478. arXiv:2104.13478.
Brown, L. G. (1992). A survey of image registration techniques. ACM computing surveys (CSUR), 24(4), 325-376. [CrossRef]
Burduja, M., & Ionescu, R. T. (2021, September). Unsupervised medical image alignment with curriculum learning. In 2021 IEEE International Conference on Image Processing (ICIP) (pp. 3787-3791). IEEE.
Chaudhary, M. F., Gerard, S. E., Wang, D., Christensen, G. E., Cooper, C. B., Schroeder, J. D., ... & Reinhardt, J. M. (2022, March). Single volume lung biomechanics from chest computed tomography using a mode preserving generative adversarial network. In 2022 IEEE 19th International Symposium on Biomedical Imaging (ISBI) (pp. 1-5). IEEE. [CrossRef]
Chen, J., Frey, E. C., He, Y., Segars, W. P., Li, Y., & Du, Y. (2022). Transmorph: Transformer for unsupervised medical image registration. Medical image analysis, 82, 102615. [CrossRef]
Chen, T., Yuan, M., Tang, J., & Lu, L. (2022). Digital Analysis of Smart Registration Methods for Magnetic Resonance Images in Public Healthcare. Frontiers in Public Health, 10, 896967. [CrossRef]
Chen, X., Diaz-Pinto, A., Ravikumar, N., & Frangi, A. F. (2021). Deep learning in medical image registration. Progress in Biomedical Engineering, 3(1), 012003. [CrossRef]
Chen, X., Wang, X., Zhang, K., Fung, K. M., Thai, T. C., Moore, K., ... & Qiu, Y. (2022). Recent advances and clinical applications of deep learning in medical image analysis. Medical Image Analysis, 79, 102444. [CrossRef]
Chen, X., Zhang, K., Abdoli, N., Gilley, P. W., Wang, X., Liu, H., ... & Qiu, Y. (2022). Transformers improve breast cancer diagnosis from unregistered multi-view mammograms. Diagnostics, 12(7), 1549. [CrossRef]
Cooper, L. A., “Mental rotation of random two-dimensional shapes,” Cognitive psychology, 7(1), 20-43(1975). [CrossRef]
Dahman, B., Bessier, F., & Dillenseger, J. L. (2022, April). Ultrasound to CT rigid image registration using CNN for the HIFU treatment of heart arrhythmias. In Medical Imaging 2022: Image-Guided Procedures, Robotic Interventions, and Modeling (Vol. 12034, pp. 246-252). SPIE. [CrossRef]
Decuyper, M., Maebe, J., Van Holen, R., & Vandenberghe, S. (2021). Artificial intelligence with deep learning in nuclear medicine and radiology. EJNMMI physics, 8(1), 81. [CrossRef]
Denton, E. L., Chintala, S., & Fergus, R. (2015). Deep generative image models using a laplacian pyramid of adversarial networks. Advances in neural information processing systems, 28.
Dey, N., Ren, M., Dalca, A. V., & Gerig, G. (2021). Generative adversarial registration for improved conditional deformable templates. In Proceedings of the IEEE/CVF international conference on computer vision (pp. 3929-3941). [CrossRef]
Dida, H., Charif, F., & Benchabane, A. (2022). Image registration of computed tomography of lung infected with COVID-19 using an improved sine cosine algorithm. Medical & Biological Engineering & Computing, 60(9), 2521-2535. [CrossRef]
Ding, W., Li, L., Zhuang, X., & Huang, L. (2022). Cross-Modality Multi-Atlas Segmentation via Deep Registration and Label Fusion. IEEE Journal of Biomedical and Health Informatics, 26(7), 3104-3115. [CrossRef]
Ding, Z., & Niethammer, M. (2022). Aladdin: Joint atlas building and diffeomorphic registration learning with pairwise alignment. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition (pp. 20784-20793). [CrossRef]
Djurabekova, N., Goldberg, A., Hawkes, D., Long, G., Lucka, F., & Betcke, M. M. (2022, October). 2D-3D motion registration of rigid objects within a soft tissue structure. In 7th International Conference on Image Formation in X-Ray Computed Tomography (Vol. 12304, pp. 518-526). SPIE.
Dossun, C., Niederst, C., Noel, G., & Meyer, P. (2022). Evaluation of DIR algorithm performance in real patients for radiotherapy treatments: A systematic review of operator-dependent strategies. Physica Medica, 101, 137-157. [CrossRef]
Dupuy, T., Beitone, C., Troccaz, J., & Voros, S. (2021, February). 2D/3D deep registration for real-time prostate biopsy navigation. In Medical Imaging 2021: Image-Guided Procedures, Robotic Interventions, and Modeling (Vol. 11598, pp. 463-471). SPIE. [CrossRef]
Estépar, R. S. J., Brun, A., & Westin, C. F. (2004). Robust generalized total least squares iterative closest point registration. In Medical Image Computing and Computer-Assisted Intervention–MICCAI 2004: 7th International Conference, Saint-Malo, France, September 26-29, 2004. Proceedings, Part I 7 (pp. 234-241). Springer Berlin Heidelberg.
Fitzpatrick, J. M., Hill, D. L., & Maurer, C. R. (2000). Image registration. Handbook of medical imaging, 2, 447-513.
Fu, H. J., Chen, P. Y., Yang, H. Y., Tsang, Y. W., & Lee, C. Y. (2022). Liver-directed stereotactic body radiotherapy can be reliably delivered to selected patients without internal fiducial markers—A case series. Journal of the Chinese Medical Association, 85(10), 1028-1032. [CrossRef]
Ganeshaaraj, G., Kaushalya, S., Kondarage, A. I., Karunaratne, A., Jones, J. R., & Nanayakkara, N. D. (2022, July). Semantic Segmentation of Micro-CT Images to Analyze Bone Ingrowth into Biodegradable Scaffolds. In 2022 44th Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC) (pp. 3830-3833). IEEE.
Gao, X., & Zheng, G. (2022, August). ACSGRegNet: A Deep Learning-based Framework for Unsupervised Joint Affine and Diffeomorphic Registration of Lumbar Spine CT via Cross-and Self-Attention Fusion. In Proceedings of the 2022 International Conference on Intelligent Medicine and Health (pp. 57-63). [CrossRef]
George, Y., Sedai, S., Antony, B. J., Ishikawa, H., Wollstein, G., Schuman, J. S., & Garnavi, R. (2021, April). Dueling deep Q-network for unsupervised inter-frame eye movement correction in optical coherence tomography volumes. In 2021 IEEE 18th International Symposium on Biomedical Imaging (ISBI) (pp. 1595-1599). IEEE. [CrossRef]
Goodfellow, I., Pouget-Abadie, J., Mirza, M., Xu, B., Warde-Farley, D., Ozair, S., ... & Bengio, Y. (2020). Generative adversarial networks. Communications of the ACM, 63(11), 139-144.
Goyal, A., & Bengio, Y. (2022). Inductive biases for deep learning of higher-level cognition. Proceedings of the Royal Society A, 478(2266), 20210068. [CrossRef]
Haskins, G., Kruger, U., & Yan, P. (2020). Deep learning in medical image registration: a survey. Machine Vision and Applications, 31, 1-18. [CrossRef]
Himthani, N., Brunn, M., Kim, J. Y., Schulte, M., Mang, A., & Biros, G. (2022). CLAIRE—Parallelized Diffeomorphic Image Registration for Large-Scale Biomedical Imaging Applications. Journal of Imaging, 8(9), 251. [CrossRef]
Hirotaki, K., Moriya, S., Akita, T., Yokoyama, K., & Sakae, T. (2022). Image preprocessing to improve the accuracy and robustness of mutual-information-based automatic image registration in proton therapy. Physica Medica, 101, 95-103. [CrossRef]
Ho, C. J., Wang, Y., Zhang, J., Nguyen, T., & An, C. (2021, October). A Convolutional Neural Network Pipeline For Multi-Temporal Retinal Image Registration. In 2021 18th International SoC Design Conference (ISOCC) (pp. 27-28). IEEE. [CrossRef]
Hoffmann, M., Billot, B., Greve, D. N., Iglesias, J. E., Fischl, B., & Dalca, A. V. (2021). SynthMorph: learning contrast-invariant registration without acquired images. IEEE transactions on medical imaging, 41(3), 543-558. [CrossRef]
Hou, Y., He, J., & She, B. (2022). Respiratory Motion Correction on PET Images Based on 3D Convolutional Neural Network. KSII Transactions on Internet and Information Systems (TIIS), 16(7), 2191-2208. [CrossRef]
Huang, J., Shlobin, N. A., Lam, S. K., & DeCuypere, M. (2022). Artificial intelligence applications in pediatric brain tumor imaging: A systematic review. World neurosurgery, 157, 99-105. [CrossRef]
Kasban, H., El-Bendary, M. A. M., & Salama, D. H. (2015). A comparative study of medical imaging techniques. International Journal of Information Science and Intelligent System, 4(2), 37-58.
Kim, W., Son, B., & Kim, I. (2021, July). Vilt: Vision-and-language transformer without convolution or region supervision. In International Conference on Machine Learning (pp. 5583-5594). PMLR.
Kujur, S. S., & Sahana, S. K. (2022). Medical image registration utilizing tissue P systems. Frontiers in Pharmacology, 13, 949872. [CrossRef]
Lai, W. S., Huang, J. B., Ahuja, N., & Yang, M. H. (2017). Deep laplacian pyramid networks for fast and accurate super-resolution. In Proceedings of the IEEE conference on computer vision and pattern recognition (pp. 624-632).
Lee, H. H., Tang, Y., Bao, S., Xu, Y., Yang, Q., Yu, X., ... & Landman, B. A. (2022, April). Supervised deep generation of high-resolution arterial phase computed tomography kidney substructure atlas. In Medical Imaging 2022: Image Processing (Vol. 12032, pp. 736-743). SPIE. [CrossRef]
Li, Y. X., Tang, H., Wang, W., Zhang, X. F., & Qu, H. (2022). Dual attention network for unsupervised medical image registration based on VoxelMorph. Scientific Reports, 12(1), 16250. [CrossRef]
Lin, T., Wang, Y., Liu, X., & Qiu, X. (2022). A survey of transformers. AI Open. [CrossRef]
Liu, P., Wang, F., Teodoro, G., & Kong, J. (2021, April). Histopathology image registration by integrated texture and spatial proximity based landmark selection and modification. In 2021 IEEE 18th International Symposium on Biomedical Imaging (ISBI) (pp. 1827-1830). IEEE. [CrossRef]
Ma, M., Xu, Y., Song, L., & Liu, G. (2022). Symmetric transformer-based network for unsupervised image registration. Knowledge-Based Systems, 257, 109959. [CrossRef]
Maillard, M., François, A., Glaunès, J., Bloch, I., & Gori, P. (2022, March). A deep residual learning implementation of metamorphosis. In 2022 IEEE 19th International Symposium on Biomedical Imaging (ISBI) (pp. 1-4). IEEE.
Meng, M., Bi, L., Fulham, M., Feng, D. D., & Kim, J. (2022). Enhancing medical image registration via appearance adjustment networks. NeuroImage, 259, 119444. [CrossRef]
Mitchell, T. M. (1980). The need for biases in learning generalizations (pp. 184-191). New Jersey: Department of Computer Science, Laboratory for Computer Science Research, Rutgers Univ.
Mitchell, W. J. (1984). What is an Image? New literary history, 15(3), 503-537.
Modat, M., Ridgway, G. R., Taylor, Z. A., Lehmann, M., Barnes, J., Hawkes, D. J., ... & Ourselin, S. (2010). Fast free-form deformation using graphics processing units. Computer methods and programs in biomedicine, 98(3), 278-284. [CrossRef]
Modersitzki, J. (2003). Numerical methods for image registration. OUP Oxford.
Mok, T. C., & Chung, A. (2022). Affine medical image registration with coarse-to-fine vision transformer. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (pp. 20835-20844).
Naik, R. R., Anitha, H., Bhat, S. N., Ampar, N., & Kundangar, R. (2022). Realistic C-arm to pCT registration for vertebral localization in spine surgery: A hybrid 3D-2D registration framework for intraoperative vertebral pose estimation. Medical & Biological Engineering & Computing, 60(8), 2271-2289.
Nazib, A., Fookes, C., Salvado, O., & Perrin, D. (2021, April). A multiple decoder CNN for inverse consistent 3D image registration. In 2021 IEEE 18th International Symposium on Biomedical Imaging (ISBI) (pp. 904-907). IEEE.
Ourselin, S., Roche, A., Subsol, G., Pennec, X., & Ayache, N. (2001). Reconstructing a 3D structure from serial histological sections. Image and vision computing, 19(1-2), 25-31. [CrossRef]
Oyallon, E., & Mallat, S. (2015). Deep roto-translation scattering for object classification. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (pp. 2865-2873).
Park, H., Lee, G. M., Kim, S., Ryu, G. H., Jeong, A., Sagong, M., & Park, S. H. (2022, March). A meta-learning approach for medical image registration. In 2022 IEEE 19th International Symposium on Biomedical Imaging (ISBI) (pp. 1-5). IEEE.
Ringel, M. J., Richey, W. L., Heiselman, J., Luo, M., Meszoely, I. M., & Miga, M. I. (2022, April). Breast image registration for surgery: insights on material mechanics modeling. In Medical Imaging 2022: Image-Guided Procedures, Robotic Interventions, and Modeling (Vol. 12034, pp. 223-230). SPIE.
Robertson, F. C., Raahil, M. S., Amich, J. M., Essayed, W. I., Lal, A., Lee, B. H., ... & Gormley, W. B. (2021). Frameless neuronavigation with computer vision and real-time tracking for bedside external ventricular drain placement: a cadaveric study. Journal of Neurosurgery, 136(5), 1475-1484. [CrossRef]
Saadat, S., Perriman, D., Scarvell, J. M., Smith, P. N., Galvin, C. R., Lynch, J., & Pickering, M. R. (2022). An efficient hybrid method for 3D to 2D medical image registration. International Journal of Computer Assisted Radiology and Surgery, 17(7), 1313-1320. [CrossRef]
Saiti, E., & Theoharis, T. (2022). Multimodal registration across 3D point clouds and CT-volumes. Computers & Graphics, 106, 259-266. [CrossRef]
Santarossa, M., Tatli, A., von der Burchard, C., Andresen, J., Roider, J., Handels, H., & Koch, R. (2022). Chronological Registration of OCT and Autofluorescence Findings in CSCR: Two Distinct Patterns in Disease Course. Diagnostics, 12(8), 1780. [CrossRef]
Schmidt, C., & Overhoff, H. M. (2023). Impact of PCA-based preprocessing and different CNN structures on deformable registration of sonograms. arXiv preprint arXiv:2301.08802. [CrossRef]
Stewart, C., Ibanez, L. (2004). Image Registration Course. Rensselaer Polytechnic Institute.
Stallings, R. (2010, April 22). Printing Lingo: What does Registration mean? Formax printing. https://www.formaxprinting.com/blog/2010/04/printing-lingo-what-does-registration-mean.
Su, S., Song, G., & Zhao, Y. (2021, November). 3D Registration of the Point Cloud Data Using Parameter Adaptive Super4PCS Algorithm in Medical Image Analysis. In 2021 4th International Conference on Digital Medicine and Image Processing (pp. 1-6). [CrossRef]
Sutton, R. S., & Barto, A. G. (1998). Introduction to reinforcement learning (Vol. 135, pp. 223-260). Cambridge: MIT Press.
Talwar, V., Chufal, K. S., & Joga, S. (2021). Artificial Intelligence: A New Tool in Oncologist's Armamentarium. Indian Journal of Medical and Paediatric Oncology, 42(06), 511-517.
Terpstra, M. L., Maspero, M., Sbrizzi, A., & van den Berg, C. A. (2022). ⊥-loss: A symmetric loss function for magnetic resonance imaging reconstruction and image registration with deep learning. Medical Image Analysis, 80, 102509.
Thirion, J. P. (1996, June). Non-rigid matching using demons. In Proceedings CVPR IEEE Computer Society Conference on Computer Vision and Pattern Recognition (pp. 245-251). IEEE.
Uneri, A., Wu, P., Jones, C. K., Ketcha, M. D., Vagdargi, P., Han, R., ... & Siewerdsen, J. H. (2021, February). Data-driven deformable 3D-2D registration for guiding neuroelectrode placement in deep brain stimulation. In Medical Imaging 2021: Image-Guided Procedures, Robotic Interventions, and Modeling (Vol. 11598, pp. 349-353). SPIE. [CrossRef]
Upendra, R. R., Hasan, S. K., Simon, R., Wentz, B. J., Shontz, S. M., Sacks, M. S., & Linte, C. A. (2021, November). Motion extraction of the right ventricle from 4D cardiac cine MRI using a deep learning-based deformable registration framework. In 2021 43rd Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC) (pp. 3795-3799). IEEE. [CrossRef]
Upendra, R. R., Simon, R., & Linte, C. A. (2021, February). Joint deep learning framework for image registration and segmentation of late gadolinium enhanced MRI and cine cardiac MRI. In Medical Imaging 2021: Image-Guided Procedures, Robotic Interventions, and Modeling (Vol. 11598, pp. 96-103). SPIE. [CrossRef]
Van Houtte, J., Audenaert, E., Zheng, G., & Sijbers, J. (2022). Deep learning-based 2D/3D registration of an atlas to biplanar X-ray images. International Journal of Computer Assisted Radiology and Surgery, 17(7), 1333-1342. [CrossRef]
Vargas-Bedoya, E., Rivera, J. C., Puerta, M. E., Angulo, A., Wahl, N., & Cabal, G. (2022). Contour Propagation for Radiotherapy Treatment Planning Using Nonrigid Registration and Parameter Optimization: Case Studies in Liver and Breast Cancer. Applied Sciences, 12(17), 8523. [CrossRef]
aswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., ... & Polosukhin, I. (2017). Attention is all you need. Advances in neural information processing systems, 30.
Vijayan, R. C., Han, R., Wu, P., Sheth, N. M., Vagdargi, P., Vogt, S., ... & Uneri, A. (2021, February). Fluoroscopic guidance of a surgical robot: pre-clinical evaluation in pelvic guidewire placement. In Medical Imaging 2021: Image-Guided Procedures, Robotic Interventions, and Modeling (Vol. 11598, pp. 393-399). SPIE. [CrossRef]
Wang, C. W., Lee, Y. C., Khalil, M. A., Lin, K. Y., Yu, C. P., & Lien, H. C. (2022). Fast cross-staining alignment of gigapixel whole slide images with application to prostate cancer and breast cancer analysis. Scientific Reports, 12(1), 11623. [CrossRef]
Wang, J., Yang, Z., Hu, X., Li, L., Lin, K., Gan, Z., ... & Wang, L. (2022). Git: A generative image-to-text transformer for vision and language. arXiv preprint arXiv:2205.14100. arXiv:2205.14100.
Wang, H. J., Lee, C. Y., Lai, J. H., Chang, Y. C., & Chen, C. M. (2022). Image registration method using representative feature detection and iterative coherent spatial mapping for infrared medical images with flat regions. Scientific Reports, 12(1), 7932. [CrossRef]
Wang, Y.; Liu, Z.; Cui, L. (2022). Research on Low Overlap Point Cloud Registration Algorithms in Medical Surgery. In Advances in Transdisciplinary Engineering. Volume 24: Advances in Machinery, Materials Science and Engineering Application. (pp. 694 - 701). [CrossRef]
Wang, Z., Xin, J., Shen, H., Chen, Q., Wang, Z., & Wang, X. (2022). Custom 3D fMRI Registration Template Construction Method Based on Time-Series Fusion. Diagnostics, 12(8), 2013. [CrossRef]
Wikipedia. 2023. “Printing registration.” Wikimedia Foundation. Last modified Jan 25, 2023. https://en.wikipedia.org/wiki/Printing_registration.
Wu, Y., Jiahao, T. Z., Wang, J., Yushkevich, P. A., Hsieh, M. A., & Gee, J. C. (2022). Nodeo: A neural ordinary differential equation based optimization framework for deformable image registration. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (pp. 20804-20813). [CrossRef]
Xiao, H., Teng, X., Liu, C., Li, T., Ren, G., Yang, R., ... & Cai, J. (2021). A review of deep learning-based three-dimensional medical image registration methods. Quantitative Imaging in Medicine and Surgery, 11(12), 4895. [CrossRef]
Xu, Z., Yan, J., Luo, J., Wells, W., Li, X., & Jagadeesan, J. (2021, April). Unimodal cyclic regularization for training multimodal image registration networks. In 2021 IEEE 18th International Symposium on Biomedical Imaging (ISBI) (pp. 1660-1664). IEEE. [CrossRef]
Yan, K., Cai, J., Jin, D., Miao, S., Guo, D., Harrison, A. P., ... & Lu, L. (2022). SAM: Self-supervised learning of pixel-wise anatomical embeddings in radiological images. IEEE Transactions on Medical Imaging, 41(10), 2658-2669. [CrossRef]
Yang, Q., Atkinson, D., Fu, Y., Syer, T., Yan, W., Punwani, S., ... & Hu, Y. (2022). Cross-Modality Image Registration Using a Training-Time Privileged Third Modality. IEEE Transactions on Medical Imaging, 41(11), 3421-3431. [CrossRef]
Yang, Q., Vercauteren, T., Fu, Y., Giganti, F., Ghavami, N., Stavrinides, V., ... & Hu, Y. (2021, April). Morphological change forecasting for prostate glands using feature-based registration and Kernel density extrapolation. In 2021 IEEE 18th International Symposium on Biomedical Imaging (ISBI) (pp. 1072-1076). IEEE. [CrossRef]
Yang, Y., Wang, F., & Guan, C. (2021). Application of Algorithm with Novel Successive Approximate Registration Method of Medical Image. In Journal of Physics: Conference Series (Vol. 1746, No. 1, p. 012043). IOP Publishing. [CrossRef]
Ye, M., Kanski, M., Yang, D., Chang, Q., Yan, Z., Huang, Q., ... & Metaxas, D. (2021). Deeptag: An unsupervised deep learning method for motion tracking on cardiac tagging magnetic resonance images. In Proceedings of the IEEE/CVF conference on computer vision and pattern recogni. [CrossRef]
Ying, J., Cattell, R., Zhao, T., Lei, L., Jiang, Z., Hussain, S. M., ... & Huang, C. (2022). Two fully automated data-driven 3D whole-breast segmentation strategies in MRI for MR-based breast density using image registration and U-Net with a focus on reproducibility. Visual Computing for Industry, Biomedicine, and Art, 5(1), 25. [CrossRef]
Zhang, J., Liu, F., Yu, X., Ma, Y., & Zhao, X. (2021, June). A 3D medical image registration method based on multi-scale feature fusion. In Journal of Physics: Conference Series (Vol. 1948, No. 1, p. 012057). IOP Publishing. [CrossRef]
Zhang, L., Zhou, L., Li, R., Wang, X., Han, B., & Liao, H. (2021, April). Cascaded feature warping network for unsupervised medical image registration. In 2021 IEEE 18th International Symposium on Biomedical Imaging (ISBI) (pp. 913-916). IEEE. [CrossRef]
Zhang, Y. N., Xia, K. R., Li, C. Y., Wei, B. L., & Zhang, B. (2021). Review of breast cancer pathologigcal image processing. BioMed research international, 2021, 1-7.tion (pp. 7261-7271). [CrossRef]
Zhu, W., Huang, Y., Xu, D., Qian, Z., Fan, W., & Xie, X. (2021, May). Test-time training for deformable multi-scale image registration. In 2021 IEEE International Conference on Robotics and Automation (ICRA) (pp. 13618-13625). IEEE.
Zitova, B., & Flusser, J. (2003). Image registration methods: a survey. Image and vision computing, 21(11), 977-1000. [CrossRef]

Figure 1. An example of printing misalignment and a crosshair on the right boundary. Crosshairs were used in the early printing industry to check misalignments like the misalignment between copies/pages.

Figure 2. Examples of mental alignment.

Figure 3. A transformation of an image from space i to space j.

Figure 4. Two representations of an image: Euclidean (left), and non-Euclidean (right).

Figure 5. An image transformation.

Figure 6. A displacement field estimated by an algorithm is used to register a moving image.

Figure 7. The displacement field transforms the domain of the moving image.

Figure 8. Examples of image interpolation.

Figure 9. Examples of deformation types.

Figure 10. Optimization phase.

Figure 11. MIR methods taxonomy.

Figure 12. Supervised MIR approaches: supervision using ground truth output image (right), and supervision using ground truth registration field (left).

Figure 13. Unsupervised MIR approach.

Figure 14. A demonstration of ICP registration.

Figure 15. Maxwell’s membrane with demons.

Figure 16. How demons work as explained in Thirion, J. P. (1996, June).

Figure 17. A demonstration of symmetry in SyN. A Transformation Tij, which rotates an image 180 degrees counterclockwise, can be decomposed into 2 symmetric rotations each of 90 degrees.

Figure 18. Invertible bidirectional Atlas-based transformations.

Figure 19. An example of a MIR model that estimates a transformation field and its inverse (InverseNet).

Figure 20. illustrates diagrams of IR in an internal correspondence space (left) and an external correspondence space (right).

Figure 23. Taxonomy of image registration stages.

Figure 24. Pyramid registration of three stages.

Figure 25. Space geometry taxonomy.

Figure 26. MIR taxonomy based on the modalities.

Figure 27. Evaluation Metrics.

Figure 28. TRE components.

Table 2. Registration in dictionaries (Oxford, Cambridge, Meriam Webster).

Dictionary	Word	Link
Oxford	Registration	https://www.oxfordlearnersdictionaries.com/definition/english/registration?q=registration
Oxford	Register (noun)	https://www.oxfordlearnersdictionaries.com/definition/english/register_2
Oxford	Register (verb)	https://www.oxfordlearnersdictionaries.com/definition/english/register_1?q=register
Cambridge	Registration	https://dictionary.cambridge.org/dictionary/english/registration
Cambridge	Register	https://dictionary.cambridge.org/dictionary/english/register
Meriam webster	Registration	https://www.merriam-webster.com/dictionary/registration
Meriam webster	Register	https://www.merriam-webster.com/dictionary/register

Table 5. Medical images datasets.

ROI	Modality	Dataset	Link
Brain	MR	OASIS: Open Access Series of Imaging Studies	https://www.oasis-brains.org/
	MR	LPBA40: The LONI Probabilistic Brain Atlas	https://www.loni.usc.edu/research/atlases
	MR	ADNI: Alzheimer’s Disease Neuroimaging Initiative	https://adni.loni.usc.edu/
	MR	IXI	https://brain-development.org/ixi-dataset/
	MR	IBIS
	MR	IBSR: The Internet Brain Segmentation Repository	https://www.nitrc.org/projects/ibsr
	MR	ADHD-200: Attention Deficit Hyperactivity Disorder	http://fcon_1000.projects.nitrc.org/indi/adhd200/
	MR	PPMI	https://www.ppmi-info.org/access-data-specimens/download-data/
	MR	CUMC12, MGH10	https://www.synapse.org/#!Synapse:syn3207203
	MR	ABIDE: Autism Brain Imaging Data Exchange	http://fcon_1000.projects.nitrc.org/indi/abide/
	MR	BraTS2017: Brain Tumor Segmentation	https://www.med.upenn.edu/sbia/brats2017/data.html
	MR	Mindboggle	https://mindboggle.info/data.html
	MR simulated	BrainWeb	https://brainweb.bic.mni.mcgill.ca/brainweb/
	MR / US	BITE: Brain Images of Tumors for Evaluation database	https://nist.mni.mcgill.ca/data/
	MR / US	CuRIOUS2018	https://curious2018.grand-challenge.org/Data/
	MR / US	RESECT: a clinical database of pre-operative MRI and intra-operative ultrasound in low-grade glioma surgeries	https://archive.norstore.no/pages/public/datasetDetail.jsf?id=10.11582/2017.00004
Prostate	MR	Prostate-3T	https://wiki.cancerimagingarchive.net/display/Public/Prostate-3T
	MR	PROMISE12: Prostate MR Image Segmentation 2012	https://zenodo.org/record/8026660
	MR	Prostate Fused-MRI-Pathology	https://wiki.cancerimagingarchive.net/pages/viewpage.action?pageId=23691514
Spine	CT, MR depending on the dataset	SpineWeb library	http://spineweb.digitalimaginggroup.ca/Index.php?n=Main.Datasets
Knee	MR	OAI	https://nda.nih.gov/oai/
Chest	CT	NLST	https://cdas.cancer.gov/datasets/nlst/
	CT	SPARE	https://image-x.sydney.edu.au/spare-challenge/
	XRAY	NIH ChestXray14	https://nihcc.app.box.com/v/ChestXray-NIHCC
	XRAY	JSRT: Japanese Society of Radiological Technology	http://db.jsrt.or.jp/eng.phphttp://imgcom.jsrt.or.jp/minijsrtdb/
	XRAY	Tuberculosis image datasets	https://lhncbc.nlm.nih.gov/LHC-downloads/downloads.html#tuberculosis-image-data-sets
Lung	CT	POPI	https://www.creatis.insa-lyon.fr/rio/popi-model_original_page
	CT	NLST	https://cdas.cancer.gov/datasets/nlst/
	CT	SPARE	https://image-x.sydney.edu.au/spare-challenge/
Heart	MR/CT	MM-WHS: Multi-Modality Whole Heart Segmentation	http://www.sdspeople.fudan.edu.cn/zhuangxiahai/0/mmwhs/
Heart	MR	SCD: The Sunnybrook Cardiac Data	https://www.cardiacatlas.org/sunnybrook-cardiac-data/
Liver	CT	sliver07	https://sliver07.grand-challenge.org/Home/
Kidney	CT	KITS23	https://kits-challenge.org/kits23/
Pancreas	CT	Pancreas-CT	https://opendatalab.com/Pancreas-CT_Datasethttps://wiki.cancerimagingarchive.net/display/public/pancreas-ct
Abdomen (kidney, liver, Spleen, Pancreas)	CT	Anatomy3	https://visceral.eu/benchmarks/anatomy3-open/
10 ROIs	MR or CT	Medical Segmentation Decathon challenge	https://decathlon-10.grand-challenge.org/

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Deep Learning in Medical Image Registration: Introduction and Survey

Abstract

1.0. Image registration etymology

1.1. Registration in Dictionaries

1.2. Registration in the printing industry

2.0. Image registration definition

2.1. IR definitions in the literature

2.2. IR definition

3.0. Introductory example

3.1. Image representations

3.2. Image transformation

3.3.1. Image deformation using a displacement field

3.3. post-processing

4.0. Review criterion

5.0. Related survey papers

6.0. Taxonomies

6.1. Deformation types

6.2. Optimization phase

6.3. MIR algorithms

6.3.1. Deep learning approaches

6.3.2. non-deep learning methods:

6.4. Correspondence space

6.5. Correspondence relation

6.6. Multistage image registration

6.6.1. Coarse-fine registration:

6.6.2. Pyramid image registration.

6.7. Space Geometry

6.8. Other taxonomies

6.8.1. Feature-based and pixel-based

6.8.2. Medical imaging modalities

7.0. Evaluation measures

7.1. Time

7.2. Distance-based measures

7.3. Segmentation measures

7.4. Correlation measures

7.5. The smoothness of the registration field

7.6. Model size

7.7. Clinical-based evaluation

8.0. Medical imaging datasets

9.0. Medical applications

9.1. Image-guided surgery

9.2. Tumor diagnosis and therapy

9.3. Motion processing

10.0. Other research directions

10.1. Transformers

10.2. No Registration

Acknowledgments

Nomenclature & Abbreviations

Appendix A.

References

MDPI Initiatives

Important Links

Subscribe