Prerpints.org logo
Preprint
Article

FPL: False Positive Loss

Altmetrics

Downloads

293

Views

84

Comments

0

Submitted:

02 September 2023

Posted:

06 September 2023

You are already at the latest version

Alerts
Abstract
When training deep neural networks tasks, the most popular choices are cross-entropy loss. On the other hand, in general speaking, a decent loss function can take on shapes that are considerably more flexible and ought to be adapted for different activities and datasets. In most of the classification tasks, generally if the true class is not correctly recognized by the network (top1), that class is placed among the five classes with the highest probability (top5). This shows that the network does not necessarily recognize the correct class with a low probability, but a class similar to it (such as 3 vs. 8 in mnist) assigns a higher probability and this causes a mistake in that task. Accordingly, we proposed a loss function deals with the error of class that the neural network incorrectly recognized as correct, in addition to the correct class error. We call our proposed loss as False Positive Loss (FPL), with the intention of viewing and designing loss functions not only through the utilization of true class but also through the utilization of the value of false positive classes. One of the core properties of our proposed loss is full adaptability, which makes False Positive Loss be fully capable of getting reformulated by using other widely used loss functions formulas based on the task or the need of the users. Extensive experimental results demonstrate that our suggested loss function outperforms other well-known losses on a variety of tasks and datasets. As can be observed, the performance of our False Positive Loss is superior to that of the cross-entropy loss when it comes to tasks involving 2D picture classification. We have compared our loss with cross entropy as the most common classification loss function on some models (such as ResNet-18, ResNet-50 and Efficientnet-V2) through classification known as a basic computer vision task. with both random or pre-trained initial weights. As a result, in some cases the models with our loss outperform the same tasks with cross entropy from the viewpoint of some metric (i.e. accuracy and FP). For example, the resnet-50 on cifar-10 dataset with random initialization indicated a top1 accuracy of 94.93 with cross entropy and 95.25 with our loss, while for top5 accuracy the results are 99.86 and 99.87, respectively.
Keywords: 
Subject: Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

1. Introduction

Optimizing neural networks hinges on the significance of loss functions. From a theoretical perspective, a loss function can be any differentiable function that transforms predictions and labels into a singular value. Nevertheless, given the extensive design scope, it’s usually tricky to devise a potent loss function, and it’s even more daunting to create a universal one that can function across diverse tasks and data sets. For instance, while L1/L2 losses are frequently employed for regression tasks, they are seldom applied in classification tasks. Focal loss and poly loss are frequently utilized to tackle the issue of overfitting of the cross-entropy loss in unevenly distributed object detection datasets [1], although their efficacy for this specific application hasn’t been proven in this study.
Designing a universal loss Numerous recent publications have investigated new loss functions by means of meta-learning, ensembles of diverse losses, or compositing various types of losses [2,3,4,5]. As we motioned, many of the well-designed, well-known, and widely used loss functions are task specific for example in Face Net [6] researchers designed their own loss function to solve the face recognition task. This could be alluded to as a drawback. According to this fact designing a new loss function which could be applied to a variety of task is a work of art. Another issue in designing a loss function which is not getting serious attention from researchers who design loss function is value ignoring for false positive classes.

1.1. Investigation over image classification loss functions

Cross-entropy loss is utilized in models for perception tasks such as categorization, detection, and semantic segmentation [7,8,9]. These models are popular and state-of-the-art now. Several other losses have been suggested as potential ways to improve cross-entropy loss [1,10,11,12]. In contrast to other publications, the purpose of this one is to develop an adaptive framework for the purpose of methodically creating a classification loss function that is superior loss for class imbalance.
Triple loss[6] involves reducing the distance between an anchor and a positive, which share the same identity, while increasing the distance between the anchor and a negative with a different identity. We suggest a simple framework for the loss function.

1.2. Loss for class imbalance

Because of class imbalance, training detection models is a tough task. This is especially true for single-stage detectors. To solve the problem of class imbalance, numerous solutions such as "hard example mining" and "reweighing" have been created [13,14,15,16,17]. Focal loss is one of these ways, and it is aimed to reduce the class imbalance issue by focusing on the difficult samples. It is also used to train cutting-edge 2D and 3D detectors [1,18,19,20,21]. By utilizing the False Positive Loss (FPL) architecture, we were able to find an improved loss function that acts in a manner that is diametrically opposed to that of focused loss. In addition to this, we present an intuitive understanding of why it is vital to create multiple loss functions utilizing the FPL framework and tailoring them to different unbalanced datasets.

1.3. Robust loss to label noise

Another path that could be pursued in research is the development of loss functions that are resistant to label noise [22,23,24,25,26]. The method of incorporating a noise-resistant loss function into cross-entropy loss, such as Mean Absolute Error (MAE), is one that is frequently utilized. MAE and cross-entropy loss are said to be unified by the Taylor cross entropy loss. The researchers showed that by eliminating higher-order polynomials, the truncated cross-entropy loss function more closely resembles MAE, which is better equipped to handle label noise on datasets with synthetic label noise. In contrast, our False Positive Loss provides a broader framework for creating loss functions for different datasets by adjusting the hyperparameters of the loss functions.

1.4. loss functions that learn

The latest research reveals that the loss function can be trained concurrently during the learning process via gradient descent or meta-learning [2,3,5,27]. Notably, Taylor GLO employs CMA-ES to optimize a multivariate Taylor parameterization of both the loss function and learning rate schedule throughout the training [4,28]. The findings suggest that adopting a four-parameter parameterization leads to a trained loss function schedule that surpasses cross-entropy loss in classification tasks, a result attributed to the expansion of the search space with the polynomial order.

2. Materials and Methods

In this paper we have introduced a novel loss function, which cares the negative class(es) along with the positive class. The first key insight of our proposed loss, False Positive Loss, is to minimize the distance between one and the prediction probability of belonging of positive class, sum with, minimize the distance between zero and prediction probability of negative class(es). Moreover, we have designed a loss function which is fully adaptive based on the task and could be easily reformulate by other loss functions formulas. Furthermore, choosing the right hyperparameters in our proposed loss makes it overcome issues such as imbalanced data. We will dive into these details in the experimental results section.

2.1. FPL definition

Based on the previous studies, to achieve more distance between classes, we have cared the positive distance and negative distance(s) simultaneously. For one sample, the positive one calculates the distance between the true class prediction and one. The negative one, on the other hand, computes the distance between the prediction of that negative class and zero, for each negative class. Our proposed loss is fully adaptive based on the need or desire of researchers. Our main goal in designing this loss was to ensure that the formulation of our proposed loss could be changed or integrated with all other well-known and widely used losses.
The general form of False Positive Loss is:
F P L ( y , y ^ ) = α T L T ( y , y ^ ) + α F L F ( y , y ^ )
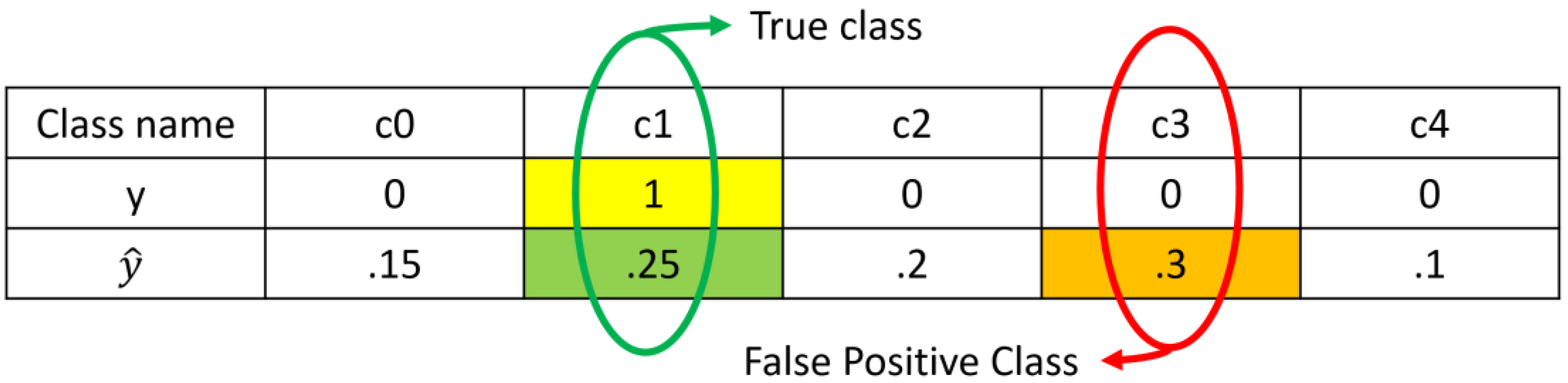
where T is true class, F is false positive class (see Figure 1), L T is loss of true class, L F is loss of false positive class, α T and α F are hyperparameters, y and y ^ are target and predicted values, respectively. As it can be seen, our proposed loss general formula consists of 4 different terms. Here, the false positive class ( F ) is one of those classes that are not true class, with maximum prediction of model. For better understanding, Figure 1 shows the false positive class for one sample that is predicted by model.
Preprints 84050 g001
Figure 1. The true class and false positive class when the model predicts one sample.
Figure 1. The true class and false positive class when the model predicts one sample.
Preprints 84050 g001
At first, L T and L F are cross entropy functions. In other words, they are defined as:
L T y , y ^ = − log ⁡ p T
where p T is the prediction of true class, and
L F y , y ^ = − log ⁡ 1 − p F
where p F is the prediction of false positive class.
On the other hand, for α T and α F we have:
( α i = N − N i N )
where N is number of total samples and N i is the number of samples in class i .

2.2. FPL and Class imbalance

Class imbalance is a serious challenge in tasks such as classification or object detection. For this purpose, we have used α i coefficients to reduce the influence of the class that has more samples than others. This is especially noticeable in the background class of object detection methods. Although the authors of this article are aware that the growth of the cross-entropy function (logarithm) in the interval [0,1] is much faster than the linear growth of α   (which makes the effect of α i weaker against the cross-entropy), but finally with We achieved favorable results with these settings.

2.3. FPL Alternatives

We have considered multiple configurations for our proposed loss. Here we discuss some of these configurations:
L T y , y ^ = 1 − p T 2
and
L F y , y ^ = p F 2
These two terms take a value based on a chosen loss. In other words, if we chose MSE for these terms, L T y , y ^ would be the part of MSE which contains the value for true class and L F y , y ^ would be the term in MSE formula which contains the value for false positive class respectively.
An alternative for α i is as follows:
α i = ( m − m i m )
where m is size of minibatch and m i is number of samples with class i in that minibatch. The advantage of recent formula is that α i is separately computed in each minibatch, which doesn’t need to get subsidiary information to compute the loss.
An alternative for false positive class is using two or more classes with high probabilities that are not true class. So, the formula of FPL could be change to:
F P L ( y , y ^ ) = α T L T ( y , y ^ ) + ∑ F α F L F ( y , y ^ )
where F = F 1 , F 2 ,   . . ,   F k is set of k false classes with highest predictions.

3. Results

Here, we compare FPL with cross-entropy loss on the cifar10 classification task over various networks like ResNet18, ResNet50, and Efficientnet. For the following experiments, we used our implementation for the cifar10[29] classification task and also we optimize the hyperparameters in the mmclassification [30] open-source platform without any tuning.

3.1. Dataset

The Cifar10 dataset [29] was utilized to assess FPL. It comprises 50,000 training examples and 10,000 testing examples across 10 classes: Airplane, Automobile, Bird, Cat, Deer, Dog, Frog, Horse, Ship, and Truck. Some examples from this dataset are depicted in Figure 1.

3.2. Evaluation metrics

The performance of FPL is evaluated using the accuracy metric, which is calculated based on FP, FN, TP, and TF. We also investigated the loss performance using the number of FP that happened for classifying each class sample. Finally, we compare the purposed loss function against cross-entropy loss employing the number of FP and accuracy. Equation 9 demonstrates how accuracy is estimated based on the abovementioned quantitative metrics.
A c c u r a c y = T P + T N T P + F P + T N + F N

3.3. Hardware Setup

The hardware that is used and parameters in training of our implementation are indicated in Table 1.
Table 1. setup of configuration.
Table 1. setup of configuration.
Hardware Spec
GPU NVIDIA® RTX A5000
CUDA version v11.3 with cuDNN v8.2.0
Framework PyTorch v1.9.1
Training parameters Value
Batch size 64
Epochs 20
Initial Learning Rate 0.001
Optimizer AdaDelta
Scheduler CosineAnnealingLR

3.4. Evaluating FPL

Table 2 compares the results of False Positive Loss (FPL) with Cross Entropy (CE) as the most common classification loss function. FPL yields 39 and 5 lower False Positive predictions compared to Cross Entropy while using Efficientnet V2 and ResNet18 as the classifier backbone, respectively. Table 3 illustrates the results of training the resnet50 classifier using FPL and CE. FPL indicated better performance regarding 0.68 in Top-1 and 0.02 in Top-5 higher classification accuracy Compared to Cross Entropy.
Table 2. Comparing the performance of False Positive Loss with Cross Entropy. Our implementation determines the results.
Table 2. Comparing the performance of False Positive Loss with Cross Entropy. Our implementation determines the results.
Network Loss False Positive Total FP
Airplane Automobile Bird Cat Deer Dog Frog Horse Ship Truck
Efficientnet V2 FPL 716 183 375 500 966 116 461 416 45 647 4425
CE 575 183 495 899 670 167 494 365 63 553 4464
Resnet18 FPL 402 131 260 883 702 69 417 281 64 322 3531
CE 411 144 359 818 631 63 381 315 58 356 3536
Table 3. Comparing the performance of the resnet50 classifier. MMCLASSIFICATION [30] repository used to train and test the method.
Table 3. Comparing the performance of the resnet50 classifier. MMCLASSIFICATION [30] repository used to train and test the method.
Network Pretrained Dataset FineTuned Dataset Loss Epochs Top-1 Top-5
ResNet50 - Cifar10 [29] FPL 200 95.25 99.87
ResNet50 - Cifar10 [29] CE 200 94.93 99.85
ResNet50 ImageNet[31] Cifar10 [29] FPL 10 94.02 99.93
ResNet50 ImageNet[31] Cifar10 [29] CE 10 94.22 99.89

3.5. Analyzing Accuracy over epochs

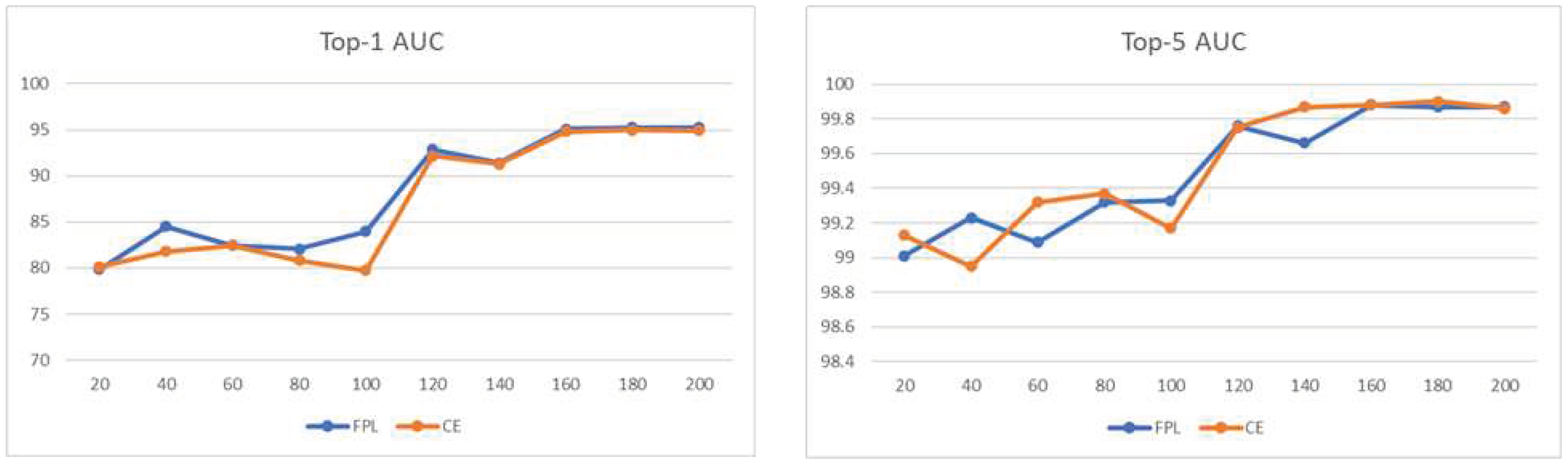
Figure 2 shows the variation of the top-1 and top-5 accuracy over epochs (Eq. 1) during the training process for resnet50 using FPL and CE. FPL provides a smoother enlargement in accuracy during the training procedure, indicating the FPL potential that led the model weights to a better local optimum. On the other hand, cross-entropy could not suppress the second maximum value, which means that our proposed modification to cross-entropy can decrease False Positives.
Preprints 84050 g002
Figure 2. Cifar10 [29] is a Tiny Images dataset subset and consists of 60000 32x32 color RGB samples.
Figure 2. Cifar10 [29] is a Tiny Images dataset subset and consists of 60000 32x32 color RGB samples.
Preprints 84050 g002
Preprints 84050 g003
Figure 3. Top-1 and Top-5 accuracy over epochs.
Figure 3. Top-1 and Top-5 accuracy over epochs.
Preprints 84050 g003

4. Discussion

In different tasks based on different needs for researchers, the terms of FPL could take different values. In other words, it is totally up to the user. For instance, any well-known loss function such as MSE, CE, etc. can be used to find the corresponding value for each term of FPL. Therefore, our proposed loss function is fully adaptive.
False Positive Loss provides a framework for designing new loss functions, which have two main properties. First as we mentioned the general formula of this proposed loss function is fully adaptive consisting of 4 different parameters. α i could take any value based on the need of research. L T and L F terms take value based on a chosen loss function such as widely used MSE. Secondly, it makes more distances between true class and false positive class by caring the importance of false positive class, which other loss functions do not allude to. For example, the cross-entropy loss does not care about the value of false positive classes, in the classification task, while out proposed loss function tries to increase the distance of true class and the maximum predicted wrong class. At this point, choosing the value for representing false positive classes is limited to the maximum predicted of false positive classes. However, it can be totally adaptive; i.e., we could use a mean or median over the value of false positive classes.
Although in all cases our loss is comparable with other ones, we had many results that we could not outperform other losses. We think tuning α i or learning it during the training phase led to achieve better results.

5. Conclusions

Cross-entropy loss is popular for deep learning categorization. A good loss function should be flexible and adaptable to varied activities and datasets.
When a class is not accurately identified by the network (top1) in the majority of classification and object detection tasks, that class is often put among the top five classes with the highest likelihood (top5). This demonstrates that network assigned a similar class a greater probability than the true class, leading to an error in classification. in this paper, we presented a loss function in which, in addition to dealing with the true class error, the loss also deals with the class that is falsely identified as positive class.
One of the key characteristics of the loss we have proposed is adaptability, which enables False Positive Loss to be recast using other widely used loss function formulae depending on the job or need of the users. FPL performs better than well-known loss Cross-entropy loss in the classification of 2D images.

Author Contributions

A.A.K., M.B. proposed the core function, A.A.K. and N.B. tuned the hyperparameters, A.A.K., M.B., S.A., N.B., and A.F. implementing the classification approach and prepared results. N.S., S.A., D.S., R.B., and A.F. participated in most of the study steps. All authors have read and approved the content of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Acknowledgments

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Lin, T.-Y.; Goyal, P.; Girshick, R.; He, K.; Dollár, P. Focal Loss for Dense Object Detection. In Proceedings of the Proceedings of the IEEE international conference on computer vision; 2017; pp. 2980–2988.
  2. Hajiabadi, H.; Molla-Aliod, D.; Monsefi, R. On Extending Neural Networks with Loss Ensembles for Text Classification. arXiv preprint arXiv:1711.05170 2017.
  3. Xu, H.; Zhang, H.; Hu, Z.; Liang, X.; Salakhutdinov, R.; Xing, E. Autoloss: Learning Discrete Schedules for Alternate Optimization. arXiv preprint arXiv:1810.02442 2018.
  4. Gonzalez, S.; Miikkulainen, R. Optimizing Loss Functions through Multi-Variate Taylor Polynomial Parameterization. In Proceedings of the Proceedings of the Genetic and Evolutionary Computation Conference; 2021; pp. 305–313.
  5. Li, C.; Yuan, X.; Lin, C.; Guo, M.; Wu, W.; Yan, J.; Ouyang, W. Am-Lfs: Automl for Loss Function Search. In Proceedings of the Proceedings of the IEEE/CVF International Conference on Computer Vision; 2019; pp. 8410–8419.
  6. Schroff, F.; Kalenichenko, D.; Philbin, J. Facenet: A Unified Embedding for Face Recognition and Clustering. In Proceedings of the Proceedings of the IEEE conference on computer vision and pattern recognition; 2015; pp. 815–823.
  7. Tan, M.; Le, Q. Efficientnetv2: Smaller Models and Faster Training. In Proceedings of the International Conference on Machine Learning; PMLR, 2021; pp. 10096–10106.
  8. Tao, A.; Sapra, K.; Catanzaro, B. Hierarchical Multi-Scale Attention for Semantic Segmentation. arXiv preprint arXiv:2005.10821 2020.
  9. Zoph, B.; Ghiasi, G.; Lin, T.-Y.; Cui, Y.; Liu, H.; Cubuk, E.D.; Le, Q. Rethinking Pre-Training and Self-Training. Advances in neural information processing systems 2020, 33, 3833–3845.
  10. Law, H.; Deng, J. Cornernet: Detecting Objects as Paired Keypoints. In Proceedings of the Proceedings of the European conference on computer vision (ECCV); 2018; pp. 734–750.
  11. Cui, Y.; Jia, M.; Lin, T.-Y.; Song, Y.; Belongie, S. Class-Balanced Loss Based on Effective Number of Samples. arXiv:1901.05555 [cs] 2019.
  12. Zhao, G.; Yang, W.; Ren, X.; Li, L.; Wu, Y.; Sun, X. Well-Classified Examples Are Underestimated in Classification with Deep Neural Networks. In Proceedings of the Proceedings of the AAAI Conference on Artificial Intelligence; 2022; Vol. 36, pp. 9180–9189.
  13. Sung, K.-K. Learning and Example Selection for Object and Pattern Detection. 1996.
  14. Felzenszwalb, P.F.; Girshick, R.B.; McAllester, D. Cascade Object Detection with Deformable Part Models. In Proceedings of the 2010 IEEE Computer society conference on computer vision and pattern recognition; Ieee, 2010; pp. 2241–2248.
  15. Shrivastava, A.; Gupta, A.; Girshick, R. Training Region-Based Object Detectors with Online Hard Example Mining. In Proceedings of the Proceedings of the IEEE conference on computer vision and pattern recognition; 2016; pp. 761–769.
  16. Liu, W.; Anguelov, D.; Erhan, D.; Szegedy, C.; Reed, S.; Fu, C.-Y.; Berg, A.C. Ssd: Single Shot Multibox Detector. In Proceedings of the European conference on computer vision; Springer, 2016; pp. 21–37.
  17. Rota Bulo, S.; Neuhold, G.; Kontschieder, P. Loss Max-Pooling for Semantic Image Segmentation. In Proceedings of the Proceedings of the IEEE conference on computer vision and pattern recognition; 2017; pp. 2126–2135.
  18. Tan, M.; Pang, R.; Le, Q.V. Efficientdet: Scalable and Efficient Object Detection. In Proceedings of the Proceedings of the IEEE/CVF conference on computer vision and pattern recognition; 2020; pp. 10781–10790.
  19. Shi, S.; Guo, C.; Jiang, L.; Wang, Z.; Shi, J.; Wang, X.; Li, H. Pv-Rcnn: Point-Voxel Feature Set Abstraction for 3d Object Detection. In Proceedings of the Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition; 2020; pp. 10529–10538.
  20. Sun, P.; Wang, W.; Chai, Y.; Elsayed, G.; Bewley, A.; Zhang, X.; Sminchisescu, C.; Anguelov, D. Rsn: Range Sparse Net for Efficient, Accurate Lidar 3d Object Detection. In Proceedings of the Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition; 2021; pp. 5725–5734.
  21. Du, X.; Lin, T.-Y.; Jin, P.; Ghiasi, G.; Tan, M.; Cui, Y.; Le, Q.V.; Song, X. Spinenet: Learning Scale-Permuted Backbone for Recognition and Localization. In Proceedings of the Proceedings of the IEEE/CVF conference on computer vision and pattern recognition; 2020; pp. 11592–11601.
  22. Ghosh, A.; Manwani, N.; Sastry, P.S. Making Risk Minimization Tolerant to Label Noise. Neurocomputing 2015, 160, 93–107.
  23. Zhang, Z.; Sabuncu, M.R. Generalized Cross Entropy Loss for Training Deep Neural Networks with Noisy Labels 2018.
  24. Wang, Y.; Ma, X.; Chen, Z.; Luo, Y.; Yi, J.; Bailey, J. Symmetric Cross Entropy for Robust Learning with Noisy Labels. In Proceedings of the Proceedings of the IEEE/CVF International Conference on Computer Vision; 2019; pp. 322–330.
  25. Oksuz, K.; Cam, B.C.; Kalkan, S.; Akbas, E. Imbalance Problems in Object Detection: A Review. IEEE transactions on pattern analysis and machine intelligence 2020, 43, 3388–3415.
  26. Menon, A.K.; Rawat, A.S.; Reddi, S.J.; Kumar, S. Can Gradient Clipping Mitigate Label Noise? In Proceedings of the International Conference on Learning Representations; 2019.
  27. Gonzalez, S.; Miikkulainen, R. Improved Training Speed, Accuracy, and Data Utilization through Loss Function Optimization. In Proceedings of the 2020 IEEE Congress on Evolutionary Computation (CEC); IEEE, 2020; pp. 1–8.
  28. Hansen, N.; Ostermeier, A. Adapting Arbitrary Normal Mutation Distributions in Evolution Strategies: The Covariance Matrix Adaptation. In Proceedings of the Proceedings of IEEE international conference on evolutionary computation; IEEE, 1996; pp. 312–317.
  29. CIFAR-10 and CIFAR-100 Datasets Available online: https://www.cs.toronto.edu/~kriz/cifar.html (accessed on 26 December 2022).
  30. MMClassification Contributors OpenMMLab’s Image Classification Toolbox and Benchmark 2020.
  31. Deng, J.; Dong, W.; Socher, R.; Li, L.-J.; Li, K.; Fei-Fei, L. ImageNet: A Large-Scale Hierarchical Image Database. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition; June 2009; pp. 248–255.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated