Prerpints.org logo
Preprint
Review

Revisiting the Probabilistic Latent Semantic Analysis: The Method, Its Extensions and Its Algorithms

Altmetrics

Downloads

189

Views

297

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

04 September 2023

Posted:

06 September 2023

You are already at the latest version

Alerts
Abstract
Probabilistic latent semantic analysis is a statistical technique developed for information retrieval and spanned many fields. It yields intuitive and solid results. However, the rigidity of the assumptions and the iterative nature derived from the Expectation-maximization algorithm generate several problems, dividing detractors and enthusiasts. In this manuscript, we first describe the Probabilistic latent semantic analysis. After, we discuss reformulations that attempt to solve these problems. We pay special attention to the works relating Probabilistic latent semantic analysis and the Singular value decomposition Theorem. Also, Probabilistic latent semantic analysis can be the basis for other techniques, such as kernelization or probabilistic transfer learning, and those that extend the descriptive character of the Principal component analysis to an inferential tool and open a window of opportunities.
Keywords: 
Subject: Computer Science and Mathematics  -   Information Systems

1. Introduction

Informally, Information Retrieval (IR) can be defined as the methods to process information to construct collections of documents. Probabilistic latent semantic analysis (PLSA) was firstly formulated as an unsupervised IR technique. This method, also known as Probabilistic latent semantic indexing (PLSI), was introduced in conference proceedings [1,2]. The classical reference is unsupervised learning by probabilistic latent semantic analysis by Hofmann [3]. PLSA is based on the ideas of Latent semantic analysis (LSA) [4] and in fact is a probabilistic remake. LSA uses cross terms and documents of a corpus to obtain a count or a table of co-occurrences. Then, arranging frequencies in a matrix, the Singular value decomposition (SVD) space span is considered a set of latent variables and interpreted as the aspect model [5]. The PLSA uses the frequencies to decompose them as mixtures or aggregate Markov models [3], and adjusted with the Expectation maximization (EM) algorithm.
Although PLSA was formulated as an IR technique, it has been used for diverse purposes. PLSA’s versatility, clarity of results, and solid statistical properties have enabled a wide range of applications, in which the concepts of words and documents are assimilated into other discrete entities, thus enabling justification of the hypotheses on which PLSA relies. However, the PLSA has several problems: ( i ) the nature of the data and the underlying hypotheses leads to a rigid model; ( i i ) the iterative nature, based on the EM algorithm, has very slow convergence; and ( i i i ) probabilistic interpretation is lacking for latent variables. Those problems translate to uneven growth, as partly determined by algorithmic and computational advances. These limitations have prompted several reformulations and a myriad of algorithms, the development of related techniques, such as Latent Dirichlet allocation (LDA), and other studies focused on the relationship between PLSA and Non-negative matrix factorization (NMF).
Exists many surveys and review articles including PLSA as a technique for IR, as [6], with a classical perspective. Other works recompile this technique as an alternative to classifying opinions from Twitter [7], or a method to detect fake news [7]. However, few reviews have focused exclusively on PLSA. One such review, by Tian [8], focuses on semantic image analysis.
In this manuscript, we pay special attention to what has been written on PLSA, the extension of this method to less restrictive data structures than co-occurrences or contingency tables, the obtained results by modifying the underlying hypotheses, and the relationship with other techniques. These results makes the PLSA a fundamental character, providing a probabilistic interpretation of the SVD.
This article is structured to reflect this point of view. The Section 3 is dedicated to the solutions of the two PLSA formulations, and the extent of their use as a supervised and semi-supervised technique. Criticism introduced by LDA is the starting point of several contributions, examined in Section 4. Mixtures in which it decomposes the PLSA relate it in a natural way to the NMF. From this viewpoint, extensions are introduced in Section 5, and are considered to represent a qualitative leap. Extensions which are conceptually relevant according to the exposed criteria, are compiled in the Section 6 and are summarized in Table 1. The works dedicated to efficiency improvement are also discussed in the Section 7. Although no studies have provided definitive results, they illustrate the efforts to construct fast and reliable computational solutions. In addition, this article has attempted to use a consistent notation.

2. Literature Review

According to our bibliographic searches (Web of Science, Scopus, Arxiv, and Google Scholar), there are a relatively large number of articles based on the PLSA. It has successfully spaned many research areas, as shown in Table 2.
The widest field of applications is Engineering, which we consider separate from Information Engineering or Computer Sciences. The applications of PLSA to this field rely on the ability of PLSA to handle discrete entities as words. Some examples are [19] seeks communication with machines and proposes to use the method to obtain a distribution. It claims that it is advantageous concerning supervised methods.
Applications of Information Engineering include syntactic structure study, quickly examined in [20]. Collaborative filtering, in which user ratings construct suitable matrices to perform PLSA algorithms [21]; or speech recognition, introducing a score concatenation matrix [22,23], cybersecurity [24] and analysis of keywords from webs related to certain topics and sentiment analysis (involving a system of definitions on which the users’ opinions and other instances, analyzed as co-occurrences) [25,26].
We adopt the Tians’ criteria for PLSA image applications. Tian classifies contributions into three types: image annotation, image retrieval, and image classification. Image annotation involves generating textual words to describe the content [27], with diverse applications including internet image filtering [28]; image retrieval, consisting of a procedure of ranking images in a database according to their posterior probabilities of being relevant to infer which visual patterns describe each object [8]; pioneering work [29]; and use in clinical image diagnosis [30,31] or facial expression semantics [32]. Image classification [33] has also enabled pain recognition [34] or autonomous driving [35]. Several variants exist, such as co-regularized PLSA, for the recognition of observed images with different perspectives [36], among many others. For applications and developments in semantic image analysis, we refer readers to the Tian (2018) review and its selected references [8].
Examples in Life Sciences can be found in bioinformatics [37,38] identificating genomic sequences with documents and some classes of genotype characteristics, such as words; neurodegenerative diseases, identifying common and non-common symptoms [39] and biology, the work [40] is devoted to the nuclear prediction and localization of proteins.
Applications in foundamental sicences include geophysics [41], instrumentation [42], spectroscopy [43]. A comparative study of PLSA, latent Dirichlet allocation (LDA), and other techniques in the framework of spectroscopy, recently published is [44].
The PLSA is a fundamental method that provides probabilistic sense to the SVD. Limitations on the original formulation compromise this assertion. Also, it causes problems of various types (described in the 4 section). We pay special attention to the works involving reformulations and those that relate to other techniques. In this manuscript, we have selected works of a methodological nature that imply a methodological contribution. We do not consider the number of citations to each work, the impact of the publication, or the interpretative orthodoxy. In this way, we equate many publications with interpretability or computability criteria, especially those that are extensions of the method.

3. The Method: PLSA Formulas

The original formulation of the PLSA, according to [3], provides a probabilistic solution to the problem of extracting a set of z k ( k = 1 , ⋯ , K ) latent variables of a data frame N ( d i , w j ) , obtained from a corpus of d i ( i = 1 , … , m ) documents when crossed with a thesaurus of w j ( j = 1 , … , n ) words. The relative frequencies
n ( d i , w j ) = N ( d i , w j ) ∑ i j N ( d i , w j )
are estimated by the joint probability P ( d i , w j ) . A key idea in this method is decomposing this probabilistic approximation as the product of conditional distributions over a set of latent variables. After some manipulations, and using the Bayes rule,
P ( d i , w j ) = P ( d i ) ∑ k P ( w j | z k ) P ( z k | d i ) ( asymmetric formulation )
= ∑ k P ( z k ) P ( w j | z k ) P ( d i | z k ) ( symmetric formulation )
where P ( d i ) and P ( z k ) are probabilities of the document d i and the latent variable z k , respectively. Formulas (2) and (3) are was called by Hofmann the asymmetric and symmetric formulations [13], or formulations I and II [45].
The discrete nature of the documents identifies each one with the probabilities of ( d 1 , … , d n ) t over the latent variables, and justifies the postulation that the mixtures P ( d i | z k ) are k independent identically distributed (iid) multinomials. Because the same occurs for the words, the objective is to determine the parameters θ and ϕ such that the conditional probabilities P ( w j | z k ) ∼ Multinomial ( θ j k ) and P ( z k | d i ) ∼ Multinomial ( ϕ k i ) for the asymmetric formulation (alternatively P ( w j | z k ) ∼ Multinomial ( θ j k ) and P ( d i | z k ) ∼ Multinomial ( ϕ i k ) for the symmetric case), with no hypothesis regarding the number or distribution of z k , which is a set of dummy variables with no probabilistic sense.
The adjustment of mixtures, given by Formulas (2) and (3), is the other key idea for obtaining a reliable probabilistic interpretation by maximizing the likelihood of the parameters. A method widely used for this purpose is the EM algorithm, which always converges [46]. The use of the EM algorithm is roughly equivalent to the problem of fitting P ( d i , w j ) to n ( d i , w j ) , but ensuring a maximum likelihood estimation of the sufficient (not necessarily minimal) parameters θ and ϕ .
In fact, the EM algorithm is a consequence of Jensen inequality [47]. For a function Q such that
Q ( M ( θ ) | θ ) ≥ M ( Q ( θ | θ ) )
where M is a map, and in statistics usages is the expectation, usually written as E. Then, for the log-likelihood L , L ( M ( θ ) ) ≥ M ( L ( θ ) ) occurs, defining a monotonically increasing sequence reaching the limit if M ( θ ) = θ . In the PLSA case, the parameters (which are not provided by the model in a closed manner) are the mixtures of relations (2) or (3).
The EM algorithm supposes two steps: expectation and maximization. Expectation (E-step) is computed on the log-likelihood
L = ∑ i j n ( d i , w j ) log P ( d i , w j )
and for parametrization (2) or (3) takes the forms
L = ∑ i j n ( d i , w j ) log P ( d i ) ∑ k P ( w j | z k ) P ( z k | d i )
= ∑ i j n ( d i , w j ) log ∑ k P ( z k ) P ( w j | z k ) P ( d i | z k )
for the asymmetric and the symmetric cases, respectively. In both cases, the expectation of L is the posterior
E ( L ) = P ( z k | d i , w j )
and after several manipulations
P ( z k | d i , w j ) = P ( z k , d i , w j ) P ( d i , w j )
The expressions for E ( L ) for both formulations are shown in the Table 3.
The calculation of expectation E ( L ) presents several complications related to the meaning of the primed index appearing in the formulas of Table 3. Interpretation requires consideration of the expression P ( z k | d i , w j ) of Formula (8). For computational purposes, the object supporting this data structure is an array containing the matrices with the estimates of P ( d i , w j ) , fixing for each one the values of z k . Then each of the elements of the array is a matrix taking the form
[ P ( d i , w j ) ] i j k ′ = vec P ( · | z k ′ ) vec P ( · | z k ′ ) t ( k ′ = 1 , 2 , ⋯ )
indicating the primed index that is fixed (it should be noticed that a vector multiplied by its transpose is a matrix. In this case are k ′ = k matrices). The vec notation has been used to better identify the scalar products of the vectors of probabilities P ( · | z k ′ ) obtained by varying z k . The entire array is
[ P ( d i , w j ) ] i j k = [ P ( d i , w j ) ] i j 1 ] | [ P ( d i , w j ) ] i j 2 | … | [ P ( d i , w j ) ] i j K
Maximization (M-step) uses Lagrange multipliers, the correspondent derivatives, to obtain the solutions maximizing probabilities after eliminating them. These solutions for each formulation yield the generative models for the figures shown in Figure 1.
The execution of adjustment of probabilities, in both formulations, involves selecting a value for k, initializing the distributions appearing in (2) or (3), and computing the E-step and M-step in an iterative process in which P ( d i , w j ) is recalculated until a certain condition is achieved. Hofmann has noted that the iterative process can end when there are no changes in the qualitative inputs, a condition called early stop [3]. A detailed, accessible derivation of the PLSA formulas and an introductory discussion of the EM algorithm convergence can be found in [45].
Another point to consider is what PLSA solutions are. Table 3 provides the formulas leading to the solutions. In many cases, providing words or documents best identify each aspect or latent variable would be more appropriate. Then, the numerical values of the columns of the involved matrices are ordered, and the corresponding labels are substituted, thus revealing the most relevant items in the respective latent class. Because the type of the desired solution has no ambiguity in the respective context, it is rarely explicit but does not confuse which result to provide. As an example, we provide two cases related to image study. For classification purposes, qualitative solutions are more suitable, and the numerical solutions are more suitable for spatial co-occurrence analysis on image regions.
Example 1. 
An example provided by Hofmann is reproduced below to illustrate the sense of word rank for interpretation of "the 4 aspects most likely generate the word “segment,” derived from a K=128 aspect model of the CLUSTER document collection. The displayed word stems are the most probable words in the class-conditional distributions P ( w j | z k ) , from top to bottom in descending order" [3].
Aspect 1 Aspect 2 Aspect 3 Aspect 4
imag video region speaker
SEGMENT sequenc contour speech
color motion boundari recogni
tissu frame descript signal
Aspect1 scene imag train
brain SEGMENT SEGMENT hmm
slice shot precis sourc
cluster imag estim speakerindepend
mri cluster pixel SEGMENT
algorithm visual paramet sound
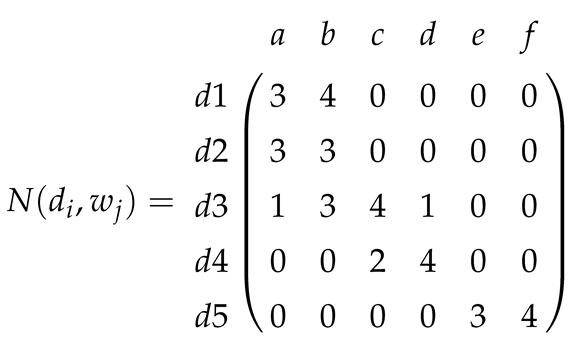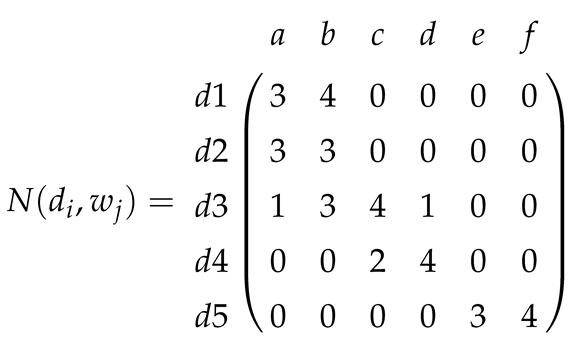In addition, we provide an artificial example to illustrate the effects of selection of K, consisting of a corpus of 5 ( d 1 to d 5 ) documents containing letters { a , b , c , d , e , f } , which we assimilate into words in a thesaurus. The co-occurrences’ data frame N isPreprints 84150 i001and the frequency matrix n
n ( d i , w j ) = . 086 . 114 0 0 0 0 . 086 . 086 0 0 0 0 . 029 . 086 . 114 . 029 0 0 0 0 . 057 . 114 0 0 0 0 0 0 . 086 . 114
If in this example, the objective is to classify documents by subject (or specialized words with the correspondent matters). Simple visual inspection indicates that they are 3. For the symmetric case formulas, running p = 1000 iterations in each case, the results are
for   k = 2 P ( d i | z k ) = 0 . 411 0 . 588 . 333 0 . 278 0 . 167 0 . 222 0 c b d a f − e − − − − − for   k = 3 P ( d i | z k ) = 0 0 . 462 0 0 . 538 . 545 0 0 . 454 0 0 0 . 429 0 0 . 571 0 c f b d e a − − − − − − − − − − − − for   k = 5 P ( d i | z k ) = . 007 0 0 . 462 0 . 347 0 0 . 538 0 . 646 . 333 0 0 0 0 . 667 0 0 0 . 0 0 . 538 0 . 419 0 0 . 462 0 . 581 c d e b f b c f a e a − − − − − − − − − − − − − − − − − − −
The characters’ matrices are the ordination of the most likely words identifying each latent variable (informally, the subjects in our toy example). Lines represent probabilities close to zero and are not useful for classification. The effect of selecting K is clear in the comparison of columns 3 and 5, which are equivalent (for k = 5 ).

3.1. Training and Prediction

The PLSA algorithm can be executed for the entire data set, providing results in the same manner as probabilistic clustering methods [48, Chap. 3]. However, to exploit the predictive power of PLSA, the model must be fitted on the available data (or training phase). Predictions for new observations are made by simply comparing them with the trained data set.
In the prediction phase, cannot assign probabilities for documents that are not in the training phase, because non-zero probabilities are needed. This problem has been solved in [49] by splitting the data set into a training group with the d i observed documents and the new unobserved documents q ∈ Q . By using probabilities P ( z k | d i ) instead of P ( d i | z k ) in (2) and expanding the logarithm, equation (6) can be rewritten as
L = ∑ i j n ( d i , w j ) log P ( d i ) + ∑ i j n ( d i , w j ) log P ( w j | d i )
To avoid a zero probability of the unseen documents in the training phase, Brants has introduced P ( d i ) > 0 , stating that the log-likelihood can be maximized, taking into account only the second term of (12), and
P ( n e w ) ( Q ) = ∏ i j P ( w j | q i )
Brants has highlighted that equation (13) does not represent the true likelihood, but if the goal is likelihood maximization, the same parameter setting is found as that when the true likelihood had been maximized [49]. The same article has proposed other methods for estimating likelihood on the basis of marginalization and splitting. Brants has also proposed PLSA folding-in, a more refined derivation of this technique [50]. A further improvement, which is more computationally efficient and is protected by a patent is [51], involves estimating the log-likelihood by spiting the data set in the training set, denoted n ′ ( d i , w j ) , and introducing the unknown documents one by one as the second term of
L ∝ ∑ i j n ′ ( d i , w j ) log P ( d ) + ∑ i j log P ( w j | d i )
In the symmetric formulation, after training on the documents by using the formulas given in Table 3, new documents can be classified by simply alternating the expressions given by [38]
P ( z k | d i , w j ) = P ( z k | d i ) P ( w j | z k ) ∑ k ′ P ( z k ′ | d i ) P ( w j | z k ′ )
P ( z k , d i ) = ∑ i n ( d i , w j ) P ( z k | d i , w j ) ∑ i j n ( d i , w j ) P ( z k | d i , w j )
In this case, binary data can be handled by entering a matrix A such that
[ A ] i j = 1 if i is annotated to j 0 otherwise
substituting n ( d i , w j ) in equations of Table 3.
PLSA can also be used as a semi-supervised learning tool, in a process known as semi-supervised PLSA [52]. Using this mode requires entering labeled and non-labeled data in the EM iterative process, and being able to split the data set into a portion in which the labels are assigned and a portion in which the labels are not assigned. A measure of similarity performs the rest of the task. Another related strategy involves introducing the link functions must-link and cannot-link in the training phase [53].

4. Criticism: The LDA and Reformulations

The work of Hofmann is not a closed contribution. The rigidity of the distributional hypotheses that limit applicability has been exploited for different purposes. In addition, several studies have related Hofmann’s work to other techniques.
One of the first criticisms was noted by Blei, who has argued that Hofmann’s work is incomplete in that it provides no probabilistic model at the level of documents. This incompleteness leads to several problems: ( i ) the number of parameters grows linearly with the size of the corpus, thus resulting in severe problems with overfitting, and ( i i ) how to assign probabilities to a document outside the training set is unclear; LDA has been proposed to solve this problem [9].

4.1. Latent Dirichlet Allocation

LDA introduces a generative Bayesian model that maps documents on topics such that the words of each document are captured by these topics. Each document is described by a topic distribution, and each topic is described by a word distribution. Introducing θ , a k dimensional Dirichlet with parameter α k , and β as an array of initialization with values P ( w | z ) , and maintaining the notation of Formulas (2) and (3),
P ( θ , z , w | α , β ) = P ( θ | α ) ∏ k P ( z h | θ ) P ( w j | z k , β )
The LDA is also a generative model. The probabilities of a document and a corpus are obtained by marginalizing (integrating) over the complete collection. Further improvements to the model, also provided by Blei, include hierarchical LDA [9] and dynamic LDA [54].
The LDA is a closely related technique that is different from PLSA. Its criticisms provided a starting point for several developments. Formal equivalence with PLSA has been shown by [55] and has led to several proposed solutions to those problems in the case of the PLSA. Although LDA is not the objective of our review, we indicate exists further developments of this technique. We underline the works of Teh in which he proposes a non-parametric approach of mixture components with a hierarchical Bayesian distribution [56]. A hierarchical nested topic model is described in [57], and more recently in [58].

4.2. Other Formulations

There are reformulations of the PLSA, mainly arising from these criticisms. These developments have the objective of relaxing distributional hypotheses and overfitting problems.

4.2.1. Extension to Continuous Data

A generalization of the PLSA for continuously evaluated responses has also been provided by Hofmann, in the context of collaborative filtering, as an alternative to the neighbor regression method [10]. The method construction assumes a set of person items y j rated v for a set of persons u i . Then,
P ( v | u , y ) = ∑ z P ( z | u ) P ( v ; μ y z , σ y z )
where μ and σ are the expectation and variance, respectively, and assuming P ( z | u ) P ( v ; μ , σ )
P ( v ; u , σ ) = 1 2 π σ exp − ( v − μ ) 2 2 σ 2
which is fitted with the EM algorithm.
Within the semantic image analysis field, the visual entities from a database are assimilated with the words from a thesaurus [59], but as discrete entities. This variant constitutes the Gaussian mixture model PLSA [60], and assumes a normal distribution of the descriptors f j (the most relevant visual words) such that f h ∼ N ( f h | μ k , Σ k ) ( h ≤ j ) . Horster has noted that this expression is difficult to train, and has proposed the alternative models shared Gaussian words PLSA and fixed shared Gaussian words PLSA. A more general treatment, in which normality is postulated for the mixtures P ( w j | d i ) , has been reported [61].

4.2.2. Randomized Probabilistic Latent Semantic Analysis

Randomized PLSA arose to address the problem of overfitting [62]. Taking a random fraction of the trained data sets, the method proceeds by folding the training data set T = { T 1 , … , T Ω } and the fraction T l ( T l < Ω ) to run the PLSA algorithm with the l samples. The average of the results is the provided output.
The basis for this statement is the work by Ho [63] on the subspace method. This method takes random subsets of the support vector machine to avoid computational complexity. In addition, the derived algorithm has been reported to be slower than the conventional PLSA implementation.

4.2.3. Tensorial Approach

Non-negative tensor factorization was introduced by [64] for n-way data structures. Peng has established the relationship with the PLSA in [65], noting that the case n = 2 corresponds to the NMF and illustrating that n = 3 allows for handling more complex data structures. The objective is to better estimate the number of latent variables, or clueters.
Peng has introduced a structure of the type
[ F ̲ ] i j l ≈ P ( d i , w j , x l )
called a tensor, and being now x l ( l = 1 , … L ) other probabilistic observations. The extension of these ideas to the PLSA is obtained by considering the factorizations
P ( d i , w j , x l ) = ∑ p P ( d i | x p ) P ( w j | z r ) P ( z k | z r ) P ( x p , y q , z k ) ( k < r )
= ∑ r P ( d i | x r ) P ( w j | x r ) P ( z k | x r ) P ( x r )
Those decompositions are the tensorial cases of the asymmetric and symmetric formulations given by Formulas (2) and (3).
Two methods exist for adjusting Formulas (22) and (23): parafrac [66] (parallel factor analysis), assuming a linear approximation of the fibers (the one-dimensional structures that can be extracted from P ( d i , w j , z k ) ) and Tucker [67], a multiway Principal component analysis (PCA). Peng has noted that both methods provide different results even when the objective function is the same [65], and has indicated that the method is useful to determine the number of latent factors. An alternative formulation has been proposed by [68].
This decomposition has several implications, mainly related to neural network applications. For details and examples of applications, we refer readers to [69, Chap. 7].

5. NMF Point of View

The algebraic object that supports the probabilities of (2) or (3) are matrices with restricted entries to the set [ 0 , 1 ] , and they are non-negative. To construct such matrices, the transformation (1) involves identifying N ( d i , w j ) to a multivariate matrix X . The matrix Y containing the probabilities P ( d i , w j ) is obtained with the transformation Y = X / ∑ i j X . This is a special case of probabilistic transformation in which probabilities are in Laplace’s sense or relative frequencies.
For matrices obtained in this way, the standard formulation of the NMF is [69, p. 131]
[ Y ] i j = [ W ] i k [ H ] k j + [ E ] i j ( k = 1 , 2 , … )
≈ [ W ] i k [ H ] k j
where E is the error matrix, and makes the NMF suitable for its use in alternative formulations of the PLSA [70]1.
Many authors attribute the introduction of this technique to the work of Paatero [74], while others do so with the publication of Lee and Seung [75]. Both approaches are not equivalent. While Paatero uses the Euclidean norm as the objective function, Lee and Seung use the I-divergence (distances d are maps that satisfy, for vectors a , b , and c , the following axioms: ( i ) symmetry, d ( a , b ) = d ( b , a ) ; ( i i ) identity d ( a , b ) = 0 if a = b ; and ( i i i ) (triangular inequality) d ( a , b ) ≤ d ( a , c ) + d ( c , b ) . A divergence D does not satisfy one of these axioms, usually symmetry, which is more suitable for measuring how densities are similar.). Furthermore, the work of Lee and Seung is focused on the clustering problem. This attribution creates conceptual errors in many works, identifying NMF techniques to classification. A previous and algebraically rigorous and sound formulation of the NMF is a debt of Chen [76]. A brief introduction to NMF as an optimization problem can be found in [77, Chap. 6]; a more standard introduction is provided in [48, Chap. 7].
On the other hand, the SVD arose from the efforts of several generations of mathematicians, from the nineteenth-century works of Beltrami [78], and independently Jordan [79], to more recent contributions regarding inequalities between eigenvalues and matrix norms by Ky-Fan [80,81]. Currently, the SVD plays a central role in algebra, constituting a field known as eigenanalysis, and serves as a basis for matrix function theory [82], and is also the basis of many multivariate methods. This research field remains active. Currently it is formulated as [77, p. 275]
Theorem 1. 
Let X ∈ ℜ m × n (or C m × n ); then orthogonal (or unitary) matrices U ∈ ℜ m × m (or U ∈ C m × m ) and V ∈ ℜ n × n (or V ∈ C m × m ) exist such that
X = U Σ V t ( o r X = U Σ V H ) Σ = Σ 1 0 0 0
where Σ 1 = d i a g ( σ 1 , … , σ r ) with diagonal entries
σ 1 ≥ , … , ≥ σ r > 0 r = r a n k ( A )
One of the first proofs can be found in [83]. The theorem as given is known as full rank SVD. The approximation for r ′ < r is known as low-rank approximation, assuming an approximation for (26) [84]. In the PLSA context, connected with probabilities, only real matrices are used.
Hofmann has related PLSA (in the symmetric formulation case) to SVD in conference proceedings [1] and [3], writing the formal equivalence
[ U ] i k ∼ P ( d i | z k )
diag ( Σ ) k ∼ P ( z k )
[ V ] k j ∼ P ( w j | z k )
where U , diag ( Σ ) , and V are related to the SVD of the matrix Y .
The relationships between the PLSA and the SVD and these relations have severe restrictions because the data are frequencies obtained from counts obeying multinomial laws, whereas SVD exists for every matrix of real entries. In addition, the conditions for the degree of adjustment of n ( d i , w j ) to Y are unclear since is not defined the approximation bound. Also, the popssibility of the use of smooth tecniques for cases that data are not frequencies, is omitted. The relations (27a)-(27c), first written by Hofmann, was considered a mere formal equivalence [3,38].
Several attempts focusing on the equivalence between PLSA and SVD, in light of NMF, have aimed to build a more rigorous relation. The explicit relationship between PLSA and NMF, stated by Gaussier, minimizes I-divergence 2 with non-negative constraints
[ · ] i j ≥ 0 ∇ D ( · ) ≥ 0 [ · ] i j ⊙ ∇ D I = 0
known as Karush-Kuhn-Tucker (KKT) conditions, where ⊙ is the Hadamard or element-wise product. KKT conditions are a widespread optimization method when divergences are used.
Solutions are [75]
[ W ] i k ← [ W ] i k ⊙ [ Y H t ] i k WH H t i k
[ H ] k j ← [ H ] k j ⊙ [ W t Y ] k j W t WH k j
and the matrix quotient is the element-wise entry division.
After adjusting equation (25) in an iterative process, consisting of selecting a value of k, switching between (28) and (29) until a satisfactory approximation degree is achieved, Gaussier has introduced diagonal matrices D 1 and D 2 of suitable dimension
[ W H ] i j = [ WD 1 − 1 D 1 ] i k [ D 2 D 2 − 1 H ] k j
= [ W D 1 − 1 ] i k diag [ D 1 D 2 ] [ D 2 − 1 H ] k j
stating that any (local) maximum solution of PLSA is a solution of the NMF with KL-divergence (I-divergence according to the nomenclature herein) [11].
Further work by Ding [86], with the same divergence, has introduced normalization for matrices W and H , such that the column stochastic matrix W ˜ = [ w ˜ 1 , ⋯ , w ˜ K ] and the row stochastic matrix H ˜ = [ h ˜ 1 , ⋯ , h ˜ K ] are obtained as
w ˜ k = w k ∑ i w i k = 1
h ˜ k = h k ∑ j h k j = 1
calling those conditions probabilistic normalizations, and writing
Y = W ˜ D W H ˜ D H
= W ˜ S H ˜ ( s . t . S = D W D H )
where the D W and D H diagonal matrices contain the column sums of the respective sub-index matrices. Ding has arrived at similar conclusions to Gaussier, and assimilated the latent variables into the space span of matrix factorization [87].
Conditions for the reverse result are shown in [18] by the KL divergence
D K L ( Y ∥ W H ) = ∑ i j [ Y ] i j log [ Y ] i j [ WH ] i j
obtaining the solutions
[ W ] i k ← [ W ] i k ⊙ [ Y ] i j [ W H ] i j [ H ] k j t
[ H ] k j ← [ H ] k j ⊙ [ W ] i k t [ Y ] i j [ W H ] i j
after proof that WH → Y if k ≥ min ( m , n ) , choosing the diagonal matrix as
t = diag [ WH ] i j t [ WH ] i j 1 / 2 trace [ WH ] i j t [ WH ] i j 1 / 2
and arranging the entries of t in decreasing order, with the same permutation on the columns of W and the rows of H , and obtaining the respective column and row stochastic matrices F ˜ and G ˜ , indicating that
[ WH ] i j = [ F ˜ ] i k diag ( t ) [ G ˜ ] k j
In this case, factorization 37 reaches the SVD of the orthonormalization of Y (see [88, p. 24] for orthonormalization process).
This procedure keeps matrix norms (also row or columns norms) [63]. Moreover, minimization of KL divergence is equivalent to maximization of the likelihood in certain cases (as can easily be seen by expanding the logarithm of the KL divergence as a difference; while the first term is a constant, the second term is the log-likelihood), but this is not exact. The minimization of the K L divergence is known as the em algorithm. In many cases, the results obtained with both methods are similar. Amari has shown that in the general case, the em solutions are asymptotes of the EM algorithm case [89].

6. Extensions

The possibility to formulate the PLSA from the NMF was early noticed by [3]. For the symmetric case, modifying the hypotheses on the nature of the data can constitute the basis for other techniques, furnishing probabilistic sense. In this section, we present them in the chronological order of appearance.

6.1. Kernelization

The dot product is used to measure similarity among instances. The transformation of the scalar products of the observations to a different space (not necessarily of the same dimension) is called kernelization and in fact is a generalization of the dot product, transforming 〈 x i 1 , x i 2 〉 to K ( x i 1 , x i 2 ) . The PLSA symmetric formulation allows for building a Fisher kernel. This approach, proposed by [3], despite computational difficulties in supporting messy data, has found practical applications in analysis of document similarity [90].
The Fisher kernel is defined as [91]
K ( y , y t ) = U θ ( y ) I F − 1 U θ ( y )
where
U θ ( y ) = − ∂ ∂ θ log P ( y | θ )
the Fisher scores, and
I F = E Y U θ U θ t
the Fisher information matrix. This kernel provides a consistent estimator of the posterior [92]. Hofmann’s proposal in [13] is
K ( d i , d i ′ ) = 〈 u ( d i ; θ ^ ) I F ( θ ^ ) − 1 ; u ( d j θ ^ ) 〉
= ∑ j P ^ ( d i , w j ) P ^ ( d i ′ , w j ) ∑ k P ( z k | d i , w j ) P ( z k | d i , w j ) P ( w j , z k )
by direct computation, and P ^ denote the documents in which the distance is measured. A later version is [90], assuming only iid mixtures.
A related technique is graph-regularized PLSA [93]. The objective of this method is to classify entities according topics, according to probabilistic criteria, to measure similarity.
In addition, NMF enables use of the generalization of the dot product to measure similarity and preserve consistency [94].

6.2. Principal Component Analysis

PCA is one of the most extended multivariate and data analysis tools. It can be considered as a particular case of the SVD, being the terms SVD and PCA sometimes interchanged. The objective is to find an orthogonal axis system in Euclidean space maximizing the variance. From a statistical point of view, this representation is a descriptive method. In addition, several attempts have been made to provide a probabilistic sense for PCA [95,96], and establishing a relationship with PLSA seems natural.
From relation (26), and restricted to the case of real matrices
Σ 2 = [ U ] i k Σ [ V ] i k t [ U ] i k Σ [ V ] i k
relates Σ 2 of the SVD theorem to the variance matrix S when X c is the centered matrix obtained from X as
[ X c ] i j = [ X ] i j − J x ¯ 1 | … | J x ¯ n i j with x ¯ j = 1 m ∑ i x i j for all j
where J is a m × 1 dimension matrix of ones, and the second term relation (47) is the expectation of X . It is immediate
Σ 2 = [ X c ] i j t [ X c ] i j
= E [ X ] i j − E ( [ X ] i j ) t E [ X ] i j − E ( [ X ] i j )
= S
PCA provides graphical representations for considering the orthogonal projections of observations on the planes formed by the consecutive pairs of columns of the matrix V , which are orthogonal as a consequence of the SVD (i.e., Σ 1 / 2 V ).
The relationship between the planes in which the PCA and the PLSA project entities was not immediately clear but has been determined in light of the NMF. However, the column vectors of the matrices of Formula (40) are not necessarily orthogonal but are non-negative. Interpreting probabilities as coordinates, Klingenberg has introduced simplicial cones Γ [15]
Γ = y j s . t . y = ∑ j α j h j with α j ≥ 0 and h j ∈ [ H ] k j
which is a convex region in the positive orthant. Figure 2 illustrates this transformation.
A formulation known as logistic PCA, described in [97], formulates the likelihood optimization problem of L ( WH )
L = P ( Y | WH )
= σ ( [ WH ] i j ∑ i j [ Y ] i j ( 1 − σ ( [ WH ] i j ) 1 − ∑ i j [ Y ] i j
being σ ( WH ) = ( 1 + e x p ( WH ) ) − 1 . Optimizing the likelihood as a Bernoulli pdf with parameters in [ 0 , 1 ] , leads to a model for dichotomous variables.
A comparison between NMF and the PCA has been provided by [98], who have noted that the PCA is capable of finding the global minimum, whereas NMF (interpreting the PCA as a dimension reduction problem and not in the full rank case) does not. In addition, the ranking of factors in the NMF is not ordered, and all are equally important. Moreover, non-negative constraints are violated by PCA.

6.3. Clustering

The relationships between the PLSA and clustering techniques, which have been satisfactorily studied, represent the classification ability of the PLSA. PLSA in fact is a probabilistic clustering method, when latent variables are identified to clusters, as has been done in several studies [12,99].
Probabilistic clustering implies that all entities belong to each cluster with different probabilities (including zero) [100], an idea shared with fuzzy clustering methods [101]. However, in the current state of the art, gaps remain concerning overlapping.
In addition, PLSA can be used for partitional clustering, relating PLSA and k-means. This process involves introducing a Bayesian classifier in the matrix W of Formula (25) [14], after proof, in the conference paper [12], the connection between NMF and PLSA, and relaxing the assumptions of non-negativity assumptions on the basis matrix [14]. Using this technique, Ding has obtained graphical representations close to the centroids of the k-means [86]. In addition, these ideas have been used to build a simplex model based on topics containing normalized data points [102].

6.4. Information Theory Interpretation

The link between PLSA and information theory is apparent when divergences are used to evaluate the similarity between distributions. It is convenient to recall the introduction of distances or divergences induces metrics when the Cauchy-Schwartz inequality ( ∥ AB ∥ ≤ ∥ A ∥ ∥ B ∥ ) is satisfied [84]. Hofmann has noted that Euclidean distance implies Gaussian distributions [13]. Although this topic is complicated and beyond the scope of this article, it notably has several implications in the symmetric PLSA interpretation.
The frequentist framework does not provides reliable estimations in some cases, as noted by Rao in population diversity studies [103,104]. Divergences satisfying the identity axiom are related to entropy after the introduction of a monotonically decreasing function J of the differences (or quotient) with parameters θ and ϕ of the same class of densities (Rao has used Jensen’s difference in [105], defined as J ( θ , ϕ ) = H ( θ , ϕ ) − λ H ( θ ) − μ H ( ϕ ) , where H is an entropy, and λ y μ scalars such that λ + μ = 1 ). On the basis of the assumption that the parameter space is a sufficiently differentiable manifold, the (dis)similarity between populations can be locally approximated by ϕ ≈ θ + d θ , known as the geodesic distance
g i j = ∑ i j ∂ 2 ∂ θ i ∂ θ j J ( θ , θ + d θ )
= ∑ i j H s . t . H ∈ Re p × p
where H is the Hessian.
Considering the development for ϕ = θ
J ( θ , θ + d θ ) = J ( θ , ϕ = θ ) + ∂ ∂ θ J ( θ , ϕ = θ ) + 1 2 ! ∂ 2 ∂ θ i ∂ θ j J ( θ , ϕ = θ ) + ⋯
the first two terms vanish, and the expectation of J is the Fisher information matrix (or the inverse variance matrix). The connection with Σ of (26) and/or (46) is
E ( H ) = I F = diag 1 / σ 1 2 , … , 1 / σ K 2
and as consequence of the Jensen inequality, the bound I F ≥ 1 / S appears.
The general treatment for connecting the divergences and underlying distributions is provided in [105]. This article reproduces the relationships between metrics and distributions obtained by [106]. A more recent treatment based on the concept of kernelization is [107].
The conference paper [16] explicitly relates the PLSA, when the KL divergence is used, to Shannon’s information, as a result of expanding the logarithm of KL divergence
D K L ( Y ∥ W H ) = ∑ i j [ Y ] i j log [ Y ] i j − [ Y ] i j log [ WH ] i j
and identifying terms
I ( Y | WH ) = H ( Y ) − H ( W | H )
where I is the mutual information. In this context, there are r ! representations (if the entries are labeled) that correspond to the indistinguishable entities (different entities that have the same values for all observational variables). A geometric interpretation of the information appears when the equivalence of the maximization of the likelihood is considered with the EM algorithm and the KL divergence. These results provide a stronger foundation for the probability space projection than for the orthogonal projection [108], as Hofmann has noted, where the divergence is the loss of information [109, p. 185].
Although Chaudiri has used this result for k-means error classification purposes, obtaining a bound for the variance expectation, the general consequence of relating divergences is a parametric estimation of the variance.

6.5. Transfer Learning

Transfer learning can be defined as the machine learning problem of trying to transfer knowledge from a source domain to a target domain [110].
PLSA can be used from the point of view of neural networks for transfer learning purposes, by solving the problem in the case in which the source domain shares only a subset of its classes (column vectors of the data matrix) for an unlabeled target data domain [17]. The log-likelihood expression is thus [17]
L = ∑ i j n ( d S , w j ) log ∑ i j P ( d S | z k S ) P ( w j | z k S ) P ( z k | z k S ) + ∑ i j n ( d T , w j ) log ∑ i j P ( d T | z k T ) P ( w j | z k T ) P ( z k | z k T )
where S indicates that a document is in the source, and T indicates the target domain. A detailed survey providing an introduction to neural networks is [111]. A similar work on the problem of transfer learning is [112].

6.6. Open Questions

The work of Gaussier and Ding has been important in relating the PLSA and the SVD; translating the conceptual framework to the context of the probabilistic interpretations of the NMF; and extending the data class domain from the non-negative integers to the non-negative reals, relaxing distributional assumptions, since no-hypothesis is done on the parameter space. This is a non-parametric method based on NMF algebra. In addition, NMF techniques mainly focus on symmetric formulation. It does not seem to be any objection preventing its use for the asymmetric one, although problems in assigning probabilities P ( d i ) in equation (2) could complicate the problem.
In addition, Ding has stated that the difference between the results of the SVD and NMF (and thus PLSA) depends on the convergence to different local optima, and it is true if k < min ( m , n ) . Ding’s work has considered SVD as a dimensional reduction problem or low-rank decomposition. In this case, the matrix WH will not be Y , but an approximation, and the SVD is not achievable with NMF. In addition, because PCA decomposition is related to the geometric multiplicities of eigenvalues, in the case of the relations obtained with NMF, it is not so clear, and it should be faced with algebraic dimensionality 3.
However, when the discussion is restricted to the symmetric formulation, questions arise, and the results depend on k and determining the equivalence of the solutions. Leaving aside the type of convergence of WH → Y , which holds in the case k ≥ min ( m , n ) , as indicated by several authors [15,18,114], suboptimality occurs when this condition is not fulfilled and implies that the SVD low-rank approximation is an ill-conditioned problem [15].
On the other hand, the similitude of PLSA and SVD presents a greater issue. Whereas SVD exists for every matrix, NMF requires the matrix entries to be restricted to non-negative values. Thus, the problem can be stated as the triplet ( Ω , A , P ) (as usual, Ω is the sample space, A is a σ -algebra, and P is the measure or probability) . In the current state of the art, Ω is restricted to R + m × n . A treatment to expand the sample space to real values could involve well-known transformations (as suggested by φ ( X ) = 1 / ( 1 + exp { X } ) ) and may be explored in the future.

7. PLSA Processing Steps and State of the Art of Solutions

PLSA is considered an effective technique but has a notable drawback in its high consumption of computing resources, in terms of both execution and internal memory. This drawback has limited its practical applications [115] and additionally makes the relationship between the SVD and PLSA curious. In the SVD case, the typical blackboard exercise of obtaining eigenvalues and eigenvectors is simple but does not occur in the same manner for moderate and large data sets. Methods for its effective computation have arisen from numerous studies and sustained efforts over several decades [116]. Currently, many program languages implement the Linear Algebra Package to facilitate SVD computation [117]. Also, solutions for PLSA are hard to obtain.
Beyond the EM algorithm problems, PLSA is highly dependent on the initialization values [118,119]. This leads to several algorithms for computational efficiency purposes, based on certain initialization conditions, and others on alternative versions of the EM algorithm, apart from those that strictly use computational techniques.
Herein, contributions to increasing the computational efficiency are examined according to the concepts on which they are based, their initialization conditions and the use of EM algorithm variants. Efforts using purely computational techniques are also discussed.

7.1. Algorithm Initialization

The dependence of the PLSA results on the initialization conditions has led to several variations. One possibility applicable only in the symmetric formulation, proposed by [118], initializes the algorithm with LSA solutions, which are the SVD solutions. Because some values can be negative, correction may be necessary (typically setting values to zero). Another strategy applicable in both formulations is execution for several random initialization distributions of the considered algorithm; after running, the higher log-likelihood value offers the best solution [119].
One algorithm is On-line belief propagation (OBP), which is based on a sequence of initializations on subsets of the data frame [119,120]. OBP segments the data frame into several parts. After initialization of the first segmentation, solutions are obtained and used in the next initialization, and so on. This technique enables the use of PLSA on large data sets.
A fundamental of the OBP is stochastic initialization [121], which consists of defining a learning function as a risk function for which the difference in conditional distributions describes a decreasing sequence between iterations [121]. The execution of this algorithm requires at least one iteration for the complete data set and selection of the most significant contributions for the first partition.

7.2. Algorithms Based on Expectation Maximization Improvement

The EM convergence rate is [122]
∥ θ ( p + 1 ) − θ ★ ∥ ≤ λ ∥ θ ( p ) − θ ★ ∥
where λ is the largest eigenvalue of the data matrix. Several methods are used to accelerate convergence, such as the descendant gradient. However, PLSA must preserve maximum log-likelihood solutions. To improve computational efficiency in such conditions, some variants and alternative algorithms have been proposed. The EM algorithm is one of the most studied in statistical environments, and many variants and simplifications exist [123]. A general description of the algorithm used in this section is [124]. An overview of the efforts is provided in Table 2. The EM algorithm is the classic optimization technique for PLSA, and some versions or modifications have been exploited to achieve PLSA solutions.

7.2.1. Tempered EM

Tempered EM uses classical concepts of statistical mechanics for computational purposes [125]. Aside from the significance in physics, the primary idea is how to achieve a posterior (E-step) close to a uniform distribution. An objective function is introduced
F β = − β ∑ i j n ( d i , w j ) ∑ k P ˜ ( z k ; d i , w j ) log P ( d i | z k ) P ( w j | z k ) P ( z k ) + ∑ i j n ( d i , w j ) ∑ k P ˜ ( z k ; d i , w j ) log P ( z k ; d i , w j )
where P ˜ ( z k ; d i , w j ) is a variational parameter defined as
P ˜ ( z k ; d i , w j ) = P ( z k ) P ( d i | z k ) P ( w j | z k ) β ∑ k P ( z k ) P ( d i | z k ) P ( w j | z k ) β
and for β < 1 , the convergence is faster [13].

7.2.2. Sparse PLSA

A proposal to improve the convergence speed has been based on sparse EM [126]. Assuming that only a subset of values is plausible for latent variables (in terms of probabilities), freezing non-significant avoids many calculations. PLSA is considered as an algebraic optimization problem of the matrix Y ∈ R m × n (which in this case is the data frame containing the relative frequencies n ( d i , w j ) ) restricted to the constraint ∑ r λ r y r y r t ( r < m ) , or unknown parameters, minimizing [127]
D q ( Y ∥ ∑ r λ r y r y r ′ ) ( with ∑ r λ r = ∥ y r ∥ 1 = ∥ y r ′ ∥ 1 = 1 , y r ∈ Y and r ′ ≠ r < n )
named Tsallis divergence [128], and computed for the r non-freezing column vectors of Y as [69, p.97]
D q ( y j ∥ λ r y r y r t ) = 1 κ ∑ i y j y j κ − ( λ r y r y r t ) κ − ∑ i y j κ y j − λ r y r y r t ( s . t . κ ≠ 0 )
This divergence solves the optimization problem of adjusting n ( d i , w j ) to P ( d i , w j ) [129]. After adjustment, probabilistic factorizations of the considered parametrization must again be obtained.

7.2.3. Incremental PLSA

Instead of global maximization, simpler contributions can be maximized. This update procedure used in the E-step for the PLSA gave rise to the incremental PLSA algorithm [130], with which results can be obtained twice as quickly. Applications in image classification can be found in [131,132].
A recursive algorithm, called recursive probabilistic latent semantic analysis, is based on the computation of the likelihood of a subset of words, as well as other words, recursively [133]. The performance has been reported to be highly similar to that obtained with the incremental PLSA.

7.3. Use of Computational Techniques

Difficulties in obtaining fast and reliable solutions for PLSA have also been approached through purely computational techniques. These advancements are a consequence of developments in computer architecture in recent decades: processing capabilities have been increased, thus resulting in a new branch of algorithms to reduce the computational time of the PLSA. The introduction of multicore processors by Intel and Sun Microsystems, in 2005, for portable machines enabled a major step toward parallel computing [134], which is now the dominant paradigm.
Parallel computing involves simultaneous execution of tasks. It requires dividing a problem into independent pieces and executing each one in a separate processing unit. The use of parallel computing techniques for the PLSA has been proposed in [135]. A current and widespread technique to support parallel capabilities is Map Reduce [136]. This technique essentially consists of dividing tasks into two phases. The first phase is a map that partitions the input data set and assigns labels to each one. The reduce phase supposes the execution of an operation on a set of previously labeled partitions. An algorithm exploiting the possibilities of Map Reduce for PLSA results has been proposed in [137].
Furthermore, graphic processing units have increased the range of capabilities, and they are useful for a broad variety of applications, particularly the simulation of complex models [138]. These capabilities have been transferred to the PLSA algorithm [139] but have not yielded definitive results.

7.4. Open Questions

The described methods do not provide fully satisfactory results, and perhaps it is one of the causes of the division between enthusiasts and indifferent regarding PLSA. The PLSA algorithms inherit the problems of EM, especially the slow convergence. Those problems are independent of the computational efficiency. There are no comparative studies on computational capability or execution time. Surprisingly, despite the EM algorithm is one of the most studied, many versions and works devoted to accelerating convergence (a recent one is [140]), there are no comparative studies.

8. Discussion

Hofmann does not provide indications as to when each formulation is applicable, the value of PLSA is clear and relatively simple: for the asymmetric formulation, it is an unsupervised learning method to train a set of latent variables with unknown number and distribution, when the data include co-occurrence or contingency tables. Also, the model can be extended to continuously evaluated entities. The use of the EM algorithm to adjust probabilities provides a maximum likelihood estimation of the parameters. This technique can be extended to semi-supervised cases. However, the symmetric formulation pales the PLSA within the fundamentals of algebra and multivariate analysis: it is the probabilistic companion of the SVD. However, there are some gaps to make full sense of this statement.
Convergence occurs for k ≥ min ( m , n ) , however, for the case k < min ( m , n ) . It has been said that the convergence limit does not necessarily occur at a global optimum [141] and does not necessarily converge to a point but can converge on a compact set [142], thus providing sub-optimal results [143]. In addition, sparse data structures can cause failures in convergence [144]. These statements are due to the interpretation of the SVD, and therefore the PCA as a low-rank approximation. However, these statements do not take into account the low-rank approximation, based on Schmidt’s approximation Theorem [145]. Establishing a bound with the help of this result is an open question.
The LDA techniques and those built on them are hierarchical models whose construction corresponds to particular fields of application. These constructions are also possible in the symmetric formulation assuming additional hypotheses on the data, like distribution, qualitative categories, or hierarchical relations. This type of treatment supposes a pre-processing of the data, preserving the content of the PLSA significance.
Furthermore, although the concept of probabilistic learning is sound, based on Vaillant’s work [146], symmetric PLSA is especially apt in the context of transfer learning. In this way, the certainty depends on the available data, as suggested by the relation (60). Then, reanalyzing a problem with new (or complementary) data or observational variables can provide learning sequences.
Although the applications of the PLSA are numerous, more surprises are likely to be encountered. However, theoretical studies from the perspective of the relationship of PLSA to SVD are scarce. Such studies are necessary for broader interpretation. In particular, data matrices of observed phenomena with real values must be related to probabilities to extend the scope of PLSA applicability.

9. Conclusion

The PLSA is a technique with a quarter of a century of existence. It has been spanned to many research areas with good results. Despite the formal equivalence of the formulations, the asymmetric formulation is an IR technique, while the symmetric formulation also allows for establishing a probabilistic relationship with the SVD. Some consequences of this relationship are that they constitu the foundation for probabilistic construction of other techniques, like kernelization, PCA, clustering, or Transfer Learning, as well as the possibility of building a Fisher kernel. However, there are some open questions, of which we highlight the approximation error when using the low-rank approximation and the poor computational efficiency.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Hofmann, T. Probabilistic latent semantic indexing. SIGIR ’99: Proceedings of the 22nd annual international ACM SIGIR conference on Research and development in information retrieval 1999.
  2. Hofmann, T. Probabilistic latent semantic analysis. Uncertainty in Artificial Intelligence, Prodeedings 1999.
  3. Hofmann, T. Unsupervised learning by probabilistic latent semantic analysis. Machine Learning 2001. [CrossRef]
  4. Deerwester, S.; Dumais, S.T.; Furnas, G.W.; Landauer, T.K.; Harshman, R. Indexing by latent semantic analysis. Journal of the American society for information science 1990, 41, 391–407. [Google Scholar] [CrossRef]
  5. Saul, L.; Pereira, F. Aggregate and mixed-order Markov models for statistical language processing. arXiv preprint cmp-lg/9706007 1997.
  6. Barde, B.V.; Bainwad, A.M. An overview of topic modeling methods and tools. 2017 International Conference on Intelligent Computing and Control Systems (ICICCS). IEEE, 2017, pp. 745–750.
  7. Ibrahim, R.; Elbagoury, A.; Kamel, M.S.; Karray, F. Tools and approaches for topic detection from Twitter streams: survey. Knowledge and Information Systems 2018, 54, 511–539. [Google Scholar] [CrossRef]
  8. Tian, D. Research on PLSA model based semantic image analysis: A systematic review. Journal of Information Hiding and Multimedia Signal Processing 2018, 9, 1099–1113. [Google Scholar]
  9. Blei, D.M.; Ng, A.Y.; Jordan, M.I. Latent Dirichlet Allocation. Journal of Machine Learning Research 2003, 3, 993–1022. [Google Scholar]
  10. Hofmann, T. Collaborative filtering via gaussian probabilistic latent semantic analysis. Proceedings of the 26th annual international ACM SIGIR conference on Research and development in informaion retrieval, 2003, pp. 259–266.
  11. Gaussier, E.; Goutte, C. Relation between PLSA and NMF and implications. In Proceedings 28th annual international ACM SIGIR conference on Research and development in information retrieval (SIGIR’05) 2005.
  12. Ding, C.; He, X.; Simon, H.D. On the equivalence of nonnegative matrix factorization and spectral clustering. Proceedings of the 2005 SIAM international conference on data mining. SIAM, 2005, pp. 606–610. [CrossRef]
  13. Hofmann, T. Learning the similarity of documents: An information-geometric approach to document retrieval and categorization. Advances in neural information processing systems, 2000, pp. 914–920.
  14. Ding, C.H.; Li, T.; Jordan, M.I. Convex and semi-nonnegative matrix factorizations. IEEE transactions on pattern analysis and machine intelligence 2008, 32, 45–55. [Google Scholar] [CrossRef] [PubMed]
  15. Klingenberg, B.; Curry, J.; Dougherty, A. Non-negative matrix factorization: Ill-posedness and a geometric algorithm. Pattern Recognition 2009, 42, 918–928. [Google Scholar] [CrossRef]
  16. Chaudhuri, A.R.; Murty, M.N. On the Relation Between K-means and PLSA. 2012 21st International Conference on Pattern Recognition 2012. [Google Scholar]
  17. Krithara, A.; Paliouras, G. TL-PLSA: Transfer learning between domains with different classes. 2013 IEEE 13th International Conference on Data Mining. IEEE, 2013, pp. 419–427. [CrossRef]
  18. Figuera, P.; García Bringas, P. On the Probabilistic Latent Semantic Analysis Generalization as the Singular Value Decomposition Probabilistic Image. Journal of Statistical Theory and Applications 2020, 19, 286–296. [Google Scholar]
  19. Bai, S.; Huang, C.L.; Tan, Y.K.; Ma, B. Language models learning for domain-specific natural language user interaction. 2009 IEEE International Conference on Robotics and Biomimetics (ROBIO), 2009, pp. 2480–2485. [CrossRef]
  20. Wang, S.; Schuurmans, D.; Peng, F.; Zhao, Y. Combining statistical language models via the latent maximum entropy principle. Machine Learning 2005, 60, 229–250. [Google Scholar] [CrossRef]
  21. Kagie, M.; Van Der Loos, M.; Van Wezel, M. Including item characteristics in the probabilistic latent semantic analysis model for collaborative filtering. Ai Communications 2009, 22, 249–265. [Google Scholar] [CrossRef]
  22. Hsieh, C.H.; Huang, C.L.; Wu, C.H. Spoken document summarization using topic-related corpus and semantic dependency grammar. 2004 International Symposium on Chinese Spoken Language Processing. IEEE, 2004, pp. 333–336. [CrossRef]
  23. Madsen, R.E.; Larsen, J.; Hansen, L.K. Part-of-speech enhanced context recognition. Proceedings of the 2004 14th IEEE Signal Processing Society Workshop Machine Learning for Signal Processing, 2004. IEEE, 2004, pp. 635–643.
  24. Tsai, F.S.; Chan, K.L. Detecting cyber security threats in weblogs using probabilistic models. Pacific-Asia Workshop on Intelligence and Security Informatics. Springer, 2007, pp. 46–57. [CrossRef]
  25. Farhadloo, M.; Rolland, E. Fundamentals of sentiment analysis and its applications. In Sentiment Analysis and Ontology Engineering; Springer, 2016; pp. 1–24.
  26. Xie, X.; Ge, S.; Hu, F.; Xie, M.; Jiang, N. An improved algorithm for sentiment analysis based on maximum entropy. Soft Computing 2019, 23, 599–611. [Google Scholar] [CrossRef]
  27. Monay, F.; Gatica-Perez, D. On image auto-annotation with latent space models. Proceedings of the eleventh ACM international conference on Multimedia, 2003, pp. 275–278.
  28. Lienhart, R.; Hauke, R. Filtering adult image content with topic models. 2009 IEEE International Conference on Multimedia and Expo. IEEE, 2009, pp. 1472–1475.
  29. Shah-Hosseini, A.; Knapp, G.M. Semantic image retrieval based on probabilistic latent semantic analysis. Proceedings of the 14th ACM international conference on Multimedia, 2006, pp. 703–706. [CrossRef]
  30. Foncubierta-Rodríguez, A.; García Seco de Herrera, A.; Müller, H. Medical image retrieval using bag of meaningful visual words: unsupervised visual vocabulary pruning with PLSA. Proceedings of the 1st ACM international workshop on Multimedia indexing and information retrieval for healthcare, 2013, pp. 75–82.
  31. Cao, Y.; Steffey, S.; He, J.; Xiao, D.; Tao, C.; Chen, P.; Müller, H. Medical image retrieval: a multimodal approach. Cancer informatics 2014, 13, CIN–S14053. [CrossRef]
  32. Fasel, B.; Monay, F.; Gatica-Perez, D. Latent semantic analysis of facial action codes for automatic facial expression recognition. Proceedings of the 6th ACM SIGMM international workshop on Multimedia information retrieval, 2004, pp. 181–188. [CrossRef]
  33. Quelhas, P.; Monay, F.; Odobez, J.M.; Gatica-Perez, D.; Tuytelaars, T.; Van Gool, L. Modeling scenes with local descriptors and latent aspects. Tenth IEEE International Conference on Computer Vision (ICCV’05) Volume 1. IEEE, 2005, Vol. 1, pp. 883–890.
  34. Zhu, S. Pain expression recognition based on pLSA model. The Scientific World Journal 2014, 2014. [Google Scholar] [CrossRef] [PubMed]
  35. Haloi, M. A novel plsa based traffic signs classification system. pre-print 2015, [1503.06643].
  36. Jiang, Y.; Liu, J.; Li, Z.; Li, P.; Lu, H. Co-regularized plsa for multi-view clustering. Asian Conference on Computer Vision. Springer, 2012, pp. 202–213. [CrossRef]
  37. Chang, J.M.; Su, E.C.Y.; Lo, A.; Chiu, H.S.; Sung, T.Y.; Hsu, W.L. PSLDoc: Protein subcellular localization prediction based on gapped-dipeptides and probabilistic latent semantic analysis. Proteins: Structure, Function, and Bioinformatics 2008, 72, 693–710. [Google Scholar] [CrossRef]
  38. Masseroli, M.; Chicco, D.; Pinoli, P. Probabilistic latent semantic analysis for prediction of gene ontology annotations. The 2012 international joint conference on neural networks (IJCNN). IEEE, 2012, pp. 1–8. [CrossRef]
  39. Pulido, A.; Rueda, A.; Romero, E. Extracting regional brain patterns for classification of neurodegenerative diseases. IX International Seminar on Medical Information Processing and Analysis; Brieva, J.; Escalante-Ramírez, B., Eds. International Society for Optics and Photonics, SPIE, 2013, Vol. 8922, p. 892208. [CrossRef]
  40. Su, E.C.Y.; Chang, J.M.; Cheng, C.W.; Sung, T.Y.; Hsu, W.L. Prediction of nuclear proteins using nuclear translocation signals proposed by probabilistic latent semantic indexing. BMC bioinformatics. Springer, 2012, Vol. 13, pp. 1–10. [CrossRef]
  41. Du, X.; Qian, F.; Ou, X. 3D seismic waveform classification study based on high-level semantic feature. 2015 1st International Conference on Geographical Information Systems Theory, Applications and Management (GISTAM). IEEE, 2015, pp. 1–5. [CrossRef]
  42. Wang, X.; Geng, T.; Elsayed, Y.; Saaj, C.; Lekakou, C. A unified system identification approach for a class of pneumatically-driven soft actuators. Robotics and Autonomous Systems 2015, 63, 136–149. [Google Scholar] [CrossRef]
  43. Kumar, K. Probabilistic latent semantic analysis of composite excitation-emission matrix fluorescence spectra of multicomponent system. Spectrochimica Acta Part A: Molecular and Biomolecular Spectroscopy 2020, 239, 118518. [Google Scholar] [CrossRef] [PubMed]
  44. Nijs, M.; Smets, T.; Waelkens, E.; De Moor, B. A Mathematical Comparison of Non-negative Matrix Factorization-Related Methods with Practical Implications for the Analysis of Mass Spectrometry Imaging Data. Rapid Communications in Mass Spectrometry 2021, e9181. [Google Scholar] [CrossRef]
  45. Hong, L. A tutorial on probabilistic latent semantic analysis. pre-print 2012, [1212.3900].
  46. Dempster, A.; Laird, N.; Rubin, D. Maximum Likelihood from Incomplete Data via the EM Agorithm. Journal of the Royal Statistical Society, Series B, Methodological 1977. [Google Scholar]
  47. Jebara, T.; Pentland, A. On reversing Jensen’s inequality. Advances in Neural Information Processing Systems 2001, 231–237. [Google Scholar]
  48. Aggarwal, C.C.; Clustering, C.R.D. Algorithms and Applications; CRC Press Taylor and Francis Group, 2014.
  49. Brants, T.; Chen, F.; Tsochantaridis, I. Topic-based document segmentation with probabilistic latent semantic analysis. Proceedings of the eleventh international conference on Information and knowledge management, 2002, pp. 211–218.
  50. Brants, T. Test data likelihood for PLSA models. Information Retrieval 2005, 8, 181–196. [Google Scholar] [CrossRef]
  51. Brants, T.; Tsochantaridis, I.; Hofmann, T.; Chen, F. Computer controlled method for performing incremental probabilistic latent semantic analysis of documents, involves performing incremental addition of new term to trained probabilistic latent semantic analysis model, 2006. US Patent Number US2006112128-A1.
  52. Zhuang, L.; She, L.; Jiang, Y.; Tang, K.; Yu, N. Image classification via semi-supervised pLSA. 2009 Fifth International Conference on Image and Graphics. IEEE, 2009, pp. 205–208.
  53. Niu, L.; Shi, Y. Semi-supervised plsa for document clustering. 2010 IEEE International Conference on Data Mining Workshops. IEEE, 2010, pp. 1196–1203.
  54. Blei, D.M.; Lafferty, J.D. Dynamic topic models. Proceedings of the 23rd international conference on Machine learning, 2006, pp. 113–120.
  55. Girolami, M.; Kabǿn, A. On an equivalence between PLSI and LDA. SIGIR 03 Proceedings of the 26th annual international ACM SIGIR conference on Research and development in information retrieval 2003.
  56. Teh, Y.W.; Jordan, M.I.; Beal, M.J.; Blei, D.M. Hierarchical Dirichlet Processes. Journal of the American Statistical Association 2006, 101, 1566–1581. [Google Scholar] [CrossRef]
  57. Mimno, D.; Li, W.; McCallum, A. Mixtures of hierarchical topics with pachinko allocation. Proceedings of the 24th international conference on Machine learning, 2007, pp. 633–640.
  58. Koltcov, S.; Ignatenko, V.; Terpilovskii, M.; Rosso, P. Analysis and tuning of hierarchical topic models based on Renyi entropy approach, 2021, [arXiv:stat.ML/2101.07598]. arXiv:stat.ML/2101.07598].
  59. Bosch, A.; Zisserman, A.; Muñoz, X. Scene classification via pLSA. European conference on computer vision. Springer, 2006, pp. 517–530.
  60. Hörster, E.; Lienhart, R.; Slaney, M. Continuous visual vocabulary modelsfor plsa-based scene recognition. Proceedings of the 2008 international conference on Content-based image and video retrieval, 2008, pp. 319–328.
  61. Li, Z.; Shi, Z.; Liu, X.; Shi, Z. Modeling continuous visual features for semantic image annotation and retrieval. Pattern Recognition Letters 2011, 32, 516–523. [Google Scholar] [CrossRef]
  62. Rodner, E.; Denzler, J. Randomized probabilistic latent semantic analysis for scene recognition. Iberoamerican Congress on Pattern Recognition. Springer, 2009, pp. 945–953.
  63. Ho, T.K. The random subspace method for constructing decision forests. IEEE Transactions on Pattern Analysis and Machine Intelligence 1998, 20, 832–844. [Google Scholar] [CrossRef]
  64. Shashua, A.; Hazan, T. Non-negative tensor factorization with applications to statistics and computer vision. Proceedings of the 22nd international conference on Machine learning, 2005, pp. 792–799.
  65. Peng, W.; Li, T. On the equivalence between nonnegative tensor factorization and tensorial probabilistic latent semantic analysis. Applied Intelligence 2011, 35, 285–295. [Google Scholar] [CrossRef]
  66. Harshman, R.A. others. Foundations of the PARAFAC procedure: Models and conditions for an explanatory multimodal factor analysis. University of California at Los Angeles Los Angeles, CA 1970.
  67. Balažević, I.; Allen, C.; Hospedales, T.M. Tucker: Tensor factorization for knowledge graph completion. pre-print 2019, [1901.09590].
  68. Yoo, J.; Choi, S. Probabilistic matrix tri-factorization. 2009 IEEE International Conference on Acoustics, Speech and Signal Processing. IEEE, 2009, pp. 1553–1556.
  69. Cichocki, A.; Zdunek, R.; A.H., P.; Amary, S. Nonnegative Matrix and Tensor Factorizations; John Willey and Sons Ltd, 2009.
  70. Shashanka, M.; Raj, B.; Smaragdis, P. Probabilistic latent variable models as nonnegative factorizations. Computational intelligence and neuroscience 2008, 2008. [Google Scholar] [CrossRef] [PubMed]
  71. Cajori, F. A history of mathematical notations; Vol. 1, Courier Corporation, 1993.
  72. Biletch, B.D.; Yu, H.; Kay, K.R. An analysis of mathematical notations: for better or for worse, 2015.
  73. Cayley, A. Remarques sur la notation des fonctions algébriques., 1855.
  74. Paatero, P.; Tapper, U. Positive matrix factorization: A non-negative factor model with optimal utilization of error estimates of data values. Environmetrics 1994, 5, 111–126. [Google Scholar] [CrossRef]
  75. Lee, D.D.; Seung, H.S. Learning the parts of objects by non-negative matrix factorization. Nature 1999, 401, 788–791. [Google Scholar] [CrossRef]
  76. Chen, J. The nonnegative rank factorizations of nonnegative matrices. Linear Algebra and its Applications 1984. [Google Scholar] [CrossRef]
  77. Zhang, X.D. Matrix analysis and applications; Cambridge University Press, 2017.
  78. Beltrami, E. Sulle funzioni bilineari. Giornale di Matematiche ad Uso degli Studenti Delle Universita 1873, 11, 98–106. [Google Scholar]
  79. Martin, C.D.; Porter, M.A. The extraordinary SVD. The American Mathematical Monthly 2012, 119, 838–851. [Google Scholar] [CrossRef]
  80. Lin, B.L. Every waking moment Ky Fan (1914–2010). Notices of the AMS 2010, 57. [Google Scholar]
  81. Moslehian, M.S. Ky fan inequalities. Linear and Multilinear Algebra 2012, 60, 1313–1325. [Google Scholar] [CrossRef]
  82. Higham, N.J.; Lin, L. Matrix functions: A short course. Matrix Functions and Matrix Equations 2013, 19, 1–27. [Google Scholar]
  83. Eckart, C.; Young, G. A principal axis transformation for non-Hermitian matrices. Bulletin of the American Mathematical Society 1939, 45, 118–121. [Google Scholar] [CrossRef]
  84. Zhang, Z. The Singular Value Decomposition, Applications and Beyond. arXiv preprint 2015, [1510.08532].
  85. Kullback, S.; Leibler, R.A. On Information and Sufficiency. The Annals of Mathematical Statistics 1951, 22, 79–86. [Google Scholar] [CrossRef]
  86. Ding, C.; T., L.; W., P. On the equivalence between non-negative matrix factorization and probabilistic latent semantic indexing. Computational Statistics & Data Analysis, 2008.
  87. Mnih, A.; Salakhutdinov, R.R. Probabilistic matrix factorization. Advances in neural information processing systems 2007, 20, 1257–1264. [Google Scholar]
  88. Khuri, A.I. Advanced calculus with applications in statistics (Second Edition); Vol. 486, John Wiley & Sons, 2003.
  89. Amari, S.I. Information geometry of the EM and em algorithms for neural networks. Neural networks 1995, 8, 1379–1408. [Google Scholar] [CrossRef]
  90. Chappelier, J.C.; Eckard, E. Plsi: The true fisher kernel and beyond. Joint European Conference on Machine Learning and Knowledge Discovery in Databases. Springer, 2009, pp. 195–210.
  91. Hofmann, T.; Schölkopf, B.; Smola, A.J. Kernel methods in machine learning. The annals of statistics 2008, 1171–1220. [Google Scholar] [CrossRef]
  92. Tsuda, K.; Akaho, S.; Kawanabe, M.; Müller, K.R. Asymptotic properties of the Fisher kernel. Neural computation 2004, 16, 115–137. [Google Scholar] [CrossRef]
  93. Wang, X.; Chang, M.C.; Wang, L.; Lyu, S. Efficient algorithms for graph regularized PLSA for probabilistic topic modeling. Pattern Recognition 2019, 86, 236–247. [Google Scholar] [CrossRef]
  94. Figuera, P.; Bringas, P.G. A Non-parametric Fisher Kernel. International Conference on Hybrid Artificial Intelligence Systems. Springer, 2021, pp. 448–459.
  95. Bishop, C.M. Bayesian pca. Advances in neural information processing systems 1999, pp. 382–388.
  96. Kim, D.; Lee, I.B. Process monitoring based on probabilistic PCA. Chemometrics and intelligent laboratory systems 2003, 67, 109–123. [Google Scholar] [CrossRef]
  97. Casalino, G.; Del Buono, N.; Mencar, C. Nonnegative matrix factorizations for intelligent data analysis. In Non-negative Matrix Factorization Techniques; Springer, 2016; pp. 49–74. [CrossRef]
  98. Schachtner, R.; Pöppel, G.; Tomé, A.; Lang, E. From binary NMF to variational bayes NMF: A probabilistic approach. In Non-negative Matrix Factorization Techniques; Springer, 2016; pp. 1–48. [CrossRef]
  99. Devarajan, K.; Wang, G.; Ebrahimi, N. A unified statistical approach to non-negative matrix factorization and probabilistic latent semantic indexing. Machine Learning 2015. [Google Scholar] [CrossRef]
  100. Dougherty, E.R.; Brun, M. A probabilistic theory of clustering. Pattern Recognition 2004, 37, 917–925. [Google Scholar] [CrossRef]
  101. Bailey, J. Alternative clustering analysis: A review. Data Clustering 2018, pp. 535–550. [CrossRef]
  102. Shashanka, M. Simplex decompositions for real-valued datasets. 2009 IEEE International Workshop on Machine Learning for Signal Processing. IEEE, 2009, pp. 1–6.
  103. Rao, C.R. Diversity and dissimilarity coefficients: a unified approach. Theoretical population biology 1982, 21, 24–43. [Google Scholar] [CrossRef]
  104. Rao, C.R. Diversity: Its measurement, decomposition, apportionment and analysis. Sankhyā: The Indian Journal of Statistics, Series A 1982, 1–22. [Google Scholar]
  105. Rao, C.R. Differential metrics in probability spaces. Differential geometry in statistical inference 1987, 10, 217–240. [Google Scholar] [CrossRef]
  106. Atkinson, C.; Mitchell, A.F. Rao’s distance measure. Sankhyā: The Indian Journal of Statistics, Series A 1981, 345–365. [Google Scholar]
  107. Sejdinovic, D.; Sriperumbudur, B.; Gretton, A.; Fukumizu, K. Equivalence of distance-based and RKHS-based statistics in hypothesis testing. The Annals of Statistics 2013, 2263–2291. [Google Scholar] [CrossRef]
  108. Uhler, C. Geometry of maximum likelihood estimation in Gaussian graphical models; University of California, Berkeley, 2011.
  109. Amari, S.i. Information geometry and its applications; Vol. 194, Springer, 2016.
  110. Chuanqi, T.; Sun, F.; Kong, T.; Zhang, W.; Yang, C.; Liu, C. A Survey on Deep Transfer Learning. arXiv preprint 2018, arXiv:cs.LG/1808.01974]. [Google Scholar]
  111. Bozinovski, S. Reminder of the first paper on transfer learning in neural networks, 1976. Informatica 2020, 44. [Google Scholar] [CrossRef]
  112. Zhao, R.; Mao, K. Supervised adaptive-transfer PLSA for cross-domain text classification. 2014 IEEE International Conference on Data Mining Workshop. IEEE, 2014, pp. 259–266.
  113. Mirsky, L. An introduction to linear algebra; Dover Publications Inc., 1990.
  114. Huang, K.; Sidiropoulos, N.D.; Swami, A. Non-Negative Matrix Factorization Revisited: Uniqueness and Algorithm for Symmetric Decomposition. IEEE TRANSACTIONS ON SIGNAL PROCESSING 2014, 62, 211. [Google Scholar] [CrossRef]
  115. Wan, R.; Anh, V.N.; Mamitsuka, H. Efficient probabilistic latent semantic analysis through parallelization. Asia Information Retrieval Symposium. Springer, 2009, pp. 432–443. [CrossRef]
  116. Golub, G.H.; Van Loan, C.F. Matrix computations. Johns Hopkins studies in the mathematical sciences; Johns Hopkins University Press, Baltimore, MD, 1996.
  117. Anderson, E.; Bai, Z.; Bischof, C.; Blackford, L.S.; Demmel, J.; Dongarra, J.; Du Croz, J.; Greenbaum, A.; Hammarling, S.; McKenney, A. others. LAPACK Users’ guide; SIAM, 1999.
  118. Farahat, A.; Chen, F. Improving probabilistic latent semantic analysis with principal component analysis. 11th Conference of the European Chapter of the Association for Computational Linguistics, 2006.
  119. Zhang, Y.F.; Zhu, J.; Xiong, Z.Y. Improved text clustering algorithm of probabilistic latent with semantic analysis [J]. Journal of Computer Applications 2011, 3. [Google Scholar] [CrossRef]
  120. Ye, Y.; Gong, S.; Liu, C.; Zeng, J.; Jia, N.; Zhang, Y. Online belief propagation algorithm for probabilistic latent semantic analysis. Frontiers of Computer Science 2013, 7, 526–535. [Google Scholar] [CrossRef]
  121. Bottou, L.; others. Online learning and stochastic approximations. On-line learning in neural networks 1998, 17, 142. [CrossRef]
  122. Watanabe, M.; Yamaguchi, K. The EM algorithm and related statistical models; CRC Press, 2003.
  123. Meng, X.L.; Van Dyk, D. The EM algorithm—an old folk-song sung to a fast new tune. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 1997, 59, 511–567. [Google Scholar] [CrossRef]
  124. Roche, A. EM algorithm and variants: An informal tutorial. pre-print 2011, [1105.1476].
  125. Hinton, G.E.; Zemel, R.S. Autoencoders, minimum description length, and Helmholtz free energy. Advances in neural information processing systems 1994, 6, 3–10. [Google Scholar]
  126. Neal, R.M.; Hinton, G.E. A view of the EM algorithm that justifies incremental, sparse, and other variants. In Learning in graphical models; Springer, 1998; pp. 355–368. [CrossRef]
  127. Hazan, T.; Hardoon, R.; Shashua, A. Plsa for sparse arrays with Tsallis pseudo-additive divergence: noise robustness and algorithm. 2007 IEEE 11th International Conference on Computer Vision. IEEE, 2007, pp. 1–8. [CrossRef]
  128. Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. Journal of statistical physics 1988, 52, 479–487. [Google Scholar] [CrossRef]
  129. Kanzawa, Y. On Tsallis Entropy-Based and Bezdek-Type Fuzzy Latent Semantics Analysis. 2018 IEEE International Conference on Systems, Man, and Cybernetics (SMC). IEEE, 2018, pp. 3685–3689. [CrossRef]
  130. Xu, J.; Ye, G.; Wang, Y.; Herman, G.; Zhang, B.; Yang, J. Incremental EM for Probabilistic Latent Semantic Analysis on Human Action Recognition. 6th IEEE International Conference on Advanced Video and Signal Based Surveillance, 2009. [Google Scholar] [CrossRef]
  131. Wu, H.; Wang, Y.; Cheng, X. Incremental probabilistic latent semantic analysis for automatic question recommendation. Proceedings of the 2008 ACM conference on Recommender systems, 2008, pp. 99–106. [CrossRef]
  132. Li, N.; Luo, W.; Yang, K.; Zhuang, F.; He, Q.; Shi, Z. Self-organizing weighted incremental probabilistic latent semantic analysis. International Journal of Machine Learning and Cybernetics 2018, 9, 1987–1998. [Google Scholar] [CrossRef]
  133. Bassiou, N.; Kotropoulos, C. Rplsa: A novel updating scheme for probabilistic latent semantic analysis. Computer Speech & Language 2011, 25, 741–760. [Google Scholar] [CrossRef]
  134. Asanovic, K.; Bodik, R.; Catanzaro, B.C.; Gebis, J.J.; Husbands, P.; Keutzer, K.; Patterson, D.A.; Plishker, W.L.; Shalf, J.; Williams, S.W. others. The landscape of parallel computing research: A view from berkeley, 2006.
  135. Hong, C.; Chen, W.; Zheng, W.; Shan, J.; Chen, Y.; Zhang, Y. Parallelization and characterization of probabilistic latent semantic analysis. 2008 37th International Conference on Parallel Processing. IEEE, 2008, pp. 628–635.
  136. Dean, J.; Ghemawat, S. MapReduce: simplified data processing on large clusters. Communications of the ACM 2008, 51, 107–113. [Google Scholar] [CrossRef]
  137. Jin, Y.; Gao, Y.; Shi, Y.; Shang, L.; Wang, R.; Yang, Y. P 2 LSA and P 2 LSA+: Two paralleled probabilistic latent semantic analysis algorithms based on the MapReduce model. International Conference on Intelligent Data Engineering and Automated Learning. Springer, 2011, pp. 385–393.
  138. gpgpu.org. General-Purpose Computation Graphics Hardware. https://web.archive.org/web/20051231024709/http://www.gpgpu.org/, 2006.
  139. Kouassi, E.K.; Amagasa, T.; Kitagawa, H. Efficient probabilistic latent semantic indexing using graphics processing unit. Procedia Computer Science 2011, 4, 382–391. [Google Scholar] [CrossRef]
  140. Saâdaoui, F. Randomized extrapolation for accelerating EM-type fixed-point algorithms. Journal of Multivariate Analysis 2023, 196, 105188. [Google Scholar] [CrossRef]
  141. Wu, C.J. On the convergence properties of the EM algorithm. The Annals of statistics 1983, 95–103. [Google Scholar] [CrossRef]
  142. Boyles, R.A. On the convergence of the EM algorithm. Journal of the Royal Statistical Society: Series B (Methodological) 1983, 45, 47–50. [Google Scholar] [CrossRef]
  143. Gupta, M.D. Additive non-negative matrix factorization for missing data. pre-print 2010, [1007.0380].
  144. Archambeau, C.; Lee, J.A.; Verleysen, M. ; others. On Convergence Problems of the EM Algorithm for Finite Gaussian Mixtures. ESANN, 2003, Vol. 3, pp. 99–106.
  145. Schmidt, Erhard. Zur Theorie der linearen und nichtlinearen Integralgleichungen. In Integralgleichungen und Gleichungen mit unendlich vielen Unbekannten; Springer, 1989; pp. 190–233.
  146. Valiant, L.G. A theory of the learnable. Communications of the ACM 1984, 27, 1134–1142. [Google Scholar] [CrossRef]
1
Notation in areas with strong mathematical content is nontrivial and has a secular history [71]. In many cases, the notation determines conceptual developments [72]. The classical matrix notation, attributed to Cayley [73], among others, remains useful today. However, in the case of NMF, it is more convenient to write, at least in elementary statements, the product WH = ∑ k w i k h k j as
[ WH ] i j = [ W ] i k [ H ] k j
making the dimension of span space explicit.
2
Several authors have referred to the Kullback-Leibler (KL) divergence as
D I ( Y ∥ W H ) = ∑ i j [ Y ] i j log [ Y ] i j [ W H ] i j − [ Y ] i j + [ WH ] i j
which we prefer to call I-divergence or generalized KL-divergence, according to [69, P. 105], reserving the term KL divergence for the mean information, following the original nomenclature of S. Kullback and R.A. Leibler [85], and given by Formula (36).
3
PCA dimension refers to the geometric multiplicity of the eigenvalues σ r of the SVD theorem and corresponds to dim E ( σ ) , with E ( σ ) = { v ∈ R m s . t Y v r = σ u y } being u r and v r vectors of U and V , respectively. The nonzero roots of σ such that det ( Y − σ I ) = 0 , or characteristic polynomial is the algebraic multiplicity . Both ideas play a fundamental role in the canonical forms [113, Chap. 10] and the interpretation of dimensionality in matrix analysis.
Preprints 84150 g001
Figure 1. Reproduced form [13]. PLSA Generative Models.. Left panel is the asymmetric formulation: ( i ) select a document d i with probability P ( d i ) ; ( i i ) pick a latent class z k with probability P ( z k | d i ) ; ( i i i ) generate a word with probability P ( w j | z k ) . Right panel is the symmetric formulation: ( i ) select a latent class z k ; ( i i ) generate documents and words with probabilities P ( d i | z k ) and P ( w j | z k ) , respectively.
Figure 1. Reproduced form [13]. PLSA Generative Models.. Left panel is the asymmetric formulation: ( i ) select a document d i with probability P ( d i ) ; ( i i ) pick a latent class z k with probability P ( z k | d i ) ; ( i i i ) generate a word with probability P ( w j | z k ) . Right panel is the symmetric formulation: ( i ) select a latent class z k ; ( i i ) generate documents and words with probabilities P ( d i | z k ) and P ( w j | z k ) , respectively.
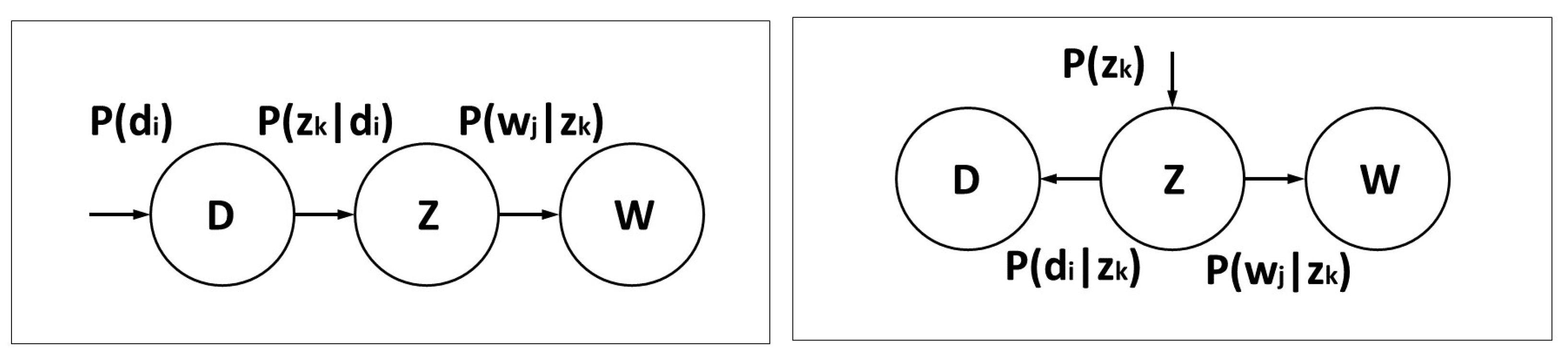
Preprints 84150 g001
Preprints 84150 g002
Figure 2. PCA and PLSA comparative. Γ -cones (dot product of the probabilistic normalized columns of H representation are the probabilistic transformation of Cartesian coordinates.
Figure 2. PCA and PLSA comparative. Γ -cones (dot product of the probabilistic normalized columns of H representation are the probabilistic transformation of Cartesian coordinates.
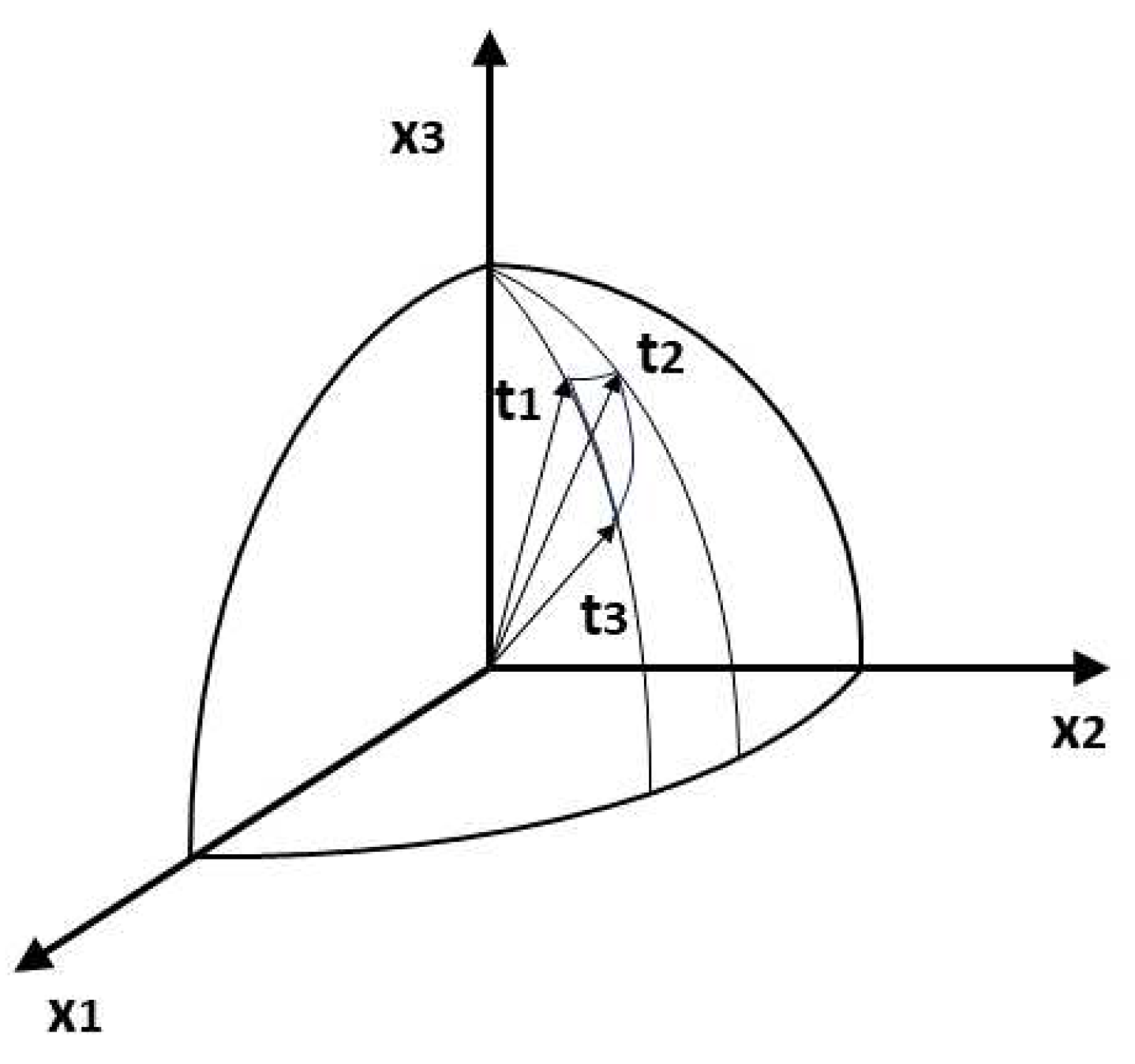
Preprints 84150 g002
Table 1. Milestones.
Table 1. Milestones.
Year Contribution Remarks
2000 PLSA PLSA formulation in conference proceedings [1,2]. [3] comments on the connections among NMF, SVD and information geometry.
2003 LDA Criticism of PLSA: LDA formulation [9].
2003 Gaussian PLSA Assumption of Gaussian mixtures [10].
2005 NMF PLSA solves the NMF problem [11]. Introduction to stochastic matrices [12].
2008 Kernelization Fisher kernel derivation from PLSA [13].
2008 k-means Equivalence between k-means and NMF [14].
2009 PCA Comparison of NMF, PLSA and PCA [15].
2012 Information Geometry Relationship between Fisher information matrix and variance from the PLSA context [16].
2018 Neural Networks Neural network interpretation of PLSA for transfer learning [17].
2020 SVD Establishment of conditions for equivalence among NMF, PLSA and SVD [18].
Table 2. PLSA Research Areas.
Table 2. PLSA Research Areas.
Discipline Research Area %
Engineering (45%) Mechanics & Robotics 37
Acoustics 4
Telecommunications & Control Theory 3
Materials Science 1
Computer Science (34%) Clustering 18
Information retireval 9
Networks 4
Machine Learning Applications 3
Semantic image analysis (10%) Image classification 4
Image retrieval 3
Image classification 3
Life Sciences (5%) Mathematical Computational Biology 2
Biochemistry Molecular Biology 2
Environmental Sciences Ecology 1
Methodological (4%) - 3
Fundamental Sciences (2%) Geochemistry Geophysics 1
Instruments Instrumentation 1
Table 3. PLSA Solutions.
Table 3. PLSA Solutions.
   Asymmetric formulation    Symmetric formulation
E-step E ( L ) = P ( w j , z k ) P ( z k , d i ) ∑ k ′ P ( w j , z k ′ ) P ( z k ′ , d i ) E ( L ) = P ( w j | z k ) P ( d i | z k ) P ( z k ) ∑ k ′ P ( w j | z k ′ ) P ( z k ′ ) P ( d i | z k ′ )
M-step P ( d i ) = ∑ j k n ( d i , w j ) P ( z k | w j , d i ) ∑ i j k n ( d i , w j ) P ( z k | w j , d i ) P ( z k ) = ∑ i j n ( d i , w j ) P ( z k | w j , d i ) ∑ i j k n ( d i , w j ) P ( z k | w j , d i )
P ( w j | z k ) = ∑ i n ( d i , w j ) P ( z k | w j , d i ) ∑ i j n ( d i , w j ) P ( z k | w j , d i ) P ( w j | z k ) = ∑ i n ( d i , w j ) P ( z k | d i , w j ) ∑ i j n ( d i , w j ) P ( z k | w j , d i )
P ( d j | z k ) = ∑ j n ( d i , w j ) P ( z k | w j , d i ) ∑ j i n ( d i , w j ) P ( z k | w j , d i ) P ( z k | d i ) = ∑ j n ( d i , w j ) P ( z k | w j , d i ) ∑ i j n ( d i , w j ) P ( z k | w j , d i )
PLSA Solutions are the M-step formulas, and they are maximum log-likelihood estimates.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated