Adaptive Synthesized Control for Solving The Optimal Control Problem

Preprint

Article

Adaptive Synthesized Control for Solving The Optimal Control Problem

This is a preprint, it has not been peer-reviewed.

Askhat Diveev^‡

Elizaveta Shmalko^*,‡

Askhat Diveev^‡

Elizaveta Shmalko^*,‡

^‡ These authors have contributed equally to this work.

This is a preprint, it has not been peer-reviewed.

Altmetrics

Downloads

Views

Comments

Submitted:

04 September 2023

Posted:

05 September 2023

You are already at the latest version

A peer-reviewed article of this preprint also exists.

Abstract

The development of artificial intelligence systems assumes that a machine can independently generate an algorithm of actions or a control system to solve the tasks. To do this, the machine must have a formal description of the problem and possess computational methods for solving it. The article deals with the problem of optimal control, which is the main task in the development of control systems, insofar as all systems being developed must be optimal from the point of view of a certain criterion. However, there are certain difficulties in implementing the resulting optimal control modes. The paper considers an extended formulation of the optimal control problem, which implies the creation of such systems that would have the necessary properties for its practical implementation. To solve it, an adaptive synthesized optimal control approach based on the use of numerical methods of machine learning is proposed. The method moves the control object, optimally changing the position of the stable equilibrium point in the presence of some initial position uncertainty. As a result, from all possible synthesized controls, he chooses one that is less sensitive to changes in the initial states. As an example, the optimal control problem of quadcopter with complex phase constraints is considered. To solve this problem? according to the proposed approach, the control synthesis problem is firstly solved to obtain a stable equilibrium point in the state space by a machine learning method of symbolic regression. After that optimal positions of the stable equilibrium point are searched according to source functional from the optimal control problem by particle swarm optimization algorithm. It is shown that such approach allows generating the control system automatically by computer basing on the formal statement of the problem and then directly implementing it onboard as far as they have already had a stabilization system inserted.

Keywords:

1. Introduction

Long ago Leonard Euler spoke about the optimal arrangement of everything in the world: "For since the fabric of the universe is most perfect and the work of a most wise Creator, nothing at all takes place in the universe in which some rule of maximum or minimum does not appear." Striving for optimality is natural in every sphere.

In order to optimally move an autonomous robot to a certain target position, currently, as a standard, engineers first solve the problem of optimal control, obtain the optimal trajectory, and then solve the additional problem of moving the robot along the obtained optimal trajectory. In most cases, the following approach is used to move the robot along a path. Initially the object is made stable relative to a certain point in the state space. Then the stability points are positioned along the desired path and the object is moved along the trajectory by switching these points from one point to another [1,2,3,4,5,6,7]. The difference between the existing methods is in solving the control synthesis problem to ensure stability relatively to some equilibrium point in the state space and in the location of these stability points.

Often, to ensure stability, the model of the control object is linearized relative to a certain point in the state space. Then, for the linear model of the object, a linear feedback control is found to arrange the eigenvalues of the closed-loop control system matrix on the left side of the complex plane. Sometimes, to improve the quality of stabilization, control channels or components of the control vector are defined that affect the movement of an object along a specific coordinate system axis of the state space. Then controllers, as a rule, PI controllers, are inserted into these channels with the coefficients that are adjusted according to the specified control quality criterion [3,4]. In some cases analytical or semi analytical methods are used to solve the control synthesis problem and building nonlinear stable control systems [5,7]. But the stability property of the nonlinear model of the control object, obtained from the linearization of this model, is generally preserved only in the vicinity of a stable equilibrium point.

The main drawback of this approach when the control object is moved along the stable points on the trajectory is that even if this trajectory is obtained as a result of solving the optimal control problem [8], then the movement itself will never be optimal. To ensure optimality, it is necessary to move along the trajectory at a certain speed, but when approaching the stable equilibrium point, the speed of the control object tends to zero.

The optimal control problem generally does not require ensuring the stability of the control object. The construction of a stabilization system that ensures the stability of the object relative to the equilibrium point in the state space is carried out by the researcher to achieve predictable behavior of the control object in the vicinity of a given trajectory.

The optimal control problem in the classical formulation is solved for a control object without any stabilization system, therefore, the resulting optimal control and the optimal trajectory will not be optimal for this object with further introduced stabilization system. It follows that the classical formulation of the optimal control problem [9] is missing something as far as its solution cannot be directly implemented in the real object, since this leads to an open-loop control. The open-loop control system is very sensitive to small disturbances, but they are always possible in real conditions, since no model accurately describes the control object. In order to achieve the optimal control in real object, it is necessary to build a feedback control system, which should provide some additional properties, for example stability relative to the trajectory or points on this trajectory. Authors [10,11] proposed an extended formulation statement of the optimal control problem, that has additional requirements established for the optimal trajectory. The optimal trajectory must have a non-empty neighborhood with a property of attraction. Performing these requirements provides implementation of the solution of the optimal control problem directly in the real control object.

In the work [12,13] an approach to solving the extended optimal control problem on the base of the synthesized control is presented. This approach ensures obtaining a solution of the optimal control problem in the class of practically implemented control functions. According to this approach, initially the control synthesis problem is solved. So the control object becomes stable in the state space relatively to some equilibrium point. In the second stage the optimal control problem is solved by determination of optimal positions of the stable equilibrium point. Switching stable points after a constant time interval ensures moving the control object from initial state to the terminal one optimally according to the given quality criterion. Optimal positions of stable equilibrium points can be far from the optimal trajectory in the state space, therefore a control object doesn’t slow down motion speed. Studies of synthesized control in various optimal control problems have shown that such control is not sensitive to perturbations and can be directly implemented in a real object [14,15].

In synthesized control the optimal control problem is solved for a control object already with a stabilization system. Other advantage of the synthesized control is a position of the stable point not changes in time interval, that is an optimal control function is solved in the class of piecewise constant functions, that simplifies a search of the optimal solution.

It is possible that piecewise constant control in the synthesized approach finds several optimal solutions with practically the same values of the quality criterion. This circumstance prompted us the idea to find among all almost optimal solutions one that is less sensitive to perturbations. This approach is called adaptive synthesized control.

In this work a principle of adaptive synthesized control is proposed in section 2, methods for solving it are discussed in section 3 and further in the section 4 a computational experiment of the solution of the optimal control problem for spatial motion of quadcopter by adaptive synthesized control is considered.

2. Adaptive Synthesized Control

Consider the principle of adaptive synthesized control for solving the optimal control problem in its extended formulation [10].

Initially, the control synthesis problem is solved to provide stability of control object relatively some point in the state space.

In the problem the mathematical model of the control object in the form of ordinary differential equation system is given.

\dot{x} = f (x, u),

(1)

where

x

is a state vector,

x \in R^{n}

u

is a control vector,

u \in U \subseteq R^{m}

U

is a compact set, that determines restrictions on the control vector.

The domain of admissible initial states is given

X_{0} \subseteq R^{n} .

(2)

To solve the problem numerically, the initial domain (2) is taken in the form of the finite number of points in the state space

{\tilde{X}}_{0} = {x^{0, 1}, \dots, x^{0, K}} .

(3)

Sometimes it is convenient to set one initial state and deviations from it:

x^{0, j} = x^{0} - Δ_{0} + 2 ⊙ {(j)}_{2} Δ_{0}, j = 1, \dots, 2^{n} - 1,

(4)

where

x^{0}

is a given initial state,

Δ_{0}

is a deviations vector,

Δ_{0} = {[Δ_{1} \dots Δ_{n}]}^{T}

, ⊙ is Hadamard product of vectors,

{(j)}_{2}

is a binary code of the number j. In this case

K = 2^{n} - 1

The stabilization point as a terminal state is given

x^{f_{1}} \in R^{n} .

(5)

It is necessary to find a control function in the form

u = h (x^{f_{1}} x) \in U,

(6)

where

h (x) : R^{n} \to R^{m}

, such that minimizes the quality criterion

J_{0} = \sum_{i = 0}^{K} (t_{f_{1}, i} + p ∥ x^{f_{1}} - x (t_{f_{1}, i}, x^{0, i}) ∥) \to min,

(7)

where

t_{f_{1}, i}

is a time of achieving the terminal state (5) from the initial state

x^{0, i}

t_{f_{1}, i}

is determined by an equation

t_{f_{1}, i} = \{\begin{matrix} t, if t < t^{+} and ∥ x^{f_{1}} - x (t, x^{0, i}) ∥ \leq ε_{0} \\ t^{+}, otherwise \end{matrix},

(8)

x (t, x^{0, i})

is a particular solution from initial state

x^{0, i}

i = 1, \dots, K

, of the differential equation (1) with inserted there control function (6)

\dot{x} = f (x, h (x^{f_{1}} - x)),

(9)

ε_{0}

is a given accuracy for hitting to terminal state (5),

t^{+}

is a given maximal time for control process, p is a weight coefficient.

Further in the principle of the synthesized optimal control the following optimal control problem is considered. The model of control object in the form (9) is used

\dot{x} = f (x, h (x^{*} - x)),

(10)

where the terminal state vector (5) is changed into the new unknown vector

x^{*}

, that will be a control vector in the considered optimal control problem.

In accordance with the classical formulation of the optimal control problem, the initial state of the object (10) is given

x^{0} \in R^{n} .

(11)

As far as in the engineering practice there can be some deviations in the initial position, therefore, in the adaptive synthesized control instead of one initial state (11) the set of initial states are used defined by the equation (4). The vector of initial deviations

Δ_{0}

is defined as a level of disturbances.

The goal of control is defined by achievement of the terminal state

x^{f} \in R^{n} .

(12)

The quality criterion is given

J_{1} = \int_{0}^{t_{f}} f_{0} (x, h (x^{*} - x)) d t \to min,

(13)

where

t_{f}

is a terminal time,

t_{f}

is not given but is limited,

t_{f} \leq t^{+}

t^{+}

is a given limit time of control process.

According to the principle of synthesized control, it is necessary to choose time interval

Δ t

and to search for optimal constant values of the control vector

x^{*, i}

for each interval

x^{*} = x^{*, i}, if (i - 1) Δ t \leq t < i Δ t, i = 1 \dots, M,

(14)

where M is a number of intervals

M = ⌊\frac{t^{+}}{Δ t}⌋,

(15)

such, that particular solution of the system (10) from the given initial state (11) reaches terminal state with optimal value of the quality criterion (13).

Algorithmically in the second stage of the adaptive synthesized control approach, the optimal values of the vector

x^{*}

are found as a result of the optimization task with the following quality criterion, which takes into account the given grid according to the initial conditions

J_{2} = \sum_{i = 1}^{K} (\int_{0}^{t_{f, i}} f_{0} (x, h (x^{*, i} - x)) d t + p ∥ x^{f} - x (t_{f, i}, x^{0, i}) ∥) \to min_{x^{*}},

(16)

where K is number of initial states,

t_{f, i}

is determined by equation (8).

3. Methods of Solving

As described in the previous section, the approach based on the principle of adaptive synthesized optimal control consists of two stages.

To implement the first stage of the approach under consideration for solving the control synthesis problem (1)–(9) any known method can be used mostly depending on the type of the model used to describe the control object. In practice, when developing a stabilization system, engineers do not use the initial performance criterion (7), since the main goal is to ensure stability. To solve the synthesis problem and obtain an equilibrium point, methods of modal control [16] can be applied for linear systems, as well as other analytical methods such as backstepping [17] or synthesis based on the application of the Lyapunov function [18]. In practice, stability is ensured through linearization of the model (1) in the terminal state and setting PI or PID-controllers in control channels [19,20]. The mathematical formulation of the stabilization problem as a control synthesis problem is needed to apply numerical methods and automatically obtain a feedback control function. Today, to solve the synthesis problem for nonlinear dynamic objects of varying complexity, modern numerical methods of machine learning can be applied [21]. In the present paper machine learning by symbolic regression [22] is used.

Symbolic regression allows to find a mathematical expression for desired function in the form of special code. All symbolic regression methods differs in the form of this code. The search for solutions is performed in the space of codes by a special genetic algorithm.

Let us demonstrate main features of symbolic regression on the example of the network operator method (NOP), that was used in this work in the computational experiment. To code a mathematical expression NOP uses an alphabet of elementary functions:

–: functions without arguments or parameters and variables of the mathematical expression;

$F_{0} = {f_{0, 1} = x_{1}, \dots, f_{0, n} = x_{n}, f_{0, n + 1} = q_{1}, \dots, f_{0, n + r} = q_{n + r}};$

(17)
–: functions with one argument

$F_{1} = {f_{1, 1} (z) = z, f_{1, 2} (z), \dots, f_{1, W} (z)};$

(18)
–: function with two arguments

$F_{2} = {f_{2, 1} (z_{1}, z_{2}), \dots, f_{2, V} (z_{1}, z_{2})} .$

(19)

Any elementary function is coded by two digits, the first one is the number of arguments, the second one is the function number in corresponding set. These digits are written as indexes of elements in the introduced sets of the alphabet (17)–(19). The set of functions with one argument must include the identity function

f_{1, 1} (z) = 1

. Functions with two arguments should be commutative, associative and have a unit element.

NOP encodes a mathematical expression in the form of an oriented graph. Source-nodes of the NOP-graph are connected with functions without arguments, other nodes are connected with functions with two arguments. Arcs of the NOP-graph are connected with functions with one argument. If on the NOP-graph some node has one input arc, then the second argument is a unit element for the function with two arguments connected with this node.

Let us define the following alphabet of elementary functions:

\begin{matrix} F_{0} & = & {f_{0, 1} = x_{1}, f_{0, 2} = x_{2}, f_{0, 3} = q_{1}, f_{0, 4} = q_{2}}, \\ F_{1} & = & {f_{1, 1} (z) = z, f_{1, 2} (z) = - z, f_{1, 3} (z) = cos (z), f_{1, 4} (z) = sin (z)}, \\ F_{2} & = & {f_{2, 1} (z_{1}, z_{2}) = z_{1} + z_{2}, f_{2, 2} (z_{1}, z_{2}) = z_{1} z_{2}} . \end{matrix}

(20)

With this alphabet the following mathematical expressions can be encoded in the form of NOP:

\begin{matrix} y_{1} & = & cos (x_{1}) sin (x_{2}) - s i n (x_{1}) cos (x_{2}), \\ y_{2} & = & cos (q_{1} x_{1} + q_{2} sin (x_{2})), \\ y_{3} & = & q_{1} sin (q_{2} x_{2}) + q_{2} cos (q_{1} x_{1}), \\ y_{4} & = & q_{1} sin (q_{2} cos (x_{1})) + q_{2} cos (q_{1} sin (x_{2})) . \end{matrix}

(21)

The NOP-graphs of these mathematical expressions are presented in Figure 1. In the computer memory the NOP-graphs are presented in the form of integer matrices.

Ψ = [ψ_{i, j}], i, j = 1, \dots, L .

(22)

As far as the NOP-nodes are enumerated in such a way that the node number from which an arc comes out is less than the node number to which an arc enters, then the NOP matrix has an upper triangular form. Every line of the matrix corresponds some node of the graph. Lines with zeros in the main diagonal corresponds to source-nodes of the graph. Other elements in the main diagonal are the function numbers with two arguments. Non zero elements above the main diagonal are the function numbers with one argument.

NOP matrices for the mathematical expressions (21) have the following forms

Ψ_{1} = [\begin{matrix} 0 & 0 & 3 & 4 & 0 \\ 0 & 0 & 4 & 3 & 0 \\ 0 & 0 & 2 & 0 & 2 \\ 0 & 0 & 0 & 2 & 1 \\ 0 & 0 & 0 & 0 & 1 \end{matrix}], Ψ_{2} = [\begin{matrix} 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 4 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 2 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 2 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 3 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \end{matrix}],

Ψ_{3} = [\begin{matrix} 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 2 & 0 & 3 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 2 & 0 & 4 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 2 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 2 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \end{matrix}], Ψ_{4} = [\begin{matrix} 0 & 0 & 0 & 0 & 3 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 4 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 2 & 0 & 4 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 2 & 0 & 3 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 2 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 2 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \end{matrix}] .

(23)

To calculate a mathematical expression by its NOP matrix, initially, the vector of nodes is determined. Number of components of the vector of nodes equals to the number of nodes in a graph. The initial vector of nodes includes variables and parameters in positions that correspond to source nodes, as well as other components equal to the unit elements of the corresponding functions with two arguments. Further every line of matrix is checked. If element of matrix doesn’t equal to zero, then corresponding element of the vector of nodes is changed. To calculate mathematical expression by the NOP matrix the following equation is used

z_{j}^{(i)} \leftarrow \{\begin{matrix} f_{2, ψ_{j, j}} (z_{j}^{(i - 1)}, f_{1, ψ_{i, j}} (z^{{(i - 1)}_{i}})), if ψ_{i, j} \neq 0 \\ z_{j}^{(i - 1)}, otherwise \end{matrix}, i = 1, \dots, L - 1, j = i + 1, \dots, L,

(24)

where

z_{i}^{(0)} = \{\begin{matrix} f_{0, i}, if ψ_{i, i} = 0 \\ e_{ψ_{i, i}}, otherwise \end{matrix},

(25)

e_{j}

is a unit element for function with two arguments

f_{2, j} (z_{1}, z_{2})

f_{2, j} (e_{j}, z) = f (z, e_{j}) = z .

(26)

Consider an example of calculating the second mathematical expression in (21) on its NOP matrix

Ψ_{2}

Initial vector of nodes is

z^{(0)} = {[x_{1} x_{2} q_{1} q_{2} 1 1 0 0]}^{T} .

Further all strings in the matrix

Ψ_{2}

are checked and non zero elements are found.

ψ_{1, 5} = 1, z_{5}^{(1)} = f_{2, 2} (z_{5}^{(0)}, f_{1, 1} (z_{1}^{(0)})) = 1 \cdot f_{1, 1} (z_{1}^{(0)}) = 1 \cdot x_{1} = x_{1},

ψ_{2, 6} = 4, z_{6}^{(2)} = f_{2, 2} (z_{6}^{(1)}, f_{1, 4} (z_{1}^{(1)})) = 1 \cdot f_{1, 4} (z^{(1)}) = 1 \cdot sin (x_{2}) = sin (x_{2}),

ψ_{3, 5} = 1, z_{5}^{(3)} = f_{2, 2} (z_{5}^{(2)}, f_{1, 1} (z_{3}^{(2)})) = x_{1} \cdot q_{1} = q_{1} x_{1},

ψ_{4, 6} = 1, z_{6}^{(4)} = f_{2, 2} (z_{6}^{(3)}, f_{1, 1} (z_{4}^{(3)})) = sin (x_{2}) \cdot q_{2} = q_{2} sin (x_{2}),

ψ_{5, 7} = 1, z_{7}^{(5)} = f_{2, 1} (z_{7}^{(4)}, f_{1, 1} (z_{5}^{(4)})) = 0 + q_{1} x_{1} = q_{1} x_{1},

ψ_{6, 7} = 1, z_{7}^{(6)} = f_{2, 1} (z_{7}^{(5)}, f_{1, 1} (z_{6}^{(5)})) = q_{1} x_{1} + q_{2} sin (x_{2}),

ψ_{7, 8} = 3, z_{8}^{(7)} = f_{2, 1} (z_{8}^{(6)}, f_{1, 3} (z_{7}^{(6)})) = 0 + cos (q_{1} x_{1} + q_{2} sin (x_{2})) = cos (q_{1} x_{1} + q_{2} sin (x_{2})) .

The last mathematical expression coincides with the needed mathematical expression for

y_{2}

(21).

So, we considered the way of codding in the NOP method. Then, to search for an optimal mathematical expression in some task, the NOP method applies a principle of small variations of a basic solution. According to this principle one possible solution is encoded in the form of the NOP matrix

Ψ_{0}

. This solution is the basic solution and it is set by a researcher as some good solution. Others possible solutions are presented in the form of sets of small variation vectors. A small variation vector consists of four integer numbers

w = {[w_{1} w_{2} w_{3} w_{4}]}^{T},

(27)

where

w_{1}

is a type of small variation,

w_{2}

the a line number of NOP-matrix,

w_{3}

is a column number of NOP-matrix,

w_{4}

is a new value of a NOP-matrix element. There are four types of small variations:

w_{1} = 0

is an exchange of the function with one argument: if

ψ_{w_{2}, w_{3}} \neq 0

, then

ψ_{w_{2}, w_{3}} \leftarrow w_{4}

;

w_{1} = 1

is an exchange of the function with two arguments: if

ψ_{w_{2}, w_{2}} \neq 0

, then

ψ_{w_{2}, w_{2}} \leftarrow w_{4}

;

w_{1} = 2

is an insertion of the additional function with one argument: if

ψ_{w_{2}, w_{3}} = 0

, then

ψ_{w_{2}, w_{3}} \leftarrow w_{4}

;

w_{1} = 3

is an elimination of the function with one argument: if

ψ_{w_{2}, w_{3}} \neq 0

and

\exists ψ_{w_{2}, j} \neq 0

j > w_{2}

j \neq w_{3}

and

\exists ψ_{i, w_{3}} \neq 0

i \neq w_{2}

, then

ψ_{w_{2}, w_{3}} \leftarrow 0

The initial population includes H possible solutions. Each possible solution

i \in {1, \dots, H}

except the basic solution is encoded in the form of the set of small variation vectors

W_{i} = (w^{i, 1,}, \dots, w^{i, d}), i \in {1, \dots, H},

(28)

where d is a depth of variations, which is set as a parameter of the algorithm.

The NOP-matrix of a possible solution is determined after application of all small variations to the basic solution

Ψ_{i} = w^{i, d} \circ \dots \circ w^{i, 1} \circ Ψ_{0}, i \in {1, \dots, H},

(29)

here small variation vector is written as a mathematical operator changing matrix

Ψ_{0}

During the search process sometimes the basic solution is replaced by the current best possible solution. This process is called a change of an epoch.

Consider an example of applying small variations to the NOP-matrix

Ψ_{3}

. Let

d = 3

and there are three following small variation vectors

w^{1} = {[0 3 5 2]}^{T}, w^{2} = {[2 5 6 3]}^{T}, w^{3} = {[2 8 9 4]}^{T}

After application of these small variation vectors to the NOP-matrix

Ψ_{3}

the following NOP-matrix is obtained

Ψ_{5} = [\begin{matrix} 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 2 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 2 & 3 & 3 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 2 & 0 & 4 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 2 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 2 & 4 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \end{matrix}] .

This NOP-matrix corresponds to the following mathematical expression

y_{5} = sin (q_{1} sin (q_{2} x_{2} cos (- q_{1} x_{1}))) + q_{2} cos (- q_{1} x_{1}) .

As a search engine for the optimal solution a genetic algorithm is used. To perform a crossover operation two possible solutions are selected randomly

\begin{matrix} W_{α} & = & (w^{α, 1}, \dots, w^{α, d}), \\ W_{β} & = & (w^{β, 1}, \dots, w^{β, d}) . \end{matrix}

(30)

A crossover point is selected randomly

c \in {1, \dots, d}

. Two new possible solutions are obtained as the result of exchanging elements of the selected possible solutions after crossover point:

\begin{matrix} W_{H + 1} & = & (w^{α, 1}, \dots, w^{α, c}, w^{β, c + 1}, \dots, w^{β, d}), \\ W_{H + 2} & = & (w^{β, 1}, \dots, w^{β, c}, w^{α, c + 1}, \dots, w^{α, d}) . \end{matrix}

(31)

The second stage of the synthesized principle under consideration is to solve the problem of optimal control via determination of the optimal position of the equilibrium points. Studies have shown [23] that for a complex optimal control problem with phase constraints, evolutionary algorithms allow to cope with such problems. Good results were demonstrated [24] by such algorithms as a genetic algorithm (GA) [25], a particle swarm optimization (PSO) algorithm [26], a grey wolf optimizer (GWO) algorithm [27] or a hybrid algorithm [28] involving one population of possible solutions and all three evolutionary transformations of GA, PSO and GWO selected randomly.

4. Computational Experiment

Consider the optimal control problem for spatial motion of a quadcopter. In the problem, the quadcopter should move in a minimum time on a closed loop circle from the given initial state to the the same terminal state, avoiding collisions with obstacles and passing through the given areas.

4.1. Mathematical Model of Spatial Movement of Quadcopter

In general case the mathematical model of quadcopter as a hard body has the following form:

\begin{matrix} \ddot{x} & = & F (cos (γ) sin (θ) cos (ψ) + sin (γ) sin (ψ)) / m, \\ \ddot{y} & = & F cos (γ) cos (θ) / m - g, \\ \ddot{z} & = & F (cos (γ) sin (θ) sin (ψ) + sin (γ) cos (ψ)) / m, \\ \ddot{γ} & = & ((I_{y y} + I_{z z}) \dot{θ} \dot{ψ} + M_{x}) / I_{x x}, \\ \ddot{ψ} & = & ((I_{z z} + I_{x x}) \dot{γ} \dot{θ} + M_{y}) / I_{y y}, \\ \ddot{θ} & = & ((I_{x x} + I_{y y}) \dot{γ} \dot{θ} + M_{z} / I_{z z}, \end{matrix}

(32)

where F is a summary thrust force of all drone screws, m is a mass of drone, g is acceleration of gravity,

g = 9.80665

M_{x}

M_{y}

M_{z}

are control moments around of respective axes.

The Figure 2 shows how angles of quadcopter turn are linked with its axes.

To transform the model (32) to a vector record the following designations are entered:

x = x_{1}

y = x_{2}

z = x_{3}

{\dot{x}}_{1} = x_{4}

{\dot{x}}_{2} = x_{5}

{\dot{x}}_{3} = x_{6}

γ = x_{7}

ψ = x_{8}

θ = x_{9}

\dot{γ} = x_{10}

\dot{ψ} = x_{11}

\dot{θ} = x_{12}

M_{1} = M_{x}

M_{2} = M_{y}

M_{3} = M_{z}

As a result the following mathematical model is received:

\begin{matrix} {\dot{x}}_{1} & = & x_{4}, \\ {\dot{x}}_{2} & = & x_{5}, \\ {\dot{x}}_{3} & = & x_{6}, \\ {\dot{x}}_{4} & = & F (cos (x_{7}) sin (x_{9}) cos (x_{8}) + sin (x_{7}) sin (x_{8})) / m, \\ {\dot{x}}_{5} & = & F (cos (x_{7}) cos (x_{9}) / m - g, \\ {\dot{x}}_{6} & = & F (cos (x_{7}) sin (x_{9}) sin (x_{8}) + sin (x_{7}) cos (x_{8})) / m, \\ {\dot{x}}_{7} & = & x_{10}, \\ {\dot{x}}_{8} & = & x_{11}, \\ {\dot{x}}_{9} & = & x_{12}, \\ {\dot{x}}_{10} & = & ((I_{y y} + I_{z z}) x_{11} x_{12} + M_{x}) / I_{x x}, \\ {\dot{x}}_{11} & = & ((I_{z z} + I_{x x}) x_{10} x_{12} + M_{y}) / I_{y y}, \\ {\dot{x}}_{12} & = & ((I_{x x} + I_{y y}) x_{10} x_{11} + M_{z}) / I_{z z}, \end{matrix}

(33)

where

x

is a state space vector,

x = {[x_{1} \dots x_{n}]}^{T}

M

is a vector of control moments,

M = {[M_{1} M_{2} M_{3}]}^{T}

As a rule quadcopters are manifactured with some angle stabilization systems. It means that a drone can be stabilize on any angle from some interval. The system of angles stabilization provides stable location of drone relatively given angles by control moments

M_{i} = w_{i} (x_{7}^{*} - x_{7}, x_{8}^{*} - x_{8}, x_{9}^{*} - x_{9}, x_{10}, x_{11}, x_{12}), i = 1, 2, 3 .

(34)

Assume that the angular stabilization system works out the given angles of the quadcopter quickly enough, at least in comparison with spatial movement. In this case we can assume that the control of the spatial movement of the quadcopter is carried out using the angular position of the drone and the thrust force. Let’s define components of the spatial control vector:

x_{7} = u_{1}

x_{8} = u_{2}

x_{9} = u_{3}

F / m = u_{4}

In result we receive the following model of spatial quadcopter movement

\begin{matrix} {\dot{x}}_{1} & = & x_{4}, \\ {\dot{x}}_{2} & = & x_{5}, \\ {\dot{x}}_{3} & = & x_{6}, \\ {\dot{x}}_{4} & = & u_{4} (cos (u_{1}) sin (u_{3}) cos (u_{2}) + sin (u_{1}) sin (u_{2})), \\ {\dot{x}}_{5} & = & u_{4} cos (u_{1}) cos (u_{3}) - g, \\ {\dot{x}}_{6} & = & u_{4} (cos (u_{1}) sin (u_{3}) sin (u_{2}) + sin (u_{1}) cos (u_{2})) . \end{matrix}

(35)

In the work this model is used in the control problem of quadcopter spatial motion.

4.2. The optimal control problem for spatial motion of quadcopter

The model (35) of control object is given. Here

x

is a state space vector,

x \in R^{6}

u

is a control vector

\in U \in R^{4}

U

is a compact set, that defines restrictions on values of control vector components,

\begin{matrix} u_{1}^{-} = - π / 12 & \leq & u_{1} & \leq & π / 12 = u_{1}^{+}, \\ u_{2}^{-} = - π & \leq & u_{2} & \leq & π = u_{2}^{+}, \\ u_{3}^{-} = - π / 12 & \leq & u_{3} & \leq & π / 12 = u_{3}^{+}, \\ u_{4}^{-} = 0 & \leq & u_{4} & \leq & 12 = u_{4}^{+} . \end{matrix}

(36)

According to the principle of synthesized control, initially the control synthesized problem (1)–(9) is solved. The model (35) is used as a model of control object. To construct the set of initial states (4) the following vector of deviations is used

Δ_{0} = {[2 2 2 0 0 0]}^{T} .

(37)

In the problem initial state and terminal state were equal

x^{0} = x^{f} = {[0 5 0 0 0 0]}^{T} .

(38)

For calculation of the quality criterion (7) the following parameters are used

t^{+} = 2

ε_{0} = 0.1

p = 2

To solve the control synthesis problem the network operator method[22] was used. NOP found the following solution

u_{i} = \{\begin{matrix} u_{i}^{+}, if {\hat{u}}_{i} > u_{i}^{+} \\ u_{i}^{-}, if {\hat{u}}_{i} < u_{i}^{-} \\ {\hat{u}}_{i}, otherwise \end{matrix}, i = 1, \dots, m = 4,

(39)

where

{\hat{u}}_{1} = μ (C),

(40)

{\hat{u}}_{2} = {\hat{u}}_{1} - {\hat{u}}_{1}^{3},

(41)

{\hat{u}}_{3} = {\hat{u}}_{2} + ρ_{19} (W + μ (C)) + ρ_{17} (A),

(42)

{\hat{u}}_{4} = {\hat{u}}_{3} + ln (| {\hat{u}}_{2} |) + sgn (W + μ (C)) \sqrt{| W + μ (C) |} + ρ_{19} (W) +

arctan (H) + sgn (F) + arctan (E) + exp (q_{2} (x_{2}^{f} - x_{2})) + \sqrt{q_{1}},

(43)

C = q_{6} (x_{6}^{f} - x_{6}) + q_{3} (x_{3}^{f} - x_{3}), W = V + tanh (G) + exp (D),

A = q_{1} (x_{1}^{f} - x_{1}) + q_{4} (x_{4}^{f} - x_{4}), H = G + tanh (F) + ρ_{18} (B),

F = E + C + arctan (D) - B, E = D + sgn (x_{5}^{f} - x_{5}) + {(x_{2}^{f} - x_{2})}^{3},

V = exp (H) + cos (q_{6} (x_{6}^{f} - x_{6})) + sgn (D) \sqrt{| D |}, G = F + \sqrt[3]{E} + sin (A),

B = sin (q_{6} (x_{6}^{f} - x_{6})) + q_{5} (x_{5}^{f} - x_{5}) + q_{2} (x_{2}^{f} - x_{2}) + cos (q_{1}) + ϑ (x_{2}^{f} - x_{2}),

D = ρ_{17} (C) + B^{3} + A + ϑ (q_{5} (x_{5}^{f} - x_{5})) + {(x_{5}^{f} - x_{5})}^{2},

μ (z) = \{\begin{matrix} z, if | z | < 1 \\ sgn (z), otherwise \end{matrix}, ρ_{17} (z) = sgn (z) ln (| z | + 1),

ρ_{18} (z) = sgn (z) (exp (| z |) - 1), ρ_{19} (z) = sgn (z) exp (- | z |),

q_{1} = 7.26709

q_{2} = 11.46143

q_{3} = 12.77026

q_{4} = 3.20630

q_{5} = 8.38501

q_{6} = 5.56250

In the second stage the optimal control problem is considered. In the problem the mathematical model (35) is given. The initial state coincides with terminal state (38).

It is necessary to find a control in the form of points in the states space (14). For synthesized control it is necessary to minimize the following quality criterion

J_{3} = t_{f} + p_{1} ∥ x^{f} - x + (t_{f}) ∥ + p_{2} \sum_{i = 0}^{N} \int_{0}^{t_{f}} ϑ (φ_{i} (x)) d t +

p_{3} \sum_{j = 1}^{S} p_{3} ϑ (min_{t} | δ_{j} (x) | - ε) \to min_{x^{*}},

(44)

where

p_{1} = 2

p_{2} = 3

p_{3} = 3

φ_{i} (x) = r_{i} - \sqrt{{(x_{i, 1} - x_{1})}^{2} + {(x_{i, 3} - x_{3})}^{2}},

(45)

i = 1, \dots, N = 4

r_{1} = r_{2} = r_{3} = r_{4} = 2

x_{1, 1} = 5

x_{1, 3} = 0

x_{2, 1} = 10

x_{2, 3} = 5

x_{3, 1} = 5

x_{3, 3} = 10

x_{4, 1} = 0

x_{4, 3} = 5

δ_{j} (x) = \sqrt{{(y_{i, 1} - x_{1})}^{2} + {(y_{j, 3} - x_{3})}^{2}},

(46)

j = 1, \dots, S = 7

y_{1, 1} = 5

y_{1, 3} = - 2

y_{2, 1} = 10

y_{2, 3} = 0

y_{3, 1} = 12

y_{3, 3} = 5

y_{4, 1} = 10

y_{4, 3} = 10

y_{5, 1} = 5

y_{5, 3} = 12

y_{6, 1} = 0

y_{6, 3} = 10

y_{7, 1} = 2

y_{7, 3} = 5

ε = 0.6

In the optimal control problem the terminal time

t_{f}

is determined by the equation (8) with

t^{+} = 14.4

ε_{0} = 0.1

. It is necessary to find coordinates of control points on each time interval,

Δ t = 0.8

. The desired vector includes

3 M

parameters, where

M = ⌊\frac{t^{+}}{Δ t}⌋ = ⌊\frac{14.4}{0.8}⌋ = 18,

(47)

that is

q^{*} = {[q_{1} \dots q_{54}]}^{T}

. The hybrid evolutionary algorithm has found the following optimal solution

\begin{matrix} x^{*, 1} = {[4.83910 1.14025 - 5.22899]}^{T}, x^{*, 2} = {[11.07056 6.79389 - 2.48647]}^{T}, \\ x^{*, 3} = {[9.19808 1.54674 15.87195]}^{T}, x^{*, 4} = {[- 0.12204 0.12276 - 1.82381]}^{T}, \\ x^{*, 5} = {[- 4.08347 2.93658 5.89553]}^{T}, x^{*, 6} = {[16.72896 2.18022 2.27907]}^{T}, \\ x^{*, 7} = {[1.18106 2.56582 14.41088]}^{T}, x^{*, 8} = {[8.67198 5.78737 - 2.90409]}^{T}, \\ x^{*, 9} = {[8.59478 2.73948 11.33252]}^{T}, x^{*, 10} {= [- 1.25924 [- 1.97448 - 1.42747]}^{T}, \\ x^{*, 11} = {[2.45445 7.42257 - 0.38164]}^{T}, x^{*, 12} = {[8.68306 - 0.78496 15.41667]}^{T}, \\ x^{*, 13} = {[0.60972 7.02724 7.66403]}^{T}, x^{*, 141} = {[- 0.59975 0.39324 - 1.31307]}^{T}, \\ x^{*, 15} = {[- 2.39004 7.95279 3.02003]}^{T}, x^{*, 16} = {[2.52642 6.69332 9.17356]}^{T} \\ x^{*, 17} = {[- 0.95896 4.42529 - 0.36318]}^{T}, x^{*, 18} = {[- 0.01193 5.02821 15.40007]}^{T} . \end{matrix}

(48)

For the found solution (48) the value of the quality criterion is

J_{3} = 14.7010

In the Figure 3 projections of the optimal trajectory on the horizontal plane

{x_{1}; x_{3}}

are presented. Here red circles are phase constraints described by the equation (45), small black circle are passing areas described by the equation (delta), small black squares are control points (48).

For the new adaptive synthesized control, proposed in this paper, the set of initial states is determined by the equation (3) with deviation vector

Δ_{0} = {[0.2 0.2 0.2 0 0 0]}^{T} .

(49)

It is necessary to find the same number of control points according to the following quality criterion

J_{4} = \sum_{k = 1}^{K} (t_{f, k} + p_{1} ∥ x^{f} - x (t_{f, i}, x^{0, i}) + p_{2} \sum_{i = 0}^{N} \int_{0}^{t_{f}} ϑ (φ_{i} (x)) d t +

p_{3} \sum_{j = 1}^{S} p_{3} ϑ (min_{t} | δ_{j} (x) | - ε)) \to min_{x^{*}},

(50)

where

K = 7

t_{f, k}

is defined by equation (8). Other parameters of the criterion are the same as for the criterion (44).

The hybrid evolutionary algorithm has found the following optimal solution

\begin{matrix} x^{*, 1} = {[17.46361 1.14030 - 8.00000]}^{T}, x^{*, 2} = {[11.07060 6.79390 - 2.48650]}^{T}, \\ x^{*, 3} = {[9.19810 2.05890 15.87207]}^{T}, x^{*, 4} = {[- 0.27800 2.51633 - 1.99493]}^{T}, \\ x^{*, 5} = {[- 3.98430 2.27048 13.40976]}^{T}, x^{*, 6} = {[17.18235 0.26253 2.19246]}^{T}, \\ x^{*, 7} = {[- 3.56784 3.44842 14.94369]}^{T}, x^{*, 8} = {[4.53881 2.20612 - 2.99328]}^{T}, \\ x^{*, 9} = {[9.06419 2.49928 11.30274]}^{T}, x^{*, 10} = {[- 0.16333 - 1.88939 - 0.75766]}^{T} . \\ x^{*, 11} = {[2.17956 6.92983 - 1.06412]}^{T}, x^{*, 12} = {[10.24873 - 0.51465 5.82840]}^{T}, \\ x^{*, 13} = {[1.12164 2.84506 7.93804]}^{T}, x^{*, 14} = {[0.10678 3.23489 - 1.55778]}^{T}, \\ x^{*, 15} = {[- 2.54374 0.99732 2.82005]}^{T}, x^{*, 16} = {[7.41006 6.49634 12.02799]}^{T}, \\ x^{*, 17} = {[- 0.67510 4.03845 - 0.28527]}^{T}, x^{*, 18} = {[- 0.18037 4.62980 6.89661]}^{T} . \end{matrix}

(51)

A value of the quality criterion (50) for one initial state

x (0) = {[0 5 0 0 0 0]}^{T}

, is

J_{4} = 15.6090

. In the Figure 4 projections of the optimal trajectory on the horizontal plane

{x_{1}; x_{3}}

found by the adaptive synthesized control (51) is presented.

Since the initial state in the problem coincided with the terminal state, in order to force the control object to move along a closed path, mandatory conditions for passing through certain areas were added to the quality criterion. For trajectories that meet the criteria for passing through the specified areas, the value of the quality criterion will not change at

p_{3} = 0

. How it is seen in the Fig.3 and the Fig.4 both trajectories pass through all specified areas.

Let’s check the sensitivity of the obtained solutions to random perturbations of the initial state

x_{i} (0) = x_{i}^{0} + β_{0} (2 ξ (t) - 1), i = 1, \dots, n = 6,

(52)

where

ξ (t)

is a function generator of random noise, returns random number from interval

(0; 1)

at every call,

β_{0}

is a constant level of noise.

In the Figure 5 and 6 the optimal (in blue) and eight perturbed trajectories (in black) for

β_{0} = 0.1

for solutions obtained by synthesized (Figure 5) and adaptive synthesized (Figure 6) control are presented.

For comparison, for a model (35) without stabilization systems (39), the problem of optimal control directly was solved, where control was sought in the form of a piece-wise linear function, taking into account restrictions (36).

u_{i} = \{\begin{matrix} u_{i}^{+}, if {\tilde{u}}_{i} > u_{i}^{+} \\ u_{i}^{-}, if {\tilde{u}}_{i} < u_{i}^{-} \\ {\tilde{u}}_{i}, otherwise \end{matrix}, i = 1, \dots, m = 4,

(53)

where

{\tilde{u}}_{i} = (q_{i + j m} - q_{i + (j - 1) m}) \frac{t - (j - 1) Δ t}{Δ t} + q_{i + (j - 1) m}, i = 1, 2, 3, 4,

(54)

(j - 1) Δ t \leq t < j Δ t

j \in {1, \dots, K + 1}

q_{i}

is a component of desired parameters vector,

i = 1, \dots, m (M + 1)

q = {[q_{1} \dots q_{m (M + 1)}]}^{T} .

(55)

In this work, we set the same time interval

Δ t = 0.8

, therefore from (15)

M = 18

, and it is necessary to find

m (M + 1) = 4 \cdot 19 = 76

parameters,

q = {[q_{1} \dots q_{76}]}^{T} .

To solve the optimal control problem the same hybrid algorithm [28] was used. As a result, the following solution was obtained

\begin{matrix} q & = & [12.57045 - 4.58471 - 2.74617 2.90422 - 9.26325 - 0.10990 \\ - 2.63222 18.36841 0.00816 - 17.35177 0.00165 4.28718 \\ - 11.81492 1.88489 - 8.01206 15.87943 10.84894 0.06505 \\ 9.65475 19.51903 2.79860 - 4.06408 - 0.88992 10.50507 \\ - 19.19030 17.90240 12.52431 19.00010 4.76513 - 11.97648 \\ 0.00010 8.85464 2.92334 0.14238 8.60919 7.83194 \\ 5.74904 - 8.35383 - 3.42757 12.87671 18.58717 15.43057 \\ 9.06137 12.55621 - 1.54628 1.47314 2.40706 8.67602 \\ 0.00091 - 11.91236 - 19.94063 17.08304 19.92640 - 1.33145 \\ - 7.77258 15.54094 - 19.93278 - 17.37121 - 9.31290 5.03257 \\ - 0.90297 - 5.22021 0.62653 4.21368 - 2.04314 - 0.53192 \\ 0.09353 14.25213 - 0.11587 9.05588 - 0.03270 11.23667 \\ {0.03826 - 16.78047 0.18220 19.81652]}^{T} . \end{matrix}

(56)

In the Figure 7 the projection of the optimal trajectory obtained by the direct method is presented.

In the table 1 values of the quality criterion (44) of ten experiments for perturbed solutions obtained by the synthesized (column Synthesized), the adaptive synthesized (column Adaptive) control, and the direct solution (Direct). In two last strings of the table average values of the functionals and standard deviations for all experiments are presented.

As can be seen from Figure 5 and 6 and the Table 1, the solutions obtained by adaptive synthesized control are less sensitive to perturbations of initial states than the solutions obtained by simple synthesized control or especially by the direct approach.

5. Results

A new method for solving the problem of optimal control in the class of implemented functions, an adaptive synthesized control principle is presented. Unlike synthesized control, the new method takes into account the perturbations of the initial state when solving the optimal control problem. Therefore, the value of quality criterion is calculated as the sum of the quality criterion values for the different initial states. As a result of this approach, a solution is chosen in such a way that for the origin initial state it may not give the best quality criterion value, but in the case of disturbances of the initial state, the quality criterion value changes slightly.

6. Discussion

Obtaining a solution based on replacing the optimal solution is less optimal, but also less sensitive to disturbances, at first glance, seems obvious and can be applied to any method of solving the optimal control problem. However, this is not the case. A direct solution to the optimal control problem results in control in the form of a time function and an open loop control system. Perturbation of the initial conditions for such a system gives large variations in quality criterion values, which cannot be reliably estimated from the average value due to the large variance.

The synthesized control method firstly makes the control object stable relative to some equilibrium point in the state space. This means that the perturbed and unperturbed trajectories at each point in time move towards a stable equilibrium point. The adaptive synthesized control method sets the positions of the equilibrium points so that all disturbed trajectories are located in some tube that does not violate phase constraints whenever possible.

In the future, when using the adaptive synthesized control method, it is necessary to assess the required size of the initial state region and reduce the number of initial state points, since this significantly increases the time for finding the optimal solution.

Author Contributions

Conceptualization, A.D. and E.S.; methodology, A.D.; software, A.D. and E.S.; validation, E.S.; formal analysis, A.D.; investigation, E.S.; resources, A.D.; writing—original draft preparation, A.D. and E.S.; writing—review and editing, E.S.; visualization, A.D.; supervision, A.D. All authors have read and agreed to the published version of the manuscript.

Funding

This research was supported by the Ministry of Science and Higher Education of the Russian Federation, project No. 075-15-2020-799.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

Egerstedt, M. Motion Planning and Control of Mobile Robots, Doctoral Thesis, Stockholm, 2000.
Walsh, G.; Tilbury, D.; Sastry, S.; Murray, R.; Laumond, J. P. Stabilization of trajectories for systems with nonholonomic constraints. IEEE Transactions on Automatic Control, 1994, 39(1) 216–222. [CrossRef]
Samir,A.; Hammad, A.; Hafez, A.; Mansour, H. Quadcopter Trajectory Tracking Control using State-Feedback Control with Integral Action. International Journal of Computer Applications (0975 - 8887), 2017, 168 (7), 1–7. [CrossRef]
Allagui, N.Y.; Abid, D.B.; Derbel, N. Autonomous navigation of mobile robot with combined fractional order PI and fuzzy logic controllers, 2019 16th International Multi-Conference on Systems, Signals & Devices (SSD), Istanbul, Turkey, 2019, pp. 78-83. [CrossRef]
Chen, B.; Cao, Y.; Feng, Y. Research on Trajectory Tracking Control of Non-holonomic Wheeled Robot Using Backstepping Adaptive PI Controller, 2022 7th Asia-Pacific Conference on Intelligent Robot Systems (ACIRS), Tianjin, China, 2022, pp. 7-12. [CrossRef]
Karnani, Ch., Raza, S., Asif, A., Ilyas, M. Adaptive Control Algorithm for Trajectory Tracking of Underactuated Unmanned Surface Vehicle (UUSV).Hindawi, Journal of Robotics, 2023, 4820479. [CrossRef]
Anh Tung Nguyen, Nguyen Xuan-Mung and Sung-Kyung Hong. Quadcopter Adaptive Trajectory Tracking Control: A New Approach via Backstepping Technique. 0Applied Sciences, 2019, 3873(9), 1–17. [CrossRef]
Lee, E.B.; Marcus, L. Foundations of Optimal Control Theory; Robert & Krieger publishing company: Malabar, Florida, 1967; 576 p. [CrossRef]
Pontryagin, L. S.; Boltyanskii, V. G.; Gamkrelidze, R. V.; Mishchenko, E. F. The Mathematical Theory of Optimal Process. L. S. Pontryagin, Selected works, vol. 4; Gordon and Breach Science Publishers: New York, London, Paris, Montreux, Tokyo, 1985; 360 p. [CrossRef]
Shmalko, E., Diveev, A. Extended Statement of the Optimal Control Problem and Machine Learning Approach to Its Solution. Mathematical Problems in Engineering, vol. 2022, Article ID 1932520, 12 pages, 2022. [CrossRef]
Diveev, A.I. Refinement of Optimal Control Problem for Practical Implementation of Its Solution. Doklady Mathematics, 2023, 107(1), pp. 28–36. [CrossRef]
Diveev, A.; Shmalko, E.Yu.; Serebrenny, V.V.; Zentay, P. Fundamentals of synthesized optimal control. Mathematics, 2020, 9(1), pp. 1–21.
Shmalko, E.Y. Feasibility of Synthesized Optimal Control Approach on Model of Robotic System with Uncertainties. Electromechanics and Robotics, 2021.
Shmalko, E. Computational Approach to Optimal Control in Applied Robotics. In: Ronzhin, A., Pshikhopov, V. (eds) Frontiers in Robotics and Electromechanics. Smart Innovation, Systems and Technologies, 2023, vol 329. Springer, Singapore.
Diveev, A.; Shmalko, E.Yu. Stability of the Optimal Control Problem Solution. In Proceedings 8th International Conference on Control, Decision and Information Technologies, CoDIT, 17-20 May, 2022, Istanbul, Turkey, pp. 33-38.
Simon J.D., Mitter S.K. A theory of modal control. Information and Control, 1968,Vol. 13, Issue 4, pp. 316-353. [CrossRef]
Zhou H.; Liu, Z. Vehicle Yaw Stability-Control System Design Based on Sliding Mode and Backstepping Contol Approach, IEEE Transactions on Vehicular Technology, vol. 59, no. 7, pp. 3674-3678, Sept. 2010. [CrossRef]
Febsya, M.R.; Ardhi, R.; Widyotriatmo, A.; Nazaruddin, Y.Y. Design Control of Forward Motion of an Autonomous Truck-Trailer using Lyapunov Stability Approach, 2019 6th International Conference on Instrumentation, Control, and Automation (ICA), Bandung, Indonesia, 2019, pp. 65-70. [CrossRef]
Zihao, S.; Bin, W.; Ting, Z. Trajectory Tracking Control of a Spherical Robot Based on Adaptive PID Algorithm, 2019 Chinese Control And Decision Conference (CCDC), Nanchang, China, 2019, pp. 5171-5175. [CrossRef]
Liu, J.; Song, X.; Gao, S.; Chen, C.; Liu K.; Li, T. Research on Horizontal Path Tracking Control of a Biomimetic Robotic Fish, 2022 International Conference on Mechanical and Electronics Engineering (ICMEE), Xi’an, China, 2022, pp. 100-105. [CrossRef]
Duriez T.; Brunton S.L.; Noack B.R. Machine Learning Control–Taming Nonlinear Dynamics and Turbulence. Springer International Publishing: Switzerland, 2017.
Diveev, A.I., Shmalko, E. Yu. Machine Learning Control by Symbolic Regression; 2021, Springer: Cham, Switzerland, 2021; 155 p.
Diveev, A.I., Konstantinov, S.V. Study of the Practical Convergence of Evolutionary Algorithms for the Optimal Program Control of a Wheeled Robot.Journal of Computer and Systems Sciences International, 2018, 57(4), 561–580. [CrossRef]
Diveev, A.; Shmalko, E. Machine Learning Feedback Control Approach Based on Symbolic Regression for Robotic Systems. Mathematics 2022, 10, 4100. [CrossRef]
Davis, L. Handbook of Genetic Algorithms.; 1991, Van Nostrand Reinhold, New York.
Eberhardt, R.C.; Kennedy, J.A. Particle Swarm Optimization, Proceedings of the IEEE International Conference on Neural Networks, 1995, Piscataway, NJ, 1942–1948.
Mirjalili, S.; Mirjalil, S.M.; Lewis, A. Grey Wolf Optimizer, Advances in Engineering Software ,2014, 69, pp 46–61.
Diveev, A. Hybrid Evolutionary Algorithm for Optimal Control Problem. Lecture Notes in Networks and Systems, LNNS, 2023 543, 726–-738.

Figure 1. NOP-graphs for mathematical expressions (21), a)

y_{1}

, b)

y_{2}

, c)

y_{3}

, d)

y_{4}

Figure 1. NOP-graphs for mathematical expressions (21), a)

y_{1}

, b)

y_{2}

, c)

y_{3}

, d)

y_{4}

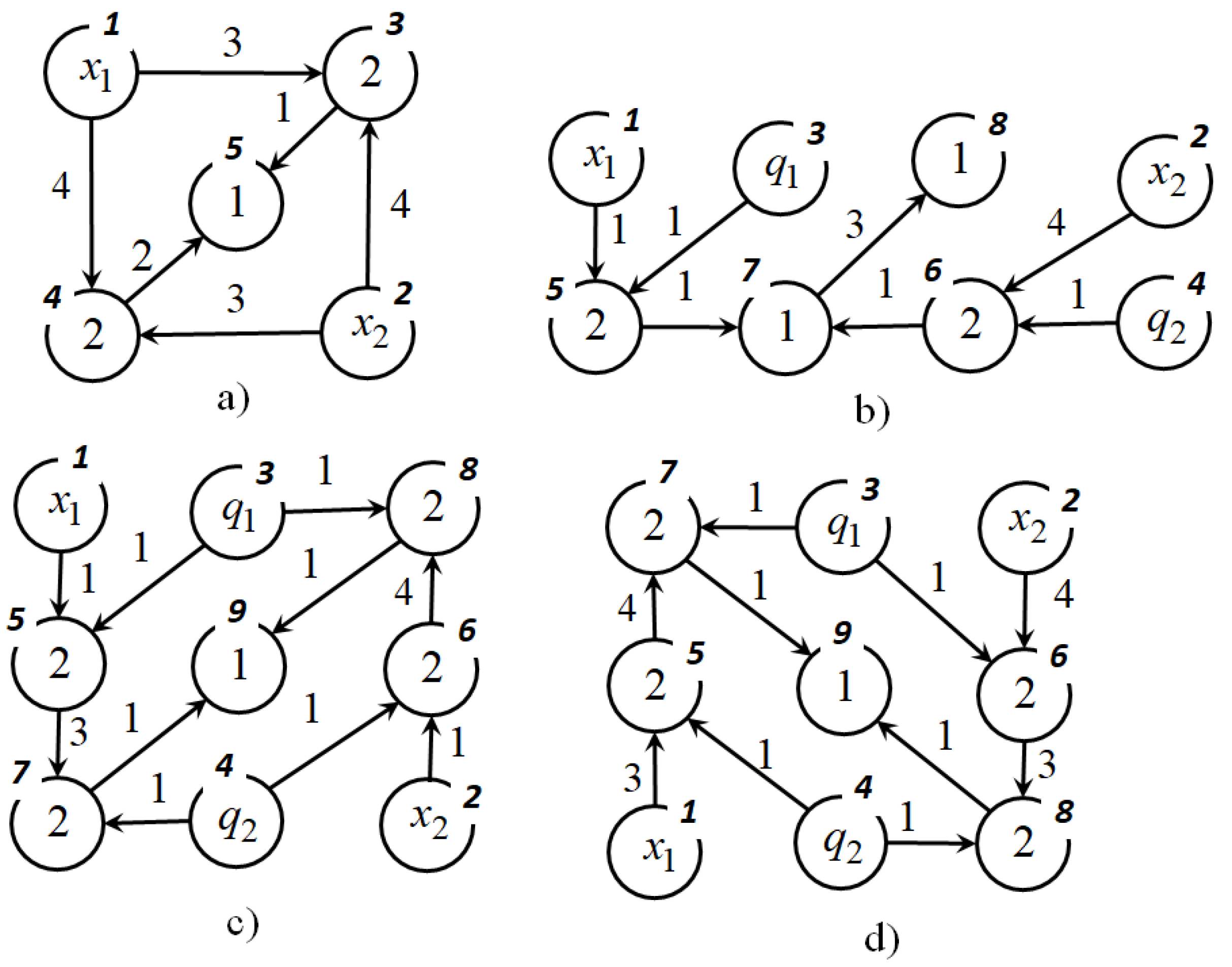
Figure 2. Inertial coordinate system for quadcopter

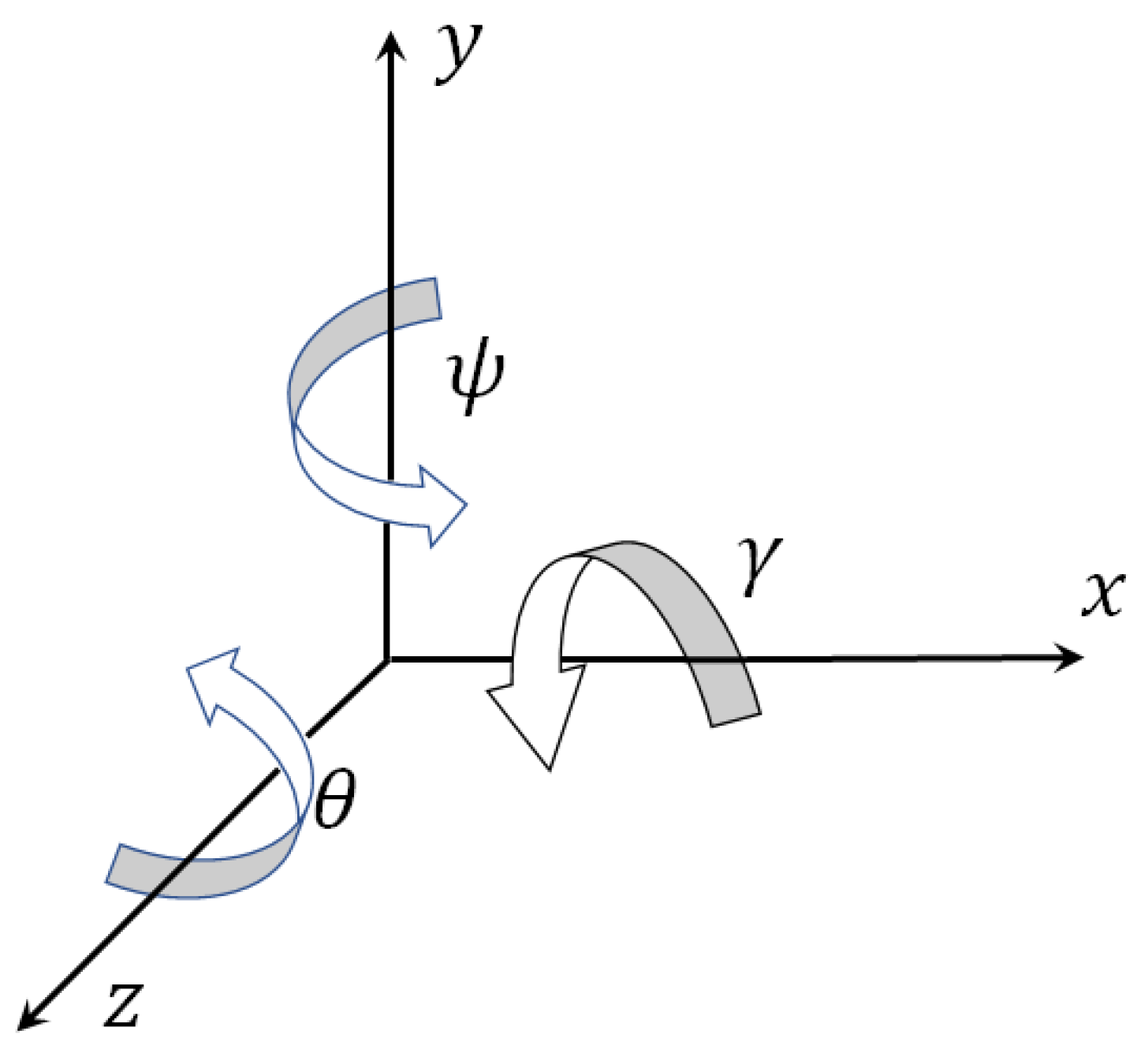
Figure 3. Optimal trajectory for synthesized control

Figure 4. Optimal trajectory for adaptive synthesized control

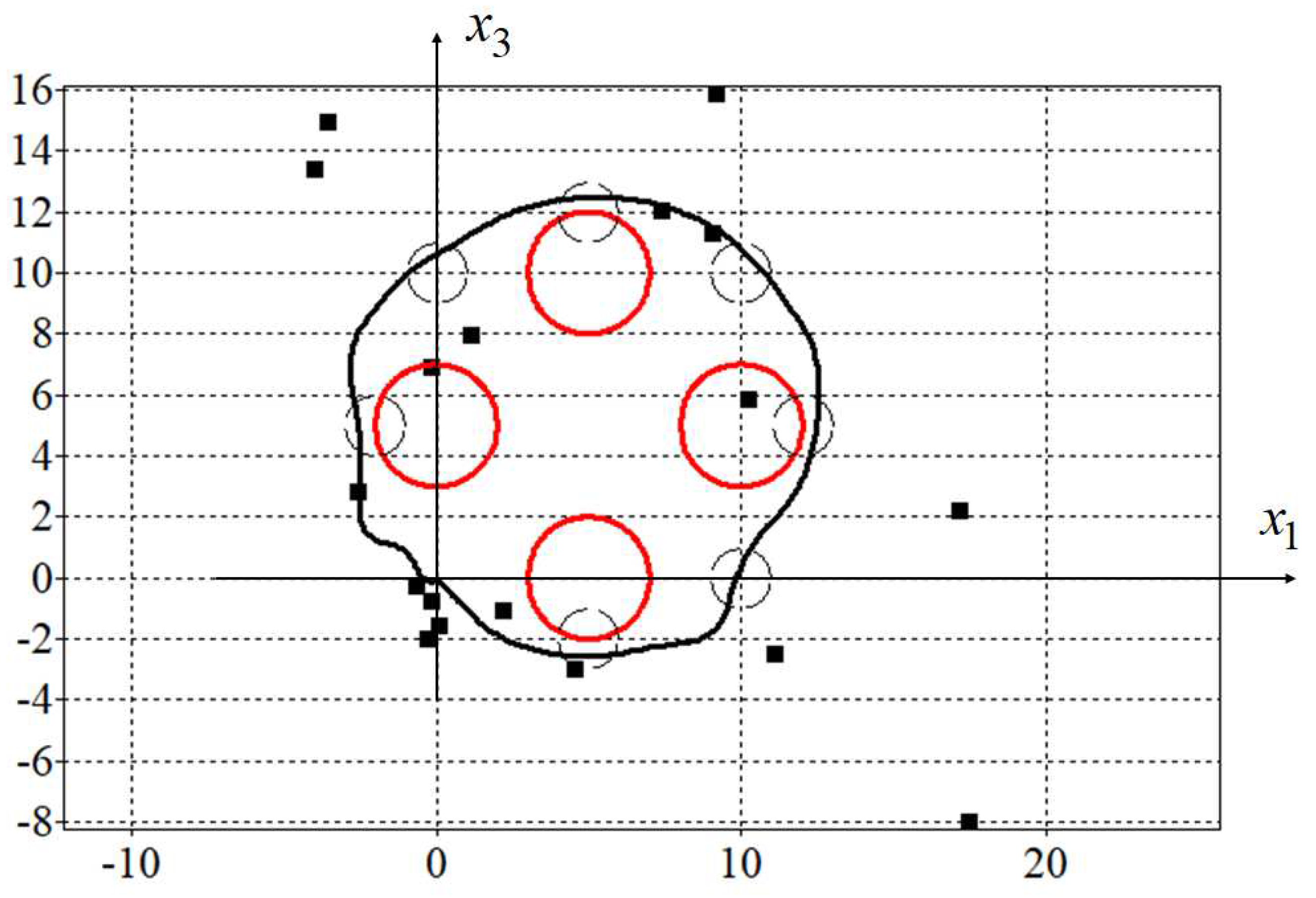
Figure 5. Optimal and eight disturbance trajectories of synthesized control

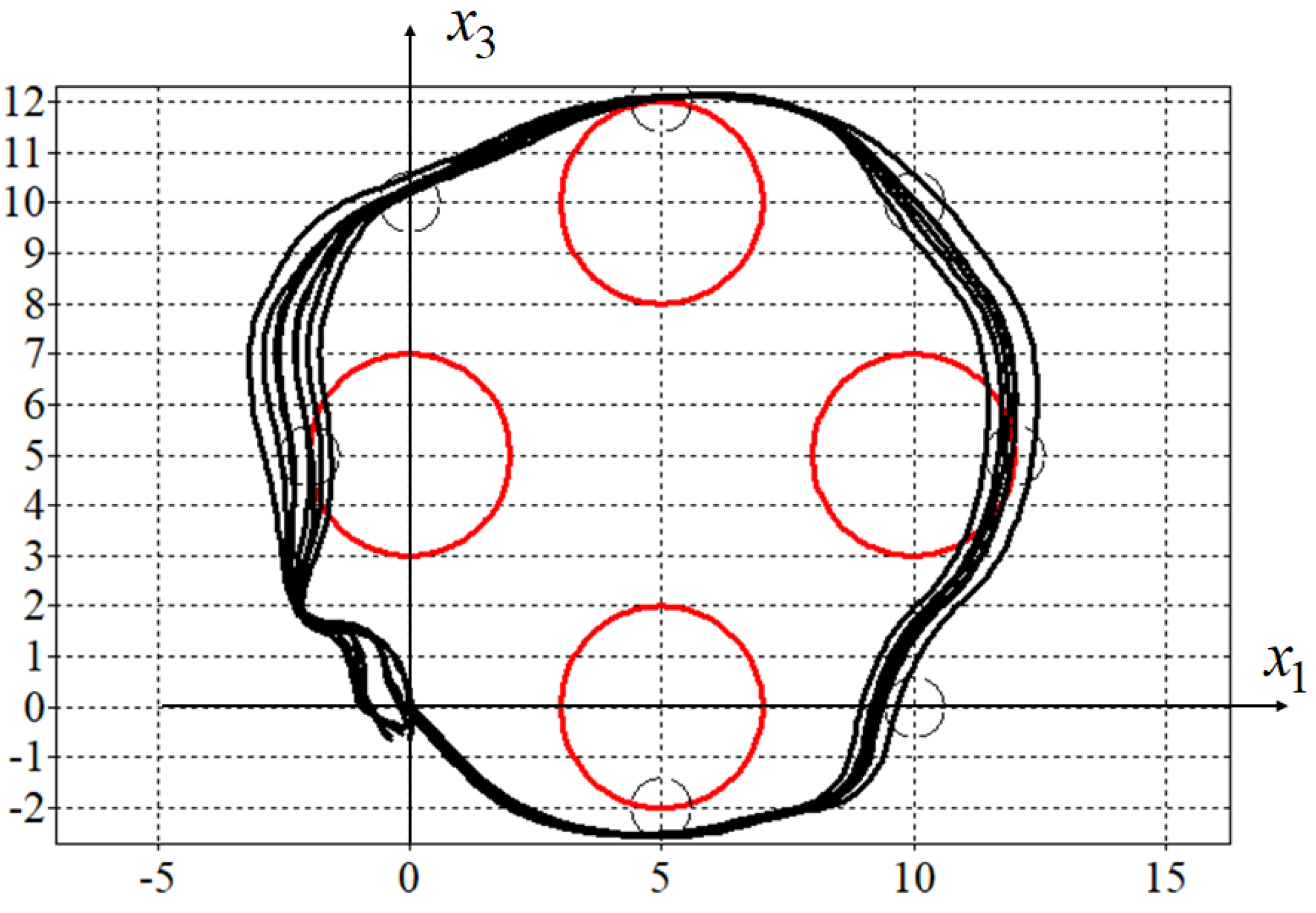
Figure 6. Optimal and eight disturbance trajectories of adaptive synthesized control

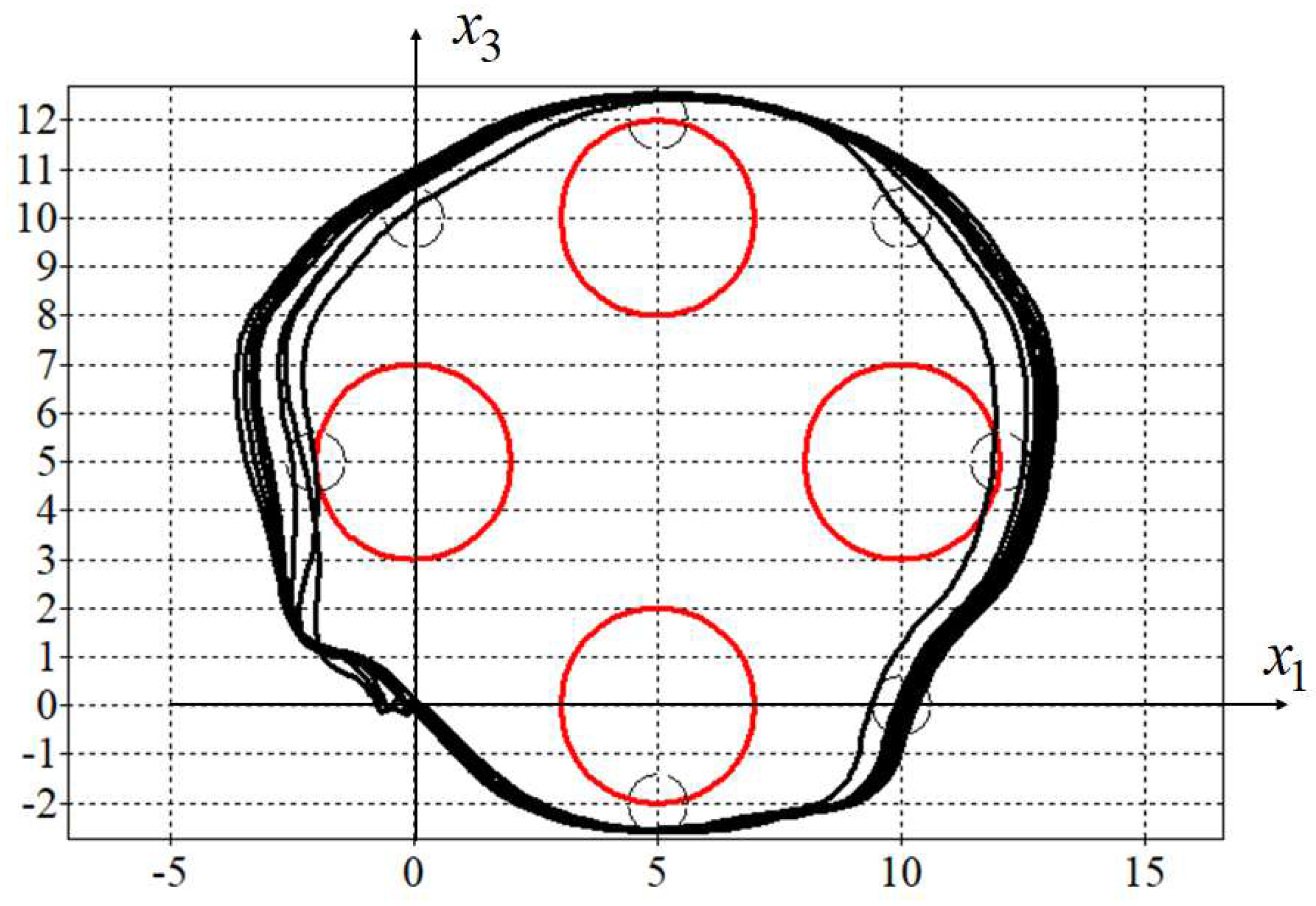
Figure 7. Optimal trajectory of direct control

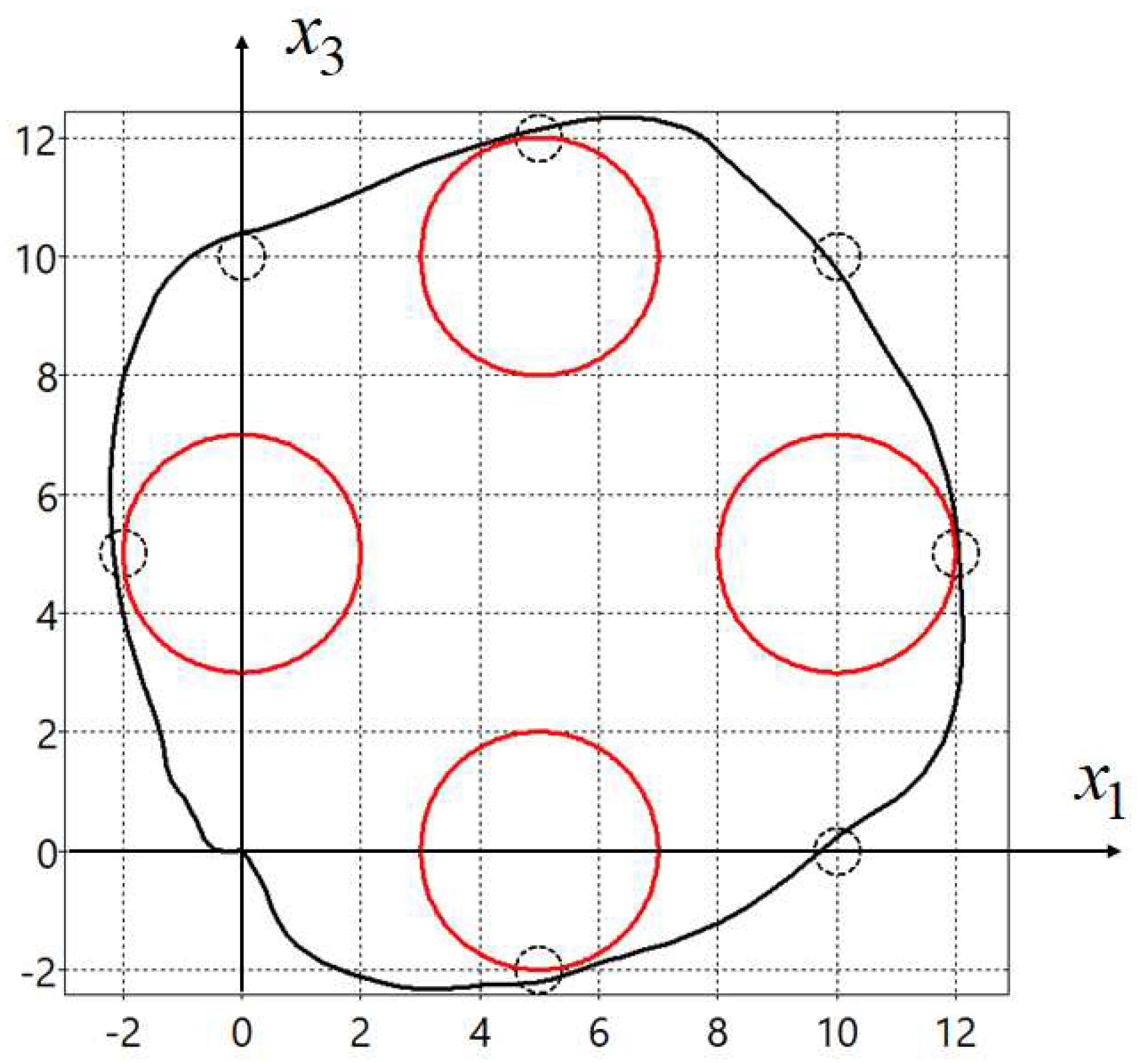
Table 1. Sensitivity of decisions to perturbations of initial states

No	Synthesized	Adaptive	Direct
1	14.7651	15.4892	19.2082
2	20.7377	15.4829	19.8854
3	15.2888	15.6947	16.7706
4	16.9743	15.4935	16.2334
5	18.6159	16.0397	19.2815
6	19.5227	15.7950	19.3866
7	20.0937	15.4178	16.8263
8	17.5416	16.1424	23.3437
9	20.1225	17.0695	19.6251
10	19.9257	15.3893	20.8163
Av	18.3588	15.8014	19.1377
SD	2.1234	0.5167	2.1285

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Alerts

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Adaptive Synthesized Control for Solving The Optimal Control Problem

Abstract

1. Introduction

2. Adaptive Synthesized Control

3. Methods of Solving

4. Computational Experiment

4.1. Mathematical Model of Spatial Movement of Quadcopter

4.2. The optimal control problem for spatial motion of quadcopter

5. Results

6. Discussion

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe