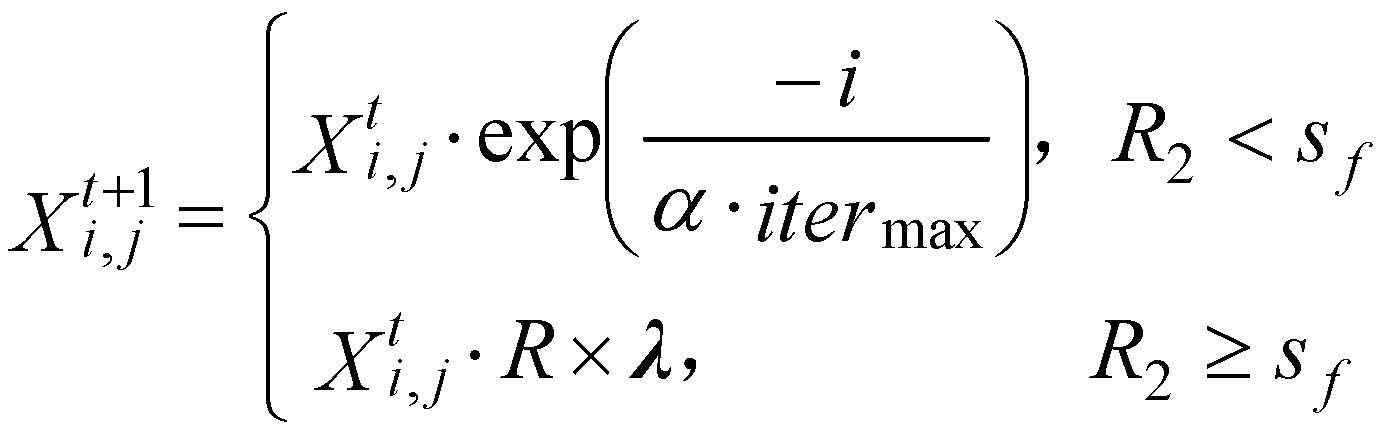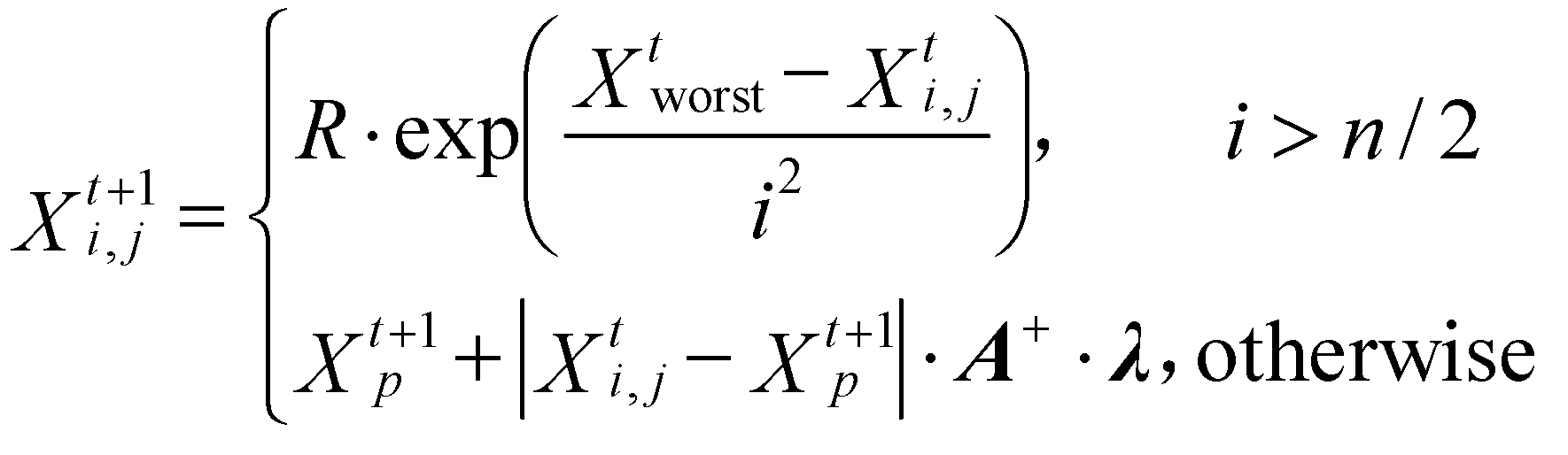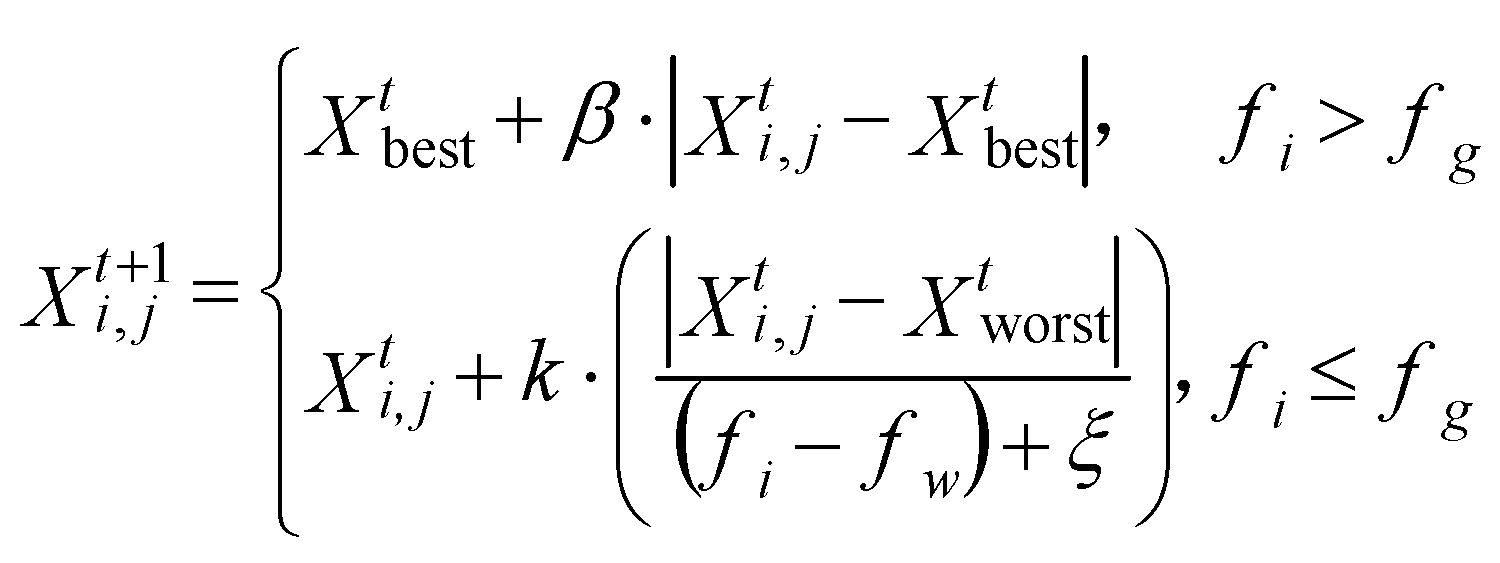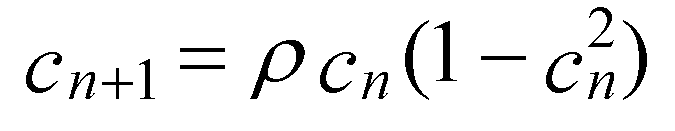Path Planning of Unmanned Surface Vehicle Based on Improved Sparrow Search Algorithm

Preprint

Article

Path Planning of Unmanned Surface Vehicle Based on Improved Sparrow Search Algorithm

Altmetrics

Downloads

102

Views

Comments

A peer-reviewed article of this preprint also exists.

Guang zhong Liu

Sheng Zhang^*,Guo jie Ma,Yi peng Pan

Guang zhong Liu

Sheng Zhang^*,Guo jie Ma,Yi peng Pan

This version is not peer-reviewed

Submitted:

30 August 2023

Posted:

06 September 2023

You are already at the latest version

Alerts

Abstract

In order to solve the problem of many constraints and complex navigation environment in the path planning of unmanned surface vehicle(USV), an improved Sparrow search algorithm com-bining Cubic chaotic map and Gaussian random walk strategy was proposed to plan it. Firstly, in the population initialization stage, Cubic chaotic map was used to replace the random generation method of the traditional sparrow search algorithm to optimize the uneven initial distribution of the population and improve the global search ability of the population. Secondly, in the late it-eration of the algorithm, the standard deviation of fitness is introduced to determine whether the population is trapped in the local optimum. If true, the Gaussian random walk strategy is used to perturb the optimal individual and assist the algorithm to escape the local optimum. Thirdly, the chosen water environment is modeled, and the navigation information of the original inland electronic navigation chart(ENC) is preprocessed, gridized, and the obstacle swelling is processed. Finally, the path planning experiments of USV are carried out in inland ENC grid environment. The experimental results show that, compared with the traditional sparrow search algorithm, the average fitness value of the path planned by improved sparrow search algorithm is reduced by 14.8%, and the variance is reduced by 49.9%. The path planned by the algorithm is of good quality and high stability, and combined with ENC, it can provide a reliable path for USV.

Keywords:

Subject: Engineering - Marine Engineering

1. Introduction

The application of unmanned ships in water transportation, environmental monitoring, life-saving, cluster investigation, and other fields is gaining popularity [1]. The key to research in unmanned ship technology lies in the three dimensions of navigation, control, and perception. Navigation is the technology used to approach or avoid obstacle targets[2], and the path planning link in the navigation section is especially crucial. Unmanned ship path planning refers to the planning of a path for an unmanned ship to reach a target point in accordance with a provided map and target points [3].

Existing algorithms for the study of the unmanned ship path planning problem include the A* algorithm, artificial potential field method, reinforcement learning method, and bionic class algorithm [4]. Each of these algorithms has its own advantages for solving the unmanned ship path planning problem, and by improving the traditional algorithms, researchers have achieved good application results under specific conditions [5] expanded the A* algorithm node search from 8 neighborhoods to 24 and 48 neighborhoods to obtain the global optimal solution in a larger optimization space and make the path smoother[6]proposed a new artificial potential field function and added the escape force factor based on Krogh's research, which solved the problems of local minima and unreachability of the target in the traditional artificial potential field method[7]solved the problem of local minima and unreachability of the target by improving the gain parameter of the potential field of Q-Learning reinforcement learning algorithm, improving the problem of high sensitivity of the parameter to the algorithm and enhancing the algorithm path planning performance[8] based on the traditional ant colony algorithm considered the uneven distribution of initial pheromone, introduced the weight factor, improved the ant colony information update rule and other methods to solve the problem that the algorithm is easy to fall into the deadlocked path. The previously mentioned ant colony algorithm is a type of bionic algorithm, and scholars have proposed a number of similar group intelligence algorithms by analysing the behaviour of biological communities in nature, including the grey wolf algorithm, the ant colony algorithm, the whale optimisation algorithm[9-11], and the sparrow search algorithm.

The sparrow search algorithm is a new population intelligence algorithm proposed by [12] in 2020. It was discovered that the algorithm outperformed the grey wolf algorithm and its equivalent type of algorithms in terms of finding accuracy, robustness, and convergence speed, and the standard test function finding results demonstrated the algorithm's superior performance[13]. Currently, the algorithm has been effectively applied to the 3D UAV trajectory optimisation problem[14], but no research has been conducted on the unmanned ship path planning problem, so a method based on the improved sparrow search algorithm is proposed: First, the Cubic chaotic mapping is used to initialise the population instead of the traditional algorithm's random generation method; then, the fitness standard deviation is introduced in the final iteration of the algorithm to determine if the population is stable. Then, in the final iteration of the algorithm, the standard deviation of fitness is introduced to determine whether the population is trapped in the local optimum, and a Gaussian random wandering strategy is used to perturb the optimal individuals to aid the algorithm in escaping the local optimum; then the selected water environment is modelled, and the original electronic route map is pre-processed, gridized, and obstacle expansion processed; finally, the enhanced algo is implemented.

2. Sparrow search algorithm

The sparrow search algorithm is an intelligent algorithm based on the foraging and anti-predation characteristics of the sparrow population, which classifies sparrows into three categories: discoverers, followers, and observers. The explorers seek sustenance for the populace and direct the foraging efforts of the followers. The following is the iterative formula for the discoverers:

(1)

Where, t is the current iteration number, X_i,j is the position information of the first sparrow population in the first dimension,

α \in r a n d (0, 1)

, iter_max is the maximum number of iterations, R is a random number obeying a normal distribution,

λ

is a 1×d matrix with all elements equal to 1, d is the dimension of the unmanned boat path planning problem,

R_{2} \in (0, 1)

, is the warning value of the sparrow population position, and

s_{f} \in (0.5, 1)

is the safety value of the sparrow population position.

When

R_{2} < s_{f}

, it indicates that there is no danger in the current foraging environment; when

R_{2} \geq s_{f}

, it indicates that there is danger in the current foraging environment that needs to be signalled, all sparrows must leave their current position and fly to a secure area. During the foraging process, the followers act in accordance with the seeker, and when the finder discovers a superior food source, the followers compete with it; if successful, they receive the finder's food. Followers update their position based on the following equation:

(2)

where X_p is the optimal population position, X_worst is the worst population position, A is 1×d matrix, each matrix cell is random-1 or 1, and A⁺=A^T(AA^T)^-1. When

i > n / 2

,the i-th follower cannot find sustenance and must seek for it elsewhere by flying. The function of scouts in sparrow populations is to be aware of danger and lead the population to a secure area, accounting for 10–20% of the total population. The iterative formula for generating the random locations of spies within the population is shown in the following equation.

(3)

Where X_best is the current global optimal position,

β

is a step control parameter that follows the standard normal distribution,

k \in [- 1, 1]

indicates the direction of individual movement, f_i is the current sparrow fitness value, f_g is the global optimal fitness value, f_w is the global worst fitness value, and

ξ

is a constant to prevent the denominator from being zero.

f_{i} > f_{g}

demonstrates that the sparrow is at the edge of the population and vulnerable to external attack;

f_{i} \leq f_{g}

demonstrates that the scout is aware of the threat and must abandon the current location.

2. Improved sparrow search algorithm

2.1. Cubic chaotic map

In comparison to other swarm intelligence algorithms, the sparrow search algorithm has superior performance. However, when solving complex optimisation problems such as unmanned ship paths, there are still issues such as slow convergence speed, reduced population diversity in the late iteration period, and a tendency to converge to local optimal solutions[15]. Taking into account the stochastic and ergodic characteristics of chaos, when the sparrow population is initialised, the majority of scholars use Logistic mapping to ensure the population distribution is uniform[16]. This paper proposes replacing the stochastic generation of the sparrow search algorithm with Cubic chaotic mapping to improve the algorithm's global search performance. Avoid premature convergence. The formula for Cubic chaotic mapping is as follows:

(4)

where -1<c_n<1，c_n≠0，n=0,1,2,…,n；

ρ

is control parameter. To analyse the effect of the value of

ρ

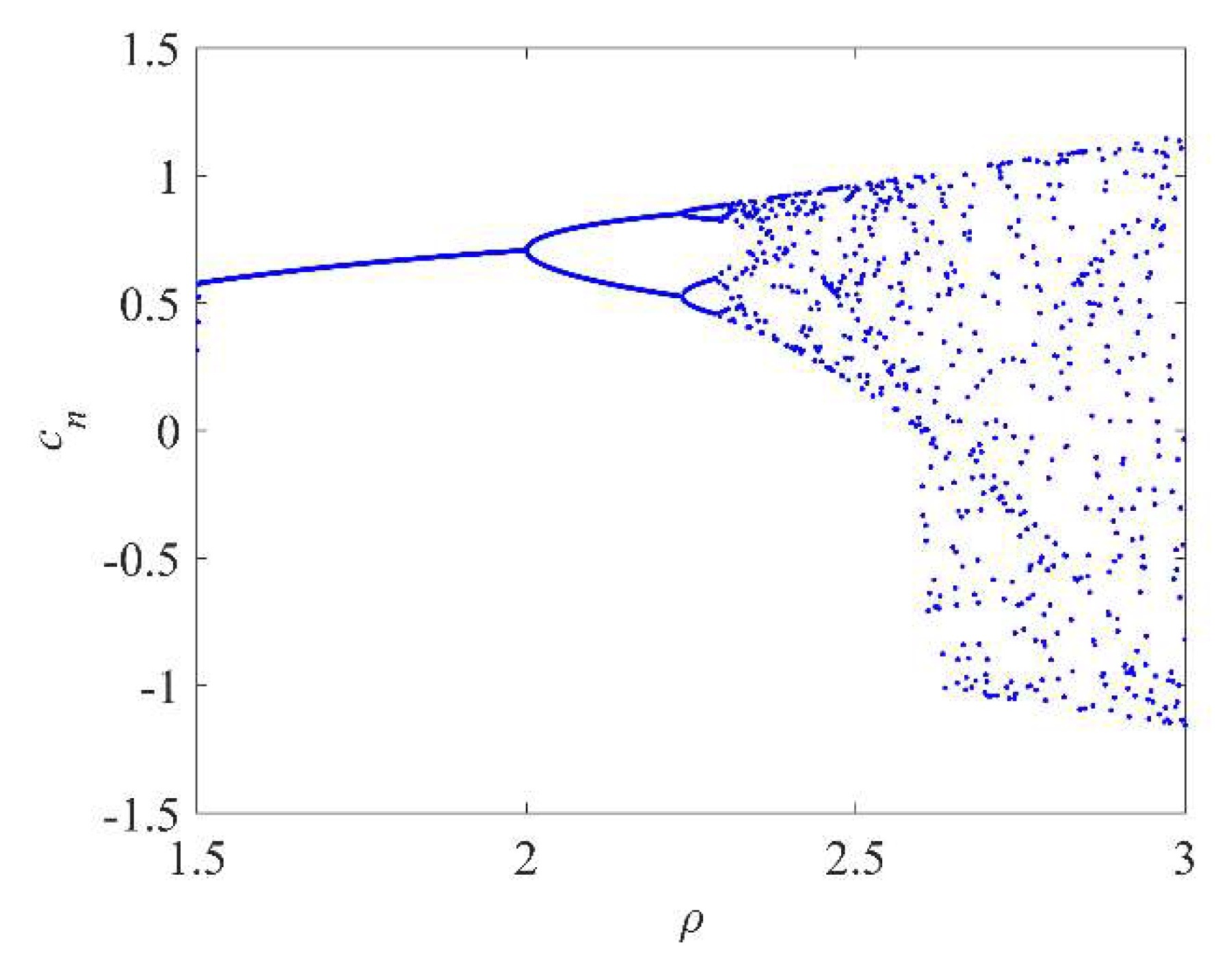
taking on the chaotic value c_n, the simulation is conducted, and the empirical initial value c₀=0.315 with a step size of 0.01 is used to acquire the chaotic results shown in Figure 1.

Based on Figure 1, when

2.595 \leq ρ \leq 3

， the chaotic value c_nhas a reasonable random distribution effect, taking the extreme value

ρ

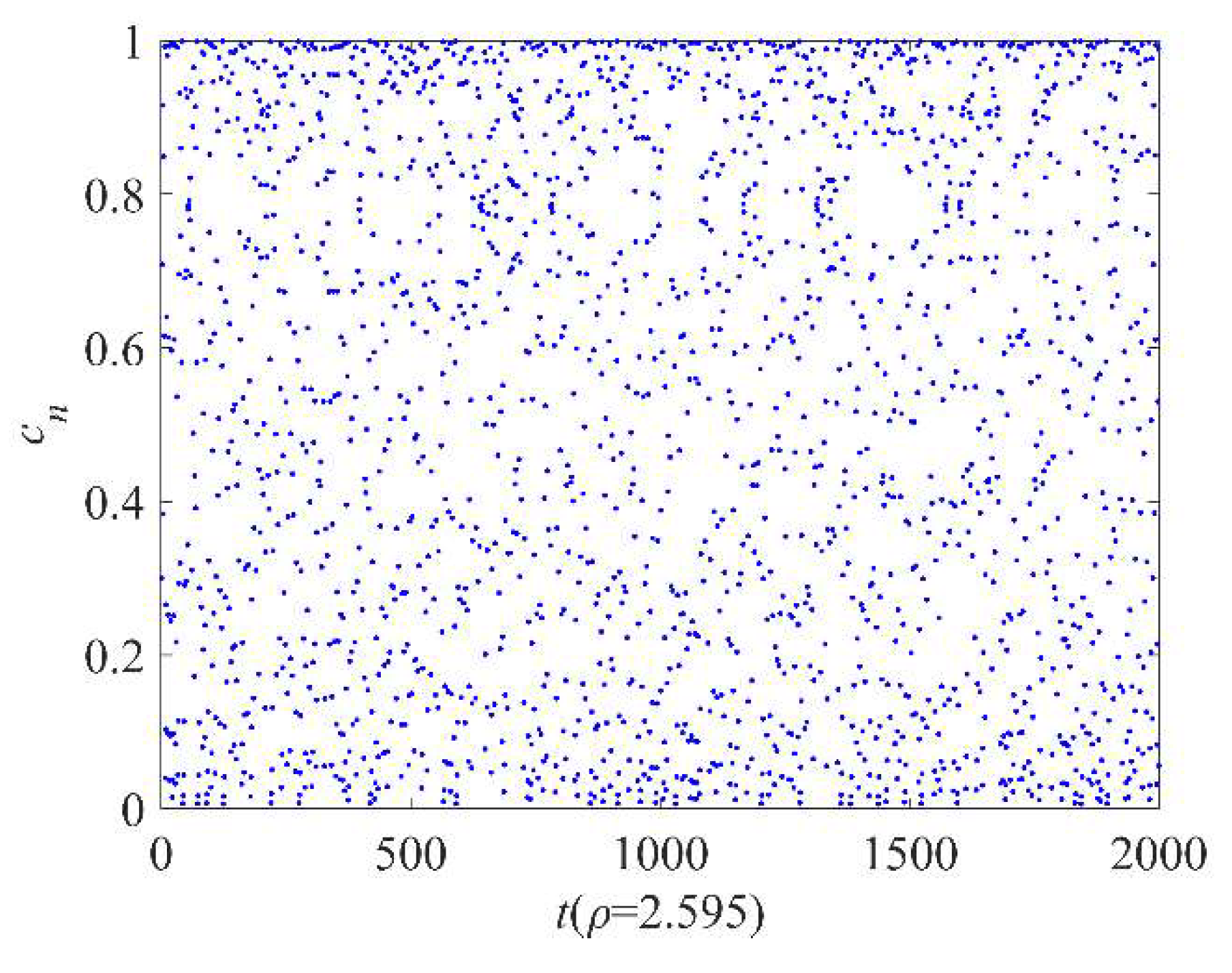
=2.595, 0<c_n<1, and the number of iterations is 2000, Figure 2 displays the results of the sequence distribution of Cubic chaotic mapping. Figure 2 demonstrates that the Cubic chaotic mapping possesses excellent uniform distribution characteristics.

The Cubic chaotic mapping establishes the sparrow population in the manner described below. The sparrow population consists of N d-dimensional sparrows and generates N d-dimensional vectors C_d before applying equation (5) to map C_d to individual sparrows：

X_{d}^{new} = \min_{d} + (\max_{d} - \min_{d}) \cdot C_{d}

(5)

Where，

\max_{d}

and

\min_{d}

are the maximum and minimum values of dth dimensional variable

X_{d}^{new}

, The result

X_{d}^{new}

obtained from Cubic chaotic mapping are used as the initial population sequence of the sparrow search algorithm, which improves the initial global search capability of the algorithm.

2.2. Gaussian random wandering strategy

The sparrow search algorithm will exist in the late iteration of the local optimum; for this problem, this paper proposes the use of a Gaussian random wandering strategy. First, the concept of fitness standard deviation is introduced to determine if the sparrow population falls into the local optimum.

σ = \sqrt{\frac{\sum_{i = 1}^{N} {(f_{i} - f_{a})}^{2}}{f}}

(6)

where fa is the mean of the overall fitness of the sparrow population, f is the control parameter of the standard deviation

σ

, and the value of f is as follows

f = \{\begin{matrix} \max \{|f_{i} - f_{a}|\}, \max \{|f_{i} - f_{a}|\} > 1 \\ 1, \max \{|f_{i} - f_{a}|\} \leq 1 \end{matrix}

(7)

If the difference between the standard deviation of fitness

σ

before and after is less than the specified value of10-3, the population is considered to have fallen into a local optimum during the iterative process. The Gaussian random walk strategy is then used to perturb the best individual of fitness fi in the sparrow population in order to help the algorithm jump out of the local optimum. The equation for the generation of new sparrow individuals is shown in the following equation:

X_{i}^{t + 1} = G a u s s (X_{i}^{t}, (- {(\frac{t}{i t e r_{\max}})}^{2} + 1) \cdot (X_{i}^{t} - X_{r}^{new} (t)))

(8)

where,

X_{r}^{new}

is the random individuals in the new sparrow population,

i t e r_{\max}

is the maximum number of iterations, and uses the property that the convex function decreases in the first quadrant: as the number of iterations t increases, the perturbation is gradually reduced. The coarse search and fine search capabilities of the algorithm are balanced.

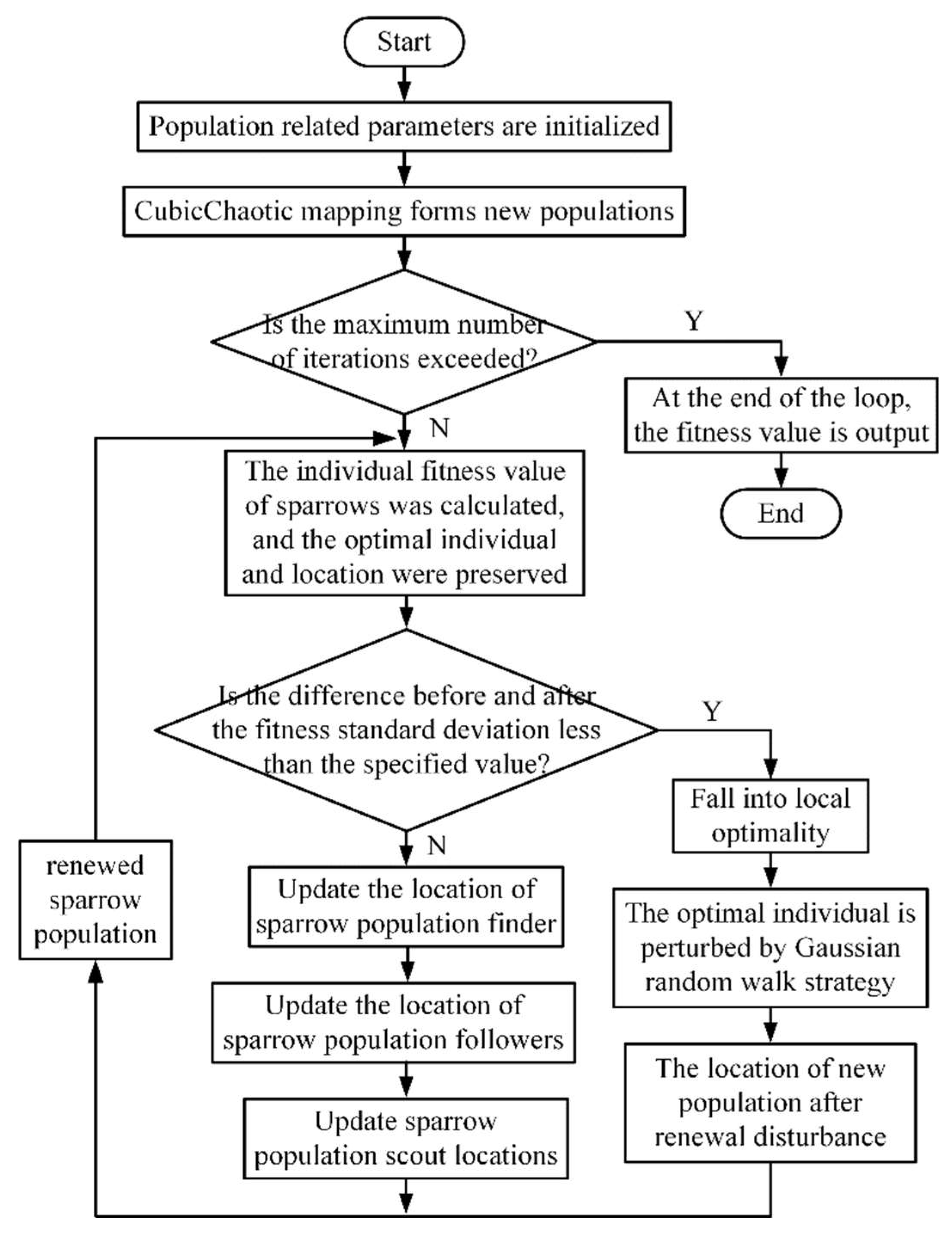
2.3. Improved sparrow search algorithm implementation process

The flow of the improved sparrow search algorithm is shown in Figure 3.

According to the implementation flow chart of the improved algorithm, the psedo-code implementation is as follows:

int main(void)

{

%cubic chaotic map initializes N sparrows and their related parameters;

N,iter_max,d,X_i_，_j,s_f,A,

β

ξ

,f_w,...

(set the basic parameters to be determined)

While(when the maximum number of iterations is not exceeded iter_max)

calculate formula (8),(1),(2),(3);

% Calculate and sort fitness values to identify the current best and worst individuals

If(calculate formula (6),(7), the standard deviation is less than the specified value 10^-3?)

{

% decide to fall into local optima

use gaussian walk strategy to perturb the optimal individual;

calculate formula (8) to obtain the perturbed new sparrow population

X_{i}^{t + 1}

;

}

else

{

calculate formula (1) to obtain the location of the sparrow-finder population;

calculate formula (2) to obtain the location of the sparrow-follower population;

calculate formula (3) to obtain the location of the sparrow-scouter population;

}

while(when the maximum number of iterations is exceeded iter_max)

output the optimal individual X_best, the optimal fitness f_g;

return 0;

}

3. Environment Modeling

Unmanned ships need to carry out environment modeling before path planning, with the purpose of representing the unmanned ship information, navigation information, and obstacle information in the navigation environment. Accurate modeling of map environment is a prerequisite for autonomous path planning of unmanned ships. An important factor to be considered in establishing an environmental model is the structure of the environmental model. If the structure is relatively simple, less data will be occupied and important environmental information may be lost. If the complexity of the modeling structure is high, the modeling time is long, and it is difficult to reflect the real-time change information of the environment. Therefore, it is particularly important to determine the model method suitable for the path planning of unmanned ships.At present, domestic and foreign research on unmanned ship environment modeling mainly includes grid method, voronoi diagram method, topological diagram method, etc [17]. Considering that the subsequent environment modeling will be based on electronic route map, in order to fit the electronic route map environment, this paper adopts grid method modeling.

3.1. Pre-processing of navigational information

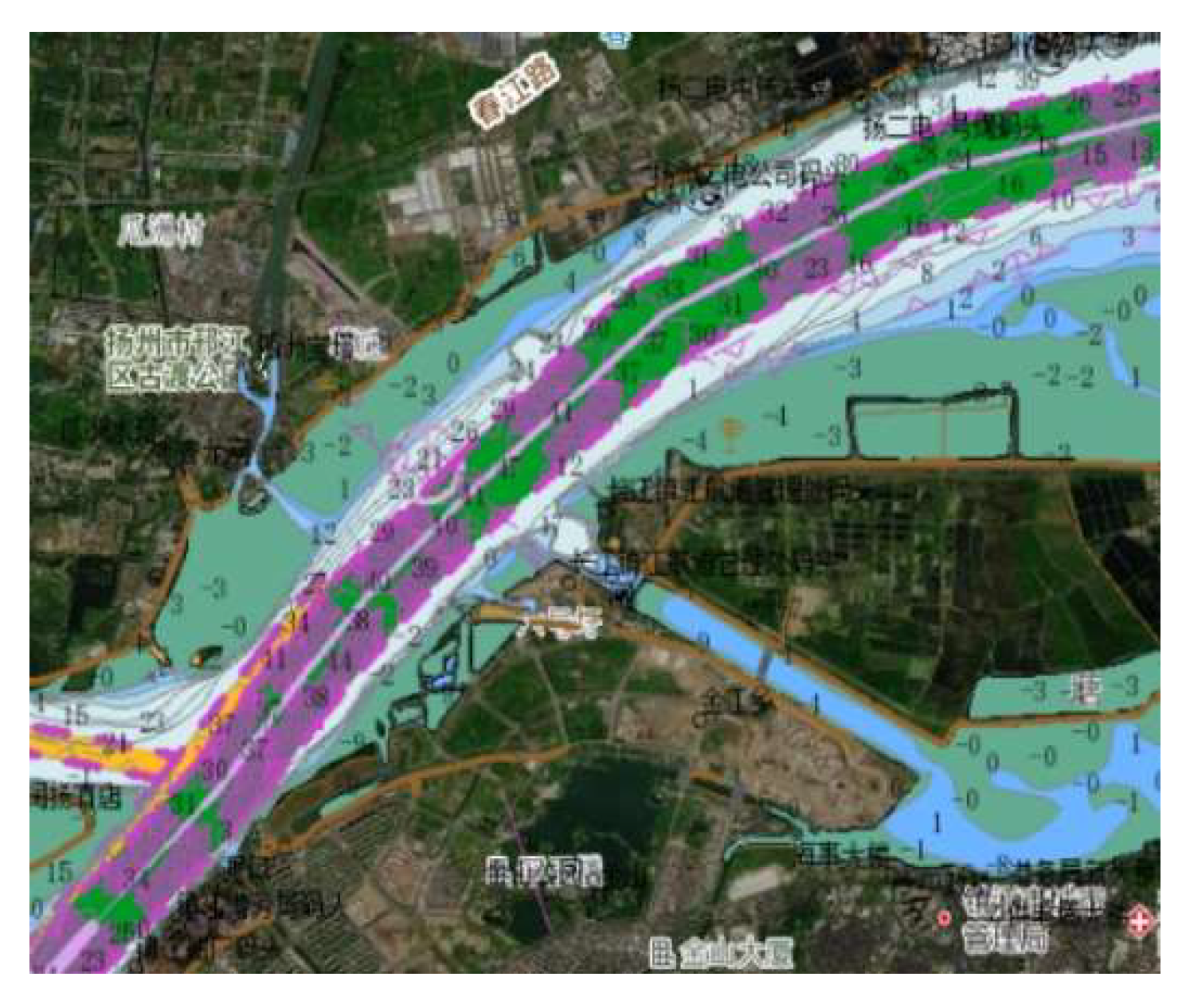
The electronic route map is a digital map that provides necessary geographic information and route information for ships during navigation. The environmental information of the section from Zhenjiang Port to Yangzhou Port is selected for study. The electronic channel map of Zhenjiang Port-Yangzhou Port section is shown in Figure 4.

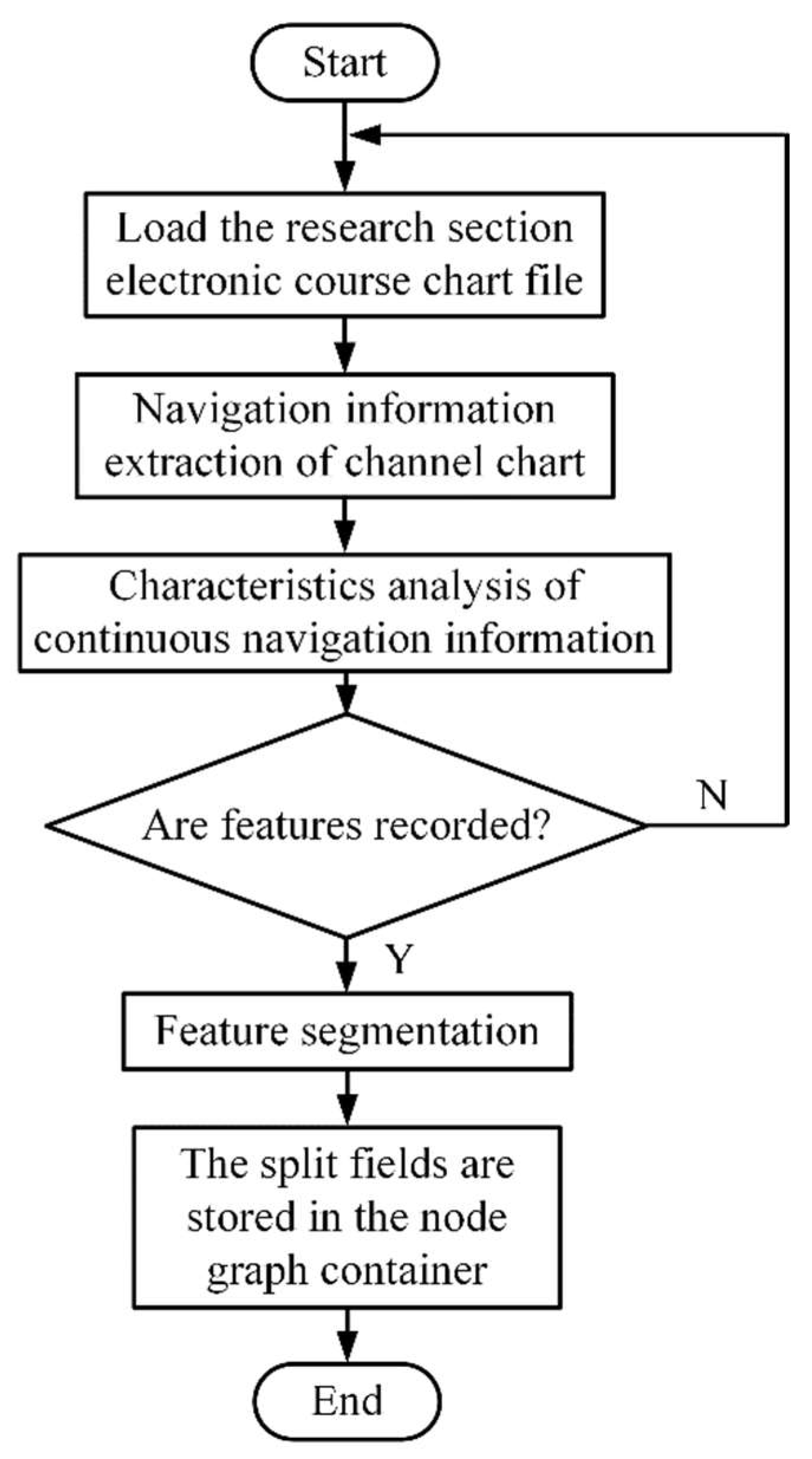
For the studied route planning problem, the channel information provided by the electronic channel chart is too comprehensive (e.g., virtual beacons, passing ships, meteorology, isobaths, etc.) to be used directly as a map for route planning; therefore, it is necessary to extract navigational feature information from the electronic channel chart, analyse the navigational information, and save it. In this paper, the fuzzy C-mean clustering algorithm is used to process the navigational information: first, the navigational information of the electronic route map is characterised, and the information applicable to unmanned vessel path planning is recorded, such as navigable water, land, etc.; segmentation is performed based on the characteristics, and the segmented fields are stored in the node graphic container; and finally, the segmented fields are stored in the node graphic container. Figure 5 is a flowchart of the extraction and analysis of electronic route information, and Figure 6 depicts the electronic route map after the aforementioned procedure has been applied.

3.2. Grid method and obstacle swelling treatment

After the pre-processed electronic channel map is obtained, the next step is to calibrate the location information of the map environment. In this paper, the grid method is used to process the map. The raster map has the advantages of easy construction, clear description of environment, unique location, etc. After the raster map data is processed, the map information is transformed from geoinformation system to information that can be solved by programming.

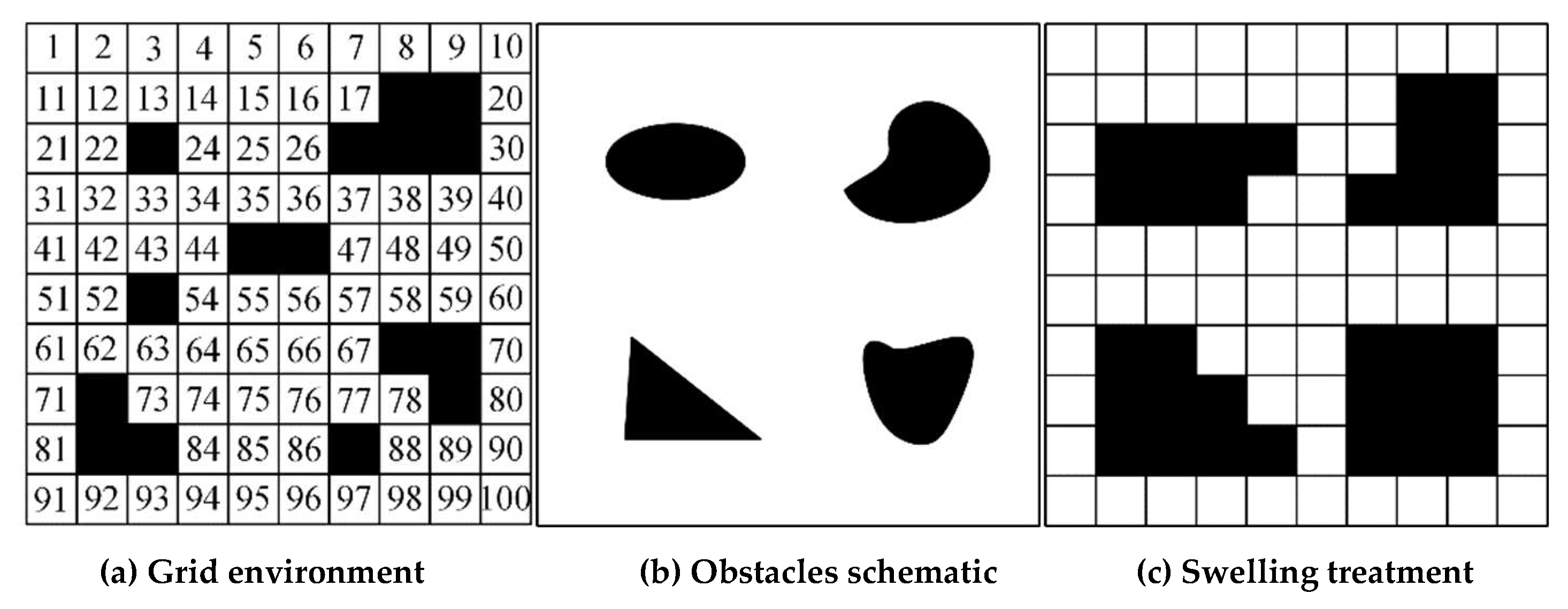
The environment modeling based on the grid method first needs to determine the coordinates of the map in the grid environment to facilitate the positioning. The grid coordinates are specified to increase from left to right and from bottom to top, set the grid number of the m×n grid as i and the grid area as 1. The coordinates of the grid center point can be obtained from the following equation

\{\begin{matrix} x = \mod (i, m) - 1 / 2 \\ y = int (i, n) + 1 / 2 \end{matrix}

(9)

where x and y represent the centre point's coordinates in the grid environment ，Figure 7(a) depicts the information of each point in the 1010 grid environment. Due to the small size of the unmanned ship in comparison to the surface navigation environment, the process of the unmanned ship performing the autonomous navigation task in the grid environment can be compared to the motion of a mass point in a two-dimensional plane for the sake of algorithm study. However, the grid size setting has a direct influence on the construction of the environment model and the affect of path planning during the actual grid processing procedure. When the determined grid is small, the grid map can clearly represent the navigation environment characteristics of the unmanned ship, but it also occupies a large amount of storage space, affecting the real-time algorithm solution, resulting in a decrease in the speed of the unmanned ship path planning, thereby reducing the manoeuvrability and flexibility of the unmanned ship; when the determined grid is large, the navigation environment characteristics of the unmanned ship are less clear. Consequently, it is essential to determine an appropriate grid size. The side length of a single gridLd is determined by 1.5 times the ship's length using this method.

To ensure that the unmanned ship does not collide with obstacles while sailing, this paper adopts expansion processing for obstacles, stipulating that in the modelling process, when the unnavigable area occupies less than one cell grid, the default expansion is one cell, stipulating that the unmanned ship is prohibited from sailing along the edge of the obstacles, and the reserved safety distance is 0.5 grid; when there is no collision between the path and the obstacle, the individual fitness value of the sparrow is equal to the sum of the length of the path and the turning energy consumption, the consumption of right-angle turning is 0.4, and the consumption of obtuse corner turning is 0.2. Figure 7(b) simulates the situation of irregular obstacles, and the raster map environment after expansion treatment is shown in Figure 7(c).

In order to save the map information into the computer as boolean form, it is necessary to obtain the black and white map before the grid method is used to model the electronic channel chart. OSTU image segmentation method is used to process Figure 6 [18]. OSTU image segmentation method has the advantages of easy implementation, small size and good stability, and has become the most widely used segmentation technology in image segmentation, especially in the range of images with different gray levels of the target and background. The principle of OSTU image segmentation is: first determine whether the feature attributes of each pixel in the map meet the pre-set threshold requirements, then determine whether the pixel in the map belongs to the target region or the background region, and finally convert the series of color images into a binary map. The segmentation threshold set by this method is 100, and the obtained binary electronic channel diagram is shown in Figure 8.

Then, the above grid method and obstacle expansion treatment are applied to Figure 8, and the binarized map is saved in the form of grid array. The grid environment model of the electronic channel chart of Zhenjiang Port and Yangzhou Port is finally obtained, as shown in Figure 9. After the grid environment model suitable for path planning of unmanned ship is obtained, the relative position information of unmanned ship during sailing (location information of individual sparrows in the population) and the horizontal and vertical coordinates of the grid map are mapped, so as to prepare for the subsequent simulation test of unmanned ship path planning.

4. Experimental simulation and evaluation

To verify the feasibility and efficacy of the constructed electronic route map grid environment model and the improved sparrow search algorithm, simulation experiments are performed on the MATLAB R2019b platform for the traditional sparrow search algorithm and the improved sparrow search algorithm. In order to demonstrate the superiority of the enhanced sparrow search algorithm over other heuristic intelligent search algorithms, the simulation portion of this paper introduces the particle swarm search algorithm as a comparison algorithm.

In order to reflect the distinctions between the traditional sparrow search algorithm and the improved sparrow search algorithm in this paper, the sparrow search algorithm's fundamental parameter settings are kept the same, as shown in Table 1.

The particle swarm search algorithm is an evolutionary computational method whose fundamental concept is to discover the optimal solution through collaboration and information sharing among a population's individuals. Each particle in the swarm possesses two types of characteristic information: velocity characteristic information and position characteristic information. Each particle autonomously investigates the local optimal solution in the search space and stores it as the extreme value of the current individual. and positional details. In this investigation, the control variable concept is utilised, and Table 2 displays the parameter settings of the particle swarm algorithm.

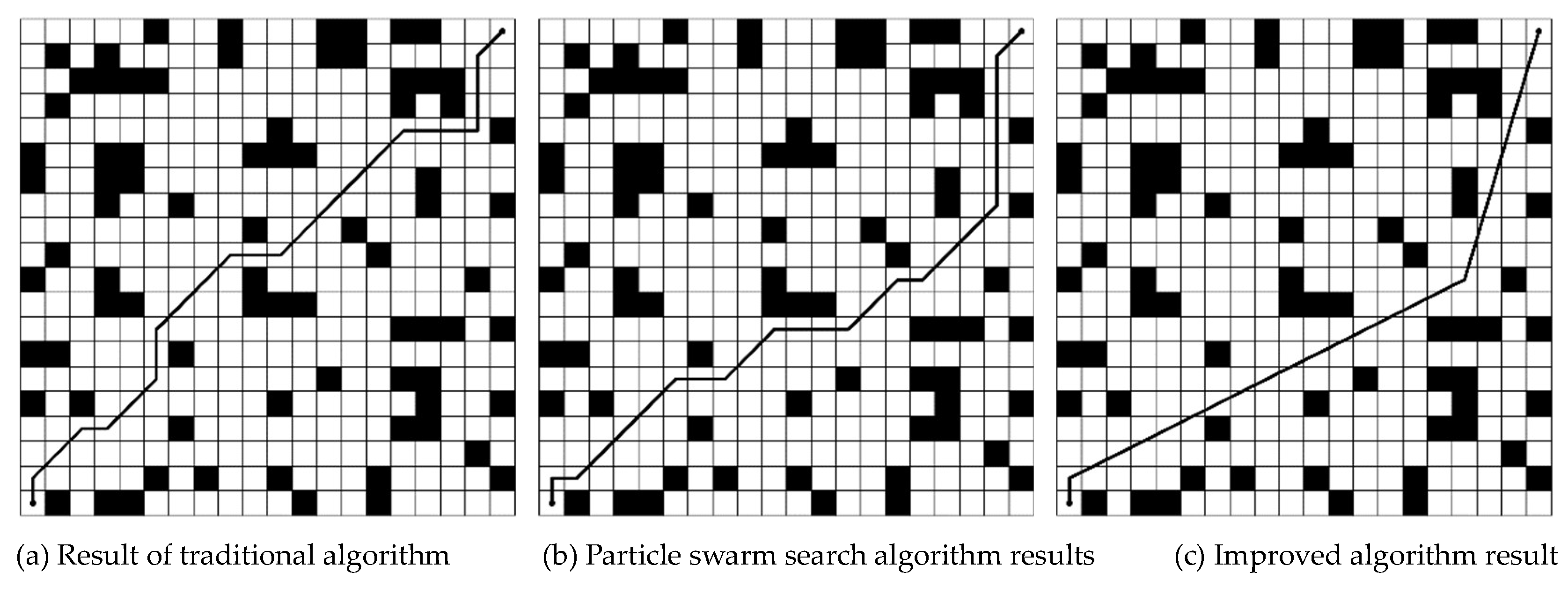
In order to compare the results of the improved sparrow search algorithm, the traditional sparrow search algorithm, and the particle swarm search algorithm, 50 simulation experiments are conducted using the 2020 grid environment model for the traditional sparrow search algorithm, the improved sparrow search algorithm, and the particle swarm search algorithm, with the same experimental starting point, end point, path evaluation method, etc. The starting point of the path is (1, 1) and the ending point is (20, 20). The path adaptation value equals the path length plus right angle turns minus 0.4 and obtuse angle turns minus 0.2. One of the simulation outcomes is depicted in Figure 3.12 and 3.13, where the optimal traditional sparrow search algorithm adaptation value is 33.17, the enhanced sparrow search algorithm adaptation value is 29.81, and the particle swarm optimisation algorithm adaptation value is 0.00. Table 3 displays a comparison of the comprehensive experimental data.

Figure 10 and Table 3 demonstrate that the improved sparrow search algorithm achieves smaller fitness values than the traditional sparrow search algorithm, as evidenced by the 10.13 percent decrease in the optimal fitness value, the 70 percent decrease in the number of turns, and the 6.3 percent decrease in the average fitness value. Specifically, the enhanced sparrow search algorithm is more stable, as demonstrated by a comparison of variance data.

The enhanced sparrow search algorithm obtained smaller fitness values than the particle swarm search algorithm, as evidenced by the 11.49% reduction in the optimal fitness value, 72.7% reduction in the number of cycles, and 7.92% reduction in the average fitness value.

In the initialization phase of the population, the Cubic chaos mapping improves the algorithm's global search capability, while the introduction of the Gaussian random walk strategy reduces the algorithm's likelihood of achieving a local optimum. Moreover, the average time spent is only 0.27 seconds slower than the traditional sparrow search algorithm and 0.34 seconds slower than the particle swarm algorithm, demonstrating that the introduction of Cubic chaos mapping to initialise the population and the Gaussian random walk strategy do not significantly increase the computation time of the improved sparrow search algorithm and meet the real-time requirement for the path planning of unmanned ships.

In order to validate the efficacy of the enhanced sparrow search algorithm in path planning under the electronic route map grid environment, simulation experiments are conducted to validate the algorithm's practicability. The results of the improved algorithm in the electronic route map grid environment are depicted in Figure 11, where the planned path begins at Zhenjiang port and ends at Yangzhou port, whose corresponding coordinates begin at (2, 2) and end at (50, 50) in Figure 11.

Figure 11 depicts the enhanced sparrow search algorithm with an adaptation value of 63.97 and an iteration time of 2.99 seconds. The fact that planning from Zhenjiang port to Yangzhou port requires only three instances of ruddering and the waypoints are reasonably distributed demonstrates the efficacy of the proposed algorithm for unmanned ship path planning in a channel chart grid environment.

Figure depicts an enhanced sparrow search algorithm with an adaptation value of 63.97 and an iteration time of 2.99 seconds. The fact that only three turns are required to plan from Zhenjiang port to Yangzhou port, and that the navigation points are reasonably distributed, demonstrates the efficacy and applicability of the proposed algorithm for unmanned vessel path planning in a channel map grid environment.

5. Conclusion

Cubic chaotic mapping is used instead of the traditional random generation of the sparrow search algorithm to optimise the problem of uneven population distribution at the initialization stage of the population; at the later stage of the iteration algorithm, the standard deviation of fitness is introduced to determine whether the population falls into the local optimum, and the Gaussian random wandering strategy is used to perturb the Since t. The simulation experiments demonstrate that the improved sparrow search algorithm has enhanced global search capability, avoids sliding into local optimum, and can produce stable and reliable navigation paths when combined with electronic route maps.

Engineering must take into account wind and current disturbances in the environment, the unmanned ship's own manoeuvrability, fuel economy, and other factors in order to realise the actual navigation. The research presented in this paper is merely a preliminary discussion in the field of unmanned ship path planning, which we hope will stimulate further research.

References

LI, S.Y. Start a new voyage and create a new future for shipping; China Communications Press, 2021. [Google Scholar]
Yu, Y.L.; Su, R.B.; Feng, X. Tracking control of backstepping adaptive path of unmanned surface vessels based on surge-varying LOS. Chinese Journal of Ship Research 2019, 14, 163–171. [Google Scholar]
HOSSAINM, A. FERDOUSI Autonomous robot path planning in dynamic environment using a new optimization technique inspired by bacterial foraging technique. Robotics and Autonomous Systems 2015, 64, 136–141. [Google Scholar] [CrossRef]
Polvara, R.; Sharma, S.; Wan, J.; et al. Obstacle avoidance approaches for autonomous navigation of unmanned surface vehicles. Journal of Navigation 2018, 71, 240–256. [Google Scholar] [CrossRef]
GAO, F.; ZHOU, H.; YANG, Z. Y. Global path planning of surface unmanned ship based on improved A* algorithm. Application Research of Computers 2020, 37, 120–121, 125. [Google Scholar]
ZHANG, Q.; TIAN, T.; LUAN, T. Y.; et al. Research on path planning of unmanned boat routes based on improved artificial potential field algorithm. Ship Science and Technology 2022, 44, 63–68. [Google Scholar]
GUO, R. X. Research on the path planning for USV based on reinforcement learning; Harbin Engineering University: Harbin, 2020. [Google Scholar]
WANG, C.; REN, J.; ZHANG, Y. Unmanned surface vessel path planning based on improved ant colony algorithm. NATURAL SCIENCE JOURNAL OF HAINAN UNIVERSITY 2021, 39, 242–250. [Google Scholar]
LIU, C. A.; WANG, X. P.; LIU, C. Y.; et al. Three-dimensional route planning for unmanned aerial vehicle based on improved grey wolf optimizer algotithm. Huazhong Univ. of Sci.&Tech.(Natural Science Edition) 2017, 45, 38–42. [Google Scholar]
WANG, S. R. Research on stanley algorithm based on improved whale optimization algorithm; Jilin University, 2022. [Google Scholar]
LIU, J. H.; YANG, J. G.; LIU, H. P.; et al. An improved ant colony algorithm for robot path planning. Soft Computing 2017, 21, 5829–5839. [Google Scholar] [CrossRef]
XUE, J.K.; SHEN, B. A novel swarm intelligence optimization approach: sparrow search algorithm. Systems Science and Control Engineering 2020, 8, 22–34. [Google Scholar] [CrossRef]
LYU, X.; MU, X. D.; ZHANG, J.; et al. Chaos sparrow search optimization algorithm. Journal of Beijing University of Aeronauticsand Astronautics 2021, 47, 1712–1720. [Google Scholar] [CrossRef]
OUYANG, C. T.; ZHU, D. L.; WANG, F. Q.; et al. UAV path planning based on refracted sparrow search algorithm. Electronics Optics & Control 2022, 29, 25–31. [Google Scholar]
GE, C.; QIAN, S. Q. Path planning of unmanned vehicle based on improved sparrow search algorithm. Journal of Navigation and Positioning 2022, 1–5. [Google Scholar]
LI, P.; CHEN, S. J.; YANG, S. S.; et al. Otsu image segmentation method optimized by fruit fly optimization algorithm based on Logistic mapping. Foreign Electronic Measurement Technology, 2022, 41, 9–17. [Google Scholar]
LI, Q. F.; YUAN, Z. J.; TANG, G. Y. Map environment modeling and path planning of unmanned boats. Proceedings of 2021 academic conference of test technology group, ship mechanics academic committee. Yunnan Kunming 2021, 490–496. [Google Scholar]
LI, P.; DING, Q. W. OSTU segmentation algorithm based on sparrow algorithm optimization. Electronic Measurement Technology 2021, 44, 148–154. (in Chinese). [Google Scholar]

Figure 1. Chaos fork.

Figure 2. Result of cubic chaotic map.

Figure 3. Flow chart of improved algorithm implementation.

Figure 4. ENC chart of Zhenjiang port - Yangzhou port.

Figure 5. Flow chart of electronic channel information analysis.

Figure 6. Pre-processed ENC.

Figure 7. Grid method and Obstacle swelling treatment.

Figure 8. ENC after OSTU segmentation.

Figure 9. ENC grid environment model.

Figure 10. Both algorithms result in a grid environment.

Figure 11. Result of the improved algorithm in ENC grid environment.

Table 1. Basic parameter settings for sparrow search algorithm.

Parameters	Value
Number of populations N	100
Number of iterations iter_max	500
Warning value R₂	0.8
Percentage of discoverers	0.3
Percentage of followers	0.2
Proportion of scouts	0.15
Solution space dimension	20

Table 2. Parameter settings for particle swarm optimization.

Parameters	Value
Number of populations N	100
Number of iterations iter_max	500
Learning factor $c_{1}$	2.5
Learning factor $c_{2}$	2.5
Inertia weights	1

Table 3. Data comparison of 50 simulation experiments.

Path metrics	Particle swarm search algorithm	Traditional sparrow search algorithm	Improved sparrow search algorithm
Optimum fitness value	33.68	33.17	29.81
Number of Turns	11	10	3
Mean value	35.96	35.34	30.11
Mean time	0.60	0.67	0.94
Variance	17.03	18.62	9.33

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Path Planning of Unmanned Surface Vehicle Based on Improved Sparrow Search Algorithm

Abstract

1. Introduction

2. Sparrow search algorithm

2. Improved sparrow search algorithm

2.1. Cubic chaotic map

2.2. Gaussian random wandering strategy

2.3. Improved sparrow search algorithm implementation process

3. Environment Modeling

3.1. Pre-processing of navigational information

3.2. Grid method and obstacle swelling treatment

4. Experimental simulation and evaluation

5. Conclusion

References

MDPI Initiatives

Important Links

Subscribe