Prerpints.org logo
Preprint
Article

A Bayesian Approach to Examine the Feasibility of Integrating Machine Learning to Recognize Households’ Eligibility in a Basic Income System

Altmetrics

Downloads

206

Views

59

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

01 September 2023

Posted:

11 September 2023

Read the latest preprint version here

Alerts
Abstract
Appeals to governments for implementing basic income systems are contemporary. The theoretical background of the basic income notion, only prescribes transferring equal amounts to individuals irrespective of their socioeconomic attributes. However, the most recent basic income initiatives all around the world are attached to certain attributes of the households to become the eligible receivers. Iran is known as the first country in the world to provide a de facto based on the definition basic income to all its citizens irrespective of their socioeconomic attributes. Since the recent years and in the face of budget constraints, the Iranian government has been attempting to consider a set of rules with regard to the welfare attributes of the receiver households to become eligible. This approach is facing significant challenges with regard to appropriate classification of the relative vulnerable from the relative wealthier groups. Can integrating machine learning contribute to reliable recognition of households’ eligibility? In this paper, we analyze this question by utilizing the official welfare statistics of one and a half million Iranian citizens and a Bayesian network approach. Our analysis provides insight into whether machine learning will forward the future of the original basic income notion towards an intelligible direction.
Keywords: 
Subject: Social Sciences  -   Government

1. Introduction

The idea of basic income, a minimum income transferred by state to each member of a society, is wide spreading. Appeals to governments for implementing basic income programs are all contemporary including the United Kingdom (Jordan , 2012; Mori, 2017), Germany (Scientific Advisory Board at the Federal Ministry, 2021; Coalition agreement SPD, The Greens and FDP, 2021) and Spain (Perkiö, 2013; De Durana & Rodrigu, 2021). In addition to the major programs and plans, there are a large number of small scale pilot projects, which are mostly revolving around several experiments in the United States (Yang et al., 2021) and serve as scientific controlled trials to capture the potential up and downs of performing the this idea (Moffitt, 2003). A complete list of the major implemented or ongoing basic income programs can be found in the world bank (Gentilini et al., 2020). Basic income systems per definition do not attach any social-demographic attributes such as age, marital status, gender, health status, social class and etc. to any individual as eligibility criteria (Bill, 1988; Van Parijs, 1991; Van der Veen, 1998; Pateman, 2004; Raventós , 2007; Widerquist, 2001). In addition, basic income shall be paid uniformly to each person of the society (Bill, 1988; Van Parijs, 1991; Van der Veen, 1998; Standing, 2012; Von Gliszczynski, 2017; Lovett, 2009; Raventós,  2007).
The idea of paying uniformly distributed basic income to all members of a society might improve the quality of life and reduce poverty, however, there are yet theoretical debates (Hoynes & Rothstein, 2019; Yang et al., 2021; Jackson, 2017; OECD, 2017; Zheng et al., 2020) regarding the financing a broad basic income program. Basically, if the equally transferred cash to all individuals be set too low, it becomes insufficient in reducing poverty. On the other hand, setting too high cash transfers payed to each individual can become extremely costly and infeasible in the face of the governments’ budget constraint (Fitzpatrick, 1999). The evidences of expansiveness’s of basic income come not only from theoretical perspective but also from empirical experiences. Hoynes & Rothstein (2019) estimate a broad basic income program not attached to social-demographic variables to be costly about twice the cost of all existing transfers in the United States. A universal no question asked public transfer to everyone would necessitate significant tax rises as well as reductions in essential existing benefits in (OECD, 2017). Jackson (2017) predicts that implementing a broad basic income program would increase tax rates for below median income workers up to 70 percent or 80 percent if the basic income level is set at one-half of Canada’s median income. Zheng et al., (2020) prognoses that if in China, in 2014, the government would have decided to pay every adult a monthly income of 336 yuan (if living in urban areas) or 231 yuan (if living in rural areas), this would have required a yearly government expenditure of 3.472 trillion yuan, equivalent to approximately 5.46% of overall Chinese GDP and almost half of the overall Chinese government expenditure.
Iran is known as the first country in the world to provide a de facto based on the definition of World bank (Gentilini et al., 2020) basic income system to all its citizens. In December 2010, Iran launched a cash transfer program that payed every Iranian residing in the country the equivalent of $40–45 a month, unconditionally.  The program, while still continuing after thirteen years, has lost much of its desired effect as the purchasing power of the transfers has been largely receding through inflation. It is now witnessed as insufficient for the vulnerable households and simultaneously as of little value for the relatively wealthier households, while worsening the government’s budget considering of its large aggregate size.
Subsequently, it has become inevitable for the Iranian administration to pursue the idea of a basic income, which incorporates a households’ eligibility application in its system. Apart from Iran’s experience, the most recent or currently ongoing basic income initiatives all around the world, are attached to certain socioeconomic conditions to select the eligible receivers (Yang et al., 2021). 
Are designing basic income systems with integrating machine learning to recognize households’ eligibility feasible? This paper investigates this question as a research gap within the existing literature of basic income. We analyze this question by utilizing the official welfare data of one and a half million Iranian citizens and a Bayesian belief network BBN approach. To our understanding information systems will forward the future of the notion of basic income in an intelligible direction.
The remainder of the paper is as follows. Section 2 explains the main welfare attributes of the individuals within the source data of the research. How the Bayesian model is constructed and evaluated, are explained in section 3. The results of the analysis are presented and deliberated in section 4. Concluding remarks are highlighted in section 5.

2. Data preparation

The anonymized welfare data of 1.5 million randomly chosen individual Iranian citizens provided by Iran’s ministry of cooperatives, labor, and social welfare are utilized in this study. The 30 distinct registered information for each individual are depicted in table 1. The source data table’s each row belongs exactly to one person containing welfare information of that person in 30 distinct columns. We did not utilize this data table directly, as we believe in a more meaningful parameter to evaluate each individuals’ welfare i.e. the aggregation of individuals’ welfare attributes within their corresponded household. Over the key identification Parent ID, we ascribed each of the 1.5 million individual persons to their corresponded unique household and came out with exactly five hundred thousand households in the total. We generated out of individual available data a new table named Household_welfare_data. In the aggregation process, we added the welfare values of individual persons (e.g. car numbers and car values) within a family together and averaged the sum over the number of family members. The aggregation carried out with the exception of person ID, parent ID, age, gender and the living place. These variables are not to be summed and hence are represented by the parent’s information in the Household_welfare_data. Finally, due to the existing of 8280 NaN values in a column related to the question of living in the city or not, we dropped the corresponded rows to come up with a data table consisting of 491,720 rows × 30 columns.

3. Bayesian Network model

A Bayesian belief network BBN model (Pearl, 1988) is a graphical network that represents probabilistic relationships among a bundle of variables. It comprises a directed acyclic graph DAG with nodes representing the variables and arcs representing conditional dependencies between the connected nodes. Bayes theorem defines the relationships between variables (Puga et. al., 2015). The main objective of BBNs is to infer the posterior probability distribution of a set of presumably not completely observable variables after observing a set of observable variables. A clear explanation of what Bayesian Belief Networks are and how they are utilized is explained in Barbrook-Johnson and Penn (2022).
In our investigation, the total of the 30 variables in the table 1 are selected to be the main components of the Bayesian network. The corresponded variable to the thirty’s row of the table 1 i.e. the average balance of the entire family members’ accounts within the period of 20.032019-20.03.2020, is the key dependent variable of our study. In a certain year, this variable represents the averaged remaining total amount of the money, which is accessible in the bank accounts of the entire members of a family through that year, after all the debits and credits have been considered. It is describing the level of accessibility of a household to cash through the year, and hence is presumed to be the possible criterion of the eligibility or not eligibility of a household to receive further cash in the form of a basic income. Hereafter, if the administration decides e.g. on 20.03.2019 upon the eligibility of a household to be the receiver of the basic income within the time period 20.032019-20.03.2020, it can look at the aggregated values of the welfare attributes of the entire members of that family by means of their banking records from 20.03.2016 until 20.03.2019 (rows 18-29 at table 1) as well as their non-banking welfare attributes of that household at the day of decision making (rows 3-17 at table 1) to assess the probabilistic posterior access of that household within the upcoming time. As the individual banking records can be interpreted as sensitive information and might not be applicable, we design experiments in this paper, once with the existence of the banking records and once without the banking records.
To construct the Bayesian network, we must go through three steps. As Bayesian networks conventionally use labeled variables, whose domain are a finite set of labels, we should discretize the space of the data for the entire variables at the first step. We do this step by splitting the data for each of 30 variables into 2 subsections, if applicable. If a variable is greater or equal than a certain threshold t h v , it becomes labeled as negative (by assumption) and if it is smaller than t h v  it becomes labeled as positive by (assumption). To experiment the impact of setting different values of t h v , we incorporate deciles. A decile is the result of splitting up the ranked data of each variable into 10 equally large subsections, so that each subsection represents 1/10 of the data of a variable. We set the splitting threshold in each experiment of our study to the 9 in-between threshold value of 10 identified deciles. Thus, the n’th decile splits the entire data related to a certain variable of the table 1 to the negatives, which represent the data part with values greater or equal than the n/10 of the ranked data of that variable and the positives, which represent the data part with values smaller than the (10-n)/10 of the ranked data of that variable. For example, the t h v ( n = 5 )  corresponded to the n=5 splits the data of a variable into the values less than the median (positives) and the values greater than the median (negatives). Note that, each time we set the threshold in line with a certain decile, we apply the same decile number n to split the data of all 30 variables. The splitting of variables is done with the exception of the gender and the living place, which are binary variables on their own.  
In the second step, we estimate a DAG that captures the dependencies between the variables given the labeled data (Neapolitan, 2003). In our study we are using the Hill Climbing Search algorithm (Tsamardinos et al., 2006). This algorithm undertakes a greedy local search that starts from a disconnected DAG consisting of the entire 30 variables and proceeds by iteratively performing single-edge manipulations that maximally increase the value of a score function. The score function maps DAGs to a numerical score, which measures how well DAGs fit to the given data table. We apply the pyAgrum 1.9.0 on Jupyter framework to compute the DAG as well as the subsequent Bayesian learning computations through our study.
In the third step, we compute the conditional probability distributions CPTs of the individual variables, given the DAG and the labeled data.
By completion of the third step, the BNN is completed and can be used to make inferences regarding the posterior probabilities of the variables of concern. In this paper we are pursuing the feasibility of obtaining reliable inferences regarding the average amount of cash, each household is going to have access on average in an upcoming year of interest, after the BNN is consulted by a set of the household’s welfare attributes. Thereby, we design experiments to split the variable average balance of the entire family members’ accounts within the period of 20.032019-20.03.2020 (, which is the key variable of our study) according to the 9 in-between threshold values of 10 deciles, each time to the corresponded negative and positive subsection and see how well the BBN can distinguish the households, who are positioned on the area larger or equal than the threshold t h v  (negatives), from the households, who are positioned on the area smaller than the threshold t h v (positives). As the BBN model outputs probabilities values linked to being negatives or positives, we must decide upon a probability threshold t h p  upon which we decide to classify a household as a positives type, if the predicted posterior probability of positives exceeds t h p  and classify a household as a negatives, if the predicted posterior probability of positives for that household through the BBN model does not exceed the t h p . The default t h p  for interpreting probabilities to class labels is 0.5. However, tuning of t h p  to increase the preciseness of predictions, necessitates observing the changes in the accuracy of the BBN model to predict each negative and positive value of the target variable while moving t h p  e.g. from 0.0 to 0.9 in small (e.g. 0.1) incremental step sizes. Thereby we apply the receiver operating characteristic (ROC) curve (Fawcett, 2006) and the precision and recall (PR) curve (Powers, 2011) as well.
Before presenting the results in section 4, we explain the applied metrics to assess the feasibility of correct eligible households’ classification by a special case in the experiment design of our investigation.

3.1. Classification of households according to above and under median cash availability

In this subsection we examine the distinguishing of the population with under median average cash access from the population with above median average cash access. The threshold t h v (n=5) is set to be the cash level larger than available for the lower n=5 deciles (positives) and less than available for the upper n=5 deciles (negatives). We split the data of the rest of the variables to the negatives and positives based on their median levels, accordingly, as described in the previous section. The BBN model is trained using the labeled data of 30 variables in line with t h v (n=5) and the Hill Climbing Search algorithm over the 80% of the 491,720 rows × 30 columns of data. The BBN’s DAG is presented in figure 1.
We use the rest of 20% of the entire data table as the test set. Left and right hand panels of the Figure 2 illustrate the ROC and PR metrics of the test set, respectively. To interpret these accuracy measures we should first note the definitions a-d, as well as the equations 1-8.
  • True negative: if the target value is negative and the predicted value is negative.
  • True positive: if the target value is positive and the predicted value is positive.
  • False negative: if the target value is positive and the predicted value is negative.
  • False positive: if the target value is negative and the predicted value is positive.
T r u e   p o s i t i v e   r a t e = T r u e   p o s i t i v e   c o u n t / ( T r u e   p o s i t i v e   c o u n t + F a l s e n e g a t i v e c o u n t )
F a l s e   p o s i t i v e   r a t e = F a l s e   p o s i t i v e   c o u n t / ( F a l s e   p o s i t i v e   c o u n t + T r u e p o s i t i v e c o u n t )
T r u e   n e g a t i v e   r a t e = T r u e   n e g a t i v e   c o u n t / ( T r u e   n e g a t i v e   c o u n t + F a l s e p o s i t i v e c o u n t )
F a l s e   n e g a t i v e   r a t e = F a l s e   n e g a t i v e   c o u n t / ( F a l s e   n e g a t i v e   c o u n t + T r u e n e g a t i v e c o u n t )
R e c a l l = T r u e   p o s i t i v e   r a t e
p r e c i s i o n = T r u e   p o s i t i v e   c o u n t / ( T r u e   p o s i t i v e   c o u n t + F a l s e n e g a t i v e c o u n t )
f 1 _ s c o r e = 2 * ( P r e c i s i o n * R e c a l l ) / ( P r e c i s i o n + R e c a l l )
a c c u r a c y t o t a l = T r u e   p o s i t i v e   c o u n t + T u r e   n e g a t i v e   c o u n t T r u e   p o s i t i v e   c o u n t + T u r e   n e g a t i v e   c o u n t + F a l s e   p o s i t i v e   c o u n t + F a l s e   n e g a t i v e   c o u n t
The ROC Curve depicts the contrast between the true positive rate and false positive rate by changing the probability thresholds t h p . The PR curve depicts the possible trade-off between the recall and the precision by changing the probability thresholds t h p . Note that the precision describes, how precise the model is, if it predicts a class to be e.g. positive, whereas the recall describes, how much the model has succeeded to cover the positives to be correctly predicted. The PR becomes more meaningful, when there are moderate to large imbalances between the number of data within the negatives and positives classes e.g. when we are seeking to distinguish the population with the lowest n=1 decile (positives) from the rest 9 deciles (negatives).
The AUC represents the integral of the area under ROC and PR curves and is a metrics for evaluating the accuracy of the model by considering the entire possible ranges of the t h p . The f1_score represents the harmonic mean of the precision and recall metrics. Note that f1_score does not incorporate the True negative count. The accuracy_total represents the overall accurateness of the model without being detailed in the negatives and positives subsections.
The blue point in Figure 2 is the optimal PR threshold that results in the best balance between the precision and recall metrics expressed in the term f1_score. The red point in the Figure 2 is the optimal ROC threshold that result in the best balance between the true and the false positive rates. The ROC and PR curves in Figure 2 show a t h p around 0.425-0.492 as the optimum threshold, which delivers a balanced accuracy and preciseness to predict the positive classes. In that t h p , we will be able to cover between 80-90 percent precisely predicted positive i.e. below median level cash accessible households. Through, by setting non-optimal  t h p threshold values deviating from the optimal value, we can increase the recognition of the true positive households up to levels higher than e.g. 90%, however, then we should take extra added false positives (in ROC), as well as a reduced precision (in PR) into the account.
Note that the most of the indicators are concerning regarding the possible fine-tuned detection of positives and not the negatives, per definition. This is to some extend legitimate in our study, as the first concern of basic income programs is the detection of positives and not negatives.
Depending on their budget constraints, the political administrations might be interested (beside the optimal thresholds) in the range of non-optimal threshold values as well, as they can choose threshold values encompassing e.g. higher than 90% recognition of True positives (, which promises a higher recognition rate of lower income groups compared to the level corresponded to optimal threshold) at the cost of accepting to allocate extra budget to be distributed to False positives. The trade-off between recognition of negatives and positives in the test set of the Iranian Household_welfare_data through altering the t h p threshold from 0.0 to 0.9 in small (0.1) incremental step sizes and its relationship with the accuracy_total is represented in Figure 3.
As the individual banking records can be interpreted as sensitive information and might not be applicable, we replicate the classification of households in the test set according to above and under median cash availability without their recent years banking records (with the exception of the average balance of the entire family members’ accounts, which is incorporated only in the training step). Note that, banking records of the recent years play a crucial role to predict the households’ cash access. This is illustrated in Figure 4.
Each panel of Figure 4 describes the change in the posterior probability of negatives and positives groups’ cash access (in the vertical axis) by providing evidences from a single explanatory variable in form of probability x for being that variable negative and 1-x for being that variable positive and incrementing x along the horizontal axis from 0.0 to 1.0 in small (0.01) incremental step sizes. The absolute difference of the maximum and the minimum of the posterior probability of negatives cash access by changing the value of the explanatory variable in the horizontal axis is depicted in the parenthesis above each explanatory variable’s panel and is a criterion for assessing how important that variable is in the shaping of a prediction for the dependent variable. The panels are sorted from the left to the right and above to below based on increasing in the importance values. As it is evident from the Figure 4, the entire banking records (rows 18-29 at table 1 and in the lower 4 rows in figure 4) play the greater role to predict the posteriors in comparison with the non-banking welfare attributes of that household (rows 3-17 at table 1 and the first 4 rows in Figure 4). Hence, it can be rationally expected that erasing banking records will reduce the model accuracy metrics.
The reduced BBN (BBN_2) model through subtraction of banking records of the recent years is trained using the labeled data of 14 variables in line with t h v (n=5) and the Hill Climbing Search algorithm over the 80% of the 491,720 rows × 14 columns of data. The BBN_2’s DAG is presented in Figure 5.
The PR and ROC curves together with AUC and f_score values in Figure 6 indicate the feasibility of obtaining relatively precise predictions by setting the t h p to optimal values. The indicators, of Figure 6, however imply lower preciseness compared to the Figure 2.
This approve our expectation regarding the reduced accuracy metrics’ level through erasing the banking records by t h v (n=5). The trade-off between recognition of negatives and positives (in the case of cutting the banking records from the households’ eligibility question in the test set of the Iranian Household_welfare_data) through altering the t h p threshold from 0.0 to 0.9 in small (0.1) incremental step sizes and its relationship with the accuracy_total is represented in Figure 7. One can see, that, in this case, the administration will have less play room in the range of non-optimal threshold values, if they e.g. decide to choose threshold values to achieve higher than 90% recognition of True positives. In this case (, which promises a higher recognition rate of lower income groups), the administration must be accepting to allocate extra budget to be distributed to more than 60% False positives, who might not be deserved to be receivers of the basic income, indeed.

4. Results

The results of examining the feasibility of distinguishing lower cash accessible groups (positives) form higher cash accessible groups(negatives) by setting various cash accessibility thresholds th(n) and various distinguishing probability thresholds tp(n), are presented in tables 2 (where banking and non-banking welfare records of households are incorporated) and 3 (where only non-banking welfare records of households are incorporated). Each column represents one distinct percentile number t h v , which can be the possible boundary of cash accessibility to define the negatives and positives. Each of the first nine rows, represent one distinct percentile number t h p , upon which we can decide to classify a household as a positives type if the predicted posterior probability of positives exceeds t h p . Each bracket within the cells within the first 9 rows and 9 columns, represents the result of the BNN models’ predictions regarding 1000 randomly chosen persons from the test set in the order of True positives, True negatives, False positives and False negatives in the bracket. The tp_ROC, tp_PR, AUC_ROC, AUC_PR, f1_score_ROC, f1_score_PR and max_accuracy represent the optimal indicators of accuracy corresponded to the entire test set within each column. The max_accuracy describes the maximum of the overall accuracy (accuracy_total) we ca achieve to deliver correct predictions within each t h v ( n ) .
The metrics reveal that, first of all, the probability of proper recognition of the entire vulnerable households without error is infinitely low. This is due to emergence of false negative counts, i.e. vulnerable households, that mistakenly are detected as wealthy classes almost in all experiments. The rare results, without false negatives being involved, comprise corner solutions consisting of e.g. tp(n=1) and th(n=9), which describe the situation, where the administration is almost next to the point approximating a basic income system for the entire population of the society.
In the both tables 2 and 3, the minimum of max_accuracy appears when the thresholds for distinguishing positives from negatives are set at the median cash accessibility level e.g. th(n=5) or next to it. The max_accuracy increases when we move towards deciding to distinguish the extreme high cash accessible groups e.g. th(n=9) from the rest of the society or to distinguish the extra low cash accessible groups e.g. th(n=1) from the rest of the society. The relatively high overall feasibility of appropriate predictions to distinguish extreme groups from the rest is also evident form the parameter AUC_ROC in both tables. However, the high total accuracies by detection of extreme groups does not mean equal preciseness with regard to positives and negatives. This is revealed through observing at f1_scores obtained at optimal threshold levels. f1_score_ROC and f1_score_PR decrease if we move from the th(n=9) to th(n=1). This mainly goes back to the increase in False negative counts and can be made evident by means of looking at the last element of each brackets (False negative counts) within each row. This means although by setting the threshold at the left hand side of the deciles range e.g. th(n=1) we are capable to recognize a relative high number of negative marked households, however, due to imbalance in the data (through higher proportion of negatives), some predictions regarding real positive household, which are the main targets of the basic income turns to be false. The problem of False negative counts becomes less severe when setting the threshold at the left hand side of the deciles range e.g. th(n=9). In this case all indicators i.e AUC_ROC, AUC_PR, f1_score_ROC, f1_score_PR and max_accuracy, are indicating satisfactory predictions. Regardless of the question of the optimum decile number t h v , the question, which probability threshold t h p , should we set to achieve the maximum accuracy of detection, can be answered to some extent by deviating from the optimal tp_ROC and tp_PR levels. A government can deviate from the optimal t h p levels, which often occur to be around 0.4 i.e. tp(n=4) in our research and set extremely soft by reducing the t h p thresholds to the levels lower than the optimum one e.g. to the tp(n=1 or 2 or 3), to achieve the minimum possible number of e.g. False negative counts. However, this tolerance often happens at the cost of accepting to allocate extra budget to be distributed to the False positives. The play room, they have to move back and forth in the range of non-optimal tp_ROC and tp_PR threshold values, in the cases of the availability of high resolution welfare attributes of the households (e.g. through integrating the bank records) is wider, compared to the cases of working with relatively limited number of welfare attributes of the households. This is because the slopes of the true positive and false positive count curves through the probability threshold axis are of a relative sharp style when incorporating less information in the Bayesian model as illustrated in figure 3 and figure 5.
Table 2. feasibility of distinguishing lower cash accessible groups (positives) form higher cash accessible groups(negatives) by setting various cash accessibility thresholds th(n) and various distinguishing probability thresholds tp(n) if bank records incorporated.
Table 2. feasibility of distinguishing lower cash accessible groups (positives) form higher cash accessible groups(negatives) by setting various cash accessibility thresholds th(n) and various distinguishing probability thresholds tp(n) if bank records incorporated.
index th(n=1) th(n=2) th(n=3) th(n=4) th(n=5) th(n=6) th(n=7) th(n=8) th(n=9)
tp(n=1) [110, 752, 109, 29] [204, 529, 247, 20] [299, 386, 293, 22] [382, 280, 321, 17] [475, 172, 342, 11] [592, 87, 319, 2] [695, 54, 245, 6] [816, 18, 164, 2] [907, 6, 87, 0]
tp(n=2) [96, 816, 45, 43] [187, 673, 103, 37] [271, 546, 133, 50] [362, 402, 199, 37] [461, 324, 190, 25] [561, 209, 197, 33] [687, 117, 182, 14] [812, 53, 129, 6] [902, 20, 73, 5]
tp(n=3) [93, 823, 38, 46] [171, 708, 68, 53] [248, 600, 79, 73] [325, 479, 122, 74] [448, 395, 119, 38] [541, 270, 136, 53] [667, 179, 120, 34] [800, 89, 93, 18] [897, 37, 56, 10]
tp(n=4) [87, 829, 32, 52] [162, 714, 62, 62] [244, 610, 69, 77] [315, 500, 101, 84] [429, 426, 88, 57] [528, 307, 99, 66] [655, 210, 89, 46] [787, 107, 75, 31] [889, 59, 34, 18]
tp(n=5) [78, 834, 27, 61] [156, 722, 54, 68] [239, 617, 62, 82] [304, 509, 92, 95] [416, 442, 72, 70] [516, 322, 84, 78] [642, 223, 76, 59] [782, 120, 62, 36] [885, 65, 28, 22]
tp(n=6) [60, 840, 21, 79] [146, 734, 42, 78] [229, 627, 52, 92] [289, 519, 82, 110] [398, 452, 62, 88] [506, 330, 76, 88] [626, 230, 69, 75] [775, 124, 58, 43] [876, 69, 24, 31]
tp(n=7) [43, 849, 12, 96] [117, 750, 26, 107] [192, 650, 29, 129] [257, 543, 58, 142] [368, 464, 50, 118] [480, 351, 55, 114] [605, 235, 64, 96] [760, 129, 53, 58] [866, 72, 21, 41]
tp(n=8) [39, 849, 12, 100] [66, 768, 8, 158] [140, 662, 17, 181] [193, 561, 40, 206] [304, 486, 28, 182] [414, 362, 44, 180] [551, 256, 43, 150] [728, 145, 37, 90] [844, 74, 19, 63]
tp(n=9) [0, 861, 0, 139] [0, 776, 0, 224] [94, 673, 6, 227] [108, 591, 10, 291] [199, 500, 14, 287] [293, 386, 20, 301] [446, 275, 24, 255] [643, 158, 24, 175] [803, 82, 11, 104]
tp_ROC 0.074391 0.185447 0.265056 0.366079 0.474387 0.627129 0.740497 0.821513 0.910046
tp_PR 0.378252 0.379527 0.397367 0.405677 0.43069 0.486599 0.463268 0.491235 0.429511
AUC_ROC 0.90767 0.897595 0.897214 0.897104 0.89446 0.897804 0.900916 0.909398 0.918033
AUC_PR 0.653285 0.760698 0.80428 0.85266 0.885026 0.917967 0.924374 0.968684 0.985953
f1_score_ROC 0.557 0.686 0.763 0.804 0.835 0.864 0.881 0.903 0.924
f1_score_PR 0.668 0.73 0.77 0.805 0.836 0.871 0.901 0.935 0.967
max_accurcy 0.916 0.88 0.856 0.815 0.858 0.838 0.865 0.902 0.95
Table 3. feasibility of distinguishing lower cash accessible groups (positives) form higher cash accessible groups(negatives) by setting various cash accessibility thresholds th(n) and various distinguishing probability thresholds tp(n) if bank records not incorporated.
Table 3. feasibility of distinguishing lower cash accessible groups (positives) form higher cash accessible groups(negatives) by setting various cash accessibility thresholds th(n) and various distinguishing probability thresholds tp(n) if bank records not incorporated.
index th(n=1) th(n=2) th(n=3) th(n=4) th(n=5) th(n=6) th(n=7) th(n=8) th(n=9)
tp(n=1) [98, 601, 274, 27] [188, 327, 469, 16] [302, 161, 534, 3] [386, 95, 514, 5] [521, 45, 430, 4] [596, 20, 383, 1] [707, 8, 284, 1] [808, 0, 192, 0] [904, 0, 96, 0]
tp(n=2) [81, 746, 129, 44] [161, 508, 288, 43] [270, 354, 341, 35] [369, 203, 406, 22] [509, 91, 384, 16] [585, 64, 339, 12] [701, 29, 263, 7] [806, 5, 187, 2] [904, 0, 96, 0]
tp(n=3) [45, 817, 58, 80] [119, 670, 126, 85] [239, 456, 239, 66] [323, 319, 290, 68] [476, 170, 305, 49] [568, 128, 275, 29] [688, 53, 239, 20] [803, 17, 175, 5] [902, 2, 94, 2]
tp(n=4) [33, 828, 47, 92] [112, 695, 101, 92] [188, 532, 163, 117] [260, 406, 203, 131] [453, 240, 235, 72] [540, 171, 232, 57] [668, 70, 222, 40] [797, 27, 165, 11] [901, 7, 89, 3]
tp(n=5) [0, 875, 0, 125] [103, 711, 85, 101] [141, 610, 85, 164] [222, 479, 130, 169] [379, 326, 149, 146] [491, 221, 182, 106] [624, 121, 171, 84] [778, 47, 145, 30] [896, 12, 84, 8]
tp(n=6) [0, 875, 0, 125] [0, 796, 0, 204] [121, 629, 66, 184] [140, 545, 64, 251] [307, 376, 99, 218] [400, 284, 119, 197] [581, 159, 133, 127] [753, 68, 124, 55] [888, 16, 80, 16]
tp(n=7) [0, 875, 0, 125] [0, 796, 0, 204] [36, 682, 13, 269] [92, 571, 38, 299] [186, 427, 48, 339] [326, 326, 77, 271] [486, 208, 84, 222] [696, 97, 95, 112] [859, 27, 69, 45]
tp(n=8) [0, 875, 0, 125] [0, 796, 0, 204] [0, 695, 0, 305] [12, 604, 5, 379] [129, 448, 27, 396] [162, 376, 27, 435] [357, 239, 53, 351] [607, 131, 61, 201] [812, 51, 45, 92]
tp(n=9) [0, 875, 0, 125] [0, 796, 0, 204] [0, 695, 0, 305] [0, 609, 0, 391] [0, 475, 0, 525] [10, 400, 3, 587] [122, 287, 5, 586] [335, 173, 19, 473] [720, 61, 35, 184]
tp_ROC 0.127837 0.255762 0.338467 0.40804 0.524492 0.609753 0.720006 0.793234 0.9331
tp_PR 0.251693 0.255762 0.311511 0.338626 0.363147 0.370657 0.416931 0.447892 0.480293
AUC_ROC 0.826763 0.794023 0.777754 0.766786 0.761776 0.758263 0.765659 0.775941 0.783671
AUC_PR 0.367298 0.50409 0.584559 0.669769 0.743793 0.798785 0.867553 0.921894 0.96335
f1_score_ROC 0.412 0.538 0.604 0.65 0.693 0.735 0.766 0.813 0.863
f1_score_PR 0.441 0.538 0.605 0.662 0.726 0.785 0.841 0.897 0.948
max_accurcy 0.875 0.814 0.751 0.701 0.705 0.712 0.745 0.825 0.908

5. Conclusion

In this paper, we examined the feasibility of integrating a data based households’ eligibility application in a basic income system. We utilized the real data of one and a half million individual persons with a Bayesian network. We converted the individual household data to household level data and set the cash availability level of a household as the criterion, upon which, we can decide, whether a household can be included in the receivers’ list of a basic income program or not. We designed experiments to see how precise we can distinguish the relative vulnerable groups of the society from the relative wealthier groups by changing the cash accessibility thresholds and classification probability thresholds. The experiments are carried out once with incorporation of a comprehensive set of households’ welfare attributes especially with considering their records of banking data and once with incorporation of a limited set of the households’ welfare attributes i.e. without considering their records of banking data. Thereby, we utilized standard machine learning metrics to evaluate the results of the experiments. The main emphasis of the metrics is put on the recognition of the relative vulnerable groups, which are marked as positives through the study. The metrics reveal that, the probability of proper recognition of the entire vulnerable households without error is infinitely low. The rare results, without false negatives being involved, comprise corner solutions, which describe the situation, where the administration is almost next to the point of approximating a basic income system for the all population of the society. However, the opportunities the achieve a balance between a highly precise recognition of relative wealthier groups and lowest possible error regarding false negative counts are obtainable. This becomes evident from different metrics applied in our study and happens if the following measures become incorporated. First, if the cash accessibility threshold is set possibly close to the deciles at the right hand side of the median level. Second, if the classification probability threshold is set possibly lower than the optimal classification probability threshold. Third, the welfare attributes profile of the households is comprehensive with consideration of the e.g. banking records. Considering these measures by applying a Bayesian network can ameliorate the budget deficiency issue of the government through confidently excluding the relative wealthy groups from a basic income program and simultaneously let the basic income program running broadly for the rest of the society. This solution might still not be a perfect one due to the existence of small percentage of false negatives, who can be falsely recognized and be disadvantaged through the households’ eligibility application within a basic income system. For that purpose, there might be some administrative workarounds, which are not a part of this research. Furthermore, we merely utilized one method i.e. Bayesian networks in our application. Using ensemble methods, which comprise the application of several machine learning methods can come out with higher accuracies to make highly reliable basic income programs. To our understanding information systems will forward the future of the notion of basic income towards an intelligible direction.

References

  1. Barbrook-Johnson, P.; Penn, A.S. Bayesian Belief Networks. 2022. [Google Scholar] [CrossRef]
  2. Koller & Friedman, Probabilistic Graphical Models - Principles and Techniques, MIT Press, 2009. Available online: http://mitp-content-server.mit.edu:18180/books/content/sectbyfn?collid=books_pres_0&id=7953&fn=9780262013192_sch_0001.pdf.
  3. Richard, E. Neapolitan, Learning Bayesian Networks. Northeastern Illinois University Chicago, Illinois, 2003. Available online: http://www.cs.technion.ac.il/~dang/books/Learning%20Bayesian%20Networks(Neapolitan,%20Richard).pdf.
  4. Tsamardinos, I.; Brown, L.E.; Aliferis, C.F. The max-min hill-climbing Bayesian network structure learning algorithm. Mach. Learn. 2006, 65, 31–78. [Google Scholar] [CrossRef]
  5. Fawcett, T. An Introduction to ROC analysis. Pattern Recogn. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
  6. Powers, David M. W. (2011). "Evaluation: From Precision, Recall and F-Measure to ROC, Informedness, Markedness & Correlation". Journal of Machine Learning Technologies. 2 (1): 37–63.
  7. Puga, J.L.; Krzywinski, M.; Altman, N. Bayes' theorem. Nat. Methods 2015, 12, 277–278. [Google Scholar] [CrossRef]
  8. Baker, J. (1992). An egalitarian case for basic income. In: Van Parijs P (ed) Arguing for basic income: ethical foundations for a radical reform. New York: Verso.
  9. Banerjee, A.; Niehaus, P.; Suri, T. Universal Basic Income in the Developing World. Annu. Rev. Econ. 2019, 11, 959–983. [Google Scholar] [CrossRef]
  10. Bartscher, A.K.; Schularick, M.; Kuhn, M.; Wachtel, P. Monetary Policy and Racial Inequality. Brookings Pap. Econ. Act. 2022, 2022, 1–63. [Google Scholar] [CrossRef]
  11. Bill, J. (1988). The prospects for basic income. Soc Policy Adm 22(2), 115–123.
  12. Bobkov V., C. E. (2020). Unconditional Basic Income: Criterial Bases, Transitional Forms and Experimental Implementation. Sotsiologicheskie issledovaniya;10 C, 84-94.
  13. Cappelen, A., Nielsen, U., Tungodden, B., Tyran, J., & Wengström, E. (2015). Fairness is intuitive. Experimental Economics volume 19, 727-740.
  14. Caterina, C. , & Flamand, S. (2019). A Review on Basic Income: A Radical Proposal for a Free Society and a Sane Economy by Philippe Van Parijs and Yannick Vanderborght. Journal of Economic Literature, 57 (3), 644-58.
  15. Coalition agreement SPD, The Greens and FDP. (2021). Mehr Fortschritt wagen. https://www.spd.de/fileadmin/Dokumente/Koalitionsvertrag/Koalitionsvertrag_2021-2025.pdf: SPD. Available online: https://www.spd.de/fileadmin/Dokumente/Koalitionsvertrag/Koalitionsvertrag_2021-2025.pdf: SPD.
  16. Davis, A. , Hirsch, D., Padley, M., & Shepherd, C. (2021). A Minimum Income Standard for the United Kingdom in 2021. Joseph Rowntree foundation. Available online: www.jrf.org.uk.
  17. De Durana, A. , & Rodrigu, G. (2021). New developments in the national guaranteed minimum income scheme in Spain. EUROPEAN SOCIAL POLICY NETWORK.
  18. De Wispelaere, J.; Stirton, L. The Many Faces of Universal Basic Income. Politi- Q. 2004, 75, 266–274. [Google Scholar] [CrossRef]
  19. Delsen, L. (2019). Empirical Research on an Unconditional Basic Income in Europe. Springer.
  20. Haddow, R.; Fitzpatrick, T. Freedom and Security: An Introduction to the Basic Income Debate. Labour / Le Trav. 2001, 47, 260. [Google Scholar] [CrossRef]
  21. Gentilini, U. , Grosh, M., Rigolini, J., & Yemtsov, R. (2020). Exploring Universal Basic Income; A Guide to Navigating Concepts, Evidence, and Practices. World Bank.
  22. Grover, J. A Literature Review of Bayes’ Theorem and Bayesian Belief Networks (BBN). 2012; 27. [Google Scholar] [CrossRef]
  23. Hoynes , H., & Rothstein, J. (2019). Universal Basic Income in the United States and Advanced Countries. Annual Review of Economics, 929-58.
  24. Jackson, A. Basic income: A social democratic perspective. Glob. Soc. Policy 2017, 17, 101–104. [Google Scholar] [CrossRef]
  25. Jenson, F. V. (1996). An introduction to Bayesian networks. Newyork: Springer.
  26. Johnson, R. , & Orme, B. (1996). How Many Questions Should You Ask in Choice-Based Conjoint Studies? Sawtooth Software, Inc.
  27. Jordan, B. (2012). The low road to basic income? Tax-beneft integration in the UK. J Soc Policy 41, 1–17.
  28. Kangas, O. , Signe, J., Miska, S., & Minna, Y. (2021). Experimenting with Unconditional Basic Income: Lessons from the Finnish BI Experiment 2017-2018. Edward Elgar Publishing.
  29. King, J.; Marangos, J. Two Arguments for Basic Income : Thomas Paine (1737-1809) and Thomas Spence (1750-1814). [CrossRef]
  30. Kulshreshtha, K. , Sharma, G., & Bajpai, N. (2021). Conjoint analysis: the assumptions, applications, concerns, remedies and future research direction. International Journal of Quality & Reliability Management.
  31. Lister, A. Reconsidering the reciprocity objection to unconditional basic income. Politi- Philos. Econ. 2020, 19, 209–228. [Google Scholar] [CrossRef]
  32. Louivere, J. (1998). Conjoint Analysis Modelling of Stated Preferences: A Review of Methods Recent Developments and External Validity. Journal of transport Economics 22(1), 93-119.
  33. Louviere, J.J.; Woodworth, G. Design and Analysis of Simulated Consumer Choice or Allocation Experiments: An Approach Based on Aggregate Data. J. Mark. Res. 1983, 20, 350. [Google Scholar] [CrossRef]
  34. Lovett, F. Domination and Distributive Justice. J. Politi- 2009, 71, 817–830. [Google Scholar] [CrossRef]
  35. Luce, R.; Tukey, J.W. Simultaneous conjoint measurement: A new type of fundamental measurement. J. Math. Psychol. 1964, 1, 1–27. [Google Scholar] [CrossRef]
  36. Marshall, D. , Bridges, J., & Hauber, B. (2010). Conjoint Analysis Applications in Health — How are Studies being Designed and Reported? Patient-Patient-Centered-Outcome-Res 3, 249–256.
  37. McFadden. (1974). Conditional logit analysis of qualitative choice behavior. In e. Zarembka P, Frontiers in Econometrics (pp. 105–142). New York: Academic Press.
  38. Moffitt, R. (2003). The Positive Income Tax and the Evolution of U.S. Welfare Policy. https://www.nber.org/: National Bureau of Economic Research, Cambridge, MA.
  39. Mori, I. (2017). Half of UK Adults Would Support Universal Basic Income in Principle. https://www.ipsos.com/ipsos-mori/en-uk/half-uk-adults-wouldsupport-: Polling commissioned by the Institute for Policy Research, University of Bath.
  40. Nguyen, L. (2021). On the implementation of the universal basic income as a response to technological unemployment. International Journal of Management Research and Economics 1(3), 1-6.
  41. Nooteboom, B. Basic Income as a Basis for Small Business. Int. Small Bus. Journal: Res. Entrep. 1987, 5, 10–18. [Google Scholar] [CrossRef]
  42. OECD. (2017). Basic income as a policy option: Can it add up?
  43. OECD. (2019). A data-driven public sector. Paris. Available online: https://www.oecd-ilibrary.org/docserver/09ab162c-en.pdf?expires=1644620690&id=id&accname=guest&checksum=08C311E2ACEE5A054D350727AC3A4873: OECD.
  44. Pateman, C. Democratizing Citizenship: Some Advantages of a Basic Income. Politi- Soc. 2004, 32, 89–105. [Google Scholar] [CrossRef]
  45. Pearl, J. (1988).. Probabilistic reasoning in intelligent systems: networks of plausible inferencee, first ed. in: Representation and Reasoning. California: Morgan Kaufmann.
  46. Peduzzi, P.; Concato, J.; Kemper, E.; Holford, T.R.; Feinstein, A.R. A simulation study of the number of events per variable in logistic regression analysis. J. Clin. Epidemiol. 1996, 49, 1373–1379. [Google Scholar] [CrossRef] [PubMed]
  47. Perkiö, J. (2013). Basic income proposals in Finland, Germany and Spain. european network for alternative thinking and political dialogue.. Available online: https://www.transform-network.net/fileadmin/_migrated/news_uploads/paper__2_13.pdf.
  48. Pulkka, V. (2017). A free lunch with robots - can a basic income stabilise the digital economy? Transf-Eur Rev Labor Res 23(3), 295–311.
  49. Raventós, D. (2007). Basic income: the material conditions of freedom. London: Pluto Press.
  50. Rawls, J. (2009). A theory of justice. Cambridge: Harvard University Press.
  51. Scientific Advisory Board at the Federal Ministry. (2021). Unconditional basic income. bmf-wissenschaftlicher-beirat.de.
  52. Standing, G. (2012). The precariat: from denizens to citizens? Polity 44(4), 588–608.
  53. Thomas, A. Full Employment, Unconditional Basic Income and the Keynesian Critique of Rentier Capitalism. Basic Income Stud. 2020, 15. [Google Scholar] [CrossRef]
  54. Van der Veen, R. (1998). Real freedom versus reciprocity: competing views on the justice of unconditional basic income. Polit Stud 46(1), 140–163.
  55. Van Parijs, P. Why Surfers Should Be Fed: The Liberal Case for an Unconditional Basic Income. 2017. [Google Scholar] [CrossRef]
  56. von Gliszczynski, M. Social protection and basic income in global policy. Glob. Soc. Policy 2016, 17, 98–100. [Google Scholar] [CrossRef]
  57. Widerquist, K. Perspectives on the Guaranteed Income, Part I. J. Econ. Issues 2001, 35, 749–757. [Google Scholar] [CrossRef]
  58. Yang, J.; Mohan, G.; Pipil, S.; Fukushi, K. Review on basic income (BI): its theories and empirical cases. J. Soc. Econ. Dev. 2021, 23, 203–239. [Google Scholar] [CrossRef]
  59. Ypma, T.J. Historical Development of the Newton–Raphson Method. SIAM Rev. 1995, 37, 531–551. [Google Scholar] [CrossRef]
  60. Zheng, Y. , Guerriero, M., Lopez, E., & Haverman, P. (2020). Universal Basic income; a working paper. UNDP China Office.
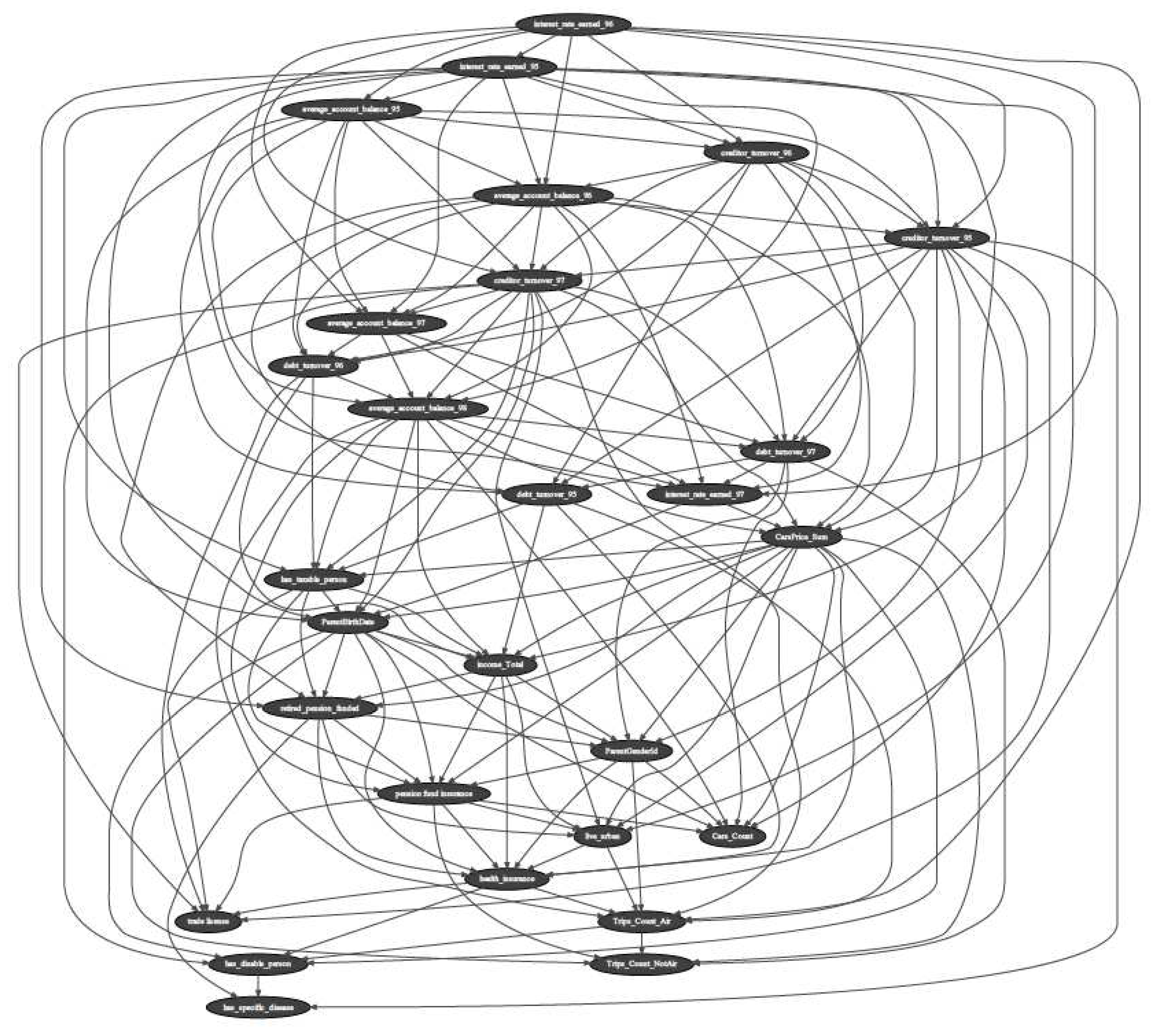
Preprints 83958 g001
Figure 1. The Bayesian belief network’s directed acyclic graph incorporating 30 welfare variables
Figure 1. The Bayesian belief network’s directed acyclic graph incorporating 30 welfare variables
Preprints 83958 g001
Preprints 83958 g002
Figure 2. The test set’s ROC and PR metrics .
Figure 2. The test set’s ROC and PR metrics .
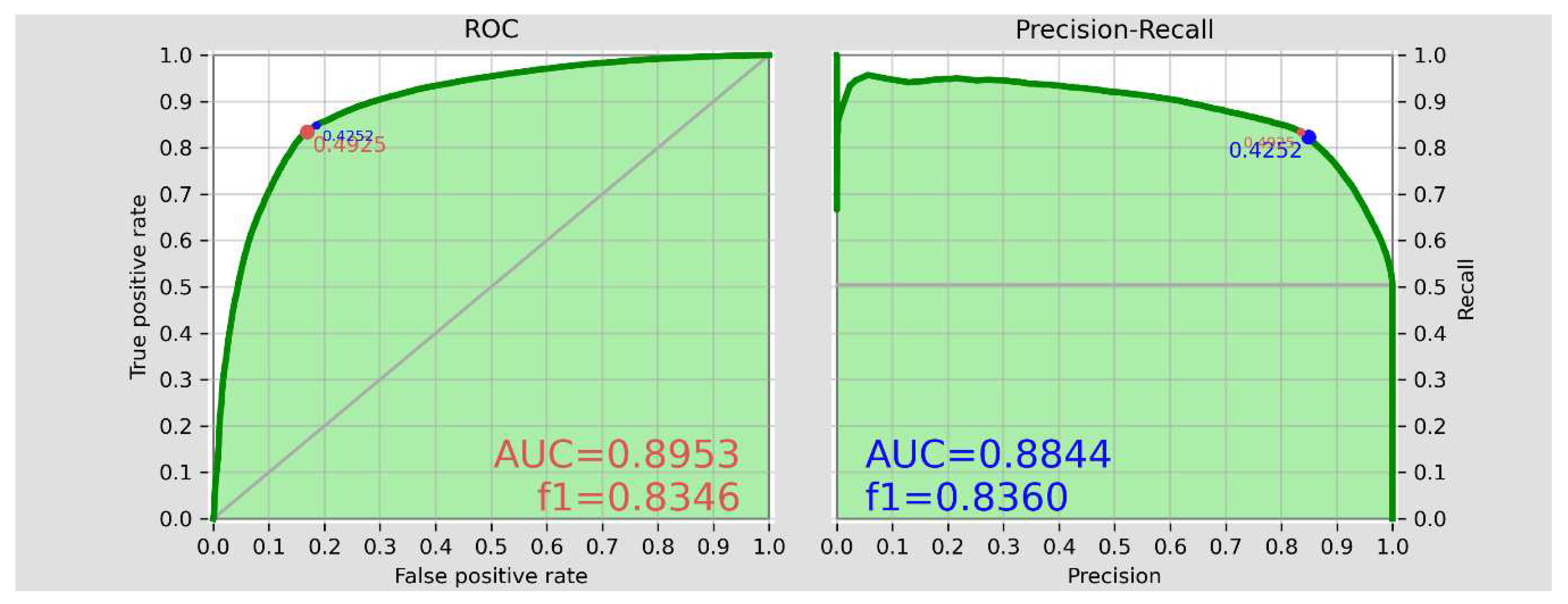
Preprints 83958 g002
Preprints 83958 g003
Figure 3. Government’s play room to recognize higher True positive rates.
Figure 3. Government’s play room to recognize higher True positive rates.
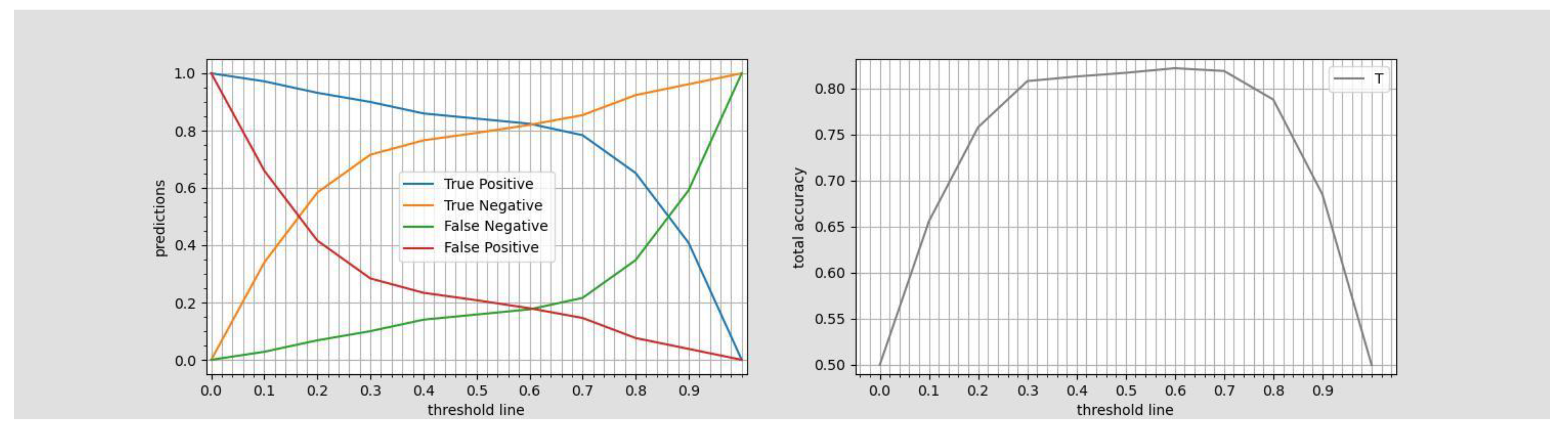
Preprints 83958 g003
Preprints 83958 g004
Figure 4. Welfare attributes importance to provide evidence regarding negative and positives.
Figure 4. Welfare attributes importance to provide evidence regarding negative and positives.
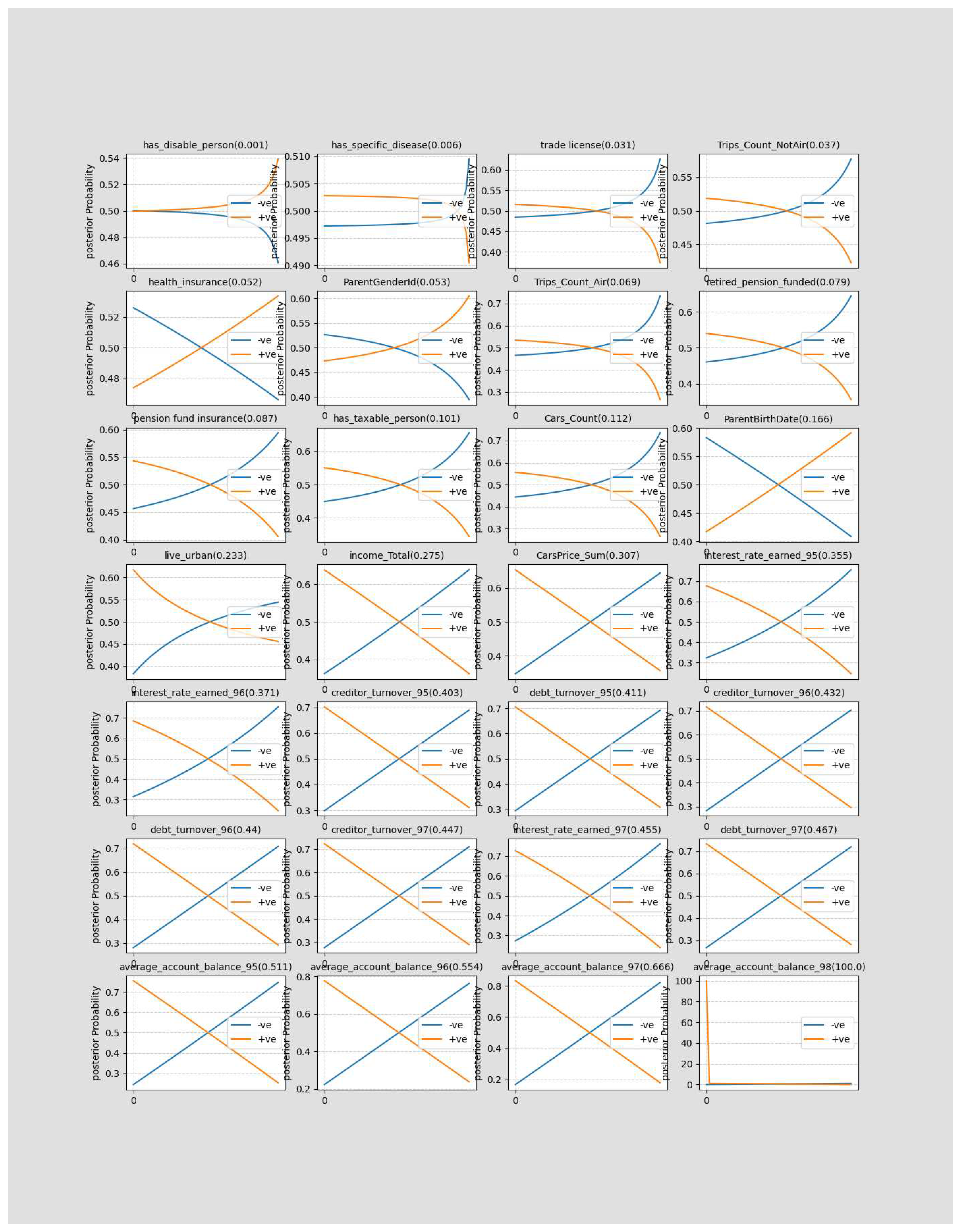
Preprints 83958 g004
Preprints 83958 g005
Figure 5. The Bayesian belief network’s directed acyclic graph incorporating non-banking welfare variables
Figure 5. The Bayesian belief network’s directed acyclic graph incorporating non-banking welfare variables
Preprints 83958 g005
Preprints 83958 g006
Figure 6. The test set’s ROC and PR metrics by incorporating non-banking welfare variables.
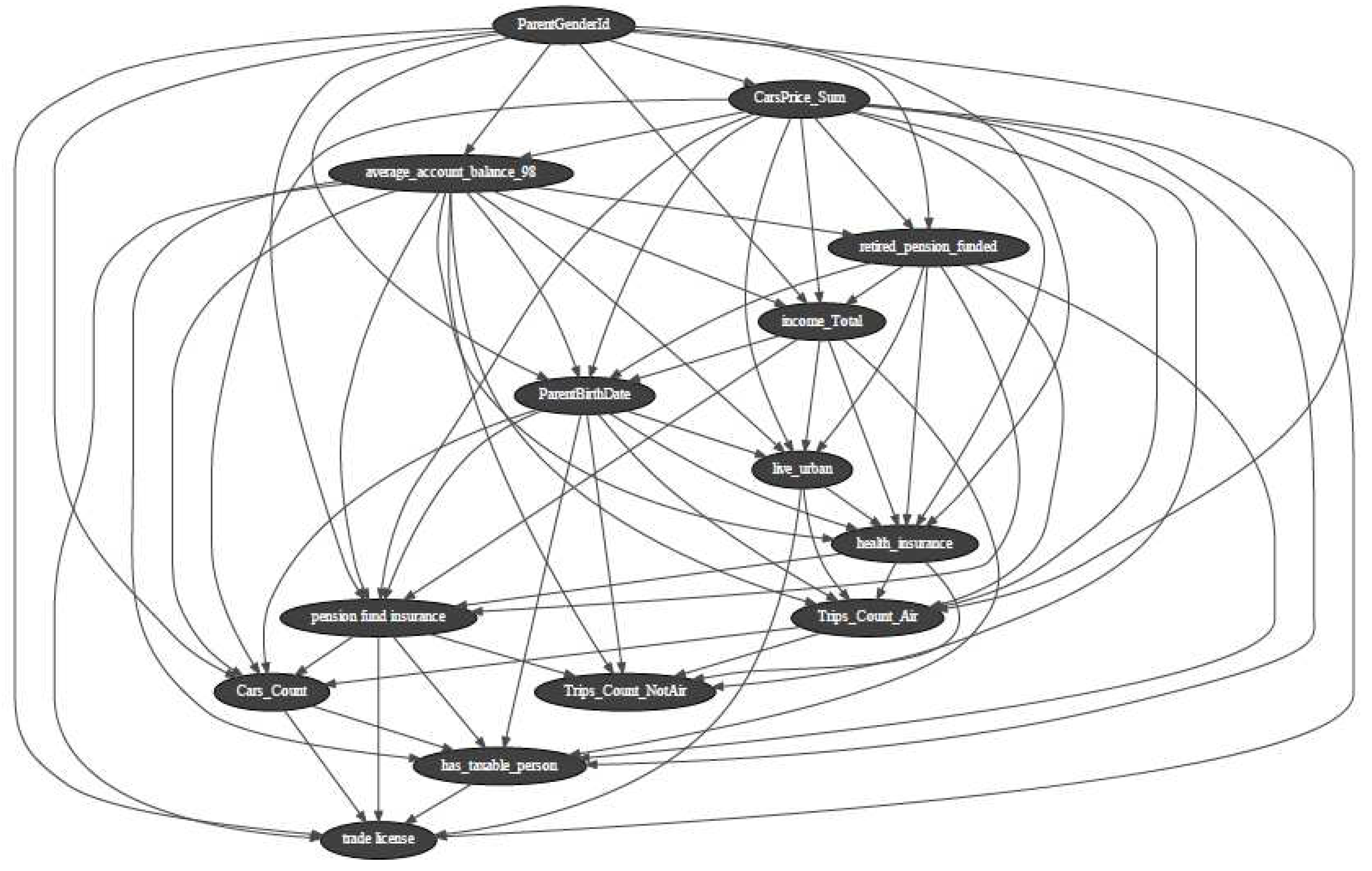
Figure 6. The test set’s ROC and PR metrics by incorporating non-banking welfare variables.
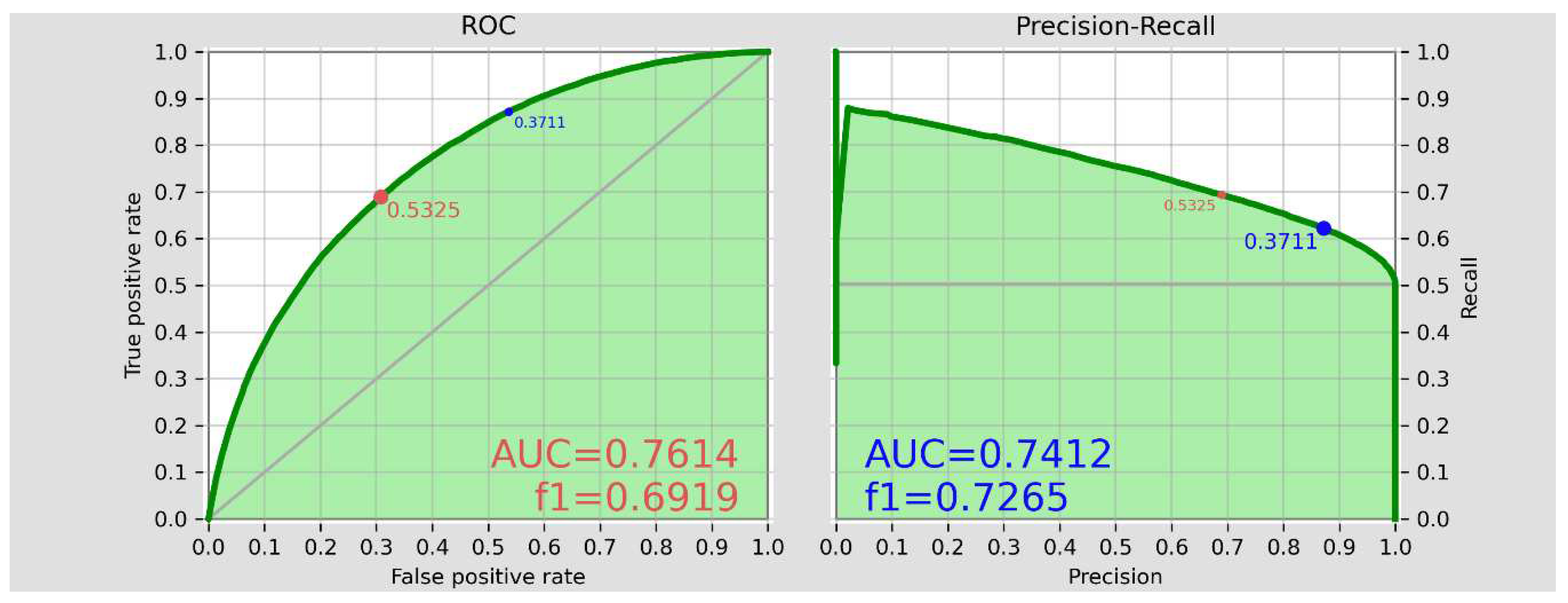
Preprints 83958 g006
Preprints 83958 g007
Figure 7. Government’s play room to recognize higher True positive rates by incorporating non-banking welfare variables.
Figure 7. Government’s play room to recognize higher True positive rates by incorporating non-banking welfare variables.
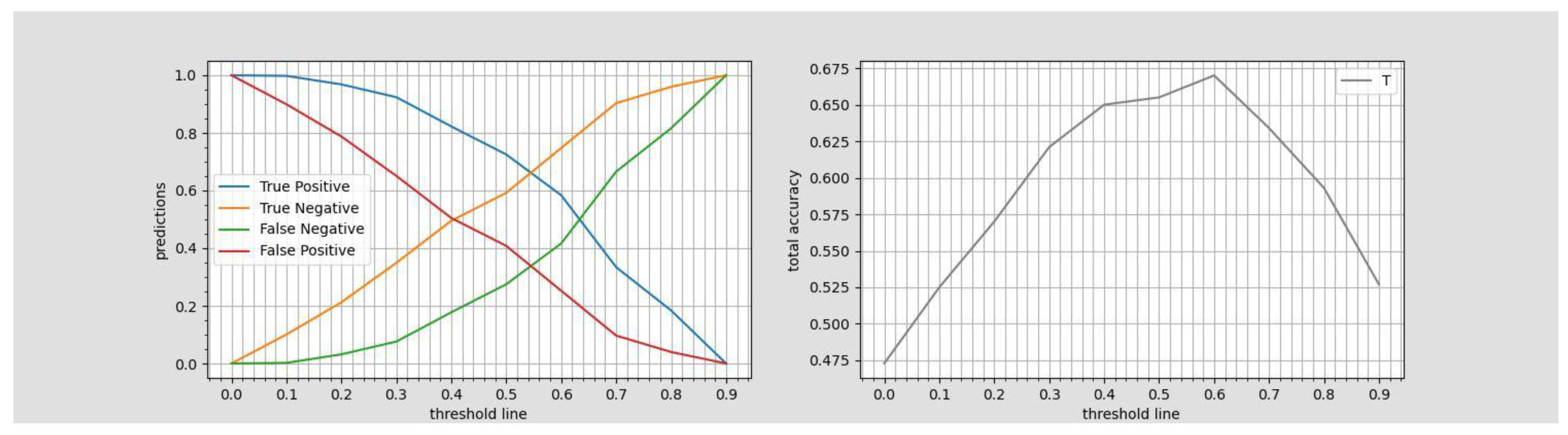
Preprints 83958 g007
Table 1. The types of 30 distinct registered information from each individual.
Table 1. The types of 30 distinct registered information from each individual.
Person’s family profile and gender
  • Person ID
2.
Parent ID
3.
Age
4.
Gender
Person’s living place
5.
live in the city or not?
Person’s income
6.
Total annual salary
7.
Has a trade union license?
8.
Is an employed taxable person?
Person’s insurance and retirement status
9.
Has health insurance?
10.
Is a pension fund insurer?
11.
Is a pension fund retiree?
Person’s transport and trips
12.
Number of foreign air trips
13.
Number of foreign land trips
14.
Total number of cars
15.
Total value of cars
Person’s special health issues
16.
Is a special patient?
17.
Is a disabled person?
Person’s bank account records of the recent years
18.
Total income from bank interest within 20.03.2016-20.03.2017
19.
Total creditor turnover within 20.03.2016-20.03.2017
20.
Total debt within 20.032016-20.03.2017
21.
Average accounts balance within 20.03.2016-20.03.2017
22.
Total income from bank interest in within 20.03.2017-20.03.2018
23.
Total creditor turnover within 20.03.2017-20.03.2018
24.
Total debt within 20.03.2017-20.03.2018
25.
Average accounts balance within 20.03.2017-20.03.2018
26.
Total income from bank interest within 20.03.2018-20.03.2019
27.
Total creditor turnover within 20.03.2018-20.03.2019
28.
Total debt within 20.03.2018-20.03.2019
29.
Average accounts balance within 20.03.2018-20.03.2019
30.
Average accounts balance within 20.03.2019-20.03.2020
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated