Prerpints.org logo
Preprint
Article

Beam Transmission (BTR) Software for Efficient Neutral Beam Injector Design and Tokamak Operation

Altmetrics

Downloads

102

Views

21

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

01 September 2023

Posted:

06 September 2023

You are already at the latest version

Alerts
Abstract
Neutral beam injection (NBI) is used for thermonuclear plasma heating, non-inductive current drive, rotation, operation scenario control, and for plasma diagnostics in nuclear fusion devices. NBI is the main source of fast particles in plasma which transmit energy to thermal plasma during their slow-down. Steady-state tokamak operation is only possible when the sub-thermal particles energy is absorbed and effectively confined in plasma volume. While NBI purposes and applications vary through different fusion systems, the engineering tasks performed during research and development (R&D) stage of neutral beamline design have much in common. The NBI studies, especially addressing long pulse and high-power operation typically include a beam transmission analysis and power loads distribution at the structural components of the beamline. Thermo-structural analysis is applied next to heat removal circuits design. ‘Beam Transmission’ (BTR) code is a dedicated tool, developed by a physicist and used by NBI physicists and engineers. BTR was created and 1st applied during R&D phase of the world’s largest tokamak ITER. BTR code is intended for public usage and routinely applied for detailed simulations of neutral beam propagation through complex beamlines. BTR is flexible and intuitive in input, user-friendly and fully interactive. Thanks to visualization and high performance BTR looks and feels like a real NB flight simulator. Despite BTR ‘mature’ age, the code is still in evolution. Support is available to all new BTR users.
Keywords: 
Subject: Engineering  -   Energy and Fuel Technology

1. Introduction

Neutral beam injection (NBI) systems are commonly used in thermonuclear fusion devices with magnetically confined plasmas (incl. tokamaks, stellarators, mirror traps, etc.) - mainly for plasma heating, current drive, rotation, pressure/current profiles control, for fast ion physics investigations, and efficient plasma parameters diagnostics. NBI is expected to be the main source of high-energy particles to maintain steady-state ‘beam-driven’ scenarios in fusion neutron source (FNS) devices based on tokamak [4,5,6]. FNS concept offers attractive possibility to cope with many specific problems of fission nuclear power engineering as well as fusion power plants. While NBI purposes can be essentially different across multiple designs and applications, the main engineering issues and scope of tasks to be performed during any NBI development and commissioning are very similar through the variety of beamlines.
Typical R&D studies of a neutral beamline, especially when addressing long pulse high-power operation include a detailed evaluation of beam transmission and power deposition at the injector surfaces [7,8]. The data sets are next used for thermal and structural analysis and finally define the engineering solutions to be adopted for the heat load removal and the entire injector design. However, during the final stage of NBI design with the geometry fixed, and also during NBI commissioning and operation in experiment, power removal issues still persist, so that the beam losses and deposition should be reviewed every time when small elements need to be installed, or their position or inclination changed, or physical conditions varied due the main device operation mode (e.g., tokamak magnetic field is different through scenarios). Besides, the machining inaccuracies in different beamline units can lead to inacceptable beam losses and overheating as well as to the material sputtering which deteriorate the overall NBI efficiency and plasma parameters in the machine.
The accelerated beam power for NBI can be very high: the peak power density across the beam cross-section can reach up to ~100 MW/m2 and hence the source beam and beamline elements need to be adjusted with an extremely high precision so that the intercepted power is minimized and no surface is burnt due to insufficient cooling. Besides, due to the tight space constraints of the main device (e.g., tokamak) configuration, a beamline design is made as compact as possible. The available space considerations result in a very long multi-parametrical optimization procedure, while NB design specifications with account of cooling requirements tend to be increasingly complex. To minimize the efforts for NBI optimization and to reduce the beam losses and heat loads along the beamline, dedicated numerical tools are required. At present, BTR code [9,10] is one of the most popular tools for NBI design and analysis [11,12,13,14,15,16,17,18,19,20,21].
The work on BTR software began during conceptual and engineering design phases of ITER project [2], so the results of BTR calculations can be found already in the ITER Design and Description Document [3] issued in 2001. The 1st version BTR-1 open for public usage was released in ~2005, when the source code moved to MS Visual C++; the earlier code versions were written in Borland Turbo Pascal 7 [22]. The successive BTR versions, including BTR-5, were developed under the aegis and with active support of ITER Organization. The primary code verification was organized by ITER heating and current drive department (H&CD); however, the paper on BTR verification was not published at the appropriate time (2008), so BTR users outside of ITER simply were unaware of the V&V document existence - and they could not refer to it when applying BTR.
BTR was intended to be maximum ‘user-friendly’; perhaps the feature which made the code especially popular (and this was especially rare among coding physicists ~20 years ago) was the interactive user interface - Windows ‘standard’ GUI - with built-in direct input control panel (so called ‘Green Panel’), and rather primitive visualization which yet offers full control over the data input and the calculation process. Due to this equipment, BTR is often used for training in the field like a primitive NBI flight-simulator. BTR supports parallel multi-thread execution; the average running time is several minutes (for single-run mode), and the best performance is naturally observed on multi-core Windows machines. The data input is flexible and highly intuitive; the entire beam and investigated injector geometry can be easily tuned for any specific beamline design. The information on the code major upgrades (2005-2020) can be found online [1].
This paper introduces basic principles of neutral beam injection and guides through BTR code main capabilities and limitations which are applicable to any NBI design and implementation process. The final NBI system efficiency depends heavily on the simulations accuracy, as well as the simulation models consistency with a real physical environment. The paper is structured as following.
NBI purposes, general structure and efficiency concerns are brought in Section II.
BTR code basic features and GUI capabilities are represented in Section III.
BTR scope and methods are discussed in Section IV.
Verification and validation (V&V) issues are considered in Section V.
The software applications in various NBI designs are illustrated in Section VI.
The main conclusions and future plans are manifested in the final Section VII.

2. NBI purpose, scheme and structure

2.1. Neutral injection purpose

Neutral beam injection is essential for thermonuclear plasma heating, current drive, rotation, plasma operation control, and plasma diagnostics in nuclear fusion devices like tokamaks and stellarators. High-energy neutral beams provide a great opportunity to enhance the operation space of the target machine by and handling the injected power and fast ion distributions in plasma volume. NBI is expected to be the main source of high-energy particles to maintain steady-state ‘beam-driven’ scenarios in fusion neutron sources (FNS) and hybrid reactors based on tokamak [4,5,6,23]. FNS concept offer attractive possibility to cope with many specific problems of fission nuclear power engineering as well as fusion power plants. While NBI purposes can be essentially different across multiple designs and applications, the main engineering issues and scope of tasks to be performed during any NBI development and implementation are similar through the beamlines.
NBI high efficiency of current drive has been proved in experiments at a large number of tokamaks; they include JET, KSTAR, DIII-D, JT-60U, Globus-M, etc. [24,25]. The experiments have confirmed the feasibility of NBI usage as one of the basic additional heating techniques in the international ITER project. However, each NBI cell takes roughly the same space as the fusion device, and the complex design makes the entire NBI cost comparable with the cost of fusion device. To keep the overall machine viability on acceptable level, NBI systems should maximize the NBI beamline performance and ensure the components ability to withstand high heat loads during a long pulsed (or steady-state) operation.
Over the past decades, the development of the NBI system for ITER has made it possible to develop and justify the techniques for the beam formation, acceleration, and transport providing injection duration of up to 3600s [7]. For almost steady-state operation mode of the injector, many key issues of both the beam generation and the heat removal from all the loaded injector elements have been worked out in detail. It has been proved that the overall NBI system efficiency is mainly defined and limited by the neutralization output, i.e., the percentage of accelerated ions which can be transformed to atoms.

2.2. Neutral injection principles and scheme

NBI main idea can be summarized as following. Positively or negatively charged hydrogen (or deuterium) ions are extracted from a beam source (BS) and accelerated to a required voltage in a multi-grid multi-aperture electrostatic accelerator, so-called ion-optical system (IOS), where the last grid (electrode) is kept at ground potential and called grounded grid (GG). The source beam optimal energy (equal to the IOS accelerating voltage) is chosen to ensure the final neutral beam capacity to penetrate deeply to plasma target; for large plasma devices (with R > 2 m) only negative-based neutral beams can be efficiently produced. In fact, the optimal beam energy is also limited by the shine-through issue, as higher energy beams penetrate deeper so they can burn the opposite wall (‘first wall’, or FW) of tokamak camera if plasma is not dense enough. The accelerated ion beam from the BS is onward neutralized by charge exchange (positive ions) or electron stripping (negative ions) processes in a neutralization cell. The source ions neutralization is achieved via the beam passage through hydrogen gas or plasma, although other techniques can become available in future, e.g., photon neutralization of the beam. A neutralizer with a gas target typically features several channels design to minimize gas flow required. Positive ions neutralization efficiency on gas drops with ion energy and becomes unacceptably low at higher beam energies [26,27] while the negative beams neutralization efficiency on gas is almost stable about ~60%. Therefore, for large fusion devices (e.g., tokamaks with R > 2 m), where neutral beam energy (Eb) is above 70 keV per nucleon (or 70 keV/amu), only negative-based neutral beams can be efficiently produced, while for smaller devices with lower energy range the usage of positive ion scheme is more beneficial [28,29]. Downstream the neutralization, the beam still contains unwanted residual charged beam fractions; the latter should be removed from the beam. For this purpose, a residual ion dump (RID) device is used, which can employ electrostatic or magnetic deflection of the ions.
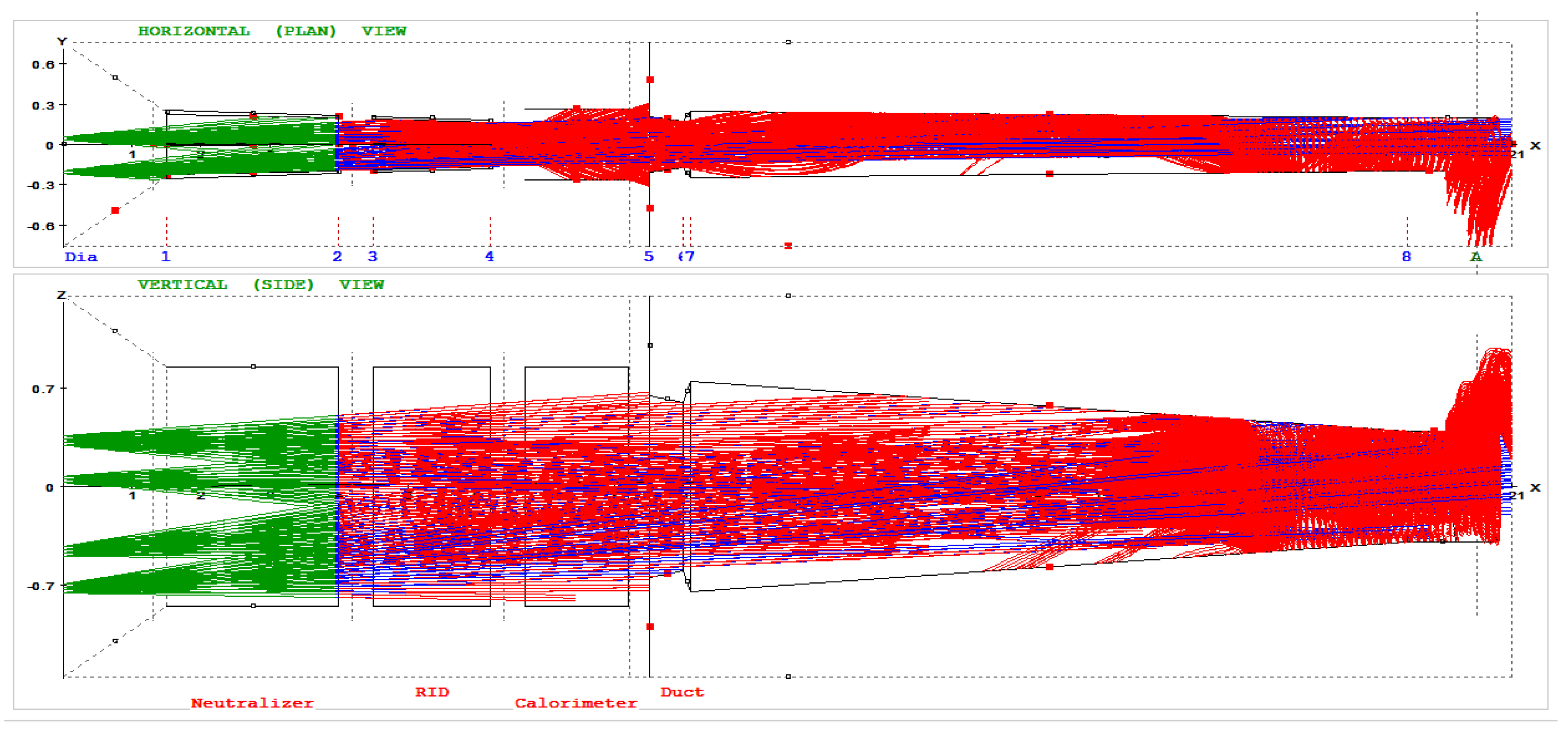
The beamline basic components used through all NBI designs are very similar, with difference associated with NB production scheme (positive or negative). The example of neutral beamline design without transmission ducts is shown in Figure 1. ‘Conventional’ NBI beamline comprises the following ‘standard’ components [7,8]: an ion beam source (BS), a neutralizer, a residual ion dump (RID), a neutral beam dump, or calorimeter, and beam transmission ducts. The source beam passes through a neutralizer and RID, and then proceeds through an exit scraper located at the exit of the beam line vessel. RID structure is typically chosen consistent with that of the neutralizer and formed by the same number of channels for beam passage. The channel structure of NBI components (neutralizer and RID) is optimal for gas supply and pumping.
The injector is connected to the tokamak vacuum chamber via a dedicated pipeline for beam passage. Downstream the NBI vessel, the neutral beam propagates to plasma through the beam transmission ducts, which are supplied with additional cooled boxes (liners) inside. In fact, there can be a large amount of elements located between the vessel and the transmission ducts (see Figure 1) like fast shutter, absolute valve, connection modules, bellow joints, and other systems; as they accept the direct neutral beam power they are often addressed as front end components (FEC). The transmission pipeline can be complex enough (see Figure 2) and include several duct modules. Outer duct pipeline (beyond the tokamak vacuum chamber) is formed by a sequence of channels (duct modules) which can be equipped by the water cooled liners. The inner part (within the tokamak chamber) is formed by the tokamak blanket elements.
The extremely tight arrangement of the tokamak systems, which include the magnetic field coils, shield and support structures lead to a relatively small aperture size available for beam input to plasma; the latter issue together with a long transmission line distance dictate severe limits on the whole NBI design requirements. These requirements implicate high precision for beam steering and focusing, as well as all the beamline channels manufacturing and alignment (fine tuning), which would ensure minimum power losses and maximum NBI efficiency for long term operation.

2.3. Neutral beamline losses and efficiency

While NBI targets and schemes can vary through different fusion designs, the engineering issues and therefore the routines to be performed during beamline development, commissioning and operation are similar. These routines, especially for the design addressing a long pulse high-power operation, typically include accurate simulations of beam generation and propagation in ‘realistic’ (reconstructed) environment, with beam power losses and thermal load deposition along the injector components; these are performed for the entire range of possible working scenarios. The beam power interception by beamline components’ surfaces can lead to unaffordable (over-critical) high power fluxes, and this justifies the need of high-fidelity beam simulations, which can be further used as base for thermo-mechanical study - for the design of cooling systems and for power facing components, even for small elements like bolt joints. Thermal power distributions obtained by NBI simulation are next applied to thermo-mechanical and structural study which finally defines the entire NBI design meeting the heat-removal requirements. And, with any minor change in the beamline design or operation conditions (like gas flow or magnetic field) or in case the experimental data disagree with initial assumptions, the power load calculations and major thermal analysis review can be essential [30,31]. Since the injector geometry is usually restricted by the tokamak systems and the injection port dimensions (see paragraph 2.2), the beamline design optimization and numerical testing routines are often complex and time consuming.
While the overall NBI system efficiency is mainly defined and limited by the neutralization output (see paragraph 2.1), the beam angular properties (divergence and focusing) together with beamline geometrical transmission play major role in the neutral beam losses and neutral power reduction before the beam reaches the tokamak plasma.
The beam angular divergence depends on the beam source plasma discharge operation [7,32] - with optimal operating point (minimal divergence) corresponding to maximum value of ion beam perveance. Operating away from this point generally leads to the beam angular widening. The beam angular width is also sensitive to the shape of the apertures and their arrangement on electrodes: the circular apertures produce elementary beams (so-called ‘beamlets’) with axially symmetrical angular divergence, while for the slit-type IOS electrodes, the beam width across the slits can be 2-3 times higher than along the slits. The beam divergence optimization and monitoring can be performed by a V-shape calorimeter during NBI commissioning. Beamlet group arrangement at GG and beamlet axes initial focusing should be also tied with the expected value of the beam divergence and beamline channels structure, this typically leads to a combined focusing: GG sections are inclined as a whole to hit the target opening in tokamak chamber, while the beamlets within each channel are focused at a shorter distance, which depends on the expected beamlet divergence; this approach leads to maximum beam transmission through the limited beamline channels cross-section. Figure 3 shows the beamlets focusing for FNS-ST neutral beamline compact design (which has one vertical channel).
The effect of the source particles distribution in space and angle which is associated with beamlets structure, internal divergence and axis inclinations is clearly observed in Figures 4ab.
Preprints 84004 g004
Figure 4a. The beam source particles statistical distribution before neutralization, left to right: (X, Y), (ϴx, ϴy), (X, ϴx), (Y, ϴy), where X, Y – horizontal and vertical position in the plane, ϴx, ϴy – horizontal and vertical angle from the beam main axis. The beam source spatial dimensions (shown in the left plot) correspond to the plasma emitter rectangle W × H = 18 × 115 cm2.
Figure 4a. The beam source particles statistical distribution before neutralization, left to right: (X, Y), (ϴx, ϴy), (X, ϴx), (Y, ϴy), where X, Y – horizontal and vertical position in the plane, ϴx, ϴy – horizontal and vertical angle from the beam main axis. The beam source spatial dimensions (shown in the left plot) correspond to the plasma emitter rectangle W × H = 18 × 115 cm2.
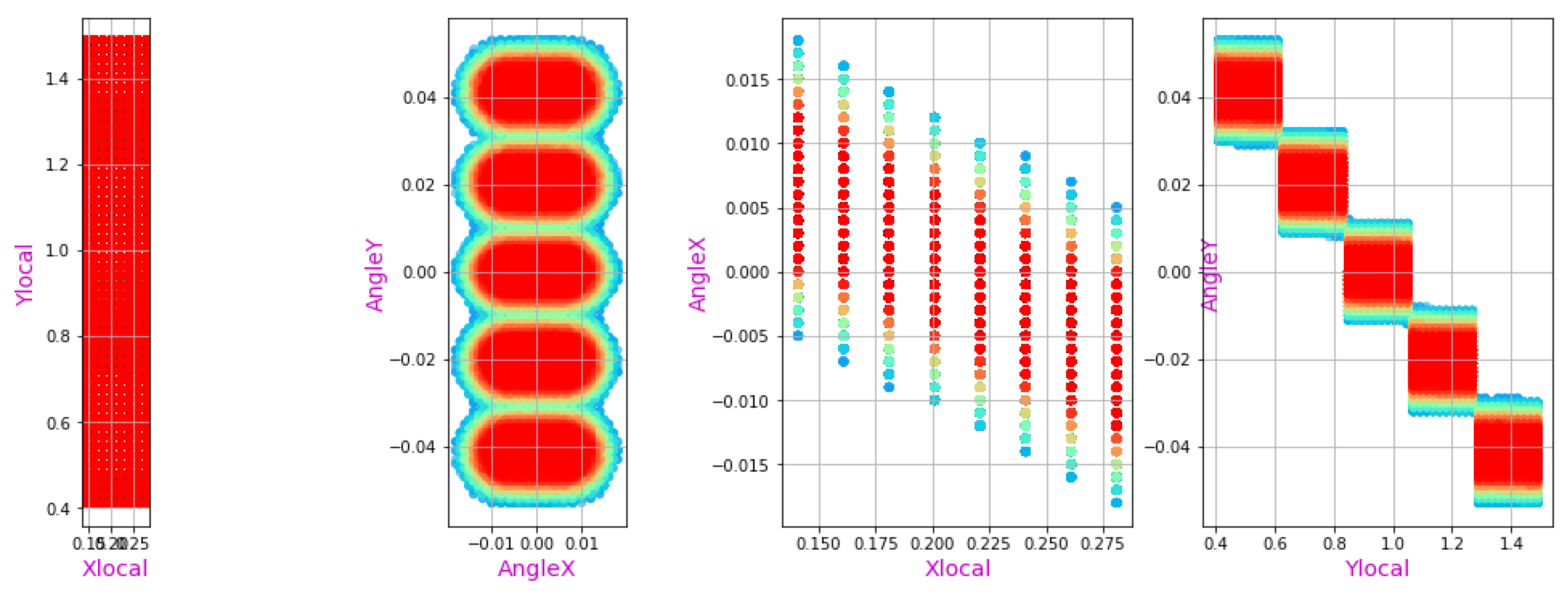
Preprints 84004 g004
Preprints 84004 g005
Figure 4b. The neutral beam distribution in the NBI port plane: (X, Y), (ϴx, ϴy), (X, ϴx), (Y, ϴy), where X, Y – horizontal and vertical position in the plane, ϴx, ϴy – horizontal and vertical angle from the beam main axis.
Figure 4b. The neutral beam distribution in the NBI port plane: (X, Y), (ϴx, ϴy), (X, ϴx), (Y, ϴy), where X, Y – horizontal and vertical position in the plane, ϴx, ϴy – horizontal and vertical angle from the beam main axis.
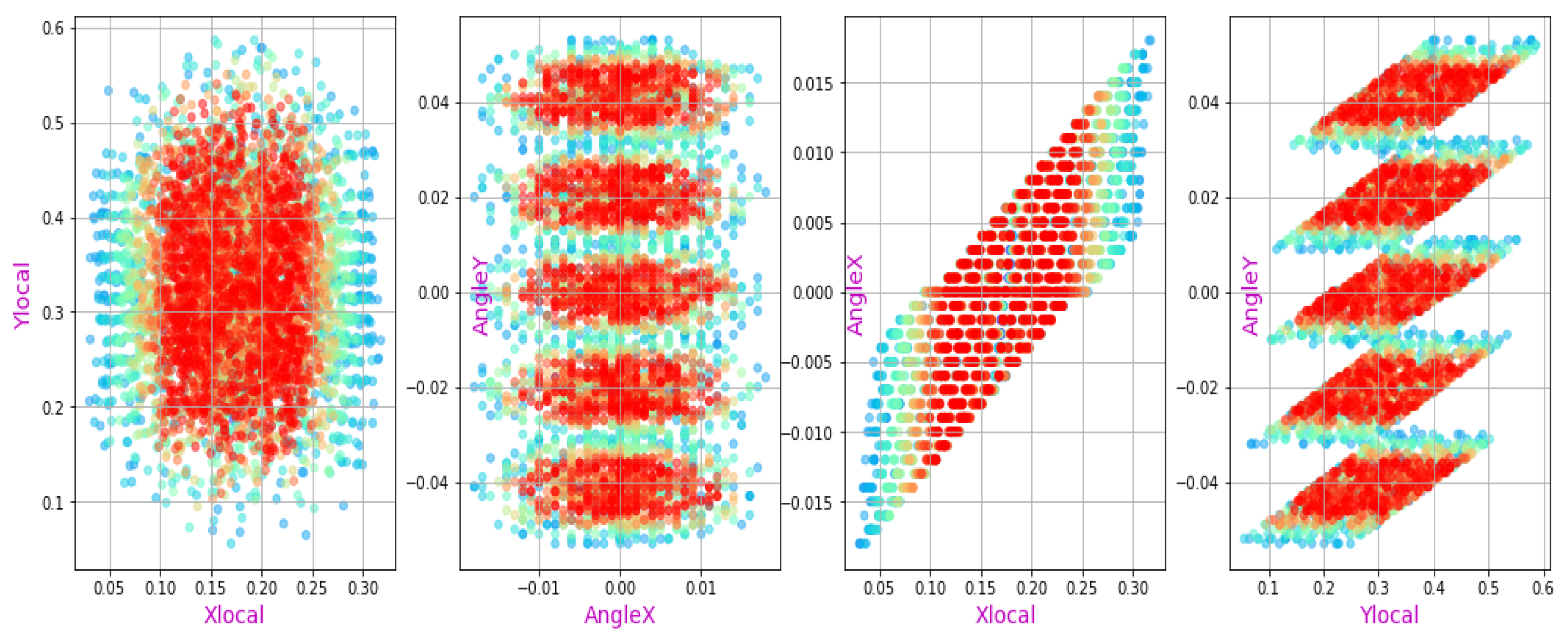
Preprints 84004 g005
The stray electromagnetic field from tokamak, if not reduced down to acceptable values deflect the source ions from their nominal straight-forward direction. The IOS high precision focusing can be violated due to many reasons. These factors cause the neutral beam higher interception and additional scattering in velocity space. Finally, when the neutral beam propagates along the long transmission line and ducts, secondary ions are born due to the neutral particles ionization on the background (residual) gas, this process leads to additional beam losses and charged power fluxes onto the beamline surfaces.
High-fidelity power flux simulation with account of background fields is essential not only for the NBI design optimization, it is also critical for the injected beam power deposition in plasma. The injected beam particles capture and behavior highly depend on the injected beam angular distribution, while the beam-plasma effects and overall NB performance in tokamak should be governed by the initial fast particle (NBI driven) source distribution in phase space. However, the latter issue is often underestimated, despite the well-known pitch-angle effect, which is the fast ions angular distribution versus the magnetic field, on the entire beam performance in plasma [33]. Through variation of the fast ion source distribution in space and velocity plasma current, pressure and toroidal rotation in tokamak can be efficiently controlled by several neutral beam injectors.
As the source beam has a finite angular width (can be ≤ 15 mrad, depending on the BS scheme), the simplest way to improve the transmission is to make the beam path as short as possible. However, the duct length is defined by tokamak systems configuration and takes roughly a half of the entire beamline length. For example, the internal duct length in ITER HNB is ~13m, while the entire beamline (from GG) is ~26m.
The next possible solution is to reduce the neutralization length, RID, and the beam dump length. However, the neutralizer length, its channels width, and the gaps between the components are coupled with the gas flow rates and pumping capacity to ensure the optimum neutralization target. In a gas neutralizer, the gas flow is defined by the target thickness needed. For reduced neutralizer length and fixed channel width, the gas throughput within the neutralization region grows up, which leads to higher gas fluxes to BS and RID and additional beam losses (due to beam collisions with gas). To reduce the gas flow from the neutralizer, it can be divided to even more sub-channels, but this will enhance the source beam direct interception, and increase the structural complexity of the injector already complicated design. The dimensions of other NBI components (RID and beam dump) are limited mainly by the high power load and local power density from the intercepted beam fractions, and by the cooling capacity too. This example is only a small illustration of the idea behind the beamlines optimization: the optimum beamline design should be consistent with the efficient beam production, ensure the lowest possible beam losses, and cope with the heat load accepted during the long or steady-state operation.
We assume the total beamline efficiency (i.e., the ratio of injected neutral power to the source beam power) is mainly defined by the beam neutralization efficiency and the beam geometrical transmission. The actual beam divergence in many cases is unknown. For example, the ITER design document [3] adopts three nominal values of negative ion beam (D-) core divergence: 3 mrad, 5 mrad, and 7 mrad; besides, according to experiments, the beam core (85% of extracted current) is accompanied by a higher divergent (~30 mrad) current fraction – ‘halo’, which carry ~15% of current. The beamline geometrical transmission for 3-7 mrad beams can vary from 70% to 90%, leading to the total beamline efficiency 35—50%.
With best affordable source beam neutralization efficiency (on gas or plasma target), and with optimized beamline geometrical transmission, the injected power to plasma can hardly exceed ~40—45% the power in accelerated source ions. The final efficiency of the beamline scheme will highly depend on the actual values of source beam divergence, which are to be defined experimentally, and on the ions deflections caused by external electro-magnetic fields.

2.4. Neutral beamline geometry in BTR

The examples of complex NBI layout are not provided in this paper, but they can be easily found in [7,8] for ITER neutral beam injectors, and also in [21,28,29] for other tokamak designs. Based on this typical layout, the default beamline input, or BTR ‘standard’ geometry consists of the following major components, see Figure 1 and Figure 2:
-
the beam source grounded grid (GG),
-
multi-channel (can be single-channel) neutralizer,
-
residual ion dump, RID (multi- or single channel),
-
neutral beam dump, or calorimeter,
-
beam transmission line, or duct, which consists of multiple modules (scrapers, FEC, liners, blanket sections, etc.).
In addition to the ‘standard’ input option, BTR allows the user to specify the list of ‘free surfaces’, which can better reproduce in more detail the beamline geometry. Free surfaces can be created either directly by the interactive input tools (GUI dialogs), or imported as text files, created manually or with dedicated software (CAD).
The beam geometry is defined as a regular array of ‘beamlets’ (elementary pencil-beams) which are emitted at BS GG plane; to be more exact, they extracted and accelerated before GG, but BTR consider the beamlet start at GG plane. A beamlet is a current cone emitted from a single aperture (GG slots can be modeled as a row of close apertures) and characterized by normal angular dispersion (divergence, or half-width of 1/e decay of amplitude) around the beamlet axis. If the NBI scheme is based on positive ion source (PIS), the source beam has different angular width in horizontal and vertical planes, due to horizontally elongated multi-slot structure of acceleration grids. Typical horizontal and vertical widths for PIS are 7-10 and 15-20 mrad respectively. The beamlet angular structure is more complicated and less defined [7] for the injectors based on negative ion sources (NIS). Experiments show, the accelerated D− beamlets consist of 2 fractions: core part (85%) and ‘halo’ (with ≈15% of current) with a divergence much higher (~30 mrad) than the beamlet core part. The characteristics of the beam from the negative ion source are still to be confirmed, therefore for design purposes the assumptions are made based on existing experimental data. For example, for ITER beamlines design for beam duration 1 h, three values of beamlet divergence are investigated, i.e., 3, 5 or 7 mrad with 15% of the power in each beamlet carried by a halo fraction with a divergence of 30 mrad.
The beamlets start positions are arranged in clusters (or BS segments, or groups) according to GG structure shown in Figure 3 (FNS-ST NBI), while the source particles distribution in space and angle are illustrated in Figure 4a (FNS-ST NBI). Standard beamlet optics is a combination of beam source groups’ steering at the injected window (NB port) center, and individual beamlet axes focusing within each group in horizontal plane — for optimal beam propagation through vertically elongated NBI channels. Finally, the entire beam envelope is inclined or tilted (as in ITER HNB, [7]) — to hit the specific tangential point in plasma and to switch between on-axis and off-axis injection with relation to the main plasma axis. For NBI design purposes it is assumed that due to the beam focusing errors the beamlets can be deviated from their optimum axes in horizontal and vertical planes, or ‘misaligned’; e.g., ITER design assumes the misfocusing tolerances ±2 mrad in horizontal and ±4 mrad in vertical plane respectively.
The example of NBI geometry and the source beam, as they appear on BTR screen, are shown in Figure 5.

3. BTR basic features and GUI

3.1. BTR general info

BTR code name is about ‘Beam Transmission (or sometimes ‘Beam Transport’) with Re-ionization’. To be short, BTR calculates the beam evolution and losses along beamlines, with account of electromagnetic field environment and the beam interactions with gas or plasma background. The beamline 3D geometry, the beam structure and focusing, and the environment form BTR input. The main BTR output consists of the 2D arrays of power density accepted by the beamline solid components and/or passed through ‘virtual’ planes (also called power load footprints). The footprints can be shown and saved as color images or in text data.
BTR simulations cover practically all known NBI designs, either simple or complicated source beam geometry. “Beamlet-based” beam structure is a large set of elementary cone-shaped beams. Channel-based beamline geometry is formed by a large set of rectangular surfaces, which can be user-defined from the direct input tool - or imported all together or partially from CAD software (as text format). At the end of each BTR single-run (from few seconds to few hours depending on the user’s claims), the heat load images and the beam power footprints for any requested surface (solid or virtual) are available, and the beam losses from various loss-channels are reported.
The Multi-Run version (BTR-5, 2020) allows automatic scenario-based restart of calculations and provides additionally Summary report after the whole session; this feature considerably reduces user efforts and time spent on matching the beamline optimization and fine-tuning all the components. The later versions of the code are also used for the optimization of beam capture in plasma. All numerical methods used by BTR are the most simple and straightforward, they are easily verified analytically; we call them briefly ‘lite neutral beam’, LNB. The important implication of LNB and BTR code availability is that verification of more sophisticated NBI models can be made by means of BTR, e.g., BTR was used for cross-checking with SAMANTHA code [18] which applies Monte-Carlo beam model.

3.2. BTR User Interface

BTR screen which appears before the user upon running BTR.exe is shown in Figure 5. The screen is divided to four major windows (by view splitting control):
  • “Config plot”, main view with NBI geometry and beam layout;
  • “Green panel” tool - BTR interactive input data processor;
  • “Loads Summary” / “Map” view switch;
  • “Running Status” / “Profiles” view switch.
The “Green panel” is the main interface tool of BTR GUI used for interactive control of input data and its diagnostics. The user directly modifies data fields in the Green panel, so that the input parameters container (configuration list or “Config”) is updated along with all the graphical representation images. The Config dataset is stored and can be next reloaded as input either for review or BTR simulations.
BTR screen is supplied with the interface tool “Main menu” on the top. The main menu commands serve the following capabilities for input/output (IO):
-
Update/Save/Import data;
-
Call dialogs for input by categories (i.e., alternative direct input way);
-
Define specific ‘Tasks’ and output options;
-
Add/Edit gas or field input profiles;
-
Select/manage visualization categories, and many other.
Apart from the main menu, there is a pop-up menu interface tool, invoked by right mouse click (not shown). It collects all the most handy and frequently used commands, including selection, zooming, switching between views, and many other.
Specific input dialogs which provide more ‘intuitive’ data input are shown in Figure 6. Rather than reviewing all the parameters in the long Green panel list (~200 lines) the user can do the same through the dialogs, where the data fields are represented by category. The dialogs are more convenient tool to set the parameters and options for calculations including the source particle species, beamlet splitting and tracking steps, particle species following choices, etc. In fact, almost all BTR I/O commands are replicated so that it is not essential for the user to keep in mind the “best” way to make anything happen: the major controls are found elsewhere despite the user’s style and behavior.
The resultant power footprints (2D color-maps) and 1D-profiles are represented by image plots, the examples of power maps are shown in Figure 7 (and through the next sections). They become available on the beam stop or pause when the user clicks on the surface of interest which can be solid or virtual (transparent). The images are interactive too: the mouse drag over map shows the local value and point-click labels the clicked point.

4. BTR models and tasks

4.1. Beam shape and the injected power

The shape of the beam and its internal structure are determined by the beamlets focusing provided by the ion-optical system (IOS) and by the beamlets internal angular dispersion. The ion beam, initially formed by plasma emitter and accelerated in a multi-grid multi-aperture IOS, consists of a large amount of beamlets (up to several hundreds) in accordance with the apertures setup across the extraction and acceleration electrodes. For example, in the beamline design for FNS-ST, which implements positive ions neutralization approach, the beam source is organized as a vertical column of five rectangular aperture clusters, with 80 beamlets per group. To ensure the efficient beam propagation to tokamak without overheating the beamline elements, the beamlets focusing is complex enough: the beamlets within the column are aimed horizontally at NBI port center-point, while in a vertical plane, the beamlets axes within each cluster are parallel to the main cluster axis with the main axes focus at NBI port plane in tokamak – this method actually works for the entire beam optimum transmission. The beamlet focusing scheme for FNS injector is shown in Figure 3.
The ion current within each beamlet, as experiments show, is well described to have a normal (Gaussian) distribution along the polar angle, and the sum of Gaussian fractions fits the beam angular shape in all NBI schemes. For example, the positive ion beam in FNS-ST injector is well matched by a 2-dimensional Gaussian profile (with different standard deviations along horizontal and vertical axes), while a negative ion beam, combined by two major angular fractions – ‘core’ and ‘halo’ parts - can be reproduced by a sum of 1-dimensional profiles versus polar angle from the beamlet axis:
j θ = 1 − H π ∆ c 2 e − θ 2 ∆ c 2 + H π ∆ h 2 e − θ 2 ∆ h 2 ,
where θ – is a polar angle from the beamlet axis, H – is so called halo fraction, Δc and Δh – the angular width of core и halo. Note: the Gaussian width in BTR notation is not the same as standard deviation σ for normal distribution.
The positive ion beams (like in FNS-ST NBI) are typically supposed to carry a single core fraction without halo (H = 0) with the core angular width ~15 mrad, which results in the effective beamlet footprint width at the NBI port plane about ~30 cm. The power delivered by the neutral beam to tokamak plasma roughly depends on the initial beam divergence and the beamline geometry transmission, but the latter property (transmission factor) is sensitive not only to the shape of the channels for beam passage, but also to the beam alignment accuracy and the risks of its deviation from nominal value (misalignment, focusing errors). The misfocusing tolerances are generally few mrad (2-6 mrad), depending on the beam divergence and NBI port dimensions. For NBI in FNS-ST, with the beamlets perfect alignment towards the center-point of the 30×60 cm2 NBI window, the calculated beam transmission efficiency is ~76%, with the injected power 3.5 MW. If the beam focusing has small errors (misaligned) about ±4 mrad in horizontal and ±6 mrad in vertical plane, the injected power to plasma reduces down to 3.3 MW (with the beam transmission ~71%), the effect is illustrated in Figure 8ab.
Since a reduced size of the injection port is highly preferred, the possibility to reduce it makes one of the high-priority issues of NBI geometry optimization. For this study the NBI port size is reduced down to the acceptable level of the beam power, so the nominal size for FNS-ST compact tokamak (with R/a = 0.5/0.3 m) with account of the chosen scheme and the beam source is 30×60 cm2, which is comparable with the tokamak camera size. If the NB port is reduced down to 20×40 cm2, the injected power drops from 3.5 MW to ~2.3 MW, or by ~30% from nominal NB power. The beam misalignment additionally reduces the NB power (down to ~2 MW). If we take into account the neutralization efficiency (~50% for the beam energy adopted), the overall NBI performance would be about 25%, so the NBI total performance is quite low. Besides, for the reduced port size design, the beam power intercepted by the beamline components becomes too high and the entire NBI design revision is needed to address the overheating issue.
One more conventional task for BTR is the investigation of the injector performance response to operation conditions change, including the impact of the beam misfocusing and presence of residual magnetic field within the neutralization region on the beamline geometrical transmission. The results of this sensitivity study form a base for the operation requirements for the beamline design; for ITER heating and diagnostic neutral beams the required magnetic field limits and the beam misfocusing range evaluated by BTR can be found in [3].
The beam particles distributions (phase diagrams) in a 4-dimensional space across the beam axis (X, Y, ϴx, and ϴy) are shown in Figures 4ab - for the IOS exit plane and for the NBI port plane (window size 30×60 cm2). The main feature which distinguishes BTR approach from the existing NBI models is that BTR calculates the injected beam statistics not only with a detailed account of the source beamlets structure, but also including the effects of background conditions (fields and gas); as a result BTR generally provides a complete and more ‘realistic’ beam losses and transmission through the injector as compared to the NBI models which typically ignore all these minor effects. However, the combination of these effects tends to be far from negligible, so during the experiments the need of a more realistic simulation becomes more evident [30,31].
The beam statistics at the tokamak NB port plane (Figure 4b) can be naturally applied to trace the fast ions ensemble in plasma until their thermalization, i.e., slow-down to thermal velocities [34]. However this task is beyond BTR scope today, although it can be implemented in future BTR versions. Fast and simple BTR methods can be applied to efficient simulation of the beam-driven effects in plasma target, among which is the beam current drive, the beam-plasma fusion rates, plasma heating and rotation in tokamak.

4.2. Beam neutralization

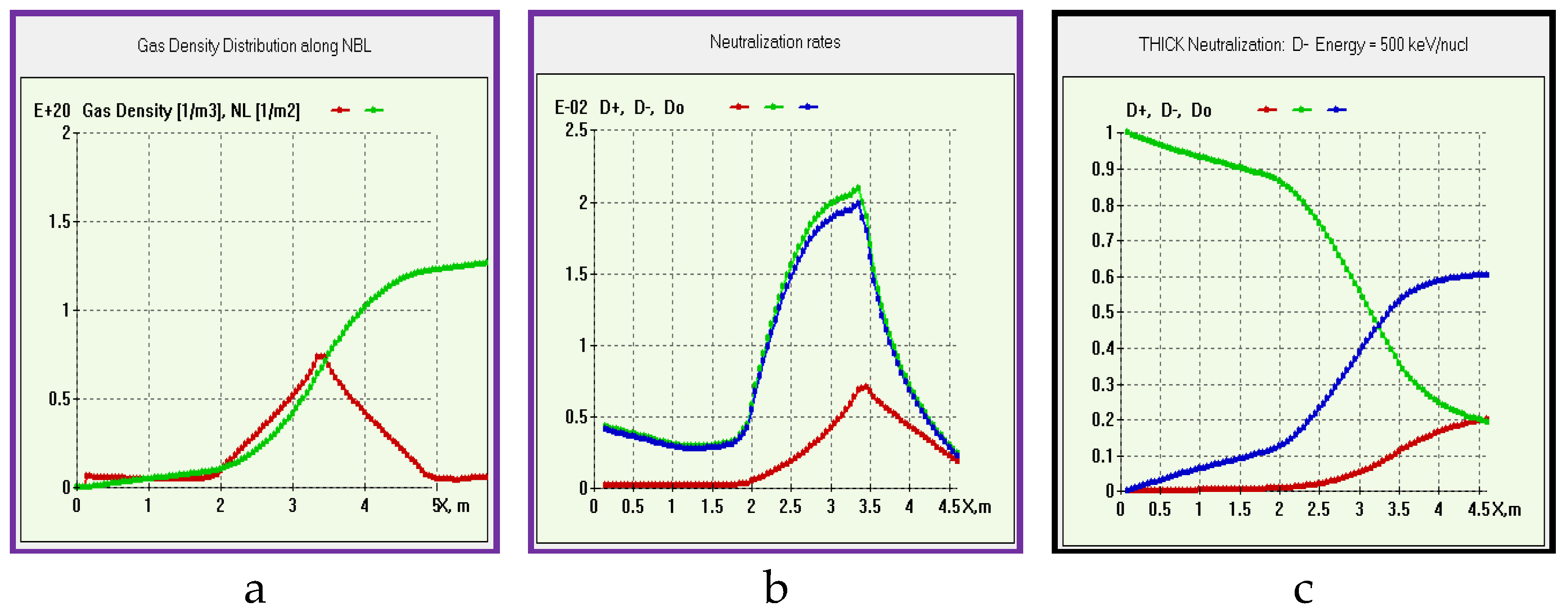
The source ions, which are either negative or positive, are converted to atoms via collisions with D2-gas in the neutralizer with relevant atomic cross-sections: 4 sigmas are involved for negative ions: σ–10 (electron stripping), σ–11 (double electron stripping), σ10 (positive ion neutralization), and σ01 (atom ionization). A positive ion neutralization process is defined by the ratio σ10 /σ01. There are two options (models) available in BTR for beam neutralization – ‘thick’ and ‘thin’. Thin model is less accurate: the total gas volume is “pushed” to a thin layer at the neutralizer exit, causing an overestimated beam deflection at the device output. However, it is by many orders of magnitude faster and finds much wider use, than thick model, which takes the real gas target distribution and produces a reduced beam deflection, and in fact to a wider test-particles divergence. The thick model (Figure 9abc) solves balance equations for beam species:
d Г − d x = − Г − ( σ − 10 + σ − 11 ) n ;
d Г 0 d x = Г - σ − 10 n + Г + σ 10 n − Г 0 σ 01 n ;
d Г + d x = Г - σ − 11 n + Г 0 σ 01 n − Г + σ 10 n .
Here Гk is the k-th species flux, n is background gas density.
Preprints 84004 g010
Figure 9. Gas target and beam fractions in the neutralizer (ITER NBI): (a) gas local density and thickness; (b) species source/sink rates; (c) species integral output.
Figure 9. Gas target and beam fractions in the neutralizer (ITER NBI): (a) gas local density and thickness; (b) species source/sink rates; (c) species integral output.
Preprints 84004 g010

4.3. Residuals deflection and dumping

The residual ions fraction, which is formed by the unwanted charged part of the beam after neutralization should be removed from the neutral beam path and accepted by a special appropriately cooled collecting device, so called residual ion dump (RID). The ions are deflected either magnetically (MRID) or electrostatically (ERID). One of BTR major tasks is to ensure the electro-magnetic field in RID deflects all the charged fractions of the beam and these are next fully intercepted by the dumping surfaces. This task requires an accurate beam statistical representation (~103-104 ions per each single BS beamlet, or 106-107 total particles) and each ion track calculation guided by the Lorenz force until the ion’s stop or escape from calculation area. BTR helps to choose the optimum configuration and magnitude of the field by scanning several NBI parameters across the nominal operation range; typically the following values are to be scanned: neutralization output, beam tilting and focusing, beam initial divergence, magnetic field profile in the neutralization region. When the optimal deflecting field is found, the expected power density maps are calculated for RID thermal cooling circuit design.
Figure 10 shows the example of the ion trajectories and power density map at one side of ERID panel for DEMO-FNS injector. The final PD footprint is formed by four vertical beam clusters (BS rectangular groups of beamlets), the clusters are focused vertically at the NBI port center, so that three PD peaks can be observed on the vertical profile shown under the map plot.

4.4. Re-ionisation on gas

The model of the neutral beam re-ionization along duct regions works quite similar to thick neutralization model: it uses the gas density distribution downstream the neutralizer and the relevant ionization cross-section σ01 (atom ionization) and σ10 (ion neutralization) both depending on the atom specific energy. In BTR each test neutral particle (‘super-atom’) produces as many secondary ions as needed given by the step of re-ionization, and the secondary positive ions are next traced until their interception by a solid surface or escape from the area, this is similar to residual ions tracking in RID area. The governing system for the process is
d Г 0 d x = Г + ∗ σ 01 ∗ n − Г − ∗ σ 10 ∗ n d Г + d x = − Г + ∗ σ 01 ∗ n + Г − ∗ σ 10 ∗ n
The secondary ions are deflected by stray electro-magnetic fields. The neutral beam re-ionization create additional NB loss channel not associated with the beam or beamline geometry; it is a result of the beam interactions with residual gas in the beamline ducts and channels. The gas is always present (not fully pumped) after neutralization region: it flows from the neutralizer and from the plasma device itself (in our case from tokamak), while the gas pumping is difficult especially along the ducts region. The main specifics of the duct region are: the stray magnetic field is not shielded, and its magnitude is many orders higher than in the RID shielded area; the gas flow from tokamak cannot be efficiently pumped, therefore the ionization rates can grow high and can produce high fluxes (hot-points) of ion power if focused in the field. Thus the essential task for the beamline ducts design is to define the expected peak PD at the duct elements and to set the heat removal requirements, given a reduced space available for cooling.
Preprints 84004 g012
Figure 11. Re-ionized particles (red) downstream the neutralizer (DEMO-FNS).
Figure 11. Re-ionized particles (red) downstream the neutralizer (DEMO-FNS).
Preprints 84004 g012

4.5. Penetration to tokamak plasma

BTR has proved to be highly effective not only for NBI beamlines design and performance study, but also for beam effects investigation in plasma and tokamak operation control. BTR most detailed beam model allows much more flexibility in reproducing the experimental data on the beam shapes and with running speed by orders higher than other known NBI models, especially those employing Monte-Carlo methods [35] BTR models were naturally extended to the beam particle tracing in plasma volume, where the beam is ionized and the resultant fast ions are captured by the magnetic field which confines the target plasma.
The neutral beam ionization in plasma is traditionally called ‘beam stopping’ (because the neutral beam intensity gradually goes down, or decays), while the following fast ions circulation and thermalization in plasma is referred as fast ion ‘slow-down’.
The atom ionization in plasma and fast ion source are obtained under Janev multi-step ionization model [36] which uses an effective stopping cross-section σs for fast atom ionization in plasma. The effective cross-section comprises all the main channels of beam ionization on plasma species including the cascade (multi-step) processes of atom ionization. Thus the neutral beam intensity (I) decay along the trajectory is written as:
d I d x = − n e σ s I ,
Where ne — the plasma target density; σs — the effective beam stopping cross-section due to ionization represented as:
σ s =   < σ i e | v − V b | > / V b +   n p n e ( σ i p +   σ cx ) +   n z n e σ z   ≈ < σ i e v > / V b +   σ i p +   σ cx +   n z n e σ i z .
Here σie, σip, σiz — are ionization cross sections of atoms in collisions with electrons, protons, and impurities of charge Z, respectively; σcx is the charge exchange cross section on hydrogen ions, brackets mean averaging over the Maxwell distribution of electron velocities. The plots showing the σs dependence on the atom energy and plasma density are shown in Figure 12abc. When the neutral beam energy is less than Eb ~ 140 keV, the NB is produced more efficiently with positive ion beam sources, so after the source ion neutralization and dissociation the beam consists of three energy fractions. From Figure 12b, it can be seen that for the lowest energy fraction (Е1/3) the stopping cross-section is up to 3 times higher than σs value for the full (maximum) energy fraction Еfull; in fact this results in more intense ionization of low-energy beam fractions (Е1/2 and Е1/3) at plasma periphery reducing the total NBI efficiency output in the plasma.
The detailed beam statistics (up to 1012 test particles) from BTR calculation produces the most accurate fast ion source distribution in space and angle, which makes an essential data for fast ion numerical studies and experimental plasma scenario control. The examples of beam ionization distributions in DEMO-FNS plasma are shown in Figure 13. The fast ion source imprints are shown in two orthogonal planes - vertical and horizontal - along the neutral beam axis direction and obtained with the beam particle statistics ~106 test-atoms, which is much smaller than BTR regular capacity. The decay of each test atom and the produced fast ion density is calculated with (6).
The comparative analysis of the beam imprints for various beam shapes has proved the beam geometry (‘shaping effect’) is essential factor for the beam deposition in plasma and for the resulting beam-driven effects. The effect is illustrated in Figure 13, where two beam geometries produce different imprints in DEMO-FNS tokamak plasma: rectangular box-shaped beam (a bunch of parallel rays) and Gaussian bell-shaped beam of 1280 beamlets with focusing and internal beamlet divergence.

4.6. Shine-through power at tokamak chamber wall

Shine-through beam power losses and the associated thermal flux onto the opposite plasma chamber wall which faces the direct power load (so-called first wall) can potentially damage the chamber and hence justify a hard limit for the choice of injected beam energy. At the same time the beam-driven current drive efficiency and nuclear fusion enhancement grow fast with the NBI energy, since the fast ions release and their deposition within plasma depend on the neutral beam penetration. The NB penetration to the hot inner core, which is most favorable for current drive and fusion, can be achieved when the average free path of fast atom before the ionization is comparable with the half-way flight distance in plasma – for toroidal tokamak geometry the flight distance is roughly the chord length along the beam axis. On the other hand, that deep beam penetration to plasma implicates a higher possibility for neutral particles to ‘shine through’ the plasma with no ionization, and thus to burn the chamber first wall.
For FNS-ST compact size tokamak (R = 0.5 m), the beam energy range 100 - 150 keV is not optimum from the point of current drive and neutron generation, but this energy level means safer tokamak operation if compared to more efficient NB energy above 200 keV. Maximum NB efficiency in tokamak is achieved normally when the energy meets the following condition: Eb/Ec = 2 - 5 [5]. For example, NB optimum energy for plasma temperature about Te = 5 keV correspond to the values of 200 - 500 keV, but the latter would be unacceptable from the point of the direct shine-through power faced by FNS-ST device first wall.
The beam ionization footprints in FNS-ST plasma which are similar to the plots in Figure 13 (for DEMO-FNS) prove the NB capture to be strongly non-uniform over the beam normal cross section. This results in high degree of shine-through power asymmetry on the tokamak first wall; the effect is especially pronounced for small aspect ratio devices and when the beam width is comparable with plasma minor radius (this is the case in FNS-ST). The resulting shine-through power density profiles on FNS-ST first wall are shown in Figure 14 for two operation cases: (a) for nominal beam alignment (ideal focus) and (b) for beam misalignment (technological error focusing) 4/-6 mrad. From Figure 14b, one can expect very small alignment errors can lead to higher direct power losses and heating within the injector beamline and, besides, produce potentially more danger for the first wall due to higher peak in shine-through power density (~1.5 times).
The beam energy and plasma target density range are restricted not only by the risk of the chamber first wall damage, but also by the physical parameters of equilibrium and stability. Within the frame of BTR simulations, the beam driven effects are considered under steady-state plasma operation, as the beam impact on the target plasma stability is beyond the basic scope of BTR applications.

5. BTR verification

Computational model verification is typically used to determine whether the verified model accurately represents the math behind the physical model. Verification can include nonexperimental testing routines such as comparison with analytic solutions, and quite often the comparisons between codes (which is called code ‘benchmarking’). The difference between model verification from validation can be expressed briefly as follows: verification solutions are already known, so they can provide a high precision standard for the solution obtained with the model, and validation is a comparison of the model with the reality object studied, this can be performed through experiment.
Software verification has to ensure that changes to the software do not invalidate a previous verification and validation (V&V) procedures; it is needed when configuration changes occur. The solution verification should ensure that the user has appropriately used the software; the solution to each problem must be verified prior to analysis. These two aspects of verification are essential parts of the entire V&V process: a solution cannot be considered true (valid) unless both the software and simulation have been confirmed.
Code verification checks the underlying code functions correctly and as intended, it generally includes the numerical verification of the solver and software quality assurance (SQA). BTR numerical verification procedure is intended to show that the underlying mathematical models are implemented appropriately. This is achieved through designing the tasks test-cases for which BTR models’ behavior and end solution are explicitly known and can be compared directly to the obtained results. The second part of BTR verification (‘input verification’) provides the information on the model sensitivity to the input parameters and the major restrictions if any, so that the users can choose the model inputs appropriately and expect the output to converge sufficiently to the desired (‘true’) solution. The input verification can be accomplished through a formal check-and-review routine.
BTR verification is performed for each individual analysis problem. The basic numerical tests include 13 ‘physical’ test-cases which allow one to compare the results with known solution by checking the particle dynamics, the beam shape in phase space, beam species transformations, and power/particles conservation and balance, as follows:
  • Neutral particle tracks
  • Charged particle motion in magnetic field
  • Charged particle motion in electric field
  • Charged particle motion in combined field
  • Beamlet current simplified profile (2D Gaussian distribution)
  • Beamlet current complex profile (core and halo fractions)
  • Positive beam source ion neutralization (H+/D+)
  • Negative beam source ion neutralization (H-/D-)
  • Neutral particles ionization on gas target (beam ducts volume)
  • Neutral particles ionization in plasma (tokamak volume)
  • Neutral beam power/particle balance after the neutralizer
  • Accelerated source beam power/particle balance without re-ionization losses
  • Accelerated source beam power/particle full balance (all processes included)
BTR input verification procedures include 5 sensitivity studies, which evaluate the solution response to the following input parameters:
  • Cut-off current input parameter effect
  • Magnetic field magnitude effect
  • Angular misfocusing effects
  • Atomic cross-sections and target density effects
  • The effects of the geometry representation accuracy, meshing and time steps, etc.
Even though code models are never 100% validated, they may be valid for a particular application problems. While the 1st group of BTR verification testing depends on the code developer, the 2nd group of tests is important for BTR valid usage, as code the final application validity always depends on the user. Hence, BTR user has to make a conclusion on whether the code is valid for a given application and how to tune the input parameters to obtain the desired accuracy. In theory, BTR code could be fully validated for every beam tracing application, but it still relies on the user to provide the appropriate inputs, mesh, and steps for the problem. If this is not done, even a valid code may produce inaccurate results. The solution must be verified for any application. BTR V&V Manual, which will be included to ‘BTR pack’ in Oct 2023, simply demonstrates the ability of the code to solve BTR application problems with acceptable accuracy.

6. BTR applications

6.1. Beamline transmission and power losses

BTR has been actively used for NBI design and engineering studies for ITER injectors [2,3]. The results of BTR analysis on beam losses and transmission performed for Heating neutral beam injector (HNB) and for the Diagnostic one (DNB) can be found in the ITER Design Description Document [DDD5.3] issued in 2001.
The results of transmission losses analysis performed for similar NBI design (for DEMO-FNS) are illustrated in Figure 15, Figure 16 and Figure 17.
A highly detailed analysis of the power loads on the Front End Components (FEC) and duct modules in ITER HNB and DNB injectors performed with BTR can be found in [8]. The analysis was carried out for various operation scenarios of ITER machine and with scanning the injector parameters which include NB energy, current and hydrogen isotope. The gas profile and the magnetic field distribution varied through the scenarios, the distributions are generally obtained from other calculations and used as input for BTR. The worst case power loads and power densities for each surface were used to study their thermomechanical behavior and manufacturing feasibility.
The importance of the obtained results is and BTR value as a tool is summarized in [8] conclusion. “BTR was successfully used to optimize the design of the front end components, the duct liner and the blanket modules for the HNB and the DNB beam lines in ITER during different phases of ITER operation (HH, HHe, DD and DT). Various scenarios of beamlet divergences, horizontal and vertical misalignments as per ITER definitions and the magnetic field variations due to changing tokamak operation scenarios have been considered in detail in these calculations. The maximum estimated total re-ionization losses are ~8% for the HNB beam line and ~20% for the DNB beam line. All the cases studied above have been summarized to obtain the maximum power loading the power density on each surface of the various components evaluated in these calculations and have formed the basis of the final design of these components. The process has been iteratively repeated till a design compatible with manufacturing feasibilities and safety requirements has been reached. Thermo-mechanical assessments are now completed and the components are in their final design stage.

6.2. Neutral injection port optimization

The injection port size issue is to be addressed almost in any NBI design. Typically a tokamak has a reduced space available for tangential injection, so that the injected beam envelope need to be minimized at the camera entrance. The source beam internal divergence and the beamline transmission reduce the bounds on the port minimum size, and small deviations from nominal beam operation reduce the actual beamline transmission. BTR is used for the injected power sensitivity analysis while the NB port size is iterated. Figure 18 illustrates the examples for DEMO-FNS tokamak. The effects of beam misfocusing and magnetic field, even within the nominal tolerance, can reduce the injected power (Pinj) by 20-30%. When the NB window width is reduced by 5 cm only, the power losses along the beam transmission become inacceptable.

6.3. Neutral beam shine-through

In addition to NBI study and optimization, BTR can be used for the injected beam efficiency optimization in plasma as well as for the evaluation of fast ions phenomena in tokamak (or any plasma confinement device). The scenarios with NBI usually feature a high contribution of fast ion population to the entire current drive, plasma rotation, nuclear fusion rates, etc. The detailed beam statistics in the NBI port plane (which takes a few seconds BTR run) can be efficiently applied to further analysis of the fast ion behavior and the entire plasma operation.
For example, when BTR is applied to simulate beam stopping and ionization in tokamak plasma volume, the user gets the 3D beam ionized power deposition footprint, as shown in Figure 13 – for DEMO-FNS. The beam deposition in plasma depends on the plasma density 3D distribution and the beam ionization cross-section (as shown in paragraph 4.5). The plasma density is normally defined along minor radius (or along the poloidal magnetic flux coordinate), so the mapping procedure for toroidal coordinates onto the beam track is used for each beam ray.
The detailed beam statistics (up to 1012 test particles) is more than sufficient for the most accurate fast ion distributions both in space and angle, which is essential for beam-driven plasma scenarios studies. The beam imprints shown in Figure 13 are calculated in the vertical and horizontal planes along the beam axis direction with the beam statistics reduced to ~106 test-atoms. The decay of each test atom is calculated with expression (6). The comparative analysis of the beam imprints has proved the shape effect to be essential for the beam deposition and resulting beam-driven quantities. The effect is clearly observed in Figure 12, where two characteristic beam geometries are compared: a rectangular beam shape (a bunch of parallel rays) and a gaussian beam shape of 1280 beamlets with realistic focusing and 7 mrad divergence, with 15% halo (30 mrad).
Finally, BTR is used to calculate the beam shine-through losses and to obtain the detailed power images at the first wall, see Figure 19. These results are important for primary optimization of the injected beam parameters and targeting geometry, as well as for plasma density range required for the effective beam capture and tokamak safe operation.

6.4. Benchmark of different numerical tools for NBI simulation

BTR code can be naturally used for cross-verification of results derived by different beam tracking software tools. One of the best examples here can be found in [18]. SAMANTHA software is recently developed for NBI design, and it mainly addresses the additional phenomena in NB lines relevant to secondary particles. While the numerical methods differ between the two codes, some results can be compared effectively. The comparison of power profiles was made for RID power density profiles, as in BTR these profiles are obtained a few seconds. Good agreement between the two codes results has shown SAMANTHA code is a reliable tool for NBI modelling, especially for the secondary particles studies which are beyond the conventional BTR scope.
Apart from the described BTR applications, the examples of BTR code usage can be found in [11,12,13,14,15,16,17,18,19,20,21]. Of course, the list of BTR references is fractional, far from being complete, as most of the papers, especially published before 2019, are citing BTR webpage [1] as the only reference to the code, or even the older page which is not active anymore [37].

7. Conclusions and outlook

BTR has a long story of development. It was conceived in 1995 and implemented in Turbo Pascal. BTR code was ‘Born-To-Run’ (i.e., ‘BTR’) - issued for open access - in 2005 being rewritten in MS Visual C++. It has got five versions so far with the last BTR-5 released in 2020. BTR is an efficient numerical tool for NBI engineers and physicists, which was developed by a NBI physicist. BTR allows the user to simulate the entire NBI beamline with help of a single software tool (not a suit of codes), rather than using different packages or building software workflows: a good example of this modelling approach can be found in [38].
BTR is created to be user-friendly and fully interactive, so its popularity despite lots of other codes developed for similar purposes can be explained mainly by the opportunity for user to quick start and then learn by touching everything - via pushing all the buttons on the screen. BTR is supplied with a variety of numerical and graphical tools for NBI accurate studies and geometry optimization. BTR is parallel, and if compared to other beam tracing models it runs faster by several orders. The code goes with a Windows-like GUI; the latter allows BTR to be applied for user training purposes like NBI flight-simulator.
BTR is able to trace up to 1010 beam test-particles in a few hours maximum on really humble old Windows systems; although its power is more evident in multi-thread execution on at least 4-8 cores. BTR numerical models are light and flexible, the calculation results are consistent and stable; the methods can be verified analytically. BTR still evolves; full support is available to BTR users. The information on BTR upgrades and code Manual can be found online [1]. Beginning from 2024, BTR Verification Manual will become also available online.

Acknowledgments

BTR was developed by author’s enthusiasm, later occasionally supported by ITER, and eventually became useful due to BTR users’ enormous patience and a strong will to make it better. In fact, waiting for the new code versions to come, the updates permanent testing and debugging required lots of time and efforts from them. Thus, all BTR users should be considered as true BTR co-authors.

References

  1. BTR code for neutral beam design. Available online: https://sites.google.com/view/btr-code/home (accessed on 08.08.2022).
  2. Hemsworth R. et al. Status of the ITER heating neutral beam system. Nucl. Fusion 49 045006 2009. [CrossRef]
  3. ITER Final Design Report, NB H&CD, DDD 5.3, 2001, Vienna, Austria, IAEA.
  4. Kuteev, B.V.; Goncharov, P.R.; Sergeev, V.Y.; Khripunov, V.I. Intense fusion neutron sources. Plasma Phys. Rep. 2010, 36, 281–317. [CrossRef]
  5. Kuteev, B.V.; Goncharov, P.R. Fusion–Fission Hybrid Systems: Yesterday, Today, and Tomorrow. Fusion Sci. Technol. 2020, 76, 836–847. [CrossRef]
  6. Kuteev B.V. et al. Status of DEMO-FNS development. — Nucl. Fusion, 2017, vol. 57, № 7, p. 076039. [CrossRef]
  7. Hemsworth R.S. et al. Overview of the design of the ITER heating neutral beam injectors. New J. Phys., 2017, vol. 19, p. 025005. [CrossRef]
  8. Singh M.J. et al. Power loads on the front end components and the duct of the heating and diagnostic neutral beam lines at ITER. AIP Conf. Proc., 2015, vol. 1655(1), p. 050011. [CrossRef]
  9. Dlougach E.D. BTR code for NBI Design and Optimization. AIP Conf. Proc., 2021, v. 2373, p.080004. [CrossRef]
  10. Dlougach E.D.; Veltri P. BTR code recent modifications for multi-run operation. AIP Conf. Proc., 2021, v. 2373, p.080010. [CrossRef]
  11. Oh B.H., Dlougach E.D. Beam transport code for the KSTAR NB heating system, 20th IEEE/NPSS Symposium on Fusion Engineering, SOFE-03. San Diego, CA, 2003. 474-477. [CrossRef]
  12. M. Bandyopadhyay, M.J. Singh, C. Rotti, A.Chakraborty, R.S. Hemsworth, B. Schunke. Beamline optimization for 100-keV diagnostic neutral beam injector for ITER, IEEE transactions on plasma science, vol. 38, no. 3, 2010. [CrossRef]
  13. E. Surrey, A. Holmes, R. McAdams, D. King Operation of the ITER Electrostatic Residual Ion Dump with a Perturbed Field, 2010, Journal of Fusion Energy 29(5): 486-498. [CrossRef]
  14. Doo-Hee Chang et al., Performance of 300 s-beam extraction in the KSTAR neutral beam injector, Current Applied Physics Volume 12, Issue 4, 2012, 1217-1222. [CrossRef]
  15. P. Veltri, P. Agostinetti, M.D. Palma, E. Sartori, G. Serianni. Evaluation of power loads on MITICA beamline components due to direct beam interception and electron backscattering, Fusion Engineering and Design 88 (2013) 1011– 1014. [CrossRef]
  16. E. Sartori, P. Veltri, E.Dlougach, R. Hemsworth, G. Serianni, M. Singh Benchmark of numerical tools simulating beam propagation and secondary particles in ITER NBI, NIBS-2014 AIP Conference Proceedings 1655, 050006 (2015). [CrossRef]
  17. R. McAdams, Beyond ITER: Neutral beams for a demonstration fusion reactor (DEMO) Review of Scientific Instruments 85, 02B319 (2014). [CrossRef]
  18. E. Sartori, P. Veltri, G. Serianni, M.D. Palma, G. Chitarin, P. Sonato. Modeling of Beam Transport, Secondary Emission and Interactions With Beam-Line Components in the ITER Neutral Beam Injector, IEEE Transactions On Plasma Science, Vol. 42, No. 3, March 2014. [CrossRef]
  19. R. McAdams, A.J.T. Holmes, D.B. King, E. Surrey, I. Turner, J. Zacks. Negative ion research at the Culham Centre for Fusion Energy (CCFE) © EURATOM/CCFE New Journal of Physics, Volume 18, December 2016. [CrossRef]
  20. Mauro Dalla Palma, Roberto Pasqualotto, Emanuele Sartori, Paolo Tinti. The beamline for the ITER heating neutral beam injectors: A case study for development and procurement of high heat flux components, Fusion Engineering and Design 171 (2021) 112559. [CrossRef]
  21. Ananyev S.S., Dlougach E.D., Krylov A.I., Panasenkov A.A., Kuteev B.V. Modeling and optimization of the neutral beam line for plasma heating and current drive for the DEMO-FNS fusion neutron source project. Fus. Eng. and Design 161, 2020, 112064. [CrossRef]
  22. https://winworldpc.com/product/turbo-pascal/7x.
  23. Kuteev B.V. et al. Steady state operation in compact tokamaks with copper coils. Nucl. Fusion 51, 2011, 073013. [CrossRef]
  24. Chernyshev, F.V. et al. Study of fast-ion losses in experiments on neutral beam injection on the Globus-M spherical tokamak, Plasma Phys. Rep. Vol. 37 No. 7, 2011. [CrossRef]
  25. Heidbrink W.W., van Zeeland M.A. et al. Initial measurements of the DIII-D off-axis neutral beams. Nucl. Fusion, 2012, vol. 52, p. 094005. [CrossRef]
  26. R.S. Hemsworth, Long pulse neutral beam injection. Nucl. Fusion 43, 2003, p. 851–861. [CrossRef]
  27. C. Hopf, G. Starnella, N. den Harder, U. Fantz. Neutral beam injection for fusion reactors: Technological constraints versus functional requirements. Nucl. Fusion 61, 2021, 106032. [CrossRef]
  28. P.P. Khvostenko et al. Tokamak T-15MD—Two years before the physical start-up. Fus. Eng. and Design. Vol. 146(3), 2019, 1108-1112. [CrossRef]
  29. Dlougach, E.D.; Panasenkov, A.; Kuteev, B.; Serikov, A. Neutral beam coupling with plasma in a compact fusion neutron source. Appl. Sci. 2022, 12, 8404. [CrossRef]
  30. A.N. Karpushov et al. Upgrade of the neutral beam heating system on the TCV tokamak – second high energy neutral beam. Fus. Eng. and Design 187, 2023, 113384. [CrossRef]
  31. F. Jaulmes et al. Numerical modelling for beam duct heat loads calculations and application to the new 1 MW neutral beam injector in the COMPASS tokamak. Plasma Phys. Control. Fusion 64, 2022, 125001. [CrossRef]
  32. A.A. Ivanov, V.I. Davydenko, Yu.I. Belchenko. Negative ion and neutral beams injectors at the Budker Institute of nuclear physics. AIP Conference Proceedings 2052, 030003, 2018. [CrossRef]
  33. Oikawa T., Park J.M. et al. Benchmarking of neutral beam current drive codes as a basis for the integrated modeling for ITER. In: Proc. of the 22nd International Conference on Fusion Energy. Geneva, Switzerland, 2008 (Vienna, IAEA, 2008), IT/P6-5.
  34. Wesson J. Tokamaks, 4th Edition 2011; Oxford: Oxford University Press.
  35. Pankin A. et al. The tokamak Monte Carlo fast ion module NUBEAM in the National Transport Code Collaboration library. Comput. Phys. Commun., 2004, vol. 159, р. 157-184. [CrossRef]
  36. Janev, R.K. ; Boley, C.D.; Post, D.E. Penetration of energetic neutral beams into fusion plasmas. Nucl. Fusion, 1989, vol. 29, p. 2125. [CrossRef]
  37. http://btr.org.ru (old page - not available anymore!).
  38. Niek den Harder, Guillermo Orozco, Irene Zammuto, Christian Hopf; et al. Modeling neutral beam transport in fusion experiments: Studying the effects of reionisation and deflection. Fus. Eng. and Design, Vol 146, 2019, 518-521. [CrossRef]
Preprints 84004 g001
Figure 1. Neutral beamline without transmission ducts.
Figure 1. Neutral beamline without transmission ducts.
Preprints 84004 g001
Preprints 84004 g002
Figure 2. Outline of NBI transmission ducts (import from CAD).
Figure 2. Outline of NBI transmission ducts (import from CAD).
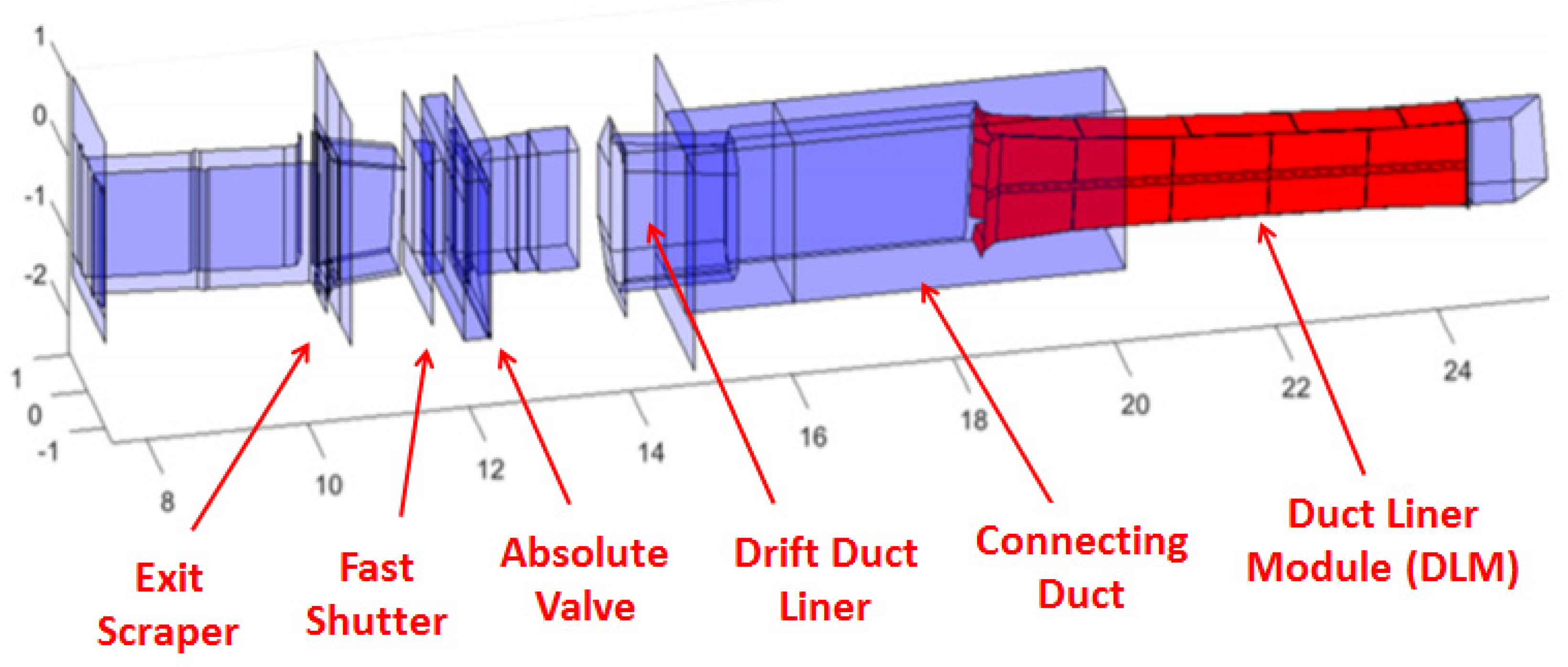
Preprints 84004 g002
Preprints 84004 g003
Figure 3. NBI beamlets axes focusing in FNS-ST compact NBI model.
Figure 3. NBI beamlets axes focusing in FNS-ST compact NBI model.
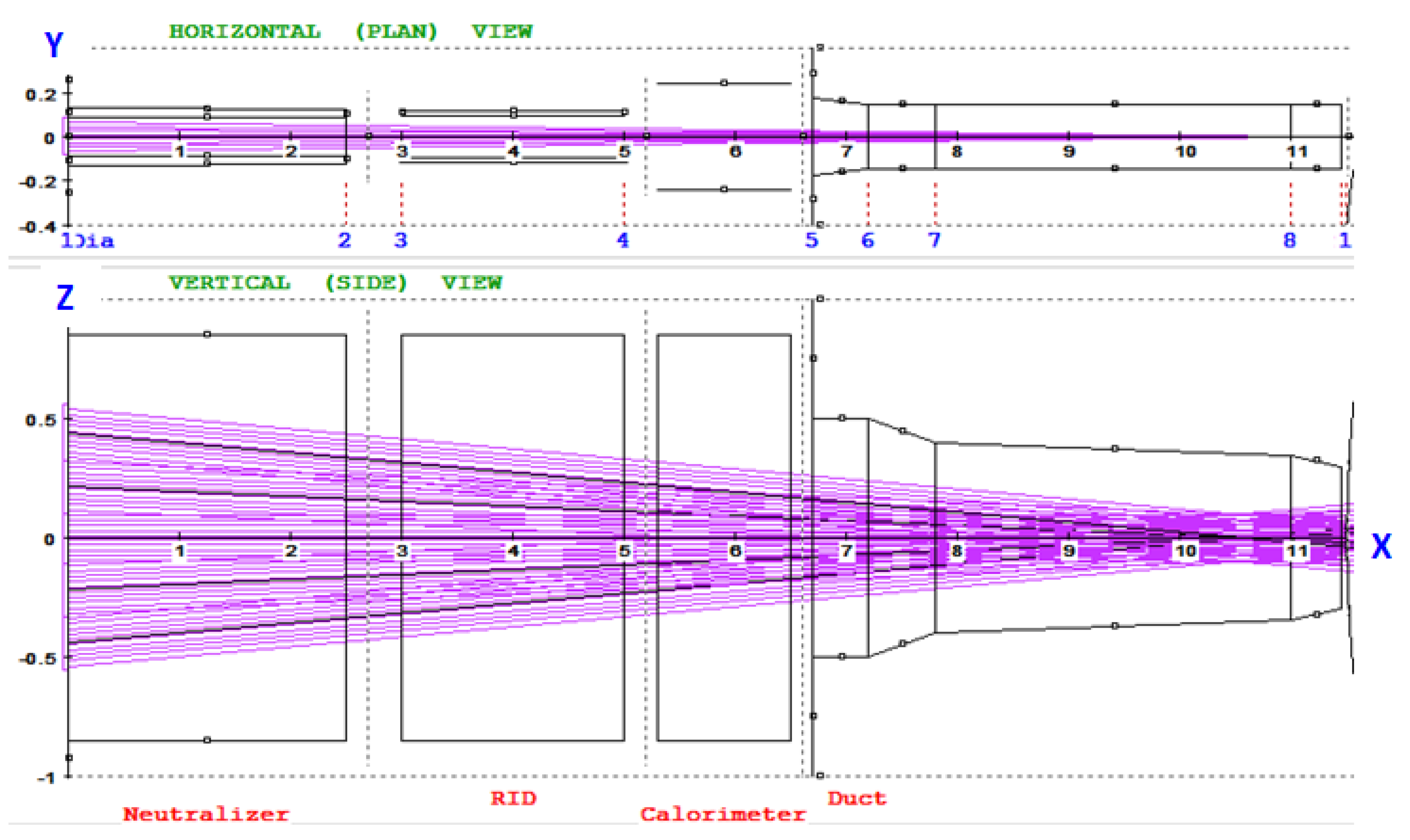
Preprints 84004 g003
Preprints 84004 g006
Figure 5. BTR screen with beamline standard ITER-like geometry and beamlets’ axes.
Figure 5. BTR screen with beamline standard ITER-like geometry and beamlets’ axes.
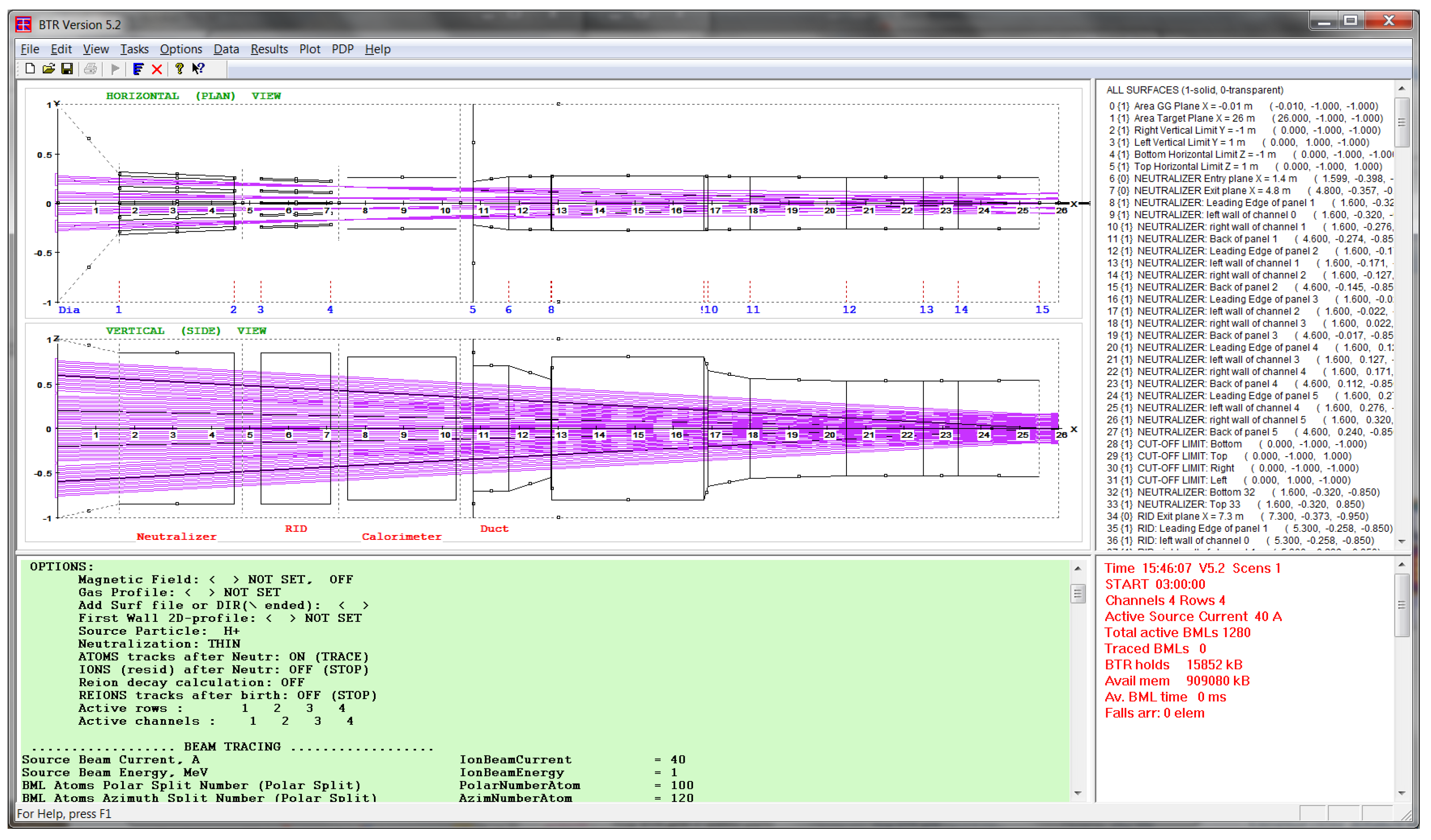
Preprints 84004 g006
Preprints 84004 g007
Figure 6. Examples of BTR dialogs for parameter input by category and input preview.
Figure 6. Examples of BTR dialogs for parameter input by category and input preview.
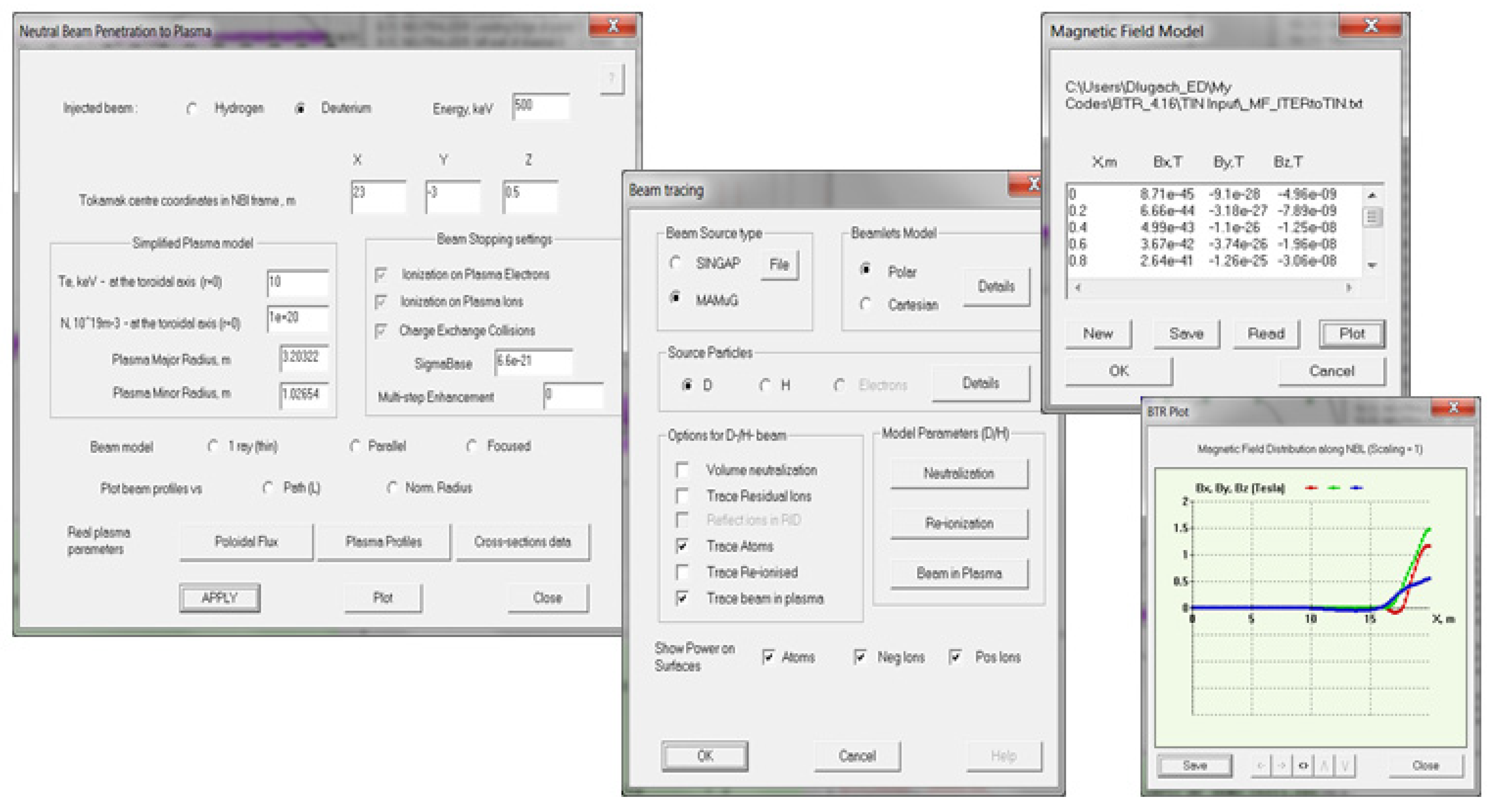
Preprints 84004 g007
Preprints 84004 g008
Figure 7. Neutral beam power density shots at virtual planes: upper – along the beamline; lower - across the beamline (taken at different distance from BS GG).
Figure 7. Neutral beam power density shots at virtual planes: upper – along the beamline; lower - across the beamline (taken at different distance from BS GG).
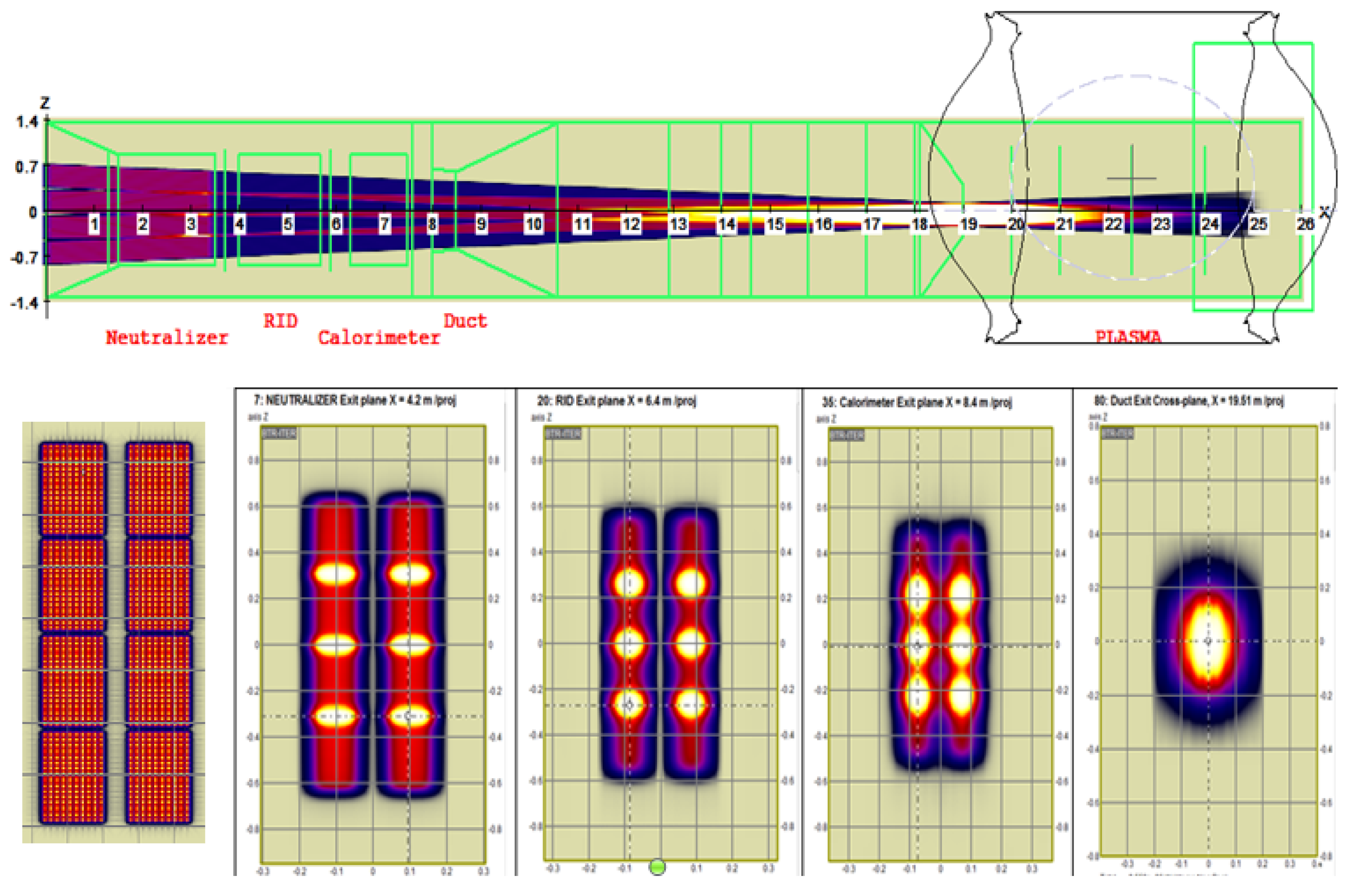
Preprints 84004 g008
Preprints 84004 g009
Figure 8. Power density (PD) maps of the injected NB footprint (maximum value is coded white, minimum - black, background area is shown olive), and correspondent power density profiles (FNS-ST, port with size 30×60cm2). The beamlets’ focus is in horizontal plane at 10.5 m: (a) ideal alignment, total power – 3.49 MW, maximum PD – 43.3 MW/m2; (b) beam misalignment 4/-6 mrad, total power – 3.27 MW, maximum PD – 43.1 MW/m2. The maps are shown in local coordinates.
Figure 8. Power density (PD) maps of the injected NB footprint (maximum value is coded white, minimum - black, background area is shown olive), and correspondent power density profiles (FNS-ST, port with size 30×60cm2). The beamlets’ focus is in horizontal plane at 10.5 m: (a) ideal alignment, total power – 3.49 MW, maximum PD – 43.3 MW/m2; (b) beam misalignment 4/-6 mrad, total power – 3.27 MW, maximum PD – 43.1 MW/m2. The maps are shown in local coordinates.
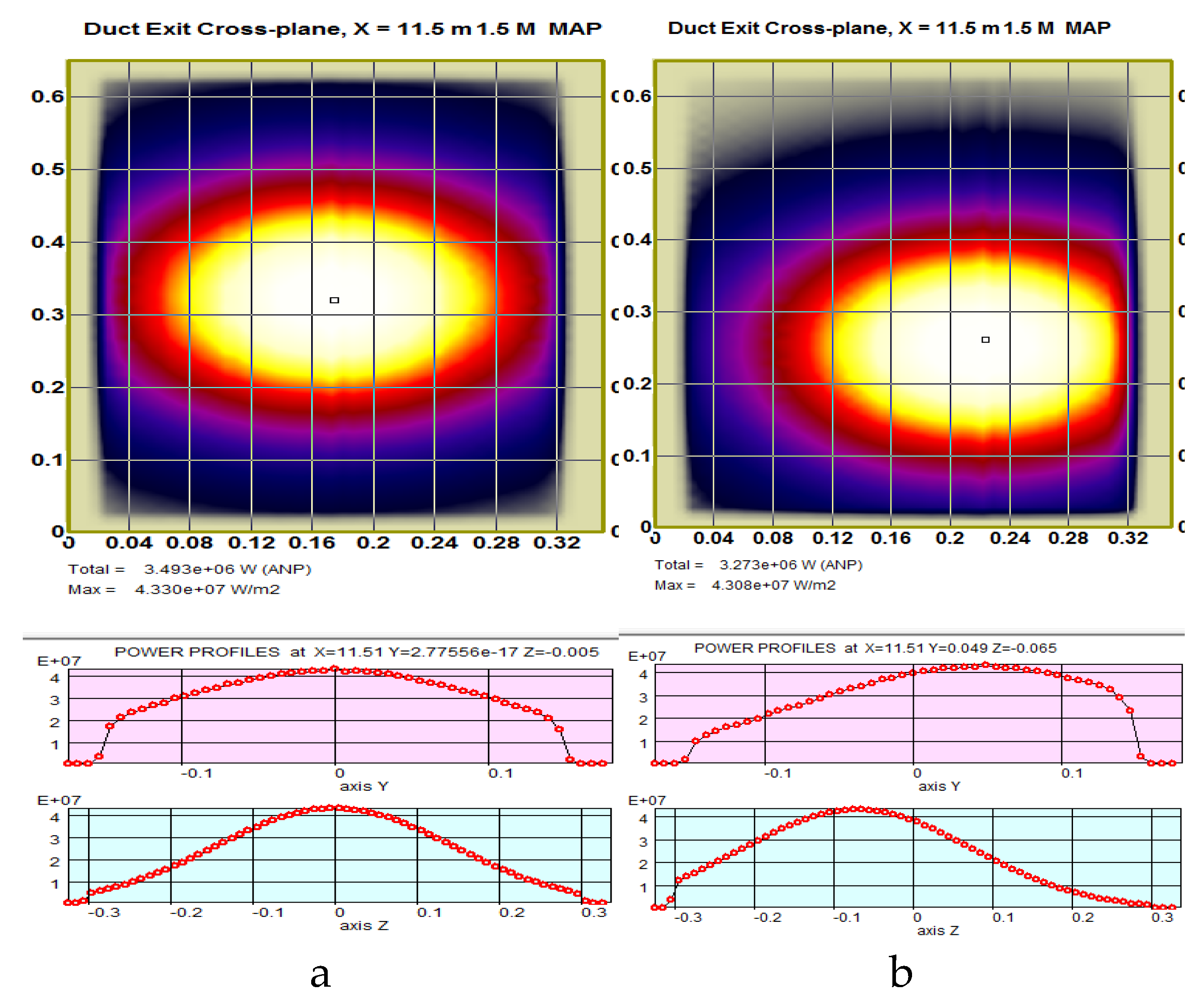
Preprints 84004 g009
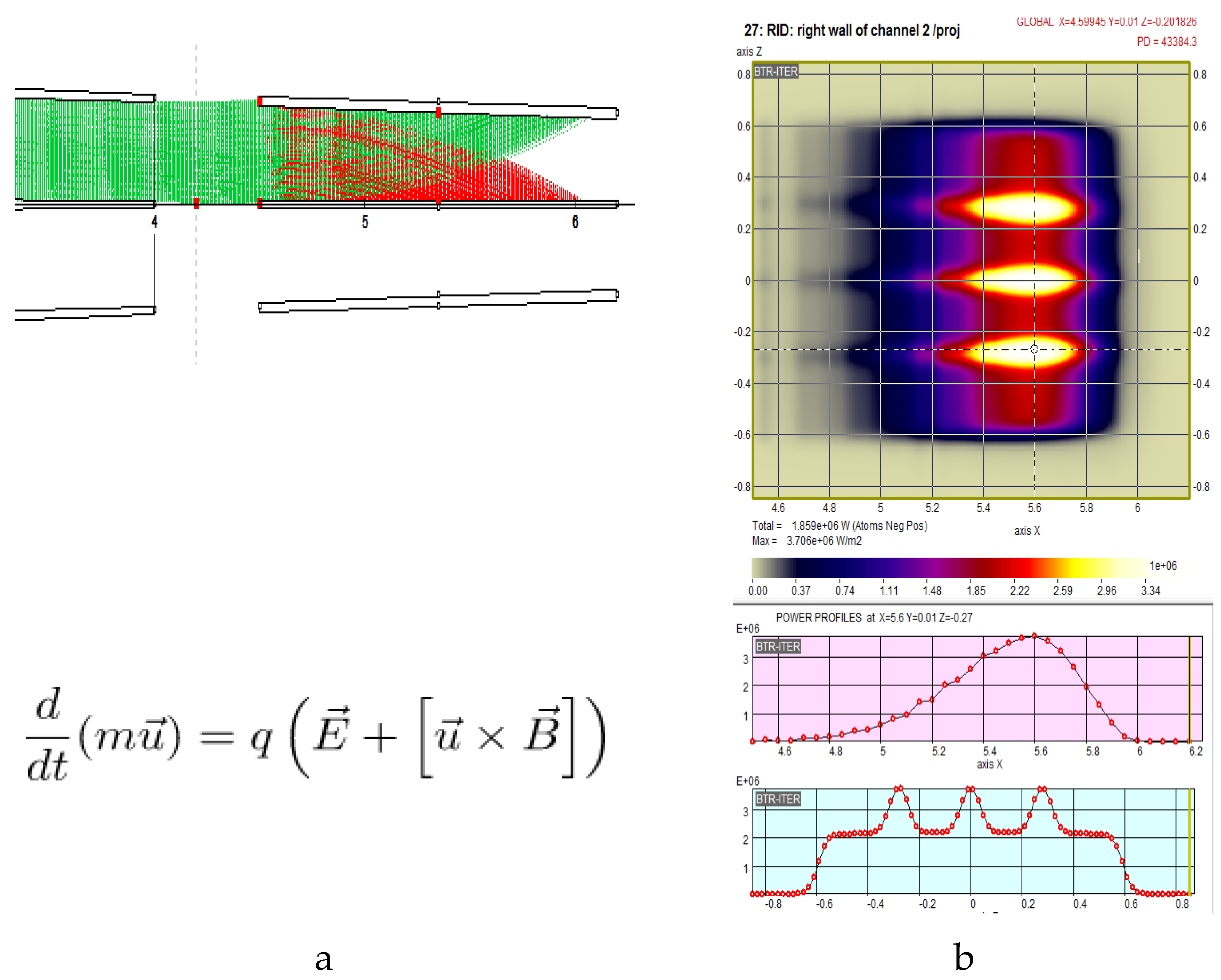
Preprints 84004 g011
Figure 10. Residual ions deflection and dumping in ERID channel (DEMO-FNS): (a) positive/negative ions trajectories; (b) power density map and profiles at the dumping panel.
Figure 10. Residual ions deflection and dumping in ERID channel (DEMO-FNS): (a) positive/negative ions trajectories; (b) power density map and profiles at the dumping panel.
Preprints 84004 g011
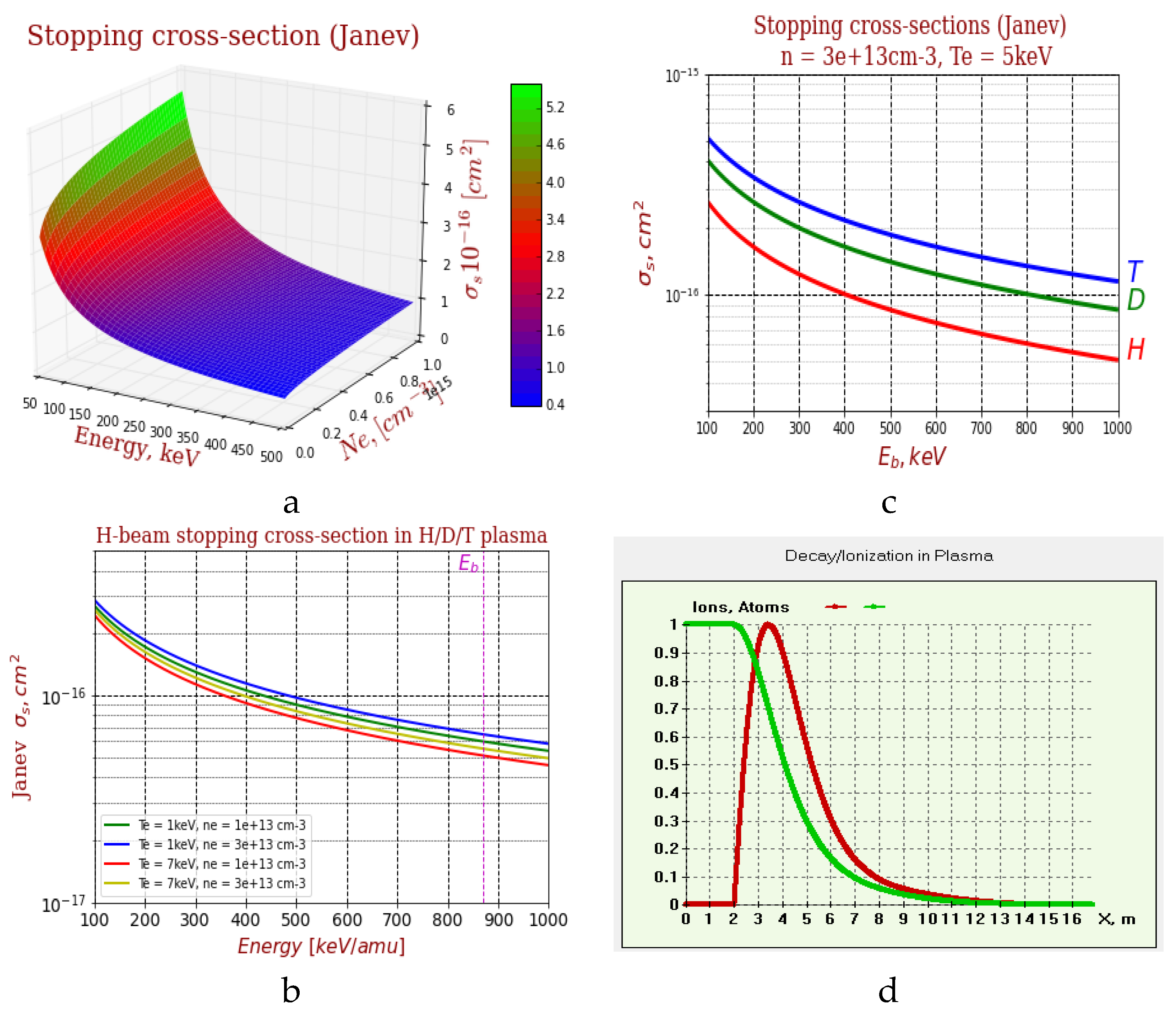
Preprints 84004 g013
Figure 12. Neutral beam stopping calculation: (a) stopping cross-section ( σ S , 10-16 cm2) vs beam energy and plasma density; (b) stopping cross-section ( σ S , 10-16 cm2) for varied temperature (Te ) and plasma density (ne); (c) stopping cross-section ( σ S , 10-16 cm2) for H/D/T beams, Te = 5 keV, ne = 0.3 ∙1020 m-3; (d) neutral beam current attenuation (green) and ion birth rate (red) along NB passage through plasma.
Figure 12. Neutral beam stopping calculation: (a) stopping cross-section ( σ S , 10-16 cm2) vs beam energy and plasma density; (b) stopping cross-section ( σ S , 10-16 cm2) for varied temperature (Te ) and plasma density (ne); (c) stopping cross-section ( σ S , 10-16 cm2) for H/D/T beams, Te = 5 keV, ne = 0.3 ∙1020 m-3; (d) neutral beam current attenuation (green) and ion birth rate (red) along NB passage through plasma.
Preprints 84004 g013
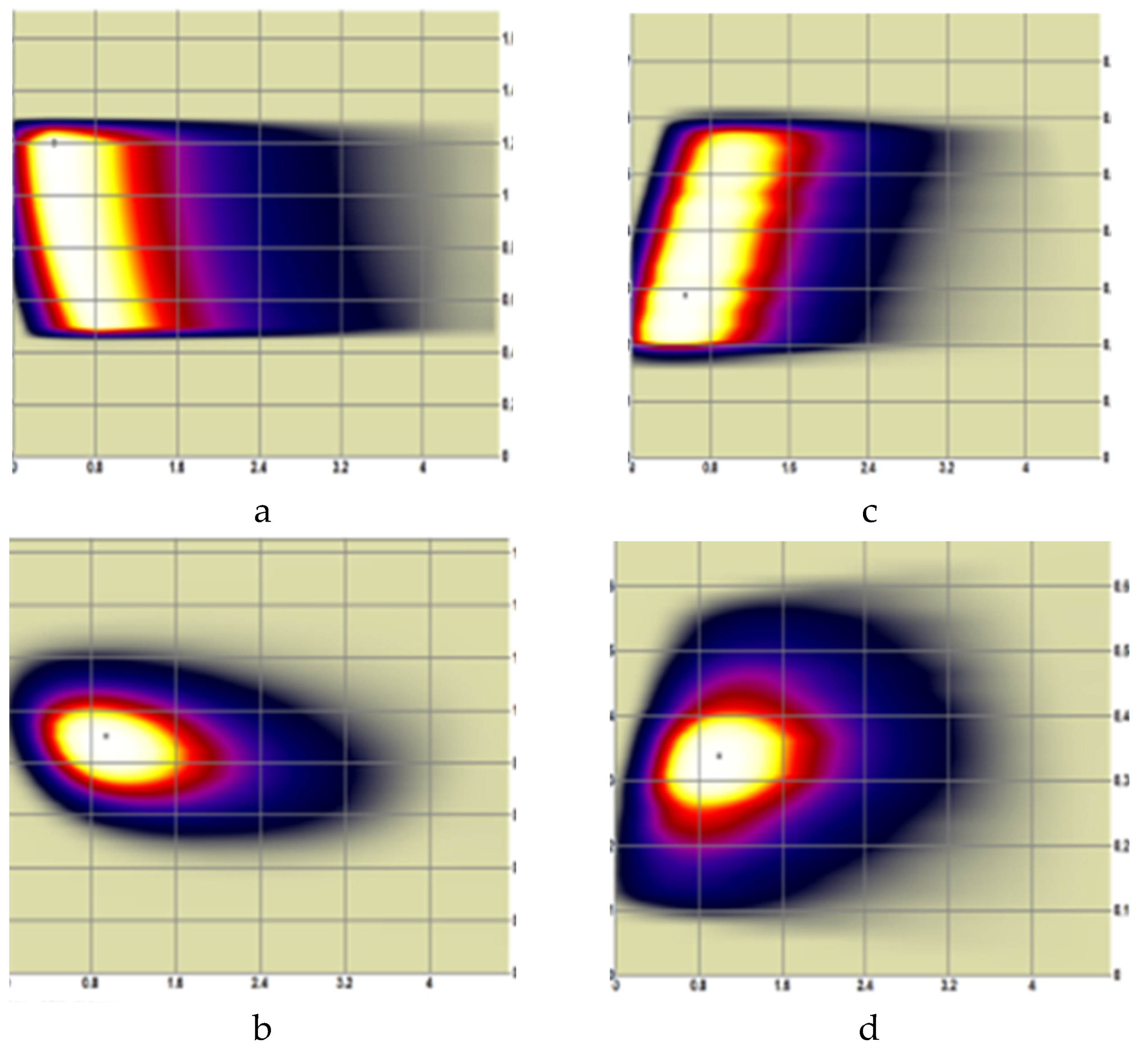
Preprints 84004 g014
Figure 13. Neutral beam spatial deposition (ionization rate intensity) in DEMO-FNS plasma (BTR plots) along the injected neutral beam axis (NB enters from the left): (a, b) vertical cross section plane, (c, d) horizontal cross section plane; (a, c) correspond to rectangular beam shape; (b, d) refer to the realistic beam shape - with divergence and beamlet focusing.
Figure 13. Neutral beam spatial deposition (ionization rate intensity) in DEMO-FNS plasma (BTR plots) along the injected neutral beam axis (NB enters from the left): (a, b) vertical cross section plane, (c, d) horizontal cross section plane; (a, c) correspond to rectangular beam shape; (b, d) refer to the realistic beam shape - with divergence and beamlet focusing.
Preprints 84004 g014
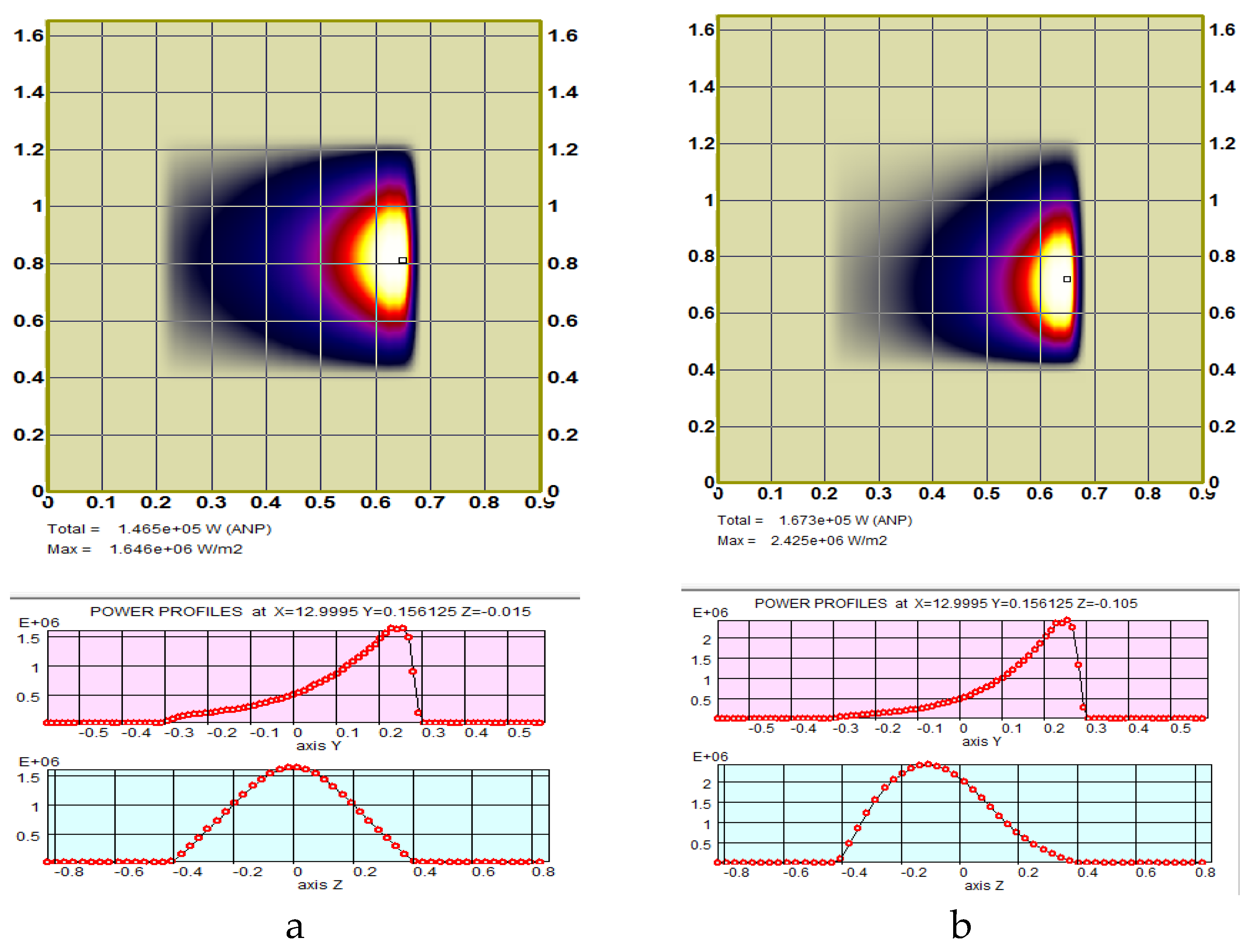
Preprints 84004 g015
Figure 14. NB shine-through PD at FNS-ST first wall (NBI port size 0.3 × 0.6 m2) for two operation cases: (a) ideal beam focus, total power – 0.147 MW, peak PD – 1.65 MW/m2; (b) beam misalignment 4/-6 mrad in horizontal and vertical planes, total power – 0.167 MW, peak PD – 2.43 MW/m2.
Figure 14. NB shine-through PD at FNS-ST first wall (NBI port size 0.3 × 0.6 m2) for two operation cases: (a) ideal beam focus, total power – 0.147 MW, peak PD – 1.65 MW/m2; (b) beam misalignment 4/-6 mrad in horizontal and vertical planes, total power – 0.167 MW, peak PD – 2.43 MW/m2.
Preprints 84004 g015
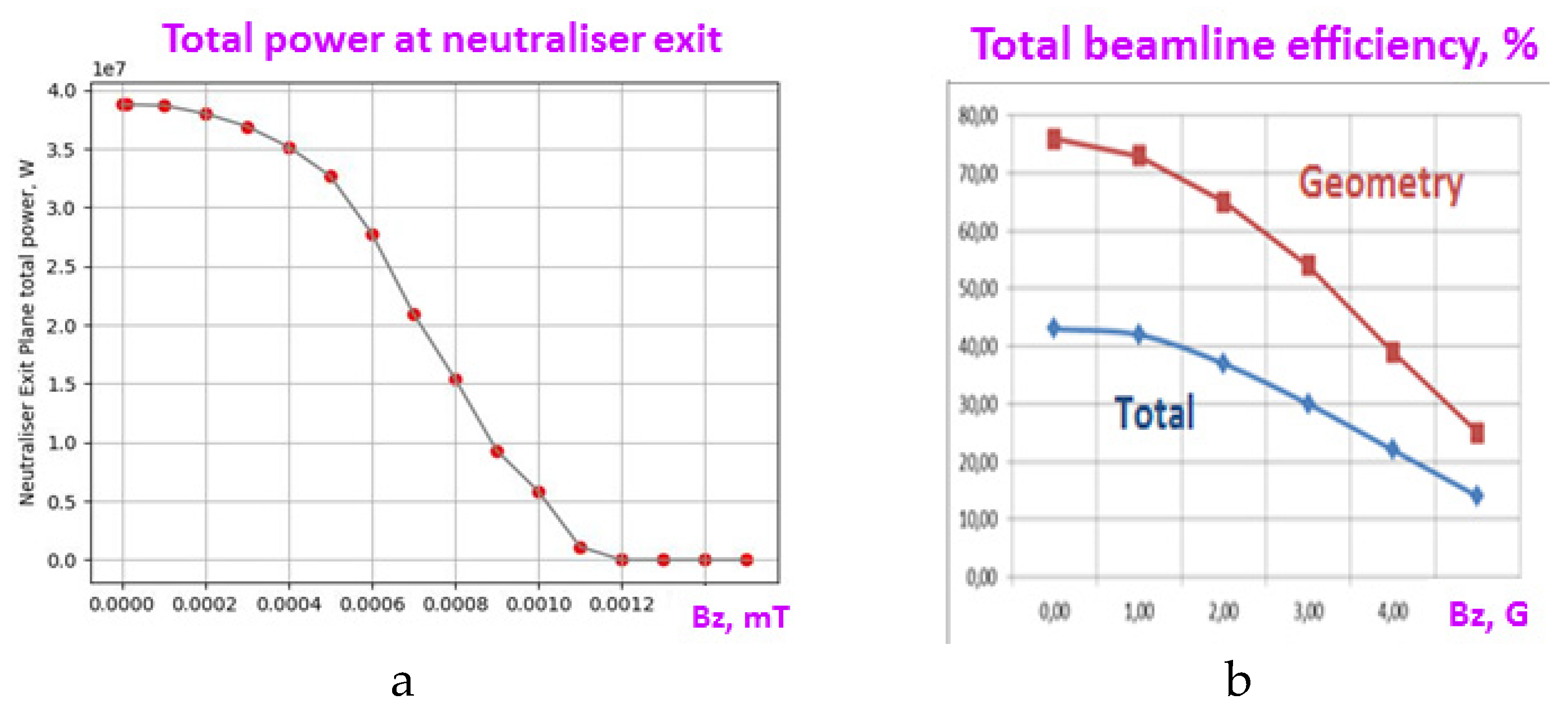
Preprints 84004 g016
Figure 15. DEMO-FNS NBI efficiency as a function of vertical magnetic field (Bz): (a) total neutral power (PNeutr) at the Neutralizer exit; (b) beamline geometry transmission (Pinj / PNeutr) and total power efficiency (Pinj / P0) shown in %.
Figure 15. DEMO-FNS NBI efficiency as a function of vertical magnetic field (Bz): (a) total neutral power (PNeutr) at the Neutralizer exit; (b) beamline geometry transmission (Pinj / PNeutr) and total power efficiency (Pinj / P0) shown in %.
Preprints 84004 g016
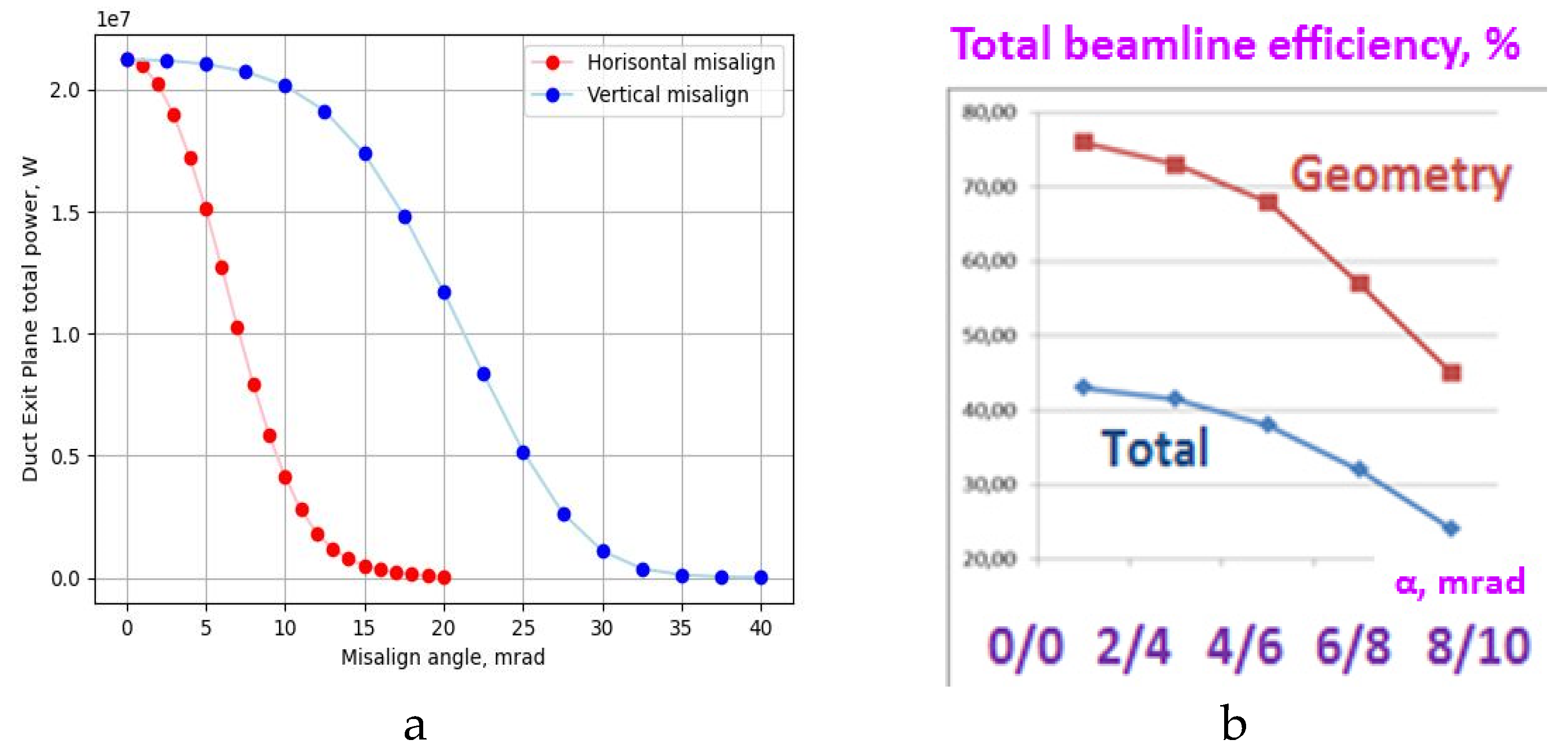
Preprints 84004 g017
Figure 16. DEMO-FNS NBI efficiency as a function of beam misalignment in horizontal and vertical planes: (a) total injected power (Pinj) at the Duct exit; (b) beamline geometry transmission (Pinj / PNeutr) and total power efficiency (Pinj / P0).
Figure 16. DEMO-FNS NBI efficiency as a function of beam misalignment in horizontal and vertical planes: (a) total injected power (Pinj) at the Duct exit; (b) beamline geometry transmission (Pinj / PNeutr) and total power efficiency (Pinj / P0).
Preprints 84004 g017
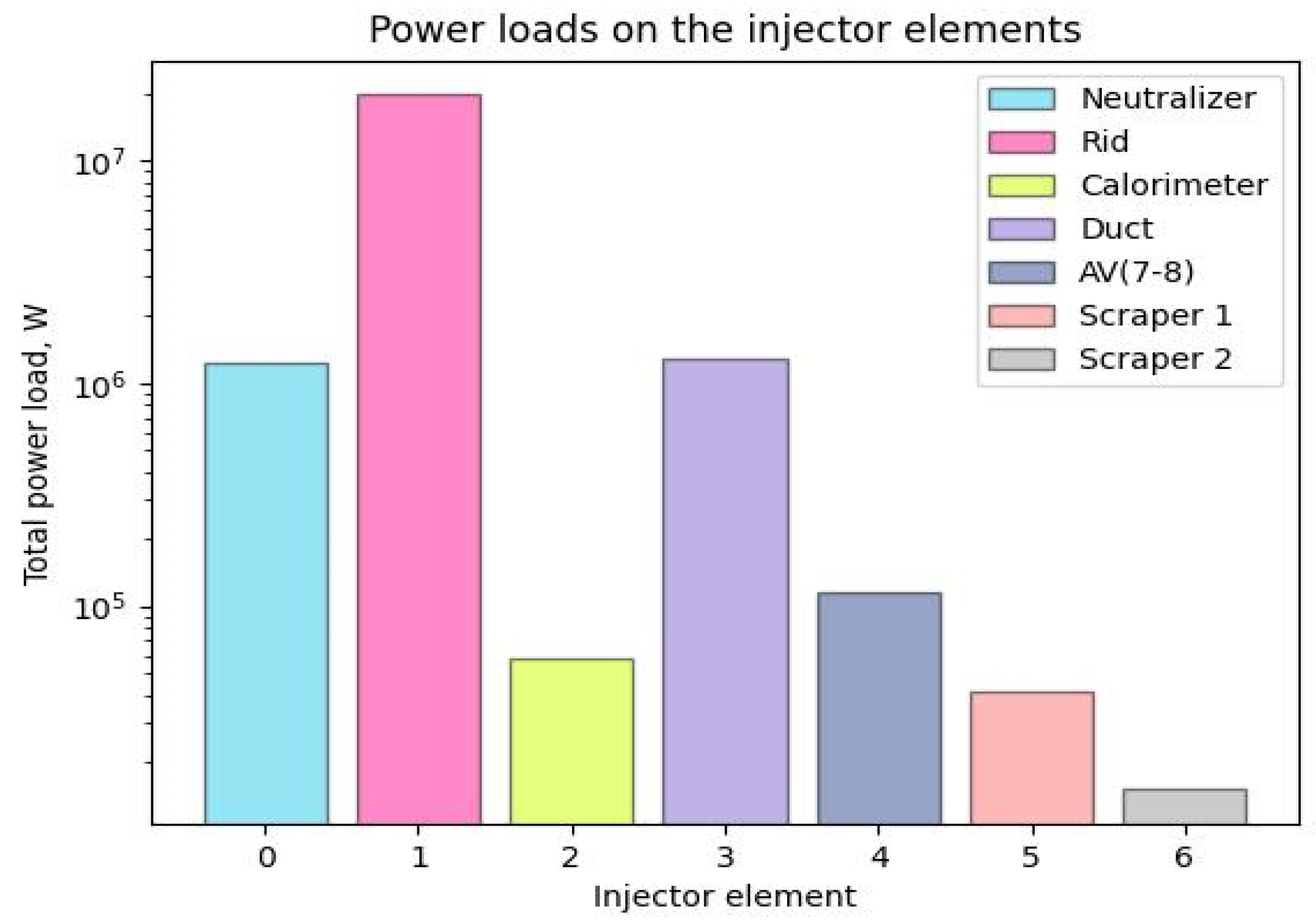
Preprints 84004 g018
Figure 17. Total power deposition at DEMO-FNS NBI major components during the beam injection to tokamak (with calorimeter is in open position).
Figure 17. Total power deposition at DEMO-FNS NBI major components during the beam injection to tokamak (with calorimeter is in open position).
Preprints 84004 g018
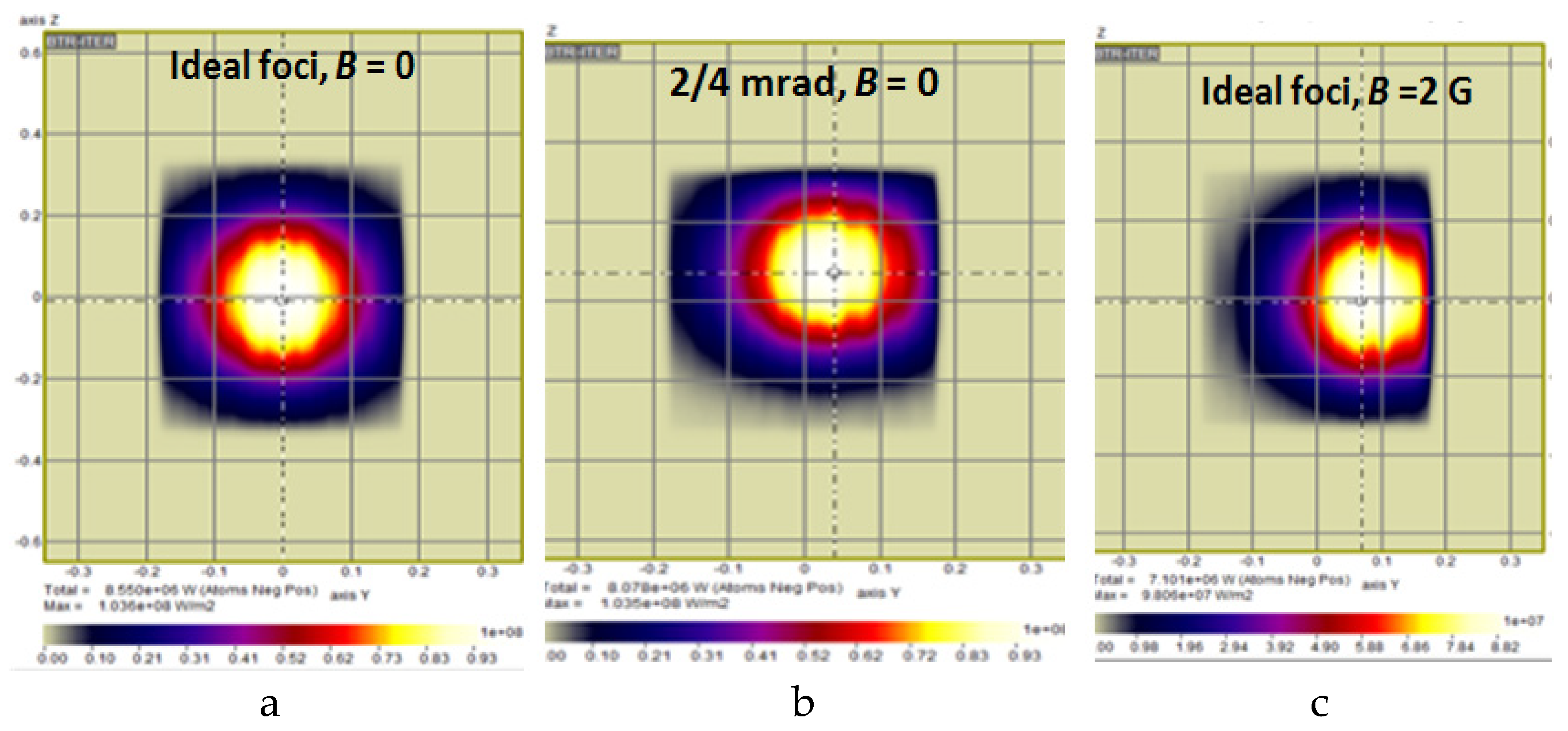
Preprints 84004 g019
Figure 18. Injected beam footprints in NB port plane illustrating the effects of the beam misfocusing and/or magnetic field in DEMO-FNS tokamak: (a) ideal non-disturbed focusing; (b) nominal source beam misalignment values in horizontal and vertical directions; (c) ideal beam focusing with vertical magnetic field.
Figure 18. Injected beam footprints in NB port plane illustrating the effects of the beam misfocusing and/or magnetic field in DEMO-FNS tokamak: (a) ideal non-disturbed focusing; (b) nominal source beam misalignment values in horizontal and vertical directions; (c) ideal beam focusing with vertical magnetic field.
Preprints 84004 g019
Preprints 84004 g020
Figure 19. Injected neutral beam stopping in DEMO-FNS tokamak for two values of plasma density maximum: (a) ne = 1020 m-3; (b) ne = 0.5∙ 1020 m-3.
Figure 19. Injected neutral beam stopping in DEMO-FNS tokamak for two values of plasma density maximum: (a) ne = 1020 m-3; (b) ne = 0.5∙ 1020 m-3.
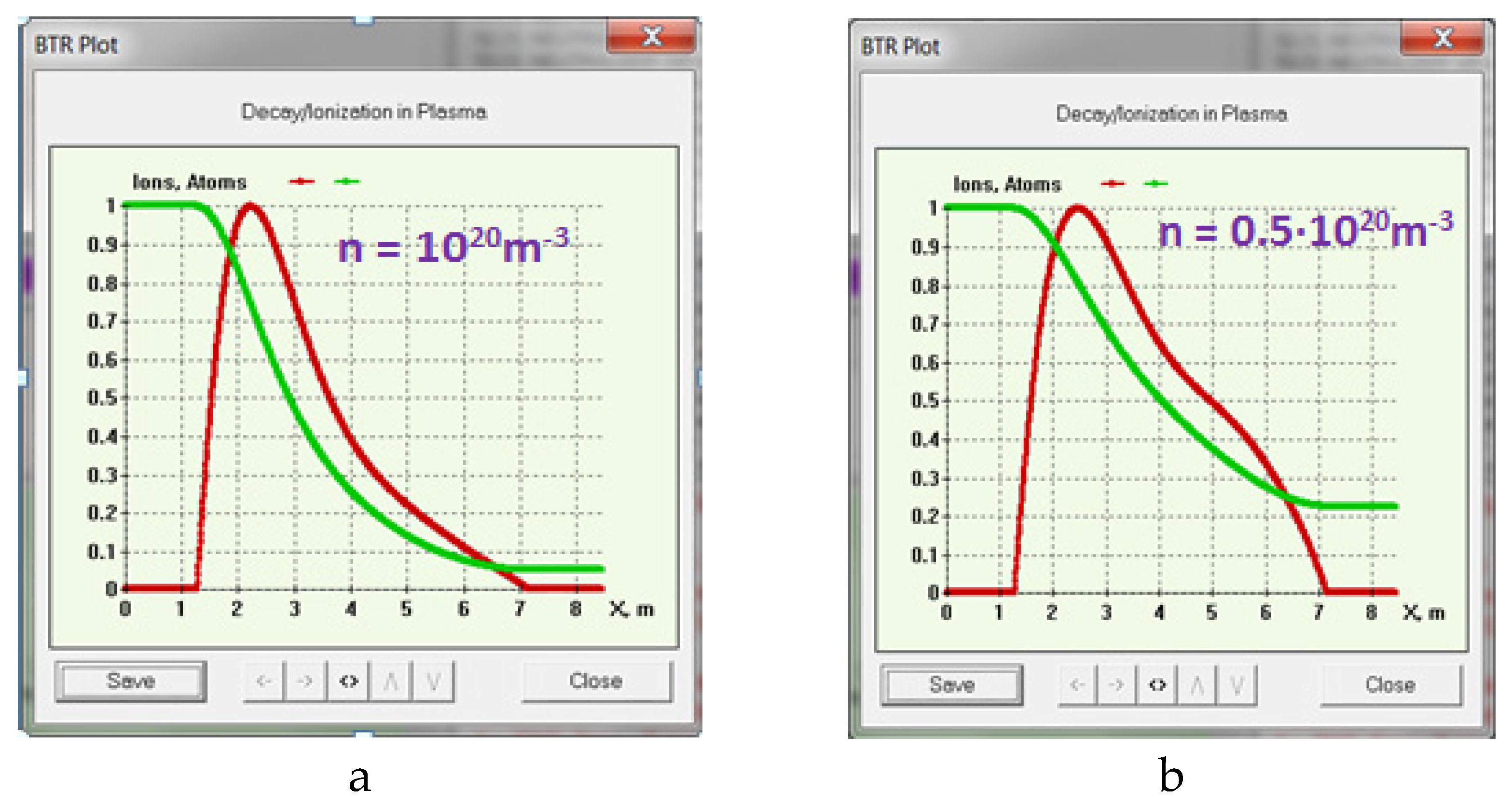
Preprints 84004 g020
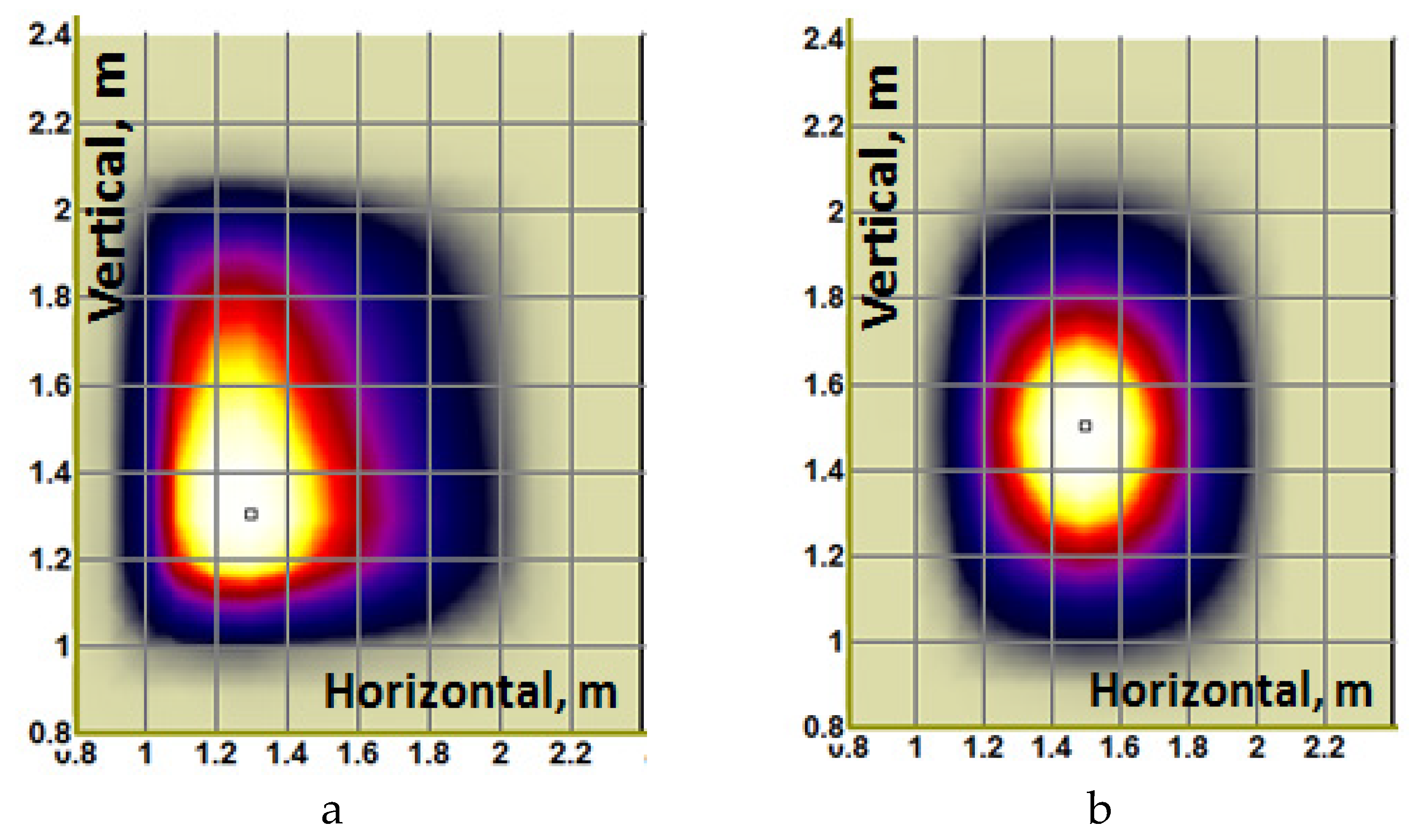
Preprints 84004 g021
Figure 20. Injected neutral beam shine-through power footprints at the first wall in DEMO-FNS tokamak : (a) rectangular beam shape; ( b) gauss beam shape.
Figure 20. Injected neutral beam shine-through power footprints at the first wall in DEMO-FNS tokamak : (a) rectangular beam shape; ( b) gauss beam shape.
Preprints 84004 g021
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated