Carbon Black Filling Amount on the Hyper-elastic Mechanical Behavior of Rubber

Preprint

Article

Carbon Black Filling Amount on the Hyper-elastic Mechanical Behavior of Rubber

Altmetrics

Downloads

101

Views

Comments

A peer-reviewed article of this preprint also exists.

Zepeng Wang,Xiulong Yao,Fangru Hu,Chuanxiang Ma,Xinyan Li,Zhanli Miao,

Junping Song^*,Lianxiang Ma,

Wei Li^*

Zepeng Wang,Xiulong Yao,Fangru Hu,Chuanxiang Ma,Xinyan Li,Zhanli Miao,

Junping Song^*,Lianxiang Ma,

Wei Li^*

This version is not peer-reviewed

Submitted:

05 September 2023

Posted:

06 September 2023

You are already at the latest version

Alerts

Abstract

We have particularly investigated the correlation law of the effect of different carbon black fillings on the hyper-elastic mechanical behavior of natural rubber by conducting uniaxial tensile tests over a wide range of deformations with different volume fractions of carbon black fillings (0%, 4.7%, 8.9%, 12.8%, 16.4%, 19.7%, 22.7%, 25.2%). The results show that the stress-strain curve for carbon black filled rubber increases with the amount of filling, meaning that the rubber gradually becomes "harder". We explore the correlation between the carbon black filling volume and the parameters of the Yeoh constitutive model by examining the Yeoh constitutive model to characterize the hyper-elastic mechanical behavior of rubber with different carbon black fillings. A quantitative relationship between the material parameters and the carbon black filling volume in the Yeoh constitutive model is presented. A method for calculating the material parameters of the Yeoh constitutive model is developed and it predicts the correlation between the hyper-elastic properties of rubber and the volume fraction of carbon black filling.

Keywords:

Subject: Chemistry and Materials Science - Materials Science and Technology

1. Introduction

Carbon black filled rubber composites are widely used in sealing, noise reduction, vibration damping and transportation applications due to their unique and excellent properties [1,2]. In addition, finite element analysis is an important means of evaluating its mechanical properties. When performing finite element analysis on rubber composites, the determination and selection of a suitable hyper-elastic constitutive model based on experimental data is fundamental and critical to the success or failure of the analysis. In order to reasonably describe the stress-strain relationship in rubber composites, different hyper-elastic constitutive models have been developed by the engineering and scientific communities. The stress-strain relationship of rubber materials is represented by the strain energy function[3]. The main hyper-elastic constitutive models of rubber are divided into two types: the image-only theoretical model based on the mechanics of continuous media and the statistical model based on molecular chain networks[4,5]. In order to study the theoretical modelling of the fundamental elastic and viscoelastic behavior of carbon black filled rubber, the Yeoh model was chosen by N. KOPROWSKI-THEISS for the reason that only uniaxial tensile tests were carried out. And the Yeoh model as an intrinsic model of fundamental elasticity is able to represent this non-linear behavior[6]. M.R. Mansouri has proposed an exponential framework of strain energy density functions for elastomers and soft biological tissues, inspired by the image-only Yeoh model. The model is simple, parametrically stable and provides more accurate predictions of the stress response of elastomers and soft tissues for a wide range of properties[7]. Zhao proposed a hyper-elasticity model for isotropic incompressible types of rubber materials in order to examine the predictive capability of the new model. He identifies the parameters of the new model, the Yeoh model and the Carroll model using experimental data for 8% vulcanized rubber and two different types of carbon black filled rubber respectively[8]. Anand determined the important fracture parameters of the NR/BR blends by experimental and finite element modelling methods, where the Yeoh model was used to characterize the hyper-elastic mechanical behavior of the material[9]. El Yaagoubi compared the life prediction capabilities of the image-only based Yeoh model and the inelastic MORPH model, but the Yeoh model does not reproduce properties such as softening effects and hysteresis losses of the material[10]. Uday has successfully modelled the hyper-elastic properties of retreaded tire rubber using the finite element method. The Yeoh and Arruda-Boyce constitutive models demonstrated parametric stability and accuracy of fit, as measured by the accuracy of test results from fitted uniaxial and planar tensile experiments[11]. He Hong evaluated the ability of 85 hyper-elastic constitutive models to reproduce experimental data for unfilled and highly filled rubber nanocomposites. He found that the image-only based Yeoh model was a good fit for the highly filled HNBR[12]. It has been shown that the Yeoh model is a good description of the mechanical response of rubber hyper-elastic materials over a wide range of deformations and that it can be applied to a wide range of practical engineering problems.

In the previously mentioned investigations, the Yeoh constitutive model has been used to describe the relationship between the shear modulus of filled rubber and its deformation. However, the amount of reinforcing agent usually determines the mechanical response of the rubber hyper-elastic material. Therefore, it would be useful to be able to develop a hyper-elastic constitutive structure model using the already existing one. And it is worth exploring if it can describe different carbon black fillings of rubber composites and also predict the mechanical characteristics of a range of different rubber formulations. The model can accurately reflect the hyper-elastic mechanical behavior of rubber composites with different carbon black contents and also to predict the mechanical response of rubber composites in terms of carbon black fillings.

This article reflects the effect of carbon black fillings on the hyper-elastic mechanical characteristics of rubber through a combination of theoretical characterization and experimental analysis. The correlation between the hyper-elastic mechanical properties of carbon black filled rubber, the volume fraction of carbon black filling, and the parameters of the Yeoh constitutive model is investigated in the paper. It can provide theoretical support and new ideas for predicting the stress-strain relationship of carbon black-filled rubber in a wide range of deformation. Section 2 introduces the strain energy density function and the stress-strain relationship equation for the Yeoh constitutive model. Section 3 describes the manufacturers of experimental materials, experimental formulations and experimental equipment. Section 4 shows the stress-strain hyper-elastic mechanical behavior of pure natural rubber and rubber with different carbon black fillings over a wide range of deformation (strain of 150%). Not only reveals the correlation between the material parameters of the Yeoh model and the volume fraction of carbon black filling, and verifies the predictive ability of the Yeoh model with explicit volume fraction of carbon black filling parameters on the hyper-elastic mechanical behavior of rubbers at different carbon black filling. Combined the relationship between the parameters of the Yeoh constitutive model and the volume fraction of carbon black filling, a Yeoh intrinsic model for explicitly characterizing the amount of carbon black filling is constructed. A summary analysis and conclusions is given at the end of the text.

2. Constitutive Models

Available rubber hyper-elastic constitutive models can be divided into statistical models based on molecular chain networks and models based on the mechanics of continuous media. The statistical models for molecular chain networks are generally the James-Guth three-chain model[13],, the Flory four-chain model[14] and the Arruda-Boyce eight-chain model[13]. They are characterized by the fact that fewer model parameters can be used to characterize the mechanical response of hyper-elastic materials in large deformation states. In contrast, image-only models based on the mechanics of continuous media usually include the Neo-Hookean model[15], the Mooney-Rivlin model[16] and the Yeoh model[17]. These constitutive models mainly reflect the hyper-elastic properties of rubber by the amount of strain invariance.Here, we have chosen to present the Yeoh constitutive model, which is applicable to a wide range of deformations and provides a good fit to uniaxial tension. Rivlin[18] expresses the strain energy function as

I_{1}

and

I_{2}

polynomials of the general form:

W = \sum_{i + j = 1}^{N} C_{i}_{j} {(I_{1} - 3)}^{i} （ I_{2} - 3)^{j}

(1)

The Yeoh model retains the higher order terms of the first strain invariant, has the ability to predict multiple modes of deformation and is practical in the medium to large range of material deformation [15]. Yeoh uses the higher order terms of 1I to correct Eq. (1) and takes the first 3 terms (

N = 3

) to obtain the reduced Yeoh polynomial model, the strain energy function of the Yeoh model is:

W = C_{10} (I_{1} - 3) + C_{20} {(I_{1} - 3)}^{2} + C_{30} {(I_{1} - 3)}^{3}

(2)

Since the Yeoh intrinsic model can accurately describe the stress-strain mechanical response of rubber materials in the medium to large deformation range, it is used to characterize the non-linear mechanical behavior of the carbon black filled rubber in the paper.

The relationship between the nominal stress

f

and the stretch ratio

λ

in a state of uniaxial tensile deformation can be expressed as follows:

f = 2 (λ^{2} - \frac{1}{λ}) [C_{10} + 2 C_{20} (λ^{2} + \frac{2}{λ} - 3) + 3 C_{30} {(λ^{2} + \frac{2}{λ} - 3)}^{2}]

(3)

where

C_{10}, C_{20}

and

C_{30}

are the material parameter of the model, which need to be obtained using data from uniaxial tensile tests.

C_{10}

in the Yeoh constitutive model represents half of the shear modulus of the rubber at the start of deformation. That is

C_{10} = μ ／ 2

.The variation of the material parameter

C_{20}

depends on the degree of softening of the rubber at medium deformation. And it usually shows negative values.

C_{30}

indicates the hardening of the rubber material when subjected to large deformations.

3. Experimental Setup

3.1. Experimental Materials

Eight rubber specimens were prepared with NR as the rubber matrix and N220 carbon black as the filler. The filler mass fractions of the eight carbon blacks were 0phr, 10phr, 20phr, 30phr, 40phr, 50phr, 60phr and 70phr respectively. The names, specifications and manufacturers of the main raw materials used in the experiments are shown in Table 1. The formulations of the eight carbon black filled rubber specimens are shown in Table 2.

3.2. Sample Preparation and Test

The preparation of rubber samples requires two stages. Firstly, the natural rubber is first put into the two-roller kneader (Model: S(X)-160A, Shanghai First Rubber Machinery Co. Ltd., Shanghai, China) for mixing, and then stopped after mixing into a flake. The mixing time is 3 minutes. The natural rubber in flake form is then added to the Hakke torque rheometer (HAAKE Germany, Germany) and after 3 minutes zinc oxide, stearic acid and antioxidant 4020 are added as minor ingredients. In order to disperse the carbon black more evenly, half of the carbon black was added after 5 minutes of running the torque rheometer and the remaining carbon black was added after 8 minutes. The total mixing time is 10 minutes. When the temperature drops to 100°C, stop the machine and discharge the material. The second mixing stage is done on a two-roller kneader. Set the temperature of the front and rear rollers of the double-roller opener to (60±5)℃, adjust the spacing between the two rollers to 3~5mm, preheat and mix a section of mixed rubber, add sulphur and accelerator NS and mix and press evenly into 3-5mm after the next piece and leave for 5h. Then, Vulcanisation characteristics were measured in accordance with GB/T9869-2014. The vulcanisation curve, minimum torque (ML), maximum torque (MH) and positive vulcanisation time (Tc90) of the rubber were recorded using a closed type rotorless rheometer. The flat Vulcanisation pressure is set to 10MPa and the vulcanisation time is the equivalent vulcanisation time (Tc90). When the temperature of the flat vulcaniser rises to 150°C, the rubber is placed in the mould for vulcanisation.. After vulcanisation the sample is cooled and left for 12h for subsequent characterisation of properties. A specimen of dumbbell type 2 was cut according to ISO 37-2017, as shown in Figure 1(a), with a thickness of 2 mm for the rubber specimen.

Quasi-static uniaxial tensile tests were carried out on the uniaxially stretched specimens (2mm thick) shown in Figure 1 using a tensile testing machine (MTS CMT4104) at 290K. To eliminate the specimen Mullins effect (The Mullins effect is the stress response of a deformation-free rubber material undergoing first loading deformation is greater than the stress response of a second loading deformation, whose deformation history affects the stress response. However, when the strain is greater than the initial strain, the stress is instead greater than the initial stress magnitude, independent of the initial deformation state.) [16], the load-unload cycle was repeated 5 times at a tensile rate of 100 mm/min before the start of the formal test, and an elongation of 150% was selected as the cyclic modulation strain. As can be seen from the Figure 2, the stress-strain curve stabilises after five modulations of the rubber specimen. The modulation temperature is 290K and the fixture is measured at a distance of 25mm. The purpose of modulating each sample is to reproduce the stress state of the tyre more accurately. The fixture used to perform the uniaxial tensile test is the double eccentric wheel fixture RA-4-1, a special tensile fixture designed to prevent the sample from slipping during the tensile test，as shown in the Figure 1(b). After modulation, the rubber specimens were left to stand for 24h to allow full recovery of elastic deformation and stable properties. The experiment was carried out five times for each condition and the average of the five experiments was taken as the final result.

4. Experimental Result and Discussion

4.1. The uniaxial tensile tests results

The uniaxial tensile stress-strain curves for natural rubber with different carbon black fillings over a wide range of deformations (150% strain) are given in Figure 3. Figure 3 shows that the stress-strain relationship for natural rubber increases overall with increasing carbon black fillings, i.e. after the addition of carbon black, the rubber stiffens and the stiffness modulus of the rubber increases due to the action of the carbon black particles. As the amount of carbon black filling increases, the stress-strain relationship for natural rubber becomes steeper and steeper, which translates into a more pronounced 'S'-shaped non-linear characteristic change. The higher the strain, the more pronounced the steepening of the curve. Although the amount of carbon black filling varies, the stress-strain relationship of natural rubber basically shows obvious "S" non-linear characteristics. The "S" nonlinearity of the stress-strain relationship of natural rubber becomes more pronounced as the amount of carbon black filling increases. The results show that filled rubber can exhibit different deformation behavior characteristics at different stages of deformation. Therefore, it is more important to study the hyper-elastic properties of carbon black filled rubber in a wide range of deformation.

In order to show more clearly the correlation law between carbon black filling and the hyper-elastic mechanical properties of rubber, Figure 3 is treated in this paper. As a result, the variation curve of stress with the volume fraction of carbon black filling for natural rubber at different constant strains was obtained, as shown in Figure 4. As can be seen from Figure 4, when the carbon black content of the rubber is increased, the stress performance of the rubber at different strains shows a non-linear growth trend. In other words, This means that as the carbon black content increases, the rubber becomes progressively stiffer, resulting in a very pronounced reinforcement of the rubber and an obvious hyper-elastic response. The mechanical properties of the rubber are also enhanced when the carbon black filling is increased, and the degree of enhancement can be observed in the upward curve at the right end of Figure 4.

To further measure the enhancement of the constant elongation stress in the rubber matrix by carbon black filling, the concept of "stress amplification factor"

α

proposed by Fukahori et al[19] is used here. It is intended to illustrate the extent to which the carbon black filling enhances the stress level of the adhesive at constant strain. As shown in the following equation:

α = σ / σ_{0}

(4)

where

σ

is the specific stress value of the filled rubber at a certain strain and

σ_{0}

is the stress value of the corresponding vulcanized natural pure rubber. The definition of Eq. (4) reflects the degree of stress enhancement in a given strain of the rubber due to the carbon black filling. This means that the stress of the carbon black filled rubber is magnified by a certain elongation ratio, which visually shows the "hardening" of the rubber under carbon black filling.

The "stress amplification factor"

α

of the filled rubber is obtained from Eq. (4) as a function of the nominal strain, as shown in Figure 5. Figure 5 shows that the 'stress amplification factor' for natural rubber with different carbon black fillings decreases and then increases with increasing tensile length. In addition, the more the amount of carbon black filled in the rubber, the more significant the change in the non-linear characteristic of "falling then rising". This indicates that the amplification of the hyper-elastic behavior of the rubber by carbon black filling at different elongation stages during the stretching process is different, and that the greater the carbon black filling the more significant the enhancement effect on the rubber. At the same time, the "stress amplification factor"

α

for the different compounds tends to be constant at nominal strains of 0.2 to 0.7. This indicates that the stress enhancement tends to be constant at this stage of deformation and increases exponentially as a function of the tensile length. Moreover, the hyper-elastic mechanical behavior of the carbon black filling on the rubber is variable at different elongation stages over a wide range of deformations.

4.2. Discussion

The experimental results of rubber specimens with different carbon black fillings (NR-0, NR-10, NR-30, NR-50, NR-70) were fitted using the Yeoh constitutive model.

The results of the study are shown in Figure 6. In order to evaluate the goodness of fit of each model, the coefficients of determination

R^{2}

are calculated.

R S S = {\sum_{i = 1}^{N} (P_{i} - \overset{\land}{P_{i}})}^{2}, T S S = {\sum_{i = 1}^{N} (P_{i} - \bar{P_{i}})}^{2}, R^{2} = 1 - R S S / T S S

(5)

where

P_{i}

is the test values,

{\hat{P}}_{i}

is the model fit values,

{\bar{P}}_{i}

is the average values of

P_{i}

N

is the number of test data.

The parameters of the Yeoh constitutive model and the coefficient of determination

R^{2}

are given in Table 3. As can be seen from Figure 6 and Table 3, the fitted curves for different carbon black fillings of rubber are in good agreement with the experimental curves (the coefficients of determination are above 0.9). This indicates that the Yeoh constitutive model is able to characterize the hyper-elastic behavior of rubber with different carbon black fillings more accurately, and has good generality in describing the hyper-elastic behavior of natural rubber.

The results of the characterization of natural rubber with different carbon black fillings only qualitatively analyze the ability of the model to characterize the hyper-elastic mechanical behavior of the filled rubber and do not directly account for the effect of the carbon black fillings on the model parameters. There is no quantitative description of the relationship between the volume fraction of carbon black filling and the hyper-elastic mechanical behavior. To address this issue, a quantitative relationship between the corresponding material parameters in the Yeoh constitutive model and the volume fraction of carbon black filling was established using macroscopic image-only theory.

The Yeoh constitutive model material parameters C10，C20 and C30 were fitted based on the experimental results of the stress-strain properties of some rubber specimens with different carbon black fillings (NR-0, NR-10, NR-30, NR-50, NR-70), as shown in Figure 7. The results of the fit show that there is a significant quadratic relationship between the material parameters C10，C20 and C30 of the Yeoh constitutive model and the volume fraction of carbon black filling. As the volume fraction of the carbon black filling increases, the rubber becomes stiffer, resulting in an increase in the modulus of the rubber. Since the material parameter C10 represents the shear modulus of the material at small deformations, it increases gradually with the volume fraction of carbon black filling. At the same time, the material parameter C20 describes the degree of softening of the rubber material in the case of moderate deformation. As the volume fraction of carbon black filling increases and the rubber becomes harder, the material parameter C20 decreases with increasing volume fraction of carbon black filling. The material parameter C30 indicates the extent to which the material starts to harden in the case of large deformations. As the volume fraction of carbon black filling increases, the material parameter C30 also becomes larger. From the above analysis, the quantitative relationship between the Yeoh constitutive model material parameters C10，C20 and C30 and the volume fraction of carbon black filling can be expressed by fitting a quadratic function numerically, as shown in Eq. (6).

\{\begin{cases} C_{10} = A_{0} + A_{1} V + A_{2} V^{2} \\ C_{20} = B_{0} + B_{1} V + B_{2} V^{2} \\ C_{30} = C_{0} + C_{1} V + C_{2} V^{2} \end{cases}

(6)

where V is the volume fraction of carbon black filling in the rubber specimen and A0, A1, A2, B0, B1, B2, C0, C1, and C2 are the fitted parameters to be determined. They are called the correlation characterization parameters for the carbon black filling volume fraction. Using the Yeoh constitutive model fitting parameters in Table 3 and Eq. (6), the correlation characterization parameters for the volume fraction of carbon black filling can be fitted and calculated, see Table 4.

Thus, the Yeoh instanton model for the filled volume fraction of apparent carbon black is obtained by combining equation (2-7) with Eq. (6).

\{\begin{cases} W = C_{10} (I_{1} - 3) + C_{20} {(I_{1} - 3)}^{2} + C_{30} {(I_{1} - 3)}^{3} \\ C_{10} = A_{0} + A_{1} V + A_{2} V^{2} \\ C_{20} = B_{0} + B_{1} V + B_{2} V^{2} \\ C_{30} = C_{0} + C_{1} V + C_{2} V^{2} \end{cases}

(7)

The stress-strain curves for NR-2, NR-4, NR-6 (20phr, 40phr, 60phr) can be obtained from Eq. (7) and the correlation characterization parameters for the volume fraction of carbon black filling in Table . This is the predicted curve of the Yeoh constitutive model for the filled volume fraction of carbon black. From Figure 8 it can be seen that the predicted and experimental curves are in good agreement. This means that the Yeoh constitutive model with apparent carbon black filling volume fraction can more accurately describe the non-linear hyper-elastic mechanical behavior of carbon black filled rubber over a range of carbon black filling volume fractions at 150% strain.

To further investigate the correlation characteristics of the hyper-elastic behavior of natural rubber with carbon black filling. Using the characterization parameters in Table and the Yeoh constitutive model with the apparent volume fraction of carbon black filling, it was possible to predict the variation of the stress in the rubber with the volume fraction of carbon black filling at constant elongation. The predicted results for the fixed extension stress are shown in Figure 9. As can be seen in Figure 9, the Yeoh constitutive model, which explicitly characterizes the volume fraction of the carbon black filling, is able to provide a more accurate indication of the stress enhancement at different constant elongations for different carbon black fillings. This means that the stress in the rubber increases with the volume fraction of the carbon black filling and shows a non-linear increasing trend. This indicates that the effect of carbon black fillings on the performance of natural rubber is gradually becoming more apparent. The degree of progression increases with increasing volume fraction of carbon black filling. For some of the more costly rubber tests in the industry, we can use this explicit Yeoh constitutive model, which characterizes the volume fraction of carbon black filling, to predict the performance of other rubber formulations over a range of deformations. This provides a highly viable forecasting method for industrial applications.

5. Conclusions

The Yeoh constitutive model for explicitly characterizing the volume fraction of carbon black filling was constructed based on the theory of continuum media mechanics，the following conclusions can be obtained:

(1) The pattern of correlation between rubber hyper-elastic properties and carbon black filling in natural rubber over a wide range of deformation is revealed. The uniaxial tensile stress-strain curve of natural rubber becomes steeper and steeper as the amount of carbon black filling increases. In other words, natural rubber becomes progressively "harder" when filled with carbon black, and the "S" non-linear characteristics of the stress-strain curve become apparent.

(2) A quantitative relationship between the Yeoh constitutive model and the volume fraction of carbon black filling was constructed to explicitly characterize the correlation between the hyper-elastic mechanical behavior of the adhesive and the carbon black filling. This further broadens the scope of application of the Yeoh constitutive model.

(3) Explicitly characterizes the Yeoh constitutive model for the volume fraction of carbon black fillings, which is able to describe more accurately the stress enhancement for different carbon black fillings at different constant elongations. It can also predict the performance of other rubber formulations within a certain range of deformation and provides a highly viable prediction method for practical applications.

Author Contributions

Conceptualization, Zepeng Wang and Wei Li; Methodology, Zepeng Wang; Software, Xiulong Yao ; Validation, Zepeng Wang and Xiulong Yao; Formal Analysis, Xiulong Yao; Investigation, Zepeng Wang and Xiulong Yao; Resources, Zepeng Wang; Data Curation, Fangru Hu, Chuanxiang Ma and Xinyan Li; Writing – Original Draft Preparation, Xiulong Yao; Writing – Review & Editing, Zepeng Wang and Zhanli Miao; Visualization , Junping Song and Lianxiang Ma; Supervision, Wei Li and Zepeng Wang. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by Natural Science Foundation of Shandong Province , China, grant number ZR2019MEM050.

References

Peng, X.; Li, L. State of the art of constitutive relations of hyperelastic materials. Chinese Journal of the Theoretical and Applied Mechanics, 2020, 52, 1221–1232. [Google Scholar]
Ding, F.; Zhang, H.; Ding, M.-M.; et al. Theoretical Models for Stress-Strain Curves of Elastomer Materials. ACTA POLYMERICA SINICA, 2019, 50, 1357–1366. [Google Scholar]
Ogden, R.W. Non-linear elastic deformations. Engineering Analysis, 1984.
Boyce, M.C.; Arruda, E.M. Constitutive models of rubber elasticity: a review. Rubber chemistry and technology, 2000, 73, 504–523. [Google Scholar] [CrossRef]
Steinmann, P.; Hossain, M.; Possart, G. Hyperelastic models for rubber-like materials: consistent tangent operators and suitability for Treloar’s data. Archive of Applied Mechanics, 2012, 82, 1183–1217. [Google Scholar] [CrossRef]
Koprowski-Theiss, N.; Johlitz, M.; Diebels, S. Characterizing the time dependence of filled EPDM. Rubber Chemistry and Technology, 2011, 84, 147–165. [Google Scholar] [CrossRef]
Mansouri, M.; Darijani, H. Constitutive modeling of isotropic hyperelastic materials in an exponential framework using a self-contained approach. International Journal of Solids and Structures, 2014, 51, 4316–4326. [Google Scholar] [CrossRef]
Zhao, Z.; Mu, X.; Du, F. Modeling and verification of a new hyperelastic model for rubber-like materials. Mathematical Problems in Engineering 2019, 2019. [Google Scholar] [CrossRef]
Poomuthu, A.; Stoček, R.; Chattopadhyay, S.; et al. Understanding fracture of a carbon black filled rubber compound using material force theory. Theoretical and Applied Fracture Mechanics, 2020, 108, 102649. [Google Scholar] [CrossRef]
El Yaagoubi, M.; Meier, J.; Juhre, D. Lifetime prediction of carbon black filled elastomers based on the probability distribution of particle using an inelastic and hyperelastic material model. Engineering Failure Analysis, 2020, 118, 104943. [Google Scholar] [CrossRef]
Gudsoorkar, U.; Bindu, R. Computer simulation of hyper elastic re-treaded tire rubber with ABAQUS. Materials Today: Proceedings, 2021, 43, 1992–2001. [Google Scholar] [CrossRef]
He, H.; Zhang, Q.; Zhang, Y.; et al. A comparative study of 85 hyperelastic constitutive models for both unfilled rubber and highly filled rubber nanocomposite material. Nano Materials Science, 2022, 4, 64–82. [Google Scholar] [CrossRef]
Arruda, E.M.; Boyce, M.C. A three-dimensional constitutive model for the large stretch behavior of rubber elastic materials. Journal of the Mechanics and Physics of Solids, 1993, 41, 389–412. [Google Scholar] [CrossRef]
James, H.M.; Guth, E. Theory of the elastic properties of rubber. The Journal of Chemical Physics, 1943, 11, 455–481. [Google Scholar] [CrossRef]
Yeoh, O.H. Some forms of the strain energy function for rubber. Rubber Chemistry and technology, 1993, 66, 754–771. [Google Scholar] [CrossRef]
Mooney, M. A theory of large elastic deformation. Journal of applied physics, 1940, 11, 582–592. [Google Scholar] [CrossRef]
Yeoh, O.H. Characterization of elastic properties of carbon-black-filled rubber vulcanizates. Rubber chemistry and technology, 1990, 63, 792–805. [Google Scholar] [CrossRef]
Rivlin, R.S. Large elastic deformations of isotropic materials. I. Fundamental concepts. Philos Tr R Soc S-A, 1948, 240, 459–490. [Google Scholar]
Fukahori, Y. The mechanics and mechanism of the carbon black reinforcement of elastomers. Rubber chemistry and technology, 2003, 76, 548–566. [Google Scholar] [CrossRef]

Figure 1. Dumbbell 2 rubber specimen(a); Double eccentric wheel fixture RA-4-1(b).

Figure 2. Stress-strain curve of modulated rubber specimen NR-0 at 290 K.

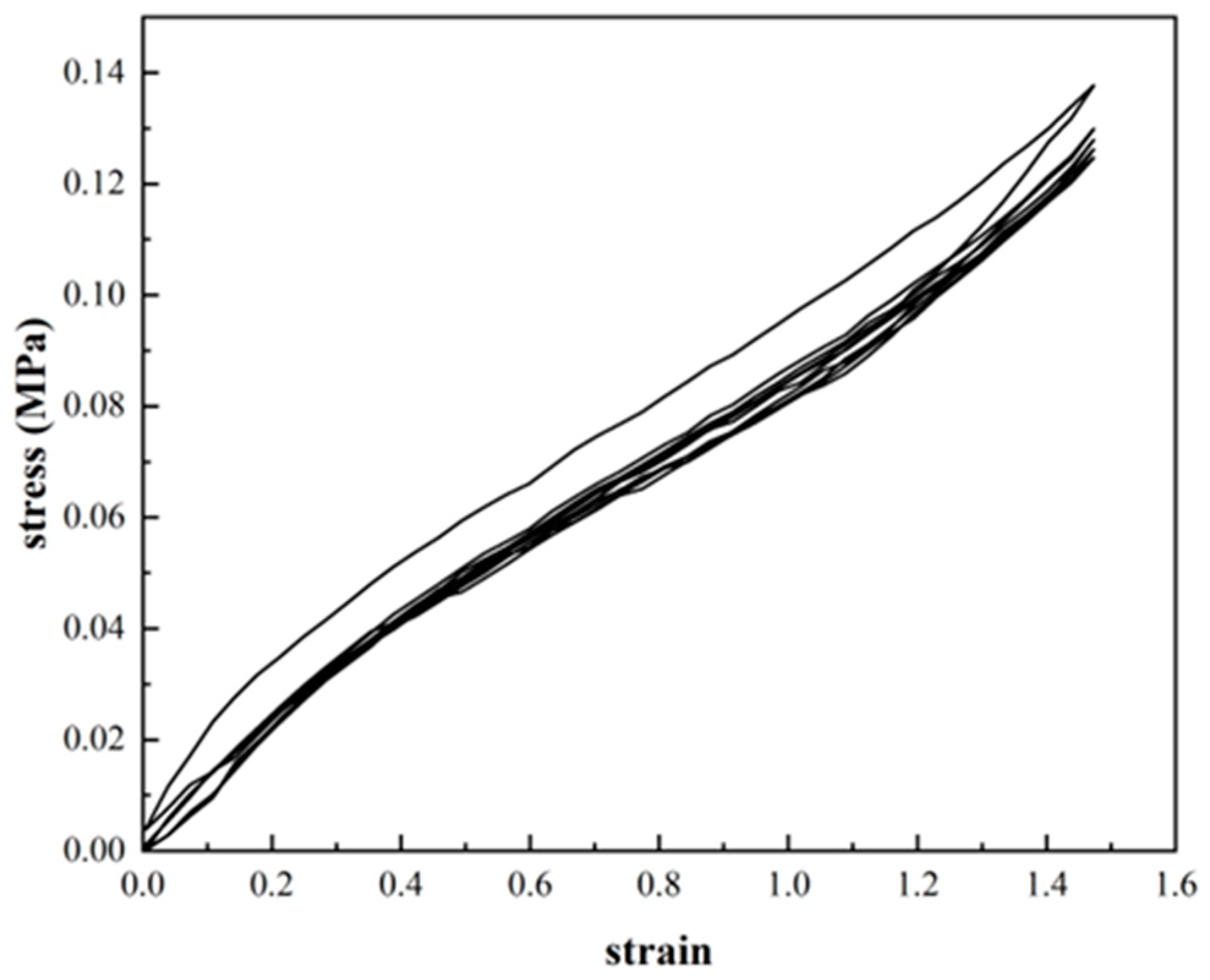
Figure 3. Uniaxial tensile stress-strain curves of natural rubber with different carbon black fillings.

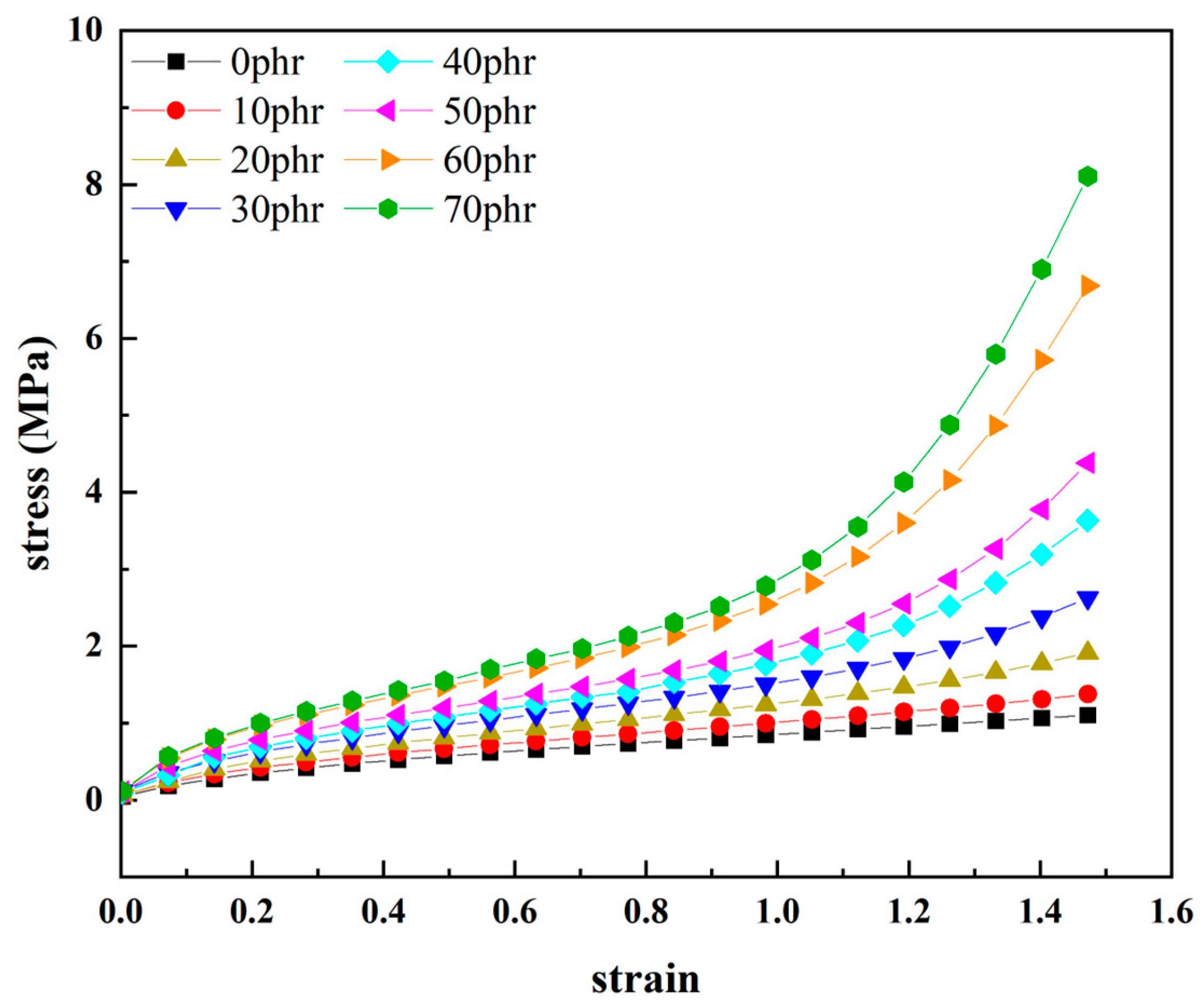
Figure 4. The variation trend of rubber stress with the volume fraction of CB under constant strain (ε is strain in the figure).

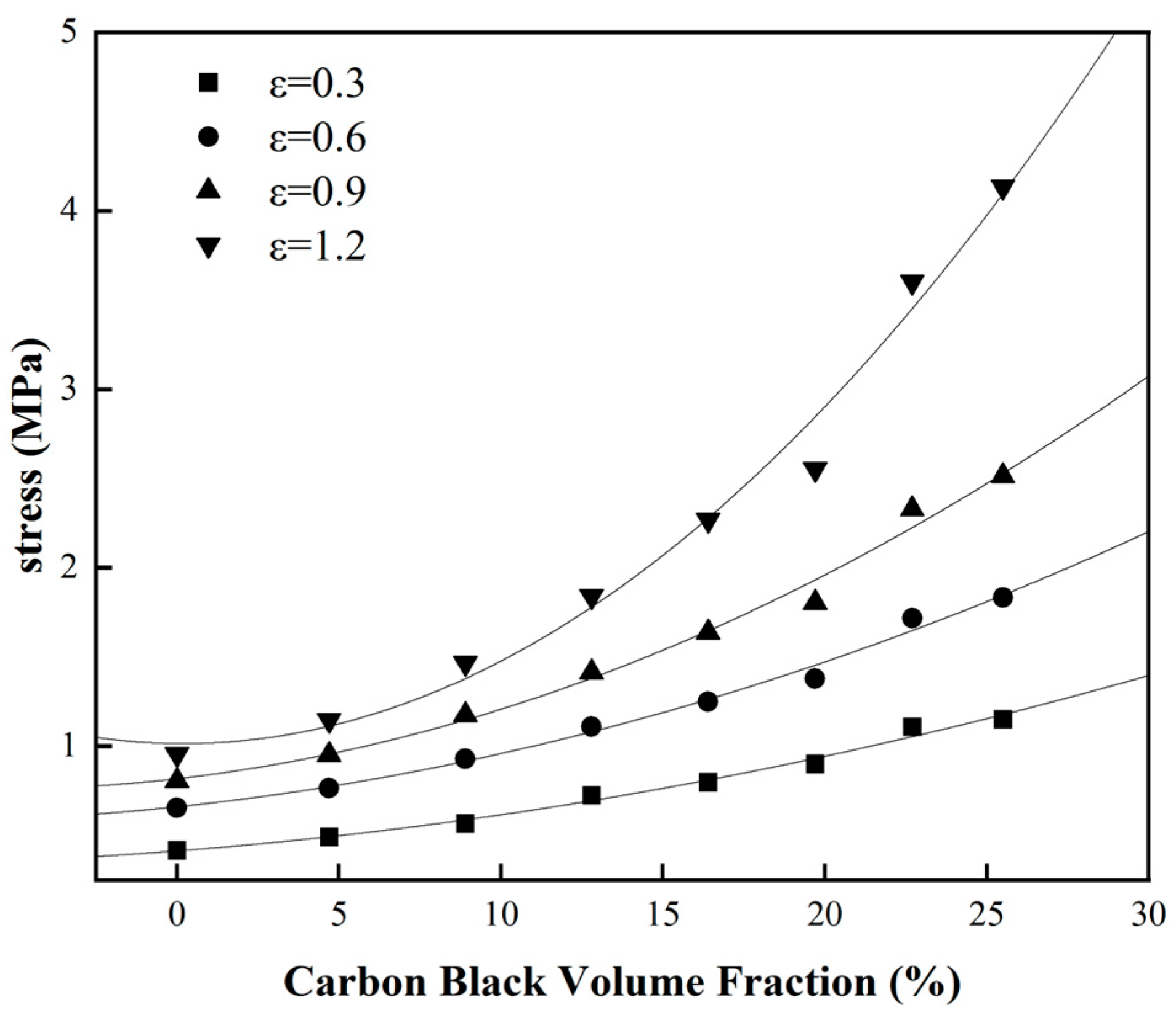
Figure 5. Stress amplification factor α versus strain of rubber with different CB filling ratios.

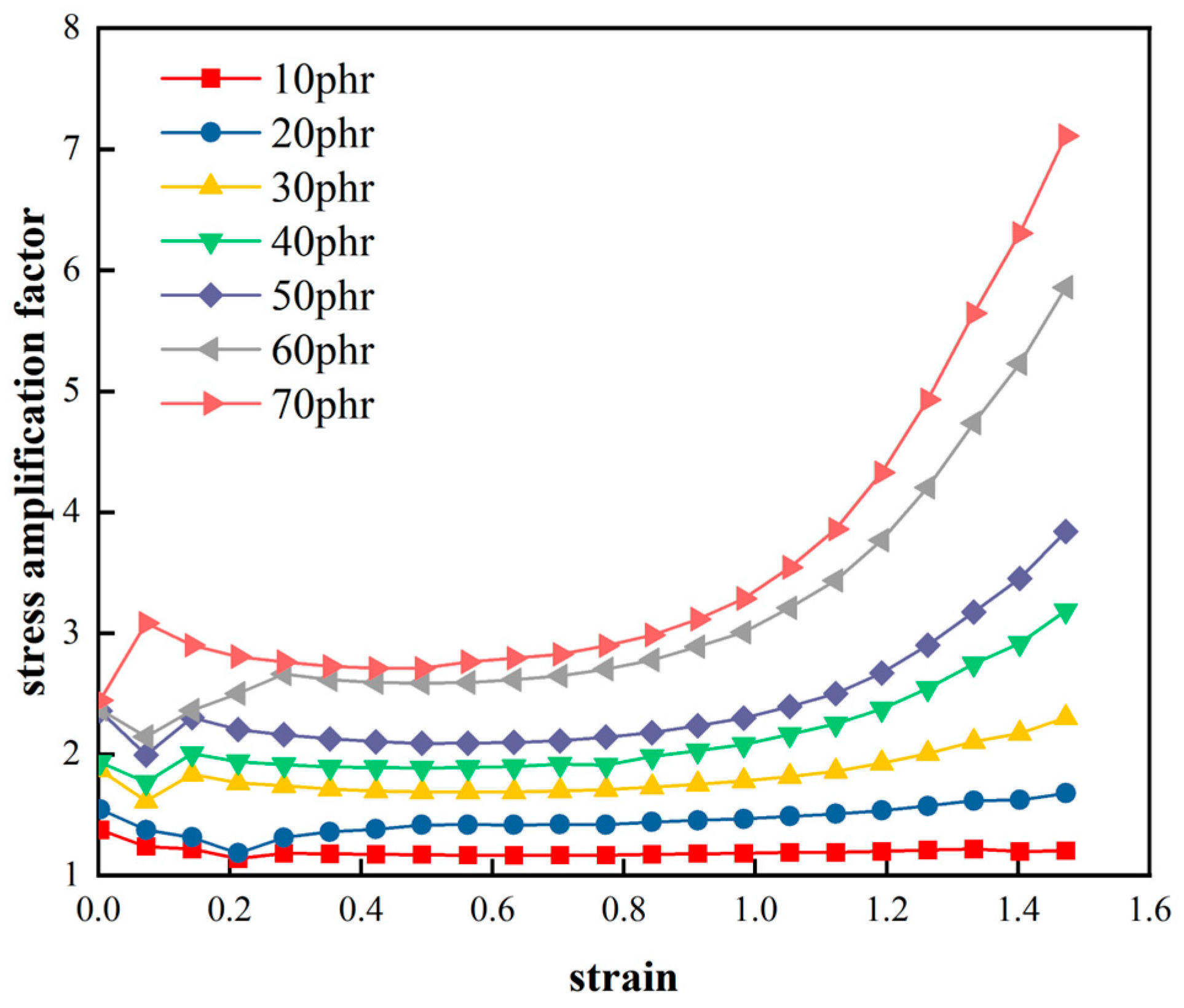
Figure 6. Fitting results of improved model for some rubbers with different CB fillings.

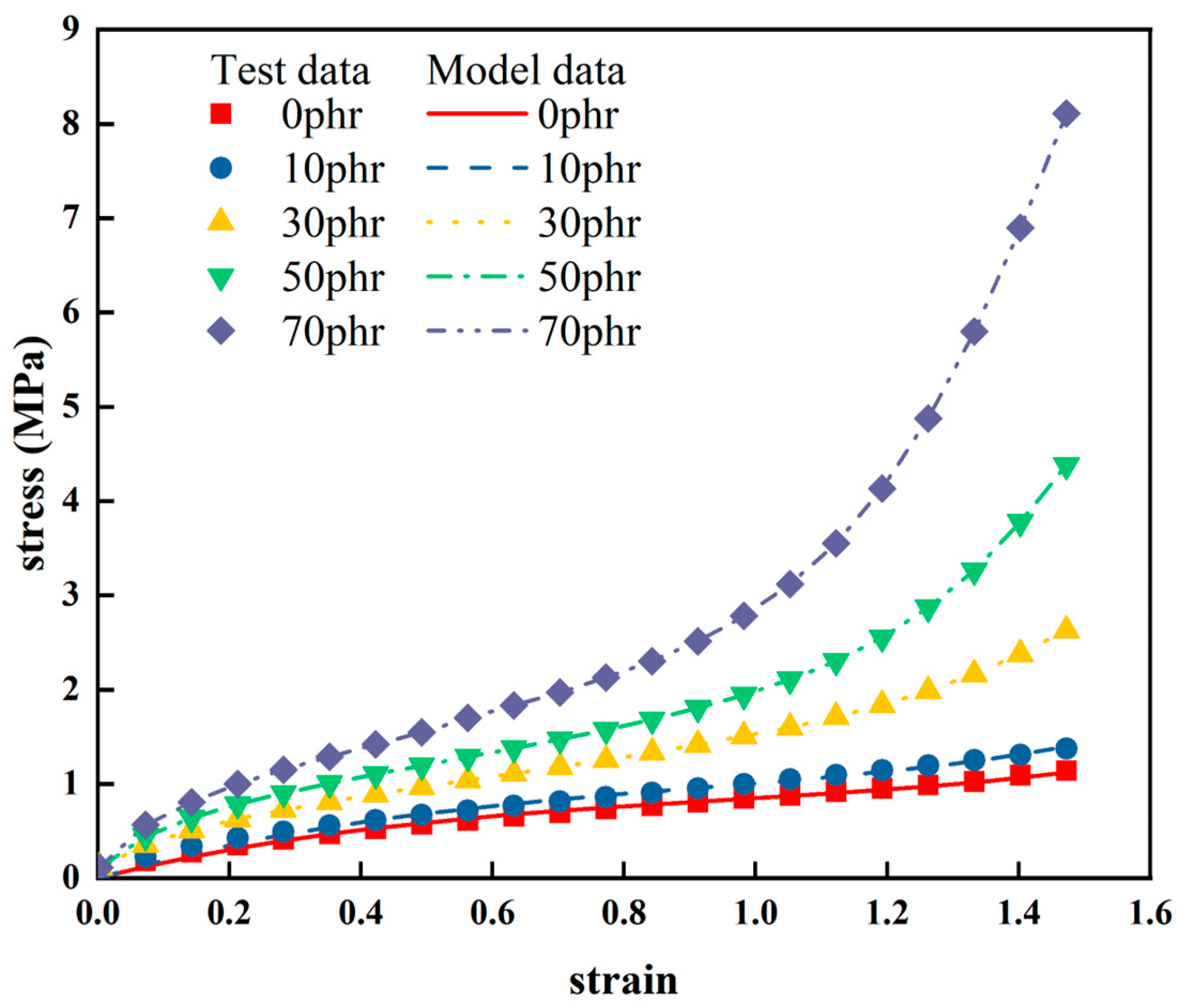
Figure 7. Variation trend of parameters of Yeoh model with CB volume fraction and the corresponding fitting curve.

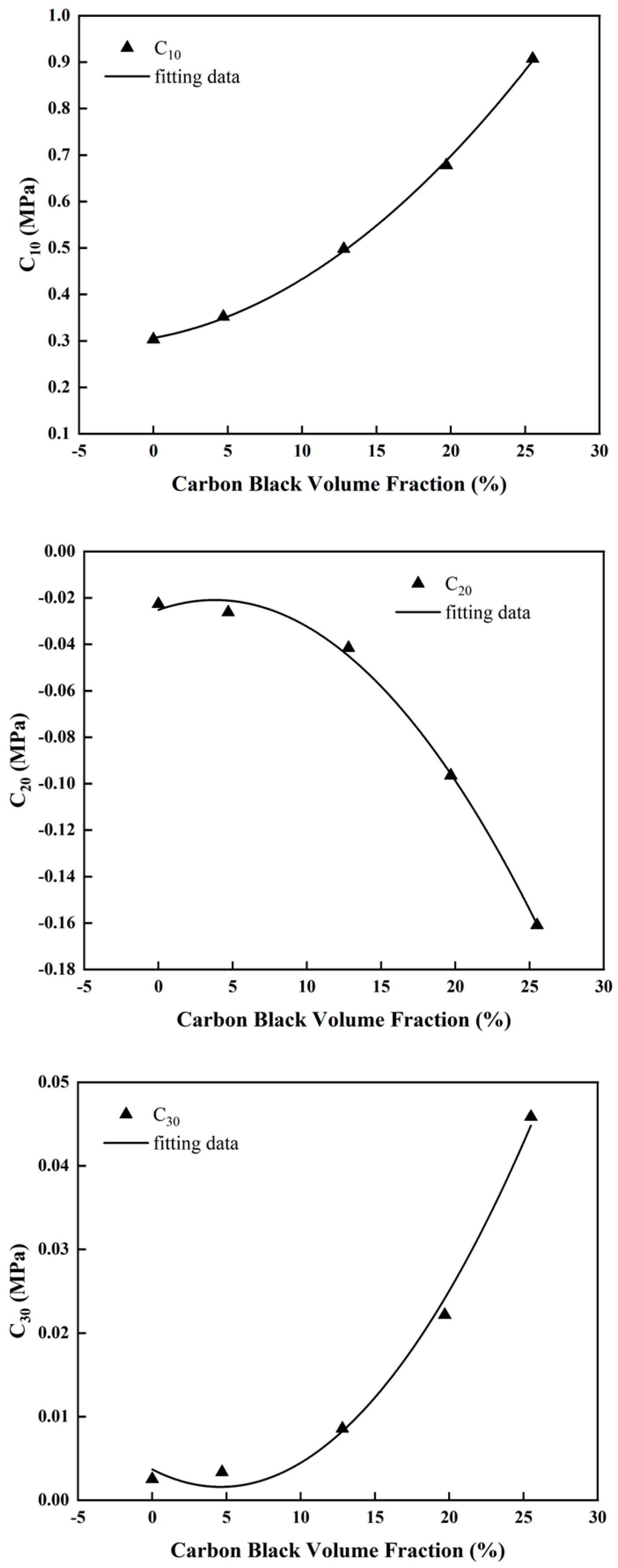
Figure 8. Predicted stress-strain curves by Yeoh model with apparent carbon black filling volume fraction.

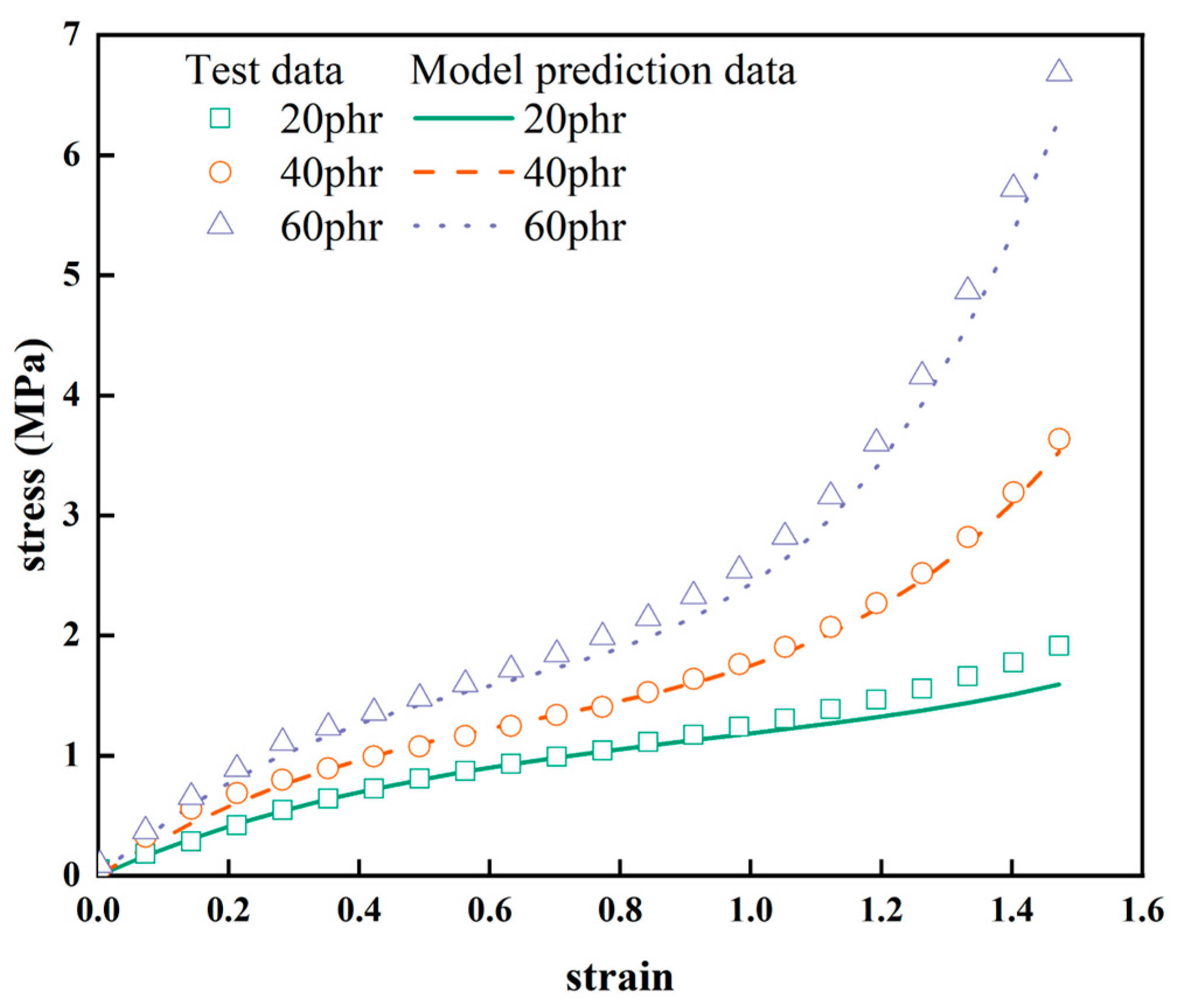
Figure 9. The variation trend of rubber stress with the volume fraction of CB under constant strain and the corresponding model prediction curve (ε is strain in the figure).

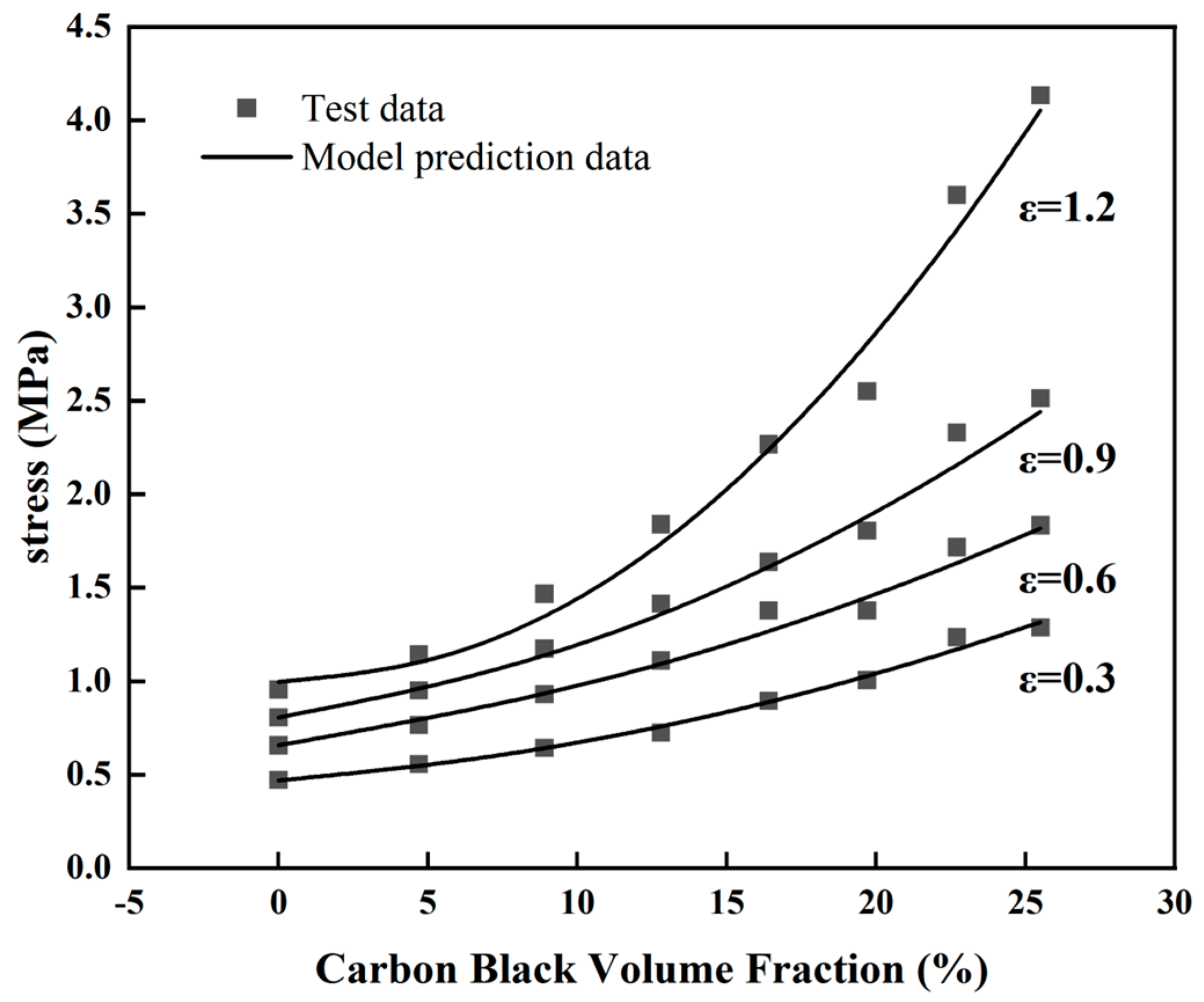
Table 1. Reagents used in the experiment.

Material name	Specification	Manufacturers
NR		Shandong Haoshun Chemical Co, Ltd. Shandong, China
CB	N220	Tianjin Zhengning New Materials Co, Ltd. Tianjin, China
Stearic acid		Industrial-grade
Zinc oxide		Industrial-grade
Sulfur		Industrial-grade
Accelerator NS		Industrial-grade
Antioxidant	4020	Industrial-grade

Table 2. Formulas and codes of eight kinds of carbon black filled vulcanized rubber (UNIT: PHR).

Specimen code	NR	CB N220	Zinc oxide	Stearic acid	Sulfur	Accelerator NS	Antioxidant 4020	Total	CB volume fraction (%)
NR-0	100	0	5	3	2	1	1.2	112.2	0
NR-1	100	10	5	3	2	1	1.2	122.2	4.7
NR-2	100	20	5	3	2	1	1.2	132.2	8.9
NR-3	100	30	5	3	2	1	1.2	142.2	12.8
NR-4	100	40	5	3	2	1	1.2	152.2	16.4
NR-5	100	50	5	3	2	1	1.2	162.2	19.7
NR-6	100	60	5	3	2	1	1.2	172.2	22.7
NR-7	100	70	5	3	2	1	1.2	182.2	25.5

Table 3. Model fitting parameters of rubber with different CB fillings.

CB（phr）	CB（vol.%）	C₁₀	C₂₀	C₃₀	R²
0	0	0.30318	-0.02264	0.00254	0.996
10	4.7	0.3521	-0.0262	0.00337	0.992
30	12.8	0.4981	-0.0415	0.008581	0.998
50	19.7	0.6781	-0.09644	0.02217	0.998
70	25.5	0.9073	-0.1609	0.04587	0.999

Table 4. Characterization parameters of volume fraction dependence of CB filling.

Model Parameter	Characterization parameters			R²
C₁₀	A₀=0.30622	A₁=0.00576	A₂=6.91E-04	0.99991
C₂₀	B₀=-0.02518	B₁=0.00225	B₂=-2.06E-04	0.99884
C30	C0=0.0037	C1=-9.12E-04	C2=9.90E-05	0.99642

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Carbon Black Filling Amount on the Hyper-elastic Mechanical Behavior of Rubber

Abstract

1. Introduction

2. Constitutive Models

3. Experimental Setup

3.1. Experimental Materials

3.2. Sample Preparation and Test

4. Experimental Result and Discussion

4.1. The uniaxial tensile tests results

4.2. Discussion

5. Conclusions

Author Contributions

Funding

References

MDPI Initiatives

Important Links

Subscribe