RCA-PixelCNN:Residual Causal Attention PixelCNN for Pulsar Candidate Image Lossless Compression

The study focuses on the crucial aspect of lossless compression for FAST pulsar search data. The deep generative model PixelCNN, stacking multiple masked convolutional layers, achieves neural network autoregressive modeling, making it one of the most excellent image density estimators. However, the local nature of convolutional networks causes PixelCNN to concentrate only on nearby information, neglecting important information at greater distances. Although deepening the network can broaden the receptive field, excessive depth can compromise model stability, leading to issues like gradient degradation. To address these challenges, the study combines causal attention modules with residual connections, proposing the Causal Residual Attention Module to enhance the PixelCNN model. This innovation not only resolves convergence problems arising from network deepening but also widens the receptive field. It effectively utilizes global features, particularly capturing vertically correlated features prominently present in subgraphs of candidates. This significantly enhances its capability to model pulsar data.In the experiments, the model is trained and validated using the HTRU1 dataset. The study compares the average negative log-likelihood score with baseline models like GMM, STM, and PixelCNN. The results demonstrate the superior performance of the our model over other models. Finally, the study introduces the practical compression encoding process by combining the proposed model with arithmetic coding.

Keywords:

Subject: Physical Sciences - Astronomy and Astrophysics

1. Introduction

The compression of astronomical big data has always been a significant research area, particularly with the activation of FAST (Five-hundred-meter Aperture Spherical radio Telescope), which employs 19 beams for observations. Following this, the daily data collection rate has reached 250TB per day. When considering 300 observation days in a year, the annual data collection amounts to 74PB, and this doesn’t even include other data storage needs. The frequent data interactions and the massive volume of data in storage make compression work exceptionally important.

Astronomical data is typically stored in the Fits (Flexible Image Transport System) file format [2] and the HDF5 (Hierarchical Data Format) format [3]. These standard file formats allow for traditional compression methods. For example, Fits files can be compressed using industrial standard algorithms such as Gzip, Rice, and HCOMPRESS. HDF5 offers compression algorithms like LZF, SZIP, and Shuffle. While these compression methods may not achieve high compression ratios, they do provide fast compression speeds.

The prerequisite for data compression is the presence of redundancy and correlation among the data. Data compression involves using fewer bits to represent frequently occurring information and more bits to represent less frequent information. In theory, any data distribution model can be subjected to lossless encoding, but the effectiveness of data compression depends on the quality of data distribution modeling. To gauge the quality of a model, it’s necessary to assess its ability to capture data correlations and minimize information entropy, which is reflected in negative log-likelihood scores.

Traditional density models like GMM (Gaussian Mixture Model) [4] and STM (Student’s T Mixture Model) [5] are capable of modeling prior distributions for low-dimensional and small-batch data but struggle with complex and high-dimensional data. With the advent of artificial intelligence methods, the use of generative models for modeling joint density distributions in complex and high-dimensional data density estimation has seen rapid development. Autoregressive models [8,9], variational autoencoders [10,11], flow models [12,13], and diffusion models [14,15] have all successfully modeled high-dimensional data. Entropy coding methods, such as arithmetic coders [16] and BB-ANS (Bits Back with Asymmetric Numeral Systems) systems [17,18,19,20], effectively combine density models for information encoding.

Research indicates that autoregressive models possess reliable density estimation capabilities. We consider using the autoregressive model PixelCNN (Pixel Convolutional Neural Networks) [9] in conjunction with an arithmetic coder to compress pulsar candidate image data. PixelCNN employs masked convolutional operations, which define network connectivity patterns and achieve localized autoregressive dependency modeling. By stacking multiple convolutional layers, PixelCNN extends the receptive field, extracting distant characteristic information to enhance its modeling capacity, showcasing strong modeling capabilities. However, the PixelCNN model has limitations. The local nature of convolutional operations constrains the receptive field. While stacking convolutional layers can expand the receptive field, these layers tend to focus on nearby information and neglect distant information. Research indicates that as network layers deepen, issues like gradient vanishing and model degradation can occur. Pulsar candidate images, with dimensions of 32x32, exhibit significant vertical correlations in time-phase subgraphs and frequency-phase subgraphs. Hence, utilizing global features for modeling pulsar candidate data becomes particularly crucial.

We propose a causal residual attention module that employs self-attention to overcome local limitations. The causal constraint of the self-attention module ensures autoregression, and the use of residual connections guarantees that deeper network layers do not degrade performance. The overall model architecture is similar to the PixelCNN model and is referred to as the RCA-PixelCNN model. The model is trained and validated on the HTRU1 dataset and fine-tuned on FAST’s pulsar candidate image data for practical compression tasks.The main innovations are as follows:

(1) Introducing the causal residual self-attention module to address the shortcomings of PixelCNN.

(2) In experiments, the proposed model is trained and validated using the HTRU1 dataset. The average negative log-likelihood values are compared with baseline models such as GMM, STM, and PixelCNN. The results indicate that the proposed model outperforms the others.

(3) Describing the practical compression encoding process by combining the proposed model with arithmetic coding.

2. Background

The FAST telescope’s search for pulsar signals generates a vast quantity of pulsar candidate images. Considering storage and network transmission requirements, it’s highly necessary to explore the compression of these pulsar candidate images using AI technology. Current AI methods in image compression are advancing rapidly. The typical approach involves utilizing generative models to model data distributions, followed by entropy coding.

The PixelCNN model, as an autoregressive model, maximizes the use of pixel dependencies. By leveraging contextual information from neighboring pixels to predict the current pixel’s probability density distribution, it demonstrates outstanding performance in data modeling. This makes it an excellent choice for lossless compression. Given its capacity to capture intricate pixel relationships, PixelCNN presents an ideal option for compressing pulsar candidate images, particularly due to their substantial volume, from both storage and network transmission perspectives.

The assumption for data compression is that there is redundancy in the data and correlation between the data. The density model for compression should be able to model the data distribution, capture correlation and obtain better log-likelihood results.

2.1. Pulsar Candidate Image

Pulsar signal search is a crucial scientific task in the sky survey observations conducted by the FAST telescope. Upon receiving pulsar signals, FAST employs search software (such as PRESTO) to undergo a series of data processing steps. For instance, pulse clipping is employed to reduce pulse interference, while dispersion removal mitigates dispersive delays. Subsequently, Fourier transformation is utilized to analyze the data in the frequency domain, thereby determining the signal period. Based on the established signal period, multiple received signals of the same period are combined to enhance the signal-to-noise ratio. The processed data is then transformed into image format, serving as samples of pulsar candidates [21]. Figure 1 illustrates pulsar candidate images processed by PRESTO.

Pulsar candidate diagnostic images are a fundamental basis for scientists to assess the significance of pulsars, and they also serve as a data source for machine learning methods used in pulsar selection. The labeled subfigures in Figure 1 include: (1)Pulsar profile curve subfigure,(2)Time-phase subfigure, (3)Frequency-phase subfigure, and (4)Period-dispersion subfigure. These subfigures provide essential reference features for astronomers when evaluating candidate samples.

With the activation of 19-beam observations and the utilization of parallel acceleration tools, FAST has significantly bolstered its search capabilities, resulting in the generation of a massive volume of pulsar candidate images. According to early statistics from the FAST data center, approximately 60,000 images are generated daily, accumulating to 60 GB per month and 800 GB per year. The exponential growth in the scale of astronomical scientific data stored in the form of image-based pulsar candidate images poses challenges in scientific data management.

Researching data compression techniques for compressing candidate images holds paramount importance. This research facilitates efficient data storage, accelerates network transmission and sharing, and contributes significantly to advancing astronomical scientific exploration and research.

2.2. PixelCNN

The autoregressive model decomposes the joint density distribution into a product of conditional distributions for multiple elements. Its formula is described as follows:

p (x) = \prod_{i = 0}^{N} p (x_{i} | x_{< i})

(1)

The autoregressive model demands a strict context structure, where for each element, only the preceding pixel information can be used to predict the current pixel’s density distribution. Models like MADE (Masked Autoregressive Model Estimator) [6], NADE (Neural Autoregressive Model Estimator) [7], and RANDE (Real Autoregressive Model Estimator) [6] implement this probability prediction function using neural networks. Image data contains spatial structural information, and simply flattening images into 1D sequences can lead to a significant loss of spatial information.

Hence, to address this, Oord et al. (2016) [8] introduced the deep generative model PixelCNN. It employs convolutional neural networks to capture structural information and models the pixel probability distribution of natural images in a z-scan order. To achieve autoregressive dependencies, Oord defined two types of masked convolutional layers, as illustrated in Figure 2. The convolution kernel of a 2D convolutional layer is multiplied by a mask matrix, which constrains network connectivity relationships, ensuring compliance with autoregressive requirements.

PixelCNN leverages the advantages of convolutional neural network operations. Convolutional layers are efficient at extracting spatially correlated information and can be parallelized for processing. This ensures both model training and data processing speed.

However, PixelCNN also has some issues and limitations. The inherent characteristics of convolutional networks determine that PixelCNN can model local correlated information effectively, yet it struggles to efficiently utilize dependencies over longer distances. Research indicates that enlarging the receptive field is crucial for enhancing model performance. To achieve this, PixelCNN stacks multiple masked convolutional layers. However, this approach also presents the following problems:

(1) Stacking multiple network layers increases the model’s parameters. As the network depth increases, the convergence speed of the model slows down, and it can even lead to a decrease in model performance or instability.

(2) Despite enlarging the receptive field, the local nature of CNNs makes the model focus more on neighboring information, often neglecting crucial information from distant areas.

3. Our Methods

To expand the receptive field and effectively utilize global image information, we introduce a self-attention module and residual connections to the PixelCNN framework, creating a novel network building block known as the causal residual self-attention module. This new model is referred to as the RCA-PixelCNN. In this section, we provide a comprehensive overview of the proposed model’s architecture, with a primary focus on a detailed analysis of the introduced causal residual self-attention module. We discuss the selected data distribution entropy model and present the integration of the proposed model with Arithmetic Coding, outlining a practical compression encoding process.

3.1. Network Architecture

As depicted in Figure 3, the proposed model primarily comprises four stages: feature extraction, residual learning, causal residual self-attention learning, and adjustment of output feature channels using 1x1 causal convolutions. Among these, the causal residual self-attention module is detailed in the orange section of the diagram. The dashed lines represent the causal attention blocks. Subsequently, masked causal convolution blocks and ReLU activation layers are stacked, and the branch outputs are connected to the input via residual connections.

3.2. Residual-Causal-Attention Block

To address the issues present in PixelCNN, we consider two approaches: residual neural networks and self-attention networks.To tackle the problem of gradient vanishing and gradient explosion caused by deep network layers, Kaiming et al. [23] introduced residual neural networks. These networks incorporate residual learning branches into the main network using skip connections. The main network approximates the target, while the residual branch learns the difference between the main network and the target. This ensures stable performance even with increased network depth. Residual connections expand the receptive field, but convolutional networks still tend to emphasize nearby information over distant information.On the other hand, self-attention models [24] utilize a square matrix of the same length as the input data sequence to store the importance of correlations between input elements. This breaks away from the convolutional bias, allowing access to long-range information indiscriminately. However, self-attention modules access all elements of the input, rather than just the pixels preceding the current pixel in the spatial position. This limitation prevents direct utilization of self-attention modules for autoregressive modeling.

Xi Chen [25] analyzed the implementation process of self-attention and introduced causal attention modules by setting specific mask matrices. This allows networks containing self-attention modules to satisfy the autoregressive property. According to a certain autoregressive order, a series of 2D feature map vectors are named as

y_{1}, y_{2}, \dots, y_{N}

. The autoregressive mapping relationship is as follows:

z_{i} = \sum_{i < j} p_{i j} f_{v a l u e} (y_{j})

(2)

p_{i} = s o f t \max ([f_{k e y} {(y_{1})}^{T} f_{q u e r y} (y_{i}), \dots, f_{k e y} {(y_{i - 1})}^{T} f_{q u e r y} (y_{i})])

(3)

The attention distribution

p_{i}

corresponds to the dependency level of all features of feature

y_{i}

. Each conditional probability is established based on accessing all pixels within the attention-constrained context

\sum_{j < i}^{} p_{i j} = 1

. As evident from Equation (2), to achieve autoregressive conditions, it is sufficient to constrain the summation terms during the summation process.

As shown in Figure 4, this is our proposed residual causal attention block. The dashed box represents the causal attention module [12], which carries essential information in the main path of the network. Below it, there are three stacked masked convolutional layers, with ReLU layers and BatchNorm layers in between. The first convolutional layer has a kernel size of

1 \times 1

, and the number of channels decreases by a factor as indicated by the downward-pointing arrow in Figure 4. The second convolutional layer has a kernel size of

3 \times 3

and maintains the same number of channels. The third convolutional layer has a kernel size of and restores the input’s original number of channels. During the process of information transmission within the network, the feature map dimensions remain unchanged. The attention module captures the importance of positional information, while the residual connection preserves detailed information in the features. Both the causal attention module and the residual branch impose connectivity constraints, ensuring the extracted information maintains autoregressive properties. The attention module can also employ a multi-head mechanism to enhance the weighting of importance. The residual causal attention module is an independent network module that can be used as a plugin within any part of an existing autoregressive network.

3.3. Entropy model

Compression encoding requires the encodable information to be discrete, corresponding to a discrete density model. Most neural networks utilize continuous models for image modeling, wherein data is first quantized inversely to learn a continuous model. Encoding with such a model involves quantizing the variables first and discretizing the learned model, which is a complex process. However, we directly model discrete pixel values; each pixel is an 8-bit integer

x \in {0, \dots, 255}

, and the pixel density model becomes a 256-way categrical distribution. For example, when we input

N \times N

image data into the model and process it through a series of network layers, we obtain prediction features with a final size of

N \times N \times 1 \times 256

. The last dimension indicates the probability of the 256 possible values for each pixel. Therefore, a softmax operation is applied to the prediction features.

s o f t \max (z_{i}) = \frac{\exp (z_{i})}{\sum_{j = 0}^{N} \exp (z_{j})}

(4)

Normalizing the last dimension of the model’s output ensures that the sum of the probability distribution is equal to 1,

\sum_{i = 0}^{255} p (z_{i}) = 1

,guaranteeing that the model’s output in this dimension represents a valid probability distribution.

The model used for data compression is denoted as

q

, while the actual distribution of the data is represented by

p

. The training objective is to minimize the distance between the model

q

and the data distribution

p

, which can be expressed as:

\begin{array}{l} D_{K L} (q (x) & | | p (x)) = p (x) (\log q (x) - \log p (x)) \\ = p (x) \log q (x) - p \log p (x) \\ = H (q, p) - H (p) \end{array}

(5)

So,the cross-entropy is given by:

H (q, p) = H (p) + D_{K L} (q | | p)

(6)

H (p)

represents the entropy of the data, and when the data is given, it remains constant. Therefore, minimizing the KL divergence is equivalent to minimizing the cross-entropy. Cross-entropy

H (q, p)

represents the amount of information required to encode data using the model and is equal to the codelength. Thus, we use cross-entropy as the training objective for the compression model. In the encoding process, the autoregressive model estimates data density, and this estimation can be computed in parallel all at once. In the decoding process, on the other hand, pixel probabilities are estimated step by step during decoding. As a result, autoregressive algorithms compress data quickly, and while decompression is slower, they offer good compression performance.

3.4. Arithmetic Coding

The most commonly used entropy coding algorithm employed in this paper is the arithmetic coding. When encoding each pixel in the image, it is necessary to know the probability distribution of the pixels. The image’s pixel sequence is then transformed into a binary sequence. Based on the size of the probabilities, pixels are assigned different numbers of coding bits. The Arithmetic Coder assigns fewer bits to pixels with higher probabilities and more bits to pixels with lower probabilities. Another reason for choosing Arithmetic Coder is its progressive coding approach, which aligns well with our progressive probability model. Based on the pixels that have already been encoded, the model predicts the probabilities of pixels to be encoded next, resulting in higher compression efficiency. The decoding process follows a similar pattern. Initially, pixels that were encoded earlier are decoded, and then subsequent pixels are decoded conditionally one by one.

4. Experiments

In this section, we first introduce the dataset of pulsar candidate diagnostic images. We also present the baseline models used for comparison against the RCA-PixelCNN model, including Gaussian Mixture Model (GMM), Student’s t Mixture Model (STM), and the PixelCNN Base Model. Subsequently, we conduct two sets of experiments. In the first set of experiments, we compare the modeling performance of the RCA-PixelCNN model against GMM, STM, and PixelCNN Base Model. We evaluate the average negative log-likelihood values. In the second set of experiments, we analyze the proposed causal residual self-attention module through various erosion experiments, investigating different settings.

4.1. Datasets

(1) The HTRU1 (High Time Resolution Universe Survey) dataset originates from observations conducted by the Parkes Telescope in Australia using multiple beams (13 beams). The central observing frequency is 1352MHz, and each beam records a bandwidth of 400MHz, with the actual data usage being in the middle 340MHz bandwidth. This dataset comprises 1196 known pulsars (positive samples) from 512 distinct sources and 89996 non-pulsar candidates (negative samples).Within the HTRU1 dataset’s HTRUS subset, there are 60000 binary classification images sized 32x32. These images include both known pulsars and non-pulsar candidates. Each image consists of two channels, analogous to the RGB channels in natural images, although the content of each channel differs from that of natural images. Channel 1 represents the period-dispersion subgraph, channel 2 corresponds to the frequency-phase subgraph, and channel 3 represents the time-phase subgraph. The left four columns in Figure 8 depict the positive samples from the HTRU1 dataset, where the first row shows the period-dispersion graph, the second row displays the frequency-phase graph, and the third row depicts the time-phase graph. In this study, the HTRU1 dataset is utilized for training, testing, and validating the models. The baseline models, including GMM and STM, require the data to be in the form of 1D tensors. Therefore, the 2D images need to be reshaped into 1D sequences before being used with these models. On the other hand, both the PixelCNN baseline model and the RCA-PixelCNN model are capable of directly processing structured image data without the need for reshaping.

(2) FAST Pulse Candidate Data: The FAST pulse candidate images are obtained from 19-beam observations using the PRESTO software processing. These image-formatted pulse candidate data files are sourced from the early data center of FAST and are intended for internal use. In practical applications, the model is initially trained using the HTRU1 dataset. Subsequently, transfer learning is applied to fine-tune the model parameters on the FAST data, ensuring the model’s better suitability for the specific application scenarios of FAST.

4.2. Baseline Models

(1) GMM: The Gaussian Mixture Model, which consists of multiple Gaussian distributions as its components. Each image is associated with a Gaussian distribution, making it suitable for data spaces with multiple central distributions. As long as the model has a sufficient number of components, it can approximate any complex distribution.

(2) STM: The Student’s t Mixture Model, similar to the GMM, employs Student’s t-distribution as its components. It is particularly well-suited for modeling data distributions with heavy tails, as seen in natural images.

(3) PixelCNN Base Model: This is a typical autoregressive model that works well for data with spatial structure. By stacking multiple masked convolutional layers, the receptive field can be expanded. In this context, the baseline model includes 1 type-A masked convolutional layer with a kernel size of 7x7, 2 type-B masked convolutional layers with kernel sizes of 3x3, and 1 type-B masked convolutional layer with a kernel size of 1x1.

4.3. Results and Analysis

4.3.1. Experiment setting and Results

The model in this paper was implemented using the PyTorch framework on an NVIDIA GeForce GTX 1080 GPU. The organizational structure of the model is as follows: The first layer is a 7x7 convolutional layer with a stride of 1 and padding of 3, which is a type A masked convolutional layer. The second layer consists of four type B Masked Conv2d+BN+ReLU residual masked convolutional layers. This is followed by a segment that includes three Res-CausalAttention blocks. The final layer is a 1x1 convolutional layer with a type B mask, aimed at converting the number of channels to the target channel quantity. The optimizer used is Adam, with an initial learning rate of 0.01 and beta parameters of 0.9 and 0.99.

In order to make a fair comparison of the density modeling abilities between RCA- PixelCNN and GMM (Gaussian Mixture Model) as well as STM (Student’s t Mixture Model), the evaluation metric used is the average negative log likelihood. Both training and testing data are sourced from the HTRU1 dataset. Our RCA-PixelCNN model directly models 2-D image matrices and 3D data volumes, whereas GMM and STM can only model 1D data sequences. Since the HTRU1 images are of size 64x64, they are flattened to 1D, resulting in a dimensionality of 4096. Due to the high dimensionality, convergence of models like GMM and STM becomes challenging. To address this issue, for the training set, we randomly extract 800,000 8x8 image patches from the training data. Through model selection experiments, we determine the optimal number of Mixture Components for GMM and STM to be 8. To avoid overfitting or underfitting, the models are trained on the training set and their performance in terms of average negative log likelihood is evaluated using the test set.As shown in Table 1, we compare the experimental results of RCA-PixelCNN with other models on the HTRU1 test dataset. The average negative log likelihood score for the Mixtures of Gaussian model is 3.51 bits per pixel (bpp), which performs well in fitting natural images. However, the Mixtures of Student T model, which is typically better suited for long-tailed distributions, performs worse than GMM, suggesting that the candidate pulse images are not following a long-tailed distribution. The PixelCNN model achieves an average negative log likelihood score of 3.11 bpp, indicating the best performance among the compared models. This highlights the superior modeling capability of neural network-based methods compared to traditional approaches. Within the PixelCNN framework, the RCA-PixelCNN model with the added Res-Causal-Attention module exhibits the best performance, outperforming the standard PixelCNN by 0.33 bpp. This demonstrates that deep learning-based modeling methods outperform traditional data distribution modeling approaches, and the inclusion of the Res-Causal-Attention module further enhances the performance of PixelCNN.

In Figure 5, we present the training curves for the PixelCNN Base Model and the RCA-PixelCNN. It is evident that the training speed of our model is slower compared to the baseline PixelCNN model. The training time per batch is approximately 10 times that of the baseline model. Additionally, our model requires higher memory resources, and due to memory limitations, the batch size for training is smaller than that of the baseline model. This can lead to greater fluctuations in the convergence during training. After adjusting the learning rate and performing subsequent training epochs, the convergence gradually stabilizes. The experimental results demonstrate that the stability and performance of our RCA-PixelCNN model significantly outperform the baseline PixelCNN model.

4.3.2. Practical coding Algorithm

In the actual data compression process, we combine the proposed RCA-PixelCNN model with Arithmetic Coding to achieve efficient data compression. The specific process is as follows:

Model Training: Firstly, we train the RCA-PixelCNN model using the HTRU1 dataset to obtain a model that accurately models the data distribution.

Density estimation:Using the trained RCA-PixelCNN model, we input the data to be compressed into the model. The model predicts the probability distribution of each pixel based on its density distribution model.

Encoding:we use the Arithmetic Coding algorithm for actual compression encoding. This algorithm maps the pixel sequence to a compact binary encoding based on the predicted probability distribution from the model. High probability pixels are assigned fewer bits, while low probability pixels are assigned more bits.

Decoding:we predict the probability distribution of each pixel using the trained model and previous decoded pixels. Then, we use the Arithmetic Coding algorithm to reverse the encoding process, recovering the original pixel sequence from the binary encoding.

In Table 2, we provide detailed pseudocode descriptions of the arithmetic encoding and decoding processes based on the RCA-PixelCNN.

4.3.3. Ablation Expermiments

In order to test the impact of specific module modifications on the overall model, we conducted a series of erosion experiments and analyses. Firstly, we compared the performance difference between the causally connected attention module without residual connections and the existing combination method. Secondly, we examined the effect of stacking different numbers of Res-Causal-Attention modules in the network on the overall model. Through these experiments, our aim was to gain a deeper understanding of how these specific module modifications affect the model’s performance.

(1) skip connection

To validate the impact of residual connections on the model, and without loss of generality, we retained the Causal-Attention part of a module and removed the Resnet Connection within the module. All connection layers were placed in the main network, maintaining the same depth and parameter count as the existing model. The comparison of training curves between the model with severed residual connections and the existing model is shown in Figure 6a. Our model achieved a negative log-likelihood score of 2.82 bpp, while the model without residual connections achieved a score of 2.99 bpp. The performance difference is 0.17 bpp. This indicates that residual connections have a significant impact on model performance. The sub-images of pulsar candidates contain a substantial amount of random noise, and the pulsar signal features exhibit subtle differences from noise, highlighting the importance of preserving details through learning.

(2) Causal-Attention

In Section 3.2, it was mentioned that the attention module can break the limit of the receptive field size in convolutional networks. It extracts information from different positions with varying degrees of attention, and computes a weighted sum of contextual information as the predicted probability distribution for the current pixel. To evaluate the role of the self-attention module in the entire network model and understand its effect on improving model performance, we conducted experiments by removing the attention module and comparing it with the existing model.

The results are shown in Figure 6(b). The model without the attention module achieved a log-likelihood value that is 0.4 bits per pixel lower than our model. The convergence speed of the network is slower, but the memory consumption is slightly reduced. This is because the test dataset, HTRU1 images, has a size of 32x32 pixels, which is of medium size. The effect of the attention module is more pronounced on larger images, and overall performance improvement is moderate. However, in practical scenarios, the images of FAST pulsar candidates that need to be compressed are larger, indicating that the impact of the attention module could be more substantial in those cases.

(3) numbers of Res-Causal-Attention

The Res-Causal-Attention module was added as a plugin module to the neural network, and different numbers of Res-Causal-Attention modules were set. The comparison of negative log-likelihood scores is shown in Table 3. In the PixelCNN network, adding 1 Res-Causal-Attention module improved the performance by 0.29 bpp, and adding 2 Res-Causal-Attention modules improved the performance by 0.33 bpp. Due to the memory-intensive nature of the attention mechanism in the Res-Causal-Attention module, and considering the limitations of the experimental environment, we stacked up to 2 Res-Causal-Attention blocks.

The experiments demonstrate that the Res-Causal-Attention module significantly improves model performance, and as the number of modules increases, the model performance continues to improve. In the experiments, we attempted to replace self-attention with multi-head self-attention and found that the multi-head mechanism also effectively enhances the model. The multi-head mechanism essentially increases the number of attention channels, achieving a similar effect as deep stacking. The significant impact of the Attention module can also be explained by the characteristics of the pulsar sub-images. For instance, the sub-integration phase image, which is a folded representation of pulsar data, exhibits clear overlapping and similarity regions in positive samples. The expanded receptive field of the convolution operation makes effective use of the vertical pixel correlations in this scenario.

4.4. Generated Positive Pulsar Candidate Samples

Pulsar observation data suffer from severe class imbalance in classification tasks. As of now, there are over 3000 confirmed pulsars, while the number of daily pulsar candidate observations reaches hundreds of thousands. Candidate selection is a crucial aspect of pulsar search efforts. Taking the HTRU1 dataset as an example, the positive-negative sample ratio is 1194:58806, with positive samples accounting for only 2% of the total. Machine learning is employed to sift through pulsar candidates, and addressing class imbalance is a primary concern21-22.

Using a class-label conditioned PixelCNN model can generate the required positive samples. We encode the class information using one-hot encoding and linearly map it to features of the same shape as the images. The label features are input to each layer. The three sub-images of each synthetic HTRU1 sample describe the same candidate’s information, and the three-channel sub-images are interdependent. As shown in the rightmost four columns of Figure 7, the positive samples generated by the class-conditioned PixelCNN model are displayed. The three rows of sub-image correspond to period-dispersion, time-phase, and frequency-phase representations. It’s evident that the generated positive samples exhibit distinct pulsar characteristics.

5. Concolusion and Discussion

In this study, we proposed an RCA-PixelCNN model with the aim of addressing the compression issue of pulsar candidate images. To fully leverage the spatial structural information in images, we introduced the concept of causal residual self-attention modules, which employ a self-attention mechanism to capture long-range relationships between pixels, thereby enhancing the modeling capability of the model. We validated our model using the HTRU1 dataset through experiments and compared it with other models, demonstrating that our model outperforms others in terms of average negative log-likelihood performance.

Through a series of ablation experiments, we conducted an in-depth analysis of the impact of the causal residual self-attention modules on model performance and the significance of residual connections. The results revealed that the inclusion of the causal residual self-attention modules significantly improved model performance, with the residual connections playing a pivotal role, especially when dealing with pulsar sub-images containing noise.

Furthermore, we addressed the issue of class imbalance. For pulsar candidate images, we employed a class-conditioned PixelCNN model to generate positive samples. By learning class information, we successfully generated images with distinct pulsar features.

Funding

This research was supported by National Natural Science Foundation of China (U1831131, U1631132, U1731238, 11743002); Chinese Academy Sciences,Astronomy Research Center FAST Major Achievements Cultivation Project (FAST [2019sr04]); National Key Research and Development Plan (2017YFA0402600); Strategic Pilot Science and Technology Project of Chinese Academy of Science (Category B) (XDB23000000); Guizhou Province Science and Technology Support General Project (QianKeHe [2023] General 333).

References

Wang, S.; Zhu, W.-W.; Li, D.; Pan, Z.-C.; Wang, P.; Cordes, J.M.; Chatterjee, S.; Yao, J.-M.; Qian, L.; Yue, Y.-L.; et al. An Arecibo follow-up study of seven pulsars discovered by Five-hundred-meter Aperture Spherical radio Telescope (FAST). Res. Astron. Astrophys. 2021, 21, 251. [Google Scholar] [CrossRef]
Pence, W. (1999). CFITSIO, v2. 0: a new full-featured data interface. In Astronomical Data Analysis Software and Systems VIII (Vol. 172, p. 487).
Cosemans, A., Batelaan, O., Louwyck, A., & Lermytte, J. (2012, April). Hierarchical data format (HDF5) for Modflow, Modpath and ZoneBudget. In EGU General Assembly Conference Abstracts (p. 8028).
Zoran, D.; Weiss, Y. Natural images, Gaussian mixtures and dead leaves. Advances in Neural Information Processing Systems 2012, 25. [Google Scholar]
van den Oord, A.; Schrauwen, B. The student-t mixture as a natural image patch prior with application to image compression. J. Mach. Learn. Res. 2014, 15, 2061–2086. [Google Scholar]
M., Gregor, K., Murray, I., & Larochelle, H. (2015, June). Made: Masked autoencoder for distribution estimation. In International conference on machine learning (pp. 881-889). PMLR.
Uria, B.; Côté, M. A.; Gregor, K.; Murray, I.; Larochelle, H. Neural autoregressive distribution estimation. The Journal of Machine Learning Research 2016, 17, 7184–7220. [Google Scholar]
Van Den Oord, A., Kalchbrenner, N., & Kavukcuoglu, K. (2016, June). Pixel recurrent neural networks. In International conference on machine learning (pp. 1747-1756). PMLR.
Van den Oord, A.; Kalchbrenner, N.; Espeholt, L.; Vinyals, O.; Graves, A. Conditional image generation with pixelcnn decoders. Advances in neural information processing systems 2016, 29. [Google Scholar]
Sønderby, C. K.; Raiko, T.; Maaløe, L.; Sønderby, S. K.; Winther, O. Ladder variational autoencoders. Advances in neural information processing systems 2016, 29. [Google Scholar]
Zhang, Z., Sun, L., Zheng, Z., & Li, Q. (2020, October). Disentangling the spatial structure and style in conditional vae. In 2020 IEEE International Conference on Image Processing (ICIP) (pp. 1626-1630). IEEE.
Levy, S.; Laloy, E.; Linde, N. Variational Bayesian inference with complex geostatistical priors using inverse autoregressive flows. Comput. Geosci. 2023, 171, 105263. [Google Scholar] [CrossRef]
Papamakarios, G.; Nalisnick, E.; Rezende, D. J.; Mohamed, S.; Lakshminarayanan, B. Normalizing flows for probabilistic modeling and inference. The Journal of Machine Learning Research 2021, 22(1), 2617–2680. [Google Scholar]
Kingma, D.; Salimans, T.; Poole, B.; Ho, J. Variational diffusion models. Advances in neural information processing systems 2021, 34, 21696–21707. [Google Scholar]
Huang, C. W.; Lim, J. H.; Courville, A. C. A variational perspective on diffusion-based generative models and score matching. Advances in Neural Information Processing Systems 2021, 34, 22863–22876. [Google Scholar]
Ezhilarasu, P.; Krishnaraj, N.; Dhiyanesh, B. Arithmetic Coding for Lossless Data Compression–A Review. International Journal of Computer Science Trends and Technology 2015, 3. [Google Scholar]
Townsend, J.; Bird, T.; Barber, D. Practical lossless compression with latent variables using bits back coding. arXiv 2019, arXiv:1901.04866. [Google Scholar]
Kingma, F., Abbeel, P., & Ho, J. (2019, May). Bit-swap: Recursive bits-back coding for lossless compression with hierarchical latent variables. In International Conference on Machine Learning (pp. 3408-3417). PMLR.
Townsend, J.; Bird, T.; Kunze, J.; Barber, D. Hilloc: Lossless image compression with hierarchical latent variable models. arXiv 2019, arXiv:1912.09953. [Google Scholar]
Ho, J.; Lohn, E.; Abbeel, P. Compression with flows via local bits-back coding. Advances in Neural Information Processing Systems 2019, 32. [Google Scholar]
Guo, P.; Duan, F.; Wang, P.; Yao, Y.; Yin, Q.; Xin, X. Pulsar candidate identification with artificial intelligence techniques. arXiv 2017, arXiv:1711.10339. [Google Scholar]
Wang, Y.-C.; Li, M.-T.; Pan, Z.-C.; Zheng, J.-H. Pulsar candidate classification with deep convolutional neural networks. Res. Astron. Astrophys. 2019, 19, 133. [Google Scholar] [CrossRef]
He, K., Zhang, X., Ren, S., & Sun, J. (2016). Deep residual learning for image recognition. In Proceedings of the IEEE conference on computer vision and pattern recognition (pp. 770-778).
Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A. N.; Polosukhin, I. Attention is all you need. Advances in neural information processing systems 2017, 30. [Google Scholar]
Chen, X., Mishra, N., Rohaninejad, M., & Abbeel, P. (2018, July). Pixelsnail: An improved autoregressive generative model. In International Conference on Machine Learning (pp. 864-872). PMLR.

Figure 1. Sample images of pulsar candidate bodies derived from FAST observations and processed using the PRESTO software.

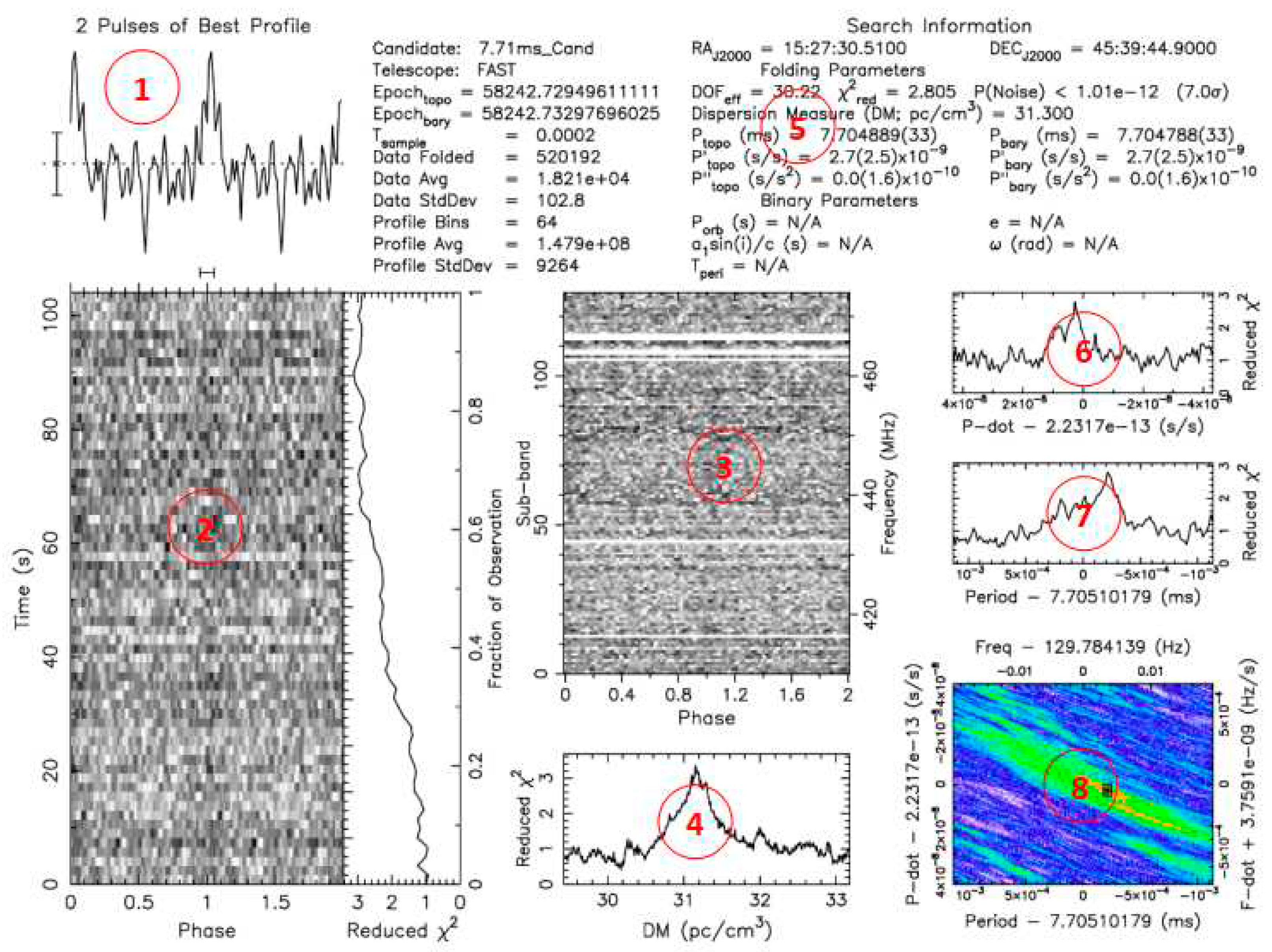
Figure 2. Two Types of Mask Matrices in PixelCNN.

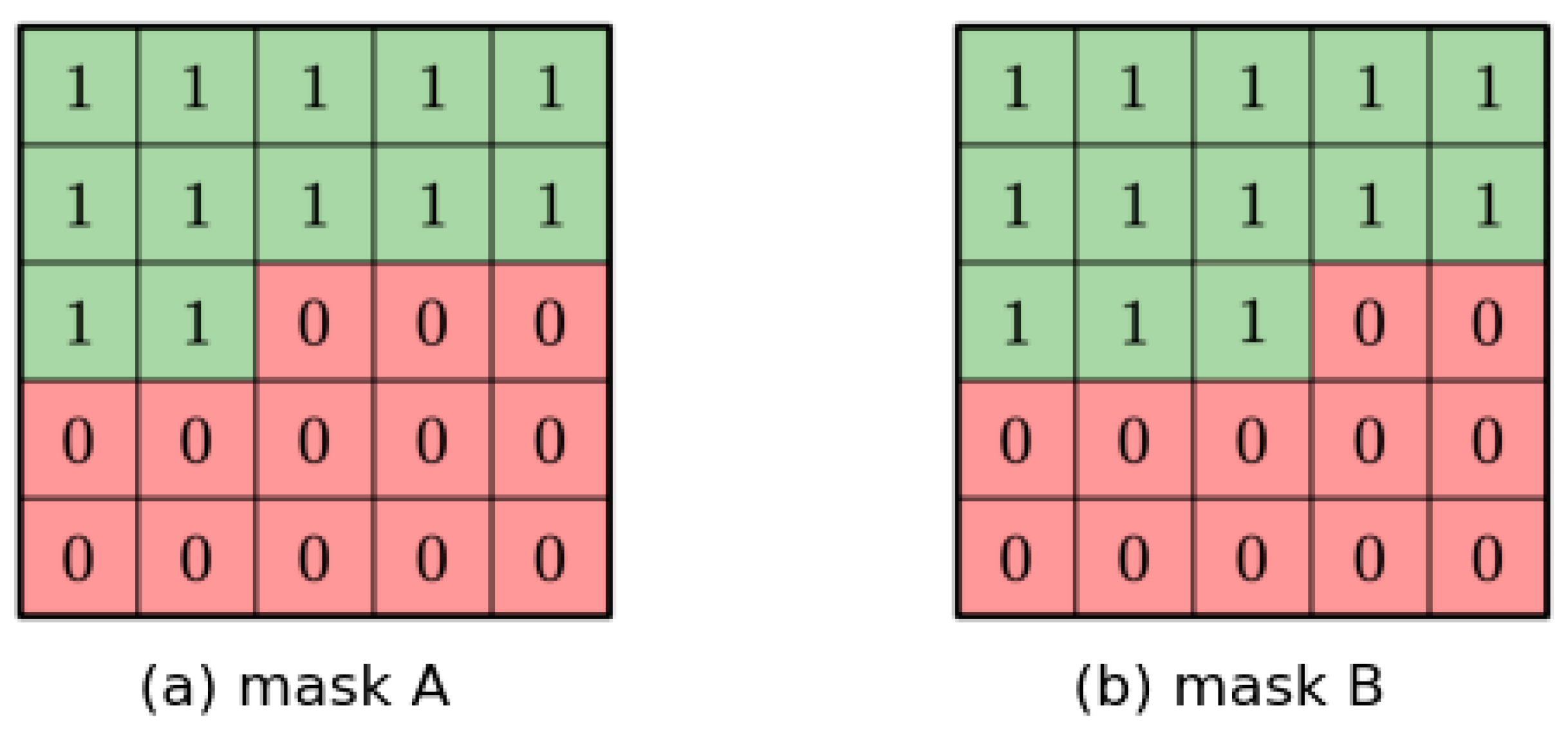
Figure 3. The network architecure of RCA-PixelCNN model.

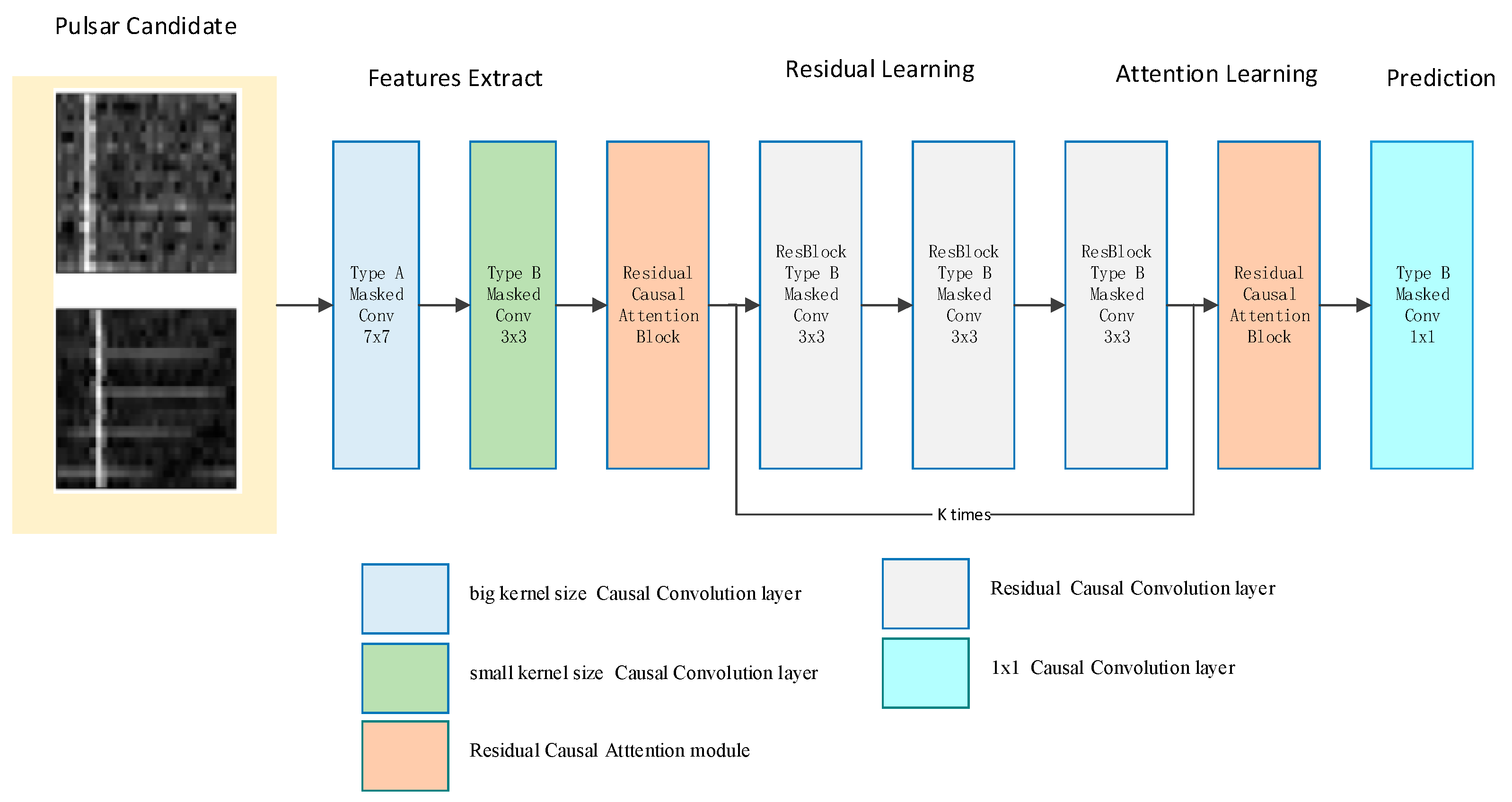
Figure 4. Residual Causal Attention Block.

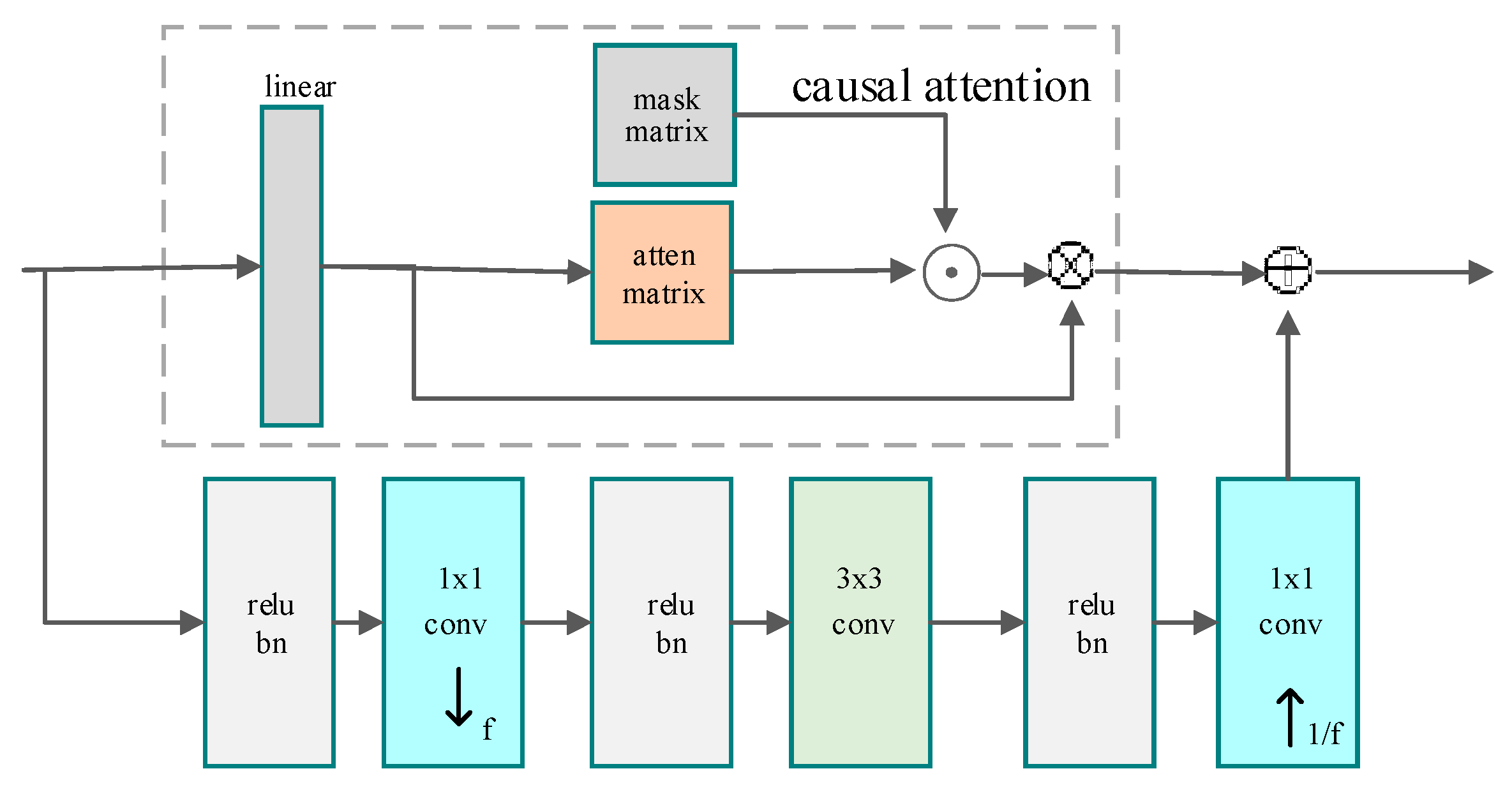
Figure 5. Training Speed and Stability Comparison between PixelCNN Base Model and RCA-PixelCNN.

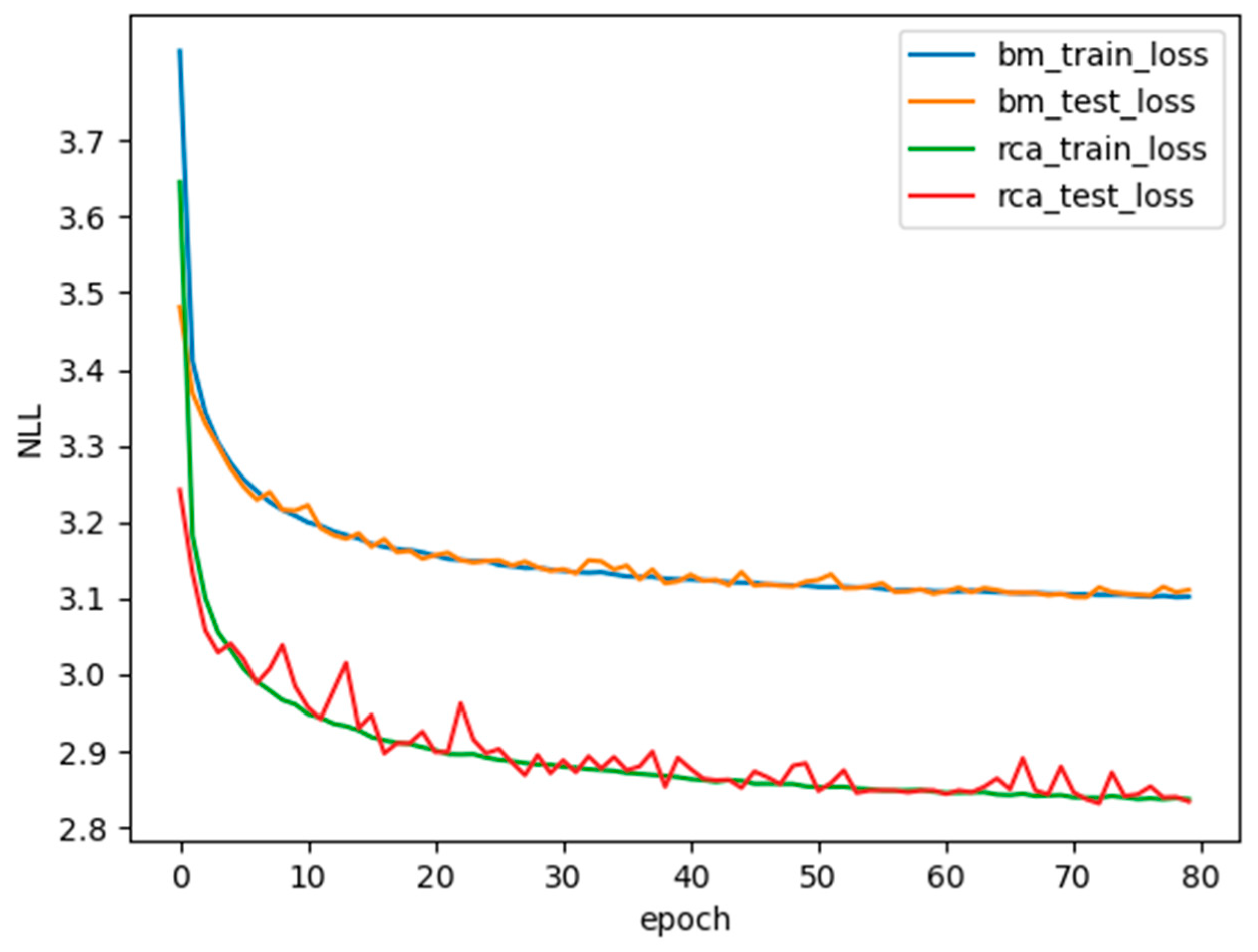
Figure 6. Impact of Modified Specific Modules on the Model.

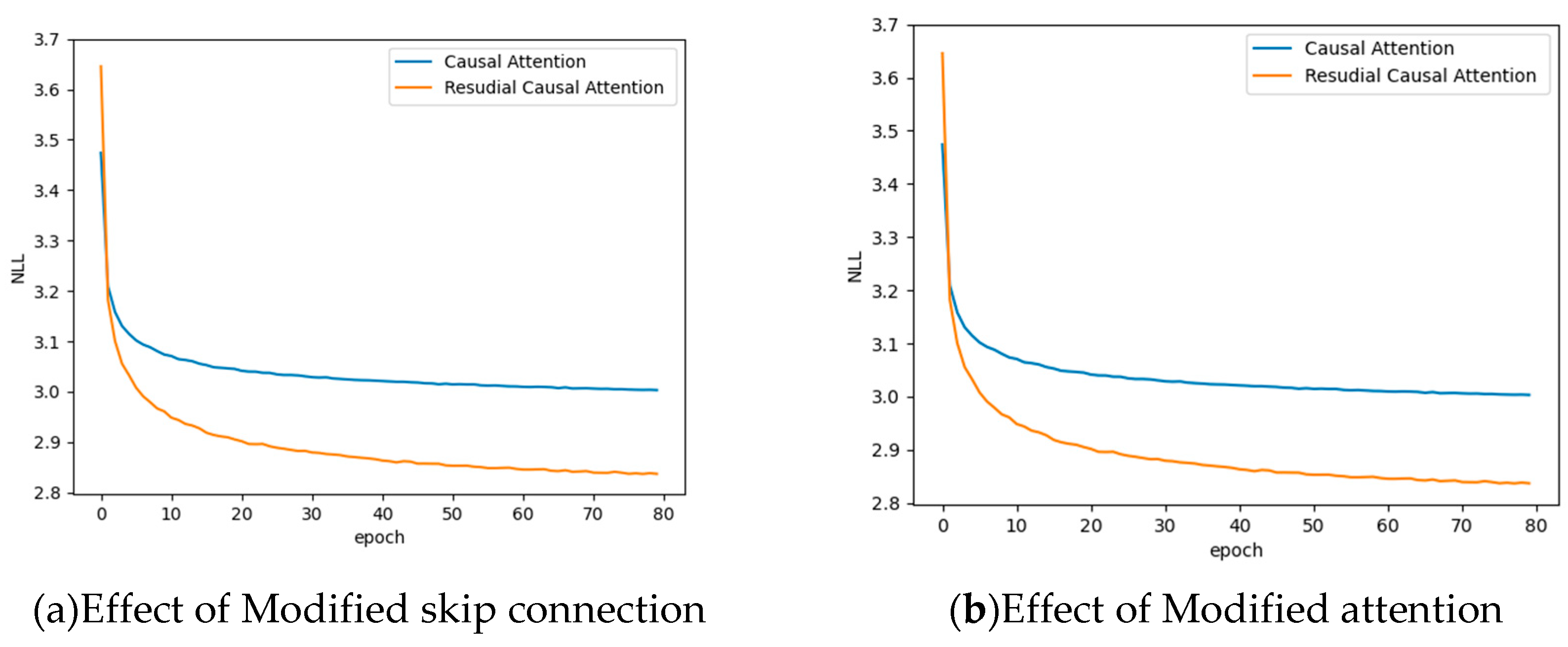
Figure 7. Positive Samples of Pulsar Candidates. The leftmost 4 columns represent HTRU1 samples, while the rightmost 4 columns represent generated samples.

Table 1. Comparison of RCA-PixelCNN with Other Models in terms of Negative Log Likelihood (NLL).

Methods	NLL
GMM	3.54
STM	4.11
PixelCNN Base Model	3.11
RCA-PixelCNN	2.82

Table 2. Arithmetic coding with RCA-PixelCNN.

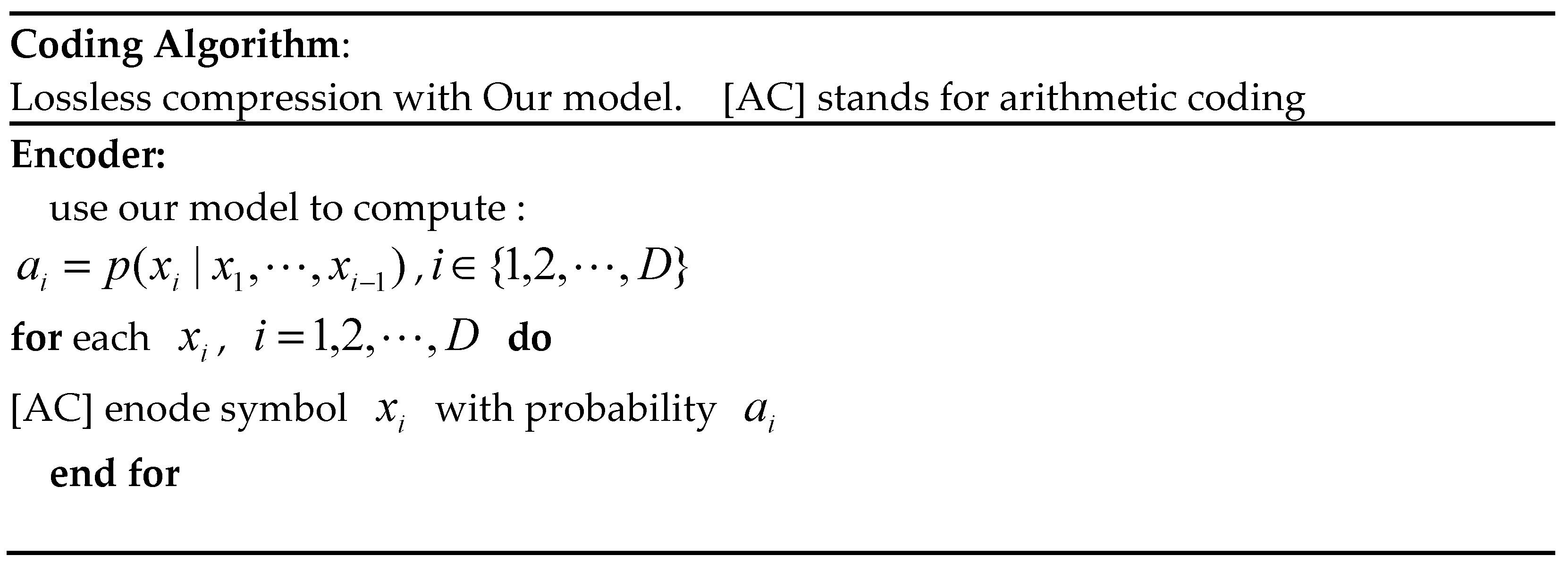
Table 3. Comparsion of model with diffferent numbers of Res-Cause-Attentino Blocks.

Methods	NLL(bpp)
PixelCNN	3.11
RCA-PixelCNN-1	2.82
RCA-PixelCNN-2	2.78

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer