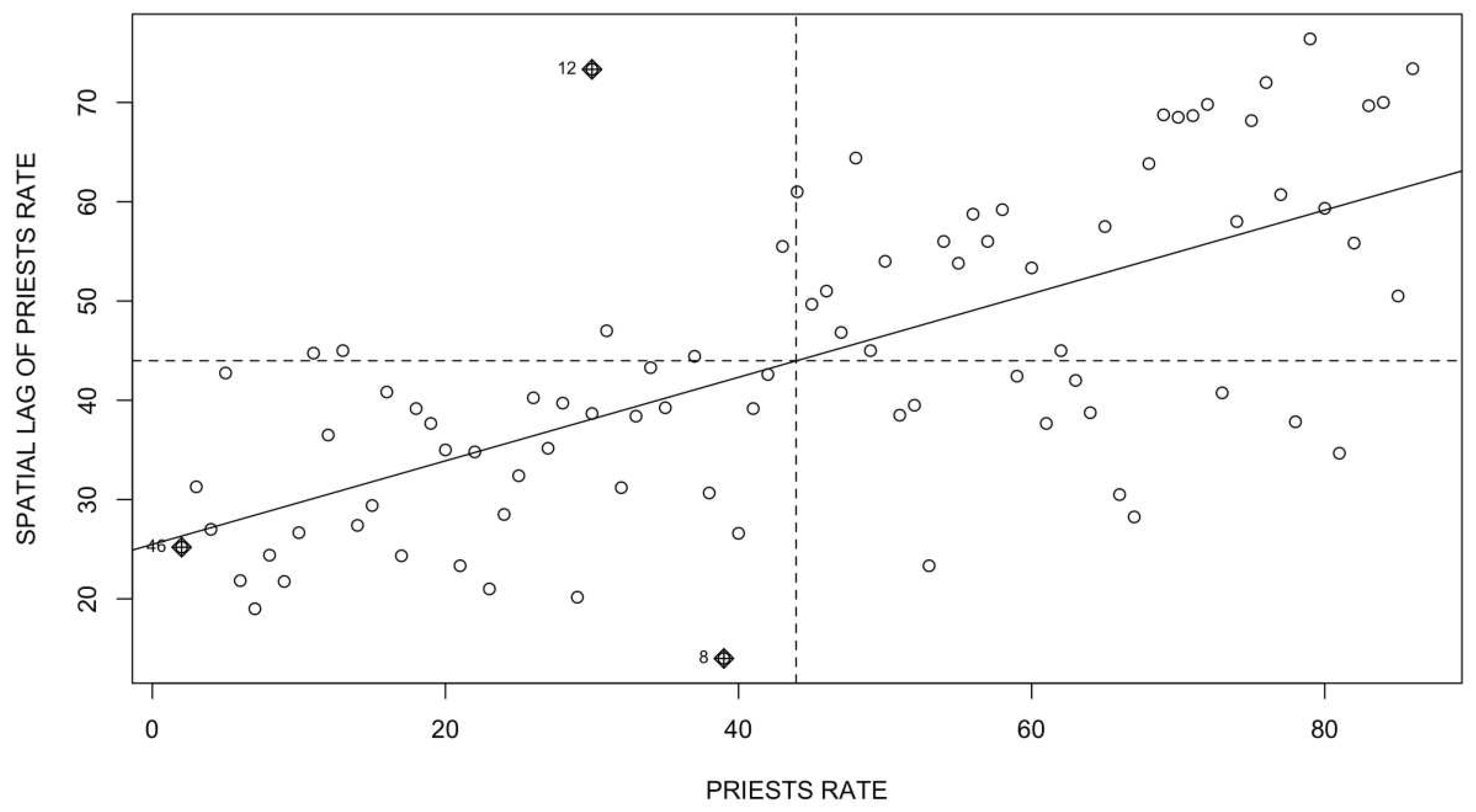
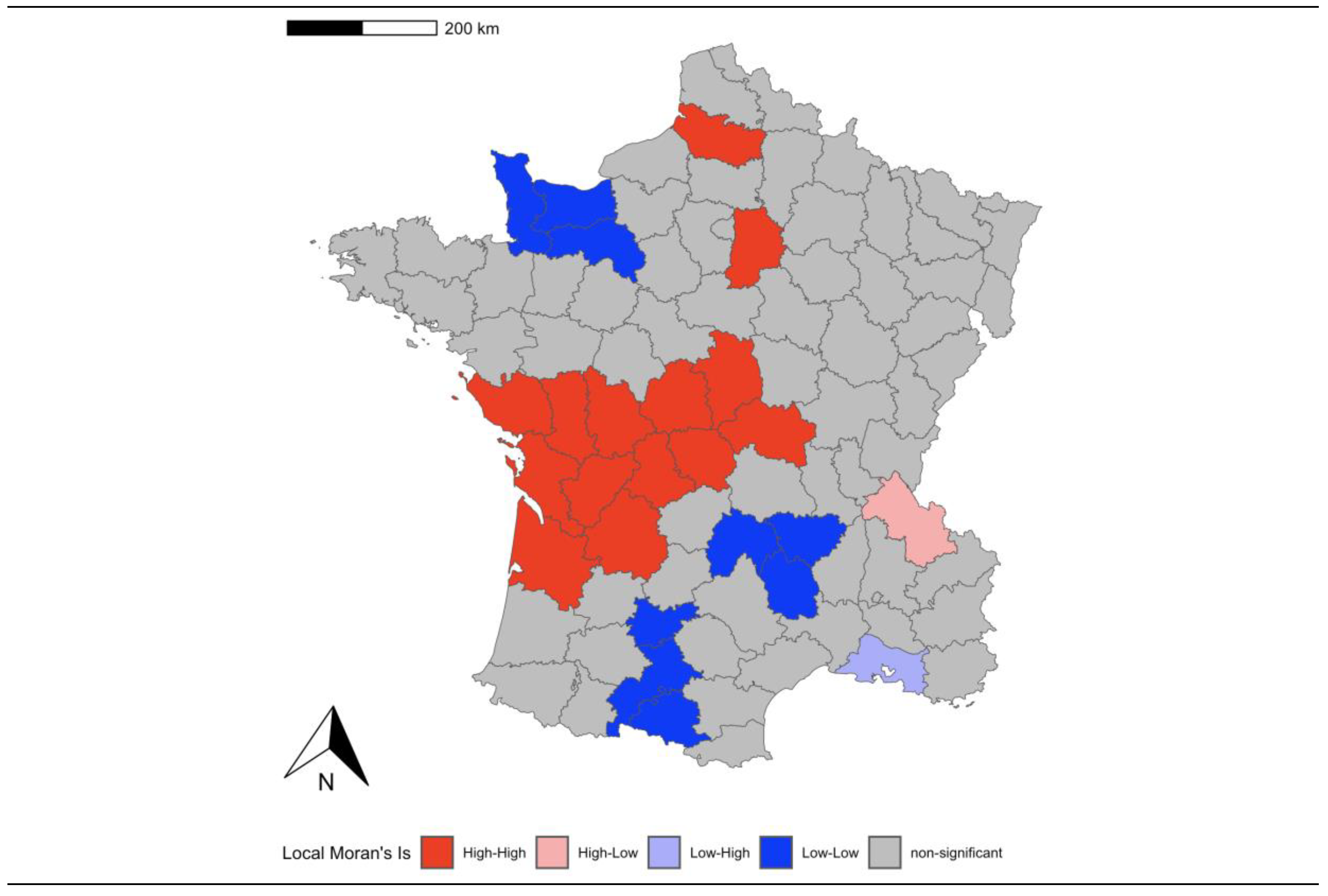
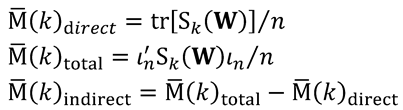Spatial cross-sectional models are a particular case of cross-sectional econometric models and, as is the case with them, they must be identified before proceeding to their estimation and testing. Hence, it is important to follow a specific identification or modelling strategy for spatial models, which allows the researcher to know the correct population parameters from the observation of a data sample.
Traditionally, spatial econometrics has solved this problem by assuming that the model specification is a priori known, either from an existing economic theory, or from the results obtained by the application of an ESDA on the variables of the model, or by applying certain strategies consisting of the comparison of several competing models. Within the latter option, we can highlight two widely used modelling strategies: the one that goes from the specific (basic model without spatial autocorrelation effects) to a general model (with spatially lagged explanatory variables), STG, and the one that starts from a general model (the spatial Durbin model) to end up in a simpler spatial autocorrelation model or the basic regression model itself without spatial effects, GTS. But, from these two previous approaches, it is possible to propose a third hybrid strategy, which considers the good properties of the previous ones.
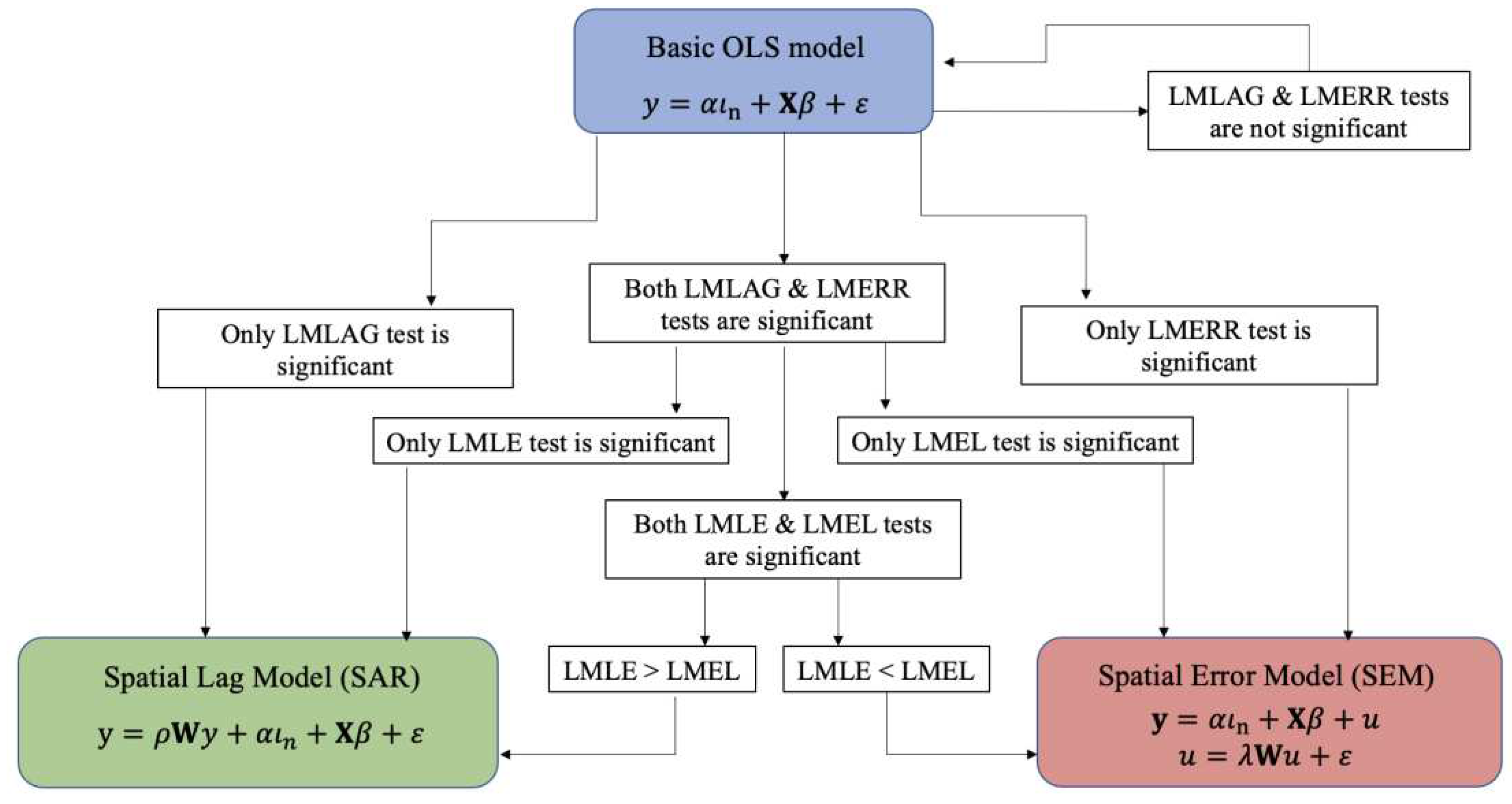
3.1.1. Anselin’s Specific-To-General Strategy (STG)
The STG strategy, also known as "classical", was proposed by Anselin ([
8]). The starting point of this strategy is a
basic linear regression model without spatial effects:
where
is the vector of the dependent variable, of order (
;
is the matrix of explanatory variables, of order (
;
is a vector of ones, of order (
;
are the set of (
parameters to be estimated; and
is the random disturbance variable, of order (
, which is distributed as
, where
is the identity matrix of order
. This model is estimated by the
Ordinary Least Squares (OLS) method.
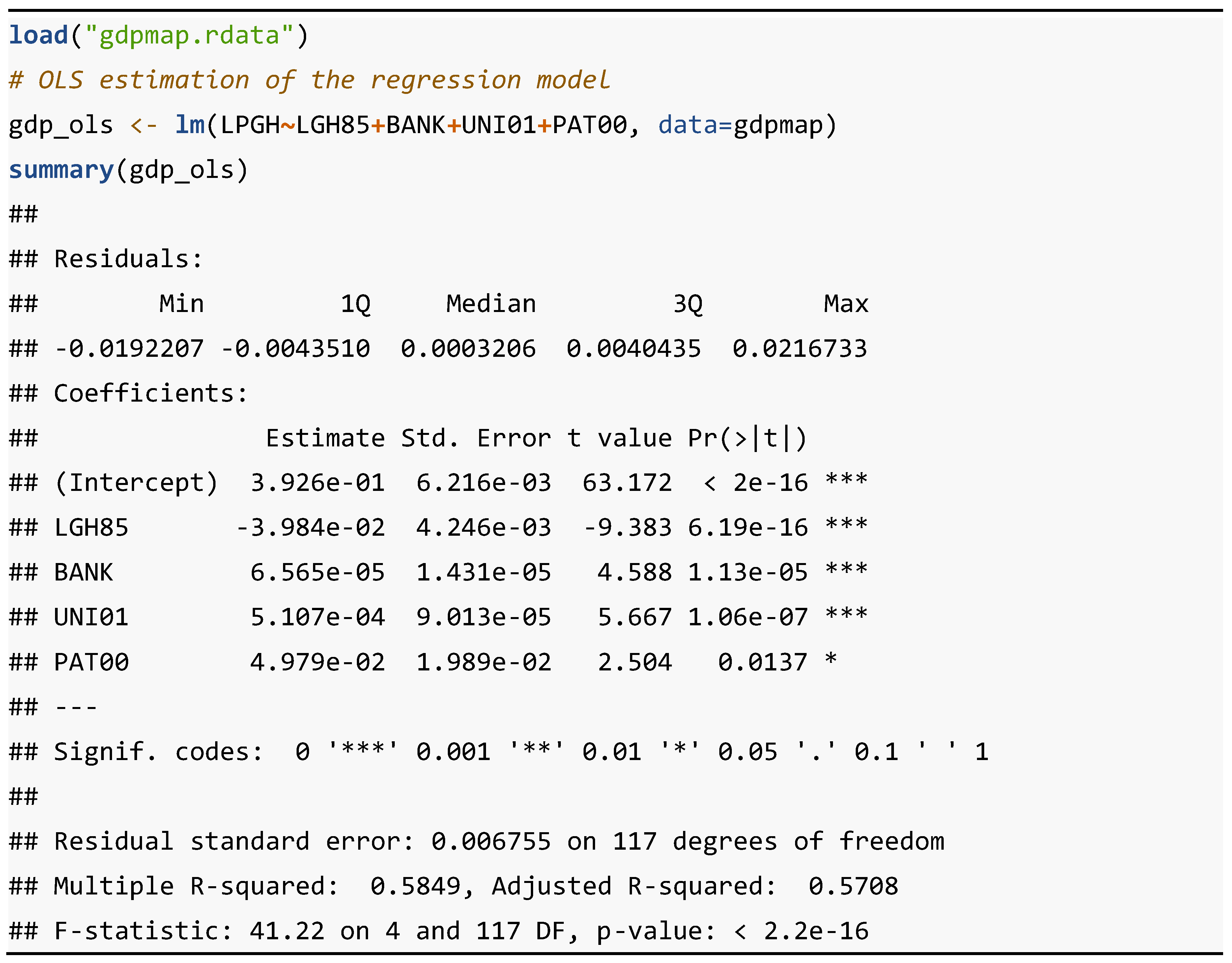
Table 12 presents the R code needed to generate the results of the OLS estimation of the basic linear regression model.
The following two libraries are required to run this code: "sp" and "stats". The main functions, not previously presented, involved in this R code are "lm" and "summary". lm {stats} is used to fit linear models, including multivariate ones. summary {base} is used to produce result summaries of the results of various model fitting functions.
The code sequences show how to estimate and test the model with a dataset of municipalities (NUTS 5) of the urban areas of Spain used in Mella and Chasco [
16]. With these data, a model of urban economic growth is formulated in which the average rate of change of GDP per capita, in logarithms, over the period 1985-2003 (LPGH), is explained as a function of GDP per capita in 1985 logarithms (LGH85), the rate of change in the number of banking institutions in the period 1985-2003 (BANK), the percentage of people with secondary and university education out of the population aged 16 and over in 2001 (UNI01) and the rate of the number of patents per inhabitant in 2000 (PAT00). As can be seen, all estimators are statistically significant at least at 99% confidence. The model has an explanatory level of 58.49%.
In order to test whether the variable of the OLS regression errors is spatially white noise,
6 the
Lagrange Multiplier (LM) tests are calculated on this variable. This basic hypothesis is rejected as soon as any of these tests, which are distributed as a Chi-square with 1 degree of freedom (
), is statistically significant. In particular, these tests are focused on a single alternative hypothesis. Thus, if the Lagrange multiplier test for the alternative hypothesis of spatially lagged dependent variable (LMLAG) is statistically significant instead of the Lagrange multiplier test for the alternative hypothesis of residual dependence (LMERR), the model that would best explain the data would be the
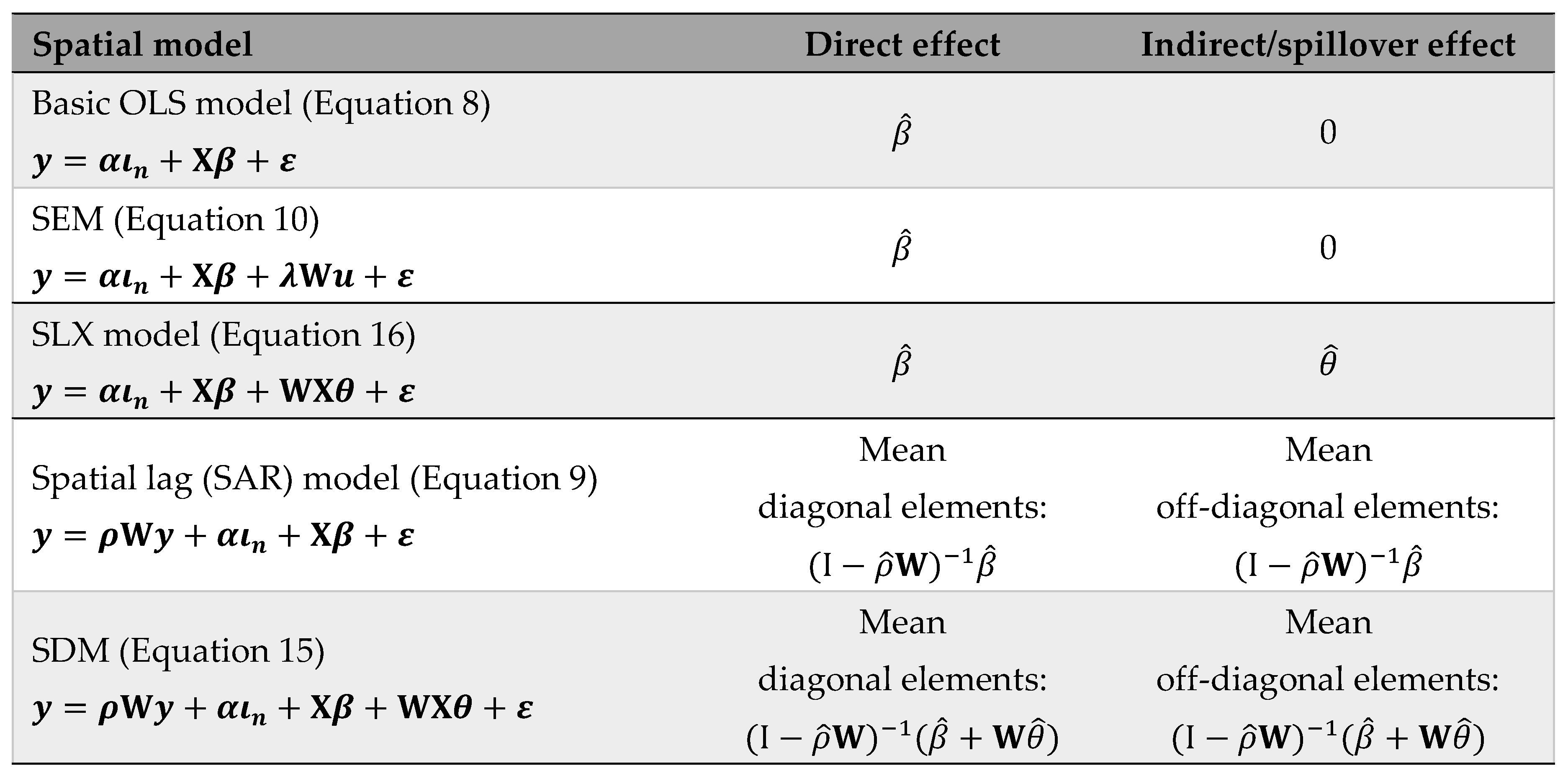
spatial lag model or spatial autoregressive model of order 1 (SAR):
being
a spatial autoregressive parameter to be estimated and
a row-standardised spatial weight matrix of order (
. But if it is the LMERR test that is statistically significant, instead of the LMLAG, the best model would be the
Spatial Error Model (SEM):
where
is a spatial autoregressive parameter to be estimated. In this case, it should be noted that
and
. Therefore, the SEM would be equivalent to a spatial lag model that includes, on the right-hand side of the equation, in addition to the terms of the basic model, the spatially lagged dependent variable and the
spatially lagged explanatory variables as follows:
The restriction
is called the
common factor (COMFAC) hypothesis and when it holds, this model is called, by Anselin [
8], as
Spatial Durbin Model (SDM).
Regarding the LM tests previously presented, it is possible that both are statistically significant because, although they are tests oriented towards an alternative spatial hypothesis or model, they are also sensitive to the existence of the other type of spatial autocorrelation. In these cases, to decide on the most appropriate spatial model, spatial lag (SAR) or SEM, Anselin, Bera, Florax and Yoon [
18] propose a solution by formulating robust versions of the LMLAG and LMERR tests, the new LMLE (a test to spatial lag dependence which is robust to ignored spatial error dependence) and LMEL (a test to spatial error robust to ignored spatial lag), respectively. If the values of LMLE > LMEL, the spatial lag (SAR) model should be selected, while if LMEL > LMLE, the SEM should be chosen.
7
Table 13 presents the R code needed to generate the results of the computation of the LM test on the OLS estimation residuals. The following three libraries are required to run this code:
"sp",
"stats" and
"spdep". The main functions, not previously presented, involved in this R code are "
coordinates" and "
lm.LMtest".
coordinates {sp} retrieves spatial coordinates from a spatial object of class
sp.
lm.LMtest {spdep} reports the estimates of the LMERR test for error dependence (which is called ‘LMerr’ by the function), the LMLAG test for a missing spatially lagged dependent variable (‘LMlag’), their corresponding robust variants LMEL (‘RLMerr’) and LMLE (‘RLMlag’), respectively, and a SARMA test, which is test for a mixed residual spatial autoregressive process (SAR) and a spatial moving average (SMA).
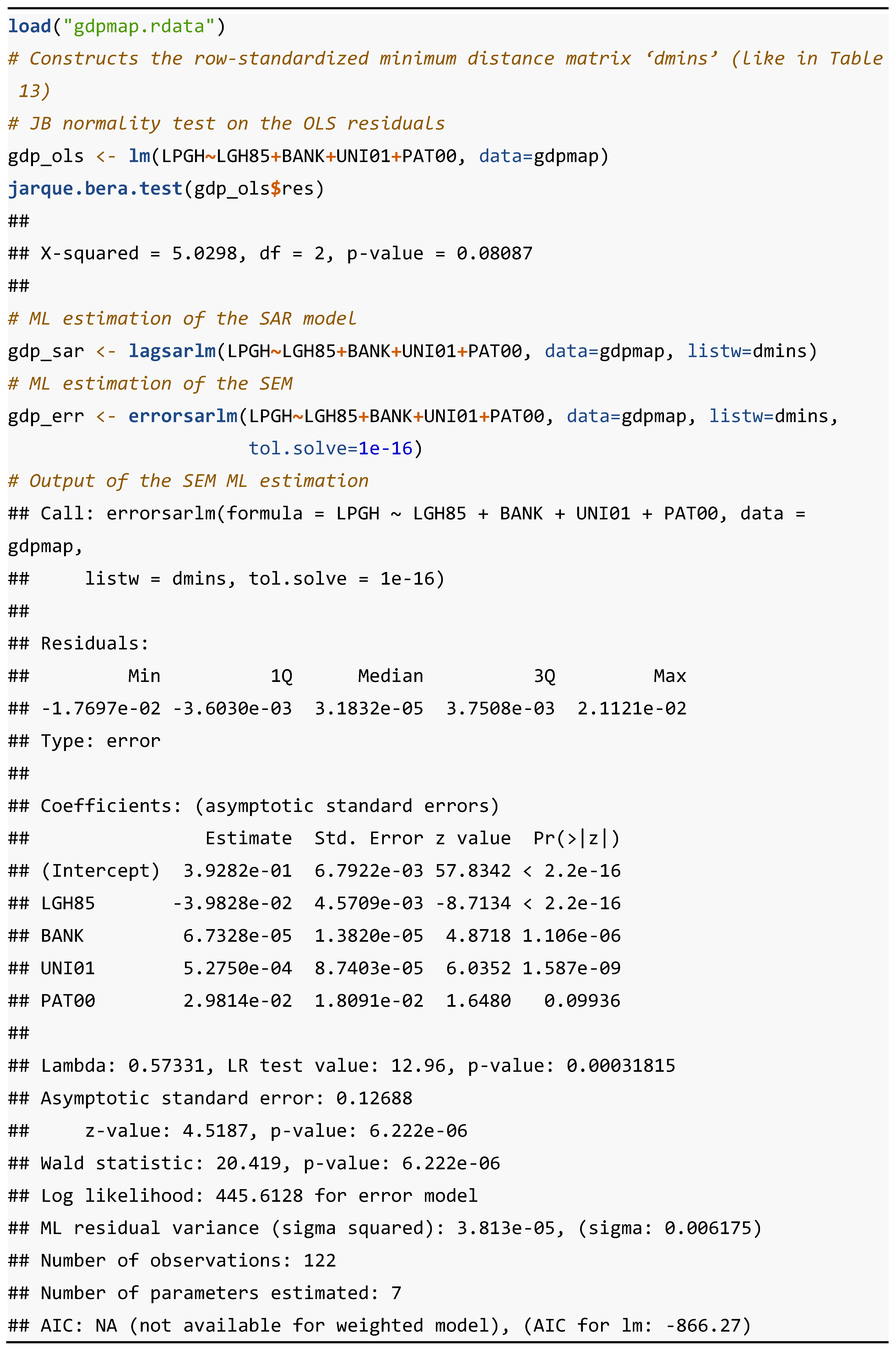
The LMLAG and LMERR tests are both highly significant, so the null hypothesis of no spatial autocorrelation must be rejected with more than 99% confidence. Additionally, of the robust tests, it is only possible to reject the null hypothesis for LMEL (not for LMLE). Therefore, according to the classic modelling strategy, the most appropriate specification for this model would be the SEM.
Since the spatial lag model (SAR) includes as an explanatory variable the spatially lagged endogenous variable (
) referred to the same moment in time as the dependent variable (
), a situation of simultaneity or contemporaneous dependence arises. Therefore, its estimation by OLS produces bias, inefficiency, and inconsistency in the estimators. As for the SEM, due to the heteroskedastic form of the variance and covariance matrix of the random disturbance
, its estimation by the OLS method results in inefficient, although consistent, estimators. Due to the problems of OLS in these spatial models, estimation by the
Maximum Likelihood (ML) method in the case of normality in the OLS error variable is recommended as more appropriate (see Anselin [
8], chap. 6).
Table 14 presents the R code needed to generate the results of the ML estimations of the spatial lag (SAR) model and the SEM. The following four libraries are required to run this code:
"sp",
"stats",
"spdep" and
"tseries".
The main functions, not previously presented, involved in this code are "jarque.bera.test”, "lagsarlm" and "errorsarlm". jarque.bera.test {tseries} tests the null of normality for a variable using the Jarque-Bera test statistic). lagsarlm {spatialreg} provides ML estimation of spatial lag (SAR) models and SDM. errorsarlm {spatialreg} provides a ML estimation of SEM.
In
Table 13, the LM tests on the OLS residuals showed the existence of spatial aucorrelation in the residuals and recommended the estimation of a SEM to correct for this problem. In
Table 14, the Jarque-Bera test cannot reject the null hypothesis of normality of the OLS error terms with more than 95% confidence, so it is possible to estimate the SEM by the ML method. For this reason, only the results of this estimation in their entirety are presented in
Table 14.
According to the STG strategy, the SEM is the model which best fits the data generation process. The value of the spatial autoregressive parameter
has no interpretation, unlike the spatial autoregressive
parameter, which is estimated in the spatial lag model (SAR). In fact, it is called by Anselin and Rey as a "nuisance" parameter and, therefore, no inference is performed for it ([
17]). All estimators of the model are statistically significant although, with respect to the estimation of the basic model (
Table 12), the estimator of the patent variable is only significant for a confidence level above 90%. In the case of the ML estimates, the R
2, as a measure of goodness of fit, is not presented, but rather the ML and information criteria (Akaike and AIC).
The modelling strategy proposed by Anselin and Rey ([
17]) is presented in
Figure 11.
When the OLS estimation errors follow a non-normal distribution, the spatial lag model (SAR) should be estimated by the
Spatial Two-Stage Least Squares method (S2SLS) which, in the version of Kelejian and Robinson [
20], consists of using the spatially lagged exogenous variables of several orders of contiguity as instruments of the spatially lagged endogenous variable, resulting in a consistent, though not very efficient, autoregressive estimator (
).
As for the SEM, Arraiz, Drukker, Kelejian and Prucha [
21] present an estimation by the
General Method of Moments (GMM), building on the initial proposal made by Kelejian and Prucha [
22]. Although, given that the estimators are unbiased and consistent, it is also considered acceptable to estimate the SEM by OLS by performing robust inference of the variance-covariance matrix of the estimators by the KP-HET method proposed by Kelejian and Prucha [
23], which takes into account the joint existence of heteroscedasticity and spatial autocorrelation in the regression errors.
Table 15 presents the R code needed to generate the results of the STSLS and GMM estimations of the spatial lag (SAR) model and the SEM, respectively. The following three libraries are required to run this code:
"sp",
"spdep" and
"spatialreg".
The main functions, not previously presented, involved in this R code are ""stsls" and "GMerrorsar". stsls {spatialreg} fits a spatial lag model (SAR) by STSLS. GMerrorsar {spatialreg} fits a SEM by the Kelejian and Prucha’s GMM.
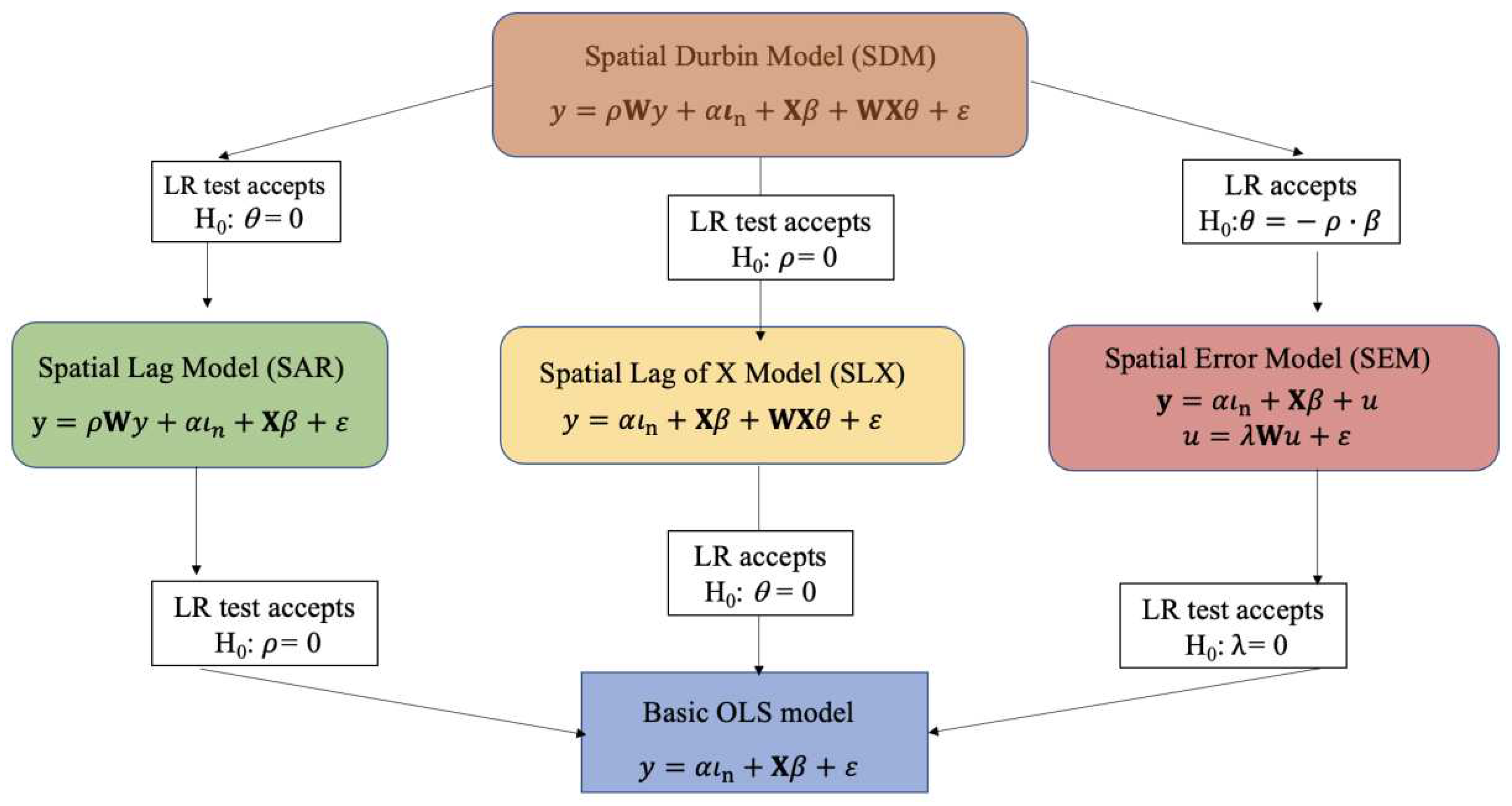
3.1.2. LeSage’s General-To-Specific Strategy (GTS)
The second strategy, GTS, is to start from the most general spatial autocorrelation model possible. According to Manski [
24], this general model is the one that includes the three possible types of spatial interaction, endogenous (
), exogenous (
) and unobserved (
) effects:
where
is a vector of
spatial autoregressive parameters. The problem with this Manski’s model is that, as the author demonstrates, it is impossible to identify its parameters. Therefore, it is necessary to reduce the three types of spatial interaction to two, which gives rise to three possible general sub-models of spatial autocorrelation. First, if we exclude the spatial endogenous effect (
), we obtain the so-called, by LeSage and Pace [
25],
Spatial Durbin Error Model (SDEM):
Secondly, if what is excluded is the spatial exogenous effect ((
), the
SARAR model or Kelejian-Prucha’s model is obtained, as it was proposed by these authors ([
22])
8:
Finally, if the spatial unobserved effect is excluded, we obtain the unconstrained
Spatial Durbin Model (SDM), where the constraint presented in Equation (11) do not hold; that is, when
. Hence:
As with the SAR model, the presence of the spatial lag of the dependent variable on the right-hand side of the equation does not result in OLS estimators with good properties, so this model must be estimated by ML.
This is the general model proposed by LeSage and Pace [
25] as a starting point for the GTS modelling strategy.
9 The SDM model fulfils the identifiability condition by including two of the three possible types of spatial interaction, endogenous and exogenous effects, and thus includes all spatially lagged explanatory variables. In this way, a possible bias in the estimators caused by the omission of any relevant spatial variable is avoided.
Additionally, LeSage and Pace demonstrated that if this model also had residual spatial autocorrelation problems, the omission of the spatially lagged error variable would lead to inefficiency, but not to bias in the estimators. The SDM model likewise has the property of nesting several models, from the basic model without spatial effects to the SAR and SEM spatial autocorrelation models (when the COMFAC hypothesis is satisfied), as well as the so-called, by LeSage and Pace [
25],
Spatial Lag of X (SLX) model, firstly called “mixed regressive-spatial cross-regressive model” by Florax and Folmer [
27].
This model can be estimated by the OLS method since, if the explanatory variables are exogenous, their corresponding spatial lags will also be exogenous. In addition, the SLX model has two more good properties: on the one hand, it is more flexible to estimate or parameterise the
W matrix and, on the other hand, it has better properties to capture spatial spillover effects when no clear theoretical model is available to support the inclusion of the endogenous spatial interaction effect (
), as shown by Halleck Vega and Elhorst [
28].
The modelling strategy proposed by LeSage and Pace ([
25]) is presented in
Figure 12.
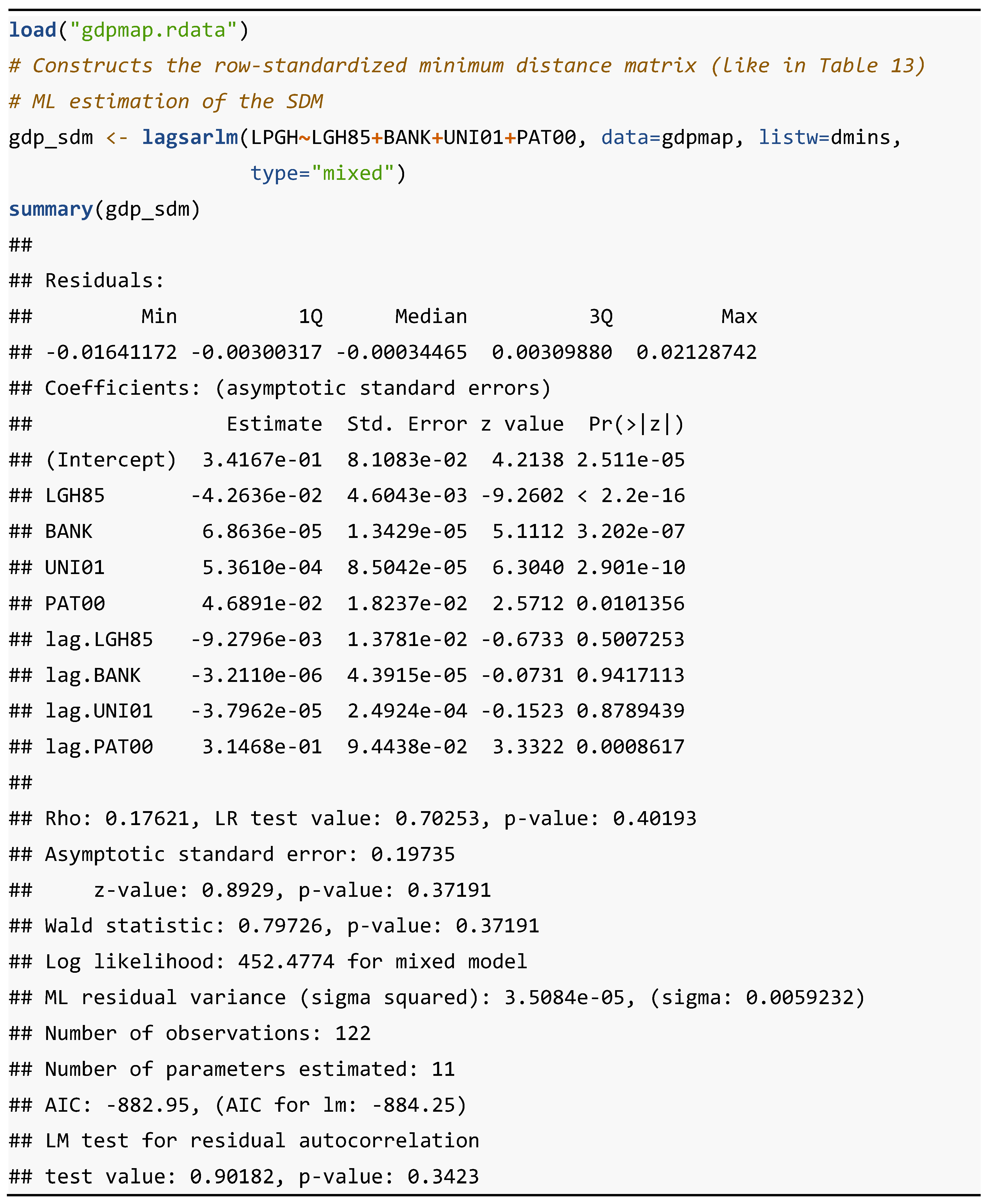
Table 16 presents the R code needed to generate the results of the ML estimation of the SDM model. The following three libraries are required to run this code:
"sp",
"spdep" and
"spatialreg". In this case, there are no new functions.
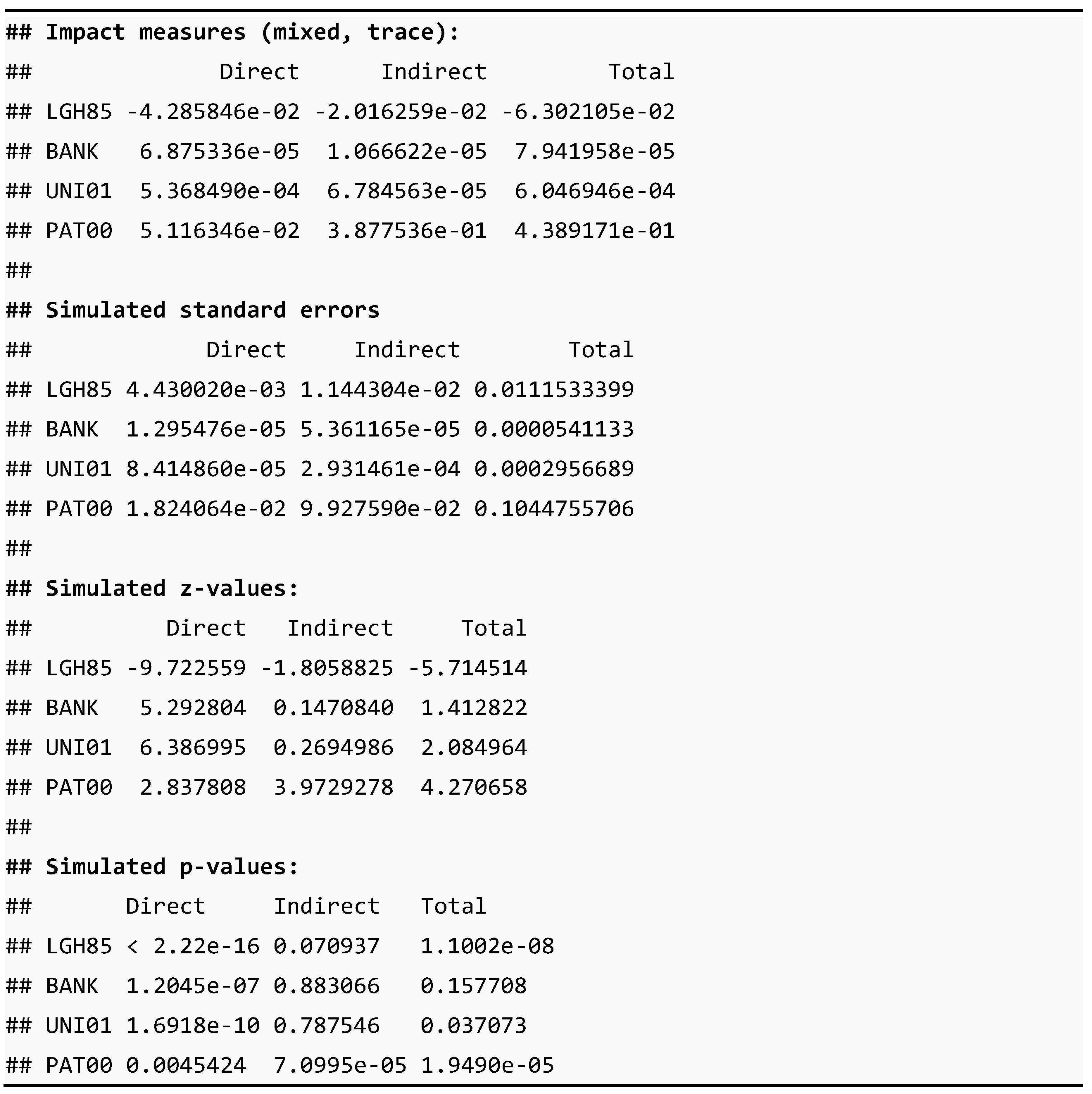
In the output, the estimation results highlight the contrast between the high statistical significance of the model's explanatory variables and the low significance of their corresponding spatial lags. The only exception is the patent variable and its corresponding spatially lagged variable, for which both coefficients are highly significant, especially in the case of the latter.
However, the lack of statistical significance of the autoregressive coefficient (p-value: 0.40193) is striking, raising doubts about the suitability of this identification as the most appropriate for the model. Finally, the function also calculates an LM test on the residuals of this regression, which is not significant, demonstrating the non-existence of spatial autocorrelation in the residuals.
As can be seen in
Figure 12, the decision on the most appropriate model for the data generating process, according to this GTS strategy, requires the calculation of several Likelihood Ratio (LR) tests, which will be discussed in more detail in the next section, where we will present a hybrid strategy, which combines the two strategies seen so far: STG and GTS.
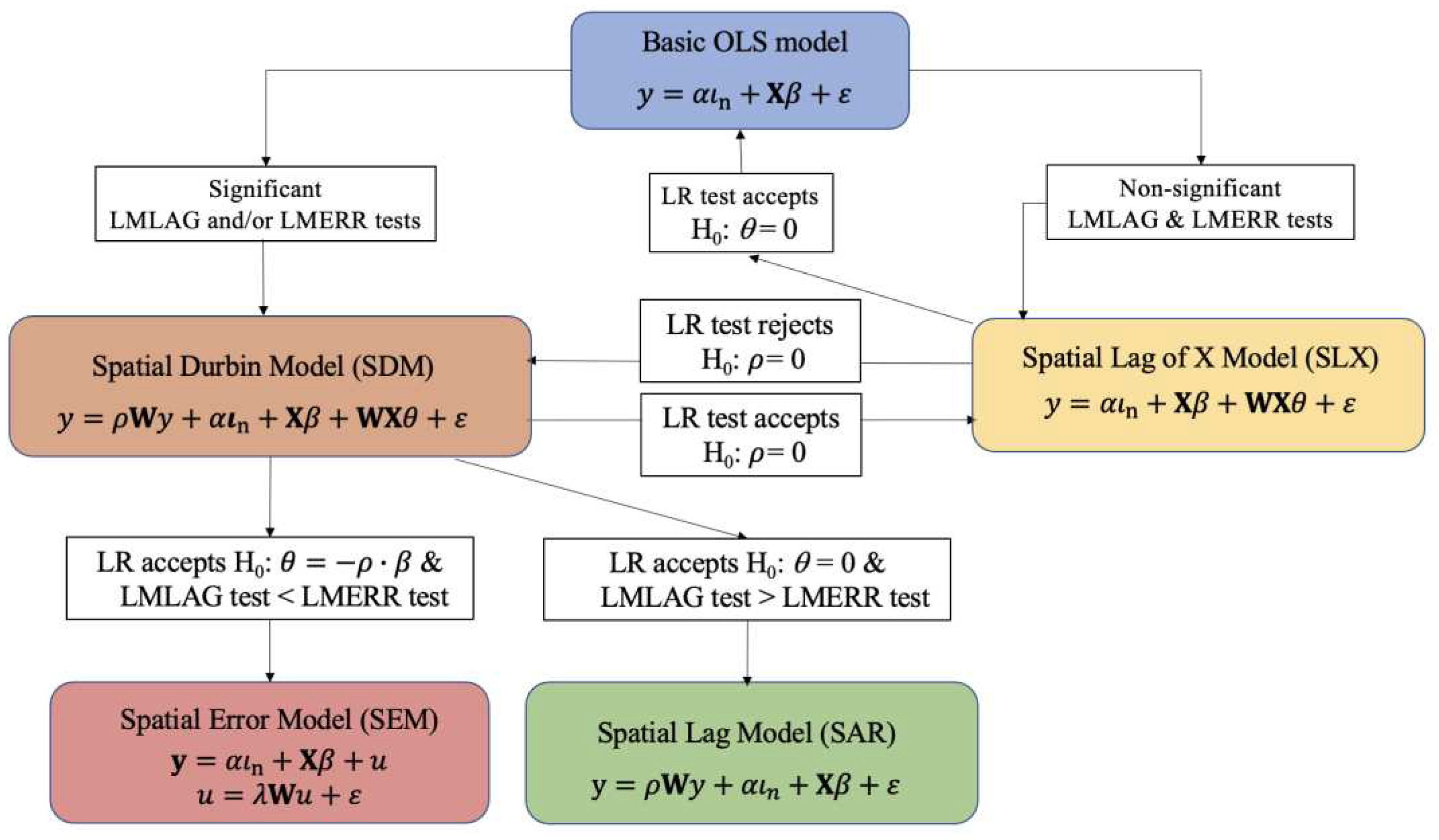
3.1.3. Elhorst’s Hybrid Strategy
Based on the two previous approaches, Elhorst [
29] proposes a hybrid strategy, which takes into account the good properties of both proposals. For this reason, this strategy will be the one we select as the most suitable for identifying spatial autocorrelation models. As presented in
Figure 13, the Elhorst’s hybrid strategy starts, like the STG strategy, with the OLS estimation of a basic model without spatial effects. The error variable of this regression is analysed with the LMLAG and LMERR tests, to check whether they are white noise. At this point, it may happen that one of the tests is statistically significant or that none of them is. Firstly, if any of the LM tests is significant, it is recommended to select the SDM model, as proposed by the GTS strategy.
The ML estimation of this model allows the likelihood ratio (LR), whose distribution follows a Chi-square with degrees of freedom (), to be used to test the null hypotheses and . If the second (COMFAC) hypothesis cannot be rejected, the SDM should be simplified to a spatial lag (SAR) model, provided that the LMLAG > LMERR tests. If the first hypothesis cannot be rejected, the SEM should be selected, provided that LMERR > LMLAG tests. If there is no agreement between the results of the LR test and the LM tests, then the SDM would be the model that best describes the data.
Secondly, if after the OLS estimation of the basic model none of the LM tests is statistically significant, then the basic model would have to be re-estimated as an SLX model, including all spatially lagged exogenous variables or a subset of them, in order to test the null hypothesis . If this hypothesis cannot be rejected, the basic model should be chosen as the one that best describes the data, i.e., there would be no evidence of the need for spatial autocorrelation effects to explain the dependent variable. But if, on the contrary, the hypothesis can be rejected, the SDM model would have to be estimated to test, again, the null hypothesis . If this hypothesis can be rejected, the selection would be the SDM; on the contrary, it should be settled that a model with spatially lagged independent variables (complete or parsimonious SLX) only suffices.
Additionally, Halleck Vega and Elhorst [
28] introduced the SLX model into the model selection process as a new SDM’s nested model (like in
Figure 12), recommending its choice when the null hypothesis
cannot be rejected. This addition may lead to differences in the final model selected, as will be seen below.
Table 17 presents the R code needed to compute the LM and LR tests necessary to determine the best model specification according to the Elhorst’s hybrid strategy. The following four libraries are required to run this code:
"sp",
"stats",
"spdep" and
"spatialreg". The main functions, not previously presented, involved in this R code are "
lmSLX" and "
LR.Sarlm".
lmSLX {spatialreg} fits a SLX model, i.e., an OLS model augmented with the spatially lagged regressor variables.
LR.Sarlm {spatialreg} is a function which provides a likelihood ratio test.
As seen in the results of the classical strategy (
Table 13), the LM tests on the OLS residuals are both statistically significant, with LMLAG < LMERR. Therefore, the SEM was identified as the most appropriate specification for the urban growth model. However, according to Elhorst's hybrid strategy, the significance of any or all of the LM tests involves estimating the SDM and then comparing it with the LR tests of their corresponding more restricted nested models. In his first version in 2010 [
29], Elhorst proposes to compare the SDM with the spatial lag model (SAR) and the SEM. As can be seen in
Table 17, the null hypothesis of the fulfilment of the COMFAC hypothesis,
, and the null hypothesis of
must be rejected. In other words, the most appropriate specification for the model is the SDM. However, if SLX is incorporated into the comparison of rival models, which is what Elhorst does in his second formulation in 2015 [
28], the null hypothesis
cannot be rejected. Therefore, the more appropriate specification for the data-generating process would be the SLX model, rather than the SDM.
10 Specifically, a more parsimonious SLX model is selected that only includes, as explanatory variables, the spatially lagged variables that are statistically significant, as shown in the last rows of the
Table 17.
Therefore, the selection of the most appropriate final model is still an open question since, as we have seen, the outcome depends on the modelling strategy adopted. In the proposed example of urban growth in Spain, if the Anselin’s classical STG strategy is followed, the selected model would be the SEM. According to the original proposal of Elhorst's hybrid strategy, the proposed model would be the SDM. Finally, according to Elhorst's second proposal, and also LeSage and Pace's GTS strategy, the model finally selected would be the SLX.
All these models must be estimated by the OLS and ML methods to be able to use the LR as a testing tool, although it should be noted that spatial autocorrelation models can also be estimated with
Bayesian methodology using the Markov Chains Monte Carlo (MCMC) approach, as explained in LeSage and Pace [
25], chapter 5.
To conclude this section on the identification of true data generation process of a dependent variable, it must be said that there is still a long way to go to create a method that considers not only the existence of the spatial autocorrelation effect, but also
spatial heterogeneity, as shown by Debarsy and Le Gallo [
30]. Spatial heterogeneity can manifest itself in various forms, such as diversity of coefficients or of the functional relationships themselves in various locations or groups of locations (spatial regimes), spatial clustering, hierarchical structures, etc. But this is a topic that will not be dealt with in this paper.