Prerpints.org logo
Preprint
Article

Impact Pressure Influence of Flood on Bridge Deck under Sediment Deposition Conditions: An Experimental Study

Altmetrics

Downloads

61

Views

7

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

05 September 2023

Posted:

07 September 2023

You are already at the latest version

Alerts
Abstract
This paper investigates the impact of sediment deposition and inflow conditions on horizontal impact pressure and frequency analysis of bridge deck vibrations during flooding. Flooding-induced pressure and vibrations contribute to bridge collapse, and sediment deposition influences water flow and impact pressure. The study explores the relationship between sediment deposition height and impact pressure, revealing a significant increase as sediment approaches 50% of bridge deck clearance. Sediment amplifies impact pressure response to flow velocity changes. The dimensionless sediment deposition height has a greater influence on impact pressure compared to the inflow Froude number. Two distinct frequencies, dominant and secondary, are identified for impact pressure and water level fluctuations. Dominant frequencies positively correlate with sediment deposition height and Froude number, indicating an increasing trend. Secondary frequencies remain stable (0.31-0.58 Hz). These findings enhance understanding of flow dynamics and bridge-flow interaction in sediment-deposited channels, providing theoretical support for evaluating and managing disasters related to bridges in such environments. Overall, this research contributes to the field of bridge engineering and supports improved design and maintenance practices for bridges exposed to sediment-deposited channels.
Keywords: 
Subject: Engineering  -   Civil Engineering

1. Introduction

Bridges are essential components of global transportation networks, serving as vital links that connect regions, facilitate trade, and foster socio-economic development. According to statistics, the USA has over 600,000 bridges [1], the UK has over 150,000 bridges [2], and China has about 500,000 road bridges alone [3]. Bridge failure can result in devastating consequences, ranging from loss of lives and injuries to disruption of critical transportation nexus, economic losses, and long-term societal implications, necessitating a comprehensive understanding of their causes and mechanisms. The primary causes of bridge collapse are categorized into internal causes and external factors. The former comprises design errors, construction flaws, and lack of maintenance, whereas the latter includes floods, earthquakes, and strong winds [4]. Lee et al. (2013) summarized 1062 bridge failures during 1980- 2012 in the USA and concludes that floods, accounting for 28.3% of all accidents, are the leading cause of bridge failure [5]. Fu et al. (2012) collected 157 bridge collapses from 2000 to 2012 in China, addressing 72 failures due to floods [6].
The failure mechanism of bridge infrastructure in a flood event is complex. Phenomena induced or exacerbated by flooding including scour, erosion, river convergence, insufficient embedment depth, softened bedrock, sand mining, debris impact, and abrasion on bridge foundations could incur the failure [7,8,9]. In mountainous areas, the geographical terrain poses unique challenges for bridge infrastructure due to the occurrence of intense rainfalls and floods, which can trigger a range of hazardous events such as slides, debris avalanches, rock falls, and spontaneous instability of steep streambeds. These natural phenomena significantly increase the risk of debris flow formation within the river channels, exacerbating the potential damage to bridges in the region [10]. For instance, the middle seven spans of the Jinshajiang Bridge (in Sichuan, China) were completely washed away, while the beams of the remaining three spans were displaced following the flood peak in 2018 [11]. Similarly, the Morandi Bridge (in Liguria, Italy) experienced a catastrophic event in the same year when its cable stays ruptured and subsequently led to a collapse during a torrential rainstorm [12]. These real-world examples underscore the critical implications of flood-related failures on bridge infrastructure in mountainous areas.
Debris flow, characterized by a downhill movement of water and particles caused by gravity, has been extensively studied in river channels. One potential damage stems from the fact that as debris flow evolves downstream, its components change, and volume and inertia increase, resulting in an exceptionally high impact pressure directly exerted on bridges [13,14] Investigations have revealed that the impact pressure of debris flows is influenced by many factors including front velocity, flow depth, bulk density, liquid volume fractions, solid volume fractions, and the interaction between debris flows and obstructions [15,16,17,18], and both laboratory experiments and in situ tests have been conducted to physically explain and quantify the impact pressure of debris flow on bridge decks, piers foundation, and abutment [10,19,20]. Additionally, numerical simulations have aided vulnerability analysis of bridge structures [21], and hybrid models have been utilized to simulate both horizontal and vertical forces exerted on bridge decks by debris flow [22]. Another possible reason for bridge destruction comes from the accumulation of debris. According to Parola et al. (2000) [23], debris collection on bridge piers and superstructures can generate large pressures. Kimura et al. (2017) [24] confirmed the increased flow pressure upstream produced by wood debris accumulation at bridges and discovered that flow pressure upstream rises with the length of the obstacle. Oudenbroek et al. (2018) [25] investigated the influence of debris on bridge hydrodynamic forces and discovered that debris is a significant contributor to bridge deck collapse.
Beyond the above two potentially destructive ways of debris flows with bridges, another significant concern lies in the debris buildup around the bridge's riverbed [26]. This buildup restricts the flow, causing a clog and subsequently increasing the horizontal pressure of water flow exerted on the bridge deck. As a result, following a sudden debris flow event, the ensuing elevation of the riverbed and continuous strong water impact could also contribute to bridge destruction. However, there remains a dearth of information concerning horizontal impact pressure under various conditions of sediment accumulation. Addressing this research gap, our study focused on exploring the hydrodynamic characteristics of the bridge deck with sediment deposited in the riverbed underneath, while investigating the influence of sediment deposition height and incoming flow conditions on the horizontal impact pressure and flow fluctuation frequency of the bridge through a channel experiment.

2. Experimental Set-up

2.1 Experimental Facility and Instrumentations

The physical experiment was conducted in a recirculated system with a rectangular glass channel with dimensions of 10 m in length, 0.5 m in width, and 0.6 m in height. A 5 m high head tank was placed at the front. The pumping water from the head tank passed through a channel equal width orifice and a current stabilizer to reach a smooth incoming flow. The current stabilizer comprised an array of PVC pipes, each with an inner diameter of 3 centimeters and a length of 1 meter. A maximum flow rate of 60 L/s could be provided by the water pump set, and a broad range of discharge could be precisely controlled by regulating the water valve. A tail weir (overshoot) with adjustable height was installed at the rear of the tank to control the water depth in the tank, thus achieving different experimental conditions. The flow rate of the model experiment was calibrated by a rectangular weir downstream (not shown in Figure 1), with a measurement error of ±1%.
The model bridge was placed 6.4 m after the inlet and 3.6 m before the tail weir, and the featured dimensions are as follows: its length measures 0.5 m, with a thickness of 0.04 m, and a width of 0.12 m. Three pressure sensors (Test Electron, TST3828E, with a precision of ±0.5%) were installed on the upstream face of the bridge deck to measure the horizontal impact pressure. Herein, one sensor is arranged in the middle of the bridge front, and the other two are symmetrically distributed on both sides. Pressure sensors were sampled simultaneously for 5 mins with a sampling frequency of 50 Hz. Two acoustic displacement meters (ADMs) (Microsonic Mic + 25/IU/TC) were installed 50cm upstream of the bridge deck and above the deck respectively to obtain the instantaneous water surface elevations. ADMs were sampled simultaneously for 2 mins for each test with a sampling frequency of 60 Hz. The flow patterns were documented from a side view near the bridge with a Nikon D750 camera and a 28 – 75 mm f/ 4S lens. The schematic diagram of the experimental setup and the layout of the upstream face measuring points of the bridge deck are shown in Figure 1.

2.2 Data Processing

The horizontal impact pressure samples taken by pressure sensors 1-3 followed a normal distribution:
f ( x ) = 1 2 π σ exp ( − ( x − μ ) 2 2 σ 2 )
where μ is the average pressure, σ is its standard deviation. The Gaussian curve is fitted by the sampled values, from which the mean voltage around the maximum sample count and the standard deviation proportional to the curve broadening are documented (shown in Figure 2). This processing method ensures the derivation of the mean pressure and fluctuation magnitude is not affected by the subjective removal of erroneous points.
The flow surface elevations were measured and recorded by ADMs, but potential contamination from splashes can lead to erroneous data. To address this issue, a robust outlier cutoff filtering approach was utilized to post-process all ADM sample data. Using the median (MED) and Median Absolute Deviation (MAD) as robust estimators for both location and variance, these estimators have a breakdown point of 50% and are more robust against outliers compared to mean and standard deviation [27,28]. The technique guarantees reasonably stable mean water elevation and fluctuation magnitude results.
2.3 Scaling Issues and Experimental Conditions
Investigating the typical debris flow that led to the destruction of bridges during the '8.13 debris flows' disaster in Sichuan, China, revealed several key features. The maximum flood flow velocity reached 5-7 m/s, while sediment in the riverbed accumulated to heights ranging from 2 to 20 m. Additionally, the channel widths ranged from 40 to 100 m. [29]. Following a length scale λL = 100, the sediment heights were set to range from 0.06 m to 0.11 m, the channel width was fixed at 0.5 m; the velocity ratio λv = λL0.5 = 10, and the incoming flow velocity V at set to 0.26 m/s-0.63 m/s.
Ten experiments divided into 3 groups of different Froude numbers (Fr = V/(gh)0.5) were conducted, as shown in Table 1. In each group, the flow discharge Q and incoming flow velocity V were kept constant and several maximum sediment deposition heights hs were adjusted. To ensure capturing the correct horizontal flow pressure value on the upstream face of the bridge deck, the sensors should be completely submerged in the water, thus the height of the bridge for the control experiment in each group was adjusted to be compatible with the flow height, viz., the mean water elevation aligns with the height of bridge deck on the top. Ordinary sediment was placed in sandbags under the bridge and ensured not to be washed away by the incoming flow.

3. Water Flow over the Bridge Deck

When exploring the impact of sediment accumulation on the characteristics of water flows, the discharge and incoming flow velocity were kept constant in the experiments. Figure 3 shows the flow conditions in the channel under different sediment deposition heights ranging from 0.06 m to 0.11 m when the discharge Q = 0.0339 m3/s, and the incoming flow velocity V = 0.47m/s. It was observed that a higher sediment deposition height silts a higher water level, primarily attributed to the gradual reduction in flow area with increasing sediment deposition height, accentuating the clogging effect.
To further quantify the interaction between sediment deposition and water flow, special attention was given to the rising height of the mean water level at the front face of bridge deck, denoted as ΔH. A linear correlation was established between the dimensionless sediment deposition height (hs/hb) and the dimensionless elevated water surface (ΔH/hb). Figure 4 illustrates this relationship, focusing on the specific case of Fr = 0.31.
Δ H / h b = 0.53 h s / h b − 0.15
When investigating the impact of flow velocity on the characteristics of water flows, the sediment deposition height was maintained. The flow conditions near the bridge deck were captured in Figure 5, under varying flow velocities of V = 0.26 m/s and V = 0.63 m/s, with sediment deposition height hs held at a constant value of 0.06 m. Evidently, as the flow velocity increased, we observed a more pronounced rise in the water level. This rise was accompanied by a greater volume of water passing through the bridge deck and a larger difference in elevation before and after the bridge. Additionally, a heightened level of turbulence on the water surface was noted downstream of the bridge. Figure 6 shows the relationship between Froude number and dimensionless elevated water surface ΔH/hb keeping sediment deposition heights hs at 0.06 m. Remarkably, this figure reveals a substantial augmentation in the influence of flow velocity as the Froude numbers escalated from 0.31 to 0.42, in comparison to the case between 0.17 to 0.31. This observation underscores the intensified impact of flow velocity on the water surface elevation, indicative of a nonlinear relationship between Froude number and water flow dynamics under constant sediment deposition heights.

4. Horizontal Impact Pressure on the Bridge Deck

Pressure sensors 1- 3 were arranged on the bridge deck facing the upstream flow. To establish a baseline reference pressure (denoted as P0), the average pressure measurement (for each sensor) for cases without sediment deposition under the bridge was utilized. It is noteworthy that, in general, the reference pressure P0 obtained at the middle of the bridge (corresponding to sensor 2) demonstrated a 20% - 35% bigger compared to the other two P0 readings obtained at the sides, which could be attributed to the wall effect.
With an increase in sediment accumulation height, there was a discernible rise in the average horizontal pressure experienced by the bridge structure. The dimensionless horizontal impact pressure P/ P0 and dimensionless sediment deposition height hs/hb present an exponential correlation. Figure 7 exhibits the case when Fr = 0.31. It is illustrated in this figure that a minor degree of blockage beneath the bridge has a negligible impact on the pressure exerted on the bridge deck. However, as blockage increases, the pressure on the bridge deck rises significantly. More specifically in this scenario, when approximately one-fourth of the space beneath the bridge deck is filled with sediments, there is no significant change in the pressure on the bridge deck. Nonetheless, when half of the space is filled, the pressure increases twofold. Subsequently, with the accumulation of another one-fourth of sediment, the pressure experiences a substantial increase, surpassing the original pressure by tenfold. These results emphasize the critical importance of timely dredging to maintain safe and optimal pressure levels on the bridge deck. The correlation could be described by:
P / P 0 = 0.36 + 0.64 e 3.92 h s / h b
Regardless of the presence of sediment deposition, it was evident that the average impact pressure values at each measurement point exhibited a consistent increase in response to rising flow velocities. When comparing scenarios under the same flow velocity, cases with sediment deposition experienced heightened impact pressures, accentuating the effect of sediment on flow dynamics. Furthermore, the discrepancies in impact pressures between cases with and without sediment deposition became more pronounced as flow velocity increased. To offer a comprehensive representation of this relationship, Figure 8 illustrates the correlation between the Froude number and the dimensionless impact pressure. The relationship could also be expressed as:
P / P 0 = 2.91 F r + 0.67
When examining the combined influence of both sediment deposition height and flow condition on the horizontal impact pressure exerted on the bridge deck, a linear regression analysis of the experimental data was conducted. As a result, it yields the following equation:
P / P 0 = 5 . 34 h s / h b + 2.85 F r − 0.76
In our experiments, the dimensionless sediment deposition height of hs/hb ranged from 0.261 to 0.478, while the Froude number Fr ranged from 0.17 to 0.42. The coefficients of these two parameters are positive, reflecting a similar growth relationship. Furthermore, the dimensionless sediment deposition height coefficient is greater than that of Froude numbers, indicating that sediment accumulation height has a more significant impact on horizontal impact pressure. It is recommended to pay more attention to sediment deposition near bridges in flood risk management and bridge safety risk management. Timely dredging should be carried out in daily management, and corresponding engineering measures can be adopted to reduce the entry of solid material sources into the river and alleviate sediment accumulation, thereby reducing the risk of bridge collapse due to flood impact.

5. Characteristic Fluctuation Frequency

Vibration has also been identified as a prominent factor contributing to bridge destruction [21,30]. The induced vibration is likely to initiate structural cracks within the bridge, leading to a decrease in its critical threshold and an augmented susceptibility to potential damage. Thus, the characteristic frequencies of the horizontal impact pressure and water level fluctuations were investigated in this study.
The water flow fluctuation characteristics were obtained by performing a Fast Fourier Transform (FFT) on the pressure signals and water level signals collected under various experimental conditions. For instance, Subtracting the average pressure from the instantaneous pressure sampled by the pressure sensor, fluctuation pressure P’ was obtained. Figure 11(a) shows the time-domain diagram of fluctuation pressure for case 3. Then an FFT transformation on the data was performed, and the frequency-domain diagram of fluctuation pressure was obtained in Figure 11(b). Smoothing the gray curve with a window width of 100 yields the dominant frequency fdom and secondary frequency fsec of fluctuation pressure, with fdom = 2.16 Hz and fsec = 0.51 Hz. Applying the same analytical procedure to the pressure signals collected in other experiments, the dominant and secondary frequencies corresponding to each condition were obtained. Figure 12 (a) shows the comparison of the dominant and secondary frequencies of fluctuation pressure under different sediment deposition heights for various Froude numbers. It can be found that the dominant fluctuation pressure increases with the increase of both the dimensionless sediment deposition height and Froude number, while the secondary fluctuation frequency is basically distributed between 0.39 - 0.58 Hz with a small variation.
Similarly, the upstream fluctuated water levels, monitored by the Acoustic Doppler Method (ADM), were subjected to data processing to ascertain their dominant and secondary fluctuation frequencies, as demonstrated in Figure 13(b). It can be seen from the figure that the dominant frequency of water level fluctuation is slightly smaller than that of pulsating pressure, and it presents a similar trend to fluctuation pressure, viz. increasing with the increase of both the dimensionless sediment deposition height and Froude number. The secondary frequency of fluctuation water level is also relatively stable, basically distributed between 0.31- 0.55 Hz.
The elevated water impact frequency and heightened flow turbulence may expedite the onset of structural issues such as cracks, corrosion, and material fatigue, ultimately compromising the bridge's strength and longevity. Concurrently, the increased water impact frequency places greater loads on the bridge deck, potentially overloading components and increasing the risk of structural damage. Furthermore, these conditions can induce vibrations that may lead to resonance phenomena, further augmenting the potential for structural harm. Therefore, especially for bridges in mountainous areas prone to flooding, the design should take these results into account.

6. Conclusions

In this study, we examined the effects of impact pressure and flow conditions on sediment accumulation under a bridge during flash floods. By testing varying sediment deposition heights and inflow conditions, we sought to unravel the intricate interplay between these factors and their consequences on horizontal pressure and flow fluctuations on the bridge deck. Based on our findings, the following conclusions can be drawn:
Firstly, we observed a direct correlation between the increase in sediment deposition height and several significant changes: elevated inflow levels, enlarged differences in water surface elevation between the bridge's front and downstream, and heightened turbulence after the bridge. These observed phenomena can be attributed to the gradual reduction in flow area due to sediment accumulation, leading to a more pronounced water-blocking effect by the sediment body and a climb over the bridge deck for the excessive water. Notably, we established an exponential correlation between dimensionless horizontal impact pressure and dimensionless sediment deposition height. As sediment accumulation height approached 50% of the bridge deck clearance height, the impact pressure surged to approximately 3 times the pressure observed in the absence of sediment accumulation.
Secondly, under similar sediment accumulation volumes, higher inflow velocities resulted in a more significant water-blocking effect and increased horizontal impact pressure. Compared to conditions prior to sediment accumulation, the magnitude of the horizontal impact pressure increment after sediment accumulation was found to be directly proportional to the flow velocity.
Thirdly, through linear regression analysis of the experimental data, we determined that the relative sediment deposition height had a more substantial influence on the horizontal impact pressure compared to the Froude number within the range of our experiments. We recommend implementing measures to mitigate sediment accumulation, as this would subsequently reduce the risk of bridge collapse during flood events.
Lastly, by conducting a Fast Fourier Transform (FFT) analysis on the pressure and water level signals, we identified two characteristic frequencies for both the horizontal impact pressure fluctuation and the bridge deck water level fluctuation: the dominant and secondary frequencies. The dominant frequency of both signals exhibited a positive correlation with the relative sediment accumulation height and the Froude number. Meanwhile, the secondary frequencies remained relatively stable, ranging from 0.31 to 0.58 Hz.
These research findings provide valuable insights into the influence of flash floods on bridge deck impact pressure under sediment accumulation conditions. They contribute to a better understanding of flow dynamics in channels with sediment accumulation and the interaction between flow and bridge structures. Furthermore, these findings offer theoretical support for engineering disaster assessment and mitigation strategies.

Author Contributions

Conceptualization, Z.N. and W.Z.; methodology, Y.L. and C.M.; software, W.Z. and C.M.; validation, H.Y., Y.L. and W.Z.; formal analysis, W.Z.; investigation, Z.N. and H.Y.; writing—original draft preparation, Y.L.; writing—review and editing, W.Z.; visualization, W.Z.; supervision, Z.N.; project administration, W.Z.; funding acquisition, W.Z. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the National Natural Science Foundation of China (52309101), China Postdoctoral Science Foundation (2023M732478), Sichuan Science and Technology Program (2023NSFSC0949, 2023NSFSC0284), Research Fund of Sichuan University for Postdoctoral Researcher (2022SCU12128), Sichuan University Postdoctoral Interdisciplinary Innovation Fund (JCXK2209), Fundamental Research Funds for the Central Universities.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Data is available on request from the corresponding author.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Dunker, K.F.; Rabbat, B.G. Why America’s Bridges Are Crumbling. Scientific American 1993, 268, 66–72. [Google Scholar] [CrossRef]
  2. Woodward, R.J; Kaschner, R.; Cremona, C.; Cullington, D. Review of Current Procedures for Assessing Load Carrying Capacity Status C. Transport Research Laboratory, Berks, UK, 1999.
  3. Yan, B.F.; Shao, X.D. Application of China Bridge Management System in Qinyuan City. In Bridge Maintenance, Safety, Management, Health Monitoring and Informatics; Koh, H.M., Ed.; Taylor & Francis: London, UK, 2008; pp. 2675–2682. [Google Scholar]
  4. Wardhana, K.; Hadipriono, F.C. Analysis of recent bridge failures in the United States. Journal of Performance of Constructed Facilities 2003, 17, 144–150. [Google Scholar] [CrossRef]
  5. Lee, G.C.; Mohan, S.B.; Huang, C. A Study of U.S. Bridge Failures (1980-2012). State University of New York at Buffalo, New York, 2013.
  6. Fu, Z.Q.; Ji, B.H. ; Cheng, M; Maeno, H. Statistical Analysis of Cause of Bridge Collapse in China. Forensic Engineering 2012.
  7. Hong, J.H.; Chiew, Y.M.; Lu, J.Y.; Lai, J.S.; Lin, Y.B. Houfeng bridge failure in Taiwan. Journal of Hydraulic Engineering 2012, 186–198. [Google Scholar] [CrossRef]
  8. Wang, H.; Hsieh, S.C.; Lin, C.; Wang, C.Y. Forensic Diagnosis on Flood-Induced Bridge Failure. I: Determination of the Possible Causes of Failure. Journal of Performance of Constructed Facilities 2014, 28, 76–84. [Google Scholar]
  9. Witzany, J.; Cejka, T.; Zigler, R. Failure resistance of historic stone bridge structure of Charles Bridge. II: Susceptibility to floods. Journal of Performance of Constructed Facilities 2008.
  10. Wang, D.P.; Chen, Z. He, S. ; Liu, Y.; Tang, H. Measuring and estimating the impact pressure of debris flows on bridge piers based on large-scale laboratory experiments. Landslides 2018, 15, 1331–1345. [Google Scholar]
  11. Zhu, H.Q.; Chen, Y.Q. Liu, LS. Dynamic responses of bridges under catastrophic floods considering fluid–soil–structure interactions. Engineering Failure Analysis 2022, 140, 106596. [Google Scholar]
  12. Malomo, D.; Scattarreggia, N.; Orgnoni, A.; Pinho, R.; Moratti, M.; Calvi, G.M. Numerical Study on the Collapse of the Morandi Bridge. Journal of Performance of Constructed Facilities. Journal of Performance of Constructed Facilities 2020, 34, 04020044. [Google Scholar] [CrossRef]
  13. Berger, C.; McArdell, B.W.; Fritschi, B.; Schlunegger, F. A novel method for measuring the timing of bed erosion during debris flows and floods. Water Resour Res 2010, 46, 228–236. [Google Scholar] [CrossRef]
  14. Iverson, R.M.; Reid, M.E.; Logan, M.; LaHusen, R.G.; Godt, J.W.; Griswold, J.P. Positive feedback and momentum growth during debris-flow entrainment of wet bed sediment. Nature Geoscience 2011, 4, 116–121. [Google Scholar] [CrossRef]
  15. Bugnion, L.; McArdell, B.W.; Bartelt, P.; Wendeler, C. Measurements of hillslope debris flow impact pressure on obstacles. Landslides 2012, 9, 179–187. [Google Scholar] [CrossRef]
  16. Li, N.; Tang, C.; Zhang, X.Z.; Chang, M.; Shu, Z.L.; Bu, X.H. Characteristics of the disastrous debris flow of Chediguan gully in Yinxing town, Sichuan Province, on August 20, 2019. Scientific Reports 2021, 11, 23666. [Google Scholar] [CrossRef]
  17. Yang, H.; Wei, F.; Hu, K.; Chernomorets, S.; Hong, Y.; Li, X.; Xie, T. Measuring the internal velocity of debris flows using impact pressure detecting in the flume experiment. Journal of Mountain Science 2011, 8, 109–116. [Google Scholar] [CrossRef]
  18. Zanuttigh, B.; Lamberti, A. Experimental analysis of the impact of dry avalanches on structures and implication for debris flows. Journal of Hydraulic Research 2006, 44, 522–534. [Google Scholar] [CrossRef]
  19. Chen, Z.; He, S.M.; Shen, W.; Wang, D.P. Effects of defense-structure system for bridge piers on two-phase debris flow wakes. Acta Geotechnica 2022, 17, 1645–1665. [Google Scholar] [CrossRef]
  20. Yan, S.X.; He, S.M.; Deng, Y.; Liu, W.; Wang, D.P.; Shen, F. A reliability-based approach for the impact vulnerability assessment of bridge piers subjected to debris flows. Engineering Geology 2020, 269, 105567. [Google Scholar] [CrossRef]
  21. Liang, Y.Z; Xiong, F. Quantification of debris flow vulnerability of typical bridge substructure based on impact force simulation. Geomatics, Natural Hazards and Risk 2019, 10, 1839–1862. [Google Scholar] [CrossRef]
  22. Shiu, W.J.; Lee, C.F.; Chiu, C.C; Weng, M.C; Yang, C.M.; Chao, W.A.; Liu, C.Y.; Lin, C.H.; Huang, W.K. ; GeoPORT Working Group. Analyzing landslide-induced debris flow and flow-bridge interaction by using a hybrid model of depth-averaged model and discrete element method. Landslides 2023, 20, 331–349. [Google Scholar]
  23. Parola, A.C.; Apelt, C.J.; Jempson, M.A. Debris forces on highway bridges. Transportation Research Board 2000, 445. [Google Scholar]
  24. Kimura, N.; Tai, A.; Hashimoto, A. Flood caused by driftwood accumulation at a bridge. International Journal of Disaster Resilience in the Built Environment 2017, 8, 466–477.
  25. Oudenbroek, K.; Naderi, N.; Bricker, J.; Yang, Y.G.; Van Der Veen, C.; Uijttewaal, W.; Moriguchi, S.; Jonkman, S. Hydrodynamic and Debris-Damming Failure of Bridge Decks and Piers in Steady Flow. Geosciences 2018, 8, 409. [Google Scholar] [CrossRef]
  26. Cook, W. Bridge failure rates, consequences, and predictive trends. PhD Thesis, Utah State University, 2014.
  27. Valero, D. On the Fluid Mechanics of Self-Aeration in Open Channel Flows. PhD thesis, Year.
  28. Zhao, W.Y; Xu, W.L.; Wang, H.; Tang, R.C.; Bai, R.D. Roller fluctuations of pre-aerated high-Froude-number hydraulic jumps. Proceedings of the Institution of Civil Engineers - Water Management 2023, 1–16.
  29. Sun, J.D.; Wan, J.H.; Zhang, B.W. Investigation of “8·13” Flash Flood and Debris Flow in Qingping township, Mianzhu, Sichuan Province. Pearl River 2015, 36, 20–24.
  30. Ju, S.H. Determination of scoured bridge natural frequencies with soil–structure interaction. Soil Dynamics and Earthquake Engineering 2013, 55, 247–254. [Google Scholar] [CrossRef]
Preprints 84281 g001
Figure 1. Schematic diagram of the experimental layout (a); the detailed layout of the experimental devices (b); the arrangement of pressure sensors on bridge deck (c).
Figure 1. Schematic diagram of the experimental layout (a); the detailed layout of the experimental devices (b); the arrangement of pressure sensors on bridge deck (c).
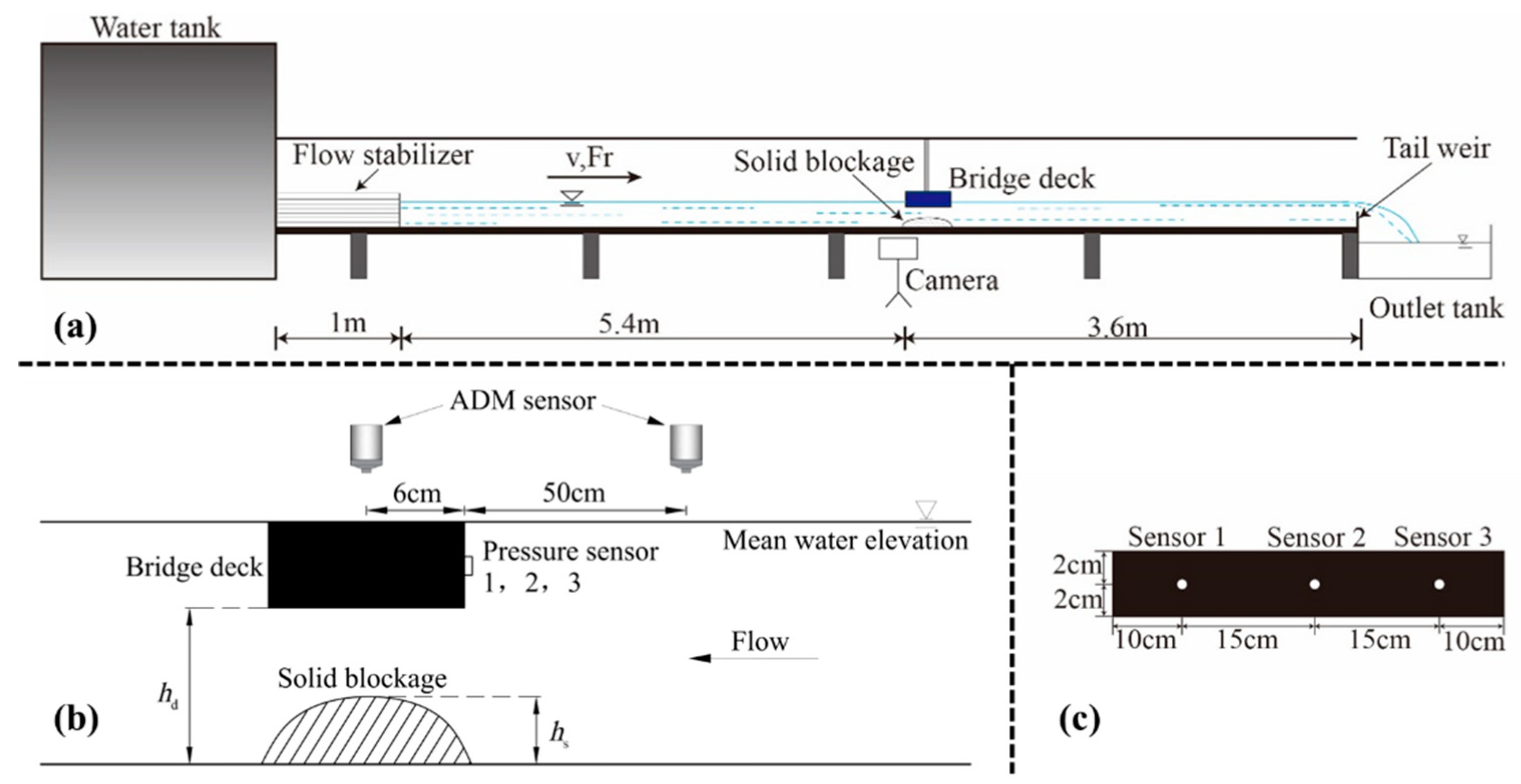
Preprints 84281 g001
Preprints 84281 g002
Figure 2. Measuring pressure count distribution of Sensor 2 (Case 3, hs/hb = 0, Fr = 0.313).
Figure 2. Measuring pressure count distribution of Sensor 2 (Case 3, hs/hb = 0, Fr = 0.313).
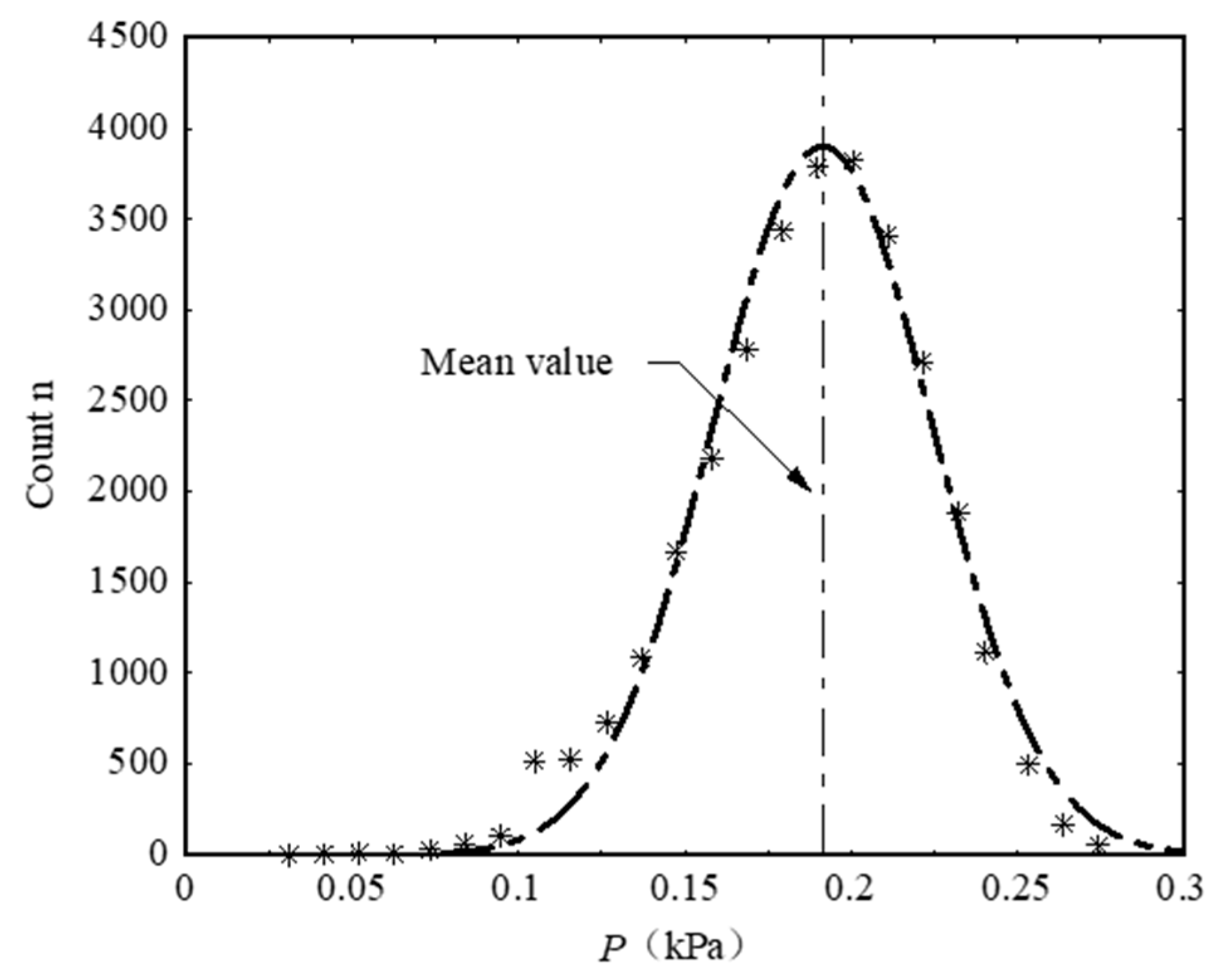
Preprints 84281 g002
Preprints 84281 g003
Figure 3. Water flow conditions (V =0.47m/s) at different sediment deposition heights: control experiment (a); hs = 0.06 m (b); hs = 0.08 m (c); hs = 0.11 m (d).
Figure 3. Water flow conditions (V =0.47m/s) at different sediment deposition heights: control experiment (a); hs = 0.06 m (b); hs = 0.08 m (c); hs = 0.11 m (d).
Preprints 84281 g003
Preprints 84281 g004
Figure 4. Relationship between dimensionless sediment deposition height and dimensionless elevated water surface.
Figure 4. Relationship between dimensionless sediment deposition height and dimensionless elevated water surface.
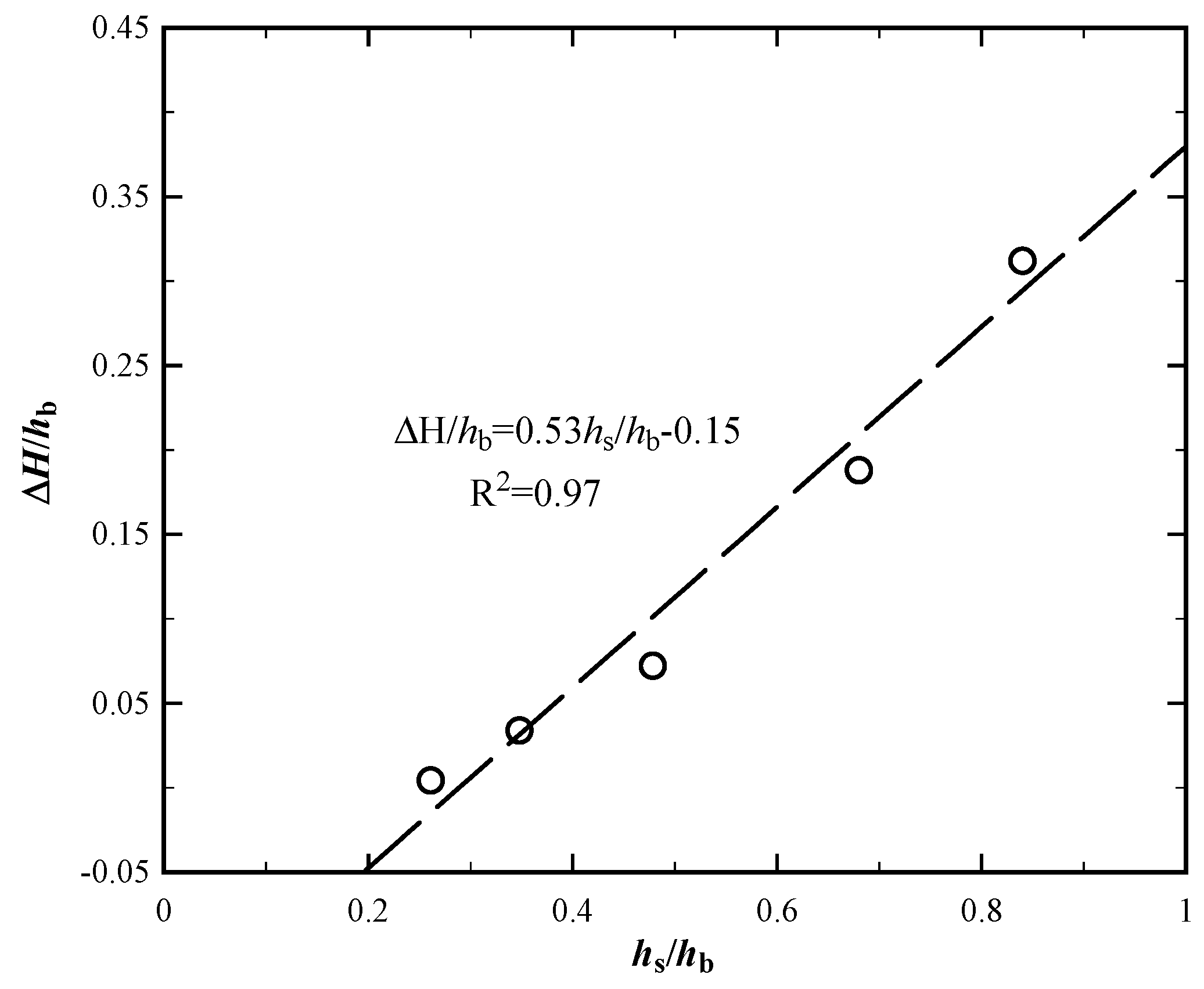
Preprints 84281 g004
Preprints 84281 g005
Figure 5. Water flow conditions with the same maximum sediment deposition height (hs=0.06m) at different flow velocities: V = 0.26 m/s (a); V = 0.63 m/s (b).
Figure 5. Water flow conditions with the same maximum sediment deposition height (hs=0.06m) at different flow velocities: V = 0.26 m/s (a); V = 0.63 m/s (b).
Preprints 84281 g005
Preprints 84281 g006
Figure 6. Relationship between Froude number and dimensionless elevated water surface.
Figure 6. Relationship between Froude number and dimensionless elevated water surface.
Preprints 84281 g006
Preprints 84281 g007
Figure 7. Relationship between dimensionless sediment deposition height and dimensionless horizontal impact pressure at each measuring point.
Figure 7. Relationship between dimensionless sediment deposition height and dimensionless horizontal impact pressure at each measuring point.
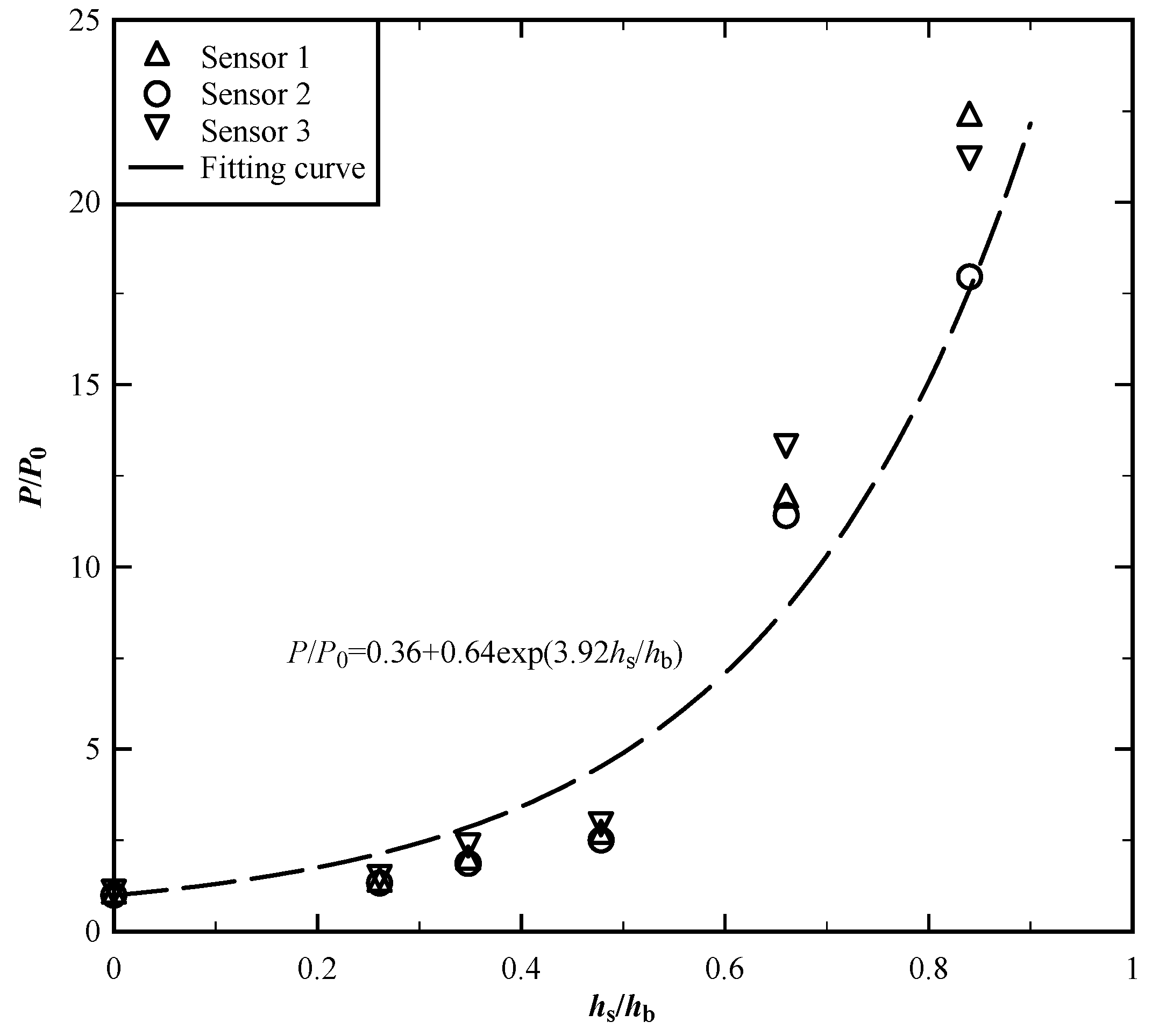
Preprints 84281 g007
Preprints 84281 g008
Figure 8. Relationship between flow velocity and pressure at each measuring point with and without sediment deposition.
Figure 8. Relationship between flow velocity and pressure at each measuring point with and without sediment deposition.
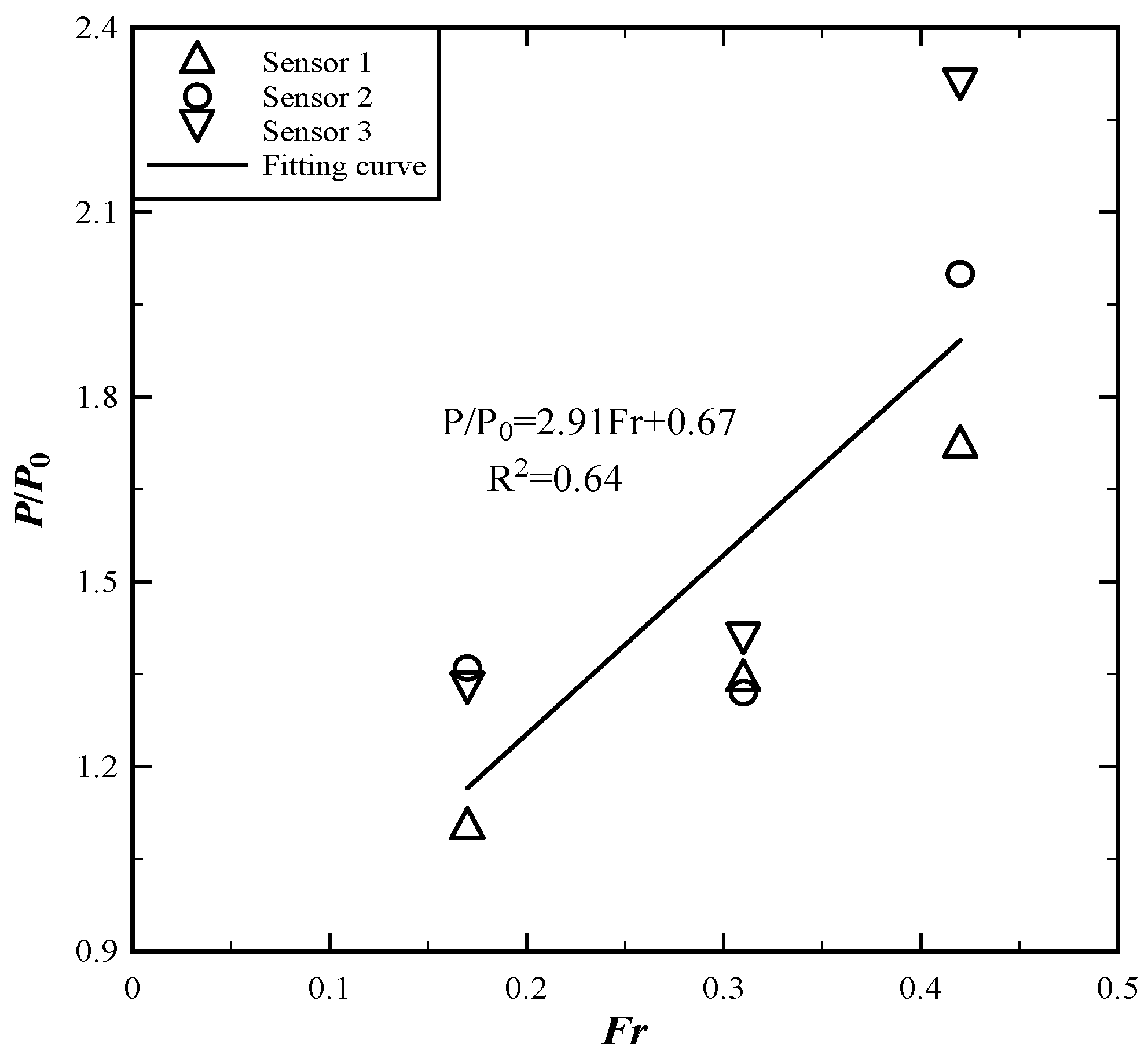
Preprints 84281 g008
Preprints 84281 g009
Figure 11. Time domain (a) and frequency domain (b) diagram of fluctuation pressure (Case 3, hs/hb = 0, Fr = 0.31).
Figure 11. Time domain (a) and frequency domain (b) diagram of fluctuation pressure (Case 3, hs/hb = 0, Fr = 0.31).
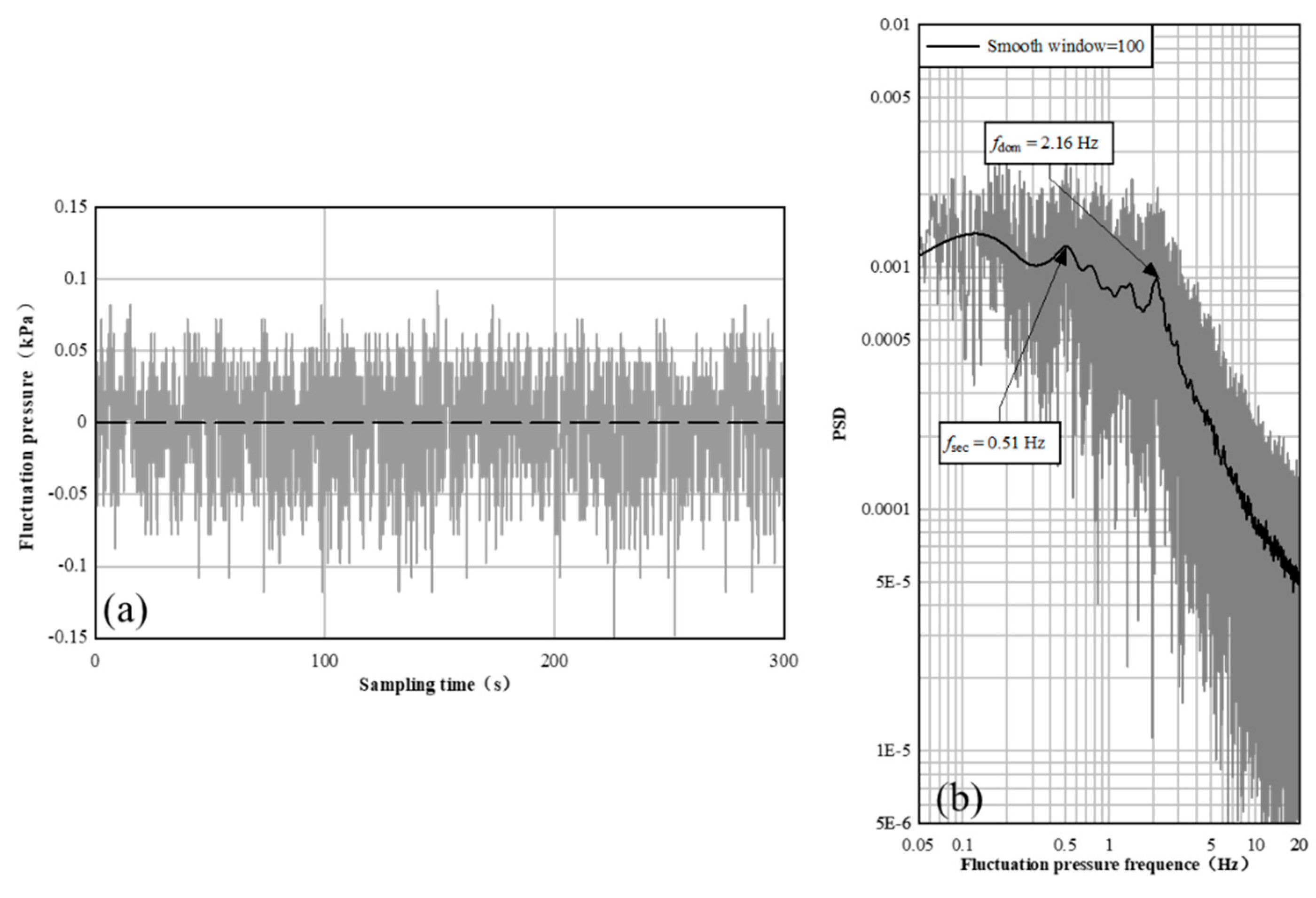
Preprints 84281 g009
Preprints 84281 g010
Figure 12. Dominant and secondary frequency of fluctuation pressure at bridge deck (a); upstream fluctuation water level (b).
Figure 12. Dominant and secondary frequency of fluctuation pressure at bridge deck (a); upstream fluctuation water level (b).
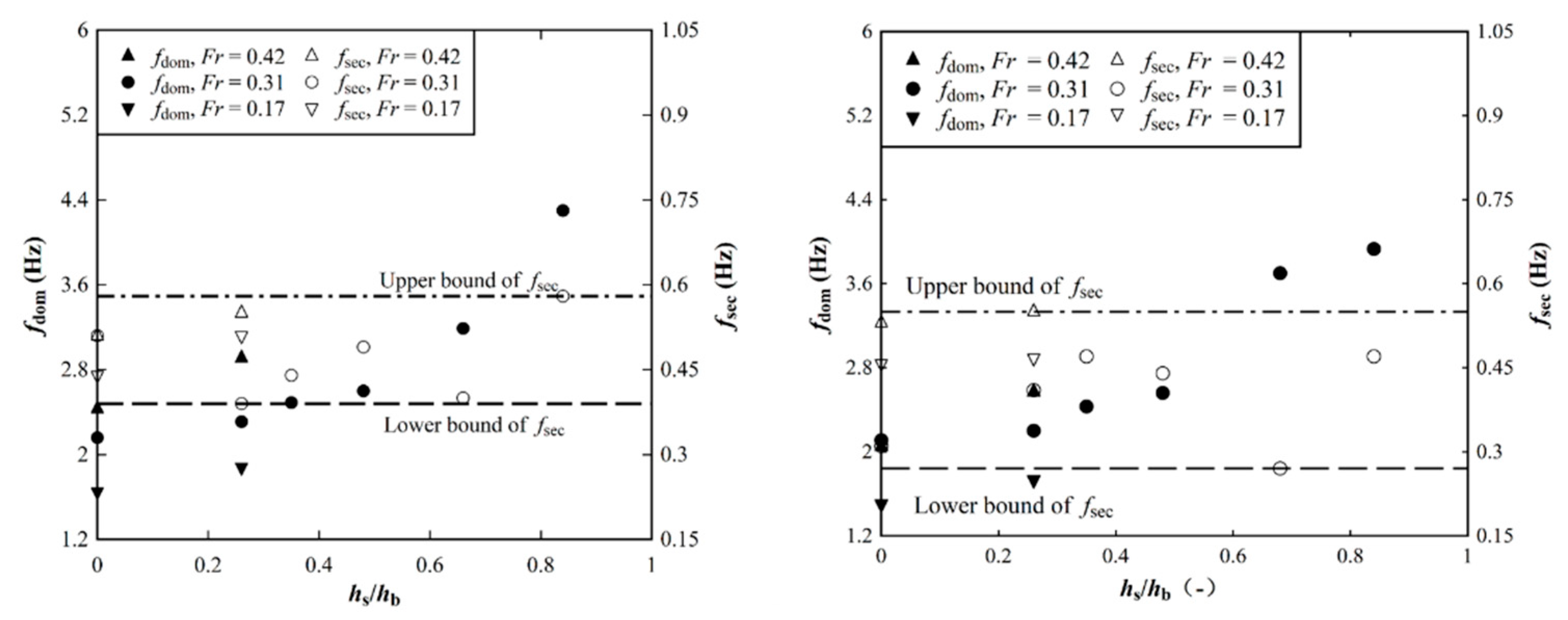
Preprints 84281 g010
Table 1. Summary of experimental conditions.
Table 1. Summary of experimental conditions.
Case hs (m) Q (m3/s) V (m/s) Fr (-)
1 0 0.0210 0.26 0.17
2 0.06
3 0 0.0339 0.47 0.31
4 0.06
5 0.08
6 0.11
7 0.17
8 0.21
9 0 0.0542 0.63 0.42
10 0.06
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated