Prerpints.org logo
Preprint
Article

Experimental Investigation of Beams Reinforced with Carbon 2D-Netzgitterträger Reinforcement

Altmetrics

Downloads

77

Views

26

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

05 September 2023

Posted:

07 September 2023

You are already at the latest version

Alerts
Abstract
The increasing popularity of carbon-reinforced concrete (CRC) is attributed to its exceptional tensile properties, low density, no corrosion phenomenon, and remarkable flexibility, allowing it to be easily shaped into various forms. This research investigates the feasibility of using a special 2D Netzgitterträger (NetzGT) reinforcement system, featuring a net-shaped fabricated textile made of multiple diagonally offset rovings with overlapping edge strands, as a viable alternative to traditional steel reinforcement in concrete beams. This reinforcement is manufactured from carbon rovings with three different diagonal angles of 50⁰, 60⁰, and 70⁰ respectively. Laboratory experiments were conducted to assess the mechanical behavior of beams reinforced with the 2D NetzGT reinforcement. Bending and shear tests were performed on beams with varying numbers of overlapped edge roving and roving angles to evaluate the tensile capacity and failure characteristics of beams. The increase in the number of overlapped edge rovings led to a noticeable increase in the maximum tensile force. Tensile tests on strands were also performed with the increasing number of overlapped rovings to analyze their tensile strength. Additionally, single yarn pull-out tests were also conducted to examine the influence of the roving angle on the bond strength between the carbon textile roving and the concrete matrix
Keywords: 
Subject: Engineering  -   Civil Engineering

1. Introduction

Cement and concrete are the necessary building components of our modern construction society. They are the most often used construction materials due to their wide resources, simplicity of usage, and adaptability. According to 2019 estimates, CO2 emissions from their usage, transportation, production, and demolition account for about 10% of all energy-related CO2 emissions worldwide [1]. The rapid expansion of population and urbanization over the coming decades world widely suggests that there is an urgent need for ways to reduce cement and concrete negative effects on the environment and climate change. Researchers have been exploring alternative materials and methods, prompting a search for more eco-friendly alternatives and innovative techniques to address the challenges of construction in a sustainable manner. For instance, one of the approaches is the use of high-strength fiber-reinforced materials that can lead to efficient resource utilization while maintaining the desired structural performance.
Concrete particularly in steel-reinforced concrete structures effectively handles compression while steel is relied upon to withstand tension. Similar to steel-reinforced concrete structures, carbon textile-reinforced concrete (CTRC) structures use carbon textile reinforcement to provide the necessary tensile strength. In carbon textile reinforcement, carbon fibers are initially produced in the form of filaments. These filaments are then grouped to form yarns or rovings and finally, rovings are then grouped in a specific pattern to form strands [2,3]. The carbon strands are arranged in a mat-like structure to provide specific mechanical properties. This CTRC composite offers several advantages over traditional steel reinforcement. Firstly, carbon fibers have a significantly higher tensile strength and lower density compared to steel, allowing for the development of lighter and more slender structural elements. The CTR exhibits a tensile strength of approximately 3500MPa, resulting in a load-bearing capacity up to six times greater than that of conventional steel reinforcement, which is approximately 550MPa. This enables the utilization of significantly reduced amounts of reinforcement material and leads to the reduced overall weight of the structure [4]. Furthermore, it offers the advantage of being corrosion resistant, as opposed to steel, which is prone to corrosion over time. As a result, concrete cover is only necessary to ensure bond strength [5]. Furthermore, the high flexibility of CTR composite also allows for easier shaping and molding of complex structural geometries [6]. These positive effects not only enhance CTR’s suitability for new construction projects but also for the repair of old buildings [7,8].
Over the past decade, there has been a surge of interest in exploring the potential of CTRC through various projects. These initiatives have aimed to investigate and utilize the capabilities of CTRC as a construction material [9]. Notably, in recent years, the findings and knowledge gained from these projects have led to the full-scale implementation of CTRC in practical applications. One impressive example is the construction of CUBE, the world’s first carbon-reinforced building. The CUBE has been recently constructed by the Institute of Concrete Structures (IMB), Technische Universität Dresden, Germany [5,10]. The extensive research and project endeavors conducted in the past decade have played a crucial role in understanding the unique properties and advantages of CTRC. These projects have likely encompassed aspects such as material characterization, structural testing, durability assessment, and performance evaluation of CTRC components. The outcomes of these investigations have provided valuable insights into the behavior, structural integrity, and potential applications of CTRC. As a result of these research efforts, CTRC has transitioned from a promising concept to a fully implemented construction material in recent years. This indicates that the knowledge and experience gained from the past decade of projects have been successfully translated into real-world applications. Furthermore, the utilization of carbon textile reinforcement provides enhanced geometrical flexibility, enabling the carbon grid-like structure to be easily molded, bent, or twisted into diverse shapes. This characteristic has sparked significant interest within the construction industry, as it allows for the creation of novel structural elements and designs, capitalizing on the advantageous properties of carbon reinforcement. One of the examples of this is the construction of an exceptionally lightweight and slender precast bridge, which has been successfully realized using CTRC as the primary material [11]. The aesthetic Pavilions in Chemnitz, Germany [12] and many other structures have been constructed by using CTRC as the primary material [13,14,15,16,17,18,19,20].
This study involved shaping carbon textile reinforcement into a specific zigzag pattern (net girder) with the intention of substituting it for traditional steel reinforcement in beams, serving as both flexural and shear reinforcement. Additionally, this 2D reinforcement was also transformed recently into a three-dimensional configuration to develop a lightweight hollow core slab system [6,21,22].

2. Materials, Test Program, and Test Setups

2.1. Materials

The experimental investigation uses a single concrete mix of grade 30/37 throughout the study. The composition of the design mix can be found in Table 1. Concrete properties were evaluated by conducting tests on 150×300mm cylinders after 29 days of curing. The average dry compressive strength achieved was 40MPa. The concrete was supplied by the local company informbeton GmbH [23]. A single batch of concrete was used for the manufacturing of single yarn pull-out specimens, bending test specimens, and shear test specimens.
Textile rovings were manufactured by the Institute of Textile Machinery and High Performance Material Technology (ITM) using carbon fiber heavy tows (CFHT) Teijin Tenax-E STS 40 F13 48K 3200tex (Teijin Carbon Europe GmbH, Wuppertal, Germany) with properties acc. to [2] in combination with impregnation material of TECOSIT CC 1000 (CHT Germany GmbH, Tübingen, Germany). Which is a polymeric dispersion with a solid content of approx. 50% [2,24]. The straight rovings were manufactured by impregnating the CFHT with the foulard technique and consolidated for 10min at approx. 180° by using infrared modules Typ IRDS750 SM 3kW 400V fast middlewave (OPTRON GmbH, Garbsen, Germany) at 90% power (2.7kW). Straight rovings were specifically produced to examine the tensile strength of rovings. Bent rovings were extracted from the 2D NetzGT reinforcement structrure with three different angles of 50⁰, 60⁰, and 70⁰ respectively to investigate the influence of the angle of roving on the bond strength.
The 2D NetzGT reinforcement is a continuous textile net-shaped non-crimp fabric reinforcement made of multiple diagonally offset carbon fiber rovings [6]. For this fundamental study 2D NetzGT reinforcement structure were produced with support of manual yarn placement of impregnated rovings on a rack and subsequent consolidation in a champer oven SV 9670/30 MK II (Arnold Schröder Industrieöfen GmbH, Flörsheim am Main, Germany) at 180°C for 30min. In principle, the textile reinforcement structure can be produced using a modified highly productive multiaxial warp knitting process in combination with the further developed warp yarn manipulation method and subsequent impregnation and consolidation of the textile structure [25]. The reinforcement is manufactured in a zigzag pattern, starting at the upper end and slanting diagonally toward the lower end. It then transitions into a straight length of 160mm, followed by a diagonal inclination from the lower end to the upper end. This pattern continues in a repeated sequence resulting in a zigzag structure as shown in Figure 1. The edge-overlapped rovings employed in the construction of NetzGT reinforcement are considered tension reinforcement, and therefore, the number of these rovings has a significant impact on the tensile strength of the reinforcement. For this reason, the investigation was carried out on strands with 1,3,4,5, and 6 overlapped rovings to examine their impact on the 2D NetzGT reinforcement.

2.2. Test Program and Test setups

2.2.1. Yarn Tension test

Tension tests were performed on the straight roving with a linear mass density of 3200tex. These specimens were labeled as “R-X,” with “R” denoting roving and “X” representing the number of roving incorporated in each strand specimen. Four distinct configurations were tested, consisting of 1, 3, 5, and 6 rovings in the specimens. Under each configuration, five specimens were taken into account for statistical analysis. For anchoring purposes, Sikadur-30, an epoxy resin-based composition from Sika company, was skillfully employed to establish a strong bond between the resin embedded rovings and metal plates [26]. The testing process involved subjecting the specimens to a controlled loading rate of 2mm/min (0.03mm/sec) while their free length remained at 100mm as shown in Figure 2. Through this testing setup, the objective was to investigate the tensile properties and behavior of the strands under varying numbers of rovings.
Table 2. Overview of different overlapped rovings.
Table 2. Overview of different overlapped rovings.
Folding The surface of single and multiple rovings Diameter [mm]
1×3200tex 3
3×3200tex 4.5
5×3200tex 5.1
6×3200tex 5.3

2.2.2. Single Yarn Pull-Out test

The single yarn pull-out (YPO) test is conducted to examine the impact of the roving angle on the bond strength and anchorage behavior of the roving in the concrete. In this test, the single rovings were embedded in concrete cubes at three different angles of 50-degree, 60-degree, and 70-degree respectively. One of the main reason on examining curved or bent roving is to assess its ability to bear loads within the center region of the NetzGT reinforcement. A total of three specimens were tested at each roving angle during the experiment. The roving used had an average diameter of 3mm. To conduct the tests, the YPO in [27] was followed with certain modifications due to the difficulties encountered in maintaining consistent dimensions; see Figure 3. Foam rubber was employed at the beginning and end of the rovings to prevent stress concentration and ensure a fixed tail length for all specimens, despite the varying angles. Furthermore, all the concrete cubes were equipped with cast-in transport bolts. These bolts served the purpose of connecting the upper- and lower parts during transportation and preparation, as well as preventing premature failure.

2.2.3. Tension test on 2D NetzGT

A four-point bending test according to RILEM RC5 [28] was performed on a beam reinforced with 2D NetzGT reinforcement to evaluate the tensile behavior of NetzGT reinforcement and failure characteristics of the beam. The test setup was modified for 2D NetzGT reinforcement with a bond breaker length of 10mm as shown in Figure 4. The beam test specimens were tested in a universal testing machine. The test specimen consists of two identical reinforced halves of a beam connected by the reinforcement for the tension test and a steel hinge for the transfer of the compressive force. The beam was reinforced with 2D NetzGT reinforcement as shown in Figure 1b. The reinforcement in the test setup was laid horizontally with a width of 300mm. The test setup uses the 2D NetzGT reinforcement with the use of three, four, and six-edge overlapped roving strands with three different roving angles of 50⁰, 60⁰, and 70⁰ respectively; see Table 3. The test specimens were labeled as B-X-Y, where the first letter B represents the “beam” specimen, X represents the angle of textile roving in the NetzGT reinforcement and Y represents the number of overlapped edge rovings. This test approach aimed to evaluate the impact of varying roving angles and the number of overlapped edge rovings on the tensile strength of NetzGT reinforcement. The beam specimens were placed on a testing apparatus specifically designed for four-point bending tests. This apparatus consisted of supports located at both ends of the beam, along with two loading points positioned between the supports. Five Linear Variable Differential Transformers (LVDTs) were used for measuring displacement at different points of the beam.

2.1.1. Shear test

Three-point bending tests were conducted on beams that were reinforced with a similar 2D NetzGT reinforcement. However, in this test, the reinforcement was placed vertically with a height of 300mm rather than horizontally; see Figure 5. The main objective of the shear test was to observe the failure behavior of the beam when the 2D NetzGT reinforcement was positioned vertically as shear reinforcement and to examine the effect of the roving angle and the number of overlapped edge rovings on the maximum load. The shear span to depth ratio (a/d = 600/320) was kept constant as 1.9 for all the test specimen. The vertical load was applied at a constant speed of 1mm/min (0.017mm/sec). The test setup uses the 2D NetzGT reinforcement with three and four overlapped edge rovings, with two different roving angles of 50⁰ and 60⁰; see Table 4. The test specimens had the same labeling as the four point bending test. i.e., B-X-Y, where the first letter B represent “beam” specimen, X represents roving angle in the NetzGT reinforcement and Y represent the number of overlapped edge rovings. Five LVDT’s were attached to the beam for measuring displacement at various points.

3. Results and Discussion

3.1. Yarn Tension test

The load-displacement curves for the strands that are tested under tension are illustrated in Figure 6. In the case of the R_1 specimen, where only one roving was used, the curves exhibited a linear behavior without having any drop in the curve, suggesting a well-distributed load over the specimen’s length. However, with an increase in the number of rovings to three in the strand (R_3 specimen), there were noticeable changes in the load-bearing behavior, resulting in sudden fluctuations in the curves. This is due to the fact that the individual yarns are not uniformly stretched within the specimen, thus not all of them contribute equally to the load transfer. Moreover the presence of multiple rovings in the strand enhanced the overall capacity of the strand, leading to an increase in the maximum force. This trend continues as the number of rovings further increased to five and six in the strand (R_5 and R_6 specimens). Additionally, it can also be seen from the curves that the stiffness increases as the number of roving in the strand increases.
It can be interpreted from Figure 7 that the increase in the number of rovings in the strands leads to a significant increase in its ultimate load-carrying capacity. The R_1 specimen with only a single roving displays a peak tensile force of 6.6kN, whereas the R_3 specimen demonstrates the tensile breaking force of 9.7kN, presenting an increase of approx. 47% compared to R_1. The R_5 specimen exhibits a maximum tensile force of 10.9kN, demonstrating a 65% increase compare to the R_1 specimen. The R_6 specimen, comprising of 6 rovings in strand achieves the highest tensile force at 13.8kN, represents a substantial increase of approx. 109% compared to R_1 specimen. The observed increase in the ultimate load-carrying capacity or the tensile force with the addition of more rovings in the strand can be attributed to the overall cross-sectional area of the strand, sharing capacity of strand, and synergistic effect of the roving. When more rovings are group together in the strand, the overall cross-sectional area of the strand increases. This means that there are more individual fibers contributing to the load-bearing capacity of the strand. Additionally, the presence of multiple rovings can enhance the load-sharing capacity of the strand. If one roving experience a localized weakness or failure, the others can compensate for it, preventing the overall failure and allowing the strand to sustain higher loads. Furthermore, the interaction between the rovings can create a synergistic effect. As the rovings are laid together, their alignment and interaction can result in improved load distribution along the length of the strand, enabling it to withstand higher forces. So, it can be concluded that the increase in the number of rovings provides more fibers to bear the load, helps in distributing the load more evenly, and provides backup if some fibers encounter failure. This combined effect leads to the significant increase in the ultimate load-carrying capacity of the strand with more rovings.
This data also clearly highlights the increase in standard deviation with an increase in the number of rovings in the strand and can be attributed to greater variability in tension distribution within the strands; see Table 5. When more rovings are incorporated to produce a strand, then each roving might experience slightly different conditions during the manufacturing process, leading to variations in their tensile properties. These variations can accumulate and result in differences in tension across the strands. As the number of roving increases, the potential for these small differences to add up also increases, which is reflected in the higher standard deviation values observed in the specimens with more roving, such as specimens R_5(2.01) and R_6(2.68) as compare to specimens R_1(0.39) and R_3(0.79).

3.2. Single Yarn Pull-Out test

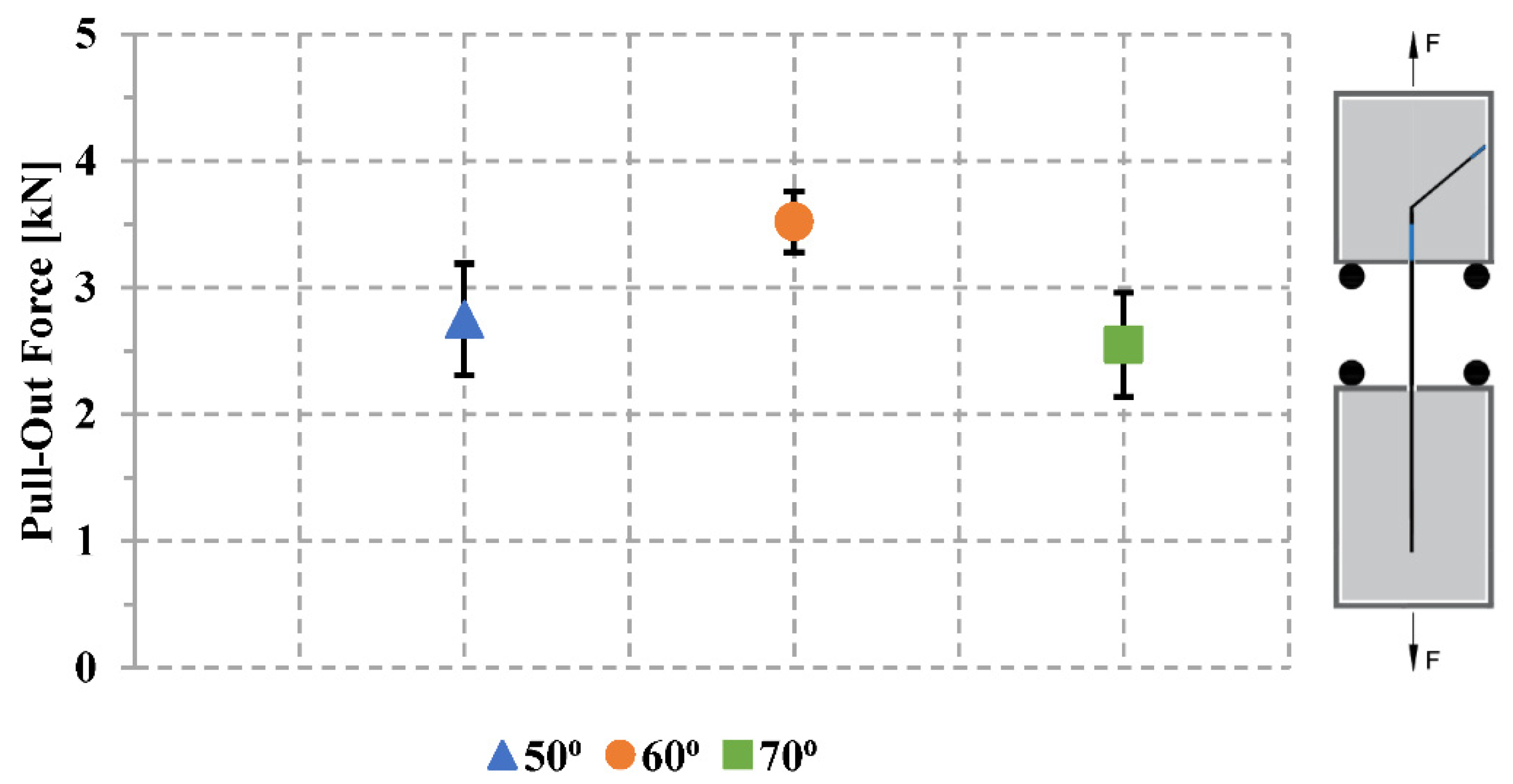
There are multiple factors that can affect the maximum pull-out load in a YPO test, such as geometry, bending radius, profile, and embedment length, steepness of the roving (angle of the roving), friction between the roving and concrete [29]. In this study, the only variable that was researched in the YPO test was the inclination of textile roving while keeping all the other parameters constant. The test details and labelling of the specimen can be found in section 2.2.2. The 50-degree roving shows an average pull-out force of 2.7kN, 60-degree roving shows 3.5kN, and 70-degree shows 2.5kN respectively. It has been observed that the force increases with increasing angle of the roving from 50⁰ to 60⁰, and then decreases with further increasing angle from 60⁰ to 70⁰.
When the embedment angle of the textile roving increases from 50-degrees to 60-degrees, the maximum pull-out force increased by 29.6%, recorded as 3.5kN at 60-degrees compared to 2.7kN at 50 degrees. This increase in force can be attributed to the increased friction and improved interlocking. As the angle of embedment increases, the frictional forces between the roving and the surrounding matrix also increases and this is due to the increase in the effective bonding surface area [30]. Also, the roving forms a more oblique or inclined orientation within the matrix at 60-degrees compare to that of 50-degrees. This inclined orientation creates a difficult path for the roving to be pulled out from the concrete matrix. Another phenomenon that can explain the increase in the pull-out force is the mechanical interlocking. The roving has a greater opportunity to interlock with the surrounding matrix with a larger embedment angle. This interlocking mechanism enhances the bond strength and subsequently increases the maximum pull-out force in 60-degrees specimen.
However, when the embedment angle of the textile roving increases further from 60-degrees to 70-degrees, the maximum pull-out force decreases by about 40%, recorded as 2.5kN at 70-degrees compared to 3.5kN at 60-degrees. The decrease in force can be attributed to the stress concentration. At steeper angles, as 70-degrees, there is a higher concentration of stress around the roving-matrix interface and thus results in a reduction in the overall pull-out force.
Therefore, it can be concluded that a 60-degree textile roving provided higher pull-out force compared to the textile roving with other angles tested in the experimental investigation. Which clearly indicates that textile roving with 60-degrees can be considered as an optimized roving angle. However, an experimental study covering a range of roving angles from 50-degrees to 70-degrees can provide valuable insights into the fluctuation of the pull-out force. By varying the roving angle within this range, it can be observed how the angle affects the pull-out force and analyze the patterns or trends that emerge.
Preprints 84282 g008
Figure 8. Pull-out forces for different angle of roving embedded in matrix.
Figure 8. Pull-out forces for different angle of roving embedded in matrix.
Preprints 84282 g008

3.3. Tension test on 2D NetzGT

The main objective of the four-point bending test is to determine the total tensile capacity of a 2D NetzGT reinforcement. The tensile forces are mainly transmitted in the overlapped edge strands, with a smaller contribution originating from the intersecting threads within the central region. So a flat 2D NetzGt can be tested to get load bearing capacity of the 3D NetzGT. By defining the inner lever arm in a bending test, the force can be determined. The inner lever arm is defined with the help of a metal joint in the compression zone, so the tensile force in the reinforcement can be determined from the bending test as shown in Figure 9. The tension strands in the NetzGT were modified by varying the number of overlapping edge rovings. Additionally the angle of orientation for the roving was also altered, with variations at 50⁰, 60⁰, and 70⁰. All of the test specimens show bending failure with a single big crack started from the bottom and grows to the steel hinge of the beam.
Figure 10 illustrates the relationship between the force and displacement for various beam specimens generated during the beam loading process. All the tested specimens exhibit a similar behavior, characterized by an initial sudden drop in force at the beginning of loading, which corresponds to the formation of the first crack. Subsequently, the force increases until reaching its maximum value. However, there are intermittent drops in force between the first crack load and the maximum load. Furthermore, all the tested specimens show an increase in the force after the occurrence of the first crack. This indicates that the NetzGT reinforcement within the beam specimens became activated, contributing to an increase in the load bearing capacity. By maintaining the identical roving angle within the specimen and increasing the number of roving in the strand, an increase in the stiffness of specimen B-60-6 compared to specimen B-60-3 can be noticed. This can be attributed to the cross-sectional area of the strand. When there are more rovings in the strand, there are more fibers providing reinforcement, leading to improved load-bearing capacity and reduced susceptibility to deformation. The increased fiber density also enhances the material’s ability to distribute and transfer loads across the strand, contributing to the increase in stiffness. These findings provide valuable insights into the tensile behavior of the NetzGT reinforced beams under bending conditions.
Effect of the number of overlapped edge rovings on the tensile capacity of NetzGT
The primary tension-resisting part of the 2D NetzGT reinforced beam consists of overlapped edge rovings, i.e., Strands. Due to this significance, it was considered important to investigate the effect of varying overlapped edge rovings on the tensile capacity of the reinforcement. The maximum tensile force in the reinforcement for each specimen was determined using equation 1, with the corresponding results presented in Table 6.
F n = ( F / 2 ) × ( l / z )
Where, Fn = Maximum tensile force in the NetzGT [kN]
F = applied load on the beam [kN]
l = known length of 300mm between the support and load; see Figure 4a
z = known inner lever arm of 95mm
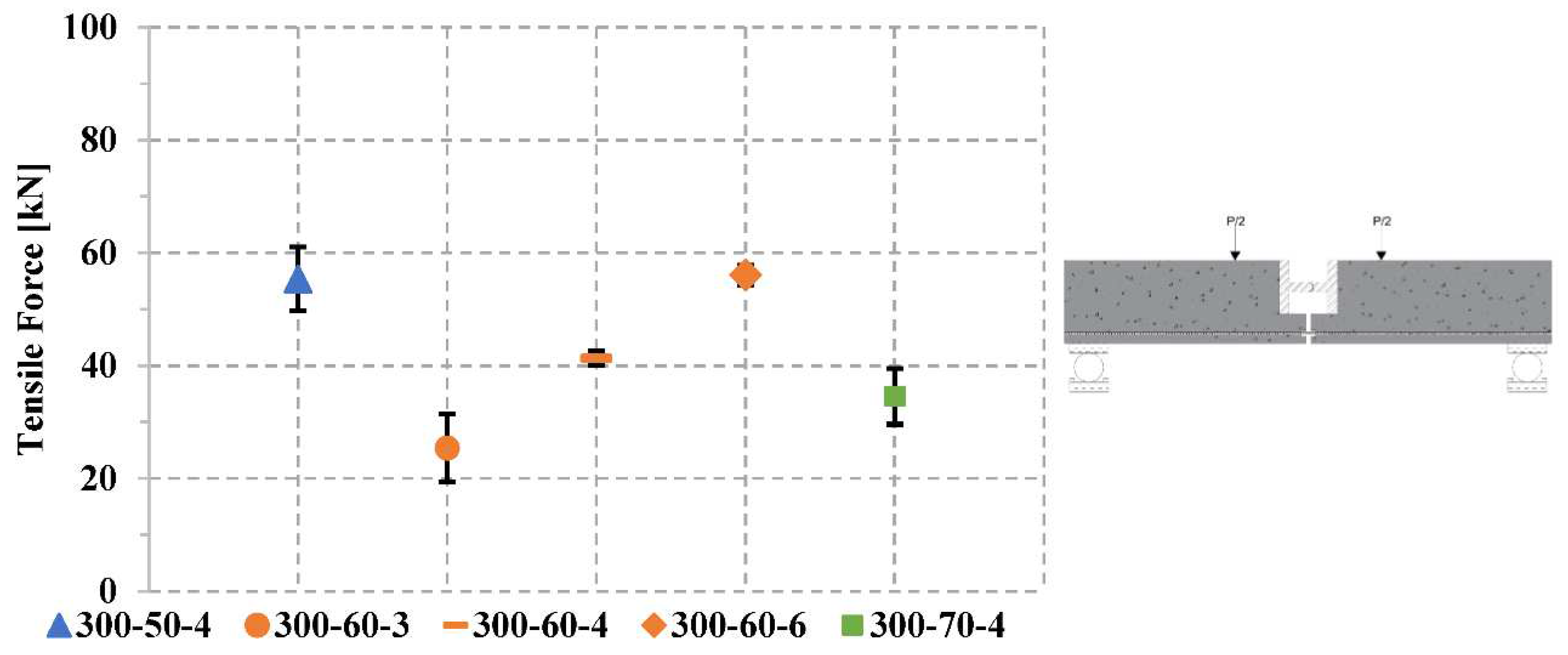
The maximum tensile force in the strands followed a specific trend, with the highest value observed for the beam specimen B-60-6 (56.1kN), followed by B-50-4 (55.4kN), B-60-4 (41.3kN), B-70-4 (34.6kN), and B-60-3 (25.4kN). The analysis reveals that maintaining the same angle of roving while increasing the number of edge overlapped rovings in the strands leads to a clear increase in the maximum tensile force. For instance, the maximum tensile force was recorded as 25.4kN for B-60-3. Subsequently, it increased by 62% to 41.3kN for B-60-4 specimen. Moreover, the tensile force further increased to 56.1kN for B-60-6, representing a 120% increase from B-60-3 and a 35% increase from B-60-4 specimen.
Effect of the roving angle on the tensile capacity of NetzGT
The effect of the textile roving angle was observed in the YPO tests, where it demonstrated an influence on the maximum pull-out force, as depicted in Figure 8. As discussed in section 2.1 regarding the construction of the 2D NetzGT reinforcement, it is important to consider that the angles of the rovings within the central region of the 2D NetzGT reinforcement can have a modest impact on the tensile force within the strands. Hence, it was important to evaluate their impact on the tensile capacity of 2D NetzGT reinforcement. By keeping the number of overlapped edge rovings constant at four such as with the specimens B-50-4, B-60-4, and B-70-4. The impact of the roving angle on tensile capacity of the reinforcement could be evaluated independently. From the results, it is evident that the maximum tensile force was observed in specimen B-60-4, followed by B-50-4, and B-70-4. There is a minimal distinction in the values between the beam specimens with 50⁰ and 60⁰ rovings. In specimens B-50-4 and B-60-4, the textile roving were more effectively activated, resulting in higher tensile force compared to B-70-4 specimen. In B-60-4 specimen, the maximum tensile force recorded as 41.3kN which is 19% higher than that of B-70-4 specimen recorded as 34.6kN. Therefore, it can be concluded based on these scientific observations that the more longitudinal alignment of the textile roving resulted in a higher activation of the roving and improved the tensile capacity of the NetzGT reinforcement.
Preprints 84282 g011
Figure 11. Maximum tensile force for strands with varying overlapped edge rovings and angle of rovings.
Figure 11. Maximum tensile force for strands with varying overlapped edge rovings and angle of rovings.
Preprints 84282 g011

3.4. Shear test

The three-point bending test was specifically designed and labeled as a shear test, with the intention of inducing shear failure in the specimen. The purpose of the shear tests was to investigate the behavior of the reinforced beams and assess the impact of the 2D NetzGT reinforcement as shear reinforcement. These tests were conducted as trial experiments, meaning they were intended to provide initial insights and gather preliminary data. The experimental setup is summarized in Figure 5. The 2D NetzGT reinforcement was embedded vertically within the beam to enhance its shear capacity. Additionally, it was aimed that shear tests would provide a broader understanding of how the vertically embedded 2D NetzGT reinforcement influence the failure of the beam.
During the shear tests on the reinforced beams, multiple cracks, including a prominent central crack, was observed in the specimens, as depicted in Figure 12. These cracks predominantly formed within the mid-span region of the beam, indicating the bending failure rather than shear failure. Additionally, it was clearly noticed that the single central crack gradually widened along the depth of the beam with the maximum average crack width of about 15mm for all the three tested specimens. The absence of shear cracks suggests that the reinforcement absorbed the shear forces within the beam, preventing shear failure. However, without testing reference beams, the exact extent of this improvement remains unknown and requires further investigation in future studies.
When examining the effect of the textile roving angle on the maximum failure load, it becomes evident that the 50-degree roving angle specimens exhibits an increase to that of 60-degree roving angle specimen. The specimens B-50-4 shows the average maximum force of 38.5kN, which is 56% greater than the B-60-3 specimen; see Table 7. However, it is important to note that the number of overlapped edge rovings in the B-50-4 specimens are greater than in the B-60-3 specimen. Consequently, it is challenging to draw a definitive conclusion regarding which factor—roving angle or the number of overlapped edge rovings—truly contributes to the increase in maximum load capacity. Furthermore, no shear failure was observed in any of the specimens. This suggests that both roving angles show an improved response to shear forces.
Furthermore, to gain a comprehensive understanding and draw confident conclusions, further studies need to investigate specimens with different roving angles as 50⁰, 60⁰ and 70⁰ and various numbers of edge overlapped rovings as illustrated in the four-point bending test (refer to section 3.3) and keeping one factor constant while systematically varying the other factor. As there is no shear failure observed in the 2D NetzGT reinforced beam, one potential approach for future studies could involve introducing longitudinal reinforcement, such as placing a rebar within the beam, to enhance its bending capacity and intentionally inducing shear failure in the beam. It is then possible to observe the formation of shear cracks and subsequently determine the effect of the roving angle on the shear failure. This research work also proposes the extension of the experimental study to encompass a wider range of tests, involving variations in the a/d ratio of the specimens. This expansion aims to examine how different a/d ratios influence the failure behavior and performance of the beam reinforced with vertically placed 2D NetzGT reinforcement.

4. Conclusions

The lightweight nature and high tensile properties of 2D NetzGT reinforcement has significant potential to serve as a replacement for traditional steel reinforcement. This work is focused on their bond strength with concrete and their initial assessment as a reinforce material in beam. The use of this reinforcement in beams need further investigation, particularly in terms of its bending and shear behavior, to establish a more confident understanding of its performance. Furthermore, the transformation of 2D NetzGT reinforcement into a 3-dimensional configuration for the production of lightweight hollow-core slab and wall systems is currently in the developmental stage and undergoing investigation. This 3D approach has also the potential to offer numerous benefits in terms of structural efficiency, material optimization and sustainable construction.
The following conclusions can be drawn from the various experimental tests conducted on various specimen types:
  • It can be concluded from the tensile tests carried on the straight strands, that increasing the number of roving in the strands substantially enhances the ultimate load capacity of the strands. For instance, R_6 specimen with 6 rovings in the strand showcases a 109% increase compared to R_1 specimen with a single roving. This increase in the tensile force can be attributed to the increased cross-sectional area of the strand, load-sharing capacity of strand, and a synergistic roving effect.
  • The YPO test examined the effect of textile roving inclination on the maximum pull-out load while keeping other parameters constant. Results showed that the maximum pull-out force increased by 29.6% when the roving angle increased from 50-degrees to 60-degrees, attributed to increased friction and improved interlocking. However, a further increase in roving angle from 60-degrees to 70-degrees led to a 40% decrease in maximum pull-out force, which can be attributed to a stress concentration. Overall, the YPO testing setup suggests that a roving angle of 60-degrees provided higher strength and can be considered as an optimized angle.
  • The four-point bending test focused on determining the total tensile capacity of 2D NetzGT reinforcement. It can be concluded from the test results that increasing the number of overlapped edge rovings increased the maximum tensile capacity of the reinforcement. Also it was found out that keeping the same number of edge overlapped rovings in the strand, the increased longitudinal alignment of the textile roving led to greater activation of the roving, thereby enhancing the tensile capacity of the NetzGT reinforcement.
  • The three-point bending test showed that the 50-degree roving angle specimens exhibited increased maximum failure load compared to the 60-degree roving angle specimens. The higher number of overlapped rovings in the 50-degree specimens likely contributed to this increase. However, to draw confident conclusions, future studies should examine one factor at one time. It is suggested from the shear test results that one potential approach could involve introducing longitudinal reinforcement to enhance bending capacity of the beam and intentionally induce shear failure to study the effect of vertically placed 2D NetzGT reinforcement.

Author Contributions

Nazaib Ur Rehman: Conceptualization, Methodology, Data curation, Investigation, Supervision, Validation, Writing – Original draft preparation. Marina Stümpel: Conceptualization, Methodology, Data curation, Investigation, Supervision, Validation, Writing – Review and Editing. Harald Michler: Conceptualization, Methodology, Supervision, Validation, Writing – Review and Editing. Paul Penzel: Resources, Validation, Writing – Review and Editing. Birgit Beckmann: Resources, Supervision, Funding acquisition, Project administration. Lars Hahn: Resources, Supervision, Validation, Writing – Review and Editing. Chokri Cherif: Resources, Supervision, Funding acquisition, Project administration. Steffen Marx: Conceptualization, Supervision, Funding acquisition, Project administration.

Funding

The IGF research project 21556 BR of the Forschungsvereinigung Forschungskuratorium Textil e. V. is funded through the AiF within the program for supporting the „Industriellen Gemeinschaftsforschung (IGF)“ from funds of the Federal Ministry for Economic Affairs and Climate Action on the basis of a decision by the German Bundestag.

Acknowledgements

The authors are thankful to Otto Mohr Laboratory (OML) team for producing testing specimens and conducting tests. Special thanks to Rene Wallschläger and Michael Liebe for their valuable input to this work.
Conflicts of interest: The authors declare that they have no conflicts of interest associated with the work presented in this paper.

References

  1. Z. Cao, E. Masanet, A. Tiwari, and S. Akolawala, “Decarbonizing Concrete: Deep decarbonization pathways for the cement and concrete cycle in the United States, India, and China,” Industrial sustainability analysis lab-Climateworks foundation, 2021.
  2. P. Penzel et al., “Bond Modification of Carbon Rovings through Profiling,” Materials, vol. 15, no. 16, p. 5581, 2022.
  3. A. Abdkader et al., “Improved Tensile and Bond Properties through Novel Rod Constructions Based on the Braiding Technique for Non-Metallic Concrete Reinforcements,” Materials, vol. 16, no. 6, p. 2459, 2023.
  4. R. Mansur de Castro Silva and F. de Andrade Silva, “Carbon textile reinforced concrete: Materials and structural analysis,” Mater Struct, vol. 53, no. 1, p. 17, 2020.
  5. M. Tietze, S. Kirmse, A. Kahnt, F. Schladitz, and M. Curbach, “The ecological and economic advantages of carbon reinforced concrete—Using the C3 result house CUBE especially the BOX value chain as an example,” Civil Engineering Design, vol. 4, no. 1–3, pp. 79–88, 2022.
  6. “DEVELOPMENT OF CARBON-REINFORCED HOLLOW CORE SLAB | Zenodo.” https://zenodo.org/record/8116760 (accessed Aug. 11, 2023).
  7. V. Mechtcherine, “Novel cement-based composites for the strengthening and repair of concrete structures,” Constr Build Mater, vol. 41, pp. 365–373, Apr. 2013. [CrossRef]
  8. JJ. Wagner et al., “Strengthening of Reinforced Concrete Structures with Carbon Reinforced Concrete— Possibilities and Challenges,” CivilEng 2022, Vol. 3, Pages 400-426, vol. 3, no. 2, pp. 400–426, May 2022. [CrossRef]
  9. D. Friese, M. Scheurer, L. Hahn, T. Gries, and C. Cherif, “Textile reinforcement structures for concrete construction applications––a review,” J Compos Mater, vol. 56, no. 26, pp. 4041–4064, 2022.
  10. “Let’s get CUBE – carbon-concrete.org.” https://carbon-concrete.org/lets-get-cube/ (accessed Nov. 09, 2022).
  11. S. Rempel, C. Kulas, N. Will, and J. Hegger, “EXTREMELY LIGHT AND SLENDER PRECAST-BRIDGE MADE OUT OF TEXTILE-REINFORCED-CONCRETE”.
  12. “Carbon Fibre-Reinforced Concrete Offers Innovative Solutions for Civil Engineering | TUCaktuell | TU Chemnitz.” https://www.tu-chemnitz.de/tu/pressestelle/aktuell/7105/en (accessed Jul. 07, 2023).
  13. H. Michler, “Segmentbrücke aus textilbewehrtem Beton–Rottachsteg Kempten im Allgäu,” Beton-und Stahlbetonbau, vol. 108, no. 5, pp. 325–334, 2013.
  14. M. Curbach, W. Graf, D. Jesse, J. Sickert, and S. Weiland, “Segmentbrücke aus textilbewehrtem Beton: Konstruktion, Fertigung, numerische Berechnung,” Beton-und Stahlbetonbau, vol. 102, no. 6, pp. 342–352, 2007.
  15. A. Scholzen, R. Chudoba, and J. Hegger, “Thin walled shell structure made of textile reinforced concrete”.
  16. “Carbon composite pedestrian bridge installed in Madrid,” Reinforced Plastics, vol. 55, no. 3, pp. 43–44, 2011. [CrossRef]
  17. “V4.2 Vorgespannter Carbonbeton für Straßenbrücken und Flächentragwerke – Carbon Concrete Composite e.V.” https://www.bauen-neu-denken.de/vorhaben/v4-2-vorgespannter-carbonbeton-fuer-strassenbruecken-und-flaechentragwerke/ (accessed Jul. 07, 2023).
  18. A. Schumann, S. May, and M. Curbach, “Design and testing of various ceiling elements made of carbon reinforced concrete,” in Proceedings, MDPI, 2018, p. 543.
  19. A. Schumann, H. Michler, F. Schladitz, and M. Curbach, “Parking slabs made of carbon reinforced concrete,” Structural Concrete, vol. 19, no. 3, pp. 647–655, 2018.
  20. M. Curbach, S. Weiland, and H. Michler, “Le béton à armature textile,” Textile Journal, vol. 125, no. 4, pp. 59–69, Oct. 2008.
  21. “Lattice girder for concrete structures,” Dec. 2016.
  22. L. Hahn et al., “New approaches to 3D non-crimp fabric manufacturing.
  23. “Das Unternehmen - informbeton.” http://www.informbeton.de/das-unternehmen.html (accessed Aug. 11, 2023).
  24. “CHT Group - sustainable specialty chemicals: CHT Group.” https://www.cht.com/en/ (accessed Aug. 11, 2023).
  25. L. Hahn, S. Rittner, C. Bauer, and C. Cherif, “Development of alternative bondings for the production of stitch-free non-crimp fabrics made of multiple carbon fiber heavy tows for construction industry,” Journal of Industrial Textiles, vol. 48, no. 3, pp. 660–681, 2018.
  26. “Sikadur®-30 | Structural Adhesives.” https://mng.sika.com/en/construction/structural-strengthening/structural-adhesives/sikadur-30.html (accessed Jul. 21, 2023).
  27. K. Schneider, A. Michel, M. Liebscher, L. Terreri, S. Hempel, and V. Mechtcherine, “Mineral-impregnated carbon fibre reinforcement for high temperature resistance of thin-walled concrete structures,” Cem Concr Compos, vol. 97, pp. 68–77, 2019.
  28. E. P. Carvalho, E. G. Ferreira, J. C. da Cunha, C. de S. Rodrigues, and N. da S. Maia, “Experimental investigation of steel-concrete bond for thin reinforcing bars,” Latin American Journal of Solids and Structures, vol. 14, pp. 1932–1951, 2017.
  29. T. Quadflieg, O. Stolyarov, and T. Gries, “Influence of the fabric construction parameters and roving type on the tensile property retention of high-performance rovings in warp-knitted reinforced fabrics and cement-based composites,” Journal of Industrial Textiles, vol. 47, no. 4, pp. 453–471, Nov. 2017. [CrossRef]
  30. J. Hartig, U. Häußler-Combe, and K. Schicktanz, “Influence of bond properties on the tensile behaviour of Textile Reinforced Concrete,” Cem Concr Compos, vol. 30, no. 10, pp. 898–906, Nov. 2008. [CrossRef]
Preprints 84282 g001
Figure 1. (a) Single textile roving with 50⁰, 60⁰, and 70⁰ roving angle (b) 2D NetzGT reinforcement for beam pull-out and shear test experiments (Top view).
Figure 1. (a) Single textile roving with 50⁰, 60⁰, and 70⁰ roving angle (b) 2D NetzGT reinforcement for beam pull-out and shear test experiments (Top view).
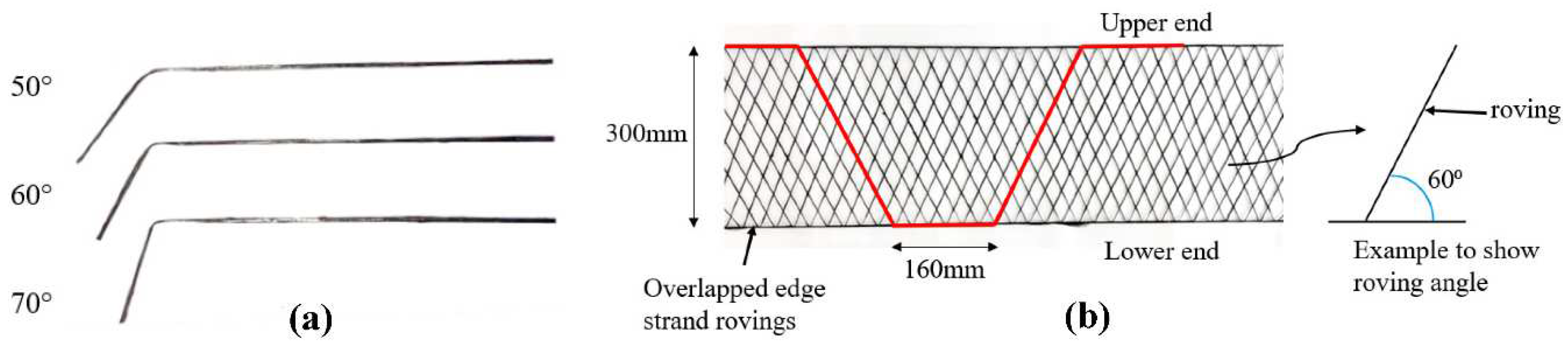
Preprints 84282 g001
Preprints 84282 g002
Figure 2. Strand prepared to be tested under tension (a), Schematic test setup for tension test on roving and strands (b). Unit is in mm.
Figure 2. Strand prepared to be tested under tension (a), Schematic test setup for tension test on roving and strands (b). Unit is in mm.
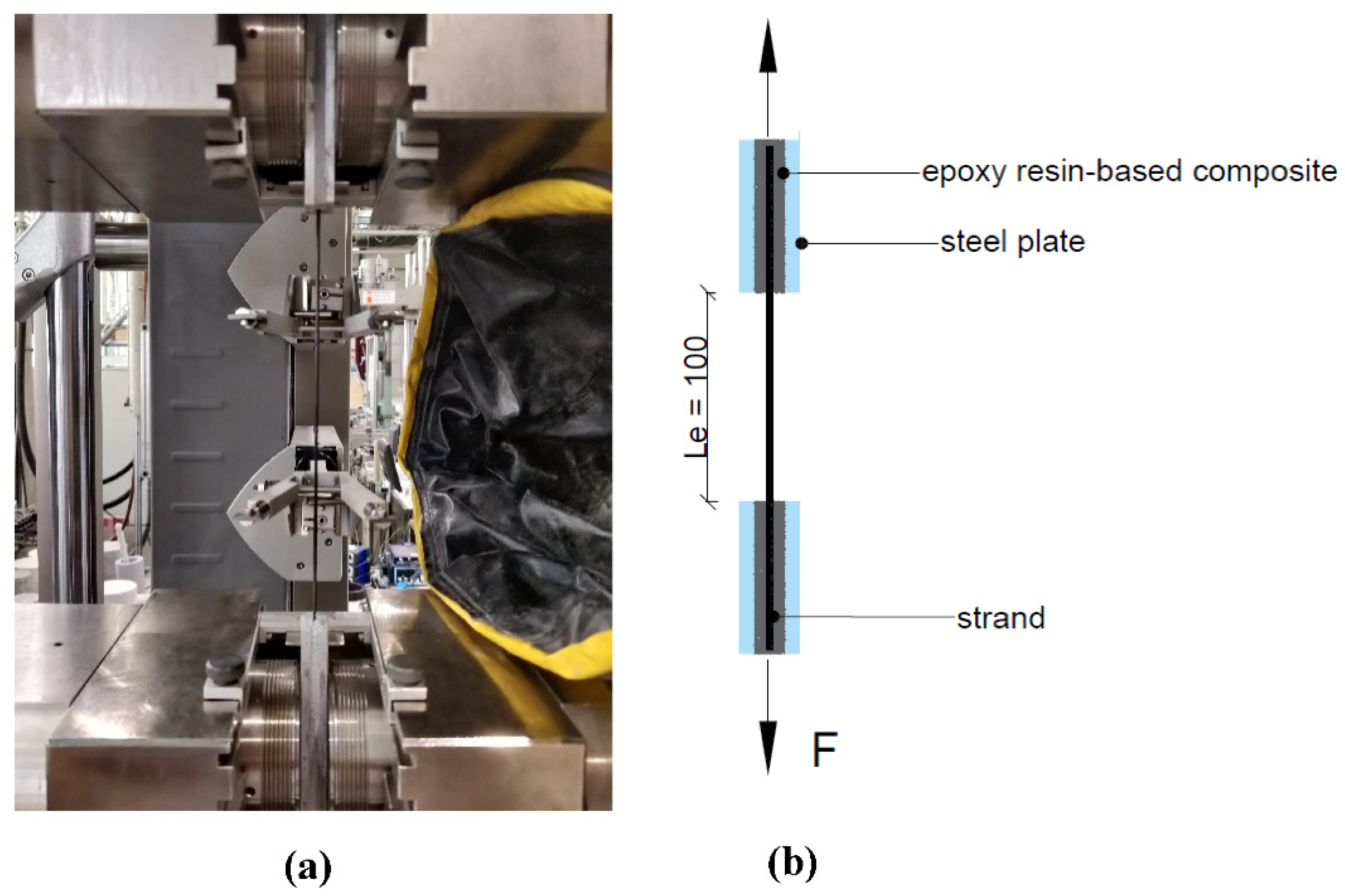
Preprints 84282 g002
Preprints 84282 g003
Figure 3. Schematic test setup for YPO test. The angle Q in the figure is the angle of roving (50⁰, 60⁰, and 70⁰). All dimensions are in mm.
Figure 3. Schematic test setup for YPO test. The angle Q in the figure is the angle of roving (50⁰, 60⁰, and 70⁰). All dimensions are in mm.
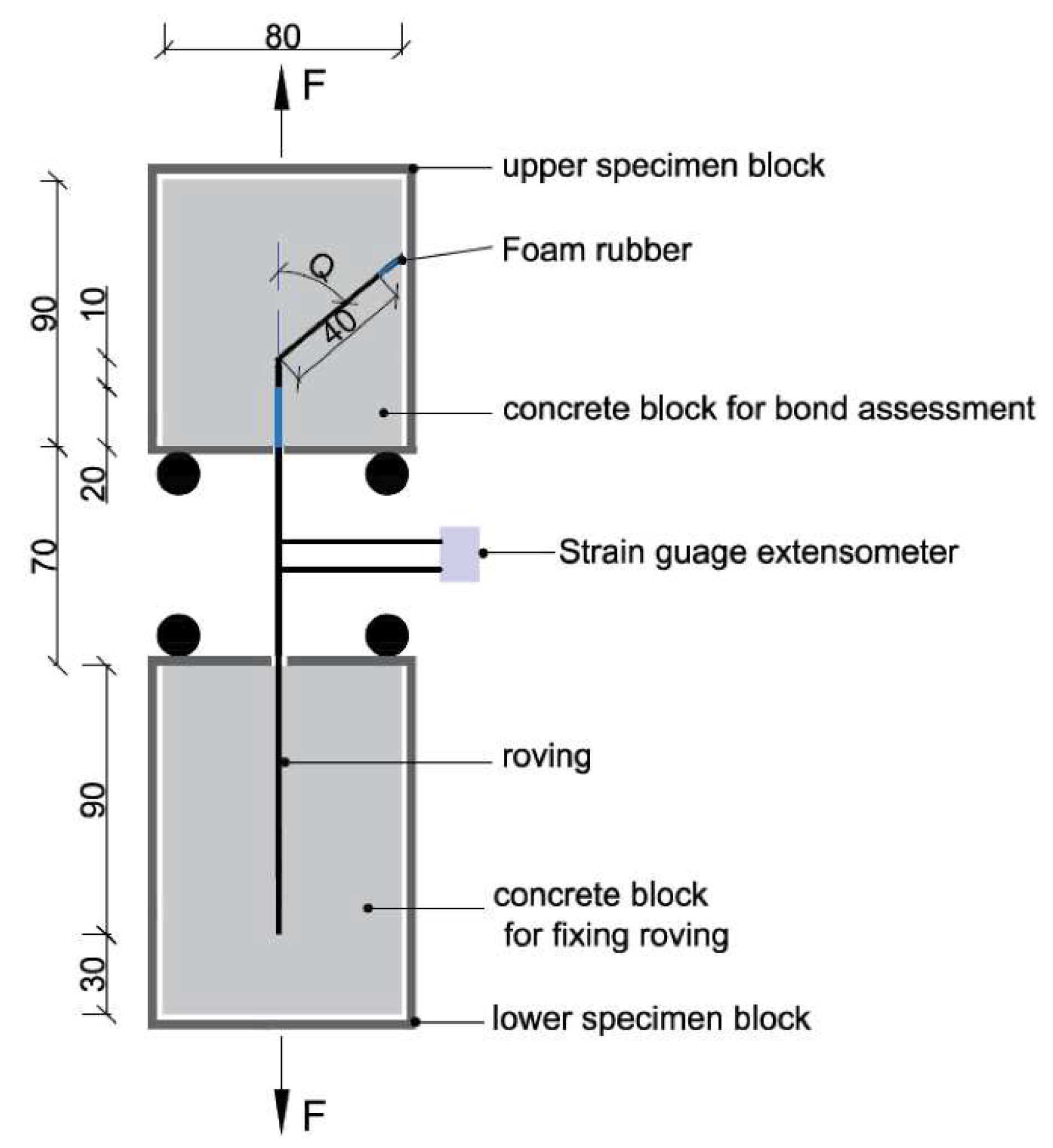
Preprints 84282 g003
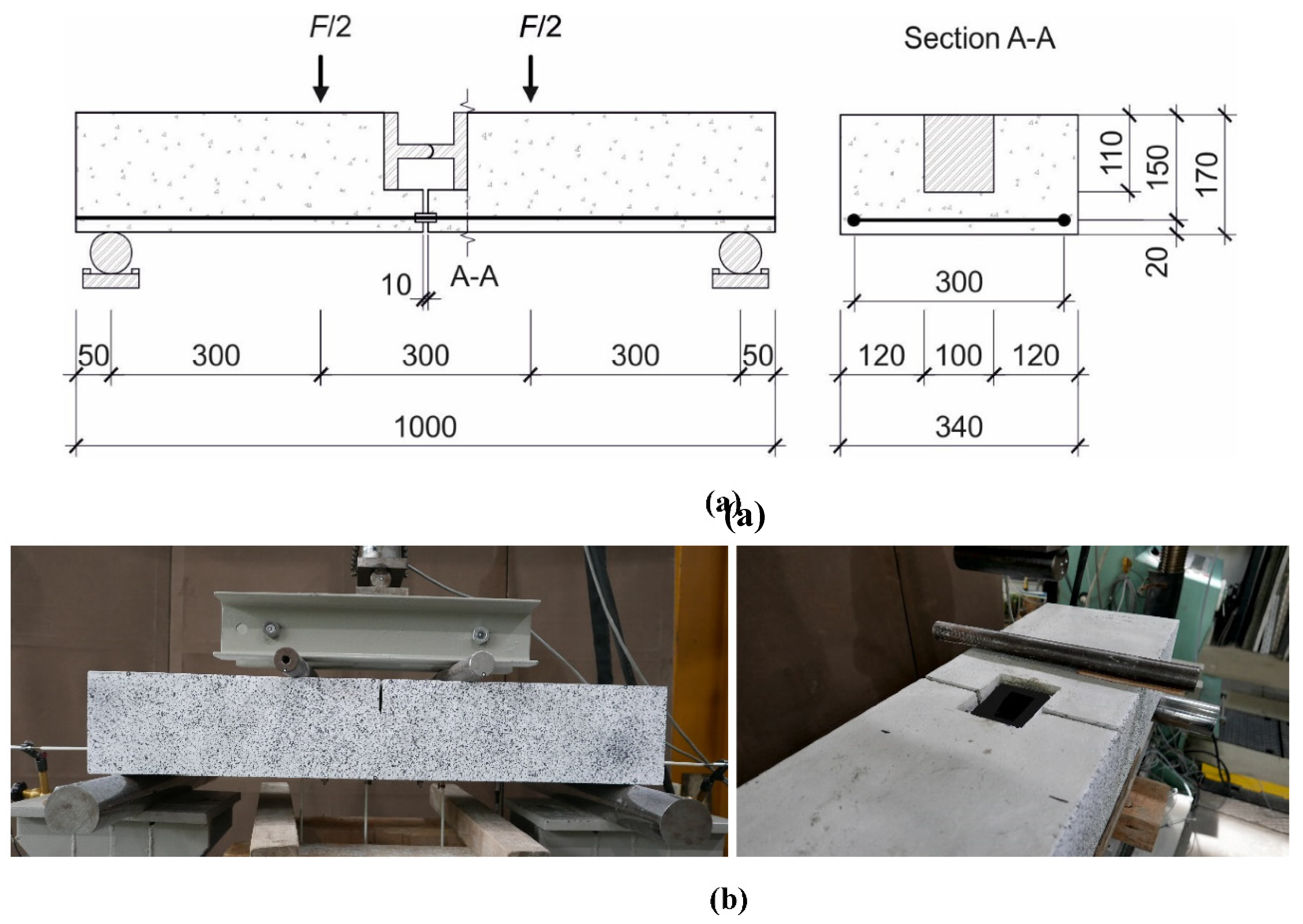
Preprints 84282 g004
Figure 4. (a) Schematic test setup for tension test on 2D NetzGT reinforcement, (b) Visualized beam specimen. All dimensions are in mm.
Figure 4. (a) Schematic test setup for tension test on 2D NetzGT reinforcement, (b) Visualized beam specimen. All dimensions are in mm.
Preprints 84282 g004
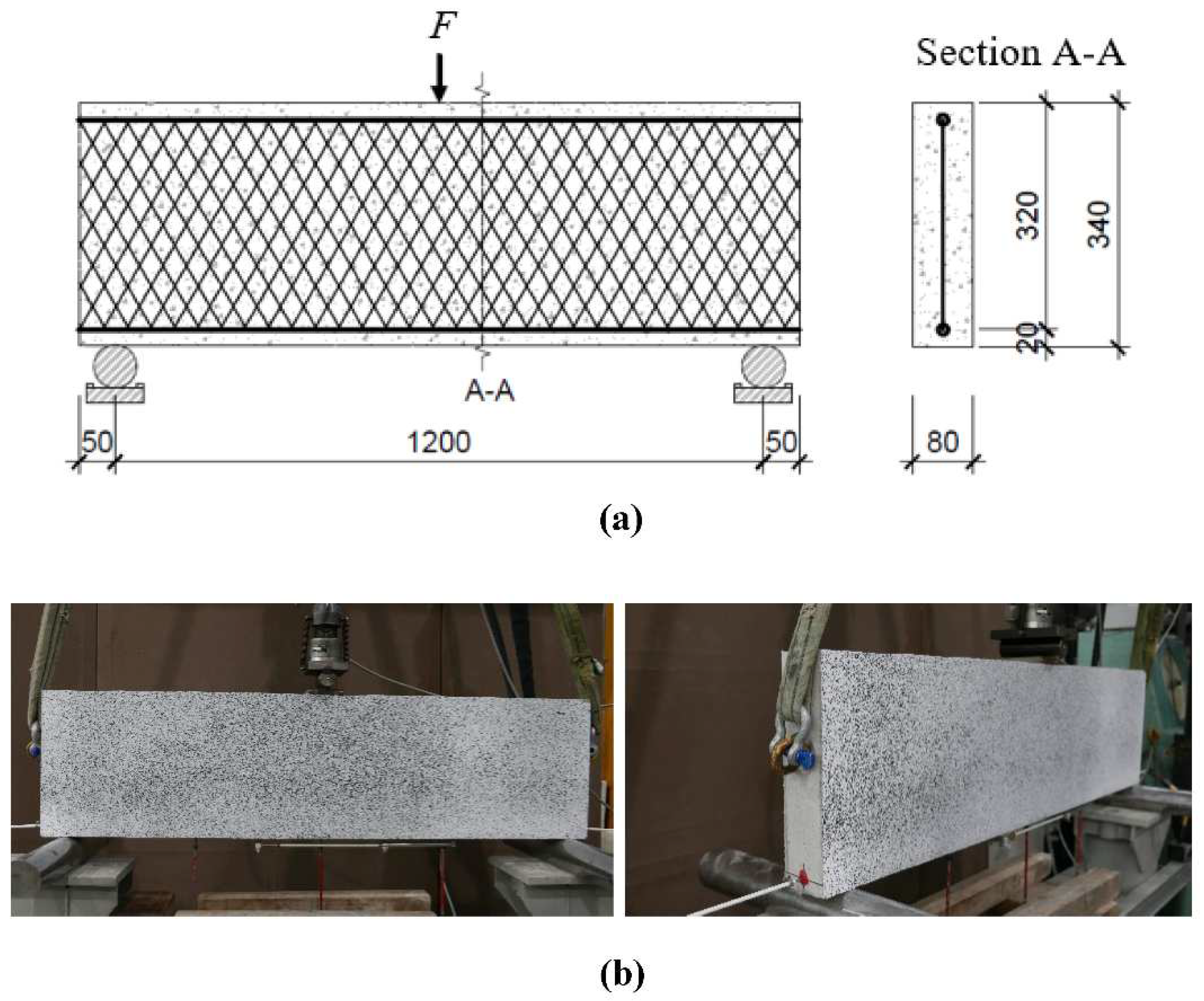
Preprints 84282 g005
Figure 5. (a) Schematic test setup for the three-point bending test. (b) Visualized beam subjected to three-point bending test. All dimensions are in mm.
Figure 5. (a) Schematic test setup for the three-point bending test. (b) Visualized beam subjected to three-point bending test. All dimensions are in mm.
Preprints 84282 g005
Preprints 84282 g006
Figure 6. Force-displacement curves for single and multiple rovings tested in tension.
Figure 6. Force-displacement curves for single and multiple rovings tested in tension.
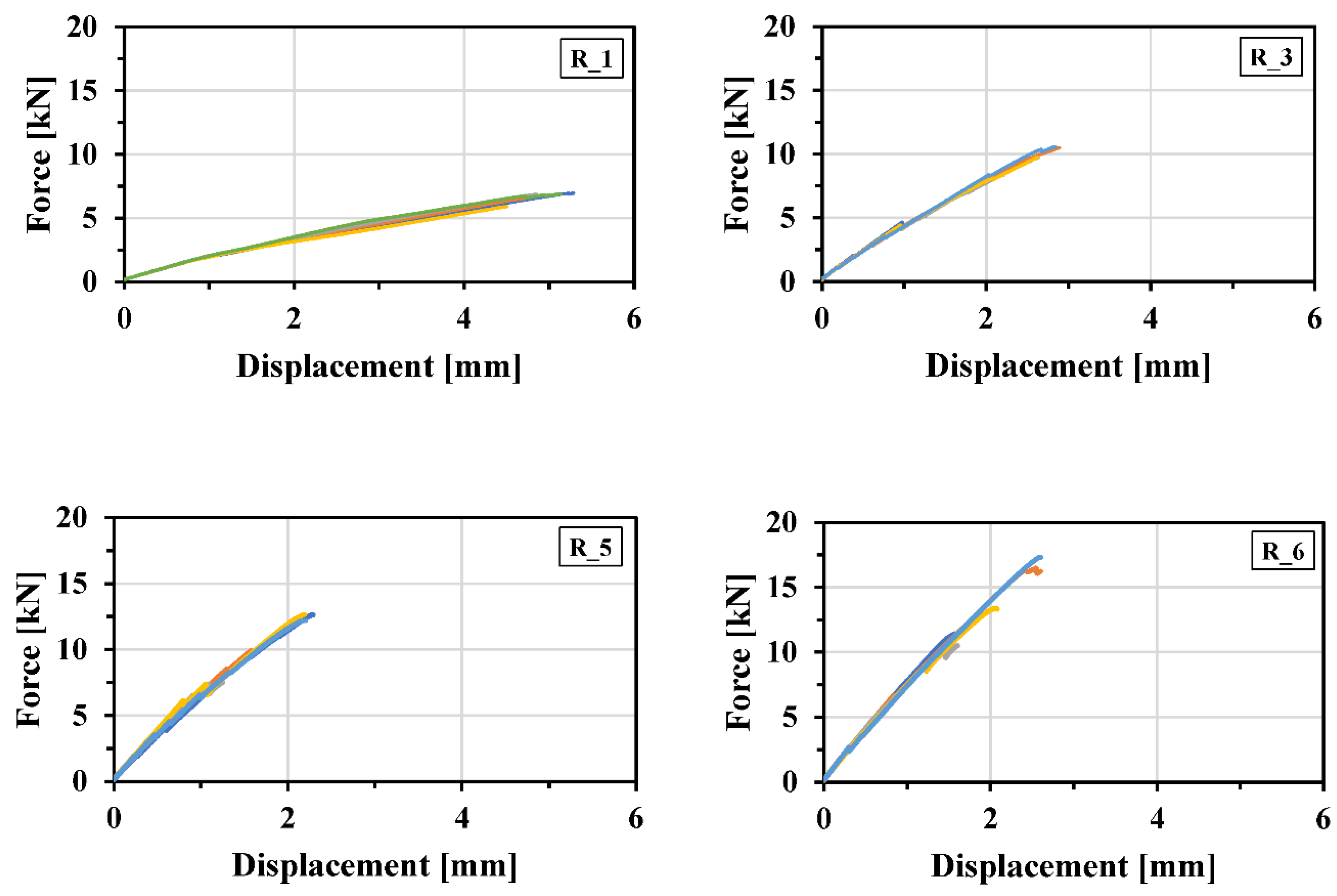
Preprints 84282 g006
Preprints 84282 g007
Figure 7. Average maximum tensile force for a single roving and strands.
Figure 7. Average maximum tensile force for a single roving and strands.
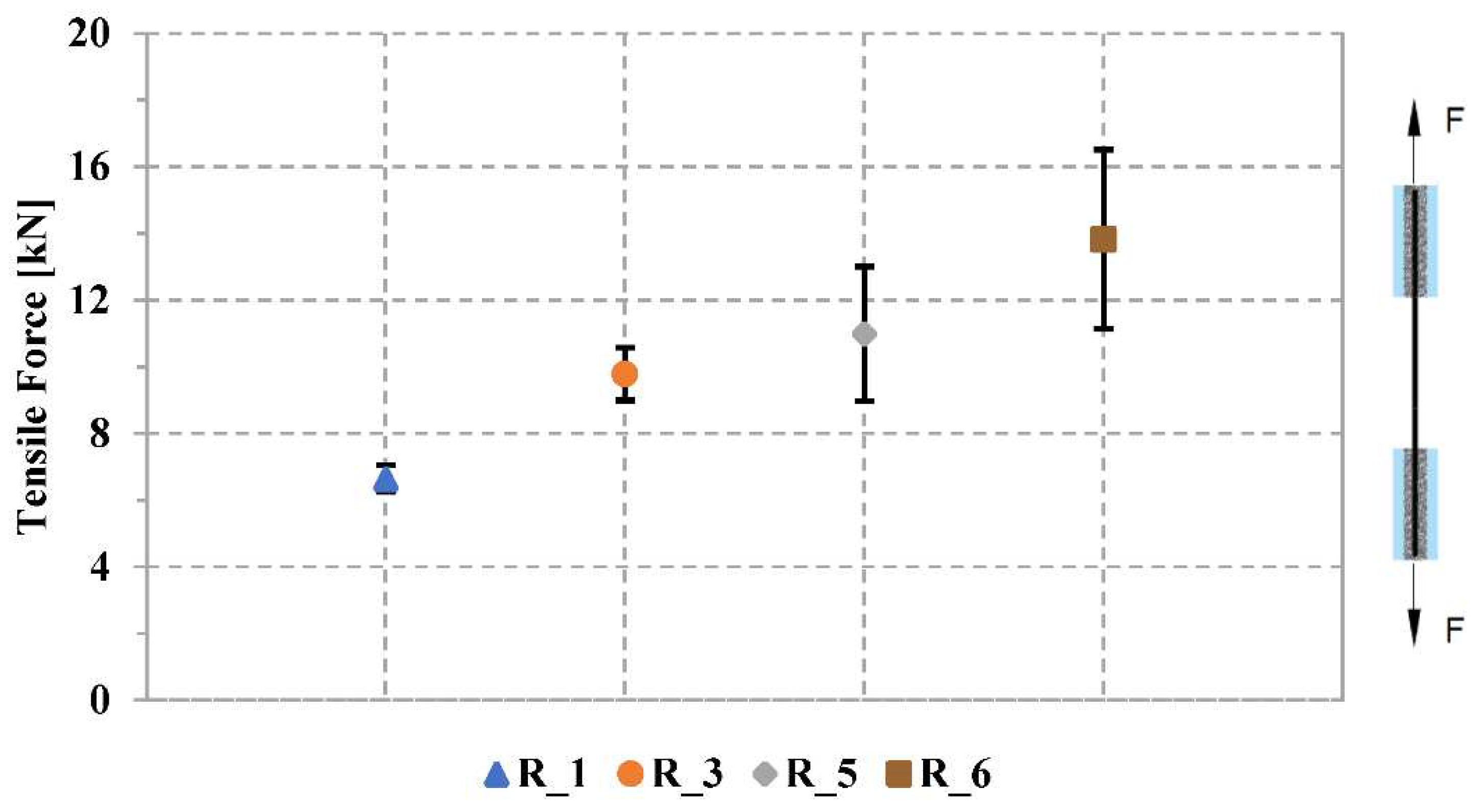
Preprints 84282 g007
Preprints 84282 g009
Figure 9. Beam subjected to four-point bending test according to RILEM RC5 with some specific modifications. Beam dimensions are L×B×D = 1000mm×340mm×170mm.
Figure 9. Beam subjected to four-point bending test according to RILEM RC5 with some specific modifications. Beam dimensions are L×B×D = 1000mm×340mm×170mm.
Preprints 84282 g009
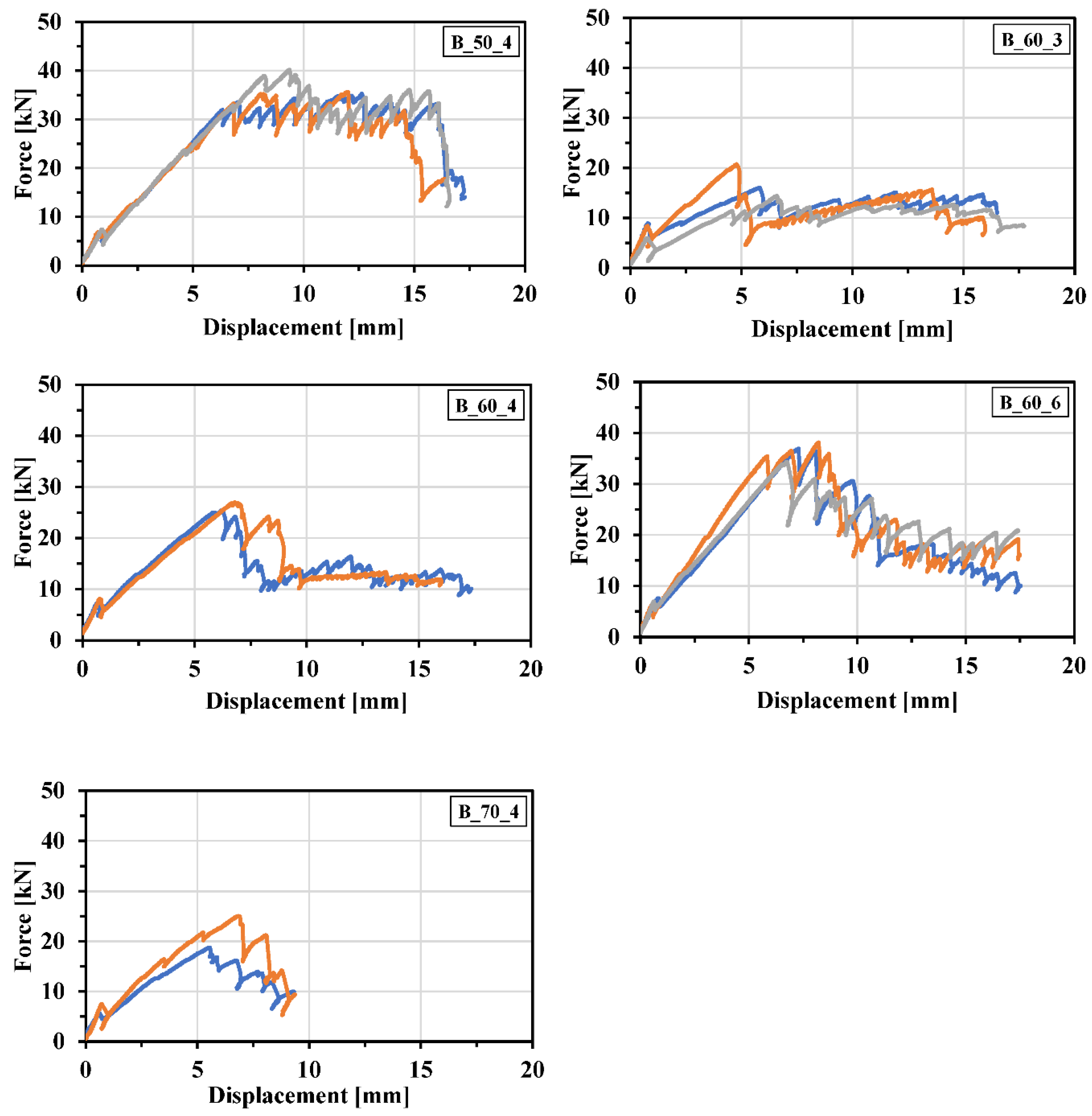
Preprints 84282 g010
Figure 10. Force-displacement curves for strands with varying edge overlapped roving’s and angle of the rovings.
Figure 10. Force-displacement curves for strands with varying edge overlapped roving’s and angle of the rovings.
Preprints 84282 g010
Preprints 84282 g012
Figure 12. Beam subjected to three-point bending test. Beam dimensions are L×B×D = 1300mm×80mm×340mm.
Figure 12. Beam subjected to three-point bending test. Beam dimensions are L×B×D = 1300mm×80mm×340mm.
Preprints 84282 g012
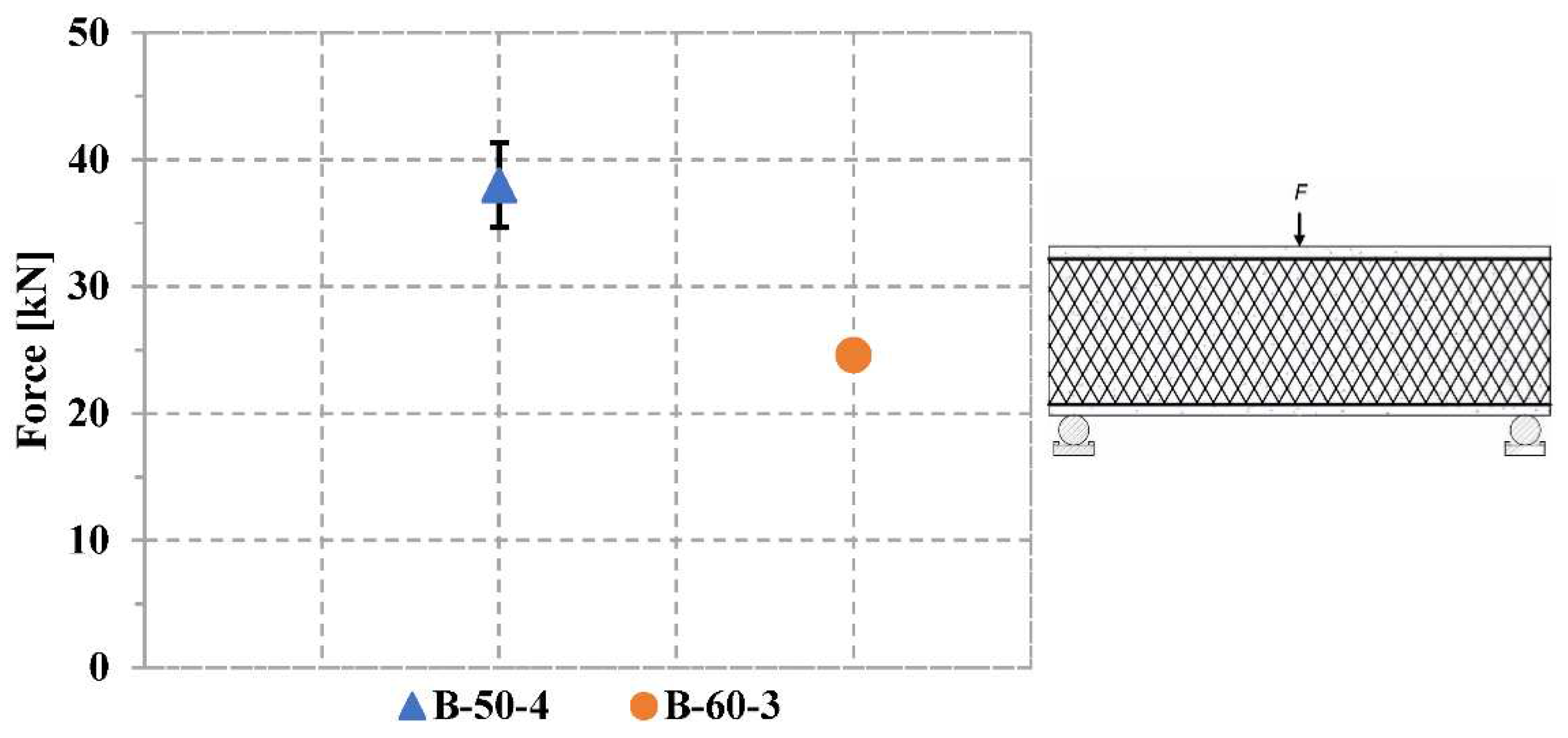
Preprints 84282 g013
Figure 13. Maximum force resulted from three-point bending test.
Figure 13. Maximum force resulted from three-point bending test.
Preprints 84282 g013
Table 1. Composition of concrete mix C30/37.
Table 1. Composition of concrete mix C30/37.
[kg/m3] CEM II/A-LL 52.5 R Limestone powder compact III Sand 0/2 Coarse aggregate 2/8 Water W/C Superplasticizer Glenium ACE 40 (FM)
- 270 155 800 900 190 0.70 approx. 4
Table 3. Test program for the four-point bending test.
Table 3. Test program for the four-point bending test.
Series B-50-4 B-60-3 B-60-4 B-60-6 B-70-4
Number of Specimens 3 3 2 3 2
Table 4. Test program for Three-point bending test.
Table 4. Test program for Three-point bending test.
Series B-50-4 B-60-3
Number of Specimens 2 1
Table 5. Strand tensile capacities manufactured with different numbers of rovings.
Table 5. Strand tensile capacities manufactured with different numbers of rovings.
Specimen Id Number of specimens Area of carbon strand [mm2] Maximum tension force [kN] Standard deviation
R_1 5 1.8 6.64 0.39
R_3 5 5.4 9.78 0.79
R_5 5 9.0 10.99 2.01
R_6 5 10.8 13.82 2.68
Table 6. Summary of the tension test on 2D NetzGT reinforcement.
Table 6. Summary of the tension test on 2D NetzGT reinforcement.
Specimen Id Number of specimens Number of rovings Diameter of roving [mm] Maximum tensile force in 2D NetzGT [kN] Standard deviation
B-50-4 3 4 4.9 55.4 5.7
B-60-3 3 3 4.5 25.4 5.9
B-60-4 2 4 4.9 41.3 1.2
B-60-6 3 6 5.3 56.1 1.7
B-70-4 2 4 4.9 34.6 4.9
Table 7. Three-point bending test results.
Table 7. Three-point bending test results.
Specimen Id Number of rovings Diameter of roving [mm] First crack load [kN] Maximum load [kN] Maximum crack width [mm]
B-50-4 4 4.9 16.5 41.8 13.9
B-50-4 4 4.9 17.3 35.1 15.4
B-60-3 3 4.5 15.7 24.6 15.4
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated