Preprint
Article
Suppressing Sidelobes in Metasurface-Based Antennas Using Cross-Entropy Method Variant and Full Wave Electromagnetic Simulations
Altmetrics
Downloads
105
Views
22
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
05 September 2023
Posted:
06 September 2023
You are already at the latest version
Alerts
Abstract
Managing sidelobe levels (SLLs) in metasurface-driven beam-steering antennas poses a significant challenge due to intrinsic factors leading to grating lobes. Our proposed method employs an equivalent model to optimize large periodic metasurfaces efficiently. This model predicts complete metasurface performance, accounting for mutual coupling between patches. We introduce an evolutionary optimization algorithm based on the Cross Entropy (CE) method to enhance PGM-based beam-steering antennas and suppress sidelobes. Two strategies were employed: first is to optimize the patch dimensions for a sidelobe-free pattern and the second is to maintain the PGM dimensions while optimizing feed array amplitudes. Both strategies effectively suppressed sidelobes, offering insights into the CE method's applicability and effectiveness for CPU-intensive electromagnetic optimization challenges. The proposed CE method variant retains its simplicity while improving monitoring capabilities, addressing this limitation. Smaller generations yield better improvements per evaluation
Keywords:
Subject: Engineering - Electrical and Electronic Engineering
1. Introduction
Metasurfaces are expansive electromagnetic structures designed by meticulously arranging sub-wavelength inclusions. These arrangements endow these structures with an extraordinary capability for precise manipulation of electromagnetic wave attributes, including amplitude, frequency, phase, and polarization [1,2,3]. This refined control over signal propagation characteristics holds significant promise across diverse wireless communication applications.
High-gain antennas are frequently integrated with phase-gradient metasurfaces (PGMs) to achieve precise control over antenna beam steering within a wide conical range [4,5]. This combination proves particularly valuable for establishing network connectivity via low/medium-earth-orbit (LEO/MEO) satellites. These configurations address the demands of satellite communications, specifically targeting scenarios involving on-the-pause or on-the-move operations. Their applications extend to providing essential connectivity in remote areas or dynamic environments such as flights, ships, and trains, where conventional terrestrial networks encounter limitations.
The phased-gradient metasurfaces are constructed using repeating supercells, each comprising a collection of unique unit cells. These individual unit cells are associated with specific phase delays, creating a comprehensive phase spectrum of 360 degrees. The arrangement of these unit cells within a supercell ensures a consistent phase difference between adjacent cells across the entire metasurface. Given the cyclical properties of phase values (after every ), the supercells exhibit repetitive patterns across the aperture of the PGM [6]. These electrically large aperture PGMs can be conceptualized as versatile devices akin to generalized reflectors or refractors, which inadvertently generate unintended diffraction orders leading to the formation of periodic lobes [7,8,9,10,11].
The presence of spurious side lobes and grating lobes can lead to signal leakage, representing significant challenges in the context of beam-scanning antennas. Achieving optimal steering performance requires an efficient metasurface with tailored amplitude and phase response corresponding to lower sidelobes and grating lobes. Effective control over these undesired lobes can be achieved by skillfully managing the arrangement of elements within the periodically repeating supercell, as well as optimizing the dimensions of the metallic features within the PGMs. This comprehensive approach contributes to enhanced antenna performance and improved beam steering capabilities [12,13].
While optimization techniques have gained traction in electromagnetic (EM) engineering, evolutionary optimization methods have been sparingly employed in the optimization of metasurfaces [14,15]. Beam-steering antenna systems based on metasurfaces often grapple with the challenge of excessive sidelobes within their radiation patterns. These sidelobes are undesirable as they lead to signal leakage and power loss. Furthermore, for applications involving satellite-on-the-move (SOTM), stringent criteria regarding directivity, bandwidth, and sidelobes must be met. In this work, we propose a variant of the Cross-Entropy (CE) method and implement it to mitigate the sidelobe levels (SLLs) within the radiation pattern of a metasurface-based beam-steering antenna. This method employs continuous monitoring and adaptive adjustments in response to the algorithm’s search progress. Furthermore, the variant with a population size of presents a close approximation to a continuous process, potentially offering greater analytical clarity compared to discrete methods.
In the traditional Cross-Entropy (CE) approach, each candidate is evaluated against others within the same generation to determine its elite status, with no consideration for the distribution of candidates in prior generations. Similar to the conventional CE method, this variant also necessitates a memory capacity of size in every iteration. However, after the initialization of the queue, which entails performance evaluations, subsequent iterations only require a single performance evaluation for each new sample. These new samples are then compared against the most recent candidates in the queue, allowing for an efficient and dynamic optimization process. Through the prompt update of the sampling distribution following each candidate evaluation, the algorithm efficiently navigates the design space. This approach obviates the need for exhaustive evaluations across the entire population, rendering it well-suited for optimizing intricate metasurface designs.
2. The Cross-Entropy Method
The concept of the Cross-Entropy (CE) method originated in 1997 [16,17]. In 1999, Rubinstein refined and applied the CE method specifically for combinatorial optimization [18], conducting extensive testing on challenging benchmark problems [19,20,21]. One outstanding feature of the CE method is its ability to rapidly converge towards the optimal or nearly optimal solution. The rules to update the parameterized probability distribution functions (PDFs) are straightforward to implement and have a solid theoretical basis rooted in information theory, providing a strong theoretical justification [22]. To estimate the optimal probability distribution that generates globally optimal solutions, the CE method follows a two-step iterative process [23,24].
- Generate a set of candidate solutions from a pre-defined parameterized probability distribution.
- Adaptively update the parameters of this probability distribution using the information extracted from the current elite candidate solutions. This adaptive update aims to guide the search towards the global optimum by minimizing the cross-entropy (or Kullback–Leibler divergence) between two sampling distributions.
The CE method is a highly versatile global stochastic learning optimization approach capable of handling both combinatorial and continuous multi-extremal, multi-objective optimization challenges. One of its distinguishing characteristics is that it operates on a parameterized probability distribution rather than directly on samples within the candidate population. The method employs an iterative process, updating the sampling distribution while minimizing the cross-entropy between the empirical distribution of the current elite sub-population and the sampling distribution of the subsequent iteration. This iterative refinement continues until the cross-entropy reaches zero, indicating that the two distributions have become identical, thereby achieving the global best solution.
The CE optimization method follows a model-based search framework, where feasible solutions stem from a parameterized probability distribution function (PDF) that gets updated based on elite candidates from the previous iteration (probability distributions are often referred to as models in the literature [25]). An elementary schematic diagram for the CE search framework is shown in Figure 1.
3. Cross-Entropy Method Variant
The CE method adopts a population-based strategy, where it evaluates all samples within a generation (population size N) before updating the sampling distribution. This process is referred to as batch processing of the population. In the traditional CE algorithm, candidates are selected only after the entire generation evaluation episode is completed. However, this approach becomes problematic when dealing with computationally expensive and time/memory-consuming problems. To address this issue, the proposed variant of the CE method performs updates immediately after each candidate is evaluated, eliminating the need to wait for the entire generation’s evaluation to be completed.
To implement the variant of the CE method, we define the problem-based performance metric over the solution space X, where for all . The goal is to estimate the parameters of the optimal probability distribution function (PDF) that generates the globally-optimal or near-optimal solution. Similar to the classical CE method, this variant starts with an initial PDF and progressively constructs a sequence of sampling distributions, focusing increasingly on a small neighborhood around the optimal solution. Finite-dimensional PDFs are used, and the choice of these PDFs depends on the nature of the design parameters associated with the optimization problem, whether they are continuous, discrete, or mixed parameters. Selecting a PDF that accurately models the problem’s structure is crucial. The optimization problems solved by the CE method are often multi-dimensional and may involve constraints. The parameters in such problems can be either continuous, discrete or even a combination of both (mixed parameters). To ensure proper sampling of candidate solutions, the PDF should appropriately support the range and type of parameters involved [26].
The first step is to sample candidates from a carefully chosen parameterized PDF. The continuous constrained parameters are usually randomly sampled using either acceptance-rejection or Gibbs sampling. The inversion method is often used to sample from a discrete distribution [27]. The second step is called parameter estimation. We use the maximum likelihood estimation (MLE) method [28] for estimating the parameters of a sampling distribution. In information theory, a natural way to estimate the parameters of the new PDF is to update the parameters of the current PDF by minimizing the Kullback–Leibler divergence (a measure of misfit between two distributions) expressed as (1) for continuous distributions and as (2) for discrete distributions:
or, analogously, by minimizing cross-entropy that can be expressed as (3) for continuous distributions and as (4) for discrete distributions:
between two PDFs, and , over . When any of the equations mentioned above, such as , equals zero, it indicates a perfect estimate of PDF parameters, resulting in both distributions becoming identical. The maximum likelihood estimation (MLE) and cross-entropy (or Kullback Liebler divergence) minimization are essentially equivalent approaches, and one can be readily derived from the other [25]. Consequently, either of these methods can be employed in optimization using the CE method.
We now introduce the necessary user-defined parameters for the CE method variant. The input parameters include Queue size , elite sub-population size , initial sampling distribution parameters, and smoothing parameter . The algorithm is initialized with a random start [29]. In each iteration, a candidate is sampled from the initial distribution, and its fitness function is evaluated. The sampled candidate, along with its fitness function value, is stored in the Queue. This sampling and storing process is repeated times until the Queue reaches its capacity. Once the Queue is full, the candidates are sorted based on their fitness values, either in ascending order if the optimizer aims to minimize the fitness function, or in descending order if the objective is to maximize it. The first candidates are then selected as the elite candidates, where is calculated as with . Additionally, the best candidates and their corresponding fitness values are recorded. The optimizer then checks the convergence or stopping criterion. If the criterion is not met, the oldest candidate is dropped from the Queue, and the iteration continues. Each candidate sampled in the following iterations will be compared against the last candidates and the decision regarding the candidate being elite can be made instantly as opposed to the traditional method where a whole population of candidates have to be evaluated before the algorithm can decide if the candidate is elite.
In each subsequent iteration, new candidates are sampled from an updated probability distribution function (PDF) and evaluated, until the stopping criterion is satisfied. The parameters of the current sampling PDF are updated based on the elite sub-population to define a new sampling distribution for the next iteration. As previously mentioned, this updating process can be achieved by minimizing the cross-entropy or by utilizing the concept of Maximum Likelihood Estimation (MLE) to find the best fit between the empirical distribution of elite candidates and the new sampling distribution. To strike a balance between exploitation and exploration, and prevent premature convergence, the algorithm incorporates a smoothing parameter . This parameter ensures a satisfactory trade-off between intensification (exploitation) and diversification (exploration). The smoothing is integrated into the updating rules as shown in the following equation:
where is the current generation PDF parameter vector, is the PDF parameter vector from the previous generation, and is the smoothed parameter vector. The smoothing parameter lies between 0 and 1. A higher value of (closer to 1) results in faster convergence, while a lower value of slows the convergence. For high-dimensional problems (more than 5), fast convergence usually results in a decreased chance of finding the global best solution. An alternate smoothing procedure known as dynamic or smoothing is followed in such cases where the smoothing results in a quick sub-optimal convergence [23].
There are several ways to define the termination criterion. Some of the popular stopping conditions are
- (1)
- when the elite sub-population consists of identical or very similar results,
- (2)
- when a specified number of maximum iterations are completed,
- (3)
- when the distance between the best-found solution and the target result becomes negligible.
An elaborate discussion on the stopping criterion is available in [30]. Several modifications of the CE method, such as Variance-Injection Method and Fully Adaptive CE method, are described in [23]. Improved CE methods and their online variants can be found in [31]. The iterative steps of this CE method variant are summarized in Algorithm 1.
| Algorithm 1: Pseudo-code for CE method variant. |
|
4. Periodic Metasurface Optimization Methodology
Because of the absence of a precise analytical model for metasurfaces, their effective optimization relies on employing a comprehensive electromagnetic simulation model. However, metasurfaces typically have electrically large apertures and a significant number of small features. As a result, simulating them becomes computationally demanding and impractical, particularly when considering population-based global optimization through conventional approaches. To mitigate the computational complexity, a more straightforward equivalent model (illustrated in Figure 2) has been put forth.
The proposed equivalent model consists of a reduced strip extracted from the original metasurface. It has the same x-axis dimension (L = 345 mm) as the original metasurface aperture and y-axis dimension (W = 7.5 mm) as small as the dimension of the constituent unit cell. Boundary conditions are appropriately assigned to this simplified structure to emulate the behavior of the complete 2D metasurface. Despite the simplification, the structure retains a high-mesh complexity (exceeding 800,000 hexahedrons), necessitating the avoidance of batch processing.
As a solution, we adopt the modified version of the CE (Cross-Entropy) method to optimize these printed metasurfaces. Our focus lies in achieving sidelobe suppression and obtaining a radiation pattern that conforms to the FCC mask (25.209) for the Ka-band. The algorithm for this customized CE method is implemented in MATLAB and linked with CST-MWS using a VBA-macro code. Through the implementation of two illustrative examples, we showcase the capability of this generalized CE approach to effectively manage computationally demanding electromagnetic challenges. This emphasizes its potency as a valuable tool for optimizing intricate metasurface designs.
4.1. Optimizing the Patch Dimension in PGM to Control SLLs
By employing the outlined CE methodology, we embark on the optimization of metasurface design with the goal of reducing sidelobe levels present in the radiation pattern of a beam-steering antenna reliant on metasurfaces. This antenna entails an electrically expansive planar configuration consisting of repeating supercells arranged along both the x- and y-axes. This arrangement orchestrates a progressive phase modulation in the electric field at the output, facilitating controlled beam tilting for the antenna’s operation.
Each supercell is composed of an array of non-identical Phase Transforming Cells (PTCs), wherein each PTC corresponds to a specific transmission phase and exhibits a substantial level of transmission magnitude. These PTCs serve as fundamental building blocks of the Phased-Gradient Metasurface (PGM), governing the spatial phase variation of the electric field as it traverses through them. Within this specific PGM design, two distinct variants of Phase Transforming Cells (PTCs) are integrated, each possessing a length equivalent to . The Type-I cell encompasses four square metal patches enveloped by three dielectric layers. These patches, denoted as , , , and , are dimensioned such that and . Conversely, the Type-II cell is characterized by three stacked dielectric layers containing a through-hole. The Taconic TLY-5 dielectric material featuring a permittivity of is employed for both variants of PTCs.
The overall structure is created by repeating a periodic supercell, which consists of five Type-I cells and one Type-II cell. This supercell has dimensions of . To cover the complete phase range from to , the dimensions of the square metal patches and the openings within the PTCs are modified accordingly. Within the supercell, the phase delay between adjacent cells is set at or radians. According to array theory, the beam tilt attained through the 1D array can be mathematically expressed using the following equation [32]:
In this context, the symbol d stands for the spacing between elements within the array, signifies the incremental phase shift contributed by each array element in radians, denotes the wavelength in free space, represents the angle of incidence concerning the surface normal, and indicates the desired beam tilt concerning the central radiation direction. Consequently, under the conditions of normal incidence, specifically when and , the metasurface achieves a beam tilt of as elucidated by (6).
We construct a 1-D metasurface, which corresponds to the highlighted strip in red within Figure 3, in CST-MWS time-domain solver and defined appropriate boundary conditions to model the response of full metasurface ("E(t) = 0" along y-axis and the "Open Add Space" boundary condition along x-axis, as depicted in Figure 2. By implementing these boundary conditions, the equivalent model offers a close approximation of the actual metasurface configuration while significantly reducing computational demands. With the supercell (comprising six individual cells) duplicated along the x-axis, the design parameters maintain the same periodic arrangement.
The optimization involves the design variables depicted in Figure 4. Within the metasurface, specific parameters are held constant, encompassing the aperture size (), cell size (/2), and the permittivity of the dielectric substrate (). In the context of the 1D metasurface model, a uniform plane wave illumination is applied through a waveguide port positioned one wavelength below the metasurface. The side lengths of the first (top) and third layer metal patches (a1, a2, a3, a4, a5) and second and fourth (bottom) layer metal patches (b1, b2, b3, b4, b5) for five consecutive cells in the supercell followed by the radius (r) of the hole constitutes an 11-parameter design vector ((7)):
The optimization problem for the metasurface design is formulated with the following inequality constraints, as shown in equation (8), based on prior knowledge:
These constraints are applied to the patch dimensions and the radius of the hole in order to ensure that the optimized metasurface design remains physically feasible and practical for fabricating a realistic and achievable design.
4.1.1. Algorithm Implementation
The described metasurface optimization process is a classic continuous optimization problem with a bounded search space. Due to the strong mutual coupling between the metallic patches, there is a significant sample correlation among the parameters within the elite sub-population. To effectively address this correlation, we utilize a multivariate Gaussian distribution to sample the 11 optimization parameters. This approach better represents the correlated continuous parameter values in each subsequent generation’s sampling distribution. The distribution parameters are, mean and co-variance such that . The probability density function (PDF) of a multivariate Gaussian distribution is expressed as:
The optimization procedure described for the metasurface represents a classical instance of continuous optimization within a constrained search space. Given the strong mutual coupling among the metallic patches, there is a significant correlation among the parameters within the distinguished sub-population. To effectively handle this correlation, we employ a multivariate Gaussian distribution to sample the 11 optimization parameters. This approach adeptly captures the correlation of continuous parameter values by refining the sampling distribution for each subsequent generation. The distribution parameters, namely the mean and the covariance , are employed such that . The probability density function (PDF) of a multivariate Gaussian distribution is expressed as:
where x is a vector of random variables of dimension d, is a vector of means, and is the co-variance matrix of dimension . In order to uphold the boundaries of the solution space, a sigmoid transformation is implemented, which maps to a viable rectangle, as detailed in [33]. This transformation ensures that the obtained samples fall within the predetermined limits. The initial distribution is characterized by a mean and a covariance , with I signifying an identity matrix. These parameters are subsequently adjusted using information from the elite sub-population following each evaluation.
The primary objective involves the minimization of Side Lobe Levels (SLLs) within the directivity pattern of the metasurface-based antenna, operating at a frequency of 20 GHz. Central to this endeavor is the precise definition of a fitness function, serving as a singular performance metric for the effective assessment of potential solutions. A novel approach has been introduced for formulating this fitness function, with a modified aim of ensuring adherence to the prescribed FCC () mask specific to the Ka-band.
The Mask function, as depicted in equation (10), establishes the upper limit for the desired gain (in dBi) across various elevation angles , spanning from to when the peak radiation aligns with the broadside direction. Each angle corresponds to an allowable gain level. Should the radiation beam be steered by degrees, the mask adjusts to align with the peak radiation direction of the beam. Consequently, the expression for the Mask function when dealing with a tilted beam transforms to ().
The algorithm aims to minimize the fitness function (FF) formulated as:
The FF value is computed across all elevation angles , spanning from to in increments of . The equation (11) ensures that the squared difference contributes to the FF value only when the directivity pattern lies above the mask, while no contribution is made when the pattern falls below the mask. The primary objective of the optimization process is to minimize the FF, thereby effectively diminishing the discrepancy between the mask and the directivity pattern whenever the pattern violates the mask’s requirements. The user-defined parameters governing the algorithm for the proposed CE method variant in the context of metasurface optimization are concisely summarized in Table 1.
The phased-gradient metasurface exhibits inherent local non-periodicity and contains sub-wavelength metallic features. As a result, conventional techniques such as transmission-line modeling and unit cell optimization [34,35] are unsuitable for comprehensively analyzing its intricate electromagnetic characteristics. To accurately investigate the complex electromagnetic behaviors, we adopt a full-wave electromagnetic simulation-driven optimization strategy. This approach serves to predict the far-field radiation pattern of the beam-steering system based on the Phased-Gradient Metasurface (PGM). To facilitate this pursuit, we employ the Cross-Entropy (CE) algorithm, which is implemented in MATLAB. This algorithm is seamlessly interfaced with CST MWS (Microwave Studio) through a macro code. This linkage establishes a dual-channel connection between MATLAB and CST, enabling smooth communication and seamless integration between the optimization algorithm and the detailed full-wave electromagnetic simulations.
4.1.2. Optimization Results
Each evaluation conducted within the CST MWS time-domain solver necessitated approximately 28 minutes, utilizing an Intel Core i7-6700 CPU clocked at GHz, accompanied by a 64 GB RAM. The entirety of the optimization procedure, which encompassed 959 function evaluations, spanned a cumulative duration of 447 hours and 48 minutes. To effectively account for alterations in patch geometry during each function evaluation, an adaptive meshing technique was implemented. The optimization cycle persisted until the maximum deviation of patch dimensions in an elite sample from the mean of all corresponding elite patch dimension samples within the Queue became less than 0.1 mm. As illustrated in Figure 5, the convergence curve reveals that the optimal solution was achieved at the 959th function evaluation. Throughout the optimization progression, once the Queue became populated with samples, the average fitness of the Queue was graphed in parallel with the best fitness attained up to that juncture. Here, "best fitness" denotes the most favorable outcome discovered in the Queue until that instance, while "average fitness" signifies the mean of fitness values for all candidates within the Queue at each function evaluation. As depicted in Figure 5, we can observe a gradual decrease in the average fitness function with an increasing number of function evaluations.
The average fitness gradually converges towards the vicinity of the best fitness, signifying the convergence of the optimization process. Notably, the curve’s central segment indicates that the degree of smoothing applied is quite pronounced, and there might be potential for reducing it to accelerate convergence. Past experience with the CE method anticipates that a higher value of would likely hasten the convergence rate. Nonetheless, it’s important to acknowledge the inherent trade-off between computational expenditure and precision. The algorithm was stopped once the diversity among the elite candidates dropped below the predefined threshold.
4.2. Optimizing Amplitude Distribution in the Feed Array of PGM to Control SLLs
In various satellite applications, metasurfaces designed for beam steering are often combined with high-gain feeding apertures, such as arrays of closely arranged low-gain antennas. These arrays create a narrow, highly focused beam directed perpendicularly (broadside) to the array plane. They achieve this with a near-uniform phase distribution across the near-electric field. However, when integrating a beam-steering metasurface that introduces a gradual phase progression within the near-electric field of the feeding array, the previously perpendicular beam of the array undergoes a tilt at an off-angle. Unfortunately, this can lead to the emergence of multiple undesired significant sidelobes in the far-field radiation pattern.
Analogies can be drawn between the theory of antenna array pattern synthesis and the control of metasurface beam steering. In this context, the methodology for designing metasurfaces can be likened to the discrete sampling process employed in antenna arrays. According to antenna array theory, effective control over the Sidelobe Level (SLL) can be achieved by utilizing appropriate amplitude distributions in the excitation field [36]. In the realm of phased arrays, techniques such as Chebyshev or Taylor amplitude distributions have been applied to regulate SLLs within the far-field pattern [37,38,39]. Building upon this concept, we posit that an optimized amplitude excitation has the potential to efficiently suppress undesired sidelobes within the far-field pattern of antennas based on metasurfaces.
To explore this concept, we use the design configuration shown in Figure 6, which offers a side view of the setup used for this investigation.
The illustration depicts an array feed situated at a half-wavelength distance beneath the metasurface, giving rise to a plane wave propagation along the z-axis. This feed encompasses an array of infinitesimal Hertzian dipoles spaced half a wavelength apart, all positioned in front of a ground plane. Uniform magnitude and phase are assigned to the feed’s elements. Each spatial phase-shifting cell within the metasurface introduces a specific phase modification, thereby establishing a consistent progressive phase disparity between adjacent cells. Consequently, the metasurface output assumes a continuous, linearly escalating phase profile. This phase profile, upon cycling every increment in phase delay, transforms into a saw-tooth phase distribution. The unchanging phase difference between neighboring cells () remains constant, where M denotes the count of unique cells in the supercell (one period within a PGM is denoted as a supercell).
The distinct phase delays () undergo periodic repetition to align with the recurring structure of a supercell within the metasurface. This linearly augmenting phase, equivalent to an unwrapped saw-tooth phase, induces beam tilting () within the far-field radiation pattern. The metasurface with an increasing electric field phase variation, shown in Figure 6, yields a steered beam but with sidelobes as well as periodic grating lobes. Ideally, the wavefront of a steered beam should have a periodically repeated saw-tooth profile [40]. However, owing to the inherent phase discretization integral to metasurface design, a stepped saw-tooth wavefront is obtained in reality. Real-world conditions introduce factors like mutual coupling, fringing fields, assumptions of periodicity in design, abrupt geometric alterations, and manufacturing imperfections, all of which collectively contribute to pattern deterioration. Consequently, deviations from the anticipated saw-tooth phase profile occur. The outcome is an elevation in sidelobe levels (SLLs) within the far-field radiation pattern. The approach to metasurface design can be analogously likened to the discrete sampling method employed in aperture-based antenna arrays.
The generalized CE algorithm is implemented to optimize the amplitude distribution within the feed array of a PGM. The primary objective is to mitigate the presence of undesirable sidelobe levels (SLLs) within the far-field radiation pattern. This study delves into leveraging amplitude variation within the feed array to proficiently govern the extent of undesired lobes in a beam-steering antenna based on a PGM. While the manipulation of phase through the metasurface facilitates main-lobe steering and control across the complete 0 to range, the optimization of excitation amplitudes within the feed array provides a strategic avenue for effective SLL management.
4.2.1. Problem Formulation
Antenna array theory has established that sidelobe levels (SLLs) can be controlled through customized amplitude distributions within the excitation field [36]. In our methodology, we harness this principle by supplying each element of the supercell with infinitesimally small Hertzian dipoles. Notably, distinct excitation amplitudes are assigned to each dipole element while maintaining a constant phase, as illustrated in Figure 7.
The design variables represent the set of feed amplitudes, which are recurrently replicated. Our objective revolves around identifying an optimal arrangement of excitation amplitudes capable of effectively mitigating SLLs to levels below the constraints stipulated in the FCC mask outlined in (10). For the purpose of optimization, the simplified 1D metasurface model depicted earlier in Figure 2 is utilized. The parameter vector consists of a periodic sequence of amplitude distributions incorporating N distinct amplitude values.
where . The fixed parameters of Hertzian dipole array fed metasurface design are the aperture size (), cell size (), the permittivity of the dielectric substrate () along with the patch and hole dimensions (a1, a2, a3, a4, a5, b1, b2, b3, b4, b5, r) whose values are listed in Table 3.
4.2.2. Algorithm Implementation
The process of optimizing the distribution of feed amplitudes constitutes a continuous optimization problem confined within a specific search space. By attributing distinct amplitude excitations to each element within the supercell, effective control over sidelobe levels within the radiation pattern is achieved. The optimization parameters () are permitted to vary continuously within the interval of 0 to 1. To maintain adherence to this range, population candidates are sampled independently and identically (i.i.d) from a beta probability distribution function () shown in Figure 8, since it naturally supports the bound within [0,1]. Initial distribution has and .
After each evaluation, the probability distribution parameters were updated using the elite population, as detailed in Algorithm 1. The fitness function (), detailed in (11), is used with the objective of ensuring that the directivity pattern aligns with the FCC mask (25.209) for Ka-band, as defined in (10). To facilitate precise full-wave EM-simulation-driven optimization, the generalized CE algorithm is implemented in MATLAB and seamlessly integrated with CST MWS. This iterative algorithm progressively minimizes the fitness function, consequently diminishing undesired sidelobe levels (SLLs) within the radiation pattern. The Chebyshev or Taylor amplitude tapering exhibits a symmetric distribution characterized by a bell-shaped profile. In order to replicate a similar pattern, we incorporated 23 distinct amplitude excitations. These excitations were duplicated in a mirrored symmetry to encompass the entire aperture, consisting of 46 elements along the x-direction. This arrangement is illustrated in Figure 9.
Table 2 lists the user-defined input parameters set in the algorithm for optimizing the feed amplitude distributions.
The entire optimization process, involving 23 design variables, spanned a duration of 198 hours and 4 minutes. During this time, a total of 566 function evaluations were executed before the termination criterion was met, leading to the algorithm’s cessation. The initial 150 function evaluations were dedicated to Queue initialization. This step involved populating the Queue with candidates and their corresponding fitness values. Following this initial phase, subsequent evaluations contributed to identifying elite candidates and subsequently updating the probability distribution parameters. This dynamic process directed the search toward the global optimum. The convergence results, as depicted in Figure 10, showcase the evolution of both the average fitness across all samples within the Queue and the best fitness observed up to that point. The graph demonstrates that the optimal solution was attained at the 508th function evaluation.
5. Electromagnetic Simulation Results
In the context of the first optimization strategy, the design characteristics of the PGM before and after optimizing the dimensions of metallic patches are presented in Table 3. The optimized design parameters were employed to construct a finite-sized 2D metasurface structure. This metasurface was subsequently subjected to simulation using the CST MWS time-domain solver, with excitation through a waveguide port and employing "Open-Add space" boundary conditions in both the x and y directions.
Table 3.
Design parameter values for the PGM before and after optimization.
| Design Parameters, mm | Before optimization | After optimization |
|---|---|---|
| 2.27, 2.25 | 2.54, 2.09 | |
| 3.30, 3.50 | 3.75, 3.47 | |
| 3.88, 3.85 | 3.65, 4.12 | |
| 4.11, 4.14 | 4.28, 3.97 | |
| 4.30, 4.20 | 4.10, 4.44 | |
| r | 3.4 | 3.68 |
| Side-lobe Level, dB | -13 | -16.5 |
| F.F, Eq. (11) | 4284 | 561 |
In Figure 11, we can observe and compare the directivity patterns obtained through full-wave electromagnetic simulation for both the initial and optimized finite-sized 2D metasurfaces.In the initial design, the directivity pattern of the PGM exhibited deviations from the FCC mask at four distinct points () within the observable range of . After undergoing the optimization process, a substantial portion of the sidelobes was effectively mitigated and the directivity pattern violated the FCC mask only at two locations, by 3.5 dB and by 0.5 dB. Furthermore, the SLL saw a reduction of 4 dB (from -13 dB to -17 dB) compared to the initial design.
Likewise, in the context of the second optimization strategy, Table 4 presents the excitation amplitude parameters of PGM both before and after the optimization process. In CST MWS, a finite-sized 2D metasurface was subject to simulation, employing "Open-Add space" boundary conditions in both the x and y directions. The metasurface was then excited using a 2D array of Hertzian dipoles featuring the optimized excitation amplitude distribution. Subsequently, the results were compared with those obtained from a simulation where a 2D array of Hertzian dipoles was uniformly excited as the source.
Figure 12 provides a comparison between the directivity patterns of the PGM before and after the optimization of excitation amplitude distribution. Notably, the optimization endeavor successfully suppressed the undesirable sidelobes, effectively keeping them below the FCC mask, with the exception of a single sidelobe situated at . Additionally, the directivity of the optimized PGM experienced a reduction of 1.4 dB. This reduction can be primarily attributed to the tapering introduced within the feed array, which played a pivotal role in achieving these improvements.
The overall directivity decreases from dBi to dBi (1.4 dB reduction) due to tapering in amplitude distribution achieved after optimization. The SLL has reduced by dB (from dB to dB).
6. Discussion
Managing sidelobe levels (SLLs) in metasurface-driven beam-steering antennas presents a formidable challenge due to the involvement of various intrinsic factors that contribute to the emergence of grating lobes. The inherent complexity of metasurface structures adds to the difficulty in achieving precise control over these sidelobes. In response to this challenge, we propose a method that leverages an equivalent model, rendering the optimization of electrically large periodic metasurfaces more feasible and computationally efficient. This model is designed to provide accurate predictions of the complete metasurface performance. It incorporates an antenna array factor calculator that duly accounts for mutual coupling between the metallic patches. By optimizing the PGM-based beam-steering antenna and strategically mitigating excessive sidelobes, we introduced a streamlined evolutionary optimization algorithm rooted in the CE method. This innovative approach effectively addresses the intricacies of sidelobe suppression, contributing to the attainment of enhanced far-field radiation pattern performance.
To achieve a beam-steered radiation pattern that complies with the FCC mask (25.209) for Ka-band applications and effectively suppresses undesired sidelobes, we adopted two distinct strategies. In the first approach, we optimized the dimensions of the patches, aiming to attain a radiation pattern devoid of spurious sidelobes. This optimization effort resulted in a notable reduction of the sidelobe levels (SLLs), thus significantly enhancing the overall metasurface performance. The second approach maintained the dimensions of the PGM constant while focusing on optimizing the amplitudes within the dipole array feed. This amplitude optimization of the feed array yielded outcomes similar to those achieved through the first approach, particularly in terms of sidelobe management.
The outcomes from these optimization cases offer valuable insights into the effectiveness and applicability of the Cross-Entropy method for CPU-intensive electromagnetic optimization challenges. Additionally, they provide essential guidance for informed decision-making when considering this optimization approach for analogous applications. A significant drawback of conventional population-based optimization methods lies in their heavy reliance on an extensive number of forward solver calls. This reliance renders them impractical when dealing with computationally demanding full-wave time-domain electromagnetic (EM) simulations, particularly in cases involving intricate EM structures that necessitate substantial computational resources and time.
In response to this challenge, the proposed variant of the Cross-Entropy (CE) method addresses this limitation by retaining the simplicity and elegance of the CE approach while simultaneously enhancing monitoring capabilities. This improvement facilitates the observation of the algorithm’s progress. Notably, it has been observed that employing smaller generations leads to more favorable expected improvements per function evaluation. This adapted version of the CE method not only demonstrates its efficiency and potential in the design and optimization of metasurfaces but also showcases its versatility across various complex EM design problems. As a result, it presents an appealing alternative to other commonly used optimization algorithms. With its favorable convergence properties, the proposed CE method establishes itself as a competitive and efficient solution for addressing computationally intensive EM optimization challenges.
References
- Singh, K.; Ahmed, F.; Esselle, K. Electromagnetic Metasurfaces: Insight into Evolution, Design and Applications. Crystals 2022, 12, 1769. [Google Scholar] [CrossRef]
- Singh, K.; Afzal, M.U.; Kovaleva, M.; Esselle, K.P. Controlling the most significant grating lobes in two-dimensional beam-steering systems with phase-gradient metasurfaces. IEEE Transactions on Antennas and Propagation 2019, 68, 1389–1401. [Google Scholar] [CrossRef]
- Singh, K.; Afzal, M.U.; Esselle, K.P. Designing efficient phase-gradient metasurfaces for near-field meta-steering systems. IEEE Access 2021, 9, 109080–109093. [Google Scholar] [CrossRef]
- Afzal, M.U.; Esselle, K.P. Steering the beam of medium-to-high gain antennas using near-field phase transformation. IEEE Transactions on Antennas and Propagation 2017, 65, 1680–1690. [Google Scholar] [CrossRef]
- Ahmed, F.; Singh, K.; Esselle, K.P. State-of-the-Art Passive Beam-Steering Antenna Technologies: Challenges and Capabilities. IEEE Access 2023. [Google Scholar] [CrossRef]
- Singh, K.; Afzal, M.U.; Lalbakhsh, A.; Esselle, K.P. Reflecting Phase-Gradient Metasurface for Radar Cross Section Reduction. 2021 IEEE Asia-Pacific Microwave Conference (APMC). IEEE, 2021, pp. 344–346.
- Lavigne, G.; Achouri, K.; Asadchy, V.S.; Tretyakov, S.A.; Caloz, C. Susceptibility derivation and experimental demonstration of refracting metasurfaces without spurious diffraction. IEEE Transactions on Antennas and Propagation 2018, 66, 1321–1330. [Google Scholar] [CrossRef]
- Chen, M.; Abdo-Sánchez, E.; Epstein, A.; Eleftheriades, G.V. Theory, design, and experimental verification of a reflectionless bianisotropic Huygens’ metasurface for wide-angle refraction. Physical Review B 2018, 97, 125433. [Google Scholar] [CrossRef]
- Zhang, L.; Wu, R.Y.; Bai, G.D.; Wu, H.T.; Ma, Q.; Chen, X.Q.; Cui, T.J. Transmission-reflection-integrated multifunctional coding metasurface for full-space controls of electromagnetic waves. Advanced Functional Materials 2018, 28, 1802205. [Google Scholar] [CrossRef]
- Singh, K.; Afzal, M.U.; Bulger, D.; Kovaleva, M.; Esselle, K.P. Optimization of beam-steering metasurfaces using modified cross-entropy algorithm. 2019 URSI International Symposium on Electromagnetic Theory (EMTS). IEEE, 2019, pp. 1–4.
- Singh, K.; Afzal, M.U.; Bulger, D.; Kovaleva, M.; Esselle, K.P. Optimizing amplitude distribution in a feed array to control side-lobe levels of a beam-steering metasurface. 2019 URSI International Symposium on Electromagnetic Theory (EMTS). IEEE, 2019, pp. 1–4.
- Boyarsky, M.; Imani, M.F.; Smith, D.R. Grating lobe suppression in metasurface antenna arrays with a waveguide feed layer. Optics Express 2020, 28, 23991–24004. [Google Scholar] [CrossRef]
- Ramaccia, D.; Barbuto, M.; Monti, A.; Vellucci, S.; Massagrande, C.; Toscano, A.; Bilotti, F. Metasurface dome for above-the-horizon grating lobes reduction in 5G-NR systems. IEEE Antennas and Wireless Propagation Letters 2022, 21, 2176–2180. [Google Scholar] [CrossRef]
- Elsawy, M.M.; Lanteri, S.; Duvigneau, R.; Brière, G.; Mohamed, M.S.; Genevet, P. Global optimization of metasurface designs using statistical learning methods. Scientific Reports 2019, 9, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Allen, K.W.; Dykes, D.J.; Reid, D.R.; Lee, R.T. Multi-Objective Genetic Algorithm Optimization of Frequency Selective Metasurfaces to Engineer Ku-Passband Filter Responses. Progress In Electromagnetics Research 2020, 167, 19–30. [Google Scholar] [CrossRef]
- De Bonet, J.S.; Isbell Jr, C.L.; Viola, P.A. MIMIC: Finding optima by estimating probability densities. Advances in neural information processing systems, 1997, pp. 424–430.
- Rubinstein, R.Y. Optimization of computer simulation models with rare events. European Journal of Operational Research 1997, 99, 89–112. [Google Scholar] [CrossRef]
- Rubinstein, R. The cross-entropy method for combinatorial and continuous optimization. Methodology and computing in applied probability 1999, 1, 127–190. [Google Scholar] [CrossRef]
- Rubinstein, R.Y. Combinatorial optimization, cross-entropy, ants and rare events. In Stochastic optimization: algorithms and applications; Springer, 2001; pp. 303–363.
- Rubinstein, R.Y.; Kroese, D.P. Combinatorial optimization via cross-entropy. In The Cross-Entropy Method; Springer, 2004; pp. 129–186.
- Singh, K.; Ahmed, F.; Esselle, K.P.; Thalakotuna, D. Cross-Entropy Method for Combinatorial Mixed-Parameter Optimization of Waveguide Polarizers for Ku-Band. 2022 5th International Conference on Communications, Signal Processing, and their Applications (ICCSPA). IEEE, 2022, pp. 1–7.
- De Boer, P.T.; Kroese, D.P.; Mannor, S.; Rubinstein, R.Y. A tutorial on the cross-entropy method. Annals of operations research 2005, 134, 19–67. [Google Scholar] [CrossRef]
- Connor, J.D. Antenna array synthesis using the cross entropy method 2008.
- Botev, Z.I.; Kroese, D.P.; Rubinstein, R.Y.; L’Ecuyer, P. The cross-entropy method for optimization. In Handbook of statistics; Elsevier, 2013; Vol. 31, pp. 35–59.
- Zlochin, M.; Birattari, M.; Meuleau, N.; Dorigo, M. Model-based search for combinatorial optimization: A critical survey. Annals of Operations Research 2004, 131, 373–395. [Google Scholar] [CrossRef]
- Joyce, D. Common probability distributions. Lecture Notes, Clark University 2006.
- Lemieux, C. Monte carlo and quasi-monte carlo sampling; Springer Science & Business Media, 2009.
- Montgomery, D.C.; Runger, G.C. Applied statistics and probability for engineers; John Wiley & Sons, 2010.
- Rahnamayan, S.; Tizhoosh, H.R.; Salama, M.M. A novel population initialization method for accelerating evolutionary algorithms. Computers & Mathematics with Applications 2007, 53, 1605–1614. [Google Scholar]
- Ghoreishi, S.N.; Clausen, A.; Jørgensen, B.N. Termination Criteria in Evolutionary Algorithms: A Survey. IJCCI, 2017, pp. 373–384.
- Szita, I.; Lorincz, A. Online variants of the cross-entropy method. arXiv preprint arXiv:0801.1988 2008.
- Gagnon, N.; Petosa, A.; McNamara, D.A. Thin phase-correcting lens antennas made using a three-layer phase-shifting surface (PSS) at Ka band. 2010 14th International Symposium on Antenna Technology and Applied Electromagnetics & the American Electromagnetics Conference. IEEE, 2010, pp. 1–4.
- Daunizeau, J. Semi-analytical approximations to statistical moments of sigmoid and softmax mappings of normal variables. arXiv preprint arXiv:1703.00091 2017.
- Hsu, L.; Dupré, M.; Ndao, A.; Yellowhair, J.; Kanté, B. Local phase method for designing and optimizing metasurface devices. Optics Express 2017, 25, 24974–24982. [Google Scholar] [CrossRef]
- Nematollahi, H.; Laurin, J.J.; Page, J.; Encinar, J.A. Design of broadband transmitarray unit cells with comparative study of different numbers of layers. IEEE Transactions on Antennas and Propagation 2015, 63, 1473–1481. [Google Scholar] [CrossRef]
- Li, H.P.; Wang, G.m.; Cai, T.; Liang, J.; Gao, X. Phase-and Amplitude-Control Metasurfaces for Antenna Main-and Side-Lobe Manipulations. IEEE Transactions on Antennas and Propagation 2018. [Google Scholar]
- Mohammed, J.R.; Sayidmarie, K.H. Synthesizing asymmetric side lobe pattern with steered nulling in nonuniformly excited linear arrays by controlling edge elements. International Journal of Antennas and Propagation 2017, 2017. [Google Scholar] [CrossRef]
- Khasim, S.N.; Krishna, M.Y.; Thati, J.; Subbarao, V.M. Analysis of different tapering techniques for efficient radiation pattern 2015.
- Hill, T.A.; Kelly, J.R. 28 GHz Taylor feed network for sidelobe level reduction in 5G phased array antennas. Microwave and Optical Technology Letters 2019, 61, 37–43. [Google Scholar] [CrossRef]
- Xiao, F.; Kong, L.; Chen, J. Beam-steering efficiency optimization method based on a rapid-search algorithm for liquid crystal optical phased array. Applied optics 2017, 56, 4585–4590. [Google Scholar] [CrossRef] [PubMed]
Figure 1.
Model-based search framework for CE method.
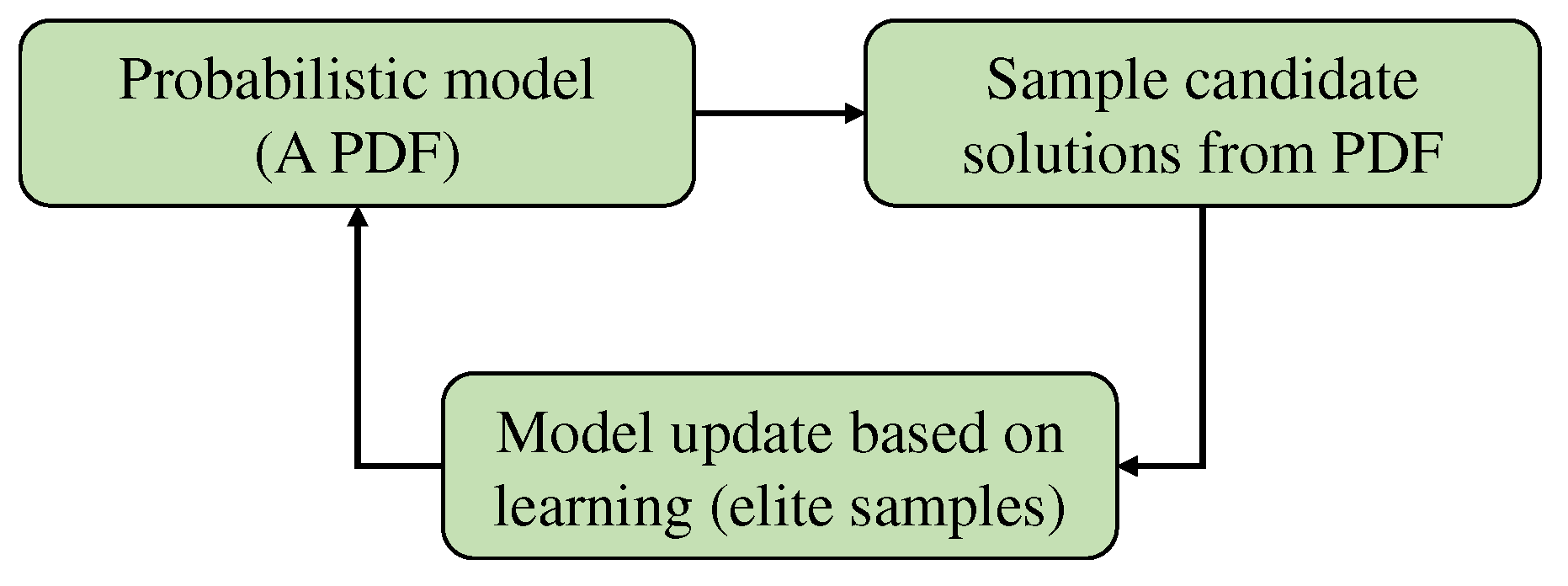
Figure 2.
Simplified equivalent model of a metasurface with boundary conditions specified to mimic a full 2D metasurface.
Figure 2.
Simplified equivalent model of a metasurface with boundary conditions specified to mimic a full 2D metasurface.

Figure 3.
Complete architecture of a PGM with a supercell and a single-cell internal composition added at the bottom for clarity.
Figure 3.
Complete architecture of a PGM with a supercell and a single-cell internal composition added at the bottom for clarity.
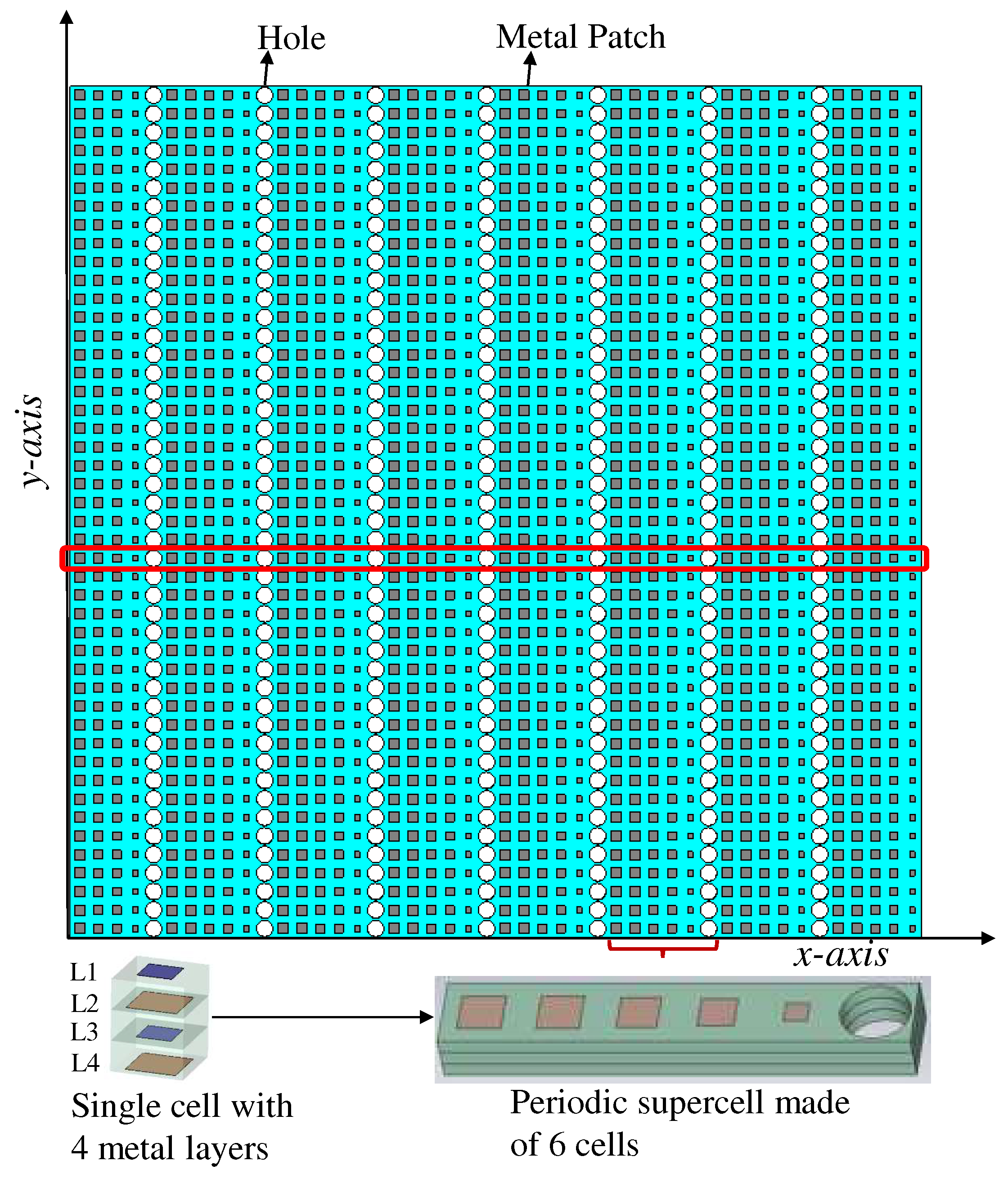
Figure 4.
The metasurface supercell showing the design parameters used in metasurface optimization.
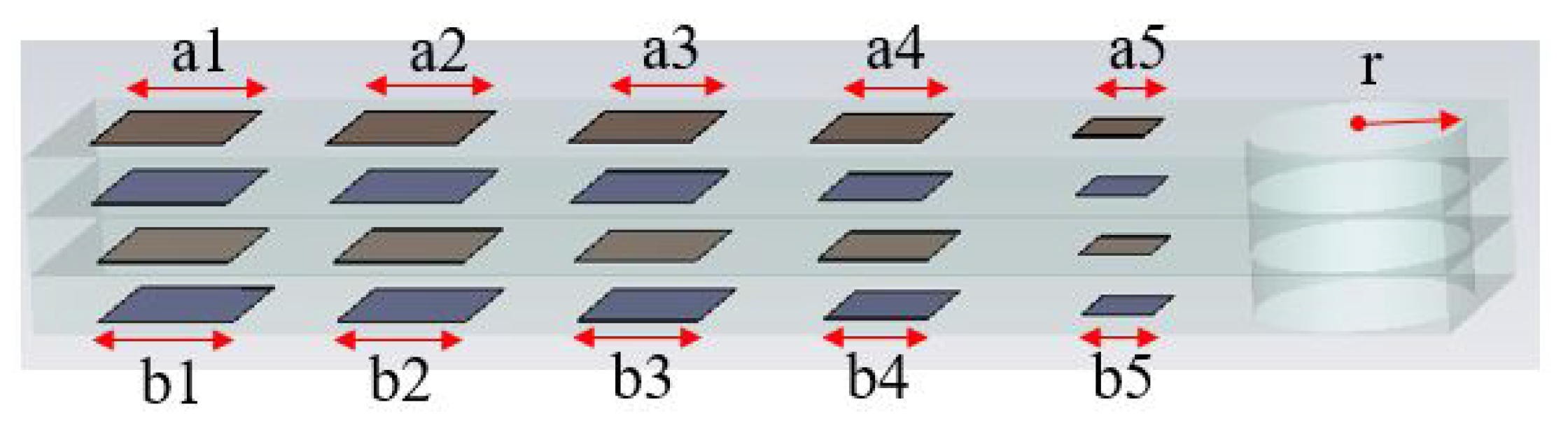
Figure 5.
Convergence curve for modified CE algorithm implemented to optimize the metallic patch dimension of the PGM. The plot compares the evolution of average fitness of the Queue with respect to the best fitness of the Queue so far.
Figure 5.
Convergence curve for modified CE algorithm implemented to optimize the metallic patch dimension of the PGM. The plot compares the evolution of average fitness of the Queue with respect to the best fitness of the Queue so far.
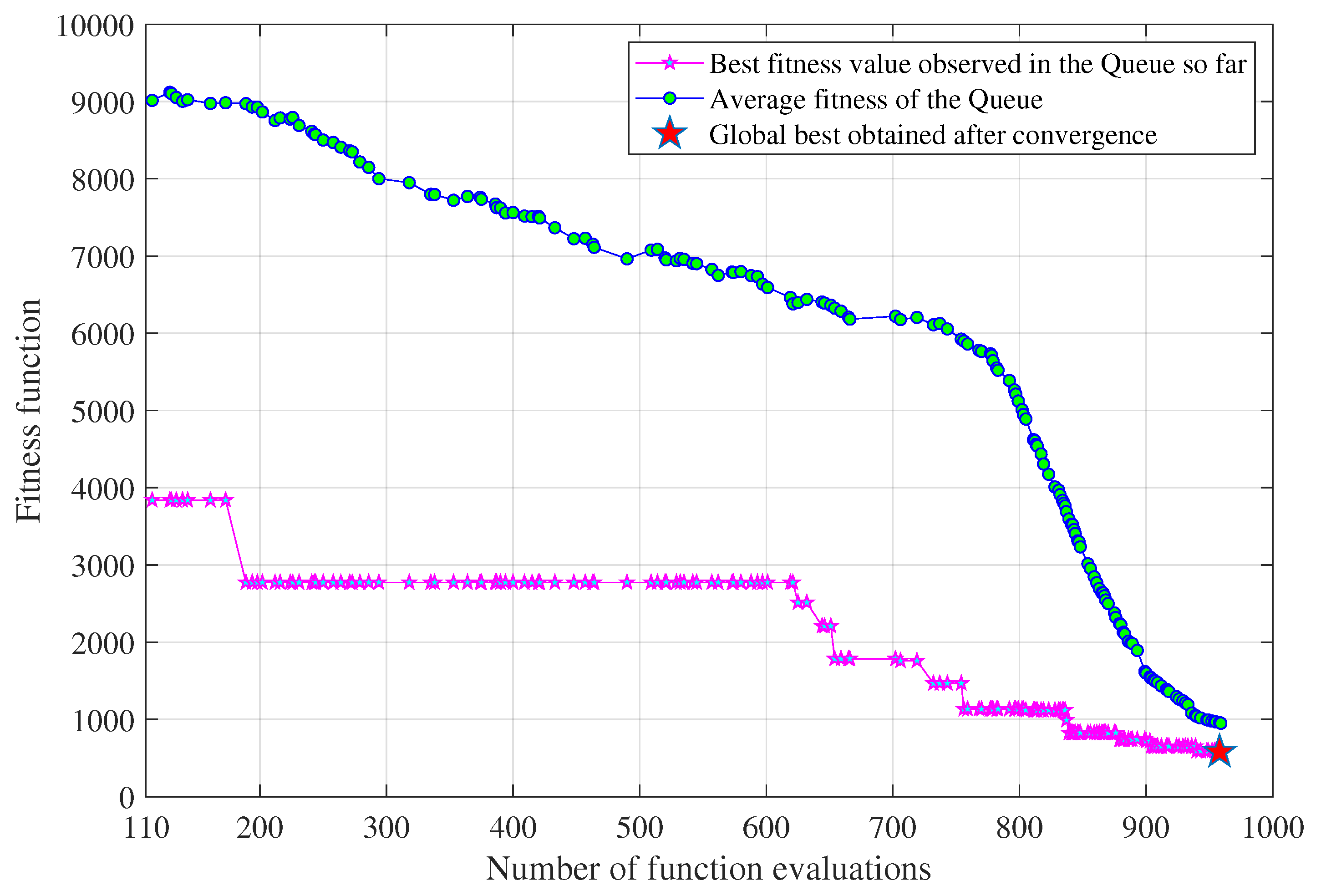
Figure 6.
Elementary diagram for the side-view of an array-fed beam-steering PGM showing a stepped saw-tooth phase profile in the near-field and a steered pattern in the far-field.
Figure 6.
Elementary diagram for the side-view of an array-fed beam-steering PGM showing a stepped saw-tooth phase profile in the near-field and a steered pattern in the far-field.
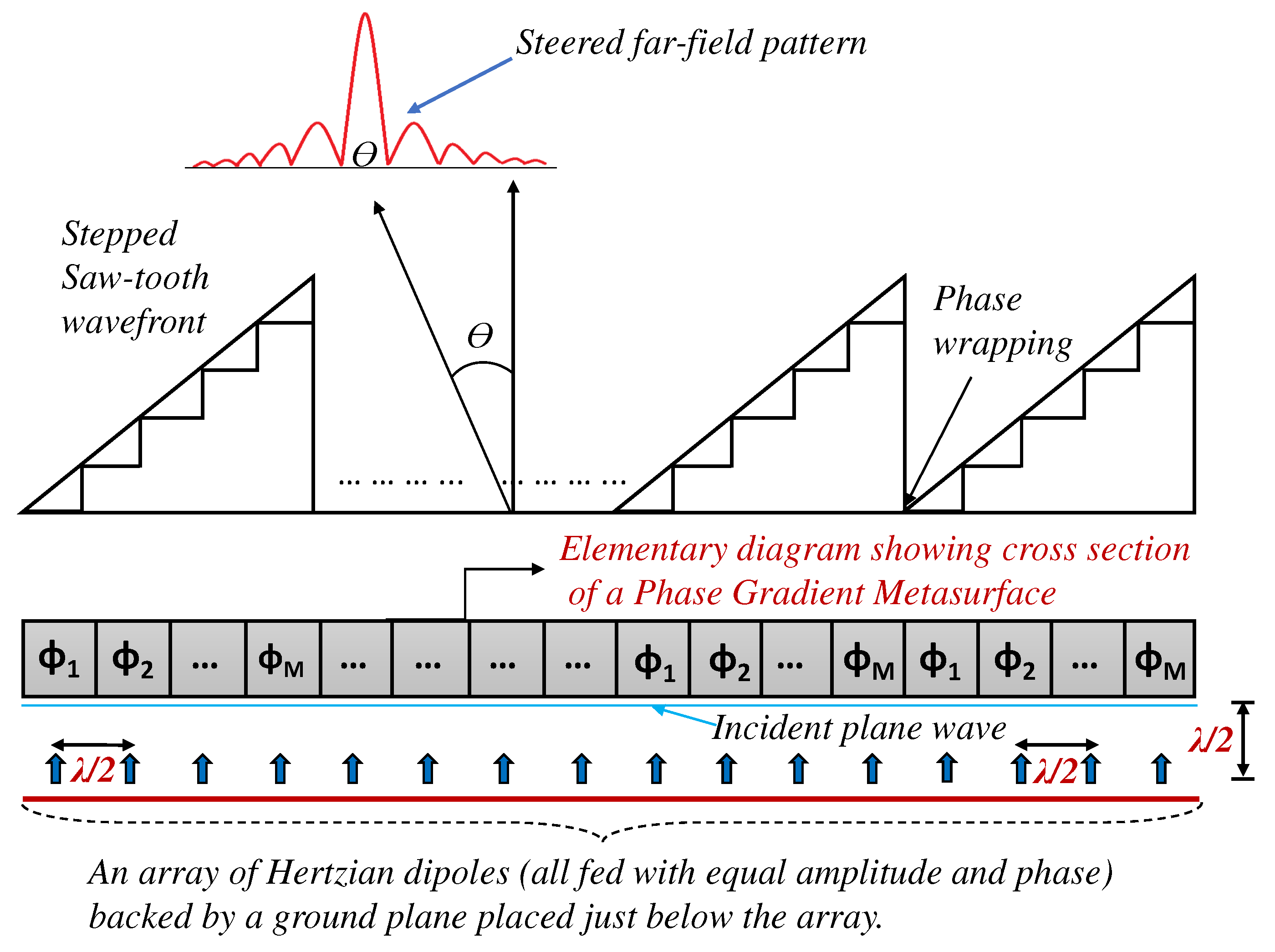
Figure 7.
Elementary diagram for the side-view of an array-fed beam-steering PGM showing a stepped saw-tooth phase profile in the near field and a steered pattern in the far field.
Figure 7.
Elementary diagram for the side-view of an array-fed beam-steering PGM showing a stepped saw-tooth phase profile in the near field and a steered pattern in the far field.
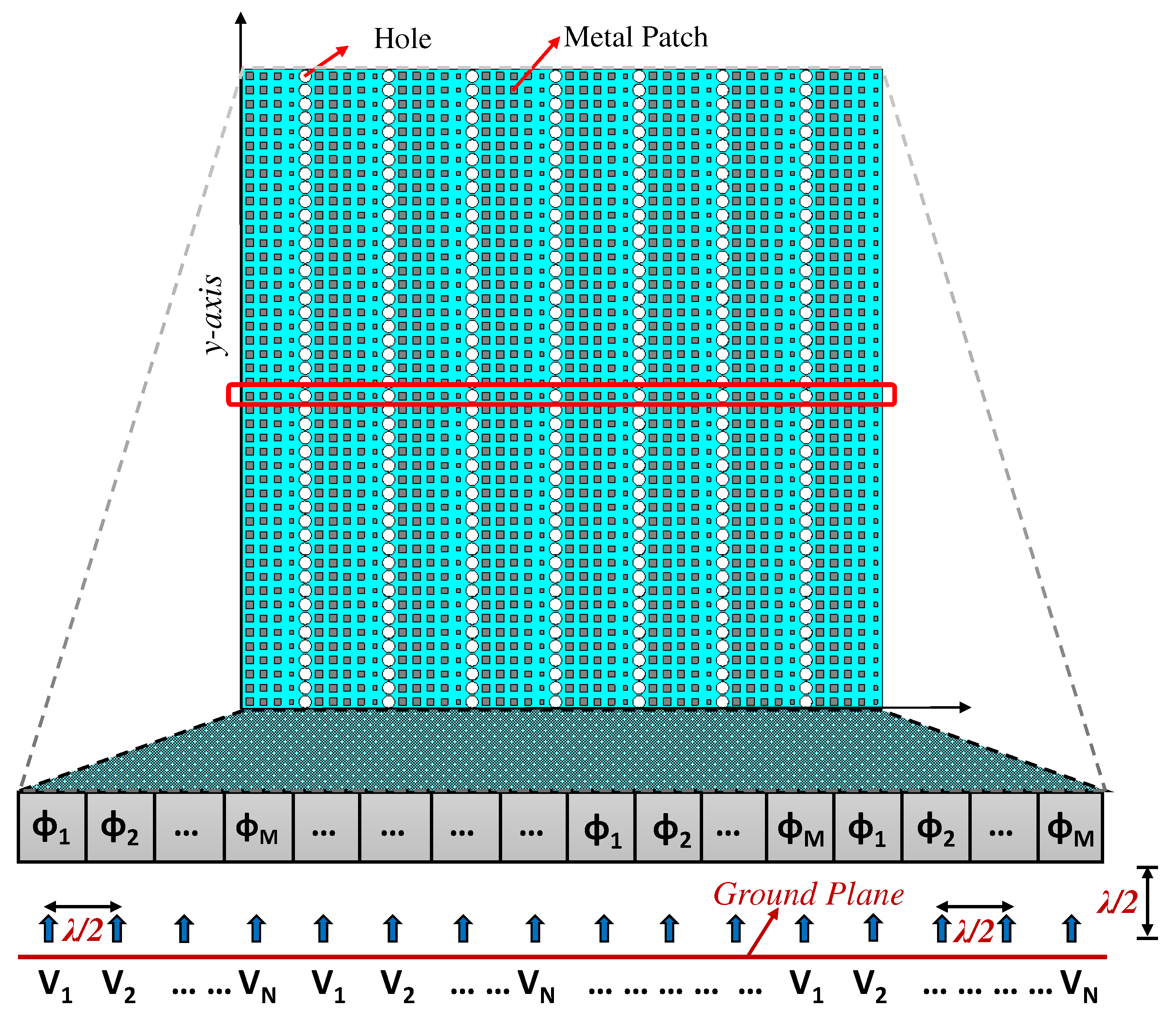
Figure 8.
Beta distribution probability density functions for different set of values of parameters and .
Figure 8.
Beta distribution probability density functions for different set of values of parameters and .
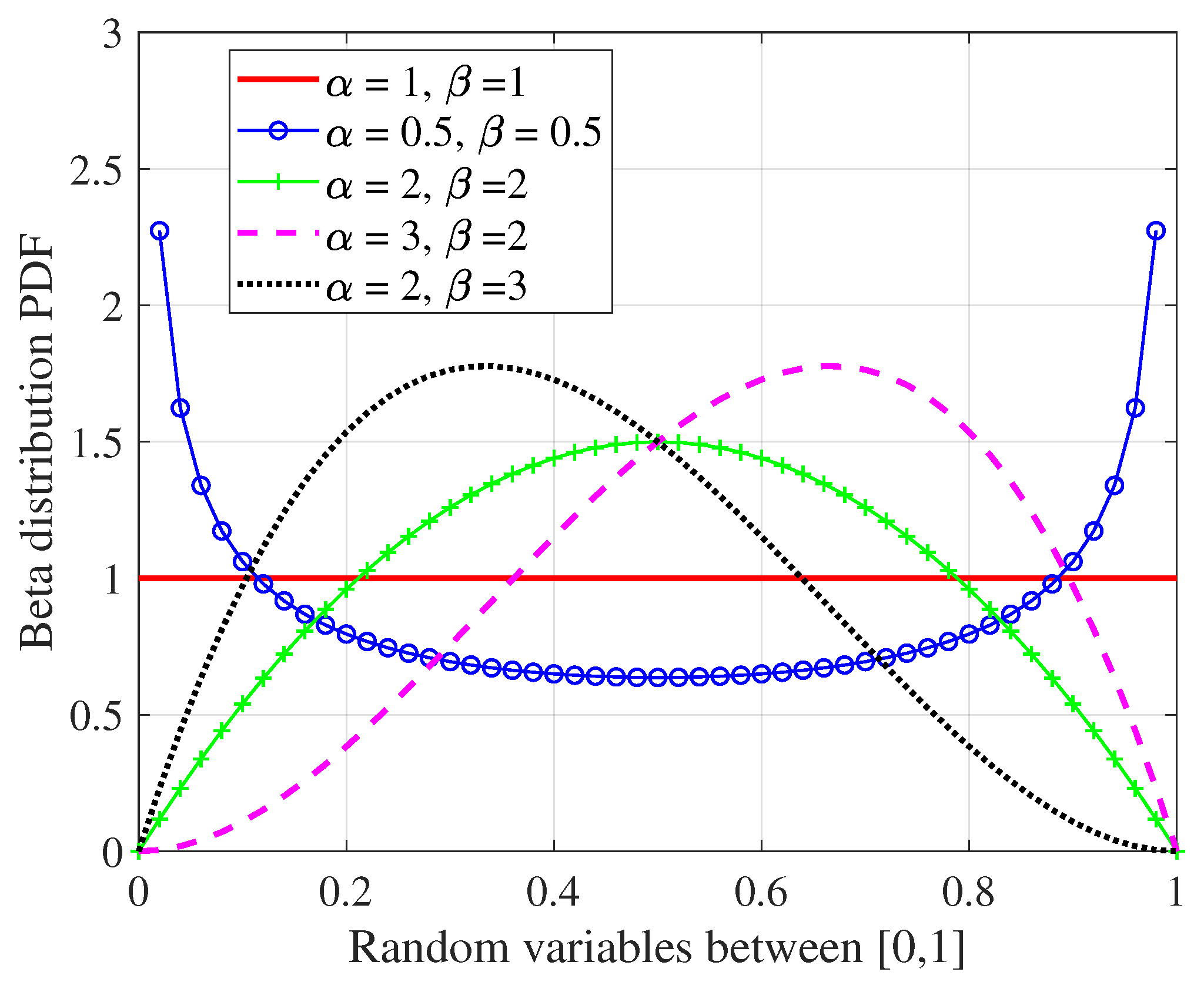
Figure 9.
A PGM fed with an array of Hertzian dipole having amplitude excitation periodicity
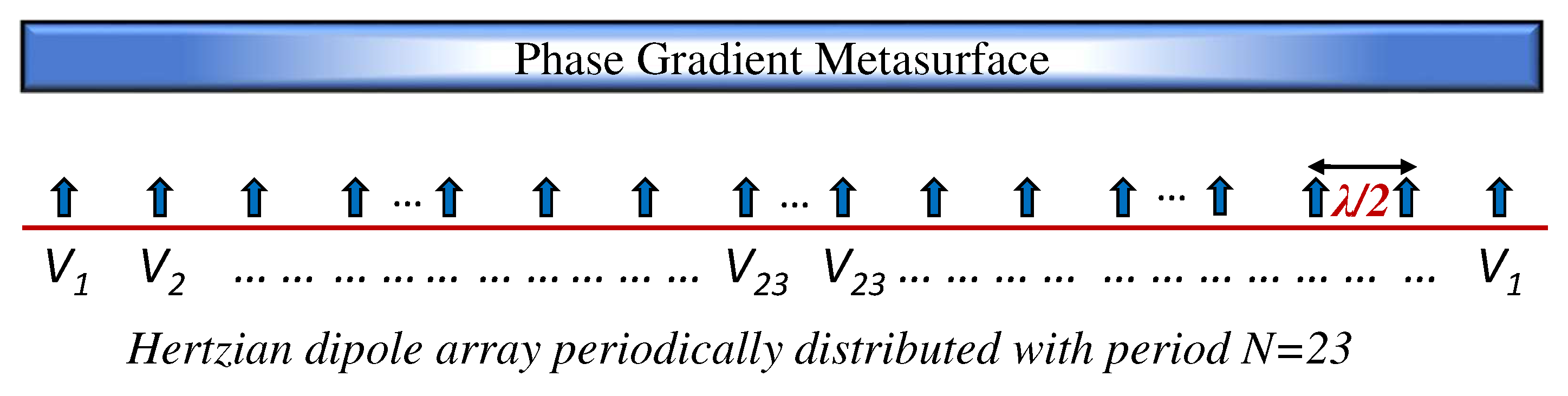
Figure 10.
Convergence results of the modified CE method for Case-II optimization of a PGM.
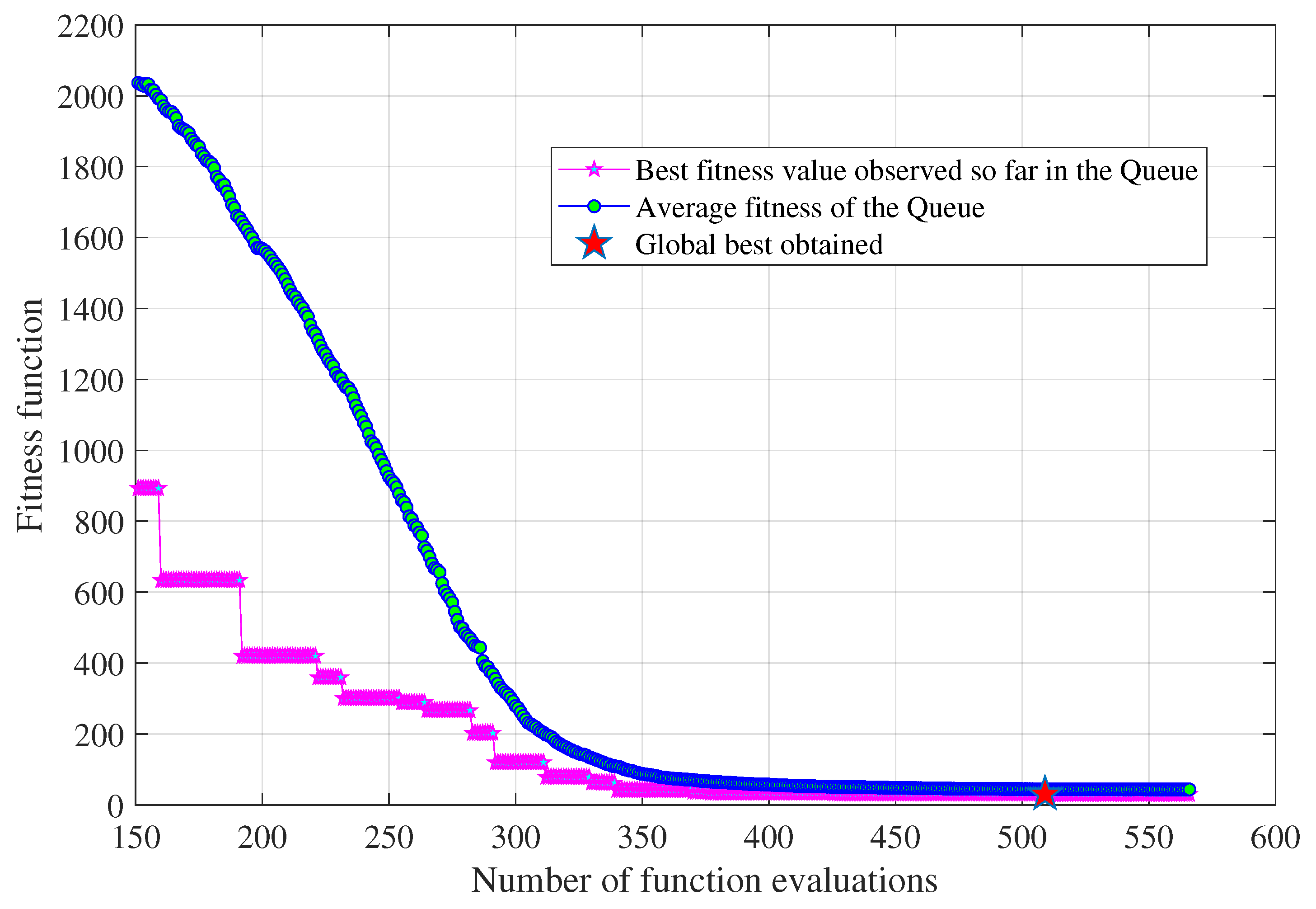
Figure 11.
Directivity pattern comparison for optimized and unoptimized PGM.

Figure 12.
Comparing the radiation pattern of a finite-sized 2D metasurface when excited by a 2D array of Hertzian dipoles showing a decrease in side-lobe levels (SLLs) following the optimization of the excitation amplitude distribution compared to a uniformly excited array.
Figure 12.
Comparing the radiation pattern of a finite-sized 2D metasurface when excited by a 2D array of Hertzian dipoles showing a decrease in side-lobe levels (SLLs) following the optimization of the excitation amplitude distribution compared to a uniformly excited array.
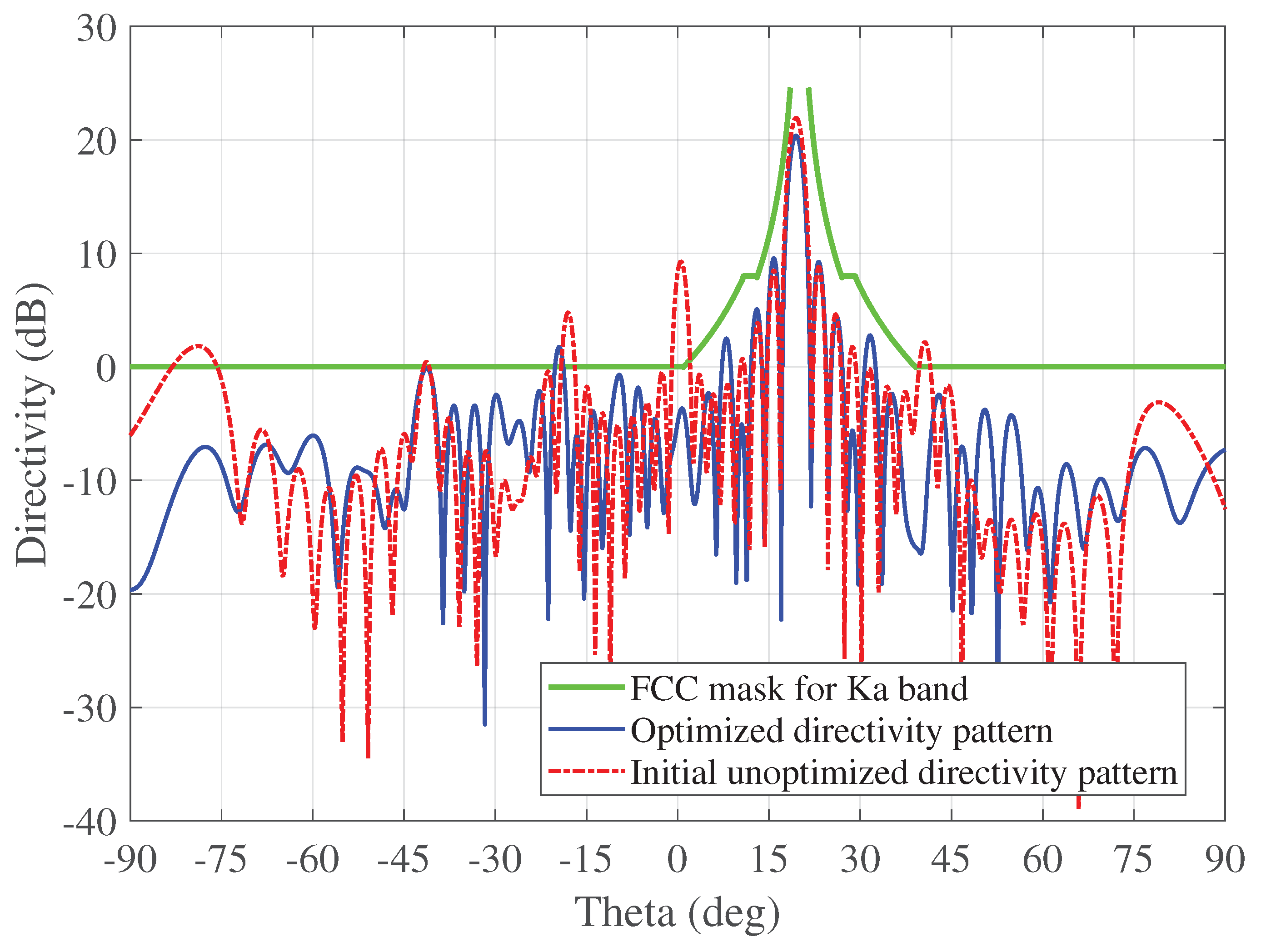
Table 1.
The CE method parameters for optimization of PGM.
| Queue size | Elite sub-population size | Smoothing |
| N | ||
| 110 | 11 | 0.2 |
Table 2.
The CE algorithm parameters for optimization of excitation amplitude distribution with periodicity , in the feed array of PGM.
Table 2.
The CE algorithm parameters for optimization of excitation amplitude distribution with periodicity , in the feed array of PGM.
| Queue size | Elite sub-population size | Smoothing |
| 150 | 15 | 0.5 |
Table 4.
Excitation amplitude distribution of feed array before and after optimization.
| Design Parameters, mm | Before optimization | After optimization |
|---|---|---|
| 1 | 0.34 | |
| 1 | 0.70 | |
| 1 | 0.65 | |
| 1 | 0.55 | |
| 1 | 0.74 | |
| 1 | 0.34 | |
| 1 | 0.70 | |
| 1 | 0.65 | |
| 1 | 0.55 | |
| 1 | 0.74 | |
| 1 | 0.34 | |
| 1 | 0.70 | |
| 1 | 0.65 | |
| 1 | 0.55 | |
| 1 | 0.74 | |
| 1 | 0.74 | |
| 1 | 0.34 | |
| 1 | 0.70 | |
| 1 | 0.65 | |
| 1 | 0.55 | |
| 1 | 0.74 | |
| 1 | 0.34 | |
| 1 | 0.46 | |
| Directivity, dBi | 21.9 | 20.5 |
| Side-lobe Level, dB | -12.4 | -19.3 |
| F.F, Eq. (11) | 1247 | 32.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated







