Preprint
Article
Biased Random Process of Randomly Moving Particles with Fixed Mean and Curl
Altmetrics
Downloads
128
Views
103
Comments
1
supplementary.pdf (280.58KB )
This version is not peer-reviewed
Submitted:
14 October 2023
Posted:
17 October 2023
You are already at the latest version
Alerts
Abstract
In this study, we investigate the behavior of randomly moving particles with a defined average energy, focusing on their biased motion around a specific point. These particles' velocity magnitudes follow a Maxwell distribution with a specific scale parameter. Our analysis derives the stochastic rotation rules for these particles and introduces the Ito equation conditions for biased stochastic rotation at a given curl value. We also consider the special relativistic-like effects in this context. The findings are validated through a representative example.
Keywords:
Subject: Physical Sciences - Mathematical Physics
Introduction
For a collection of particles with a defined average energy, their magnitudes of velocities follow a Maxwell distribution characterized by a specific parameter. When a subset of the particles exhibits biased motion in their movement direction, they can be characterized as three distinct and prevalent types of biased stochastic motion (At an extremely large particle count and scale, even scenarios with exceedingly low probabilities can manifest with notable frequency within a specific region). These biased motions encompass: () stochastic movement with a preferential direction while maintaining equal probabilities in other directions; () stochastic movement favoring a specific spatial point but equiprobable in alternative directions; and () stochastic movement with a predilection for revolving around a designated rotational center. Within these scenarios of biased stochastic motion, systems exhibiting characteristics of the first situation display the special relativistic-like effects[1,2]. On the other hand, biased stochastic motions with higher probabilities directed towards or revolving around a specific center incorporate these special relativistic-like effects into processes of spatial aggregation[3] or rotational phenomena[4].
For the rotational effect produced by biased randomly moving particles, the constituent particles of the rotating body inherently experience a displacement in linear velocity. Consequently, such motion should also exhibit special relativistic-like effects. Previous research[4] has investigated the rotational behavior generated by a group (radius is R) of randomly moving particles with consistent linear velocities c. The conclusion drawn is that the magnitude of the angular velocity produced by k randomly moving particles follows a Maxwell distribution with a scale parameter of . In actual physical systems, it is more common for these particles to not have perfectly consistent linear speeds. Instead, when the energy is fixed, their speeds follow a Maxwell distribution determined by a specific parameter. Furthermore, nearly every celestial body in the universe is rotating. The underlying mechanism for this rotation might be a result of the collective actions of particles whose speeds follow a Maxwell distribution. In summary, it is essential to thoroughly investigate the distribution of angular speeds generated by particles with speeds following a Maxwell distribution as they move randomly in space. Based on this premise, when the magnitude of the angular velocity is a specific value, particles undergoing pure random motion transition to biased random motion. Presenting the corresponding Itô equation expression under this scenario is the primary objective of this study.
With the aid of mathematical packages, certain complex theoretical problems can be effortlessly addressed. Currently, among the world’s most powerful symbolic computation packages are Maple (Cybernet Systems Co. Ltd., Japan) and Mathematica (Wolfram Research Inc., USA). The intricately designed algorithms within these platforms have facilitated the work of countless scientists and engineers worldwide. However, these mathematical packages are neither universal nor omnipotent. Real-world problems are often intricate, and relying solely on one specific package might not provide an optimal solution. It is essential to utilize a combination of software tools and appropriately decompose the actual problem to achieve a comprehensive resolution. In this study, Mathematica v13.2 was employed for theoretical derivations, while Maple v2023 was utilized for solving the system of partial differential equations.
This study first examines the distribution of rotational angular velocity magnitudes in a particle system with a defined average energy, where the magnitudes of the particle velocities follow a Maxwell distribution with a specific scale parameter. Subsequently, a set of Itô equations that describe the motion characteristics of biased moving particles with rotational effects is introduced. Finally, an illustrative example is provided to further elucidate the characteristics of these Itô equations. The biased moving particles discussed in this study, which exhibit special relativistic-like effects, differ from the conventional understanding where particle motion must follow the constraints of special relativity. This study assumes that these particles move at relatively low speeds, essentially unaffected by special relativistic effects, or they represent ideal particles completely unaffected by special relativistic effects. In this study, the average speed c represents the mean magnitude of particle velocities rather than the speed of light. These biased moving particles can exhibit common significant phenomena. Understanding their essence is crucial for comprehending the effects of special relativity and the inherent nature behind rotations influenced by special relativistic effects.
Results and Discussion
For particle assemblies with consistent magnitudes of velocity and directions arbitrarily dispersed within a three-dimensional domain, the resultant rotational effects in space have been comprehensively examined in our prior publication[4]. This study primarily investigates the rotational behavior in space exhibited by particle assemblies under identical conditions, where the magnitudes of their velocities follow a Maxwell distribution. Analogous to the investigative approach presented in reference [4], we first examine the distribution of the magnitude of the random angular velocity generated by a random vector with its origin uniformly distributed on a unit sphere S, where the magnitude of follows a Maxwell distribution with a mean of c (Figure 1). Assuming is the radius of the unit sphere S, then
Let us establish a 3-dimensional Cartesian coordinate system for . Suppose that the disk is perpendicular to the z-axis and consider the random variables and . Then, the magnitude of the random vector obtained by projecting the uniformly distributed points on sphere onto disc is
Therefore, the probability of is
Assuming is one coordinate X that is equivalent to the three coordinates of . By taking a product of random variables, we can obtain the probability density of X, which represents one of the three equivalent coordinates of the angular velocity contributed by the random vector , specifically,
The probability density of equivalent coordinate of contributed by which is uniformly distributed throughout the whole unit ball enclosed by the sphere S is
Thus, the distribution function of the contribution of to one of the equivalent coordinates of is obtained. Next, is integrated over the whole unit ball and the probability density of the contribution of in the whole unit ball to an equivalent coordinate X of the angular velocity can be obtained:
Next, we extend the analysis to the case in which the radius of the ball has an arbitrary value R. The probability density of the contribution of the random vector to the single equivalent coordinate X of angular velocity is
the standard deviation of which is . Therefore, when k independent and identically distributed random vectors move randomly in space, according to the central limit theorem (when they are grouped together), the magnitude of the average angular velocity generated by all of their components relative to their total centroid follows a Maxwell distribution with scale parameter .
Building upon this foundation, we delve into the representation of this stochastic rotation behavior using the Itô equation, specifically discussing scenarios where the curl assumes a defined value of , where . For particle assemblies with a defined energy, the magnitudes of their velocities follow a Maxwell distribution characterized by specific parameters. Previous research has provided the form of the Itô equation for particles exhibiting biased random motion in a particular direction, incorporating the special relativistic-like effects[2]. In this study, we further incorporate the special relativistic-like effects into the stochastic rotation.
For any given particle, the biased motion around a specific point fundamentally remains a movement with a linear velocity. Consequently, it still adheres to the velocity reduction inherent of special relativistic-like. Assuming that at a specific time t, the linear velocity of a particle at position is , its projections onto the three coordinate axes are and . As per the description method in the literature[2], the Itô equation at time t can be expressed as:
where . Differing from the literature, here we replace and with and . From a macroscopic perspective, if the system exhibits rotational effects, then at a given time t, the velocity u should also be a function of the position . Then, the sum of integrals of the curl of the velocity over all possible closed loops (s) is not zero, that is,
We will not delve extensively into this issue here; instead, we will examine the scenarios in the microscopic domain when particles show indications of rotation. At a given time t, the velocity u should also be a function of the position . Then, the velocity components along the three axes should satisfy the condition that a non-zero curl, meaning and are subject to the following constraints:
We will focus on the form of the Itô equation when the curl is specified.
To elucidate this problem further, we present a concrete example. Assuming these particles rotate within the plane around the axis , resulting in a curl value of , and the magnitude of the particle’s linear velocity remains constant at u. We proceed to solve the following equation:
Subsequently, we select a particular solution from the aforementioned equation to illustrate the issue:
Substituting Eq. 12 into Eq. 8 and omitting the time term, we obtain
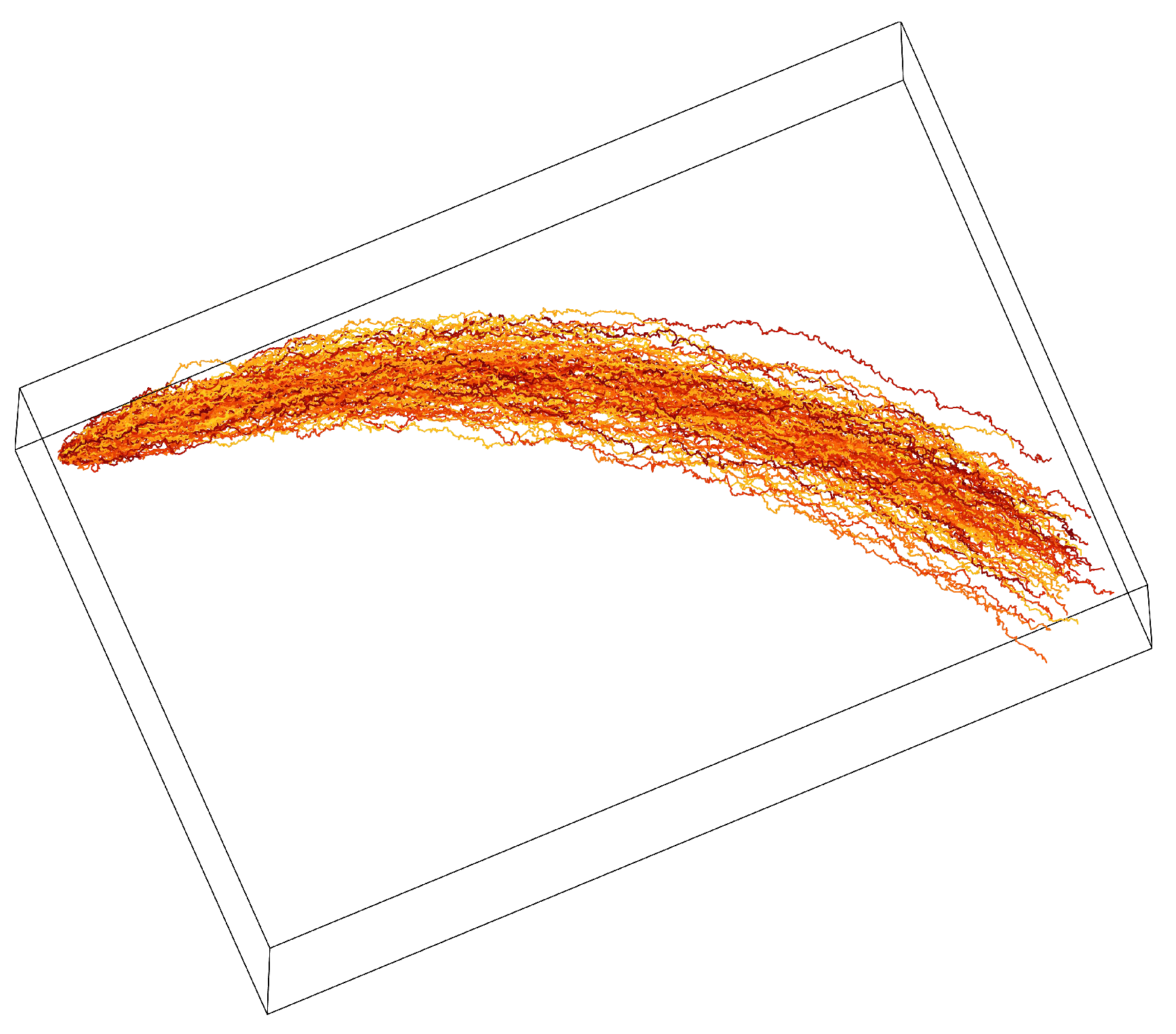
We substitute the values , and into Eq. 13 and simulate with a sample of 100 particles. The results are depicted in Figure 2:
In Figure 2, although only the motion of 100 particles starting from the same point is depicted, it is not difficult to infer the motion scenarios at various points when the starting positions are distributed across the entire plane. We will not elaborate further with additional examples here.
Conclusions
For a set of k particles with a defined average energy, when their velocity magnitudes follow a Maxwell distribution characterized by the parameter (average speed is c), their random motion can lead to angular velocity magnitudes that follow a Maxwell distribution with the parameter . Specifically, when the curl of the particles maintains a certain value, their motion must satisfy the biased conditions defined by Eq. 8 and 10. Notably, akin to the scenario where the particle group moves linearly, these rotation effects are also constrained by the special relativistic-like effects.
Supplementary Materials
The following supporting information can be downloaded at the website of this paper posted on Preprints.org. Mathematica code for necessary calculation process and graphics. The following file is available free of charge. Supporting Information.
Data Availability Statement
All data generated or analysed during this study are included in this published article and its supplementary information files.
Acknowledgments
The author is thankful for Maplesoft Inc. and Wolfram Inc.
Conflicts of Interest
There are no conflicts to declare.
References
- Guo, T. Study on the average speed of particles from a particle swarm derived from a stationary particle swarm. Scientific Reports 2021, 11, 1–4. [Google Scholar] [CrossRef]
- Guo, T. Biased Random Process of Randomly Moving Particles with Fixed Mean and Group Velocities. Preprints 2023, p. [Google Scholar] [CrossRef]
- Guo, T. Dynamics of stochastic-constrained particles. Scientific Reports 2023, 13, 2759. [Google Scholar] [CrossRef]
- Yang, T.; Guo, T. The angular speed distribution of randomly moving-particle group. AIP Advances 2022, 12, 045005. [Google Scholar] [CrossRef]
Figure 1.
Schematic diagram of the generation method for the vector . The radius of denotes the mean of magnitudes of the spatial vectors that follow a Maxwell distribution with a parameter .
Figure 1.
Schematic diagram of the generation method for the vector . The radius of denotes the mean of magnitudes of the spatial vectors that follow a Maxwell distribution with a parameter .
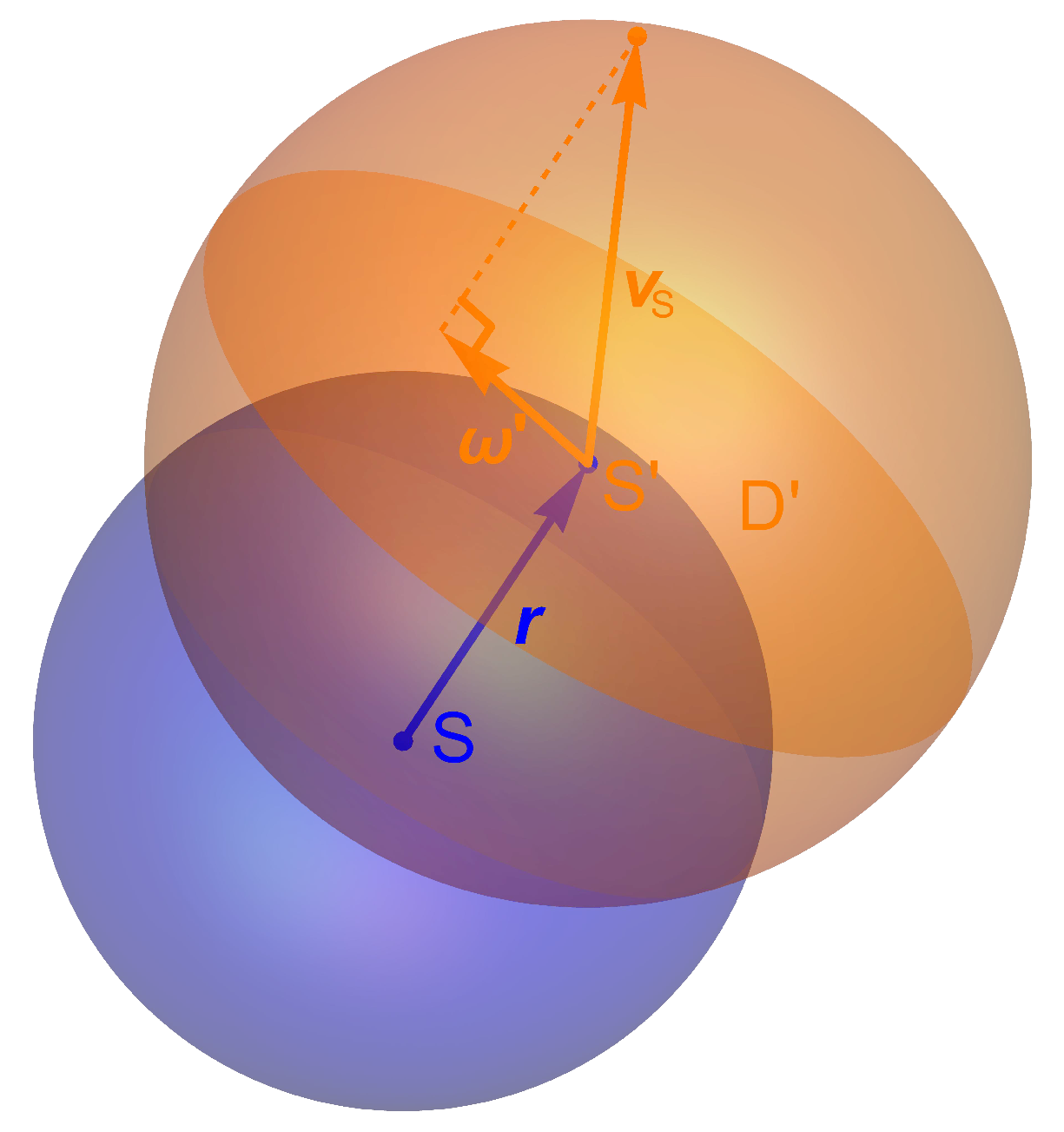
Figure 2.
Simulation results of the trajectories of 100 particles randomly moving for 10 s (, and ).
Figure 2.
Simulation results of the trajectories of 100 particles randomly moving for 10 s (, and ).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated