Prerpints.org logo
Preprint
Article

Smart Energy Borrowing and Relaying in Wireless Powered Networks: A Deep Reinforcement Learning Approach

Altmetrics

Downloads

103

Views

35

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

05 September 2023

Posted:

07 September 2023

You are already at the latest version

Alerts
Abstract
Wireless energy harvesting (EH) communication has long been considered a sustainable networking solution. However, it has been limited in efficiency, which has been a major obstacle. Recently, strategies such as energy relaying and borrowing have been explored to overcome these difficulties and provide long-range wireless sensor connectivity. In this article, we examine the reliability of the wireless-powered communication network by maximizing the net bit rate. To accomplish our goal, we focus on enhancing the performance of hybrid access points and information sources by optimizing their transmit power. Additionally, we aim to maximize the use of harvested energy by energy-harvesting relays for both information transmission and energy relaying. However, this optimization problem is complex as it involves non-convex variables and requires combinatorial relay selection indicators optimization for decode and forward (DF) relaying. To simplify this problem, we utilize the Markov decision process and deep reinforcement learning framework based on the deep deterministic policy gradient algorithm. This approach enables us to tackle this non-tractable problem, which conventional convex optimisation techniques would be difficult to solve in complex problem environments. The proposed algorithm significantly improves the end-to-end net bit rate of the smart energy borrowing and relaying EH system by 13.22%,27.57%, and 14.12% compared to the benchmark algorithm based on borrowing energy with an adaptive reward for Quadrature Phase Shift Keying, 8-PSK, and 16-Quadrature amplitude modulation schemes, respectively.
Keywords: 
Subject: Engineering  -   Electrical and Electronic Engineering

1. Introduction

The deployment of ultra-low-power electronic sensors has increased significantly with the advancement of wireless communication technology. These sensors are used for various applications, such as the Internet of Things (IoT) and wireless sensor networks (WSNs) [1]. However, the lifetime of these networks is limited by the battery constraints of the individual sensor devices. To address this issue, dedicated radio frequency energy transfer (RF-ET) has emerged as a potential solution to ensure uninterrupted long-duration network operation by providing controllable on-demand energy replenishment of sensor devices [2]. Radiative RF-ET has appealing features, including long-range beamforming capabilities for energy harvesting (EH), joint energy, and information transfer provisioning over the same signal [3]. This introduces two attractive research domains: wireless-powered communication networks (WPCN) and simultaneous wireless information and power transfer (SWIPT). In WPCN, the uplink information transfer (IT) is governed by downlink ET from the hybrid access point (HAP), whereas SWIPT supports IT and ET simultaneously in the same direction.
The RF-EH system can operate independently in remote and harsh locations, but it has some limitations. These include low energy sensitivity, low rectification efficiency at lower input power, high attenuation due to path loss, and energy dispersion loss [4]. Additionally, the energy harvested from ambient sources cannot be accurately predicted dynamically because the channel conditions are constantly changing [5]. Therefore, it is necessary to have a backup power supply, such as a power grid (PG), to facilitate energy cooperation. This secondary power supply can efficiently handle energy transactions when EH devices require additional power for uninterrupted WPCN operation. This paper investigates the artificial intelligence (AI) enabled smart energy sharing and relaying in cooperative WPCN to enhance the end-to-end system performance.

1.1. Related Works

Several studies, including those referenced in citations [6,7,8,9,10,11,12,13], have explored implementing autonomous cooperative energy harvesting (EH) techniques with unknown channel gains. These techniques involve energy-constrained sensor devices transmitting information using harvested energy in wireless power transfer networks (WPCN). For instance, one study proposed an optimization model in [6] to maximize two-hop radio frequency energy transfer efficiency with optimal relay placement. In [8], the overall bit rate was maximized by jointly optimizing time and power allocation for downlink energy transfer and uplink information transfer and relaying. Another study by Chen et al. in [9] approximated the closed-form expression of average throughput for wireless-powered cooperative networks using the harvest-then-cooperate protocol. In addition to fixed relaying approaches in [8] and [9], an adaptive transmission protocol in [10] dynamically determines whether the information source (IS) should access the point (AP) directly or cooperatively with relays based on estimated channel state information (CSI). Beamforming optimization was performed in [11] to maximize received power for evaluating the performance of relay-assisted schemes under EH efficiency constraints. In [12], a generalized frequency division multiplexing (GFDM) based cooperative relaying system was developed to improve the quality of experience (QoE) of cell-edge users. In [13], Wei et al. proposed an iteration-based wireless power transfer (WPT) to enhance spectral efficiency (SE) by jointly optimizing time slot duration, subcarriers, and the transmit power of the source and relay. However, the harvested energy from WPT at sensor device batteries cannot transmit data over long distances. Therefore, energy cooperation and sharing strategies are necessary to overcome dynamic green energy arrival conditions for perpetual WPCN operation.
In network optimization, [14] proposed a method to minimize network delay through simplified energy management and conservation constraints for fixed data and energy routing topologies. Meanwhile, [15] explored various energy-sharing mechanisms among multiple EH devices within the network. When data transmission is possible, but there is insufficient energy in the device battery, external energy supply from nearby secondary power sources must be considered. [16] addressed this issue by examining the external energy supply provided by PG to EH devices in WPCN. In contrast, [17] proposed that EH devices borrow energy from PG for information transmission and return it with additional interest as a reward. Sun et al. developed a schedule [18] to maximize system throughput through energy borrowing and returning. However, these approaches rely on predefined statistical parameters and dynamics, whereas in reality, channel gains and harvested energy are subject to random variation. Therefore, a decision-making deep reinforcement learning (DRL) algorithm is needed to determine current network parameters based on previously gained knowledge of the environment.
Wireless network management has recently seen an increase in deep reinforcement learning (DRL) use as part of machine learning (ML) due to its decision-making capabilities through a trial-and-error approach. The sophisticated combination of neural networks (NNs) in DRL makes it ideal for handling complex situations with high-dimensional problems. Qie et al. used DRL based on the deep deterministic policy gradient (DDPG) algorithm to develop an optimal energy management strategy for an EH wireless network. Resource allocation policies were also developed using DRL in [22] to maximize achievable throughput, considering EH, causal information of the battery state, and channel gains. DRL based on the borrowing energy with an adaptive reward (BEAR) algorithm was proposed in [23] for energy scheduling policy to optimize energy borrowing from a secondary power source and efficient data transfer utilizing harvested energy. In [24], cooperative communications with adaptive relay selection in WSN was investigated as a Markov decision process (MDP), and deep-Q-network (DQN) was proposed to evaluate network performance based on outage probability, system capacity, and energy consumption. DRL based on the actor-critic method was used in [25] and [26] to maximize the energy efficiency (EE) of a heterogeneous network for optimal user scheduling and resource allocation. However, the impact of energy scheduling and transmit power allocation of IS to maximize the transmission rate of an energy borrowing and relaying aided WPCN is still a research gap that needs to be explored.

1.2. Motivation and Key Contributions

In current EH cooperative relaying techniques for WPCN, such as those mentioned in references [10,11,12,13], having complete knowledge of the CSI at the receiver is necessary. However, such simplified channel models fail to account for the dynamic communication environment, which is crucial for optimizing resource allocation and analyzing system performance. Alternative approaches, like energy scheduling and management methods, have been adopted in references [15,16,17,18], which assume a practical probability distribution model for energy arrival. However, these methods do not consider optimal power allocation, energy borrowing, and returning schedules for harvested energy relaying for IT. Only the authors of reference [21] have considered a practical EH channel model, where a single EH relay wirelessly transfers energy to the IS. However, this model does not apply to multiple EH relay-assisted WPCN, where maximizing throughput and minimizing transmission delay are essential. Our article addresses these issues by exploring the RF-powered joint information and energy relaying (JIER) protocol for WPCN, which efficiently allocates resources to maximize system reliability. Specifically, we consider an EH-HAP that effectively manages energy transactions with the PG and transmits RF energy to the IS through multiple EH relays. It then receives information from the source via uplink DF-relay-assisted channels. This timely investigation focuses on maximizing the efficacy of EH in WPCN by optimally utilising the available energy resources by enabling intelligent energy relaying and borrowing. Our specific contribution is four-fold, which can be summarized as follows:
  • Considering a novel smart energy borrowing and relaying-enabled EH communication scenario, we investigate the end-to-end net bit rate maximization problem in WPCN. Here, we jointly optimize the transmit power of HAP and IS, fractions of harvested energy transmitted by the relays, and the relay selection indicators for DF relaying within the operational time.
  • As the original formulated problem is non-convex and combinatorial, we decompose it into multi-period decision-making steps using MDP. Specifically, we propose a nontrivial transformation where the state represents the current onboardonboard battery energy level and the instantaneous channel gains. In contrast, the corresponding action indicates the transmit power allocations. Since HAP selects the relay based on the maximum achievable signal-to-noise ratio (SNR) among all the relays for receiving the information, the instantaneous transmission rate attained by HAP is treated as an immediate reward.
  • We observed that the initial joint optimization problem was analytically intractable to be solved using traditional convex optimization techniques due to the realistic parameter settings of complex communication environments. Therefore, we suggest a DRL framework using the DDPG algorithm to train the DNN model, enabling the system to discover the best policy in an unfamiliar communication environment. The proposed approach determines the current policy using the Q-value for all state-action pairs. Additionally, we have examined the convergence and complexity of the proposed algorithm to improve the learning process.
  • Our analysis is validated by the extensive simulation results, which offer valuable insights into the impact of key system parameters on optimal decision-making. Additionally, we compared the performance of various modulation schemes, including QPSK, 8-PSK, and 16-QAM, that leverage the same algorithm. Our resource allocation technique significantly improved the net bit rate of the system compared to the BEAR-based benchmark algorithm.
The rest of the article is organized as follows: Section 2 presents the system model of efficient WPCN. Section 3 elaborates on the mathematical formulation of our objective. Section 4 introduces the DRL approach and the proposed DDPG algorithm for resource allocation corresponding to the optimal policy. Section 5 gives insights into extensive simulation results for performance evaluation. Finally, the conclusion is outlined in Section 6, followed by references.
Notation: We use bold letters to denote vector quantity; . represents the magnitude of a complex quantity; erfc . stands for complementary error function; CN λ , ω denotes a circularly symmetric complex Gaussian random variable with mean λ and variance ω ; and O . denotes the big-O notation.

2. System Model

Consider a JIER-assisted WPCN consisting of a PG and three types of transceiver modules such as a HAP, two RF-EH relays, and an IS, as depicted in Figure 1. HAP can harvest energy from ambient sources, such as RF power signals, and subsequently store the harvested energy in its internal battery of finite capacity. We assume that IS can only harvest energy into its small-size battery storage from the RF energy transfer mode as it has no direct external energy supply. When IS accumulates sufficient energy, it can transmit information to relays and HAP. Furthermore, HAP can borrow the required energy from the PG while it faces the potential energy shortage for RF energy transmission towards relays and IS. To reduce PG’s additional burden, HAP returns the borrowed energy to PG along with interest based on the borrowing price, where no energy leakage is considered within the energy transmission deadline [27]. For ease of calculation, we discretize the operational period into N equally spaced time slots, each of duration δ . Let, at the nth n ∈ N = 1 , 2 , … , N time slot, the battery energy level of HAP is B n and its harvested energy from the ambient sources is E H n , where E H n follows the Gaussian distribution of mean μ H and variance σ H 2 . The instantaneous channel gain between source and destination also follows the Gaussian distribution of mean μ h and variance σ h 2 [28].

2.1. JIER Protocol

We consider that HAP can transfer energy to IS by the two RF-EH relays, i.e., R 1 and R 2 via full-duplex two-hops downlink channel and then IS transmits data to the HAP via uplink half-duplex decode and forward (DF) relaying channel. The entire protocol is divided into four phases as follows:
Phase 1: Energy is harvested at R 1 , R 2 and IS for N − 3 time slots by the directly transmitted RF signals from the HAP.
Phase 2: Energy is further harvested at IS in N − 2 th time slot by energy relaying from R 1 and R 2 where the relays transmit a fraction of harvested energy from phase 1. Let σ 1 n and σ 2 n are the fractions of the harvested energy transmitted by R 1 and R 2 respectively.
Phase 3: At N − 1 th time slot, IS directly transmits information to R 1 , R 2 and HAP using the harvested energy stored in its onboard battery.
Phase 4: Finally, at Nth time slot, the information is transmitted to HAP from R 1 or R 2 via DF relaying using the remaining harvested energy stored in the relays’ battery. HAP receives information from a single relay at a time and selects that relay depending on the maximum achievable SNR among all the relays.

2.2. Energy Scheduling

The instantaneous battery energy level of HAP depends on its current harvesting energy, energy borrowing, and returning energy to PG, which can be expressed as [27]
B n = min B n − 1 + E H n , B max + E B n − E R n − δ P H n .
where B max is the maximum battery capacity of HAP, E B n represents the instantaneous borrowed energy from PG, E R n denotes the returned energy to PG at nth time slot, and P H n is the instantaneous transmit power of HAP.

2.2.1. Energy Borrowing

If HAP’s current energy level is less than its energy consumption at a slot while transmitting with the power of P H n , HAP borrows the required energy from the PG, which can be expressed as [27]
E B n = δ P H n − B n − 1 + E H n , if δ P H n > B n − 1 + E H n 0 , otherwise

2.2.2. Energy Returning

Since sometimes HAP borrows the required energy from PG according to (2), it has to be returned to PG along with the interest based on the borrowing price. Hence, HAP returns it by utilizing the harvested energy at future time slots. The energy-returning schedule at nth time slot is defined as [23]
E U n = ς E E n , if E U n − 1 > E E n ς E U n − 1 , Otherwise ,
where E E n = B n − 1 + E H n + E B n − δ P H n is the excess energy at the nth time slot, ς denotes the energy transfer efficiency from HAP to PG, and E U n indicates the unreturned energy at nth time slot, which can be expressed as [23]
E U n = E U n − 1 + E B n , if δ P H n > B n − 1 + E H n E U n − 1 + E I n − E R n , if δ P H n ≤ B n − 1 + E H n and E R n ≤ E U n − 1 + E I n 0 , Otherwise . .
where E I n = ϱ E U n − 1 is the cost incurred in the form of interest because of delay in returning the borrowed energy, and ϱ denotes the rate of interest. To restrict excessive energy borrowing, we set the threshold E max as the upper bound of unreturned energy during the entire energy transmission process, which is expressed as E U n < E max .

2.3. RF Energy Harvesting

As we mentioned earlier in Section 2.1 that energy is harvested in R 1 and R 2 and IS during the first two phases, we employ a linear harvesting model in this case. According to this model, instantaneous stored harvested energies at R 1 , R 2 and IS are calculated as [28]
E H R 1 n = η δ P H n h 1 n 2 ,
E H R 2 n = η δ P H n h 2 n 2 ,
E H S n = η δ P H n h 3 n 2 + η 2 P H n σ 1 n h 1 n 2 h 4 n 2 + σ 2 n h 2 n 2 h 5 n 2 .
where η is RF-EH efficiency, h 1 n , h 2 n , h 3 n , h 4 n , and h 5 n are the instantaneous channel gains between the links of HAP to R 1 , HAP to R 2 , HAP to IS, R 1 to IS, and R 2 to IS respectively.

3. Problem Definition

3.1. DF Relay Assisted Information Transfer

We consider instantaneous bit rate as the performance metric for the proposed WPCN. The bit rate refers to the number of bits transmitted per unit of time over the communication channel. Various factors, including the modulation scheme, channel bandwidth, coding scheme, and the presence of any error correction or data compression techniques, influence the bit rate. At nth time slot, can be expressed as [28]
R n = ξ ρ ζ 1 − P e n ξ ρ ,
where ξ is the number of bits per symbol, ρ represents the number of symbols per packet, ζ denotes the packet duration, and P e n is the instantaneous end-to-end bit error rate (BER), which can be expressed for DF relaying system as [27]
P e n = ∑ d w m , d 1 2 erfc z m , d P R 1 n h 1 n 2 + P S n h 4 n 2 + P S n h 3 n 2 2 N 0 , if R 1 is selected ∑ d w m , d 1 2 erfc z m , d P R 2 n h 2 n 2 + P S n h 5 n 2 + P S n h 3 n 2 2 N 0 , if R 2 is selected ∑ d w m , d 1 2 erfc z m , d P S n h 3 n 2 2 N 0 , if direct transmission without any relay ,
where erfc . denotes complementary error function, P S n is the instantaneous transmit power of IS, P R 1 n = 1 − σ 1 n E H R 1 n / δ and P R 2 n = 1 − σ 2 n E H R 2 n / δ are the instantaneous transmit power of R 1 and R 2 respectively to relay the information toward HAP, N 0 is noise power received at R 1 , R 2 , and HAP. w m , d and z m , d are two modulation-related parameters whose values are provided in Table 1. Here, d stands for the particular constant that modulation index m determines in the nth time slot. Furthermore, as HAP receives information from a single relay at a time slot, we define relays R 1 and R 2 selection indicators at nth time slot respectively as
Ω 1 n = 1 , if P R 1 n h 1 n 2 / N 0 > Υ and P R 1 n h 1 n 2 > P R 2 n h 2 n 2 0 , Otherwise
Ω 2 n = 1 , if P R 2 n h 2 n 2 / N 0 > Υ and P R 2 n h 2 n 2 > P R 1 n h 1 n 2 0 , Otherwise .

3.2. Optimization Formulation

To improve the reliability of the proposed WPCN, we maximize its performance metric i.e., the end-to-end net bit rate from IS to HAP by finding the optimal transmit power of HAP and IS, fractions of harvested energy transmitted by relays, and relay selection indicator for DF relaying within the operational period. The associated problem is formulated as
OP : max P H n , P S n , σ 1 n , σ 2 n , Ω 1 n , Ω 2 n ∀ n ∈ N ∑ n = 1 N R n , Subject to ( C 1 ) : P H n ≥ B n / δ , ∀ n ∈ N , ( C 2 ) : 0 ≤ P S n ≤ B S n + E H S n , ∀ n ∈ N , ( C 3 ) : E B n ≥ 0 , ∀ n ∈ N , ( C 4 ) : E R n ≥ 0 , ∀ n ∈ N , ( C 5 ) : E U N = 0 , E U n ≤ E max , ∀ n ∈ N , n ≠ N , ( C 6 ) : 0 ≤ σ 1 n ≤ 1 , 0 ≤ σ 2 n ≤ 1 , ∀ n ∈ N , ( C 7 ) : Ω 1 n , Ω 2 n ∈ 0 , 1 , ∀ n ∈ N .
Here, C 1 , C 2 , C 3 , and C 4 set the boundary conditions for HAP and IS’s transmit power, borrowing, and returning energy of HAP, respectively, at nth time slot; C 5 implies that the unreturned energy of HAP at the end of the operation has to be zero, but it should not exceed the certain threshold during the operation; C 6 specify the fractions of harvested energy transmitted by the relay R 1 and R 2 ; and C 7 verifies the relay selection indicators.
The formulated problem is combinatorial because the fractions of the harvested energy transmitted by relays at phase 2 are related to their transmit power at phase 4, which also associates with HAP’s transmit power at phase 1. Furthermore, since the optimization problem is nontrivial due to the nonlinear structure of the objective function and non-convex constraints, traditional convex optimization makes several approximation steps to obtain suboptimal solutions. In addition, the channel gain and energy arrival rate are unpredictable in a practical wireless communication environment. Hence, we propose a DRL model with the help of the DDPG algorithm, which supports the states and actions in the continuous domain to maximize the objective value in the long run and guarantees fast convergence.

4. Proposed Solution Methodology

The original optimization problem has multiple decision variables, making it combinatorial and originating several nonconvexity issues. Hence, we formulate an MDP-based DRL framework in which the system interacts with the unknown environment to learn the best decision-making policy for improving the objective value.

4.1. MDP-Based DRL Framework

We consider a centralized controller executing the DRL framework while simultaneously connecting PG, HAP, EH relays and IS. Here, MDP governs the sequential decision-making policy where the current network state depends only on the immediate past state value.

4.1.1. State Space

Since the transmit powers, fractions of harvested energy, and relay selection depend on current channel gains, battery level, and harvested energy, the state vector at nth time slot is defined as
s n = [ h 1 n 2 , h 2 n 2 , h 3 n 2 , h 4 n 2 , h 5 n 2 , B n , B R 1 n , B R 2 n ,
B S n , E H n , E H R 1 n , E H R 2 n , E H S n ] ,
where B R 1 n ∈ 0 , B max R 1 , B R 2 n ∈ 0 , B max R 2 , and B S n ∈ 0 , B max S are the instantaneous battery level of the relay R 1 , R 2 , and IS respectively, B max R 1 , B max R 2 , and B max S are their respective maximum battery capacity.

4.1.2. Action Space

According to the decision-making policy, the optimizing variables’ values are determined. Therefore, these are characterized by the transmit power of HAP and IS, fractions of harvested energy transmitted by relays, and relay selection indicators at every instance. Hence, the action vector at the current time slot is defined as:
a n = P H n , P S n , σ 1 n , σ 2 n , Ω 1 n , Ω 2 n ,

4.1.3. Reward Evaluation

Reward defines the quality of an action taken at a particular state. To maximize the end-to-end net bit rate from IS to HAP by jointly adjusting the transmit power of HAP and IS, fractions of harvested energy transmitted by relays, and relay selection indicators, the immediate reward function is defined, which is modelled as the instantaneous objective value, expressed as:
r s n , a n = R n ,

4.1.4. State Transition

It is defined as the probability that is obtained for the transition from state s n to s n + 1 after taking action a n at the current time slot. In our model, channel gains and harvested energy are uncertain and must be learned during decision-making. As these decision variables mostly follow Gaussian distribution, we must estimate their distribution parameters, such as mean and variance, over the simulation episode to maximize the cumulative long-term reward. We define the instantaneous channel gain values and harvested energy according to their current distribution parameters as h 1 n ∼ CN μ h 1 n , σ h 1 2 n , h 2 n ∼ CN μ h 2 n , σ h 2 2 n , h 3 n ∼ CN μ h 3 n , σ h 3 2 n , h 4 n ∼ CN μ h 4 n , σ h 4 2 n , h 5 n ∼ CN μ h 5 n , σ h 5 2 n , and E H n ∼ CN μ H n , σ H 2 n respectively. Depending on their values, battery levels at the next time slot are measured as
B S n + 1 = min B S n + E H S n , B max S − δ P S n ,
B R 1 n + 1 = min B R 1 n + E H R 1 n , B max R 1 − σ 1 n E H R 1 n − δ P R 1 n ,
B R 2 n + 1 = min B R 2 n + E H R 2 n , B max R 2 − σ 2 n E H R 2 n − δ P R 2 n .

4.2. Decision-Making Policy

The system builds up its knowledge about the surrounding environment through interaction to obtain a sub-optimal decision-making policy. As the system does not know the communication environment initially, it tentatively selects action at a given state, gets the Q s n , a n value for the state-action pair and immediately receives reward r s n , a n . Then the current state s[n] is updated to the next state s n + 1 where the expected mapping value between state and action can be expressed using the Bellman equation as [28]:
Q s n , a n = E ∑ n = n ∞ γ n − n r s n , a n | s n , a n , Π .
where E . is the expectation operator, γ ∈ 0 , 1 denotes the discount factor, and Π represents a deterministic policy for the decision-making process.

4.3. DRL using DDPG Algorithm

DDPG is an RL framework that can handle the continuous state and action spaces based on policy and Q-value evaluation. It employs a direct policy search method for obtaining action value at a time slot as a n = μ s n | θ μ . Here μ . is the policy evaluation NN with parameter θ μ , that takes the state vector s n as input and outputs corresponding action vector a n . Being a feed-forward NN, μ s n | θ μ consists of an input layer of thirteen neurons, three successive hidden layers of N 1 , N 2 , and N 3 neurons, and an output layer of six neurons. As the normalized action vector can only be a positive value for a given positive value state vector, we apply the sigmoid activation function to better tune the policy NN model. After taking action a n at the current state s n , the immediate reward r s n , a n is generated and the current state is updated to the next state s n + 1 . Then, the sample data tuple s n , a n , r s n , a n , s n + 1 is stored in the experience memory. During the training phase, a mini-batch of N B random samples is selected from the memory to train another NN, i.e., Q s n , a n | θ Q . Here, Q . is Q-value evaluation NN with parameter θ Q that takes the state and action vectors as input and provides the state-action value Q s n , a n as output. Being a feedforward NN, Q s n , a n | θ Q consists of an input layer of nineteen neurons, three successive hidden layers of N 4 , N 5 , and N 6 neurons, and an output layer of one neuron. As the desired output Q value is always a positive number, we apply the sigmoid activation function to tune the Q value NN. The policy and Q-value target NNs, respectively represented by μ ′ s n | θ μ ′ and Q ′ s n , a n | θ Q ′ with parameters θ μ ′ and θ Q ′ replicating the same structure as the policy and Q-value evaluation NNs respectively are applied to stabilize the training process. The parameter of the Q-value evaluation NN, θ Q , is updated by minimizing the temporal difference (TD) error loss, which is expressed as [21]:
L θ Q = 1 N B ∑ n Y ¯ n − Q s n , a n | θ Q 2 ,
where Y ¯ n , the output of the Q-value target NN is calculated using the output of the policy target network as [21]:
Y ¯ n = r s n , a n + γ Q ′ s n + 1 , μ ′ s n + 1 | θ μ ′ | θ Q ′ ,
where γ is the discount factor. The parameters of policy evaluation NN can be updated through the deterministic policy gradient method, which is given as [21]:
∇ θ μ J θ μ = 1 N B ∑ n ∇ μ Q s , a | θ Q | s = s n , a = μ s n | θ μ ∇ θ μ μ s | θ μ | s = s n ,
Finally, the parameters of the target NNs are updated slowly with respect to learning rate τ ≪ 1 as [21]:
θ μ ′ ← τ θ μ + 1 − τ θ μ ′ ,
θ Q ′ ← τ θ Q + 1 − τ θ Q ′ .

4.4. Implementation Details

Algorithm 1 implements the step-by-step training process for the end-to-end net bit rate maximization in the proposed EH relay-assisted WPCN. In the beginning, the four NNs, namely, policy evaluation NN, policy target NN, Q-value evaluation NN, and Q-value target NN, are initialized with random weight vectors. Then, inside the main loop, policy evaluation NN takes the current state as input for each time slot and approximates the action value. In order to keep exploration, we add Gaussian noise of variance ϵ to the current action. After choosing the action, the system updates to a new state and generates an immediate reward by (14). Then, the transition data set, consisting of the current state, action, reward, and the next state, is stored in experience memory to train the DRL model. When the filled memory length is greater than the batch size, randomly sample a mini-batch of transition data from memory, calculate the loss values, and update the parameters of policy and Q-value evaluation NNs by (21) and (19), respectively. Then, the algorithm updates the parameters of the target NNs by (22) and (23) and also updates the current state as the next state. Finally, the running episode is terminated when the system elapsed maximum operational time steps, and the obtained policy corresponding to the last episode makes optimal decision variables.
The centralized controller implements the proposed algorithm to train the NNs mentioned above configuration. The proposed algorithm’s computational complexity depends entirely on the defined NN structures and the number of operations in the network model. The dimension of inputs determines it, the number of neurons in each layer of the NNs, the number of fully connected layers, and the output dimension. Let W 1 and W 2 denote the number of fully connected layers in the policy and Q-value NNs, respectively. In each time slot, the total transition made by policy evaluation NN is calculated as ∑ u = 0 W 1 − 1 Θ u P Θ u + 1 P , where Θ u P is the neurons of the u-th layers of the policy NN. Similarly, the total transition faced by Q-value NN can be obtained as ∑ w = 0 W 2 − 1 Θ w Q Θ w + 1 Q , where Θ w Q is the neurons of the w-th layer of the Q-value NN. Therefore, after experiencing N timeslots in each of the T episodes successively, the computational complexity of the proposed algorithm will be O N T ∑ u = 0 W 1 − 1 Θ u P Θ u + 1 P + ∑ w = 0 W 2 − 1 Θ w Q Θ w + 1 Q . According to this expression, the computational complexity of the proposed algorithm increases with the operational period.
Algorithm 1:DRL based on DDPG for end-to-end net bit rate maximization
Require: 
N, T, N B , N 0 , η , δ , ξ , ρ , ζ
Ensure: 
P H n , P S n , σ 1 n , σ 2 n , Ω 1 n , Ω 2 n , ∀ n ∈ N
1:
Initialize policy evaluation and target NNs, Q-value evaluation, and target NNs as μ s n | θ μ , μ ′ s n | θ μ ′ , Q s n , a n | θ Q , Q ′ s n , a n | θ Q ′ , and corresponding parameters are θ μ ′ = θ μ and θ Q ′ = θ Q , respectively.
2:
Initialize an empty experience buffer memory as M E = where initial memory length is set as | M E | = 0 .
3:
for t = 1 , 2 , . . . , T do
4:
    Reset the state vector at the initial condition as s 1
5:
    for  n = 1 , 2 , . . . , N  do
6:
        Obtain the current normalized action vector as a n = μ s n | θ μ + CN 0 , ϵ
7:
        Obtain next state vector s n + 1 by (1), (15), (16), (17)
8:
        Get immediate reward r s n , a n by (14)
9:
        
9:
 Store state, action, and reward transition data in the experience memory
9:
 buffer as a tuple of s n , a n , s n + 1 , r s n , a n
10:
         | M E | = | M E | + 1
11:
        if  | M E | ≥ N B  then
12:
            Randomly sample a batch of data from memory
13:
           
13:
     Update parameters of policy and Q-value evaluation NNs by
13:
     (21) and (19) respectively
14:
           
14:
     Update the parameters of policy and Q-value target NNs by
14:
    (22) and (23), respectively.
15:
        end if
16:
        Update the current state vector as s n = s n + 1 .
17:
    end for
18:
    Update action noise as ϵ = ϵ 1 − t / T
19:
end for
20:
Obtain the optimal policy as P H n , P S n , σ 1 n , σ 2 n , Ω 1 n , Ω 2 n , ∀ n ∈ N

5. Simulation Results

In this section, we validate the effectiveness and convergence of the proposed algorithm through various simulation results. We use the Pytorch 1.10.1 module in Python 3.7.8 to build the DDPG environment and conduct the simulations on a high computing system with a specification of Intel® Core™ i7-9700 CPU 3.00 GHz and 16 GB RAM. The Adam optimizer is applied to update the parameters of policy and Q value evaluation NNs. We compare the performance of the proposed methodology with the benchmark BEAR algorithm [23], where the underlying transmission power allocation is modelled by parameterized Gaussian distribution, ensuring maximum sum bit rate over a given time slot while learning the EH rate and channel conditions. Furthermore, the primary simulation parameters are taken from [23] and [28] which are given as: B max = B max R 1 = B max R 2 = B max S = 3 Joul, E max = 5 Joul, N = 100 , ς = 0.8 , ϱ = 0.1 , η = 0.6 , ρ = 1000 , ζ = 0.01 s, δ = 1 s, Υ = 15 dB, μ h 1 = μ h 2 = μ h 3 = μ h 4 = μ h 5 = μ H = 0.5 , σ h 1 2 = σ h 2 2 = σ h 3 2 = σ h 4 2 = σ h 5 2 = σ H 2 = 0.75 , N B = 128 , M E = 50000 , γ = 0.9 , τ = 0.001 , ϵ = 0.1 , T = 3000 , N 1 = 128 , N 2 = 64 , N 3 = 32 , N 4 = 64 , N 5 = 128 , and N 6 = 32 .

5.1. Convergence Analysis

Figure 2 demonstrates the converging behaviour of the training performance at − 25 dB noise power for various learning rates under the QPSK modulation scheme. According to this figure, the end-to-end net bit rate increases with each episode and eventually converges. If we choose a low learning rate, the training process runs slowly because the low learning rate updates NNs’ weights on a small scale. However, if we set a high learning rate, the loss function of NNs encounters undesirable divergence. Consequently, NNs experience high oscillation during training, but the objective value converges quickly. This figure shows that fluctuations and convergence rates over the training episode increase when the learning rate varies from 1 × 10 − 5 to 5 × 10 − 3 . Hence, considering the model’s stability, we set the learning rate as 5 × 10 − 4 for the subsequent simulations.
In order to analyze the performance of proposed and benchmark algorithms corresponding to different modulation schemes, we present the variation of end-to-end net bit rate over the training episodes in Figure 3. At the same time, the noise power is set as − 25 dB. This figure shows that the converged objective value increases with the lower modulation schemes because it requires less power and fewer signal points to transmit the same amount of data, which allows more efficient use of the available frequency spectrum. Therefore, QPSK achieves a higher end-to-end net bit rate than 8-PSK and 16-QAM. Furthermore, as the benchmark BEAR algorithm faces more computational complexity due to the off-policy samples from the replay buffer, the achievable performance metric corresponding to the BEAR algorithm is less than the proposed DDPG algorithm. Hence, according to this figure, the DDPG algorithm outperforms the BEAR algorithm by 20.67 % , 16.21 % , and 26.38 % in cases of QPSK, 8-PSK, and 16-QAM modulation schemes, respectively.

5.2. Performance Evaluation

We plot the transmit power variation of HAP in Figure 4 corresponding to the proposed and benchmark algorithms for different modulation schemes. It can be observed that the average transmit power of HAP increases for the higher modulation schemes because they require more peak-to-average power ratios and higher transmit power levels to generate complex signal constellations. On the other hand, the conventional BEAR algorithm updates the parameters of policy evaluation NN by distributional shift correction method to reduce the overestimation of the Q-value. This limits the ability of the algorithm to explore the search space and find optimal policies in complex environments. From Figure 4, it is clear that the proposed methodology reduces the average transmit power of HAP by 19.12 % , 17.69 % , and 11.58 % as compared to the BEAR algorithm in the cases of QPSK, 8-PSK, and 16-QAM modulation schemes, respectively over the operational period.
Figure 5 illustrates the end-to-end net bit rate for different modulation schemes under various noise power levels at the receiver. This figure shows that the 16-QAM modulation scheme performs better than 8-PSK and QPSK at lower noise power, whereas QPSK outperforms 8-PSK and 16-QAM at higher noise power. This is because higher modulation schemes encode more bits per symbol, which allows higher data rates to be transmitted over a given channel bandwidth. However, since they typically use more complex signal constellations with smaller distances between signal points, they are highly susceptible to distortion caused by noise or channel impairments. On the other hand, the lower modulation techniques are more straightforward to implement than the higher modulation techniques. This makes them more suitable for low-power at low-complexity systems, making them more bandwidth efficient at higher noise power. From Figure 3 and Figure 4, we have justified that the benchmark BEAR algorithm faces several challenges in finding the optimal policy; therefore, our proposed algorithm effectively improves the performance metric by 13.22 % , 27.57 % , and 14.12 % as compared to the BEAR algorithm in the cases of QPSK, 8-PSK, and 16-QAM modulation schemes respectively.
The variation of allotted IS’s transmit power with respect to the noise power under different modulation techniques is shown in Figure 6. It is observed that the transmit power of IS increases with the noise power because IS utilizes more transmit power to achieve a minimum SNR and BER value for higher noise power, which also maintains the adequate quality of service (QoS). Since we have mentioned earlier that higher modulation techniques are more susceptible to distortion caused by channel noise impairments, 16-QAM requires more transmit power at higher noise power levels as compared to 8-PSK and QPSK modulation techniques. Moreover, as the benchmark algorithm is less effective in this case, the proposed technique reduces the transmit power of IS by 15.17 % , 9.94 % , and 8.18 % compared to the BEAR algorithm in the cases of QPSK, 8-PSK, and 16-QAM modulation schemes respectively.

6. Conclusion

Facing the grand challenges of reliable WPCN, this article introduced a JIER protocol that allocates resources efficiently for effective energy management in EH wireless networks. Specifically, the formulated joint optimization of HAP and IS transmit power, the fraction of harvested energy transmitted by relays, and relay selection indicators maximized the end-to-end net bit rate of the system under energy borrowing and returning scheduling constraints. The formulated problem was highly non-convex, nontrivial, and difficult to solve directly. Hence, we leveraged the DRL framework that decomposed the objective problem into multiple sequential decision-making sub-problems based on MDP and then proposed the DDPG algorithm to find the optimal policy. Simulation results validated the proposed scheme and enhanced the end-to-end net bit rate of the system by 13.22 % , 27.57 % , and 14.12 % compared with the BEAR algorithm for QPSK, 8-PSK, and 16-QAM modulation schemes, respectively. In the future, we will extend this work for energy borrowing and returning strategy in multi-user and multi-antenna relay-assisted EH systems using multi-agent DRL.

References

  1. Lin, H. C.; Chen, W. Y. An approximation algorithm for the maximum-lifetime data aggregation tree problem in wireless sensor networks. IEEE Trans. Wireless Commun. 2017, 16, 3787–3798. [Google Scholar] [CrossRef]
  2. Lu, X.; Wang, P.; Niyato, D.; Kim, D. I.; Han, Z. Wireless charging technologies: fundamentals, standards, and network applications. IEEE Commun. Surveys Tuts. 2016, 18, 1413–1452. [Google Scholar] [CrossRef]
  3. Mishra, D.; De, S.; Jana, S. , Basagni, S.; Chowdhury, K, Ed.; Heinzelman, W. Smart RF energy harvesting communications: Challenges and opportunities. IEEE Communications Magazine, 2015. [Google Scholar] [CrossRef]
  4. Hsieh, P. H.; Chou, C. H.; Chiang, T. An RF energy harvester with 44.1% PCE at input available power of -12 dbm. IEEE Transactions on Circuits and Systems, 1528. [Google Scholar] [CrossRef]
  5. Tutuncuoglu, K.; Yener, A. Energy harvesting networks with energy cooperation: procrastinating policies. IEEE Transactions on Communications, 4525. [Google Scholar] [CrossRef]
  6. Mishra, D.; De, S. Optimal relay placement in two-hop RF energy transfer. IEEE Transactions on Communications, 1635. [Google Scholar] [CrossRef]
  7. Mishra, D. , De, S. Energy Harvesting and Sustainable M2M Communication in 5G Mobile Technologies. Internet of Things (IoT) in 5G Mobile Technologies; Springer: Cham, Switzerland, 2016, 8, 99–125. [Google Scholar] [CrossRef]
  8. Ju, H.; Zhang, R. User cooperation in wireless powered communication networks. IEEE Global Communications Conference, 1430. [Google Scholar] [CrossRef]
  9. Chen, H.; Li, Y.; Rebelatto, J. L.; Uchoa-Filho, B. F.; Vucetic, B. Harvest-then-cooperate: wireless-powered cooperative communications. IEEE Transactions on Signal Processing, 2015, 63, 1700–1711. [Google Scholar] [CrossRef]
  10. Gu, Y.; Chen, H.; Li, Y.; Vucetic, B. An adaptive transmission protocol for wireless-powered cooperative communications. IEEE International Conference on Communications (ICC), 4223. [Google Scholar] [CrossRef]
  11. Sarma, S.; Ishibashi, K. Time-to-recharge analysis for energy-relay-assisted energy harvesting. IEEE Access, 2019, 7, 139924–139937. [Google Scholar] [CrossRef]
  12. Na, Z.; Lv, J.; Zhang, M.; Peng, B.; Xiong, M.; Guan, M. GFDM based wireless powered communication for cooperative relay system. IEEE Access, 2019, 7, 50971–50979. [Google Scholar] [CrossRef]
  13. Wei, Z.; Sun, S.; Zhu, X.; Kim, D. I.; Ng, D. W. K. Resource allocation for wireless-powered full-duplex relaying systems with nonlinear energy harvesting efficiency. IEEE Transactions on Vehicular Technology, 2019, 68, 12079–12093. [Google Scholar] [CrossRef]
  14. Gurakan, B.; Ozel, O.; Ulukus, S. Optimal energy and data routing in networks with energy cooperation. IEEE Transactions on Wireless Communications, 2016, 15, 857–870. [Google Scholar] [CrossRef]
  15. Huang, X.; Ansari, N. Energy sharing within EH-enabled wireless communication networks. IEEE Wireless Communications, 2015, 22, 144–149. [Google Scholar] [CrossRef]
  16. Hu, C.; Gong, J.; Wang, X.; Zhou, S.; Niu, Z. Optimal green energy utilization in MIMO systems with hybrid energy supplies. IEEE Transactions on Vehicular Technology, 2015, 64, 3675–3688. [Google Scholar] [CrossRef]
  17. Sun, Z.; Dan, L.; Xiao, Y.; Wen, P.; Yang, P.; 0Li, S. Energy borrowing: an efficient way to bridge energy harvesting and power grid in wireless communications. IEEE 83rd Vehicular Technology Conference. [CrossRef]
  18. Sun, Z.; Dan, L.; Xiao, Y.; Yang, P.; Li, S. Energy borrowing for energy harvesting wireless communications. IEEE Communications Letters, 2016, 20, 2546–2549. [Google Scholar] [CrossRef]
  19. Cui, J.; Ding, Z.; Deng, Y.; Nallanathan, A.; Hanzo, L. Adaptive UAV-trajectory optimization under quality of service constraints: a model-free solution. IEEE Access, 2020, 8, 112253–112265. [Google Scholar] [CrossRef]
  20. Challita, U.; Saad, W.; Bettstetter, C. Interference management for cellular-connected UAVs: a deep reinforcement learning approach. IEEE Transactions on Wireless Communications, 2019, 18, 2125–2140. [Google Scholar] [CrossRef]
  21. Qiu, C.; Hu, Y.; Chen, Y.; Zeng, B. Deep deterministic policy gradient (DDPG)-based energy harvesting wireless communications. IEEE Internet of Things Journal, 2019, 6, 8577–8588. [Google Scholar] [CrossRef]
  22. Zhao, B.; Zhao, X. Deep reinforcement learning resource allocation in wireless sensor networks with energy harvesting and relay. IEEE Internet of Things Journal, 2022, 9, 2330–2345. [Google Scholar] [CrossRef]
  23. Sachan, A.; Mishra, D.; Prasad, G. BEAR: reinforcement learning for throughput aware borrowing in energy harvesting systems. IEEE Global Communications Conference (GLOBECOM). [CrossRef]
  24. Su, Y.; Lu, X.; Zhao, Y.; Huang, L.; Du, X. Cooperative communications with relay selection based on deep reinforcement learning in wireless sensor networks. IEEE Sensors Journal, 2019, 19, 9561–9569. [Google Scholar] [CrossRef]
  25. Wei, Y.; Yu, F. R.; Song, M.; Han, Z. User scheduling and resource allocation in hetnets with hybrid energy supply: an actor-critic reinforcement learning approach. IEEE Transactions on Wireless Communications, 2018, 17, 680–692. [Google Scholar] [CrossRef]
  26. Masadeh, A.; Wang, Z.; Kamal, A. E. An actor-critic reinforcement learning approach for energy harvesting communications systems. International Conference on Computer Communication and Networks. [CrossRef]
  27. Reddy, G. K.; Mishra, D.; Devi, L. N. (2020). Scheduling protocol for throughput maximization in borrowing-aided energy harvesting system. IEEE Networking Letters, 2020, 2, 171–174. [Google Scholar] [CrossRef]
  28. Kumari, M.; Prasad, G.; Mishra, D. Si2ER protocol for optimization of RF powered communication using deep learning. IEEE Wireless Communications and Networking Conference (WCNC). [CrossRef]
Preprints 84272 g001
Figure 1. System model of WPCN.
Figure 1. System model of WPCN.
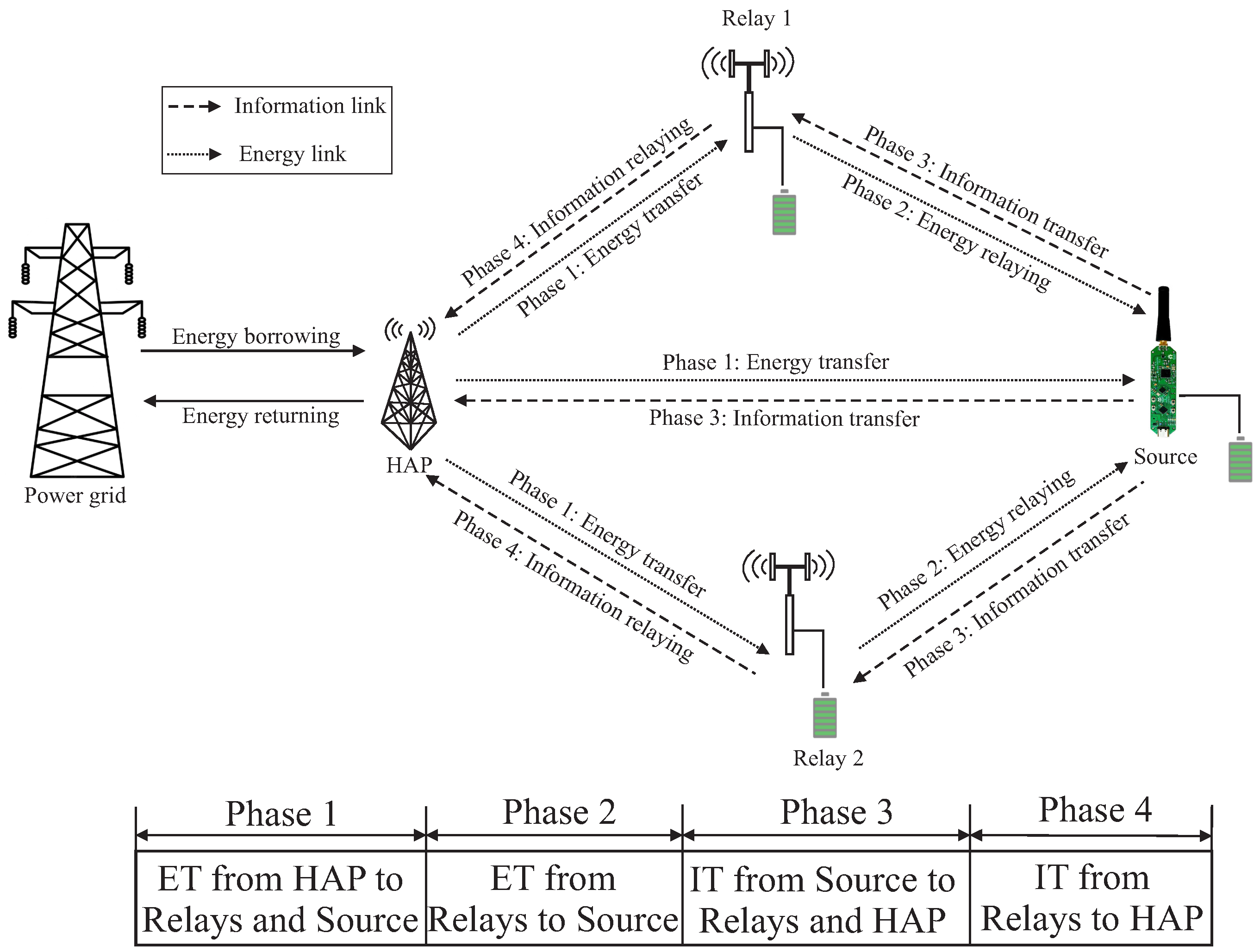
Preprints 84272 g001
Preprints 84272 g002
Figure 2. Impact of different learning rate values on convergence.
Figure 2. Impact of different learning rate values on convergence.
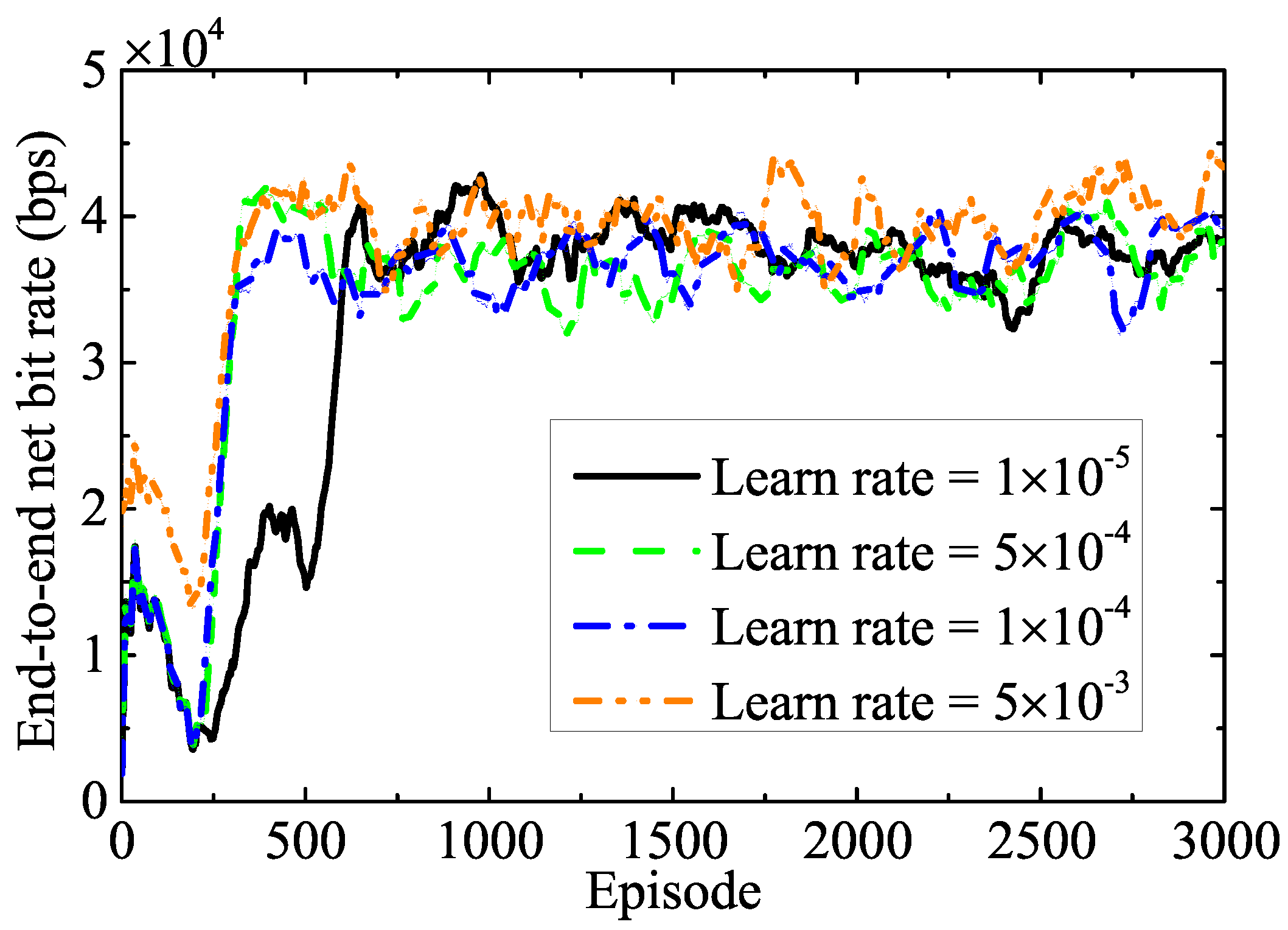
Preprints 84272 g002
Preprints 84272 g003
Figure 3. Performance comparison of DDPG and BEAR algorithm for various modulation schemes.
Figure 3. Performance comparison of DDPG and BEAR algorithm for various modulation schemes.
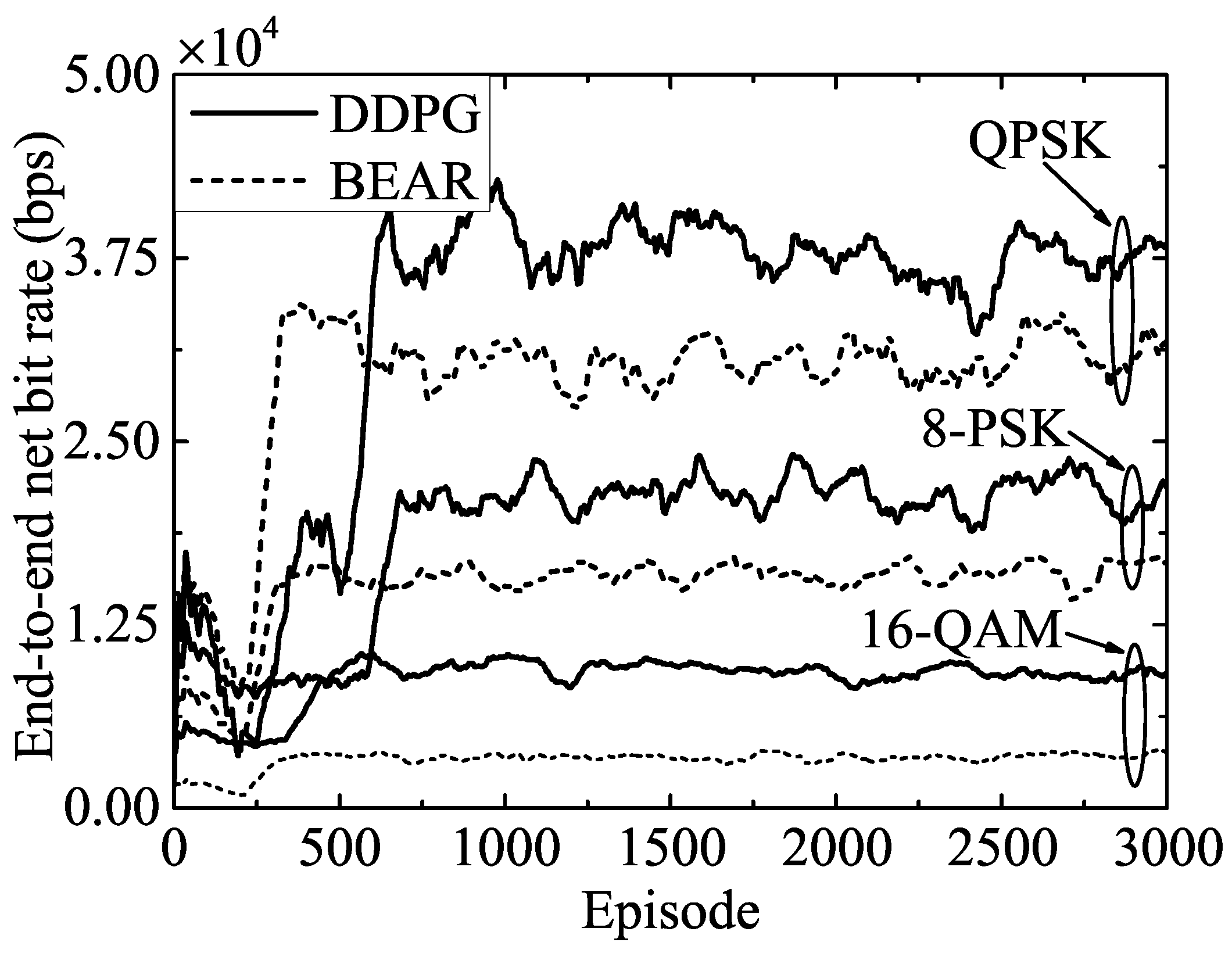
Preprints 84272 g003
Preprints 84272 g004
Figure 4. Transmit power variation of HAP over the operational period.
Figure 4. Transmit power variation of HAP over the operational period.
Preprints 84272 g004
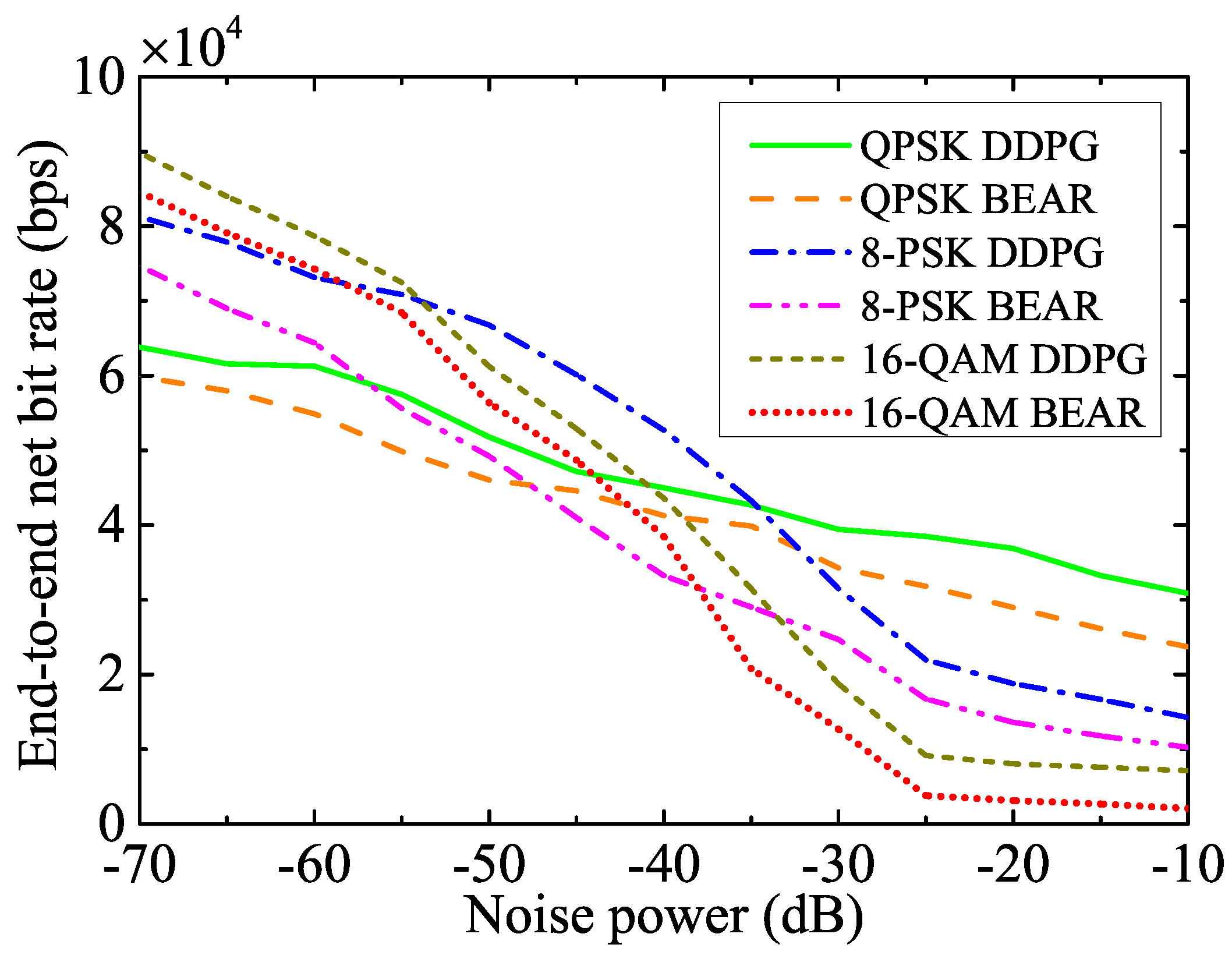
Preprints 84272 g005
Figure 5. End-to-end net bit rate by different modulation schemes for a wide range of noise power.
Figure 5. End-to-end net bit rate by different modulation schemes for a wide range of noise power.
Preprints 84272 g005
Preprints 84272 g006
Figure 6. Transmit power variation of IS by different modulation schemes for various noise power.
Figure 6. Transmit power variation of IS by different modulation schemes for various noise power.
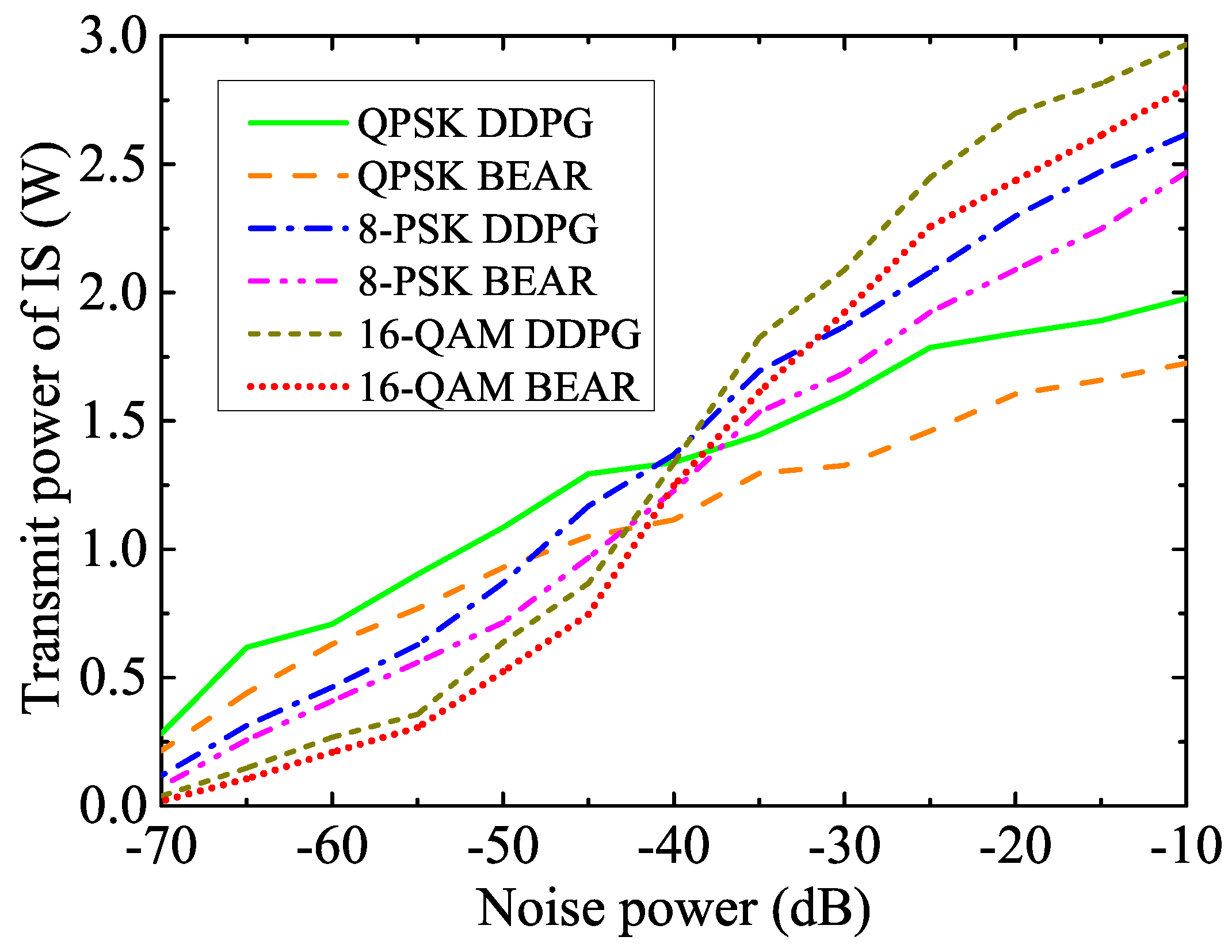
Preprints 84272 g006
Table 1. Value of parameters m , d for three modulations
Table 1. Value of parameters m , d for three modulations
Modulation w m , d , z m , d
QPSK w m , 0 , z m , 0 = 1 , 1
8-PSK w m , 0 , z m , 0 = 2 3 , 2 sin 2 π 8
w m , 1 , z m , 1 = 2 3 , 2 sin 2 3 π 8
16-QAM w m , 0 , z m , 0 = 3 4 , 1 5
w m , 0 , z m , 0 = 1 2 , 9 5
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated