Preprint

Article

Sustainable Cooperation between Schools, Enterprises, and Government: An Evolutionary Game Theory Analysis

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Chao Liu,Hexin Wang,

Yu Dai^*

Chao Liu,Hexin Wang,

Yu Dai^*

This version is not peer-reviewed

Submitted:

05 September 2023

Posted:

07 September 2023

You are already at the latest version

Alerts

Abstract

Promoting close and sustainable cooperation between schools, enterprises, and government has become an important concern in many countries. Based on evolutionary game theory, this paper constructs a tripartite evolutionary game model of schools, enterprises, and government in order to analyze the stability of strategies of the different players. The results show that the main factor that influences the stability of the strategies of schools and enterprises is the reward of positive cooperation from sources other than the government, and the main factor that influences the stability of the strategy of the government is the benefit of positive cooperation strategy under the scenario where schools cooperate with enterprises. Therefore, the government should focus on implementing more effective policies, such as increasing the incentives and penalties, improving the mechanism for managing conflicts, ensuring the fairness of benefits distribution, and clarifying the responsibilities of different departments; schools should focus on providing more practical curricula and programs for students, training high-quality teachers, and perfecting talent cultivation to meet the needs of enterprises; and enterprises should focus on providing job experiences for students and transforming the results of schools’ teaching and theoretical research into practical productivity.

Keywords:

Subject: Social Sciences - Education

1. Introduction

In many models of economic development, the development of the economy depends on human capital (talent). Schools can be viewed as the producers of such capital and enterprises as the consumers. Thus, strengthening the relationship between schools and enterprises is crucial to maintaining a dynamic balance between the supply and demand of talent and promoting the growth of the economy. In addition, the government plays an important role in facilitating the connection between schools and enterprises. For example, the German government has established a series of laws, regulations, and management systems to ensure that students can acquire theoretical knowledge in school and develop practical skills in enterprise [1]. The U.S. government has also passed the Strengthening Career and Technical Education (CTE) for the 21st Century Act to support partnerships among various schools and enterprises [2], and the Chinese government has enacted Several Opinions on Deepening the Integration of Industry and Education to promote the supply-side structural reform of talent and improve the synergy of educational resources and regional industries [3]. Promoting close and sustainable cooperation between schools, enterprises, and government has clearly become an important concern in these countries.

However, the reality is that the cooperation between schools, enterprises, and government has not been very effective. This is due to the differences in goals and culture between schools and enterprises, as well as disputes over the ownership of intellectual property. The differences in organizational attributes and social functions of schools and enterprises lead two types of social division of labor, which results in the differences in the goals of both of these types of institutions [4,5,6]. The goals of schools include cultivation, education, and theoretical research, and the primary goal of enterprises is to maximize profits. These differences in goals also lead to differences in culture between schools and enterprises, such as in organization and management, behavioral patterns, and approaches to schedules [7,8,9]. In addition, there are some differences regarding the ownership of intellectual property. For example, researchers at schools tend to publish research results in order to increase their influence and push the frontier of knowledge, but enterprises are incentivized to keep their core technology and know-how secret in order to monopolize the market [10]. All these factors can impede the cooperation between schools, enterprises, and government. Therefore, the question of how to promote this cooperation deserve careful study.

In this paper, we consider schools, enterprises, and government as players in an evolutionary game to study the emergence and evolution of their cooperative behavior, explore the main factors that influence their strategies, and to analyze effective ways to facilitate cooperation between them. The rest of the paper is organized as follows: Section 2 reviews the relevant literature. Section 3 constructs the tripartite evolutionary game model. Section 4 analyzes the stability of different combinations of game strategies. Section 5 summarizes the main conclusions and provides some suggestions for sustainable cooperation between schools, enterprises, and government in the real world.

2. Literature Review

The cooperation between schools and enterprises has been explored extensively in the existing literature. Many scholars have already investigated various school-enterprise cooperation models, such as the Dual System, Cooperative Education, and Sandwich Courses. The Dual System is considered to be the driving force of Germany’s post-war economic recovery and has become an exemplary case of school-enterprise cooperation. Theuerkauf and Weiner summarized 5 major characteristics of the Dual System, including a broadly-based basic education, combined technical training and theory, training directed at acquiring key qualifications, a standardized system, and a planned changing from schools to the training system [11]. The Federal Ministry of Education and Research of Germany (BMBF) has also published a book to introduce the origins, features, and training processes of the Dual System in detail [12].

Pleshakova analyzed the genesis and development of the Dual System in Germany from a historical perspective [13]. Given the advantages of the Dual System, some scholars have discussed the practice of Dual System in countries other than Germany, such as Russia [14,15], Ukraine [16], and China [17,18,19]. However, there are also some weaknesses with the Dual System. Pritchard pointed out that the Dual System is permeated with tensions emanating from individuals, schools, firms, and various influential interest groups [20] that can limit competition in the labor market, delay adult status in the labor market, and fail to guarantee employment [21].

Compared to the German Dual System in which the government and enterprises are deeply involved, American Cooperative Education and British Sandwich Courses are driven by schools, with little responsibility from government or enterprises [22]. Cooperative Education is a model of school-enterprise cooperation in America that refers to an educational program that combines classroom learning with work experience, and Younis and Pierrakos et al. argued that Cooperative Education is essential for both students and society [23,24]. Cooperative Education has also been found to have a positive impact on students’ early career success and self-efficacy [25,26]. Students who enroll in Cooperative Education programs can learn professional knowledge and skills and gain practical on-the-job experience [27,28].

Sandwich Courses is a British model of school-enterprise cooperation that involves a pattern in which periods of school study alternate with periods of industrial training or experience [29]. Sandwich Courses have been recognized as an effective method for accumulating sustained, structured work experience and improving employment chances [30,31,32].

The motivations and factors of cooperation between schools and enterprises have also attracted the attention of scholars. Lee and Win (2004) summarized the motivations of schools for cooperating with enterprises, such as assessing the needs of the economy and developing talent accordingly, placing students in industry to connect classroom learning with practical experience, conducting both fundamental and applied research, accessing protected markets, enhancing the business stature, improving the implementation of new technology, developing new products and patents, and saving production costs [33]. Arza (2010) divided the motivations of schools into economic motivation and research motivation [34]. Similarly, Lam (2011) argued that “gold”, “ribbons”, and “puzzles” are the motivators of researchers in schools for cooperating with enterprises and found that few academic researchers are driven by economic motivation [35]. Reducing transaction costs [36,37], obtaining human capital, technology, education, and equipment [38], and establishing a network of cooperation [39] have all been argued to be motivators of enterprises for cooperating with schools. Moreover, the factors influencing the cooperation between schools and enterprises, such as the scale of schools and enterprises [40,41], trust and mutual benefits between schools and enterprises [42,43], and culture differences [44], have also been widely explored in the literature.

In addition, evolutionary game theory is an effective tool for analyzing the strategic interactions between different parties [45] and has been used in various disciplines, including economics [46,47], public policy [48], and environmental science [49,50,51]. Some scholars have also introduced evolutionary game theory into education. For example, Zhu and Wang (2022) built an evolutionary game model involving government, universities, and students to explore the development the choice between innovation and entrepreneurship in education [52], and Li and Wang (2022) discussed the management of primary and secondary school students’ online learning during COVID-19 lockdowns by constructing two game models involving “schools and students” and “schools, students, and parents” [53]. Zhang and Zeng (2022) analyzed the manifestation of both the instrumental and human value of education for sustainable development, and proposed that a country’s education for sustainable development should start from those concrete education issues that urgently need to be solved within the theory of sustainable development [54].

Although the above research has provided some theoretical and methodological support for the study of cooperation between schools, enterprises and government, there are still some shortcomings. (1) There are very limited studies that use evolutionary game theory to analyze the cooperation between schools and enterprises. (2) The role government plays in this cooperation has yet to be sufficiently revealed. To address these shortcomings, in this paper we construct a tripartite evolutionary game model. Based on stability strategy analysis, we then put forward some effective ways to promote cooperation between schools, enterprises, and government.

3. Methodology

In this section a tripartite evolutionary game model of schools, enterprises, and government is established to investigate the evolution of cooperative behavior among these three stakeholders.

3.1. Model Assumptions

Assumption 1. There are three populations: schools, enterprises, and government, all of which have bounded rationality.

Assumption 2. Each population has two strategies, a positive cooperation strategy and a negative cooperation strategy. x, y, and z represent the probability of selecting the positive cooperation strategy for schools, enterprises, and government, respectively, and 1 – x, 1 – y, and 1 – z represent the probability of selecting the negative cooperation strategy of schools, enterprises, and government, respectively.

Assumption 3. We assume that schools can receive some benefits in terms of discipline construction, knowledge innovation, and talent cultivation, denoted by M, before cooperating with enterprises. When schools choose the positive cooperation strategy, some costs will be spent on the development of teachers and the adjustment of talent cultivation to meet the needs of enterprises, denoted by C₁. In return, schools obtain some rewards from the government such as political and financial support, denoted by G₁. Beyond that, if enterprises also choose the positive cooperation strategy, schools will produce more high-quality talents. These talents not only bring direct economic benefits to schools, such as alumni donations, but also bring indirect benefits, such as improving the social reputation of the schools. We use R₁ to denote the additional benefits to schools from cooperating with enterprises. However, when schools choose the negative cooperation strategy, they receive some punishment from the government, denoted by P₁. In order to reflect the binding force of punishment, we assume P₁ > C₁ + G₁ + R₁.

Assumption 4. We assume that enterprises can receive some benefits from the cooperation process, denoted by N, before cooperating with schools. When enterprises choose the positive cooperation strategy, some costs will be spent on providing internships and salaries for students, as well as training and managing students, denoted by C₂. In return, enterprises obtain some rewards from the government such as political and financial support, denoted by G₂. Beyond that, if schools choose the positive cooperation strategy, enterprises will have access to cheap labor and technical support from schools, which can improve their social reputation. We use R₂ to denote the additional benefits to enterprises from cooperating with schools. However, when enterprises choose the negative cooperation strategy, they receive some punishment from the government, denoted by P₂, and we assume P₂ > C₂ + G₂ + R₂.

Assumption 5. When the government chooses the positive cooperation strategy, some costs will be spent on aligning the interests of various parties and issuing relevant policies to regulate and facilitate the cooperative behaviors of schools and enterprises, denoted by C₃. In return, if both schools and enterprises choose the positive cooperation strategy, the government will gain more outstanding talents, better development of the economy, and a higher social reputation, denoted by B₁. Moreover, when the government chooses the negative cooperation strategy, and both schools and enterprises choose the positive cooperation strategy, the government will still receive the benefits of talent cultivation, economic development, and social reputation as a result of the cooperation between schools and enterprises, denoted by B₂. In order to reflect the effect of the government’s support, we assume B₁ > B₂. However, when the government chooses the negative cooperation strategy, and at least one of schools or enterprises chooses the negative cooperation strategy, the government suffers losses of talents cultivation, economic development and social reputation, denoted by P₃. Consistent with the previous assumption, we also stipulate P₃ > C₃ + G₃ + R₃.

In order to understand the model assumptions clearly, we list the meanings of the aforementioned symbols in Table 1.

3.2. Model Construction

Based on the above assumptions, we draw a tree diagram to show all the combinations of strategies among schools, enterprises, and government in Figure 1.

As shown in Figure 1, there are 8 strategy combinations, labeled as S₁ (schools’ positive cooperation strategy, enterprises’ positive cooperation strategy, government’s positive cooperation strategy), S₂ (schools’ positive cooperation strategy, enterprises’ positive cooperation strategy, government’s negative cooperation strategy), S₃ (schools’ positive cooperation strategy, enterprises’ negative cooperation strategy, government’s positive cooperation strategy), S₄ (schools’ positive cooperation strategy, enterprises’ negative cooperation strategy, government’s negative cooperation strategy), S₅ (schools’ negative cooperation strategy, enterprises’ positive cooperation strategy, government’s positive cooperation strategy), S₆ (schools’ negative cooperation strategy, enterprises’ positive cooperation strategy, government’s negative cooperation strategy), S₇ (schools’ negative cooperation strategy, enterprises’ negative cooperation strategy, government’s positive cooperation strategy), S₈ (schools’ negative cooperation strategy, enterprises’ negative cooperation strategy, government’s negative cooperation strategy).

According to the previous assumptions and strategy combinations, we construct the tripartite evolutionary game payoff matrix of schools, enterprises, and government, as shown in Table 2.

Each entry in Table 2 contains 3 values, the first represents the schools’ payoff, the middle represents the enterprises’ payoff, and the last represents the government’s payoff. We adopt a replicator dynamics equation, one of the most fundamental methods in evolutionary game theory, to indicate the evolution mechanism of cooperative behavior [55]. Here, we set U_A1 and U_A2 as the expected payoff of schools’ positive and negative cooperation strategies, respectively. According to the tripartite evolutionary game payoff matrix and the probability of different strategies among schools, enterprises, and government, U_A1 and U_A2 can be calculated as follows:

U_{A 1} = y z (M - C_{1} + G_{1} + R_{1}) + y (1 - z) (M - C_{1} + R_{1}) + (1 - y) z (M - C_{1} + G_{1}) + (1 - y) (1 - z) (M - C_{1})

(1)

U_{A 2} = y z (M - P_{1}) + y (1 - z) M + (1 - y) z (M - P_{1}) + (1 - y) (1 - z) M

(2)

\bar{U_{A}}

denotes the average expected payoff of schools, which can be simplified as:

\bar{U_{A}} = x U_{A 1} + (1 - x) U_{A 2}

(3)

Similarly, we use U_B1 and U_B2 to represent the expected payoff of enterprises’ positive and negative cooperation strategies, respectively and use

\bar{U_{B}}

to represent the average expected payoff of enterprises, which are simplified below.

U_{B 1} = x z (N - C_{2} + G_{2} + R_{2}) + x (1 - z) (N - C_{2} + R_{2}) + (1 - x) z (N - C_{2} + G_{2}) + (1 - x) (1 - z) (N - C_{2})

(4)

U_{B 2} = x z (N - P_{2}) + x (1 - z) N + (1 - x) z (N - P_{2}) + (1 - x) (1 - z) N

(5)

\bar{U_{B}} = y U_{B 1} + (1 - y) U_{B 2}

(6)

Finally, we use U_C1 and U_C2 in the same way to represent the expected payoff of the government’s positive and negative cooperation strategies, respectively and use

\bar{U_{C}}

to represent the average expected payoff of the government:

U_{C 1} = x y (- C_{3} - G_{1} - G_{2} + B_{1}) + x (1 - y) (- C_{3} - G_{1} + P_{2}) + (1 - x) y (- C_{3} - G_{2} + P_{1}) + (1 - x) (1 - y) (- C_{3} + P_{1} + P_{2})

(7)

U_{C 2} = x y B_{2} + x (1 - y) (- P_{3}) + (1 - x) y (- P_{3}) + (1 - x) (1 - y) (- P_{3})

(8)

\bar{U_{C}} = z U_{C 1} + (1 - z) U_{C 2}

(9)

Thus, the replicator dynamics equations of schools, enterprises, and government, which are denoted by

\frac{d x}{d t}

\frac{d y}{d t}

, and

\frac{d z}{d t}

, respectively, can be obtained as follows:

F (x) = \frac{d x}{d t} = x (U_{A 1} - \bar{U_{A}}) = x (1 - x) [y R_{1} + z (G_{1} + P_{1}) - C_{1}]

(10)

F (y) = \frac{d y}{d t} = y (U_{B 1} - \bar{U_{B}}) = y (1 - y) [x R_{2} + z (G_{2} + P_{2}) - C_{2}]

(11)

F (z) = \frac{d z}{d t} = z (U_{C 1} - \bar{U_{C}}) = z (1 - z) [x y (B_{1} - B_{2} - P_{3}) + x (- G_{1} - P_{1}) + y (- G_{2} - P_{2}) - C_{3} + P_{1} + P_{2} + P_{3}]

(12)

In the next section, we analyze the stability of the strategies of each population by solving the replicator dynamics equations, constructing the Jacobian matrix, and calculating the eigenvalues of the Jacobian matrix at different equilibrium points.

4. Strategy Stability Analysis

First of all, we let F(x) = 0, F(y) = 0, and F(z) = 0, and define the system of simultaneous equations as:

\{\begin{array}{l} F (x) = x (1 - x) [y R_{1} + z (G_{1} + P_{1}) - C_{1}] = 0 \\ F (y) = y (1 - y) [x R_{2} + z (G_{2} + P_{2}) - C_{2}] = 0 \\ F (z) = z (1 - z) [x y (B_{1} - B_{2} - P_{3}) + x (- G_{1} - P_{1}) + y (- G_{2} - P_{2}) - C_{3} + P_{1} + P_{2} + P_{3}] = 0 \end{array}

(13)

By solving the equations in (13), 14 equilibrium points can be obtained: E₁ (0, 0, 0), E₂ (0, 0, 1), E₃ (0, 1, 0), E₄ (0, 1, 1), E₅ (1, 0, 0), E₆ (1, 0, 1), E₇ (1, 1, 0), E₈ (1, 1, 1), E₉ (0,

\frac{C_{3} - P_{1} - P_{2} - P_{3}}{{- G}_{2} - P_{2}}

\frac{C_{2}}{G_{2} + P_{2}}

), E₁₀ (1,

\frac{{G_{1} + C}_{3} - P_{2} - P_{3}}{B_{1} - B_{2} - P_{2} - P_{3} - G_{2}}

\frac{C_{2} - R_{2}}{G_{2} + P_{2}}

), E₁₁ (

\frac{C_{3} - P_{1} - P_{2} - P_{3}}{- G_{1} - P_{1}}

, 0,

\frac{C_{1}}{G_{1} + P_{1}}

), E₁₂ (

\frac{{G_{2} + C}_{3} - P_{1} - P_{3}}{B_{1} - B_{2} - P_{1} - P_{3} - G_{1}}

, 1,

\frac{C_{1} - R_{1}}{G_{1} + P_{1}}

), E₁₃ (

\frac{C_{2}}{R_{2}}

\frac{C_{1}}{R_{1}}

, 0), and E₁₄ (

\frac{C_{2} - G_{2} - P_{2}}{R_{2}}

\frac{C_{1} - G_{1} - P_{1}}{R_{1}}

, 1). However, the solution of the replicator dynamics system in a multi-agent evolutionary game must be a strict Nash equilibrium solution [55]. Hence, we select only the pure strategy combinations E₁ , E₂, E₃, E₄, E₅, E₆, E₇, and E₈ (1, 1, 1) as the possible stable equilibrium points.

Next, we adopt Friedman’s replication dynamics system stability analysis method [56] to construct the Jacobian matrix of the “schools-enterprises-government” tripartite game.

J = (\begin{matrix} \frac{\partial F (x)}{\partial x} & \frac{\partial F (x)}{\partial y} & \frac{\partial F (x)}{\partial z} \\ \frac{\partial F (y)}{\partial x} & \frac{\partial F (y)}{\partial y} & \frac{\partial F (y)}{\partial z} \\ \frac{\partial F (z)}{\partial x} & \frac{\partial F (z)}{\partial y} & \frac{\partial F (z)}{\partial z} \end{matrix}) = (\begin{matrix} J_{11} & J_{12} & J_{13} \\ J_{21} & J_{22} & J_{23} \\ J_{31} & J_{32} & J_{33} \end{matrix})

(14)

where

J₁₁ = (1 – 2x) [y R₁ + z (G₁ + P₁) – C₁]

J₁₂ = x (1 – x) R₁

J₁₃ = x (1 – x) (G₁ + P₁)

J₂₁ = y (1 – y) R₂

J₂₂ = (1 – 2y) [x R₂ + z (G₂ + P₂) – C₂]

J₂₃ = y (1 – y) (G₂ + P₂)

J₃₁ = z (1 – z) [y (B₁ – B₂ – P₃) + (– G₁ – P₁)]

J₃₂ = z (1 – z) [x (B₁ – B₂ – P₃) + (– G₂ – P₂)]

J₃₃ = (1 – 2z) [x y (B₁ – B₂ – P₃) + x (– G₁ – P₁) + y (– G₂ – P₂) – C₃ + P₁ + P₂ + P₃]

According to Lyapunov stability theory, the stability at an equilibrium point can be judged by analyzing the eigenvalues of the Jacobian matrix [57]. Specifically, for any equilibrium point, if there are no positive eigenvalues, that point is stable. If there are any positive eigenvalues, the equilibrium point is unstable, and if the eigenvalues cannot be estimated, the equilibrium point is a saddle point. The results of substituting each of the 8 equilibrium points into the Jacobian matrix and calculating the eigenvalues of the Jacobian matrix at different equilibrium points are shown in Table 3.

In Table 3, “N” means that the sign of the eigenvalue cannot be determined, “+” means that the eigenvalue is positive, and “–” means that the eigenvalue is negative.

As can be seen from Table 3, there are 2 saddle points (E₇ and E₈) in the system. When the equilibrium point is E₇(1, 1, 0), when both schools and enterprises choose the positive cooperation strategy, and the government chooses the negative cooperation strategy, the conditions for stability of the system are R₁ > C₁, R₂ > C₂ and C₃ > B₁ – B₂ – G₁ – G₂. When this occurs, the positive cooperation strategy rewards of both schools and enterprises received from sources other than the government are greater than their cost, and the cost of the government’s positive cooperation strategy is greater than the difference between the benefit of the government’s positive cooperation strategy, the benefit of the government’s negative cooperation strategy, and the incentives given to schools and enterprises by the government.

When the equilibrium point is E₈(1, 1, 1), when all populations cooperate, the condition for stability of the system is C₃ < B₁ – B₂ – G₁ – G₂. When this occurs, the cost of the government’s positive cooperation strategy is lower than the difference between the benefit of the government’s positive cooperation strategy, the benefit of the government’s negative cooperation strategy, and the incentives given to schools and enterprises by the government. Comparing the two equilibrium points shows that the main factor that influences the stability of the strategies of schools and enterprises is the reward for the positive cooperation strategy from sources other than the government, and the main factor that influences the stability of the strategy of the government is the benefit from the positive cooperation strategy under the condition of schools cooperating with enterprises.

5. Conclusions

In this paper we studied cooperation between schools, enterprises, and government from the perspective of evolutionary game theory by establishing a tripartite evolutionary game model. Based on our strategy stability analysis, we found several effective ways to promote the cooperation between schools, enterprises, and government, and reached the following conclusions.

(1) There are two equilibrium points, E₇ (1, 1, 0) and E₈ (1, 1, 1), at which the system can reach a stable state.

(2) The main factor that influences the stability of the strategies of schools and enterprises is the reward for positive cooperation from sources other than the government. When schools and enterprises can receive enough rewards from sources other than the government because, the system can reach a stable state regardless of whether the government chooses the positive or negative cooperation strategy. The nongovernmental effects of the cooperation between schools and enterprises are greater than the governmental effects. That is, the current influence of government on school-enterprise cooperation is not obvious. Therefore, the government should focus on implementing more effective policies, such as increasing the incentives and penalties, improving the mechanism for managing conflicts, ensuring the fairness of benefits distribution, and clarifying the responsibilities of different departments, in order to provide the best possible environment to facilitate the cooperation between schools and enterprises.

(3) The main factor that influences the stability of the strategy of the government is the benefit from the positive cooperation strategy under the condition of schools cooperating with enterprises. When the government can receive enough benefit from the cooperation of schools and enterprises as a result of positive cooperation strategy, the system is can reach a stable state. Therefore, the effectiveness should be emphasized when schools cooperate with enterprises. Schools should focus on providing more practical curricula and programs for students, training high-quality teachers, and perfecting talent cultivation to meet the needs of enterprises. Similarly, while enterprises should focus on providing job experiences for students and transforming the results of schools’ teaching and theoretical research into practical productivity.

References

https://www.bibb.de/en/77214.php.
https://careertech.org/Perkins.
https://www.gov.cn/gongbao/content/2018/content_5254308.htm.
Cyert, R. M.; Goodman, P. S. Creating effective university-industry alliances: an organizational learning perspective. Organizational Dynamics 1997, 25(4), 45-57. [CrossRef]
Wright, M.; Clarysse, B.; Lockett, A.; Knockaert, M. Mid-range universities’ linkages with industry: Knowledge types and the role of intermediaries. Research policy 2008, 37(8), 1205-1223. [CrossRef]
Bergman, E. M. Knowledge links between European universities and firms: a review. Papers in regional science 2010, 89(2): 211-222. [CrossRef]
Harrison, R.; Leitch, C. Enterpreneurial learning: researching the interface between learning and the entrepreneurial context. Entrepreneurship theory and practice 2005, 29(4), 351-371.
Plewa, C. Exploring organizational culture difference in relationship dyads. Australasian marketing journal 2009, 17(1), 46-57. [CrossRef]
Galan, M. V.; Plewa, C. What drives and inhibits university-business cooperation in Europe? A comprehensive assessment. R & D Management 2016, 46(2), 369-382.
Perkmanna, M.; Tartari, V.; McKelvey, M.; et al. Academic engagement and commercialisation: A review of the literature on university-industry relations. Research policy 2013, 43(2), 423-442. [CrossRef]
Theuerkauf, W. E.; Weiner, A. The German Dual System of Vocational Education and Implications for Human Resource Development in America. Oxford Review of Education 2002, 1, 53-73.
BMBF. Vocational training in the dual system in Germany [M]. Bonn: Federal Ministry of Education, Science, Research and Technology, Public Relations Division, 1997.
Pleshakova, AY. Dual System of Education in Germany: Historical Context. Nauchnyi Dialog 2018, 10, 301-312. [CrossRef]
Remington, T. F. Business-Government Cooperation in VET: A Russian Experiment with Dual Education. Post-Soviet Affairs 2017, 33(4), 313-333. [CrossRef]
Dudyrev, F.; Romanova, O.; Shabalin, A. Dual Education in Regions of Russia: Models, Best Practices, Growth Prospects. Voprosy Obrazovaniya-Educational Studies Moscow 2018, 2, 117-138.
Pyliavets, M.; Protas, O.; Martinets, L.; Lyaskevich, A.; Babyshena, M.; Chumak, L.; Lazorko, O. A Comparative Analysis of Peculiarities of Vocational Education in Ukraine and Germany. Revista Romaneasca Pentru Educatie Multidimensionala 2020, 12(3), 200-212. [CrossRef]
Cai, Y. A Study on the Education Model of Dual System in Comprehensive Universities in Germany. Studies in Foreign Education 2010, 37(7), 80-85 (in Chinese).
Liang, L. Inspiration of German “Dual System” on the Cooperation with Enterprises in Application-oriented Universities. Scientific Management Research 2014, 32(6), 128-131 (in Chinese).
Yang, R.; Sun, S. A Study and Reference of the Dual System of Education Governance in Germany: An Analysis Based on Cultural-Historical Activity Theory. Journal of Beijing Administration Institute 2021, 4, 99-107 (in Chinese).
Pritchard, R. M. O. The German Dual System: Educational Utopia? Comparative Education 1992, 28(2), 131-143.
Shackleton, J. R. Training in Germany: a view from abroad. Education & Training 1997, 39(8), 303-308. [CrossRef]
Li, J.; Li, D. International Comparative Analysis of Industry-Education Integration in Vocational Education. Research in Higher Education of Engineering 2019, 4, 159-164.
Younis, N. Cooperative education impact on enhancing mechanical engineering curriculum. America Society for Engineering Education. 2012.
Pierrakos, O.; Borrego, M.; Lo, J. Preliminary findings from a quantitative study: What are students learning during cooperative education experiences? ASEE Annual Conference and Exposition, Conference Proceeding. 2008.
Schuurman, M. K.; Pangborn, R. N.; McClintic, R. D. Assessing the Impact of Engineering Undergraduate Work Experience: Factoring in Pre-work Academic Performance. Journal of Engineering Education 2008, 97(2), 207-212. [CrossRef]
Raelin, J. A.; Bailey, M. B.; Hamann, J. C.; Pendleton, L.K.; Raelin, J.; Reisberg, R.; Whitman, D. The Effect of Cooperative Education on Change in Self-Efficacy Among Undergraduate Students: Introducing Work Self-Efficacy. Journal of Cooperative Education and Internships 2011, 45(2), 17-35.
Rowe, P. M. Work Experience, the Scientist-Practitioner Model, and Cooperative Education. Canadian Psychology-Psychologie Canadienne 2018, 59(2), 144-150.
Chopra, S.; Golab, L. Undergraduate engineering applicants’ perceptions of cooperative education: A text mining approach. International Journal of Work-Integrated Learning 2022, 23(1), 95-112.
Baldwin, C. T. Sandwich courses in the universities. Physics Bulletin 1969, 20, 486. [CrossRef]
Jones, B.; Healey, M.; Matthews, H. The thick sandwich: still on the menu. Journal of Geography in Higher Education 1995, 19(2), 23.
Santiago, A. Impact of Sandwich Course Design on First Job Experience. Asia-Pacific Education Researcher 2009, 18(2), 205-217. [CrossRef]
Brooks, R.; Youngson, P. L. Undergraduate work placements: an analysis of the effects on career progression. Studies In Higher Education 2016, 41(9), 1563-1578. [CrossRef]
Lee, J.; Win, H. N. Technology transfer between university research centers and industry in Singapore. Technovation 2004, 24(5), 433-442. [CrossRef]
Arza, V. Channels, benefits and risks of public — private interactions for knowledge transfer: conceptual framework inspired by Latin America. Science and public policy 2010, 37(7), 473-484. [CrossRef]
Lam, A. What motivates academic scientists to engage in research commercialization: ‘Gold’, ‘ribbon’ or ‘puzzle’? Research policy 2011, 40(10), 1354-1368.
Mowery, D. C.; Sampat, B. N. The Bayh-Dole Act of 1980 and university-industry technology transfer: a model for other OECD government? The Journal of Technology Transfer 2004, 30(1), 115-127.
Eom, B. Y.; Lee, K. D. Determinants of industry-academy linkages and their impact on firm performance: the case of Korea as a latecomer in knowledge industrialization. Research policy 2010, 39(5), 625-639. [CrossRef]
Santoro, M. D.; Chakrabarti, A. K. Firm size and technology centrality in industry-university interactions. Research policy 2002, 31(7), 1163-1180. [CrossRef]
Perkmann, M.; Neely, A.; Walsh, K. How should firms evaluate success in university-industry alliances? A performance measurement system. R & D Management 2011, 41(2), 202-216. [CrossRef]
de Moraes Silva, D. R.; Furtado, A. T.; Vonortas, N. S. University-industry R&D cooperation in Brazil: a sectoral approach. Journal of Technology Transfer 2018, 43(2), 285-315. [CrossRef]
Laursen, K.; Reichstein, T.; Salter, A. Exploring the effect of geographical proximity and university quality on university-industry collaboration in the United Kingdom. Regional studies 2011, 45(4), 507-523. [CrossRef]
Numprasertchai, S.; Igel, B. Managing knowledge through collaboration: multiple case studies of managing research in university laboratories in Thailand. Technovation 2005, 25(10), 1173-1182. [CrossRef]
Rosendo-Rios, V.; Ghauri, P. N.; Zhang, Y. Empirical analysis of the key factors that can contribute to university-industry cooperational success from a relationship marketing approach. European Journal of International Management 2016, 10(6), 647-677.
Li, Z.; Wang, D.; Li, X. Status quo and influence factors of university industry collaboration: evidence of Zhejiang Province. Science & Technology Progress and Policy 2012, 29(21), 150-154 (in Chinese).
Shan, H.; Yang, J. Sustainability of photovoltaic poverty alleviation in China: An evolutionary game between stakeholders. Energy 2019, 181, 264–280. [CrossRef]
Zhao, R.; Zhou, X.; Han, J.J.; Liu, C. For the sustainable performance of the carbon reduction labeling policies under an evolutionary game simulation. Technol. Forecast. Soc. Chang. 2016, 112, 262–274. [CrossRef]
Babu, S.; Mohan, U. An integrated approach to evaluating sustainability in supply chains using evolutionary game theory. Comput. Oper. Res. 2018, 89, 269–283. [CrossRef]
Congleton, R.D. Game theory and public policy—By Roger, A. McCain. Public Adm. 2013, 91, 248–250.
Hui, E.; Bao, H. The logic behind conflicts in land acquisitions in contemporary China: A framework based upon game theory. Land Use Policy 2013, 30, 373–380. [CrossRef]
Estalaki, S.M.; Abed-Elmdoust, A.; Kerachian, R. Developing environmental penalty functions for river water quality management: Application of evolutionary game theory. Environ. Earth Sci. 2015, 73, 4201–4213. [CrossRef]
Wu, B.; Liu, P.; Xu, X. An evolutionary analysis of low-carbon strategies based on the government–enterprise game in the complex network context. J. Clean. Prod. 2017, 141, 168–179. [CrossRef]
Zhu, H.; Wang, Q. The Development Dilemma and Path Choice of Innovation and Entrepreneurship Education Based on Game Theory. Advances in Multimedia 2022, 2022, 1-11. [CrossRef]
Li, D.; Wang, W. Online Learning Management for Primary and Secondary Students during the COVID-19 Epidemic: An Evolutionary Game Theory Approach. Sustainability 2022, 14, 12416.
Zhang, H.; Zeng, Y. The Education for Sustainable Development, Online Technology and Teleological Rationality: A Game between Instrumental Value and Humanistic Value. Sustainability 2022, 14, 2101. [CrossRef]
Ritzberger, K.; Weibull, J.W. Evolutionary selection in normal form games. Econometrica 1995, 63, 1371–1399. [CrossRef]
Friedman, D. Evolutionary Games in Economics. Econometrica 1991, 59, 637–666. [CrossRef]
Lyapunov, A. M. The general problem of the stability of motion. International Journal of Control 1992, 55(3), 531-534. [CrossRef]

Figure 1. Tree diagram of the strategy combinations among schools, enterprises, and government.

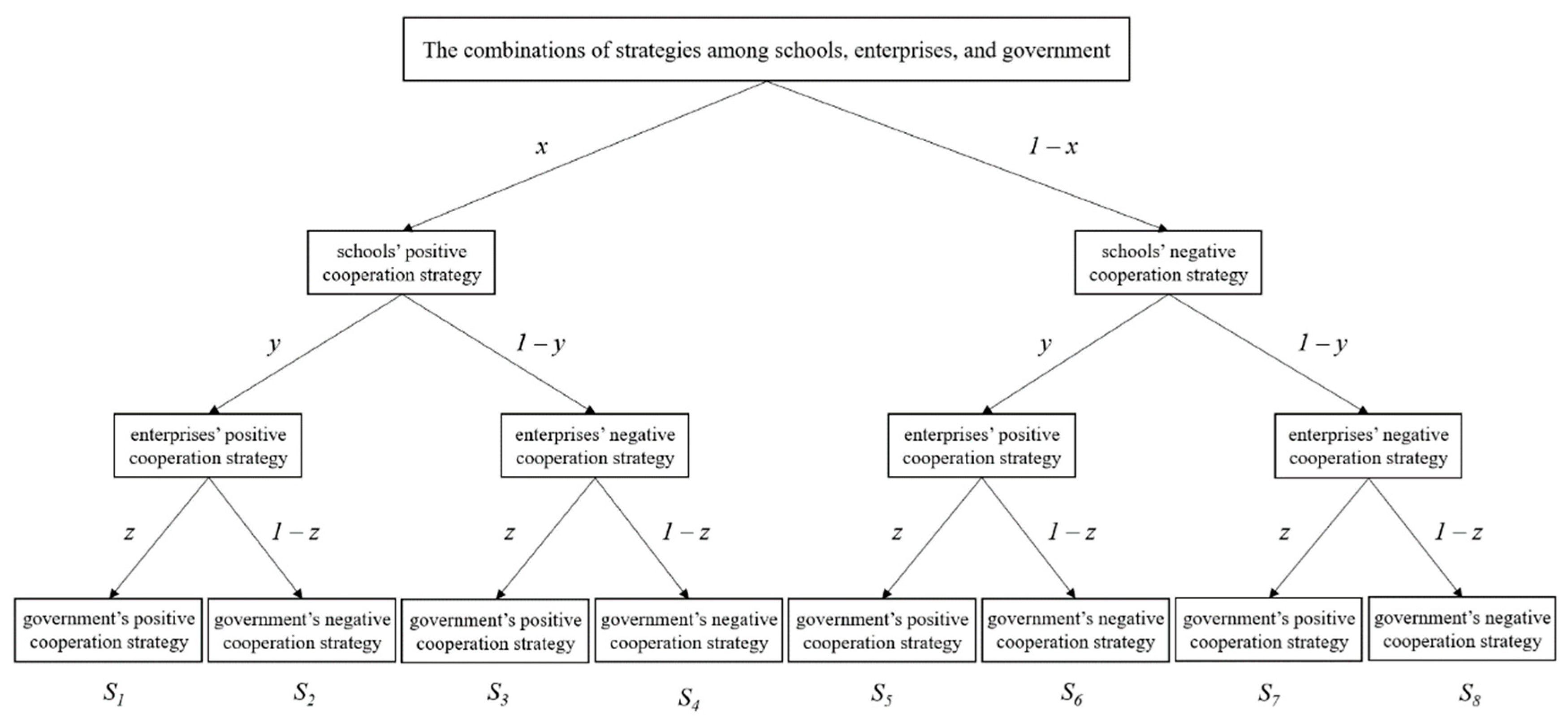
Table 1. Notation of symbols.

Symbol	Meaning
M	The benefit of schools before cooperating with enterprises.
N	The benefit of enterprises before cooperating with schools.
C₁	The cost of schools’ positive cooperation strategy.
C₂	The cost of enterprises’ positive cooperation strategy.
C₃	The cost of government’s positive cooperation strategy.
G₁	The reward for schools’ positive cooperation strategy from the government.
G₂	The reward for enterprises’ positive cooperation strategy from the government.
R₁	The additional rewards of schools’ positive cooperation strategy from sources other than the government.
R₂	The additional rewards of enterprises’ positive cooperation strategy from sources other than the government.
B₁	The benefits of the government’s positive cooperation strategy.
B₂	The benefits of the government’s negative cooperation strategy.
P₁	The punishment for schools’ negative cooperation strategy from the government.
P₂	The punishment for enterprises’ negative cooperation strategy from the government.
P₃	The punishment for the government’s negative cooperation strategy.

Table 2. Payoff matrix of the tripartite evolutionary game between schools, enterprises, and government.

				government
				positive cooperation strategy	negative cooperation strategy
schools	positive cooperation strategy	enterprises	positive cooperation strategy	M – C₁ + G₁ + R₁, N – C₂ + G₂ + R₂, – C₃ – G₁ – G₂ + B₁	M – C₁ + R₁, N – C₂ + R₂, B₂
			negative cooperation strategy	M – C₁ + G₁, N – P₂, – C₃ – G₁ + P₂	M – C₁, N, – P₃
	negative cooperation strategy	enterprises	positive cooperation strategy	M – P₁, N – C₂ + G₂, – C₃ – G₂ + P₁	M, N – C₂, – P₃
			negative cooperation strategy	M – P₁, N – P₂, – C₃ + P₁ + P₂	M, N, – P₃

Table 3. Eigenvalues and stability of equilibrium points.

equilibrium point	λ₁	symbol	λ₂	symbol	λ₃	symbol	state
E₁ (0, 0, 0)	– C₁	–	– C₂	–	P₁ + P₂ + P₃ – C₃	+	unstable
E₂ (0, 0, 1)	G₁ + P₁ – C₁	+	G₂ + P₂ – C₂	+	C₃ – P₁ – P₂ – P₃	–	unstable
E₃ (0, 1, 0)	R₁ – C₁	N	C₂	+	P₁ + P₃ – G₂ – C₃	+	unstable
E₄ (0, 1, 1)	R₁ + G₁ + P₁ – C₁	+	C₂ – G₂ – P₂	–	G₂ + C₃ – P₁ – P₃	N	unstable
E₅ (1, 0, 0)	C₁	+	R₂ – C₂	N	P₂ + P₃ – G₁ – C₃	N	unstable
E₆ (1, 0, 1)	C₁ – G₁ – P₁	–	R₂ + G₂ + P₂ – C₂	+	G₁ + C₃ – P₂ – P₃	N	unstable
E₇ (1, 1, 0)	C₁ – R₁	N	C₂ – R₂	N	B₁ – B₂ – G₁ – G₂ – C₃	N	saddle
E₈ (1, 1, 1)	C₁ – R₁ – G₁ – P₁	–	C₂ – R₂ – G₂ – P₂	–	B₂ + G₁ + G₂ + C₃ – B₁	N	saddle

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.