1. Introduction
This work uses a new approach to investigate the Riemann hypothesis, drawing conclusions about its trueness. It is based on the more general method presented in a very recent publication [
20], by the same author, showing in detail how to approach that very well-known and interesting problem.
The Riemann hypothesis is the conjecture that the Riemann zeta function has nontrivial zeros just in the set of complex numbers with real part 1/2 (critical line in ). Several researchers consider it as the most important unsolved problem in pure mathematics, being very significant in analytic number theory because of its connections with the distribution of prime numbers. The so-called trivial zeros occur at all negative even integers {-2, -4, -6, -8, -10, -12, ...}, and the (supposedly found) nontrivial roots occur at certain points on the critical line. The Riemann hypothesis is concerned with the locations of these nontrivial zeros, stating:
The real part of every nontrivial zero of the Riemann zeta function is 1/2.
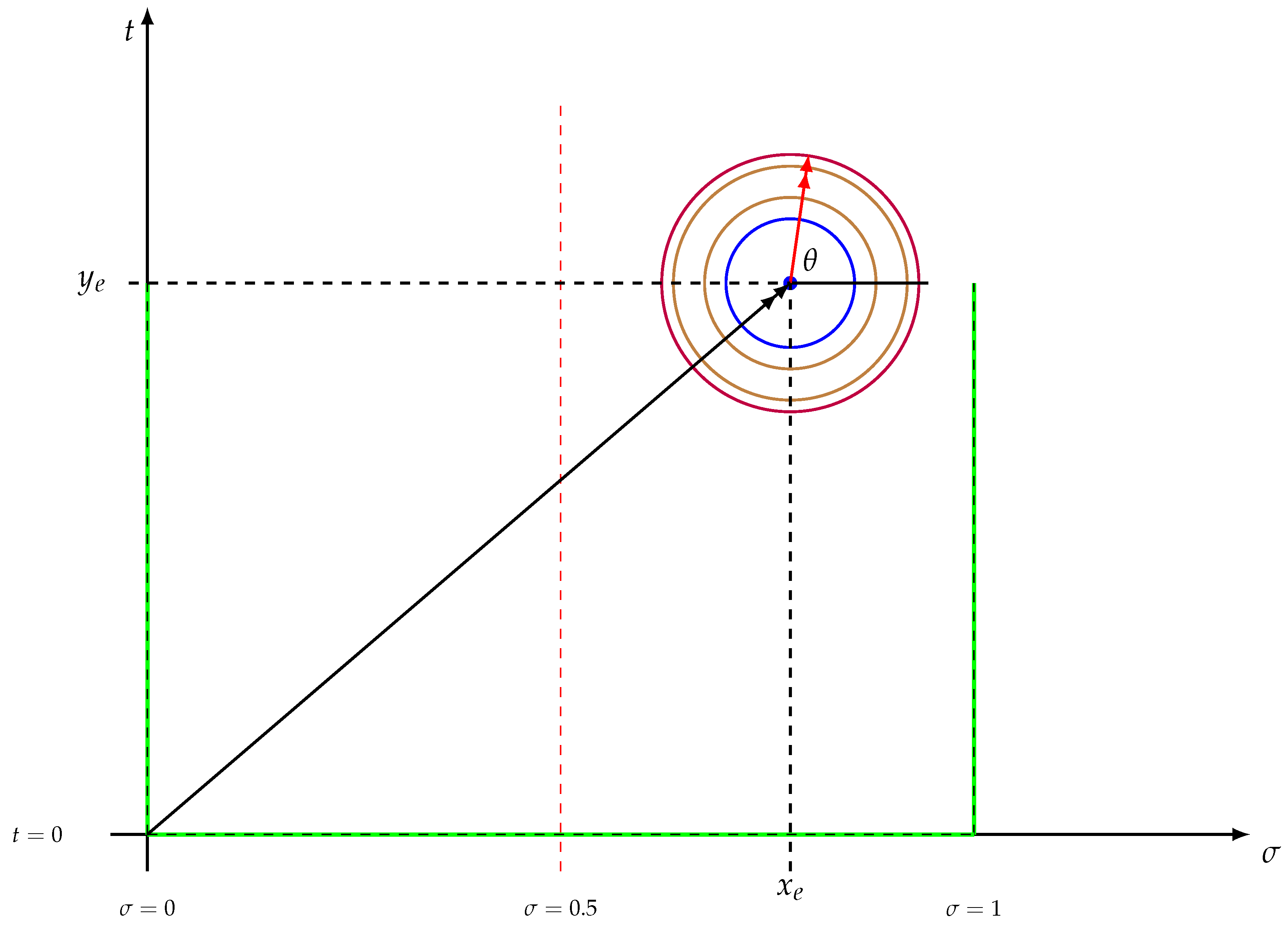
Figure 1.
Part of open critical strip and critical line
Figure 1.
Part of open critical strip and critical line
In this fashion, if the hypothesis is true, all nontrivial zeros must be located on the critical line, that is, the subset of with real part equal to 1/2 .
In order to start the investigation, it is important to establish the expressions for eta and zeta in terms of the complex variable
s :
So, considering the clean relationship between zeta (
) and eta (
) functions, often it may be easier to work with eta, considering the coincidence of their roots inside the critical strip. They are related by:
Furthermore, as cited above, the study will be conducted only in the open half-strip
. This is valid because roots are vertically symmetric (the conjugate of a zero is a zero as well), and horizontally symmetric relatively to the critical line - please, for more details, refer to [
4] Therefore, the discovery of one root in
results in finding four roots, symmetrically located relatively to the x axis and the critical line.
In general lines, the underlying idea in this work is to face the eta function as a mapping, associating to each element of
A one vector in
, that is to say, a 2-dimensional vector field usually referred to as the field associated to
[
15], namely,
, using the same designation for both entities. This unusual viewpoint gives rise to a nonlinear autonomous system
which will be the basis for the development of the proof.
Obviously, the state space of system (
4) can be extended to the full domain of
.
2. Dirichlet Eta Function and Associated Vector Field
By identifying
and
, the Dirichlet Eta function can be written
already seen as a vector field with components given by its real and imaginary parts, restricted to and , due to posterior developments.
As is widely known,
is a holomorphic function, therefore its components are
and have partial derivatives of all orders. In addition, it satisfies Cauchy-Riemann equations [
15].
The total differentials of
f and
g are given by
and taking into account that
we have
3. Poincaré Index for 2-Dimensional Dynamical Systems
Given a 2-dimensional vector field
V, defined in a simply connected region
, consider any closed curve
C fully contained in it and not enclosing any equilibrium points of the dynamical system originated by
V in its interior.
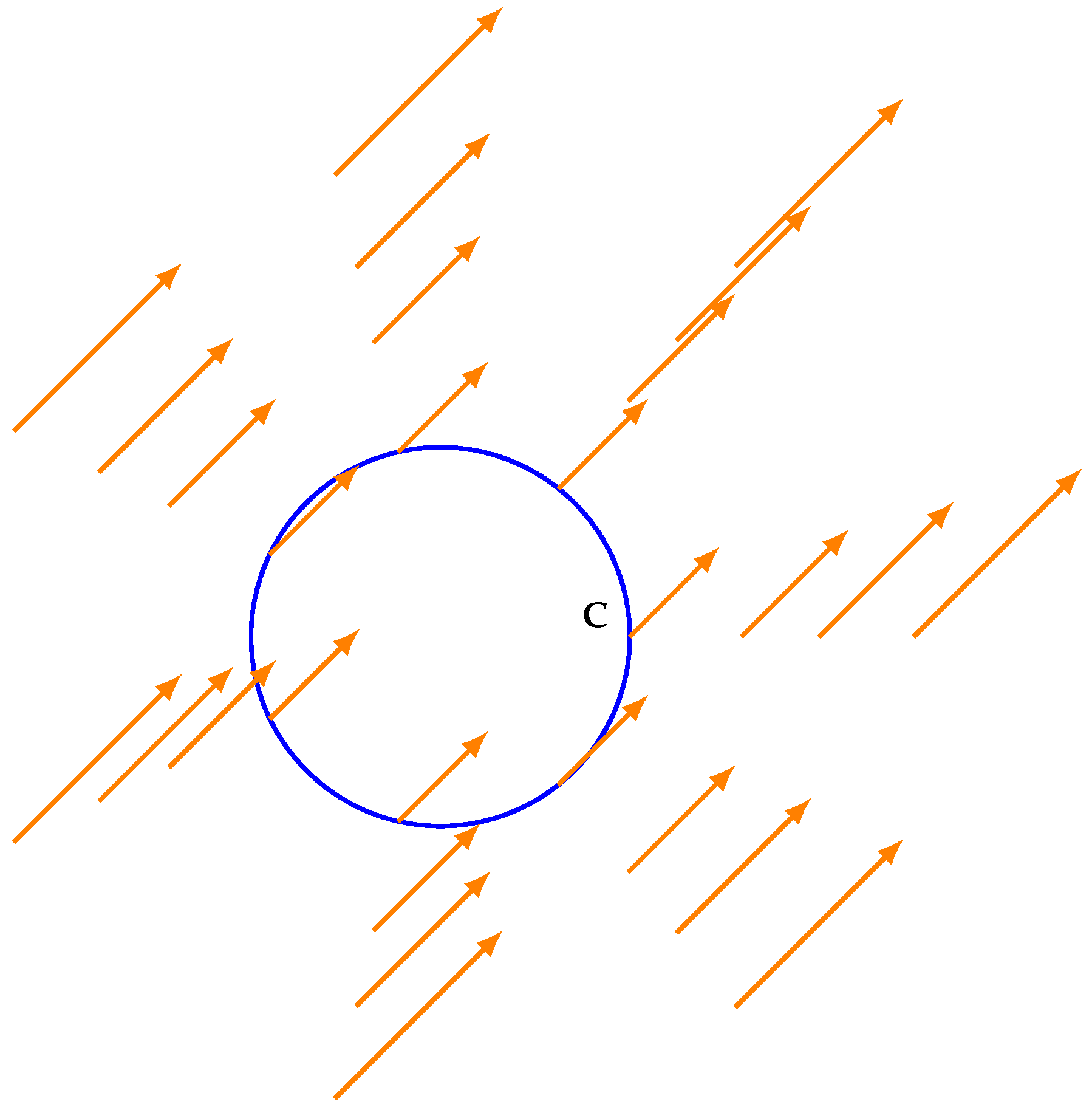
By restricting
V to the closed curve
C we obtain a vector field along it, as displayed in
Figure 2.
In general, after moving along C in the anti-clockwise, positive sense, the vectors with origin in C rotate and, after a full excursion, an angle is traversed, where - the integer k is called the Poincaré index of the curve C . The index of a closed curve with no equilibria inside it can be obtained by integrating the change in the angle of the vectors at each point of C.
For a vector field given by
the index of
C is
The Poincaré index of an equilibrium point of V, , is defined to be the index of a closed curve C which surrounds only this specific point, not existing equilibria on the closed curve.
The Poincaré index features some very significant properties [
1,
2,
17,
21,
23]:
It is invariant under homotopical transformations of C, provided equilibria do not "clash" with curves.
When C is a simple closed curve, V is a vector field defined on C and its interior, and there are no critical points of V inside C , the index of C relative to V is 0.
The index of a sink, a source, or a center is +1.
The index of a periodic orbit is +1.
The index of a hyperbolic saddle point is -1.
Figure 3.
One isolated equilibrium (center) inside the closed curve ⇒ index = 1
Figure 3.
One isolated equilibrium (center) inside the closed curve ⇒ index = 1
Figure 4.
One isolated equilibrium (source) inside the closed curve ⇒ index = 1
Figure 4.
One isolated equilibrium (source) inside the closed curve ⇒ index = 1
Figure 5.
One isolated equilibrium (sink) inside the closed curve ⇒ index = 1
Figure 5.
One isolated equilibrium (sink) inside the closed curve ⇒ index = 1
Figure 6.
No equilibrium point inside the closed curve ⇒ index = 0
Figure 6.
No equilibrium point inside the closed curve ⇒ index = 0
4. Detailed Proof
4.1. Preliminary Information and Proof Directives
The proof will be by contradiction (principle of non-contradiction). Therefore, it will be assumed that there is a nontrivial and isolated zero
of the
function, located outside the critical line (and inside the open and simply connected region
), and the proof will proceed until a contradiction arises, demonstrating that the assumption is false, and the inexistence of nontrivial roots of
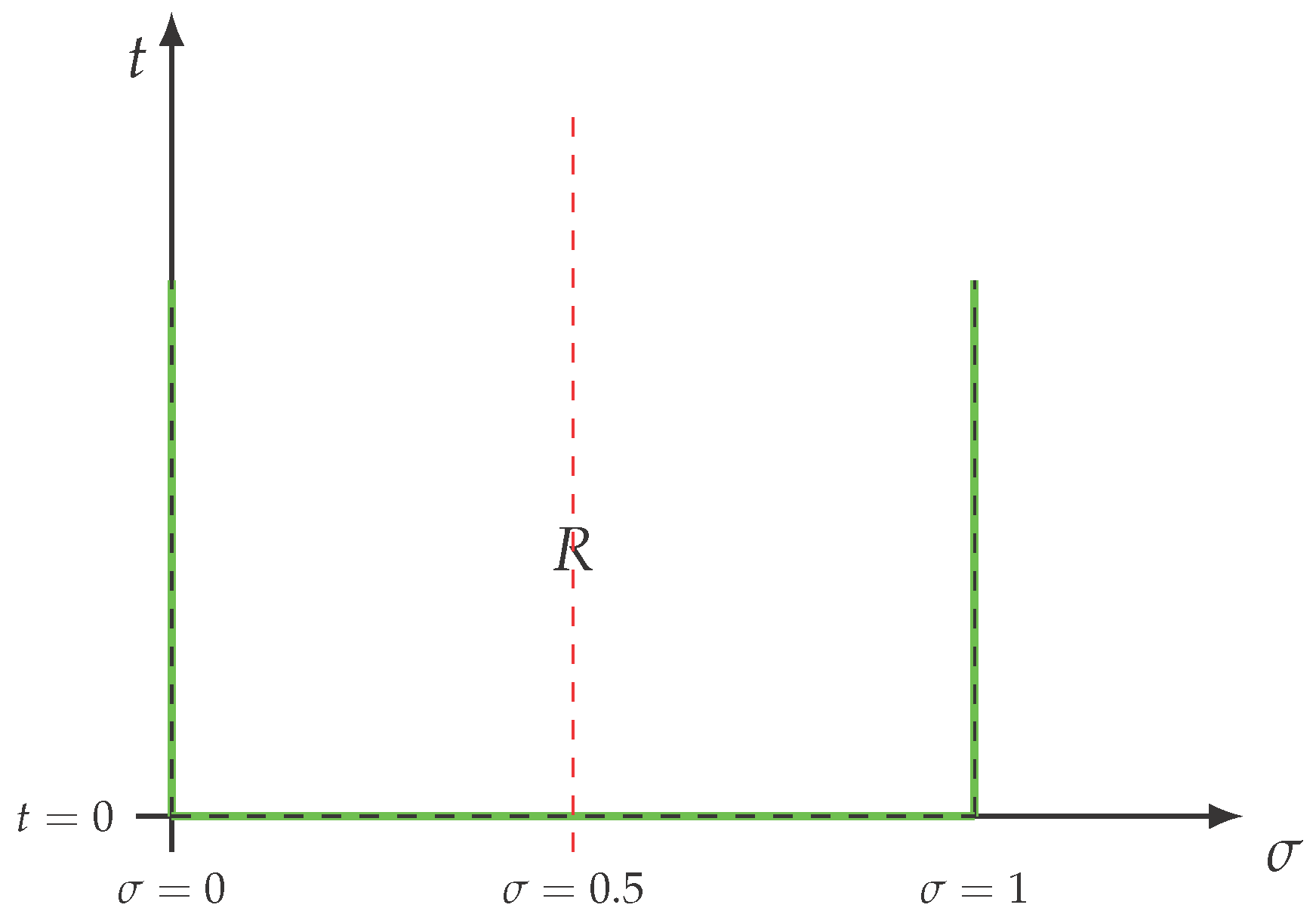
and
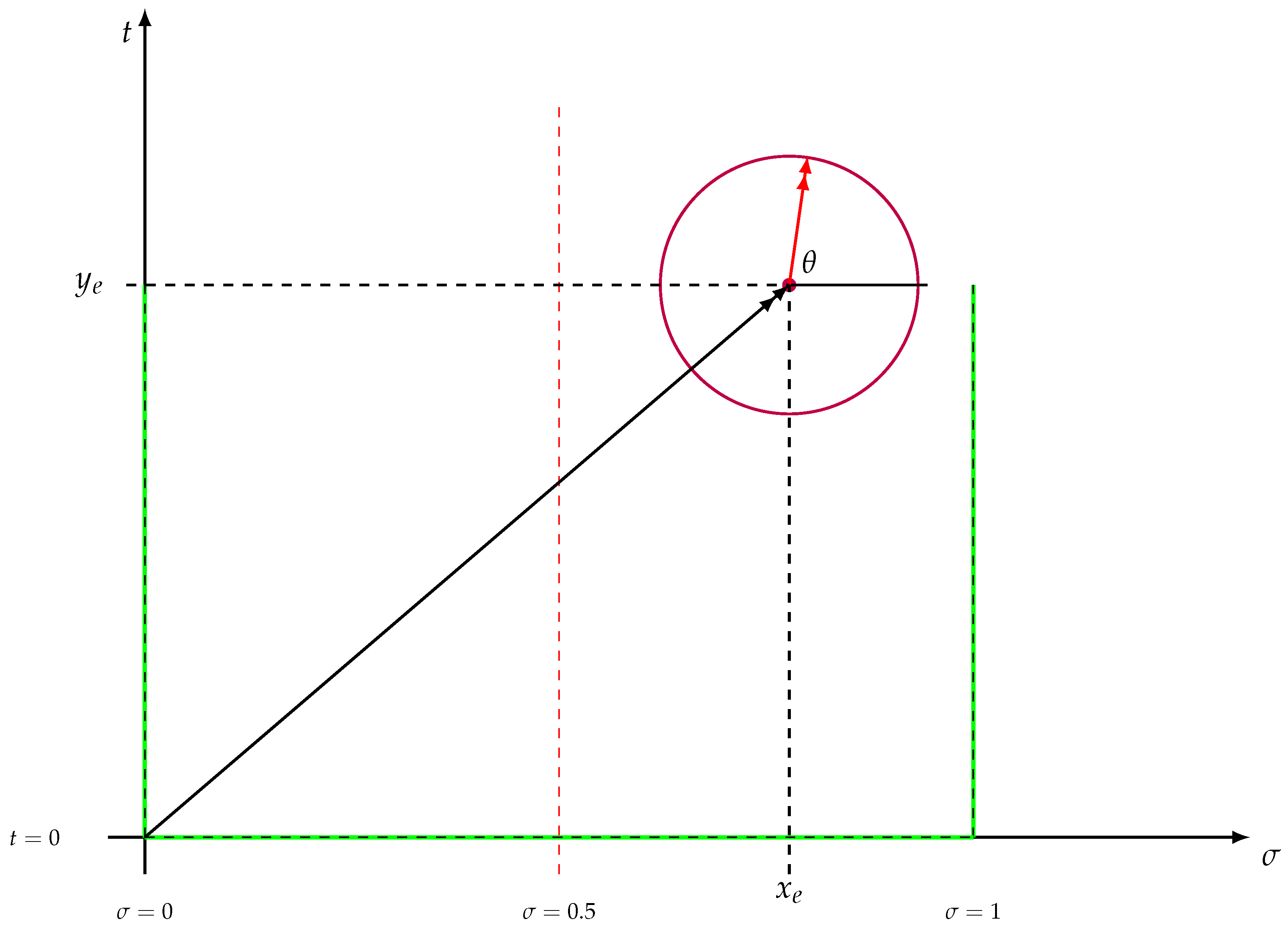
functions outside the critical line. In addition, the curve
C will be a circle with center at
, radius
R, and parameterized by the angle
, indicated in
Figure 7. In this fashion, we have
where
s is a generic point in
C.
4.2. Final Transformation
Now, a final change of variables is about to take place, and it will allow us to arrive at the final expression for the Poincaré index, this time including
and further relevant parameters. Please, note that for the sake of better understanding, a notation "overloading" occurs in the following - although
f and
g are 2-variable functions, the same identification is kept for both after the change of variables, replacing
, is done. For example,
and
are formally distinct as functions, but related as objects.
or
In order to further simplify the previous expression, the well-known formulas for cos and sin of sums will be used below. By establishing
In order to certify that series (35) and (36)
converge, some traditional convergence tests will be used, Dirichlet’s (page 152 of [
16]) and direct calculations, for instance.
Starting with (35), define
According to Dirichlet’s test, if is monotonic and converges to 0, and is bounded for all N, ( or expression (35) ) converges.
The condition on
is also provided by Stolz-Cesàro theorem [
18], considering that it is monotonic,
, and
The condition on
is satisfied as well - rearranging
as the summation
and using
we obtain an expression for the new general term of
As the third factor of
converges to zero, the decreasing increments keep the sum
bounded, as demanded by Dirichlet’s test. This concludes the proof of convergence for (
34).
A similar reasoning holds for () and is presented below.
For the case of (), define
According to Dirichlet’s test, if is monotonic and converges to 0, and is bounded for all N, ( or expression () ) converges.
The condition on was proved above.
The condition on
is true as well because, by writing
as
and using
we obtain an expression for the new general term of
As the third factor of converges to zero, the decreasing increments keep the sum bounded, as demanded by Dirichlet’s test. This concludes the proof of convergence for ().
Instead of using the somewhat unconventional expressions (
38) and (
42), an alternative way to convey the same ideas could be achieved by defining another general term
by
and working with it in the above calculations.
4.3. Considerations About the Index of Surrounded by the Circle C
As defined in expressions (
18), the Poincaré index of an equilibrium point
of a given planar vector field, is defined to be the index (
k) of a closed curve
C which surrounds only this specific point, not existing equilibria on the closed curve. It is given by
and, when used in the present case, assumes a very interesting form, mainly because
C is a circle with radius
R and center
, as described above.
Some aspects are worth mentioning:
Any concentric circle with radius smaller than
R will result in the same index for
, because they are homotopic and enclose only one and the same isolated equilibrium, by hypothesis [
17]. So, even for arbitrarily small and positive values of the radius,
k remains constant.
-
According to the particular expression for , formula (30), the integrand may be written , resulting in the following formulation for the index k, where H is a function.
-
By analysing the function
H, it is possible to see that it is composed of some convergent series and also expressions like
and
, which approach constant values when
R gets near zero, although always positive. Therefore, expressions like
will tend to
, where
is a constant. Hence, the expression in (41) to the right of
R may be made practically independent of
R for sufficiently small radiuses. In addition, the expression
is bounded, considering its analytical composition, and there must exist a real, positive constant RC such that
for all
R, provided the respective circle remains located inside the correct region. Choosing
and multiplying the previous expression by it, we obtain
As by definition, it must be equal to zero.
Figure 8.
Contracting circles with fixed center at
Figure 8.
Contracting circles with fixed center at
But, as an isolated equilibrium, must have nonzero Poincaré index,.
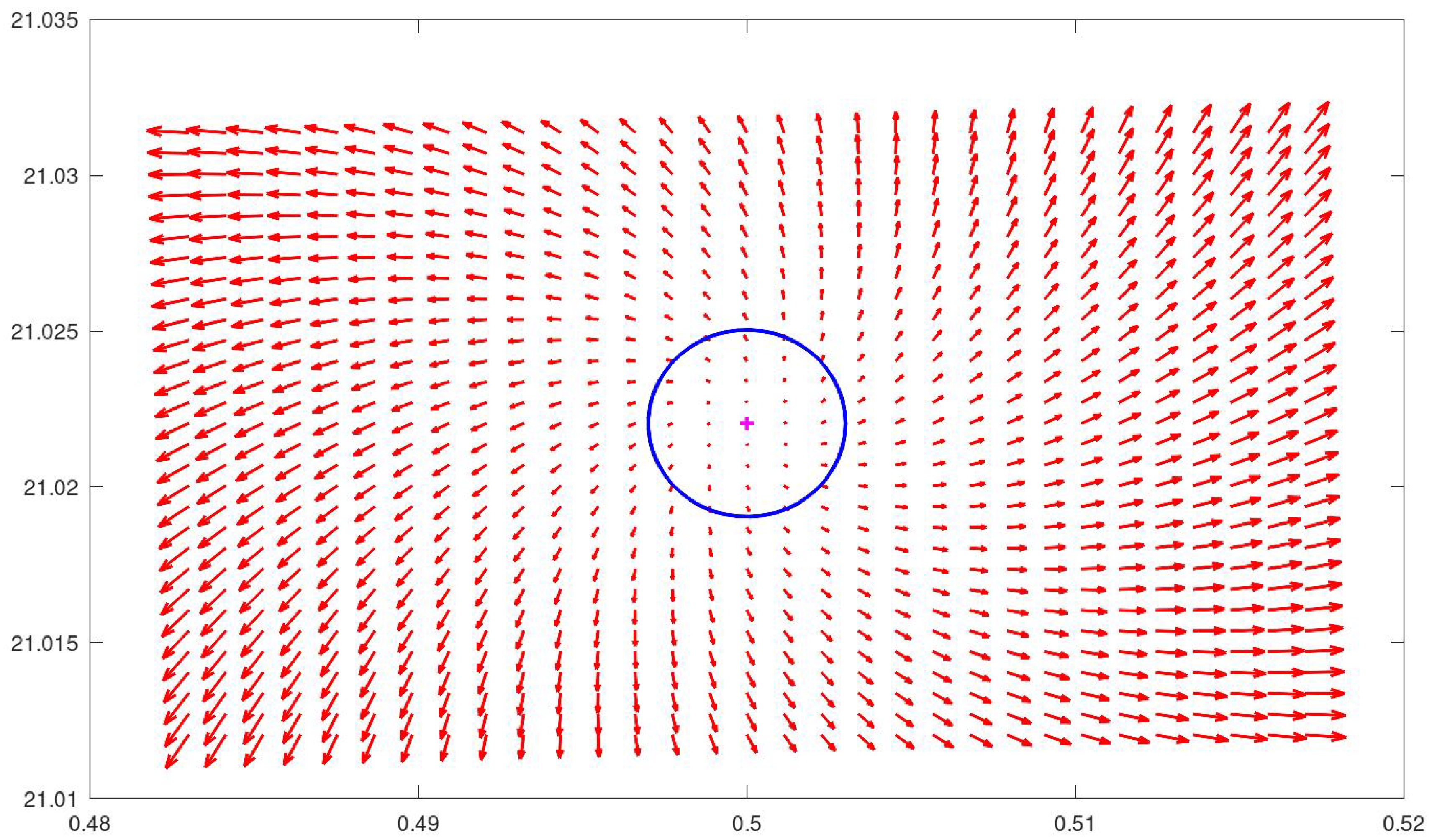
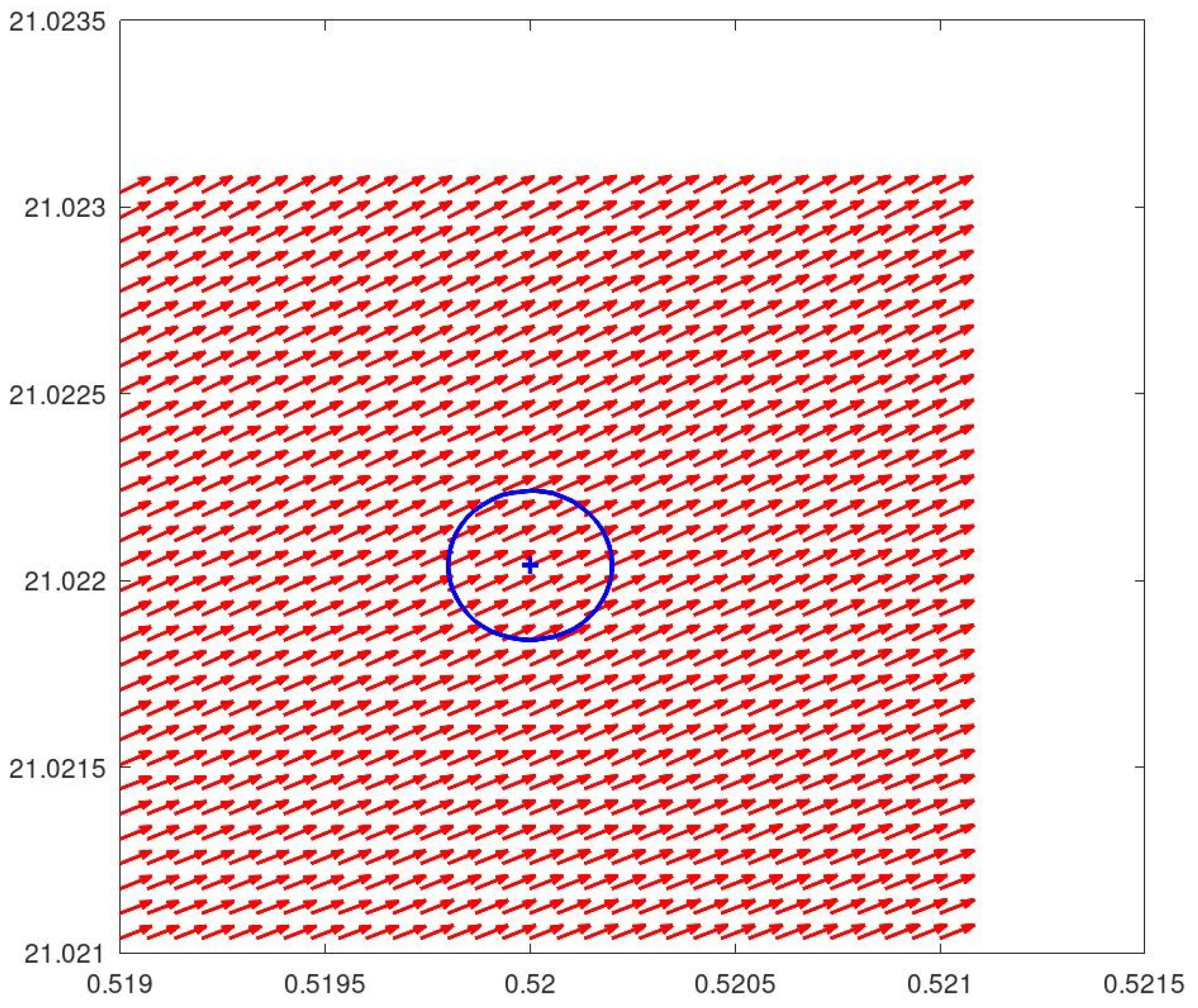
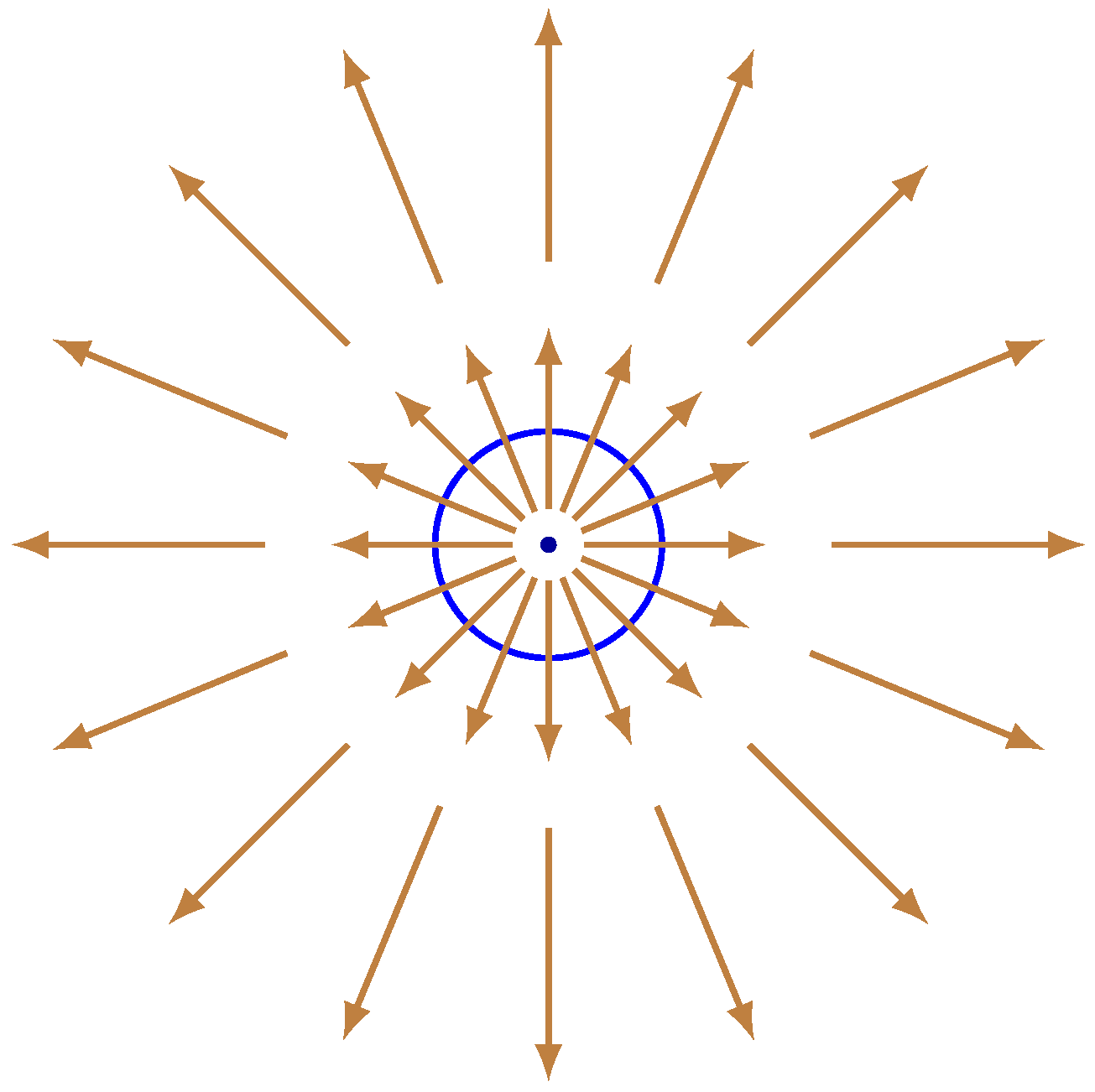
For the sake of illustration,
Figure 9 displays the vector field around the equilibrium corresponding to the zero ( 0.5 , 21.0220396387715549926284 ) of
and
. It is possible to infer that it represents a source for the overall dynamical system.
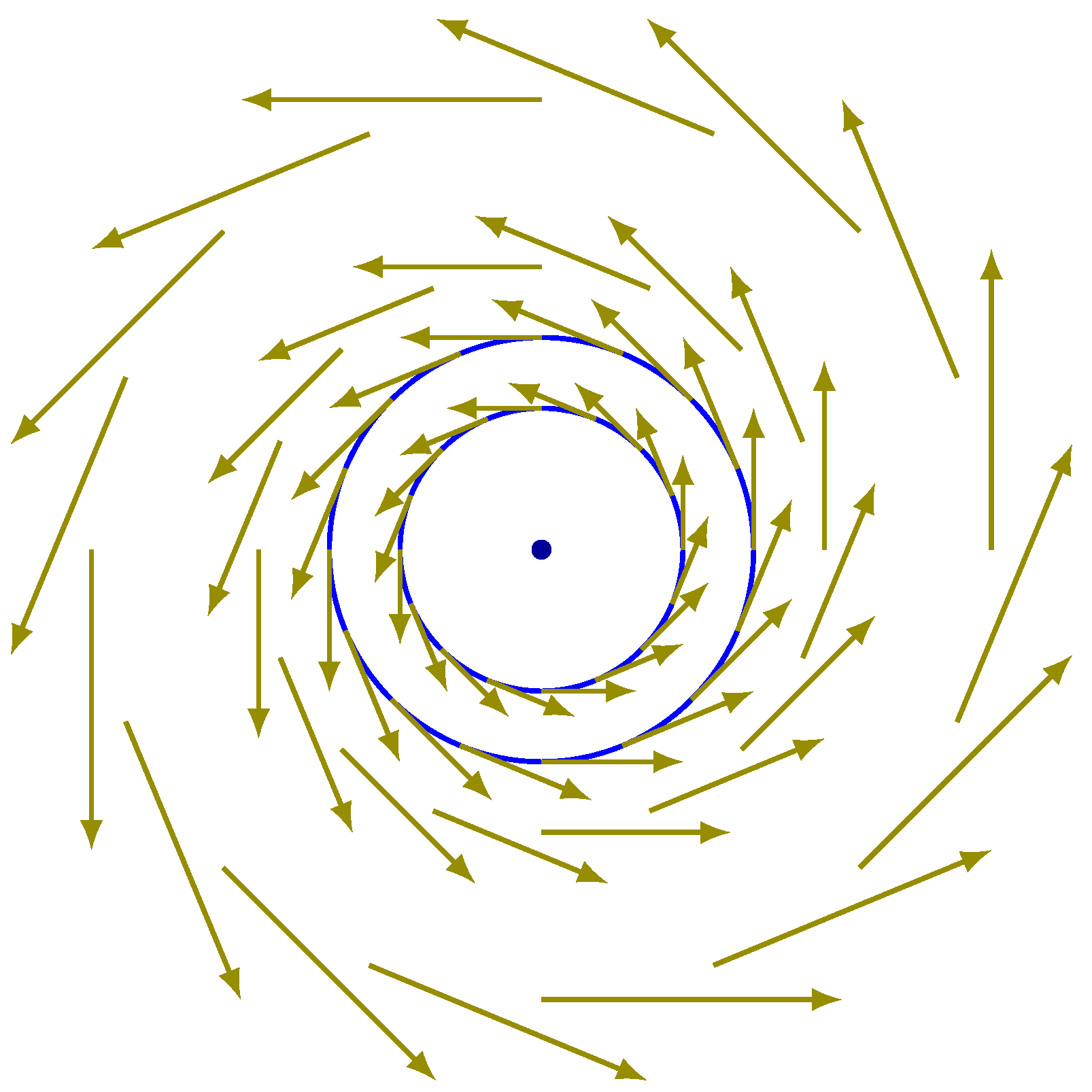
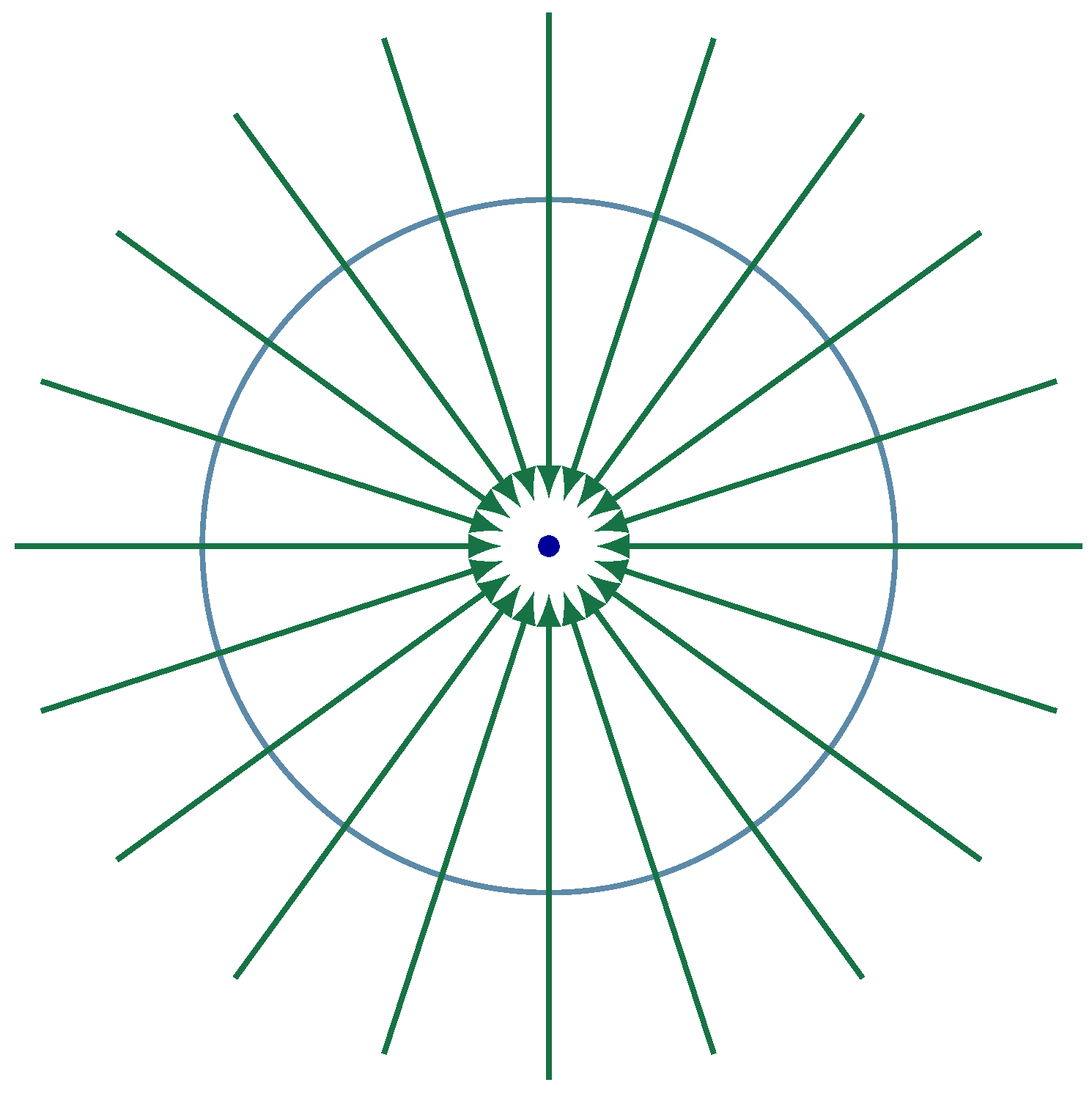
Now,
Figure 10 displays the vector field corresponding to
in a region without equilibria. It is possible to infer that the Poincaré index of the circle is zero.
5. Conclusions
By leaving the complex numbers’ realm it was possible to arrive at a satisfactory conclusion about the Riemann hypothesis. By using concepts of the theory of dynamical systems and a specific vector field constructed with basis in the Dirichlet eta function, the negation of the Riemann hypothesis provoked a logical contradiction, leading to the conclusion it is true.
The underlying method used in this paper may be directed to any complex function, provided it satisfies certain (not very restrictive) regularity conditions, including Dirichlet L-functions and so many others [
20].
References
- ALEKSANDROV, Alexander G. The Poincaré index and its applications. Universe, v. 8, n. 4, p. 223, 2022.
- A. A. Andronov, E. A. Leontovich, I. I. Gordon and A. G. Maier, Qualitative Theory of Second-Order Dynamic Systems. Halsted Press, New York, 1973.
- A. A. Andronov, E. A. Leontovich, I. I. Gordon and A. G. Maier, Theory of Bifurcations of Dynamical Systems on a Plane. Wiley, New York, 1973.
- N. ARWASHAN, THE RIEMANN HYPOTHESIS AND THE DISTRIBUTION OF PRIME NUMBERS, Nova Science Publisher Inc, 2021.
- V. I. Arnold, Mathematical Methods of Classical Mechanics, Springer, New York, 1989.
- V. I. Arnold, Geometrical Methods in the Theory of Ordinary Differential Equations, Springer, New York, 1983.
- D. K. Arrowsmith and C. M. Place, Ordinary Differential Equations. A Qualitative Approach with Applications. Chapman & Hall, London, 1982.
- F. Brauer, J. A. Nohel, The Qualitative Theory of Ordinary Differential Equations: An Introduction. Courier Corporation, New York,1989.
- J. Derbyshire, Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics. New York, Penguin, 2004.
- Edwards, H. M. Riemann’s Zeta Function. New York: Dover, 2001.
- J. Guckenheimer and P. Holmes, Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields, Springer, New York, 2013.
- J. K. Hale, Ordinary Differential Equations. Robert E. Krieger Publishing Co. Inc., New York,1980.
- P. Hartman, Ordinary Differential Equations. John Wiley & Sons, New York, 1964.
- K. Knopp, Theory and Application of Infinite Series, Dover, 1990.
- S. Lang, Complex Analysis, 4th ed., Springer-Verlag, 1999.
- C. H.C. Little, K. L. Teo, B. van Brunt, Real Analysis via Sequences and Series, Springer, New York, 2015.
- R. Marangell, Index Theory Lecture Notes, University of Sydney, 2017.
- M. Mureşan, A Concrete Approach to Classical Analysis, Springer-Verlag, New York, 2009.
- Z. Nitecki, Differentiable Dynamics - An Introduction to the Orbit Structure of Diffeomorphisms. The MIT Press, New York, 1971.
- H. Oliveira. Existence of Zeros for Holomorphic Complex Functions: A Dynamical Systems Approach. Preprints 2023, 2023090357. [CrossRef]
- L. Perko, Differential Equations and Dynamical Systems. Springer Science & Business Media, New York, 2001.
- E. C. Titchmarsh. The Theory of the Riemann Zeta Function, 2nd edition, Oxford University Press, 1986.
- S. Wiggins. An introduction to applied nonlinear dynamical systems and chaos 2nd ed., Springer, 2003.
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

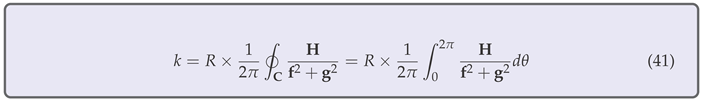
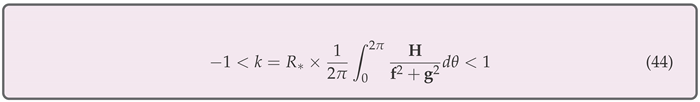 As by definition, it must be equal to zero.
As by definition, it must be equal to zero.