Flow Governed by Generalized Brinkman’s Equation through an Inclined Porous Channel

Preprint

Article

Flow Governed by Generalized Brinkman’s Equation through an Inclined Porous Channel

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

04 September 2023

Posted:

07 September 2023

You are already at the latest version

Alerts

Abstract

Unidirectional flow of a fluid with pressure-dependent viscosity through a porous structure is considered when the viscosity-pressure relationship is an exponential function of a pressure power function in order to investigate effects of the viscosity-pressure relation on the flow characteristics. The flow is governed by the generalized Brinkman’s equation with constant permeability, and a model flow domain of flow down an inclined porous channel is chosen for the sake of studying flow behaviour. Although the current work considers flow in a constant permeability porous structure, it does represent a first step in studying the more general, flow through a variable permeability porous channel. The arising governing equations are solved numerically using MATLAB and the flow is simulated to illustrate the effects of fluid properties as well as flow and medium parameters on the velocity profiles and shear stress.

Keywords:

Subject: Engineering - Mechanical Engineering

1. Introduction

The main objective of this work is to study the effects of viscosity variations due to pressure on the flow through a porous structure of an incompressible fluid, governed by the generalized Brinkman equation. In particular, viscosity,

μ

, is taken as an exponential function of pressure,

p

, of the form:

μ (p) = f (p) = μ_{0} e^{({(\frac{p}{p_{0}})}^{n} - 1)}

(1)

where

α \geq 0

p_{0} > 0

n \geq - 1

, and

μ_{0} = f (p_{0}) > 0

is the constant viscosity when

α = 0

and

p = p_{0}

The realization that changes in flow conditions (such as changes in temperature and pressure) result in corresponding changes in the viscosity of a flowing fluid dates back to the works of Stokes, [1], and Barus, [2]. With increasing temperature, viscosity of a fluid decreases, while an excessive increase in pressure could result in an increase in fluid viscosity. Barus, [2], suggested that viscosity is an exponentially increasing function of pressure of the form:

μ = μ_{0} e^{α (p - p_{0})}

(2)

For small values of

α

or small pressure differences, relationship (2) between viscosity and pressure can be expressed as, [3]:

μ = μ_{0} [1 + α (p - p_{0})]

(3)

It has been customary to assume that in the flow of Newtonian liquids in the absence of temperature variations, shear viscosity is constant (cf. [4] and the references therein). This assumption ignores the effects of pressure on viscosity when the fluid pressure is of the order of 1000 atm., [3,5].

While the above relationships, (2) and (3), are suitable for fluids with small molecules, long chain molecules (the likes of polymers and some oil mixtures) require other forms of viscosity-pressure relations, [3,6,7]. It has also been realized that the effect of pressure on density of a fluid is small as compared to the effect of pressure on viscosity, [6,7,8]. Accordingly, it suffices in many applications to study incompressible fluid flow with pressure-dependent viscosity as governed by the equation of continuity and the Navier-Stokes equations, written here for steady flow, in the absence of body forces, in the following forms, [3,9,10], respectively:

\nabla \cdot \vec{u} = 0

(4)

ρ \vec{u} \cdot \nabla \vec{u} = - \nabla p + \nabla \cdot \vec{T} + ρ \vec{g}

(5)

where

\vec{T} = - p \vec{I} + 2 μ (p) \vec{K}

(6)

is the Cauchy stress tensor in which

\vec{K} = \frac{1}{2} (\nabla \vec{u} + (\nabla \vec{u})^{T})

(7)

is the symmetric part of the velocity gradient,

\vec{u}

is the velocity field,

ρ

is the constant fluid density, and

ρ \vec{g}

is the gravitational force per unit volume.

Governing equations (4) and (5), with

\vec{T}

and

\vec{K}

defined by (6) and (7), represent an underdetermined system of four equations in the five unknowns

\vec{u} = (u, v, w)

p

and

μ

. In the absence of additional conservation principles to provide an additional equation, viscosity can be expressed as a function of pressure (such as in (2) and (3)) to provide an additional condition to render the governing system of equations determinate.

In addition to the flow conditions’ influence on viscosity, there are flow domain conditions that could result in changes in viscosity of a flowing fluid. For instance, in fluid flow through domains with constrictions and in porous structures, it has been suggested by a large number of researchers that the effective viscosity of a fluid in a porous structure is different than the viscosity of the base fluid (cf. [11] and the references therein). It can be argued that Brinkman’s equation accounts for viscosity change due to domain constrictions by introducing an effective viscosity term. However, it does not explicitly take into account spatial variations of viscosity, or viscosity variations due to changes in pressure, which is a function of position, (cf. [12] and the references therein).

When the flow is taken through a porous medium, Navier-Stokes equations are valid microscopically in the pore space. However, they are hard to track due to the complexity of the pore space. Furthermore, changes in flow quantities at the microscopic scale are at times insignificant at the macroscopic scale. The equations governing the flow of a fluid with pressure-dependent viscosity through a porous structure are the continuity equation, of the form of (4), and the momentum equation proposed by Rajagopal et.al, [10], referred to as the generalized Brinkman’s equation. For the purposes of this work, the generalized Brinkman’s equation is conveniently written in the following form:

ρ (\vec{u} \cdot \nabla) \vec{u} = - \nabla p + \nabla \cdot μ (\nabla \vec{u} + {(\nabla u)}^{T}) - Γ (p) \vec{u} + ρ \vec{g}

(8)

where

\vec{u}

in (4) and (8) now stands for the Brinkman velocity vector,

μ = μ (p)

, and

Γ (p)

is the pressure-dependent drag coefficient. Both

μ (p)

and

Γ (p)

control variations in viscosity due to pressure, and variations in pressure due to variations in porous parameters. In particular, Subramanian and Rajagopal, [13], identified

μ (p)

with the measure of resistance between fluid layers while

Γ (p)

is a measure of friction between solid and fluid at the pore.

Various forms and combinations of

μ (p)

and

Γ (p)

have been suggested and used in the literature, popular among which are the following forms, [14]:

μ (p) = A e^{a p} Γ (p) = B e^{b p}

(9)

μ (p) = A e^{a p} Γ (p) = B {(\frac{p}{p_{0}})}^{m}

(10)

μ (p) = A {(\frac{p}{p_{0}})}^{n} Γ (p) = B e^{b p}

(11)

μ (p) = A {(\frac{p}{p_{0}})}^{n} Γ (p) = B {(\frac{p}{p_{0}})}^{m}

(12)

wherein

A

B

a, b, m, n

are constants.

Considering that flow through a porous structure is influenced in part by permeability to the flow, Alharbi et.al., [11], suggested that

Γ (p) = \frac{μ (p)}{k}

, where k is the permeability, and provided the following form of momentum equation (8):

ρ (\vec{u} \cdot \nabla) \vec{u} = - \nabla p + \nabla \cdot μ (\nabla \vec{u} + {(\nabla \vec{u})}^{T}) - \frac{μ (p)}{k} \vec{u} + ρ \vec{g}

(13)

It is conceivable that the use of (8) or (13) is predicated by the type of practical application being considered, and by the porous microstructure. In general, flow through porous media has well established applications that include the study of groundwater movement, oil and gas recovery, flow through membranes and kidney dialysis, air conditioning and heat transfer, and the drying of solids, (cf. [15] and the references therein). Flow with high pressures arise in a number of industrial applications that involve chemical and process technologies, such as medical tablet production, crude and fuel oil pumping, food processing, fluid-film lubrication theory, and in microfluidics, [3 ,4,5,16,17,18,19,20]. The form of governing equations used must accommodate and describe the different types of fluid flow, flow conditions, and the anticipated porous structure, [12,21,22].

In the current work, the objective is to study the effects of porous medium permeability, and the form of dependence of viscosity on pressure, on characteristics of the flow. In particular, relationship (1) between viscosity and pressure is employed in this work in order to study the effects of

n

. Cases where

n

is a positive integer are investigated, together with the case when

n = - 1

, which results in a decrease in the exponent with increasing pressure distribution. For comparison, the case of

n = 0

is considered. This case corresponds to flow with constant fluid viscosity.

To accomplish the above objective, model equation (13) will be used under the assumption of a constant permeability at this stage, while the more realistic variable permeability considerations will be considered in future work and after quantification of constant permeability influence on the flow. In order to quantify the effects of relationship (1) on the flow characteristics, unidirectional flow through an inclined porous channel is considered under variations in six parameters. The six parameters to be investigated are the angle of inclination of the channel to the horizontal; pressure-control parameter,

α

; medium permeability,

k

; constant reference pressure,

p_{0}

(taken as atmospheric pressure at upper channel wall); constant reference viscosity,

μ_{0}

, taken as the value of viscosity at pressure

p_{0}

; and variations in

n

(namely, the values -1, 0, 1, 2, and 3).

All solutions and simulations used in this work have been carried out using MATLAB software package, version R2022a. However, for the sake of comparison and validation of the numerical results, the analytic solution to the flow problem at hand is obtained for the case of

n = 1

. Comparisons of flow characteristics obtained using the analytic solution and those obtained using MATLAB are made.

2. Problem Formulation

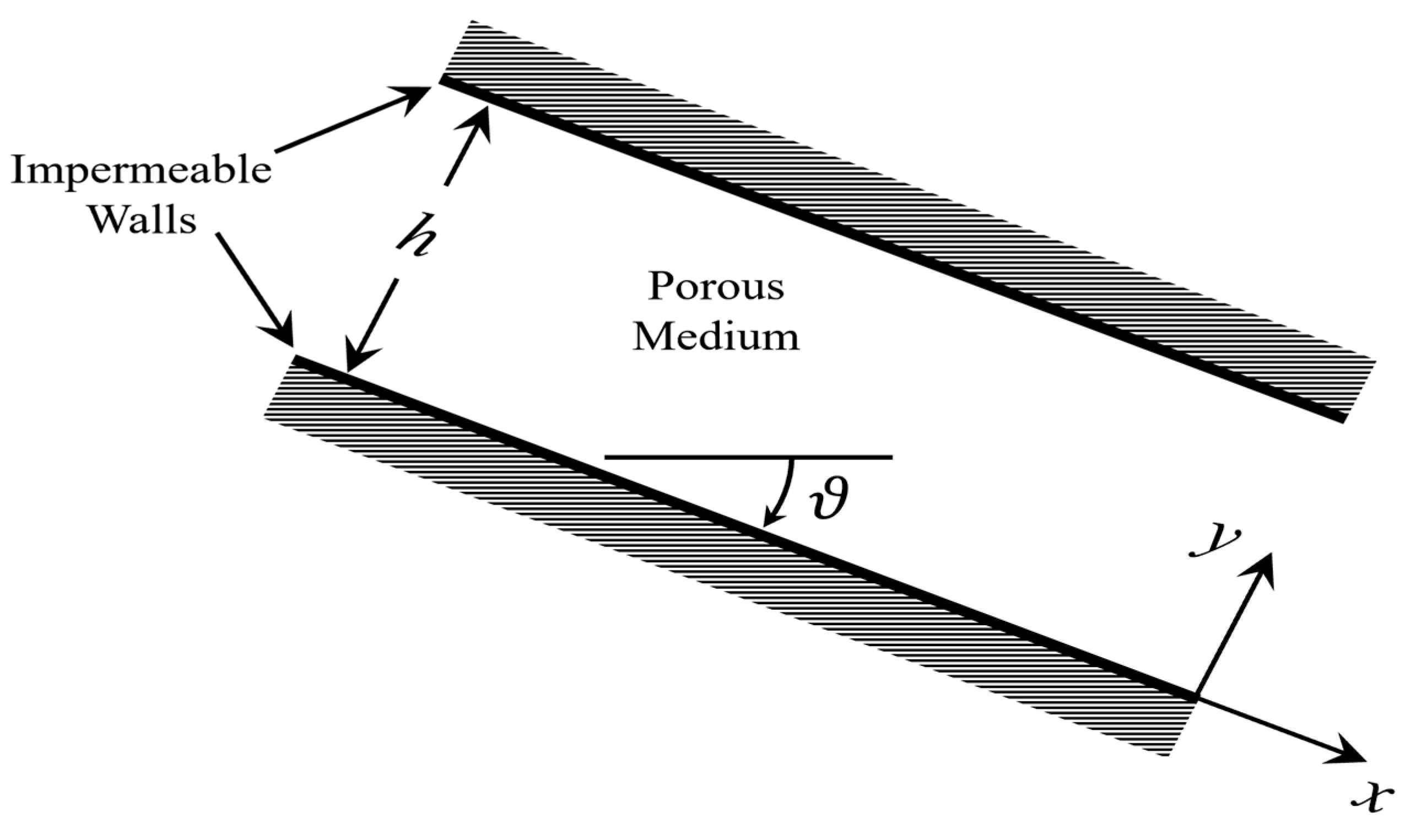
Consider the flow of a fluid with pressure-dependent viscosity through a porous sediment of depth h inclined at angle

ϑ

to the horizontal. The flow configuration is illustrated in Figure 1 which shows the orientation of the coordinate system used. It is assumed that the sediment is bounded by impermeable, solid walls on which the no-slip condition is applied.

Flow in the above domain is governed by the equation of continuity (4) and momentum equations (13), which reduce to the following set of equations, wherein

u = u (y)

is the tangential velocity component and

g

is acting vertically downward:

- \frac{d p}{d x} + μ \frac{d^{2} u}{{d y}^{2}} + \frac{d μ}{d y} \frac{d u}{d y} + ρ g s i n ϑ - \frac{μ}{k} u = 0

(14)

- \frac{d p}{d y} - ρ g c o s ϑ = 0

(15)

with boundary conditions given by zero-slip on the solid boundaries

y = 0

and

y = h

, and a prescribed pressure at

y = h

(such as atmospheric pressure, say

p_{0}

). Boundary conditions are thus given as:

u (0) = 0, u (h) = 0, p (h) = p_{0}

(16)

Introducing the dimensionless quantities defined as:

y^{*} = \frac{y}{h}; u^{*} = \frac{u}{\sqrt{g h}}; p^{*} = \frac{p}{ρ g h}; μ^{*} = \frac{μ}{ρ h \sqrt{g h}}; k^{*} = \frac{k}{h^{2}}

(17)

then boundary conditions, (16), and governing equations (14) and (15) take the following dimensionless forms, respectively, after dropping the asterisks “*”:

u (0) = 0, u (1) = 0, p (1) = p_{0}

(18)

μ \frac{d^{2} u}{{d y}^{2}} + \frac{d μ}{d y} \frac{d u}{d y} + s i n ϑ - \frac{μ}{k} u = 0

(19)

\frac{d p}{d y} = - c o s ϑ

(20)

We note that in (17), the velocity scale has been set to

\sqrt{g h}

, which renders the resulting solution readily applicable as the velocity scale depends on physical parameters of the problem. Furthermore, since

\sqrt{g h}

is the velocity scale,

u^{*}

is the local Froude number and

μ^{*} = \frac{1}{R e}

, where

R e

is the Reynolds number.

The general solution to (20) takes the form

p = c - y c o s ϑ

(21)

where c is an arbitrary constant.

Using pressure condition

p (1) = p_{0}

we find that

c = p_{0} + c o s ϑ

and (21) takes the form

p = p_{0} + (1 - y) c o s ϑ

(22)

In order to solve (19) for

u (y)

, we assume that the viscosity varies with pressure. We thus let

μ (p) = f (p)

(23)

where

f (p)

is a function of

p

(to be specified).

From (23), we obtain

\frac{d μ}{d y} = \frac{d μ}{d p} \frac{d p}{d y} = f^{'} (p) \frac{d p}{d y}

(24)

From (22), we obtain

\frac{d p}{d y} = - c o s ϑ

(25)

Using (25) in (24), we obtain

\frac{d μ}{d y} = {- c o s ϑ f}^{'} (p)

(26)

Using (23) and (26) in (19), we obtain

f (p) \frac{d^{2} u}{{d y}^{2}} {- c o s ϑ f}^{'} (p) \frac{d u}{d y} + s i n ϑ - \frac{f (p)}{k} u = 0

(27)

\frac{d^{2} u}{{d y}^{2}} - c o s ϑ \frac{f^{'} (p)}{f (p)} \frac{d u}{d y} - \frac{u}{k} = - \frac{s i n ϑ}{f (p)}

(28)

Equation (28) is a general differential equation that governs the flow of a fluid with pressure-dependent viscosity through a porous domain down an inclined plane. Given

f (p)

and

k

, specific forms of (28) are obtained. A form of interest to this work from a fundamental analysis point of view is the following:

f (p) = μ_{0} e^{α ({(\frac{p}{p_{0}})}^{n} - 1)} = {A μ}_{0} e^{{(\frac{p}{p_{0}})}^{n}}

(29)

where

A = e^{- α}

α > 0, μ_{0} = f (p_{0}) > 0 i s t h e v i s c o s i t y a t y = 1, w h e r e p = p_{0} > 0

, and

n \geq - 1

is an integer.

Using (29) in (28), the following governing differential equation is obtained:

\frac{d^{2} u}{{d y}^{2}} - c o s ϑ \frac{α n (p)^{n - 1}}{{(p}_{0})^{n}} \frac{d u}{d y} - \frac{u}{k} = - \frac{s i n ϑ}{A μ_{0} e^{α {(\frac{p}{p_{0}})}^{n}}}

(30)

Letting

P = \frac{p}{p_{0}}

(31)

then (17) can be written as:

P = \frac{p}{p_{0}} = B - C y

(32)

where

B = 1 + C

and

C = \frac{c o s ϑ}{p_{0}}

Using (31) and (32), equation (30) can be written as:

\frac{d^{2} u}{{d y}^{2}} - α n C (B - C y)^{n - 1} \frac{d u}{d y} - \frac{u}{k} = - \frac{s i n ϑ}{A μ_{0} e^{α (B - C y)^{n}}}

(33)

Equation (33) is to be solved subject to no-slip conditions in (16). Solution to (33) is obtained numerically using MATLAB. However, when

n = 1

, (33) reduces to

\frac{d^{2} u}{{d y}^{2}} - α C \frac{d u}{d y} - \frac{u}{k} = - \frac{s i n ϑ}{A μ_{0} e^{α B}} e^{α C y}

(34)

whose general solution takes the form:

u = b_{1} e^{m_{1} y} + b_{2} e^{m_{2} y} + \frac{k s i n ϑ e^{α C y}}{A μ_{0} e^{α B}}

(35)

Using (35) and (16), the following solution to the boundary value problem is obtained:

u = \frac{k s i n ϑ}{A μ_{0} e^{α B}} \{[\frac{e^{α C} {- e}^{m_{2}}}{e^{m_{2}} - e^{m_{1}}}] e^{m_{1} y} + [\frac{{e^{m_{1}} - e}^{α C}}{e^{m_{2}} - e^{m_{1}}}] e^{m_{2} y} + e^{α C y}\}

(36)

where

m_{1} = \frac{α C - \sqrt{α^{2} C^{2} + \frac{4}{k}}}{2}

(37)

m_{2} = \frac{α C + \sqrt{α^{2} C^{2} + \frac{4}{k}}}{2}

(38)

Using (36), vorticity,

ω

, is obtained as:

ω = - \frac{d u}{d y} = - \frac{m_{1} k s i n ϑ}{A μ_{0} e^{α B}} \{[\frac{e^{α C} {- e}^{m_{2}}}{e^{m_{2}} - e^{m_{1}}}] e^{m_{1} y} - m_{2} [\frac{{e^{m_{1}} - e}^{α C}}{e^{m_{2}} - e^{m_{1}}}] e^{m_{2} y} - α C e^{α C y}\}

(39)

and the shear stress,

τ

, takes the following form:

τ = μ \frac{d u}{d y} = - μ ω = {- A μ}_{0} e^{α (B - C y)^{n}} ω

(40)

Total shear stress is given by

\frac{d}{d y} (μ \frac{d u}{d y}) = \frac{d}{d y} (- μ ω) = {\frac{d}{d y} {- A μ}_{0} e^{α (B - C y)^{n}} ω}

(41)

3. Results and Discussion

The solution given by equation (36) was tabulated for the Reference Case given in Table 1 and compared to the numerical solution calculated with MATLAB. The magnitude of the difference in the values of

u

between the two solutions across the channel was less than

4 \times 1 0^{- 17}

Equation (33) was solved numerically using the bvp5c algorithm in MATLAB R2022a which is described by Kierzenka and Shampine [23] with the relative and absolute tolerances set to

1 \times 10^{- 12}

. Results have been obtained for the ranges of flow and domain parameters given in Table 1:

Table 1. Ranges of Flow and Domain Parameters.

Case	1	2	3	4	5	6
Parameter			Reference Case
$ϑ$	$15^{°}$	$30^{°}$	$45^{°}$	$60^{°}$	$75^{°}$	$90^{°}$
$μ_{0}$	$10^{- 1}$	$10^{- 0.5}$	1	$10^{0.5}$	$10^{1}$	-
$p_{0}$	$10^{- 1}$	$10^{- 0.5}$	1	$10^{0.5}$	$10^{1}$	-
$α$	$10^{- 1}$	$10^{- 0.5}$	1	$10^{0.5}$	$10^{1}$	-
$n$	-1	0	1	2	3
$k$	$10^{- 4}$	$10^{- 3}$	$10^{- 2}$	$10^{- 1}$	1	-

The column with Reference Case heading in Table 1 is used to isolate phenomena and contains the fixed values of parameters when a particular parameter is under investigation. The graphical results for the Reference Case appear in all of the parametric studies to facilitate comparison. For instance, to study the effects of changes in

α

, its values are varied as listed in the horizontal row labelled

α

in Table 1, namely

α

takes the range of values 10^-1, 10^-0.5, 1, 10^0.5, and 10¹, while other parameters’ fixed values are listed in the reference case column, namely

ϑ = 45^{°}

μ_{0} = 1

p_{0} = 1

n = 1

, and

k = 10^{- 2}

In the discussion that follows, effects of the parameters of Table 1 on viscosity and pressure distributions, velocity profiles, shear stress and viscous drag and resistance to the flow are discussed.

Six parametric studies will be presented in the following order:

ϑ, μ_{0}, p_{0}, α, n

, and

k

. The results for each parametric study include (1) velocity profiles,

u (y)

; (2) viscosity profiles,

μ (y)

; (3) Darcy friction profiles,

- μ (y) (\frac{u (y)}{k})

; (4) the net force on a differential fluid element due to variation of the shear strain rate across the fluid element,

μ (\frac{d^{2} u}{d y^{2}})

; (5) the net force on a differential fluid element due to variation of the viscosity across the fluid element,

(\frac{d μ}{d y}) (\frac{d u}{d y})

; and (6) the dimensionless volumetric flowrate in the channel,

Q

Items (3)-(5) show the spatial variation each of the forces present in the dimensionless force balance given by equation (19) and must sum to

- \sin (ϑ)

, the component of the fluid’s weight acting along the incline. Presentation of the results in this manner aids in the development of an understanding of the physical phenomena involved in the resulting velocity profiles. Note that in some instances semi-logarithmic axes are used to better illustrate the results when the quantity in question varies over orders of magnitude.

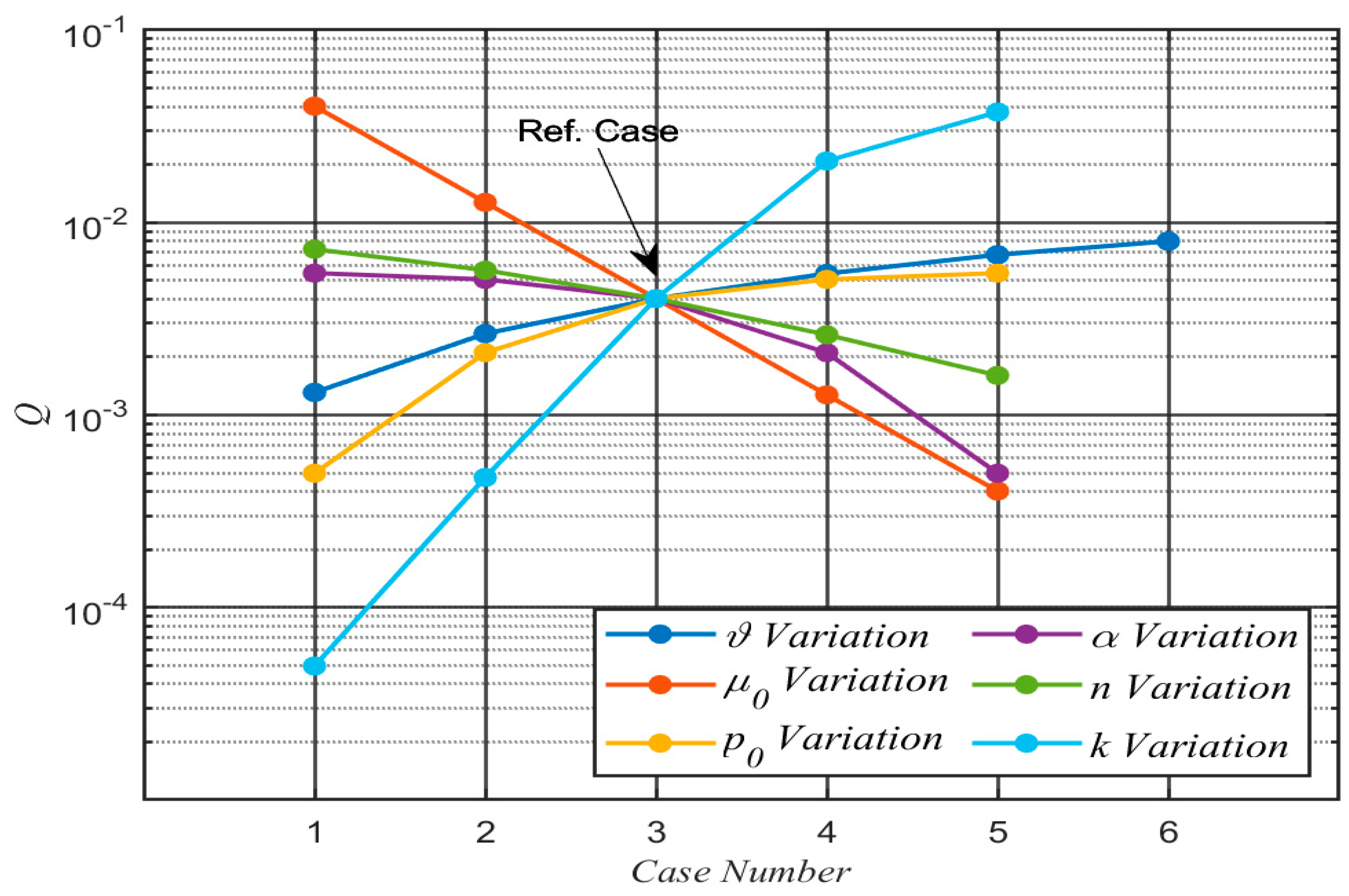
A visual display of the ranges of Table 1 is shown in Figure 2, below, to demonstrate increase and decrease of the chosen values for the parameters relative to each other and how they influence the dimensionless volumetric flowrate in the channel,

Q

. Figure 2 shows that an increases in

μ_{0}

results in a linear decrease in

Q

. It also illustrates the expected largest rate of increase in

Q

with increasing permeability,

k

3.1. Pressure and Viscosity Distributions

Prior to discussion of the resulting velocity and force profiles, the effects of the parameters on the pressure distribution, and hence the viscosity distributions, will be presented. Plots of the pressure across the channel are not included as they vary linearly according to equation (22).

In this work viscosity is taken to be a function of pressure as defined by equation (29), wherein parameters

n

and

α

are the viscosity distribution control parameters. Therefore, as the pressure varies due to hydrostatic forces, the fluid’s viscosity also varies across the channel. In practice, the values of

p_{0}

and

μ_{0}

n

and

α

can adjusted to reproduce the appropriate variation of the viscosity for the problem at hand. In the present study, their chosen ranges guarantee realistic viscosity values yet are varied enough to illustrate their effects on the flow. Other than the permeability,

k

, variations in all other parameters listed in Table 1 have a direct influence on viscosity across the channel, as discussed in what follows.

3.2. Effects of $ϑ$

Viscosity is assumed to be a function of pressure as given by (29) while the pressure in the channel is given by (22), namely

p (y) = p_{0} + (1 - y) c o s ϑ

. From this equation it is observed that the pressure has its smallest value,

p_{0}

, at the upper wall and increases linearly with decreasing

y

until it reaches its maximum

p_{0} + c o s ϑ

at the lower wall. Changes in pressure across the channel affect the viscosity distribution across the channel, and result in a maximum viscosity at the lower wall and a minimum at the upper wall (in all but one case, when

n = - 1

). Effects of

ϑ

u,

μ

Q

- \frac{μ u}{k}

μ \frac{d^{2} u}{d y^{2}}

, and

(\frac{d μ}{d y}) (\frac{d u}{d y})

are illustrated in Figure 3.

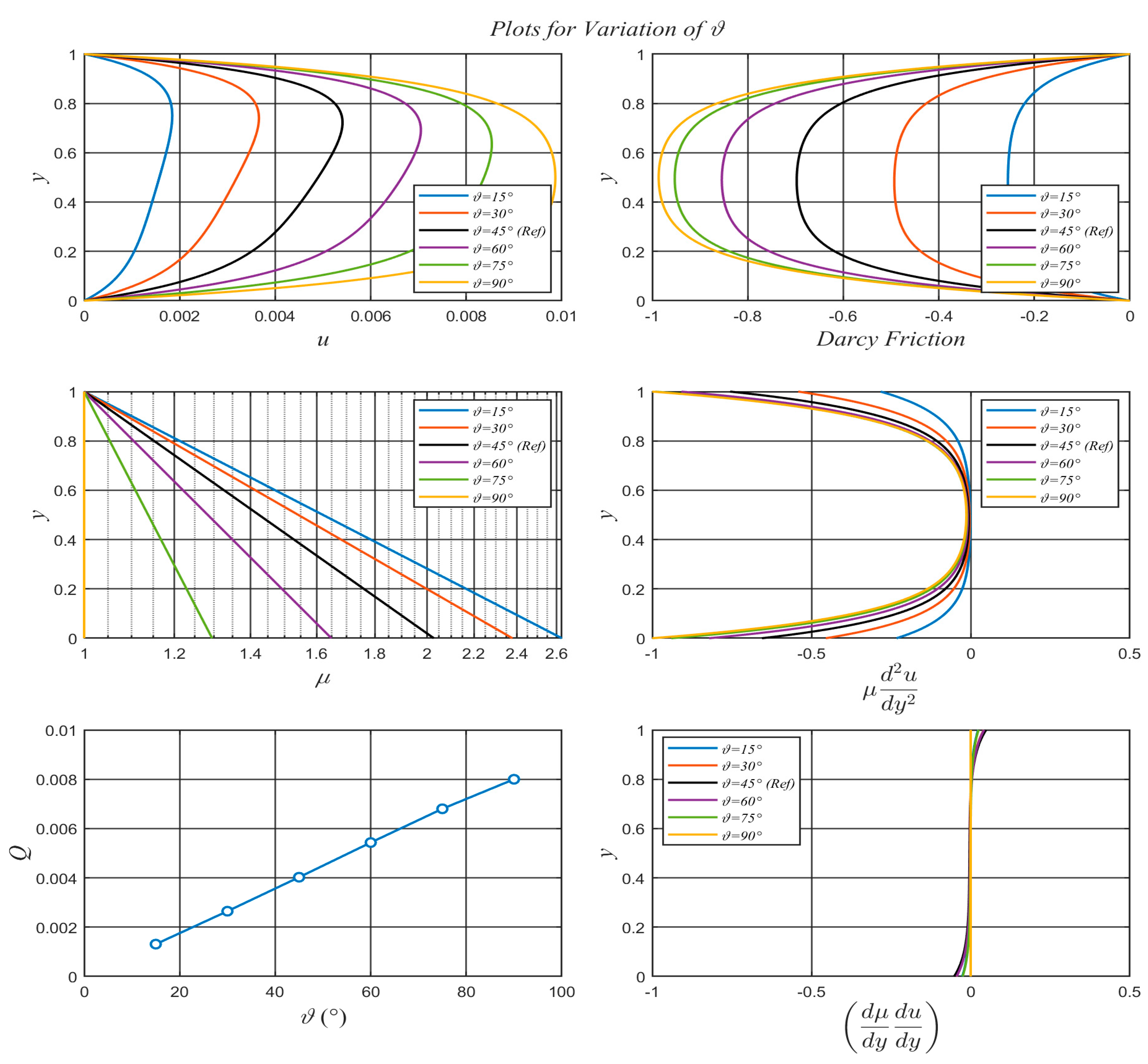
The inclinations of the flow domain used were

ϑ = 15 °, 30 °, 45 °, 60 °, 75 °, a n d 90 °

while all other parameters take on the values identified in the Reference Case given in Table 1. The variation of the angle has two distinct effects on the flow: the first is the variation of the pressure across the channel, and thereby the variation of the viscosity; the second effect is the variation of the component of gravitational acceleration along the incline, and therefor the driving force for the flow. When

ϑ = 0 °

the variation of the pressure across the channel is maximized but does not produce flow as there is no component of gravity acting along the incline. When the angle of inclination is

90^{°}

, equations (22) and (29) render

p (y) = p_{0}

and

μ (y) = μ_{0}

meaning the viscosity is constant across the channel.

The plots of the velocity profiles, which can be found in Figure 3 show that for the case of

ϑ = 90 °

, the velocity profile is symmetric about the center of the channel. This is a result of the unform pressure, and therefore uniform viscosity, across the channel. As

ϑ

decreases, the component of gravitational acceleration along the direction of flow decreases thereby reducing the overall driving force behind the flow. Furthermore, the higher viscosity as at the bottom of the channel, illustrated in Figure 3 causes the velocity to be lower near the bottom of the channel resulting in the asymmetry in the velocity profiles which becomes more pronounced at smaller values of

ϑ

. Despite the lower velocity, Figure 3 shows that the Darcy friction is significant and nearly symmetric across the channel with the low-speed regions corresponding to regions of high viscosity. As mentioned previously, when

ϑ = 90 °

there is no variation in pressure, and therefore viscosity, across the channel so

\frac{d μ}{d y} = 0

and a symmetric velocity profile and, therefor, symmetric distributions of Darcy friction and

μ (\frac{d^{2} u}{d y^{2}})

. Examining the cases of

ϑ \neq 90 °

, small asymmetries can be seen in all of the forces and in the case of

(\frac{d μ}{d y}) (\frac{d u}{d y})

, changes in direction of the force can be seen through the channel.

3.3. Effects of $μ_{0}$

Equation (29) suggests that

μ_{0}

is a “multiplier” of

μ (y)

, the dimensionless viscosity, across the channel. At

y = 1

, or the upper channel wall,

μ (1) = μ_{0}

, therefore, increasing

μ_{0}

results in increasing

μ (1)

. At the lower channel wall,

y = 0

, values of

μ (0)

are also dependent on

μ_{0}

, as calculated using (29) and (32), for a given value of

ϑ

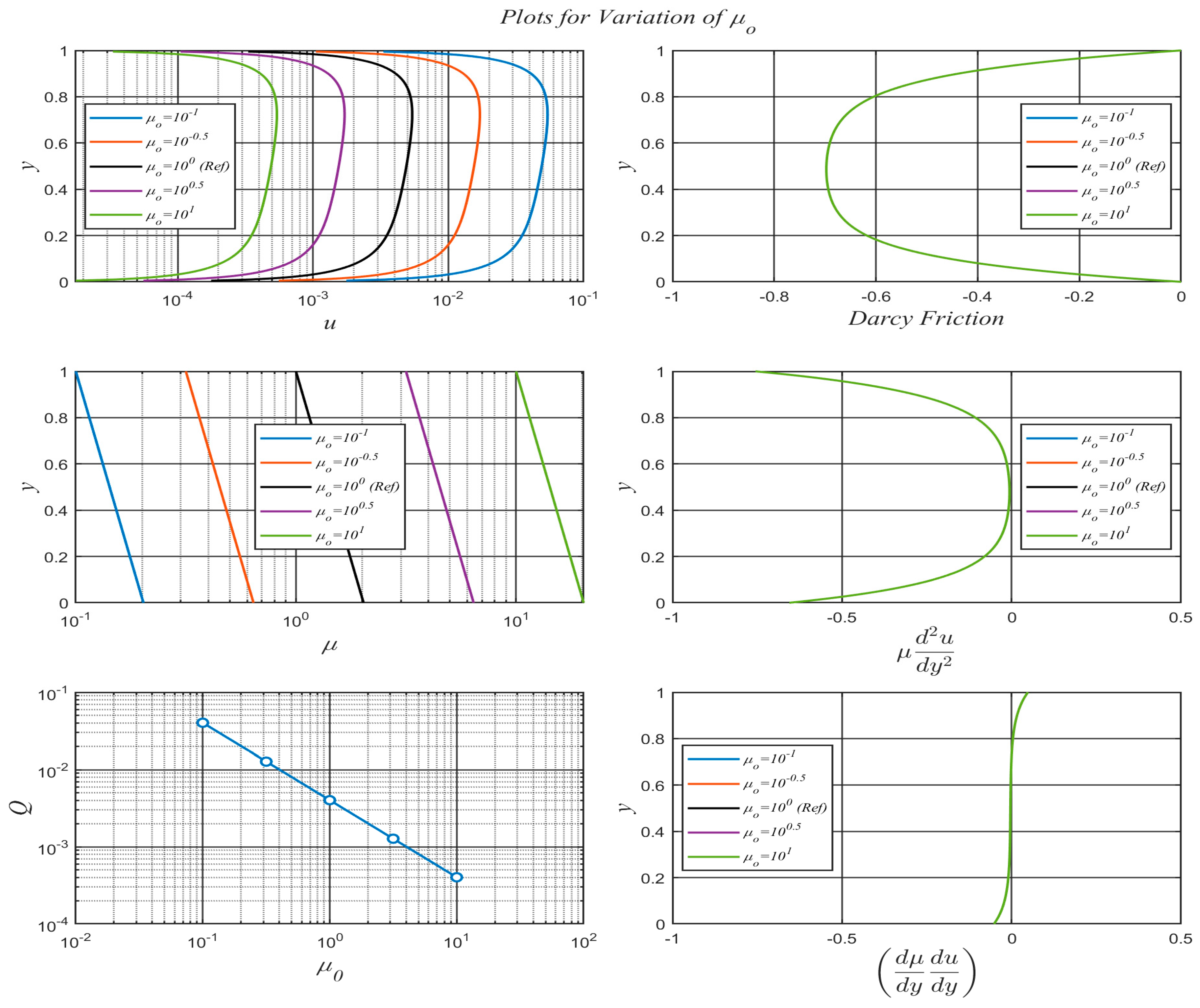
The results for logarithmically evenly spaced values of

μ_{0}

can be found in Figure 4 where

μ_{0} = 1 0^{- 1}, 10^{- 0.5}, 1, 10^{0.5}, a n d 1 0^{1}

while all other parameters take on the values identified in the Reference Case given in Table 1. Note that the velocity profiles are shown on a semi-log scale due to the significant reduction caused by the high viscosity flows. In terms of

μ

being the inverse of Reynolds number, an increase in

μ

implies a decrease in Reynolds number, hence a slower flow. As seen in Figure 4, the variation of

μ_{0}

produces a scaling of the velocity profile (and therefore

(\frac{d u}{d y}

) and

(\frac{d^{2} u}{d y^{2}})

) by a factor of

\frac{1}{μ_{0}}

. This is a result of each of these quantities being multiplied by

μ_{0}

in equation (27) or, as seen more directly in equation (33), the division of the RHS by

μ_{0}

. These effects combine to produce identical Darcy friction and viscous forces profiles for all values of

μ_{0}

. As a result of the velocity profiles scaling by the factor of

\frac{1}{μ_{0}}

, the dimensionless flowrate, Q, becomes a straight line when plotted on log-log axis. Since the profile of

(\frac{d μ}{d y}) (\frac{d u}{d y})

is not symmetric, the Darcy friction and

μ (\frac{d^{2} u}{d y^{2}})

also contain some slight asymmetry.

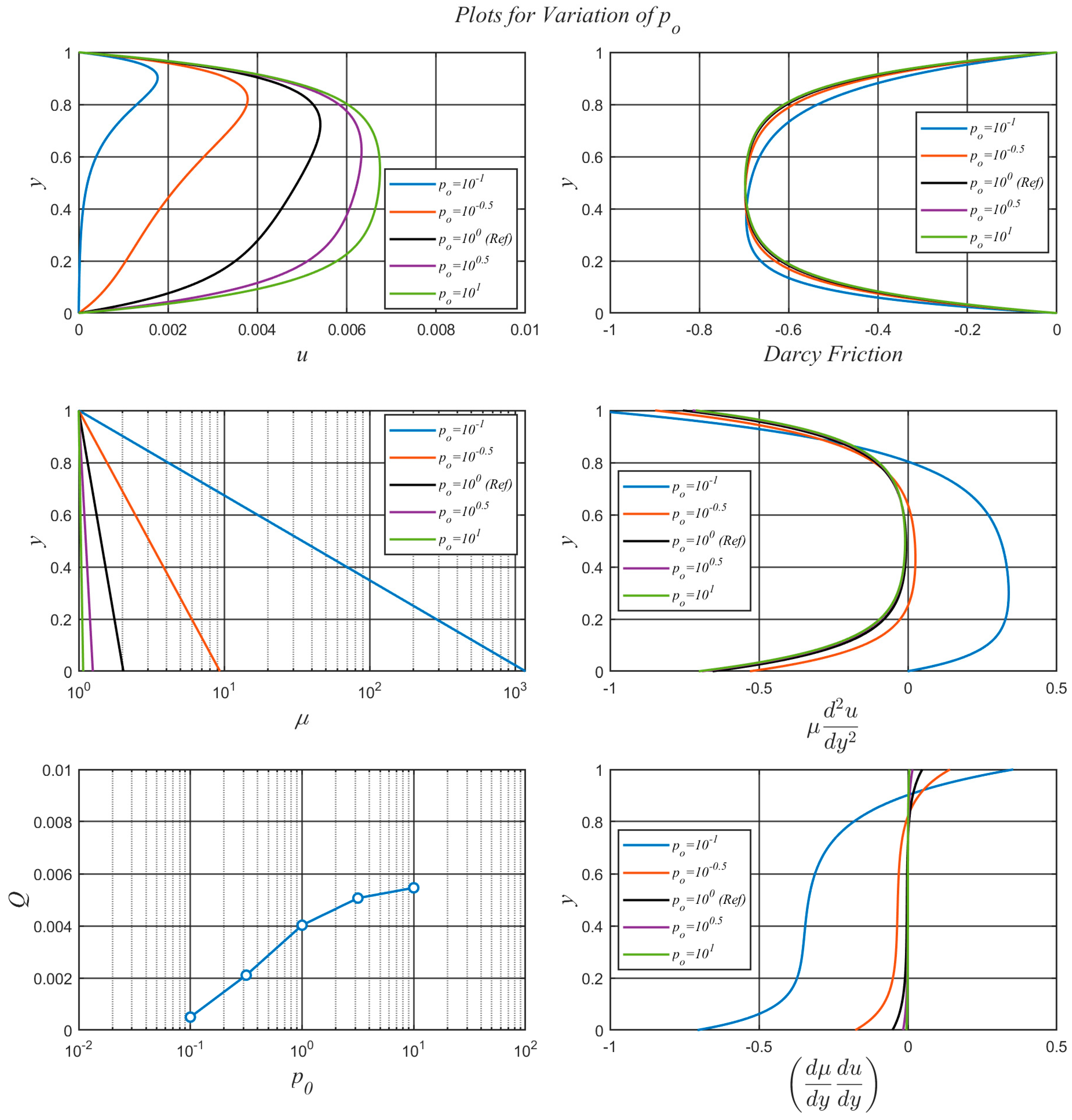
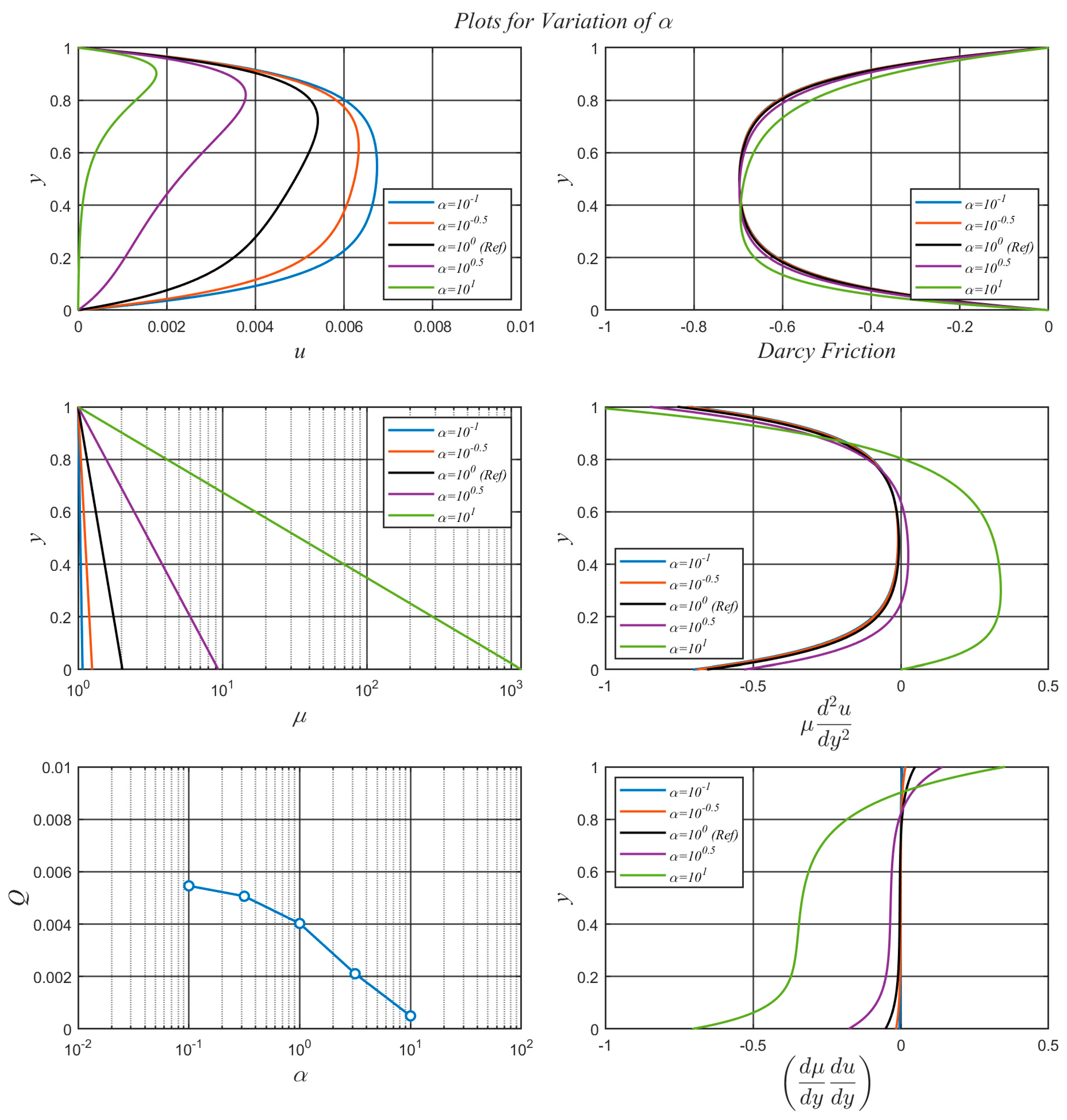
3.4. Effects of $p_{0}$ and $α$

The value of

p_{0}

is the value of pressure at the upper channel wall but also affects the pressure distribution across the channel as seen in equation (22). In equation (29),

p_{0}

appears in the denominator of the exponent that defines viscosity.

Parameter

α

is a viscosity-control parameter which, when varied on its own, adjusts the rate at which the viscosity changes with pressure. As seen in equation (29), an increase in

α

results in an increase in the exponent that defines viscosity as a function of pressure. Since the value of the viscosity on the upper channel wall is set via

μ_{0}

, increasing the value of

α

results in increasing the viscosity in the lower portion of the channel.

The effects of increasing

p_{0}

on viscosity distribution are, therefor, opposite to the effects of increasing

α

The results for the variation of

p_{0}

and

α

can be seen in Figure 5 and Figure 6, respectively, while all other parameters take on the values identified in the Reference Case given in Table 1. Increasing

p_{0}

translates into a higher value of pressure on the upper channel wall, due to pressure boundary condition there. At the lower channel wall,

y = 0

, equation (22) gives

{p (0) = p}_{0} + c o s ϑ

which, for a given

ϑ

, increases with increasing

p_{0}

. Pressure distribution across the channel, therefore, decreases from

{p (0) = p}_{0} + c o s ϑ

{p (1) = p}_{0}

. Clearly, the higher the value of

p_{0}

, the lower the ratio

P = \frac{p}{p_{0}}

that appears in equation (29). This implies that the viscosity across the channel decreases and offers less resistnce to the flow. The end result is that flow velocity increases with increasing

p_{0}

The effect of low

p_{0}

(high

α

) is to cause the viscosity to vary more rapidly throughout the channel thereby decreasing the flow’s velocity in the lower, highly viscous, regions of the domain. Furthermore, this rapid variation of viscosity across the channel causes significant variation of the shear force across a differential fluid element as seen in the plot of

(\frac{d μ}{d y}) (\frac{d u}{d y})

in Figure 5, and a corresponding change in

μ (\frac{d^{2} u}{d y^{2}})

; the latter developing a significant region of reversal of direction caused by the region of inflection in the velocity profile.

α \to 0^{+}

μ (y) \to μ_{0}

as can be seen from equation (29). When viscosity is constant across the channel, the velocity profile is near symmetric about the longitudinal centreline of the channel. As

α

increases, viscosity distribution across the channel decreases with increasing

y

, and the flow experiences more resistance in the lower parts of the channel. Velocity therefore decreases with decreasing

y

, accompanied with greater deviations from symmetry in the velocity profile. This behaviour is demonstrated in Figure 6 when

α

increases from 0.01 to 10.

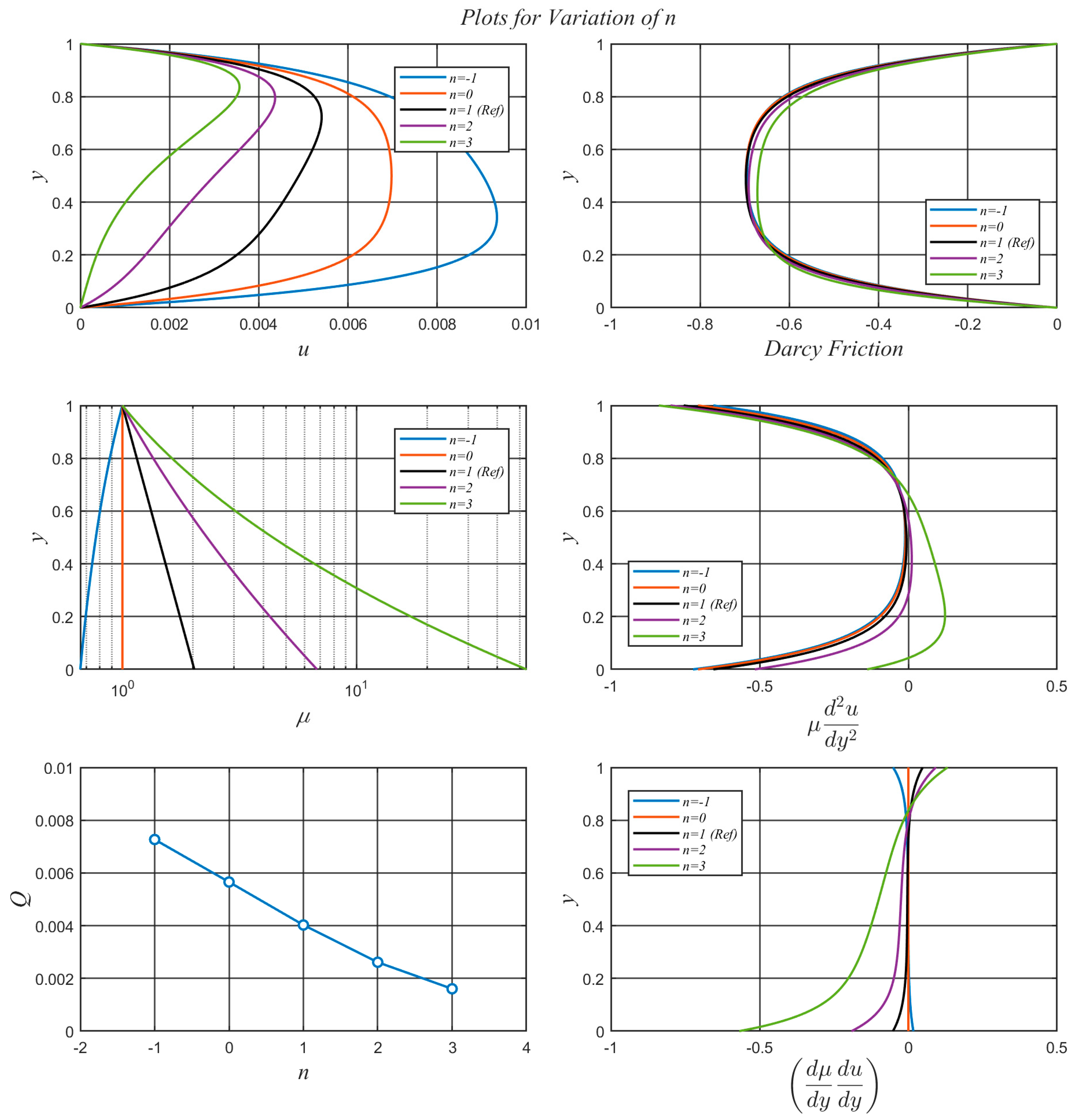
3.5. Effects of $n$

Effects of variations in

n

on the viscosity distribution

μ (y)

across the porous channel are illustrated in Figure 2 for the values of parameters identified in Table 1 as Reference Case. Figure 2 shows that at the upper channel wall,

y = 1

, viscosity is independent of

n

. This can be seen from equation (29) where at the upper wall

p = p_{0}

, hence

μ (1) = f (p_{0}) = μ_{0} = 1

for all values of

n

At the lower channel bounding wall,

y = 0

, equation (22) gives the pressure

p (0) = p_{0} + c o s 45^{°} = 1 + \frac{1}{\sqrt{2}} .

The quantity

\frac{p (0)}{p_{0}} = 1 + \frac{1}{\sqrt{2}}

results in increasing

μ (y)

with increasing

n

, as can be seen from equation (29). This translates into increasing

μ (0)

and an associated nonlinear increase in the viscosity profiles across the channel with increasing

n

The results from the variation of

n

can be found in Figure 7 for

n = - 1, 0, 1, 2, a n d 3

while all other parameters take on the values identified in the Reference Case given in Table 1. for the case of

n = 0

(\frac{d μ}{d y}) = 0

so the resulting flow is simply that of a constant viscosity fluid and corresponding symmetric velocity, Darcy friction, and

μ (\frac{d^{2} u}{d y^{2}})

profiles.

For the cases of

n > 0

μ

increases with depth thereby producing a reduction in the velocity in the lower part of the channel. In the extreme case of

n = 3

, a significant region of inflection is present in the velocity profile with a corresponding sign reversal of the viscous shear term

μ (\frac{d^{2} u}{d y^{2}})

. Furthermore, the dramatic variation of the viscosity is also seen to produce significant variation of

(\frac{d μ}{d y}) (\frac{d u}{d y})

across the domain.

For the case of

n = - 1

(\frac{d μ}{d y}) > 0

meaning that, unlike all of the other flows considered in this work, the viscosity decreases with depth. The reduction in viscosity with depth results in less resistance to flow in the lower portion of the channel and, therefore, higher velocities there.

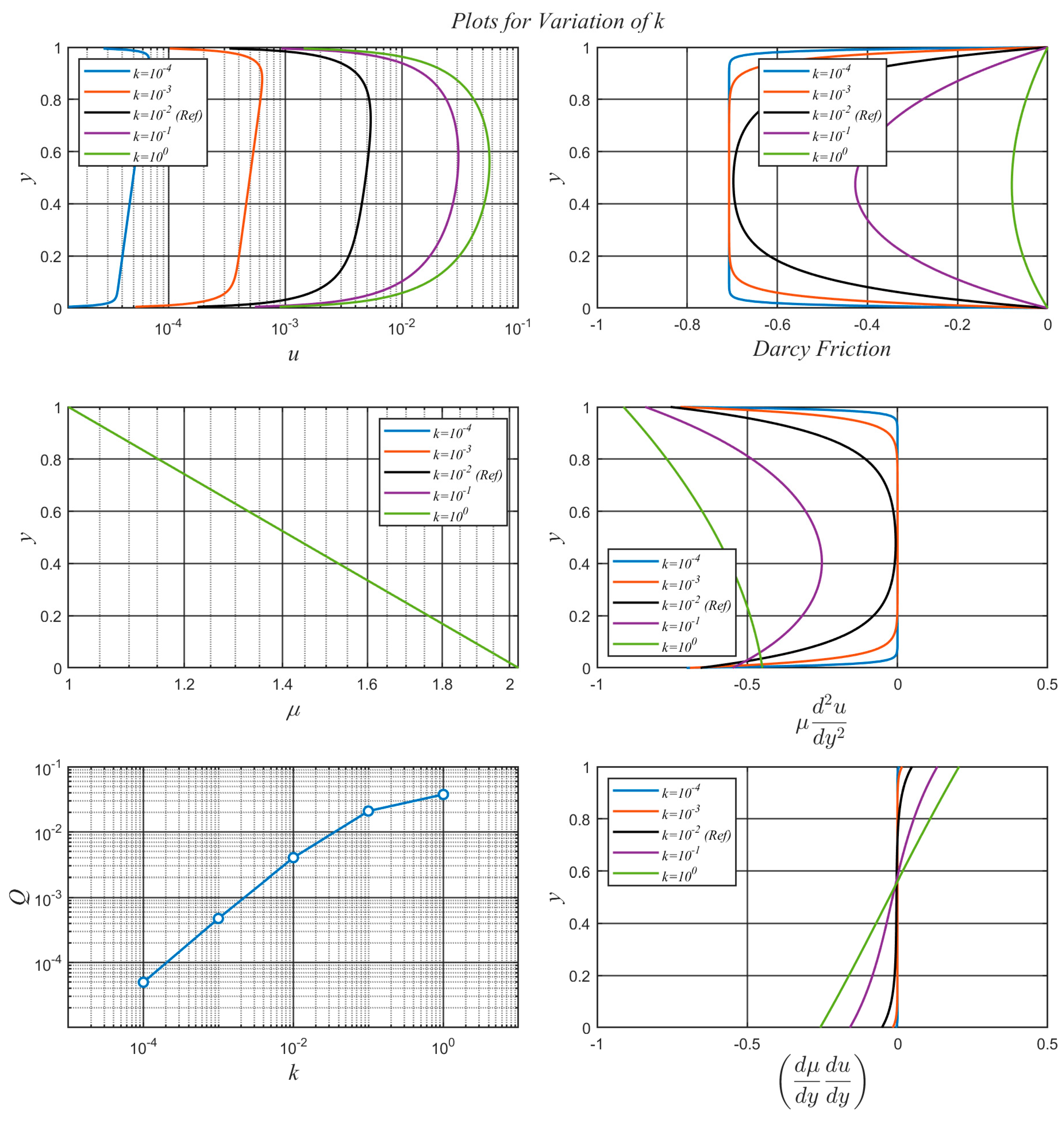
3.6. Variation of $k$

The results for the variation of the dimensionless permeability,

k

, can be found in Figure 8 while all other parameters take on the values identified in the Reference Case given in Table 1. Note that the velocity profiles are shown on a semi-log scale due to the significant reduction caused by the low permeability flows.

For the higher permeability flows the velocity profiles tend towards Navier-Stokes behaviour with a variable viscosity. As

k

decreases, however, the resistance to flow through the porous medium increases resulting in a flow that is dominated by the Darcy friction. Taking equation (28) in the limit of small

k

and then substituting for

f (p)

from equation (29) and rearranging gives:

u (y) = \frac{k \sin ϑ}{{A μ}_{0} e^{{(\frac{p}{p_{0}})}^{n}}}

(43)

which, for the Reference Case with

n = 1

, will produce an inverse exponentially varying velocity profile across the channel. Near the edges of the channel, where the solution must satisfy the boundary conditions, the viscous shear terms become significant. As

k

becomes progressively small, the region of flow dominated by Darcy-type behaviour increases. As seen in Figure 8 the Darcy friction profiles are relatively symmetric and, as

k

becomes small, become nearly constant across the channel except near the boundaries. For small values of

k

the viscous shear term,

μ (\frac{d^{2} u}{d y^{2}})

, is nearly zero except near the walls and shows significant deviation from the constant value that would be expected in non-porous channel flow that would produce a parabolic velocity profile. The plot of the variation of

(\frac{d μ}{d y}) (\frac{d u}{d y})

can be found in Figure 8 where, since the variation of

μ

is the same in all flows, the differences in the profiles are due directly to the changes in the velocity profiles that result from the variation of

k

. Note that this force changes sign approximately at the midpoint of the channel where

(\frac{d u}{d y})

changes sign to meet the no-slip boundary condition.

4. Conclusion

In this work, unidirectional flow of a fluid with pressure-dependent viscosity through a porous structure has been considered when the viscosity-pressure relationship is an exponential function of a pressure power function in order to investigate effects of the viscosity-pressure relation on the flow characteristics. This form of dependence is given by equation (1), above, when n takes on the values -1, 0, 1, 2, and 3. To accomplish this study, momentum equations governing the flow are given by (13), which have the realistic advantage of taking into account medium permeability in the drag term. It is realistic since one is dealing with flow through a porous structure. All solutions and simulations used in this work have been carried out using MATLAB software package, version R2022a. Effects of the six flow and medium parameters,

ϑ, μ_{0}, p_{0}, α, n

, and

k

on: (1) velocity profiles,

u (y)

; (2) viscosity profiles,

μ (y)

; (3) Darcy friction profiles,

- μ (y) (\frac{u (y)}{k})

; (4) the net force on a differential fluid element due to variation of the shear strain rate across the fluid element,

μ (\frac{d^{2} u}{d y^{2}})

; (5) the net force on a differential fluid element due to variation of the viscosity across the fluid element,

(\frac{d μ}{d y}) (\frac{d u}{d y})

; and (6) the dimensionless volumetric flowrate in the channel,

Q

, have been studied and analysed. Future work includes extension of the current constant permeability model to one of variable permeability, and contrasting the results with current ones.

References

Stokes, G.G., On the theories of the internal friction of fluids in motion, and of the equilibrium and motion of elastic solids, Trans. Camb. Philos. Soc., Vol. 8, 1845, pp. 287-305. [CrossRef]
Barus, C.J., (1891). Note on dependence of viscosity on pressure and temperature. Proceedings of the American Academy. 27, 13-19, 1891. [CrossRef]
Housiadas, K.D., Georgiou, G.C. and Tanner, R.I., A note on the unbounded creeping flow past a sphere for Newtonian fluids with pressure-dependent viscosity, International Journal of Engineering Science, Vol. 86, 2015, pp. 1–9. [CrossRef]
Fusi, L., Farina, A. and Rosso, F., Mathematical models for fluids with pressure-dependent viscosity flowing in porous media, International Journal of Engineering Science, Vol. 87, 2015, pp. 110-118. [CrossRef]
Martinez-Boza, F.J., Martin-Alfonso, M.J., Callegos, C. and Fernandez, M., High-pressur behavior of intermediate fuel oils, Energy Fuels, Vol. 25, 2011, pp. 5138-5144. [CrossRef]
Hron, J., Malek, J. and Rajagopal, K.R., Simple flows of fluids with pressure-dependent viscosities, Proceedings of the Royal Society, Vol. 457, 2001, pp. 1603-1622. ttps://doi.org/10.1098/rspa.2000.0723.
Málek, J. and Rajagopal, K.R., Mathematical properties of the solutions to the equations governing the flow of fluids with pressure and shear rate dependent viscosities, in: Handbook of Mathematical Fluid Dynamics, Elsevier, 2007. [CrossRef]
Rajagopal, K.R., Saccomandi, G. and Vergori, L., Flow of fluids with pressure- and shear-dependent viscosity down an inclined plane, Journal of Fluid Mechanics, Vol. 706, 2012, pp. 173-189. [CrossRef]
Lanzendörfer, M., On steady inner flows of an incompressible fluid with the viscosity depending on the pressure and the shear rate, Nonlinear Analysis: Real World Applications, Vol. 10, 2009, pp. 1943-1954. [CrossRef]
Savatorova, V.L. and Rajagopal, K.R., Homogenization of a generalization of Brinkman’s equation for the flow of a fluid with pressure dependent viscosity through a rigid porous solid, ZAMM, Vol. 91 No. 8, 2011, pp. 630-648. [CrossRef]
Alharbi, S.O., Alderson, T.L. and Hamdan, M.H., Flow of a fluid with pressure-dependent viscosity through porous media, Advances in Theoretical and Appl. Mechanics, Vol. 9, No. 1, 2016, pp.1-9. [CrossRef]
M.S. Abu Zaytoon, S. Jayyousi-Dajani and M.H. Hamdan, Effects of the Porous Microstructure on the Drag Coefficient in Flow of a Fluid with Pressure-Dependent Viscosity, International Journal of Mechanics, Vol. 15, pp. 136-144, 2021. [CrossRef]
Subramanian, S.C. and Rajagopal, K.R., A note on the flow through porous solids at high pressures, Computers and Mathematics with Applications, Vol. 53, 2007, pp. 260–275. [CrossRef]
Kannan, K. and Rajagopal, K.R., Flow through porous media due to high pressure gradients, Applied Mathematics and Computation, Vol. 199, 2008, pp. 748-759. [CrossRef]
Nield, D.A. and Bejan, A.,.
Bridgman, P.W., The Physics of High Pressure, MacMillan, New York, 1931.
Housiadas, K.D. and Georgiou, G.C., New analytical solutions for weakly compressible Newtonian Poiseuille flows with pressure-dependent viscosity, International Journal of Engineering Science, Vol. 107, 2016, pp. 13-27. [CrossRef]
Singh, A.K., Sharma, P.K. and Singh, N.P., Free convection flow with variable viscosity through horizontal channel embedded in porous medium, The Open Applied Physics Journal, Vol. 2, 2009, pp. 11-19. [CrossRef]
Szeri, A.Z., Fluid Film Lubrication: Theory and Design, Cambridge University Press, 1998.
Vergne, P.H., Pressure viscosity behavior of various fluids, High Press. Res., Vol. 8, 1991, pp. 451–454. [CrossRef]
Abu Zaytoon, M.S., Allan, F.M., Alderson, T.L. and Hamdan, M.H., Averaged equations of flow of fluid with pressure-dependent viscosity through porous media”, Elixir Appl. Math. 96, 2016, pp. 41336-41340.
Alzahrani, S.M., Gadoura,I., and Hamdan, M.H., Flow down an inclined plane of a fluid with pressure-dependent viscosity through a porous medium with constant permeability, Journal of Modern Technology and Engineering, Vol. 2 #2, 2017, pp. 155-166.
Kierzenka, J., and Shampine, L.F., A BVP Solver that Controls Residual and Error, Journal of Numerical Analysis, Industrial and Applied Mathematics, Vol. 3, No. 1-2, 2008, pp. 27-41.

Figure 1. Representative sketch.

Figure 2. Visual Display of Parameters’ Variations and their Effects on the dimensionless volumetric flowrate in the channel,

Q

Figure 2. Visual Display of Parameters’ Variations and their Effects on the dimensionless volumetric flowrate in the channel,

Q

Figure 3. Effects of

ϑ

u,

μ

Q

- \frac{μ u}{k}

μ \frac{d^{2} u}{d y^{2}}

, and

(\frac{d μ}{d y}) (\frac{d u}{d y})

Figure 3. Effects of

ϑ

u,

μ

Q

- \frac{μ u}{k}

μ \frac{d^{2} u}{d y^{2}}

, and

(\frac{d μ}{d y}) (\frac{d u}{d y})

Figure 4. Effects of

μ_{0}

u,

μ

Q

- \frac{μ u}{k}

μ \frac{d^{2} u}{d y^{2}}

, and

(\frac{d μ}{d y}) (\frac{d u}{d y})

Figure 4. Effects of

μ_{0}

u,

μ

Q

- \frac{μ u}{k}

μ \frac{d^{2} u}{d y^{2}}

, and

(\frac{d μ}{d y}) (\frac{d u}{d y})

Figure 5. Effects of

p_{0}

u,

μ

Q

- \frac{μ u}{k}

μ \frac{d^{2} u}{d y^{2}}

, and

(\frac{d μ}{d y}) (\frac{d u}{d y})

Figure 5. Effects of

p_{0}

u,

μ

Q

- \frac{μ u}{k}

μ \frac{d^{2} u}{d y^{2}}

, and

(\frac{d μ}{d y}) (\frac{d u}{d y})

Figure 6. Effects of

α

u,

μ

Q

- \frac{μ u}{k}

μ \frac{d^{2} u}{d y^{2}}

, and

(\frac{d μ}{d y}) (\frac{d u}{d y})

Figure 6. Effects of

α

u,

μ

Q

- \frac{μ u}{k}

μ \frac{d^{2} u}{d y^{2}}

, and

(\frac{d μ}{d y}) (\frac{d u}{d y})

Figure 7. Effects of

n

u,

μ

Q

- \frac{μ u}{k}

μ \frac{d^{2} u}{d y^{2}}

, and

(\frac{d μ}{d y}) (\frac{d u}{d y})

Figure 7. Effects of

n

u,

μ

Q

- \frac{μ u}{k}

μ \frac{d^{2} u}{d y^{2}}

, and

(\frac{d μ}{d y}) (\frac{d u}{d y})

Figure 8. Effects of

k

u,

μ

Q

- \frac{μ u}{k}

μ \frac{d^{2} u}{d y^{2}}

, and

(\frac{d μ}{d y}) (\frac{d u}{d y})

Figure 8. Effects of

k

u,

μ

Q

- \frac{μ u}{k}

μ \frac{d^{2} u}{d y^{2}}

, and

(\frac{d μ}{d y}) (\frac{d u}{d y})

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Flow Governed by Generalized Brinkman’s Equation through an Inclined Porous Channel

Abstract

1. Introduction

2. Problem Formulation

3. Results and Discussion

3.1. Pressure and Viscosity Distributions

3.2. Effects of ϑ

3.3. Effects of μ 0

3.4. Effects of p 0 and α

3.5. Effects of n

3.6. Variation of k

4. Conclusion

References

MDPI Initiatives

Important Links

Subscribe

3.2. Effects of $ϑ$

3.3. Effects of $μ_{0}$

3.4. Effects of $p_{0}$ and $α$

3.5. Effects of $n$

3.6. Variation of $k$