Mapping Geodesic Orbits around Cosmic Strings using Iterated Maps and Correlation with Disclination Intensity

Preprint

Article

Mapping Geodesic Orbits around Cosmic Strings using Iterated Maps and Correlation with Disclination Intensity

Altmetrics

Downloads

105

Views

Comments

This version is not peer-reviewed

Submitted:

31 August 2023

Posted:

07 September 2023

You are already at the latest version

Alerts

Abstract

Cosmic strings can arise from spontaneous phase transitions during the inflationary period and are describable as disclination topological defects in spacetime. Analytical integration of the geodesic equations for a particle around a cosmic string reveals distinct orbit patterns dependent on the disclination intensity $\beta_{0}$. After its interaction with the cosmic string, the particle's behavior becomes random. To categorize these patterns, we describe the geodesic motion as iterated maps of a discrete parameter. Through the stabilization values of these functions, we correlate the scattering angle and the number of loops for the particle with $\beta_{0}$. Therefore, we interpret the gravitational field mathematically as an instructor of a particle's next position, given its previous one. We find that the radial function in the small displacement limit is similar to the logistic map. This leads us to conjecture the potential of the discrete parameter being a multiple of Planck's time, suggesting a method for the geometric discretization of spacetime around a cosmic string.

Keywords:

Subject: Physical Sciences - Theoretical Physics

1. Introduction

Each material has a standard crystalline structure, with its atoms forming symmetric patterns in a planar or spatial distribution. When the material is subjected to tension, reaching its elastic limit or undergoing a phase transition, its crystalline structure can undergo abrupt changes. These changes in the topological structure of the crystal are known as topological defects. These defects have a significant impact on the material’s properties and functionality. They can alter essential thermodynamic properties such as free energy, entropy, thermal and electrical conductivity, as well as its mechanical properties. The study of topological defects is crucial as it provides a deeper understanding of the underlying mechanisms and their implications in materials science, including metallurgy.

Topological defects can be broadly categorized into three types: point defects, where an atom is removed or an impurity is added; line defects, in which a line of atoms is displaced; and planar defects, affecting an entire plane of atoms. Line defects can be further divided into dislocations and disclinations, each with distinct structural characteristics [1]. A dislocation occurs when an entire semi-plane of atoms is displaced, and a disclination occurs when a line of atoms is removed, resulting in an angular deficit in the topology of the material. The relationship between line defects and the tension applied to the crystal is described by the Volterra process [2], a crucial concept for understanding the behavior of defects in crystals.

It is believed that a spontaneous phase transition in the early universe during the inflationary period [3,4] may have caused topological defects in spacetime itself. These defects are called cosmic strings [5,6,7]. The Volterra process may be adapted in order to construct general topological defects in spacetime [8]. By doing so, one finds ten types of linear defects: four temporal and six spatial. Half of the spatial ones are dislocations and the other half are disclinations. When the disclination occurs around a symmetry axis, it can be used to describe a cosmic string [8]. Geometrically, it is found that the density of topological defects is related to the spacetime torsion. Hence, topological defects are widely studied in gravitational theories whose geometries yield a non-zero torsion tensor, e.g., the Cartan and Weitzenböck geometry [9,10,11,12,13].

The geodesic motion of particles around cosmic strings is somewhat similar to the Newtonian motion of a two-body system in the sense that a particle may perform an elliptic-like trajectory or a parabolic-like or a time-limited bounded one. For the same set of initial conditions for the particle, but with different disclinations, the motion can exhibit these distinct behaviors as well as secondary ones. When the trajectory is a time-limited bounded one, the number of loops seems arbitrary in the intensity of the disclination, as the direction where the particle escapes the defect. These apparently random effects are difficult to be mapped by means of equations of motion alone, as their inversion and elimination of the affine parameter is not direct. The coordinate time can be used as an affine parameter, and the equations of motion involve quadratic quantities of time.

The appearance of quadratic quantities in gravitational fields are interesting, as can be exemplified in the simple case of the motion of a particle in a constant Newtonian gravitational field. Let us consider the case of a particle with initial vertical velocity

v_{0}

placed in a vertical uniform gravitational field

- g

. The equations of motion are

y = - \frac{1}{2} g t^{2} + v_{0} t .

By adjusting the unit system, we can write the former equation as

y = - r_{g} x^{2} + r_{g} x

and compare it with the logistic map

x_{n + 1} = - r x_{n}^{2} + r x_{n}

. Hence, y acts as the next position

x_{n + 1}

depending on the previous position [14].

The occurrence of the logistic function in physical phenomena is not a new feature, being found analogies between the logistic equation and the standard cosmological model [15] to describe the time evolution of lasers with free electrons [16], and other applications in condensed matter and chemical physics [17,18]. Ergo, we can see that patterns such as the logistic map are present in nature and can lead to better understanding of the physical phenomena.

Given the occurrence of patterns similar to the logistic-type pattern in physics and its applications in describing phenomena of nature, in this article we pursuit the idea of describing the motion of a particle around a cosmic string as a problem of iteration, i.e., we construct iterated maps out of the equations of motion arising from the geodesic equations of GR. Thus, we obtain a simple iterated map that describes the coordinates of the particle independently, i.e., two separated iterated maps. We test the precision of the description by comparing it with the values arising from the equations of motion and we obtain a very precise relation. With the aid of this maps, we analyze the pattern of the time-limited bounded orbits and the scattering angle, both as a functions of the disclination intensity. We find an oscillatory stabilization value for the map representing the radial coordinate, similar to that of the logistic map. By considering a small displacement from the initial position, we show that the map obtained reduces to the logistic map.

This article is divided as follows. In Section 2, we review the fundamental mathematical concepts of a cosmic string-type disclination and we present the equations of motion of a free particle around the cosmic string. In Section 3, we iterate the equations of motion and construct the iterated map for the radial and azimuthal coordinates and represent graphically the results and discuss the behavior of the iterated maps. Finally, in Section 4, we present our conclusions.

2. Cosmic Strings as Disclinations in Spacetime

Cosmic strings can be viewed as one type of disclination defect arising as a topological defect in a disordered scalar field during a phase transition [19]. The Volterra process can be used to construct this defect by cutting out a region of spacetime, removing the resulting piece, and then joining the two new edges. When this process is performed around the z-axis, we obtain [8]

d s^{2} = - d t^{2} + d r^{2} + β {(r)}^{2} r^{2} d ϕ^{2} + d z^{2},

(1)

where the function

β = β (r)

represents the defect, with

β = 1

corresponding to Minkowski spacetime.

The function

β

’s dependence on r can be modeled as a disclination core along the z-axis using the function [13]

β (r) = \{\begin{matrix} β_{0}, & r > a, \\ 1, & r \leq a, \end{matrix}

(2)

where a denotes the disclination core, i.e., the radius of the "cylinder" along the z-axis. By taking the limit

a \to 0

, we can recover the cosmic string.

From the line element (1), the metric tensor gives us the non-zero components for the Riemann tensor

\begin{matrix} R^{1}_{221} & = β (r) \partial_{r} (r^{2} β^{'} (r)), \end{matrix}

(3)

\begin{matrix} R^{2}_{112} & = \frac{\partial_{r} (r^{2} β^{'} (r))}{r^{2} β (r)}, \end{matrix}

(4)

with primes denoting differentiation with respect to r. Examining (3,), we find that spacetime is flat everywhere except at the border

r = a

. This indicates that the cosmic string’s spacetime outside the dislocation core is locally flat but not globally flat. When

r > a

, we can compute the length of a circumference with radius R as

L = \int_{0}^{2 π} \sqrt{g_{22}} R d ϕ = 2 π β_{0} R .

(5)

From (5), we see that the length evaluates to

2 π R

only when

β_{0} = 1

. In this case,

R^{λ}_{ρ μ ν} = 0

everywhere, and Minkowski spacetime is recovered. Thus, the parameter

β_{0}

corresponds to the percentage angle deficit, e.g., if

β_{0} = 1 / 2

, then

L = π R

The geodesic equation for massive particles can be easily derived from (1). For the coordinates t and z, we have

\ddot{t} = 0

and

\ddot{z} = 0

, where the dot indicates differentiation with respect to an affine parameter. Consequently, we can use the coordinate time t as an affine parameter and analytically integrate the remaining equations, thus obtaining

\begin{matrix} r^{2} (t) & = {(r_{0} + v_{0 r} t)}^{2} + \frac{β_{0}^{2} l^{2}}{r_{0}^{2}} t^{2}, \end{matrix}

(6)

\begin{matrix} ϕ (t) & = ϕ_{0} - \frac{1}{β_{0}} {tan}^{- 1} (\frac{r_{0} v_{0 r}}{β_{0} l}) + \frac{1}{β_{0}} {tan}^{- 1} (\frac{r_{0}^{3} v_{0 r} + (β_{0}^{2} l^{2} + r_{0}^{2} v_{0 r}^{2}) t}{β_{0} l r_{0}^{2}}), \end{matrix}

(7)

where we identified

r_{0}

v_{0 r}

, and

ϕ_{0}

as the initial conditions for the radial and azimuthal coordinates, respectively, at

t = 0

, and l as the angular momentum per unit mass of the particle also at

t = 0

. The angular momentum l is conserved. By choosing a zero initial longitudinal velocity, the motion is restricted to a plane

z = constant

, and we can analyze it as a motion in the 2-space orthogonal to the cosmic string.

The trajectory given by (1,2) results in a straight line for a non-zero initial velocity, as in ordinary Minkowski spacetime. The presence of the defect

β (r)

causes the particle to undergo a small displacement from a straight line if

β_{0}

is close to unity. As we decrease

β_{0}

, i.e., increase the angular deficit, this deviation becomes more significant and starts to look like a hyperbolic orbit in a scattering pattern. For

β_{0} = 1 / 2

, we have a trajectory similar to a parabola. For

β_{0}

smaller than

1 / 2

, the particle undergoes loops around the cosmic string and eventually escapes to infinity. The number of loops depends on the choice of

β_{0}

, with smaller values implying a bigger number of loops. The particle undergoes a bounded orbit for a limited time, which can be made as big as we want by demanding that

β_{0}

be small enough. Hence, summarizing, we have, approximately, (i) hyperbolic orbit for

1 / 2 < β_{0} < 1

; (ii) parabolic orbit for

β_{0} = 1 / 2

; (iii) bounded orbit for

0 < β_{0} < 1 / 2

The residual effect of the particle’s interaction with the cosmic string seems chaotic, i.e., the number of loops and the scattering angle seem to be very sensitive to variations in

β_{0}

. Hence, in order to investigate possible patterns, we construct iterated maps for the coordinates in the next section and analyze their stabilization.

3. Iterated maps for the cosmic string

In order to create an iterated map for the coordinates, we perform some simplifications by choosing the initial radial position and angular momentum of the particle to be

r_{0} = l = 1 / β_{0}

. These choices merely simplify the mathematical problem and do not reduce the validity of our method for a particular case.

We choose to iterate the time t discretely, i.e.,

t \to n

, where

n = 0, 1, 2, \dots

. From (6), we have

r_{n}^{2} = \frac{1}{β_{0}^{2}} + \frac{2 v_{0 r}}{β_{0}} n + (v_{0 r}^{2} + β_{0}^{2}) n^{2} .

(8)

We define a new positive variable

{\bar{r}}_{n} \equiv r_{n}^{2} / β_{0}^{2}

(9)

and rewrite (8) as

{\bar{r}}_{n} = [\frac{1}{β_{0}^{4}} + \frac{2 v_{0 r}}{β_{0}^{3}} n + (\frac{v_{0 r}^{2}}{β_{0}^{2}} + 1) n^{2}] .

(10)

The sequence (10) generates

\begin{matrix} {\bar{r}}_{0} = & 1 / β_{0}^{4}, \\ {\bar{r}}_{1} = & {\bar{r}}_{0} + 1 + \frac{2 v_{0 r}}{β_{0}^{3}} + \frac{v_{0 r}^{2}}{β_{0}^{2}}, \\ {\bar{r}}_{2} = & {\bar{r}}_{1} + 3 + \frac{2 v_{0 r}}{β_{0}^{3}} + \frac{3 v_{0 r}^{2}}{β_{0}^{2}}, \\ {\bar{r}}_{3} = & {\bar{r}}_{2} + 5 + \frac{2 v_{0 r}}{β_{0}^{3}} + \frac{5 v_{0 r}^{2}}{β_{0}^{2}}, \\ {\bar{r}}_{4} = & {\bar{r}}_{3} + 7 + \frac{2 v_{0 r}}{β_{0}^{3}} + \frac{7 v_{0 r}^{2}}{β_{0}^{2}}, \\ ⋮ \\ {\bar{r}}_{n + 1} = & {\bar{r}}_{n} + \frac{2 v_{0 r}}{β_{0}^{3}} + (2 n + 1) (1 + \frac{v_{0 r}^{2}}{β_{0}^{2}}) . \end{matrix}

(11)

In equation (11), we can eliminate the iterated parameter n by solving (10) and obtaining

n = \frac{\pm \sqrt{β_{0}^{4} {\bar{r}}_{n} + β_{0}^{2} r_{n} v_{0 r}^{2} - 1} - v_{0 r} / β_{0}}{v_{0 r}^{2} + β_{0}^{2}},

(12)

where the positive sign indicates

v_{0 r} > 0

and the negative sign indicates

v_{0 r} < 0

. Hence, by choosing the negative one and substituting (12) into (11), we finally obtain

\begin{matrix} {\bar{r}}_{n + 1} & = {\bar{r}}_{n} + \frac{2 v_{0 r}}{β_{0}^{3}} + (1 + \frac{v_{0 r}^{2}}{β_{0}^{2}}) (1 - 2 \frac{\sqrt{(β_{0}^{4} + β_{0}^{2} v_{0 r}^{2}) {\bar{r}}_{n}^{2} - 1} - v_{0 r} / β_{0}}{v_{0 r}^{2} + β_{0}^{2}}) \\ = {\bar{r}}_{n} + \frac{β_{0}^{2} + 2 \sqrt{β_{0}^{2} {\bar{r}}_{n} (β_{0}^{2} + v_{0 r}^{2}) - 1} + v_{0 r}^{2}}{β_{0}^{2}} . \end{matrix}

(13)

We can further simplify expression (13) by choosing

v_{0 r} = - β_{0}

, thus obtaining

{\bar{r}}_{n + 1} = {\bar{r}}_{n} + 2 - \frac{2 \sqrt{2 β_{0}^{4} {\bar{r}}_{n} - 1}}{β_{0}^{2}} .

(14)

Equation (14) represents the subsequent radial coordinate of the particle as a function of the previous one.

For the azimuthal coordinate

ϕ

, we define

\bar{ϕ} \equiv β_{0} ϕ

(15)

and we can choose the same initial conditions as before with

v_{0 r} = - β_{0}

since the beginning, in order to simplify our analysis. By using the formula

{tan}^{- 1} u + {tan}^{- 1} v = {tan}^{- 1} [\frac{u + v}{1 - u v}]

and identifying

t \to n

, together with the initial conditions, we can simplify (7) to

{\bar{ϕ}}_{n} = {tan}^{- 1} (\frac{β_{0}^{2} n}{1 - β_{0}^{2} n}) .

(16)

By defining

A_{n} \equiv \frac{β_{0}^{2} n}{1 - β_{0}^{2} n}

, we may write (16) as

{\bar{ϕ}}_{n + 1} = ϕ_{n} + {tan}^{- 1} A_{n} .

(17)

Thus, for

A_{n}

we have

\begin{matrix} A_{0} = & 0, \\ A_{1} = & \frac{β_{0}^{2}}{1 - β_{0}^{2}}, \\ A_{2} = & \frac{β_{0}^{2}}{1 - 5 β_{0}^{2} + 12 β_{0}^{4}}, \\ A_{3} = & \frac{β_{0}^{2}}{1 - 7 β_{0}^{2} + 24 β_{0}^{4}}, \\ A_{4} = & \frac{β_{0}^{2}}{1 - 9 β_{0}^{2} + 40 β_{0}^{4}}, \\ A_{5} = & \frac{β_{0}^{2}}{1 - 11 β_{0}^{2} + 60 β_{0}^{4}}, \\ ⋮ \\ A_{n} = & \frac{β_{0}^{2}}{1 - (2 n + 1) β_{0}^{2} + 2 n (n + 1) β_{0}^{4}} . \end{matrix}

(18)

Isolating n in (16) we obtain

n = \frac{tan {\bar{ϕ}}_{n}}{β_{0}^{2} (1 + tan {\bar{ϕ}}_{n})} .

(19)

Finally, by replacing (19) in (18), we obtain the iterated map

{\bar{ϕ}}_{n + 1} = {\bar{ϕ}}_{n} + {tan}^{- 1} (\frac{β_{0}^{2} (1 + sin (2 {\bar{ϕ}}_{n}))}{1 - β_{0}^{2} cos (2 {\bar{ϕ}}_{n})}) .

(20)

The iterated maps (13) and (20) represent the kinematics of a particle in geodesic motion in the presence of a cosmic string.

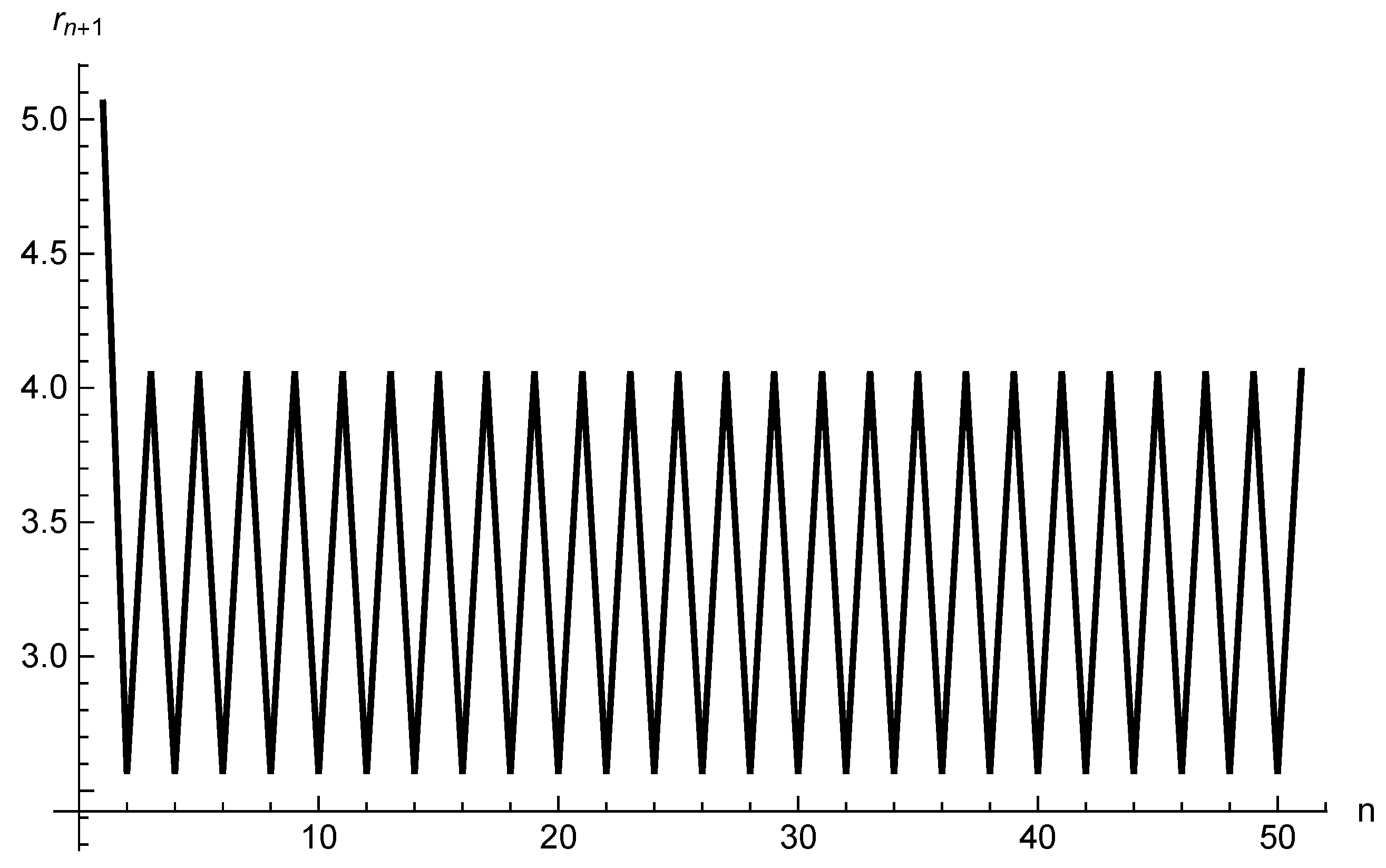
The iterated map (14) gives the radial position

\bar{r}

given a previous one independently of the value of

\bar{ϕ}

. Similarly, we can track the azimuthal position independently of

\bar{r}

. Thus, the 2-dimensional motion can be separated into two 1-dimensional motions that are completely independent. The evolution of the iterated map (14) can be seen in Figure 1. We observe that

\bar{r}

decreases as expected, since we have a negative initial radial velocity. However, for larger values of n, we observe a stabilization at a specific value. Upon closer analysis of the stabilization region in Figure 2, we observe that there are two stable values that oscillate periodically between them. The points are connected by lines to illustrate the trend of the function.

The behavior of

\bar{ϕ}

can be seen in Figure 3. It is clear that the azimuthal coordinate does not exhibit an oscillatory behavior.

To recover the original coordinates

(r, ϕ)

from

(\bar{r}, \bar{ϕ})

, we can use equations (9) and (15). The accuracy of the iteration process can be observed in Figure 4, where we compare the continuous trajectory given by the geodesic equations (6) and (7) represented by a solid line, with the corresponding points obtained from the iterated maps (14) and (20).

The relationship between the number of loops and the cosmic string parameter

β_{0}

is depicted in Figure 5.

It is observed that the number of loops increases with

β_{0}

until reaching a maximum, after which it decreases. This unexpected maximum suggests the existence of an ideal value of

β_{0}

that allows the particle to remain bound for a longer period of time, even for a fixed set of initial conditions in relation to

β_{0}

Furthermore, it is noted that particles with the same initial conditions escape the cosmic string at different angles depending on the value of

β_{0}

. By examining the final scattering angle as a function of

β_{0}

, we can observe the behavior shown in Figure 6. The scattering angle exhibits oscillations with variable amplitude and period until eventually decaying monotonically towards the limit of flat spacetime at

β_{0} = 1

Figure 5. Number of laps N versus

β_{0}

Figure 5. Number of laps N versus

β_{0}

Figure 6. Scattering angle

ϕ_{e s c}

versus

β_{0}

. The units are in multiples of

π

and the points joined.

Figure 6. Scattering angle

ϕ_{e s c}

versus

β_{0}

. The units are in multiples of

π

and the points joined.

Considering equation (14) in the limit of small displacements from the initial position (

r_{n} - r_{0} ≪ 1

), we have

β_{0}^{4} {\bar{r}}_{n} \approx 1

. Expanding to the second order around

β_{0}^{4} {\bar{r}}_{n} = 1

, we obtain

{\bar{r}}_{n + 1} = 2 + β_{0}^{- 2} - (4 β_{0}^{2} - 1) {\bar{r}}_{n} + β_{0}^{6} {\bar{r}}_{n}^{2} .

(21)

For

β_{0} > 1 / 2 \Rightarrow 4 β_{0}^{2} - 1 > 0

, equation (21) exhibits similarity to the logistic map. We can express it as

{\bar{r}}_{n + 1} = A - B {\bar{r}}_{n} + C {\bar{r}}_{n}^{2},

(22)

where

A \equiv 2 + β_{0}^{- 2}

B \equiv (4 β_{0}^{2} - 1)

C \equiv β_{0}^{6}

are positive constants. In this case, for small values of

{\bar{r}}_{n}

, the negative linear term dominates, while for larger values, the positive quadratic term becomes more significant. This balance results in a pattern similar to that of the logistic map, as shown in Figure 7 for equation (14).

Figure 7. Dependence of

{\bar{r}}_{n}

on n for

β_{0} = 2 / 3

Figure 7. Dependence of

{\bar{r}}_{n}

on n for

β_{0} = 2 / 3

Therefore, the limit that creates the logistic-type map corresponds precisely to the threshold that separates open orbits from time-limited closed orbits around a cosmic string.

4. Conclusions

In this article, we have reviewed the concept of cosmic strings as disclination topological defects and derived the equations of motion in a plane perpendicular to the string using the geodesic equations. These equations were expressed as two iterated maps, where a particle’s next position depends only on its previous position. This interpretation allows us to mathematically view spacetime as an instructor that determines the future position based on the present position.

In Section 3, we analyzed the behavior of the iterated maps and observed a decrease in the radial coordinate followed by stabilization for a larger number of iterations. The stabilization pattern observed in Figure 2 resembled that of the logistic map, where the parameter oscillates between two values.

To assess the accuracy of our description, we compared the equations of motion (6) and (7) with the continuous trajectory and the corresponding iterated maps (14) and (20). This comparison, shown in Figure 4, demonstrated remarkable precision. Although the motion equations for r and

ϕ

are coupled through the coordinate time t, evaluating the coordinates using the iterated maps allows us to treat the 2-dimensional motion as two independent 1-dimensional motions. This suggests that by iterating the motion of a particle and a gravitational field, we can mathematically treat a higher dimension as a composition of several independent dimensions. This intriguing possibility may extend beyond the spacetime of cosmic strings and deserves further investigation.

The study of topological defects in spacetime has not only provided a description of large-scale structures such as cosmic strings but also offered the potential for a geometrical quantization of spacetime. Previous research in the late 1980s and early 1990s explored the idea of a purely geometrical quantum theory of gravity [20,21,22]. One approach considered describing a gravitational field as a dislocation in spacetime, or as a collection of dislocations, with the Burgers vector (describing the dislocations) being a multiple of the Planck length. While this idea is interesting, it is not possible to describe all gravitational fields solely as dislocation defects. Certain known solutions of general relativity, such as the pp-wave solution, lead to disclination defects instead [23]. A complete description of quantum gravity would need to account for all solutions. However, when we describe the equations of motion of a particle using the sequences (10) and (16), we impose that time is a positive integer. Consequently, we obtain the discrete iterated positions (14) and (20), and by discretizing time, we obtain a corresponding discretization in space. Thus, if we assume

t = n t_{p}

, where

t_{p}

is the Planck time, we can introduce a quantization of time and, as a consequence, obtain a discrete space. Therefore, it is possible that discretizing time could lead to a more robust model of geometrical quantum gravity than solely focusing on spatial discretization.

If large-scale topological defects exist in nature, their primary detection would likely come from observing the motion of particles around them. By studying the behavior of particles near the topological defect discussed in this article, one could measure the scattering angle, which would be a more realistic observable compared to the number of loops, as the loop time may exceed our lifetime. A graphic similar to Figure 6 could be constructed, and the disclination parameter

β_{0}

could be determined by fitting the curve to experimental data. Thus, the results presented in this paper can contribute to the improvement of future theories and experimental methods for detecting topological defects.

Furthermore, the iterated maps (14) and (20), particularly equation (14) due to its simpler form, can also be subject of interesting mathematical investigations. These maps exhibit intriguing behaviors and patterns, resembling the logistic map and offering potential for further mathematical analysis. Exploring the properties, dynamics, and mathematical implications of these iterated maps can lead to valuable insights and contribute to the broader field of dynamical systems and iterative processes.

In conclusion, our study has provided insights into the behavior of particles around cosmic strings, treating spacetime as an instructor that determines future positions based on present positions. The precision of the description, as demonstrated by the comparison between continuous trajectories and iterated maps, highlights the effectiveness of this approach. The findings presented here not only have implications for the understanding of cosmic strings but also open up possibilities for investigating the nature of spacetime, the quantization of spacetime, and the detection of topological defects in a broader context. Future research in this direction, including the search for universal properties of this system, can deepen our understanding of fundamental physics and contribute to the development of theories such as geometrical quantum gravity.

Author Contributions

Conceptualization, M.P.L. and F.L.C; Investigation, M.P.L. and F.L.C, M.P.L. and F.L.C.; Writing—review & editing, M.P.L. and F.L.C. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

Smallman, R.E. Modern physical metallurgy; Elsevier, 2016.
Volterra, V. Sur l’équilibre des corps élastiques multiplement connexes. In Proceedings of the Annales scientifiques de l’École normale supérieure, 1907, Vol. 24, pp. 401–517.
Linde, A. Inflation and quantum cosmology. Physica Scripta 1991, 1991, 30. [CrossRef]
Guth, A.H. Inflationary universe: A possible solution to the horizon and flatness problems. Physical Review D 1981, 23, 347. [CrossRef]
Hindmarsh, M.B.; Kibble, T.W.B. Cosmic strings. Reports on Progress in Physics 1995, 58, 477.
Copeland, E.J.; Kibble, T.W.B. Cosmic strings and superstrings. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences 2010, 466, 623–657.
Vilenkin, A. Cosmic strings. Physical Review D 1981, 24, 2082.
Puntigam, R.A.; Soleng, H.H. Volterra distortions, spinning strings, and cosmic defects. Classical and Quantum Gravity 1997, 14, 1129.
de Andrade, L.C.G. Einstein–Cartan non-supersymmetric spin-polarised nucleons wall dynamos. Annals of Physics 2021, 431, 168558. [CrossRef]
Rahaman, F.; Mandal, S.; Bhui, B.C. Vacuumless global monopole in Einstein-Cartan theory. FIZIKA B-ZAGREB- 2003, 12, 291–298.
Ruggiero, M.L.; Tartaglia, A. Einstein–Cartan theory as a theory of defects in space–time. American Journal of Physics 2003, 71, 1303–1313.
de Andrade, L.C.G. Chiral and non-chiral spinning string dynamo instability from quantum torsion sources. Annals of Physics 2022, 436, 168666. [CrossRef]
Maluf, J.W.; Goya, A. Space–time defects and teleparallelism. Classical and Quantum Gravity 2001, 18, 5143.
Lobo, M.P. Chaotic logistic map, parabola, and gravity. Open Journal of Mathematics and Physics 2019, 19, 1-3.
Dussault, S.; Faraoni, V.; Giusti, A. Analogies between logistic equation and relativistic cosmology. Symmetry 2021, 13, 704.
Dattoli, G. Logistic function and evolution of free-electron-laser oscillators. Journal of applied physics 1998, 84, 2393–2398. [CrossRef]
Olemskoĭ, A.I.; Flat, A.Y. Application of fractals in condensed-matter physics. Physics-Uspekhi 1993, 36, 1087. [CrossRef]
Ferretti, A.; Rahman, N.K. A study of coupled logistic map and its applications in chemical physics. Chemical physics 1988, 119, 275–288. [CrossRef]
Vilenkin, A.; Shellard, E.P.S. Cosmic strings and other topological defects; Cambridge University Press, 1994.
Magnon, A.M.R. Spin-plane defects and emergence of Planck’s constant in gravity. Journal of mathematical physics 1991, 32, 928–931. [CrossRef]
De Sabbata, V.; Sivaram, C.; Borzeszkowski, H.H.; Treder, H.J. Quantum general relativity, torsion and uncertainty relations. Annalen der Physik 1991, 503, 497–502. [CrossRef]
Ross, D.K. Planck’s constant, torsion, and space-time defects. International journal of theoretical physics 1989, 28, 1333–1340.
Carneiro, F.L.; Ulhoa, S.C.; Maluf, J.W.; da Rocha-Neto, J.F. Non-linear plane gravitational waves as space-time defects. The European Physical Journal C 2021, 81, 1–9. [CrossRef]

Figure 1. Relationship between the iterated map (14) and the index n for a cosmic string parameter

β_{0} = 1 / 32

Figure 1. Relationship between the iterated map (14) and the index n for a cosmic string parameter

β_{0} = 1 / 32

Figure 2. Relationship between the iterated map (14) and the index n for a cosmic string parameter

β_{0} = 1 / 32

. The points are connected by lines to illustrate the trend of the function.

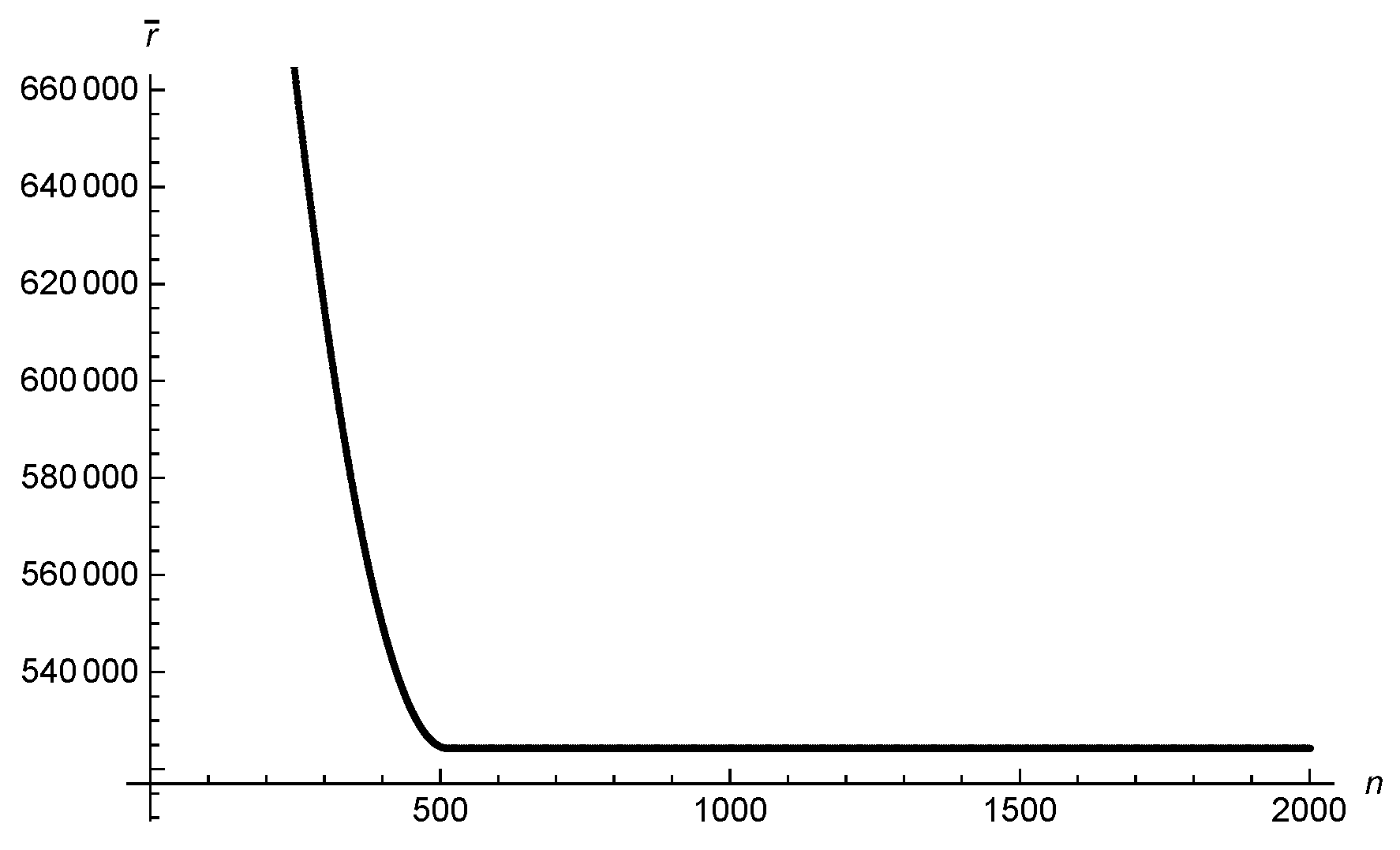
Figure 2. Relationship between the iterated map (14) and the index n for a cosmic string parameter

β_{0} = 1 / 32

. The points are connected by lines to illustrate the trend of the function.

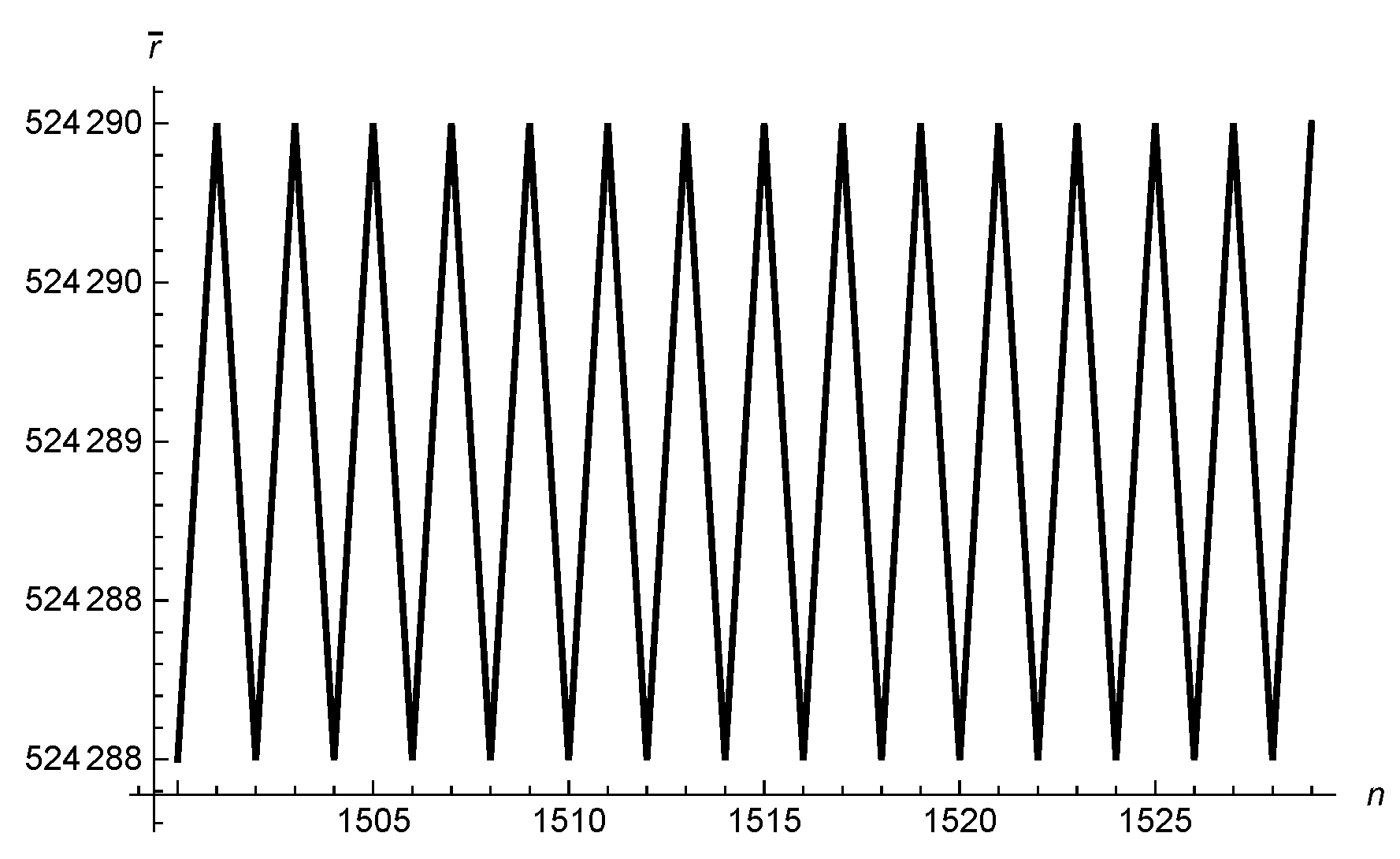
Figure 3. Relation of the iterated map (20) with the index n for

β_{0} = 1 / 32

Figure 3. Relation of the iterated map (20) with the index n for

β_{0} = 1 / 32

Figure 4. Geodesic trajectory of a particle in the presence of a cosmic string with a parameter

β_{0} = 1 / 32

depicted by a continuous line. The dots represent the resulting values of the iterated coordinates, showcasing the positions of the particle along the trajectory.

Figure 4. Geodesic trajectory of a particle in the presence of a cosmic string with a parameter

β_{0} = 1 / 32

depicted by a continuous line. The dots represent the resulting values of the iterated coordinates, showcasing the positions of the particle along the trajectory.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Mapping Geodesic Orbits around Cosmic Strings using Iterated Maps and Correlation with Disclination Intensity

Abstract

1. Introduction

2. Cosmic Strings as Disclinations in Spacetime

3. Iterated maps for the cosmic string

4. Conclusions

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe