SigML++: Supervised Log Anomaly with Probabilistic Polynomial Approximations

Preprint

Article

SigML++: Supervised Log Anomaly with Probabilistic Polynomial Approximations

Altmetrics

Downloads

113

Views

Comments

A peer-reviewed article of this preprint also exists.

Devharsh Trivedi^*

,Aymen Boudguiga,

Nesrine Kaaniche,Nikos Triandopoulos

Devharsh Trivedi^*

,Aymen Boudguiga,

Nesrine Kaaniche,Nikos Triandopoulos

This version is not peer-reviewed

Submitted:

07 September 2023

Posted:

08 September 2023

You are already at the latest version

Alerts

Abstract

Log collection and storage is a crucial process for enterprises around the globe. Log analysis helps identify potential security breaches and, in some cases, is required by law for compliance. However, enterprises often delegate these responsibilities to third-party Cloud Service Providers (CSPs), where the logs are collected and processed for anomaly detection and stored in a data warehouse for archiving. Prevalent schemes rely on plain (unencrypted) data for anomaly detection. More often, these logs can reveal sensitive information about an organization or the customers of that organization. Hence, it is best to keep it encrypted at all times. This paper presents "SigML++," an extension of work done in "SigML." We utilize Fully Homomorphic Encryption (FHE) with the Cheon-Kim-Kim-Song (CKKS) scheme for supervised log anomaly detection on encrypted data. We use an Artificial Neural Network (ANN) based probabilistic polynomial approximations using a Perceptron with linear activation. We probabilistically approximate the Sigmoid activation function (σ(x)) in the encrypted domain for the intervals [−10,10] and [−50,50]. Experiments show better approximations for Logistic Regression (LR) and Support Vector Machine (SVM) for low-order polynomials.

Keywords:

Subject: Computer Science and Mathematics - Computer Science

1. Introduction

Information security tools like Intrusion Detection Systems (IDS), Intrusion Prevention Systems (IPS), and Security Information and Event Management (SIEM) are designed to help organizations defend against cyberattacks. A Security Operations Center (SOC) uses these security tools to analyze logs collected from endpoints, such as computers, servers, and mobile devices. The logs can contain information about system events, user activity, and security incidents. The SOC uses this information to identify anomalies and potential threats. The SOC may generate an alert to notify the appropriate personnel if an anomaly is detected. The logs collected from endpoints are typically unstructured textual data. This data can be challenging to analyze manually. SIEM tools can help automate these logs’ analysis and identify potential threats. SIEM tools collect logs from various sources, known as Security Analytics Sources (SAS). SAS can be a mobile or stationary host or an information and data security tool such as an IDS. SIEM tools use this data to monitor for security threats in near real-time. If a threat is detected, the SIEM tool can generate an alert and take appropriate action, such as blocking traffic or isolating an infected system.

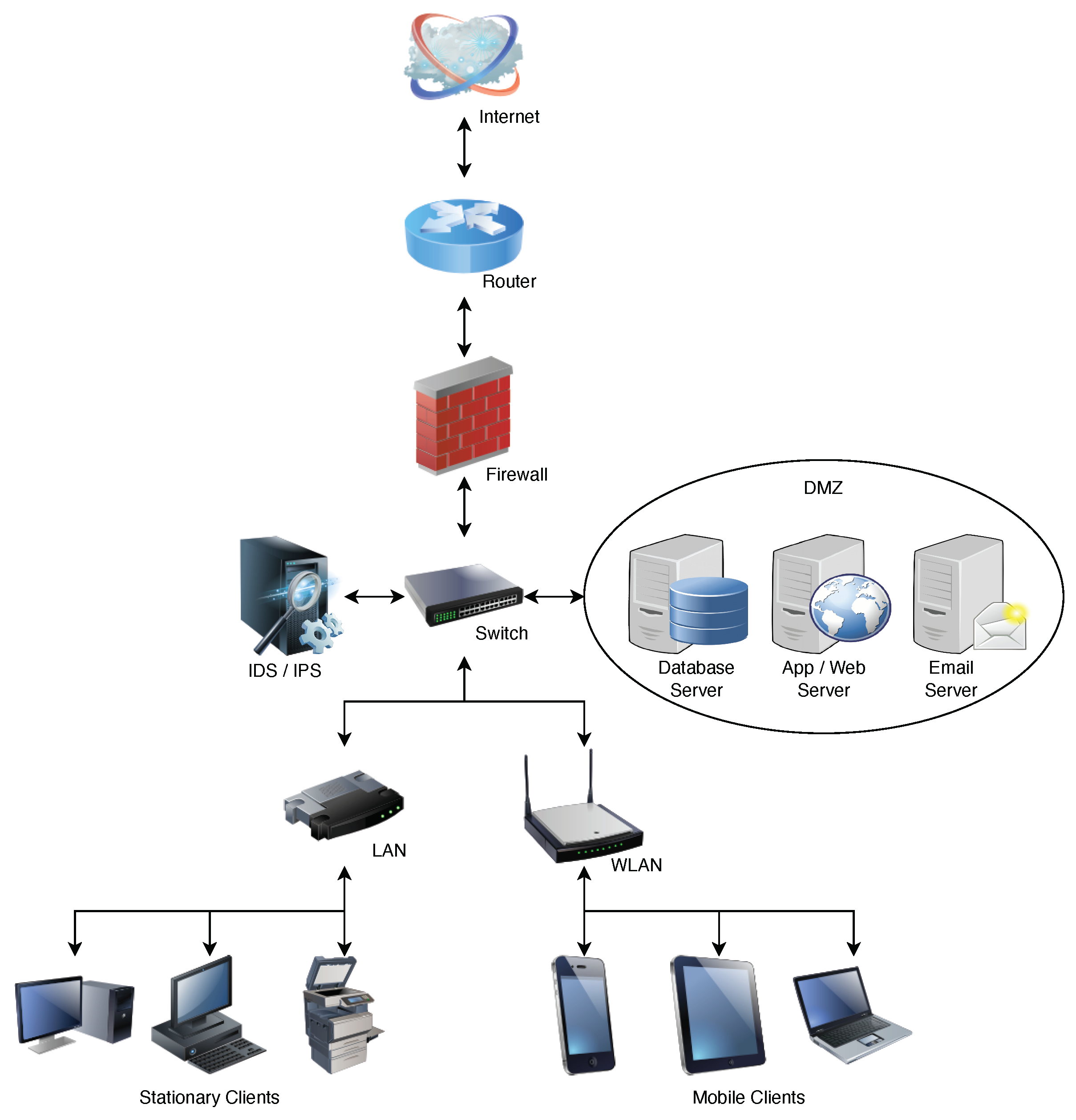
As shown in Figure 1, a typical corporate network is connected to the Internet behind a firewall, which is divided into a Local Area Network (LAN), Wide Area Network (WAN), and Demilitarized zone (DMZ). A SAS client is typically a LAN or WAN endpoint that transmits security or audit logs to a SIEM. A SIEM could be placed in the network along with IDS/IPS or placed externally out of the network and connected via the Internet. There are three types of endpoints in any organization based on the isolation from the Internet: (i) Edge nodes or gateways or machines with public IP, (ii) Machines on LAN or WAN like high-power consumption devices like Servers and Laptops, mid-power devices like Smartphones, and low-power Internet of Things (IoT) or embedded devices and (iii) Machines on a Demilitarized zone (DMZ) like Email or FTP servers.

A Firewall is the first line of defense in a typical corporate network, and an IDS or IPS can accompany it. Additionally, we can have antivirus software running on endpoints. An Advanced Persistent Threat (APT) attacker is assumed to be outside the network and compromises and gains unauthorized access to one of the endpoints. Log anomaly detection aims to trace the trail left behind by the APT attacker while gaining unauthorized access. This trail is called IoC and is identified from the device logs. Logs from different devices are collected and fed to a central SIEM server outside the corporate network for storage and anomaly detection. These logs are collected, parsed, and correlated to generate alerts if anomalies are detected. An example of correlation in logs is to detect new DHCP servers that use UDP protocols on specific ports.

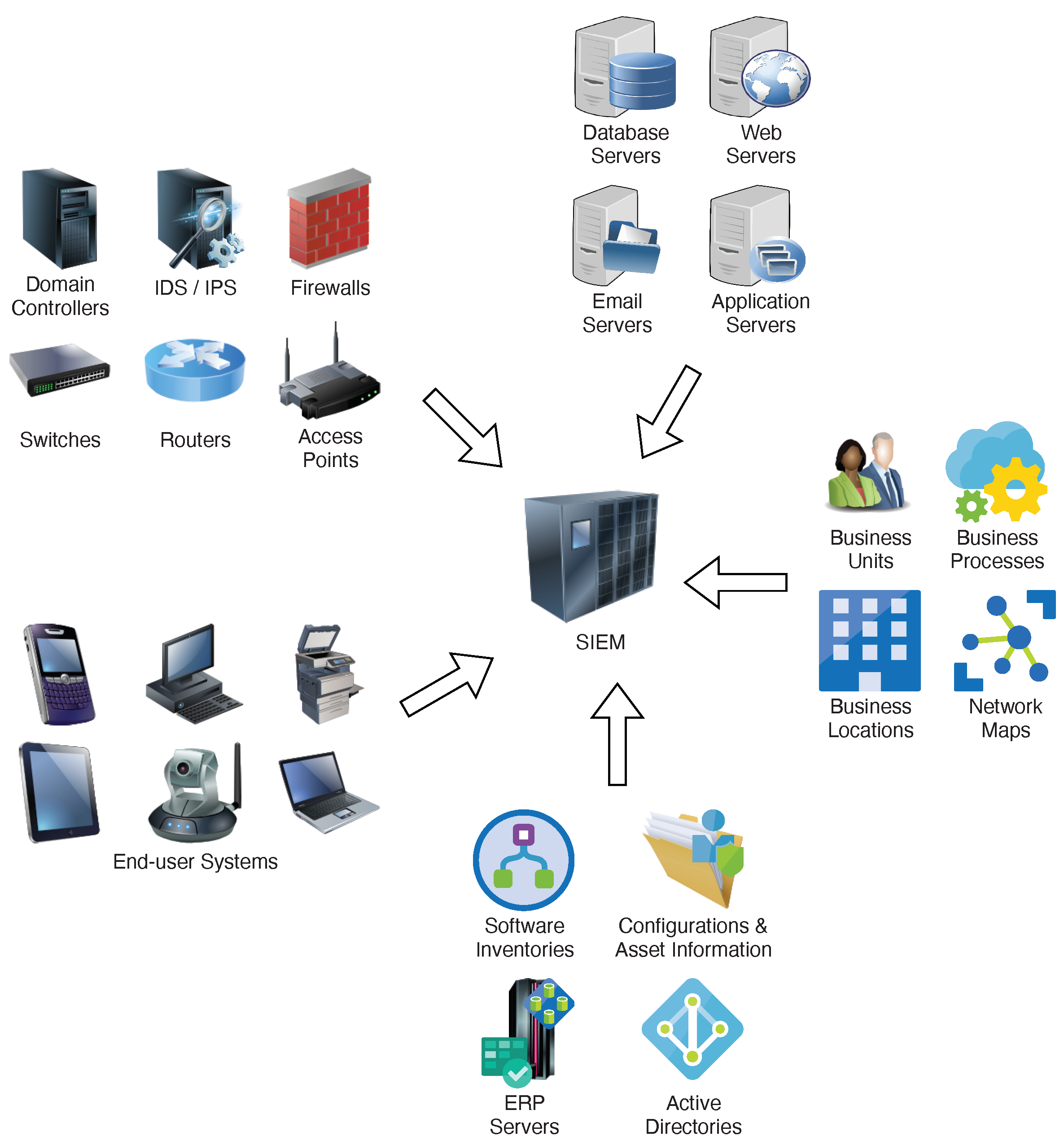
Besides the logs collected from network devices, application servers, and end-user systems, SIEM may collect other confidential organization information (Figure 2), such as business locations, active directory information, and ERP server data. These SAS inputs contain a lot of sensitive data, so protecting the security and privacy of data collected for anomaly detection is imperative. 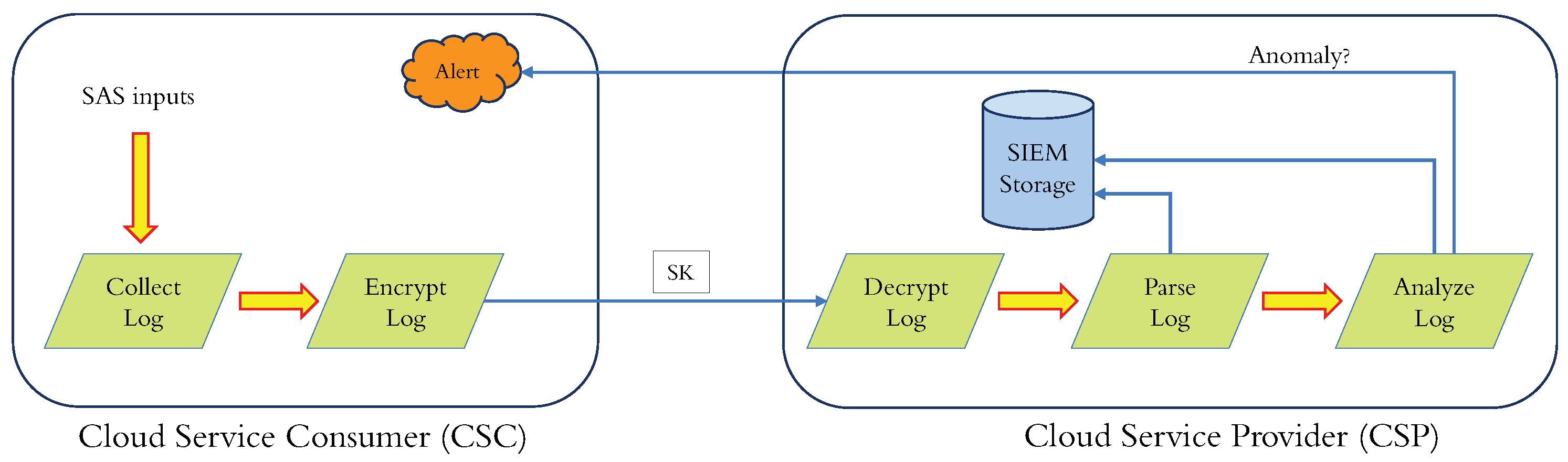As shown in Figure 3, a typical log anomaly (or intrusion) detection scheme consists of the following components:

A "Log Collector" to collect logs from diverse applications operating on an SAS.
A "Transmitter" to send logs to SIEM, which is usually encrypted to safeguard against eavesdropping in the communication channel.
A "Receiver" to amass, store, and ascertain the transmitted logs’ integrity.
A "Parser" to convert the data in a structured form used by the SIEM vendor to process the decrypted logs.
An "Anomaly Detector" using proprietary algorithms to render and transmit alerts.

Enterprises frequently employ a third-party cloud vendor for SOC. Third-party cloud services lessen complexity and deliver flexibility for organizations. Nonetheless, Cloud Service Consumers (CSCs) must commission their data - and their customer’s data - to Cloud Service Providers (CSPs), who are often incentivized to monetize these data. Meanwhile, ordinances such as the US Consumer Online Privacy Rights Act (COPRA) [1], the US State of California Consumer Privacy Act (CCPA) [2], and the EU General Data Protection Regulation (GDPR) [3] strive to safeguard consumers’ privacy. Non-compliant institutions are subjected to stringent fines and deteriorated reputations. This outcome is a tradeoff between data utility and privacy.

Exporting log data to an SIEM deployed on a third-party CSP is perilous, as the CSP requires access to plaintext (unencrypted) log data for alert generation. Moreover, the CSP may have adequate incentives to accumulate user data. These data are stored in the CSP’s servers and thus encounter diverse privacy and security threats like data leakage and misuse of information [4,5,6,7,8,9]. Thus, shielding these logs’ privacy and confidentiality is crucial. We present the use of Fully Homomorphic Encryption (FHE) to permit CSC to assure privacy without sabotaging their capability to attain insights from their data.

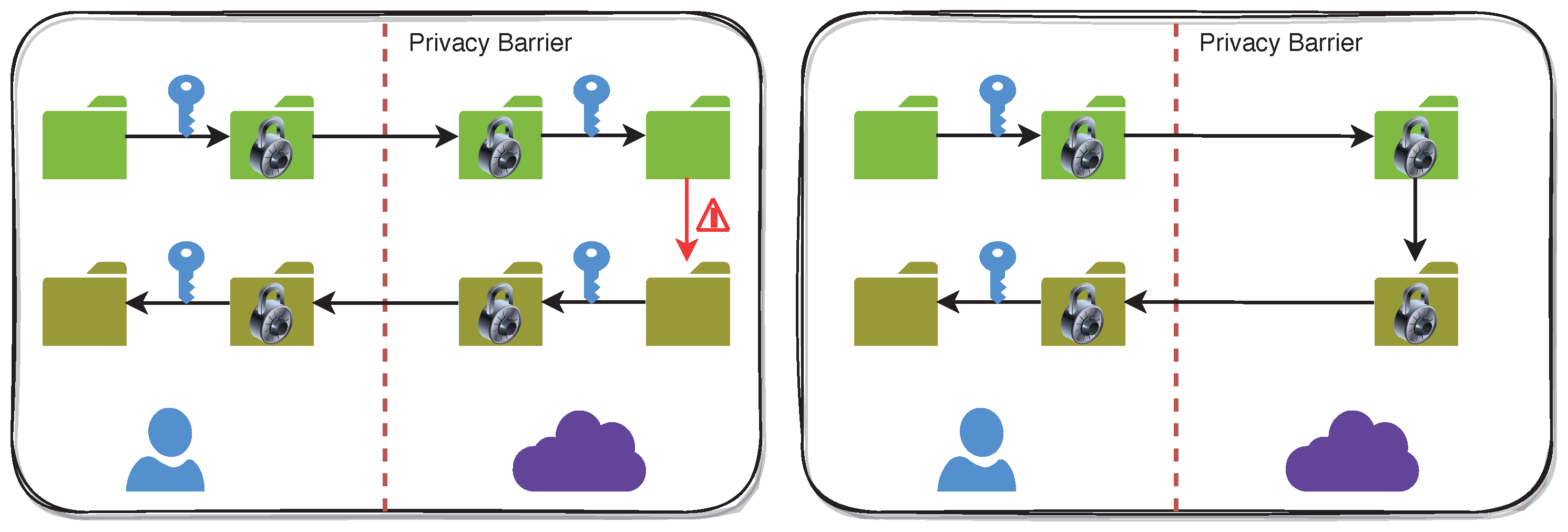
Traditional cloud storage and computation approaches using contemporaneous cryptography mandate customer data to be decrypted before operating on it. Thus, security policies are deployed to avert unauthorized admission to decrypted data. CSCs must entrust the Access Control Policies (ACP) incorporated by their CSPs for data privacy (Figure 4). With FHE, data privacy is accomplished by the CSC via cryptography, leveraging rigid mathematical proofs. As a consequence, the CSP will not have admission to unencrypted customer data for computation and storage without a valid Secret Key (SK).

FHE allows calculations to be performed on encrypted data without decrypting it first. The results of these computations are stored in an encrypted form. Still, when decrypted, they are equivalent to the results that would have been obtained if the computations had been performed on the unencrypted data. Plaintexts are unencrypted data, while ciphertexts are encrypted data. FHE can enable privacy-preserving storage and computation and process encrypted data in commercial cloud environments. It is a promising technology with a wide range of potential applications.

For privacy-preserving log anomaly detection, we can use a hardware-based solution (e.g., Trusted Execution Environment (TEE)) or a software-based approach (e.g., FHE). SGX-Log [10] and Custos [11] showed private log anomaly detection using TEE with Intel SGX. However, TEEs have limitations on how much data can be stored. For example, Intel SGX has a limit of 128 MB. Hence, bit-wise FHE schemes like TFHE [12] or word-wise FHE schemes like BFV [13,14] and CKKS [15] are better for larger data. Concrete-ML from Zama [16] uses TFHE, which is efficient for smaller arithmetic. Still, it is inefficient for larger arithmetic operations (while amortized performance in CKKS can be improved with batching). For word-wise FHE schemes, we have BFV for integers and CKKS for approximate arithmetic. Hence, for Machine Learning (ML) tasks, CKKS is a better choice. Aymen et al. [17] used BFV for SVM with linear kernel. They experimentally calculate the best scaling factor value to convert floats to integers for better accuracy, which is not required in CKKS. SigML [18] used CKKS for LR and SVM.

1.1. Contributions

Our contributions can be summarized as follows:

First, we formulate a supervised binary classification problem for log anomaly detection and implement it with the CKKS cryptosystem.
Second, we propose novel ANN-based third-degree Sigmoid approximations in the intervals $[- 10, 10]$ and $[- 50, 50]$ .
Third, we evaluate the performance of various Sigmoid approximations in the encrypted domain, and our results show better accuracy and sum ratio.

1.2. Organization

This paper is organized as follows. First, we describe the building blocks of our protocols in Section 2, where we review FHE in Section 2.1 and present polynomial approximations for the Sigmoid function in Section 3. Next, we describe our methodology in Section 4. Then, we review the previous work in Section 5. Finally, we discuss our experimental results in Section 6.

2. Background

This section details CKKS, a Fully Homomorphic Encryption scheme, and deterministic and probabilistic polynomial approximation schemes.

2.1. Fully Homomorphic Encryption

This work utilizes the CKKS [15] as a fully homomorphic encryption scheme. CKKS varies from other FHE schemes (such as BFV [13,14], BGV [19], and TFHE [12]) in the way that it interprets encryption noise. Indeed, CKKS treats encryption noise as part of the message, similar to how floating-point arithmetic approximates real numbers. This means the encryption noise does not eliminate the Most Significant Bits (MSB) of the plaintext m as long as it stays small enough. CKKS decrypts the encryption of message m as an approximated value

m + e

, where e is a slight noise. The authors of CKKS suggest multiplying plaintexts by a scaling factor

Δ

prior to encryption to lessen precision loss after adding noise during encryption. CKKS also sustains batching, a process for encoding many plaintexts within a single ciphertext in a Single Instruction Multiple Data (SIMD) fashion. We describe CKKS as a set of probabilistic polynomial-time algorithms regarding the security parameter

k

. The algorithms are:

$CKKS . Keygen$ : Generates a key pair.
$CKKS . Enc$ : Encrypts a plaintext.
$CKKS . Dec$ : Decrypts a ciphertext.
$CKKS . Eval$ : Evaluates an arithmetic operation on ciphertexts.

The level of a ciphertext is l if it is sampled from

Z_{q_{l}} [X] / (X^{N} + 1)

. Let

L, q_{0}

and

Δ

be integers. We set

q_{l} = Δ^{l} \cdot q_{0}

for any l integer in

〚 0, L 〛

$(e v k, p k, s k) \leftarrow CKKS . Keygen (1^{k}, L)$ : generates a secret key ( $s k$ ) for decryption, a public key ( $p k$ ) for encryption, and a publicly available evaluation key ( $e v k$ ). The secret key ( $s k$ ) is a sample from a random distribution over $Z_{3} [X] / (X^{N} + 1)$ . The public key ( $p k$ ) is computed as:

$p k = ({[- a \cdot s k + e]}_{q_{L}}, a) = (p_{0}, p_{1})$

where a is sampled from a uniform distribution over $Z_{q_{L}} [X] / (X^{N} + 1)$ , and e is sampled from an error distribution over $Z_{q_{L}} [X] / (X^{N} + 1)$ . $e v k$ is utilized for relinearisation after the multiplication of two ciphertexts.
$c \leftarrow CKKS . {Enc}_{p k} (m)$ : encrypts a message m into a ciphertext c utilizing the public key ( $p k$ ). Let v be sampled from a distribution over $Z_{3} [X] / (X^{N} + 1)$ . Let $e_{0}$ and $e_{1}$ be small errors. Then the message m is encrypted as:

$c = {[(v \cdot p k_{0}, v \cdot p k_{1}) + (m + e_{0}, e_{1})]}_{q L} = (c_{0}, c_{1}) .$
$m \leftarrow CKKS . {Dec}_{s k} (c)$ : decrypts a message c into a plaintext m utilizing the secret key ( $s k$ ). The message m can be recovered from a level l ciphertext thanks to the function $m = {[c_{0} + c_{1} \cdot s k]}_{q_{l}}$ . Note that with CKKS, the capacity of a ciphertext reduces each time a multiplication is computed.
$c_{f} \leftarrow CKKS . {Eval}_{e v k} (f, c_{1}, \dots, c_{k})$ : estimates the function f on the encrypted inputs $(c_{1}, \dots, c_{k})$ using the evaluation key $evk$ .

2.2. Polynomial Approximations

This section describes commonly used function interpolation techniques like (i) Taylor, (ii) Fourier, (iii) Pade, (iv) Chebyshev, (v) Remez, and (vi) probabilistic ANN scheme.

2.2.1. Taylor

The Taylor series (Eq. (1)) is a mathematical expression approximating a function as an infinite sum of terms expressed in terms of the function’s derivatives at a single point a, called the center of the Taylor series. The Maclaurin series is a particular case of the Taylor series where the center of the series is

a = 0

. In other words, a Maclaurin series is a Taylor series centered at zero. It is a power series that permits the calculation of an approximation of a function

f (x)

for input values near zero, given that the values of the successive derivatives of the function at zero are known. The Maclaurin series can be used to find the antiderivative of a complicated function, approximate a function, or compute an uncomputable sum. In addition, the partial sums of a Maclaurin series provide polynomial approximations for the function.

\sum_{n = 0}^{\infty} f^{(n)} (a) \frac{{(x - a)}^{n}}{n!} = f (a) + f^{'} (a) (x - a) + \frac{f^{''} (a)}{2!} {(x - a)}^{2} + \dots + \frac{f^{(k)} (a)}{k!} {(x - a)}^{n} + \dots

(1)

2.2.2. Fourier

The Fourier series can be represented in sine-cosine, exponential, and amplitude-phase forms. For a sine-cosine form, coefficients are

\begin{matrix} A_{0} = \frac{1}{P} \int_{- P / 2}^{P / 2} f (x) d x \\ A_{n} = \frac{2}{P} \int_{- P / 2}^{P / 2} f (x) cos (\frac{2 π n x}{P}) d x \\ B_{n} = \frac{2}{P} \int_{- P / 2}^{P / 2} f (x) sin (\frac{2 π n x}{P}) d x \end{matrix}

(2)

With these coefficients, the Fourier series is

f (x) \sim A_{0} + \sum_{n = 1}^{\infty} A_{n} cos (\frac{2 π n x}{P}) + B_{n} sin (\frac{2 π n x}{P})

(3)

For an exponential form, coefficients are

\begin{matrix} c_{0} = A_{0} \\ c_{n} = (A_{n} - i B_{n}) / 2, for n > 0 \\ c_{n} = (A_{- n} + i B_{- n}) / 2, for n < 0 \end{matrix}

(4)

By substituting Eq. 2 into Eq. 4

c_{n} = \frac{1}{P} \int_{- P / 2}^{P / 2} f (x) e^{- \frac{2 π i n x}{P}} d x

(5)

With these definitions, we can write Fourier series in exponential form

f (x) = \sum_{n = - \infty}^{\infty} c_{n} \cdot e^{\frac{2 π i n x}{P}}

(6)

2.2.3. Pade

Given a function f and two integers

m \geq 0

and

n \geq 1

, the Pade approximant of order

[m / n]

is the rational function

R (x) = \frac{Σ_{j = 0}^{m} a_{j} x^{j}}{1 + Σ_{k = 1}^{n} b_{k} x^{k}} = \frac{a_{0} + a_{1} x + a_{2} x^{2} + \dots + a_{m} x^{m}}{1 + b_{1} x + b_{2} x^{2} + \dots + b_{n} x^{n}}

(7)

which agrees with

f (x)

to the highest possible order, which amounts to

\begin{matrix} f (0) = R (0), \\ f^{'} (0) = R^{'} (0), \\ f^{''} (0) = R^{''} (0), \\ ⋮ \\ f^{(m + n)} (0) = R^{(m + n)} (0) \end{matrix}

(8)

Equivalently, if

R (x)

is expanded in a Taylor series at 0, its first

m + n

terms would cancel the first

m + n

terms of

f (x)

, and as such

f (x) - R (x) = c_{m + n + 1} x^{m + n + 1} + c_{m + n + 2} x^{m + n + 2} + \dots

(9)

2.2.4. Chebyshev

The Chebyshev polynomial of degree n is denoted

T_{n} (x)

, and is given by the formula

T_{n} (x) = cos (n arccos x)

(10)

The first few Chebyshev polynomials of the kind are

\begin{matrix} T_{0} (x) = 1 \\ T_{1} (x) = x \\ T_{2} (x) = 2 x^{2} - 1 \\ \dots \\ T_{n + 1} (x) = 2 x T_{n} (x) - T_{n - 1} (x) \end{matrix}

(11)

f (x)

is an arbitrary function in the interval

[- 1, 1]

, and if N coefficients

c_{j}, j = 0, \dots, N - 1

, are defined by

c_{j} = \frac{2}{N} \sum_{k = 1}^{N} f (x_{k}) T_{j} (x_{k}) = \frac{2}{N} \sum_{k = 1}^{N} f [cos (\frac{π (k - \frac{1}{2})}{N})] cos (\frac{π j (k - \frac{1}{2})}{N})

(12)

Then, we get the approximation formula

f (x) \approx [\sum_{k = 0}^{N - 1} c_{k} T_{k} (x)] - \frac{1}{2} c_{o}

(13)

2.2.5. Remez

Given a function

f (x)

to be approximated and a set X of

n + 2

points

x_{1}, x_{2}, \dots, x_{n + 2}

in the approximation interval, usually the extrema of Chebyshev polynomial linearly mapped to the interval. The Remez algorithm is the following:

Solve the system of linear equations

$b_{0} + b_{1} x_{i} + \dots + b_{n} x_{i}^{n} + {(- 1)}^{i} E = f (x_{i}); i = 1, 2, \dots, n + 2$

(14)

for the unknowns $b_{0}, b_{1}, \dots, b_{n}$ and E.
Use the $b_{i}$ as coefficients to form a polynomial $P_{n}$ .
Find the set M of points of local maximum error $| P_{n} (x) - f (x) |$ .
If the errors at every $m \in M$ are alternate in sign (+/-) and of equal magnitude, then $P_{n}$ is the minimax approximation polynomial. If not, replace X with M and repeat the steps as described above.

2.2.6. ANN

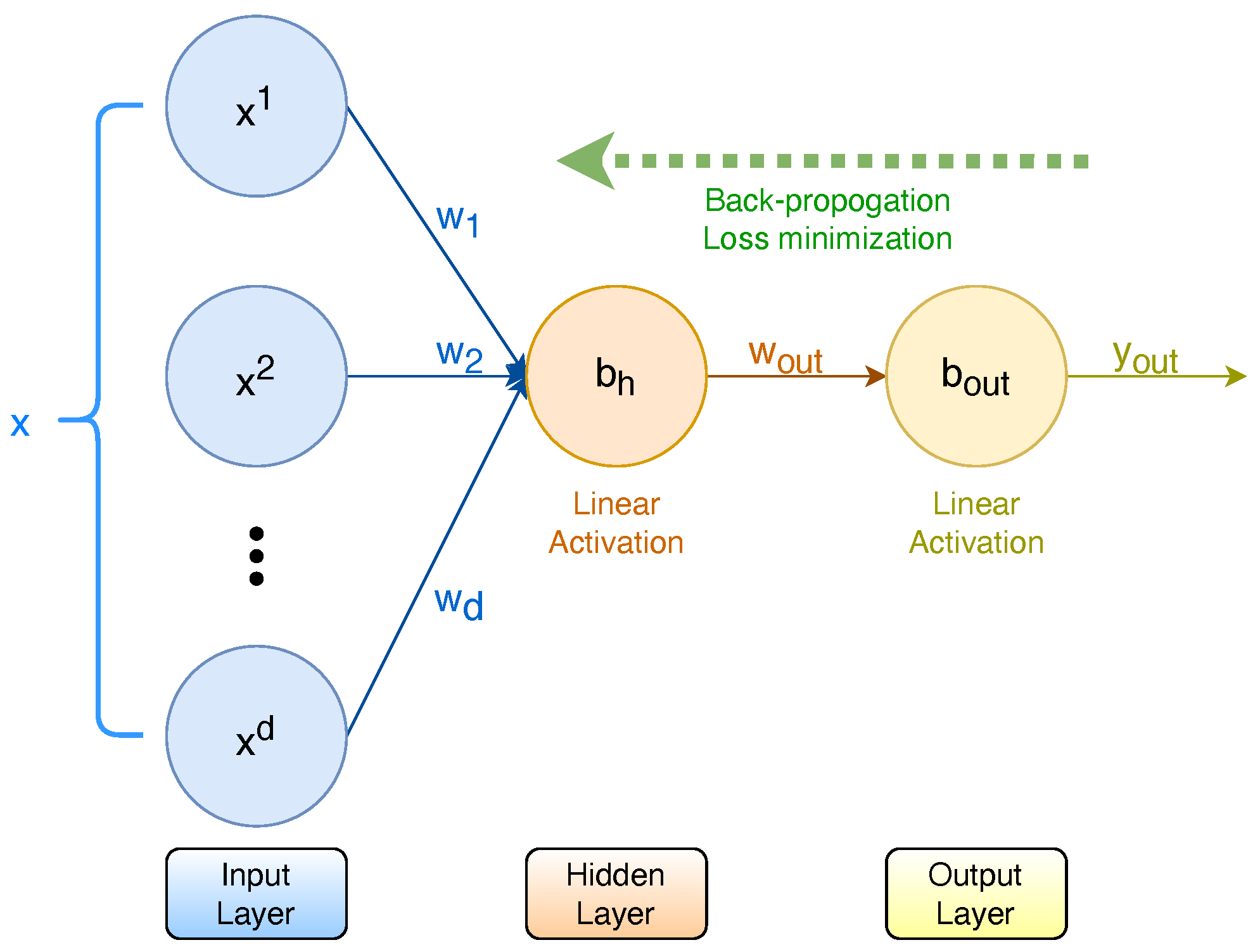
While Artificial Neural Networks (ANNs) are known for their universal function approximation properties, they are often treated as a black box and used to calculate the output value. We propose to use a basic 3-layer Perceptron (Figure 5) consisting of an input layer, a hidden layer, and an output layer; both hidden and output layers having linear activations to generate the coefficients for an approximation polynomial of a given order. In this architecture, the input layer is dynamic, with the input nodes corresponding to the desired polynomial degrees. While having a variable number of hidden layers is possible, we fix it to a single layer with a single node to minimize the computation. We show coefficient calculations for a third-order polynomial (

d = 3

) for a univariate function

f (x) = y

for an input x, actual output y, and predicted output

y_{o u t}

. Input layer weights are

{w_{1}, w_{2}, \dots, w_{d}} = {w_{1}, w_{2}, w_{3}} = {x, x^{2}, x^{3}}

and biases are

{b_{1}, b_{2}, b_{3}} = b_{h}

. Thus, the output of the hidden layer is

y_{h} = w_{1} x + w_{2} x^{2} + w_{3} x^{3} + b_{h}

The predicted output is calculated by

y_{o u t} = w_{o u t} \cdot y_{h} + b_{o u t} = w_{1} w_{o u t} x + w_{2} w_{o u t} x^{2} + w_{3} w_{o u t} x^{3} + (b_{h} w_{o u t} + b_{o u t})

(15)

where the layer weights

{w_{1} w_{o u t}, w_{2} w_{o u t}, w_{3} w_{o u t}}

are the coefficients for the approximating polynomial of order-3 and the constant term is

b_{h} w_{o u t} + b_{o u t}

3. Sigmoid Approximation

Barring message expansion and noise growth, implementing the Sigmoid activation function is a substantial challenge in implementing ML with FHE. Sigmoid is used in LR and SVM during classification, so we determined to make it homomorphic. We further describe techniques to approximate this activation function with a polynomial for word-wise FHE and compare various polynomial approximations in terms of Accuracy, Precision, Recall, F1-Score, and the

Σ

-Ratio of the predicted sum from Sigmoid values to the sum of all actual binary labels for the test dataset. We denote

M_{i}^{d}

, where

M

is an approximation method like Taylor (

T

), Remez (

R

), Chebyshev (

C

), or ANN (

A

d

is degree and

i

is the interval

[- i, i]

of the polynomial. We approximate the class

C [a, b]

of continuous functions on the interval

[a, b]

by order-n polynomials in

P_{n}

using the

L^{\infty}

-norm to measure fit. This is directed to as minimax polynomial approximation since the best (or minimax) approximation solves:

p_{n}^{*} = arg min_{p_{n} \in P_{n}} max_{a \leq x \leq b} | f (x) - p_{n} (x) |

(16)

A minimax approximation is a technique to discover the polynomial p in Eq. (16), i.e., the Remez algorithm [20] is an iterative minimax approximation and outputs the following results [21] for the interval [-5,5] and order 3:

R_{5}^{3} (x) = 0.5 + 0.197 x - 0.004 x^{3}

(17)

Taylor series (around point 0) of degree 3 is given by

T^{3} (x) = 0.5 + 0.25 x - 0.0208333 x^{3}

(18)

Chebyshev series of degree 3 for the interval

[- 10, 10]

0.5 + 0.139787 x + (3.03084 e - 26) x^{2} - 0.00100377 x^{3}

We omit the term for

x^{2}

to get

C_{10}^{3} (x) = 0.5 + 0.139787 x - 0.00100377 x^{3}

(19)

Similarly, we obtain the Chebyshev series of degree 3 for the interval

[- 50, 50]

C_{50}^{3} (x) = 0.5 + 0.0293015 x - (8.65914 e - 6) x^{3}

(20)

We derive the ANN polynomials of degree 3 for

[- 10, 10]

A_{10}^{3} (x) = 0.49961343 + 0.12675145 x - 0.00087002286 x^{3}

(21)

and for the interval

[- 50, 50]

A_{50}^{3} (x) = 0.49714848 + 0.026882438 x - (7.728304 e - 06) x^{3}

(22)

4. Proposed Solution

Our threat model considers SAS (CSC) and SIEM (CSP) for simplicity. SAS is the client that wants to generate anomaly alerts from logs while preserving its privacy. Consequently, the SIEM server should be oblivious to the data received and refrain from comprehending the log information. On the other hand, SIEM also desires to shield the weights and coefficients of the ML model used to detect intrusion anomalies and generate alerts. Thus, SAS should not learn about the model information. For log analysis using FHE, log parsing shifts from SIEM to SAS. Instead of SIEM decrypting and parsing the logs, SAS collects and parses unstructured log to a structured form and normalize the data. Data normalization helps to enhance ML model prediction.

SAS uses FHE to generate an encryption key (

p k / s k

), a decryption key (

s k

), and an evaluation key (

e v k

). The parsed log inputs are encrypted using the public key (

p k

) or secret key (

s k

). We use the CKKS scheme for FHE, better suited for floating-point value calculations. CKKS is more suited for arithmetic on real numbers, where we can have approximate but close results, while BFV is more suited for arithmetic on integers. The SIEM performs homomorphic computations on the encrypted inputs and the ML model’s coefficients in plaintext, using the evaluation key (

e v k

) generated by SAS. The encrypted result(s) are then passed to SAS. SAS decrypts the result(s) with the secret key (

s k

), infers whether there was an anomaly, and generates an alert accordingly.

We present (i) "Ubiquitous" and (ii) "Aggregate" configurations similar to SigML. While the "Ubiquitous" configuration is similar to prevalent research works, the "Aggregate" configuration reduces the computation and communication requirements of the SAS. Both configurations differ in how SIEM results are generated and processed at SAS:

Ubiquitous - SIEM sends one encrypted result per encrypted user input.
Aggregate - Only one result is sent in the encrypted domain for all inputs. This technique helps reduce communication costs and uses much fewer resources on SAS to decrypt a single encrypted result than one encrypted result per encrypted input.

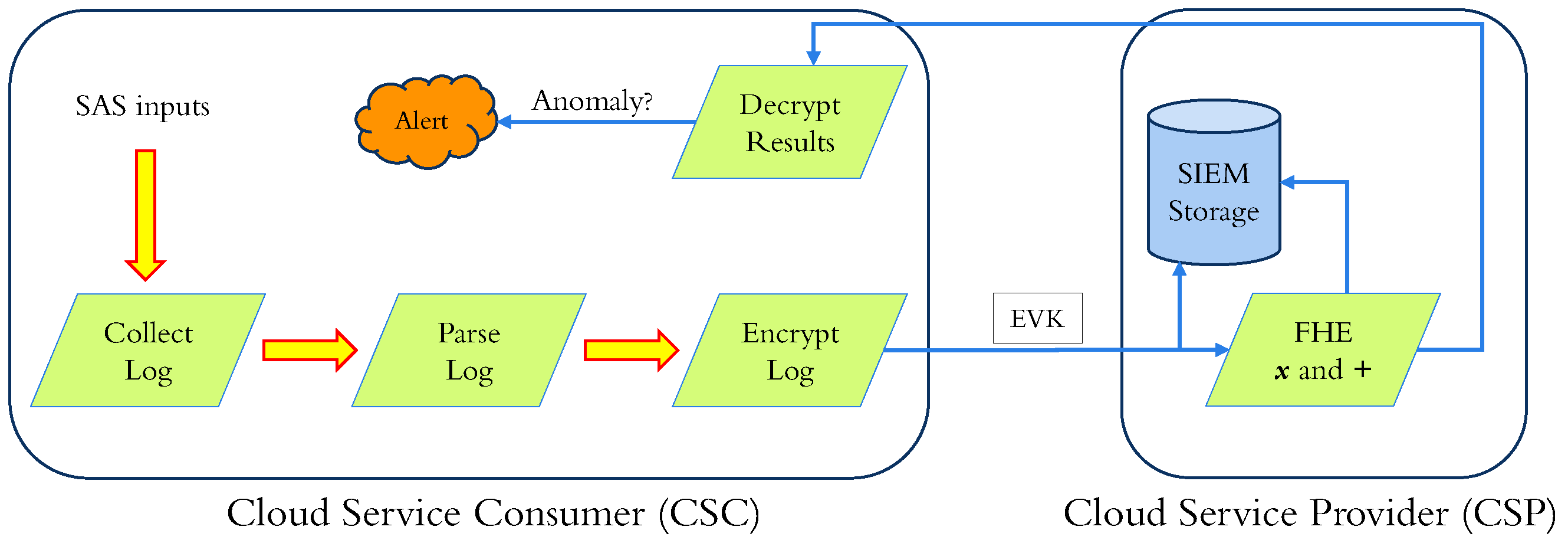
In the "Ubiquitous" configuration (Figure 6), SAS sends encrypted parsed inputs to SIEM for analysis, and SIEM performs homomorphic calculations on encrypted inputs and unencrypted weights. SIEM sends one encrypted result for every encrypted log entry in the received block to SAS. SAS decrypts all the results and evaluates the labels for all the individual log entries. In this configuration, the disadvantage is leaking the data used for training or the model weights, as a dishonest client can perform inference attacks.

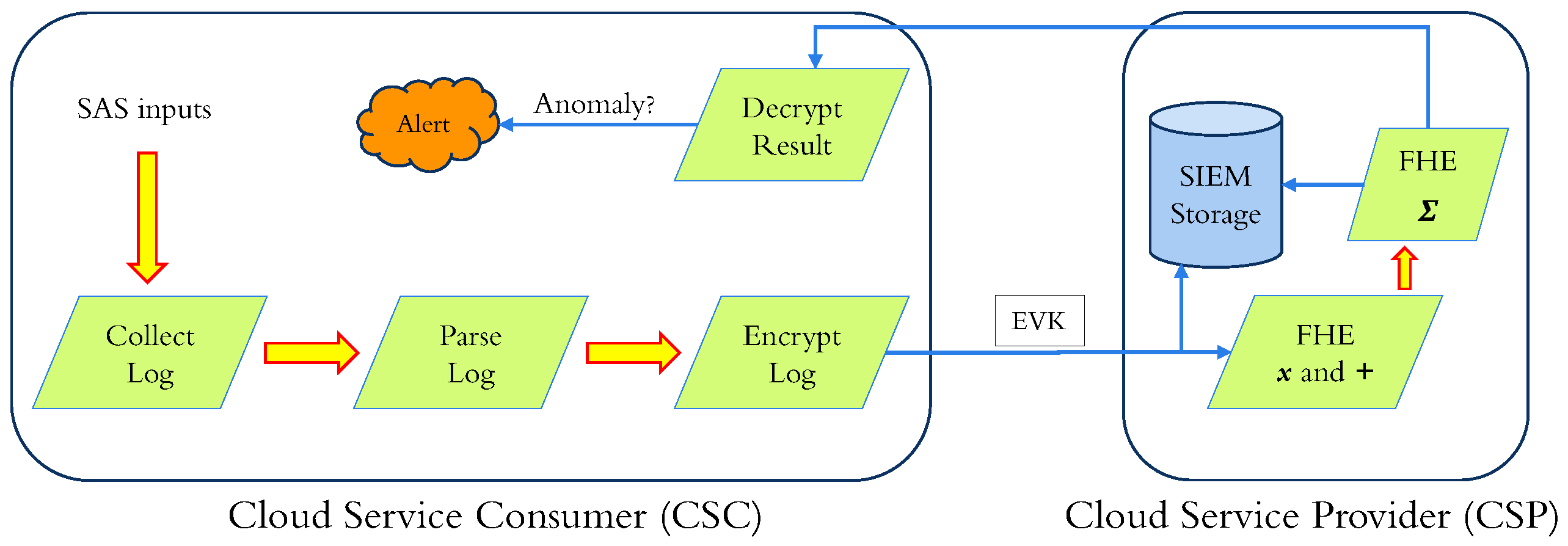
In the "Aggregate" configuration (Figure 7), SAS sends a block of encrypted parsed inputs as before. SIEM performs homomorphic computation with plaintext model weights for each input in the received block, applies Sigmoid approximation on individual encrypted results, and sums (homomorphic additions) all encrypted results.

The sigmoid activation is a mathematical function that approximates the outputs of a machine learning model in the

[0, 1]

range. In log anomaly detection, a label of 0 corresponds to a "normal" class, and a 1 corresponds to an "anomalous" class. In the proposed procedure, the SAS receives only one result per block of messages. This saves network bandwidth, as the SAS does not need to receive individual ciphers (encrypted labels) for each message. Additionally, the SAS only needs to decrypt one cipher (encrypted total) per block, which saves storage and computation overhead. The SAS decrypts the result and assesses the sum for the block of messages. If there are no abnormalities in the block, the totality should be 0. Otherwise, it should be the count of anomalous inputs.

Another advantage of this configuration is utilizing an anomaly score per block of log entries, and it functions as a litmus test for log anomalies. For example, a SOC engineer may prefer to examine the block of logs with a higher anomaly score than a block with a much lesser score. Furthermore, if there are successive blocks with higher than usual anomaly scores, it may function as an IoC. The drawback of this configuration is that SAS can not pinpoint which entry in the block is anomalous.

As shown in Table 1, n is the number of logs,

T_{E} (p)

is the time taken to encrypt a single message,

S_{E} (p)

is bytes occupied by a single ciphertext,

T_{D} (c)

is the time taken to decrypt a single ciphertext, and

S_{D} (c)

is bytes occupied by a single (decrypted) message. We first train the ML models using LR and SVM in plaintext and perform inference on encrypted data as the inputs to the model are encrypted. The calculations are performed on plaintext weights of the model, yielding the encrypted results. This also helps to create a baseline to compare the performance of various approximations in encrypted domains.

5. Related Work

This section discusses previous research on privacy-preserving log management architectures. Zhao et al. [22] proposed a system called Zoo to minimize latency in data processing and reduce the amount of raw data exposed to the Cloud Service Provider (CSP). Zoo is deployed on Customer-owned Edge Devices (CEDs) rather than on the cloud, and it supports the composition, construction, and easy deployment of Machine Learning (ML) models on CEDs and local devices. Zoo is implemented in the OCaml language on top of the open-source numerical computing system Owl [23]. In addition to CEDs, Zoo can be deployed on cloud servers or a hybrid of both. This can further reduce the data exposed to the CSP and the communication costs associated with it. Repositioning ML-based data analytics to edge devices from the cloud poses hurdles such as resource limitations, scarcity of usable models, and difficulty deploying user services. Additionally, deploying services on a CED environment introduces problems for the CSP, as the privacy of ML models (weights) must be shielded from the CED.

Ray et al. [24] proposed a set of protocols for anonymous upload, retrieval, and deletion of log records in the cloud using the Tor [25] network. Their scheme addresses integrity and security issues throughout the log management, including log collection, transmission, retrieval, and storage. Yet, their logging client is operating system-specific, and privacy is not guaranteed because logs can be identified by their tag values.

Zawoad et al. [26,27] presented Secure Logging as a Service (SecLaaS), which stores and provides access to logs generated by Virtual Machines (VMs) running in the cloud. SecLaaS ensures the confidentiality and integrity of these logs, which the CSCs own. SecLaaS encrypts some of the Log Entry (LE) information utilizing a shared public key of the security agents to ensure confidentiality. The private key to decrypt the log is shared among the security agents. An auditor can verify the integrity of the logs utilizing the Proof of Past Log (PPL) and the Log Chain (LC). However, SecLaaS cannot encrypt all the fields of the LE, as the CSP needs to be able to search the storage by some fields. Additionally, using a shared public key violates the CSC’s data privacy.

Rane and Dixit [28] presented BlockSLaaS, a Blockchain-assisted Secure Logging-as-a-Service system for cloud environments. BlockSLaaS aims to make the cloud more auditable and forensic-friendly by securely storing and processing logs while tackling multi-stakeholder collusion problems and ensuring integrity and confidentiality. The integrity of logs is assured by utilizing the immutable property of blockchain technology. Cloud Forensic Investigators (CFIs) can only access the logs for forensic investigation through BlockSLaaS, which preserves the confidentiality of logs. To assure the privacy of the CSC, the Node Controller (NC) encrypts each log entry utilizing the CFI’s public key,

C F I_{P K}

. The CFI can then utilize its secret key,

C F I_{S K}

, to decrypt the logs, preserving the confidentiality of the CSC’s logs. However, this scheme utilizes the CFI’s public key, which violates the data privacy of the CSC. A more privacy-preserving scheme would use a different keying mechanism, such as a private blockchain or a Trusted Execution Environment (TEE).

Bittau et al. [29] presented a principled systems architecture called Encode, Shuffle, Analyze (ESA) for performing large-scale monitoring with high utility while safeguarding user privacy. ESA guarantees the privacy of monitored users’ data by processing it in a three-step pipeline:

Encode: The data is encoded to control its scope, granularity, and randomness.
Shuffle: The encoded data is shuffled to break its linkability and guarantee that individual data items get "lost in the crowd" of the batch.
Analyze: The anonymous, shuffled data is analyzed by a specific analysis engine that averts statistical inference attacks on analysis results.

The authors implemented ESA as a system called PROCHLO, which develops new techniques to harden the three steps of the pipeline. For example, PROCHLO uses the Stash Shuffle, a novel, efficient, and scalable oblivious-shuffling algorithm based on Intel’s SGX, a TEE. TEEs provide isolated execution environments where code and data can be protected from the host system. However, using a TEE like Intel SGX may only be practical for some devices and infeasible for legacy and low-resourced systems. Additionally, TEEs limit the data amount that can be secured.

Paul et al. [30] presented a Collective Learning protocol, a secure protocol for sharing classified time-series data within entities to partially train the parameters of a binary classifier model. They approximated the Sigmoid activation function (

σ (x)

) to a polynomial of degree 7. They presented a Collective Learning protocol to apply Homomorphic Encryption (HE) to fine-tune the last layer of a Deep Neural Network (DNN) securely. However, the degree-7 approximation using an HE method is counterproductive for resource-constrained machines, such as wireless sensors or Internet-of-Things (IoT) devices.

The most comparative work to ours on log confidentiality during transmission and analysis using FHE techniques is presented by Boudguiga et al. [17]. In their scheme, the authors examine the feasibility of using FHE to furnish a privacy-preserving log management architecture. They utilize Support Vector Machines (SVMs) with a linear kernel to assess the FHE classification of Intrusion Detection System (IDS) alerts from the NSL-KDD dataset. In their scheme, they encrypt the input data from SAS using the BFV scheme and perform FHE calculations on the encrypted data using the SIEM weights in plaintext. The encrypted results for each log entry are then sent back to the SAS for decryption. However, this approach can be vulnerable to inference attacks by malicious SAS, such as attribute inference, membership inference, and model inversion attacks. Our "Aggregate" scheme helps prevent most of these attacks, as it only sends a total anomaly score (sum) per block instead of predictions or labels per input, thus minimizing the data inferred by the attacker.

SigML, proposed by Trivedi et al. [18], uses the CKKS scheme and presents:

Ubiquitous configuration: This is similar to other works and sends an encrypted result for every log entry.
Aggregate configuration: This reduces communication and computation requirements by sending a single result for a block of log entries.

SigML compares three approximations of the sigmoid function:

σ^{1} (x), σ^{3} (x), σ^{5} (x)

. These approximations are used for a Logistic Regression (LR) and Support Vector Machine (SVM) model. The authors observed that the LR and SVM models trained from scikit-learn [31] did not perform well with the sigmoid activation for the "Aggregate" configuration. Therefore, they designed Sigmoid-LR (

σ_{L R}

) to improve performance. Sigmoid-LR uses a kernel

A = X \cdot W + b

to reduce the errors of

S i g m o i d (a)

with the learning rate

r_{l e a r n}

and the number of iterations

r_{i t e r}

. The inputs and labels are

X, Y \in [0, 1]

. This paper presents "SigML++," an extension of SigML [18]. SigML++ improves the results of SigML with LR and SVM models using a novel

A N N

approximation. SigML++ also evaluates third-order polynomials in the

[- 10, 10]

and

[- 50, 50]

6. Experimental Analysis

The experiments were conducted on a 2.4 GHz Quad-Core MacBook Pro with an Intel Core i5 processor and 2133 MHz 8 GB LPDDR3 memory. We used the SEAL-Python [32] library for Python3 to furnish CKKS encryption. Moreover, we have used sklearn [33] APIs for binary classifiers.

6.1. Evaluation Criteria

We compared the performance of the models using the following metrics: Precision, Recall, Accuracy, and F1-score for the "Ubiquitous" configuration and

Σ

-Ratio for the "Aggregate" configuration. We repeated the experiments on both the NSL-KDD and the balanced HDFS datasets.

Precision is the proportion of correctly predicted positive results (True Positives, TP) to the total predicted positive results (TP + False Positives, FP). It is also known as positive predictive value.
Recall is the proportion of correctly predicted positive results (TP) to the total actual positive results (TP + False Negatives, FN). It is also known as sensitivity or specificity.
Accuracy is the proportion of all correct predictions (TP + TN) to the total number of predictions made (TP + FP + TN + FN). It can be calculated as "Precision" divided by "Recall" or $1 - \frac{F a l s e N e g a t i v e R a t e (F N R)}{F a l s e P o s i t i v e R a t e (F P R)}$ .
F1-Score is a measure that considers both "Precision" and "Recall." It is calculated as the harmonic mean of "Precision" and "Recall."
Sum ratio is a measure used for the Sigmoid activation function with binary outcomes. It is calculated as the sum of all predicted labels to the sum of all actual labels.

P r e c i s i o n = \frac{T P}{T P + F P}

(23)

R e c a l l = \frac{T P}{T P + F N}

(24)

A c c u r a c y = \frac{T P + T N}{T P + F P + T N + F N}

(25)

F 1 - S c o r e = 2 * \frac{P r e c i s i o n * R e c a l l}{P r e c i s i o n + R e c a l l}

(26)

Σ - R a t i o = \frac{\sum_{i = 1}^{n} Predicted y_{i}}{\sum_{i = 1}^{n} Actual y_{i}}, where y_{i} \in {0, 1}

(27)

Table 2. Return-1 model performance for NSL-KDD and HDFS.

Dataset	Type	Accuracy	Precision	Recall	F1-Score	$Σ$ -Ratio
NSL-KDD	Full (100%)	0.4811	0.4811	1.0000	0.6497	2.0782
	Test (20%)	0.4832	0.4832	1.0000	0.6515	2.0695
HDFS	Full (100%)	0.4999	0.4999	1.0000	0.6666	2.0000
	Test (20%)	0.5016	0.5016	1.0000	0.6681	1.9934

6.2. Datasets

Log datasets are often imbalanced, with most samples belonging to one class. This can lead to overfitting and a "pseudo-high" accuracy for the trained model. To avoid this, we propose to use balanced datasets. We first used a "Return-1 Model" to verify the balance of classes in our log anomaly datasets. This model always classifies samples as "anomalous." We achieved an Accuracy of 48.11% and a

Σ

-ratio of 2.07 for the NSL-KDD dataset and an Accuracy of 49.99%, and a

Σ

-ratio of 2.00 for the HDFS dataset. We also achieved a Recall 100% for both datasets, as the model always outputs 1 for "anomaly." The NSL-KDD [34] dataset is a modified version of the KDD’99 [35] dataset that solves some of its intrinsic problems. It contains 148,517 inputs with 41 features and two observations for Score and Label. We modified the labels to make it a binary classification problem, with all attack categories consolidated into label-1. This resulted in 77,054 inputs with label-0 ("normal") and 71,463 inputs classified to label-1 ("anomalous"). The testing set comprised 29,704 inputs, with 14,353 of label-1 and 15,351 of label-0. The HDFS_1 [36] labeled dataset from Logpai is 1.47 GB of HDFS logs forged by running Hadoop-based map-reduce jobs on over 200 Amazon EC2 nodes for 38.7 hours. Hadoop domain experts labeled it. Of the 11,175,629 log entries accumulated, 288,250 (

\sim 2.58 %

) data are anomalous. We used Drain [37], a log parser, to convert our unstructured log data into a structured format. For brevity, we skip the details of textual log data parsing. We created a more undersized, balanced dataset of 576,500 inputs with seven observations equally distributed among the "normal" and "anomaly" classes. We used 20% of the total dataset as testing data, with 115,300 inputs, out of which 57,838 inputs belonged to label-1 and 57,462 belonged to label-0.

6.3. Test Results

Foremost, we constructed baselines with plain (unencrypted) data, and the results are exhibited in Table 3. For the NSL-KDD dataset, we accomplished 93.52% Accuracy, 95.02% Precision, and 0.99

Σ

-Ratio with LR and 93.30% Accuracy, 95.50% Precision, and 1.06

Σ

-Ratio with SVM. Likewise, for the HDFS (balanced) dataset, we accomplished 96.83% Accuracy, 94.12% Precision, and 1.00

Σ

-Ratio with LR and 96.81% Accuracy, 94.02% Precision, and 0.86

Σ

-Ratio with SVM.

Next, we compare third-order sigmoid approximations as shown in Equations 17, 18, 19, 20, 21, and 22 in terms of performance metrics and execution time. We empirically show that our

A N N

-based polynomials performed better in most instances. For the NSL-KDD dataset and LR model with a CKKS scaling factor of

2^{30}

, the Chebyshev polynomial

C_{10}^{3}

in the range

[- 10, 10]

(Eq. 19) yielded 93.30% Accuracy, 94.86% Precision, 91.08% recall, 92.93% f1-score and 1.06

Σ

-ratio. While

A N N

approximation

A_{10}^{3}

in the same range (Eq. 21) had 93.42% accuracy, 95.02% precision, 91.16% recall, 93.05% f1-score and 1.06

Σ

-ratio. Thus,

A_{10}^{3}

resulted in 0.13% improvement in accuracy and 0.17% in precision over

C_{10}^{3}

We also experimented with different scaling factors of

2^{30}

and

2^{40}

. While it did not significantly impact the NSL-KDD dataset, we observed improvements for HDFS. For

C_{50}^{3}

with the SVM model, Accuracy improved from 92.63% to 96.81%, Precision from 93.85% to 94.02%, Recall from 91.30% to 100%, and f1-score also improved from 92.56% to 96.92% when increasing scaling factor. We also observed improvements for

Σ

-ratio, for

A_{10}^{3}

it reduced from 7.45 to 7.43 (ideal value is close to 1).

We also improve the results reported in SigML. For instance, $A_{10}^{3}$ performed much better than $R_{5}^{3}$ . For NSL-KDD, with LR, Accuracy was improved from 79.23% to 93.42%, precision from 92.72% to 95.02%, recall from 61.86% to 91.16%, f1-score from 74.21% to 93.05% and

Σ

-ratio from 0.63 to 1.06. However, like SigML, our approximations did not yield good results for HDFS datasets, specifically for

Σ

-ratio. It would be interesting to approximate sigmoid in the

[- 20, 20]

and

[- 30, 30]

to get better results.

We also measured the average time taken for encryption, decryption, and sigmoid operations, as shown in Table 4. We did not see any significant impact of different datasets, models, scales, or methods on average time taken in seconds. We also measured the total User CPU and System CPU time for different configurations for completeness. $A_{10}^{3}$ was observed to be faster than other methods.

Table 3. Comparing performance metrics for sigmoid approximations.

Dataset	Model	Scale	Method	Accuracy	Precision	Recall	F1-Score	$Σ$ -Ratio
NSL-KDD	LR		Plain	0.9352	0.9502	0.9138	0.9317	0.9966
			$R_{5}^{3}$	0.7923	0.9272	0.6186	0.7421	0.6336
		$2^{30}$	$T^{3}$	0.3865	0.3083	0.2167	0.2545	-2.1720
			$C_{10}^{3}$	0.9330	0.9486	0.9108	0.9293	1.0633
			$C_{50}^{3}$	0.9351	0.9498	0.9139	0.9315	1.0753
			$A_{10}^{3}$	0.9342	0.9502	0.9116	0.9305	1.0667
			$A_{50}^{3}$	0.9120	0.9213	0.8942	0.9076	1.0666
		$2^{40}$	$T^{3}$	0.3870	0.3087	0.2169	0.2548	-2.1649
			$C_{10}^{3}$	0.9341	0.9501	0.9115	0.9304	1.0634
			$C_{50}^{3}$	0.9352	0.9502	0.9138	0.9317	1.0752
			$A_{10}^{3}$	0.9341	0.9501	0.9115	0.9304	1.0668
			$A_{50}^{3}$	0.9350	0.9537	0.9096	0.9311	1.0660
	SVM		Plain	0.9330	0.9550	0.9039	0.9287	1.0614
			$R_{5}^{3}$	0.9326	0.9550	0.9031	0.9283	1.0993
		$2^{30}$	$T^{3}$	0.7743	0.9262	0.5790	0.7126	0.7872
			$C_{10}^{3}$	0.9312	0.9522	0.9029	0.9269	1.1190
			$C_{50}^{3}$	0.8426	0.8194	0.8649	0.8649	1.0569
			$A_{10}^{3}$	0.9239	0.9407	0.8993	0.9195	1.1110
			$A_{50}^{3}$	0.9311	0.9574	0.8974	0.9264	1.0489
		$2^{40}$	$T^{3}$	0.7762	0.9302	0.5804	0.7148	0.7876
			$C_{10}^{3}$	0.9330	0.9550	0.9039	0.9287	1.1189
			$C_{50}^{3}$	0.9330	0.9550	0.9039	0.9287	1.0566
			$A_{10}^{3}$	0.9329	0.9551	0.9036	0.9287	1.1111
			$A_{50}^{3}$	0.9318	0.9604	0.8958	0.9270	1.0489
HDFS	LR		Plain	0.9683	0.9412	0.9992	0.9693	1.0001
			$R_{5}^{3}$	0.5308	0.5167	0.9992	0.6812	292.6803
		$2^{30}$	$T^{3}$	0.3616	0.4178	0.6928	0.5213	1545.6206
			$C_{10}^{3}$	0.5561	0.5306	0.9993	0.6931	71.6765
			$C_{50}^{3}$	0.8899	0.8203	0.9995	0.9011	0.7862
			$A_{10}^{3}$	0.5560	0.5305	0.9994	0.6931	62.0974
			$A_{50}^{3}$	0.8932	0.8249	0.9992	0.9037	0.7784
		$2^{40}$	$T^{3}$	0.3616	0.4178	0.6927	0.5212	1542.8804
			$C_{10}^{3}$	0.5564	0.5307	0.9992	0.6932	71.5496
			$C_{50}^{3}$	0.8908	0.8216	0.9992	0.9018	0.7835
			$A_{10}^{3}$	0.5565	0.5308	0.9992	0.6933	61.9845
			$A_{50}^{3}$	0.8930	0.8247	0.9992	0.9036	0.7794
	SVM		Plain	0.9681	0.9402	1.0000	0.9692	0.8649
			$R_{5}^{3}$	0.5605	0.5330	1.0000	0.6953	36.6039
		$2^{30}$	$T^{3}$	0.5513	0.5278	1.0000	0.6910	198.8704
			$C_{10}^{3}$	0.6356	0.5793	0.9988	0.7333	8.5442
			$C_{50}^{3}$	0.9263	0.9385	0.9130	0.9256	0.6254
			$A_{10}^{3}$	0.6397	0.5820	1.0000	0.7358	7.4514
			$A_{50}^{3}$	0.9682	0.9406	0.9998	0.9693	0.6478
		$2^{40}$	$T^{3}$	0.5518	0.5281	1.0000	0.6912	198.5042
			$C_{10}^{3}$	0.6357	0.5793	1.0000	0.7336	8.5288
			$C_{50}^{3}$	0.9681	0.9402	1.0000	0.9692	0.6253
			$A_{10}^{3}$	0.6399	0.5821	1.0000	0.7359	7.4376
			$A_{50}^{3}$	0.9682	0.9404	1.0000	0.9693	0.6482

7. Conclusion

We implemented a FHE-based solution for supervised binary classification for log anomaly detection. FHE is a cryptographic technique that allows computations on encrypted data without decrypting it. This makes it a promising approach for privacy-preserving machine learning applications, such as log anomaly detection. In our solution, we used the CKKS algorithm, which is a popular FHE scheme. We also approximated the Sigmoid activation function, a commonly used function in machine learning, with novel low-order polynomials. This allowed us to reduce our solution’s communication and computation requirements, making it more suitable for wireless sensors and IoT devices. Chebyshev approximations of low order for FHE are widely used in many privacy-preserving tasks. We compared our ANN-based polynomials with Chebyshev regarding performance metrics and timings. We empirically show that our polynomials performed better in most cases for the same amount of computation and multiplication depth. However, comparing our approximations with composite (iterative) polynomials [38,39] would make an interesting study. Our evaluation of FHE for supervised binary classification was limited to linearly separable problems. In future work, we plan to implement FHE with other ML models, such as Recurrent Neural Networks (RNN) and Random Forests (RF). We also plan to use Chimera [40] and combine TFHE/BFV for assessing the Sigmoid activation function by approximating it by the Signum (Sign) operation furnished by the TFHE bootstrapping.

Author Contributions

All authors contributed to this study’s conceptualization and methodology. D.T. contributed to writing—original draft preparation. All authors contributed to writing—review and editing. D.T. contributed to visualization. A.B. contributed to supervision. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

No new data were created or analyzed in this study. Data sharing does not apply to this article.

Conflicts of Interest

The authors declare no conflict of interest.

References

S.3195 - Consumer Online Privacy Rights Act, 2021.
TITLE 1.81.5. California Consumer Privacy Act of 2018 [1798.100 - 1798.199.100], 2018.
EUR-Lex - 02016R0679-20160504 - EN - EUR-Lex, 2016.
Durumeric, Z.; Ma, Z.; Springall, D.; Barnes, R.; Sullivan, N.; Bursztein, E.; Bailey, M.; Halderman, J.A.; Paxson, V. The Security Impact of HTTPS Interception. In Proceedings of the NDSS, 2017.
Principles for the processing of user data by Kaspersky security solutions and technologies | Kaspersky.
Nakashima, E. Israel hacked Kaspersky, then tipped the NSA that its tools had been breached, 2017.
Perlroth, N.; Shane, S. How Israel Caught Russian Hackers Scouring the World for U.S. Secrets, 2017.
Temperton, J. AVG can sell your browsing and search history to advertisers, 2015.
Taylor, S. Is Your Antivirus Software Spying On You? | Restore Privacy, 2021.
Karande, V.; Bauman, E.; Lin, Z.; Khan, L. SGX-Log: Securing system logs with SGX. In Proceedings of the Proceedings of the 2017 ACM on Asia Conference on Computer and Communications Security, 2017, pp. 19–30.
Paccagnella, R.; Datta, P.; Hassan, W.U.; Bates, A.; Fletcher, C.; Miller, A.; Tian, D. Custos: Practical tamper-evident auditing of operating systems using trusted execution. In Proceedings of the Network and distributed system security symposium, 2020.
Chillotti, I.; Gama, N.; Georgieva, M.; Izabachène, M. Faster Fully Homomorphic Encryption: Bootstrapping in Less Than 0.1 Seconds. In Proceedings of the Advances in Cryptology – ASIACRYPT 2016; Cheon, J.H.; Takagi, T., Eds.; Springer Berlin Heidelberg: Berlin, Heidelberg, 2016; pp. 3–33.
Brakerski, Z. Fully Homomorphic Encryption Without Modulus Switching from Classical GapSVP. In Proceedings of the Proceedings of the 32Nd Annual Cryptology Conference on Advances in Cryptology — CRYPTO 2012 - Volume 7417; Springer-Verlag New York, Inc.: New York, NY, USA, 2012; pp. 868–886. [CrossRef]
Fan, J.; Vercauteren, F. Somewhat Practical Fully Homomorphic Encryption. Cryptology ePrint Archive, Report 2012/144, 2012. https://eprint.iacr.org/2012/144.
Cheon, J.H.; Kim, A.; Kim, M.; Song, Y. Homomorphic Encryption for Arithmetic of Approximate Numbers. Cryptology ePrint Archive, Report 2016/421, 2016. https://eprint.iacr.org/2016/421.
Frery, J.; Stoian, A.; Bredehoft, R.; Montero, L.; Kherfallah, C.; Chevallier-Mames, B.; Meyre, A. Privacy-Preserving Tree-Based Inference with Fully Homomorphic Encryption. arXiv preprint arXiv:2303.01254 2023.
Boudguiga, A.; Stan, O.; Sedjelmaci, H.; Carpov, S. Homomorphic Encryption at Work for Private Analysis of Security Logs. In Proceedings of the ICISSP, 2020, pp. 515–523.
Trivedi, D.; Boudguiga, A.; Triandopoulos, N. SigML: Supervised Log Anomaly with Fully Homomorphic Encryption. In Proceedings of the International Symposium on Cyber Security, Cryptology, and Machine Learning. Springer, 2023, pp. 372–388.
Brakerski, Z.; Gentry, C.; Vaikuntanathan, V. Fully Homomorphic Encryption without Bootstrapping. Cryptology ePrint Archive, Paper 2011/277, 2011. https://eprint.iacr.org/2011/277.
Remez, E.Y. Sur le calcul effectif des polynomes d’approximation de Tschebyscheff. CR Acad. Sci. Paris 1934, 199, 337–340.
Chen, H.; Gilad-Bachrach, R.; Han, K.; Huang, Z.; Jalali, A.; Laine, K.; Lauter, K. Logistic regression over encrypted data from fully homomorphic encryption. BMC medical genomics 2018, 11, 3–12. [CrossRef]
Zhao, J.; Mortier, R.; Crowcroft, J.; Wang, L. Privacy-preserving machine learning based data analytics on edge devices. In Proceedings of the Proceedings of the 2018 AAAI/ACM Conference on AI, Ethics, and Society, 2018, pp. 341–346.
Wang, L. Owl: A General-Purpose Numerical Library in OCaml, 2017, [arXiv:cs.MS/1707.09616].
Ray, I.; Belyaev, K.; Strizhov, M.; Mulamba, D.; Rajaram, M. Secure logging as a service—delegating log management to the cloud. IEEE systems journal 2013, 7, 323–334. [CrossRef]
The Tor Project | Privacy & Freedom Online.
Zawoad, S.; Dutta, A.K.; Hasan, R. SecLaaS: secure logging-as-a-service for cloud forensics. In Proceedings of the Proceedings of the 8th ACM SIGSAC symposium on Information, computer and communications security, 2013, pp. 219–230.
Zawoad, S.; Dutta, A.K.; Hasan, R. Towards building forensics enabled cloud through secure logging-as-a-service. IEEE Transactions on Dependable and Secure Computing 2015, 13, 148–162. [CrossRef]
Rane, S.; Dixit, A. BlockSLaaS: Blockchain assisted secure logging-as-a-service for cloud forensics. In Proceedings of the International Conference on Security & Privacy. Springer, 2019, pp. 77–88.
Bittau, A.; Erlingsson, Ú.; Maniatis, P.; Mironov, I.; Raghunathan, A.; Lie, D.; Rudominer, M.; Kode, U.; Tinnes, J.; Seefeld, B. Prochlo: Strong privacy for analytics in the crowd. In Proceedings of the Proceedings of the 26th symposium on operating systems principles, 2017, pp. 441–459.
Paul, J.; Annamalai, M.S.M.S.; Ming, W.; Al Badawi, A.; Veeravalli, B.; Aung, K.M.M. Privacy-Preserving Collective Learning With Homomorphic Encryption. IEEE Access 2021, 9, 132084–132096. [CrossRef]
Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. Journal of Machine Learning Research 2011, 12, 2825–2830.
Huelse. Huelse/Seal-Python: Microsoft seal 4.x for Python. https://github.com/Huelse/SEAL-Python, 2022. [Released: May 9, 2022].
Buitinck, L.; Louppe, G.; Blondel, M.; Pedregosa, F.; Mueller, A.; Grisel, O.; Niculae, V.; Prettenhofer, P.; Gramfort, A.; Grobler, J.; et al. API design for machine learning software: experiences from the scikit-learn project. In Proceedings of the ECML PKDD Workshop: Languages for Data Mining and Machine Learning, 2013, pp. 108–122.
for Cybersecurity, C.I. NSL-KDD | Datasets | Research | Canadian Institute for Cybersecurity. https://www.unb.ca/cic/datasets/nsl.html, 2019.
Tavallaee, M.; Bagheri, E.; Lu, W.; Ghorbani, A.A. A detailed analysis of the KDD CUP 99 data set. In Proceedings of the 2009 IEEE symposium on computational intelligence for security and defense applications. Ieee, 2009, pp. 1–6.
He, S.; Zhu, J.; He, P.; Lyu, M.R. Loghub: A Large Collection of System Log Datasets towards Automated Log Analytics, 2020. [CrossRef]
He, P.; Zhu, J.; Zheng, Z.; Lyu, M.R. Drain: An online log parsing approach with fixed depth tree. In Proceedings of the 2017 IEEE international conference on web services (ICWS). IEEE, 2017, pp. 33–40.
Cheon, J.H.; Kim, D.; Kim, D.; Lee, H.H.; Lee, K. Numerical method for comparison on homomorphically encrypted numbers. In Proceedings of the International Conference on the Theory and Application of Cryptology and Information Security. Springer, 2019, pp. 415–445.
Lee, E.; Lee, J.W.; No, J.S.; Kim, Y.S. Minimax approximation of sign function by composite polynomial for homomorphic comparison. IEEE Transactions on Dependable and Secure Computing 2021, 19, 3711–3727. [CrossRef]
Boura, C.; Gama, N.; Georgieva, M.; Jetchev, D. CHIMERA: Combining Ring-LWE-based Fully Homomorphic Encryption Schemes. Cryptology ePrint Archive, Report 2018/758, 2018. https://eprint.iacr.org/2018/758.

Figure 1. A typical corporate network architecture.

Figure 2. Security Analytics Sources (SAS) of a SIEM.

Figure 3. Log anomaly detection with contemporary encryption schemes.

Figure 4. Traditional cloud model (left) v/s FHE cloud model (right).

Figure 5. Polynomial approximation using

A N N

Figure 5. Polynomial approximation using

A N N

Figure 6. Encrypted log anomaly detection in Ubiquitous mode.

Figure 7. Encrypted log anomaly detection in Aggregate mode.

Table 1. Comparing "Ubiquitous" and "Aggregate" configurations.

Configuration	Encryption		Decryption
	Time	Size	Time	Size
Ubiquitous	$n \cdot T_{E} (p)$	$n \cdot S_{E} (p)$	$n \cdot T_{D} (c)$	$n \cdot S_{D} (c)$
Aggregate			$T_{D} (c)$	$S_{D} (c)$

Table 4. Time taken in seconds for sigmoid approximations.

Dataset	Model	Scale	Method	Average			Total (CPU)
				Encryption	Decryption	Sigmoid	User	System
NSL-KDD	LR	$2^{30}$	$T^{3}$	15.9451	1.2736	25.0283	21229.5304	31.1183
			$C_{10}^{3}$	15.8492	1.2750	24.8478	14151.9965	21.6079
			$C_{50}^{3}$	16.3591	1.3128	25.6645	57907.9974	192.8575
			$A_{10}^{3}$	15.9845	1.2882	25.1456	7098.8882	12.2847
			$A_{50}^{3}$	16.4581	1.3294	25.8525	50652.5642	173.5452
		$2^{40}$	$T^{3}$	16.5453	1.3044	26.1130	21864.5342	86.9118
			$C_{10}^{3}$	16.3382	1.2872	25.6880	14527.2336	63.9331
			$C_{50}^{3}$	16.2095	1.2866	25.3791	72326.0694	229.5827
			$A_{10}^{3}$	16.4056	1.2930	25.8025	7249.1064	44.1778
			$A_{50}^{3}$	16.2132	1.2683	25.5183	65122.4439	209.3589
	SVM	$2^{30}$	$T^{3}$	15.9461	1.2854	25.1386	21342.9889	37.2623
			$C_{10}^{3}$	16.0024	1.2769	25.1158	14240.9221	27.7670
			$C_{50}^{3}$	16.3930	1.3225	25.7013	34780.6294	69.3801
			$A_{10}^{3}$	16.1102	1.2971	25.3295	7138.4435	17.5237
			$A_{50}^{3}$	16.0584	1.2954	25.1713	79472.3131	241.1018
		$2^{40}$	$T^{3}$	16.0374	1.2567	25.0808	43369.0540	144.5788
			$C_{10}^{3}$	15.9906	1.2657	25.0830	36270.2810	133.6592
			$C_{50}^{3}$	16.1845	1.2751	25.3623	41969.1462	86.2903
			$A_{10}^{3}$	16.4235	1.3000	25.8985	29143.3392	110.3346
			$A_{50}^{3}$	15.9473	1.2531	25.1184	93679.2789	260.7503
HDFS	LR	$2^{30}$	$T^{3}$	16.3908	1.2578	25.4707	28191.8944	96.0272
			$C_{10}^{3}$	16.4117	1.2704	25.3694	56176.0993	249.5097
			$C_{50}^{3}$	16.2385	1.3113	25.1131	83989.0793	355.9741
			$A_{10}^{3}$	16.1082	1.2582	24.9673	27724.1933	75.9279
			$A_{50}^{3}$	15.9611	1.2891	24.7696	55177.6614	119.2686
		$2^{40}$	$T^{3}$	16.0785	1.1416	24.8503	27533.3271	43.9969
			$C_{10}^{3}$	16.1325	1.1467	24.6902	28002.8715	42.0600
			$C_{50}^{3}$	16.1544	1.1475	24.7477	55939.1609	88.9075
			$A_{10}^{3}$	16.0655	1.1504	25.0016	82767.8606	171.9368
			$A_{50}^{3}$	16.4731	1.1875	25.5487	110748.7027	309.8314
	SVM	$2^{30}$	$T^{3}$	16.3642	1.2677	25.4733	82902.0987	212.2604
			$C_{10}^{3}$	16.0238	1.2588	24.7493	27494.7062	61.8813
			$C_{50}^{3}$	15.9412	1.2864	24.7108	54953.8687	107.4183
			$A_{10}^{3}$	16.1825	1.2757	25.0942	138438.5341	379.7756
			$A_{50}^{3}$	16.3706	1.3089	25.4166	35159.2336	121.3245
		$2^{40}$	$T^{3}$	16.6737	1.1933	25.8361	83201.7236	274.1485
			$C_{10}^{3}$	15.9010	1.1333	24.5346	27335.2857	46.0062
			$C_{50}^{3}$	16.0024	1.1422	24.6981	54971.1042	97.4169
			$A_{10}^{3}$	15.9279	1.1375	24.6168	27384.4133	46.0062
			$A_{50}^{3}$	15.9141	1.1383	24.5868	27388.0323	43.6415

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

SigML++: Supervised Log Anomaly with Probabilistic Polynomial Approximations

Abstract

1. Introduction

1.1. Contributions

1.2. Organization

2. Background

2.1. Fully Homomorphic Encryption

2.2. Polynomial Approximations

2.2.1. Taylor

2.2.2. Fourier

2.2.3. Pade

2.2.4. Chebyshev

2.2.5. Remez

2.2.6. ANN

3. Sigmoid Approximation

4. Proposed Solution

5. Related Work

6. Experimental Analysis

6.1. Evaluation Criteria

6.2. Datasets

6.3. Test Results

7. Conclusion

Author Contributions

Funding

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe