Submitted:
29 November 2023
Posted:
30 November 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Related Work
3. Classification of jamming Attacks
- Constant Jamming: This attack sees the intruder ceaselessly emitting random radio signals over the communication channel, neglecting the MAC protocol. Consequently, valid users mistakenly perceive the channel as occupied when it's available.
- Deceptive Jamming: This type of interference, unlike persistent ECM attacks, involves attackers not merely sending random bit sequences but transmitting semi-coherent information packets. The header of these packets appears valid, but the data they carry is essentially worthless. Such deceptive maneuvers often make channels appear perpetually engaged to genuine users, severely hampering authentic communication.
- Random Jamming: This strategy is less power-consuming than the two mentioned before. Attackers using random jamming alternate between periods of active interference (attack mode) and non-interference (sleep mode). The energy used up in the attack corresponds to the ratio of these two modes. This method gives a clear perspective on how random jamming attacks function and their energy dynamics.
- Reactive Jamming: Here, the attacker springs into action, jamming only when they identify an ongoing communication within the network. They prioritize jamming the receiver rather than the transmitter, ensuring minimal resource expenditure. In vehicular networks, this usually takes the form of nodes emitting potent disruptive signals, drowning out legitimate communications. This results in receivers either failing to capture signals or experiencing drastic reductions in reception quality, categorizing this as a predominant form of direct interference attack.
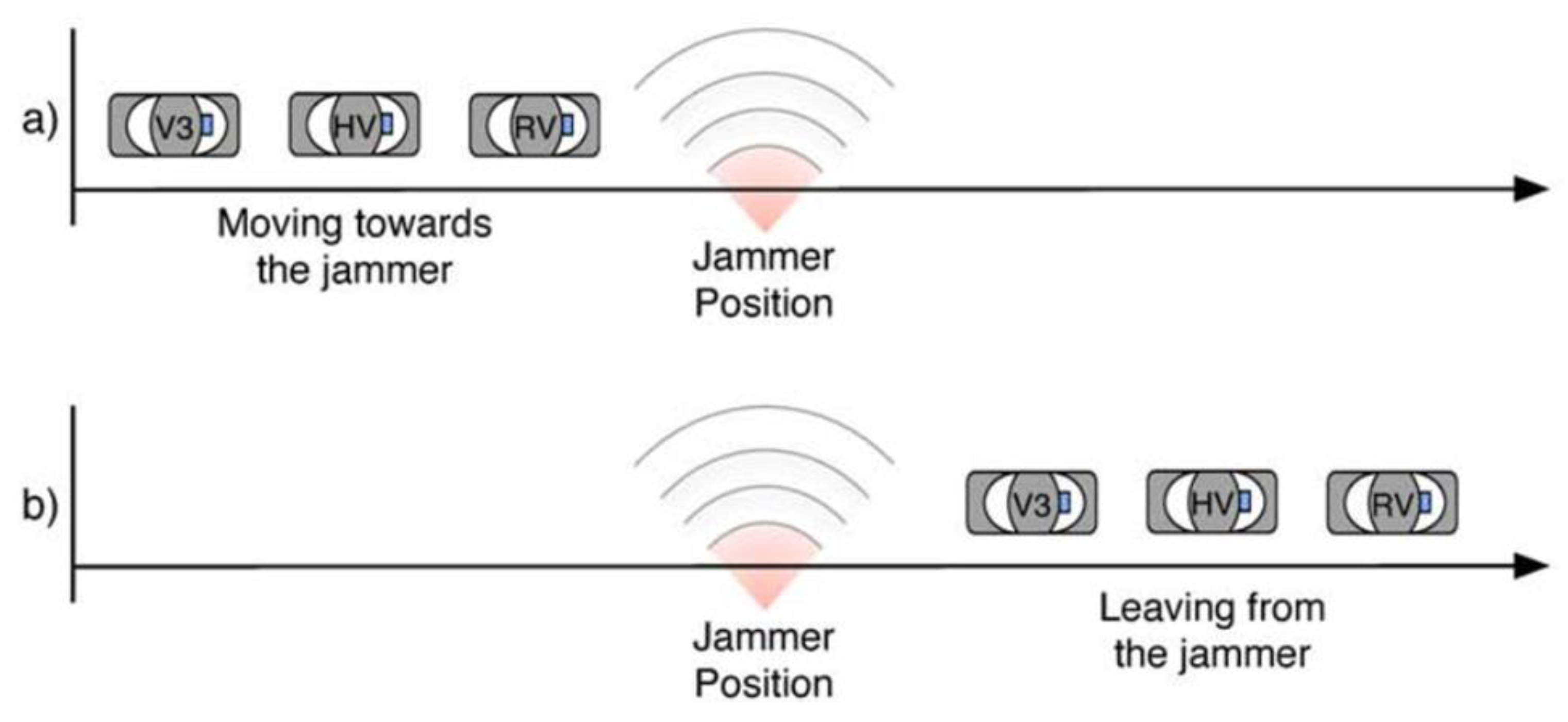
4. Jamming Detection and Description Scenario
4.1. Predication Location
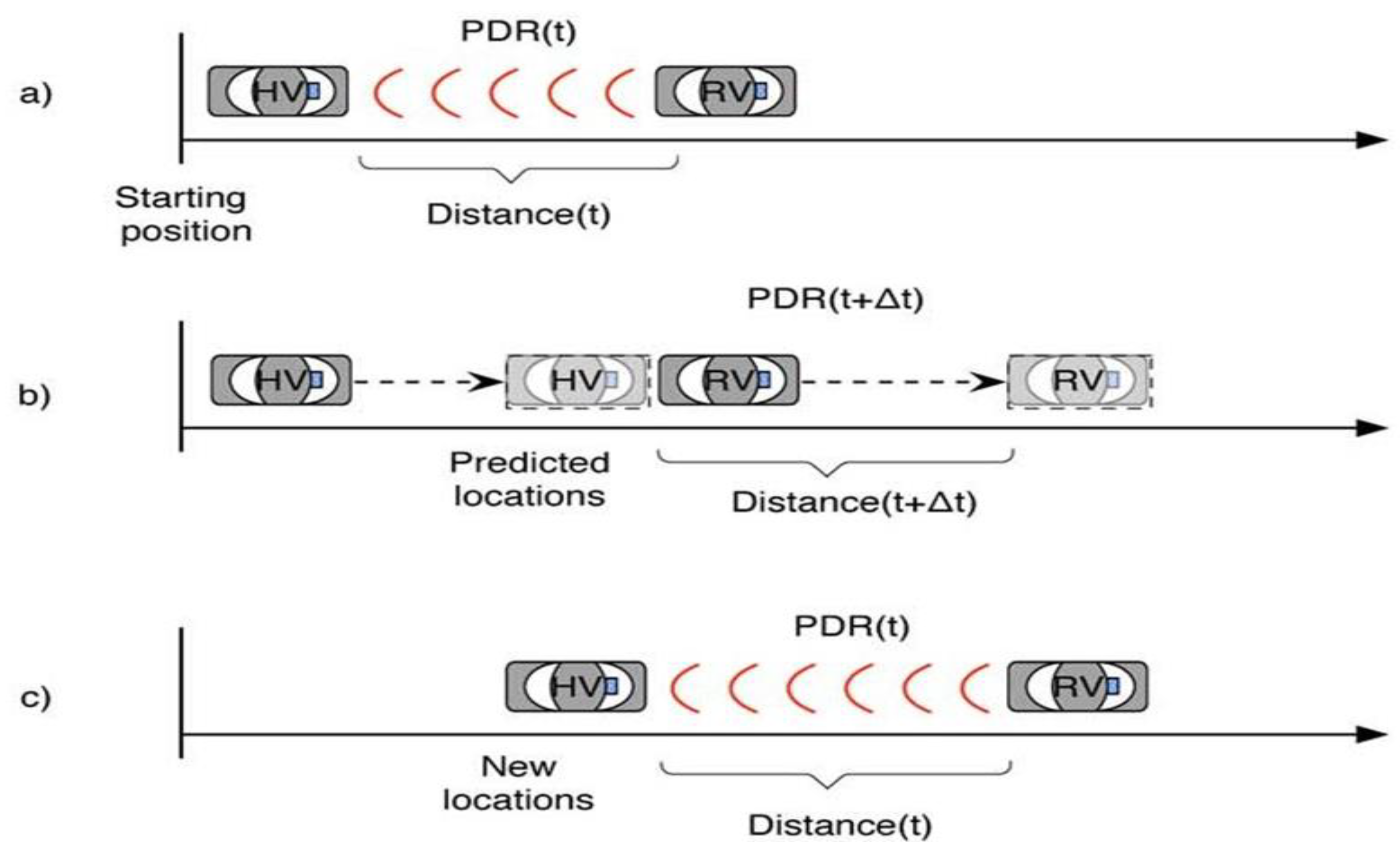
4.2. PDR Evaluation
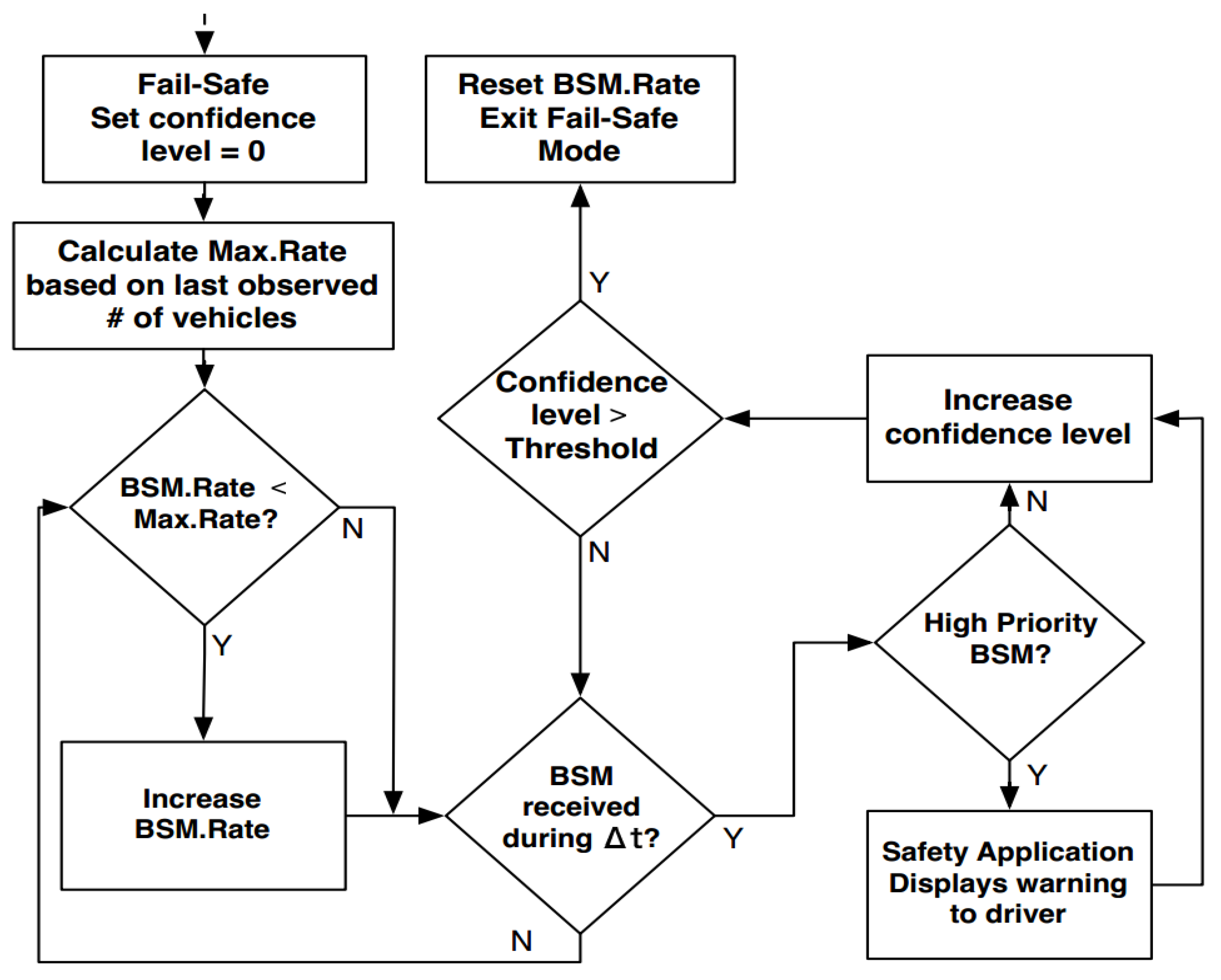
5. Model designed to detect jamming attacks on VANETs.
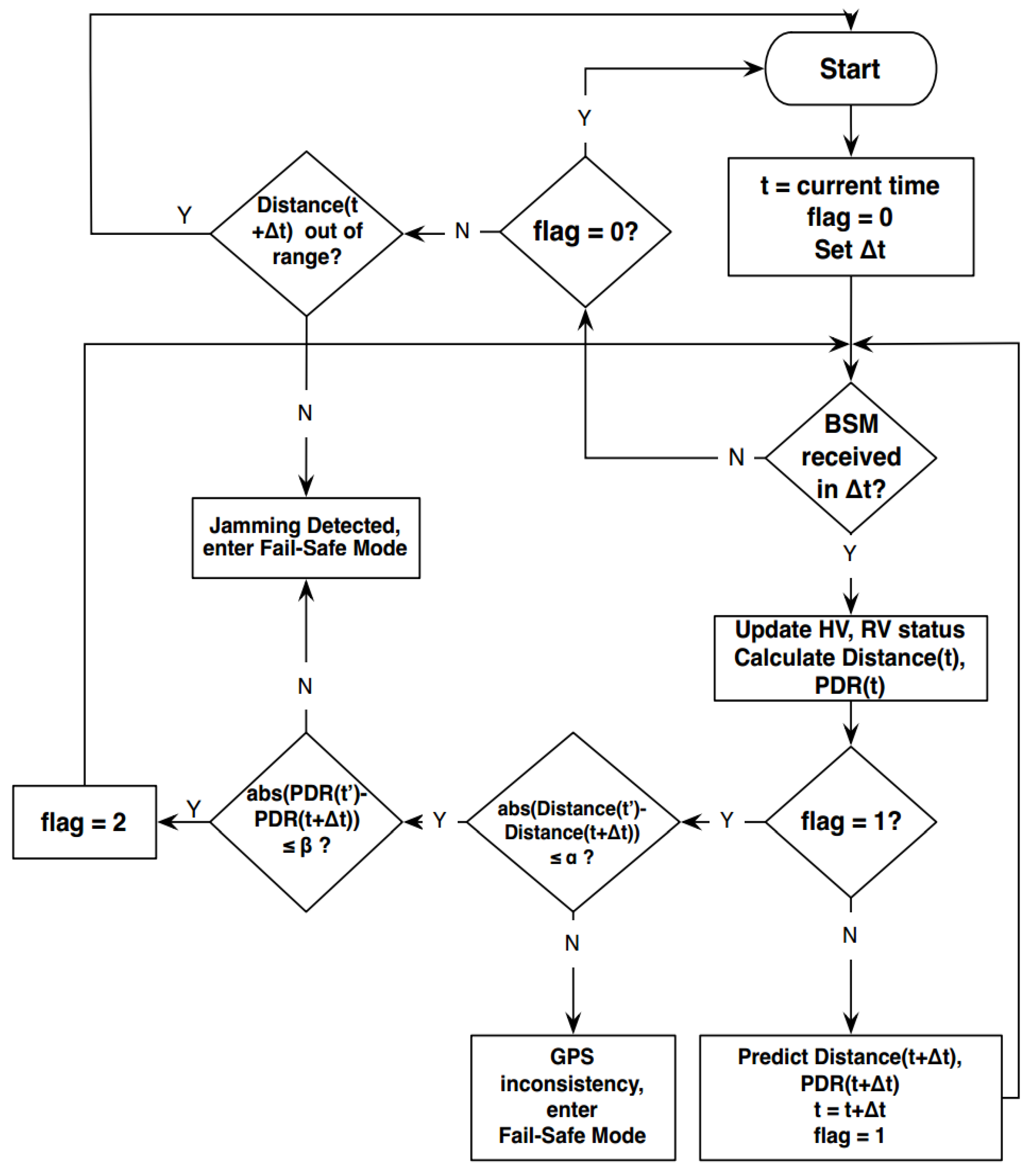
6. Jamming Attack Recovery Algorithm for Dedicated Short-Range Communications (DSRC) Safety Applications in Vehicular Ad-Hoc Networks (VANET).
6.1. Reliability and Redundancy
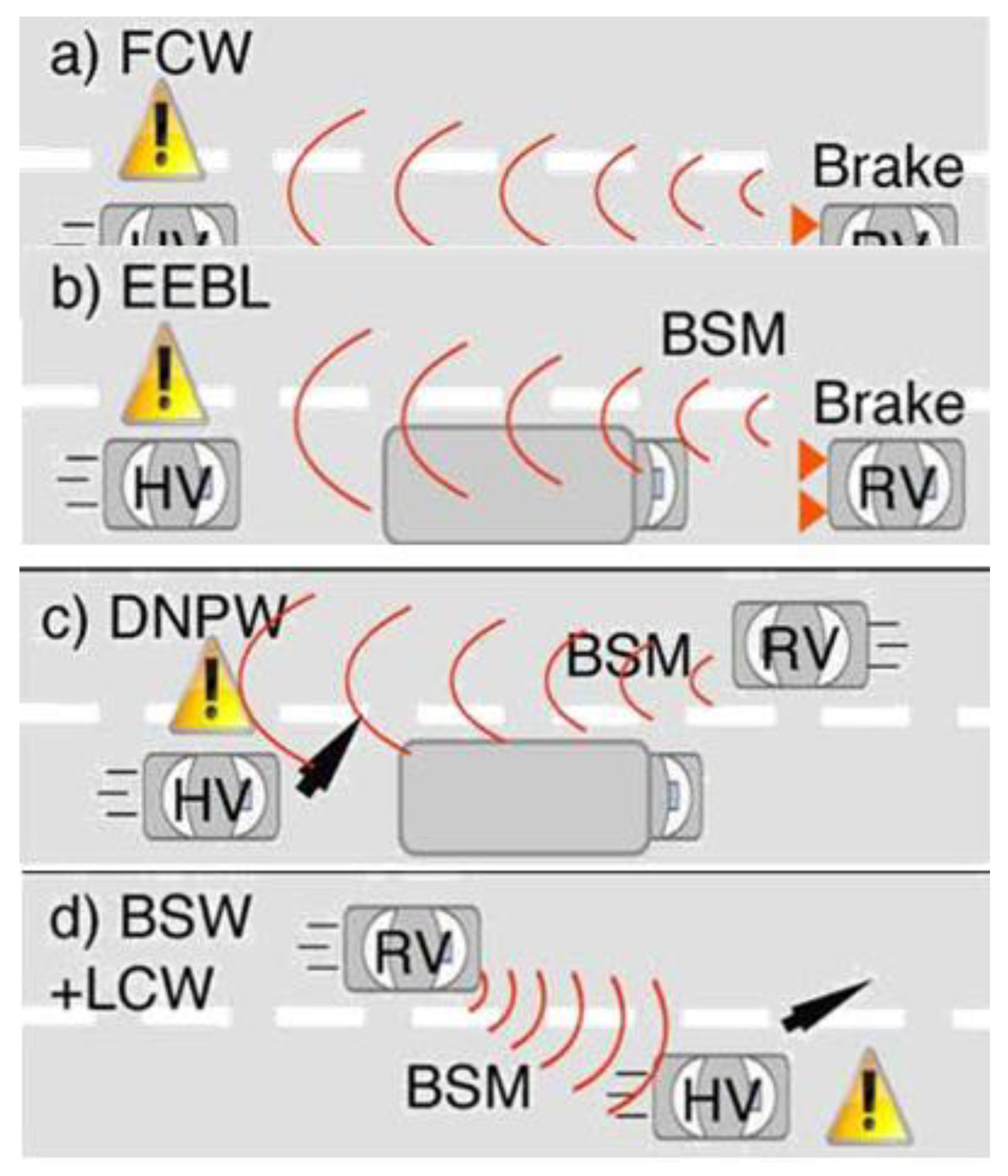
- Figure 3 showcases several vital Safety Applications, which we'll delve into below:
- Forward Collision Warning (FCW) – Pictured in Figure 3a, the FCW alerts the driver of the Host Vehicle (HV) about a potential rear-end collision with a Rear Vehicle (RV) ahead, moving in the same lane and direction. This system proves especially valuable when the HV is closing in on a vehicle that's either decelerating or has come to a halt.
- Emergency Electronic Brake Lights (EEBL) – As illustrated in Figure 3b, the EEBL is somewhat of a toned-down version of FCW. Upon receiving data that an RV ahead is braking sharply, it prompts the HV driver to slow down. The significance of this feature is amplified when an obstruction (like a big truck) limits the HV driver's view.
- Do Not Pass Warning (DNPW) – Depicted in Figure 3 c, DNPW sounds an alert to the HV driver during an overtaking maneuver if there's an incoming vehicle from the opposite direction.
- Blind Spot Warning + Lane Change Warning (BSW+LCW) – Demonstrated in Figure 3d, this Safety Application cautions the HV driver wanting to switch lanes if another vehicle—moving in the same direction—is present in their blind spot.
- It's imperative to note that the success and reliability of these DSRC Safety Applications are heavily dependent on the Basic Safety Messages (BSM) from the RV. If the HV doesn't receive these messages or they aren't frequent enough, the effectiveness of the application may be compromised.
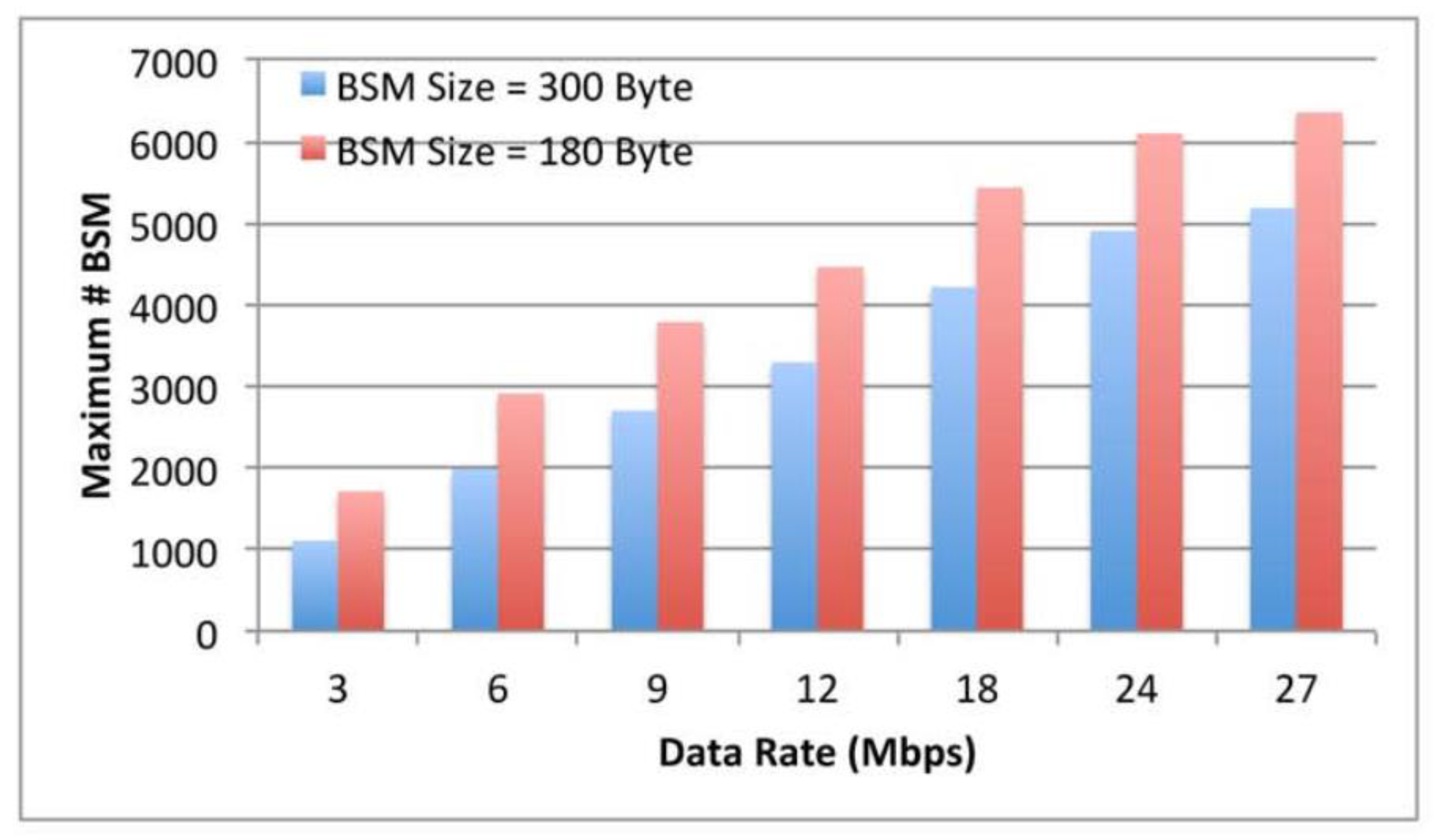
6.2. Effectiveness of various BSM Rates.
| Average number of back-off slots, W | I6 |
| Transmission range, R | 6oo m |
| DIFS time | 64 micro s |
| Data rate | 6 Mbps |
| BSM rates | IO, 2o and 3o BSM/s |
| BSS size | i8o Bytes |
| Vehicle density | z-zoo vehicles/km |
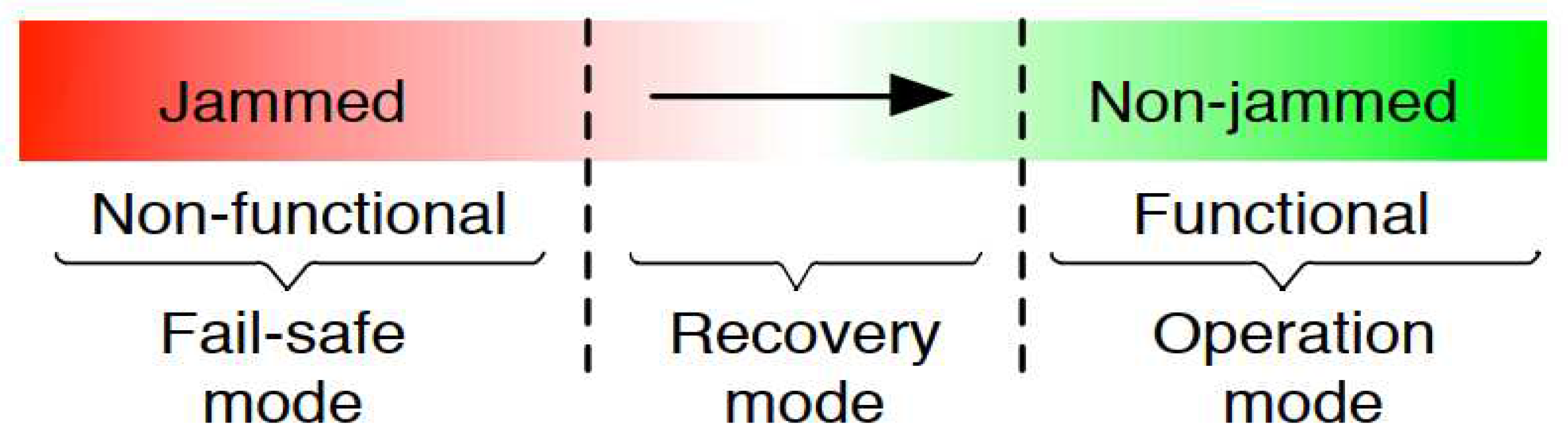
7. Jammer Fail-Safe Mode and Recovery Algorithm
8. Performances Evaluation
| Vehicle speed | 16.6 m/s |
| OBU | Arada Systems LocoMate Classic |
| Length test range | 1.53 km |
| Test range | Straight of 2-lane road |
| Rate of BSM | 10 BSM/s (the BSM for every 100ms) |
| Jammer position | 700 m from starting point |
| Effective bandwidth | 8.3 MHz |
| Channel | Safety Channel 172 |
| Rate of Data | 6and 3 Mbps |
| Power Transmitter | 19 dBm |
| Data rates jammer | 3, 6,, 12 Mbps |
| Jammer power | 18 dBm |
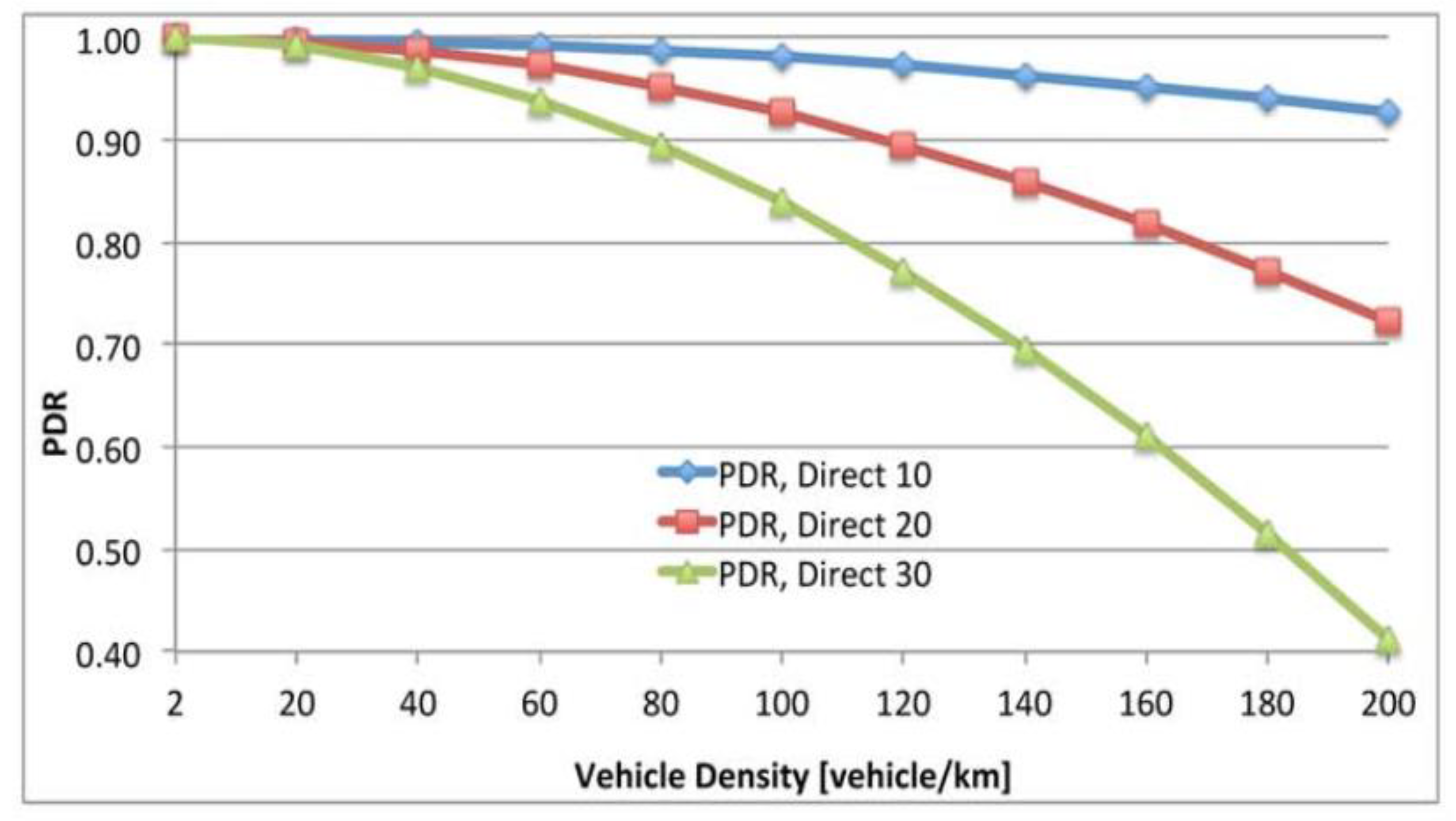
8.1. Indigenous PDR
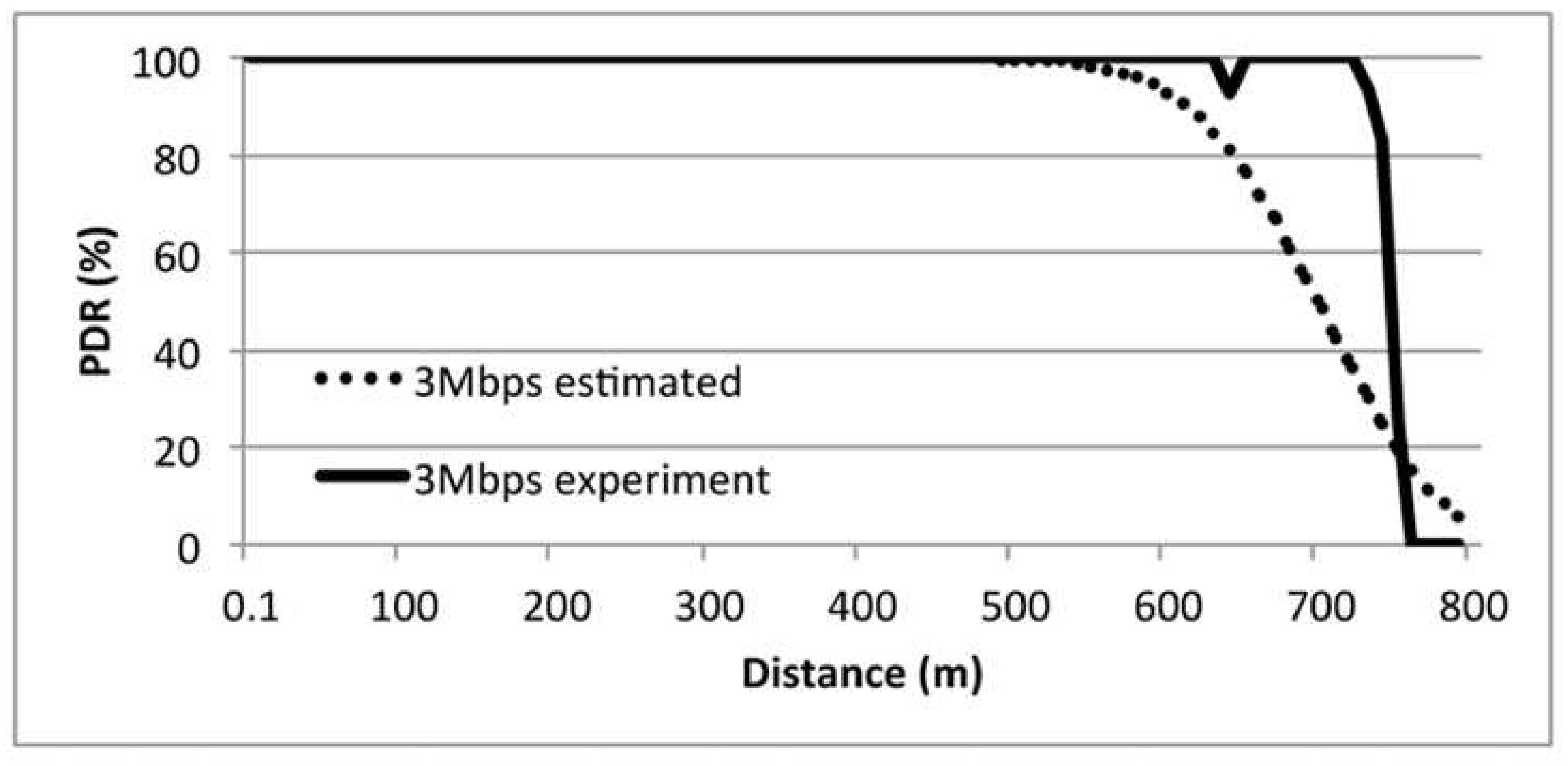
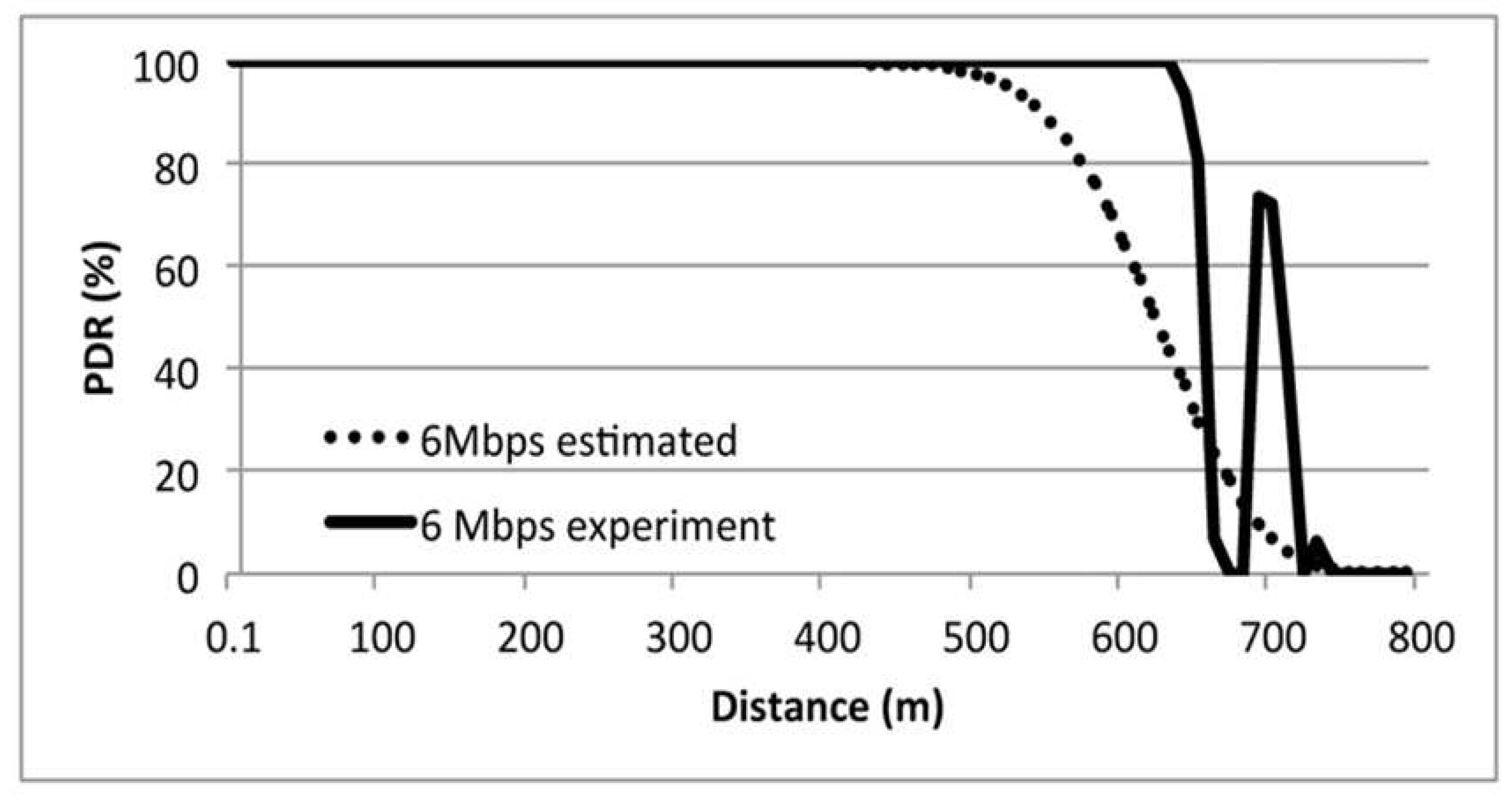
8.2. The Effect Jamming for PDR
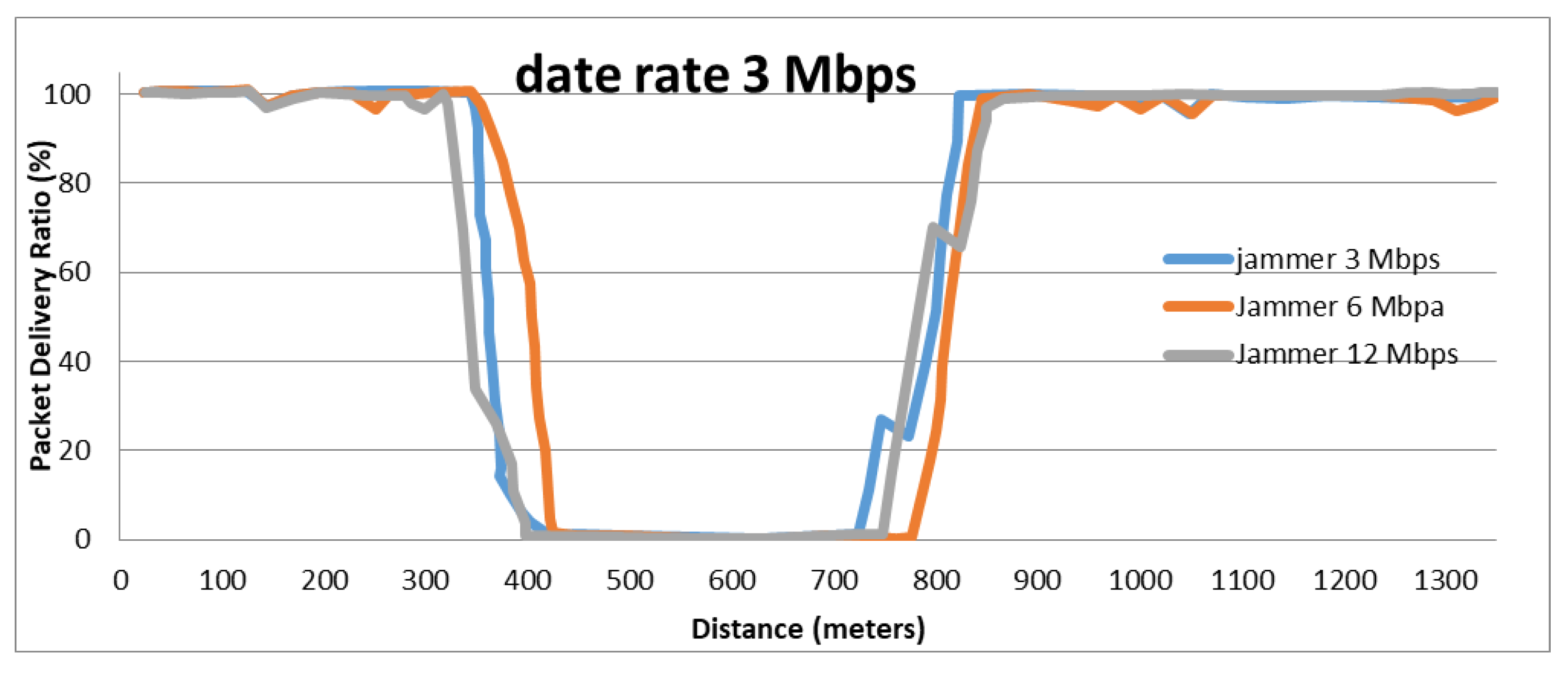

8.3. Jamming Detection Evaluation of Algorithm
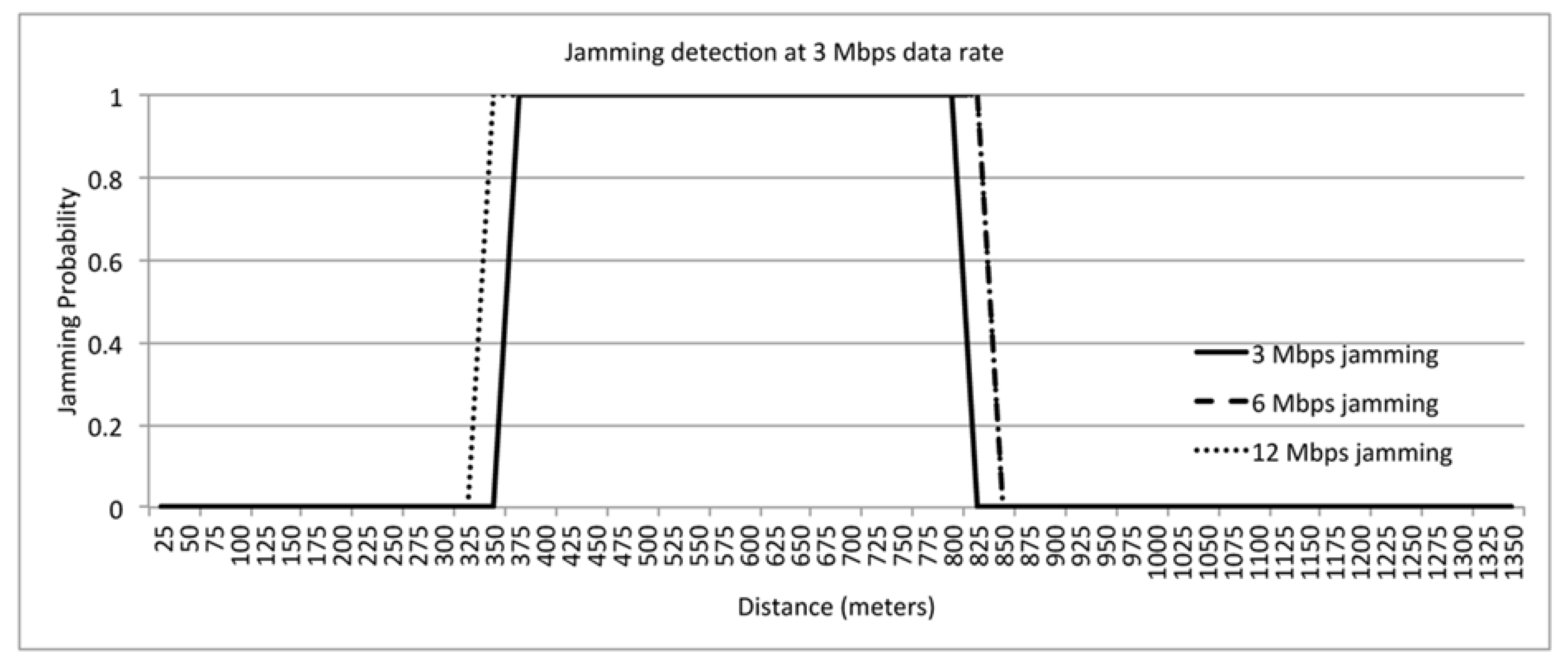
9. Discussion and Results
9.1. Constant Jammer
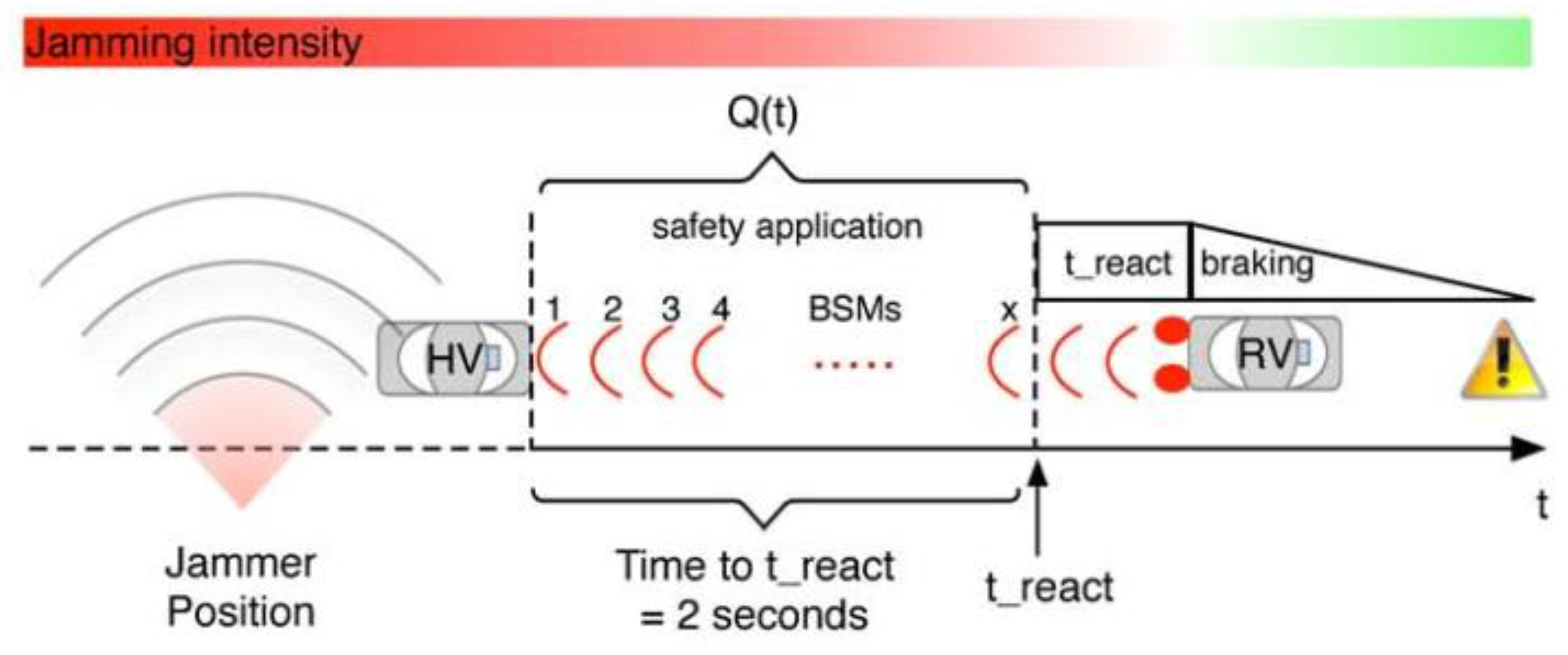
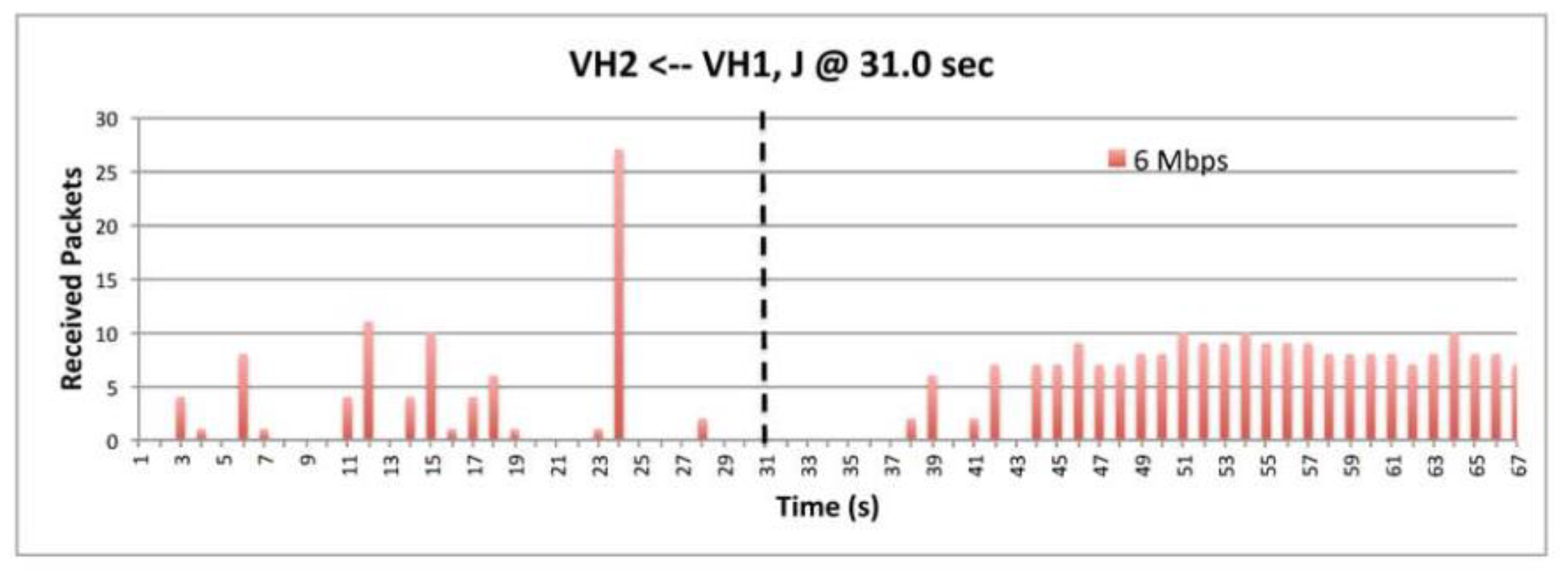
9.2. The Impact of BSM Rats
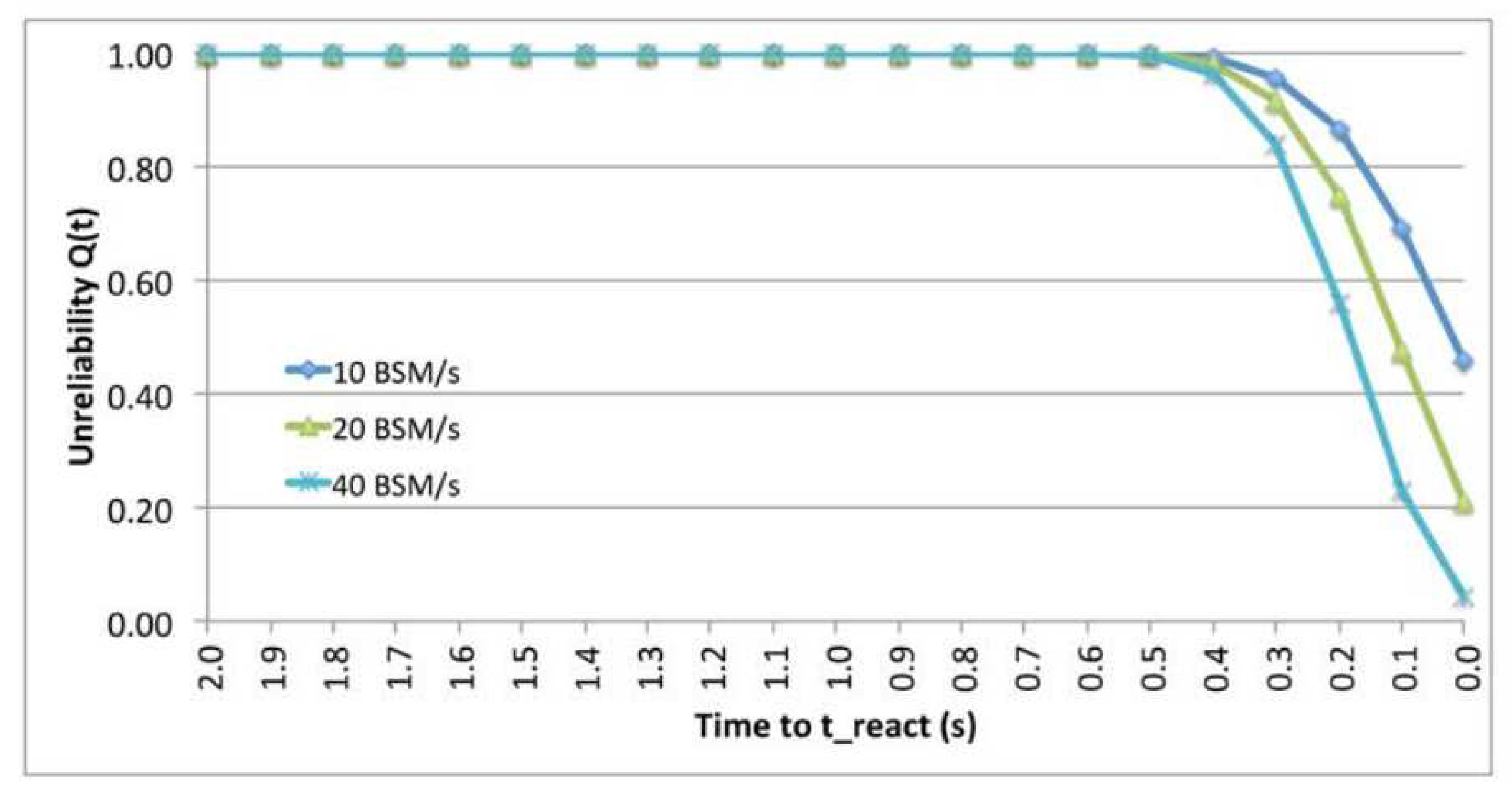
9.2. The effect of Transmission Power.
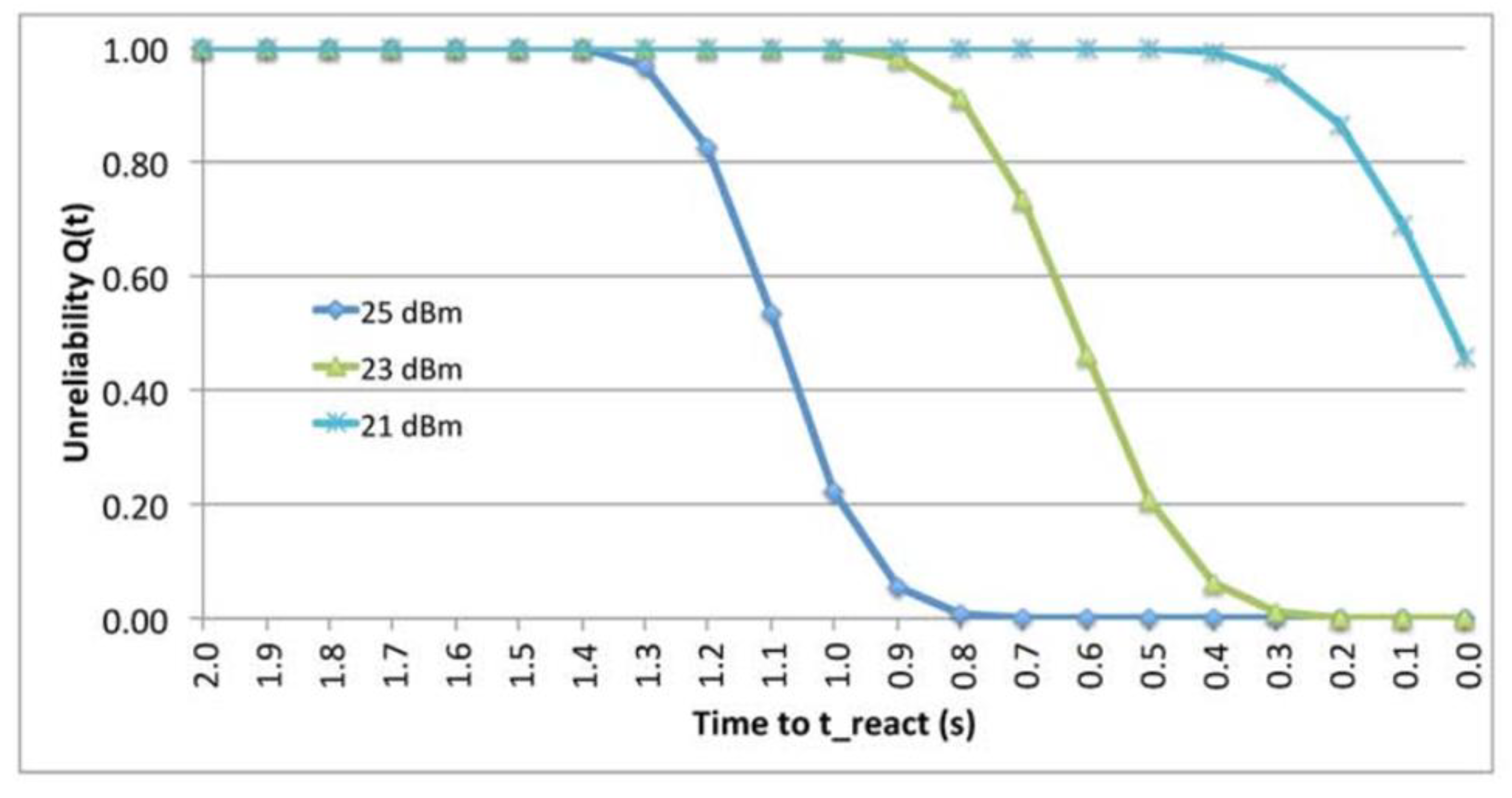
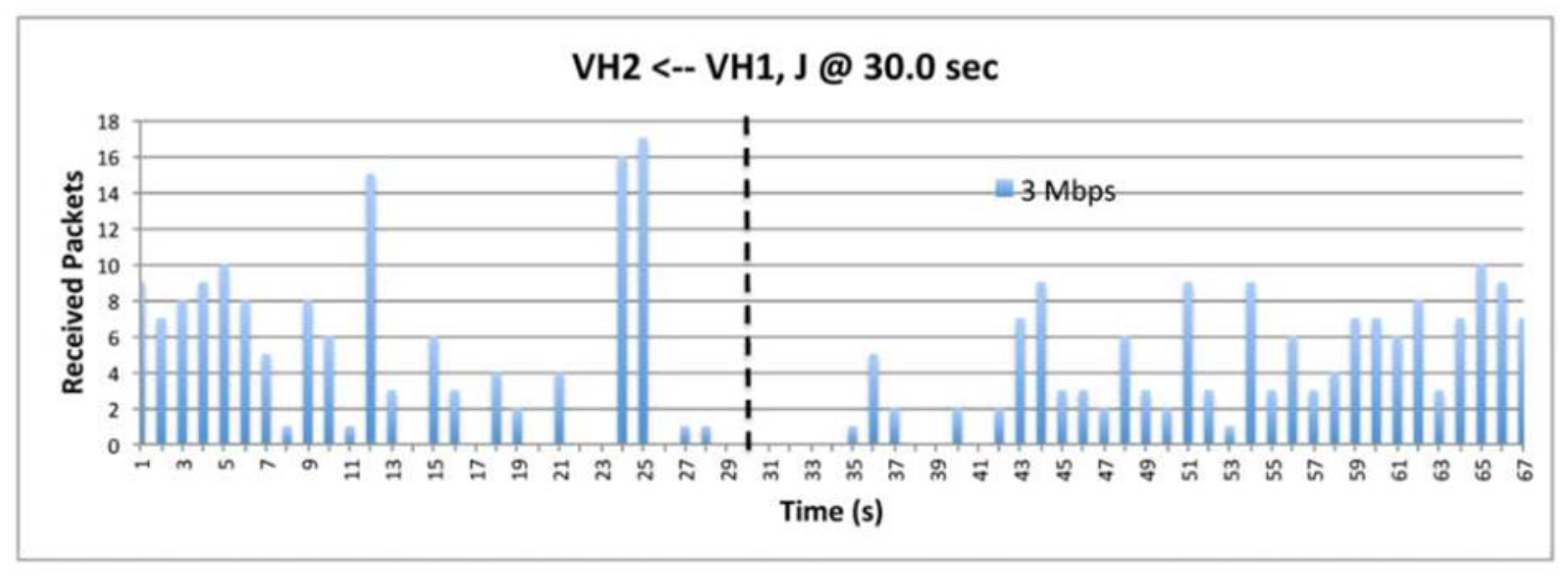
9.2. The effect of Data Rate.
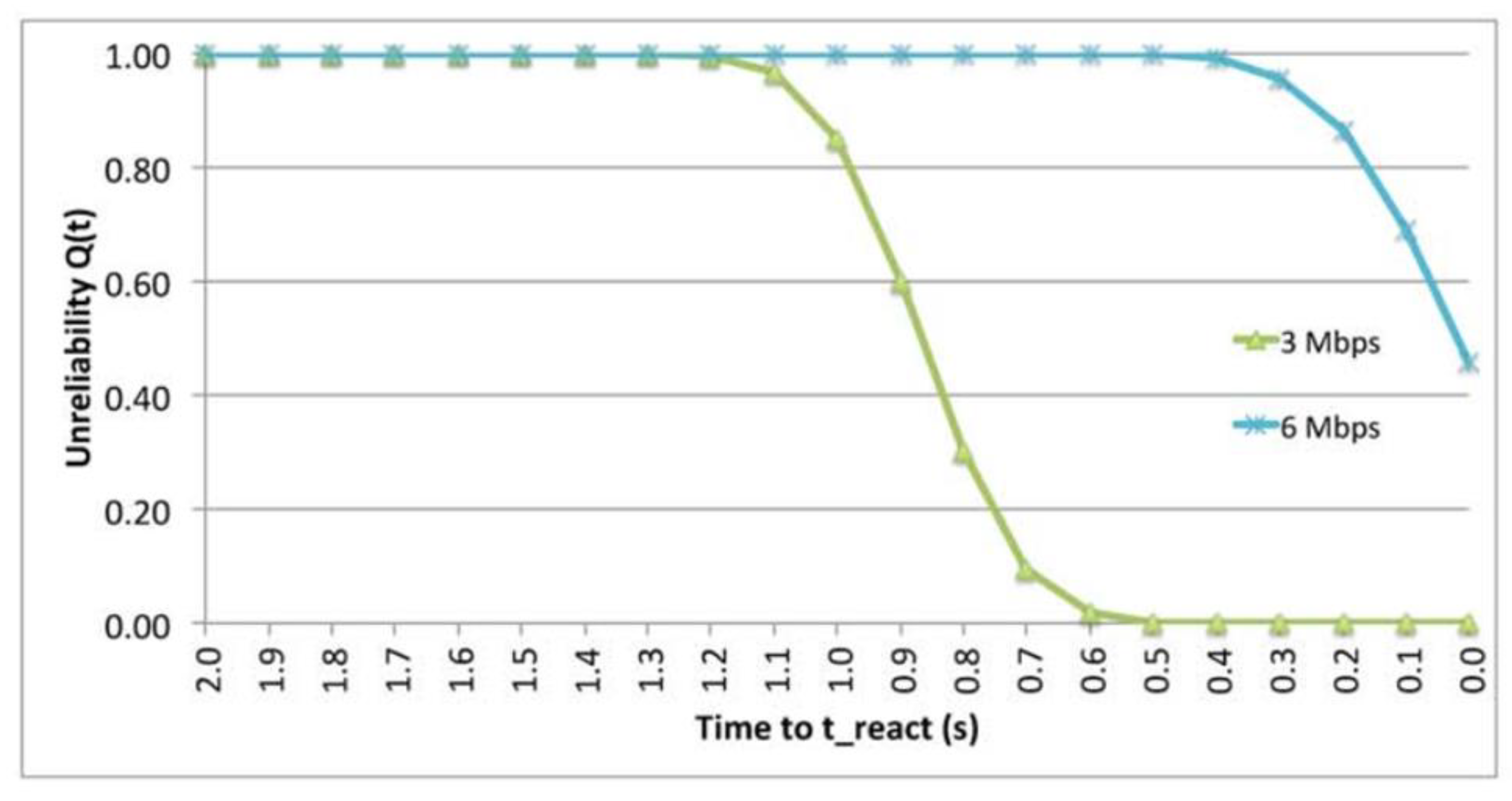
9.5. Deceptive Jammer.
| OBU Model | Arada Systems LocoMate Classic |
| Vehicle speed | 20 m/s |
| Range test | Two lines for the road |
| Test range length | 1000 m |
| Jammer position | 500 m from starting point |
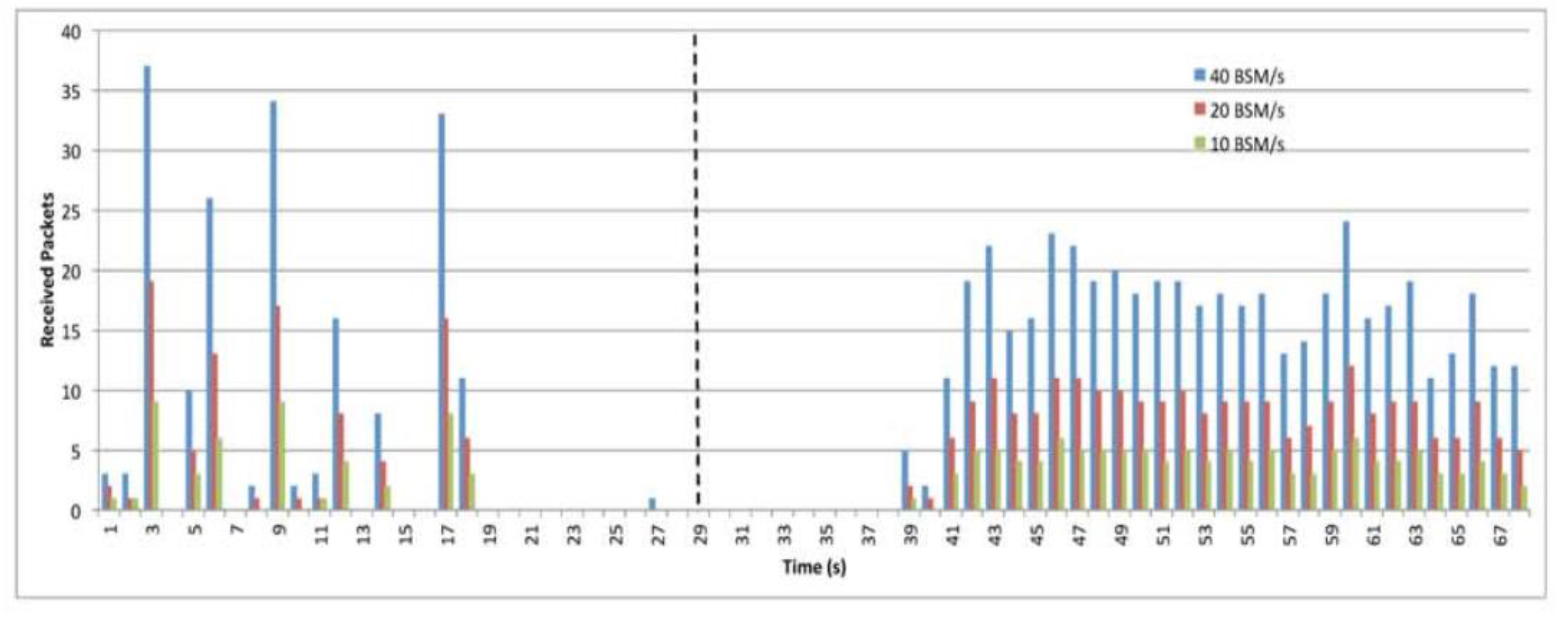
| BSM generation | 10,20 and 40 BSM/s |
| Channel | Safety Channel 172 |
| Effective bandwidth | 8.3 MHz |
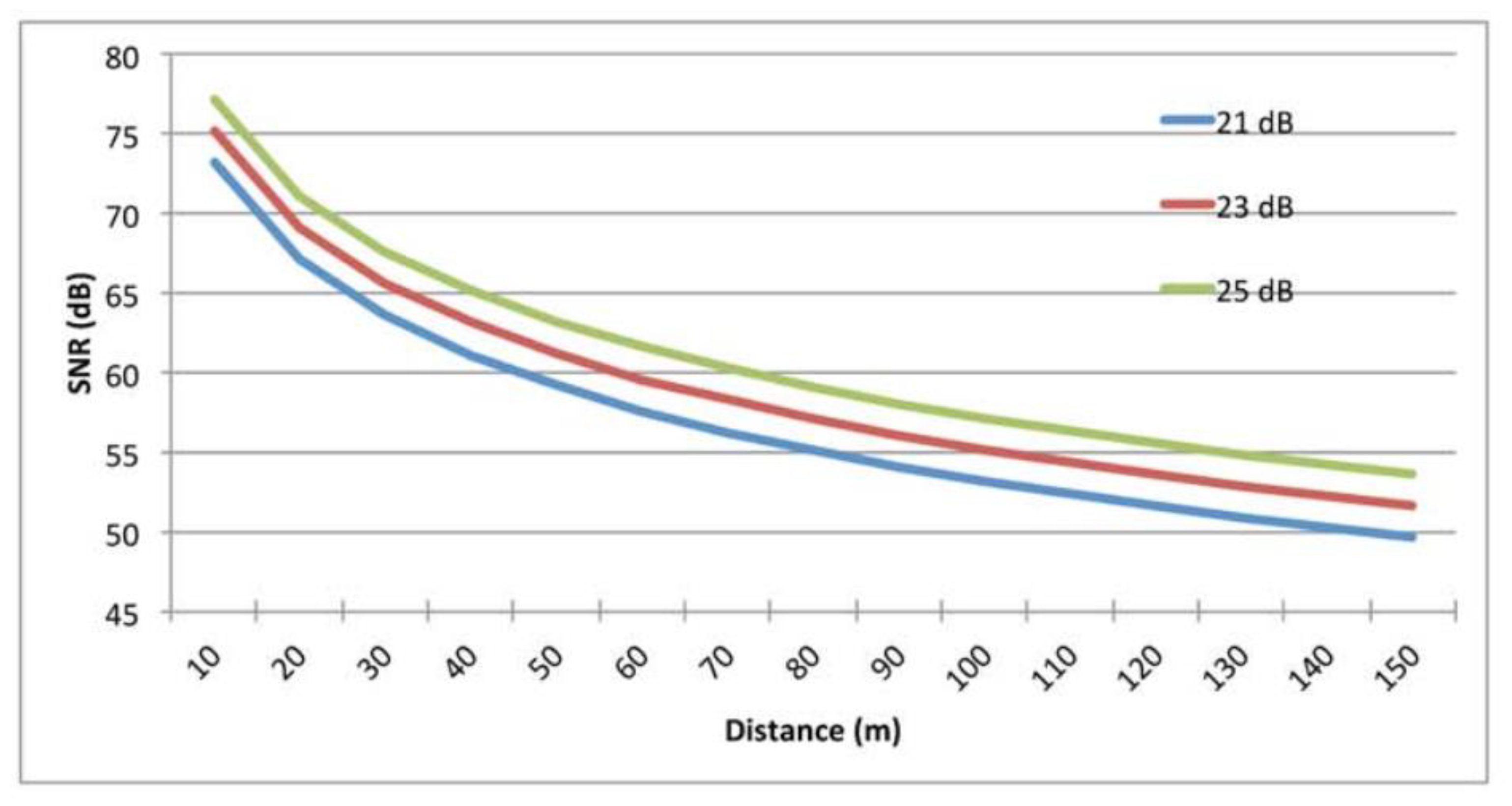
| Transmitter power | 21,23 and 25 dBm |
| Data rate Transmission | 3 and 6 Mbps |
| Data rate Jammer power | 6 Mbps and 18 dBm |
9.6. The Impact of BSM Rates.
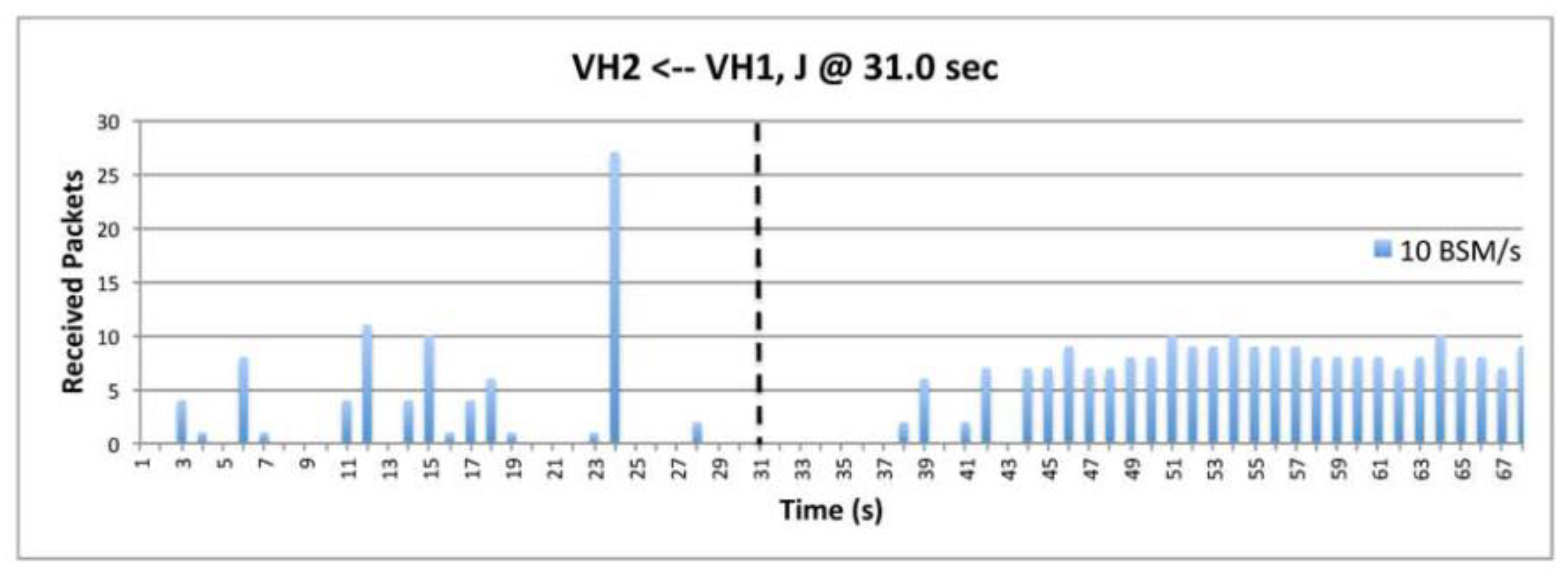
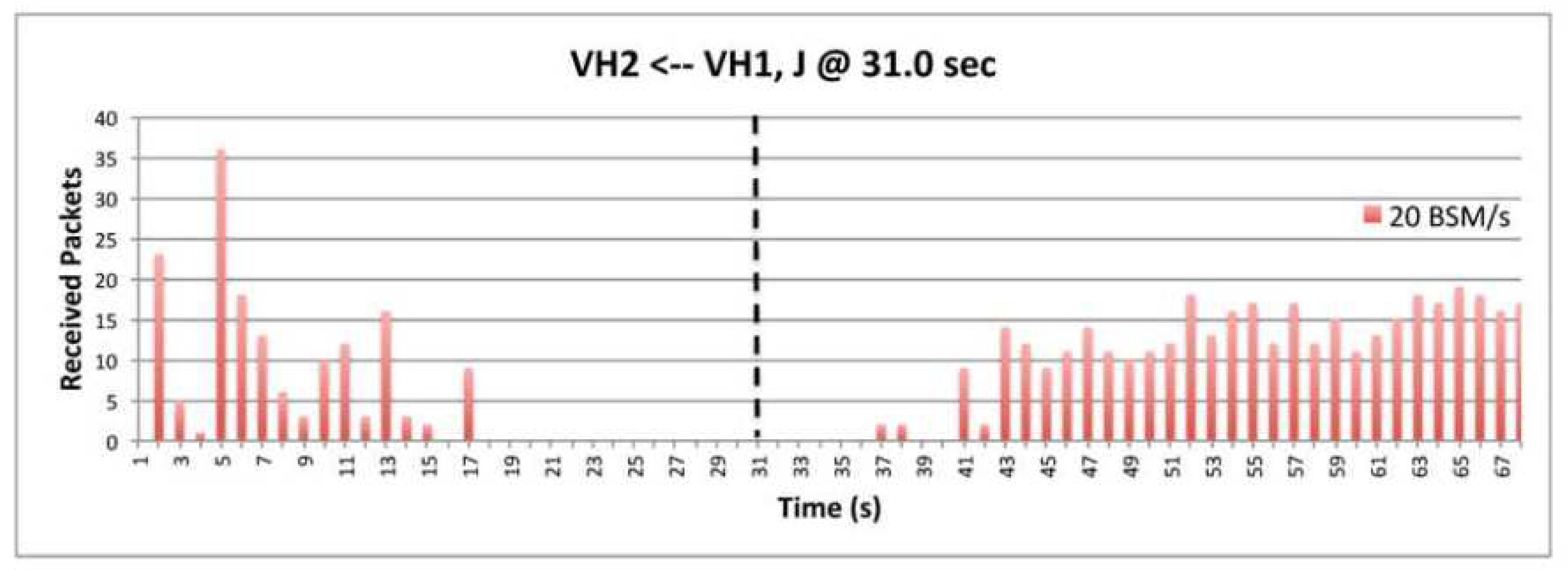
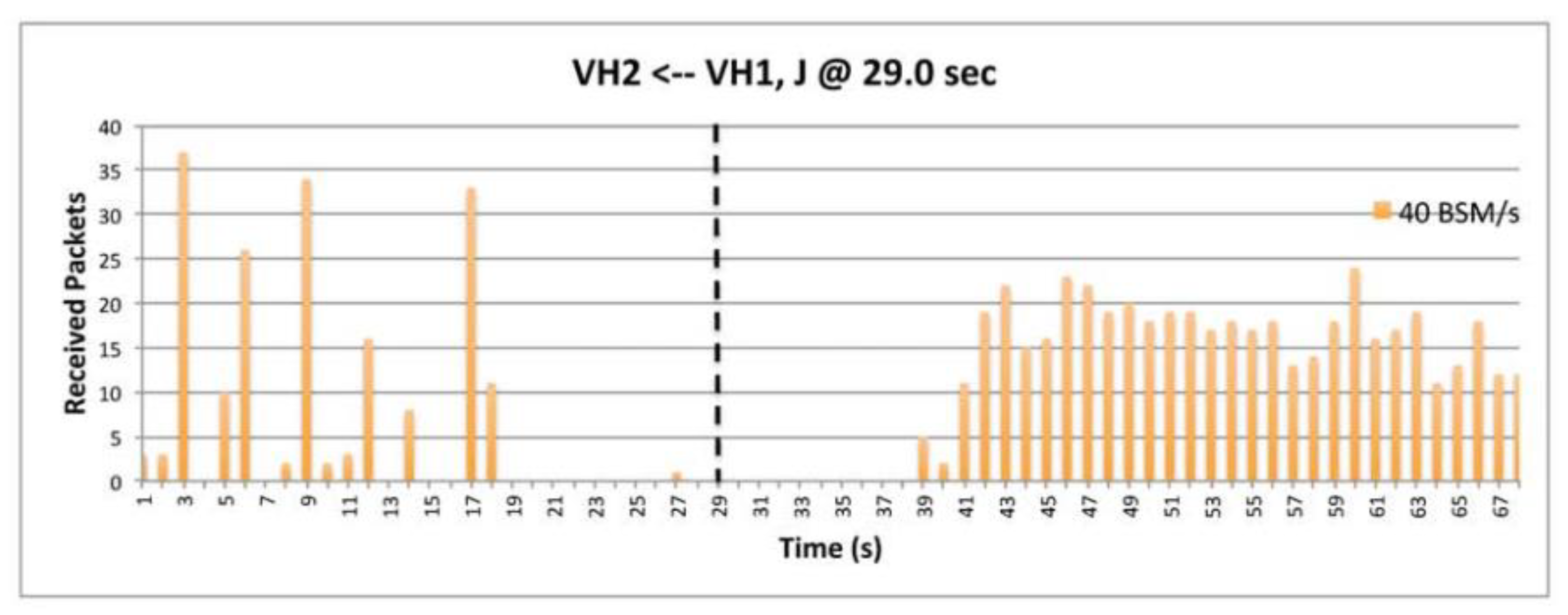
9.7. The Impact of Transmission Power.
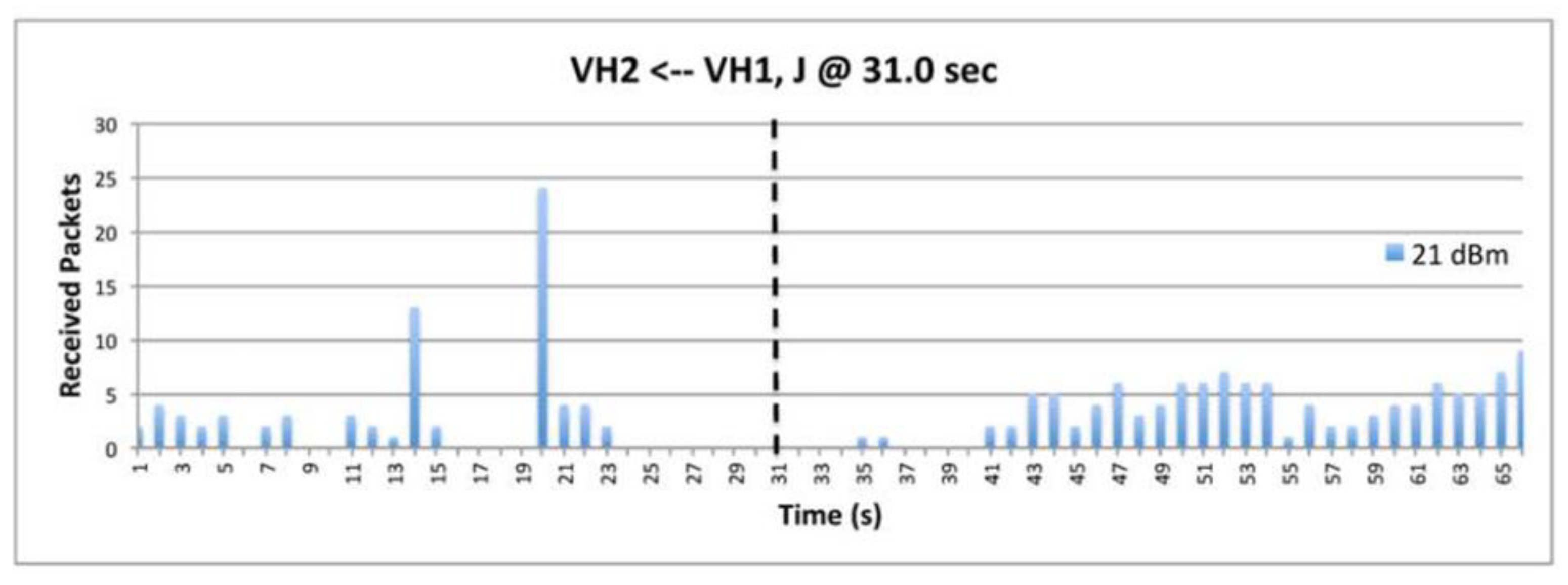
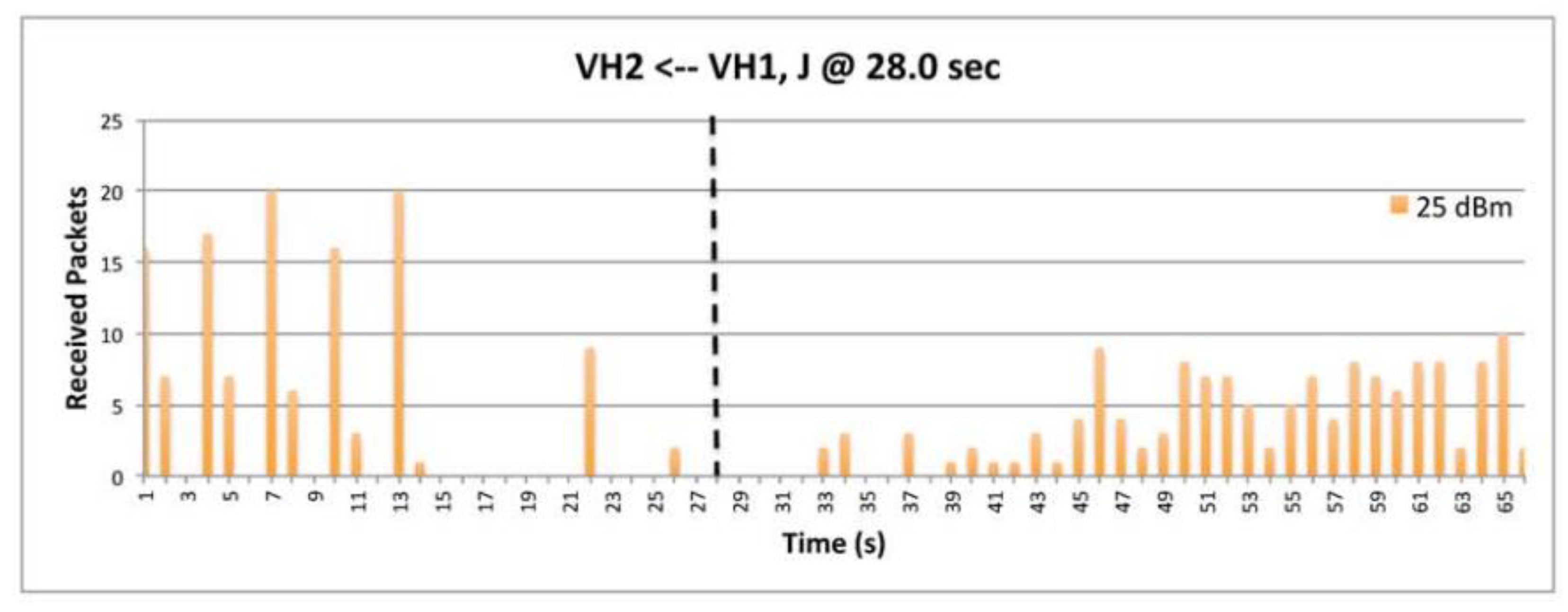
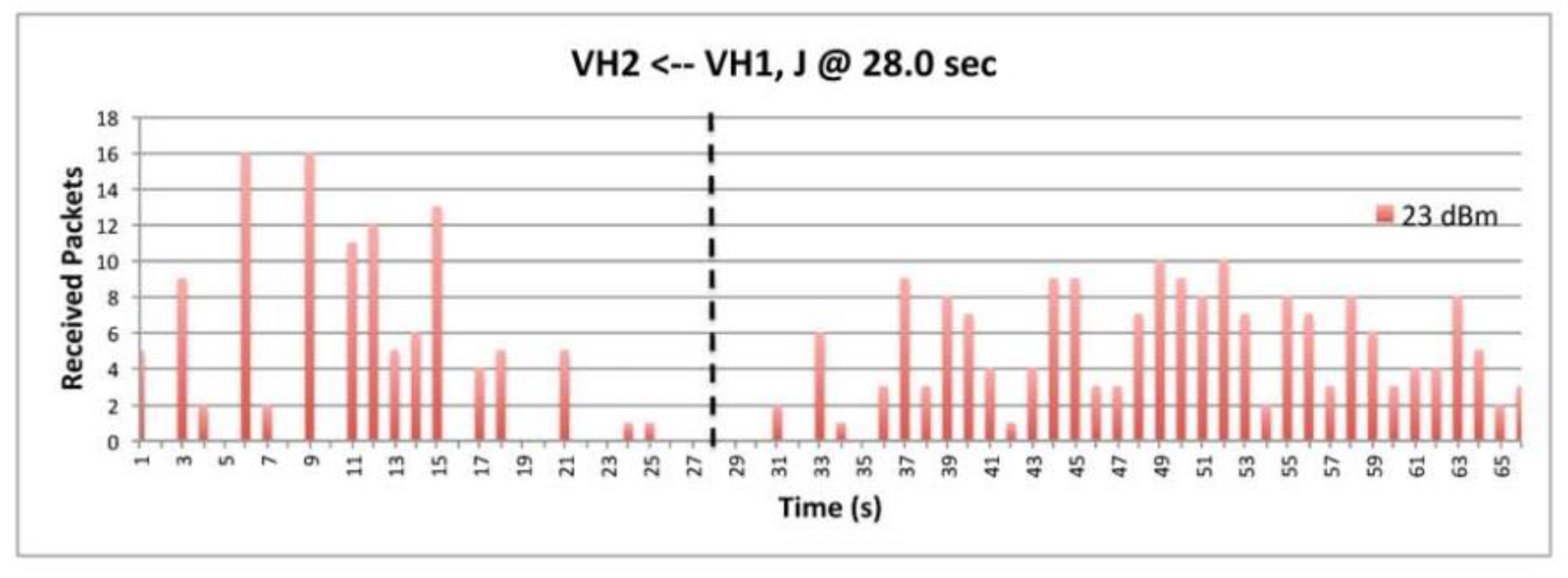
9.8. The Impact of Data.
| Deceptive Jammer (Field Experiment} | BSM /s | Power (dBm) |
Data Rate (Mbps) |
|||||
| 10 | 20 | 40 | 21 | 23 | 25 | 3 | 6 | |
| Recovery Time (Seconds) | 12.0 | 9.0 |
|
9.0 | 7.0 | 10.0 | 11.0 | 12.0 |
| Distance (meters) |
145 | 115 | 125 | 106 | 68.5 | 120 | 125 | 150 |
10. Conclusion
Author Contributions
Funding
Conflicts of Interest
References
- N. 2015. ] Traffic Safety Facts: Crash Stats, U.S. Department of Transportation, National Highway Traffic Safety Administration, DOT HS 812 219, “No Title.”.
- “J. B. Kenney, Dedicated Short-Range Communications (DSRC) Standards in the United States, Proceedings of the IEEE, vol. 99, no. 7, pp. 1162-1182, 2011.”. [CrossRef]
- “No TitleIEEE Standard for Wireless Access in Vehicular Environments - Security Services for Applications and Management Messages, IEEE Std 1609.2TM, 2018.”.
- Mahmood A. Al-Shareeda; Selvakumar Manickam, “A Systematic Literature Review on Security of Vehicular Ad-Hoc Network (VANET) Based on VEINS Framework,” IEEE 66th Veh. Technol. Conf., vol. 11, pp. 46218–46228, 2023. [CrossRef]
- S. Blessy, A.M.C., Brindha, “Energy-efficient fuzzy management system using tri-parametric methodology in vanet,” IEEE, vol. 14, 2023. [CrossRef]
- G. Ayoob, A., Su, G. and Al, “Hierarchical Growing Neural Gas Network (HGNG)-Based Semi cooperative Feature Classifier for IDS in Vehicular Ad Hoc Network (VANET,” J. Sens. Actuator Networks, vol. 7, no. 3, p. 41, 2018. [CrossRef]
- Jinsong Zhang; Kangfeng Zheng; Dongmei Zhang; Bo Yan, “AATMS: An Anti-Attack Trust Management Scheme in VANET,” IEEE Access, vol. 8, no. 10, 2020. [CrossRef]
- M. Hadded, P. Muhlethaler, A. Laouiti, R. Zagrouba, and L. A. Saidane, “TDMA-Based MAC Protocols for Vehicular Ad Hoc Networks: A Survey, Qualitative Analysis, and Open Research Issues,” IEEE Commun. Surv. Tutorials, vol. 17, no. 4, pp. 2461–2492, 2015. [CrossRef]
- G. Lu, Vasukidevi, “A Survey on Security and Key Management in,” IJIRST –International J. Innov. Res. Sci. Technol., vol. 3, no. 08, pp. 107–111, 2017.
- Y. Hu, A. Perrig, and D. B. Johnson, “Ariadne : A Secure On-Demand Routing Protocol for Ad Hoc Networks,” Wirel. Networks 11, vol. 5, pp. 21–38, 2015. [CrossRef]
- F. , Xu Hao , J. Hortelano , Sakiz and S. Sen, “Ad Hoc Networks Survey paper A survey of attacks and detection mechanisms on intelligent transportation systems : VANETs and IoV,” Ad Hoc Networks, vol. 61, pp. 33–50, 2017. [CrossRef]
- H. M. Maier, “Florida State University Libraries Nutritional Status and the Relationship of Dietary and Serum Advanced Glycation End-Products with Inflammation , Oxidative Stress and Healing of Diabetic Foot Ulcers,” 2013.
- S. I. Sou and O. K. Tonguz, “Enhancing VANET connectivity through roadside units on highways,” IEEE Trans. Veh. Technol., vol. 60, no. 8, pp. 3586–3602, 2017. [CrossRef]
- E. F. Ahmed Elsmany, M. A. Omar, T. C. Wan, and A. A. Altahir, “EESRA: Energy efficient scalable routing algorithm for wireless sensor networks,” IEEE Access, vol. 7, pp. 96974–96983, 2019. [CrossRef]
- J. Puñal, Ó., Pereira, C., Aguiar, A., & Gross, “Experimental characterization and modeling of RF jamming attacks on VANETs.,” IEEE Trans. Veh. Technol., vol. 64, no. 2, pp. 524–540, 2015. [CrossRef]
- Y. Shi, “LTE-V: A Cellular-Assisted V2X Communication Technology,” 2019.
- F. B. and A. P. A. Studer, E. Shi, “TACKing Together Efficient Authentication, Revocation, and Privacy in VANETs, in Sensor, Mesh and Ad Hoc Communications and Networks,” Access IEEE, pp. 1–9, 2018. [CrossRef]
- H. L. and M. G. Jie Li, “A Novel Authentication Framework with Conditional Privacy-Preservation and Non-Repudiation for VANETs,” IEEE Trans. Parallel Distrib. Syst., vol. 26, pp. 938–948, 2019. [CrossRef]
- J. P. and Z. Mammeri, “Authentication and Consensus Overhead in Vehicular Ad Hoc Networks, in Telecommunication systems,” IEEE 66th Veh. Technol. Conf., vol. 52, no. 4, pp. 2699–2712, 2015. [CrossRef]
- M. G. and Z. C. Z. Cao, J. Kong, U. Lee, “Proof-of-relevance: Filtering False Data via Authentic Consensus in Vehicle Ad-hoc Networks, in IEEE INFOCOM,” Workshops, vol. 20815, pp. 1–6.
- U. Rajput, F. Abbas, H. Eun, and H. Oh, “A Hybrid Approach for Efficient Privacy Preserving Authentication in VANET,” IEEE Access, vol. 3536, no. c, pp. 1–1, 2017. [CrossRef]
- P. Donadio, A. Cimmino, and G. Ventre, “Enhanced Intrusion Detection Systems in ad hoc networks using a Grid based agnostic middleware,” Proc. Int. Conf. Pervasive Serv. ICPS 2008 2nd Int. Work. Agent-Oriented Softw., pp. 15–19, 2008.
- R. G. Engoulou, M. Bellaïche, S. Pierre, and A. Quintero, “VANET security surveys,” Comput. Commun., vol. 44, 2014. [CrossRef]
- F. Anjum, D. Subhadrabandhu, and S. Sarkar, “Signature based intrusion detection for wireless ad-hoc networks: a comparative study of various routing protocols,” 2003 IEEE 58th Veh. Technol. Conf., vol. 3, 2003.
- Y. Hu, A. Perrig, and D. B. Johnson, “Rushing Attacks and Defense in Wireless Ad Hoc Network Routing Protocols,” [Computer Commun. Networks, vol. 3.
- T. O. Address, U. In, and H. Times, “by Maria Isabel Portal Palomo A Thesis Submitted to the Faculty of The College of Engineering and Computer Science in Partial Fulfillment of the Requirements for the Degree of Master of Science Florida Atlantic University Boca Raton , Florida,” no. May, 2013.
- and C. S. B. Awerbuch, A. Richa, “A Jamming-Resistant MAC Protocol for Single-Hop Wireless Networks, in Proceedings of the twenty-seventh ACM symposium on Principles of distributed computing,” ACM/Springer Mob. Networks Appl., vol. 2015.
- Y. P. and K. H. R. C.D. Jung, C. Sur, “A Robust Conditional Privacy-Preserving Authentication Protocol in VANET, in Security and Privacy in Mobile Information and Communication Systems,” Springer Berlin Heidelb., p. 35-45, 2014. [CrossRef]
- A. H. and J. Ben-Othman, “IEEE International Conference on Communications, Dresden,” in Detection of Jamming Attacks in Wireless Ad Hoc Networks Using Error Distribution, 2015, pp. 877–889.
- K. Sampigethaya, M. Li, L. Huang and R. Poovendran, “Robust Location Privacy Scheme for VANET,” IEEE J. Sel. Areas Commun., vol. 25, no. 8, pp. 569–1589. [CrossRef]
- Mokdad, L., Ben-Othman, J., & Nguyen, “DJAVAN: Detecting jamming attacks in Vehicle Ad hoc Networks,” Perform. Eval., vol. 87, pp. 47–59, 2015. [CrossRef]
- M. I. A. S., “Radio Jamming Attacks Against Two Popular Mobile Networks.,” Semin. Netw. Secur., vol. 11( 2), pp. 135–142, 2000.
- Alasmary, W.; Zhuang, “Public safety application for approaching emergency vehicle alert and accident reporting in VANETs using WAVE,” Ad Hoc Netwowking, vol. 10, p. 90, 2012.
- W. Chen, R. K. Guha, T. J. Kwon, J. Lee, and Y. Hsu, “A survey and challenges in routing and data dissemination in vehicular ad hoc networks,” Wirel. Commun. Mob. Comput., vol. 15, no. October 2009, pp. 787–795, 2011.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





