Preprint
Review
Neutrino Masses in Supersymmetric Models with R-Symmetry
Altmetrics
Downloads
108
Views
41
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
06 September 2023
Posted:
07 September 2023
You are already at the latest version
Alerts
Abstract
In this article, we give a brief review of the origin of the neutrino mass in some interesting non-linear supersymmetric models with R-symmetry. These models are able to address and solve the most important problems of the particle physics and provide mechanisms for neutrino mass generation and their mixing parameters in agreement with the current experimental data. Their prediction could be experimentally tested in the near future by collider experiments.
Keywords:
Subject: Physical Sciences - Particle and Field Physics
1. Introduction
The internal symmetries of the Standard Model (SM) are described by the gauge group
where the subscripts and Y refer to color, left chirality and weak hypercharge, respectively. At the weak scale, the electroweak symmetry subgroup
is spontaneously broken to
This spontaneous symmetry breakdown is driven by an doublet of the scalar Higgs field defined as
with the following vacuum expectation value (vev)
The Yukawa coupling
induces Dirac masses for all charged leptons except for neutrinos which is massless at all perturbative level due to the lack of a right-handed neutrino component.
The SM successfully describes the particle phenomenology across the energy scales probed by Large Hadron Collider (LHC). However, SM also has some relevant problems such as
- The coupling constants do not meet at a single definite value.
- The mass hierarchy problem ().
- The naturalness or fine tuning problem.
- The CP-violation and matter anti-matter asymmetry.
Within the framework of particle physics, one promising class of theories that could solve the problems of the SM is formed by the supersymmetric (SUSY) extensions of the SM. SUSY arose in theoretical papers more than 30 years ago with the Minimal Supersymmetric Standard Model (MSSM) proposed by Pierre Fayet in [1]. (see, for more details, e. g. [1,2]).
The arguments in favour of SUSY are based on the belief that more fundamental a theory is, a higher internal symmetry it should have [3,4,5]. This construct is amply used in string theory where SUSY is promoted to a local symmetry and the supergravity obtained in this way represents a formal unification of gravity with the field theory. However, the SUSY is useful to particle physics without involving the string theory, as it provides a simple and natural mechanism for the cancelling of the quadratic divergences. Indeed, since SUSY is a symmetry between the bosonic states and the fermionic states , there is a negative sign fermionic contribution at one-loop to the radiative correction of the scalar mass
The cutoff no longer needs fine tuning across a energy scale. In order to stabilize the mass hierarchy, one has to set (electroweak scale) which is the main reason to search for masses of superparticles in this range. This has an additional benefit, since it is a predicted mass scale by some Dark Matter models, where the best candidates are the lighest neutralinos or sneutrinos. Among other useful features of SUSY, one should mention its helpfulness in solving the coupling constant problem in the framework of the Grand Unification Theories (GUT). As is well known, GUT models based on and gauge groups do not have an intersection point of the three gauge couplings, display a proton instability and have a GUT hierarchy problem that involves the electroweak (light) and the GUT (heavy) Higgs bosons. In the supersymmetric GUT models, the first two problems above are improved by placing the predictions within the experimental bounds while the GUT hierarchy problem is completely solved.
Also, concerning the CP-violation, it is known that in the SM, the CP-violation originates in the quark sector. On the other hand, in the SUSY models, there are several new -violation phases, coming from gluino [6] and neutralino [4] sectors as well as from the Higgs sector [7,8].
Another reason to search for theories and models beyond the SM are some experimental and observational results which have not found a satisfactory explanation within the SM framework, e. g.
- Neutrinos are massive and they oscillate.
- The muon anomalous magnetic moment.
- Dark Matter.
- Dark Energy.
The shortcomings of the SM invite to build extensions of it that could solve its problems. From a different angle, a fundamental theory should predict the unification of the gravitational interaction with the other three fundamental interactions and should address all the above mentioned puzzles as well as questions usually raised in General Relativity such as the Dark Energy which can be addressed and possibly solved in SUSY models [9,10].
In this paper, we review the relation between the neutrinos and the R-symmetry in several non-minumal SUSY models: MSSM with R-Parity violation, NMSSM, MSSM3RHN, SM, SUSYB-L, SUSYLR and two SUSYGUTS models. (For a detailed discussion of one of these models see [12]). With the recent experimental bounds in the minimal SUSY models from the LHC, there has been a revival of interest in non-minimal models with R-symmetry [13,14]. Beside addressing the neutrino problems, the R-symmetric models also provide a fruitful framework to model Dark Matter with gaugino acquiring mass through R-symmetry breaking process [15].
2. Neutrinos Mass
Historically, the main phenomenological reason to introduce the neutrinos mass was the solar neutrino problem which basically states that the ration between the flux of electron neutrinos detected by the electron neutrinos predicted is roughly around one half, but can be as low as one third [16] (for a recent review, see e. g. [17]). Several crucial experiments have supported the idea that there are three neutrino flavours of low masses at scale () and they participate to weak and gravitational interactions. Since the neutrino is a spin-half electrically neuter particle, it can be described by a Majorana field with the anti-neutrino characterized by the opposed helicity. The unknown nature of the neutrino that could be a Dirac or a Majorana spinor is under current experimental investigation at CUORE [18], GERDA [19], MAJORANA [20], SNO+ [21] and EXO [22]. The experimental results suggest that the neutrinos have non-zero masses and oscillations. The best-fit values at error level for the neutrino oscillation parameters in the three-flavour framework are [23]
3. R-Symmetry
We start off by recalling the important remark that the SM has two accidental symmetries and , namely the lepton and baryon numbers, besides its gauge symmetries. The and are responsible for the stability of the nucleons under decay into light leptons and the existence of Dirac neutrinos. In general, the conservation of implies that the neutrinos are Dirac, while if the is broken, the breaking pattern determines the nature of the neutrinos [24]. In the SM model, all the interactions conserve both discrete symmetries. However, models beyond SM do not need to conserve or as is the case with several SUSY models that contain interactions that violate both or , or both. Therefore, one has to impose a discrete symmetry to get a model where all the interactions do not violate L and B conservation. This discrete symmetry is known today as R-symmetry and it was introduced independently by A. Salam and J. Strathdee [13] and P. Fayet [14].
Let us recall the R-symmetry. Consider the commutation relations involving the fermionic generators of the super-Poincaré algebra
The R-symmetry is a symmetry of the super-algebra (9) defined by the following commutation relations
From the above commutators we conclude that
which means that the R-charges of Q and are and , respectively.
In order to construct models with R-symmetry, it is necessary to define the action of the operator on the superspace and superfields. Let us denote the generator of R-symmetry by and the superspace coordinates by [25]. Then the action of on the fermionic coordinates and is given by the following relations
Hence, the R-charges are and . These charges are summarized in the following table
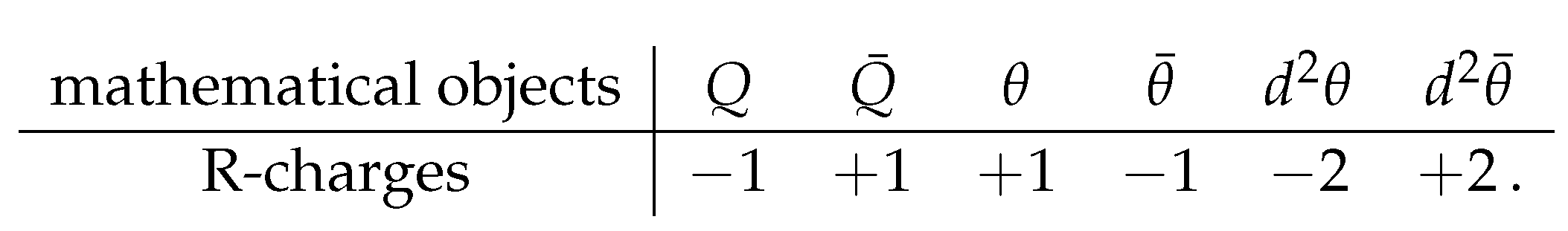 The superfields on the superspace are the basic objects of the SUSY models. The operator acts on the chiral , anti-chiral and vector superfields as follows
where is the R-charge of the above chiral superfield while the vector superfield is invariant under this symmetry. The above relations show that in general the terms of the superpotential have charges 2, which is two times the charge of . Here and in what follows we are using the conventions and basic results from the standard reference [25].
The superfields on the superspace are the basic objects of the SUSY models. The operator acts on the chiral , anti-chiral and vector superfields as follows
where is the R-charge of the above chiral superfield while the vector superfield is invariant under this symmetry. The above relations show that in general the terms of the superpotential have charges 2, which is two times the charge of . Here and in what follows we are using the conventions and basic results from the standard reference [25].
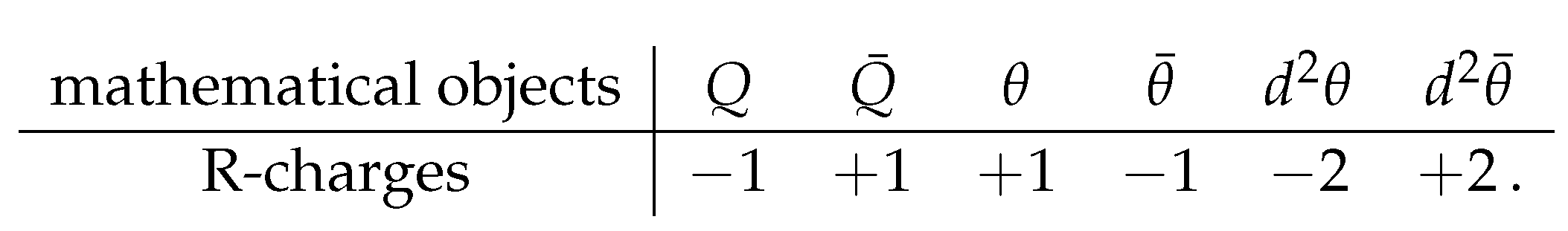
The relations (17) show that proposals of discrete R-symmetries based on groups are constrained by the allowed values of the R-charges of superfields and their components. Consider, for example, the chiral superfield defined by the equation
which has the following decomposition
The relation between the charges and , and is the following
Thus, the superpotential that corresponds to the factor has charge either or which prohibits the use of as R-symmetry group.
The Master Lagrangian of a supersymmetric model has the following general form
where the first term is known as the Kähler potential and has the general form , is the superpotential and the last term describes the supersymmetric Yang-Mills action with
The Master Lagrangian is invariant under R-Symmetry. By expanding the action from the Equation (21), we obtain
where and are parameters symmetric in all their indices and … stands for terms from the Yang-Mills lagrangian. The Equation (24) displays the invariance of the Käller potential under R-symmetry. On the other hand, the R-symmetry can be broken by the superpotential term.
One important SUSY model is the supersymmetric quantum electrodynamics that contains two chiral superfields that have the following transformation properties under the R-symmetry
Here, is another chiral superfield and e is the charge. The lagrangian of the supersymmetric quantum electrodynamics is given by the following equation [25]
One can easily verify that is invariant under R-Symmetry defined by the Equations (17) and (25) above.
3.1. Continuous R-Symmetry in MSSM
The simplest SUSY model is the MSSM that extends the field content of the SM by a minimal set of fields and has been used as a main model in the investigations of the supersymmetry. The superpotential of MSSM has two terms
In order to analyse the R-symmetry of MSSM, one makes the assumption that
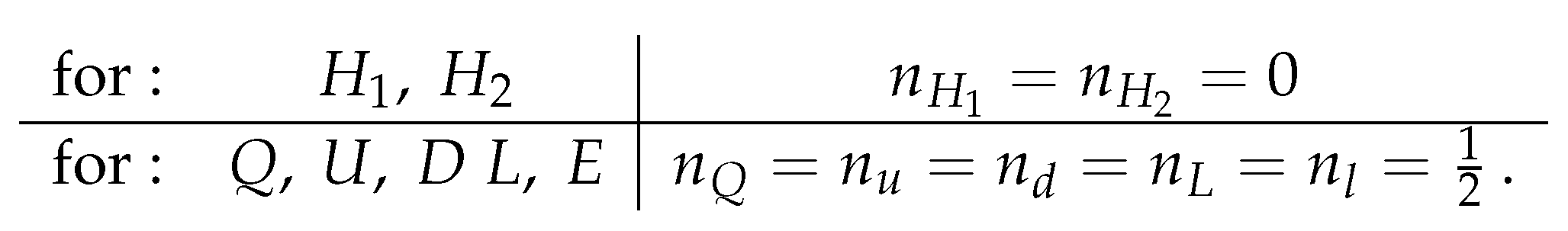 Then the R-symmetry acts on the components of the fields as follows
Then the R-symmetry acts on the components of the fields as follows
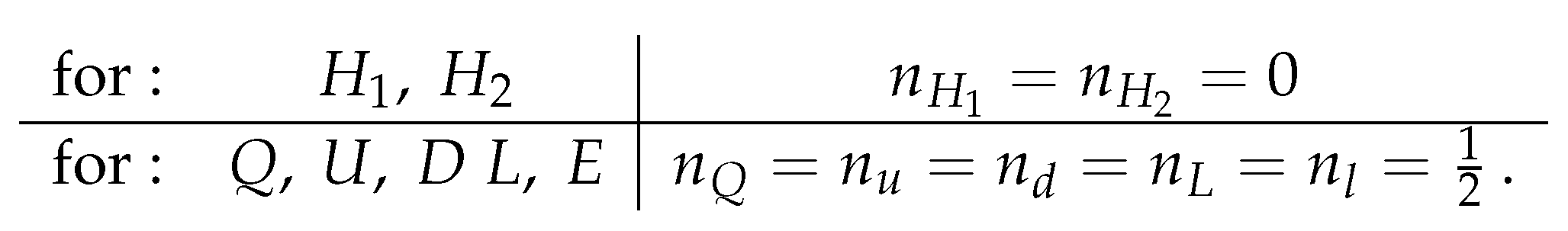
This shows that the scalars and all the standard fermions are invariant under R-symmetry. One can easily see that the conserving R-symmetry terms from the superpotential are
It is important to note here that, in this case, all charged fermions get masses at tree-level. However, the neutrinos are massless as in the SM.
The neutrinos can be given masses in the presence of the unbroken R-symmetry in a Minimal R-Supersymmetric Standard Model (MRSSM) that generalizes MSSM. In MRSSM, both have and the particle content of the MSSM is enlarged in the following way
The adjoint chiral superfields and and their R-charge are zero. The superpotential of this model is
where the complex triplet is defined as follows
3.2. A Problem of Continuous R-Symmetry. Discrete R-Parity
We already mentioned that the vector superfield V is invariant under R-Symmetry. However, the field components of the vector superfield transform as
In order to break the supersymmetry, Girardello introduced a mass term for gauginos of the following form [30]
that transforms under the R-symmetry (35) as follows
From the relations (35) one can see that the mass term given by the Equation (36) is not invariant under the R-symmetry.
The soft breaking of supersymmetry suggests to replace the continuous R-symmetry, by a discrete R-symmetry called R-parity denoted by which solves the above problem by setting . In the supersymmetry models with R-parity, the gluinos and other gauginos become massive.
For the following values of R-charges
the allowed terms in the superpotential are
The above superpotential defines the known MSSM, and as in Equation (30) all the neutrinos are massless at all orders of perturbations. However, by choosing the following charges
the terms in the superpotential allowed by this new R-parity are the following ones
As shown in [31,32,33], the superpotential (41) generates neutrino masses as showed numerically at [34]. We can, also, reproduce the mixing parameters [35].
The R-parity plays an important role in the baryon B and lepton L numbers violation in the MSSM. The most general superpotential of the MSSM contains interacting terms that violate the baryon and lepton numbers. In order to remove these terms that are not allowed by the SM, the R-parity is introduces. The general form of the R-parity in terms of B and L numbers is
where M is the matter parity and takes the following values
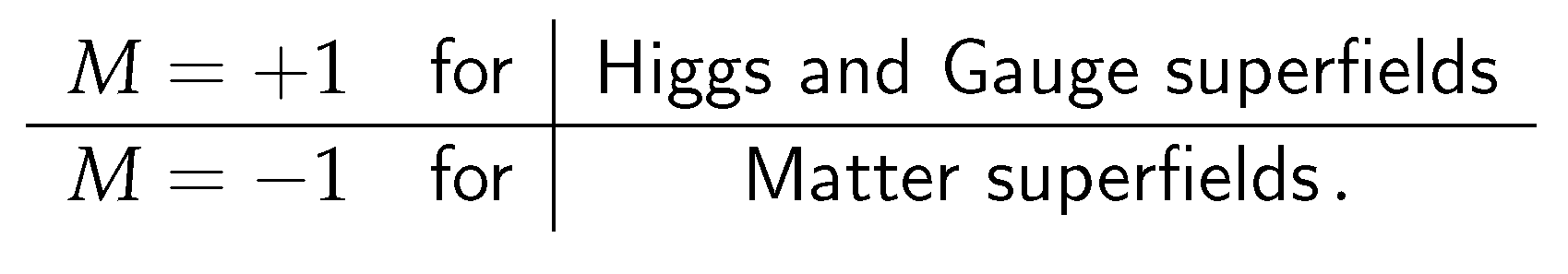
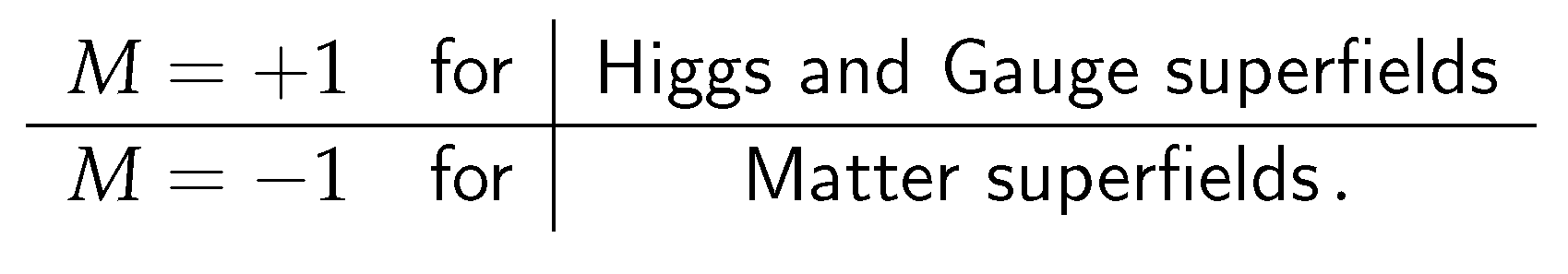
This remark is important for the construction of the SUSYB-L models.
3.3. Nelson-Seiberg Theorem
Since the SUSY is not directly observed in nature, one has to consider that it is a broken symmetry. One important class of models that display the dynamical SUSY breaking of strongly-coupled gauge theories at low-energies are the generalized O’Raifeartaigh models which are weakly-coupled Wess-Zumino models in which the SUSY is broken by vacuum expectation values of tree-level F-term [36]. The generalized O’Raifeartaigh models are a particular case of generic calculable models that obey the Nelson-Seiberg theorem [37]
Theorem(Nelson-Seiberg) The necessary and sufficient conditions for SUSY breaking at the true vacuum in a Wess-Zumino model with a generic superpotential are:
- Necessary: The model must have an R-symmetry.
- Sufficient: The R-symmetry should be spontaneously broken.
Here, the term generic refers to the property that the superpotential must contain all renormalizable terms with complex coefficients. The Nelson-Seiberg theorem has been revisited lately in [38,39] and counterexamples have been found in [40,41].
The theorem relates the global to the SUSY- breaking by the following argument. Since the superpotential R-charge is 2, then it has the following form
where denotes the fields. However, the SUSY vacuum is a stationary point of the system
for all . Then it is easy to see that the effective equations (44) reduce to a system of equations with n unknowns which does not admit a solution, in general. Therefore, one cannot determine a supersymmetric vacuum. That leads to the conclusion that in the presence of the R-symmetry, the SUSY must be spontaneously broken.
4. Next to Minimal Standard Model
The NMSSM is characterized by the following new singlet superfielfield
given as a chiral superfield [12]
Here, the vev of the scalar field S is taken to be
The fermionic field , defined by the Equation (46), is known as singlino.
The most general superpotential that contains the singlet extension of MSSM is given by the following relation [42]
where is defined by the Equation (41). The parameters and are dimensionless while the parameters and have mass dimension.
The the Next-to-the-Minimal Supersymmetric Standard-Model (NMSSM) can be obtained either from super-GUT models or from super-string models [12,42]. To get NMSSM, one needs to set
Then the superpotential takes the following form
The superpotential that generates neutrino masses in NMSSM was given in [43] where the following function was proposed
From , just one massive neutrino is generated as in MSSM with R-Parity violation terms. All conclusions presented after Equation (41) still hold in this case.
An important conclusion is that if we want to generate masses for all neutrinos at tree level, we need to introduce three right-handed neutrinos. We discuss this case in some detail below.
5. Minimal Supersymmetric Standard Model with three right-handed Neutrinos
The simplest supersymmetric model to explain the masses of the left-handed neutrinos is known as the Minimal Supersymmetric Standard Model with three generation Right-Handed neutrinos (MSSMRH). The particle content of this model is the same as MSSM with the addition of the right-handed neutrinos (see, e. g. [4,44,45,46]). The superpotential of the MSSMRH is given by
where is defined by the Equation (41). For this model, the R-charges described by the Equation (40) together with the condition .
In this MSSMRH, the masses of neutrinos are obtained from the terms
Here, the symmetric matrices are the Majorana masses and are the source of the Dirac masses. This model is interesting because it can generate mass to all neutrinos at tree level and also to explain all mixing data about neutrinos, as shown in [47].
If we consider the symmetry that acts on the chiral superfields by a real phase
where is an entire number, then the Majorana masses can be avoided and only the Dirac mass term survives
In order to explain the lightness of the neutrino masses, one must have [48].
6. from Supersymmetric Standard Model (SSM)
The MSSM and also the MSSMRH suffer from the -problem [49] that can be formulated as the generation of a coupling in the term of the order of the electro-weak scale. The -problem is solved by the Next-to-the-Minimal Supersymmetric Standard-Model (NMSSM). From the point of view of neutrino oscillations, NMSSM is not interesting because its neutrinos are massless [4]. Nevertheless, one can construct a non-minimal SUSY model that solves the -problem and at same time gives masses to all neutrinos. This is called the " from Supersymmetric Standard Model" (SSM) and it was proposed in [50].
The superpotential of SSM can be obtained by requiring that it be invariant under -symmetry, see Equation (54). This leads to the following formula
This superpotential is consistent with the phenomenological models derived from the superstring theory. From it, one can see that the neutralino mass matrices have the general form
The neutrinos are Majorana in this model. Therefore, several processes as the double beta decay, can take place without neutrinos. More details can be found in [12].
7. Supersymmetric Model
The TeV scale right-handed neutrino is naturally obtained in supersymmetric (SUSYB-L) extension of the SM which is one of the simplest non-linear class of models beyond the SM that provide a viable and testable solution to the neutrino mass. Also, it can account for the experimental results of the light neutrino masses and their large mixing angles.
The B-L number defined as the baryon minus lepton numbers can be obtained from a gauge symmetry that is broken at TeV scale [51,52]. Recall that this is the SUSY breaking scale necessary to explain the hierarchy problem in MSSM. In the SUSYB-L, as happen in the MSSM, the Higgs potential receives large radiative corrections that induce spontaneous symmetry breaking at TeV scale, in analogy to the electroweak symmetry breaking in MSSM [51].
One interesting properties of this kind of model is the new complex phases in the leptonic sector that can generate lepton asymmetry that is converted to baryon asymmetry [52]. The relevant terms from the Lagrangian that are responsible for that are the soft SUSY-breaking terms [53,54]
The above Lagrangian describes the mixing between the sneutrino and the anti-sneutrino . The CP violation phase in this mixing generates lepton asymmetry in the final states of the -decay and it is converted to baryon asymmetry through the sphaleron process [55].
7.1. The Minimal Supersymmetric Model
The light neutrino masses can be obtained from the minimal gauged that is invariant under the following gauge group
In this model, we have R-parity violation [56]. The matter chiral supermultiplets for leptons and their , and quantum numbers are given by
With this matter content, the superpotential can be defined as follows
Once the R-parity is broken, the neutralinos and neutrinos can mix as in MSSM. Due to this mixing, the masses to all the neutrinos is generated via the see-saw mechanism. Let us briefly review the basic arguments for the generation of light neutrino masses given in [56]. By breaking the R-parity, the mixing of the neutralinos and neutrinos fields takes place. These fields are
One particular simple case is given by the vev and . Then
where the vev’s of the Higgs doublets are
and is the see-saw contribution and is from the R-parity violation. These two contributions have the following form
where
Here, is the neutralino mass matrix as calculated in the MSSM. This shows that the light neutrino masses is obtained from the R-symmetry breaking in the minimal model. For more details, we refer to the original paper [56].
8. Supersymmetric Left-Right Model
The minimal SUSYB-L model discussed in the above section is not the only one that can explain the light neutrinos. The SUSYLR is a different proposal which can also solve the strong CP problem [57]. In the SUSYLR model, the gauge symmetry group is
The lepton content of SUSYLR is different from the lepton content of MSSM where the left-handed fermions belong to the doublet representation while the right-handed fermions are singlets of . Here, both left-handed and right-handed leptons are doublets in the corresponding gauge groups
In the literature, two different SUSYLR models have been discussed: the first one uses triplets (SUSYLRT) [58] and the second one has doublets (SUSYLRD) [59]. Since the neutrinos in SUSYLRD are massless, we will not discuss the details of this model here.
8.1. Triplet Model (SUSYLRT)
The scalars fields of this model are
The most general superpotential W is given by [58]
where are the Yukawa couplings for the leptons. This model can be embedded in a supersymmetric grand unified theory (SUSYGUT) with , some of which will be briefly discussed in the next section.
The masses of neutrinos in the SUSYLRT are given by the following matrix [61]:
This result is in agreement with the one given in [60] for .
9. Supersymmetric Grand Unification Theory
In the standard minimal SUSYGUT scenario, the models possess both the supersymmetry and the unified gauge symmetry at the unification scale. The main properties of a finite SUSYGUT are [62]
- The number of generations is fixed by the requirement of finiteness.
- There are various realistic possibilities given by the gauge groups , , and .
The last point above leads to a huge class of models compatible with the SUSYGUT. Below, we are going to give a very brief highlight of two supersymmetric grand unification models that give masses to neutrinos, namely and .
9.1. grand unified model with right-handed neutrinos
There are very nice reviews of the SUSY model are given at [63,64]. The SUSYGUT model with gauge group meets observational difficulties that come from the proton decay channel [65]
Also, the neutrinos are massless and the lepton sector must be changed to provide a mechanism that can generate masses for neutrinos. For a discussion of the challenges posed by the models, see [66].
Let us focus now on the grand unified model with right-handed neutrinos . Similarly to the minimal model, we can introduce the charged lepton1 as . Also, we have to introduce the right-handed neutrinos which are as . The scalars of the model are given by and . Then the superpotential is given by [67,68]:
where only the terms that give neutrinos masses are written explicitly. Here, is the Majorana mass matrix for right-handed neutrinos and is the Dirac mass. Both masses are generated via the see-saw mechanism.
9.2. Minimal SO(10) Supersymmetric Model
The supersymmetric models are extensively reviewed in [69,70]. Since our focus is the generation of the neutrinos masses, we can exemplify the group with the model presented in [71,72]. Here, the lepton is introduced as representation of and the Higgs fields in the representations and of . The terms of the superpotential that are responsible for the lepton masses, are given by the following relation
where h and f are symmetric matrices in that denote generation indices. The neutrino masses can be calculated in this model from
where is a new parameter of the model responsible for non-null CKM mixing angles [71].
The Supersymmetric Model has a second mass generating mechanism which produces the neutrino masses from the scalar of the 126 representations of . A large mass mixing in the channel imposes to the low energy Majorana neutrino mass matrix the following form [73]
which has the following eigenvalues in units
By making assumptions about the texture of the Dirac mass matrix (that is, its form to be of the up-quark mass matrix), one has the other Majorana mass matrices
with , and
with
Here, one has the following expressions
The see-saw mechanism imposes the following equation
It is important to note that this model provides a large mixing and a large mass splitting by postulating the general form of the Dirac mass matrix. Also, it generates a hierarchical mass matrix for the right-handed neutrinos with a small mixing. For more details on this interesting SUSYGUT model, see [73].
10. Conclusions
We have reviewed the connection between the neutrino masses and the R-symmetry in some interesting non-linear SUSY models. The interest in this ideas, some older and some new, has been revived by the results obtained at recent collider experiments and by the atmospheric, astronomical and cosmological observations. More important, all the models presented here can be tested in high energy experiments.
The R symmetry can be used to solve the -problem since the later can be connected with the supersymmetry breaking process and allows constructing models with viable neutrino masses. The fermion mass hierarchies can be explained by constructing models with pseudo-anomalous symmetry. Discrete non-abelian symmetries based on can be used to obtain the neutrino mixing. These models solve the fermion mass hierarchies and the hierarchy problem without fine-tuning while modelling a neutrino mixing by a non-abelian flavour symmetry. For details on these models, see [74].
To conclude, non-linear extensions of the SUSY with R-symmetry are to solve the main problems of the particle physics beyond SM, and represent viable theories for addressing other fundamental problems of quantum field theory and gravity, such as the Dark Matter and Dark Energy. These models can be tested experimentally, which makes them inviting for both theoretical and experimental explorations.
Author Contributions
The authors contributed to this work as follows: conceptualization, M. C. R. and I. V. V; review of phenomenological results, M. C. R.; review of theoretical concepts, M. C. R. and I. V. V.; writing—original draft preparation, M. C. R. and I. V. V.; writing—review and editing, M. C. R. and I. V. V. . All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
We acknowledge R. Rosenfeld for hospitality at ICTP-SAIFR where part of this work was accomplished.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Fayet, P. About the origins of the supersymmetric standard model. Nucl. Phys. Proc. Suppl. 2001, 101, 81. [Google Scholar] [CrossRef]
- Rodriguez, M. C. History of Supersymmetric Extensions of the Standard Model. Int. J. Mod. Phys. 2010, A24, 1091. [Google Scholar] [CrossRef]
- Drees, M. Godbole, R. M. and Royr P. Theory and Phenomenology of Sparticles, 1st ed.; World Scientific Publishing: Singapore, 2004. [Google Scholar]
- Baer, H. Godbole, and Tata X. Weak scale supersymmetry: From superfields to scattering events, 1st ed.; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Chung, D. J. H. Everett , L. L. Kane , G. L. King , S. F. Lykken , J. D. and Wang , L. T. The Soft Supersymmetry-Breaking Lagrangian: Theory and Applications. Phys. Rept. 2005, 407, 1. [Google Scholar] [CrossRef]
- Heinemeyer ,S. and Schappacher C. Gluino Decays in the Complex MSSM: A Full One-Loop Analysis. Eur. Phys. J. 2012, C72, 1905. [Google Scholar]
- Carena, M. Ellis , J. Lee , J. S. Pilaftsis A. and Wagner , C. E. M. CP Violation in Heavy MSSM Higgs Scenarios. JHEP 2016, 1602, 123. [Google Scholar] [CrossRef]
- Christova, E. Eberl , H. Ginina , E. and Majerotto , W. CP violation in charged Higgs decays in the MSSM. JHEP 2007, 02, 075. [Google Scholar] [CrossRef]
- Bilic, N. Vacuum fluctuations in a supersymmetric model in FRW spacetime. Phys. Rev. 2011, D83, 105003. [Google Scholar]
- Bilic, N. Supersymmetric dark energy. Rom. J. Phys. 2012, 57, 793. [Google Scholar]
- Dimopoulos, S. Raby , S. and Wilczek , F. Supersymmetry and the scale of unification. Phys. Rev. 1981, D24, 1681. [Google Scholar]
- Rodriguez, M. C.; Vancea, I. V. Flat Directions and Leptogenesis in a "New" μνSSM.Available online: https://arxiv.org/abs/1603.07979.
- Salam, A. and Strathdee , J. Supersymmetry and fermion-number conservation. Nucl. Phys. 1975, B87, 85. [Google Scholar]
- Fayet, P. Supergauge invariant extension of the Higgs mechanism and a model for the electron and its neutrino. Nucl. Phys. 1975, B90, 104. [Google Scholar] [CrossRef]
- Hatanaka, H. Inami , T. Lim , C. S. The gauge hierarchy problem and higher-dimensional gauge theories. Mod. Phys. Lett. 1992, A13, 2601. [Google Scholar]
- Pontecorvo, B. Mesonium and antimesonium. JETP 1958, 6, 429. [Google Scholar]
- Bilenky, A. M. Prehistory of neutrino oscillation. In Proceedings of the International Conference on History of the Neutrino: 1930-2018, Paris, France, 5-7 September 2018. [Google Scholar]
- Dompè , V, Adams , D. Q. Alduino , C. Alfonso , K. Avignone , F. T. Azzolini , O Bari , G. Bellini , F. Benato , G. and Beretta , M. Expected sensitivity to 128Te neutrinoless double beta decay with the CUORE TeO2 cryogenic bolometers. J. Low Temp. Phys. 2022, 209, 788. [Google Scholar]
- Biancacci, V. The GERDA Experiment in the Search for Neutrinoless Double-Beta Decay. Moscow Univ. Phys. Bull. 2022, 77, 359. [Google Scholar] [CrossRef]
- Arnquist, I. J. et al. Final Result of the Majorana Demonstrator’s Search for Neutrinoless Double-β Decay in Ge76. Phys. Rev. Lett. 2023, 130, 062501. [Google Scholar] [CrossRef]
- Tam, B. The SNO+ Experiment: Reactor & Solar ν Prospects. In Proceedings of the Neutrino Oscillation Workshop 2022, Ostuni, Brindisi, Italy, 4-11 September 2022. PoS NOW20222023, 033.
- Fu, Y. C.; Song, L. M.; Ding, G. Q.; Ge, M. Y.; Tuo, Y. L.; Zhang, S.; Zhang, S. N.; Hou, X.; Qu, J. L.; Zhang, J. Timing analysis of EXO 2030+375 during its 2021 giant outburst observed with Insight-HXMT. Mon. Not. Roy. Astron. Soc. 2023, 521, 893. [Google Scholar] [CrossRef]
- Schwetz, T. Tortola , M. and Valle , J. W. F. Three-flavour neutrino oscillation update. New J. Phys. 2008, 10. [Google Scholar] [CrossRef]
- Hirsch, M. Srivastava , R. and Valle , J. W. F. Can one ever prove that neutrinos are Dirac particles? Phys. Lett. 2018, B781, 302–305. [Google Scholar] [CrossRef]
- Wess,J. and Bagger, J. Supersymmetry and Supergravity., 2nd ed.; Princeton University Press: Princeton, USA, 1992. [Google Scholar]
- Kribs, G. D. Poppitz , E. and Weiner , N. Flavor in supersymmetry with an extended R-symmetry. Phys. Rev. 2008, D78, 055010. [Google Scholar]
- Diessner, P. Kalinowski , J. Kotlarski , W. and Stöckinger , D. Higgs boson mass and electroweak observables in the MRSSM JHEP 2014, 12, 124. [Google Scholar]
- Diessner, P. and Weiglein , G. Precise prediction for the W boson mass in the MRSSM. JHEP 2019, 07, 011. [Google Scholar]
- Athron, P. Bach , M. Jacon , D. H. J. Kotlarski , W. Stöckinger , D. and Voigt , V. Precise calculation of the W boson pole mass beyond the Standard Model with Flexible SUSY. Phys.Rev. 2022, D106, 9. [Google Scholar]
- Girardello ,L. and Grisaru , M. T. Soft breaking of supersymmetry. Nucl. Phys. 1982, B194, 65. [Google Scholar]
- Hall, L. J. and Suzuki , M. Explicit R-parity breaking in supersymmetric models. Nucl. Phys. 1984, B231, 419. [Google Scholar]
- Banks, T. Grossman , Y. Nardi ,E. and Nir , Y. Supersymmetry without R parity and without lepton number. Phys. Rev. 1995, D52, 5319. [Google Scholar]
- Diaz, M. A. Romão , J. C. and Valle , J. W. F. Minimal supergravity with R-parity breaking. Nucl. Phys. 1998, B524, 23. [Google Scholar]
- Montero, J. C. Pleitez , V. and Rodriguez , M. C. Lepton masses in a supersymmetric 3-3-1 model. Phys. Rev. 2002, D65, 095008. [Google Scholar]
- Rodriguez, M. C. The Minimal Supersymmetric Standard Model (MSSM) with R-Parity Violation.Available online: https://arxiv.org/abs/2204.05348.
- Intriligator, K. A. Seiberg , N. and Shih , D. Dynamical SUSY breaking in meta-stable vacua. JHEP 2006, 04, 021. [Google Scholar]
- Nelson, A. E. and Seiberg , N. R-symmetry breaking versus supersymmetry breaking. Nucl. Phys. 1994, B416, 46–62. [Google Scholar] [CrossRef]
- Kang, Z. Li , T. and Sun , Z. The Nelson-Seiberg theorem revised. JHEP, 2013, 12, 093. [Google Scholar]
- Li, Z.; Sun, Z. The Nelson-Seiberg theorem generalized with nonpolynomial superpotentials. Adv. High Energy Phys. 2020, 3701943. [Google Scholar] [CrossRef]
- Sun, Z. Tan , Z. and Yang , L. A counterexample to the Nelson-Seiberg theorem. JHEP 2020, 10, 072. [Google Scholar]
- Amariti, A. and Sauro , D. On the Nelson-Seiberg theorem: generalizations and counter-examples. Nucl.Phys. 2020, B989, 116075. [Google Scholar]
- Rodriguez, M. C. The Minimal Supersymmetric Standard Model (MSSM) and General Singlet Extensions of the MSSM (GSEMSSM), a short review. Available online: https://arxiv.org/abs/1911.13043.
- Abada, A. and Moreau , G. An origin for small neutrino masses in the NMSSM. JHEP 2006, 0608, 044. [Google Scholar]
- Langacker, P. Nucl. Phys. Proc. Suppl. 2001, 100, 383. [CrossRef]
- Baek, S. Goto ,T. Okada , Y. Okumura , K.-I. Muon anomalous magnetic moment, lepton flavor violation, and flavor changing neutral current processes in supersymmetric grand unified theory with right-handed neutrinos. Phys.Rev. 2001, D64, 095001. [Google Scholar]
- Sato, J. Tobe , K. Yanagida , T. A constraint on Yukawa-coupling unification from lepton-flavor violating processes. Phys.Lett. 2001, B498, 189. [Google Scholar]
- Rodriguez, M. C. Short review about the MSSM with three right-handed neutrinos (MSSM3RHN). Available online: https://arxiv.org/abs/2003.04638.
- Allahverdi, R. Dutta , B. and Mazumdar , A. Unifying inflation and dark matter with neutrino masses. Phys. Rev. Lett. 2007, 99, 261301. [Google Scholar] [CrossRef]
- Kim, J. E. and Nilles , H. P. The μ problem and the strong CP problem. Phys. Lett. 1984, B138, 150. [Google Scholar]
- Lopez-Fogliani, D. E. and Muñoz , C. Proposal for a Supersymmetric Standard Model. Phys. Rev. Lett. 2006, 97, 041801. [Google Scholar] [CrossRef] [PubMed]
- Khalil, S. and Masiero , A. Radiative B-L symmetry breaking in supersymmetric models. Phys. Lett. 2008, B665, 374. [Google Scholar]
- Khalil, S. Low scale B - L extension of the Standard Model at the LHC. J. Phys. 2008, G35, 055001. [Google Scholar]
- Khalil, S. Lepton flavor violation in supersymmetric B-L extension of the standard model. Phys. Rev. 2010, D81, 035002. [Google Scholar]
- Kajiyama, Y. Khalil , S. and Raidal , M. Electron EDM and soft leptogenesis in supersymmetric B-L extension of the standard model. Nucl. Phys. 2009, B820, 75. [Google Scholar]
- Kuzmin, V. A. Rubakov , V. A. and Shaposhnikov , M. E. Phys. Lett. 1985, 155, 36. [Google Scholar]
- Barger, V. Fileviez Perez , P. and Spinner , S. Minimal gauged U(1)B-L model with spontaneous R-parity violation. Phys. Rev. Lett. 2009, 102, 181802. [Google Scholar] [CrossRef]
- Frank, M. Turan , I. and de Oña , A. C. CP-odd phase effects in a left-right symmetric chargino sector Phys. Rev. 2005, D72, 075008. [Google Scholar]
- Huitu, K. Maalampi , J. and Raidal , M. Supersymmetric left-right model and its tests in linear colliders. Nucl. Phys. 1994, B420, 449. [Google Scholar]
- Babu, K. S. Dutta , B. and Mohapatra , R. N. Solving the strong CP and the supersymmetry phase problems with parity symmetry. Phys.Rev. 2002, D65, 016005. [Google Scholar]
- Frank, M. Neutrino masses in the left–right supersymmetric model. Phys. Lett. 2002, B540, 269. [Google Scholar] [CrossRef]
- Maekawa, C. M. and Rodriguez , M. C. Masses of fermions in supersymmetric models. JHEP 2006, 04, 031. [Google Scholar]
- Dimopoulos, S. Georgi , H. Softly broken supersymmetry and SU(5). Nucl.Phys. 1981, B193, 150. [Google Scholar]
- Bagnaschi, E. et al. Likelihood Analysis of Supersymmetric SU(5) GUTs. Eur. Phys. J. 2017, C77, 104. [Google Scholar]
- de Boer, W. Ehret , R. and Kazakov , D. I. Predictions of SUSY masses in the minimal supersymmetric grand unified theory. Z. Phys. 1995, C67, 647. [Google Scholar]
- Murayama ,H. and Pierce , A. Not even decoupling can save the minimal supersymmetric SU (5) model. Phys.Rev. 2002, D65, 055009. [Google Scholar]
- Bajc, B. Lavignac , S. and Mede , T. Challenging the minimal supersymmetric SU(5) model. In Proceedings, Workshop on Dark Matter, Neutrino Physics and Astrophysics CETUP 2013: 7th International Conference on Interconnection between Particle Physics and Cosmology (PPC 2013) : Lead/Deadwood, South Dakota, USA, July, 8-13, 2013, 297-304. Published in: AIP Conf.Proc. 2015, 1604, 297–304. [Google Scholar]
- Causse, M. B. Neutrino radiative decay and lepton flavor violation in supersymmetric models.Available online: https://arxiv.org/abs/hep-ph/0202096.
- Causse, M. B. Supersymmetric penguin contributions to the process B/d –> Phi K(S) in SUSY GUT with right-handed neutrino.Available online: https://arxiv.org/abs/hep-ph/0207070.
- Blažek, T. Dermíšek , R. and Raby , S. Predictions for Higgs and Supersymmetry Spectra from SO(10) Yukawa Unification with μ>0. Phys. Rev. Lett. 2002, 88, 111804. [Google Scholar] [CrossRef]
- Raby, S. Phenomenology of the minimal SO(10) SUSY model. Pramana 2004, 62, 523. [Google Scholar] [CrossRef]
- Goh, H. S. Mohapatra , R. N. and Ng , S. P. Minimal SUSY SO(10) model and predictions for neutrino mixings and leptonic CP violation. Phys. Rev. 2003, D68, 115008. [Google Scholar]
- Goh, H. S. Mohapatra , R. N. Nasri , S. and Ng , S. P. Proton decay in a minimal SUSY SO(10) model for neutrino mixings. Phys. Lett. 2004, B587, 105. [Google Scholar]
- Chen, M. C. and Mahanthappa , K. T. From the CKM matrix to the Maki-Nakagawa-Sakata matrix: A model based on SO(10)×U(2)F supersymmetric symmetry. Phys.Rev. 2000, D62, 113007. [Google Scholar]
- Chen, M. C. Fallbacher , M. Omura , Y. Ratz , M. and Staudt , C. Predictivity of models with spontaneously broken non-Abelian discrete flavor symmetries. Nucl.Phys. 2013, B873, 343. [Google Scholar]
| 1 | The representation of and the indices , as usual, denote generations, and A is index that runs from 1 to 5. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated





