Prerpints.org logo
Preprint
Article

Investigating Formation Factor—Hydraulic Conductivity Relations in Complex Geologic Environments: A Case Study in Taiwan

Altmetrics

Downloads

66

Views

15

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

06 September 2023

Posted:

08 September 2023

You are already at the latest version

Alerts
Abstract
The development of cost-effective methods for estimating hydraulic conductivity profiles has been an ongoing effort in the field of engineering practice, which can be used to increase availability to clarify the hydrogeological complexity of fractured rock aquifers for the aid of solving groundwater-related problems. A methodology is presented, which combines electrical well logs, fluid conductivity logs, double packer hydraulic tests, Archie’s law, and the Kozeny-Carman-Bear equation to investigate relations between formation factor and hydraulic conductivity. This method was applied to develop hydraulic conductivity profiles based on the data collected from 88 boreholes in Taiwan's mountainous areas. The investigation results include: (1) Well logging signals were suggested to be categorized by rock types to establish effective relationships with hydraulic conductivity. (2) Removing the mud-bearing section data with two proposed data clustering techniques could effectively enhance the correlation between the formation factor and hydraulic conductivity. (3) The predictive models for estimating hydraulic conductivity have been developed for sandstone, schist, and slate. (4) The prevalence of clay content in most of Taiwan's mountainous rock formations has been found, which implies that careful consideration of clay-related issues in complex geologic formations is essential while applying Archie's law theory.
Keywords: 
Subject: Engineering  -   Civil Engineering

1. Introduction

Hydraulic conductivity plays an essential role in controlling the distribution, flow path, and storage of groundwater in the formation, especially in complex geological environments where this parameter is highly heterogeneous and, as generally recognized, may vary with spatial locations [1,2,3,4]. Therefore, if detailed and continuous hydraulic conductivity along boreholes can be obtained during the site investigation [5], it will be constructive to clarify the hydrogeological complexity of rock formations [6]. However, such detailed information is not easily obtained due to the limitations of budget, manpower, and exploration methods. Most of the projects only take the representative data as the basis to characterize hydrogeological conditions of a site for the assistance of engineering planning and design. When the representative data cannot deal with the complexity of an engineering system, construction accidents may occur, such as large groundwater inflow accidents during tunnel construction [7]. In addition, limited access to detailed data may lead to undiscovered scientific problems related to hydrogeology, or the possible cross-disciplinary applications may be limited by insufficient observed information. Thus, there is a demand for detailed and continuous hydrogeological information for handling vertical heterogeneity in engineering practice and science.
Traditionally, direct field hydraulic tests with the fixed-interval approach can be adopted to determine the hydraulic conductivity profile along a borehole in a geologically complex formation [8]. Although this method can provide detailed information concerning hydraulic conductivity with accurate results, the method is labor-intensive, time-consuming, and costly, as mentioned above. To improve the limitation, down-hole logging tools, such as flowmeter [9,10,11], electrical well logging [5,12,13], the liner profiling method [14], or NMR (nuclear magnetic resonance) logging [15] have been studied to explore profiles of the hydraulic properties of formations surrounding boreholes. Although these down-hole logging tools can provide higher resolutions, not all tools have the advantage of low cost while estimating hydraulic conductivity. Besides, geophysical data measured from these tools still need to combine transform functions to obtain hydraulic conductivity, and these studies have not yet been fully developed [5,10,12,14,15].
Inexpensive and less time-consuming methods with high resolution for estimating such a profile increase their worth in practical applications. Among these logging tools, electrical well logging meets the criteria of relatively inexpensive survey costs and high resolution. Although most of the downhole electrical logging signals are mainly used to identify the profiles of lithology, porosity, hydraulic property, cementation, strength, and water-bearing zones of a formation in a qualitative way, a few studies have attempted to utilize such data to estimate hydraulic conductivity.
Since 1951, studies have focused on exploring electrical-hydraulic relationships for groundwater exploration [16]. In the early time, previous studies utilized electrical well logging data to calculate values of the formation factor [17], and then establish direct relationships between electrical data and hydraulic conductivity [17,18,19,20]. The later studies used a two-step approach to construct the electrical-hydraulic relationship. First, electrical well logging data were utilized to calculate values of the formation resistivity factor and then estimate the porosity using Archie's law [17,21]. Second, the predicted porosity is typically used in conjunction with the Kozeny-Carman model to estimate hydraulic conductivity. The abovementioned methodology has been presented in the literature [5,12,13,22,23]. These studies also pointed out that Archie’s law and Kozeny-Carman model are only validated in sandy strata. If clayed or shaley formations are present in the analysis, estimation results are inferior. To improve electrical-hydraulic relationships in response to the effect of clay mineralogy, the modification of Archie’s law was proposed by Waxman and Smits [24]. Few studies have considered the new law to improve electrical estimations from hydraulic conductivity [5,12]. In addition, electrical-hydraulic relationships developed from most of the previous studies were focused on unconsolidated formations. Such relationships are less well developed in fractured rock formations. Due to their geologic complexity, obtaining a good result on the electrical-hydraulic relationship could become challenging.
In this study, relations between hydraulic conductivity and electrical data in complex geologic environments of Taiwan, where fractured rock aquifers with diverse lithologies are commonly present, were investigated. Available geophysical and hydraulic data measured from 88 boreholes using the electrical well logging tools and double packer hydraulic test were collected to perform the correlation studies. The main tasks include (a) inspection of the quality of the geophysical data by comparing the existing drilling core data with the consistency of actual lithology; (b) investigation of correlations between hydraulic conductivity and geophysical parameters (spontaneous potential, short normal resistivity, long normal resistivity, point resistivity, natural gamma, and fluid conductivity); (c) classification of collected data with/without clay contents by using two proposed clustering approaches; (d) feasibility studies for establishing the relationship between the formation factor and hydraulic conductivity over various lithologies in fractured rock formations.

2. Study Area and data sources

A twelve-year program related to groundwater resource explorations in Taiwan's mountainous areas was initiated by the Central Geological Survey of Taiwan in 2010 [25]. The main objective of this program is to explore the potential of using groundwater extracted from fractured rock formations as alternative water resources against drought. To understand the feasibility of this concept, hydrogeologic data in regolith-bedrock aquifers over the entire Taiwan mountain areas through various hydrogeological investigation tests were collected and analyzed to support the purpose of this program. 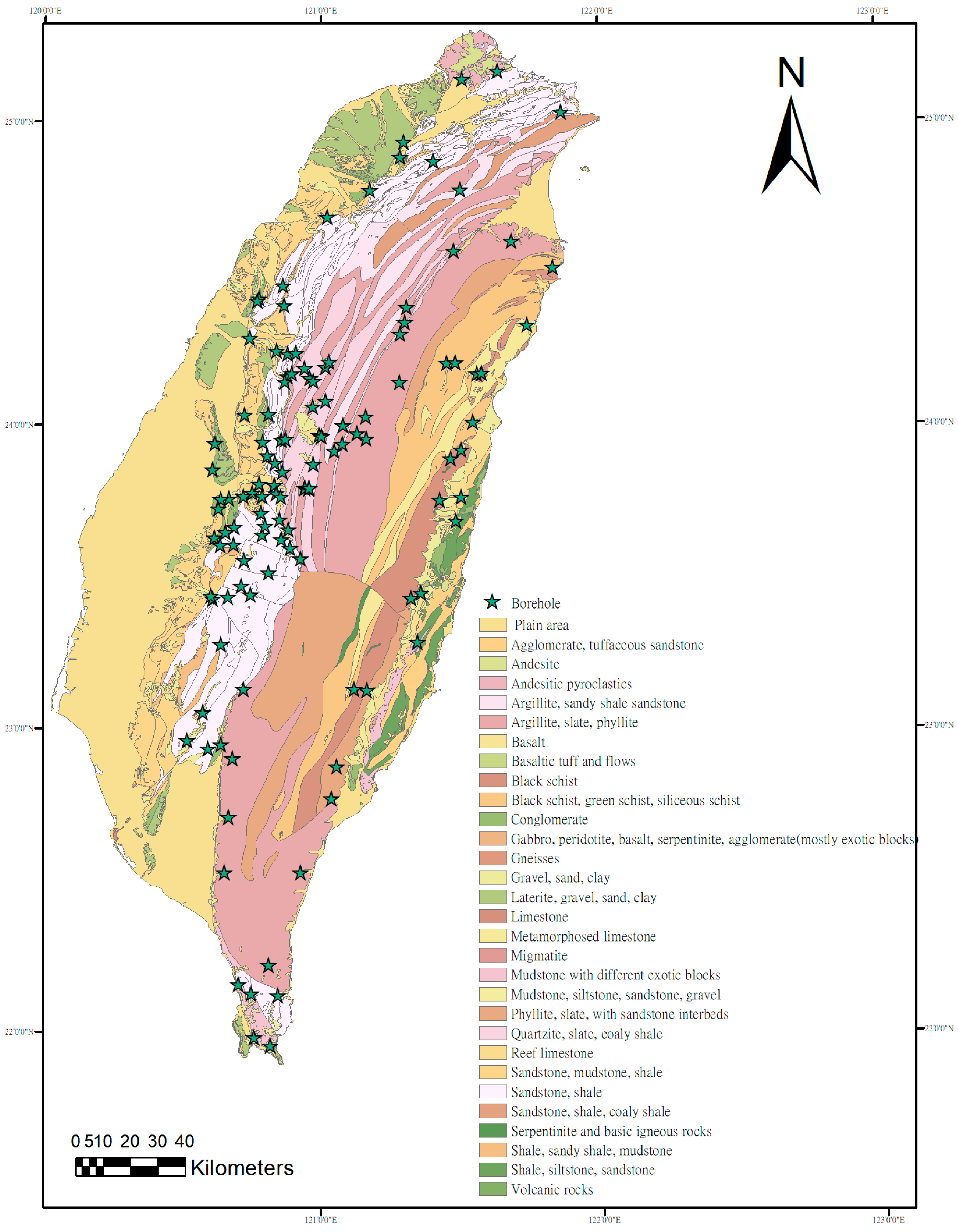Figure 1 shows the distribution of the investigated borehole locations in the mountainous area of Taiwan for the program mentioned above from 2010 to 2021. Each investigated borehole conducted seven in-situ hydrogeological tests, including electrical well logging, fluid conductivity logging, temperature logging, groundwater velocity logging, borehole imaging, double-packer hydraulic test, and pumping test. The total investigated boreholes and the depth of each borehole are 88 and 100 meters, respectively.
To develop a model for determining hydraulic conductivity of mountainous formations along a borehole, this study collected samples from a part of the above-mentioned hydrogeological tests. The analyzed data mainly aimed at survey data from the electrical well logging (spontaneous potential, short normal resistivity, long normal resistivity, point resistivity, and natural gamma), fluid conductivity logging, and double-packer hydraulic test. Data samples for each borehole were selected from the borehole sections by performing double-packer hydraulic tests (the test interval of 1.5 m). A total of 396 double-packer hydraulic test samples were collected. In addition, the electrical well logging and fluid conductivity logging have one-centimeter data sampling, which can meet this study's research goal of high resolution. Finally, each borehole's drilling core logs and image data confirmed whether the geophysical values can reflect the lithology presented.
The lithological environment covered by the collected data samples includes quartz sandstone, sandstone, sandstone interbedded with shale, silty sandstone, sandy shale, shale, alternations of sandstone and shale, mudstone, siltstone, argillaceous siltstone, andesite, volcanic agglomerate, phyllite, marble, slate, schist, gneiss, argillite, quartzite, metasandstone, and argillite interbedded with some sandstone. The number of data samples collected for each sub-lithology is shown in Table 1. Among the analyzed data, the five most abundant rock types include sandstone, slate, alternations of sandstone and shale, schist, and shale. The above data collected can construct electrical parameters to hydraulic conductivity, followed by statistical techniques to possibly develop reliable models for predicting hydraulic properties of various subsurface formations. Due to the wide range of geological environments covered by the data sources collected, the formation factor-hydraulic conductivity relation can be investigated more comprehensively.

3. Methods

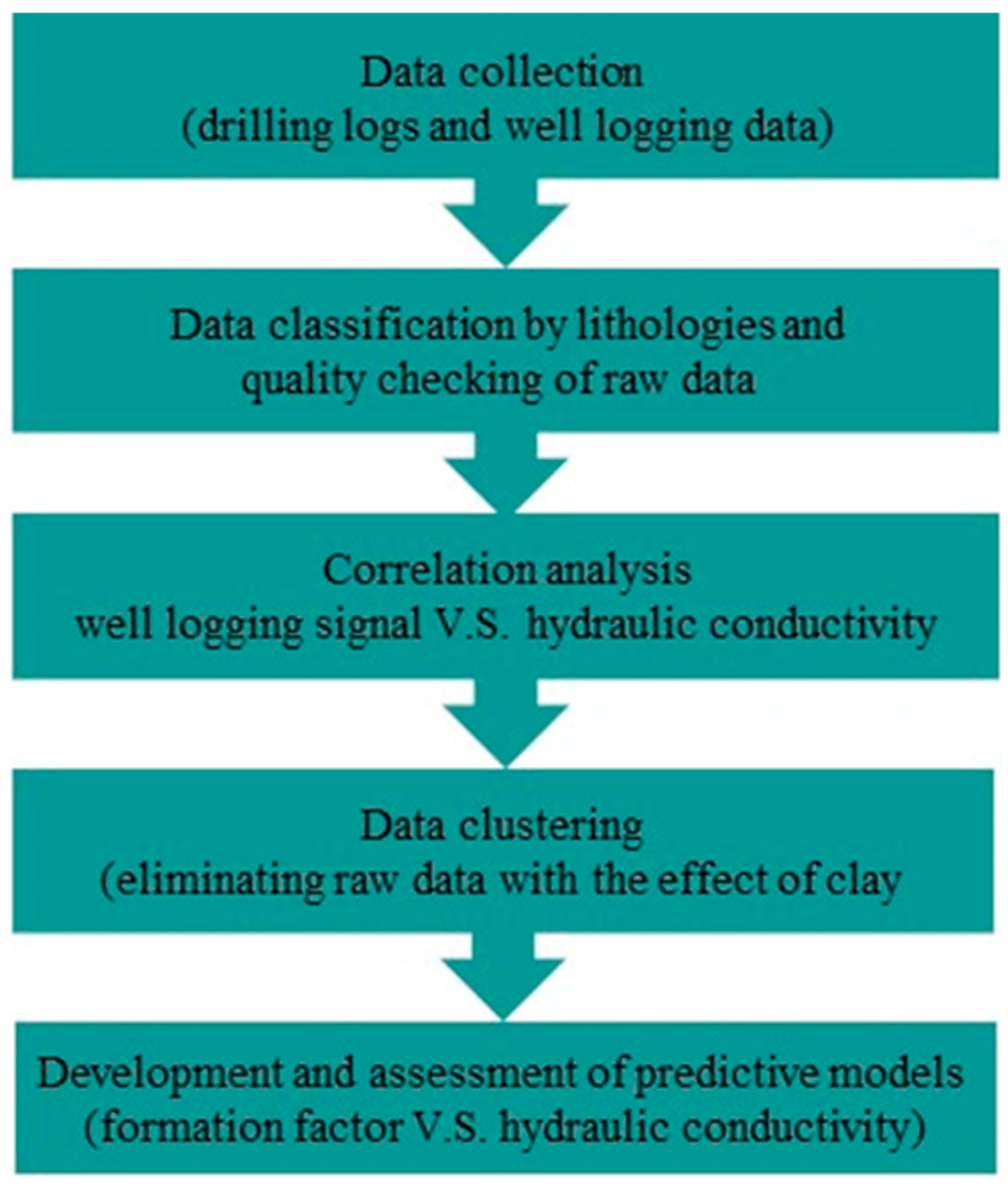
To provide a cost-effective approach for producing hydraulic conductivity profiles along boreholes, this study intends to explore relationships between the formation factor and hydraulic conductivity using the resistivity data of formation and fluid obtained from the most commonly used electrical well logging in drilling construction and the theory of Archie's law. A flowchart summarizing the implementation of this study for developing the estimation of hydraulic conductivity is shown in Figure 2. Five investigation stages are illustrated, including (1) collecting borehole data, including drilling logs and a variety of well logging data (spontaneous potential, short normal resistivity, long normal resistivity, point resistivity, natural gamma, and fluid conductivity), (2) classifying the raw data by lithology as well as examining the quality of the collected data compared with the existing rock core logs, (3) performing correlation analysis by investigating relations between hydraulic conductivity and each geophysical parameter, (4) proposing two data clustering methods to eliminate raw data with the effect of clay contents, and (5) establishing the relationship between the formation factor and hydraulic conductivity according to the clustered data as well as evaluating the feasibility of the developed models.

3.1. Data processing and classification

Generally, the electrical well logging signal data are used to infer the stratum's lithology by using geophysics principles on an indirect basis, which is different from geologists' direct visual recording of lithology. Both methods have their own advantages and disadvantages. The electrical signal data are recorded every centimeter, while the artificial core description is recorded every 20 cm, so the resolution of the latter data is much rougher than that of the former. Taking the 1.5 m test section of the double-packer hydraulic test as an example, geologists can only describe the main lithological features in the test section. Also, due to the visual identification method, it is impossible to describe the lithology for the finer parts. However, the electrical measurement data can be used to infer the difference in lithology in a test interval through variations of the signal value.
To confirm whether numerical changes of these signals correctly reflect the actual lithology, this study collected five types of signals (including spontaneous potential (SP), long normal (LON), short normal (SHN), single-point resistivity (SPR), and natural gamma ray (NGAM)) of double-packer test sections in different boreholes with different depths. A total of 150 points were measured for each signal in the 1.5 m double-packer test interval. For each test section at a given signal, the average value and standard deviation (SD) value of all samples were calculated. For the section with a large SD value, the data were compared and verified by core logs and photos to confirm that lithology rather than artificial errors caused the greater deviation. 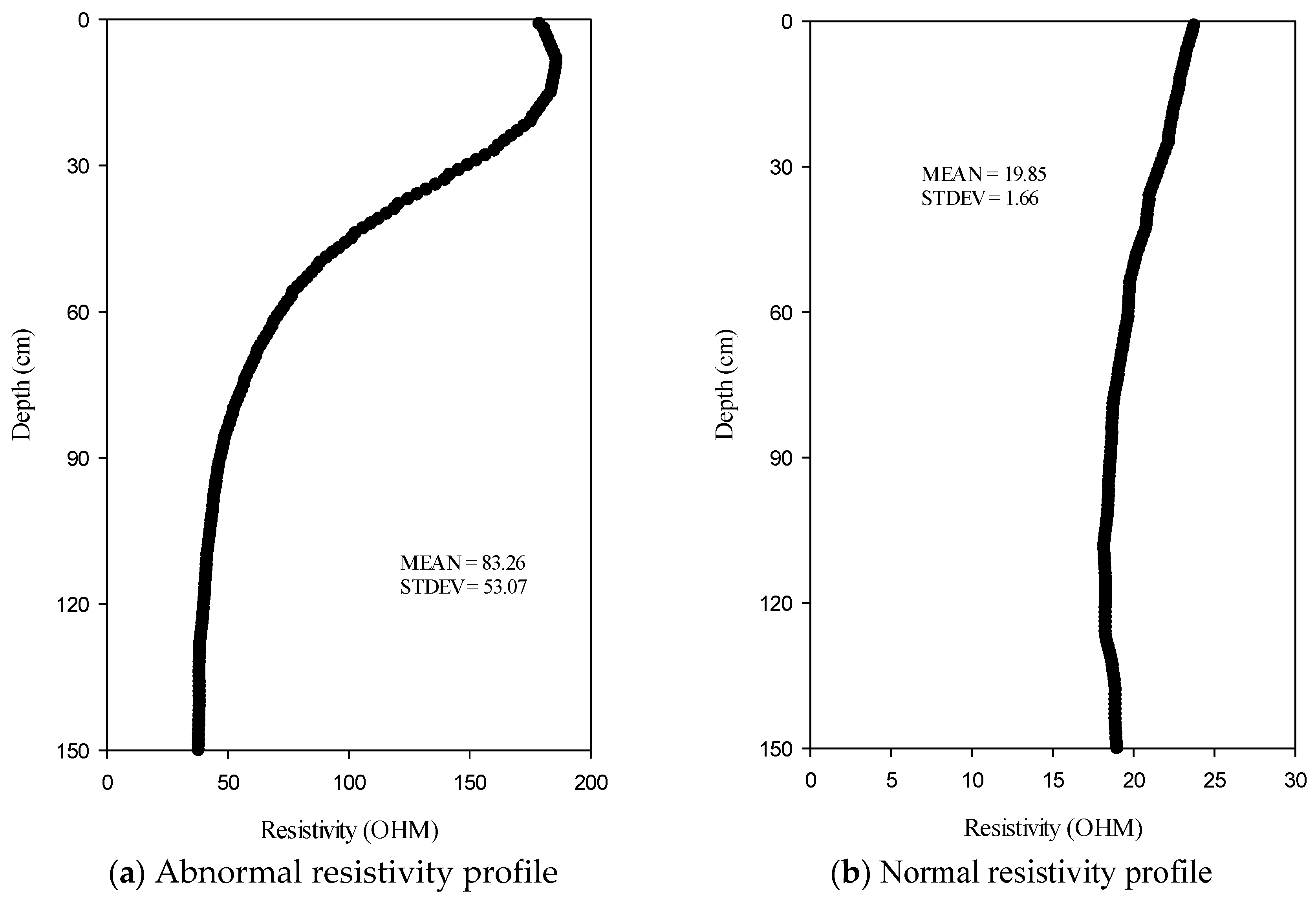Figure 3 shows the short normal resistivity profiles at two different double-packer intervals (1.5 m), and the geologists described the cores of both intervals as fine-grained sandstone. However, while comparing Figure 3(a) and 3(b), the resistivity value of the entire vertical interval in Figure 3(b) has little difference (SD value is about 1.66), but the resistivity value of the whole vertical section in Figure 3(a) shows a larger variation (SD value is about 53.07). Thus, Figure 3(b) may be more in line with the result of the lithological description, so the signal quality of the double-packer interval in Figure 3(a) should be rechecked. In particular, the signal results obtained in a relatively complex geological environment need to be compared carefully with the existing core data to confirm the correctness of the collected signal data so that the signal values used can appropriately reflect the hydraulic conductivity value of the formation. After the quality control of the data, the confirmed data can be classified into a different group by lithology and used for subsequent statistical analysis.

3.2. Theory of formation factor- hydraulic conductivity relation for clay-free formations

Formation factor F, or formation resistivity factor, was initially presented by Archie [17] and defined as the ratio of the resistivity of a fully water-saturated granular reservoir rock (Ro) to the resistivity of the water saturating the pores (Rw). Archie [17] also proposed the relation between F and porosity n. Since 1942, the F-n relation has been confirmed empirically in a variety of singular formations. The relation is commonly expressed in the following form [21].
F = R o R w = a n − m
where a is the tortuosity constant or lithology constant, and m is the cementation factor. The values of m and a have been reported for different formations by different investigators [26]. The reported ranges for two parameters in a specific lithology are variable. The reason for such variations can be attributed to several factors, including size, packing and sorting of grains, degree of cementation, porosity, pressure, tortuosity, wettability of rock surface, and clay content. Especially, the last factor is significant due to violating Archie’s original experimental conditions. Thus, a meaningful evaluation for Equation (1) is based on accounting for the clay content effect. Additionally, if a is equal to one, Equation (1) is called Archie’s first law. While applying both equations, discussions on the difference between Equation (1) and Archie’s first law can be referred to the study of Glover [27].
Based on the above relation of Equation (1), n can be theoretically obtained from F. However, valid relations between F and K generally do not exist. However, several studies have developed for the valid relations between K and n, which can be found in a textbook [5,12]. One of the famous relations comes from the Kozeny-Carman-Bear equation given by Bear [28] and Domenico and Schwartz [29].
K = δ w g μ · d 2 180 · n 3 1 − n 2
wherew is the dynamic viscosity; g is the acceleration gravity;  is the fluid density; d is the mean grain size; n is the porosity. Equation (2) is developed by the concept of the capillary tubes and often estimates the saturated K for most soils [30].
Since formation factor F and hydraulic conductivity K are both functions of porosity n, integrating Equations (1) and (2) links the two parameters F and K. The functional relationship between K and F can be assumed to be established and given as:
K = F u c t i o n ( F )
In fact, such a relationship has been used in previous studies to estimate hydraulic conductivity [5,12,22,31,32]. However, the relationship was confirmed with a small size of data and a clay-free lithology. Thus, this study applied the functional relationship to investigate formation factor—hydraulic conductivity relations in various complex geologic environments.

3.3. Data clustering for eliminating data containing clay content

Since Archie’s law is only applicable to the clay-free formation, the application of Equation (3) for establishing the relationship between F and K for the study area in the relatively complex geological conditions of the Taiwan mountains requires testing the data first for clustering those that are compatible with the original theory. Accordingly, this study proposes two different clustering methods to screen the data samples less affected by clay minerals to conform to the theoretical formula of Archie’s law. The clustering methods and theories are detailed as follows:
(a)
natural gamma ray threshold
The natural gamma ray (NGAM) has the characteristic of strongly distinguishing the clay mineral in a formation. Therefore, the natural gamma ray may be used to design the threshold value for recognizing clay minerals. When the average NGAM value of a formation sample is larger than the threshold value, the sample may contain clay minerals. Such a sample should be excluded in the subsequent analysis of the correlation with hydraulic conductivity. Using natural gamma ray thresholds to confirm whether a formation is affected by clay mineral effects has been investigated by Kaleris and Zioga[5] at a site in Greece. His study suggested that strata are less affected by the clay mineral effect when the natural gamma ray value in API (American Petroleum Institute) is less than 35. According to the previous study, the design of the NGAM threshold may be the key to determining the presence of clay minerals.
The NGAM threshold can be obtained by dichotomy to group data samples into two categories, which may contain clay or non-clay content, to find a possible NGAM threshold value. Then, the correlation of F and K can be performed on the grouped data with the non-clay content. If the correlation outcome is good, it implies that Archie’s law can apply to the analyzed data set. The NGAM value of splitting into two groups can be the threshold for recognizing clay content. However, this splitting method does not consider the nature of the distribution of the data itself. Thus, the frequency distribution of NGAM in the collected data set was utilized to summarize the information on the number of occurrences of class intervals in a given NGAM range. The number of class intervals can be calculated as the following equation.
P = 5 × log 10 ⁡ ( N )
where N is the total amount of collected samples. P is the number of class intervals. If P is a decimal number, rounding this decimal number to the nearest whole number is needed. Based on the rounded P number, the frequency of data belonging to each class interval is plotted in a frequency distribution figure, which is also called Histogram. Each data set collected in this study was able to use this technique to obtain the frequency pattern of NGAM. The higher class interval has larger NGAM values, which may be more likely to contain clay minerals. Subsequently, a stepwise deletion process of sample data from the class interval (starting from the highest class interval) was carried out, and correlations between F and K were performed for each group of screened samples. The analyzed correlation levels were used to determine the natural gamma ray threshold value that could recognize the existence of clay minerals in the samples.
(b)
Modified Archie’s law
Initially, Archie's law does not consider the influence of clay minerals in a formation. For the geological environment where clay mineral exists, applying this theory to predict porosity generally does not work well [26]. The main reason is that clay mineral has a high degree of ion exchange and a high specific surface area [24,33]. Formations with higher clay minerals may reduce the correlation between resistivity and hydraulic conductivity. Later, some studies based on Archie's law [24,26] proposed a modified Archie's equation incorporating the effect of clay minerals, which is given below.
F a = F c × ( 1 + B Q v R w ) − 1
Among them, Fa is the apparent formation factor; Fc is the corrected formation factor; Rw is the resistivity of the water saturating the pores; Qv is the cation exchange capacity; and B is the equivalent conductivity of each cation. After proper rearrangement, Equation (5) can be presented as a linear relationship between 1/Fa and Rw.
1 F a = 1 F c + B Q v F c R w
BQv/Fc stands for the gradient [26]; the data of Rw (x-axis) and 1/Fa (y-axis) are plotted, and then the simple linear regression formula is obtained by using regression analysis. The intercept of the regression formula is 1/Fc, and its value is calculated by inversion to obtain Fc.
Afterward, a dimensionless value (Fa/Fc) is calculated by dividing the uncorrected apparent formation factor (Fa) and the corrected formation factor (Fc) calculated by the correction method addressed above. A clay-free formation may be expected if Fa/Fc is greater than or equal to 0.9 [26]. The criterion indicated by Worthington [26] can be used to separate the collected samples into clay-bearing and clay-free sample groups for data clustering. The clay-free sample group can meet the original Archie`s law theory hypothesis, and the samples can be utilized to establish relations between the formation factor and hydraulic conductivity.
Therefore, data samples in complex geological environments clustered by the above two techniques (a) and (b) can be used to recognize the clay-free conditions of the samples. It may assist in improving the establishment of estimation models for predicting hydraulic conductivity through downhole resistivity data.

4. Results and discussion

4.1. Data processing result

In this study, the data quality control procedures mentioned in section 3.1 were used to eliminate the samples whose electrical signal data were inconsistent with the actual lithology, and the consistent samples were subjected to basic descriptive statistical analysis. Five data samples out of 396 were not included in the subsequent analyses. For the remaining 391 data samples, the sample data of various electrical signals in the 1.5 m double-packer hydraulic test section with different depths in different boreholes were compiled. One hundred fifty measurements in the test section were recorded for each signal sample, and each sample's mean and standard deviation were calculated. Then, all samples were classified into three group data categories: singular lithology, three major rock types, and entire data. The mean and standard deviation for each group type of data were calculated as shown in Table 2.
When comparing the standard deviations of the three categories, most of the singular lithology categories have relatively small standard deviations. A greater standard deviation means that the dispersion of the data is relatively large. If these data are used to develop a hydraulic conductivity predictive model, the prediction model's performance may not be good. Therefore, the statistical results of the underlying data imply the importance of data classification or clustering in the development of the estimation model. In addition, comparing the differences in the standard deviations of various signals, it is found that the standard deviation of the NGAM signal is smaller than other signals in each classification group. It is speculated that this signal is less susceptible to the external factors of the well (borehole size, the effect of the invasion of the mud filtrate into the formation, the heterogeneity of geologic formation, the salinity or conductivity of groundwater), while other signals are more affected by these external factors of the well. The standard deviation of the COND signal has the largest variation value, indicating that the mud may affect the fluid in the borehole. The variation of the SHN signal is larger than that of the LON signal, probably because the SHN signal reflects the resistivity value of the mud-infiltrated area and is more significantly affected by the mud. However, the LON signal reflects the formation resistivity and is less affected by mud. Therefore, the standard deviation variation can be used to understand the geology heterogeneity and the signal's degree of influence by external factors in each double-packer test section.
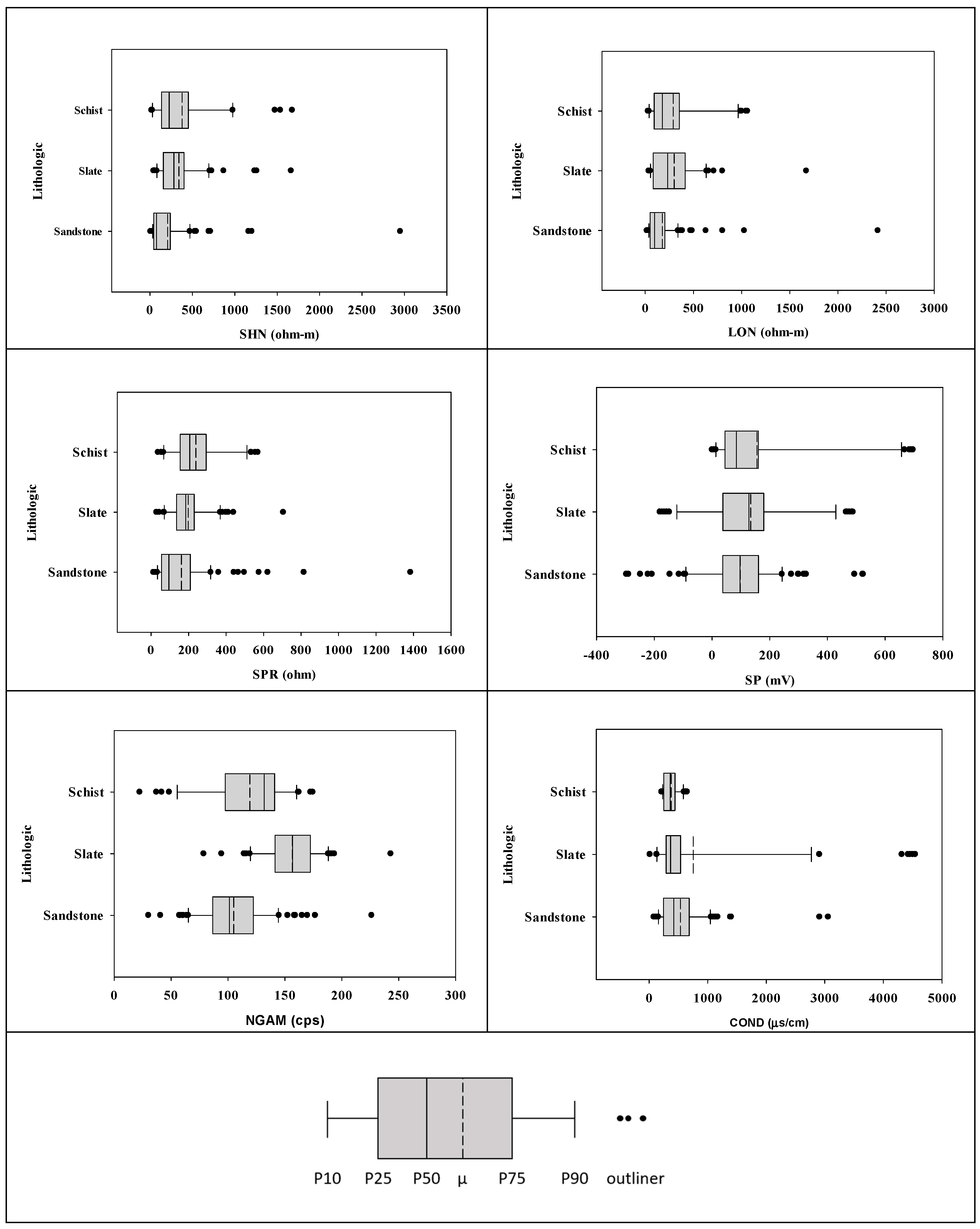
Furthermore, box plots were used to demonstrate the distributions of numeric signal data values and the comparisons between multiple groups. First, the selection of box plot data is based on a single lithological group with a sample size of more than 20 and no mud or shale contents. The single lithology groups that meet these selection criteria include sandstone, slate, and schist. Then, six different signal box plots were drawn for the three single lithological groups, as shown in Figure 4. The outlier points shown in Figure 4 lie outside the 10th and 90th percentiles as black circle symbols. The number of outliers and the dispersion of the primary data points for the three lithological groups were compared from the box plots of the five signals, which were used to determine the lithology of the strata. This comparison reveals that the numerical value distribution of sandstone data is more dispersive than the other two lithologies. This result is consistent with the results of the standard deviation analysis in Table 2. However, the comparison for the signal of determining the formation's fluid conductivity reveals that the slate data points are the most scattered, followed by sandstone. This result can be used to explain how strongly the formation fluid was affected by the drilling mud fluid in the borehole at the time of the test. Therefore, for the samples with the same lithology recorded manually, the results of the box plots drawn from the downhole exploration data with higher resolution data can be used to identify whether there is geological heterogeneity in the samples, which can help the development of estimation models.
Based on the analysis results of the collected data, it can be concluded that (1) preliminary data quality control is of great importance because these signal data are susceptible to external factors; (2) these signal data can help further investigate the heterogeneity of the rock formations than the visual description data recorded by geologists; (3) the high degree of geological heterogeneity of the study site has been found, and this result suggests that it is more appropriate to establish the hydraulic conductivity estimation model based on a single lithology type.
Table 2. Table 2 Descriptive statistics of six well logging signals for various rock types (1/2).
Table 2. Table 2 Descriptive statistics of six well logging signals for various rock types (1/2).
Signal Type SP (V) NGAM (cps) COND (ohm.m)
Category N μ S.D. μ S.D. μ S.D.
All lithologic types 388 141.81 155.80 121.02 38.61 598.91 704.94
Sedimentary Rock 230 127.49 129.31 114.77 30.93 634.64 608.68
Sandstone 90 97.59 147.39 105.02 31.42 238.39 479.28
Shale 30 147.15 97.09 129.37 20.23 810.53 393.21
Sandy Shale 3 112.41 2.73 135.09 5.46 357.70 10.84
Sandstone interbedded with Argillite 10 182.97 88.13 150.42 13.17 475.71 433.32
Mudstone 8 153.16 12.01 75.20 43.42 660.81 177.84
Siltstone 14 127.85 81.40 125.69 14.60 1430.85 1018.14
Silty Sandstone 20 179.10 168.03 102.14 22.45 324.68 129.65
Alternations of Sandstone & Shale 44 135.32 104.48 124.28 27.52 468.51 374.78
Argillaceous Siltstone 5 61.72 6.04 106.40 7.05 476.60 10.33
Quartz Sandstone 6 182.97 216.57 123.38 41.24 2100.29 1459.38
Igneous Rock 13 238.67 168.08 43.35 26.55 359.45 96.49
Andesite 7 124.80 66.79 59.53 7.32 329.46 63.19
Vocanic Agglomerate 6 371.52 152.05 24.48 28.88 394.43 121.77
Metamorphic Rock 145 155.86 186.87 137.85 39.11 563.72 859.02
Phyllite 6 458.57 17.38 155.20 4.95 861.69 55.67
Slate 57 133.41 165.13 157.13 26.16 782.87 1213.49
Schist 41 155.60 202.61 119.14 35.60 375.59 120.84
Marble 6 130.69 15.25 46.27 15.65 244.82 46.86
Gneiss 5 -55.84 22.01 143.68 5.69 269.90 142.64
Argillite 18 203.31 169.42 157.10 23.74 277.10 225.91
Metasandstone 3 463.68 4.05 136.56 34.48 131.96 12.33
Argillite interbedded with som sandstone 2 49.03 70.90 153.44 18.23 168.15 2.17
Quartzite 7 30.03 127.06 96.60 42.01 1186.50 1339.26
Note: The COND in this table is the reciprocal of the original COND, which was transformed into electrical resistivity.
Table 2. Descriptive statistics of six well logging signals for various rock types (2/2).
Table 2. Descriptive statistics of six well logging signals for various rock types (2/2).
Signal SHN (ohm.m) LON (ohm.m) SPR (ohm.m)
Category N μ S.D. μ S.D. Μ S.D.
All lithologic types 388 288.70 596.58 243.23 446.49 182.30 260.95
Sedimentary Rock 230 124.45 254.45 123.47 214.02 106.12 140.89
Sandstone 90 207.92 366.58 176.30 289.81 161.32 193.35
Shale 30 35.69 33.42 56.02 48.89 40.64 28.14
Sandy Shale 3 30.40 7.35 38.85 6.28 58.89 7.84
Sandstone interbedded with Argillite 10 277.11 228.22 330.14 247.94 176.69 100.96
Mudstone 8 14.27 4.93 17.66 2.94 28.19 11.50
Siltstone 14 27.87 11.44 47.34 27.40 31.32 13.51
Silty Sandstone 20 60.82 82.72 104.34 148.53 73.49 58.88
Alternations of Sandstone & Shale 44 63.51 79.04 87.46 135.64 82.45 69.08
Argillaceous Siltstone 5 9.54 1.15 12.09 1.21 21.00 1.22
Quartz Sandstone 6 225.83 222.09 105.54 85.37 148.34 173.97
Igneous Rock 13 375.77 590.63 254.86 373.40 217.36 209.74
Andesite 7 618.32 739.84 399.87 474.51 330.52 232.63
Vocanic Agglomerate 6 92.78 43.96 85.68 25.45 85.35 42.46
Metamorphic Rock 145 541.43 846.39 433.46 627.32 300.01 352.76
Phyllite 6 523.33 120.23 513.80 79.44 190.98 42.20
Slate 57 314.15 250.56 290.28 261.60 188.74 93.86
Schist 41 379.55 417.83 289.07 305.18 238.53 139.27
Marble 6 3973.34 1417.58 2864.96 1171.03 1606.99 850.91
Gneiss 5 1329.79 327.79 1031.72 195.14 737.45 118.70
Argillite 18 315.24 316.01 226.36 171.24 291.30 186.95
Metasandstone 3 373.64 134.02 384.41 125.77 312.53 39.43
Argillite interbedded with sandstone 2 211.48 141.82 216.72 81.60 205.53 75.00
Quartzite 7 598.84 467.85 491.71 393.95 270.94 181.78

4.2. Correlation analysis for various well logging signals with hydraulic conductivity

The correlation analysis for well logging signals was performed for (1) exploring possible correlations between singular signal and hydraulic conductivity and (2) examining the resolution level of the formation resistivity used in the formation factor. This study correlated each signal with hydraulic conductivity. Normality tests for each signal were conducted to determine parametric or non-parametric statistical methods utilized to quantify the level of association between the various signals and hydraulic conductivity. The bivariate correlation analysis, then, was adopted to examine correlations between the various signals and hydraulic conductivity.
Firstly, the normal testing outcomes pointed out that the null hypothesis for a sample from a normally distributed population was rejected for most of the signals. However, most of the signals did not pass the normality test. Thus, Spearman’s correlation was used to quantify the association between each signal and hydraulic conductivity. In addition, a significance level (p-value) of 0.05 with the two-tailed test was used for all correlation results in this study. If the results of significance testing show that the p-value is greater than 0.05, the correlation value is not meaningful.
Table 3 lists various signals that were analyzed for the correlation study. The correlation analysis items include hydraulic conductivity vs. SP, SHN, LON, SPR, NGAM, and COND. The analyzed data herein were selected from Table 1 for different lithological data groups, including all lithological rocks, sedimentary rock, igneous rock, metamorphic rock, sandstone, slate, and schist. In addition, Table 3 marks the correlation coefficient as a hyphen symbol if the significant testing does not pass. Based on meaningful correlation results for the all-lithologic type, the correlation results of SP and NGAM signals are insignificant among the six signal types. The possible main reason is that the formula for calculating the formation factor needs to come from the formation resistivity. Although the correlation between NGAM and K values is not meaningful, the NGAM signal is a crucial indicator for determining the presence of mud in the geological strata. Therefore, in the subsequent data clustering process, the NGAM values were used as the threshold to categorize the data samples into mud-containing and free groups for data clustering purposes.
In addition, the meaningful correlation coefficients shown in Table 3 exist in SHN, LON, SPR, and COND signals. According to Cohen’s guideline [34] for interpreting the level of correlation from Spearman’s coefficient, the strength of the relation for SHN, SPR, and COND reaches the medium strength (0.3-0.5). The strength of the relation for LON belongs to the low strength (0.3-0.1). While looking at other data groups for specific lithology, the strength of the relation for these meaningful signals may increase. The increased correlation strength, which is up to the level of the strong strength, depends on the lithology. The correlation analysis results regarding the three electrical resistivity signals (SPR, SHN, and LON) show that the strength of their associations, from best to worst, is in the order of SPR, SHN, and LON. The electrical resistivity value is commonly used as an essential parameter for estimating the formation factor (F) of formation. Based on the correlation strength of electrical resistivity results, theoretically, F should be calculated using the best-correlated signal, SPR. However, the electrical well logging data from SPR is typically used only as a supplementary tool to determine the presence of fractures and groundwater flow in rock formations. The electrical resistivity values for lithological characterization are usually determined by SHN and LON signals. Therefore, the SHN signal was adopted in this study, which showed a stronger correlation with K for estimating the F values. The correlation of SHN that is better than that of LON was also confirmed by previous studies [5,13]. For estimating the formation factor, SHN is utilized as it assures a greater resolution of the formation than LON.
Finally, the correlation between COND and K revealed a certain degree of negative correlation. The connection between these two parameters was not expected, as the COND values were initially intended to understand the water quality around a drilling well. However, a plausible explanation for this connection is that higher COND values indicate relatively more polluted water quality, possibly due to the poor permeability of the strata, resulting in the groundwater flowing poorly in the stratum. As a result, the analysis shows a negative correlation where higher COND values correspond to smaller K values. Although COND may correlate with K, COND is not directly used to estimate K. Instead, The reciprocal of COND was transformed into electrical resistivity, which is used as the resistivity of the water saturating the pores (Rw), as shown in Equation (1). It is then combined with SHN to calculate F.

4.3. Data clustering results

To address the influence of clay minerals on the correlation between F and K, this study first utilized the findings from Section 4.2, which showed a higher correlation between single lithological well logging data and hydraulic conductivity as the basis for data samples classification. Furthermore, two data clustering methods from Section 3.3 were employed to progressively eliminate data samples containing clay minerals from each single lithological group. The remaining samples can be the basis for constructing models to estimate K from F. The detailed outcomes of the two data clustering methods are summarized below.

4.3.1. Outcomes from the natural gamma threshold method

This study classified the data population based on individual lithological data (Table 2). Three individual lithological groups were selected among these data groups, namely sandstone, slate, and schist. The selected criteria were based on the data group with a sample size of more than 20 and did not contain clay minerals in lithological compositions. These filtered groups were subjected to the NGAM threshold clustering analysis. 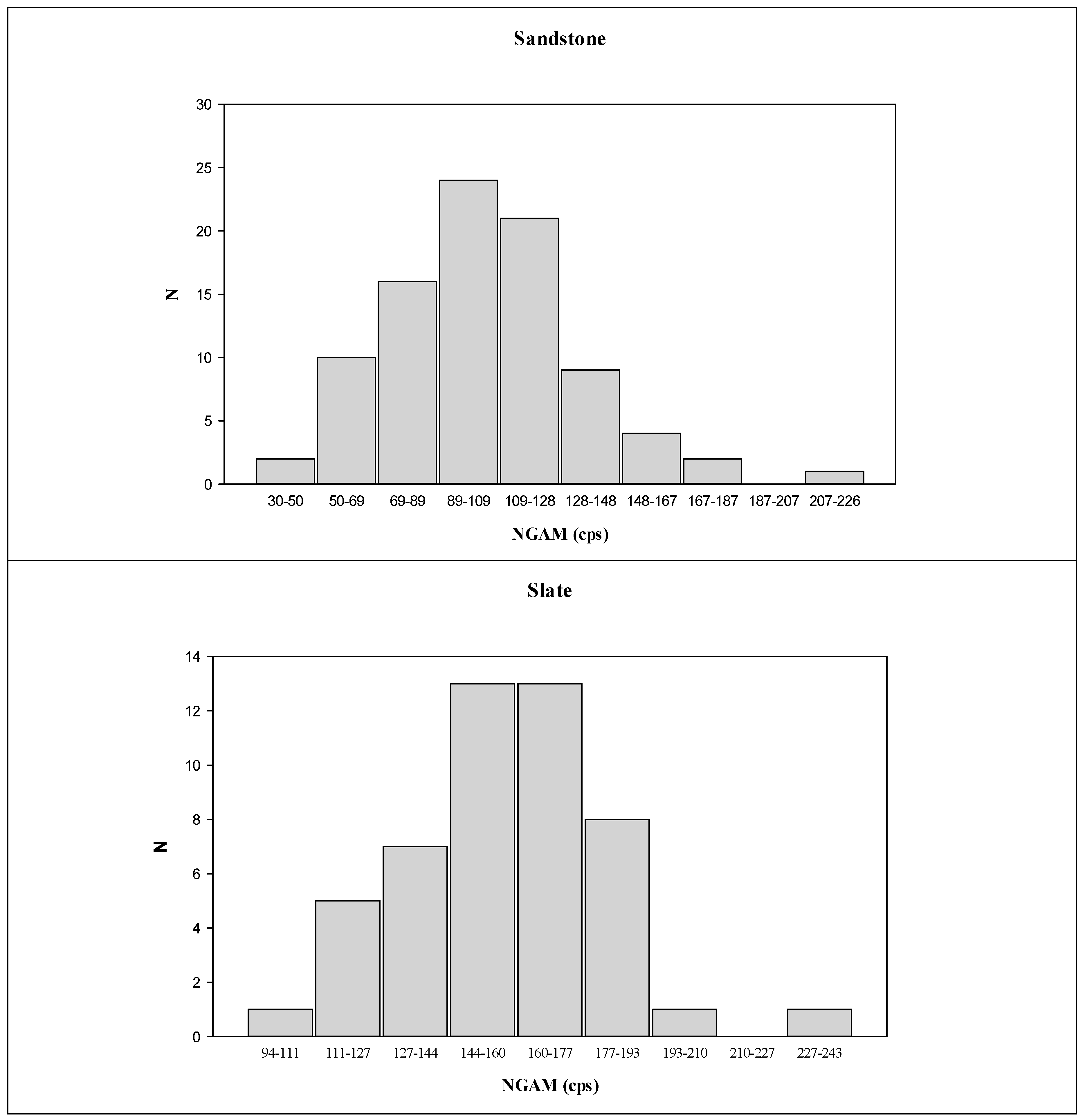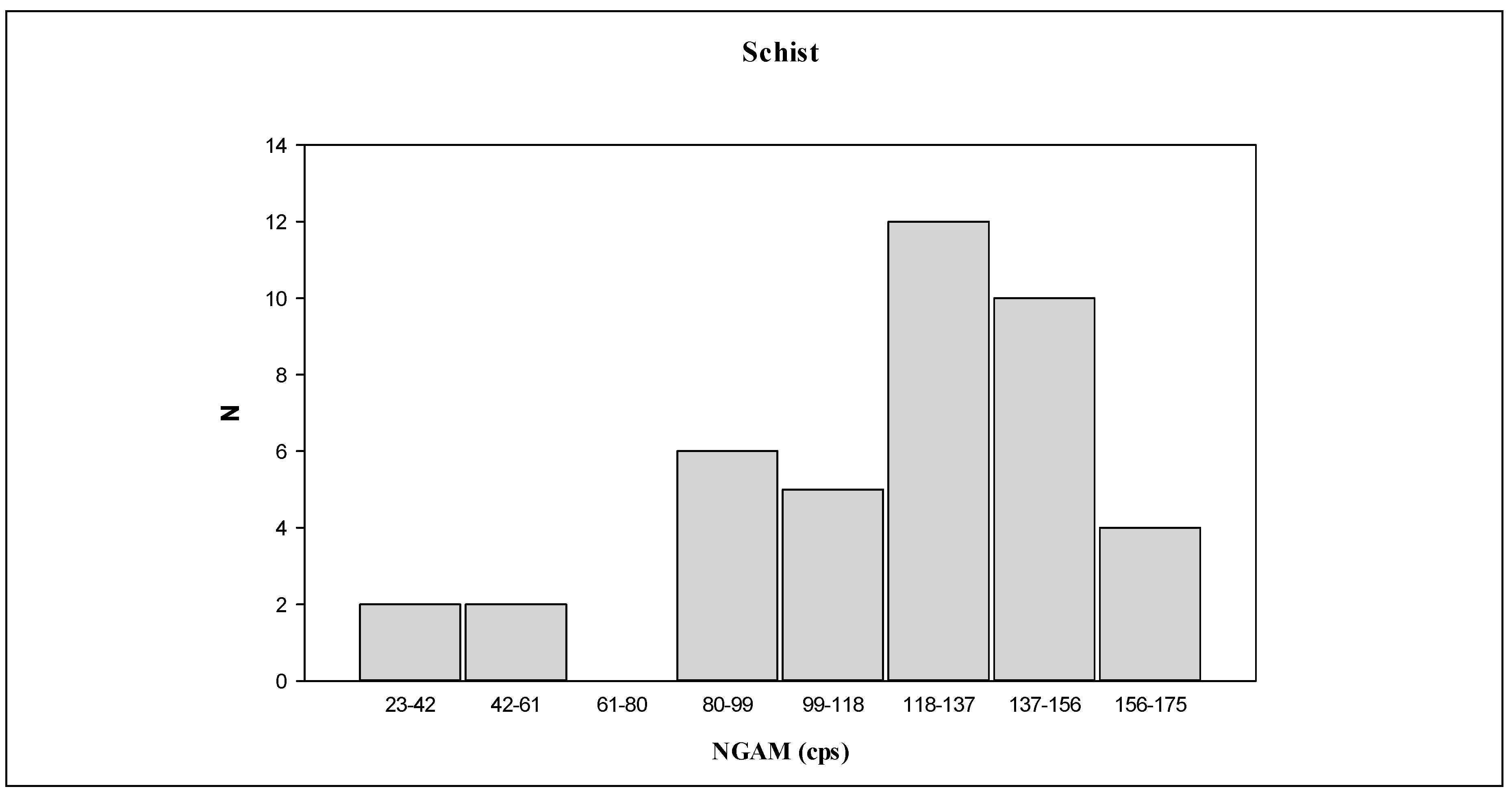Using Equation (4), the frequency distribution figure of NGAM for each single lithology type was plotted in Figure 5. Based on each Histogram, the higher class interval was supported to have a greater NGAM value that may contain clay minerals. A relatively better correlation can gradually be found by deleting clay-contained data samples from the highest-class interval with performing correlation analysis between F and K for each filtered data group. Table 4, Table 5 and Table 6 show the process of correlation variations with different data groups for sandstone, slate, and schist, respectively. As seen in Table 4, the correlation coefficient of Spearman between F and K gradually increased by deleting samples with higher NGAM values. When the NGAM value of the data is between 30 and 90, Spearman's coefficient is greater than 0.5, which reaches the minimum lower limit of the strong strength according to Cohen’s guideline [34]. The Spearman’s correlation coefficient increased from 0.159 (all data samples) to 0.572 ([30,89] data samples), and the maximum correlation coefficient value is statistically significant (The P-value is less than 0.05). Therefore, in this case, NGAM equal to 89 is used as the threshold value for sandstone clustering. Values above this threshold indicate intervals containing mud, while values below suggest intervals with very low mud content or being clean. However, the correlation coefficient between F and K shows a positive relationship, meaning that as F increases, K also increases. This contradicts the theory of Archie’s law and Kozeny-Carman-Bear equation, implying that the samples selected using NGAM equal to 89 as the threshold might still contain some muddy samples or incomplete data of clean sand, which may include some quantities of mud. However, such an empirical relationship requires more data to be proved.
Table 5 shows the correlation variations with various filtered data sets for the slate group. The Spearman’s correlation coefficients between F and K gradually increased by deleting samples with higher NGAM values. When the NGAM value of the data is between 94 and 127, the spearman's coefficient is -0.455, which is the maximum value and belongs to the medium strength according to Cohen’s guideline [34]. The Spearman’s correlation coefficient increased from -0.125 (all data samples) to -0.455 ([94,127] data samples). However, the maximum correlation coefficient value is not statistically significant (The P-value is greater than 0.05). The insignificant result of F vs. K is that the sample size may not be sufficient. The applicability of this clustering method to the slate group needs further confirmation with more data. Finally, Table 6 shows the correlation variations with various filtered data sets for the schist group. The Spearman’s correlation coefficients between F and K gradually increased by deleting samples with higher NGAM values. When the NGAM value of the data is between 23 and 118, the Spearman's coefficient is -0.643, which is the maximum value and belongs to the strong strength according to Cohen’s guideline [34]. The Spearman’s correlation coefficient increased from -0.102 (all data samples) to -0.643 ([23,118] data samples), and the maximum correlation coefficient value is statistically significant (The P-value is less than 0.05). Therefore, in this case, NGAM equal to 118 is used as the threshold value for schist clustering. Values above this threshold indicate intervals containing mud, while values below suggest intervals with very low mud content or being clean.

4.3.2. Outcomes from the modified Archie’s law method

To understand the mud content within the specific interval of a formation, this study establishes an alternative clustering approach different from directly using the NGAM signal to classify intervals into muddy/clean zones based on a threshold value. Instead, this study first constructed the apparent formation factor (Fa) using formation resistivity (Ro) and the inverse of formation fluid conductivity (Rw). Then, the modified formation factor (Fc) was computed by means of Equations (5) and (6) in Section 3.3. The Fa and Fc values are divided to obtain a dimensionless parameter Fa/Fc, and data samples where the Fa/Fc value falls in the [0.9,1.0] interval as the clean segments [26]. Finally, conducting a correlation analysis between the corrected formation factor (Fc) and hydraulic conductivity (K) within the clean zones allows this study to understand the benefits of the improved correlation between Fc and K resulting after being corrected by this clustering approach.
To obtain Fc values for each sample under a single lithologic classification using the techniques described in Section 3.3, a scatter plot with 1/Fa and Rw values was created using 150 downhole signal data points for each sample section (1.5 m double-packer test interval). Furthermore, simple linear regression analysis was applied to determine the regression equation's intercept (representing Fc) and slope. However, if the obtained intercept or slope from the data points is negative, it would contradict the theoretical expectations. Such samples from the analysis will be excluded from the subsequent correlation analysis between Fc and K. Based on the analysis as mentioned above criteria, each sample's (Fa, Fc) data was obtained for each individual lithological type. Simultaneously, the Fa/Fc ratio was calculated for each sample. The correlation between Fc and K was then analyzed for different ranges of the Fa/Fc ratio. This analysis aimed to investigate the relationship between the ratio and the correlation of Fc vs. K. Theoretically, as the Fa/Fc ratio increases, the sample's mud content decreases, aligning better with Archie's law's theoretical assumptions.
Table 7 shows the correlation analysis between modified formation factor (Fc) and hydraulic conductivity (K) for different lithological types. According to the study by Worthington [26], the Fa/Fc value of the clean and mud-free formation interval should be greater than 0.9. However, the analysis results in the table show that very few samples of different lithological types meet the criterion of Fa/Fc greater than 0.9. Only a few sandstone samples can exceed this 0.9 threshold. Using this approach to separate samples from muddy and clean sections of the formation, it is clear that relatively few lithological samples in the Taiwan region meet the requirements of Archie's law well.
In addition, the smaller the Fa/Fc ratio, the higher the probability of containing mud. Table 7 also shows sample groups for different ranges of Fa/Fc ratios along with the correlation analysis results between Fc and K. Taking sandstone as an example, the correlation between Fc and K improves as the Fa/Fc ratio increases. Similar trends were observed for most other lithological types. However, upon comparing these trends with the results of the correlation coefficient trends for each lithological type, this clustering approach suggests that sedimentary rock types have a better chance of yielding mud-free samples. On the other hand, slates in metamorphic rocks are more challenging to screen for mud-free samples. This conclusion aligns with the findings in the analysis of Section 4.3.1.
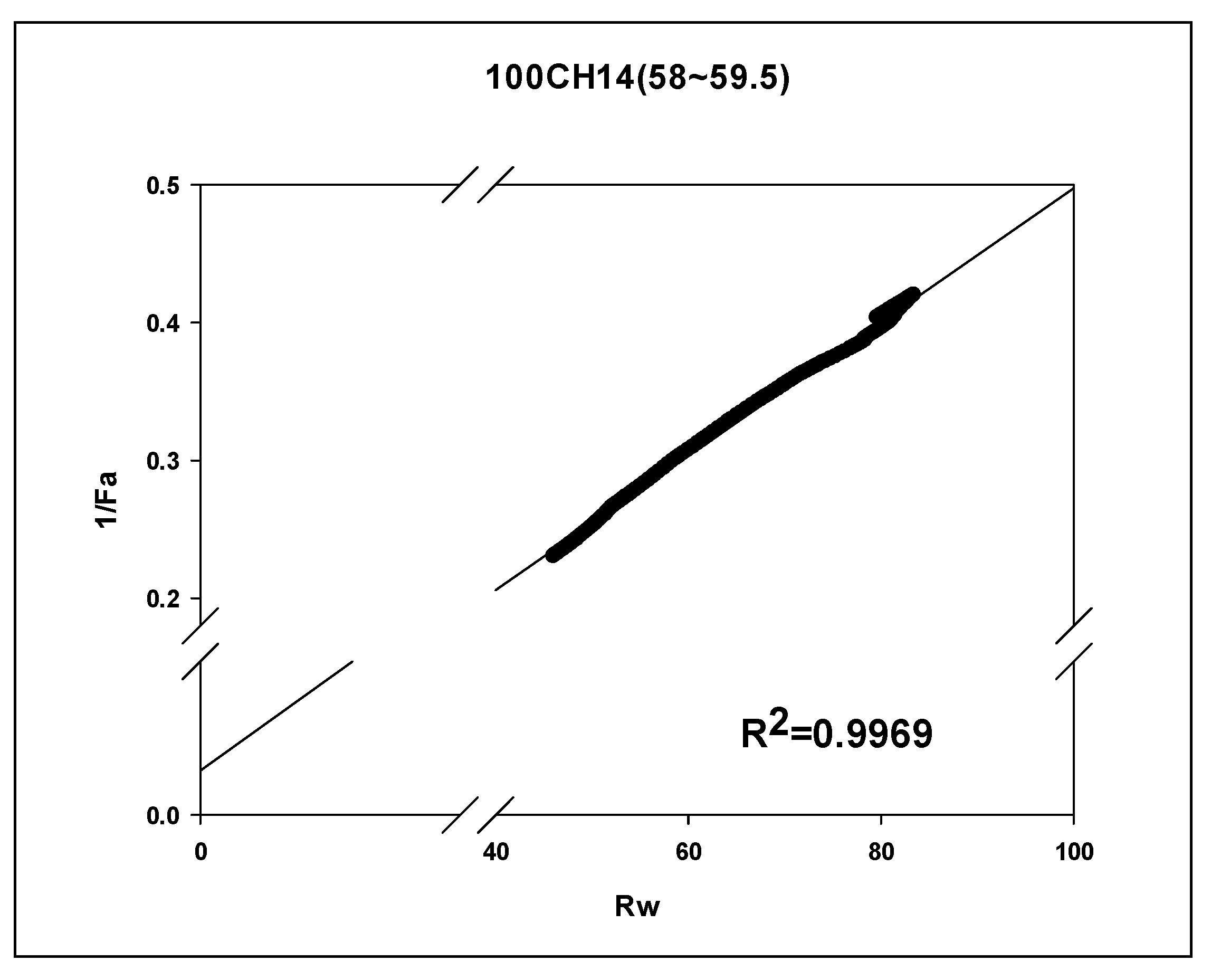
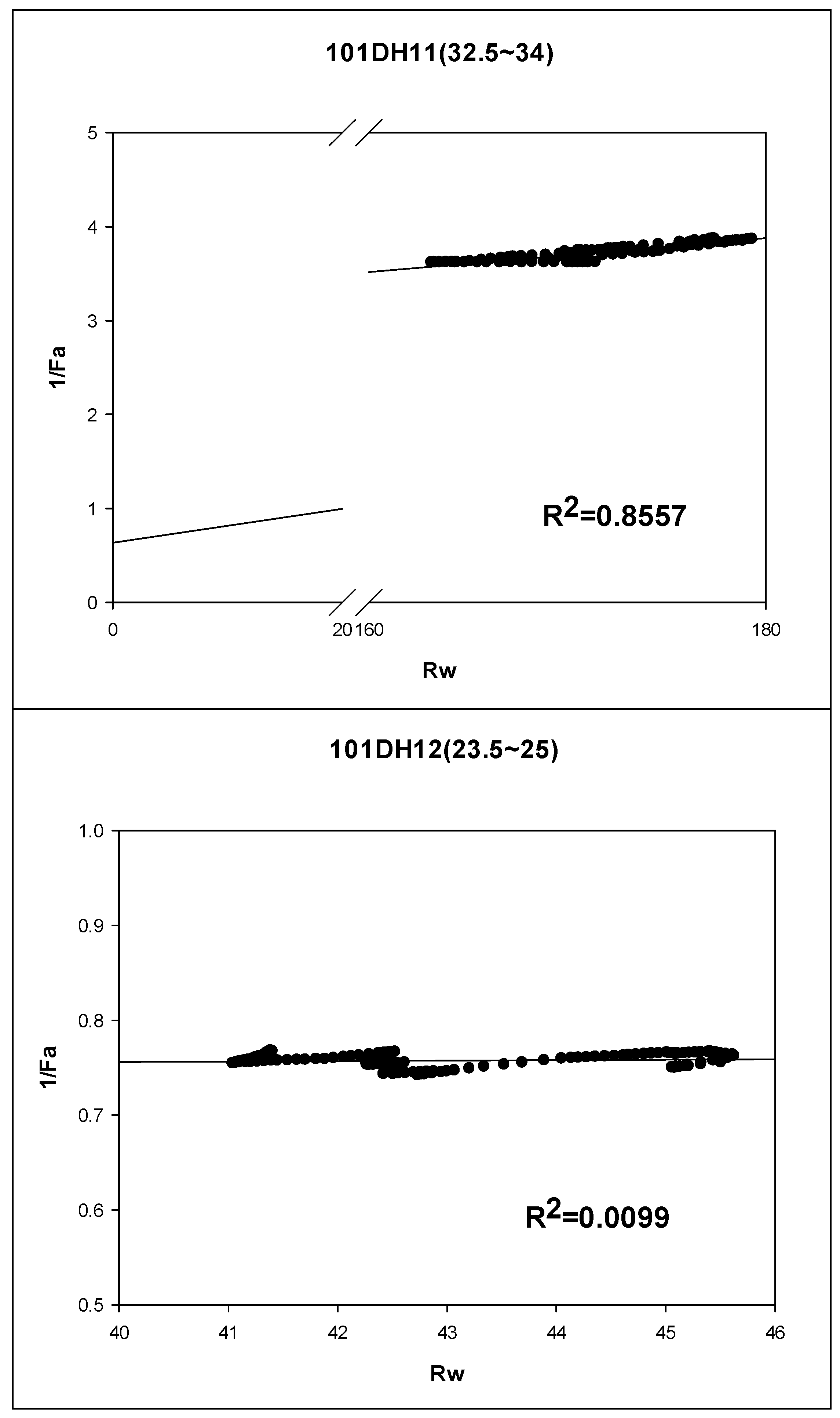
Finally, concerning the proposed method for calculating Fc in this study, the estimated quality of Fc data deserves discussion, as it determines the reliability of the correlation analysis results between Fc and K. Figure 6 displays scatter plots and regression curves for three different sample sets of 1/Fa against Rw. The corresponding regression coefficients (R2) for the three sample sets are 0.9969, 0.8557, and 0.0099, respectively. The first sample set exhibits the highest R2 value and a concentrated point distribution, indicating a strong matching degree and concentrated point set. The estimated Fc value from this kind of well-matching and concentrated point distribution samples may belong to higher-quality data. Conversely, the point distribution in the last sample set is more scattered, suggesting lower-quality data for the estimated Fc value. Thus, the quality of Fc estimation has a specific impact on the quality of subsequent correlation analysis results between Fc and K. Therefore, there is room for improvement in the feasibility of this clustering method for determining mud-containing intervals.

4.4. Establishment of hydraulic conductivity estimation models

Using the two clustering methods outlined in Section 4.3, a preliminary selection of potential mud-free samples conforming to Archie's law theory has been conducted based on the collected sample data. This serves as a foundation for further establishing estimation formulas for predicting hydraulic conductivity based on the formation factor. Regarding the outcomes of the natural gamma-ray threshold clustering method, the analysis primarily focuses on results from three individual lithological types: sandstone, schist, and slate. Initially, an examination was performed to check for anomalies in short normal resistivity and fluid conductivity values within each set of individual lithological samples. These anomalies were verified against expected short normal resistivity and fluid conductivity values based on the hydraulic conductivity value. Theoretically, both short normal resistivity and fluid conductivity values should be small for samples with high permeability. Conversely, for low permeability samples, both values should be larger. When the raw data signals were rechecked for anomalies, these abnormal data samples were considered an outlier within that set. Finally, regression analysis between hydraulic conductivity and formation factors and the construction of hydraulic conductivity estimation models were performed exclusively for samples with signals conforming to the theoretical values.
During the process of model establishment, it was observed that each lithological type had outliers after data quality checking. Simultaneously, the R2 values of regression analyses between original data points and checked data points showed significant differences between the two sets of analysis results. The accuracy of hydraulic conductivity estimation models can be greatly enhanced by re-evaluating the rationality of data signals. Regression analysis results with the removal of outliers revealed R2 values of 0.63, 0.60, and 0.83 for sandstone, schist, and slate regression models, respectively. For these three lithological types, the hydraulic conductivity estimation models best matched the power law model. Equations (7), (8), and (9) show the estimation equations for sandstone, schist, and slate, respectively. Through the established estimation models, the steps for estimating hydraulic conductivity are: (1) selecting the appropriate lithological estimation model, (2) collecting short normal resistivity and fluid conductivity data from borehole electrical logging, (3) obtaining the formation factor (F) using Archie's law theory, and (4) estimating hydraulic conductivity using the calculated F value and equations (7), (8), or (9).
K = 7 × 10 − 8 F 1.3033
K = 6 × 10 − 4 F − 2.422
K = 2 × 10 − 6 F − 3.055
Although this study utilized the statistical method in Section 3.3 to rapidly screen for valid data samples, there were still some samples for which abnormal signals could not be entirely screened out. However, further scrutiny of well-logging signals allowed the selection of ultimately analyzable samples. Improvements can be made to the screening method in Section 3.3 in the future.
Regarding the outcomes of the modified Archie's law screening method, only the single lithological type of sandstone can reach the criterion of Fa/Fc ≥ 0.9 after clustering. This clustering method is relatively stringent and theoretically grounded for identifying mud-containing formation intervals. After undergoing this clustering process, the sample count was reduced from 41 to only three that met the clustering criterion. Finally, regression analysis between K and Fc and the establishment of hydraulic conductivity estimation models was performed for samples conforming to theoretical signal values. The regression analysis results for sandstone indicated that this lithological type's hydraulic conductivity estimation model exhibited the best match with the power law model, with an R2 value of 0.98. Equation (10) presents the estimation equation for sandstone.
K = 4 × 10 − 6 F − 7.591

5. Conclusions

Given the need for information on the continuous hydraulic conductivity of rock mass vertically required for scientific questions or the development planning of rock engineering, this study performs a feasibility investigation for estimating hydraulic properties of rock formations in complex geologic environments using downhole electrical signals. Summarizing the various research findings of this study, the following conclusions can be drawn, along with potential research directions for future efforts.
  • This study collected hydrogeological test data from 88 boreholes of the groundwater resources investigation project in Taiwan's mountainous areas. These data included results from double-packer hydraulic tests, electrical well logging, and fluid conductivity logging. Based on data from 396 double-packer hydraulic test sections, methods such as Archie’s law, Kozeny-Carman-Bear equation, and data clustering techniques (natural gamma ray threshold and modified Archie’s law) were employed to develop estimation models of hydraulic conductivity.
  • Basic descriptive statistics were successfully used in this study to inspect the data quality of well-logging signals (SP, LON, SHN, SPR, NGAM, and COND). Statistical analysis showed that single rock types exhibited better aggregation, aiding anomaly data verification.
  • Without rock type classification and data clustering, the correlation analysis between each well logging signal and hydraulic conductivity revealed that the three types of resistivity and fluid conductivity signals had better correlation performance. This better performance may be due to the fact that the resistivity and fluid conductivity parameters are required to be composed of the formation factor (F). Among six signals, single-point resistivity and short-normal resistivity performed the best, while natural potential and natural gamma ray showed weaker correlations.
  • To address the impact of clayey formation sections on the correlation between F and K, this study proposed the natural gamma ray threshold clustering and modified Archie’s law clustering methods to filter clayey data. Results showed that the natural gamma ray threshold clustering method achieved better recognition results for clayey sections in sandstone and schist, while the modified Archie’s law clustering method exhibited superior recognition only in sandstone. Moreover, the modified Archie’s law clustering method filtered out more clayey samples for the same rock type than the natural gamma ray threshold clustering method, indicating the former's stricter criteria. After aggregating well-logging signal data, formation sections with very low clay content or being clean were identified, forming the basis for building hydraulic conductivity estimation models.
  • Through the natural gamma ray threshold clustering and modified Archie’s law clustering methods, it was observed that removing clayey sections could effectively enhance the correlation between formation factor and hydraulic conductivity. However, to satisfy Archie’s law's theoretical requirements, many data entries for various rock types needed to be removed, indicating that Taiwan's mountainous rock formations are complex and often contain significant clay content. Therefore, careful consideration of clay-related issues in formation layers is essential in practical engineering applications in mountainous regions.
  • Based on the natural gamma ray threshold clustering method results, this study performed regression analysis for hydraulic conductivity and formation factor on sandstone, shale, and slate and built hydraulic conductivity estimation models. The regression analysis indicated that the hydraulic conductivity estimation models for each rock type best matched the power law model. The R2 values for regression analysis were 0.63 for sandstone, 0.60 for schist, and 0.83 for slate.
  • According to the modified Archie’s law clustering method results, only the single rock type of sandstone met the criteria of Fa/Fc≧0.9. This is primarily because the modified Archie’s law clustering method is more rigorous in screening clayey formation sections and is based on sound theoretical principles. Finally, regression analysis for hydraulic conductivity and formation factor was performed on samples that matched theoretical signal values. The regression analysis results for sandstone showed that the hydraulic conductivity estimation model is best represented by a power law model with an R2 value of 0.98. However, the high R2 value can be attributed to the limited number of analyzed samples, highlighting the need for more data to construct the hydraulic conductivity estimation model for sandstone and the prevalence of clay content in Taiwan's mountainous sandstone formations.
  • During the exploration of electrical well logging data, it was found that the clay effect is present in most rock formations in Taiwan. To enhance the utilization of a mathematical model for estimating hydrogeological parameters of individual rock types using single resistivity signals, more data collection is required to ensure the reliability of the model. Furthermore, for hydrogeological parameter estimation models applicable to multiple rock types, it is recommended to consider recombining the collected signals. This approach could yield novel signal indicators, enabling the construction of new relationships between indicators and different hydrogeological parameters.

Author Contributions

S.-M.H. developed the conceptualization, processed data, and wrote the manuscript; G.-Y.L. worked on the correlation studies; M-C.D. worked on data clustering; Y.-F.L. analyzed the well-logging data and the data curation; G.-S.L. worked on well logging data preparation; All authors have read and agreed to the published version of the manuscript.

Acknowledgments

This work was supported by the National Science and Technology Council of Taiwan [MOST 110-2116-M-019-004 -]. Additionally, the authors express their gratitude to the Central Geological Survey, Ministry of Economic Affairs (MOEA) of Taiwan, for offering hydrogeological investigation data used in this study.

Conflicts of Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

References

  1. Chen, Y.C.; Tsai, J.P.; Chang, L.C.; Chang, P.Y.; Lin, H. Estimating hydraulic conductivity fields in composite fan delta using vertical electrical sounding. Water. 2018, 10(11). [CrossRef]
  2. Dou, Z.; Zhou, Z.; Tan, Y.; Zhou, Y. Numerical study of the influence of cavity on immiscible liquid transport in varied-wettability fractures. Journal of Chemistry. 2015, 1-10. [CrossRef]
  3. Hsu, S.M.; Hsu, J.P.; Ke, C.C.; Lin, Y.T.; Huang, C.-C. Rock mass permeability classification schemes to facilitate groundwater availability assessment in mountainous areas: a case study in Jhuoshuei river basin of Taiwan. Geosciences Journal. 2019. [CrossRef]
  4. Zhan, S.S.; Wang, T.T.; Huang, T.H. Variations of hydraulic conductivity of fracture sets and fractured rock mass with test scale: Case study at Heshe well site in Central Taiwan. Engineering Geology. 2016, 206, 94-106. [CrossRef]
  5. Kaleris, V.K.; Ziogas, A.I. Using electrical resistivity logs and short duration pumping tests to estimate hydraulic conductivity profiles. Journal of Hydrology. 2020, 590(), 125277–. [CrossRef]
  6. Hsu, S.M. Quantifying hydraulic properties of fractured rock masses along a borehole using composite geological indices: A case study in the mid- and upper-Choshuei river basin in central Taiwan. Eng. Geol. 2021, 284. [CrossRef]
  7. Sousa, R.L.; Einstein, H.H. Lessons from accidents during tunnel construction. Tunnelling and Underground Space Technology. 2021, 113, 103916. [CrossRef]
  8. Sara, M.N. Site assessment and remediation handbook (2nd edn.). Environmental Geology. 2003, 45, 144-145.
  9. Kaleris, V.; Hadjitheodorou, C.; Demetracopoulos, A.C. Numerical simulation of field methods for estimating hydraulic conductivity and concentration profiles. Journal of hydrology. 1995, 171(3-4), 319-353. [CrossRef]
  10. Lo, H.C.; Chen, P.J.; Chou, P.Y.; Hsu, S.M. The combined use of heat-pulse flowmeter logging and packer testing for transmissive fracture recognition. Journal of Applied Geophysics. 2014, 105, 248-258. [CrossRef]
  11. Molz, F.J.; Morin, R.H.; Hess, A.E.; Melville, J.G.; Güven, O. The impeller meter for measuring aquifer permeability variations: evaluation and comparison with other tests. Water Resources Research. 1989, 25(7), 1677-1683. [CrossRef]
  12. Asfahani, J. Porosity and hydraulic conductivity estimation of the basaltic aquifer in Southern Syria by using nuclear and electrical well logging techniques. Acta Geophysica. 2017, 65, 765-775. [CrossRef]
  13. Kaleris, V.K.; Ziogas, A.I. Estimating hydraulic conductivity profiles using borehole resistivity logs. Procedia Environmental Sciences. 2015, 25, 135-141. [CrossRef]
  14. Keller, C.E.; Cherry, J.A.; Parker, B.L. New method for continuous transmissivity profiling in fractured rock. Groundwater. 2014, 52(3), 352-367. [CrossRef]
  15. Ren, S.; Parsekian, A.D.; Zhang, Y.; Carr, B.J. Hydraulic conductivity calibration of logging NMR in a granite aquifer, Laramie Range, Wyoming. Groundwater. 2019, 57(2), 303-319. [CrossRef]
  16. Jones, P.H.; Buford, T.B. Electric logging applied to ground-water exploration. Geophysics. 1951, 16(1), 115-139. [CrossRef]
  17. Archie, G.E. The electrical resistivity log as an aid in determining some reservoir characteristics. Transactions of the AIME. 1942, 146(01), 54-62. [CrossRef]
  18. Huntley, D. Relations between permeability and electrical resistivity in granular aquifers. Groundwater. 1986, 24(4), 466-474. [CrossRef]
  19. Worthington, P.F. Influence of matrix conduction upon hydrogeophysical relationships in arenaceous aquifers. Water Resources Research. 1977, 13(1), 87–92. [CrossRef]
  20. Slater, L.; Lesmes, D.P. Electrical-hydraulic relationships observed for unconsolidated sediments. Water resources research. 2002, 38(10), 31-1. [CrossRef]
  21. Winsauer, W.O.; Shearin Jr, H.M.; Masson, P.Y.; Williams, M. Resistivity of brine-saturated sands in relation to pore geometry. AAPG bulletin. 1952, 36(2), 253-277. [CrossRef]
  22. Khalil, M.A.; Ramalho, E.C.; Monteiro Santos, F.A. Using resistivity logs to estimate hydraulic conductivity of a Nubian sandstone aquifer in southern Egypt. Near Surface Geophysics. 2011, 9(4), 349–356. [CrossRef]
  23. Shen, B.; Wu, D.; Wang, Z. A new method for permeability estimation from conventional well logs in glutenite reservoirs. Journal of Geophysics and Engineering. 2017, 14(5), 1268-1274. [CrossRef]
  24. Waxman, M.H.; Smits, L.J.M. Electrical conductivities in oil-bearing shaly sands. Society of Petroleum Engineers Journal. 1968, 8(02), 107-122. [CrossRef]
  25. Central Geological Survey of Taiwan. Ground-water resources investigation P\program for mountainous region of Central Taiwan (1/4). Ministry of Economic Affairs: Taipei, Taiwan. 2010.
  26. Worthington, P.F. The uses and abuses of the Archie equations, 1: The formation factor-porosity relationship. Journal of Applied Geophysics. 1993, 30(3), 215-228. [CrossRef]
  27. Glover, P.W. Archie's law–a reappraisal. Solid Earth. 2016, 7(4), 1157-1169. [CrossRef]
  28. Bear, J. Dynamics of fluids in porous media: Elsevier. 1972.
  29. Domenico, P.A.; Schwartz, F.W. Physical and chemical hydrogeology. John wiley & sons. 1997.
  30. Chapuis, R.P.; Aubertin, M. On the use of the Kozeny Carman equation to predict the hydraulic conductivity of soils. Canadian Geotechnical Journal. 2003, 40(3), 616-628. [CrossRef]
  31. Khalil, M.A.; Santos, F.A.M. Hydraulic conductivity estimation from resistivity logs: a case study in Nubian sandstone aquifer. Arabian Journal of Geosciences. 2013, 6, 205-212. [CrossRef]
  32. Rahman, A. A GIS based DRASTIC model for assessing groundwater vulnerability in shallow aquifer in Aligarh, India. Applied geography. 2008, 28(1), 32-53. [CrossRef]
  33. Vinegar, H.J.; Waxman, M.H. Induced polarization of shaly sands: Geophysics. 1984.
  34. Cohen, J.; Cohen, P.; West, S.G.; Aiken, L.S. Applied multiple regression/correlation analysis for the behavioral sciences. Routledge. 2013.
Preprints 84406 g001
Figure 1. The study area and locations of investigated boreholes.
Figure 1. The study area and locations of investigated boreholes.
Preprints 84406 g001
Preprints 84406 g002
Figure 2. Flowchart for investigating formation factor-hydraulic conductivity relationships.
Figure 2. Flowchart for investigating formation factor-hydraulic conductivity relationships.
Preprints 84406 g002
Preprints 84406 g003
Figure 3. The short normal resistivity profiles at two different double-packer intervals.
Figure 3. The short normal resistivity profiles at two different double-packer intervals.
Preprints 84406 g003
Preprints 84406 g004
Figure 4. Box plots for demonstrating the distributions of various signals with three major lithologies.
Figure 4. Box plots for demonstrating the distributions of various signals with three major lithologies.
Preprints 84406 g004
Preprints 84406 g005aPreprints 84406 g005b
Figure 5. Histogram of NGAM for three lithologies (sandstone, slate, and schist, respectively).
Figure 5. Histogram of NGAM for three lithologies (sandstone, slate, and schist, respectively).
Preprints 84406 g005aPreprints 84406 g005b
Preprints 84406 g006aPreprints 84406 g006b
Figure 6. Demonstration on the quality of estimated Fc values for three types of levels.
Figure 6. Demonstration on the quality of estimated Fc values for three types of levels.
Preprints 84406 g006aPreprints 84406 g006b
Table 1. Statistics of lithology for the data samples collected from the double packer hydraulic test.
Table 1. Statistics of lithology for the data samples collected from the double packer hydraulic test.
Main lithology Sub-lithology Amount
Sedimentary rock Sandstone 93
Shale 31
Sandy Shale 3
Sandstone interbedded with Argillite 2
Mudstone 8
Siltstone 14
Silty Sandstone 20
Alternations of Sandstone & Shale 44
Argillaceous Siltstone 5
Quartz Sandstone 6
Igneous rock Andesite 7
Metamorphic rock Volcanic Agglomerate 6
Phyllite 6
Slate 61
Schist 41
Marble 6
Gneiss 5
Argillite 18
Metasandstone 3
Argillite interbedded with some sandstone 10
Quartzite 7
Total 396
Table 3. Correlation outcomes between k and various signal types with various lithologic groups.
Table 3. Correlation outcomes between k and various signal types with various lithologic groups.
Signal
type		 All lithologic type Sedimentary rock Igneous rock Metamorphic rock Sandstone Slate Schist
Sample quantity 391 230 13 148 90 60 41
SP - - -.613 - - - -
SHN .343 .575 .732 - .442 - -
LON -.277 .480 - - .397 - -
SPR -.378 .549 .765 .245 .490 - -
NGAM - - - - - - -
COND -.308 -.281 - -.355 -.338 - .345
Note: “-” stands for “ the significant testing fails”.
Table 4. Correlation variations with various filtered data sets for the lithological group of sandstone.
Table 4. Correlation variations with various filtered data sets for the lithological group of sandstone.
F-Sandstone
K Data
sets		 All
Data		 [187-30] [167-30] [148-30] [128-30] [109-30] [89-30]
r .180 .180 .213 .217 .254 .377 .554
Sig. .089 .094 .049 .050 .030 .006 .002
N 90 88 86 82 73 52 28
Table 5. Correlation variations with various filtered data sets for the lithological group of slate.
Table 5. Correlation variations with various filtered data sets for the lithological group of slate.
F-Slate
K Data
sets		 All Data [210-94] [193-94] [177-94] [160-94] [144-94] [127-94]
r -.125 -.089 -.101 -.161 -.283 -.321 -.455
Sig. .392 .546 .501 .327 .161 .285 .365
N 49 48 47 39 26 13 6
Table 6. Correlation variations with various filtered data sets for the lithological group of schist.
Table 6. Correlation variations with various filtered data sets for the lithological group of schist.
F-Schist
K Data
sets		 All Data [156-23] [137-23] [118-23]
r -.102 -.102 -.461 -.643
Sig. .526 .550 .015 .01
N 41 37 27 15
Table 7. Correlation analysis of corrected formation factor (Fc) and hydraulic conductivity (K) of different lithology under different Fa/Fc ratio ranges.
Table 7. Correlation analysis of corrected formation factor (Fc) and hydraulic conductivity (K) of different lithology under different Fa/Fc ratio ranges.
Rock
Types		 Sandstone Slate Schist
Fa/Fc r No. of samples r No. of samples r No. of samples
0-1 -0.1 41 0.168 32 -0.085 16
0.2-1 0.003 21 -0.115 22 -0.297 10
0.4-1 0.245 12 -0.291 13 0.353 6
0.6-1 0.406 10 -0.066 8 0.936 3
0.8-1 -0.800 4 3 N.A. 1
0.9-1 -1.000 3 N.A. 2 N.A. 1
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated