Preprint
Communication
Impedance Variation of a Coaxial Coil Encircling a Metal Tube Adapter
Altmetrics
Downloads
76
Views
24
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
07 September 2023
Posted:
11 September 2023
You are already at the latest version
Alerts
Abstract
. The impedance change of an induction coil surrounding a metal tube adapter is investigated by the truncated region eigenfunction expansion (TREE) method. Conventional TREE method is inapplicable to this problem as a consequence of the numerical overflow of eigenfunctions of the air-metal multi-subdomain regions. The difficulty is surmounted by a normalization procedure for the numerical eigenfunctions obtained from the finite element method (FEM). Efficient algorithm is devised by the Clenshaw-Curtis quadrature rule for integrals involving the numerical eigenfunctions. Numerical results of the TREE and FEM simulation coincide very well in all cases, and the efficiency of the proposed method is also confirmed.
Keywords:
Subject: Physical Sciences - Applied Physics
1. Introduction
A tube adapter is a component connecting two tubes of different diameters. The standard analytical method of Dodd and Deeds [1] is unable to investigate the interaction of an induction coil with a metal tube adapter, due to the end effects involved in this problem. The truncated region eigenfunction expansion (TREE) method, pioneered by Hannakam and Tepe [2], and developed by Theodoulidis, Kriezis and Bowler [3-9] for modeling of the eddy current nondestructive testing (EC NDT), is capable of analyzing the end effects and establishing analytical models. However, successful implementation of TREE for the model of end effects depends on the solution of relevant eigenvalue equations, which are transcendental and complex roots should be determined. Conventionally, the Newton-Raphson algorithm [10-13] or contour integral based on the Cauchy’s theorem [14-17] are applied to solve the eigenvalue equations. A novel method based on the Sturm-Liouville theory and Galerkin approach has been proposed recently [18, 19], which greatly simplifies the process of locating the complex eigenvalues.
Unfortunately, the TREE cannot be used immediately for the problem of this work, even with the novel approach. The bottleneck lies in the numerical issues for the regions composed of multiple air-metal subdomains, more specifically, the numerical overflow occurs constantly when the symbolic eigenfunctions are employed for the n-subdomain ( ) regions. Admittedly, for certain three-subdomain problems, the overflow can be suppressed by splitting the model into even and odd parts [6, 8, 20-22], but the technique is merely available for the problems with additional symmetry.
More recently, the difficulties of overflow have been overcome in [23] by an innovative approach based on the FEM solution of the Sturm-Liouville equation. By this method, no numerical overflow arises in the solving process, therefore, many new models can be dealt with the TREE. According to [23], the Clenshaw-Curtis quadrature rule is appropriate for the evaluations of the integrals involving the numerical eigenfunctions, to obtain an efficient algorithm. The investigation of this work will be based on the approach.
In Section 2, the TREE solution is given for the metal tube adapter surrounding by a coaxial coil. The permeability of the metal is not restricted to μ0 in comparison with [23]. In Section 3, the numerical eigenfunctions are obtained by the FEM solution of the Sturm-Liouville equations and normalized, and the Clenshaw-Curtis quadrature rule is applied to the computation of the integrals involving the numerical eigenfunctions. In Section 4, the TREE results are compared with those from the FEM simulation.
2. Formulation
A metal tube adapter of conductivity σ and permeability (μr is supposed to be constant), is encircled by a coaxial induction coil excited by a time harmonic current of frequency ω and amplitude I (See Figure 1). The geometry of the coil and tube adapter is shown in Figure 2. Perfect electric boundary is imposed at z=0 and z=b to discretize the eigenvalues of this boundary value problem (BVP).
The solution domain is divided into 5 regions along the r-axis (See Figure 2). The vector potentials A1 to A5 satisfy the Laplace or Helmholtz equations in the corresponding regions:
where is the wavenumber of the metal.
Only the φ-component of the vector potential exists, due to the axisymmetry of the BVP, i.e. , and the vector Laplacian of equations (1) and (2) is reduced to
2.1. Vector Potential of the Source Coil
The formulation of source vector potential can be obtained by the source expansion of the Poisson equation [24, 25]. The vector potential of the coil can be written in the form (See Figure 3)
where the source vector V(r) is
with the elements
where , and Ln(x) is the modified Struve function of order n, and
Other matrices and vectors in (4a)-(4c) are
where In(x) and Kn(x) are the modified Bessel functions of the first and second kinds of order n, respectively, and ,,, are coefficients to be determined. With the interface conditions of Br and Hz at r=r1 and r=r2, the coefficients can be found:
where
For the function χ(x) used for the subsequent analysis, it is advisable to adopt an alternative form for the practical evaluations, namely
Expression (9) is obtained by the Maclaurin and asymptotic expansions of Ln(x) [26], and high accuracy can be achieved by setting m0=23 and m1=10, respectively.
2.2. Impedance Change of the Coil Encircling the Metal Tube Adapter
The vector potentials in the 5 regions of Figure 2 are expansible by the separation of variables
where P1, P2 and P3 are the eigenvalue matrices of the Regions 2, 3 and 4, respectively,
and
are the axial eigenfunctions satisfying the relevant Sturm-Liouville equations:
and
with
and
Taking account of the interface conditions of Br and Hz at r=a1, r=a2, r=a3 and r=a4, the following equations for the coefficients , , , , and can be derived
where
In (13a)-(13h), the orthogonalities of the eigenfunctions
have been adopted, where I is the identity matrix, and
The orthonormalization relations of (18b)-(18d) will be expounded in Section III.
Matrix algebra of (13a)-(13h) yields the equation system
where
with
Solving equation (20) will give the coefficients C2, D2, C4 and D4, and other coefficients can be found by
The coefficient required for calculation of ΔZ is
Accordingly, the coil impedance variation is given by
where the current density J has been omitted (letting J=1) to simplify the expression.
3. Eigenfunctions and the Associated Integrals of the Multi-Subdomain Regions
The conventional TREE method is limited to the two-subdomain problems, apart from certain three-subdomain problems which can be split in the even and odd parts. In general, it is impossible to evade the numerical overflow of the symbolic eigenfunctions of Regions 2, 3 and 4. Accordingly, the approach of [23] will be applied to cope with F(z), G(z) and H(z). In accord with [18, 19], the eigenvalues of (11a) can be obtained by the solution of a generalized eigenvalue equation
where K is the stiffness matrix with the elements
and W is the damping matrix of the elements
where φm and φn are FEM functions consisting of the Lagrange polynomials defined on the reference interval (the shape functions).
Sparse matrix K will be generated from the FEM basis. Hence, equation (28) can be solved by the efficient algorithm such as Arnoldi iteration [27]. The solution provides both the eigenvalues p1,i and the eigenvectors Ui, which are the discrete eigenfunctions . Moreover, denoting
and by virtue of the vector normalization
the eigenfunction normalization
can be established automatically. Equations (32) and (33) can be validated by inspecting the diagonal entries of , and taking equation (30) into account. Consequently, the orthonormality of (18b)-(18d) can be established.
The requirement of the accurate and efficient algorithm leads to the choice of high order Lagrange polynomials for the FEM basis. Here, we choose the cubic Lagrange polynomials
The cubic interpolation of the eigenfunction is
where are successive 4 entries of , Ne(z) is obtained by (34) with the change of variable
where za and zb are the mesh nodes corresponding to the reference interval. The numerical overflow of is eliminated by this procedure. They are consequently well adapted for the subsequent integral computation. Furthermore, it appears to be very effective to evaluate directly the integrals (14)-(17) with the Clenshaw-Curtis quadrature rule, which is quoted here for completeness [28-30]
where the weights wk are given by
and the quadrature nodes are
with
It follows from equations (37)-(41) that the matrix elements of T1 can be computed by
where
The matrix elements of T2 are likewise given by
where
The same analysis is also applicable to the matrix elements of T3 and T4.
4. Numerical Validation
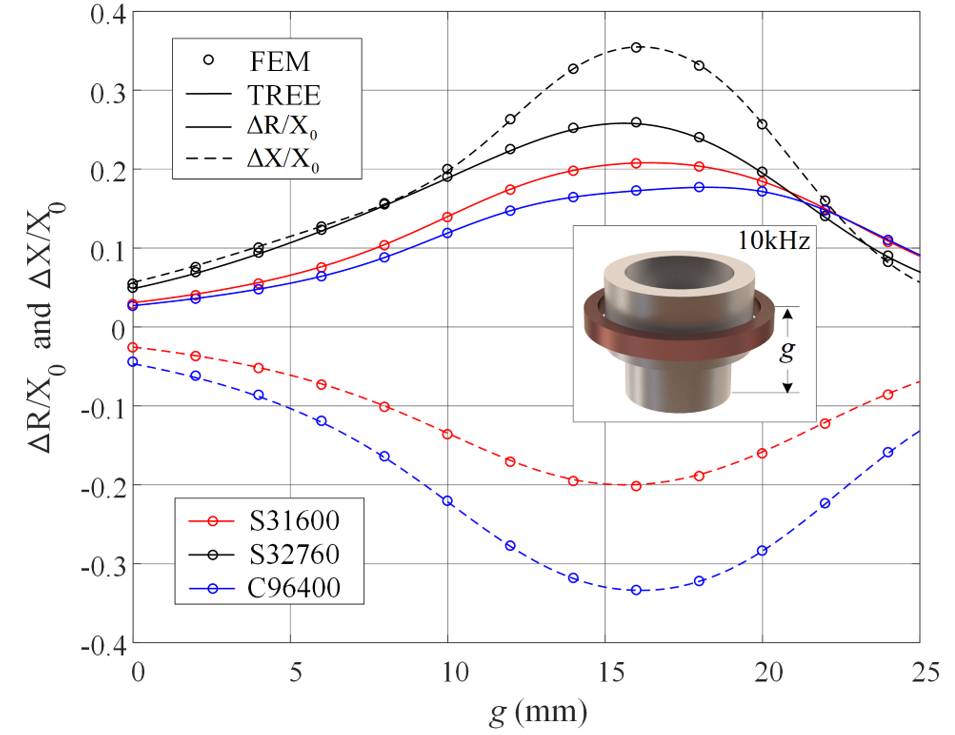
The proposed method will be verified with the parameters of the metal tube adapter and the induction coil given in Table 1, Table 2 and Table 3. The nonmagnetic alloy UNS (Unified Numbering System) C96400 (70-30 Copper-Nickel), and the magnetic stainless steels S31600 (austenitic) and S32760 (super duplex) [31] are used for the numerical validation. The coil impedance variations are calculated and plotted for these metal materials, with different coil positions. The TREE results are compared with those from the FEM simulation of Comsol Multiphysics®, shown in Figure 4, where the theoretical and FEM data are denoted by solid lines and circles, respectively. The reactance of the isolated induction coil is X0=ωL0, with L0=4.104132mH, which can be found by the method such as in [32, 33].
Further calculations are carried out for the coil impedance variation with respect to the frequencies. For the alloys of lower μr (C96400 and S31600), the calculation frequency ranges from 1kHz to 100kHz, for higher μr (S32760) the frequency interval [100Hz, 10kHz] is chosen. The results are shown in Figure 5 and Figure 6, where the TREE data are plotted by solid lines, in connection with the circles representing the data of FEM simulation. Other parameters are referred to the Table 2 and 3.
Very good agreement is obtained between the TREE and FEM results in the numerical comparisons. The calculations were implemented on a personal computer of a 4.2 GHz processor (Intel® Core i7-7700K) and 16 GB RAM. Additional algorithm details are shown in Table 4, where the frequencies, summation terms (matrix size), mesh elements and quadrature nodes used in the computation are listed. The execution time of the eigenvalue and eigenfunction computation, and the total execution time of TREE evaluation are also provided. No more than 1.5 seconds (including the time consumed by the calculation of eigenvalues and eigenfunctions) are consumed for a TREE evaluation. The satisfactory algorithm efficiency is in evidence.
5. Conclusions
The interaction of an eddy-current coil with a metal tube adapter has been investigated by the TREE method. The numerical overflow for symbolic eigenfunctions of air-metal multi-subdomain regions has been removed by the normalization of the eigenvectors, and satisfactory computational speed is achieved by Clenshaw-Curtis quadrature rule applied to the integrals associated with the numerical eigenfunctions. The calculation accuracy has been verified by the numerical comparisons, and the efficiency of our approach has also been confirmed. Considerable potential has been shown for the developing of new analytical models with the aid of the proposed approach.
Author Contributions
Conceptualization, Y. L. and X.Y.; methodology, Y.L.; software, Y.L. and X.Y.; data curation, X.Y.; writing—original draft preparation, Y.L.; writing—review and editing, Y.L. and X.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding
Institutional Review Board Statement
Not applicable.
Data Availability Statement
Data sharing not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Dodd, C. V.; Deeds, W. E. Analytical solutions to eddy current probe-coil problems. J. Appl. Phys. 1968, 39, 2829–2838. [Google Scholar] [CrossRef]
- Hannakam, L.; Tepe, R. Feldschwächung durch leitende Rechteckzylinder im Luftspalt. Archiv für Elektrotechnik. 1979, 61, 137–144. [Google Scholar] [CrossRef]
- Theodoulidis, T.; Kriezis, E. Eddy Current Canonical Problems (With Applications to Nondestructive Evaluation). Forsyth, GA: Tech Science Press, 2006.
- Theodoulidis, T. Model of ferrite-cored probes for eddy current nondestructive evaluation. J. Appl. Phys. 2003, 93, 3071–3078. [Google Scholar] [CrossRef]
- Theodoulidis, T.; Bowler, J. Eddy current coil interaction with a right-angled conductive wedge. Proc. R. Soc. A. 2005, 461, 3123–3139. [Google Scholar] [CrossRef]
- Bowler, J.; Theodoulidis, T. Eddy currents induced in a conducting rod of finite length by a coaxial encircling coil. J. Phys. D: Appl. Phys. 2005, 38, 2861–2868. [Google Scholar] [CrossRef]
- Theodoulidis, T.; Kriezis, E. Series expansions in eddy current nondestructive evaluation models. J. Mater. Process. Technol. 2005, 161, 343–347. [Google Scholar] [CrossRef]
- Theodoulidis, T.; Bowler, J. Eddy-current interaction of a long coil with a slot in a conductive plate. IEEE Trans. Magn. 2005, 41, 1238–1247. [Google Scholar] [CrossRef]
- Bowler, J.; Theodoulidis, T. Coil impedance variation due to induced current at the edge of a conductive plate. J. Phys. D: Appl. Phys. 2006, 39, 2862–2868. [Google Scholar] [CrossRef]
- Hannakam, L.; Kost, A. Leitender Rechteckkeil im Felde einer Doppelleitung. Archiv für Elektrotechnik. 1982, 65, 363–368. [Google Scholar] [CrossRef]
- Hannakam, L.; Orglmeister, R. Induzierte Wirbelstrombelag an ausgeprägten Massivpolen hoher Permeabilität bei Wanderfelderregung. Archiv für Elektrotechnik. 1984, 67, 49–55. [Google Scholar] [CrossRef]
- Filtz, M.; Nethe, A. Bemerkung zur Lösung des dreidimensionalen Wirbelstromproblems in Kreiszylindern endlicher Länge. Archiv für Elektrotechnik. 1993, 76, 195–200. [Google Scholar] [CrossRef]
- Filtz, M.; Nethe, A. Anregung dreidimensionaler Wirbelströme in massiven Kreizylindern endlicher Länge durch ein homogenes magnetisches Wechselfeld beliebiger Ausrichtung. Archiv für Elektrotechnik. 1990, 73, 227–237. [Google Scholar] [CrossRef]
- Theodoulidis, T.; Bowler, J. Interaction of an eddy-current coil with a right-angled conductive wedge. IEEE Trans. Magn. 2010, 46, 1034–1042. [Google Scholar] [CrossRef]
- Delves, L.; Lyness, J. A numerical method for locating the zeros of an analytic function. Math. Comput. 1967, 21, 543–560. [Google Scholar] [CrossRef]
- Tytko, G.; Dawidowski, L. Locating complex eigenvalues for analytical eddy-current models used to detect flaws. COMPEL. 2019, 36, 1800–1809. [Google Scholar] [CrossRef]
- Vasic, D.; Ambrus, D.; Bilas, V. Computation of the eigenvalues for bounded domain. IEEE Trans. Magn. 2016, 52, 7004310. [Google Scholar] [CrossRef]
- Yang, X.; Luo, Y.; Kyrgiazoglou, A.; Tytko, G.; Theodoulidis, T. An analytical model of an eddy-current coil near the edge of a conductive plate. IET Electr. Power Appl. 2022, 16, 1017–1029. [Google Scholar] [CrossRef]
- Theodoulidis, T.; Skarlatos, A.; Tytko, G. Computation of eigenvalues and eigenfunctions in the solution of eddy current problems. Sensors 2023, 23, 3055. [Google Scholar] [CrossRef]
- Stahlmann, H. D. Der Differentialtransformator als induktiver Stellungsmelder. Archiv für Elektrotechnik. 1983, 66, 277–281. [Google Scholar] [CrossRef]
- Sun, H.; Bowler, J.; Theodoulidis, T. Eddy currents induced in a finite length layered rod by a coaxial coil. IEEE Trans. Magn. 2005, 41, 2455–2461. [Google Scholar] [CrossRef]
- Skarlatos, A.; Theodoulidis, T. Calculation of the eddy-current flow around a cylindrical through-hole in a finite-thickness plate. IEEE Trans. Magn. 2015, 15, 6201507. [Google Scholar] [CrossRef]
- Luo, Y.; Yang, X. Impedance variation of an induction coil above a metal disk with a borehole and an annular slot. IEEE Sens. J. in preparation.
- Luo, Y. Field and inductance calculations for coaxial circular coils with magnetic cores of finite length and constant permeability. IET Electr. Power Appl. 2017, 11, 1254–1264. [Google Scholar] [CrossRef]
- Courant, R.; Hilbert, D. Methoden der Mathematischen Physik I. New York: Springer-Verlag, 1968.
- Abramowitz, M.; Stegun, A. Handbook of Mathematical Functions. New York: Dover, 1972.
- Arnoldi, W. E. The principle of minimized iterations in the solution of the matrix eigenvalue problem, Q. Appl. Math. 1951, 9, 17–29. [Google Scholar] [CrossRef]
- Olver, F.; Lozier, D.; Boisvert, R.; Clark, C. NIST Handbook of Mathematical Functions. New York: Cambridge University Press, 2010.
- Clenshaw, C.; Curtis, A. A method for numerical integration on a automatic computer. Numer. Math. (Heidelb.) 1960, 2, 197–205. [Google Scholar] [CrossRef]
- Hildebrand, F. B. Introduction to Numerical Analysis. New York: Dover Publications,1987.
- Boniardi, M.; Casaroli, A. Rostfreie Edelstähle. [Online]. Available: http://www.fa-fe.com/files/pdf/libri_articoli/de/1-Rostfreie_Edelstahle.pdf.
- Luo, Y.; Chen, B. Improvement of self-inductance calculations for circular coils of rectangular cross section. IEEE Trans. Magn. 2013, 49, 1249–1255. [Google Scholar] [CrossRef]
- Luo, Y.; Wang, X.; Zhou, X. Inductance calculations for circular coils with rectangular cross section and parallel axes using inverse Mellin transform and generalized hypergeometric functions. IEEE Trans. Power Electron. 2017, 32, 1367–1374. [Google Scholar] [CrossRef]
Figure 1.
A metal tube adapter encircled by a coaxial coil.

Figure 2.
Side view of a metal tube adapter encircled by a coaxial coil.
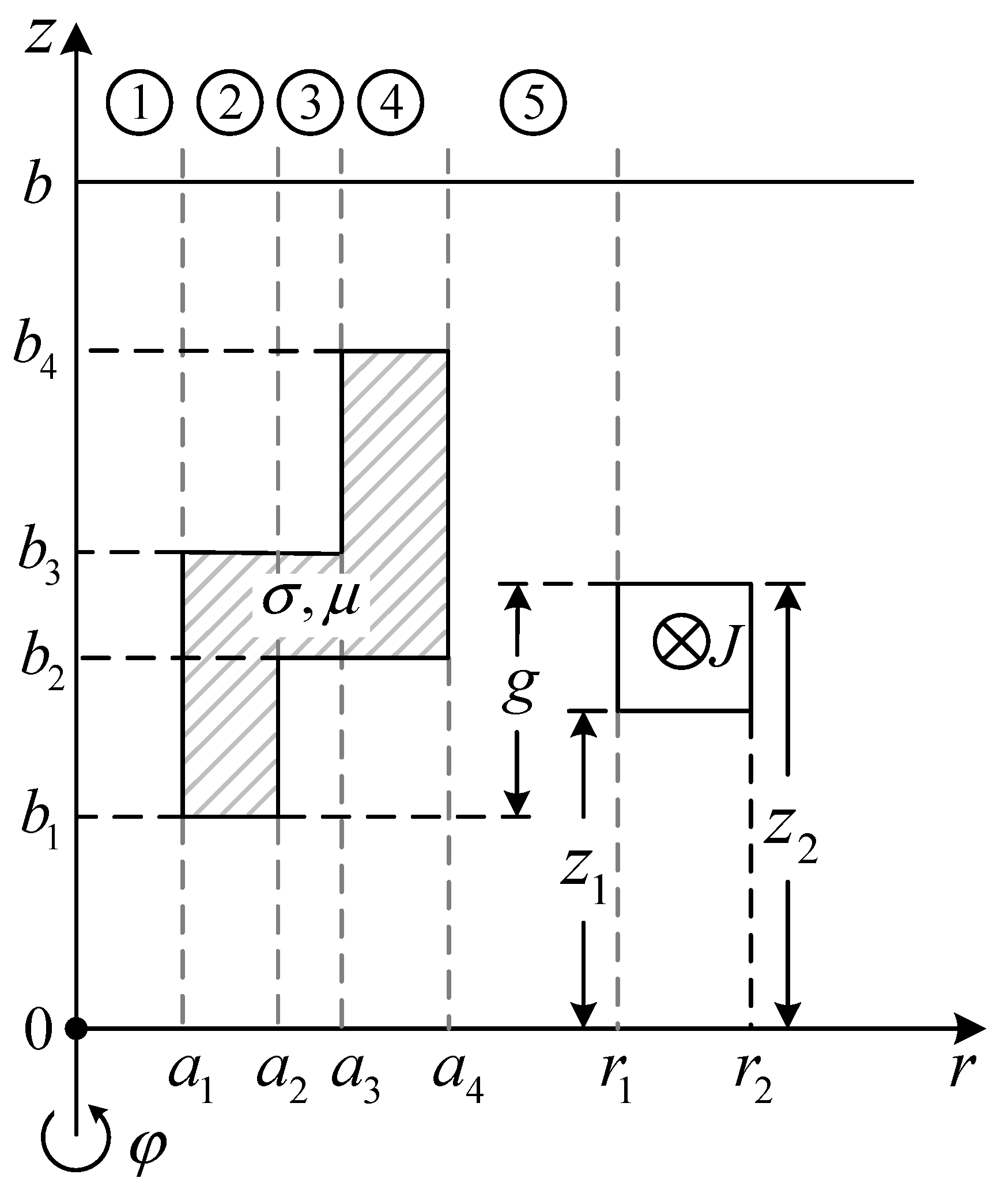
Figure 3.
Side view of an isolated coil with truncation boundary.
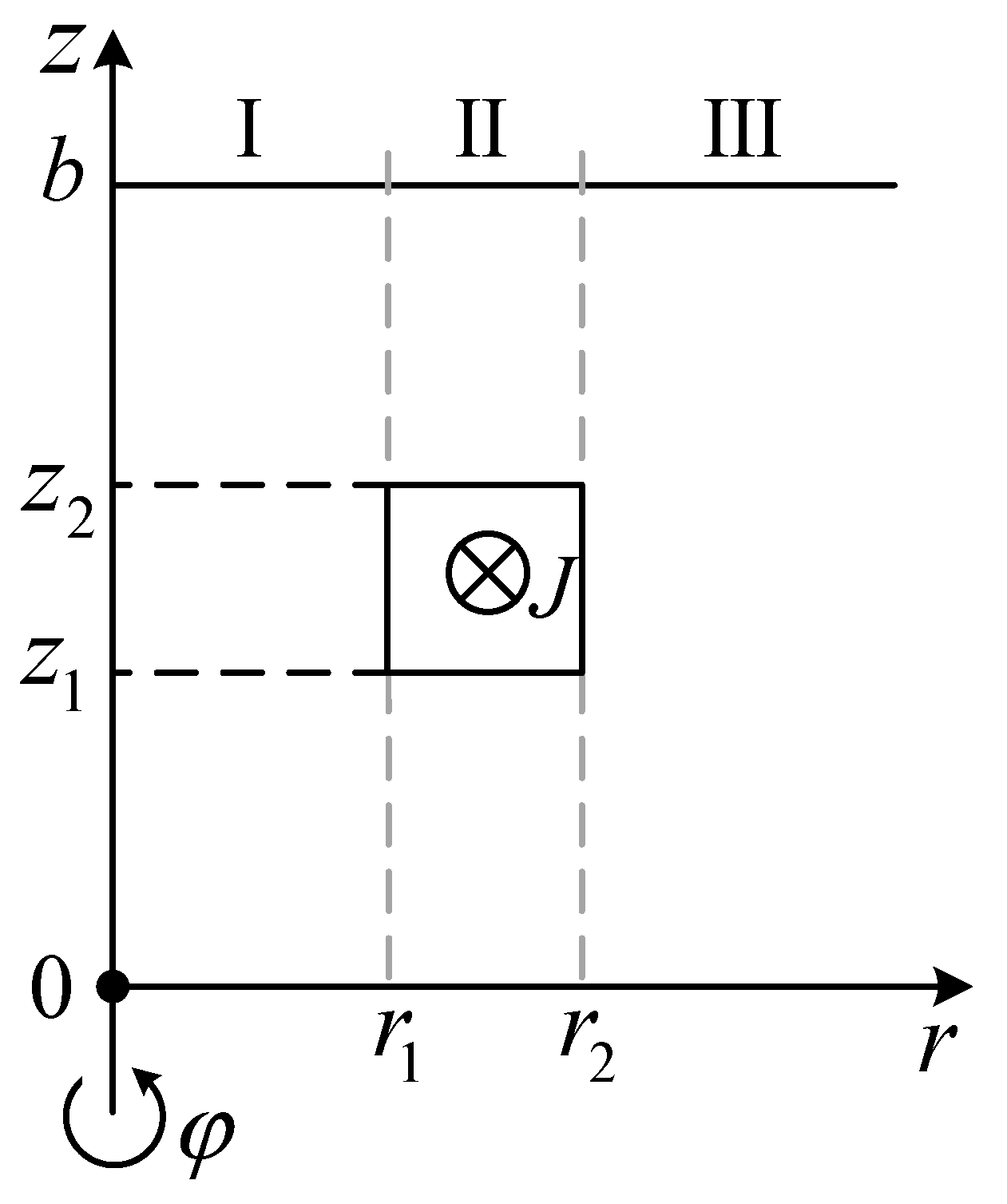
Figure 4.
Normalized impedance variations with the abscissa representing the parameter g. (a) The resistance variation. (b) The reactance variation.
Figure 4.
Normalized impedance variations with the abscissa representing the parameter g. (a) The resistance variation. (b) The reactance variation.
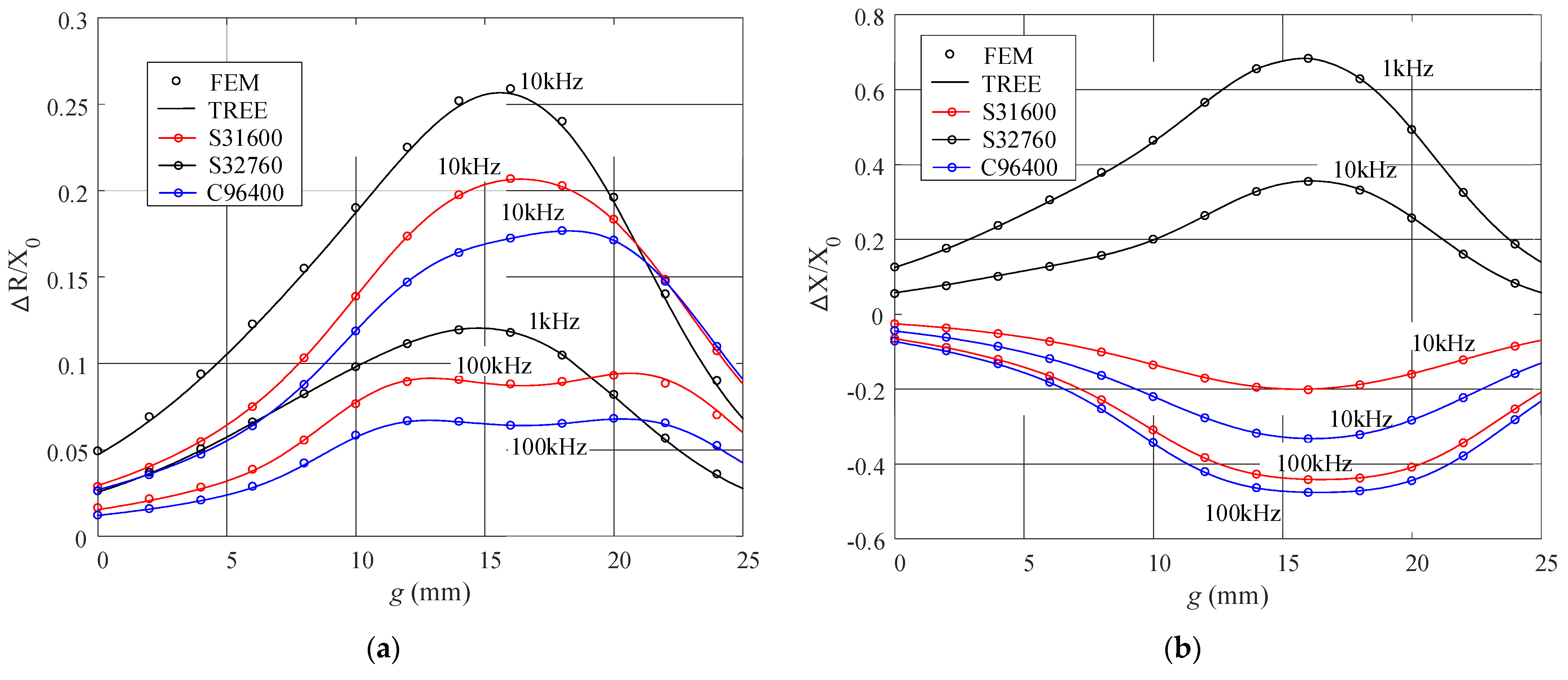
Figure 5.
Normalized impedance variations with the abscissa representing the frequency. The alloys are C96400 and S31600. (a) The resistance variation. (b) The reactance variation.
Figure 5.
Normalized impedance variations with the abscissa representing the frequency. The alloys are C96400 and S31600. (a) The resistance variation. (b) The reactance variation.

Figure 6.
Normalized impedance variations with the abscissa representing the frequency. The alloy is S32760. (a) The resistance variation. (b) The reactance variation.
Figure 6.
Normalized impedance variations with the abscissa representing the frequency. The alloy is S32760. (a) The resistance variation. (b) The reactance variation.
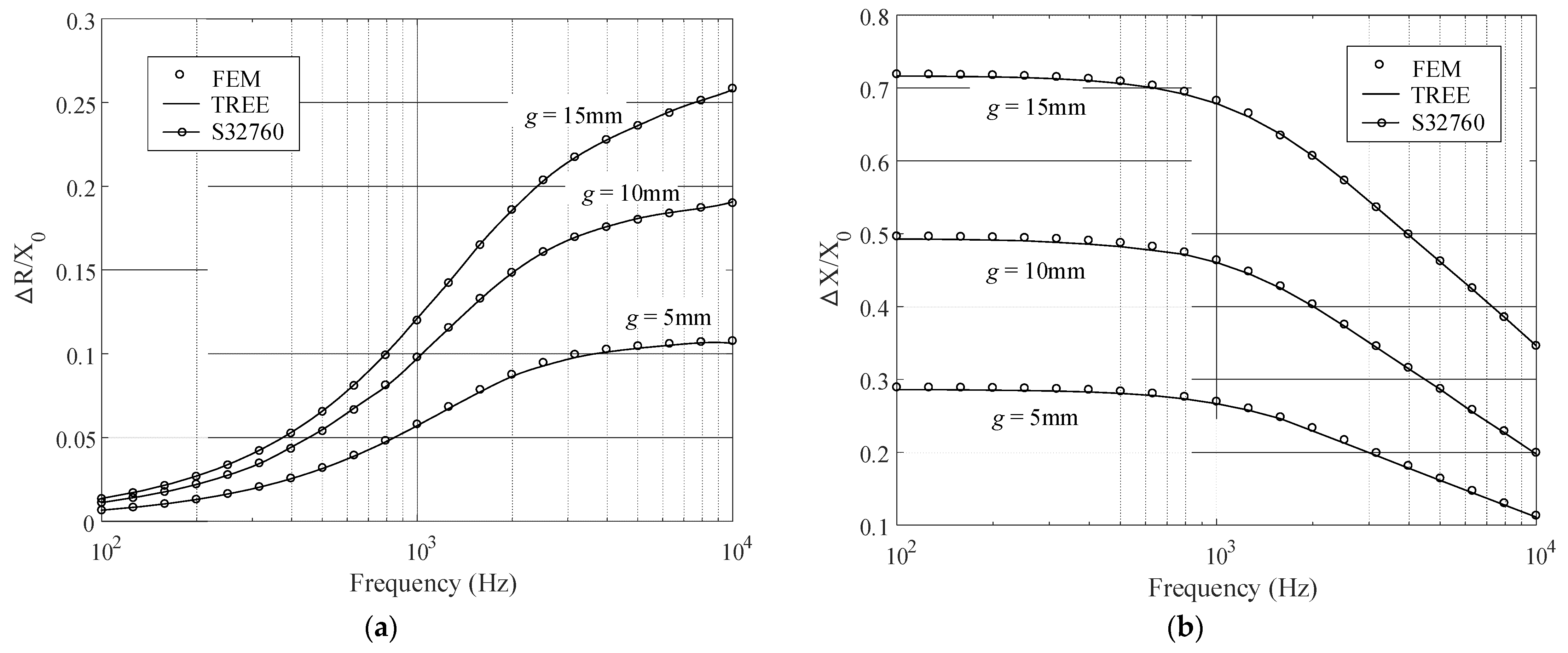
Table 1.
Metals used for the tube adapter.
| Metal(UNS) | Conductivity σ (MS/m) | Relative Permeability μr |
|---|---|---|
| C96400 | 2.9 | 1 |
| S31600 | 1.33 | 1.02 |
| S32760 | 1.25 | 29 |
Table 2.
Geometry of the metal tube adapter.
| Parameter | Parameter | ||
|---|---|---|---|
| a1(mm) | 5 | b1(mm) | 40 |
| a2(mm) | 8 | b2(mm) | 48 |
| a3(mm) | 11 | b3(mm) | 51 |
| a4(mm) | 14 | b4(mm) | 59 |
| b(mm) | 100 |
Table 3.
Parameters of the induction coil.
| Parameter | |
|---|---|
| Inner radius r1(mm) | 5 |
| Outer radius r2(mm) | 8 |
| Axial length z2-z1(mm) | 11 |
| Number of turns | 14 |
Table 4.
Computation configuration and execution time of TREE method.
| Metal (UNS) |
Frequency | Summation terms | Quadrature nodes | Mesh elements |
Execution time of eigenvalue and eigenfunction computation | Total execution time |
|---|---|---|---|---|---|---|
| S31600 | 10kHz | 30 | 80 | 510 | 0.19s | 0.55s |
| 100kHz | 40 | 80 | 510 | 0.26s | 0.73s | |
| S32760 | 1kHz | 55 | 80 | 510 | 0.36s | 1.00s |
| 10kHz | 70 | 90 | 510 | 0.54s | 1.30s | |
| C96400 | 10kHz | 30 | 80 | 510 | 0.19s | 0.56s |
| 100kHz | 50 | 80 | 510 | 0.34s | 0.90s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated





