Prerpints.org logo
Preprint
Article

A Fractional (q, q′) Non-extensive Information Dimension of Complex Networks

Altmetrics

Downloads

79

Views

25

Comments

0

A peer-reviewed article of this preprint also exists.

supplementary.docx (144.63KB )

Submitted:

08 September 2023

Posted:

11 September 2023

You are already at the latest version

Alerts
Abstract
This article introduces a new fractional approach to the concept of information dimension of complex networks, based on a (q,q′)-entropy proposed in the literature. The q parameter measures how far is the number of subsystems (for a given size ε) from the mean number of overall sizes. The q′ (interaction index) measures when the interactions between subsystems are greater (q′>1), lesser (q′<1) or equal to the interactions into these subsystems. The computations of the proposed information dimension are carried out on several real-world and synthetic complex networks. The results from the proposed information dimension are compared with those from the information dimension based on the Shannon entropy.
Keywords: 
Subject: Computer Science and Mathematics  -   Mathematics

1. Introduction

Entropy is a crucial measure of the uncertainty of the state in physical systems that would be needed to specify the state of disorder, randomness, or uncertainty in the micro-structure of the system. Due to this fact, researchers in many scientific fields have continually extended, interpreted, and applied the notion of entropy (introduced by Clausius [1] in thermodynamics).
Several generalizations of celebrated Shannon entropy, originally related to the processes information [2], have been introduced in the literature. For a deeper gather entropy measures, the reader is referred to [3,4,5,6,7,8].
Given a probability distribution P = { p 1 , p 2 , … , p N } under a probability space X = { x 1 , x 2 , … , x N } , under P (see [9]) is generated as:
I = lim t → − 1 d d t ∑ i = 1 N p i − t = − ∑ i = 1 N p i ln p i ,
where N is the total number of (microscopic) possibilities p i and ∑ i = 1 N p i = 1 .
Similarly, Tsallis entropy (also called q-entropy) [10,11,12] is generated by the same procedure but using Jackson’s q-derivative operator D q t f ( t ) = f ( q t ) − f ( t ) ( q − 1 ) t , t ≠ 0 , [13], see also [9,14,15] and it is given by
I T = lim t → − 1 D q t ∑ i = 1 N p i − t = − ∑ i = 1 N p i l n q p i ,
where q − logarithm is defined by
l n q ( p i ) = p i 1 − q − 1 1 − q ,
( p i > 0 , q ∈ R , q ≠ 1 , l n 1 p i = l n p i ).
Tsallis entropy is connected to the Shannon entropy through the limit
lim q → 1 I T = I ,
which being the reason it is considered one parameter extension of Shannon entropy.
Several entropy measures have been revealed following the same procedure above and using appropriate fractional order differentiation operators on the generative function ∑ i = 1 N p i − t concerning variable t and then letting t → − 1 , see for instance [16,17,18,19,20,21,22,23].
A new measure of information, called extropy, has been introduced by Lad, Sanfilippo and Agrò [24] as the dual version of Shannon entropy. In the literature, this measure of uncertainty has received considerable attention in the last years [25,26,27]. The entropy and the extropy of a binary distribution ( N = 2 ) are identical.
In recent years, complex networks and systems have been extensively studied since they are applied to describe a wide range of systems in many disciplines to solve practical problems [28].
In the study of the structure of complex networks has been considered the method of fractional order information dimension by combining the fractional order entropy and information dimension, see for instance [29,30] and the references given there.
This article proposes a fractional two-parameter non-extensive information dimension of complex networks based on fractional order entropy proposed in [31]. This new information dimension is computed on real-world and synthetic complex networks. The contents of the sections of the paper, besides this introduction, are described as follows. Section 2 introduces the reader to a fractional entropy measure and the information dimension of complex networks. Then, the new definitions of fractional information dimension are introduced in Section 3. Section 4 focuses on applying the new measure to several real complex networks. Finally, the findings of this study and the conclusion are given in Section 4.

2. Preliminaries

2.1. Fractional ( q , q ′ ) − entropy

Following the same produce to obtain Shannon and Tsallis entropies, a generalized nonextensive two-parameter entropy, named fractional ( q , q ′ ) − entropy, is developed in [31] and obtained by the action of a derivative operator already proposed by Chakrabarti and Jagannathan [32]:
I q , q ′ : = lim t → − 1 D q , q ′ t ∑ i = 1 N p i − t = ∑ i = 1 N p i q ′ − p i q q − q ′ ,
where D q , q ′ t of a function f is given by D q , q ′ t f ( t ) = f ( q t ) − f ( q ′ t ) ( q − q ′ ) t .
Following the general idea that extropy is the complementary dual version of entropy, we present the ( q , q ′ ) − extropy for a discrete random variable X as
J q , q ′ = ∑ i = 1 N ( 1 − p i ) q ′ − ( 1 − p i ) q q − q ′ .
An easy computation shows that Eq. (5) can be expressed in terms of Tsallis entropy
I q , q ′ = ( 1 − q ′ ) I T − ( 1 − q ) I T q − q ′ .
The I q , q ′ ≥ 0 , ∀ q , q ′ and I q , q ′ = W 1 − q − W 1 − q ′ q ′ − q for p i = 1 / W , ∀ i . Consider a system composed of two independent subsystems, A and B, with factorized probabilities p i , A and p i , B then
I q , q ′ = I q , q ′ A + I q , q ′ B + ( 1 − q ) I q , q ′ A I q , 1 B + ( 1 − q ′ ) I q , q ′ B I q , 1 A ,
where, I ( q , 1 ) entropy resembles Tsallis entropy Eq. (2) and I ( 1 , 1 ) the Shannon entropy Eq. (1). Thus, I ( q , q ′ ) is non-additive for q , q ′ ≠ 1 .

2.2. Information dimensions of complex networks

The information dimensions measuring the topological complexity of a given network are sketched briefly. Let us consider the Shannon entropy Eq. (1); a definition of the information dimension is introduced in [33] as follows
d I = − lim ε → 0 I ( ε ) ln ε = lim ε → 0 ∑ i = 1 N b p i ( ε ) ln p i ( ε ) ln ε ,
where p i ( ε ) = n i ( ε ) n , n i ( ε ) is the mass of the ith box of size ε , n is the number of nodes of complex networks, and N b is the minimum number of boxes to cover the network. The reader is referred to [34,35] for in-depth details on obtaining N b .
Applying Eq. 9, we can assert that
I ( ε ) ∼ − d I ln ε + β ,
for some constant β , where ε is diameter of the boxes to perform the covering of the network.

3. Fractional ( q , q ′ ) information dimension of complex

Now we proceed to the primary goal of this article, which is to introduce the fractional ( q , q ′ ) information dimension of complex network denoted by d q , q ′ as follows:
d q q ′ = − lim ε → 0 I q , q ′ ( ε ) ln ε = lim ε → 0 ∑ i = 1 N b p i q ′ ( ε ) − p i q ( ε ) q − q ′ ln ε ,
where p i ( ε ) = n i ( ε ) n , n i ( ε ) is the mass of the ith box of size ε , n is the number of nodes of the network, and N b is the minimum number of boxes to cover the network. The parameters q , q ′ depend on the minimal covering of the network; thus, the maximal entropy minimal covering principle was adopted as in previous research on complex network [29,30,36,37,38] to the computation for ε = [ 2 , Δ ] , where Δ means the diameter of the network.
For some constant β , the Eq. (12) is deduced from Eq. (11)
I ( ε ) ∼ − d q , q ′ ln ε + β ,

3.1. Computation of q , q ′

The computation of parameter q relies on the idea that considers the networks as a system that can be divided into several subsystems. This division is based on the formation of minimum boxes by the box-covering algorithm. Hence, the number of subsystems equals the number of boxes N b for a given size ε .
For a given box size ε , the value of q is determined as the average of q ε , denoted by q ¯ ε , where
q ε : = ( Δ − 1 ) N b ( ε ) ∑ ε = 2 Δ N b ( ε ) ,
Note that q ε = ( q 2 , q 3 , . . . , q Δ ) .
This approximation measures how far the number of subsystems (for a given size ε ) is from the mean number of overall sizes, which is the baseline.
Now, to quantify the interactions among the elements that conform the subsystems (nodes) and among these subsystems (boxes), the α and β were introduced in [30]:
α ε , i = 1 − | S i | i n d e g ( S i ) n ∑ i = 1 N b i n d e g ( S i ) ,
β ε , i = 1 − o u t d e g ( S i ) ε Δ ∑ i = 1 N b o u t d e g ( S i ) ,
where | S i | is the number of nodes in S i , n is the number of nodes of the network, i n d e g ( G i ) are the edges among the nodes that are in S i , o u t d e g ( S i ) are the edges among the sub-networks S i , ε is the diameter of the box to compute the sub-network S i and Δ is the diameter of the network.
Finally, q ′ is defined by
q ′ = β ¯ ε , i α ¯ ε , i
where β ¯ ε , i , α ¯ ε , i are the mean of β ε , i and α ε , i , respectively, since they are vectors ( a ε , 1 , a ε , 2 , … , a ε , N b ) . The Eq. (16) is the interaction index [30] that shows if β is equal to ( q ′ = 1 ), greater ( q ′ > 1 ) or lesser ( q ′ < 1 ) than α ; hence, it reflects which type of interactions is stronger: inner subsystems interaction ( α ), outer them ( β ) or if both are balanced.
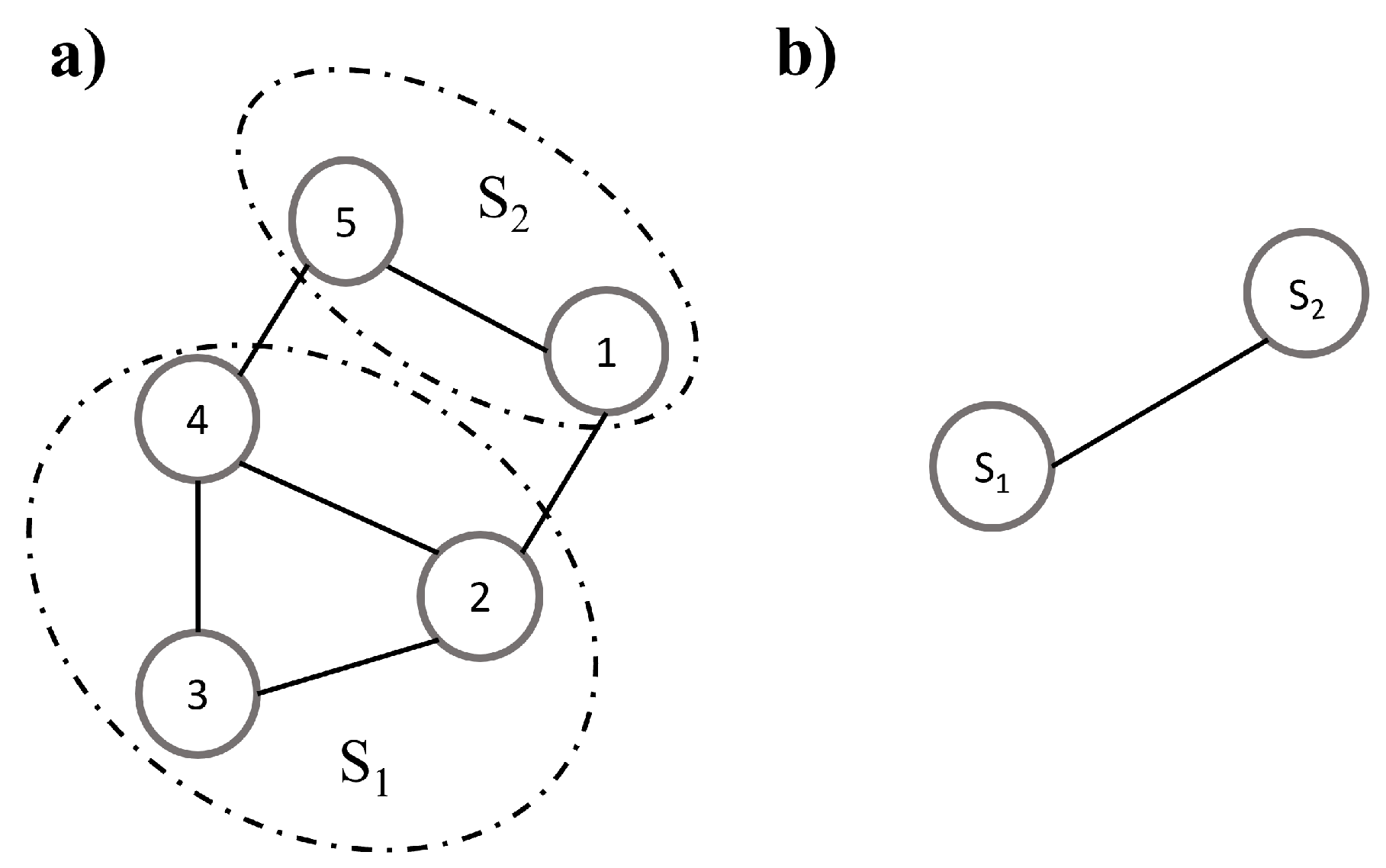
Figure 1 show an example α , β computations. Once a box covering is performed, using the approach in [35], for ε = 2 , see Figure 1a), the re-normalization agglutinates the nodes into the boxes in a super node (subsystem) S 1 , S 2 as shown in Figure 1b). Since Δ = 2 , in the example, q = q ¯ ε = q 2 = 1 . Furthermore, i n d e g ( S 1 ) = 3 , i n d e g ( S 2 ) = 1 and o u t d e g ( S 1 ) = 1 , o u t d e g ( S 2 ) = 1 which is the degree of the nodes of the re-normalized network in Figure 1b).
Since n = 5 , the result of Eq. (14) are α 2 , S 1 = 0.55 , α 2 , S 2 = 0.9 and β 2 , S 1 = 0.5 , β 2 , S 2 = 0.5 from Eq. (15); thus, q ′ = 0.689 . The networks included have a diameter greater than the example shown above, so the steps to estimate q ε and q ε ′ are repeated by each box size ε resulting in two vectors that are averaged to obtain q and q ′ .

4. Results

4.1. Real-world networks

The fractional ( q , q ′ ) information dimension Eq.(11) and the classical information dimension Eq.(9) were computed on 28 real-world networks that were gathered from [30,39], see Table 1 for number of nodes, edges, diameter and source. These networks cover several domains, such as biological, social, technological, and communications, so they are representative.
Next, the models of Eq.(10) and Eq.(12) –that corresponds to the classical information dimension and the fractional ( q , q ′ ) information model, respectively– were approximated using Nonlinear Regression [40] in MATLAB R2022a. The best model is selected by summed Bayesian information criterion with bonuses (SBICR)[41]. The SBICR penalize the complex models (that were estimated independently) and the size of the data sets employed to approximate the parameters; hence, the model with the largest SBICR score must be selected.
Table 2 shows the fit of information model Eq.(10) and fractional ( q , q ′ ) model Eq.(12) on the information and fractional ( q , q ′ ) information, respectively. The results of SBICR, d I , d q , q ′ , q, q ′ computations are also shown. The column S B I C R I and S B I C R q , q ′ show that the Eq.(12) is better than Eq.(10) for all networks except for PG and POW (in bold). Additionally, q > 1 means that the number of subsystems for a given ε is higher than the baseline (mean subsystems found for all ε ). On the other hand, for 12 networks, the interaction between subsystems ( q ′ > 1 )(in bold) is stronger and for 16 networks, the interaction between the elements of the subsystems named inner interactions ( q ′ < 1 ) are higher than those between subsystems (outer interactions).
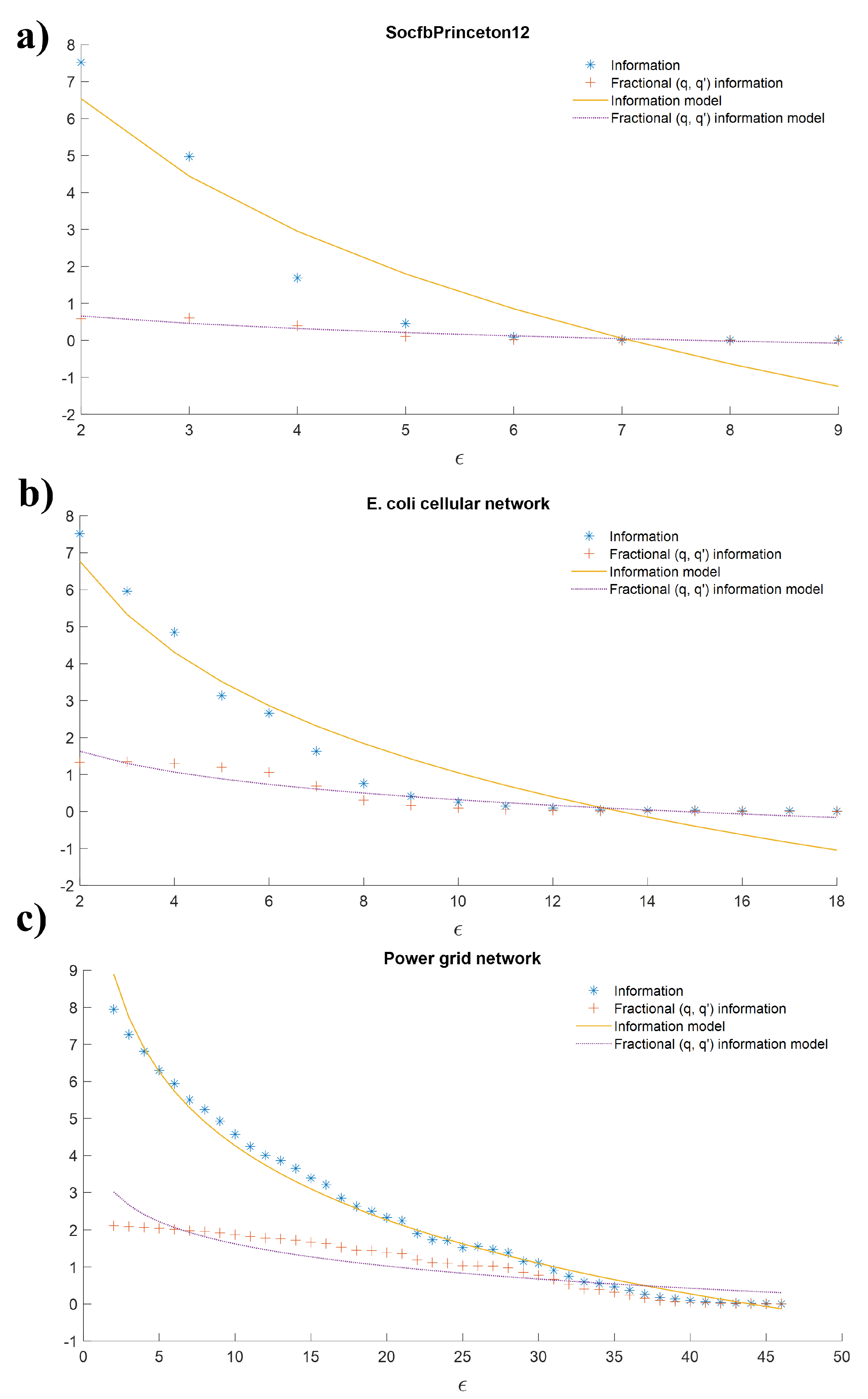
Figure 2 a) show the SocfbPrinceton12 network, were fractional ( q , q ′ ) model (dotted line) is closer to fractional ( q , q ′ ) information (+) than information model (solid line) to information(*). It is rather difficult to appreciate in Figure 2 b), so the SBICR is a valuable tool. The opposite occurs in Figure 2 c) where the information model is better than the fractional ( q , q ′ ) model since the value of S B I C R I is higher than the value S B I C R ( q , q ′ ) for Power grid network (PG), see Table 2.

4.2. Synthetic networks

The same produce was followed on networks generated by Barabasi-Albert (BA) [42], Song, Havlin and Makse (SHM) [43], and Watts and Strogatz (WS) models [44]. First, d I , d q , q ′ were computed and then the best models of Eq.(10) and Eq.(12) were chosen based on the SBICR. The BA networks were 225, 211 for SHM and 216 for WS. Table 3 summarise the nodes, edges, d I , d q , q ′ and the information model selected between Eq.(10) and Eq.(12). See the supplementary material for the details on the parameters of each model to generate the networks as well as the specific S B I C R I , S B I C R ( q , q ′ ) , d I , d q , q ′ , q and q ′ .
A remarkable finding on real and synthetic networks is that d q , q ′ < d I . The fractional ( q , q ′ ) model fitted better for all BA and WS networks and about 71% of the SHM. Table 4 summarises the parameter of the SHM model that produces 29 % ( 153 ) networks for which the information model fits better; see the supplementary material for the meaning of each parameter. The values of the SHM parameters are influenced by the assortativity ( M O D E = 1 ) and hub repulsion ( M O D E = 2 ), so the only conditions that intersect on M O D E = 1 and M O D E = 2 were G = 2 M = 3 I B = 0 B B = . 4 , G = 3 M = 2 I B = 0 B B = 1 , and G = 3 M = 2 I B = . 4 B B = . 8 .
Additionally, for BA, the average node degree ( a d ) equal to 1 produces networks with stronger outer interactions than inner one q ′ > 1 . It occurs no matter what the number of initial nodes ( n 0 ) and total nodes(n) values were chosen; see Table S1 of the supplementary material. On the other hand, for SHM three networks: SHM_G-3 M-4 IB-0.40 BB-0.00 MODE-2, SHM_G-4 M-3 IB-0.00 BB-0.40 MODE-2, SHM_G-4 M-3 IB-0.40 BB-0.00 MODE-2 and for WS a network: WS-2000-2-0.400000 obtained q ′ > 1 , see Tables S2 and S3. These results suggest that the fractional ( q , q ′ ) information dimension captures the complexity of the network topology since the SHM model tunes the links between nodes into the boxes ( I B ) and the connections between boxes through B B . This capability is not in BA and WS models.

5. Conclusion

This article introduced complex networks’ fractional ( q , q ′ ) − information dimension. The rationale of the definition is that the network can be divided into several subsystems. Hence, q measures how far the number of subsystems (for a given size ε ) is from the mean number of overall sizes, which is the baseline. On the other hand, q ′ (interaction index) measures if the interactions between subsystems are greater( q ′ > 1 ), lesser ( q ′ < 1 ) or equal to the interactions into these subsystems ( q ′ = 1 ).
Starting from the experimental results on real networks and synthetic networks, a glance at the interaction of the subsystems shows that clear interconnection patterns emerge, especially in the networks generated by the SHM model, where its parameters play a crucial role in obtaining networks for which the information model best fit. The initial nodes parameter of BA model generated networks where the outer interactions are stronger than inner ones q ′ > 1 , no matter what value takes the remaining parameters. Finally, our experiments reveal that d q , q ′ < d I in both types of networks.
We have enough evidence to state that the fractional ( q , q ′ ) − information dimension of complex networks based on ( q , q ′ ) − extropy seems to be a complementary dual statistical index of the fractional ( q , q ′ ) − information dimension. It is an exciting area for future research to prove to what extent the new formulations will be helpful.

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org, Table S1: The SBICR of information model Eq.(8) and the fractional ( q , q ’ ) information model Eq.(10), d I , d q , q ′ and the q, q ′ values of BA networks; Table S2: The SBICR of information model Eq.(8) and the fractional ( q , q ′ ) information model Eq.(10), d I , d q , q ′ and the q, q ′ values of SHM networks; Table S3: The SBICR of information model Eq.(8) and the fractional ( q , q ′ ) information model Eq.(10), d I , d q , q ′ and the q, q ′ values of WS networks.

Author Contributions

Conceptualization, J.B.-R. and A.R.-A.; formal analysis, A.R.-A. and J.B.-R.; investigation, J.-S.D.-l.-C.-G.; methodology, A.R.-A. and J.-S.D.-l.-C.-G.; supervision, J.B.-R.; writing—original draft, A.R.-A. and J.B.-R.; writing—review & editing, A.R.-A. and J.B.-R. All authors have read and agreed to the published version of the manuscript

Funding

This research was funded by Instituto Politécnico Nacional grant number 20230066.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

The following abbreviations are used in this manuscript:
SBICR Bayesian Information Criterion with Bonuses
BA Barabasi-Albert
SHM Song, Havlin and Makse
WS Watts and Strogatz

References

  1. Clausius, R. The Mechanical Theory of Heat: With Its Applications to the Steam-Engine and to the Physical Properties of Bodies; Creative Media Partners: Sacramento, CA, USA, 1867. [Google Scholar]
  2. Shannon, C.E. A mathematical theory of communication. Bell system technical journal 1948, 27, 379–423. [Google Scholar] [CrossRef]
  3. Beck, C. Generalized information and entropy measures in physics. Contemporary Physics 2009, 50, 495–510. [Google Scholar] [CrossRef]
  4. Esteban, M.D. A general class of entropy statistics. Applications of Mathematics 1997, 42, 161–169. [Google Scholar] [CrossRef]
  5. Esteban, M.D.; Morales, D. A summary on entropy statistics. Kybernetika 1995, 31, 337–346. [Google Scholar]
  6. Ribeiro, M.; Henriques, T.; Castro, L.; Souto, A.; Antunes, L.; Costa-Santos, C.; Teixeira, A. The entropy universe. Entropy 2021, 23, Paper No. 222, 35. [Google Scholar] [CrossRef]
  7. Lopes, A.M.; Tenreiro Machado, J.A. A review of fractional order entropies. Entropy 2020, 22, Paper No. 1374, 17. [Google Scholar] [CrossRef]
  8. Amigó, J.M.; Balogh, S.G.; Hernández, S. A brief review of generalized entropies. Entropy 2018, 20, Paper No. 813, 21. [Google Scholar] [CrossRef]
  9. Abe, S. A note on the q-deformation-theoretic aspect of the generalized entropies in nonextensive physics. Physics Letters A 1997, 224, 326–330. [Google Scholar] [CrossRef]
  10. Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. Journal of Statistical Physics 1988, 52, 479–487. [Google Scholar] [CrossRef]
  11. Tsallis, C.; Tirnakli, U. Non-additive entropy and nonextensive statistical mechanics – Some central concepts and recent applications. Journal of Physics: Conference Series 2010, 201, 012001. [Google Scholar]
  12. Tsallis, C., Introduction to non-extensive Statistical Mechanics: Approaching a Complex World; Springer, 2009; chapter Thermodynamical and Nonthermodynamical Applications, pp. 221–301.
  13. Jackson, D.O.; Fukuda, T.; Dunn, O.; Majors, E. On q-definite integrals. Quart. J. Pure Appl. Math, 1910, pp. 193–203.
  14. Johal, R.S. q calculus and entropy in nonextensive statistical physics. Physical Review E 1998, 58, 4147. [Google Scholar] [CrossRef]
  15. Lavagno, A.; Swamy, P.N. q-Deformed structures and nonextensive-statistics: a comparative study. Physica A: Statistical Mechanics and its Applications 2002, 305, 310–315. [Google Scholar] [CrossRef]
  16. Shafee, F. Lambert function and a new non-extensive form of entropy. IMA journal of applied mathematics 2007, 72, 785–800. [Google Scholar] [CrossRef]
  17. Ubriaco, M.R. Entropies based on fractional calculus. Physics Letters A 2009, 373, 2516–2519. [Google Scholar] [CrossRef]
  18. Ubriaco, M.R. A simple mathematical model for anomalous diffusion via Fisher’s information theory. Physics Letters A 2009, 373, 4017–4021. [Google Scholar] [CrossRef]
  19. Karci, A. Fractional order entropy: New perspectives. Optik 2016, 127, 9172–9177. [Google Scholar] [CrossRef]
  20. Karci, A. Notes on the published article “Fractional order entropy: New perspectives” by Ali KARCI, Optik-International Journal for Light and Electron Optics, Volume 127, Issue 20, October 2016, Pages 9172–9177. Optik 2018, 171, 107–108. [Google Scholar] [CrossRef]
  21. Radhakrishnan, C.; Chinnarasu, R.; Jambulingam, S. A Fractional Entropy in Fractal Phase Space: Properties and Characterization. International Journal of Statistical Mechanics 2014, 2014. [Google Scholar] [CrossRef]
  22. Ferreira, R.A.C.; Tenreiro Machado, J. An Entropy Formulation Based on the Generalized Liouville Fractional Derivative. Entropy 2019, 21. [Google Scholar] [CrossRef]
  23. Ferreira, R.A.C. An entropy based on a fractional difference operator. Journal of Difference Equations and Applications 2021, 27, 218–222. [Google Scholar] [CrossRef]
  24. Lad, F.; Sanfilippo, G.; Agrò, G. Extropy: complementary dual of entropy. Statist. Sci. 2015, 30, 40–58. [Google Scholar] [CrossRef]
  25. Xue, Y.; Deng, Y. Tsallis eXtropy. Comm. Statist. Theory Methods 2023, 52, 751–762. [Google Scholar] [CrossRef]
  26. Liu, J.; Xiao, F. Renyi extropy. Comm. Statist. Theory Methods 2023, 52, 5836–5847. [Google Scholar] [CrossRef]
  27. Buono, F.; Longobardi, M. A dual measure of uncertainty: the Deng extropy. Entropy 2020, 22, Paper No. 582, 10. [Google Scholar] [CrossRef] [PubMed]
  28. Newman, M.E.J. The structure and function of complex networks. SIAM Rev. 2003, 45, 167–256. [Google Scholar] [CrossRef]
  29. Ramirez-Arellano, A.; Sigarreta-Almira, J.M.; Bory-Reyes, J. Fractional information dimensions of complex networks. Chaos: An Interdisciplinary Journal of Nonlinear Science 2020, 30, 093125. [Google Scholar] [CrossRef]
  30. Ramirez-Arellano, A.; Hernández-Simón, L.M.; Bory-Reyes, J. Two-parameter fractional Tsallis information dimensions of complex networks. Chaos, Solitons & Fractals 2021, 150, 111113. [Google Scholar]
  31. Borges, E.P.; Roditi, I. A family of nonextensive entropies. Physics Letters A 1998, 246, 399–402. [Google Scholar] [CrossRef]
  32. Chakrabarti, R.; Jagannathan, R. A (p, q)-oscillator realization of two-parameter quantum algebras. Journal of Physics A: Mathematical and General 1991, 24, L711. [Google Scholar] [CrossRef]
  33. Wei, D.; Wei, B.; Hu, Y.; Zhang, H.; Deng, Y. A new information dimension of complex networks. Physics Letters A 2014, 378, 1091–1094. [Google Scholar] [CrossRef]
  34. Song, C.; Havlin, S.; Makse, H.A. Self-similarity of complex networks. Nature 2005, 433, 392. [Google Scholar] [CrossRef] [PubMed]
  35. Song, C.; Gallos, L.K.; Havlin, S.; Makse, H.A. How to calculate the fractal dimension of a complex network: the box covering algorithm. Journal of Statistical Mechanics: Theory and Experiment 2007, 2007, P03006. [Google Scholar] [CrossRef]
  36. Rosenberg, E. Maximal entropy coverings and the information dimension of a complex network. Physics Letters A 2017, 381, 574–580. [Google Scholar] [CrossRef]
  37. Ramirez-Arellano, A.; Hernández-Simón, L.M.; Bory-Reyes, J. A box-covering Tsallis information dimension and non-extensive property of complex networks. Chaos, Solitons & Fractals 2020, 132, 109590. [Google Scholar]
  38. Ramirez-Arellano, A.; Bermúdez-Gómez, S.; Hernández-Simón, L.M.; Bory-Reyes, J. d-summable fractal dimensions of complex networks. Chaos, Solitons & Fractals 2019, 119, 210–214. [Google Scholar]
  39. Rossi, R.A.; Ahmed, N.K. The Network Data Repository with Interactive Graph Analytics and Visualization. AAAI, 2015.
  40. Seber, G.; Wild, C. Nonlinear Regression; Wiley Series in Probability and Statistics, Wiley, 2003.
  41. Dudley, R.M.; Haughton, D. Information criteria for multiple data sets and restricted parameters. Statistica Sinica 1997, 265–284. [Google Scholar]
  42. Barabási, A.L.; Albert, R. Emergence of scaling in random networks. Science 1999, 286, 509–512. [Google Scholar] [CrossRef]
  43. Song, C.; Havlin, S.; Makse, H.A. Origins of fractality in the growth of complex networks. Nature physics 2006, 2, 275. [Google Scholar] [CrossRef]
  44. Watts, D.J.; Strogatz, S.H. Collective dynamics of ‘small-world’ networks. Nature 1998, 393, 440. [Google Scholar] [CrossRef]
Preprints 84689 g001
Figure 1. The box covering of a) network and b) network re-normalization for ε = 2 .
Figure 1. The box covering of a) network and b) network re-normalization for ε = 2 .
Preprints 84689 g001
Preprints 84689 g002
Figure 2. The box covering of a) network and b) network renormalization for ε = 2 .
Figure 2. The box covering of a) network and b) network renormalization for ε = 2 .
Preprints 84689 g002
Table 1. Diameter, number of nodes, source, d I and d q , q ′ of real-world networks.
Table 1. Diameter, number of nodes, source, d I and d q , q ′ of real-world networks.
Network Full name Source Diameter Nodes Edges
ACF American college football [30] 4 115 613
BCEPG Bio-CE-PG [30] 8 1692 47309
BGP Bio-grid-plant [30] 26 1272 2726
BGW Bio-grid-worm [30] 12 16259 762774
CEN C. elegant neural network [30] 5 297 2148
CNC Ca-netscience [30] 17 379 914
COL SocfbColgate88 [39] 6 3482 155044
DRO Drosophilamedulla1 [39] 6 1770 33635
DS Dolphins social network [30] 8 62 159
ECC E. coli cellular network [30] 18 2859 6890
EM Email [30] 8 1133 5451
IOF Infopenflights [39] 14 2905 30442
JM Jazz-musician [30] 6 198 2742
JUN Jung2015 [39] 16 2989 31548
LAS Lada Adamic’s network [30] 8 350 3492
LDU Labanderiadunne [39] 6 700 6444
MAR Marvel [39] 11 19365 96616
MIT SocfbMIT [39] 8 6402 251230
PAIR Pairdoc [39] 14 8914 25514
PG Power grid network [30] 46 4941 6594
PGP Techpgp [39] 24 10680 24340
POW Powerbcspwr10 [39] 49 5300 13571
PRI SocfbPrinceton12 [39] 9 6575 293307
TC Topology of communications [30] 7 174 557
USAA USA airport network [30] 7 500 2980
WHO TechWHOIS [39] 8 7476 56943
YEAST Protein interaction [30] 11 2223 7046
ZCK Zachary’s karate club [30] 5 34 78
Table 2. The SBICR of information model Eq.(10) and the fractional ( q , q ′ ) information model Eq.(12), d I , d q , q ′ and the q, q ′ values.
Table 2. The SBICR of information model Eq.(10) and the fractional ( q , q ′ ) information model Eq.(12), d I , d q , q ′ and the q, q ′ values.
Network S B I C R I S B I C R ( q , q ′ ) d I d q , q ′ q q ′
ACF -10.135 -7.348 1.913 .93 2.976 .442
BCEPG -35.38 -20.988 1.828 1.004 6.109 1.814
BGP -95.919 -95.442 1.591 1.037 3.558 .817
BGW -64.525 -42.927 1.949 1.006 2.437 1.219
CEN -13.897 -12.103 1.822 .988 3.253 .805
CNC -58.166 -49.747 1.835 1.014 3.606 .733
COL -25.187 -18.343 2.679 1.001 3.655 1.364
DRO -23.34 -18.202 1.443 .998 5.856 .662
DS -17.868 -14.616 1.498 .989 3.959 .788
ECC -87.426 -66.706 1.625 1.029 5.044 1.442
EM -34.459 -31.15 1.547 1.001 4.663 .915
IOF -65.328 -51.656 1.736 1.028 4.846 1.112
JM -19.449 -13.532 2.805 .986 2.659 .726
JUN -63.643 -58.511 2.485 1.006 5.95 1.105
LAS -30.269 -21.898 2.103 1.02 3.459 .365
LDU -20.75 -20.091 1.85 .998 2.879 .864
MAR -52.612 -46.428 1.644 1.003 3.976 .9
MIT -39.208 -25.351 2.295 1.006 4.353 1.165
PAIR -68.947 -57.065 1.582 1.004 2.726 .67
PG -186.322 -199.049 1.463 .999 5.221 1.324
PGP -117.159 -100.827 1.573 1.013 2.93 1.666
POW -186.721 -206.691 1.589 .994 5.176 .489
PRI -45.866 -27.325 2.533 1.016 6.338 1.234
TC -22.759 -22.025 1.57 .991 5.494 1.143
USAA -26.655 -18.497 1.678 .996 2.358 .626
WHO -36.125 -29.873 1.675 1.002 4.751 1.28
YEAST -48.576 -43.622 1.533 1.006 6.5 .594
ZCK -9.77 -3.672 1.5 .95 5.094 .696
Table 3. The nodes (max-min), edges (max-min), d I (max-min), d q , q ′ (max-min) and the percentage of information model for synthetic networks. I=Eq.(10) and q , q ′ = Eq.(12)
Table 3. The nodes (max-min), edges (max-min), d I (max-min), d q , q ′ (max-min) and the percentage of information model for synthetic networks. I=Eq.(10) and q , q ′ = Eq.(12)
Network model Nodes Edges d I d q , q ′ Model
BA 2000-4500 2685-40455 3.93-7.41 .86-1.73 q , q ′ (100%)
SHM 10-36480 9-880475 .83-12.69 .01-2.43 q , q ′ (70.83%)-I(29.17%)
WS 2000-4000 4000-40000 .96-7.36 .01-1.54 q , q ′ (100%)
Table 4. The parameter of SHM model that produce networks for which the information model fitted better
Table 4. The parameter of SHM model that produce networks for which the information model fitted better
G M I B B B M O D E
2 2 0 .4 1
2 2 .4 .4 1
2 3 0 .4 1
2 3 .4 [ 0 , 1 ] 1
2 4 0 .8 1
3 2 0 [ 0 , 1 ] 1
3 2 .4 [ . 2 , . 8 ] 1
3 3 [ 0 , . 4 ] ≤ . 8 1
3 4 0 1 1
4 [ 2 , 3 ] 0 .4 1
2 2 0 [ 0 , . 2 , . 8 ] 2
2 2 .4 [ 0 , 1 ] 2
2 2 1 ≤ . 8 2
2 3 0 ≤ . 4 2
2 3 .4 .2 2
3 2 0 [ 2 , . 6 , 1 ] 2
3 2 .4 .8 2
3 4 0 .4 2
4 2 0 ≤ . 2 2
4 2 .4 [ . 4 , . 2 ] 2
4 3 0 .8 2
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated