Preprint
Article
Horava-Lifshitz $F(\bar{R})$ Theories and the Swampland
Altmetrics
Downloads
57
Views
23
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
08 September 2023
Posted:
11 September 2023
You are already at the latest version
Alerts
Abstract
The compatibility between the de Sitter Swampland conjecture and Ho\v{r}ava-Lifshitz $F(\bar{R})$ theories with a flat FLRW metric is studied. We first study the standard $f(R)$ theories and show that the only way in which the dS conjecture can be made independent of $R$ is by considering a power law of the form $f(R)\sim R^{\gamma}$. The conjecture and the consistency of the theory puts restrictions on $\gamma$ to be greater but close to $1$. For the $F(\bar{R})$ theories described by its two parameters $\lambda$ and $\mu$ we use the equations of motion to construct the function starting with an ansatz for the scale factor in the Jordan frame of the power law form. By doing a conformal transformation on the three metric to the Einstein frame we can obtain an action of gravity plus a scalar filed by relating the parameters of the theory. The non-projectable and projectable cases are studied and the differences are outlined. The $F(\bar{R})$ function obtained consists of terms of the form $\bar{R}^{\gamma}$ with the possibility of having negative power terms. The dS conjecture leads to inequalities for the $\lambda$ parameter, in both versions it gets restricted to be greater but close to $1/3$. For the general case in which $\mu$ and $\lambda$ are considered as independent, the action contains an extra term but we propose that the conjecture is still applicable. Once again the non-projectable and projectable cases are studied. The $F$ function obtained has the same form as before, the consistency of the theory and the dS conjecture lead to a set of inequalities on both parameters that are studied numerically. In all cases $\lambda$ is restricted by $\mu$ around $1/3$ and we obtain $\lambda\to1/3$ if $\mu\to0$. Finally we consider the $f(R)$ limit $\mu,\lambda\to1$ and we obtain consistent results.
Keywords:
Subject: Physical Sciences - Theoretical Physics
1. Introduction
One fundamental aspect of any physical theory is the agreement that it must hold with experiment. However, it has been known from the beginning that any approach to a quantum theory of gravity would have severe issues with this aspect and string theory is not an exception. Decades have passed since the first string theory was proposed. In that amount of time the theory has been improved vastly leading to a framework with a vast scenario of possible realizations. One of the most controversial issues that string theory possesses in this regard is the choice of a vacuum for the theory, since the physical constants on any string theory come from vacuum expectation values for scalar fields, the choice of such a vacuum is fundamental. However, at present none mechanism to choose dynamically such a vacuum exists. Instead, there is a very big number of possible vacua that can be compatible, the so called Landscape of string theory. If we have a full quantum theory of gravity, any model constructed within it will lead to an effective theory in the low energy limit. However the opposite is not in general true, and thus the idea that it should be possible to distinguish an effective theory that can be completed to a correct quantum theory of gravity in the ultraviolet (UV) from those which cannot is an important subject. The theories that can be completed in this sense are said to belong to the mentioned Landscape. In contrast if an effective theory in the infrared (IR) cannot be completed in this sense is said to belong to the Swampland. In order to pursue conditions on an effective field theory containing gravity to be completed in the UV a set of Swampland conjectures have been proposed recently [1,2,3,4,5,6]. They describe some behaviours found generically on string theoretic realizations that seem to be key elements of a quantum gravity theory. Although features derived from string theory models are used as guidelines, these conjectures are expected to be valid in a general sense independently of string theory.
There is a vast number of constructions in string theory aiming to describe a cosmological scenario compatible with observation. For example from the inflationary point of view string theory have many proposals for the inflaton field (see for example [7]). However, it has been found very difficult to obtain a dS background with a complete construction on the higher dimensional theory. This seemingly impossibility led to the dS conjecture that now claims that it is not possible to obtain such a background [8,9,10,11,12]. There are other Swampland conjectures in this sense such as the Distance conjecture, the Transplanckian Censorship conjecture, etc. but in this article we will focus exclusively on the dS conjecture. When we only have one scalar field coupled to gravity as standard in inflationary models, this conjecture is written as inequalities on the scalar field potential. However, it is known that the dS conjecture is not compatible with the standard cosmological picture of an inflationary universe driven by a scalar field that obeys the slow-roll conditions on General Relativity (GR) [13,14,15], since those conditions are expressed in terms of the scalar field potential and they are the opposite of the dS conjecture among other problems. There are various ways out of this inconsistency such as considering Warm Inflation[16], Multi-field inflation [17] or variations of the gravitational theory such as theories [18,19,20] among other proposals [21,22,23,24,25]. In this work we will be interested on studying the compatibility of this conjecture with another modification of the gravitational theory known as Hořava-Lifshitz theories.
It is known that GR must be the theory of gravity on the low energy regime. String theory of course fulfils this condition. However, instead of modifying the theory of gravity at the fundamental level to discover its quantum description, there is also the possibility of improving GR to obtain such description in a closer way to the original theory. In this sense, inspired on the Lifshitz scaling of condensed matter systems, Petr Hořava proposed to modify the Einstein-Hilbert action by incorporating spatial higher-derivative terms compatible with an anisotropic scaling of space and time variables [26,27,28,29,30]. These terms break the Lorentz symmetry in the UV but makes the theory power counting renormalizable and thus it represents a better candidate to a quantum UV completion of gravity. The IR limit of this theory was found to be troublesome but it led to new relevant cosmological behaviours such as bouncing universes [31,32,33] or the appearance of a dark energy term as a constant of integration [34] to name a few of them. This theory has been generalized in a number of ways in order to improve the issues in the IR limit that the original theory has. For example in [35,36] an extra field was added. It has also been proposed a generalization of such a theory in the same way as to theories are a generalization of the standard Einstein-Hilbert action, this has led to the Hořava-Lifshitz theories [37,38]. These theories describe new scenarios that do not appear in standard theories and thus they are relevant to be further explored. In the present article we perform an analysis of the compatibility of these theories with the Swampland conjectures. In particular we are going to focus on the dS conjecture as explained before.
The outline of this article is as follows. In Section 2 we are going to summarize the way in which standard theories are studied in the light of the dS conjecture. We will particularly focus on the way in which this conjecture can be made independent of R. In Section 3 we present the theories and in Section 4 we perform the full analysis of their compatibility with the dS conjecture. Finally in Section 5 we present our final remarks section.
2. Swampland conjectures in theories
In this section we briefly overview the situation of the Swampland dS conjectures in the context of theories. Our aim is not to be exhaustive but just introduce conventions and notation which will be necessary in the further sections.
We consider the theory of gravity coupled to a scalar field, the dS conjecture was written originally in the following form (first dS conjecture) [8,9,10,11,12]
where V is the scalar field potential, is the derivative of the potential with respect to the scalar field which we are considering to be unique and c is an order 1 constant. Later this conjecture was refined to incorporate another possibility which is written as (second dS conjecture)
where is another order 1 constant. Thus the dS conjecture is expressed now as the statement that either one of the two inequalities, the first or the second dS conjecture must hold.
Let us give a general picture of how can we study the Swampland conjectures in the light of theories [18]. These theories are a generalization of GR by considering the gravitational action in the Jordan frame as1
where is some well behaved function of the curvature scalar R and no matter component has been considered. In this scenario it is thought that the action for GR is just the first term on a Taylor expansion of the f function around a small curvature. These theories are of great interest since they lead to many new interesting cosmological behaviours [39]. In order to transform this action into a form suitable to investigate its compatibility with the conjectures we consider the equivalent action [39,40]
where is just an auxiliary field and . Then we can perform a conformal transformation in order to describe the dynamics in the Einstein frame in the form
with . We then obtain the following action
which represents just the action of gravity plus a scalar field where the scalar field is given by
with potential
Let us remark that in the Einstein frame we have the action of gravity plus a canonically coupled scalar field although in the Jordan frame we have not considered any matter contribution. This scalar field originated in the process of getting to the Einstein frame by a conformal transformation and thus the field and its potential are entirely defined by geometry. However since the dS conjecture is expected to hold for any scalar field that is canonically coupled to gravity, we can apply the conjecture in this scenario as well. We will not consider any matter content in the Jordan frame since as we will see by considering only gravity we can use the conjectures to constraint the parameters of the gravitational theory and thus the allowed solutions.2 We note from (1) that if the potential is negative the conjecture is satisfied immediately. Therefore we are interested in the scenario where the potential is positive. In this case from (8) we see therefore that we have to impose the condition
And from (7) we also note that we need . Using these definitions we can obtain the derivative of the potential with respect to the scalar field as
With this setup the first dS conjecture (1) takes the general form
and the second dS conjecture (2) is written as
From these expressions the conjectures were studied in a general way in [18] finding the constraints on the f function that makes it compatible with the conjectures. In [19] particular attention was put in a function of the form where is a small number, it was found that the conjectures were compatible with the region of of phenomenological interest. Finally in [20] the first dS conjecture was found to be in good agreement with numerical data.
We expect that in general (11) will lead to inequalities involving R. However since we want to use the conjectures to constraint the theory in this article we will be interested in a scenario where the conjecture could be made independent of R and thus valid for all values of R. We can achieve this by imposing the condition
where A is any constant that should be positive in order to fulfil (9). Let us remark that this is an ansatz and therefore it is not the only way to fulfil (11), but it is the only way to fulfil it independently of R. We have therefore two possibilities regarding the sign of the term inside the absolute value. If (13) leads to
where with . In order to have a well-defined scalar field and not ghostly gravitons we require that and in order to have positive mass of the curvature fluctuations we also require [39]. The expression (14) fulfils both conditions for . Substituting this form in the first dS conjecture we obtain that is restricted to be
In particular for this leads to . Thus the conjecture leads to a restriction on the exponent of the f function that can not be the GR value but it is restricted to be close.
For the case we obtain the same form but in this case and thus . This form can also fulfil the two conditions and for . However in this range of values the first dS conjecture can not be fulfilled.
On the other hand, substituting the form (14) into (2) we obtain that the second dS conjecture is written as
which is independent of R but cannot be fulfilled for any value of . Therefore this form for the f function is incompatible with the second dS conjecture. This is not a great deal since we only need to fulfil one of the two versions of the conjecture.
Thus we conclude that in theories the only way to fulfil the first dS conjecture independently of R is to take f as a power term of R. The conjecture restricts the exponent of this function to be close to the GR value and the second dS conjecture is never valid.
In the following sections we will describe the Hořava-Lifshitz theories and investigate if a similar procedure as the one just described can be applied to them to look for the viability of the Swampland conjectures.
3. Hořava-Lifshitz theories
This section will be devoted to briefly overview Hořava-Lifshitz theory of gravity in the context of modified gravity. We will consider the ADM decomposition of spacetime in which we write the metric in the general form
where N is the lapse function, the shift functions and the three-metric. We note that the Friedmann-Lemaitre-Robertson-Walker (FLRW) metric has this form with vanishing shift functions and it is always possible to choose the lapse function to be equal to one.
In the Hořava-Lifshitz theory of gravity the metric is naturally written in an ADM form and the action for the gravitational part can be written as [26,27,28,29,30]
where is the extrinsic curvature, is a parameter and is a potential term for gravity. In the general scenario this term will contain the scalar curvature of the three-metric and seven constants accompanying higher spatial derivative terms written in terms of the Ricci scalar of the spatial three-metric. If the detailed balanced condition is proposed this term is derived from a geometrical action and the number of constants is reduced. However, for the flat FLRW metric which will be of interest to us this term will always be zero since in that case the three-metric is just the scale factor times the three dimensional euclidean flat metric. Thus in the following we will not be concerned with the specific form for this term. As can be easily seen, the IR limit will be obtained in the limit and it is obtained . The lapse function appearing in the action can lead to different versions of the theory depending on the variables in which it may depend on. If the projectability condition is used, the lapse function only depends on the time variable and thus the hamiltonian constraint is a global constraint contrary to the case in which the lapse function is allowed to depend also in the spatial variables. Since we will deal with the FLRW metric we will choose but in general the global nature of the hamiltonian constraint leads to an integration constant and thus a new term in the equations of motion absent in the other scenario [28,34]. Thus even though in both cases we can choose the lapse function to be 1 the equations of motion will be different. This will be an important remark later on.
In [41] the Swampland conjectures have been studied when a nonlinear dispersion relation is taken into account. Such feature comes naturally from HL gravity and its possible extensions (such as [35]). However, for an FLRW flat metric the equations of motion are almost identical in all types of HL theories as the ones obtained in GR and thus the problem of the incompatibility of the slow roll criteria is still present. Therefore in the following we will consider a generalization of HL theory in the same line as theories and investigate the compatibility with the Swampland conjectures.
As we can see from the form of the action (18) it is natural to generalize the HL theories in the same way as the generalization leading to the theories described in the previous section. In this case it has been proposed a more general action in the form
where now can be understood as a generalization of R which includes the new terms of spatial derivatives which is proposed to have the form [37,38]
where is a constant. The term containing is usually omitted in the standard proposal since it turns out to be a total derivative term. However it is necessary for these theories. As we can see for the above definitions the limit , of this theory will lead to the standard theory used in the previous section. This theory was originally proposed in a series of papers [37,38] using the detailed balanced condition. The resulting cosmological scenarios were found to describe new and interesting behaviours for the flat FLRW metric such as solutions with two periods of accelerating expansion. In [42] the Ekpyrotic scenario was studied for these theories. In [43] the detailed balanced condition was abandoned. However for the flat FLRW metric, as we have pointed out earlier, the equations of motion are the same. A hamiltonian analysis for these theories was performed in [44] and the relation to general scalar tensor HL theories was investigated in [45]. An extension to include a field was performed in [46]. However as in the latter case the equations of motion found for the FLRW flat metric is the same as in the original scenario with or without the detailed balanced condition. Thus, if we consider only the flat FLRW metric at the level of equations of motion, all the versions proposed for the metric will lead to the same results. Therefore the following analysis will be valid in all these scenarios.
Let us consider then a flat FLRW metric in the form
With this metric we obtain from (20) the following result
where is the Hubble parameter. In contrast the standard curvature scalar in this case is
and thus the difference between both theories for this metric are just the appearance of the two parameters and and thus at least for the flat FLRW metric the interpretation of can be considered as related to the curvature. However we will see that although both expressions differ only by constants they will lead to very important differences.
Considering only gravity the first equation of motion obtained through the hamiltonian constraint is [37]
where , and where is an integration constant in the projectable version of the theory which can be considered to represent dark matter for the way in which it appears in the equations of motion when it takes positive values [34]. In the non-projectable version of the theory we have . This is the only difference between both versions of the theory that will be of importance to us. Varying with respect the three-metric the second equation of motion is obtained [37]
As stated before we note from these equations and (20) that the limit in which we can recover the standard theories is . If we put an ansatz of the form in the above equations and squared or cubic polynomials form for the function the cosmological solutions describe exponential acceleration for two different periods [37,38]. This behaviour is exclusive of these theories since it is removed in the mentioned limit. This is one of the reasons that shows the importance of these kind of theories.
Before continue let us remark an important point. The Swampland conjectures were proposed originally in theories with Lorentz invariance. However HL theories, as well as their generalizations, break this invariance in the UV so one may worry about the applicability of the conjectures to these kind of theories. If we apply the conjectures and find that they are incompatible we may conclude that Lorentz invariance is a key requirement of the conjectures. However in the next section we will discover that the conjectures are indeed compatible with these theories and they actually lead to some expected behaviours. Thus we can support the idea that the conjectures may be applicable to more scenarios that originally thought considering our results as one indication a posteriori supporting this idea. In [25] the compatibility of the conjectures with a cosmologcal setup with explicit breaking of Lorentz invariance was studied with positive results as well.
4. Swampland conjectures for theories
In the same way that we need to perform a conformal transformation to the theory in order to obtain an action of GR plus a scalar field in the Einstein frame, we will perform a conformal transformation in the three-metric of the above theories and then we will be able to study the compatibility with the Swampland conjectures. Let us start by considering the action
with . This action is equivalent to (19) with an auxiliary field. Then we perform a conformal transformation only on the three-metric of the form
and choose and as in the flat FLRW metric, which leads to the action in the Einstein frame [38,43] given by
with
In order to eliminate the term that combines the metric with the scalar field and to obtain a canonically coupled scalar field (that is that it appears as in standard scalar theories) we choose
Thus we perform the redefinition of the scalar field as
where
then we finally obtain in the Einstein frame the action in the following form
Moreover in the Einstein frame we obtain an action of gravity plus a canonically coupled scalar field. We note that we do not obtain the HL theory of gravity since in this case there is no higher derivative terms of the scalar field, however since the general form is the one of gravity plus a scalar field we can use this action to investigate the compatibility with the Swampland conjectures of the theories. We do not worry that the gravity part of the action is not GR since we only need to describe a theory of gravity. For example in [23] the conjectures are studied with a Gauss-Bonnet term in the action. We note that since we made the choice (30), we can no longer recover the theories in any limit. We first study this case since this simplification allows a complete analytic analysis. The general scenario where this special choice is not required will be studied in Subsection 4.4 .
With this set up and using (10) with , the first dS conjecture (1) is given in the general form
which can be written as
and the condition for the scalar field to be positive is
On the other hand the second dS conjecture takes the general form
We note that similarly as what happened with the theories the way in which the above expressions are to be independent of is by considering as some power of . However, since these theories have not been studied as extensively as the theories we will proceed in a different way. Instead of choosing some form for the F function, we will use the system of equations of motion in the Jordan frame with an ansatz for the Hubble parameter which is of cosmological interest and then construct the function. Finally we will check if this function can fulfil the conjectures at the same time that leads to cosmological interesting solutions.
With this choice we also obtain
Thus, the general procedure will be to use this system of equations to construct the function with an interesting cosmological behaviour. Since the constant C will change the possible solutions we will consider separately the two different scenarios, namely the case in which it can be eliminated, that is the non-projectable case and the case in which it has to be different from zero which is the projectable case.
4.1. Non-projectable case
Let us begin firstly with the non-projectable case in which . We could start by proposing the simplest ansatz of cosmological interest, namely a constant Hubble parameter which describes a universe with an exponential acceleration ideal for an inflationary era. With this proposal in [37] it was shown that these theories could result on a solution with two different periods of accelerated expansion. However with the reduced system of equations (that is after choosing the value of ) this proposal will lead us to a vanishing value for the F function. Therefore we will propose instead an ansatz that describes an accelerated expanding universe but in the form of a power law with the time parameter, that is we propose that the scale factor in the Jordan frame has the form
where n is a constant that will be considered as positive. Thus the Hubble parameter is . With this ansatz using Eq. (40) we obtain that is related to the time variable as
We note from (31) that we must always have in order to have the scalar field properly defined. We will generally be interested on values of n that describes accelerating expanding universes and therefore from the above we note that considering positive values for we obtain the condition . We note from this expression that grows inversely with time with a behaviour similar to what we could expect of the curvature. In this scenario Eq. (41) is written as
which leads to the solution
where and are integration constants and
The other equations on the system are immediately satisfied. Using (43) we can find the form of F as a function of , we obtain in this way
where we have defined the positive constants
The last inequality follows from the condition in both cases and we have also defined
We note that our general solution contains two terms of powers of and thus we expect that it can fulfil the dS conjecture for any of the terms taken independently. The condition to have a non-negative potential for the scalar field in the Einstein frame (36) in this case takes the form
Furthermore from (48) we obtain that
Thus the condition (50) can be easily fulfilled by taking positive values for the integration constants and . In this case we obtain
Since there is a minus sign in the first term the F function cannot have a definite sign for all values of , and thus we cannot fulfil the dS conjecture for all values of if we consider both terms at the same time as we anticipated. Thus let us consider each term separately.
First let us consider the positive power factor on , that is we choose and , then the first dS conjecture (35) leads to
In the other case if we consider the negative power factor on by choosing and the conjecture leads to
In both cases the condition (36) is satisfied. Thus the dS conjecture leads in both cases to an inequality for the HL parameter . We also note that the faster we want the expansion to be, that is the bigger the value of n, the closer we get to the value . Thus in order to fulfil the conjecture independently of and to have a fast expansion, we obtain that must be bigger but close to and thus away for its IR limit value. We also note that since in both cases the first dS conjecture leads to a region of validity for the parameter and neither nor in (47) depend on , the form of the function is not constrained by the conjecture, it only depends on n, and thus we have the freedom to choose any positive values of interest for these terms, in contrast to the standard case.
On the other hand, the second dS conjecture (37) in this case is written in general as
Taking the positive powers of , that is taking this leads to
which can never be fulfilled because the term on the left hand side is always positive. Taking now the negative powers of , that is taking we obtain the condition
which again is never fulfilled. Thus we obtain that the second dS conjecture is never compatible with the obtained function.
In summary, we have obtained that in these theories we can describe universes with a power law scale factor that describe expanding universes in the Jordan frame and this behaviour leads naturally to power law terms for the function. In the Einstein frame we obtain a scalar field in which we can apply the Swampland conjectures. The first one of the dS conjectures can be fulfilled for each term on the solution of F independently of leading to an inequality for the HL parameter which is in agreement with the difficulties of achieving this scenario in GR since it leads us to the opposite limit of GR that is it leads us to the UV limit for rapidly expanding universes. We also obtain that the second dS conjecture can never be valid for this form of the function.
Finally we would like to explore what is the behaviour described by these solutions on the Einstein frame where we have the scalar field coupled to gravity. For this we note that since both frames are related by the transformation (27) in the Einstein frame we also have a flat FLRW metric, but now the scale factor is given by
Let us consider each term separately as previously done. For the negative powers of we choose and . Thus the scale factor is
We note that does not depend on and therefore the result (54) derived from the dS conjecture will not restrict the range of values that it can take. We obtain in this case that the exponent will always be positive, and thus the universe will always be expanding.
On the other hand, for the positive power term of we choose and . Thus the scale factor is given by
Once again is independent of and always takes positive values describing expanding universes. It can be shown that in general
Thus, for negative powers of in F we have in the Einstein frame a more rapidly expanding universe than in the Jordan frame for . On the contrary, for positive powers we have an slower expanding universe. For small time values this behaviour is flipped and the fastest expanding universe corresponds to positive powers of . We show the behaviour just described for in Figure 1.
4.2. Projectable case
Let us consider now the projectable case in which we take in the system of equations (38)-(41). We are going to propose the same ansatz as before that is the scale factor as a power law on the time variable. Thus Eq. (43) is still valid. In this case Eq. (41) leads to
The solution of this equation consists of the homogeneous solution (the same as before with ) and a particular solution, in this form we obtain the solution
where we note that we must exclude the possible roots of the polynomial , which are . In this case the function takes the form
where we have defined
The condition for the positivity of the scalar field potential (36) leads in this case to
Since Eqs. (51) hold we note that in order to fulfil this condition for all values of we need , thus . Therefore we have two possibilities:
- and .
- and .
We note that in this case
Since the last term will always be present, if we take the function F will not have a definite sign for all values of and thus it will not fulfil the dS conjecture for all values of . Thus we will consider only the positive power and take . In this case we could fulfil the dS conjecture for all positive values of but not independently of it as we have stated before. The first dS conjecture in this case leads to
Moreover we note that in order to fulfil this inequality for all values of we must ask each term within square brackets to be positive, in this form we obtain the two inequalities
We note that (69) is the same as the one obtained in the non-projectable case (53). However since both inequalities are on the same parameter, we only need to impose the stronger one. It turns out that (69) is more restrictive than (70) only if . Thus for most of the values of n the dS conjecture will be satisfied by (70) for every value of . Then, considering leads us to a stronger condition for the parameter for most cases.
Thus since we have for all . However we have from these expressions that
which does not have a definite sign for all values of . Therefore the second dS conjecture (37) can not be studied in general for all values of in this case.
In summary in the projectable case the first dS conjecture can still be fulfilled for all positive values of but not independently of it. The conjecture also leads to an inequality for the parameter and for most values of n this condition is more restrictive than the non-projectable case.
Once again the metric in the Einstein frame will also be a flat FLRW metric. In this case taking the scale factor will be
Thus in the projectable case the scale factor has a dependence on and the dS conjecture leads to a lower bound for it. Since both terms are positive, the universe is always expanding. In Figure 2 we plot this scale factor choosing , and for different values of C. Since in order to fulfil the conditions mentioned we need to take negative values for C, thus we write . We see that the effect of projectability, that is of values for different than zero is that as increases, the scale factor increases, making the expansion faster.
Finally let us note from (64) that taking and we have two terms of positive powers of . Thus we could hope to write this function in a form that resembles an approximation of an Einstein-Hilbert term plus corrections. We also note from the dS conjecture inequality (69) that if n is close to its limiting value we can have access to the IR limit . Thus let us study what form do our solutions take for n close to . We write
with . In this case we can take and the most restrictive inequality is (69). From (64) taking , and (75) we obtain
For we can make the approximation [19]
Thus we obtain
with the correction term
Consequently the scale factor in the Einstein frame (74) takes the form
In this case we can take values of greater than 1 and the resulting universes are always expanding. However let us point out a subtle issue with this IR limit. From (40) we obtain
We note that this value does not coincide with the GR value of R (23). Thus since we chose the IR limit does not correspond to GR. In order to perform a correct GR limit in SubSection 4.4 we are going to avoid this choice and consider the conjectures in the general case.
4.3. Constraints on
As we have shown in the previous subsections, in the particular case () the first dS conjecture leads to constraints on the parameter in both the projectable as well as the non-projectable case. In order to visualize in a graphical form these constraints we plot in Figure 3 for the non-projectable case the upper values (53) and (54) for different values of n. We note that values of bigger than 1 are allowed only when n is small but as n grows the allowed region is reduced in both cases. In general we note that for positive power terms in the function the allowed region is bigger than for negative power terms. For the projectable case we show the behaviour of the corresponding upper bound coming from (69) and (70). We choose the most restrictive constraint as we vary n. It is shown that for small values of n the constraint is the same as the one obtained in the non-projectable case. However when n is big enough, the constraint coming from this scenario is more restrictive and thus the allowed range of gets smaller and decreases inversely with n. In all cases we choose .
4.4. The general case
In the general scenario in which we consider and as independent parameters the action has the form (28) and the scalar field is defined by (31). We note that in general we do not have an action that can be divided into a sum of an action for gravity plus the action of a scalar field because of the third term in the action that combines the metric with the scalar field. However we do have an explicit definition for a scalar field with the correct form of the kinetic term in the action as before and we also have a definition for its corresponding potential. Thus we propose that the dS conjectures are still applicable for this action. A similar scenario was presented in [24] were the conjectures were studied with an scalar field that is non canonically coupled to gravity as well.
In order to have a correct definition of the scalar field we need the parameter defined in (32) to be a real number which leads to
We are going to consider and , use the same ansatz for the scale factor in the Jordan frame as before, that is and consider the non-projectable case (). Thus the latter reduces to
With this ansatz from (22) we obtain
with . As a result, we can still interpret as related to the curvature. In the particular case we considered only positive values for which led us to a lower bound for n compatible with expanding universes. For consistency and later convenience we will also ask in the general case for positive values of , consequently we obtain the condition which leads to
from where we obtain . Thus, as a result of considering only a correct definition of the scalar field and positive values for we have obtained upper bounds for . Now let us proceed as in the particular case by solving (84) and construct the function. The general solution of (84) is
with
where we have defined
The condition for the scalar field potential to be positive in this case takes the form
which is the same as in (50) with substituted by . Therefore, in order to fulfil this condition for all values of we ask each term to be positive. We choose and and we are left with the conditions and . The first condition is fulfilled with (86) whereas the second leads to
From (86) and (93) it can be proven that we always have and therefore the function in the general case (90) always consists of a negative power term of and one with positive exponent. The negative power term has a negative coefficient whereas the posite power term has a positive coefficient as in the particular case studied before.
Thus, in the general case we have 3 inequalities (82), (86) and (93) that constraint the values of . Since the three are constraints on the same parameter it suffices to take the most restringent one, then these inequalities lead to
We note that the closer is to zero, the closer gets to its limiting value . We also note that in order to correctly fulfilled the inequalities and therefore the simpler version of theories that do not take into account this term are inconsistent with this conformal transformation and thus the generalization of [37] is needed.
The first dS conjecture has the form (35) with the function (90). In order to fulfil this conjecture independently of we take once again each term separately. For the negative power term we take and the conjecture leads to
On the other hand for the positive power term we choose and the conjecture leads to
In general both expressions (95) and (96) lead to a region of validity for the parameter in terms of and thus we can compare the resulting bounds with (94) to investigate the region of compatibility. However the expression are complicated to solve analytically and thus we carry out a numerical analysis.
For the negative power term upper and lower bounds coming from (95) are found numerically. In Figure 4 these bounds are shown for , and varying the parameter. We also show the upper and lower bounds coming from (94). We note that in order to fulfil both expressions, we need the upper bound from (94) to be bigger than the lower bound from (95) and thus is bounded from above and consequently the allowed values of increase as increases but not above a maximum value. For smaller values of n or bigger values of c the restriction on is more severe and gets closer to .
For the positive power term in we find with a numerical analysis that for small values of (96) leads to an upper bound for that is bigger than the one coming from (94) and thus the conjecture is satisfied as a consequence of (94). On the other hand, for values of big enough (96) leads to two regions of validity, one is an upper bound which is smaller than (94) and one is a region with an upper and lower bounds bigger than (94) and therefore inconsistent. Thus, for big values of the dS conjecture is more restrictive than (94). In any case, both upper bounds grows with and thus, in this scenario we can have access to bigger values of . It only gets restricted to be close to if is small enough. In Figure 5 we show this behaviour for and . For smaller values of n or bigger values of c the region where the dS conjecture is more restrictive than (94) is found for smaller values of .
The second dS conjecture leads to (55) with instead of and thus for the positive power term we have (56) with and for the negative power term we have (57) with . Therefore, the second dS conjecture is never fulfilled in the general scenario as well.
In the general case the metric in the Einstein frame will also have the FLRW form with the scale factor given by
Thus, for the negative power term we choose and and the scale factor takes the form
with
Similarly for the positive power term we choose and and the scale factor takes the form
with
In the general scenario the scale factor will depend on and and therefore the inequalities (94) and the region coming from the first dS conjecture will restrict it. Moreover it can be proven that we always have and thus we always have expanding universes.
Thus, the general scenario is similar to the particular case, that is, in order to have a properly defined scalar field and to fulfil the first dS conjecture gets restricted in terms of around and the resulting description in the Einstein frame are expanding universes. For the positive power term however we can have access to bigger values of by increasing the values of which will be important to consider the limit of interest in the following. In this case we also obtain that the second dS conjecture is never fulfilled.
Furthermore, the general scenario allows us to correctly perform the limit which as stated before should correspond to standard . In this limit (82) and (93) are automatically satisfied whereas (86) leads to . The fist dS conjecture will correspond to upper bounds for n.
For the negative power term (95) leads to which is inconsistent with c being an order 1 constant. For the positive power term (96) leads to
The biggest upper value is obtained in and corresponds to approximately . Using (88) we obtain for the allowed values of the exponent in the F function to be
The allowed region (103) must be compared to the one obtained in the standard case (15). The lower bound from (103) comes from the dependence of on n and the condition coming from (86). Since the system of equations (24) and (25) reduces to standard in the limit , , after proposing the ansatz , the same form of the f function (90) should emerge and thus, after imposing in the standard theories we will obtain the same lower bound. The upper bound in contrast is different. This comes from the fact that although in the Jordan frame the theory recovers standard in the mentioned limit, the transformation to the Einstein frame for theories is only on the three-metric (27) whereas in standard the conformal transformation used is in the complete 4-metric (5). Thus the resulting scalar field and scalar potential are different and therefore the first dS conjecture has a different form. It is interesting however that even though the analytic form of both upper bounds are different, their maximum value are not too far. In standard we get approximately whereas in we get approximately . Thus theory allows a bigger region for the exponent although it is still not too far from 1. Therefore in the limit the theories lead to a consistent result with the standard theories, that is, the power of gets restricted to be bigger than 1 (actually bigger than ) but not too big, smaller than approximately . From (101) we obtain that in this limit the scale factor has the form (100) with
Thus, there is enough room for accelerated expansion in the Einstein frame.
Finally, let us study the projectable case. Since the obtained form for the F function has the same form as the one obtained in the particular case, it only changes the specific form of the exponents, the projectable case can be treated as it was done in SubSection 4.2. In this case the F function is written as
The condition for a positive potential is written analogously to (66) and it can also be fulfilled for all values of by taking the coefficient for the new term to be positive and . Once again we take , then the first dS conjecture is written with two terms as in (68) and thus in order to fulfil the conjecture for all values of we obtain two inequalities. The first is the same as in (96) whereas the second is
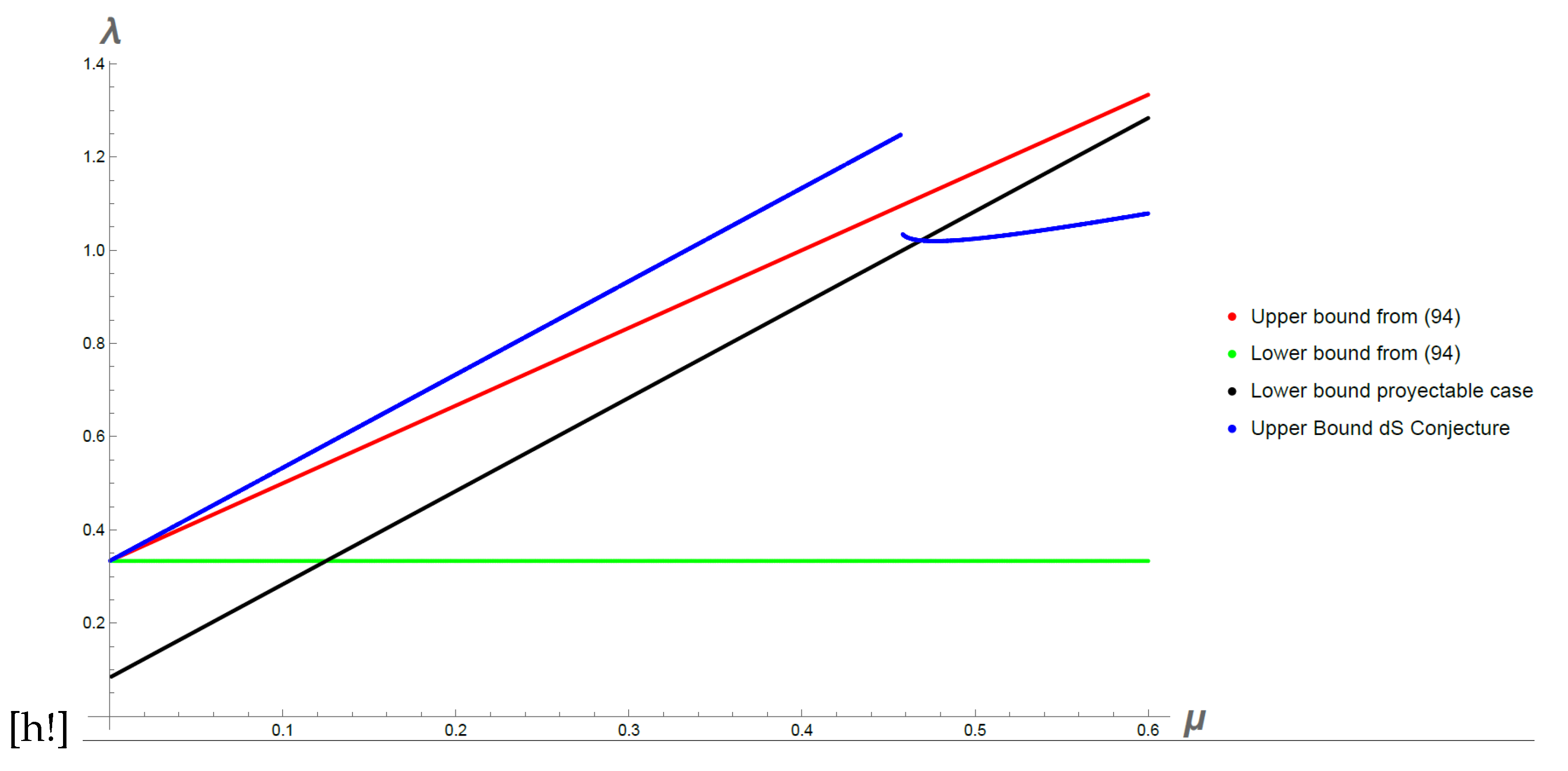
Thus we obtain an extra inequality that has to be taken at the same time with (94) and (96) but now it is a lower bound for . In Figure 6 we show the bounds shown earlier for (94) and (96) but we now add the bound coming from (106) for and . We note that in order to fulfil the complete system of inequalities there is an upper bound for and thus gets restricted once again to be close to .
In the limit (106) reduces to
the upper bound gets it maximum value at and corresponds to approximately . Thus in the proyectable case, the upper bound on n is more restrictive than in the non-proyectable case, this leads to
Thus we get bounds that are even more restrictive than standard in this case. However, the form of the F function has an extra power term with a exponent of . If we take small values of n around we can write this function as GR plus correction terms as in (78) (the only difference will be the coefficients of each term and the exponent of the second term in (79)) since in this case we can obtain consistently in the mentioned limit.
5. Final Remarks
In the present article we have presented an analysis of the compatibility of the Hořava-Lifshitz theories with the Swampland conjectures, focusing on the dS conjecture and using a flat FLRW metric.
We first presented the analysis for the standard theories which was previously done. In the Jordan frame we had the action and we needed to perform a conformal transformation to the Einstein frame where it was obtained an action of gravity plus a canonically coupled scalar field. It was in this frame where the Swampland conjectures could be applied to the scalar field which is defined in terms of the function. We particularly focused on the way in which the dS conjecture can be made independent of R. It was found that the only way in which such scenario can be obtained is when the f function is a power term on R. With this form the dS conjecture and consistency of the theory led to conditions on the power of R that has to be greater than 1 (consequently not GR) but close to it since the upper bound was found to be around . In this scenario the second dS conjecture could never be fulfilled.
We then moved on to study the Hořava-Lifshitz theories that represent a generalization to the HL gravity theory in the same way as standard theories generalize GR. The analysis was performed using a flat FLRW metric and thus it is valid for all the different versions of this theory and its generalizations whose equations of motion for this metric are the same. In order to obtain a scalar field in the Einstein frame it was also performed a conformal transformation but this time only on the three metric as it has been previously established. In this sense it can be obtained a scalar field and its corresponding potential in terms of the function. From this it was easily seen that in order to fulfil the conjecture independently of we would also need a power term in the F function. However the general strategy was to propose an ansatz for the scale factor in the form of , consider positive values of and then use the equations of motion to construct the F function and finally investigate the compatibility with the dS conjecture. However, in the Einstein frame the action contained an extra term that is written in terms of derivatives of the three-metric and of the scalar field. This term could be eliminated with an appropriate choice of the parameters of the theory, putting in terms of and thus staying with only one parameter left.
We first studied this particular case that allowed us to have an action of gravity plus a scalar field canonically coupled and thus be able to apply the dS conjecture. The projectability condition of the theory was found to be relevant, since it adds an extra term in the equations of motion. We first studied the non-projectable case in which this term can be ignored. In this case the function was found to consist of two power terms, one with a positive exponent and positive coefficient and one with a negative exponent and negative coefficient. In order to fulfil the dS conjecture independently of we studied each term separately. In both cases the conjecture led to upper bounds for the parameter around its UV value of , the faster the expansion, the closer got to this extreme value. In this case the second dS conjecture was also never fulfilled. In the projectable case there is an extra positive power term in the F function and thus the conjecture could not be fulfilled independently of . However it could be fulfilled for all positive values of , the conjecture led to another upper bound for which makes it closer to , we showed these upper bound for the two cases in Figure 3. In this case the second dS conjecture could not lead to a result for all values of . In both cases the metric in the Einstein frame had the same flat FLRW form and it is always expanding. In the non-projectable case the scale factor only depends on n and we showed the general behaviour in Figure 1, it is found that for the most rapidly expanding universe is the one with the positive power term and the least one is the one with the negative power, however for the situation is reversed. For the projectable case the scale factor got a dependence on and thus it is subjected to the dS conjecture, in Figure 2 we showed this behaviour. It was found that the scale factor increases as increases.
Finally we proposed that in the general scenario in which and were considered as independent parameters and the action could not be put in the form of gravity plus a scalar field, the dS conjecture can still be applicable since we do have a well-defined scalar field and its corresponding potential. By doing the same procedure as before we considered the non-projectable case and found the same general form for the F function but the exponents were found to depend on and . In this case there were more inequalities to consider in order to have a correct description in the Einstein frame which led to upper bounds for the parameter in terms of the parameter. If these bounds made . The dS conjecture could be studied in general for each term on the F function and led to regions of validity in terms of and but in order to find regions of compatibility of both expressions we had to rely on a numerical analysis. In Figure 4 we showed these bounds for different values of for the negative power term. It was found that in order to fulfil both inequalities an upper bound for appeared, and thus got restricted around as well. These upper bounds were found to become more restrictive as n decreases or c increases. However in Figure 5 we showed these bounds for different values of for the positive power term. In this case the bounds of could get bigger as increases. Thanks to this behaviour it was possible to perform the limit . In this limit it was found that the only possible form of compatible with the dS conjecture was a a positive exponent which has to be greater than and less than around . The lower bound came from the specific ansatz used and can arise in the standard case as well. The upper bound on the contrary is different since the conformal transformation used in this case is only in the three-metric, however in general we can say that it is in agreement with the case studied before since the numbers are not too far apart. Since the F function has the same general form as in the particular case, the projectable version could be studied in the same way and it led to the same form as in the particular case. Once again the dS conjecture could be valid for all values of but not independently of it. In this case we obtained a new lower bound for that originated an upper bound for and those got restricted once again to a region not far from . This behaviour was shown in Figure 6. The limit could be studied in this case as well and we obtained a more restrictive condition on n which could allow us to write the f function as a GR term plus corrections.
In summary our results show that by assuming that the dS conjecture holds we have obtained restrictions on the parameters of the theories that are in general agreement with the UV behaviour of the theories. Thus we can conclude that our results support the idea that the dS conjecture may be encoding key aspects of quantum gravity. We also point out that since these theories break Lorentz invariance in the UV but we are still obtaining consistent results, the dS conjecture are found to be applicable to theories without general covariance a posteriori (as was also considered before in [25]) and thus they may be in fact more general than originally thought.
Finally, let us mention a possible scenario to extend this work in the future. The metric of most interest in building cosmological models is the flat FLRW metric. It is in this metric that the description of an inflationary universe with a scalar field in GR is usually performed and where the dS conjecture is not fulfilled. That is the main reason that we used it throughout this work. However, it would be interesting to use a closed or open FLRW metric or even other anisotropic metrics that will lead to different equations of motion between the different versions of the Hořava-Lifshitz theory and thus they will lead to different scenarios regarding the dS conjecture. This could be used in principle to get a better sense on which version of the theory is the most useful using the dS conjecture as a guideline.
Acknowledgments
D. Mata-Pacheco and L. Zapata would like to thank CONACyT for a grant.
References
- C. Vafa, “The String landscape and the swampland,”[arXiv:hep-th/0509212 [hep-th]].
- T. D. Brennan, F. Carta and C. Vafa, “The String Landscape, the Swampland, and the Missing Corner,” PoS TASI2017 (2017), 015 [arXiv:1711.00864 [hep-th]].
- H. Ooguri and C. Vafa, “On the Geometry of the String Landscape and the Swampland,” Nucl. Phys. B 766 (2007), 21-33 [arXiv:hep-th/0605264 [hep-th]]. [CrossRef]
- E. Palti, “The Swampland: Introduction and Review,” Fortsch. Phys. 67 (2019) no.6, 1900037 [arXiv:1903.06239 [hep-th]]. [CrossRef]
- M. van Beest, J. Calderón-Infante, D. Mirfendereski and I. Valenzuela, “Lectures on the Swampland Program in String Compactifications,” Phys. Rept. 989, 1-50 (2022) [arXiv:2102.01111 [hep-th]]. [CrossRef]
- M. Graña and A. Herráez, “The Swampland Conjectures: A Bridge from Quantum Gravity to Particle Physics,” Universe 7, no.8, 273 (2021) [arXiv:2107.00087 [hep-th]].
- D. Baumann and L. McAllister, “Inflation and String Theory,” Cambridge University Press, 2015, ISBN 978-1-107-08969-3, 978-1-316-23718-2 [arXiv:1404.2601 [hep-th]]. [CrossRef]
- G. Obied, H. Ooguri, L. Spodyneiko and C. Vafa, “De Sitter Space and the Swampland,”[arXiv:1806.08362 [hep-th]].
- H. Ooguri, E. Palti, G. Shiu and C. Vafa, “Distance and de Sitter Conjectures on the Swampland,” Phys. Lett. B 788 (2019), 180-184 [arXiv:1810.05506 [hep-th]]. [CrossRef]
- D. Andriot, “On the de Sitter swampland criterion,” Phys. Lett. B 785 (2018), 570-573 [arXiv:1806.10999 [hep-th]]. [CrossRef]
- P. Agrawal, G. Obied, P. J. Steinhardt and C. Vafa, “On the Cosmological Implications of the String Swampland,” Phys. Lett. B 784 (2018), 271-276 [arXiv:1806.09718 [hep-th]]. [CrossRef]
- C. Roupec and T. Wrase, “de Sitter Extrema and the Swampland,” Fortsch. Phys. 67 (2019) no.1-2, 1800082 [arXiv:1807.09538 [hep-th]]. [CrossRef]
- S. K. Garg and C. Krishnan, “Bounds on Slow Roll and the de Sitter Swampland,” JHEP 11 (2019), 075 [arXiv:1807.05193 [hep-th]]. [CrossRef]
- I. Ben-Dayan, “Draining the Swampland,” Phys. Rev. D 99 (2019) no.10, 101301 [arXiv:1808.01615 [hep-th]]. [CrossRef]
- W. H. Kinney, S. Vagnozzi and L. Visinelli, “The zoo plot meets the swampland: mutual (in)consistency of single-field inflation, string conjectures, and cosmological data,” Class. Quant. Grav. 36 (2019) no.11, 117001 [arXiv:1808.06424 [astro-ph.CO]]. [CrossRef]
- M. Motaharfar, V. Kamali and R. O. Ramos, “Warm inflation as a way out of the swampland,” Phys. Rev. D 99 (2019) no.6, 063513 [arXiv:1810.02816 [astro-ph.CO]]. [CrossRef]
- A. Achúcarro and G. A. Palma, “The string swampland constraints require multi-field inflation,” JCAP 02 (2019), 041 [arXiv:1807.04390 [hep-th]]. [CrossRef]
- M. Artymowski and I. Ben-Dayan, “f(R) and Brans-Dicke Theories and the Swampland,” JCAP 05 (2019), 042 [arXiv:1902.02849 [gr-qc]]. [CrossRef]
- M. Benetti, S. Capozziello and L. L. Graef, “Swampland conjecture in f(R) gravity by the Noether Symmetry Approach,” Phys. Rev. D 100 (2019) no.8, 084013 [arXiv:1905.05654 [gr-qc]]. [CrossRef]
- E. Elizalde and M. Khurshudyan, “Swampland criteria for f(R) gravity derived with a Gaussian process,” Eur. Phys. J. C 82 (2022) no.9, 811 [arXiv:1807.06581 [hep-th]]. [CrossRef]
- F. Denef, A. Hebecker and T. Wrase, “de Sitter swampland conjecture and the Higgs potential,” Phys. Rev. D 98 (2018) no.8, 086004. [CrossRef]
- O. Trivedi, “Swampland conjectures and single field inflation in modified cosmological scenarios,”[arXiv:2008.05474 [hep-th]].
- Z. Yi and Y. Gong, “Gauss–Bonnet Inflation and the String Swampland,” Universe 5 (2019) no.9, 200 [arXiv:1811.01625 [gr-qc]]. [CrossRef]
- S. Brahma and M. W. Hossain, “Dark energy beyond quintessence: Constraints from the swampland,” JHEP 06 (2019), 070 [arXiv:1902.11014 [hep-th]]. [CrossRef]
- O. Trivedi, “Lorentz violating inflation and the swampland,” Eur. Phys. J. Plus 137 (2022) no.4, 507 [arXiv:2106.03578 [hep-th]]. [CrossRef]
- P. Horava, “Quantum Gravity at a Lifshitz Point,” Phys. Rev. D 79 (2009), 084008 [arXiv:0901.3775 [hep-th]]. [CrossRef]
- O. Bertolami and C. A. D. Zarro, “Hořava-Lifshitz Quantum Cosmology,” Phys. Rev. D 84 (2011), 044042 [arXiv:1106.0126 [hep-th]]. [CrossRef]
- T. P. Sotiriou, “Hořava-Lifshitz gravity: a status report,” J. Phys. Conf. Ser. 283, 012034 (2011) [arXiv:1010.3218 [hep-th]]. [CrossRef]
- E. Kiritsis and G. Kofinas, “Hořava-Lifshitz Cosmology,” Nucl. Phys. B 821 (2009), 467-480 [arXiv:0904.1334 [hep-th]]. [CrossRef]
- S. Mukohyama, “Hořava-Lifshitz Cosmology: A Review,” Class. Quant. Grav. 27, 223101 (2010) [arXiv:1007.5199 [hep-th]]. [CrossRef]
- G. Calcagni, “Cosmology of the Lifshitz universe,” JHEP 09 (2009), 112 [arXiv:0904.0829 [hep-th]]. [CrossRef]
- R. Brandenberger, “Matter Bounce in Hořava-Lifshitz Cosmology,” Phys. Rev. D 80 (2009), 043516 [arXiv:0904.2835 [hep-th]]. [CrossRef]
- E. Czuchry, “The Phase portrait of a matter bounce in Hořava-Lifshitz cosmology,” Class. Quant. Grav. 28 (2011), 085011 [arXiv:0911.3891 [hep-th]]. [CrossRef]
- S. Mukohyama, “Dark matter as integration constant in Hořava-Lifshitz gravity,” Phys. Rev. D 80 (2009), 064005 [arXiv:0905.3563 [hep-th]]. [CrossRef]
- T. Zhu, F. W. Shu, Q. Wu and A. Wang, “General covariant Hořava-Lifshitz gravity without projectability condition and its applications to cosmology,” Phys. Rev. D 85 (2012), 044053 [arXiv:1110.5106 [hep-th]]. [CrossRef]
- Y. Huang, A. Wang and Q. Wu, “Inflation in general covariant theory of gravity,” JCAP 10 (2012), 010 [arXiv:1201.4630 [gr-qc]]. [CrossRef]
- M. Chaichian, S. Nojiri, S. D. Odintsov, M. Oksanen and A. Tureanu, “Modified F(R) Hořava-Lifshitz gravity: a way to accelerating FRW cosmology,” Class. Quant. Grav. 27 (2010), 185021 [erratum: Class. Quant. Grav. 29 (2012), 159501] [arXiv:1001.4102 [hep-th]]. [CrossRef]
- E. Elizalde, S. Nojiri, S. D. Odintsov and D. Saez-Gomez, “Unifying inflation with dark energy in modified F(R) Hořava-Lifshitz gravity,” Eur. Phys. J. C 70 (2010), 351-361 [arXiv:1006.3387 [hep-th]]. [CrossRef]
- A. De Felice and S. Tsujikawa, “f(R) theories,” Living Rev. Rel. 13 (2010), 3 [arXiv:1002.4928 [gr-qc]]. [CrossRef]
- V. Faraoni and S. Capozziello, “Beyond Einstein Gravity: A Survey of Gravitational Theories for Cosmology and Astrophysics,” Springer, 2011, ISBN 978-94-007-0164-9, 978-94-007-0165-6 [arXiv:1912.05145 [gr-qc]]. [CrossRef]
- Q. Wu and T. Zhu, “Inflationary Cosmology with Quantum Gravitational Effects and Swampland Conjectures,” Commun. Theor. Phys. 71 (2019) no.9, 1115-1120 . [CrossRef]
- A. J. Lopez-Revelles, R. Myrzakulov and D. Saez-Gomez, “Ekpyrotic universes in F(R) Hořava-Lifshitz gravity,” Phys. Rev. D 85 (2012), 103521 [arXiv:1201.5647 [gr-qc]]. [CrossRef]
- S. Carloni, M. Chaichian, S. Nojiri, S. D. Odintsov, M. Oksanen and A. Tureanu, “Modified first-order Hořava-Lifshitz gravity: Hamiltonian analysis of the general theory and accelerating FRW cosmology in power-law F(R) model,” Phys. Rev. D 82 (2010), 065020 [erratum: Phys. Rev. D 85 (2012), 129904] [arXiv:1003.3925 [hep-th]]. [CrossRef]
- M. Chaichian, M. Oksanen and A. Tureanu, “Hamiltonian analysis of non-projectable modified F(R) Hořava-Lifshitz gravity,” Phys. Lett. B 693 (2010), 404-414 [erratum: Phys. Lett. B 713 (2012), 514] [arXiv:1006.3235 [hep-th]]. [CrossRef]
- J. Kluson, “Note About Equivalence of and Scalar Tensor Hořava-Lifshitz Gravities,” Phys. Rev. D 84 (2011), 104014 [arXiv:1107.5660 [hep-th]]. [CrossRef]
- J. Kluson, S. Nojiri, S. D. Odintsov and D. Saez-Gomez, “U(1) Invariant Hořava-Lifshitz Gravity,” Eur. Phys. J. C 71 (2011), 1690 [arXiv:1012.0473 [hep-th]]. [CrossRef]
| 1 | Throughout this work we will use units where . |
| 2 | This remark is similar to the scenario in string theory where the action in the string frame has not a canonically coupled scalar field and a conformal transformation is performed to the Einstein frame to obtain a canonically coupled scalar field. The only difference is that in our scenario the field is absent in the Jordan frame and it is defined by geometry. |
Figure 1.
Scale factor with in the Jordan frame (Red curve) and in the Einstein frame with negative powers of in F (Blue curve) and with positive powers (Black curve).
Figure 1.
Scale factor with in the Jordan frame (Red curve) and in the Einstein frame with negative powers of in F (Blue curve) and with positive powers (Black curve).
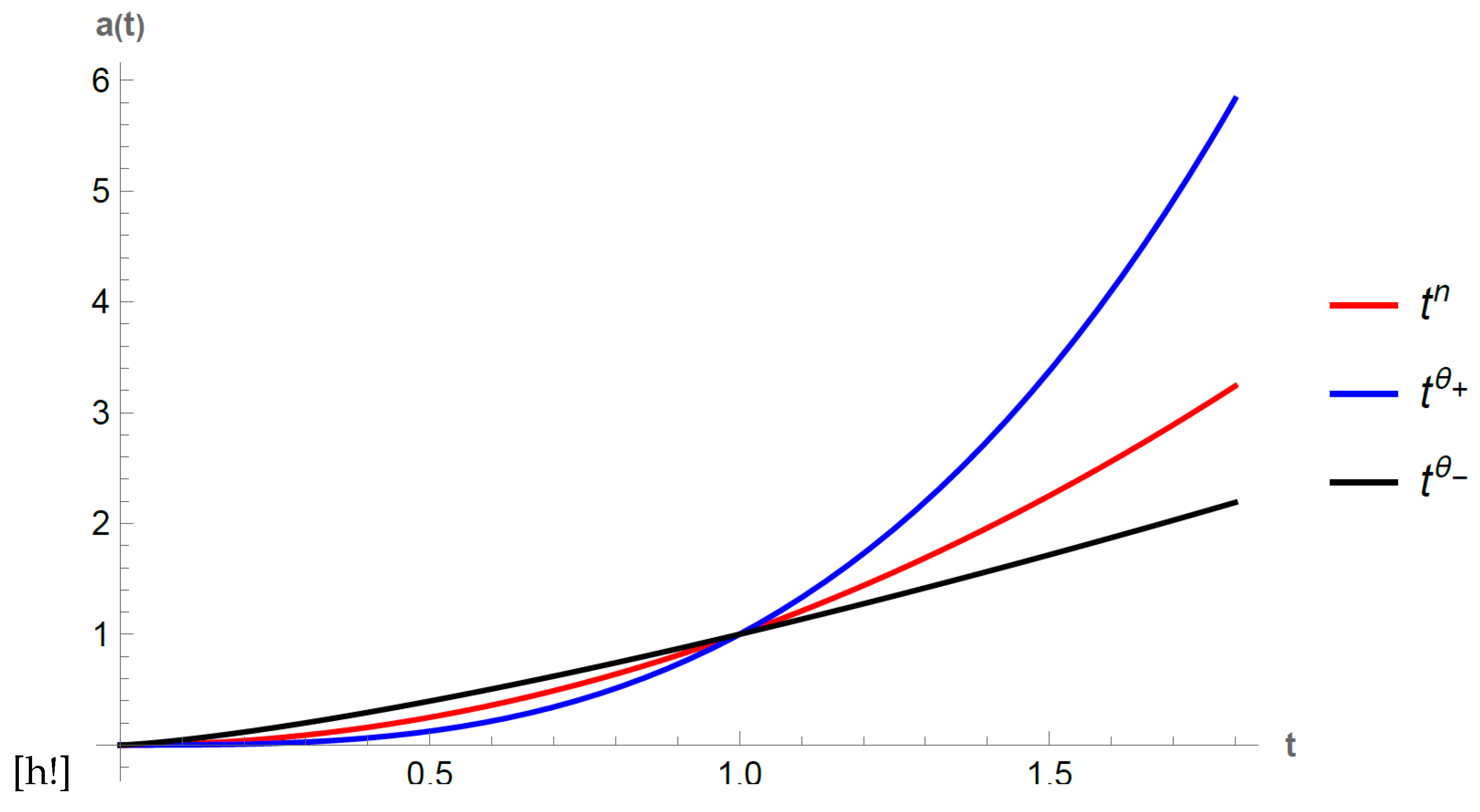
Figure 2.
Scale factor in the Einstein frame for the projectable case with , , and choosing for (Black curve) (Non-projectable case), (Green curve) and (Brown curve). In all cases we have expanding universes.
Figure 2.
Scale factor in the Einstein frame for the projectable case with , , and choosing for (Black curve) (Non-projectable case), (Green curve) and (Brown curve). In all cases we have expanding universes.
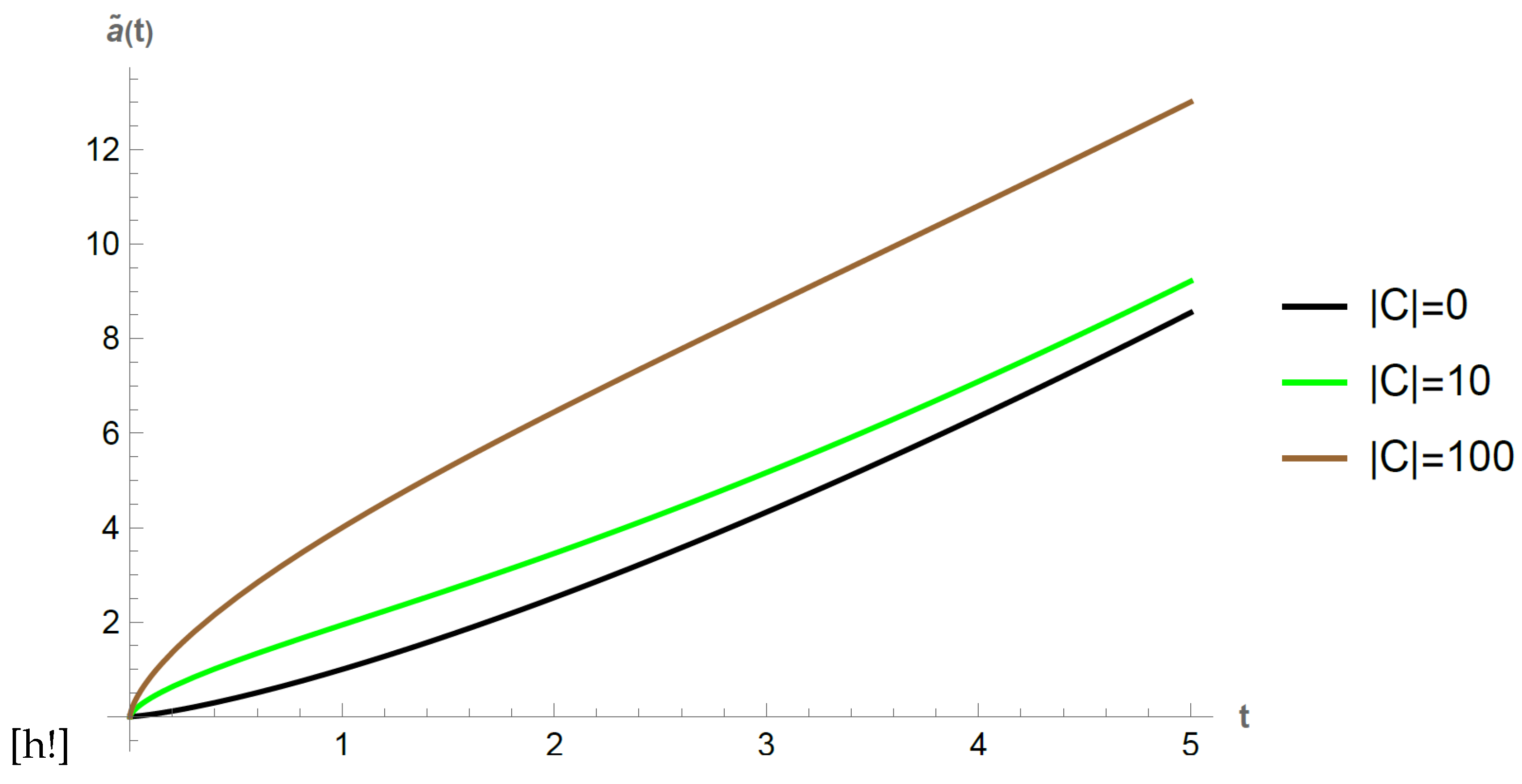
Figure 3.
Allowed values for in agreement with the dS conjecture with . The black horizontal line indicates the lower bound . For the non-projectable case we have . The upper bounds for the non-projectable case are shown when (Blue curve) and when (Red curve). For the projectable case we have the additional term in with and . The corresponding upper bound is shown as well (Yellow curve).
Figure 3.
Allowed values for in agreement with the dS conjecture with . The black horizontal line indicates the lower bound . For the non-projectable case we have . The upper bounds for the non-projectable case are shown when (Blue curve) and when (Red curve). For the projectable case we have the additional term in with and . The corresponding upper bound is shown as well (Yellow curve).
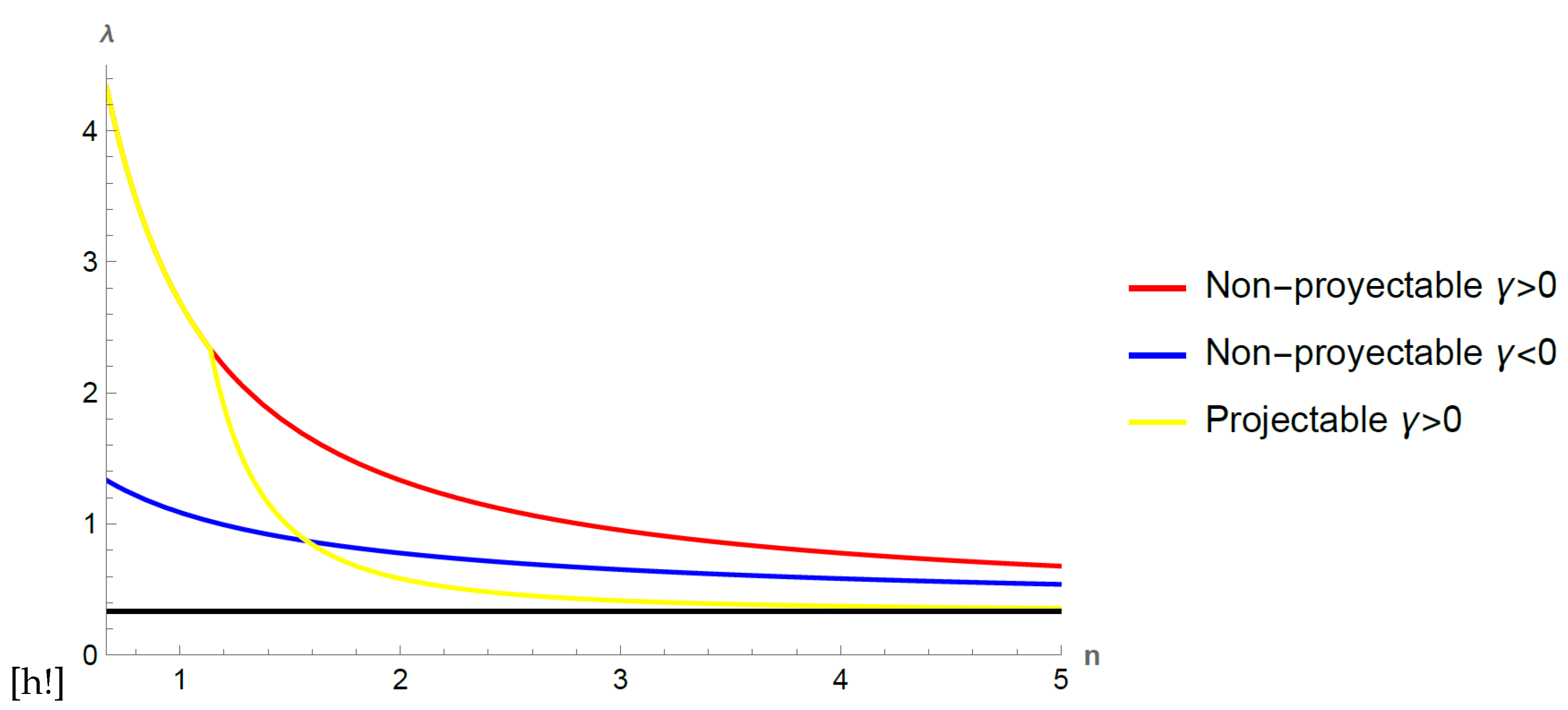
Figure 4.
Allowed values for in the non-projectable general scenario for the negative power term in for and . The lower and upper bounds from the dS conjecture are shown with the red and blue curve respectively. The lower () and upper bound coming from (94) is also shown with the green and black curves respectively. The allowed values of is restricted to the region when the red curve shows smaller values than the black one.
Figure 4.
Allowed values for in the non-projectable general scenario for the negative power term in for and . The lower and upper bounds from the dS conjecture are shown with the red and blue curve respectively. The lower () and upper bound coming from (94) is also shown with the green and black curves respectively. The allowed values of is restricted to the region when the red curve shows smaller values than the black one.
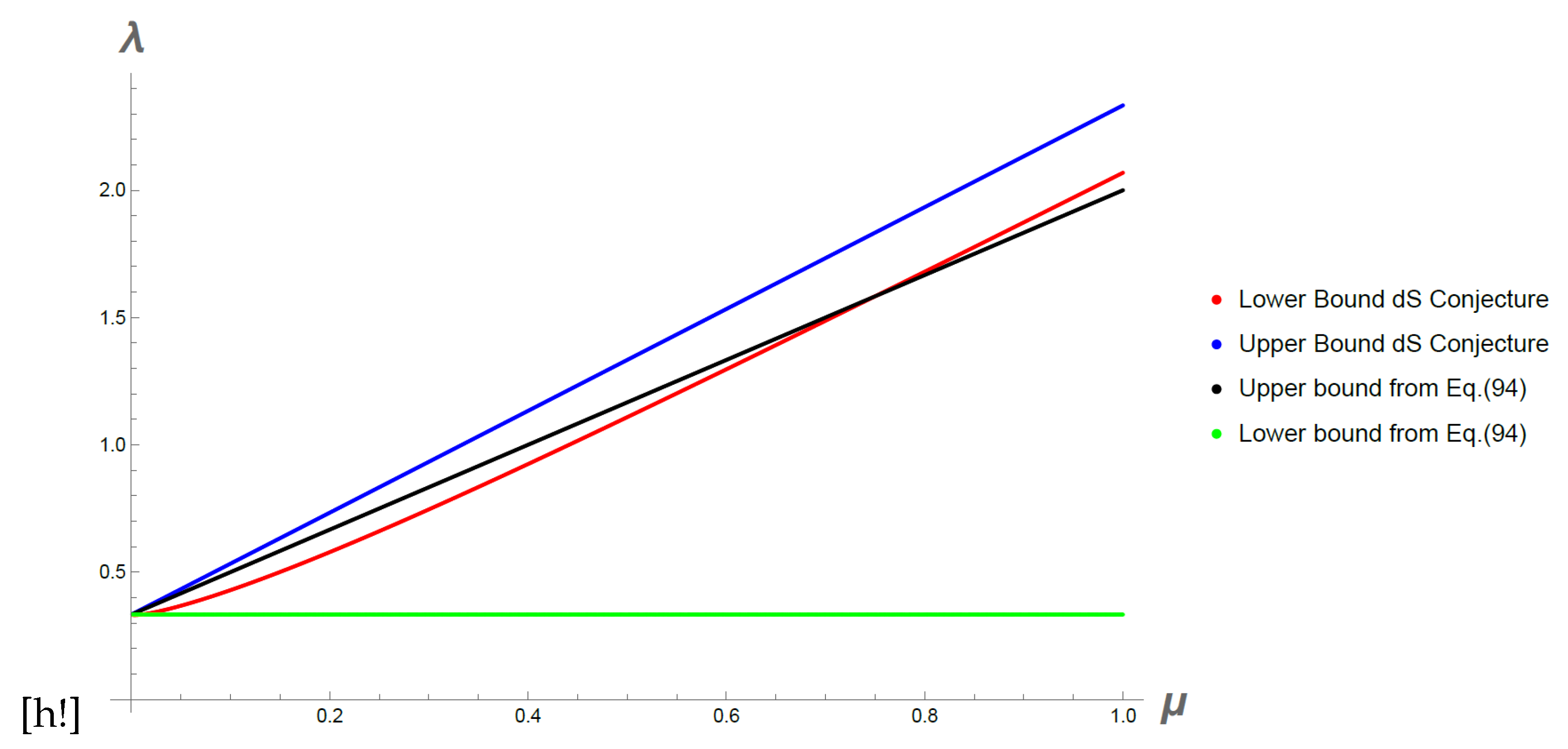
Figure 5.
Allowed values for in the non-projectable general scenario for the positive power term in for and . The lower () and upper bounds from (94) is shown with the green and red curves respectively. The upper bound from the dS conjecture is shown with the blue curve. For big enough values of there is two allowed regions, we show only the lowest upper bound since the other region is inconsistent with (94).
Figure 5.
Allowed values for in the non-projectable general scenario for the positive power term in for and . The lower () and upper bounds from (94) is shown with the green and red curves respectively. The upper bound from the dS conjecture is shown with the blue curve. For big enough values of there is two allowed regions, we show only the lowest upper bound since the other region is inconsistent with (94).
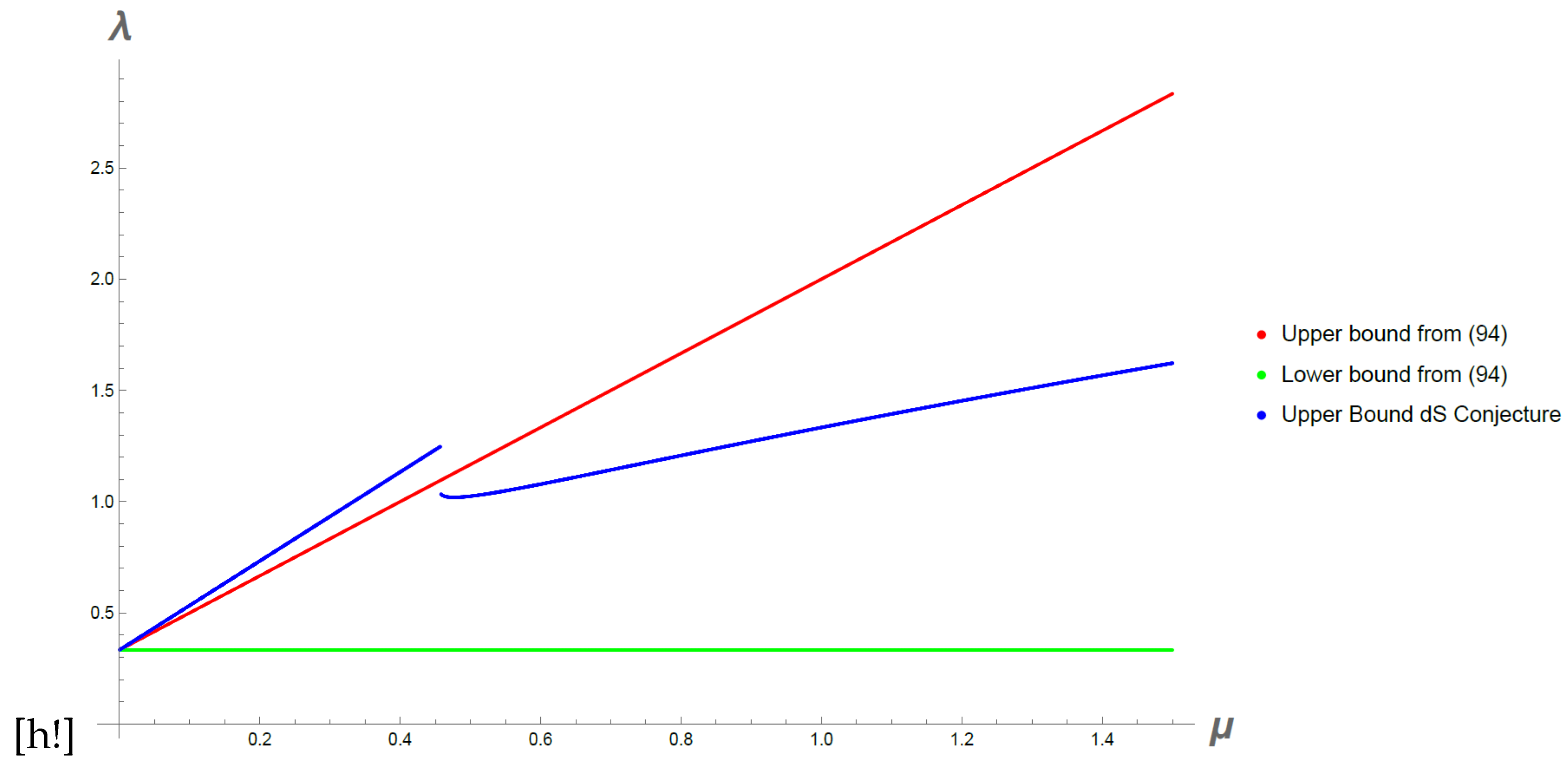
Figure 6.
Allowed values for in the general scenario with proyectability for and . The lower () and upper bounds from (94) is shown with the green and red curves respectively. The upper bound from the dS conjecture is shown with the blue curve. The lower bound from (106) is shown with the black curve. The allowed values for is restricted to the region when the black curve gives smaller values than the blue or red curves.
Figure 6.
Allowed values for in the general scenario with proyectability for and . The lower () and upper bounds from (94) is shown with the green and red curves respectively. The upper bound from the dS conjecture is shown with the blue curve. The lower bound from (106) is shown with the black curve. The allowed values for is restricted to the region when the black curve gives smaller values than the blue or red curves.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated





