Prerpints.org logo
Preprint
Article

Theoretical Study of Measuring Moving MEGs with 83Kr Based Atomic Co-Magnetometer

Altmetrics

Downloads

114

Views

52

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

09 September 2023

Posted:

12 September 2023

You are already at the latest version

Alerts
Abstract
K-Rb-83Kr based atomic co-magnetometer for measuring moving MEGs is theoretically studied in this paper. Parameters such as the spin exchange rates, the spin dephasing rates and the polarization of the nuclear spins are studied to configure the co-magnetometer. Results show that the nuclear spin could generate around 700 nT magnetic field under which the nuclear spin could compensate wide range of magnetic fields. We also showed the hybrid optical pumping vapor cell fabrication process in this paper. Alkali metals were mixed in a glove box and then was connected to the alkali vapor cell fabrication system. The vapor cell fabrication process is illustrated in this paper.
Keywords: 
Subject: Physical Sciences  -   Optics and Photonics

1. Introduction

MEGs recordings have found various applications, including the source localization of epilepsy-related seizures to aid in planning epilepsy surgery[1,2], studying brain’s response to specific external stimuli which helps map motor system[3], sensory areas[4], language, vision, etc. MEGs signal recordings could also be used for early stage of Alzheimer’s disease diagnosis[5] and cerebral networks of the tremor syndromes[6]. Traditional MEGs measurement equipment is typically SQUID(super conducting quantum interference device) in which very large helmet with liquid helium are used which limits the application of the magnetometer to the motor system such as freely moving of a person’s head as the MEGs is measured[7,8].
With the development of Optically Pumped Magnetometer(OPM) which could work under room temperature as well as reach sensitivity to that of a SQUID magnetometer[9], the future MEGs equipment could be wearable[10,11,12]. A wearable OPM system together with EEGs(electroencephalography) have been combined for the brain function study[13]. This could reinforce more application of the MEGs equipment such as the motor system related space navigation of the brain, MEGs of visual-motor integration.
Even though the OPMs are wearable and movable, a quite important technique problem should be considered. Different from the EEGs in which there is no large background electric field in the environment, the MEGs recording are recorded on the earth which means that the geomagnetic field could affect the MEGs recording. We know that the brain magnetic field is quite weak compared with the geomagnetic field. Thus magnetic field shield rooms(MSR) are typically used for suppression of the environment magnetic field. Moreover, the penetration of magnetic field into the MSR still could affect the MEGs recording. In order to record the moving MEGs, a large bi-planar coil was used for the moving related background magnetic field compensation[14]. A person could only move in a small area as well as very tiny movement could be done such as drinking water during the MEGs recording[8]. In order to overcome the head movements bluring of the topography of the neuronal sources, a novel method based on monitors head position was developed. An offline analysis method that takes into account the head position time-series[15] was considered. In order to enable ambulatory movement in wearable MEGs, a matrix coil active magnetic shielding was used[16]. Some other method based on magnetic field compensation was also studied[17,18,19]. Magnetic field differential method also can be used for background magnetic field suppression[20].
Even though so many methods have been developed for moving MEGs measurement, most of these methods based on magnetic field compensation in the space of the movement. Large compensation coils are required which could make the system very complicate. Moreover, the compensation method could not compensate the magnetic field for each sensor head and some of the sensors could be over compensated or under compensated.
As we understand, the crucial aspect of moving MEGs lies in compensating for fluctuations in the magnetic field. The method based on hyperpolarized nuclear spins could also be used[7]. The nuclear spin method could compensation magnetic field in-situ as well as automatically compensated fluctuation magnetic field in each of the OPMs. Complicated compensation coils are not needed, resulting in a significant reduction in the system’s volume.
The hyperpolarized nuclear spins include 3 He, 21 Ne, 129 Xe, 131 Xe. The first demonstration of the moving MEGs measurement is with 21 Ne[7]. There is a large spin exchange rate between 21 Ne and alkali atoms such as K or Rb. 21 Ne nuclear spin could be easily polarized even though it owns a very large quadrupolar relaxation rate[21]. 21 Ne nuclear spins are widely used for rotation sensing or studying of fundamental Physics[22,23,24,25,26]. However, due to the very low natural abundance of isotope enriched 21 Ne nuclear spins, it is very expensive to buy such gases. The 3 He nuclear spins owns a very small spin exchange optical pumping rate with the alkali metals, thus it is very hard to polarize the 3 He nuclear spins. Moreover, the 3 He nuclear spins are pretty sensitive to magnetic field gradients and can be easily depolarized in a holding magnetic field. Even the stem of a vapor cell could affect the spin polarization of the nuclear spins[27,28,29]. 129 Xe, 131 Xe could also be used. However, due to the large collision relaxation with the container walls, it is hard to polarize the nuclear spins[30,31,32]. For 83 Kr nuclear spins whose atom mass is much smaller than that of the Xe atoms, we could estimate a smaller wall relaxation as well as a weaker interaction strength between the alkali atoms. 83 Kr could be a good candidate for the moving MEGs measurement. In this paper, we will focus on the study of 83 Kr nuclear spins for fluctuation background magnetic field compensation in the moving MEGs measurement.

2. Theory

2.1. Relaxation of 83 Kr

The nuclear spin based field compensation method for moving MEGs is heavily related to the nuclear spin polarization which is closely related to the spin relaxation of the nuclear spins. The 83 Kr atom owns a nuclear spin of I = 7 / 2 and thus it owns a quadrupole moment. We can estimate that the quadrupolar relaxation would be the main relaxation process of the nuclear spins. Moreover, the container wall related quadrupolar relaxation of the nuclear spins as well as the quarupolar relaxation between 83 Kr- 83 Kr collision are the main relaxation process.
The quadrupolar relaxation between 83 Kr- 83 Kr collision is related to the number density of the 83 Kr atoms. The higher number density of the nuclear spins, the faster of the relaxation which is caused by the quadrupolar interaction. It is reported that the relationship between the quadrupolar relaxation time T 1 and the number density of the nuclear spins ρ in Amagat(1 Amagat is 2.69 × 10 19 / c m 3 ) is 1 / T 1 = ρ ( 2.13 ± 0.05 ) × 10 − 3 s − 1 [33]. For a typical condition of 50Torr gas was used, the relaxation rate of the gas phase 83 Kr collision is 1.4 × 10 − 4 s − 1 .
The quadrupolar relaxation with the container wall and the spin exchange relaxation with the alkali atoms are the main relaxation processes which is around an order higher than that of the 83 Kr- 83 Kr collision process. Since 83 Kr owns a quadrupole moment, the nuclear spins could be relaxed as them collide with the container wall of the vapor cell on which the impurities in the wall could produces electric field gradients(EFGs). The spin exchange optical pumping process with the alkali atoms could also cause the decay of the nuclear spin polarization. Spin momentum could transfer between alkali atoms and 83 Kr atoms. Note that the spin exchange process could also be the pumping process which could made the nuclear spins be polarized. We define the total relaxation rate of the 83 Kr nuclear spins[31] to be:
( 1 T 2 ) m , n = f m , n < ω Q 2 > J ( 0 ) + σ e x v ¯ n R b ,
m and n represent the energy level and in our study we typically consider the m=1/2 and n=-1/2 sublevels. For the 83 Kr nuclear spins we can calculate f m , n = 5 / 4 in the equation 118 of the reference[34].
< ω Q 2 > = ( 3 e 2 Q ( 1 − γ ∞ ) 2 ℏ I ( 2 I − 1 ) ) 2 < q 2 > ,
includes that mean square of the local quadrupole coupling-constant < e 2 q Q ( 1 − γ ∞ ) h − 1 > 2 as a measure of the mean interaction strength at the surface wall site. In the reference, the coupling-constant is measured to be 5.6MHz for the 83 Kr atoms on the typical Duran glass[31]. I is the nuclear spin quantum number of 83 Kr. ℏ is the Planck’s constant. Note that q is equal to < q 2 > which is defined to be the root mean square of the electric field gradient. With the parameters, we can calculate < ω Q 2 > which is approximately not temperature dependent. J ( 0 ) is defined to be the spectral density function at zero frequency. It is related to the stochastic sequence of the wall collisions and the thermally activated surface diffusion. In our experiment condition, it is believed diffusion along the surface is strongly hindered and the quadruple relaxation is governed by the adsorption and desorption processes.
J ( 0 ) ≈ τ s 2 τ v ∝ e x p ( 2 E A / k B T )
where τ v equals to v ¯ S / 4 V which is the average time of the nuclear spin move to the wall. 8 k B T / π M is the average velocity of the nuclear spins. V is the volume of the vapor cell and S is the over all surface of the vapor cell. k B is the Boltzmann constant. E A is the activation energy of desorption. We could not directly get τ s which is defined to be the adsorption time of the nuclear spins on the surface wall. However, we can use the squared phase angle < θ 2 > in the reference[31] to acquire τ s . Use the relation τ s 2 = ( τ 0 e x p ( 2 E A / k B T ) ) 2 = < θ 2 > / < ω Q 2 > , we can calculate τ s with the measured < θ 2 > under 373K to be 4.9 × 10 − 8 r a d 2 .
The total relaxation of 83 Kr also includes the spin exchange interaction with the Rb atom spins which will be considered in our study. The spin exchange interaction cross section σ e x , the velocity v ¯ and the number density of Rb n R b will determine the relaxation rate. Based on the spin exchange term σ e x v ¯ 2 = 1.9 × 10 − 12 c m 4 s − 2 measured in the reference[31], we can get a numerical simulation of the total relaxation rate in Figure 1.

2.2. Polarization of 83 Kr

The polarization of the nuclear spin is very important because it could determine the magnetic field experienced by the electron spins. With the relaxation and the spin exchange optical pumping rate between alkali atoms and the nuclear spins, we can determine the polarization of the nuclear spins. In Equation. (1), the term σ e x v ¯ n R b also can be defined to be the spin exchange optical pumping rate between Rb and the nuclear spins. The polarization of the nuclear spins can be defined to be:
P n = P e σ e x v ¯ n R b f m , n < ω Q 2 > J ( 0 ) + σ e x v ¯ n R b ,
Where P e is the polarization of the electron spin. We can see that the highest polarization of the nuclear spin could reach that of the electron spins. It is known that the polarization of the electron spin could be 0.5 under which the magnetometer owns a highest sensitivity. Thus, we can let P e to be 0.5. We can do a numerical simulation for the polarization of the nuclear spins with the change of the temperature. Figure 2a shows the results.
In order to compensate for the fluctuation background magnetic field experienced by the electron spins used in brain magnetic field sensing, it is necessary to calculate the magnetic field generated by the nuclear spins. B n . We can estimate that the larger the nuclear spin magnetic field, the higher compensation ability of the nuclear spins. The magnetic field produced by the nuclear spins could be defined to be:
B n = 8 3 π k 0 μ K r n K r P n ,
In which k 0 is the Fermi Contact interaction enhancement factor and it is equal to 270 for R b − 83 K r pair[35,36]. μ K r is the magnetic moment of the 83 K r nuclear spin. n K r is the number density of the nuclear spins. We suppose that the partial pressure of 83 K r gas inside the vapor cell is 50Torr. We can do a simulation of the nuclear spin magnetic field with the change of the temperature. Figure 2b shows the result.

2.3. Relaxation of Rb and fundamental sensitivity

The relaxation of Rb need to be considered because it is related to the spin projection noise of the co-magnetometer. Since Rb is used for the detection of the brain’s magnetic field as well as the nuclear spins’ compensation magnetic field. The sensitivity of the magnetometer could greatly be determined by the relaxation of Rb. The relaxation of Rb caused by several collision processes such as the collision with itself, the collision with the N 2 quenching buffer gas and the collision with 83 K r nuclear spins[37]. These collision relaxation rates are closely related to the collision cross sections and number densities of the gases. We do a simulation about the relaxation rates and Figure 3 shows the results. We change the temperature of the vapor cell and thus both of the Rb-Rb spin destruction relaxation and Rb- 83 Kr spin exchange relaxation changes with the temperature. The spin destruction rate of Rb- N 2 is weakly temperature dependent. We also show the relationship between the temperature and the Rb- 83 Kr spin exchange relaxation rates.
After we have got the total relaxation of Rb electron spins, then we can calculate the fundamental sensitivity of the co-magnetometer which is limited by the spin projection noise. The fundamental sensitivity of the co-magnetometer is limited by the total relaxation of the atomic spins, the number density of the spins and the volume of the vapor cell. The fundamental sensitivity of the co-magnetometer is defined to be δ B :
δ B = 1 γ e Q ( P e ) R t o t n R b V ,
In which γ e is the gyro-magnetic ratio of the electron spin. Q ( P e ) is the slow down factor of the Rb electron spins[9]. R t o t is the total relaxation of the Rb spins which has been calculated in the last subsection. n R b is the number density of Rb which is related to the temperature of the vapor cell. V is the interact vulume of the Rb atoms with the laser light. With the equation, we can calculate the fundamental sensitivity of the co-magnetometer with the changes of temperature and the interact volume. Figure 4 shows the results. We can see that even in a very small volume(0.002 c m 3 ), we can get more than 10fT sensitivity if the temperature of the vapor cell is high enough. This means that we can fabricate very small sensor head for the MEGs detection. The space resolution is quite high if we use relatively high temperature of the vapor cell.

3. Cell Fabrication

3.1. K-Rb mixture preparation

In order to achieve very high nuclear spin polarization as well as reduce the spin exchange relaxation between the Rb and 83 K r nuclear spins, hybrid optical pumping is a good solution. If we want to achieve very high nuclear spin polarization, we need to rise the vapor cell temperature. However, the high temperature vapor cell could lead to very large optical depth and thus the laser light could not easily pass the medium. The polarization of the nuclear spins could be decreased. Hybrid optical pumping is need. We can achieve very high nuclear spin polarization.
We need to prepare the alkali vapor cell before the experiment could be done. The hybrid optical pumping cell need mixture of alkali metals to be filled. Before the vapor cell was filled with K-Rb mixture by torch flame on the fabrication apparatus, the K-Rb mixture with intended Mole Fraction Ratio(MFR) should be prepared in the glove box first.
When preparing the K-Rb mixture, the mass ratio of K and Rb should be determined first. The mass ratio is defined to be M r = m K / ( m R b + m K ), where m K is the mass of K and m R b is the mass of Rb. The mass ratio determines the MFR and density ratio of K and Rb in a Hybrid Pumping Cell(HPC)[38]. In a K − R b − 87 K r co-magnetometer, the density ratio Dr of K to Rb could be controlled for improving the uniformity of the spin polarization at the operation temperature. For example, we could prepare the groups of the mixture with the density ratios of 1/212 and 1/109 at 463K after the cell was filled with them respectively. In order to reach to the intended Dr, Table 1 shows the mass of K and Rb which should be mixed together in the glove box.
The calculation of the mass of K and Rb determines the amount of alkali metal which should be mixed together in the glove box. Before the mixing of the alkali metals, the glass wares used in this experiment were cleaned before they were put into the glove box to pretend the alkali metals from impurities. All of the glass wares were immersed into piranha solution and cleaned by the ultrasonic cleaner for 5 minutes. Several times of rinsing with deionized water were implied to rinse away the residual piranha solution. After the cleaning, the glass wares were quickly put into a drying box for several hours to get rid of water on the glass wares. When the glass wares were put into the transfer chamber of the glove box, the gases in the chamber were pumped away to further dry the glass ware.
The mixing of the K-Rb metals were done after the low concentration of oxygen condition in glove box was realized. The commercial Rb and K ampoules were broken open. A homemade glass spoon was used to scoop the Rb and K metal out of the ampoules. The glass knife cut the metals to small pieces in the petri dish. A piece of weighting paper was put on the analytical balance to weight the pieces of alkali metals. According the calculation results in Table 1, 30mg of K and 2.13g of Rb were added to the homemade break seal ampoule to get the 1/212 D r at 463K in a hybrid pumping cell. A Teflon valve and an O-ring sealed the alkali metal mixture in the ampoule to protect the mixture from air when the ampoule was taken out of the glove box. To seal the mixture in the glass ampoule and protect the mixture from air, a vacuum pump was used to pump out the gases in the ampoule. Methane flame was used to seal the glass at the neck of the ampoule as the pumping was on. The mixture was finally sealed in the glass ampoule. Figure 5 shows this process. For HPCs with small MFRs, we used glass knife to cut the alkali metal into small pieces whose weight was about 30mg. Moreover, we used a valve and pumping technique to protect the mixture from oxygen and water after the ampoules were moved out of the glass box.

3.2. Alkali Chasing and Gas filling

The mixture break seal ampoule was attached to the alkali vapor cell fabrication apparatus and the cell fabrication process began after the ampoule was ready. Figure 6 shows the method of filling the vapor cells with the K-Rb mixture. The K-Rb mixture ampoule was connected to the alkali fabrication apparatus by a glass tube. An iron hammer was sealed in the vertical glass tube which was connected with the ampoule to break the seal. The vapor cell was connected to the glass tube and the glass tube was connected to the vacuum pumping system and the gas line system. The vacuum pumping system pumped the whole system and the gas line system supplied the vapor cell with gases such as 21 N e , 131 Xe, 129 Xe, 83 K r , N 2 . The gas line system and the vacuum pumping system were similar to the system described in this reference[39]. All the glass wares were cleaned by piranha solution and deionized water as that of the glass wares used to make the mixture ampoule. To further clean the surface of the glass wares, after they were connected to the fabrication system, an oven can was used to heat the glass wares at about 473K when the pumping system was on. After 2 to 3 days’ heating and pumping, the vacuum pressure reached 10 − 5 Pa level. The vapor cells were filled with K-Rb mixture when the vacuum reached to 10 − 5 Pa level. Then the K-Rb mixture was chased by flame into the retort slowly for thoroughly mixing the K-Rb alloy and purifying the alloy. The ampoule was firing off at the small neck of the glass tube after the mixture was chased into the retort. After that, the mixture was chased into the vapor cell and experiment results showed that Rb moves faster than K for the lower melting point of Rb. As a result, special chasing method was developed to ensure the MFR in the HPC was right. Most of the mixture was chased into the cell and then chased out of the cell to leave the amount of alloy that was needed. This process could ensure that the MFR in the cell were close to the MFR in the ampoule. Figure 6 shows the schematic of the filling process.
After the vapor cells were filled with alkali metal mixtures, the vapor cells were filled with gases by the gas line. In some of the experiment, the vapor cell is filled with about 2 Atm gases. For sealing the glass by flame, the cell can’t be until the inner pressure is lower than the pressure outside. Liquid nitrogen was used to fill the cell with gases more than 1 Atm.
Figure 6 shows the schematic of the filling the glass cell with gas whose pressure was more than 1 Atm. The liquid nitrogen trap was taken down and the temperature of the trap raise to room temperature before the gas filling. The needle valve handled the gas into the cell and the pressure gauge measured the pressure of the cell. When reaching the intended pressure P 0 , the gas line was shut down. The homemade dewar was filled with liquid nitrogen and the dewar was lift by a lifting platform to immerse the cell into liquid nitrogen. The pressure decreased and settled down to a lower pressure P 1 . Torch flame was used to fire off the stem of the cell and the pressure raise a little to P 2 . This phenomenon was due to the rising of the temperature of the cell when the flame was used to fire off the cell from the glass tube. In order to know exactly the pressure of the cell after it was fired off from the glass tube and the temperature of the cell raise to the room temperature, the ideal gas equation was used to calculate the pressure. The volume of the cell was measured to be V c and the volume of the glass tube and the gas line tube was measured to be V g (the measurement method is described below). The pressure of the cell at room temperature should be:
P c = P 0 + ( P 0 − P 2 ) V g V c
V g was measured by the ideal gas equation either and a standard calibration volume was used to measure it. Suppose that the standard calibration volume was V c a l and the calibration volume was pumped to vacuum state. Gas was filled in V g and the pressure is P g 0 . After opening the angle valve of the calibration volume, the pressure changed into P g 1 . The volume of the glass tube and the gas line was calculated to be:
V g = P g 1 V c a l P g 0 − P g 1
After the volume V g was measured, the cell pressure P c was calculated by Eq.(6) finally. P c is the pressure of the gases in the vapor cell at room temperature.

4. Discussion

This paper theoretically studied the 83 Kr based atomic co-magnetometer which is promising for moving MEGs recording. Due to the large fermi contact interaction with Rb electron spins, the compensation field produced by the nuclear spin is quite large. A wide compensation range can be achieved, which is of utmost importance for effectively compensating for fluctuation background magnetic fields in the future. Due to the small destruction collision relaxation rate with the 83 Kr atoms, Rb magnetometer could reach very high sensitivity. Experimental setup is under way to configure a K-Rb- 83 Kr co-magnetometer. Moreover, this is the first time that a 83 Kr based co-magnetometer studied.
As we know that the co-magnetometer is also sensitive to rotation velocity. For the 83 Kr based atomic co-magnetometer, the nuclear spin is 7 / 2 and we can estimate a very small gyro-magnetic ratio which means that the co-magnetometer is quite sensitive to the rotations. As we measure the moving related MEGs, we may only measure movement without rotations. Anyway, further experiment need to be done to study this. The study of 83 Kr based atomic co-magnetometer also contribute to the gyroscope study.
The relaxation rate, polarization and fundamental sensitivity are quite important parameters for atomic co-magnetometer. Note that the 83 Kr nuclear spin relaxation is quite complicated since the quadupolar relaxation with wall as well as with the nuclear spin itself should be considered. Especially collision with the wall, the desorption energy, the collision related average angle should be studied. The quadrupolar interaction process makes the simulation more complicated. Our results give very concrete evidence for the future co-magnetometer design.
At the last part of the paper, we shows the alkali fabrication process. Especially, the hybrid optical pumping is need. We gives the details on how to make a hybrid pumping vapor cell. We also gives the alkali fabrication process with the glass blowing technique.

5. Conclusions

In conclusion, we have theoretically designed a new kind of atomic co-magnetoemter which is based on 83 Kr nuclear spins. Compared with 21 Ne, 3 He and 129 Xe based atomic co-magnetometers, the new co-magnetometer have the merits of high sensitivity, relatively lower temperature and large compensation field range. We conclude that 83 Kr based co-magnetometer is quite promising for moving MEGs recording. This is the first time that such atomic co-magnetometer has been designed. We give the key parameters for the design of the co-magnetometer such as the spin relaxations and polarization. These parameters are highly important for the future experimental results. Considering that the alkali vapor cell is quite important for the co-magnetometer, we show the method to develope hybrid optical pumping vapor cells. The study in this paper prove to be highly valuable for the future experimental setup.

Author Contributions

Conceptualization, Yao Chen; methodology, Ruyang Guo and Jiyang Wang; investigation, Mingzhi Yu and Man Zhao; writing—original draft preparation, Yao Chen; supervision, Libo Zhao. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by National Natural Science Foundation of China under grant number 62103324, China Postdoctoral Science Foundation under grant number 2020M683462, National key research and development program under grant number 2022YFB3203400. We want to thank for all these agency for the supporting.

Data Availability Statement

Data underlying the results presented in this paper are not publicly available at this time but may be obtained from the authors upon reasonable request.

Acknowledgments

We want to give special thanks for Prof. Libo Zhao’s supervising of this study.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Knowlton, R.C.; Shih, J. Magnetoencephalography in Epilepsy. Epilepsia 2004, 45, 61–71. [Google Scholar] [CrossRef] [PubMed]
  2. Englot, D.J.; Nagarajan, S.S.; Imber, B.S.; Raygor, K.P.; Honma, S.M.; Mizuiri, D.; Mantle, M.; Knowlton, R.C.; Kirsch, H.E.; Chang, E.F. Epileptogenic zone localization using magnetoencephalography predicts seizure freedom in epilepsy surgery. Epilepsia 2015, 56, 949–958. [Google Scholar] [CrossRef] [PubMed]
  3. Boon, L.I.; Geraedts, V.J.; Hillebrand, A.; Tannemaat, M.R.; Contarino, M.F.; Stam, C.J.; Berendse, H.W. A systematic review of MEG-based studies in Parkinson’s disease: The motor system and beyond. Human Brain Mapping 2019, 40, 2827–2848. [Google Scholar] [CrossRef] [PubMed]
  4. Lin, C.H.; Tierney, T.M.; Holmes, N.; Boto, E.; Leggett, J.; Bestmann, S.; Bowtell, R.; Brookes, M.J.; Barnes, G.R.; Miall, R.C. Using optically pumped magnetometers to measure magnetoencephalographic signals in the human cerebellum. The Journal of Physiology 2019, 597, 4309–4324. [Google Scholar] [CrossRef] [PubMed]
  5. López-Sanz, D.; Serrano, N.; Maestú, F. The Role of Magnetoencephalography in the Early Stages of Alzheimer’s Disease. Frontiers in Neuroscience 2018, 12. [Google Scholar] [CrossRef] [PubMed]
  6. Timmermann, L.; Gross, J.; Butz, M.; Kircheis, G.; Haussinger, D.; Schnitzler, A. Pathological oscillatory coupling within the human motor system in different tremor syndromes as revealed by magnetoencephalography. Neurology & clinical neurophysiology : NCN 2004, 2004, 26. [Google Scholar]
  7. Chen, Y.; Zhao, L.; Ma, Y.; Yu, M.; Wang, Y.; Zhang, N.; Wei, K.; Jiang, Z. Spin exchange optically pumped nuclear spin self compensation system for moving magnetoencephalography measurement. Biomed. Opt. Express 2022, 13, 5937–5951. [Google Scholar] [CrossRef] [PubMed]
  8. Boto, E.; Holmes, N.; Leggett, J.; Roberts, G.; Shah, V.; Meyer, S.S.; Muñoz, L.D.; Mullinger, K.J.; Tierney, T.M.; Bestmann, S. Moving magnetoencephalography towards real-world applications with a wearable system. Nature 2018, 555, 657. [Google Scholar] [CrossRef]
  9. Kominis, I.; Kornack, T.; Allred, J.; Romalis, M.V. A subfemtotesla multichannel atomic magnetometer. Nature 2003, 422, 596–599. [Google Scholar] [CrossRef]
  10. Xia, H.; Ben-Amar Baranga, A.; Hoffman, D.; Romalis, M. Magnetoencephalography with an atomic magnetometer. Applied Physics Letters 2006, 89, 211104. [Google Scholar] [CrossRef]
  11. Shah, V.K.; Wakai, R.T. A compact, high performance atomic magnetometer for biomedical applications. Physics in Medicine & Biology 2013, 58, 8153. [Google Scholar]
  12. Borna, A.; Carter, T.R.; Colombo, A.P.; Jau, Y.Y.; McKay, J.; Weisend, M.; Taulu, S.; Stephen, J.M.; Schwindt, P.D. Non-invasive functional-brain-imaging with an OPM-based magnetoencephalography system. Plos one 2020, 15, e0227684. [Google Scholar] [CrossRef] [PubMed]
  13. Boto, E.; Seedat, Z.A.; Holmes, N.; Leggett, J.; Hill, R.M.; Roberts, G.; Shah, V.; Fromhold, T.M.; Mullinger, K.J.; Tierney, T.M.; Barnes, G.R.; Bowtell, R.; Brookes, M.J. Wearable neuroimaging: Combining and contrasting magnetoencephalography and electroencephalography. NeuroImage 2019, 201, 116099. [Google Scholar] [CrossRef] [PubMed]
  14. Holmes, N.; Leggett, J.; Boto, E.; Roberts, G.; Hill, R.M.; Tierney, T.M.; Shah, V.; Barnes, G.R.; Brookes, M.J.; Bowtell, R. A bi-planar coil system for nulling background magnetic fields in scalp mounted magnetoencephalography. Neuroimage 2018, 181, 760–774. [Google Scholar] [CrossRef] [PubMed]
  15. Stolk, A.; Todorovic, A.; Schoffelen, J.M.; Oostenveld, R. Online and offline tools for head movement compensation in MEG. NeuroImage 2013, 68, 39–48. [Google Scholar] [CrossRef]
  16. Holmes, N.; Rea, M.; Hill, R.M.; Leggett, J.; Edwards, L.J.; Hobson, P.J.; Boto, E.; Tierney, T.M.; Rier, L.; Rivero, G.R.; Shah, V.; Osborne, J.; Fromhold, T.M.; Glover, P.; Brookes, M.J.; Bowtell, R. Enabling ambulatory movement in wearable magnetoencephalography with matrix coil active magnetic shielding. NeuroImage 2023, 274, 120157. [Google Scholar] [CrossRef] [PubMed]
  17. Rea, M.; Holmes, N.; Hill, R.M.; Boto, E.; Leggett, J.; Edwards, L.J.; Woolger, D.; Dawson, E.; Shah, V.; Osborne, J.; Bowtell, R.; Brookes, M.J. Precision magnetic field modelling and control for wearable magnetoencephalography. NeuroImage 2021, 241, 118401. [Google Scholar] [CrossRef]
  18. Mellor, S.; Tierney, T.M.; O’Neill, G.C.; Alexander, N.; Seymour, R.A.; Holmes, N.; López, J.D.; Hill, R.M.; Boto, E.; Rea, M.; Roberts, G.; Leggett, J.; Bowtell, R.; Brookes, M.J.; Maguire, E.A.; Walker, M.C.; Barnes, G.R. Magnetic field mapping and correction for moving OP-MEG. IEEE Transactions on Biomedical Engineering 2021. [Google Scholar] [CrossRef]
  19. Tierney, T.M.; Alexander, N.; Mellor, S.; Holmes, N.; Seymour, R.; O’Neill, G.C.; Maguire, E.A.; Barnes, G.R. Modelling optically pumped magnetometer interference in MEG as a spatially homogeneous magnetic field. NeuroImage 2021, 244, 118484. [Google Scholar] [CrossRef]
  20. Pratt, E.J.; Ledbetter, M.; Jiménez-Martínez, R. ; others. Kernel Flux: a whole-head 432-magnetometer optically-pumped magnetoencephalography (OP-MEG) system for brain activity imaging during natural human experiences. Optical and Quantum Sensing and Precision Metrology. International Society for Optics and Photonics, 2021, Vol. 11700, p. 1170032.
  21. Chen, Y.; Quan, W.; Zou, S.; Lu, Y.; Duan, L.; Li, Y.; Zhang, H.; Ding, M.; Fang, J. Spin exchange broadening of magnetic resonance lines in a high-sensitivity rotating K-Rb-21Ne co-magnetometer. Scientific reports 2016, 6, 36547. [Google Scholar] [CrossRef]
  22. Brown, J.M.; Smullin, S.J.; Kornack, T.W.; Romalis, M.V. New Limit on Lorentz- and CPT-Violating Neutron Spin Interactions. Physical Review Letters 2010, 105, 151604. [Google Scholar] [CrossRef] [PubMed]
  23. Li, R.; Fan, W.; Jiang, L.; Duan, L.; Quan, W.; Fang, J. Rotation sensing using a K-Rb-21Ne comagnetometer. Physical Review A 2016, 94, 032109. [Google Scholar] [CrossRef]
  24. Fang, J.; Chen, Y.; Zou, S.; Liu, X.; Hu, Z.; Quan, W.; Yuan, H.; Ding, M.; Physics, O. Low frequency magnetic field suppression in an atomic spin co-magnetometer with a large electron magnetic field. Journal of Physics B: Atomic, Molecular 2016, 49, 065006. [Google Scholar] [CrossRef]
  25. Duan, L.; Quan, W.; Chen, Y.; Jiang, L.; Fan, W.; Ding, M.; Wang, Z.; Fang, J. Rotation sensing decoupling of a dual-axis K-Rb-21Ne atomic comagnetometer. Applied optics 2018, 57, 1611–1616. [Google Scholar] [CrossRef] [PubMed]
  26. Ji, W.; Chen, Y.; Fu, C.; Ding, M.; Fang, J.; Xiao, Z.; Wei, K.; Yan, H. New Experimental Limits on Exotic Spin-Spin-Velocity-Dependent Interactions by Using SmCo5 Spin Sources. Phys. Rev. Lett. 2018, 121, 261803. [Google Scholar] [CrossRef] [PubMed]
  27. Kornack, T.; Ghosh, R.; Romalis, M.V. Nuclear spin gyroscope based on an atomic comagnetometer. Physical review letters 2005, 95, 230801. [Google Scholar] [CrossRef]
  28. Vasilakis, G.; Brown, J.; Kornack, T.; Romalis, M. Limits on New Long Range Nuclear Spin-Dependent Forces Set with a K-3He Comagnetometer. Phys. Rev. Lett. 2009, 103, 261801. [Google Scholar] [CrossRef]
  29. Kornack, T.; Romalis, M. Dynamics of two overlapping spin ensembles interacting by spin exchange. Physical review letters 2002, 89, 253002. [Google Scholar] [CrossRef]
  30. Wu, Z.; Happer, W.; Kitano, M.; Daniels, J. Experimental studies of wall interactions of adsorbed spin-polarized 131xe nuclei. Physical Review A 1990, 42, 2774. [Google Scholar] [CrossRef]
  31. Butscher, R.; Wäckerle, G.; Mehring, M. Nuclear quadrupole surface interaction of gas phase 83Kr: comparison with 131Xe. Chemical Physics Letters 1996, 249, 444–450. [Google Scholar] [CrossRef]
  32. Chen, Y.; Yu, M.; Ma, Y.; Wang, Y.; Guo, J.; Lin, Q.; Zhang, N.; Jiang, Z.; Zhao, L. Quadrupolar interaction induced frequency shift of 131Xe nuclear spins on the surface of silicon. Journal of Physics D: Applied Physics 2022, 55, 355102. [Google Scholar] [CrossRef]
  33. Brinkmann, D.; Kuhn, D. Nuclear magnetic relaxation of 83Kr in krypton gas. Phys. Rev. A 1980, 21, 163–167. [Google Scholar] [CrossRef]
  34. Wu, Z.; Schaefer, S.; Cates, G.D.; Happer, W. Coherent interactions of the polarized nuclear spins of gaseous atoms with the container walls. Phys. Rev. A 1988, 37, 1161–1175. [Google Scholar] [CrossRef] [PubMed]
  35. Walker, T.G. Estimates of spin-exchange parameters for alkali-metal – noble-gas pairs. Physical Review A 1989, 40, 4959–4964. [Google Scholar] [CrossRef] [PubMed]
  36. Walker, T.G.; Happer, W. Spin-exchange optical pumping of noble-gas nuclei. Reviews of Modern Physics 1997, 69, 629. [Google Scholar] [CrossRef]
  37. Chen, Y.; Zhao, L.; Zhang, N.; Yu, M.; Ma, Y.; Han, X.; Zhao, M.; Lin, Q.; Yang, P.; Jiang, Z. Single beam Cs-Ne SERF atomic magnetometer with the laser power differential method. Optics Express 2022, 30, 16541–16552. [Google Scholar] [CrossRef]
  38. Chen, W.C.; Gentile, T.R.; Walker, T.G.; Babcock, E. Spin-exchange optical pumping of 3He with Rb-K mixtures and pure K. Phys. Rev. A 2007, 75, 013416. [Google Scholar] [CrossRef]
  39. Chen, W.C.; Gentile, T.R.; Fu, C.B.; Watson, S.; Jones, G.L.; McIver, J.W.; Rich, D.R. Polarized 3He cell development and application at NIST. Journal of Physics: Conference Series 2011, 294, 012003. [Google Scholar] [CrossRef]
Preprints 84714 g001
Figure 1. The relaxation rate of the nuclear spins changes with the temperature of the vapor cell. Under low temperature, the 83 Kr will be adsorbed on the surface walls for longer time and the fluctuation EFGs will cause the relaxation of the nuclear spin. As the temperature is higher, the relaxation between the collision with Rb atoms will be larger because the number density of the Rb will be larger. More alkali atoms will depolarize the nuclear spins. The spin exchange relaxation will dominant under high temperature since the atoms will stay on the surface for a short time and the quadrupolar relaxation can be neglected.
Figure 1. The relaxation rate of the nuclear spins changes with the temperature of the vapor cell. Under low temperature, the 83 Kr will be adsorbed on the surface walls for longer time and the fluctuation EFGs will cause the relaxation of the nuclear spin. As the temperature is higher, the relaxation between the collision with Rb atoms will be larger because the number density of the Rb will be larger. More alkali atoms will depolarize the nuclear spins. The spin exchange relaxation will dominant under high temperature since the atoms will stay on the surface for a short time and the quadrupolar relaxation can be neglected.
Preprints 84714 g001
Preprints 84714 g002
Figure 2. (a)The relationship between the temperature and the nuclear spin’s polarization P n . As the temperature of the vapor cell change we can estimate the rising of the spin exchange optical pumping of the nuclear spins as well as a decreasing of the quadrupolar relaxation. Thus, the polarization of the nuclear spins increases with the rising of the temperature.(b) The relationship between the temperature and the magnetic field produced by the nuclear spin B n . As the magnetic field produced by the nuclear spin is directly related to the nuclear spin polarization and thus we can estimate a similar change of the B n with the temperature.
Figure 2. (a)The relationship between the temperature and the nuclear spin’s polarization P n . As the temperature of the vapor cell change we can estimate the rising of the spin exchange optical pumping of the nuclear spins as well as a decreasing of the quadrupolar relaxation. Thus, the polarization of the nuclear spins increases with the rising of the temperature.(b) The relationship between the temperature and the magnetic field produced by the nuclear spin B n . As the magnetic field produced by the nuclear spin is directly related to the nuclear spin polarization and thus we can estimate a similar change of the B n with the temperature.
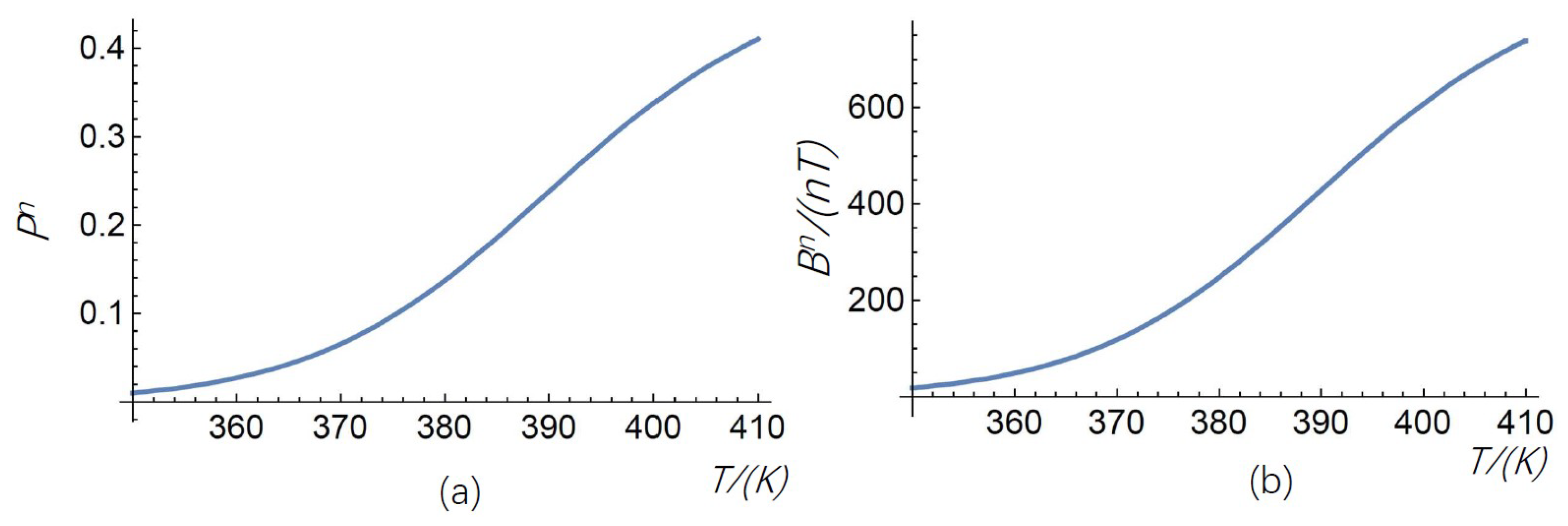
Preprints 84714 g002
Preprints 84714 g003
Figure 3. The relationship between the temperature and the relaxation of Rb which is used to polarize the nuclear spins. ’SE Relaxation’ stands for ’Spin Exchange Relaxation’. The total relaxation includes the spin destruction relaxation between Rb and N 2 , the spin destruction relaxation between Rb and Rb, the spin transfer rate from Rb to 83 K r . The SE relaxation only includes the transfer rate of Rb electron spin to the nuclear spins.
Figure 3. The relationship between the temperature and the relaxation of Rb which is used to polarize the nuclear spins. ’SE Relaxation’ stands for ’Spin Exchange Relaxation’. The total relaxation includes the spin destruction relaxation between Rb and N 2 , the spin destruction relaxation between Rb and Rb, the spin transfer rate from Rb to 83 K r . The SE relaxation only includes the transfer rate of Rb electron spin to the nuclear spins.
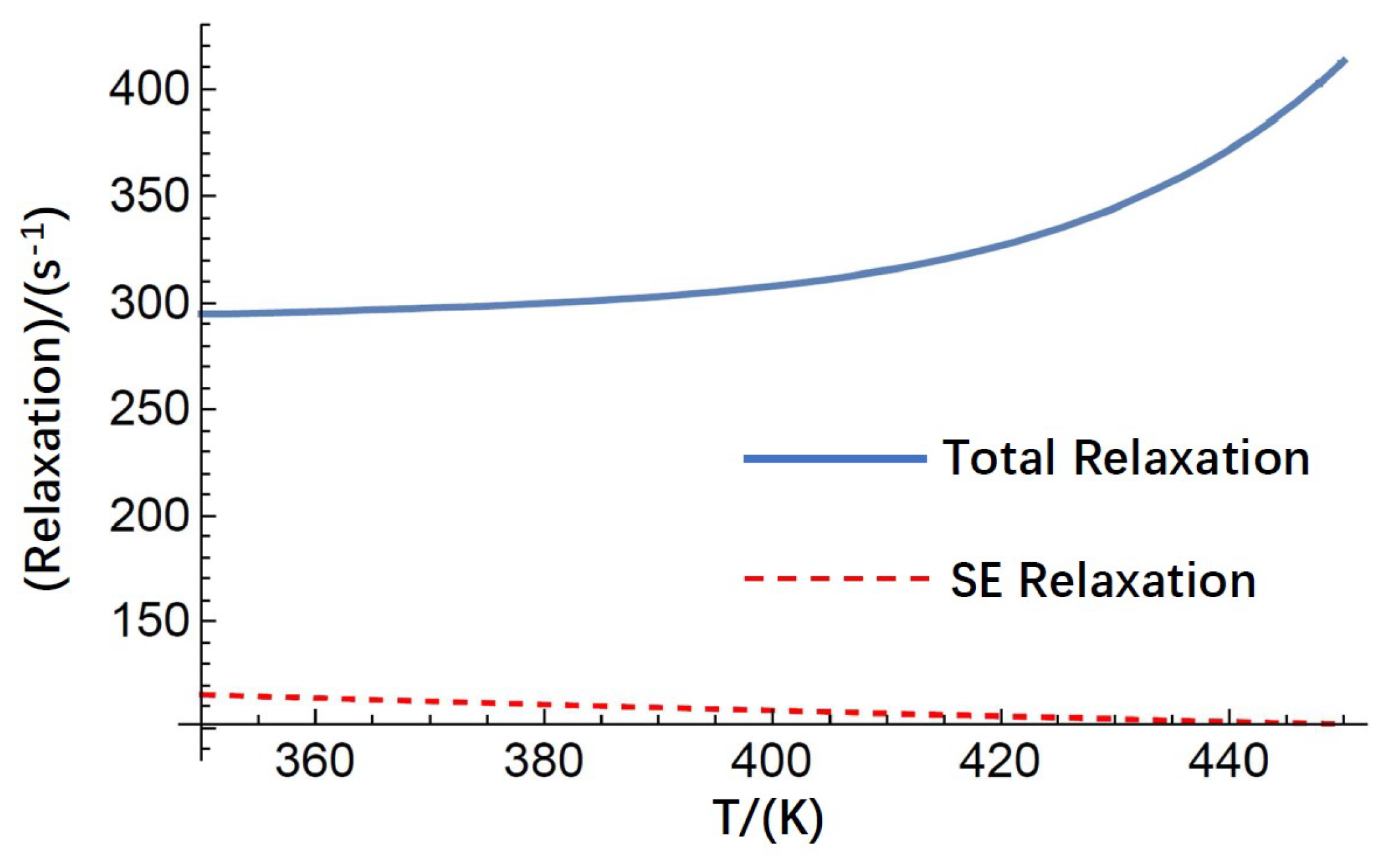
Preprints 84714 g003
Preprints 84714 g004
Figure 4. The fundamental sensitivity of the magnetometer. The temperature of the vapor cell is changed and thus the number density of the Rb atoms changes. As the temperature is higher, we estimate higher sensitivity. We also change the active volume of the vapor cell in which the laser light interactive with the Rb atom spins and then the fundamental sensitivity of the co-magnetometer was calculated. As the volume is larger, the fundamental sensitivity is higher.
Figure 4. The fundamental sensitivity of the magnetometer. The temperature of the vapor cell is changed and thus the number density of the Rb atoms changes. As the temperature is higher, we estimate higher sensitivity. We also change the active volume of the vapor cell in which the laser light interactive with the Rb atom spins and then the fundamental sensitivity of the co-magnetometer was calculated. As the volume is larger, the fundamental sensitivity is higher.
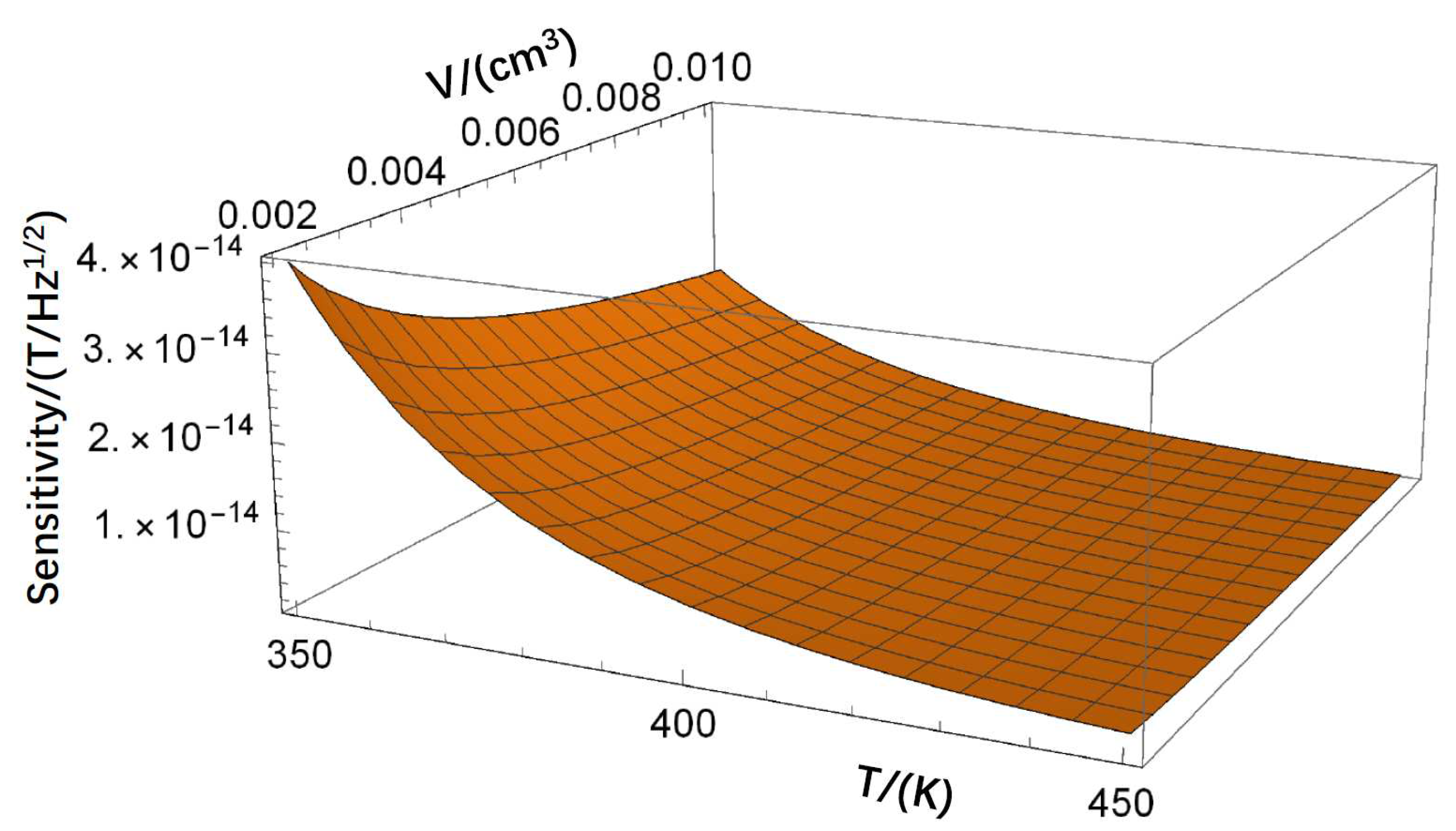
Preprints 84714 g004
Preprints 84714 g005
Figure 5. The process of preparing the K-Rb mixture in the glove box.
Figure 5. The process of preparing the K-Rb mixture in the glove box.
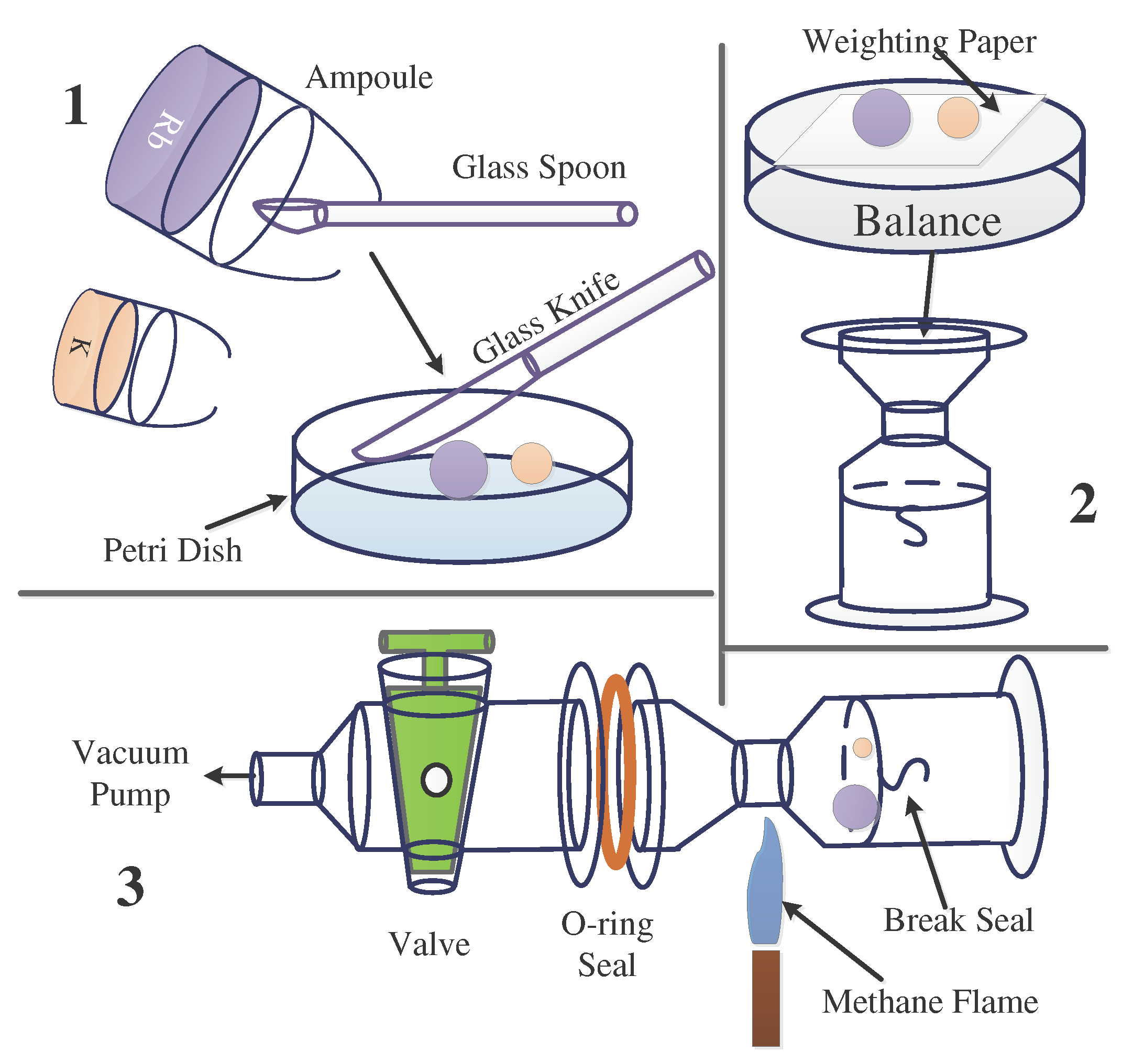
Preprints 84714 g005
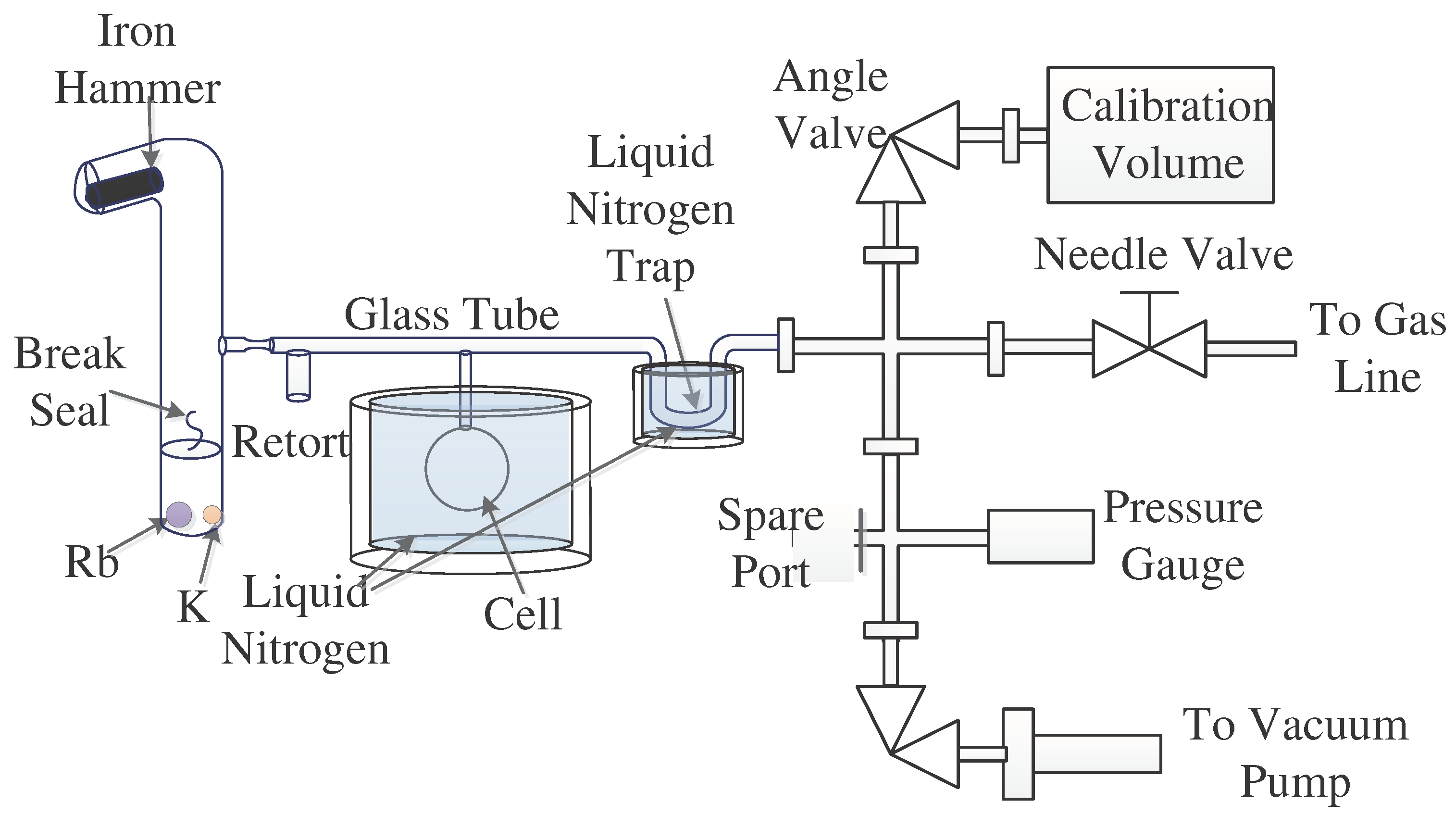
Preprints 84714 g006
Figure 6. Schematic of filling the vapor cell with K-Rb mixture and gases.
Figure 6. Schematic of filling the vapor cell with K-Rb mixture and gases.
Preprints 84714 g006
Table 1. The calculation of mass of K and Rb which should be mixed together to reach the intended D r .
Table 1. The calculation of mass of K and Rb which should be mixed together to reach the intended D r .
Intended D r @463K M r m K (mg) m Rb (g) MFR of K
1/212 0.014 30 2.13 0.029
1/109 0.026 41 1.54 0.055
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated