Prerpints.org logo
Preprint
Article

A Phenomenological Model for Creep and Creep-fatigue Crack Growth Behavior in Ferritic Steels

Altmetrics

Downloads

121

Views

41

Comments

0

This version is not peer-reviewed

Advanced Processes in Metallurgical Technologies

Submitted:

11 September 2023

Posted:

13 September 2023

You are already at the latest version

Alerts
Abstract
A model to rationalize the effects of test temperature and microstructural variables on the creep crack growth (CCG) and creep-fatigue crack growth (CFCG) rates in ferritic steels is described. The model predicts that as the average spacing between grain boundary particles that initiate creep cavities decrease, the CCG and CFCG rates increase. Further, CCG data at several temperatures collapse into a single trend when a temperature compensated CCG rate derived from the model is used. CCG and CFCG behavior measured at different temperatures is used to assess the effects of variables such as differences between basemetal (BM), weldmetal (WM) and the heat-affected zone (HAZ) regions. The model is demonstrated for Grade 22 and Grade 91 steels using data from literature. It is shown that differences between the CCG behavior of Grade 22 steel in new and ex-service conditions are negligible in the BM and WM regions but not in the HAZ region. The CCG behavior of Grade 91 steels can be separated into creep-ductile and creep-brittle regions. The creep-brittle tendency is linked to the presence of excess trace element concentrations in the material chemistry. Significant differences found in the CCG rates between BM and the WM and HAZ regions of Grade 91 steel were explained.
Keywords: 
Subject: Engineering  -   Metallurgy and Metallurgical Engineering

1. Introduction

The rates at which cracks in structural components are expected to grow under high temperature creep and creep-fatigue conditions are a critical aspect of fitness for service (FFS) evaluations, making crack growth rate an essential input for a temporal understanding of when fracture is expected to occur or when an inspection of the component is warranted [1,2]. Creep crack growth (CCG) and creep-fatigue crack growth (CFCG) behaviors in two ferritic materials used extensively in power plants are discussed in this paper, Grade 22 (2.25Cr-1Mo) and Grade 91 (9Cr-1Mo-V-Nb-N).
Many power generation high temperature components such as seam-welded and seamless piping, steam outlet headers, and large casings and forgings are fabricated from Grade 22 and Grade 91 materials. CCG data for these steels obtained from literature is analyzed using a phenomenological model that consolidates data over a range of temperatures and service histories. Equations for CCG and CFCG rates are provided for use in design and fitness-for-service assessments for components made from these steels.

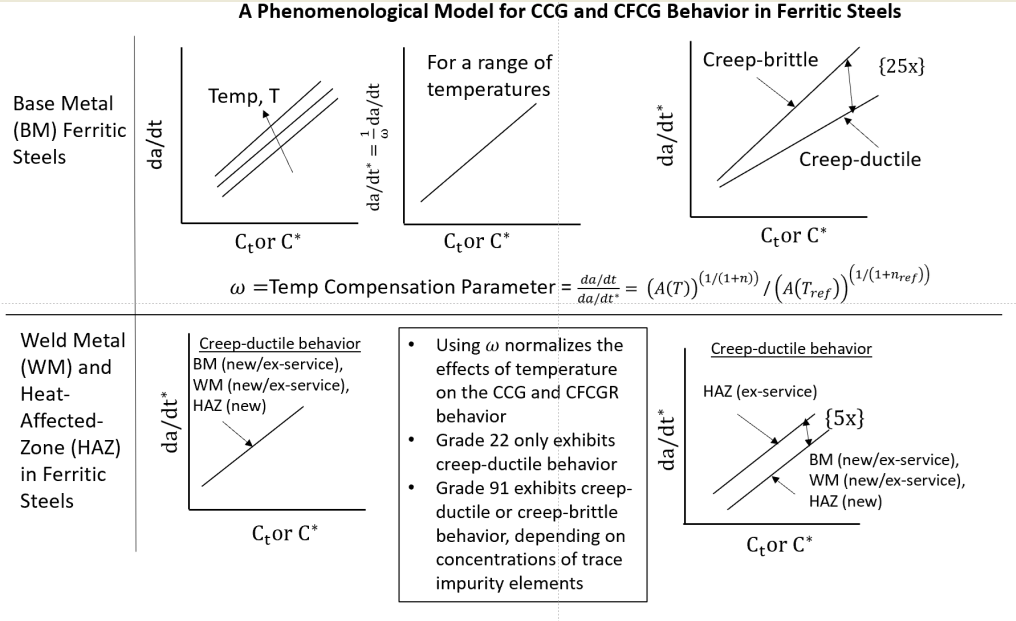
2. Phenomenological Model for Creep Crack Growth

The model presented here evaluates the effects of variables that are expected to influence the CCG behavior. This model was first proposed by Wilkinson and Vitek [3], developed further by Saxena and Bassani [4], and is further refined in this paper. In the model, it is assumed that steady-state creep deformation conditions given in equation (1) prevail in the cracked body
ε ˙ s s = A σ n
Where, A and n are empirically determined constants obtained from creep deformation tests conducted on uniaxial samples. Under these conditions, the CCG behavior is represented by da/dt versus crack tip parameters C* or Ct [5,6,7,8]. In this regime, C* and Ct are identical [8].
Figure 1a schematically shows the idealized development of creep damage ahead of the crack tip in the form of an array of creep cavities with radii of ρ 1 , ρ 2 … . ρ i … ρ N that are spaced by a center-to-center distance of 2b. The cavities are assumed to nucleate on the grain boundary facets, Figure 1b, that are aligned normal to the loading direction and have an initial diameter of ρ N , which corresponds to the radius of the nucleating particle. These cavities grow at a rate that is constrained by power-law creep, equation (1), in the crack tip stress environment. When the cavity closest to the crack tip approaches a critical radius, it coalesces with the crack tip and the crack is believed to have advanced by a distance 2b. All successive cavities grow and move closer to the crack tip while the one nearest becomes part of the crack. A steady-state crack growth rate is established and described by equation (2) [3,4]
d a d t = 2 b 2 n + 3 n + 1 3 d . A 1 n + 1 2.5 ρ c 3 − ρ N 3 ∑ m = 1 m 1 m n n + 1 C * I n σ ^ y y 90 0 ,   n n n + 1
2b = inter-cavity spacing
m = number of cavities in the process zone ahead of the crack tip that grow due to creep deformation (approximately between 3 to 5)
ρ i = radius of the i t h cavity from the crack tip
ρ c = critical cavity radius
ρ N = cavity radius at nucleation
d = grain diameter
σ ^ y y 90 0 , n = crack tip field quantity that depends on n and evaluated at an angle of 90 degrees to the crack plane and has a value on the order of 1.
I n = 6.568 − 0.4744 n + 0.0404 n 2 − 0.00262 n 3
If it is assumed that for creep-ductile materials, ρ c ≫ ρ N , and ρ c ≈ b . Equation (2) then reduces to:
d a d t = β α n A 1 n + 1 C * b n n + 1
where, α n = 2 2 n + 3 n + 1 ( 1.2 ) I n n n + 1 and β = d σ ^ y y 90 0 , n n n + 1 ∑ m = 1 m 1 m n n + 1
The constant β , as seen above, also includes the angular terms in the crack tip stress fields and can be made part of a consolidated constant. α n   ≈ 1.3 for 5 ≤ n ≤ 10 and the term ∑ m = 1 m 1 m n n + 1   ≈ 13.0 for 5 ≤ m 1 ≤ 10 can also be merged into the same consolidated constant. If b 0 represents the inter-cavity spacing at which the da/dt asymptotically approaches a lower bound value where ρ c ≈ b 0 , implying a highly creep-ductile material, equation (3) can be written as:
d a d t = c 1 A 1 n + 1 b 0 / b n n + 1 C * n n + 1
Where, c 1 = α n β b 0 n n + 1 .
In equation (4), the term A 1 n + 1 compensates the CCG rate behavior for temperature. For b less than b0, the CCG rates are expected to be higher. Thus, a microstructural length dimension is explicitly included in the CCG rate equation. This microstructural parameter could also evolve during service and account for changes in CCG properties due to exposure to high temperatures during service. For example, if during service, new grain boundary particles form due to exposure to service temperatures and reduce the value of b, the CCG rate is expected to increase, and the material is expected to embrittle during service.
A ductility exhaustion model has been proposed by Nikbin, Smith, and Webster (NSW) [7] that relates creep ductility to the CCG behavior as shown in equation (5) below:
d a d t = n + 1 ε f * A 1 n + 1 C * I n n n + 1 r c 1 n + 1
Where, ε f * is the multi-axial creep ductility, and rc is the process zone size of the material that depends on microstructural characteristics and the crack tip constraint. There are similarities among the two models as both equations can be reduced to the following form. The WVSB model explicitly contains microstructural terms while the NSB model is based on notional parameters, such as rc.
d a d t = c 1 A T 1 n + 1 C * n n + 1
The constant A is a strong function of temperature. However, when it is raised to a power of 1/(n+1), where n ranges between 5 and 13 for ferritic steels, the dependence of da/dt on A becomes weak, but still significant. Further, we can replace C* with a more general parameter Ct in equation (6) [8] that is also applicable to small-scale-creep conditions and becomes identical to C* under steady-state creep conditions. This parameter also permits the inclusion of CFCG rates at various hold times on the same plot [9]. We next define a reference temperature, Tref, that is equal to say a commonly used temperature for the material and for which CCG data are available.
At Tref,
d a / d t r e f = c 1 A T r e f 1 / 1 + n r e f C t q
In equation (7), n/(n+1) is replaced by an empirically determined material constant, q. The value of n/(n+1) ranges from 0.75 to 0.9 for n values between 4 and 10 and compares well with the range of values of q found in the CCG data for a wide variety of steels.
Next, we divide equation (6) by equation (7) to get:
ω T = d a / d t d a / d t r e f = A T 1 / 1 + n A T r e f 1 / 1 + n r e f
and
d a / d t = ω d a / d t r e f
We can write:
d a * d t = 1 ω d a d t = c 1 A T r e f 1 / 1 + n r e f C t q
The parameter ω T , a function of temperature, is referred to as the temperature compensation parameter and is applied to CCG and CFCG data at a variety of temperatures, so the effects of temperature can be separated from the effects of other variables on CCG and CFCG rates. Thus, the CCG equation can be written as:
da / dt *   = 1 ω d a d t = c 1 A T r e f 1 / 1 + n r e f C t q = c C t q
where, c = c 1 A T r e f 1 / 1 + n r e f
The values of c and q are empirically determined constants from CCG and CFGG data that correspond to the reference temperature. To determine c, CCG data from several temperatures can be expressed as da/dt* (by dividing da/dt with ω as in equation (9)) and Ct and pooled together for the purposes of the regression analysis leading to c and q values. Such analysis is shown for Grade 22 and Grade 91 steels in the subsequent section.

3. CCG in Grade 22 and Grade 91 Materials

3.1. CCG Behavior of Grade 22 Materials:

CCG and CFCG data were collected from the literature for Grade 22 materials [10,11,12,13,14,15,16]. Crack growth data were identified separately for new and ex-service basemetals (BM), new and ex-service weldmetals (WM), and for new and ex-service heat-affected zone regions (HAZ) in the temperature range from 538 0C to 594 0C. These data were plotted using the temperature compensated CCG rates to identify variables other than temperature that are relevant to the CCG rates in this material. The secondary creep constants, A, and n were obtained from the studies that reported the CCG data and are summarized in Table 1. The value of ω (equation 8) at each temperature is also reported in Table 1.
Figure 2 shows the correlation between the CCG rates at various temperatures for Grade 22 basemetal in new and ex-service conditions at various temperatures. In Figure 3, the same data are plotted as temperature compensated crack growth rates referenced to a temperature of 540 0C. All data over several orders of magnitude in growth rates fall within a narrow scatter band in Figure 2 but is even better consolidated in Figure 3. In Figure 2, the crack growth rates at 594 0C are seen to be consistently higher than at other lower temperatures but when plotted in the temperature compensated plot, they become indistinguishable from the data at other temperatures. No significant differences were found in the data trends in Figure 3 for new and ex-service BM also. Thus, the mean and upper bound (UB) and lower bound (LB) values of c in Table 2 were determined from the pooled data consisting of all the new and ex-service BM. This allows direct comparisons of CCG data in WM and HAZ regions with the BM. Table 2 lists the constants c and q in equation (10) that describe the mean, the upper bound (UB) and the lower bound (LB) trends in the various regions of the weldment.
The CCG rates for samples taken from the weldmetal (WM) and heat-affected-zone (HAZ) regions of Grade 22 material are plotted in Figure 4. Data obtained at various temperatures are adjusted for 540 0C using the temperature compensation parameter, ω . For comparison, the 95% confidence interval for the base material in Figure 3 is also superimposed in Figure 4 and the 95% CI band for just the service exposed HAZ region. The CCG rates in new and ex-service WM lie in the center of the BM band, but there is a clear difference in the CCG rates between ex-service and new materials when samples are taken from the heat-affected zone (HAZ) regions. Exposure to service temperatures appear to degrade the CCG rates in the HAZ regions while apparently not affecting the BM and WM. This observation is consistent with the service experience where the instance of cracking is most frequently found at the interface of BM and WM in seam-welded steam pipes but not in the BM and WM regions, and not in seamless piping made from Grade 22 material[13,17].
In summary, there are no distinctions in the temperature compensated CCG behavior between new BM, ex-service BM, new WM, ex-service WM, and new HAZ regions for Grade 22 material. However, the CCG rates in ex-service HAZ regions were found to be higher than the new HAZ region. The CCG kinetics are listed in Table 2 for all regions of Grade 22 weldments.

3.2. CCG Behavior of Grade 91 Materials

CCG behavior of BM, WM, and HAZ regions of Grade 91 steels have been reported in references [18,19,20,21,22,23,24,25,26] in the temperature range of 538 0C to 650 0C. The data at 538 0C, 593 0C [18], 6000C [19,22], and 6250C [20] on BM were available in excel format. The data at 650 0C [21] and some at 600 0C [23,24] were available as regression constants for the CCG data. The latter were included in the CCG plots as data points estimated from equations at Ct/C* values of 0.01, 0.1, 1, 10, and 50 J/m2h to document the reported trend but are not used in regression analyses for determining the CCG constants because they are not measured values.
Table 3 lists the steady-state or secondary creep behavior for Grade 91 material at various temperatures ranging from 538 0C to 650 0C, covering the range of temperatures for which the CCG data were available in the literature. The Table also provides the computed ω T values for the various temperatures. The temperature compensated CCG rates are shown in shown in Figure 5 for basemetal regions of Grade 91 steel. At temperatures of 538 0C, 594 0C, 600 0C, and 650 0C, the CCG tests were conducted using new plate material while the tests conducted at 625 0C were performed on a material taken from an ex-service pipe; but the pipe section used for testing was heat treated prior to testing to rejuvenate its microstructure to the original state [25,26]. The latter should, therefore, also be considered a new material. Large variability in the CCG rates were observed between various data sets with the rates being much higher for some of the 600 0C [19, Yatomi et al.] and all the 625 0C tests [20, Shingledecker] compared to the other conditions reported. No systematic variations were observed in the CCG rates with temperature since the crack growth rates plotted are compensated for temperature. At 600 0C, the data reported by Yatomi et al. [19] showed much higher CCG rates than by Kim et al. [23]. Such large variability cannot simply be attributed to random experimental scatter and therefore deserves a more in-depth discussion.
Parker and Siefert [27] have conducted an exhaustive study on the levels of certain trace elements that include S, Cu, Sn, As, Sb, and Pb present in Grade 91 steels as impurities and their effect on the creep behavior, specifically the creep ductility. They have reported a tendency of components made from heats containing more than critical levels of the trace elements to develop early cracking during elevated temperature service. They separated heats of Grade 91 material between what they termed as creep damage resistant and creep damage prone and related them to chemistry, particularly the amounts of the above trace elements.
Table 4a lists the chemical composition of the heat of Grade 91 steel that experienced early cracking during service used by Shingledecker [20] in his CCG studies in service exposed but rejuvenated condition. Thus, after removal from service, the material was heat treated to rejuvenate its microstructure to the original form prior to machining CCG samples that were tested at 625 0C [20,24,25,26]. Table 4b lists the actual levels of trace elements, S, Cu, Sn, As, Sb, and Pb along with levels that were seen to result in creep damage resistant and creep damage prone behaviors in the Parker and Seifert study; in other words, creep-ductile or creep-brittle behavior, respectively. The compositions shown in Table 4b clearly show that the levels of several trace elements in the heat of Grade 91 that exhibited creep-brittle behavior did exceed or had comparable levels of trace elements known to cause creep-brittle behavior consistent with the experimental observations.
In Figure 6, all tests yielding creep-ductile trend in Figure 5 were plotted using one type of marker and tests yielding creep-brittle trends were plotted using a different marker. The difference between the two trends are obvious in the plot. Separate 95% CI bands were also developed for each of the two conditions as shown in Figure6. Creep-brittle behavior also leads to higher scatter in the CCG data compared to creep-ductile behavior. The CCG constants for creep-ductile and creep-brittle conditions are listed in Table 5 for Grade 91 steels.
In Figure 7, additional CCG data at temperatures of 550 0C, 600 0C, and 650 0C from the literature on [21,22,23] on Grade 91 BM are plotted. The markers in this figure are values derived from equations representing mean trends in the various sets of data. All CCG rates appear to fall within the 95% CI band for creep-ductile materials in Fig, 6 with the 650 0C CCG data laying near the upper scatter band for creep-ductile materials. The chemistry of the base metals used for these CCG tests conducted at 650 0C by Hyde et al. [21] and at 600 0C and 550 0C conducted by Kim et al. [22,23] are provided in Table 4. However, the chemical analysis for trace elements was not reported in either of these studies, thus, judgements about whether creep-ductile or creep-brittle behavior is expected in these experiments cannot be made. Based on just the CCG data trend, these materials are classified as creep-ductile. Next, the CCG trends in the WM and HAZ regions of weldments that use the above materials as BM are discussed.
Figure 8 shows the CCG trends in the WM and HAZ regions of welds in Grade 91 steel in the temperature range of 550 0C to 650 0C [22,23]. The WM and HAZ regions have nearly identical CCG behaviors at 550 0C and 600 0C [22,23] but the rates were somewhat higher when compared to the BM at those temperatures. At 650 0C, the CCG rates taken from a different study [21] in the HAZ region of the weldment show much higher crack growth rates compared to the BM at that temperature. The CCG rates in the HAZ region in this latter study [21] are in the creep-brittle regime, and significantly higher than at 550 0C and 600 0C data for WM, HAZ, and BM. However, it cannot be concluded that it is the temperature that causes the creep-brittle behavior because these data were obtained on a different P91 Grade steel. The WM and BM chemistry of the weldments are shown in Table 4 but the amounts of trace elements are missing. Therefore, the higher CCG rates at 650 0C in the HAZ region cannot also be attributed to higher content of trace elements in the composition of the weld or base metal and the cause remains an unanswered question.

4. CFCG in Grade 22 and Grade 91 Steels

4.1. CFCG in Grade 22 Steel

In Figure 2 and Figure 3, the CFCG data available for Grade 22 material for a hold time of 50 seconds at a temperature of 594 0C are also included [10]. The time rate of crack growth, (da/dt)avg during the hold time were correlated with the average value of the Ct parameter, referred to as (Ct)avg. The reported CFCG rates are also temperature compensated in Figure 3 like the CCG data. The (da/dt)avg and (Ct)avg data were obtained primarily under small-scale-creep (SSC) conditions, but are seen to blend with the CCG data, especially in Figure 3 after temperature compensation. Thus, no separate correlation for CFCG is needed for this material. The cyclic crack growth rate for a hold time th can simply be estimated by multiplying the (da/dt) value with th. This observation is significant for evaluating the lives of components that are periodically cycled during service such as high-pressure equipment.

4.2. CFCG in Grade 91 Steel

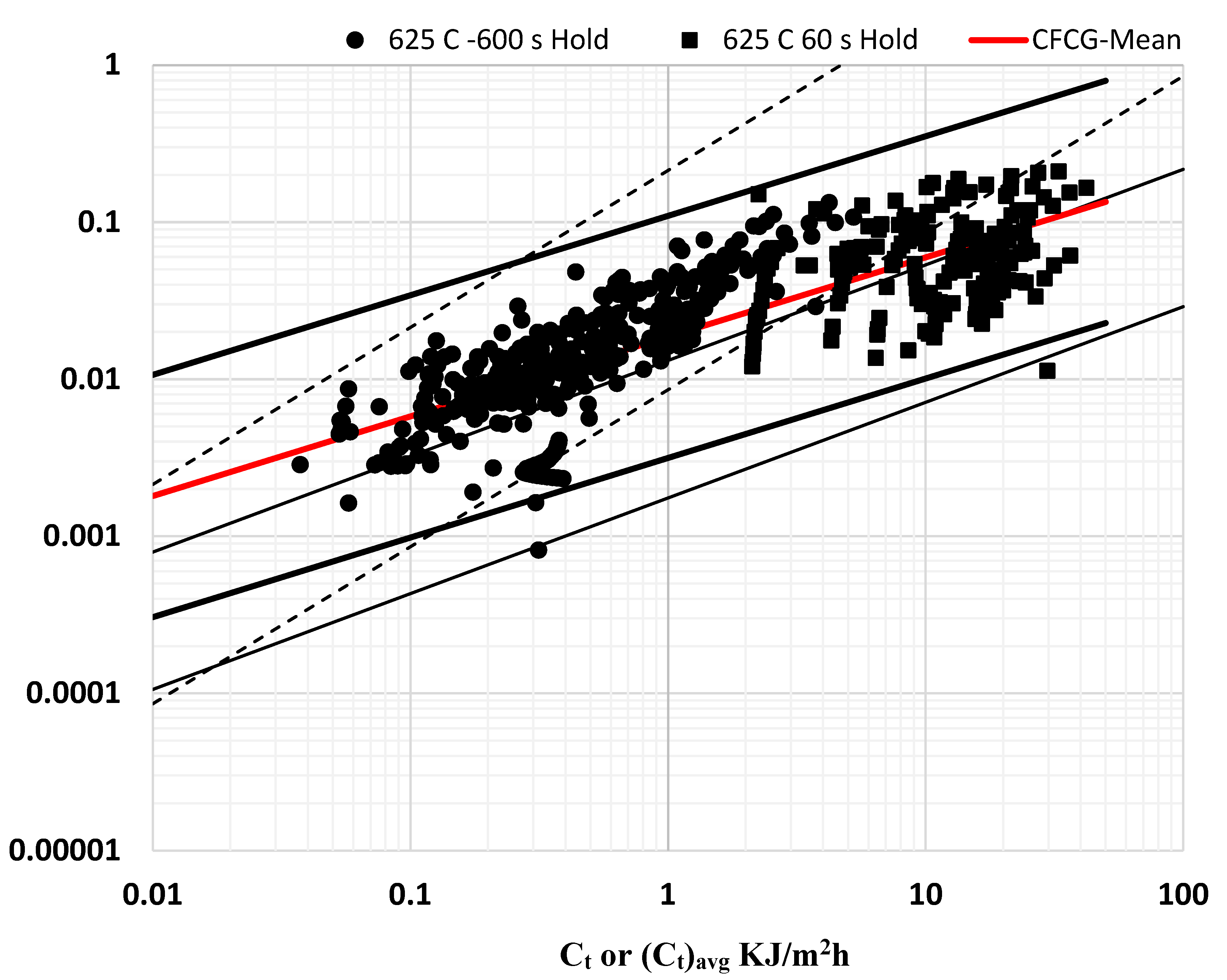
There is large scatter in the CFCG data, similar to that observed in the CCG rates on the same heat of Grade 91 steel in the rejuvenated ex-service condition. Some of this scatter may be attributed to tests being conducted by 13 laboratories around the world with different levels of prior experience in conducting CFCG testing, but a significant portion must also be from the material itself. All CCG data shown in Figure 5 at 625 0C show considerable scatter even when all tests were conducted by a single, highly experienced laboratory. The 60 s hold time data seem to show somewhat lower CFCG rates compared to the 600 s hold time. These differences, if there, are small in comparison to the general scatter in the data. For regression analyses to obtain the mean and 95% confidence intervals, the data from both hold times were pooled. The constants representing the mean and upper and lower bounds of the 95% confidence intervals for the CFCG behavior are listed in Table 3. The reason for large scatter in the CCG rates in Grade 91 steel at 625 0C were discussed previously as embrittlement caused by higher concentrations of trace elements in the chemistry of the steel. Same factors are expected to contribute to the scatter in the CFCG trend.
The CFCG trend lies between the creep-ductile and creep-brittle CCG trends for Grade 91 steel. The slope is better aligned with the creep-ductile trend than with the creep-brittle trend and the crack growth rates are closer to the upper bound creep-ductile behavior. It appears that under cyclic loading, the crack growth behavior tends more toward creep-ductile behavior. Cyclic softening of the material in the crack tip region may be responsible for the tendency toward creep-ductile behavior.

5. Recommendations for Future Work and Conclusions

The collection of CCG and CFCG data reported in this study provides a new way to report CCG and CFCG data such that it is compensated for effects due to temperature. The temperature compensation parameter has been derived based on a phenomenological model presented as part of this paper and evaluated extensively using data from several prior studies. Some recommendations for future work are listed below.
  • Conduct a round-robin study of CCGR and C-FCGR testing consisting of several laboratories and using well-established cavitation resistant material with well documented creep deformation behavior, tensile data, well characterized microstructure, documented chemistry including levels of trace elements that cause embrittlement, and cyclic stress-strain data. This will more definitively establish the expected levels of scatter in the data from experimental sources.
  • A standard protocol should be established to report chemical composition and microstructure of the test material as part of testing. Principles of quantitative metallography and the capabilities of automated imaging equipment should be utilized fully to obtain statistically meaningful results.
  • Changes to the ASTM standards for CCG and CFCG testing must be made to include results from the proposed study.
  • Document a procedure for qualifying test equipment used by participants for testing prior to commencing the tests.

6. Summary and Conclusions

Following is a summary and conclusions can be gleaned for this study:
  • A phenomenological model for rationalizing the effects of temperature and microstructural characteristics on the CCG and CFCG behavior of ferritic steels is proposed in this paper and was evaluated using extensive amounts of data gathered from the literature. The ability of the model to rationalize the effects of temperatures is clearly demonstrated in the paper. The model contains a characteristic microstructural parameter that can only be determined by quantitative microstructural evaluation of the test materials, typically not reported in CCG studies.
  • Basemetal (BM) CCG and CFCG data for Grade 22 steels in new and ex-service materials in the temperature range of 538 to 594 0C were indistinguishable.
  • The weldmetal (WM) CCG data for Grade 22 steels in new and ex-service conditions on average followed the same trend as the BM.
  • CCG rates in the heat-affected zone (HAZ) region of Grade 22 materials are comparable to the CCG rates in BM and WM, but the CCG rates after service exposure were on average approximately four times higher.
  • CFCG and CCG behaviors in Grade 22 steels were indistinguishable from each other.
  • Extensive amounts of BM CCG and CFCG data for new and rejuvenated ex-service Grade 91 steels in the temperature range of 538 0C to 650 0C are reported from the literature. The tests were conducted on four separate heats of material.
  • The variability among the BM CCG behavior in Grade 91 steels was significantly higher than found in Grade 22 steels.
  • It was observed that the CCG in the BM of Grade 91 steels at temperatures of 538 0C, 593 0C, and some at 600 and at 650 0C follow creep-ductile tendencies implying higher CCG resistance than those under creep-brittle behavior observed in some heats tested at 600 0C and 625 0C. It is hypothesized, based on results from a study conducted by Parker and Seifert [27], that subtle chemical compositions among the trace impurity elements cause creep-brittle tendencies. This strongly suggests the need for reporting the full chemistry including levels of trace elements as standard practice when reporting CCG and CFCG test results.
  • CCG constants for Grade 22 and Grade 91 steels representing the mean, upper bound (UB), and lower bound (LB) trends were calculated and reported in the paper. For Grade 91, the constants were reported separately for creep-ductile and creep-brittle trends.

7. Acknowledgements

The author wishes to acknowledge partial financial support from the Electric Power Research Institute (EPRI) for the study and useful discussions with Jonathan Parker, John Shingledecker, John Siefert and Thomas Sambor, all from EPRI. Assistance from Santosh Narasimhachary of Siemens Technology is also gratefully acknowledged.

References

  1. API 579-1/ASME FFS-1 (2016), Fitness for Service, American Petroleum Institute, USA.
  2. BS 7910:2013+A1, (2015), Guide to Methods for Assessing the Acceptability of Flaws in Metallic Structures” British Standard, UK.
  3. Wilkinson DS and Vitek, V., (1982), Propagation of Cracks by Cavitation- A General Theory”, Acta Metallurgica, 30:1723-1732. [CrossRef]
  4. Saxena, A and Bassani, JL (1984), Time-Dependent Fatigue Crack Growth Behavior at Elevated Temperature, in Fracture: Interactions of Microstructure, Mechanisms and Mechanics, TMS-AIME, Warrendale, PA 357-383.
  5. Saxena A (1980), Evaluation of C* for Characterization of Creep Crack Growth Behavior of 304 Stainless-Steel”, in Fracture Mechanics: Twelfth Conference, ASTM STP 700, American Society for Testing and Materials, Philadelphia, 131–151.
  6. Landes JD and Begley JA (1976), A Fracture Mechanics Approach to Creep Crack Growth, Mechanics of Crack Growth, ASTM STP 590, American Society for Testing and Materials, Philadelphia, 128-148.
  7. Nikbin KM, Smith DJ, and Webster GA, (1986), An Engineering Approach to the Prediction of Creep Crack Growth, J. Engineering Materials and Technology, ASME, 108: 186-191. [CrossRef]
  8. Saxena A (1986), Creep Crack Growth under Non-steady State Conditions, Fracture Mechanics: Seventeenth Volume, ASTM STP 905, American Society for Testing and Materials, Philadelphia, 185-201.
  9. Yoon KB, Saxena, A., and Liaw PK (1993), Characterization of Creep-Fatigue Crack Growth Behavior under Trapezoidal Wave Shape Using Ct Parameter, International J of Fracture, 59: 95-114. [CrossRef]
  10. Grover PS and Saxena, A (1995), Characterization of Creep-Fatigue Behavior in 2.25Cr-1Mo Steel Using (Ct)avg Parameter, International J. Fracture, 73: 273-286. [CrossRef]
  11. Saxena, A., Han, J. and Banerji, K., (1988) Creep Crack Growth Behavior in Power Plant Boiler and Piping Materials, Journal of Pressure Vessel Technology, Vol. 110, pp. 137-146. [CrossRef]
  12. Riedel, H, Detampel, V, (1987) Creep Crack Growth in Ductile, Creep-resistant Steels, International Journal of Fracture, Vol 33, pp 239-262. [CrossRef]
  13. Liaw, P.K., Saxena, A. and Schaffer, J., (1989) Determination of Inspection Criterion for Seam Welded Steam Pipes, Part I: Mechanical Properties, Engineering Fracture Mechanics, vol. 32, pp. 675-708. [CrossRef]
  14. Norris, RH (1994), Creep Crack growth Behavior in Weld Metal/Base Metal/Fusion Zone Regions in Chromium Molybdenum Steels, PhD Dissertation, Georgia Institute of Technology.
  15. Grover PS and Saxena, A, (1995) Characterization of Creep-Fatigue Crack Growth Behavior in 2.25 cr-1 Mo Steels, International Journal of Fracture, Vol. 73, pp 273-286. [CrossRef]
  16. Liaw, PK, Rao, GV, Burke, MG, (1991) “Creep Fracture Behavior of 2 1/4Cr-1Mo Welds from a 31-year-Old Fossil Power Plant, Materials Science and Engineering A, Vol. 131, pp 187-201. [CrossRef]
  17. Bangs, S, (1986) When Welds Fail, Welding Design and fabrication, Vol. 59, pp 79-82.
  18. Jaske, CE and Swindeman, RW, (1987) Long-term-creep and creep-crack-growth behavior of 9Cr-1Mo-V-Nb steel, Advances in Material Technology for Fossil Power Plants, Viswanathan, R. and Jaffe, R.I. Editors, ASM International, Metals Park, OH, pp 231-241.
  19. Yatomi M, Yoshida K, Kimura T, (2011), “Difference of creep crack growth behavior for base, heat-affected zone and welds of modified 9Cr – 1Mo steel”, Materials at High Temperature, 28: 109-113. [CrossRef]
  20. Shingledecker, J, (2018) “Creep Crack Growth Behavior of P91 Material at 6250C” unpublished data, Electric Power Research Institute, Charlotte, NC.
  21. Hyde, TH, Saber, M, and Sun, W, (2010) Creep Crack Growth Data and Prediction for P91 Weld at 650 0C, International Journal of Pressure Vessel and Piping. Vol. 87, pp 721-729. [CrossRef]
  22. Kim, WG, Park, JY, Lee, HY, Kim, ES, Kim, SJ, (2018), Assessment of Creep Crack Growth Rates for Grade 91 Weld Joint at 550 0C, Proceedings of the ASME 2018 Pressure Vessel and Piping Conference, PVP2018, July 15 – 20, 2018, Prague, Czech Republic.
  23. Kim W.G., Park, JY, Lee, HY, Hong, SD, Kim, YW, Kim, SY, (2013), International Journal of Pressure Vessel and Piping, Vol. 110, pp 66-71.
  24. Saxena A and Narasimhachary, SB, (2019) Accounting for Crack Tip Cyclic Plasticity and Creep Reversal in Estimating (Ct)avg During Creep-Fatigue Crack Growth, Fatigue and Fracture of Engineering Materials and Structures. [CrossRef]
  25. Narasimhachary SB and Saxena A, (2013) “Crack Growth Behavior of 9 Cr-1 Mo Steel under Creep-fatigue Conditions”, International Journal of Fatigue, 56, 106-113. [CrossRef]
  26. Saxena A and Narasimhachary SB, (2018), “Creep-fatigue Crack Growth Testing of P91 Steel: Results of the Round Robin for Assessing ASTM Standard E 2760-10” EPRI, Palo Alto, CA, 3002014273.
  27. Parker J and Siefert J, “Metallurgical and Stress State Factors Which Affect the Creep and Fracture Behavior of 9%Cr Steels”, (2018) Advances in Materials Science and Engineering. [CrossRef]
Preprints 84854 g001
Figure 1. (a) Array of cavities ahead of a growing creep crack and (b) Creep cavities located on grain boundary facets normal to the loading axis.
Figure 1. (a) Array of cavities ahead of a growing creep crack and (b) Creep cavities located on grain boundary facets normal to the loading axis.
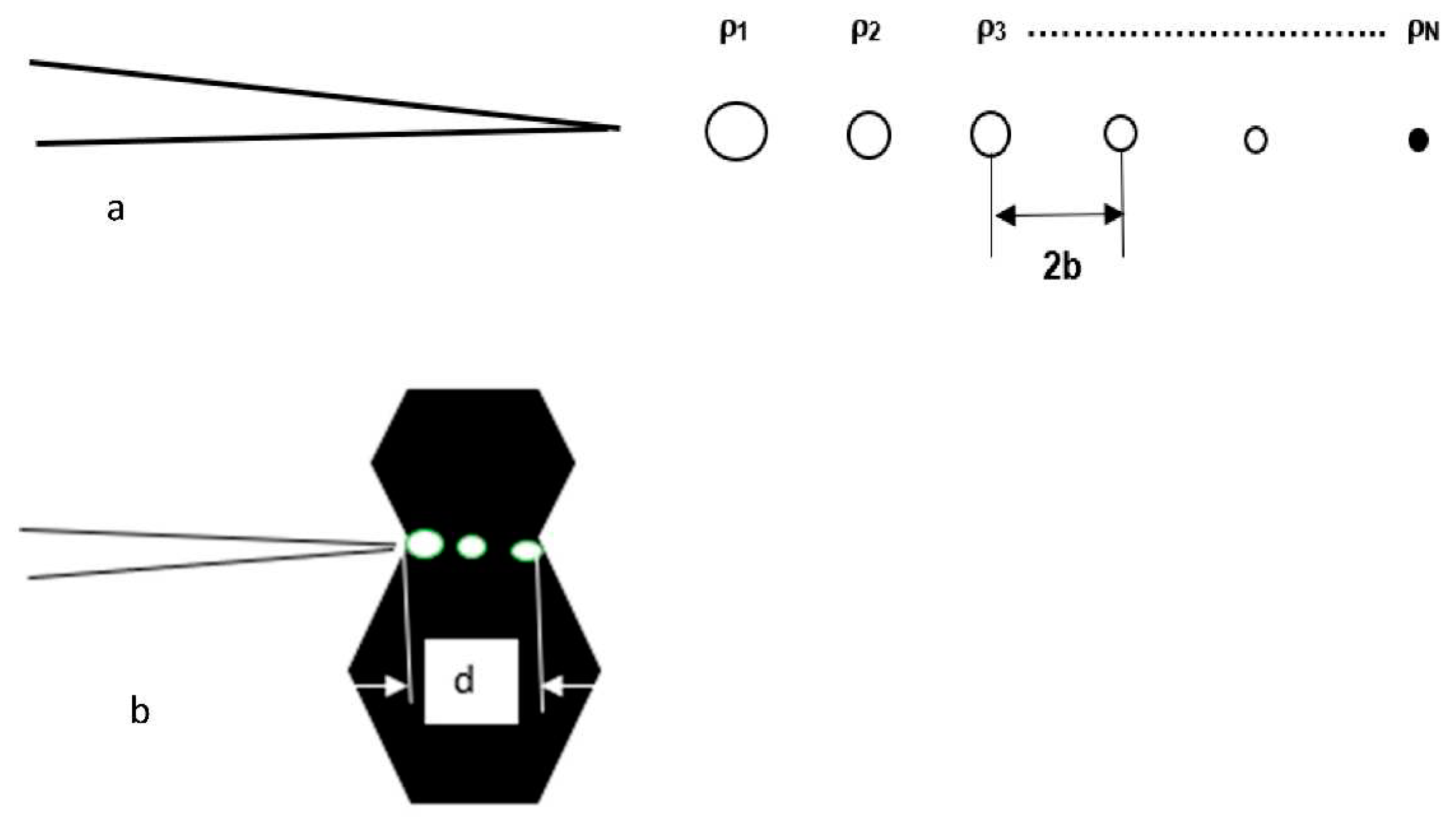
Preprints 84854 g001
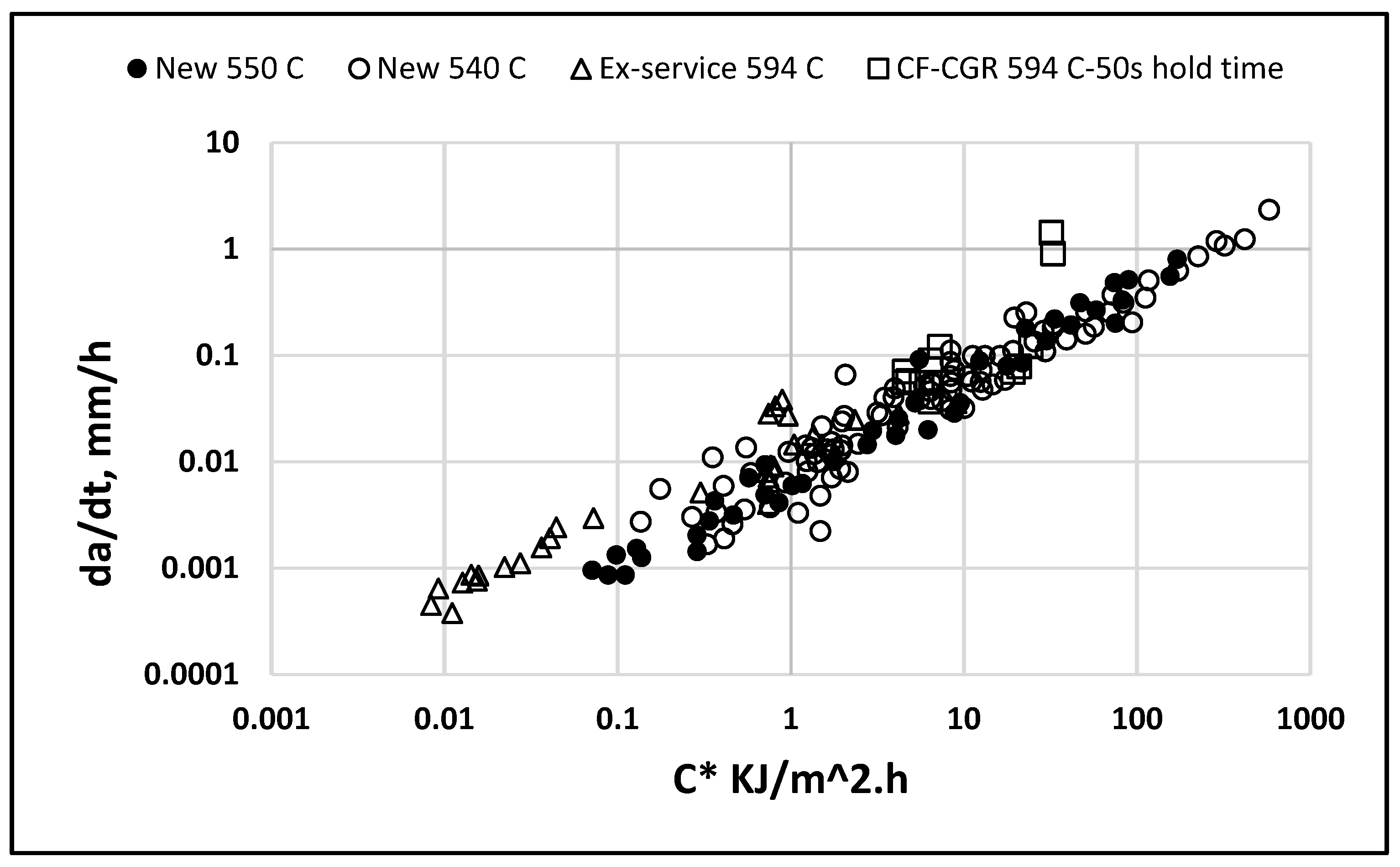
Preprints 84854 g002
Figure 2. Base metal CCGR and CF-CGR behavior as a function of Ct for hold times of 50s for Grade 22 steels at various temperatures in new and ex-service conditions.
Figure 2. Base metal CCGR and CF-CGR behavior as a function of Ct for hold times of 50s for Grade 22 steels at various temperatures in new and ex-service conditions.
Preprints 84854 g002
Preprints 84854 g003
Figure 3. Temperature compensated base metal CCG and CFCG behavior at a hold time of 50 s as a function of Ct or C* for Grade 22 steels at various temperatures plotted using temperature compensated rates.
Figure 3. Temperature compensated base metal CCG and CFCG behavior at a hold time of 50 s as a function of Ct or C* for Grade 22 steels at various temperatures plotted using temperature compensated rates.
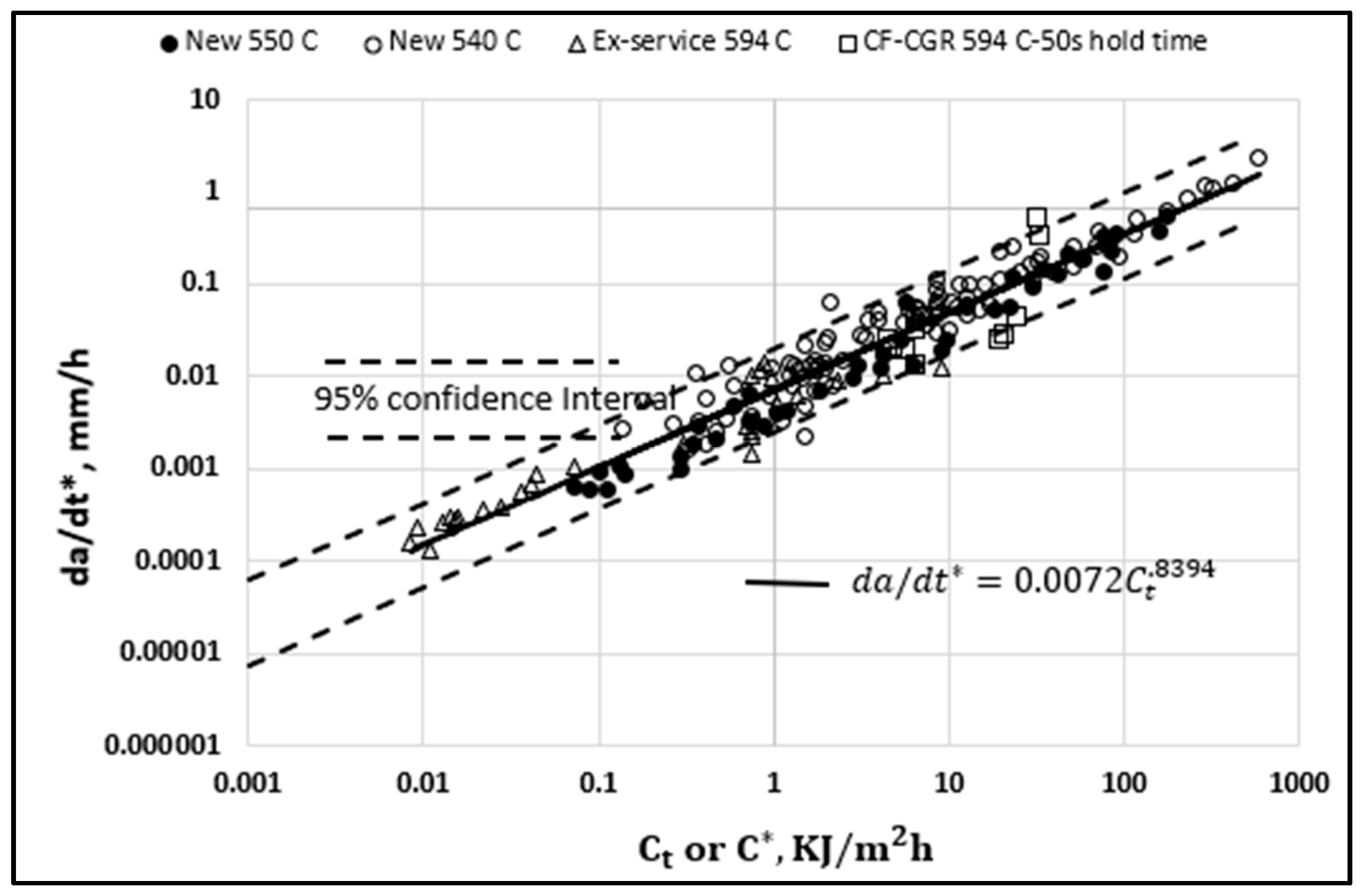
Preprints 84854 g003
Preprints 84854 g004
Figure 4. CCG behavior of Grade 22 steel in the WM and HAZ regions of weldments in new and ex-service conditions compared to BM. All CCG rates are plotted as temperature compensated values using a reference temperature of 540 0C.
Figure 4. CCG behavior of Grade 22 steel in the WM and HAZ regions of weldments in new and ex-service conditions compared to BM. All CCG rates are plotted as temperature compensated values using a reference temperature of 540 0C.
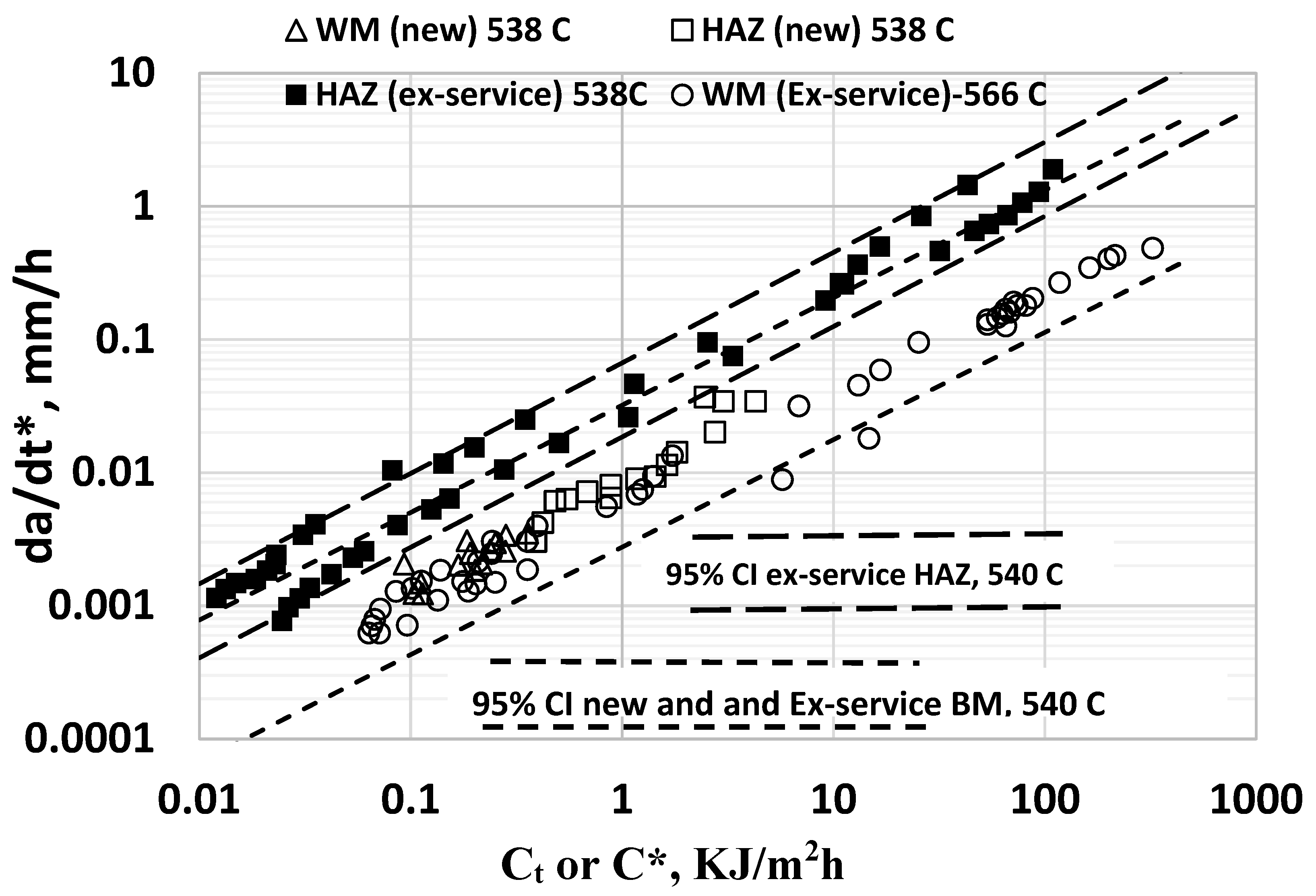
Preprints 84854 g004
Preprints 84854 g005
Figure 5. Temperature compensated CCG rates in Grade 91 BM in new and service exposed but rejuvenated conditions.
Figure 5. Temperature compensated CCG rates in Grade 91 BM in new and service exposed but rejuvenated conditions.
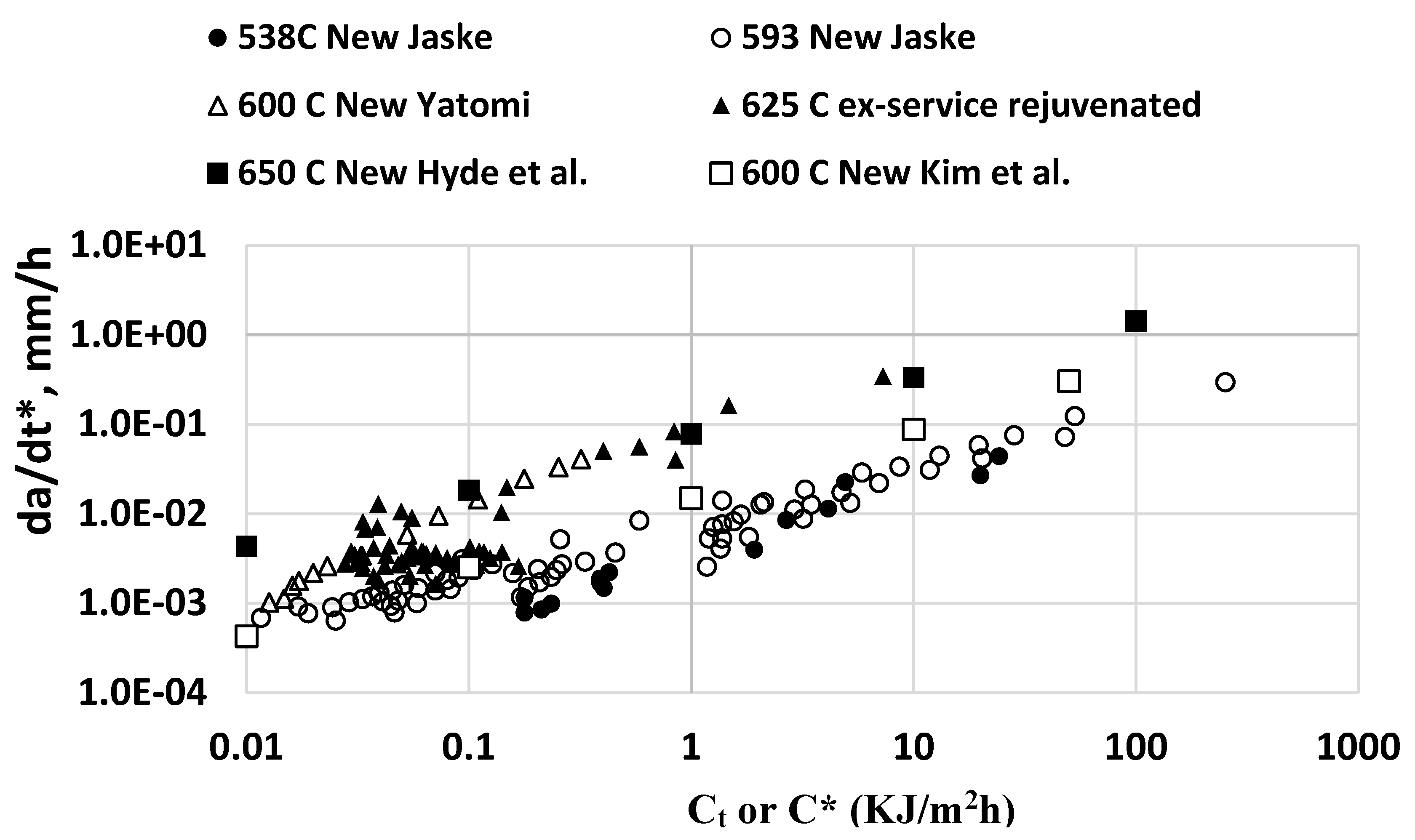
Preprints 84854 g005
Preprints 84854 g006
Figure 6. 95% confidence interval bands for temperature compensated CCG rates in Grade 91 BM in the temperature range from 538 0C to 650 0C for conditions exhibiting creep-ductile and creep-brittle behavior. All CCG rates are referenced to 538 0C.
Figure 6. 95% confidence interval bands for temperature compensated CCG rates in Grade 91 BM in the temperature range from 538 0C to 650 0C for conditions exhibiting creep-ductile and creep-brittle behavior. All CCG rates are referenced to 538 0C.
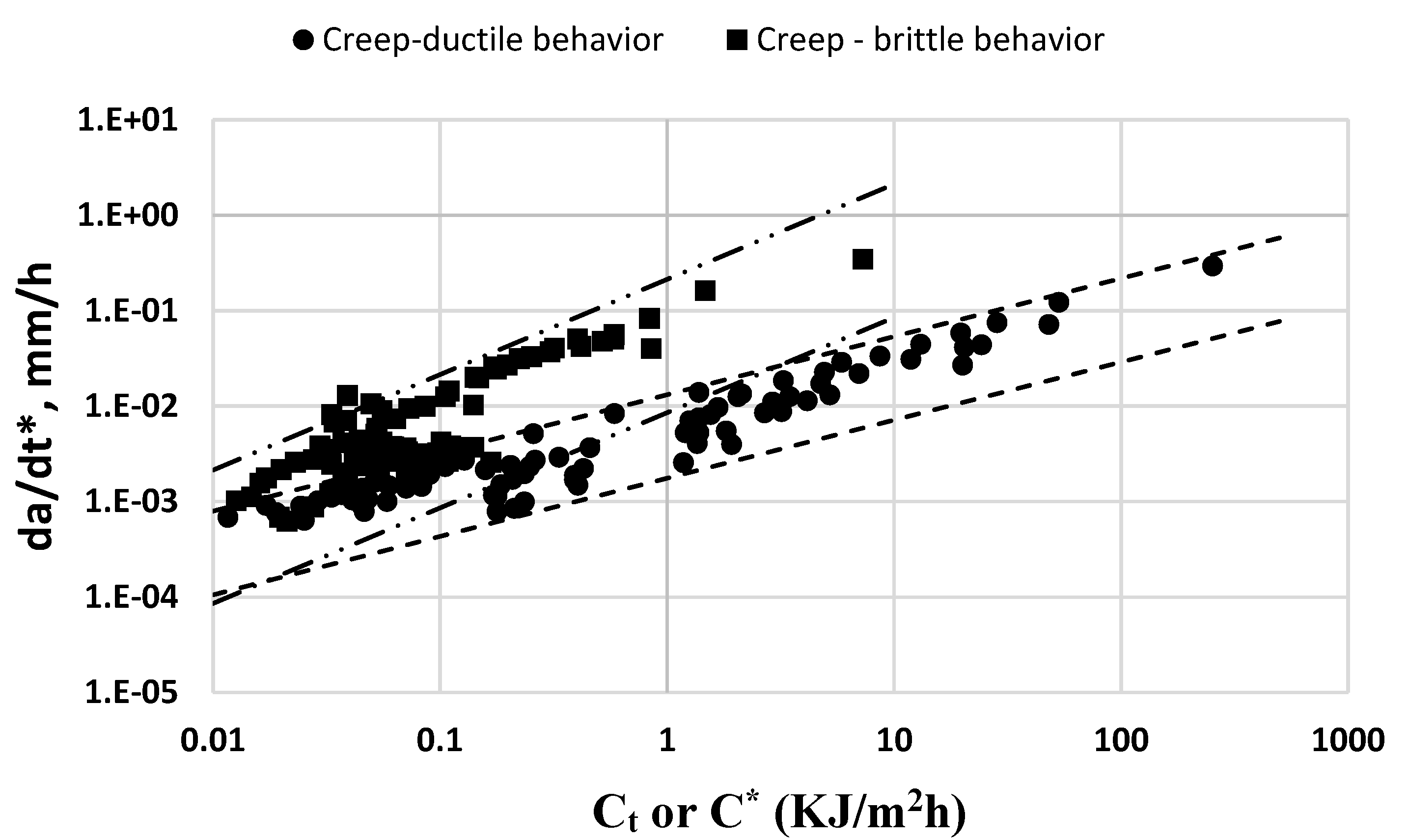
Preprints 84854 g006
Preprints 84854 g007
Figure 7. Additional Grade 91 BM data in the temperature range of 550 0C, 600 0C, and 650 0C compared to the 95% CI bands for creep-ductile and creep-brittle shown in Figure 6.
Figure 7. Additional Grade 91 BM data in the temperature range of 550 0C, 600 0C, and 650 0C compared to the 95% CI bands for creep-ductile and creep-brittle shown in Figure 6.
Preprints 84854 g007
Preprints 84854 g008
Figure 8. CCG behavior of the WM and HAZ regions of Grade 91 steel welds in the temperature range of 550 0C to 650 0C and compared to the CCG of the base metal used in fabricating the weldments.
Figure 8. CCG behavior of the WM and HAZ regions of Grade 91 steel welds in the temperature range of 550 0C to 650 0C and compared to the CCG of the base metal used in fabricating the weldments.
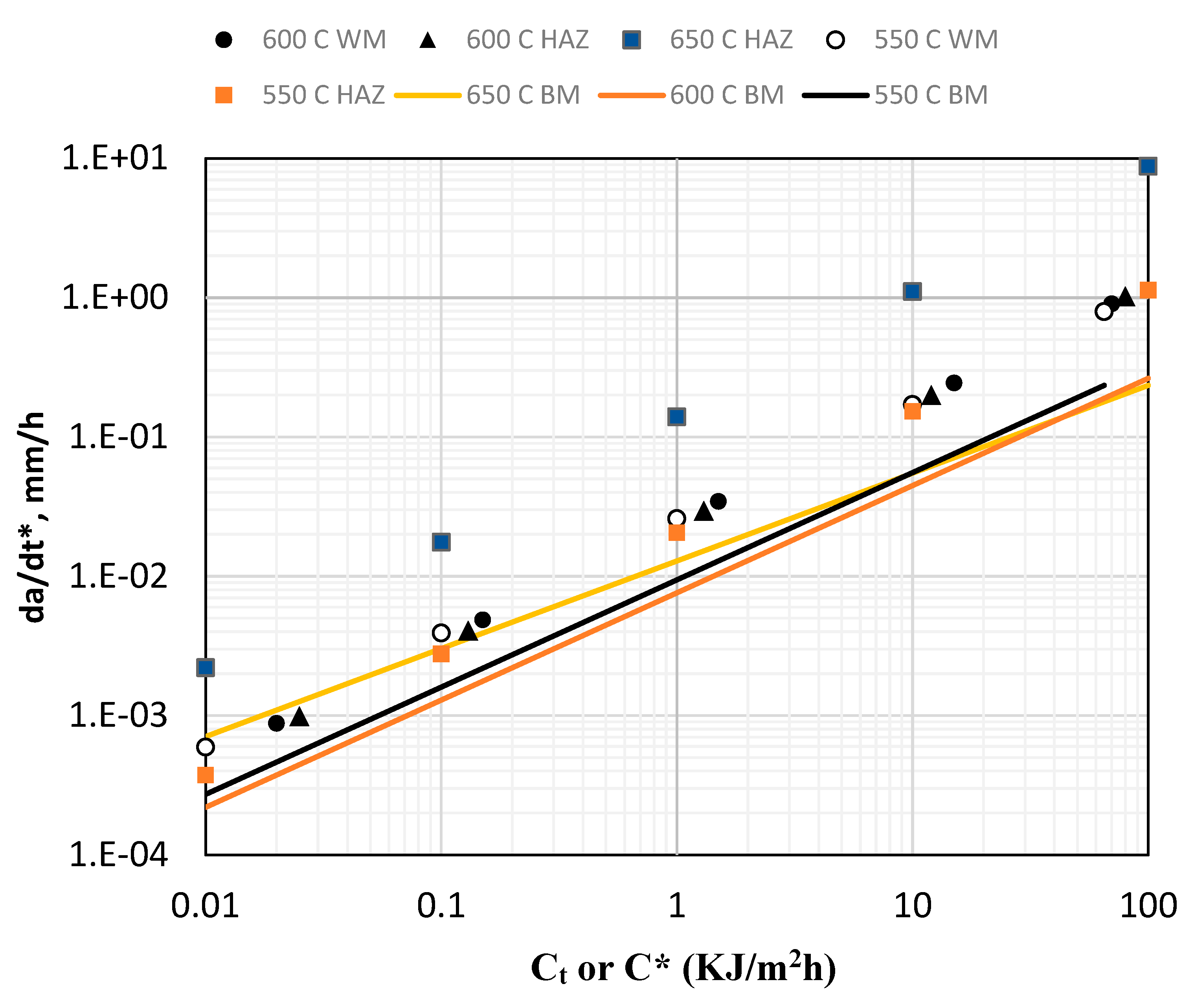
Preprints 84854 g008
Preprints 84854 g009
Figure 9. Temperature compensated CFCG behavior of Grade 91 steel at 625 0C at hold times of 60 s and 600 s. the 95% CI bands for creep-ductile and creep-brittle CCG behavior are superimposed on the CFCG data for comparison.
Figure 9. Temperature compensated CFCG behavior of Grade 91 steel at 625 0C at hold times of 60 s and 600 s. the 95% CI bands for creep-ductile and creep-brittle CCG behavior are superimposed on the CFCG data for comparison.
Preprints 84854 g009
Table 1. Secondary creep constants for Grade 22 steel at three temperatures [10,11,12,13,14,15,16].
Table 1. Secondary creep constants for Grade 22 steel at three temperatures [10,11,12,13,14,15,16].
T 0C ε ˙ s s = A T σ n A T 1 / 1 + n ) ω T from equation (8)
A(T) n
540 (Ref Temp, Tref) 2.2x10-20 6.6 0.00259 1
550 3.94x10-22 7.79 0.00367 1.41
566 6.36x10-23 9.36 0.007243 2.78
594 1.94x10-24 10.08 0.00724 2.8
Table 2. CCG and CFCG constants for Grade 22 steels. The values of Ct/C* are in KJ/m2h and crack growth rates are in mm/h. All constants are referenced to a temperature of 540 0C.
Table 2. CCG and CFCG constants for Grade 22 steels. The values of Ct/C* are in KJ/m2h and crack growth rates are in mm/h. All constants are referenced to a temperature of 540 0C.
Material Temperature 0C Mean/Upper Bound c q
BM/Ex-service BM 540 -594, referenced to 540 Mean 0.0072 0.8394
UB 0.0205
LB 0.0025
New and ex-service WM, New HAZ 540, referenced to 540 Mean 0.0072 0.8394
UB 0.02050
LB 0.0025
Ex-service HAZ 538, assumed to be same as at 540 Mean 0.037 0.8294
UB 0.00666
LB 0.0185
Table 3. Measured minimum creep rate at a stress of 200 MPa at various temperatures and the estimated values of the temperature compensation parameter for CCGR behavior of Grade 91 steel.
Table 3. Measured minimum creep rate at a stress of 200 MPa at various temperatures and the estimated values of the temperature compensation parameter for CCGR behavior of Grade 91 steel.
Temperature (0C) ε ˙ s s = A T σ n A T 1 / 1 + n ) ω T
A(T) n
538 (Ref Temp) 4 x 10-47 17.536 0.00313 1.00
550 (BM) 1.29 x 10-37 13.7 0.00309 0.989
550 (WM) 1.07 x 10-31 11.4 0.00318 1.016
550 (HAZ) 2.45 x 10-35 12.9 0.003236 1.034
575 6 x 10-31 11.202 0.003336 1.066
593 1 x 10-36 14.195 0.004274 1.365
600 1 x 10-26 9.834 0.003982 1.272
625 1 x 10-22 8.383 0.004522 1.445
650 (BM) 1.092 x 10-20 8.462 0.007706 2.46
650 (WM) 1.37 x 10-20 7.65 0.05054 1.615
650 (HAZ) 2.3 x 10-20 8.462 0.008404 2.685
Table 4. a. Actual and nominal chemical composition of test material (in weight%): NR = Not Reported.
Table 4. a. Actual and nominal chemical composition of test material (in weight%): NR = Not Reported.
c Si Mn P S Ni Cr Mo As V Nb Al Cu N Sb,Sn Fe
Shingledecker 0.11 0.31 0.45 0.011 0.009 0.19 8.22 0.94 .005 0.21 0.07 .006 0.16 .039 .001 Bal
Hyde et al. BM 0.11 0.022 0.36 NR NR NR 8.74 0.98 NR 0.21 0.12 NR 0.08 0.048 NR Bal
Hyde et al. WM 0.087 0.28 1.04 NR NR NR 8.6 1.02 NR 0.22 0.24 NR 0.03 0.04 NR Bal
Kim et al. BM 0.115 0.23 0.415 0.012 0.014 0.22 8.9 0.87 NR .0194 0.073 0.02 0.038 0.0513 NR Bal
Nominal 0.1 0.38 0.46 0.02 .002 0.33 8.1 0.92 - 0.18 0.073 0.034 - 0.049 - Bal
Table 4. b. Actual trace element content compared to levels that are known to cause creep damage resistant and creep damage prone conditions in Grade 91 steels.
Table 4. b. Actual trace element content compared to levels that are known to cause creep damage resistant and creep damage prone conditions in Grade 91 steels.
S Cu Sn As Sb Pb
Actual 0.009 0.16 0.001 0.005 0.001 ?
Damage Prone 0.01 0.19 0.008 0.0128 0.0023 0.00075
Damage Resistant 0.002 0.05 0.003 0.0042 0.00063 0.00003
Table 5. CCG rate constants for creep-ductile and creep-brittle behaviors in Grade 91 steels. All constants are for a reference temperature of 538 0C for Ct expressed in KJ/m2h and da/dt* in mm/h.
Table 5. CCG rate constants for creep-ductile and creep-brittle behaviors in Grade 91 steels. All constants are for a reference temperature of 538 0C for Ct expressed in KJ/m2h and da/dt* in mm/h.
Material Temperature 0C Mean/Upper Bound c q
CCG-Creep-ductile behavior 538 – 593, referenced to 538 Mean 0.0048 0.6093
UB 0.01314
LB 0.001752
CCG-Creep-brittle behavior 600 -625, referenced to 538 Mean 0.0427 0.9991
UB 0.2130
LB 0.008557
CFCG 625 but referenced to 538 Mean 0.0186 0.5061
UB 0.1099
LB 0.003149
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated