Prerpints.org logo
Preprint
Article

Evolution of a Stratified Turbulent Cloud under Rotation

Altmetrics

Downloads

74

Views

9

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

12 September 2023

Posted:

14 September 2023

You are already at the latest version

Alerts
Abstract
Localized turbulence is common in geophysical flows, where the roles of rotation and stratification are paramount. In this study, we investigate the evolution of a stratified turbulent cloud under rotation. Recognizing that a turbulent cloud is composed of vortices of varying scales and shapes, we start our investigation with a single eddy. Compared to an eddy under pure rotation, the stratified eddy shows the physical manifestation of a known potential vorticity mode, appearing as a static stable vortex. In addition, the expected shift from inertial waves to inertial-gravity waves is observed. In our numerical simulations of the turbulent cloud, carried out at a constant Rossby number over a range of Froude numbers, stratification causes columnar structures to deviate from vertical alignment. This deviation increases with increasing stratification, slowing the expansion rate of the cloud. The observed characteristics of these columnar structures are consistent with the predictions of linear theory, particularly in their tilt angles and vertical growth rates, suggesting a significant influence of inertial-gravity waves. Using Lagrangian particle tracking, we have identified regions where wave activity dominates over turbulence. In scenarios of milder stratification, these inertial-gravity waves are responsible for a significant energy transfer away from the turbulent cloud, a phenomenon that attenuates with increasing stratification.
Keywords: 
Subject: Physical Sciences  -   Fluids and Plasmas Physics

1. Introduction

Localized turbulence is common in both atmospheric and oceanic flows, which are strongly influenced by the Earth’s rotation and stable density stratification [1,2,3,4,5]. Understanding the evolution of these turbulent patches under the combined effects of rotation and stratification is crucial for gaining deeper insights into various geophysical phenomena. A key mechanism behind the generation of such turbulence is the local breakdown of internal waves [6,7]. In particular, the resulting turbulence often exhibits horizontal scales that are significantly larger than their vertical counterparts. Empirical observations from deep waters and the equatorial pycnocline also reveal pronounced differences in horizontal and vertical scales of turbulent patches [2,3]. Furthermore, mixing induced by internal wave breaking tends to weaken local stratification. Such reduced stratification is also observed in turbulent regions within the ocean mixed layer [8]. With these characteristics in mind, our present study is concerned with a horizontally extended turbulent cloud within a vertically stably stratified, rotating fluid system, where the effects of rotation dominate over the stratification. Our focus is on understanding the formation of flow structures and analysing the associated energy dispersion patterns.
While numerous studies have highlighted the dominance of waves in spatially uniform and stationary scenarios of rotating/stratified turbulence [9,10,11], the dynamics of localized turbulent patches has also attracted considerable attention. In particular, under rotation, these turbulent patches often give rise to columnar vortices parallel to the axis of rotation, associated with inertial waves [12,13,14,15]. For example, in their oscillating-grid turbulence experiments, Dickinson and Long [13] found that, for a Rossby number close to unity, the boundary between perturbed and quiescent regions moves at speeds related to certain wave velocities. Similarly, Davidson et al. [14] showed experimentally that the leading edges of columnar vortices under rotation align with inertial wave group velocities. Using direct numerical simulations (DNS), Ranjan and Davidson [15] observed these columnar structures, attributed their formation to inertial waves, and emphasized their role in significant energy dissipation from localized turbulence.
Analogous to turbulent patches under rotation, the presence of internal wave radiation is clearly evident in localized turbulence within stratified fluids [16,17,18,19], such as wakes caused by object motion [20,21]. The flow structures in these scenarios are predominantly wave-dominated. In addition, these waves contribute significantly to energy reorganization, highlighting their fundamental role in the atmosphere and oceans [22]. Anisotropic structures and wave propagation are observed in both rotating and stratified turbulent flows. These phenomena highlight the complex interplay between rotation and stratification in geophysical flows [23,24,25]. While many studies have investigated the turbulent patch behavior in rotating and stratified fluids, the emphasis has often been on aspects such as lateral intrusions, Thorpe scales and the vertical expansion of the patch [26,27,28,29]. However, the waves emitted by these disturbances often receive less attention. One notable exception [30] used DNS to study a buoyant cloud subjected to vertical rotation and horizontal gravity, reminiscent of equatorial conditions. It was confirmed that the formation of columnar structures was due to inertial waves arising from the buoyant cloud.
Building on previous work, we explore an under-explored area: the evolution of a horizontal turbulent cloud under vertical rotation and stratification. This has significant relevance in geophysical contexts such as the high latitudes of the atmosphere and oceans [31] and the deep Arctic waters [32,33]. In particular, our study examines scenarios where rotation effects outweigh stratification, in contrast to many typical geophysical flows where stratification predominates. In this context, we address three key questions: First, how does stratification affect the resulting flow structures, as opposed to purely rotating scenarios? Second, are these structures influenced by inertial-gravity waves, and how does different stratification affect their formation? Third, what fraction of the cloud’s energy is transferred to waves at different stratification levels?

2. The evolution of a single stratified eddy under rotation

In this section, we study the evolution of a single stratified eddy under rotation. This is motivated by the fact that a turbulent cloud can be considered as a sea of randomly oriented vortex blobs with different scales. First, we introduce internal-inertial gravity waves under the Boussinesq approximation. Second, we solve analytically the initial value problem of a compact vortex blob in a rapidly rotating stratified environment. Finally, a numerical simulation is performed to validate the analytical solution. It is shown that as the eddy evolves, part of the energy is retained in the eddy by the potential vorticity (PV) mode, while the other part is carried away from the eddy by inertial-gravity waves.

2.1. Internal-inertial gravity waves

The Boussinesq set of equations for a linearly stratified fluid under system rotation can be written as:
∇ · u = 0 ,
∂ u ∂ t + u · ∇ u = − 1 ρ 0 ∇ p + 2 u × Ω − N ϕ e z + ν ∇ 2 u ,
∂ ϕ ∂ t + u · ∇ ϕ = N u z + κ ∇ 2 ϕ ,
where u is the velocity vector, u z is the z-component of the velocity, p is the modified pressure incorporating a centrifugal term, Ω = Ω e z represents the rotation vector, N is the Brunt-Väisälä frequency, and ν and κ are the kinematic viscosity and the diffusion coefficient, respectively. We define ϕ = g / ρ 0 N ρ ′ , which has the dimension of the velocity, and ρ ′ is the density perturbation from the ambient density.
Inertial-gravity waves can be obtained after a linearization of the Boussinesq equations. Neglecting the molecular diffusion and the second-order terms of u , w and ϕ one obtains:
∂ ω ∂ t + ∇ × ( 2 Ω × u ) = − N ∇ ϕ × e z ,
∂ ϕ ∂ t = N u z ,
from which one finds [see [34], p. 56]
∂ 2 ∂ t 2 ∇ 2 u z + 4 Ω 2 ∂ 2 u z ∂ z 2 + N 2 ∂ 2 u z ∂ x 2 + ∂ 2 u z ∂ y 2 = 0 .
This equation admits inertial-gravity waves with the dispersion relation given as
ϖ = ± N 2 k h 2 + 4 Ω 2 k z 2 / k ,
where ϖ is the frequency, while k h = k x 2 + k y 2 and k = k x 2 + k y 2 + k z 2 are the horizontal wavenumber and the total wavenumber, respectively. The group velocity is c g = ∇ ϖ , whose z-component is
c g , z = ∂ ϖ ∂ k z = ± 4 Ω 2 − N 2 k h 2 k z N 2 k h 2 + 4 Ω 2 k z 2 k 3 .

2.2. Analytical study of a single eddy

Following Davidson et al. [14], we consider the evolution of an eddy in a stratified fluid under rotation, assuming that the process is axisymmetric with respect to the eddy axis. In this context, in a cylindrical coordinate system ( r , θ , z ) , an axisymmetric velocity field u can be decomposed into azimuthal and poloidal components
u = Γ / r e θ + ∇ × ψ / r e θ ,
where Γ = u θ r is the angular momentum and ψ is the Stokes streamfunction. We substitute Equation (9) into the linearized inviscid vorticity equation (4) and the linearized non-diffusive Equation (5) to obtain
∂ Γ ∂ t = 2 Ω ∂ ψ ∂ z , ∂ ∂ t r ω θ = 2 Ω ∂ Γ ∂ z + N r ∂ ϕ ∂ r , ∂ ϕ ∂ t = N r ∂ ψ ∂ r ,
where ∇ * 2 ψ = r ∂ / ∂ r r − 1 ∂ ψ / ∂ r + ∂ 2 ψ / ∂ z 2 = − r ω θ , ∇ * 2 being the Stokes operator. Combining the equations in (10) yields
∂ ∂ t ∂ 2 ∂ t 2 ∇ * 2 Γ + 2 Ω 2 ∂ 2 ∂ z 2 + N 2 r ∂ ∂ r ∂ r ∂ r Γ = 0 .
Equation (11) can be readily solved by using the Hankel-cosine transform
u ^ θ = 1 2 π 2 ∫ 0 ∞ ∫ 0 ∞ r u θ J 1 k r r cos k z z d r d z ,
where J 1 is the Bessel function of the first kind of order 1. Here, k r and k z represent the wavenumbers in the r-direction and the z-direction, respectively, with 0 ≤ k r , k z < ∞ . Given the initial conditions u ^ θ = u ^ θ 0 , ψ = 0 and ϕ = 0 , we can derive that
u ^ θ = u ^ θ 0 / N 2 k r 2 + 2 Ω 2 k z 2 N 2 k r 2 + 2 Ω 2 k z 2 cos N 2 k r 2 + 2 Ω 2 k z 2 t / k ,
from which we obtain
u θ = 4 π ∫ 0 ∞ ∫ 0 ∞ N 2 k r 3 u ^ θ 0 / α 2 J 1 k r r cos k z z d k r d k z ︸ PV mode + 2 π ∫ 0 ∞ ∫ 0 ∞ 2 Ω 2 k r k z 2 u ^ θ 0 / α 2 J 1 k r r cos k z z − α t / k + cos k z z + α t / k d k r d k z ︸ inertial - gravity waves ,
where we introduce α = N 2 k r 2 + 2 Ω 2 k z 2 for conciseness. In the absence of stratification (i.e. when N = 0 ), Equations (13) and (14) are consistent with the results presented in Davidson et al. [14], which consider only the rotation of the system. However, the inclusion of stratification introduces a new time-independent term and changes the frequencies of the previously identified wave-like components. Note that the phase velocities of the wave-like components, given by ± α / k , closely match those of the inertial-gravity waves according to equation (7), provided we replace k r with k h . This alignment strongly suggests that these wave-like components are indeed manifestations of the inertial-gravity waves. In a periodic domain with spatially uniform rotating stratified flows, Smith and Waleffe [35] identified the linear eigenmodes as two inertial-gravity waves and a PV mode, suggesting that the time-independent term in (14) is consistent with the zero-frequency PV mode. However, our solution shows how these PV mode and inertial-gravity waves manifest in a localized, non-uniform turbulent background - an aspect not addressed in previous studies. Later in Section 2.3, we will explore the associated flow structures and elucidate their role in energy dispersion.

2.3. Numerical validation of the analytical results

To assess the applicability of the analytical results in Section 2.2 and to develop a better understanding of the evolution of a single eddy in a rotating stratified fluid, a simple initial velocity field of the Gaussian-eddy form is chosen:
u = Λ r exp − r 2 + z 2 δ 2 e θ ,
for which Davidson et al. [14] have given an analytical solution when only the rotation is considered. In this equation, Λ is the characteristic angular rotation rate and δ is the characteristic size. The corresponding Rossby and Froude numbers are defined by R o = Λ / ( 2 Ω ) and F r = Λ / N , respectively. To validate our analytical solutions, we chose parameters R o = 0.02 and F r = 0.16 , corresponding to a vortex characterized by Λ = 0.422 and δ = 0.125 . The analytical solution is then obtained by substituting (15) into (14). We then performed a DNS to study the evolution of this Gaussian eddy. Equations (1)-(3) are solved using a parallelized pseudo-spectral code in a 512 3 periodic box of size l b o x = 2 π , where the fourth-order Runge-Kutta time-stepping scheme is employed. The linear terms caused by rotation and stratification, together with the viscous and diffusive terms, are integrated exactly using an integrating factor technique. A combination of phase-shifting and truncation is used to de-alias the nonlinear terms [see e.g. [36].
Figure 1(a) and (b) show contours of u θ 2 (normalized by its maximum value) in the x − z plane passing through the axis of the Gaussian eddy at t / t f = 13.5 . These are results from the analytical solution and the DNS respectively. Here t f = 1 / ( 2 Ω ) denotes the rotation time scale. The DNS result, which takes into account the full Navier-Stokes equations, is still in close agreement with the analytical counterpart. A prominent region of u θ 2 near the origin stands out, which is absent in the unstratified scenario [Figure 3 [30]. This region is indicative of the PV mode, while the other intense regions represent inertial-gravity waves.
To illustrate the evolution of the flow structures and their corresponding energy dispersion, Figure 2 shows iso-surfaces of the vertical vorticity, ω z = 0.1 Λ , color-coded with ϕ , at times t / t f = 13.5 and 16.9 . As the system begins to evolve, a central vortex appears at the origin, flanked by two vortices, one above and one below (Figure 2(a)). Over time, the central vortex undergoes minor changes, while the flanking vortices become smaller and their centers move further away from the origin (Figure 2(b)). This behavior is in stark contrast to the purely rotating case [30], where only two columnar structures emerge, progressively moving away from each other as they elongate. The shifts in the flow structures can be attributed to the interplay between the Coriolis and buoyancy forces. In Figure 2(a), all three cyclonic vortices ( w z > 0 ) are influenced by the Coriolis force, causing them to stretch horizontally. For the central vortex, ϕ has negative values at the top and positive ones at the base. This distribution results in a vertical stretch from the buoyancy force, which counteracts the Coriolis force due to the incompressibility of the fluid. As a result, this vortex remains relatively stable, maintaining a nearly consistent energy distribution over time. For each flanking vortex, ϕ retains its sign, showing larger absolute values for smaller magnitudes of | z | . This implies that the buoyancy force is acting to move these vortices away from the origin and to compress them vertically. The interaction of the Coriolis and buoyancy forces causes these vortices to recede and decrease in size, resulting in energy dispersion and potential-kinetic energy exchange. It is worth noting that a similar phenomenon to the central vortex has been documented in homogeneous rotating stratified turbulence, where it correlates with a pronounced exchange between kinetic and potential energy [37].

3. A stratified turbulent cloud under rotation

In this section, we move from the study of a single eddy to the nonlinear evolution of a turbulent cloud. Using DNS, we study the flow structures and observe characteristics consistent with inertial-gravity waves. Finally, we calculate the energy radiated from the turbulent cloud by these waves to understand their role in energy transfer for localized turbulent patches.

3.1. DNS of a turbulent cloud

Following the procedure described by Davidson [38], we performed DNS on fully developed homogeneous isotropic turbulence to obtain the initial velocity field for the turbulent cloud study. We then selected a velocity field corresponding to a specific moment characterized by an integral length scale of l 0 ≈ 0.04 l b o x and a Reynolds number R e 0 = u 0 l 0 / ν ≈ 169 , where u 0 is the r.m.s. velocity. To numerically generate a horizontal turbulent cloud, the resulting velocity field was spatially filtered with
f z = exp − 10 a z − π m ,
as shown in Figure 3(a). Here we set a = 4 and m = 9 , resulting in a cloud thickness of l c = 0.13 l b o x , approximately three times the integral length scale l 0 . The buoyancy field was initialized with ϕ = 0 throughout the computational domain, which ensures a uniformly linear density profile, indicating no initial mixing within the cloud. Figure 3(b) shows the initial turbulent cloud as indicated by the velocity module, and its spectrum in the x-y plane, averaged over its central part in the z-direction, is shown in Figure 3(c).
To investigate the effect of different stratification on the evolution of a turbulent cloud under rotation, we conducted DNS with a constant Rossby number, R o = 0.11 , and five different Froude numbers: F r = ∞ (corresponding to N = 0 , a purely rotating scenario), 0.88 , 0.44 , 0.22 and 0.11 . The simulation parameters are given in Table 1, where R o = u 0 / ( 2 Ω l 0 ) and F r = u 0 / ( N l 0 ) . With the exception of the purely rotating case R0.11, the simulations are denoted by their Froude numbers, e.g. the case F0.88 corresponds to F r = 0.88 .

3.2. Evolution of flow structures

To show the evolution of the turbulent cloud structures, Figure 4 shows iso-surfaces of u z for all simulations at different times. For the case R0.11 under pure rotation, Figure 4(a) shows the emergence of vertical columnar structures from the turbulent cloud, which extend into the quiescent region, in agreement with previous experimental results [14] and numerical study [15]. For the weakly stratified case F0.88, Figure 4(b) shows subtle differences in the flow structures at t / t f = 8.4 and more pronounced variations at t / t f = 12.7 compared to the case R0.11.
For the moderately stratified cases F0.44 and F0.22, Figure 4(c) and (d) show that the columnar structures tend to deviate from a purely vertical orientation as they extend into the quiescent region. This tilt becomes more pronounced with increasing stratification. A comparison of Figure 4(a)-(e) shows that, at equivalent time intervals, the vertical growth of these structures decreases with decreasing F r . This suggests that strong density stratification limits the vertical expansion of the cloud, consistent with the observation in experiments [27].
In the case F0.11 (Figure 4(e)), the rotation frequency and the Brunt-Väisälä frequency are identical. As a result, no structures emerge from the turbulent cloud, suggesting minimal energy emission from the cloud. This behavior mirrors the case without both rotation and stratification, as documented in [15]. A plausible interpretation is that the stratification strength is sufficient to completely inhibit the vertical expansion of the turbulent cloud in the presence of system rotation. It is noteworthy that Equation (7) for this scenario yields ϖ = 2 Ω = N , implying uniform frequencies of inertial-gravity waves in all directions. Thus, in the absence of both rotation and stratification, the system exhibits isotropy.

3.3. Are the flow structures formed by inertial-gravity waves?

Columnar structures from a turbulent cloud under rotation have been identified as inertial waves [15], while the large-scale pancake structures from a stratified turbulent cloud are recognized as internal gravity waves [22]. This section examines whether the flow structures discussed in Section 3.2 from the stratified turbulent cloud under rotation can be attributed to inertial-gravity waves.
In all simulations, the growth of flow structures in different directions leads to the expansion of turbulent clouds in the vertical direction, which can be quantified by tracking the boundary of the | u z | iso-surfaces with time. The reason we choose u z to indicate structure is that it satisfies the wave equation as described by (6). In particular, given a threshold | u z b | , the upper and lower boundaries of the cloud can be obtained from the positions where | u z | = | u z b | . We can therefore calculate the vertical extent of the cloud, h ( x , y , t ) , for each point on the x − y plane and time t. The mean wave-cloud thickness h ¯ ( t ) is defined as the average of h ( x , y , t ) over x and y. Figure 5 shows the mean wave-cloud thickness for all the simulations where we choose | u z b | = 0.35 u 0 . The results remain robust when the threshold varies around this value, and this threshold is used consistently throughout the analysis in this paper. For the purely rotating case R0.11, the mean wave-cloud thickness shows a linear growth with time, resulting from the inertial waves with k z = 0 traveling at the group velocity c g = 2 Ω ⁄ k h [15]. For the case F0.88 with weak stratification, the mean wave-cloud thickness is close to that in the case R0.11 at t ≤ 0.2 , indicating that the stratification does not affect the cloud before t = 0.2 . This is because that the linear time scale corresponding to the rotation, t f = 1 / ( 2 Ω ) , is smaller than that corresponding to the stratification, t N = 1 / N . When t > 0.2 , the mean wave-cloud thickness shows a smaller linear growth rate. For the cases F0.44 and F0.22 with stronger stratification, the behavior of the mean wave-cloud thicknesses can be interpreted as the superposition of a linear growth and an oscillation with a fixed frequency over time. In addition, the frequency is larger in the case F0.22. The mean wave-cloud thickness in the case F0.11 is almost constant with time, consistent with the observation in Figure 4(e).
To investigate whether the flow structures are closely related to the inertial-gravity waves, we compare the results from the DNS with those predicted by the linear theory. Since the initial turbulent cloud can be viewed as a distribution of random vortex blobs of different shapes and sizes, we consider the linear evolution of a Gaussian vortex satisfying Equation (15) under the same Rossby and Froude numbers. We set Λ = 2.31 , δ = 0.125 , and utilize | u z b | = 0.002 Λ δ to determine the vertical extent of the eddy, h e . This extent is defined as the largest vertical distance between the positions where | u z | = | u z b | . Figure 5(b) shows that the results for h e align qualitatively with those of h ¯ in Figure 5(a), suggesting that the expansion of the turbulent cloud may be prominently influenced by the linear mechanism.
We now show quantitatively that the flow structures are closely related to inertial-gravity waves. For a vortex blob in the initial turbulent cloud, suppose it is characterized by a length scale of 1 / k . Then its rescaled group velocity in the vertical direction is
c ˜ g , z = k c g , z = ± 2 Ω ( 1 − ( N / ( 2 Ω ) ) 2 ) ( k z / k h ) ( N / ( 2 Ω ) ) 2 + ( k z / k h ) 2 ( 1 + ( k z / k h ) 2 ) .
Given the ratio of the Brunt-Väisälä frequency to the rotation frequency N / ( 2 Ω ) , it is determined that when
k z k h 2 = 1 4 − ( N / ( 2 Ω ) ) 2 + ( N / ( 2 Ω ) ) 4 + 8 ( N / ( 2 Ω ) ) 2 ,
c ˜ g , z reaches the maximum c ˜ g , z m a x , which is the vertical growth rate of the turbulent cloud predicted by the linear inertial-gravity waves. Furthermore, the corresponding value of k z / k h = ( k z / k h ) 0 characterizes the tilt angle of the flow structure. The vertical growth rate of the turbulent cloud in the DNS can be determined from the growth rate of the mean wave-cloud thickness, h ¯ ( t ) , as shown in Figure 5(a). The rate is calculated using a linear fitting method. In Figure 6(a) we present two vertical growth rates: α D N S derived from DNS and α L T derived from linear theory. To facilitate comparison, both rates are normalized by their values at N / 2 Ω = 0 . Figure 6(b) shows the angle between the flow structure and the vertical direction, θ = arctan [ ( k z / k h ) 0 ] , predicted by linear theory for different N / ( 2 Ω ) . The results are consistent with Figure 4, where the angle becomes larger as N / ( 2 Ω ) increases. For quantitative comparison, we also plot cones in the third columns of Figure 4(b), (c) and (d), where the angle between the cone surface and the vertical axis is equal to θ . It is notable that there is a strong agreement between the DNS results and the predictions of linear theory. However, for the case F0.22, both α and θ are slightly underestimated by the linear theory. This discrepancy could be due to the interactions between waves and turbulence, especially given the small vertical expansion of the cloud in this case. It is important to note that in scenarios where both rotation and stratification are present, the frequency of the inertial-gravity waves (7) tied to c ˜ g , z m a x is not zero. This explains the oscillatory component observed in h ¯ for the cases F0.44 and F0.22. When only rotation or stratification is present, the maximum group velocity always coincides with inertial (or gravity) waves of zero frequency. Under these circumstances, tools such as two-dimensional energy spectrum analysis can be used effectively, given the consistent phase of u z [15] or u x [22] at the edge of the turbulent cloud.

3.4. Wave-dominated and turbulence-dominated regions

In Section 3.3 it is highlighted that the flow structures emerging from the turbulent cloud show a strong association with inertial-gravity waves. In stratified turbulence, PV has been used to identify turbulent/non-turbulent interfaces [22,39]. Our study, however, uses Lagrangian particle tracking to measure the vertical extent of turbulent advection [15]. Lagrangian particles act as passive tracers, with their position r at time t given by d r / d t = u ( r , t ) . In this relationship, u represents the velocity of the fluid. To determine u at the particle positions, we use a 6th-order Lagrange interpolation. Furthermore, the positions of these particles are integrated using a 2nd-order Adams-Bashforth scheme.
Tracer particles with a number N p = 65536 are initialized randomly from a uniform distribution throughout the initial turbulent cloud, the vertical range of which is denoted as [ z 0 , z 1 ] . Let N p o u t be the number of particles outside of the range of the initial turbulent cloud. The r.m.s. distance of these particles to the initial turbulent cloud can be calculated as
d r m s = 1 N p o u t ∑ p = 1 N p o u t d p 2 ,
where
d p = z p − z 1 , z p > z 1 z 0 − z p , z p < z 0
represents the distance of the particle p to the initial turbulent cloud. We consider [ z 0 − d r m s , z 1 + d r m s ] as the vertical range of the turbulence-dominated region and the other domain as the wave-dominated region. Figure 7 shows the ratio of particles outside the initial turbulent cloud, N p o u t / N p , and d r m s normalized with the initial cloud thickness l c . For the case R0.11, both N p o u t / N p and d r m s / l c increase with time, while for the cases F0.88 and F0.44 both quantities first increase and then decrease after reaching the maximum values, probably due to the stable stratification. However, in the cases F0.22 and F0.11, where the stratification is strong, both quantities immediately reach stationary states around small values.
Table 2 presents the maximum values of N p o u t / N p and d r m s / l c for all cases, where max ( d r m s / l c ) can also be interpreted as the maximum vertical expansion of the initial turbulent cloud. It is observed that both quantities become smaller with increasing stratification, indicating the limitation of vertical turbulent advection by stratification.
Once the regions dominated by waves and turbulence are identified, we can determine the energy of the turbulent cloud carried away by the inertial-gravity waves, denoted as E w a v e . This energy is equal to the energy within the wave-dominated region. Figure 8(a) shows that for cases where R o < F r , the ratio E w a v e / E exhibits a monotonic increase with time. In particular, for a given time point, a decrease in F r results in smaller values of E w a v e / E . This suggests that under stronger stratification, inertial-gravity waves contain a smaller fraction of the energy. In contrast, for the scenario where R o = F r , the ratio E w a v e / E oscillates with a fixed pattern. Its values fluctuate between nearly zero and a peak of about 15 % , indicating that the inertial-gravity waves only sporadically extract a small fraction of energy from the turbulent cloud. Thus, while inertial waves account for a significant fraction of the energy in a system dominated by rotation alone, this energy contribution diminishes with the introduction of stratification. Figure 8(b) shows the ratio of potential energy to total energy in the wave-dominated region, E P w a v e / E w a v e . As stratification increases, potential energy becomes increasingly dominant and varies more frequently with time. This highlights the increasing importance of the kinetic-potential energy exchange and suggests that the dominant inertial-gravity waves exhibit greater phase velocities under increased stratification. It is worth noting that a similar kinetic-potential energy exchange phenomenon has been reported in homogeneous rotating stratified turbulence [40].

4. Discussion and Conclusions

In this study, we investigate the evolution of a stratified turbulent cloud influenced by rotation. By analyzing the behavior of a single eddy under both rotation and stratification, we observe clear deviations from the purely rotating scenario. In particular, within the stratified environment, we detect a spatial manifestation of a known PV mode, characterized as a stable vortex at the origin. Furthermore, the system transitions from exhibiting inertial waves to producing inertial-gravitational waves, whose propagation relations depend on both rotation and stratification.
Numerical simulations have been performed to investigate the nonlinear evolution of the turbulent cloud influenced by different degrees of stratification under rotation. In cases where R o < F r , columnar structures emerge spontaneously from the turbulent cloud. These structures are vertically oriented in the case of pure rotation, but deviate from the vertical as stratification is introduced. As F r decreases, the tilt angle increases and the rate of cloud expansion decreases. Conversely, in the R o = F r system, the turbulent cloud remains devoid of distinct structures, reminiscent of scenarios without rotation and stratification. The flow structures are observed to have characteristics consistent with inertial-gravity waves. This observation is supported by the agreement between DNS and linear theory, which give consistent predictions for the vertical growth rates of the turbulent cloud and the tilt angles of these structures. Using Lagrangian particle tracking, we distinguish between wave-dominated and turbulence-dominated regions. It is found that the inertial gravity waves emitted by the cloud can transport a substantial fraction of the energy to the neighbouring quiescent fluid, which decreases with increasing stratification. This suggests the central role of inertial-gravity waves in energy transfer processes within atmospheres and oceans, particularly around regions of localized turbulence.
The present study elucidates the effects of stratification on localized turbulence under system rotation. First, compared to the purely rotating case, the presence of stratification introduces the zero-frequency PV mode, whose energy distribution barely changes with time. While this mode is not new, our finding is its distinct spatial manifestation within a non-uniformly turbulent background. Second, as the stratification intensifies, the dominant inertial-gravity waves exhibit increased tilting and reduced vertical group velocity. In combination, these phenomena limit the energy emitted by the initial turbulent cloud. It should be noted that this study focuses on the parameter regime where R o < F r . While the R o > F r regime is thought to dominate in the Earth’s atmosphere and oceans [6], the R o < F r regime is relevant for several geophysical flows, such as in the deep sea where the influence of stratification is weak but rotation effects are prominent [41,42,43,44,45]. Furthermore, the observed flow structures can be conceptualized as Fourier modes with phase coherence. This provides an alternative perspective: the evolution of these turbulent clouds could be seen as the evolving phase coherence of Fourier modes influenced by both rotation and stratification, which is an avenue for future research.

Author Contributions

Conceptualization, T.L., M.W. and S.C.; methodology, T.L.; formal analysis, T.L.; investigation, T.L.; resources, M.W. and S.C.; data curation, T.L.; writing—original draft preparation, T.L.; writing—review and editing, M.W. and S.C.; visualization, T.L.; supervision, M.W. and S.C.; project administration, M.W. and S.C.; funding acquisition, M.W. and S.C. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by NSFC Basic Science Center Program, grant number 11988102; NSFC, grant number 91752201; Department of Science and Technology of Guangdong Province, grant number 2019B21203001; Shenzhen Science and Technology Innovation Commission, grant number KQTD20180411143441009; and European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme, grant agreement number 882340.

Institutional Review Board Statement

Not applicable.

Data Availability Statement

The data and code used in this study are available on request from the corresponding author.

Acknowledgments

Numerical simulations were supported by the Center for Computational Science and Engineering of Southern University of Science and Technology. T.L. extends gratitude to Vikrant Gupta for proofreading the manuscript. M.W. acknowledges the support from Centers for Mechanical Engineering Research and Education at MIT and SUSTech.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

The following abbreviations are used in this manuscript:
DNS Direct numerical simulation
PV Potential vorticity

References

  1. Grant, H.; Moilliet, A.; Vogel, W. Some observations of the occurrence of turbulence in and above the thermocline. Journal of Fluid Mechanics 1968, 34, 443–448. [Google Scholar] [CrossRef]
  2. Nasmyth, P.W. Oceanic turbulence. PhD thesis, University of British Columbia, 1970.
  3. Wijesekera, H.W.; Dillon, T.M. Internal waves and mixing in the upper equatorial Pacific Ocean. Journal of Geophysical Research: Oceans 1991, 96, 7115–7125. [Google Scholar] [CrossRef]
  4. Nash, J.; Alford, M.; Kunze, E.; Martini, K.; Kelly, S. Hotspots of deep ocean mixing on the Oregon continental slope. Geophysical Research Letters 2007, 34. [Google Scholar] [CrossRef]
  5. Yang, C.F.; Chi, W.C.; van Haren, H. Deep-sea turbulence evolution observed by multiple closely spaced instruments. Scientific Reports 2021, 11, 1–12. [Google Scholar] [CrossRef] [PubMed]
  6. Riley, J.J.; Lelong, M.P. Fluid motions in the presence of strong stable stratification. Annual review of fluid mechanics 2000, 32, 613–657. [Google Scholar] [CrossRef]
  7. Sutherland, B.R. Internal gravity waves; Cambridge university press, 2010.
  8. Thorpe, S.A. The turbulent ocean; Cambridge University Press, 2005.
  9. Yarom, E.; Sharon, E. Experimental observation of steady inertial wave turbulence in deep rotating flows. Nature Physics 2014, 10, 510–514. [Google Scholar] [CrossRef]
  10. Savaro, C.; Campagne, A.; Linares, M.C.; Augier, P.; Sommeria, J.; Valran, T.; Viboud, S.; Mordant, N. Generation of weakly nonlinear turbulence of internal gravity waves in the Coriolis facility. Physical Review Fluids 2020, 5, 073801. [Google Scholar] [CrossRef]
  11. Monsalve, E.; Brunet, M.; Gallet, B.; Cortet, P.P. Quantitative experimental observation of weak inertial-wave turbulence. Physical Review Letters 2020, 125, 254502. [Google Scholar] [CrossRef]
  12. Hopfinger, E.; Browand, F.; Gagne, Y. Turbulence and waves in a rotating tank. Journal of Fluid Mechanics 1982, 125, 505–534. [Google Scholar] [CrossRef]
  13. Dickinson, S.C.; Long, R.R. Oscillating-grid turbulence including effects of rotation. Journal of Fluid Mechanics 1983, 126, 315–333. [Google Scholar] [CrossRef]
  14. Davidson, P.; Staplehurst, P.; Dalziel, S. On the evolution of eddies in a rapidly rotating system. Journal of Fluid Mechanics 2006, 557, 135–144. [Google Scholar] [CrossRef]
  15. Ranjan, A.; Davidson, P. Evolution of a turbulent cloud under rotation. Journal of Fluid Mechanics 2014, 756, 488–509. [Google Scholar] [CrossRef]
  16. Thorpe, S. On the layers produced by rapidly oscillating a vertical grid in a uniformly stratified fluid. Journal of Fluid Mechanics 1982, 124, 391–409. [Google Scholar] [CrossRef]
  17. Browand, F.; Guyomar, D.; Yoon, S.C. The behavior of a turbulent front in a stratified fluid: Experiments with an oscillating grid. Journal of Geophysical Research: Oceans 1987, 92, 5329–5341. [Google Scholar] [CrossRef]
  18. De Silva, I.; Fernando, H. Some aspects of mixing in a stratified turbulent patch. Journal of Fluid Mechanics 1992, 240, 601–625. [Google Scholar] [CrossRef]
  19. De Silva, I.; Fernando, H.J. Experiments on collapsing turbulent regions in stratified fluids. Journal of Fluid Mechanics 1998, 358, 29–60. [Google Scholar] [CrossRef]
  20. Gilreath, H.; Brandt, A. Experiments on the generation of internal waves in a stratified fluid. AIAA journal 1985, 23, 693–700. [Google Scholar] [CrossRef]
  21. Rowe, K.; Diamessis, P.; Zhou, Q. Internal gravity wave radiation from a stratified turbulent wake. Journal of Fluid Mechanics 2020, 888, A25. [Google Scholar] [CrossRef]
  22. Maffioli, A.; Davidson, P.; Dalziel, S.; Swaminathan, N. The evolution of a stratified turbulent cloud. Journal of Fluid Mechanics 2014, 739, 229–253. [Google Scholar] [CrossRef]
  23. Veronis, G. The analogy between rotating and stratified fluids. Annual Review of Fluid Mechanics 1970, 2, 37–66. [Google Scholar] [CrossRef]
  24. Pedlosky, J. Geophysical fluid dynamics; Springer Science & Business Media, 2013.
  25. Vallis, G.K. Atmospheric and oceanic fluid dynamics; Cambridge University Press, 2017.
  26. Manins, P. Intrusion into a stratified fluid. Journal of fluid mechanics 1976, 74, 547–560. [Google Scholar] [CrossRef]
  27. Davies, P.A.; Fernando, H.J.; Besley, P.; Simpson, R.J. Generation and spreading of a turbulent mixed layer in a rotating, stratified fluid. Journal of Geophysical Research: Oceans 1991, 96, 12567–12585. [Google Scholar] [CrossRef]
  28. Folkard, A.M.; Davies, P.A.; Fernando, H.J. Measurements in a turbulent patch in a rotating, linearly-stratified fluid. Dynamics of atmospheres and oceans 1997, 26, 27–51. [Google Scholar] [CrossRef]
  29. Wells, J.R.; Helfrich, K.R. A laboratory study of localized boundary mixing in a rotating stratified fluid. Journal of Fluid Mechanics 2004, 516, 83–113. [Google Scholar] [CrossRef]
  30. Ranjan, A.; Davidson, P. DNS of a Buoyant Turbulent Cloud under Rapid Rotation. In Advances in Computation, Modeling and Control of Transitional and Turbulent Flows; World Scientific, 2016; pp. 452–460.
  31. Emery, W.; Lee, W.; Magaard, L. Geographic and seasonal distributions of Brunt-Väisälä frequency and Rossby radii in the North Pacific and North Atlantic. J. Phys. Oceanogr 1984, 14, 294–317. [Google Scholar] [CrossRef]
  32. Jones, E.; Rudels, B.; Anderson, L. Deep waters of the Arctic Ocean: origins and circulation. Deep Sea Research Part I: Oceanographic Research Papers 1995, 42, 737–760. [Google Scholar] [CrossRef]
  33. Woodgate, R.A.; Aagaard, K.; Muench, R.D.; Gunn, J.; Björk, G.; Rudels, B.; Roach, A.; Schauer, U. The Arctic Ocean boundary current along the Eurasian slope and the adjacent Lomonosov Ridge: Water mass properties, transports and transformations from moored instruments. Deep Sea Research Part I: Oceanographic Research Papers 2001, 48, 1757–1792. [Google Scholar] [CrossRef]
  34. Lesieur, M. Turbulence in fluids: stochastic and numerical modelling; Nijhoff Boston, MA, 1987.
  35. Smith, L.M.; Waleffe, F. Generation of slow large scales in forced rotating stratified turbulence. Journal of Fluid Mechanics 2002, 451, 145–168. [Google Scholar] [CrossRef]
  36. Canuto, C.; Hussaini, M.Y.; Quarteroni, A.; Thomas Jr, A. ; others. Spectral methods in fluid dynamics, 2012. [Google Scholar]
  37. Li, T.; Wan, M.; Wang, J.; Chen, S. Flow structures and kinetic-potential exchange in forced rotating stratified turbulence. Physical Review Fluids 2020, 5, 014802. [Google Scholar] [CrossRef]
  38. Davidson, P. Turbulence: an introduction for scientists and engineers; Oxford University Press, 2015.
  39. Watanabe, T.; Riley, J.J.; de Bruyn Kops, S.M.; Diamessis, P.J.; Zhou, Q. Turbulent/non-turbulent interfaces in wakes in stably stratified fluids. Journal of Fluid Mechanics 2016, 797, R1. [Google Scholar] [CrossRef]
  40. Li, T.; Wan, M.; Wang, J.; Chen, S. Spectral energy transfers and kinetic-potential energy exchange in rotating stratified turbulence. Physical Review Fluids 2020, 5, 124804. [Google Scholar] [CrossRef]
  41. Wingate, B.A.; Embid, P.; Holmes-Cerfon, M.; Taylor, M.A. Low Rossby limiting dynamics for stably stratified flow with finite Froude number. Journal of fluid mechanics 2011, 676, 546–571. [Google Scholar] [CrossRef]
  42. Heywood, K.J.; Garabato, A.C.N.; Stevens, D.P. High mixing rates in the abyssal Southern Ocean. Nature 2002, 415, 1011–1014. [Google Scholar] [CrossRef] [PubMed]
  43. Van Haren, H.; Millot, C. Gyroscopic waves in the Mediterranean Sea. Geophysical Research Letters 2005, 32. [Google Scholar] [CrossRef]
  44. Timmermans, M.L.; Melling, H.; Rainville, L. Dynamics in the deep Canada Basin, Arctic Ocean, inferred by thermistor chain time series. Journal of physical oceanography 2007, 37, 1066–1076. [Google Scholar] [CrossRef]
  45. Timmermans, M.L.; Rainville, L.; Thomas, L.; Proshutinsky, A. Moored observations of bottom-intensified motions in the deep Canada Basin, Arctic Ocean. Journal of Marine Research 2010, 68, 625–641. [Google Scholar] [CrossRef]
Preprints 84922 g001
Figure 1. Contours of u θ 2 / ( u θ 2 ) m a x in the x − z plane through the axis of the Gaussian eddy at t / t f = 13.5 . Results are from (a) the analytical solution (14) and (b) the DNS.
Figure 1. Contours of u θ 2 / ( u θ 2 ) m a x in the x − z plane through the axis of the Gaussian eddy at t / t f = 13.5 . Results are from (a) the analytical solution (14) and (b) the DNS.
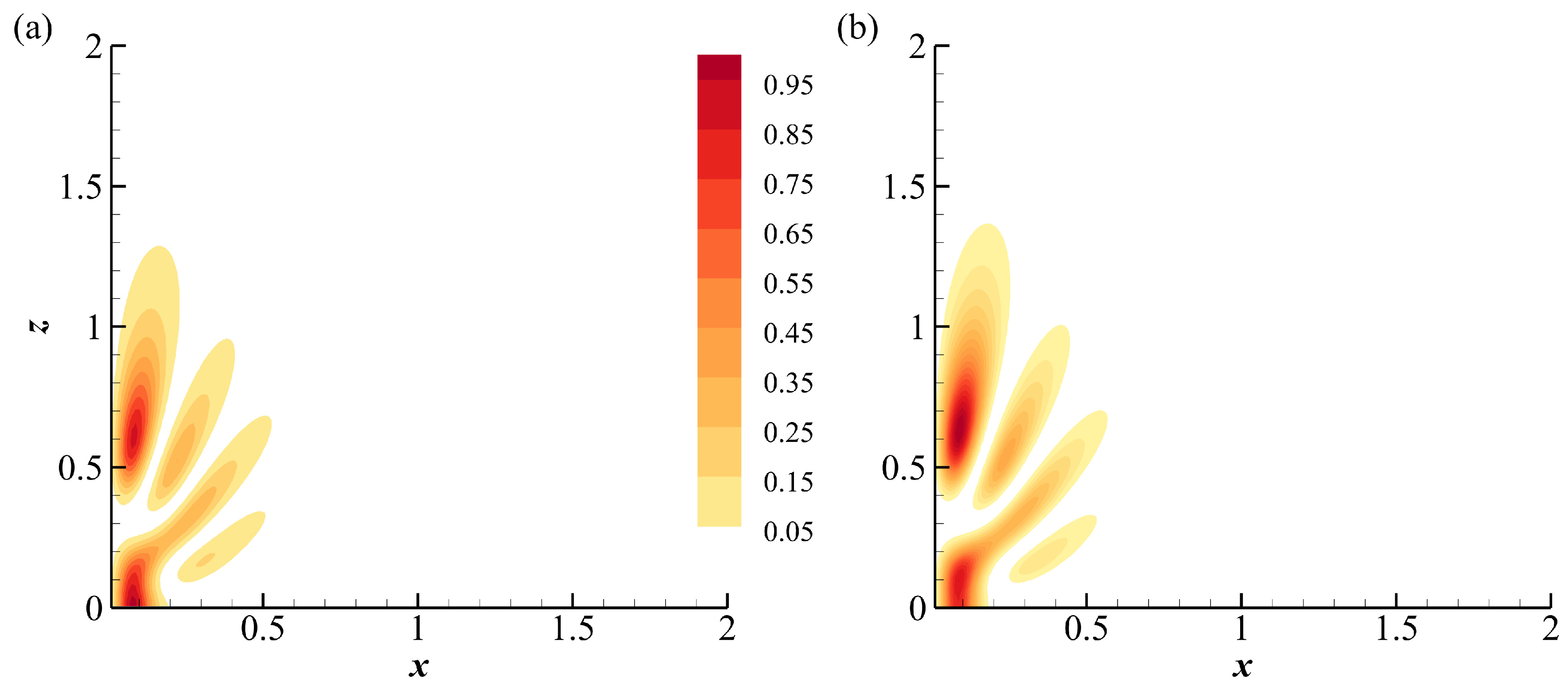
Preprints 84922 g001
Preprints 84922 g002
Figure 2. The iso-surfaces of ω z = 0.1 Λ (front view) color-coded with ϕ obtained from the DNS at (a) t / t f = 13.5 and (b) t / t f = 16.9 .
Figure 2. The iso-surfaces of ω z = 0.1 Λ (front view) color-coded with ϕ obtained from the DNS at (a) t / t f = 13.5 and (b) t / t f = 16.9 .
Preprints 84922 g002
Preprints 84922 g003
Figure 3. (a) The spatial filter given by f z = exp − 10 a z − π m with a = 4 and m = 9 . (b) Initial turbulent cloud visualized by the velocity module. (c) Energy spectrum in the x-y plane, averaged over different z values around the center of the cloud.
Figure 3. (a) The spatial filter given by f z = exp − 10 a z − π m with a = 4 and m = 9 . (b) Initial turbulent cloud visualized by the velocity module. (c) Energy spectrum in the x-y plane, averaged over different z values around the center of the cloud.
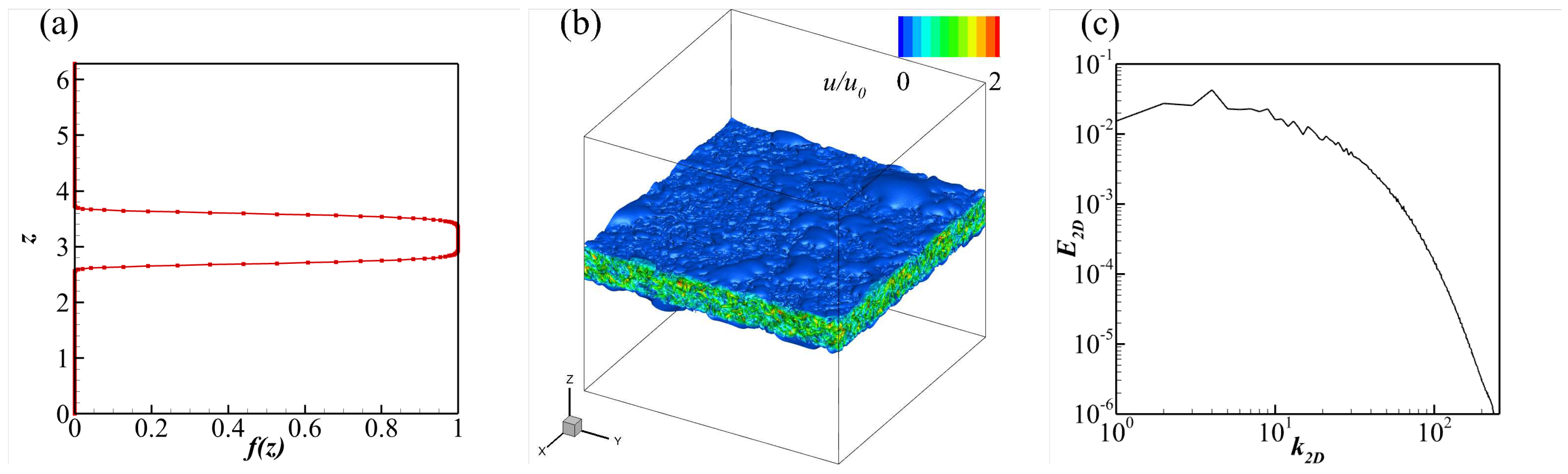
Preprints 84922 g003
Preprints 84922 g004
Figure 4. The evolution of the iso-surfaces of u z for the cases: (a) R0.11, (b) F0.88, (c) F0.44, (d) F0.22 and (e) F0.11 at t / t f = 4.2 (left), 8.4 (middle) and 12.7 (right). The color scheme is as follows: 0.24 u 0 in yellow, 0.50 u 0 in red, − 0.24 u 0 in cyan and − 0.50 u 0 in blue. Cones are plotted to indicate the predicted tilt angle of flow structures from the linear theory.
Figure 4. The evolution of the iso-surfaces of u z for the cases: (a) R0.11, (b) F0.88, (c) F0.44, (d) F0.22 and (e) F0.11 at t / t f = 4.2 (left), 8.4 (middle) and 12.7 (right). The color scheme is as follows: 0.24 u 0 in yellow, 0.50 u 0 in red, − 0.24 u 0 in cyan and − 0.50 u 0 in blue. Cones are plotted to indicate the predicted tilt angle of flow structures from the linear theory.
Preprints 84922 g004
Preprints 84922 g005
Figure 5. (a) The mean wave-cloud thickness h ¯ of turbulent clouds in the DNS. (b) The vertical extent h e of a Gaussian eddy evolving under the same R o and F r as those in the DNS.
Figure 5. (a) The mean wave-cloud thickness h ¯ of turbulent clouds in the DNS. (b) The vertical extent h e of a Gaussian eddy evolving under the same R o and F r as those in the DNS.
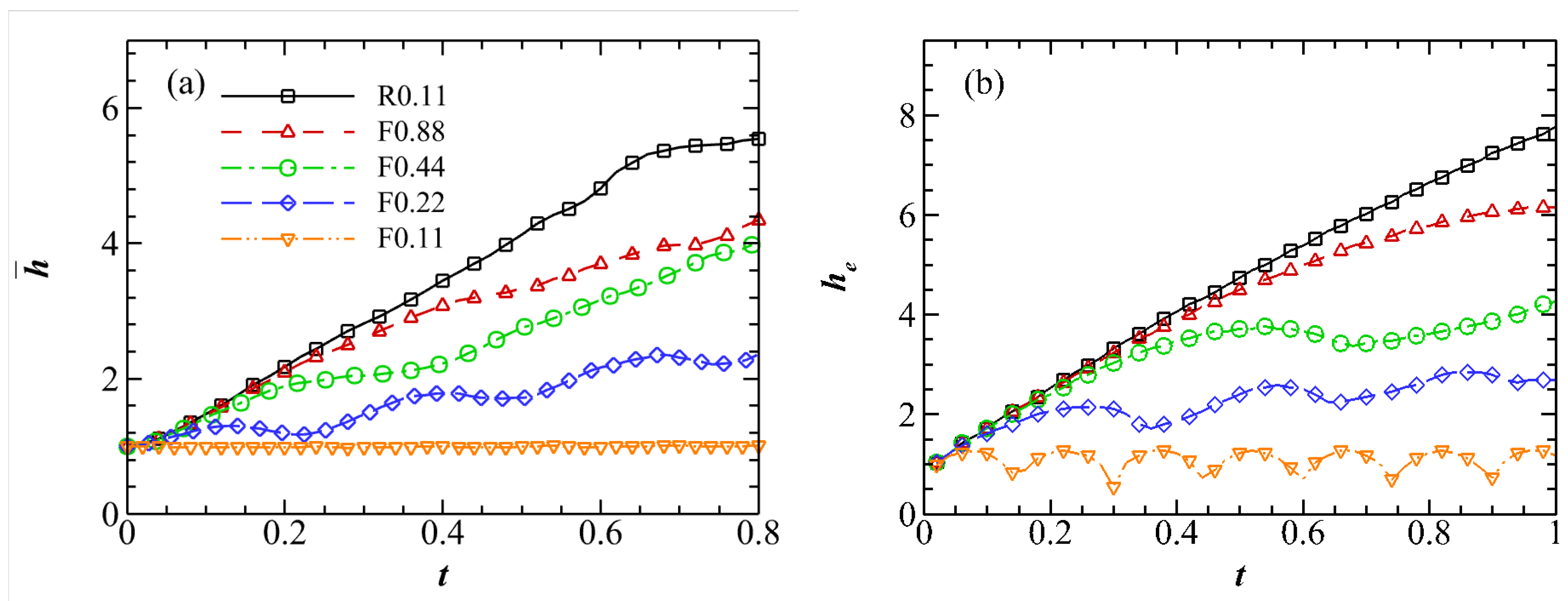
Preprints 84922 g005
Preprints 84922 g006
Figure 6. (a) Normalized vertical growth rates of the turbulent cloud, α , obtained from the DNS results and the linear theory. (b) The angle θ between the flow structure and the vertical direction as predicted by the linear theory.
Figure 6. (a) Normalized vertical growth rates of the turbulent cloud, α , obtained from the DNS results and the linear theory. (b) The angle θ between the flow structure and the vertical direction as predicted by the linear theory.
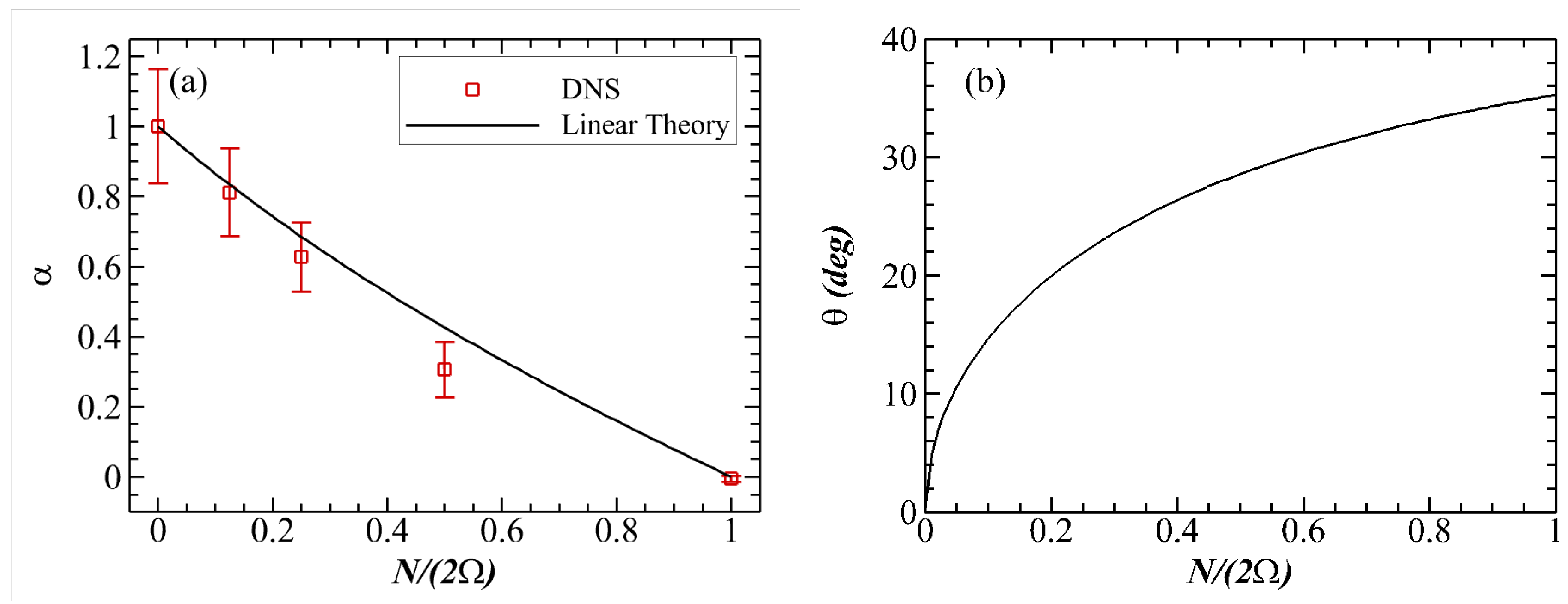
Preprints 84922 g006
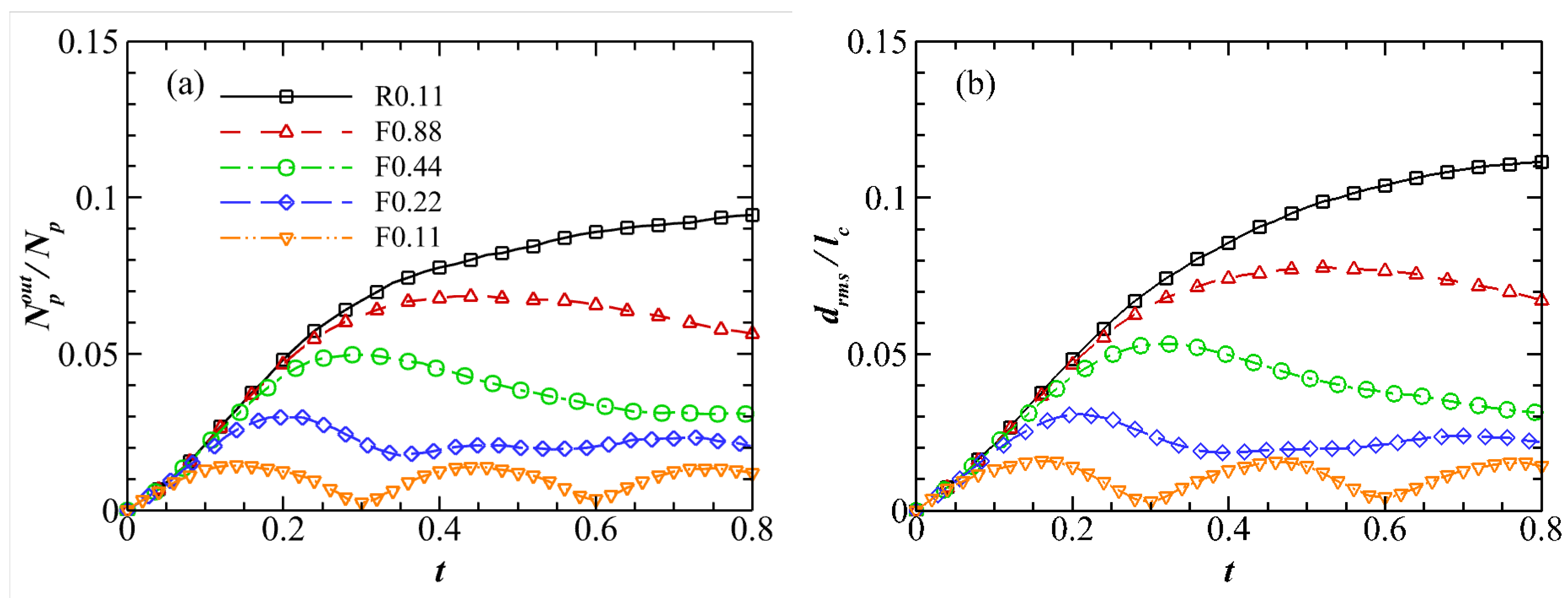
Preprints 84922 g007
Figure 7. (a) The ratio of particles outside the initial turbulent cloud. (b) The r.m.s. distance of particles outside the initial turbulent cloud to its boundary.
Figure 7. (a) The ratio of particles outside the initial turbulent cloud. (b) The r.m.s. distance of particles outside the initial turbulent cloud to its boundary.
Preprints 84922 g007
Preprints 84922 g008
Figure 8. (a) The energy ratio within the inertial-gravity waves. (b) The ratio of potential energy to total energy in the wave-dominated region.
Figure 8. (a) The energy ratio within the inertial-gravity waves. (b) The ratio of potential energy to total energy in the wave-dominated region.
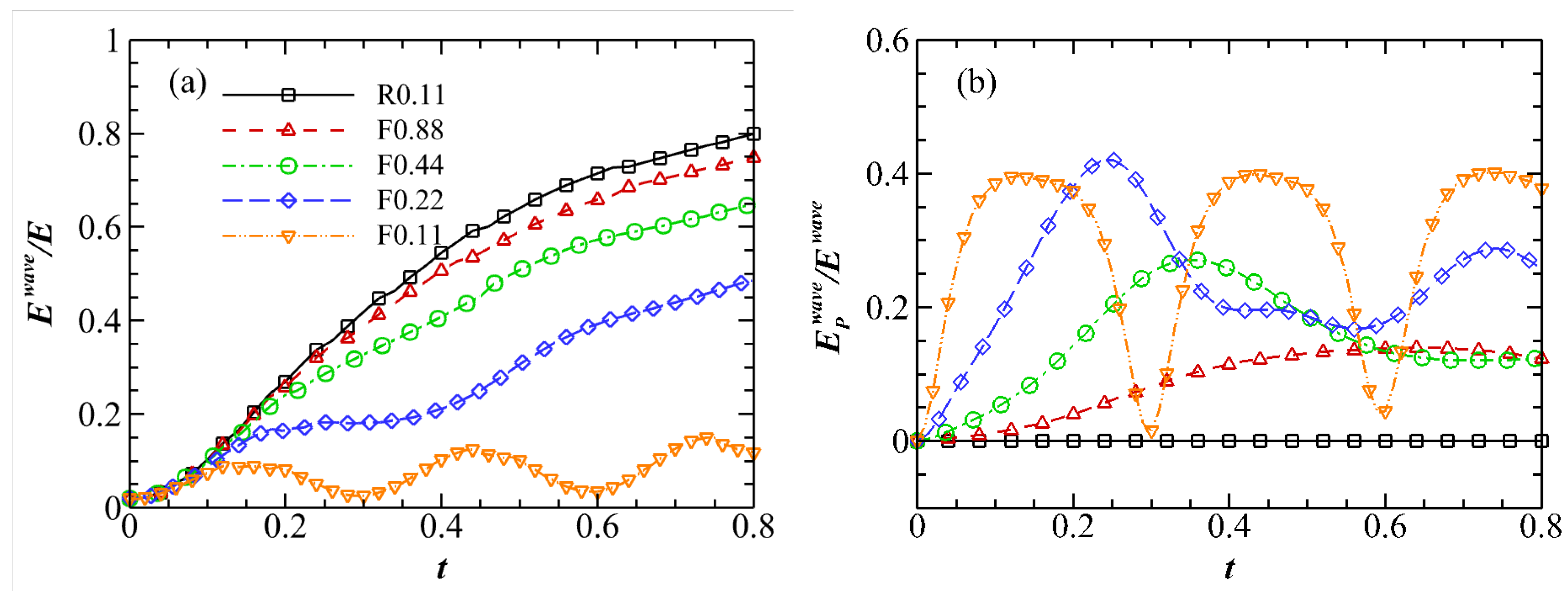
Preprints 84922 g008
Table 1. Simulation parameters for the DNS of a turbulent cloud.
Table 1. Simulation parameters for the DNS of a turbulent cloud.
Case Resolution R o 2 Ω F r N l c / l b o x l c / l 0 ν κ
R0.11 512 3 0.11 21.1 ∞ 00.0 0.13 3 0.001 0.001
F0.88 512 3 0.11 21.1 0.88 02.6 0.13 3 0.001 0.001
F0.44 512 3 0.11 21.1 0.44 05.3 0.13 3 0.001 0.001
F0.22 512 3 0.11 21.1 0.22 10.6 0.13 3 0.001 0.001
F0.11 512 3 0.11 21.1 0.11 21.1 0.13 3 0.001 0.001
Table 2. Maximum proportion of particles located outside the initial turbulent cloud, and the maximum vertical cloud expansion for the different cases.
Table 2. Maximum proportion of particles located outside the initial turbulent cloud, and the maximum vertical cloud expansion for the different cases.
Case R0.11 F0.88 F0.44 F0.22 F0.11
max ( N p o u t / N p ) 9.45 % 6.86 % 4.98 % 2.99 % 1.44 %
max ( d r m s / l c ) 11.16 % 7.77 % 5.33 % 3.08 % 1.57 %
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated