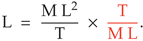Understanding the Often Ignored, but Ever-Present Natural Units

Preprint

Article

Understanding the Often Ignored, but Ever-Present Natural Units

Altmetrics

Downloads

109

Views

Comments

A peer-reviewed article of this preprint also exists.

Supplementary Material

supplementary.xlsx (1.09MB )

David Humpherys^*

This version is not peer-reviewed

Submitted:

13 September 2023

Posted:

14 September 2023

You are already at the latest version

Alerts

Abstract

The natural units of measure lauded by Max Planck more than 100 years ago are rarely used today. But many physical constants, including Planck's constant, the gravitational constant, the speed of light, vacuum permittivity, and vacuum permeability, consist of natural units in their unit dimensions. The natural units are present in all formulas containing these constants. The defining characteristic of the natural units is an alignment of unit values at the Planck scale. This alignment gives a computational basis of proportionality from which the correlated properties and dynamics of elementary particles, including wavelength, period, mass, momentum, and energy, manifest in equal or inversely proportional ratios of the Planck scale. These correlations explain many of the defining equations of quantum mechanics, classical gravity, and electromagnetism.

Keywords:

Subject: Physical Sciences - Theoretical Physics

1. Introduction

The present-day International System of Units (SI) defines units of length, mass, and time that were largely decided centuries ago. Base units of meters, seconds, and kilograms correspond with everyday physical phenomena, but the magnitudes of these units were selected arbitrarily and not from fundamental constants of nature. While the choice of units does not affect the underlying physics, natural units have certain advantages over other unit systems. Max Planck lauded the uniqueness of these units when he introduced formulas for calculating their values from the universal constants

... it is possible to set up units for length, mass, time and temperature, which are independent of special bodies or substances, necessarily retaining their meaning for all times and for all civilizations, including extraterrestrial and non-human ones, which can be called "natural units of measure."

Planck combined the values and dimensions of c, G, and ℏ into ratios that isolate each unit dimension. His approach presumes that the universal constants contain natural units in their compound unit dimensions [2]. This is why the universal constants can be expressed in natural units as [3,4,5,6,7]

c = \frac{l_{P}}{t_{P}} = 2.997 924 \times 10^{8} m / s .

(1)

ℏ = \frac{m_{P} l_{P}^{2}}{t_{P}} = m_{P} l_{P} c = 1.054 572 \times 10^{- 34} k g m^{2} / s

(2)

G = \frac{l_{P}^{3}}{m_{P} t_{P}^{2}} = \frac{l_{P}}{m_{P}} c^{2} = 6.674 30 \times 10^{- 11} m^{3} / k g s^{2}

(3)

Because the natural units are calculated from ratios of the three universal constants, their precision is limited by the precision of G which has a relative standard uncertainty of

2.2 \times 10^{- 5}

[8,9]. However, the intensive ratios of certain unit pairs, such as Planck length to Planck time, have been measured with much greater precision [10,11]. The advantage of working in natural units is the correlations they reveal and not their utility in everyday experiments.

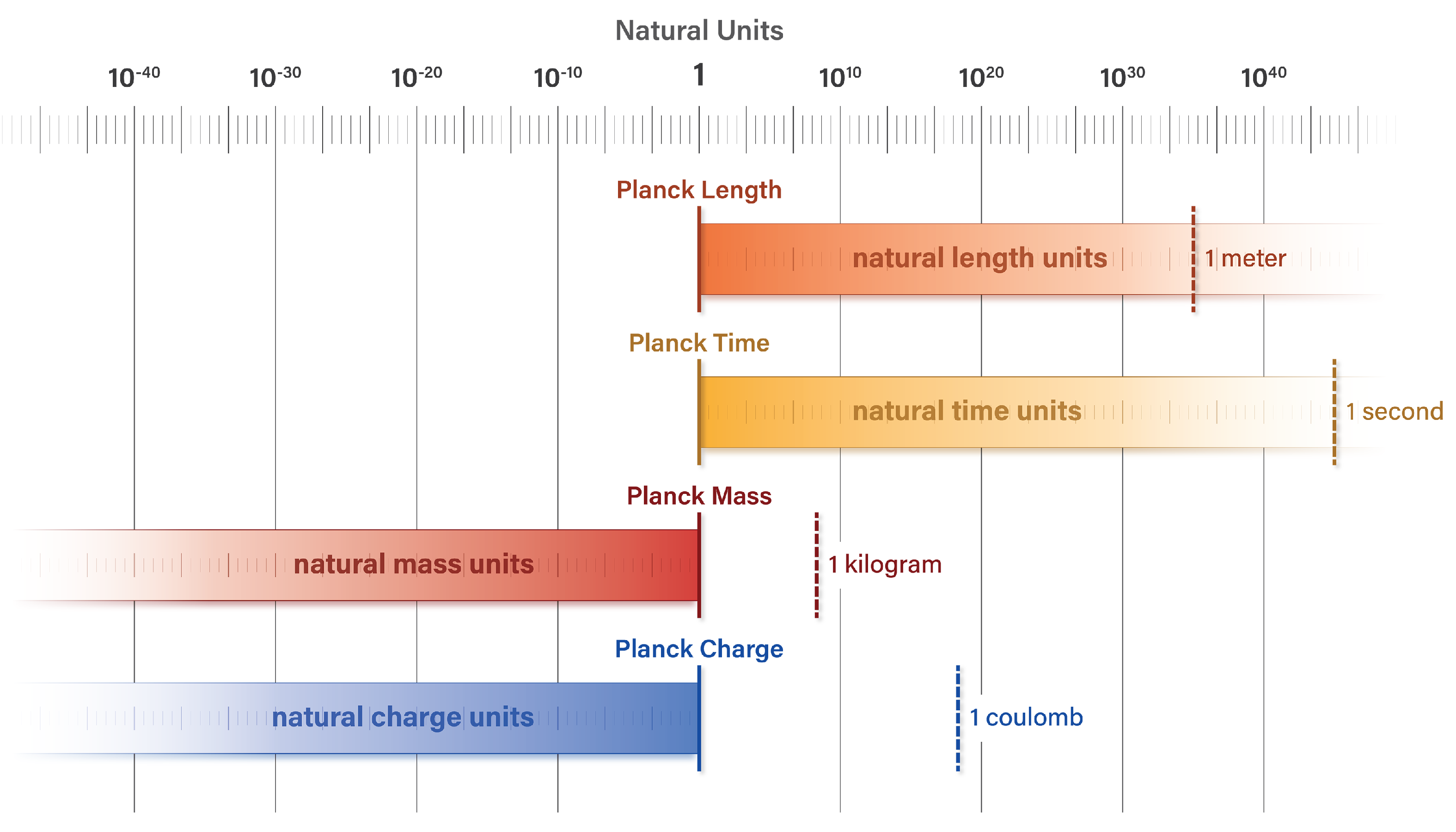
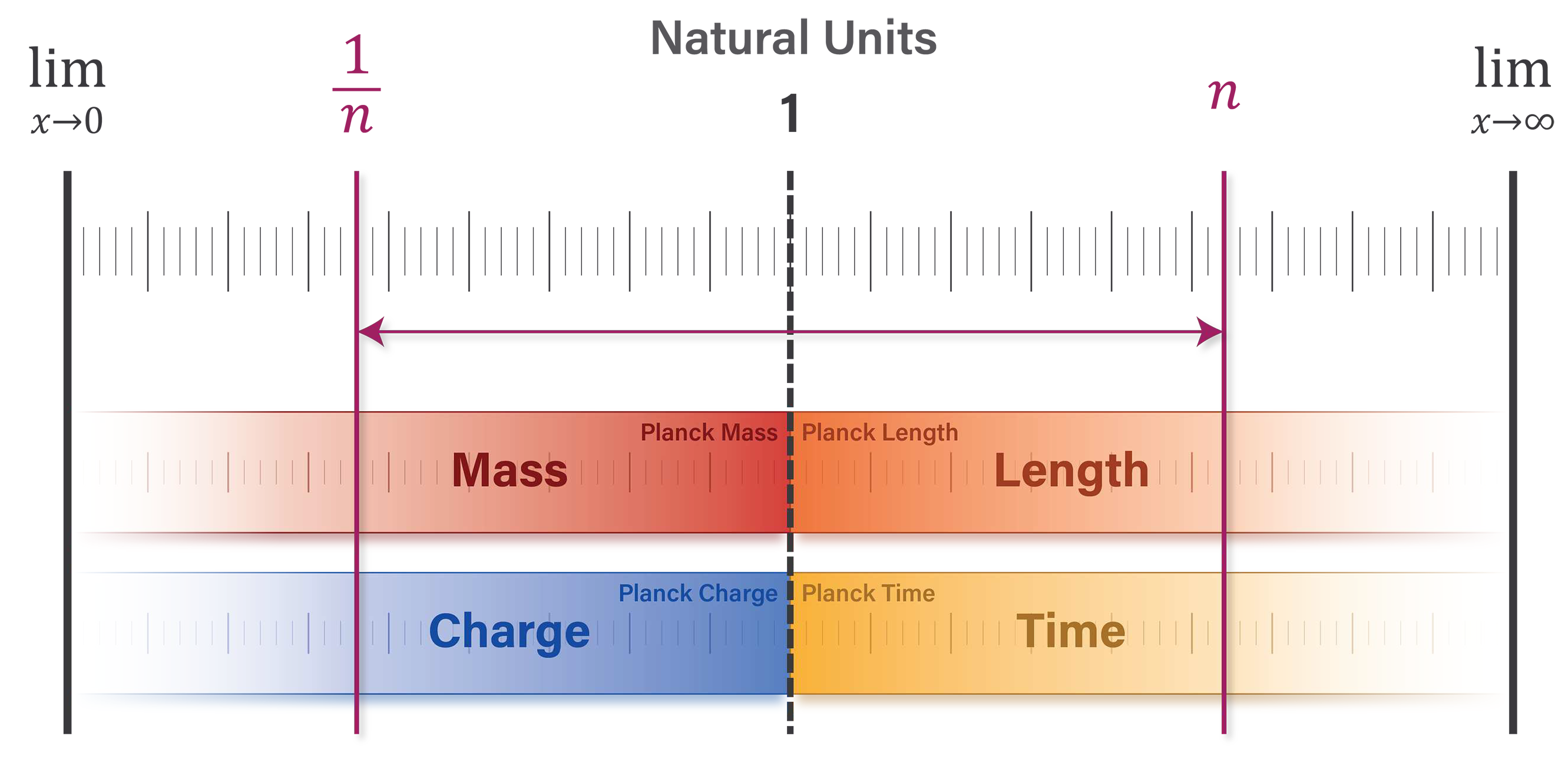
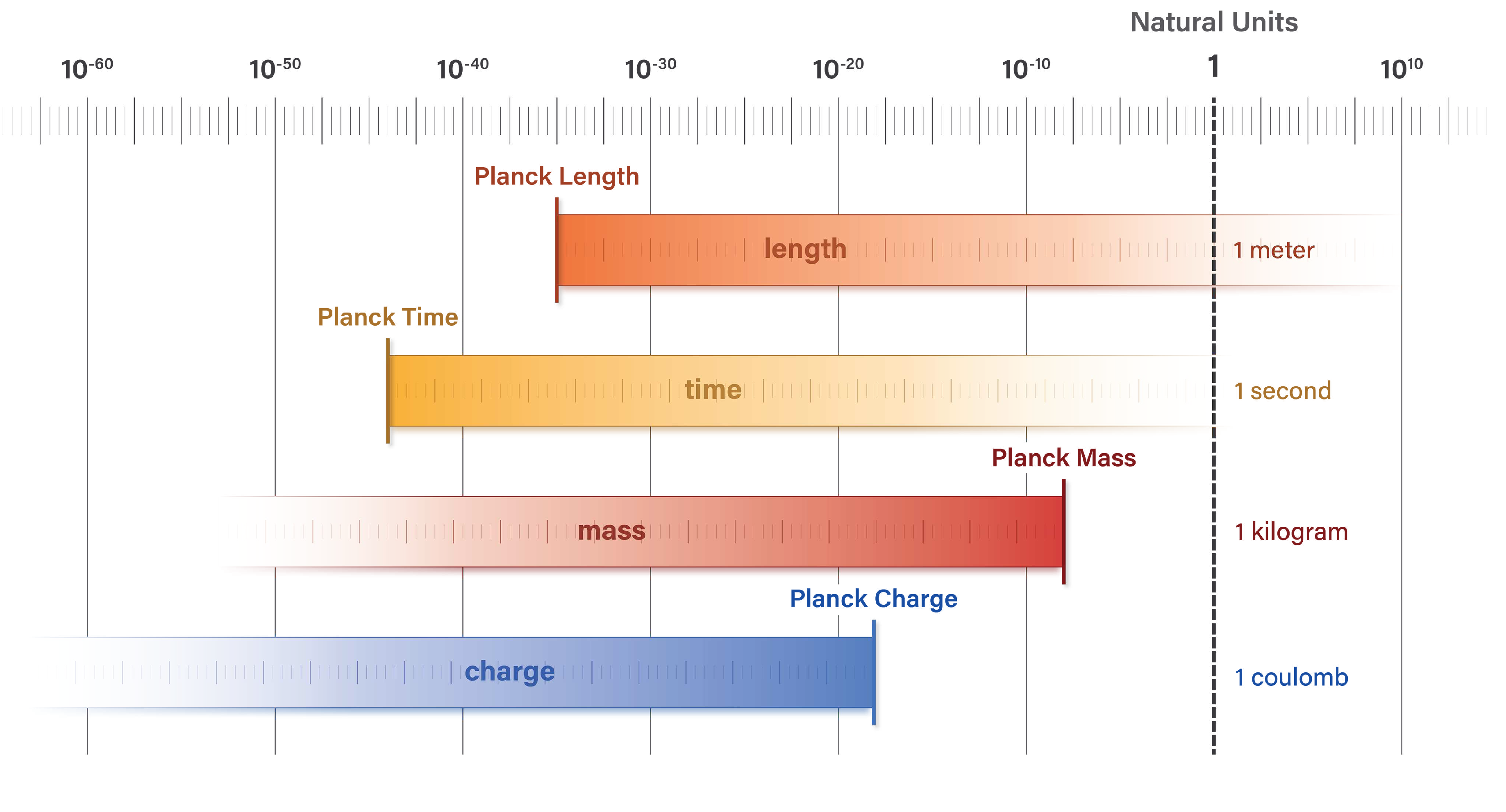
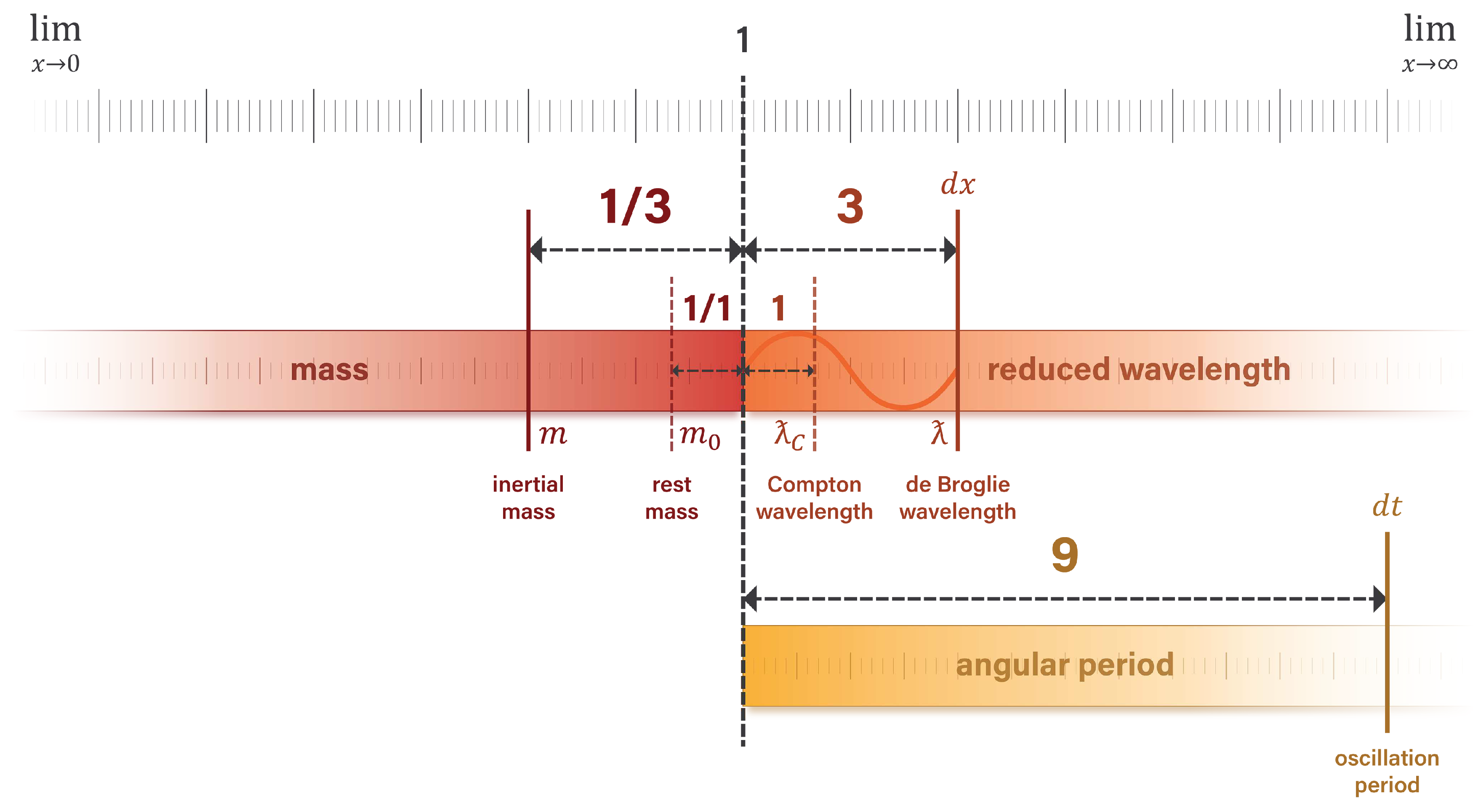
1.1. The natural unit scale

The characteristic feature of natural units is the alignment of unit values at the Planck scale. Each unit dimension has a value of 1 and asymptotically approaches a limit of zero or infinity. Unit dimensions of length and time have minimum values of 1 and maximum values approaching infinity. With respect to discrete quanta, unit dimensions of mass and charge have maximum values of 1 and minimum values approaching zero [12,13,14]. Figure 1 illustrates this natural structure.

The Planck scale acts as a basis of proportionality for quantifying physical phenomena in natural units. For certain correlated pairs, a quantity of length or time n on the right side of the scale corresponds with an inversely proportional quantity

1 / n

on the left side. An example of this natural structure is the relationship between the electron mass and Compton wavelength. In SI units, the electron has a rest mass of

9.109 \times 10^{- 31} k g

and a reduced Compton wavelength of

3.862 \times 10^{- 13} m

. Restating these quantities in natural units shows that the two electron properties are inversely proportional. The number of natural length units is determined by the ratio

\frac{ƛ_{C}}{l_{P}} = \frac{3.861 593 \times 10^{- 13} m}{1.616 255 \times 10^{- 35} m} = 2.389 222 \times 10^{22}

(4)

and the natural unit value of the electron’s mass is

\frac{m_{0}}{m_{P}} = \frac{9.109 384 \times 10^{- 31} k g}{2.176 434 \times 10^{- 08} k g} = \frac{1}{2.389 222 \times 10^{22}} .

(5)

The natural structure shown in Figure 1 produces proportionally meaningful insights by setting the Planck units—and certain collections of Planck units such as the universal constants—equal to 1. However, the occasional practice of setting universal constants equal to 1 gives an opaque view of this natural structure compared to the clarity obtained by stating the universal constants in natural units. These insights are presented in the following sections.

The relationship between electron mass and wavelength, and many similar correlations found in nature, are poorly understood today because of the incongruence between SI unit values and natural units. Figure 2 illustrates this misalignment. In the figure, limits of mass and charge pertain to discrete quanta and not to large-scale systems.

SI units of meter, second, kilogram, and coulomb obfuscate natural correlations that become evident when equations are stated in natural units. The following sections demonstrate these correlations and highlight the crucial role of natural units in the equations.

2. The laws of physics in natural units

The universal constants appear in many equations that describe the elementary structures of nature. Their contributions to the formulas include a single value and multiple unit dimensions—two, four, and six unit dimensions for c, ℏ, and G respectively. An impressive quality of the universal constants is that they consistently satisfy the following two requirements:

Formulas with universal constants produce the correct unit dimensions of the physical phenomenon you are solving for (i.e. momentum, energy, force, etc.)
The formulas produce the correct magnitude of the phenomenon from the given inputs.

Planck’s constant appears regularly in formulas describing the quantized behavior of matter and radiation, correctly predicting the mechanical properties and dynamics of elementary particles. Evaluating the formulas in each unit dimension reveals the role of natural units in the mathematical transformations. For example, the de Broglie wavelength formula combines Planck’s constant with inputs of mass and velocity (inputs are highlighted in red)

λ = \frac{h}{mv} .

(6)

The first requirement of the function is to reduce seven unit dimensions to one

Three unit dimensions in the numerator and three in the denominator reduce the dimensionality to

L = (\frac{M}{M}) \times (\frac{L}{L}) \times (\frac{T}{T}) \times L .

The second requirement of the function is to obtain the correct magnitude of wavelength from the given inputs. Restating Equation 6 in natural units accounts for the mathematical transformation in each unit dimension and shows how formula inputs produce the corresponding magnitude of particle wavelength

ƛ = \frac{ℏ}{m_{0} v} = \frac{l_{P} m_{P} c}{m_{0} v} = (\frac{m_{P}}{m_{0}}) (\frac{c}{v}) l_{P}

(7)

The physical meaning of the dimensionless ratios in Equation 7 is evaluated throughout this study. For now, we can summarize the role of natural units in quantifying the de Broglie wavelength in two parts:

The Planck length serves as a minimum limit or computational basis from which observable quantities of wavelength are calculated.
A matter particle’s inverse-reduced wavelength is the same ratio of the Planck scale as its momentum.

Rearranging Equation 7 as an equality emphasizes the second point

\frac{ƛ}{l_{P}} = (\frac{m_{P}}{m_{0}}) (\frac{c}{v})

(8)

The natural structure of Equation 8 explains why the formula produces a proportionally significant result. This structure allows the discovery of one attribute or dynamic from a known quantity of a correlated attribute or dynamic. Another example of this natural structure is the formula for photon energy

E = \frac{h c}{λ} = \frac{l_{P} m_{P} c^{2}}{ƛ} = (\frac{l_{P}}{ƛ}) E_{P} .

(9)

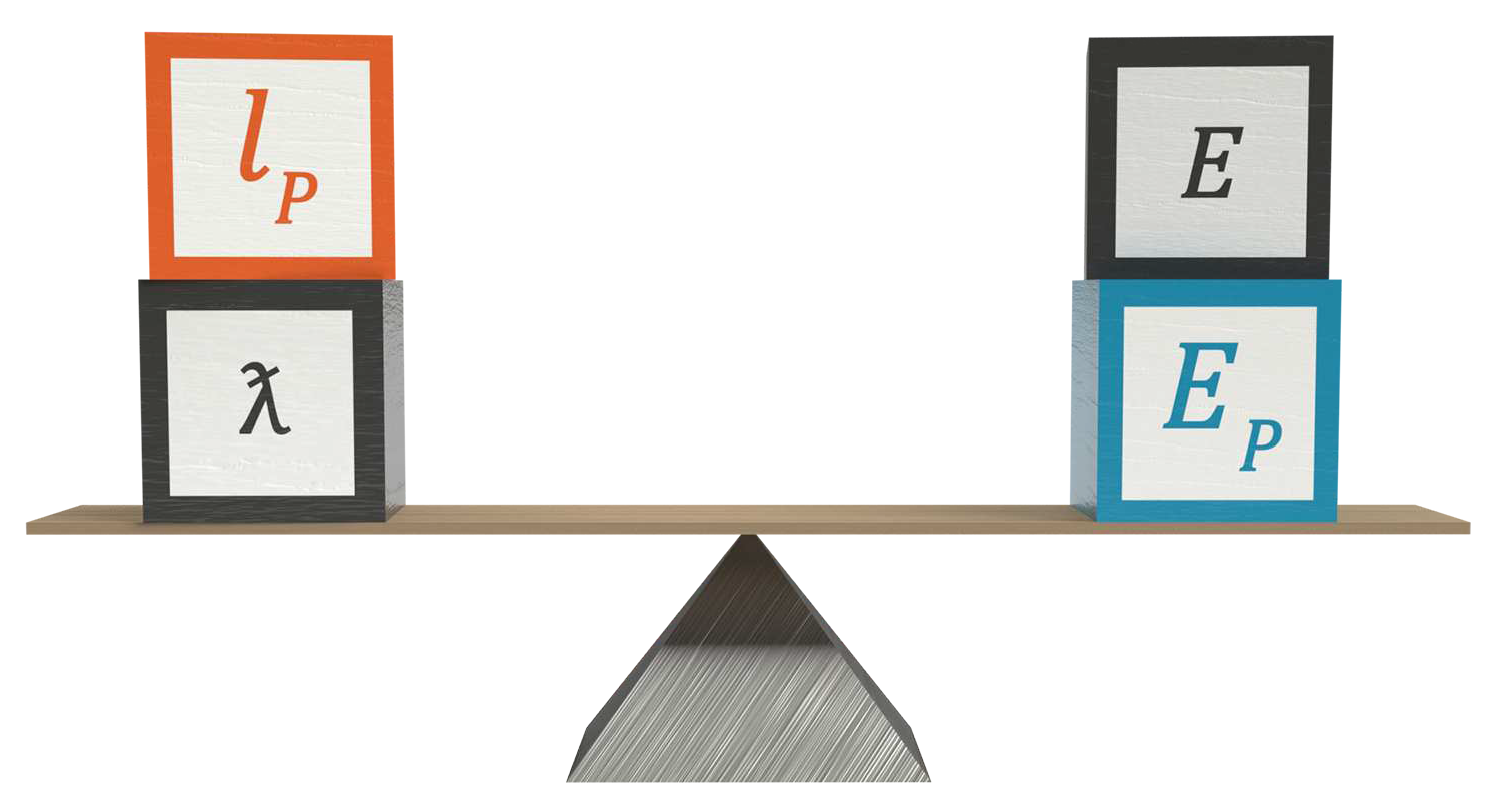
Arranging the natural unit formula as an equality shows why the formula works

\frac{l_{P}}{ƛ} = \frac{E}{E_{P}} .

(10)

The natural unit formulas demonstrate that the reason we can calculate a photon’s energy from its wavelength is because the ratio of Planck length to reduced wavelength is equal to the ratio of energy to Planck energy.

Figure 3. The physical properties and dynamics of elementary particles are correlated.

These equalities suggest that the function of universal constants is to inject natural units into the formulas to exploit correlations between the physical properties and dynamics of elementary particles and systems. It is not simply that photon momentum and energy are proportional to Planck’s constant. Rather, the momentum and energy of a photon are proportional to the Planck momentum and Planck energy. This pattern consistently explains the correlations, constants, and equations.

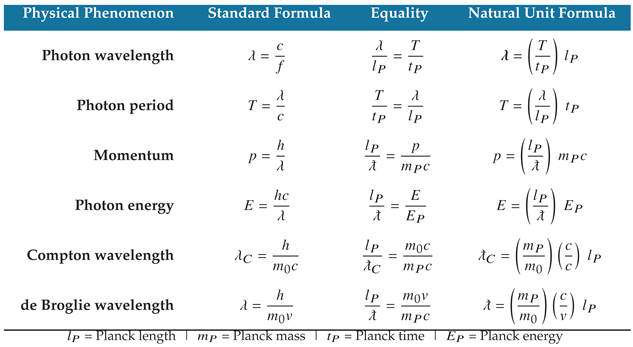
Table 1, Table 7, and Table 9 present natural unit formulas and equalities for several defining equations of quantum mechanics, classical gravity, and electromagnetism. The natural unit formulas are computationally equivalent to the standard formulas within the limits of their measured uncertainties, and they reveal the natural structure underpinning the mathematics.

An important benefit of the natural unit formulas in Table 1, Table 7, and Table 9 is that they characterize the physical properties of natural phenomena in unit dimensions of length, mass, and time. For example, the Planck energy can be characterized by a Planck-length photon moving at the speed of light.

2.1. Independent units of measure

The ratio of photon wavelength to Planck length produces a dimensionless number of natural length units when the wavelength and Planck length are both quantified in meters. To retain the dimensionality of these natural quantities, it is the practice throughout this study to label such quantities using the dimensional notation L, M, and T for natural units of length, mass, and time; and the symbol Q for natural units of electric charge.

Natural unit quantities of length and time appear regularly in the formulas in Table 1, Table 7, and Table 9. For example, the relationship between a photon’s wavelength, oscillation period, and frequency is given by

λ = \frac{c}{f} = c T .

(11)

Restating c in natural units produces natural unit equations for wavelength and period

λ = (\frac{T}{t_{P}}) l_{P}

(12)

and

T = (\frac{λ}{l_{P}}) t_{P} .

(13)

Equation 12 finds the photon’s wavelength by determining the equivalent number of natural time units and multiplying this by a single unit of length. Equation 13 similarly finds the photon period from the number of natural length units. The two formulas may be summarized by the equality

\frac{λ}{l_{P}} = \frac{T}{t_{P}} .

(14)

While the speed of light is an intensive ratio that can be stated equivalently at different length and time scales (including meters per second), the natural units produce a unique quantity of photon wavelength and period that remains the same in any unit system. This is because natural unit values of length and time are produced from SI unit ratios. Changing the unit scale would change the nominal values, but the ratios would remain the same.

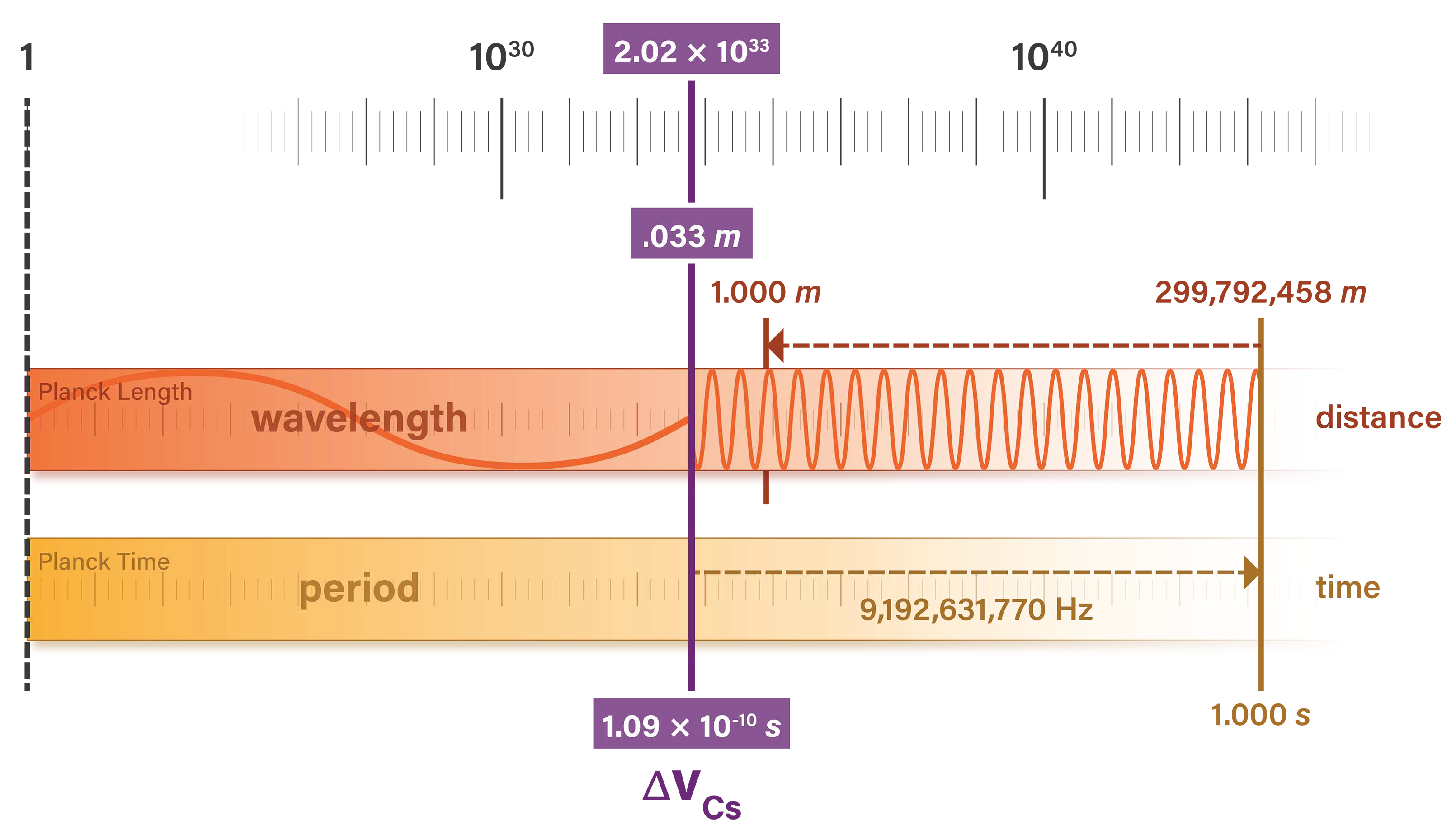
This independence of natural units from arbitrary unit systems is evident in the properties of a specific photon. The unperturbed ground-state hyperfine transition frequency of cesium 133 produces a specific amount of radiation that is used in the SI definitions of the second, meter, and kilogram [15]. The photon has an oscillation period measured in seconds of

T = \frac{1}{f} = \frac{1}{9, 192, 631, 770 H z} = 1.087 827 757 \times 10^{- 10} s

(15)

which can be stated in natural time units as

\frac{T}{t_{P}} = \frac{1.087 827 \times 10^{- 10} s}{5.391 247 \times 10^{- 44} s} = 2.017 767 \times 10^{33} T .

(16)

The photon also has a wavelength in meters

\frac{c}{Δ v_{C s}} = \frac{299, 792, 458 m / s}{9, 192, 631, 770 H z} = . 032 612 256 m

(17)

which can be stated in natural length units as

\frac{λ}{l_{P}} = \frac{. 032 6122 m}{1.616 255 \times 10^{- 35} m} = 2.017 767 \times 10^{33} L .

(18)

If we were to redefine the meter as precisely one-half of its present-day value, we would measure the photon wavelength to be twice its current nominal value, or

0.065 m^{'}

. We would also measure the speed of light as approximately

600, 000, 000 m^{'} / s

and the Planck length as

3.232 \times 10^{- 35} m^{'}

. So the natural unit value of the hyperfine transition frequency radiation would remain the same

λ = \frac{0.065 m^{'}}{3.232 \times 10^{- 35} m^{'}} = 2.017 767 \times 10^{33} L .

(19)

The natural length and time units in Equations 16 and 18 are the natural units of measure Planck referred to which retain their meaning for all times and all civilizations including extraterrestrial and non-human ones. An alien civilization is unlikely to quantify length and time in units equivalent to meters and seconds, but any unit system they devise will produce the same natural unit value of wavelength and oscillation period for the hyperfine transition frequency of cesium 133.

Figure 4 illustrates the alignment of length and time units at the Planck scale, and the relationship between SI and natural units.

The Planck scale is at the left of the figure, where natural units of length and time are equal to one. The speed of light is a 1:1 ratio between length and time units and may be represented anywhere in the figure by a vertical line.

The figure shows the relationship between the hyperfine transition radiation and the second which it defines. The unit definition is a precise integer multiple of the photon oscillation cycle and has the identity

1 s = \frac{1 s}{9, 192, 631, 770 H z} \times 9, 192, 631, 770 H z

(20)

The meter is defined as a fraction of the distance that light travels in a vacuum over one second. Taking the defined value of the second, the meter is precisely

1 / 299, 792, 458

the distance light travels in this time. The meter has the identity

1 m = 299, 792, 458 m / s \times \frac{1}{3.335 640 95 \times 10^{- 9}} s

(21)

The natural unit value

2.018 \times 10^{33}

is an invariant measure of the photon wavelength and period. It is the same value regardless of how we define units of length and time.

2.2. Arbitrary unit systems

The natural unit formulas in Table 1, Table 7, and Table 9 demonstrate that the equations of physics are based on correlations between the physical properties and dynamics of elementary particles and fields, and not on the unit system or nominal values of measurement. Changing the unit scale will change the measured values in that scale, including the universal constants, but the equations will remain the same.

For example, one insightful unit system we could devise would retain current definitions of the meter and kilogram but redefine a unit of time

s^{'}

as the time required for light to travel one meter. A unit of time

s^{'}

would be precisely

1 / 299, 792, 458

times one second, and the revised Planck time would be

t_{P}^{'} = 1.616 \times 10^{- 35} s^{'} .

(22)

All three universal constants include at least one natural unit of time and would be re-quantified using

t_{P}^{'}

\begin{matrix} c^{'} & = \frac{l_{P}}{t_{P}^{'}} = 1 m / s^{'} \end{matrix}

(23)

\begin{matrix} G^{'} & = \frac{l_{P}}{m_{P}} c^{' 2} = 7.426 \times 10^{- 28} m^{3} / k g s^{' 2} \end{matrix}

(24)

\begin{matrix} ℏ^{'} & = l_{P} m_{P} c^{'} = 3.518 \times 10^{- 43} k g m^{2} / s^{'} \end{matrix}

(25)

This hypothetical unit system highlights the one-to-one ratio between length and time units at the speed of light, and states all quantities of velocity as a fraction of the speed limit. Furthermore, in this unit system, the Planck constant and gravitational constant are equal to the product and quotient of natural length and time units, respectively.

The important takeaway is that measuring natural phenomena with the new time unit

s^{'}

and using the revised universal constants will produce the same results. The oscillation period of

Δ v_{C s}

in this system would be

T = \frac{λ}{c^{'}} = . 03261 s^{'}

(26)

and the number of natural time units in the hyperfine transition frequency would still be

\frac{T}{t_{P}^{'}} = 2.017 767 \times 10^{33} T .

(27)

The physical meaning of the universal constants is not found in the values acquired from a particular unit system, but from correlations of natural phenomena that remain constant in any unit system. A better understanding of the equations follows from a better understanding of the correlations driving the mathematical machinery.

2.3. The kilogram

The 2019 redefinition of SI base units changed the kilogram definition from a physical artifact to a relationship among three physical constants ℏ, c, and

Δ v_{C s}

[15]. The new standard is sometimes referred to as the quantum kilo because it defines a standard unit of mass in relation to Planck’s constant. Instrumental in the new kilogram definition is a quantity of mass produced by the ratio of hyperfine transition radiation energy

E = h Δ v_{C s} = 6.091 102 297 \times 10^{- 24} k g m^{2} / s^{2}

(28)

and the speed of light squared

\frac{h Δ v_{C s}}{c^{2}} = 6.777 265 312 \times 10^{- 41} k g .

(29)

The kilogram is defined by the identity between this exactly defined mass and its reciprocal

1 k g = 6.777 265 312 \times 10^{- 41} k g \times 1.475 521 400 \times 10^{40} .

(30)

It is the modern practice to define units of measure in relation to physical constants, while the experimental realization of those units may be achieved using measurable applications of those constants. The kilogram is therefore measured experimentally using the Kibble balance and not by measuring the hyperfine transition radiation [16].

Of paramount importance to our understanding of equation 29 and the quantum kilo definition is whether a compound dimensional phenomenon such as energy has characteristic quantities in each of its unit dimensions

E = {ML}^{2} T^{- 2} .

If so, the photon has only one unit dimension, M, to account for changes in energy as the photon wavelength changes. This form of electromagnetic mass-energy equivalence was introduced by Henri Poincare in his 1900 article La theorie de Lorentz et le Principe de reaction, in which he uses the relation

m = E / c^{2}

to account for the recoil of a Hertzian oscillator [17,18]. This description of electromagnetic mass, or inertial mass, lost favor to a more abstract representation that does not endeavor to explain the presence of mass in unit dimensions of photon energy. Nor does it reconcile incompatible conceptual descriptions of classical and quantum mechanical momentum.

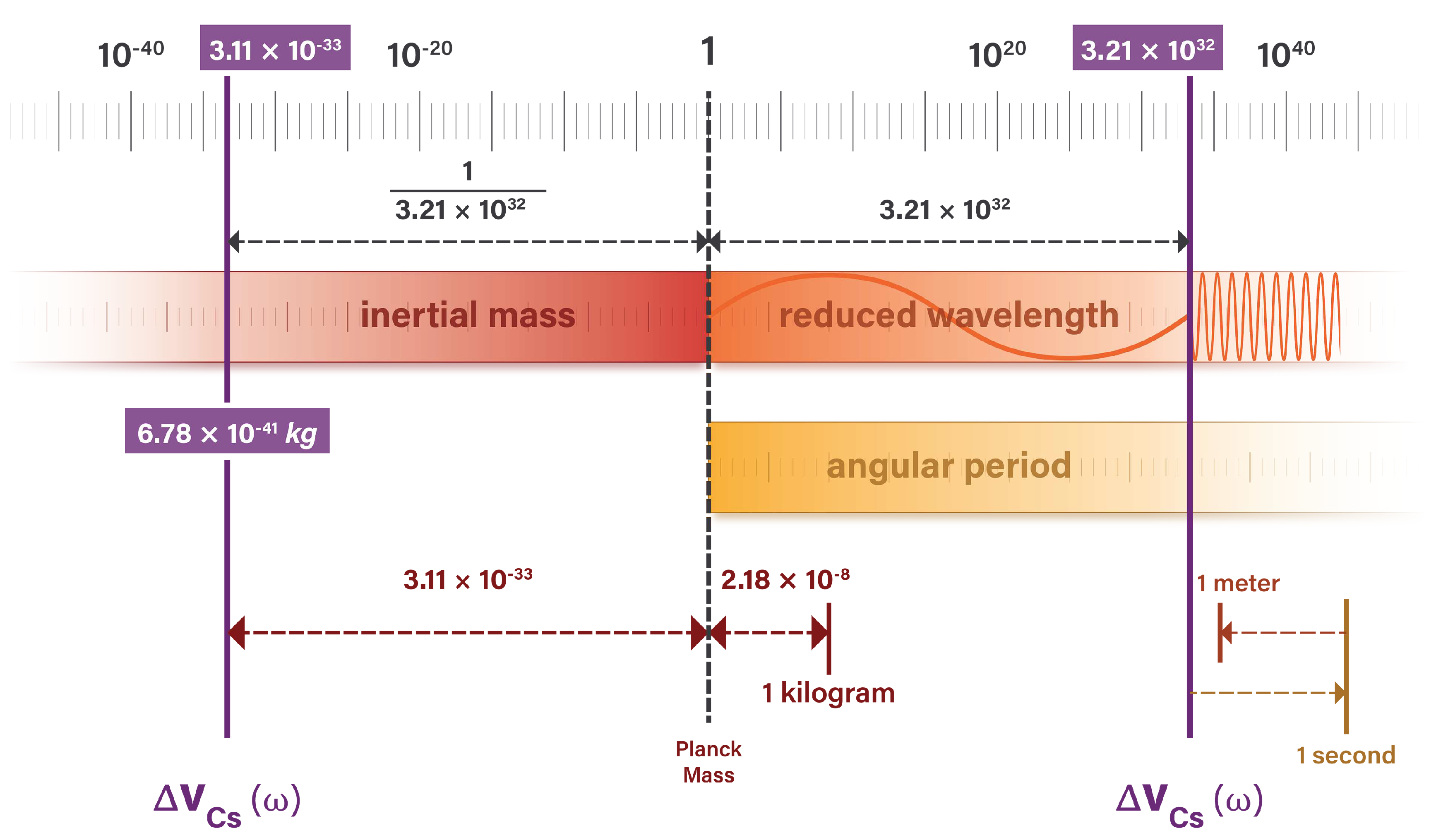
The natural unit structure of the formulas provides evidence in favor of Poincare’s view. In the case of the hyperfine transition frequency, the photon’s inertial mass m in natural units is

\frac{m}{m_{P}} = \frac{6.777 265 \times 10^{- 41} k g}{2.176 434 \times 10^{- 8} k g} = \frac{1}{3.211 375 \times 10^{32}} M

(31)

which is inversely proportional to the photon’s reduced wavelength ƛ and angular period

τ

. Furthermore, the wavelength, inertial mass, and period are each proportional or inversely proportional to the photon energy

\frac{l_{P}}{} = \frac{m}{m_{P}} = \frac{t_{P}}{τ} = \frac{E}{E_{P}} = \frac{1}{3.211 375 \times 10^{32}} .

(32)

Equation 32 explains why Planck’s constant is

2 π

larger than the reduced Planck constant. Because the inverse mass and energy are equal to the reduced wavelength and period in natural units, the constant

2 π

is included in h to reduce

λ

and T

h = 2 π ℏ = 2 π l_{P} m_{P} c .

(33)

Table 2 lists the SI and natural unit values of the wavelength, inertial mass, oscillation period, and energy of radiation produced by the unperturbed ground-state hyperfine transition frequency of cesium 133.

The natural unit values in Table 2 demonstrate the highly correlated properties and dynamics of radiation. Dimensionally, the hyperfine transition frequency energy can be stated as

E = \frac{1}{3.211 375 \times 10^{32}} m_{P} (\frac{3.211 375 \times 10^{32} l_{P}}{3.211 375 \times 10^{32} t_{P}}) (\frac{3.211 375 \times 10^{32} l_{P}}{3.211 375 \times 10^{32} t_{P}}) = \frac{1}{3.211 375 \times 10^{32}} E_{P}

(34)

Figure 5 illustrates the correlated photon properties on the natural scale with Poincare’s inertial mass

E / c^{2}

in unit dimension M.

The hyperfine transition frequency counts the oscillations of a photon with a reduced wavelength and angular period of

3.211 375 \times 10^{32}

natural length and time units, shown in unit dimensions of length and time in the figure. The photon’s reduced wavelength produces an inversely proportional quantity of inertial mass

1 / 3.211 375 \times 10^{32}

natural mass units shown in unit dimensions of mass in the figure.

The wavelength, period, and inertial mass of a photon are limited by the Planck scale; and one kilogram exceeds this limit by a multiple of

1 / m_{P}

. Therefore, the kilogram definition, based on the hyperfine transition radiation, takes the product of the photon’s inertial mass

3.113 \times 10^{- 33}

and the ratio of 1 kilogram to Planck mass

2.176 \times 10^{- 8}

. This is expressed in equations as

\begin{matrix} \frac{h Δ v_{C s}}{c^{2}} & = \frac{l_{P} m_{P} c}{c^{2}} Δ v_{C s} \end{matrix}

(35)

\begin{matrix} = m_{P} t_{P} Δ v_{C s} \end{matrix}

(36)

\begin{matrix} = (\frac{t_{P}}{τ}) m_{P} \end{matrix}

(37)

\begin{matrix} = (3.114 \times 10^{- 33}) \times (2.176 \times 10^{- 8} k g) \end{matrix}

(38)

\begin{matrix} = 6.777 265 \times 10^{- 41} k g . \end{matrix}

(39)

The defined values of h, c and

Δ v_{C s}

give a precise definition of the kilogram, whereas individual Planck units are less precise. But it is the natural correlations between photon wavelength, inertial mass, and oscillation period that relate SI units of meter, second, and kilogram in the SI definitions.

3. Correlations of matter

The correlated photon properties characterized in natural units are simple and symmetrical; a single ratio quantifies a photon’s wavelength, period, inertial mass, and energy. The quantum mechanical properties of matter are also highly correlated but not as symmetrical as those of radiation. Like the photon correlations, these correlations become clearer in natural units.

3.1. Rest mass

The reduced Compton wavelength of a matter particle is inversely proportional to its rest mass, as evidenced by the Compton wavelength formula [19,20,21]

ƛ_{C} = \frac{ℏ}{m_{0} c} = \frac{l_{P} m_{P} c}{m_{0} c} = (\frac{m_{P}}{m_{0}}) l_{P} .

(40)

The formula gives an equality between length and mass

\frac{l_{P}}{ƛ_{C}} = \frac{m_{0}}{m_{P}} .

(41)

In the language of natural units, the inverse-reduced Compton wavelength is equal to the natural unit quantity of rest mass. At the Planck scale, Equation 41 states that a reduced Compton wavelength of one Planck length would produce a rest mass of one Planck mass.

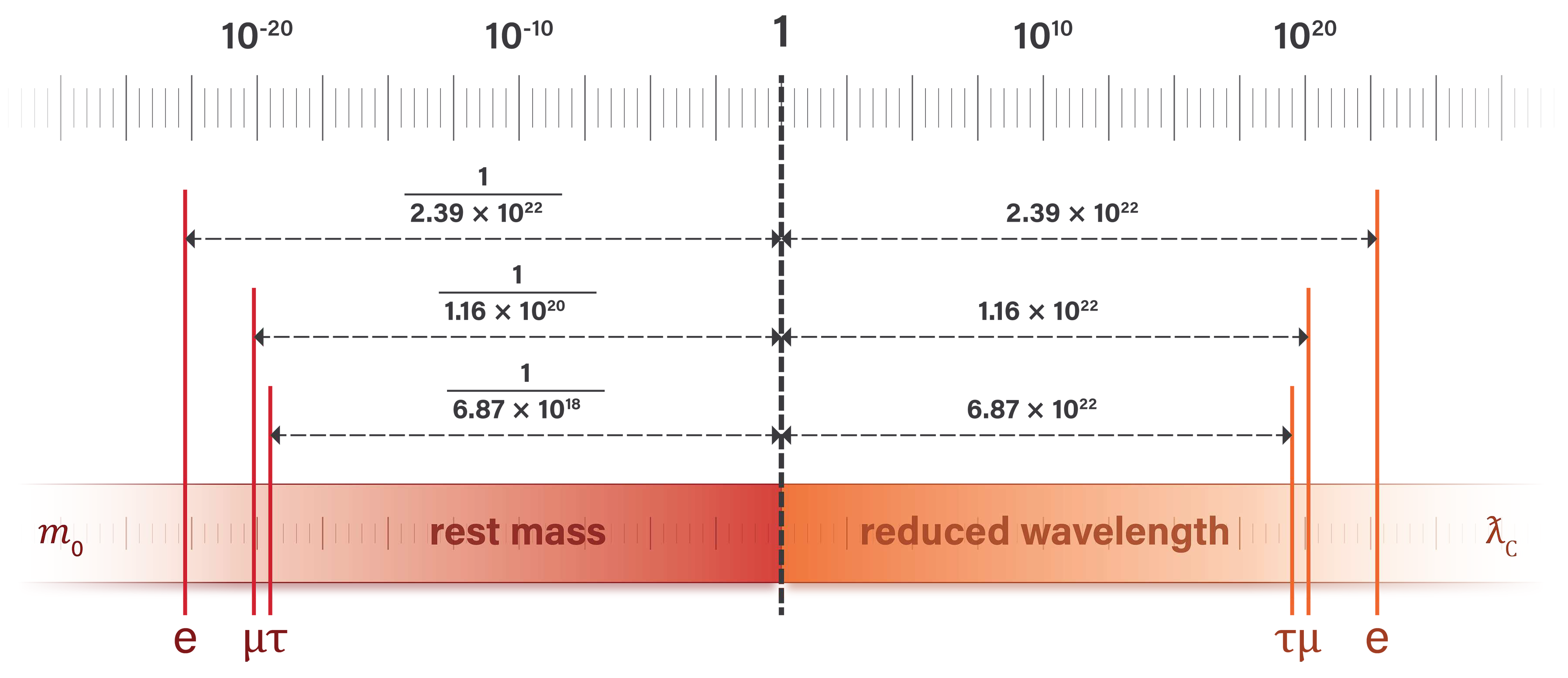
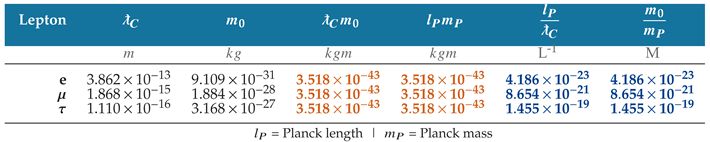
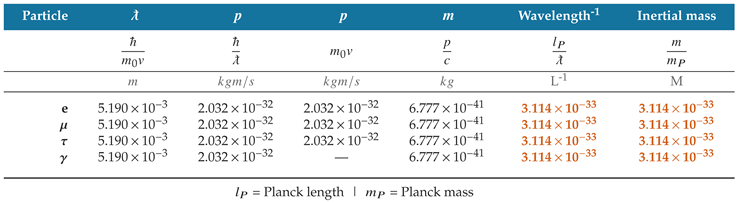
The relationship between rest mass and Compton wavelength is shown in Table 3 using the current values of the charged leptons.

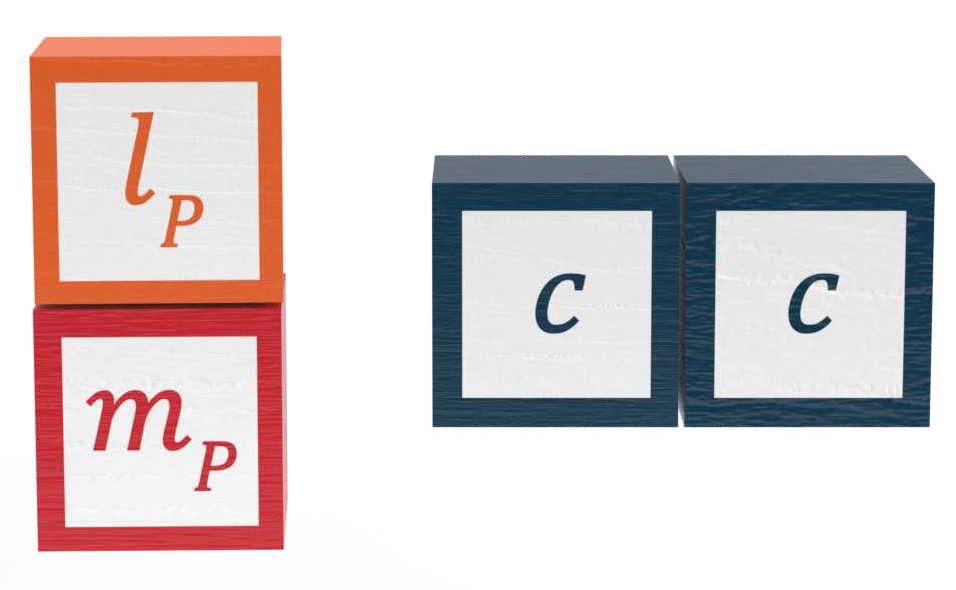
The inversely proportional relationship gives a constant product of Compton wavelength and rest mass, which is equal to the product of Planck length and Planck mass

ƛ_{C} m_{0} = l_{P} m_{P} = 3.517 673 \times 10^{- 43} k g m .

(42)

The constant

l_{P} m_{P}

is equal to the ratio of two universal constants with defined SI values and thereby inherits a defined value in SI units

l_{P} m_{P} = \frac{ℏ}{c} = 3.517 672 9418 \times 10^{- 43} k g m .

(43)

Furthermore, the correlation between rest mass and Compton wavelength is so strong that the electron mass and Compton wavelength produce Planck’s constant with a precision comparable to measurements performed with the Kibble balance [11]

ℏ = ƛ_{C} m_{0} c = 1.054 571 8176 \times 10^{- 34} k g m^{2} / s .

(44)

Figure 6 illustrates the alignment of length and mass units at the Planck scale and the inversely proportional relationship between the reduced Compton wavelength and rest mass of the charged leptons.

The reduced Compton wavelengths for the electron, muon, and tau particles are plotted in the length dimension, with longer wavelengths extending further to the right. The corresponding, inversely proportional rest masses are shown in the unit dimension of mass, with rest mass decreasing further to the left.

3.2. Momentum

While the Compton wavelength is inversely proportional to the rest mass of a matter particle, the de Broglie wavelength is inversely proportional to its momentum. The physical meaning of the two wavelengths characterizing a single particle may become clear in time and with further investigation; however, the mathematical relationships—the correlations in these particle attributes—are etched into the equations.

The de Broglie hypothesis presumes the equivalence of classical and quantum mechanical momentum [22], relating the two formulas by

p = m_{0} v = \frac{ℏ}{ƛ}

(45)

where denotes the reduced de Broglie wavelength. The natural structure that makes this statement true is found in the unit dimensions of the equality. Stating Planck’s constant in natural units yields

m_{0} v = \frac{l_{P} m_{P} c}{ƛ}

(46)

which can be arranged into a dimensionless equality

(\frac{m_{0}}{m_{P}}) (\frac{v}{c}) = \frac{l_{P}}{ƛ} .

(47)

The corresponding natural unit equation for the de Broglie wavelength is

ƛ = (\frac{m_{P}}{m_{0}}) (\frac{c}{v}) l_{P} .

(48)

A consequence of the de Broglie hypothesis is that we can determine a quantum mechanical property of matter by making a classical observation. Given a particle’s rest mass and by measuring its velocity, we can determine the particle’s de Broglie wavelength.

However, Equation 48 is not the only way to represent the de Broglie wavelength. Evaluating the Compton and de Broglie wavelength formulas 40 and 48 in their standard form or in natural units shows that

\frac{ƛ_{C}}{ƛ} = \frac{v}{c} .

(49)

Furthermore, the two equalities 41 and 49 give the following combined relationship

(\frac{m_{0}}{m_{P}}) (\frac{v}{c}) = (\frac{l_{P}}{ƛ_{C}}) (\frac{ƛ_{C}}{ƛ}) = \frac{l_{P}}{ƛ} .

(50)

Therefore, it is mathematically equivalent, according to de Broglie’s conjecture, to state the momentum of a matter particle as

p = (\frac{l_{P}}{ƛ}) m_{P} c = \frac{ℏ}{ƛ} .

(51)

DeBroglie’s hypothesis suggests that classical momentum may simply be a convenient way of quantifying the wavelengths of constituent matter particles in a classical system. Given Equation 49, the role of velocity in classical momentum may be to quantify a particle’s inertial mass—the Poincare mass—from a proportional quantity of rest mass. With this assumption, the energy-momentum relation gives a vector sum of the two masses where

m = p / c

E = \sqrt{m_{0}^{2} + m^{2}} c^{2}

(52)

Table 4 compares the physical properties of the three charged leptons and a photon when the wavelength of each particle is equal to the wavelength of

Δ v_{C s}

As shown in the table, the momentum of all four particles is the same when the particles have the same wavelength; this is true regardless of whether a particle has rest mass or whether its velocity is constant. The quantum mechanical momentum formula and description apply equally to quanta of matter and radiation, whereas the classical formula only describes matter.

The concept of inertial mass provides a general statement about the relationship between mass and wavelength, which is rooted in the natural unit formulas, and gives a consistent account of the transformations in each unit dimension. It explains how momentum is a single, consistent phenomenon for matter and radiation and suggests that classical and quantum mechanical formulas describe the same underlying physical structure.

Perhaps the most compelling evidence for the Poincare view is that it shows how classical and quantum mechanical energy are the same phenomenon—each one a function of particle frequency. By treating one of the velocity terms in the classical kinetic energy formula as a proportional substitute for quantifying the de Broglie wavelength, we remove the redundancy of a second velocity term. This gives a product of de Broglie wavelength and velocity that is equal to the frequency or inverse period of the matter particle.

3.3. Correlated mechanics

Irrespective of one’s view on the Poincare mass, correlations appear in classical and quantum mechanical formulas that are not contingent on whether the formulas are written in natural units or universal constants. Figure 7 illustrates these correlations, and Table 5 and Table 6 show the relationships under two scenarios.

Changes in the inertial mass and velocity of a matter particle are proportional to the ratio of Compton wavelength to de Broglie wavelength. The two wavelengths converge at the non-relativistic limit of the particle’s velocity, the speed of light. At this limit, the non-relativistic energy

E = m_{0} c^{2}

is equal to the energy of a photon with the same wavelength.

As the de Broglie wavelength increases with respect to the Compton wavelength, inertial mass and velocity decrease in equal proportions. For example, a matter particle with a de Broglie wavelength that is three times the Compton wavelength has one-third the inertial mass and its velocity is one-third the speed of light. The combined result is a 9x increase in the oscillation period and a 9x decrease in the kinetic energy. The following two expressions quantify the combined change in kinetic energy

\frac{v^{2}}{c^{2}}

(53)

and

(\frac{ƛ_{C}}{ƛ}) (\frac{v}{c}) .

(54)

Table 5 and Table 6 demonstrate these correlated mechanics under two scenarios. The first scenario is the electron state illustrated in Figure 7, where the de Broglie wavelength is three times the Compton wavelength. The second scenario is the electron ground state in which the de Broglie wavelength is equal to the Compton wavelength divided by the fine-structure constant. Table 6 approximates this ratio as

1 / 137

4. Classical gravity in natural units

The correlations examined thus far pertain to the quantum mechanical properties of matter and radiation, including large-scale manifestations of quantum attributes in classical systems. An investigation into the natural unit structure of the gravitational constant and the equations of classical gravity reveal similar correlations between the physical attributes of massive bodies and the gravitational field. In these formulas, the Planck scale plays a pivotal role in quantifying gravity.

The classical two-body gravity formulas stated in natural units show that G can be characterized in two parts:

The ratio $l_{P}$ / $m_{P}$ gives a Planck scale basis of proportionality for quantifying the gravitational field generated by mass M and distance r.
The quantity $c^{2}$ included in the gravitational constant is the computational basis for stating gravitational field potentials in terms of the momentum and velocity of a test particle or second body.

Figure 8. The gravitational constant is the ratio of Planck length to Planck mass and the speed of light squared.

Beneath the compound unit dimensions of G, the classical formulas compare a body’s mass and radius with the Planck scale basis of Planck mass and Planck length. Two signature inputs into the formulas—mass in the numerator and radius in the denominator—produce a dimensionless ratio

\frac{l_{P}}{r} \frac{M}{m_{P}}

(55)

which is the correct ratio for quantifying gravitational field strength on a scale of 0 to 1, where 1 represents the Planck scale. This quantity of radial density provides the definition of the Schwarzschild radius and appears in each of the classical gravity formulas shown in Table 7.

Table 7. The ratio between a massive body’s radial density and the ratio of Planck length to Planck mass (highlighted in orange) determines the gravitational field strength at distance r.

Similar to the quantum mechanical formulas in Table 1, classical gravity equations are characterized by equalities between the physical attributes of the system and the phenomena they induce.

The formulas suggest that

l_{P} / m_{P}

quantifies a lower boundary on the possible values of radius for a given quantity of mass. This relationship is true whether the formulas are written with G or natural units. The classical Schwarzschild radius formula stated in natural units is

\begin{matrix} R_{s} & = 2 G \frac{M}{c^{2}} \end{matrix}

(56)

\begin{matrix} = 2 [\frac{l_{P}}{m_{P}} c^{2}] \frac{M}{c^{2}} \end{matrix}

(57)

\begin{matrix} = 2 (\frac{M}{m_{P}}) l_{P} . \end{matrix}

(58)

Rearranging 58 defines the Schwarzschild radius as one-half of the density limit

\frac{l_{P}}{R_{s}} \frac{M}{m_{P}} = \frac{1}{2} .

(59)

Equation 59 reflects a known property of black holes. Because the relationship between the Schwarzschild radius and mass is constant, the volumetric density of a black hole decreases as its radius increases. Although the formula does not indicate how the mass of a black hole is distributed, it is consistent with the view that black holes are not singularities.

The equalities in Table 7 show that gravitational potentials are proportional to the natural unit limit regardless of whether the body is a black hole. For example, the escape velocities of the Earth and Sun are proportional to the ratio of their mass and radius to

l_{P} / m_{P}

Table 8 compares the radial densities of several massive bodies, each stated in terms of the Schwarzschild radius, or twice the natural unit limit. Ratios for black holes were calculated using the Schwarzschild radius formula, while the ratios of other bodies were calculated using recent values of mass and radius [23,24,25,26,27,28].

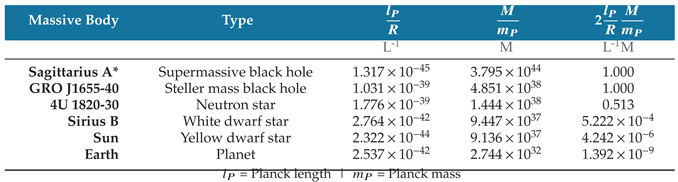
Table 8. The ratio between a massive body’s real or hypothetical Schwarzschild radius and surface R quantifies its gravitational field. The table compares this ratio for several classes of massive bodies.

A simple way to understand the ratio in the last column is to consider that each body’s mass is constant. For the given mass of each body, the radial density ratio is equal to the ratio of the Schwarzschild radius to the surface radius. For example, multiplying Earth’s radius by twice its radial density ratio in Table 8 produces the Schwarzschild radius

(6, 371, 000 m) \times (1.39229 \times 10^{- 9}) = . 008 870 m .

(60)

The radial density ratio accounts for both the size and density of the massive body. While the Earth and Sun have similar volumetric densities, the Sun’s radial density ratio is about four orders of magnitude larger. The larger radius of the Sun gives it a larger surface area and greater volume accommodating more mass per unit of radial distance than the Earth.

Perhaps the most interesting insights gained from the natural unit formulas are descriptions of how the gravitational field is related to the mechanical properties induced on a second body. One such example is gravitational potential energy. Setting the energy potential equal to the kinetic energy of a second body gives

[\frac{l_{P}}{r} \frac{M}{m_{P}}] m c^{2} = \frac{1}{2} m v^{2}

(61)

where v is equal to the escape velocity. At the Schwarzschild radius, the potential energy is ½

m c^{2}

and decreases with distance. Simplifying Equation 61 provides an insightful relationship between the radial density of a first body and the momentum and velocity of a second body

2 [\frac{l_{P}}{r} \frac{M}{m_{P}}] = \frac{v^{2}}{c^{2}} .

(62)

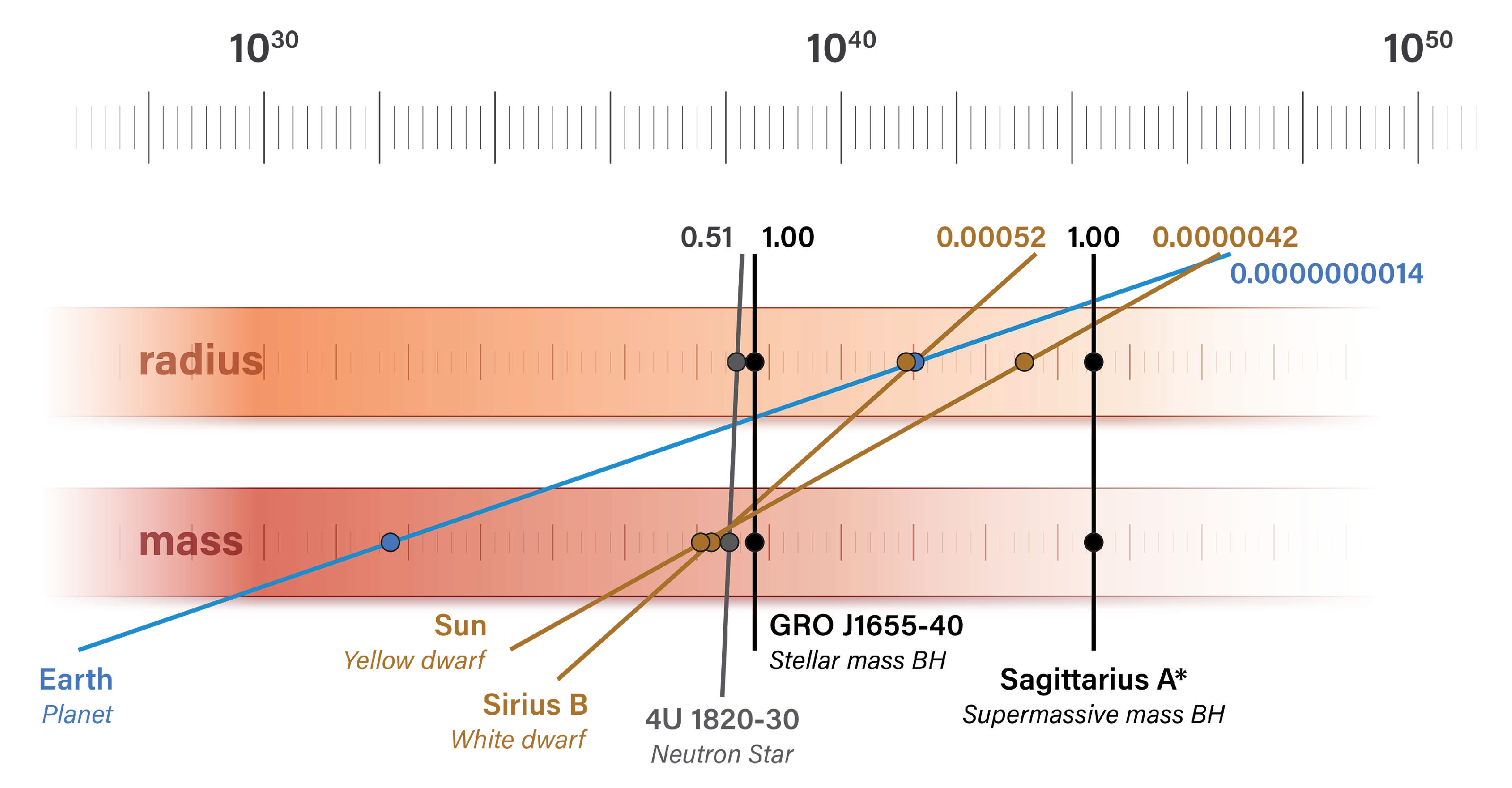
Figure 9 illustrates the relationship between natural units of radius and mass for the massive bodies in Table 8.

The mass and radius of each body are plotted in natural units and normalized to a Schwarzschild radius value of one. The slope of each line represents the ratio between the body’s mass and radius in natural units. Black holes have a vertical line between their mass and radius, and the slope decreases as the radius of the body increases with respect to mass. More massive bodies appear further to the right of the illustration.

Different classes of massive bodies appear in different colors: black holes are shown in black, a neutron star in gray, dwarf stars in yellow, and planet Earth in blue.

5. Electromagnetism

The same natural structure underlying quantum mechanics and classical gravity is also found in the constants and equations of electromagnetism. Electromagnetic phenomena include a unit dimension of electric charge that aligns with unit dimensions of length, mass, and time at the Planck scale. The ratio between electric charge and Planck charge plays a pivotal role in the equations.

5.1. Electrostatic force

Coulomb’s law gives the electrostatic force acting between a pair of charged particles. The Coulomb constant transforms inputs of charge and distance into the resulting electrostatic force. Like the universal constants, Coulomb’s constant contains natural units in its unit dimensions

M L^{3} T^{- 2} Q^{- 2} .

Inserting natural units of length, mass, time, and charge into the unit dimensions of Coulomb’s constant demonstrates the natural unit structure

k_{e} = \frac{m_{P} l_{P}^{3}}{t_{P}^{2} q_{P}^{2}} = F_{P} {(\frac{l_{P}}{q_{P}})}^{2} = 8.988 \times 10^{9} k g m^{3} s^{- 2} C^{- 2} .

(63)

The standard form of the electrostatic force equation

F = k_{e} \frac{q_{1} q_{2}}{r^{2}}

(64)

can be expressed in natural units by combining 63 and 64

F = F_{P} {(\frac{l_{P}}{r})}^{2} (\frac{q_{1}}{q_{P}}) (\frac{q_{2}}{q_{P}}) .

(65)

The corresponding equality between the electrostatic force, charge, and distance is

\frac{F}{F_{P}} = {(\frac{l_{P}}{r})}^{2} (\frac{q_{1}}{q_{P}}) (\frac{q_{2}}{q_{P}}) .

(66)

The natural unit equalities and formulas for Coulomb’s law and several defining equations of electromagnetism are shown in Table 9.

Table 9. Several defining equations of electromagnetism are stated in natural unit equalities and formulas. The Planck scale and natural units play the same role in quantifying electromagnetic phenomena.

The electrostatic force can be understood further by inserting the elementary charge into the formula

F = k_{e} \frac{e^{2}}{r^{2}} = F_{P} {(\frac{l_{P}}{r})}^{2} {(\frac{e}{q_{P}})}^{2} .

(67)

and then simplifying based on the ratio of elementary charge to Planck charge

\frac{e}{q_{P}} = \frac{1.602 176 634 \times 10^{- 19} C}{1.875 546 038 \times 10^{- 18} C} = 0.085 424 543 132 = \sqrt{α} .

(68)

The electrostatic force between a pair of elementary charges is therefore reduced to

F = α {(\frac{l_{P}}{r})}^{2} F_{P} .

(69)

The formula can be stated simply in terms of the fine-structure constant and the natural unit distance between charges, giving a dimensionless determinant on a scale of 0 to 1

F = \frac{α}{L^{2}} F_{P}

(70)

The natural unit formula suggests that two factors determine the strength of electrostatic force between a pair of electric charges. Given the basis of Planck force, the fine-structure constant provides a fixed reduction in force between charges, and the inverse square of the distance provides a variable reduction in force.

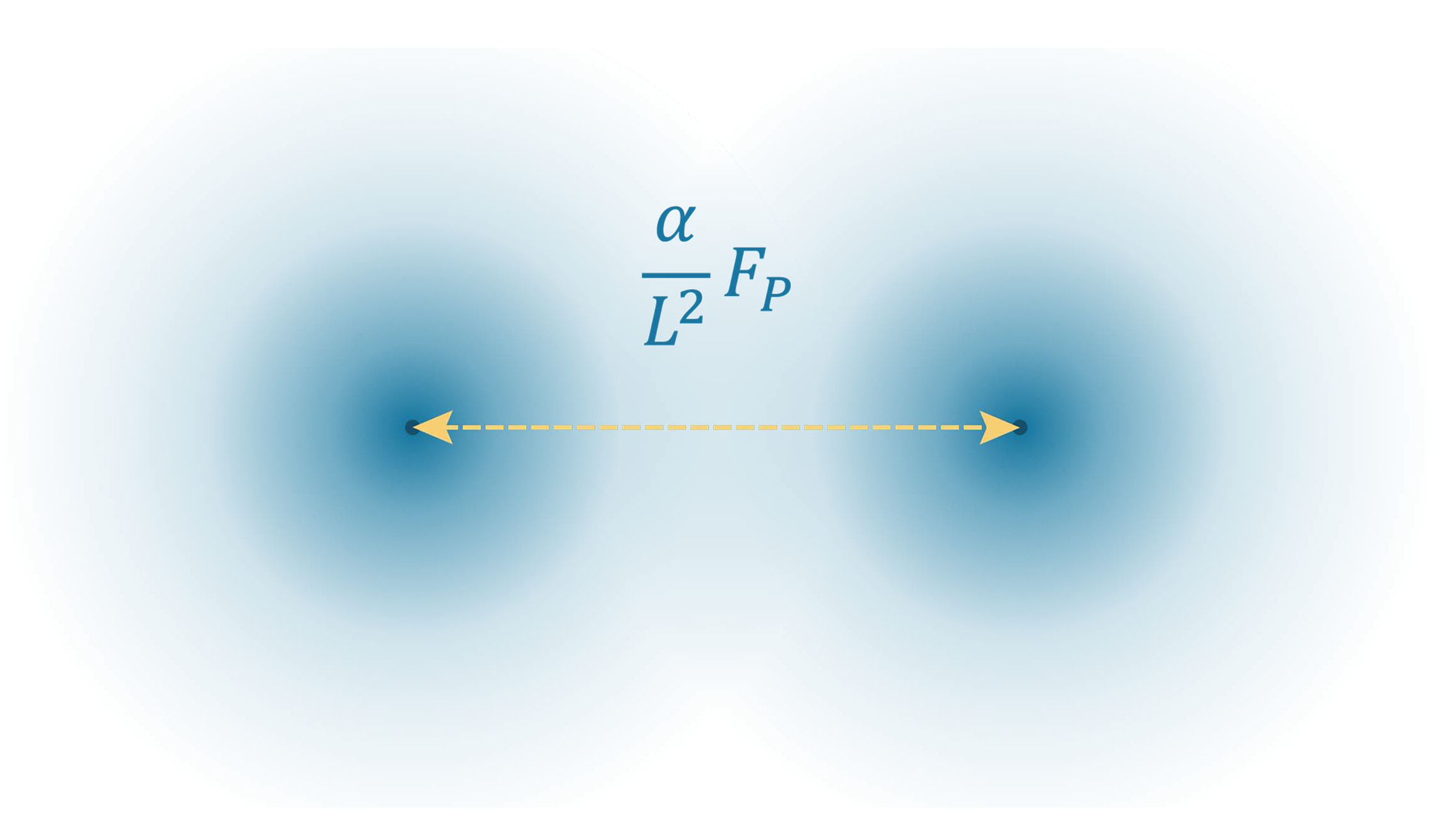
Figure 10. The electrostatic force between a pair of charged particles is proportional to the Planck force. The dimensionless fine-structure constant and distance squared in natural units determine the strength of the electrostatic force.

At a distance of one Planck length, the force between a pair of electric charges is less than the Planck force by a simple factor of

α

F = α F_{P} .

(71)

5.2. Vacuum permittivity

The relationship between Coulomb’s constant and the vacuum electric permittivity gives the natural unit definition of the electric constant as

ϵ_{0} = \frac{1}{4 π F_{P}} {(\frac{q_{P}}{l_{P}})}^{2} = 8.854 19 \times 10^{- 12} C^{2} s^{2} k g^{- 1} m^{- 3} .

(72)

The natural unit form of the constant distinguishes between the Planck scale basis required by the equations (the Planck force) and additional units of Planck length and charge that convert SI inputs of length and charge into natural units.

While the vacuum permittivity is conveniently structured for calculating force, it can also be used to calculate energy such as the potential energy between a pair of point charges

\begin{matrix} U_{E} & = \frac{e^{2}}{4 π ϵ_{0} r} \end{matrix}

(73)

\begin{matrix} = \frac{e^{2}}{4 π r} 4 π F_{P} \frac{l_{P}^{2}}{q_{P}^{2}} . \end{matrix}

(74)

The formula cleverly restructures the Planck force into Planck energy and produces the fine-structure constant using Equation 68

\begin{matrix} U_{E} & = \frac{4 π}{4 π} F_{P} l_{P} (\frac{l_{P}}{r}) (\frac{e^{2}}{q_{P}^{2}}) \end{matrix}

(75)

\begin{matrix} = α (\frac{l_{P}}{r}) E_{P} . \end{matrix}

(76)

Table 10 lists the natural unit form of several electromagnetic constants in dimensions of length, mass, time, and charge. Each natural unit value of a constant is equivalent to the standard value within the uncertainty limits of the Planck units. The Planck charge has a much more precise value than the other Planck units because it can be calculated with the precision of the fine-structure constant or electric permittivity.

5.3. Vacuum permeability

The vacuum permeability is related to the vacuum permittivity by

μ_{0} = \frac{1}{ϵ_{0} c^{2}}

(77)

which gives a natural unit equation for the magnetic constant

μ_{0} = 4 π F_{P} {(\frac{t_{P}}{q_{P}})}^{2} = 1.256 637 \times 10^{- 6} N A^{- 2}

(78)

Similar to the electric constant, the magnetic constant has a basis of Planck force. However, units of Planck charge and Planck time included in the constant make it more suitable for equations with inputs of electric current.

Because the magnetic constant has two units of Planck time in both the numerator and denominator, it can be reduced to

μ_{0} = 4 π \frac{l_{P} m_{P}}{q_{P}^{2}} k g m C^{- 2}

(79)

which is equivalent to the formula used for calculating the CODATA value [8,9]

μ_{0} = 4 π \frac{α ℏ}{e^{2} c} .

(80)

Replacing Planck’s constant with natural units gives

μ_{0} = 4 π \frac{α l_{P} m_{P} c}{e^{2} c}

(81)

and the ratio

e^{2} / α

can be replaced with the Planck charge squared, as shown in Equation 68

μ_{0} = 4 π \frac{l_{P} m_{P}}{q_{P}^{2}} .

(82)

5.4. Electromagnetic potentials

The equations of electromagnetism use the Planck scale as a basis of proportionality for determining the correlated attributes of charged particles and systems. The Planck scale potentials listed in Table 11 are therefore important physical constants. Each physical phenomenon in the table is a Planck scale electromagnetic potential designated by subscript p.

6. Putting it all together

The natural units of measure which retain their meaning for all times and for all civilizations provide a single, unifying principle behind the values and dimensions of all the constants and equations in Table 1, Table 7, Table 9, Table 10, Table 11, and Table 12. Restating compound-dimensional constants in natural units unveils a natural structure underpinning the mathematics, aligning each unit dimension at the Planck scale, and revealing the highly correlated properties and dynamics of elementary particles and fields.

Natural unit formulas establish a coherent connection between the mathematical formulations and physical dimensions of natural phenomena. In light of this natural structure, is it still reasonable to consider the universal constants fundamental? The natural units are decidedly more elemental than the universal constants, having a single value and dimension for each unit. And while it is widely presumed that natural units of length, mass, and time are “derived” from three fundamental universal constants, it is difficult to imagine how the following combinations of universal constants give conceptual meaning to length, mass, and time

Planck length = \sqrt{\frac{ℏ G}{c^{3}}} = \sqrt{\frac{l_{P}^{2} m_{P}}{t_{P}} \frac{l_{P}^{3}}{m_{P} t_{P}^{2}} \frac{t_{P}^{3}}{l_{P}^{3}}} = l_{P}

(83)

Planck mass = \sqrt{\frac{ℏ c}{G}} = \sqrt{\frac{l_{P}^{2} m_{P}}{t_{P}} \frac{l_{P}}{t_{P}} \frac{m_{P} t_{P}^{2}}{l_{P}^{3}}} = m_{P}

(84)

Planck time = \sqrt{\frac{ℏ G}{c^{5}}} = \sqrt{\frac{l_{P}^{2} m_{P}}{t_{P}} \frac{l_{P}^{3}}{m_{P} t_{P}^{2}} \frac{t_{P}^{2} t_{P}^{3}}{l_{P}^{5}}} = t_{P} .

(85)

In the orthodox view of these equations, one is left wondering what role the square root of the speed of light to the fifth power plays in defining a single unit of time. On the other hand, it is easy to see that the universal constants are compound collections of natural units. The peculiar ratios of universal constants in Equations 83, 84, and 85 are simply what is required to isolate each unit dimension from the compound-dimensional constants.

It is often the case that equations stated in compound-dimensional constants are unnecessarily complex. These formulas contain extraneous and enigmatic ratios of physical constants to produce the correct combination of natural units. For example, a particularly extraneous form of the Rydberg constant

R_{\infty}

R_{\infty} = \frac{m_{e} e^{4}}{8 ϵ_{0}^{2} h^{3} c} .

(86)

The formula produces a high precision value of

R_{\infty}

which is essential for experimental research; but the equation conveys little representational meaning about the constant. Stating the constants in natural units reduces the formula to more elemental components

\begin{matrix} R_{\infty} & = \frac{m_{e}}{8} (q_{P}^{4} α^{2}) (\frac{16 π^{2} l_{P}^{6} m_{P}^{2}}{t_{P}^{4} q_{P}^{4}}) (\frac{t_{P}^{3}}{8 π π^{2} l_{P}^{6} m_{P} m_{P}^{2}}) (\frac{t_{P}}{l_{P}}) \end{matrix}

(87)

\begin{matrix} = \frac{m_{e} α^{2}}{4 π l_{P} m_{P}} . \end{matrix}

(88)

Restating the compound-dimensional constants in natural units explains why Equation 86 gives the same result as other equations that produce the constant. A more efficient equation [29] that still produces a high precision value is

\begin{matrix} R_{\infty} & = \frac{m_{e} α^{2} c}{2 h} \end{matrix}

(89)

\begin{matrix} = \frac{m_{e} α^{2}}{2} (\frac{l_{P}}{t_{P}}) (\frac{t_{P}}{2 π l_{P} l_{P} m_{P}}) \end{matrix}

(90)

\begin{matrix} = \frac{m_{e} α^{2}}{4 π l_{P} m_{P}} . \end{matrix}

(91)

The physical significance of the Rydberg constant can be understood by its use in atomic spectroscopy. Multiplying the Rydberg constant by Planck’s constant and the speed of light produces the ground-state electron energy, but the universal constants do not explain why. Restating the formula in natural units yields

\begin{matrix} h c R_{\infty} & = \frac{1}{4 π} \frac{m_{e} α^{2}}{l_{P} m_{P}} h c \end{matrix}

(92)

\begin{matrix} = \frac{1}{4 π} \frac{m_{e} α^{2}}{l_{P} m_{P}} (\frac{2 π l_{P}^{2} m_{P}}{t_{P}}) (\frac{l_{P}}{t_{P}}) \end{matrix}

(93)

\begin{matrix} = \frac{1}{2} m_{e} α^{2} c^{2} . \end{matrix}

(94)

which produces the CODATA Rydberg energy formula [9]. The correlations of matter particle properties shown in Section 3 and the role of the fine-structure constant in quantifying electrostatic energy shown in Section 5 explain why

v = α c

and why Equation 94 gives the ground state energy

h c R_{\infty} = \frac{1}{2} m_{e} v^{2} .

(95)

6.1. Luminosity

The transformation of a star’s temperature into the corresponding quantity of radiant power is a good test of an equation’s ability to explain the underlying physics. The standard formula uses the Stefan-Boltzmann constant

σ = \frac{π^{2} k^{4}}{60 ℏ^{3} c^{2}} W m^{- 2} K^{- 4}

(96)

and determines radiant power by the formula

L = σ A T^{4} .

(97)

Given a surface temperature of 5,778 K and a radius of 696,156,000 m, the Sun’s luminosity is

\begin{matrix} L & = (5.670 \times 10^{- 8} W m^{- 2} K^{- 4}) \times (4 π \times 696, 156, 000 m^{2}) \times {(5778 K)}^{4} \end{matrix}

(98)

\begin{matrix} = 3.849 \times 10^{26} W . \end{matrix}

(99)

The function gives little indication of how inputs of temperature and radius are transformed into the corresponding amount of radiant power. The surface area clearly acts as a scaling factor for some amount of radiant power produced from the temperature. But it is not clear how this quantity of power is determined.

The same formula restated in natural units provides a physical explanation in each dimension of space and time. The natural unit equality and formula in Table 12 provide an outline of the transformation.

Table 12. The natural unit luminosity formula explains how temperature is translated into radiant power.

P_{p}

= maximum power potential =

E_{P} / t_{P}

The function determines radiant power in two steps: first, by translating the average kinetic energy into a corresponding quantity of radiant power at the Planck scale, and then by rescaling that power over the surface area of a star. The relevant quantities for this example are

Apart from the constant, the function contains two dimensionless (or naturally dimensionful) ratios and the Planck scale basis of Planck energy per Planck time. The three quantities are calculated as follows

Surface area

The function rescales the radiant power per Planck area to the Sun’s surface area using the ratio

\frac{A}{l_{P}^{2}} = \frac{4 π \times 696, 156, 000^{2} m^{2}}{{(1.616 \times 10^{- 35} m)}^{2}} = 2.331 \times 10^{88} L^{2}

(100)

Power potential

The Planck scale power potential is the ratio of Planck energy to Planck time. This is the basis against which the correlated photon properties produce a given quantity of radiant power

P_{p} = \frac{E_{P}}{t_{P}} = \frac{1.956 \times 10^{9} J}{5.391 \times 10^{- 44} s} = 3.628 \times 10^{52} W .

(101)

Ratio of radiant power to Planck area

The challenge in converting temperature to luminosity is converting the average kinetic energy per particle into the correct magnitude of radiant power over a given area. This is demonstrated by the natural unit formula. First, the photon energy equivalent is calculated in natural units as a ratio of the Planck energy

\frac{k_{B} T}{E_{P}} = \frac{E}{E_{P}} = \frac{7.977 \times 10^{- 20} J}{1.956 \times 10^{9} J} = 4.078 \times 10^{- 29} E .

(102)

According to 32, this gives inversely proportional quantities of wavelength and oscillation period which quantify the energy in dimensions of space and time

\frac{E}{E_{P}} = \frac{l_{P}}{ƛ} = \frac{t_{P}}{τ} = 4.078 \times 10^{- 29} .

(103)

The amount of radiant power per unit of Planck length is therefore the ratio of energy per time

\frac{E}{τ} = {(4.078 \times 10^{- 29})}^{2} = 1.663 \times 10^{- 57} E T^{- 1}

(104)

and the corresponding radiant power per Planck area is

\frac{P}{P_{P}} = {(4.078 \times 10^{- 29})}^{4} = 2.766 \times 10^{- 114} E T^{- 1} .

(105)

Multiplying the natural unit power by 101 gives the radiant power per Planck area, and 100 rescales it to the surface area. The following steps illustrate how the natural unit formula is equivalent to the standard formula stated in universal constants

\begin{matrix} L & = σ A T^{4} \end{matrix}

(106)

\begin{matrix} = (\frac{π^{2} k_{B}^{4}}{60 ℏ^{3} c^{2}}) A T^{4} \times (\frac{c}{c}) \end{matrix}

(107)

\begin{matrix} = \frac{π^{2}}{60} (\frac{{(k_{B} T)}^{4}}{E_{P}^{3}}) (\frac{A}{l_{P}^{2}}) (\frac{1}{t_{P}}) \end{matrix}

(108)

\begin{matrix} = \frac{π^{2}}{60} (\frac{E^{4}}{E_{P}^{3}}) (\frac{A}{l_{P}^{2}}) (\frac{1}{t_{P}}) \times (\frac{E_{P}}{E_{P}}) \end{matrix}

(109)

\begin{matrix} = \frac{π^{2}}{60} (\frac{E^{4}}{E_{P}^{4}}) (\frac{E_{P}}{t_{P}}) (\frac{A}{l_{P}^{2}}) \end{matrix}

(110)

Equations 106 through 110 show that it is not only the case that compound-dimensional constants insert superfluous natural units into the formulas; it is also sometimes the case that reduced formulas conceal natural units in the numerator and denominator of the equations which produce the required correlations.

Restating the Stefan-Boltzmann constant and the luminosity formula in natural units shows how inputs of area and temperature produce the corresponding amount of radiant power. Such explanations are generally hidden by the traditional form of the constants and equations.

7. Conclusion

Many compound-dimensional constants provide high-precision values that are important for experimental and applied physics. However, from a theoretical perspective, the natural units provide a more granular representation of the physical constants and equations.

The natural units of measure are independent of unit systems. They reveal hidden correlations in the physical attributes and dynamics of natural phenomena that explain why the equations produce meaningful results—transforming formula inputs into the expected quantities and dimensions of formula outputs.

The importance of such correlations was extolled by John Bell who exclaimed “The scientific attitude is that correlations cry out for explanations.” [30] With respect to the universal constants, however, the scientific attitude is overtaken by philosophical prejudice and historical bias. The present-day attitude is that deeper meaning should not be investigated or ascribed to the “fundamental” constants of nature.

In light of the deeper significance of natural units demonstrated throughout this study, the established philosophy argues that somehow less is more—that we should ignore the more granular, accordant natural structure and simply embrace the abstractness of h and G.

In his celebrated paper on the role of mathematics in physics, Eugene Wigner contemplates a scenario in which conflicting theories cannot be resolved experimentally. Such a situation is possible, he says because “fundamentally, we do not know why our theories work so well. Hence, their accuracy may not prove their truth and consistency.” [31]

The present situation offers an alternative conceptual explanation of the equations that cannot be resolved by experiment. The computations are equivalent within the measurement uncertainties of the constants. Furthermore, the very assumption on which Planck calculated the natural units is their equivalence with the universal constants in their compound unit dimensions. The challenge lies in adjudicating between different mathematical formulations that produce the same computational result.

Unlike Wigner’s scenario, the natural units offer a less abstract description of nature than the orthodox depictions derived from the universal constants. The natural units hold the equations accountable for transformations in each unit dimension, placing constraints on the choice of symbols when there are multiple, equivalent ways of arriving at the same result.

The natural units offer a rare opportunity to re-evaluate the physical meaning of the standard model which has grown stagnant over the past half-century. They challenge the assumption that classical and quantum physics are distinct and incompatible descriptions of nature, providing a common language for interpreting classical and quantum mechanics, classical gravity, and electromagnetism; and they may illuminate a pathway to quantum gravity.

The natural units have been an integral part of the constants and equations from the beginning, but they are still waiting to be acknowledged and understood.

Appendix A. Natural unit alignment

Figure A1 aligns unit dimensions of length, mass, time, and charge at the Planck scale, where each unit has a value of 1. Units of length and time approach a limit of infinity whereas mass and charge approach a limit of 0 in the context of discrete quanta. SI units of meters, seconds, kilograms, and coulombs are shown for comparison.

Figure A1. Unit dimensions of length, mass, time, and charge are aligned at the Planck scale. SI units of meter, second, kilogram, and coulomb are shown for comparison.

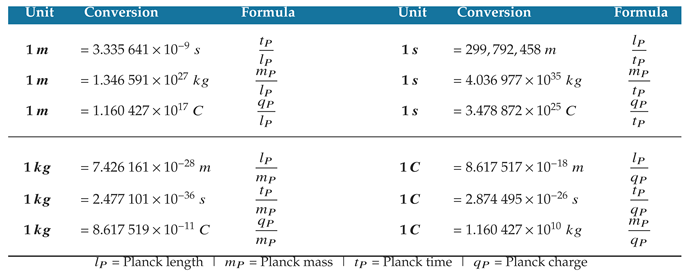
The Planck-scale alignment of natural units gives a ratio for each pair of unit values in SI units, which is useful for recognizing natural scale alignments such as the speed of light. Table A1 provides each ratio which serves as an SI unit conversion from one unit dimension to another.

Table A1. Natural unit ratios give a conversion between unit dimensions in SI units.

References

Max Planck. Über irreversible strahlungsvorgänge. Sitzungsberichte der Königlich Preußischen Akademie der Wissenschaften zu Berlin 1899, 5, 440–480. [Google Scholar]
David Humpherys. The Implicit Structure of Planck’s Constant. European Journal of Applied Physics 2022, 4, 22–25. [Google Scholar] [CrossRef]
Espen Gaarder Haug. Progress in the Composite View of the Newton Gravitational Constant and Its Link to the Planck Scale. Universe 2022, 8, 454. [Google Scholar] [CrossRef]
Barton Zwiebach. A First Course in String Theory; Cambridge university press, 2004. [Google Scholar]
V.A. Nastasenko. Otkrutie predelno vozmojnuh volnovuh parametrov: Theoria and tehnica peredachi, priema i pererabotki informacii. Proceedings of the 10-ja Jubilejnaja Megdunarodnaja Conferencia, Kharkov, Ukraine, 1, 2004.
Claude Mercier. Several Ways to Calculate the Universal Gravitational Constant G Theoretically and Cubic Splines to Verify Its Measured Value. Journal of Modern Physics 2020, 11, 1428–1465. [Google Scholar] [CrossRef]
Jody A Geiger. Measurement Quantization Describes History of Universe—Quantum Inflation, Transition to Expansion, CMB Power Spectrum. Journal of High Energy Physics, Gravitation and Cosmology 2020, 6, 186–224. [Google Scholar] [CrossRef]
C. Rothleitner and S. Schlamminger. Invited Review Article: Measurements of the Newtonian constant of gravitation, G. Review of Scientific Instruments 2017, 88, 111101. [Google Scholar] [CrossRef] [PubMed]
Fundamental Physical Constants. 2018. https://physics.nist.gov/cuu/Constants/index.html.
DA Jennings, RE Drullinger, KM Evenson, CR Pollock, and JS Wells. The continuity of the meter: the redefinition of the meter and the speed of visible light. Journal of Research of the National Bureau of Standards 1987, 92, 11. [Google Scholar] [CrossRef]
David Humpherys. Measuring Planck’s Constant With Compton Scattering. Applied Physics Research 2023, 15, 24–29. [Google Scholar] [CrossRef]
K.A. Tomilin. Natural system of units. To the centenary anniversary of the Planck system. Proceedings of the XXII Workshop on High Energy Physics and Field Theory, 1999.
M.A. Markov. Supplement of the Progress of Theoretical Physics. Commemoration Issue for 30th Anniversary of Meson Theory by Dr. H. Yukawa, page 85, 1965.
Saulo Carneiro. Elementary charge and neutrino’s mass from planck length. Foundations of Physics 2020, 50, 1376–1381. [Google Scholar] [CrossRef]
BIPM. Resolution 1 of the 26th CGPM (2018): On the revision of the International System of Units (SI). Bureau international des poids et mesures, 2018.
Miguel A Martin-Delgado. The new SI and the fundamental constants of nature. European Journal of Physics 2020, 41, 063003. [Google Scholar] [CrossRef]
Henri Poincaré. La théorie de Lorentz et le Principe de réaction. 1900.
Moylan, P. Poincare on mass-energy equivalence. Bulgarian Journal of Physics 2019, 46, 81–93. [Google Scholar]
David Humpherys. Natural Planck Units and the Structure of Matter and Radiation. International Journal of Quantum Foundations: Quantum Speculations 2021, 3. [Google Scholar]
Espen Gaarder Haug. Extraction of the Planck Length from Cosmological Redshift without Knowledge of G or h. International Journal of Quantum Foundations: Quantum Speculations 2022, 4. [Google Scholar]
Gordon R Kepner. Relating the de Broglie and Compton Wavelengths to the Velocity of Light? Applied Physics Research 2014, 4. [Google Scholar]
Louis de Broglie. Xxxv. A tentative theory of light quanta. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science 1924, 47, 446–458. [Google Scholar] [CrossRef]
Roberto Abuter, A Amorim, M Bauböck, JP Berger, H Bonnet, W Brandner, Y Clénet, V Coudé Du Foresto, PT De Zeeuw, J Dexter, et al. A geometric distance measurement to the galactic center black hole with 0.3% uncertainty. Astronomy & Astrophysics 2019, 625, L10. [Google Scholar]
SE Motta, TM Belloni, L Stella, T Muñoz-Darias, and R Fender. Precise mass and spin measurements for a stellar-mass black hole through x-ray timing: the case of gro j1655- 40. Monthly Notices of the Royal Astronomical Society 2014, 437, 2554–2565. [Google Scholar] [CrossRef]
Tolga Güver, Patricia Wroblewski, Larry Camarota, and Feryal Özel. The mass and radius of the neutron star in 4u 1820- 30. The Astrophysical Journal 2010, 719, 1807. [Google Scholar] [CrossRef]
Jay B Holberg, MA Barstow, FC Bruhweiler, AM Cruise, and AJ Penny. Sirius b: A new, more accurate view. The Astrophysical Journal 1998, 497, 935. [Google Scholar] [CrossRef]
Mustapha Meftah, Thierry Corbard, Alain Hauchecorne, Frédéric Morand, R Ikhlef, Bertrand Chauvineau, Catherine Renaud, Alain Sarkissian, and Luc Damé. Solar radius determined from picard/sodism observations and extremely weak wavelength dependence in the visible and the near-infrared. Astronomy & Astrophysics 2018, 616, A64. [Google Scholar]
Numerical Standards for Fundamental Astronomy Astronomical Constants: Current Best Estimates (cbes). Technical report, IAU Division I Working Group.
Eite Tiesinga, Peter J Mohr, David B Newell, and Barry N Taylor. Codata recommended values of the fundamental physical constants: 2018. Journal of Physical and Chemical Reference Data 2021, 50. [Google Scholar]
John S Bell. Bertlmann’s socks and the nature of reality. Le Journal de Physique Colloques 1981, 42, C2–41. [Google Scholar]
Eugene, P. Wigner. The Unreasonable Effectiveness of Mathematics in the Natural Sciences. Richard Courant lecture in mathematical sciences delivered at New York University, may 11, 1959. Communications on Pure and Applied Mathematics 1960, 13, 1–14. [Google Scholar] [CrossRef]

Figure 1. Unit dimensions have a defined limit at one end of the scale and asymptotically approach limits of zero or infinity at the opposite end. Mass and charge are inversely proportional to length and time.

Figure 2. SI units of meter, kilogram, second, and coulomb are incongruent with the natural unit scale. Natural units of length, mass, time, and electric charge coincide at the Planck scale where each unit has a value of 1.

Figure 4. Natural unit measures of photon wavelength and period are equivalent. These values are independent of unit system.

Figure 5. The hyperfine transition radiation has a quantity of mass that is inversely proportional to its wavelength and period in natural units. This quantity is instrumental in the SI definition of the kilogram.

Figure 6. The inversely proportional relationship between Compton wavelength and rest mass is shown for the charged leptons.

Figure 7. Physical attributes of matter particles are highly correlated. The ratio of Compton wavelength to de Broglie wavelength explains correlations in the wavelength, mass, period, velocity, and energy of matter particles.

Figure 9. The mass and radius of several massive bodies are plotted in natural units (not plotted to scale). The Schwarzschild radius is the distance at which the number of natural length units is twice the number of natural mass units.

Table 1. Correlations in the attributes and dynamics of physical phenomena explain how the equations of physics produce proportionally significant results.

Table 2. Properties and dynamics of the hyperfine transition radiation, which defines the units of meter, second, and kilogram, are shown in SI and natural units. Natural unit values indicate that these quantities are proportional or inversely proportional to each other.

Table 3. The product of the Compton wavelength and rest mass is equal to the product of Planck length and Planck mass. The inversely proportional relationship between wavelength and mass is shown in SI and natural units.

Table 4. Particle wavelength gives a single, consistent description of momentum for matter and radiation.

Table 5. Physical properties and dynamics of three electron states are shown in the table. In each scenario, the ratio of Compton wavelength to de Broglie wavelength quantifies the correlations.

Table 6. Correlations in the physical properties and dynamics of matter are shown for the electron states in Table 5. The ratio of Compton wavelength to de Broglie wavelength quantifies the correlations.

Table 10. Electromagnetic constants have natural units of length, mass, time, and charge in their unit dimensions.

Table 11. Electromagnetic phenomena are proportional to the Planck scale, making these natural unit potentials important physical constants.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Understanding the Often Ignored, but Ever-Present Natural Units

Abstract

1. Introduction

1.1. The natural unit scale

2. The laws of physics in natural units

2.1. Independent units of measure

2.2. Arbitrary unit systems

2.3. The kilogram

3. Correlations of matter

3.1. Rest mass

3.2. Momentum

3.3. Correlated mechanics

4. Classical gravity in natural units

5. Electromagnetism

5.1. Electrostatic force

5.2. Vacuum permittivity

5.3. Vacuum permeability

5.4. Electromagnetic potentials

6. Putting it all together

6.1. Luminosity

7. Conclusion

Appendix A. Natural unit alignment

References

MDPI Initiatives

Important Links

Subscribe