Prerpints.org logo
Preprint
Article

Tunable Helmholtz Resonators using Multiple Necks

Altmetrics

Downloads

112

Views

39

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

14 September 2023

Posted:

15 September 2023

You are already at the latest version

Alerts
Abstract
One of the uses of Helmholtz resonators is as sound absorbers for room acoustic applications, especially for the low frequency range. Their efficiency is centered around their resonance frequency which is mainly depended on elements of their geometry such as the resonator volume and neck dimensions. Incorporating additional necks on the body of a Helmholtz resonator (depending on whether they are open or closed) has been found to alter the resulted resonance frequency. For this study, tunable Helmholtz resonators to multiple resonance frequencies, are proposed and investigated utilizing additional necks. The resonance frequencies of various multi-neck Helmholtz resonators are first modeled with the use of finite element method (FEM), then calculated with the use of an analytical approach and the results of the two approaches are finally compared. Results of this study show that Helmholtz resonators with multiple resonances at desired frequencies are achievable with the use of additional necks, while FEM and analytical methods can be used for the estimation of the resonance frequencies. Analytical and FEM approach results show a good agreement in cases of small number of additional necks, while the increasing differences in cases of higher neck additions, were attributed to the change in effective length of the necks as demonstrated by FEM. The proposed approach can be useful for tunable sound absorbers for room acoustics applications according to the needs of a space. Also, this approach can be applied in cases of additional tunable air resonances of acoustic instruments (e.g. string instruments).
Keywords: 
Subject: Physical Sciences  -   Acoustics

1. Introduction

In architectural acoustics, the acoustic properties of the materials that make up a space largely determine its acoustic behavior. The sound absorption affects all the acoustic parameters which in turn define aspects of the acoustic behavior of a space [1]. In addition, for computational acoustics approaches, the knowledge of sound absorption of materials is necessary in order to model the acoustics of a space.
There are generally three categories of absorptive materials used in architectural acoustics applications [2]: porous absorbers, panel absorbers, and resonant absorbers. Porous absorbers are the most widely used due to their abundance of materials [3] (e.g. fiberglass, mineral fiber products) and in turn also come in many categories [4]. Panel absorbers are usually nonporous lightweight sheets, with an air cavity behind them forming a resonant oscillating mass-spring system. They can be solid or perforated [5], and the air volume can potentially be partly or completely filled with materials such as mineral wool or foam. Finally, resonant absorbers are usually Helmholtz resonators or similar enclosures, which are effective around their resonant frequency or partitions vibrating at their mass-air-mass resonance [2].
A Helmholtz resonator is a very important type of acoustic absorber with various applications in numerous fields. In general, a Helmholtz resonator is a container of gas (usually air) with a neck or an open hole. The compressible fluid inside the resonator acts as a spring [6], for the resonance frequency which depends on the volume of the resonator and the dimensions of the neck. The sound energy loss in a Helmholtz resonator occurs due to viscous loss at the wall of the neck, at the front wall of the resonator, at the edges of the neck and thermal loss in the resonator cavity [7]. Helmholtz resonators having a relatively small volume can be effective absorbers at low frequencies, unlike porous absorbers which are usually effective at medium and high frequencies [8]. This fact is very important, as the combination of these types of absorbers can cause a uniform absorption throughout the frequency range in a space.
Many architectural acoustics applications of the Helmholtz resonator can be found in the literature. Helmholtz resonators have been used as sound absorbers in churches [9,10,11] and also in ancient theatres [12]. They have been used also in the acoustic treatment of broadcasting studios [13] and conference rooms [14]. They have also been used to suppress specific eigenmodes in a room [15] and also to form a construction as a suspended ceiling [16]. Their sound absorption has been extensively studied [17,18] and various improvements have been proposed [19,20]. Also, various combinations with porous absorbers have been found to improve their acoustic performance [21]. Their sound absorption can be evaluated with appropriate sources [22,23] and excitation signals [24]. Beside architectural acoustics applications, various other applications exist for Helmholtz resonators such as in musical acoustics [25,26] or for sound speaker manufacturing [27]. Additionally, also for acoustic energy harvesting [28], noise control in aircrafts [29] and gas turbines [30], and also as an acoustic metamaterial [31].
As presented before, in general, a Helmholtz resonator is a container of gas with an additional neck or opening. However, there are many variations regarding the shape of the neck (e.g. spiral [32,33], tapered [34], angled [35], petal shape [36]), or regarding the shape of the container [37,38]. An important and useful variation is the one where the Helmholtz resonator has more than one neck (usually called multi-neck Helmholtz resonators [39]). The result when you add more necks to the resonator body is that the resonance frequency changes which depends on the geometry and number of necks [40]. The same can be observed when there is a leak or a gap in the body of the resonator [40,41], therefore the understanding of the phenomenon is important for predicting the acoustic behavior of the resonator. For the numerical investigation of multi-neck Helmholtz resonators, various methods have been applied such as Boundary Element Method (BEM) [40] and Finite Element Method (FEM) [42] [43]. Among computational methods, FEM is probably the most widely used in the field of noise control [44], in architectural and environmental acoustics [45] and also in the frequency and the time domain [46,47].
This study set to propose and investigate a tunable Helmholtz resonator to multiple resonance frequencies, utilizing additional necks. For this reason, tunable multi-neck Helmholtz resonators are modeled with the use of FEM and also the resonance frequencies are calculated with an analytical formulation.
This paper has been organized as follows: Section 2 presents the methodology employed for the analytical and the FEM approach. Section 3 includes the findings of the research, while the discussion section analyzes the data, addresses the research question and identifies areas for further research. Finally, the conclusion section gives a brief summary of this research and contextualizes the study.

2. Methods

2.1. Theoretical formulation (single-neck, multi-neck)

2.1.1. Single-Neck

The resonance frequency of a single neck Helmholtz resonator can be calculated as follows [48]:
f 0 = c 0 2 π ρ 0 S 1 V 0 M 1
In the formula, c0 and ρ0 are the speed of sound and density of the air inside the body of the resonator, respectively. Vo is the cavity volume and S1 is the cross-sectional area of the neck. M1 is assumed to be the inertial mass of the air volume of the neck. For a cylindrical neck with diameter d1, and length   l 1 , the M1 can be estimated as: M 1 = ρ 0 l 1 + a 1 d 1 . Where ai is the end correction coefficient which accounts for the ‘induced mass’ in the oscillatory flow in the vicinity of the two ends of the neck [49]. Values for the end correction can be found in the literature (e.g. circular aperture: π / 4 ( ≈ 0.785 . . ) [50], unflanged pipe: 0.75 [51], flanged pipe: 0.85 [51]).

2.1.2. Multi-Neck

A recent study [39] introduced a theoretical formulation for the calculation of the resonance frequency of a Helmholtz resonator with multiple necks. It was considered that the volume change inside the body of the resonator causes a compression of the fluid resulting in a pressure amplitude. Thus, pressure inside the cavity can be calculated with the use of the bulk modulus of the fluid according to [52]. After a rigorous mathematical process, the following formula was proposed for the calculation of the resonance frequency of a multi-neck Helmholtz resonator:
f 0 = c 0 2 π ρ 0 V 0 ∑ i = 1 N S i M i
For this formulation, a total of N necks is assumed to be connected to the cavity of the resonator, each neck i, with 1 ≤ i ≤ N . Si is the cross-sectional area of each neck. Finally, as mentioned before, Mi can be interpreted as the inertial mass of the neck air volume. In the case of cylindrical necks with diameter di, as presented before, the neck air volume mass Mi can be approximated as: M i = ρ 0 l i + a i d i . It should be also noted that Eq. (2) can be expressed by introducing the resonance frequencies which correspond to the Helmholtz resonance frequencies with all, except the i-th, openings closed. Thus, Eq. (2) becomes:
f i = c 0 2 π ρ 0 V 0 S i M i
f l e a k s = c 0 2 π ρ 0 V 0 ∑ i = 2 N S i M i
f 0 = ∑ i = 1 N f i 2 = f 1 2 + f l e a k s 2
Eq. (5) shows that the resonance frequency of a Helmholtz resonator with multiple necks is given by the square root of the sum of the squared resonance frequency without leaks f 1 2 and the squared resonance frequency with leaks only ( f l e a k s 2 ).

2.2. FEM formulation

For the FEM formulation, the Helmholtz equation was used. In the equation, p is the acoustic pressure and k is the wave number. The equation is formed as:
∆ p x + k 2 p x = 0
According to the following equation, the normal derivative of the acoustic pressure p is associated to the normal fluid particle velocity u f :
u f x = 1 i ω ρ f ∂ p ( x ) ∂ n ( x )
In this equation n x is the outward normal vector at a field point x and ρ f is the average density of the fluid.
As a next step a weak formulation with weighting function χ ( x ) was used, and the equation is formed as follows [53]:
∫ Ω χ x ∆ p x + k 2 p x d Ω x     = ∫ Γ χ x i ω ρ f u f x d Γ x + ∫ Ω ∇ χ x ∇ p x − k 2 χ x p x d Ω x = 0
In this notation , Ω and Γ are the domain and boundary respectively. Therefore, the acoustic pressure and particle velocity are shown as follows [49]:
p x = ∑ n = 1 N Φ n x p n
u f x = ∑ n = 1 N Φ n x u n
Finally, Φ n ( x ) is a basis function and p n and u n are the discrete acoustic pressure and fluid particle velocity at point x . Adding eq. 9 to eq. 8 [53]:
K − i k C − k 2 M p = f
K , C and M are the stiffness, damping and mass matrices. Vector f accounts for the source and vector and p accounts for the sound pressure values at the nodal locations.

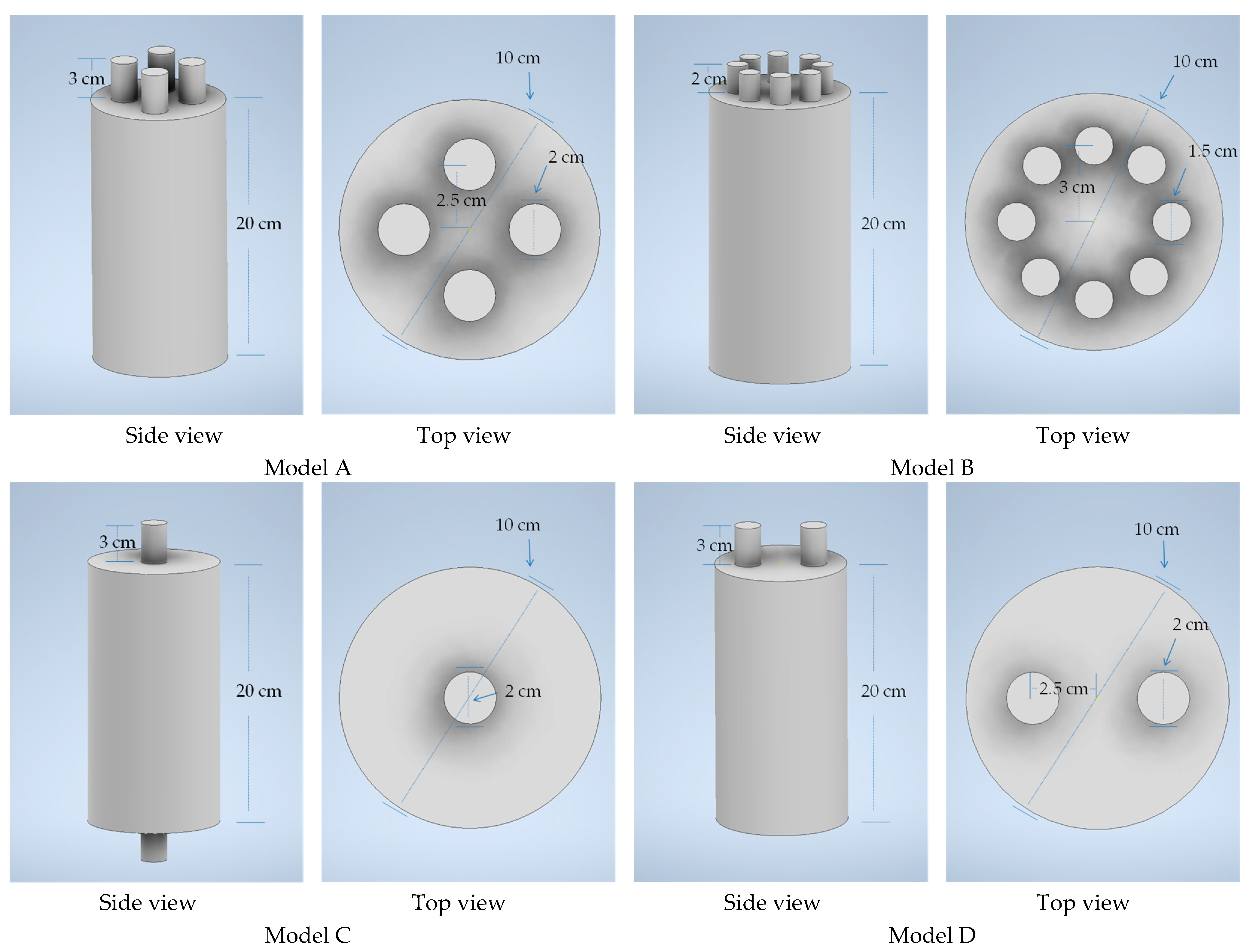
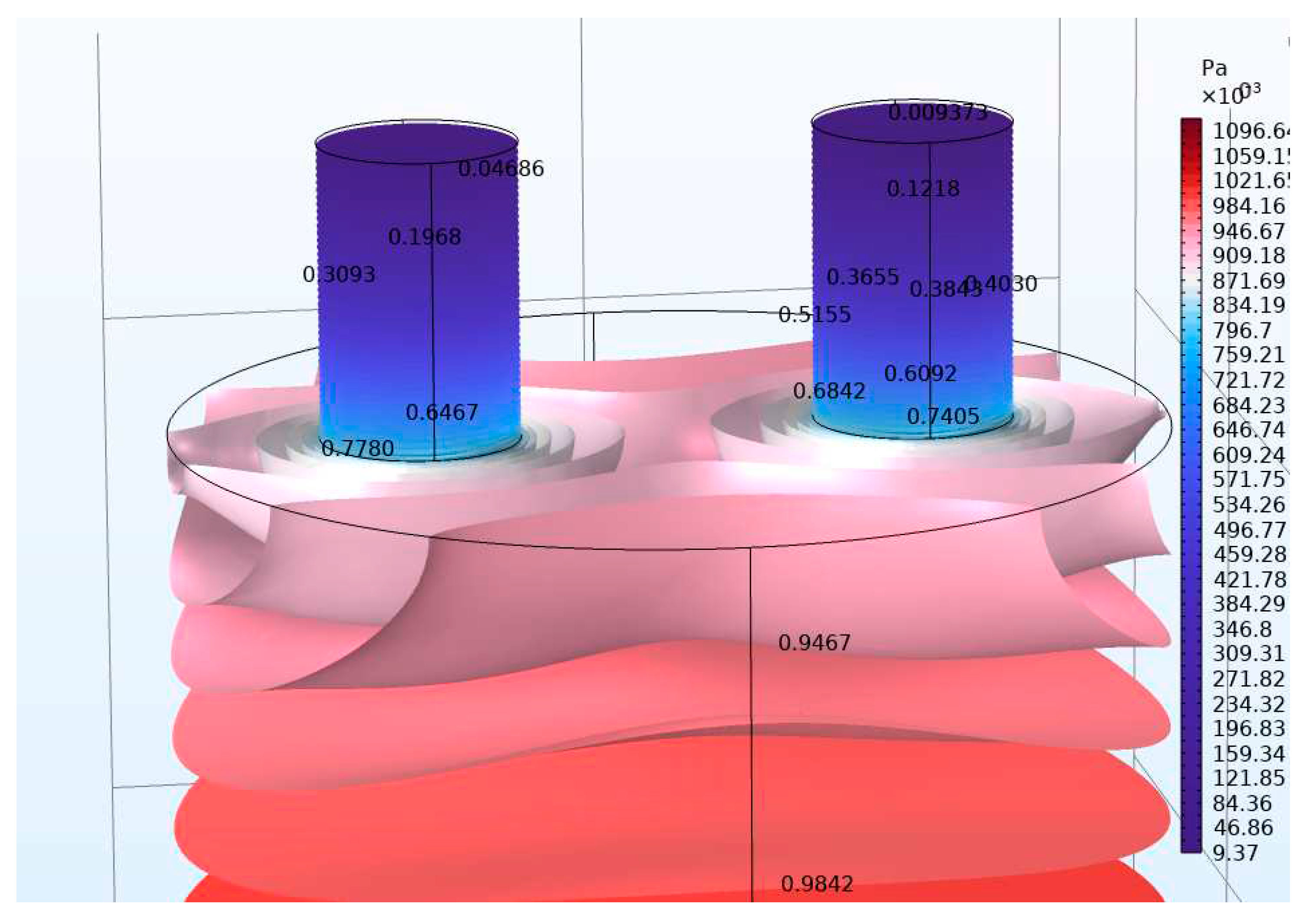
2.3. 3D Model and setup

For the modeling of the multi-neck Helmholtz resonators, the software Inventor v.2024 (Autodesk, San Francisco, U.S.) was used. The shape and dimensions of the models are shown in Figure 1. Four different models were made, Model A and Model B, with 4 and 8 necks respectively and Models C and D with 2 necks. The Models C and D were chosen, in order to have a comparison between resonators containing the same number of necks, placed in different positions on the body of the resonator.
For the FEM, the software Comsol v.6 (Comsol inc., Burlington, USA) was used. In Figure 2, the 3D meshes for the models are presented. Five elements per wavelength were applied, typical for similar FEM modeling [54]. For all FEM models and formulae, the speed of sound was set to 343 m/s and the density of air to ρ=1.2 kg/m3.

3. Results

Figure 3 and Figure 4 present the results of FEM modeling for Models A and B respectively. For Model A (Figure 3), acoustic pressure levels and sound pressure levels are presented in the Helmholtz resonator (body and neck) for five different cases (a-e). In each case there is an opening or openings in the top of the necks of the Helmholtz resonators.
The necks with the openings in each case can be seen with the colored differences in acoustic pressure and sound pressure levels compared to the other necks. In cases b and c, two variations of the case with two openings in necks are presented (necks next to each other, necks opposite). The reason these variations were studied, is to investigate whether there are differences in the measured resonance frequencies.
Similarly for Model Β (Figure 4), acoustic pressure levels and sound pressure levels are presented in the Helmholtz resonator for eight different cases (a-h). In each case there is an opening or openings in the top of the necks of the Helmholtz resonators. The necks with the openings in each case can be seen with the colored differences in acoustic pressure and sound pressure levels compared to the other necks.
In Table 1 and Table 2, comparison of the results of the resonance frequency for Models A and B respectively, is presented, calculated with the analytical approach and with FEM. Error of calculation is also presented.

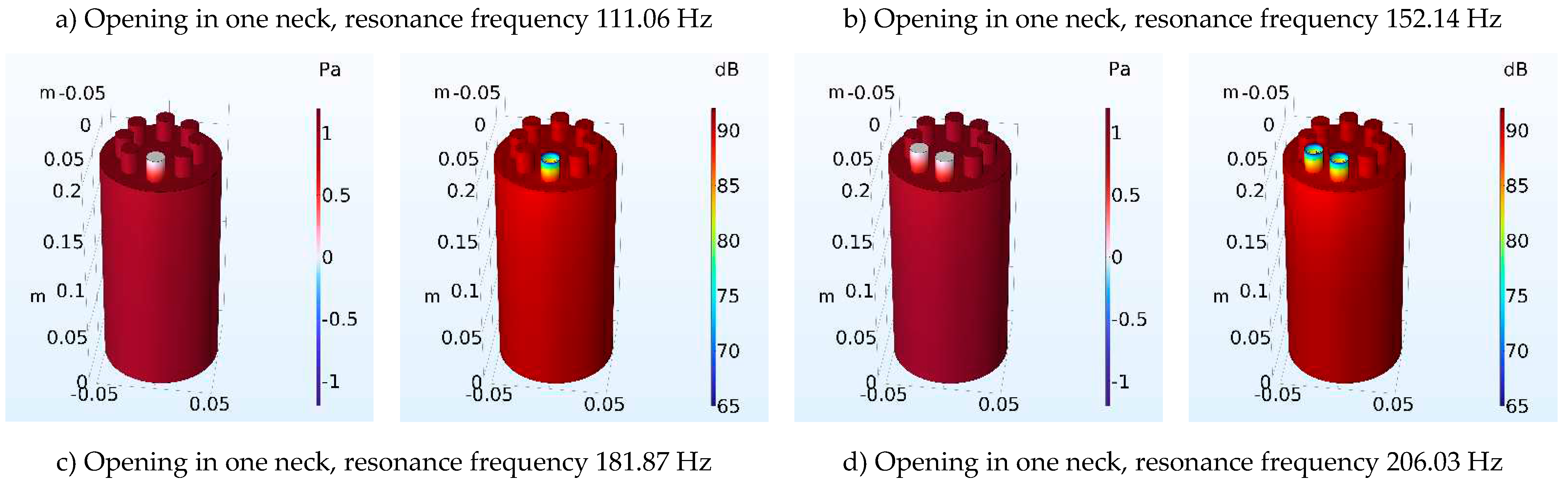
3.1 Multi-neck Helmholtz resonators with same number of necks

As stated in methods section, in order to have a comparison between resonators containing the same number of necks, but necks placed in different places on the body of the resonator, the Models C and D were investigated. The body and necks geometry of both resonators are identical. The differences in the resonators are focused on the location of the necks. In Model C the necks are on opposite surfaces, while in Model D they are on the same surface. In Model C the necks are in the center of the resonator, while in Model D the necks are equidistant from the center of the surface.
Figure 5 shows a comparison of the acoustic pressure distribution inside the resonators, in the case that both necks have openings. For the presentation of the acoustic pressure, isosurfaces were used so that the differences are more apparent. In addition, the same color legend was used for both cases.
In Figure 6 and Figure 7, the acoustic pressures in the neck area of models C and D respectively are presented, so that the differences are more clearly visible. The acoustic pressure values are shown at points on the resonator and especially in the neck area. Again, for the presentation of the acoustic pressure, isosurfaces were used. Color legends were used to make the differences more apparent. It is evident that the acoustic pressure values in the neck area have differences in Figure 6 and Figure 7. For example, the differences are clearly seen at the base of the neck, where model C has a higher value (0.9127 Pa) than model D (0.7780 Pa). In Table 3 and Table 4, comparison of the results of the resonance frequency for Models C and D respectively, is presented, calculated with the analytical approach and with FEM. Error of calculation is also presented. All of the above will be discussed in the next section.

4. Discussion

The FEM modeling results for Models A and B were presented in Figure 3 and Figure 4 and also the results for the resonance frequency for analytical method and FEM were presented in Table 1 and Table 2. The proposed Helmholtz resonators have resonance frequencies that are spaced apart by frequency differences that depend on the dimensions of the resonator necks. The different variations show that it is possible to make tunable Helmholtz resonators at any desired frequency. For example, to achieve small variations, suitably sized resonators (e.g. smaller neck diameter) can be added. As mentioned in the introduction, such resonators can be used as absorbers in various applications [13,14,16]. Additionally, the ability of the resonators to be tunable, makes them suitable for applications such as suppressing specific eigenmodes in a room [15].
The FEM modeling results (acoustic pressure, sound pressure level) for the Models A and B are presented in Figure 3 and Figure 4. The figures show the acoustic pressure and sound pressure level distribution inside the resonator using color grading. It is evident that in the body of the resonator the pressure has maximum values while in the neck the pressure has the smallest values. An important observation is that in the necks of the resonators which are closed, the pressure has a large value similar to the body of the resonator. During the analytical approach calculations, the volume of the necks with closed openings, was considered as part of the body of the resonator.
Regarding the comparison of the results between the analytical approach and the FEM, there are several observations that can be made. In the initial case where a single neck is utilized in the Helmholtz resonator, the error of calculation is very small. This result is in agreement with previous studies (e.g. [55]) that have used FEM to estimate the resonance frequency of a resonator. In the case of multi-necks in the Helmholtz resonator, in general, the results show a good agreement between the analytical method and the FEM. It is evident that the resonance frequency increases with the addition of necks in the Helmholtz resonator, as has also been seen in related investigations [39,40]. Comparison of the results between FEM and analytical method shows small differences, especially for a small number of necks. This outcome is significant as the analytical method has been validated with the help of experimental data [39]. This in turn shows that the result of FEM modeling is most likely to correspond to experimental results. However, regarding a larger number of necks, there seems to be an increasing difference of the results between the analytical and the FEM formulation. This is discussed further in the next section.

4.1 Analytical and FEM approach differencies

For Models A and B, regarding a larger number of necks, there seems to be an increasing difference of the results between the analytical and the FEM formulation. In order to explore further these results, Models C and D were investigated. As stated in methods section, for Models C and D, the body and necks geometry of both resonators are identical. The differences in the resonators are focused on the location of the necks. In Model C the necks are on opposite surfaces, while in Model D they are on the same surface. In Model C the necks are in the center of the resonator, while in Model D the necks are equidistant from the center of the surface. As can be seen in Table 3, the differences between analytical method and FEM for Model C are small. However, the differences between analytical method and FEM for model D, in the case of openings in both necks, seem to increase, similarly with Models A and B.
A possible explanation may be due to the initial assumptions in determining the analytical equation. It is stated that [39] ‘p (pressure) can be assumed to be uniform inside the cavity and calculated with the bulk modulus of the fluid’. However, it can be seen, especially in Figure 7 (Model D) that the pressure is not uniform inside of the cavity. Since the two necks (in Model D) are in close proximity, there seems to be an interaction in the acoustic pressure around the end of the necks resulting in a non-uniform acoustic pressure for Model D in that area compared to Model C. For model C, in contrast, there is no interaction due to the necks being on opposite surfaces. The above shows us that the exact determination of the resonance frequency of a Helmholtz resonator depends on many parameters. The determination of all these parameters is beyond the scope of this text. Research is being conducted to determine all the parameters to better calculate the resonance frequency. Further work needs to be carried out to establish the effectiveness of the method in a wide range of cases.

5. Conclusions

For this study, a tunable Helmholtz resonator utilizing multiple necks was proposed and investigated. Initially, the various resonance frequencies of a multi-neck Helmholtz resonator are first calculated with the use of a theoretical approach. In addition, the Helmholtz resonator is modeled with the use of finite element method (FEM) and the results of the theoretical and the FEM modeling resonance frequencies are compared. The results of the two approaches show a very good agreement, with differences less than 1%.
This study demonstrated that with the utilization of appropriate number of necks, the Helmholtz resonator can be tunable to various desirable frequencies depended on the resonators geometry. The proposed approach can be useful for tunable sound absorbers for room acoustics applications according to the needs of a space. Also, this approach can be useful in cases of tunable air resonance of acoustic instruments.

Author Contributions

Conceptualization, N.P. and G.S.; methodology, N.P.; software, N.P.; validation, N.P. and G.S.; formal analysis, N.P. and G.S.; investigation, N.P. and G.S; resources, N.P.; data curation, N.P. and G.S.; writing—original draft preparation, N.P.; writing—review and editing, G.S.; visualization, N.P.; supervision, G.S.; project administration, N.P. and G.S.. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding

Data Availability Statement

The data presented in this study are available on request from the corresponding author.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. ISO: Geneva, S. ISO 3382-1: 2009. Measurement of Room Acoustic Parameters - Part 1: Performance spaces. 2009.
  2. Long, M. Architectural acoustics. 2005, 208.
  3. Cao, L.; Fu, Q.; Si, Y.; Ding, B.; Yu, J. Porous materials for sound absorption. Composites Communications 2018, 10, 25-35. [CrossRef]
  4. Kalauni, K.; Pawar, S. A review on the taxonomy, factors associated with sound absorption and theoretical modeling of porous sound absorbing materials. Journal of Porous Materials 2019, 26, 1795-1819. [CrossRef]
  5. Carbajo, J.; Ramis, J.; Godinho, L.; Amado-Mendes, P. Perforated panel absorbers with micro-perforated partitions. Applied Acoustics 2019, 149, 108-113. [CrossRef]
  6. Rossing, T.D.; Rossing, T.D. Springer handbook of acoustics; Springer: 2014.
  7. Komkin, A.; Mironov, M.; Bykov, A. Sound absorption by a Helmholtz resonator. Acoustical Physics 2017, 63, 385-392. [CrossRef]
  8. Padhye, R.; Nayak, R. Acoustic textiles; Springer: 2016.
  9. Kanev, N. Resonant Vessels in Russian Churches and Their Study in a Concert Hall. In Proceedings of the Acoustics, 2020; pp. 399-415. [CrossRef]
  10. Mijic, M.; Sumarac-Pavlovic, D. Analysis of contribution of acoustic resonators found in Serbian Orthodox churches. Building Acoustics 2004, 11, 197-212. [CrossRef]
  11. Desarnaulds, V.; Loerincik, Y.; Carvalho, A.P. Efficiency of 13th-century acoustic ceramic pots in two Swiss churches. In Proceedings of the Proceedings of the 2001 National Conference on Noise Control Engineering, 2001.
  12. Pöhlmann, E. Vitruvius De Architectura V: Resounding Vessels in the Greek and Roman Theatre and Their Possible Afterlife in Eastern and Western Churches. Greek and Roman Musical Studies 2021, 9, 157-174. [CrossRef]
  13. Gilford, C. Helmholtz resonators in the acoustic treatment of broadcasting studios. British Journal of Applied Physics 1952, 3, 86. [CrossRef]
  14. Namvar Arefi, H.; Ghiasi, S.M.A.; Ghaffari, S.M.; Ramezanghorbani, F.; Sharifpour, S.; Irajizad, P.; Ghoreishi Langroudi, S.D.; Amjadi, A. Conference room reverberation time correction using helmholtz resonators lined with absorbers. Shock and Vibration 2014, 2014. [CrossRef]
  15. Klaus, J.; Bork, I.; Graf, M.; Ostermeyer, G.-P. On the adjustment of Helmholtz resonators. Applied acoustics 2014, 77, 37-41. [CrossRef]
  16. Asakura, T. Numerical investigation of the sound-insulation effect of a suspended ceiling structure with arrayed Helmholtz resonators by the finite-difference time-domain method. Applied Acoustics 2021, 172, 107601. [CrossRef]
  17. Kanev, N. Maximum sound absorption by a Helmholtz resonator in a room at low frequencies. Acoustical Physics 2018, 64, 774-777. [CrossRef]
  18. Herrero-Durá, I.; Cebrecos, A.; Picó, R.; Romero-García, V.; García-Raffi, L.M.; Sánchez-Morcillo, V.J. Sound absorption and diffusion by 2D arrays of Helmholtz resonators. Applied Sciences 2020, 10, 1690. [CrossRef]
  19. Huang, S.; Fang, X.; Wang, X.; Assouar, B.; Cheng, Q.; Li, Y. Acoustic perfect absorbers via Helmholtz resonators with embedded apertures. The Journal of the Acoustical Society of America 2019, 145, 254-262. [CrossRef]
  20. Mahesh, K.; Kumar Ranjith, S.; Mini, R. Inverse design of a Helmholtz resonator based low-frequency acoustic absorber using deep neural network. Journal of Applied Physics 2021, 129. [CrossRef]
  21. Vergara, E.; Almeida, G.; Barbosa, L.; Lenzi, A.; Carvalho de Sousa, A. Broadband and low-frequency sound absorption of modified Helmholtz resonator combined with porous layer addition. Journal of Applied Physics 2022, 132. [CrossRef]
  22. Papadakis, N.M.; Stavroulakis, G.E. Review of Acoustic Sources Alternatives to a Dodecahedron Speaker. Applied Sciences 2019, 9, 3705. [CrossRef]
  23. Papadakis, N.M.; Stavroulakis, G.E. Handclap for Acoustic Measurements: Optimal Application and Limitations. Acoustics 2020, 2, 224-245. [CrossRef]
  24. Papadakis, N.M.; Antoniadou, S.; Stavroulakis, G.E. Effects of Varying Levels of Background Noise on Room Acoustic Parameters, Measured with ESS and MLS Methods. Acoustics 2023, 5, 563-574. [CrossRef]
  25. Nia, H.T.; Jain, A.D.; Liu, Y.; Alam, M.-R.; Barnas, R.; Makris, N.C. The evolution of air resonance power efficiency in the violin and its ancestors. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences 2015, 471, 20140905. [CrossRef]
  26. Papadakis, N.M.; Stavroulakis, G.E. FEM Investigation of the Air Resonance in a Cretan Lyra VIbration 2023.
  27. Garcia-Alcaide, V.; Palleja-Cabre, S.; Castilla, R.; Gamez-Montero, P.J.; Romeu, J.; Pamies, T.; Amate, J.; Milán, N. Numerical study of the aerodynamics of sound sources in a bass-reflex port. Engineering Applications of Computational Fluid Mechanics 2017, 11, 210-224. [CrossRef]
  28. Yuan, M.; Cao, Z.; Luo, J.; Chou, X. Recent developments of acoustic energy harvesting: A review. Micromachines 2019, 10, 48. [CrossRef]
  29. Kone, C.T.; Ghinet, S.; Panneton, R.; Dupont, T.; Grewal, A. Multi-tonal low frequency noise control for aircraft cabin using Helmholtz resonator with complex cavity designs for aircraft cabin noise improvement. INTERNOISE-2021 2021.
  30. Wang, J.; Rubini, P.; Qin, Q.; Houston, B. A model to predict acoustic resonant frequencies of distributed Helmholtz resonators on gas turbine engines. Applied Sciences 2019, 9, 1419. [CrossRef]
  31. Fang, N.; Xi, D.; Xu, J.; Ambati, M.; Srituravanich, W.; Sun, C.; Zhang, X. Ultrasonic metamaterials with negative modulus. Nature materials 2006, 5, 452-456. [CrossRef]
  32. Cai, C.; Mak, C.-M.; Shi, X. An extended neck versus a spiral neck of the Helmholtz resonator. Applied Acoustics 2017, 115, 74-80. [CrossRef]
  33. Shi, X.; Mak, C.M. Helmholtz resonator with a spiral neck. Applied Acoustics 2015, 99, 68-71. [CrossRef]
  34. Tang, S.K. On Helmholtz resonators with tapered necks. Journal of sound and vibration 2005, 279, 1085-1096. [CrossRef]
  35. Ramos, D.; Godinho, L.; Amado-Mendes, P.; Mareze, P. Experimental and numerical modelling of Helmholtz Resonator with angled neck aperture. In Proceedings of the INTER-NOISE and NOISE-CON Congress and Conference Proceedings, 2020; pp. 37-47.
  36. Duan, M.; Yu, C.; He, W.; Xin, F.; Lu, T.J. Perfect sound absorption of Helmholtz resonators with embedded channels in petal shape. Journal of Applied Physics 2021, 130. [CrossRef]
  37. Chanaud, R. Effects of geometry on the resonance frequency of Helmholtz resonators. Journal of Sound and Vibration 1994, 178, 337-348. [CrossRef]
  38. Chanaud, R. Effects of geometry on the resonance frequency of Helmholtz resonators, part II. Journal of sound and vibration 1997, 204, 829-834. [CrossRef]
  39. Langfeldt, F.; Hoppen, H.; Gleine, W. Resonance frequencies and sound absorption of Helmholtz resonators with multiple necks. Applied Acoustics 2019, 145, 314-319. [CrossRef]
  40. Selamet, A.; Kim, H.; Huff, N.T. Leakage effect in Helmholtz resonators. The Journal of the Acoustical Society of America 2009, 126, 1142-1150. [CrossRef]
  41. Lee, I.; Jeon, K.; Park, J. The effect of leakage on the acoustic performance of reactive silencers. Applied acoustics 2013, 74, 479-484. [CrossRef]
  42. Papadakis, N.M.; Stavroulakis, G.E. FEM Investigation of a Multi-Neck Helmholtz Resonator. Applied Sciences 2023.
  43. Li, M.; Wu, J.H.; Yuan, X.Y. Metasurface zero-impedance matching mechanism for aerodynamic noise reduction. Journal of Sound and Vibration 2022, 536, 117147. [CrossRef]
  44. Zolfagharian, A.; Noshadi, A.; Khosravani, M.R.; Zain, M.Z.M. Unwanted noise and vibration control using finite element analysis and artificial intelligence. Applied Mathematical Modelling 2014, 38, 2435-2453. [CrossRef]
  45. Sakuma, T.; Sakamoto, S.; Otsuru, T. Computational simulation in architectural and environmental acoustics; Springer: 2014.
  46. Papadakis, N.M.; Stavroulakis, G.E. Finite Element Method for the Estimation of Insertion Loss of Noise Barriers: Comparison with Various Formulae (2D). Urban Science 2020, 4, 77. [CrossRef]
  47. Papadakis, N.M.; Stavroulakis, G.E. Time domain finite element method for the calculation of impulse response of enclosed spaces. Room acoustics application. Mechanics of Hearing: Protein to Perception: 12th International Workshop on the Mechanics of Hearing 2015, 1703, 100002. [CrossRef]
  48. Blackstock, D.T. Fundamentals of physical acoustics. 2001.
  49. Ingard, U. Notes on acoustics; Laxmi Publications, Ltd.: 2010.
  50. Kuttruff, H. Room acoustics. 2016. [CrossRef]
  51. Crocker, M.J.; Arenas, J.P. Engineering acoustics: noise and vibration control; John Wiley & Sons: 2021.
  52. Beranek, L.L.; Mellow, T. Acoustics: sound fields and transducers; Academic Press: 2012.
  53. Marburg, S.; Nolte, B. Computational acoustics of noise propagation in fluids: finite and boundary element methods; Springer: 2008; Volume 578.
  54. Ihlenburg, F. Finite element analysis of acoustic scattering; Springer Science & Business Media: 2006; Volume 132.
  55. Jena, D.; Dandsena, J.; Jayakumari, V. Demonstration of effective acoustic properties of different configurations of Helmholtz resonators. Applied Acoustics 2019, 155, 371-382. [CrossRef]
Preprints 85094 g001
Figure 1. 3D models (side and top view) of the multi-neck Helmholtz resonators (Models A-D).
Figure 1. 3D models (side and top view) of the multi-neck Helmholtz resonators (Models A-D).
Preprints 85094 g001
Preprints 85094 g002
Figure 2. 3D models with meshes of the multi-neck Helmholtz resonators (Models A-D).
Figure 2. 3D models with meshes of the multi-neck Helmholtz resonators (Models A-D).
Preprints 85094 g002
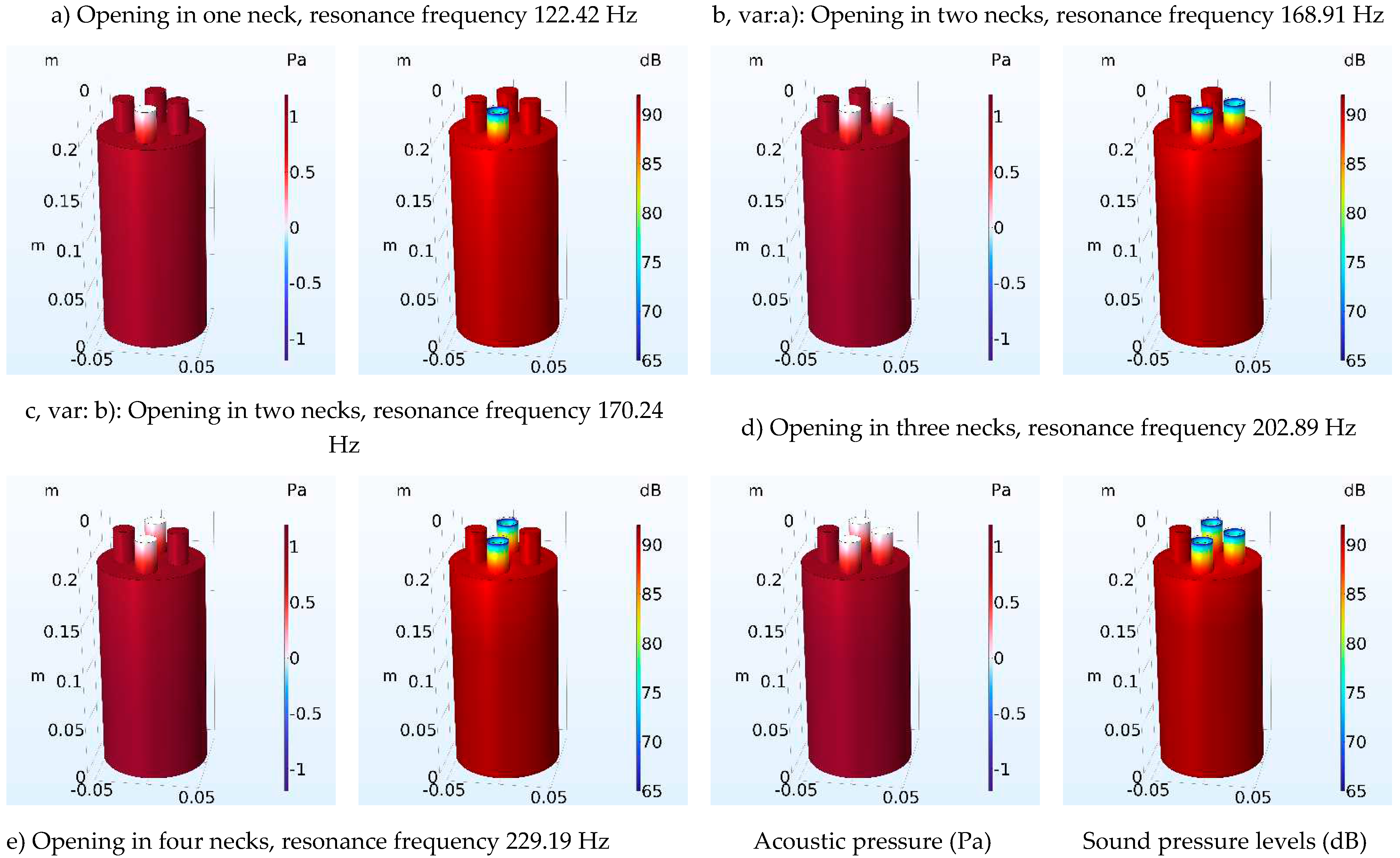
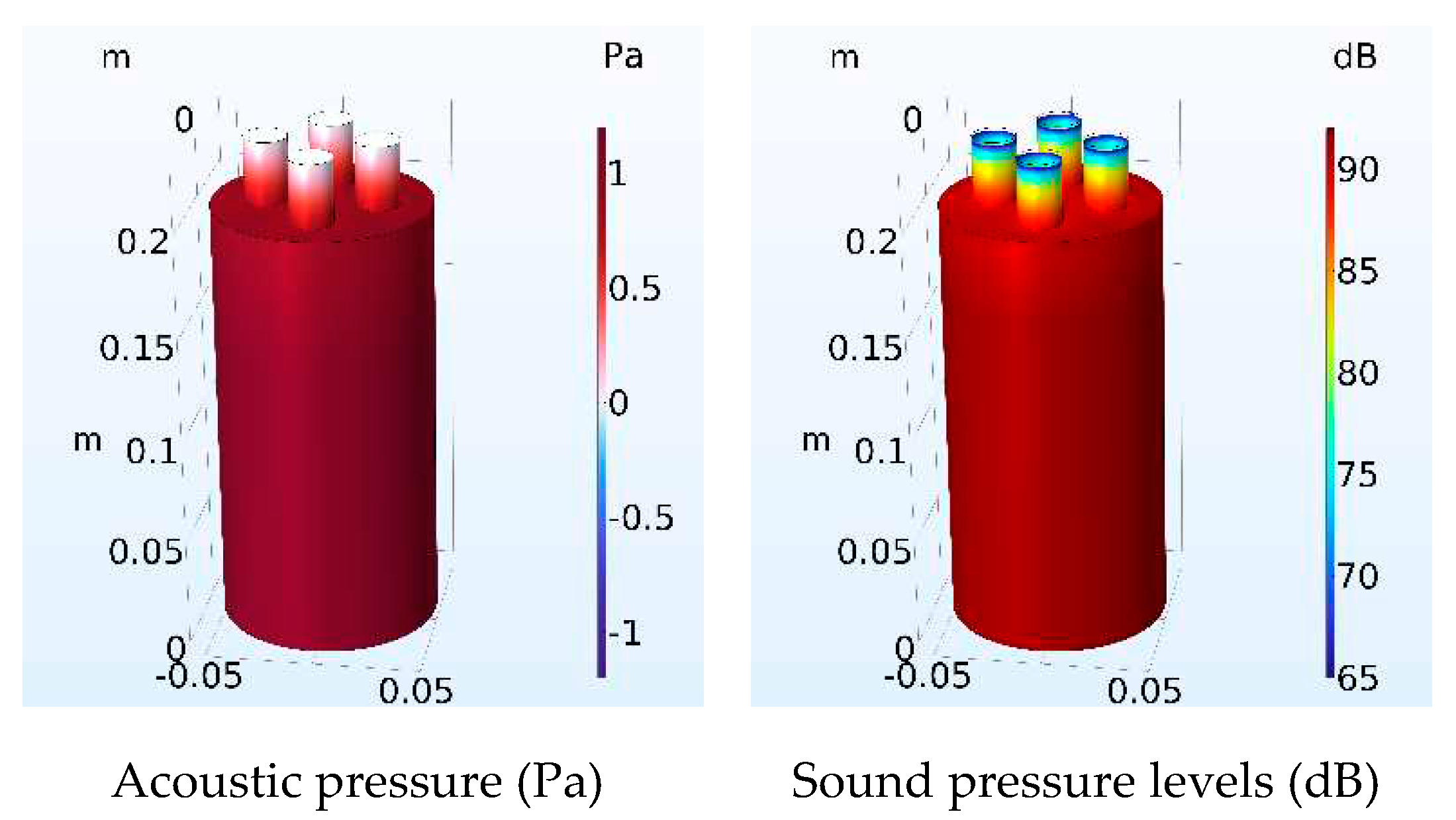
Preprints 85094 g003aPreprints 85094 g003b
Figure 3. Helmholtz resonator (Model A): Acoustic pressure levels and sound pressure levels are presented for five different cases (a-e). In each case there is an opening or openings in the top of the necks of the Helmholtz resonator. The necks with the openings can be distinguished by color differences in acoustic pressure and sound pressure levels in relation to the other necks. Cases b and c have same number of neck openings (2), but with different configurations.
Figure 3. Helmholtz resonator (Model A): Acoustic pressure levels and sound pressure levels are presented for five different cases (a-e). In each case there is an opening or openings in the top of the necks of the Helmholtz resonator. The necks with the openings can be distinguished by color differences in acoustic pressure and sound pressure levels in relation to the other necks. Cases b and c have same number of neck openings (2), but with different configurations.
Preprints 85094 g003aPreprints 85094 g003b
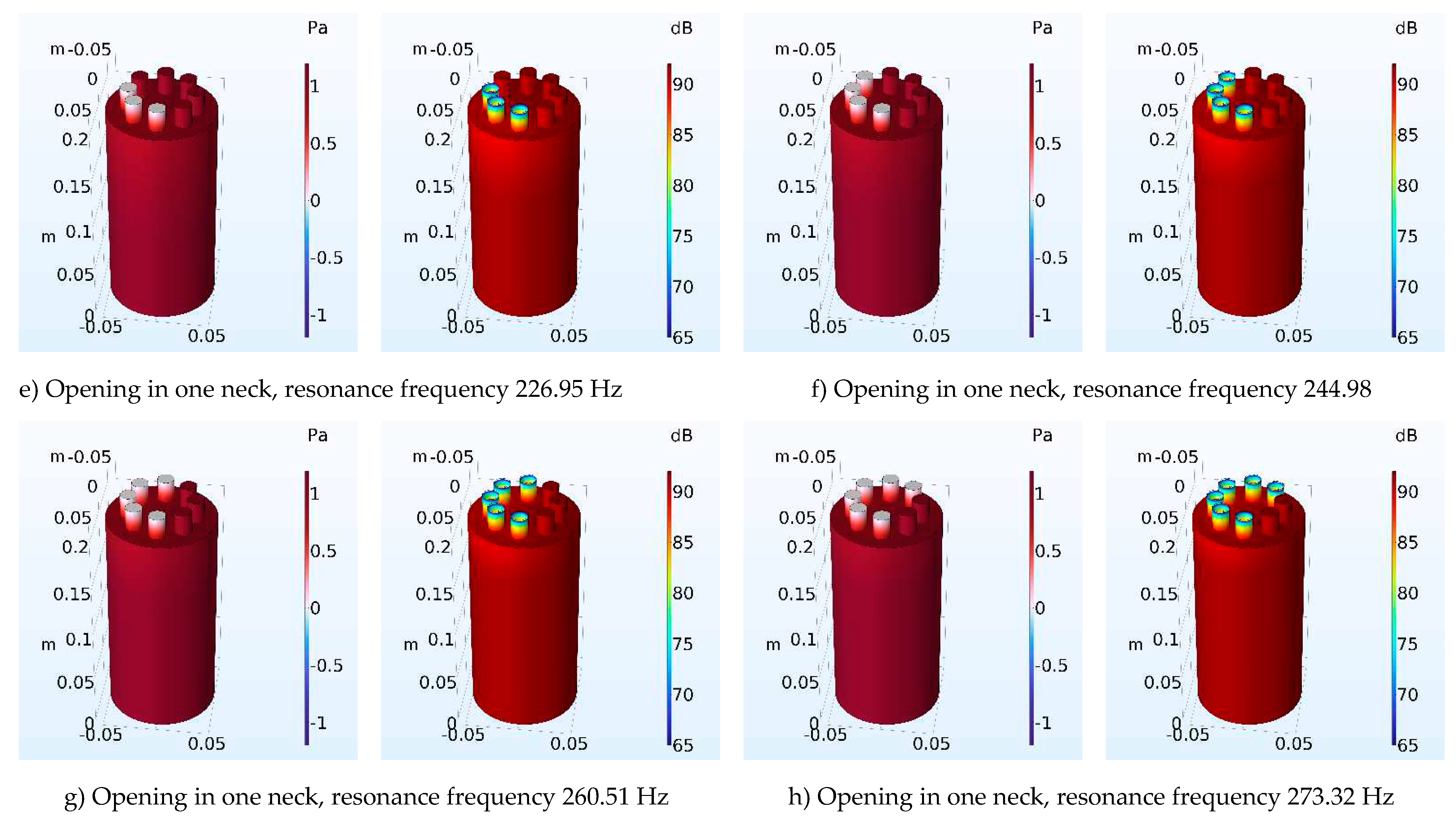
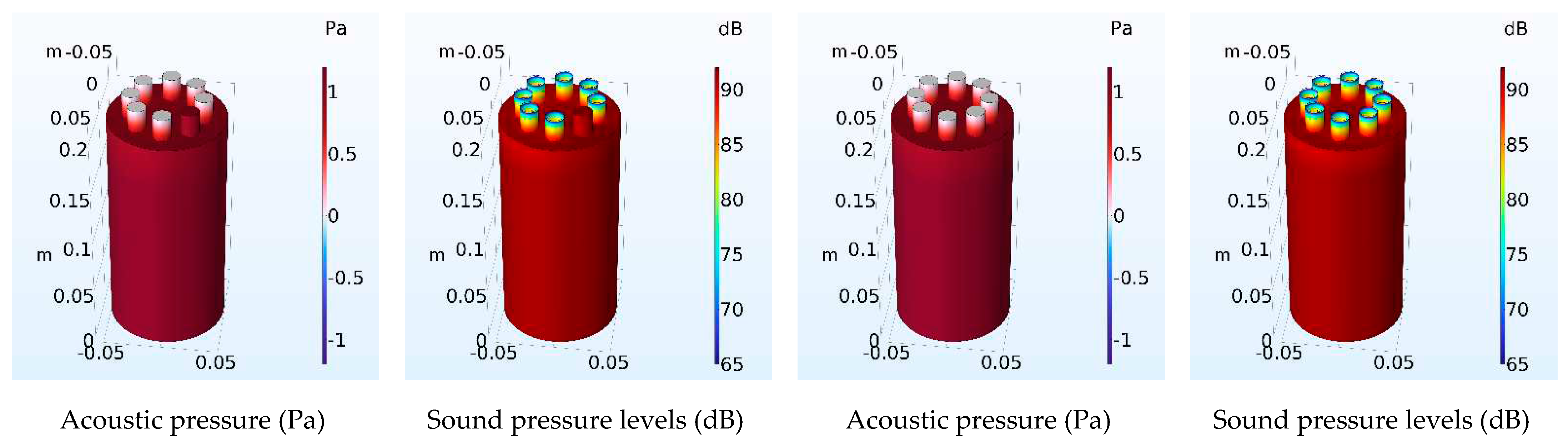
Preprints 85094 g004aPreprints 85094 g004bPreprints 85094 g004c
Figure 4. Helmholtz resonator (Model A): Acoustic pressure levels and sound pressure levels are presented in the Helmholtz resonator for four different cases (a-d). In each case there is an opening or openings in the top of the necks of the Helmholtz resonators. The necks with the openings in each case can be seen with the colored differences in acoustic pressure and sound pressure levels compared to the other necks.
Figure 4. Helmholtz resonator (Model A): Acoustic pressure levels and sound pressure levels are presented in the Helmholtz resonator for four different cases (a-d). In each case there is an opening or openings in the top of the necks of the Helmholtz resonators. The necks with the openings in each case can be seen with the colored differences in acoustic pressure and sound pressure levels compared to the other necks.
Preprints 85094 g004aPreprints 85094 g004bPreprints 85094 g004c
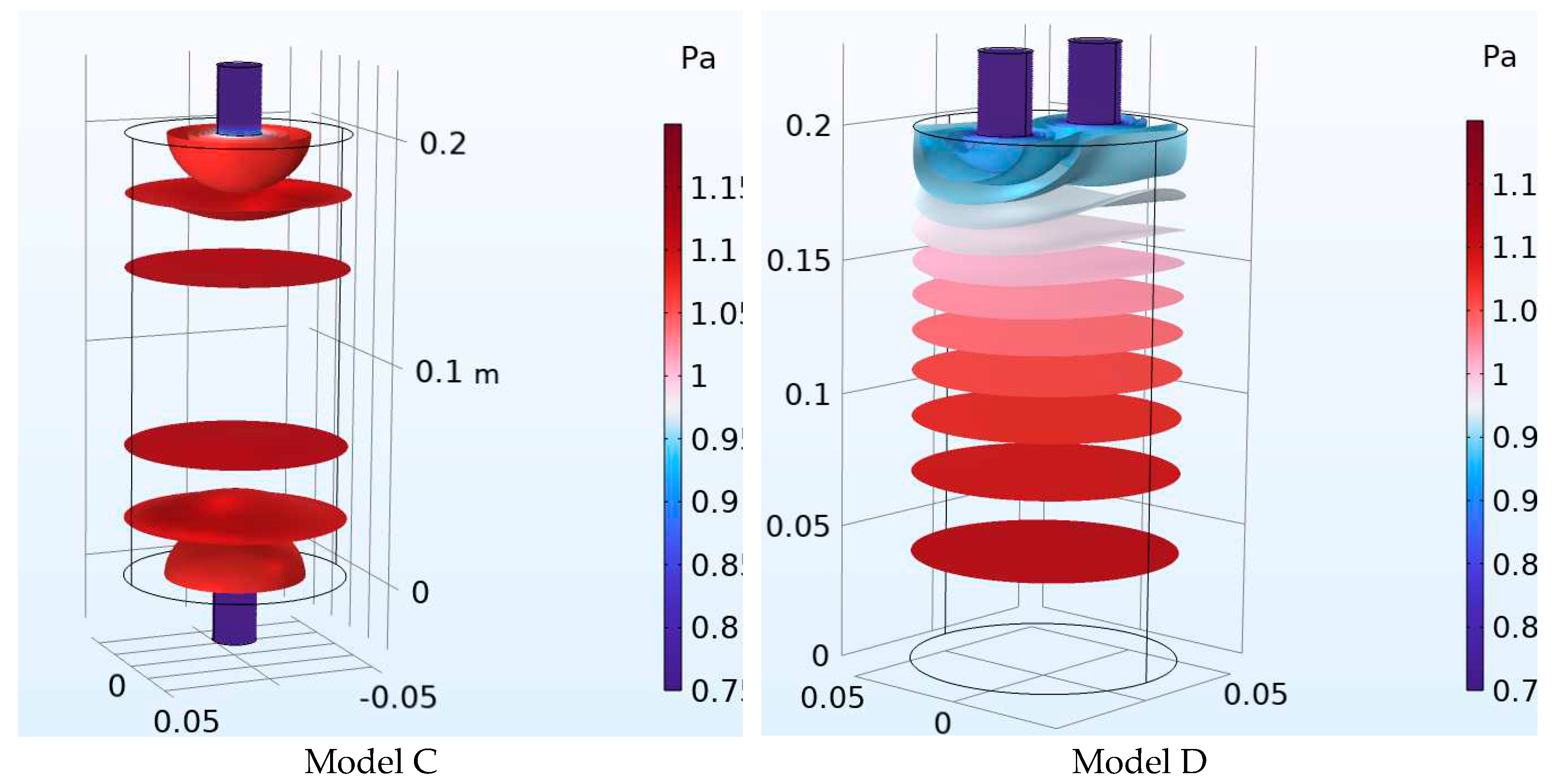
Preprints 85094 g005
Figure 5. Helmholtz resonators (Model C and D): Acoustic pressure levels are presented in the Helmholtz resonators in the form of isosurfaces. In each case there are openings in the top of the necks of the Helmholtz resonators. The same color legend was used for both Models.
Figure 5. Helmholtz resonators (Model C and D): Acoustic pressure levels are presented in the Helmholtz resonators in the form of isosurfaces. In each case there are openings in the top of the necks of the Helmholtz resonators. The same color legend was used for both Models.
Preprints 85094 g005
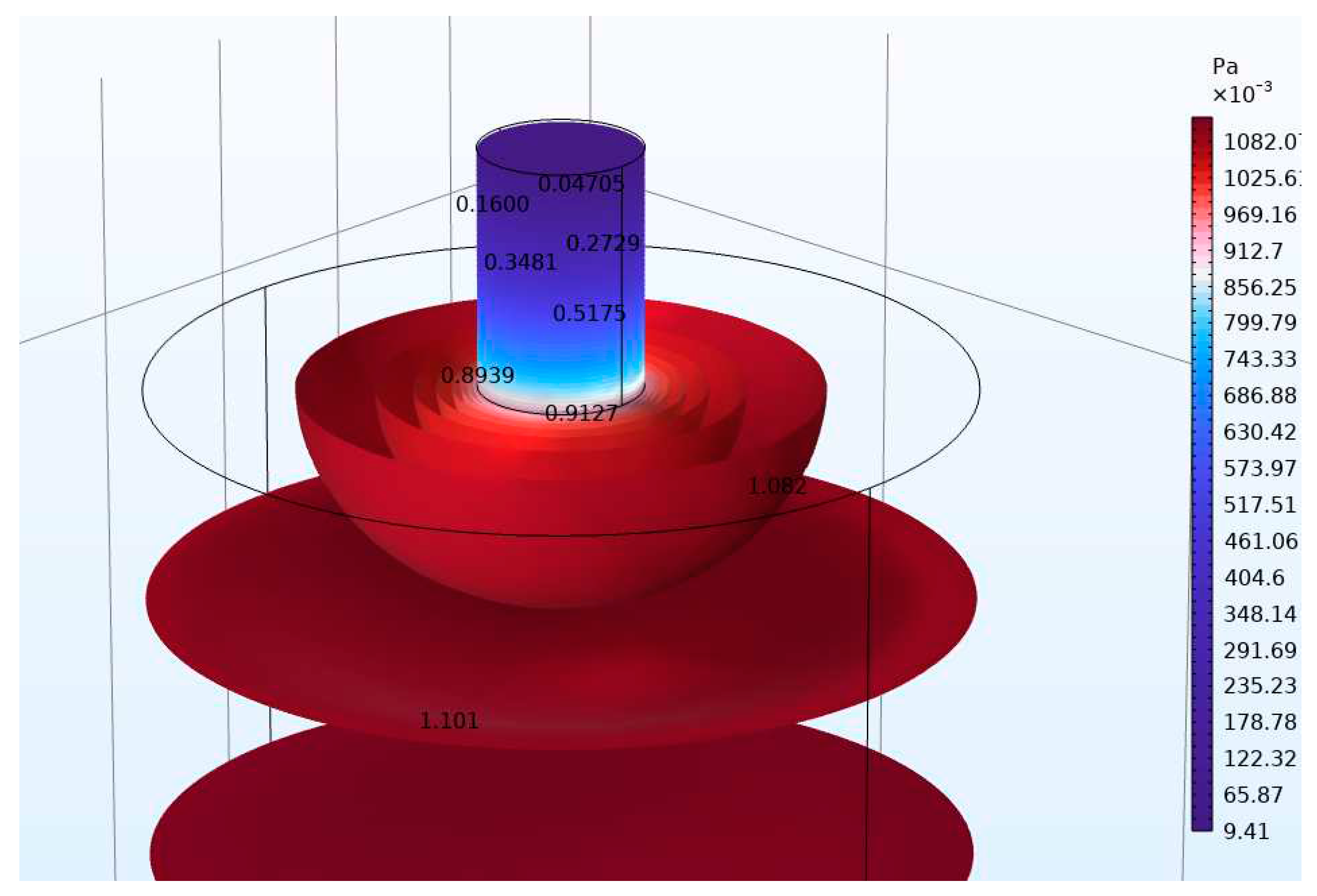
Preprints 85094 g006
Figure 6. Helmholtz resonator (Model C): Acoustic pressure is presented in the Helmholtz resonator in the form of isosurfaces. There are openings in the top of both necks of the Helmholtz resonator (also the one in the bottom that is not visible). The acoustic pressure values are shown at points on the resonator and especially in the neck area. Color legends were used to make the differences more apparent.
Figure 6. Helmholtz resonator (Model C): Acoustic pressure is presented in the Helmholtz resonator in the form of isosurfaces. There are openings in the top of both necks of the Helmholtz resonator (also the one in the bottom that is not visible). The acoustic pressure values are shown at points on the resonator and especially in the neck area. Color legends were used to make the differences more apparent.
Preprints 85094 g006
Preprints 85094 g007
Figure 7. Helmholtz resonator (Model D): Acoustic pressure is presented in the Helmholtz resonator in the form of isosurfaces. There are openings in the top of both necks of the Helmholtz resonator. The acoustic pressure values are shown at points on the resonator and especially in the neck area. Color legends were used to make the differences more apparent.
Figure 7. Helmholtz resonator (Model D): Acoustic pressure is presented in the Helmholtz resonator in the form of isosurfaces. There are openings in the top of both necks of the Helmholtz resonator. The acoustic pressure values are shown at points on the resonator and especially in the neck area. Color legends were used to make the differences more apparent.
Preprints 85094 g007
Table 1. Comparison of the results of the resonance frequency for Model A, calculated with the analytical approach and with FEM. Error of calculation is also presented. The positions of the necks with openings (2) in variations a and b, can be seen in Figure 3.
Table 1. Comparison of the results of the resonance frequency for Model A, calculated with the analytical approach and with FEM. Error of calculation is also presented. The positions of the necks with openings (2) in variations a and b, can be seen in Figure 3.
Number of Necks Resonant frequency Analytical (Hz) Resonant frequency FEM (Hz) Error of calculation (%) Analytical-FEM
1 124.37 122.42 1.56
2 (var. a) 176.15 168.91 4.11
2 (var. b) 176.15 170.24 3.35
3 216.06 202.89 6.10
4 249.85 229.19 7.91
Table 2. Comparison of the results of the resonance frequency for Model B, calculated with the analytical approach and with FEM. Error of calculation is also presented.
Table 2. Comparison of the results of the resonance frequency for Model B, calculated with the analytical approach and with FEM. Error of calculation is also presented.
Number of Necks Resonant frequency Analytical (Hz) Resonant frequency FEM (Hz) Error of calculation (%) Analytical-FEM
1 112.91 111.06 1.16
2 159.77 152.14 4.78
3 195.79 181.87 7.11
4 226.20 206.03 8.92
5 253.04 226.95 10.31
6 277.35 244.98 11.67
7 299.73 260.51 13.09
8 320.61 273.32 14.78
Table 3. Comparison of the results of the resonance frequency for Model C, calculated with the analytical approach and with FEM. Error of calculation is also presented.
Table 3. Comparison of the results of the resonance frequency for Model C, calculated with the analytical approach and with FEM. Error of calculation is also presented.
Number of Necks Resonant frequency Analytical (Hz) Resonant frequency FEM (Hz) Error of calculation (%) Analytical-FEM
1 125.11 123.86 0.99
1 125.11 123.86 0.99
2 176.73 178.78 1.19
Table 4. Comparison of the results of the resonance frequency for Model D, calculated with the analytical approach and with FEM. Error of calculation is also presented.
Table 4. Comparison of the results of the resonance frequency for Model D, calculated with the analytical approach and with FEM. Error of calculation is also presented.
Number of Necks Resonant frequency Analytical (Hz) Resonant frequency FEM (Hz) Error of calculation (%) Analytical-FEM
1 125.11 123.11 0.99
1 125.11 123.11 0.99
2 176.73 171.12 3.17
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated