Prerpints.org logo
Preprint
Article

Three-Stage Sampling Algorithm for Highly Imbalanced Multi-Classification Time Series Data Sets

Altmetrics

Downloads

96

Views

26

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

12 September 2023

Posted:

14 September 2023

You are already at the latest version

Alerts
Abstract
Purpose To alleviate the data imbalance problem caused by subjective and objective reasons, scholars have developed different data preprocessing algorithms, among which undersampling algorithms are widely used because of their fast and efficient performance. However, when the number of samples of some categories in a multi-classification dataset is too small to be processed by sampling, or the number of minority class samples is only 1 to 2, the traditional undersampling algorithms will be weakened. Methods This study selects 9 multi-classification time series datasets with extremely few samples as the objects, fully considers the characteristics of time series data, and uses a three-stage algorithm to alleviate the data imbalance problem. Stage one: Random oversampling with disturbance items increases the number of sample points; Stage two: On this basis, SMOTE (Synthetic Minority Oversampling Technique) oversampling; Stage three: Using dynamic time warping distance to calculate the distance between sample points, identify the sample points of Tomek Links at the boundary, and clean up the boundary noise.Results This study proposes a new sampling algorithm. In the 9 multi-classification time series datasets with extremely few samples, the new sampling algorithm is compared with four classic undersampling algorithms, ENN (Edited Nearest Neighbours), NCR (Neighborhood Cleaning Rule), OSS (One Side Selection) and RENN (Repeated Edited Nearest Neighbours), based on macro accuracy, recall rate and F1-score evaluation indicators. The results show that: In the 9 datasets selected, the dataset with the most categories and the least number of minority class samples, FiftyWords, the accuracy of the new sampling algorithm is 0.7156, far beyond ENN, RENN, OSS and NCR; its recall rate is also better than the four undersampling algorithms used for comparison, at 0.7261; its F1-score is increased by 200.71%, 188.74%, 155.29% and 85.61%, respectively, relative to ENN, RENN, OSS, and NCR; In the other 8 datasets, this new sampling algorithm also shows good indicator scores.Conclusion The new algorithm proposed in this study can effectively alleviate the data imbalance problem of multi-classification time series datasets with many categories and few minority class samples, and at the same time clean up the boundary noise data between classes.
Keywords: 
Subject: Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

1. Introduction

In the processing of data imbalance methods, the sampling algorithm of data preprocessing plays an important role[1]. By obtaining balanced classes through sampling methods, the learning time can be reduced and the algorithm can be executed faster[2]. The core idea of oversampling is to artificially synthesize to increase the scale of the minority class, so as to obtain a balanced two classes. Oversampling algorithms can be traced back to random oversampling, which randomly replicates samples. Although the sample scale of the class has increased, random oversampling has the main problem of overfitting due to repeated sampling[3]. To solve this type of problem, SMOTE (Synthetic Minority Oversampling Technique) came into being, and SMOTE has since become one of the most representative algorithms in oversampling[4]. Based on SMOTE, many new algorithms have been extended, such as Borderline-SMOTE, DBSMOTE (Density-Based Synthetic Minority Over-sampling Technique), etc[5,6].
On the contrary, undersampling algorithms balance classes by extracting samples, and the remaining samples are ignored, and the training speed is faster[7]. Undersampling can be traced back to Wilson’s nearest neighbor rule, which editing nearest neighbor rule becomes the basis for many subsequent undersampling algorithms. Later undersampling algorithms include Chawla’s NCR ((Neighborhood Cleaning Rule), which focuses on retaining instances of the majority class, and Kubat’s OSS (One Side Selection) algorithm, which uses two undersampling algorithms to balance classes while cleaning boundary noise[8].
To date, more sampling algorithms are seeking targeted solutions to some other problems, such as using multiple sampling algorithms to deal with the problem of dealing with noise data and class data at the same time[9]. Most of the sampling algorithms for balancing data are designed based on the imbalanced dataset of binary classification, when processing the imbalanced dataset of multi-classification, will face the situation of extremely missing samples of some categories. If traditional undersampling algorithms are used for extremely few samples, the imbalanced dataset will be undersampled to only 1 to 2, so that the performance of the processed dataset in the classifier will not increase but decrease. Therefore, the best method to choose will depend on the specific characteristics of the dataset [10,11]. This study proposes a new algorithm for extreme imbalanced multi-class time series datasets, which improves the data imbalance problem through three stages and cleans boundary noise in the process. (1) First, use a random oversampling with disturbance items to increase the number of sample points in the minority class by repeatedly replicating minority class samples; (2) Next, use the traditional SMOTE algorithm to generate more minority class samples; (3) Finally, to clean up the fuzzy boundary data that may be caused by these newly generated minority class samples, use the dynamic time warping DTW (Dynamic Time Warping) method to calculate the distance between the data, and use Tomek Links to clean up the boundary noise.

2. Application

For extremely imbalanced time sequence multi-class classification datasets, this three-stage sampling algorithm is combined with the border noise cleaning by DTW and Tomek Links after random oversampling and SMOTE. The three-stage sampling algorithm proposed in this study has targeted advantages in each stage: the use of random oversampling with perturbation can solve the problem of the extremely sparse number of sample points in the minority class, which makes it difficult to generate sample points; SMOTE can make the balance between subsets; the bilateral cleaning of TLDTW (Tomek Links combined with Dynamic Time Warping) maximizes the removal of noise caused by oversampling; the details of the three stages are described below. Warping) bilateral cleaning maximizes the noise removal caused by oversampling, and the specifics of the three stages are described below.

2.1. Step one: increase the number of minority class sample points

By randomly oversampling an insufficient number of minority class samples to the K value, the number of minority class samples that are insufficient for further sampling can be increased. Random oversampling(ROS) is a method of randomly replicating minority class samples for sample generation, and this repetition of minority class samples may make the classifier prone to overfitting in such a dataset. Set the training set as S = x i , y i , i = 1 , 2 , … , N , y i ϵ + , − , defining the number of samples of instances belonging to the majority class to be N − , and the number of samples of instances belonging to the minority class to be N + , where N = N + + N − . Also define the sampling ratio as f and the imbalance ratio as I R = N − N + .
When the oversampling algorithm is implemented, the number of samples of instances belonging to the minority category is generated as N + × f ; when the undersampling algorithm is implemented, the number of samples of instances belonging to the majority category is deleted as N − × f f + 1 , f ∈ ( 0 , I R − 1 ] , and the number of samples in the training set of the over- or undersampling when f = I R − 1 is is N + = N − .
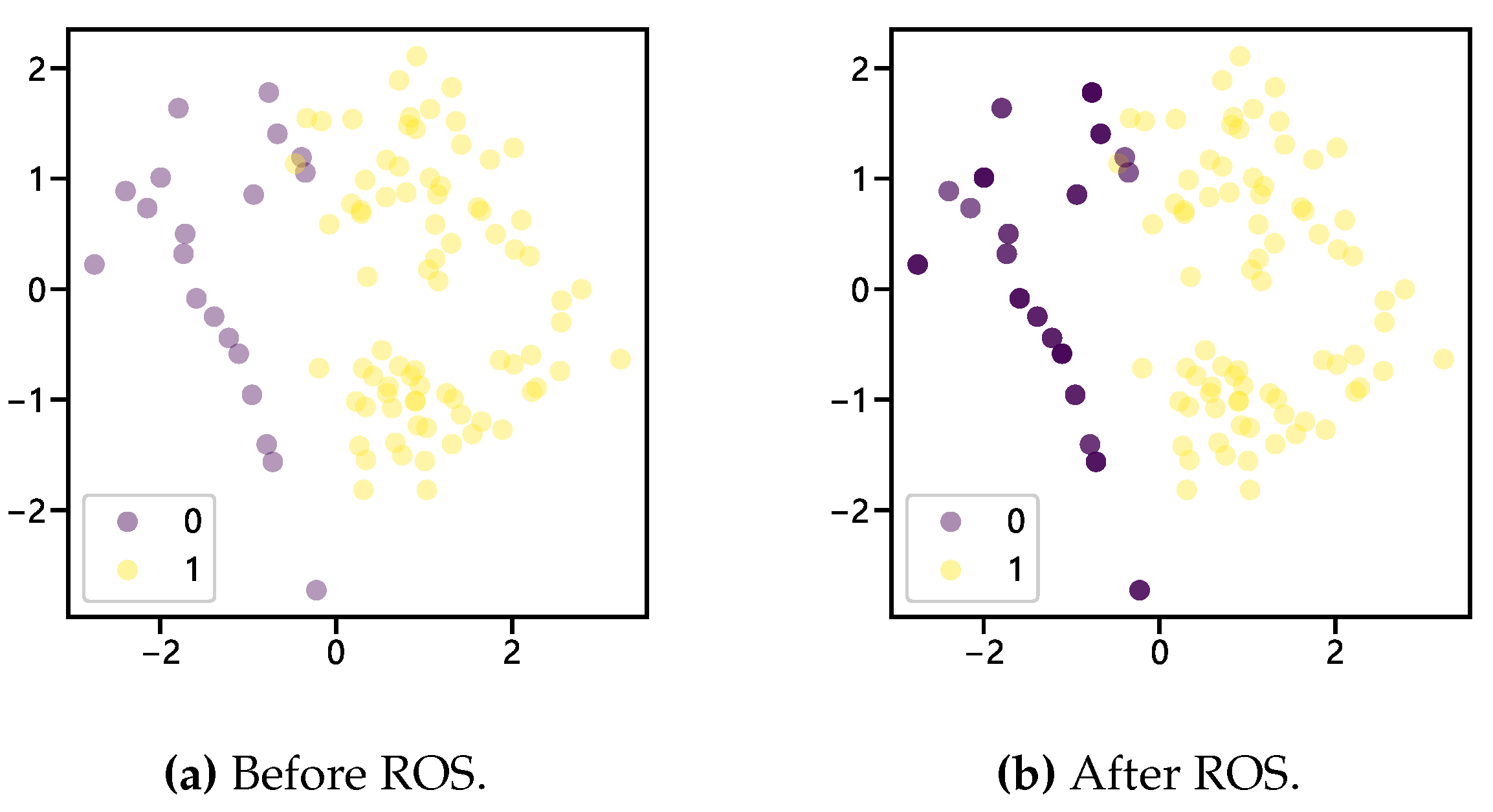
In ordinary random oversampling, when too many synthetic samples are introduced in the majority class samples, the main idea is to copy some random samples from the minority class, which does not add any new information and may make the classifier overfitted. As shown in Figure 1(a), "0" and "1" represent the sample category labels, minority class and majority class, respectively. A repeated generation of samples makes the newly generated minority class samples overlap with each other, and the color of the example sample points in Figure 1(b) deepens. To mitigate this problem, this study generates random noise at each randomly generated sample point using a smoothed Bootstrap, i.e., sampling from the kernel density estimate of the data points[12]. Assuming that K is a symmetric kernel density function with variance 1, the standard kernel density estimate of f(x) is:
f ^ n ( x ) = 1 n h ∑ i = 1 n K ( x − X i h )
where h is the smoothing parameter. The corresponding distribution function is:
F ^ n ( x ) = ∫ ( − ∞ ) X f ^ n ( t ) d t
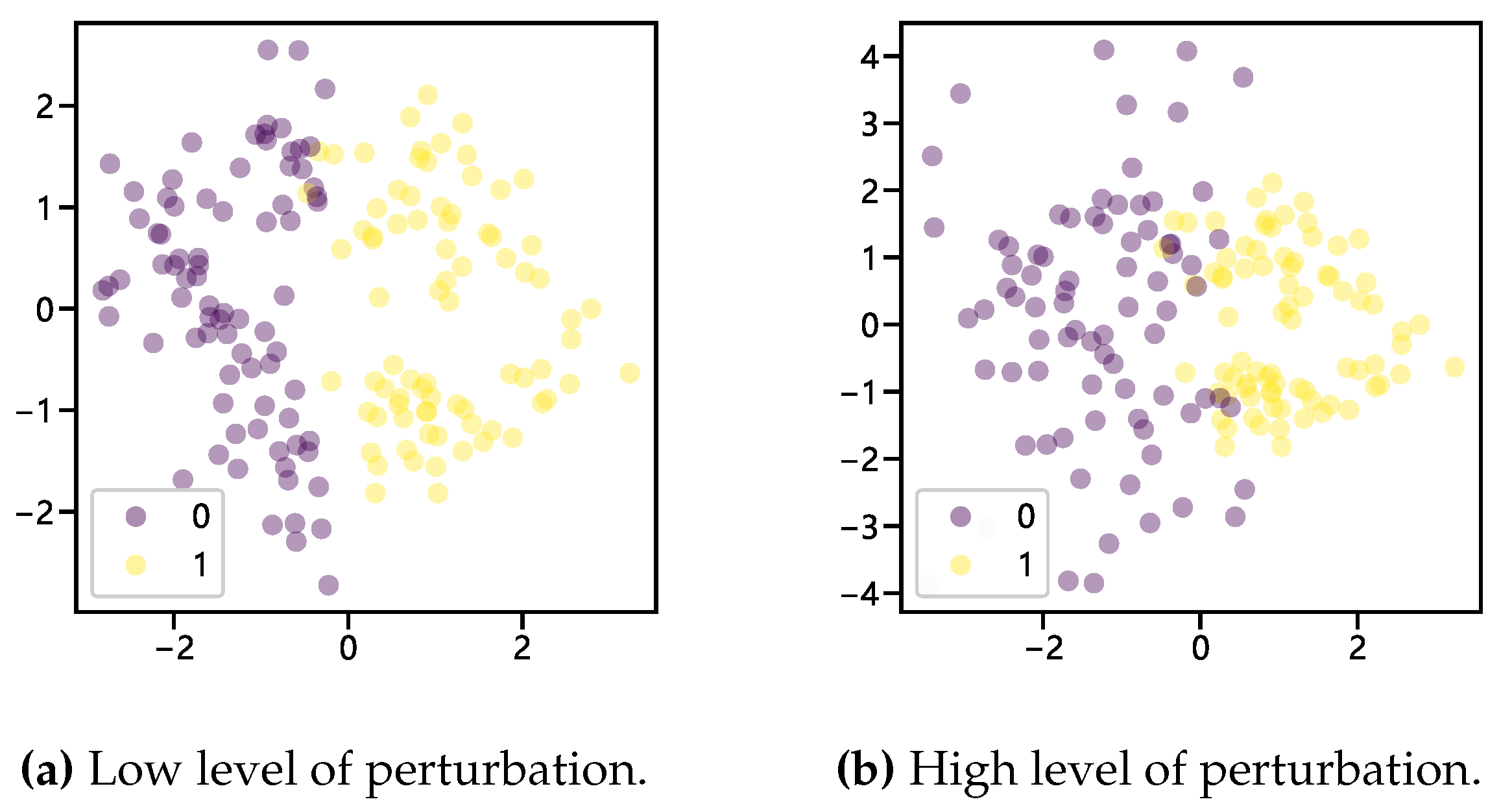
After adding a perturbation factor to the random oversampling to allow for small perturbations in the randomly generated samples, the sample points generated are shown in Figure 2, representing two degrees of perturbation. After the parameter is perturbed by adding a small amount of noise, the randomly generated samples no longer overlap.

2.2. Step two: balanced data subset

Because of its convenience and robustness in the sampling process, SMOTE is widely used to deal with imbalanced data. SMOTE has had a profound impact on supervised learning, unsupervised learning, and multi-class categorization, and it is an important benchmark in algorithms for imbalanced data[13]. SMOTE creates interpolation between the samples of the minority class instances in the defined neighborhood by obtaining K nearest neighbors of sample X in the minority class, randomly selecting one of the samples in the set of nearest neighbors, denoted as X i , and the newly generated minority class samples are:
X n e w = X o r i g i n + r a n d × X i − X o r i g i n , i = 1 , 2 , … , n
where r a n d is a randomly selected number in ( 0 , 1 ) that generates minority class samples at a rate of approximately 1 R − 1 , R = p o s i t i v e s a m p l e s n e g a t i v e s a m p l e s . The process of SMOTE can be summarized as:
1
Select random data from a small number of classes.
2
Calculate the distance of this random data from the K nearest neighbors.
3
Multiply the distance with a random number between 0 and 1 and generate a sample, add the generated sample to the minority class.
4
Repeat until the sample set is balanced.

2.3. Step three: clear boundary noise

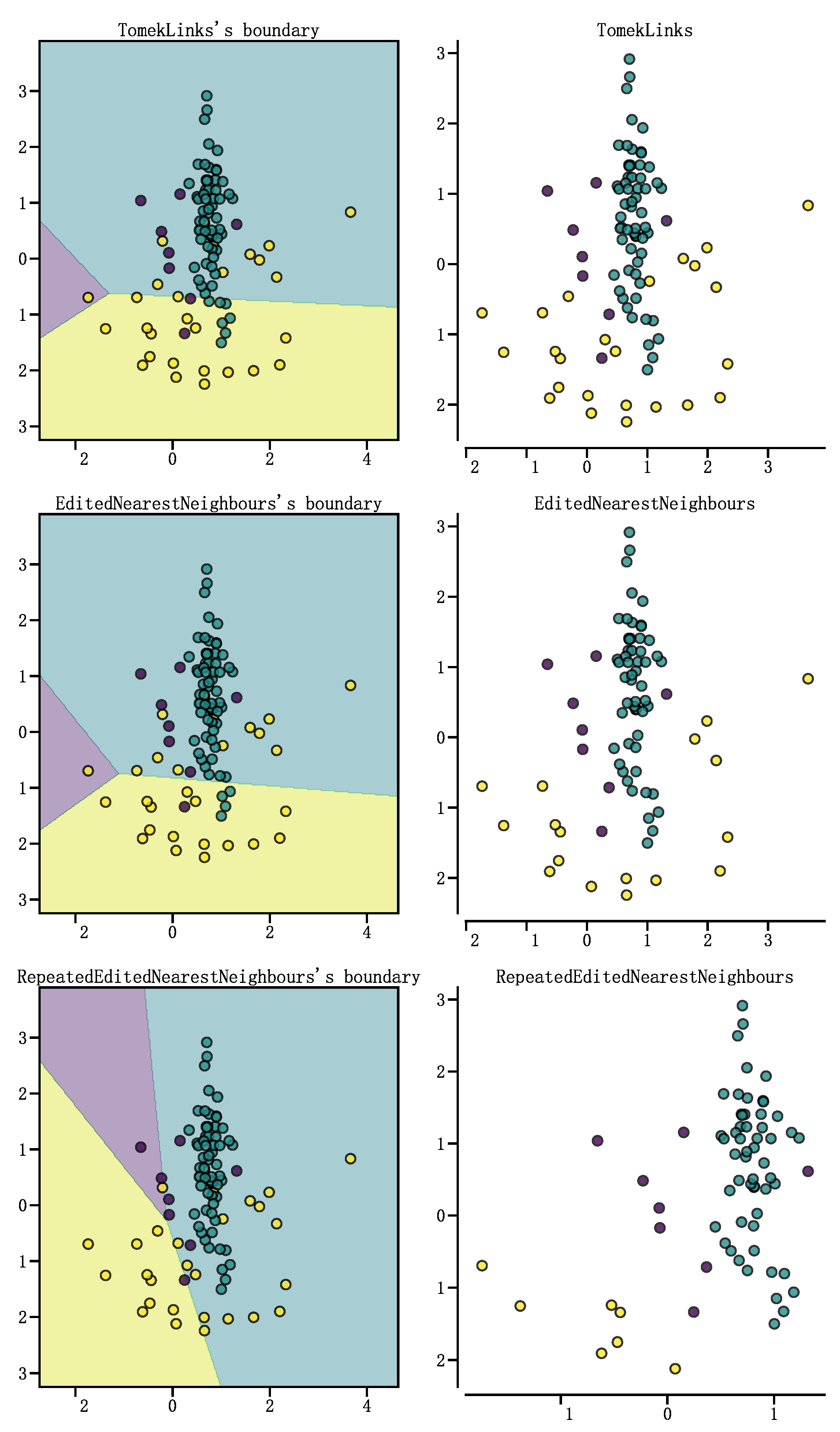
Random oversampling and SMOTE with the addition of perturbation ensures that sufficient minority class samples are generated, while undersampling removes samples in the majority class, which corrects for the excess noise generated during both oversampling processes. If the instance samples are labeled as Tomek Links, then the pair of instance samples are either located near the classification boundary or are noisy instance samples.The characteristics of Tomek Links allow for the deletion of samples that retain more sample points relative to other deletion forms of undersampling. As shown in Figure 3, three algorithms for selecting deleted sample points for undersampling are compared, and the undersampling algorithms used from top to bottom are, Tomek Links, ENN (Edited Nearest Neighbours), RENN (Repeated Edited Nearest Neighbours ). As can be seen in Figure 3, Tomek Links has the shallowest degree of undersampling of the sample set compared to the two types of undersampling, ENN and RENN. In order to ensure as much sample size as possible and to remove useless samples, after random oversampling and SMOTE, this study uses a Tomek Links algorithm that uses Dynamic Temporal Distance Warping as a distance metric.Dynamic Temporal Warping (DTW) is an algorithm used to measure the similarity of two time series.DTW allows for a certain amount of deformation of a time series in the temporal dimension, and is therefore more suitable than the traditional Euclidean distance is more suitable for measuring the similarity of time series[8,14].The algorithm for DTW is as follows:
1
Constructs a matrix in which each element represents the distance between two time series at the corresponding position.
2
Start at the top left corner of the matrix and traverse the matrix along the diagonal to the bottom right corner.
3
At each position, select the distance at which d is minimized.
4
Repeat steps 2-3 until you reach the lower right corner of the matrix.
5
The element in the lower right corner of the matrix is the DTW distance between the two time series.
The TLDTW undersampling algorithm extended to time series data removes boundary noise from time series data to better create balanced classes. Like Tomek Links, TLDTW also has the option of unilateral or bilateral undersampling, and bilateral TLDTW undersampling is used in SMOTE TLDTW.
Using SMOTE and TLDTW will output the data matrix X f , the flow is shown in the algorithm 1. In the Experiments section, the three-stage sampling algorithm of this paper will be analyzed.
Preprints 84954 g010

3. Experiments

3.1. Data Description

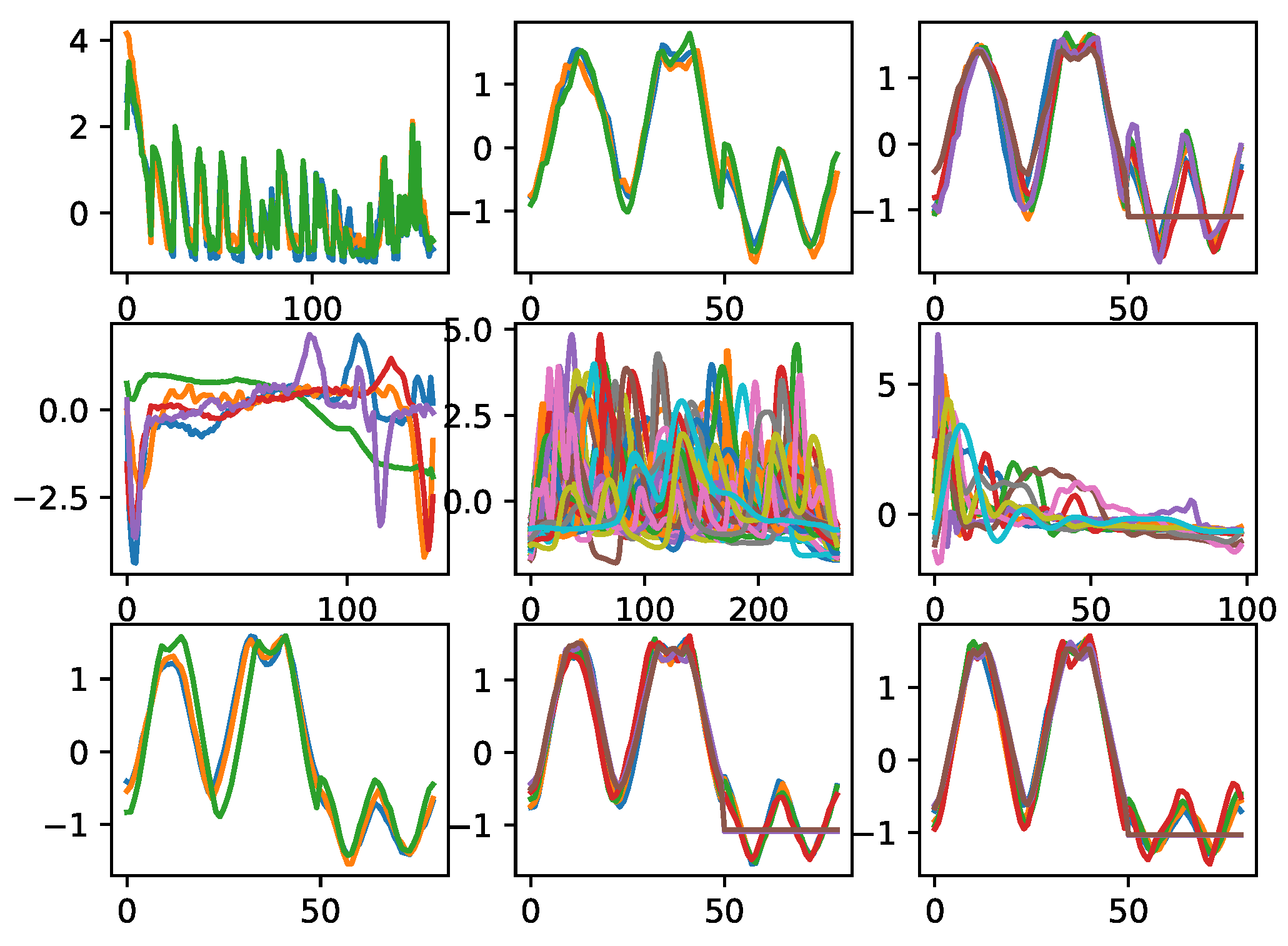
Nine datasets from the UCR dataset were used in this study, and their visualizations are shown in Figure 4[15]. The horizontal axis in Figure 4 represents the sequence and the vertical axis represents the values taken from the time series.The nine multicategorical datasets have different numbers of categories as well as disparate majority-to-minority ratios, and the degree of data imbalance in these multicategorical time series datasets ranges from slight to severe. Table 1 shows the imbalance rate of the multicategorical imbalanced time series dataset, the imbalance rate IR is calculated using the number of samples of the maximum majority class and the number of samples of the minimum minority class, I m b a l a n c e d r a t e ( I R ) = number of the maximum majority class number of the minimum minority class , which can reflect the degree of imbalance in the data set. In the nine datasets used for experiments in this study, FiftyWords has the largest number of sample classes, 49, and the smallest number of samples, only 1. In addition to FiftyWords, there are some minority classes in the ECG5000 dataset that have a very small number of samples, with the smallest minority class having a sample size of 2, and their data distributions are shown in Figure 5.

3.2. Metrics

Decomposing a multi-class classification problem into a binary classification problem is a common way[16,17,18].
When dealing with multi-classified data, SMOTE TLDTW is consistent with the TLDTW algorithm in its decomposition approach, using the OVR (One VS Rest) decomposition, where a few classes are randomly oversampled to the set K value of SMOTE at each decomposition, and for better generation of the samples, SMOTE is then used to generate the sample size of the minority classes up to the number of the maximum number of classes in the datasets. In order to correspond to the calculation of precision, recall and F1-scores for multi-classification, the macro average precision, recall recall and F1-scores shown below are used correspondingly[19].
P r e c i s i o n = T P T P + F P
R e c a l l = T P T P + F N
F 1 − s c o r e = 2 × P r e c i s i o n × R e c a l l P r e c i s i o n + R e c a l l
M a c r o P r e c i s i o n = 1 N ∑ i = 1 N P r e c i s i o n c l a s s = i
M a c r o R e c a l l = 1 N ∑ i = 1 N R e c a l l c l a s s = i
M a c r o F 1 − s c o r e = 1 N ∑ i = 1 N F 1 − s c o r e c l a s s = i

3.3. Other Undersampling Algorithms,Classifier and Parameter

The four most representative undersampling algorithms, ENN, RENN, OSS, and NCR, are selected for comparison. OSS and NCR combine the ideas of selecting deleted samples and selecting retained samples. OSS selects retained samples through the CNN algorithm and deleted samples through Tomek Links; NCR selects retained samples through the CNN algorithm and deleted samples through the ENN; NCR selects retained samples by the CNN algorithm and deleted samples by ENN. The undersampling algorithm selected in this paper is an algorithm for undersampling by selecting deleted samples. In the three-stage sampling algorithm of this paper, TLDTW is the third step of SMOTE TLDTW, so TLDTW also comes to be used for making comparisons.
The parameters are set according to the most stable and commonly used values for each type of algorithm. TLDTW uses one-sided undersampling and only the majority class is censored. OSS uses the nearest neighbor of K=1, K=5 is set in SMOTE TLDTW, and the insufficient number of minority class samples are randomly oversampled up to the level of K=5, and then SMOTE oversampling is performed, and the noisy data is cleaned using the two-sided TLDTW. The number of nearest neighbors of NCR is set to K=3. The ROCKET (Random Convolutional Kernel Transform) classifier has a neural network structure but only one hyperparameter K. Compared to the other classifiers, the impact of the hyperparameter is relatively small, and thus it is chosen as the predictive model with the parameter set to 500 [20].

4. Experiment Results

Table 2 shows that the performance of SMOTE TLDTW for the minority classes of imbalanced time series multiclassification datasets with very small sample sizes are all improved, with the highest precision, recall, and F1-scores in the dataset MedicalImages at 0.7507, 0.7397, and 0.7311, respectively.
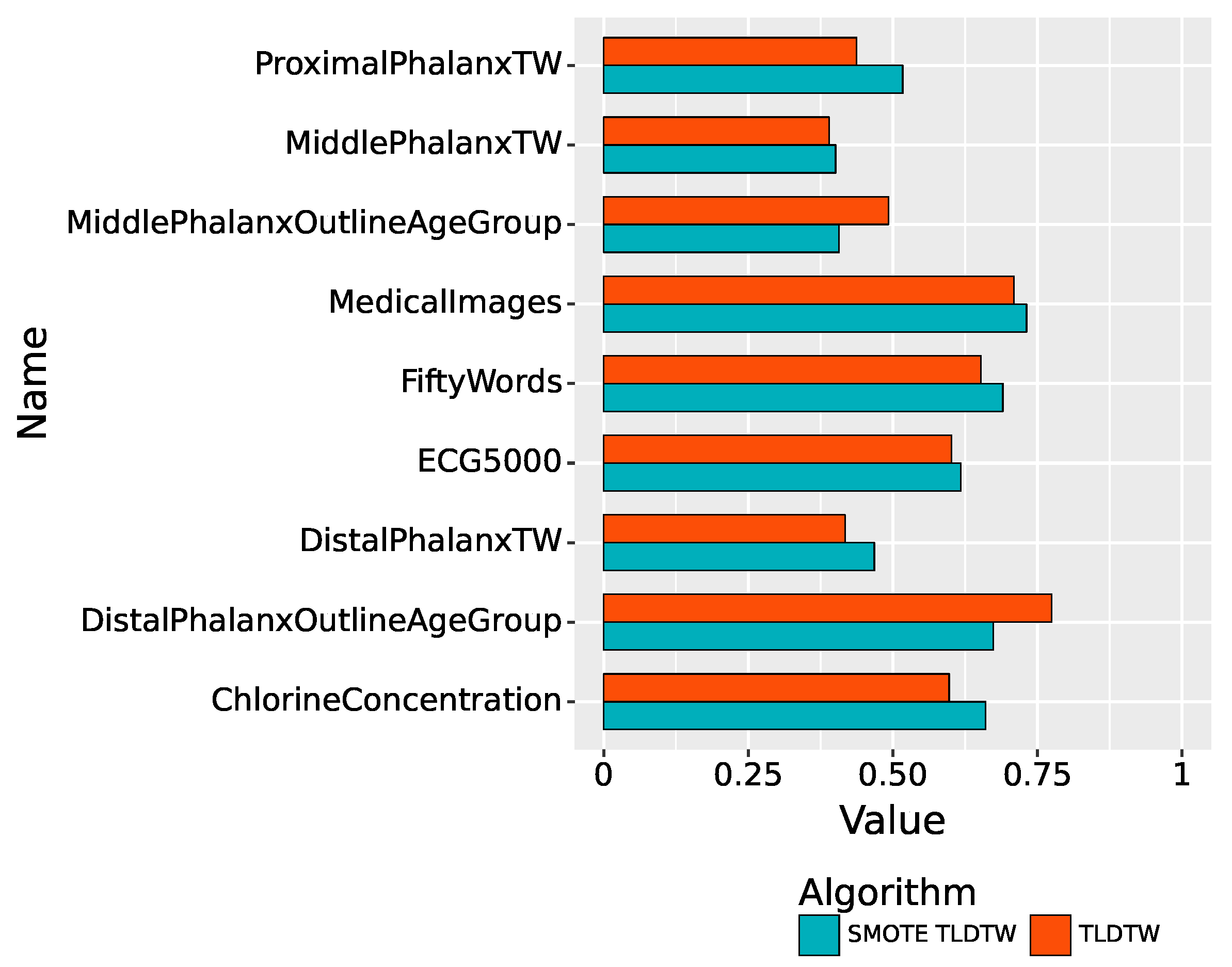
The F1-scores of the two sampling algorithms, TLDTW and SMOTE TLDTW, for the imbalanced multiclassified time series datasets are shown in Figure 6. In the nine imbalanced time series multiclassification datasets, TLDTW outperforms SMOTE TLDTW in the two datasets DistalPhalanxOutlineAgeGroup and MiddlePhalanxOutlineAgeGroup with more samples from a few classes, with F1-scores of 0.7746 and 0.4922, respectively; SMOTE TLDTW has higher F1-scores in the remaining seven datasets. It can be seen that TLDTW has better F1-scores than SMOTE TLDTW in a few datasets with large sample sizes, but in a few datasets with severely insufficient sample sizes, such as ProximalPhalanxTW, ECG5000, and FiftyWords, which have only 16, 2, 1, and 6 samples, respectively, in a few categories, MedicalImages and other datasets, the F1-score of SMOTE TLDTW performs better than that of TLDTW, which is 0.5170, 0.6171, 0.6901, and 0.7311 for the above datasets, respectively.
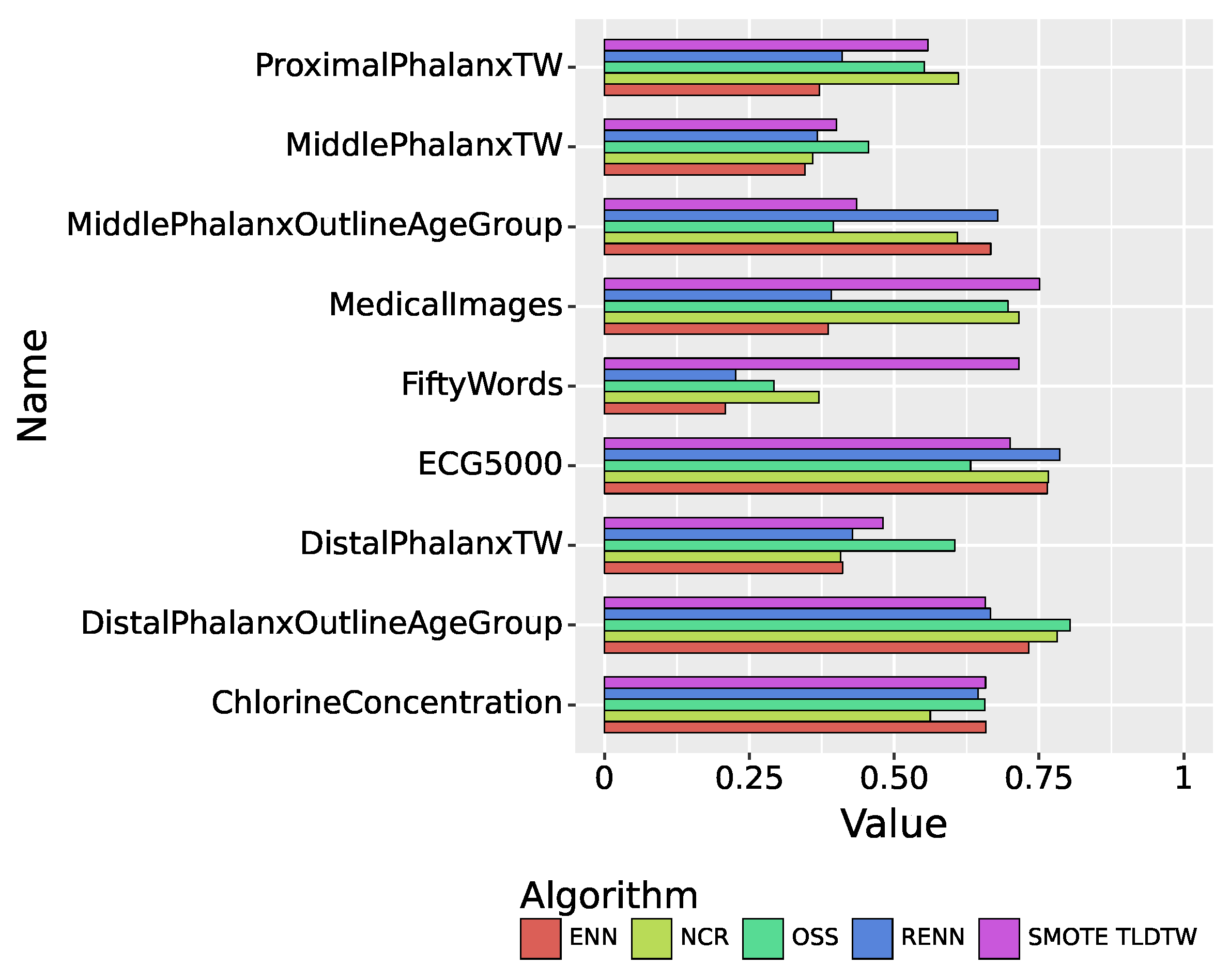
As shown in Figure 7, in the multiclassified datasets, the precision of SMOTE TLDTW in the dataset FiftyWords, which has many categories and a small number of minority classes, is much better than ENN, RENN, OSS, and NCR, with a precision of 0.7156.
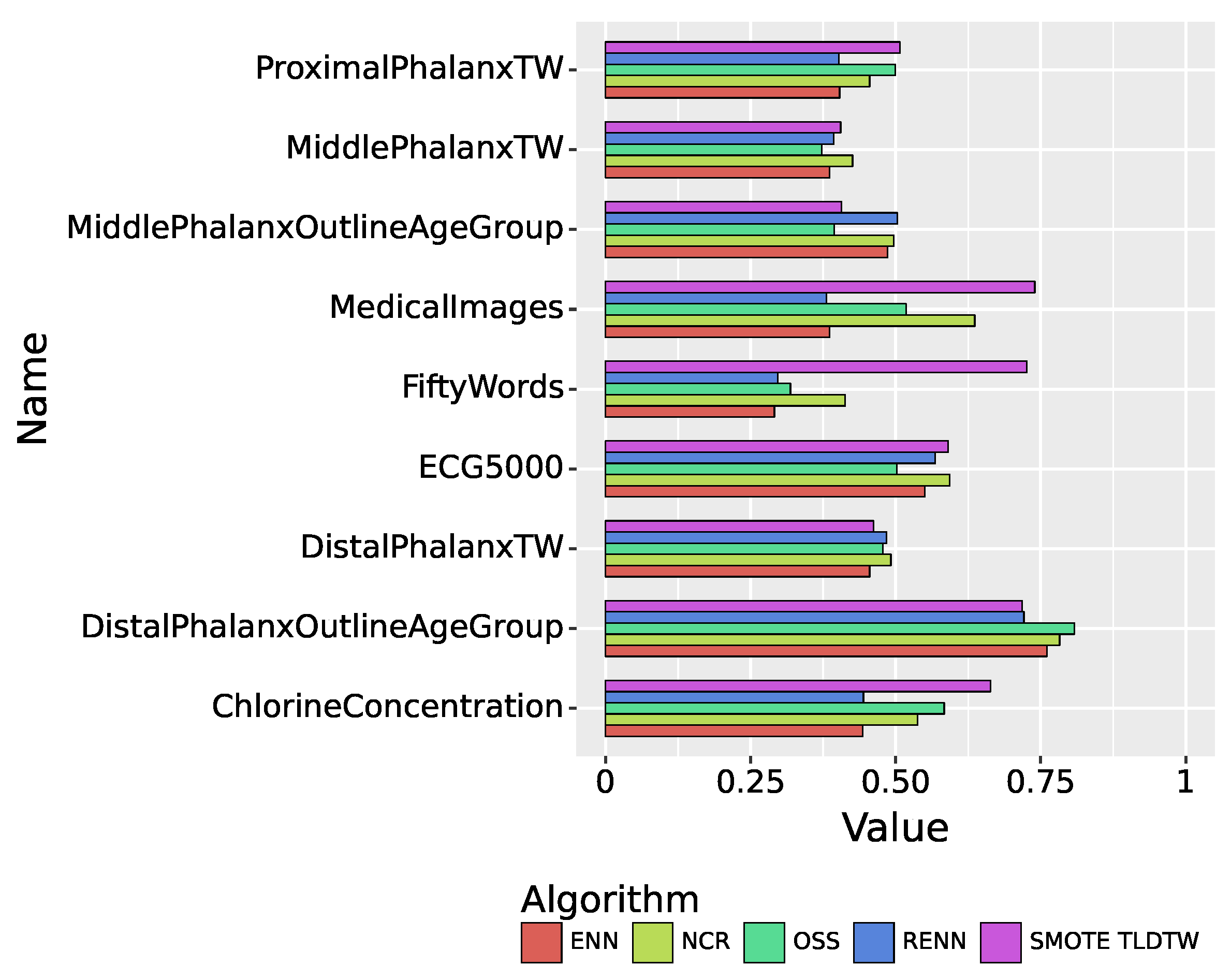
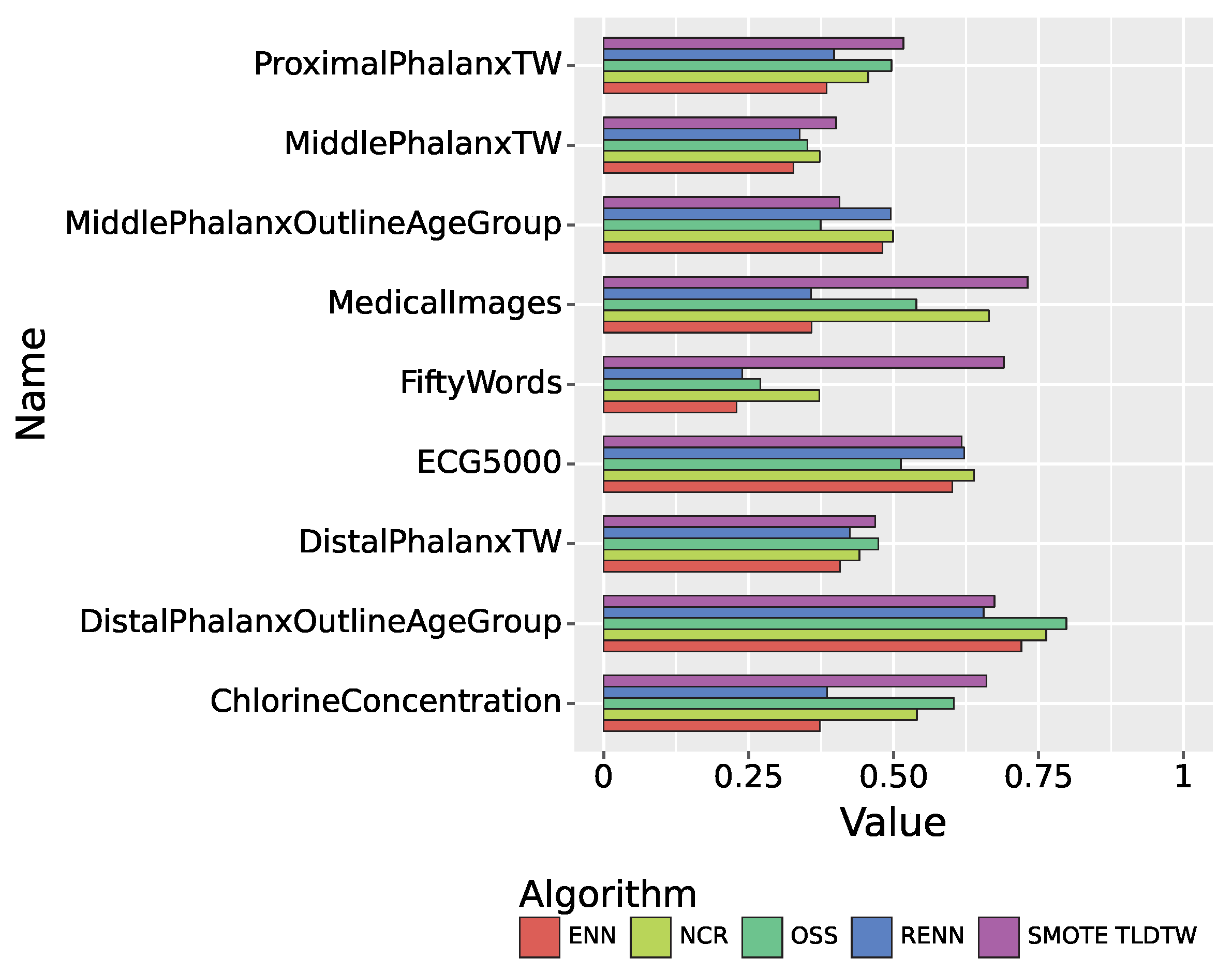
Figure 8 summarizes the recall performance of the five sampling algorithms. In the multiclassified dataset, SMOTE TLDTW still significantly outperforms the other four undersampling algorithms in FiftyWords and MedicalImages, which have a large number of categories and a sparse minority of categories. The F1-score comparison results of the five sampling algorithms are shown in Figure 9, summarizing the results of the nine imbalanced time series datasets. SMOTE TLDTW outperforms the other four undersampling algorithms in five datasets, namely, MedicalImages, FiftyWords, ChlorineConcentration, ProximalPhalanxTW, and MiddlePhalanxTW. The F1-scores of the SMOTE TLDTW algorithm in these five datasets are 0.7311, 0.6901, 0.6602, 0.5170, and 0.4010, respectively. In the nine imbalanced time series multiclassified datasets, for the most categorized FiftyWords, SMOTE TLDTW provided an increase of 200.71%, 188.74%, 155.29%, and 85.61% relative to ENN, RENN, OSS, and NCR, respectively.

5. Conclusion

In this study, we propose the TLDTW undersampling approach for time series data based on the concept of Tomek Links so that it retains clearer boundaries without losing too much information. It is found that the combination of Tomek Links and time series metric distance DTW can better remove the boundary noise samples. When the number of training sets is insufficient, this sampling method makes the accuracy of the classifier decrease; when the amount of data in the training sets is enough, this sampling method makes the classifier boundaries clearer and better. In the experiments, compared with the other three undersampling algorithms, TLDTW outperforms at least two undersampling algorithms in eight imbalanced multiclassification datasets, and TLDTW works well. The two undersampling strategies of TLDTW do not differ significantly under the ROCKET classifier. This study will provide more ideas for further data multi-class algorithms for imbalanced time series in the future.

Author Contributions

The author contributed to all aspects of the research and writing of the paper.

Funding

This research received no external funding

Data Availability Statement

The datasets analysed during the current study are available in the [The UCR Time Series Classification Archive] repository, https://www.cs.ucr.edu/~eamonn/time_series_data_2018/

Conflicts of Interest

As the paper contains only one author, there can be no competing interests.

References

  1. Thabtah, F.; Hammoud, S.; Kamalov, F.; Gonsalves, A. Data Imbalance in Classification: Experimental Evaluation. Information Sciences 2020, 513, 429–441. [Google Scholar] [CrossRef]
  2. Cao, L.; Zhai, Y. Imbalanced Data Classification Based on a Hybrid Resampling SVM Method. 2015 IEEE 12th Intl Conf on Ubiquitous Intelligence and Computing and 2015 IEEE 12th Intl Conf on Autonomic and Trusted Computing and 2015 IEEE 15th Intl Conf on Scalable Computing and Communications and Its Associated Workshops (UIC-ATC-ScalCom); IEEE: Beijing, 2015; pp. 1533–1536. [Google Scholar] [CrossRef]
  3. Ganganwar, V. An Overview of Classification Algorithms for Imbalanced Datasets. International Journal of Emerging Technology and Advanced Engineering 2012, 2, 42–47. [Google Scholar]
  4. Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic Minority Over-sampling Technique. Journal of Artificial Intelligence Research 2002, 16, 321–357. [Google Scholar] [CrossRef]
  5. Han, H.;Wang,W.Y.; Mao, B.H. Borderline-SMOTE: A New Over-Sampling Method in Imbalanced Data Sets Learning. Advances in Intelligent Computing; Huang, D.S.; Zhang, X.P.; Huang, G.B., Eds.; Springer: Berlin, Heidelberg, 2005; Lecture Notes in Computer Science, pp. 878–887. [CrossRef]
  6. Bunkhumpornpat, C.; Sinapiromsaran, K.; Lursinsap, C. DBSMOTE: Density-Based Synthetic Minority Over-sampling TEchnique. Applied Intelligence 2012, 36, 664–684. [Google Scholar] [CrossRef]
  7. Devi, D.; Biswas, S.K.; Purkayastha, B. A Review on Solution to Class Imbalance Problem: Undersampling Approaches. 2020 International Conference on Computational Performance Evaluation (ComPE), 2020, pp. 626–631. [CrossRef]
  8. Kubat, M.; Matwin, S. Addressing the Curse of Imbalanced Training Sets: One-Sided Selection. In Proceedings of the Fourteenth International Conference on Machine Learning. Morgan Kaufmann; 1997; pp. 179–186. [Google Scholar]
  9. Koziarski, M.; Woźniak, M.; Krawczyk, B. Combined Cleaning and Resampling Algorithm for Multi-Class Imbalanced Data with Label Noise. Knowledge-Based Systems 2020, 204, 106223. [Google Scholar] [CrossRef]
  10. Kaur, H.; Pannu, H.S.; Malhi, A.K. A Systematic Review on Imbalanced Data Challenges in Machine Learning: Applications and Solutions. ACM Computing Surveys 2019, 52, 79:1–79:36. [Google Scholar] [CrossRef]
  11. Aguiar, G.; Krawczyk, B.; Cano, A. A Survey on Learning from Imbalanced Data Streams: Taxonomy, Challenges, Empirical Study, and Reproducible Experimental Framework. Machine Learning 2023. [Google Scholar] [CrossRef]
  12. Wang, S. Optimizing the Smoothed Bootstrap. Annals of the Institute of Statistical Mathematics 1995, 47, 65–80. [Google Scholar] [CrossRef]
  13. Fernandez, A.; Garcia, S.; Herrera, F.; Chawla, N.V. SMOTE for Learning from Imbalanced Data: Progress and Challenges, Marking the 15-Year Anniversary. Journal of Artificial Intelligence Research 2018, 61, 863–905. [Google Scholar] [CrossRef]
  14. Keogh, E.; Ratanamahatana, C.A. Exact Indexing of Dynamic Time Warping. Knowledge and Information Systems 2005, 7, 358–386. [Google Scholar] [CrossRef]
  15. Dau, H.A.; Bagnall, A.; Kamgar, K.; Yeh, C.C.M.; Zhu, Y.; Gharghabi, S.; Ratanamahatana, C.A.; Keogh, E. The UCR Time Series Archive. IEEE/CAA Journal of Automatica Sinica 2019, 6, 1293–1305. [Google Scholar] [CrossRef]
  16. Knerr, S.; Personnaz, L.; Dreyfus, G. Single-Layer Learning Revisited: A Stepwise Procedure for Building and Training a Neural Network. In Neurocomputing; Soulié, F.F., Hérault, J., Eds.; Springer Berlin Heidelberg: Berlin, Heidelberg, 1990; pp. 41–50. [Google Scholar] [CrossRef]
  17. Clark, P.; Boswell, R. Rule Induction with CN2: Some Recent Improvements. Machine Learning—EWSL-91; Kodratoff, Y., Ed.; Springer: Berlin, Heidelberg, 1991; Lecture Notes in Computer Science, pp. 151–163 [CrossRef]
  18. Anand, R.; Mehrotra, K.; Mohan, C.; Ranka, S. Efficient Classification for Multiclass Problems Using Modular Neural Networks. IEEE Transactions on Neural Networks 1995, 6, 117–124. [Google Scholar] [CrossRef] [PubMed]
  19. Gowda, T.; You, W.; Lignos, C.; May, J. Macro-Average: Rare Types Are Important Too. Proceedings of the 2021 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, 2021, pp. 1138–1157, [arxiv:cs/2104.05700]. [CrossRef]
  20. Dempster, A.; Petitjean, F.; Webb, G.I. ROCKET: Exceptionally Fast and Accurate Time Series Classification Using Random Convolutional Kernels. Data Mining and Knowledge Discovery 2020, 34, 1454–1495, [1910.13051]. [CrossRef]
Preprints 84954 g001
Figure 1. Comparison before and after random oversampling.
Figure 1. Comparison before and after random oversampling.
Preprints 84954 g001
Preprints 84954 g002
Figure 2. Two degress perturbation of ROS.
Figure 2. Two degress perturbation of ROS.
Preprints 84954 g002
Preprints 84954 g003
Figure 3. three undersampling algorithm
Figure 3. three undersampling algorithm
Preprints 84954 g003
Preprints 84954 g004
Figure 4. Visualization of multi classification time series data
Figure 4. Visualization of multi classification time series data
Preprints 84954 g004
Preprints 84954 g005
Figure 5. The distribution map of ECG500 and FifyWords
Figure 5. The distribution map of ECG500 and FifyWords
Preprints 84954 g005
Preprints 84954 g006
Figure 6. The distribution map of ECG500 and FifyWords
Figure 6. The distribution map of ECG500 and FifyWords
Preprints 84954 g006
Preprints 84954 g007
Figure 7. The precision of 9 imbalanced time-series multiple datasets
Figure 7. The precision of 9 imbalanced time-series multiple datasets
Preprints 84954 g007
Preprints 84954 g008
Figure 8. The recall of 9 imbalanced time-series multiple datasets
Figure 8. The recall of 9 imbalanced time-series multiple datasets
Preprints 84954 g008
Preprints 84954 g009
Figure 9. The F1-score of 9 imbalanced time-series multiple datasets
Figure 9. The F1-score of 9 imbalanced time-series multiple datasets
Preprints 84954 g009
Table 1. The imbalanced rate of datasets
Table 1. The imbalanced rate of datasets
Datasets Imbalance rate
ChlorineConcentration 2.88
DistalPhalanxOutlineAgeGroup 8.57
DistalPhalanxTW 11.83
ECG5000 146.00
FiftyWords 52.00
MedicalImages 33.83
MiddlePhalanxOutlineAgeGroup 4.31
MiddlePhalanxTW 6.40
ProximalPhalanxTW 11.25
Table 2. The performance of SMOTE TLDTW
Table 2. The performance of SMOTE TLDTW
Datasets Precision Recall F1-score
ChlorineConcentration 0.6577 0.6633 0.6602
DistalPhalanxOutlineAgeGroup 0.6576 0.7178 0.6739
DistalPhalanxTW 0.4803 0.4622 0.4680
MedicalImages 0.7507 0.7397 0.7311
MiddlePhalanxOutlineAgeGroup 0.4351 0.4064 0.4070
MiddlePhalanxTW 0.4004 0.4052 0.4010
ProximalPhalanxTW 0.5583 0.5075 0.5170
ECG5000 0.6998 0.5904 0.6171
FiftyWords 0.7156 0.7261 0.6901
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated