1. Introduction
Interest in applications of drone swarms is rising rapidly due to the development of robotic technologies. Scientists worldwide propose and research new control algorithms that can be implemented to execute specific tasks or improve existing solutions. Many of them are theoretical dissertations not transferred to practical applications. The research provided in this paper focuses on an attempt to simulate the real-life swarm of UAVs with all its physical parameters.
Deployment of a real-life swarm system requires many robots to be built, programmed, and launched. The time and cost of those processes can grow significantly, especially for testing and prototyping[
1]. This makes simulations the first stage in preparing a complex system [
2]. Implementing a virtual system allows for conducting a series of tests with different conditions having only a PC. Such tests are not dependent on the weather, do not require robot maintenance, and can be terminated if any malfunction appears[
3]. Prototyping an algorithm for a swarm of maneuvering, real-life UAVs can be dangerous for the surroundings and the swarm itself[
4].
Most of the research focuses on control algorithms, a set of rules that defines how swarm agents propagate throughout the area. Tests using virtual simulations provide the mathematical output of the swarm’s behavior, and often, their physical parameters are either not addressed or simplified. The more precise data implemented in the simulation, the more realistic its output is. In the case of simulating swarm behavior, not only the commanding algorithm matters but also the movement of a single agent in the swarm. Simulation of a UAV in the swarm requires knowledge of its physical parameters and dynamics. Every neglection or simplification at such an early research stage can lead to incorrect conclusions, affecting further real-life applications[
5].
In the case of practical applications, energy consumption is a crucial factor in the usage of autonomous robots, especially UAVs[
6]. The energy used to perform the task is often neglected in the research, while UAVs depend highly on their battery life. A power source defines their performance, such as velocities, altitude, capacity, etc. [
7,
8].
This paper presents an approach to identify dynamic models for rotary-wing UAVs. Experimental flights were performed, which allowed the collection of flight data for the UAVs and thus helped to improve the precision of data used in simulations. Such an approach permitted performing simulations close to the actual behavior of swarm agents without solving complex mathematical formulas regarding quadrotors. This was especially useful when the consumption of energy was calculated. Also, the algorithm implemented the collision avoidance feature to imitate real-life drones better.
2. Materials and Methods
The main goal of the presented research was to build a control system for UAV swarm. The study was divided into five stages as follows:
Prepare a simulation program executing a desired algorithm;
Conduct experimental flights with real-life UAVs to collect flight data for the identification of dynamic models;
Identify dynamic models of UAVs in examined flight stages;
Implement obtained dynamic models into the simulation. Conduct tests and gather and analyze results.
All study stages were described in more detail in the other parts of this paper.
2.1. Physical Parameters in Simulations of UAV Swarm
Before launching a real-life swarm system, the first step was to test it in virtual simulations. This stage required models of the objects to be implemented into the simulation as a representation of real-life objects. The more accurate those models were, the more realistic the simulation output was.
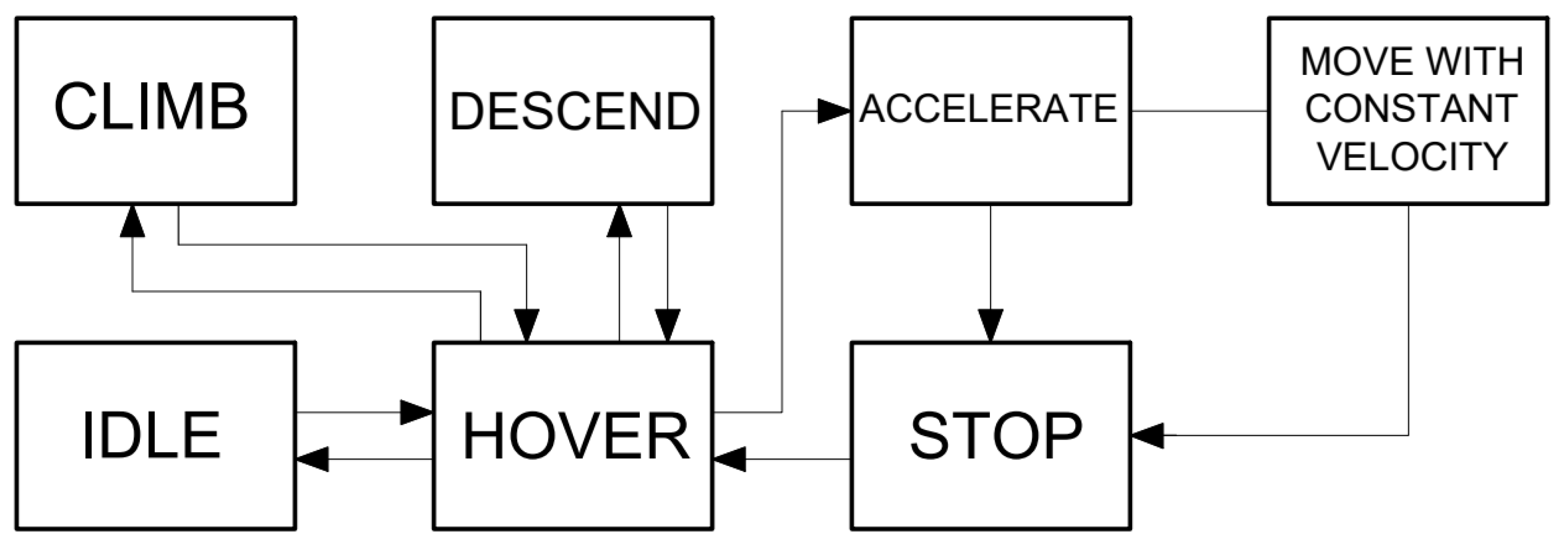
For two reasons, knowing the drones’ dynamic models was vital in conducting the simulations. Firstly, it allowed to correctly measure the time and energy consumed by the swarm while performing the mission. Those two factors were significant for the optimization of the performance. Drones operated in different flight stages during the simulation, as presented in
Figure 1. During all of them, they consumed energy at different rates and knowing those rates enabled calculating total energy consumption. UAV systems are known for their relatively low battery capacities, and optimizing swarm systems according to energy consumption is one of the main factors to include in research. Secondly, the time required to complete transition states (accelerating, climbing, etc.) and maximal velocities enabled us to derive the total time needed to finish the task.
The second reason for identifying dynamic models of the drones was the safety of the swarm and the fluency of its movement. Due to the collision avoidance feature, knowing the distance required to accelerate or decelerate was necessary because it was vital for the path planning of the drones. The distance covered during stopping was crucial as the algorithm needed to compute when the drones had to start decelerating to avoid a collision if such a situation appeared.
2.3. Experimental Flights and Data Collection
The mathematical models can be estimated by the identification method. This method uses time series models such as ARX, AR, and ARMAX. The transfer function can be estimated from the ARX model:
where:
– is the
transform of an output signal,
– is the
transform of an input signal,
– is the
transform of the white noise,
is a transfer function in terms of
z operator, and
– is a color filter in terms of
z operator.
are polynomials in terms of
z operator. The transfer function of an identified model can be converted from a digital model to an analog model. The continuous transfer function is equal:
where:
the sampling period. The authors for the stochastic recovery paths simulation need a model of teak-off, landing and cruise flight, acceleration, and deacceleration of the UAV. We assume that the swarm of UAVs will not change altitude at the operational zone. The UAV class quadrotor was used to conduct the identification experiment. The quadrotor is presented in
Figure 2.
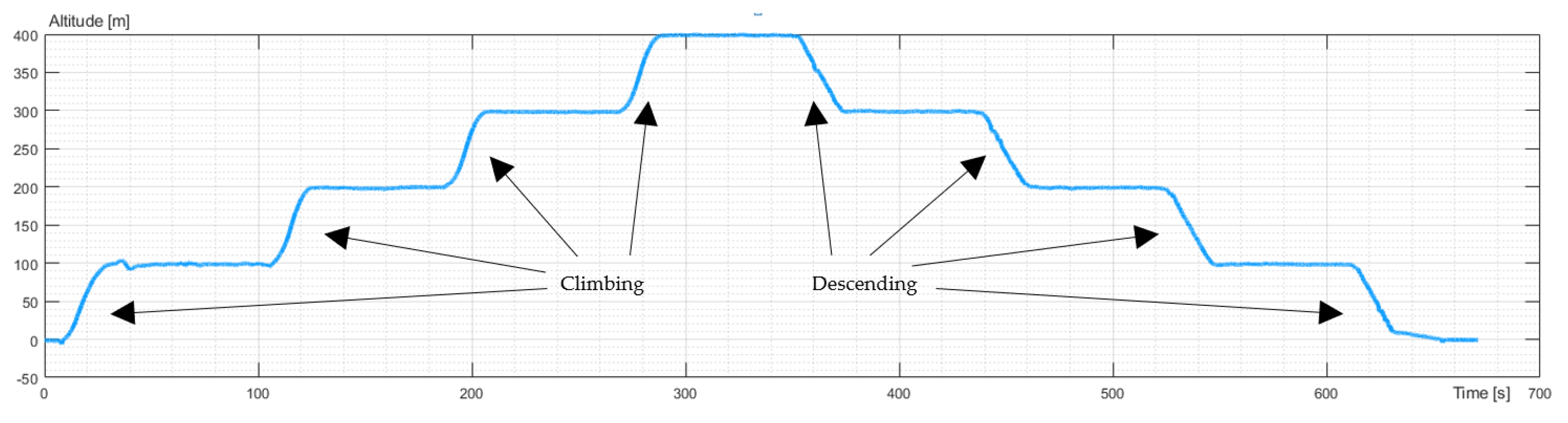
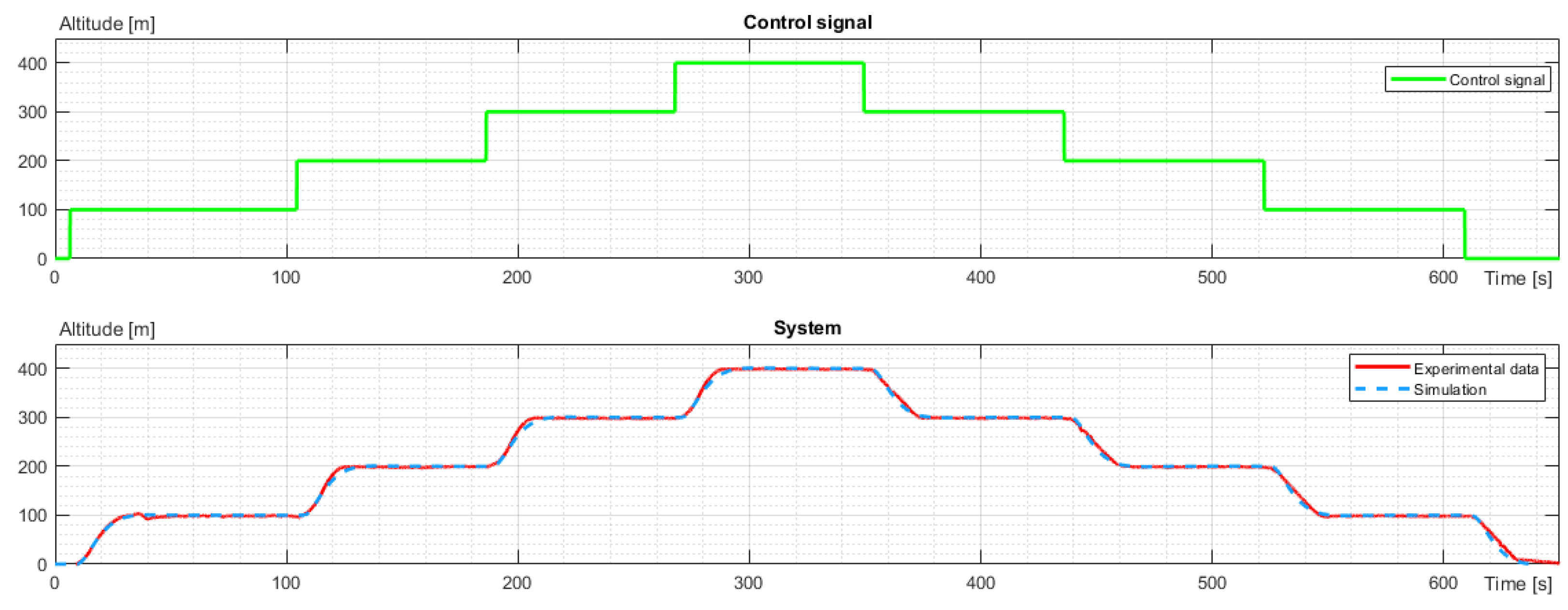
The experiments were divided into the vertical and horizontal movement of the UAV. The vertical move study included take-off to an altitude of 100 m. Next, the altitude increased to 200 m, 300 m, and 400 m and decreased to 300 m, 200 m, and 100 m. The last point of the study was landing. The UAV hovered at each point of the study. It took the same position (latitude and longitude), and the flight controller stabilized and corrected the angular orientation of the UAV. The altitude flight is presented in
Figure 3.
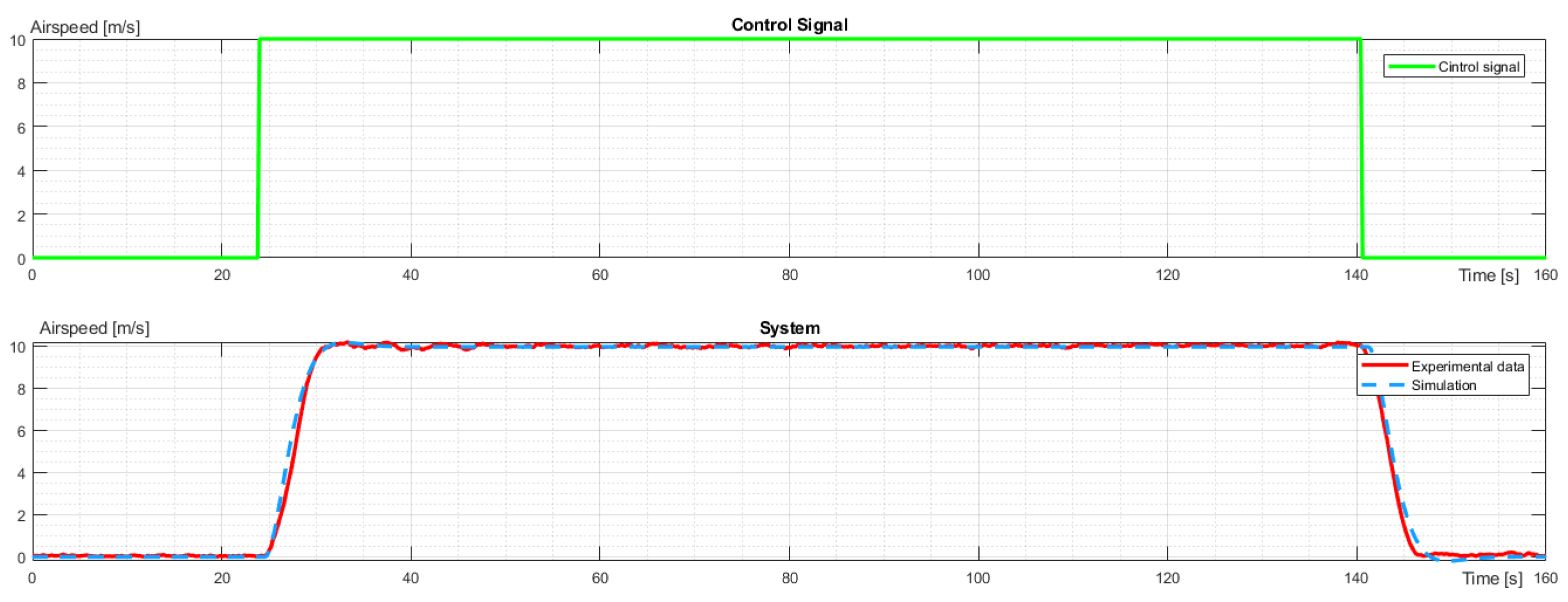
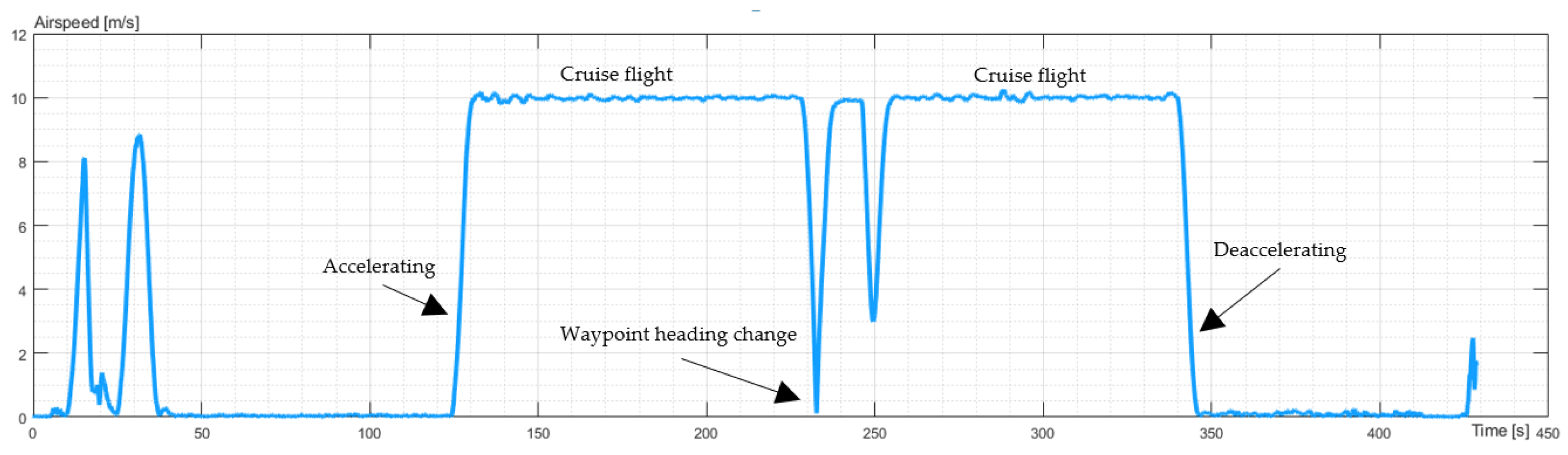
The next experiment applied to horizontal movement. The UAV took off to an altitude of 200 m and moved to the waypoint. There, the UAV changed the heading and returned to the point of take-off, and the UAV landed. The UAV had defined latitude, longitude, and altitude of the take-off and waypoint. The maximum airspeed was 10 m/s, as defined in the flight plan. The airspeed profile is presented in
Figure 4.
The mechanical and electrical parameters were recorded during identification experiments. The voltage, current, airspeed, vertical speed, altitude, latitude, longitude, and reference airspeed and altitude were recorded. The experiment enabled us to obtain the transfer function between the reference value and energy. The transfer functions were estimated for the take-off, climbing, descending, cruise, and landing of the UAV.
3. Results
3.1. Identify Dynamic Models
When experimental data was collected, it was possible to identify dynamic models for every flight state. The models were identified according to a section of gathered data corresponding to the same state in actual flight. Then, to verify it, dynamic models were compared to a suitable part of data from other flights. At last, the entire flight was simulated using identified models mimicking the real-life test, and it allowed us to compare the total energy consumption and scale of errors.
Identification was performed in Matlab. Input data was a control signal from the flight controller, and output data was registered flight parameters. Identified parameters were a change of Power over time, vertical displacements, and horizontal velocities over time during every considered flight state. The dynamic models were presented as a continuous time transfer function.
The only difference was hover, in which the power was calculated as the average power required to hover at a given altitude. Then, knowing the result for a few different altitudes, the dependence of power on time was approximated with function. According to Rotratu [
9], the power required to hover is given by:
where: T – total thrust force,
A – total area swept by rotors,
ρ – air density.
Assuming that during hover, T and A are constant, power depends on air density, which in International Standard Atmosphere [
10] can be approximated as revered exponential proportional to flight altitude H. In this case, the power required to hover can be written as:
where:
z – proportion exponent.
Using collected data, the equation describing power required to hover on flight altitude H was approximated with:
3.1.1. Vertical Movement Models
The first dynamic models to identify were vertical movements: ascending and descending. The data for the process was four subsequent climbs by 100 meters from 0 to 400m for ascending. Analogically, there were four subsequent decreases by 100m from 400m to 0 for the descent. Models for the altitude changes were identified together for both states, and models of power were created separately. A comparison of experimental data and identified models for altitude change was shown in
Figure 5.
As seen in
Figure 5, the simulated characteristic matches the experimental data; hence, the simulation can be assumed to mimic the vertical movement of the drone with sufficient precision. The following transfer function described the identified model:
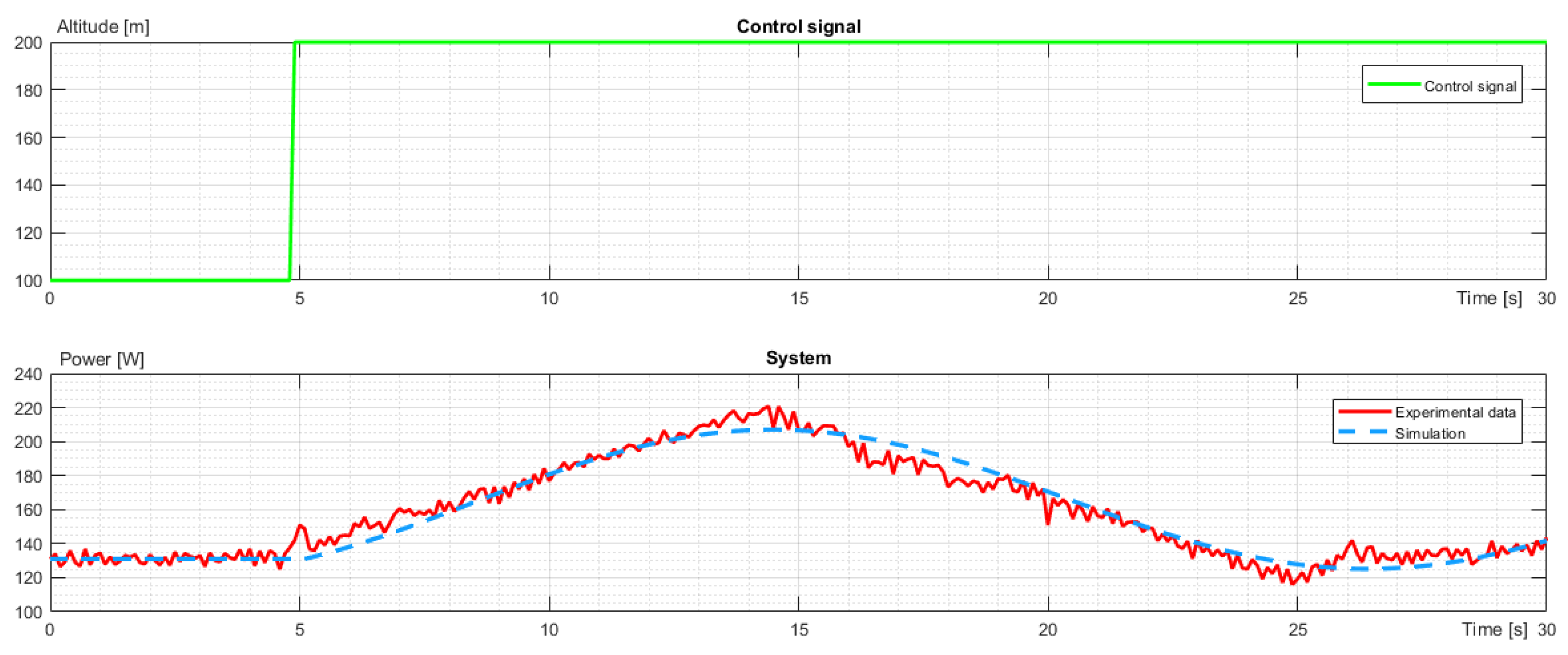
The second part of the identification was made for the power required to climb and descend on a 100m difference in altitude. As the system was assumed to be linear, offsets were brought to 0 not to break homogeneity and superposition principles. Then, it was added to the stable state power required for hover. The power characteristics for climb and descent were shown in
Figure 6 and
Figure 7.
As can be seen, at the beginning of the climb, the power rapidly increased as the drone had to accelerate upwards. At some point, the UAV reached sufficient speed to reach the desired altitude, requiring less and less thrust. Hence, the power started to decrease. At the climb’s final stage, the drone had to lose gathered speed using a force of gravity. At that point, the power dropped below a stable state shortly after stabilizing to the value required to hover. The identified model for power during the climb was presented below:
When the drone needed to descend, power first dropped, and reduced thrust became lower than gravity force, making the drone accelerate downwards. From some point, the power rose to slow the rate of descent. Subsequently, the thrust had to grow over the force of gravity for some time to lose downward velocity and stabilize the flight to hover at the desired altitude. The transfer function for power during descent was presented below:
In both cases, the experimental data was distorted by a noise that could not be seen in the simulated response. Optical evaluation allowed us to conclude that the signal trends were similar in both cases, yet further validation of the models had to be done.
3.1.2. Horizontal Movement Identification
Analogical identification was performed for horizontal movement. The flight states were accelerating, moving with constant velocity, and decelerating (stopping). The energy consumption had linear dependence on acceleration and flying with constant velocity. While accelerating, the temporal power grew proportionally to velocity, and during the constant speed movement, the energy consumption was settled around a constant value. This value was calculated as an average take from the segment where the drone flew with constant velocity. The identified model for horizontal flight was presented below:
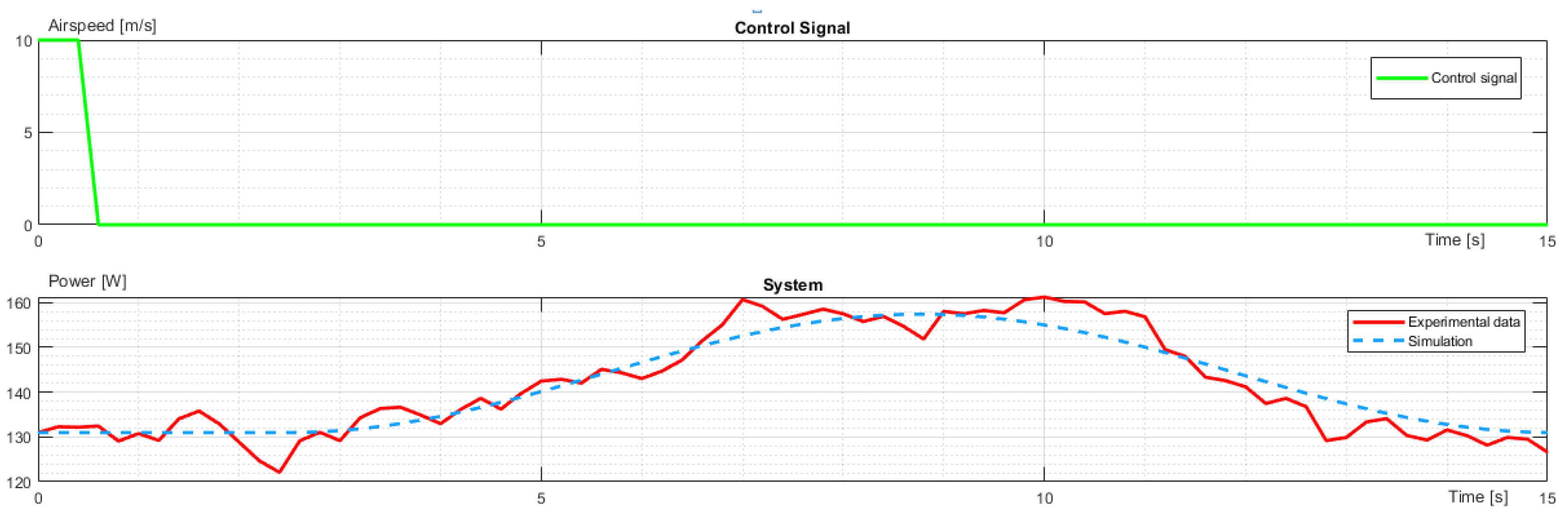
When the drone was commanded to stop, the desired velocity was instantly changed to 0, so the UAV not only aborted the flying forward but also tried to stop in the shortest time. Hence, it rotated backward and created counter thrust to its movement direction, creating backward force. The power change for deacceleration was shown in
Figure 9.
Figure 8.
The control signal and characteristic comparison of experimental data and simulation for airspeed during horizontal flight.
Figure 8.
The control signal and characteristic comparison of experimental data and simulation for airspeed during horizontal flight.
Figure 9.
The control signal and characteristic comparison of experimental data and simulation for power during deacceleration.
Figure 9.
The control signal and characteristic comparison of experimental data and simulation for power during deacceleration.
As can be seen after being commanded to stop, the power consumption rapidly increased as the drone started the backward rotation and increased the thrust. Then, it rotated forward, decreasing the power to settle in the hover. Below, the identified transfer function for power change during deacceleration was presented:
3.2. Models Verification
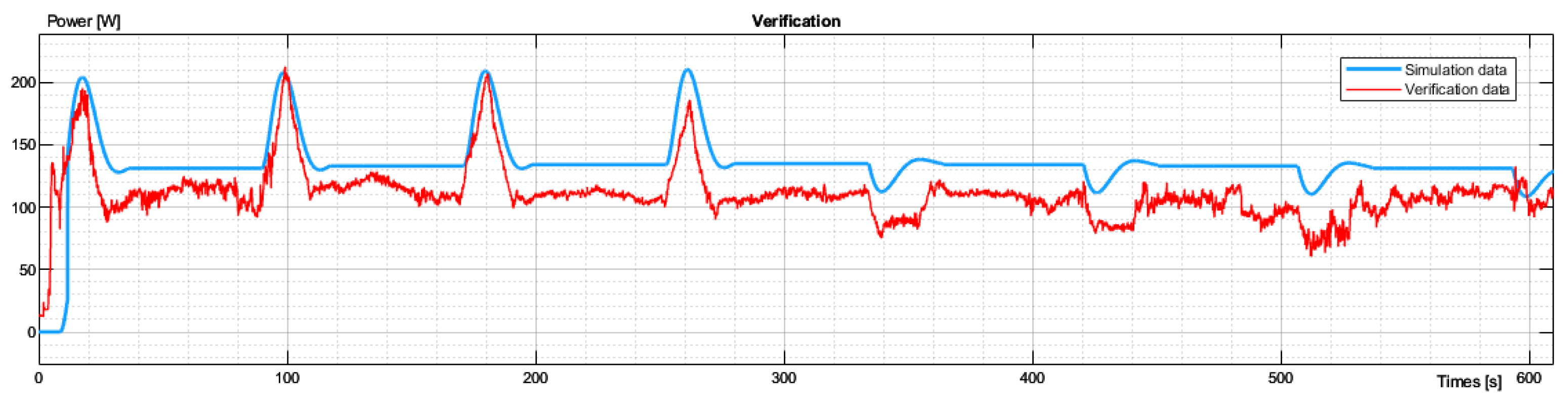
After identifying the dynamic models, the next step is their verification. This is required to prove that identified models represent different cases. The other experimental flight was taken into consideration, and its flight plan was recreated in simulation. Next, the experimental and simulated data were compared.
As seen in
Figure 10., the nature of both characteristics was the same. Flat segments and peaks were synchronized and had a similar magnitude. Yet, the charts were not perfectly aligned as their height is mainly defined by the constant power required to remain at altitude. This value depends on many factors such as atmospheric conditions, winds, etc., so if in compared attempts they were different, the average power required to hover also differed.
Nevertheless, such comparisons proved that most of the identification was performed correctly. It also showed how vital for UAVs is the Power required to hover and how volatile that variable is.
4. Discussion
The article describes a method for identifying dynamic models of UAV flight. As shown in the paper, obtaining dynamic models of certain maneuvers of quadrotor robots is possible without deriving a complete mathematical model, which is complex for such objects. Properly conducted experimental flights with data recording are required to perform identification.
This method comes into use, especially regarding energy consumption and temporal power during flight stages. Battery capacity is one of the most significant challenges of present UAVs, and energy characteristic is integral to mission planning. The presented method allows us to quickly identify the power characteristics of flying UAVs.
In the case of rotary-wing UAVs, the most critical flight state is remaining at a constant altitude. During a hover or while performing maneuvers, a significant part of the generated thrust had to be directed down to counteract the force of gravity. The presented results show that the gross amount of temporal energy had to be consumed so the robot would not fall. Therefore, correctly identifying this power is crucial in preparing a UAV flight model.
Identified models for certain flight states can be implemented into virtual simulations of the swarm. This way, simulations become more realistic while remaining in the virtual process. Kinematic models allowed us to mimic the movement of the UAVs, which helps to reproduce the acceleration and stopping distances, which are crucial in path planning and collision avoidance. Power parameters models allow us to derive energy consumption for the entire flight.
Simulating and deriving the power characteristics throughout the entire flight of the UAV allows for calculating the total energy that must be consumed to fulfill the planned mission. Such a study improves the path planning process with another factor, especially significant for rotary-wing UAVs. Thanks to that, it is possible to optimize the count of the agents in the swarm by optimizing the total energy consumption of the entire group.
References
- Sanchez-Lopez, Jose Luis, et al. "A reliable open-source system architecture for the fast designing and prototyping of autonomous multi-uav systems: Simulation and experimentation." Journal of Intelligent & Robotic Systems 84 (2016): 779-797. [CrossRef]
- Soria, Enrica, Fabrizio Schiano, and Dario Floreano. "SwarmLab: A MATLAB drone swarm simulator." 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). IEEE, 2020. [CrossRef]
- de Winter J.C.F., van Leeuwen P.M., Happee R. “Advantages and Disadvantages of Driving Simulators: A Discussion” Proceedings of Measuring Behavior 2012 8 th International Conference on Methods and Techniques in Behavioral Research Utrecht, August 28-31, 2012, p. 47-49.
- Higgins, Fiona, Allan Tomlinson, and Keith M. Martin. "Threats to the swarm: Security considerations for swarm robotics." International Journal on Advances in Security 2.2&3 (2009), p. 288-297.
- Popov, Luben Nikolaev. Drone swarm simulation. 2020. PhD Thesis. University of Houston, page 8.
- Li, Jing, et al. "A path planning method for sweep coverage with multiple UAVs." IEEE Internet of Things Journal 7.9 (2020): 8967-8978. [CrossRef]
- Dudek, Magdalena, et al. "Hybrid fuel cell–battery system as a main power unit for small unmanned aerial vehicles (UAV)." Int. J. Electrochem. Sci 8.6 (2013): 8442-8463.
- Cesare, Kyle, et al. "Multi-UAV exploration with limited communication and battery." 2015 IEEE international conference on robotics and automation (ICRA). IEEE, 2015. [CrossRef]
- Rotaru, C., Todorov, M.(2018), Helicopter Flight Physics. In Flight Physics Models, Techniques and Technologies; Volkov, K., Ed.; IntechOpen: London, UK; ISBN 978-953-51-3807-5.
- Cavcar M. (2000) The International Standard Atmosphere (ISA), Import from: https://scholar.google.com/citations?user=WpEp_wcAAAAJ&hl=en , date of import: 30.08.2023.
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).