Preprint
Article
Navigating through Noise Comparative Analysis of using Convolutional Codes Vs. Other Coding Methods in GPS Systems
Altmetrics
Downloads
104
Views
23
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
14 September 2023
Posted:
18 September 2023
You are already at the latest version
Alerts
Abstract
This research highlights the importance of error-correcting codes in ensuring secure and efficient data transmission over noisy channels. It discusses the application of Convolutional codes and the Viterbi algorithm for error detecting and correcting in applications where the data rate is high and the error probability is relatively low. This research extends beyond previous studies by conducting a comparative analysis of Convolutional codes, the Viterbi algorithm, and alternative coding methods utilized in satellite communication systems, by evaluating their effectiveness and efficiency relative to other coding approaches like BCH, LDPC, and turbo codes. The evaluation encompasses key performance metrics including error correction capabilities, computational complexity, and robustness against various error types. Additionally, practical implementation factors such as power consumption, computational requirements, and compatibility with existing hardware are considered. The analysis sheds light on the advantages and disadvantages of each coding method, offering insights into why convolutional codes and the Viterbi algorithm are particularly suitable for GPS systems.
Keywords:
Subject: Computer Science and Mathematics - Security Systems
1. Introduction
Global Positioning System (GPS) is a crucial technology for navigation and communication systems that rely on satellite communications. GPS has emerged as a valuable tool in both military and civilian applications. From aircraft navigation and surveying to automotive applications and recreational activities like hiking and camping, GPS has proven its versatility and utility. GPS has been in use for providing positioning, navigation and timing (PNT) services in many parts of the world.
The demands on GPS receiver performance are as varied as the applications. For example, the hiker is not interested in millimeter-level positioning, but a compact, low-weight, long battery-life unit is highly desirable. Surveying units may take advantage of the increased accuracy which can be achieved by exploiting the low-level of dynamics of the receiver. Although the specific requirements vary significantly, the most fundamental aspects remain unchanged. Every GPS application ultimately involves the determination of platform position, velocity, and/or time.
However, the GPS signals are often susceptible to noise (Thermal Noise, Receiver Noise), interference (Electromagnetic Interference, Multipath Interference, Atmospheric Interference), attenuation, and errors during transmission, which can cause the bit flip errors at the binary level of the transmitted information. The impact of bit flip errors can range from minor deviations to significant shifts or complete loss of satellite lock, resulting in unreliable navigation information.
In order to over-come these challenges, various coding techniques are used to improve the reliability and robustness of GPS signals. Among these coding techniques, Convolutional codes and Viterbi algorithm have emerged as some of the most effective methods for error correction in GPS systems [1,2]. These techniques use a systematic approach to encoding and decoding data, based on the generation and evaluation of polynomials, ensuring that errors are corrected with high precision and minimized signal distortion.
The most challenge (causes bit flip error) exists in the channels used in Global Positioning System (GPS) and the Convolutional code and Viterbi algorithm can deal with, is representing in multipath fading [3].
When a signal is transmitted from a satellite, it can travel to the receiver in multiple paths, because of reflections off buildings, towers, and other objects. These paths can have different delays and attenuation levels, causing the signal to interfere with previous signals and distort itself at the receiver. This mean that the receiver will receive one message, but this message may be affected by Multipath fading, which can cause errors and distortions in the signal, or in other word, the receiver would receive only one message affected by multipath fading, and the different signals paths would combine at the receiver to create one composite signal that includes both the original message and the effects of multipath fading [4].
Despite these limitations, Convolutional codes and the Viterbi algorithm are still widely used in satellite communications today, particularly in Low-Earth orbit (LEO) satellite systems where communication delays are low and the channel conditions are relatively stable.
Specifically, Viterbi decoding is used in LEO satellite systems to mitigate the effect of multipath fading, which can cause severe errors in the received signal.
The main objective of the article is to assess and compare Convolutional codes and the Viterbi algorithm to other coding techniques employed in satellite communication systems. Focusing specifically on GPS systems, the article will evaluate their ability to correct errors, the level of computational complexity involved, power consumption considerations, and compatibility with existing hardware. Through this analysis, the article seeks to provide a deeper understanding of why Convolutional codes and the Viterbi algorithm are especially well-suited for GPS systems.
Other notable satellite communication systems that use Convolutional codes and the Viterbi algorithm include the Integrated Services Digital Broadcasting-Satellite (ISDB-S) system used in Japan, the Advanced Television Systems Committee (ATSC) standard used in North America, and the European Space Agency’s (ESA) EUMETSAT Meteorological Satellites.
While prior investigations have examined the application of Convolutional codes and the Viterbi algorithm in satellite communication systems, this study surpasses previous work by evaluating various performance metrics. These metrics encompass error correction capabilities, computational complexity, and resilience to diverse forms of errors. Furthermore, practical implementation factors such as power consumption, computational requirements, and compatibility with existing hardware are taken into account. Through shedding light on the strengths and weaknesses associated with each coding method, this analysis delivers clear insights into the suitability of Convolutional codes and the Viterbi algorithm for GPS systems.
The paper is structured as follows: In Section 2, a comprehensive review of existing research pertaining to error detection and correction codes utilized in satellite communications is presented. This section not only focuses on the efficiency assessment of various codes within communication systems but also includes comparisons between them. Additionally, Section 3 offers a detailed functional description of Convolutional Codes and the Viterbi algorithm employed for encoding and decoding information, as well as an exploration of potential error types encountered during signal transmission, such as single bit errors, random bit errors, and burst bit errors. In Section 4, the advantages of Convolutional Codes and the Viterbi algorithm are discussed in relation to other code types commonly employed in satellite communication systems. Finally, Section 5 and 6 provide a concise summary of the findings and draw general conclusions based on the research conducted.
2. Literature review
This literature review aims to synthesize and critically examine previous research on the efficacy of Convolutional Codes and the Viterbi Algorithm in GPS systems, in comparison to other coding techniques. Despite a paucity of studies specifically addressing this topic, it is important to note that many researches has been conducted on the efficiency of error detection and correction codes, including comparisons between various codes within the context of communication systems. This study will draw upon these prior investigations to elucidate the rationale for the selection of Convolutional Codes in GPS systems.
NASA has conducted a study that aims to achieve dependable communications at lower signal-to-noise ratios [5]. The research demonstrates simulation outcomes outlining the comparison between modified Convolutional codes with sequential decoding and NRBO (Non-Return-to-Zero Bit-Level One) codes. Showing that the Convolutional codes with sequential decoding achieve nearly the same performance as Turbo codes, but with improved computational complexity, as well as other aspects such as free and open architectures. Nevertheless, they did need large block sizes and high computational complexity to attain this performance. These advantages mentioned in the results of this paper, illustrate one of the reasons that makes Convolutional codes with sequential decoding a promising option for GPS communications systems, which require reliable and efficient communication over long distances.
Another study by Chopra, S.R., Kaur, J., and Monga, H. (2016) [6] provides a detailed analysis of different types of channel coding techniques, including block coding and Convolutional coding, and their performance in reducing bit error rates. The authors compared the performance of Hamming code, Reed Solomon code, and Convolution codes using bit error rate (BER) versus Eb/No performance with Binary Phase Shift Keying (BPSK) modulation. The simulation results showed that Convolution codes have better error controlling and correction capabilities in comparison to block codes, and among the block codes, the performance of Reed Solomon code is better comparatively.
Another study by Wang et al. (2021) [7] proposed a novel deep learning-based approach for identifying Convolutional codes with high accuracy and robustness, particularly in low signal-to-noise ratio (SNR) scenarios. The approach employs deep residual networks, eliminating the need for manual feature extraction. Experimental results indicate recognition accuracy exceeding 88% for 17 distinct forms of Convolutional codes. The approach is advantageous for applications such as cognitive radios and signal interception, where low SNR is a prevalent issue. Further investigation is necessary to ascertain its applicability to GPS systems .
In another study by Pandey and Pandey (2015) [8] conducted a comparative analysis of three types of error correction codes: BCH, Hamming, and convolution codes. Their results showed that for larger block sizes, Convolution codes outperformed both BCH and Hamming codes in terms of bit error rate (BER). However, for smaller block sizes, Hamming code performed better than both BCH and Convolution codes . The results of this paper have highlighted a number of advantages that lend credence to the viability of adopting Convolutional codes with sequential decoding as a viable solution for GPS communications systems that demand dependable and efficient communication across long distances.
In another study by Ayibapreye K. Benjamin and Collins E. Ouserigha (2020) [9] concludes that the implemented Convolutional codes with Viterbi decoding scheme can effectively improve the BER performance in satellite communication systems. The coding gain obtained for different coding rates demonstrates the effectiveness of the design.
Overall, in comparative studies, Convolutional codes and the Viterbi algorithm consistently outperform other coding methodologies like LDPC codes, turbo codes, and BCH codes in terms of complexity, efficiency, resistance to burst errors, and stream decoding capability. These advantages make them suitable for GPS communication systems with high data rates and relatively low error probability.
This study aims to provide a comprehensive assessment of the advantages and disadvantages of each coding method employed in satellite communication systems. By doing so, it offers valuable insights into why convolutional codes and the Viterbi algorithm are suitable for GPS systems.
3. General encoding and decoding algorithm
Convolutional codes are error correcting codes where the data streams of indefinite lengths are encoded before transmission over noisy channels. The message streams are encoded by the sliding application of Boolean functions that generate a sequence of output bits.
Convolutional codes and block codes do differ, with Convolutional codes incorporating memory in the encoding process. An (n, k, K) Convolutional code can be implemented with a k-input, n-output linear sequential circuit and "constraint length" K which defined as is defined as (K = m + 1, 1 represents the input bit encoded along with the bits stored in the m shift registers )[10], where m is the maximum number of stages (memory size) in any shift register. The encoder of convolution code for a binary (2, l, 3) code is shown in Figure 1. All Convolutional encoders can be implemented using a linear feedforward shift register of this type [11].
In practice, Convolutional codes are often designed based on a tradeoff between code performance and complexity. The choice of the specific number of bits or the length of the shift registers depends on factors such as the desired coding efficiency, the available hardware resources, and the complexity of the communication system being designed.
The code rate of a Convolutional code refers to the ratio of output bits to input bits. Together, the constraint length and code rate of a Convolutional code determine its error-correction capabilities. A longer constraint length and higher code rate generally result in better error correction, at the expense of increased computational complexity and bandwidth utilization [12]. The choice of the length of the shift registers determines the number of bits to be stored, which in turn determines the number of bits used to compute the output bits. Longer shift registers provide more memory and can result in better coding performance, but they also increase the complexity of the encoding and decoding processes. On the other hand, shorter shift registers provide less memory, and hence, less coding performance, but they also simplify the encoding and decoding processes [13] .
In the case of the GPS system’s Convolutional code, the constraint length is 7, which means that the encoder uses 7 previous input bits to generate the current output bit [14,15]. For the GPS system’s Convolutional code, the code rate is 1/2, which means that for every 2 input bits, the encoder generates 1 output bit. This results in a redundancy in the transmitted signal that makes it less susceptible to errors. As an example of constraint length size utilized in Convolutional codes, which has been employed since the Voyager program, possesses a constraint length of 7 and a rate of 1/2. In the case of the Mars Pathfinder, Mars Exploration Rover, and Cassini probe to Saturn, a code with a constraint length of 15 and a rate of 1/6 is employed. In the context of GSM, an error correction technique is utilized that employs a Convolutional code with a constraint length of 2 and a rate of 1/2 [16].
The encoding in convolutional codes can be represented in various equivalent ways, namely the Generator, Tree Diagram, State Diagram, and Trellis Diagram representations. However, our research will utilize the Trellis Diagram Representation.
- Trellis Diagram
Trellis diagram is a graphical representation of the code’s encoding process. The trellis diagram is a directed, a cyclic graph that displays all possible paths that the encoding process can take for a given input sequence. The trellis diagram consists of a set of nodes or state points that correspond to the internal state of the encoder and a set of branches that connect the state points. The branches represent the encoder’s output bits as they change from one state to another. Each state point in the trellis diagram represents a possible encoder state, and the branches emanating from each state point represent the possible output bits. The trellis diagram is arranged in such a way that the transitions between the state points correspond to the sequence of input bits being encoded.
To demonstrate the process of encoding using Convolutional codes through the Trellis Diagram, consider a scenario where the circuit is employed to encode the message (11011) and (k = 1, n = 2 and K = 2). Figure 2 shows a Convolutional Trellis Diagram encoder with k = 1, n = 2 and K = 2.
By utilizing the Convolutional Trellis Diagram encoder, the resulting codeword is depicted in Figure 3 and 4. This example has been selected due to its ability to clearly demonstrate the underlying principles of the aforementioned concept.
So, the codeword that the sender will send equal to 11,01,01,00,01,01,11, and that last zero bits are to flush the Flip flop shift registers and make them value equal to zero to prepare the encoder circuit for next encoding operation.
- Viterbi Algorithm
The trellis diagram is an essential tool for decoding Convolutional codes using the Viterbi algorithm. In the Viterbi algorithm, the trellis diagram is also used to determine the most likely sequence of input bits that produced a particular output sequence, based on the concept of finding the path with the minimum Hamming distance. In this paper, definitions have been established for two metrics, namely the branch metric (BM) and the path metric (PM). The branch metrics are Hamming distances/Euclidean distances/probabilities depending on the type of encoding. The path metric is a value associated with a state in the trellis. The equation used to update the path metric in the Viterbi algorithm is as follows [17]:
It is used to calculate the new path metric for each state in the trellis diagram, based on the previous path metrics and the branch metrics, where:
- PM [s, i+1] is the new path metric for state (s) at time i+1. It represents the likelihood of the most likely path through the trellis diagram that ends in state (s) at time i+1.
- PM [, i] is the previous path metric for state at time i. It represents the likelihood of the most likely path through the trellis diagram that ends in state at time i.
- B [, i] is the branch metric for transitioning from state at time i to state (s) at time i+1. It represents the similarity between the received signal and the expected signal for this state transition.
As mentioned, the equation calculates the new path metric for each state in the trellis diagram, based on the previous path metrics and the branch metrics. This process is repeated for each time step in the trellis diagram, until the final state is reached. The path metric for the final state represents the likelihood of the most likely path through the trellis diagram, and is used to determine the decoded sequence of bits.
The efficiency of this code is evaluated within the following conditions:
- 1.
-
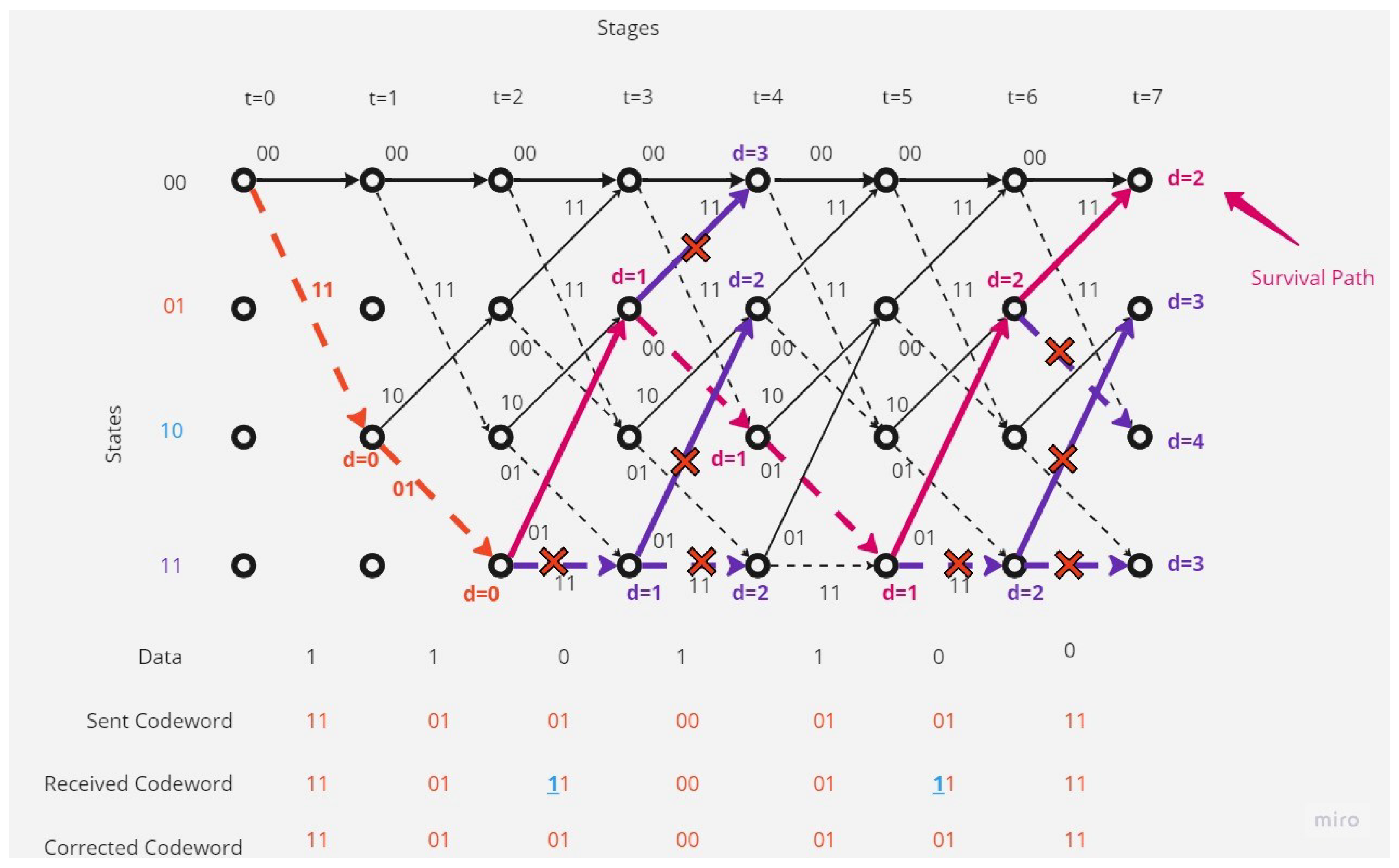
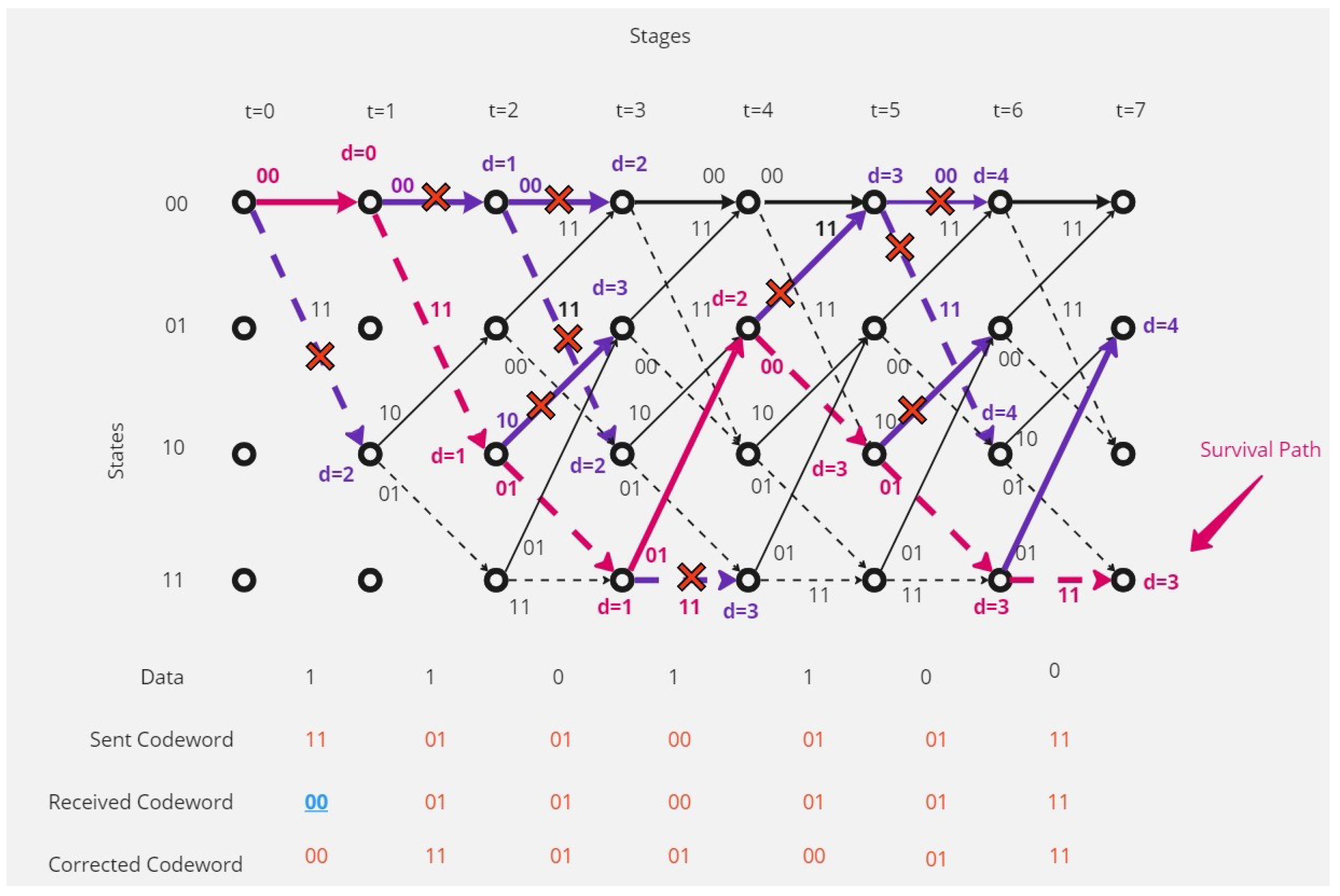
There is no error in the received codeword.In this case the decoding operation at the receiver point will as shown in the Figure 5:The receiver and depending on Viterbi algorithm found the correct code depending on the survival path (path with minimum hamming distance value, here it equal to 0).
- 2.
-
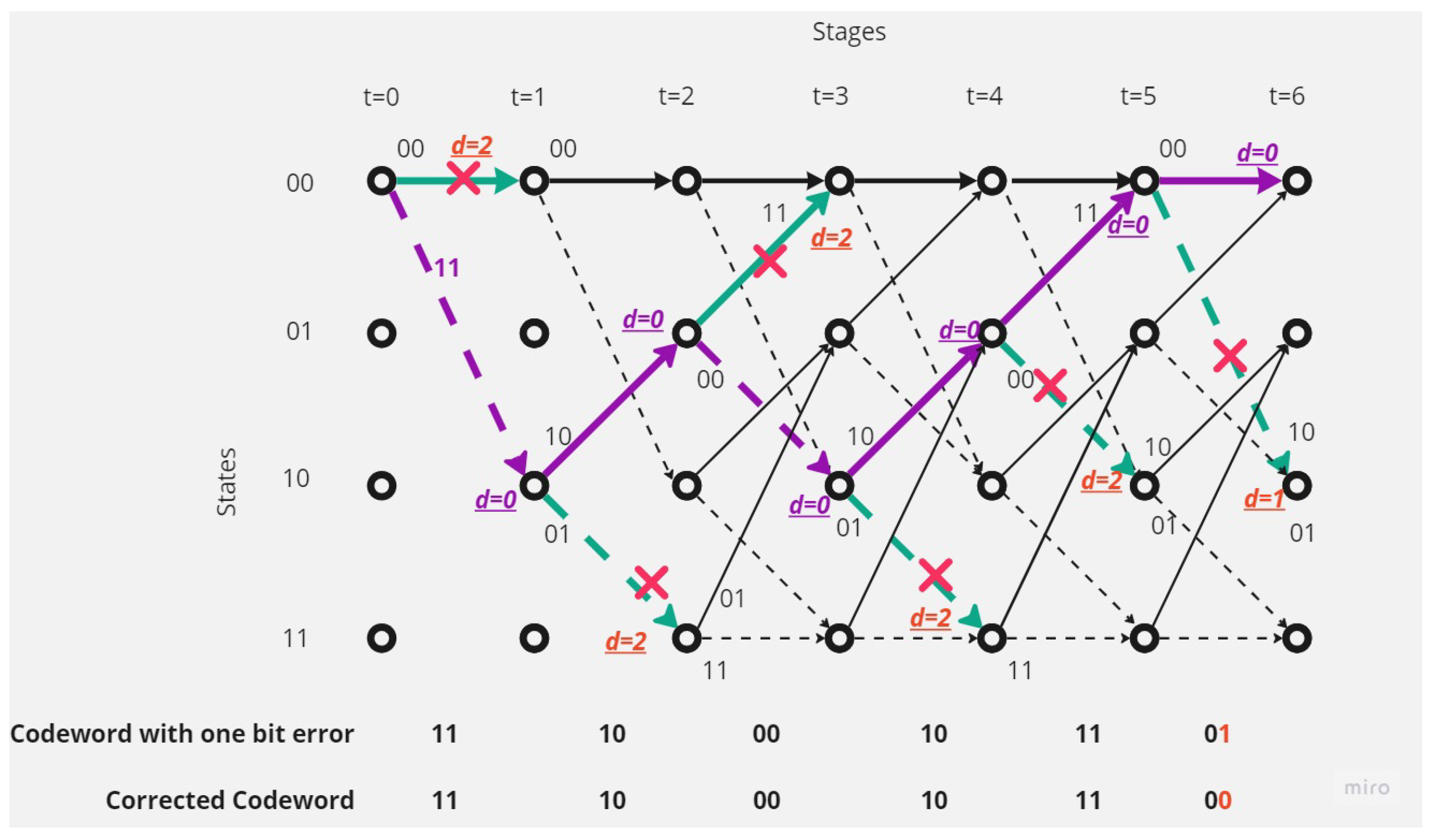
There is one error in the received codeword.Figure 6 shows that the receiver received a codeword with one-bit error.The receiver and depending on Viterbi algorithm found the error bit and corrected code depending on the survival path (path with minimum hamming distance value, here it is 1).
- 3.
-
There are separated errors in the received codeword.Figure 7 show that the receiver received a codeword with a separated two-bit error.The receiver and depending on Viterbi algorithm found the error bit and corrected code depending on the survival path (path with minimum hamming distance value, here it is 2).
- 4.
-
There are continuous (contiguous) errors in the received codeword.Figure 8 show that the receiver received a codeword with continuous errors.The receiver in this situation couldn’t detect the errors and the receiver could correct only 64.29% of the received codeword, and there are 35.71% of the received code word couldn’t correct it, and this shows the disadvantages of this type of coding and decoding method.
4. Comparative analysis Convolutional codes with LDPC codes, BCH codes and Turbo codes
Viterbi decoding algorithm is designed to mitigate errors caused by these signal distortions. It works by estimating the most likely data sequence that the satellite transmitted based on the observed received signal and the knowledge of the encoder. This involves searching a large number of possible data sequences and selecting the one that has the highest likelihood of being the transmitted data.
In the case of multipath fading, Viterbi decoding algorithm can track and compensate for the different signal delays and interference levels caused by the multiple signal paths. By comparing the decoded data sequence with the original data sequence, it can also detect and correct any errors that may have occurred due to signal distortions.
There are other types of codes that are used in satellite communications in addition to Convolutional codes [18,19], such as (LDPC codes, BCH codes, Turbo codes).
The question is, why can’t use one of these codes instead of Convolutional Code and Viterbi algorithm in GPS Systems?
Satellite communication systems often face challenges such as limited bandwidth, noise, and interference [20]. Convolutional codes and the Viterbi algorithm are well-suited to address these challenges, and their use in GPS communication systems is based on several requirements [21]:
- High data rate: Satellite communication systems typically need to transmit high volumes of data over long distances. Convolutional codes are efficient error-correcting codes that can operate at high data rates. They can be implemented in hardware or software and enable reliable transmission of large amounts of data.
- Channel characteristics: Satellite communication channels often suffer from fading and interference, which can cause errors and degradation of the transmitted signal. Convolutional codes and the Viterbi algorithm are designed to deal with such channel impairments. Convolutional codes are powerful because their encoding and decoding processes involve comparing the received signal with the expected signal. The Viterbi algorithm can estimate the most likely transmission sequence from a received signal in spite of channel distortions.
- Low computational complexity: Satellite communication systems often have limited computational resources due to power and size constraints. Convolutional codes and the Viterbi algorithm are computationally efficient and require relatively few resources, making them suitable for use in satellite communication systems.
- Real-time processing: Satellite signals must be processed in real-time to provide real-time communication services. The algorithm used for the decoding needs to be fast and efficient, which is another reason why the Viterbi algorithm is often used. The algorithm has been proven to decode signals in real-time, making it a good fit for satellite communication systems.
- Compatibility with modulation schemes: Convolutional codes can be used with a variety of modulation schemes, including phase-shift keying (PSK) and quadrature amplitude modulation (QAM). This makes them a versatile choice for satellite communication systems, where different modulation schemes may be used depending on the specific requirements of the system.
Based on the requirements of high data rate, channel characteristics, low computational complexity, real-time processing and Compatibility with modulation schemes, Convolutional codes with the Viterbi algorithm are well-suited to use in GPS systems.
4.1. Convolutional codes VS. LDPC codes
LDPC codes are known for their efficiency; however, decoding LDPC codes is more challenging compared to decoding Convolutional codes. Furthermore, LDPC codes require a larger memory capacity to store the parity check matrix used in the decoding process than Convolutional codes.
To comprehend the reasons behind the higher memory requirements for LDPC codes in comparison to Convolutional codes, we can observe the following:
In LDPC codes [22,23], the code matrix, denoted as the parity matrix H, plays a vital role in establishing the relationship between the message and the codeword. The parity matrix consists of (N-K) rows and N columns, where N represents the block length and K represents the message length. This matrix is essential for both encoding and decoding procedures, as it guides the transformation of messages into codewords and vice versa. The memory required to store the code matrix is directly proportional to the number of elements in the matrix, which is (N-K)xN.
The decoding process for LDPC codes involves the utilization of the message passing algorithm. This decoding method employs the parity matrix H and specific rules to update the probabilities of each bit in the codeword. Iterations of these updates continue until a solution is reached or a maximum limit is attained. The memory needed for decoding the code using the message passing algorithm is proportional to the number of elements in the matrix H, multiplied by the number of iterations I, which yields ((N-K)xN) · I.
In Convolutional codes [10,24], the generator matrix G is a (k,n) matrix consisting of polynomial entries. The generator matrix G defines the combination of input bits and shift register bits to generate the output bits. Each row in G corresponds to one output bit, and each column represents one input bit or one shift register bit. For example, if G=, it implies that the encoder has k = 2 output bits, n = 1 input bit, and m=2 shift register bits, and this because the generator matrix for a convolutional code is a matrix that describes how the input bits are encoded into output bits by using shift registers and modulo-2 additions. The number of rows of the generator matrix is equal to the number of output bits per input bit, which is denoted by k. The number of columns of the generator matrix is equal to the number of input bits plus the number of shift register bits, which is denoted by . The degree of each row of the generator matrix is equal to the number of feedback connections from the shift registers to that output bit [25].
In previous example, the generator matrix has two rows, so k = 2. It has three columns, so = 3. Since the first row has degree 1 and the second row has degree 2, there are two feedback connections in total, so m = 2. Therefore, n = 1.
The memory required to store the generator matrix G of the Convolutional code is depend on the size of the matrix. In general, the size of the matrix is determined by the rate and constraint length of the code.
To provide an example, let’s consider a rate 1/2 Convolutional code with s=64 states (m = 6 bits) and LDPC code with rate and a block length of N = 2048 bits. In this case, the generator matrix would have 2 rows and 12 columns. This is because each input bit is mapped to two output bits, and the encoder uses the current input bit as well as the five previous input bits to generate each pair of output bits. Therefore, the generator matrix will be 2 x 7. This is because k = 2 (the number of output bits per input bit) and n = 1 (the number of input bits). The number of columns is , which is 1 + 6 = 7. The size of memory needed for saving this matrix in Convolutional code depends on the data type and the format of the matrix. For example, if the matrix is stored as a binary array of 0s and 1s, then each element would take 1 bit of memory. The total size of the matrix would be 2 x 7 = 14 bits.
Conversely, the memory required to store the parity matrix H of the LDPC code is proportional to (N-K)xN = 2097152 bits. Clearly, the LDPC code demands significantly more memory to store the code matrix compared to the Convolutional code. The block length is the same for LDCP and Convolutional code in this example, but in encoding operation in Convolutional code the memory required to store the generator matrix G of the convolutional code depends only on the number of memory elements m and not on the block length.
The memory requirements for decoding also depend on the decoding algorithm employed. For Viterbi decoding of Convolutional codes, the memory needed is proportional to s· N = 131072. The result s · N = 131072 comes from multiplying the number of states s=64 by the block length N = 2048. This is the memory required to store the survivor paths in the Viterbi decoding algorithm. Each survivor path is a sequence of N bits that represents a possible input to the Convolutional encoder. The Viterbi decoder keeps track of s survivor paths at each decoding step and chooses the one with the minimum path metric as the most likely input. So as we mentioned before, the block length is important in encoding operation and its not in encoding operation. In message passing decoding of LDPC codes, the memory required [26] is proportional to (N-K)xN · I = 209715200. The result (N-K)xN · I = 209715200 comes from multiplying the number of parity bits (N-K) = 1024 by the block length N = 2048 by the number of iterations I = 100. This is the memory required to store the messages in the message passing decoding algorithm. Each message is a vector of N real numbers that represents the likelihood ratio of a bit being 0 or 1. The message passing decoder exchanges messages between the variable nodes and the check nodes in each iteration and updates the posterior probabilities of the bits. The number of iterations I = 100 is an arbitrary choice. It depends on the desired decoding performance and complexity. The more iterations, the better the performance, but also the higher the complexity. There is no fixed rule for choosing the number of iterations, but some common values are 10, 50, or 100.
Through this comparison, it becomes evident that the memory necessary for decoding LDPC codes is considerably higher than that required for Convolutional codes. Thus, the limited memory and in addition to other factors such as processing power available in GPS receivers makes it difficult to use LDPC codes. On the other hand, the Viterbi algorithm used with Convolutional codes provides less memory requirment and a low complexity alternative [27] and good balance of error correction performance and computational efficiency for GPS receivers Compared with LDPC codes. These are number of the advantages of using Convolutional codes over LDPC codes in GPS systems, while there are many more advantages to consider.
4.2. Convolutional codes VS. BCH codes
BCH codes are a class of cyclic error-correcting codes that are constructed using polynomials over a finite field. They have precise control over the number of symbol errors correctable by the code and can be decoded easily using an algebraic method known as syndrome decoding. They are used in various applications such as satellite communications, DVDs, QR codes and quantum-resistant cryptography.
One way to compare the complexity of BCH codes and Convolutional codes is to look at their encoding and decoding algorithms.
In order to explicate the intricacies involved, we shall consider a (15, 7) BCH code and a (2, 1, 2) Convolutional code as illustrative examples. These codes have been chosen due to their comparable error correcting capabilities. This is solely a simplified illustration, and the actual complexity may vary depending on the implementation and the code parameters.
BCH codes: They are a class of cyclic error-correcting codes that are constructed using polynomials over a finite field. They have precise control over the number of symbol errors correctable by the code and can be decoded easily using an algebraic method known as syndrome decoding. They are used in various applications such as satellite communications, DVDs, QR codes and quantum-resistant cryptography.
BCH encoding: It is the process of finding a polynomial that is a multiple of the generator polynomial, which is defined as the least common multiple of the minimal polynomials of some consecutive powers of a primitive element. The encoding can be either systematic or non-systematic, depending on how the message is embedded in the codeword polynomial.
To encode a message using BCH code, need to choose a finite field GF(q), a code length n, and a design distance d. Then need to find a generator polynomial g(x) that has ∝, ,…, as roots, where ∝ is a primitive element of GF() and n = - 1. Can be used the table of minimal polynomials in [28] to find g(x) as the least common multiple of some of them. Then multiply the message polynomial m(x) by g(x) to get the codeword polynomial c(x).
BCH decoding: It is the process of finding and correcting the errors in the received codeword using the syndromes, which are formed by evaluating the received polynomial at some powers of a primitive element. There are several algorithms for decoding BCH codes, such as Peterson’s algorithm, Forney algorithm, Sugiyama’s algorithm and Euclidean algorithm. They involve finding the error locator polynomial and the error values, and then subtracting them from the received codeword to recover the original one.
To decode a received word r(x) using BCH code, need to calculate the syndromes =r() for j = 1, 2, …, 2t, where t is the number of errors that can be corrected. Then use an algorithm such as Peterson’s algorithm or Euclidean algorithm to find the error locator polynomial that has the error locations as roots. Then use another algorithm such as Forney’s algorithm to find the error values at those locations. Finally, correct the errors by subtracting them from the received word to get the original codeword.
For example, suppose we want to encode the message [1 0 1 0] using a binary BCH code with n = 15 and d = 7, it is recommended to choose GF(2) as the finite field and use the reducing polynomial +z+1 and the primitive element =z as in [28]. Then can find the generator polynomial g(x) as:
Please note that the lcm, which stands for least common multiple, is responsible for ensuring that g(x) contains all the necessary roots required for BCH encoding.
Now, The message polynomial is m(x) =+x, so the codeword polynomial is
c(x) = m(x)g(x) = (+x)(++++1) =+++++x
The codeword is [0 0 0 0 1 0 1 1 1 0 1 1 0 0 0].
Suppose receive the word r(x) = [0 0 0 0 1 0 1 0 1 0 1 1 0 0 0], which has two errors at positions = 8 and = 10. The syndromes can be computed as follows:
= = ∝ = = ∝ = = ∝ = = ∝ = = ∝ = = ∝
Peterson’s algorithm can be used to find the error locator polynomial and as following:
while Forney’s algorithm can be employed to find the error values, and as follwoing:
To fix the errors, you can subtract them from the received word, and as following:
This is the same as the original codeword.
The complexity and the number of operations required for encoding and decoding BCH codes depend on the parameters of the code, such as the code length, the design distance, and the number of errors. Here are some general formulas for estimating the complexity:
For encoding, the complexity is proportional to the degree of the generator polynomial g(x), which is at most (), where m is the extension degree of the finite field and t is the number of errors that can be corrected. The number of operations is O() for binary BCH codes and O( log q) for non-binary BCH codes, where q is the size of the finite field.
For decoding, the complexity is proportional to the number of syndromes that need to be computed and processed, which is () for binary BCH codes and t for non-binary BCH codes. The number of operations is O( log n) for binary BCH codes and O( log q) for non-binary BCH codes, where N is the code length.
The given example is a binary BCH code because the finite field used is GF(2), which has only two elements (0 and 1).
Our objective entails the determination of the computational workload involved in both encoding and decoding a message within the provided example. The ultimate goal is to assess the inherent complexity embedded within the BCH code and subsequently conduct a comparative analysis between such complexity and the counterpart system comprised of Convolutional codes.
To know the number of encoding operation in BCH in the given example, we need to multiply the message polynomial m(x) by the generator polynomial g(x) to get the codeword polynomial c(x). The degree of g(x) is 8, which is equal to (), where and . The number of operations is O() = O() = for binary BCH codes. This means that you need at most 16 operations in GF(2) to encode the message.
For decoding, need to calculate the syndromes, find the error locator polynomial, find the error values, and correct the errors. The number of operations depends on the number of errors and the algorithm used. For binary BCH codes, the number of operations is O() for calculating the syndromes, O() for finding the error locator polynomial using Peterson’s algorithm or O() using Euclidean algorithm, O() for finding the error values using Forney’s algorithm, and O() for correcting the errors. The total number of operations is O() for Peterson’s algorithm or O() for Euclidean algorithm. In this example, and , so the total number of operations is at most 128 for Peterson’s algorithm or 64 for Euclidean algorithm(note, this is the maximum number of operation, this means that the number of operation may be less than these numbers).
On the other hand, to encode the message [1 0 1 0] using a convolutional code (2, 1, 2), it is necessary to utilize the State Transition Table and the encoder circuit illustrated in Figure 3. Subsequently, the following operations need to be performed:
- Set all memory registers to zero.
- Feed the input bits one by one and shift the register values to the right.
- Calculate the output bits using the generator polynomials = (1,1,1) and = (1,0,1).
- Append two zero bits at the end of the message to flush the encoder.
For each input bit, we need to perform two additions and no multiplications. The total number of operations for encoding a message of length N plus m (m for the number of zeros that need to flush the shift registers), therefore the total number of operations for encoding a message of length N is 2N + m.
Figure 9, shows the encoding operation using Trellis diagram :
Figure 10, shows the decoding operation using Viterbi algorithm:
Figure 9.
Message encoding using convolutional code (2,1,2).
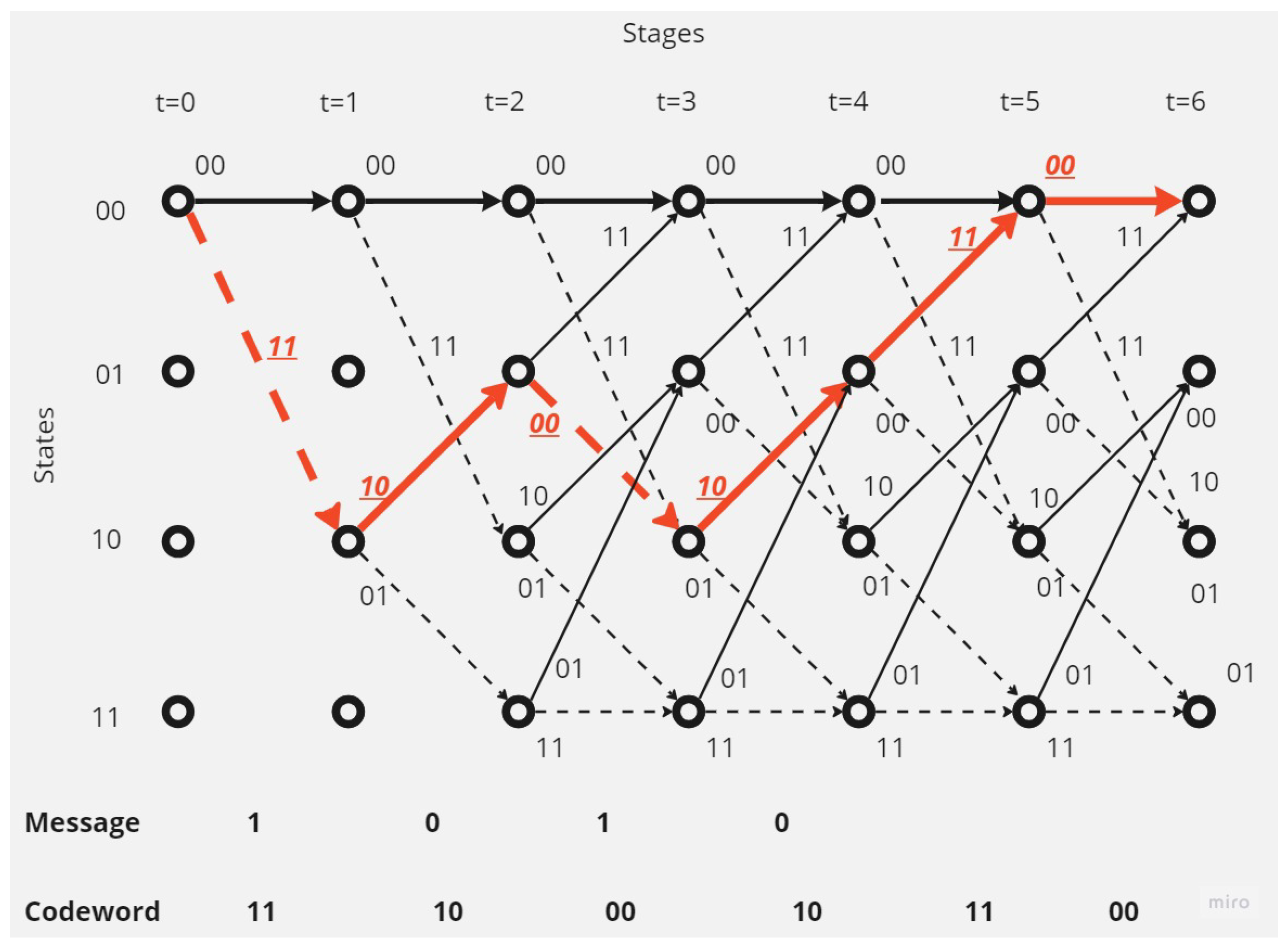
Figure 10.
Codeword decoding operation using Viterbi Algorithm.
For encoding a message of length N = 4, we need to perform 2N+2 = 10 additions and no multiplications. For decoding a message of length N = 4+2 = 6 with four states in the trellis diagram, we need to perform approximately =96 additions and 48 comparisons (there are 8 possible transitions per time step and 6 time steps for a message of length 4+2=6). Therefore, there are =48 comparisons for these time steps (note, that the total of comparisons is less than 48, because the comparisons number in time step 1 and 2 is less than 8).
Another way to compare the complexity of BCH codes and Convolutional codes is to look at their codeword lengths. BCH codes tend to produce longer codewords than Convolutional codes for the same message length and error-correcting capability. This is because BCH codes have a fixed codeword length that depends on the size of the finite field, while Convolutional codes have a variable codeword length that depends on the constraint length and the code rate. For example, a (63,51) BCH code can correct up to 2 errors per codeword, while a (3,1) Convolutional code with constraint length 7 can correct up to 5 errors per codeword. However, the BCH code has a codeword length of 63 bits, while the Convolutional code has a codeword length of 21 bits for a message length of 7 bits [29,30].
When comparing the encoding and decoding operations, it is evident that Convolutional codes require fewer steps compared to BCH codes. Additionally, the mathematical operations involved in BCH codes are more complicated than in Convolutional codes. However, Convolutional codes still face a fundamental issue known as exponential complexity. Despite this drawback, Convolutional codes are considered the most appropriate choice for GPS communication systems.
Overall, the high complexity associated with BCH codes makes them unsuitable for implementation in GPS systems and real-world applications. Consequently, Convolutional codes with Viterbi decoding, which are less computationally complex, are preferred over BCH codes..
4.3. Convolutional codes VS. Turbo codes
Turbo codes are a type of forward error correction codes that use two or more Convolutional codes in parallel with an interleaver [19]. They have high performance and can achieve near-Shannon limit error correction capacity [31]. However, they also have some drawbacks, and two of them are:
First Drawback:Turbo codes require complex encoding and decoding algorithms that require significant computing power.
The encoding process involves two or more Convolutional encoders and an interleaver, while the decoding process involves soft-input soft-output decoders that use either the log-MAP or the max-log-MAP algorithm. Numerous studies have focused on addressing the issue of power consumption caused by Turbo codes. For instance, a study conducted by Oliver Yuk-Hang Leung, Chung-Wai Yue, Chi-ying Tsui, and Roger S. Cheng at Hong Kong University of Science and Technology [32], examined the complexities and high power consumption associated with decoding Turbo codes in receivers. The authors presented potential solutions to this problem in their research.
Second Drawback:The use of a turbo code may increase the processing time of the GPS receiver, which may result in a delay in receiving and processing GPS signal data.
This is because the decoding algorithm requires multiple iterations to converge to a reliable solution, and each iteration involves matrix operations and logarithmic calculations, and this because the computational complexity involved in Turbo codes leads to increased power consumption. In computer science and engineering, it is widely recognized that there is a trade-off between complexity, power, and time. More complex codes or models require additional resources such as memory, processing power, and energy for storage and operation, resulting in longer execution times and higher power consumption. The complexity of Turbo codes compared to Convolutional codes has been explored in various studies, including a research conducted by David J.C. MacKay [33].
Thus, GPS systems often use Convolutional codes due to their lower computational complexity (compared to other codes types using satellite communications systems) and faster decoding time, yet they are effective for error correction.
In addition to information mentioned, one of the most Reasons that makes Convolutional codes suitable for GPS Systems is that block codes are typically slower than Convolutional codes for the following reasons:
- Block codes require larger block sizes to achieve the same level of error protection as convolutional codes. The larger block size means more bits need to be processed, which can slow down the system.
- Block codes require more complex encoding and decoding algorithms than Convolutional codes, which can also slow down the system. Convolutional codes use a shift register and some XOR gates to generate the parity bits, which is a simpler process than the matrix multiplication required for block codes.
- Error detection and correction are more efficient in Convolutional codes than block codes. Convolutional codes can detect and correct errors in real-time, while block codes require the entire block to be received before errors can be corrected.
Overall, while block codes can offer more robust error correction, they require more complex algorithms and larger block sizes, which can make them slower than convolutional codes in some applications like GPS systems. Therefore, BCH, LDPC, and turbo codes are not suitable for GPS systems. Also, difficulties in LDPC, BCH, Turbo codes make them require:
- More memory to store the parity check matrix used for decoding;
- Significant processing power, which can be problematic for low-power and low-cost GPS devices that are commonly used in commercial applications;
- Slow encoding and decoding operation.
On the other hand, Convolutional codes and the Viterbi algorithm can offer a favorable balance of computational efficiency and error correction performance specifically suited for Global Positioning System (GPS) receivers.
5. Conclusions
Convolutional codes and the Viterbi algorithm are two efficient methods used for error-correction in satellite communication systems, particularly in GPS systems. Convolutional codes are effective error-correcting codes that can work at high data rates and demand relatively few resources, thus making them a suitable choice for employment in GPS systems. In contrast, the Viterbi algorithm is computationally efficient and can estimate the most probable transmission sequence from a received signal in real-time, making it an appropriate choice for GPS systems. Other efficient coding methods, such as LDPC codes and Turbo codes, which have a high computational complexity and memory requirements, may not be compatible with the limited processing power and low-cost devices used in commercial applications, making them less well-suited for GPS systems.
Over all the advantage of Convolutional codes is that they can achieve high coding gains with relatively low decoding complexity. However, the performance of Convolutional codes can be limited by their constraint length (the number of bits that each input bit is dependent on), and they may not be able to correct bursts of errors as effectively as other error-correcting codes.
Acknowledgments
This research was funded by the Ministry of Science and Higher Education of the Russian 128 Science Foundation (Project "Goszaadanie" No 075-01024-21-02 from 29.09.2021, FSEE-2021-0015).
Abbreviations
The following abbreviations are used in this manuscript:
| LDPC codes | Low-Density Parity Check (LDPC) codes |
| BCH codes | The Bose, Chaudhuri, and Hocquenghem (BCH) codes |
| EUMETSAT | European Organisation for the Exploitation of Meteorological Satellites (EUMETSAT) |
References
- Ripa, H.; Larsson, M. A Software Implemented Receiver for Satellite Based Augmentation Systems. Master’s thesis, Luleå University of Technology, 2005.
- Wikipedia contributors. GPS signals — Wikipedia, The Free Encyclopedia, 2023. [Online; accessed 30-August-2023].
- Gao, Y.; Cui, X.; Lu, M.; Li, H.; Feng, Z. The analysis and simulation of multipath error fading characterization in different satellite orbits. China Satellite Navigation Conference (CSNC) 2012 Proceedings. Springer, 2012, pp. 297–308.
- Gao, Y.; Yao, Z.; Cui, X.; Lu, M. Analysing the orbit influence on multipath fading in global navigation satellite systems. IET Radar, Sonar & Navigation 2014, 8, 65–70. [Google Scholar]
- Morakis, J. A comparison of modified convolutional codes with sequential decoding and turbo codes. 1998 IEEE Aerospace Conference Proceedings (Cat. No.98TH8339), 1998, Vol. 4, pp. 435–439 vol.4. [CrossRef]
- Chopra, S.R.; Kaur, J.; Monga, H. Comparative Performance Analysis of Block and Convolution Codes. Indian Journal of Science and Technology 2016, 9, 1–6. [Google Scholar] [CrossRef]
- Wang, J.; Tang, C.; Huang, H.; Wang, H.; Li, J. Blind identification of convolutional codes based on deep learning. Digital Signal Processing 2021, 115, 103086. [Google Scholar] [CrossRef]
- Pandey, M.; Pandey, V.K. Comparative Performance Analysis of Block and Convolution Codes. International Journal of Computer Applications 2015, 119, 43–7. [Google Scholar] [CrossRef]
- Benjamin, A.K.; Ouserigha, C.E. Implementation of Convolutional Codes with Viterbi Decoding in Satellite Communication Link using Matlab Computational Software. European Scientific Journal (ESJ) 2021, 17, 1. [Google Scholar] [CrossRef]
- Huang, F.h. Convolutional Codes; Springer, 2010.
- Ass.Prof.Dr.Thamer. Convolution Codes. https://uotechnology.edu.iq/dep-eee/lectures/4th/Communication/Information%20theory/4.pdf, Unknown. Accessed on: [Insert date here].
- G. DAVID FORNEY, J. G. DAVID FORNEY, J. The Viterbi Algorithm. PDF file, 1973.
- Ivaniš, P.; Drajić, D. Information Theory and Coding-Solved Problems; Springer, 2017.
- Dafesh, P.; Valles, E.; Hsu, J.; Sklar, D.; Zapanta, L.; Cahn, C. Data message performance for the future L1C GPS signal. Proceedings of the 20th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2007), 2007, pp. 2519–2528.
- Corraro, F.; Ciniglio, U.; Canzolino, P.; Garbarino, L.; Gaglione, S.; Nastro, V. An EGNOS Based Navigation System for Highly Reliable Aircraft Automatic Landing.
- Wikipedia contributors. Convolutional code — Wikipedia, The Free Encyclopedia, 2023. [Online; accessed 31-July-2023].
- Dalal, D. Convolutional Coding And Viterbi Decoding Algorithm.
- Wikipedia contributors. BCH code — Wikipedia, The Free Encyclopedia, 2023. [Online; accessed 31-July-2023].
- Wikipedia contributors. Turbo code — Wikipedia, The Free Encyclopedia. https://en.wikipedia.org/w/index.php?title=Turbo_code&oldid=1106388136, 2022. [Online; accessed 31-July-2023].
- Al-Hraishawi, H.; Chatzinotas, S.; Ottersten, B. Broadband non-geostationary satellite communication systems: Research challenges and key opportunities. 2021 IEEE International Conference on Communications Workshops (ICC Workshops). IEEE, 2021, pp. 1–6. [CrossRef]
- Chen, C.L.; Rutledge, R.A. Error Correcting Codes for Satellite Communication Channels. IBM Journal of Research and Development 1976, 20, 168–175. [Google Scholar] [CrossRef]
- Lee, J.S.; Thorpe, J. Memory-efficient decoding of LDPC codes. Proceedings. International Symposium on Information Theory, 2005. ISIT 2005., 2005, pp. 459–463. [CrossRef]
- Wikipedia contributors. Low-density parity-check code — Wikipedia, The Free Encyclopedia, 2023. [Online; accessed 3-September-2023].
- Lahtonen, J. Convolutional Codes. https://www.karlin.mff.cuni.cz/~holub/soubory/ConvolutionalCodesJyrkiLahtonen.pdf, 2004. [Online; accessed 3-September-2023].
- Petac, E.; Alzoubaidi, A.R. Convolutional codes simulation using Matlab. 2004 IEEE International Symposium on Signal Processing and Information Technology. IEEE, 2004, pp. 573–576. [CrossRef]
- Kurkoski, B. Introduction to Low-Density Parity Check Codes. http://www.jaist.ac.jp/~kurkoski/teaching/portfolio/uec_s05/S05-LDPC%20Lecture%201.pdf, 2005. Accessed on: [Insert date here].
- Tahir, B.; Schwarz, S.; Rupp, M. BER comparison between Convolutional, Turbo, LDPC, and Polar codes. 2017 24th international conference on telecommunications (ICT). IEEE, 2017, pp. 1–7. [CrossRef]
- Wikipedia contributors. BCH code — Wikipedia, The Free Encyclopedia, 2023. [Online; accessed 7-September-2023].
- Jiang, Y. Analysis of Bit Error Rate Between BCH Code and Convolutional Code in Picture Transmission. 2022 3rd International Conference on Electronic Communication and Artificial Intelligence (IWECAI), 2022, pp. 77–80. [CrossRef]
- FEC Codes bch code, 2023. Accessed: Sun, 03 Sep 2023.
- Hrishikesan, S. Error Detecting and Correcting Codes in Digital Electronics, 2023.
- Leung, O.H.; Yue, C.W.; Tsui, C.Y.; Cheng, R. Reducing power consumption of turbo code decoder using adaptive iteration with variable supply voltage. Proceedings. 1999 International Symposium on Low Power Electronics and Design (Cat. No.99TH8477), 1999, pp. 36–41. [CrossRef]
- MacKay, D.J. Information Theory, Inference, and Learning Algorithms, 2003. Accessed on [insert date here].
Figure 1.
Convolution code for a binary (2, l, 3).
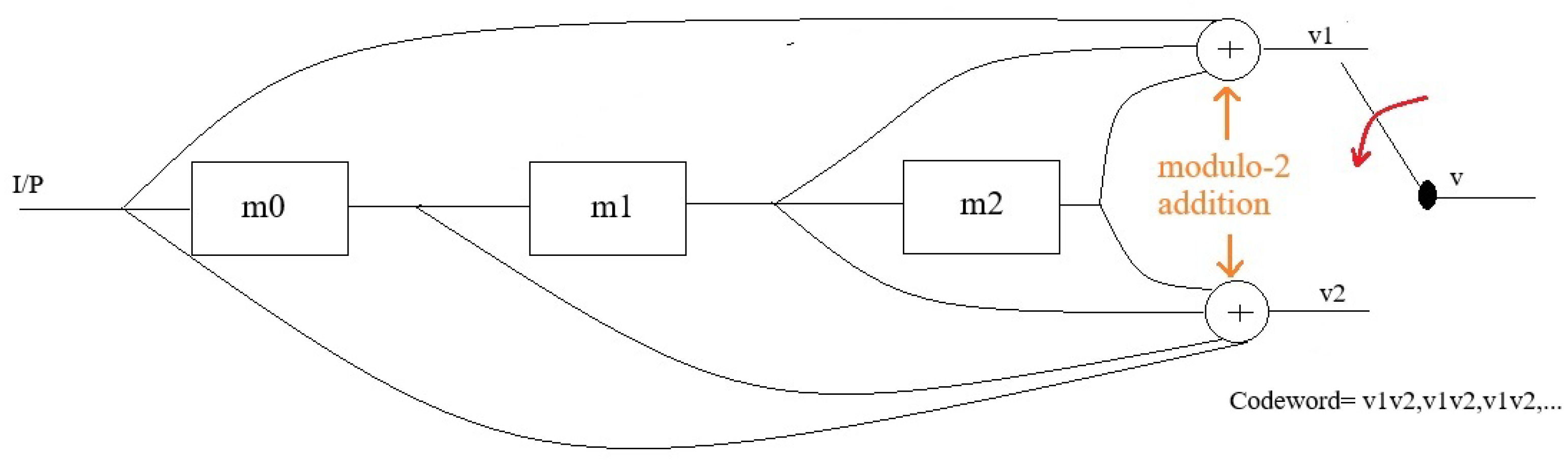
Figure 2.
Convolutional Trellis Diagram encoder.
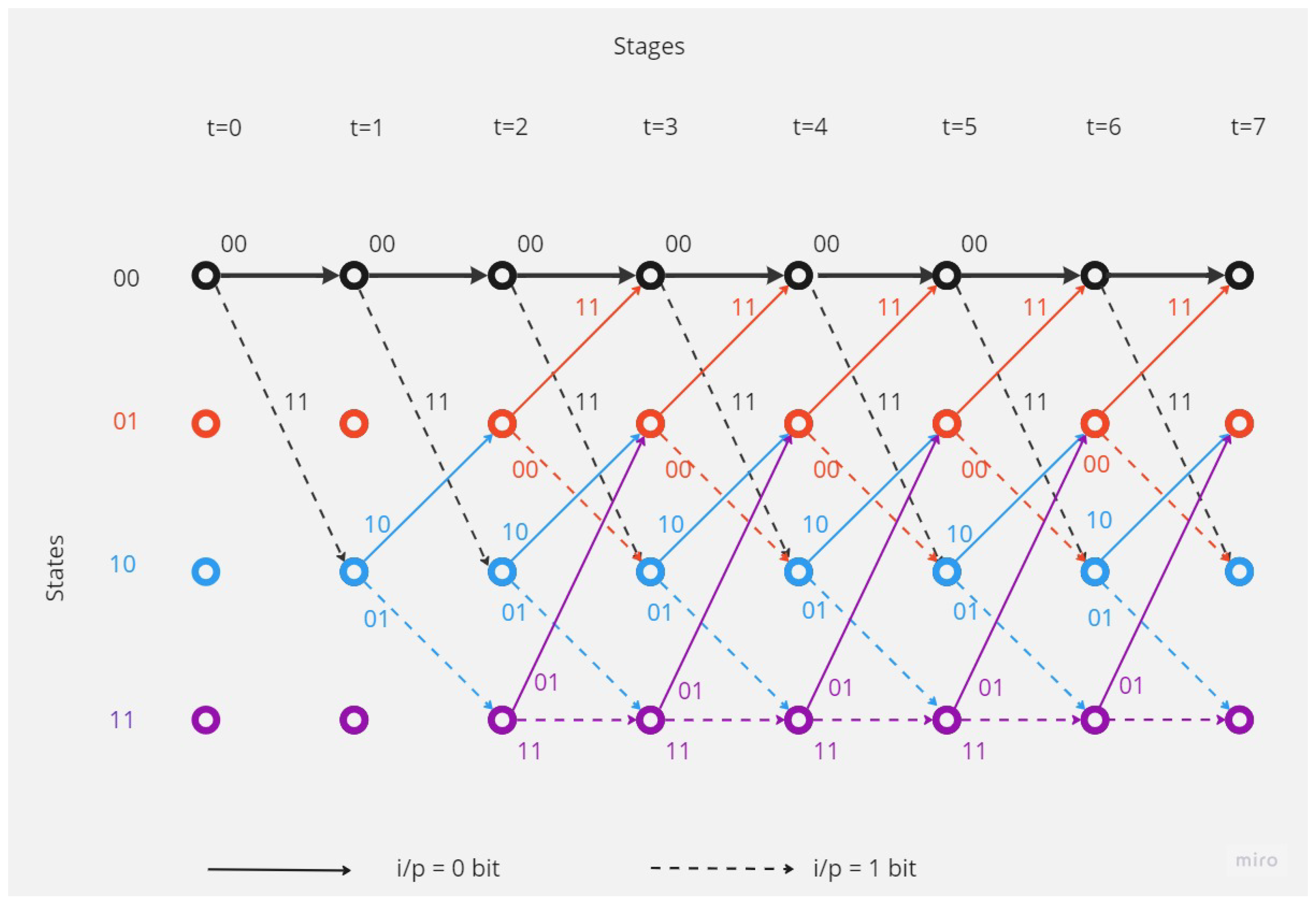
Figure 3.
Convolutional Trellis Encoder Circuit and the State Translation Table.
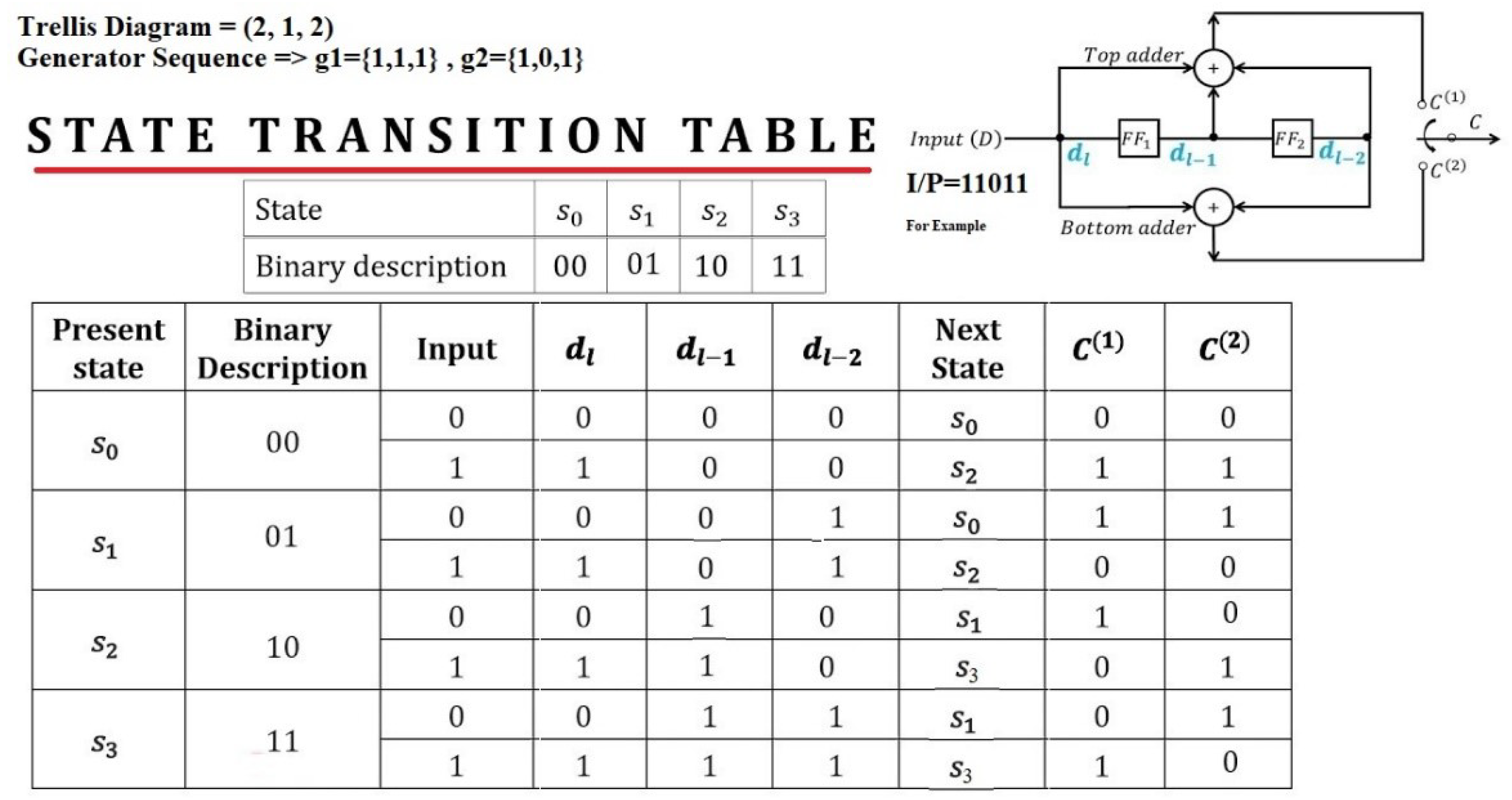
Figure 4.
Convolutional Encoding Message Operation.
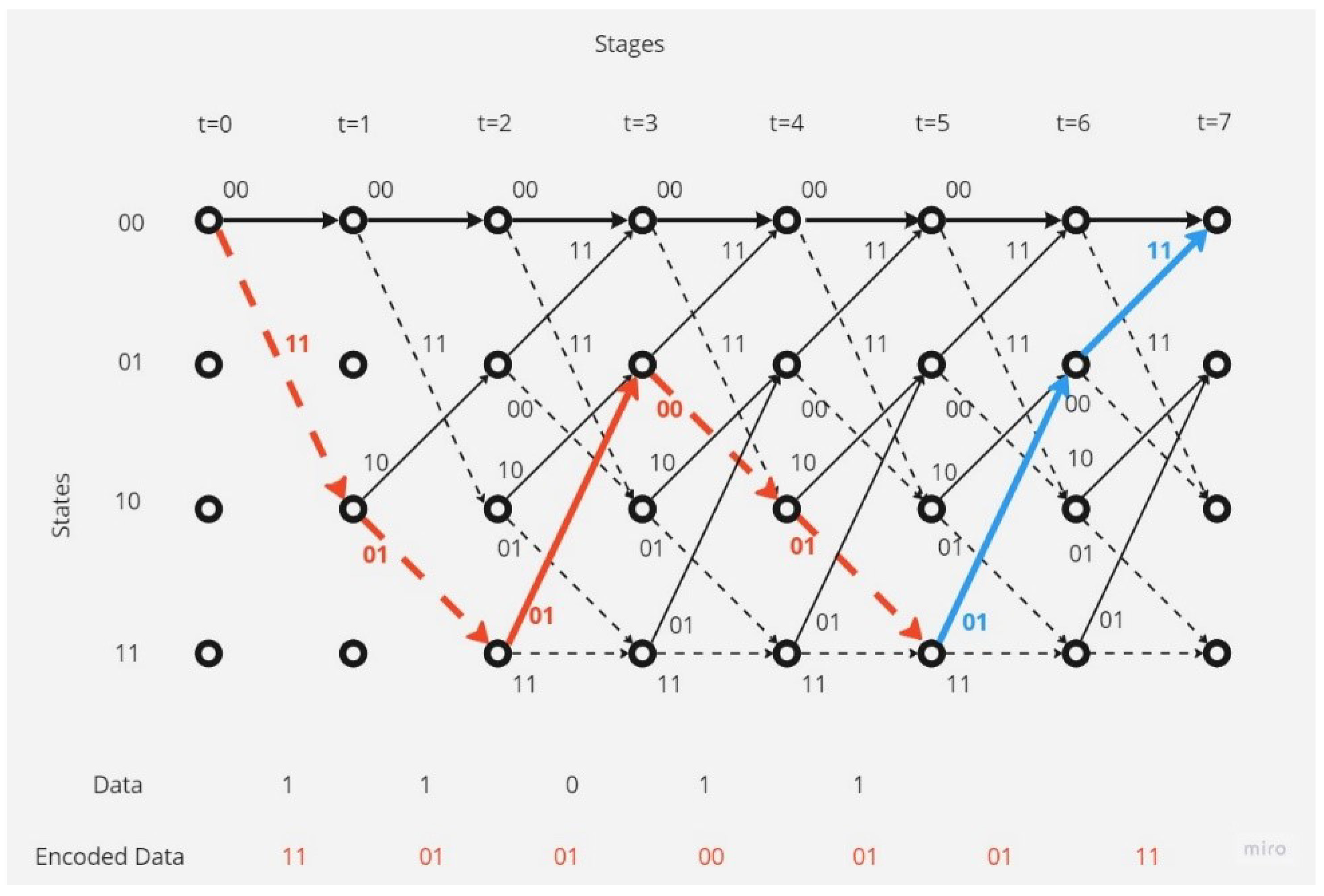
Figure 5.
Convolutional Decoding operation through Viterbi algorithm.
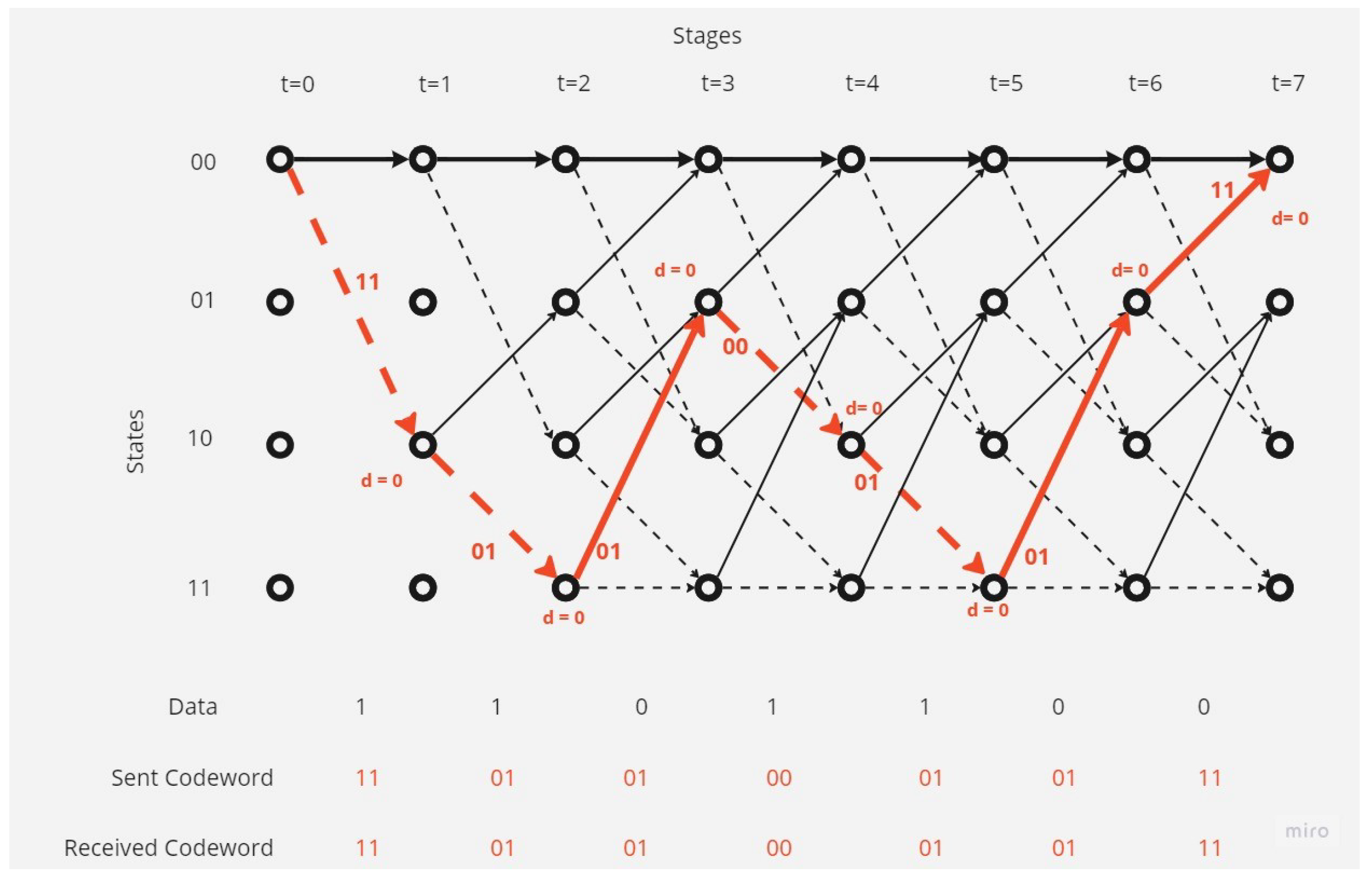
Figure 6.
Received a codeword with one-bit error.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated