Novel Method for Ranking Generalized Fuzzy Numbers Based on Normalized Height Coefficient and Benefit and Cost Areas

Preprint

Article

Novel Method for Ranking Generalized Fuzzy Numbers Based on Normalized Height Coefficient and Benefit and Cost Areas

Altmetrics

Downloads

108

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

15 September 2023

Posted:

18 September 2023

You are already at the latest version

Alerts

Abstract

To avoid loss of information and incorrect ranking, this paper proposes a method for ranking generalized fuzzy numbers, which guarantees both horizontal and vertical values are important parameters affecting the final ranking score. In this method, the normalized height coefficient is introduced to evaluate the influence of the height of fuzzy numbers on the final ranking score. The higher the normalized height coefficient of a fuzzy number is, the higher its ranking. The left area and the right area are presented to calculate the impact of vertical value on the final ranking score. The left area is considered the benefit area. The right area is considered the cost area. The fuzzy number is preferred if the benefit area is larger and the cost area is smaller. The proposed method can be employed to rank both normal and non-normal fuzzy numbers without normalization or height minimization. Numerical examples and comparison with other methods highlight the feasibility and robustness of the proposed method, which can overcome the shortcomings of some existing methods and can support decision-makers to select the best alternative.

Keywords:

Subject: Computer Science and Mathematics - Applied Mathematics

1. Introduction

Ranking fuzzy numbers is a very important issue in fuzzy sets theory and applications and has been extensively researched (Wang & Luo, 2009). Some ranking methods have been reviewed and compared by Bortolan & Degani (1985), Brunelli & Mezei (2013), and Chu & Kysely (2021). Nevertheless, none of these methods can always guarantee a consistent result in every situation, and some are even unintuitive and indiscriminate (Chou et al., 2011). Especially, when fuzzy numbers are non-normal, some methods used height minimization (

\min w_{i}

) or normalization, which leads to information loss (Yu et al., 2013; Chi & Yu, 2018). Methods used

\min w_{i}

include the maximizing set and minimizing set for ranking fuzzy numbers (Chen, 1985), and the rank and mode approach for ranking generalized fuzzy numbers (Kumar et al., 2011). The method used the normalization is ranking fuzzy numbers with integral value (Liou & Wang, 1992).

It is impossible to define the boundary of the membership function of a fuzzy number in normal form. Thus, most recent studies have focused on taking into account the height of the fuzzy number to avoid loss of information, and incorrect ranking (Chi & Yu, 2018). However, such studies have some limitations. Chen & Chen (2009) pointed out that three factors affect ranking score: the defuzzified value, height, and spread. The defuzzified value and height of a generalized fuzzy number are the major factors determining its ranking score; the spread is only a minor factor. However, Kumar et al., (2011) indicated that the ranking function proposed by Chen & Chen (2009) does not satisfy the reasonable property

\tilde{A} ≻ \tilde{B} \Rightarrow (\tilde{A} - \tilde{B}) ≻ (\tilde{B} - \tilde{A})

for the ordering of fuzzy quantities which is a contradiction according to Wang & Kerre (2001) (see Example 1 in Section 2.3). Chen & Sanguansat (2011) considered the areas on the positive side, the areas on the negative side and the height of the generalized fuzzy numbers to evaluate the ranking score of the generalized fuzzy numbers. Xu et al. (2012) pointed out that in the situation when the score is zero, the results of the Chen and Sanguansat’s ranking method (2011) ranking method are unreasonable. Chi & Yu (2018) proposed ranking generalized fuzzy numbers based on the centroid and rank index, which prevents the truncation of heights during comparison. To avoid information loss, the original height of given fuzzy number is retained and considered an important factor to affect the ranking of the generalized fuzzy numbers. However, this considers three factors, namely, the centroid, rank and mode, and height, as discrete factors, with height being the least influential, leading to incorrect final ranking results (see Example 2 in Section 2.3). De et al. (2020) indicated that the height of fuzzy numbers plays essential role in preventing information loss. This study considers centroid point, rank index, and height for ranking interval type-2 fuzzy numbers. However, this method cannot be used to rank fuzzy numbers with different centroids and heights (see Example 3 in Section 2.3). Revathi & Valliathal (2021) used centroid method for ordering non-normal fuzzy numbers with more parameters is investigated using level analysis, which gives flexibility to the expert’s opinion. Nguyen & Chu (2023) proposed a DEMATEL-ANP-Based fuzzy PROMETHEE II to rank startups in which areas based on a subject confidence level was suggested and height was not considered. He et al. (2023) introduced a new fuzzy distance based on a novel interval distance that considers all points within the intervals by using the concept of integration to calculate the average distance between all points belonging to two intervals, respectively.

Jain (1977) proposed maximizing set to rank fuzzy numbers and restricted the membership function

f_{A} (x)

to the normal form. Chen (1985) developed the maximizing set and minimizing set for generalized fuzzy numbers. However, this paper chose

w_{i} = \sup_{x} f_{A_{i}} (x), w = \inf w_{i}

, this method fails to rank the same fuzzy numbers with different heights (see Example 4 in Section 2.3). Wang et al. (2009) based on maximizing set and minimizing set developed the deviation degree method. According to Chutia (2017) the expectation value of the centroid points involved in the epsilon deviation degree method does not influence the heights of fuzzy numbers, which leads to an incorrect ranking of non-normal fuzzy numbers (illustrated in Example 4 in Section 2.3). Furthermore, in the case where

λ = 0 and 1 - λ = 0

, when the left deviation degree and the right deviation degree are multiplied by these values, they become valueless (Nejad & Mashinchi, 2011b). Wang & Luo (2009) proposed ranking indices based on areas and considered maximizing set and minimizing set as positive ideal point and negative ideal point, respectively. However, this study does not consider the height of fuzzy numbers, therefore it fails to rank non-normal fuzzy numbers (as shown in Example 4 in Section 2.3). Asady (2010) revised the deviation degree method with the new left and right areas. However, Hajjari & Abbasbandy (2011) pointed out that Asady’s revision has a shortcoming the same as Wang’s (2009) method. Nejad & Mashinchi (2011) proposed ranking fuzzy numbers based on the areas on the left and the right sides. To prevent the values of

λ = 0 and 1 - λ = 0

, and

S_{i}^{R} = 0 and S_{i}^{L} = 0

, in any collection including the fuzzy number

A_{i}, i = 1, 2, ....., n

, two triangular fuzzy numbers,

A_{0} and A_{n + 1}

, are added. Yu et al. (2013) pointed out that Asady (2010) and Nejad & Mashinchi (2011) redefined the deviation degree of a fuzzy number to overcome the shortcomings of Wang et al. (2009). However, most methods based on the deviation degree approach exhibit the same limitations due to neglect of the decision-makers’ attitude, incoherent transfer coefficient formulas, and unreliable ranking index computation. Chutia (2017) proposed a method for ranking fuzzy numbers by using value and angle in the epsilon-deviation degree method. This method also has some limitations, which are illustrated in Example 5 in Section 2.3. The historical timeline of the aforementioned research is presented in the following chart.

To overcome the aforementioned obstacles, this paper proposes a method for ranking generalized fuzzy numbers based on the left area (benefit area), the right area (cost area) and a normalized height coefficient. In this method, the left area denotes the area from

x_{\min}

x^{L}

and is bounded by the maximizing membership function

f_{M}

and minimizing membership function

f_{G}

. A ranking is higher if the left area is larger; therefore, the left area is considered the benefit area. The right area denotes the area from

x_{\max}

x^{R}

and is bounded by the maximizing membership function

f_{M}

and minimizing membership function

f_{G}

. A ranking is higher if the right area is smaller; therefore, the right area is considered the cost area. The normalized height coefficient reflects the influence of the height of fuzzy numbers on their final ranking scores. The proposed method can rank both normal and non-normal fuzzy numbers without normalization or height minimization, thereby avoiding information loss and incorrect final ranking results.

The main contributions of this study to bridge these gaps are briefly as follows:

(I): This research develops a new coefficient to calculate the impact of the height of fuzzy numbers on the final ranking score.
(II): The new areas considered as benefit and cost are introduced to reflect the influence of vertical values on the final ranking score.
(III): A new index is proposed to guarantee that both vertical and horizontal values of a fuzzy number are important parameters that impact the final ranking score.
(IV): The proposed method can rank both normal and nonnormal fuzzy numbers without normalization or height minimization, thereby avoiding information loss and incorrect final ranking results.
(V): The proposed method can overcome the shortcomings of some existing methods and can be applied to many fuzzy MCDM model to support decision-makers to select the most suitable alternative in the decision-making process.

This paper is organized as follows. In Section 2, some basic definitions are introduced. Section 2 also provides an overview of the deviation degree method and explores the shortcomings of recent methods. In Section 3, the proposed method ranking of generalized fuzzy numbers based on the normalized height coefficient and benefit and cost areas is presented. In Section 4, numerical examples and comparisons are presented. Finally, we provide concluding remarks in Section 5.

2. Preliminary

2.1. Definitions and notions

Definition 1. Fuzzy Sets

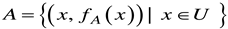, where U is the universe of discourse, x is an element in U, A is a fuzzy set in U, f_A (x) is the membership function of A at x (Kaufmann and Gupta, 1991). The larger, f_A (x) the stronger the grade of membership for x in A.

Definition 2. Fuzzy Numbers

A real fuzzy number A is described as any fuzzy subset of the real line R with membership function F_A which possesses the following properties (Dubois and Prade, 1978):

(a) F_A is a continuous mapping from R to [0,1];

(b)

;

(d)

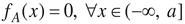; (e) F_A is strictly decreasing on [c,d];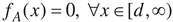

(f)

, where a ≤ b ≤ c ≤ d, A can be denoted as [a,b,c,d;w]. The membership function F_A of the fuzzy number A can also be expressed as follows: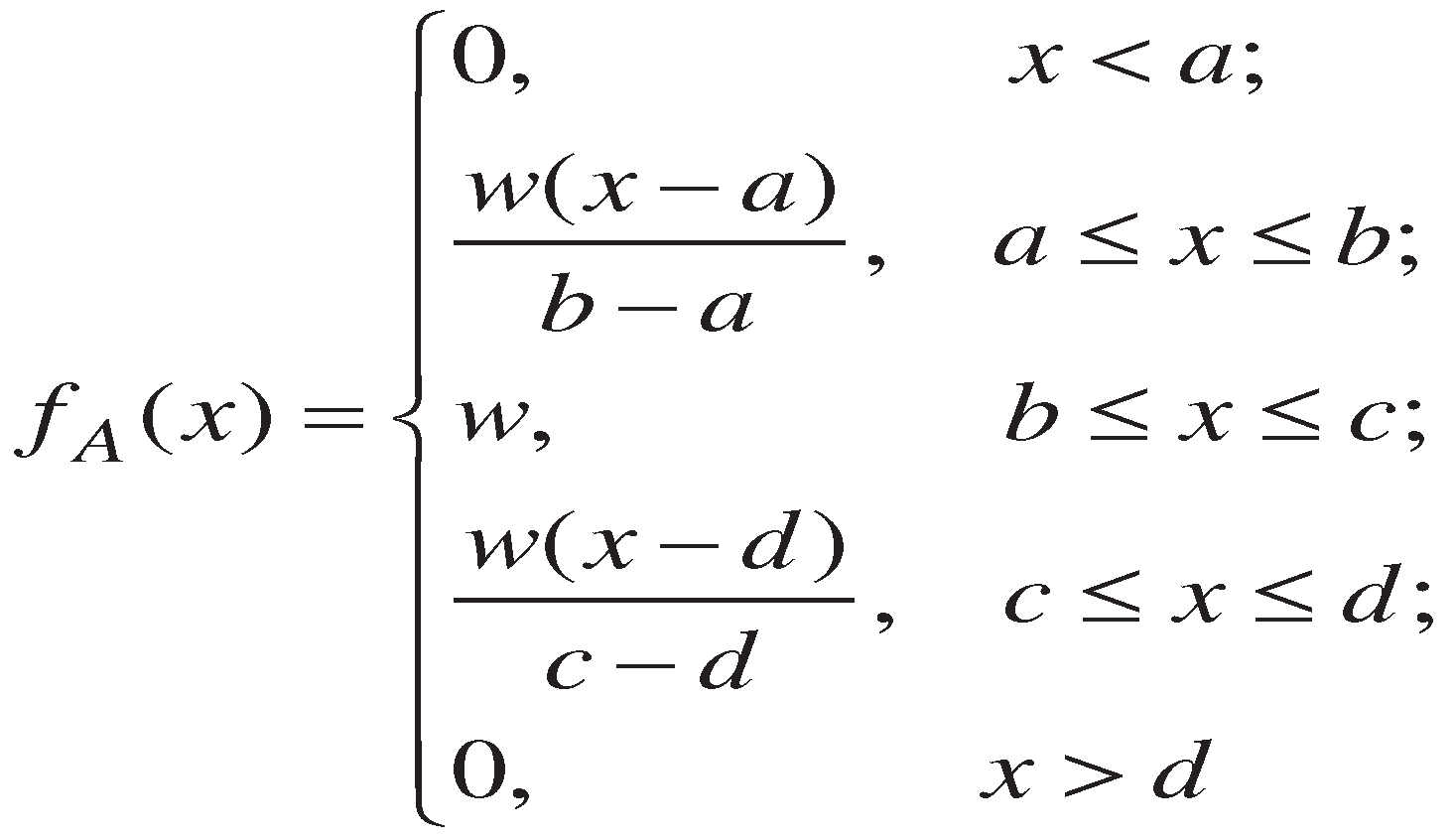

(1)

This trapezoidal fuzzy set, A = (a,b,c,d;w), 0 ≤ w ≤ 1, as shown in Figure 1.

Figure 1. A trapezoidal fuzzy set.

Definition 3. The arithmetic operations between two generalized trapezoidal fuzzy numbers

A₁ = (a₁,b₁,c₁,d₁;w₁) and A₂ = (a₂,b₂,c₂,d₂;w₂) are defined as below:

(2)

(3)

(4)

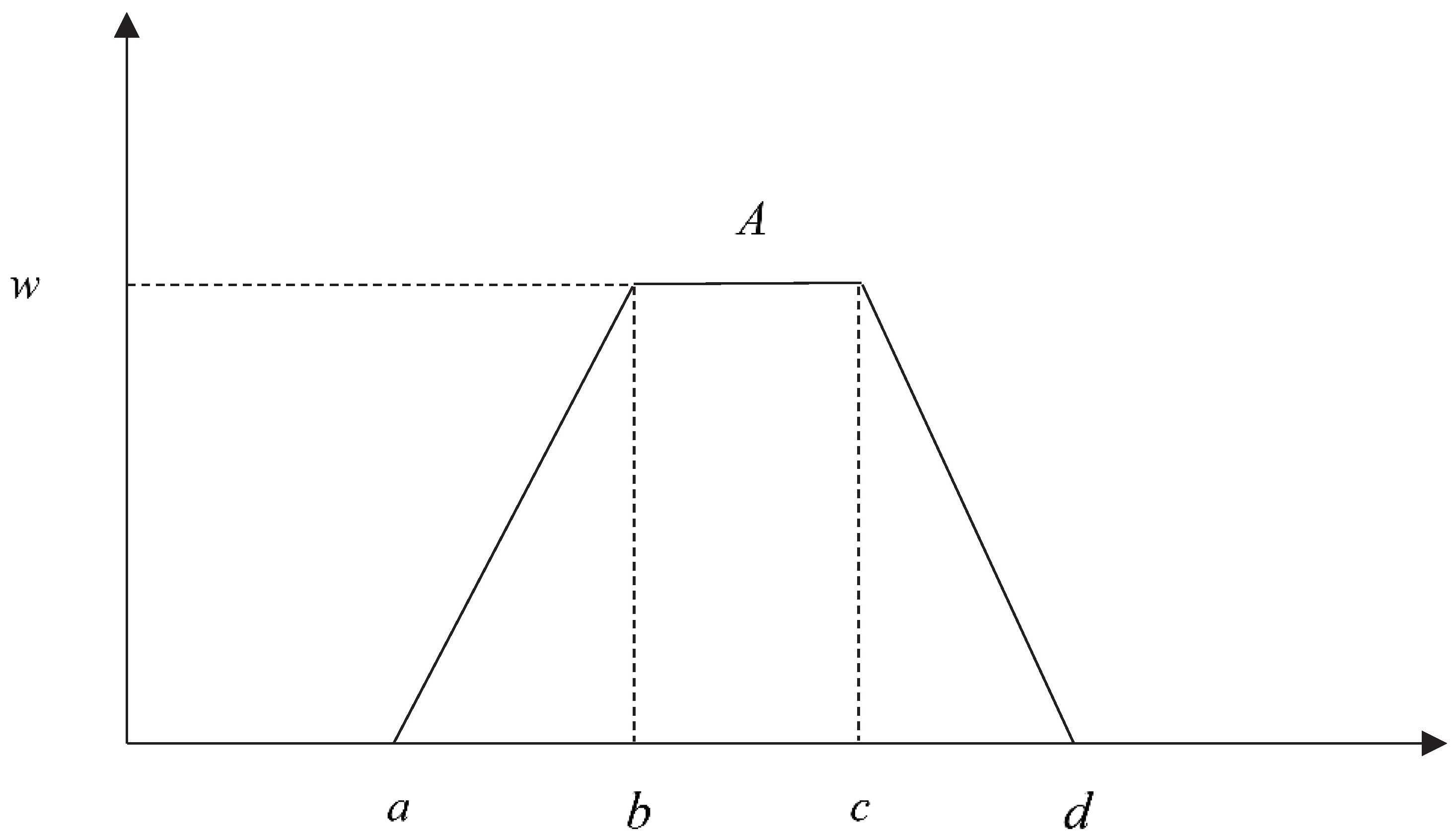
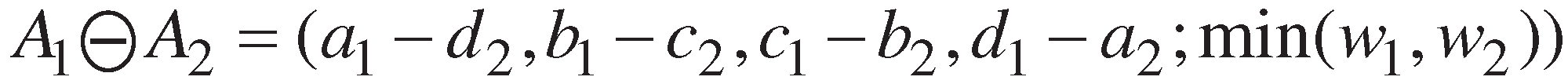
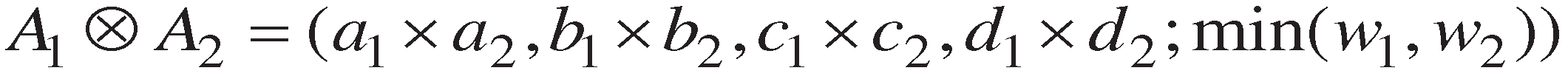
2.2. A review of the deviation degree method

In this section, firstly the minimal and maximal reference sets are reviewed. Then, based on the minimal and maximal reference sets, the left and right deviation degree (L–R deviation degree) is defined. Moreover, the transfer coefficient which measures the relative variation of L–R deviation degree of fuzzy numbers is quoted.

Definition 4. For any group of fuzzy numbers, A₁, A₂, ... A_n, let be the infimum and supremum of the support set of these fuzzy numbers. Then, A_min and A_max are the minimal reference set and maximal reference set of these fuzzy numbers, respectively, and their membership functions are given by

(5)

(6)

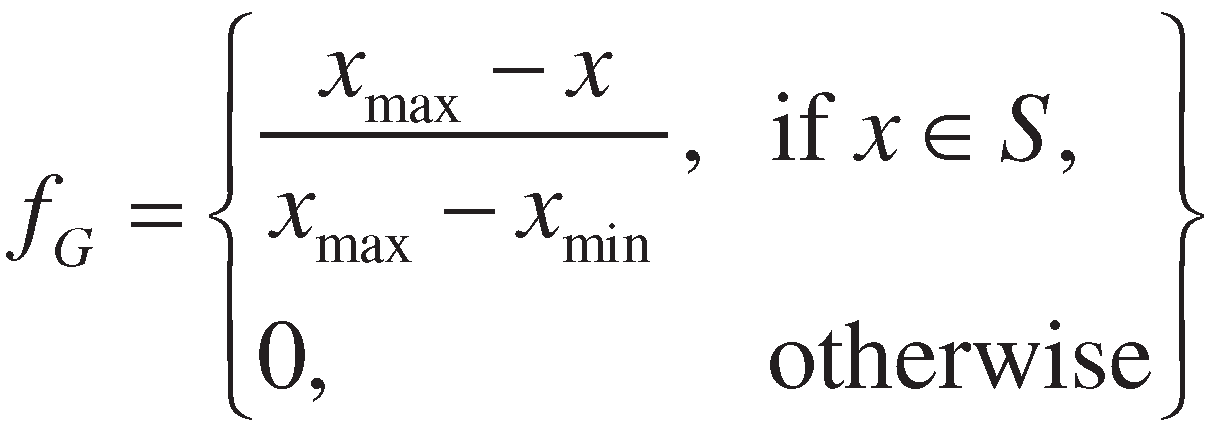
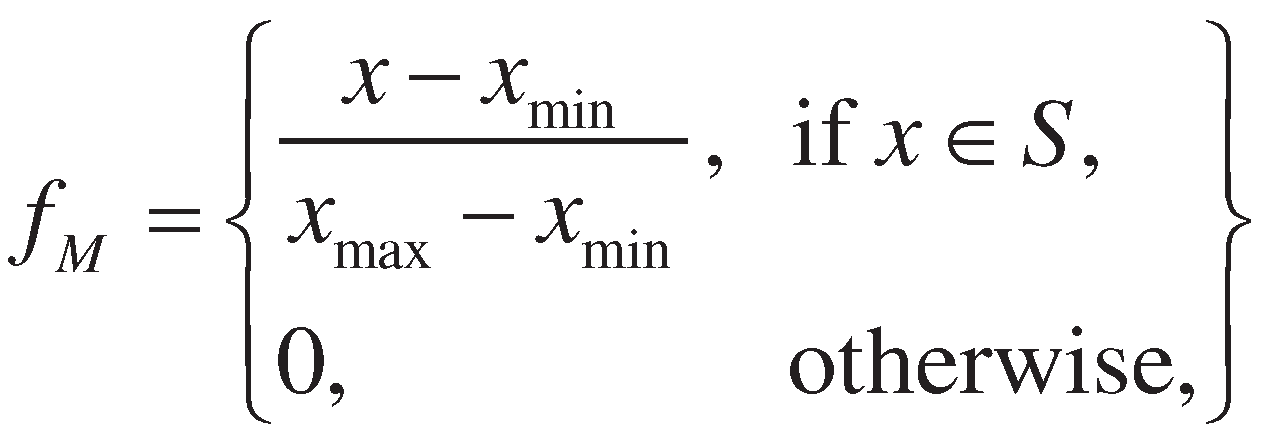
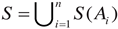
Where S is the support set of these fuzzy numbers, i.e., Preprints 85249 i012

Definition 5. For any group of fuzzy numbers A₁, A₂, ... A_n, let A_min and A_max be the minimal reference set and maximal reference set of these fuzzy numbers, respectively. Then, the left deviation degree and right deviation degree of A_i, i = 1,2,...,n are defined as follows:

(7)

(8)

Where

x_{A_{i}}^{L}

and

x_{A_{i}}^{R}

, i = 1,2,...n, are the abscissas of the crossover points of

f_{A_{i}}^{L}

and f_G, and

f_{A_{i}}^{R}

and f_M respectively.

Definition 6. For any fuzzy number A_i = (a_i,b_i,c_i,d_i,w_i), its expectation value of centroid is defined as follows:

(9)

Definition 7. For any fuzzy numbers A_i = (a_i,b_i,c_i,d_i,w_i), the transfer coefficient of A_i, i = 1,2,...,n is given by

(10)

Where M_max = max {M₁,M₂,...M_n} and M_min = min {M₁,M₂,...M_n}

Definition 8. The ranking index value of fuzzy number A_i, i = 1,2,...,n is given by:

(11)

Now, by using d_i given in Eq.(11), for any two fuzzy numbers A_i and A_j, their orders are determined based on the following rules:

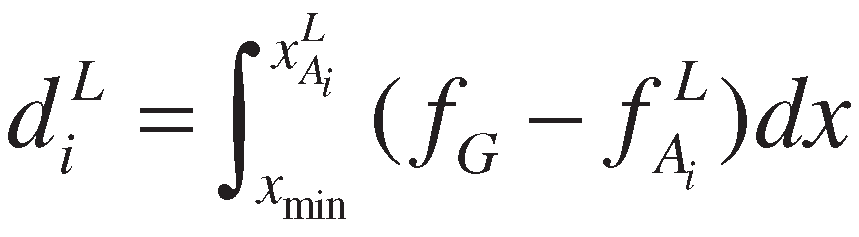
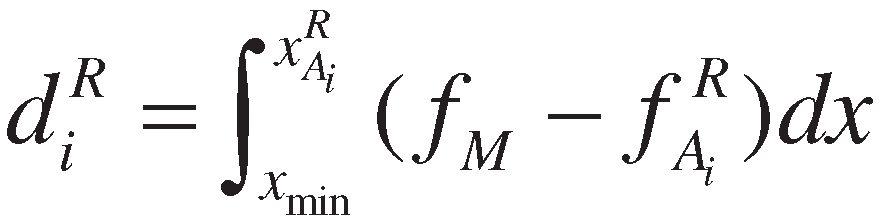
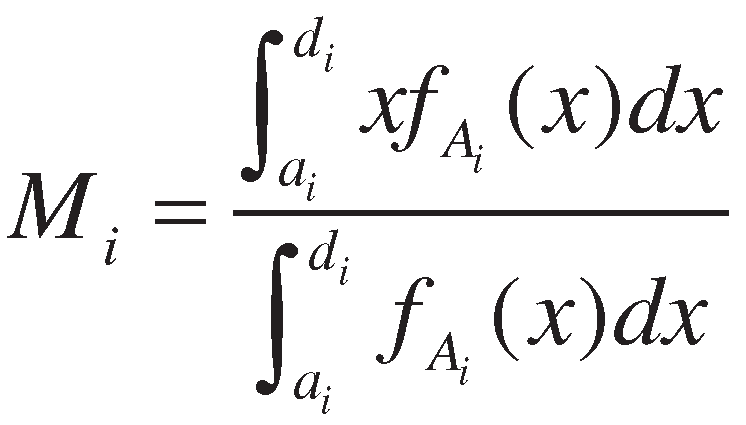
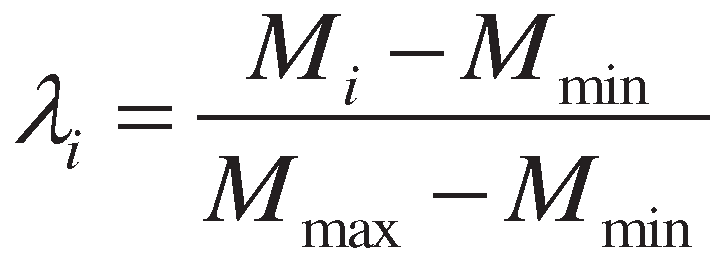
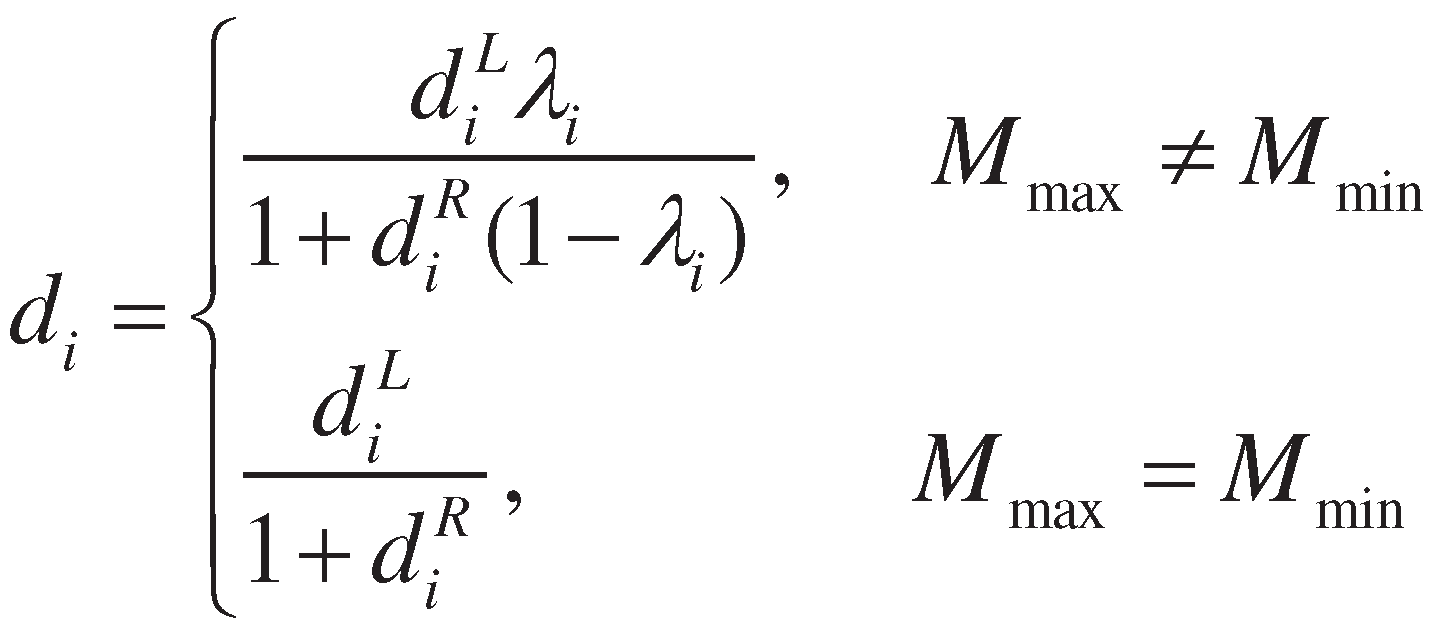
(1): A_i ≻ A_j, if and only if d_i ≻ d_j
(2): A_i ≺ A_j, if and only if d_i ≺ d_j
(3): A_i ~ A_j, if and only if d_i = d_j

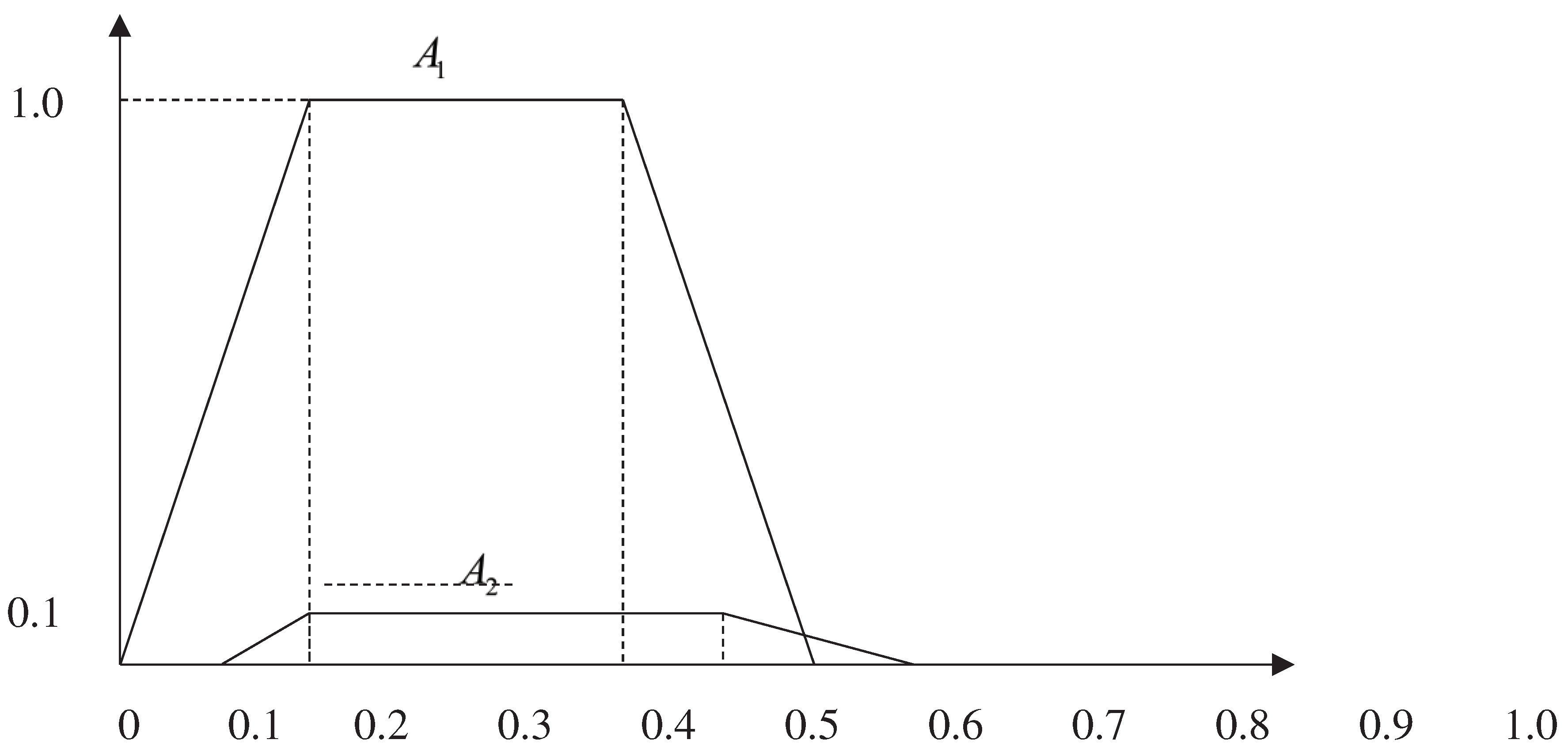
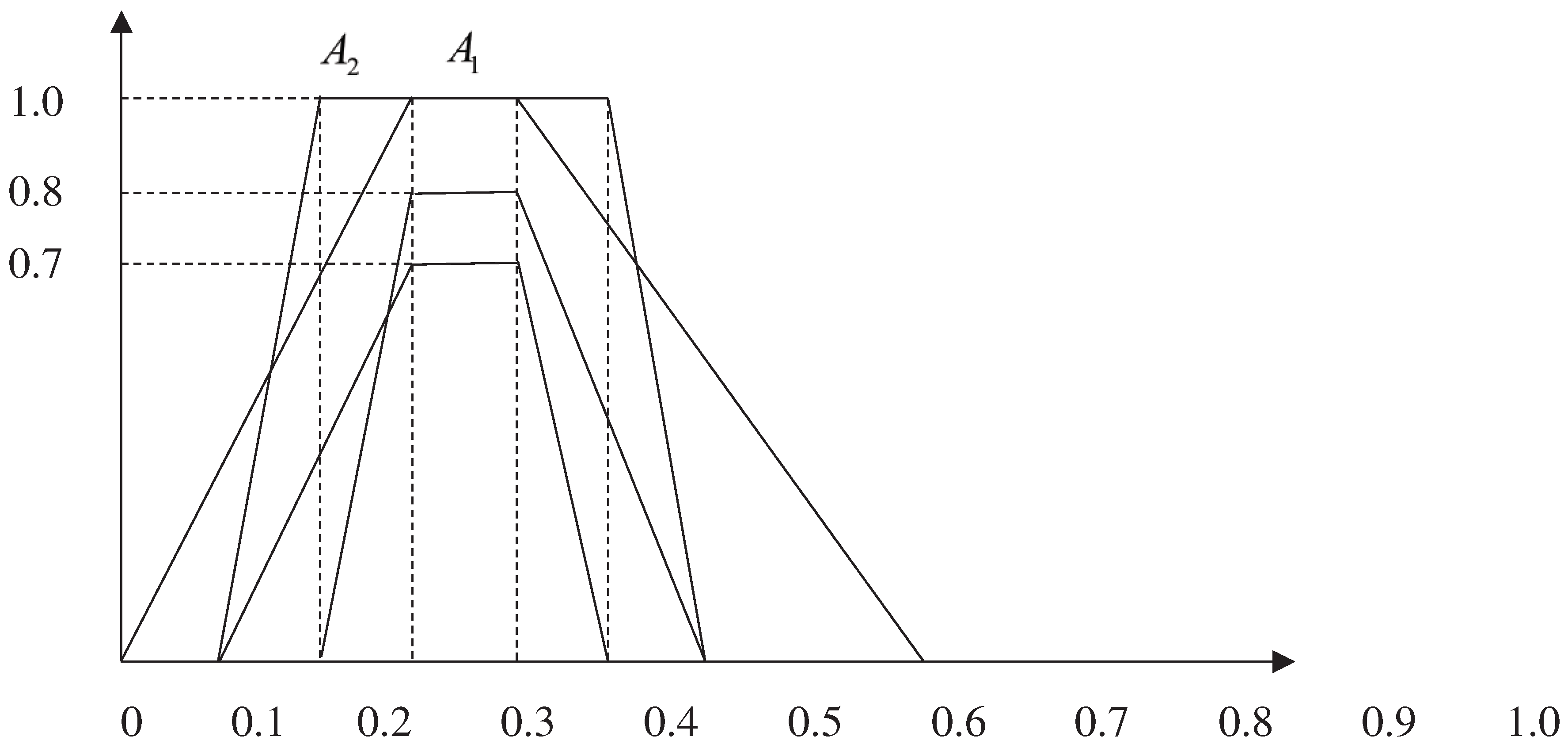
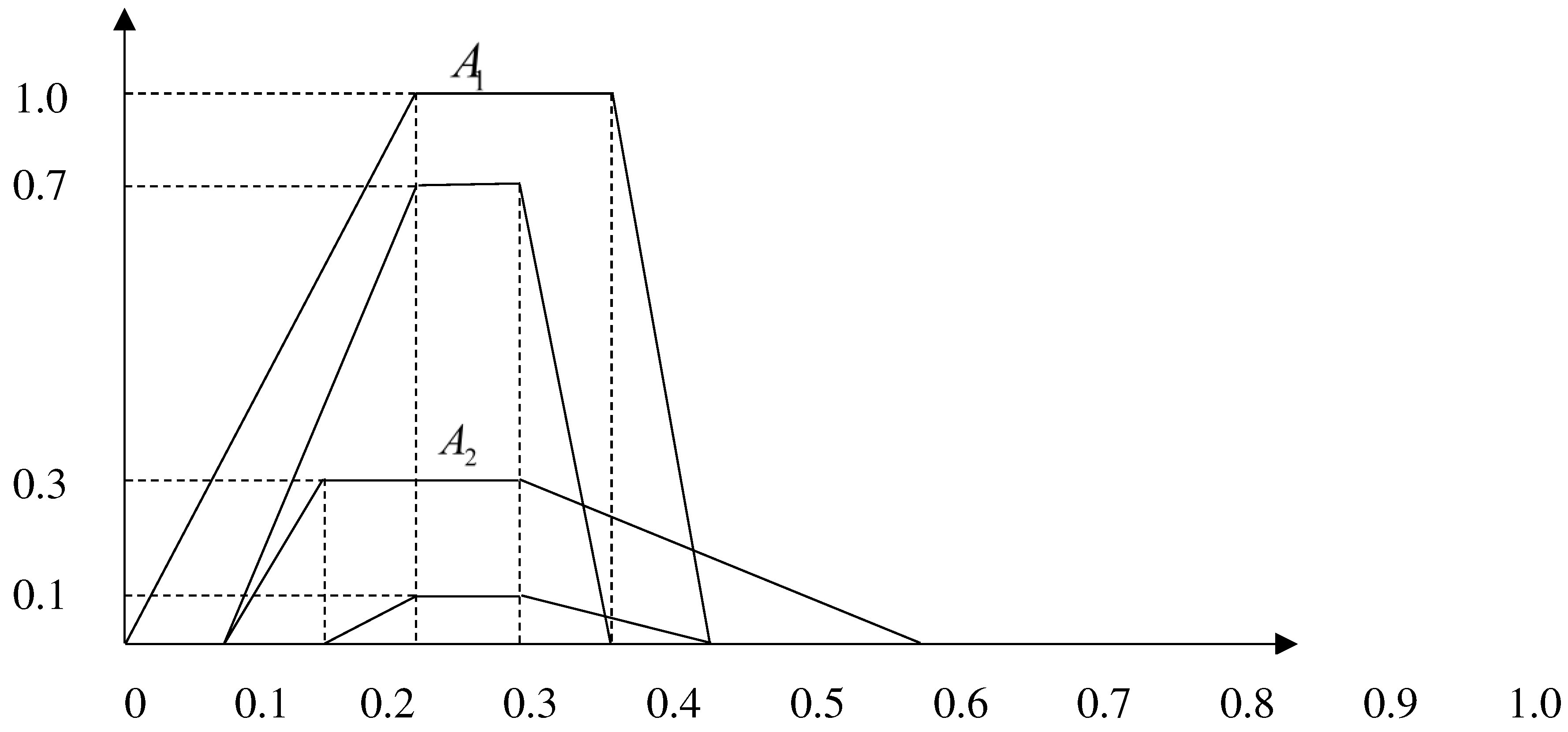
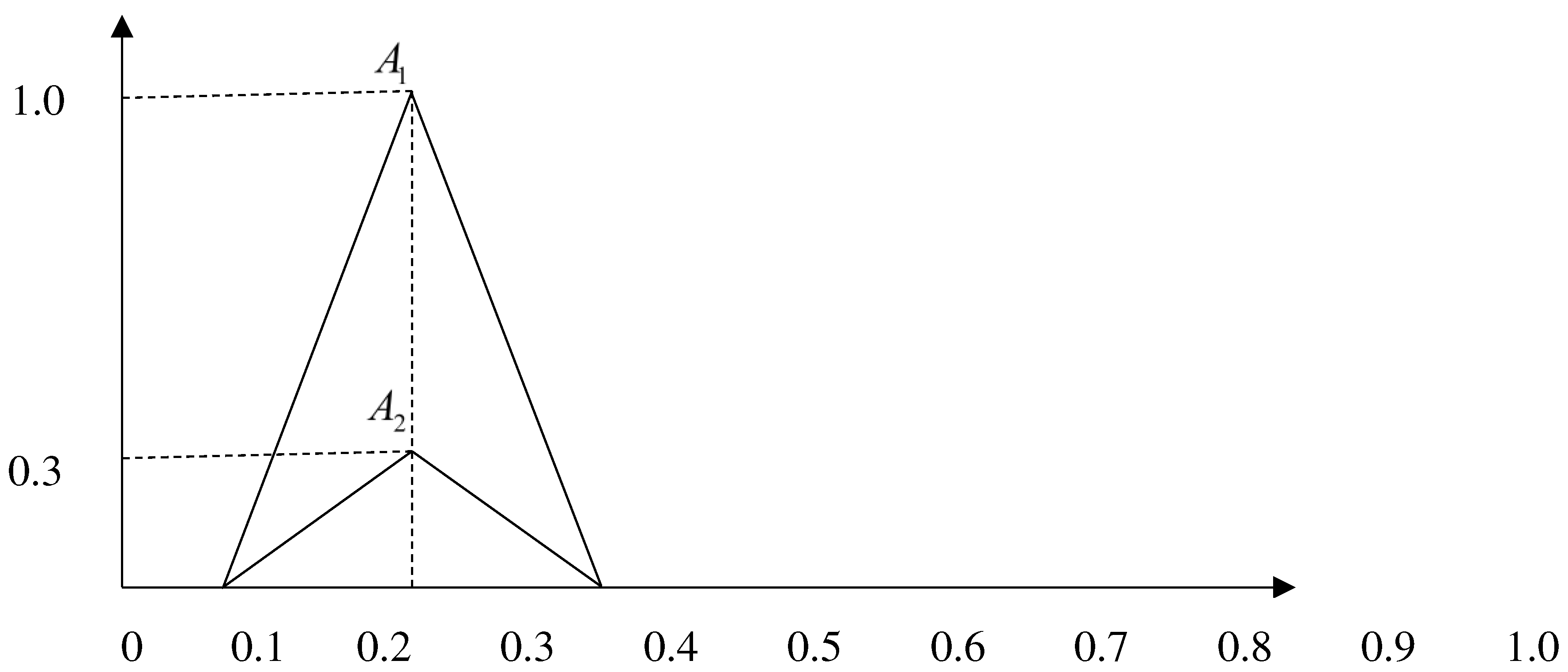
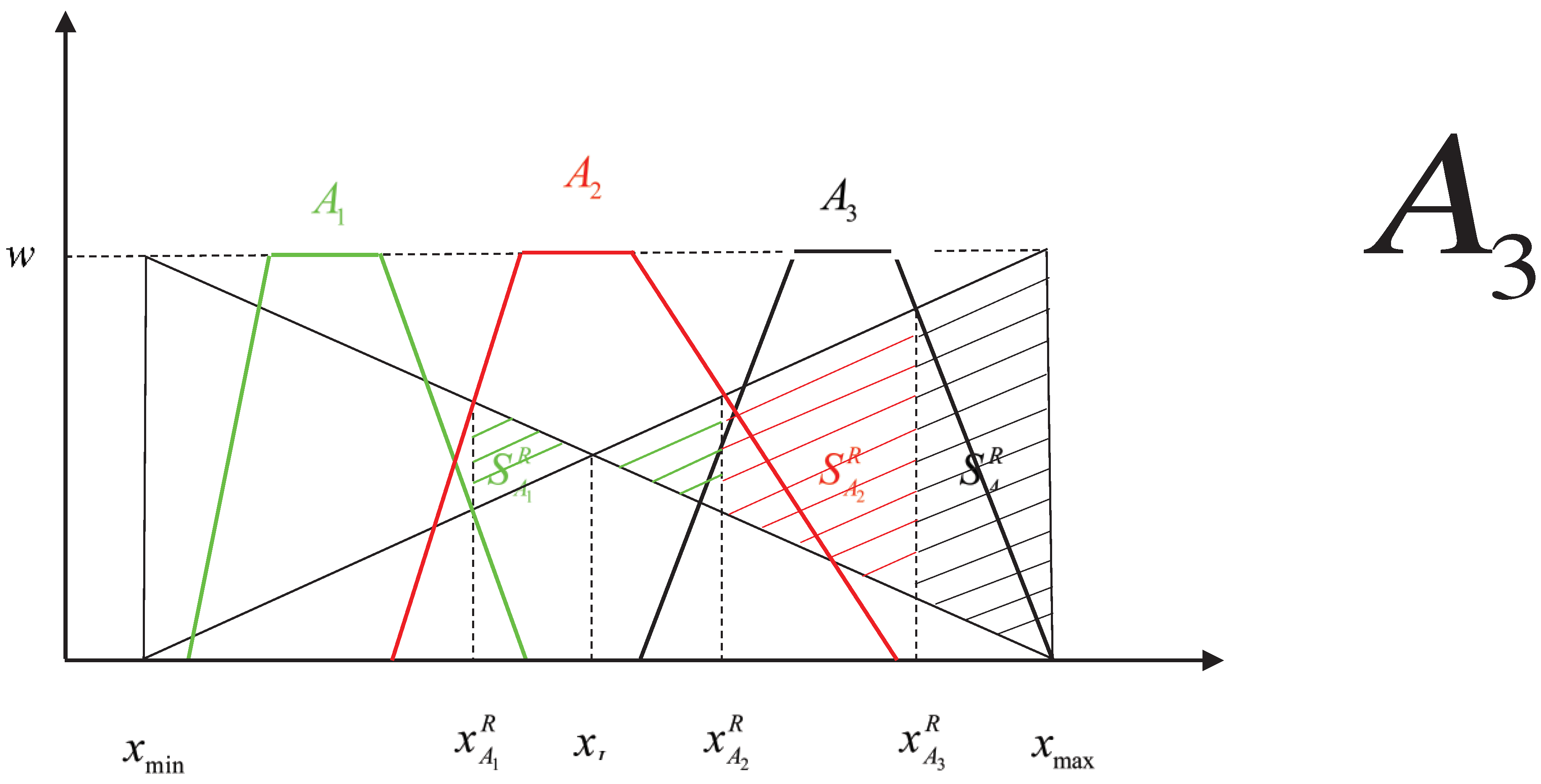
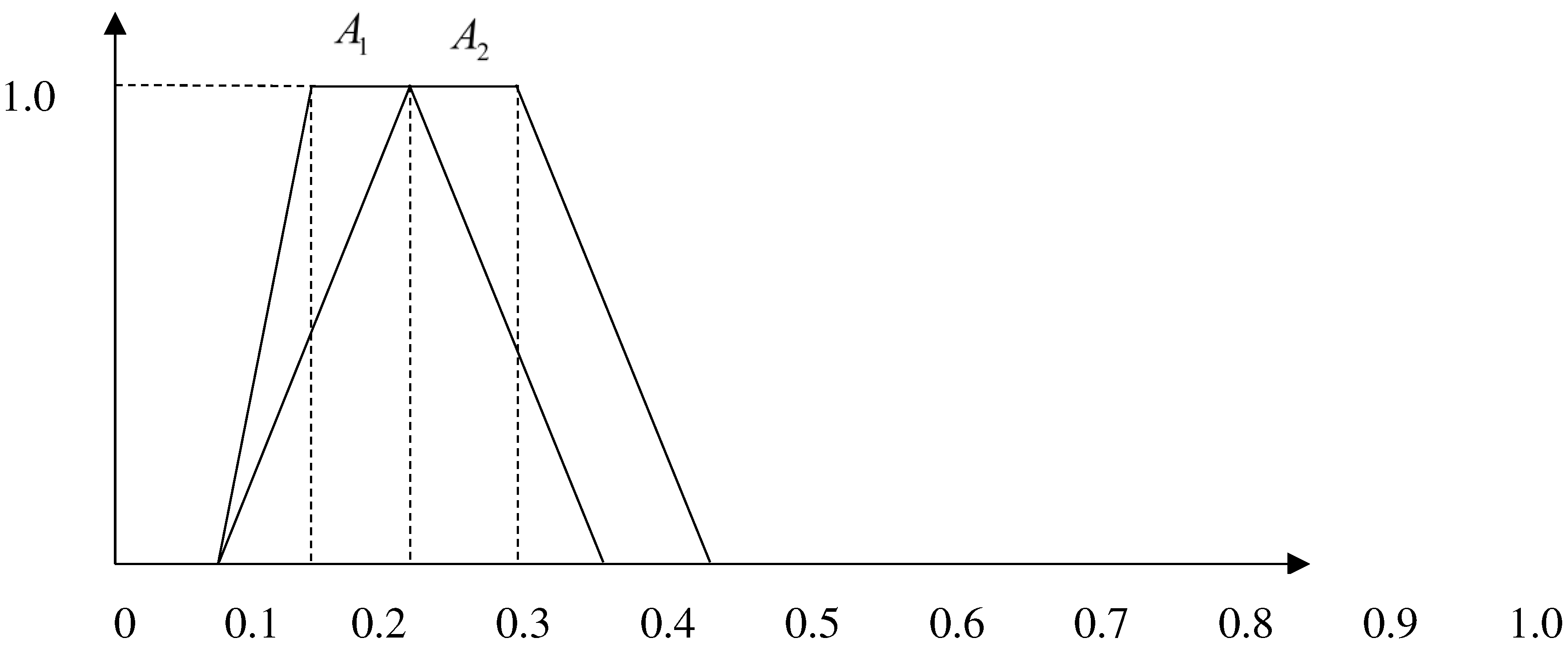
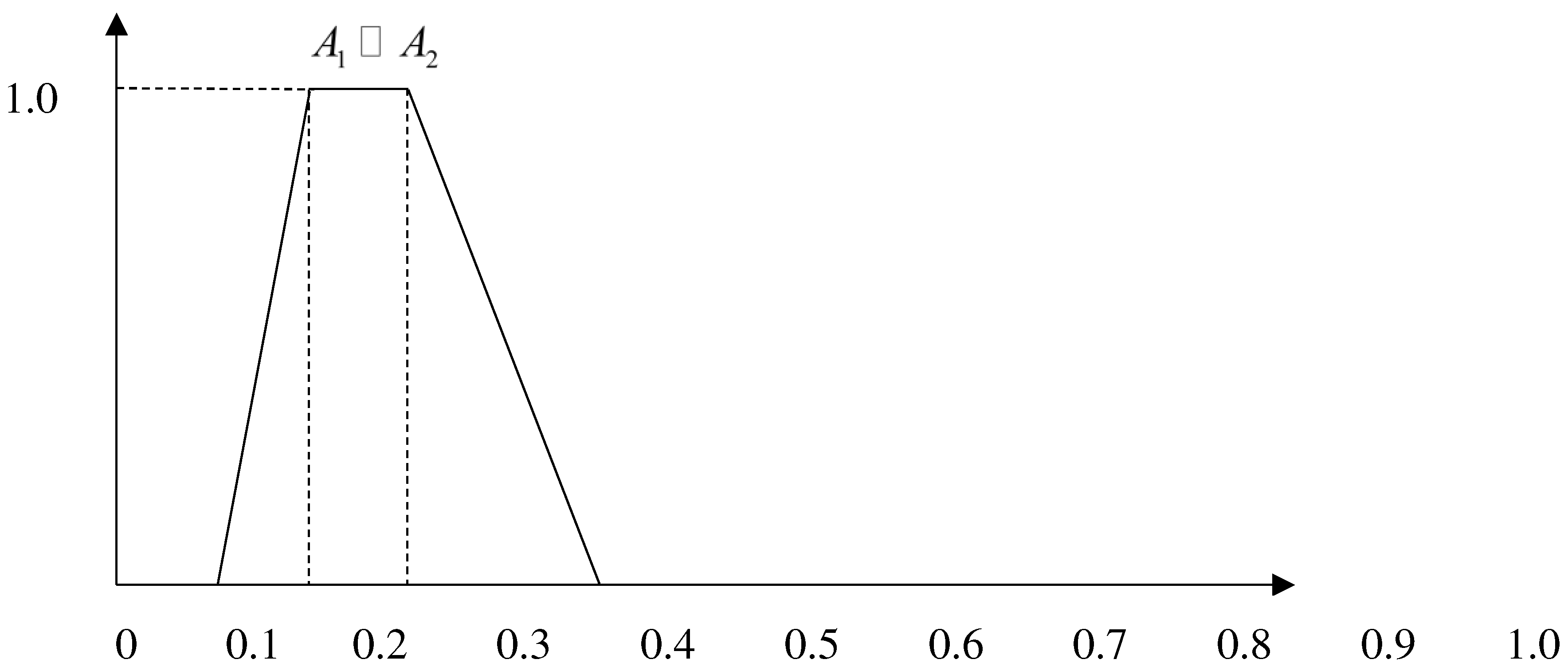
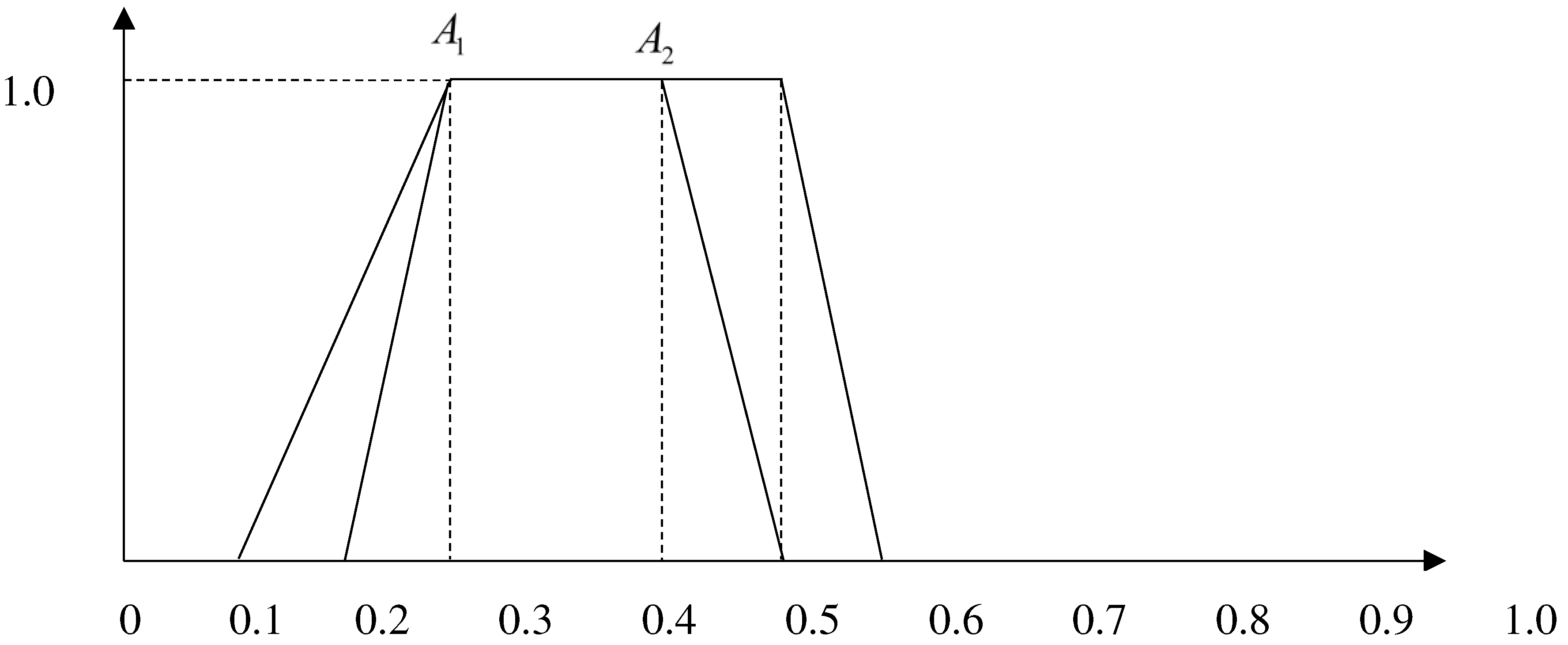
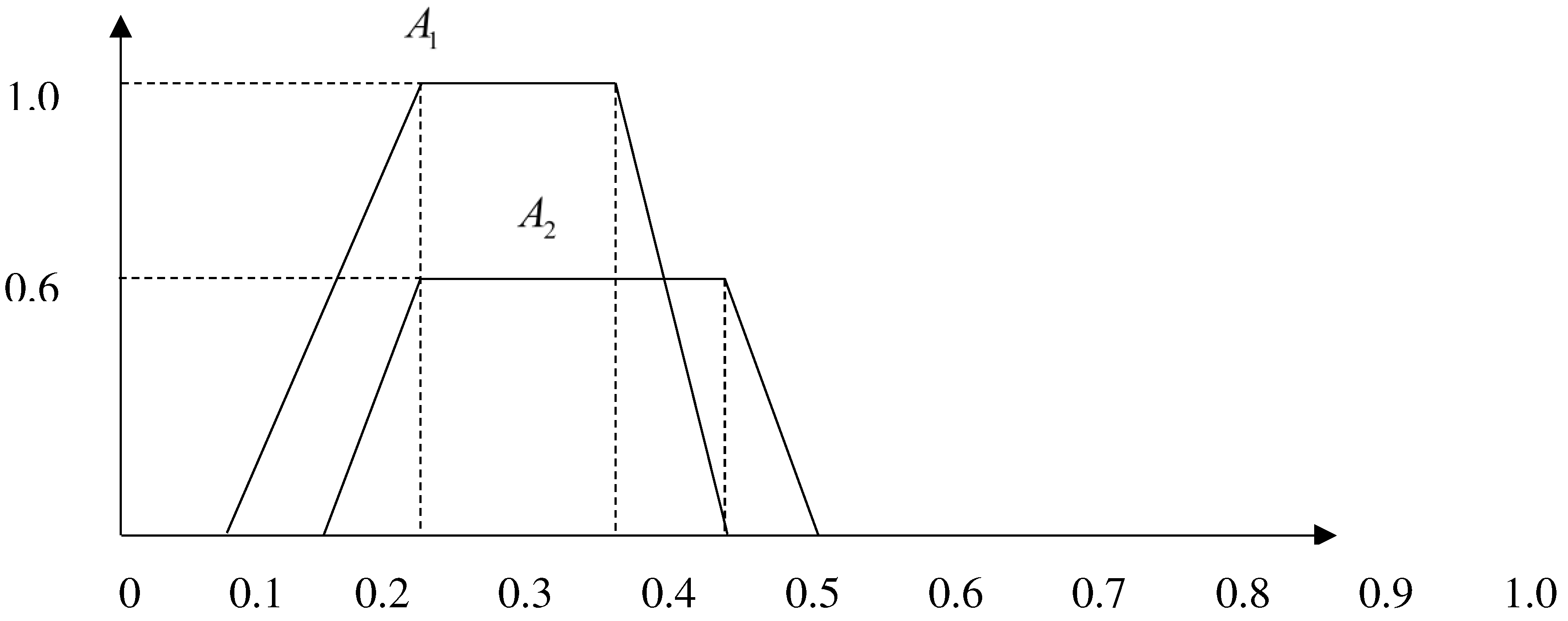
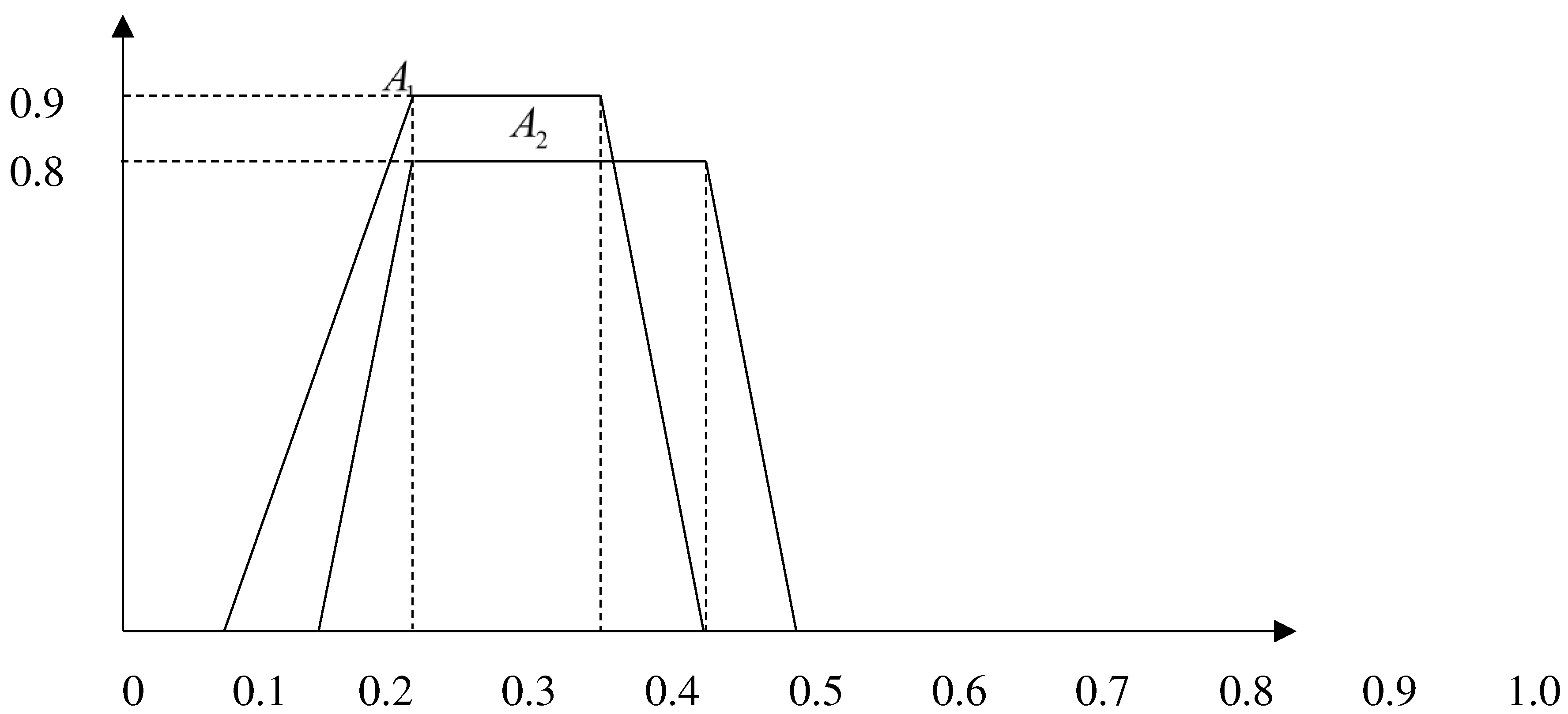
2.3. Limitations and shortcomings of existing methods

Example 1. Consider two generalized trapezoidal fuzzy numbers

A_{1} = (0.2, 0.4, 0.6, 0.8; 0.35)

and

A_{2} = (0.1, 0.2, 0.3, 0.4; 0.7)

adopted from Kumar et al. (2011). According to Chen & Chen, (2009) approachA₂ ≻ A₁. However, Kumar et al., (2011) noted that A₂ − A₁ ≻ A₁ − A₁, which is unreasonable and a contradiction, according to Wang & Kerre (2001).

Example 2.Consider two sets; each set comprises two type-1 trapezoidal fuzzy numbers (Figure 2 and Figure 3) as follows:

Set 1 comprises

A_{1} = (0, 0.2, 0.5, 0.7; 1)

and

A_{2} = (0.1, 0.2, 0.6, 0.8; 1)

Set 2 comprises

A_{1} = (0, 0.2, 0.5, 0.7; 1)

and

A_{2} = (0.1, 0.2, 0.6, 0.8; 0.1)

Based on Chi & Yu (2018) the final ranking of Set 1 and Set 2 are the same: A₂ ≻ A₁, which shows that the height does not affect the final ranking. These two sets have fuzzy numbers with the same support but different heights; in Set 2, the height of

A_{2}

is only 0.1.

Figure 2. Fuzzy number A₁ and A₂ of set 1 in example 2.

Figure 3. Fuzzy number

A_{1} and A_{2}

of set 2 in example 2.

Figure 3. Fuzzy number

A_{1} and A_{2}

of set 2 in example 2.

Example 3. Consider two sets, each comprising two type-2 trapezoidal fuzzy numbers (Figure 4 and Figure 5) as follows:

Set 3 comprises

A_{1} = ((0, 0.3, 0.5, 0.6; 1)

;

(0.1, 0.3, 0.4, 0.5; 0.7))

and

A_{2} = ((0.1, 0.2, 0.4, 0.8; 1)

;

(0.2, 0.3, 0.4, 0.6; 0.8))

Set 4 comprises

A_{1} = ((0, 0.3, 0.5, 0.6; 1)

;

(0.1, 0.3, 0.4, 0.5; 0.7))

and

A_{2} = ((0.1, 0.2, 0.4, 0.8; 0.3)

;

(0.2, 0.3, 0.4, 0.6; 0.1))

Based on De et al., (2020) the final rankings of Set 3 and Set 4 are the same: A₂ ≻ A₁. Therefore, height does not affect the final ranking. These two sets have fuzzy numbers with the same support but different heights; in Set 4, the heights of the upper and lower trapezoidal fuzzy numbers of

A_{2}

are only 0.3 and 0.1, respectively.

Example 4. Consider two trapezoidal fuzzy numbers (Figure 6) as follows:

A_{1} = (0.1, 0.3, 0.3, 0.5; 1)

and

A_{2} = (0.1, 0.3, 0.3, 0.5; 0.3)

These two fuzzy numbers have the same support, but the height of

A_{2}

is lower than that of

A_{1}

. However, the final ranking according to Chen (1985); Wang & Luo (2009) is A₁ ~ A₂, which is counterintuitive, thus illustrating a shortcoming in ranking nonnormal fuzzy numbers. According to Wang et al., (2009) the final ranking result A₂ ≺ A₁ which is inconsistent with human intuition.

Example 5. Consider three fuzzy numbers,

A_{1} = (0.3, 0.5, 0.5, 0.7; 1)

A_{2} = (0.3, 0.5, 0.5, 0.9; 1)

, and

A_{3} = ((0.3, 0.5, 0.8, 0.9; 1)

. Seghir (2021) pointed out that all the compared and proposed methods provide the correct rankingA₃ ≻ A₂ ≻ A₁, which is intuitive. However, the ranking A₃ ≻ A₂ ≻ A₁ of Chutia (2017) is incorrect and counterintuitive.

3. Proposed method

This study proposes a method that considers maximizing and minimizing sets to be reference sets, the left area to be the benefit area, and the right area to be the cost area. Additionally, the normalized height coefficient is used to determine the influence of height on the final ranking score, thus enabling the ranking of both normal and nonnormal fuzzy numbers without normalization or height minimization, which avoids information loss and incorrect final rankings.

To guarantee that the vertical value is considered an important parameter that impacts the final ranking score, the left area and the right area are evaluated. Assume there are n fuzzy numbers A_i = (a_i,b_i,c_i,d_i,w_i,), i = 1,2,...n. The left area denotes the area from x_min to

x_{A_{i}}^{L}

and is bounded by the maximizing membership function f_M and minimizing membership function f_G. Where

x_{A_{i}}^{L}

is the intersection of the crossover point of the minimizing membership function f_G and the left membership function

f_{A_{i}}^{L} x

. The left area is shown in Figure 7 and is described by Eqs. (12) and (13).

(12)

(13)

(14)

(15)

(16)

In Figure 7 the left areas of fuzzy number

A_{1}

and fuzzy number

A_{2}

are in the case of

x^{L} \leq x_{I}

. Therefore, applying Eq. (12), the left area of fuzzy number

A_{1}

is the green area, the left area of fuzzy number

A_{2}

is the green area adding the red area. The left area of fuzzy number

A_{3}

is in the case of

x^{L} ≻ x_{I}

, applying Eq. (13) the left area of fuzzy number

A_{3}

is the green area adding the red area adding the black area.

The right area denotes the area from x_max to

x_{A_{i}}^{R}

and is bounded by the maximizing membership function f_M and minimizing membership function f_G. Where

x_{A_{i}}^{R}

is the intersection of the crossover point of the maximizing membership function f_M and the right membership function

f_{A_{i}}^{L} x

. The right area is shown in Figure 8 and is described by Eqs. (17) and (18).

(17)

(18)

(19)

(20)

In Figure 8 the right areas of fuzzy number

A_{3}

and fuzzy number

A_{2}

are in the case of

x^{R} \geq x_{I}

. Therefore, applying Eq. (17), the right area of fuzzy number

A_{3}

is the black area, and the left area of fuzzy number

A_{2}

is the black area adding the red area. The right area of fuzzy number

A_{3}

is in the case of

x^{R} ≺ x_{I}

, applying Eq. (18) the right area of fuzzy number

A_{1}

is the black area adding the red area adding the green area.

Herein, x_min = inf a_i is considered the negative ideal solution, and x_man = sup d_i is considered the positive ideal solution,

x_{I}

is the intersection of the maximizing membership function f_M and minimizing membership function f_G. In the proposed method, the left and right areas are new areas that are simple to calculate and provide greater consistency and robustness in comparison with other methods.

The fuzzy number A_i is preferred if it is the farthest from the negative ideal solution x_min and closest to the positive ideal solution x_man. If

S_{A_{i}}^{L}

is larger, the fuzzy number A_i is farther from the negative ideal solution and closer to the positive ideal solution. Therefore,

S_{A_{i}}^{L}

is considered a benefit; thus, larger

S_{A_{i}}^{L}

is better. Conversely, if

S_{A_{i}}^{R}

is smaller, A_i is farther from the negative ideal solution and closer to the positive ideal solution. Therefore,

S_{A_{i}}^{R}

is considered a cost; thus, smaller

S_{A_{i}}^{R}

is better. In other words, larger

S_{A_{i}}^{L}

and smaller

S_{A_{i}}^{R}

indicate a larger fuzzy number A_i.

To guarantee that horizontal value is also considered an important parameter to influence the final ranking, the normalized height coefficient is defined in Eq. (21) to reflect the influence of the height of a fuzzy number on the final ranking score. The higher the normalized height coefficient of fuzzy number A_i , the higher the ranking of A_i is.

(21)

The final ranking score (RS) for fuzzy number A_i is defined as in Eq. (22):

(22)

If A_i and A_j are two fuzzy numbers, then the ranking score leads to the following decisions:

(23)

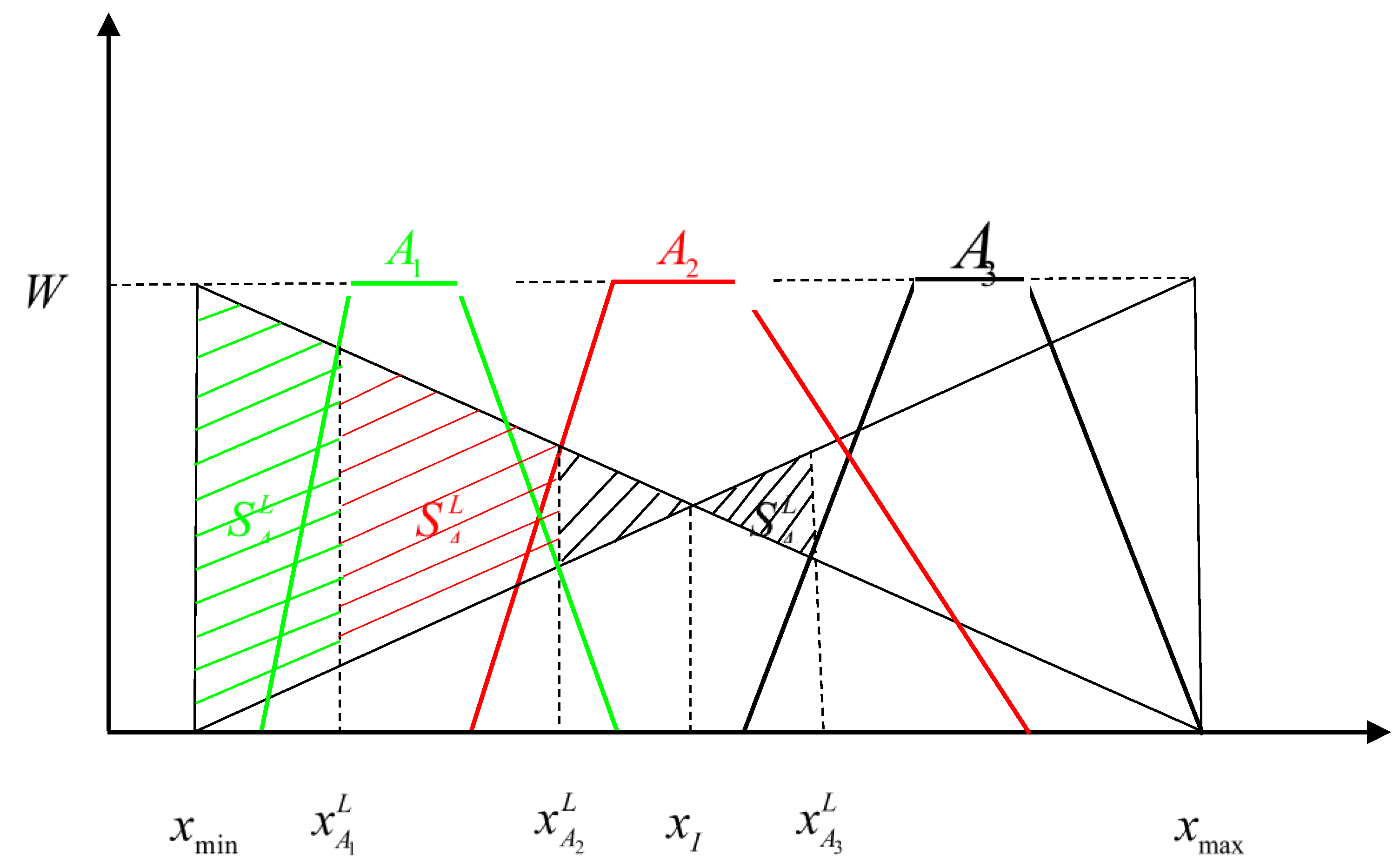
A flowchart in Figure 9 as below is used to present the procedure of the proposed method.

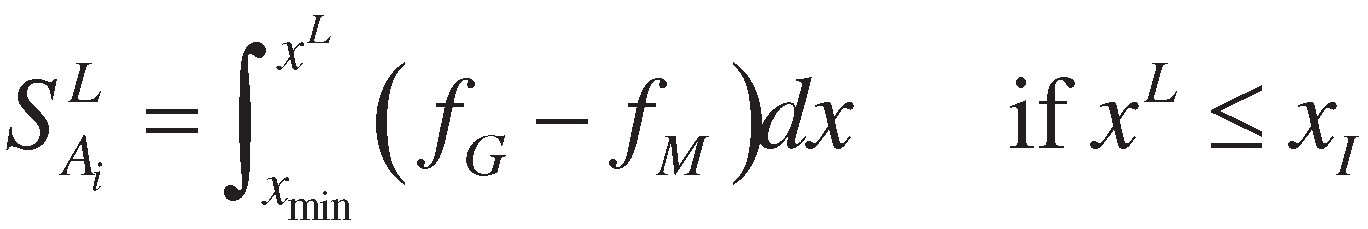
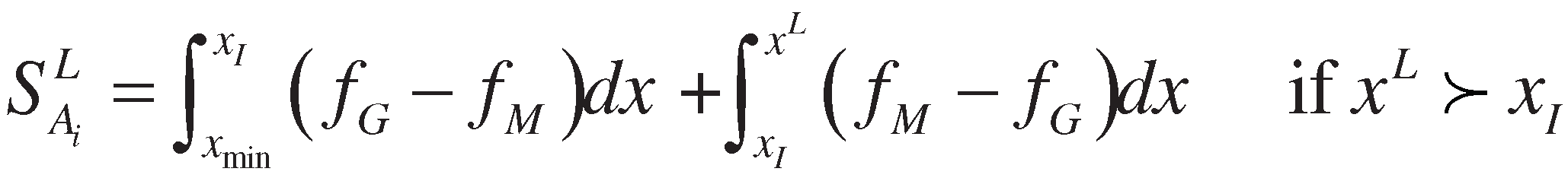
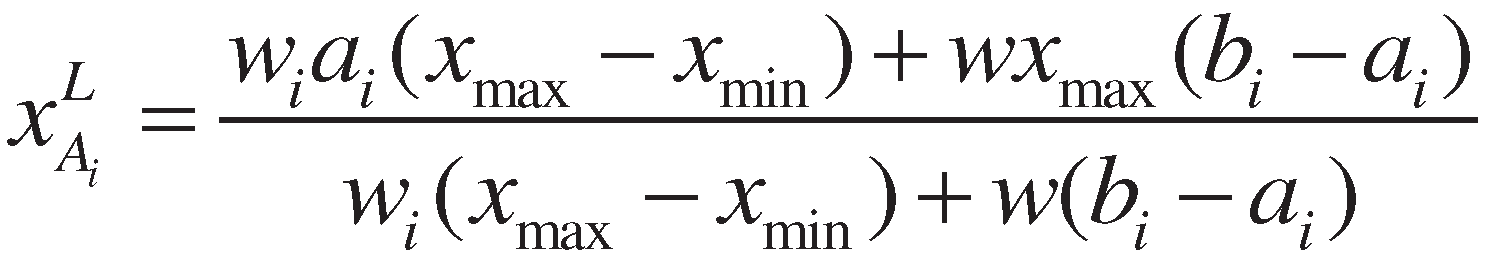
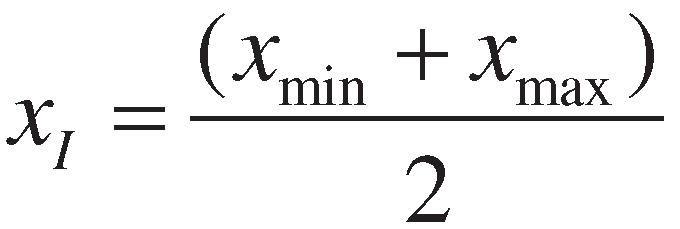
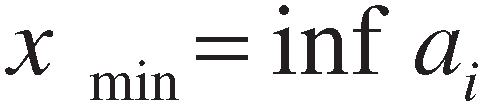
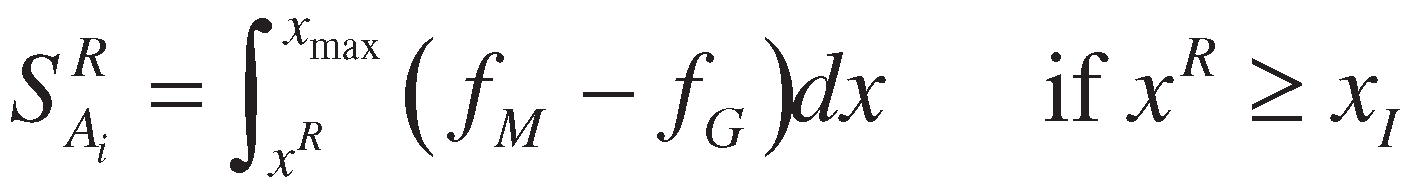
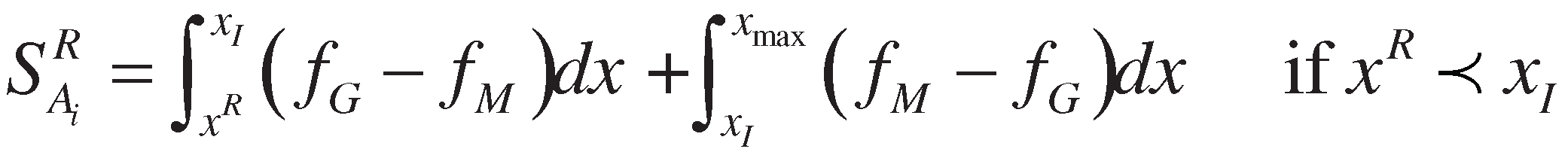
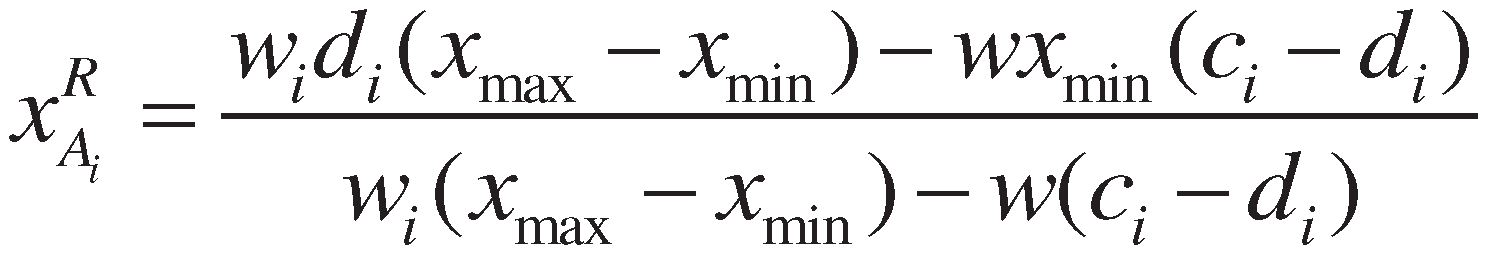
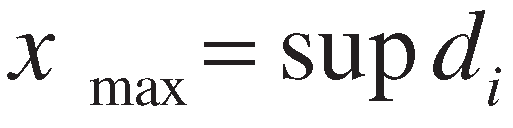
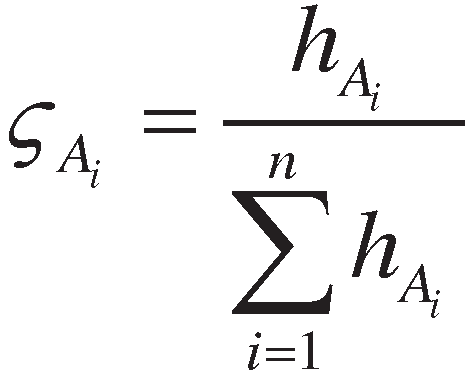
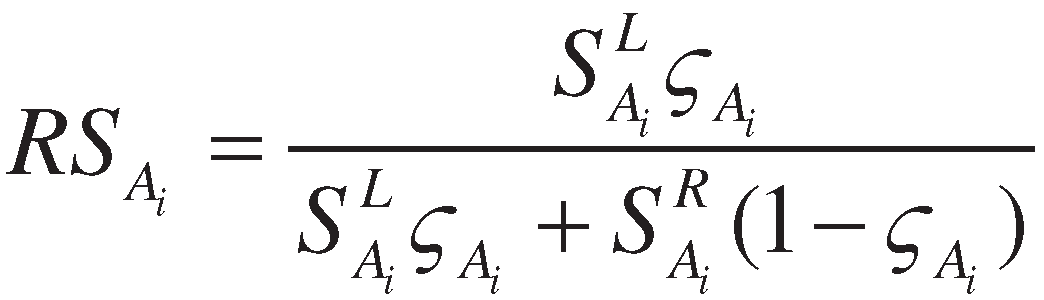
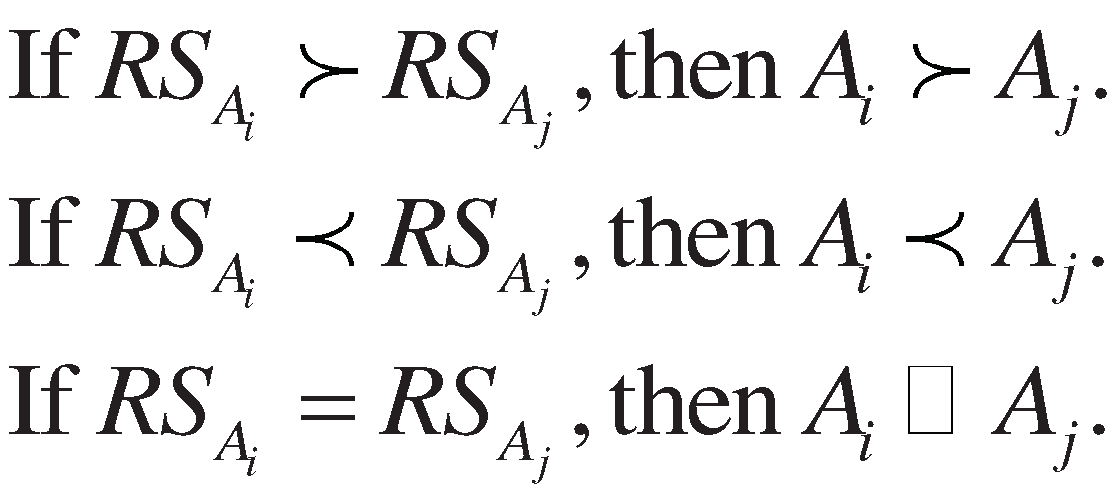
4. Numerical example and comparative study

4.1. Examples

To highlight the advantages, consistency, and robustness of this method, numerical examples are used. Step-by-step, this example demonstrates the simple computation and application of the proposed method.

Example 6. Consider two trapezoidal fuzzy numbers A₁ = (0.1,0.2,0.3,0.5;1) and A₂ = (0.1,0.3,0.4,0.6;1) (Figure 10). According to the proposed method, the final ranking is determined to be A₂ ≺ A₁ as follows:

Step 1: Based on Eqs. (16) and (20), x_min = 0.1, x_max = 0.6

Step 2: Based on Eqs. (14) and (19), the

x_{A_{i}}^{L}

and

x_{A_{i}}^{R}

of fuzzy number A₁ are

x_{A_{1}}^{L}

= 0.18333 and

x_{A_{1}}^{R}

= 0.38571. The

x_{A_{i}}^{L}

and

x_{A_{i}}^{R}

of fuzzy number A₂ are

x_{A_{2}}^{L}

= 0.24286 and

x_{A_{2}}^{R}

= 0.45714.

Step 3: Based on Eqs. (12) and (17), the

S_{A_{i}}^{L} and S_{A_{i}}^{R}

of fuzzy number A₁ are

S_{A_{1}}^{L} = 0.06944 and S_{A_{1}}^{R} = 0.12245

. The

S_{A_{i}}^{L} and S_{A_{i}}^{R}

of fuzzy number A₂ are

S_{A_{2}}^{L} = 0.10204 and S_{A_{2}}^{R} = 0.10204

Step 4: Based on Eq. (21), the normalized height coefficient of fuzzy number A₁ and fuzzy number A₂ are

ς_{A_{1}} = 0.5 and ς_{A_{2}} = 0.5

, respectively.

Step 5: Based on Eq. (22), the ranking score (RS) of fuzzy number A₁ and fuzzy number A₂ are

R S_{A_{1}} = 0.36189 and R S_{A_{2}} = 0.5000

Step 6: Based on Eq. (23) the final ranking is A₁ ≺ A₂ .

The following numerical examples (Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16 and Figure 17) are calculated step-by-step as in Example 6; the results are shown in Table 1.

Example 7. Consider two normal trapezoidal fuzzy numbers A₁ = (0.1,0.2,0.3,0.5;1), and A₂ = (0.1,0.2,0.3,0.5;1) (Figure 11). These fuzzy numbers are the same, so the ranking scores are equal and the final ranking is A₁ ~ A₂.

Example 8. Consider the normal trapezoidal fuzzy numberA₁ = (0.1,0.2,0.3,0.5;1) and non-normal trapezoidal fuzzy number A₂ = (0.1,0.2,0.3,0.5;0.8) (Figure 12). These fuzzy numbers share the same support, but the ranking scores are different because of different heights. The final ranking result is A₁ ≻ A₂ . This example indicates that the proposed method can rank both normal and non-normal fuzzy numbers.

Example 9. Consider two normal trapezoidal fuzzy numbers A₁ = (0.1,0.3,0.5,0.6;1) and A₂ = (0.2,0.3,0.6,0.7;1) (Figure 13). The final ranking result is A₁ ≺ A₂.

Example 10. Consider the normal trapezoidal fuzzy numberA₁ = (0.1,0.3,0.5,0.6;1) and nonnormal trapezoidal fuzzy number A₂ = (0.2,0.3,0.6,0.7;1) (Figure 14). These two fuzzy numbers share the same support as in Example 9, but the height of

A_{2}

is 0.6. Therefore, the final ranking is A₂ ≻ A₁. This example demonstrates that height is an important parameter affecting the final ranking score.

Example 11. Consider two nonnormal trapezoidal fuzzy numbers, A₁ = (0.1,0.3,0.5,0.6;0.9) and

A_{2} = (0.2, 0.3, 0.6, 0.7; 0.8)

(Figure 15). These two fuzzy numbers have the same support as in Example 9; however, the height of A₁ is 0.9, and the height of A₂ is 0.8. Therefore, the final ranking is A₂ ≺ A₁. This example also indicates that the final ranking is sensitive to height

Example 12. Consider two normal trapezoidal fuzzy numbers, A₁ = (0.1,0.2,0.3,0.5;1) and A₂ = (−0.5,−0.3,−0.2,−0.1;1) (Figure 16). The final ranking is A₂ ≻ A₁. This example shows that the proposed method can be used to rank positive and negative fuzzy numbers.

Example 13. Consider three normal trapezoidal fuzzy numbers, A₁ = (0.1,0.2,0.3,0.5;1), A₂ = (0.1,0.3,0.5,0.6;1), and A₃ = (0.2,0.3,0.6,0.7;1) (Figure 17). The final ranking is. A₁ ≺ A₂ ≺ A₃. This example reveals that the proposed method be used to rank sets comprising more than two fuzzy numbers.

4.2. Comparison

For objective comparison, fuzzy sets are adopted from Chen & Chen (2007). This section presents a comparison of the proposed method based on ranking score (RS) with the methods based on maximizing and minimizing set method (E_T) Chen (1985); deviation degree (DD) Wang et al., (2009); area ranking based on positive and negative ideal points (RIA) Wang & Luo (2009); revised method of deviation degree (RDD) Asady (2010); areas on the left and right sides of fuzzy number (SLR) Nejad & Mashinchi (2011); and the value and angle in the epsilon-deviation degree (MEDD) Chutia (2017), the final ranking results and comparison are presented in Table 2 where R is final ranking.

Table 2 illustrates that the final ranking of Set 7 by the proposed method is consistent with the rankings generated by the methods based on revised method of deviation degree (RDD), the areas on the left and right sides of fuzzy number (SLR), and the value and angle in the epsilon-deviation degree (MEDD); thus, our method is intuitive for ranking nonnormal fuzzy numbers. The methods based on maximizing set and minimizing set (U_T), the area ranking based on positive and negative ideal points (RIA) equally rank the fuzzy numbers, which is counterintuitive because the two fuzzy numbers share the same score support but differ in height. Furthermore, the final ranking based on deviation degree (DD) is unreasonable because the fuzzy number with lower height has a higher ranking, making it counterintuitive. These final rankings of Sets 5, 6, 8, and 9 generated by proposed method are consistent with those by the other methods. The final ranking of Set 10 is the same as that generated by most other methods, namely, maximizing set and minimizing set (U_T), the area ranking based on positive and negative ideal points (RIA), the revised method of deviation degree (RDD), and the value and angle in the epsilon-deviation degree (MEDD). Thus, the final ranking generated by proposed method is consistent with those of other methods for normal fuzzy numbers. Additionally, the proposed method can be used to rank the nonnormal fuzzy numbers described in Set 7 without normalization or height minimization (

\min w_{i}

5. Conclusion

This paper proposes an approach for ranking generalized fuzzy numbers on the basis of a normalized height coefficient and benefit and cost areas. In this method, the left area denotes the area from x_min to

x_{A_{i}}^{L}

and is bounded by the maximizing membership function f_M and minimizing membership function f_G. The right area denotes the area from x_max to

x_{A_{i}}^{R}

and is bounded by the maximizing membership function f_M and minimizing membership function f_G.

S_{A_{i}}^{L}

is considered as the benefit, larger is better.

S_{A_{i}}^{R}

is considered as the cost, smaller is better. In other words, larger

S_{A_{i}}^{L}

and smaller

S_{A_{i}}^{R}

mean bigger fuzzy number A_i. The normalized height coefficient is designed to reflect the influence of the height of fuzzy numbers on the final ranking score. The higher the normalized height coefficient of a fuzzy number, the higher its ranking is. The numerical example and comparison presented herein demonstrate the feasibility and robustness of the proposed method.

The proposed ranking method can be applied to fuzzy multicriteria decision-making MCsDM to support decision-makers to select the best alternative. Future research can extend this ranking method to develop other ranking methods for fuzzy numbers, including interval type-2 fuzzy numbers, intuitionistic fuzzy numbers and hesitant fuzzy numbers etc., to solve more complex decision-making problems in practice.

Funding

This work was supported in part by the National Science and Technology Council, Taiwan, under Grant MOST 112-2410-H-218-005.

References

Asady B (2010) The revised method of ranking LR fuzzy number based on deviation degree. Expert Systems with Applications, 37(7), 5056–5060. [CrossRef]
Bortolan G, Degani R (1985) A review of some methods for ranking fuzzy subsets. Fuzzy Sets and Systems, 15(1), 1–19. [CrossRef]
Brunelli M, Mezei J (2013) How different are ranking methods for fuzzy numbers ? A numerical study. International Journal of Approximate Reasoning, 54(5), 627–639. [CrossRef]
Chen SH (1985) Ranking fuzzy numbers with maximizing set and minimizing set. Fuzzy Sets and Systems, 17(2), 113–129. [CrossRef]
Chen SJ, Chen SM (2007) Fuzzy risk analysis based on the ranking of generalized trapezoidal fuzzy numbers. Applied Intelligence, 26(1), 1–11.
Chen SM, Chen JH (2009) Fuzzy risk analysis based on ranking generalized fuzzy numbers with different heights and different spreads. Expert Systems with Applications, 36, 6833–6842. [CrossRef]
Chen SM, Sanguansat K (2011) Analyzing fuzzy risk based on a new fuzzy ranking method between generalized fuzzy numbers. Expert Systems with Applications, 38, 2163–2171. [CrossRef]
Chi HTX, Yu VF (2018) Ranking generalized fuzzy numbers based on centroid and rank index. Applied Soft Computing Journal, 68, 283–292. 68. [CrossRef]
Chou SY, Dat LQ, Yu VF (2011) A revised method for ranking fuzzy numbers using maximizing set and minimizing set. Computers and Industrial Engineering, 61(4), 1342–1348. 1342. [CrossRef]
Chu TC, Kysely M (2021) Ranking objectives of advertisements on Facebook by a fuzzy TOPSIS method. Electronic Commerce Research. 21(4), 881-916. [CrossRef]
Chutia R (2017) Ranking of fuzzy numbers by using value and angle in the epsilon-deviation degree method. Applied Soft Computing Journal, 60, 706–721. [CrossRef]
De A, Kundu P, Das S, Kar S (2020) A ranking method based on interval type-2 fuzzy sets for multiple attribute group decision making. Soft Computing, 24(1), 131–154. [CrossRef]
Dubois D, Prade H (1978) Operations on fuzzy numbers. International Journal of Systems Science 9(6):613-626. 6: International Journal of Systems Science 9(6).
Hajjari T, Abbasbandy S (2011) A note on “the revised method of ranking LR fuzzy number based on deviation degree.” Expert Systems with Applications, 38(10), 13491–13492. [CrossRef]
He W, Rodríguez RM, Takáč Z, Martínez L (2023) Ranking of Fuzzy Numbers on the Basis of New Fuzzy Distance. International Journal of Fuzzy Systems. [CrossRef]
Jain R (1977) A procedure for multiple-aspect decision making using fuzzy sets. International Journal of Systems Science, 8(1), 1–7. [CrossRef]
Kaufmann A, Gupta MM (1985, 1991) Introduction to fuzzy arithmetic: theory and application. Van Nostrand Reinhold, New York. [CrossRef]
Kumar A, Singh P, Kaur P, Kaur A (2011) RM approach for ranking of L-R type generalized fuzzy numbers. Soft Computing, 15(7), 1373–1381. 1373. [CrossRef]
Liou TS, Wang MJJ (1992) Ranking fuzzy numbers with integral value. Fuzzy Sets and Systems, 50(3), 247–255. [CrossRef]
Nejad AM, Mashinchi M (2011) Ranking fuzzy numbers based on the areas on the left and the right sides of fuzzy number. Computers and Mathematics with Applications, 61(2), 431–442. [CrossRef]
Nguyen HT, Chu TC (2023) Ranking startups using DEMATEL-ANP-Based fuzzy PROMETHEE II, Axioms, 12(6), 1-34. [CrossRef]
Revathi M, Valliathal M (2021) Non-normal fuzzy number analysis in various levels using centroid method for fuzzy optimization. Soft Computing, 25(14), 8957–8969. [CrossRef]
Seghir F (2021) FDMOABC: Fuzzy discrete multi-objective artificial bee colony approach for solving the non-deterministic QoS-driven web service composition problem. Expert Systems with Applications, 167(2021), 114413. [CrossRef]
Wang X, Kerre EE (2001) Reasonable properties for the ordering of fuzzy quantities ( I ). Fuzzy Sets and Systems 118(2001), 375–385. [CrossRef]
Wang YM, Luo Y (2009) Area ranking of fuzzy numbers based on positive and negative ideal points. Computers and Mathematics with Applications, 58(9), 1769–1779. [CrossRef]
Wang ZX, Liu YJ, Fan ZP, Feng B (2009) Ranking L-R fuzzy number based on deviation degree. Information Sciences, 179(13), 2070–2077. [CrossRef]
Xu P, Su X, Wu J, Sun X, Zhang Y, Deng Y (2012). A note on ranking generalized fuzzy numbers. Expert Systems with Applications, 39(7), 6454–6457. [CrossRef]
Yu VF, Chi HTX, Dat LQ, Phuc PNK, Shen CW (2013) Ranking generalized fuzzy numbers in fuzzy decision making based on the left and right transfer coefficients and areas. Applied Mathematical Modelling, 37(16–17), 8106–8117. [CrossRef]
Yu VF, Chi HTX, Shen CW (2013) Ranking fuzzy numbers based on epsilon-deviation degree. Applied Soft Computing Journal, 13(8), 3621–3627. [CrossRef]

Figure 4. Fuzzy number

A_{1} and A_{2}

of set 3 in example 3.

Figure 4. Fuzzy number

A_{1} and A_{2}

of set 3 in example 3.

Figure 5. Fuzzy number

A_{1} and A_{2}

of set 4 in example 3.

Figure 5. Fuzzy number

A_{1} and A_{2}

of set 4 in example 3.

Figure 6. Fuzzy number

A_{1} and A_{2}

of set 4 in example 3.

Figure 6. Fuzzy number

A_{1} and A_{2}

of set 4 in example 3.

Figure 7. The left area.

Figure 8. The right area.

Figure 9. The graphical abstract of the proposed method.

Figure 10. Fuzzy number

A_{1} and A_{2}

in example 6.

Figure 10. Fuzzy number

A_{1} and A_{2}

in example 6.

Figure 11. Fuzzy number

A_{1} and A_{2}

in example 7.

Figure 11. Fuzzy number

A_{1} and A_{2}

in example 7.

Figure 12. Fuzzy number

A_{1} and A_{2}

in example 8.

Figure 12. Fuzzy number

A_{1} and A_{2}

in example 8.

Figure 13. Fuzzy number

A_{1} and A_{2}

in example 9.

Figure 13. Fuzzy number

A_{1} and A_{2}

in example 9.

Figure 14. Fuzzy number

A_{1} and A_{2}

in example 10.

Figure 14. Fuzzy number

A_{1} and A_{2}

in example 10.

Figure 15. Fuzzy number

A_{1} and A_{2}

in example 11.

Figure 15. Fuzzy number

A_{1} and A_{2}

in example 11.

Figure 16. Fuzzy number

A_{1} and A_{2}

in example 12.

Figure 16. Fuzzy number

A_{1} and A_{2}

in example 12.

Figure 17. Fuzzy number

A_{1} and A_{2}

in example 13.

Figure 17. Fuzzy number

A_{1} and A_{2}

in example 13.

Table 1. Numerical Examples.

	Fuzzy numbers	S^L	S^R	ȝ	RS	Rank
Ex.6	A₁ (0.1,0.2,0.3,0.5;1)	0.069	0.122	0.500	0.362	2
Ex.6	A₂(0.1,0.3,0.4,0.6;1)	0.102	0.102	0.500	0.500	1
Ex.7	A₁(0.1,0.2,0.3,0.5;1)	0.064	0.089	0.500	0.419	1
Ex.7	A₂(0.1,0.2,0.3,0.5;1)	0.064	0.089	0.500	0.419	1
Ex.8	A₁ (0.1,0.2,0.3,0.5;1)	0.044	0.065	0.556	0.460	1
Ex.8	A₂(0.1,0.2,0.3,0.5;0.8)	0.051	0.071	0.444	0.365	2
Ex.9	A₁(0.1,0.3,0.5,0.6;1)	0.113	0.122	0.500	0.479	2
Ex.9	A₂(0.2,0.3,0.6,0.7;1)	0.122	0.073	0.500	0.625	1
Ex.10	A₁(0.1,0.3,0.5,0.6;1)	0.050	0.066	0.625	0.558	1
Ex.10	A₂(0.2,0.3,0.6,0.7;0.6)	0.073	0.044	0.375	0.500	2
Ex.11	A₁(0.1,0.3,0.5,0.6;0.9)	0.085	0.096	0.529	0.499	2
Ex.11	A₂(0.2,0.3,0.6,0.7;0.8)	0.098	0.059	0.471	0.597	1
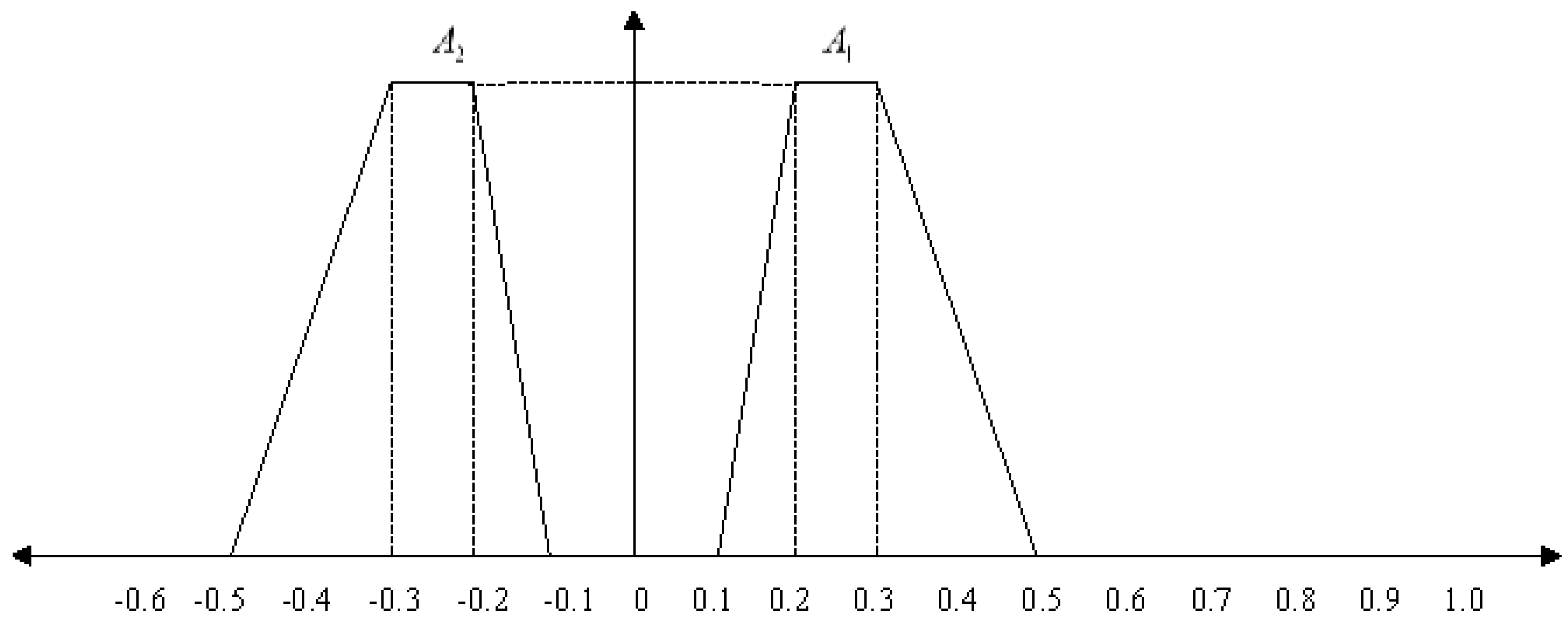
Ex.12	A₁(0.1,0.2,0.3,0.5;1)	0.231	0.139	0.500	0.625	1
Ex.12	A₂(-0.5,-0.3,-0.2,-0.1;1)	0.139	0.231	0.500	0.375	2
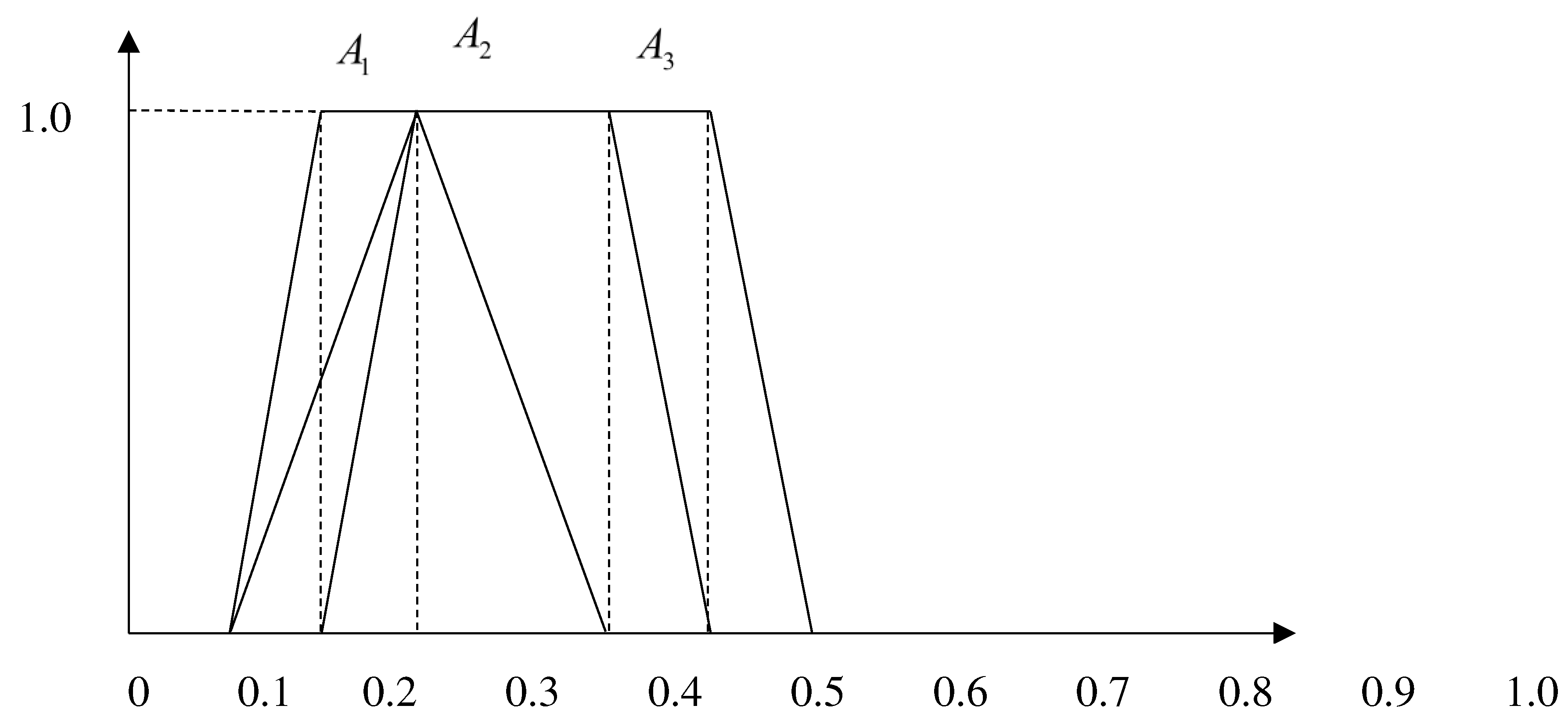
Ex.13	A₁(0.1,0.2,0.3,0.5;1)	0.073	0.150	0.333	0.197	3
	A₂(0.1,0.3,0.5,0.6;1)	0.113	0.122	0.333	0.315	2
	A₃(0.2,0.3,0.6,0.7;1)	0.122	0.073	0.333	0.455	1

Table 2. Comparison of the proposed method with other methods.

Set	FNs	Ut	R	DD	R	RIA	R	RDD	R	SLR	R	MEDD	R	RS	R
Set 5	A₁(0.1,0.3,0.3,0.5;1)	0.375	2	0.000	2	0.250	2	0.222	2	0.075	2	0.041	2	0.429	2
Set 5	A₂(0.3,0.5,0.5,0.7;1)	0.625	1	0.300	1	0.750	1	0.571	1	0.303	1	24.462	1	0.571	1
Set 6	A1(0.1,0.3,0.3,0.5;1)	0.500	1	0.063	1	0.500	1	0.286	1	0.130	1	1.000	1	0.500	1
Set 6	A₂(0.1,0.3,0.3,0.5;1)	0.500	1	0.063	1	0.500	1	0.286	1	0.130	1	1.000	1	0.500	1
Set 7	A₁(0.1,0.3,0.3,0.5;0.8)	0.400	1	0.063	1	0.500	1	0.242	2	0.242	2	0.126	2	0.444	2
Set 7	A₂(0.1,0.3,0.3,0.5;1)	0.400	1	0.061	2	0.500	1	0.286	1	0.286	1	9.488	1	0.556	1
Set 8	A₁(-0.5,-0.3,-0.3,-0.1;1)	0.250	2	0.000	2	0.125	2	0.154	2	0.035	2	0.015	2	0.333	2
Set 8	A₂(0.1,0.3,0.3,0.5;1)	0.750	1	1.333	1	0.875	1	1.143	1	0.679	1	65.091	1	0.667	1
Set 9	A₁(0.3,0.5,0.5,1.0;1)	0.503	1	0.327	1	0.545	1	0.514	1	0.285	1	1.185	1	0.502	1
Set 9	A₂(0.1,0.6,0.6,0.8;1)	0.497	2	0.000	2	0.455	2	0.436	2	0.196	2	0.844	2	0.498	2
Set 10	A₁(0.0,0.4,0.6,0.8;1)	0.517	3	0.000	3	0.500	3	0.474	3	0.229	3	0.087	3	0.349	3
	A₂(0.2,0.5,0.5,0.9;1)	0.554	2	0.313	1	0.636	2	0.600	2	0.363	1	0.498	2	0.363	2
	A₃(0.1,0.6,0.7,0.8;1)	0.614	1	0.207	2	0.700	1	0.647	1	0.362	2	2.176	1	0.434	1

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Novel Method for Ranking Generalized Fuzzy Numbers Based on Normalized Height Coefficient and Benefit and Cost Areas

Abstract

1. Introduction

2. Preliminary

2.1. Definitions and notions

2.2. A review of the deviation degree method

2.3. Limitations and shortcomings of existing methods

3. Proposed method

4. Numerical example and comparative study

4.1. Examples

4.2. Comparison

5. Conclusion

Funding

References

MDPI Initiatives

Important Links

Subscribe