Preprint
Article
Physics of Ice Nucleation and Antinucleation: Action of Antifreeze Proteins and Ice Nucleators
Altmetrics
Downloads
168
Views
89
Comments
0
Submitted:
14 September 2023
Posted:
18 September 2023
You are already at the latest version
Alerts
Abstract
Ice-binding proteins are crucial for adaptation of various organisms to low temperatures. Some of these, called antifreeze proteins, are usually thought to inhibit growth and/or recrystallization of ice crystals. However, prior to these events, ice must somehow appear in the organism, either coming from outside or forming inside through the nucleation process. Unlike most other works, our paper is focused on ice nucleation rather than the behavior of the already existing ice. The nucleation kinetics is studied both theoretically, with special attention paid to ice nucleation on ice-binding surfaces, and experimentally. For experimental studies, we use the ice-binding protein mIBP83, a previously constructed mutant of a spruce budworm Choristoneura fumiferana antifreeze protein. We show that mIBP83 does not affect the ice nucleation temperature in the buffer in test tubes, but hinders the impact of potent ice nucleators of various chemical natures, namely CuO powder and ice-nucleating bacteria Pseudomonas syringae. Additional experiments on human cells show that mIBP83 is concentrated in some regions, but only in cooled cells. Thus, the antifreeze protein not only binds to ice, but also blocks various sites that act or can act as ice nucleators. Such ice-preventing binding may be the crucial biological task of antifreeze proteins.
Keywords:
Subject: Biology and Life Sciences - Biophysics
1. Introduction
Many organisms on Earth must deal with temperatures below 0 °C, and hence, with a potentially hazardous process of water freezing.
To control the formation of ice, the organisms use different substances varying from low-molecular ones, such as polyols and sugars [1,2], to macromolecules like ice-binding proteins (IBPs; for reviews, see, e.g. [3,4,5]. IBPs are perhaps the most interesting case, because their effect requires a 200–500 times less molecular concentration than that of low-molecular substances [6,7], being a specific, “non-colligative” effect [8].
Of the ice-binding proteins, the most studied group is termed antifreeze proteins (AFPs), which inhibit the growth and/or recrystallization of ice crystals [8,9,10,11,12]. The antifreeze proteins were first found in the blood of fish living in the Arctic and Antarctic waters [13,14]. Then such proteins were found in other animals [15] including insects [6,16,17], as well as in many other organisms from bacteria [18,19] and other microorganisms [20,21] to fungi [18,22] and plants [23,24].
Though AFPs are rather extensively studied, the detailed mechanism of their action is still far from being clear [25,26,27], but it is commonly believed that AFPs act on already existing ice crystals, binding to certain planes of the crystal [9,11,12,28,29]. However, prior to this, ice must somehow appear in the organism. Except for inoculative freezing when ice enters the organism from outside [1,30,31,32], ice can only result from nucleation within the organism, and namely the latter phenomenon we consider here.
It is well-known that water per se does not start to freeze at 0 °C and stays supercooled at small and moderate negative temperatures (see, e.g., [33,34]). In a biologically reasonable time, the emergence of an ice seed (the smallest stable piece of arising ice), can occur in bulk water only at temperatures below –30 °C – –40 °C [35,36]. For kinetic reasons, at higher but still negative temperatures, some “ice nucleators” are required to initiate the freezing [37,38,39,40,41,42,43]. These ice nucleators could serve as the targets for “antinucleators”, including antifreeze proteins [44,45].
Here, we show that an ice-binding protein does not lower the ice nucleation temperature for a standard buffer in plastic test tubes but lowers the ice nucleation temperature for the buffer with some ice nucleators like copper(II) oxide (CuO) powder or bacteria Pseudomonas syringae [43]. Lastly, we show that living cells have regions where antifreeze protein molecules concentrate at a temperature close to 0 °C; these regions may be able to act as ice nucleators, but definitely did not evolve as such, because these were human cells.
2. Results
2.1. Ice Nucleation and Its Hindering in the Presence of an Ice-Binding Protein
We have studied the action of an antifreeze protein on the temperature of initiation of ice formation in the presence and in the absence of potent ice nucleators.
The ice-binding protein used in our experiments is the mutant mIBP83 [46,47] of the natural ice-binding protein cfAFP isoform 337 [48,49,50]; the cfAFP is an antifreeze protein from a spruce budworm Choristoneura fumiferana, a moth whose larvae winter at temperatures below –30 °C [51]. This mutant was used because while retaining the ability of ice-binding [46,47], it is less susceptible to aggregation during isolation and purification than the wild-type cfAFP, thus being more convenient for experiments. The mutant mIBP83 has one SS bond vs. four of the wild-type cfAFP and a slightly truncated C-terminus (for details, see [46,47]).
To visualize the results of some of our experiments, we used the fusion protein mIBP83-GFP [46,47], where “GFP” means the cycle3 mutant form of the green fluorescent protein [52]. The cycle3 mutant remains monomeric and fluorescent under our experimental conditions [53].
The fusion protein mIBP83-GFP, as well as mIBP83 itself, was expressed in E. coli cells, isolated, and purified [46,47]. The ice-binding ability of this fusion protein and the lack of such ability of GFP (Figure 1A) have already been shown by some of us [46,47].
Experiments on sample freezing in the thermostat (the device was described in detail at [56], see also Materials and Methods) show the impact of mIBP83 on ice nucleation. The experiments were carried out as follows (for details, see Materials and Methods). In the thermostat, a plastic (polypropylene) test tube with 1 mL of a sample was cooled from +10 °C to –18 °C at a rate of 0.24 °C/min and then heated at the same rate; the temperature was measured in the center of the sample. In Figure 1B, we show the change in temperature of sodium phosphate water buffer without any protein in several cooling/heating cycles using the same sample portion and the same test tube. Freezing of the sample can be noticed as a sharp increase in the sample temperature during the cooling because the sample starts to receive the latent heat released by the freezing liquid. The beginning of each peak, i.e., the nucleation event, is indicated by an arrow. After the ice freezing is completed, the temperature drops back to the thermostat temperature. One can see that all three nucleation events shown in Figure 1B occur at a temperature of about –10 °C. These nucleation temperatures are very well reproducible from cooling to cooling, provided neither the sample portion nor the test tube has been changed during the experiment.
Similar experiments—with similar results [54]—were performed by two of us previously with distilled water.
In Figure 1C, four blue curves stand for freezing of the same buffer, but with different 1 mL portions of the sample in different test tubes. We present an individual freezing curve for each portion of the sample; the point of ice nucleation, i.e., the beginning of the temperature peak, is indicated with a blue arrow. One can see that here, the range of nucleation temperatures is wider than in the case of several nucleation events observed for one and the same sample portion (Figure 1B). Four red curves with red arrows correspond to the solution of the antifreeze mIBP83 in the same buffer. There is no significant change in the average nucleation temperature between the sole buffer and the buffer with added mIBP83 (Figure 1C, Table 1).
Similar experiments with the same results were performed, as a control, with 0.6 mg/mL solution of carbonic anhydrase B, a protein that has never been considered as an antifreeze protein, in the same phosphate buffer: again, we saw no change in the nucleation temperature between the sole buffer and the buffer with carbonic anhydrase B.
In contrast, in the presence of the nucleating agents CuO and P. syringae, we observed significant changes in the nucleation temperature upon the addition of mIBP83 (see Figures 1D, 1E, and Table 1).
The ranges of nucleation temperatures for all studied samples are given in Table 1. This Table and Figure 1 show that the antifreeze protein mIBP83 decreases the ice initiation temperature in the presence of a potent ice nucleating agent.
It follows from Figure 1 and Table 1 that the freezing of all studied solutions occurs not at 0 °C but, in the absence of nucleators, below –7.9 °С. This means, by the way, that in the absence of nucleators, the blood freezing per se cannot happen to any polar fish since the ocean temperature is never below –2 °C [57]; see also the “Temperature of Ocean Water” website: https://www.windows2universe.org/earth/Water/temp.html.
In all the above cases, the initiation of freezing occurred in supercooled liquids. The phenomenon of liquid supercooling before freezing is well-known [38,39]. Below, it is discussed in association with the ice nucleation kinetics.
To elucidate the mechanism of freezing initiation and especially functioning of ice-binding proteins, i.e., antifreeze proteins and ice-nucleators, we address the theory of the first order phase transitions [38,39,40,41] describing the nucleation of crystals, e.g., ice. We use this theory to evaluate the rate of ice formation in water, as well as in bodily fluids, at different temperatures, and in particular, “biological” ones.
We focus on the nucleation, which is a crucial step of ice formation (because “there is no pregnancy without conception”) and pay little attention to the growth of ice, which, at “biological” temperatures, usually takes much less time than the ice nucleation event [43].
2.2. Ice Nucleation: A Theoretical Consideration
We consider the ice nucleation in conditions that are most interesting for biology: at high subzero temperatures, i.e., just below 0 °C (=273 K), where the ice and the liquid water phases are close to the equilibrium; and we ignore shock waves which are rare in organisms but, in principle, can trigger the freezing in supercooled liquids [37]).
As reported previously [38,39,42,43,54,58], the "3-dimensional case" of ice nucleation—nucleation within a body of bulk water—can only happen, for kinetic reasons, at rather low temperatures (experimentally: below ≈–35 °C [59]), which are not of interest here.
Therefore, we consider the most “biology-related” case of ice formation that occurs at high subzero temperatures on the surfaces that are in contact with water. The basic estimates of the nucleation time of this "2-dimensional case" of the first order phase transition can be obtained using the classical theory of nucleation [40,60,61,62]. To do so, one must find the activation free energy corresponding to the transition state, i.e., the maximum value of the free energy that changes with growing n, the number of particles in the d-dimensional (d = 3 or 2) piece of the new phase:
here is the chemical potential of a molecule in the “new” (arising) solid phase minus that in the “old” (liquid) one (so that at the point of thermodynamic equilibrium of phases), is the additional free energy of one molecule on the border of the “new” phase, i.e., on its surface for the 3-dimensional () or perimeter for the 2-dimensional () case, and (where , , see [43]) is the number of molecules on the border of a compact piece of the new phase of particles. Then and , while the diameter of the ice “seed” (i.e., the minimal stable piece of arising ice) is
in both cases [43], 3Å being the size of an H2O molecule.
The value of the temperature-depended term is estimated as follows. At the temperature (=273 K, i.e., 0 °C, is the water/ice equilibrium point, and ), according to the classical thermodynamics, where and are the entropy and enthalpy of water freezing per 1 molecule at the absolute temperature . Taking and values from [63], we obtain [43]:
being the Boltzmann constant. Thus,
with the value ≈ 0.85 that follows from the experimental value of the ice/water interface free energy ≈32 erg/cm2 [64] and the fact that an H2O molecule occupies ≈10 Å2 of the interface, we obtain
The time of appearance of the ice seed around one given H2O molecule is
where τ (the time of the border H2O molecule diffusive inclusion in or exclusion from the ice surface at about 0 °C) is a fraction of a microsecond [39,43]. It is clear that is the main temperature-depended term here (when →0 and thus →0, i.e., close to 0 °C, can be huge), while the temperature dependence of the term is relatively weak [43] and can be ignored.
The time of nucleation, i.e., of appearance of an ice seed around some one of the N water molecules contained in (at d=3) the vessel or on its borders (at d=2) is
and is much larger than the time of ice growth after the seeding, especially close to 0 °C. Both theoretically and experimentally, the growth of ice in a ~1 mL test tube at ≈–10 °C usually takes seconds, while the ice nucleation time () at temperatures higher than –10 °C is usually minutes, hours or much more [39,43,54].
Note that if, as observed experimentally, the time of ice appearance in a test tube, , is much longer than seconds, and which corresponds to the volume of a tiny droplet or the water layer on walls of a ~1 mL test tube, then , the appearance of the ice seed around one given H2O molecule, takes billions of years, like a decay of a uranium nucleus. Comparison of this years with the experimental times of ice nucleation in a ~1 mL test tube ( seconds at the temperature of ice nucleation, see the end of this Section and Section 2.2.2) and the subsequent ice growth time there (also ~10 seconds, see [54]) shows that all ice in a ~1 mL test tube usually arises from one or two, rarely three ice seeds.
If the time of appearance of the ice seed around one given H2O molecule is , the probability that a seed does not appear around the given H2O molecule in time t is , and the probability that a seed arises around this H2O molecule is if . Under the condition that , the probability of the appearance of m seeds in time t in an ensemble of N water molecules follows from the Poisson probability distribution = , which gives the average expected value of m as , and its variance as . Thus, the expected value of m is . So, at , is the range of expected seed numbers at the characteristic moment (see Equation (5)) of the appearance of the first ice seed in the ensemble. This means that the expected characteristic time range of appearance of the first ice seed at a fixed temperature is approximately .
2.2.1. Ice Nucleation in Bulk Water Is Only Possible at Rather Low Temperatures
For the 3-dimensional case corresponding to the ice nucleation in a body of bulk water, the transition state free energy is:
[43]; where ≈0.85, see above.
Equations (4), (6) show that the time of ice appearance is extremely temperature-sensitive: it turns to infinity when →0, and, unlike most molecular processes, the freezing is accelerated not with increasing but with decreasing temperature, at least, when it is not too far from 0 °C.
The time of ice appearance within 1 mL of resting pure water containing H2O molecules not surrounded by solid walls (e.g., inside a water droplet), should take (theoretically) very many years at about –35 °C, and a fraction of microsecond at about –50 °C [43]; this is in agreement with numerous experimental observations that ice never appears within a droplet of resting pure water at –35 °C and above [59].
2.2.2. Ice Nucleation on the Ice-Binding Surfaces at High Subzero Temperatures
Now we address a more biologically interesting case of ice formation on the ice-binding walls of a vessel filled with water or on the surfaces of ice-binding dust particles in water. Unlike the ice nucleation inside a body of bulk water, the ice nucleation on a surface can occur at rather high subzero temperatures [38,39,41,43].
On the ice-binding surface, an ice nucleus (and seed) arises not as a 3d (Figure 2A) but as a 2d (Figures 2B, 2C) object. This (cf. Equation (6) with Equation (7) below) drastically decreases [43] the transition state free energy when :
If it is assumed that for a 2d nucleus, as it is for the 3d one, then , and, according to Equations (4, 5), the characteristic time of appearance of an ice seed somewhere on the 1 mL vessel walls accommodating 1015 water molecules is
where and, at ,
This means that with , the freezing of water in a 1 mL vessel should, theoretically, take a second at ≈6°, that is, at a temperature of –6 °C, and a minute at –5.5 °C. Thus, any ice-binding surface can be considered as a kind of ice nucleator. The time is highly temperature-sensitive: at a temperature of 1° higher than –6 °C, the appearance of an ice seed would take hours, while at a temperature of 1° lower than –6 °C, it would take a millisecond.
However, the experimentally measured [64] value represents the average free energy of the ice/water interface per interface molecule, while different facets of an ice crystal may have somewhat different values of this interface free energy due to different orientation of molecules relative to different crystal facets [39,65]. Then, if, for instance, , we have instead of in Equation (8), and theoretically, the initiation of water freezing in a 1 mL vessel should take seconds at about –10 °C and minutes at about –9 °C (the freezing initiation temperature of –9 ÷ –10 °C was observed in our experiments, see Figure 1B). With , Equation (8) has the form
The value of can be experimentally measured at a given fixed temperature . However, our experiments on water cooling use a constant decrease in temperature with time t, where and with (see Section 2.1). Therefore, the total time from the beginning of the experiment to the appearance of an ice seed at a temperature of can be calculated as . The minimum of this calculated time must correspond to the experimental value of .
The first derivative of with respect to equals to , which must be equal to zero at the extremum of . With , this extremum corresponding just to is the minimum because the second derivative of with respect to is positive. At , the optimal time of freezing nucleation calculated from Eq. (8a) is about 40 seconds.
2.2.3. Ice-Binding Surfaces
As mentioned above, the emergence of ice is catalyzed by ice-binding surfaces, i.e., the surfaces that bind ice stronger than liquid water. However, the catalytic effect is not affected by the strength of ice binding to the “non-ice” underlay, so far as this binding is stronger than the binding of liquid water. This is because the second and all further layers of ice form on the ice already bound to the “non-ice” underlay, and, if the ice strongly binds to the “non-ice” underlay, a monomolecular ice layer exists even at temperatures > 0 °C; but a massive ice growth, our sole interest, can arise on this icy underlay only at temperatures below 0 °C.
Thus, any ice-binding surface, including that of a plastic test tube or some dust particles, serves as an ice nucleator but its catalytic effect on the ice emergence is determined solely—see Equations (8), (8a)—by the temperature and the free energy of the border of the arising ice, i.e., by the B2 factor. The latter depends on the orientation of molecules forming the layer of ice arising on the underlay. A special shape of the underlay (cf. Figure 2C with Figure 2B) can significantly weaken the contacts between ice molecules inside the newly arising ice layer, and accordingly, reduce the values of the boundary factors. In turn, the smaller strongly decreases the freezing temperature, thereby drastically shortening the freezing time at a given temperature. The faster ice formation on surfaces corrugated at an atomic scale has been already experimentally observed [66]. Thus, a special atomic structure of the underlay can create a strong “ice nucleator”—like, e.g., CuO powder [43]—unlike while "weak ice nucleators”, such as plastic walls of test tubes.
If strong ice nucleators are added to water in a test tube with ice-binding walls, then there are two parallel freezing nucleation reactions: one is generated by the walls of the test tube, and the other by the added nucleators. If the initiation time of the freezing generated by the tube walls alone is , and the initiation time of the freezing generated by the added nucleators alone is , then the initiation time of the freezing in the test tube with added nucleators is
Here, is the number of water molecules on the tube walls, is the number of water molecules on the surfaces of the added nucleators, and , are the activation free energies for nucleation on the tube walls and on the added nucleators, respectively. If is large enough and is small enough, then the freezing time is determined mainly by the added ice nucleators.
If the antifreeze protein is added, it reduces in proportion to the antifreeze concentration and the antifreeze-wall binding constant, and it reduces in proportion to its concentration and the antifreeze-nucleator binding constant.
2.2.4. Can an Antifreeze Protein Bind to Something That Was Not Evolved to Be an Ice Nucleator?
Since the activity of the antifreeze protein so clearly manifests itself in the blocking of ice nucleators, we hypothesized that antifreeze proteins could evolve to bind to any surfaces which are or may serve as ice nucleators. Some ice nucleators (e.g., in P. syringae) are thought to be used as a weapon [67] or, in some plants, as a natural thermostat utilizing, in frost, the latent heat released during the nucleators-induced freezing to save other parts of the plant [68]. But one cannot expect that ice nucleators could evolve, e.g., in mice, though it has been already shown [69] that ice arises in tails of mice at –22 °C (while ice cannot arise at temperatures higher than –35 °C without nucleators, see above), and that an antifreeze protein induced by transfection protects the mice tails from frostbite damage. Thus, the observed ice-nucleating activity in mice is apparently an incidental side effect of something with another function.
In this connection, we checked if human cells have binding sites for mIBP83.
Since mIBP83-GFP allows visualization of the mIBP83 location, we transfected human breast cancer cells SKBR-3 by plasmids encoding either the fused protein mIBP83-GFP or sole GFP as a control. The transfected cells were cultured under standard conditions (see Experiments with the Human Cell Culture in Materials and Methods).
To test the response of the transfected cells to cold, they were kept at +37 °C and then incubated at +2 °C for 2 hours, followed by immediate fixation with 4% formaldehyde to prevent protein redistribution during the imaging procedure. The temperature of +2 °C was chosen as the lowest temperature at which the cells remained spread out, attached to the substrate, and accordingly, convenient for the research using a laser scanning microscope, see Materials and Methods.
The pattern of intracellular location of mIBP83-GFP clearly differs from that of the sole GFP namely at a low positive (+2 °C) temperature (Figure 3). At +37 °C, both proteins do not show a clear location in the cell. The cooling down to +2 °C leads to drastic changes in the mIBP83-GFP but not in the GFP distribution. The amount of diffusely distributed mIBP83-GFP decreases, and it accumulates mainly in central regions of the cytoplasm, including a part of the perinuclear regions. Although no region in the considered cells evolved as a natural target for the given antifreeze protein, mIBP83-GFP is concentrated in small areas that are clearly visible in the cells. This suggests that mIBP83-GFP binds to some cellular structures upon the cooling down to almost zero.
3. Discussion
The ice-binding properties of various surfaces, mainly of technical use, have been studied (see, e.g., [70,71] and references therein). However, we don't know very much about the ice-binding properties of surfaces of biological origin which can be targets for AFPs; thus, the identification of such surfaces and the study of their properties will be the next step in the investigation of the action of ice nucleators and their interaction with antifreeze proteins.
The results obtained in the experiments with living cells (Figure 3) are in line with our hypothesis that at temperatures of about 0 °C, cells may contain some potentially ice-nucleating surfaces to which antifreeze proteins can bind.
3.1. Notes on Antifreeze Protein Functions
It is worth emphasizing that our work supports a new view on the functioning of antifreeze proteins. Their main task may be other than just ice crystal binding and preventing its further growth. Instead, they may aim to bind—directly or through a thin layer of water molecules—to those cell or tissue surfaces where the ice nuclei can form, thus preventing the ice formation completely. The blockage of these ice-nucleating surfaces is the only way to prevent freezing using a small number of antifreeze molecules.
It is known that there are several classes of antifreeze proteins, and some antifreeze proteins bind to some facets of ice crystals and to some nucleators, while others bind to other facets and other partners [11,72,73].
Occasionally, ice particles can penetrate inside the organism through the body surface, guts, gills, etc. This has been experimentally observed for fishes, insects, turtles, and some other organisms [17,30,31,74,75]. These particles initiate the inoculative freezing process which can also be blocked by ice-binding proteins.
Besides, the IBPs binding to some cell surfaces may contribute to their stabilization, thereby protecting them from hypothermic cold shock damage even at a temperature above 0 °C when there is no possibility of ice emergence; this is demonstrated, in particular, by a protection of human hepatoma cells by a fish AFP at +4 °C [76]. It has been experimentally shown that expression of a tick antifreeze glycoprotein enhances cold tolerance in Drosophila melanogaster [77].
The proposed binding of IBPs to cell surfaces can explain both experimentally observed phenomena [29,78]: (i) the survival during strong (below 0 °C) cooling that could result in ice formation but was avoided due to the IBP-induced inhibition of ice crystal formation, and (ii) the tolerance of cells to the cold shock under moderate cooling to almost 0 °C by the stabilization of cell surfaces due to their binding to IBPs.
It should be noted that the prevention of ice formation and binding to cell surfaces (and, of course, the blocking of the ice itself—in case it still appears, one way or another, say, by the inoculative freezing) are not the only properties of IBPs. Since mIBP83 binds to ice (Figure 1A), it can stabilize the ice, and so it does indeed, i.e., increases the ice melting temperature [54,75]; thus, an IBP can serve not only as an antifreeze but also as an ice-stabilizing or even ice-nucleating protein. However, as follows from the above calculations (see Equation (2b)), the diameter of an ice-nucleating surface must be not less than ~130 nm at and ~20 nm at . This agrees with the data that a large (164 kDa) antifreeze glycoprotein can initiate the formation of ice nuclei, and its ice-nucleation ability is diminished after removal of carbohydrate (92 kDa in total) from it, while this removal did not noticeably alter its antifreeze activity [79]. Moreover, there is a correlation of ice-nucleator “power” (that is, the maximal nucleation temperature) with the ice-nucleator's size [80,81]. In general, it has been shown that the size is a good predictor of the temperature of ice nucleation by different IBPs [78,82], and one can change—and even switch—the behavior of the ice-binding molecule (or molecular complex) by changing its size [83].
3.2. Notes on Ice Nucleators
According to the literature, the ice nucleators known to date are very different both in their chemical nature and in the “nucleation power”. Most of them act at temperatures below –10 °C, while some induce freezing at a temperature above –4 °C. Among the most potent ice nucleators, there are inorganic substances such as the powder of famous AgI [84,85], powders of various organic substances, including some steroids [86], long-chain alcohols [87], and amino acids [88], some macromolecules and whole biological objects like pollen [89] and bacteria [90,91]. The bacterium P. syringae is an extremely potent ice nucleator that induces water freezing at temperatures up to –2 °C and even above [90].
Along with the relatively well-studied [91,92] bacterial ice nucleators which are large proteinaceous complexes situated on the bacterial membrane, somewhat less is known about the chemical nature of ice nucleators acting in other organisms [68,93]. Some insects have ice nucleators, both lipoproteins and proteins, in their hemolymph in summer and lose these, especially the most potent ones, during the cold season [93,94]. The loss of ice nucleators is also observed in turtles, and these nucleators are probably ingested soil bacteria like P. syringae [95]. Ice-nucleating lipoproteins from the cranefly Tipula trivittata are not anchored to membranes but aggregate into long chains [96]. Long filamentous aggregates are also formed by the bacterial ice nucleators (of P. syringae and P. borealis) expressed in Escherichia coli [97,98]. In winter rye (Secale cereale) leaves, ice nucleators seem to be complexes of proteins, carbohydrates, and phospholipids [99]. It is known that membrane vesicles of Erwinia herbicola bacteria have ice-nucleating activity [100] which can be inhibited by an antifreeze glycoprotein, and it is hypothesized [101] that cell membranes by themselves could be ice nucleators, especially in animal cells, because they have a large fraction of cholesterol known as a good ice nucleator in a solid state [86,102]. Also, the pool of ice nucleators includes cellulose, which is the major component of plant cell walls [103], and even some (especially large) antifreeze proteins [78,79], see the end of the Section 3.1 above.
3.3. Ice Nucleators and Antifreeze Proteins
Although it is yet impossible to directly observe the interaction between ice nucleators and antinucleating proteins, the hindering of the ice-nucleating activity unambiguously hints at a connection between them.
Some data on interactions between ice nucleators and antifreeze proteins are available in the literature. It was shown that antifreeze proteins from larvae of a beetle Dendroides canadensis inhibit some, but not all, tested ice nucleators [94,104,105]. An antifreeze glycoprotein from Antarctic toothfish (Dissostichus mawsoni) was demonstrated to inhibit the ice-nucleating activity of membrane vesicles from the bacterium Erwinia herbicola [98]. A bacterium Acinetobacter calcoaceticus was shown to produce an anti-nucleating protein that demonstrated various specificities for various ice-nucleating bacteria and AgI [106]. Fish antifreeze protein type III was reported to inhibit the ice nucleation process by adsorbing onto the surfaces of both ice nuclei and dust particles [44]. Fish antifreeze proteins (AFP I and AFP III) and some simpler organic compounds like poly(vinyl alcohol), poly(vinyl pyrrolidone), and poly(ethylene glycol) inactivated the ice nucleating activity of AgI [45]. A recombinant antifreeze protein derived from the perennial ryegrass plant Lolium perenne suppressed the ice nucleation point of ice nucleators of P. syringae, while a recombinant fish antifreeze protein had no such effect [107]. An evaluation of the effects of five different antifreeze proteins on the activity of bacterial ice nucleators showed that bacterial ice nucleating proteins are inhibited by certain antifreeze proteins, while other antifreeze proteins produce no such effect [73].
Thus, it can be stated that our mIBP83 protein is not the only one with the antinucleating ability. At least some other antifreeze proteins, in addition to inhibiting ice growth and/or recrystallization, are shown to inhibit the action of ice nucleators, thus being able to completely prevent formation of ice.
4. Materials and Methods
4.1. Freezing Experiments Equipment
Experiments on freezing were carried out using a Julabo F-25 thermostat, Germany. The thermostat and measuring thermometers (thermocouples) were checked using an LT-300-N, TERMEX laboratory thermometer, Russia, resolution 0.01 °C, accuracy ±0.05 °C. In detail, the experimental device is described in [56].
The experiments used standard plastic (polypropylene) microcentrifuge test tubes (1.7 mL, Cat. No. 3621, Costar®). The liquid volume was always 1 mL.
In experiments with added nucleators, we added either 0.5 mg of copper(II) oxide or 0.05 mL of suspension of P. syringae with a cell density of 1.0 optical units.
Copper(II) oxide (CuO) was from Reachem (Moscow, Russia). During the course of our experiment, this non-soluble CuO powder was at the bottom of the test tubes.
P. syringae cells (Pseudomonas syringae pv. syringae) were grown on medium L (yeast extract 5.0 g/L; peptone 15.0 g/L; NaCl 5.0 g/L) at +37 °C. The cells were grown in the liquid medium to a cell density of 1.0 optical units (by absorption at 600 nm), and then precipitated on a centrifuge at 6000 g, and washed twice with a solution of 20 mM Tris-HCl (pH 7.5). Lastly, the buffer of the same composition was added to obtain the desired cell density (1.0 optical units). The concentration of P. syringae cells in the experiments was controlled by absorption at 600 nm.
The test tubes shown in Figure 1A were illuminated using an ecx-f20.m VILBER transilluminator, France.
4.2. Experiments with the Human Cell Culture
The human breast adenocarcinoma cells SKBR–3 (ATCC® HTB 30™) were cultured in McCoy's medium (PanEco, Russia) with 10% (v/v) fetal calf serum (HyClone, USA) in 5% CO2 at +37 °C.
For transient expression of fluorescent proteins, we used the plasmid vectors pTag-2N encoding the gene of mIBP83-GFP or sole GFP (cycle3 GFP) under the control of cytomegalovirus promoter and the gene of resistance to the antibiotic G418. The cells were transfected using the Lipofectamin 3000 transfection reagent (Invitrogen, USA) according to the manufacturer's instructions. The transfection was followed by cultivation in a selective G418-containing medium for several passages.
Cooling of the cells was performed using a solid-state ThermoStat Plus (Eppendorf®, Germany) with precise temperature control. The cells were cultured in Falcon® 96-well black/blear flat-bottom TC-treated imaging microplates or Eppendorf® glass-bottom cell imaging dishes. To test the response to cold, the cell cultures were incubated at +2 °C for 2 h and then immediately fixed with 4% formaldehyde. The experimental temperature was +2 °C because, at lower temperatures, the cells would separate from the substrate, thus becoming inconvenient for the microscopic research.
The images were obtained using an Axio Observer Z1 LSM–710 DUO NLO laser scanning microscopy system (Carl Zeiss, Germany). The GFP fluorescence was excited at 488 nm and registered in a wide spectral range of 500–735 nm.
5. Conclusions
Concerning the biological action of ice-binding proteins, we conclude that if a cell, a tissue, a blood vessel, etc. has ice-binding, i.e., potentially ice-nucleating surfaces, then certain antinucleating molecules, including antifreeze proteins, are required to bind to these surfaces, thereby blocking ice nucleation at subzero temperatures. And the surfaces of ice crystals (if they nonetheless appear—say, by inoculation) can be considered as a special case surfaces on which ice can form, and therefore such surfaces should also be blocked by antifreeze proteins.
Our goal for future work is a detailed investigation of the targets for IBP binding in various cell types and tissues. In particular, we plan to investigate ice nucleators from those cells and organisms which naturally must avoid freezing, and thus the interaction of their ice nucleators with some antifreeze proteins can naturally occur.
Author Contributions
Conceptualization, theory, writing, and editing, A.V.F.; conceptualization and experimental investigations, B.S.M.; data analysis, writing, and editing, S.O.G.; genetic engineering, K.A.G.; human cell investigation, visualization, E.A.S.; human cell investigation, visualization, data analysis, writing, I.V.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Russian Science Foundation, grant # 21-14-00268.
Acknowledgments
We are grateful to G. Fermi, A.Yu. Grosberg, M.D. Frank-Kamenetsky, E.G. Malenkov, E.I. Shakhnovich, D. Frenkel, and A.N. Gavrishev for fruitful discussions, and to G.S. Nagibina, Yu.D. Okulova, E.N. Samatova for assistance in experiments, and O.A. Eremeeva and E.V. Serebrova for assistance in paper editing.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Salt, R.W. Principles of insect cold-hardiness. Annu. Rev. Entomol. 1961, 6, 55–74. [Google Scholar] [CrossRef]
- Storey, K.B.; Storey, J.M. Biochemistry of cryoprotectants. In Insects at Low Temperatures. Lee, R.E., Denlinger, D., Eds.; Chapman & Hall: New York, USA, 1991; pp. 64–93. [Google Scholar]
- Davies, P.L. Ice-binding proteins: A remarkable diversity of structures for stopping and starting ice growth. Trends Biochem Sci. 2014, 39, 548–555. [Google Scholar] [CrossRef] [PubMed]
- Bar Dolev, M.; Braslavsky, I.; Davies, P.L. Ice-binding proteins and their function. Annu. Rev. Biochem. 2016, 85, 515–542. [Google Scholar] [CrossRef] [PubMed]
- Białkowska, A.; Majewska, E. , Olczak, A.; Twarda-Clapa, A. Ice binding proteins: Diverse biological roles and applications in different types of industry. Biomolecules 2020, 10, 274. [Google Scholar] [CrossRef]
- Duman, J.G. The role of macromolecular antifreeze in the darkling beetle, Meracantha contracta. J. Comp. Physiol. B 1977, 115, 279–286. [Google Scholar] [CrossRef]
- Harding, M.M.; Ward, L.G.; Haymet, A.D. Type I ‘antifreeze’ proteins. Structure–activity studies and mechanisms of ice growth inhibition. Eur. J. Biochem. 1999, 264, 653–665. [Google Scholar] [CrossRef]
- Raymond, J.A.; DeVries, A.L. Adsorption inhibition as a mechanism of freezing resistance in polar fishes. Proc. Natl Acad. Sci. USA 1977, 74, 2589–2593. [Google Scholar] [CrossRef]
- DeVries, A.L. Glycoproteins as biological antifreeze agents in Antarctic fishes. Science 1971, 172, 1152–1155. [Google Scholar] [CrossRef]
- Knight, C.A.; Duman, J.G. Inhibition of recrystallization of ice by insect thermal hysteresis proteins: A possible cryoprotective role. Cryobiology, 1986, 23, 256–262. [Google Scholar] [CrossRef]
- Drori, R.; Celik, Y.; Davies, P.L.; Braslavsky, I. Ice-binding proteins that accumulate on different ice crystal planes produce distinct thermal hysteresis dynamics. J. R. Soc. Interface 2014, 11, 20140526. [Google Scholar] [CrossRef]
- Rahman, A.T.; Arai, T.; Yamauchi, A.; Miura, A.; Kondo, H.; Ohyama, Y.; Tsuda, S. Ice recrystallization is strongly inhibited when antifreeze proteins bind to multiple ice planes. Sci. Rep. 2019, 9, 2212. [Google Scholar] [CrossRef] [PubMed]
- DeVries, A.L.; Wohlschlag, D.E. Freezing resistance in some Antarctic fishes. Science 1969, 163, 1073–1075. [Google Scholar] [CrossRef] [PubMed]
- DeVries, A.L.; Komatsu, S.K.; Feeney, R.E. Chemical and physical properties of freezing point-depressing glycoproteins from Antarctic fishes. J. Biol. Chem. 1970, 245, 2901–2908. [Google Scholar] [CrossRef]
- Theede, H.; Schneppenheim, R.; Béress, L. Frostschutz-Glykoproteine bei Mytilus edulis? Mar. Biol. 1976, 36, 183–189, [in German]. [Google Scholar] [CrossRef]
- Duman, J.G. Thermal-hysteresis-factors in overwintering insects. J. Insect Physiol. 1979, 25, 805–810. [Google Scholar] [CrossRef]
- Duman, J.G. Antifreeze and ice nucleator proteins in terrestrial arthropods. Annu. Rev. Physiol. 2001, 63, 327–357. [Google Scholar] [CrossRef]
- Duman, J.G.; Olsen, T.M. Thermal hysteresis protein activity in bacteria, fungi, and phylogenetically diverse plants. Cryobiology 1993, 30, 322–328. [Google Scholar] [CrossRef]
- Sun, X.; Griffith, M.; Pasternak, J.J.; Glick, B.R. Low temperature growth, freezing survival, and production of antifreeze protein by the plant growth promoting rhizobacterium Pseudomonas putida GR12-2. Can. J. Microbiol. 1995, 41, 776–784. [Google Scholar] [CrossRef]
- Bayer-Giraldi, M.; Uhlig, C.; John, U.; Mock, T.; Valentin, K. Antifreeze proteins in polar sea ice diatoms: Diversity and gene expression in the genus Fragilariopsis. Environ. Microbiol. 2010, 12, 1041–1052. [Google Scholar] [CrossRef]
- Gwak, I.G.; Jung, W.S.; Kim, H.J.; Kang, S.H.; Jin, E. Antifreeze protein in Antarctic marine diatom, Chaetoceros neogracile. Mar. Biotechnol. (NY) 2010, 12, 630–639. [Google Scholar] [CrossRef]
- Hoshino, T.; Kiriaki, M.; Ohgiya, S.; Fujiwara, M.; Kondo, H.; Nishimiya, Y.; Yumoto, I.; Tsuda, S. Antifreeze proteins from snow mold fungi. Canad. J. Bot. 2003, 81, 1175–1181. [Google Scholar] [CrossRef]
- Griffith, M.; Ala, P.; Yang, D.S.; Hon, W.C.; Moffatt, B.A. Antifreeze protein produced endogenously in winter rye leaves. Plant Physiol. 1992, 100, 593–596. [Google Scholar] [CrossRef] [PubMed]
- Urrutia, M.E.; Duman, J.G.; Knight, C.A. Plant thermal hysteresis proteins. Biochim. Biophys. Acta 1992, 1121, 199–206. [Google Scholar] [CrossRef] [PubMed]
- Hudait, A.; Moberg, D.R.; Qiu, Y.; Odendahl, N.; Paesani, F.; Molinero, V. Preordering of water is not needed for ice recognition by hyperactive antifreeze proteins. Proc. Natl Acad. Sci. USA 2018, 115, 8266–8271. [Google Scholar] [CrossRef]
- Sun, Y.; Maltseva, D.; Liu, J.; Hooker II, T.; Mailänder, V.; Ramløv, H.; DeVries, A.L.; Bonn, M.; Meister, K. Ice recrystallization inhibition is insufficient to explain cryopreservation abilities of antifreeze proteins. Biomacromolecules 2022, 23, 1214–1220. [Google Scholar] [CrossRef] [PubMed]
- Tas, R.P.; Hendrix, M.M.R.M.; Voets, I.K. Nanoscopy of single antifreeze proteins reveals that reversible ice binding is sufficient for ice recrystallization inhibition but not thermal hysteresis. Proc. Natl Acad. Sci. USA 2023, 120, e2212456120. [Google Scholar] [CrossRef] [PubMed]
- Celik, Y.; Drori, R.; Pertaya-Braun, N.; Altan, A.; Barton, T.; Bar-Dolev, M.; Groisman, A.; Davies, P.L.I.; Braslavsky, I. Microfluidic experiments reveal that antifreeze proteins bound to ice crystals suffice to prevent their growth. Proc. Natl Acad. Sci. USA 2013, 110, 1309–1314. [Google Scholar] [CrossRef]
- Kuramochi, M.; Takanashi, C.; Yamauchi, A.; Doi, M.; Mio, K.; Tsuda, S.; Sasaki, Y.C. Expression of ice-binding proteins in Caenorhabditis elegans improves the survival rate upon cold shock and during freezing. Sci. Rep. 2019, 9, 6246. [Google Scholar] [CrossRef]
- Scholander, P.F.; Dam, L.V.; Kanwisher, J.W.; Hammel, H.T.; Gordon, M.S. Supercooling and osmoregulation in arctic fish. J. Cell. Comp. Physiol. 1957, 49, 5–24. [Google Scholar] [CrossRef]
- Frisbie, M. P.; Lee, R.E., Jr. Inoculative freezing and the problem of winter survival for freshwater macroinvertebrates. J. North Am. Benthol. Soc. 1997, 16, 635–650. [Google Scholar] [CrossRef]
- Praebel, K.; Hunt, B.; Hunt, L.H.; DeVries, A.L. The presence and quantification of splenic ice in the McMurdo Sound notothenioid fish, Pagothenia borchgrevinki (Boulenger, 1902). Comp. Biochem. Physiol. A Mol. Integr. Physiol. 2009, 154, 564–569. [Google Scholar] [CrossRef] [PubMed]
- Dorsey, N.E. The freezing of supercooled water. Trans. Am. Phil. Soc. 1948, 38, 247–328. [Google Scholar] [CrossRef]
- Langham, E.J.; Mason, B.J. The heterogeneous and homogeneous nucleation of supercooled water. Proc. R. Soc. Lond. A 1958, 247, 493–504. [Google Scholar] [CrossRef]
- Pruppacher, H.R.; Klett, J.D. Microphysics of Clouds and Precipitation; Springer: New York, USA, 2010; Chapter 7. [Google Scholar]
- Murray, B.J.; Broadley, S.L.; Wilson, T.W.; Bull, S.J.; Wills, R.H.; Christenson, H,K.; Murray, E.J. Kinetics of the homogeneous freezing of water. Phys. Chem. Chem. Phys. 2010, 12, 10380–10387. [Google Scholar] [CrossRef]
- Zeldovich, J.B. Toward the theory of formation of a new phase. Cavitation. J. Exp. Theor. Phys. 1942, 12, 525–538. [Google Scholar]
- Ubbelohde, A.R. Melting and Crystal Structure; Clarendon Press: Oxford, UK, 1965; Chapter 14. [Google Scholar]
- Chernov, A.A. Modern Crystallography III. Springer Berlin: Heidelberg, Germany, 1984. [CrossRef]
- Slezov, V.V. Kinetics of First Order Phase Transitions, 1st ed.; Wiley-VCH: Weinheim, Germany, 2009; Chapter 3. [Google Scholar]
- Ruckenstein, E.; Berim, G. Kinetic Theory of Nucleation; CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2016. [Google Scholar]
- Finkelstein, A.V. Some peculiarities of water freezing at small sub-zero temperatures. arXiv:2008.13682v1 [Preprint], 2020. Available at: https://doi.org/10.48550/arXiv.2008.13682 (Accessed on August 29, 2023). [CrossRef]
- Finkelstein, A.V.; Garbuzynskiy, S.O.; Melnik, B.S. How can ice emerge at 0 °C? Biomolecules 2022, 12, 981, Correction - in Biomolecules, 2023, in press. [Google Scholar] [CrossRef]
- Du, N.; Liu, X.Y.; Hew, C.L. Ice nucleation inhibition: Mechanism of antifreeze by antifreeze protein. J. Biol. Chem. 2003, 278, 36000–36004. [Google Scholar] [CrossRef]
- Inada, T.; Koyama, T.; Goto, F.; Seto, T. Inactivation of ice nucleating activity of silver iodide by antifreeze proteins and synthetic polymers. J. Phys. Chem. B 2012, 116, 5364–5371. [Google Scholar] [CrossRef]
- Glukhova, K.A.; Okulova, J.D.; Melnik, B.S. Designing and studying a mutant form of the ice-binding protein from Choristoneura fumiferana. bioRxiv [Preprint], 2020. Available at: https://doi.org/10.1101/2020.08.31.275651 (Accessed on August 29, 2023). [CrossRef]
- Deeva, A.A.; Glukhova, K.A.; Isoyan, L.S.; Okulova, Y.D.; Uversky, V.N.; Melnik, B.S. Design and analysis of a mutant form of the ice-binding protein from Choristoneura fumiferana. Protein J. 2022, 41, 304–314. [Google Scholar] [CrossRef]
- Tyshenko, M.G.; Doucet, D.; Davies, P.L.; Walker, V.K. The antifreeze potential of the spruce budworm thermal hysteresis protein. Nature Biotechnol. 1997, 15, 887–890. [Google Scholar] [CrossRef]
- Leinala, E.K.; Davies, P.L.; Doucet, D.; Tyshenko, M.G.; Walker, V.K.; Jia, Z. A β-helical antifreeze protein isoform with increased activity. J. Biol. Chem. 2002, 277, 33349–33352. [Google Scholar] [CrossRef] [PubMed]
- Leinala, E.K.; Davies, P.L.; Jia, Z. Crystal structure of β-helical antifreeze protein points to a general ice binding model. Structure 2002, 10, 619–627. [Google Scholar] [CrossRef] [PubMed]
- Sanders, C.J. Biology of North American spruce budworms. In Tortricid Pests, their Biology, Natural Enemies and Control; van der Geest, L.P.S., Evenhuis, H.H., Eds.; Elsevier Science Publishers B.V.: Amsterdam, the Netherlands, 1991. [Google Scholar]
- Fukuda, H.; Arai, M.; Kuwajima, K. Folding of green fluorescent protein and the cycle3 mutant. Biochemistry 2000, 39, 12025–12032. [Google Scholar] [CrossRef]
- Glukhova, K.F.; Marchenkov, V.V.; Melnik, T.N.; Melnik, B.S. Isoforms of green fluorescent protein differ from each other in solvent molecules “trapped” inside this protein. J. Biomol. Struct. Dyn. 2017, 35, 1215–1225. [Google Scholar] [CrossRef]
- Melnik, B.S.; Finkelstein, A.V. Physical basis of functioning of antifreeze protein. Mol. Biol. (Moscow) 2022, 56, 297–305. [Google Scholar] [CrossRef]
- Doucet, D.; Tyshenko, M.G.; Kuiper, M.J.; Graether, S.P.; Sykes, B.D.; Daugulis, A.J.; Davies, P.L.; Walker, V.K. Structure-function relationships in spruce budworm antifreeze protein revealed by isoform diversity. Eur. J. Biochem. 2000, 267, 6082–6088. [Google Scholar] [CrossRef]
- Veselova, V.R.; Majorina, M.A.; Melnik, B.S. An experimental technique for accurate measurement of the freezing point of solutions and ice melting in the presence of biological objects on the examples of P. syringae and E. coli. Opera Med. Physiol. 2022, 9, 19–30. [Google Scholar] [CrossRef]
- Pawlowicz, R. Key physical variables in the ocean: temperature, salinity, and density. Nature Education Knowledge 2013, 4, 13. [Google Scholar]
- Melnik, B.S.; Glukhova, K.A.; Sokolova, E.A.; Balalaeva, I.V.; Finkelstein, A.V. A novel view on the mechanism of biological activity of antifreeze proteins. bioRxiv [Preprint], 2021. Available at: https://doi.org/10.1101/2021.09.22.461391 (Accessed on August 29, 2023). [CrossRef]
- Koop, T.; Murray, B.J. A physically constrained classical description of the homogeneous nucleation of ice in water. J. Chem. Phys. 2016, 145, 211915. [Google Scholar] [CrossRef]
- Gibbs, J.W. Graphical methods in the thermodynamics of fluids. Trans. Conn. Acad. 1873, 2, 309–342. [Google Scholar]
- Becker, R.; Döring, W. Kinetic treatment of grain-formation in super-saturated vapors. Ann. Phys. 1935, 416, 719–752. [Google Scholar] [CrossRef]
- Eyring, H. The activated complex in chemical reactions. J. Chem. Phys. 1935, 3, 107–115. [Google Scholar] [CrossRef]
- Lide, D.R. CRC Handbook of Chemistry and Physics on CD; CRC Press: Boca Raton, FL, USA, 2005; Section 6. [Google Scholar]
- Hillig, W.B. Measurement of interfacial free energy for ice/water system. J. Cryst. Growth 1998, 183, 463–468. [Google Scholar] [CrossRef]
- Zaragoza, A.; Conde, M.M.; Espinosa, J.R.; Valeriani, C.; Vega, C.; Sanz, E. Competition between ices Ih and Ic in homogeneous water freezing. J. Chem. Phys. 2015, 143, 134504. [Google Scholar] [CrossRef] [PubMed]
- Lin, C.; Corem, G.; Godsi, O.; Alexandrowicz, G.; Darling, G.R.; Hodgson, A. Ice nucleation on a corrugated surface. J. Am. Chem. Soc. 2018, 140, 15804–15811. [Google Scholar] [CrossRef]
- Lindow, S.E.; Arny, D.C.; Upper, C.D. Bacterial ice nucleation: A factor in frost injury to plants. Plant Physiol. 1982, 70, 1084–1089. [Google Scholar] [CrossRef]
- Krog, J.; Zachariassen, K.E.; Larsen, B.; Smidsrød, O. Thermal buffering in Afro-alpine plants due to nucleating agent-induced water freezing. Nature 1979, 282, 300–301. [Google Scholar] [CrossRef]
- Heisig, M.; Mattessich, S.; Rembisz, A.; Acar, A.; Shapiro, M.; Booth, C.J.; Neelakanta, G.; Fikrig, E. Frostbite protection in mice expressing an antifreeze glycoprotein. PLoS One 2015, 10, e0116562. [Google Scholar] [CrossRef]
- Raraty, L.E.; Tabor, D. The adhesion and strength properties of ice. Proc. R. Soc. Lond. A 1958, 245, 184–201. [Google Scholar] [CrossRef]
- Work, A.; Lian, Y. A critical review of the measurement of ice adhesion to solid substrates. Prog. Aerosp. Sci. 2017, 98, 1–26. [Google Scholar] [CrossRef]
- Antson, A.A.; Smith, D.J.; Roper, D.I.; Lewis, S.; Caves, L.S.; Verma, C.S.; Buckley, S.L.; Lillford, P.J.; Hubbard, R.E. Understanding the mechanism of ice binding by type III antifreeze proteins. J. Mol. Biol. 2001, 305, 875–889. [Google Scholar] [CrossRef] [PubMed]
- Schwidetzky, R.; Kunert, A.T.; Bonn, M.; Pöschl, U.; Ramløv, H.; DeVries, A.L.; Fröhlich-Nowoisky, J.; Meister, K. Inhibition of bacterial ice nucleators is not an intrinsic property of antifreeze proteins. J. Phys. Chem. B. 2020, 124, 4889–4895. [Google Scholar] [CrossRef] [PubMed]
- Packard, G.C.; Packard, M.J. Cold acclimation enhances cutaneous resistance to inoculative freezing in hatchling painted turtles, Chrysemys picta. Funct. Ecol. 2003, 17, 94–100. [Google Scholar] [CrossRef]
- Cziko, P.A.; DeVries, A.L.; Evans, C.W.; Cheng, C.-H.C. Antifreeze protein-induced superheating of ice inside Antarctic notothenioid fishes inhibits melting during summer warming. Proc. Natl Acad. Sci. USA 2014, 111, 14583–14588. [Google Scholar] [CrossRef]
- Hirano, Y.; Nishimiya, Y.; Kowata, K.; Mizutani, F.; Tsuda, S. Construction of time-lapse scanning electrochemical microscopy with temperature control and its application to evaluate the preservation effects of antifreeze proteins on living cells. Anal. Chem. 2008, 80, 9349–9354. [Google Scholar] [CrossRef] [PubMed]
- Neelakanta, G.; Hudson, A.M.; Sultana, H.; Cooley, L.; Fikrig, E. Expression of Ixodes scapularis antifreeze glycoprotein enhances cold tolerance in Drosophila melanogaster. PLoS One 2012, 7, e33447. [Google Scholar] [CrossRef] [PubMed]
- Bissoyi, A.; Reicher, N.; Chasnitsky, M.; Arad, S.; Koop, T.; Rudich, Y.; Braslavsky, I. Ice nucleation properties of ice-binding proteins from snow fleas. Biomolecules 2019, 9, 532. [Google Scholar] [CrossRef]
- Xu, H.; Griffith, M.; Patten, C.L.; Glick, B. R. Isolation and characterization of an antifreeze protein with ice nucleation activity from the plant growth promoting rhizobacterium Pseudomonas putida GR12−2. Can. J. Microbiol. 1998, 44, 64–73. [Google Scholar] [CrossRef]
- Govindarajan, A.G.; Lindow, S.E. Size of bacterial ice-nucleation sites measured in situ by radiation inactivation analysis. Proc. Natl Acad. Sci. USA 1988, 85, 1334–1338. [Google Scholar] [CrossRef]
- Ling, M.L.; Wex, H.; Grawe, S.; Jakobsson, J.; Löndahl, J.; Hartmann, S.; et al. Effects of ice nucleation protein repeat number and oligomerization level on ice nucleation activity. J. Geophys. Res. Atmos. 2018, 123, 1802–1810. [Google Scholar] [CrossRef]
- Eickhoff, L.; Dreischmeier, L.; Zipori, A.; Sirotinskaya, V.; Adar, C.; Reicher, N.; Braslavsky, I.; Rudich, Y.; Koop, T. Contrasting behavior of antifreeze proteins: Ice growth inhibitors and ice nucleation promoters. J. Phys. Chem. Lett. 2019, 10, 966–972. [Google Scholar] [CrossRef] [PubMed]
- Kobashigawa, Y.; Nishimiya, Y.; Miura, K.; Ohgiya, S.; Miura, A.; Tsuda, S. A part of ice nucleation protein exhibits the ice-binding ability. FEBS Lett. 2005, 579, 1493–1497. [Google Scholar] [CrossRef] [PubMed]
- Vonnegut, B. The nucleation of ice formation by silver iodide. J. Appl. Phys. 1947, 18, 593–595. [Google Scholar] [CrossRef]
- Marcolli, C.; Nagare, B.; Welti, A.; Lohmann, U. Ice nucleation efficiency of AgI: Review and new insights. Atmos. Chem. Phys. 2016, 16, 8915–8937. [Google Scholar] [CrossRef]
- Head, R. Steroids as ice nucleators. Nature 1961, 191, 1058–1059. [Google Scholar] [CrossRef]
- Popovitz-Biro, R.; Wang, J.L.; Majewski, J.; Shavit, E.; Leiserowitz, L.; Lahav, M. Induced freezing of supercooled water into ice by self-assembled crystalline monolayers of amphiphilic alcohols at the air-water interface. J. Am. Chem. Soc. 1994, 116, 1179–1191. [Google Scholar] [CrossRef]
- Power, B.; Power, R. Some amino-acids as ice nucleators. Nature 1962, 194, 1170–1171. [Google Scholar] [CrossRef]
- Gute, E.; Abbatt, J.P.D. Ice nucleating behavior of different tree pollen in the immersion mode. Atmos. Environ. 2020, 231, 117488. [Google Scholar] [CrossRef]
- Maki, L.R.; Galyan, E.L.; Chang-Chien, M.M.; Caldwell, D.R. Ice nucleation induced by Pseudomonas syringae. Appl. Microbiol. 1974, 28, 456–459. [Google Scholar] [CrossRef]
- Gurian-Sherman, D.; Lindow, S.E. Bacterial ice nucleation: Significance and molecular basis. FASEB J. 1993, 7, 1338–1343. [Google Scholar] [CrossRef]
- Roeters, S.J.; Golbek, T.W.; Bregnhøj, M.; Drace, T.; Alamdari, S.; Roseboom, W.; Kramer. G.; Šantl-Temkiv, T.; Finster, K.; Pfaendtner, J.; Woutersen, S.; Boesen, T.; Weidner, T. Ice-nucleating proteins are activated by low temperatures to control the structure of interfacial water. Nature Commun. 2021, 12, 1183. [Google Scholar] [CrossRef] [PubMed]
- Zachariassen, K.E.; Kristiansen, E. Ice nucleation and antinucleation in nature. Cryobiology 2000, 41, 257–279. [Google Scholar] [CrossRef] [PubMed]
- Olsen, T.M.; Duman, J.G. Maintenance of the supercooled state in overwintering pyrochroid beetle larvae, Dendroides canadensis: Role of hemolymph ice nucleators and antifreeze proteins. J. Comp. Physiol. B 1997, 167, 105–113. [Google Scholar] [CrossRef]
- Packard, G.C.; Packard, M.J. To freeze or not to freeze: Adaptations for overwintering by hatchlings of the North American painted turtle. J. Exp. Biol. 2004, 207, 2897–2906. [Google Scholar] [CrossRef] [PubMed]
- Yeung, K.L.; Wolf, E.E.; Duman, J.G. A scanning tunneling microscopy study of an insect lipoprotein ice nucleator. J. Vac. Sci. Technol. B 1991, 9, 1197–1201. [Google Scholar] [CrossRef]
- Hartmann, S.; Ling, M.; Dreyer, L.S.A.; Zipori, A.; Finster, K.; Grawe, S.; Jensen, L.Z.; Borck, S.; Reicher, N.; Drace, T.; Niedermeier, D.; Jones, N.C.; Hoffmann, S.V.; Wex, H.; Rudich, Y.; Boesen, T.; Šantl-Temkiv, T. Structure and protein-protein interactions of ice nucleation proteins drive their activity. Front. Microbiol. 2022, 13, 872306. [Google Scholar] [CrossRef] [PubMed]
- Hansen, T.; Lee, J.C.; Reicher, N.; Ovadia, G.; Guo, S.; Guo, W.; Liu, J.; Braslavsky, I.; Rudich, Y.; Davies, P.L. Ice nucleation proteins self-assemble into large fibers to trigger freezing at near 0 °C. bioRxiv [Preprint], 2023. Available at: https://doi.org/10.1101/2023.08.03.551873 (Accessed on September 11, 2023). [CrossRef]
- Brush, R. A.; Griffith, M.; Mlynarz, A. Characterization and quantification of intrinsic ice nucleators in winter rye. Plant. Physiol. 1994, 104, 725–735. [Google Scholar] [CrossRef]
- Parody-Morreale, A.; Murphy, K.P.; Di Cera, E.; Fall, R.; DeVries, A.L.; Gill, S.J. Inhibition of bacterial ice nucleators by fish antifreeze glycoproteins. Nature 1988, 333, 782–783. [Google Scholar] [CrossRef]
- Sosso, G.C.; Whale, T.F.; Holden, M.A.; Pedevilla, P.; Murray, B.J.; Michaelides, A. Unravelling the origins of ice nucleation on organic crystals. Chem. Sci. 2018, 9, 8077–8088. [Google Scholar] [CrossRef]
- Fukuta, N.; Mason, B.J. Epitaxial growth of ice on organic crystals. J. Phys. Chem. Solids 1963, 24, 715–718. [Google Scholar] [CrossRef]
- Hiranuma, N.; Möhler, O.; Yamashita, K.; Tajiri, T.; Saito, A.; Kiselev, A.; Hoffmann, N.; Hoose, C.; Jantsch, E.; Koop, T.; Murakami, M. Ice nucleation by cellulose and its potential contribution to ice formation in clouds. Nature Geosci. 2015, 8, 273–277. [Google Scholar] [CrossRef]
- Duman, J.G.; Xu, L.; Neven, L.G.; Tursman, D.; Wu, D.W. Hemolymph proteins involved in insect low temperature tolerance: Ice nucleators and antifreeze proteins. In Insects at Low Temperatures. Lee, R.E., Denlinger, D., Eds.; Chapman & Hall: New York, USA, 1991; pp. 94–127. [Google Scholar]
- Olsen, T.M.; Duman, J.G. Maintenance of the supercooled state in the gut fluid of overwintering pyrochroid beetle larvae, Dendroides canadensis : Role of ice nucleators and antifreeze proteins. J. Comp. Physiol. B 1997, 167, 114–122. [Google Scholar] [CrossRef]
- Kawahara, H.; Nagae, I.; Obata, H. Purification and characterization of a new anti-nucleating protein isolated from Acinetobacter calcoaceticus KINI-1. Biocontrol Sci. 1996, 1, 11–17. [Google Scholar] [CrossRef]
- Tomalty, H.E.; Walker, V.K. Perturbation of bacterial ice nucleation activity by a grass antifreeze protein. Biochem. Biophys. Res. Commun. 2014, 452, 636–641. [Google Scholar] [CrossRef] [PubMed]
Figure 1.
(A) A comparison of two test tubes with pieces of ice in solutions with mIBP83-GFP (+IBP) and solely with GFP (–IBP). As seen, mIBP83-GFP binds to ice while GFP does not; see also [47]. (B, C, D, E) Experiments on ice nucleation in different samples in a thermostat. The arrows indicate the moment of ice nucleation. (B) 20 mM sodium phosphate buffer, pH 7.0. Cooling alternates with heating. The ice melting (corresponding to the shoulder on the rising part of the curve, corresponding to heating) was briefly discussed in [54]. But here we are only interested in the ice nucleation (see the beginnings of the sharp peaks indicated by arrows) that occurs during cooling. Throughout this experiment, the sample and the test tube remained unchanged, and, as seen, the nucleation temperature is practically the same for all cycles. Analogous "nucleation peaks" (indicated by arrows) for different samples in different test tubes are shown separately in panels C, D, E. (C) Four blue lines: cooling of the buffer without mIBP83 (–IBP); four red lines: the same buffer supplemented with 0.6 mg/mL of mIBP83 (+IBP); 0.6 mg/mL is a typically used antifreeze protein concentration, see, e.g., [55]). The nucleation temperature is seen to be only approximately reproduced after changing the test tube and sample, and this temperature is virtually the same for both –IBP and +IBP. (D, E) The same experiments with the nucleators CuO and P. syringae, in the same buffer. The antifreeze mIBP83 is seen to reliably decrease the nucleation temperature. Concentrations/amounts of all substances are given in the Footnote to Table 1.
Figure 1.
(A) A comparison of two test tubes with pieces of ice in solutions with mIBP83-GFP (+IBP) and solely with GFP (–IBP). As seen, mIBP83-GFP binds to ice while GFP does not; see also [47]. (B, C, D, E) Experiments on ice nucleation in different samples in a thermostat. The arrows indicate the moment of ice nucleation. (B) 20 mM sodium phosphate buffer, pH 7.0. Cooling alternates with heating. The ice melting (corresponding to the shoulder on the rising part of the curve, corresponding to heating) was briefly discussed in [54]. But here we are only interested in the ice nucleation (see the beginnings of the sharp peaks indicated by arrows) that occurs during cooling. Throughout this experiment, the sample and the test tube remained unchanged, and, as seen, the nucleation temperature is practically the same for all cycles. Analogous "nucleation peaks" (indicated by arrows) for different samples in different test tubes are shown separately in panels C, D, E. (C) Four blue lines: cooling of the buffer without mIBP83 (–IBP); four red lines: the same buffer supplemented with 0.6 mg/mL of mIBP83 (+IBP); 0.6 mg/mL is a typically used antifreeze protein concentration, see, e.g., [55]). The nucleation temperature is seen to be only approximately reproduced after changing the test tube and sample, and this temperature is virtually the same for both –IBP and +IBP. (D, E) The same experiments with the nucleators CuO and P. syringae, in the same buffer. The antifreeze mIBP83 is seen to reliably decrease the nucleation temperature. Concentrations/amounts of all substances are given in the Footnote to Table 1.
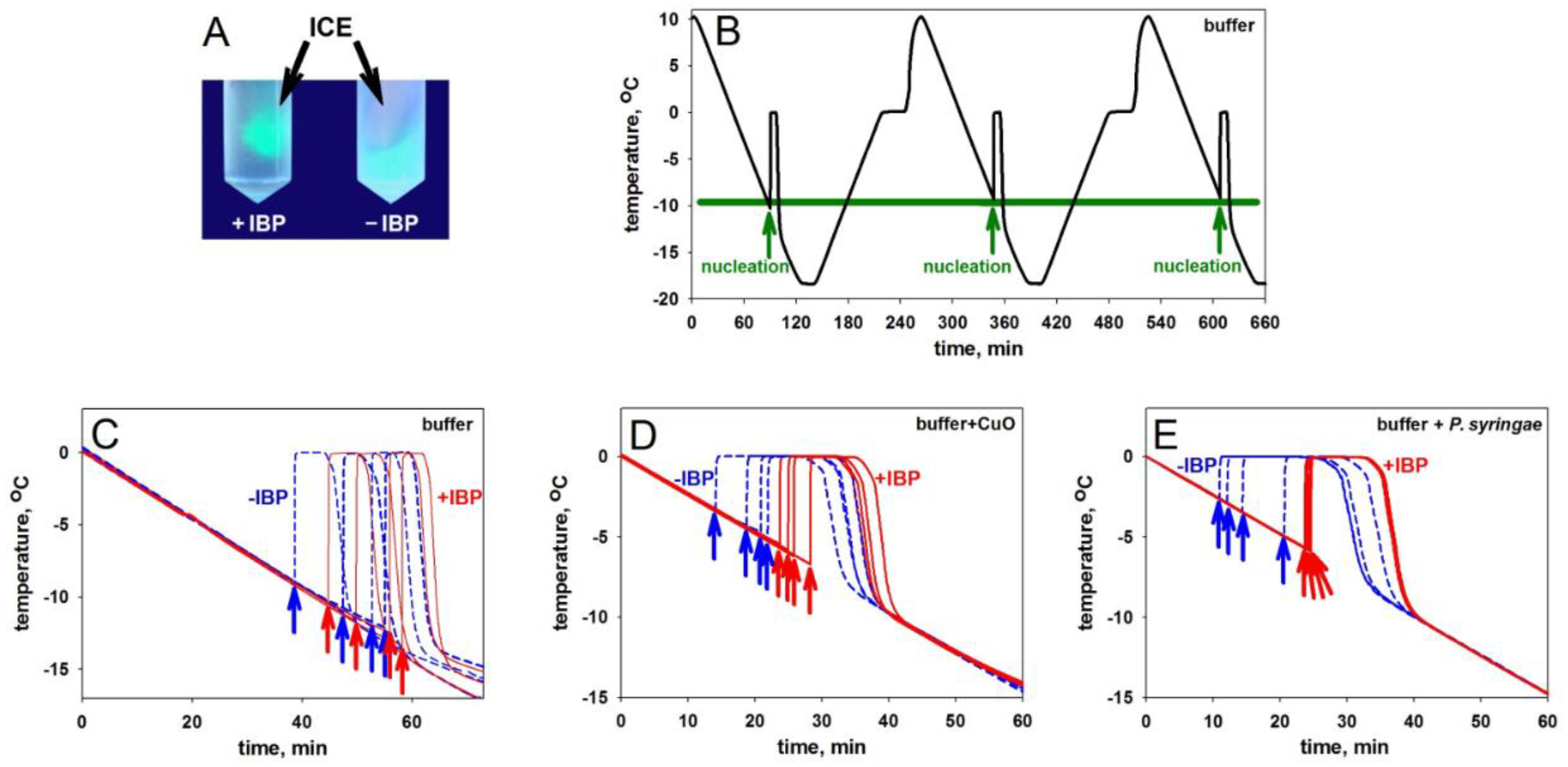
Figure 2.
Schematic drawings of a 3-dimensional (3d) ice nucleus (A), and two kinds (B, C) of 2-dimensional (2d) ice nuclei on underlays of different shapes. The water molecules in ice are shown as light-blue cubes, the surrounding liquid water molecules are shown as light-blue balls, and ice-binding surfaces (underlays) are shown in dark-blue or black. Additional free energies of molecules on different facets of the 3d ice nucleus, in principle, may be somewhat different, since these molecules may have different orientations relative to different facets [39,65]. The 2d nuclei arise on the underlying ice-binding (or ice) surfaces. In extreme cases, the underlays may be smooth (B) or corrugated (C); side views (see insets) show that contacts between the ice molecules inside a layer formed on a smooth underlay are strong, while contacts between the ice molecules inside a layer formed on a corrugated underlay are weak, while the contact of this ice layer with the underlay is stronger in the case (C) than in the case (B). Respectively, the additional free energy of a border molecule of the layer arising on a smooth underlay is high, while the additional free energy of a border molecule of the layer arising on a corrugated underlay is low. Thus, ice nucleation time drastically decreases on the corrugated surfaces as compared to the smooth ones.
Figure 2.
Schematic drawings of a 3-dimensional (3d) ice nucleus (A), and two kinds (B, C) of 2-dimensional (2d) ice nuclei on underlays of different shapes. The water molecules in ice are shown as light-blue cubes, the surrounding liquid water molecules are shown as light-blue balls, and ice-binding surfaces (underlays) are shown in dark-blue or black. Additional free energies of molecules on different facets of the 3d ice nucleus, in principle, may be somewhat different, since these molecules may have different orientations relative to different facets [39,65]. The 2d nuclei arise on the underlying ice-binding (or ice) surfaces. In extreme cases, the underlays may be smooth (B) or corrugated (C); side views (see insets) show that contacts between the ice molecules inside a layer formed on a smooth underlay are strong, while contacts between the ice molecules inside a layer formed on a corrugated underlay are weak, while the contact of this ice layer with the underlay is stronger in the case (C) than in the case (B). Respectively, the additional free energy of a border molecule of the layer arising on a smooth underlay is high, while the additional free energy of a border molecule of the layer arising on a corrugated underlay is low. Thus, ice nucleation time drastically decreases on the corrugated surfaces as compared to the smooth ones.

Figure 3.
Localization of the fused protein mIBP83-GFP (+IBP) and GFP alone (–IBP) in SKBR-3 cells. The cells were kept at +37 °C or incubated at +2 °C for 2 h, then fixed and imaged using a laser scanning microscope. The fluorescence images (black background) and the merged “transmittance + fluorescence” images (gray background) are presented for each experiment. The nuclei of some individual cells are marked as nu. The white arrows indicate some of the most pronounced mIBP83-GFP accumulations in some regions of the cooled cells. It is seen that the well-defined accumulation of mIBP83-GFP (and not GFP alone) is only observed at a temperature close to 0 °C.
Figure 3.
Localization of the fused protein mIBP83-GFP (+IBP) and GFP alone (–IBP) in SKBR-3 cells. The cells were kept at +37 °C or incubated at +2 °C for 2 h, then fixed and imaged using a laser scanning microscope. The fluorescence images (black background) and the merged “transmittance + fluorescence” images (gray background) are presented for each experiment. The nuclei of some individual cells are marked as nu. The white arrows indicate some of the most pronounced mIBP83-GFP accumulations in some regions of the cooled cells. It is seen that the well-defined accumulation of mIBP83-GFP (and not GFP alone) is only observed at a temperature close to 0 °C.
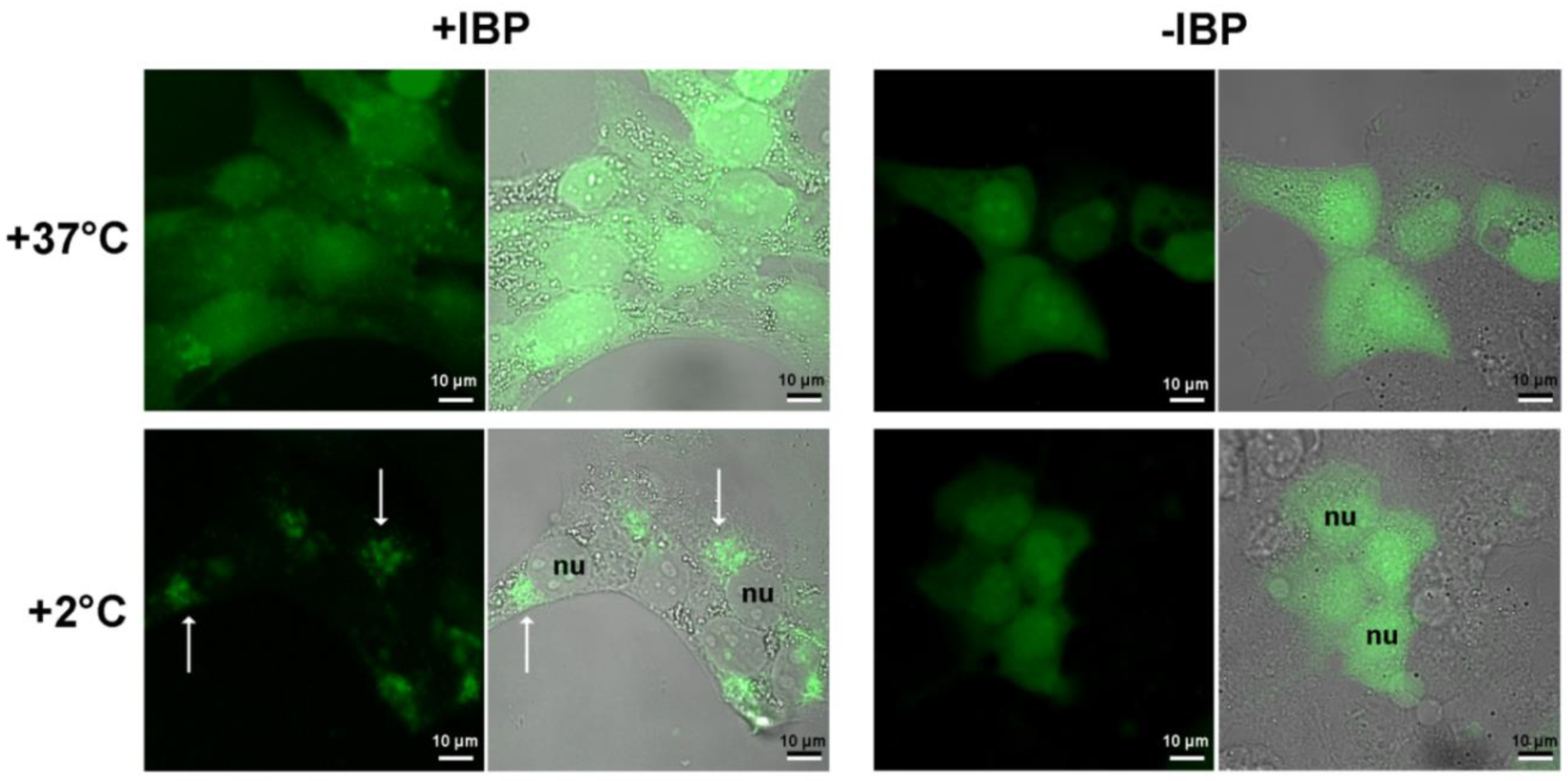
Table 1.
Ice nucleation Temperatures for explored samples.
| Sample | Range of nucleation temperatures, °C | Number of measurements |
|---|---|---|
| Sodium phosphate buffer | from –8 to –13 | 30 |
| mIBP83 † in phosphate buffer | from –11 to –14 | 15 |
| CuO* in the buffer | from –3 to –6 | 15 |
| CuO* + mIBP83 † in the buffer | from –6 to –8 | 15 |
| P. syringae* in the buffer | from –2 to –5 | 15 |
| P. syringae* + mIBP83 † in the buffer | from –5 to –7 | 15 |
| Carbonic anhydrase B in the buffer | –10.0±0.4 & –10.5±0.3 | 2 |
Footnote: Concentrations/amounts per 1 mL of liquid in a polypropylene test tube: sodium phosphate buffer, 20 mM, pH 7.0; carbonic anhydrase B, 0.6 mg/mL; mIBP83, 0.6 mg/mL; CuO powder, 0.5 mg; suspension of P. syringae, 0.05 mL with the optical density OD = 1. † Antifreeze. *Nucleator.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated








