Prerpints.org logo
Preprint
Article

Short- and Medium-Term Electricity Consumption Forecasting Using Prophet and GRU

Altmetrics

Downloads

147

Views

29

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

18 September 2023

Posted:

19 September 2023

You are already at the latest version

Alerts
Abstract
This study proposes a short- and medium-term electricity consumption prediction algorithm by combining the GRU model suitable for long-term forecasting and the Prophet model suitable for seasonality and event handling. (1) Manufacturing Company B's Electricity consumption data and meteorological data in Naju, Jeollanam-do, South Korea are collected and preprocessed. (2) The preprocessed data proposes the Prophet model in the first step for seasonality and event handling prediction. (3) In the second step, seven multivariate data are experimented with GRU. Specifically, the seven multivariate data consist of six meteorological data and the residuals between the predicted data from the proposed Prophet model in Step 1 and the observed data. These are utilized to predict electricity consumption at 15-minute intervals. (4) Electricity consumption is predicted for short-term (2 days and 7 days) and medium-term (15 days and 30 days) scenarios. The experimental results demonstrate that the proposed method outperforms the conventional Prophet model by more than 23 times and the modified GRU model by more than 2 times in terms of MAPE.
Keywords: 
Subject: Computer Science and Mathematics  -   Computer Science

1. Introduction

Building Energy Management System (BEMS) covers the entire electricity system, from power generation to consumption, including generation, transmission, distribution, and consumption. Energy management software, implemented in areas with high energy usage such as households, buildings, and factories, analyzes energy consumption to determine whether energy is being consumed appropriately by energy source, heat source, system, and major equipment. The goal is to establish an efficient energy management system, leading to cost savings from energy conservation, reviewing appropriate energy usage of energy sources, reducing carbon emissions through optimal operation, decreasing facility operation and maintenance costs, extending equipment lifespan, and improving facility operation efficiency, all of which contribute to increased building value [1,2].
Despite the numerous advantages of BEMS, reliable forecasting of electricity consumed in buildings is essential. Electricity consumption forecasting can be categorized into very short-term, short-term, medium-term, and long-term forecasts [3,4,5]. Very-short term electricity consumption forecasting predicts power consumption and demand in real time by performing predictions for 1 hour, 15 min, and 30 min to stably operate power. Short-term electricity consumption forecasting covers predictions ranging from hourly to a few weeks using algorithms such as Exponential Smoothing [6] and Auto Regressive Integrated Moving Averages (ARIMA) [7]. Conversely, medium-term electricity consumption forecasting spans a few weeks to several months and utilizes various variables such as meteorological data, event information, and economic indicators to predict power consumption. Different algorithms such as linear regression, multiple regression, polynomial regression [8], neural networks [9], deep learning [10], and Long Short-term Memory (LSTM) [11] are used. Long-term electricity consumption forecasting involves predictions spanning three months to a year, and it requires consideration of more variables and system elements than short-term and medium-term forecasts. Time series analysis, ARIMA models, and ensemble techniques can help predict the trends and patterns of long-term power consumption.
ARIMA is effective for short-term forecasts but challenging to apply to data with seasonality or non-stationarity, and it struggles to predict long-term patterns. Exponential Smoothing is useful for short-term forecasting but faces challenges in predicting long-term trends and incorporating other factors. The Prophet is suitable for medium-term forecasting and can handle seasonality and events, but it struggles to predict long-term trends. LSTM is suitable for long-term forecasting as it learns long-term dependencies in time series data, but it is sensitive to the quantity and quality of data and requires significant computational resources for training and prediction [12,13,14].
Recent electricity consumption forecasting algorithms combine various techniques based on data characteristics and forecasting objectives [15,16,17,18,19,20]. For example, combining Prophet and LSTM shows improved accuracy and performance in short-term and long-term electricity consumption predictions [15,16]. Other studies propose combining ARIMA and XGBoost for short-term electricity consumption forecasting [17] and ARIMA and Bi-LSTM models for smart grid parameters [18]. Additionally, a combination of ARIMA-LSTM and ARIMA-GRU models uses ARIMA to model trends and seasonality in time series data and LSTM to improve prediction performance [19,20]. The previously mentioned studies have evaluated the strengths, weaknesses, and performance of the models, thereby establishing criteria for model selection. However, the complexity of parameter configuration and the training process associated with the combination of these two models can be intricate. Furthermore, the performance may vary based on the application domain, as well as the characteristics of the data.
This study proposes a method for short- and medium-term electricity consumption prediction by combining the GRU model, suitable for long-term forecasting, and the Prophet model, suitable for capturing seasonality and events. In this study, simulation data collected from July 1, 2018, to October 31, 2019, in 15-minute intervals represents the electricity consumption of Company B in Naju, Jeollanam-do. Meteorological data is collected hourly from a weather observation point closest to Naju, Gwangju.
The proposed methodology is as follows:
(1) Collect and preprocess electricity consumption data and meteorological data.
(2) Utilize the preprocessed data to propose the Prophet model in the first step for handling seasonality and events.
(3) In the second step, simulate seven multivariate datasets, consisting of six meteorological data variables and observed electricity consumption data, using the GRU model.
(4) Predict electricity consumption at 15-minute intervals using the residuals between the data predicted by the proposed Prophet model in Step 1 and the observed data, along with the six meteorological data variables.
(5) Conduct experiments for short-term (2 days and 7 days) and medium-term (15 days and 30 days) electricity consumption predictions.
The study's structure is as follows: Section 2 discusses related research on the Prophet and GRU models. Section 3 addresses the problems of the existing Prophet and proposes solutions. Section 4 explains the algorithm and experimental results of the proposed method. Finally, Section 5 concludes the study.

2. Related works

2.1. Prophet model

The Prophet model, an open-source time series forecasting library developed by Facebook [21], stands as a robust solution for predicting time series data with dynamic temporal changes. Its applicability spans across a wide array of domains, including marketing, advertising, demand projection, energy consumption forecasting, and financial prediction. The Prophet model is structured with three fundamental components, as represented by equation (1).
𝑦(𝑡) = 𝑔(𝑡) + 𝑠(𝑡) + ℎ(𝑡) + 𝜖(𝑡)
In equation (1), y(t) signifies the observed value at the time point t. The component g(t) embodies the trend, elucidating the overarching long-term growth or decline trends within the time series. s(t) characterizes the seasonality component, adept at capturing recurrent patterns and oscillations. h(t) assumes the role of the holidays component, adeptly accounting for singular events or exceptional incidents that may influence the time series. Finally, ε(t) represents the error term, accommodating any stochastic or irregular variations present in the data. Prophet's versatility and adeptness in accommodating diverse time series patterns make it an immensely popular and potent tool for time series forecasting across a multitude of industries.
Figure 1 depicts the electricity consumption data of Company B collected from July 1, 2018, to October 31, 2019, in this study.
Figure 2 and Figure 3 illustrate the results of applying the basic Prophet model with only the holiday effect considered to the training data for one year (July 2018 to June 2019). In Figure 2, the blue line represents the model's predicted values, and the black dots represent the observed data values.
Figure 3 displays the components (trend, holiday, weekly, and daily) of the fitted model. From Figure 3, we can observe that the trend and holidays exhibit relatively stable trends every month. The weekly component shows that electricity consumption occurs from Monday to Friday but not on weekends. The daily component shows that electricity consumption happens during working hours, from 8 AM to 8 PM, and remains low during the rest of the day.

2.2. GRU model

GRU, which stands for Gated Recurrent Unit, is a type of Recurrent Neural Network (RNN) used for processing sequence data [22]. It provides similar functionality to LSTM but has a simpler structure, as depicted in Figure 4. GRU addresses the vanishing gradient problem while learning long-term dependencies in sequence data and offers the advantage of reducing computational costs compared to LSTM.
The components of GRU include the update gate, reset gate, and hidden state. Equation (2) represents the mathematical formulation of GRU. In Equation (2),   r t denotes the reset gate, z t represents the update gate, h t is the hidden state, and   x t signifies the current input. W z and   W r are the weights for the update and reset gates, respectively.
z t = σ W z · h t − 1 , x t r t = σ W r · h t − 1 , x t h t ˜ = t a n h W · r t ∗ h t − 1 , x t h t = 1 − z t ∗ h t − 1 + z t ∗ h t
GRU's simplicity and effectiveness in handling long-term dependencies have made it a popular choice for various sequence data processing tasks. It overcomes some limitations of traditional RNNs and is widely used in natural language processing, time series analysis, and other fields that involve sequential data processing.

2.2.1. Update gate

The update gate determines how much information to retain based on the current input and the previous hidden state. It is represented as a value between 0 and 1, where a value closer to 0 indicates that more past information will be forgotten, and a value closer to 1 indicates that more information will be retained.

2.2.2. Reset gate

The reset gate determines how much of the past information to forget based on the current input and the previous hidden state. It is represented as a value between 0 and 1, where a value closer to 0 indicates that more past information will be discarded, and a value closer to 1 indicates that more past information will be preserved.

2.2.3. Hidden state

GRU computes a new hidden state based on the previous hidden state and the current input. It uses the update gate and the reset gate to control the combination of past and current information, resulting in the generation of a new hidden state.

3. Basic prophet model’s problem and solution

3.1. Basic prophet model’s problem

The advantage of the Prophet model is its ability to incorporate seasonality and events (holidays and public holidays) into the predictions. However, as shown in Figure 5, when applying the Prophet model from September 1st to September 30th, 2019, there is a drawback where the observed values (y) during the 4-day thank-giving day (September 12th to September 15th) are close to zero, but the Prophet model fails to accurately predict this.
Therefore, when using the basic prophet model, it is necessary to set parameters specifically for holiday information (duration, name) and consider the impact of holidays on electricity consumption before and after the holiday. Adjusting the flexibility of the trend and setting appropriate parameters for yearly seasonality are also necessary to better predict electricity consumption accurately.

3.2. Prophet model’s solution

Figure 6 represents the errors between the prophet model (Prophet) and the observed values (y) for July 1st, 2019 (in 15-minute intervals). To address these errors, the study utilizes GRU, which is suitable for mid-term predictions, by incorporating meteorological data that influence building electricity consumption.
While applying GRU with the collected electricity consumption and meteorological data, the study acknowledges the limitation of not handling information related to holidays and events. To overcome this limitation, the proposed approach combines Prophet, which is effective in handling holidays and events for long-term predictions, with GRU for short-term predictions. By doing so, the strengths of each model can be leveraged to improve the accuracy and performance of electricity consumption forecasting.

4. Proposed methods

The flow chart of the proposed method in this study is shown in Figure 7. Section 4.1 explains how to collect data, Section 4.2 describes the pre-processing method for collected data, Section 4.3 describes how to divide data for learning and testing, Section 4.4 describes the proposed method using prophet and GRU, and finally, the study concludes with error measurements and visualizations.

4.1. Data collection

In this study, the electricity consumption data used is collected from a company, B Corporation (machinery manufacturing), located in Naju, Jeollanam-do, South Korea. The data spans from July 1, 2018, to October 31, 2019, with a time interval of 15 minutes.
To enhance the accuracy of electricity consumption predictions, various factors, including Korean holidays (alternative holidays, election days, national holidays, etc.), are taken into account. The Workalendar package is utilized to generate the Korean holiday data. Additionally, meteorological data such as temperature, precipitation, wind speed, humidity, sunshine duration, and cloud cover are collected at hourly intervals from the Korea Meteorological Administration's weather data portal (http://www.weather.go.kr).

4.2. Data pre-processing

The meteorological data is then resampled using linear interpolation to match the 15-minute intervals of the electricity consumption data. To handle missing values in both power and meteorological data, they are filled with zeros. To minimize the impact of outliers, the RobustScaler method [23] is applied to normalize the data scale, as shown in equation (3).
X s c a l e d = x − Q 1 x Q 3 x − Q 1 x
In equation (3), X s c a l e d is the scaled data, x is the original data, Q1(x) is the first quartile of the data, and Q3(x) is the third quartile of the data. By using RobustScaler, we ensure that the data is normalized while being less sensitive to the influence of outliers.

4.3. Data partition for training and test data

The training data spans from July 1, 2018, to June 31, 2019, and the test data covers the period from July 1, 2019, to October 31, 2019. The data is split into a 75% portion for training and a 25% portion for testing to conduct the experiments.

4.4. Proposed prophet model

The experimental training data used in this study consists of electricity consumption data collected from July 2018 to May 2019. The modified Prophet model was simulated with components including trends, seasonality, holidays, flows, and others, as outlined in Table 1. Notably, the 'df' variable in the holiday parameters was adjusted to account for substitute holidays in this study. Both regular holidays and substitute holidays, such as election days and traditional holidays, within this time frame were taken into consideration to enhance the accuracy of electricity consumption predictions.
The simulation results are shown in Figure 8 and Figure 9.
In this study, the correlation coefficient was used as shown in Equation (4) to evaluate the accuracy of the long-term and short-term predictions [24].
r X , Y = 1 n ∑ i = 1 n x i − x ¯ y i − y ¯ σ x σ y
In Equation (4), x ¯ and y ¯ represent the mean of X and Y, respectively, and σ x and σ y represent the standard deviation of X and Y, respectively, while n represents the number of data points.
For long-term predictions (1-year period) and short-term predictions (2 days), the correlation coefficients between the predicted electricity consumption and the observed consumption were found to be 0.67 and 0.87, respectively. This indicates that the modified Prophet model performs poorly for long-term electricity consumption predictions. However, the correlation coefficient of 0.87 for short-term predictions indicates that the model performs better than for long-term predictions. Therefore, the proposed Prophet model was used for short-term electricity consumption predictions.

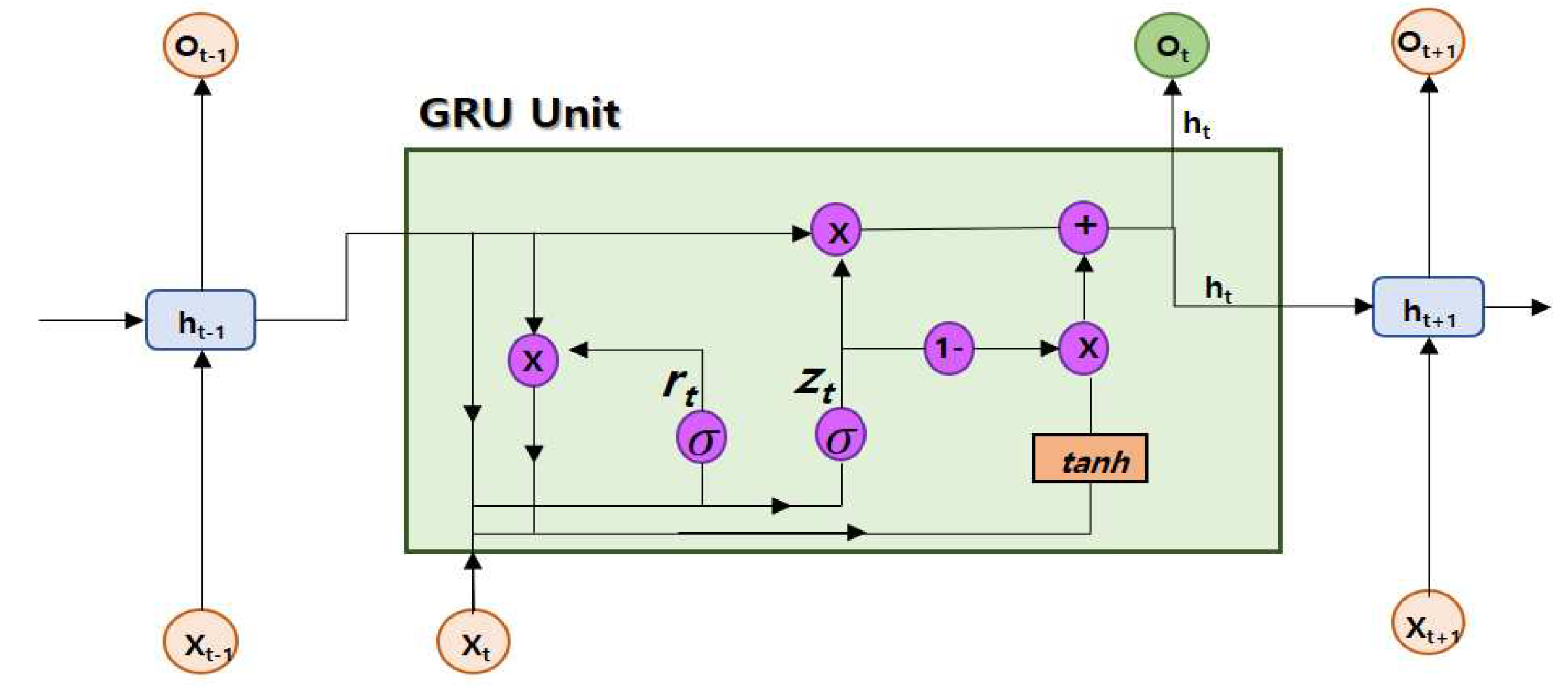
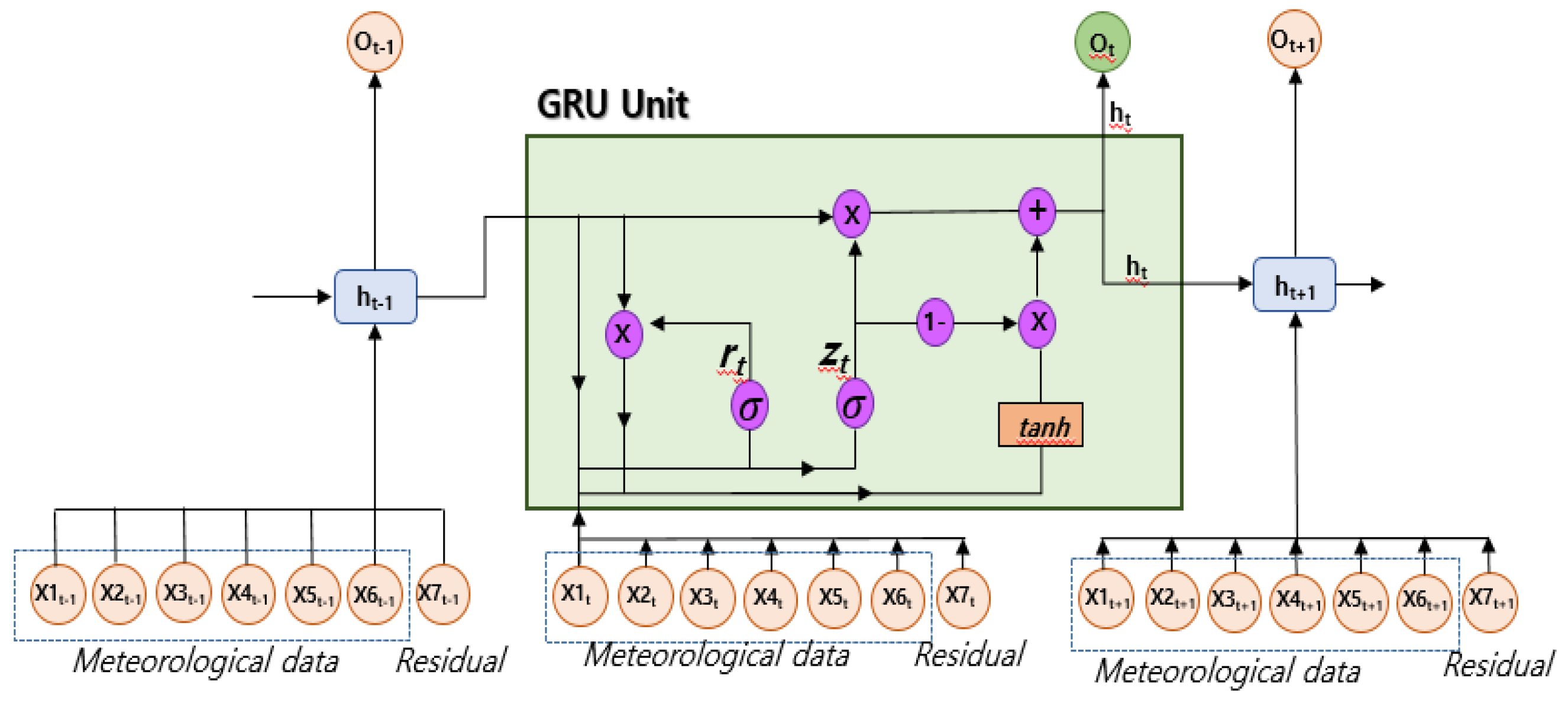
4.5. Proposed GRU model

To reduce the errors between Prophet's predictions and observed values, we propose incorporating GRU, as shown in Figure 10. Among various meteorological data that influence electricity consumption forecasting, the study adopted and utilized the six (temperature, precipitation, wind speed, humidity, sunshine duration, and cloud cover) most impactful variables for this study [25]. The input data consists of multiple variables, including meteorological data (temperature, precipitation, wind speed, humidity, sunshine duration, and cloud cover) and the residual (the difference between the predictions and observed values obtained from the Prophet model in the first step), totaling 7 variables.
In Figure 10, x 1 t − 1 to x 6 t − 1 represent the meteorological data from the previous time point (t-1), i.e., temperature, precipitation, wind speed, humidity, sunshine duration, and cloud cover. x 7 t − 1 represents the residual. The traditional GRU prediction model typically targets the entire consumption data for electricity consumption predictions. However, in this study, we apply the residuals of the long-term trend (yearly and monthly) predictions to the GRU model, as shown in Equation (5), to predict electricity consumption and reduce error rates.
R e s i d u a l = P r o p h e t p r e d − y
In Equation (5), "Residual" denotes the residual, "Prophetpred" represents the predictions obtained from the original Prophet model, and "y" is the observed consumption value. The GRU model's training and validation data are derived from the same dataset. The input layer of the GRU model consists of 7 variables, which include 6 meteorological data variables (temperature, precipitation, wind speed, humidity, sunshine duration, cloud cover), and 1 residual variable. The hidden layer of the GRU model contains 7 nodes. The initial learning rate is set to 0.005, and the maximum number of iterations is 50,000. The mean square error (MSE) is used as the loss function, and the ADAM optimizer (Adaptive Moment Estimation) is employed during training and testing.

5. Test environment and simulation results

5.1. Test environment and software

To verify the Prophet model, GRU, and proposed methods, the experiments were performed on a workstation computer equipped with an Intel Xeon (R) W-2133 CPU, boasting a clock speed of 3.60 GHz CPU, and 3.60 GHz, and complemented by a generous 32 GB of RAM (Dell Precision 5820 Tower Workstation). The operating system was Windows 10 Pro for the workstations (64-bit). To conduct the experiments in this study, we employed the following approaches:
(1) Utilizing Time Series Prediction Libraries: For time series forecasting, essential libraries such as scikit-learn [26], pandas [27], numpy [28], plotly [29], and others were employed. These libraries offer comprehensive tools for data manipulation, analysis, visualization, and modeling.
(2) Implementing the Prophet Model: The implementation of the Prophet model was facilitated by employing the fbprophet library [30]. This dedicated library offers functionalities tailored for the Prophet forecasting framework, streamlining the process of working with seasonal and event-driven data.
(3) GRU and Proposed Method Implementation: To experiment with GRU and the proposed hybrid method, we leveraged the Tensorflow [31] and Keras libraries [32]. These libraries are widely used in deep learning research and provide a platform for building, training, and evaluating neural network models like GRU.
By integrating these tools, we were able to effectively carry out the experiments outlined in the study, encompassing various aspects of time series analysis, forecasting, and model evaluation.

5.2. Evaluation metrics

To validate the proposed method in this study, error metrics including correlation coefficient (CC), Mean Absolute Percentage Error (MAPE) [33], and Symmetric Mean Absolute Percentage Error (SMAPE) [34] were adopted. These metrics were utilized to assess the performance and accuracy of the proposed approach compared to other methods. Equations (6) and (7) are MAPE and SMAPE, respectively.
M A P E = 100 n × ∑ i = 1 n y i − y i ¯ y i
S M A P E = 100 n × ∑ i = 1 n y i − y i ¯ y i + y i ¯ / 2
In equations (6) and (7), y i is the actual value, y i ¯ is the predicted value, and n is the number of data points

5.3. Simulation results

Table 2 shows the performance comparison of the Prophet, GRU, and proposed methods. The Prophet model utilized the approach proposed in step 1, while GRU consisted of 7 simulations (6 meteorological datasets and 1 observed consumption dataset). The proposed method is a hybrid of steps 1 and 2. The performance evaluation methods employed were the correlation coefficient (CC), MAPE (%), and SMAPE (%). The correlation coefficient of the Prophet model decreased as the forecast period lengthened, whereas the correlation coefficients of GRU and the proposed method were consistently higher than that of the Prophet model regardless of the forecast period. The MAPE of the Prophet model was 4-9 times higher than that of GRU and 9-23 times higher than that of the proposed method. Furthermore, the MAPE of GRU was more than twice as high as that of the proposed method. Hence, the proposed method performed better than the Prophet and GRU models.
Figure 11, Figure 12, Figure 13 and Figure 14 present the short-term electricity consumption forecasting comparisons for 2 days (July 1, 2019, to July 2, 2019), 7 days (August 1, 2019, to August 7, 2019), 15 days (September 1, 2019, to September 15, 2019), and 30 days (October 1, 2019, to October 30, 2019), respectively. In these figures, ‘y’ represents the observed consumption data measured during the specified periods, ‘Prophet’ denotes the modified Prophet model in Section 4.4, ‘GRU’ represents the predicted values based on meteorological data and observed consumption data, and ‘Proposed’ signifies the predicted electricity consumption using the proposed method.
In Figure 11, Figure 12, Figure 13 and Figure 14, the proposed method and ‘GRU’ closely resemble the observed consumption data (y), while ‘Prophet’ exhibits high errors compared to the observed data (y). ‘GRU’ shows intermittent spikes in prediction errors as indicated in the "E" part. Even in times when energy consumption was minimal, ‘GRU’ made many high predictions. The reason for prediction errors in ‘GRU’ is due to the inability to accurately predict the occurrence of consecutive holidays or events (substitute holidays, holidays, and vacations). On the other hand, the proposed method closely aligns with the observed consumption data (y).

6. Conclusion

The electricity consumption forecasting is crucial in the electricity industry and energy system operations as it helps improve efficiency and stability. It provides valuable information to energy companies, power suppliers, network operators, and other stakeholders involved in energy management. This study proposes a short- and medium-term forecasting algorithm, combining the Prophet and GRU models, for predicting building electricity consumption over 2 days, 7 days, 15 days, and 30 days. The proposed method outperforms both the modified Prophet and GRU using multivariate.
Our proposed method offers a versatile and effective solution for optimizing energy management within Building Energy Management Systems, with the potential for substantial cost savings, improved energy source utilization, reduced carbon emissions, and enhanced operational efficiency, ultimately increasing the overall value of the building.

Author Contributions

Y.J.Shin; collected and analyzed the data and summarized the results, N.R.Son; supervision.

Funding

This study received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Acknowledgments

This research was supported by the MSIT (Ministry of Science and ICT), Korea, under the National Program for Excellence in SW (2021-0-01409) supervised by the IITP (Institute for Information & Communication Technology Planning & Evaluation).

Conflicts of Interest

Not applicable.

References

  1. International Renewable Energy Agency. Renewable Capacity Statistics; International Renewable Energy Agency: Masdar City, United Arab Emirates, 2020. [Google Scholar]
  2. Rethink energy site. Available online: https://www.letsrethinkenergy.com/ (accessed on 1 August 2023).
  3. Grazioli, G.; Chlela, G.; Selosse, S.; Maïzi, N. The Multi-Facets of Increasing the Renewable Energy Integration in Power Systems. Energies 2022, 15, 6795. [Google Scholar] [CrossRef]
  4. Xue, B.; Keng, J. Dynamic transverse correction method of middle and long term energy forecasting based on statistic of forecasting errors. In Proceedings of the Conference on Power and Energy IPEC, Ho Chi Minh City, Vietnam; 2012; pp. 253–256. [Google Scholar]
  5. Enea, M. A review of machine learning algorithms used for load forecasting at micro-grid level. In Sinteza 2019-International Scientific Conference on Information Technology and Data Related Research; Singidunum University: Belgrade, Serbia, 2019; pp. 452–458. [Google Scholar]
  6. Brown, R.G. Smoothing Forecasting and Prediction of Discrete Time Series; Prentice-Hall: Englewood Cliffs, NJ, USA, 1963. [Google Scholar]
  7. Ohtsuka, Y.; Oga, T.; Kakamu, K. Forecasting electricity demand in Japan: A Bayesian spatial autoregressive ARMA approach. Comp. Stat. Data Anal. 2010, 54, 2721–2735. [Google Scholar] [CrossRef]
  8. Holt, C.E. Forecasting Seasonal and Trends by Exponentially Weighted Average; Carnegie Institute of Technology: Pittsburgh, PA, USA, 1957. [Google Scholar]
  9. Kalogirou, S.A.; Neocleous, C.C.; Schizas, C.C. Building heating load estimation using artificial neural networks. In Proceedings of the 17th International Conference on Parallel Architectures and Compilation Techniques, San Francisco, CA, USA, 10–14 November 1997. [Google Scholar]
  10. Bagnasco, A.; Fresi, F.; Saviozzi, M.; Silvestro, F.; Vinci, A. Electrical consumption forecasting in hospital facilities: An application case. Energy Build 2015, 103, 261–270. [Google Scholar] [CrossRef]
  11. Gers, F.; Schmidhuber, J.; Cummins, F. Learning to Forget: Continual Prediction with LSTM. In Proceedings of the 9th International Conference on Artificial Neural Networks, Edinburgh, UK; 1999; pp. 850–855. [Google Scholar]
  12. Valenzuela, P.; Gorricho, J.; de la Iglesia. Automatic model and feature selection for time series forecasting: Achieving good performance and interpretability. Information Sciences 2018, 423, 157–174. [Google Scholar]
  13. Sanguansat, P.; Klomjit, N. A comparative study of machine learning techniques for short-term load forecasting. Energies 2019, 12. [Google Scholar]
  14. Fung, G.; Shih, E. Evaluating the Forecasting Performance of Facebook's Prophet Model for Time Series Data. Journal of Open Source Software 2019, 4. [Google Scholar]
  15. Tasarruf, B.; Chen, H. Short-term electricity load forecasting using hybrid prophet-LSTM model optimized by BPNN. Energy Reports 2022, 8, 1678–1686. [Google Scholar]
  16. Serdar, A. A hybrid forecasting model using LSTM and Prophet for energy consumption with decomposition of time series data. PeerJ Computer Science 2022, 8. [Google Scholar]
  17. Pin, L.; Zhang, J.S. A New Hybrid Method for China’s Energy Supply Security Forecasting Based on ARIMA and XGBoost. Energies 2018, 11. [Google Scholar]
  18. Yuanhua, C.; Muhammad, S.B.; Muhammad, A.; Dingtian, X. Evaluation of Machine Learning Models for Smart Grid Parameters: Performance Analysis of ARIMA and Bi-LSTM. Sustainability 2023, 15. [Google Scholar]
  19. Zhang, G.P. Time Series Forecasting using a Hybrid ARIMA and neural network model. Neurocomputing 2003, 50, 159–175. [Google Scholar] [CrossRef]
  20. Agbessi, A.P.; Salami, A.A.; Agbosse, K.S.; Birregah, B. Peak Electrical Energy Consumption Prediction by ARIMA, LSTM, GRU, ARIMA-LSTM and ARIMA-GRU Approaches. Energies 2023, 16, 4739. [Google Scholar]
  21. Taylor, S.J.; Letham, B. Prophet: Forecasting at scale. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining; 2017; pp. 1389–1397. [Google Scholar]
  22. Cho, K.; Merriënboer, B.V.; Bahdanau, D.; Bengio, Y. On the properties of neural machine translation: Encoder-decoder approaches. Eighth Workshop on Syntax, Semantics and Structure in Statistical Translation, 2014.
  23. RobustScaler documentation in scikit-learn. Available online: https://www.itl.nist.gov/div898/software/dataplot/refman2/auxillar/iqrange.htm (accessed on 26 August 2023).
  24. Sethna, James P. Chapter 10: Correlations, response, and dissipation. In Statistical Mechanics: Entropy, Order Parameters, and Complexity; Oxford University Press, 2006; ISBN 978-0198566779. [Google Scholar]
  25. Son, N. Comparison of the Deep Learning Performance for Short-Term Power Load Forecasting. Sustainability 2021, 13, 12493. [Google Scholar] [CrossRef]
  26. Scikit-learn.org. Machine learning in Python. Available online: https://scikit-learn.org/ (accessed on 26 August 2023).
  27. Pandas.org. Data structure for statistical computing in Python. Available online: https://pandas.pydata.org/ (accessed on 26 August 2023).
  28. Numpy.org. Array programming with NumPy. Available online: https://numpy.org/ (accessed on 26 August 2023).
  29. Plotly.org. Interactive web-based data visualization with R, plot, and shiny. Available online: https://plotly.org/ (accessed on 26 August 2023).
  30. Fbprophet.org. Forecasting at scale. Available online: https://facebook.github.io/prophet/ (accessed on 26 August 2023).
  31. Tensorflow.org. Deep Learning Library Developed by Google. Available online: https://www.tensorflow.org/ (accessed on 26 August 2023).
  32. Keras.io. The Python Deep Learning Library. Available online: https://keras.io/ (accessed on 26 August 2023).
  33. MAPE. Available online: https://en.wikipedia.org/wiki/Mean_absolute_percentage_error (accessed on 26 August 2023).
  34. SMAPE. Available online: https://en.wikipedia.org/wiki/Symmetric_mean_absolute_percentage_error (accessed on 26 August 2023).
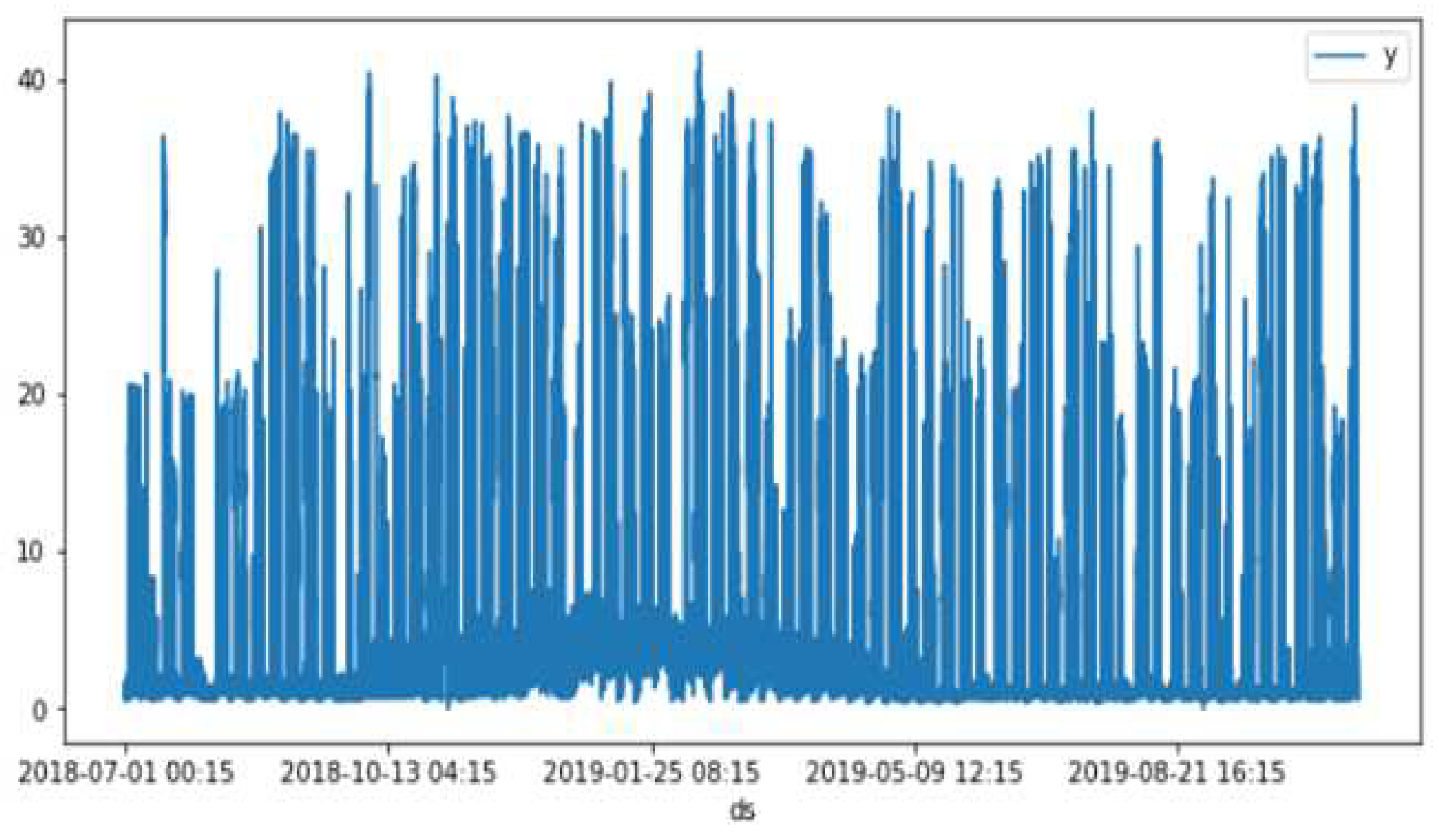
Preprints 85415 g001
Figure 1. Electricity consumption data of Company B collected from July 1, 2018, to October 31, 2019.
Figure 1. Electricity consumption data of Company B collected from July 1, 2018, to October 31, 2019.
Preprints 85415 g001
Preprints 85415 g002
Figure 2. A basic Prophet model that only considers the holiday effect on the training data for one year (July 2018 to June 2019).
Figure 2. A basic Prophet model that only considers the holiday effect on the training data for one year (July 2018 to June 2019).
Preprints 85415 g002
Preprints 85415 g003
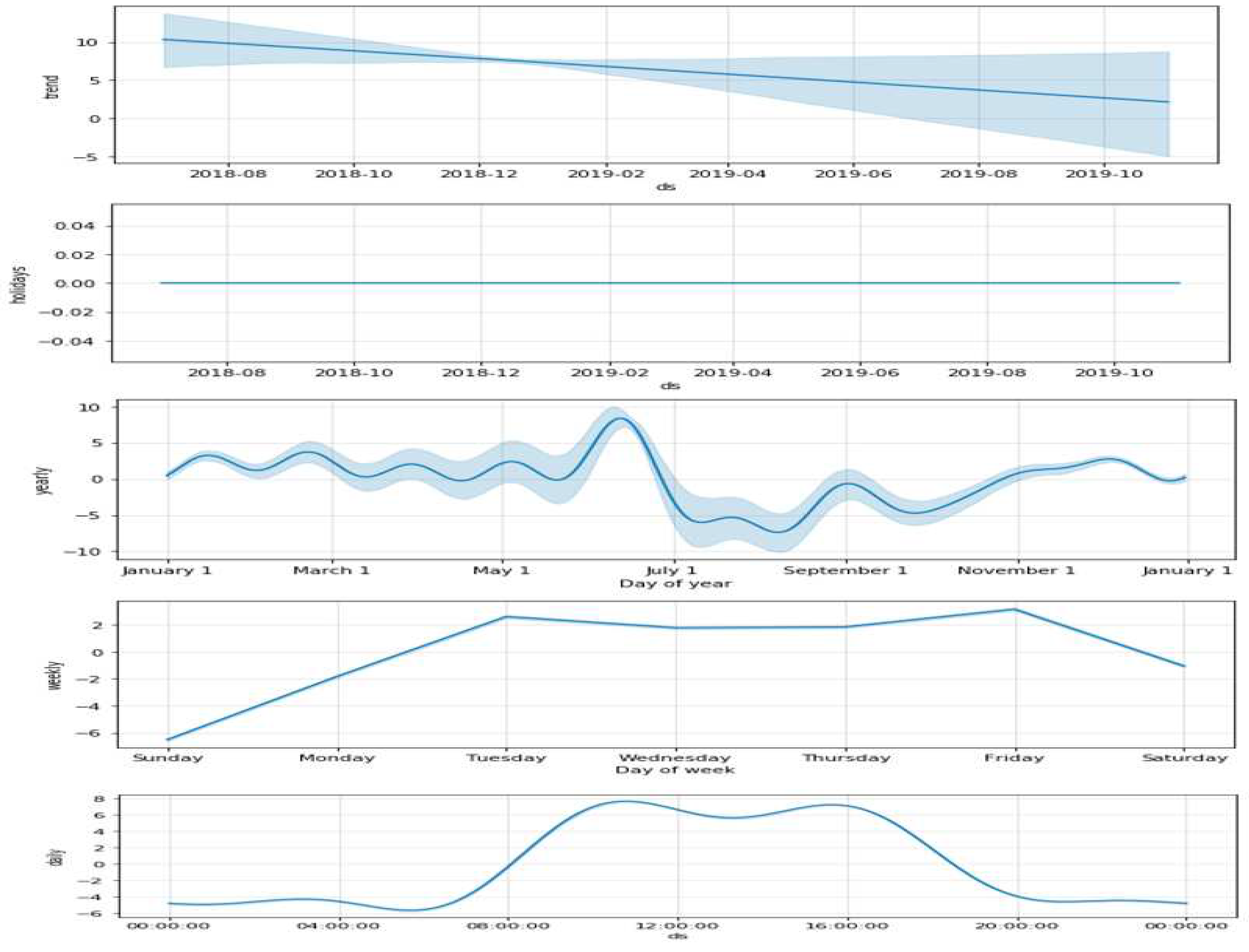
Figure 3. Trend, holidays, weekly, and daily prediction analysis of basic prophet model. The blue line shows the trend the model fits from the test data, and the light blue shade shows the predicted trend.
Figure 3. Trend, holidays, weekly, and daily prediction analysis of basic prophet model. The blue line shows the trend the model fits from the test data, and the light blue shade shows the predicted trend.
Preprints 85415 g003
Preprints 85415 g004
Figure 4. GRU structure.
Figure 4. GRU structure.
Preprints 85415 g004
Preprints 85415 g005
Figure 5. Performance comparison between observed value (y) and basic prophet model (basic prophet) from July 1st to 30th, 2019.
Figure 5. Performance comparison between observed value (y) and basic prophet model (basic prophet) from July 1st to 30th, 2019.
Preprints 85415 g005
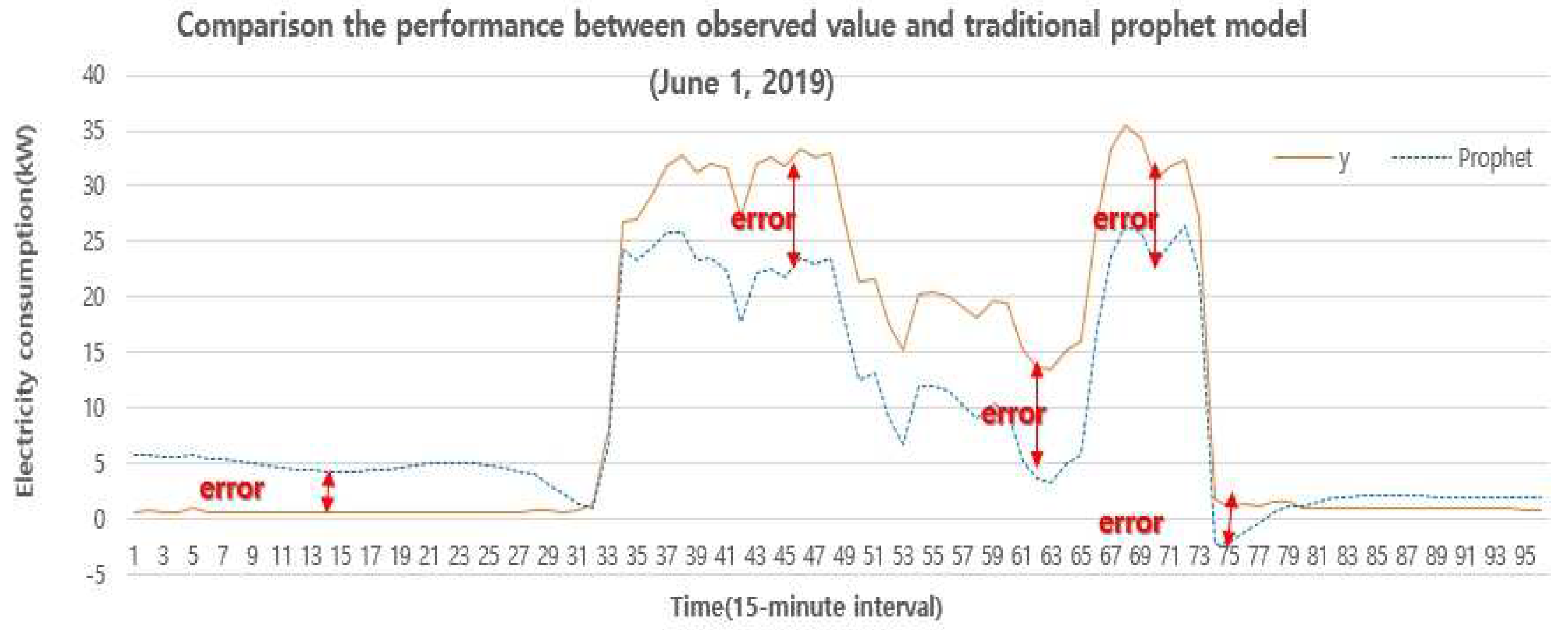
Preprints 85415 g006
Figure 6. Performance comparison between the observed value (y) and the basic prophet model’s value (Prophet) on July 1st, 2019.
Figure 6. Performance comparison between the observed value (y) and the basic prophet model’s value (Prophet) on July 1st, 2019.
Preprints 85415 g006
Preprints 85415 g007
Figure 7. The flowchart of the proposed method.
Figure 7. The flowchart of the proposed method.
Preprints 85415 g007
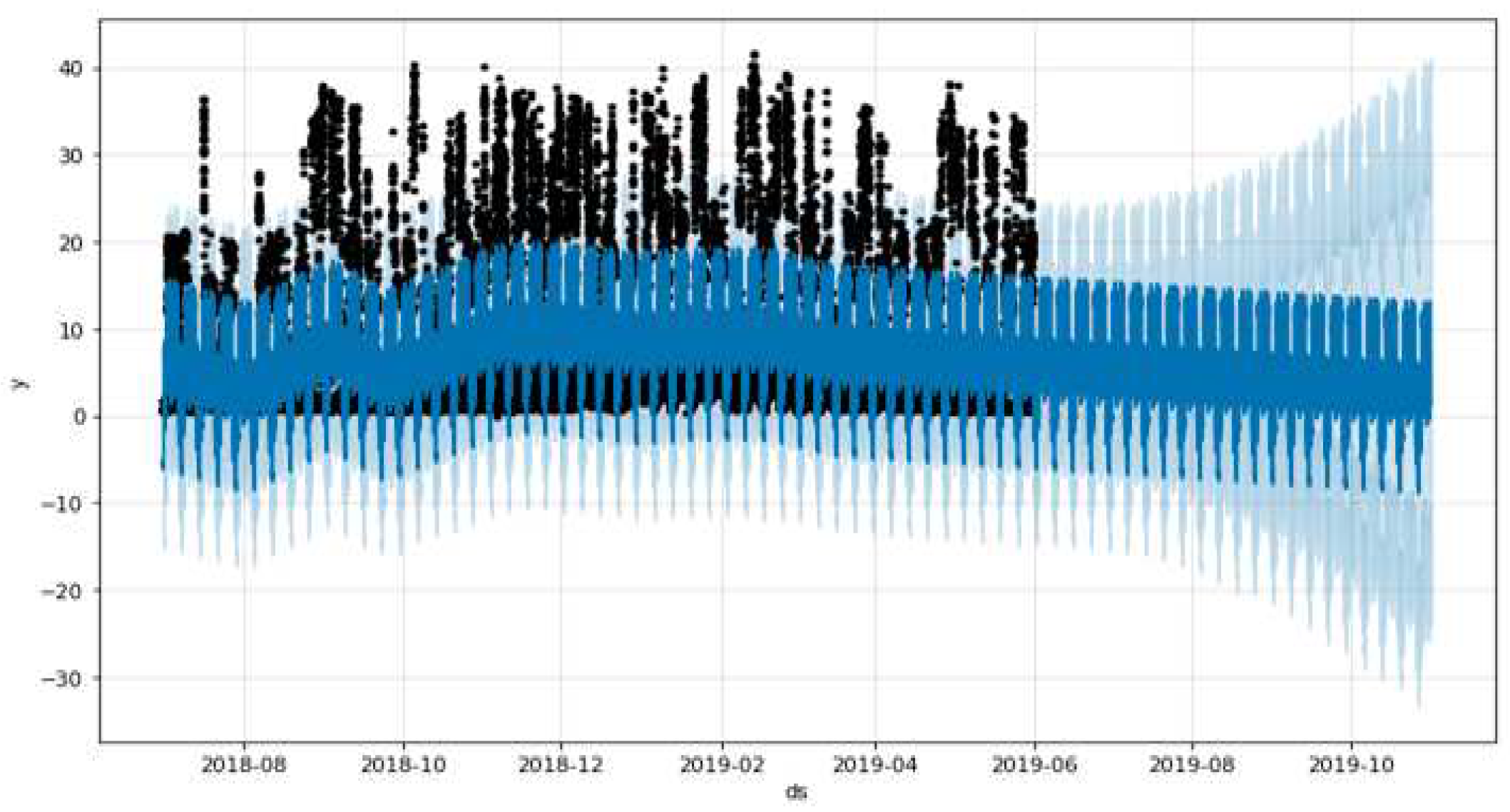
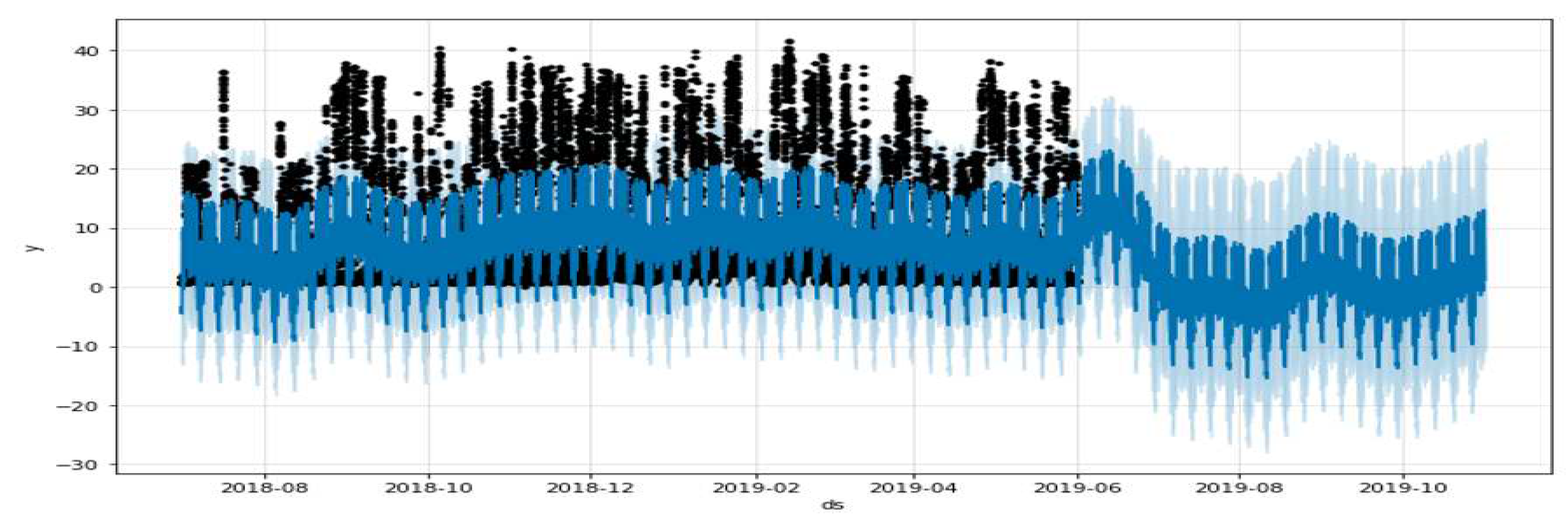
Preprints 85415 g008
Figure 8. Error forecast of the proposed Prophet model. The black dots represent the historical input data, the blue line represents the predicted trend line after model fitting, and the light blue area above and below the blue curve represents the confidence interval.
Figure 8. Error forecast of the proposed Prophet model. The black dots represent the historical input data, the blue line represents the predicted trend line after model fitting, and the light blue area above and below the blue curve represents the confidence interval.
Preprints 85415 g008
Preprints 85415 g009
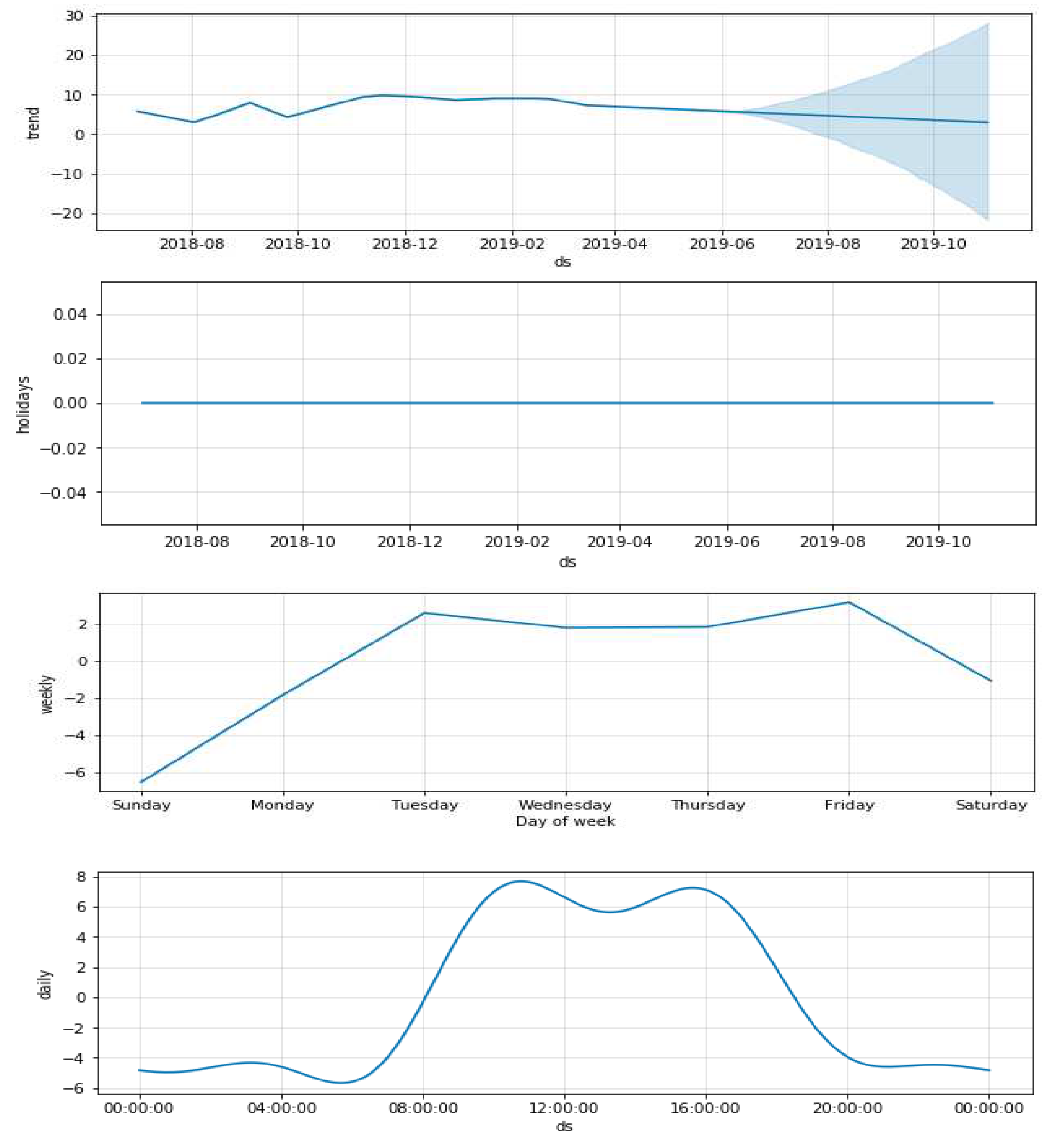
Figure 9. Trend, holidays, weekly, and daily prediction analysis of the proposed prophet model. The blue line shows the trend the model fits from the test data, and the light blue shade shows the predicted trend.
Figure 9. Trend, holidays, weekly, and daily prediction analysis of the proposed prophet model. The blue line shows the trend the model fits from the test data, and the light blue shade shows the predicted trend.
Preprints 85415 g009
Preprints 85415 g010
Figure 10. Structure of proposed GRU model.
Figure 10. Structure of proposed GRU model.
Preprints 85415 g010
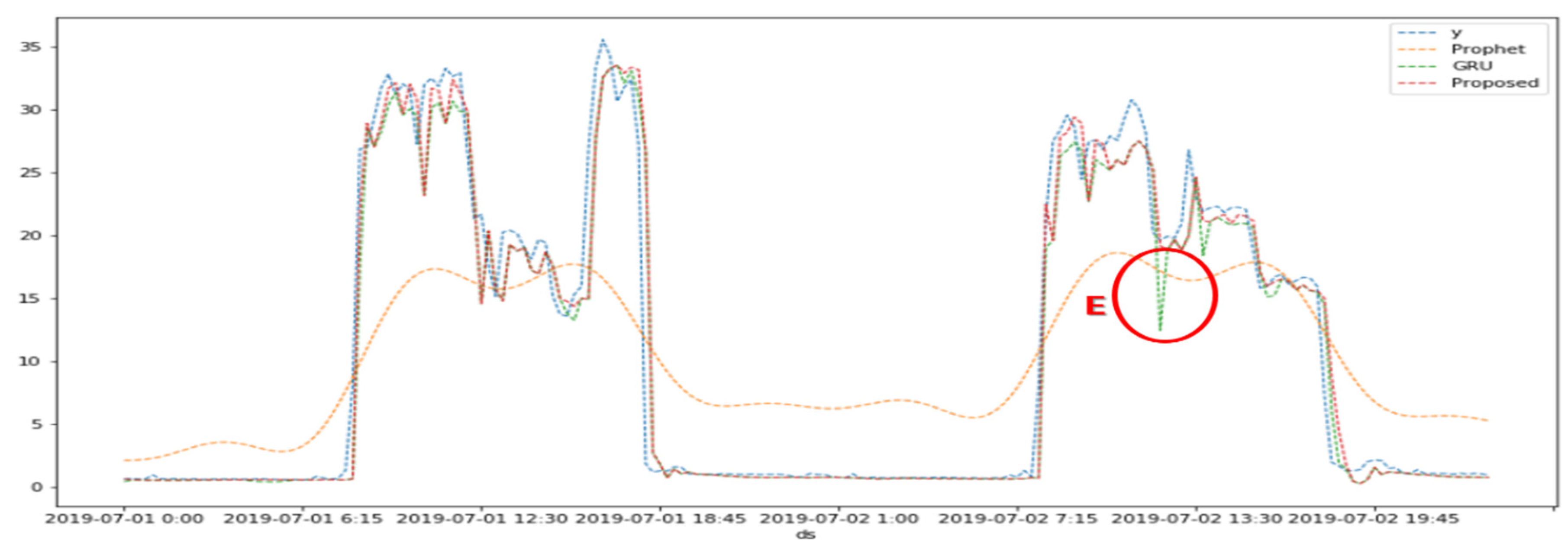
Preprints 85415 g011
Figure 11. Comparison of graphic visualization performance between observed values (y) and other methods (modified Prophet, GRU using multivariate, and Propose) from July 1 to July 2, 2019.
Figure 11. Comparison of graphic visualization performance between observed values (y) and other methods (modified Prophet, GRU using multivariate, and Propose) from July 1 to July 2, 2019.
Preprints 85415 g011
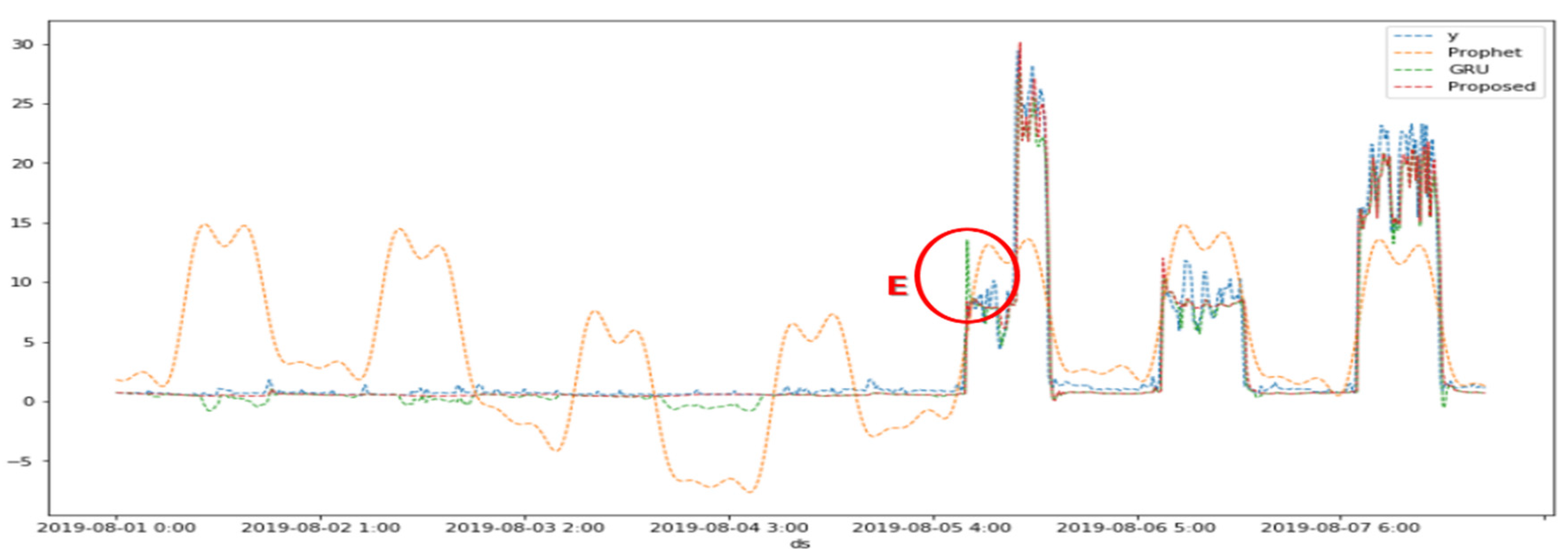
Preprints 85415 g012
Figure 12. Comparison of graphic visualization performance between observed values (y) and other methods (modified Prophet, GRU using multivariate, and Propose) from Aug. 1 to Aug. 7, 2019.
Figure 12. Comparison of graphic visualization performance between observed values (y) and other methods (modified Prophet, GRU using multivariate, and Propose) from Aug. 1 to Aug. 7, 2019.
Preprints 85415 g012
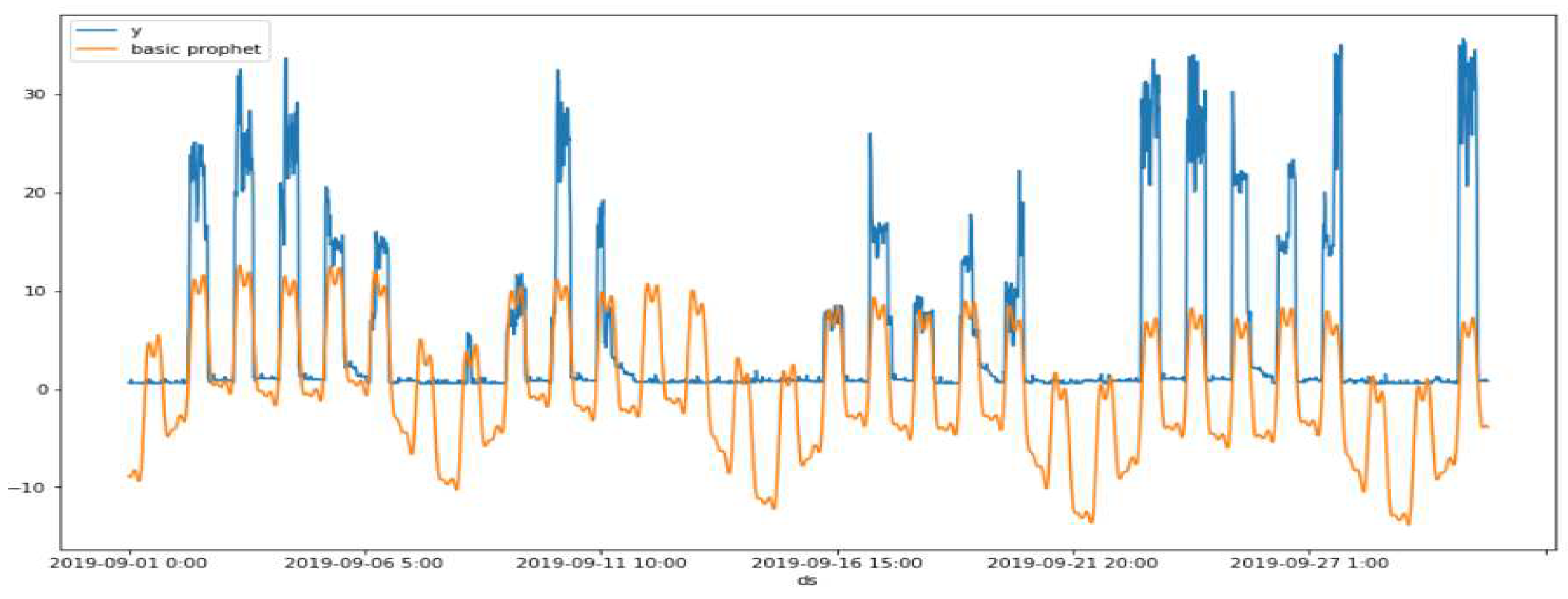
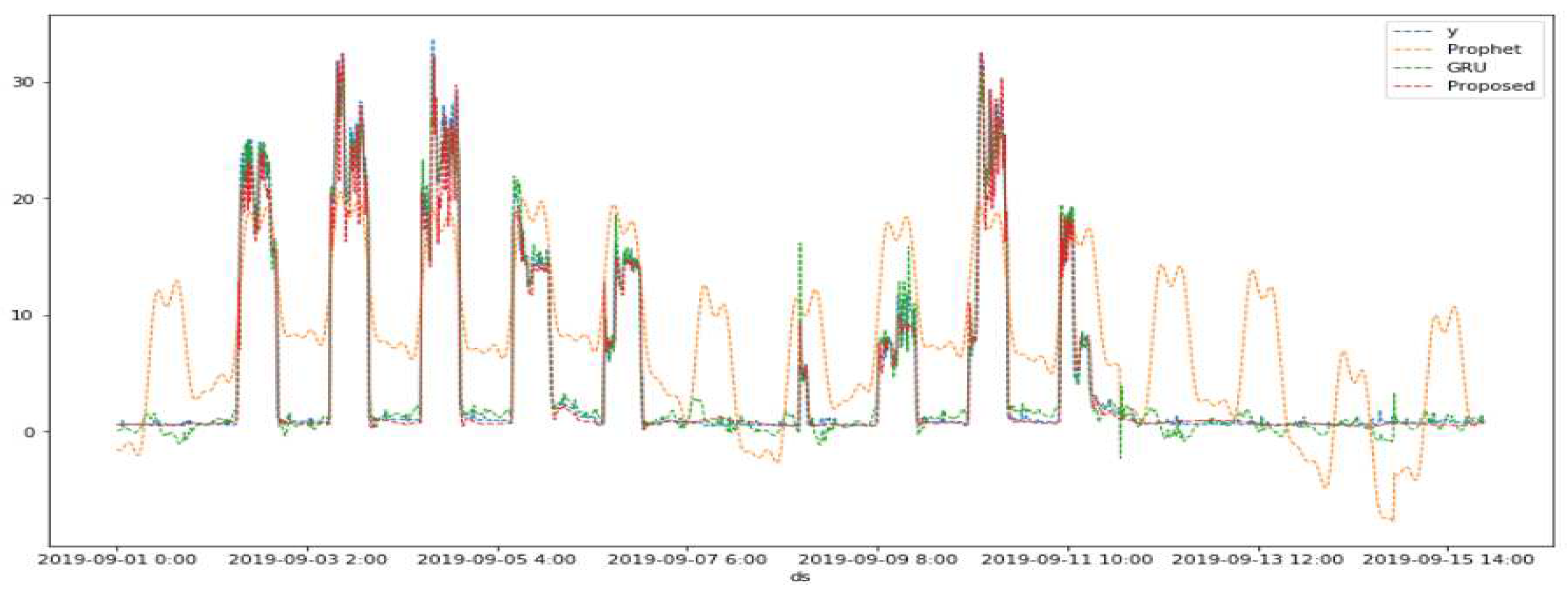
Preprints 85415 g013
Figure 13. Comparison of graphic visualization performance between observed values (y) and other methods (modified Prophet, GRU using multivariate, and Propose) from Sep. 1 to Sep. 15, 2019.
Figure 13. Comparison of graphic visualization performance between observed values (y) and other methods (modified Prophet, GRU using multivariate, and Propose) from Sep. 1 to Sep. 15, 2019.
Preprints 85415 g013
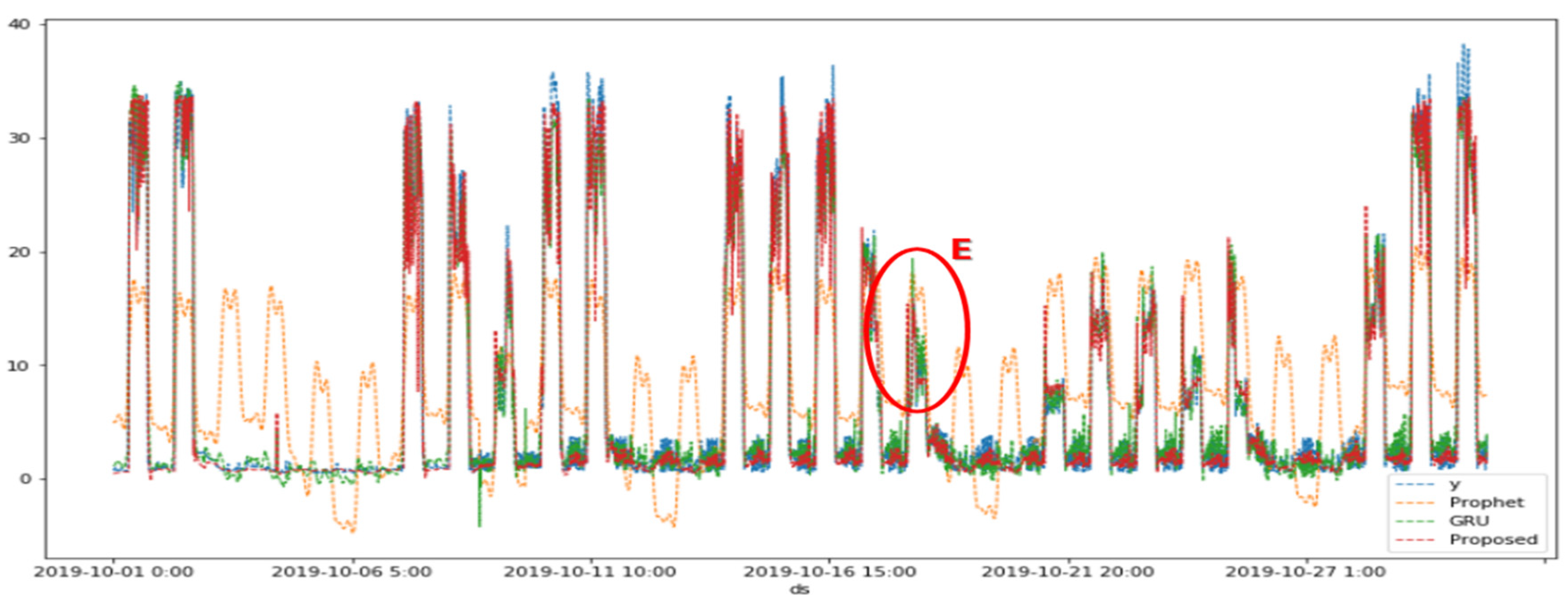
Preprints 85415 g014
Figure 14. Comparison of graphic visualization performance between observed values (y) and other methods (modified Prophet, GRU using multivariate, and Propose) from Oct. 1 to Oct. 30, 2019.
Figure 14. Comparison of graphic visualization performance between observed values (y) and other methods (modified Prophet, GRU using multivariate, and Propose) from Oct. 1 to Oct. 30, 2019.
Preprints 85415 g014
Table 1. Proposed prophet model parameter setting.
Table 1. Proposed prophet model parameter setting.
Parameter Nature Parameter Name Value
Trend Parameters growth linear
changepoints None
n_changepoints 25
changepoint_range 0.8
changepoint_prior_scale 0.01
Seasonality parameters yearly_seasonality 10
weekly_seasonality False
daily_seasonality False
seasonality_mode multiplicative
seasonality_prior_scale 10
Holidays parameters holidays
Holidays_prior_scale 		df
0.25
Flow parameters flow flow
flow_prior_scale 10
Other parameters mcmc_samples 0
interval_width 0.8
Table 2. Comparison of the performance of modified Prophet, GRU, and proposed method.
Table 2. Comparison of the performance of modified Prophet, GRU, and proposed method.
Term Metrics Prophet GRU Proposed
Short-
term		 2 days
(July 1~2)		 CC 0.88 0.97 0.97
MAPE (%) 316.56 25.09 24.57
SMAPE (%) 97.58 20.53 19.72
7 days
(Aug. 1~7)		 CC 0.51 0.97 0.98
MAPE (%) 526.62 48.07 27.32
SMAPE (%) 123.01 59.07 30.09
Medium-
term		 15 days
( Sep. 1~15)		 CC 0.70 0.98 0.98
MAPE (%) 579.80 42.55 24.61
SMAPE (%) 125.98 50.76 22.58
30 days
(Oct. 1~30)		 CC 0.67 0.97 0.98
MAPE (%) 348.06 37.66 34.37
SMAPE (%) 103.92 42.48 33.28
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated