Tricyclic Graph with Minimum Randić Index

Preprint

Article

Tricyclic Graph with Minimum Randić Index

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

16 September 2023

Posted:

19 September 2023

You are already at the latest version

Alerts

Abstract

The Randić index of a graph G is the sum of (dG(u)dG(v))−1/2 over all edges uv of G, where dG(u) denotes the degree of vertex u in G. In this paper, we investigate a few graph transformations that decrease Randić index of graph. By applying those transformations, we determine the minimum Randić index on tricyclic graphs, and characterize the corresponding extremal graphs.

Keywords:

Subject: Chemistry and Materials Science - Theoretical Chemistry

1. Introduction

In this paper we are concerned with undirected simple connected graphs, unless otherwise specified. Let

G = (V, E)

be such a graph with n vertices and m edges, which is addressed as an

(n, m)

-graph in what follows. A graph is cyclic if it contains at least one cycle, otherwise acyclic. More specifically, an

(n, n + k)

-graph is tree, unicyclic, bicyclic, tricyclic or tetracyclic, if

k = - 1, 0, 1, 2, 3

respectively. Denote

N_{G} (v)

the neighbors of vertex v in G, and

d_{G} (v) = | N_{G} (v) |

the degree of v. As usual, let

Δ (G) = max {d_{G} (v) | v \in V}

and

δ (G) = min {d_{G} (v) | v \in V}

. A pendant vertex (or leaf) is a vertex of degree one. The star

S_{n}

is tree with

n - 1

pendant vertices, and the path

P_{n}

is tree with two pendant vertices. For vertex v, we call

N_{G}^{1} (v) = {u \in N_{G} (v) | d_{G} (u) = 1}

pendant neighbors of v, and

N_{G}^{2} (v) = {u \in N_{G} (v) | d_{G} (u) > 1}

non-pendant neighbors. Furthermore, let

d_{G}^{1} (v) = | N_{G}^{1} (v) |

and

d_{G}^{2} (v) = | N_{G}^{2} (v) |

. If

\tilde{E}

is an edge set, then

G - \tilde{E}

denotes the graph formed from G by deleting edges in

\tilde{E}

, while

G + \tilde{E}

means the graph from G by adding edges in

\tilde{E}

. If graph G and H are isomorphic, we can write it as

G ≅ H

The Randić index(or R index for short) of G is defined as

R (G) = \sum_{u v \in E} \frac{1}{\sqrt{d_{G} (u) d_{G} (v)}} .

This structural descriptor was proposed as branching index[11] by Milan Randić in 1975. Since then, mathematical properties of R index have been studied extensively. For a comprehensive survey, see [6,8,9].

From the view of extremal graph theory, Bollobas and Erdӧs [1] first proved that

S_{n}

is the unique graph with the minimum R index for all n-vertex graphs and n-vertex trees. Trees with the second to the fourth minimum R indices have been determined by Zhao and Li in [10]. Caporossi et al [2] and P. Yu [12] showed that

P_{n}

attains the maximum R index in trees of order n. In [2], trees and unicyclic graphs with the first and the second maximum R indices and bicyclic graphs with the maximum R index are also considered. The unique unicyclic graph with the minimum R index has been determined by Gao and Lu in [7]. Du and Zhou [5] investigated more minimum and maximum R indices of trees, unicyclic and bicyclic graphs, for instance the second to the fifth maximum and the second minimum R indices of bicyclic graphs. Furthermore, the tricyclic and tetracyclic graphs with the maximum and the second maximum R indices have been determined in [3,4], while the counterparts with the minimum Randić indices are still unidentified for now.

In this paper, we investigate a few graph transformations which decrease R index of graphs. With the aid of these transformations, we derive tricyclic graph with the minimum Randić index as follows.

Theorem 1.

If G is a tricyclic graph of order

n \geq 4

, then

R (G) \geq \frac{n - 4 + \sqrt{3}}{\sqrt{n - 1}} + 1

. And the equality holds if and only if

G ≅ T R_{n}^{★}

, where

T R_{n}^{★}

is obtained by attaching

n - 4

pendant vertices to one vertex of a complete graph

K_{4}

shown as Figure 1.

2. Preliminaries

The following lemmas are required mainly for characterizing transformations in the next section.

Lemma 1.

Suppose

f (x)

is twice differentiable, and

f^{″} (x) > 0

. Let

S = f (a) - f (b) - f (c) + f (d)

with

a + d = b + c

a \leq b \leq d

and

a \leq c \leq d

. Then

S \geq 0

with equality holding if and only if

a = b

a = c

Proof.

a = b

, then

d = c

from

a + d = b + c

, thereby

S = 0

. Similarly

S = 0

a = c

. Without loss of generality, we may assume that

a < b \leq c < d

. Thus we obtain

S = f^{'} (ξ_{1}) (a - b) + f^{'} (ξ_{2}) (d - c) = (b - a) (f^{'} (ξ_{2}) - f^{'} (ξ_{1})) = (b - a) (ξ_{2} - ξ_{1}) f^{″} (η) > 0,

where

a < ξ_{1} < b \leq c < ξ_{2} < d

and

ξ_{1} < η < ξ_{2}

. Therefore the lemma holds clearly. □

Lemma 2.

x \geq 2, y \geq 2

, then

f (x, y) = \frac{y - 2 + \frac{2}{\sqrt{x}}}{\sqrt{y}} - \frac{y - 1 + \frac{1}{\sqrt{x}}}{\sqrt{y + x - 1}} > 0 .

Proof.

Let

g (x, y) = f (x, y) (\frac{y - 2 + \frac{2}{\sqrt{x}}}{\sqrt{y}} + \frac{y - 1 + \frac{1}{\sqrt{x}}}{\sqrt{y + x - 1}}) y (x + y - 1) = (x - 3 + \frac{2}{\sqrt{x}}) y^{2} + (4 \sqrt{x} - 4 x + 7 + \frac{3}{x} - \frac{10}{\sqrt{x}}) y + 4 x - \frac{4}{x} + \frac{8}{\sqrt{x}} - 8 \sqrt{x}

with

x \geq 2

and

y \geq 2

. Note that it suffices to show that

g (x, y) > 0

Observe that

{(x - 3 + \frac{2}{\sqrt{x}})}^{'} = 1 - \frac{1}{x^{\frac{3}{2}}} > 0

, so

x - 3 + \frac{2}{\sqrt{x}} \geq 2 - 3 + \frac{2}{\sqrt{2}} > 0

. Hence

\frac{\partial g (x, y)}{\partial y} = 2 y (x - 3 + \frac{2}{\sqrt{x}}) + (4 \sqrt{x} - 4 x + 7 + \frac{3}{x} - \frac{10}{\sqrt{x}}) \geq 4 (x - 3 + \frac{2}{\sqrt{x}}) + (4 \sqrt{x} - 4 x + 7 + \frac{3}{x} - \frac{10}{\sqrt{x}}) = 4 \sqrt{x} + \frac{3}{x} - \frac{2}{\sqrt{x}} - 5 \geq 4 \sqrt{2} + \frac{3}{2} - \frac{2}{\sqrt{2}} - 5 > 0

since

{(4 \sqrt{x} + \frac{3}{x} - \frac{2}{\sqrt{x}} - 5)}^{'} = \frac{2}{\sqrt{x}} + \frac{1}{x^{\frac{3}{2}}} - \frac{3}{x^{2}} > 0

. As a consequence,

g (x, y) \geq g (x, 2) = 2 + \frac{2}{x} - \frac{4}{\sqrt{x}} \geq 2 + \frac{2}{2} - \frac{4}{\sqrt{2}} > 0

{(2 + \frac{2}{x} - \frac{4}{\sqrt{x}})}^{'} = \frac{2}{x^{\frac{3}{2}}} - \frac{2}{x^{2}} > 0

. Hence the lemma holds easily. □

Lemma 3.

x \geq 3, y \geq 3

and

k \geq \frac{2}{\sqrt{5}}

, and let

f (x, y) = \frac{x - 3}{\sqrt{x}} + \frac{y - 3}{\sqrt{y}} + \frac{1}{\sqrt{x} \sqrt{y}} - \frac{x + y - 5}{\sqrt{x + y - 1}} + (\frac{k}{\sqrt{x}} - \frac{k}{\sqrt{x + y - 1}}) .

Then

f (x, y) > 0

and

f (y, x) > 0

Proof.

Since

f (x, y) \geq \frac{x - 3}{\sqrt{x}} + \frac{y - 3}{\sqrt{y}} + \frac{1}{\sqrt{x} \sqrt{y}} - \frac{x + y - 5}{\sqrt{x + y - 1}} + \frac{2}{\sqrt{5}} (\frac{1}{\sqrt{x}} - \frac{1}{\sqrt{x + y - 1}}) = h (x, y)

, then we only have to show

h (x, y) > 0

. Consider the gradient

\begin{matrix} \frac{\partial h (x, y)}{\partial y} & = \frac{1}{2} (\frac{1}{\sqrt{y}} - \frac{1}{\sqrt{x + y - 1}}) + \frac{3 - \frac{1}{\sqrt{x}}}{2 y^{\frac{3}{2}}} - \frac{4 - \frac{2 \sqrt{5}}{5}}{2 {(x + y - 1)}^{\frac{3}{2}}} \\ \geq \frac{x - 1}{4 η^{\frac{3}{2}}} + \frac{3 - \frac{1}{\sqrt{3}}}{2 y^{\frac{3}{2}}} - \frac{4 - \frac{2 \sqrt{5}}{5}}{2 {(x + y - 1)}^{\frac{3}{2}}} \\ \geq \frac{(\frac{3 - 1}{2} + 3 - \frac{1}{\sqrt{3}}) - (4 - \frac{2}{\sqrt{5}})}{2 {(x + y - 1)}^{\frac{3}{2}}} = \frac{\frac{2}{\sqrt{5}} - \frac{1}{\sqrt{3}}}{2 {(x + y - 1)}^{\frac{3}{2}}} > 0, \end{matrix}

where

y < η < x + y - 1

, hence

h (x, y) \geq h (x, 3)

Let

g (x) = x (x + 2) (\frac{x - 3 + \frac{1}{\sqrt{3}} + \frac{2}{\sqrt{5}}}{\sqrt{x}} + \frac{x - 2 + \frac{2}{\sqrt{5}}}{\sqrt{x + 2}}) h (x, 3) = \frac{2 \sqrt{3}}{3} x^{2} + \frac{4 \sqrt{15} + 12 \sqrt{5} - 100 - 10 \sqrt{3}}{15} x + \frac{304 + 8 \sqrt{15} - 72 \sqrt{5} - 60 \sqrt{3}}{15} .

Since the axis of symmetry of

g (x)

- \frac{4 \sqrt{15} + 12 \sqrt{5} - 100 - 10 \sqrt{3}}{15} / \frac{2 \sqrt{3}}{3} / 2 \approx 2.16493 < 3

, hence

g (x) \geq g (3) = - 12 \sqrt{5} / 5 + 4 / 15 + 4 \sqrt{15} / 3 \approx 0.06408 > 0

, implying

h (x, 3) > 0

Analogously, it can be shown that

f (y, x) > 0

holds. Therefore the lemma follows immediately. □

Lemma 4.

x \geq 3, y \geq 4

, then

\begin{matrix} f (x, y) & = \frac{x - 3}{\sqrt{x}} + \frac{1}{\sqrt{x} \sqrt{y}} - \frac{x - 2}{\sqrt{x + y - 1}} + \frac{1}{\sqrt{2}} (\frac{1}{\sqrt{x}} - \frac{1}{\sqrt{x + y - 1}}) \geq 0 . \end{matrix}

Proof.

Consider the gradient

\frac{\partial f (x, y)}{\partial y} = \frac{x - 2 + \frac{\sqrt{2}}{2}}{2 {(x + y - 1)}^{\frac{3}{2}}} - \frac{1}{2 \sqrt{x} y^{\frac{3}{2}}}

. Since

\begin{matrix} \frac{\partial f (x, y)}{\partial y} (\frac{x - 2 + \frac{\sqrt{2}}{2}}{2 {(x + y - 1)}^{\frac{3}{2}}} + \frac{1}{2 \sqrt{x} y^{\frac{3}{2}}}) (4 {(x + y - 1)}^{3} x) \\ = x {(x - 2 + \frac{\sqrt{2}}{2})}^{2} - \frac{{(x + y - 1)}^{3}}{y^{3}} \geq x {(x - 2 + \frac{\sqrt{2}}{2})}^{2} - \frac{{(x + 3)}^{3}}{4^{3}} \\ = \frac{63 (x - 3) + (60 \sqrt{2} - 76)}{64} x^{2} + (\frac{252}{64} - 2 \sqrt{2}) x + \frac{9 (x - 3)}{64} > 0, \end{matrix}

where the last inequality holds by

x \geq 3

, and consequently

\frac{\partial f (x, y)}{\partial y} > 0

Therefore, it is sufficient to show

f (x, 4) \geq 0

. Let

q (x) = f (x, 4) x (x + 3) (\frac{x - 3 + \frac{1}{2} + \frac{\sqrt{2}}{2}}{\sqrt{x}} + \frac{x - 2 + \frac{\sqrt{2}}{2}}{\sqrt{x + 3}}) = 2 x^{2} + \frac{10 \sqrt{2} - 51}{4} x + \frac{81 - 30 \sqrt{2}}{4} .

Since the axis of symmetry of

q (x)

(- \frac{10 \sqrt{2} - 51}{4}) / 4 \approx 2.3 < 3

, then

q (x) \geq q (3) = 0

. Note that

q (x)

and

f (x, 4)

have the same sign, so the proof is complete. □

Lemma 5.

Let

x_{1}, x_{2}, y

be integers with

y \geq 3

, and let

f (x_{1}, x_{2}, y) = \frac{x_{1} + \frac{1}{\sqrt{2}} + k}{\sqrt{x_{1} + x_{2}}} + \frac{y - 2 + \frac{1}{\sqrt{2}}}{\sqrt{y}} + \frac{1}{\sqrt{y (x_{1} + x_{2})}} - \frac{x_{1} + y - 2 + \sqrt{2} + k}{\sqrt{x_{1} + x_{2} + y - 2}} - \frac{1}{2},

then

f (x_{1}, x_{2}, y) > 0

, if either of the following is satisfied: (1)

x_{1} \geq 1, 2 \leq x_{2} \leq 10, k = 0

; (2)

x_{1} = 0, 2 \leq x_{2} \leq 6, k = \frac{1}{\sqrt{3}}

Proof.

(1). Let

h (t) = \frac{t - \sqrt{2} + 2 x_{2}}{2 {(t + x_{2})}^{\frac{3}{2}}}

with

t \geq 1

. Note that

h^{^{'}} = \frac{- \frac{t}{2} - 2 x_{2} + \frac{3 \sqrt{2}}{2}}{2 {(t + x_{2})}^{\frac{5}{2}}} < 0

. Then we have

\frac{\partial f (x_{1}, x_{2}, y)}{\partial x_{1}} = \frac{x_{1} - \sqrt{2} + 2 x_{2} + (\frac{1}{\sqrt{2}} - \frac{1}{\sqrt{y}})}{2 {(x_{1} + x_{2})}^{\frac{3}{2}}} - \frac{(x_{1} + y - 2) - \sqrt{2} + 2 x_{2}}{2 {((x_{1} + y - 2) + x_{2})}^{\frac{3}{2}}} > h (x_{1}) - h (x_{1} + y - 2) > 0,

hence it suffices to prove

f (1, x_{2}, y) > 0

Let

A = \frac{y - 2 + \frac{1}{\sqrt{2}}}{\sqrt{y}} + \frac{1}{\sqrt{y (1 + x_{2})}} + \frac{1 + \frac{1}{\sqrt{2}}}{\sqrt{1 + x_{2}}} - \frac{1}{2}

, and

B = \frac{y - 1 + \sqrt{2}}{\sqrt{x_{2} + y - 1}}

. First note that

\frac{1 + \frac{1}{\sqrt{2}}}{\sqrt{1 + x_{2}}} - \frac{1}{2} \geq \frac{1 + \frac{1}{\sqrt{2}}}{\sqrt{1 + 10}} - \frac{1}{2} > 0

, which means

A > 0

. Let

g (x_{2}, y) = f (1, x_{2}, y) (A + B) y (x_{2} + 1) (x_{2} + y - 1) = (A^{2} - B^{2}) y (x_{2} + 1) (x_{2} + y - 1) = a_{1} y^{\frac{5}{2}} + a_{2} y^{2} + a_{3} y^{\frac{3}{2}} + a_{4} y + a_{5} y^{\frac{1}{2}} + a_{6}

. It is easy to see

f (1, x_{2}, y) > 0

g (x_{2}, y) > 0

Now let

b_{1} = a_{1}

, and

b_{i} = \sqrt{3} b_{i - 1} + a_{i}

for

i = 2, 3, 4, 5, 6

. With assistance of computer, one can get all values of

b_{i}

for

2 \leq x_{2} \leq 10

as shown in Table 1, and conclude that

b_{i} > 0

for each i.

We find that

g (x_{2}, y) = b_{1} y^{\frac{5}{2}} + a_{2} y^{2} + a_{3} y^{\frac{3}{2}} + a_{4} y + a_{5} y^{\frac{1}{2}} + a_{6} \geq \sqrt{3} b_{1} y^{2} + a_{2} y^{2} + a_{3} y^{\frac{3}{2}} + a_{4} y + a_{5} y^{\frac{1}{2}} + a_{6} = b_{2} y^{2} + a_{3} y^{\frac{3}{2}} + a_{4} y + a_{5} y^{\frac{1}{2}} + a_{6}

. By repeating this process, we arrive at

g (x_{2}, y) \geq b_{6} > 0

. Therefore

f (x_{1}, x_{2}, y) > 0

holds.

(2) Since the result in this case can be proved by a similar argument as (1), so we omit the details and only give the values of

b_{i}

in Table 2.

The lemma therefore follows easily. □

Lemma 6.

y \geq z \geq 2

, then

f (y, z) = (\frac{1}{\sqrt{y z}} - \frac{1}{\sqrt{(y + 1) (z - 1)}}) - (\frac{1}{\sqrt{z}} + \frac{1}{\sqrt{y}} - \frac{1}{\sqrt{z - 1}} - \frac{1}{\sqrt{y + 1}}) > 0 .

Proof.

Observe that

f (y, z) = (1 - \frac{1}{\sqrt{z}}) (1 - \frac{1}{\sqrt{y}}) - (1 - \frac{1}{\sqrt{z - 1}}) (1 - \frac{1}{\sqrt{y + 1}}) .

It is obvious that

f (y, 2) = (1 - \frac{1}{\sqrt{2}}) (1 - \frac{1}{\sqrt{y}}) > 0

Now we consider the case

y \geq z > 2

. Let

h (y, z) = ln (1 - \frac{1}{\sqrt{z}}) (1 - \frac{1}{\sqrt{y}}) - ln (1 - \frac{1}{\sqrt{z - 1}}) (1 - \frac{1}{\sqrt{y + 1}})

with

y \geq z > 2

. Note that

f (y, z)

has the same sign with

h (y, z)

since

ln (x)

is increasing for

x > 0

. Let

g (t) = - ln (1 - \frac{1}{\sqrt{t}})

for

t > 1

, and

g^{^{″}} (t) = \frac{3 \sqrt{t} - 2}{4 t^{2} {(\sqrt{t} - 1)}^{2}} > 0

. Hence we obtain

h (y, z) = g (z - 1) - g (z) - g (y) + g (y + 1) > 0

by Lemma 1. Therefore the lemma holds easily. □

Lemma 7.

Let

f (y, z) = \frac{y + k}{\sqrt{y}} + \frac{z + k}{\sqrt{z}} + \frac{k^{'}}{\sqrt{y z}}

with

y \geq z \geq 2

, then

f (y, z) > f (y + 1, z - 1)

if it meets one of the following conditions: (1)

k \leq 0

and

k^{'} = 0

; (2)

k \leq - 1

k^{'} = 1

Proof.

(1). Let

g (t) = - \frac{t + k}{\sqrt{t}}

with

t \geq 1

, and note that

g^{^{″}} (t) = \frac{t - 3 k}{4 t^{\frac{5}{2}}} > 0

. Then we have

f (y, z) - f (y + 1, z - 1) = g (z - 1) - g (z) - g (y) + g (y + 1) > 0

by Lemma 1.

(2) Let

h (t) = - \frac{t + k + 1}{\sqrt{t}}

with

t \geq 1

, and note that

h^{^{″}} (t) = \frac{t - 3 k - 3}{4 t^{\frac{5}{2}}} > 0

. By Lemma 6, we have

f (y, z) - f (y + 1, z - 1) \geq (\frac{z + k}{\sqrt{z}} + \frac{y + k}{\sqrt{y}} - \frac{z - 1 + k}{\sqrt{z - 1}} - \frac{y + 1 + k}{\sqrt{y + 1}}) + (\frac{1}{\sqrt{z}} + \frac{1}{\sqrt{y}} - \frac{1}{\sqrt{z - 1}} - \frac{1}{\sqrt{y + 1}}) = h (z - 1) - h (z) - h (y) + h (y + 1) > 0,

where the last inequality follows from Lemma 1. □

Lemma 8.

x \geq 4, y \geq 4

, then

f (x, y) = \frac{y - 3 + \frac{\sqrt{3}}{3} + \frac{\sqrt{2}}{2} + \frac{1}{\sqrt{x}}}{\sqrt{y}} + \frac{x - 4 + \frac{\sqrt{3}}{3} + \sqrt{2}}{\sqrt{x}} - \frac{x + y - 7 + \frac{2 \sqrt{3}}{3} + \sqrt{2}}{\sqrt{x + y - 3}} - (\frac{1}{3} + \frac{1}{\sqrt{6}}) > 0

Proof.

Since

\begin{matrix} \frac{\partial f (x, y)}{\partial x} & = \frac{4 - \sqrt{2} - \frac{\sqrt{3}}{3} - \frac{1}{\sqrt{y}}}{2 x^{\frac{3}{2}}} - \frac{4 - \sqrt{2} - \frac{2 \sqrt{3}}{3}}{2 {(x + y - 3)}^{\frac{3}{2}}} + (\frac{1}{2 \sqrt{x}} - \frac{1}{2 \sqrt{x + y - 3}}) \\ > \frac{4 - \sqrt{2} - \frac{\sqrt{3}}{3} - \frac{1}{\sqrt{4}}}{2 x^{\frac{3}{2}}} - \frac{4 - \sqrt{2} - \frac{2 \sqrt{3}}{3}}{2 {(x + y - 3)}^{\frac{3}{2}}} > \frac{\frac{\sqrt{3}}{3} - \frac{1}{2}}{2 {(x + y - 3)}^{\frac{3}{2}}} > 0, \end{matrix}

hence

f (x, y) \geq f (4, y)

. And moreover,

\begin{matrix} \frac{\partial f (4, y)}{\partial y} & = \frac{\frac{5}{2} - \frac{\sqrt{3}}{3} - \frac{\sqrt{2}}{2}}{2 y^{\frac{3}{2}}} - \frac{4 - \frac{2 \sqrt{3}}{3} - \sqrt{2}}{2 {(y + 1)}^{\frac{3}{2}}} + (\frac{1}{2 \sqrt{y}} - \frac{1}{2 \sqrt{y + 1}}) \\ = \frac{\frac{5}{2} - \frac{\sqrt{3}}{3} - \frac{\sqrt{2}}{2}}{2 y^{\frac{3}{2}}} + \frac{1}{4 η^{\frac{3}{2}}} - \frac{4 - \frac{2 \sqrt{3}}{3} - \sqrt{2}}{2 {(y + 1)}^{\frac{3}{2}}} > \frac{\frac{1}{\sqrt{3}} + \frac{1}{\sqrt{2}} - 1}{2 {(y + 1)}^{\frac{3}{2}}} > 0, \end{matrix}

where

y < η < y + 1

. Therefore

f (x, y) \geq f (4, 4) \approx 0.05036 > 0

. □

3. Transformations Decreasing Randić Index

To find tricyclic graphs with small Randić index, we provide some transformations which decrease Randić index of graphs. It is worth noting that all transformations defined here preserve the number of vertices and edges of a graph. For simplicity, we will not repeat this property in the sequel.

Theorem 2

(Transformation I). Suppose G is a graph with given two adjacent vertices u and v such that

N_{G} (v) \cap N_{G} (u) = \emptyset

. Let graph

G^{'} = G - {v w | w \in N_{G} (v) ∖ u} + {u w | w \in N_{G} (v) ∖ u}

, and we write the transformation as

G^{'} = Γ (G, u, v)

. Then

R (G) > R (G^{'})

if G meets one of the following conditions:

(1): v has only one non-pendant neighbor u and $d_{G} (v) \geq 2$ ;
(2): v has two non-pendant neighbors u and w with $d_{G} (u) \geq d_{G} (w)$ ;
(3): v has three non-pendant neighbors $u, v_{1}, v_{2}$ and u has three non-pendant neighbors $v, u_{1}, u_{2}$ such that $\frac{1}{\sqrt{d_{G} (u_{1})}} + \frac{1}{\sqrt{d_{G} (u_{2})}} + \frac{1}{\sqrt{d_{G} (v_{2})}} + \frac{1}{\sqrt{d_{G} (v_{2})}} \geq \frac{2}{\sqrt{5}}$ ;
(4): $d_{G} (v) \geq 4$ and u has three non-pendant neighbors $v, u_{1}, u_{2}$ with $\frac{1}{\sqrt{d_{G} (u_{1})}} + \frac{1}{\sqrt{d_{G} (u_{2})}} \geq \frac{1}{\sqrt{2}}$ .

Proof.

Let

\tilde{E}

be the edge set of G that are not incident with u or v, and

\tilde{R} = \sum_{p q \in \tilde{E}} \frac{1}{\sqrt{d_{G} (p) d_{G} (q)}}

. And let

x = d_{G} (u)

y = d_{G} (v)

Δ = R (G) - R (G^{'})

. Then

\begin{matrix} R (G) & = \tilde{R} + \sum_{z \in N_{G} (u) ∖ v} \frac{1}{\sqrt{x d_{G} (z)}} + \sum_{z \in N_{G} (v) ∖ u} \frac{1}{\sqrt{y d_{G} (z)}} + \frac{1}{\sqrt{x y}} \\ R (G^{'}) & = \tilde{R} + (\sum_{z \in N_{G} (u) ∖ v} \frac{1}{\sqrt{d_{G} (z)}} + \sum_{z \in N_{G} (v) ∖ u} \frac{1}{\sqrt{d_{G} (z)}} + 1) \frac{1}{\sqrt{x + y - 1}} . \end{matrix}

(1) Note that

x, y \geq 2

and v has

y - 1

pendant neighbors. Then

\begin{matrix} Δ & = \frac{y - 1}{\sqrt{y}} + \frac{1}{\sqrt{x y}} - \frac{y}{\sqrt{x + y - 1}} + \sum_{z \in N_{G} (u) ∖ v} \frac{1}{\sqrt{d_{G} (z)}} (\frac{1}{\sqrt{x}} - \frac{1}{\sqrt{x + y - 1}}) \\ \geq \frac{y - 1}{\sqrt{y}} + \frac{1}{\sqrt{x y}} - \frac{y}{\sqrt{x + y - 1}} \\ = (\frac{y - 2 + \frac{2}{\sqrt{x}}}{\sqrt{y}} - \frac{y - 1 + \frac{1}{\sqrt{x}}}{\sqrt{x + y - 1}}) + (1 - \frac{1}{\sqrt{x}}) (\frac{1}{\sqrt{y}} - \frac{1}{\sqrt{x + y - 1}}) > 0, \end{matrix}

where the last inequality holds by Lemma 2 and

\frac{1}{\sqrt{y}} > \frac{1}{\sqrt{x + y - 1}}

(2) Notice that

x \geq 2

y \geq 2

d_{G} (w) \leq x

, and v has

y - 2

pendant neighbors in this case. Then

\begin{matrix} Δ & \geq \frac{y - 2}{\sqrt{y}} + \frac{1}{\sqrt{x y}} - \frac{y - 1}{\sqrt{y + x - 1}} + \frac{1}{\sqrt{d_{G} (w)}} (\frac{1}{\sqrt{y}} - \frac{1}{\sqrt{y + x - 1}}) \\ + \sum_{z \in N_{G} (u) ∖ v} \frac{1}{\sqrt{d_{G} (z)}} (\frac{1}{\sqrt{x}} - \frac{1}{\sqrt{x + y - 1}}) \\ \geq \frac{y - 2}{\sqrt{y}} + \frac{1}{\sqrt{x y}} - \frac{y - 1}{\sqrt{y + x - 1}} + \frac{1}{\sqrt{x}} (\frac{1}{\sqrt{y}} - \frac{1}{\sqrt{y + x - 1}}) \\ = \frac{y - 2 + \frac{2}{\sqrt{x}}}{\sqrt{y}} - \frac{y - 1 + \frac{1}{\sqrt{x}}}{\sqrt{y + x - 1}} > 0, \end{matrix}

where the last inequality holds by Lemma 2.

(3) Let

k_{1} = \frac{1}{\sqrt{d_{G} (u_{1})}} + \frac{1}{\sqrt{d_{G} (u_{2})}}

k_{2} = \frac{1}{\sqrt{d_{G} (v_{1})}} + \frac{1}{\sqrt{d_{G} (v_{2})}}

, and

p (x, y) = \frac{x - 3}{\sqrt{x}} + \frac{y - 3}{\sqrt{y}} + \frac{1}{\sqrt{x} \sqrt{y}} - \frac{x + y - 5}{\sqrt{x + y - 1}}

. Note that

x, y \geq 3

and

k_{1} + k_{2} \geq \frac{2}{\sqrt{5}}

from the condition. Then

\begin{matrix} Δ & = p (x, y) + (\frac{k_{1}}{\sqrt{x}} - \frac{k_{1}}{\sqrt{x + y - 1}}) + (\frac{k_{2}}{\sqrt{y}} - \frac{k_{2}}{\sqrt{x + y - 1}}) \\ = \frac{k_{1}}{k_{1} + k_{2}} [p (x, y) + (\frac{k_{1} + k_{2}}{\sqrt{x}} - \frac{k_{1} + k_{2}}{\sqrt{x + y - 1}})] \\ + \frac{k_{2}}{k_{1} + k_{2}} [p (x, y) + (\frac{k_{1} + k_{2}}{\sqrt{y}} - \frac{k_{1} + k_{2}}{\sqrt{x + y - 1}})] > 0, \end{matrix}

where the last inequality holds by Lemma 3.

(4) Obviously

x \geq 3

y \geq 4

and

N_{G} (v) ∖ u \neq \emptyset

. Then

\begin{matrix} Δ & = \frac{x - 3}{\sqrt{x}} + \frac{1}{\sqrt{x} \sqrt{y}} - \frac{x - 2}{\sqrt{x + y - 1}} \\ + \sum_{z \in N_{G} (v) ∖ u} \frac{1}{\sqrt{d_{G} (z)}} (\frac{1}{\sqrt{y}} - \frac{1}{\sqrt{x + y - 1}}) \\ + (\frac{1}{\sqrt{d_{G} (u_{1})}} + \frac{1}{\sqrt{d_{G} (u_{2})}}) (\frac{1}{\sqrt{x}} - \frac{1}{\sqrt{x + y - 1}}) \\ > \frac{x - 3}{\sqrt{x}} + \frac{1}{\sqrt{x} \sqrt{y}} - \frac{x - 2}{\sqrt{x + y - 1}} + \frac{1}{\sqrt{2}} (\frac{1}{\sqrt{x}} - \frac{1}{\sqrt{x + y - 1}}) \geq 0, \end{matrix}

where the last inequality holds by Lemma 4. □

Theorem 3

(Transformation II). Suppose G is a graph, and there is a cycle

C = v_{0} v_{1} v_{2} v_{0}

in G with

d_{G}^{1} (v_{1}) \geq 1

and

d_{G}^{2} (v_{1}) = 2

. Let

G^{'}

arise from G by moving all pendant neighbors from

v_{1}

v_{0}

. Then

R (G) > R (G^{'})

if either of the following is satisfied:

(1): $d_{G}^{1} (v_{0}) \geq 1, 2 \leq d_{G}^{2} (v_{0}) \leq 10$ ;
(2): $2 \leq d_{G}^{2} (v_{0}) \leq 6$ and there is a vertex $u \in N_{G} (v_{0}) ∖ {v_{1}, v_{2}}$ with $d_{G} (u) \leq 3$ .

Proof.

Let

x_{1} = d_{G}^{1} (v_{0})

x_{2} = d_{G}^{2} (v_{0})

and

y = d_{G} (v_{1})

. Let

f (x) = \frac{1}{\sqrt{x}}

, then

f^{″} (x) = \frac{3}{4 x^{\frac{5}{2}}} > 0

. And note that

2 + (x_{1} + x_{2} + y - 2) = y + (x_{1} + x_{2})

2 \leq x_{1} + x_{2} \leq (x_{1} + x_{2} + y - 2)

and

2 \leq y \leq (x_{1} + x_{2} + y - 2)

, then we get

\frac{1}{\sqrt{2}} - \frac{1}{\sqrt{x_{1} + x_{2}}} - \frac{1}{\sqrt{y}} + \frac{1}{\sqrt{x_{1} + x_{2} + y - 2}} \geq 0

by Lemma 1. Then

\begin{matrix} R (G) - R (G^{'}) \\ = \frac{x_{1}}{\sqrt{x_{1} + x_{2}}} + \frac{y - 2}{\sqrt{y}} + \frac{1}{\sqrt{y (x_{1} + x_{2})}} - \frac{x_{1} + y - 2 + \frac{1}{\sqrt{2}}}{\sqrt{x_{1} + x_{2} + y - 2}} \\ + \sum_{z \in N_{G}^{2} (v_{0}) ∖ {v_{1}, v_{2}}} \frac{1}{\sqrt{d_{G} (z)}} (\frac{1}{\sqrt{x_{1} + x_{2}}} - \frac{1}{\sqrt{x_{1} + x_{2} + y - 2}}) \\ - \frac{1}{\sqrt{d_{G} (v_{2})}} (\frac{1}{\sqrt{2}} - \frac{1}{\sqrt{x_{1} + x_{2}}} - \frac{1}{\sqrt{y}} + \frac{1}{\sqrt{x_{1} + x_{2} + y - 2}}) \\ \geq \frac{x_{1}}{\sqrt{x_{1} + x_{2}}} + \frac{y - 2}{\sqrt{y}} + \frac{1}{\sqrt{y (x_{1} + x_{2})}} - \frac{x_{1} + y - 2 + \frac{1}{\sqrt{2}}}{\sqrt{x_{1} + x_{2} + y - 2}} \\ + \sum_{z \in N_{G}^{2} (v_{0}) ∖ {v_{1}, v_{2}}} \frac{1}{\sqrt{d_{G} (z)}} (\frac{1}{\sqrt{x_{1} + x_{2}}} - \frac{1}{\sqrt{x_{1} + x_{2} + y - 2}}) \\ - \frac{1}{\sqrt{2}} (\frac{1}{\sqrt{2}} - \frac{1}{\sqrt{x_{1} + x_{2}}} - \frac{1}{\sqrt{y}} + \frac{1}{\sqrt{x_{1} + x_{2} + y - 2}}), \end{matrix}

where the last inequality follows by

d_{G} (v_{2}) \geq 2

(1) Note that

x_{1} \geq 1

2 \leq x_{2} \leq 10

and

y \geq 3

. Then

\begin{matrix} R (G) - R (G^{'}) \\ \geq \frac{x_{1}}{\sqrt{x_{1} + x_{2}}} + \frac{y - 2}{\sqrt{y}} + \frac{1}{\sqrt{y (x_{1} + x_{2})}} - \frac{x_{1} + y - 2 + \frac{1}{\sqrt{2}}}{\sqrt{x_{1} + x_{2} + y - 2}} \\ - \frac{1}{\sqrt{2}} (\frac{1}{\sqrt{2}} - \frac{1}{\sqrt{x_{1} + x_{2}}} - \frac{1}{\sqrt{y}} + \frac{1}{\sqrt{x_{1} + x_{2} + y - 2}}) \\ = \frac{x_{1} + \frac{1}{\sqrt{2}}}{\sqrt{x_{1} + x_{2}}} + \frac{y - 2 + \frac{1}{\sqrt{2}}}{\sqrt{y}} + \frac{1}{\sqrt{y (x_{1} + x_{2})}} - \frac{x_{1} + y - 2 + \sqrt{2}}{\sqrt{x_{1} + x_{2} + y - 2}} - \frac{1}{2} > 0, \end{matrix}

where the last inequality holds by (1) of Lemma 5.

(2) Obviously, the assertion holds if

d_{G}^{1} (v_{0}) \geq 1

by (1). Hence we only need to consider the case

d_{G}^{1} (v_{0}) = 0

. Note that

x_{1} = 0, 2 \leq x_{2} \leq 6, y \geq 3, d_{G} (u) \leq 3

, then

\begin{matrix} R (G) - R (G^{'}) \\ \geq (\frac{y - 2}{\sqrt{y}} + \frac{1}{\sqrt{y x_{2}}}) - \frac{y - 2 + \frac{1}{\sqrt{2}}}{\sqrt{x_{2} + y - 2}} + \frac{1}{\sqrt{d_{G} (u)}} (\frac{1}{\sqrt{x_{2}}} - \frac{1}{\sqrt{x_{2} + y - 2}}) \\ - \frac{1}{\sqrt{2}} (\frac{1}{\sqrt{2}} - \frac{1}{\sqrt{x_{2}}} - \frac{1}{\sqrt{y}} + \frac{1}{\sqrt{x_{2} + y - 2}}) \\ \geq \frac{\frac{1}{\sqrt{2}} + \frac{1}{\sqrt{3}}}{\sqrt{x_{2}}} + \frac{y - 2 + \frac{1}{\sqrt{2}}}{\sqrt{y}} + \frac{1}{\sqrt{y x_{2}}} - \frac{y - 2 + \sqrt{2} + \frac{1}{\sqrt{3}}}{\sqrt{x_{2} + y - 2}} - \frac{1}{2} > 0, \end{matrix}

where the last inequality holds by (2) of Lemma 5. □

Theorem 4

(Transformation III). Suppose G is a graph with given two vertices u and v such that

d_{G} (u) \geq d_{G} (v) \geq 2

and

d_{G}^{1} (u) \geq d_{G}^{1} (v) \geq 1

. Let

G^{'}

be graph obtained from G by moving one pendant neighbor of v to u, then

R (G) > R (G^{'})

d_{G}^{2} (v) = d_{G}^{2} (u)

and

\sum_{z \in N_{G}^{2} (u) ∖ v} \frac{1}{\sqrt{d_{G} (z)}} = \sum_{z \in N_{G}^{2} (v) ∖ u} \frac{1}{\sqrt{d_{G} (z)}}

Proof.

Let

\tilde{E}

be the edge set of G that are not incident with u or v, and

x = d_{G} (u) \geq 2

y = d_{G} (v) \geq 2

. And observe that

- | d_{G}^{2} (u) | + \sum_{z \in N_{G}^{2} (u) ∖ v} \frac{1}{\sqrt{d_{G} (z)}} = - | d_{G}^{2} (v) | + \sum_{z \in N_{G}^{2} (v) ∖ u} \frac{1}{\sqrt{d_{G} (z)}}

, denoted by k.

If u and v are not adjacent, then

k = \sum_{z \in N_{G}^{2} (u)} (\frac{1}{\sqrt{d_{G} (z)}} - 1) \leq 0

, so

\begin{matrix} R (G) & = \sum_{p q \in \tilde{E}} \frac{1}{\sqrt{d_{G} (p) d_{G} (q)}} + \sum_{z \in N_{G}^{2} (u)} \frac{1}{\sqrt{x d_{G} (z)}} + \frac{x - | N_{G}^{2} (u) |}{\sqrt{x}} \\ + \sum_{z \in N_{G}^{2} (v)} \frac{1}{\sqrt{y d_{G} (z)}} + \frac{y - | N_{G}^{2} (v) |}{\sqrt{y}} \\ = \sum_{p q \in \tilde{E}} \frac{1}{\sqrt{d_{G} (p) d_{G} (q)}} + \frac{x + k}{\sqrt{x}} + \frac{y + k}{\sqrt{y}} \\ R (G^{'}) & = \sum_{p q \in \tilde{E}} \frac{1}{\sqrt{d_{G} (p) d_{G} (q)}} + \frac{x + 1 + k}{\sqrt{x + 1}} + \frac{y - 1 + k}{\sqrt{y - 1}} . \end{matrix}

Therefore we get

R (G) > R (G^{'})

by (1) of Lemma 7.

If u and v are adjacent, then

k = - 1 + \sum_{z \in N_{G}^{2} (u) ∖ v} (\frac{1}{\sqrt{d_{G} (z)}} - 1) \leq - 1

, so

\begin{matrix} R (G) & = \sum_{p q \in \tilde{E}} \frac{1}{\sqrt{d_{G} (p) d_{G} (q)}} + \sum_{z \in N_{G}^{2} (u) ∖ v} \frac{1}{\sqrt{x d_{G} (z)}} + \sum_{z \in N_{G}^{2} (v) ∖ u} \frac{1}{\sqrt{y d_{G} (z)}} \\ + \frac{x - | N_{G}^{2} (u) |}{\sqrt{x}} + \frac{y - | N_{G}^{2} (v) |}{\sqrt{y}} + \frac{1}{\sqrt{x y}} \\ = \sum_{p q \in \tilde{E}} \frac{1}{\sqrt{d_{G} (p) d_{G} (q)}} + \frac{x + k}{\sqrt{x}} + \frac{y + k}{\sqrt{y}} + \frac{1}{\sqrt{x y}} \\ R (G^{'}) & = \sum_{p q \in \tilde{E}} \frac{1}{\sqrt{d_{G} (p) d_{G} (q)}} + \frac{x + 1 + k}{\sqrt{x + 1}} + \frac{y - 1 + k}{\sqrt{y - 1}} + \frac{1}{\sqrt{(x + 1) (y - 1)}}, \end{matrix}

hence we have

R (G) > R (G^{'})

by (2) of Lemma 7. Thus the proof is complete. □

Lemma 9.

Suppose G is a graph with two vertices u and v such that

N_{G}^{2} (u) ∖ v = N_{G}^{2} (v) ∖ u

and

d_{G}^{1} (u) > 0, d_{G}^{1} (v) > 0

. Let

G^{'}

be a graph obtained from G by moving all pendant neighbors of v to u, then

R (G) > R (G^{'})

Proof.

Observe that if we exchange pendant neighbors of v and u,

R (G)

does not change. Hence the assertion holds easily from Theorem 4. □

4. Main Results

4.1. Undeletable subgraph and Classification of tricyclic graphs

We need the following important definition to start our analysis.

Definition 1.

Suppose G is a cyclic graph, then the undeletable subgraph

ϕ (G)

of G is defined as a maximum subgraph without pendant vertex, i.e., the subgraph arising from G by deleting all pendant vertices recursively.

Obviously that

ϕ (G)

is connected and

δ (ϕ (G)) \geq 2

. Moreover, undeletable subgraph of a graph is unique. And it is easy to verify that the undeletable subgraph of a unicyclic graph is a cycle.

With the definition and Theorem 2, we are able to prove the following crucial lemma:

Lemma 10.

Suppose G is a cyclic

(n, m)

-graph with undeletable subgraph

ϕ (G)

. Then there exists a

(n, m)

-graph

G^{'}

such that

R (G) > R (G^{'})

if there is a vertex

w \in V (G) ∖ V (ϕ (G))

with

d_{G} (w) > 1

Proof.

Let

\hat{G} = G - E (ϕ (G))

by deleting all edges of

ϕ (G)

. By the definition of

ϕ (G)

\hat{G}

contains no cycle, i.e.,

\hat{G}

is a forest.

Let T be the tree of

\hat{G}

containing w. We claim that T contains exactly one vertex of

V (ϕ (G))

. First, assume that T contains no vertex of

V (ϕ (G))

, then T is not connected with vertices of

V (ϕ (G))

in G, thereby G is disconnected which is a contradiction. Now assume that T contains at least two vertices of

V (ϕ (G))

, and denote two of which by x and y, then there is a unique path in T that connects them containing a vertex

z \notin V (ϕ (G))

since

E (T) ⋂ E (ϕ (G)) = \emptyset

. And there exists a path in

ϕ (G)

that connects u and v since

ϕ (G)

is connected. Therefore vertex z lies on a cycle of G, implying that it belongs to

V (ϕ (G))

, which contradicts the fact

z \notin V (ϕ (G))

. So T contains exactly one vertex of

V (ϕ (G))

, say

v_{0}

Let

P = v_{0} v_{1} \dots v_{h}

be the longest path from

v_{0}

to all other vertices in T. Note that

h \geq 2

because a path from

v_{0}

to a pendant vertex containing w is of length at least two. Hence

d_{G} (v_{h - 1}) \geq 2

d_{G} (v_{h - 2}) \geq 2

, and

v_{h - 2}

is the only non-pendant neighbor of

v_{h - 1}

. Then by (1) of Theorem 2, there is an

(n, m)

-graph

G^{'} = Γ (G, v_{h - 2}, v_{h - 1})

such that

R (G) > R (G^{'})

. □

For a graph G with undeletable subgraph

ϕ (G)

, if

d_{G} (w) = 1

for each

w \in V (G) ∖ V (ϕ (G))

, i.e., each

v \in V (ϕ (G))

only has pendant neighbors in

V (G) ∖ V (ϕ (G))

, it is said to be a pendant-maximized graph.

Lemma 11.

Suppose G is a pendant-maximized tricyclic

(n, n + 2)

-graph with undeletable subgraph

ϕ (G)

. If there is a vertex

v \in V (ϕ (G))

with exactly two non-adjacent neighbors in

ϕ (G)

, then there is an

(n, n + 2)

-graph

G^{'}

such that

R (G) > R (G^{'})

; otherwise,

ϕ (G)

must be one of the 15 graphs as shown in Figure 2,Figure 3,Figure 4 up to isomorphism.

Proof.

(1). We first prove the “if" part. Without loss of generality, let the neighbors of v in

ϕ (G)

be u and w with

d_{G} (u) \geq d_{G} (w)

. Observe that

d_{G}^{2} (v) = 2

because G is pendant-maximized and v has two neighbors in

ϕ (G)

. Hence

N_{G} (v) \cap N_{G} (u) = \emptyset

since u and w are non-adjacent. Therefore, there is an

(n, n + 2)

-graph

G^{'} = Γ (G, u, v)

such that

R (G) > R (G^{'})

by (2) of Theorem 2.

(2) Now the “otherwise" part. By the definition of undeletable subgraph,

ϕ (G)

is a tricyclic graph, that is,

| E (ϕ (G)) | = | V (ϕ (G)) | + 2

and

δ (ϕ (G)) \geq 2

. In the remaining argument, all degree and neighbors are constrained in

ϕ (G)

We claim that

4 \leq | V (ϕ (G)) | \leq 10

, where the lower bound is obvious by checking graphs of order 1 to 4. We first show there are at most 6 vertices of degree 2 in

ϕ (G)

. Notice that each vertex v of degree 2 must lie on a cycle of length 3 because the neighbors of v must be adjacent. Moreover, each cycle of length 3 contains at most 2 vertices of degree 2, otherwise the cycle is disconnected with other parts of

ϕ (G)

. Since there are at most 3 edge-disjoint cycles in a tricyclic graph, thereby at most 3 edge-disjoint cycles of length 3. Hence by Handshaking Lemma, we have

2 \times 6 + 3 \times (| V (ϕ (G)) | - 6) \leq (| V (ϕ (G)) | + 2) \times 2

, implying

| V (ϕ (G)) | \leq 10

Therefore we can list all possible graph structures for

ϕ (G)

with

4 \leq | V (ϕ (G)) | \leq 10

, which are exactly those shown in Figure 2,Figure 3,Figure 4. Thus the proof is complete. □

Let

{TR}_{i}^{j} (n)

be the set of n-vertex tricyclic graphs obtained from

U_{i}^{j}

by attaching

n - | V (U_{i}^{j}) |

pendant vertices to

U_{i}^{j}

. It is evident that graphs belonging to

{TR}_{i}^{j} (n)

are pendant-maximized. On the other hand, if a pendant-maximized tricyclic graph G with

ϕ (G) ≅ U_{i}^{j}

, then

G \in {TR}_{i}^{j} (n)

4.2. Relations between ${TR}_{i}^{j} (n)$

Suppose

A

and

B

are two graph sets, and if for any graph

G \in A

, there is a graph

G^{'} \in B

such that

R (G) > R (G^{'})

, then this relation is written as

R (A) > R (B)

R (B) < R (A)

. Our remaining task is to figure out the above described relations between all

{TR}_{i}^{j} (n)

Lemma 12.

R ({TR}_{7}^{4} (n)) > R ({TR}_{7}^{3} (n)) > R ({TR}_{7}^{2} (n)) > R ({TR}_{7}^{1} (n))

Proof.

We prove the results in the order of left to right.

(1) Suppose G is a graph in

{TR}_{7}^{4} (n)

with undeletable subgraph labelled as

U_{7}^{4}

in Figure 4. It may be assumed that

d_{G}^{1} (v_{4}) = 0

; otherwise, by Lemma 9, pendant neighbors of

v_{4}

can be moved to

v_{3}

without increasing

R (G)

since

N_{G}^{2} (v_{3}) ∖ v_{4} = N_{G}^{2} (v_{4}) ∖ v_{3}

. Moreover, we may assume

d_{G}^{1} (v_{6}) = 0

by similarly reasoning. Then clearly,

d_{G} (v_{4}) = d_{G} (v_{6}) = 2

Consider first when

d_{G}^{1} (v_{2}) > 0

. If

d_{G}^{1} (v_{3}) > 0

, by (1) of Theorem 3, moving pendant neighbors of

v_{3}

v_{2}

reduces

R (G)

. So we may assume

d_{G}^{1} (v_{3}) = 0

. Since

d_{G}^{2} (v_{2}) = d_{G}^{2} (v_{1}) = 3

, and

\frac{1}{\sqrt{v_{3}}} + \frac{1}{\sqrt{v_{4}}} + \frac{1}{\sqrt{v_{7}}} + \frac{1}{\sqrt{v_{8}}} > \frac{2}{\sqrt{2}} > \frac{2}{\sqrt{5}}

, therefore graph

G^{'} = Γ (G, v_{1}, v_{2})

satisfies

R (G) > R (G^{'})

appealing to (3) of Theorem 2.

Now we turn to the case of

d_{G}^{1} (v_{2}) = 0

, that is,

d_{G} (v_{2}) = 3

. Note that

d_{G}^{2} (v_{7}) = d_{G}^{2} (v_{1}) = 3

, and

\frac{1}{\sqrt{v_{2}}} + \frac{1}{\sqrt{v_{8}}} + \frac{1}{\sqrt{v_{5}}} + \frac{1}{\sqrt{v_{6}}} > \frac{1}{\sqrt{2}} + \frac{1}{\sqrt{3}} > \frac{2}{\sqrt{5}}

, thus graph

G^{''} = Γ (G, v_{1}, v_{7})

satisfies

R (G) > R (G^{″})

again by (3) of Theorem 2. It is not difficult to check that

G^{'}

and

G^{″}

both belong to

{TR}_{7}^{3} (n)

. Thus we have

R ({TR}_{7}^{4} (n)) > R ({TR}_{7}^{3} (n))

(2) Let

G \in {TR}_{7}^{3} (n)

be a graph with undeletable subgraph as

U_{7}^{3}

in Figure 4. As before, we may assume

d_{G}^{1} (v_{4}) = 0

. Let

G^{'} = Γ (G, v_{2}, v_{1})

, and obviously

G^{'} \in {TR}_{7}^{2} (n)

. Since

d_{G} (v_{1}) \geq 4

d_{G}^{2} (v_{2}) = 3

and

\frac{1}{\sqrt{v_{3}}} + \frac{1}{\sqrt{v_{4}}} \geq \frac{1}{\sqrt{2}}

, then we get

R (G) > R (G^{'})

by (4) of Theorem 2. Thus

R ({TR}_{7}^{3} (n)) > R ({TR}_{7}^{2} (n))

holds.

(3) Using similar arguments as (2), there is a graph

G^{'} = Γ (G, v_{2}, v_{1}) \in {TR}_{7}^{1} (n)

such that

R (G) > R (G^{'})

. Hence

R ({TR}_{7}^{3} (n)) > R ({TR}_{7}^{2} (n))

. □

Lemma 13.

R ({TR}_{6}^{3} (n)) > R ({TR}_{6}^{2} (n)) > R ({TR}_{6}^{1} (n))

Proof.

We prove the relations from left to right.

(1) Let

G \in {TR}_{6}^{3} (n)

be a graph with

ϕ (G)

U_{6}^{3}

in Figure 4. As before, we assume that

d_{G}^{1} (v_{6}) = 0

Let

S = \frac{1}{\sqrt{v_{2}}} + \frac{1}{\sqrt{v_{3}}} + \frac{1}{\sqrt{v_{5}}} + \frac{1}{\sqrt{v_{6}}}

. If

d_{G}^{1} (v_{2}) = 0

, then

S > \frac{1}{\sqrt{2}} + \frac{1}{\sqrt{3}} > \frac{2}{\sqrt{5}}

. And if

d_{G}^{1} (v_{2}) > 0

, we may assume

d_{G}^{1} (v_{3}) = 0

; otherwise

R (G)

can be reduced by moving pendant neighbors of

v_{3}

v_{2}

according to (1) of Theorem 3. Then we have

S > \frac{1}{\sqrt{2}} + \frac{1}{\sqrt{2}} > \frac{2}{\sqrt{5}}

. Moreover,

d_{G}^{2} (v_{1}) = d_{G}^{2} (v_{4}) = 3

, hence there is a graph

G^{'} = Γ (G, v_{1}, v_{4})

with

R (G) > R (G^{'})

from (3) of Theorem 2. And it is evident that

G^{'} \in {TR}_{6}^{2} (n)

, thus we obtain

R ({TR}_{6}^{3} (n)) > R ({TR}_{6}^{2} (n))

(2) Suppose G is a graph in

{TR}_{6}^{2} (n)

with undeletable subgraph as

U_{6}^{2}

in Figure 4. Using analogous arguments as (1), we can show that

\frac{1}{\sqrt{v_{1}}} + \frac{1}{\sqrt{v_{3}}} + \frac{1}{\sqrt{v_{4}}} + \frac{1}{\sqrt{v_{5}}} > \frac{1}{\sqrt{2}} + \frac{1}{\sqrt{4}} > \frac{2}{\sqrt{5}}

. Additionally, note that

d_{G}^{2} (v_{2}) = d_{G}^{2} (v_{6}) = 3

. By (3) of Theorem 2, there is a graph

G^{'} = Γ (G, v_{2}, v_{6}) \in {TR}_{6}^{1} (n)

such that

R (G) > R (G^{'})

. So it follows

R ({TR}_{6}^{2} (n)) > R ({TR}_{6}^{1} (n))

easily. □

Lemma 14.

R ({TR}_{4}^{2} (n)) > R ({TR}_{4}^{1} (n))

R ({TR}_{7}^{1} (n)) > R ({TR}_{4}^{1} (n))

R ({TR}_{6}^{1} (n)) > R ({TR}_{4}^{1} (n))

Proof.

We prove the three relations in the order of left to right.

(1) Let

G \in {TR}_{4}^{2} (n)

with undeletable subgraph as

U_{4}^{2}

in Figure 3. As before, we assume

d_{G}^{1} (v_{6}) = 0

, i.e.,

d_{G} (v_{6}) = 2

. And notice that

d_{G} (v_{4}) \geq 4, d_{G}^{2} (v_{7}) = 3

. Then by (4) of Theorem 2, graph

G^{'} = Γ (G, v_{4}, v_{7}) \in {TR}_{4}^{1} (n)

satisfies

R (G) > R (G^{'})

. Thus

R ({TR}_{4}^{2} (n)) > R ({TR}_{4}^{1} (n))

holds clearly.

(2) Let

G \in {TR}_{7}^{1} (n)

with undeletable subgraph as

U_{7}^{1}

in Figure 4. As before, we assume

d_{G}^{1} (v_{3}) = d_{G}^{1} (v_{5}) = 0

. Note that

d_{G}^{2} (v_{1}) = 6

and

v_{5} \in N_{G} (v_{1}) ∖ {v_{2}, v_{3}}

. If

d_{G}^{1} (v_{2}) > 0

, then by (2) of Theorem 3,

R (G)

can be reduced by moving pendant neighbors of

v_{2}

v_{1}

. Similarly, it holds for

v_{4}

. So we may assume

d_{G}^{1} (v_{2}) = d_{G}^{1} (v_{4}) = 0

Let

d_{i} = d_{G} (v_{i})

, and we have

d_{2} = d_{3} = d_{4} = d_{5} = 2

and

d_{1} \geq 6

. Let

G^{'} = G - v_{2} v_{3} + v_{2} v_{5}

, then

R (G) - R (G^{'}) = (\frac{1}{\sqrt{d_{1} d_{3}}} + \frac{1}{\sqrt{d_{1} d_{5}}} + \frac{1}{\sqrt{d_{2} d_{3}}} + \frac{1}{\sqrt{d_{4} d_{5}}}) - (\frac{1}{\sqrt{d_{1}}} + \frac{1}{\sqrt{d_{1} (d_{5} + 1)}} + \frac{1}{\sqrt{d_{2} (d_{5} + 1)}} + \frac{1}{\sqrt{d_{4} (d_{5} + 1)}}) = \frac{1}{\sqrt{d_{1}}} (\sqrt{2} - 1 - \frac{1}{\sqrt{3}}) + 1 - \frac{2}{\sqrt{6}} \geq \frac{1}{\sqrt{6}} (\sqrt{2} - 1 - \frac{1}{\sqrt{3}}) + 1 - \frac{2}{\sqrt{6}} \approx 0.1169 > 0

. It is easy to check that

G^{'} \in {TR}_{4}^{1}

. Thus

R ({TR}_{7}^{1} (n)) > R ({TR}_{4}^{1} (n))

follows.

(3) Let

G \in {TR}_{6}^{1} (n)

with undeletable subgraph as

U_{6}^{1}

in Figure 4. As before, we assume

d_{G}^{1} (v_{5}) = d_{G}^{1} (v_{7}) = 0

. Moreover, we may assume

d_{G}^{1} (v_{3}) = 0

; Otherwise, note that

d_{G}^{2} (v_{1}) = 4

and

v_{5} \in N_{G} (v_{1}) ∖ {v_{2}, v_{3}}

with

d_{G} (v_{5}) = 2

, then appealing to (2) of Theorem 3, moving pendant neighbors of

v_{3}

v_{1}

will decrease

R (G)

Now notice that

d_{G}^{2} (v_{2}) = 4

d_{G} (v_{3}) = 2

and

v_{3} \in N_{G} (v_{2}) ∖ {v_{6}, v_{7}}

, we can decrease

R (G)

by moving pendant neighbors of

v_{6}

v_{2}

d_{G}^{1} (v_{6}) > 0

. Hence we only have to consider the case

d_{G} (v_{6}) = d_{G} (v_{7}) = 2

Let

d_{i} = d_{G} (v_{i})

, and notice that

d_{1} \geq 4, d_{2} \geq 4

. Let

G^{'} = G - v_{6} v_{7} + v_{6} v_{1}

, then

R (G) - R (G^{'}) > (\frac{1}{\sqrt{d_{2} d_{7}}} + \frac{1}{\sqrt{d_{6} d_{7}}}) - (\frac{1}{\sqrt{d_{2}}} + \frac{1}{\sqrt{d_{6} (d_{1} + 1)}}) = \frac{1}{\sqrt{d_{2}}} (\frac{1}{\sqrt{2}} - 1) + \frac{1}{2} - \frac{1}{\sqrt{2 (d_{1} + 1)}} \geq \frac{1}{\sqrt{4}} (\frac{1}{\sqrt{2}} - 1) + \frac{1}{2} - \frac{1}{\sqrt{10}} > 0 .

It is easy to see that

G^{'} \in {TR}_{4}^{1} (n)

, thus

R ({TR}_{6}^{1} (n)) > R ({TR}_{4}^{1} (n))

holds. □

Lemma 15.

R ({TR}_{5}^{2} (n)) > R ({TR}_{5}^{1} (n)) > R ({TR}_{3}^{1} (n))

R ({TR}_{4}^{1} (n)) > R ({TR}_{3}^{1} (n))

R ({TR}_{3}^{2} (n)) > R ({TR}_{3}^{1} (n))

Proof.

We prove the assertions from left to right.

(1) Let

G \in {TR}_{5}^{2} (n)

with undeletable subgraph as

U_{5}^{2}

in Figure 3. As before, we assume

d_{G}^{1} (v_{6}) = 0

. Observe that

N_{G}^{2} (v_{1}) ∖ v_{2} = N_{G}^{2} (v_{2}) ∖ v_{1} = {v_{3}, v_{4}}

. By Lemma 9, we can move pendant neighbors of

v_{2}

v_{1}

and do not increase

R (G)

d_{G}^{1} (v_{2}) > 0

. Therefore we may assume that

d_{G}^{1} (v_{2}) = 0

. Notice that

d_{G}^{2} (v_{4}) = d_{G}^{2} (v_{7}) = 3

and

\frac{1}{\sqrt{v_{1}}} + \frac{1}{\sqrt{v_{2}}} + \frac{1}{\sqrt{v_{5}}} + \frac{1}{\sqrt{v_{6}}} > \frac{1}{\sqrt{2}} + \frac{1}{\sqrt{3}} > \frac{2}{\sqrt{5}}

, hence there is

G^{'} = Γ (G, v_{4}, v_{7}) \in {TR}_{5}^{1} (n)

such that

R (G) > R (G^{'})

from (3) of Theorem 2. Thus we obtain

R ({TR}_{5}^{2} (n)) > R ({TR}_{5}^{1} (n))

(2) Let

G \in {TR}_{5}^{1} (n)

with undeletable subgraph as

U_{5}^{1}

in Figure 3. By analogous arguments as (1), we may assume that

d_{G}^{1} (v_{6}) = d_{G}^{1} (v_{2}) = 0

, that is,

d_{G} (v_{6}) = 2, d_{G} (v_{2}) = 3

. And note that

d_{G}^{2} (v_{4}) = 4

and

v_{2} \in N_{G} (v_{4}) ∖ {v_{5}, v_{6}}

. Then according to (2) of Theorem 3, moving pendant neighbors of

v_{5}

v_{4}

reduces

R (G)

d_{G}^{1} (v_{5}) > 0

. So we may assume that

d_{G}^{1} (v_{5}) = 0

Let

G^{'} = G - v_{5} v_{6} + v_{5} v_{1}

, and let

d_{i} = d_{G} (v_{i})

. Note that

d_{1} \geq 3, d_{4} \geq 4, d_{G} (v_{5}) = d_{G} (v_{6}) = 2

. Then

R (G) - R (G^{'}) > (\frac{1}{\sqrt{d_{4} d_{6}}} + \frac{1}{\sqrt{d_{5} d_{6}}}) - (\frac{1}{\sqrt{d_{4}}} + \frac{1}{\sqrt{(d_{1} + 1) d_{5}}}) = \frac{1}{\sqrt{d_{4}}} (\frac{1}{\sqrt{2}} - 1) + \frac{1}{\sqrt{4}} - \frac{1}{\sqrt{2 (d_{1} + 1)}} \geq \frac{1}{\sqrt{4}} (\frac{1}{\sqrt{2}} - 1) + \frac{1}{\sqrt{4}} - \frac{1}{\sqrt{2 (3 + 1)}} = 0

. It is easy to verify that

G^{'} \in {TR}_{3}^{1} (n)

. Therefore

R ({TR}_{5}^{1} (n)) > R ({TR}_{3}^{1} (n))

holds.

(3) Let

G \in {TR}_{4}^{1} (n)

with undeletable subgraph as

U_{4}^{1}

in Figure 3. Using similar arguments as (2), we may assume that

d_{G}^{1} (v_{2}) = d_{G}^{1} (v_{5}) = d_{G}^{1} (v_{6}) = 0

, i.e.,

d_{G} (v_{2}) = d_{G} (v_{5}) = d_{G} (v_{6}) = 2

Let

G^{'} = G - v_{3} v_{2} + v_{3} v_{6}

, and let

d_{i} = d_{G} (v_{i})

. Note that

d_{4} \geq 5

. Then

R (G) - R (G^{'}) > (\frac{1}{\sqrt{d_{2} d_{4}}} + \frac{1}{\sqrt{d_{4} d_{6}}} + \frac{1}{\sqrt{d_{2} d_{3}}} + \frac{1}{\sqrt{d_{5} d_{6}}}) - (\frac{1}{\sqrt{d_{4}}} + \frac{1}{\sqrt{d_{4} (d_{6} + 1)}} + \frac{1}{\sqrt{d_{3} (d_{6} + 1)}} + \frac{1}{\sqrt{d_{5} (d_{6} + 1)}}) = \frac{1}{\sqrt{d_{4}}} (\sqrt{2} - 1 - \frac{1}{\sqrt{3}}) + \frac{1}{\sqrt{d_{3}}} (\frac{1}{\sqrt{2}} - \frac{1}{\sqrt{3}}) + \frac{1}{\sqrt{4}} - \frac{1}{\sqrt{6}} \geq \frac{1}{\sqrt{5}} (\sqrt{2} - 1 - \frac{1}{\sqrt{3}}) + \frac{1}{\sqrt{4}} - \frac{1}{\sqrt{6}} \approx 0.01879 > 0 .

It is clear that

G^{'} \in {TR}_{3}^{1} (n)

. Therefore we obtain

R ({TR}_{4}^{1} (n)) > R ({TR}_{3}^{1} (n))

as desired.

(4) Let

G \in {TR}_{3}^{2} (n)

with undeletable subgraph as

U_{3}^{2}

in Figure 2. Let

S = \frac{1}{\sqrt{v_{2}}} + \frac{1}{\sqrt{v_{3}}}

. If

d_{G}^{1} (v_{2}) = 0

, i.e.,

d_{G} (v_{2}) = 3

, then clearly

S \geq \frac{1}{\sqrt{3}}

. Otherwise, note that

d_{G}^{2} (v_{2}) = 3, d_{G}^{1} (v_{2}) > 0

, according to (1) of Theorem 3, moving pendant neighbors of

v_{3}

v_{2}

decreases

R (G)

d_{G}^{1} (v_{2}) > 0

. So

S \geq \frac{1}{\sqrt{2}}

in this case. As a consequence, we have

S \geq \frac{1}{\sqrt{3}}

by the above argument. Similarly,

\frac{1}{\sqrt{v_{5}}} + \frac{1}{\sqrt{v_{6}}} \geq \frac{1}{\sqrt{3}}

, implying that

\frac{1}{\sqrt{v_{2}}} + \frac{1}{\sqrt{v_{3}}} + \frac{1}{\sqrt{v_{5}}} + \frac{1}{\sqrt{v_{6}}} > \frac{2}{\sqrt{5}}

. And notice that

d_{G}^{2} (v_{1}) = d_{G}^{2} (v_{4}) = 3

and

N_{G} (v_{1}) ⋂ N_{G} (v_{4}) = \emptyset

. Appealing to (3) of Theorem 2, graph

G^{'} = Γ (G, v_{1}, v_{4})

satisfies

R (G) > R (G^{'})

with

G^{'} \in {TR}_{3}^{1} (n)

. Therefore we have

R ({TR}_{3}^{2} (n)) > R ({TR}_{3}^{1} (n))

. □

Before proceeding with more relations, let us define some essential functions and graph classes. Let

\begin{matrix} F_{1} (n) & = \frac{n - 4 + \sqrt{3}}{\sqrt{n - 1}} + 1, F_{2} (n) = \frac{n - \frac{9}{2} + \frac{3 \sqrt{2}}{2}}{\sqrt{n - 1}} + \frac{3 \sqrt{2}}{4}, \\ F_{3} (n) & = \frac{n - 5 + \frac{2 \sqrt{3}}{3} + \sqrt{2}}{\sqrt{n - 1}} + \frac{1 + \sqrt{6}}{3} . \end{matrix}

For

i = 1, 2, 3

, let

T R_{i}^{*} (n)

be n-vertex graphs in

{TR}_{i}^{1} (n)

with a vertex of degree

n - 1

. It is worth noting that all pendant vertices of

T R_{i}^{*} (n)

are adjacent to a single vertex. Further, it can be verified easily that

T R_{1}^{*} (n) ≅ T R_{n}^{★}

Lemma 16.

G \in {TR}_{1}^{1} (n)

, then

R (G) \geq F_{1} (n)

with equality if and only if

G ≅ T R_{1}^{*} (n)

Proof.

G ≅ T R_{1}^{*} (n)

, then clearly

R (G) = F_{1} (n)

. If

G ≇ T R_{1}^{*} (n)

, at least two vertices of

ϕ (G)

have pendant neighbors. Suppose the undeletable subgraph

ϕ (G)

is labelled as

U_{1}^{1}

in Figure 2. Without loss of generality, we may assume that

d_{G}^{1} (v_{1}) \geq d_{G}^{1} (v_{2}) \geq d_{G}^{1} (v_{3}) \geq d_{G}^{1} (v_{4})

. Note that

N_{G}^{2} (v_{1}) ∖ v_{2} = N_{G}^{2} (v_{2}) ∖ v_{1} = {v_{3}, v_{4}}

. By Lemma 9, moving pendant neighbors of

v_{2}

v_{1}

will decrease

R (G)

d_{G}^{1} (v_{2}) > 0

. Similarly, this holds for

v_{3}

and

v_{4}

. So we can conclude that

R (G) > F_{1} (n)

G ≇ T R_{1}^{*} (n)

. So the proof is complete. □

Lemma 17.

G \in {TR}_{2}^{1} (n)

, then

R (G) \geq F_{2} (n)

with equality if and only if

G ≅ T R_{2}^{*} (n)

Proof.

Suppose the undeletable subgraph

ϕ (G)

is labelled as

U_{2}^{1}

in Figure 2. If

G ≅ T R_{2}^{*} (n)

, i.e., one of

v_{1}, v_{2}

is adjacent to all pendant neighbors, then obviously

R (G) = F_{2} (n)

. Then let us consider the case

G ≇ T R_{2}^{*} (n)

Case 1.

d_{G}^{1} (v_{1}) > 0, d_{G}^{1} (v_{2}) > 0

d_{G}^{1} (v_{3}) = d_{G}^{1} (v_{4}) = d_{G}^{1} (v_{5}) = 0

It is easy to see that

N_{G}^{2} (v_{1}) ∖ v_{2} = N_{G}^{2} (v_{2}) ∖ v_{1} = {v_{3}, v_{4}, v_{5}}

. By Lemma 9,

R (G)

can be reduced by moving pendant neighbors of

v_{2}

v_{1}

, implying

R (G) > F_{2} (n)

Case 2. one of

v_{3}, v_{4}, v_{5}

has pendant neighbors.

We may assume that

d_{G}^{1} (v_{3}) > 0, d_{G}^{1} (v_{4}) = d_{G}^{1} (v_{5}) = 0

. Notice that

d_{G}^{2} (v_{1}) = 4, d_{G} (v_{4}) = 2

, and

v_{4} \in N_{G} (v_{1}) ∖ {v_{2}, v_{3}}

. By (2) of Theorem 3, we can move pendant neighbors of

v_{3}

v_{1}

to reduce

R (G)

. Thus we have

R (G) > F_{2} (n)

Case 3. at least two of

v_{3}, v_{4}, v_{5}

have pendant neighbors.

Suppose

d_{G}^{1} (v_{3}) > 0, d_{G}^{1} (v_{4}) > 0

without loss of generality. Note that

N_{G}^{2} (v_{3}) ∖ v_{4} = N_{G}^{2} (v_{4}) ∖ v_{3} = {v_{1}, v_{2}}

. Then again appealing to Lemma 9, pendant neighbors of

v_{4}

can be moved to

v_{3}

with

R (G)

decreased. Then we arrive at Case 2, thus

R (G) > F_{2} (n)

Therefore, it completes the proof. □

Lemma 18.

G \in {TR}_{3}^{1} (n)

, then

R (G) \geq F_{3} (n)

with equality if and only if

G ≅ T R_{3}^{*} (n)

Proof.

Suppose the undeletable subgraph

ϕ (G)

is labelled as

U_{3}^{1}

in Figure 2. If

G ≅ T R_{3}^{*} (n)

, i.e.,

v_{1}

is adjacent to all pendant vertices, then obviously

R (G) = F_{3} (n)

. So we suppose that

G ≇ T R_{3}^{*} (n)

Case 1.

d_{G}^{1} (v_{2}) = d_{G}^{1} (v_{3}) = 0

Consider first

d_{G}^{1} (v_{5}) > 0

. And observe that

d_{G}^{2} (v_{1}) = 4, d_{G} (v_{2}) = 2

and

v_{2} \in N_{G} (v_{1}) ∖ {v_{3}, v_{5}}

. Then by (2) of Theorem 3, we can move pendant neighbors of

v_{5}

v_{1}

and get

R (G)

smaller. Likewise, this holds for

d_{G}^{1} (v_{4}) > 0

. Therefore we obtain

R (G) > F_{3} (n)

Case 2. one of

d_{G}^{1} (v_{2}) > 0, d_{G}^{1} (v_{3}) > 0

holds. Without loss of generality, suppose

d_{G}^{1} (v_{2}) > 0, d_{G}^{1} (v_{3}) = 0

Subcase 2.1.

d_{G}^{1} (v_{4}) = d_{G}^{1} (v_{5}) = 0

. Let

G^{'}

be obtained from G by moving pendant neighbors of

v_{2}

v_{1}

. Observe that

d_{G} (v_{4}) = d_{G} (v_{5}) = 2, d_{G} (v_{3}) = 3

. Let

x = d_{G} (v_{1}) \geq 4

and let

y = d_{G} (v_{2}) = d_{G}^{1} (v_{2}) + d_{G}^{1} (v_{2}) \geq 4

. So

R (G) - R (G^{'}) = (\frac{\sqrt{6}}{6} + \frac{y - 3 + \frac{\sqrt{3}}{3} + \frac{\sqrt{2}}{2} + \frac{1}{\sqrt{x}}}{\sqrt{y}} + \frac{x - 4 + \frac{\sqrt{3}}{3} + \sqrt{2}}{\sqrt{x}}) - (\frac{\sqrt{6}}{3} + \frac{1}{3} + \frac{x + y - 7 + \frac{2 \sqrt{3}}{3} + \sqrt{2}}{\sqrt{x + y - 3}}) = \frac{y - 3 + \frac{\sqrt{3}}{3} + \frac{\sqrt{2}}{2} + \frac{1}{\sqrt{x}}}{\sqrt{y}} + \frac{x - 4 + \frac{\sqrt{3}}{3} + \sqrt{2}}{\sqrt{x}} - \frac{x + y - 7 + \frac{2 \sqrt{3}}{3} + \sqrt{2}}{\sqrt{x + y - 3}} - (\frac{1}{3} + \frac{1}{\sqrt{6}}) > 0

, where the last inequality holds by Lemma 8. Thus we obtain

R (G) > F_{3} (n)

Subcase 2.2.

d_{G}^{1} (v_{4}) > 0, d_{G}^{1} (v_{5}) = 0

. Observe that

d_{G}^{2} (v_{4}) = 2, d_{G}^{2} (v_{2}) = 3

, moving pendant neighbors of

v_{4}

v_{2}

will reduce

R (G)

from (1) of Theorem 3. Then we arrive at Subcase 2.1.

Subcase 2.3.

d_{G}^{1} (v_{4}) = 0, d_{G}^{1} (v_{5}) > 0

. By analogous argument as Case 1, we can move pendant neighbors of

v_{5}

v_{1}

, so we get to Subcase 2.1.

Subcase 2.4.

d_{G}^{1} (v_{4}) > 0, d_{G}^{1} (v_{5}) > 0

. Similarly as Subcase 2.2, pendant neighbors of

v_{4}

can be moved to

v_{2}

and

R (G)

will decrease. Then we arrive at Subcase 2.3.

According to the 4 subcases, we obtain

R (G) > F_{3} (n)

in this case.

Case 3.

d_{G}^{1} (v_{2}) > 0, d_{G}^{1} (v_{3}) > 0

Subcase 3.1.

d_{G}^{1} (v_{4}) = d_{G}^{1} (v_{5}) = 0

. Note that

d_{G}^{2} (v_{2}) = d_{G}^{2} (v_{3}) = 3

and

\sum_{u \in N_{G}^{2} (v_{2}) ∖ v_{3}} \frac{1}{\sqrt{d_{G} (u)}} = \sum_{u \in N_{G}^{2} (v_{3}) ∖ v_{2}} \frac{1}{\sqrt{d_{G} (u)}} = \frac{1}{\sqrt{d_{G} (v_{4})}} + \frac{1}{\sqrt{d_{G} (v_{1})}}

. By Theorem 9,

R (G)

can be reduced by moving pendant neighbors of

v_{3}

v_{2}

. Then we get the Subcase 2.1.

Subcase 3.2.

d_{G}^{1} (v_{4}) + d_{G}^{1} (v_{5}) > 0

. Notice that

d_{G}^{2} (v_{2}) = 3, d_{G}^{2} (v_{4}) = 2

. By (1) of Theorem 3, pendant neighbors of

v_{4}

can be moved to

v_{2}

with

R (G)

decreased if

d_{G}^{1} (v_{4}) > 0

. Analogously, this holds for

v_{5}

. Thus we arrive at Subcase 3.1.

Now, we can conclude that

R (G) > F_{3} (n)

if vertices other than

v_{1}

ϕ (G)

have pendant neighbors. Thus the proof is complete. □

Lemma 19.

R ({TR}_{3}^{1} (n)) > R ({TR}_{2}^{1} (n)) > R ({TR}_{1}^{1} (n))

Proof.

Suppose

A, B

are two graph sets with

{min}_{G \in A} R (G) < {min}_{G \in B} R (G)

. Let

G_{A} \in A

be a graph satisfying

R (G_{A}) = {min}_{G \in A} R (G)

. Then for any graph

G_{B} \in B

, we have

R (G_{B}) \geq {min}_{G \in B} R (G) > R (G_{A})

, that is,

R (A) < R (B)

So by Lemma 16, 17, 18, it suffices to show that

F_{3} (n) > F_{2} (n) > F_{1} (n)

. Observe that

n \geq 5

for

G \in {TR}_{3}^{1} (n)

G \in {TR}_{2}^{1} (n)

. Hence

F_{3} (n) - F_{2} (n) = \frac{1 + \sqrt{6}}{3} - \frac{3 \sqrt{2}}{4} + \frac{\frac{2}{\sqrt{3}} - \frac{1}{2} - \frac{1}{\sqrt{2}}}{\sqrt{n - 1}} \geq \frac{1 + \sqrt{6}}{3} - \frac{3 \sqrt{2}}{4} + \frac{\frac{2}{\sqrt{3}} - \frac{1}{2} - \frac{1}{\sqrt{2}}}{\sqrt{4}} \approx 0.06297 > 0

. And

F_{2} (n) - F_{1} (n) = \frac{3 \sqrt{2}}{4} - 1 + \frac{\frac{3}{\sqrt{2}} - \frac{1}{2} - \sqrt{3}}{\sqrt{n - 1}} \geq \frac{3 \sqrt{2}}{4} - 1 + \frac{\frac{3}{\sqrt{2}} - \frac{1}{2} - \sqrt{3}}{\sqrt{4}} \approx 0.005295 > 0

. Therefore the assertion holds clearly. □

We draw all the relations mentioned here in Figure 5, in which

A \to B

represents

R (A) < R (B)

4.3. The proof of Theorem 1

Now we are ready to prove our main result.

Proof of Theorem 1.

First note that

F_{1} (n) = \frac{n - 4 + \sqrt{3}}{\sqrt{n - 1}} + 1

and

T R_{1}^{*} (n) ≅ T R_{n}^{★}

, so it is equivalent to show that

R (G) \geq F_{1} (n)

with equality if and only if

G ≅ T R_{1}^{*} (n)

. Let

F = ⋃ {TR}_{i}^{j} (n)

be the union of all

{TR}_{i}^{j} (n)

G ≅ T R_{1}^{*} (n)

, it is clear that

R (G) = F_{1} (n)

G \in {TR}_{1}^{1} (n) ∖ {T R_{1}^{*} (n)}

, we have

R (G) > F_{1} (n)

by Lemma 16.

G \in F ∖ {TR}_{1}^{1} (n)

, by Lemma 12, 13, 14, 15, 19 together, we obtain

R (G) > R (T R_{1}^{*} (n)) = F_{1} (n)

G \notin F

and G is pendant-maximized, by Lemma 11, we can find a graph

G^{'} \in F

such that

R (G) > R (G^{'}) \geq F_{1} (n)

G \notin F

and G is not pendant-maximized, by Lemma 10 and 11, we will again find a graph

G^{'} \in F

such that

R (G) > R (G^{'}) \geq F_{1} (n)

Therefore the theorem holds clearly. □

5. Conclusions

In the current work, we investigate three kinds of graph transformations decreasing Randić index of graphs, which may be valuable for studying relations between Randić index and structure of graphs. For instance, Theorem 4 implies that the pendant neighbors of two vertices of a graph connects to its Randić index predictably. By applying these transformations systematicaly, the minimum Randić index of tricyclic graphs is determined with the corresponding extremal graphs. In fact, the minimum Randić index of trees, unicyclic and bicyclic graphs could be obtained by the analogous method without much effort.

Author Contributions

Conceptualization, L.T. and Z.S.; methodology, L.T. and Z.S.; software, L.T.; validation, L.T., Z.S. and M.L.; formal analysis, Z.S.; investigation, M.L.; writing—original draft preparation, L.T.; writing—review and editing, Z.S.; visualization, Z.S.; supervision, M.L.; project administration, L.T.; funding acquisition, L.T. and Z.S. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by Hunan Provincial Natural Science Foundation of China grant number 2019JJ40005, Science and Technology Plan Project of Hunan Province grant number 2016TP1020, Double First-Class University Project of Hunan Province grant number Xiangjiaotong[2018]469, Open Fund Project of Hunan Provincial Key Laboratory of Intelligent Information Processing and Application for Hengyang Normal University grant number IIPA19K02, and Shenzhen higher education stability support program grant number 20220820085638002.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

Bollobás, B.; Erdös, P. Graphs of extremal weights. Ars Combin. 1998, 50, 225–233. [Google Scholar] [CrossRef]
Caporossi, G.; Gutman, I.; Hansen, P.; Pavlović, L. Graphs with maximum connectivity index. Comput. Biol. Chem. 2003, 27, 85–90. [Google Scholar] [CrossRef]
Dehghan-Zadeh, T.; Ashrafi, A.R.; Habibi, N. Maximum and Second Maximum of Randić Index in the Class of Tricyclic Graphs. MATCH Commun. Math. Comput. Chem. 2015, 74, 137–144. [Google Scholar]
Dehghan-Zadeh, T.; Ashrafi, A.R.; Habibi, N. Tetracyclic graphs with extremal values of Randić index. Boll. Unione Mat. Ital. 2015, 8, 1–8. [Google Scholar] [CrossRef]
Du, Z.; Zhou, B. On Randić indices of trees, unicyclic graphs, and bicyclic graphs. Int. J. Quantum Chem. 2011, 111, 2760–2770. [Google Scholar] [CrossRef]
Gutman, I.; Furtula, B. (Eds.) Recent Results in the Theory of Randić Index; Univerzitet Kragujevac: Kragujevac, Serbia, 2008. [Google Scholar]
Gao, J.; Lu, M. On the Randić index of unicyclic graphs. MATCH Commun. Math. Comput. Chem. 2005, 53, 377–384. [Google Scholar]
Li, X.; Gutman, I. Mathematical Aspects of Randić-Type Molecular Structure Descriptors; Univerzitet Kragujevac: Kragujevac, Serbia, 2006. [Google Scholar]
Li, X.; Shi, Y. A survey on the Randić index. MATCH Commun. Math. Comput. Chem. 2008, 59, 127–156. [Google Scholar]
Li, X.; Zhao, H. Trees with small Randić connectivity indices. MATCH Commun. Math. Comput. Chem. 2004 51, 167–178.
Randić, M. On characterization of molecular branching. J. Amer. Chem. Soc. 1975, 97, 6609–6615. [Google Scholar] [CrossRef]
Yu, P. An upper bound on the Randić index of trees. J. Math. Study 1998, 31, 225–230. (in Chinese). [Google Scholar]

Figure 1. The structure of

T R_{n}^{★}

Figure 1. The structure of

T R_{n}^{★}

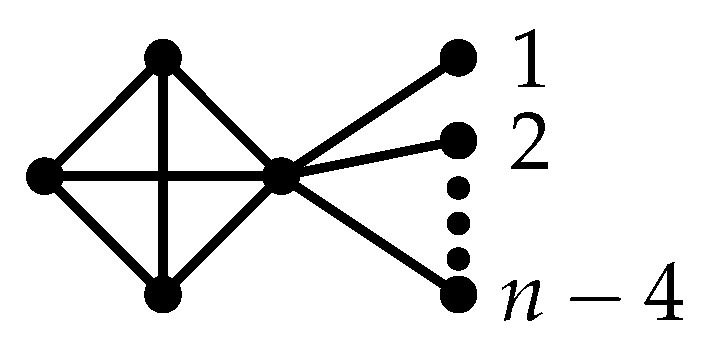
Figure 2. graphs containing no edge-disjoint cycle

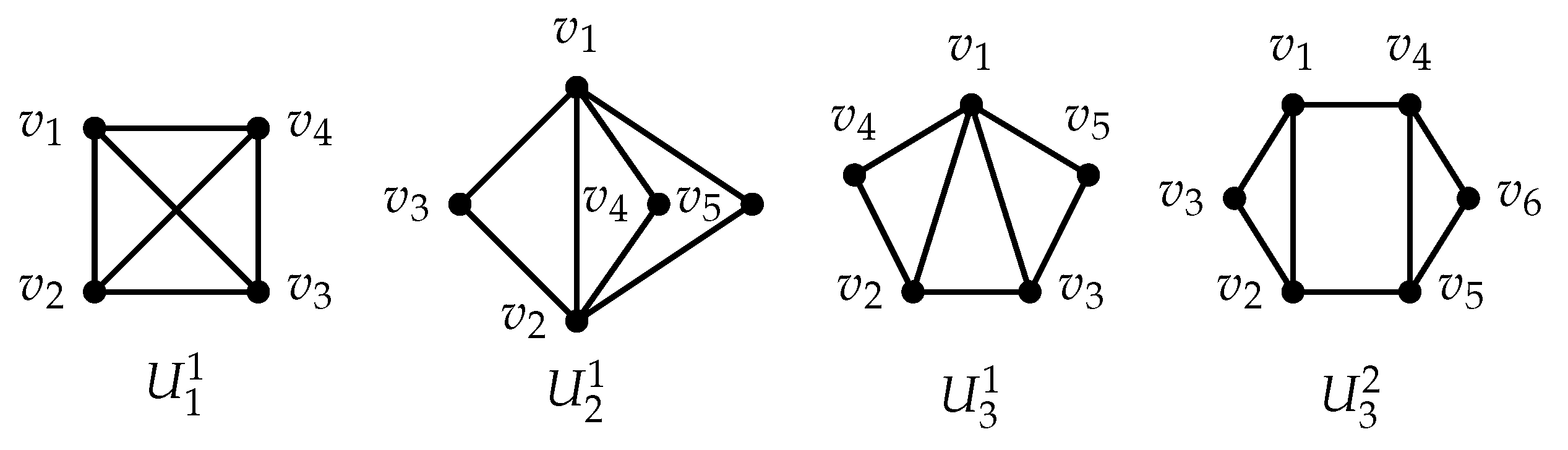
Figure 3. graphs containing one edge-disjoint cycle

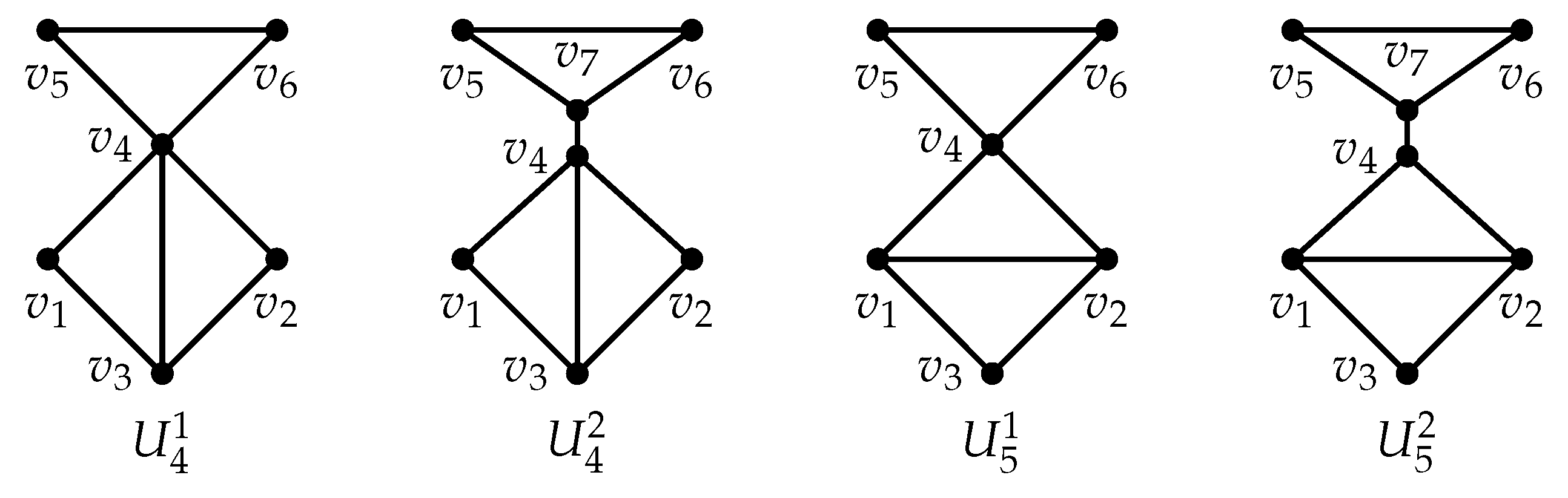
Figure 4. graphs containing three edge-disjoint cycles

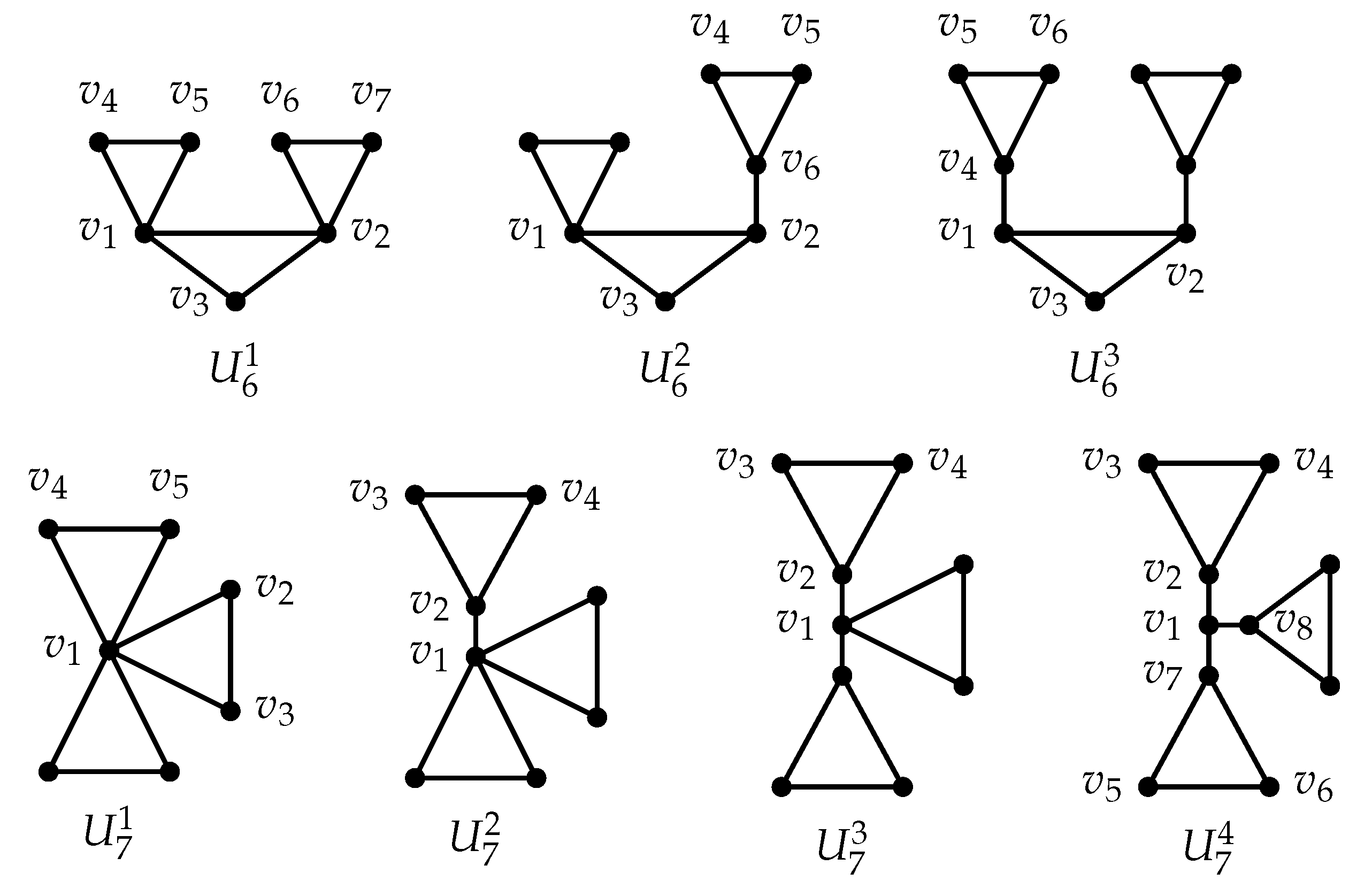
Figure 5. Relations between all

{TR}_{i}^{j} (n)

Figure 5. Relations between all

{TR}_{i}^{j} (n)

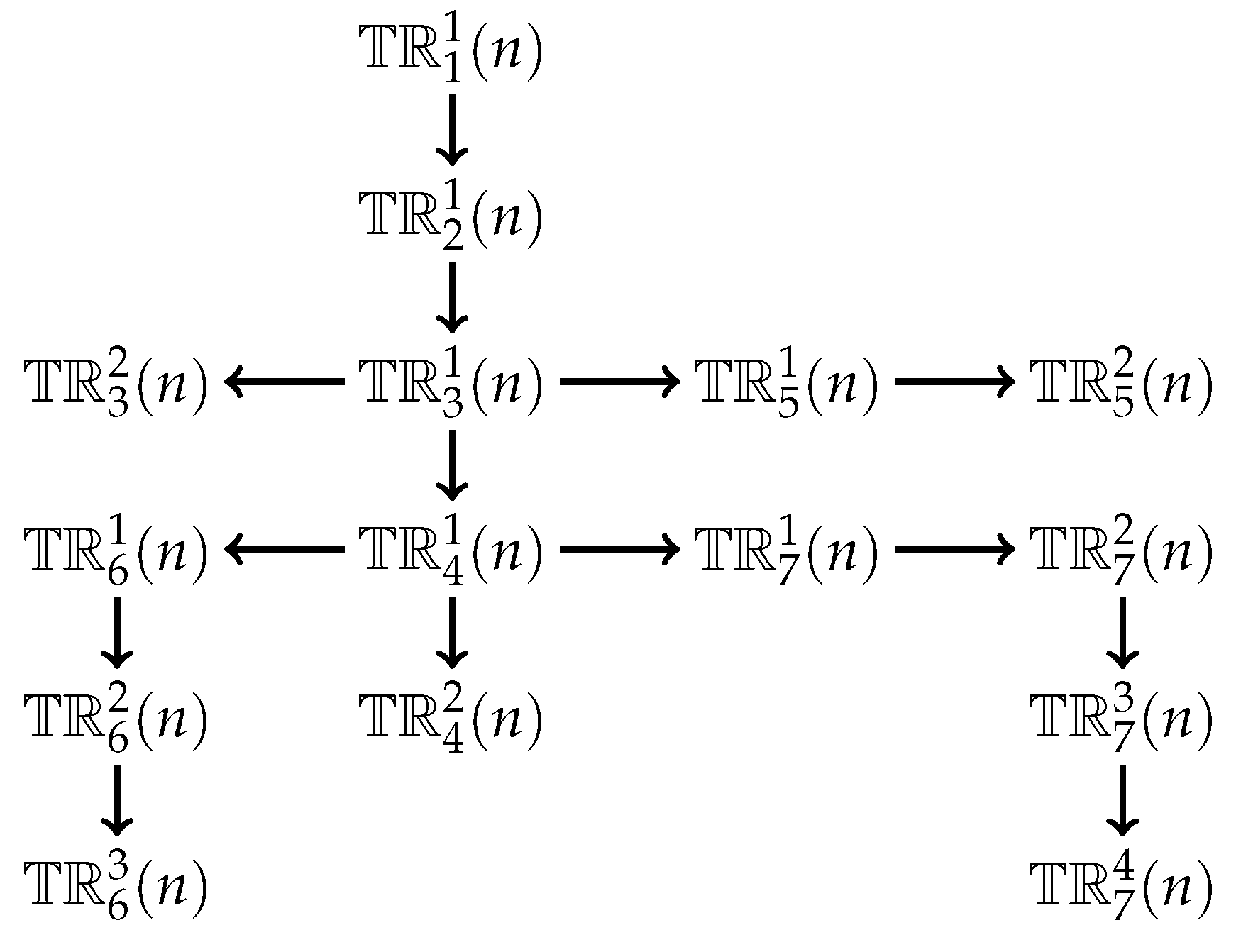
Table 1. values of

b_{i}

calculated by computer

Table 1. values of

b_{i}

calculated by computer

$x_{2}$	$b_{1}$	$b_{2}$	$b_{3}$	$b_{4}$	$b_{5}$	$b_{6}$
2	2.914	1.975	4.250	4.797	6.224	12.32
3	2.828	3.742	9.896	7.282	8.128	19.11
4	2.634	7.311	18.34	10.15	10.90	29.61
5	2.363	12.74	29.43	13.10	14.33	43.61
6	2.033	20.06	43.05	15.92	18.28	60.95
7	1.657	29.30	59.13	18.44	22.61	81.51
8	1.243	40.47	77.60	20.54	27.23	105.2
9	0.7967	53.58	98.40	22.11	32.07	131.9
10	0.3237	68.64	121.5	23.06	37.06	161.5

Table 2. values of

b_{i}

calculated by computer

Table 2. values of

b_{i}

calculated by computer

$x_{2}$	$b_{1}$	$b_{2}$	$b_{3}$	$b_{4}$	$b_{5}$	$b_{6}$
2	1.633	0.8524	0.5197	1.586	2.748	4.759
3	1.449	1.443	2.912	2.461	3.225	7.122
4	1.138	3.776	7.914	3.697	4.599	13.00
5	0.7443	7.944	15.36	4.898	6.596	22.15
6	0.2925	14.00	25.15	5.812	9.032	34.43

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Tricyclic Graph with Minimum Randić Index

Abstract

1. Introduction

2. Preliminaries

3. Transformations Decreasing Randić Index

4. Main Results

4.1. Undeletable subgraph and Classification of tricyclic graphs

4.2. Relations between TR i j ( n )

4.3. The proof of Theorem 1

5. Conclusions

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe

4.2. Relations between ${TR}_{i}^{j} (n)$