1. Introduction

2. Related Work

3. Methodology

Figure 1. Audio file from the RAVDESS dataset.

Figure 1. Audio file from the RAVDESS dataset.

Figure 2. MFCCs of the RAVDESS dataset audio file in Figure 1.

Figure 2. MFCCs of the RAVDESS dataset audio file in Figure 1.

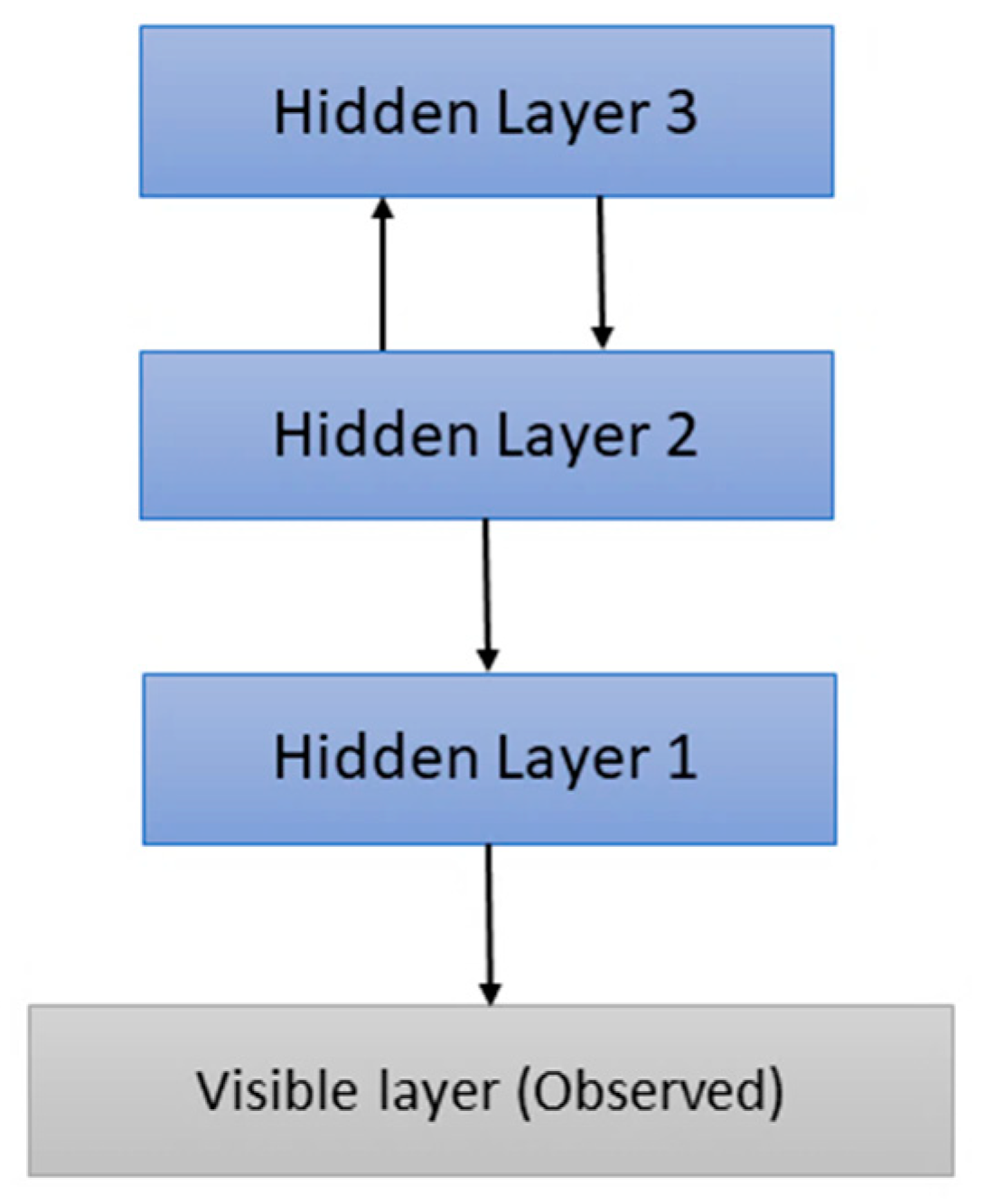
3.1. Deep Belief Network (DBN)

The model of our Deep Belief network (DBN) is shown in Figure 3. The code of the deep-belief-network-1.0.3 package from the Github repository (https://github.com/albertbup/deep-belief-network/) was used as the basis for the implementation of this model.

Figure 3. Deep Belief Network Model.

Figure 3. Deep Belief Network Model.

We created a DBN with three hidden layers (Figure 3) with a size of 128 nodes each, which receives as input the time average of the 40 MFCCs. Each hidden layer can be considered a Restricted Bolzman Machine (RBM), with the hidden layer being the first layer of the next RBM. The values of the hyperparameters of the model we adopted are: 0.005 for the learning rate of the RBM hidden layers, 0.05 for the learning rate of the neural network output, 50 for the number of epochs of the RBM hidden layers. Also, we adopted the value 1000 for the number of iterations for the backpropagation algorithm, used by the neural network’s stochastic gradient descent algorithm, and 32 for the batch size. Finally, we used the Dropout normalization technique, which is a thoughtful (or random) zeroing of a percentage of connections (which in our case is 20%), between neurons (i.e., setting the output of the neuron next to 0) of two fully connected layers, as well as the ReLU activation function.

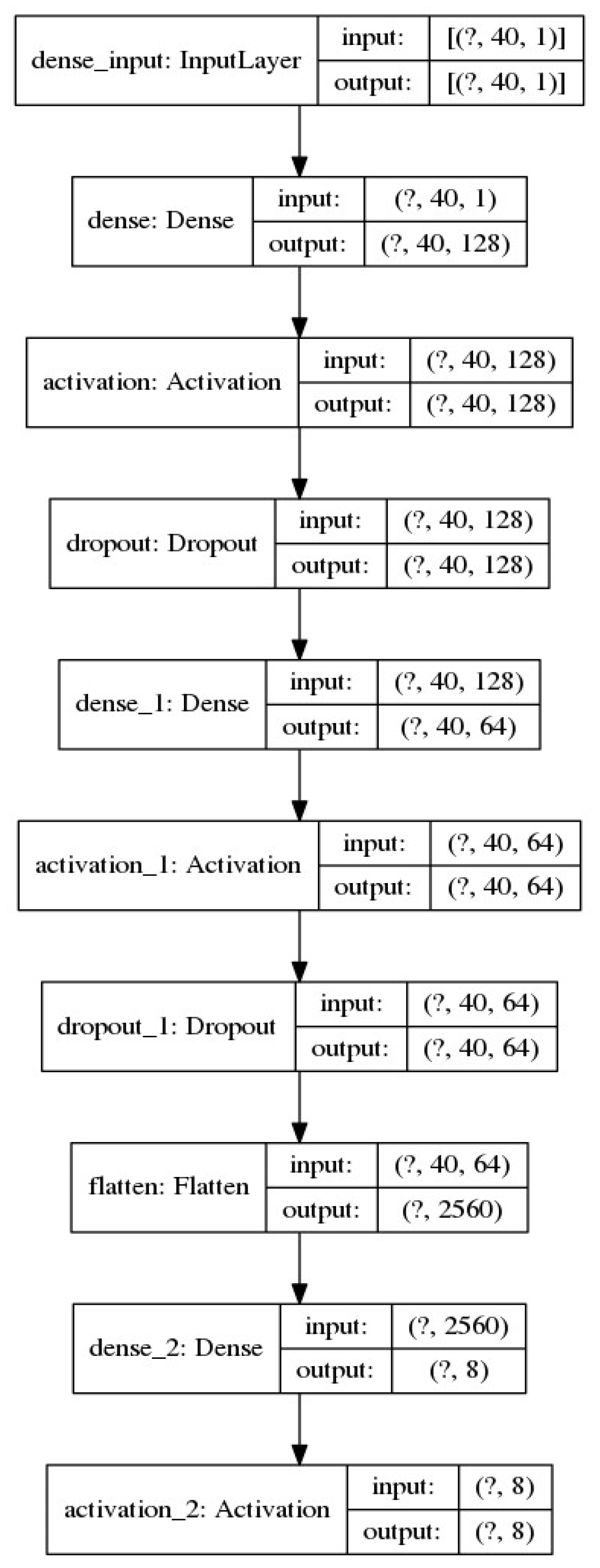
3.2. Simple Deep Neural Network (SDNN)

The model of our simple deep neural network is depicted in Figure 4.

Figure 1. Simple Deep Neural Network model.

Figure 1. Simple Deep Neural Network model.

The diagram in Figure 4 shows a deep neural network model that receives the average time of the 40 MFCCs as input. Because we want to implement a DNN model in its simplest form, we use Dense layers, for which it is true that each input neuron is connected to the output neuron and that the parameter units simply define the dimension of the output neuron. For the first (hidden) layer of the network we use a dense layer that receives as input a tensor of dimensions (40, 1), due to the 40 MFCCs, and produces an output tensor of dimensions (40,128), due to the number of 128 parameters we defined. We use the ReLU activation function, for this layer. Also, we employ the dropout normalization technique, with 10% dropout rate. The reason for it is that in each iteration it trains a modified model that ignores the existence of some of the neurons of previous or even next layers, and this results in different groups of network parameters being trained without being affected from other parameters that have been reset, each time the code is run. Thus, our network avoids the problem of “overfitting”.

For the second (hidden) layer of the network, we use a dense layer that receives as input the output of the previous layer, a tensor (40, 128), and an output neuron of dimension (40, 64), due to the number of 64 parameters we defined for this layer. The ReLU activation function and the dropout of 10% are also used. Successively, we use the flatten function, which reshapes the tensor to have a shape equal to the number of elements contained in the tensor. In our case the number of elements included in the tensor is 2560.

The third network layer is also a dense layer that receives as input the flattened tensor (of 2560 elements), and produces a tensor of size 8 or 7, depending on the database on which we train the model. Essentially, it categorizes the 2560 elements into those 8 or 7 emotion classes. We use the “Softmax” activation function here that returns a probability distribution over the targeted classes in the multi-class classification problem.

3.3. LSTM based network (LSTM)

As a third model, we configure a DNN, which uses LSTM (Long Short-Term Memory layer) layers that have been found to achieve very good results in problems with sequential data. The architecture is depicted in Figure 5.

Here, instead of entering the average of the MFCCs over the file in the model, we enter the sequence of the different MFCCs over the length of the file. As the first layer of the network, we use an LSTM layer that receives as input a tensor of dimensions (228, 40) for the RAVDESS, and (308, 40) for the SAVEE database, due to the sequence size of the 40 MFCCs (228 and 308 respectively) for each database. It produces an output tensor (228, 100) and (308, 100) respectively, due to the number of parameters (100) that we defined.

As the second layer of the network, we use an LSTM layer that receives as input the output of the previous layer, and produces its output tensor of dimension 50, due to the number of 50 parameters (cells) that we defined. We use here the dropout normalization technique to reset 50% of the connections, and then the flatten function, which reshapes the tensor to have a shape equal to the number of elements contained in the tensor (50).

The third network layer is a dense layer that receives as input the flattened tensor, of 50 elements, and produces a tensor of 8 or 7 components, depending on the database we use to train the model, categorizing the 50 elements in those 8 or 7 classes of emotions. Finally, we use the “Softmax” activation function that returns a probability distribution over the targeted classes in the multi-class classification problem.

Figure 2. LSTM Based Neural Network model.

Figure 2. LSTM Based Neural Network model.

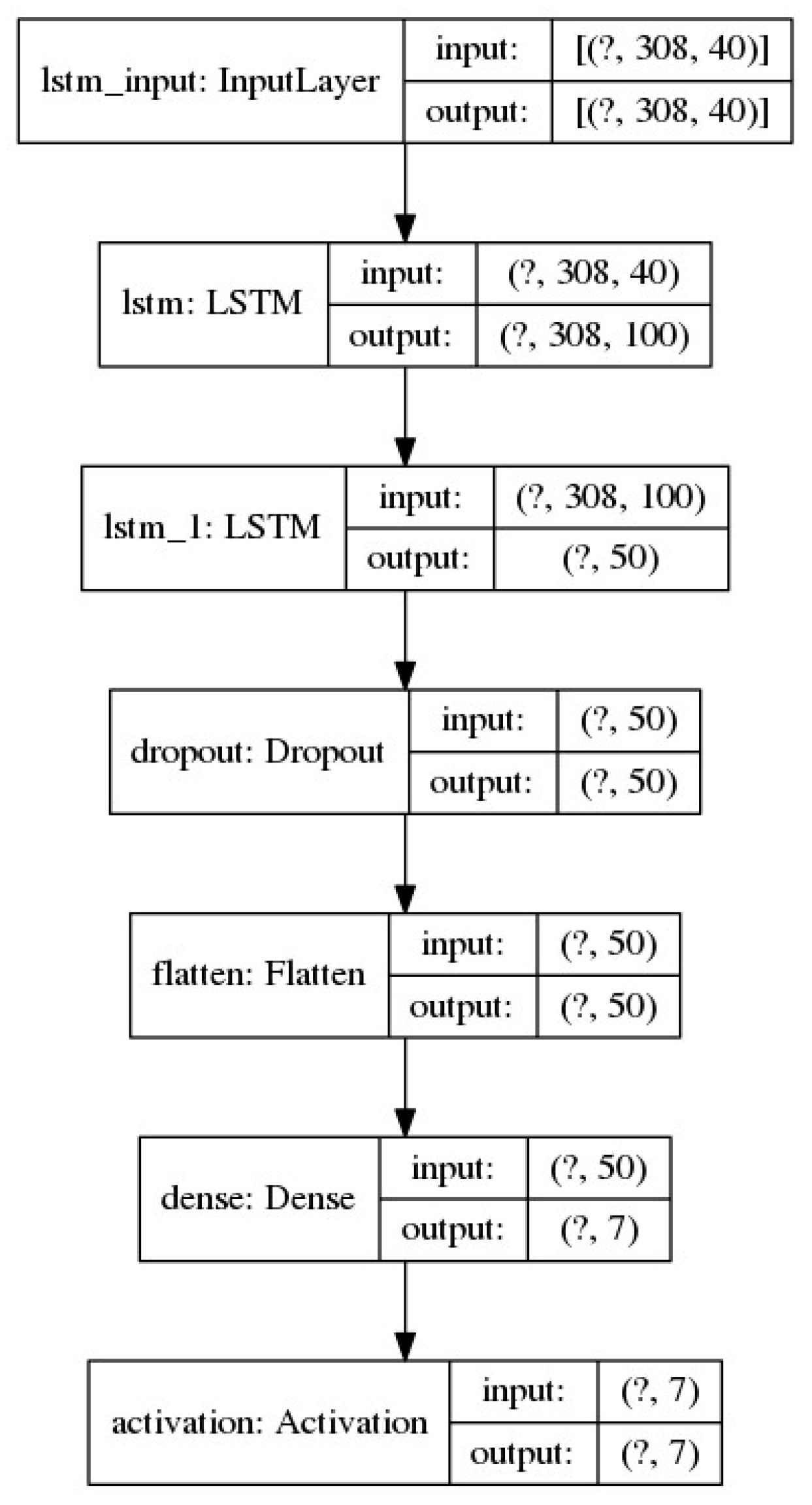
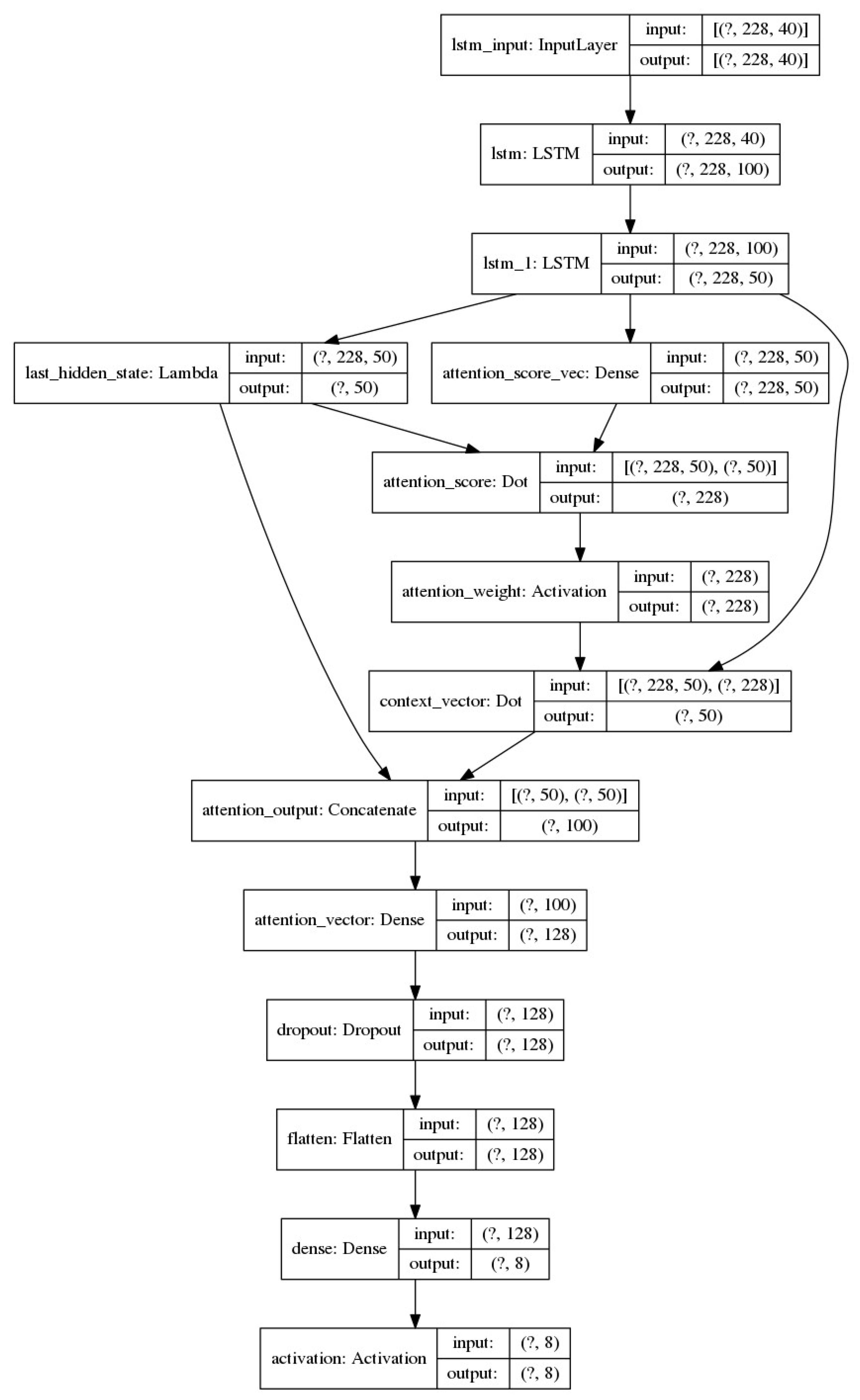
3.4. LSTM based Network with Attention Mechanism (LSTM-ATN)

In the previous LSTM model, we add an attention mechanism, and the new created architecture is presented in Figure 6. As in the previous LSTM based model, we enter the sequence of the different MFCCs in the file duration. As the first layer of the network, we use a same LSTM layer as the one in the previous model (see Figure 5).

As the second layer of the network, we use a same LSTM layer as in the previous model, but without using dropout normalization and the flatten function.

Next, we introduce the attention layer, which applies the dot-product attention mechanism, as it is referred to in Luong [25]. The dot-product attention mechanism calculates scores through the dot product between the current/last target state ${\mathit{h}}_{\mathit{t}}$ and all previous source states ${\tilde{\mathit{h}}}_{\mathit{s}}$. At each time step t, in the decoding phase, this approach first takes as input the hidden state ${\mathit{h}}_{\mathit{t}}$ at the top layer of a stacking LSTM. The goal is then to draw a context vector ${\mathit{c}}_{\mathit{t}}$ that retains relevant source information to help in predicting the current target-word ${\mathit{y}}_{\mathit{t}}$. The scoring function is calculated by $score\left(h_t,{\tilde{h}}_s\right)=h_t^T{\tilde{h}}_s$. In this attention model, an alignment vector of variable length ${\mathit{a}}_{\mathit{t}}$, whose size is equal to the number of time steps in the source side, is obtained by comparing the current hidden target state ${\mathit{h}}_{\mathit{t}}$ with any hidden source state ${\tilde{\mathit{h}}}_{\mathit{s}}$:

$$a_t\left(s\right)=align\left(h_t,{\tilde{h}}_s\right)=\frac{\exp \left(score\left[h_t,{\tilde{h}}_s\right]\right)}{\sum _{s^{\prime }}\mathrm{e}\mathrm{x}\mathrm{p}\left(score\left(h_t,{\tilde{h}}_{s^{\prime }}\right)\right)}$$

Given the alignment vector as weights, the context vector ${\mathit{c}}_{\mathit{t}}$ is calculated as the dot product of the weighted average over the previous hidden state ${\tilde{\mathit{h}}}_{\mathit{s}}$. Given the current target state ${\mathit{h}}_{\mathit{t}}$ and the context vector ${\mathit{c}}_{\mathit{t}}$, we use a simple concatenation to combine information from both vectors to create an attentional hidden state as follows: ${\tilde{h}}_t=\mathit{tan}h\left(w_c\left[c_t;h_t\right]\right)$. Next, we use the dropout normalization technique to reset the order of 50% of the connections and then the flatten function, which receives the tensor with the attentional vector ${\tilde{\mathit{h}}}_{\mathit{t}}$, which reshapes it to have a shape equal to the number of elements contained in the tensor. In our case, the number of elements in the tensor is 128.

The third layer of the network is the same as in the previous model (see Figure 5).

Figure 3. Deep LSTM Based Neural Network with attention mechanism model.

Figure 3. Deep LSTM Based Neural Network with attention mechanism model.

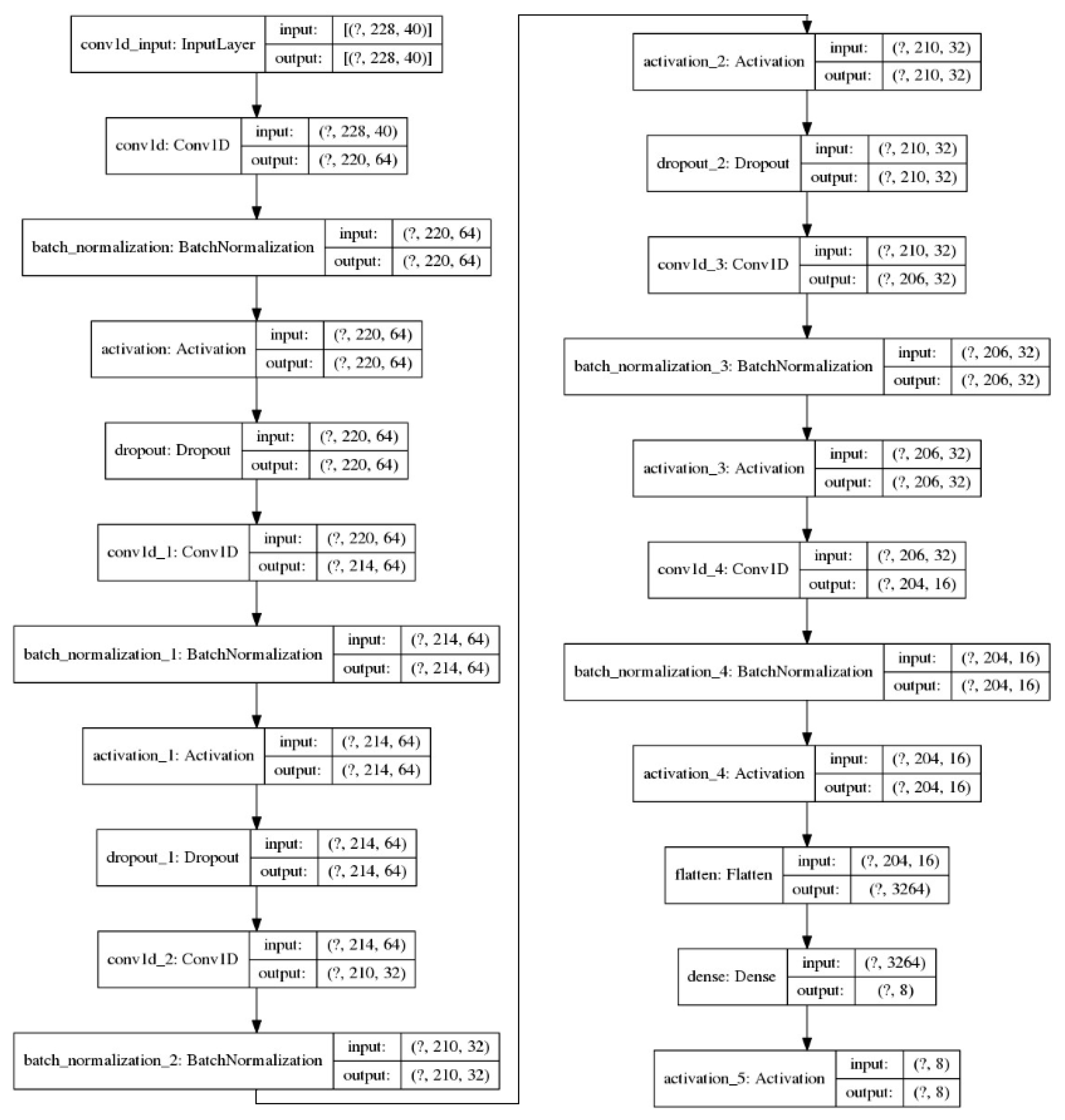
3.5. Convolutional Neural Network (CNN)

Our next model is a convolutional network that also considers the dimension of time. The architecture of the convolutional network is depicted in Figure 7.

Here, we enter the sequence of the different MFCCs in the file duration too. As the first layer of the network, we use a one-dimension convolutional layer (Conv1D), which receives as input a tensor of the dimensions (228, 40) for the RAVDESS, and (308, 40) for the SAVEE database, as previously. For the analysis of the model, we use the case of training it with the RAVDESS database, as shown in Figure 7. The first convolutional layer, in this case, will produce an output tensor of dimensions (220, 64), due to the number of 64 filters we have defined. Additionally, we set the kernel size, which refers to the size of the convolution window, to 9, as we work with a convolutional layer of one dimension. Next, we use the batch-normalization layer that speeds up training, as it allows the use of higher learning rates, given that activations are now less “sensitive” to changes in parameters. Finally, we use the ReLU activation function and the dropout normalization technique at a rate of 50%.

As the second layer of the network, we use a convolutional layer of one dimension (Conv1D), which receives as input a tensor of dimensions (220, 64) and produces an output tensor of dimensions (214, 64), due to the number of 64 filters that we defined. Additionally, we set the kernel size to 9, as explained above. Next, we use the batch-normalization layer, which speeds up training, using the ReLU activation function and a dropout of 50%.

The third layer of the network is implemented as a convolutional layer of one dimension (Conv1D), which receives as input a tensor of dimensions (214, 64) and produces an output tensor of dimensions (210, 32), due to the number of 32 filters that we defined. Additionally, we set the kernel size 7, and use the batch-normalization layer, to speed up training, using the ReLU activation function, and a dropout normalization at the rate of 50%.

The fourth layer of the network is the same as the third one.

The fifth layer of the network is implemented as a convolutional layer of one dimension (Conv1D), which receives as input a tensor of dimensions (206, 32), and produces an output tensor of dimensions (204, 16), due to the number of 16 filters that we defined. Additionally, we set the kernel size to 5, and use the batch-normalization layer, to speed up training, using the ReLU activation function.

In the sequel, we use the flatten function (in this case, the tensor contains 3264 elements). Next, a dense layer that receives as input the flattened tensor (hence it has 3264 elements), produces a tensor of size 8 or 7, depending on the database we train the model, categorizing the 3264 elements into their 8 or 7 emotion classes. Finally, we use the “Softmax” activation function.

Figure 4. Deep CNN model.

Figure 4. Deep CNN model.

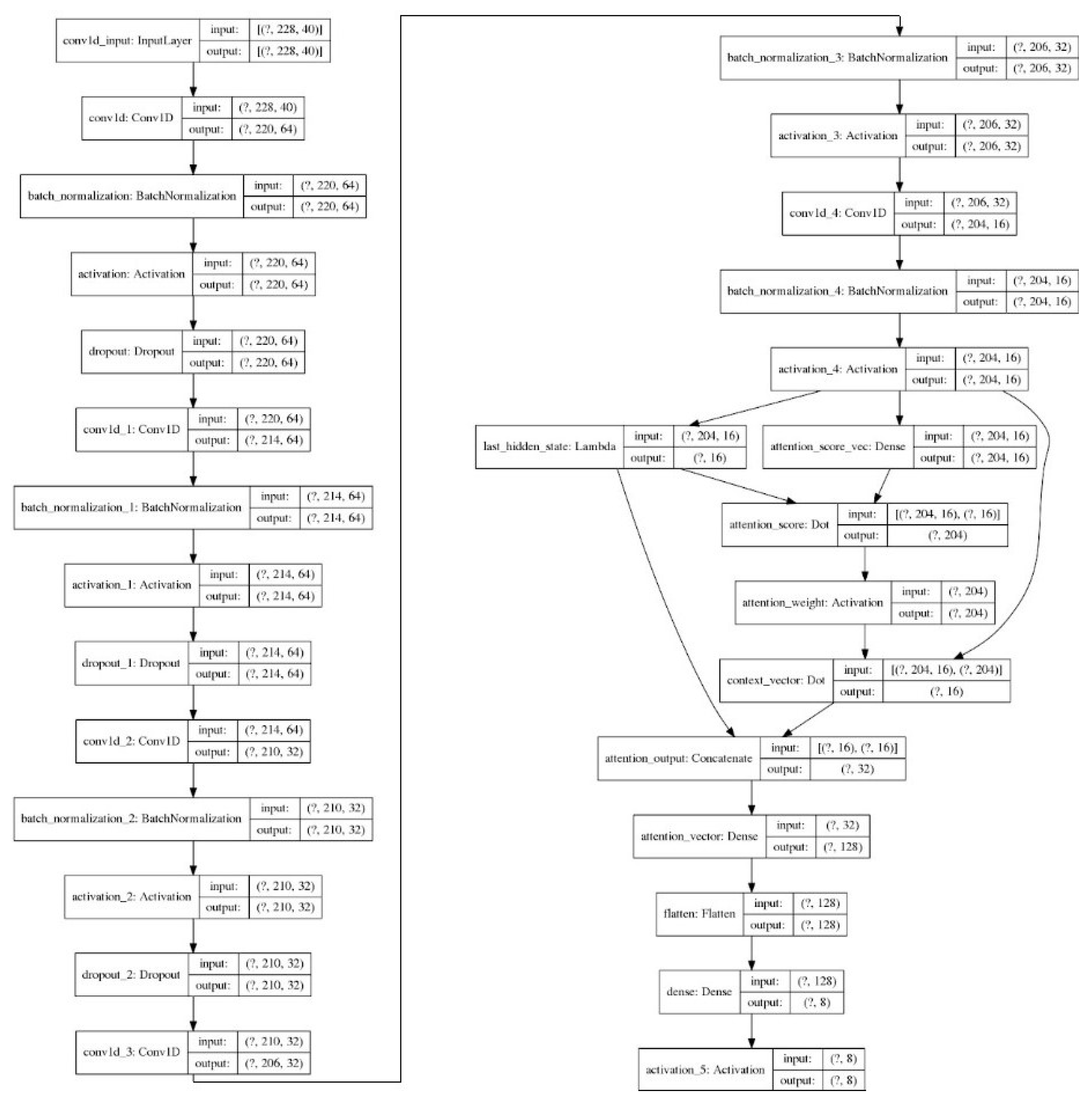
3.6. Convolutional Neural Network with Attention mechanism (CNN-ATN)

Our last model is a deep convolution network with the addition of an attention mechanism, as presented in Figure 8.

Figure 5. Deep CNN Neural Network with attention mechanism model.

Figure 5. Deep CNN Neural Network with attention mechanism model.

Here, we again enter the sequence of the different MFCCs in the file duration. Τhe first, the second, and the third layers of the network are the same as those of the plain CNN model.

The fourth layer of the network is implemented as a convolutional layer of one dimension (Conv1D), which receives as input a tensor of dimensions (210, 32) and produces an output tensor of dimensions (206, 32). The first dimension (210) is the result of reducing the input one, due to the elimination of zero values, whereas the second dimension is the number of 32 filters we have defined. Additionally, we set the kernel size to 7. Next, we use the batch-normalization layer, which speeds up training, using the ReLU activation function.

The fifth layer of the network is the same as the fifth layer of the simple CNN.

After that, we enter the attention layer, which applies the dot-product attention mechanism, in the same way as in section 3.4. An alignment vector of variable length ${\mathit{a}}_{\mathit{t}}$ is calculated by the same formula. Next, we use the flatten function, which receives the tensor with the attentional vector ${\tilde{\mathit{h}}}_{\mathit{t}}$, which reshapes it to have a shape equal to the number of elements contained in the tensor (128 in our case).

Then, a dense layer is used, which receives as input the flattened tensor that has 128 elements and produces an 8 or 7 components tensor, as in previous models, where the “Softmax” activation is used.

4. Experimental Study and Results

4.2. Experimental Results-Accuracy and Loss Curves

In the sequel, we present the results in the form of graphs for the accuracy and loss of our six models, through Figures 9 to 24. Where there is need, we add some comments. It is important to note here that compared to the other models, the Deep Belief Network (DBN) algorithm package provides only loss information, so we have only one graph for each dataset.

Figure 6. DBN loss training charts for RAVDESS (left) and SAVEE (right) databases.

Figure 6. DBN loss training charts for RAVDESS (left) and SAVEE (right) databases.

Figure 7. DNN training charts for RAVDESS database.

Figure 7. DNN training charts for RAVDESS database.

Figure 8. DNN training charts for SAVEE database.

Figure 8. DNN training charts for SAVEE database.

Figure 9. LSTM network training charts for RAVDESS database.

Figure 9. LSTM network training charts for RAVDESS database.

Figure 10. LSTM network training charts for SAVEE database.

Figure 10. LSTM network training charts for SAVEE database.

Figure 11. LSTM network with attention mechanism training charts for RAVDESS database.

Figure 11. LSTM network with attention mechanism training charts for RAVDESS database.

Figure 12. LSTM network with attention mechanism training charts for SAVEE database.

Figure 12. LSTM network with attention mechanism training charts for SAVEE database.

Figure 13. CNN network training charts for RAVDESS database.

Figure 13. CNN network training charts for RAVDESS database.

Figure 14. CNN network training charts for SAVEE database.

Figure 14. CNN network training charts for SAVEE database.

The model of Figure 13 and Figure 14 uses the batch-normalization and dropout techniques with a reset of 50%, to prevent large overfitting of the model, but still no good generalization is achieved. For this reason, two more variations of our model were tested.

Initially, zero padding was tested on the input vectors at the hidden levels. This was to keep the dimensions of the vector containing the input sequence the same as the model proceeds to the next hidden levels (for RAVDESS 228, and for SAVEE 308). This test was performed on the RAVDESS database, and the accuracy and loss curves are presented in Figure 18.

As we can see from the graphics of the test with zero padding compared to our model in Figure 16, it is obvious that the accuracy remains the same (70.5%), as well as the overfit (30%). However, comparing the graph of the loss between the two implementations, we observe that the error from epoch 50 onwards, in the zero-padding test, gradually increases and does not stabilize after epoch 100 on 2, as is done with the model in Figure 16. On the contrary, it continues to grow and exceeds 2.

Then, after the first test for the RAVDESS database had not yielded the desired results, a second test was performed using zero padding in combination with the replacement of the ReLU activation function by the LeakyReLU. The ReLU activation function sets, all negative values to zero. This makes our network adaptable to ensure that the most important neurons have positive values (> 0). However, this can also be a problem, as the gradient of 0 is 0 and therefore neurons that reach large negative values cannot recover and stick to 0. This causes the neurons to die and for this reason this phenomenon is called “The dying ReLU problem”.

Figure 15. CNN network training charts for RAVDESS database with zero padding.

Figure 15. CNN network training charts for RAVDESS database with zero padding.

To avoid this phenomenon, LeakyReLU was proposed, according to which negative values instead of zero are multiplied by a factor of 0.01:

$$f\left(x\right)=\left\{\begin{array}{c}0.01,ifx<0\\ x_{,}x\ge 0\end{array}\right.$$

Comparing it with ReLU, we can see that LeakyReLU has a slight negative slope, avoiding the entrapment of neurons with negative values at 0. There have generally been reports of success adopting this activation function, but the results are not always consistent. The reason we want to apply it to the CNN model is that through its operation we reduce the phenomenon of overfitting a little more, and stabilize more the instabilities of our system, which appear as abrupt changes (spikes) in the graphics.

This test was performed on RAVDESS and SAVEE databases and the accuracy and loss curves are depicted in Figure 19 and Figure 20 respectively.

Figure 16. CNN network training charts for RAVDESS database with zero padding and LeakyReLU.

Figure 16. CNN network training charts for RAVDESS database with zero padding and LeakyReLU.

Figure 17. CNN network training charts for SAVEE database with zero padding and LeakyReLU.

Figure 17. CNN network training charts for SAVEE database with zero padding and LeakyReLU.

As we can see from the graphs of the test with zero padding and LeakyReLU in the RAVDESS base, compared to our model in Figure 16, it is obvious that the accuracy decreases slightly (67%) and the overfitting increases slightly (33%). Comparing the graphs of loss between the two implementations, we notice that the instability (spikes) of the system has been improved. However, the error from epoch 50 onwards, in the test with zero padding and LeakyReLU, increases gradually and does not stabilize after epoch 100 on 2, as it is done with the model in Figure 16. On the contrary, it continues to increase, approaching values such as 3 and 4.

Comparing now the graph of test accuracy with zero padding and LeakyReLU on the SAVEE base with that of Figure 17, we notice that the accuracy increases dimly (55.7%) compared to the model in Figure 17 (55.2%), so there is a very minimal reduction in overfitting, of 0.5%. Then comparing the loss graphs between the two implementations, we notice that the instability (spikes) of the system has been slightly improved. The error from epoch 50 onwards, in the test with zero padding and LeakyReLU, increases gradually and does not stabilize, approaching 3.5. This is a small improvement of the system as the loss in Figure 17 approaches 4.5 in epoch 200, but from epoch 200 onwards stabilizes.

The above comparison of the two tests with the implementation of Figure 16 in the RAVDESS database concludes that our model with the use of ReLU and without zero padding gives overall better results in terms of accuracy and loss. Regarding the comparison of the test with zero padding and LeakyReLU with the implementation of Figure 17 for the SAVEE base, we observe that the test with zero padding and LeakyReLU achieves faintly improved overall results, in terms of both accuracy and loss. This may be due to the fact that this database has a smaller number of samples than RAVDESS. Therefore, we conclude that the model implemented with ReLU and without zero padding performs in general better and that the techniques tested do not give the desired results, i.e. reduce the overfitting effect and the loss to a significant degree.

Figure 18. CNN network with attention training charts for RAVDESS database.

Figure 18. CNN network with attention training charts for RAVDESS database.

Figure 19. CNN network with attention training charts for SAVEE database.

Figure 19. CNN network with attention training charts for SAVEE database.

Because we see that the models show a degree of overfitting that cannot be further reduced, we performed a test, where we removed the dropout normalization technique from the model, so that only the batch-normalization technique remained, to see the effects. The results of this model (without the dropout) for the RAVDESS and SAVEE databases are depicted in Figure 23 and Figure 24, respectively.

Figure 20. CNN network with attention training charts for RAVDESS database without Dropout.

Figure 20. CNN network with attention training charts for RAVDESS database without Dropout.

Figure 21. CNN network with attention training charts for SAVEE database without Dropout.

Figure 21. CNN network with attention training charts for SAVEE database without Dropout.

It is obvious that with the removal of the dropout function, the model shows a significant increase in the overfitting effect, given that for both the RAVDESS and SAVEE datasets we observe a significant reduction in the accuracy of the model and some increase in loss. More specifically, for the RAVDESS dataset, the model without the dropout function achieves 65% accuracy, in contrast to the model of Figure 21, which achieves 77% accuracy. This means that the model without the dropout technique overfits to a percentage of 45% on this dataset. Also, the loss of the model without the dropout technique fluctuates (spikes) around 2.5, while the model of Figure 21 fluctuates (spikes) around 1.5, and from epoch 100 onwards revolves around 1, with a minimal upward trend to 1.2.

For the SAVEE dataset, the model without the dropout technique achieves an accuracy of 47%, in contrast to the model of Figure 22, which achieves an accuracy of 74%. This means that the model without the dropout technique overfits to a percentage of 63% on this dataset. Also, the loss of the model without the dropout technique from epoch 25 onwards has a steady upward trend from 1.3 to 1.6, while the model in Figure 22 fluctuates (spikes) around 1.5. From the above it is obvious that proposed CNN-Attention model applying the dropout technique against overfitting is the best possible option.

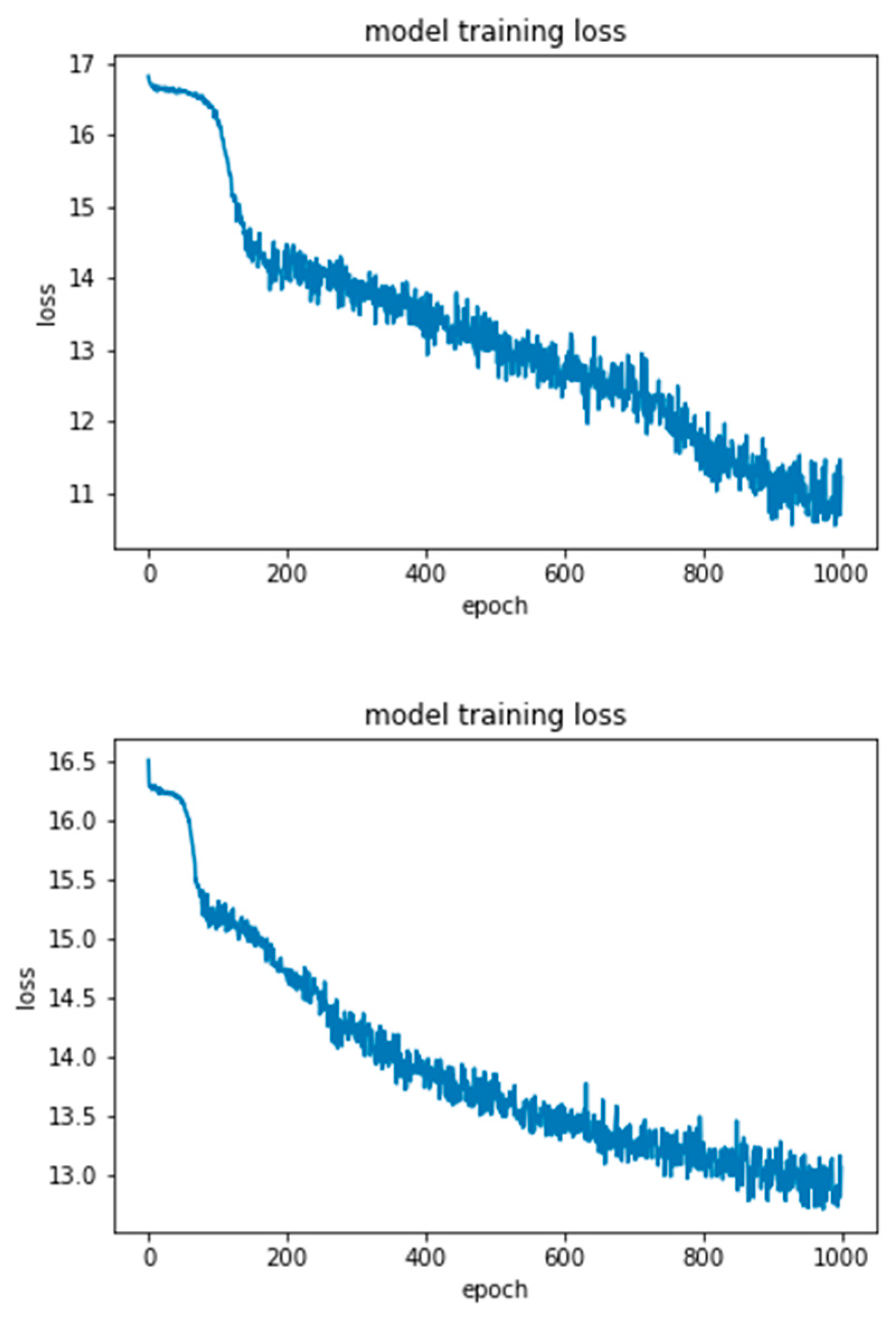
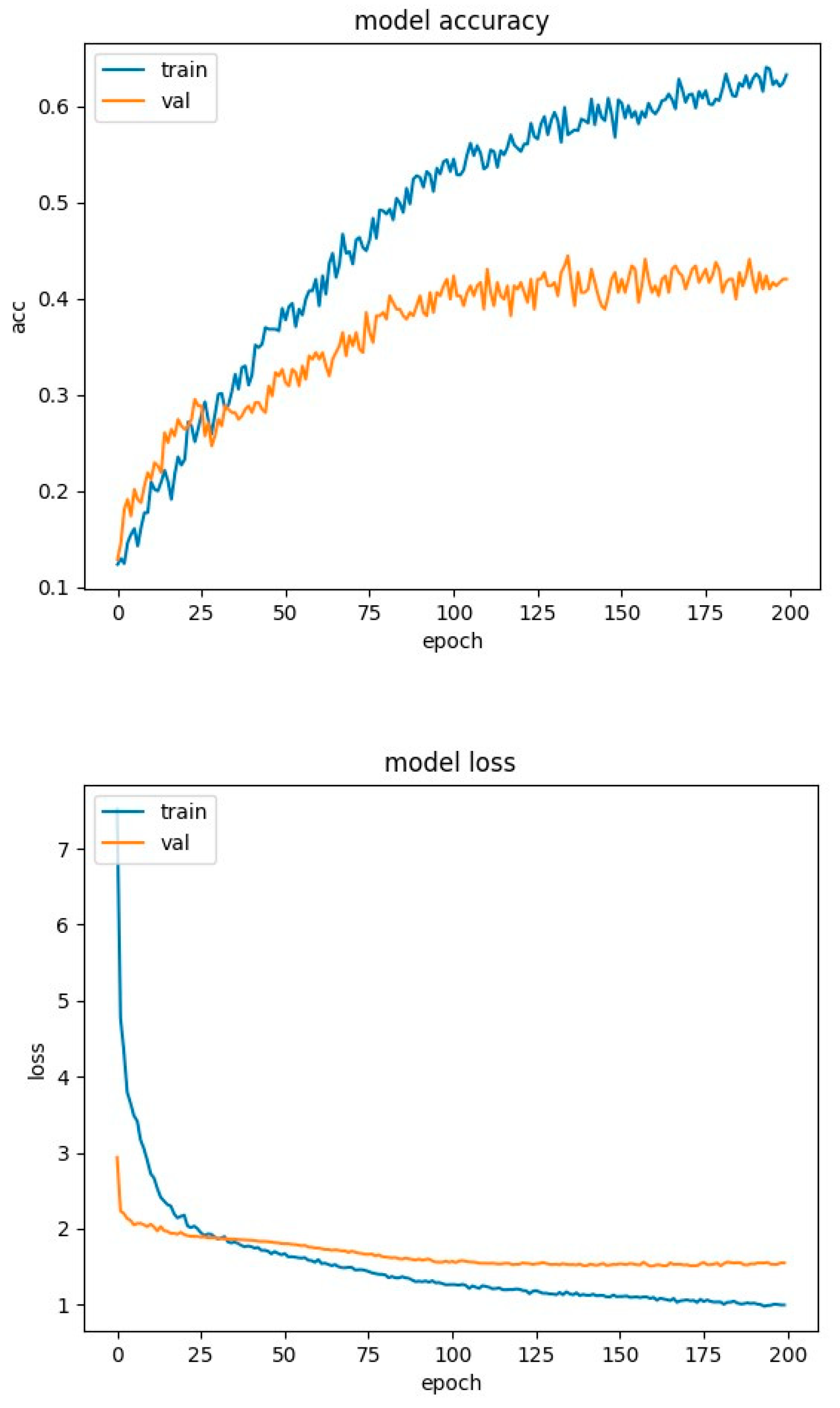
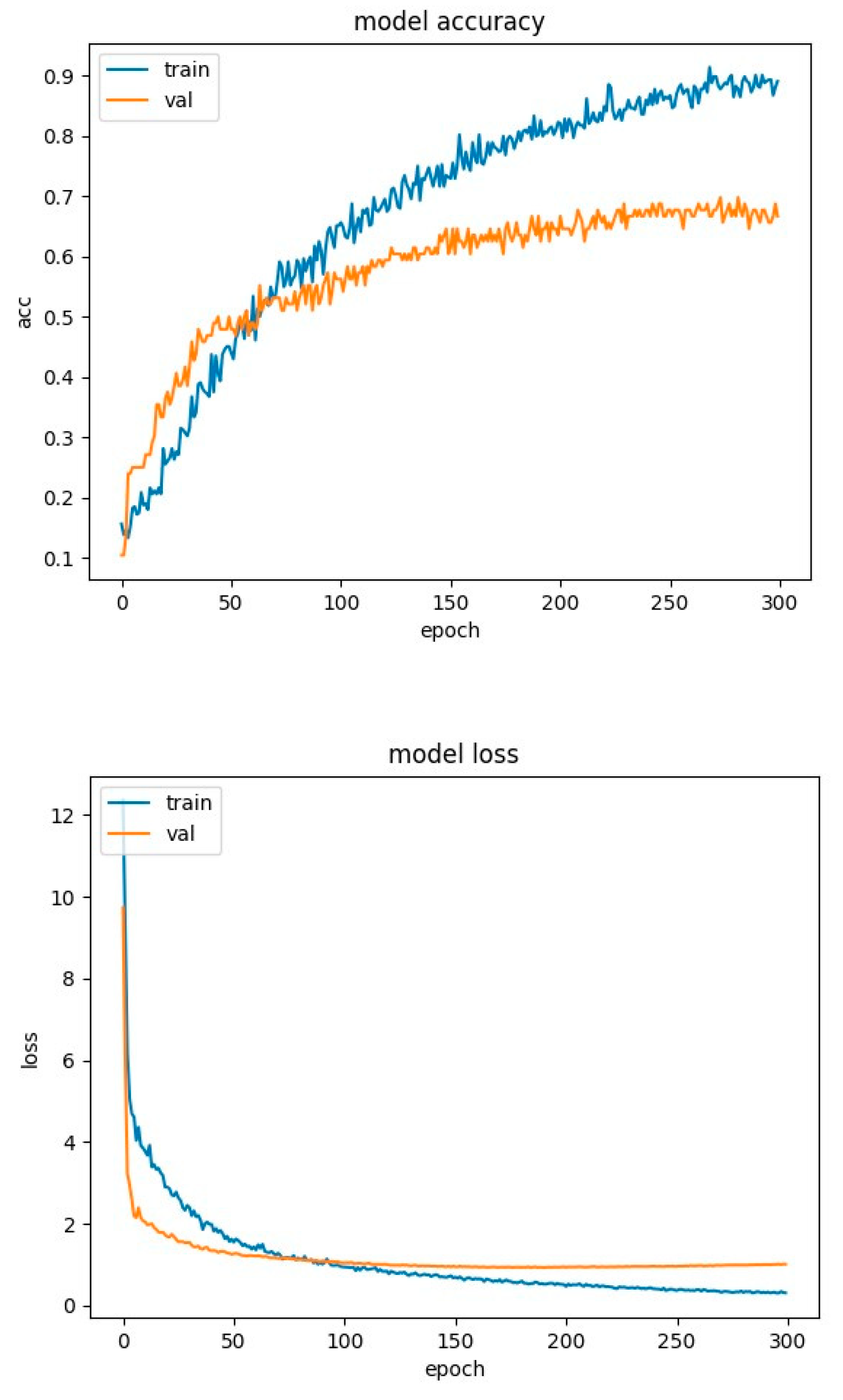
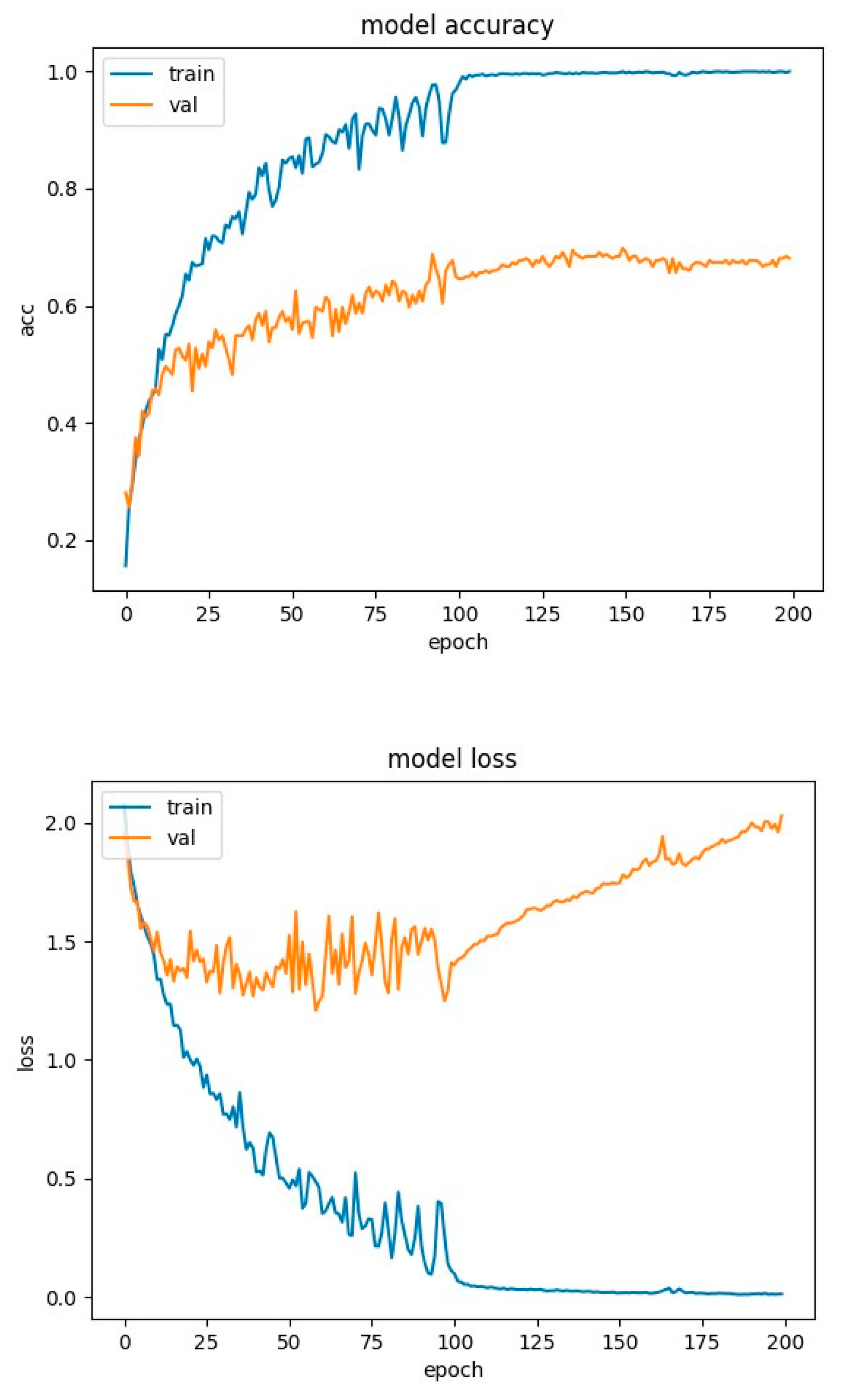
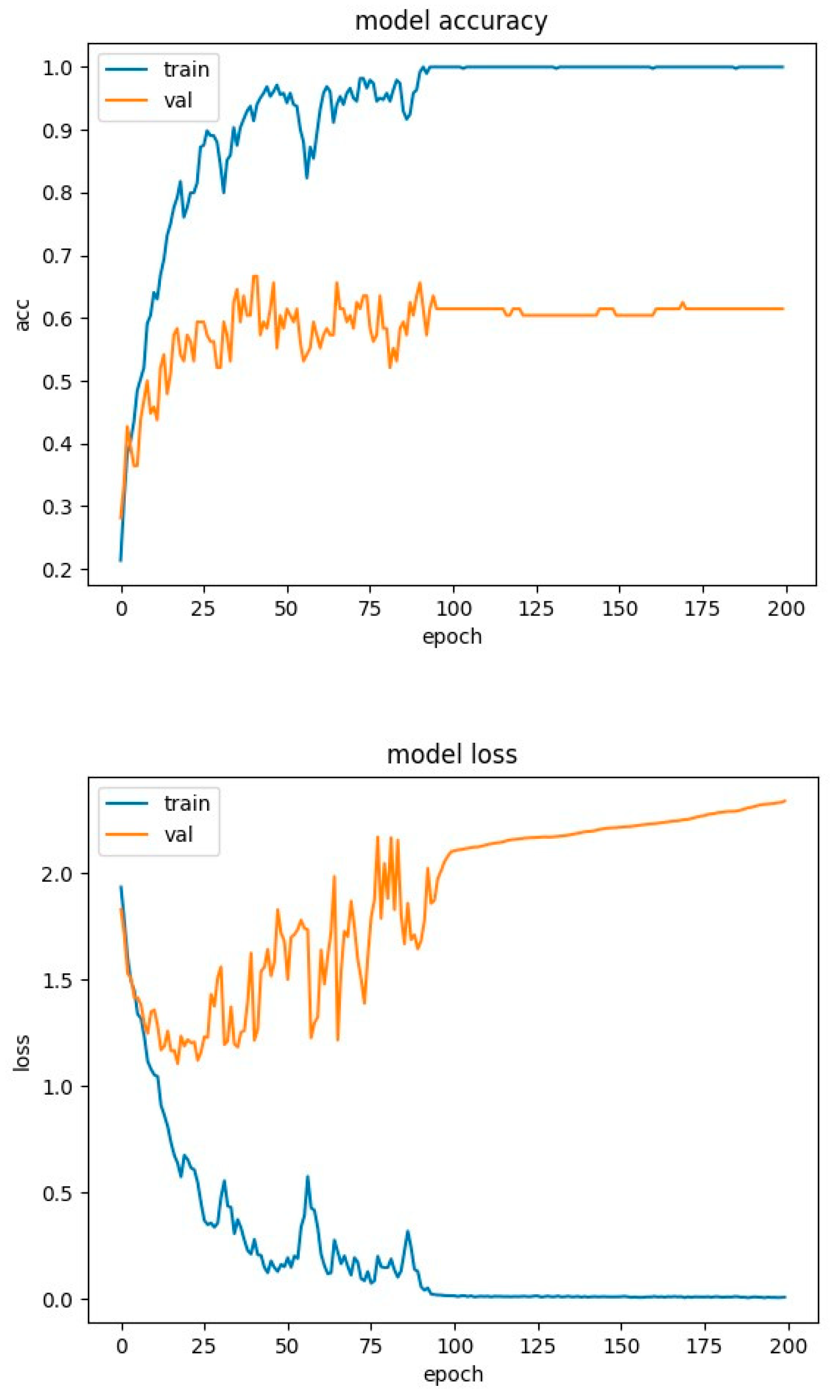
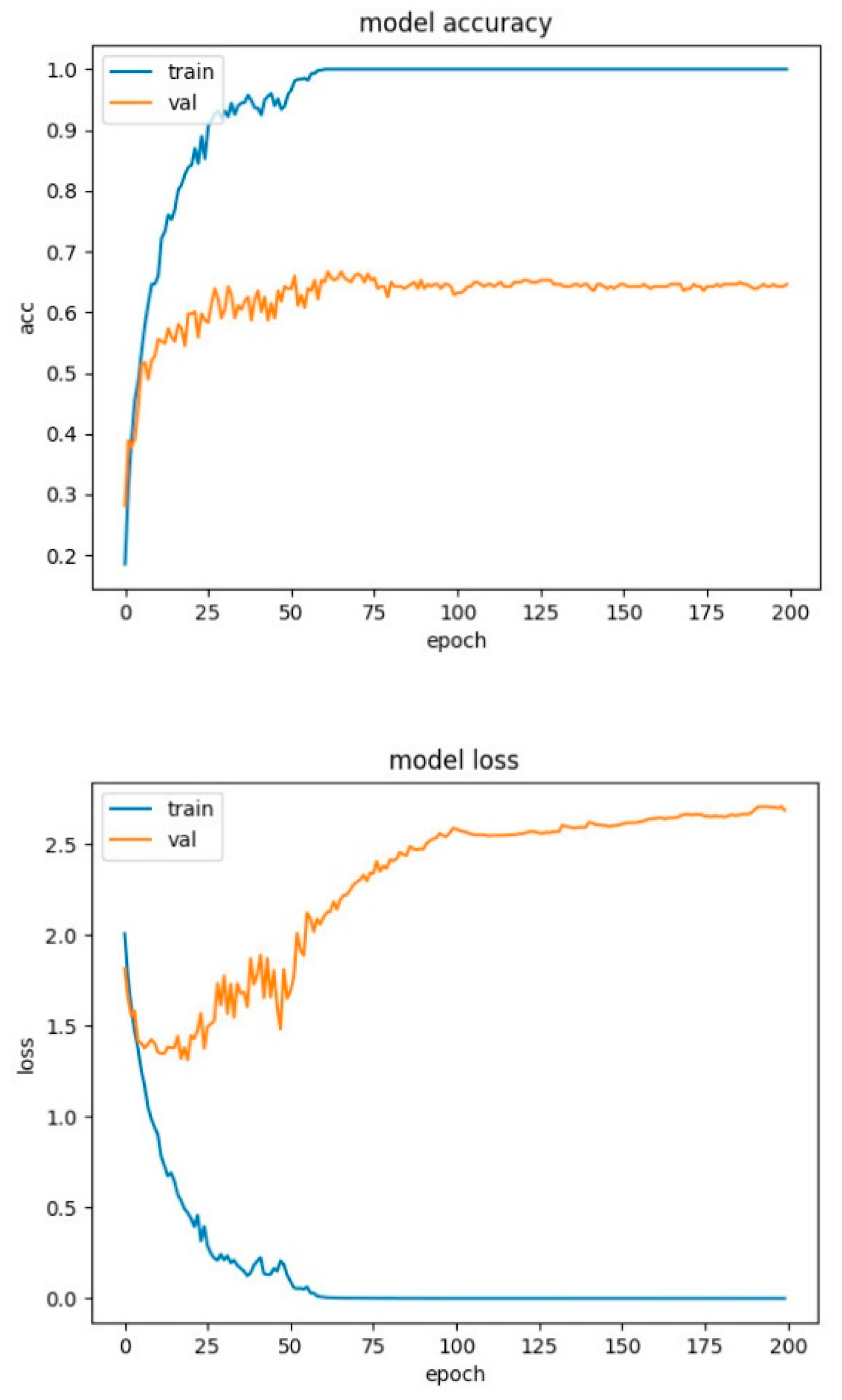
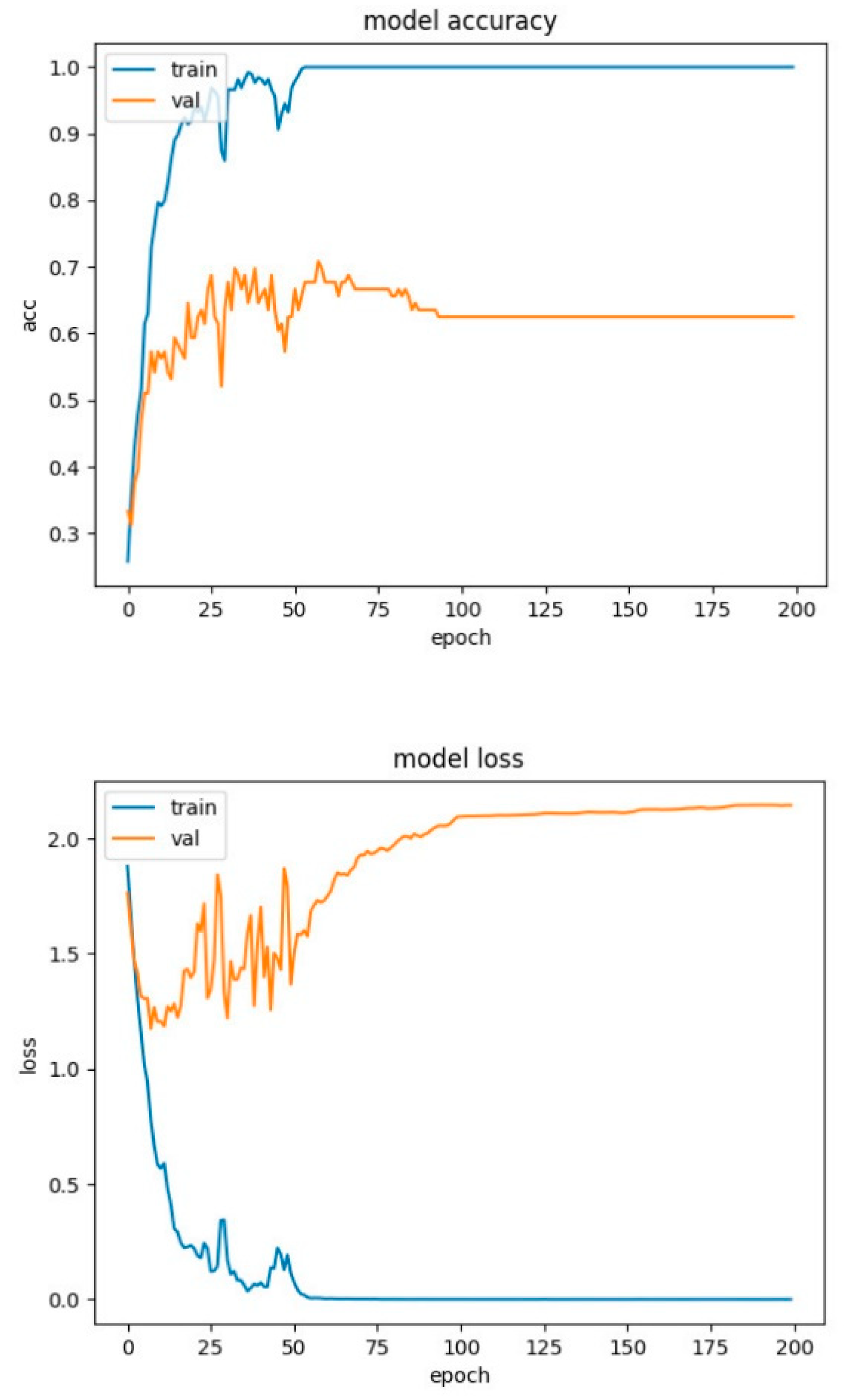
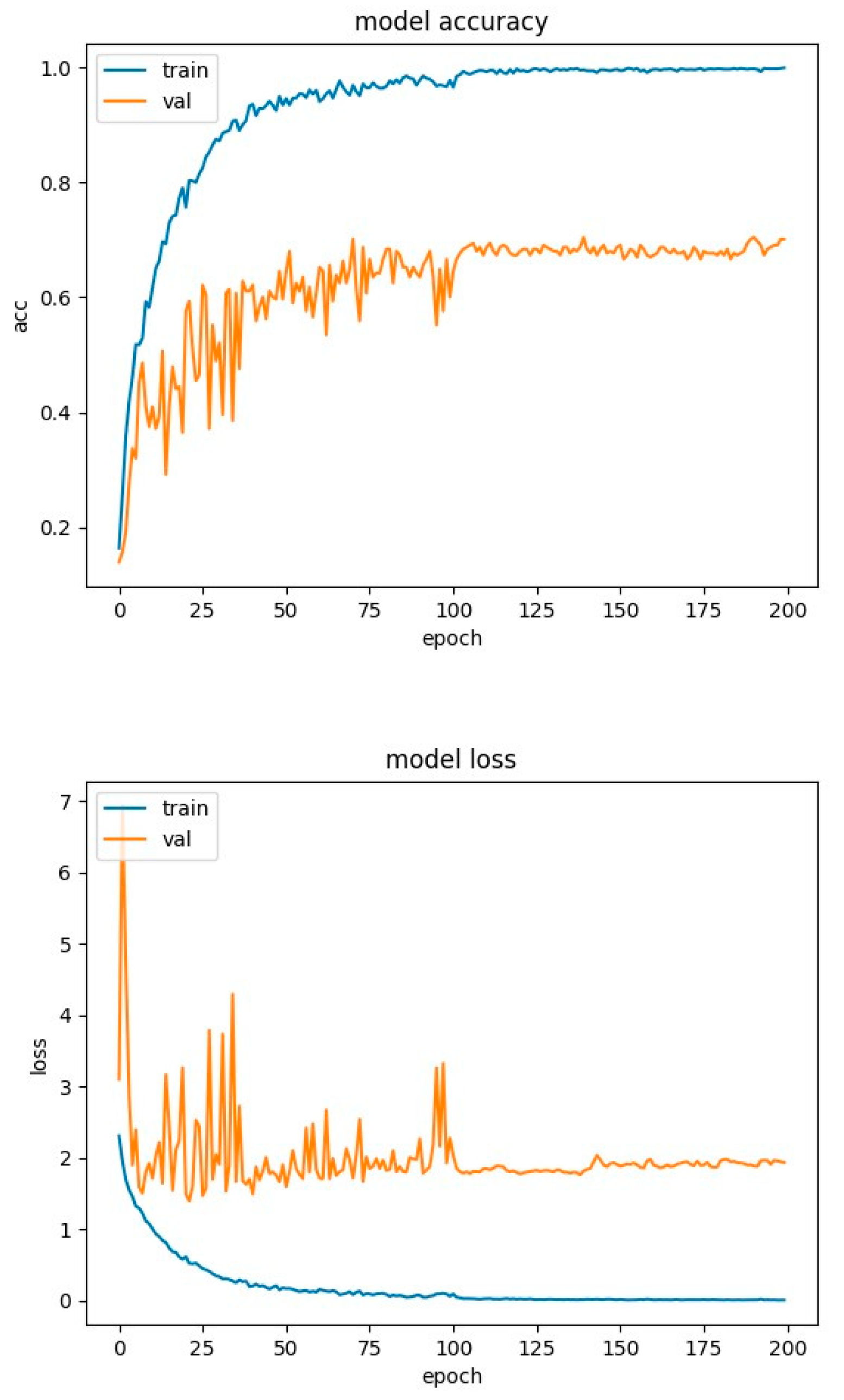
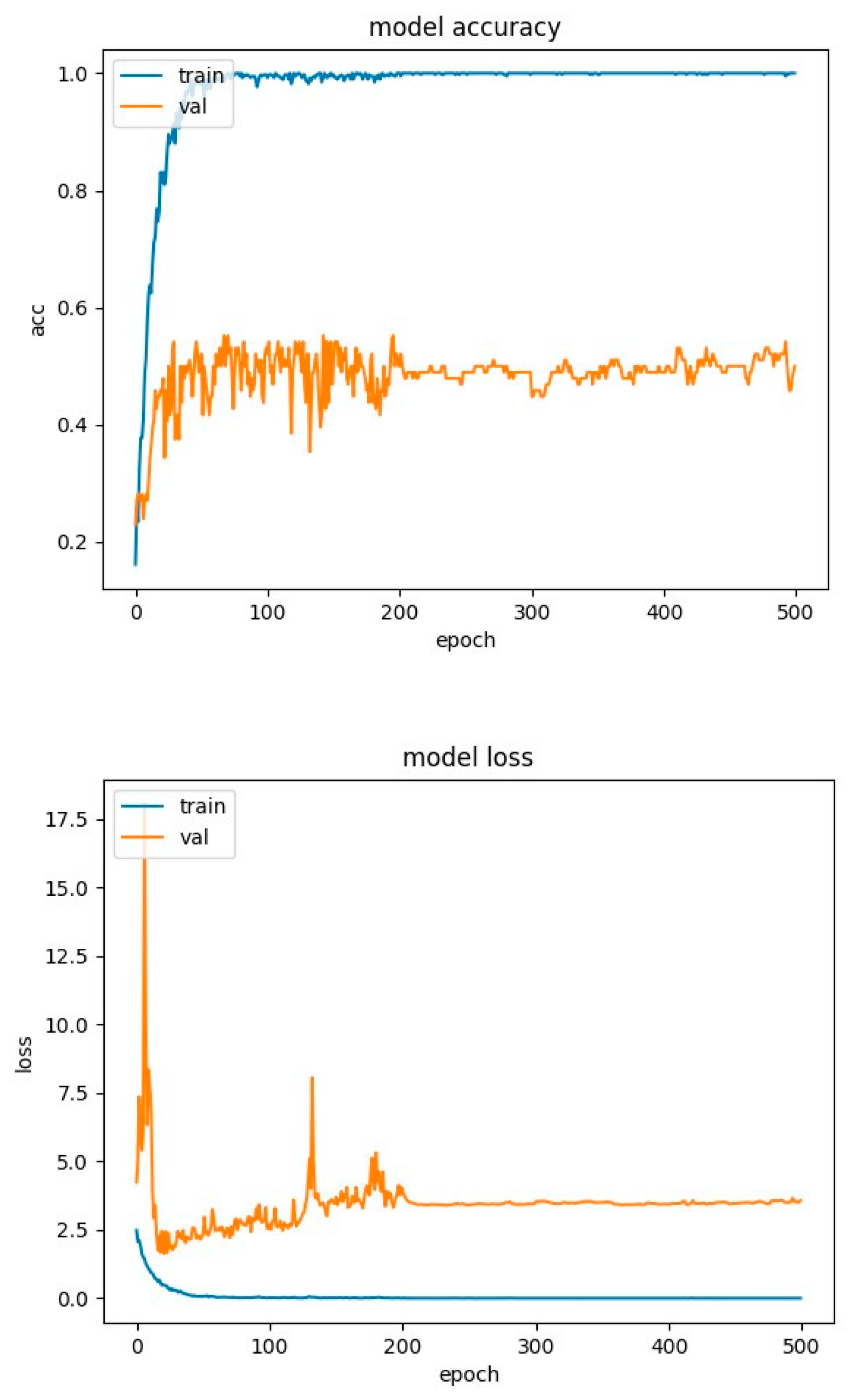
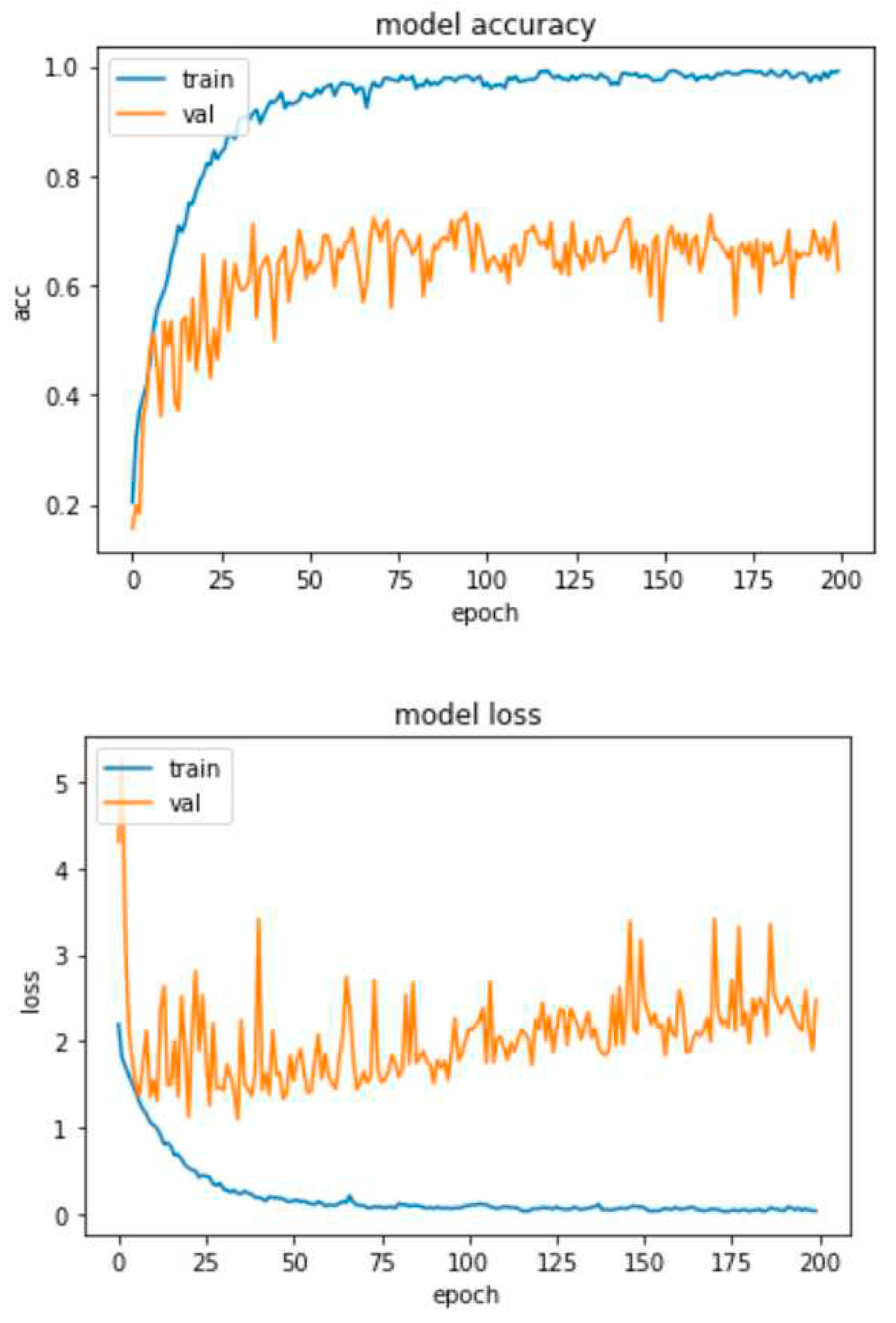
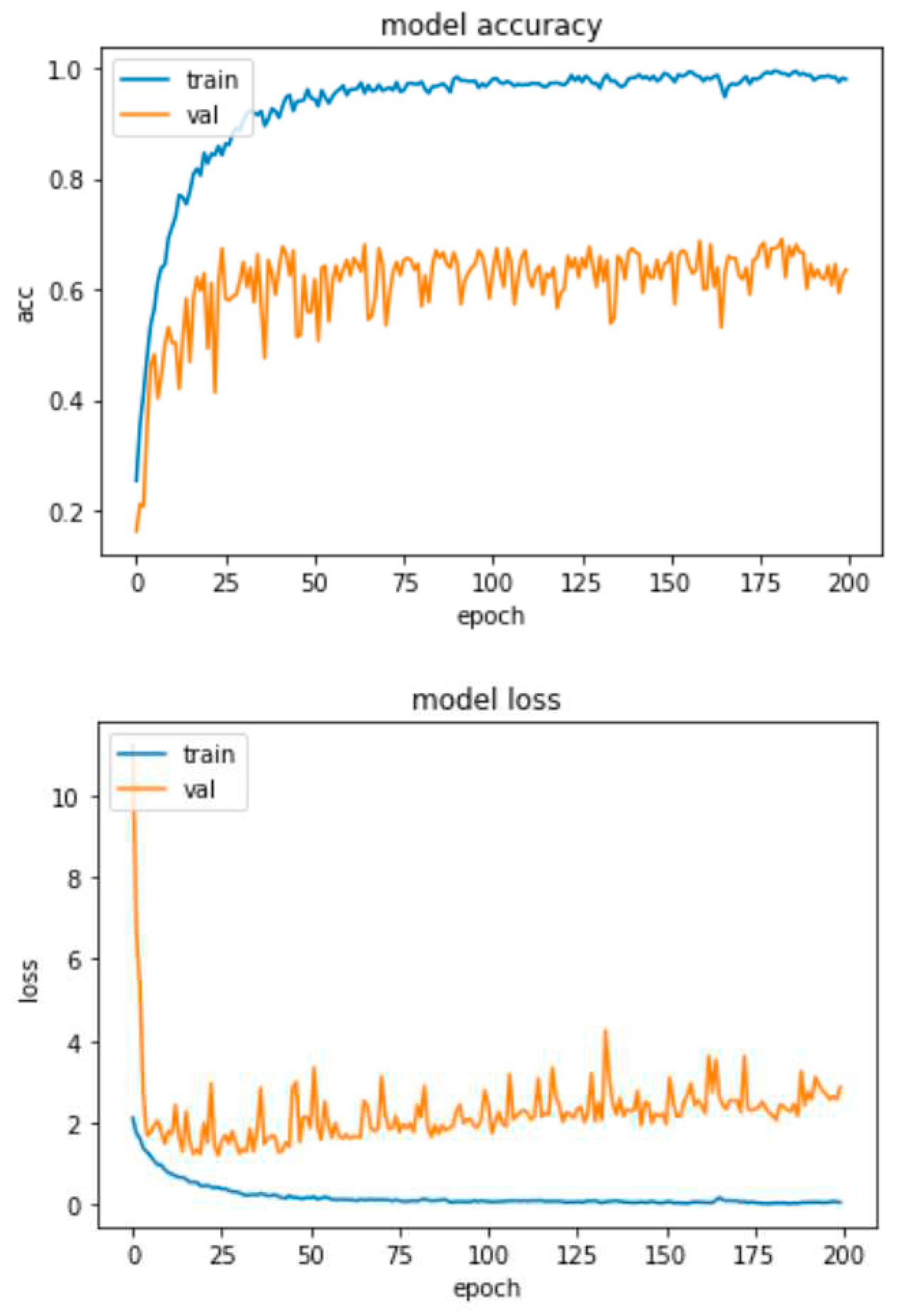
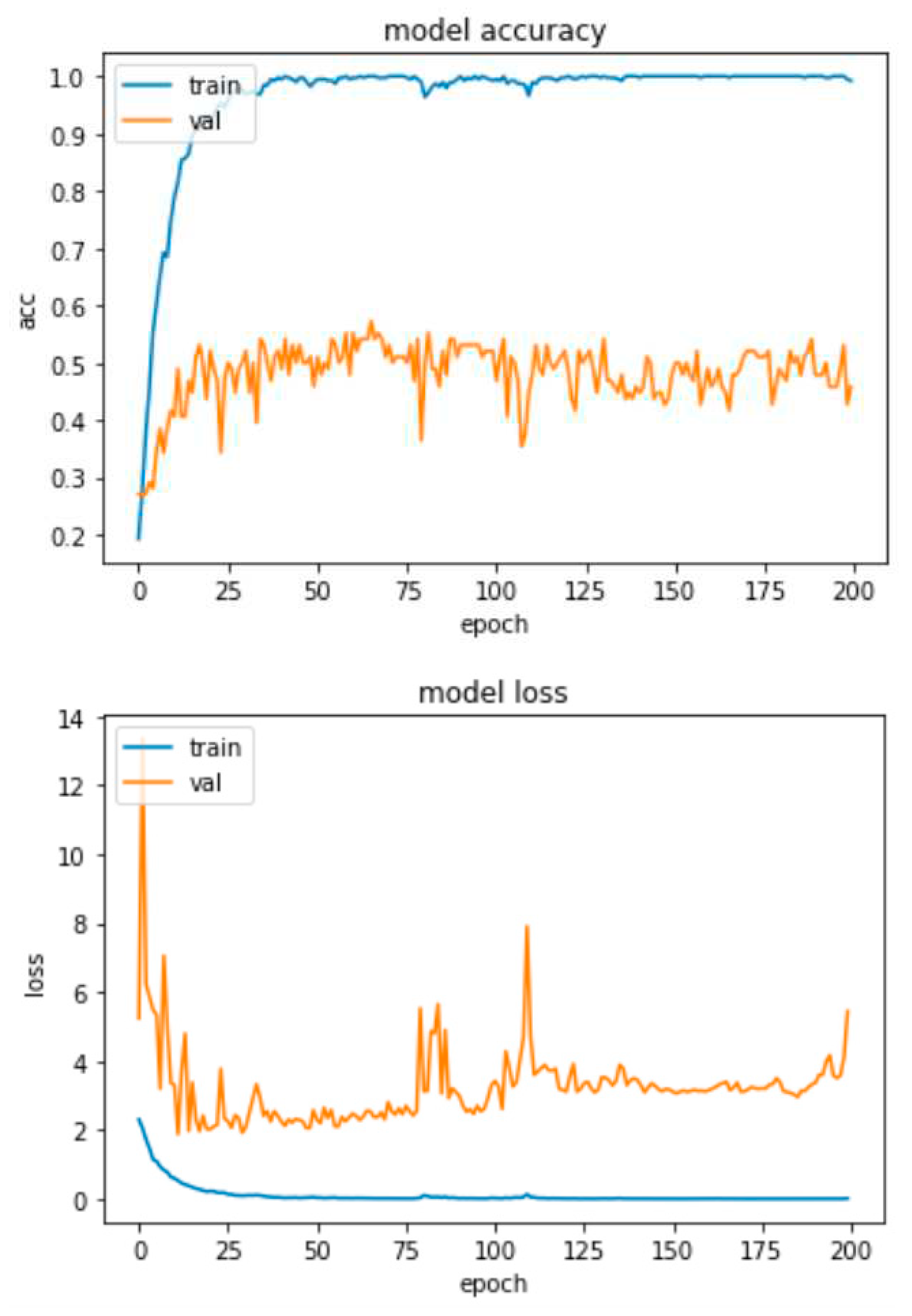
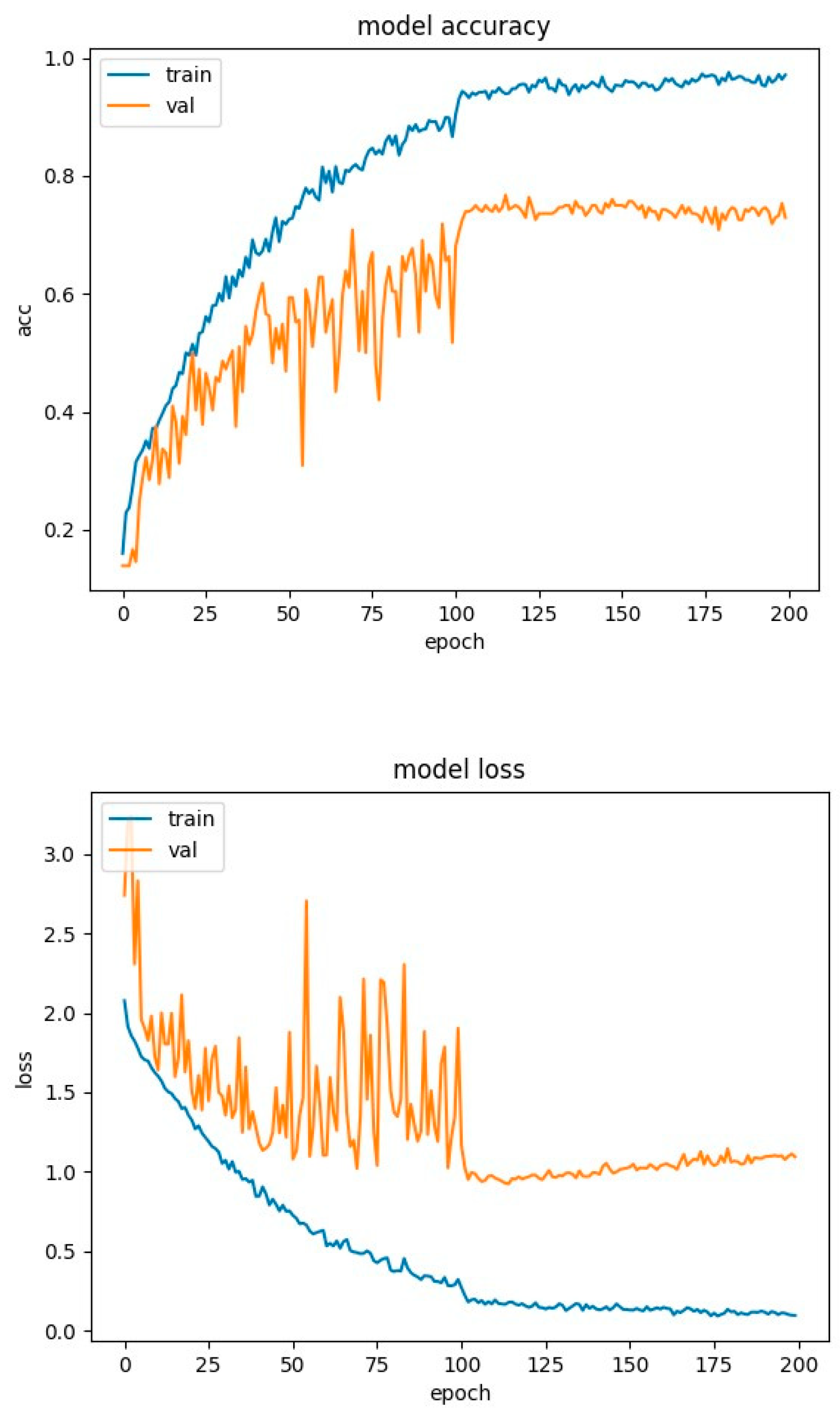
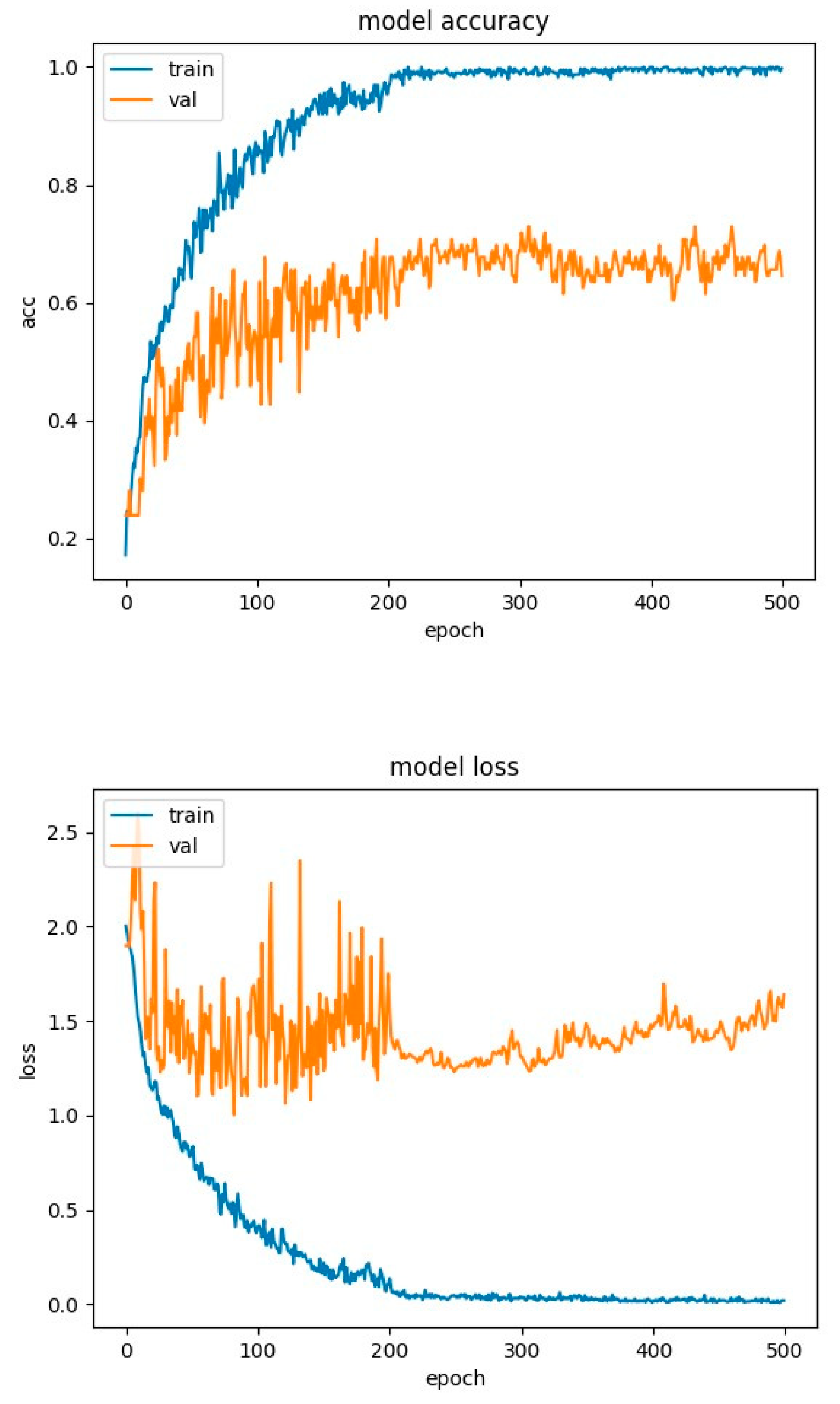
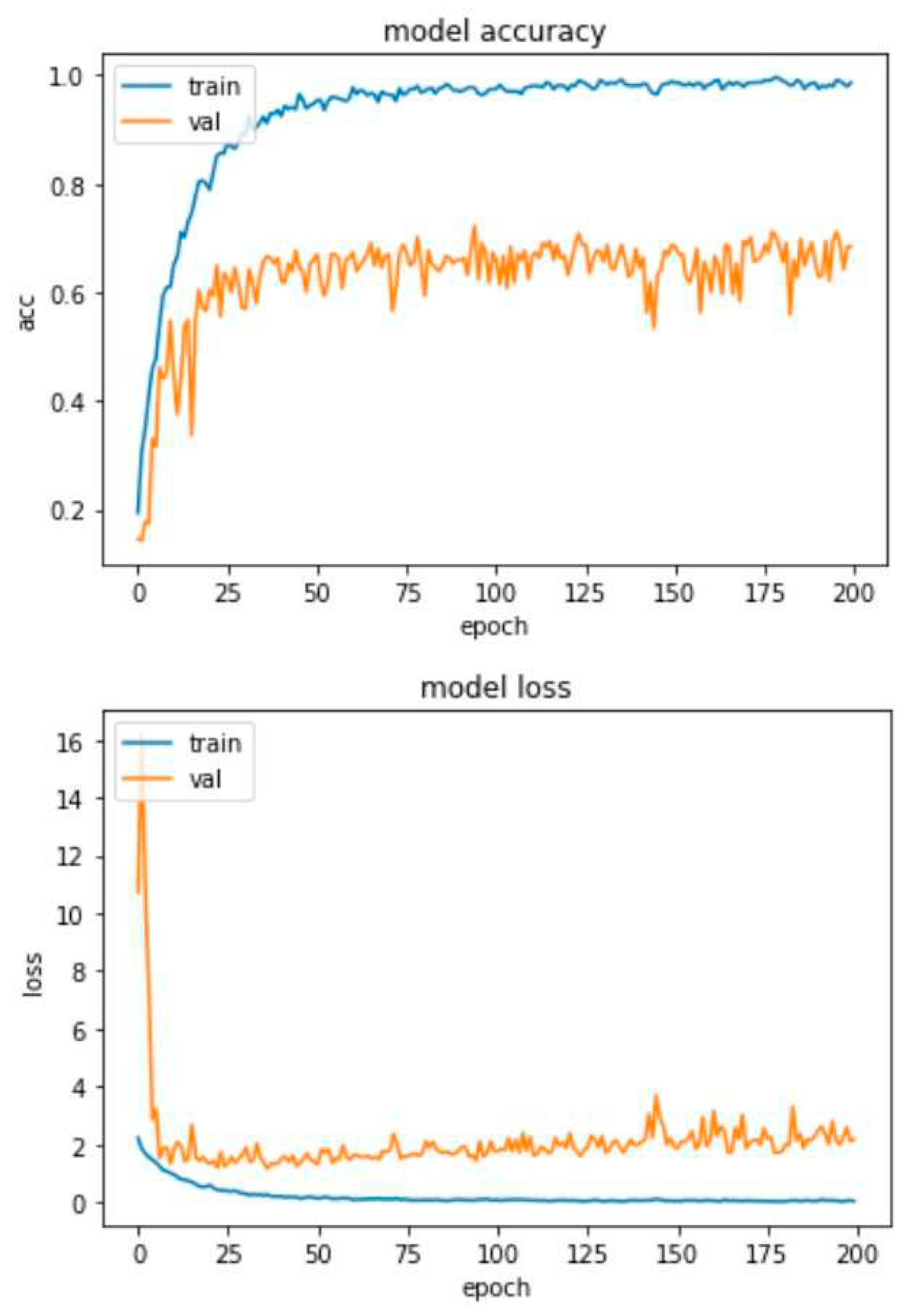
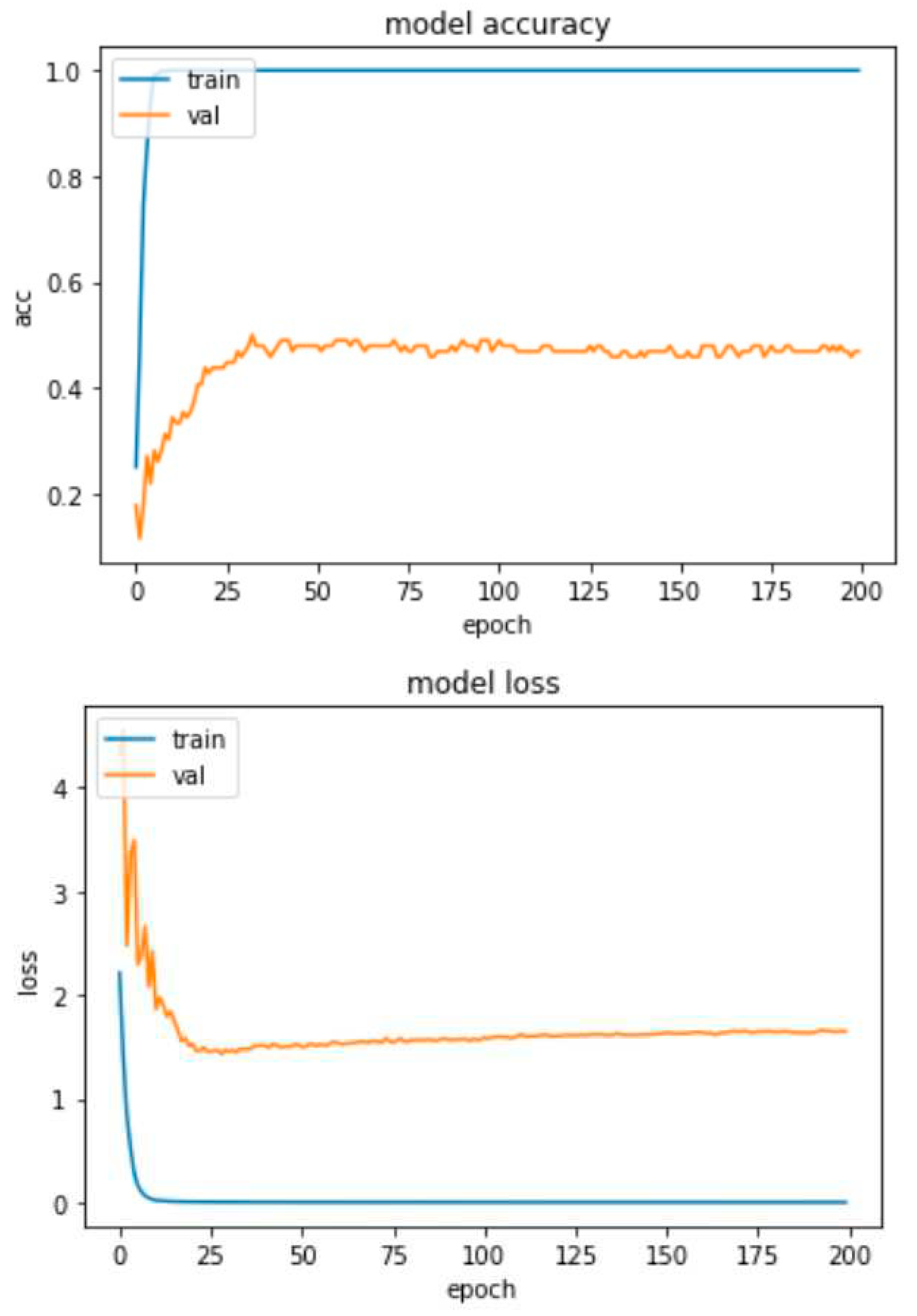
4.4. Experimental Results-Confusion Matrices

For the six implemented models, the confusion matrices for each of the RAVDESS and SAVEE datasets are presented in this subsection, via the Figures 25 to 30. The confusion matrices, as it is well known, contain information about the success rate of the models’ predictions for each emotion of the selected datasets separately. Table 1 shows the correspondence between the labels in confusion matrices and the two datasets.

From the confusion matrix of DBN for the RAVDESS dataset (Figure 25), we can conclude that the ‘neutral’ and the ‘angry’ emotions of the dataset yields the lowest success rate (0%), as the ‘neutral’ emotion is most often confused with the emotion of ‘calm’ {in 9 out of 20 samples} and the emotion of ‘anger’ is most often confused with the emotion of ‘surprise’ {in 27 out of 36 samples}. In contrast, the emotion of ‘surprise’ receives the best success rate (80.5%) compared to the rest, as it identifies 33 out of 41 samples.

Figure 22. DBN confusion matrices for RAVDESS (left) and SAVEE (right).

Figure 22. DBN confusion matrices for RAVDESS (left) and SAVEE (right).

From the confusion matrix of DBN for the SAVEE dataset (Figure 25), we can conclude that the ‘anger’ emotion of the dataset yields the lowest success rate (25%) by identifying only 3 of the 12 samples, as it confuses most times with the emotion of ‘sadness’ {in 8 out of 12 samples}. In contrast, the emotion of ‘surprise’ receives the best success rate (66.7%) compared to the rest, as it identifies 8 out of 12 samples.

In the confusion matrix of DNN for the RAVDESS dataset (Figure 26), we can see that the ‘neutral’ emotion yields the lowest success rate (14.3%), as it is most often confused with the ‘sad’ emotion {in 5 out of 21 samples} and the emotion of ‘disgust’ {in 5 out of 21 samples}. In contrast, the emotion of ‘surprise’ receives the best success rate (61%) compared to the rest, as it identifies 25 out of 41 samples.

Similarly, in the confusion matrix of DNN for the SAVEE dataset (Figure 26), we can see that the emotion of ‘surprise’ yields the lowest success rate (33.3%) identifying only 4 out of the 12 samples, as it is confused most often with the feeling of ‘fear’ {in 5 out of the 12 samples}. In contrast, the ‘neutral’ emotion receives the best success rate (91.3%) compared to the rest, as it identifies 21 out of 23 samples.

Figure 23. DNN confusion matrices for RAVDESS (left) and SAVEE (right).

Figure 23. DNN confusion matrices for RAVDESS (left) and SAVEE (right).

Figure 24. LSTM network confusion matrices for RAVDESS (left) and SAVEE (right).

Figure 24. LSTM network confusion matrices for RAVDESS (left) and SAVEE (right).

From the confusion matrix of LSTM for the RAVDESS dataset (Figure 27) we can conclude that the ‘happy’ emotion and the ‘neutral’ emotion of the dataset yield the lowest success rates achieving 44.8% and 66.7%, respectively. This is because the ‘happy’ emotion is most often confused with the emotion of ‘fearful’ {in 7 out of 29 samples} and the ‘neutral’ emotion is sometimes confused with the ‘sad’ emotion {in 3 out of 21 samples}. In contrast, the emotions of ‘calm’ and ‘surprise’ receive the best success rates (80% and 78%), as they identify 32 out of 40 and 32 out of 41 samples, respectively.

From the confusion matrix of LSTM for the SAVEE dataset (Figure 27) we can conclude that the emotion of ‘happiness’ yields the lowest success rate (36.4%) identifying only 4 out of 11 samples, as it is confused several times with both the emotion of ‘anger’ and the emotion of ‘surprise’ {in 3 out of 12 samples for each}. In contrast, the ‘neutral’ emotion receives the optimal success rate (95.6%) compared to the rest, as it identifies 22 of the 23 samples.

Figure 25. LSTM network with attention mechanism confusion matrices for RAVDESS (left) and SAVEE (right).

Figure 25. LSTM network with attention mechanism confusion matrices for RAVDESS (left) and SAVEE (right).

From the confusion matrix of LSTM-ATN for the RAVDESS dataset (Figure 28), we can conclude that the ‘sad’ emotion achieves the lowest success rate (50%) by identifying only 22 out of 44 samples, as it is sometimes confused with the emotion of ‘disgust’ {in 6 out of 44 samples}. In contrast, the ‘calm’ emotion receives the optimal success rate (95%) compared to the rest, as it identifies 38 out of 40 samples.

From the confusion matrix of LSTM-ATN for the SAVEE dataset (Figure 28), we can conclude that the emotion of ‘happiness’ yields the lowest success rate (27.3%) identifying only 3 of the 11 samples, as it is most often confused with the emotion of ‘surprise’ {in 3 out of 11 samples}. In contrast, the neutral emotion receives the optimal success rate (95.6%) compared to the rest, as it identifies 22 out of 23 samples.

Figure 26. CNN network confusion matrices for RAVDESS (left) and SAVEE (right).

Figure 26. CNN network confusion matrices for RAVDESS (left) and SAVEE (right).

From the confusion matrix of CNN for the RAVDESS dataset (Figure 29), we can conclude that the ‘neutral’ emotion achieves the lowest success rate (28.6%) by identifying only 6 of the 21 samples, as it is most often confused with the emotion of ‘calm’ {in 8 out of 21 samples}. In contrast, the emotion of ‘calm’ receives the optimal success rate (85%) compared to the rest, as it identifies 34 out of 40 samples.

From the confusion matrix of CNN for the SAVEE dataset (Figure 29), we can conclude that the emotion of ‘disgust’ yields the lowest success rate (10%) by identifying only 1 out of 10 samples, as is confused several times with both the emotion of ‘sadness’ {in 4 out of 10 samples} and the ‘neutral’ emotion {in 3 out of 10 samples}. In contrast, the ‘neutral’ emotion receives the optimal success rate (82.6%) compared to the rest, as it identifies 19 out of 23 samples.

Figure 27. CNN network with attention mechanism confusion matrices for RAVDESS (left) and SAVEE (right).

Figure 27. CNN network with attention mechanism confusion matrices for RAVDESS (left) and SAVEE (right).

From the confusion matrix of CNN-ATN for the RAVDESS dataset (Figure 30), we can conclude that ‘neutral’ emotion yields the lowest success rate (57%) as it is often confused with the emotion of ‘calm’ {in 9 out of 21 samples}. In contrast, the ‘calm’ emotion receives the optimal success rate (97%) compared to the rest, as it identifies 39 out of 40 samples.

From the confusion matrix of CNN-ATN for the SAVEE dataset (Figure 30), we can conclude that the emotion of ‘disgust’ yields the lowest success rate (60%) by identifying 6 out of 10 samples, as it is confused a few times with the ‘neutral’ emotion {in 2 out of 10 samples}. In contrast, both the emotion of ‘anger’ and the emotion of ‘sadness’ receive the best success rate (91.6%) compared to the rest, as it identifies 11 out of 12 samples.

In conclusion, from all the above we observe that for the RAVDESS base our models can on average perceive more successfully the emotions of ‘calm’ and ‘surprise’, while they find it difficult to determine the ‘neutral’ emotion. This may be due to the fact that in this database there are two basic emotions that approach the ‘neutral’ emotion, one from a negative point of view and the other from a positive point of view, making it difficult to determine the right emotion. Regarding the SAVEE database, we observe that our models can perceive the ‘neutral’ emotion more successfully, as in this database it is unique, while they find it difficult to identify the emotions of ‘happiness’ and ‘disgust’.

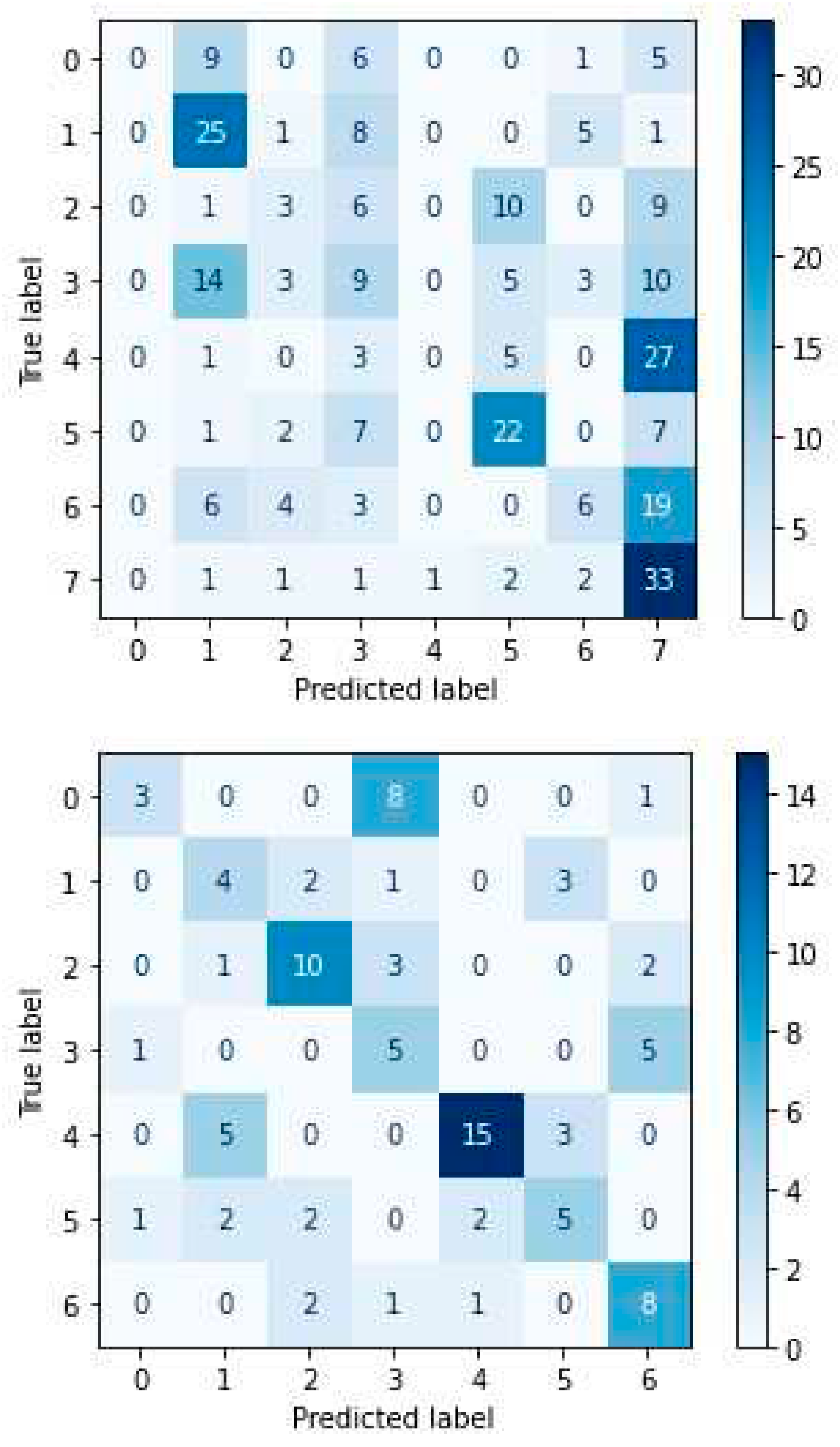
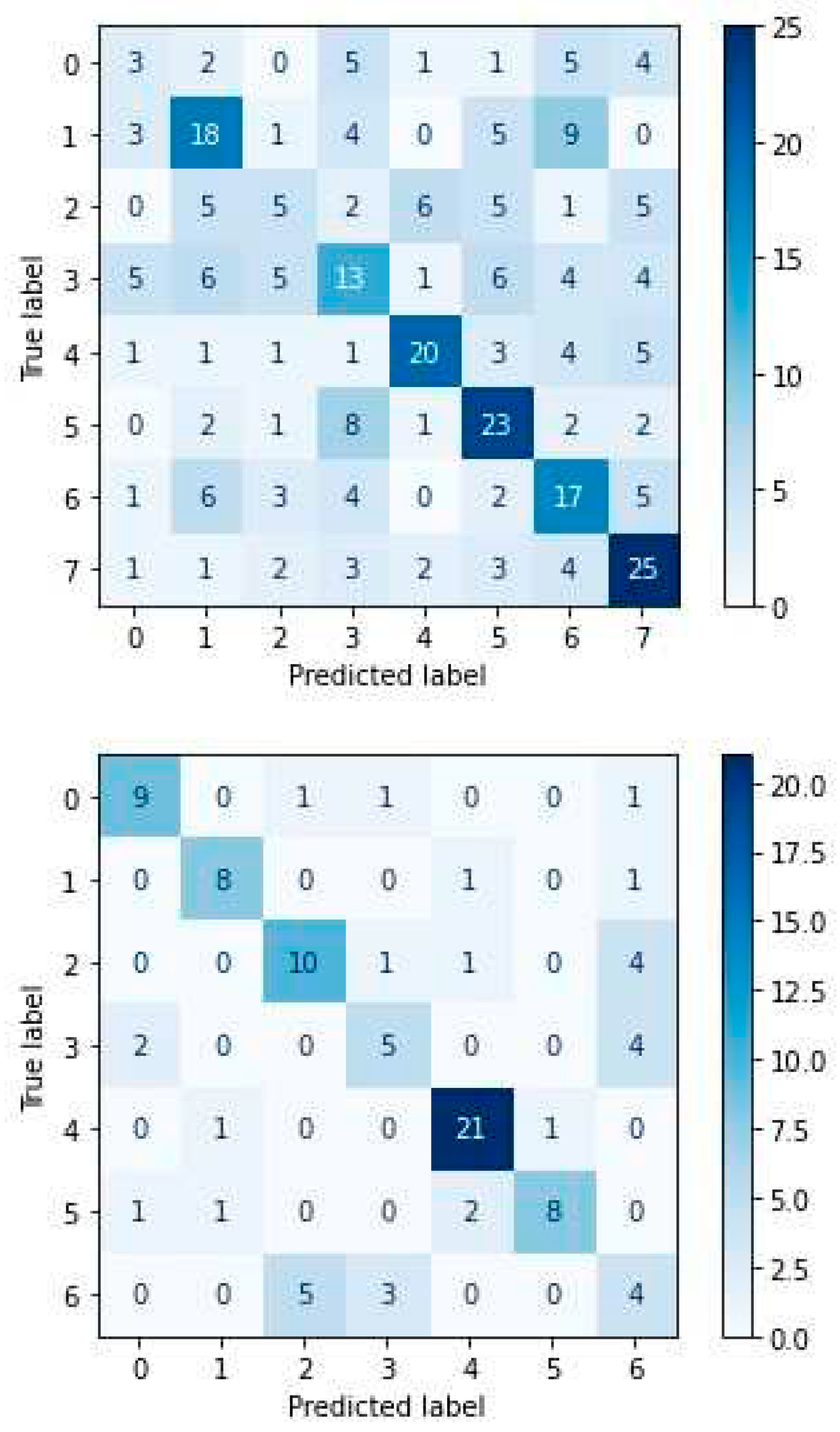
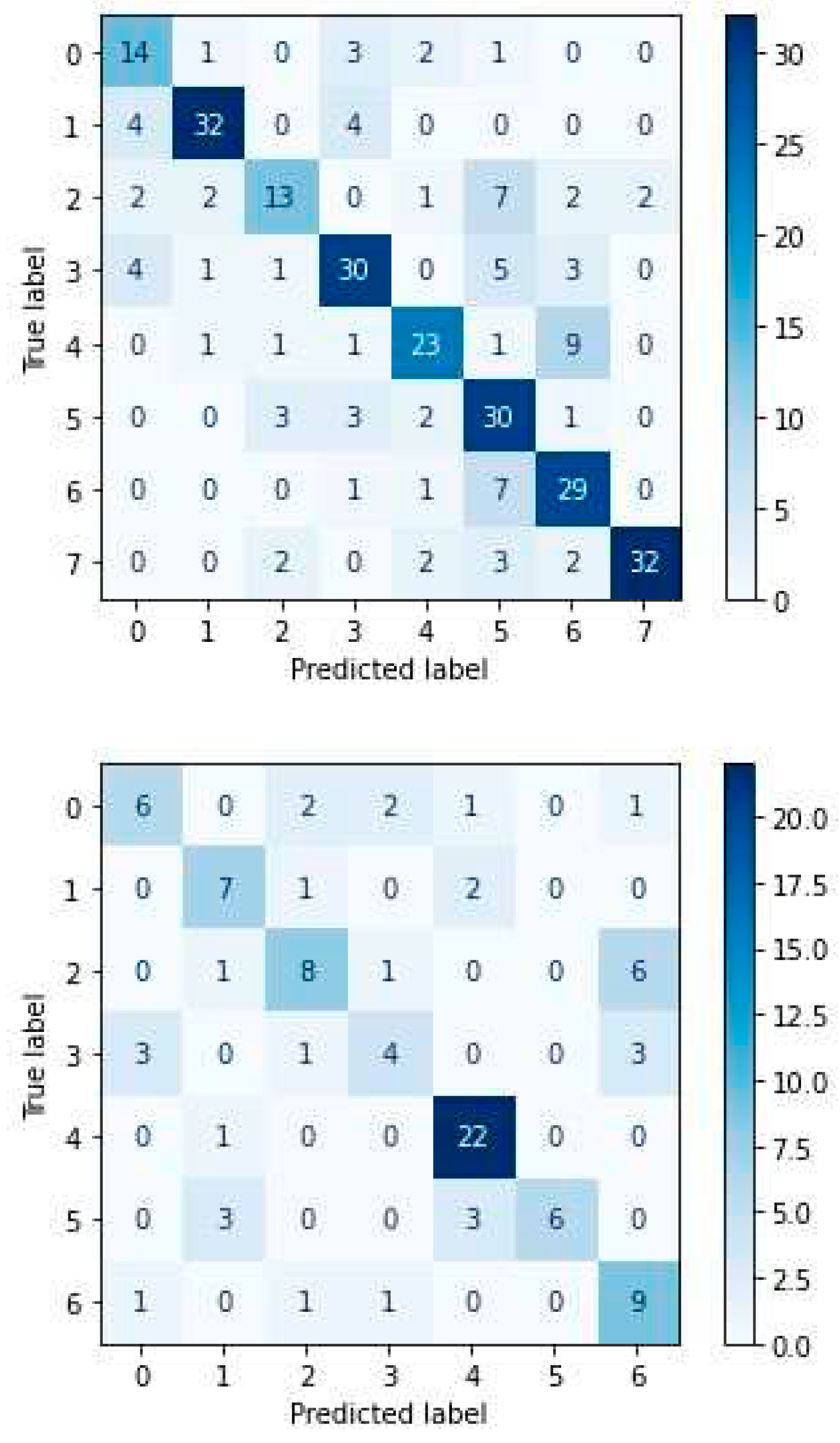
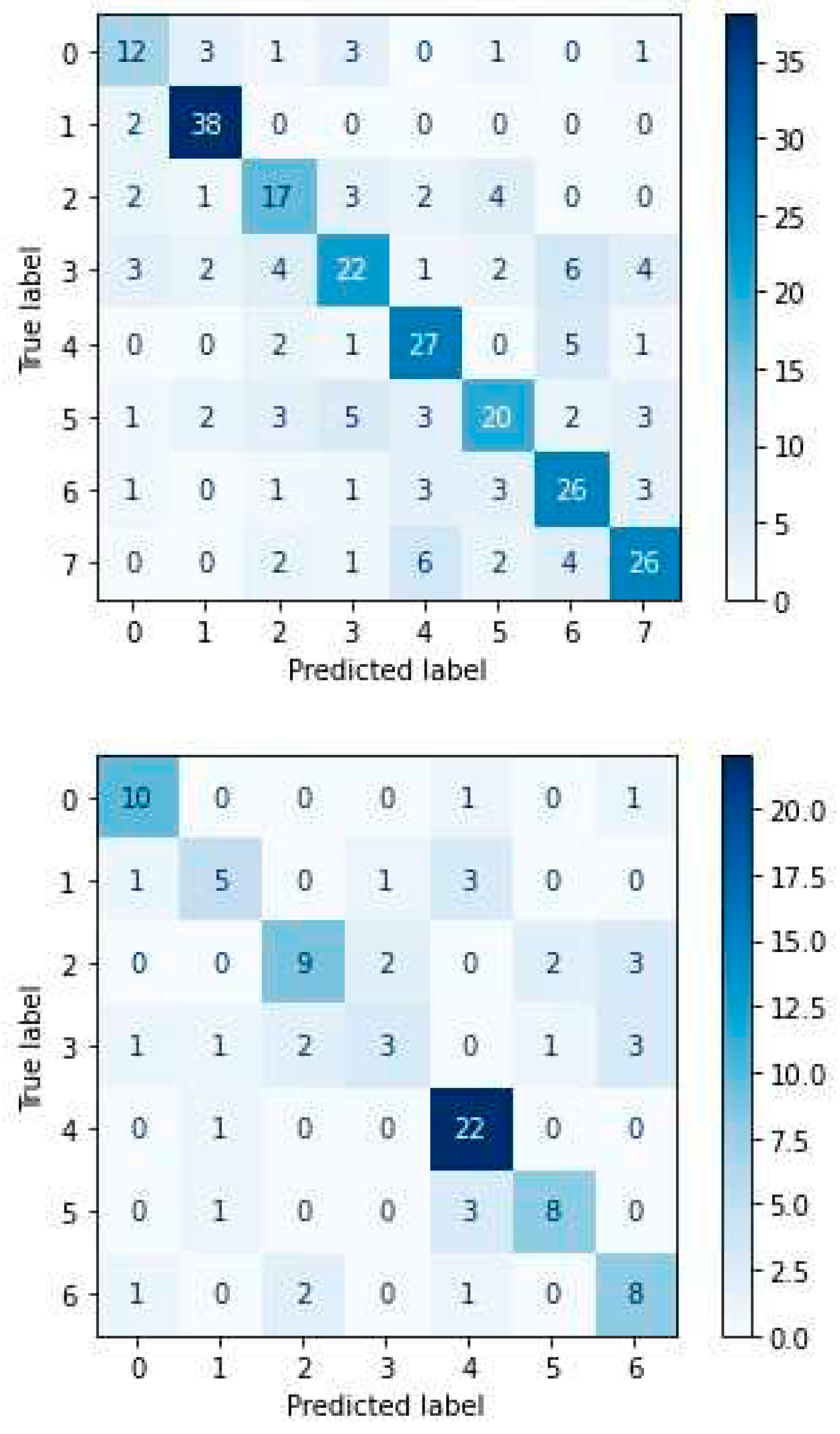
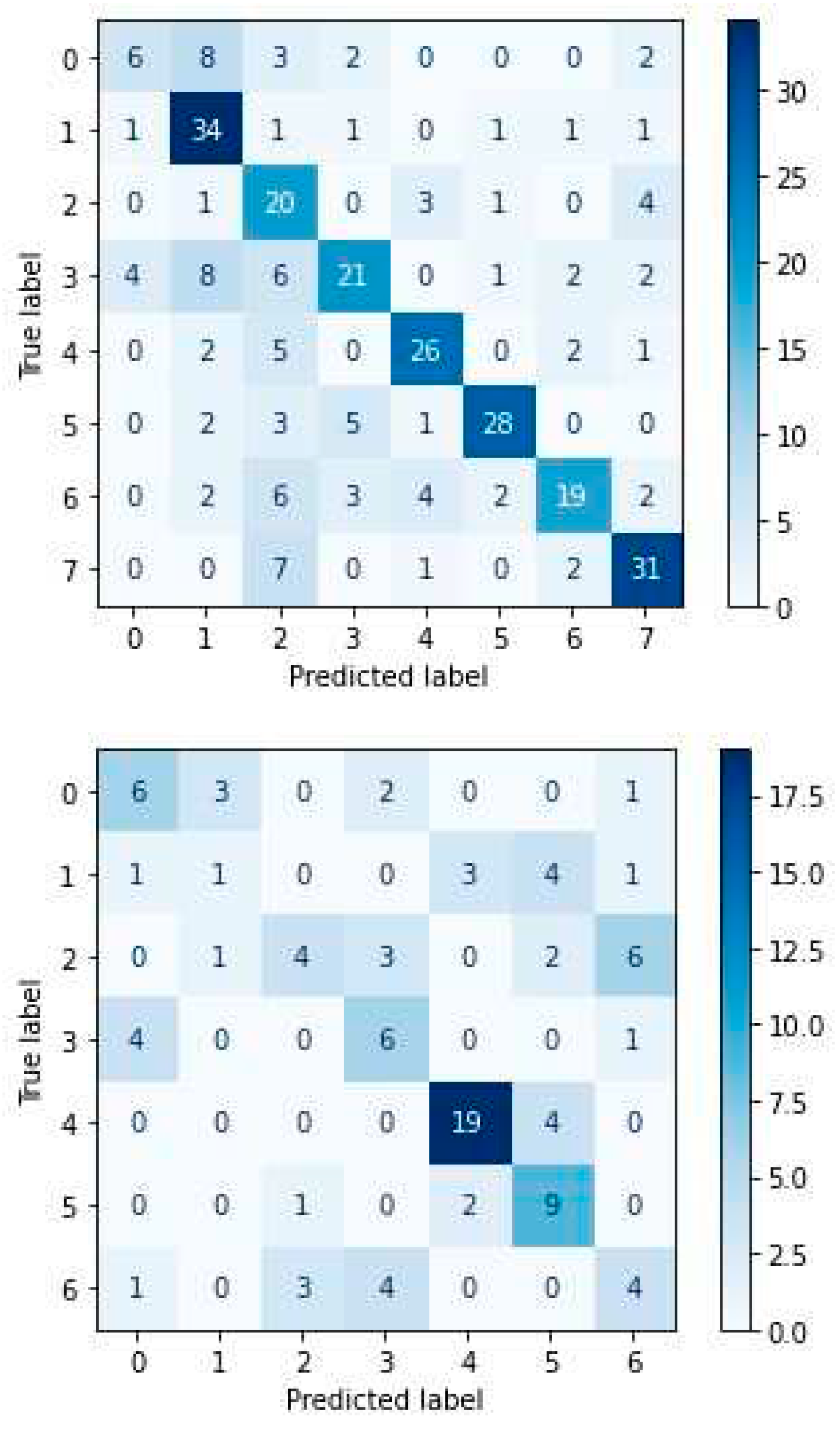
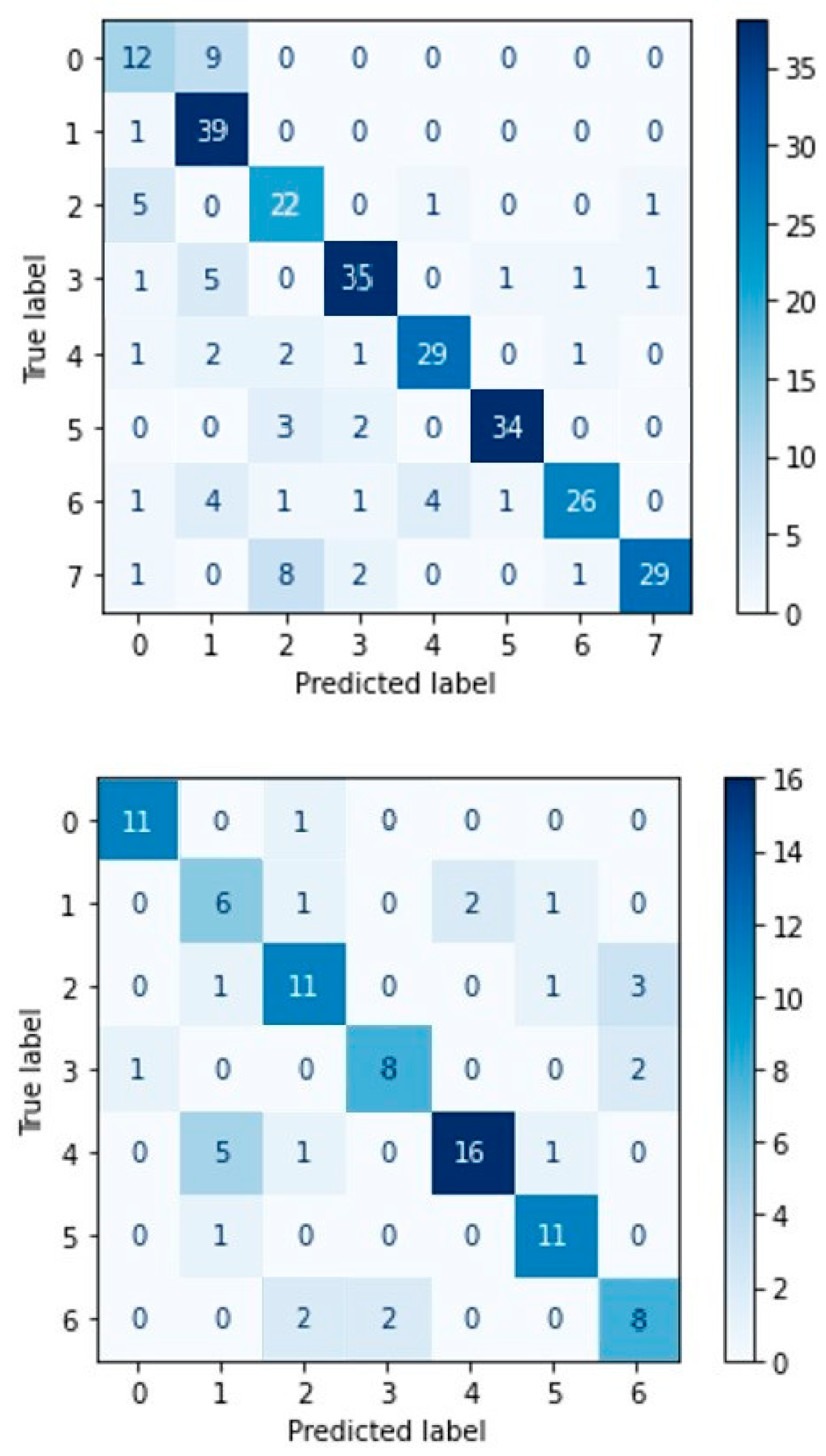
4. Discussion

Table 2. Prediction results of the models in Ravdess and Savee Databases (weighted accuracy).

5. Conclusions

References

1. Wang, X.; Zhang, Y.; Yu, S.; Liu, X.; Yuan, Y.; Wang, F. E-learning recommendation framework based on deep learning. In Proceedings of the 2017 IEEE International Conference on Systems, Man, and Cybernetics (SMC); 2017; pp. 455–460. [Google Scholar] [CrossRef]
2. Jelena Gligorijevic, Djordje Gligorijevic, Martin Pavlovski, Elizabeth Milkovits, Lucas Glass, Kevin Grier, Praveen Vankireddy, Zoran Obradovic. Optimizing clinical trials recruitment via deep learning. Journal of the American Medical Informatics Association 2019, 26, 1195–1202. [Google Scholar] [CrossRef]
3. Davatzikos, C.; Ruparel, K.; Fan, Y.; Shen, D.; Acharyya, M.; Loughead, J.; Gur, R.; Langleben, D.D. Classifying spatial patterns of brain activity with machine learning methods: Application to lie detection. NeuroImage 2005, 28, 663–668. [Google Scholar] [CrossRef]
4. Justesen, N.; Bontrager, P.; Togelius, J.; Risi, S. Deep Learning for Video Game Playing. IEEE Transactions on Games 2020, 12, 1–20. [Google Scholar] [CrossRef]
5. Lavrentyeva, G.; Novoselov, S.; Malykh, E.; Kozlov, A.; Kudashev, O.; Shchemelinin, V. Audio Replay Attack Detection with Deep Learning Frameworks. Proc. Interspeech 2017, 82–86. [Google Scholar] [CrossRef]
6. Uchechukwu Ajuzieogu. The Role of AI In Modern Computing and Education”, Computer Education Seminar 2019, UNN, A seminar approach to understanding the underlying principles of AI and its relevance to Education, in the 21st Century, 2019.
7. Jalal, M.A.; Loweimi, E.; Moore, R.K.; Hain, T. Learning Temporal Clusters Using Capsule Routing for Speech Emotion Recognition. Proc. Interspeech 2019, 1701–1705. [Google Scholar] [CrossRef]
8. Mustaqeem; Kwon, S. A CNN-Assisted Enhanced Audio Signal Processing for Speech Emotion Recognition. Sensors 2020, 20, 183. [Google Scholar]
9. Singh, Y.B.; Goel, S. A systematic literature review of speech emotion recognition approaches. Neurocomputing 2022, 492, 245–263. [Google Scholar] [CrossRef]
10. Wani, T.M.; Gunawan, T.S.; Qadri, S.A.A.; Kartiwi, M.; Ambikairajah, E. A comprehensive review of speech emotion recognition systems. IEEE access 2021, 9, 47795–47814. [Google Scholar] [CrossRef]
11. Khalil, R.A.; Jones, E.; Babar, M.I.; Jan, T.; Zafar, M.H.; Alhussain, T. Speech emotion recognition using deep learning techniques: A review. IEEE Access 2019, 7, 117327–117345. [Google Scholar] [CrossRef]
12. Abbaschian, B.J.; Sierra-Sosa, D.; Elmaghraby, A. Deep learning techniques for speech emotion recognition, from databases to models. Sensors 2021, 21, 1249. [Google Scholar] [CrossRef]
13. Wen, G.; Li, H.; Huang, J.; Li, D.; Xun, E. Random Deep Belief Networks for Recognizing Emotions from Speech Signals. Computational Intelligence and Neuroscience 2017, 2017, 1945630. [Google Scholar] [CrossRef]
14. Badshah, A.M.; Ahmad, J.; Rahim, N.; Baik, S.W. Speech Emotion Recognition from Spectrograms with Deep Convolutional Neural Network. In Proceedings of the 2017 International Conference on Platform Technology and Service (PlatCon); 2017; pp. 1–5. [Google Scholar] [CrossRef]
15. Zhao, J.; Mao, X.; Chen, L. Speech emotion recognition using deep 1D & 2D CNN LSTM networks. Biomed. Signal Process. Control. 2019, 47, 312–323. [Google Scholar]
16. Lee, C.; Song, K.Y.; Jeong, J.; Choi, W.Y. Convolutional Attention Networks for Multimodal Emotion Recognition from Speech and Text Data. arXiv 2019, arXiv:1805.06606. [Google Scholar]
17. Tang, D.; Zeng, J.; Li, M. An End-to-End Deep Learning Framework for Speech Emotion Recognition of Atypical Individuals. Proc. Interspeech 2018, 162–166. [Google Scholar] [CrossRef]
18. Chen, M.; He, X.; Yang, J.; Zhang, H. 3-D Convolutional Recurrent Neural Networks With Attention Model for Speech Emotion Recognition. IEEE Signal Processing Letters 2018, 25, 1440–1444. [Google Scholar] [CrossRef]
19. Li, P.; Song, Y.; Mcloughlin, I.; Guo, W.; Dai, L. An Attention Pooling Based Representation Learning Method for Speech Emotion Recognition. Interspeech 2018. [Google Scholar]
20. Jiang, W.; Wang, Z.; Jin, J.S.; Han, X.; Li, C. Speech Emotion Recognition with Heterogeneous Feature Unification of Deep Neural Network. Sensors 2019, 19, 2730. [Google Scholar] [CrossRef]
21. Huang, K.; Wu, C.; Hong, Q.; Su, M.; Chen, Y. Speech Emotion Recognition Using Deep Neural Network Considering Verbal and Nonverbal Speech Sounds. In Proceedings of the ICASSP 2019 - 2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, United Kingdom; 2019; pp. 5866–5870. [Google Scholar] [CrossRef]
22. Issa, D.; Demirci, M.; Yazici, A. Speech emotion recognition with deep convolutional neural networks. Biomedical Signal Processing and Control 2020, 59, 101894. [Google Scholar] [CrossRef]
23. Makhmudov, F.; Kutlimuratov, A.; Akhmedov, F.; Abdallah, M.S.; Cho, Y.I. Modeling Speech Emotion Recognition via Attention-Oriented Parallel CNN Encoders. Electronics 2022, 11, 4047. [Google Scholar] [CrossRef]
24. Abdul, Z.K.; Al-Talabani, A.K. Mel Frequency Cepstral Coefficient and its applications: A Review. IEEE Access 2022. [Google Scholar] [CrossRef]
25. Luong, M.T.; Pham, H.; Manning, C.D. Effective Approaches to Attention-based Neural Machine Translation. arXiv 2015, arXiv:1508.04025. [Google Scholar]
26. Jackson, P.; Haq, S. Surrey Audio-Visual Expressed Emotion (SAVEE) database. 2011. Available online: http://kahlan.eps.surrey.ac.uk/savee/Database.html.
27. Livingstone, S.R.; Russo, F.A. The Ryerson Audio-Visual Database of Emotional Speech and Song (RAVDESS): A dynamic, multimodal set of facial and vocal expressions in North American English. PLoS ONE 2018, 13, e0196391. [Google Scholar] [CrossRef] [PubMed]
28. Sivanagaraja, T.; Ho, M.K.; Khong, A.W.H.; Wang, Y. End-to-end speech emotion recognition using multi-scale convolution networks. In Proceedings of the 2017 Asia-Pacific Signal and Information Processing Association Annual Summit and Conference (APSIPA ASC), Kuala Lumpur; 2017; pp. 189–192. [Google Scholar] [CrossRef]
29. Latif, S.; Rana, R.; Younis, S.; Qadir, J.; Epps, J. Transfer Learning for Improving Speech Emotion Classification Accuracy. arXiv 2018, arXiv:1801.06353. [Google Scholar]
30. HFayek, M.; Lech, M.; Cavedon, L. Towards real-time Speech Emotion Recognition using deep neural networks. In Proceedings of the 2015 9th International Conference on Signal Processing and Communication Systems (ICSPCS), Cairns, QLD; 2015; pp. 1–5. [Google Scholar] [CrossRef]
31. Chenchah, F.; Lachiri, Z. Acoustic Emotion Recognition Using Linear and Nonlinear Cepstral Coefficients. International Journal of Advanced Computer Science and Applications (IJACSA) 2015, 6. [Google Scholar] [CrossRef]
32. Rajak, R.; Mall, R. Emotion recognition from audio, dimensional and discrete categorization using CNNs. In Proceedings of theTENCON 2019 - 2019 IEEE Region 10 Conference (TENCON), Kochi, India; 2019; pp. 301–305. [Google Scholar] [CrossRef]
33. Venkataramanan, K.; Rajamohan, H.R. Emotion Recognition from Speech. arXiv 2019, arXiv:1912.10458. [Google Scholar]
34. Mohanty, H.; Budhvant, S.; Gawde, P.; Shelke, M. Implementation of Mood Detection through Voice Analysis using Librosa and CNN. In Proceedings of the International Research Journal of Engineering and Technology (IRJET), Thane, Maharashtra, India, 6 June 2020; pp. 5876–5879. [Google Scholar]
35. Huang, A.; Bao, P. Human Vocal Sentiment Analysis. arXiv 2019, arXiv:1905.08632. [Google Scholar]
36. Wagner, J.; et al. Dawn of the Transformer Era in Speech Emotion Recognition: Closing the Valence Gap. IEEE Transactions on Pattern Analysis and Machine Intelligence 2023, 45, 10745–10759. [Google Scholar] [CrossRef]