Prerpints.org logo
Preprint
Article

Multifractal Characteristics of Uranium Grade Distribution and Spatial Regularities in a Sandstone Type Uranium Deposit in Xinjiang, China

Altmetrics

Downloads

66

Views

20

Comments

0

A peer-reviewed article of this preprint also exists.

supplementary.docx (21.43KB )

This version is not peer-reviewed

Submitted:

15 September 2023

Posted:

19 September 2023

You are already at the latest version

Alerts
Abstract
Based on the analysis of the spatial distribution of uranium grade in 348 boreholes of a uranium deposit in Xinjiang, the enrichment and spatial variation of uranium ore in two stopes of the deposit are discussed by using multifractal theory. The distribution characteristics of uranium ore of the two stopes are studied by multifractal parameters: the scaling exponent of mass , the scaling exponent of each sub-set and its corresponding fractal dimension , the fractal dimension D0 and information dimension D1. The differences of uranium distribution in two stopes can be well quantified by multifractal spectrum and multifractal parameters( , , ).10m×10m is defined as a fence unit, and the window sizes are respectively set, the singularity exponent of the two stopes are calculated by this element concentration-area(C-A) method. The results show that the multifractal theory and model can organically combine spatial structure information, scale change information and anisotropy information to obtain low-grade and weak mineral resources information, and can effectively distinguish complex and superimposed anomalies. This will provide a basis for local concentration and spatial variation rules of uranium distribution and the design of the parameters of leaching uranium mining well site.
Keywords: 
Subject: Engineering  -   Mining and Mineral Processing

1. Introduction

Nonlinear theory and complexity theory are regarded as some of the core contents of scientific research in the 21st century. The application of modern nonlinear theory and complexity theory, especially chaos theory, fractal/multifractal theory [1,2,3,4] and self-organized criticality theory, to the basic research of earth system science and the application of research on natural resources has shown good prospects [5,6]. The fractal method is an effective method for studying self-similarities or statistical self-similarities and describing the singularity of field values [7,8,9]. The fractal method can reveal some hidden laws from complex and irregular phenomena. A large number of research results at home and abroad show that it is of great significance to describe the self-similar hierarchical structure of objective things through various methods and reveal the similarities between the local and the whole in the aspects of structure, function, information, time, space and other forms of statistical significance. The fractal method is widely used in the fields of physics [10], minerals processing [11,12,13], uranium mining [14], medicine [15], and geotechnical engineering [16,17], and obtained a good application effect. In recent years, fractals have also been widely used in the distribution of geochemical elements; the study of the distribution law of geochemical elements is an important way to explore mineralization enrichment and spatial variation laws [18]. The study of the distribution law of geochemical elements is an important way to explore the mineralization enrichment and spatial variation law of elements, and the statistical characteristics of geochemical element data can be used to describe the spatial and temporal distribution laws of geochemical elements. However, the multi-dimensional fractal method is an effective method for studying the distribution law of self-similarities or statistical self-similarities and describing the singularity of field values.
In terms of metallurgy and geostatistics, studying the distribution of mineral deposits can reasonably determine the exploration network, underground engineering sampling spacing and well site process parameters, and improve the efficient mining and recovery of mineral resources. Many scholars have used fractal theory and models to study the mineral distribution characteristics of some mineral deposits and mining areas [19,20,21]. Shen et al. [22] discussed the fractal dimension characteristics of a gold deposit and its geological significance, and the results showed that the fractal dimension D could quantitatively characterize the complexity of the ore body and the degree of spatial heterogeneity in the gold grade of the studied gold deposit. Wang et al. [23] used the studied deposit to confirm that the correlation coefficients of the multifractal parameters R (spectrum symmetry parameter) and f are relatively higher, indicating that the spatial accumulation patterns are almost the same during the ore-forming process. Zhao et al. [24] showed that the geochemical distribution patterns can be characterized by multifractal parameters such as singular exponent α , as well as τ and Δ α . Seyedrahimi et al. [25] explained that the fractal method could separate one phase of change based on the fractal dimension with high-concentration areas of the Au element in the studied deposit. Tao et al. [26] analyzed the grades of ore elements in the studied deposit using fractal and multifractal methods. Zuo et al. [27] collected 10 mineralized boreholes and 1 non-mineralized borehole from the Qulong copper deposit, Tibet, western China, to identify the vertical distribution properties of Cu values using fractal models. The fractal methods can describe the distribution, mineralization, enrichment and anomalies of some mineral deposits [28,29,30,31]. These studies fully demonstrate the good application prospects of fractal methods and models in the fields of geostatistics and metallurgy.
Compared with traditional geostatistics methods, fractal methods are linked to the concepts of self-similarity, reformation, and scaling laws in physics, which can measure the complexity and inhomogeneity of spatial structure and physical processes and the probability distribution of masses, and can also effectively portray the complex context of mineral distribution within a deposit, with areas of mineral enrichment formed by local superposition [32]. Shen [33] investigated the fractal characteristics and geological significance of the gold grade distribution of a gold mine in Xinjiang in detail. Kusák [34] discussed how to describe the drainage patterns of the Blue Nile Basin in Ethiopia using the fractal method. The geochemical distribution patterns and migration characteristics of the major and trace elements can be well demonstrated by the multifractal method and multifractal parameters [35]. Based on the model of multifractals, scholars have used many methods to calculate the distribution singularity exponent of geochemical elements to separate the geochemical anomalies from the background. Xiao et al. [36] proposed a novel batch sliding window (BSW) based on the singularity mapping method to improve the accuracy of the calculation of singularity exponent. Wang et al. [37] discussed U-statistics and singularity mapping as two efficient approaches for the separation of geo-anomaly and background. Liu et al. [38] presented an efficient method that combines a sequential indicator co-simulation with local singularity analysis to identify uncertainty propagation in geochemical elements’ anomalies. Xu et al. [39] presented a window-based local singularity mapping through a comprehensive analysis of multiple parameters, including the average concentration calculation algorithm. Mohammadi et al. [40] used U-statistics and the fractal concentration–area model for the separation and detection of anomalous areas of the background. Wen et al. [41] made a summarization to the C-A, concentration–distance (C-D), spectrum–area (S-A), multifractal singular-value decomposition (MSDV) methods, and the presented multifractal model is meaningful for the anomaly separation of the geochemical elements.
Although many studies show how to use multifractal and its parameters to describe the spatial distribution law of geochemical elements, few studies focus on how to transform macroscopic regional element content distribution into calculable mass distribution. As a strategic energy source, uranium is the most valuable source of natural wealth in the world, and it is also an extremely relevant resource for China [42]. In this paper, the coordinates of the boreholes of the studied deposit are marked in detail to obtain an accurate floor plan of the distribution of uranium ore grade of the deposit. The gray-scale map of uranium-ore-grade value is further obtained, and the fractal characteristics of uranium ore distribution in NO.11 and NO.12 stopes are obtained by further analysis and calculation. The local enrichment information of uranium ore content is also extracted. This has certain significance for the research on metallogeny and mineral resources’ exploitation, including mineral rock structure, a description of mineral deposit and ore body characteristics, mineral resources’ distribution simulation, element enrichment and agglomeration laws, and mineral resources’ information.

2. Preliminaries and Method

2.1. Fractal theory

In fractal theory, if the mass of a set is uniformly distributed, we have Equation (1): [8]
N ( r ) ∼ 1 r D   or   D ∼ log N ( r ) log ( 1 / r ) ,
where r is the ruler of the measure, N ( r ) is the number of boxes of the measure, and, given that the mass is uniformly distributed, each section of mass can be expressed as
P i = r i α ,
where α is the scale exponent.
For the non-uniform fractal object, to reflect the non-uniformity of its mass, we use the q-order moment ∑ i p i q of mass to represent the boxes’ number N , which be weighted. To reflect that the length of the ruler is not uniform, we assume that this mass number (or q-order moment) is not proportional to r − D but is proportional to r τ ( q ) ; that is,
∑ i p i q ∼ r τ ( q ) ,
and
− τ ( q ) = log ∑ i = 1 N p i q log ( 1 / r ) ,
where τ ( q ) can be called the scale exponent of the mass moment (q-order).
Obviously, if the set is of uniform mass, its q-order moment ∑ i p i q will be proportional to r α q , while, for the non-uniform set, the scale exponent of the mass moment is τ ( q ) , and the scale exponent α ( q ) of each subset and its corresponding fractal dimension f ( α ) are derived as Equations (5)-(10). For each segment, the number of boxes covered by boxes with scale r will be:
ρ ( α ) d α ⋅ r − f ( α ) ,
where ρ ( α ) d α is the number of sets in segment d α . For ∑ p i q , we can obtain
∑ p i q = ∫ ρ ( α ) r − f ( α ) ⋅ r α q d α .
It can be obtained by combining equations (3) and (5)
τ ( q ) = α ( q ) q − f ( α ( q ) ) .
It is not difficult to prove that the curve f ( α ) is a convex shape, and it can be further obtained that the slope value of the function f ( α ) is the order of the q-order moment. Therefore, there is
d τ d q = α ( q ) .
Equation (7) shows that if the scale exponent α ( q ) and its corresponding dimension f ( α ( q ) ) are given, the scale exponent τ ( q ) of its q-order moment can be obtained. Otherwise, if τ ( q ) is known, the scale exponent α ( q ) can be known by Equation (8), and then f ( α ) will be determined by Equation (7).
The highest point of the curve f ( α ) is an extreme point, the slope of this point is d f / d α = 0 , and the value of the function f ( α ) of this point can be obtained from Equation (6)
− τ ( o ) = f ( α ( o ) ) ,
the value f ( α ( ο ) ) is the fractal dimension D0 of the set.
If the box with size r is used to measure the fractal set, Shannon's information is proportional to log ( 1 / r ) . If the fractal dimension of the set is D1, then its information is log ( 1 / r ) times of D1, i.e.,
D 1 = I 1 log ( 1 / r ) = − ∑ i = 1 N P i ⋅ l o g P i log ( 1 / r ) ,
where D1 is called the information dimension.
For the uniform fractal object,
P i = 1 N ,
Then,
D 1 = I 1 log ( 1 / r ) = − ∑ i = 1 N P i ⋅ l o g P i log ( 1 / r ) = D 0 ,
that is , for the uniform fractal object, information dimension D1 is the same thing as fractal dimension D0
For the non-uniform fractal object, we should consider the q-order moment ∑ i p i q of mass, similar to definition (10) of information dimension D1; the generalized Renyi dimension Dq is defined as
D q = I q log ( 1 / r ) = 1 1 − q log ∑ i = 1 N P i q log ( 1 / r ) .
Combining Equations (4) and (13), we obtain [8]
D q = τ ( q ) q − 1 ,
D q is defined by Equation (13) obviously including D 0 and D 1 . Taking q=0 in Equation (13), D 0 is the fractal dimension; taking q=1, and using Robita's rule for the limit q → 1 , we can obtain the information dimension D1. Therefore, the difference between D 0 and D 1 reflects the uniformity of the fractal. By combining the equations given in this paper, we can calculate the special values of τ ( q ) , α ( q ) , f ( α ( q ) ) and D q , which could help us judge and analyze the characteristics of the fractal object.

2.2. Overview of the ore deposit

The studied uranium deposit belongs to the sandstone uranium deposit controlled by interlayer oxidation zone, in Yili Basin, Xinjiang, China. It is the first in-service mine to have carried out a series of experimental works, and has become the first uranium production base of underground leaching and mining in China. Accordingly, a relatively complete underground leaching technology system has been established [43], which has made important contributions to the production of natural uranium in the country. The sandstone uranium resources, which had been regarded as "dull ore" in the past, have become a kind of ground-leachable uranium resource. In recent years, the sandstone-type uranium resources discovered and proved in the north have been increasing, and the resource reserves have exceeded the hard rocks in the south. Many scholars have discussed the characteristics, reserves and pore characteristics of uranium sandstone in Xinjiang, China [44].
The studied deposit is located in the western section of the southern slope belt of the Yili Basin [45], and its tectonic position belongs to the east of the Yili microplate, which is sandwiched between the Kazakhstan plate and the Tarim plate. Yili Basin is a large meso-Cenozoic intermountain depression basin. Its basement is composed of Proterozoic and Paleozoic, and its cap beds are composed of Triassic, Jurassic, Cretaceous, Tertiary and Quaternary. The geological map of uranium deposits in the mining area is shown in Figure 1.
In the studied deposit, we selected stopes No. 11 and No. 12 as research objects, with a thickness of 13.4 m to 27.0 m and an average thickness of 19.5 m. The mineralization is controlled by the interlayer oxidation–reduction transition zone, which extends along the front of the oxidation zone in the plane as a serpentine strip, and in the profile, has a short head and long tail curl or long head and short tail curl. The ore deposit is divided into two parts: coil head and wing. The length of the ore body in coil head part in No.11 and No.12 stopes ranges from 45 m to 205 m, with an average of 115 m. The ore body in the wing part is mainly the upper wing ore body, with a length of from 50 m to 587 m, with an average of 204 m. The ore body is buried from 110 m to 240 m, the occurrence is basically the same as that of the sand body, and the dip angle is 5° to 15°. The thickness of the ore body ranges from 0.5 m to 12.3 m, with an average of 3.7 m. The thickness of the coil head ore body ranges from 1.1m to 12.3 m, with an average of 5.0 m. The thickness of the upper wing ore body ranges from 0.5 m to 5.5 m, with an average of 2.7 m. The ore grade varies greatly from the coil head to the wing. The ore grade of the coil head ranges from 0.015% to 0.142% with an average of 0.086%. The ore grade in the wing ranges from 0.015% to 1.521%, averaging 0.090%. The area of stopes No. 11 and No. 12 of the studied deposit is 233,657 m2, and the total number of boreholes is 338, among which, the No.11 stope has an area of 10,7102 m2, with 161 boreholes; No.12 stope has an area of 126555 m2, with 177 boreholes. The boreholes of the deposit are arranged in a determinant (or formation), with rows spaced from 25 m to 40m apart, most of which are from 25 m to 30m apart. The boreholes’ distribution of the two stopes is shown in Figure 2 . Based on the geological data, the average grade isogram of uranium ore revealed by borehole logging in the No. 11 and 12 stopes of the deposit is shown in Figure 3.

3. Results and discussion

The ore grade of an ore body in a mining area can be seen as the combined product of geological and mineralization processes in the area, with each geological and mineralization action potentially leading to the enrichment or depletion of certain trace elements in the rock, and the superposition of such repeated mineralization in space will eventually form a complex spatial distribution pattern of trace elements with multiple fractal distribution characteristics[22,23,27,29]. Combined with the distribution characteristics of 338 boreholes in the No. 11 and No. 12 stopes of the studied mining area, the multifractal detrended fluctuation analysis method and Equation (6), Equation (8), Equation (12) and Equation (14) are used to analyze and calculate the uranium grade value, and the multifractal parameter diagrams shown in Figure 4 and Figure 5 can be obtained.
In this paper, the multifractal method is used to analyze the spatial distribution characteristics of uranium grade in the studied deposit. Based on the further analysis of the multifractal spectrum function f ( α ) and its parameters in Figure 4 and Figure 5, the relevant parameter values of the multifractal spectrum, as shown in Table 1 and Table 2, can be calculated.

3.1. Multifractal spectrum and multifractal parameters

It can be seen from Figure 4(a, b) and Figure 5(a, b) that the average uranium grade in the two stopes of the deposit has obvious scale invariance when q ∈ [ − 50 , 50 ] , ln ( ξ ) ∈ [ − 5.6 , − 0.6 ] , which shows obvious multifractal characteristics. The relationship between the generalized Renyi dimension Dq (include D0 and D1) and order q is shown in Figure 4(b) and Figure 5(b); it is obvious that Dq changes with the change in q. Furthermore, in Figure 4(c) and Figure 5(c), we can obtain the relationship between q ∼ α ( q ) and q ∼ f ( q ) and, from that, we determined the multifractal spectrum parameter values of the average grade of uranium ore at q = 0 ， 1 ， ± ∞ ; the multifractal spectrum parameter values are shown in Table 1 and Table 2. The following results are obtained: α max in No.11 stope and No.11 stope are 2.60 and 2.64, respectively; α min in No.11 stope and No.12 stope are 1.68 and 1.52, respectively; f max in No.11 stope and No.11 stope are 1.98 and 1.93 respectively’ f max represents the value of D0. All the results in Table 1 and Table 2 prove that there are some differences in the distribution of uranium ore in the two stopes, which require further analysis. In fractal theory, if the mass of a set is uniformly distributed, only one scaling exponent α and its corresponding fractal dimension D0 are needed to describe it, while for the set with non-uniform mass, new parameters should be determined to reflect the non-uniform structure. As can be seen in Figure 4(b) and Figure 5(b), the average grade fractal dimension and information dimension of uranium ore in the No.11 stope are 1.98 and 1.87, respectively, while those in the No. 12 stope are 1.92 and 1.83, respectively. The difference between D0 and D1 reflects the non-uniformity of fractal, and indicates that the mineralization in the No.11 stope is more uniform. If there is a high grade value of the ore body, it is more likely that the ore body is rich. In Figure 4(d) and Figure 5(d), we can also learn the singularity exponent α of the average grade of uranium in the two stopes of the deposit changes in a wide range, and the multifractal spectral function f ( α ) is not a point on the plane f ∼ α , but basically presents a continuous distribution, and reaches the maximum in α = 2.15 and α = 2.05 , respectively. This also further confirms the existence of multifractal characteristics of uranium distribution in this deposit.
In addition, the multifractal spectrum curves of uranium grade in the two stopes are both convex and asymmetric images, which indicate that the uranium ore in this deposit has undergone the local superposition of different sources and different degrees in the process of mineralization.
According to Figure 4(d) and Figure 5(d), the multifractal spectra f ( α ) of the average grade of uranium in the two stopes show different degrees of asymmetry, and the singularity exponent α = 2 divides the spectral function curve f ( α ) into two parts. The α < 2 part indicates that the content of chemical elements is enriched; the α > 2 part indicates that the content of chemical elements is depleted; α = 2 reflects the normal background distribution. Therefore, according to the spectral function curves of Figure 4(d) and Figure 5(d), the average grade of uranium in the two stopes is enriched to a certain extent.
If the value of the right end point of the multifractal spectrum f ( α ) is higher than that of the left end point, and its shape is like a right hook, this means that there are more small values, that is, the probability of being in the region of low value is higher than that of being in the region of high value. On the contrary, if the multifractal spectrum has a left hook shape, the large value is dominant. It can be seen from Figure 4 and Figure 5 that the multifractal spectrums of the average grade of uranium ore in both stopes are right-skewed, and this means the large grade value is dominant.

3.2. Multifractal spectrum parameters analysis of uranium grade

After analyzing the basic features of the multifractal spectral function curve f ( α ) , the practical significance of the spectral function f ( α ) image features is further analyzed by the parameters[27,28,29]. Therefore, the parameters of each multifractal spectrum are calculated according to the fractal spectral function f ( α ) , as shown in Table 1, Table 2 and Table 3.

3.2.1. The opening width of multifractal spectrum ( Δ α )

The parameter Δ α ( Δ α = α max − α min ) reflects the singularity and uniformity of the distribution of the research object on the whole measure. The larger parameter Δ α , the more uneven the distribution of the research object, and the greater the singularity. As can be seen from Table 3, the average uranium-grade fractal spectrum parameters of stope 11 and 12 are 0.74 and 0.72, respectively. The opening width of the fractal spectrum of stope 11 is greater than that of stope 12, which means that the distribution of uranium grade in stope 11 is more singular. The internal structure of uranium ore in this area is more complex, and uranium ore is more likely to be enriched, which is consistent with the distribution of mean uranium grades in the two areas of the deposit revealed in Figure 3 (the isogram reveals that the average grade value of uranium ore in stope 11 is higher than that in stope 12), suggesting that multiple fractals can quantitatively characterize the spatial distribution pattern of the anomaly, reflecting its spatial coverage and geometric properties.

3.2.2. The width Δ α L

of the left half and the width Δ α R of the right half of the curve f ( α ) In general, the multifractal spectrum curve f ( α ) is completely symmetric, but the superposition of any low-content region or high-content region will affect the symmetry of the spectrum curve, resulting in the left or right deviation of the curve f ( α ) .The curve  is bounded by α 0 (the highest point of singularity exponent of f ( α ) ), and Δ α will be divided into two parts. The left part length is Δ α L （ Δ α L = α 0 - α min ） and the right part length is Δ α R （ Δ α R = α max - α 0 ） ; their lengths have practical significance. When Δ α L < Δ α R , the spatial average density difference between the high-value parts of chemical elements is larger; when Δ α L > Δ α R , this indicates that the lower-value part of chemical elements has greater spatial singularity.
According to the data in Table 2, the average-grade multifractal spectrum curves f ( α ) of uranium ore in both stopes are satisfied, Δ α L < Δ α R , indicating that the high content of uranium is more singular than the low content of uranium in the whole deposit.

3.2.3. The spectral height difference Δ f

of the curve f ( α ) The inhomogeneity and complexity of the spatial distribution of chemical element content can be analyzed by analyzing the spectral height difference Δ f in the multifractal spectral curves f ( α ) . According to the data in Table 2, the parameters Δ f of the average grade of uranium ore in the two stopes are 0.19 and 0.34, respectively, and the fractal spectrum curves both show a left hook shape, indicating that the content distribution of uranium ore elements in the deposit is dominated by higher values.
The discussion of the shape characteristics and parameters on the multifractal spectrum f ( α ) of the two stopes is helpful to summarize the spatial distribution and enrichment rule of uranium grade, and to estimate the uranium element value and deposit reserves.

3.2.4. The skew coefficient R of the multifractal spectrum

In the calculation of multifractal spectrum, the skew coefficient R is defined as Equation (15) [46].
R = ( α 0 − α min ) − ( α max − α 0 ) α max − α min
According to the definition of Equation (15), the skew coefficient R ∈ [ − 1 , 1 ] ; when R < 0 , the multifractal spectrum is left-hooked; when R > 0 , the multifractal spectrum is right-hooked; when R = 0 , the multifractal spectrum is bell-shaped. When R → 1 , this represents that there are more areas where the mass of the fractal is dense. When R → − 1 , this means that there are more sparse areas of mass distribution. The data in Table 3 show that the multifractal spectrum deflection coefficients R of uranium ore grade in stopes 11 and 12 are -0.30 and -0.56, respectively, both of which are less than 0, indicating that the multifractal spectrum is left-hooked and there are not many densely distributed areas of uranium ore in the two stopes. Moreover, − 0.30 > − 0.56 , indicating that the uranium ore grade distribution in stope 11 is more densely distributed than that in stope 12.

3.3. Uranium distribution information by multifractal local singularity exponent

Q-Q plot is one of the most commonly used methods to test the statistical frequency distribution characteristics of elements, which can test whether the elements follow normal or lognormal distribution. As shown in Figure 6, the Q-Q plots of uranium-grade values in the two stopes show an approximate linear form, indicating that the distribution of uranium grade values basically follows a lognormal distribution, except for higher outliers. The data that meet the statistical normal distribution or lognormal distribution of geochemical elements are usually the normal values or background values, while, for the outliers that deviate from the straight line, the fractal distribution is satisfied. According to the data of the two stopes, the C-A double-log plot of uranium grade of the two stopes can be obtained using Equation (2), as shown in Figure 7.
In this paper, the local singularity exponent α in multifractal theory is used to analyze the uranium-grade distribution in the deposit. The local self-similarity of value α can reveal the degree of singularity in the distribution of geochemical elements and the local scale characteristics of anomalies so as to identify and extract the abnormal regions of geochemical elements’ distribution. Using the local singularity exponent α to analyze the statistical characteristics of the elements varying with scale in space, which is different from the traditional statistical methods, can intuitively distinguish different kinds of information from the background[39,40,41]. The singularity exponent α of an element indicates the information of a local enrichment region. For singularity exponent α , local self-similar features can be used for characterization [32]:
ρ ( ε ) ∝ ε α − 2
where α is the local singularity exponent, ε is the scale range, and ρ ( ε ) is the average density of element content within the range ε . α can be calculated by the element concentration–area (C-A) method.
According to the spacing between uranium holes in the deposit and the actual terrain and the geomorphology, 10m*10m is defined as a fence unit, and the window sizes ε = 3 , 6 , 9 ⋯ , 45 are respectively set to calculate the average density value ρ ( ε ) of uranium grade within the range of square windows of different scales, ε . The singularity number of each point is calculated by fitting the double logarithmic map using the least square method. The slope value of the line fitted by the double logarithmic plot plus 2 is the singularity exponent α . The singularity exponents of two stopes in the ore deposit are calculated by this sliding window algorithm. Figure 8 illustrates the distributions of the singularity exponents of the two stopes.
According to the power rate-law and multifractal theory, the singularity exponent α can reveal the enrichment and dilution characteristics of elements[36,37,38]. When α < 2 , the element content in this region indicates enrichment, and then the element density increases with the reduction in the distribution range. The smaller the value α , the higher the degree of singularity will be; when α is close to 2, this indicates a normal background area, indicating that this area is normal and not much affected by mineralization, and the element density does not change with the reduction in the distribution range. In this case, the elements in the corresponding area are evenly distributed; when α > 2 , this indicates that the element content in this area is depleted, and the element density decreases with the reduction in the distribution range.
It can be seen from Figure 7 that the abnormal concentration characteristics of uranium grade in the two stopes of the deposit are significant. There is a certain correlation between the uranium content distribution and the singularity exponent distribution in the two stopes, which can be seen by comparing the grade isogram (Figure 3) and singularity exponent distribution map (Figure 7). When α < 2 , the average grade value of uranium ore is obviously larger, indicating that the high content value partly corresponds to the abnormal area where α is less than 2, and there is an enrichment phenomenon of uranium ore in this area. However, the region where α > 2 reflects the uranium dilution of the uranium; the region where α is close to 2 reveals the background field.
Through an analysis of the singularity exponent α distribution of uranium grade in the No. 11 and No. 12 stopes, we found that the distribution areas of α < 2 are different. The areas of α < 2 in the No. 11 stope are mainly concentrated in the northeast and central areas, while the areas of α < 2 in the No. 12 stope are mainly concentrated in the northwest and central areas, indicating that uranium ore is relatively enriched in these areas. There are regions where α > 2 in the two stopes: there are small areas in the upper part of the northwestern and eastern edges of the No. 11 stope, and small areas on the right of the northeastern and southern edges of the No. 12 stope, respectively, indicating that the two stopes are relatively depleted in these areas. The area with α > 2 in stope No. 11 is smaller than that in stope No. 12, indicating that the depleted area in stope No. 11 is smaller than that in stope No. 12. In addition, area α = 2 is the area with the largest proportion of the two stopes, indicating that most areas of the two stopes are background areas.

4. Conclusion

Based on the multifractal theory, the parameter difference of multifractal reflects the structure of spatial distribution of mineral grade to a certain extent[22,27]. For example, fractional dimension D0 can characterize the degree of sample deviation from normal distribution, while other parameters, such as parameters D q , α ( q ) and f ( α ) , can also reflect the non-uniformity of mineral distribution. After a comprehensive multifractal distribution analysis of uranium ore, we combine local singularities and correlations of the spatial distribution of geochemical elements, which can be used to extract the enrichment depletion information of geochemical elements from the anomalous values of local singularities. The following conclusions can be drawn:
(1) A group of uranium-grade values and their plane distribution maps are obtained from the ore deposit, the uranium-grade grid data covering the area are formed by interpolating the uranium-grade values at these points, the data are processed by ash, and the macroscopic distribution problem of geochemical elements is reduced to a microscopic distribution problem.
(2) A multifractal model of uranium ore distribution is established, and the multifractal spectra and multifractal parameters of uranium grade in two stopes (No.11 and No.12 stopes) are obtained by numerical calculation. These spectral function images are almost parabolic shapes. Fractal dimension D0 and information dimension D1 of the uranium-grade distribution of stope No.11 are 1.98 and 1.97, respectively, and fractal dimension D0 and information dimension D1 of the uranium grade distribution of stope No.12 are 1.92 and 1.91. The skew coefficient R of the uranium-grade fractal spectrum of the two stopes is -0.30 and -0.56, respectively. The relationship between q ∼ D q , q ∼ α ( q ) and q ∼ f ( q ) parameters shows that the average grade distribution of uranium ore in the two stopes has multi-fractal characteristics, and the differences in the multifractal parameters between the two areas are compared. After comparison, fractal dimension D0 and information dimension D1 of mining area No. 11 are both larger than the corresponding values of mining area No. 12. Similarly, the spectral width Δ α and the left-half spectrum width Δ α L values of stope No. 11 are also larger than those of stope No. 12. Moreover, the skew coefficient R of the two stopes satisfies − 0.30 > − 0.56 , indicating that the uranium-ore-grade distribution in stope No.11 is more densely distributed than that in stope No.12. The results after comparison all show that that the singularity of uranium-grade distribution in No. 11 stope is greater, the internal structure of uranium ore in this stope is more complex, and uranium ore is easier to enrich. The multical method can effectively indicate the local anomalies in the geochemical elements.
(3) Singularity exponent distribution maps of uranium grade in the two stopes are obtained using the element content–area method. The spatial distribution region of the calculated singularity exponent ( α < 2 ) has a strong correlation with the uranium-grade enrichment region, and the singularity exponent can be used to accurately decompress and identify uranium-grade anomalies and background information. This is indicative for element content estimation, deposit reserve prediction and mineral resource information acquisition.
In this paper, the characteristics of uranium ore distribution are described by using multifractal theory and a model from the perspective of statistical data analysis. The multifractal parameters of uranium-grade distribution are related not only to the calculation method used for the dimension, but also to the collection of samples. The sampling range, sampling spacing, sampling adequacy and local geological conditions of the used data used affect the calculation results. In view of the complex geological conditions and metallogenic factors, more indicators need to be explored in future studies, such as considering the chemical mechanism, to improve the acquisition and recognition of the multifractal spectrum of two-dimensional data in this method, and improve the accuracy when indicating anomalies in physical and chemical fields and background fields.

Author Contributions

Conceptualization, Q.E.Cai,K.X.Tan and S.Zeng; dtata curation,J.J.Zhu;formal analysis,Q.E.Cai;funding acquisition,S.Zeng; investigation, A.C.;methodology, J.J.Zhu ;Q.E.Cai; project administration, S.Zeng; resources, K.X.Tan ;software, Q.E.Cai and J.J.Zhu; supervision, K.X.Tan ;validation K.X.Tan;visualization, J.J.Zhu ;writing—original draft, Q.E.Cai; writing—review and editing, S.Zeng . All authors have read and agreed to the published version of the manuscript.

Data Availability Statement

Data sharing not applicable.

Acknowledgement

This study was supported by the National Natural Science Foundation of China(Grant No. U1703123), Hunan Provincial Department of Education Foundation of China (Grant No. 19C1609), Educational science project in Hunan Province, China(Grant No.ND207843).

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

References

  1. Mandelbrot, Benoit B. The Fractal Geometry of Nature. Am J Phys, 1998, 51, 286–287.
  2. Kenneth, F.; Xiong, J. Dimension conservation for self-similar sets and fractal percolation. Int Math Res Notices. 2015, 24. [Google Scholar] [CrossRef]
  3. Albeverio, S.; Torbin, G. Fractal properties of singular probability distributions with independent q*-digits. B Sci Math. 2005, 129, 356–367. [Google Scholar] [CrossRef]
  4. Hall, P.; Roy, R. On the Relationship Between Fractal Dimension and Fractal Index for Stationary Stochastic Processes. Ann. Appl. Probab. 1994, 4, 241–253. [Google Scholar] [CrossRef]
  5. Yang, S.; Liang, M.; Yu, B.; Zou, M. Permeability model for fractal porous media with rough surfaces. Microfluid. Nanofluidics 2014, 18, 1085–1093. [Google Scholar] [CrossRef]
  6. Zhao,J.;Chen,S.;Zuo,R.;Zhao,M.Controls on and prospectivity mapping of volcanic-type uranium mineralization in the pucheng district, nw fujian, china. Ore Geology Reviews: Journal for Comprehensive Studies of Ore Genesis and Ore Exploration. 2019,112. [CrossRef]
  7. Lovejoy,S.;Schertzer, D.;Ladoy,P. Fractal characterization of inhomogeneous geophysical measuring net-works.Nature.1987,319,43 -44.
  8. Salat, H.; Murcio, R.; Arcaute, E. Multifractal methodology, J. Physica A: Statistical mechanics and its applications.2017,473,467-487.
  9. Zhang, J.; Hu, Q.; Wu, H.; Su, J.; Zhao, P. Application of Fractal Dimension of Terrestrial Laser Point Cloud in Classification of Independent Trees. Fractal Fract. 2021, 5, 14. [Google Scholar] [CrossRef]
  10. Cai, J.; Hu, X.; Xiao, B.; Zhou, Y.; Wei, W. Recent developments on fractal-based approaches to nanofluids and nanoparticle aggregation. Int. J. Heat Mass Transf. 2017, 105, 623–637. [Google Scholar] [CrossRef]
  11. Ma, D.; Duan, H.; Liu, J.; Li, X.; Zhou, Z. The role of gangue on the mitigation of mining-induced hazards and environmental pollution: An experimental investigation. Sci. Total. Environ. 2019, 664, 436–448. [Google Scholar] [CrossRef]
  12. Li, Q.; Liu, D.; Cai, Y.; Zhou, Y.; Yin, T. Investigation on the Methane Adsorption Capacity in Coals: Considerations from Nanopores by Multifractal Analysis. Energy Fuels 2021, 35, 6633–6643. [Google Scholar] [CrossRef]
  13. Mahamud, M.M.; Novo, M.F. The use of fractal analysis in the textural characterization of coals. Fuel 2008, 87, 222–231. [Google Scholar] [CrossRef]
  14. Wang, F.; Zeng, F.; Wang, L.; Hou, X.; Cheng, H.; Gao, J. Fractal Analysis of Tight Sandstone Petrophysical Properties in Unconventional Oil Reservoirs with NMR and Rate-Controlled Porosimetry. Energy Fuels 2021, 35, 3753–3765. [Google Scholar] [CrossRef]
  15. Makevi, V.; Milovanovich, I.D.; Popovac, N.; Jankovi, R.; Trajkovi, J.; Vukovi, A.; Milosevi, B.; Jevti, J.; de Luka, S.R.; Ili, A. Fractal Parameters as Independent Biomarkers in the Early Diagnosis of Pediatric Onset Inflammatory Bowel Disease. Fractal Fract. 2023, 7, 619. [Google Scholar] [CrossRef]
  16. Lai, J.; Wang, S.; Wang, G.; Shi, Y.; Zhao, T.; Pang, X.; Fan, X.; Qin, Z.; Fan, X. Pore structure and fractal characteristics of Ordovician Majiagou carbonate reservoirs in Ordos Basin, China. AAPG Bull. 2019, 103, 2573–2596. [Google Scholar] [CrossRef]
  17. Dou, W.; Liu, L.; Xu, Z.; Wang, M.; Chen, Y.; Wang, X. Surface fractal analysis of pore structure of tight sandstones: Comparison of different models based on mercury intrusion porosimetry. AAPG Bull. 2021, 105, 1491–1509. [Google Scholar] [CrossRef]
  18. Agterberg, F.P. Multifractal Modeling of the Sizes and Grades of Giant and Supergiant Deposits. Int. Geol. Rev. 1995, 37, 1–8. [Google Scholar] [CrossRef]
  19. Nazarpour, A.; Omran, N.R.; Paydar, G.R. Application of multifractal models to identify geochemical anomalies in Zarshuran Au deposit, NW Iran. Arab. J. Geosci. 2013, 8, 877–889. [Google Scholar] [CrossRef]
  20. Monecke, T.; Gemmell, J.B.; Monecke, J. Fractal distributions of veins in drill core from the Hellyer VHMS deposit, Australia: constraints on the origin and evolution of the mineralising system. Miner. Deposita 2001, 36, 406–415. [Google Scholar] [CrossRef]
  21. Behnam,S.;Parviz Moarefvand,P.A.;Amir, B.Y.; Lili, D.S. Application of fractal models to outline mineralized zones in the Zaghia iron ore deposit, Central Iran. J Geochem Explor .2012, 122, 9-19. [CrossRef]
  22. Shen,B.; Shen,Y. Fractal characteristics of a gold deposit in Xinjiang and its geological significance. Sci China Ser B.1993,23,297-302.
  23. Wang, Q.F.; Deng, J.; Wan, L.; Zhao, J.; Gong, Q.J.; Yang, L.Q.; Zhou, L.; Zhang, Z.J. Multifractal Analysis of Element Distribution in Skarn-type Deposits in the Shizishan Orefield, Tongling Area, Anhui Province. Acta Geologica Sinica. 2008, 82, 896–905. [Google Scholar] [CrossRef]
  24. Zhao, J.; Chen, S.; Zuo, R. Identification and mapping of lithogeochemical signatures using staged factor analysis and fractal/multifractal models. Geochem. Explor. Environ. Anal. 2017, 17, 239–251. [Google Scholar] [CrossRef]
  25. Seyedrahimi-Niaraq, M.; Hekmatnejad, A. The efficiency and accuracy of probability diagram, spatial statistic and fractal methods in the identification of shear zone gold mineralization: a case study of the Saqqez gold ore district, NW Iran. Acta Geochim. 2020, 40, 78–88. [Google Scholar] [CrossRef]
  26. Tao; Sun,L.;Liu. Delineating the complexity of cu–mo mineralization in a porphyry intrusion by computational and fractal modeling: a case study of the chehugou deposit in the chifeng district, inner mongolia, china. J Geochem Explor. 2014. [CrossRef]
  27. Zuo, R.; Cheng, Q.; Xia, Q. Application of fractal models to characterization of vertical distribution of geochemical element concentration. J. Geochem. Explor. 2009, 102, 37–43. [Google Scholar] [CrossRef]
  28. Peyman, A.;Younes,F.A.; Parviz, M.; Nematolah, R.O.; Hooshang Asadi Haroni. Application of power-spectrum–volume fractal method for detecting hypogene, supergene enrichment, leached and barren zones in kahang cu porphyry deposit, central iran. J Geochem Explor. 2012,112,131-138. [CrossRef]
  29. Ahad, N.; Behnam,S.; Martiya,S. Application of fractal models to characterization and evaluation of vertical distribution of geochemical data in zarshuran gold deposit, nw iran. J Geochem Explor.2015,148,60-70. [CrossRef]
  30. Asadi, H.H.; Kianpouryan, S.; Lu, Y.-J.; McCuaig, T.C. Exploratory data analysis and C–A fractal model applied in mapping multi-element soil anomalies for drilling: A case study from the Sari Gunay epithermal gold deposit, NW Iran. J. Geochem. Explor. 2014, 145, 233–241. [Google Scholar] [CrossRef]
  31. Deng, J.; Wang, Q.; Wan, L.; Yang, L.; Gong, Q.; Zhao, J.; Liu, H. Self-similar fractal analysis of gold mineralization of Dayingezhuang disseminated-veinlet deposit in Jiaodong gold province, China. J. Geochem. Explor. 2009, 102, 95–102. [Google Scholar] [CrossRef]
  32. Cheng,Q. Multifractal and geostatistic methods for characterizing local structure and singularity properties of exploration geochemical anomalies. J Earth Sci-china. 2001,026, 161-164.
  33. Shen,B. Fractal structure factor and its application in geology. Acta Petrol Sin.1993,9,267-276. [CrossRef]
  34. Kusk,M. Application of fractal and multifractal analysis on Blue Nile drainage patterns in the morphostructural analysis of the Ethiopian highlands, Ethiopia. Prog Phys Geog.2022,46,357-370. [CrossRef]
  35. Liu, Y.; Cheng, Q.; Zhou, K. New Insights into Element Distribution Patterns in Geochemistry: A Perspective from Fractal Density. Nat. Resour. Res. 2018, 28, 5–29. [Google Scholar] [CrossRef]
  36. Xiao, F.; Chen, Z.; Chen, J.; Zhou, Y. A batch sliding window method for local singularity mapping and its application for geochemical anomaly identification. Comput. Geosci. 2016, 90, 189–201. [Google Scholar] [CrossRef]
  37. Wang, W.; Zhu, M.; Zhao, J.; Chen, Z.; Cheng, Q. Joint Modeling Based on Singularity Mapping and U-statistical Methods for Geo-Anomaly Characterization. Nat. Resour. Res. 2022, 31, 1909–1923. [Google Scholar] [CrossRef]
  38. Liu, Y.; Carranza, E.J.M. Uncertainty Analysis of Geochemical Anomaly by Combining Sequential Indicator Co-simulation and Local Singularity Analysis. Nat. Resour. Res. 2022, 31, 1889–1908. [Google Scholar] [CrossRef]
  39. Xu, S.; Hu, X.; Carranza, E.J.M.; Wang, G. Multi-parameter Analysis of Local Singularity Mapping and Its Application to Identify Geochemical Anomalies in the Xishan Gold Deposit, North China. Nat. Resour. Res. 2020, 29, 3425–3442. [Google Scholar] [CrossRef]
  40. Mohammadi,N.M.; Hezarkhani,A.; Saljooghi,B.S. Separation of a geochemical anomaly from background by fractal and U-statistic methods, a case study: Khooni district, Central Iran.Geochemistry: Interdisciplinary Journal for Chemical Problems of the Geosciences and Geoecology. 2016,76, 491-499. [CrossRef]
  41. Wen,Z.;Liu,H.;Gao,X.Geochemical and Geophysical anomaly separation and anomaly analyses based on multifractal.Chinese Journal Progress in geophysics. 2007,22, 972- 978.
  42. Shang,D.; Geissler B.; Mew M.;Satalkina,L.; Haneklaus, N.Unconventional uranium in China's phosphate rock: Review and outlook.Renew. Sust Energ Rev. 2021, 140,110740. [CrossRef]
  43. Zeng, S.; Shen, Y.; Sun, B.; Zhang, N.; Zhang, S.; Feng, S. Pore structure evolution characteristics of sandstone uranium ore during acid leaching. Nucl. Eng. Technol. 2021, 53, 4033–4041. [Google Scholar] [CrossRef]
  44. Sun, B.; Hou, S.-S.; Zeng, S.; Bai, X.; Zhang, S.-W.; Zhang, J. 3D characterization of porosity and minerals of low-permeability uranium-bearing sandstone based on multi-resolution image fusion. Nucl. Sci. Tech. 2020, 31, 1–20. [Google Scholar] [CrossRef]
  45. Liu, X.; Yuan, S.; Bai, X.; Jiang, J.; Li, Y.; Liu, J. Tectonic uplift of the Tianshan Mountains since Quaternary: evidence from magnetostratigraphy of the Yili Basin, northwestern China. Int. J. Earth Sci. 2023, 112, 1–11. [Google Scholar] [CrossRef]
  46. de Benicio, R.B.; Stošić, T.; de Figueirêdo, P.; Stošić, B.D. Multifractal behavior of wild-land and forest fire time series in Brazil. Phys. A: Stat. Mech. its Appl. 2013, 392, 6367–6374. [Google Scholar] [CrossRef]
Preprints 85274 g001
Figure 1. Geological map of uranium deposits in Yili Basin and adjacent areas.
Figure 1. Geological map of uranium deposits in Yili Basin and adjacent areas.
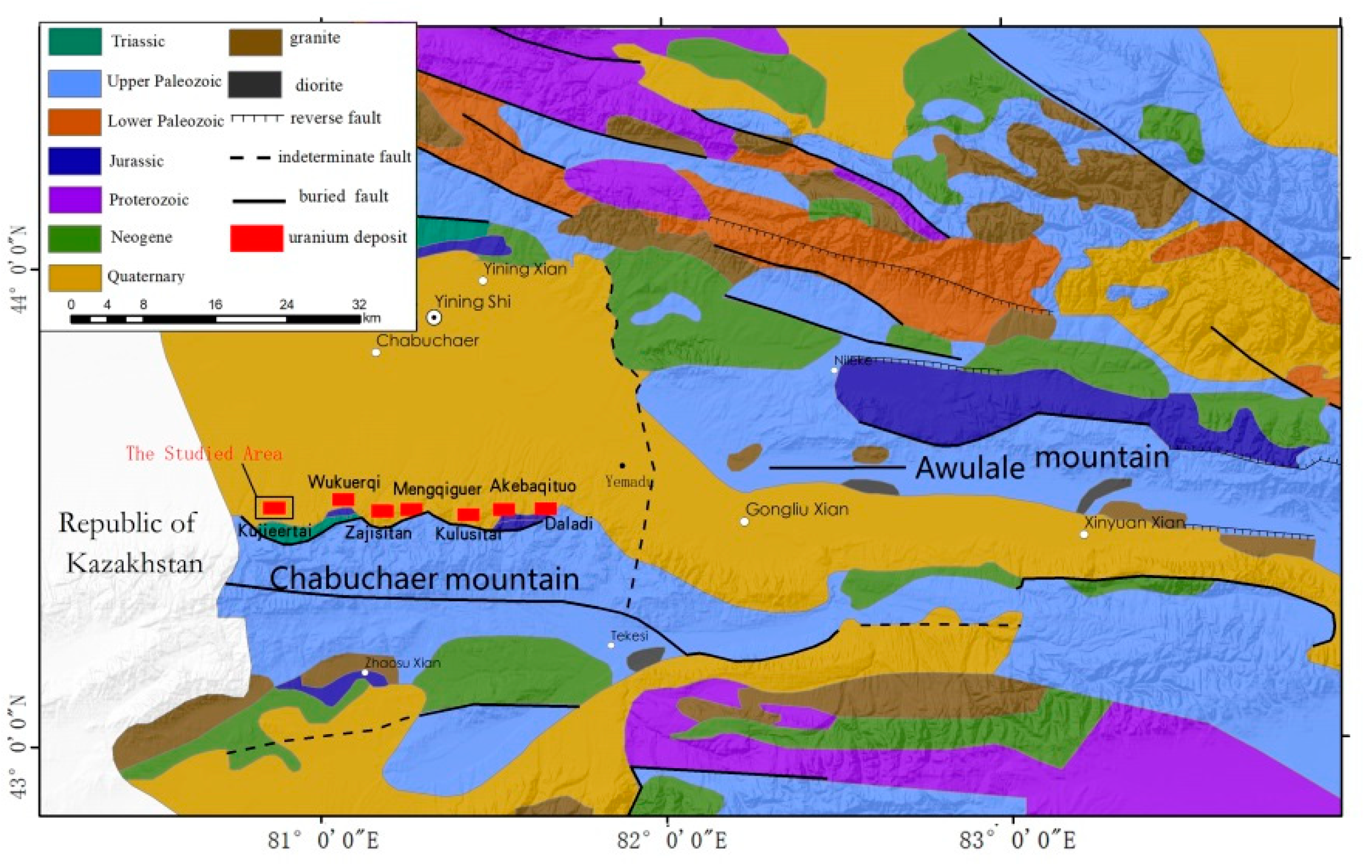
Preprints 85274 g001
Preprints 85274 g002
Figure 2. Distribution and arrangement of test boreholes of the studied ore deposit. ( No. 11 stope is on the right, No.12 stope is on the left).
Figure 2. Distribution and arrangement of test boreholes of the studied ore deposit. ( No. 11 stope is on the right, No.12 stope is on the left).
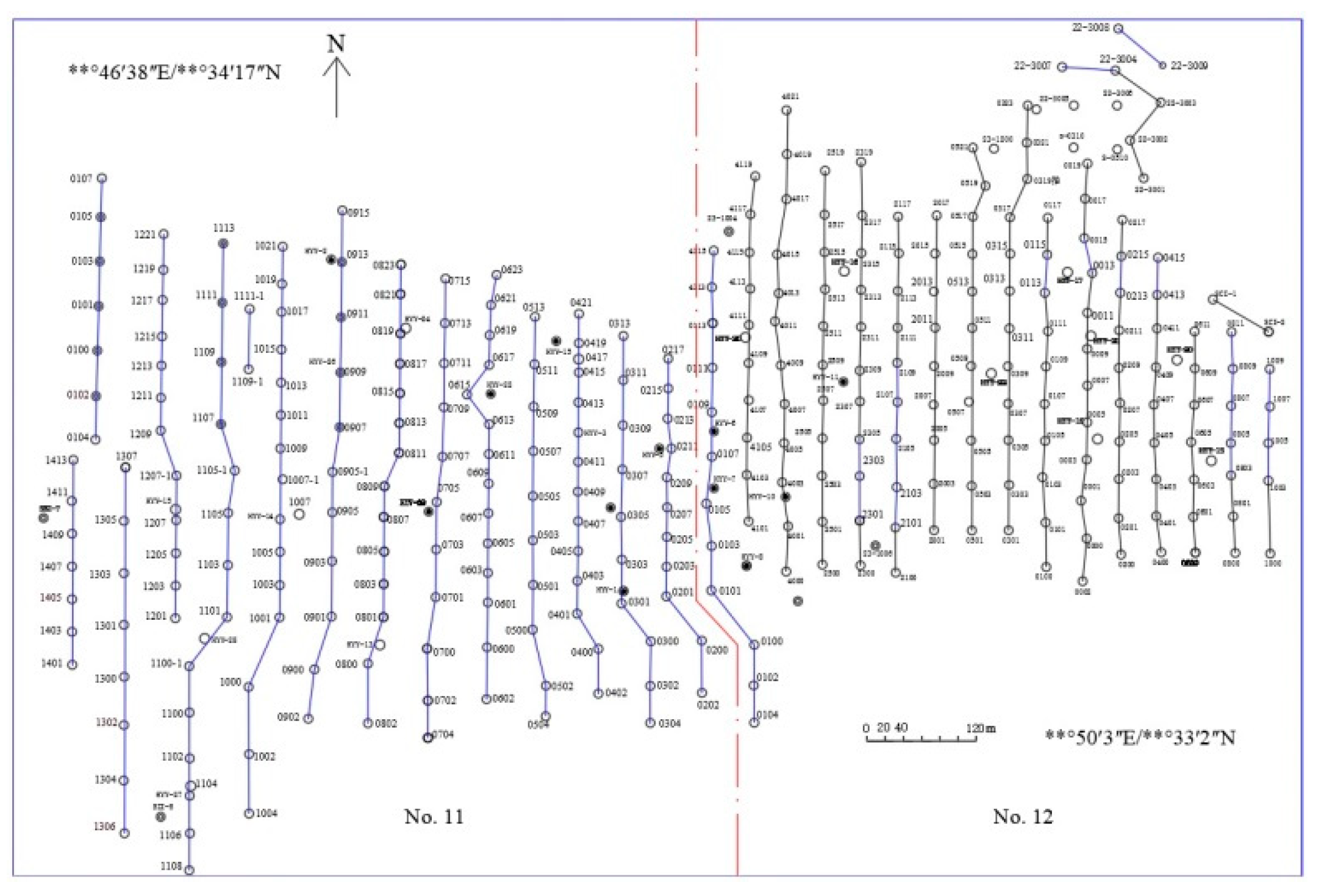
Preprints 85274 g002
Preprints 85274 g003
Figure 3. Average uranium grade isogram revealed by borehole logging of the deposit. ( No.11 stope is on the top, No.12 stope is on the bottom. Unit: percentage).
Figure 3. Average uranium grade isogram revealed by borehole logging of the deposit. ( No.11 stope is on the top, No.12 stope is on the bottom. Unit: percentage).
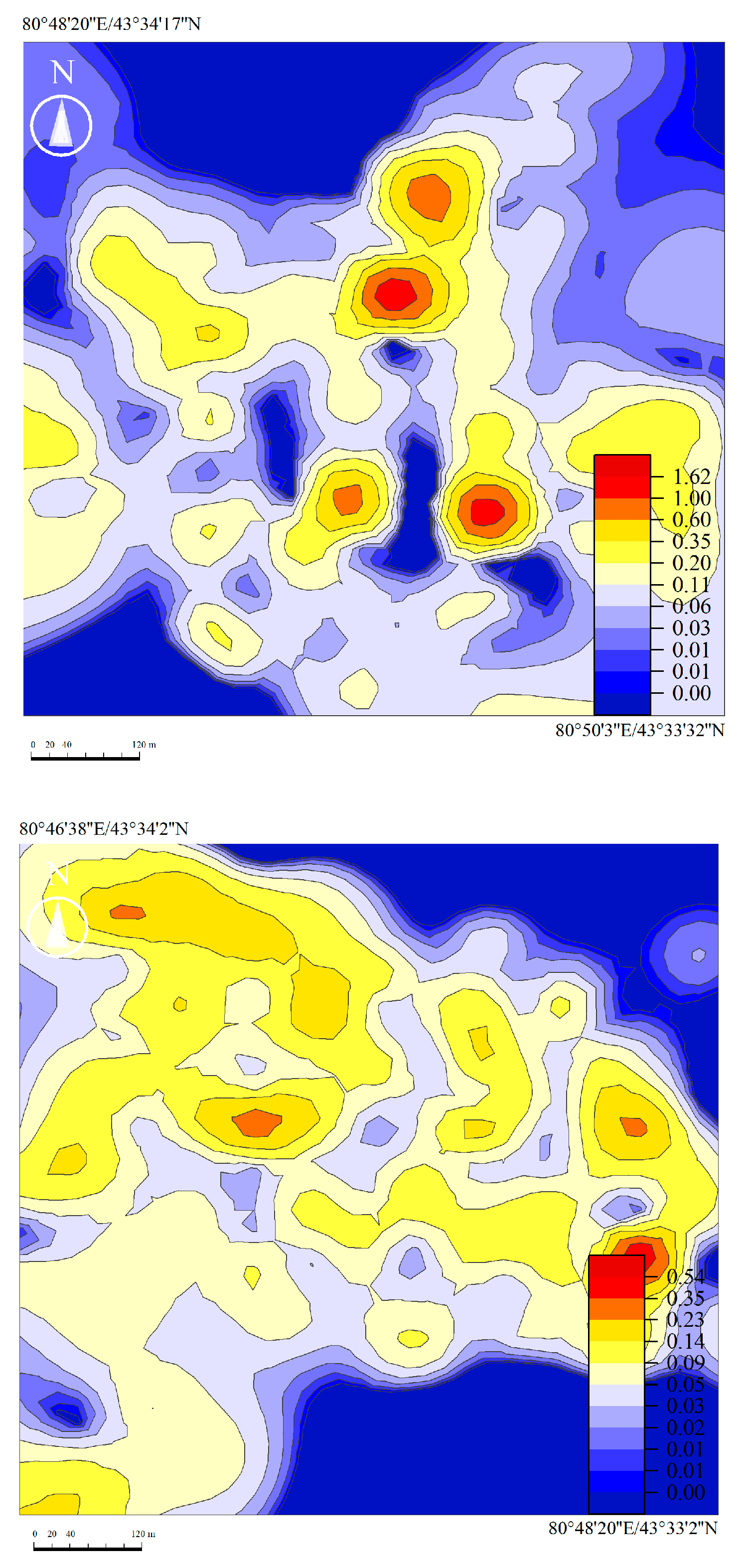
Preprints 85274 g003
Preprints 85274 g004
Figure 4. Analysis results of average grade of uranium ore in No.11 stope by multifractal method. (a) uranium ore average grade ln X q ( ξ ) ∼ ln ( ξ ) map; (b) uranium ore average grade q ∼ D q map; (c) uranium ore average grade q ∼ α ( q ) and q ∼ f ( q ) map; (d) uranium ore average grade α ∼ f ( α ) map.
Figure 4. Analysis results of average grade of uranium ore in No.11 stope by multifractal method. (a) uranium ore average grade ln X q ( ξ ) ∼ ln ( ξ ) map; (b) uranium ore average grade q ∼ D q map; (c) uranium ore average grade q ∼ α ( q ) and q ∼ f ( q ) map; (d) uranium ore average grade α ∼ f ( α ) map.
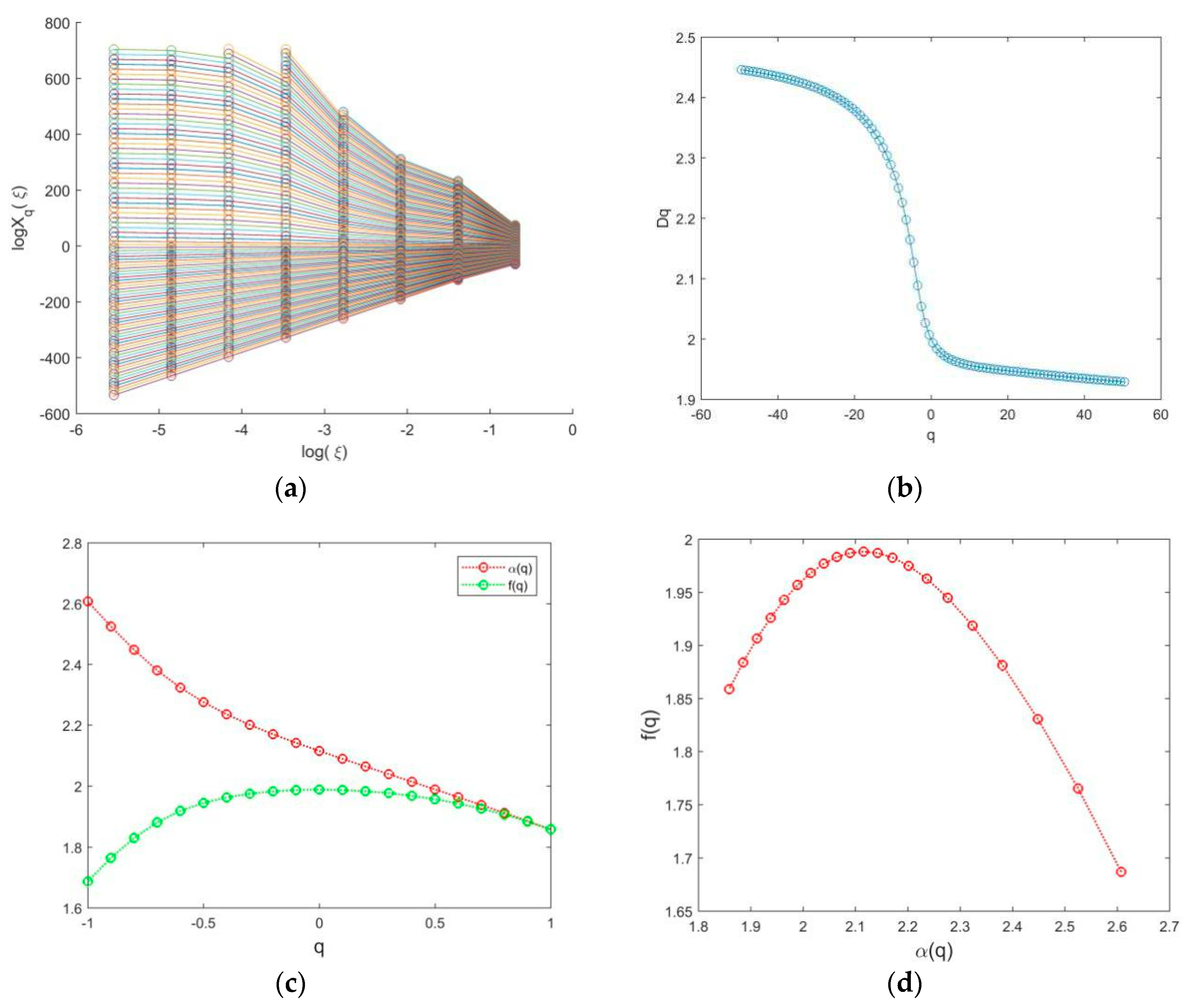
Preprints 85274 g004
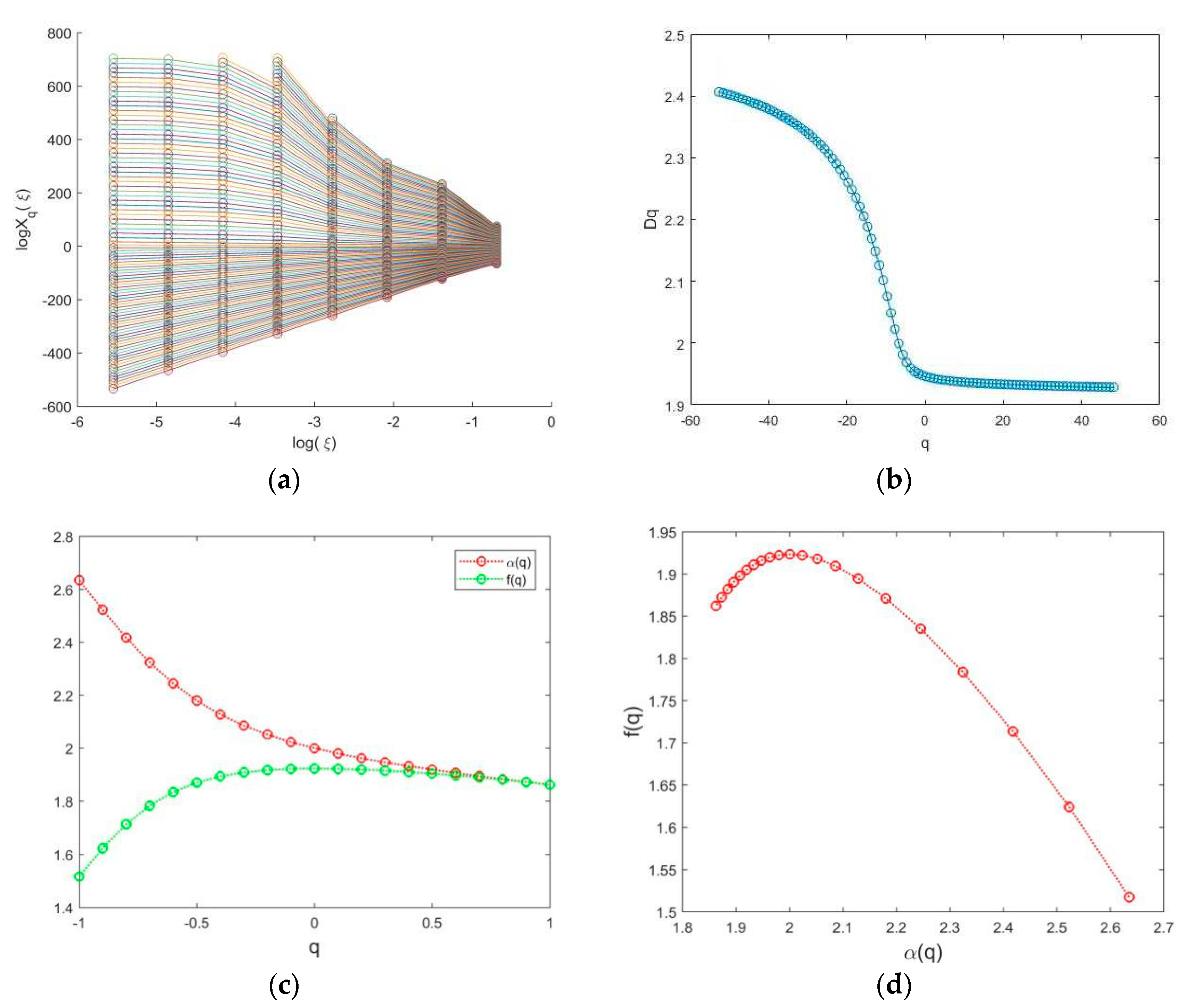
Preprints 85274 g005
Figure 5. Analysis results of average grade of uranium ore in No.12 stope by multifractal method. (a) uranium ore average grade ln X q ( ξ ) ∼ ln ( ξ ) map; (b) uranium ore average grade q ∼ D q map; (c) uranium ore average grade q ∼ α ( q ) and q ∼ f ( q ) map; (d) uranium ore average grade α ∼ f ( α ) map.
Figure 5. Analysis results of average grade of uranium ore in No.12 stope by multifractal method. (a) uranium ore average grade ln X q ( ξ ) ∼ ln ( ξ ) map; (b) uranium ore average grade q ∼ D q map; (c) uranium ore average grade q ∼ α ( q ) and q ∼ f ( q ) map; (d) uranium ore average grade α ∼ f ( α ) map.
Preprints 85274 g005
Preprints 85274 g006
Figure 6. Q-Q plot of average grade of uranium ore in two stopes of the deposit( No. 11 is on the left, No.12 is on the right).
Figure 6. Q-Q plot of average grade of uranium ore in two stopes of the deposit( No. 11 is on the left, No.12 is on the right).
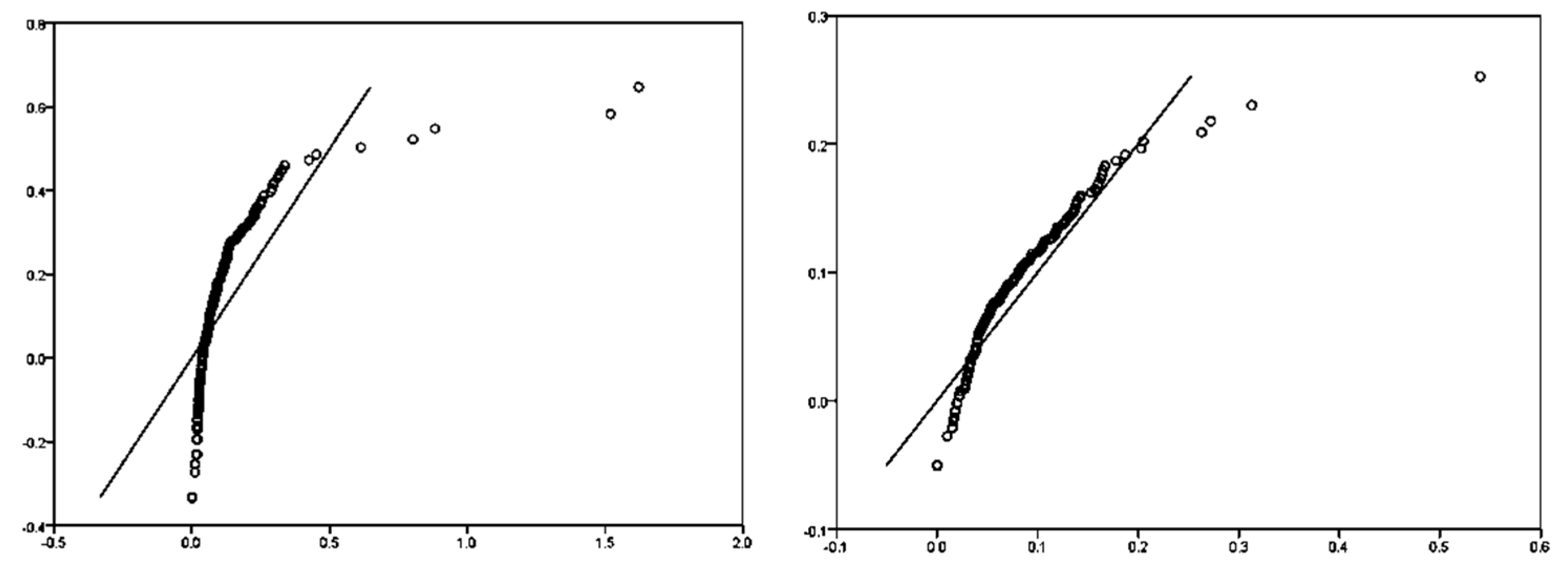
Preprints 85274 g006
Preprints 85274 g007
Figure 7. C-A double-log plot of average grade of uranium ore( No. 11 stope is on the left, No.12 stope is on the right).
Figure 7. C-A double-log plot of average grade of uranium ore( No. 11 stope is on the left, No.12 stope is on the right).
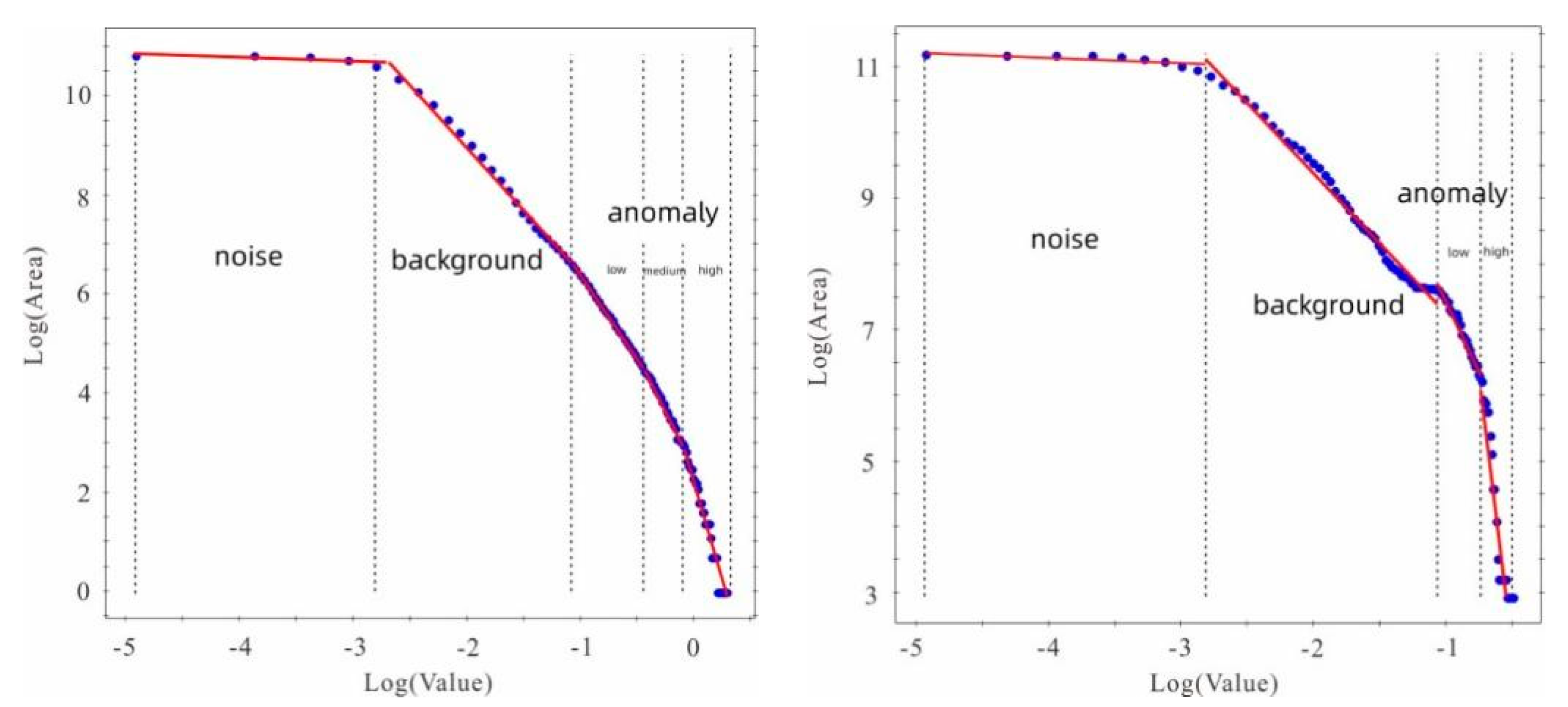
Preprints 85274 g007
Preprints 85274 g008aPreprints 85274 g008b
Figure 8. Singularity exponent distribution of uranium grade value of the deposit. ( No. 11 stope is on the top, No.12 stope is on the bottom).
Figure 8. Singularity exponent distribution of uranium grade value of the deposit. ( No. 11 stope is on the top, No.12 stope is on the bottom).
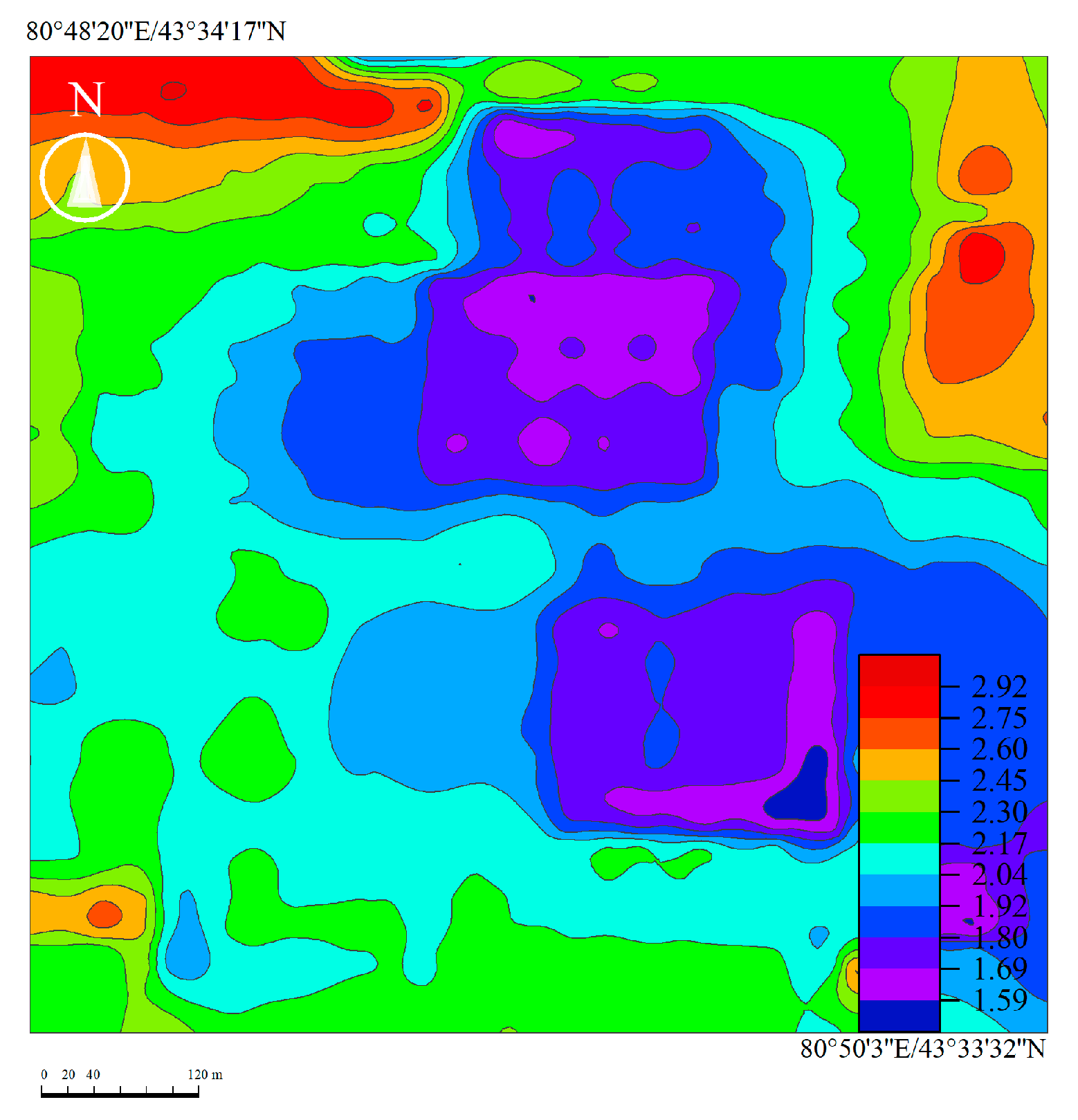
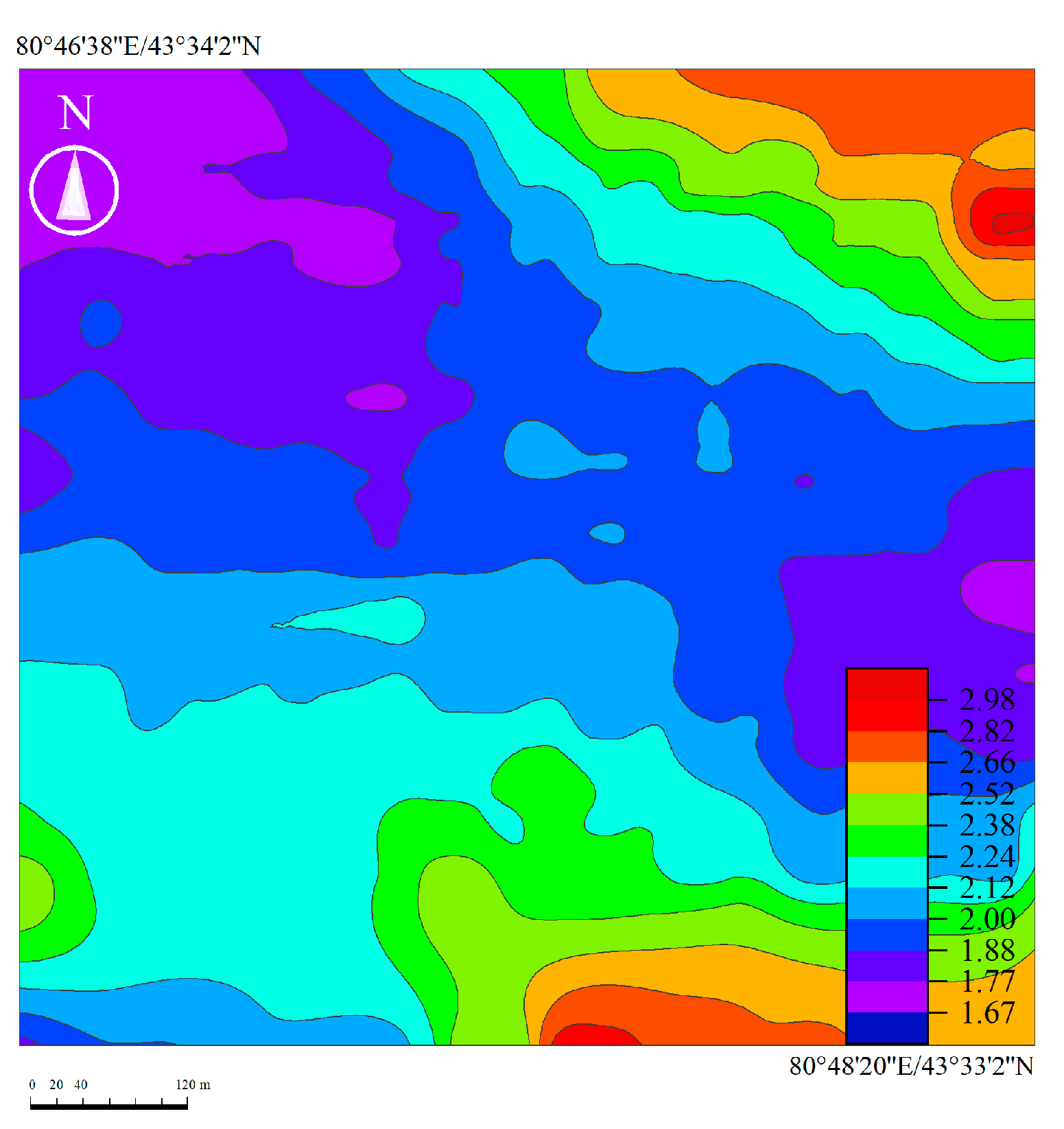
Preprints 85274 g008aPreprints 85274 g008b
Table 1. Multifractal spectrum parameter values of average grade of uranium ore in No. 11 stope at q = 0 ， 1 ， ± ∞
Table 1. Multifractal spectrum parameter values of average grade of uranium ore in No. 11 stope at q = 0 ， 1 ， ± ∞
q τ ( q ) α = d τ d q f ( α ) = α q − τ ( q ) D q
− ∞ q α max 2.60 0 2.60
0 -1.98 2.12 1.98 1.98
1 0 1.87 1.87 1.97
+ ∞ q α m i n 1.68 0 1.68
Table 2. Multifractal spectrum parameter values of average grade of uranium ore in No. 12 stope at q = 0 ， 1 ， ± ∞
Table 2. Multifractal spectrum parameter values of average grade of uranium ore in No. 12 stope at q = 0 ， 1 ， ± ∞
q τ ( q ) α = d τ d q f ( α ) = α q − τ ( q ) D q
− ∞ q α max 2.64 0 2.64
0 -1.92 2.05 1.92 1.92
1 0 1.86 1.86 1.91
+ ∞ q α m i n 1.52 0 1.52
Table 3. Multifractal spectrum parameters of average grade of uranium ore.
Table 3. Multifractal spectrum parameters of average grade of uranium ore.
stope α 0   Δ α Δ f Δ α R Δ α L R
NO.11 2.12 0.74 0.19 0.48 0.26 -0.30
NO.12 2.05 0.72 0.34 0.56 0.16 -0.56
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated