Wind Speed Spectrum of a Moving Vehicle Under Turbulent Crosswinds

Preprint

Article

Wind Speed Spectrum of a Moving Vehicle Under Turbulent Crosswinds

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Qingsong Duan^*

This version is not peer-reviewed

Submitted:

16 September 2023

Posted:

19 September 2023

You are already at the latest version

Alerts

Abstract

Wind loads have become one of the key influence factors for the running safety of vehicles and comfort of passengers. Investigation on the wind speed spectrum characteristics of a moving vehicle under turbulent crosswinds is of great influence. Expressions of the wind speed spectrum of a moving vehicle was obtained from the von Kármán spectrum based on Taylor’s frozen flow hypothesis. The influence factors, including the ratio of the vehicle speed to the wind speed and the wind yaw angle from 15° to 175°, were analyzed. The maximum value of the wind speed spectrum and the corresponding frequency were studied as well. The results show that the maximum values of the wind speed spectrum of the moving vehicle were larger than those of the static vehicle. The maximum value of the wind speed spectrum corresponding to the moving vehicle first increased and then decreased as the wind yaw angle increased. Some of the frequencies corresponding to the longitudinal wind speed spectrum values of the moving vehicles were smaller than those of the static vehicle. For moving vehicles, the frequency values corresponding to the maximum values of the longitudinal wind speed spectrum first increased and then decreased as the ratio of the vehicle speed to the wind speed and the wind yaw angle increased.

Keywords:

Subject: Engineering - Civil Engineering

1. Introduction

China is one of the few countries in the world that is prone to severe wind disasters. It may influence the running speed limit of a vehicle, affect its transportation capacity, even cause vehicle shutdown or accidents (Guo, 2006; Zhang, 2016; Yan, 2018; Duan, 2018). In 2007, the Lanzhou-Xinjiang Line crossed the Gobi gale area in Xinjiang, China. A train vehicle was derailed by strong winds. 11 cars were overturned, 34 passengers died and the southern Xinjiang line was interrupted for nine hours. On February 24, 2008, 48 Japanese trains were stopped, and 183 trains were delayed due to a serious wind disaster which affected about 140000 people. Also, the wind has left the train vehicle late in some conditions. High speed wind could turn the running cars driving on the highway, causing casualties, and the general response strategy is to reduce the running speed of the car. Obviously, every year many people die around the world due to vehicle accidents under strong wind, and the economic losses caused by the influence of wind disasters are huge. Influence of crosswind on a moving vehicle deserves constant attention. Wind loads have become one of the key influence factors for the coupling vibration of wind-vehicle-bridge system which could evaluate the running safety and comfort effectively, and related studies are of great influence. Wind speed spectra of a moving vehicle should be obtained.

Figure 1. Train vehicles overturned in crosswinds.

The aerodynamic characteristics of vehicles under crosswind has been experimentally investigated considering the aerodynamic coupling effect between the static train vehicle and bridge girder section (Li, 2005, 2016, 2017; Duan, 2018). Mostly, the vehicles are running on girders. The wind speed spectrum characteristics of a moving vehicle or a point should be studied experimentally or numerically. Originally, the total wind speed of a moving vehicle was obtained based on the wind speed spectrum of the static point from the traditional wind field simulation method. The wind flow field is artificially divided into several relevant wind speed intervals along the vehicle running direction. While, the wind field mutational effect would occur and leads to deviation in the calculation results which is also inconsistent with the actual situation (Li et al., 2005; Xu et al., 2006; Cai et al., 2004). Investigation of the wind speed spectrum of a moving point that consist with the actual situation is of great significance, which provide a parametric basis for the analysis of wind-vehicle-bridge coupling systems.

Many scholars have studied the characteristics of the wind spectrum of moving train vehicles. Cooper (1984) theoretically derived the longitudinal wind speed spectrum of a moving vehicle. The derivation of the wind speed spectrum has been recognized by many scholars. However, the derivation only targets working conditions in which the angle between the wind speed and the train vehicle running direction is 90°, which could not be widely applied. Obviously, the angle is varied. More working conditions should be studied.

The on-road turbulent wind environment was measured utilizing a vehicle instrumented with mast-mounted cross-wire and propeller-vane anemometers (Watkins, 1990; Watkins et al., 1995). For vehicle’s moving speed is of 27.8m/s and the wind speed is from 1 to 9 m/s, the measured longitudinal and lateral turbulence intensities of the moving point were 2.5%~5% and 2%~10%, respectively. Watkins (Watkins et al., 1995) developed a mathematical model of the turbulence intensities perceived by a moving vehicle. At the same time, the relative turbulence was investigated from field measurement (Watkins et al., 2006).

Wu (2014; 2015) numerically studied the correlation characteristics of a moving vehicle was obtained (Taylor, 1938). Li et al. (2016, 2017) and Hu (2018) developed another analytical model of the wind velocity spectra. Yu (2016) computed the unsteady aerodynamic load on a moving vehicle. However, the difference between the wind spectrums of the static and moving points was not analyzed comprehensively. The necessity for specialized studies of the moving-point wind spectrum is not highlighted in the study. Li and Su (2020) experimentally investigated the wind spectrum of a moving point under crosswind in wind tunnel and the results were compared to those of Balzer’s (1973; 1977) and Cooper’s models (Cooper, 1938). However, the cross-correlation characteristics of two moving points were not investigated. The cross-correlation characteristics of two moving points have not been studied in depth.

Study of wind characteristics of a moving vehicle and its mathematical model is conducted. Based on the above study, an analytical expression of the wind speed spectrum based on the Cooper wind speed spectrum theory was deduced in a new analytical model. Influence of the wind yaw angle, the ratios between wind speed to vehicle running speed at the peak of the wind speed spectrum and the scaling coefficient of the corresponding frequency were fully discussed. The analytical expression of the stationary point von Kármán spectrum and the running vehicle wind velocity spectrum are firstly given. Secondly, the turbulent field is obtained by wind tunnel test. Thirdly, the wind velocity spectrum of a running point corresponding to the simulated turbulent field is derived, and its relevant characteristics are analyzed. The cross-correlation characteristics of two moving points are also studied.

2. Wind Speed Spectrum Models

2.1. Wind Speed Spectrum of a Static Vehicle

The correlation characteristics of two points in a turbulent flow field can be expressed in terms of the correlation functions f(r) and g(r), where f(r) is the cross-correlation function of the wind speeds for two points apart from r along the axis of the two points (Figure 2 (a)), and g(r) is the cross-correlation function of two points apart from r which are perpendicular to the axis (see Figure 2 (b)).

f (r) = 〈u_{1} (x) u_{1} (x + r)〉 / u_{1}^{2} (x)

(1)

g (r) = 〈u_{2, 3} (x) u_{2, 3} (x + r)〉 / u_{2, 3}^{2} (x)

(2)

where

u_{1}

，

u_{2}

and

u_{3}

are the fluctuating wind speeds in the x，y and z directions at a point in the spatial turbulent flow field, respectively.

The longitudinal and vertical wind speed spectra can be obtained by the two following formulas:

S_{11} (k_{1}) = 4 σ_{11}^{2} \int_{0}^{\infty} f (r) \cos (k_{1} r) d r

(3)

S_{33} (k_{1}) = 4 σ_{33}^{2} \int_{0}^{\infty} g (r) \cos (k_{1} r) d r

(4)

where

σ_{11}^{}

and

σ_{33}

are the root mean square of the fluctuating wind speed，

σ_{11}^{2} = \int_{0}^{\infty} S_{11} (k_{1}) d r

σ_{33}^{2} = \int_{0}^{\infty} S_{33} (k_{1}) d r

;

k_{1} = w / U

w = 2 π f

, f is the frequency value and U is the incoming mean wind speed.

Von Kármán (1948) derived the relationship between g(r) and f(r) based on the spherical symmetry assumption.

g (r) = f (r) + (r / 2) \frac{d}{d r} f (r)

(5)

Bullen derived the mathematical models of the main correlation functions based on the isotropic turbulence theory:

f (r) = [{(r / a)}^{n} / 2^{n - 1} / Γ (n)] K_{n} (r / a)

(6)

g (r) = [{(r / a)}^{n} / 2^{n} / Γ (n)] [2 K_{n} (r / a) - (r / a) K_{n - 1} (r / a)]

(7)

where a and n are parameters controlling the shape and scale, respectively; K_n and K_n-1 are the second type of Bessel function；Γ is the Gamma function.

In the isotropic turbulence field, the relationship between the turbulence integral scale L and the parameter a is satisfied as follows:

L = [\sqrt{π} \cdot Γ (n + \frac{1}{2}) / Γ (n)] \cdot a

(8)

Respectively putting Eq. (6) and Eq. (7) into Eq. (3) and Eq. (4) yields

S_{11} (k_{1}) = \frac{4 σ_{11}^{2} L / U}{{[1 + {(a k_{1})}^{2}]}^{n + 1 / 2}}

(9)

S_{33} (k_{1}) = \frac{2 σ_{33}^{2} (L / U) [1 + 2 a^{2} k_{1}^{2} (n + 1)]}{{[1 + {(a k_{1})}^{2}]}^{n + 3 / 2}}

(10)

When n=1/3, the von Kármán wind spectrum is as follows：

\frac{f S_{11} (k_{1})}{σ_{11}^{2}} = \frac{4 X_{u}}{{[1 + 70.8 X_{u}^{2}]}^{5 / 6}}

(11)

\frac{f S_{33} (k_{1})}{σ_{33}^{2}} = \frac{2 X_{u} [1 + 188.8 X_{u}]}{{[1 + 70.8 X_{u}^{2}]}^{11 / 6}}

(12)

Where

X_{u} = k_{1} L / 2 π

，

k_{1} = f / U

f

is the frequency and

U

is the incoming wind speed.

2.2. Wind Speed Spectrum of a Moving Vehicle

Figure 3 shows two points (Points P and P') fixed on a vehicle and the corresponding equivalent points. The moving vehicle travels at a constant speed V_T along the straight line ON, which passes through the origin of the overall coordinate system O-xyz. The angle between the line ON and the x-axis is

ϕ

, which is the wind yaw angle. The overall coordinate system is fixed to the ground and the moving coordinate system N-ξηζ is fixed to the moving vehicle. The η-axis is the moving direction of the vehicle, and the ζ-axis is parallel to the z axis. Points P and P' are the fixed points on the moving vehicle, whose coordinates in the local coordinate system N-ξηζ are (0, η, ζ) and (0, η',ζ'), respectively. In the overall coordinate system O-xyz, the position vector of point P at t and t+τ moments could be accessible.

The time delay

τ

can be transformed into an equivalent spatial interval

τ \bar{V}

according to Taylor's freezing hypothesis. Thus, for the physical point P' (at time t+τ), there are corresponding equivalent points

P_{e}^{'}

in the frozen turbulent flow field (at time t). The cross-correlation characteristics between point P and P' that move with the vehicles could be equivalent to the cross-correlation between point P and points

P_{e}^{'}

in the frozen turbulent flow field.

In the frozen turbulent flow field, the equivalent interval between point P and points

P_{e}^{'}

could be the projected distances on the x axis, y axis and z axis, respectively:

\begin{array}{l} Δ x_{e} = (η' - η - V_{T} τ) \cos ϕ - \bar{V} τ \\ Δ y_{e} = (η' - η - V_{T} τ) \sin ϕ \\ Δ z_{e} = ζ^{'} - ζ \end{array}

(13)

Where

\bar{V}

is the mean wind speed of the incoming flow.

The cross-correlation function between the two points on a moving vehicle could be expressed as follows:

ρ_{u u} (r, r', τ) = c_{u} f (\tilde{r}) + (1 - c_{u}) g (\tilde{r})

(14)

where

c_{u} = {(Δ x_{e} / Δ r_{e})}^{2}

，

Δ r_{e} = {(Δ x_{e}^{2} + Δ y_{e}^{2} + Δ z_{e}^{2})}^{1 / 2}

；

\tilde{r} = α \frac{Δ r_{e}}{L_{u}}

，

L_{u} / α = a

，

a = Γ (1 / 3) / [\sqrt{π} \cdot Γ (5 / 6)] \approx 1.339 L

α

=0.747 and

L_{u} = {[\begin{array}{l} {(^{x} L_{u} Δ x_{e} / Δ r_{e})}^{2} + {(^{y} L_{u} Δ y_{e} / Δ r_{e})}^{2} \\ + {(^{z} L_{u} Δ z_{e} / Δ r_{e})}^{2} \end{array}]}^{1 / 2}

When point P and point P' coincide, Eq. (13) becomes as follows:

\begin{array}{l} Δ x_{e} = (- V_{T} τ) \cos ϕ - \bar{V} τ \\ Δ y_{e} = (- V_{T} τ) \sin ϕ \\ Δ z_{e} = 0 \end{array}

(15)

Where

Δ r_{e} = τ V_{R}

V_{R} = {({\bar{V}}^{2} + V_{T}^{2} + 2 \bar{V} V_{T} \cos ϕ)}^{1 / 2}

In the turbulent flow field, the turbulent power spectral density function of a single moving point can be obtained from the autocorrelation function by Fourier transform.

\begin{matrix} S_{u u} (f) = 4 σ_{u}^{2} \int_{0}^{\infty} ρ_{u u} (τ) \cos 2 π f τ d τ \\ = 4 σ_{u}^{2} c_{u} \int_{0}^{\infty} f (\tilde{r}) \cos (2 π f τ) d τ + 4 σ_{u}^{2} (1 - c_{u}) \int_{0}^{\infty} g (\tilde{r}) \cos (2 π f τ) d τ \end{matrix}

(16)

According to

S_{u} (f) = 4 σ_{u}^{2} \int_{0}^{\infty} f (\tilde{r}) \cos 2 π f \tilde{r} d \tilde{r}

and

S_{w} (f) = 4 σ_{w}^{2} \int_{0}^{\infty} f (\tilde{r}) \cos 2 π f \tilde{r} d \tilde{r}

, thus

4 σ_{u}^{2} \int_{0}^{\infty} f (\tilde{r}) \cos 2 π f τ d τ = (\frac{L_{u}}{α V_{R}}) S_{u} (\hat{f})

(17)

4 σ_{w}^{2} \int_{0}^{\infty} g (\tilde{r}) \cos 2 π f τ d τ = (\frac{L_{u}}{α V_{R}}) S_{w} (\hat{f})

(18)

Where

\hat{f} = f L_{u} / α V_{R}

When Eq. (17) and Eq. (18) are put into Eq. (16), Eq. (16) becomes as follows:

\begin{array}{l} 4 σ_{u}^{2} c_{u} \int_{0}^{\infty} f (\tilde{r}) \cos (2 π f τ) d τ + 4 σ_{u}^{2} (1 - c_{u}) \int_{0}^{\infty} g (\tilde{r}) \cos (2 π f τ) d τ \\ = c_{u} (\frac{L_{u}}{α V_{R}}) S_{u} (\hat{f}) + (1 - c_{u}) (\frac{L_{u}}{α V_{R}}) S_{w} (\hat{f}) \end{array}

(19)

For the von Kármán wind spectrum,

α

=0.747.

The parameter values of the power spectral density function of a moving point are as follows:

\tilde{r} = α \frac{τ V_{R}}{L_{u}}

(20)

L_{u} = {}_{x}L_{u} {[c_{u} + (1 - c_{u}) {(2 {}_{y}L_{u} / {}_{x}L_{u})}^{2}]}^{1 / 2}

(21)

c_{u} = {[(V_{T} / V_{R}) \cos ϕ + (\bar{V} / V_{R})]}^{2}

(22)

When the wind speed spectrum at a static point is the von Kármán wind spectrum, the corresponding wind spectrum of a moving point can be obtained.

S_{u u} (\hat{f}) = c_{u} (\frac{L_{u}}{α V_{R}}) S_{u} (\hat{f}) + (1 - c_{u}) (\frac{L_{u}}{α V_{R}}) S_{w} (\hat{f})

(23)

Therefore, based on the theoretical derivation process of the wind velocity spectrum of a static point and the corresponding moving point, a general equation of the wind speed spectrum for a moving point can be obtained. For the von Kármán wind speed spectrum of a static point, the corresponding wind speed spectrum of a moving point can be obtained. The derivation process of the transverse wind velocity spectrum at the moving point is similar to that of the longitudinal wind velocity spectrum. The difference is mainly related to c_i (i = u, v), L_u and V_R. In this study, the investigation mainly focuses on the longitudinal wind velocity spectrum of a moving point.

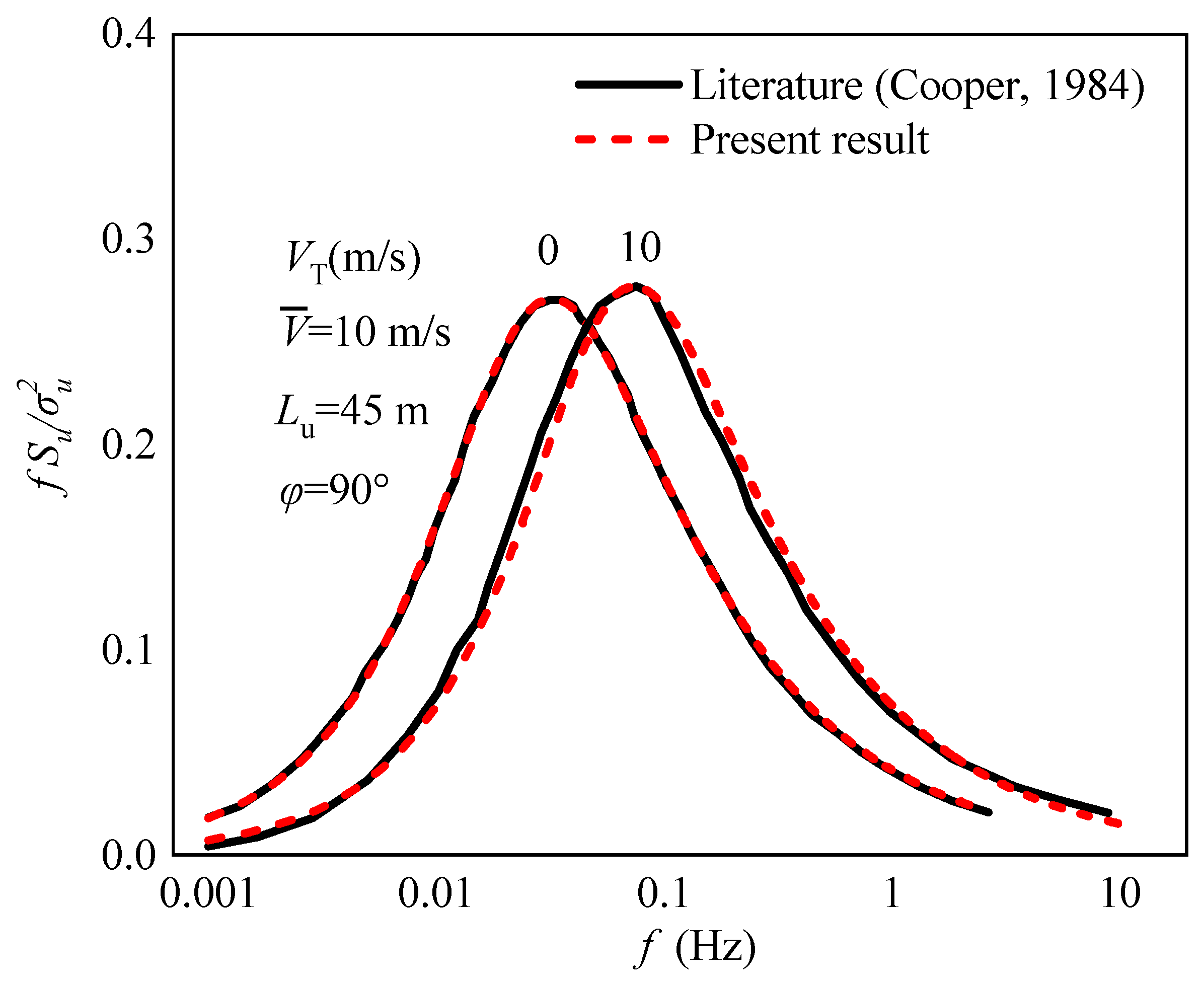
2.4. Validation of the Proposed Model

To verify the validation of the derivation process, Figure 3 shows the comparison curve of Cooper’s results and the results derived in section 2.2. The train vehicle running velocity is 0 m/s and 10 m/s and the longitudinal turbulence integral scale is 45 m. The incoming wind flow is perpendicular to the running direction of the train vehicle. In Figure 3, the horizontal axis coordinates are in log form. It is known that the derived results align well with Cooper’s results, which verifies that the derivation procedure presented in this paper is accurate.

Figure 4. Validation verification of wind speed spectrum of a moving vehicle based on von Kármán spectrum.

3. Turbulent Wind Flow Characteristics in Wind Tunnel

3.1. Wind Tunnel Tests

The experimental campaign was conducted at the XNJD-3 wind tunnel located at Southwest Jiaotong University in China, which is built in 2008, and the wind tunnel is currently the world's largest boundary layer wind tunnel. The atmospheric boundary layer flows were produced using a combination of spires, fences and cubes. The setup covers roughly 25 m of the floor of the wind tunnel.

One typical form of atmospheric boundary layer flow is simulated in this study. The turbulent wind field was generated using 13 rectangular spires with a distance interval of 0.16m (Figure 5). The wind characteristics of the simulated flows was measured by a Cobra probe (Turbulent Flow Instrument series 100). The sampling frequency is set to 256 Hz and the sampling time is 180s. The Cobra Probe was placed at the middle of wind tunnel in width direction. The mean and turbulent wind characteristics along the horizontal direction are basically consistent.

3.2. Turbulent Wind Flow Characteristics

Table 1 tabulates the values of the turbulence intensity and integral length scales. Figure 6 shows the comparison between the normalized stream-wise longitudinal velocity Power Spectral Density (PSD) measured in mean turbulence conditions and the interpolation of the real wind normalized PSD provided by von Kármán as a function of the reduced frequency. The curves in Figure 6 align well.

4. Wind Speed Spectra of a Moving Vehicle

4.1. Results

By putting the parameter results from Table 1 into Eq. (23), the wind speed spectrum of a moving point can be obtained. Figure 7 shows the spectrum results of a moving point corresponding to the static point in the wind tunnel simulated turbulence field at a wind yaw angle of 15° ~ 175° for 12 total working conditions. In Figure 7, V_T is the vehicle running speed,

\bar{V}

is the incoming wind speed and

ϕ

is the wind yaw angle. When the vehicle running speed is 0, it is the wind speed spectrum of the static point corresponding to the spire turbulent flow field in the wind tunnel tests. The turbulent integral scale adopts the results of Table 1.

The ratios of the vehicle running speed to the incoming wind speeds are 0 ~ 5. If the train vehicle running speed is 200 km/h and the wind speed is 11 m/s, the

V_{T} / \bar{V}

value can reach 5. For a running car on highway, the running speed is 120 km/h and the wind speed is 11 m/s, so the

V_{T} / \bar{V}

value is about 3.3. The once-in-a-century wind speed in mountainous areas can reach 30 m/s or higher. The ratio of the vehicle running speed to the wind speed is thus about 2. Therefore, ratios of 0~6 are considered in this investigation.

As can be seen in Figure 7, the basic shape of the wind velocity spectrum varies little. The main differences are found at the wind speed spectrum peaks and the corresponding frequencies.

(1) When

V_{T} / \bar{V}

=1 and the wind yaw angle

ϕ

=15°, the wind speed spectrum peak is the same as that of the static point, while the frequency corresponding to the peak is larger than that of the static point. The wind speed spectrum peak of the moving point gradually becomes larger than that of the static point. As the wind yaw angle

ϕ

increases, the wind velocity spectrum peak and the corresponding frequency of the moving point also gradually increase. At different wind yaw angles, the wind speed spectrum peak of the moving point gradually moves to higher frequencies.

(2) When the wind yaw angle

ϕ

is 15° ~ 45°, the peak wind speed spectrum values of the moving point remain unchanged as the

V_{T} / \bar{V}

values increase. The wind spectrum peak just corresponds to a larger frequency. When the wind yaw angle

ϕ

is 60°, the peak values and the corresponding frequencies increase as the

V_{T} / \bar{V}

value increases. The wind yaw angle continues to increase, and the peaks also gradually increase. When the wind yaw angle is 135°, the frequencies corresponding to the wind spectrum peak gradually decrease. When the wind yaw angle is 175°, the wind speed spectrum in conditions

V_{T} / \bar{V}

=2 and

V_{T} / \bar{V}

=0 roughly coincide.

4.2. Discussion on Wind Speed Spectrum Peak

Figure 8 shows the change regulation of the wind speed spectrum peak at different wind yaw angles and different

V_{T} / \bar{V}

values, in which the amplification coefficient ε represents the ratio of the peak between the moving point and the static point.

Generally, the wind speed spectrum peak changes with the wind yaw angles into the sinusoidal curve.

When the

V_{T} / \bar{V}

value is 0.1 or 0.3, the wind speed spectrum peak of the moving point roughly coincides with the peak of the static point at different wind yaw angles. That is, when the vehicle running speed is small, the influence of movement can be neglected.

When

V_{T} / \bar{V}

is 0.5 and φ is 120°, the wind speed spectrum peak is at the maximum and reaches the minimum at 15° and 175°. The influence of the vehicle running speed should be considered and the maximum increase rate of the wind speed spectrum peak could be 0.6%.

When

V_{T} / \bar{V}

is 0.75 and φ is 135°, the wind speed spectrum peak is at the maximum and reaches the minimum at 15° and 175°. The maximum increase rate of the wind speed spectrum peak could be 2.7%.

When

V_{T} / \bar{V}

is 1 and φ is 175°, the wind speed spectrum peak is at the maximum and is at the minimum at 15°. The maximum increase rate of the wind speed spectrum peak is 7.6%.

When

V_{T} / \bar{V}

is 2, the wind speed spectrum peak is at the minimum at a wind yaw angle of 15° and is at the maximum at 120°. The maximum increase rate of the wind speed spectrum peak could be 7.6%.

When

V_{T} / \bar{V}

increases to 5 from 3, the wind speed spectrum peak is at the minimum at 15° and reaches the maximum at 105°. The maximum increase rate of the wind speed spectrum peak could be 7.5%. That is, when

V_{T} / \bar{V}

is small, the influence of the vehicle running speed is low, and the wind speed spectrum is close to that of the static point.

If the train vehicle running speed is 200 km/h (roughly 55.6m/s) and the wind speed is 11 m/s, the

V_{T} / \bar{V}

value is about 5. Obviously, the influence of movement cann’t be neglected. For a running car, if the running speed is 120 km/h (roughly 33m/s) and the wind speed is 11 m/s, the

V_{T} / \bar{V}

value is about 3.3. Also, the influence of movement should not be neglected. Once-in-a-century wind speeds in mountainous areas could reach to 20 m/s or larger. The ratio of the vehicle running speed to the wind speed is about 2. That is, in a natural wind environment, the influence of the vehicle movement must be considered and the wind speed spectrum peak could be increased by 8% at a wind yaw angle of 105°, which is the worst working condition. That is, in this working condition, the wind speed may be the largest, and wind loads on the train vehicle is most unfavorable.

The wind speed spectrum peak of a moving point is larger than that of a static point. With the increase of the wind yaw angles, the wind speed spectrum peaks of the moving point could be divided into two regions, as is shown in Figure 9 (a): the increasing region I and the decreasing region II.

The change law is shown in Figure 9 (b). As the

V_{T} / \bar{V}

value increases, the wind yaw angle corresponding to the maximum value of ε was firstly increased and then decreased. When the

V_{T} / \bar{V}

value is smaller than 1, the frequencies corresponding to the wind speed spectrum peak are increased with the increasing

V_{T} / \bar{V}

values. When the

V_{T} / \bar{V}

value is larger than 1, the frequencies corresponding to the wind spectrum peak was decreased and then keep unchanged for

V_{T} / \bar{V}

is larger than 3. As the

V_{T} / \bar{V}

value increases, the wind yaw angle corresponding to the maximum value of ε was firstly increased and then decreased.

In Figure 9 (c), the maximum wind speed spectrum peak increase rate is shown. Under the condition that the

V_{T} / \bar{V}

value is larger than 1, the wind speed spectrum peaks increase by 8% and exhibit little change. The wind speed spectrum of a moving point could be considered to have just moved to the right, with small changes in the values. Under the condition that the

V_{T} / \bar{V}

value is smaller than 1, the maximum wind speed spectrum peak is increased with the increasing

V_{T} / \bar{V}

It is obviously known that, for different

V_{T} / \bar{V}

values, the worst working condition is not at a wind yaw angle of 90°. In a natural wind environment, the ratio of the train vehicle running speed to the wind speed could reach to 5 or larger. The most adverse working conditions are found under a wind yaw angle of 105°.

4.3. Discussion on Frequencies Corresponding to Wind Speed Spectrum Peak

In Figure 10, the scaling coefficients of frequencies corresponding to the wind speed spectrum peak are shown. Generally, the scaling coefficients are increased. That is, for a moving point, the frequencies corresponding to the wind speed spectrum peak are larger than those of a static point. Scale coefficients β represent the frequency corresponding to the maximum value of the wind spectrum of a moving vehicle to the static.

From Figure 10(a), when

V_{T} / \bar{V}

is 0.1 and the wind yaw angle is 105°, 120°, 135°, 160° or 175°, the frequencies corresponding to the wind speed spectrum peak of a moving point are smaller than those of a static point. The frequencies show little change as the wind yaw angles increase. When

V_{T} / \bar{V}

is 0.5 and the wind yaw angle is 135°, 150°, 165° or 175°, the same rule is true. The frequency increases as the wind yaw angle increases. When the

V_{T} / \bar{V}

value is 1 and the wind yaw angle is 150°, 165° or 175°, the frequency corresponding to the wind speed spectrum peak of a moving point is smaller than that of a static point. That is, the scaling coefficient is smaller than 1. When the wind yaw angle is 45°, the frequency corresponding to the wind speed spectrum peak of a moving point is the same as that of a static point. In addition, the frequency increases as the wind yaw angle increases. When the wind yaw angle is small, the wind speed spectrum peak of the moving point is mainly caused by the longitudinal wind speed spectrum, and the influence of the transverse wind speed spectrum is little. As the wind yaw angle gradually increases, the influence of the transverse wind speed spectrum also gradually increases.

From Figure 10(c), when

V_{T} / \bar{V}

is 2, 3, 4 or 5, the frequencies corresponding to the wind speed spectrum peak first are firstly increased and then decreased. When the wind yaw angle is 90°, the frequency corresponding to the wind spectrum peak of a moving vehicle is at the maximum. The maximum scaling coefficient β can reach to 10 and the minimum coefficient β can reach to 6 when

V_{T} / \bar{V}

value is 5. When the

V_{T} / \bar{V}

value is 0.1 or 0.5, the maximum scaling coefficient β is smaller than 2 at different wind yaw angles. That is, when the wind direction is perpendicular to the vehicle running direction, the frequencies corresponding to the wind spectrum peak of a moving vehicle are at their largest.

5. Coherence Function

The cross-correlation function of the wind speed at points P and P´ in Figure 3 can be written as follows:

ρ_{u u} (Δ η, τ) = E [u (0, η, t) u (0, η', t + τ)]

(29)

where

u (0, η, t)

and

u (0, η', t + τ)

are respectively the longitudinal wind speeds at points P and P’ at time t and

t + τ

The time delay

τ

can be transformed into an equivalent spatial interval

τ \bar{V}

according to Taylor's freezing hypothesis in Figure 3. Eq. 29 can be presented as the correlation characteristics of points P and

P_{e}^{'}

ρ_{u u} (Δ η, τ) = E [u (0, η, t) u (0, Δ y_{e} + η, t + τ + τ')] = R_{u u} (Δ y_{n}, τ + τ')

(30)

\begin{array}{l} Δ x_{n} = (η' - η - V_{T} τ) \cos ϕ \\ Δ y_{n} = (η' - η - V_{T} τ) \sin ϕ \end{array}

(31)

ρ_{u u} (Δ η, τ) = ρ_{u u} (Δ y_{n}, τ + τ') = \int_{0}^{\infty} S_{u u} (Δ y_{n}, f) \cos [2 π f (τ + τ')] d f

(32)

S_{u u} (Δ y_{n}, f) = C_{o h} (Δ y_{n}, f) S_{u} (f)

(33)

where

S_{u u} (Δ η, f)

is the cross-power spectral density of two points on a moving vehicle with a distance

Δ η

S_{u u} (f)

is the power spectral density of a single point.

By substituting Eq. (32) into Eq. (33), Eq. (32) can be written as follows:

ρ_{u u} (Δ η, τ) = ρ_{u u} (Δ y_{n}, τ + τ') = \int_{0}^{\infty} S_{u} (f) C_{o h} (Δ y_{n}, f) \cos [2 π f (τ + τ')] d f

(34)

C_{o h} (Δ y_{n}, f) = \frac{S_{u u} (Δ y_{n}, f)}{S_{u} (f)}

(35)

C_{o h} (Δ y_{n}, f)

can be presented as follows:

C_{o h} (Δ y_{n}, f) = \exp (- \frac{f C u |Δ y|}{U})

(36)

In Eq. (36), Cu is the correlation coefficient which could not evaluate the influence of the turbulence integral scale on the correlation characteristics. Jakobsen proposed an empirical model with appropriate corrections as follows:

\begin{array}{l} C_{o h} (Δ y_{n}, f) = \exp (- A_{J} Δ y) \\ A_{J} = {(c_{2}^{2} + {(c_{3} f / 2 π U)}^{2})}^{0.5 c_{^{1}}} \end{array}

(37)

where c₁、c₂ and c₃ are the parameters to be fitted. The parameters are dimensioned and Eq. (38) can be corrected as follows:

\begin{array}{l} C_{o h} (Δ y_{n}, f) = \exp (- A_{J_{w}} Δ y) \\ A_{J_{w}} = {(c_{2}^{2} + {(c_{3} f L_{w} / 2 π U)}^{2})}^{0.5 c_{^{1}}} / L_{w} \end{array}

(38)

The correlation coefficients can then be obtained from Eq. (34). However, the most important problem is that the expression for a correlation function cannot be obtained easily. Yan (2018) and Wu (2014) obtained the change law of the correlation function using an integral approach. Considering the wind spectrum peak, when the

V_{T} / \bar{V}

value is larger than 1, the increasing rate could reach 8%. After comprehensive consideration, when the vehicle running speed is larger than the wind speed, the wind spectrum and correlation characteristics should be considered.

In Figure 11, some of the coherence function of points on the vehicle at different running speeds are showed. It could be known that the coherence function increases with the increasing speed ratio of the vehicle running speed to the wind speed. The correlation characteristics on the moving vehicles, which are of great influence, could be investigated by wind tunnel tests.

6. Practical Application

If the train vehicle running speed is 200 km/h (roughly 55.6 m/s), wind speed is 10 m/s, the ratio

V_{T} / \bar{V}

value is about 5.6. In condition the wind speed is smaller than 10 m/s, the ratio

V_{T} / \bar{V}

value is larger than 5.6. The corresponding wind spectrum peak is larger. On high-speed way, if the running speed of a car is 120 km/h (roughly 33 m/s), and in condition the wind speed is 10 m/s, the

V_{T} / \bar{V}

value is about 3.3. While, Once-in-a-century wind speeds in mountainous areas could reach to 20 m/s or larger. The ratio of the train vehicle or car running speed to the wind speed is respectively 2.8 and 1.7. In this condition, influence of running speed of vehicles should not be ignored. At this moment, the wind yaw angle that corresponding to the wind spectrum peak is 105° and not at wind yaw angle 90°. That is, the wind spectrum of a moving vehicle should not be applied by that for a static vehicle. Considering the influence of the bridge deck wind environment, the situation may be even worse.

After obtaining the wind speed spectrum of a moving vehicle, the wind speed could be obtained by numerical analysis method from the wind speed spectrum. From the coherence function, the spatial distribution law of wind speed in the longitudinal direction of moving vehicles. This is largely in line with previous studies. Next, computational analysis based on wind-vehicle-bridge coupling vibration analysis may be conducted.

7. Conclusion

(1) When

V_{T} / \bar{V}

=1 and

ϕ

=15°, the wind speed spectrum peak is equal to that of the static point. As the wind yaw angle

ϕ

increases, the wind velocity spectrum peak and the corresponding frequency of the moving point gradually increase as well. At different wind yaw angles, the wind speed spectrum peak of the moving point gradually moves to higher frequencies.

(2) The wind speed spectrum peak changes with the wind yaw angles into the sinusoidal curve. When the

V_{T} / \bar{V}

value is 0.1, the wind speed spectrum peak of the moving point gradually coincides with the peak of the static point at different wind yaw angles. When

V_{T} / \bar{V}

is 1 and

ϕ

is 175°, the wind speed spectrum peak is at the maximum, and is at the minimum at 15°. The maximum increase rate of the wind speed spectrum peak is 7.5%. When

V_{T} / \bar{V}

increases to 5 from 3, the wind speed spectrum peak is at the minimum at 15° and reaches the maximum at 105°.

(3) When the wind yaw angle is small, the wind speed spectrum peak of the moving point is mainly caused by to the longitudinal wind speed spectrum, and the influence of the transverse wind speed spectrum is low. As the wind yaw angle gradually increases, the influence of the transverse wind speed spectrum also gradually increases. When

V_{T} / \bar{V}

is 2, 3, 4 or 5, the frequency corresponding to the wind speed spectrum peak first increased and then decreased.

(4) The increases in both coherence and the power spectrum contribute to the larger aerodynamic forces and wind-induced vehicle vibration as the speed ratio increases. The correlation characteristics on the moving vehicles, which are of great influence, could be investigated by wind tunnel tests.

Funding

The author(s) disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: The research described in this article was financially supported by the Natural Science Foundation of China (grant no.: 52078438) and the China Postdoctoral Science Foundation (grant no: 2019M663897XB) and Natural Science Foundation of Southwest University of Science and Technology (grant no: 21ZX7148).

Declaration of Conflicting Interests

The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.

References

Balzer, L.A. A Study of an Active Suspension for Trucked Hovercraft and of the Relevant Disturbances. Doctoral dissertation, University of Cambridge, 1973. [Google Scholar]
Balzer, L.A. Atmospheric turbulence encountered by high-speed ground transport vehicles. Journal of Mechanical Engineering Science 1977, 19, 227–235. [Google Scholar] [CrossRef]
Cai, C.S.; Chen, S.R. Framework of vehicle-bridge wind dynamic analysis. Journal of wind engineering and Industrial aerodynamics 2004, 92, 579–607. [Google Scholar] [CrossRef]
Cooper, R.K. Atmospheric Turbulence with Respect to Moving Ground Vehicles. Journal of Wind Engineering and Industrial Aerodynamics 1984, 17, 215–238. [Google Scholar] [CrossRef]
Duan, Q.S. Investigation on the aerodynamic forces characteristics of railway vehicles in turbulent crosswinds. Ph.D. Thesis, Southwest Jiaotong University, China, 2018. [Google Scholar]
Guo, W.W.; Xia, H. Dynamic responses of long-span bridges and running safety of trains under wind action. China Railway Science 2006, 2, 137–139. [Google Scholar] [CrossRef]
Hu, P.; Lin, W.; Yang, D.G.; et al. Fluctuating wind speed spectrum of a moving vehicle under crosswinds. China Journal Highway Transportation 2018, 31, 101–109. [Google Scholar]
Kármán, T.V. Progress in the statistical theory of turbulence. Physics 1948, 34, 530–539. [Google Scholar] [CrossRef]
Li, Y.L.; Qiang, S.Z.; Liao, H.L.; et al. Dynamic of wind-rail vehicle-bridge system. Journal of wind engineering and Industrial aerodynamics 2005, 93, 483–507. [Google Scholar] [CrossRef]
Li, X.Z.; Xiao, J.; Liu, D.J.; et al. An Analytical Model for the Fluctuating Wind Velocity Spectra of a Moving Vehicle. Journal of wind Engineering and Industrial Aerodynamics 2017, 164, 34–43. [Google Scholar] [CrossRef]
Li, X.Z.; Xiao, J.; Liu, D.J.; et al. Fluctuating wind velocity spectra of moving vehicle under horizontal crosswind. Sci Sin Tech 2016, 46, 1263–1270. [Google Scholar] [CrossRef]
Su, Y.; Li, M.S.; Yang, Y.; et al. Experimental investigation of turbulent fluctuation characteristics observed at a moving point under crossflows. Journal of wind Engineering and Industrial Aerodynamics 2020, 197, 1–12. [Google Scholar] [CrossRef]
Taylor, G.I. The spectrum of turbulence. Proceeding of the Royal Society of London 1938, 164, 476–490. [Google Scholar] [CrossRef]
Watkins, S. Wind-tunnel modelling of vehicle aerodynamics: With emphasis on turbulent wind effects on commercial vehicle drag. Ph.D. Thesis, Victorian University of Technology, Australia, 1990. [Google Scholar]
Watkins, S.; Saunders, J.W.; Hoffemann, P.H. Turbulence Experienced by Moving Vehicles. Part I. Introduction and Turbulence Intensity. Journal of wind Engineering and Industrial Aerodynamics 1995, 57, 1–17. [Google Scholar] [CrossRef]
Watkins, S.; Milbank, J.; Loxton, B.J.; et al. Atmospheric Winds and Their Implications for Micro air Vehicles. Aiaa Journal 2006, 44, 2591–2600. [Google Scholar] [CrossRef]
Wu, M.X. Effects of sudden change of wind loads on rail vehicle running performance in crosswind conditions. Ph.D. Thesis, Southwest Jiaotong University, China, 2015. [Google Scholar]
Wu, M.X.; Li, Y.L.; Chen, X.Z.; et al. Wind spectrum and correlation characteristics relative to vehicles moving through cross wind field. Journal of wind Engineering and Industrial Aerodynamics 2014, 133, 92–100. [Google Scholar] [CrossRef]
Xu, Y.L.; Zhang, N.; Xia, H. Vibration of coupled train and cable-stayed bridge system in crosswinds. Engineering Structures 2006, 26, 1389–1406. [Google Scholar] [CrossRef]
Yan, N.J. Wind turbulence and aerodynamic forces relative to moving vehicle and its overturning risk under crosswind. Ph.D. Thesis, Southwest Jiaotong University, China, 2018. [Google Scholar]
Yu, M.; Liu, J.; Liu, D.; Chen, H.; Zhang, J. Investigation of aerodynamic effects on the high-speed train exposed to longitudinal and lateral wind velocities. Journal of Fluids and Structures 2016, 61, 347–361. [Google Scholar] [CrossRef]
Zhang, T. Study on running safety of trains and windproof measures for high-speed railway bridges in strong wind field. Ph.D. Thesis, Beijing Jiaotong University, China, 2013. [Google Scholar]

Figure 2. Correlation functions.

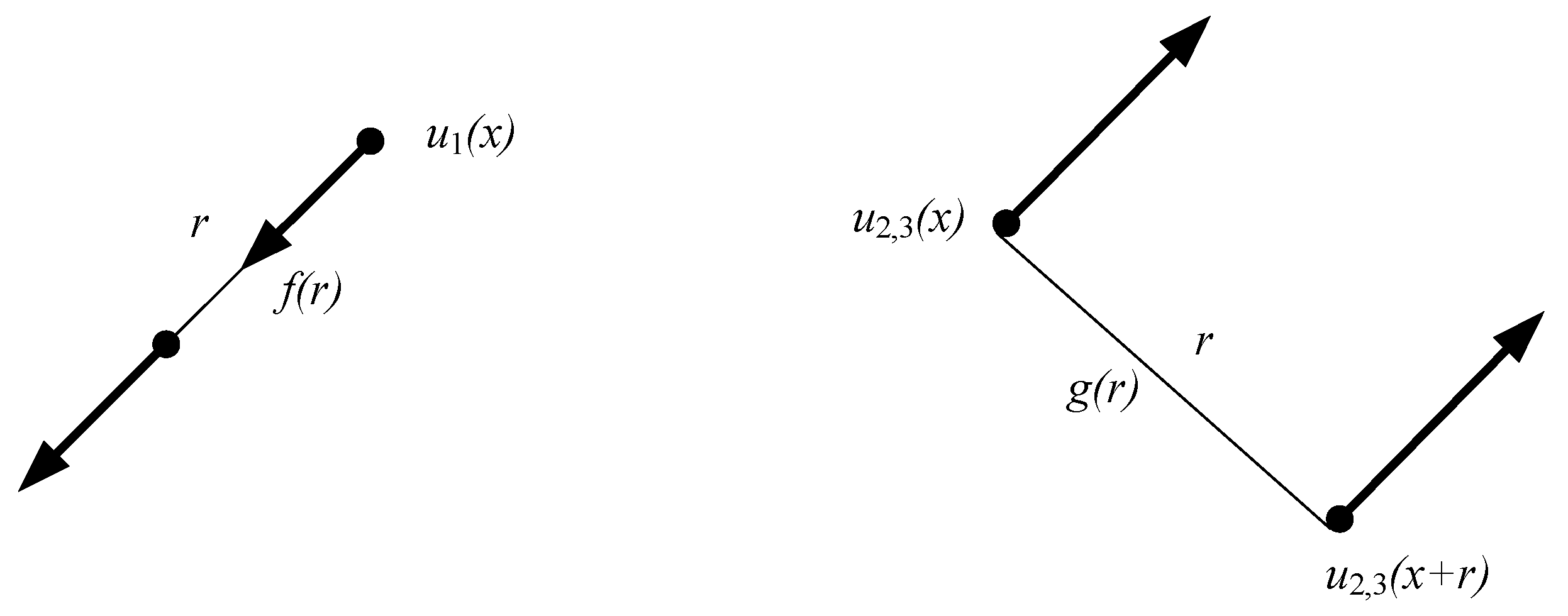
Figure 3. Two points and their equivalent points on a moving vehicle.

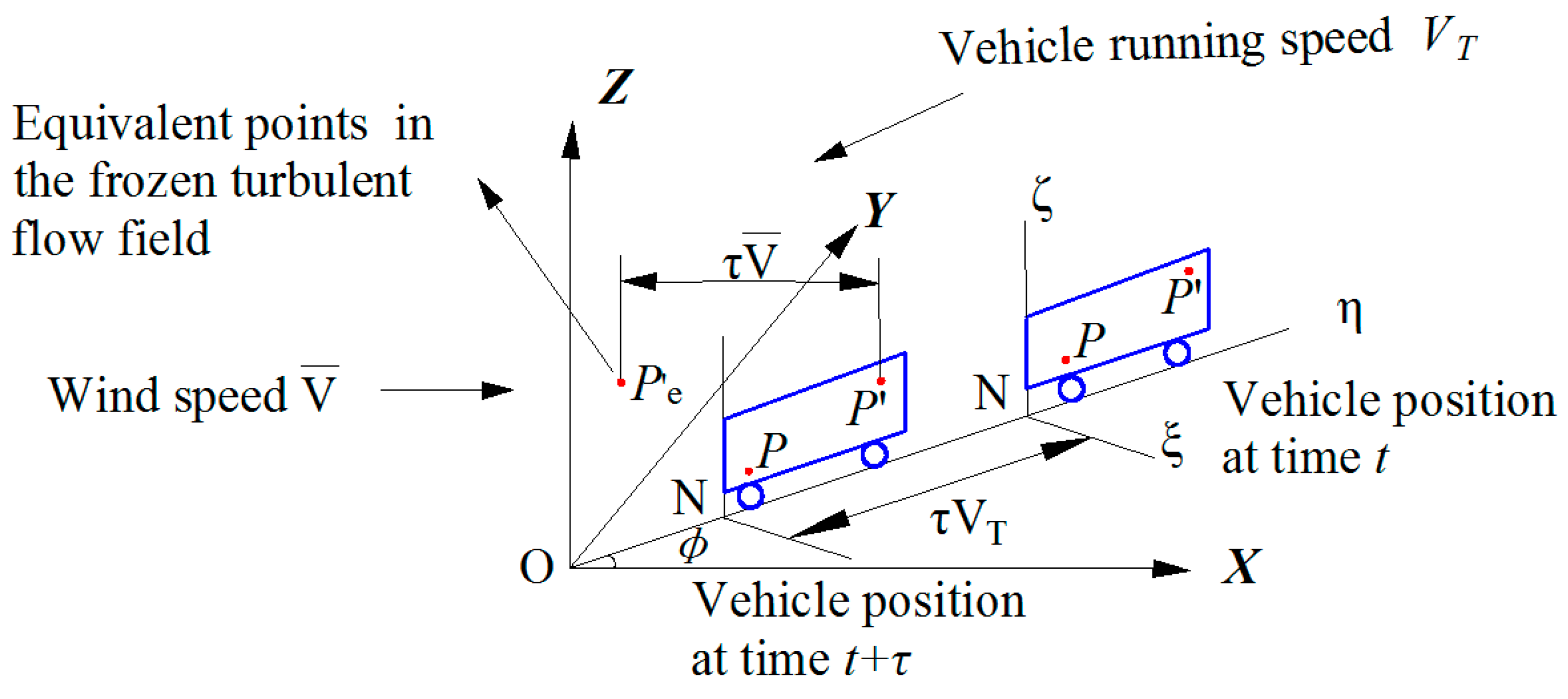
Figure 5. Experimental setups for the wind fields (unit: cm).

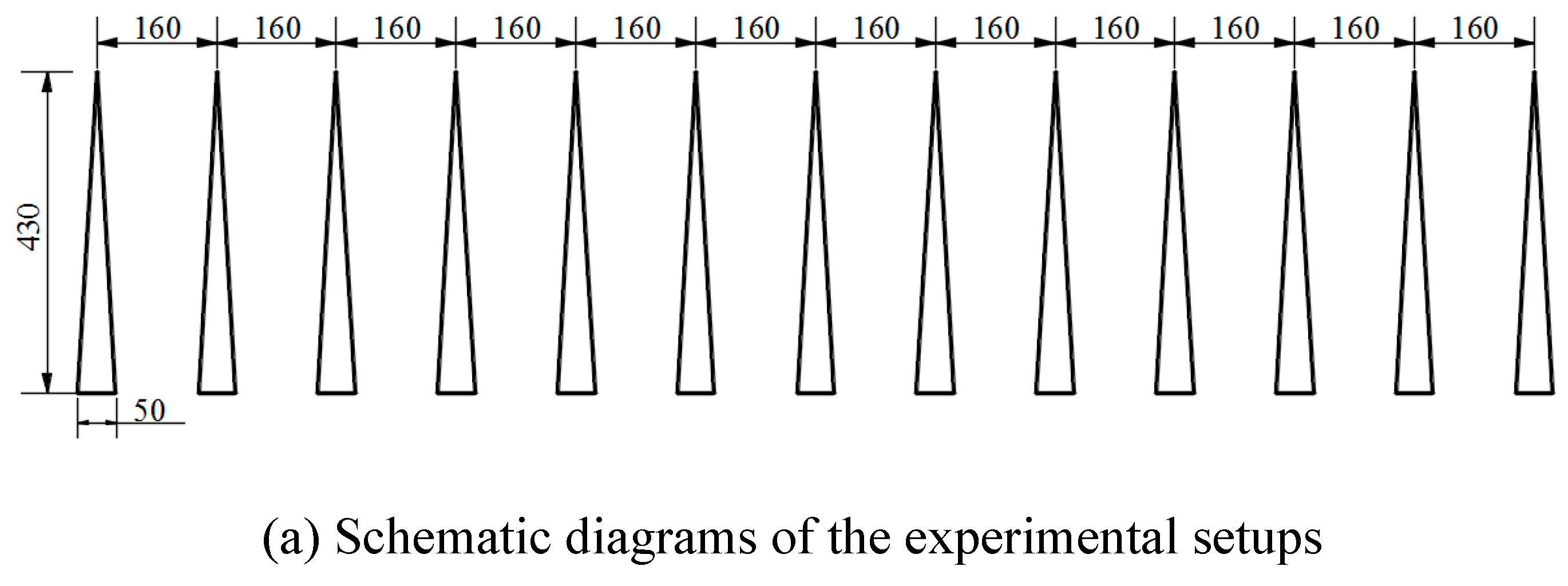
Figure 6. Comparison of the turbulence flow PSD and von Kármán PSD.

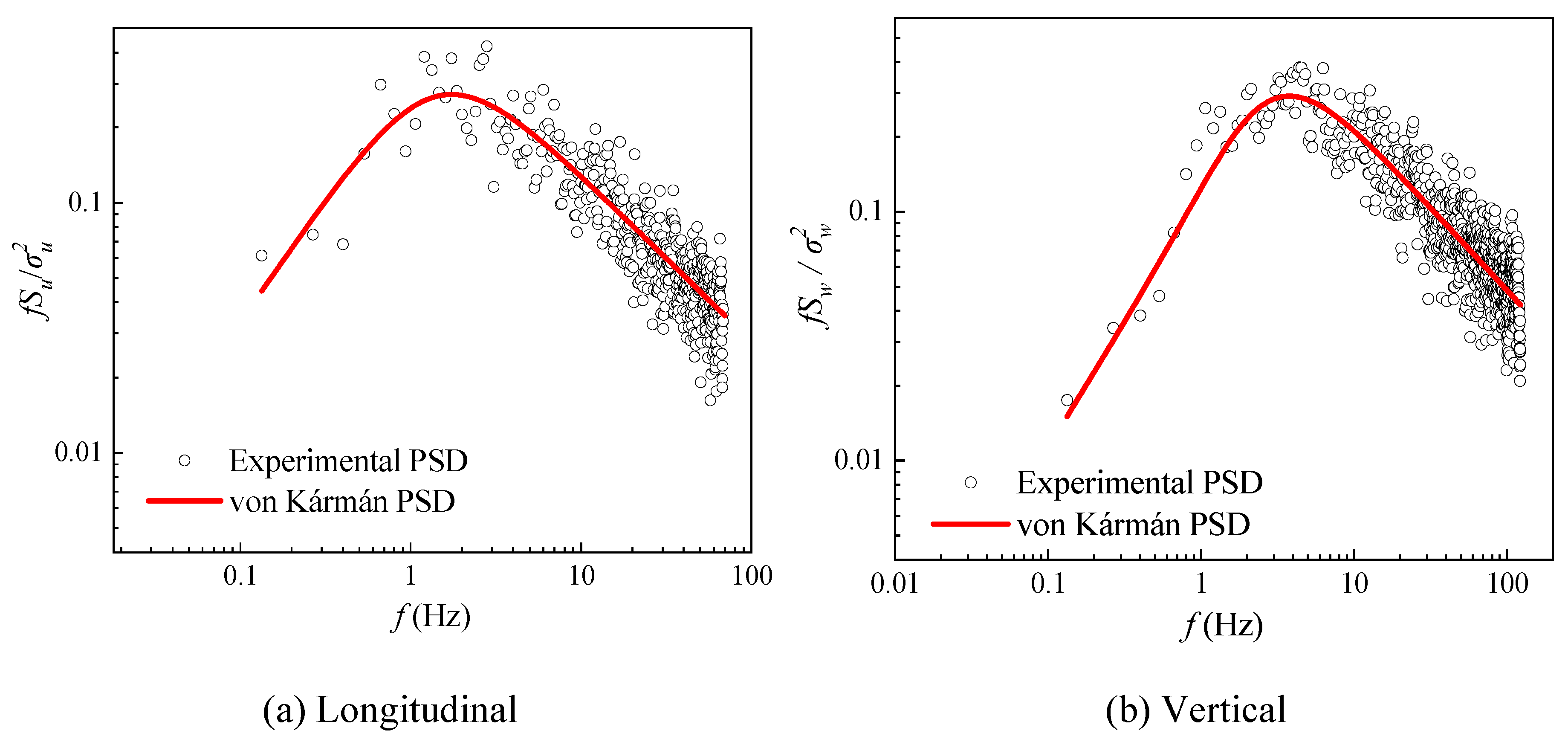
Figure 7. Wind speed spectra of a moving vehicle.

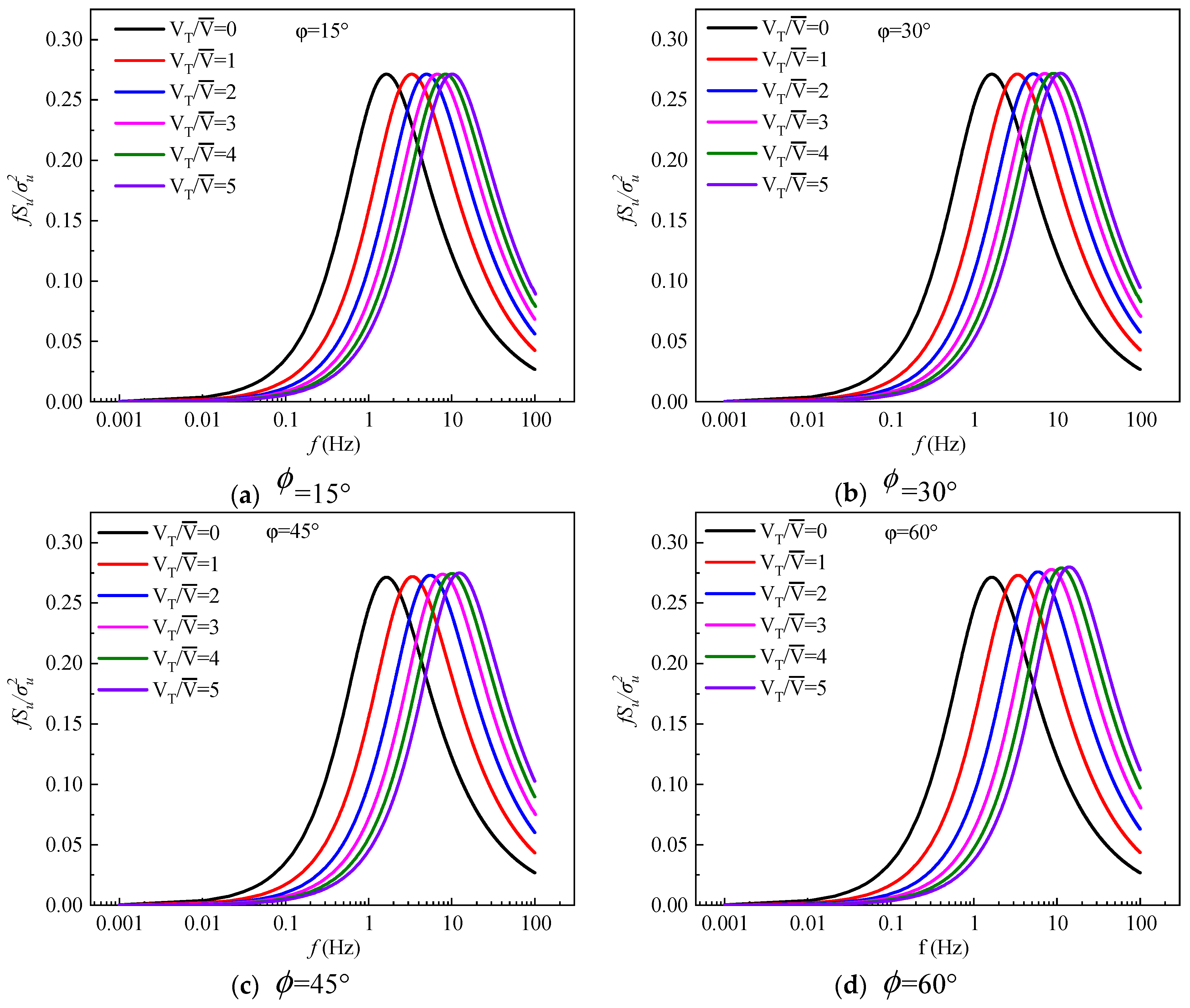
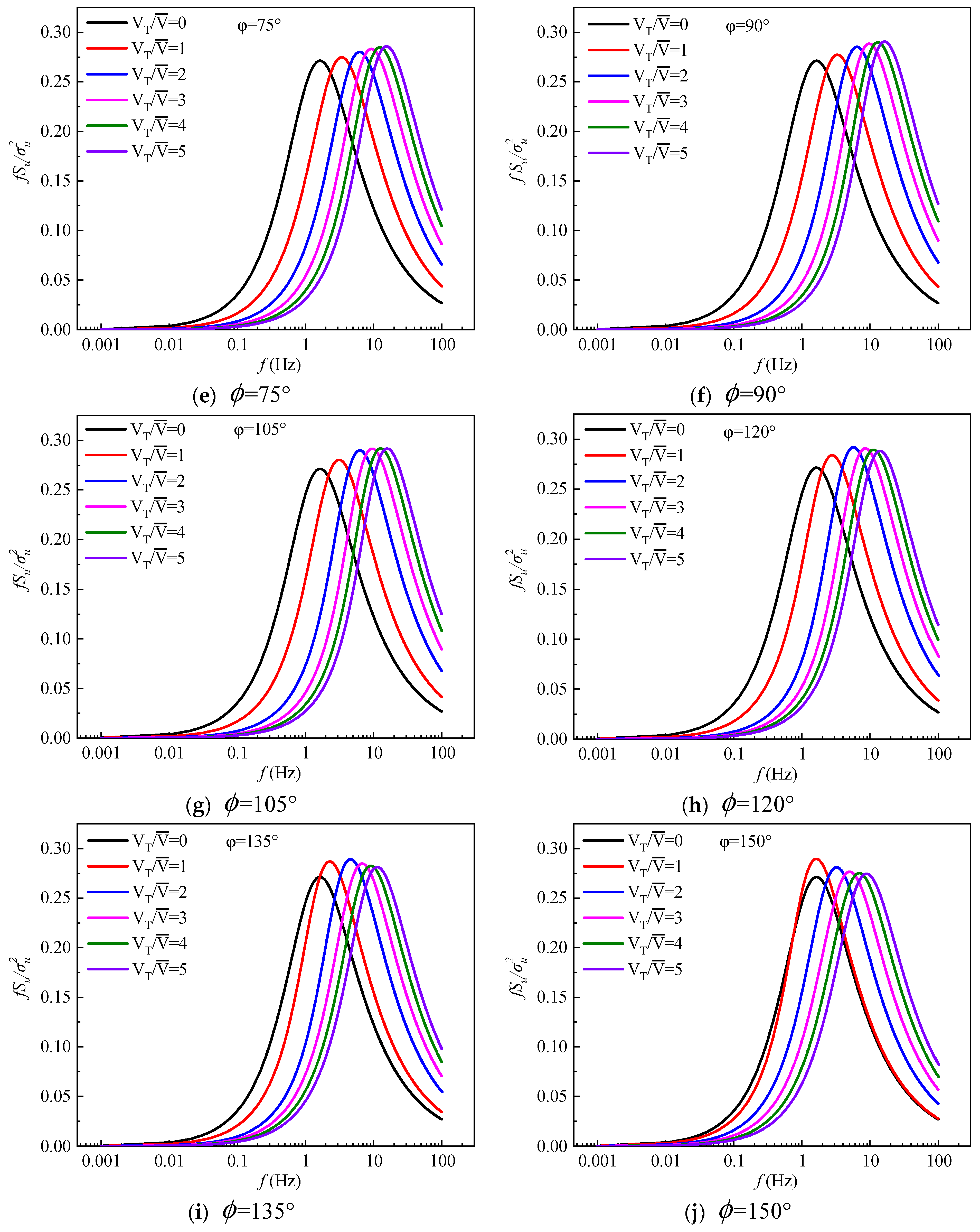
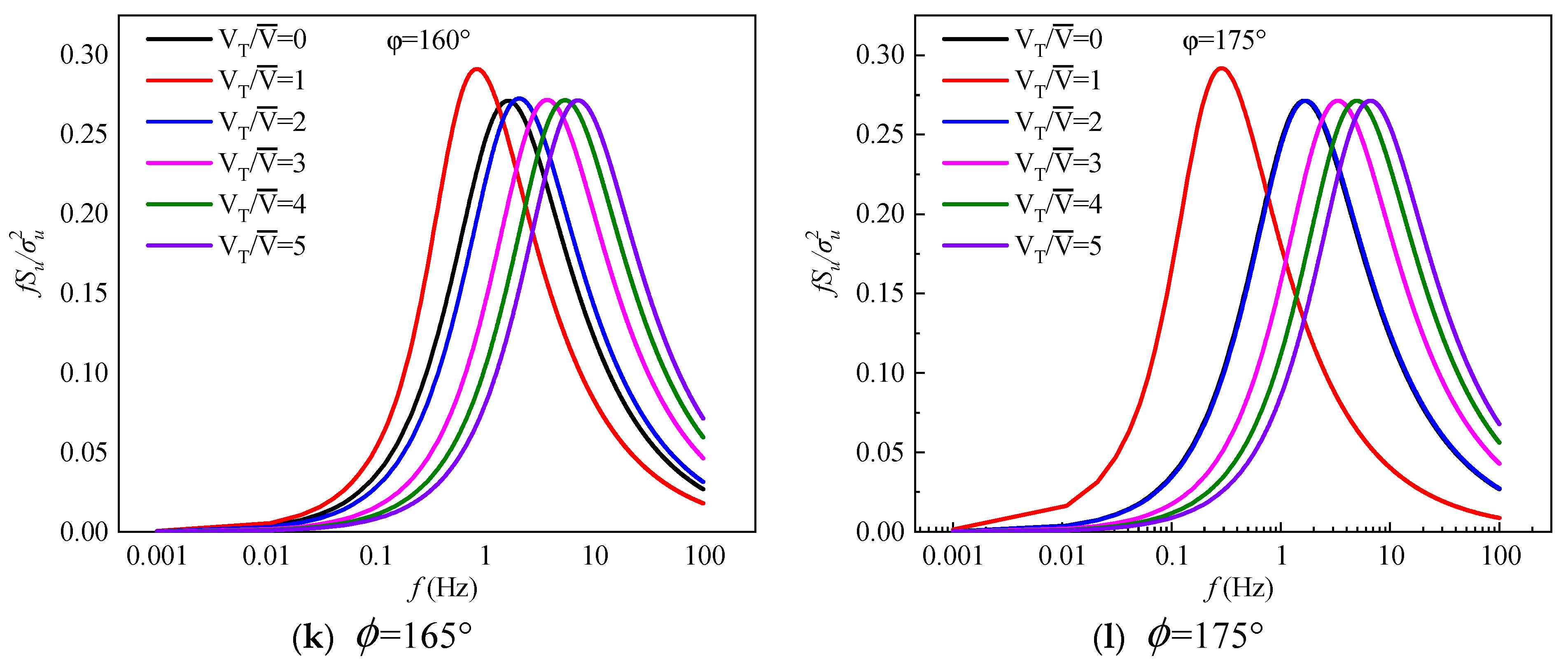
Figure 8. Wind speed spectrum peak coefficients.

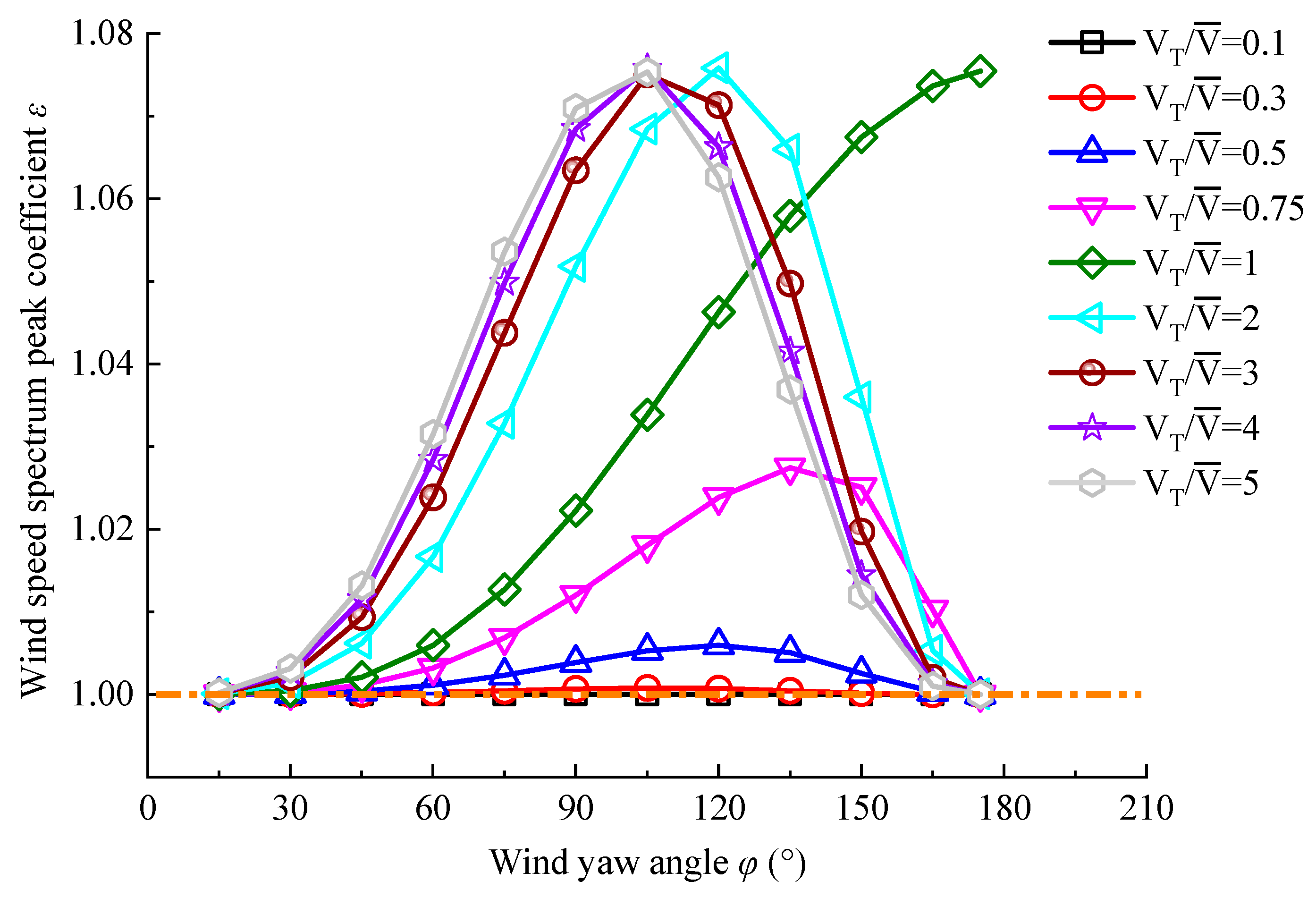
Figure 9. Change law of wind speed spectrum peak coefficients (a) Wind speed peak spectrum coefficients (b) Maximum wind speed spectrum peak at different wind yaw angles and

V_{T} / \bar{V}

Figure 9. Change law of wind speed spectrum peak coefficients (a) Wind speed peak spectrum coefficients (b) Maximum wind speed spectrum peak at different wind yaw angles and

V_{T} / \bar{V}

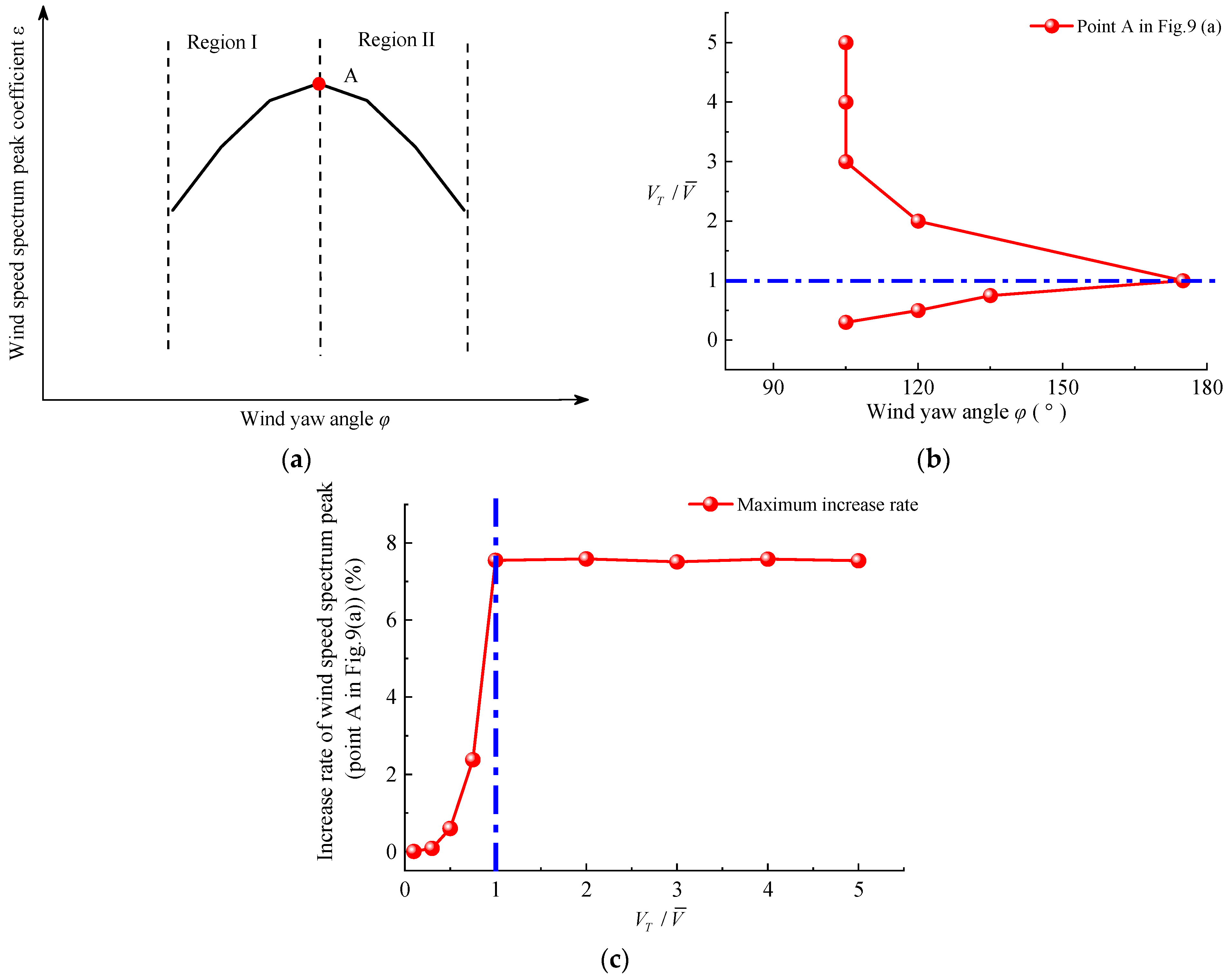
Figure 10. The frequency corresponding to the wind speed spectrum peak.

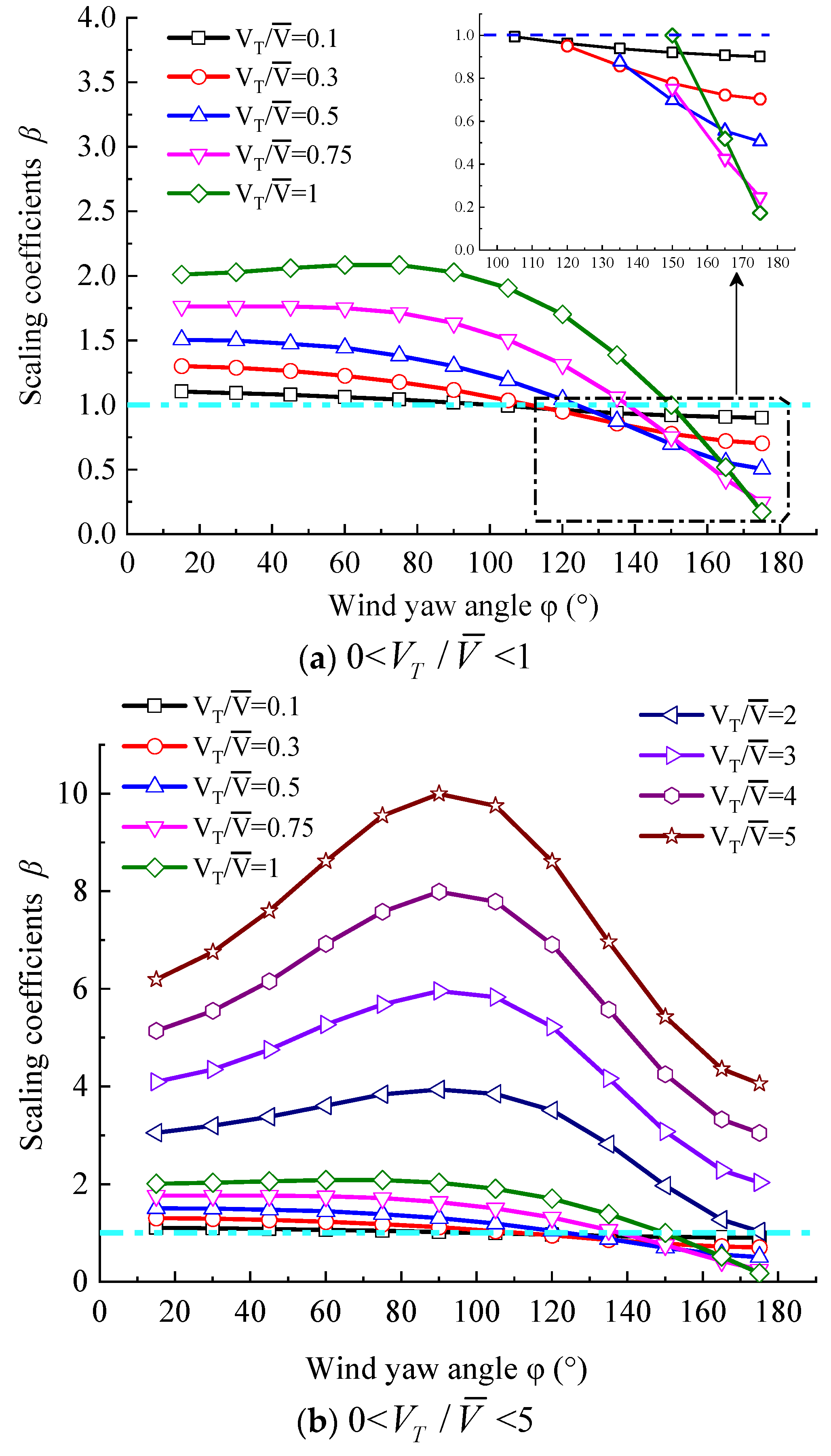
Figure 11. Coherence function of points on vehicle at different running speeds.

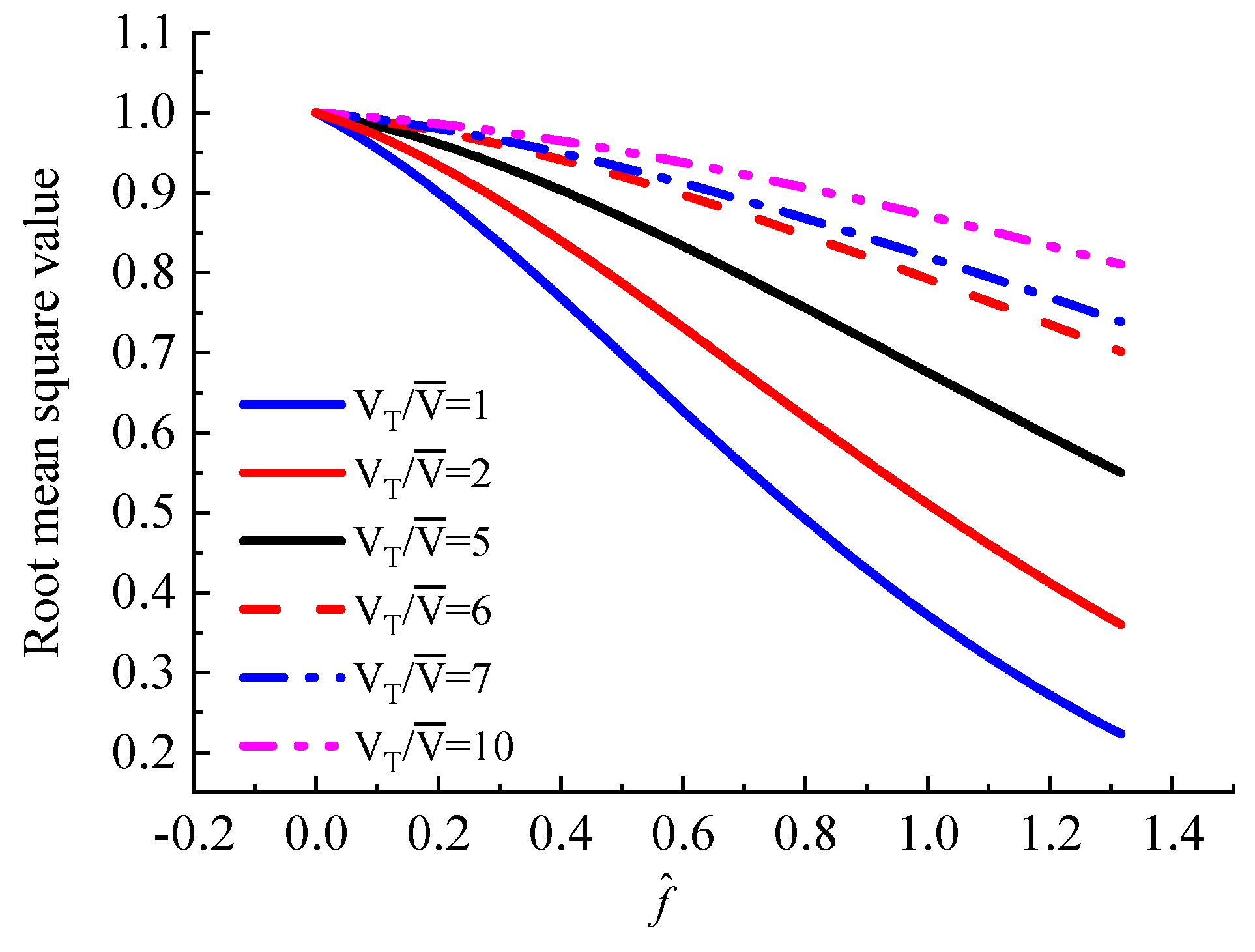
Table 1. Characteristics of the typical types of turbulent flows.

Mean wind speed (m/s)	Turbulence integral scale			Turbulence intensity
Mean wind speed (m/s)	L_u (m)	L_v (m)	L_w (m)	I_u (%)	I_v (%)	I_w (%)
7.770	0.685	0.245	0.217	8.634	7.757	6.944

Note:

u

represents the longitudinal direction;

v

represents the transversal direction;

w

represents the vertical direction.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Wind Speed Spectrum of a Moving Vehicle Under Turbulent Crosswinds

Abstract

1. Introduction

2. Wind Speed Spectrum Models

2.1. Wind Speed Spectrum of a Static Vehicle

2.2. Wind Speed Spectrum of a Moving Vehicle

2.4. Validation of the Proposed Model

3. Turbulent Wind Flow Characteristics in Wind Tunnel

3.1. Wind Tunnel Tests

3.2. Turbulent Wind Flow Characteristics

4. Wind Speed Spectra of a Moving Vehicle

4.1. Results

4.2. Discussion on Wind Speed Spectrum Peak

4.3. Discussion on Frequencies Corresponding to Wind Speed Spectrum Peak

5. Coherence Function

6. Practical Application

7. Conclusion

Funding

Declaration of Conflicting Interests

References

MDPI Initiatives

Important Links

Subscribe