Preprint

Article

Semi-Analytical Prediction of Shield Tunneling Induced Ground Surface Heave Considering Three-Dimensional Space Effect

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

18 September 2023

Posted:

19 September 2023

You are already at the latest version

Alerts

Abstract

The ground surface deformation induced by shield tunnels passing through enclosure structure of existing tunnels is a particular underground construction scenario, which is encountered in Wuhan metro line 12 engineering cases in China. The classic ground deformation theory is difficult to accurately predict this ground deformation. This paper develops a semi-analytical method to predict ground heave considering space effect in this engineering condition. Based on improved ground deformation theory, a novel deformation prediction method of ground and enclosure structure is derived combined with Kirchhoff plate theory. Comparing with field deformation measurements, the maximum difference between measured and calculated deformation is 14.6%, which demonstrating that the proposed method can be used to predict the ground heave induced by shield tunnels passing through the enclosure structure of existing tunnels. The parameters of underground diaphragm wall used in Wuhan metro line 12 are further studied in detail. The results show that the ground heaves have positive correlation with embedded ratio of diaphragm wall, but negative correlation with its elastic modulus and thickness. But the thickness and embedded ratio has a limited effect on ground heaves. This study provides a technical reference for optimization setting of enclosure structure in protecting existing building.

Keywords:

Subject: Engineering - Civil Engineering

1. Introduction

In the process of subway tunnel shielding in urban, it would disturb the original stress state of surrounding soil [1,2], which may lead to the cracking, tilting and even collapse of preexisting buildings [3,4,5,6,7]. Therefore, it is essential to protect buildings from damage during shielding excavation. Engineers need to master enough specialized knowledge for estimating the potential ground movements, so that they can assess whether the damage of neighboring buildings is serious.

Early studies focus on using elastic mechanics and soil mechanics to solve the analytical solutions of ground deformation considering simplified tunnel excavation boundary [8]. For example, Mindlin [9] used Galerkin method to derive the formation of stress field and displacement field under the action of concentrated forces in elastic half space. Based on this form, Timoshenko (1970) proposed a general solution in the form of Airy's function to describe the ground deformation caused by tunnel excavation. Sagaseta [10] assumed that the soil was an incompressible, isotropic, elastic semi-infinite body, and adopted the mirror image method to eliminate the influence of the top free boundary. The soil strain and stress field caused by formation loss at a depth below the surface was then analyzed. Verruijt [11] adopted complex function method to derive the analytical deformation solution of ground caused by circular tunnel excavation in elastic half space. Empirical solutions can extend application conditions of proposed analytical solution. The empirical formula for predicting ground settlement caused by tunnels excavation was first proposed by Peck [12], and the Gaussian normal distribution curve was used to describe the ground settlement profile. Later, many scholars further improved Peck (1969) equation according to different geological conditions, such as Zhao et al. [13], Moh et al. [14] and Atkinson et al. [15]. Finno et al. [16] pointed out that Peck (1969) equation and it modified forms have unavoidable calculation error due to not consider soil three-dimensional (3D) space effect. 3D numerical simulation method is gradually developed to analyze ground deformation [17,18,19,20]. Although numerical method has advantages in simulating complex boundary conditions and capturing the 3D space effect, it has high time-consuming and modeling-difficult shortcoming. Therefore, it is desirable to develop a simple and practical method for calculating the ground movements straightforward.

In addition, large soil-tunnel structure unbalance caused by shield tunnels underpassing existing tunnels is another common and important problem, which studied by many scholars [21,22,23,24,25]. Klar et al. [26] studied the effect of shield excavation on existing pipelines by using the boundary integral method, and gave the normalized solution of calculating the maximum bending moment and angle. Zhang et al. [27] studied the soil disturbance caused by multi-line tunnels and the complex overlapping interaction mechanism of adjacent tunnels. Combined with the field monitoring data of tunnels in Shanghai, the theoretical solution of response of the existing tunnel is obtained. He et al. [28] pointed out that shield tunneling affected the stability of existing tunnels, and it was curial to make reasonable supporting scheme. At present, the protection measures for existing tunnels are enclosure structure to cut off building and existing tunnels [29,30] and grouting strength surrounding soil [28,31]. Grout fluid is difficult to be controlled and easy to lose, so enclosure structure can better control soil and existing tunnels deformation. Shield tunneling would produce additional thrust acted on enclosure structure. If additional thrust is too large, enclosure structure may cause large squeeze deformation, which leads to ground heave. However, how to predict the enclosure structure deformation and ground heave induced by shield tunnels passing through enclosure structure is still unsolved challenges.

This paper aims to derive a simple, explicit solution for predicting the ground heave induced by shield tunnels passing through enclosure structure of existing tunnels considering 3D space effect. To fulfill this objective, the relationships between the deformation volume of enclosure structure and ground deformation volume are firstly established. Furthermore, the ground heave solutions considering 3D space effect are obtained. The validity and applicability of the proposed method is checked with field deformation monitoring results of preexisting Yuanlin road station when metro line 12 passing through line 4. The proposed method may offer some insights in evaluating the ground heaves induced by tunnels passing through enclosure structure in protecting existing building.

2. Problem description

2.1. Engineering background

Wuhan metro line 12, China is only a loop line in Wuhan metro network, with a total length of 59.9 km and consisting of 37 stations. Single line and double hole scheme are adopted in line 12. The diameter of tunnel is 6.8m, and its thickness is 400mm. The route map of Wuhan metro line 12 is shown in Figure 1. At the position of planned Yuanlin road station, line 12 need to underpass through Yuanlin road station of metro line 4.

The Yuanlin road station of line 4 is a single-column and double-span box structure, and has been in operation for many years. The covering thickness of the station is 2.9m, the buried depth of the bottom plate is 15.46m, and the width of the station foundation pit is 19.7m. The base of the station is located in the silty sand layer. The distance between the line 12 and bottom plate of Yuanlin road station is only 2.34m. Hence, it is very dangerous for line 12 passing through Yuanlin road station of metro line 4.

In order to ensure line 12 pass through Yuanlin road station of line 4 in safe, underground diaphragm wall with the thickness of 1200mm and length of 41m is considered. Diaphragm wall is a wide used enclosure structure in Urban underground engineering construction with high stiffness, good anti-seepage performance and little effects on surrounding environment. C30 concrete is used to construct diaphragm wall. The bottom of the wall into the weathered silty mudstone 2m. The I-steel joint is adopted to bond each wall segment. However, Under the protection of underground diaphragm wall, large deformation, even destruction induced by tunneling additional thrust may occur in Yuanlin road station, when line 12 passing through underground diaphragm wall. Figure 2 shows the space relationship of metro line 12, line 4 and underground diaphragm wall. Hence, it is important to accurately evaluate the deformation of Yuanlin road station to determine if more supporting schemes adopted.

2. 2 Engineering geological conditions

The proposed project site locates in river accumulation plain area and belongs to the first-class terrace of the Yangtze River. The terrain of the site is low in the west and high in the east, and the ground elevation variables between 20.8 and 21.6m. The strata of site from top to bottom are mainly ①1 miscellaneous fill, ③1 silty clay, ④1 silty sand and ④2 silty sand, shown in Figure 2. Line 12 is located in silty sand layer. The physical parameters of soils are listed in Table 1, which originates from survey and design files of metro line 12.

3. Prediction method of ground heave considering 3d space effect

3.1. Basic assumptions

This section illustrates the prediction method of shield tunneling induced ground heave considering 3D space effect. Some assumptions are introduced to establish the deformation calculation method, which are as follows:

(1) Under the process of tunneling, the soil volume behind underground diaphragm wall keeps constant.

(2) Ground heave is induced by lateral deformation of underground diaphragm wall, which shown in Figure 3.

(3) Diaphragm wall deformation volume V_W has a proportional relationship with deformation volume V_S,

This is example 1 of an equation:

V_S = μV_W,

(1)

where μ is coefficient proportionality, which depends on compressibility of soil [32]. Considering silty clay used in metro line 12, the value of μ can be set as 0.8.

(4) In order to simplify calculation, the weighted average method is used to homogenize multilayer soil.

(5) Diaphragm wall follows Kirchhoff plate theory [33]. The reason is that the ratio of width and depth of wall is 1.2 m/41 m, which far less than 1/5. Hence, this wall is a typical Kirchhoff plane.

(6) Due to large strength of diaphragm wall, only elastic deformation is considered in wall, which is widely adopted. Additionally, diaphragm wall is considered as isotropic material.

Based on above assumptions, a calculation model of ground heave induced by diaphragm wall deformation is established.

3.2. Deformation volume of diaphragm wall

In our engineering case, the deformation of diaphragm wall is induced by additional thrust during shield tunneling. This can simply as a rectangular thin-plate bending with four edges simply supported, shown in Figure 4.

Navier [33] thinks the deflection of Kirchhoff plate w as double Fourier Series,

w = \sum_{m = 1}^{\infty} \sum_{n = 1}^{\infty} A_{m n} \sin \frac{m π y}{L} \sin \frac{n π z}{H}

(2)

where A_mn is Fourier coefficient. m and n are positive integer. Considering all boundary conditions, the value of A_mn can be obtained. The deflection w for additional thrust P acting on diaphragm wall is induced. The more detailed derivation process is seen in Appendix. The deformation volume V_W of wall can be further calculated,

V_{W} = \int_{0}^{L} \int_{0}^{H} w d y d z

(3)

Equation (3) is expanded, a primary expression is obtained,

V_{W} = \sum_{m = 1}^{\infty} \sum_{n = 1}^{\infty} A_{m n} \frac{L H}{m n π^{2}} (\cos m π - 1) (\cos n π - 1)

(4)

3.3. Ground deformation volume

Due to space effect of ground deformation considered, transverse deformation curve (x-direction) perpendicular to the diaphragm wall and longitudinal deformation curve (y-direction) parallel to the diaphragm wall should be introduced to calculate deformation volume. Many experimental and numerical results show transverse deformation curve has a good agreement with normal distribution [3,32], shown in Figure 5a. Hence, the expression of transverse deformation curve is,

S_{x} = S_{x \max} e^{- π {(x - x_{m})}^{2} / {(x_{0} - x_{m})}^{2}}

(5)

where S_xmax is maximum value of transverse deformation, x₀ is influence range of transverse deformation and x_m is distance from position where has maximum deformation value. Based on field monitoring and theoretical results, Peck (1969) [12] raised that ground deformation of sandy and clay is in range of 2 times excavated depth, and soft soil in 2.5 to 5 times excavated depth. Peck suggestion does not give the value of influence range of deformation. Bowles (1988) [32] studied ground and wall movements induced by excavation of foundation pit. They developed an empirical expression to determine the value x0 of ground movement,

x_{0} = H \tan (45^{\circ} - φ / 2)

(6)

where φ is friction angle of soil. It is also used by Fan et al. [3], Kung [34], Clough and ORourke [35]. Likewise, the x_m can be calculated with an empirical expression,

x_{m} = \frac{H}{\tan (82^{°} - 2.36 φ)}

(7)

Longitudinal deformation curve can be fitted better with Boltzmann function, based on a large number of measured data of ground deformation in Beijing, China [36]. Figure 5b shows the longitudinal deformation calculated model. Hence, ground longitudinal deformation can be expressed as,

S_{y} = S_{y \max} \frac{1}{1 + e^{(y - y_{0} / 2) / 12}}

(8)

where S_ymax is maximum value of longitudinal deformation, y₀ is influence range of longitudinal deformation. Taking x₀ as reference, the value of y₀ can be determined as,

y_{0} = H \tan (45^{\circ} - φ / 2) + L

(9)

where L is the width of diaphragm wall. Considering transverse deformation and longitudinal deformation, the deformation S at any point in ground is,

S = S_{\max} e^{- π {(x - x_{m})}^{2} / {(x_{0} - x_{m})}^{2}} \frac{1}{1 + e^{(y - y_{0} / 2) / 12}}

(10)

where S_max is the maximum value of deformation. In influence range of deformation, integrating Equation (10) to obtain the deformation volume V_S,

V_{S} = \int_{0}^{x_{0}} \int_{0}^{y_{0}} S_{\max} e^{- π {(x - x_{m})}^{2} / {(x_{0} - x_{m})}^{2}} \frac{1}{1 + e^{(y - y_{0} / 2) / 12}} d x d y

(11)

Equation (11) does not have primary form, but can be solved by double numerical integration function using Matlab code.

3.4. Deformation calculation

Figure 6 plots the flowchart of ground heave calculation induced by tunnels passing through underground diaphragm wall. Firstly, the geometrical and mechanical parameters of tunnels and diaphragm wall are substituted into Equation (10), the deformation volume of diaphragm wall V_W is obtained. According to properities of soil, the coefficient of proportionality μ in Equation (1) is determined. Then, the ground heave volume V_S is calculated using Equation (1). Based on the value of V_S, the numerical solution of Equation (11) using Matlab code is obtained to calculate maximum value of ground heave S_max. Finally, ground heave S in any points can be calculated using Equation (10).

4. Field monitoring setting

To investigate the influence of shield tunnels of line 12 passing through diaphragm wall on Yuanlin road station of line 4, the deformation monitoring, diaphragm wall top deformation and horizontal displacement monitoring and axial force monitoring are arranged to evaluate the deformation of Yuanlin road station and diaphragm wall. Figure 7 shows the layout of monitoring points in Yuanlin road station.

The arrangement of deformation monitoring points aimed to monitor the overall deformation of Yuanlin road station. DINI03 electronic level, Tianbao, China and indium steel ruler are used in deformation monitoring. 10 ground observation piers are installed on different positions of Yuanlin road station, as denoted DB-1 to DB-10 in Figure 7. DB-1, DB-2, DB-3, DB-4 and DB-5 points are arranged on monitoring section A-A’, which located upward side of left tunnel. And DB-6, DB-7, DB-8, DB-9 and DB-10 are arranged on monitoring section B-B’, which located upward side of right tunnel. These points are installed by sleeve burying method, shown in Figure 8a.

TCA2003 total station and DINI03 electronic level are employed to monitor the vertical deformation (points ZL-1, ZL-2, ZL-3 and ZL-4) and horizontal displacement (points CX-1, CX-2, CX-3, CX-4, CX-5 and CX-6) of wall top, respectively. Monitoring points are installed by screw-thread steel in diaphragm wall top with length of 100 mm and diameter of 16mm, plotted in Figure 8b. The buried depth of screw-thread steel is 100 mm, and master prism is installed on steel top. The layout of monitoring points is shown in Figure 7.

5. Results and discussion

5.1. Field monitoring results

All monitoring instruments installation finishes before shield tunneling from starting well. The deformation of diaphragm wall and ground heave data is recorded from starting tunnel to passing through diaphragm wall.

Figure 9 shows the variation of ground heave of some typical deformation monitoring points (DB-1, DB-2, DB-3, DB-4 and DB-5) with time. Because the monitoring section A-A’ is symmetrical to section B-B’, monitoring points DB-1, DB-2, DB-3, DB-4 and DB-5 are selected to analyze the deformation mechanism of Yuanlin road station when line 12 passes through underground diaphragm wall. The ground shows s tendency of upward deformation in process of shield tunneling. Additionally, three deformation stages of slope were observed from Figure 9 namely, initial deformation stage, rapid deformation stage and slow deformation stage. In the initial shield excavation stage, the ground deformed at a low rate because of small volume of excavation. After 7 days, the tunnel line 12 is excavated rapidly, and close to Yuanlin road station of line 4, which leads to deformation rate at the surface monitoring points increasing dramatically. When tunnels pass through diaphragm wall, the ground heave suddenly increases, and then shows a temporarily stable. After tunnel line 12 passing through diaphragm wall, the deformation values of monitoring points DB-1, DB-2, DB-3, DB-4 and DB-5 are 4.1mm, 6.2mm, 7.53mm, 7.92mm and 6.72mm, respectively. Overall, the ground heave is small, which not affect stability of line 4.

Likewise, the monitoring results of wall top vertical deformation of CX-1, CX-2, CX-3 and CX-4 are plotted in Figure 10. Overall, three deformation stages are observed which are same with that of ground heave. Initial small deformation lasts 25 days, which is longer than that of ground heave. The main reason is that large stiffness of diaphragm wall leads to its smaller deformation response, compared with ground heave response. Additionally, diaphragm wall produces large deformation when line 12 passing through wall. As shown in Figure 10, after tunnel line 12 passing through diaphragm wall, the vertical deformation values of monitoring points CX-1, CX-2, CX-3 and DB-4 are 0.21mm, 0.1mm, 0.15mm, and 0.5mm, respectively.

Figure 11 shows horizontal deformation result of typical monitoring points ZL-1 and ZL-2 in section A-A’ during tunneling of line 12. The main horizontal deformation of diaphragm wall tendency of monitoring points is consistent with vertical deformation. The direction of horizontal deformation of diaphragm wall is towards to adjacent Yuanlin road station. At tunneling of 43 days, the horizontal deformations of monitoring points ZL-1 and ZL-2 are 6.81mm and 4.71mm, respectively.

5.2. Field monitoring results

According to the proposed deformation calculation method, the deformation of diaphragm wall and Yuanlin road station of line 4 is determined. The value of additional thrust P can be taken as 20 kPa [37]. Table 2 lists the calculated mechanical parameters of ground deformation. The value of m and n in Equation (4) affects the calculation accuracy of proposed method. To determine optimum value of m and n, more than 100 trial calculations are conducted. The values of m and n variable from 3 to 20 in trial calculations. Figure 12 shows the deformation of wall acting of additional thrust under different m and n. The variation of calculated results is small when the values of m and n are greater than 10. It is shown that the values of m and n are 11, which is sufficient in terms of computational accuracy.

Deformation monitoring points DB-1, DB-2, DB-3, DB-4 and DB-5, and horizontal deformation monitoring point CX-1 in Monitoring section A-A’ is selected to verify the accuracy of proposed method. Figure 13 shows the comparisons of deformation of diaphragm wall and ground measured by monitoring points and calculated by proposed method. The calculated horizontal deformation of diaphragm wall top is 0.6 mm, which has small difference from measured value. The calculated deformation values for DB-1, DB-2, DB-3, DB-4 and DB-5 are 3.74mm, 5.95mm, 7.44mm, 7.64mm, 6.31mm, respectively. The maximum difference between measured and calculated deformation is 14.6%, which is acceptable for engineering analysis. Additionally, the measured ground heave is greater than calculated value, plotted in Figure 13. The reason is that the vertical deformation of diaphragm wall is not considered in proposed model. Actually, deformation of wall would affect surrounding ground heave. However, the measured deformation of diaphragm wall is 0.2mm, which value is too small to obviously affect accuracy of proposed model. Hence, it is indicated that the proposed method can be used to analyze the ground heave induced by shield tunnel passing through building envelope.

Based on ground heave calculation results, 3D ground heave of Yuanlin road station is plotted in Figure 14. The groove shape is observed in whole ground heave. The maximum deformation is 7.64mm, which located in center of two tunnels. And the value of deformation become small, as being away from tunnels.

5.3. Parametric study of underground diaphragm wall

The main factors that affecting the ground heave induced by tunnels passing through diaphragm wall is thickness b, elasticity modulus E and depth H of diaphragm wall. But how those factors affect the ground heave is not known, which should be studied.

Based on the proposed method, the thickness of diaphragm wall of 600mm, 800mm, 900mm, 1000mm, 1100mm and 1200mm is used to calculate ground heave, and other parameters are same with that in section 5.2. Figure 15 plots the ground heave under different thickness of diaphragm wall at center section of twin tunnels. As the thickness of diaphragm wall increases, the ground heave decreases gradually. The maximum deformation values are 8.1mm, 7.64mm, 7.26mm, 7.03mm, 6.88mm and 6.84mm for thickness of 600mm, 800mm, 900mm, 1000mm, 1100mm and 1200mm, respectively. Compared with maximum deformation value of thickness of 600mm, the decrements of 0.46mm, 0.84mm, 1.07mm, 1.22mm and 1.26mm are for the thickness of 800mm, 900mm, 1000mm, 1100mm and 1200mm, respectively. It is indicating that the ground heave trends to stable as thickness increases. Hence, the large thickness of diaphragm wall can control the ground heave, but the effect of larger thickness is limited. Reasonable selection of thickness of diaphragm wall is significant.

The effects of elastic modulus of diaphragm wall on ground heave is shown in Figure 16. The values of elastic modulus E are selected as 15GPa, 20GPa, 25GPa, 30GPa and 35GPa, and other parameters are same with that in section 5.2. As the elastic modulus increases, the deformation gradually decreases, meanwhile, the ground heave curve is getting much narrower and shallower. Further analysis shows that compared with maximum deformation value of elastic modulus of 15GPa, the decrements of 0.39mm, 0.77mm, 1.16mm, 1.55mm are for the elastic modulus of 20GPa, 25GPa, 30GPa, 35GPa, respectively. Hence, the stiff diaphragm wall facilitates the control of ground heave, and the facilitation is significant.

To discuss the effect of the embedded length of diaphragm wall on ground heave, an embedded ratio r_e is defined as,

r_{e} = \frac{H_{e}}{H}

(12)

where H_e is the length between bottom of tunnels and top of diaphragm wall.

The effect of the embedded ratio r_e of diaphragm wall on ground heave is shown in Figure 17. The length of diaphragm wall H is set as 41m, 49.2m, 61.5m, 82.0m and 123m and He keep constant value of 24.6m. It is shown that as the embedded ratio increases, the ground heave gradually increases. The increase degree for r_e of 0.3, 0.4, 0.5 and 0.6 is 1.02%, 2.15%, 7.83% and 13.5%, respectively. It is indicating that the embedded length of diaphragm wall is beneficial to control ground heave, but when the embedded length reaches a certain value, it has little effect on the surface deformation.

6. Conclusions & discussion

This paper develops a semi-analytical method to predict ground heave induced by shield tunnels passing through enclosure structure of existing tunnels considering space effect. The proposed method is based on improved ground deformation theory combined with Kirchhoff plate theory. The proposed method is verified by comparing with the field measurements. The main conclusions are drawn as follows:

(1) The relationships between the deformation volume of underground diaphragm wall and ground deformation volume are firstly established. The deformation volume of diaphragm wall is calculated by Kirchhoff plate theory, and the ground deformation volume is evaluated by transverse deformation curve and longitudinal deformation curve. Further, the ground heave solutions at arbitrary position are obtained.

(2) The proposed method is verified by field measurements from Wuhan metro tunnel cases, China. In general, a good agreement has been observed for shield excavation induced ground heave profile and the prediction is good for normalized ground heave profile. The maximum error is 14.6%, which is acceptable. Hence, the proposed method can be used as a feasible approach for estimation of deformations induced by shield excavations.

(3) The parameters of underground diaphragm wall are studied using the proposed deformation calculation method to determine reasonable design scheme of underground diaphragm wall. The elastic modulus of diaphragm wall has significant effects on ground heaves, while the thickness and embedded ratio of diaphragm wall has limited effects on ground heaves. As elastic modulus and thickness of diaphragm wall increase, the ground heaves gradually decrease. And the effects of embedded ratio show a positive correlation. But when the thickness and embedded ratio reaches a certain value, it has little effect on the ground heaves.

(4) The presence of underground water has non-ignorable influences on ground deformation. So, a new ground heaves prediction method should be derived considering underground water seepage in the future.

Author Contributions

Methodology, J.Q. and F.L.; software, J.Q.; validation, J.Q. and G.Z.; formal analysis, L.S. and P.Z.; investigation, J.Z. and L.S.; data curation, F.L. and F.Z.; writing, J.Q. and G.Z.; supervision, Y.J.; project administration, Y.J.; funding acquisition, Y.J. and G.Z. All authors have read and agreed to the published version of the manuscript.

Funding

This research was sponsored by the National Natural Science Foundation of China (Grant Nos.: 41920104007, 42227805).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Data available on request due to restrictions eg privacy or ethical The data presented in this study are available on request from the corresponding author. The data are not publicly available due to business reasons.

Conflicts of Interest

The authors declare no conflict of interest.

Appendix A

Deflection solution for diaphragm wall with additional thrust P

For arbitrary loading q, Navier [33] gives the value of A_mn in Equation (2),

A_{m n} = \frac{4 \int_{0}^{L} \int_{0}^{H} q \sin \frac{m π y}{L} \sin \frac{n π z}{H} d y d z}{π^{4} L H D {(\frac{m^{2}}{L^{2}} + \frac{n^{2}}{H^{2}})}^{2}}

(A1)

where D is bending stiffness of thin-plate, which is calculated as,

D = \frac{E b^{3}}{12 (1 - μ^{2})}

(A2)

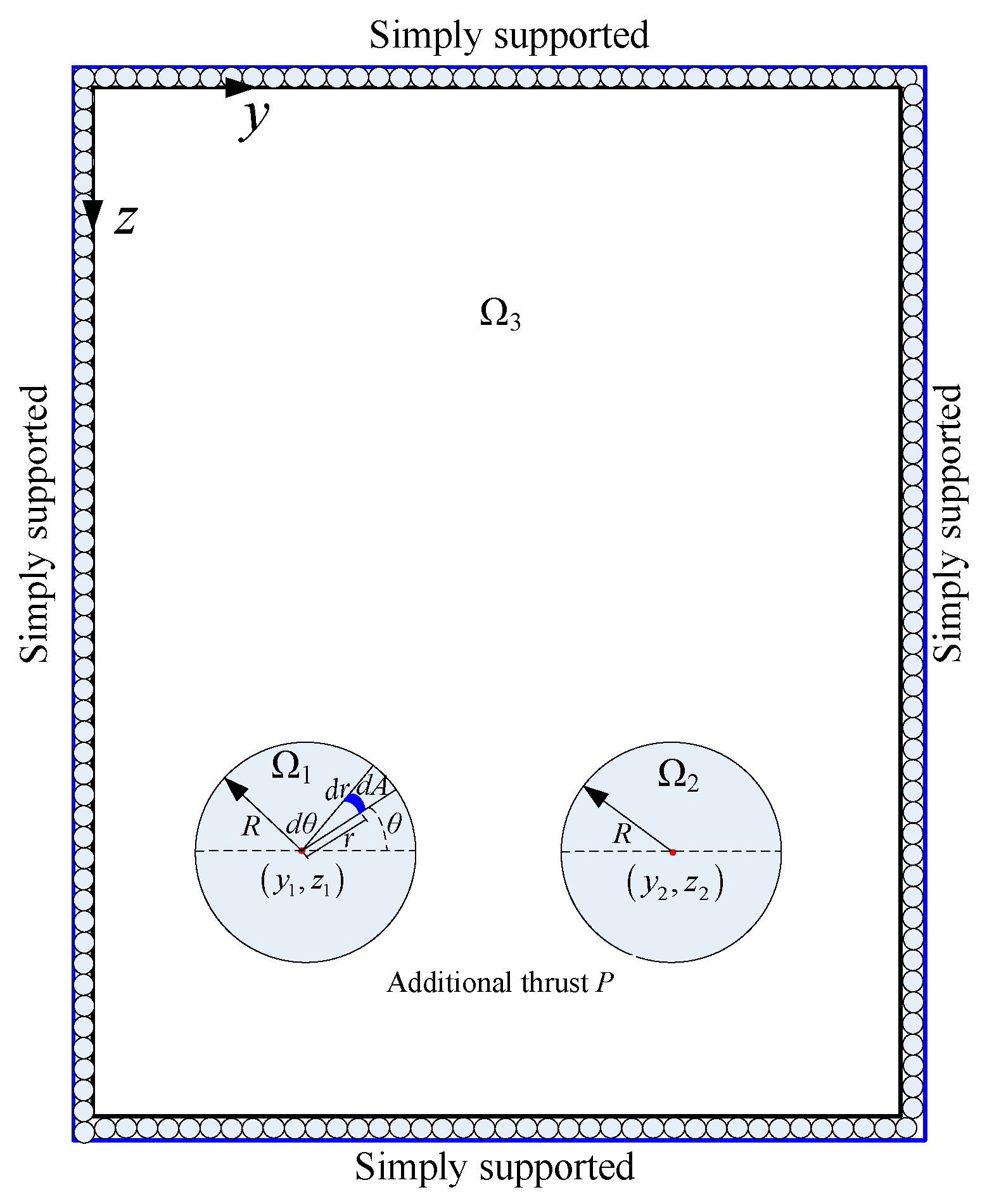
in which, E is elasticity modulus of plate and μ is Poisson's ratio of plate. In our condition, two circle zones (tunnels) in thin-plate is sufficient to additional thrust P. In local coordiate, the positions of two circle are

({x^{'}}_{1}, {z^{'}}_{1})

and

({x^{'}}_{2}, {z^{'}}_{2})

, and have same radius of R. Figure A1 shows the schematic diagram of diaphragm wall with additional thrust. Hence, the A_mn can be written as,

A_{m n} = \frac{4}{π^{4} L H D {(\frac{m^{2}}{L^{2}} + \frac{n^{2}}{H^{2}})}^{2}} \int_{Ω_{1} + Ω_{2} + Ω_{3}} q \sin \frac{m π y}{L} \sin \frac{n π z}{H}

(A3)

Due to no any force acting on zone Ω₃, the Equation (A3) can be simplified as,

A_{m n} = \frac{4}{π^{4} L H D {(\frac{m^{2}}{L^{2}} + \frac{n^{2}}{H^{2}})}^{2}} \int_{Ω_{1} + Ω_{2}} q \sin \frac{m π y}{L} \sin \frac{n π z}{H}

(A4)

Adopting polar coordinate trnaform (r, θ) to solve double integral,

y^{'} = r \cos θ

z^{'} = r \sin θ

and dA=rdrdθ is substituted into Equation (A4). Equation (A4) becomes,

A_{m n} = \frac{4}{π^{4} L H D {(\frac{m^{2}}{L^{2}} + \frac{n^{2}}{H^{2}})}^{2}} \int_{0}^{2 π} \int_{0}^{R} P r (\sin \frac{m π (y_{1} + r \cos θ)}{L} \sin \frac{n π (z_{1} + r \sin θ)}{H} + \sin \frac{m π (y_{2} + r \cos θ)}{L} \sin \frac{n π (z_{2} + r \sin θ)}{H}) d r d θ

(A5)

Equation (A4) doesn’t have primary solution. MATLAB commerical software provides a double numerical integration function. The value of A_mn can be calculated using MATLAB code, which are listed as,

close all; clear all; clc

f=@(r, theta) P*r*(sin(m*pi*(y1+r*cos(theta))/L)* sin(n*pi*(z1+r*sin(theta))/H)+

sin(m*pi*(y2+r*cos(theta))/L)* sin(n*pi*(z2+r*sin(theta))/H));

Amn=4/(pi^4*L*H*D*(m^2/L^2+n^2/H^2))*dblquad(f,0,2*pi,0,R,1.0e-3,’quadl’);

Figure A1. Calculated model of diaphragm wall with additional trust.

References

Schuster, M.; Kung, G.; Juang, C.; Hashash, Y. Simplified model for evaluating damage potential of buildings adjacent to a braced excavation. Journal of Geotechnical and Geoenvironmental Engineering. 2009, 135, 1823–1835. [Google Scholar] [CrossRef]
Hsiao, E.; Schuster, M.; Juang, C.; Kung, G. Reliability analysis and updating of excavation-induced ground settlement for building serviceability assessment. Journal of Geotechnical and Geoenvironmental Engineering. 2008, 134, 1448–1458. [Google Scholar] [CrossRef]
Fan, X.; Phoon, K.; Xu, C.; Tang, C. Closed-form solution for excavation-induced ground settlement profile in clay. Computers and Geotechnics. 2021, 137, 104266. [Google Scholar] [CrossRef]
Cao, L.; Zhang, D.; Fang, Q. Semi-analytical prediction for tunnelling-induced ground movements in multi-layered clayey soils. Tunneling and Underground Space Technology. 2020, 102, 103446. [Google Scholar] [CrossRef]
Dalgoc, K.; Hendriks, M.; Ilki, A. Building response to tunneling and excavation-induced ground movements: using transfer functions to review the limiting tensile strain method. Structure & Infrastructure Engineering: Maintenance, Management, Life-Cycle Design & Performance. 2018, 14, 766–779. [Google Scholar] [CrossRef]
Park, K. Elastic solution for the tunneling-induced ground movements in clays. International Journal of Geomechanics. 2004, 4, 310–318. [Google Scholar] [CrossRef]
Bobet, A. Analytical solutions for shallow tunnels in saturated ground. Journal of Engineering Mechanics. 2001, 127, 1258–1266. [Google Scholar] [CrossRef]
Kong, F.; Lu, D.; Du, X. Elastic analytical solution of shallow tunnel owing to twin tunnelling based on a unified displacement function. Appl. Math. 2019, 68, 422–442. [Google Scholar] [CrossRef]
Mindlin, R. Force at a point in the interior of a semi-infinite solid. Physics. 1936, 7, 195–202. [Google Scholar] [CrossRef]
Sagaseta, C. Analysis of undrained soil deformation due to ground loss. Geotechnique. 1987, 37, 301–320. [Google Scholar] [CrossRef]
Verruijt, A. A complex variable solution for a deforming circular tunnel in an elastic half-plane. International Journal for Numerical and Analytical Methods in Geomechanics. 1997, 21, 77–89. [Google Scholar] [CrossRef]
Peck, R. Deep excavation and tunneling in soft ground. Proceedings of the 7th International conference on soil mechanics and foundation engineering, State-of-the-Art. Mexico city, 1969; pp. 225–290.
Zhao, C.; Lavasan, A.; Barciaga, T. Mechanized tunneling induced ground movement and its dependency on the tunnel volume loss and soil properties. International Journal for Numerical and Analytical Methods in Geomechanics. 2019, 43, 781–800. [Google Scholar] [CrossRef]
Moh, Z.; Ju, H.; Hwang, R. Ground movements around tunnels in soft ground. Proceedings of the International symposium on geotechnical aspects of underground construction in soft ground. Rotterdam: Balkema, 1996; pp. 268–273.
Atkinson, J.; Potts, D. Stability of a shallow circular tunnel in cohesionless soil. Geotechnique. 1977, 27, 203–215. [Google Scholar] [CrossRef]
Finno, R.; Blackburn, J.; Roboski, J. Three-dimensional effects for supported excavations in clay. Journal of Geotechnical and Geoenvironmental Engineering. 2007, 133, 30–36. [Google Scholar] [CrossRef]
Liu, C.; Peng, Z.; Pan, L.; Pan, L.; Liu, H.; Yang, Y.; Chen, W. Influence of tunnel boring machine (TBM) advance on adjacent tunnel during ultra-rapid underground pass (URUP) tunneling: a case study and numerical investigation. Applied Sciences. 2020, 10, 3746–3770. [Google Scholar] [CrossRef]
Shah, R.; Lavasan, A.; Peila, D. Numerical study on backfilling the tail void using a two-component grout. Journal of Materials in Civil Engineering. 2018, 30, 4018003–40180011. [Google Scholar] [CrossRef]
Fu, J. Modelling ground movement and associated building response due to tunneling in soils. Technische Universitaet Bergakademie Freiberg, Freiberg, Germany, 2014.
Franzius, J.; Potts, D. Influence of mesh geometry on three-dimensional finite-element analysis of tunnel excavation. International Journal of Geomechanics. 2005, 5, 256–266. [Google Scholar] [CrossRef]
Gan, X.; Yu, J.; Gong, X.; Liu, N.; Zheng, D. Behaviours of existing shield tunnels due to tunneling underneath considering asymmetric ground settlements. Underground Space. 2022, 7, 882–897. [Google Scholar] [CrossRef]
Zhang, J.; Gao, Y.; Liu, X.; Zhang, Z.; Yuan, Y.; Mang, H. A shield tunneling for enlarging the diameter of existing tunnels: Experimental investigations. Tunneling and Underground Space Technology. 2022, 128, 104605. [Google Scholar] [CrossRef]
Liu, B.; Yu, Z.; Zhang, R.; Han, Y.; Wang, Z.; Wang, S. Effects of undercrossing tunneling on existing shield tunnels. International Journal of Geomechanics. 2021, 21, 1–12. [Google Scholar] [CrossRef]
Lin, X.; Chen, R.; Wu, H.; Cheng, H. Deformation of behaviors of existing tunnels caused by shield tunneling undercrossing oblique angle. Tunneling and Underground Space Technology. 2019, 89, 78–90. [Google Scholar] [CrossRef]
Chakeri, H.; Hasanpour, R.; Hindistan, M. Analysis of interaction between tunnels in soft ground by 3D numerical modeling. Bulletin of Engineering Geology and the Environment. 2011, 70, 439–448. [Google Scholar] [CrossRef]
Klar, A.; Vorsster, T.; Soga, K.; Mair, R. Soil-pipe interaction due to tunnelling: comparison between Winkler and elastic continuum solutions. Geotechnique. 2005, 55, 461–466. [Google Scholar] [CrossRef]
Zhang, H.; Huang, M. Geotechnical influence on existing subway tunnels induced by multiline tunneling in Shanghai soft soil. Computers and Geotechnics. 2014, 56, 121–132. [Google Scholar] [CrossRef]
He, S.; Lai, J.; Wang, L.; Wang, K. A literature review on properties and applications of grouts for shield tunnel. Construction and Building Materials. 2020, 239, 117782. [Google Scholar] [CrossRef]
Zhao, Y.; Chen, X.; Hu, B.; Wang, P.; Li, W. Evolution of tunnel uplift induced by adjacent long and collinear excavation and an effective protective measure. Tunnelling and Underground Space Technology. 2023, 131, 104846. [Google Scholar] [CrossRef]
Wei, G.; Qi, Y.; Chen, C.; Zhang, S.; Qian, C.; Zhou, J. Analysis of the protective effect of setting isolation piles outside the foundation pit on the underpass tunnel side. Transportation Geotechnics. 2022, 35, 100791. [Google Scholar] [CrossRef]
Liang, X.; Ying, K.; Ye, F.; Su, E.; Xia, T.; Han, X. Selection of backfill grouting materials and ratios for shield tunnel considering stratum suitability. Construction and Building Materials. 2022, 314 (Part A), 125431. [Google Scholar] [CrossRef]
Bowles, J. Foundation Analysis and Design. McGraw-Hill, New York, 1988.
Simo, J.; Hughes, T. Interdisciplinary Applied Mathematics, Springer, 1998.
Kung, G.; Juang, C.; Hsiao, E.; Hashash, Y. Simplified model for wall deflection and ground-surface settlement caused by braced excavation in clays. Journal of Geotechnical and Geoenvironmental Engineering. 2007, 133, 731–747. [Google Scholar] [CrossRef]
Clough, G.; O’Rourke, T. Construction induced movements of in situ walls. In: Proc., Design and Performance of Earth Retaining Structures. ASCE, New York, 1990. pp. 439–470.
Feng, C.; Zhang, D. The general deformation mode and its application of subway station foundation pit in sandy cobble stratum. Chinese Journal of Rock Mechanics and Engineering. 2018, 37, 4395–4405. [Google Scholar] [CrossRef]
Huang, M.; Zhang, C.; Li, Z. A simplified analysis method for the influence of tunneling on ground piles. Tunneling and Underground Space Technology. 2009, 125, 207–215. [Google Scholar] [CrossRef]

Figure 1. Location of metro line 12 in Wuhan city, China.

Figure 2. Space relationship of metro line 4 and line 12.

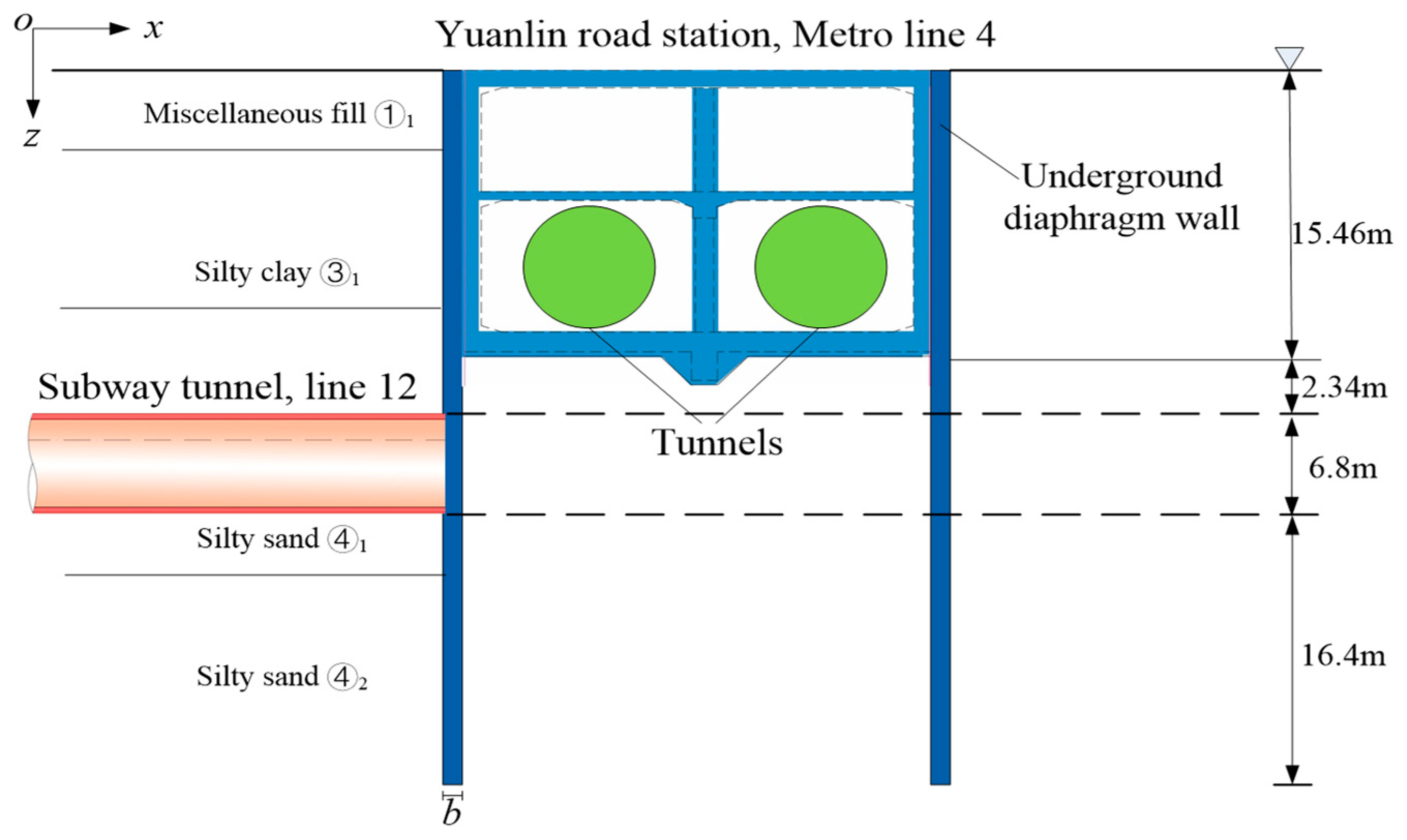
Figure 3. Calculation model of ground heave induced by diaphragm wall deformation.

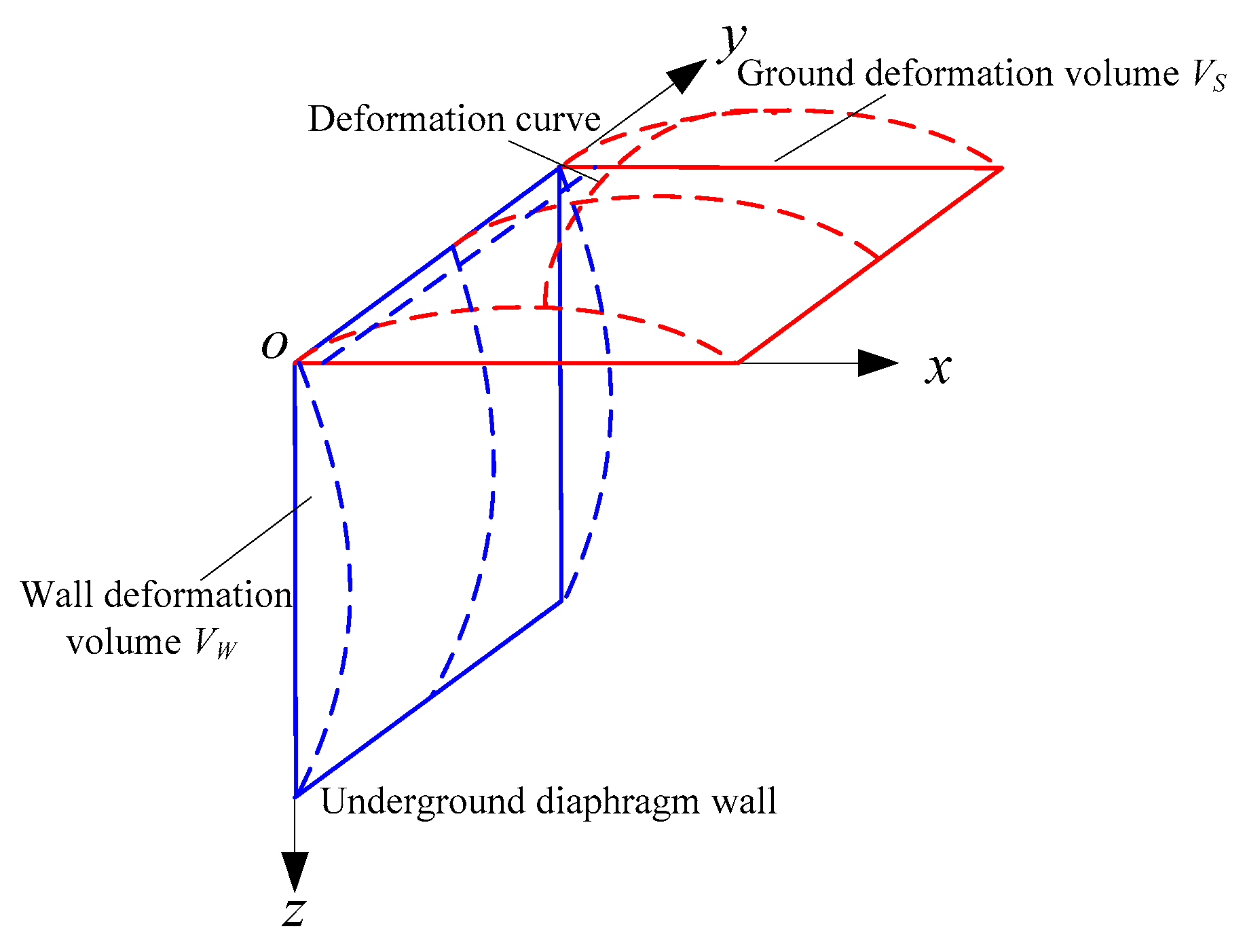
Figure 4. The simplified calculation model of tunnel line 12 passing through diaphragm wall.

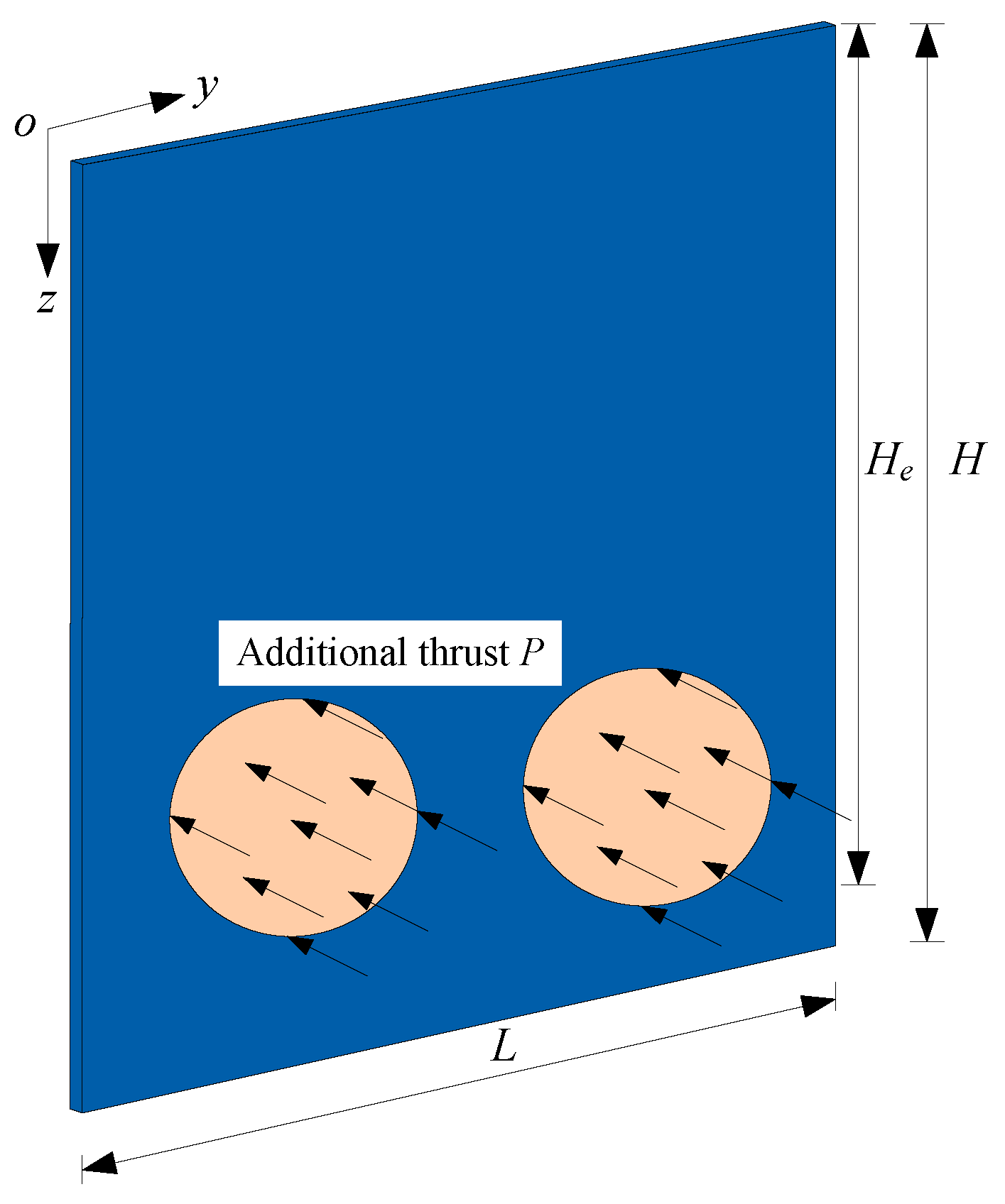
Figure 5. (a) Calculation model of transverse deformation curve; (b) Calculation model of longitudinal deformation curve.

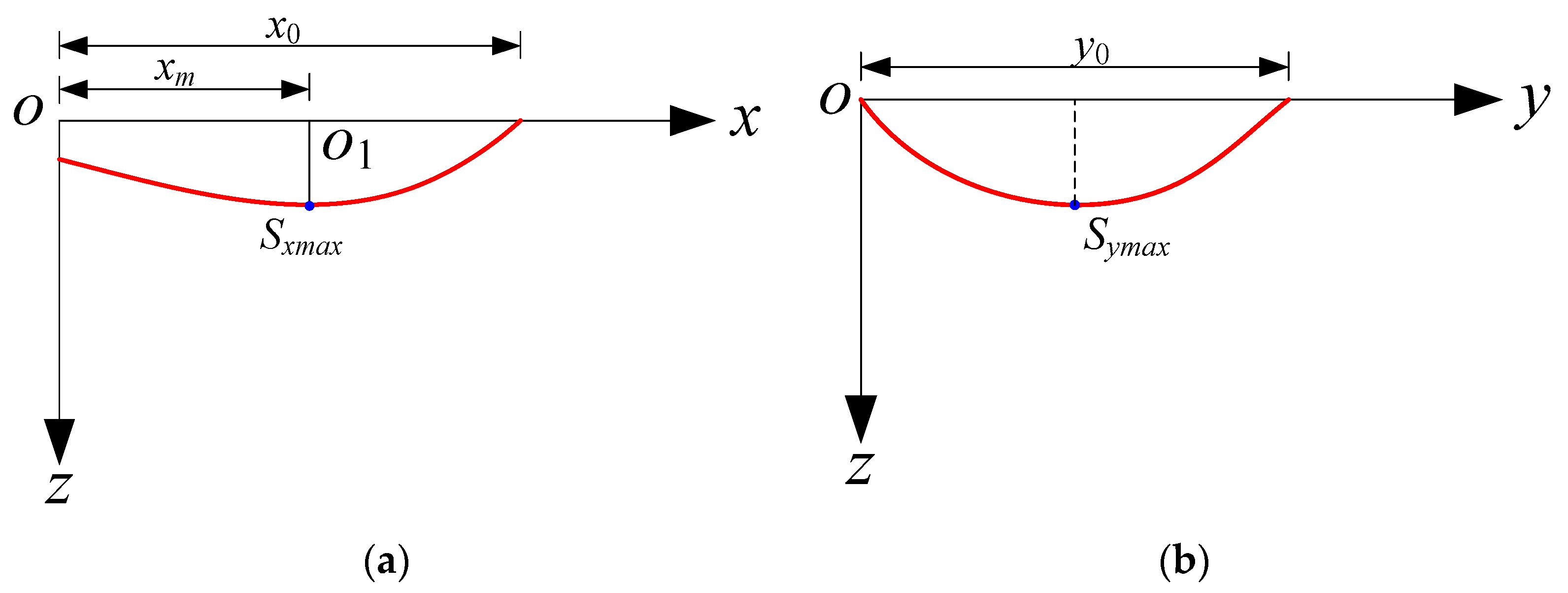
Figure 6. Flowchart of ground heave calculation.

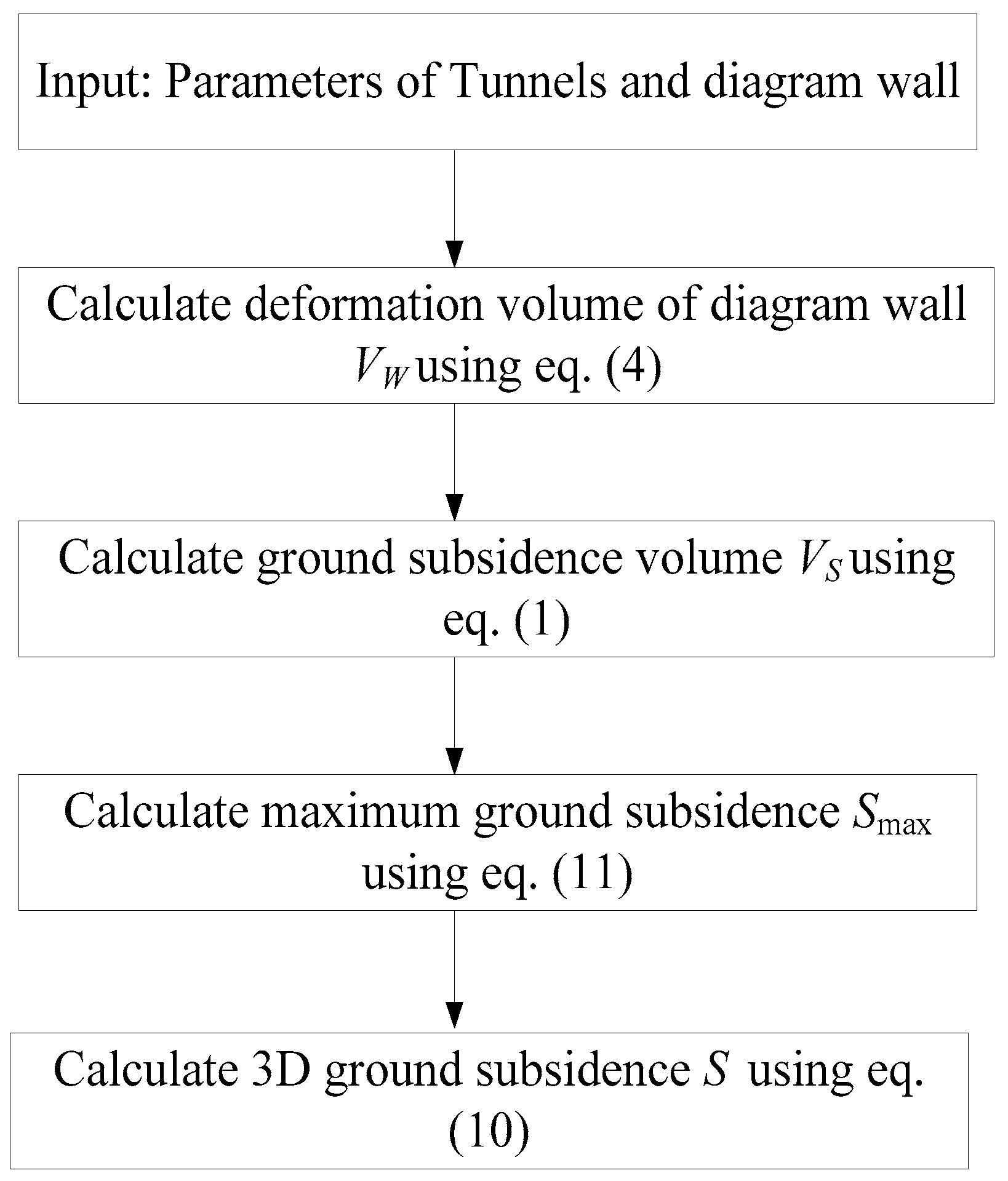
Figure 7. Layout of field monitoring points. Red circle represents deformation monitoring point, red triangle represents diaphragm wall top deformation and horizontal displacement monitoring points.

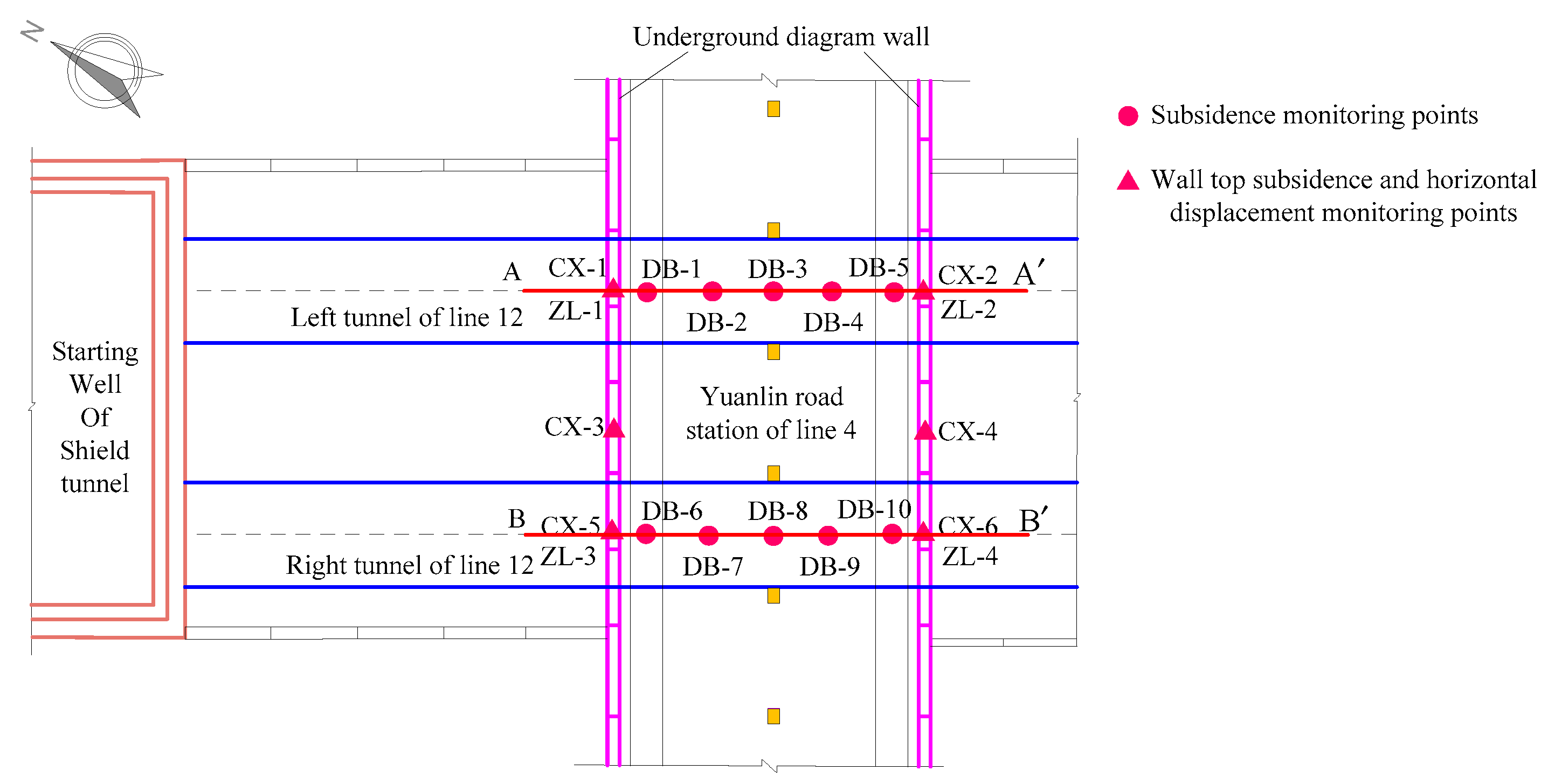
Figure 8. (a) Installation instruction of deformation monitoring points; (b) Installation instruction of diaphragm wall top monitoring points.

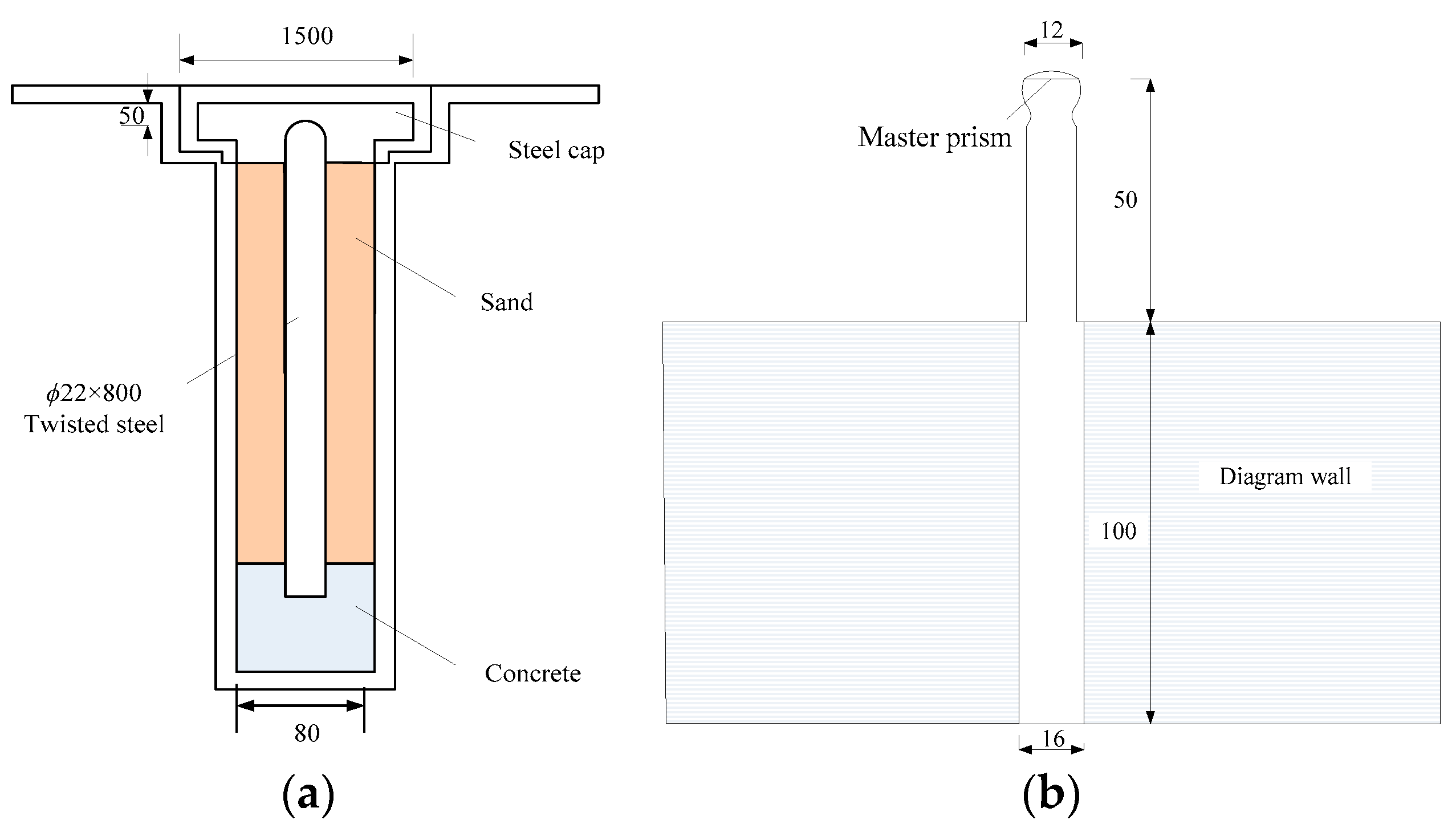
Figure 9. The monitoring results of ground heave of DB1~DB5. Day 38 is when line 12 passing through underground diaphragm wall.

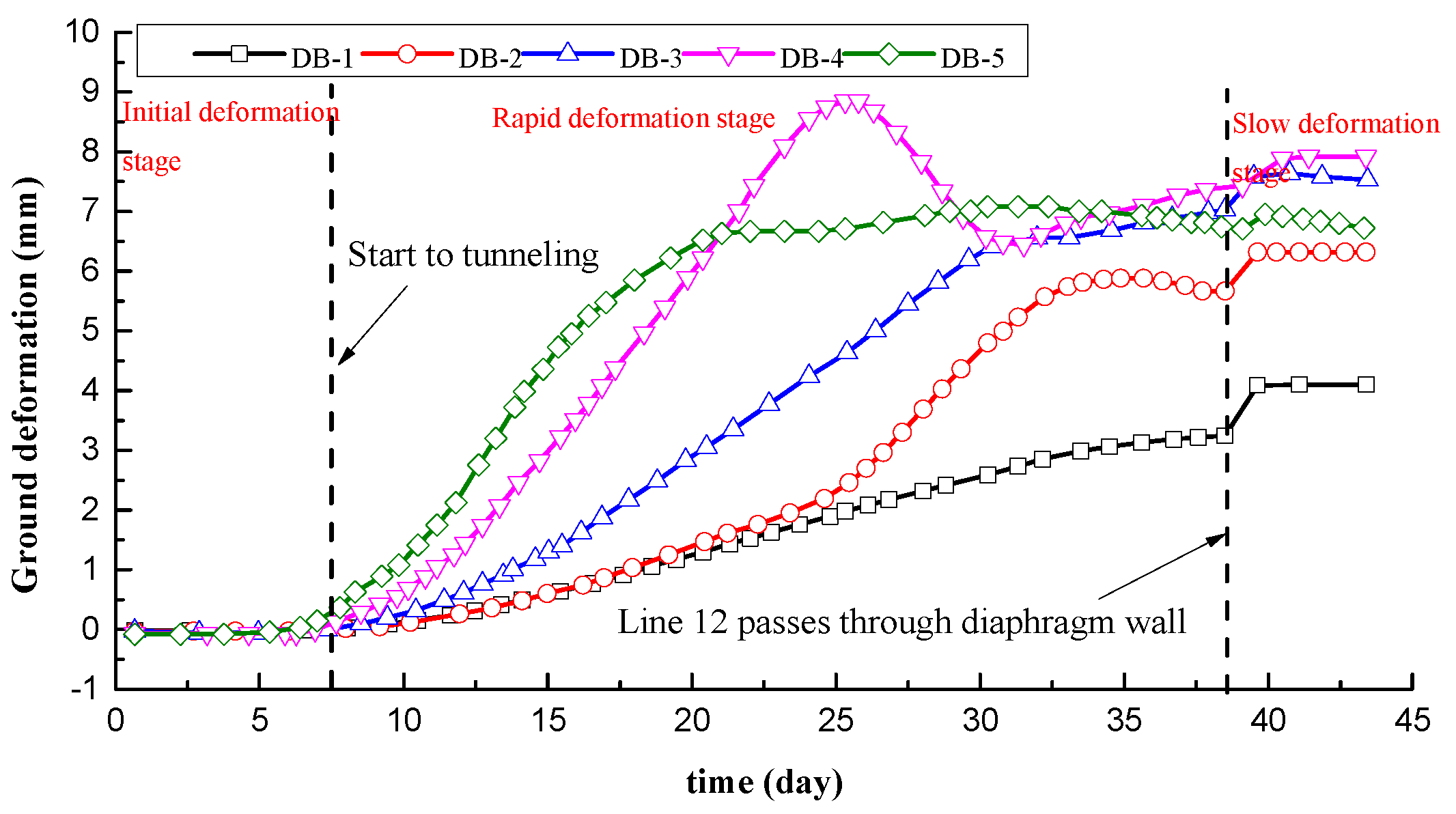
Figure 10. The monitoring results of wall top vertical deformation of CX1~CX4.

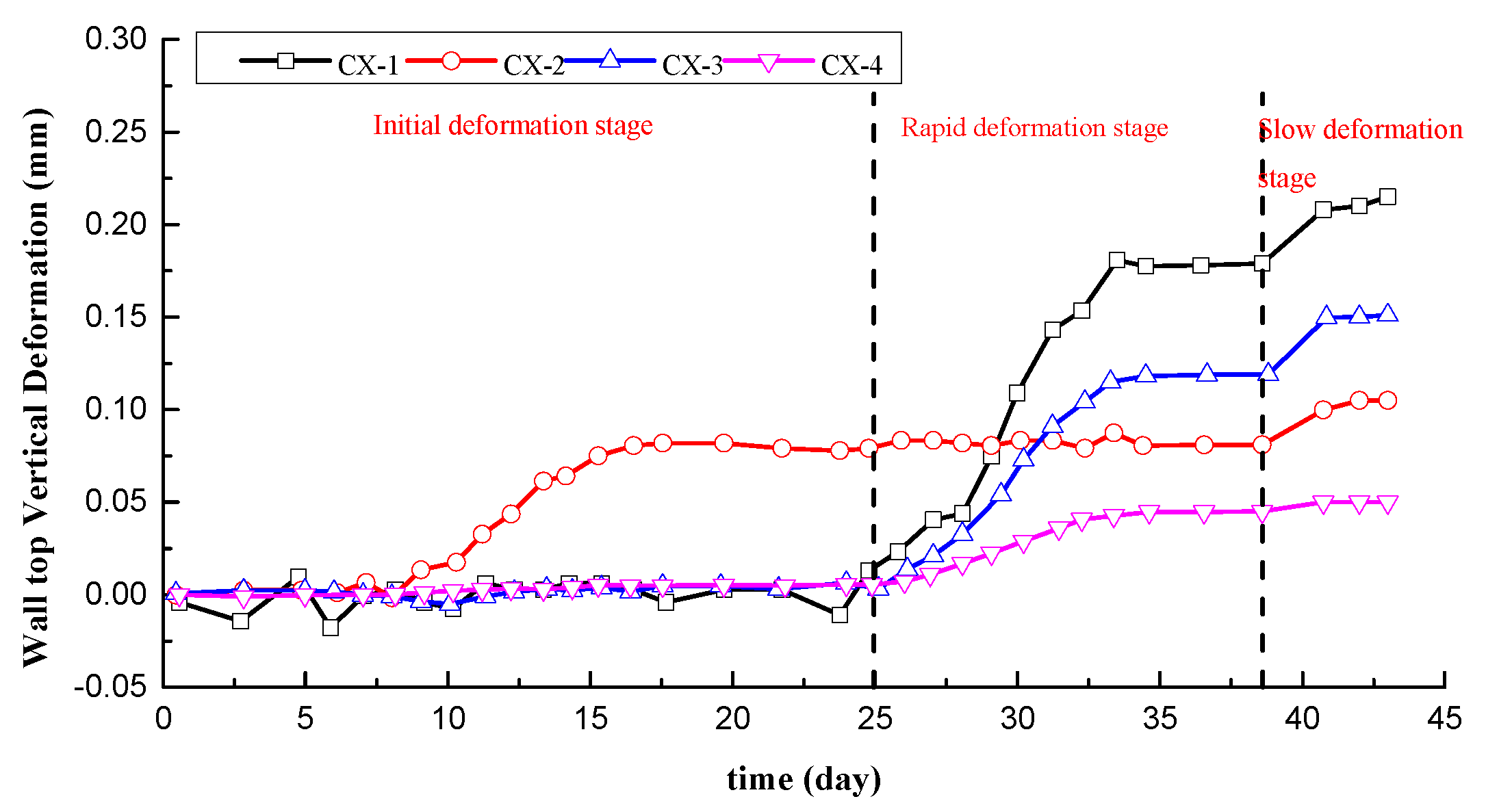
Figure 11. The monitoring results of wall top horizontal deformation of ZL1~ZL2.

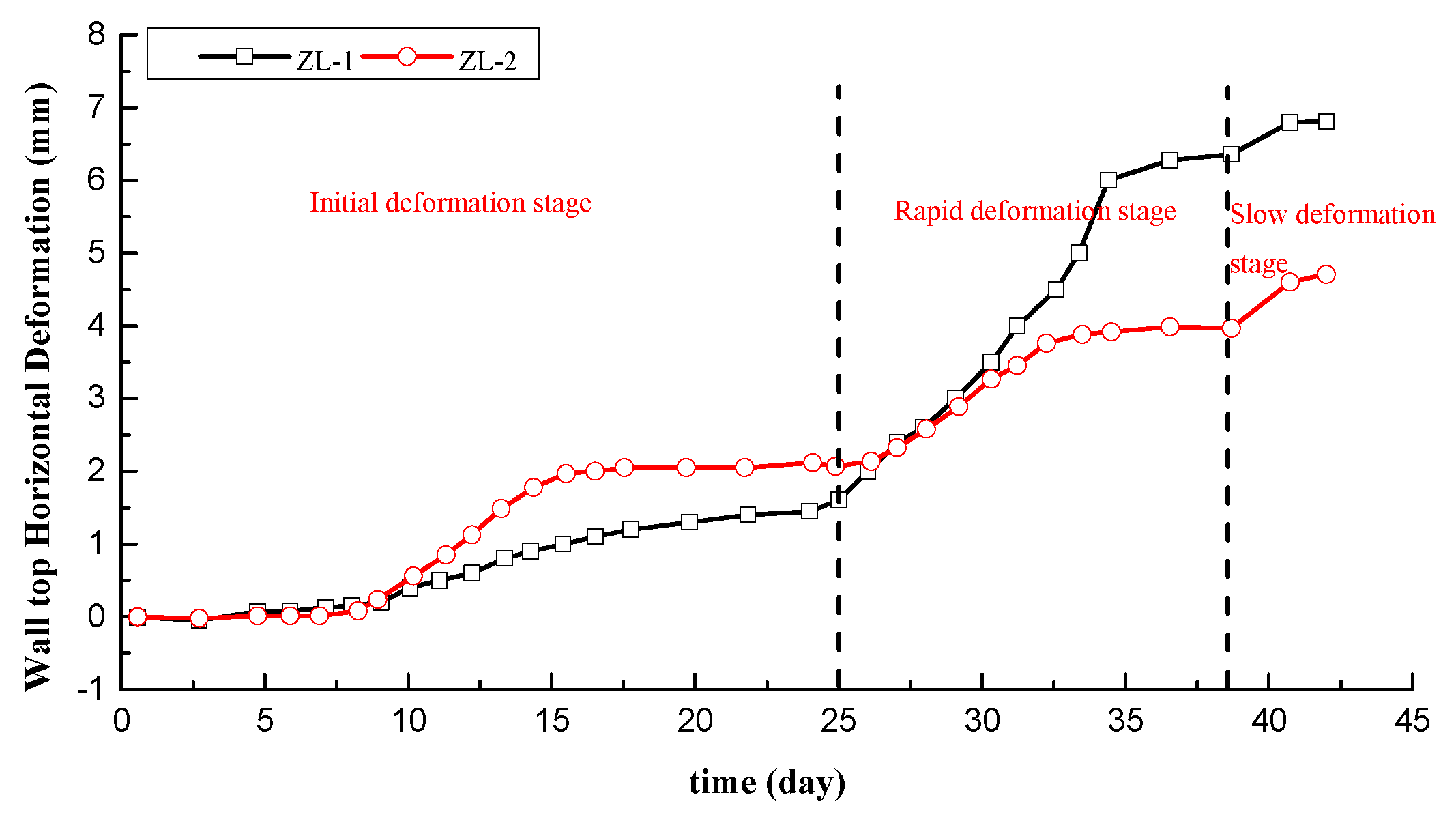
Figure 12. Calculated deformation of underground diaphragm wall acting of additional thrust P.

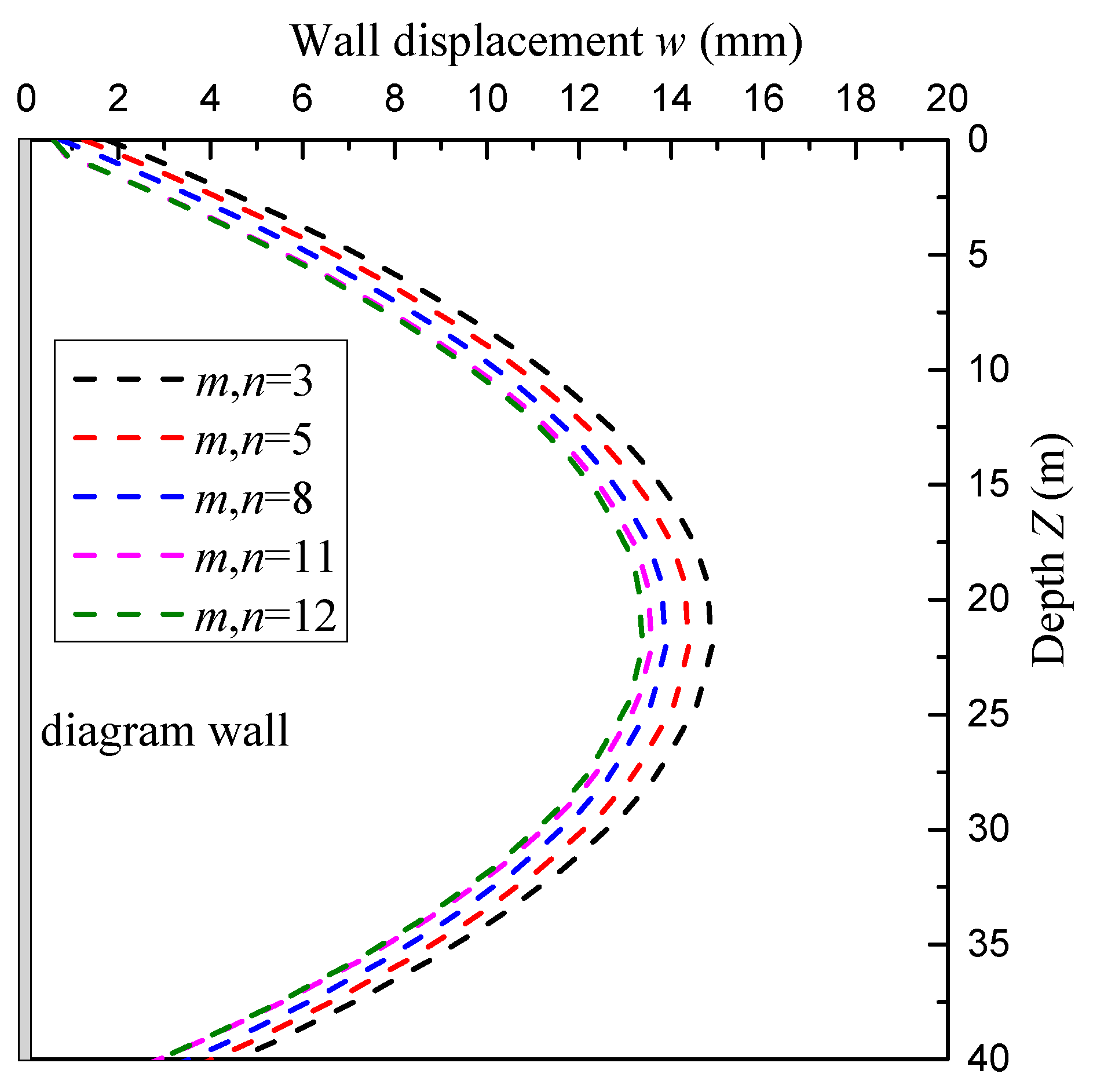
Figure 13. Deformation of diaphragm wall and ground. Solid line is ground heave calculated by proposed method, dash line is horizontal deformation of diaphragm wall, solid square is measured deformation and open square is measure horizontal deformation of diaphragm wall.

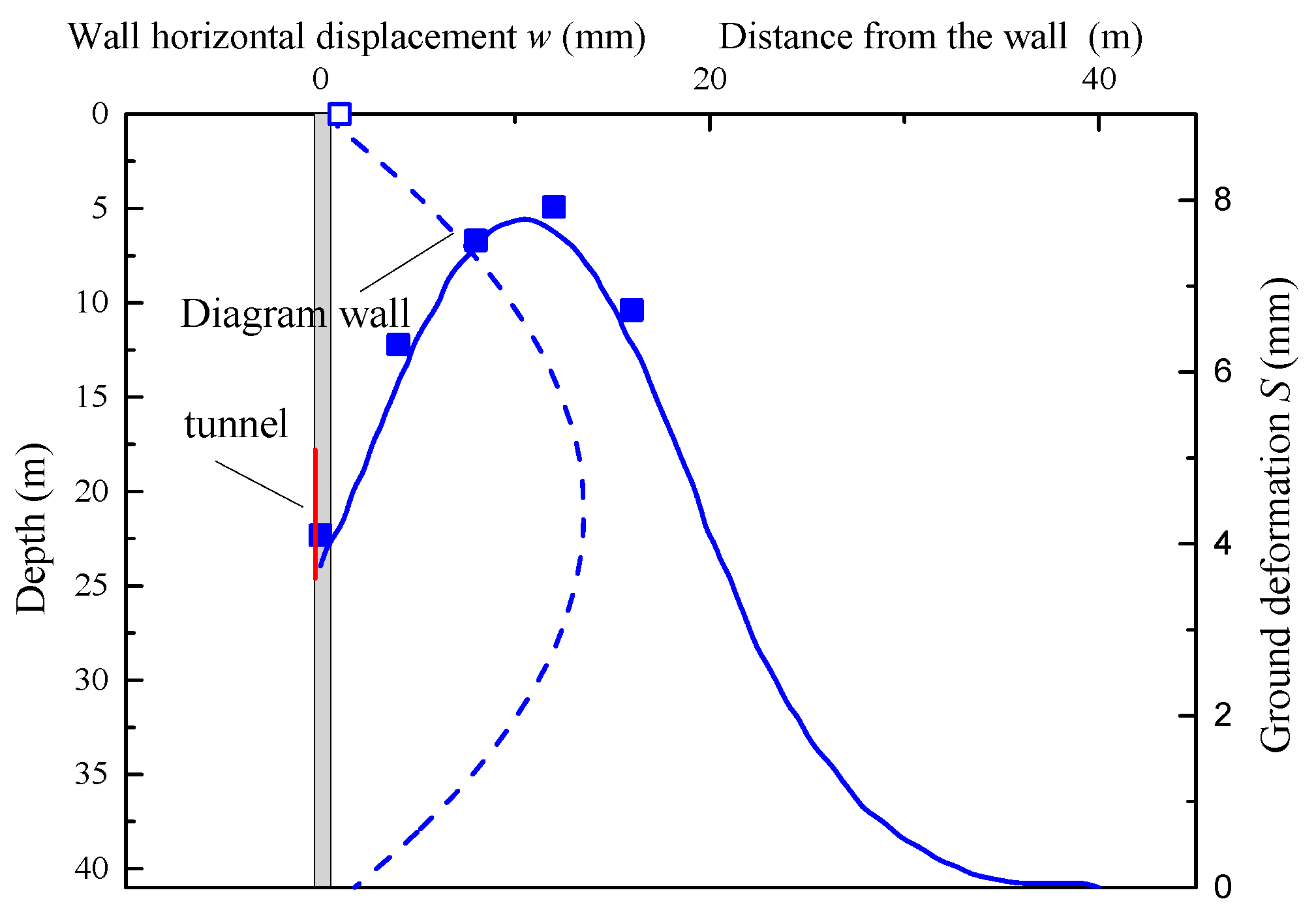
Figure 14. 3D Ground heave distribution by proposed method.

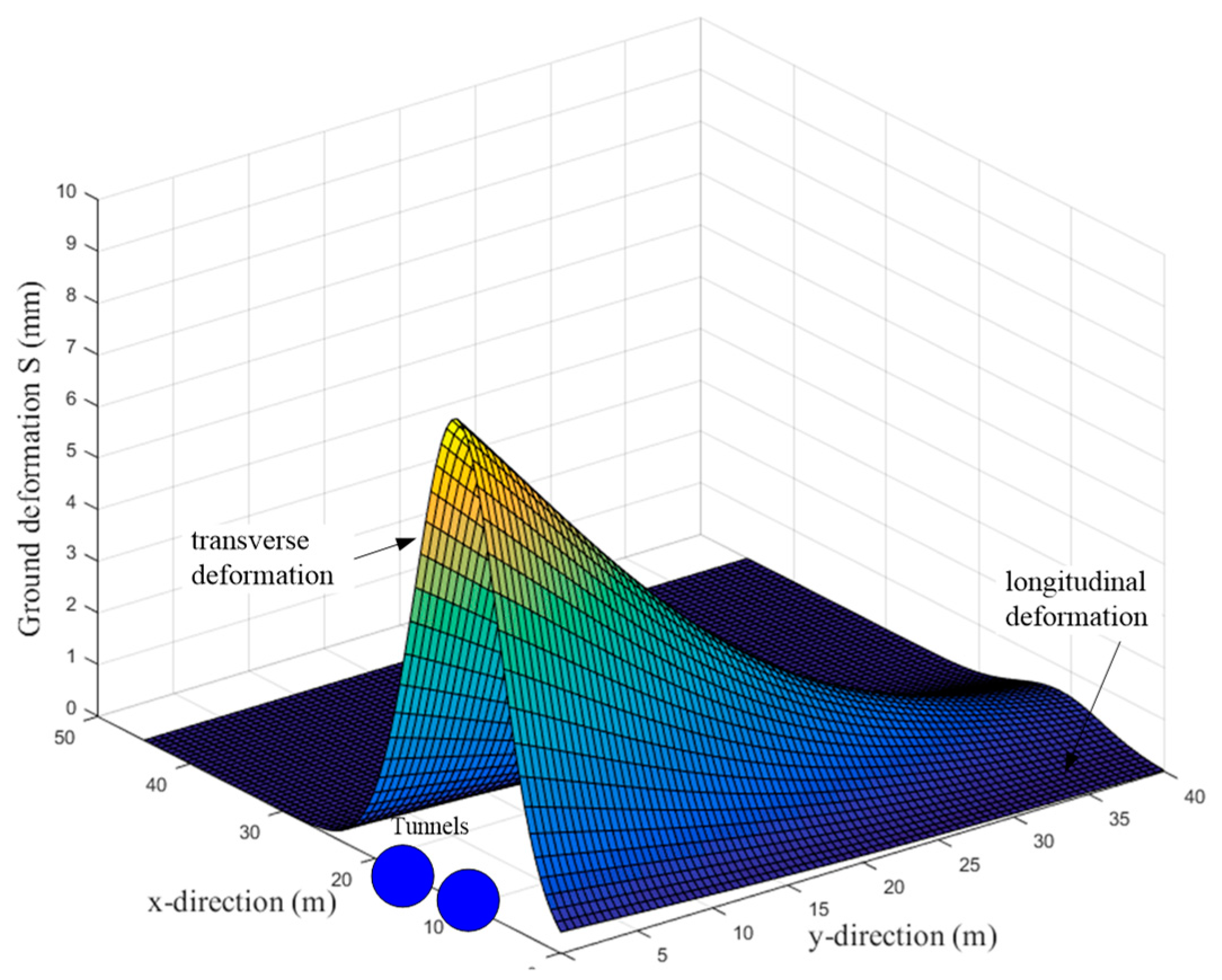
Figure 15. The effects of thickness of diaphragm wall b on ground heave.

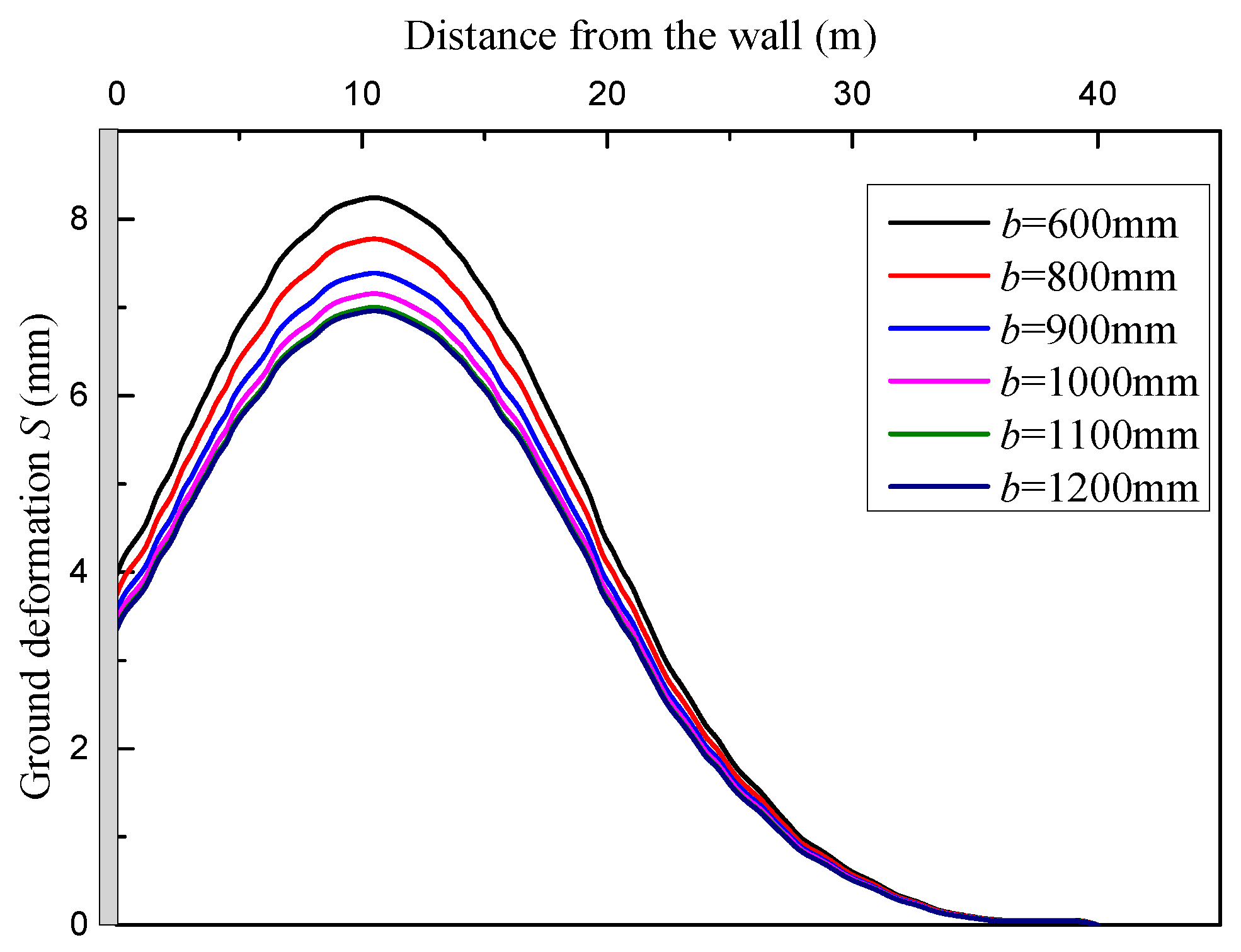
Figure 16. The effects of elasticity modulus E of diaphragm wall on ground heave.

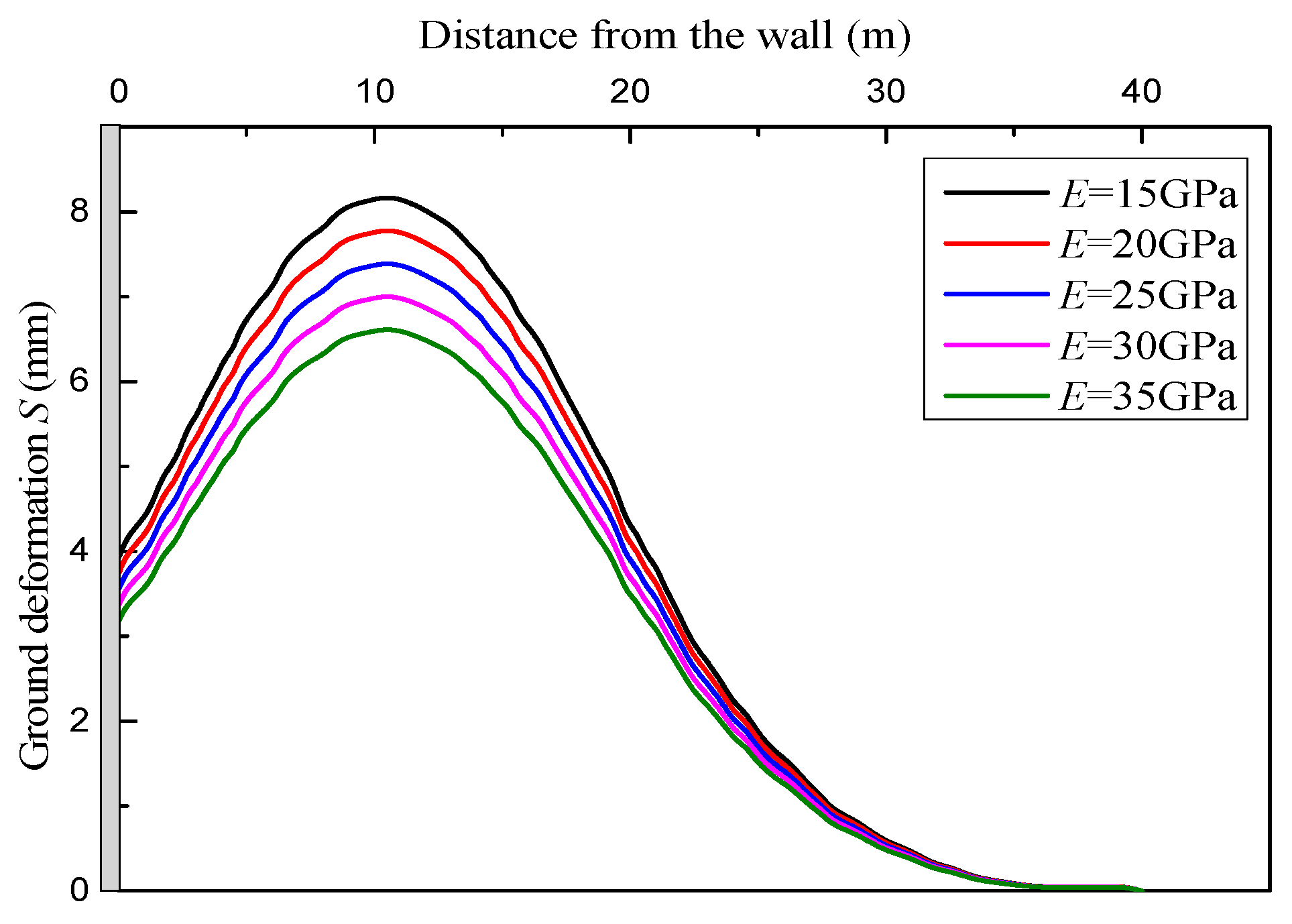
Figure 17. The effects of embedded ratio re of diaphragm wall on ground heave.

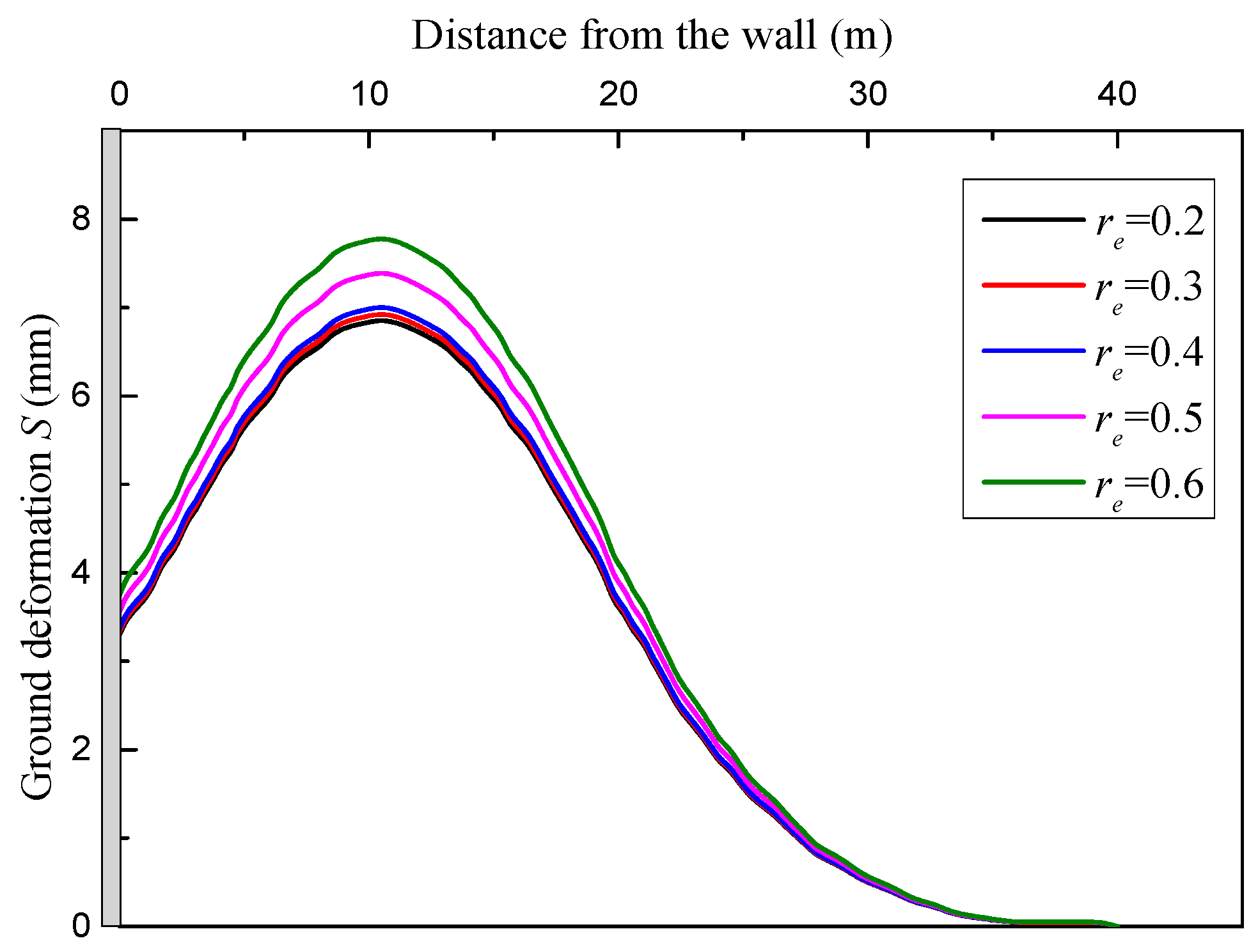
Table 1. Physical parameters of soil layers.

Soil	Weight γ (kN/m³)	Bearing capacity f_ak (kPa)	Friction angle φ (°)	modulus of compression Es (MPa)	Poisson ratio μ	Permeability coefficient k (cm/s)
miscellaneous fill ①₁	20.0	-	18	-	0.25	5.0e-3
silty clay ③₁	19.1	123	11	4.5	0.3	3.5e-3
silty sand ④₁	19.0	155	33.4	13.5	0.3	2.8e-3
silty sand ④₂	19.5	206	35.2	18.6	0.3	3.1e-3

Table 2. Calculated parameters used in proposed model.

	Modulus of elasticity E (GPa)	Poisson ratio μ	Friction angle φ (°)
Diaphragm wall	20	0.1	50
Equivalent soil	12.2	0.3	25

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer