Prerpints.org logo
Preprint
Communication

Reliability Analysis of A MEMS Flow Sensor with Accelerated Degradation Test

Altmetrics

Downloads

92

Views

38

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

18 September 2023

Posted:

19 September 2023

You are already at the latest version

Alerts
Abstract
With the wide application of flow sensor, their reliability under extreme conditions has been concerned in recent years. The reliability of a Micro Electro Mechanical Systems flow sensor under temperature (Ts) is researched in this paper. Firstly, the Step-stress accelerated degradation test is designed. Because this flow sensor consists flow sensor chip and signal processing system, the accelerated degradation testing is implemented, respectively. While the results show that the biggest drift is 3.15% for flow sensor chips with 150℃ conditions, and 32.91% for this flowmeter. By analysis, it could be found that the attenuation of the signal processing system is significant to the degeneration of this flowmeter. The minimum drift of the signal processing system accounts for 82.01% of this flowmeter. Secondly, using the Coffin-Manson model, the relationship between cycle-index and Ts is established. And the lifetime with different Ts is estimated by the Arrhenius model. In addition, the Weibull distribution is applied to evaluate the lifetime distribution. Finally, the reliability function of the Weibull distribution is demonstrated, and the survival rate within one year is 87.69% with 85℃ conditions. Thus, by the application of accelerated degradation testing, the acquired results are innovative and original. This research illustrates the reliability research, which provides a relational database for the application of this flow sensor.
Keywords: 
Subject: Engineering  -   Electrical and Electronic Engineering

1. Introduction

Flow sensor has been widely used in metrology and industry as a fundamental device [1,2,3]. It has received continuous attention and in-depth research of worldwide researchers with Micro Electro Mechanical Systems (MEMS) technology [4,5,6]. In this paper, this flow sensor has consisted of MEMS sensor chip and signal processing system (SPS), which requires analog sub-systems such as amplifiers, comparators, filters, digital-analog and analog-digital converters. As is known, the MEMS flow sensor has the advantages of low cost and high sensitivity. Moreover, the application of a MEMS flow sensor is good industrialization prospect. With the progress of science and technology, the efficient and intelligent flow sensor is often used in a high-temperature or high-humidity environments. [7,8,9,10]. Especially with the continuous development of MEMS Flow sensor, the application field is more and more extensive. Unfortunately, the high performance and integrated functions get superabundant attention, and the reliability tends to be forgotten. However, the MEMS sensor chip, as the core of the whole flow sensor system, suffers from degradation and reduced reliability, which constitutes a major hazard to the safety performance of the system. Thus, the reliability of flow sensor under extreme conditions has been paid much more attention in recent years [11,12,13,14,15,16,17,18,19]. In addition, the reliability of electronic devices system, especially on their performance with concerning for SPS had been reported very little frequently, even though the fact that the SPS was one of the weakest components in the entire system [20,21,22]. Consequently, ensuring the reliability of flow sensor under extreme conditions cannot be ignored for their future operating characteristic and commercialization. Accelerated degradation testing (ADT) has been widely applied as an efficient strategy to obtain the reliability (life) information of the assets in a shorter-than-normal period time by exposing the assets to higher-than-normal stresses [9]. The ADT is a good way to study the devices under extreme conditions, especially Step-stress accelerated degradation test (SSADT) can set different temperatures during a finite test period time [10,11,12,13,14,15].
In this paper, a MEMS flow sensor lifetime and reliability is reported. Based on the SSADT of temperature stress ( T s ) , the influences of T s on MEMS sensor chips, SPS, and entire flow sensor are discussed, respectively. The acquired results are innovative and original, and the lifetime of MEMS flow sensor is estimated. Using Coffin-Manson illustrated the relationship between cycle-index and T s . And lifetime is estimated with the Arrhenius model. Finally, the Weibull distribution (WD) is applied to analyze the lifetime distribution. This paper is organized as follows. Section 2 elaborates on the experiment steps and methods. The experiment results of SSADT are obtained and discussed in Section 3. Section 4 estimates the lifetime distribution and predicts reliability with WD.

2. Materials and Methods

As the Figure 1 shows, the flow sensor consists of a MEMS flow sensor chip and the SPS. Meanwhile, the MEMS flow sensor includes three parts: Micro-heater, sensitive area and a silicon substrate. By the way, the polysilicon resistor was simultaneously used as a heating structure (Micro-heater) and sense structure (up/down-downstream thermopile).
For this MEMS flow sensor, the physical principles of thermoelectric generation are based on Seebeck effect. As shown in Equation (1), Seebeck coefficient is an important actor for this MEMS sensing chip.
α a b = d Θ a b d T ( μ V / K )
α a b is coefficient of Seebeck. Θ a b is potential (electric) force of Seebeck. T is temperature of Micro-heater. When voltage is applied to the Micro-heater, the Micro-heater will generate heat to warm up the surroundings. The hot junctions of two thermopiles are heated. Then generate initial thermoelectric voltage. When there was air flow, the thermal field distribution is changed, leading to the initial voltage of the thermopile be changed accordingly [23,24,25,26,27].
Before ADT, the resistance of Micro-heater (RHG) and the resistance of the up-downstream thermopile (RUG, RDG) were test separately. The average value (AVG) of output voltage at 100 sccm and 500 sccm were shown in Table 1. And the resistors value was acquired too, as shown in Table 2. On the other hand, the operation voltage is 3.3V for Flow sensor. As the Finite element simulation results shown in Figure 2 (a), the maximum temperature is 184℃, but the SPS cannot withstand for long periods of time. Thus, to complete the accelerated experimental data in a short time and obtain effective experimental phenomena and data. SSADT with the 85℃-120℃-150℃ T s is performed.
As showed in Figure 2, the ADT is carried out on the flow sensor chip and flow sensor simultaneously, which is set up in climatic chamber. Figure 2 (b)-(d) show the assets have been put into the climatic chamber. The test period for every temperature gradient of SSADT is 500 hours, each cycle takes 3000 hours, as shown in Figure 2 (d).

3. ADT Description

3.1. ADT Results

As is shown in Figure 1, considering the structure of this MEMS flow sensor, the output voltage changes as the drifts of characteristic parameters for the flow sensor, and the changes of resistors is acquired as the drifts of characteristic parameters for the sensor chip. The results of drifts of the characteristic parameters were presented. Specifically, the resistance drifts of 85℃, 120℃, and 150℃ T s of RHG, RDG, and RUG were tested. As shown in Figure 3 (a)-(c), where Δ R is the changes of resistor and R 0 is the initial resistor. After 3000 hours aging, the biggest drift of 85℃, 120℃, and 150℃ were 1.35%, 2.09%, and 3.15%. It could be found that with the increases of T s , the Δ R ∕ R 0 was more obvious.
On the other hand, the drift of this flow sensor was acquired too. V 0 is the initial output voltage of various flow rates and Δ V corresponds to changes. Comparing Figure 4 (a)-(c), it could be found the higher T s the stronger attenuation. In addition, the attenuation of the larger flow rate was enhanced obviously. The biggest drift was -32.91% at 500 sccm with 150℃.
To further analyzed the attenuation of SPS in MEMS flow sensor system. The SPS before and after the ADT test were calculated. As is shown in Table 3, taking the flow rate of 500 sccm as an example, ADT-C is the initial value of the MEMS flow chip and ADT-S is initial value of SPS. C-ADT is aging value of the MEMS flow chip and S-ADT is aging value of SPS. By comparison, it finds that the attenuation of SPS in ADT is significantly greater than that of the MEMS flow chip. The minimum drift of SPS accounts for 82.01% of this MEMS flow sensor system.

3.2. Modelling Description

As is known, the resistance tends to produce a thermally drift, which is a function of time t and temperature T . Because there are thermal cycles in this SSADT, it is necessary to incorporate a Coffin-Manson component. The Coffin Manson model reflects the fatigue failure of products under thermal sequential stress, and has also been successfully used to simulate the crack propagation process of solder joints subjected to temperature impact [28,29,30,31]. Thus, it can be used to describe the relationship between thermal fatigue failure and temperature cyclic stress of products. The resistance drift based on Coffin-Manson dependency had been proposed.
∆ R R 0 = e x p − ∆ E K B · 1 T 1 − 1 T 2
ε = A 0 ∆ T β 1   ·   1 f β 2     ·   e x p Δ Ε K B T m a x
K B is the Boltzmann’s constant 8.36 × 10 − 5 e V / ° K . T m a x is the maximum temperature. Δ Ε is activation energy of two different ADT stress. ∆ R is drift. t is the time of ADT. T 1 and T 2 are different environmental temperature. ε is cycle-index. ∆ T is operation temperature. f is cycle frequency. A 0 , β 1 , and β 2 is undetermined constant.
From Figure 3 and Figure 4, the drift rate could be calculated. For MEMS sensor chip, we could get the Δ Ε of assets with different stress via the drift. Furthermore, the drift of RHG was more stable with a maximum average drift rate in various assets groups. Consequently, the activation energy of each group tested assets could be acquired by calculating the RHG drift rate with different ADT conditions. Then, the activation energy of 85℃ ( ∆ E 25 ℃ − 85 ℃ ), 120℃ ( ∆ E 25 ℃ − 120 ℃ ) and 150℃ ( ∆ E 25 ℃ − 150 ℃ ) of sensor chip were obtained by Equation (4) with the maximum average drift was 1.01%, 1.47% and 2.04%, respectively.
∆ E T 1 − T 2 = 8.36 × 10 − 5 e V / K · l n ∆ R R H G R R H G 0 1 T 1 − 1 T 2
                                                    ∆ E 25 ℃ − 85 ℃ = 8.36 × 10 − 5 e V / K · l n 1.01 1 298 K − 1 358 K = 0.0015   e V
                                                    ∆ E 25 ℃ − 120 ℃ = 8.36 × 10 − 5 e V / K · l n 1.47 1 298 K − 1 393 K = 0.039   e V
                                                        ∆ E 25 ℃ − 150 ℃ = 8.36 × 10 − 5 e V / K · l n 2.04 1 298 K − 1 423 K = 0.060   e V
Meanwhile, the parameter of Coffin-Manson is obtained with Δ Ε   of SSADT. As shown in Table 4, the value is 2.303 for A 0 , 0.154 for β 1 , and 0.187 for β 2 . Based on the above research, the ∆ E of different SSADT of this flow sensor can be estimated without having to go to calculate the ∆ R .
Similarly, the E a of this MEMS Flow sensor with different stress via the drift can be obtained. Thus, activation energy could be calculated with the maximum average drift was 1.21%, 11.15%, and 16.82%, respectively by flow rate was 500 sccm. Then, the activation energy of 85℃ ( ∆ E 25 ℃ − 85 ℃ ), 120℃ ( ∆ E 25 ℃ − 120 ℃ ), and 150℃ ( ∆ E 25 ℃ − 150 ℃ ) of Flow sensor were obtained by Equation (5) with the maximum activation energy was 0.028 eV, 0.359 eV, and 0.421 eV, respectively. At the same way, the parameter of Coffin-Manson of Flow sensor is obtained with Δ Ε of SSADT. As shown in Table 5, the value is 1.764 for A 0 , 0.235 for β 1 , and 0.298 for β 2 , as shown in Table 5.
∆ E 25 ℃ − 85 ℃ = 8.36 × 10 − 5 e V / K · l n 1.21 1 298 K − 1 358 K = 0.028 e V
∆ E 25 ℃ − 120 ℃ = 8.36 × 10 − 5 e V / K · l n 11.15 1 298 K − 1 393 K = 0.249 e V
∆ E 25 ℃ − 150 ℃ = 8.36 × 10 − 5 e V / K · l n 16.82 1 298 K − 1 423 K = 0.238 e V
According to the ∆ E had obtained by the drifts and the lifetime would be estimated. And ε had obtained from Coffin-Manson modeling. Specifically, Arrhenius lifetime model is employed in the degradation model, which had been widely used in the reliability literature [31,32,33,34].
N 1 = l 1 l 1 ′ = e x p ∆ E K B · 1 S 1 − 1 S ′
N 1 is Arrhenius accelerator. l 1 is the lifetime of S 1 . l 1 ′ is the lifetime of S ′ . The lifetime at various conditions could be estimated. For this MEMS flow sensor system, the lifetime was calculated, as shown in Table 6. It could be found that the lifetime shrunk more obviously from 8.290 years to 0.594 years in a range of 85℃ to 150℃. But for sensor chip, the change was 29.702 to 14.724 years. In addition, the lifetime of other conditions was acquired with obtained lifetime-stress data fitting. As is shown in Figure 5 (a) and (b), the predicted lifetime distributions are presented.

4. Reliability Description

Reliability engineering has become a powerful tool to determine the behavior of devices over time. One of the most ingrained concepts within reliability is the description of survival rate through the lifetime distribution modeling. For further exploring, it was necessary for us to evaluate the lifetime distribution. As we can see from the introduced publications, there are many methods for the description of lifetime distribution, Exponential distribution (ED), Weibull distribution (WD), Gamma, and Gaussian distribution [35,36,37,38]. Each lifetime distribution model contains a cumulative distribution function and a reliability function.
Considering numerous versions and types, we select the WD model to be a reliability model. On account of WD modifications have been proposed through diverse mathematical techniques to ensure that the behavior described is closest to the most of devices [39,40,41]. The cumulative distribution function F(t) and the reliability function R(t) could be calculated. The reliability-related parameters of the F(t) and R(t) are crucial adjective.
F t = 1 − exp ⁡ − t α 0 β
R t = exp ⁡ − t α 0 β
The α 0 is the scale factor or characteristic function. β is the shape factor or shape parameter. α 0 and β and could be obtained by fitting procedure [37,38,39,40,41,42]. t is working time.
After obtaining the modeling, the results were analyzed as shown in Figure 6(a)- (c). The log time of accelerated was displayed in horizontal coordinate axis and the ln[-ln(1-F(t)] in the vertical. The results at each stress level were fit in straight lines. Therefore, it could be considered that the failure time of this Flow sensor was obeyed to WD under different temperature stresses. The R-squared of 85℃, 120℃, and 150℃ were displayed in Table 7. In addition, α 0 , β , and the R t were acquired, respectively, with 3000 hours aging time. As shown in Table 7, the R t of this Flow sensor was 87.69% with 85℃. At the same time, the R t was 32.77% for 120℃ and 19.39% for 150℃. Thus, the reliability of this Flow sensor with different T s was acquired.

5. Conclusions

In this paper, the reliability of a MEMS flow sensor with T s is estimated. The degradation characteristics of the MEMS flow sensor chip and the Flow sensor with SSADT are acquired. The biggest drift of 85℃, 120℃, and 150℃ are 1.35%, 2.09%, and 3.15% for the MEMS flow sensor chip. For flow sensor, the biggest drift is -32.91% at 500 sccm with 150℃. By analysis, it can be found that the attenuation of SPS is significant. The minimum drift of the signal processing system accounts for 82.01% of whole system. To obtain the lifetime of this flow sensor, the activation energy of 85℃,120℃, and 150℃ are calculated. The maximum activation energy is 0.028 eV, 0.359 eV, and 0.421 eV, respectively. By using the Coffin-Manson model, the relationship between cycle-index and T s with SSADT is established. And the lifetime of MEMS flow sensor chip and flow sensor with different T s is estimated by the Arrhenius. Furthermore, the reliability with WD is demonstrated. The R t is 87.69% for 85℃, 32.77% for 120℃, and 19.39% for 150℃.
To sum up, the content illustrates the reliability study of a MEMS flow sensor with T s . The results are innovative and original, and lay a foundation for this MEMS flow sensor to work under extreme temperature environment. Based on this research, the reliability database is set up. Moreover, we will further analysis the causes of degradation to instruct the design of this MEMS flow sensors system and make them more practical circumstances in complex conditions.

References

  1. Wang, S.; Wang, J.; Li, X. Sensitivity Improvement of P+Si/Au Thermopile-Based Gas Flow Sensor by Optimizing Heat-Sink and Thermal-Insulation Configuration. In Proceedings of the 2020 IEEE 33rd International Conference on Micro Electro Mechanical Systems (MEMS); 2020. [Google Scholar] [CrossRef]
  2. Kaltsas, G.; Nassiopoulos, A.; Nassiopoulou, A. Characterization of a silicon thermal gas-flow sensor with porous silicon thermal isolation. IEEE Sensors J. 2002, 2, 463–475. [Google Scholar] [CrossRef]
  3. Sturm, H.; Dumstorff, G.; Busche, P.; Westermann, D.; Lang, W. Boundary Layer Separation and Reattachment Detection on Airfoils by Thermal Flow Sensors. Sensors 2012, 12, 14292–14306. [Google Scholar] [CrossRef]
  4. Fang, B.; Lu, A.; Sun, J.; Li, X.; Shen, T. The Simulation of Extremely Low Cycle Fatigue Fracture Behavior for Pipeline Steel (X70) Based on Continuum Damage Model. Metals 2023, 13, 1238. [Google Scholar] [CrossRef]
  5. Escobar, L.A.; Meeker, W.Q. A Review of Accelerated Test Models. Stat. Sci. 2006, 21, 552–577. [Google Scholar] [CrossRef]
  6. Hnommel, M.; Knab, H.; et al. Electric properties of graphene-based conductive layers from DC up to terahertz range. Microelectronics Reliability 2021, 126, 1–6. [Google Scholar]
  7. Heo, J.; Park, M.; Kim, J.-M.; Jang, D.-W.; Han, J.-H. Effect of Flexible Operation on Residual Life of High-Temperature Components of Power Plants. Processes 2023, 11, 1679. [Google Scholar] [CrossRef]
  8. George, B.; Muthuveerappan, N. Life assessment of a high temperature probe designed for performance evaluation and health monitoring of an aero gas turbine engine. Int. J. Turbo Jet-Engines 2020, 40, 139–146. [Google Scholar] [CrossRef]
  9. Wang, Z.; Cheng, X.; Liu, J. Time-dependent concurrent reliability-based design optimization integrating experiment-based model validation. Struct. Multidiscip. Optim. 2017, 57, 1523–1531. [Google Scholar] [CrossRef]
  10. Ali, S.; Ali, S.; Shah, I.; Khajavi, A.N. Reliability analysis for electronic devices using beta generalized Weibull distribution. Iranian Journal of Science and Technology, Transactions A: Science 2019, 43, 2501–2514. [Google Scholar] [CrossRef]
  11. Raghavan, V.A.; Roggeman, B.; Meilunas, M.; Borgesen, P. Effects of ‘latent damage’ on pad cratering: reduction in life and a potential change in failure mode. Microelectron. Reliability 2013, 53, 303–313. [Google Scholar] [CrossRef]
  12. Romdhane, E.B.; Guédon-Gracia, A.; Pin, S.; Roumanille, P.; Frémont, H. Impact of crystalline orientation of lead-free solder joints on thermomechanical response and reliability of ball grid array components. Microelectron. Reliability 2020, 114, 113812. [Google Scholar]
  13. Limon, S.; Yadav, O.P.; Liao, H. A literature review on planning and analysis of accelerated testing for reliability assessment. Qual. Reliab. Eng. Int. 2017, 33, 2361–2383. [Google Scholar] [CrossRef]
  14. Shen, D.; Liu, T.; Zhang, L.; et al. A novel ADT design considering stress optimization. Clust. Comput. 2018, 20, 1–10. [Google Scholar]
  15. Escobar, L.A.; Meeker, W.Q. A Review of Accelerated Test Models. Stat. Sci. 2006, 21, 552–577. [Google Scholar] [CrossRef]
  16. Lu, C.J.; Meeker, W.O. Using Degradation Measures to Estimate a Time-to-Failure Distribution. Technometrics 1993, 35, 161–174. [Google Scholar] [CrossRef]
  17. Wu, S.-J.; Chang, C.-T. Optimal design of degradation tests in presence of cost constraint. Reliab. Eng. Syst. Saf. 2002, 76, 109–115. [Google Scholar] [CrossRef]
  18. Wang, Z.W.; Liu, G.; et al. Electric properties of graphene-based conductive layers from DC up to terahertz range. Microelectronics Reliability 2021, 124, 1–9. [Google Scholar]
  19. Liao, C.M.; Tseng, S.T.; et al. A novel optimal accelerated degradation test design method considering multiple decision variables. IEEE Trans. Reliab. 2016, 55, 59–66. [Google Scholar] [CrossRef]
  20. Cortes, F.P.; Fabris, E.; Bampi, S. Analysis and design of amplifiers and comparators in CMOS 0.35 μm technology. Microelectronics Reliability 2004, 44, 657–664. [Google Scholar] [CrossRef]
  21. Jagtap, S.; Sharma, D.; Gupta, S. Design of SET tolerant LC oscillators using distributed bias circuitry. Microelectron. Reliab. 2015, 55, 1537–1541. [Google Scholar] [CrossRef]
  22. Chiozzi, D.; Bernardoni, M.; Delmonte, N.; Cova, P. A simple 1-D finite elements approach to model the effect of PCB in electronic assemblies. Microelectron. Reliab. 2016, 58, 126–132. [Google Scholar] [CrossRef]
  23. Chen, C.; Hu, H.; Wang, J.J. Numerical Study of the Thermal Thermopile Flow Sensor. In Proceedings of the 2018 IEEE International Conference on Mechatronics and Automation (ICMA); 2018. [Google Scholar]
  24. Zhou, H.; Kropelnicki, P.; Tsai, J.M.; Lee, C. Development of a thermopile infrared sensor using stacked double polycrystalline silicon layers based on the CMOS process. J. Micromechanics Microengineering 2013, 23. [Google Scholar] [CrossRef]
  25. Dijkstra, M.; Lammerink, T.; de Boer, M.; Wiegerink, R.; Elwenspoek, M. Ambient Temperature-Gradient Compensated Low-Drift Thermopile Flow Sensor. In Proceedings of the IEEE International Conference on Micro Electro Mechanical Systems; 2009. [Google Scholar] [CrossRef]
  26. Randjelović, D.; Frantlović, M.; Miljković, B.; Rosandić, B.; Jakšić, Z.; Popović, B. Intelligent Thermopile-Based Vacuum Sensor. Procedia Eng. 2011, 25, 575–578. [Google Scholar] [CrossRef]
  27. Randjelovic, D.; Popovic, B.; Poljak, P.; Jaksic, O. Sensing Gas Type and Pressure with Multipurpose Device Based on Seebeck Effect. 2019 International Semiconductor Conference (CAS); 2019. [Google Scholar] [CrossRef]
  28. Shi, X.; Pang, H.; Zhou, W.; Wang, Z. Low cycle fatigue analysis of temperature and frequency effects in eutectic solder alloy. Int. J. Fatigue 2000, 22, 217–228. [Google Scholar] [CrossRef]
  29. Ma, Z.; Li, C.; Zhang, W.; Wang, S.; Li, J.; Zhao, H.; Ren, L. Modified Coffin-Manson equation to predict the fatigue life of structural materials subjected to mechanical-thermal coupling non-coaxial loading. J. Mater. Sci. Technol. 2023, 160, 118–127. [Google Scholar] [CrossRef]
  30. Ding, L.; Song, R.; Zhao, S.; Wang, J.; Mantooth, H.A. Active Peltier Effect Heat Sink for Power Semiconductor Device Thermal Stability Enhancement. IEEE Trans. Power Electron. 2023, PP, 1–14. [Google Scholar] [CrossRef]
  31. Roy, P.; Kurre, M.; Nannam, H.C.; Banerjee, A. Reliability evaluation of carrier-based pulse width modulated three-level F-type neutral point clamped inverter with power loss analysis. Int. J. Circuit Theory Appl. 2023. [Google Scholar] [CrossRef]
  32. Liu, D.; Wang, S. Reliability estimation from lifetime testing data and degradation testing data with measurement error based on evidential variable and Wiener process. Reliab. Eng. Syst. Saf. 2020, 205, 107231. [Google Scholar] [CrossRef]
  33. Limon, S.; Yadav, O.P.; Liao, H. A literature review on planning and analysis of accelerated testing for reliability assessment. Qual. Reliab. Eng. Int. 2017, 33, 2361–2383. [Google Scholar] [CrossRef]
  34. Meeker, W.Q.; Escobar, L.A.; Lu, C.J. Accelerated degradation tests: Modeling and analysis. Technometrics 1998, 40, 89–99. [Google Scholar] [CrossRef]
  35. Ding, Y.; Yang, Q.; King, C.B.; Hong, Y. A General Accelerated Destructive Degradation Testing Model for Reliability Analysis. IEEE Trans. Reliab. 2019, 68, 1272–1282. [Google Scholar] [CrossRef]
  36. Ali, S.; Ali, S.; Shah, I.; Siddiqui, G.F.; Saba, T.; Rehman, A. Reliability Analysis for Electronic Devices Using Generalized Exponential Distribution. IEEE Access 2020, 8, 108629–108644. [Google Scholar] [CrossRef]
  37. Hani, D.B.; Athamneh, A.L. Reliability modeling of the fatigue life of lead-free solder joints at different testing temperatures and load levels using the Arrhenius model. SCIENTIFIC REPORTS 2023, 13, 463–472. [Google Scholar] [CrossRef]
  38. Liu, B.; Teng, Y.; Huang, Q. RETRACTED: A novel imprecise reliability prediction method for incomplete lifetime data based on two-parameter Weibull distribution. Proc. Inst. Mech. Eng. Part O: J. Risk Reliab. 2018, 234, 208–218. [Google Scholar] [CrossRef]
  39. Bender, E.; Bernstein, J.; Bensoussan, A. Reliability prediction of FinFET FPGAs by MTOL. Microelectron. Reliab. 2020, 114, 113809. [Google Scholar] [CrossRef]
  40. Acovic, A.; Rosa, G.L.; et al. A review of hot-carrier degradation mechanisms in MOSFETs. Microelectronics Reliability 1996, 36, 845–869. [Google Scholar] [CrossRef]
  41. Kohout, J. Three-parameter Weibull distribution with upper limit applicable in reliability studies and materials testing. Microelectron. Reliab. 2022, 137. [Google Scholar] [CrossRef]
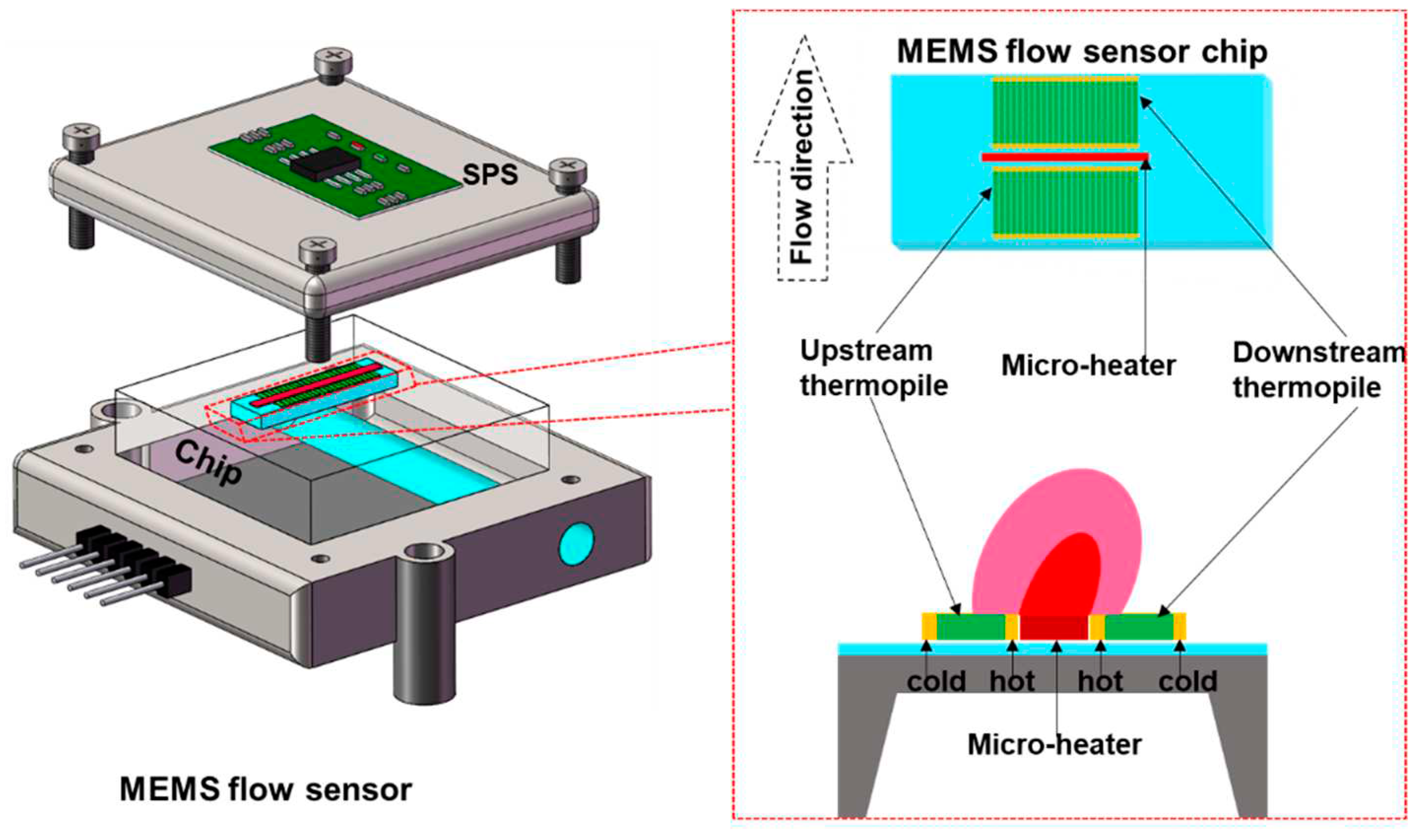
Preprints 85389 g001
Figure 1. MEMS Flow sensor.
Figure 1. MEMS Flow sensor.
Preprints 85389 g001
Preprints 85389 g002
Figure 2. Experiment facilities. (a) Temperature distribution with voltage by Finite element simulation; (b). Climatic chamber and tested assets; (c). ADT process; (d). Example of testing cycle for ADT.
Figure 2. Experiment facilities. (a) Temperature distribution with voltage by Finite element simulation; (b). Climatic chamber and tested assets; (c). ADT process; (d). Example of testing cycle for ADT.
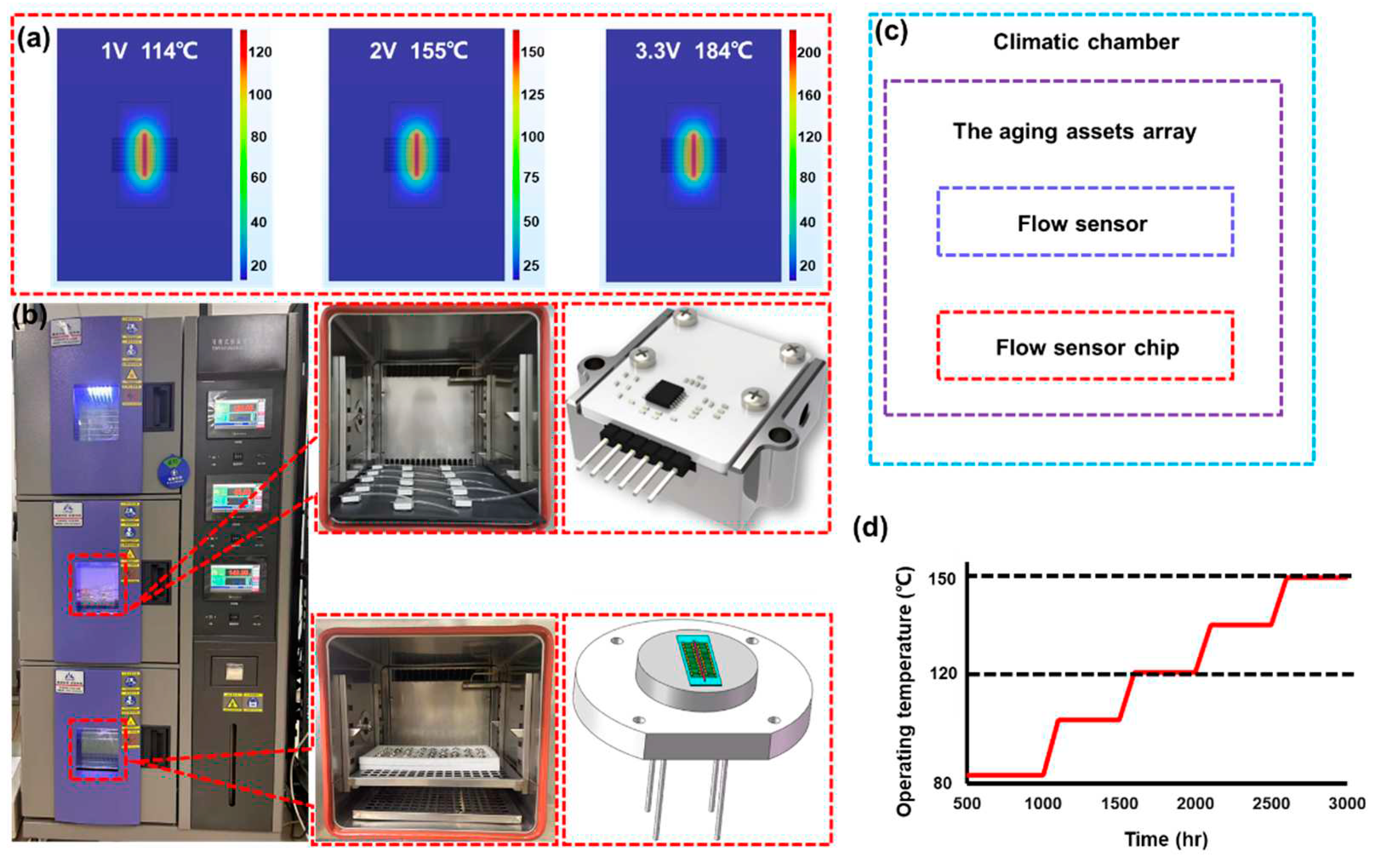
Preprints 85389 g002
Preprints 85389 g003
Figure 3. The ADT results of flow sensor chip with SSADT. (a) The maximum drift was 1.45% for 85℃; (b). The maximum drift was 2.09% for 120℃; (c). The maximum drift was 3.15% for 150℃.
Figure 3. The ADT results of flow sensor chip with SSADT. (a) The maximum drift was 1.45% for 85℃; (b). The maximum drift was 2.09% for 120℃; (c). The maximum drift was 3.15% for 150℃.
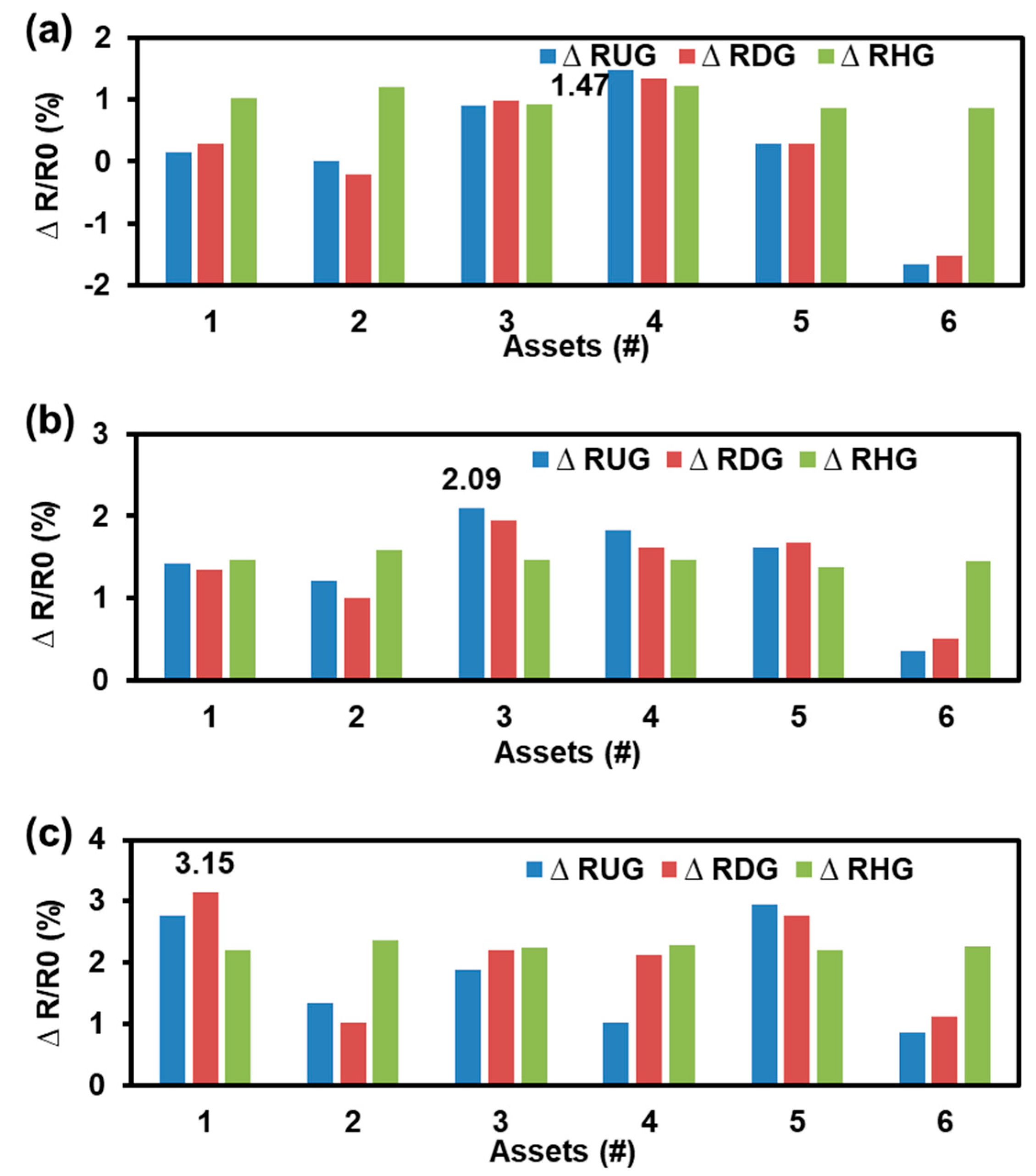
Preprints 85389 g003
Preprints 85389 g004
Figure 4. The ADT results of flow sensor with SSADT. (a) The maximum drift was 3.32% for 85℃; (b). The maximum drift was 11.55% for 120℃; (c). The maximum drift was 32.19% for 150℃.
Figure 4. The ADT results of flow sensor with SSADT. (a) The maximum drift was 3.32% for 85℃; (b). The maximum drift was 11.55% for 120℃; (c). The maximum drift was 32.19% for 150℃.
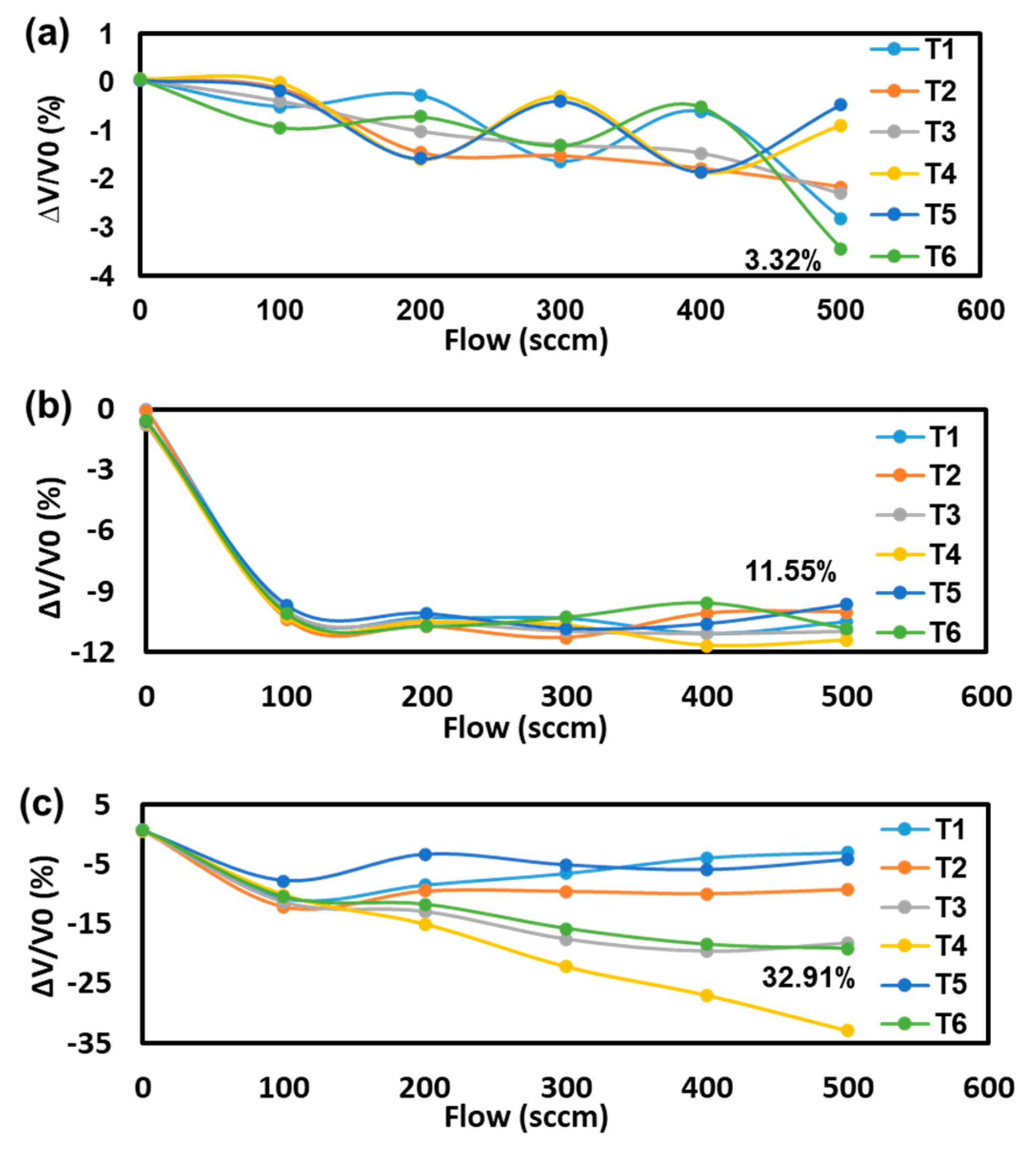
Preprints 85389 g004
Preprints 85389 g005
Figure 5. The ADT results of lifetime-stress. (a) The lifetime-stress of MEMS sensor chip; (b). The lifetime-stress of MEMS sensor.
Figure 5. The ADT results of lifetime-stress. (a) The lifetime-stress of MEMS sensor chip; (b). The lifetime-stress of MEMS sensor.
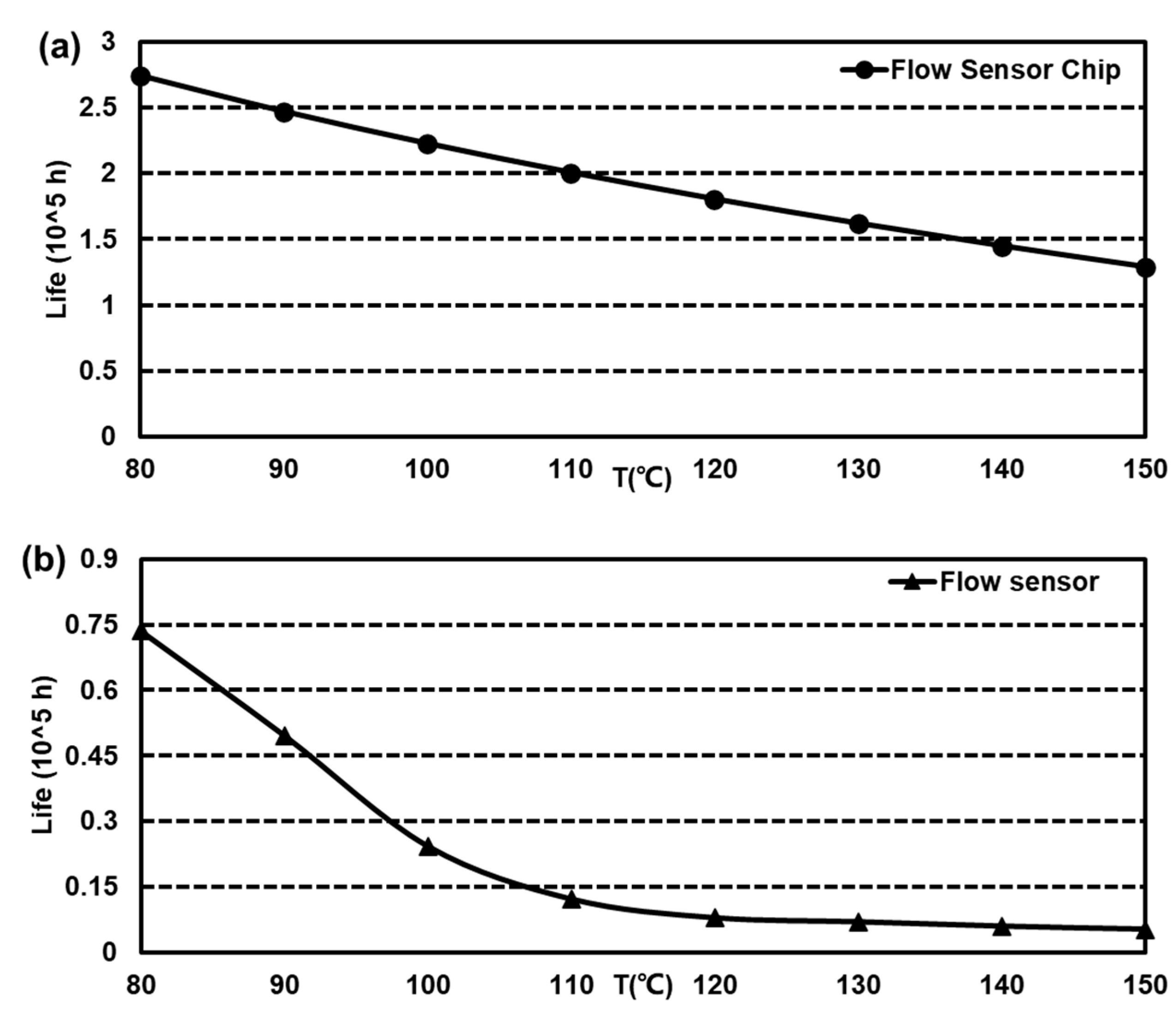
Preprints 85389 g005
Preprints 85389 g006
Figure 6. The fitting results of MEMS flow sensor with WD distribution. (a) The WD distribution result of 85℃; (b). The WD distribution result of 120℃; (a) The WD distribution result of180℃.
Figure 6. The fitting results of MEMS flow sensor with WD distribution. (a) The WD distribution result of 85℃; (b). The WD distribution result of 120℃; (a) The WD distribution result of180℃.
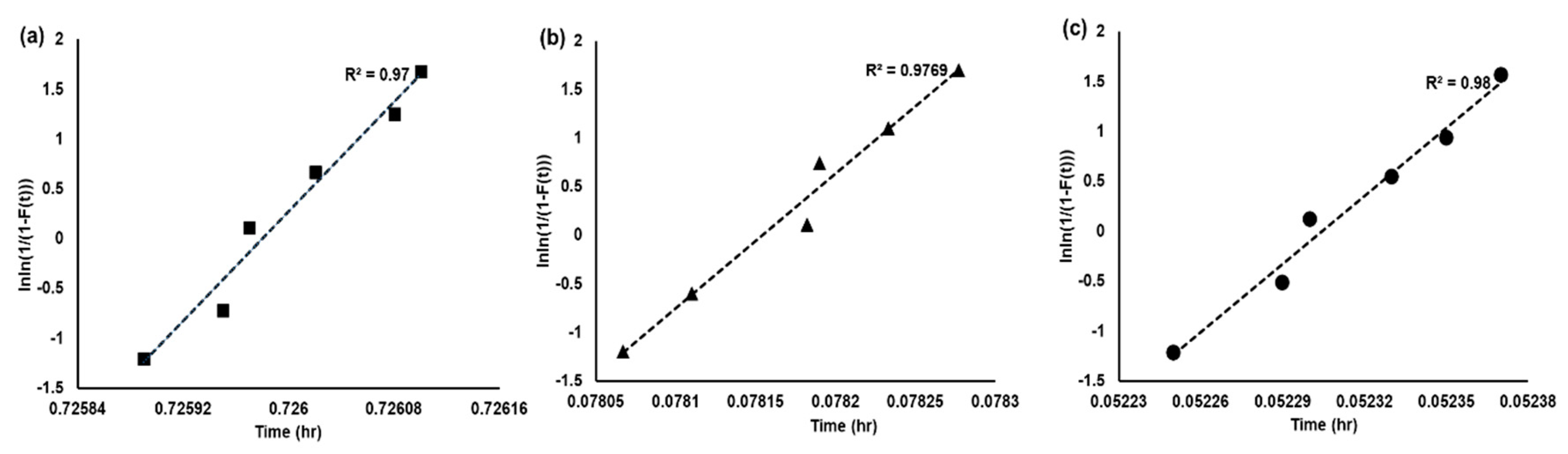
Preprints 85389 g006
Table 1. Repeatability and Consistency of Flow sensor
Table 1. Repeatability and Consistency of Flow sensor
Flow Index #1 #2 #3 #4 #5 #6
100 sccm Avg(V) 1.868 1.873 1.856 1.863 1.844 1.867
500 sccm Avg(V) 4.801 4.856 4.885 4.894 4.872 4.893
Table 2. Repeatability and Consistency of Flow sensor chip
Table 2. Repeatability and Consistency of Flow sensor chip
Index #1 #2 #3 #4 #5 #6
RUG Avg(KΩ) 119.7 118.1 122.5 121.1 121.3 115.8
RDG Avg(KΩ) 116.5 122.2 114.7 120.2 122.8 120.2
RHG Avg(Ω) 704.3 703.6 704.5 705.3 704.6 703.7
Table 3. The ADT Results of Flow Sensor and SPS
Table 3. The ADT Results of Flow Sensor and SPS
Index #1 #2 #3 #4 #5 #6
ADT-C (mV) 9.533 9.752 9.634 9.607 9.611 9.664
C-ADT (mV) 9.529 9.751 9.621 9.603 9.591 9.657
Drift (%) 17.29 0.81 1.37 1.925 17.98 3.43
ADT-S (V) 4.801 4.856 4.894 4.893 4.893 4.816
S-ADT (V) 4.778 4.733 3.943 4.685 4.782 4.612
Drift (%) 82.70 99.19 98.63 98.07 82.01 96.56
Table 4. The Parameter Estimation of Coffin-Manson Results of Flow Sensor Chip
Table 4. The Parameter Estimation of Coffin-Manson Results of Flow Sensor Chip
Index ε f ∆ T ( K ) T m a x ( K ) Δ Ε (eV) A 0 β 1 β 2
25 ℃ − 85 ℃ 2 0.5 60 85 0.0015 2.303 0.154 0.187
25 ℃ − 120 ℃ 2 0.5 95 120 0.039 2.303 0.154 0.187
25 ℃ − 150 ℃ 2 0.5 125 150 0.060 2.303 0.154 0.187
Table 5. The Parameter Estimation of Coffin-Manson Results of Flow Sensor
Table 5. The Parameter Estimation of Coffin-Manson Results of Flow Sensor
Index ε f ∆ T ( K ) T m a x ( K ) Δ Ε (eV) A 0 β 1 β 2
25 ℃ − 85 ℃ 2 0.5 60 85 0.028 1.764 0.235 0.298
25 ℃ − 120 ℃ 2 0.5 95 120 0.249 1.764 0.235 0.298
25 ℃ − 150 ℃ 2 0.5 125 150 0.238 1.764 0.235 0.298
Table 6. The Estimation of Lifetime
Table 6. The Estimation of Lifetime
Index Tem (℃) E a (eV) Lifetime (years)
Sensor-chip-RHG 85℃ 0.0015 eV 29.702
120℃ 0.039 eV 20.548
150℃ 0.060 eV 14.724
Flow sensor-500 sccm 85℃ 0.028 eV 8.290
120℃ 0.249 eV 0.893
150℃ 0.238 eV 0.594
Table 7. The Parameter Estimation of Reliability
Table 7. The Parameter Estimation of Reliability
Index 85℃ 120℃ 150℃
α 0   ( · 10 5 ) 0.726 0.0781 0.0523
β 0.96 0.96 0.96
R t (%) 87.69 32.77 19.39
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated