1. Introduction
Soliton theory based on water waves, plasmas, optical fibers etc., was developed in 1960-1970. This is significant branch of applied mathematics as well as mathematical physics. It has significant uses in non-linear optics, fluid mechanics, plasmas etc. This theory is applied in various natural sciences, including telecommunication, biology, chemistry, mathematics and many fields of physics including fluid dynamics, condensed matter, plasma physics etc. Distinct kinds of naturally occurring phenomenon are shown as a non-linear fractional partial differential equations (NLFPDEs). Distinct schemes are made to attain exact results of non-linear partial differential equations i.e modified direct algebraic technique [
1], modified Khater scheme [
2], Kudryashov technique [
3], novel
-expansion method [
4], extended mapping scheme [
5].
In our study we use three simple, useful and significant methods named as modified simplest equation method, Sardar sub-equation method and generalized Kudryashov method. There are various uses of these methods. Instantly; some solitary wave solutions of BBM and Chan-Hilliard equations by utilizing modified simplest equation method [
6], exact solitons of Boussinesq and coupled Boussinesq equations have been attained by using this technique in [
7]. Some solitons solutions of perturbed Fokas-lenells model have been obtained with the help of Sardar sub-equation technique [
8], new kind of solitons of (2+1)-dimensional Sawada-Kotera (SK) model have been gained by this method [
9], some exact wave solitons of new Hamiltonian Ampltude equation have been attained [
10], the dark, bright and singular optical solitons of higher order non-linear Schrödinger have been gained by utilizing Sardar sub-equation scheme [
11], the singular, bright, dark, periodic singular, combined solitons and other solutions of strain wave model have been achieved with the use of this technique [
12]. Similarly, the bell, anti-bell, dark, kink, flat kink and other wave solutions of Fokas-Lenelles by applying generalized Kudryashov technique [
13], exact solitons of KdV-Burger model are obtained in [
14] etc.
Our mathematical physical important model is the (1+1)-dimensional non-linear simplified Modified Camassa-Holm model (SMCHM). Different types of exact solitons of our concerned model have been achieved with the use of different methods. Likely, some distinct kind of travelling wave solitons of SMCHM have been attained with the help of generalized
-expansion scheme in [
15], solitary wave solitons are gained through Exp-function technique in [
16], different types of wave solutions have been gained by utilizing the Riccati-Bernoulli sub-ODE scheme in [
17] etc.
The purpose of our research is to discover the new types of M-fractional wave solitons to the (1+1)-dimensional non-linear simplified Modified Camassa-Holm model by utilizing modified simplest equation, Sardar sub-equation and generalized Kudryashov techniques.
The paper have distinct sections; In section 2: we explain the our concerned model and it’s mathematical analysis. In section 3: we describe the modified simplest equation technique and it’s application to obtain the soliton solutions. In section 4: we explain the Sardar sub-equation technique and apply it to gain the new soliton solutions of our concerned model. In section 5: we describe the generalized Kudryashov technique and it’s application to obtain the soliton solutions. In section 6: we explain the some obtained solutions through 2-dimensional, 3-dimensional and contour plots. In section 7: we give a conclusion of our research work.
2. The concerning model and It’s mathematical analysis
Let’s assume the non-linear M-fractional simplified Modified Camassa-Holm model from the family of important equations known as the modified
-equations explained by Wazwaz [
18].
here g=g(x,t) represents the wave profile while
and
are nonzero parameters. Putting
in the Eq.(
1), we get
This form is called modified Camassa-Holm model. Furthermore simplified form is of Eq.(
2) given in [
19].
here
where
is the truncated Mittag-Leffler (ML) function of one parameter shown in [
20,
21].
Assume the wave transformation given as follows:
where
and
are the nonzero constants. By substituting the Eq.(
5) into Eq.(
3) we attain
3. Modified simplest equation technique
The fundamental points of this scheme are given as:
Step 1:
Consider a NLPDE:
here
represents wave profile.
Consider the wave transformation:
Inserting Eq. (
8) into Eq. (
7), we gain a NLODE:
Step 2:Consider Eq.(
9) has below shape solution:
where
are undetermined and
.
A new profile
fulfil below ODE:
where
is a parameter.
Eq.(
11) have solutions for different cases of
:
Step 3:
Putting Eq.(
10) into Eq.(
9) with Eq.(
11) and collecting the coefficients of every order of
. Substituting co-efficients of equal to 0, we obtain a set of equations involving
,
,
. Manipulating the gained set of equations, we gain results for parameters.
Step 4:
Inserting Eq.(
9) of which
,
,
has been obtained into Eq.(
10), we attain solutions of Eq.(
7).
3.1. New soliton solutions of Eq.(6) by MSET
Eq.(
10) changes into given form for m=1:
Using Eq.(
23) into Eq.(
6) with Eq.(
11). By collecting coefficients of every order of
and taking equal to 0, we obtain a system of equations. Manipulating the achieved set by Mathematica software, we attain sets.
4. Description of Sardar sub-equation technique
Here, we explain the fundamental points of Sardar sub-equation method [
22]. Assume the nonlinear fractional PDE:
here
is a wave profile.
Substituting a wave transformation shown as:
We obtain a non-linear ODE shown as:
Consider Eq.(
50) posses the results in the given shape:
here
fulfill the ODE shown as:
here
and
are constants.
Using Eq.(
51) into Eq.(
50) along Eq.(
52) and collecting the coefficients of every power of
. Inserting co-efficient of every power equal to 0, we achieve a set of equations having
,
,
. Solving the achieved set of equation, we gain the results for unknowns.
Case 1: if
and
, we have
where,
,
Case 2: if
and
, we have
where,
,
Case 3: if
and
, we have
where,
,
Case 4: if
and
, we have
where,
,
4.1. Solutions through Sardar sub-equation method
Eq.(
51) changes into given form for m=1.
Putting Eq.(
67) into Eq.(
6) by using Eq.(
52). Collecting co-efficients of every power of
and taking equal to 0, we attain a set of equations. Solving the attained set of equations by Mathematica tool, we gain a set.
5. The generalized Kudryashov technique
The basic steps of this technique are given as [
23,
24]:
Step 1:
Take a nonlinear PDE:
here q is a wave profile.
Assume the transformation given as:
Inserting Eq. (
84) into Eq. (
83), we gain the nonlinear ODE:
Step 2:
Consider the roots of Eq. (
85) is of form:
here
and
,
are undetermined parameters and
is a new wave profile of
that is a root of the general Riccati equation shown as:
where a, b and c are the constants. The roots of Eq.(
87) are given in the below cases [
25]:
Case 1: If all a, b and c are nonzero, we have
is shown by
Case 2:If a=0 and
, we have
Case 3:If b=0 and
, we have
Case 4:If c=0 and
, then
Step 3:
By substituting Eq.(
86) into Eq.(
85) and collecting co-efficients of every order of
. Leting the co-efficient of every order equal to 0, we attain a set of equations containing
and
,
and other parameters. By manipulating the attain set by Mathematica tool, we achieve the results for undetermined.
Set 4:
By substituting results of
and
,
into Eq.(
86) and using Eq.(
88)-Eq.(
104), we gain results for Eq.(
6).
5.1. New wave solutions through generalized Kudryashov technique
For
, Eq. (
86) changes into:
here
and
, are unknowns. Inserting Eq. (
105) into Eq. (
6) along Eq. (
87) and collecting the co-efficients every power of
, we obtain the set of equations having
,
and other parameters. With the Mathematica tool, we achieve the set given as:
6. Physical explanation
Here, we explain some of our obtained solutions through different kind of graphs. The effect of fractional order is also shown through the graphs.
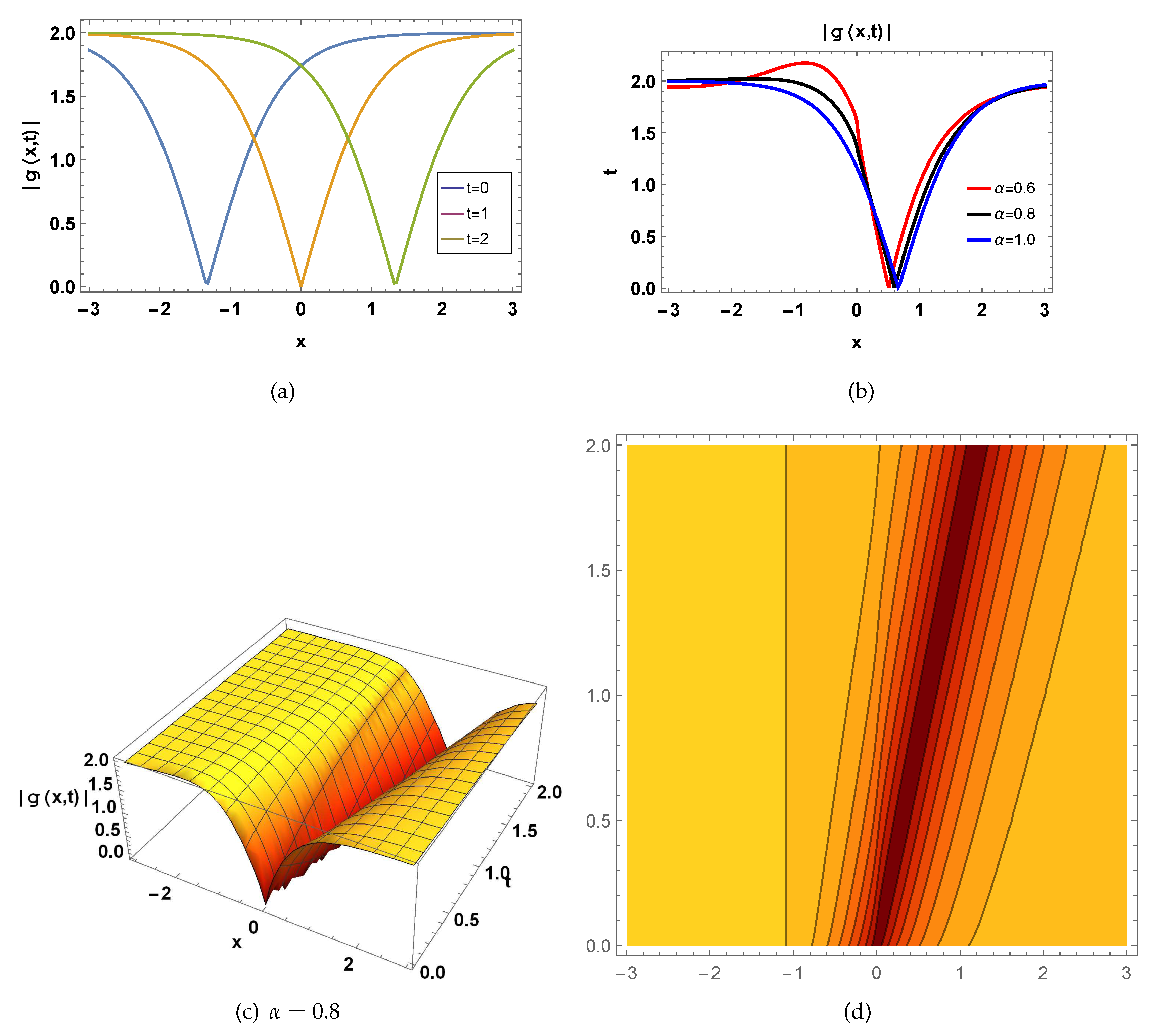
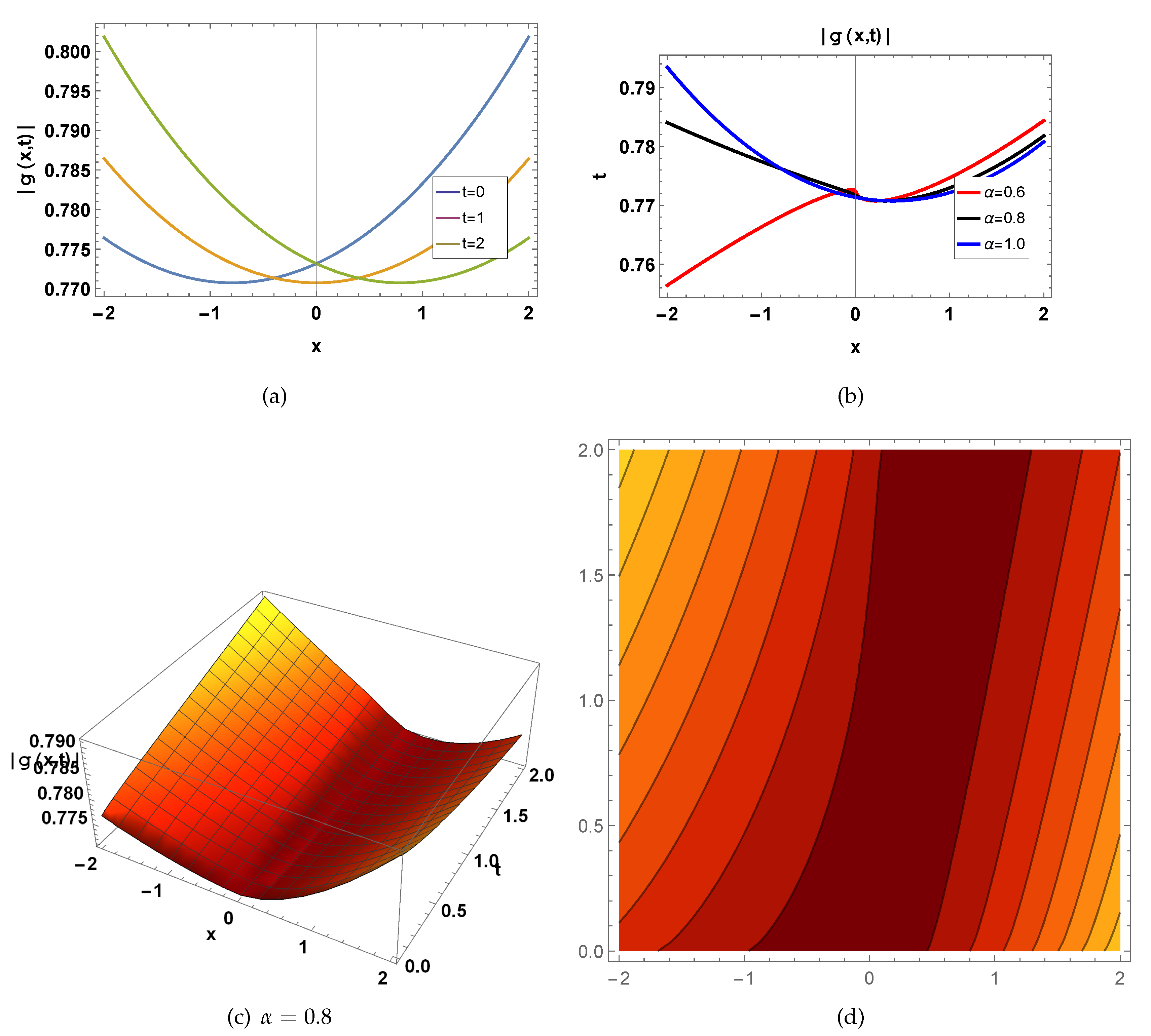
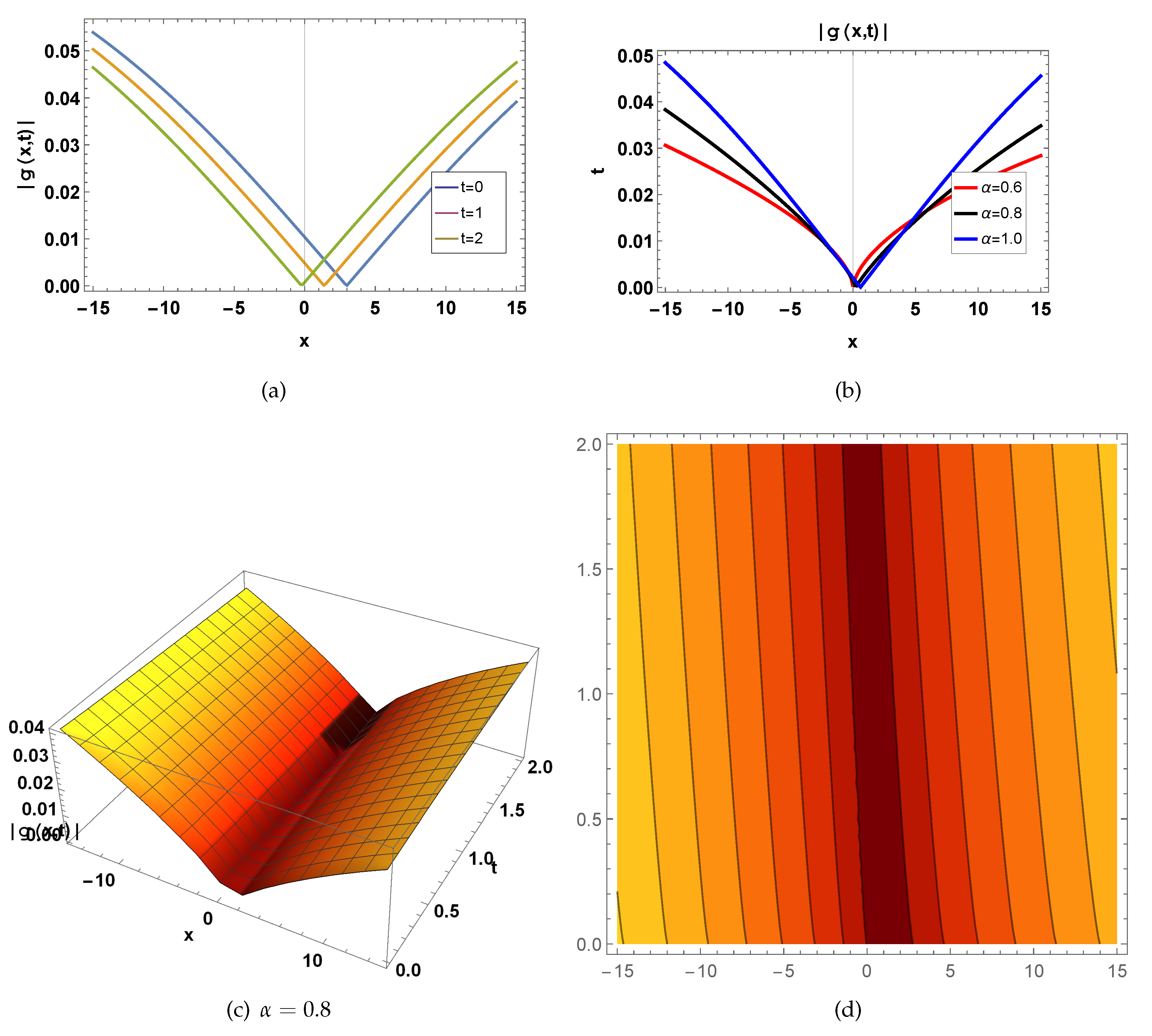
Figure 1.
represents a wave function of
shown in Eq.(
25) for
, fig(a)
in 2D for
, blue curve draw for
, orange curve draw for
, green curve draw for
, fig(b)
in 2D for
, red curve draw for
, black curve draw for
, blue curve draw for
, fig(c) in 3D for
and
, and fig(d) in contour for
and
.
Figure 1.
represents a wave function of
shown in Eq.(
25) for
, fig(a)
in 2D for
, blue curve draw for
, orange curve draw for
, green curve draw for
, fig(b)
in 2D for
, red curve draw for
, black curve draw for
, blue curve draw for
, fig(c) in 3D for
and
, and fig(d) in contour for
and
.
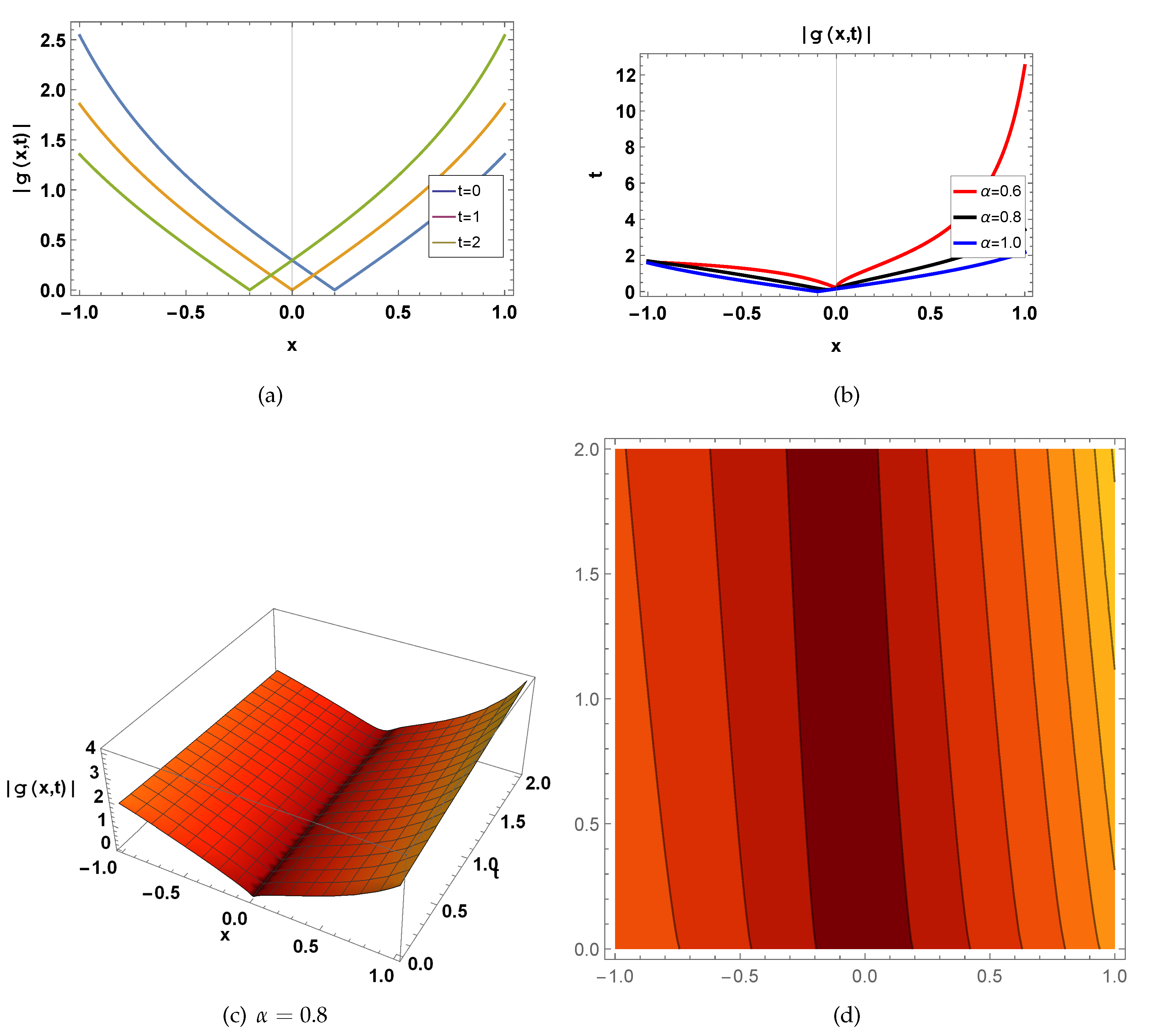
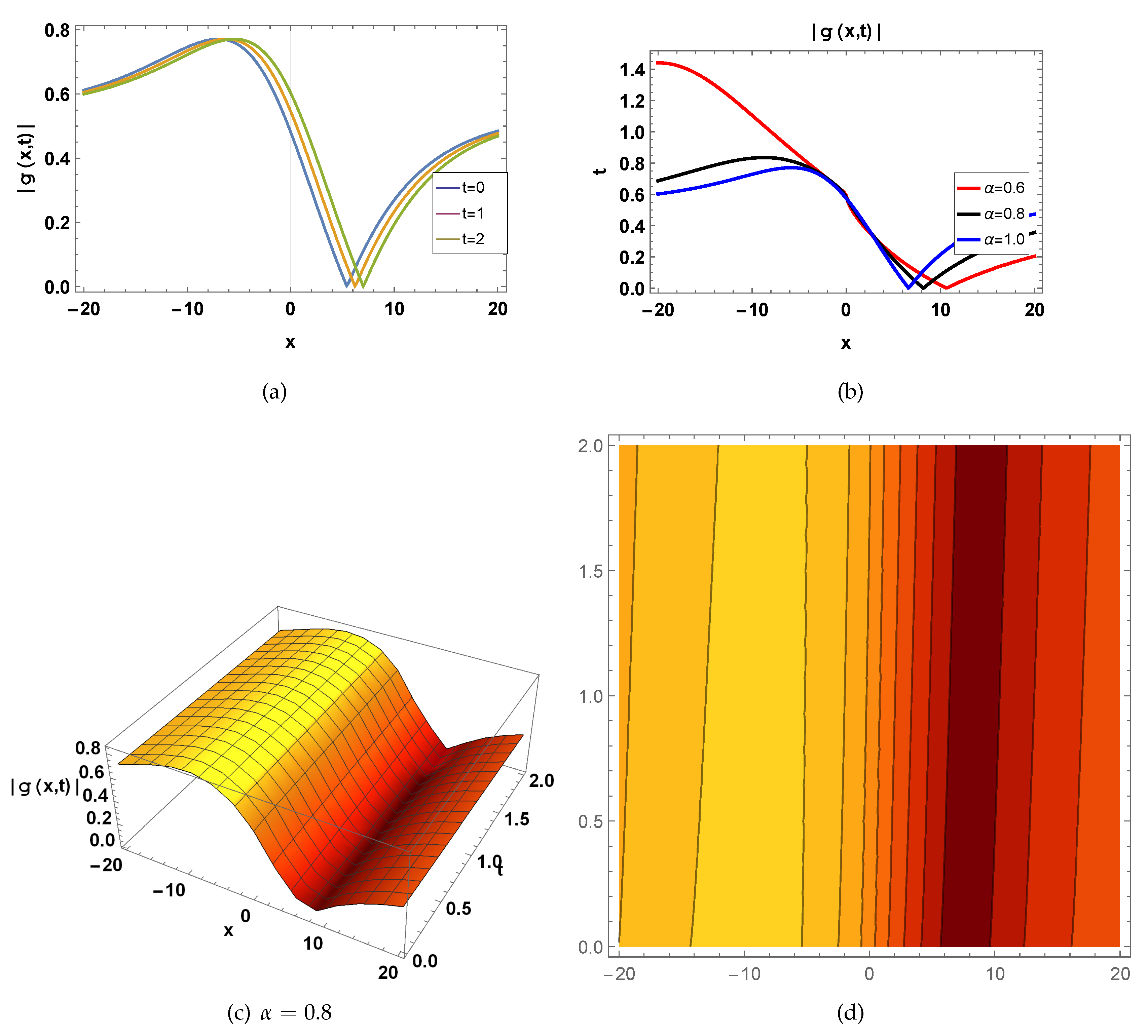
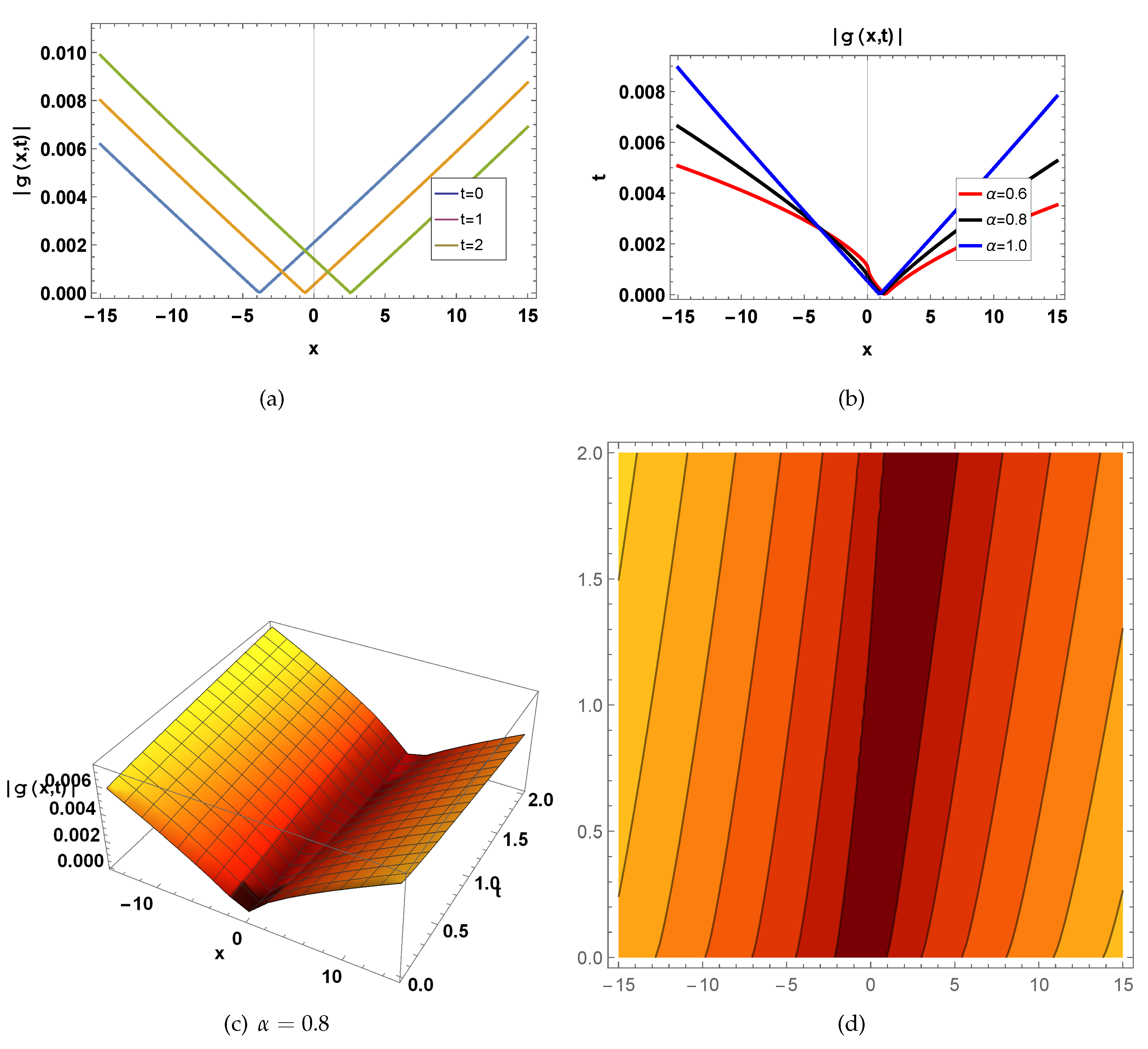
Figure 2.
represents a wave function of
shown in Eq.(
30) for
, fig(a)
in 2-D for
, blue curve draw for
, orange curve draw for
, green curve draw for
, fig(b)
in 2-D for
, red curve draw for
, black curve draw for
, blue curve draw for
, fig(c) in 3-D for
and
, and fig(d) in contour for
and
.
Figure 2.
represents a wave function of
shown in Eq.(
30) for
, fig(a)
in 2-D for
, blue curve draw for
, orange curve draw for
, green curve draw for
, fig(b)
in 2-D for
, red curve draw for
, black curve draw for
, blue curve draw for
, fig(c) in 3-D for
and
, and fig(d) in contour for
and
.
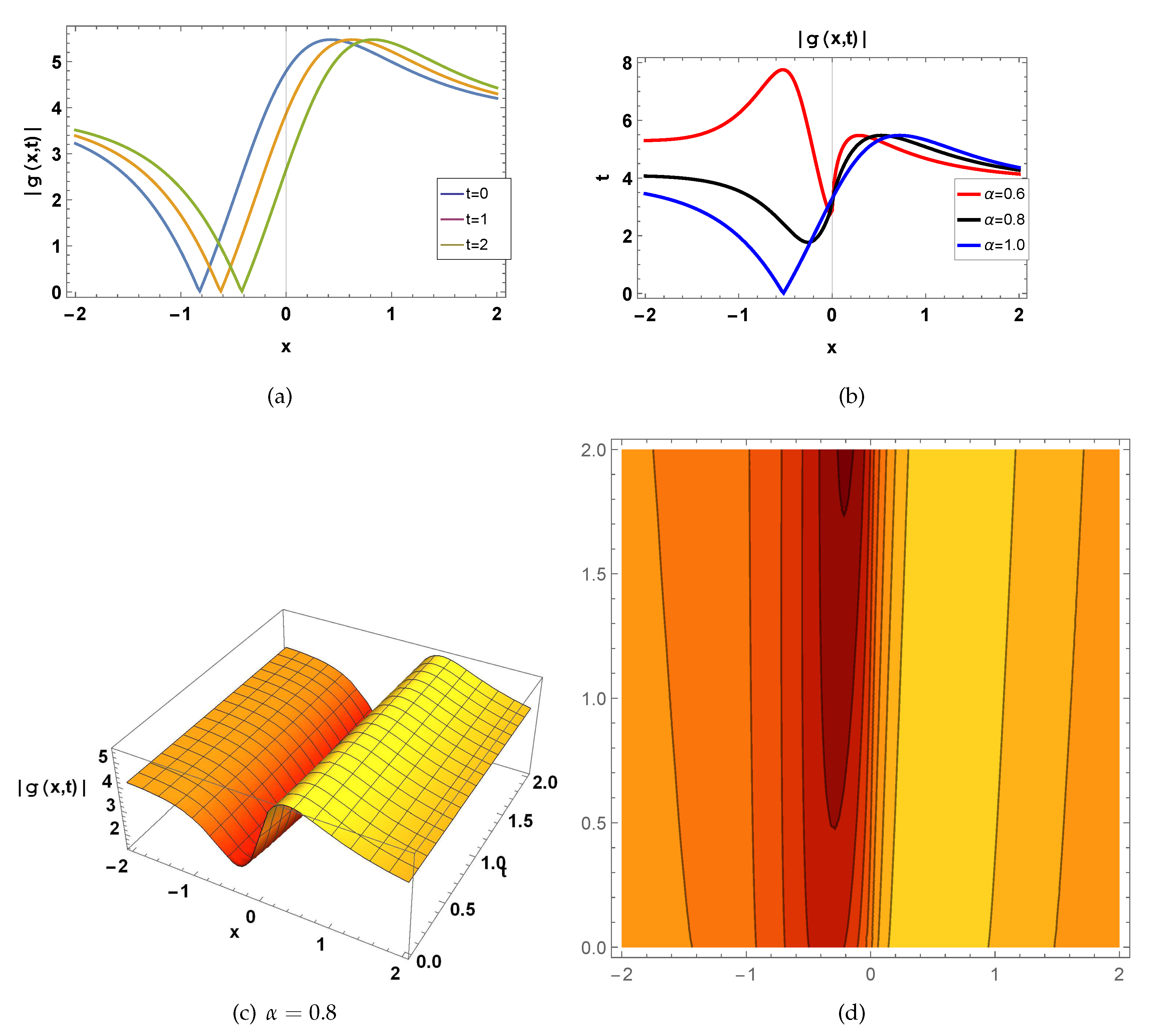
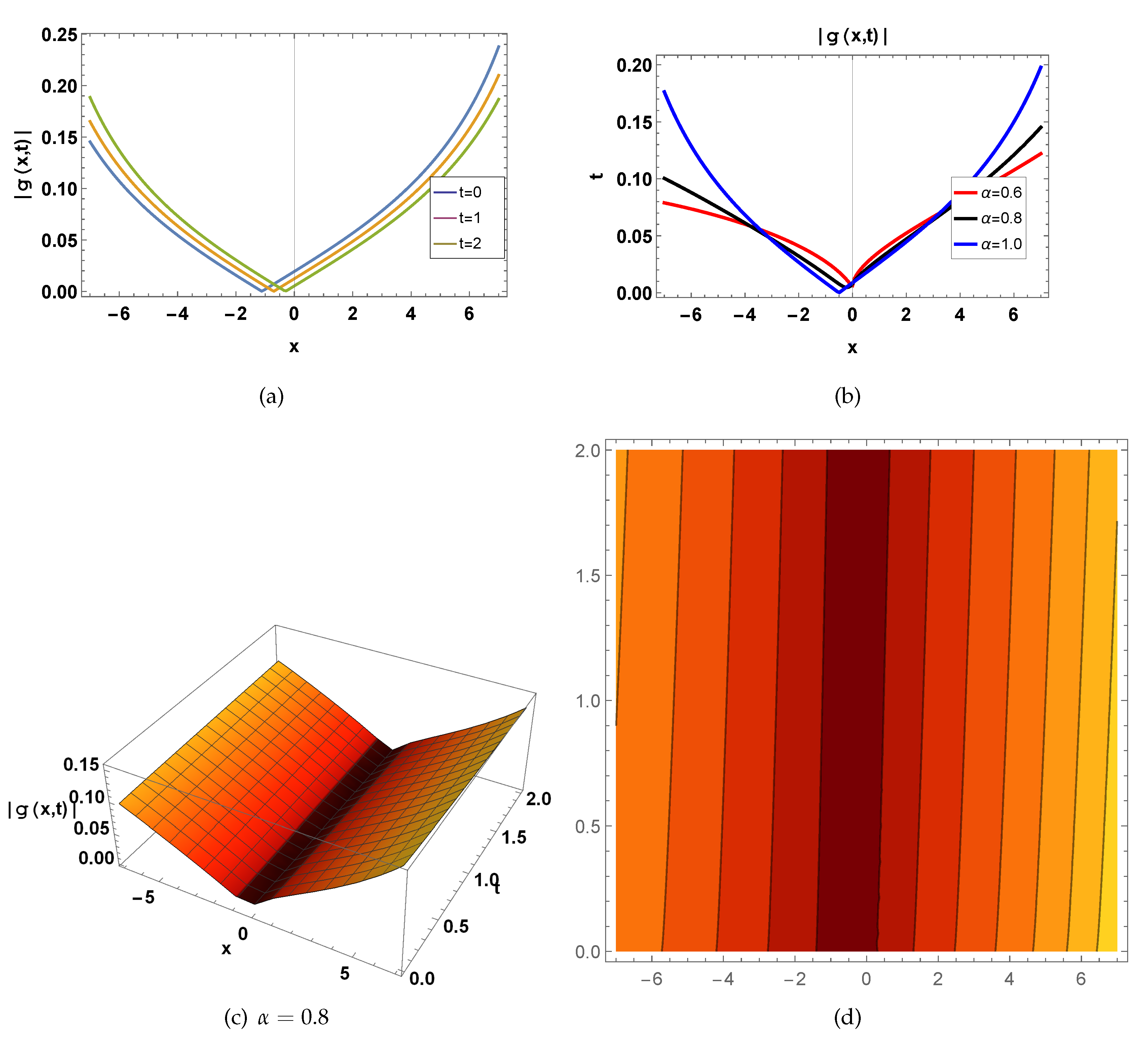
Figure 3.
represents a wave function of
shown in Eq.(
37) for
, fig(a)
in 2-D for
, blue curve draw for
, orange curve draw for
, green curve draw for
, fig(b)
in 2-D for
, red curve draw for
, black curve plotted at
, blue curve draw for
, fig(c) in 3-D for
and
, and fig(d) in contour for
and
.
Figure 3.
represents a wave function of
shown in Eq.(
37) for
, fig(a)
in 2-D for
, blue curve draw for
, orange curve draw for
, green curve draw for
, fig(b)
in 2-D for
, red curve draw for
, black curve plotted at
, blue curve draw for
, fig(c) in 3-D for
and
, and fig(d) in contour for
and
.
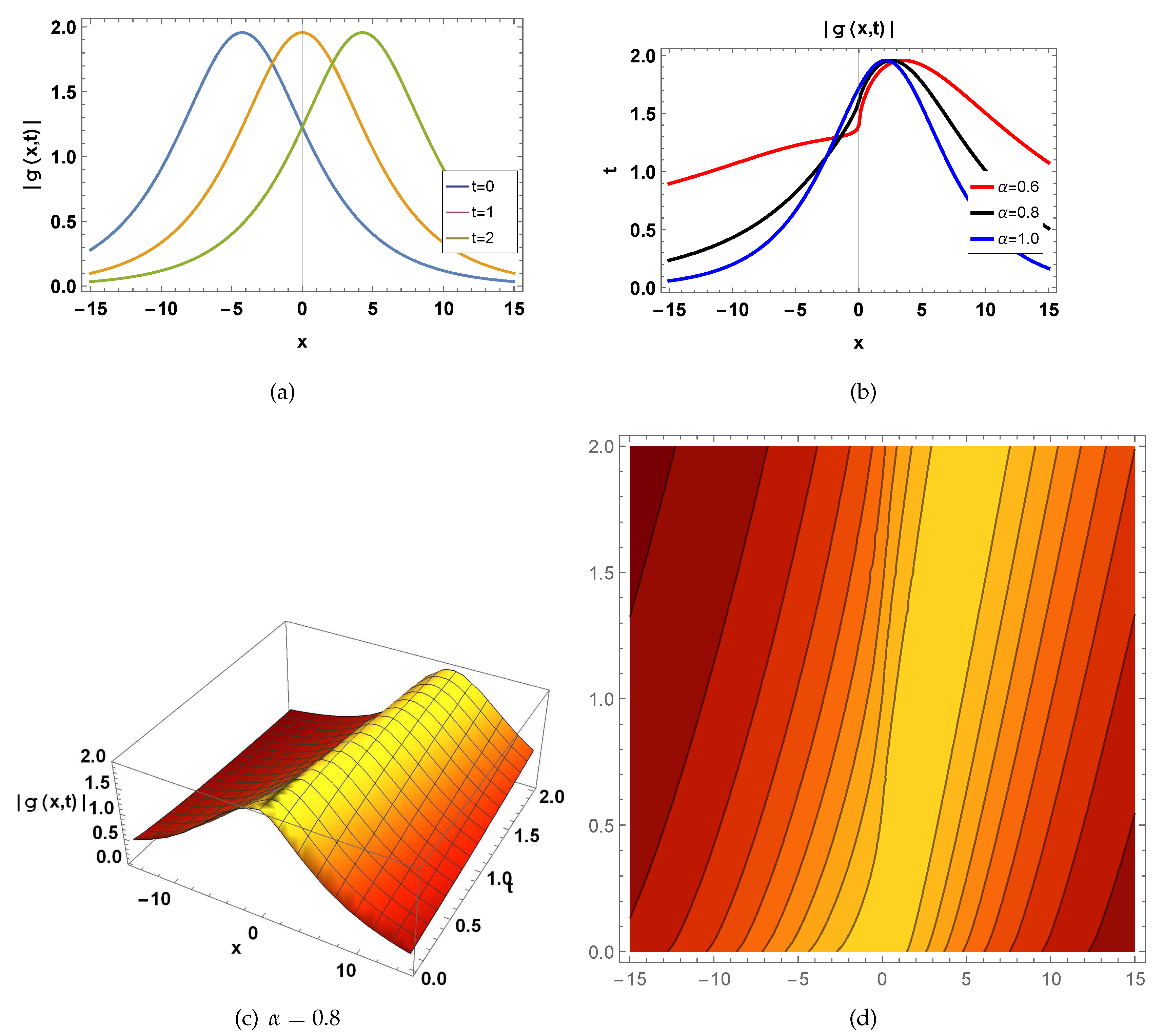
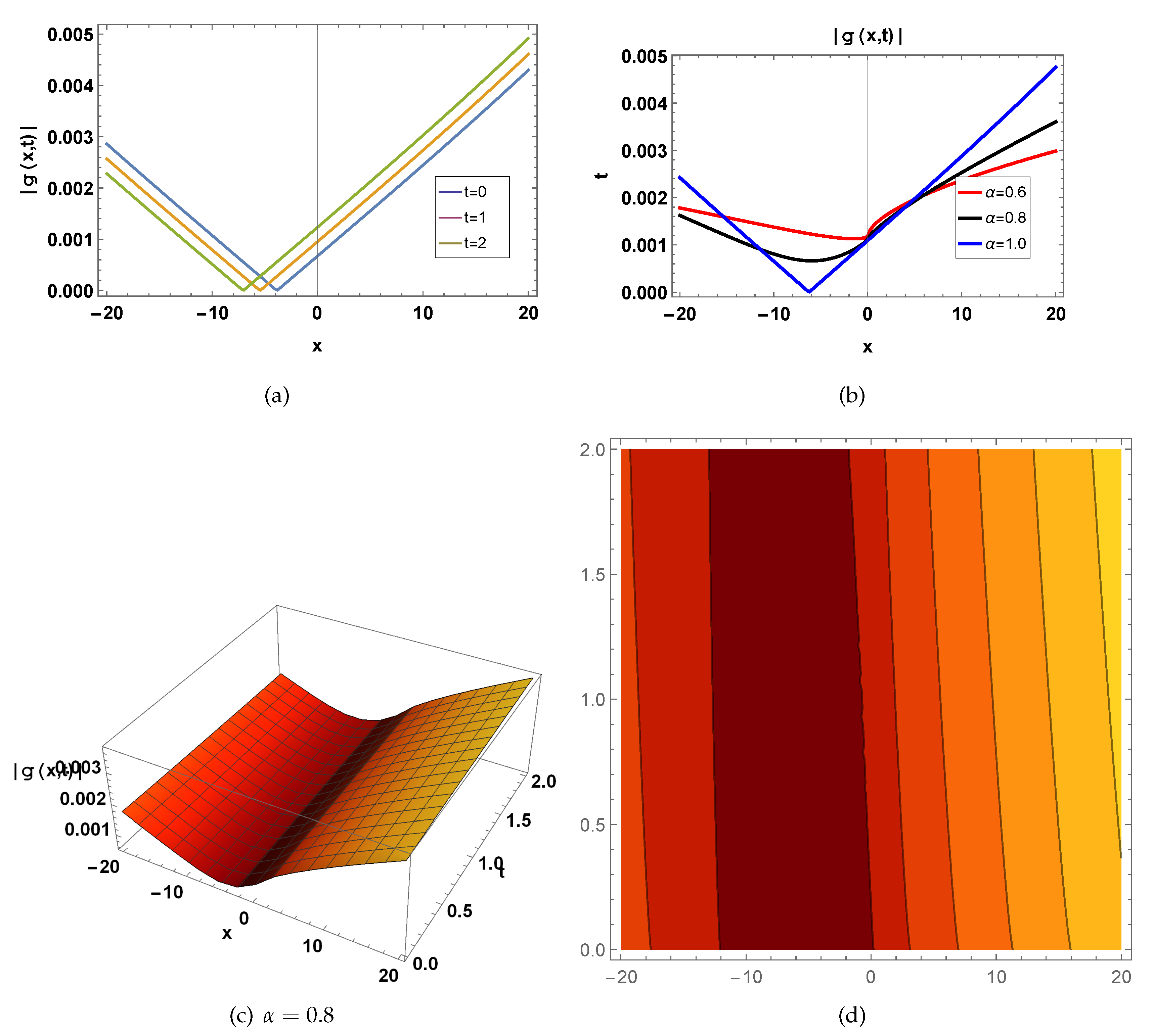
Figure 4.
represents a wave function of
shown in Eq.(
69) for
, fig(a)
in 2-D for
, blue curve draw for
, orange curve plotted at
, green curve draw for
, fig(b)
in 2-D for
, red curve draw for
, black curve draw for
, blue curve draw for
, fig(c) in 3-D for
and
, and fig(d) in contour for
and
.
Figure 4.
represents a wave function of
shown in Eq.(
69) for
, fig(a)
in 2-D for
, blue curve draw for
, orange curve plotted at
, green curve draw for
, fig(b)
in 2-D for
, red curve draw for
, black curve draw for
, blue curve draw for
, fig(c) in 3-D for
and
, and fig(d) in contour for
and
.
Figure 5.
represents a wave function of
shown in Eq.(
71) for
, fig(a)
in 2-D for
, blue curve draw for
, orange curve draw for
, green curve draw for
, fig(b)
in 2-D for
, red curve draw for
, black curve draw for
, blue curve draw for
, fig(c) in 3-D for
and
, and fig(d) in contour for
and
.
Figure 5.
represents a wave function of
shown in Eq.(
71) for
, fig(a)
in 2-D for
, blue curve draw for
, orange curve draw for
, green curve draw for
, fig(b)
in 2-D for
, red curve draw for
, black curve draw for
, blue curve draw for
, fig(c) in 3-D for
and
, and fig(d) in contour for
and
.
Figure 6.
represents a wave function of
shown in Eq.(
75) for
, fig(a)
in 2-D for
, blue curve draw for
, orange curve draw for
, green curve draw for
, fig(b)
in 2-D for
, red curve draw for
, black curve draw for
, blue curve draw for
, fig(c) in 3-D with
and
, and fig(d) in contour for
and
.
Figure 6.
represents a wave function of
shown in Eq.(
75) for
, fig(a)
in 2-D for
, blue curve draw for
, orange curve draw for
, green curve draw for
, fig(b)
in 2-D for
, red curve draw for
, black curve draw for
, blue curve draw for
, fig(c) in 3-D with
and
, and fig(d) in contour for
and
.
Figure 7.
represents a wave function of
shown in Eq.(
79) for
, fig(a)
in 2-D for
, blue curve draw for
, orange curve draw for
, green curve draw for
, fig(b)
in 2-D for
, red curve draw for
, black curve draw for
, blue curve draw for
, fig(c) in 3-D for
and
, and fig(d) in contour for
and
Figure 7.
represents a wave function of
shown in Eq.(
79) for
, fig(a)
in 2-D for
, blue curve draw for
, orange curve draw for
, green curve draw for
, fig(b)
in 2-D for
, red curve draw for
, black curve draw for
, blue curve draw for
, fig(c) in 3-D for
and
, and fig(d) in contour for
and
Figure 8.
represents a wave function of
shown in Eq.(
108) for
, fig(a)
in 2-D for
, blue curve draw for
, orange curve draw for
, green curve draw for
, fig(b)
in 2-D with
, red curve draw for
, black curve draw for
, blue curve draw for
, fig(c) in 3-D for
and
, and fig(d) in contour for
and
.
Figure 8.
represents a wave function of
shown in Eq.(
108) for
, fig(a)
in 2-D for
, blue curve draw for
, orange curve draw for
, green curve draw for
, fig(b)
in 2-D with
, red curve draw for
, black curve draw for
, blue curve draw for
, fig(c) in 3-D for
and
, and fig(d) in contour for
and
.
Figure 9.
represents a wave function of
shown in Eq.(
113) for
, fig(a)
in 2-D for
, blue curve draw for
, orange curve draw for
, green curve draw for
, fig(b)
in 2-D for
, red curve draw for
, black curve draw for
, blue curve draw for
, fig(c) in 3-D for
and
, and fig(d) in contour with
and
.
Figure 9.
represents a wave function of
shown in Eq.(
113) for
, fig(a)
in 2-D for
, blue curve draw for
, orange curve draw for
, green curve draw for
, fig(b)
in 2-D for
, red curve draw for
, black curve draw for
, blue curve draw for
, fig(c) in 3-D for
and
, and fig(d) in contour with
and
.
Figure 10.
represents a wave function of
shown in Eq.(
119) for
, fig(a)
in 2-D for
, blue curve draw for
, orange curve draw for
, green curve draw for
, fig(b)
in 2-D with
, red curve draw for
, black curve draw for
, blue curve draw for
, fig(c) in 3-D for
and
, and fig(d) in contour for
and
.
Figure 10.
represents a wave function of
shown in Eq.(
119) for
, fig(a)
in 2-D for
, blue curve draw for
, orange curve draw for
, green curve draw for
, fig(b)
in 2-D with
, red curve draw for
, black curve draw for
, blue curve draw for
, fig(c) in 3-D for
and
, and fig(d) in contour for
and
.
7. Conclusion
We succeed to contributes to our understanding of the truncated M-fractional (1+1)-dimensional non-linear simplified Modified Camassa-Holm model and provides a useful methods for handling nonlinear fractional partial differential equations. This paper describes the successful application of modified simplest equation, Sardar sub-equation and generalized Kudryashov techniques to explore new type of M-fractional soliton solutions for the truncated M-fractional (1+1)-dimensional non-linear simplified Modified Camassa-Holm model. The obtained solutions are fruitful for further studies of the concerned model. The modified simplest equation, Sardar sub-equation and generalized Kudryashov techniques are shown to be a simple, fruitful, and reliable techniques for handling nonlinear fractional partial differential equations. The solutions are verified and also described graphically through 2-dimensional, 3-dimensional and contour graphs using Mathematica software.
Author Contributions
The authors declare that the study was realized in collaboration with equal responsibility. All authors read and approved the final manuscript.
Funding
Authors bear publishing costs.
Institutional Review Board Statement
There is no conflict between the authors and anyone.
Informed Consent Statement
The authors agree to publish.
Data Availability Statement
Data sharing not applicable to this article as no datasets were generated or analyzed during the current study.
Acknowledgments
Not applicable.
Conflicts of Interest
The authors declare that they have no competing interests.
References
- Bilal, Muhammad and Ahmad, Jamshad and others; New exact solitary wave solutions for the 3D-FWBBM model in arising shallow water waves by two analytical methods, Results in Physics, 25, 104230, (2021). [CrossRef]
- Alshahrani, B and Yakout, HA and Khater, Mostafa MA and Abdel-Aty, Abdel-Haleem and Mahmoud, Emad E and Baleanu, Dumitru and Eleuch, Hichem; Accurate novel explicit complex wave solutions of the (2+ 1)-dimensional Chiral nonlinear Schrödinger equation, Results in Physics, 23, 104019, (2021). [CrossRef]
- Kudryashov, Nikolay A; Method for finding highly dispersive optical solitons of nonlinear differential equations, Optik, 206, 163550, (2020). [CrossRef]
- Hafez, Mohammad Golam and Alam, Md Nur and Akbar, M Ali; Exact traveling wave solutions to the Klein–Gordon equation using the novel (G′/G)-expansion method, Results in Physics, 4, 177–184, (2014). [CrossRef]
- Seadawy, Aly R and Alamri, Sultan Z; Mathematical methods via the nonlinear two-dimensional water waves of Olver dynamical equation and its exact solitary wave solutions, Results in Physics, 8, 286–291, (2018). [CrossRef]
- Razzaq, Waseem and Habib, Mustafa and Nadeem, Muhammad and Zafar, Asim and Khan, Ilyas and Mwanakatwea, Patrick Kandege; Solitary Wave Solutions of Conformable Time Fractional Equations Using Modified Simplest Equation Method, Complexity, 2022, (2022). [CrossRef]
- Razzaq, Waseem and Zafar, Asim and Akbulut, Arzu; The modified simplest equation procedure for conformable time-fractional Boussinesq equations, International Journal of Modern Physics B, 36, 17, 2250095, (2022). [CrossRef]
- Cinar, Melih and Secer, Aydin and Ozisik, Muslum and Bayram, Mustafa; Derivation of optical solitons of dimensionless Fokas-Lenells equation with perturbation term using Sardar sub-equation method, Optical and Quantum Electronics, 54, 7, 402, (2022).
- Debin, Kong and Rezazadeh, Hadi and Ullah, Najib and Vahidi, Javad and Tariq, Kalim U and Akinyemi, Lanre; New soliton wave solutions of a (2+ 1)-dimensional Sawada-Kotera equation, Journal of Ocean Engineering and Science, (2022). [CrossRef]
- Raheel, Muhammad and Zafar, Asim and Cevikel, Adem and Rezazadeh, Hadi and Bekir, Ahmet; Exact wave solutions of truncated M-fractional new hamiltonian amplitude equation through two analytical techniques, International Journal of Modern Physics B, 37, 01, 2350003, (2023). [CrossRef]
- Faisal, Khalida and Abbagari, Souleymanou and Pashrashid, Arash and Houwe, Alphonse and Yao, Shao-Wen and Ahmad, Hijaz; Pure-cubic optical solitons to the Schrödinger equation with three forms of nonlinearities by Sardar subequation method, Results in Physics, 48, 106412, (2023). [CrossRef]
- Ur Rehman, Hamood and Awan, Aziz Ullah and Habib, Azka and Gamaoun, Fehmi and El Din, ElSayed M Tag and Galal, Ahmed M; Solitary wave solutions for a strain wave equation in a microstructured solid, Results in Physics, 39, 105755, (2022). [CrossRef]
- Barman, Hemonta Kumar and Roy, Ripan and Mahmud, Forhad and Akbar, M Ali and Osman, MS; Harmonizing wave solutions to the Fokas-Lenells model through the generalized Kudryashov method, Optik, 229, 166294, (2021). [CrossRef]
- PANDIR, Yusuf and Sahragül, EREN; Exact solutions of the two dimensional KdV-Burger equation by generalized Kudryashov method, Journal of the Institute of Science and Technology, 11, 1, 617–624, (2021).
- Alam MN, Akbar MA. Some new exact travelling wave solutions to the simplified MCH equation and the (1+1)-dimensional combined KdV-mKdV equations. J Assoc Arab Univ Basic Appl Sci., 17, 6–13, (2015). [CrossRef]
- Zulfiqar Aniqa, Ahmad Jamshad. Exact solitary wave solutions of fractional modified Camassa–Holm equation using an efficient method. Alexandra Eng. J., (2020). [CrossRef]
- Hassan SZ, Abdelrahman MA. Solitary wave solutions for some nonlinear time-fractional partial differential equations, Pramana, 91(5),67, (2018).
- Wazwaz AM. Solitary wave solutions for modified forms of Degasperis–Procesi and Camassa–Holm equations. Phys. Lett A, 352, 500–4, (2006). [CrossRef]
- Asim Zafar, M. Raheel, Kamyar Hosseini, Mohammad Mirzazadeh, Soheil Salahshour, Choonkil Park, Dong Yun Shin; Diverse approaches to search for solitary wave solutions of the fractional modified Camassa–Holm equation, Results in Physics, 31, 104882, (2021). [CrossRef]
- Tukur Abdulkadir Sulaiman, Gulnur Yel and Hasan Bulut; M-fractional solitons and periodic wave solutions to the Hirota- Maccari system, Modern Physics Letters B, 1950052, (2019). [CrossRef]
- J. Vanterler D A C. Sousa, and E. Capelas D E Oliveira; A new truncated M-fractional derivative type unifying some fractional derivative types with classical properties, International Journal of Analysis and Applications, 16, 1 , 83-96, (2018).
- Ullah, Naeem and Asjad, Muhammad Imran and Awrejcewicz, Jan and Muhammad, Taseer and Baleanu, Dumitru; On soliton solutions of fractional-order nonlinear model appears in physical sciences, AIMS Mathematics, 7, 5, 7421–7440, (2022). [CrossRef]
- N.A. Kudryashov, One method for finding exact solutions of nonlinear differential equations, Commun. Nonlinear Sci. Numer. Simul. 17, (6), 2248-2253, (2012). [CrossRef]
- A .A . Gaber , A .F. Aljohani , A . Ebaid , J.T. Machado , The generalized Kudryashov method for nonlinear space-time fractional partial differential equations of burgers type, Nonlinear Dyn. 95, (1), 361-368, (2019).
- C.A. Gómez, A.H. Salas, Special symmetries to standard Riccati equations and applications, Appl. Math. Comput. 216, (10), 3089-3096, (2010). [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).