Preprint
Article
Theoretical and Non-dimensional Investigations on Vibration Control Using Viscoelastic and Endochronic Elements
Altmetrics
Downloads
69
Views
23
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
19 September 2023
Posted:
20 September 2023
You are already at the latest version
Alerts
Abstract
Abstract: Theoretical and non-dimensional investigations have been performed to study the vibration control potential of approaches that can be based on viscoelastic but also on endochronic elements. The latter are known from the endochronic theory of plasticity and provide the possibility to establish rate-independent schemes for vibration control. The main question that has to be answered is: Can rate-independent damping be efficiently used to reduce mechanical vibrations? To answer this question non-dimensional models for dynamical systems are derived and analyzed numerically in time-domain as well as in frequency-domain. The results are used to compare the performance of an optimally tuned endochronic absorber to the performance of an optimally tuned dynamic absorber with viscoelastic damping. Based on a novel closed form representation for non-linear systems with endochronic elements, it has been possible to prove that rate-independent control of vibration results in an overall control profit that is close to the control profit obtained by the application of well-established approaches. It has also been found that the new concept is advantageous if anti-resonances have to be considered in broadband vibration control. Based on these novel findings, a practical realization in the context of active vibration control is proposed in which the rate-independent control law is implemented on an appropriate signal processing hardware.
Keywords:
Subject: Engineering - Mechanical Engineering
1. Introduction
In order to attenuate mechanical vibrations it is possible to use passive, semi-active or active noise treatments that can either be designed to reduce dominant single harmonics present in the disturbance signal or to suppress unwanted vibrations in a broad frequency range acting as dynamic absorber (DA). For this purpose it is common to assume viscoelastic damping that is proportional to the velocity of the vibration and therefore describes a rate-dependent material behavior. The basic principles as well as design guidelines for optimally tuned DA that are still relevant for a broad range of applications in mechanical engineering were published by Den Hartog [1]. However, semi-active and active vibration control based on the principle of dry-friction damping was suggested as an alternative concept [2,3]. This approach is more sophisticated, because one has carefully to distinguish between the state of stick and the state of slip that results in a non-linear characteristic because a switch is integrated in the control concept.
To overcome this problem it is possible to introduce the rate-independent concept of endochronic material behavior (materials with internal time scale) that avoids the need to distinguish between stick and slip into the field of vibration control. This new approach is presented for the first time. The elastoplastic theory of endochronic materials was proposed by Valanis [4] and applied to metallic materials [5]. However, a thermodynamically consistent framework based on integral equations was developed by Haupt [6]. For practical applications the description of endochronic material behavior based on differential equations as proposed by Krawietz [7] can to be taken into account.
Examples, considering non-linear but quasi-static deformation behavior of rotary shaft seals made of polytetrafluoroethylene (PTFE), can be found in [8] and [9]. This paper presents new and basic results considering rate-independent damping behavior modelled with endochronic elements in the field of vibration control. These results are compared to the classical approach, in which of rate-dependent viscoelastic elements, known as Maxwell element (spring and dashpot in serial connection) or Kelvin element (spring and dashpot in parallel connection), are applied to dissipate energy.
In order to support the theoretical investigations by numerical simulations a non-dimensional form will be introduced for all algebraic and differential equations used to describe the analyzed systems in time-domain as well as in frequency-domain. This is also advantageous, if the reader wants to scale engineering problems in order to compare them with the theoretical findings presented in this contribution.
The paper is structured as follows: All aspects of analytical and numerical modelling, necessary to describe and investigate vibration control using viscoelastic and endochronic elements considering lumped systems, are described in section 2. The results of the numerical investigations are presented and discussed in section 3. Especially the overall control profit (CP), the reduction of the vibration level, will be analyzed for different excitation signals to quantify the reduction of the vibration level. The main findings are summarized in the conclusions, sections 4.
2. Modelling lamped systems with viscoelastic and elastoplastic elements
2.1. Modelling energy dissipation considering viscoelastic and endochronic material behavior
The main difference between damping caused by viscoelastic elements (used to model rate-dependent material behavior) and damping caused by endochronic elements (used to model rate-independent material behavior) can easily be analyzed, if hysteresis curves are compared. For this purpose it is advantageous to concentrate on rheological models that have an identical topological structure such as the Maxwell model (Figure 1, left) and the endochronic model (Figure 1, right).
Both models represent a serial connection, combining a linear elastic spring and a dissipative element. This yields to an additive decomposition of the total displacement into elastic and inelastic parts. The external force represents the system input to both systems. For the Maxwell element we define an additive decomposition of into the elastic displacement and the displacement of the viscous dashpot , compare (1). The elastic law is given by (2), where is the stiffness of the spring. The evolution of the viscous displacement is determined by (3), where is the viscosity of the dashpot
For the endochronic element the decomposition of is given by (4), where is the plastic displacement. The linear elastic law is given by (5), and the evolution of the inelastic deformation is described by (6), where the constant has the dimension of a force. It should be noticed that using the endochronic theory of plasticity the increment of plastic deformation only depends on the increment of the total deformation , but not on the speed of the deformation process. For this reason a rate-independent material behavior (without relaxation properties) is described by the endochronic approach
In case of quasi-static tension as well as considering the initial condition , it is possible to find a closed form solution for the problem given by (4)-(6)
This result shown in (7) proves that (without further modelling of hardening effects) the constant determines the maximum amount of force that can be transmitted though the endochronic element, if the plastic flow is fully developed. It is also interesting to notice that a non-linear elastic law is described by (7). Thus, endochronic elements cannot be seen as linear time-invariant (LTI) systems that is (to the best knowledge of the author) reported in this clearness for the first time. However, assuming time-harmonic fluctuation for all quantities, it is possible to derive the following force-displacement relations
for both rheological models, where is the angular frequency, is the complex magnitude of the internal force , is the complex magnitude of the total displacement , and is the imaginary unit. While a rate-dependent material behavior is defined by (8) for the Maxwell element, a rate-independent material behavior is described by (9) for the endochronic element. To evaluate these two equations numerically, it is advantageous to introduce non-dimensional formulations such as
where a tilde indicates non-dimensional quantities in the non-dimensional formulations for the Maxwell element (10) and the endochronic element (11).
To define the normalized quantities given in (12), it is in a first step necessary to choose reference values ( - for the angular frequency, - for the total displacement, and - for the spring stiffness). Based on these reference values it is in a second step possible to define non-dimensional quantities such as
Associated results for cyclic loading are presented and discussed in subsection 3.1.
2.2. Vibrations models for dynamic systems with one degree of fredom
In order to compare the behavior of dynamic systems with viscoelastic damping on the one hand to the behavior of dynamic systems with endochronic damping mechanisms on the other hand, the classical harmonic oscillator (Figure 2, left) is compared to a one degree of freedom system considering an endochronic element (Figure 2, right).
In both systems, the displacement of the mass is caused by the external force that is reduced by a force . Thus, the balance of linear momentum reads
where the term represents d’Alembert’s force while is the elastic force in the spring with stiffness , compare (13). Depending on the damping mechanism the force is given by
in order model the viscous force in the dashpot that is proportional to the vibration velocity, compare (14), or in case of the endochronic element by the elastic law
where is the stiffness of the endochronic element, while the internal variable describes the amount of plastic displacement. The evolution of the internal variable , compare (15), is given by the non-linear but rate-independent flow rule (16)
where the constant controls the evolution of the plastic deformation during the dynamic process. To develop a non-dimensional formulation for the equations of motion, it is necessary to introduce the dimensionless time such as
where is the angular natural frequency of the undamped system. As a consequence the first and second time derivatives are given by
Furthermore, critical damping , a non-dimensional stiffness ratio as well as non-dimensional displacements and , a non-dimensional excitation force , and the non-dimensional force constant for the endochronic element are introduced such as
where is a reference displacement. Considering these normalized quantities, defined in (19), the resulting non-dimensional equation of motion for the harmonic oscillator reads
while the set of non-dimensional equations of motion for the oscillator with the rate-independent endochronic element are given by
It should be noticed that (19) represents a non-dimensional representation of a LTI system, while (20)-(21) describe a non-linear system, because of the non-linear endochronic flow rule. The response of both systems is purely elastic, if the relative velocity between the mass and the base tends to zero, because stress relaxation is not covered by the Kelvin model as well as by the endochronic model proposed in this study. Furthermore, the response of both systems is identical, if damping can be neglected such as and the stiffness ratio is set to . The impulse response as well as the magnitude response of both system models is discussed in subsection 3.2.
2.3. Virbration models for coupled systems with two degrees of freedom
Because control of vibration by passive, semi-active or active systems requires a coupling between the vibrating system and the device used to attenuate the disturbance, it is necessary to analyze the dynamics of coupled systems. A situation in which two degrees of freedom have to be taken into account is shown in Figure 3, where the mass that is excited by the external force is coupled to vibration reduction devices. The latter are represented by the mass . While a viscoelastic system is shown in Figure 3 (left), a non-linear endochronic system is presented in Figure 3 (right).
For both systems, the balance of linear momentum is given by (22) and (23), considering D’Alembert’s forces as well as linear elastic laws for every spring
However, as for the single degree of freedom systems, the definition of the force depends on the damping mechanism that has to be described. In case of viscoelastic damping this quantity is given by the relative velocity in the dashpot, as shown in (24)
If damping is modeled using the rate-independent endochronic approach, the force is given by the elastic law (25), while the evolution of the plastic displacement is described by the flow rule (26)
Considering an elastic coupling between and the force could also be applied by a proper actuator (compare Figure 4) driven by the control signal . The latter is calculated by the controller based on sensor signals. These are the transducer force and the measure of the relative velocity that can also be integrated in the control unit. This remark is important, because it answers the question how endochronic elements can be realized in practical applications.
However, the main intention of this contribution is to analyze the noise control potential of viscoelastic and endochronic noise control devices attached to a dynamic system in a general way. To proceed it is again advantageous to develop a non-dimensional version of the equations of motion. At first the non-dimensional time is re-defined considering the angular frequency as shown in (27)
As a consequence the first and second time derivatives are now given by
for both degrees of freedom. Furthermore, it is necessary to define a mass ratio as well as to introduce two modified stiffness ratios such as presented in (29)
Critical damping is now defined by (30)
Furthermore, non-dimensional variables for the external force and the two degrees of freedom are introduced in (31)
where is again a reference displacement. Finally the non-dimensional constant for the endochronic element has to be re-defined such as
Using the definitions given by (27)-(32) it is possible to derive the following sets of non-dimensional equations. At first the non-dimensional model of the viscoelastic system (compare Figure 3, left) is presented in (33)
The non-dimensional model for the two degree of freedom system with the endochronic element (compare Figure 3, right) is given by
where the evolution equation for the non-dimensional plastic displacement is defined by (35) such as
The models defined by (33) as well as by (34)-(35) can be used to analyze the behavior of both systems numerically. It should be noticed that (33) represents a time-domain model of a LTI system, while the set of equation summarized in (34)-(35) describes a non-linear system. The response of both systems is identical, if damping can be neglected, i.e. and . It is easy to prove that for time-harmonic fluctuation of all quantities a frequency-domain representation can be derived from (33) for the viscoelastic system that is given in (36)
where a hat indicates the complex magnitude of a non-dimensional quantity. However, if (25) is not used to eliminate the force in the balance of linear momentum (22)-(23) it is, after some algebraic manipulations, also possible to derive a non-linear frequency-domain model for time-harmonic analysis of the system with the endochronic element such as
where the complex magnitude of the non-dimensional force is given by
With (37)-(38) the present paper proposes for the first time a non-linear and non-dimensional model of coupled dynamical systems that enables an efficient way of analyzing vibration control with endochronic elements considering time-harmonic excitation in frequency-domain. The time-domain models as well as the frequency-domain system representations have been used for numerical investigations. The associated results are presented in subsection 3.3.
3. Results of numerical investigations and discussion of noise control potential
3.1. Energy dissipation described by viscoelastic and endochronic rheological models
The analytical models (10) and (11) derived for the Maxwell element (Figure 1, left) and the endochronic element (Figure 1, right) have been analyzed considering two normalized angular frequencies and , compare (12). Furthermore, the following non-dimensional constants have been used to specify the non-dimensional stiffness, the non-dimensional viscosity, and the non-dimensional force such as , , .
The simulation results for the endochronic element are shown in Figure 5 (left), while the results for the Maxwell element are presented in Figure 5 (right). As illustrated by Figure 5 (left) rate-independent material behavior is described by the endochronic element, because the shape of the hysteresis curves are independent on frequency.
The presented results also prove that both magnitude response as well as phase response of the endochronic element described by (11) are independent on frequency. This is an interesting result that is presented in this form for the first time. The same is however not true for the Maxwell element, compare Figure 5 (right), that can be applied to model rate-dependent hysteresis effects as well as relaxation and creep in quasi-static deformation processes.
3.2. Dynamic behaviour of systems with one degree of freedom
In order to study the behavior of dynamic systems with viscoelastic damping and dissipation caused by plastic deformation, the mathematical models for the harmonic oscillator (20) and the oscillator with an endochronic element (21) have been analyzed numerically considering a unit impulse as system input such as . A self-implemented 4th-order Runge-Kutta scheme with fixed step size has been applied for numerical integration considering 25000 time steps. To apply the Runge-Kutta schema, the set of equation has been transformed to a set ODE’s containing only first derivatives with respect to the non-dimensional time . All initial conditions have been set to zero. To fulfill Shannon’s criteria, the non-dimensional sampling frequency has been set to , where is the normalized resonance frequency according to (17).
For the harmonic oscillator described by (20), critical damping has been set to . In order to match the resonance of the harmonic oscillator, the system parameter of the non-linear oscillator described by (21) have been set to and . The associated simulation results are presented in Figure 6 and in Figure 7.
For both systems, the impulse response curves are shown in Figure 6 (left), while the normalized magnitude response curves are presented in Figure 6 (right) using a semi-logarithmic scale. As typical for viscoelastic systems, an exponential decay of the normalized displacement has been simulated for the model of the harmonic oscillator, compare Figure 6 (left). A significant (but not exponential) decay of the impulse response has also been found for the non-linear oscillator with the endochronic element, compare Figure 6 (left).
The magnitude response curves of both systems are nearly identical for normalized frequencies above the resonance, compare Figure 6 (right). It should be noticed that for quasi-static excitation (low normalized frequencies below the resonance) the force transmitted though the dashpot of the harmonic oscillator is close to zero. For this reason, the magnitude response of the system described by (20) covers a static deflection for very low normalized frequencies.
This is not true for the non-linear system described by (21), because the force transmitted through the endochronic element is rate-independent as discussed in the previous subsection. For this reason a plastic flow is induced also at very low normalized frequencies and causes an attenuation of the excitation that can be observed in the magnitude response curve, compare in Figure 6 (right).
In order to illustrate the non-linear effects caused by the endochronic element that have also been discussed for static loading, the reader is referred to the discussion of (7), the evolution of the plastic displacement is shown in Figure 7 (left) considering a small section of the time series. It is interesting to note that the evolution of the plastic displacement is a non-linear process. The higher-harmonics that contribute to the evolution of the plastic displacement are uneven multiples of the normalized natural frequency. Especially the first higher harmonic contributes significantly to the time-domain response of the endochronic element. For the chosen set of parameter, the non-linear characteristic is not to be found in the frequency response of the total displacement, compare Figure 7 (right).
3.3. Discussion of dynamic behaviour and evaluation of control profit for coupled systems
In order to evaluate the vibration control potential of dynamic absorber that are based on viscoelastic and plastic dissipation, it is necessary to analyze the dynamical behavior of coupled systems. In the present contribution the DA, compare Figure 3 (left), is used as a reference. Its time-domain representation is given by (33), while the associated frequency-domain model is given by (36). The CP, compare (42), that can be obtained by the application of an optimally tuned DA is compared to the CP that is estimated for an optimally tuned endochronic absorber (EA), compare Figure 3 (right). The time-domain model for the coupled system with the EA is given by (34)-(35). Its frequency-domain counterpart is given by (37)-(38).
As in the previous subsection, a self-implemented 4th-order Runge-Kutta schema with fixed step size has been used to perform numerical integration other 50000 time steps considering initial conditions that have been set to zero for all quantities. To fulfill Shannon’s criteria, the non-dimensional sampling frequency has been set to , where is a normalized frequency according to (27).
For both models, the mass ratio has been set to . The optimal values for the DA, compare (39), have been calculated following the procedure proposed in [1]
To simulate the EA, the stiffness ratio has been set to the optimal value of the DA given in (39) such as . The remaining normalized constants for the endochronic element have been set to
The constants given in (40) have been determined by genetic optimization limiting the parameter space for both constants by the lower bound 0.0 and the upper bound 2.0. The cost function (41)that has been applied to find these constants (defining an optimally tuned EA) has been defined as the sum of the squared normalized magnitudes of the system mass and the so called tilger mass such as
considering 300 normalized frequencies in the range . To solve the non-linear set of equations given by (37)-(38) the Levenberg-Marquardt algorithm has been applied. The results calculated for the optimally tuned DA and the optimally tuned EA will be compared to results that have been calculated for a system without damping considering only the system mass and the tilger mass , the two springs characterized by and as well as the ratios and .
3.3.1. Time-harmonic analysis of coupled systems
Numerical results obtained for (i) the undamped system, (ii) the optimally tuned DA, and (iii) the optimally tuned EA considering time-harmonic excitation acting at the system mass are presented in Figure 8.
The normalized response of the system mass due to excitation acting at the system mass is shown in Figure 8 (left). The curve indicating the system without damping illustrates three characteristic frequencies. These are the two resonance frequencies that are located at and as well as the anti-resonance that is to be found at . The latter is identical to the normalized natural frequency of the undamped single degree of freedom system. The normalized magnitude response of the tilger mass caused by the excitation acting on is shown in Figure 8 (right). The resonance frequencies and can also be detected in the associated curve.
This is not possible by following the response curves representing the systems with the optimally tuned DA and the optimally tuned EA because a significant and broadband reduction of the vibration level is simulated for both approaches. Furthermore, as known from the theory of mechanical vibrations, the effect of damping lowers the CP outside the resonances – especially around the anti-resonance.
It should be noticed that using the set of parameter determined for the optimally tuned DA and the optimally tuned EA, the CP realized with the DA exceeds the CP that is realized with the EA around the resonance frequencies. However, the results presented in Figure 8 (left) also prove that the increase in vibration level around the anti-resonance is lower, if the EA is used to attenuate the vibration at the system mass .
3.3.2. System analysis considering broadband and time-varying excitation signals
In order to analyze the response of coupled systems caused by more sophisticated input signals, numerical simulations have also been performed using (i) linear chirp signal, (ii) white Gaussian noise, and (iii) a step signal as system input. However, in contrast to the results of the time-harmonic analysis presented in Figure 8, the magnitude response is now presented as a 1/3 octave band analysis. For this purpose, the octave bands defined in [10] have been used considering an upscaling of the normalized sampling frequency by the factor 1000 by calculating the 1/3 octave band analysis using the Matlab® command poctave.
Furthermore, all 1/3 octave band plots have been adjusted by multiplying the data on the x-aches by the factor 6.2 in order to match the anti-resonance in the normalized representation for the non-dimensional frequency range. Because the CP is especially relevant for the system mass the 1/3 octave band analysis has been limited to the magnitude response of normalized displacement .
Figure 9 presents numerical results that have been obtained by analyzing the dynamics of coupled systems using a linear chirp as input signal. The latter has been designed in such a way that the maximum value of the normalized frequency has been reached at the end of the simulation. Figure 9 (left) presents this input signal considering the first 5% of the total time scale. The associated 1/3 octave response curves of the system mass are shown in Figure 9 (right) considering the full time scale.
As for the excitation with time-harmonic signals, it is possible to identify the two resonance frequencies and as well as the anti-resonance at by analyzing the curve for the undamped system.
Furthermore, it is possible to validate that vibration control based on an optimally tuned DA lowers the magnitude response around the resonance frequencies but increases the magnitude response around the anti-resonance. The application of an optimally tuned EA improves the CP at the anti-resonance. But, the CP obtained around the resonance frequency is smaller compared to the CP that is obtained by the application of an optimally tuned DA. However, by comparing the results presented in subsection 3.3.1. to the results presented in subsection 3.3.2. it must be taken into account that Fourier spectra are presented in subsection 3.3.1., while 1/3 octave band power spectra are presented in subsection 3.3.2.
Numerical results that have been obtained by simulating the system response using white Gaussian noise as input signal are presented in Figure 10. The input signal is shown in Figure 10 (left) for the first 5% of the total time scale. The associated 1/3 octave response curves of the system mass are shown in Figure 10 (right). These results are in very good agreement with the results presented in Figure 9 (right). Small deviations in magnitude are caused by the fact that only one (time-limited) realization of a stochastic process has been considered. The data are therefore not identical to results obtained by using deterministic signals, even if an identical frequency range is excited.
Figure 11 presents results that have been obtained by analyzing the response of coupled systems considering a step input signal. The latter is shown in Figure 11 (left). It is both, deterministic and broadband, but can also be classified as transient. It has been considered in order to investigate the response to a short time and non-stationary excitation signal. In contrast to the input signal shown in Figure 11 (left), the chirp signal shown in Figure 9 (left) changes relatively slow in time. Furthermore, the white Gaussian noise signal shown in Figure 10 (left) can be classified as a stationary signal that enables the system that is excited a stationary response (known as forced vibration), if the amount of damping is significant.
The 1/3 octave band magnitude response curves caused by the step input signal are shown in Figure 11 (right). Because of the transient character of the input signal, these results differ from the results shown in Figure 9 (right) and Figure 10 (right).
It can be seen that the CP around the resonances is more significant, if the optimally tuned DA is coupled to the systems mass . This is especially true for . However, it is easy to explain why the CP realized with the optimally tuned EA is in the same range of magnitude compared to the CP realized with the optimally tuned DA around . In order to generate plastic dissipation, a relative motion is required between the systems mass and the tilger mass . This relative motion is more significant for a mode shape in which both masses vibrate out-of-phase.
This is typical for the second resonance frequency but not for the first resonance frequency . Thus, it can be concluded that the short time step input used in this analysis is more capable of exciting the out-of-phase vibration instead of the first mode shape that is characterized by an in-phase displacement of system mass and tilger mass .
Nevertheless, it has been found that the application of an optimally tuned EA also enables a significant CP, if the excitation signal has a transient character. An amplification of the dynamic response around resonances has not been detected.
3.3.3. Discussion of noise control potential
In order to discuss the noise control potential it is necessary to define an appropriate measure for the CP. The latter can be established as the difference of the overall vibration level of the uncontrolled and the controlled system such as
where the overall vibration level for the uncontrolled system and the overall level for the controlled system , compare (42), have to be calculated according to the usual approach
considering a proper reference value . Following this approach, the CP has been evaluated for all types of input signals. Table 1 contains the numerical data that have been calculated for every frequency line (sine) and every 1/3 octave band frequency (chirp, white Gaussian noise, step). However, by comparing the absolute values it must be taken into account that the results obtained from the time-harmonic analysis (sine) are taken from a narrow-band Fourier spectrum, while the results obtained for all remaining input signals are evaluated as 1/3 octave band power spectra.
The results shown in Table 1 (first row) prove that the overall CP is nearly identical, if time-harmonic excitation is relevant as system input. This finding is in fair agreement with the results presented in Figure 8 (left). The data presented in the second, third, and fourth row prove that a significant CP can be achieved, if optimally tuned absorber are applied. Also these data are in good agreement with the simulation results presented in Figure 9 (right), Figure 10 (right), and Figure 11 (right).
It can be concluded that the CP is reduced, if the system input becomes stochastic and transient. For the chirp signal the CP obtained with the optimally tuned EA is nearly identical to the CP that is obtained with the optimally tuned DA. However, if random excitation and shock has to be considered, the overall CP obtained with the optimally tuned EA is still significant, even if, the overall CP obtained with the optimally tuned DA has a benefit close to 12dB.
If an electronic realization of the control approach is applied (compare Figure 4), it is also possible to switch between the characteristic of an optimally tuned DA and an optimally tuned EA. Furthermore, it is possible to combine both approaches to vibration control using the same actuator. This can be relevant, if the control profit has to be concentrated to a specific mode shape as discussed for the optimally tuned EA regarding the out-of-phase mode at the second resonance frequency and the transient (step) input signal. In addition, the combination of these two control approaches can be advantageous, if broadband control has to be realized around anti-resonances. It has been shown, compare Figure 9 (right) and Figure 10 (right), that vibration control based on an optimally tuned EA performs better at the anti-resonance frequency comparted to the optimally tuned DA.
5. Conclusions
For the first time a detailed vibration analysis and vibration control potential evaluation has been presented considering plastic damping modeled by endochronic elements. All findings have been compared to classical approaches based on viscoelastic damping modeled by Maxwell elements or Kelvin elements. By analyzing rheological models it has been found that elastoplastic material behavior described by the endochronic theory of plasticity results in a rate-independent approach that is capable of providing a hysteresis that is independent on frequency.
Also for the first time it has been shown that modelling of rate-independent damping effects using endochronic elements results in a non-linear system behavior that can especially be found in the development of the plastic displacement. Furthermore, a new closed form analytical model has been presented that allows for time-harmonic analysis of coupled systems including non-linear effects caused by endochronic elements.
Based on this novel finding it has been possible to compare the well-established concept of vibration control based on an optimally tuned DA to the new approach that is based on an optimally tuned EA. It has been found that the new approach is capable of realizing an overall CP that is comparable to the overall CP of the established viscoelastic approach, if time-harmonic excitation signals and chirp signals (varying slowly in time) are responsible for the disturbance. It has also been found that the overall CP that can be realized with an optimally tuned EA is significant for stochastic as well as transient disturbances. Independent on the type of the excitation signal, vibration control based on an optimally tuned EA has to be found more effective around anti-resonances comparted to broadband vibration control based on an optimally tuned DA.
Even if a mechanical realization of an endochronic material has not been reported in literature so far, it is nowadays possible to realize an endochronic approach to vibration control using the concept of active vibration reduction by implementing a rate-independent control law on a proper signal processing unit. Considering the concept of self-adaptive control the concept of active damping based on the endochronic theory of plasticity therefore also offers new possibilities for research on non-linear adaptive control.
All results that have been presented are based on non-dimensional and therefore normalized quantities. This is not only advantageous for numerical simulation and evaluation of mathematical models. It is also helpful in order to scale results and to condense the number of system parameter.
Supplementary Materials
Please contact the author, if supplementary material is helpful for your academic work.
Funding
“This research received no external funding.
Data Availability Statement
Please contact the author, if data exchange is helpful for your academic work.
Acknowledgments
The author gratefully acknowledges the inspiring work of his teachers Albrecht Bertram and Uwe Schomburg.
References
- Den Hartog, J.P. Mechanische Schwingungen, 1st ed.; Springer: Berlin, Germany, 1936. [Google Scholar]
- Stammers, C.W.; Sireteanu, T. Vibration control of machines by use of Semi-active dry friction damping. J. Sound and Vibration 1998, 209, 671–684. [Google Scholar] [CrossRef]
- Gaul, L.W.; Nitsche, R. Friction control for vibration suppression. Mechanical Systems and Signal Processing 2000, 14, 139–150. [Google Scholar] [CrossRef]
- Valanis, K. A theory of viscoplasticity without a yield surface, Part I: General theory. Archive of Applied Mechanics 1971, 23, 517–533. [Google Scholar]
- Valanis, K. A theory of viscoplasticity without a yield surface, Part I: Application to mechanical behaviour of metals. Archive of Applied Mechanics 1971, 23, 535–551. [Google Scholar]
- Haupt, P. Viskoelastizität und Plastizität. Thermodynamisch konsistente Materialgleichungen, 1st ed.; Springer: Berlin, Germany, 1977. [Google Scholar]
- Krawietz, A. Materialtheorie. Mathematische Beschreibung des phänomenologischen thermomechanischen Verhaltens, 1st ed.; Springer: Berlin, Germany, 1986. [Google Scholar]
- Kletschkowski, T.; Bertram, A.; Schomburg, U. Endochronic viscoplastic material models for filled PTFE. Mechanics of Materials 2002, 34, 795–808. [Google Scholar] [CrossRef]
- Albrecht, F.; Kletschkowski, T. Simulation von Wellendichtringen mit einer Vielteilchenmethode. Proceedings of 19th ISC Int. Sealing Conference, Stuttgart, Germany, 2016., October 12-13.
- Specification for Octave-Band and Fractional-Octave-Band Analog and Digital Filters. ANSI Standard S1.11-2004. Melville, NY: Acoustical Society of America, 2004.
Figure 1.
Rheological models. Left: Maxwell element. Right: Endochronic element.
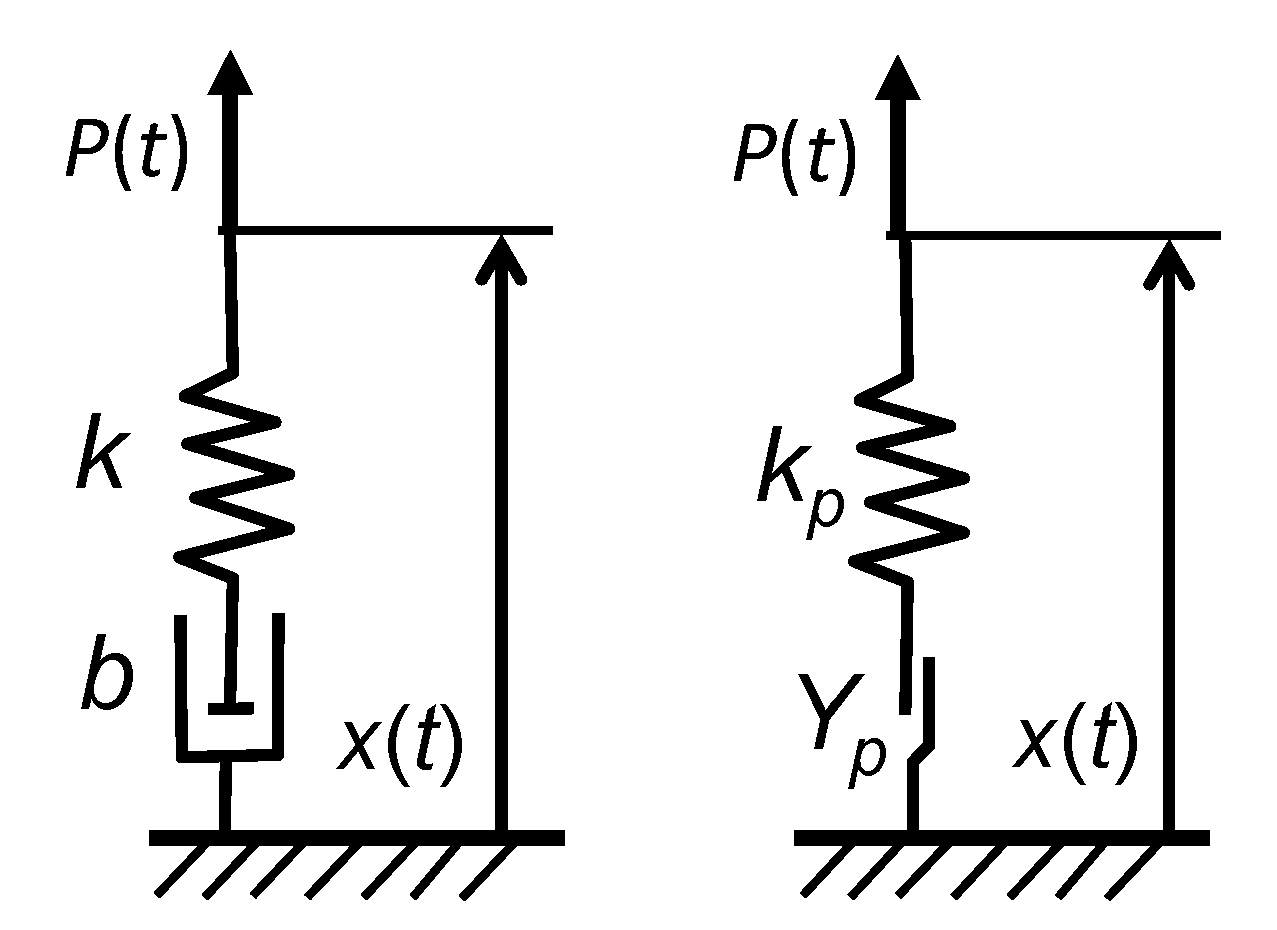
Figure 2.
Dynamic systems with one degree of freedom. Left: Lumped mass supported by spring and dashpot. Right: Lumped mass supported by spring and endochronic element.
Figure 2.
Dynamic systems with one degree of freedom. Left: Lumped mass supported by spring and dashpot. Right: Lumped mass supported by spring and endochronic element.
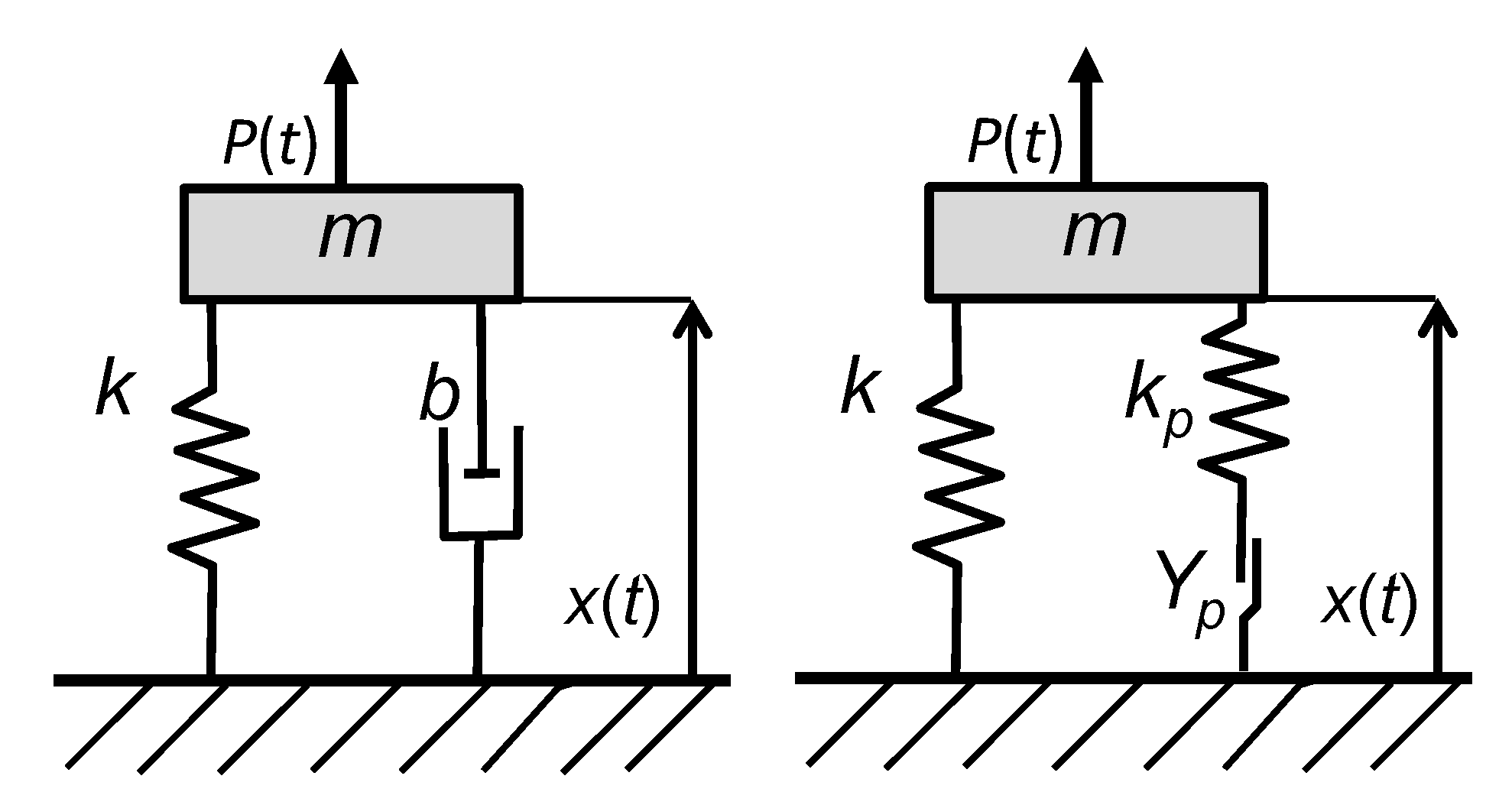
Figure 3.
Dynamic systems with two degrees of freedom. Left: Viscoelastic system. Right: Elastoplastic system.
Figure 3.
Dynamic systems with two degrees of freedom. Left: Viscoelastic system. Right: Elastoplastic system.
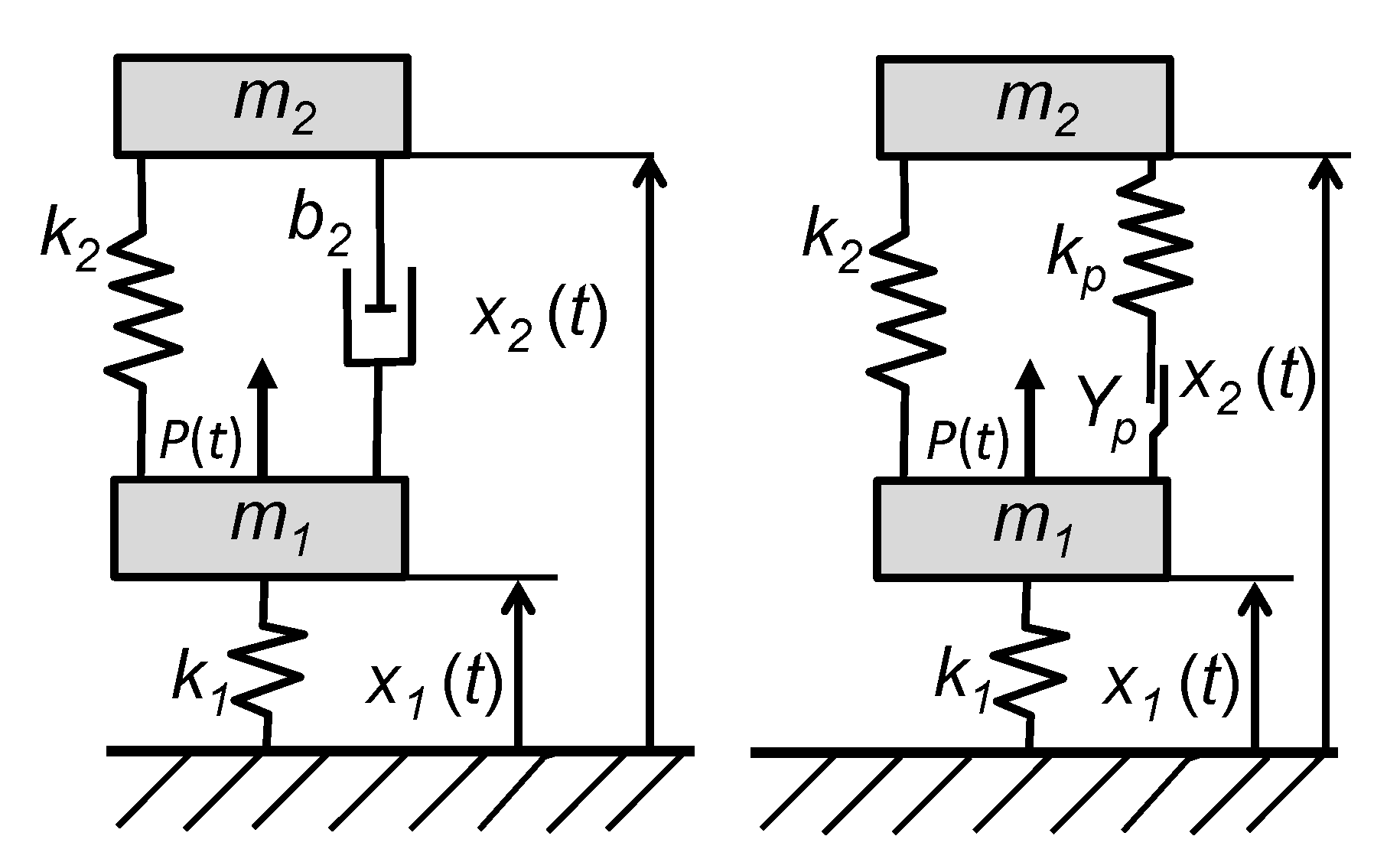
Figure 4.
Dynamic systems with two degrees of freedom and active control element.
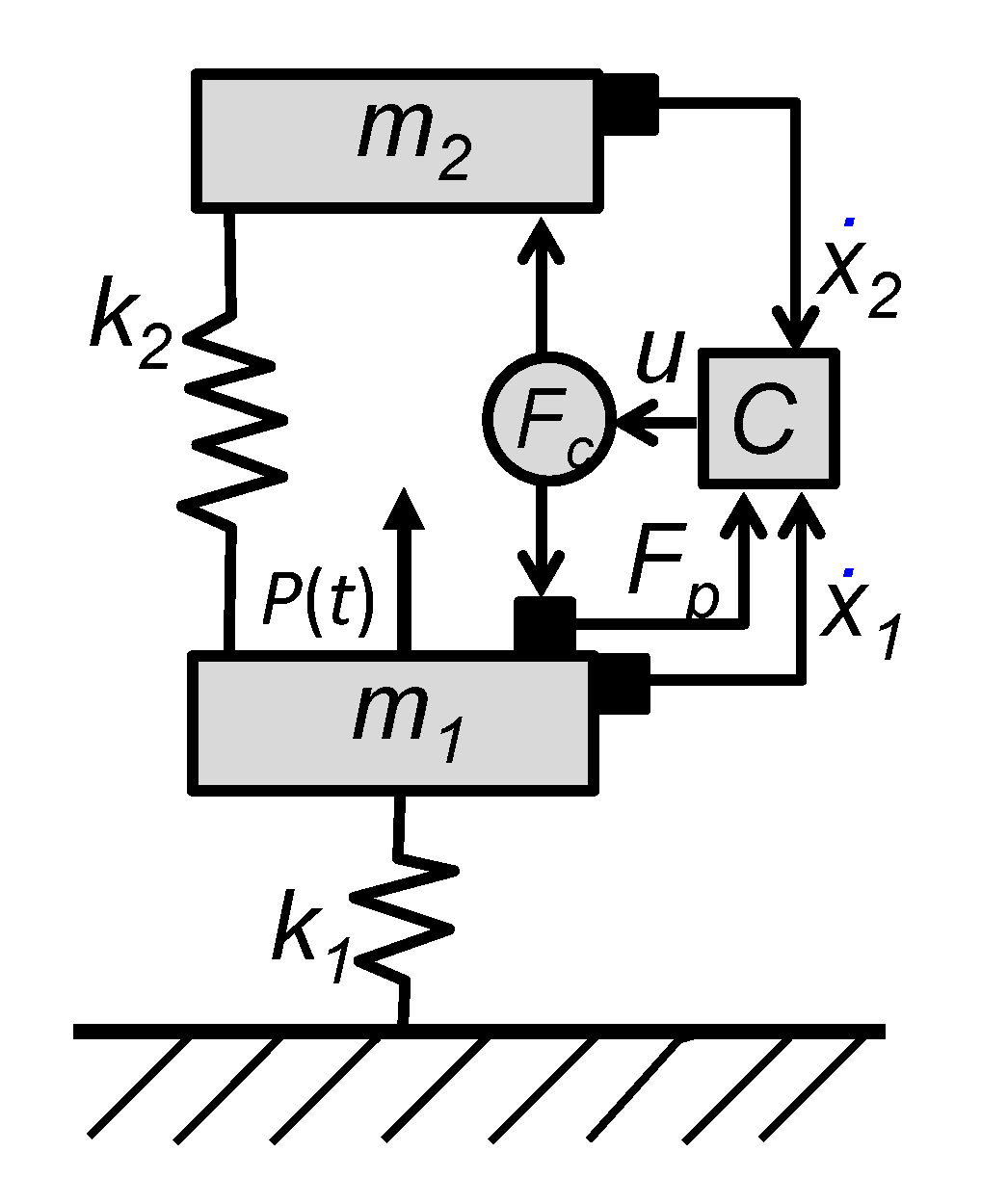
Figure 5.
Energy dissipation for time-harmonic excitation. Left: Endochronic element. Right: Maxwell element.
Figure 5.
Energy dissipation for time-harmonic excitation. Left: Endochronic element. Right: Maxwell element.
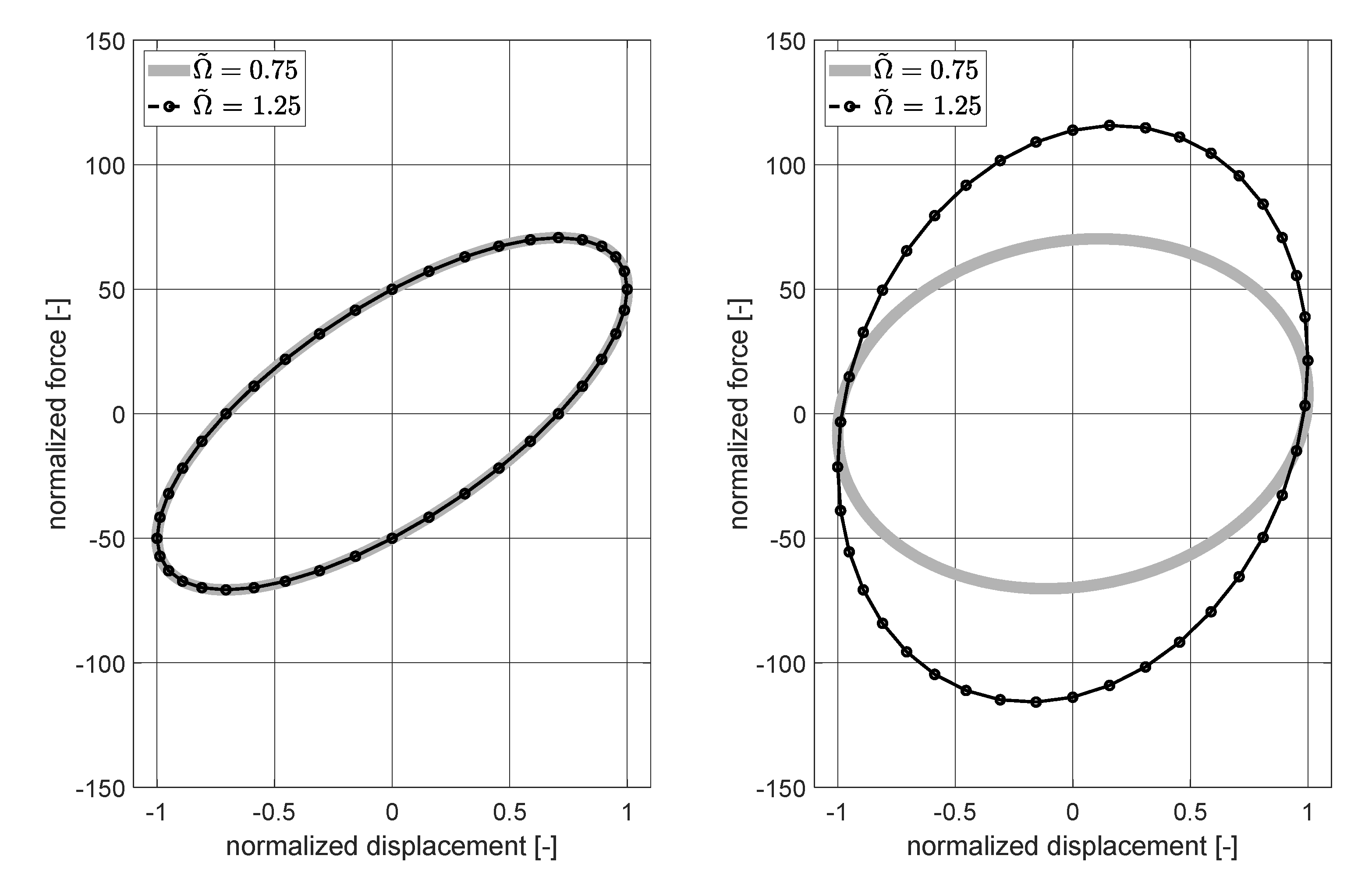
Figure 6.
Response of systems with one degree of freedom to a unit impulse. Left: Impulse response. Right: Magnitude response.
Figure 6.
Response of systems with one degree of freedom to a unit impulse. Left: Impulse response. Right: Magnitude response.
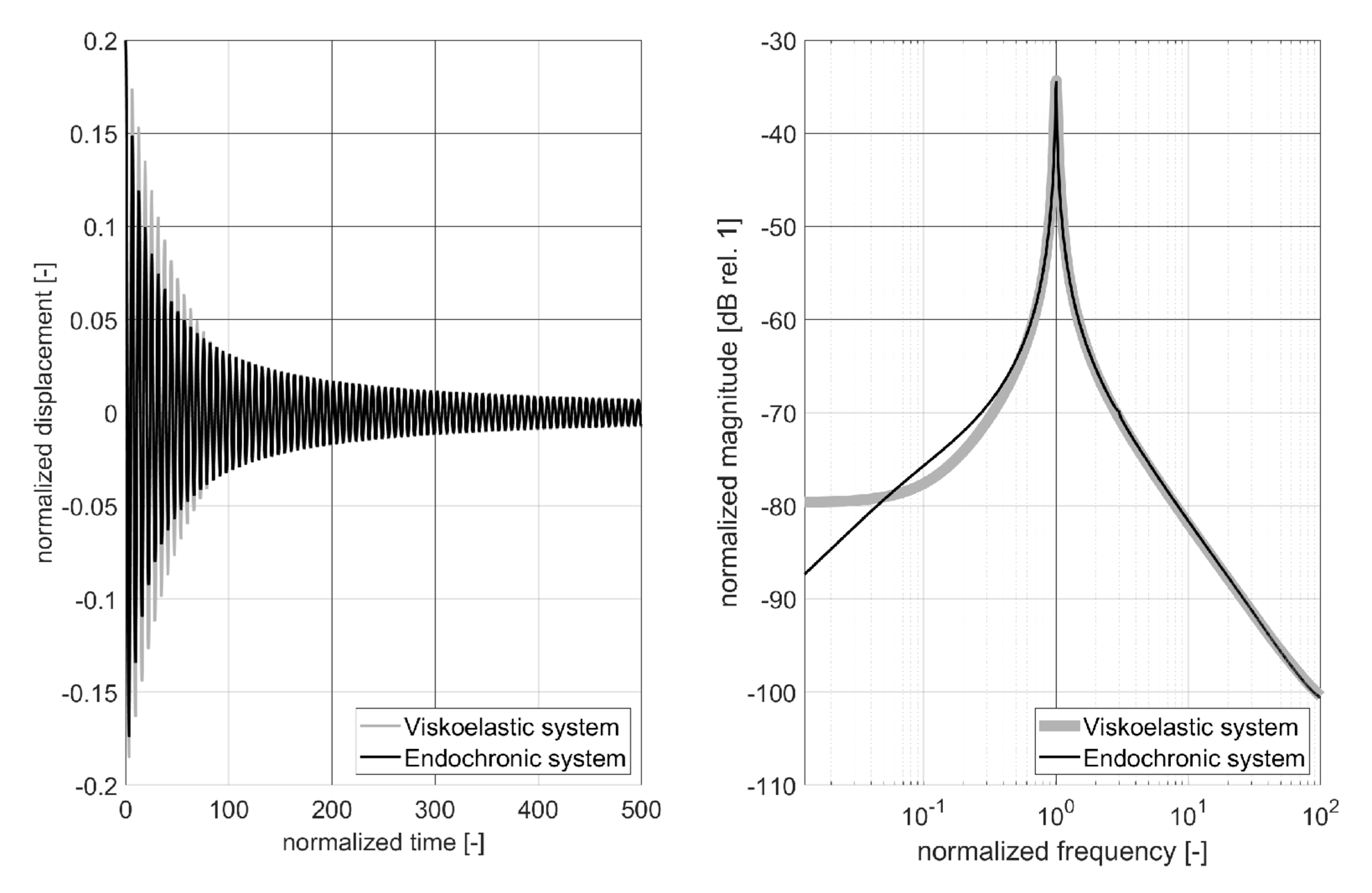
Figure 7.
Response of the elastoplastic system with one degree of freedom to a unit impulse. Left: Total displacement and plastic deformation. Right: Magnitude response for total displacement and plastic deformation.
Figure 7.
Response of the elastoplastic system with one degree of freedom to a unit impulse. Left: Total displacement and plastic deformation. Right: Magnitude response for total displacement and plastic deformation.
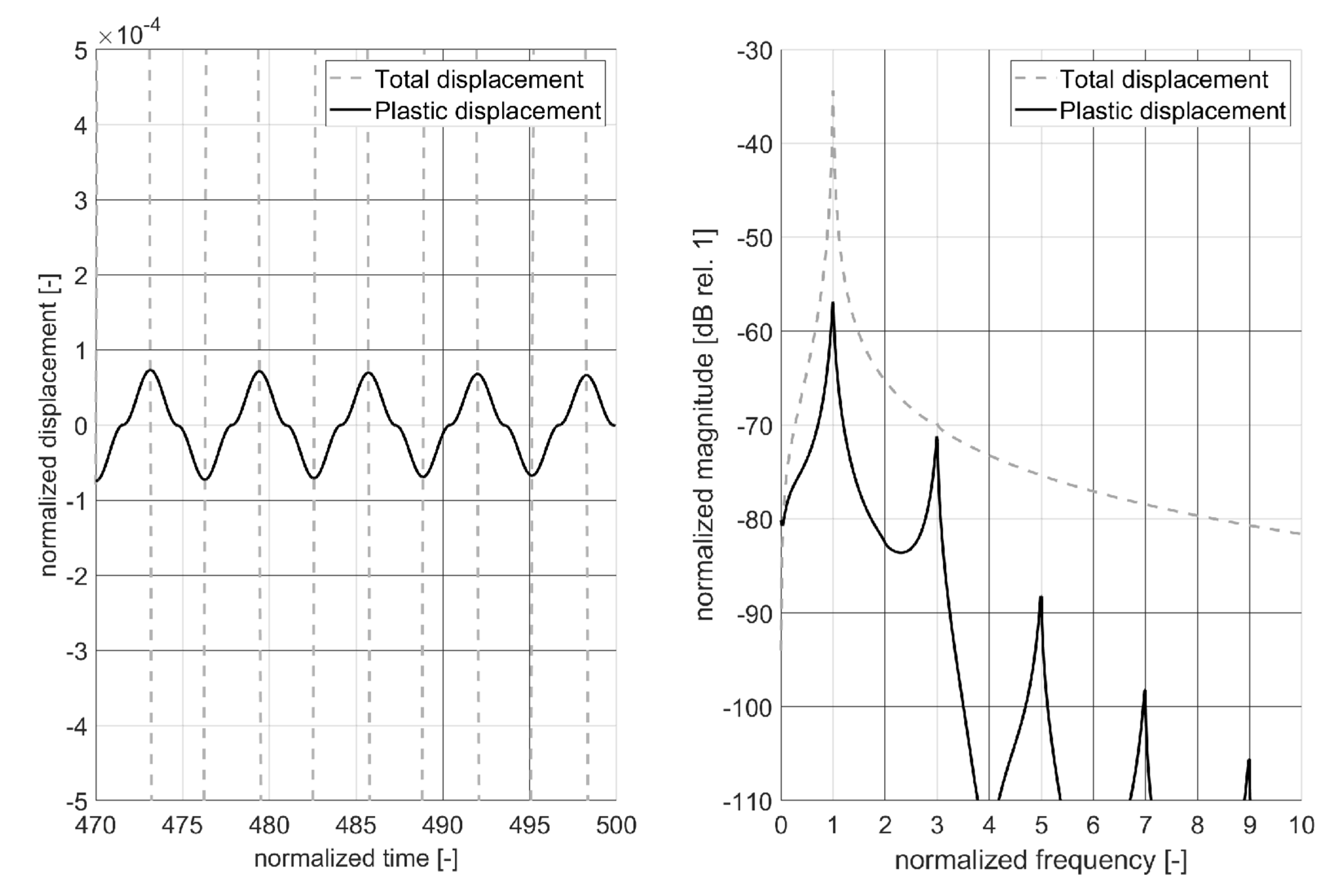
Figure 8.
Narrow-band frequency response of systems with two degrees of freedom due to time-harmonic excitation. Left: Response at m1 due to excitation at m1. Right: Response at m2 due to excitation at m1.
Figure 8.
Narrow-band frequency response of systems with two degrees of freedom due to time-harmonic excitation. Left: Response at m1 due to excitation at m1. Right: Response at m2 due to excitation at m1.
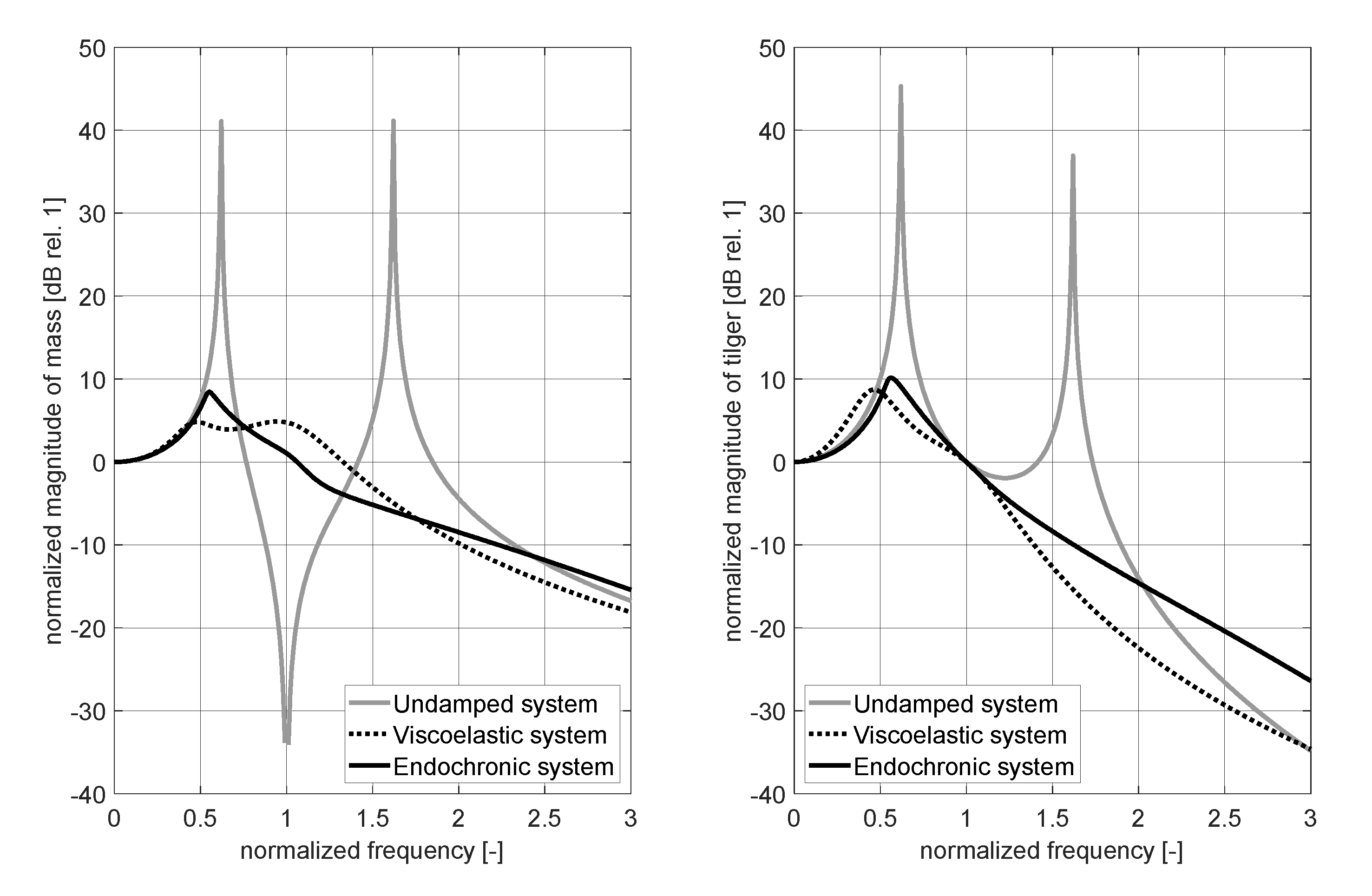
Figure 9.
Broadband analysis of systems with two degrees of freedom using linear chirp signal. Left: Chirp signal applied at m1. Right: Magnitude response at m1 due to excitation at m1 presented in 1/3 octave bands.
Figure 9.
Broadband analysis of systems with two degrees of freedom using linear chirp signal. Left: Chirp signal applied at m1. Right: Magnitude response at m1 due to excitation at m1 presented in 1/3 octave bands.
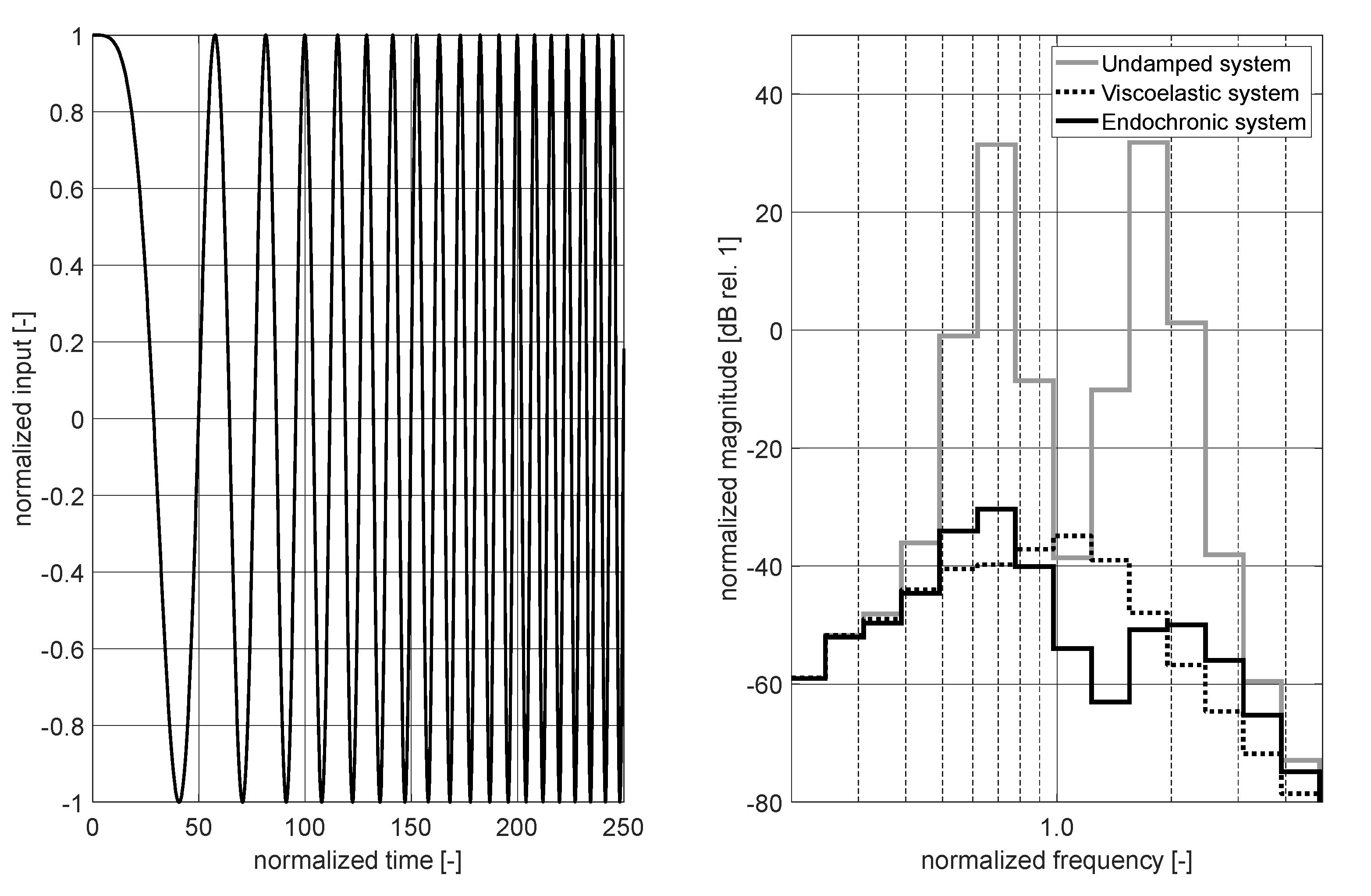
Figure 10.
Broadband analysis of systems with two degrees of freedom using white Gaussian noise. Left: White Gaussian noise applied at m1. Right: Magnitude response at m1 due to excitation at m1 presented in 1/3 octave bands.
Figure 10.
Broadband analysis of systems with two degrees of freedom using white Gaussian noise. Left: White Gaussian noise applied at m1. Right: Magnitude response at m1 due to excitation at m1 presented in 1/3 octave bands.
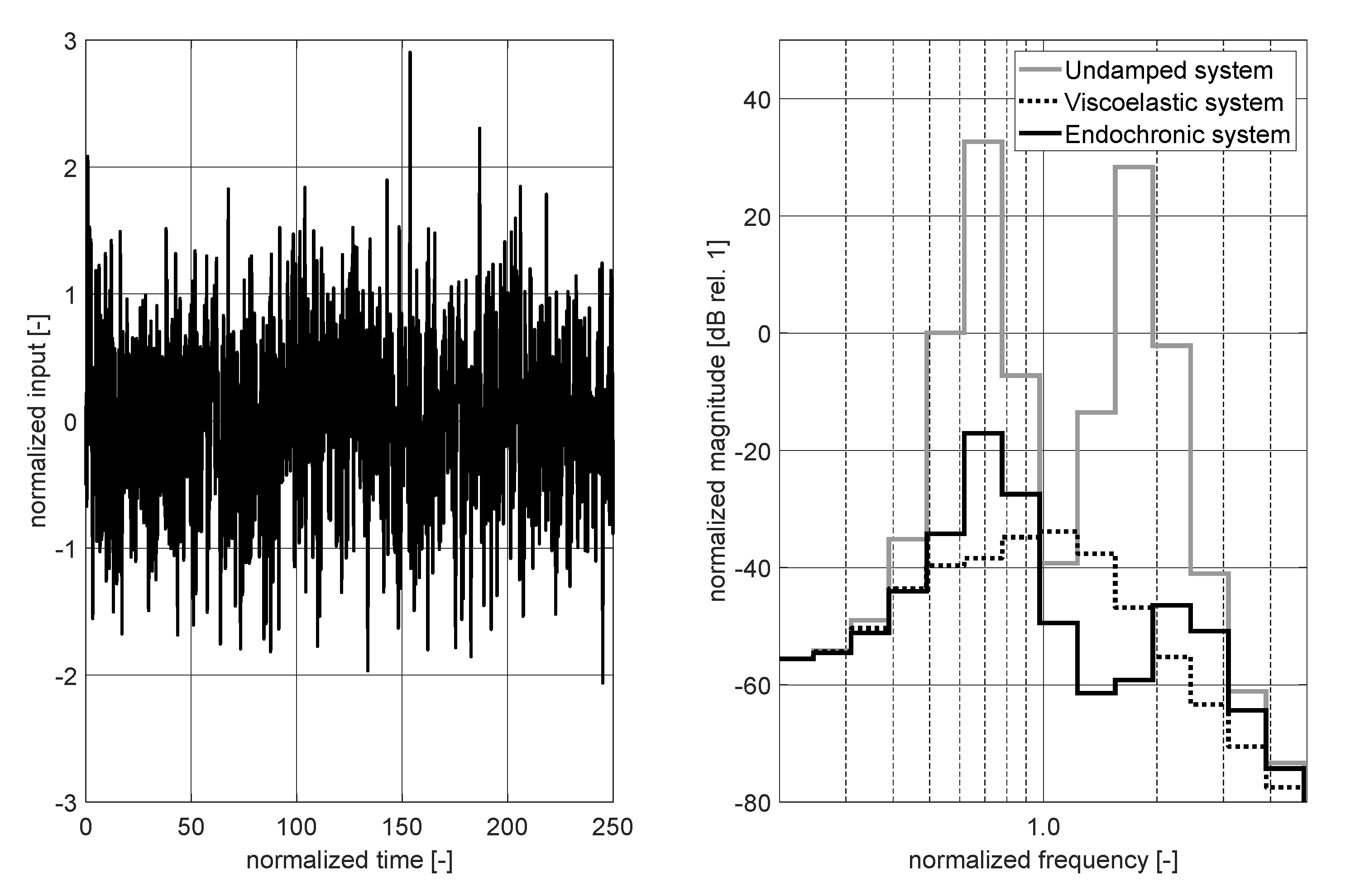
Figure 11.
Transient analysis of systems with two degrees of freedom using step input signal. Left: Step signal applied at m1. Right: Magnitude response at m1 due to excitation at m1 presented in 1/3 octave bands.
Figure 11.
Transient analysis of systems with two degrees of freedom using step input signal. Left: Step signal applied at m1. Right: Magnitude response at m1 due to excitation at m1 presented in 1/3 octave bands.
Table 1.
Overall control profit for different excitation signals shown for the optimally tuned dynamic absorber (DA) and the optimally tuned endochronic absorber (EA).
Table 1.
Overall control profit for different excitation signals shown for the optimally tuned dynamic absorber (DA) and the optimally tuned endochronic absorber (EA).
| Type of input signal | Control profit DA | Control Profit EA |
|---|---|---|
| sine | 19.7 dB | 20.9 dB |
| chirp | 65.0 dB | 62.9 dB |
| white Gaussian noise | 58.8 dB | 46.6 dB |
| shock | 46.9 dB | 35.4 dB |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






