Prerpints.org logo
Preprint
Article

Revisiting The Raman Spectra of Carbonate Minerals

Altmetrics

Downloads

151

Views

45

Comments

0

A peer-reviewed article of this preprint also exists.

supplementary.docx (17.61MB )

Submitted:

19 September 2023

Posted:

20 September 2023

You are already at the latest version

Alerts
Abstract
This work presents a new discussion about the vibrational properties of the carbonate ion displayed in several different environments, not only the microparameters introduced by cation substitution and different crystal lattices but also the crystal aggregation, showing how their active Raman modes are affected by these changes by using data obtained with four different laser excitation sources. New Raman spectra excited at 1064 nm are reported for calcite, aragonite, and dolomite groups, also including magnesite, witherite, rhodochrosite, siderite, malachite and azurite. These new data contribute to the discussion and understanding of these materials and their spectra, bringing new observations based on the Raman modes, focusing on the internal symmetrical and asymmetrical stretching and bending modes of the carbonate ion, highlighting the differences observed in the relative intensity and width of the bands. The results indicate some evidence of the influence of the crystal habit and/or the growth of the mineral itself in the Raman spectrum. In addition, the data show the influence of the cation substitution upon the Raman band width and that small cations contribute to less rigid crystalline structures and, consequently, larger Raman bandwidths.
Keywords: 
Subject: Environmental and Earth Sciences  -   Geochemistry and Petrology

1. Introduction

Common carbonate minerals can be classified into four groups: the calcite group, the dolomite group, the aragonite group, and an OH-bearing group. The first two are comprised of minerals with a rhombohedral structure, the third is of minerals with an orthorhombic structure, and the last one is comprised of minerals with a monoclinic crystal structure [1]. The idea of a periodic crystal structure comes from observing the faces and cleavage of crystals, that arise from the bonding forces between atoms [2]. In 1773, Bergmann studied the regular cleavage of calcite and suggested that small fragments could be the building blocks of crystals, and in 1824, Ludwig August Seeber introduced the term "lattice" for a periodic structure where each point has the same environment and orientation [2]. The unit cell is a parallelepiped formed by eight lattice points, the crystal structure is the atomic arrangement within it and the macroscopic crystal is made by repeating the unit cell [2].
The four carbonate groups differ in themselves not only because of their crystal structures, but by the cations present in the chemical composition [1]. Comparing the calcite and dolomite groups, the main difference between these minerals is that the first one is composed of carbonate ions associated with only one type of cation, while the second is composed of carbonate ions associated with more than one cation, maintaining the rhombohedral structure [3,4,5]. For these two groups, the structure is based upon alternating layers of carbonate ions and cations, comprising planes of carbonate ions parallel to planes of cations [6]. The position of the carbonate is repeated every six layers due to its triangular geometry and the 6-fold coordination of the cations [1]. For dolomite, the cation layers are alternating, that is, Ca2+ and Mg2+ fill alternating planes separated by planar carbonate groups [3,4,5,6,7,8].
Generically, the orthorhombic structure is favored for cations whose radius is larger than 1.1 Å in octahedral coordination, and the rhombohedral structure is favored for smaller cations [1,2,6]. Ca2+ has an ionic radius of 1.14 Å in octahedral coordination, so it can provide minerals in both structural cases [1,6]. That is also the case for the aragonite group. When exposed to high pressure, calcium carbonate is formed like aragonite, as an orthorhombic polymorph [6].
A characteristic feature of crystals is ‘‘directionality’’: specific directions in crystals are inherently different, and these differences are implicit in the lattice structure [1,2]. If the growth velocity were equal in all directions, crystals would occur as spheres [2]. Instead, they display a regular morphology with planar surfaces [2]. Crystal growth leads to various crystal morphologies expressed by specific combinations of crystal forms and states of aggregation that reflect the kinetic conditions [2].
The morphology and state of aggregation depends on the nucleation rate, the number of nucleation sites and on the growth rate [2]. All of these are complicated functions of many parameters, including temperature, chemical composition, trace amounts, and defects in the crystal structure, and in most cases, the relationships are not very well known [2]. The external appearance of a crystal, its combination of crystal forms, and the relative development of these forms are collectively called the crystal habit [1,2]. Even though the complexities of crystal growth processes lead to morphologies that are not perfect regular polyhedral, there is nevertheless a characteristic shape to many minerals, and it is used in mineral identification [2]. The same mineral may occur with an equant, acicular or fibrous habit, depending upon the conditions under which it grows [2].
Raman spectroscopy has proved to be a very powerful characterization technique for carbonate minerals in different kind of samples and for many purposes [3,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45]. For the rhombohedral groups, CO32- has five Raman active modes: three internal modes of CO32- and two external vibrations of the crystal lattice [9]. For the orthorhombic minerals (aragonite group), there are thirty Raman active fundamental phonons [13,20,21]. The vibrational modes of carbonate ion are directly affected by all these changes in the environment, not only within each of the groups, but also seen as changes between the groups.
In this work, a discussion of the vibrational characterization for the carbonate ion is presented, featured in several different environments, not only the microparameters such as cation substitution and different crystal lattice, but also the crystal aggregation. The focus of this work is in the three main regions of the internal modes of the carbonate ion: 1420 to 1460 cm-1 corresponding to the asymmetrical stretching mode, 1060 to 1090 cm-1 corresponding to the symmetrical stretching mode, and 700 to 740 cm-1 corresponding to the bending mode. Also, the use of different laser lines for excitation, showing how their Raman modes are affected by such changes, using data obtained with 1064 nm excitation (an interferometric instrument), and visible laser lines (785, 632.8 and 532 nm, from a dispersive system). Finally, it is discussed how these data can assist in the presentation of a different approach for the Raman analysis of some important carbonate minerals.

2. Methods

A total of 20 samples of different carbonate minerals were analyzed. Some of these samples were donated by the Centre of Mineral Technology (CETEM, Rio de Janeiro, Brazil), others were purchased from specialized mineral stores. With the object to compare the behavior of the samples in different conditions and using different excitation sources, a Bruker FT-Raman spectrometer was used, with an excitation line of 1064 nm and 500 mW of power and with 1 cm-1 of spectral resolution and 512 accumulated spectra. A Brucker SENTERRA Raman dispersive spectrometer was also used, making use of 785, 632.8 and 532 nm lasers as excitation sources, a spectral resolution of 3 cm-1, 10 seconds of spectral accumulation and 10 spectra in addition, using 100mW (785 nm) and 20 mW (632.8 and 532 nm) of laser power at the sample. All spectra were obtained at least twice for each sample to avoid thermal or photochemical damage, comparing the position and intensity for each one of the Raman bands in the spectra. All the samples were also submitted to analysis by energy dispersive spectroscopy (EDS) coupled to a Hitachi 3000 tabletop scanning electronic microscopy instrument, and the results are presented in Figures S1 to S30. The samples were placed directly on the sample compartment in the instrument, without any pre-treatment being undertaken.

3. Vibrational Analysis

The results and discussion in this work will be based on the similarity of structures and crystal parameters for the investigated series. Further details will then follow on the Raman spectrum of each mineral, exploring the behavior of the structure and chemical bonds against the interaction with the excitation source under different spectral conditions. The primary goal of this work is the clearer understanding of the vibrational modes of CO32-.
In the calcite group, classified as rhombohedral minerals, there are 27 vibrational modes:
Γ = A 1 g + 2 A 1 u + 3 A 2 g + 3 A 2 u + 4 E g + 5 E u
Five of these 27 vibrational modes are Raman active, and the carbonate ion presents three main vibrational modes: one near 1400 - 1450 cm-1, related to the asymmetrical stretching of the C-O bond (Eg symmetry), one around 1080 cm-1 related to the symmetrical stretching of the C-O bond (A1g symmetry) and one around 700-750 cm-1 related to the COO bending mode (Eg symmetry); the other two Eg modes correspond to libration and translation lattice modes [9].
In the aragonite group, classified as orthorhombic minerals, there are 57 vibrational modes:
Γ = 9 A g + 6 A u + 6 B 1 g + 8 B 1 u + 9 B 2 g + 5 B 2 u + 6 B 3 g + 8 B 3 u
Thirty of these modes are Raman active, and for the internal modes of carbonate ion there are seven vibrational modes: one near 1450 - 1460 cm-1, related to the asymmetrical stretching of the C-O bond (B1g symmetry), one around 1080 cm-1 related to the symmetrical stretching of the C-O bond (Ag symmetry), and three around 700-720 cm-1 related to COO bending mode (two with B3g and one Ag symmetry); in addition, one mode occurs around 800 cm-1, with Ag symmetry, which is not observed at room temperature [13]. The other twenty-three modes correspond to lattice modes of the orthorhombic structure [13].
Similar to calcite, for dolomite, which is also a rhombohedral mineral, there are calculated 18 vibrational modes:
Γ = 4 E g + 4 A g + 5 E u + 5 A u
Eight of these modes are Raman active: the asymmetrical stretching of the C-O bond (Eg symmetry), appears around 1440 cm-1; the symmetrical stretching of the C-O bond (Ag symmetry), appears around 1100 cm-1, and for the COO bending mode, there are two bands with Eg and Ag symmetries, appearing around 720 and 880 cm-1, respectively. All the other vibrational modes correspond to lattice movements [3,4,10,33].
The azurite (monoclinic mineral) Raman spectrum can be divided into three types of modes: the CO32- , OH- and Cu-O modes [16,43]. Taking into account only the carbonate ions in the azurite structure, there are 24 vibrational modes:
Γ = 6 A g + 6 B g + 6 A u + 6 B u
where 12 of these modes are Raman active. For the asymmetrical stretching of the C-O bond, there are three bands, observed at 1416 cm-1 (Ag symmetry), 1428 cm-1 (Bg symmetry), 1456 (Ag symmetry). For the symmetrical stretching of the C-O bond, there is one band at 1094 cm-1 (Ag symmetry), and for the COO bending mode, there are four bands at 740 cm-1 (Bg symmetry), 763 cm-1 (Ag symmetry), 814 cm-1 (Bg symmetry) and 837 cm-1 (Ag symmetry) [16,43].
Further, for malachite (a monoclinic mineral) there are 15 vibrational modes:
Γ = 3 A g + 1 B g + 1 B 2 g + 1 B 3 g + 3 B u + 3 B 2 u + 3 B 3 u
Associated with the internal modes of carbonate ion, there are six Raman active modes. For the asymmetrical stretching of the C-O bond, there are two bands at 1460 cm-1 (Bg symmetry) and 1490 cm-1 (Ag symmetry). For the symmetrical stretching of the C-O bond, there are two bands at 1066 cm-1 (Ag symmetry) and 1100 cm-1 (Bg symmetry), and for the COO bending mode, there are three bands which can be seen at 719 cm-1 (Ag symmetry), 750 cm-1 (Bg symmetry), and 818 cm-1 (Ag symmetry) [43].

4. Results and Discussion

As said before, this work reports new data for the Raman spectra of some carbonate minerals using 1064 nm excitation with a spectral resolution of 1.0 cm-1. Figure 1 shows the data for one sample of each mineral. The information about the samples and the results for EDS analysis can be seen in the supplementary material. For siderite, azurite and malachite it was not possible to obtain the Raman spectra for 1064 nm excitation. Siderite shows a bigger interference of thermal background, whereas azurite and malachite show photothermal decomposition, even with very small incident laser power. For a better understanding of the related parameters, the discussion will follow considering each one of the main vibrational modes for the carbonate ion: symmetrical, asymmetrical, and bending modes.
Two parameters can be investigated when we compare samples of the same mineral and the minerals themselves: the shift of the Raman band, caused by the cation substitution and the intensity of the Raman bands. For the first parameter the chemical composition and the presence of different cations in the structure must be considered but for the relative intensity of the bands some other variables must also be considered. Since the relative intensity of a band is influenced by the optical orientation of the crystals, the comparison between the spectra will be made by using as reference modes the ones from the same symmetry. For example, in calcite group, the asymmetrical stretching and the bending modes of CO32- belong to the same symmetry (Eg), so the differences in relative intensity must be made using this reference, since both modes are affected in the same way by the optical orientation. For spectra obtained using FT-Raman (1064 nm), the Ge detector shows the same response in the whole spectral range, so that comparison between the relative intensity of the Raman modes considering the same symmetry can be made also including the low wavenumber region frequencies. For the other lasers (dispersive instrument), the standard comparison must be more cautious because the CCD detector does not show the same response for all the spectral range, mainly for the 785 nm laser source.
The first observation to be made concerns the shift observed for the vibrational mode, which is already known in the literature: for cations bigger than calcium, the Raman band shifts to a lower wavenumber (witherite), and for cations smaller than calcium, the Raman band shifts to a higher wavenumber (magnesite) [9]. Thus, the smaller the cation, the greater the electron density in the region, which can lead to an increase in the value of the bond strength force constant. For rhodochrosite (MnCO3) and siderite (FeCO3) this pattern has not been observed, since the presence of the half-filled d orbital for the transition metal ions can create a different influence, explained by the additional and more concentrated negative charge located at the transition metal ions, since they are cations with a smaller radius than calcium, then leading to the opposite effect [26,28,31,34,38,39,42]. Such changes were studied previously by Zhang and collaborators, showing that the substitution of calcium ions by a transition metal cation leads to differences in the vibrational properties [42], such as shifts to lower wavenumbers for the symmetrical vibrational modes. In the dolomite spectrum, the band shift to a higher wavenumber should be less than that expected for a total replacement (which can be seen in the case of magnesite), due to a partial replacement of calcium for magnesium ions. This shift is observed for all Raman bands, except for the symmetric stretching of the carbonate ion; it is important to understand that the partial cation replacement leads to a loss of symmetry in the crystal lattice unit cell, as observed in the case of dolomite and predicted by the theoretical approach [3,4,10,33].
It is significant to point out the differences in the band widths for the stretching modes. Calcite, aragonite and witherite present the narrowest bands, while dolomite and siderite are intermediary, and magnesite shows the widest bands. Comparing the spectra for different samples, the bands show similar band widths for the same minerals, implying that this is a characteristic derived from the mineral unit cell and cannot be associated with macroscopic parameters such as the crystal aggregation in the sample or even the anisotropy. The width of a Raman band can be associated with small variations in the transition energy values associated with the vibrational modes, in addition to other parameters. Based on thermodynamic parameters, the bandwidth can be interpreted as a consequence of the entropy; therefore, it is possible to propose that the replacement of the calcium ion by smaller cations, leads to a broadening of the Raman band. This fact can be understood mainly for cations of similar electronic charge, such as magnesium, in the rhombohedral system. This replacement also allows the thermodynamic and entropic variation of the transition energy value of the vibrational mode, then a combination of several different factors influencing the broadening of the Raman band. Some previous studies have shown that positional disorder of carbonate ions creates a broadening of the Raman band, a parameter that can also be interpreted as a consequence of the smaller crystal size of biogenic Mg-calcite, for example [30,37]. In this specific case, the greater degree of disorder associated with a higher Mg content may be responsible for a higher chemical reactivity during diagenesis [30,37]. The proposition of this work follows the same theory. Figure 2 shows that observation, using as an example the 633 nm Raman spectra.
The crystal optical orientation is a crucial parameter in the recording of the Raman spectrum. There are two main parameters that contribute to the intensity of a Raman band, the frequency of the excitation source and the polarizability tensor. For crystals, the incident angle of the laser source favors some symmetries, making the relative intensity of the Raman band variable depending upon the crystal optical orientation. For raw minerals, the crystal aggregation characterizes an anhedral system, so different crystals with different orientations contribute to the scattering and to the intensity and width of the Raman band. If in the crystal growth process of a mineral there is more available space, when compared to another with space restriction or even a high-pressure condition, there will be a variation in energy associated with the vibrational modes of chemical bonds, which may be greater for the mineral that presents less restriction, leading to an oscillation in the relative intensity of the Raman band. Such differences are observed by the growth of different mineral habits and are affected by temperature, pressure, concentration etc. For example, calcite crystals grown in the presence of an excess of Ca2+ ions exhibit an elongated habit, whereas with an excess of CO32- ions the habit varies from thick to fine tabular [46]. These differences in the crystal habit for rhombohedral calcite allows us to identify how old a mineral is, based on the morphogenetic Kalb´s order, that proposes the observation of some pattern for crystal growth in some cases, allowing the identification of which crystal was formed first [46]. Based on the bandwidth comparison discussion, it is important to emphasize that the observation can be made for all the samples of a same mineral, i.e., bandwidth is the same for all the samples of a same mineral. Then, the parameter is an intrinsic property of the composition and not a consequence of the measurement conditions or minimal differences between the samples.
For comparison purposes, as said before, the intensities of the Raman bands were normalized using modes of the same symmetry. Then, for the calcite samples, fixing upon the asymmetrical stretching intensity, differences can be observed in the relative intensity of the bending mode. In addition, all samples are raw anhedral minerals which makes it possible to disregard the crystal orientation influence upon the Raman band intensity, at least for 1064 nm excitation, where the laser spot over the sample area is big enough to include diverse crystal units in several orientations and the Raman spectrum then is an average of all the orientations over the sample spot region. As can be seen in the Raman spectra, the asymmetrical C-O stretching mode is relatively weak and in some cases, depending on the quality of the spectrum, can be imperceptible for some carbonate minerals. In such cases, it is possible to compare the relative intensity based on the low wavenumber region frequency, since the parameters of instrumental response previously discussed do not interfere in the analysis. Normalizing the asymmetrical stretching, some small differences are observed in the relative intensity for the calcite samples (Figure 3). The major difference between the samples is the crystal habit (a macroscopic visual parameter) of the mineral and its visual color. It is difficult to suggest that the data obtained are influenced by the presence of very small quantities of different cations and the intensity of the Raman band can be more easily associated with the permissibility of the motion, which can be related to the available space, in other words, the ease of performance of the vibrational movement when the chemical species are in these particular chemical environments. It is interesting to point out that the euhedral system (Sample A) does not show the higher relative intensity.
Figure 4 shows the MEV images of the samples to illustrate their different textures. The main difference observed in the MEV images for calcite samples is the changes in depth and the cleavage marks. Comparing the sample with higher value of relative intensity, sample A, and the sample with the lowest, sample A, more evident marks of different depths are observed and the straight lines of crystal growth are seen for sample A, while sample D shows smooth variations of depth and almost no straight lines of crystal growth.
These first observations are very small and there is a need for more samples with crystal habit, but the analysis is also limited by the vibrational modes and the number of bands that are available for comparison. In the aragonite case these relations will be more evident.
This approach can be made comparing samples of the same mineral but also for samples of different minerals, wherein we can consider a cation substitution; Figure 5 shows a comparison between calcite, magnesite and dolomite using the C-O bending mode as a reference. There are some observations that can be made here : dolomite exhibits the higher intensity for the asymmetrical stretching and this is different from the stretching modes, the bending mode is shifted in the order of wavenumber δ O C O M g C O 3 > δ O C O C a M g C O 3 2 > δ O C O C a C O 3 ; the differences between the T and L modes in the low wavenumber region are also noteworthy ; the shift caused by the cation substitution is the same observed in the bending mode, however, the intensity of the L mode compared to the T mode is greatest in the magnesite spectrum. The decrease of symmetry in this case (when comparing dolomite, calcite and magnesite) affects differently each Raman mode; considering that the dolomite structure is the less symmetric of the three minerals, it is also the one that exhibits the highest intensity for the asymmetric stretching mode. Magnesite, on other hand, has the same symmetry as calcite but the structure is more flexible due the smaller cation, so we can observe wider bands. Lastly, the increase in intensity from calcite to magnesite is really noteworthy and can be associated with the permissibility of the movement, since these modes are correlated to collective vibrational movements.
For the aragonite samples, the symmetrical stretching mode at 1086 cm-1 has the same symmetry as the bending mode at 705 cm-1 (Ag). Hence we can make a comparison between the relative intensities of the aragonite modes for the three samples using four different normalizations, one for each vibrational symmetry. Figure 6 shows the spectra for all the aragonite samples at 1064 nm for each Raman mode. Normalizing to the νsym(CO), there can be seen differences in the intensity of the 705 cm-1 band. The samples do not show any trace of a different cation (according to the EDS analysis, Figures S1-S30); The spectra in Figure 6 are normalized to the Ag symmetry, so here it is possible to compare the changes in the bands related to that symmetry: 1086, 705, 217, 164 and 145 cm-1. Curiously, the aragonite samples show differences in the bandwidth only for the symmetrical stretching: for sample C the band is narrower than the band for samples A and B. The 705 cm-1 relative intensity increases in the order C<A<B, but for the Ag modes in the low wavenumber region do not change at all. Normalizing by other symmetries, for B1g for example, it is possible to compare the 1462 and 155 cm-1 bands and normalizing to the 1462 cm-1 band an increase in intensity for the 155 cm-1 band can be observed. Normalizing the B2g (717, 208 and 182 cm-1) bands or B3g symmetry (701 and 193 cm-1 bands), no difference is observed, which is the expected behavior according to the theory. The differences observed for the relative intensities are small, but we can suggest that two modes are affected: the symmetrical Ag mode and the B1g mode. The Raman data strongly suggest the same approach that was used for the calcite samples, i.e. the relative intensity of the Raman band is being influenced by the crystallization degree of the mineral samples or, similarly, to the arrangement of the crystal growth/habit. The spectra using the B1g, B2g, B3g modes can be seen in the Figure S30 in the supplementary material.
Dolomite samples show the same Raman shift for all the carbonate modes despite their variable elemental composition, in agreement with the literature as previously suggested [reference]. Comparing the relative intensities (Figure S31), the differences are largest for the external modes, mainly for the T mode. A shoulder at the symmetrical stretching mode (Figure S32) for all the samples is seen at 1078 cm-1. An important reference work for the dolomite Raman spectra in the literature was published by Farsang and collaborators, the same shoulder is also observed for their sample, which implies that this information is intrinsic to the dolomite structure [11]. This Raman mode is not predicted theoretically and an explanation is that it would arise from the possible appearance of different carbonate species in the solid state due to different chemical interactions with the magnesium and calcium ions in the structure. For magnesite samples (Figure S33), of the Eg modes, only the L mode changes from sample A to B, but this is not a significant observed change.
Comparing aragonite and witherite, normalizing the spectra to the B1g symmetry mode, almost no difference is observed between the bands in the spectra. For the Ag symmetry, normalized to the symmetric stretching mode, the bands at 145 and 164 cm-1 (in aragonite) are shifted to 136 and 160 cm-1, respectively (in witherite), and show an increase in the relative intensity when compared to the bands of same symmetry in the spectra of the two minerals. For the band at 217 cm-1, the shift is to a high wavenumber in witherite (225 cm-1), but the intensity is almost the same. For the B2g symmetry, normalized to the bending mode (717 in aragonite and 700 cm-1 in witherite), both bands decrease in relative intensity in the witherite spectrum, but the one at 182 cm-1 is shifted to a low wavenumber (180 cm-1) in witherite, whilst the 208 cm-1 band is shifted to a high wavenumber value (218 cm-1). For the B3g symmetry, normalized to the bending mode (703 in aragonite and 690 cm-1 in witherite), the 193 cm-1 band is shifted to 196 cm-1 and decreased in relative intensity. Figure 7 show the spectra at 1064 nm for the Ag normalization, the other symmetries are shown in Figure S34. The explanation here follows the idea of the cation substitution discussed previously in the Calcite/Dolomite/Magnesite case. The CO32- internal modes are shifted to a low wavenumber due the increase of the cation ratio. The same pattern is not observed for the external modes that also show changes in the relative intensities of the bands. The limited number of samples precludes a better understanding of the structure of witherite, but it is possible to affirm that these changes in the relative intensity are clear enough to be classified as an intrinsic characteristic of witherite.
For azurite, the Raman spectrum shows a set of Raman bands assigned to the carbonate ion asymmetric stretching mode (Figure 8). There are three bands: 1457, 1427, 1419 cm-1 for spectra with 633 nm excitation. For 532 nm excitation, an additional band is observed at 1492 cm-1. Fundamental changes in the relative intensity of these bands are observed when the excitation source is changed, not only between these three bands, but also when they are compared to other bands in the spectrum. The data strongly suggest a resonant Raman effect is in operation, but the sample is sensitive to two of the four available excitation wavelength sources used in this work and new and more refined data to contribute to a Raman profile are required. Curiously, it is observed that the asymmetrical stretching became more intense than the symmetrical stretching; the reasonable explanation would be this chemical system has an electronic excited state which is degenerate, leading to a change of the polarizability according to Albrecht’s approach [47]. For malachite, three bands are observed at 1364, 1460 and 1490 cm-1 (Figure 8). With 633 nm excitation, the band at 1460 cm-1 is very weak, but the bands at 1364 and 1490 cm-1 have a greater intensity. For 633 nm excitation, the band at 1490 cm-1 is more intense, and with 532 nm excitation, the band at 1364 cm-1 is more intense. Likewise in the azurite case, changing the excitation source results in changes in the relative intensity of these bands and the data for that mineral also suggest that a resonance Raman effect is occurring. Malachite is also a sensitive mineral to two of the four available excitation sources used here, and as stated previously, new and more refined data for a Raman profile are required.
Specifically, for malachite and azurite, two minerals showing a dependence upon the excitation radiation, the C-O symmetrical stretching mode undergoes a split due the loss of symmetry when compared with calcite; their spectra can be seen in Figure 8. For the symmetrical stretching mode in azurite, the band shifts to a higher wavenumber (1094 cm-1), and the symmetry (Ag) is maintained similar to calcite (A1g), but the bandwidth is greater for azurite than it is for calcite. These observations are expected for the loss of symmetry (from D3d in calcite to C2h in azurite). For malachite, Frost and collaborators described the free carbonate ions on the basis of a D3h point group [16]; however, Bissengaliyeva has shown in a theorical approach that the carbonate ion oxygen atoms of malachite are situated in triangular vertices where the valence angles at carbon are noticeably different from 120°, displaying a symmetry which is somewhat different from the equilateral triangle symmetry D3h [43]. In this last study, Bissengaliyeva has given three different force constants values for O-C-O bonds in three different environments: 0,80, 0,82 and 1,00 mdyn/Å [43]. For malachite, the symmetrical stretching mode splits, becoming three bands: at 1100, 1066, 1008 cm-1 . This last one was only seen in the Raman spectrum at 532 nm excitation. According to Bissengaliyeva’s work, the carbonate ion is not an equilateral triangle in both malachite and azurite; however, for azurite, also three values of the force constants have been evaluated for six different carbonate ions in different environments (1,40, 1,50 and 1,60 mdyn/Å) [43], yet only one band is observed in the Raman spectrum for the symmetrical stretching mode (1094 cm-1). There is clearly some contradiction here, but the Raman spectra described in this present work are more consistent with the description of Frost and clearly more detailed work needs to be done for these minerals [16].
For rhodochrosite, comparing with calcite (Figure 9) and using the normalization by the Eg symmetry with the asymmetric stretching as a reference, it is possible to observe that the bending mode is clearly more intense, and the same observation can be made about the T mode. For the L mode, both the Raman shift and relative intensity are similar. In this case, the differences between these minerals seems to affect mainly the Raman shift, because the frequencies show a shift slightly different to that expected from the cation substitution. In terms of the relative intensity, these observations suggest that, despite the cation substitution, the structure of rhodochrosite seems to behave similarly to calcite.
A comparison between the rhodochrosite samples was not possible, due to the similarity of the two available samples; their spectra also did not show any notable difference in Raman shift and relative intensity.
For siderite, some experimental difficulties were found due to the thermal background and low Raman signal at 1064nm. Hence, the comparison with the calcite spectrum here is made using the 523 nm excitation source (Figure 10). Using as reference the bending mode, all the Eg symmetry modes show very similar intensities except for the L mode, which exhibits a clear increase of intensity. In fact, for both rhodochrosite and siderite, the expectations are of a very similar structure, however, this is not observed. Rhodochrosite shows T and L modes that are very similar to calcite, but this is not observed in the siderite spectrum. It is known that the siderite Raman spectrum has a strong temperature dependence and the shoulder observed in the bending mode for siderite corresponds to a vibrational mode that is shown to be infrared active in the vibrational analysis, but the flexibility of the structure of this mineral allows that this mode also becomes Raman active depending on the temperature [11,28,39,48]. Curiously, that dependence is not observed in the same way for rhodochrosite [11,36,39]. Data strongly suggest that these systems are completely different and unique, and the cation substitution cannot be used in the same way as in the non-transition metals case. The temperature associated with the flexibility of the crystalline lattice is noted in the literature: the small Fe atom allows distortion that leads to the appearance of an unusual mode that is only infrared allowed [11,28,39,48]. Interestingly, until this moment, siderite (FeCO3) is expected to have a more flexible crystalline lattice than rhodochrosite (MnCO3), because of the appearance in the Raman spectrum of the active modes in the IR. This flexibility-temperature relationship is not seen in the Raman spectrum at different temperatures for these two minerals. Rhodochrosite presents a variation of the Raman bands, both in displacement and intensity, much greater than siderite, that is, rhodochrosite would be more flexible if this justification were considered [11,36,39]. The contradiction exists in the literature [11,28,36,39,48] and the interaction of the carbonate anion with the transition metal is unique in each system, making these structures not comparable to each other.
In addition to the discussion about the influence of the crystal habit, the spectra of a sample can be compared at different excitation sources. The data show that, even using the same region of the sample in the measurement, changing the laser source leads to some change in the relative intensities, mainly in the low wavenumber region. This observation was made for the aragonite samples, because the same behavior was not observed for the three different samples using different excitation sources. It is possible that the laser spot size (which is different for the wavelength of the laser excitation) changes with the average contribution of the crystal optic orientations. Mapping the samples, it is observed that the relative intensity in the low wavenumber region changes more significantly for samples A and C, but not for sample B, which implies that there is a more homogeneous average contribution of crystal orientations in this specific sample. This fact implies that this sample has more crystals organized in the same way; upon changing the laser, and consequently minimizing the spot size, the differences are clearly seen. Figure 10 shows the comparison between the spectra for aragonite B; it is important to highlight that the spectrum at 1064 nm in Figure 10 was obtained in a macroscopic configuration.
Changes in the external modes are also observed for rhodochrosite. For both the T and L modes presenting the same Eg symmetry, the mapping of the sample shows significant changes in the relative intensity of these bands, where an inversion of the intensity can be observed depending on the region of the sample where the measurement was made (Figure 12). Firstly, these differences can be related to the optical orientation of the crystals in the sample, however, both modes present the same symmetry, so they are influenced in the same way by this parameter and an inversion of the relative intensity should not be expected.

5. Conclusions

The acquisition of new Raman data excited at 1064 nm for carbonate minerals contributes to the discussion and understanding of these materials and their spectra, bringing to light new observations. Perhaps the major contribution here is the indication of the influence of the crystal habit and the growth of the mineral itself to the relative intensities observed in the Raman spectrum, suggesting that different relationships between unit cells entropically affects the system, leading to changes in the relative intensities of the asymmetric stretching, bending modes of the carbonate ion and the external modes. In addition, this work has opened the discussion about the influence of the cation substitution to the Raman band width, showing that small cations contribute to less rigid crystalline structures and, consequently, broader Raman bands. The identification of these minerals by their Raman spectra non-destructively demonstrates the benefits of the technique and this revisitation of their spectra brings a proposal on how best to obtain a quality Raman spectrum: the best conditions for obtaining these spectra and how this can vary not only from one mineral to another, but from one sample to another, are explored. It is worth emphasizing that the relevance of this study of carbonate minerals for the discussion of the theory of inelastic light scattering itself, shows new results associated with how thermodynamic parameters that influence the growth of a mineral, dispersed in different geological eras in the Earth's crust, can leave marks on its crystalline macrostructure that can reflect upon their vibrational spectra. In addition, the new data open the studies of how, for anhedral minerals, the same region where the measurement is obtained can lead to different Raman spectra depending on the laser wavelength due to differences in the size of the laser spot. In the case of carbonate minerals, at least for the ones investigated here, the smaller the laser spot the better the visualization of the structural details of the sample. Finally, this contribution sheds some light on the development of new studies of carbonate minerals that can improve the geological information underlying these valuable materials.

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org. Table S1: Samples information; Figures S1 to S30: Results of EDS analysis; Figure S31: Raman spectra normalized by the Eg symmetry for dolomite samples; Figure S32: Raman spectra normalized by the Eg symmetry for dolomite samples showing the bands at 1078 cm-1 and 882 cm-1; Figure S33: Raman spectra normalized by the Eg symmetry for magnesite samples; Figure S34: Raman spectra normalized by the B1g, B2g and B3g symmetries for a comparison between aragonite and witherite samples; Figure S35: samples photographs.

Author Contributions

Conceptualization, J.F.A. and L.F.C.O.; methodology, J.F.A.; software, J.F.A.; validation, J.F.A., A.K. and L.F.C.O.; formal analysis, J.F.A., L.F.C.O., H.G.M.E and A.K.; investigation, J.F.A.; resources, L.F.C.O.; data curation, J.F.A., H.G.M.E.; writing—original draft preparation, J.F.A.; writing—review and editing, L.F.C.O., H.G.M.E. and A.K.; visualization, J.F.A.; supervision, L.F.C.O.; project administration, L.F.C.O.; funding acquisition, L.F.C.O. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by FAPEMIG, grant number APQAPQ-03079-23, and CNPq grant numbers 406853/2021-5 and 303569/2022-0. AK was supported by state assignment project IGM SB RAS (122041400241-5).

Data Availability Statement

Publicly available datasets were analyzed in this study. This data can be found here: [link/accession number].

Acknowledgments

Authors are in debt with CNPq, FAPEMIG, CAPES, FINEP (Brazilian agencies)for instrumental facilities. JFA acknowledges Petrobras for a scholarship.

Conflicts of Interest

“The authors declare no conflict of interest.”.

References

  1. Nesse, W.D. Introduction to Optical Mineralogy, 3rd ed.; Oxford University Press: New York, USA, 2017. [Google Scholar]
  2. Wenk, H.R.; Bulakh, A. Minerals. Their Constitution and Origin., 2nd ed.; Cambridge University Press: Cambridge, 2016. [Google Scholar]
  3. Sun, J.; Wu, Z.; Cheng, H.; Zhang, Z.; Frost, R.L. A Raman Spectroscopic Comparison of Calcite and Dolomite. Spectrochim Acta A Mol Biomol Spectrosc 2014, 117, 158–162. [Google Scholar] [CrossRef]
  4. Teoh, C.P.; Laya, J.C.; Rose, K.; Kaczmarek, S. The effects of magnesium concentration in high-magnesium calcite allochems on dolomitization: insights from high-temperature dolomite synthesis experiments. Journal of Sedimentary Research 2022, 92, 134–143. [Google Scholar] [CrossRef]
  5. Allen, B.L.; Hajeck, B.F. Mineral occurrence in soil environments, in Minerals in soil environments, 2nd ed.; Dixon, J., Weed, S.B., Eds.; Soil Science Society of America: Madison, USA, 1989. [Google Scholar]
  6. Yoder, C.H. Ionic Compounds Applications of Chemistry to Mineralogy, 1st ed.; John Wiley & Sons: New Jersey, USA, 2006. [Google Scholar]
  7. Kaczmarek, S.E.; Thornton, B.P. The effect of temperature on stoichiometry, cation ordering, and reaction rate in high-temperature dolomitization experiments. Chem Geol 2017, 468, 32–41. [Google Scholar] [CrossRef]
  8. Gunasekaran, S.; Anbalagan, G.; Pandi, S. Raman and infrared spectra of carbonates of calcite structure. Journal of Raman Spectroscopy 2006, 37, 892–899. [Google Scholar] [CrossRef]
  9. Dufresne, W.J.B.; Rufledt, C.J.; Marshall, C.P. Raman spectroscopy of the eight natural carbonate minerals of calcite structure. Journal of Raman Spectroscopy 2018, 49, 1999–2007. [Google Scholar] [CrossRef]
  10. Biellmann, C.; Gillet, P. High-pressure and high-temperature behavior of calcite, aragonite and dolomite: a Raman spectroscopic study. European Journal of Mineralogy 1992, 4, 389–394. [Google Scholar] [CrossRef]
  11. Farsang, S.; Facq, S.; Redfern, S.A.T. Raman modes of carbonate minerals as pressure and temperature gauges up to 6 GPa and 500 °C. American Mineralogist 2018, 103, 1988–1998. [Google Scholar]
  12. Tomić, Z.; Makreski, P.; Gajić, B. Identification and spectra-structure determination of soil minerals: Raman study supported by IR spectroscopy and x-ray powder diffraction. Journal of Raman Spectroscopy 2010, 41, 582–586. [Google Scholar] [CrossRef]
  13. De La Pierre, M.; Carteret, C.; Maschio, L.; André, E.; Orlando, R.; Dovesi, R. The Raman spectrum of caco3 polymorphs calcite and aragonite: a combined experimental and computational study. Journal of Chemical Physics 2014, 140. [Google Scholar] [CrossRef]
  14. Kim, Y.; Caumon, M.C.; Barres, O.; Sall, A.; Cauzid, J. Identification and composition of carbonate minerals of the calcite structure by Raman and infrared spectroscopies using portable devices. Spectrochim Acta A Mol Biomol Spectrosc 2021, 261. [Google Scholar] [CrossRef]
  15. Shi, W.; Fleet, M.E.; Shieh, S.R. High-pressure phase transitions in Ca-Mn carbonates (Ca, Mn)CO3 studied by Raman spectroscopy. American Mineralogist 2012, 97, 999–1001. [Google Scholar] [CrossRef]
  16. Frost, R.L.; Martens, W.N.; Rintoul, L.; Mahmutagic, E.; Kloprogge, J.T. Raman Spectroscopic Study of Azurite and Malachite at 298 and 77 K. Journal of Raman Spectroscopy 2002, 33, 252–259. [Google Scholar] [CrossRef]
  17. Yu, B.S.; Fang, J.N.; Huang, E.P. Characteristics of the Raman spectra of archaeological malachites. Journal of Raman Spectroscopy 2013, 44, 630–636. [Google Scholar] [CrossRef]
  18. Jehlička, J.; Culka, A.; Košek, F. Obtaining Raman spectra of minerals and carbonaceous matter using a portable sequentially shifted excitation raman spectrometer – a few examples. Journal of Raman Spectroscopy 2017, 48, 1583–1589. [Google Scholar] [CrossRef]
  19. Farfan, G.A.; Boulard, E.; Wang, S.; Mao, W.L. Bonding and electronic changes in rhodochrosite at high pressure. American Mineralogist 2013, 98, 1817–1823. [Google Scholar] [CrossRef]
  20. Wang, X.; Ye, Y.; Wu, X.; Smyth, J.R.; Yang, Y.; Zhang, Z.; Wang, Z. High-temperature Raman and FTIR study of aragonite-group carbonates. Phys Chem Miner 2019, 46, 51–62. [Google Scholar] [CrossRef]
  21. Krishnamurti, D. The Raman spectra of aragonite, strontianite and witherite. Proceedings of the Indian Academy of Sciences. Section A 1960, 51, 285–295. [Google Scholar] [CrossRef]
  22. Bersani, D.; Lottici, P.P. Raman spectroscopy of minerals and mineral pigments in archaeometry. Journal of Raman Spectroscopy 2016, 47, 499–530. [Google Scholar] [CrossRef]
  23. Frech, R.; Wang, E.C.; Bates, J.B. The i. r. and Raman Spectra of CaCO3 (Aragonite); Spectrochim Acta A Mol Biomol Spectrosc 1980, 36, 915–919. [Google Scholar] [CrossRef]
  24. Carteret, C.; Dandeu, A.; Moussaoui, S.; Muhr, H.; Humbert, B.; Plasari, E. Polymorphism studied by lattice phonon Raman spectroscopy and statistical mixture analysis method. Application to calcium carbonate polymorphs during batch crystallization. Cryst Growth Des 2009, 9, 807–812. [Google Scholar] [CrossRef]
  25. Fong, M.Y.; Nicol, M. Raman spectrum of calcium carbonate at high pressures. J Chem Phys 1971, 54, 575–578. [Google Scholar] [CrossRef]
  26. Boulard, E.; Guyot, F.; Fiquet, G. The influence on Fe content on Raman spectra and unit cell parameters of magnesite-siderite solid solutions. Phys Chem Miner 2012, 39, 239–246. [Google Scholar] [CrossRef]
  27. Liu, L.; Lv, C.; Zhuang, C.; Yi, L.; Liu, H.; Du, J. Effects of differential stress on the structure and Raman spectra of calcite from first-principles calculations. American Mineralogist 2016, 101, 1892–1897. [Google Scholar] [CrossRef]
  28. Müller, J.; Efthimiopoulos, I.; Jahn, S.; Koch-Müller, M. Effect of temperature on the pressure-induced spin transition in siderite and iron-bearing magnesite: a Raman spectroscopy study. European Journal of Mineralogy 2017, 29, 785–793. [Google Scholar] [CrossRef]
  29. Aru, M.; Burgio, L.; Rumsey, M.S. Mineral impurities in azurite pigments: artistic or natural selection? Journal of Raman Spectroscopy 2014, 45, 1013–1018. [Google Scholar] [CrossRef]
  30. Borromeo, L.; Zimmermann, U.; Andò, S.; Coletti, G.; Bersani, D.; Basso, D.; Gentile, P.; Schulz, B.; Garzanti, E. Raman spectroscopy as a tool for magnesium estimation in Mg-calcite. Journal of Raman Spectroscopy 2017, 48, 983–992. [Google Scholar] [CrossRef]
  31. Farfan, G.; Wang, S.; Ma, H.; Caracas, R.; Mao, W.L. Bonding and structural changes in siderite at high pressure. American Mineralogist 2012, 97, 1421–1426. [Google Scholar] [CrossRef]
  32. Xu, J.; Kuang, Y.; Zhang, B.; Liu, Y.; Fan, D.; Zhou, W.; Xie, H. High-pressure study of azurite Cu3(CO3)2(OH)2 by synchrotron radiation X-Ray diffraction and Raman spectroscopy. Phys Chem Miner 2015, 42, 805–816. [Google Scholar] [CrossRef]
  33. Wang, F.; Zhao, C.; Xu, L.; Liu, J. Effects of hydrostaticity and Mn-substitution on dolomite stability at high pressure. American Mineralogist 2022, 107, 2234–2241. [Google Scholar] [CrossRef]
  34. Müller, J.; Speziale, S.; Efthimiopoulos, I.; Jahn, S.; Koch-Müller, M. Raman Spectroscopy of siderite at high pressure: evidence for a sharp spin transition. American Mineralogist 2016, 101, 2638–2644. [Google Scholar] [CrossRef]
  35. Liu, J.; Caracas, R.; Fan, D.; Bobocioiu, E.; Zhang, D.; Mao, W.L. High-pressure compressibility and vibrational properties of (Ca, Mn)CO3. American Mineralogist 2016, 101, 2723–2730. [Google Scholar] [CrossRef]
  36. Zhao, C.; Li, H.; Jiang, J.; He, Y.; Liang, W. Phase transition and vibration properties of MnCO3 at high pressure and high-temperature by Raman Spectroscopy. High Press Res 2018, 38, 212–223. [Google Scholar] [CrossRef]
  37. Perrin, J.; Vielzeuf, D.; Laporte, D.; Ricolleau, A.; Rossman, G.R.; Floquet, N. Raman characterization of synthetic magnesian calcites. American Mineralogist 2016, 101, 2525–2538. [Google Scholar] [CrossRef]
  38. Cerantola, V.; McCammon, C.; Kupenko, I.; Kantor, I.; Marini, C.; Wilke, M.; Ismailova, L.; Solopova, N.; Chumakov, A.; Pascarelli, S.; et al. High-pressure spectroscopic study of siderite (FeCO3) with a focus on spin crossover. American Mineralogist 2015, 100, 2670–2681. [Google Scholar] [CrossRef]
  39. Wang, C.; Ren, L.; Walters, J.B.; Zhang, L.; Tao, R. In situ Raman vibrational spectra of siderite (FeCO3) and rhodochrosite (MnCO3) up to 47 GPa and 1100 K. American Mineralogist 2023, 108, 312–325. [Google Scholar] [CrossRef]
  40. Jorge-Villar, S.E.; Edwards, H.G.M. green and blue pigments in roman wall paintings: a challenge for Raman spectroscopy. Journal of Raman Spectroscopy 2021, 52, 2190–2203. [Google Scholar] [CrossRef]
  41. Ulian, G.; Valdrè, G. The effect of long-range interactions on the infrared and Raman spectra of aragonite (CaCO3, pmcn) up to 25 GPa. Sci Rep 2023, 13, 2725. [Google Scholar] [CrossRef]
  42. Zhang, J.; Martinez, I.; Guyot, F.; Reeder, R.J. Effects of Mg-Fe+2 Substitution in Calcite-Structure Carbonates: Thermoelastic Properties; American Mineralogist, 1998, 83, 280-287. 83.
  43. Bissengaliyeva, M.R. Calculations of the structural and thermodynamic characteristics of copper carbonates by quantum-chemical methods. Russian Journal of Physical Chemistry A 2009, 83, 238–244. [Google Scholar] [CrossRef]
  44. Porto, S.P.S.; Giordmaine, J.A.; Damen, T.C. Depolarization of Raman Scattering in Calcite. Physical Review 1966, 147, 608–611. [Google Scholar] [CrossRef]
  45. Warr, L.N. a new collection of clay mineral ‘crystallinity’ index standards and revised guidelines for the calibration of Kübler and Árkai indices. Clay Miner 2018, 53, 339–350. [Google Scholar] [CrossRef]
  46. Kirov, G.K.; Vesselinov, I.; Cherneva, Z. Conditions of formation of calcite crystals of tabular and acute rhombohedral habits. Kristall und Technik 1972, 7, 497–509. [Google Scholar] [CrossRef]
  47. Clark, R.J.H.; Dines, T.J. Resonance Raman spectroscopy, and its application to inorganic chemistry. new analytical methods (27). Angewandte Chemie International Edition in English 1986, 25, 131–158. [Google Scholar] [CrossRef]
  48. Langille, D.B.; O’Shea, D.C. ; Raman spectroscopy studies of antiferromagnetic FeCO3 and related carbonates, J. Phys. Chem. Solids, 1977, 38, 1161–1171. [Google Scholar] [CrossRef]
Preprints 85586 g001
Figure 1. Raman spectra for one sample of each studied mineral in 1064 nm excitation source, calcite (a), aragonite (b), dolomite (c), magnesite (d), rhodochrosite (e) and witherite (f).
Figure 1. Raman spectra for one sample of each studied mineral in 1064 nm excitation source, calcite (a), aragonite (b), dolomite (c), magnesite (d), rhodochrosite (e) and witherite (f).
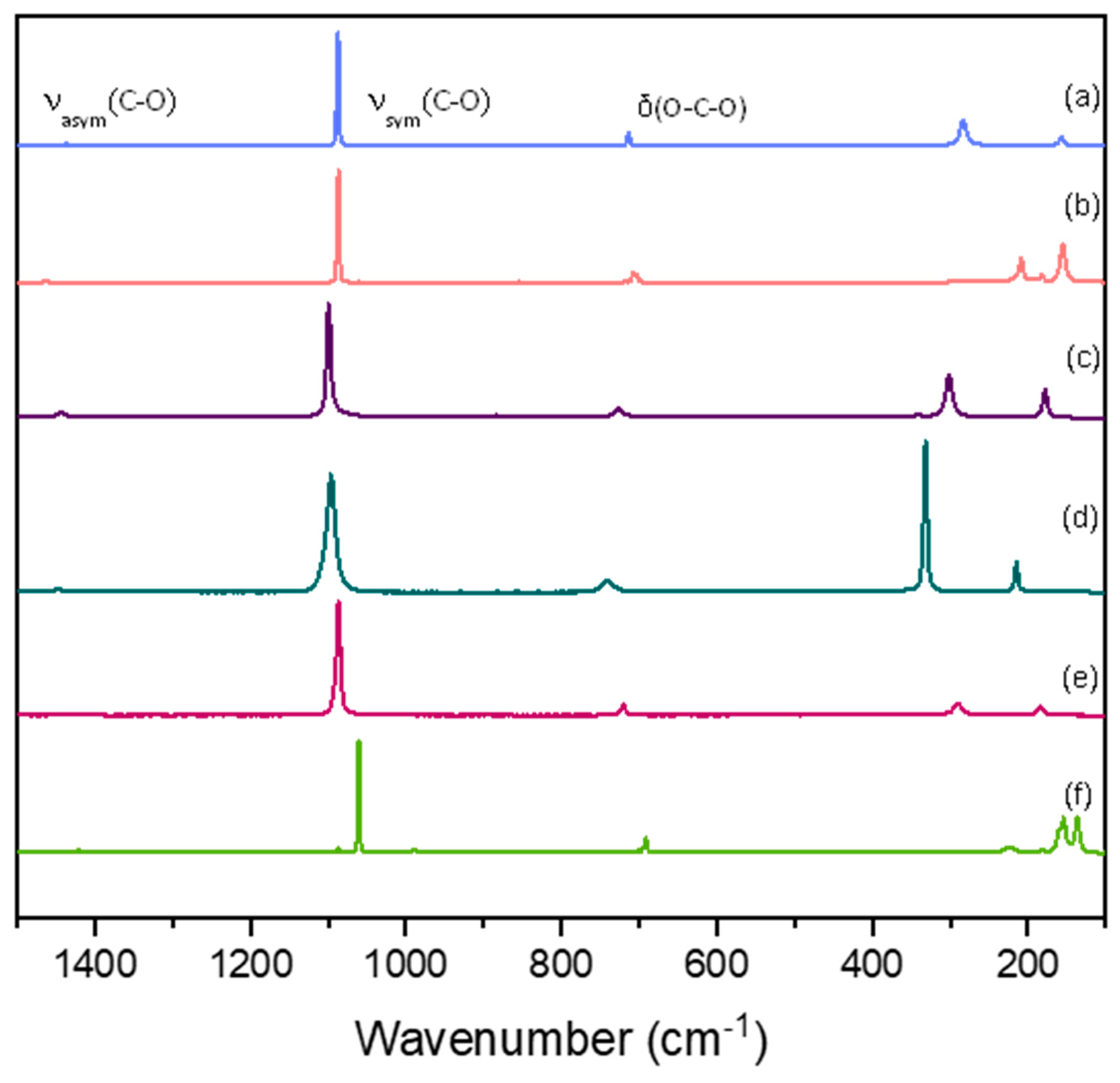
Preprints 85586 g001
Preprints 85586 g002
Figure 2. Raman spectra for the stretching mode at 633 nm excitation source for calcite, dolomite and magnesite.
Figure 2. Raman spectra for the stretching mode at 633 nm excitation source for calcite, dolomite and magnesite.
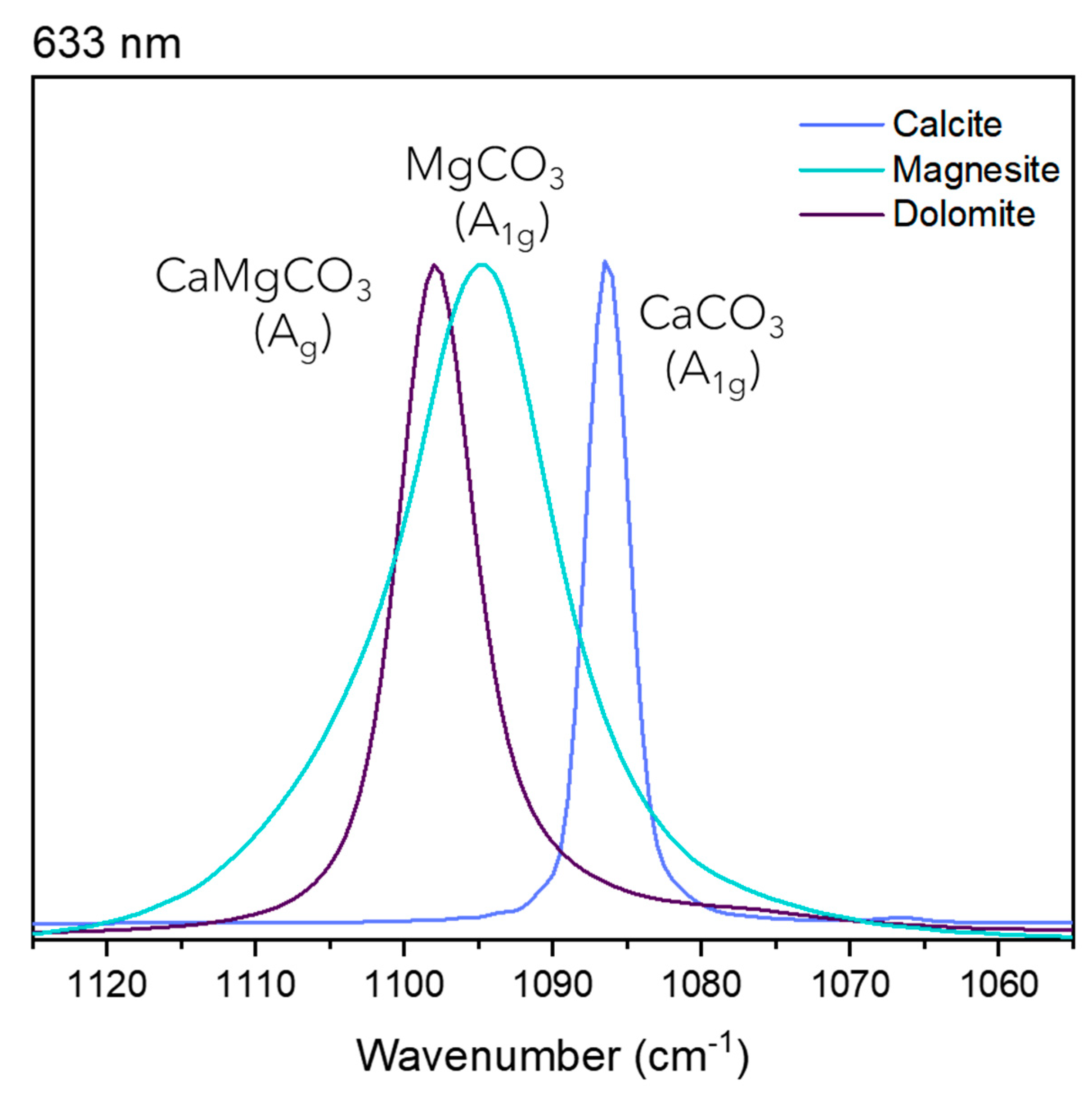
Preprints 85586 g002
Preprints 85586 g003
Figure 3. Raman at 1064 nm excitation source for calcite samples A, B, D and E. Sample C was omitted due the poor signal/noise ratio.
Figure 3. Raman at 1064 nm excitation source for calcite samples A, B, D and E. Sample C was omitted due the poor signal/noise ratio.
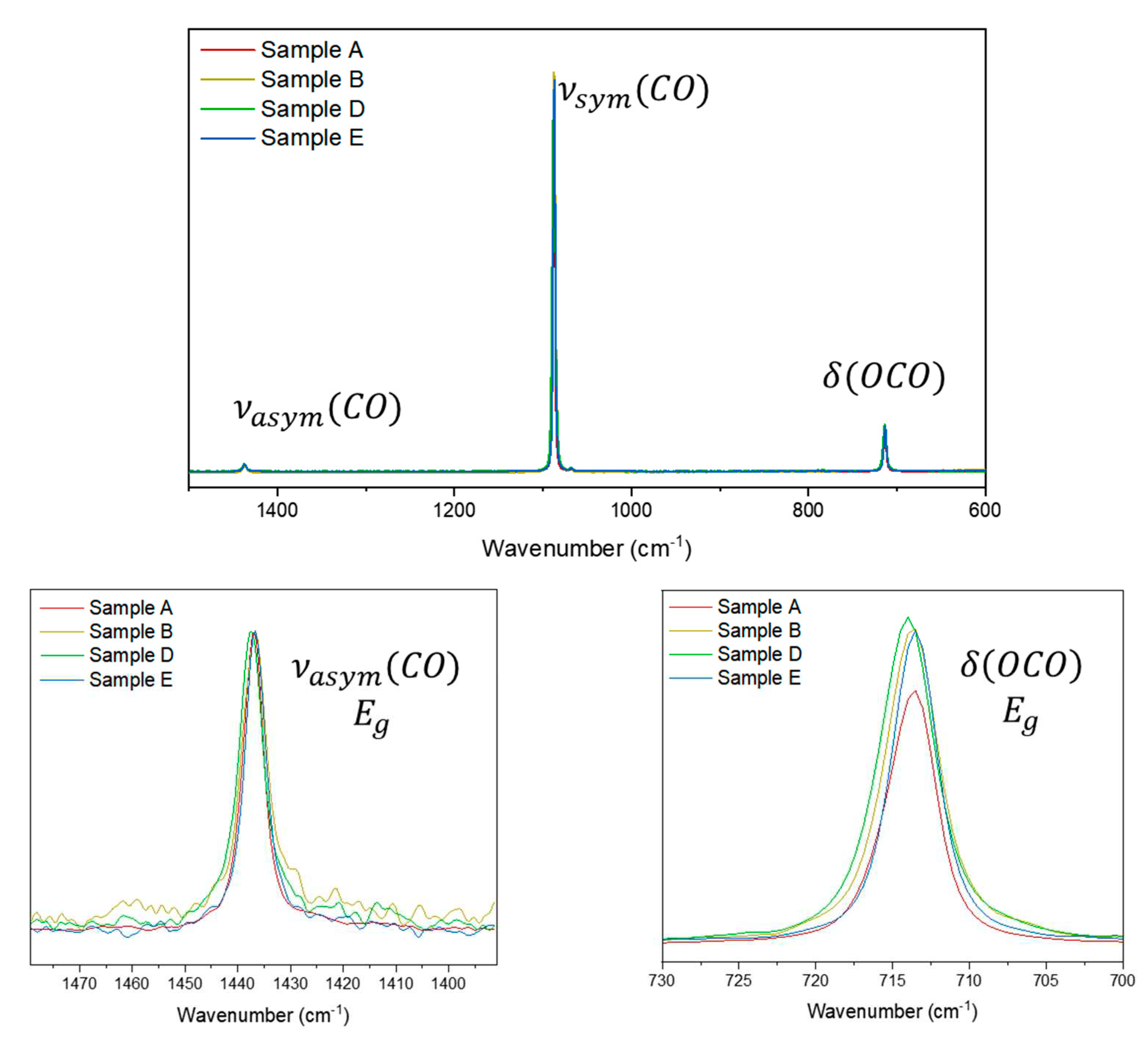
Preprints 85586 g003
Preprints 85586 g004
Figure 4. MEV images for calcites samples A, B, C, D and E at one of the two regions analyzed.
Figure 4. MEV images for calcites samples A, B, C, D and E at one of the two regions analyzed.
Preprints 85586 g004
Preprints 85586 g005
Figure 5. Raman spectra at 532 nm for calcite, magnesite and dolomite.
Figure 5. Raman spectra at 532 nm for calcite, magnesite and dolomite.
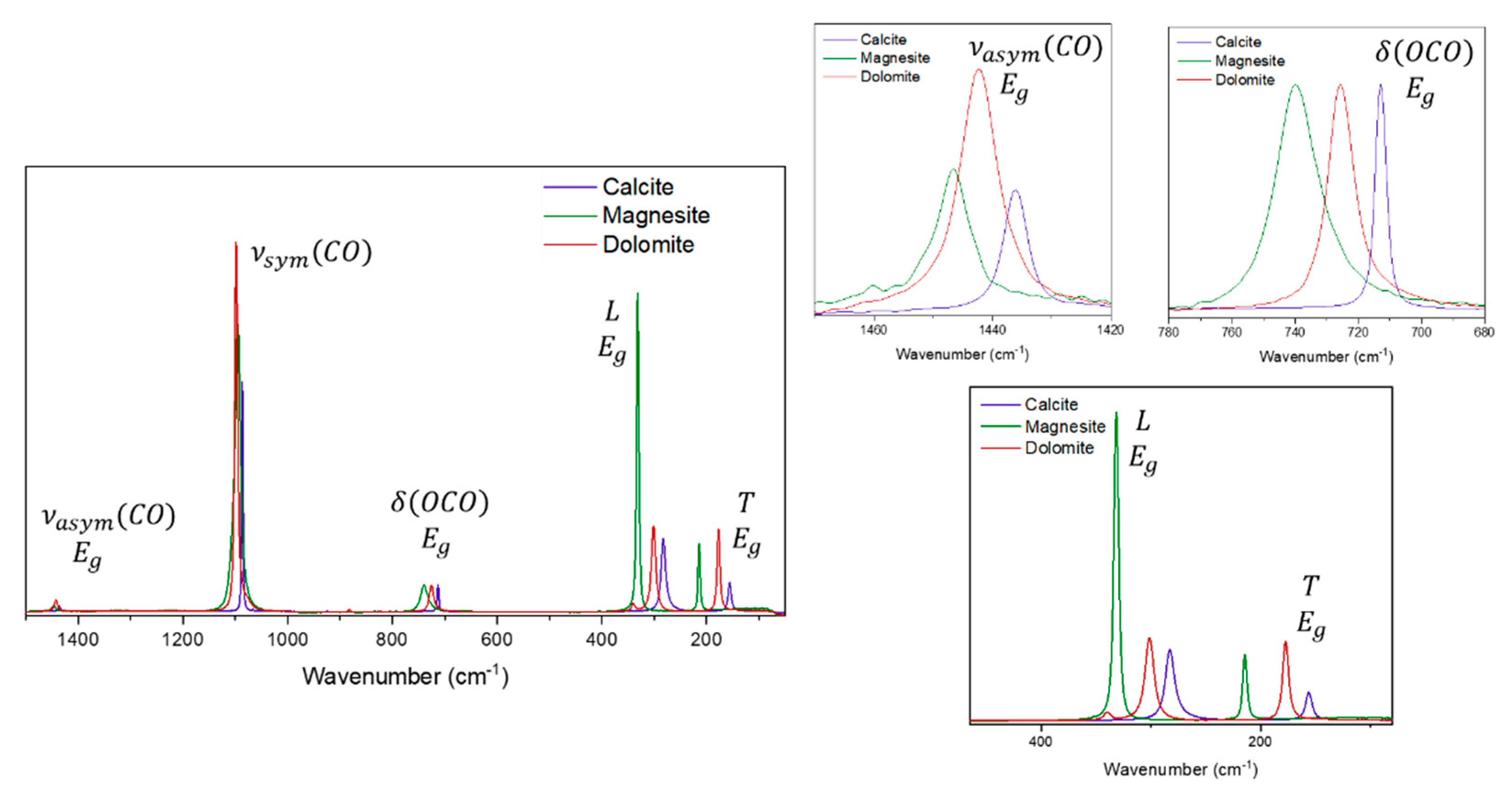
Preprints 85586 g005
Preprints 85586 g006
Figure 6. Raman spectra for aragonite samples A, B and C at 1064 nm excitation source, normalized by the Ag mode at 1086 cm-1. The symmetry of each mode presented was based on De La Pierre and collaborators’ work [13].
Figure 6. Raman spectra for aragonite samples A, B and C at 1064 nm excitation source, normalized by the Ag mode at 1086 cm-1. The symmetry of each mode presented was based on De La Pierre and collaborators’ work [13].
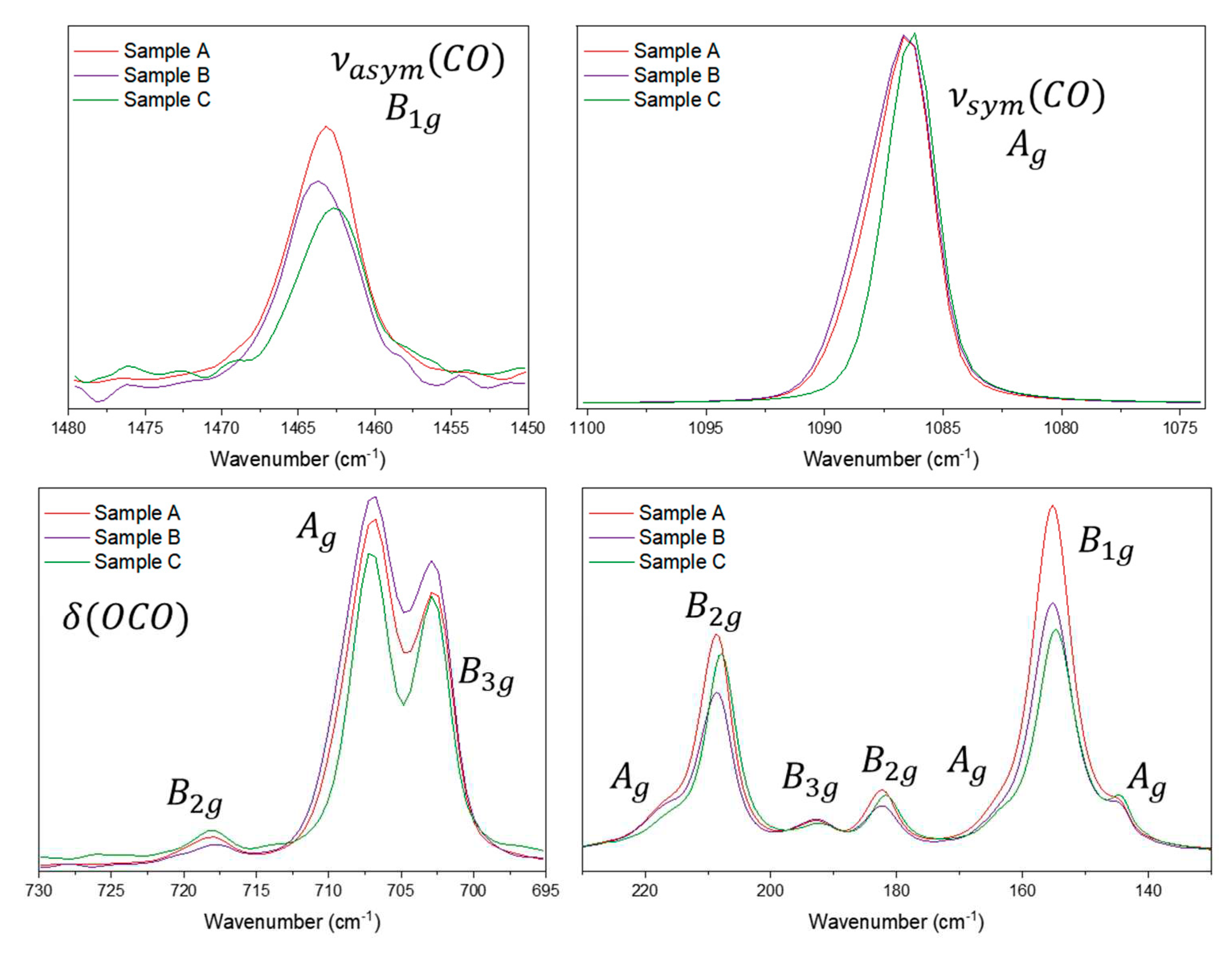
Preprints 85586 g006
Preprints 85586 g007
Figure 7. Raman spectra for aragonite and witherite samples at 1064 nm excitation source, normalized by the Ag mode.
Figure 7. Raman spectra for aragonite and witherite samples at 1064 nm excitation source, normalized by the Ag mode.
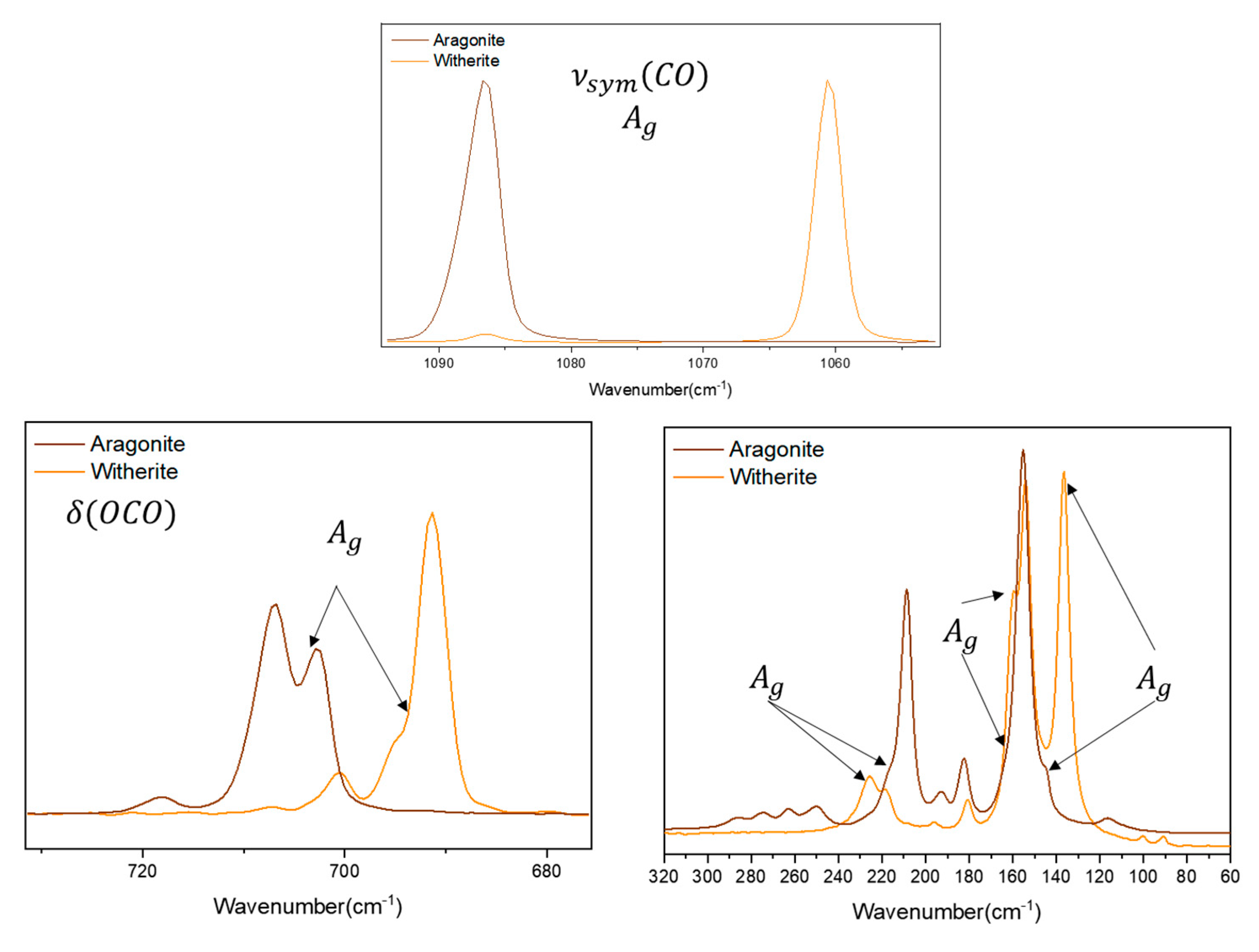
Preprints 85586 g007
Preprints 85586 g008
Figure 8. Raman spectra of azurite and malachite samples at 1520-900 cm-1 region, the arrow indicates the symmetric stretching mode, used to normalize the spectra.
Figure 8. Raman spectra of azurite and malachite samples at 1520-900 cm-1 region, the arrow indicates the symmetric stretching mode, used to normalize the spectra.
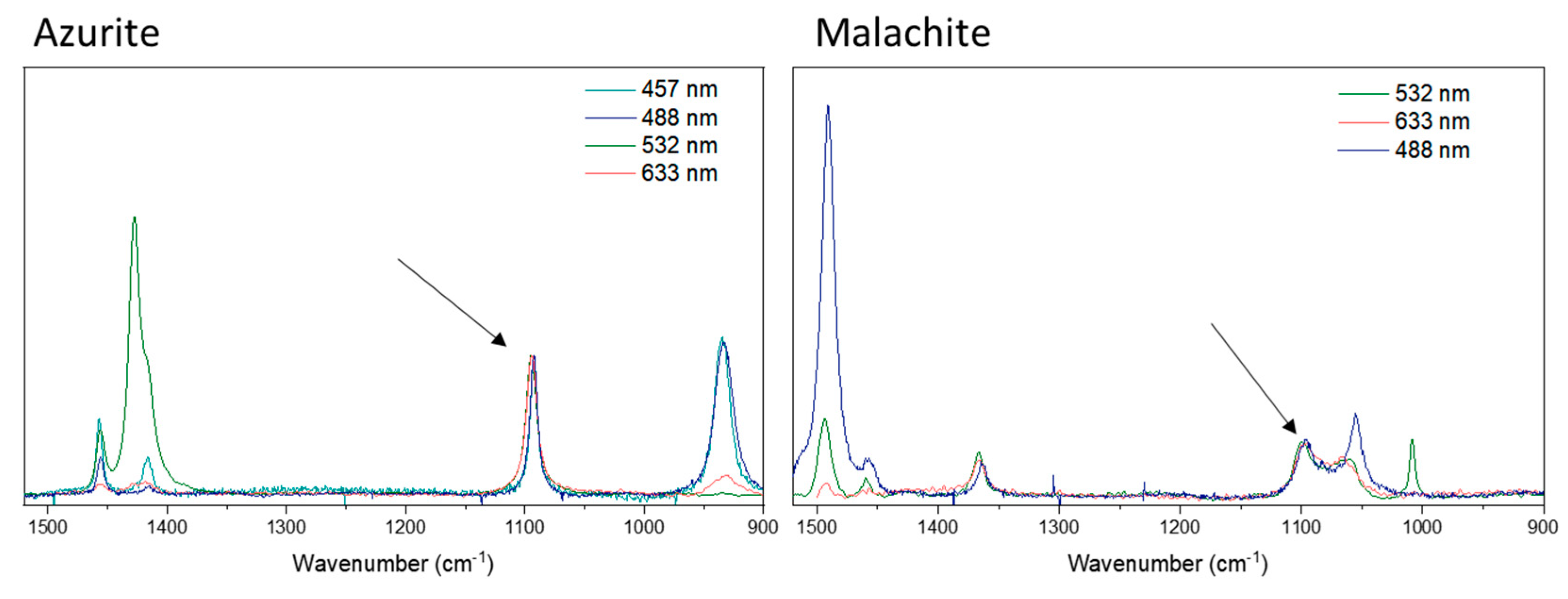
Preprints 85586 g008
Preprints 85586 g009
Figure 9. Raman spectra of calcite and rhodochrosite at 1064 nm excitation source.
Figure 9. Raman spectra of calcite and rhodochrosite at 1064 nm excitation source.
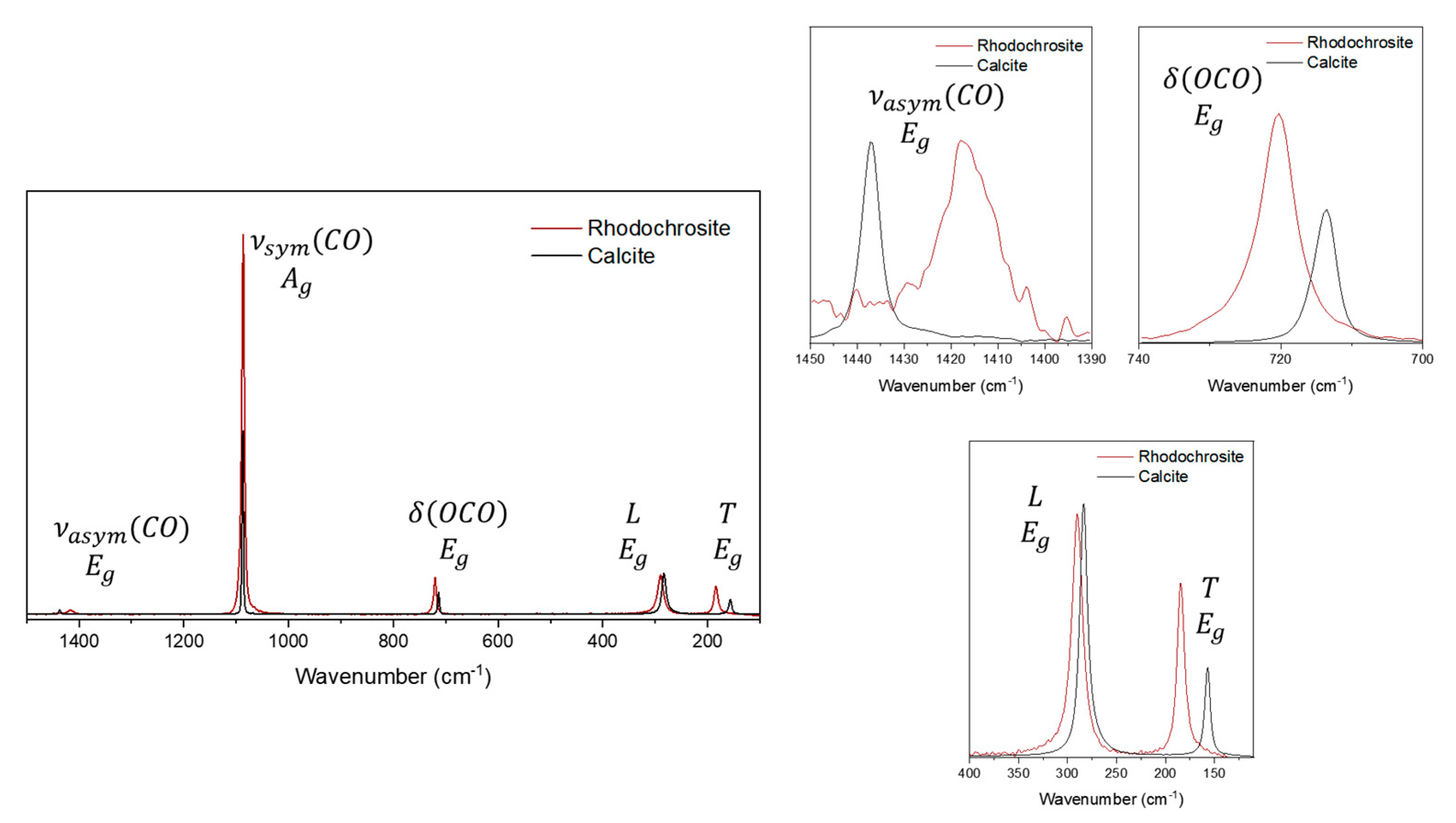
Preprints 85586 g009
Preprints 85586 g010
Figure 10. Raman spectra of siderite sample in comparison calcite. In this region, it is observed the bending mode next to 700 cm-1 and the external modes.
Figure 10. Raman spectra of siderite sample in comparison calcite. In this region, it is observed the bending mode next to 700 cm-1 and the external modes.
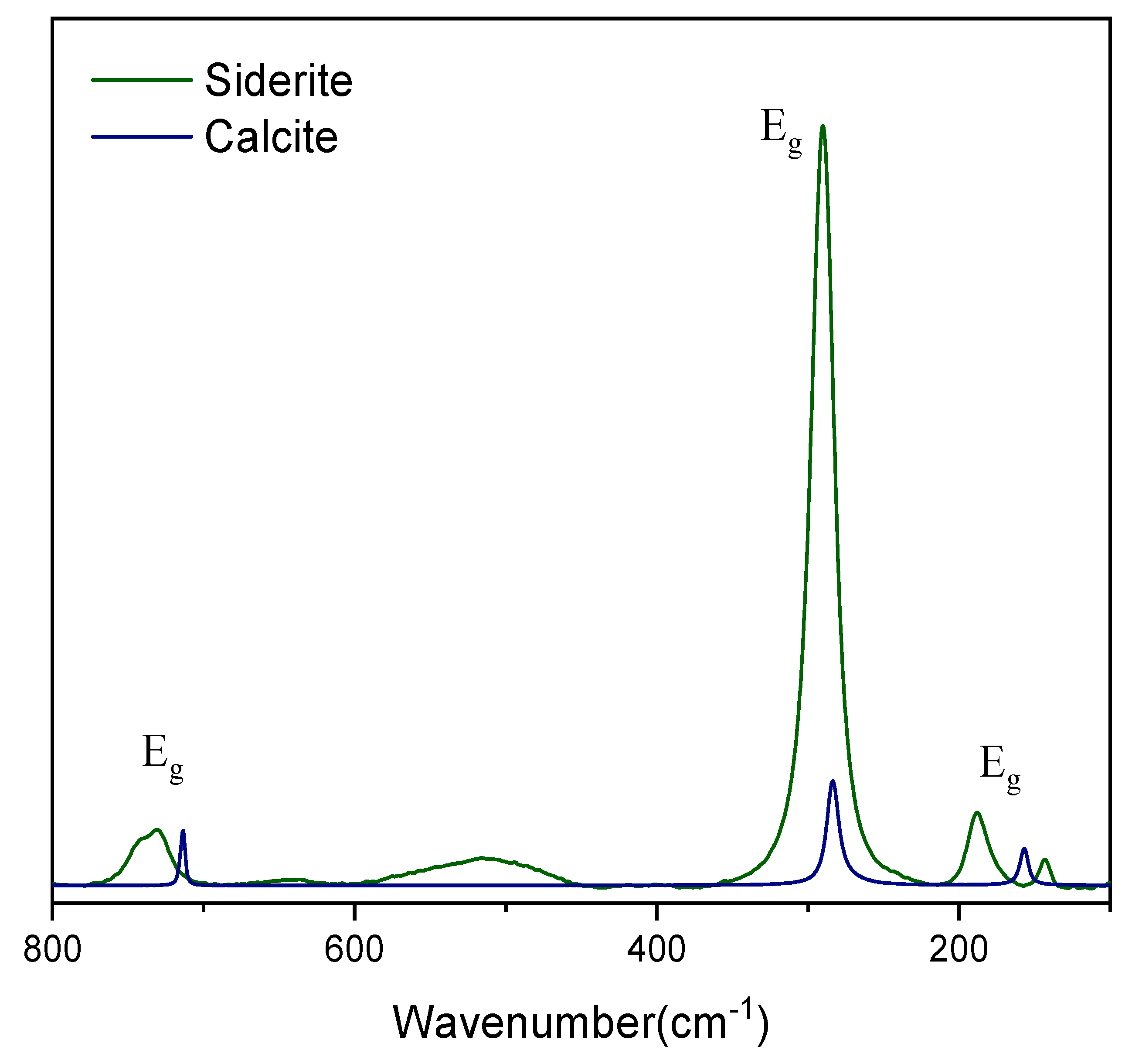
Preprints 85586 g010
Preprints 85586 g011
Figure 11. Raman spectra of Aragonite sample B for different excitation sources.
Figure 11. Raman spectra of Aragonite sample B for different excitation sources.
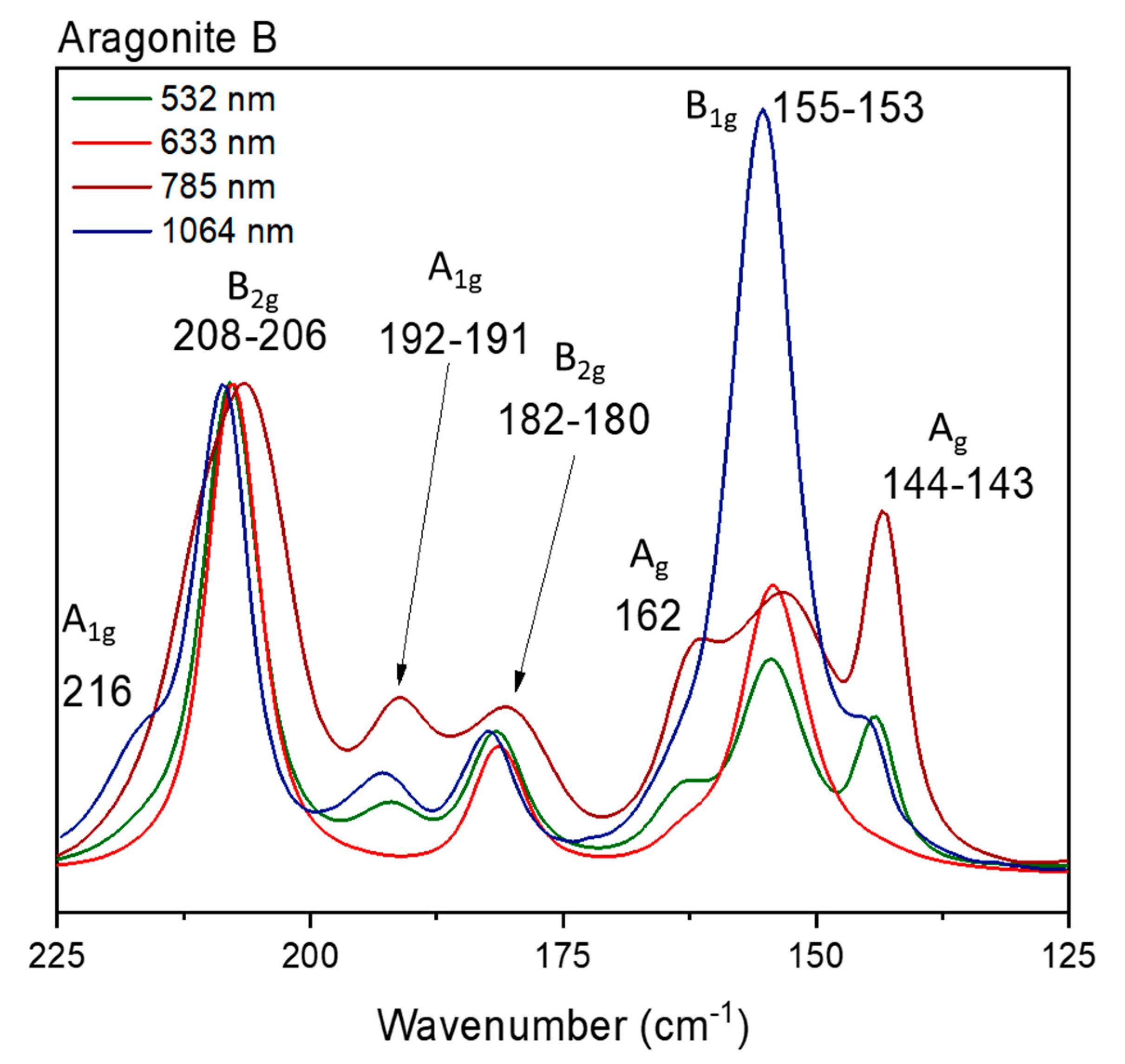
Preprints 85586 g011
Preprints 85586 g012
Figure 12. Mapping with 16 points of the Rhodochrosite sample B, at 532 nm excitation source, showing the low region spectra.
Figure 12. Mapping with 16 points of the Rhodochrosite sample B, at 532 nm excitation source, showing the low region spectra.
Preprints 85586 g012
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated