Prerpints.org logo
Preprint
Article

Global and Local Approaches for Forecasting of Long-Term Natural Gas Consumption in Poland Based on Hierarchical Short Time Series

Altmetrics

Downloads

149

Views

140

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

19 September 2023

Posted:

21 September 2023

You are already at the latest version

Alerts
Abstract
This study presents a novel approach for predicting hierarchical short time series. In this article, our objective was to formulate long-term forecasts for household natural gas consumption by considering the hierarchical structure of territorial units within a country's administrative divisions. For this purpose, we utilized natural gas consumption data from Poland. The length of the time series was an important determinant of the data set. We contrast global techniques, which employ a uniform method across all time series, with local methods that fit a distinct method for each time series. Furthermore, we compare the conventional statistical approach with a machine learning (ML) approach. Based on our analyses, we devised forecasting methods for short time series that exhibit exceptional performance. We have demonstrated that global models provide better forecasts than local models. Among ML models, neural networks yielded the best results, with the MLP network achieving comparable performance to the LSTM network while requiring significantly less computational time.
Keywords: 
Subject: Business, Economics and Management  -   Econometrics and Statistics

1. Introduction

The energy mix of a country determines sustainability of its energy sources, which in turn significantly affects the environmental, economic, and social facets of energy production and consumption. This mix is largely shaped by a nation's geographical location and historical context. In case of Poland, its energy infrastructure has traditionally been coal-centric, making its energy sector the sixth largest in Europe. Roughly 49% of Poland's energy originates from hard coal, followed by 26% from lignite, and about 8% from the combustion of natural gas. When contrasted with the energy mix of the European Union, distinct differences emerge: in 2019, renewable energy sources comprised 35%, nuclear energy accounted for 25.5%, and natural gas stood at 21.7%. The smallest proportion, 14.7%, was attributed to energy produced through coal combustion [1].
Although Poland's energy mix has remained largely unchanged for the past three decades, the next thirty years might see a significant shift due to evolving EU policies. Particularly noteworthy in this context is the role of natural gas, which is being viewed as a transitional fuel in the journey towards a greener Polish energy sector. Consequently, there's a growing need to develop more sophisticated tools for analyzing gas consumption patterns.
In Poland, the industrial sector consumes 65% of the natural gas, with the remaining 35% linked to household (domestic) consumption. This consumption meet the needs over 7.2 million private consumers, who represent more than 93% of the gas recipients in Poland [1]. The annual natural gas consumption trends in Poland are illustrated in Figure 1. In this article, we focus on building methods for forecasting gas consumption in the household sector (individual consumers and small industry).
Forecasting long-term household natural gas consumption is intrinsically more challenging than its industrial counterpart. This complexity stems from various factors. First, the ongoing expansion of the gas network infrastructure influences consumption patterns. As of 2017, gas was accessible in only 58% of Polish municipalities. However, the strategic plan of the Polish Gas Company, the primary distribution operator in the country, aims to extend it. The goal is to bring gas to an additional 300 municipalities, raising the penetration rate to about 70%, thereby covering 90% of Poland's populace [2]. Second, population migrations between regions cause shifts in local gas consumption, even if the overall national consumption remains unchanged. The next limitation lies in the length and level of aggregation of time series provided by the Polish Statistical Office [3]. A potential solution is the decomposition of this time series into lower administrative levels, but this approach comes with its own challenges. Specifically, such data is often noisy, making it scientifically challenging to develop an effective method for forecasting hierarchical, short time series. The political transformations in Central Europe were not just a systemic change but also marked a shift in data collection methodologies. Consequently, many time series from the Central Statistical Office are short. Moreover, climate change introduces added complexity by causing temperature fluctuations that influence gas consumption. Within homes, natural gas is mainly used for heating and cooking.
The above-mentioned reasons highlight two main challenges faced by the authors of the article. The first is building a method for long-term forecasting of gas consumption in the household sector within the territorial divisions of Poland. The second challenge relates to the dataset structure, particularly the hierarchy of short time series. This article aims to find a method that can effectively forecast for this kind of data. There are two main approaches to forecast hierarchical time series [5,6]. The first is the local (series-by-series) approach, which handles each time series separately. However, in our dataset this approach can face issues like limited number of observations and the risk of overfitting. The second approach, known as the global or cross-learning approach, assumes that all time series in the dataset comes from the same stochastic process. This can lead to better forecasting accuracy because of the larger sample size. Even though the global approach might seem limiting, recent studies show it works well even with heterogenous datasets (time series comes from different objects). A challenge with using the global approach for such datasets is the wide variation in time series, which arises from different consumption patterns of Polish territorial units.
Recently, there's been a debate in scientific literature about the best forecasting methods for hierarchical time series – whether traditional statistical methods like ARIMA and ETS applied to local model or machine learning methods like LSTM applied to global model are more effective. In [7], the authors found that for univariate hierarchical time series forecasting, statistical methods are often more accurate than machine learning methods. However, [8] showed that this is mostly true for shorter time series. As the time series gets longer, or when more series are considered, machine learning methods start performing better. In [9] similar research for hierarchical time series founds that machine learning methods outperformed others, both in the series-by-series and cross-series approaches. Unfortunately, individual time series in these datasets were quite lengthy (over 100 observations), and machine learning generally excels in such situations. There are no studies in the literature for hierarchy of short time series.
To develop a forecasting method for such a dataset, the authors needed to address four research questions.
  • A common approach to forecasting abovementioned dataset involves using classical statistical methods series-by-series. The first hypothesis sought to answer the question: Can classical statistical forecasting methods, when applied locally, ensure accurate predictions for multiple hierarchy levels and short time series?
  • Methods based on Machine Learnings, which typically struggle with short time series, might surpass the results of classical statistical methods when using a global model. The next hypothesis aimed to verify whether employing the global approach would enhance forecast accuracy in such datasets.
  • Subsequently, the authors tested if using the local approach, along with explanatory variables, could improve the model's performance.
  • The next hypothesis assessed whether incorporating multiple explanatory variables would notably enhance forecast accuracy compared to the time series predictions alone. Lastly, the study evaluated if the LSTM network might outperform other forecasting techniques for short time series.

2. Literature review

2.1. Natural gas forecasting research

Forecasting methodology of natural gas consumption is frequently created for individual countries. Some important studies for particular countries include: [10] (decomposition method), [11] (neural networks, Belgium), [12] (Spain, stochastic diffusion models), [13] (Poland, logistic model), [14] (Turkey, machine learning, neural networks), [15] (Turkey, Gray models), [16] (Argentina, aggregation of short- and long-run models), [17] (China, grey model). However, these models are usually country specific which makes it difficult to use for other countries.
Short-term natural gas consumption is the main area of research in forecasting. Short-term consumption forecasts, traditionally use time series forecasting models like ETS family [18] or ARIMA/SARIMA [19]. The use of BATS/TBATS models is a relatively new approach [20,21]. Traditional time series models are often replaced by artificial neural networks, among others, deep neural networks and Long Short-Term Memory (LSTM) [22,23,24]. Long-term forecasting is the research area in only about 20% of studies [25,26,27,28]. Usually, long-term forecasts are constructed using models with dependent macroeconomic variables (GDP, population, unemployment rate etc.), without distinguishing between spatial and types of gas consumption (private-industrial), what is the core of our analysis in this paper. Exceptions are the forecasts for Iran [29] (logistic regression and genetic algorithms) and Argentina [16] (logistic models, computer simulation and optimization models), [30] (regression, elasticity coefficients). While, medium-term forecasting of natural gas incorporates mainly economic and temperature variables [31].
Traditionally, econometric and statistical models have been frequently used in forecasting. The most popular group of models are econometric models (e.g. [32,33], and statistical models [10,34]. Recent researches have focused attention on artificial intelligence methods [11,35,36,37]. One of the latest research [26] compares the accuracy of more than 400 models of energy demand forecasting. The authors of this study found that statistical methods work better in short- and medium-term models, while in the long-term models based on computational intelligence are more appropriate. One of the reasons is, that computational intelligence methods are more advantageous for poorly cleaned data. Typical data sets used in gas demand forecasts are: gas consumption profiles, macro- and microeconomic data (e.g., households) and climatic data [38].
Forecasting natural gas consumption in households (or domestic, residential) has been the subject of not much scientific studies. For example, Szoplik [39] used neural networks to construct medium-term forecasts for households located at a single urban area. Bartels and others [38] used gas consumption profiles of households and their economic characteristics, macro- and microeconomic data including regional differences in natural gas consumption and climatic data. Cieślik and others [40] studied the impact of infrastructural development (electrical network, water supply, sewage system) on natural gas consumption in Polish counties. Sakas et al. [41] proposed a methodology for modeling energy consumption, including natural gas, in the residential sector in the medium term, taking into account economic, weather and demographic data.
A common practice is forecasting the demand for gas for business purposes for distribution companies. An example of such forecasts are studies on gas demand for eastern and south-eastern Australia [42]. Similar forecasts are made for Polska Spółka Gazownictwa – the main Polish distribution company. Commercial forecasts consider detailed data on existing customers and their past gas consumption. The challenge remains in accounting for future changes in the number of recipients and their gas consumption characteristics.

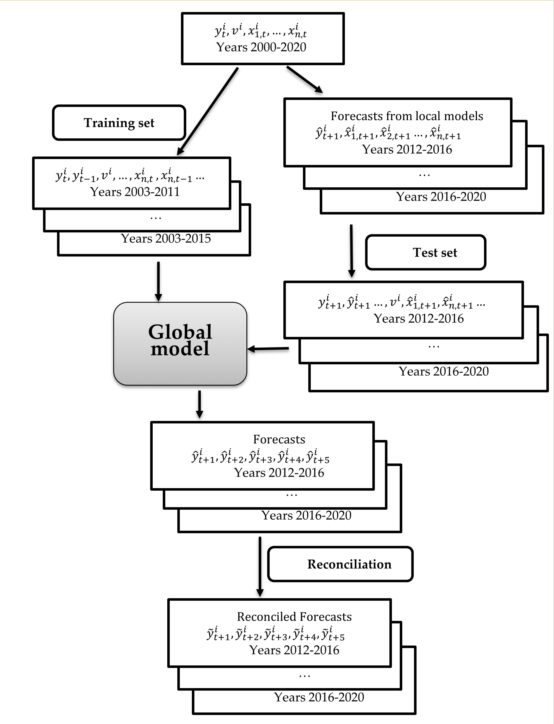
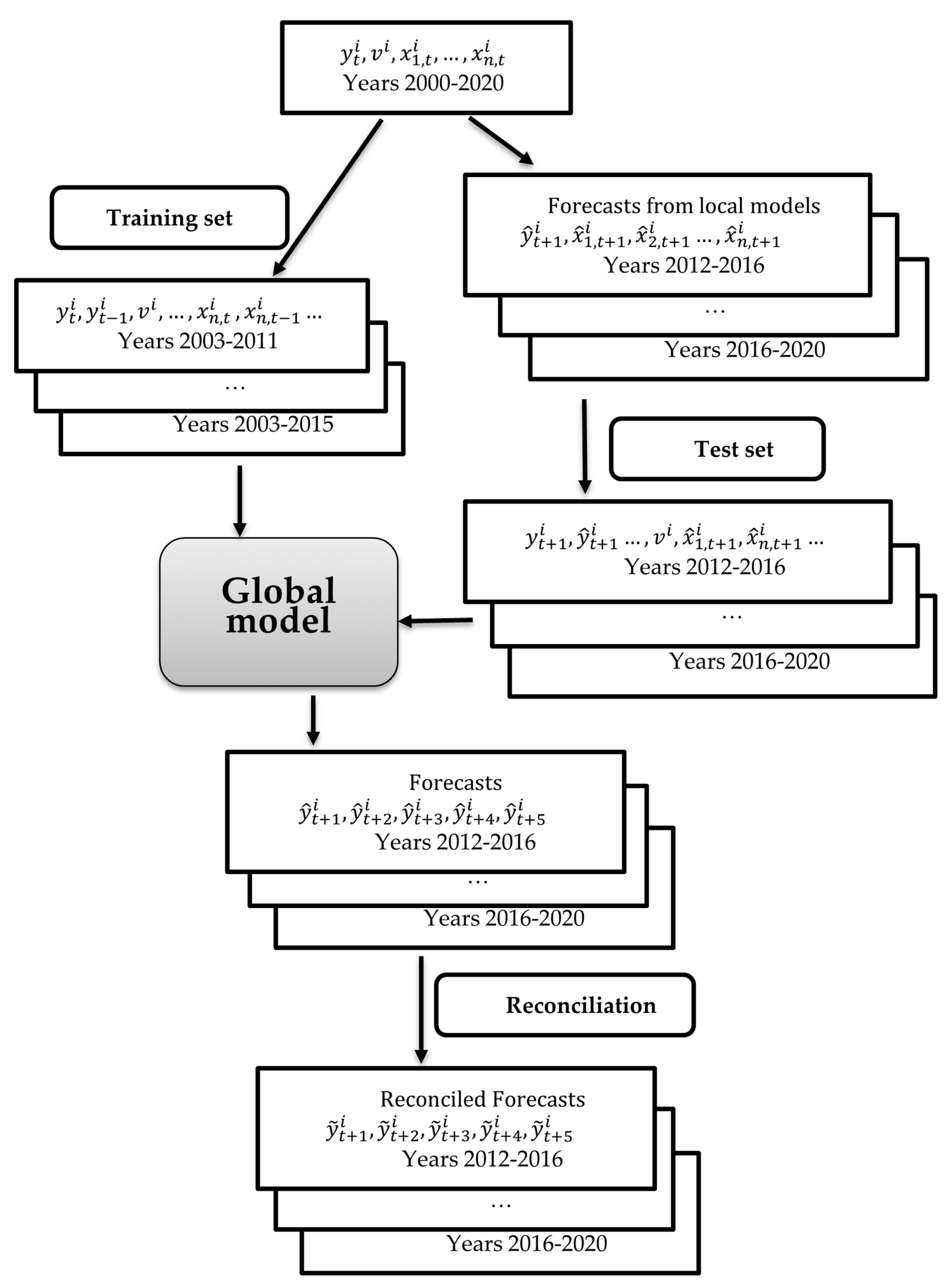
2.2. Hierarchical forecasting of short time series

A time series is typically represented as a sequence of observations, given by Y = { y t , … , y t , … , y T } . When forecasting a time series, the goal is to estimate the future values y T + 1 , … , y T + h , where h represents the forecasting horizon. The forecast is typically denoted as y ^ T + h . There are two primary group of forecasting. The univariate method predicts future observations of a time series based solely on its past data. In contrast, multivariate methods expand on univariate techniques by including additional time series as explanatory variables.
In the literature, univariate methods are generally classified into three main groups. The first group comprises simple forecasting methods that are often used as benchmarks. The most common example is the naive method, which predicts future values of the time series based on the most recent observation:
y ^ T + h = y T .
Other methods in this group are mean, seasonal naive, or drift.
Statistical group encompass classical techniques such as the well-known ARIMA and ETS families of methods. The ARIMA model, which stands for autoregressive integrated moving average, represents a univariate time series using both autoregressive AR and moving average MA components. The AR(p) component predicts future observations as a linear combination of past p observations using the equation:
y ^ T + h = c + ∑ i = 0 p − 1 ϕ i y t − i + ε t ,
where c is constant, ϕ i represents the model’s parameters and ε t is white noise.
The MA(q) component, on the other hand, models the time series using past errors. It can be represented as:
y ^ T + h = μ + ε t + ∑ i = 0 q − 1 θ i ε t − i ,
where μ denote the mean of the observation and θ i models’ parameters.
Selecting parameters manually for ARIMA models can be challenging, particularly with forecasting numerous time series simultaneously. However, the auto-ARIMA method provides a solution by automatically testing multiple parameter combinations to identify the model with the lowest AIC (Akaike Information Criterion).
The ETS family is a smoothing technique that use weighted averages of past values, with the weights decreasing exponentially for older data points. Each component of ETS: Error, Trends and Seasonality is modelled by one recursive equation. The auto-ETS procedure, analogous to auto-ARIMA, automates the process of identifying the best-fitting ETS model for a given time series [43].
An important aspect of statistical forecasting is stationarity, which refers to a time series whose statistical properties, such as mean and variance, remain constant over time. Many real-world processes lack stationary structures. While models like ETS do not require constant stationarity, others, like ARIMA, use differencing transformations to achieve it.
The third group is Machine Learning (ML) models. In this approach, time series forecasting corresponds to the task of autoregressive modeling AR(p). This necessitates transforming the time series into a dataset format. Let x i , y i constitute a set of observations referred to as the training set. Transformation between time series and training set is modelled by equation:
x i = y i − 1 , … . , y i − p , y i ∈ Y .
The xi is called feature vector.
Machine learning (ML) in time series forecasting, learn relationships between input features and an output variable. In general, the assumptions of ML models which leads to multiple regression problems.
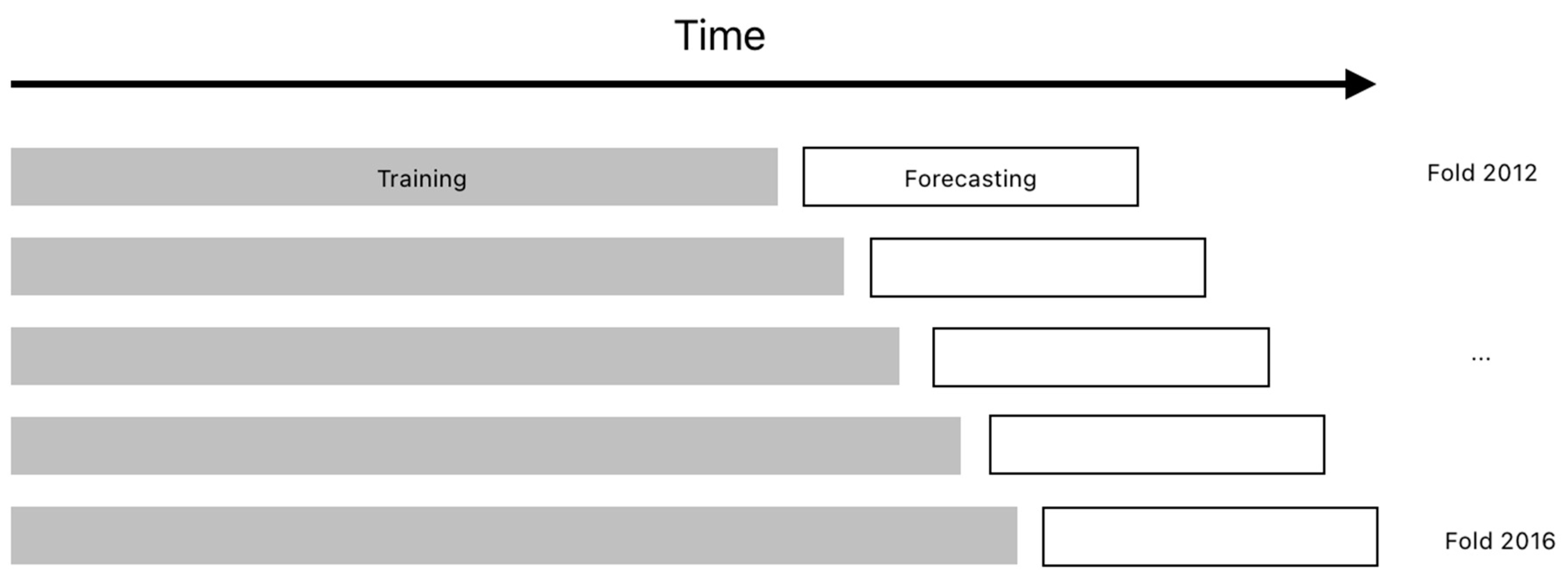
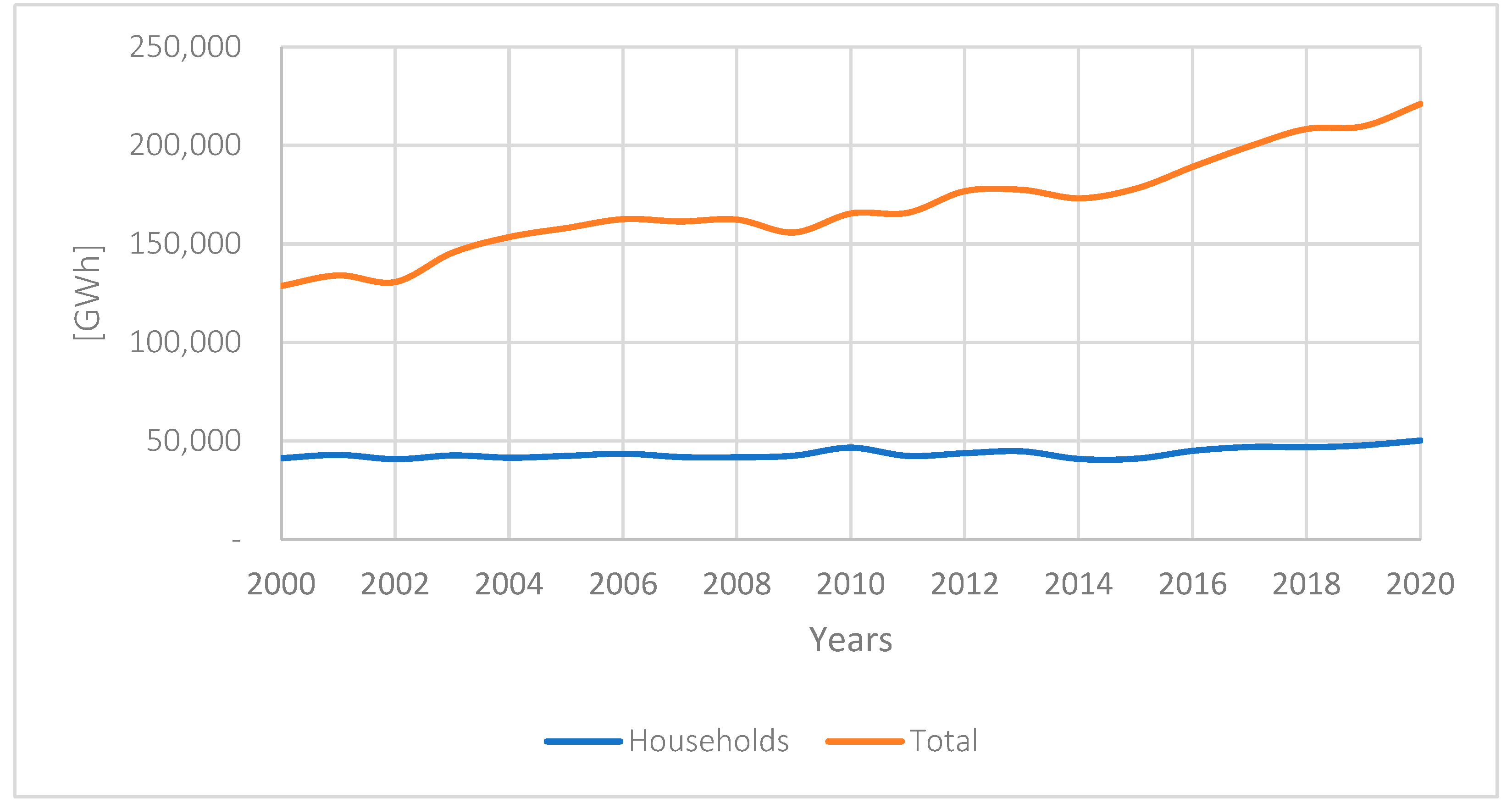
Regardless of the chosen approach, time series forecasting is strongly influenced by the number of available observations. Gas consumption data for households in Poland constitute a short time series due to the limited historical data available. Forecasting with this kind of time series can be tricky. As noted by Hyndman [9], two rules should be met when utilizing a short time series for forecasting: firstly, the number of parameters in the model should be fewer than the number of observations; secondly, forecast intervals should be limited. The literature on short time series forecasting is limited. The comprehensive article "Forecasting: Theory and Practice" [44] does not mention short time series. The literature suggests [45,46] that uncomplicated models such as ARIMA, ETS, or regression perform exceptionally well with small time series.
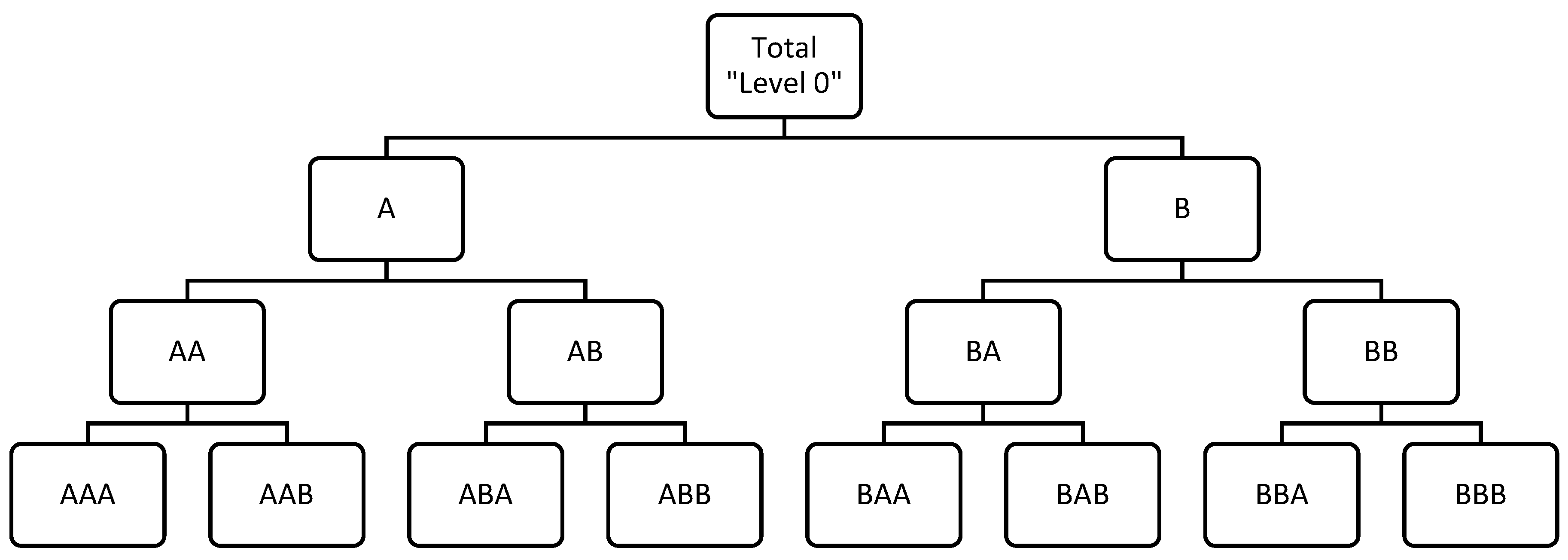
Time series often follow a structured system called hierarchical time series (HTS) where each unique time series is arranged into a hierarchy based on dimensions like geographical territory or product categories (Figure 2). Many studies, like [47,48,49,50], discuss forecasting HTS. In HTS, level 0 consists of a completely aggregated main time series. Level 1 to k-2 breaks down this main series by features. The k-1 level contains disaggregated time series. The hierarchy vector of time series can be described as follows:
y t h t s = y t 0 y t 1 ⋮ y t k − 1 .
where y t 0 is an observation of the highest level, and y t k − 1 vector of observations at the bottom level. The summing matrix S defines structure of hierarchy:
y t h t s = S y t k − 1
When forecasting with HTS, it's important to get consistent results at every level. Firstly, each series is predicted on its own, creating base forecasts. Then, these forecasts are reconciliated to be coherent [51]. Traditionally, there are four strategies for reconciling forecasts: the top-down, bottom-up, middle-out and min-T. The top-down strategy begins by forecasting at the highest level of the hierarchy and then breaks down the forecasts for lower-level series using weighting systems. This disaggregation is done using the proportion vector p = ( p 1 , … , p j , … , p m k − 1 ) T , which represents the contribution of each time series. Typical ways to calculate p are:
averages of historical proportions
p j = 1 T ∑ t = 1 T y i , t k − 1 y t 0 ,
average of the historical values
p j = ∑ t = 1 T y i , t k − 1 T ∑ t = 1 T y t 0 T ,
or proportions of forecasts
p j = ∏ k = 0 K − 2 y ^ t , i k S ^ t , i k + 1 ,
where y ^ t , i k is base forecast of the series that corresponds to the node, which is k levels above the node j, and S ^ t , i k + 1 is sum of the base forecasts below the series that is k levels above node j.
Let y ~ t is a vector of reconciled, forecasted observations. The top-down approach can be expressed as
y ~ h = p S y h 0 .
Similarly, the bottom-up approach produces forecasts at the bottom level k-1 and then aggregates them to upper-levels:
y ~ h = S y ^ h k − 1 .
Another approach, known as the middle-out strategy, combines elements of both the top-down and bottom-up strategies. It estimates models from an intermediary stage of the hierarchy where predictions are most reliable. Forecasts at higher levels than this are synthesized using a bottom-up approach, while forecasts for observations below this midpoint are calculated using a top-down approach. One of the most promising reconciliation methods is the min-T [52]. In this approach, the total joint variance of all obtained consistent forecasts is minimized. The approach described here is usually called local.
The local approach has two drawbacks [5]. The size of a single time series can lead to the situation that individual forecasting models for each time series becoming too specialized and suffer from over-fitting. Temporal dependencies that may not be adequately modelled by algorithms. To avoid this problem, analysts should manually input their knowledge to algorithms what is time consuming and makes the models less accurate, harder to scale up and time consuming, as each time series needs human supervision. There's another way to approach this problem, known as the global [53] or cross-learning [54]. In the global approach, all the time series data is treated as a single comprehensive group. This approach assumes that all the time series data originates from objects that behave in a similar manner. Some researchers have found that the global approach can yield surprisingly effective results, even for sets of time series that don't seem to be related. [55] demonstrates that even if this assumption doesn't hold true, the methods still provide better performance than the local approach.
In the global approach, a single prediction model is created using all the available data, which helps mitigate overfitting due to the larger dataset for learning. However, this approach has its own limitations: it employs the same model for all time series, even when they exhibit differences, potentially lacking the flexibility of the local approach.

3. Materials and Methods

3.1. Dataset description

The dataset details the consumption of natural gas by households in Poland, categorized by territorial units. The dataset contained data at 4 levels of hierarchy: country, provinces (voivodships), counties (poviats), and municipalities (communes). The information used to forecast natural gas consumption in Poland from 2000 to 2020 came from the Polish Central Statistical Office's local database (known as GUS – Local Data Bank, 2022). Each time series included yearly data, and the longest series had 20 observations. Given the short length of these series, it's not possible to identify seasonality. Table 1 presents the structure of the dataset.
In the analyzed period, the average annual gas consumption for a single county was approximately 149,917 MWh. Individual observation ranged from 0 MWh to 3,508,184 MWh, with the latter being for the county with the highest natural gas consumption. For individual provinces, the average consumption stood at 3,189,765 MWh, while a single commune had an average consumption of 27,603 MWh. In 2000, the total gas consumption for all territorial units covered in our study was 45,888,090 MWh, which increased to 58,584,611 MWh by 2020.

3.1.1. Data preprocessing

Before forecasting, the input dataset required preparation. The raw data was collected in various units of measurement. Up until 2014, data in the dataset was recorded in volume units (m3). Starting from 2014, data was provided in megawatt hours (MWh). To ensure consistency, volume data from the preceding period was converted to MWh using the average calorific value of natural gas.
Territorial units with either a lifespan shorter than 15 years or less than 15 years of gas network coverage were omitted from the research sample. Additionally, territorial units affected by division or aggregation due to changes in territory were also excluded. These exclusions were necessary to maintain the dataset's integrity and alignment with the research objectives.
The final dataset comprises a total of 46,297 observations, representing natural gas consumption in the investigated territorial units. However, it's important to note that this count is slightly lower than the theoretical count of territorial units multiplied by the number of analyzed years. This discrepancy arises due to the formation, combination, or dissolution of certain counties during the study period.

3.1.2. Explanatory Variables

The dataset for natural gas consumption was expanded to include several explanatory variables to enhance forecast performance. Initially chosen variables are listed in Table 2 and were selected based on their availability in hierarchical form and their potential significant impact on the dependent variable. We chose the variables most strongly correlated with the dependent variable and having the highest impact on the dependent variable based on entropy estimation from k-nearest neighbors distances [56,57]. Consequently, we selected the variables: population, households with gas access, and number of dwellings. Descriptive statistics of selected explanatory variables are presented in Table 3. In the further part of the article, we will be using two data sets – univariate refers to forecasting using only data on household gas consumption, while univariate also includes explanatory variables.

3.2. Methodology

In the current state of scientific knowledge, no consensus has been reached regarding whether statistical models or machine learning (ML) models offer superior accuracy in hierarchical time series forecasting. Makridakis demonstrated in [7,9] that the choice of model depends on the characteristics of the dataset. After analyzing the two aforementioned works, it was hard to determine which approach would be more suitable for our dataset. On one hand, the dataset comprises numerous short time series, which suggests that statistical models might be appropriate. On the other hand, the relationships between the series, the similarities in individual series' behaviors, and the dataset's size indicate that ML methods might perform better. Therefore, the decision was made to compare the predictive capabilities of two approaches: a local approach based on statistical models and a global approach utilizing machine learning models. Consequently, three models were build: local univariate statistical model, a global univariate ML model, and a global ML multivariate model.

3.2.1. Local univariate model

As stated below, the local model assumes that an individual forecasting model is estimated for each time series. The optimal hyperparameters for such a model are obtained through an automated procedure that minimizes the Akaike Information Criterion. Given the number of parameters to be estimated during forecasting, we limited the tested models to univariate statistical models. Due to the length of individual series, we couldn't employ ARIMAX or LSTM networks because the number of parameters to be estimated exceeds the number of observations in a single time series. To construct the classical hierarchical approach, we considered the following families of forecasting models as base forecast:
  • NAÏVE – naïve forecast (benchmark),
  • 3MA – moving average using three last observations,
  • ARIMA – The auto-regressive integrated moving average model,
  • ETS – The exponential smoothing state-space model.
Due to the absence of seasonality in the data, other automated forecasting models like TBats were omitted. The selection of methods for generating forecasts was conducted based on an analysis of the literature [58].
In the next step, best base forecast is reconciled by four common reconciliation algorithms: bottom-up, top-down, middle-out, and Minimum Trace. The outcomes of the reconciled models were compared against two global models – univariate and multivariate.
The benchmark time series models described above were implemented using the ‘fable’ package in R [59]. The ‘hts’ R package was employed for conducting hierarchical time series forecasting [60]. Additionally, the ‘fable’ package was utilized to automatically fine-tune the parameters for ARIMA and ETS.

3.2.2. Global univariate and multivariate models

To create univariate and multivariate global models, we employed following machine learning algorithms:
  • Multilayer Perceptron (MLP): An artificial neural network architecture with multiple layers capable of learning complex patterns across various data types.
  • Long Short-Term Memory (LSTM): A form of recurrent neural network designed to capture sequential dependencies, making it effective for tasks involving sequences and time-series data.
  • LightGBM: A high-performance gradient boosting framework used for structured/tabular data, utilizing ensemble learning to enhance predictive accuracy.
Both LSTM and MLP networks were implemented using the TensorFlow library in Python, and lightGBM in R (library ‘lightgbm’). The LSTM is very popular for forecasting time series. We also used a classic perceptron neural network. While the feed-forward network is not as adept at forecasting time series as the LSTM network, short time series might not provide sufficient data for the LSTM network to showcase its advantages. LightGBM is a gradient boosting framework that utilizes tree-based algorithms. Although not intrinsically designed for time series, LightGBM's ability to handle large datasets, rapid training speed, and efficiency in feature selection make it a versatile choice for forecasting tasks.
In both variants of the global model, the dataset was divided into training and testing data using the cross-validation methodology. In the univariate variant, we employed three regressors representing lags up to 3 periods. The univariate model for natural gas consumption in any territorial unit i in period t can be expressed as:
y ^ t i = f y t − 1 i , … , y t − 3 i
We set the lag based on the analysis of the automatically tuned ARIMA models. In multivariate models, explanatory variables also include lagged values up to 3 periods. Explanatory variables in multivariate models were natural gas consumption, population, households with gas access, and the number of dwellings. Additionally, the set of explanatory variables was expanded to include the following regressor: province code. A detailed explanation of these variables is included in subchapter 3.1.2. Due to nonlinear activation, the data is scaled before training using min-max scaling. The multivariate model for natural gas consumption in any territorial unit i in period t is as follows:
y ^ t i = f y t − 1 i , … , y t − p i , v i , x 1 , t i , x 1 , t − 1 i , … , x 1 , t − p i , … , x n , t i , x n , t − 1 i , … , x n , t − p i ,
where xn is n-th explanatory variable and vi is the province (voivodeship) code for i-th territorial unit.
To obtain training and testing sets for machine learning algorithms, we needed to create variables representing the lag in gas consumption over time. In the context of the global model, increasing the lag by subsequent years extended the length of the training series but decreased the size of the training set. For instance, for the training set spanning 2000 to 2015, using the entire time series produced only one observation for each territorial unit. Yet, incorporating a 3-year lag as delayed variables resulted in 13 observations for each unit. This decision yielded 28,626 observations from 2003 to 2015 in the training set for forecasts spanning 2016 to 2020, and 19,790 observations in the training set for forecasts from 2012 to 2016.
A further consideration was how to obtain lagged variables for gas consumption in the testing set. For 5-year forecasts, the last four years must be forecasts. Two strategies were possible here. The first, a rolling approach, involves populating the testing set with forecasts from the global model for the forthcoming years, necessitating the creation of five global models. Alternatively, the second approach involves forecasting the explanatory variables – in this scenario, gas consumption – using time series forecasting methods for the entire testing set. Thus, the global model is constructed only once. This methodology is both quicker and less labor-intensive, making it a more pragmatic option. We adopted this latter approach, with gas consumption forecasts derived from the ARIMA model. It also enabled a standardized forecasting methodology in comparison to the multidimensional model with explanatory variables, elaborated upon in the subsequent subsection. A comprehensive overview of the forecasting procedure can be seen in Figure 3. The entire process of forecasting global model is outlined by the following steps:
  • Select potential explanatory variables.
  • Preprocess data: fill in missing data, correct outliers, and consider territorial unit divisions, mergers, and formations.
  • Conduct explanatory variable selection, retaining variables with the greatest impact on the explained variable.
  • Forecast the explanatory variables for h forecast years using the selected forecasting method.
  • Introduce additional explanatory variables into the model, representing lagged values of selected variables for 1, 2, ..., p prior years.
  • Normalize the variables.
  • Add variables indicating affiliation to level of territorial hierarchy (e.g., provinces). Apply one-hot encoding for region codes.
  • Divide the dataset into training and testing sets. Multiple splits for the training and test sets can be achieved using fixed-origin or rolling-origin setups. Alternatively, employ expanding-window or rolling-window setups for cross-validation [61,62].
  • Train the model on the entire training set to obtain a global model.
  • Generate forecasts for each territorial unit independently using the global model and the test set data.
  • Reconcile forecasts using the selected method.
  • Evaluate models and results [62].
All steps describe the construction of the global multivariate model. For the global univariate model, the procedure is limited to steps 3-5 and 8-11.
Both LSTM and MLP networks were constructed with a single hidden layer, generally deemed suitable for time series forecasting. The learning rate parameter, which prevents getting stuck in local minima during learning, was set to the default for the Adam optimizer, which is 0.001. The number of neurons in the input layer was determined using results from the SciKit Learn library with grid search. We began with the guideline that the number of neurons in the input layer should be roughly half of the total input variables, and that the number in the hidden layer should be the average of neurons in the input and output layers. The final count of neurons was optimized using the SciKit Learn library. The same library determined the dropout rate for each layer—a parameter essential for curtailing model overfitting and enhancing generalization. This parameter defines the likelihood that some layer cells will be temporarily omitted during neural network training. The optimizer parameter, which determines the method for error function optimization, was selected empirically. It governs how weights are adjusted throughout the neural network training. In line with our methodology, the built-in RMSprop optimizer from the Keras library produced the most optimal outcomes. The number of epochs was evaluated experimentally: beginning with a range from 50 down to 10 epochs, we observed that the learning error stabilized after just 10 epochs. Bearing in mind the need to shorten learning time, we fixed the number of epochs at 20. The hyper-parameters of both neural networks are presented in Table 4.
LightGBM, as a gradient boosting framework, has numerous hyperparameters that users can tune to optimize model performance. We use ‘keras’ library to choose best combination of parameters. For this dataset the most important parameters (most impact of solution): ‘max_depth’: 3, ‘learning_rate’: 0.01, boosting_type: ‘gbdt’. For hierarchical reconciliation we used ‘hierarchical forecast library’ [63].

3.2.3. Model selection

To evaluate models, we divided the data into two sets: training (in-sample) and testing (out-of-sample). The forecasting horizon (h) was set to 5. The training set was used for estimating hyper-parameters, while the test data helped determine performance metrics. We employed the rolling origin out-of-sample cross-validation technique [62,64] to assess our model's robustness. This technique maintains the forecast length constant but shifts the forecast's starting point over time. a forecast length but adjusts the forecast's starting point over time. We segmented our dataset into five folds spanning 2012 to 2016, with each fold representing a split point into training and testing data (Figure 4). This created multiple train/test partitions. For each fold, the best-performing model was retrained using the in-sample data. Forecasts are then recursively generated for the out-of-sample period. By averaging the errors across these folds, we were able to derive a robust estimate of the model's error.
To evaluate forecasting performance, we use two metrics, root mean square error (RMSE):
R M S E = 1 T − t ∑ i = t + 1 T y i − y i ^ 2
and mean absolute percentage error (MAPE):
M A P E = 1 T − t ∑ i = t + 1 T y i − y ^ i y i .
The MAPE and RMSE are scale independent, so they can also be used to compare the performance of forecasts across different series. Therefore, by averaging their values from multiple series, we can get a single measure of how accurately the forecasts predict a group of series.
We also analyzed execution time of methods. The execution time of algorithm are averaged between fold.

4. Results and Discussion

4.1. Local univariate model

Table 5 showcases the comparison between benchmark and local statistical models without reconciliation. The table underscores the difficulties of forecasting short time series. In the training sample, exponential smoothing methods excel, aligning with findings from [58]. Yet, when comparing results from test and training samples, a notable discrepancy emerges, suggesting the model's overfitting to the training data. All methods have similar outcomes with an average error around 15% on testing set.
Ultimately, the best model was the ETS family. In terms of matching, the simple models (M,N,N) and (A,N,N) were the best, accounting for 90% of the fitted local models. This is also consistent with literature results, where simple exponential smoothing is typically the best solution for short time series (e.g., [58]). Based on those results, the ETS model was adopted as the base forecast.
In the subsequent step, we reconciled the base forecast, as shown in Table 6. Reconciliation doesn't substantially improve the forecasting performance. The average MAPE for the local model stands at just over 15%. This means that statistical models cannot be used to build an accurate prediction for the analyzed dataset.

4.2. Global univariate and multivariate model

In the next step, we compared the performance between the best local model and the global univariate (Global) and multivariate models (with explanatory variables – Global ex). Table 7 summarize results. Figure 5 presents boxplots depicting the distribution of MAPE mean errors for individual folds. The boxplot indicates that the distribution of MAPE errors for ETS is significantly narrower than for benchmark, although average MAPE are practically the same. Global models overperforms local one but choosing the best global univariate model is not easy.
Univariate LSTM and MLP neural network models have a similar average; however, the errors from the MLP model exhibit greater volatility. LightGBM, despite obtaining an average MAPE higher than methods based on neural networks, yields result with low variability. It's challenging to determine which ML model is superior, the LSTM model has shorter whiskers, while the MLP model's box is slightly lower in position. Furthermore, it is evident that the MLP model fails in several folds, as indicated by the outliers on the boxplot. Global, univariate models outperform local ones, although distinguishing between the two can be difficult. Based on the variability of results, it seems that the LSTM models offer the best performance, but average MAPE and RMSE is slightly lower for MLP.
We use the Nemenyi test [65] to compare how well different methods perform. This test ranks the methods in each fold, then averages those ranks and produces confidence bounds (CI) for those means. The means of ranks correspond to medians, so this means that by using this test, we compare the medians of errors of different methods. If CI for different methods overlap, it means their medians are statistically the same. The results are presented in the Figure 6. The forecasting methods are sorted vertically according to the MAPE mean rank. The graph shows that the MLP Global ex, LSTM Global ex, LSTM global, and MLP global have similar medians at the 95% confidence level (because their bounds intersect). For these methods, we conducted another Nemenyi test for each hierarchy levels in all folds. So we evaluated 20 forecasts (5 (folds) times 4 (methods) times 1 (time series)) at country levels, 320 forecasts at voivodship level, 6820 forecasts at county levels, and 37020 forecast at commune levels. The results are presented in Figure 7 and in Table 8. This meant evaluating 20 forecasts at the country level (5 folds x 4 methods x 1 time series), 320 at the voivodship level, 6,820 at the county level, and 37,020 at the commune level. Detailed results can be found in Figure 7 and Table 8.
These results highlight that models’ performances vary significantly across the hierarchy and are influenced by the hierarchical level. Only at the country level are the differences between methods statistically insignificant. Interestingly, the univariate LSTM and multivariate MLP models show comparable performance. As we go deeper into the hierarchy, the multivariate MLP method consistently outperforms the others, with the advantage becoming more pronounced at lower levels. Comparing the univariate models, LSTM consistently outperforms MLP, with this advantage increasing at lower hierarchical levels. Comparison of results for different folds used in cross validation procedure is presented in Table 9. The overall result of hierarchical forecasts for all 16 provinces (voivodeships) for the period 2016-2020 obtained using the MLP network is presented in Figure 8.
Using the prepared dataset, we additionally assessed the performance of classical econometric models, such as linear regression and panel data models. However, these methods proved to be inadequate for forecasting territorial gas consumption, yielding MAPE errors of over 30%. This is likely due to the nonlinear relationship between the explanatory variables and the forecasted variable. It would be worth exploring the addition of higher-order variables, logarithmic transformations, or variable interactions in these models. Nevertheless, the classical and labor-intensive econometric approaches, which do not guarantee success, are clearly outperformed by neural network models. However, the interpretability of the impact of individual variables on the dependent variable is compromised in neural network models.
Finally, we compared the execution times of the algorithms. The results are as expected: statistical methods outpace ML methods in terms of speed. The computation time for the global univariate MLP model is significantly faster than that of the LSTM, further emphasizing the advantages of this model over others. Calculations were performed on a Dell PowerEdge R440 computer, 2 Intel Xeon Silver 4210 2.2 Ghz processors, 128 GB RAM, Operating system: Windows Server 2019 Datacenter. Comparison of computational time for all models is presented in Table 10.

Conclusions and future studies

In this article, we address forecasting on large hierarchical datasets with short individual series. Our insights can be used to forecasting scenarios with limited information. We demonstrate that, for this dataset, classical forecasting methods implemented locally, even when reconciled, are surpassed by ML global models. Global models, such as LSTM or MLP, can produce coherent forecasts. Importantly, the right ML methods have distinct pros and cons depending on the situation. We discussed different scenarios for using them.
Global ML methods outperform their statistical counterparts in hierarchical forecasting. For a univariate approach, the LSTM has a slight edge over the MLP. Multivariate methods surpass univariate ones, but the significance of this advantage becomes apparent only when considering hierarchical levels. Bottom-level series are noisy and challenging to predict, yet univariate MLP methods handle them effectively. Incorporating additional explanatory variables also enhances forecasting accuracy.
Proposed approach proves effective in forecasting domestic natural gas consumption, with the resulting errors acceptable for long-time planning. However, our approach exhibits significant forecast variability at lower hierarchical levels. More research could target optimizing bottom levels and investigating reconciliation at different aggregation tiers.
For future work, exploring the structural aspects of hierarchy—including the number of levels, series, and other elements like correlations between territories at different levels—would be beneficial. There's a need for more research to select the best forecasting model not only for size of time series but also considering such criteria like hierarchical level, time series characteristic (like variability) and forecast horizon. Integrating these as features in a global ML model could help pinpoint the best forecasting and reconciliation methods.
While our proposed method can generate five-year forecasts, further studies should focus on multi-step forecasting techniques. Lastly, our findings indicate that ML approaches in hierarchical forecasting excel for point forecasting. A potential avenue for future research is to expand this evaluation to forecasting uncertainty.

Author Contributions

Both authors contributed substantially to all aspects of this article. All authors have read and agreed to the published version of the manuscript.

Funding

The APC was funded under subvention funds for the Faculty of Management and by- program “Excellence Initiative—Research University” for the AGH University in Krakow.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Publicly available datasets were analyzed in this study. This data can be found here: https://bdl.stat.gov.pl/bdl/dane/podgrup/temat (accessed on 10 March 2022), https://ec.europa.eu/eurostat/data/database (accessed on 27 August 2023)

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Report – Natural gas. Dolnośląski Instytut Studiów Energetycznych 2020.
  2. Gaz-System, S.A. Krajowy dziesięcioletni plan rozwoju systemu przesyłowego. 2019. [Google Scholar]
  3. GUS - Bank Danych Lokalnych (Local Data Bank). Available online: https://bdl.stat.gov.pl/bdl/dane/podgrup/temat (accessed on 10 March 2022).
  4. Database - Eurostat. Available online: https://ec.europa.eu/eurostat/data/database (accessed on 27 August 2023).
  5. Montero-Manso, P.; Hyndman, R.J. Principles and Algorithms for Forecasting Groups of Time Series: Locality and Globality. International Journal of Forecasting 2021, 37, 1632–1653. [Google Scholar] [CrossRef]
  6. Buonanno, A.; Caliano, M.; Pontecorvo, A.; Sforza, G.; Valenti, M.; Graditi, G. Global vs. Local Models for Short-Term Electricity Demand Prediction in a Residential/Lodging Scenario. Energies 2022, 15, 2037. [Google Scholar] [CrossRef]
  7. Makridakis, S.; Spiliotis, E.; Assimakopoulos, V. Statistical and Machine Learning Forecasting Methods: Concerns and Ways Forward. PLOS ONE 2018, 13, e0194889. [Google Scholar] [CrossRef]
  8. Cerqueira, V.; Torgo, L.; Soares, C. Machine Learning vs Statistical Methods for Time Series Forecasting: Size Matters 2019.
  9. Spiliotis, E.; Makridakis, S.; Semenoglou, A.-A.; Assimakopoulos, V. Comparison of Statistical and Machine Learning Methods for Daily SKU Demand Forecasting. Oper Res Int J 2022, 22, 3037–3061. [Google Scholar] [CrossRef]
  10. Sanchez-Ubeda, E.F.; Berzosa, A. Modeling and Forecasting Industrial End-Use Natural Gas Consumption. Energy Economics 2007, 29, 710–742. [Google Scholar] [CrossRef]
  11. Suykens, J.; Lemmerling, Ph.; Favoreel, W.; de Moor, B.; Crepel, M.; Briol, P. Modelling the Belgian Gas Consumption Using Neural Networks. Neural Process Lett 1996, 4, 157–166. [Google Scholar] [CrossRef]
  12. Gutiérrez, R.; Nafidi, A.; Gutiérrez Sánchez, R. Forecasting Total Natural-Gas Consumption in Spain by Using the Stochastic Gompertz Innovation Diffusion Model. Applied Energy 2005, 80, 115–124. [Google Scholar] [CrossRef]
  13. Siemek, J.; Nagy, S.; Rychlicki, S. Estimation of Natural-Gas Consumption in Poland Based on the Logistic-Curve Interpretation. Applied Energy 2003, 75, 1–7. [Google Scholar] [CrossRef]
  14. Olgun, M.; ÖZDEMİR, G.; Aydemir, E. Forecasting of Turkey’s Natural Gas Demand Using Artifical Neural Networks and Support Vector Machines. Energy, Education, Science and Technology 2011, 30, 15–20. [Google Scholar]
  15. Boran, F.E. Forecasting Natural Gas Consumption in Turkey Using Grey Prediction. Energy Sources, Part B: Economics, Planning, and Policy 2015, 10, 208–213. [Google Scholar] [CrossRef]
  16. Gil, S.; Deferrari, J. Generalized Model of Prediction of Natural Gas Consumption. Journal of Energy Resources Technology 2004, 126, 90–98. [Google Scholar] [CrossRef]
  17. Zeng, B.; Li, C. Forecasting the Natural Gas Demand in China Using a Self-Adapting Intelligent Grey Model. Energy 2016, 112, 810–825. [Google Scholar] [CrossRef]
  18. Hyndman, R.; Koehler, A.B.; Ord, J.K.; Snyder, R.D. Forecasting with Exponential Smoothing: The State Space Approach; Springer Science & Business Media, 2008.
  19. Jeong, K.; Koo, C.; Hong, T. An Estimation Model for Determining the Annual Energy Cost Budget in Educational Facilities Using SARIMA (Seasonal Autoregressive Integrated Moving Average) and ANN (Artificial Neural Network). Energy 2014, 71, 71–79. [Google Scholar] [CrossRef]
  20. De Livera, A.M.; Hyndman, R.J.; Snyder, R.D. Forecasting Time Series With Complex Seasonal Patterns Using Exponential Smoothing. Journal of the American Statistical Association 2011, 106, 1513–1527. [Google Scholar] [CrossRef]
  21. Naim, I.; Mahara, T.; Idrisi, A.R. Effective Short-Term Forecasting for Daily Time Series with Complex Seasonal Patterns. Procedia Computer Science 2018, 132, 1832–1841. [Google Scholar] [CrossRef]
  22. Merkel, G.; Povinelli, R.; Brown, R. Deep Neural Network Regression for Short-Term Load Forecasting of Natural Gas. International Symposium on Forecasting 2017. [Google Scholar] [CrossRef]
  23. Marziali, A.; Fabbiani, E.; De Nicolao, G. Forecasting Residential Gas Demand: Machine Learning Approaches and Seasonal Role of Temperature Forecasts. IJOGCT 2021, 26, 202. [Google Scholar] [CrossRef]
  24. Wei, N.; Li, C.; Peng, X.; Li, Y.; Zeng, F. Daily Natural Gas Consumption Forecasting via the Application of a Novel Hybrid Model. Applied Energy 2019, 250, 358–368. [Google Scholar] [CrossRef]
  25. Soldo, B. Forecasting Natural Gas Consumption. Applied Energy 2012, 92, 26–37. [Google Scholar] [CrossRef]
  26. Tamba, J.G.; Essiane, S.N.; Sapnken, E.F.; Koffi, F.D.; Nsouandélé, J.L.; Soldo, B.; Njomo, D. Forecasting Natural Gas: A Literature Survey. International Journal of Energy Economics and Policy 2018, 8, 216–249. [Google Scholar]
  27. Scarpa, F.; Bianco, V. Assessing the Quality of Natural Gas Consumption Forecasting: An Application to the Italian Residential Sector. Energies 2017, 10, 1879. [Google Scholar] [CrossRef]
  28. Gaweł, B.; Paliński, A. Long-Term Natural Gas Consumption Forecasting Based on Analog Method and Fuzzy Decision Tree. Energies 2021, 14, 4905. [Google Scholar] [CrossRef]
  29. Forouzanfar, M.; Doustmohammadi, A.; Menhaj, M.B.; Hasanzadeh, S. Modeling and Estimation of the Natural Gas Consumption for Residential and Commercial Sectors in Iran. Applied Energy 2010, 87, 268–274. [Google Scholar] [CrossRef]
  30. Khan, M.A. Modelling and Forecasting the Demand for Natural Gas in Pakistan. Renewable and Sustainable Energy Reviews 2015, 49, 1145–1159. [Google Scholar] [CrossRef]
  31. Liu, J.; Wang, S.; Wei, N.; Chen, X.; Xie, H.; Wang, J. Natural Gas Consumption Forecasting: A Discussion on Forecasting History and Future Challenges. Journal of Natural Gas Science and Engineering 2021, 90, 103930. [Google Scholar] [CrossRef]
  32. Bianco, V.; Scarpa, F.; Tagliafico, L.A. Analysis and Future Outlook of Natural Gas Consumption in the Italian Residential Sector. Energy Conversion and Management 2014, 87, 754–764. [Google Scholar] [CrossRef]
  33. Bianco, V.; Scarpa, F.; Tagliafico, L.A. Scenario Analysis of Nonresidential Natural Gas Consumption in Italy. Applied Energy 2014, 113, 392–403. [Google Scholar] [CrossRef]
  34. Erdogdu, E. Natural Gas Demand in Turkey. Applied Energy 2010, 87, 211–219. [Google Scholar] [CrossRef]
  35. Šebalj, D.; Mesarić, J.; Dujak, D. Predicting Natural Gas Consumption–a Literature Review. In Proceedings of the Central European Conference on Information and Intelligent Systems; Faculty of Organization and Informatics Varazdin, 2017; pp. 293–300. [Google Scholar]
  36. Paliński, A. Data Warehouses and Data Mining in Forecasting the Demand for Gas and Gas Storage Services. Nafta-Gaz 2018, 74, 283–289. [Google Scholar] [CrossRef]
  37. Paliński, A. Forecasting Gas Demand Using Artificial Intelligence Methods. Nafta-Gaz 2019, 75. [Google Scholar] [CrossRef]
  38. Bartels, R.; Fiebig, D.G.; Nahm, D. Regional End-Use Gas Demand in Australia*. Economic Record 1996, 72, 319–331. [Google Scholar] [CrossRef]
  39. Szoplik, J. Forecasting of Natural Gas Consumption with Artificial Neural Networks. Energy 2015, 85, 208–220. [Google Scholar] [CrossRef]
  40. Cieślik, T.; Kogut, K.; Metelska, K.; Narloch, P.; Szurlej, A.; Wnęk, P. Wpływ wybranych czynników na zużycie gazu ziemnego w powiatach. Rynek Energii 2019, 143. [Google Scholar]
  41. Sakkas, N.; Yfanti, S.; Daskalakis, C.; Barbu, E.; Domnich, M. Interpretable Forecasting of Energy Demand in the Residential Sector. Energies 2021, 14, 6568. [Google Scholar] [CrossRef]
  42. Gas Statement of Opportunities GSOO. Available online: https://aemo.com.au/energy-systems/gas/gas-forecasting-and-planning/gas-statement-of-opportunities-gsoo (accessed on 27 July 2023).
  43. Hyndman, R.J.; Athanasopoulos, G. Forecasting: Principles and Practice; OTexts, 2018; ISBN 978-0-9875071-1-2.
  44. Petropoulos, F.; Apiletti, D.; Assimakopoulos, V.; Babai, M.Z.; Barrow, D.K.; Ben Taieb, S.; Bergmeir, C.; Bessa, R.J.; Bijak, J.; Boylan, J.E.; et al. Forecasting: Theory and Practice. International Journal of Forecasting 2022, 38, 705–871. [Google Scholar] [CrossRef]
  45. Hyndman, R.J.; Kostenko, A.V. MINIMUM SAMPLE SIZE REQUIREMENTS FOR SEASONAL FORECASTING MODELS.
  46. Thomakos, D.; Wood, G.; Ioakimidis, M.; Papagiannakis, G. ShoTS Forecasting: Short Time Series Forecasting for Management Research. British Journal of Management 2023, 34, 539–554. [Google Scholar] [CrossRef]
  47. Gross, C.W.; Sohl, J.E. Disaggregation Methods to Expedite Product Line Forecasting. Journal of Forecasting 1990, 9, 233–254. [Google Scholar] [CrossRef]
  48. Athanasopoulos, G.; Gamakumara, P.; Panagiotelis, A.; Hyndman, R.J.; Affan, M. Hierarchical Forecasting. In Macroeconomic Forecasting in the Era of Big Data: Theory and Practice; Fuleky, P., Ed.; Advanced Studies in Theoretical and Applied Econometrics; Springer International Publishing: Cham, 2020; pp. 689–719. ISBN 978-3-030-31150-6. [Google Scholar]
  49. Hyndman, R.J.; Athanasopoulos, G. Forecasting: Principles and Practice (3rd Ed), 3rd ed.; OTexts: Melbourne, 2021. [Google Scholar]
  50. Spiliotis, E.; Abolghasemi, M.; Hyndman, R.J.; Petropoulos, F.; Assimakopoulos, V. Hierarchical Forecast Reconciliation with Machine Learning. Applied Soft Computing 2021, 112, 107756. [Google Scholar] [CrossRef]
  51. Mancuso, P.; Piccialli, V.; Sudoso, A.M. A Machine Learning Approach for Forecasting Hierarchical Time Series. Expert Systems with Applications 2021, 182, 115102. [Google Scholar] [CrossRef]
  52. Wickramasuriya, S.L.; Athanasopoulos, G.; Hyndman, R.J. Optimal Forecast Reconciliation for Hierarchical and Grouped Time Series Through Trace Minimization. Journal of the American Statistical Association 2019, 114, 804–819. [Google Scholar] [CrossRef]
  53. Salinas, D.; Flunkert, V.; Gasthaus, J.; Januschowski, T. DeepAR: Probabilistic Forecasting with Autoregressive Recurrent Networks. International Journal of Forecasting 2020, 36, 1181–1191. [Google Scholar] [CrossRef]
  54. Dudek, G.; Pelka, P.; Smyl, S. A Hybrid Residual Dilated LSTM and Exponential Smoothing Model for Midterm Electric Load Forecasting. IEEE Trans. Neural Netw. Learning Syst. 2022, 33, 2879–2891. [Google Scholar] [CrossRef] [PubMed]
  55. Oreshkin, B.N.; Carpov, D.; Chapados, N.; Bengio, Y. N-BEATS: Neural Basis Expansion Analysis for Interpretable Time Series Forecasting 2020.
  56. Ross, B.C. Mutual Information between Discrete and Continuous Data Sets. PLOS ONE 2014, 9, e87357. [Google Scholar] [CrossRef]
  57. Sklearn.Feature_selection.SelectKBest. Available online: https://scikit-learn/stable/modules/generated/sklearn.feature_selection.SelectKBest.html (accessed on 22 July 2023).
  58. ShoTS Forecasting: Short Time Series Forecasting for Management Research - Thomakos - 2023 - British Journal of Management - Wiley Online Library. Available online: https://onlinelibrary.wiley.com/doi/abs/10.1111/1467-8551.12624 (accessed on 24 July 2023).
  59. Forecasting Models for Tidy Time Series. Available online: https://fable.tidyverts.org/ (accessed on 22 August 2023).
  60. Hierarchical and Grouped Time Series. Available online: https://pkg.earo.me/hts/ (accessed on 22 August 2023).
  61. Tashman, L.J. Out-of-Sample Tests of Forecasting Accuracy: An Analysis and Review. International Journal of Forecasting 2000, 16, 437–450. [Google Scholar] [CrossRef]
  62. Hewamalage, H.; Ackermann, K.; Bergmeir, C. Forecast Evaluation for Data Scientists: Common Pitfalls and Best Practices. Data Min Knowl Disc 2023, 37, 788–832. [Google Scholar] [CrossRef] [PubMed]
  63. Hierarchicalforecast - Hierarchical Forecast 👑. Available online: https://nixtla.github.io/hierarchicalforecast/ (accessed on 30 August 2023).
  64. Bergmeir, C.; Benítez, J.M. On the Use of Cross-Validation for Time Series Predictor Evaluation. Information Sciences 2012, 191, 192–213. [Google Scholar] [CrossRef]
  65. Demšar, J. Statistical Comparisons of Classifiers over Multiple Data Sets. Journal of Machine Learning Research 2006, 7, 1–30. [Google Scholar]
Preprints 85581 g001
Figure 1. Natural gas consumption in Poland, own study based on [3,4].
Figure 1. Natural gas consumption in Poland, own study based on [3,4].
Preprints 85581 g001
Preprints 85581 g002
Figure 2. Simple hierarchy structure.
Figure 2. Simple hierarchy structure.
Preprints 85581 g002
Preprints 85581 g003
Figure 3. Forecasting process scheme.
Figure 3. Forecasting process scheme.
Preprints 85581 g003
Preprints 85581 g004
Figure 4. Procedure of cross-time validation.
Figure 4. Procedure of cross-time validation.
Preprints 85581 g004
Preprints 85581 g005
Figure 5. Comparison of boxplots of the accuracy between the local and global models.
Figure 5. Comparison of boxplots of the accuracy between the local and global models.
Preprints 85581 g005
Preprints 85581 g006
Figure 6. Nemenyi test results at 95% confidence level for all 5 folds of the dataset.
Figure 6. Nemenyi test results at 95% confidence level for all 5 folds of the dataset.
Preprints 85581 g006
Preprints 85581 g007
Figure 7. Nemenyi test for each level of hierarchy. The forecasting methods are sorted vertically according to the MAPE mean rank.
Figure 7. Nemenyi test for each level of hierarchy. The forecasting methods are sorted vertically according to the MAPE mean rank.
Preprints 85581 g007
Preprints 85581 g008
Figure 8. Reconciled MLP forecasts and actual values of natural gas consumption of Polish provinces for the fold 2016.
Figure 8. Reconciled MLP forecasts and actual values of natural gas consumption of Polish provinces for the fold 2016.
Preprints 85581 g008
Table 1. Hierarchy of the dataset.
Table 1. Hierarchy of the dataset.
Level Number of series Total observations per level
Country 1 21
Province (voivodship) 16 361
County 341 7,149
Municipality (commune) 1,851 38,791
Table 2. Preselected variables for forecasting natural gas consumption.
Table 2. Preselected variables for forecasting natural gas consumption.
Variable Explanation
population Total number of inhabitants of a given territorial unit
households Number of households in a given territorial unit
households with gas access Number of households with access to the gas network
dwellings Number of apartments or single-family homes in a territorial unit
dwellings built in a given year Number of apartments or single-family homes commissioned in a given year in the area of a given unit
length of a gas network Total length of the gas distribution network in a given territorial unit
* - The value of the variable for the superior unit is the sum of the values of the subordinate units.
Table 3. Descriptive statistics of explanatory variables.
Table 3. Descriptive statistics of explanatory variables.
Level
Variable Country Province County Municipality
Gas consumption [MWh] avg 52,095,287 3,255,956 152,773 28,145
std 3,152,298 2,626,010 261,999 103,042
max 58,584,612 11,920,993 3,508,185 3,508,185
min 47,861,391 477,309 16 3
population avg 35,470,005 2,216,876 104,018 19,163
std 176,351 1,310,045 129,364 58,184
max 35,603,931 5,100,691 1,794,166 1,794,166
min 35,158,436 594,578 4,302 1,021
households with gas access avg 8,408,569 525,536 24,659 4,543
std 428,245 343,761 46,467 20,823
max 9,522,706 1,608,416 687,908 687,908
min 7,938,363 113,846 1 0
dwellings avg 13,061,565 816,348 38,304 7,057
std 661,606 507,996 61,718 27,915
max 14,200,526 2,300,920 1,020,433 1,020,433
min 12,067,040 209,748 1,694 243
Table 4. Parameters of neuron networks.
Table 4. Parameters of neuron networks.
Parameter LSTM, MLP local LSTM, MLP global
Input layer – number of neurons 9 16
Hidden layer – number of neurons 6 8
Drop out rate 0.4 0.4
Learning rate 0.001 0.001
Number of epochs 20 20
Table 5. Average performance of local models without reconciliation.
Table 5. Average performance of local models without reconciliation.
avMAPE [%] avRMSE
Train
auto ARIMA 12.2 7,325
auto EST 10.7 7,745
NAIVE 13.2 8,716
3-MA 14.5 8,748
Test
auto ARIMA 17.2 10,476
auto EST 15.6 9,423
NAIVE 15.0 10,068
3-MA 15.2 9,120
Table 6. Average performance of ETS local models with different reconciliation methods.
Table 6. Average performance of ETS local models with different reconciliation methods.
MAPE RMSE
Top down 15.6 9,423
Bottom up 15.6 9,370
Min-T 15.4 9,368
Middle out 15.5 9,348
Table 7. Average performance of global models for hierarchical forecast reconciled with middle out approach.
Table 7. Average performance of global models for hierarchical forecast reconciled with middle out approach.
Method Approach MAPE [%] RMSE
LightGBM Global Global univariate 9.8 7,729
LSTM Global Global univariate 8.5 5,476
MLP Global Global univariate 9.2 7,264
LightGBM Global ex Global multivariate 9.2 7,189
LSTM Global ex Global multivariate 7.8 5,478
MLP Global ex Global multivariate 7.1 4,970
Table 8. Detailed performance of global models for different levels of hierarchical forecast reconciled with middle out approach.
Table 8. Detailed performance of global models for different levels of hierarchical forecast reconciled with middle out approach.
Method Approach Level 0Country Level 1Province Level 2County Level 3Commune
MAPE [%]
LSTM Global univariate 3.5 4.3 6.5 8.8
MLP Global univariate 5.1 5.6 7.3 9.6
LSTM Global ex Global multivariate 3.7 4.3 6.1 8.1
MLP Global ex Global multivariate 3.3 4.0 5.6 7.3
RMSE
LSTM Global univariate 2,104,511 156,496 10,266 2,153
MLP Global univariate 3,251,453 221,999 12,928 2,611
LSTM Global ex Global multivariate 2,321,036 168,800 10,116 2,046
MLP Global ex Global multivariate 1,971,673 147,538 9,192 1,897
Table 9. Average performance of global models for hierarchical forecast reconciled with middle out approach in consecutive folds.
Table 9. Average performance of global models for hierarchical forecast reconciled with middle out approach in consecutive folds.
Method Fold 2012 2013 2014 2015 2016
MAPE [%] Approach
LSTM Global univariate 9.1 9.4 9.8 7.6 6.4
MLP Global univariate 8.3 8.7 10.8 12.0 6.1
LSTM Global ex Global multivariate 9.7 8.7 6.7 6.8 6.8
MLP Global ex Global multivariate 7.9 7.9 6.9 6.3 5.9
RMSE
LSTM Global univariate 5,321 6,163 6,939 5,088 3,866
MLP Global univariate 5,767 6,898 7,922 11,874 3,857
LSTM Global ex Global multivariate 6,392 6,468 4,419 5,359 5,112
MLP Global ex Global multivariate 5,775 5,740 5,260 4,651 3,537
Table 10. Comparison of computational time.
Table 10. Comparison of computational time.
Method Approach Computational Time [h]
Benchmark Local 0.02
ETS with reconciliation Local 0.04
LightGBM Global univariate 0.06
LSTM Global Global univariate 0.30
MLP Global Global univariate 0.25
LSTM Global ex Global multivariate 0.80
MLP Global ex Global multivariate 0.40
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions, or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated